Dynamic System Identification via Randomized Stochastic Optimization Under Unknown-but-Bounded Noise

Discretization in time and in the state space of the system leads to the necessity to solve the parameter identification problems for dynamic systems in a limited time (at a finite time interval) using observations obtained under the influence of unknown-but-bounded noise. Finding the solution in this case is more difficult compared to traditional identification problem setting which considers random independent zero-mean noise. For system parameter identification problem under unknown-but-bounded noise, a randomized stochastic optimization algorithm is given in the paper, estimates for the mean square values of the residuals for a finite observation interval are obtained. An example of application of the given method to the problem of tuning the parameters of a multi-mirror telescope is considered.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

An exact solution to any problem is possible with an accurate formulation of the problem, but connections and relationships in the real world are so complex and diverse that it is almost impossible to describe many phenomena strictly in mathematical language. A typical approach in theory is to select a mathematical model close to real processes and include various noises related, on the one hand, to the roughness of the mathematical model and, on the other hand, characterizing uncontrolled external disturbances affecting the considered object or system. For all mathematical models, the result of the experiment is a mathematical object: a number, a set of numbers, a curve, etc. From a mathematical point of view, a significant range of applied problems aims to restore characteristics from experimental data (parameters) of the object. At the same time, real systems are rarely described thoroughly by limited mathematical models. When choosing a model to solve a real problem, it is common to consider so-called systematic error (model error), which can be quantified by the distance from the real operator to the selected model. Another type of error that an experimenter may encounter is associated with measurement errors. Such errors are called statistical errors (random errors). The process of selecting characteristics (parameters) of a model from a given class of models to describe the results in a best way is one of the general definitions of estimation. In practice the estimation process can often be related to some quantitative characteristic of the quality of estimation and, it is natural while choosing the estimates, to try to minimize the negative impact of errors, both statistical and, if possible, systematic [2]. Examples include:

formation of multiscale vortex structures in turbulent fluid flows and plastic flow of solids under pulsed load;
clustering in a stream of concentrated dispersive mixtures;
propagation of the shock wave front inside the substance;
transition layers near interphase boundaries;
processes of protein formation in cells;
hierarchy of structures in living systems;
processes of fission of heavy elements nuclei;
thermonuclear fusion;
as well as the behavior of groups of people.

2. Discretization in System State Space

Among new directions in distributed systems research connections between distributed systems theory on the one hand, and canonical problems in turbulence and statistical mechanics on the other could be suggested. In one class of problems, spatio-temporal dynamical analysis clarifies old and complex questions in the theory of shear flow turbulence. In another class of problems, structured, distributed control design exhibits dimensionality-dependence and phase transition phenomena similar to those in statistical mechanics.

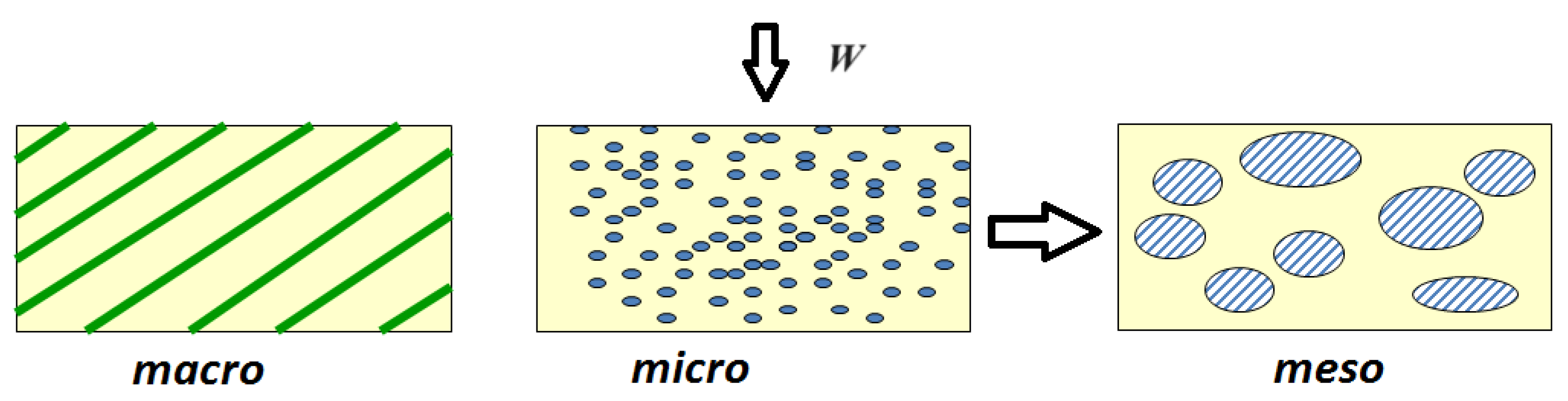
Figure 1. Mesoscale system structure can occur as a result of external influence at the system with microscale structure. It exhibits the properties of both micro- and macroscale structure. On the one hand, the clusters at meso-scale can be considered as a set of different structures, as single particles at microscale but of larger size. On the other hand each cluster could be viewed as a rigid structure, as a macroscale object but of smaller size.

Assume that (unidirectional) time t is introduced, and consider non-isolated systems consisting of elements. Evolution of each system over time is determined by the current states of both the system itself and other elements of the system. The evolution is also affected by external disturbing influences W (the absence of influence can be interpreted as zero impact). External influences W can be formally included in the general set of system states. The inclusion of W into of the system state can significantly complicate the descriptive model. External influences W naturally fall into two groups:

W = (\begin{matrix} u \\ w \end{matrix}),

(1)

controlled ones u (or simply, control) and uncontrolled ones w.

It is usually assumed that at time t the system state

X (t)

is finite-dimensional, and to describe the dynamics of the system a system of differential equations is used

{\dot{x}}_{i} = g_{i} (X, W), X = {x_{i}}, i \in M = {1, 2, \dots, m}

(2)

with some functions

g_{i} (\cdot)

and external disturbances W. In models of complex systems of this type, consisting of a huge number of components, it is customary to assume a large dimension n of state space. But, on the one hand, the choice of the threshold for n significantly limits the “upper bound” of complexity, and, on the other hand, does not allow to take possible “flexibility” of the system into account during its changing process. We will assume that the system consists of a continuum of elements

X = {x_{γ}}

, parameterized by

γ \in [0, 1]

, and the evolution of each of the elements is described by equation

{\dot{x}}_{γ} = g_{γ} (X, W), X = {x_{γ}}, γ \in M = [0, 1] .

(3)

Such setups can occur, for instance, in stochastic games with many players [3] and mean-field games with almost infinitely many players [4]. Additionally, we assume that the external influence W for all its arbitrariness at each moment of time k has a structure

s_{k}

of finite order. Finite structure of external influence after some transition process causes discretization of spatial elements (clustering) in the considered complex system

X_{s_{k}} = {X_{1}, X_{2}, \dots, X_{m_{s_{k}}}} : X = \cup_{i = 1, 2, \dots, m_{s_{k}}} X_{i}, X_{i} \subset X .

(4)

Discretization occurs due to the self-organization of groups of elements and their synchronization. For clusters

i = 1, \dots m_{s_{k}}

, a set of

m_{s_{k}} \in N

variables

{\bar{x}}_{i}

averaged over cluster

X_{i}

is naturally introduced. Set of

{\bar{x}}_{i}

i = 1, \dots, m_{s_{k}}

could be generalized as a set of some integrals over the clusters. Such approach is usually applied to simplify physical models (dimension reduction). The general integral characteristics of clusters of elements with similar properties are introduced and dynamic models in reduced state spaces are considered. Experiments show that such simplifications are justified and often give good results.

Typically, the process of clustering (self-organization) in a system is not “one-shot”, but is constantly reproduced due to changes in external influences and critical changes in internal states. But at the same time we will assume that a change in the structure of external influences does not occur permanently, but in some time instants

T_{0}, T_{1}, T_{2}, \dots .

This leads to the necessity to consider the dynamic processes under condition of state space structure change over time.

So, when the structure of external influence changes, the discretization of spatial elements may change. Let us assume that this transient process takes a duration of time no longer than some

δ \geq 0

(see Figure 2). We will assume that

δ

is many times smaller than the intervals between successive changes in the structure of external influences:

δ < < ζ = min_{k} | T_{k + 1} - T_{k} |

(5)

In addition to discretizing spatial variables we obtain time sampling, neglecting duration of transient process intervals. After such discretization in many practical applications the system of differential equations describes the dynamics of changes in the original complex system over the time interval from

T_{k} + δ

T_{k + 1}

\dot{\bar{x_{i}}} = {\bar{g}}_{i} (\bar{X}, u, w, θ_{s_{k}}), i = 1, 2, \dots, m_{s_{k}},

(6)

where

{\bar{x}}_{i}

is aggregated state

{x_{i}}

{x_{γ}}

from cluster

X_{i}

\bar{X} = c o l ({\bar{x}}_{1}, {\bar{x}}_{2}, \dots, {\bar{x}}_{m_{s_{k}}})

θ_{s_{k}}

is a finite set of current parameters at time interval

[T_{k} + δ, T_{k + 1})

3. Control Problem and Discretization on Time

Consider a control problem of choosing the strategy of control minimizing the cost function comprised of local cost functions computed at different parts of the system:

L ({u}) = \sum_{i \in M} l (x_{i}, u) \to min_{u}

or, in case the system consists of continuum elements (3):

L ({u}) = \int_{M} l (x_{γ}, u) d γ \to min_{u} .

Previously it was assumed perturbation W has a “finite structure” at each moment, and the structure of

s_{k}

changes at times

T_{0}, T_{1}, T_{2}, \dots

, causing clustering of the state space:

X_{s_{k}} = {X_{1}, X_{2}, \dots, X_{m_{s_{k}}}} : X = \cup_{i = 1, 2, \dots, m_{s_{k}}} X_{i}, X_{i} \subset X

(7)

where

{\bar{x}}_{i}

is aggregated state

{x_{i}}

{x_{γ}}

of cluster

X_{i}

\bar{X} = c o l ({\bar{x}}_{1}, {\bar{x}}_{2}, \dots, {\bar{x}}_{m_{s_{k}}})

θ_{s_{k}}

is finite set of current parameters. We assume that for any k the dimension of

θ_{s_{k}}

is bounded by d. For

t \in [T_{k} + δ, T_{k + 1})

due to integral (sum) additive property the loss function could be changed to:

L = \int_{M} l (x_{γ}, u) d x_{γ} \approx \sum_{i}^{m_{s_{k}}} {\bar{l}}_{k} ({\bar{x}}_{k}, u, θ_{s_{k}}) = {\bar{L}}_{k} (\bar{X}, u, θ_{s_{k}}) .

Assume that control strategy u are piece-wise constant and changing in the end of each time interval of length h,

u (t) = u_{n}, t \in [(n - 1) h, n h) .

The feedback u will be computed on the base of noised observations of the loss function

\tilde{L}

. After sampling in time and space, we obtain an observation model for the loss function:

y_{n} = {\tilde{L}}_{k} ({\bar{X}}_{n}, u_{n}, θ_{s_{k}}) + ξ_{n},

(8)

where

t_{n} \in [T_{K} + δ, T_{k + 1})

{\tilde{L}}_{k} (\cdot)

are functions from

{\bar{X}}_{n} = \bar{X} (t_{n}), u_{n} = u (t_{n}), θ_{s_{k}},

ξ_{n} = ξ_{n}^{'} + ξ_{n} (s_{k}) "

is discrepancy (error) composed of some random noise

ξ_{n}^{'}

independent of current system structure

s_{k}

, and systematic error

ξ_{n} (s_{k}) "

which is, in general, is some function of the current system state.

4. Parameter Identification Problem

Estimation of system parameters values can be formulated as an optimization problem. The discrepancy between estimated and real parameter values could be expressed in terms of some loss function value and thus to solve the system identification problem one has to minimize given loss function. To identify the system structure it is required to choose such control formation strategy

{u}

, which minimizes some loss function.

Suppose that for a given parameter vector

θ_{s_{k}} \in R^{d}

the optimal control strategy

{u_{n}} = U (θ_{s_{k}})

is known. After substituting it in (8), we get the problem of minimizing the function

f_{s_{k}} (θ) = {\tilde{L}}_{k} ({\bar{X}}_{n}, U (θ), θ_{s_{k}})

when observing its values against under the influence of noise

ξ_{n}

. Under the assumptions made, the minimum of the function

f_{s_{k}} (θ)

is reached when

θ = θ_{s_{k}}

. To solve the formulated problem, the method from [5] can be used.

The distributed optimization task can be formulated in terms of finding the method of constructing cluster (meso-) control, in which the same control action is applied to all elements of the cluster. In this case, the discretized loss function can be represented as a distributed functional

f_{s_{k}} (θ) = \sum_{i = 1}^{m_{s_{k}}} {\tilde{l}}_{k} ({\bar{X}}_{n}^{i}, U^{i} (θ), θ_{s_{k}}) .

This problem could be solved by appliying the stochastic optmimization type method from [15].

The considered problem setting is a particular case of more general problem of minimizing a non-stationary differentiable function with respect to

θ

. Let

F_{n - 1}

be the

σ

-algebra of all probabilistic events which happened during time interval

n - 1

before start of time interval n. Hereinafter

E_{F_{n - 1}}

is a symbol of the conditional mathematical expectation with respect to the

σ

-algebra

F_{n - 1}

E

is a symbol of the mathematical expectation. The minimum point

θ_{s_{k}}

of function

F_{n} (θ) = E_{F_{n - 1}} f_{s_{k}} (θ) \to min_{θ}

needs to be estimated.

More precisely, using the observations

y_{1}, y_{2}, \dots, y_{n}

and inputs

θ_{1}, θ_{2}, \dots, θ_{n}

, construct an estimate

{\hat{θ}}_{n}

of an unknown vector

θ_{s_{k}}

minimizing the time-varying mean-risk functional.

4.1. Assumptions

Let us formulate Assumptions about disturbances and functions

f_{s_{k}} (θ), F_{n} (θ)

For $n = 1, 2, \dots$ , the successive differences ${\bar{ξ}}_{n} = ξ_{n}^{+} - ξ_{n}^{-}$ of observation noise are bounded: $| {\bar{ξ}}_{n} | \leq c_{ξ} < \infty$ , or $E {\bar{ξ}}_{n}^{2} \leq c_{ξ}^{2}$ if a sequence ${ξ_{n}}$ is random, where $ξ_{n}^{+}$ , $ξ_{n}^{-}$ are observation noises occurred during the same time interval n but at different time instants.
Functions $F_{n} (\cdot)$ have unique minimum points $θ_{s_{k}}$ and $\forall θ 〈 θ - θ_{s_{k}}, E_{F_{n - 1}} \nabla f_{s_{k}} (θ) 〉 \geq μ {∥ θ - θ_{s_{k}} ∥}^{2}$ with a constant $μ > 0$ . Here and further $〈 \cdot, \cdot 〉$ is a scalar product of two vectors.
The gradient $\nabla f_{s_{k}}$ is uniformly bounded in the mean-squared sense at the minimum points $θ_{t} : E {∥ \nabla f_{s_{k}} (θ_{t}) ∥}^{2} \leq g^{2}$
$\forall s_{k} \in S$ the gradient $\nabla f_{s_{k}} (θ)$ satisfies the Lipschitz condition: $\forall θ^{'}, θ^{''}$

$∥ \nabla f_{s_{k}} (θ^{'}) - \nabla f_{s_{k}} (θ^{''}) ∥ \leq M ∥ θ^{'} - θ^{''} ∥$

with a constant $M \geq μ$ .
$\forall n \geq 1$ random vector $Δ_{n}$ does not depend on ${\bar{w}}_{n}$ , random vectors ${\bar{w}}_{n}, Δ_{n}$ do not depend on ${\bar{w}}_{1}, \dots, {\bar{w}}_{n - 1}$ ; if ${{\bar{v}}_{n}}$ are random variables, then ${\bar{w}}_{n}, Δ_{n}$ also do not depend on ${\bar{v}}_{1}, \dots, {\bar{v}}_{n}$ .

Using available observations, it is necessary to construct a sequence of estimates

{\hat{θ}}_{n}

of the unknown vector

θ_{s_{k}}

that minimizes the function

f_{s_{k}} (θ)

. To solve the problem, we will use an iterative algorithm with two measurements.

Let the trial simultaneous disturbance

Δ_{n}, n = 1, 2, \dots

be an observable (set or user-controlled) sequence of independent random vectors with known distribution functions

P_{n} (\cdot)

— and specified vector functions

K_{n} (\cdot) : R^{d} \times R^{d} \to R^{1}

, satisfy the conditions

\int K_{n} (x) P_{n} (d x) = 0; \int K_{n} (x) x^{T} P_{n} (d x) = I,

(9)

sup_{n} \int {∥ K_{n} (x) ∥}^{2} P_{n} (d x) < \infty, n = 1, 2, \dots .

(10)

4.2. Algorithm

Let’s choose an arbitrary initial estimate vector

{\hat{θ}}_{0} \in R^{d}

and scalar parameters

α

β

for an iterative algorithm

\{\begin{matrix} θ_{n}^{+} = {\hat{θ}}_{n - 1} + β Δ_{n}, θ_{n}^{-} = {\hat{θ}}_{n - 1} - β Δ_{n} \\ y_{n}^{+} = f_{n} (θ_{n}^{+}) + ξ_{n}^{+}, y_{n}^{-} = f_{n} (θ_{n}^{-}) + ξ_{n}^{-} \\ {\hat{θ}}_{n} = {\hat{θ}}_{n - 1} - \frac{α}{2 β} K_{n} (Δ_{n}) (y_{n}^{+} - y_{n}^{-}) . \end{matrix}

(11)

4.3. Main Result

Let us introduce the following notation:

ν = α (0.5 - μ - \frac{L α C_{τ}}{2}), ϕ = α γ + \frac{L}{2} α^{2} C_{σ}, γ = 0.5 {(C_{1} β)}^{2}, ψ = \frac{ϕ}{ν}

Here

C_{τ}

C_{σ}

could be chosen to satisfy inequation

E ∥ \frac{1}{2 β} (f_{n} (θ + β Δ_{n}) + ξ_{n}^{+} - f_{n} (θ - β Δ_{n}) - ξ_{n}^{-}) ∥^{2} \leq C_{σ} + C_{τ} {∥ θ - θ_{s_{k}} ∥}^{2}

and

C_{1} \geq \int ∥ K_{n} {(x) ∥ M ∥ x ∥}^{2} P_{n} (d x)

and

α

chosen to satisfy following conditions:

\begin{matrix} 0 \leq α \leq \frac{4 μ - 2}{L C_{τ}}, α \leq \frac{2 μ - 1 - \sqrt{{(2 μ - 1)}^{2} - 2 L C_{τ}}}{L C_{τ}} \\ α \geq \frac{2 μ - 1 + \sqrt{{(2 μ - 1)}^{2} - 2 L C_{τ}}}{L C_{τ}} . \end{matrix}

(12)

Theorem 1.

Let Assumptions 1–5 and conditions for kernels

K

(9)-(10) and α (12) be satisfied. Set

{\hat{θ}}_{0}

, choose interval size parameter k

E {∥ {\hat{θ}}_{n} - θ_{s_{k}} ∥^{2}} \leq E {∥ {\hat{θ}}_{0} - θ_{s_{k}} ∥^{2}} {(1 - ν_{i})}^{n} + ψ (1 - {(1 - ν_{i})}^{n}) .

(13)

Proof. To analyze the convergence of the algorithm (11) estimates, a method from [10] is used. Choose

V ({\hat{θ}}_{n}) = \frac{1}{2} {∥ {\hat{θ}}_{n} - θ_{s_{k}} ∥}^{2}

(14)

as Lyapunov function. To prove the theorem (13) is true it is sufficient to show the following six propositions are satisfied.

Proposition 1. The iterative process

Y_{n}

, which defines the direction of the estimate change, is a Markov process, i.e. the distribution of the random vector

Y_{n}

depends only on

{\hat{θ}}_{n}

and n:

Y_{n} = \frac{1}{2 β} K (Δ_{n}) (y_{n}^{+} - y_{n}^{-})

(15)

For algorithm (11) we have

E {Y_{n}} = E {K_{n} (Δ_{n}) \frac{y_{n}^{+} - y_{n}^{-}}{2 β} | F_{n - 1}},

where the right hand side depends only on

{\hat{θ}}_{n}

and n in the sense that

Δ_{n}

does not depend on any other random variables. Proposition is true.

Proposition 2.

V ({\hat{θ}}_{n}) \geq 0

inf V ({\hat{θ}}_{n}) = 0

V ({\hat{θ}}_{n})

has first-order derivative, and its gradient satisfies Lipshitz condition:

∥ \nabla V (x) - \nabla V (θ) ∥ \leq L ∥ x - θ ∥ \forall x, θ \in R^{d} .

The proposition is valid due to the choice of Lyapunov function (14).

Proposition 3. Pseudo-gradient condition:

〈 \nabla V ({\hat{θ}}_{n}), E {Y_{n}} 〉 \geq δ_{n} V ({\hat{θ}}_{n}) - γ_{n}, δ_{n} > 0, γ_{n} \geq 0 .

(16)

At first consider

E {Y_{n}}

. Due to (11) pseudo-gradient (15) after using Assumption 5 becomes

E {Y_{n}} = E {K_{n} (Δ_{n}) \frac{1}{2 β} (f_{s_{k}} (θ_{n}^{+}) - f_{s_{k}} (θ_{n}^{-})) | F_{n - 1}}

(17)

Consider the expression under mathematical expectation. Using Taylor series representation it could be written as:

\begin{matrix} \frac{1}{2} \nabla F_{n} ({\hat{θ}}_{n}) + \frac{1}{2 β} \int K_{n} (x) x^{T} \int_{0}^{1} (\nabla_{x} f_{s_{k}} ({\hat{θ}}_{n} + t β x) - \nabla f_{s_{k}} ({\hat{θ}}_{n})) d t P_{n} (d x) + \\ + \frac{1}{2} \nabla F_{n} ({\hat{θ}}_{n}) - \frac{1}{2 β} \int K_{n} (x) x^{T} \int_{0}^{1} (\nabla f_{s_{k}} ({\hat{θ}}_{n} - t β x) - \nabla f_{s_{k}} ({\hat{θ}}_{n})) d t P_{n} (d x) \end{matrix}

Estimate absolute value of the sum of integral elements in the obtained expression. After using (9), Assumption 4 we get

| \int (\cdot) P_{n} (d x) | + | \int (\cdot) P_{n} (d x) | \leq \frac{2 β^{2}}{2 β} \int ∥ K_{n} (x) ∥ ∥ x ∥ M ∥ x ∥ P_{n} (d x) \leq C_{1} β .

(18)

Substitute the estimate, elements containing gradients of

F_{n}

and (14) into (16), regard the relation

\int (\cdot) P_{n} (d x) \geq - | \int (\cdot) P_{n} (d x) |

and Cauchy–Bunyakovsky–Schwarz inequality:

〈 {\hat{θ}}_{n} - θ_{s_{k}}, E {Y_{n}} 〉 \geq 〈 {\hat{θ}}_{n} - θ_{s_{k}}, \nabla F_{n} ({\hat{θ}}_{n}) 〉 - ∥ {\hat{θ}}_{n} - θ_{s_{k}} ∥ C_{1} β .

Apply Assumption 2 and estimate

∥ {\hat{θ}}_{n} - θ_{s_{k}} ∥ C_{1} β \leq \frac{1}{2} (∥ {\hat{θ}}_{n} - θ_{s_{k}} ∥^{2} + {(C_{1} β)}^{2}) :

〈 {\hat{θ}}_{n} - θ_{s_{k}}, E {Y_{n}} 〉 \geq (2 μ - 1) \frac{1}{2} {∥ {\hat{θ}}_{n} - θ_{s_{k}} ∥}^{2} - \frac{1}{2} C_{1}^{2} β^{2}

Proposition is true for

μ > 1 / 2

Proposition 4.

E {∥ Y_{n} ∥^{2}} \leq σ_{n}^{2} + τ V (x), σ_{n} \geq 0, τ_{n} \geq 0 .

Using (10), Cauchy–Bunyakovsky–Schwarz inequality, Assumptions 1 and 3 it could be shown that

\begin{matrix} E {∥ Y_{n} ∥^{2}} & \leq \frac{1}{2} sup_{x} K_{n} {(x)}^{2} E {{(ξ_{n}^{+})}^{2} + {(ξ_{n}^{-})}^{2} | F_{n - 1}} + \\ + \int {(f_{s_{k}} ({\hat{θ}}_{n}^{+}) - f_{s_{k}} ({\hat{θ}}_{n}^{-}))}^{2} ∥ K_{n} {(x) ∥}^{2} P_{n} (d x) \leq C_{2} β^{2} (∥ {\hat{θ}}_{n - 1} - θ_{s_{k}} ∥^{2}) + C_{3} β^{4} + C_{4} ξ_{n}^{2} \end{matrix}

Proposition holds true with

τ = 2 C_{2} β^{2}

σ_{n}^{2} = C_{3} β^{4} + C_{4} ξ_{n}^{2}

Proposition 5.

E V ({\hat{θ}}_{0}) < \infty .

Proposition is valid due to arbitrariness of initial approximation

{\hat{θ}}_{0}

choice and an assumption regarding final order

s_{k}

of the external disturbance W affecting the system and thus the final order of the system state vector.

Proposition 6.

0 \leq ν \leq 1

;

\sum_{n} ν = \infty, n \to \infty

The first inequality could be met by choice of α and the second one is true since ν is constant. Proposition is true.

The fulfillment of the given propositions allow to prove the theorem using the result in [10]. □

Remark 1.

After the algorithm converges the parameter estimates

{\hat{θ}}_{n}

continue to fluctuate around the true parameter value

θ_{s_{k}}

until the new change of system structure and value of

θ_{s_{k}}

Remark 2.

The most common problem setup for unknown-but-bound disturbances in existing works is formulated as follows. It is required to minimize the value of the objective function

f (θ)

with some adversarial deterministic noise

ξ (θ)

such that

| ξ (θ) | \leq ξ

and

ξ > 0

\tilde{f} (θ) = f (θ) + ξ (θ) .

The considered setup implies that external noise depends on system state

s_{k}

which is not a direct function of θ but rather is affected by values of

θ_{t}

during some time period

[t - d, t)

\tilde{f} (θ) = f (θ) + ξ (s_{k}) .

Value

s_{k}

is formed on basis of previous values of θ.

5. Application for Orientation Improvement of Radio Telescope’s Elements

For astronomers, an urgent task was to obtain images of objects that can’t be recorded using optical telescopes, which are situated on earth or in space. This problem was largely solved using radio telescopes [11]. The main tasks of the telescope are: to collect radiation that falls on the mirror system with minimal losses, and also obtain the most accurate image of the object [6]. There are various ways to solve this problem, consider for example, [8]. One of them is improving the quality of the device [12], which collects radiation for obtaining images. Another one is combining radio telescopes into systems [9]. If the radiation is collected with significant errors, then the image will have disturbances [27].

An important and time-consuming part of image acquisition is the precise tuning of the radio telescope antenna (or systems consisting of such antennas) [13]. The quality of the image obtained on a radio telescope directly depends on the quality of the construction of a reflecting system of mirrors that focuses the radiation coming from outside. To improve the image quality, it is necessary to focus the radiation of the device in such a way that it works as accurately as possible, especially if it is located in space [14]. Traditional antenna tuning algorithms are sufficient for the task. However, they lose their effectiveness under uncontrolled unpredictable external influences. We consider the case when these are deformations of the radio telescope shields that arise due to environmental influences such as temperature changes, wind and other influences.

In practice, radiation is subject to various distorting influences, and as a result the quality of the observed image decreases, despite the presence of various stabilizers and filters [11]. One of the ways to solve such a problem is using randomized stochastic optimization algorithms [15]. A method for improving image quality by improving the tuning characteristics of the radio telescope mirror system is considered in [25].

In an ideal antenna system, the signal is reflected from different mirror plates and assembled at one point. Deformations of radio telescope structures, external temperature, wind, mechanical influences lead to deviation of the optical path lengths of the rays from the required ones. As a result, the focus point on the plane of the receiver shifts [12]. To improve reflection accuracy on the surface of radio telescope mirrors, the following methods are used: autocollimation [22], telescope calibration by spectral density radiation flux, synchronous calibration method [21], laser geodetic measurements [6], improvement of the kinematics of antenna elements [19], radio holography physical method [24]. The goal is to develop a stochastic optimization type algorithm to improve the quality of the settings of the radio telescope mirror system model which could be used in a system similar to Radioastron [20,26]. The main criterion for efficiency is the recording power of the desired signal and the time required for adjusting the parameters.

The antenna segments can be set to the optimal position to improve the quality of image recording. Consider an irradiator (radiation generator), a receiver and a mirror system of a radio telescope, consisting of identical plates that reflect the incoming signal (

i = 1, \dots, N, N = 895

in the RATAN-600 installation). Radiation is created in the irradiator, which, falling on the plates and focused in the receiver. Let’s divide the number axis into time intervals of duration

δ

, starting from some moment

t_{0}

, where

T_{k}

is the k-th time interval k is the index of the time interval. Assume that we know:

1) the position (orientation) of each i-th plate, which is specified by the vector of parameters

{(a_{i}, b_{i}, c_{i})}^{T}

, where

a_{i}

is the rotation angle of the i-th reflective element horizontally;

b_{i}

is the vertical rotation angle,

c_{i}

is the forward horizontal displacement of the i-th reflecting element. Let

θ_{k}

be a vector that contains all parameters of the mirror system in a given time interval k,

θ_{k} = {(a_{1}, a_{2}, . . ., a_{N}, b_{1}, b_{2}, . . ., b_{N}, c_{1}, c_{2}, . . ., c_{N})}^{T},

2) radiation coming from each mirror (

z_{i}

3) the common signal coming from all mirrors to the receiver

Z (θ_{k}) = \sum_{i = 1, \dots, N} (z_{i})

4) characteristics of the signal in the generator.

The front of a signal is the sum of harmonics that comes to us with different phases from a certain direction. The perfect placement of the plates brings all radiation from the objects into focus. We obtain the signal as a sum of sines with phases. Different

z_{i}

arrive at different times with different phases. Let us evaluate the difference between the signals from an ideal antenna and from a real one (with deformations). Signals reflected from ideal mirror segments will have the same phase

ϕ_{i}

(

ϕ_{1} = ϕ_{2} = \dots = ϕ_{N}

). The signals from segments with deformations will look like this:

z_{1} = sin (ω t + ϕ_{1}), z_{2} = sin (ω t + ϕ_{2}), \dots z_{i} = sin (ω t + ϕ_{i})

(19)

The objective function of the problem

(F (θ)

is the signal power) is defined as follows:

F (θ) = \bar{{lim}_{k}} \int_{t \in T_{k}} {| Z (θ, t) |}^{2} d t .

(20)

It is required to maximize the objective function:

F (θ) \to max_{θ}

(21)

We consider the problem of optimizing the position of mirrors in the limit over time (not over a specific time interval).

The reflective elements of the antenna are made exactly the same, so they provide equivalent observations in all directions.

At the same time, if one moves along an ideal reflective surface, its local characteristics change. Therefore, a real reflective surface composed of identical elements will repeat deviations from the ideal surface from element to element. These deviations will be greater, if the shape of the surface of the element differs from the shape of that portion of the ideal surface which this element should represent. If the size of the reflective elements increases, then the deviations naturally increase. These deviations are an error distributed over the reflector of a variable profile antenna, which, at large values, creates unacceptable distortions reducing the efficiency of the antenna. We will call

v_{k}

the signal power measurement errors arising due to unknown and uncontrolled deformations in the reflective elements of the antenna caused by weather, wind, and temperature changes.

After conventional procedures for adjusting the inclination angles and positions of the radio telescope mirrors, we obtain an initial approximation

{\hat{θ}}_{0}

to the optimal tuning values. Then there is still the possibility of “tuning” in a certain neighborhood T containing

{\hat{θ}}_{0}

and the optimal value

θ^{★}

corresponding to the maximum power of the received signal. We use a stochastic optimization algorithm with two measurements per iteration, which allows us to reduce the negative impact of various disturbances on the power of the recorded signal [7]:

Select

θ_{0} .

n - 1 \to n

We sequentially generate vectors

Δ_{n}

with components from +/-1, which are chosen with equal probability.

We measure the power values for two positions of the antenna system:

(θ_{n} + β Δ_{n})

and

(θ_{n} - β Δ_{n}) .

Measurements are obtained with noise

v_{2 n}

and

v_{2 n - 1}

y_{2 n} = P_{2 n} (θ_{2 n} + β Δ_{n}) + ξ_{2 n};

(22)

y_{2 n - 1} = P_{2 n - 1} (θ_{2 n - 1} - β Δ_{n}) + ξ_{2 n - 1};

(23)

Next, we form the following estimate

θ_{2 n}

according to the rule:

θ_{2 n} = P_{T} (θ_{2 n - 1} + \frac{α K_{n} (Δ_{n})}{2 β} (y_{2 n} - y_{2 n - 1})),

(24)

where

α, β

are the parameters of the algorithm,

P_{T}

is the projection onto the set

T

To construct the kernels

K_{0} (\cdot)

and

K_{1} (\cdot)

on the interval

[- 1 / 2, 1 / 2]

orthogonal Legendre polynomials could be used. In this case, for initial values

ℓ = 1, 2

(i.e.

2 \leq γ \leq 3

) the type of kernels is as follows:

K_{0} (q) = 12 q, K_{1} (q) = 1, ∣ q ∣ \leq 1 / 2,

for

ℓ = 3, 4

(i.e.

3 < γ \leq 5

K_{0} (q) = 5 q (15 - 84 q^{2}), K_{1} (q) = 9 / 4 - 15 q^{2}, ∣ q ∣ \leq 1 / 2,

and for

| q | > 1 / 2

both functions are equal to zero.

The test disturbance is formed in such a way that

\forall n \geq 1

random vector

Δ_{n}

does not depend on

{\bar{v}}_{1}, \dots, {\bar{v}}_{k}

and

E {{(v_{2 n} - v_{2 n - 1})}^{2} / 2} \leq σ_{2}^{2}, (E {v_{n}^{2}} \leq σ_{1}^{2});

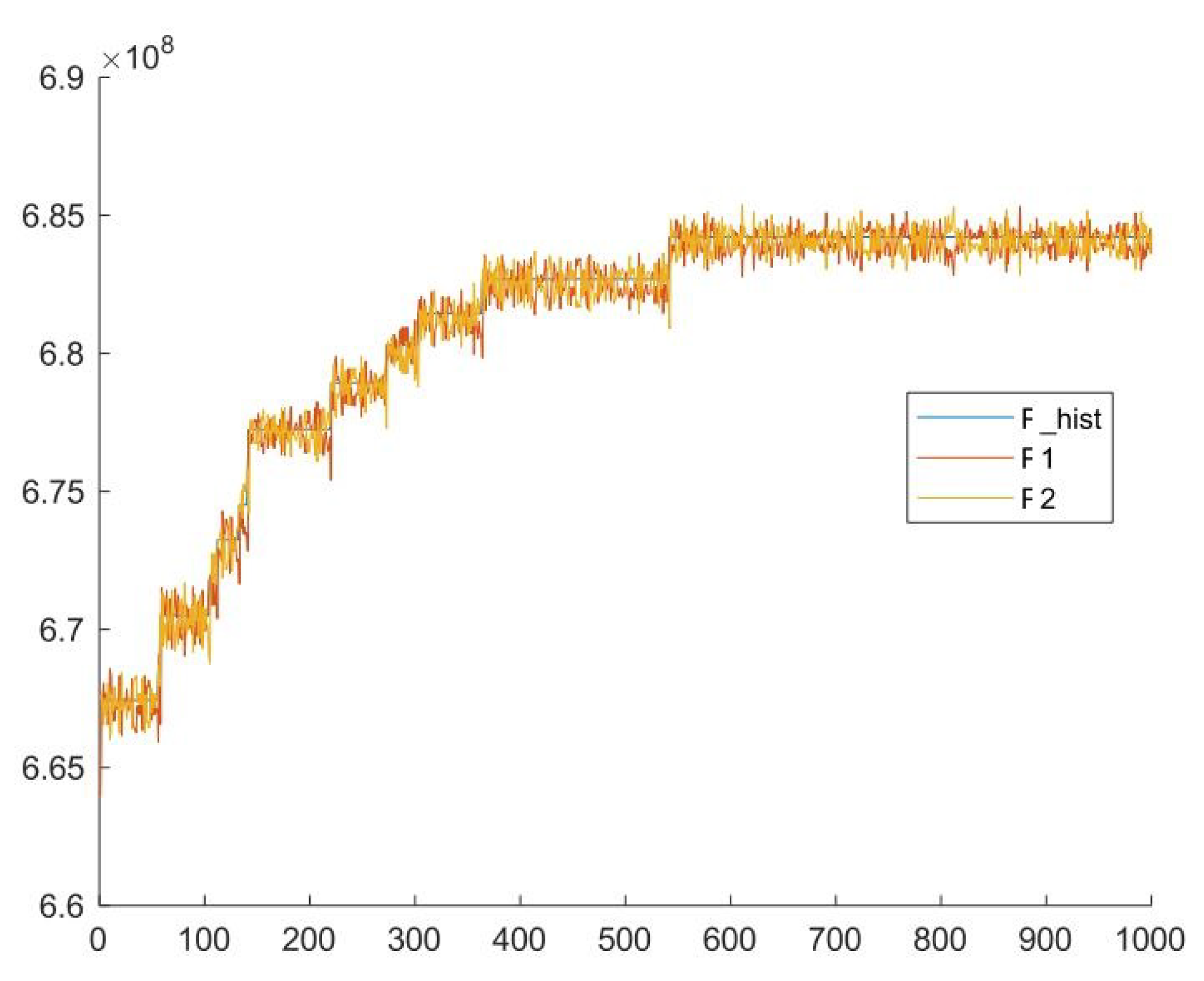
The main element that reflects the incoming signal is the segment of the mirror system. It is important to configure these shields so that the signal comes into focus. The system allows to customize the required dimensions of the reflective shield and its curvature. Stochastic optimisation algorithm (11) can be applied for tuning a system which consists of a large number of telescopes in space under conditions of interference and also when individual elements of the system are deformed. About 3000 parameters of the mirror surfaces are adjusted, during focusing of the mirror system.The faster setting up of the mirrors is very important for the accuracy of observations. For acceleration, it is proposed to use the Nesterov acceleration method in distributed form [16,17,18]. In Figure 3 on page 11, the dependence of the signal power on the number of iterations of the algorithm is given.

Author Contributions

Conceptualization, O.G.; methodology, O.G.; software, K.D.; formal analysis, Y.I.; writing—original draft preparation, K.D. and Y.I.; writing—review and editing, O.G, and Y.I.; visualization, K.D.; All authors have read and agreed to the published version of the manuscript.

Funding

The work was supported by the IPME RAS by Russian Science Foundation (project no. 21-19-00516).

Conflicts of Interest

The authors declare no conflict of interest.

References

Granichin, O.; Uzhva, D.; Volkovich, Z. Cluster Flows and Multiagent Technology. Mathematics 2021, 9, 22. [Google Scholar] [CrossRef]
Granichin, O. What is an Actual Structure of Complex Information-Control Systems? Stochastic optimization in informatics. 2016. Is. 12, No 1.
Parilina, E.; Petrosyan, L. On a Simplified Method of Defining Characteristic Function in Stochastic Games. Mathematics 2020, 8, 1135. [Google Scholar] [CrossRef]
Achdou, Y. , Cardaliaguet, P., Delarue, F., Porretta, A. and Santambrogio, F., 2021. Mean Field Games: Cetraro, Italy 2019 (Vol. 2281). Springer Nature.
Granichin, O. and Amelina, N., 2014. Simultaneous perturbation stochastic approximation for tracking under unknown but bounded disturbances. IEEE Transactions on Automatic Control, 60(6), pp.1653-1658. [CrossRef]
Ermakov A., N. , Kovalev Yu. A. Project “RadioAstron”. Calibration of a space telescope in flight - automation of measurement processing of the ASC FIAN, Moscow, Russia, Proceedings of the Institute of Applied Astronomy of the Russian Academy of Sciences, vol. 54. 2020. [Google Scholar]
Granichin, O.N. , Polyak B.T. Randomized estimation and optimization algorithms under almost arbitrary noise. M.: Nauka, 2003. 291 p.
Droszcz, A. , J˛edrzejewski, K. , Kłos, J., Kulpa, K., Pozoga M. Beamforming of LOFAR Radio-Telescope for Passive Radiolocation Purposes. Remote Sens. 2021, 13, 810. [Google Scholar] [CrossRef]
Leonid I. Gurvits. Advances in Space Research Volume 65, Issue 2, 15 January 2020, Pages 868-876 Space VLBI: from first ideas to operational missions Author links open overlay panel.
Polyak, B.T. Convergence and rate of convergence in iterative stochastic processes. I. The general case. 1976. Avtomatika i telemekhanika, No. 12, pp.83-94.
Kardashev, N.S. and others. “RADIOASTRON”: results of the implementation of the scientific research program for 5 years of flight // Bulletin of NPO im. S.A. Lavochkina. 2016. No. 3. P. 4-24.
Dubarenko, V.V. , Kuchmin A.Yu., Artemenko Yu.N., Shishlakov V.F. Millimeter-wave radio telescopes with adjustable mirror surfaces: monograph. – St. Petersburg: GUAP, 2019.
Monakhova, U.V. , Ivanov D.S. Formation of a swarm of nanosatellites using decentralized aerodynamic control taking into account communication restrictions // Preprints of the Institute for Problems of Materials Science. M.V.Keldysh. 2018. No. 151. 32 p. [CrossRef]
Bentum, M.J. , Verma M.K., Rajan R.T., Boonstra A.J., Verhoeven C.J.M., Gill E.K.A., van der Veen A.J., Falcke H., Klein Wolt M., Monna B., Engelen S., Rotteveel J., Gurvits L.I. A Roadmap towards a Space-based Radio Telescope for Ultra-Low Frequency Radio Astronomy. [CrossRef]
Granichin, O.N. , Erofeeva V.A., Ivanskiy Y.V., Jiang Y. Simultaneous Perturbation Stochastic Approximation-Based Consensus for Tracking Under Unknown-But-Bounded Disturbances. IEEE Transactions on Automatic Control 2021, Vol. 66, Is. 8 PP. 3710–3717. [CrossRef]
Rogozin, A. , Yarmoshik D., Kopylova K. Gasnikov A. P: Decentralized Strongly-Convex Optimization with Affine Constraints: Primal and Dual Approaches 2022.
Nesterov, Y. A method of solving a convex programming problem with convergence rate o(1/k 2 ). Soviet Mathematics Doklady, 27(2):372–376, 1983.
Nesterov, Y. Introductory Lectures on Convex Optimization: a basic course. Kluwer Academic Publishers, Massachusetts, 2004.
Zharov, V.I. , Sotnikova Yu.V. Methodology for determining the kinematic characteristics of the elements of the main mirror of the RATAN-600 radio telescope using modern laser measuring systems. Astrophysical Bulletin, 2017. Vol. 72, No. 4, pp. 520–526.
Moisheev, A.A. Creation of space segments of astrophysical observatories. Bulletin 2.
Sotnikova, Yu.V. , Kovalev Yu.A., Erkenov A.K., Method of synchronous calibration of RATAN-600 using 2 of its sectors. Astrophysical Bulletin, 2019. Vol. 74, No. 4, pp. 535–543. [CrossRef]
Khaikin, V.B. , Bursov N.N. Autocollimation automatic adjustment and control of the efficiency of elements of the RATAN-600 radio telescope. Journal of Radioelectronics, 2016, pp. 1684-1719.
Mingaliev, M.G. RATAN-600 - current state and prospects. Abstracts of the report. Conf. RT-2002, in Pushchino, 2002. P. 80.
Khaikin, V.B. , Lebedev M.K., Ripak A.M. A method for radio-holographic monitoring of the surface of the main mirror of the RATAN-600 radio telescope with radial movement of the support element. Journal of Radioelectronics, 2016, pp. 1684-1719.
Kopylova, K.D. , Granichin O.N. Minimizing the systematic error of a radio astronomy telescope using a randomized stochastic optimization algorithm. Proceedings of the 13th multi-conference on management issues, 2020.
Kovalev, Yu.A. , Sotnikova Yu.V., Erkenov A.K., Popkov A.V., Volvach L. N., Vasilkov V. I., Lisakov M. M., Semenova T. A., Tsybulev P. G. Features of calibration of the space radio telescope "RadioAstron" and the radio telescope RATAN-600. // Proceedings of the IPA RAS. – St. Petersburg: IPA RAS, 2018. Issue. 47.- pp. 38-42.
Minchenko, B.S. Synthesis of radio images on the RATAN-600 radio telescope Izv. universities Radiophysics. 1983. T. 26, No. 11. P. 1463–1471.

Figure 2. State space structure change at time interval

[T_{k}, T_{k} + δ]

. Up to time instant

T_{k}

the system has the structure

s_{k - 1}

. After

T_{k}

the system structure changes as a result of some disturbance. During time period

δ

the system transformation to a new state happens and from time instant

T_{k} + δ

the system has new structure

s_{k}

Figure 2. State space structure change at time interval

[T_{k}, T_{k} + δ]

. Up to time instant

T_{k}

the system has the structure

s_{k - 1}

. After

T_{k}

the system structure changes as a result of some disturbance. During time period

δ

the system transformation to a new state happens and from time instant

T_{k} + δ

the system has new structure

s_{k}

Figure 3. Convergence of the algorithm.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dynamic System Identification via Randomized Stochastic Optimization Under Unknown-but-Bounded Noise

Abstract

1. Introduction

2. Discretization in System State Space

3. Control Problem and Discretization on Time

4. Parameter Identification Problem

4.1. Assumptions

4.2. Algorithm

4.3. Main Result

5. Application for Orientation Improvement of Radio Telescope’s Elements

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe