Dynamics of Fricke-Painlevé VI surfaces

1. Introduction

Free groups $F_r$ of rank $r=2$ and 3 have been found to be important in our earlier work about topological quantum computing (TQC) [1] and biology at the DNA/RNA genomic scale [2]. In the first context, one motivation is that an elementary link, the Hopf link $L=L2a1$ made of two unknotted curves may serve as naive approach of TQC, corresponding to one qubit on either curves, as in [3]. Representation theory of the fundamental group ${\pi }_1(L)$ over the group $S{L}_2(\mathbb{C})$ puts the punctured torus $T_1^1$ whose group is ${\pi }_1(T_1^1)\cong F_2$ into focus. In the second context, at least in a first approximation, a finitely generated group $f_p$ defined from an appropriate DNA/RNA sequence turns out to be close to $F_2$ (for a sequence built from two distinct nucleotides) or to $F_3$ (for a sequence built from three distinct nucleotides). The $S{L}_2(\mathbb{C})$ character variety of such a $f_p$ group favors the topology of the triply punctured sphere $S_2^{(3)}$ (respectively the quadruply punctured sphere $S_2^{(4)}$) whose fundamental groups are $F_2$ (respectively $F_3$).

Both free groups $F_2$ and $F_3$ are related when studying the fibrations of the Painlevé VI (or $P_{VI}$) equation, a second order differential equation governing the isomonodromic deformations (monodromy preserving deformations) of linear rank two Fuchsian systems [4].

In Section 2, we first briefly describe the mathematics establishing the connection between the topology of free groups $F_2$ and $F_3$, isomonodromy deformations, $S{L}_2(\mathbb{C})$ representations, the Painlevé VI equation and the so-called Fricke-Painlevé surfaces. In Section 3 and Section 4, we use the parametric forms of some algebraic solutions of $P_{VI}$ and provide log-log plots of some of them for the first time. In Section 5, we discuss the applications of Painlevé VI to the character varieties of finitely generated groups encountered in TQC and genetics, and provide perspectives.

2. Materials and Methods

There is the notion of a flat connection on a fibre bundle $M\to B$, where the base B is the three-punctured sphere $B=S_2^{(3)}={\mathbb{P}}^1\setminus \{0,1,\infty \}$ and for each point $t\in B$ there exists a corresponding four-punctured sphere $P_t=S_2^{(4)}={\mathbb{P}}^1\setminus \{0,1,t,\infty \}$. Let $M_t$ be the fibre of M over the base point $t\in B$, the monodromy action is described by the action of the fundamental group of the base on the fiber thanks to the homomorphism ${\pi }_1(B)\to Aut(M_t)$ [4].

The space of conjugacy classes of $S{L}_2(\mathbb{C})$ representations for the fundamental group ${\pi }_1(P_t)$ is the character variety

$$\mathcal{C}=\mathrm{Hom}({\pi }_1(P_t),G)/G,\mathrm{with}G=S{L}_2(\mathbb{C}).$$

The connection is described by $P_{VI}$ equation as follows

$$\begin{array}{cc}& y_{tt}=\frac{1}{2}(\frac{1}{y}+\frac{1}{y-1}+\frac{1}{y-t})y_t^2-(\frac{1}{t}+\frac{1}{t-1}+\frac{1}{y-t})y_t\\ & +\frac{y(y-1)(y-t)}{2t^2{(t-1)}^2}\{{\alpha }_4^2-{\alpha }_1^2\frac{t}{y^2}+{\alpha }_2^2\frac{t-1}{{(y-1)}^2}+(1-{\alpha }_3^2)\frac{t(t-1)}{{(y-t)}^2}\}\\ \hfill \end{array}$$

(1)

with $y_t=\frac{dy}{dt}$ and parameters ${\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4$.

2.1 The Fricke-Painlevé VI surface

Let the boundary components of $P_t$ be A, B, C, D, then ${\pi }_1(P_t)=〈A,B,C,D|ABCD〉\cong F_3$. A $S{L}_2(\mathbb{C})$ representation of ${\pi }_1$ is the quadruple $\alpha =\rho (A)$, $\beta =\rho (B)$, $\gamma =\rho (C)$, $\delta =\rho (D)$ with $\alpha \beta \gamma \delta =I.$ Taking the four boundary traces $a=tr(\rho (\alpha ))$, $b=tr(\rho (\beta ))$, $c=tr(\rho (\gamma ))$, $d=tr(\rho (\delta ))$ and the three traces x, y, z of elements $AB$, $BC$, $CA$ representing simple loops on $P_t$, we obtain the character variety for $P_t$ [5], Section 5.2, [6], Section 2.1, [7], Section 3B, [8], Eq. 1.9, [9], Eq. (39), [10]

$$V_{a,b,c,d}(x,y,z)=x^2+y^2+z^2+xyz-{\theta }_{1}x-{\theta }_{2}y-{\theta }_{3}z-{\theta }_4=0,$$

(2)

with ${\theta }_1=ab+cd$, ${\theta }_2=ad+bc$, ${\theta }_3=ac+bd$ and ${\theta }_4=4-a^2-b^2-c^2-d^2-abcd.$

From now, the 3-dimensional cubic surface $V_{a,b,c,d}(x,y,z)$ with 3 variables and 4 parameters is called the Fricke-Painlevé VI surface (or simply Fricke-Painlevé surface) due to the established correspondence between the automorphisms of such a surface and Painlevé VI equation.

Looking at the nonlinear monodromy of Painlevé VI we get the relation between parameters a, b, c, d of $V_{a,b,c,d}(x,y,z)$ and parameters ${\alpha }_i$, $i=1..4$, of Painlevé VI equation as [8], Theorem 3, [9], Section 4.2, [10], Eq. 13

$$(a,b,c,d)=[2cos(\pi {\alpha }_1),2cos(\pi {\alpha }_2),2cos(\pi {\alpha }_3),2cos(\pi {\alpha }_4)].$$

(3)

The Cayley’s nodal cubic surface

The most famous Fricke-Painlevé surface follows from the fundamental group of the knot complement ${\pi }_1(S_3\setminus L2a1)=〈a,b|[a,b]〉={\mathbb{Z}}^2$, where $S_3$ is the three sphere, $[a,b]=a^{-1}{b}^{-1}ab$ is the group theoretical commutator and $L2a1$ the Hopf link. The character variety is given by the polynomial

$${\kappa }_4(x,y,z)=x^2+y^2+z^2-xyz-4,$$

(4)

where the notation ${\kappa }_4(x,y,z)=V_{0,0,0,0}(x,y,z)$ is for the unique surface of the Fricke-Painlevé family, known as the Cayley nodal cubic surface, exhibiting four isolated singularities. A plot can be found in [1], Figure 1.

Solutions of the corresponding Painlevé VI equation, attributed to Picard (in 1889), can be explicitly expressed in terms of the Weierstrass elliptic function [10], Proposition 51, p. 155, [11].

3. Algebraic solutions of Painlevé VI equation mapping to algebraic surfaces

Following the description of [12], an algebraic solution $y(t)$ of $P_{VI}$ equation should be specified by a polynomial equation $F(y,t)=0$ with rational coefficients and a set of four parameters ${\alpha }_i$, $i=1..4$.

More precisely, an algebraic solution of Painlevé VI is a compact (possibly singular) algebraic curve $\Pi$ together with two rational functions y and t: $\Pi \to {\mathbb{P}}_1$ providing a rational parametric representation ($y(s),t(s))$ such that (a) t is a Belyi map, with its branch locus being a subset of $\{0,1,\infty \}$ and (b) y solves $P_{VI}$ for some parameters ${\alpha }_i$.

All algebraic solutions of $P_{VI}$ have been classified in [13] and [10] building upon significant earlier contributions, including [14,15,16]. In [13], all algebraic solutions of $P_{VI}$, if not of the dihedral, tetrahedral or octahedral type, are refered to as isosahedral solutions as they can be derived from the finite monodromy subgroup $\Gamma$ of $G=S{L}_2(\mathbb{C})$, where $\Gamma$ is the binary icosahedral group. Such solutions, governing the isomonodromic deformations of $P_{VI}$, have finite branching, with a number of branches ranging from 5 to 72.

Mapping an algebraic Fricke-Painlevé surface with integer parameters ${\theta }_i$ to an algebraic solution of Painlevé VI equation is one to one except for parameters ${\theta }_i=(1,0,0,2)$ (yielding three distinct solutions) and ${\theta }_i=(0,0,0,3)$ (yielding two distinct solutions) [10]. In the first exceptional case the surface is a degree 3 del Pezzo surface of type $A_1$ (with one isolated singularity) while in the later case it is a degree 3 del Pezzo surface without a simple singularity. Detailed information about the 12 solutions ($3+2+7$) is provided in this section.

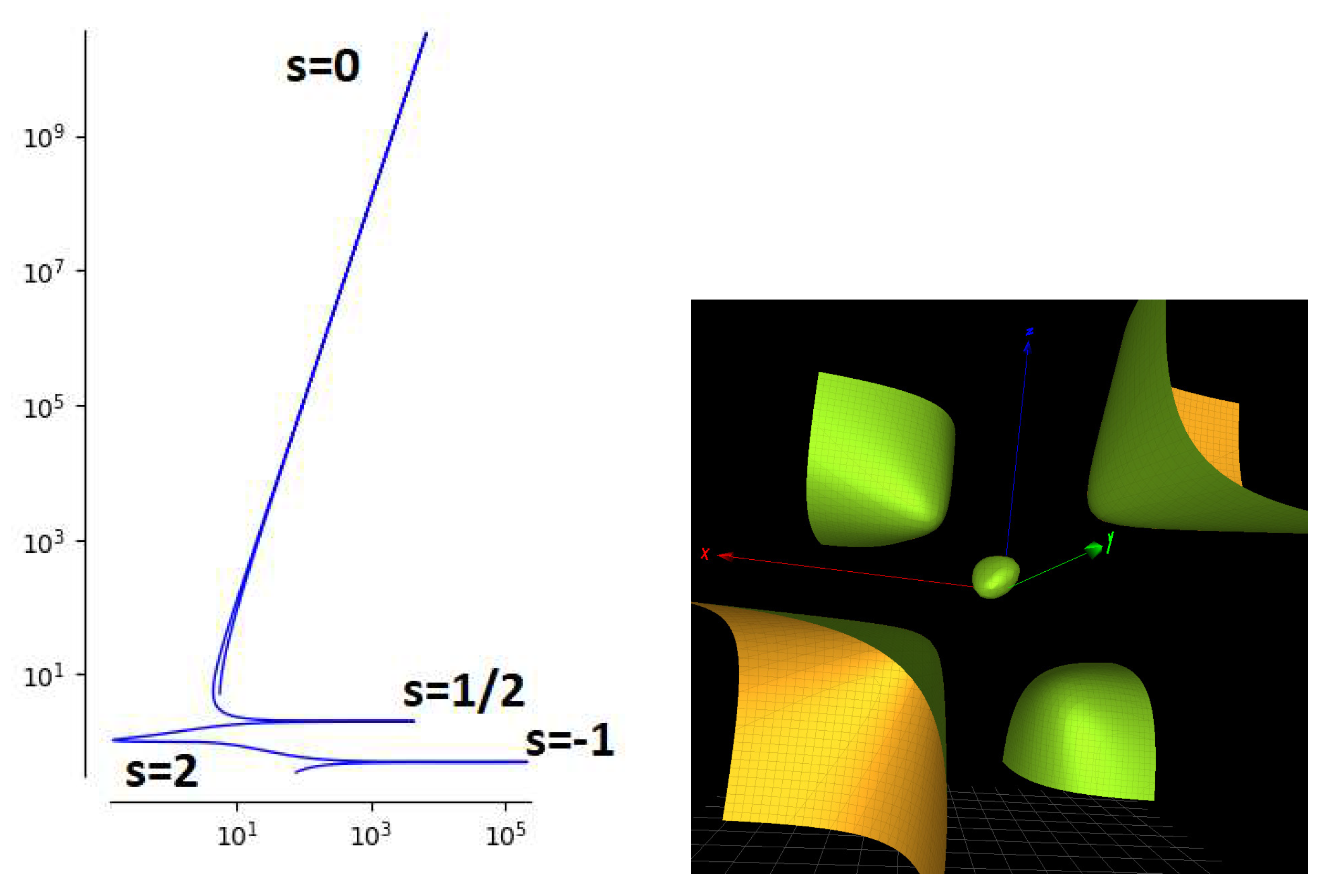
3.1. The Klein surface

The Klein surface, obtained with parameters $({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=(1,1,1,0)$ [10], solution 8, has the parametric form

$$y(s)=\frac{(5s^2-8s+5)(7s^2-7s+4)}{s(s-2)(s+1)(2s-1)(4s^2-7s+7)},t(s)=\frac{{(7s^2-7s+4)}^2}{s^3{(4s^2-7s+7)}^2}$$

(5)

It corresponds to the complex reflection group 24 in the Shephard-Todd list. The solution has 7 branches and parameters ${\alpha }_i=(2/7,2/7,2/7,4/7)$. It is shown in Figure 1.

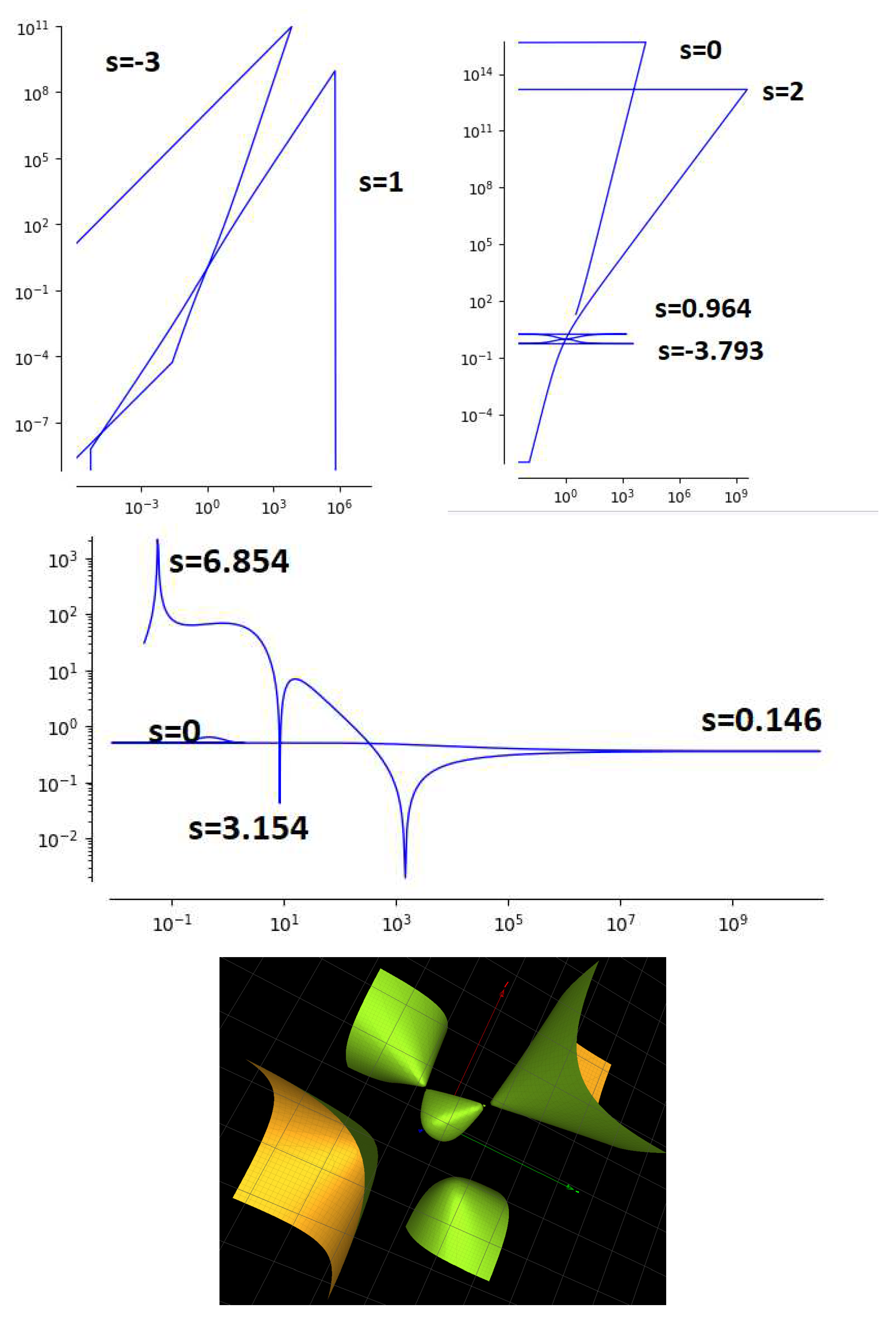
3.2. Solutions with parameters $({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=(1,0,0,2)$

There are three solutions of $P_{VI}$ corresponding to the algebraic surface $xyz+x^2+y^2+z^2-x-2=0$. They are referred to as solution 3 (a tetrahedral solution with 6 branches), solution 21 with 12 branches and solution 42 with 36 branches in [10]. The surface is a degree 3 del Pezzo surface with an isolated singularity of type $A_1$. It is depicted at the bottom of Figure 2.

The parametric form of the tetrahedral solution 3 is

$$y(s)=\frac{-s(s+1){(s-3)}^2}{3(s+3){(s-1)}^2},t(s)=\frac{-{(s+1)}^3{(s-3)}^3}{{(s-1)}^3{(s+3)}^3}$$

(6)

The parametric forms for solutions 21 and 42 are found in [10]. The log-log plots of the solutions are given in Figure 2.

The parametric form of solution 3 has poles at $s=1$ and 3 which are evident as discontinuities in the log-log plot. For solution 21, there are poles at $s=0$, 2, $-\sqrt{2}\pm 2.2^{1/4}$ (i.e. $s\sim 0.964$ and $-3.793$). For solution 42, there are poles at $s={10}^{1/3}+1\sim 3.154$ and $(7\pm \sqrt{5})/2$ (i.e. $s\sim 6.854$ and $0.146$).

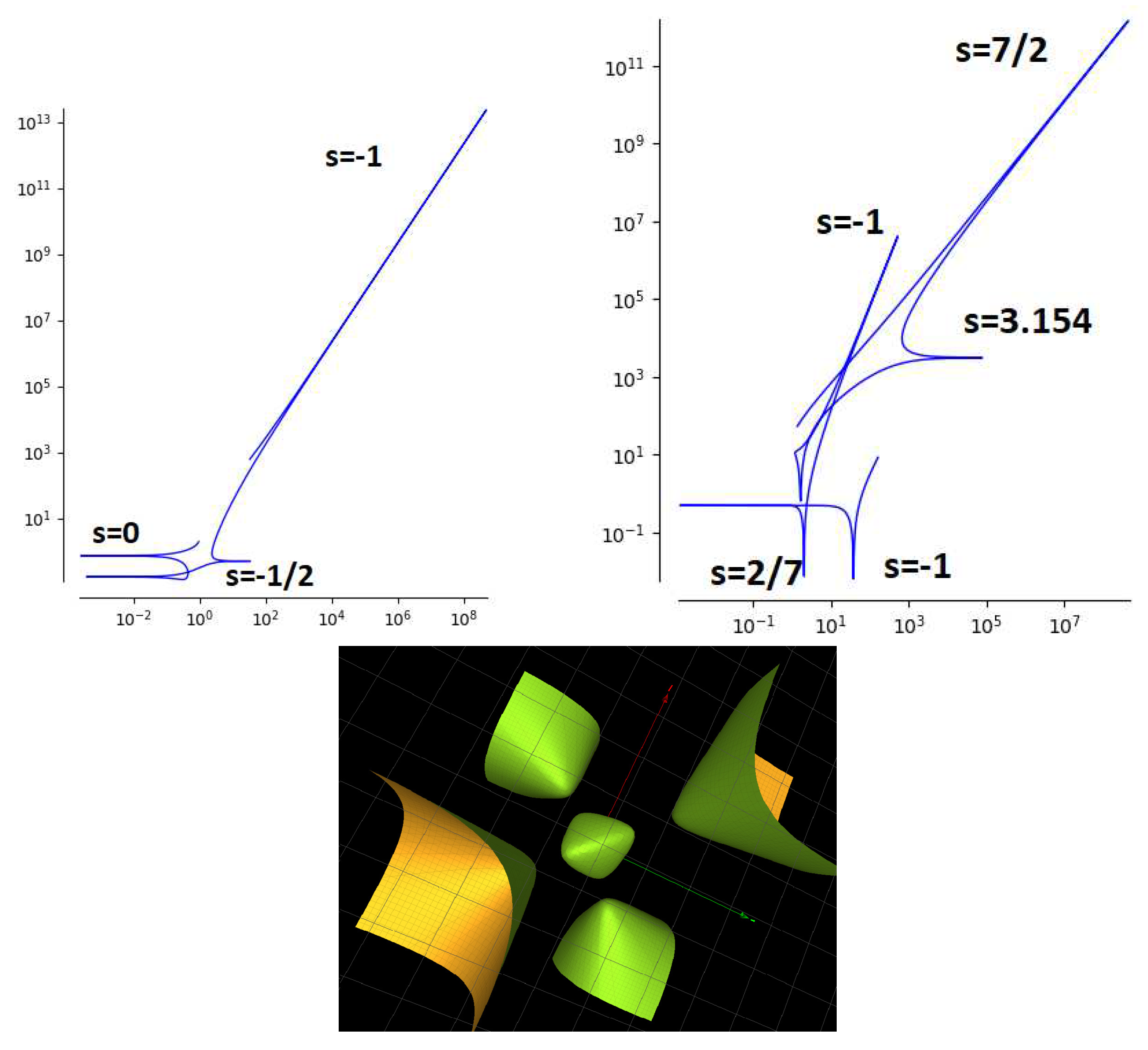
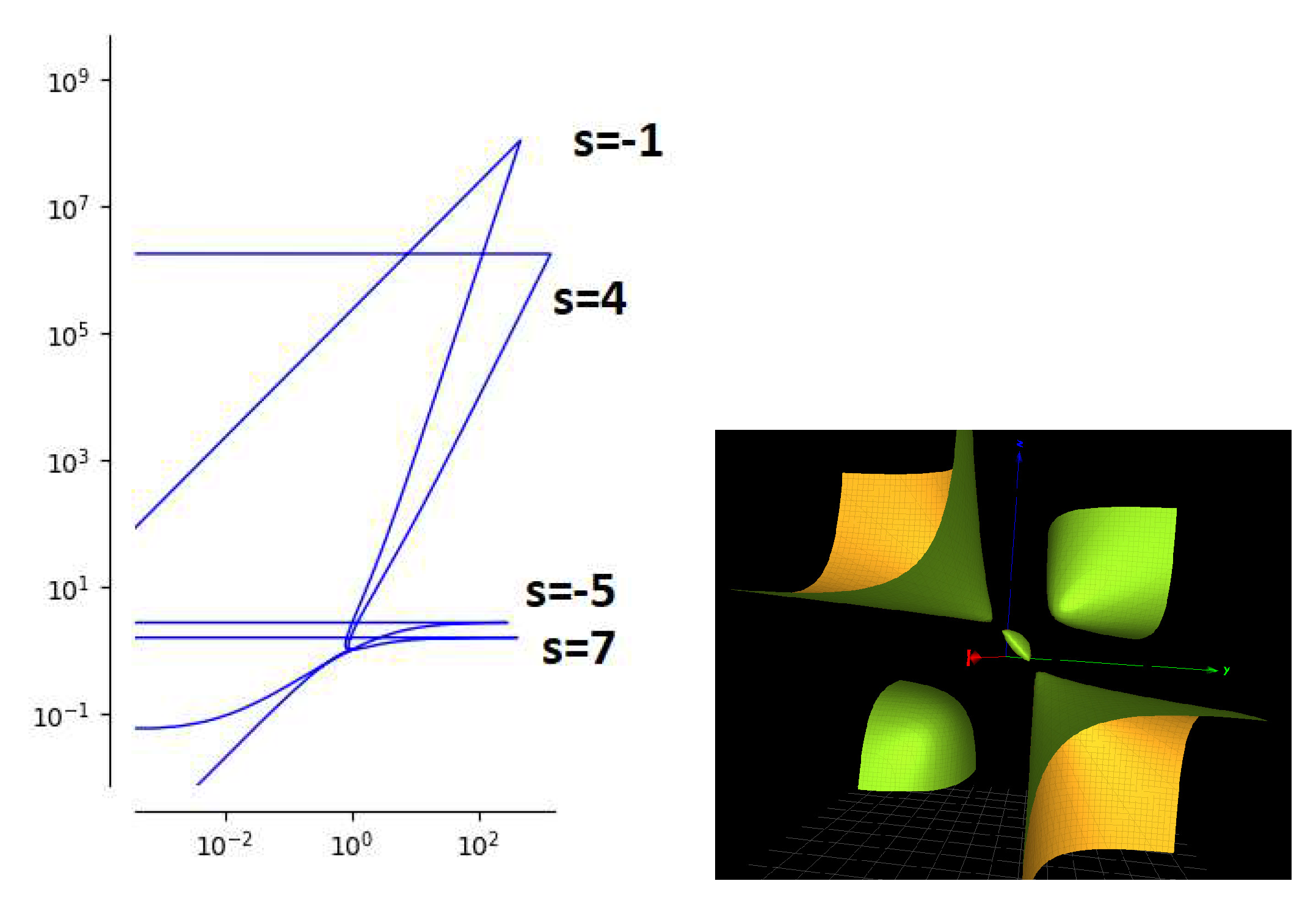
3.3. Solutions with parameters $({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=(0,0,0,3)$

There are two solutions of $P_{VI}$ corresponding to the algebraic surface $xyz+x^2+y^2+z^2-3=0$. They are referred to as solution 20 (an octahedral solution with 12 branches) and solution 45 with 72 branches in [10]. The surface is of a degree 3 del Pezzo type devoid of an isolated singularity. It is depicted at the bottom of Figure 3.

The parametric form of the octahedral solution 20 is

$$\begin{array}{cc}& y(s)=\frac{1}{2}+\frac{45s^6+20s^5+95s^4+92s^3+39s^2-3}{4(5s^2+1){(s+1)}^{2}u(s)}\\ & t(s)=\frac{1}{2}+\frac{s{(2s+1)}^2(27s^4+28s^3+26s^2+12s+3)}{{(s+1)}^{3}u{(s)}^3}\\ & u{(s)}^2=(2s+1)(9s^2+2s+1)\\ \hfill \end{array}$$

(7)

The parametric forms for solution 45 is given in [10]. The log-log plots of the solutions are presented in Figure 3. The parametric form of solution 20 reveals two poles at $s=-1$ and $-1/2$ and another discontinuity at $s=0$. For solution 45, there are poles at $s=\pm 1$, $2/7$, $7/2$ and ${10}^{1/3}+1$.

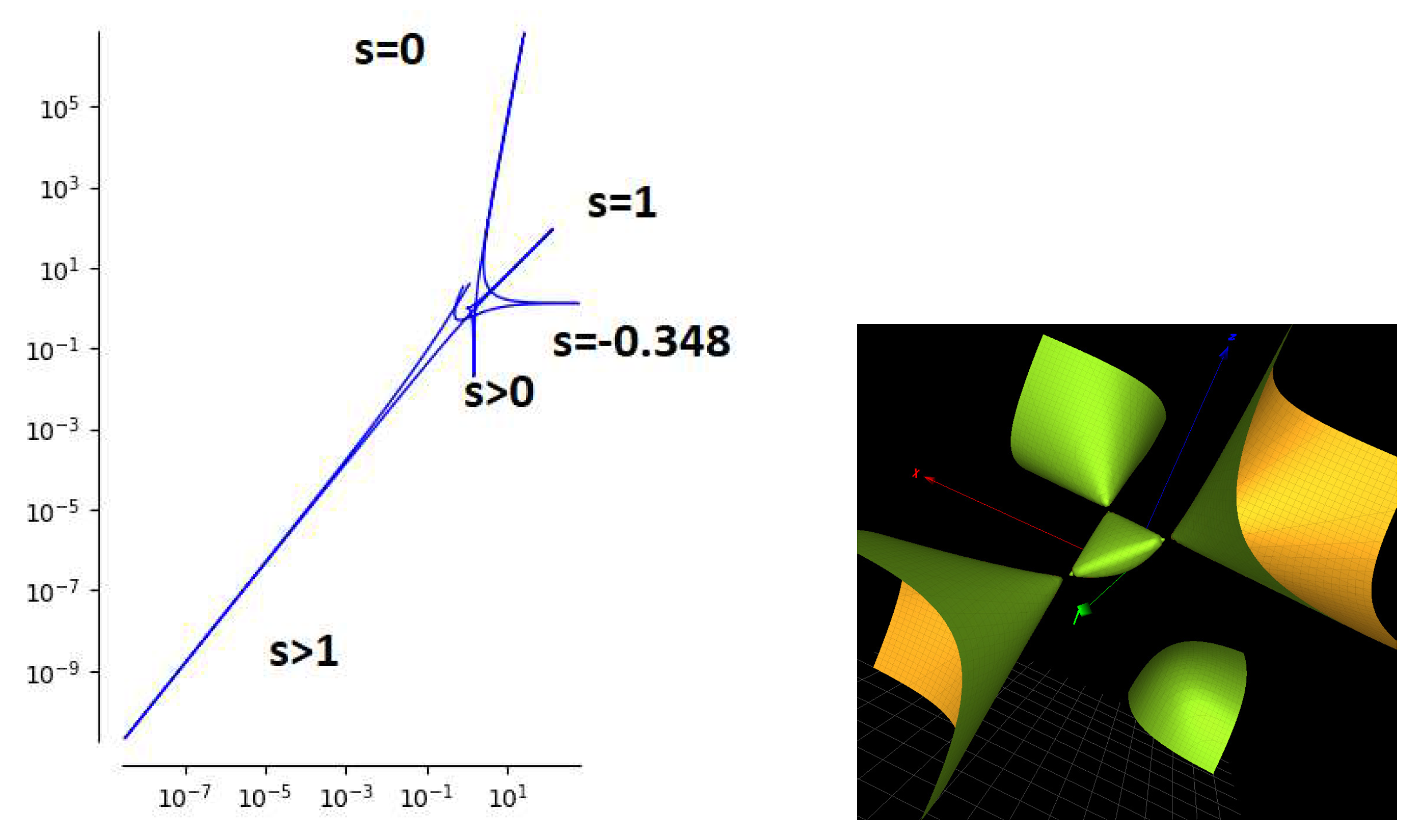
3.4. The great dodecahedron solution

The great dodecahedron solution, obtained with parameters $({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=(2,2,2,-1)$ [10], solution 31, has the parametric form

$$\begin{array}{cc}& \frac{1}{2}-\frac{8s^7-28s^6+75s^5+31s^4-269s^2+318s^2-166s+56}{18u(s)(s-1)(3s^3-4s^2+4s+2)}\\ & \frac{1}{2}+\frac{(s+1)(32(s^8+1-320(s^7+s)+1112(s^6+s^2)-2420(s^5+s^3)+3167s^4}{54u{(s)}^{3}s(s-1)}\\ & u{(s)}^2=s(8s^2-11s+8)\\ \hfill \end{array}$$

(8)

The solution has 18 branches and parameters ${\alpha }_i=(1/3,1/3,1/3,1/3)$. A log-log plot for the modulus of solution 31 is shown in Figure 4 (Left) where the three poles at $s=(4-2.{10}^{2/3}+{10}^{1/3})/9\sim -0.348$, $s=0$ and 1 are shown. The corresponding algebraic surface is a degree 3 del Pezzo of type $3A_1$.

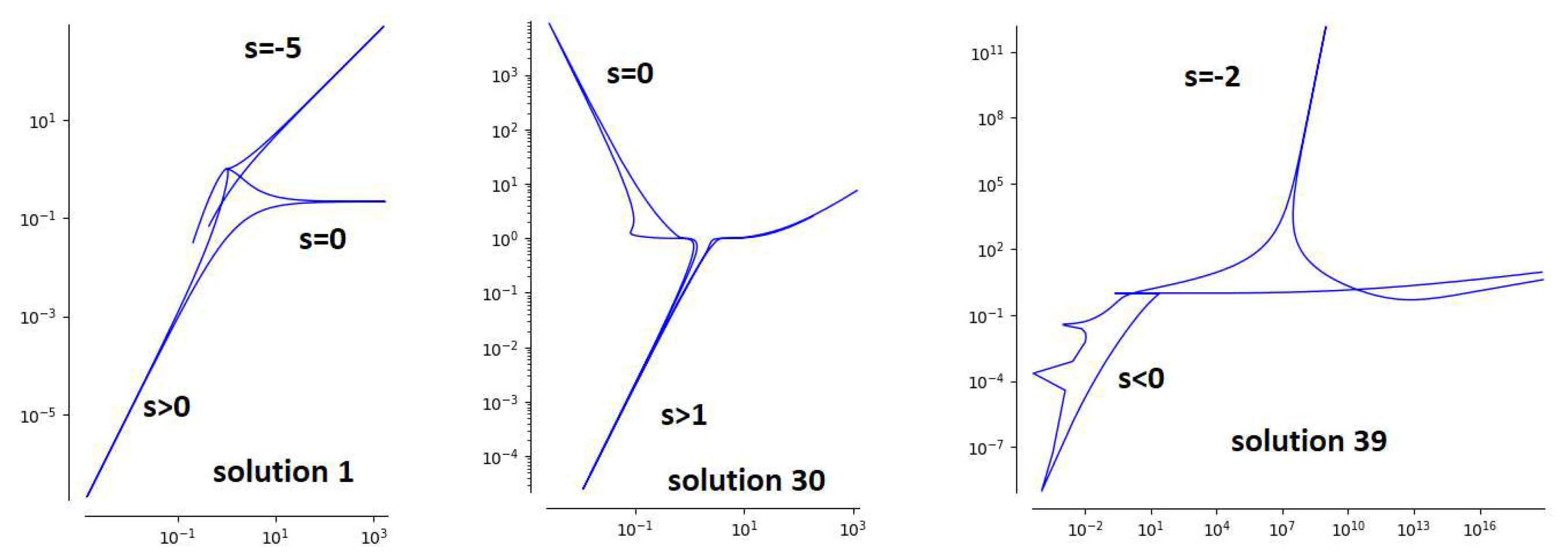
3.5. Three extra solutions leading to an algebraic Fricke-Painlevé surface

There are three extra solutions corresponding to an algebraic Fricke-Painlevé surface. They correspond to the unique solutions with parameters $({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=(0,1,1,0)$ (solution 1 with 5 branches), $(0,0,0,3)$ (solution 30 with 16 branches), and $(1,1,1,1)$ (solution 39 with 24 branches). The parametric expressions are in [10]. The log-log plots are found in Figure 5. The corresponding Fricke-Painlevé surfaces are degree 3 del Pezzo and devoid of isolated singularities.

4. Further algebraic solutions of Painlevé VI equation

From now, we list further algebraic solutions of $P_{VI}$ not related to an algebraic Fricke-Painlevé surface.

4.1. The icosahedral solution 7

The surface, obtained with parameters $({\alpha }_i=(1/5,2/5,1/5,1/3))$, that is $({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=((1+\sqrt{5},(3+\sqrt{5})/2,(3+\sqrt{5})/2,-2-\sqrt{5})$ [10], solution 7, has six branches and parametric form

$$y(s)=\frac{-54s(s-7)}{(s-4)(s+1)(s^4-20s^2-35)},t(s)=\frac{432s}{(s+5){(s+1)}^3{(s-4)}^2}$$

(9)

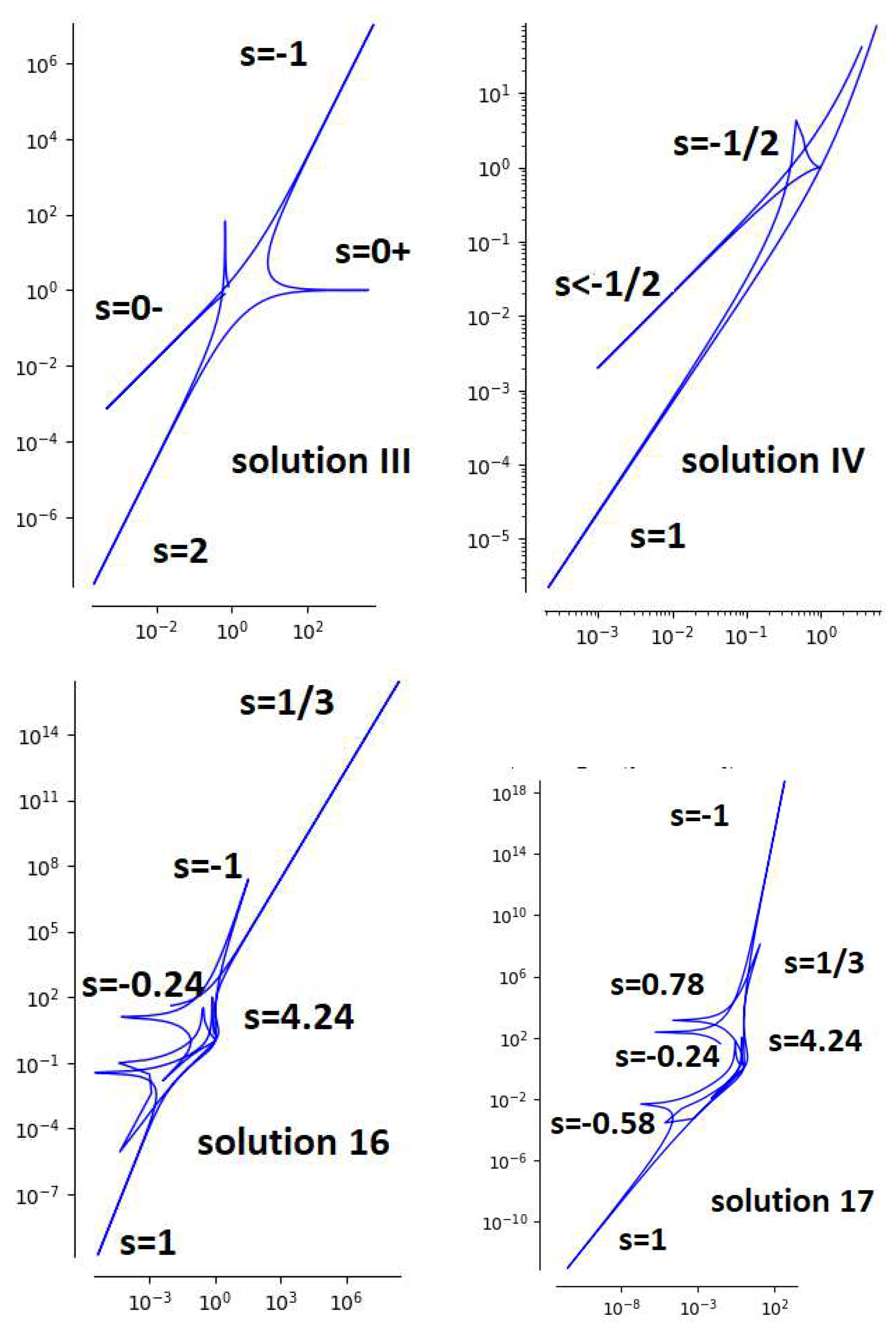
4.2. Dubrovin-Mazzocco platonic solutions

In [14], some platonic solutions of Painlevé VI equation are explored. These include the tetrahedral solution (solution III in [10] with 3 branches), the dihedral solution (solution IV in [10] with 4 branches), icosahedral solutions (solution 16 and 17 with 10 branches in [10]) and the great dodecahedron solution (solution 31 in [10]). These solutions are obtained for parameters ${\alpha }_i=(0,0,0,2/3)$, $(0,0,0,1/2)$, $(0,0,0,-4/5)$, $(0,0,0,-2/5)$ and $(1/3,1/3,1/3,1/3)$, respectively. The great dodecahedron solution was previously mentioned in subsection 3.4 and the parametric forms of other solutions are depicted in Figure 7. The explicit parametric forms can be found in the aforementioned papers.

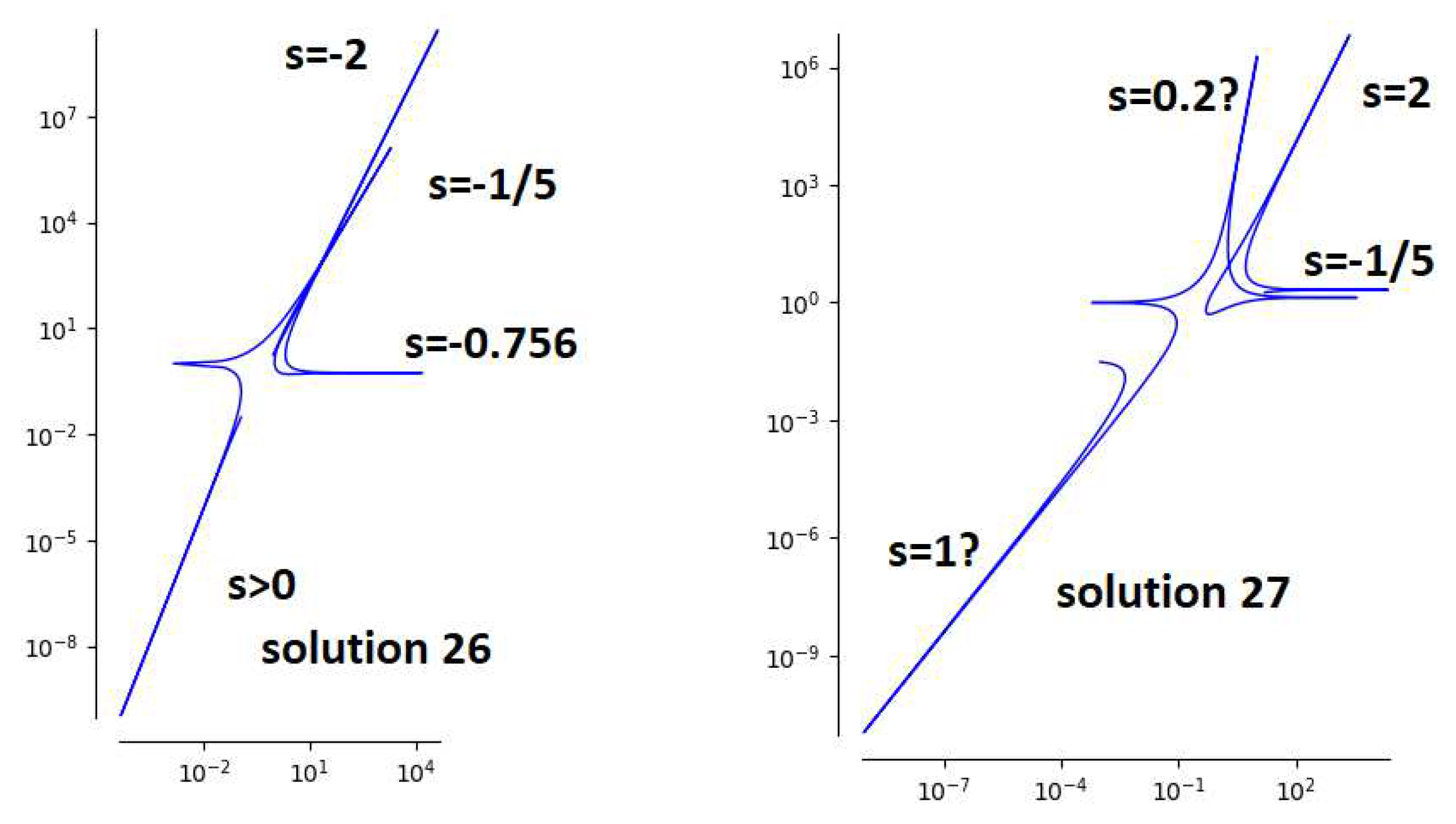
4.3. Solutions related to the Valentiner group

The Valentiner group is the three-dimensional complex reflection group 27 with an order of 2160 in the Shephard-Todd list. Three solutions of $P_{VI}$ are built upon this symmetry [4], Theorem D. One of them is solution 39 described in subSection 3.5. The other two are solutions 26 and 27 (with parameters ${\alpha }_i=(1/3,1/3,1/3,3/5)$ and $(1/3,1/3,1/3,1/5)$), representing ${\theta }_i=((3\mp \sqrt{5})/2,(3\mp \sqrt{5})/2,(3\mp \sqrt{5})/2,\pm \sqrt{5}+1)$ and 15 branches.

The solutions are plotted in Figure 8

4.4. Two extra icosahedral solutions

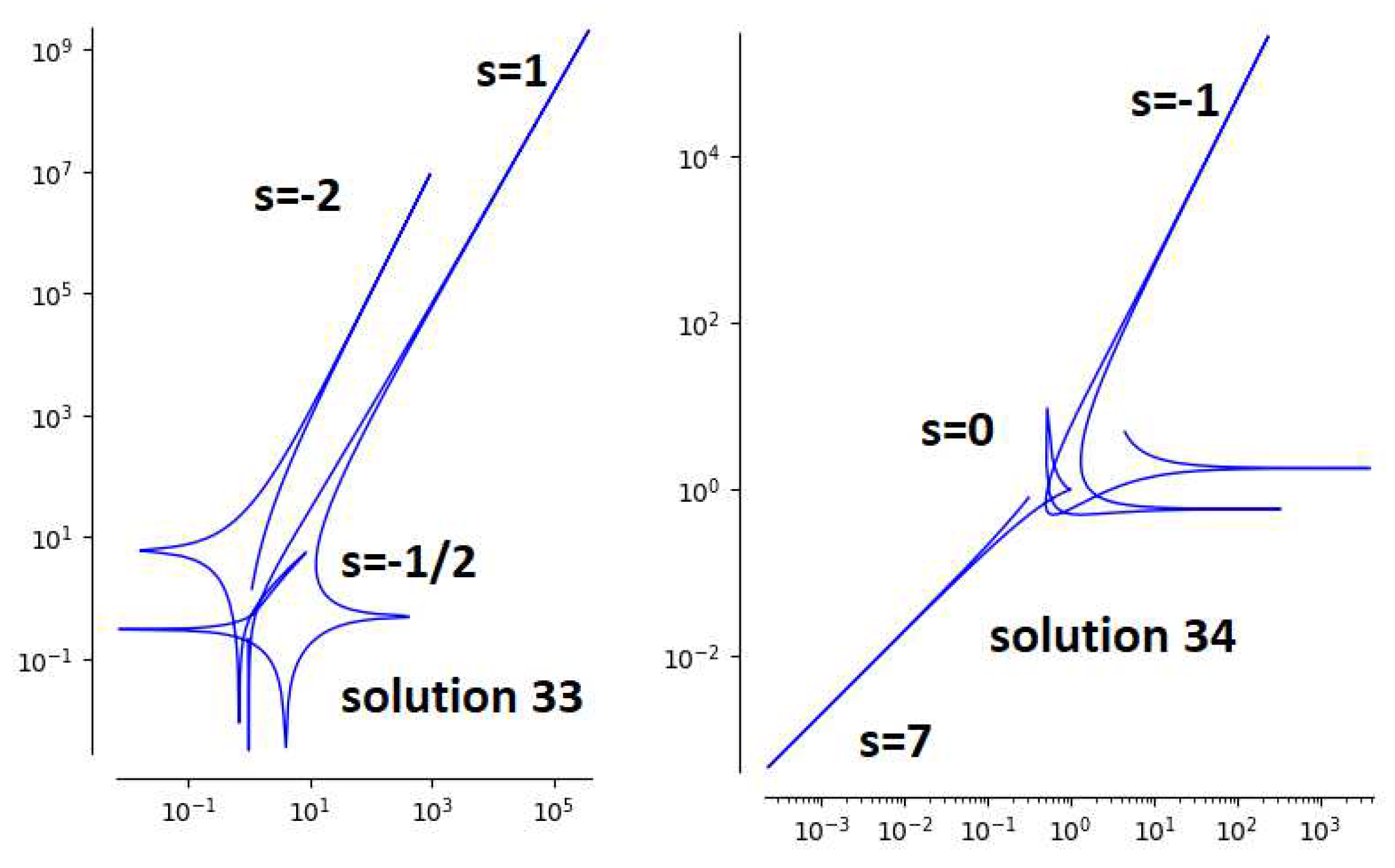
Solutions 33 (with parameters ${\alpha }_i=(1/3,1/7,1/7,6/7)$) first found in [16] and 34 (with parameters ${\alpha }_i=(2/7,2/7,2/7,1/3)$) are closed to each other. Their parametric forms are plotted in Figure 9.

5. Discussion

5.1. Application to $S{L}_2(\mathbb{C})$ character varieties of finitely generated groups

Our interest in Painlevé VI arises from our exploration of $S{L}_2(\mathbb{C})$ representations of finitely generated groups $f_p$ encountered in models of topological quantum computing (TQC) [1,17] and the investigation of DNA/RNA short sequences crucial in transcriptomics [2,18]. A model of TQC can commence with a link such as the Hopf link $L2a1$, whose character variety is the Cayley cubic surface ${\kappa }_4(x,y,z)$ [4]. This surface is associated with the Picard solution of $P_{VI}$, as mentioned at the end of the introduction. Other links, such as $L7a4$ or $L6a1=6_3^2$[1], Figure 2, whose character varieties contain the Fricke-Painlevé surfaces ${\kappa }_d(x,y,z)$ for $d=2$ and 3 can be utilized. To these surfaces one can attach solution 30 of Painlevé VI (see subsection 3.5 for the former case), and solutions 20 or 45 (see subsection 3.3 for the latter case).

It has been observed that the Groebner basis of four-letter $f_p$ groups encountered in the context of DNA/RNA sequences contains algebraic surfaces ${\kappa }_d(x,y,z)$ for $d=3$ and 4 as mentioned above, as well as the surface $V_{1,1,1,1}(x,y,z)$[2]. This surface corresponds to Fricke-Painlevé solution 31, with parameters ${\theta }_i=(2,2,2,-1)$, associated with the symmetry of the great dodecahedron (see subsection 3.4). The surface with parameters ${\theta }_i=(1,0,0,2)$ is also part of the Groebner basis for four-letter $f_p$ groups. This reveals that many algebraic solutions of $P_{VI}$, the Picard solution for the Cayley cubic ${\kappa }_4(x,y,z)$, solutions 20 and 45 associated to ${\kappa }_3(x,y,z)$, solutions 3, 21 and 42 for parameters ${\theta }_i=(1,0,0,2)$ and the great dodecahedron solution 31 should play a role in genetics at the genome scale.

5.2. Perspectives

Isomonodromic deformation is a concept dating back to the nineteenth century, pioneered by P. Painlev’ and subsequently studied by Fuchs, Schlesinger, Jimbo, and numerous other scholars [19]. This concept is underpinned by crucial mathematical properties of isomonodromy equations, including the Painlev’ property, indicating that essential singularities remain fixed while poles may shift; transcendence, implying that solutions are non-classical; the existence of a symplectic structure, a twistor structure, and a Gauss-Manin connection. Isomonodromic deformation finds applications across various fields, such as random matrix theory, statistical physics, topological quantum field theory, nonlinear partial differential equations, Einstein field equations, and mirror symmetry.

While this paper primarily delves into the exploration of algebraic solutions of the Painlev’ VI equation, it is noteworthy that the chaotic dynamics of $P_{VI}$ has also received attention [20]. Further generalizations can be explored, as presented in [21]. In this latter paper, the role of $P_{VI}$ is assumed by a differential equation governing the divergences in a formulation of renormalization in quantum field theory. The concept of a flat connection on a fiber bundle over the three-punctured sphere is significantly extended to a `flat equisingular bundle’ within a tensor category. The underlying symmetries are no longer discrete but are described by a motivic Galois group, also referred to as the `cosmic Galois group’, in line with ’Cartier’s dream’ [22].