1. Introduction
Power electronics play a fundamental role in efficient energy conversion and control in various applications, ranging from consumer electronics applications to electric propulsion systems and integrating renewable energy resources in microgrids [
1,
2,
3]. For instance, electric mobility applications demand the implementation of voltage inverter systems for the power supply and control of AC motors for electric traction, such as those reported in [
4,
5]. Likewise, DC-AC inverters assume a crucial role by allowing the conversion of direct current voltages into alternating current, thus facilitating the integration of DC sources into conventional electrical grids or the power supply of AC loads. Inverter systems are also used in applications of injection of renewable energy in DC into the conventional grid in AC, such as the works reported in [
6,
7]. However, optimizing and controlling inverters remains a substantial challenge, as it involves both ensuring the quality of the output waveform and the energy efficiency of the conversion [
8].
More broadly, a significant body of knowledge has been accumulated within the scope of application of DC-AC inverters. Oh et al. [
9] presented an innovative approach using an integrated Z-source DC-AC inverter controlled by symmetrical and asymmetrical voltages, contributing to the advancement of high-performance power converters. Research, such as that of Hsieh et al. [
10], has explored the design and implementation of a novel 7-level output voltage inverter, achieving a notable decrease in harmonics upon conversion with an efficiency greater than 96%. Regarding the use of DC-AC inverters in microgrid applications, Engelhardt et al. [
6] carried out the optimized control of a DC microgrid with a busbar array for high-power electric vehicle charging keeping the DC-AC conversion out of the control. Furthermore, Huynh et al. [
11] explored the design and implementation of modified three-level reverse-phase inverters for powering three-phase loads. Villanueva et al. [
12] investigated the reliability of transformerless DC/AC photovoltaic converters based on the mission profile, contributing to the development of robust and efficient solutions.
In the context of the control algorithms of DC-AC voltage inverters and their applications, control techniques based on fuzzy logic and its different variants have demonstrated their effectiveness. Lim et al. [
13] proposed a fuzzy PI controller for energy management and zero power flow between the main and local grid in photovoltaic systems. Javadi et al. [
14] introduced a fuzzy logic-controlled intelligent transformer for current imbalance compensation in a power grid. Furthermore, Srikanth et al. [
7] presented a bidirectional operation of a dual-mode PV inverter for seamless power transfer between DC and AC loads along with the grid interface. The research of Rodríguez-Flores et al. [
15] is cited for expanding the use of fuzzy logic in electrical applications, who demonstrated the application of a proportional-integral controller and a proportional controller based on Mandani fuzzy logic and connected in cascade to determine the reference generation power and the reference phase shift of the generator in order to perform synchronization between the main grid and a decentralized microgeneration system through a 140 [kVA] inverter.
This paper presents a comprehensive approach for designing a 10 [kW] transformer-isolated DC-AC inverter controlled by a fuzzy PI controller with anti-windup mitigation techniques. The proposed methodology fuses fuzzy control principles with anti-windup mitigation techniques [
16,
17,
18], intending to improve both the quality of the output waveform and the transient response of the inverter. Throughout this study, the theoretical aspects, the design, and control implementation of the inverter will be detailed, as well as the results obtained and their meaning in the context of efficient and high-quality DC-AC energy conversion, contrasting the data obtained from open and closed loop performance assessment. In particular, the effect of anti-windup in the controller on the output AC signal's total harmonic distortion (THD) are discussed.
3. Discussion
Considering the final effect at the design and performance levels of the boost and inverter system, from to RMS, it can be observed that, when comparing Tables II, VI, VIII, and XIII, the harmonic distortion factor is affected by the regulation process, averaging . However, the harmonic distortion factor is without regulation at full load.
By developing a comparison among Figures 8, 19, 23, and 27, it can be concluded that there is a significant reduction in electrical stress on components and an increase in electrical safety for loads connected to the power system, which is due to a decrease in transient voltage and current spikes, though settling time is increased for the nominal voltage and current values of the to RMS conversion system.
Beyond comparing transient responses, where extreme values must be considered for both voltage and current of the power source, the normalized spectral study has significantly contributed to evaluating statistical behaviors. These could represent a judgment criterion in the performance evaluation process.
If the behavior of the voltage variation or ripple is evaluated, at the DC level, it can be concluded that at the frequency of it is around and at is . On the other hand, when a test is carried out with load variation, the voltage ripple at is around and at is 0.06%. The inverter system presents more sensitivity in the current, that is, in open loop at nominal load the current ripple at is and at is . However, when the inverter system operates in closed loop, the current ripple at is and at is . Besides, when the inverter system operates in closed loop, but with load variation, the current ripple at is and at is . This is a great variation compared to the previous cases and even more so if the case of closed loop regulation is considered with varying the source voltage of the battery pack. In this last case, the current ripple at is and at is .
The simulated study, carried out with a rigid model, allowed the evaluation of details and the application of offline training criteria associated with the fuzzy control system, particularly the fuzzy PI control system with anti-windup. Otherwise, online training could have been risky for both experimenters and the integrity of the power electronics system and its associated components.
Figures 22(b) and 26(b), representing the deviation of control action per unit (p.u.) in response to variations, either in load or source voltage, respectively, demonstrate an improved capability of the fuzzy PI controller with anti-windup to compensate for variations caused by source voltage disturbances than for load variations. However, both situations will occur, and not necessarily separately, as it is an inherent operating condition for the considered light electric vehicle power supply system.
4. Conclusions
In this paper, the mathematical modeling of the power electronics of the inverter system and its switched and non-linear operation was carried out, allowing the develop of a detailed simulation that shows the possibility of evaluating aspects associated with the proposed fuzzy PI control and its optimal operation.
The quantitative evaluation related to the converter's performance was carried out through the discrete treatment of the voltage and current samples using spectral techniques as well as filtering considerations and evaluation of limit cycle for the determination of the system's stability with the proposed control strategy. The THD at the output of the filter (transformer and capacitor) was around and at nominal load in open loop and closed loop, respectively.
The behavior of the system power source is stable enough to operate the connected system (no need for control). However, the difficulty of guaranteeing nominal voltage at the output of the equipment rises when the inversion system is without load or with a load close to the nominal value, events for which the fuzzy PI control is capable of reacting to maintain the system's stability.
The study yields conclusions highlighting the parameterization of the dynamic components of the system because the load variation around the nominal value does not cause significant control action. However, significant variations in the ripple occur at the level of the DC rise voltage prior to the inverter process, highlighting (in the spectral studies) two ripple frequencies, one at the switching frequency in the voltage rise process and another at the double the frequency of the inversion system. In open loop and nominal load, the current ripple at is and at is . However, when the inverter system operates in closed loop, the current ripple at is and at is The design of an optimized fuzzy PI control with anti-windup action was possible by replicating a known behavior and incorporating the variants do not present in a linear regulator (in this case, a classic PI). The development of the fuzzy PI controller, with anti-windup, showed more sensitivity to the source voltage variation of the battery pack than to the load variation.
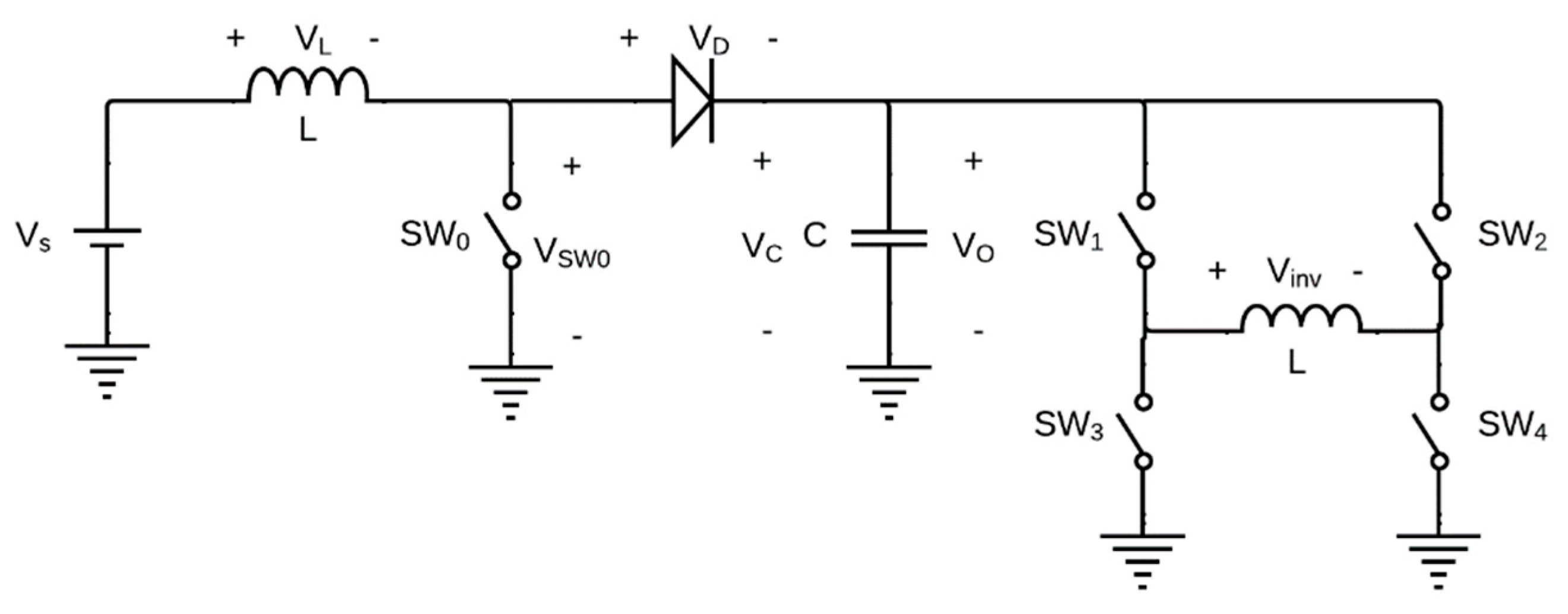
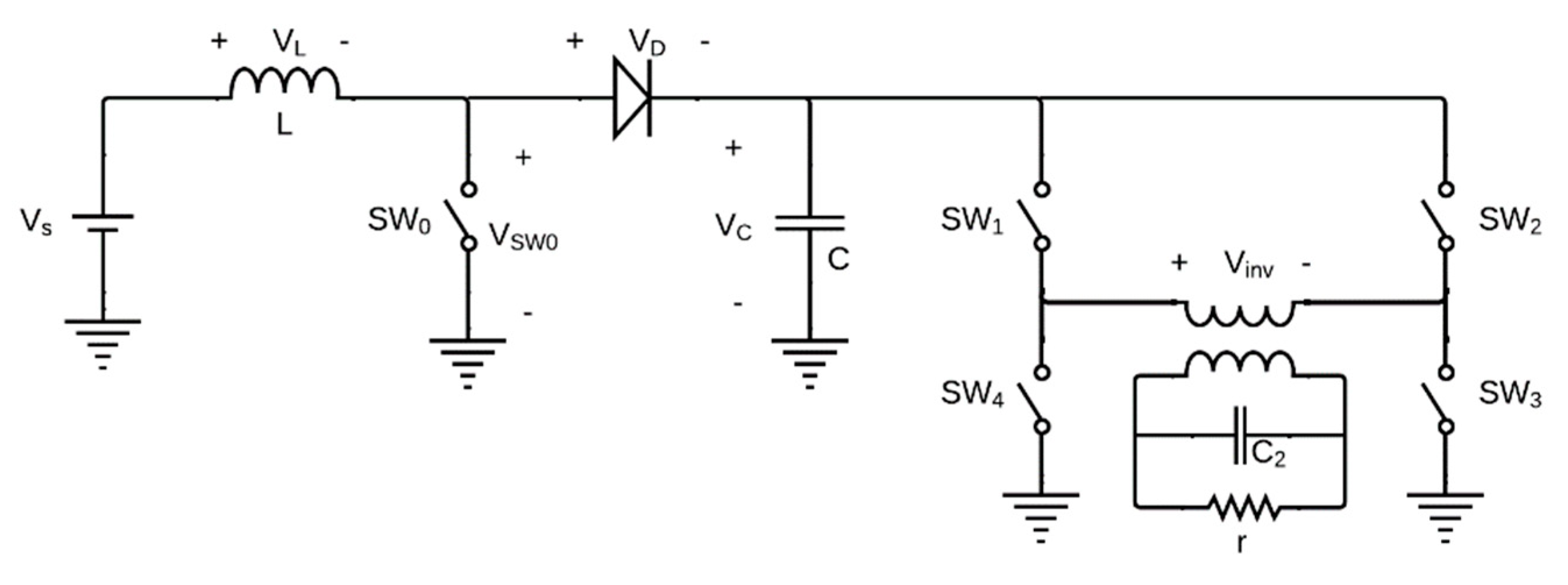
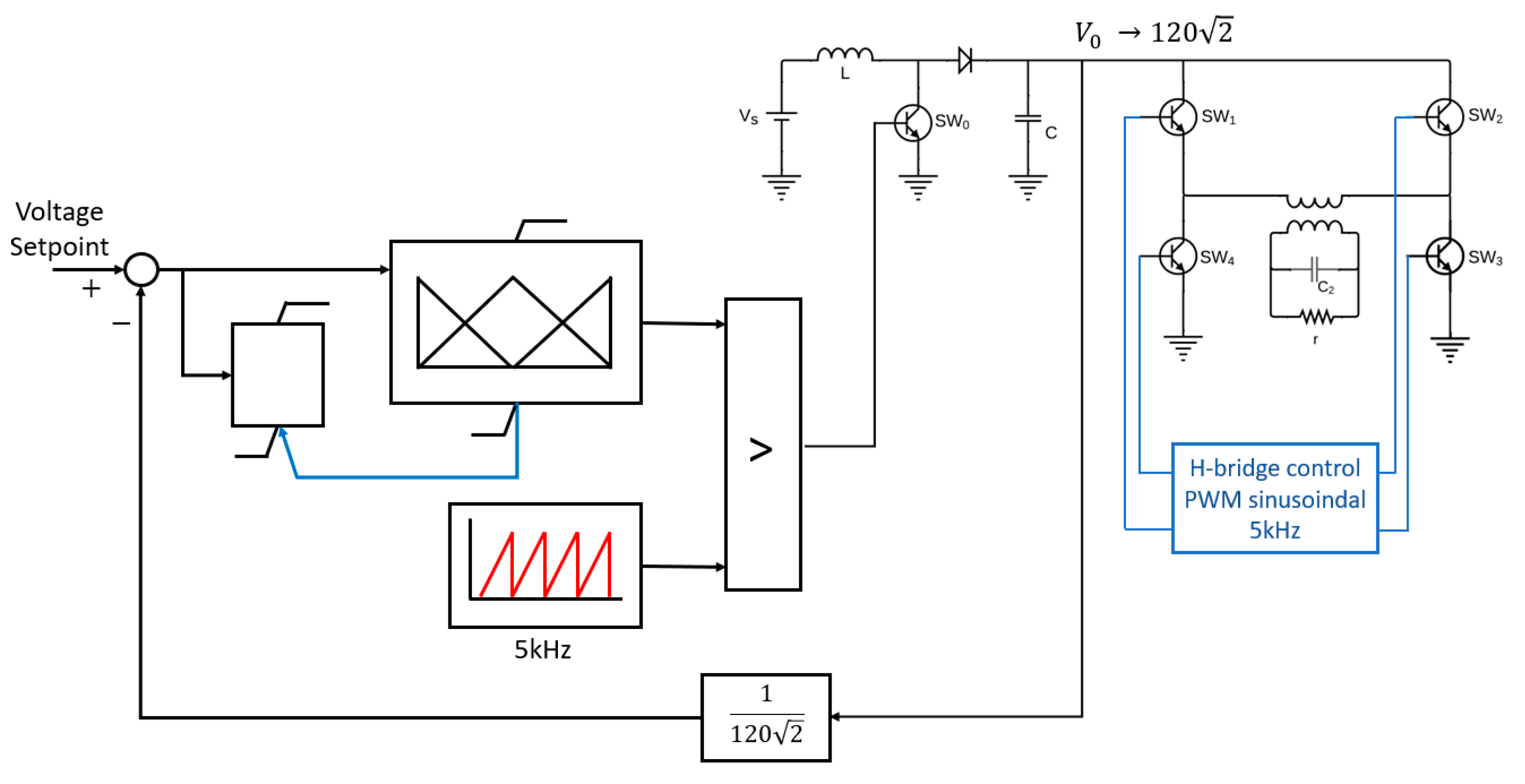
Figure 1.
Simplified topology of the 48 [V] DC to 120 [V] RMS voltage boost and inverter system.
Figure 1.
Simplified topology of the 48 [V] DC to 120 [V] RMS voltage boost and inverter system.
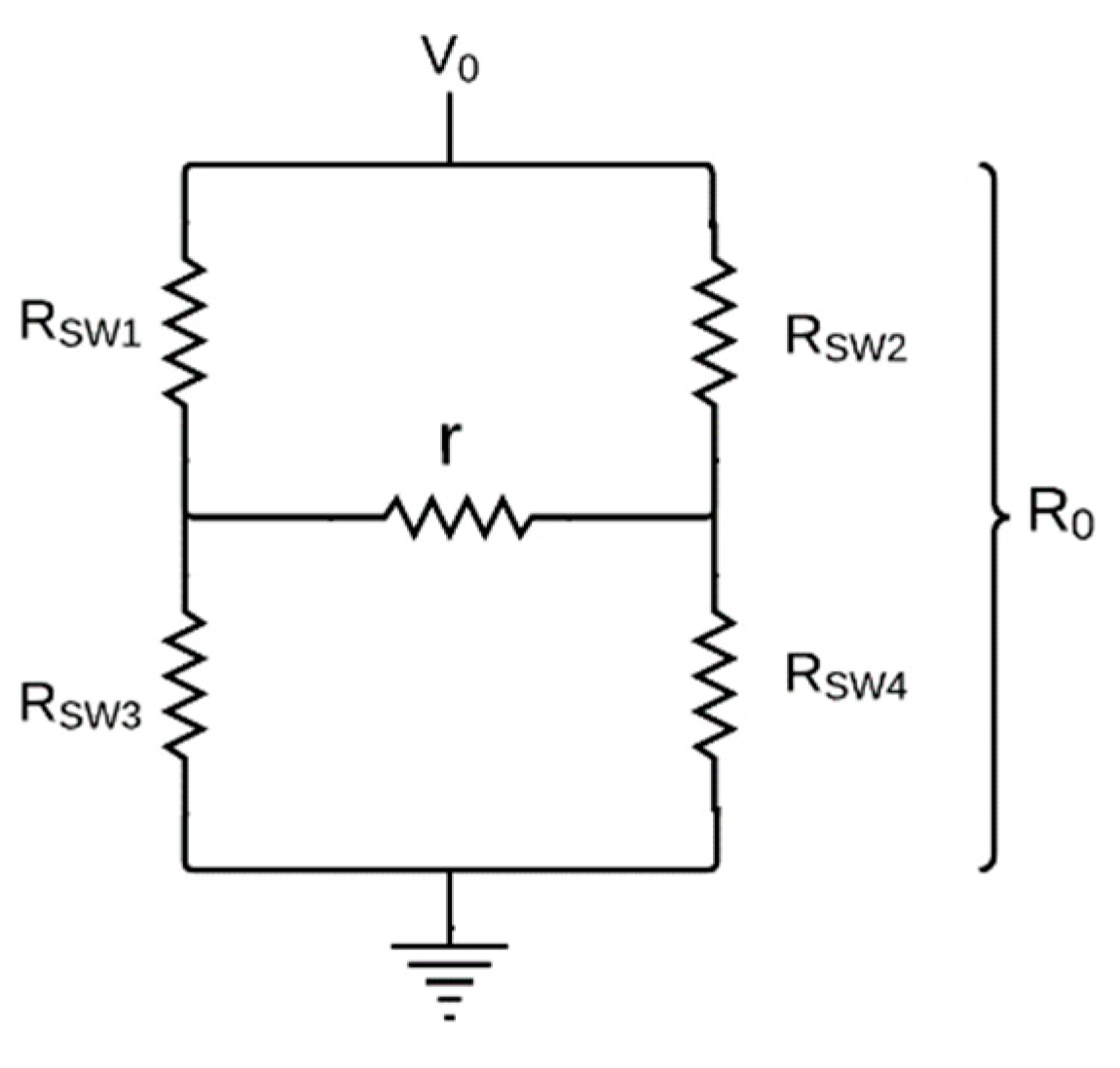
Figure 2.
The output stage of the DC-DC source and the AC inverter system schematic for determining the equivalent resistive load .
Figure 2.
The output stage of the DC-DC source and the AC inverter system schematic for determining the equivalent resistive load .
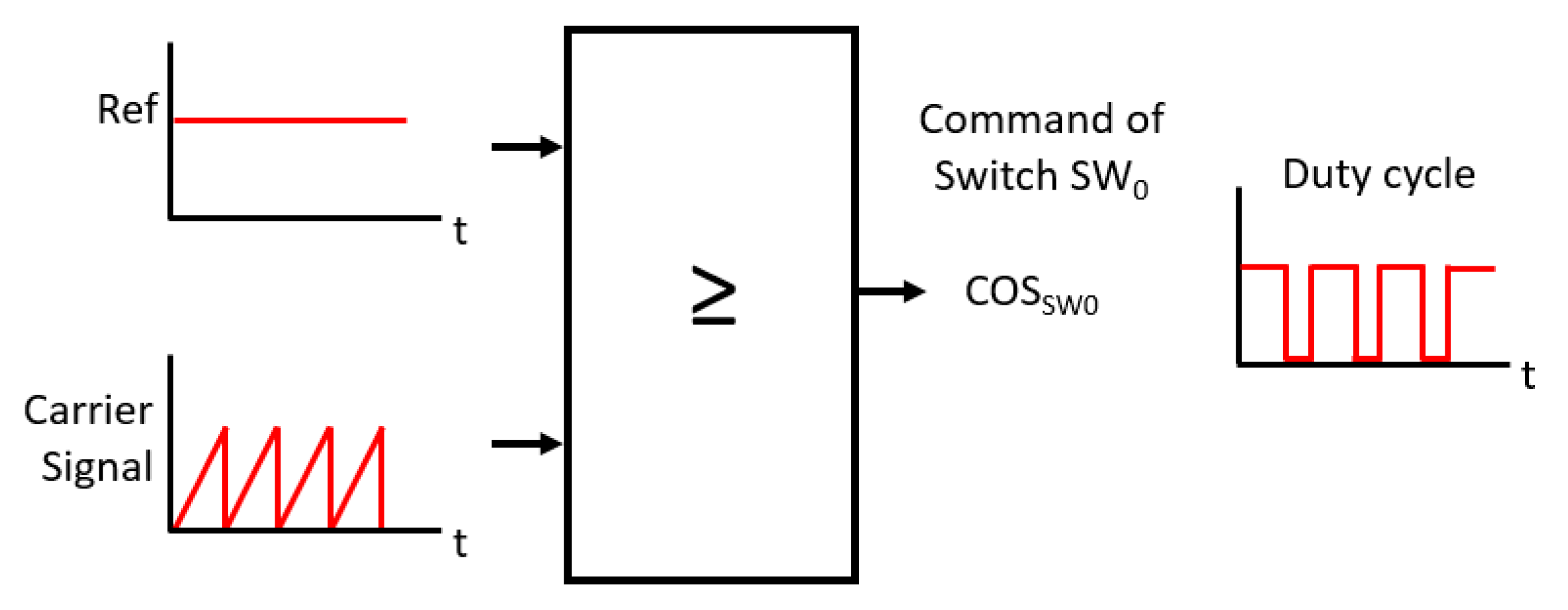
Figure 3.
Comparison criteria for generating the COS for , which corresponds to the duty cycle.
Figure 3.
Comparison criteria for generating the COS for , which corresponds to the duty cycle.
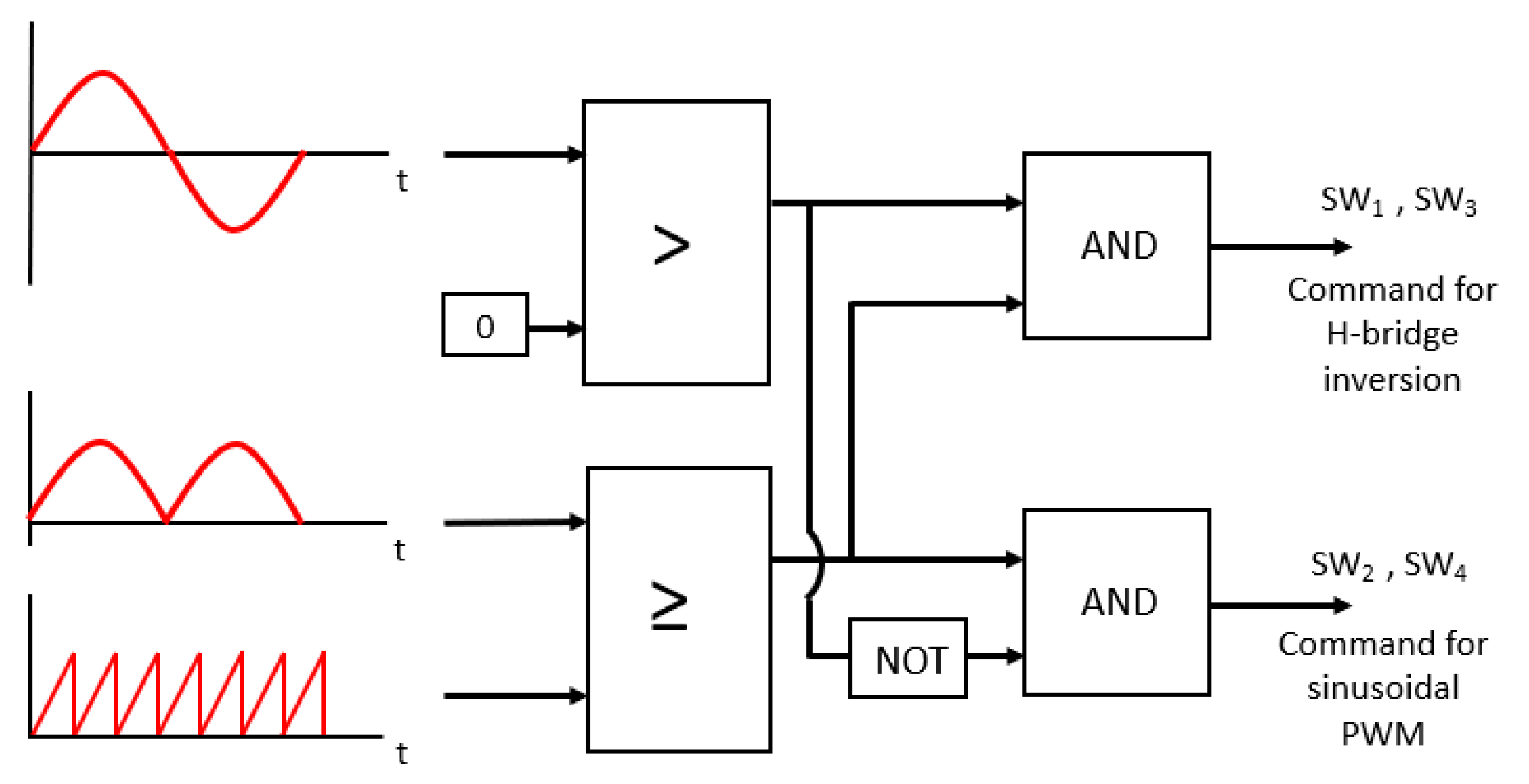
Figure 4.
Generation of pulse width modulation commands and the inverter system.
Figure 4.
Generation of pulse width modulation commands and the inverter system.
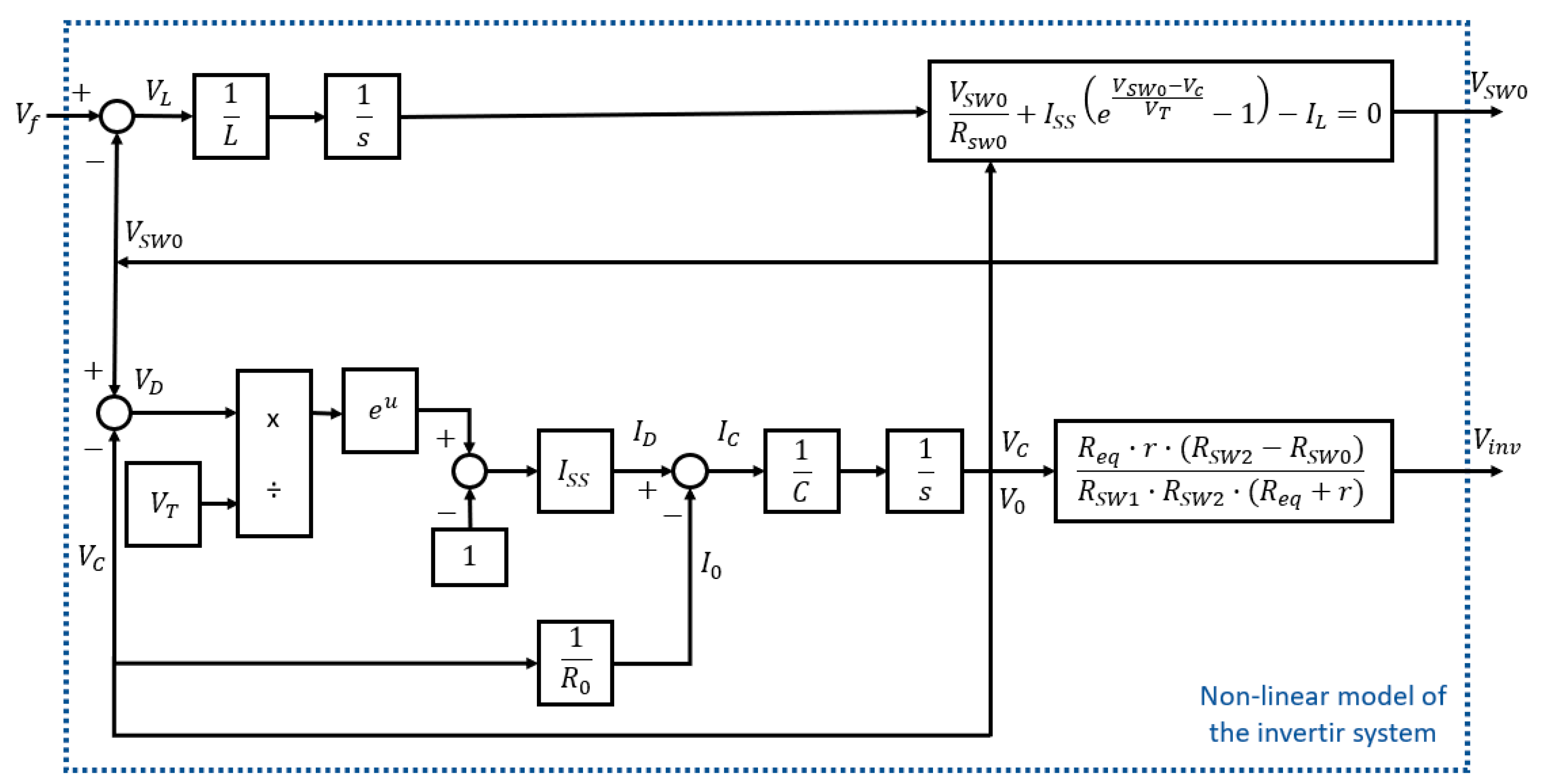
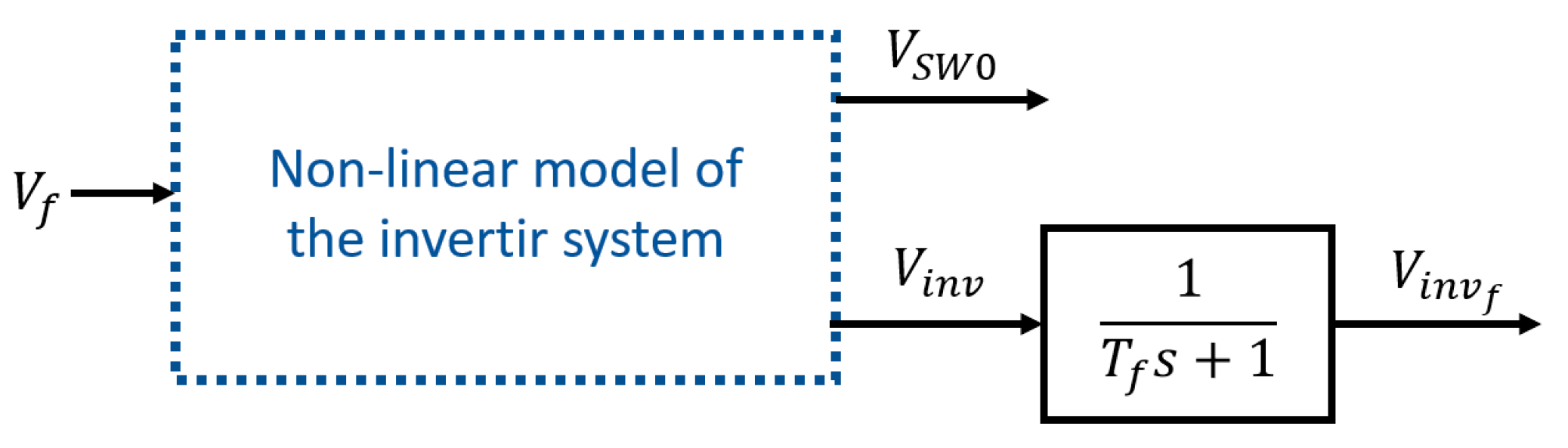
Figure 5.
Simplified nonlinear diagram of the dynamics of the boost and inverter system.
Figure 5.
Simplified nonlinear diagram of the dynamics of the boost and inverter system.
Figure 6.
Simplified topology of the 48 [V] DC to 120 [V] rms boost and inverter system with coupling transformer and filtering.
Figure 6.
Simplified topology of the 48 [V] DC to 120 [V] rms boost and inverter system with coupling transformer and filtering.
Figure 7.
Simplified nonlinear diagram of the dynamics of the boost and inverter system with the coupling transformer and filtering.
Figure 7.
Simplified nonlinear diagram of the dynamics of the boost and inverter system with the coupling transformer and filtering.
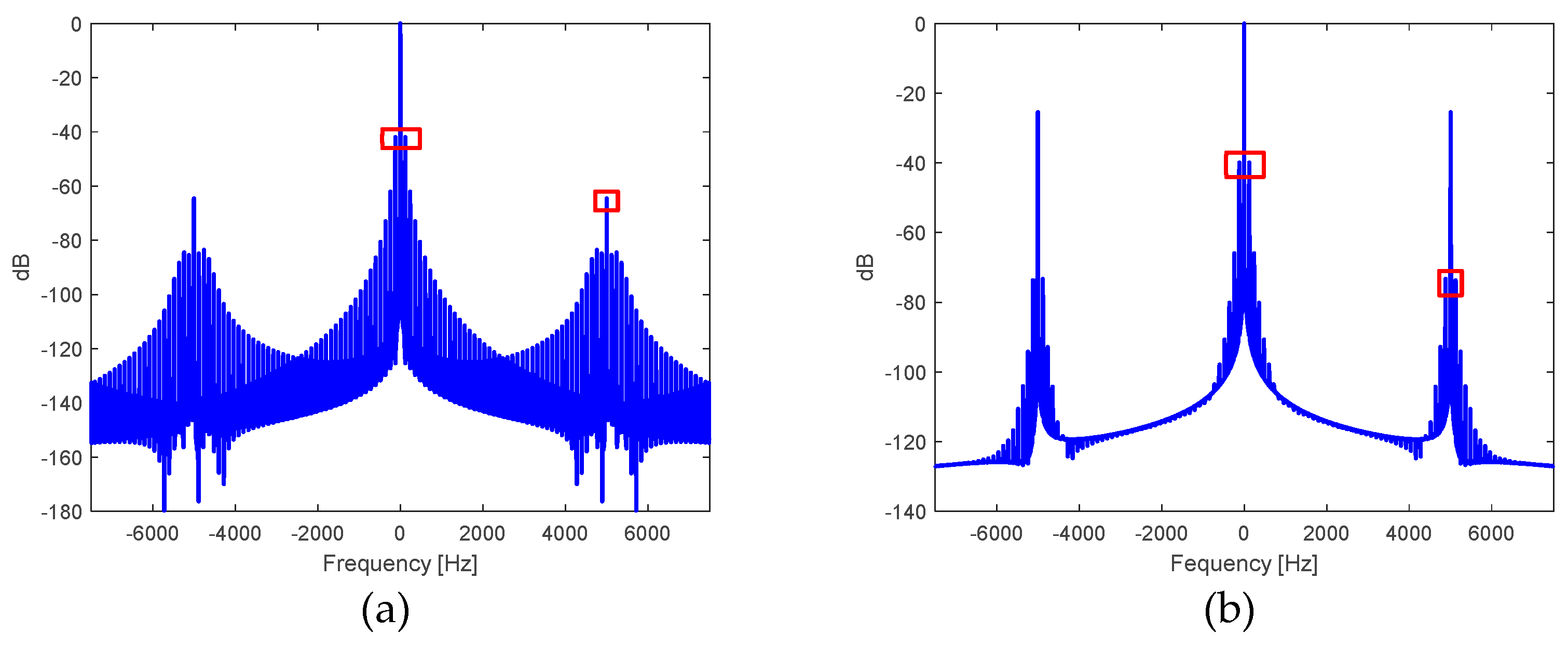
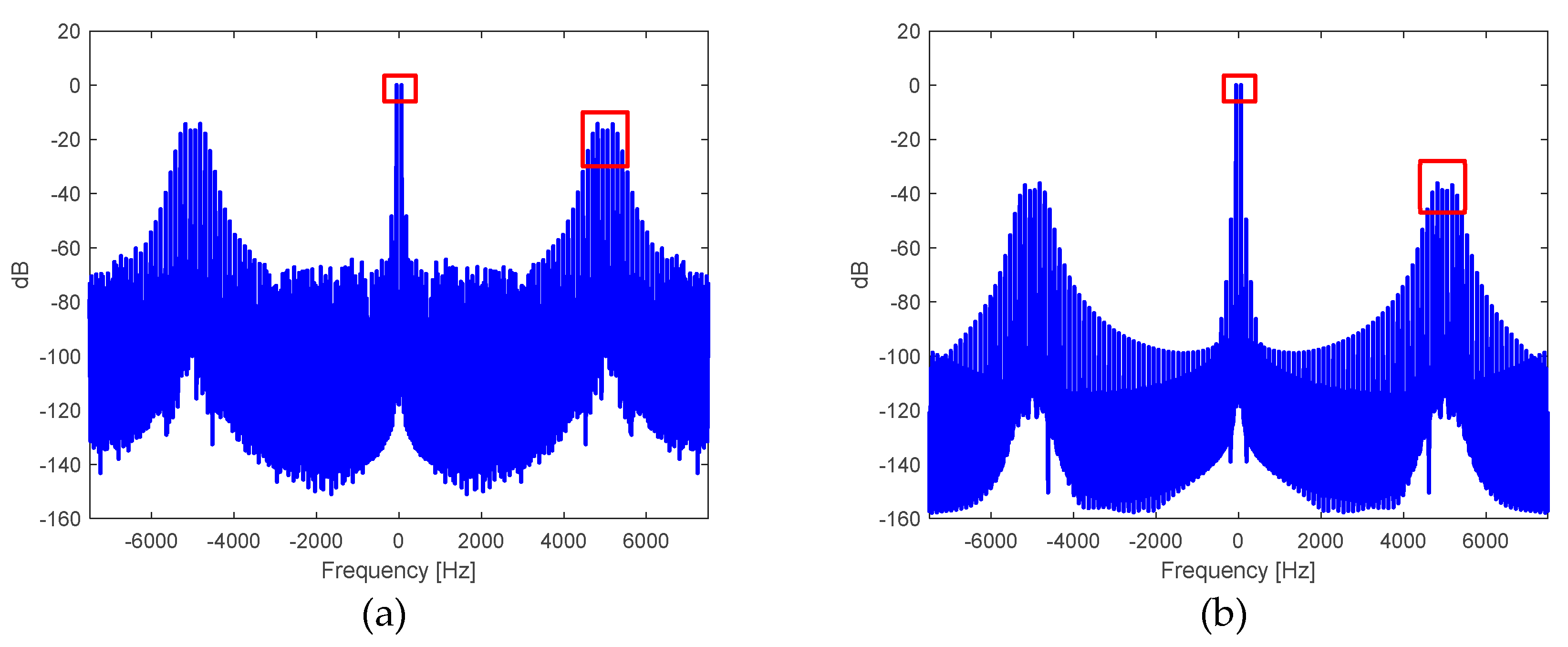
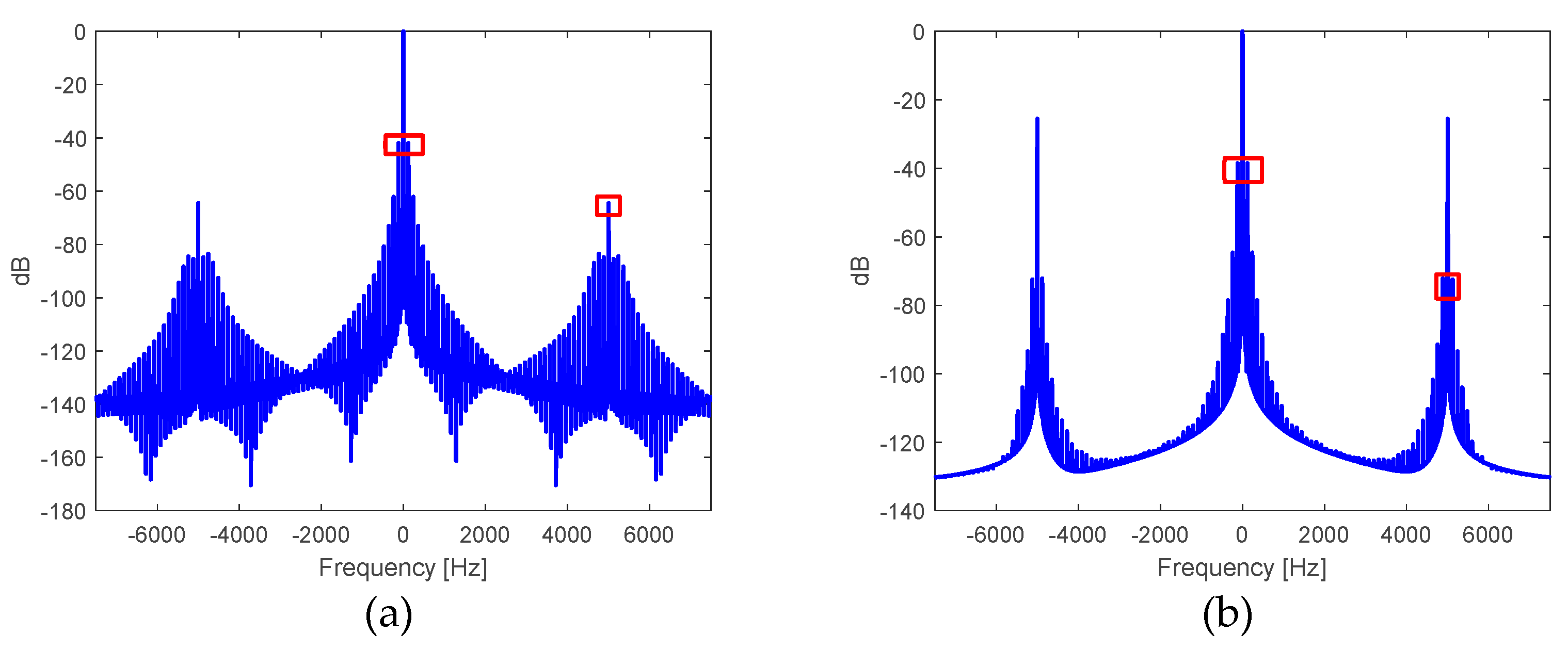
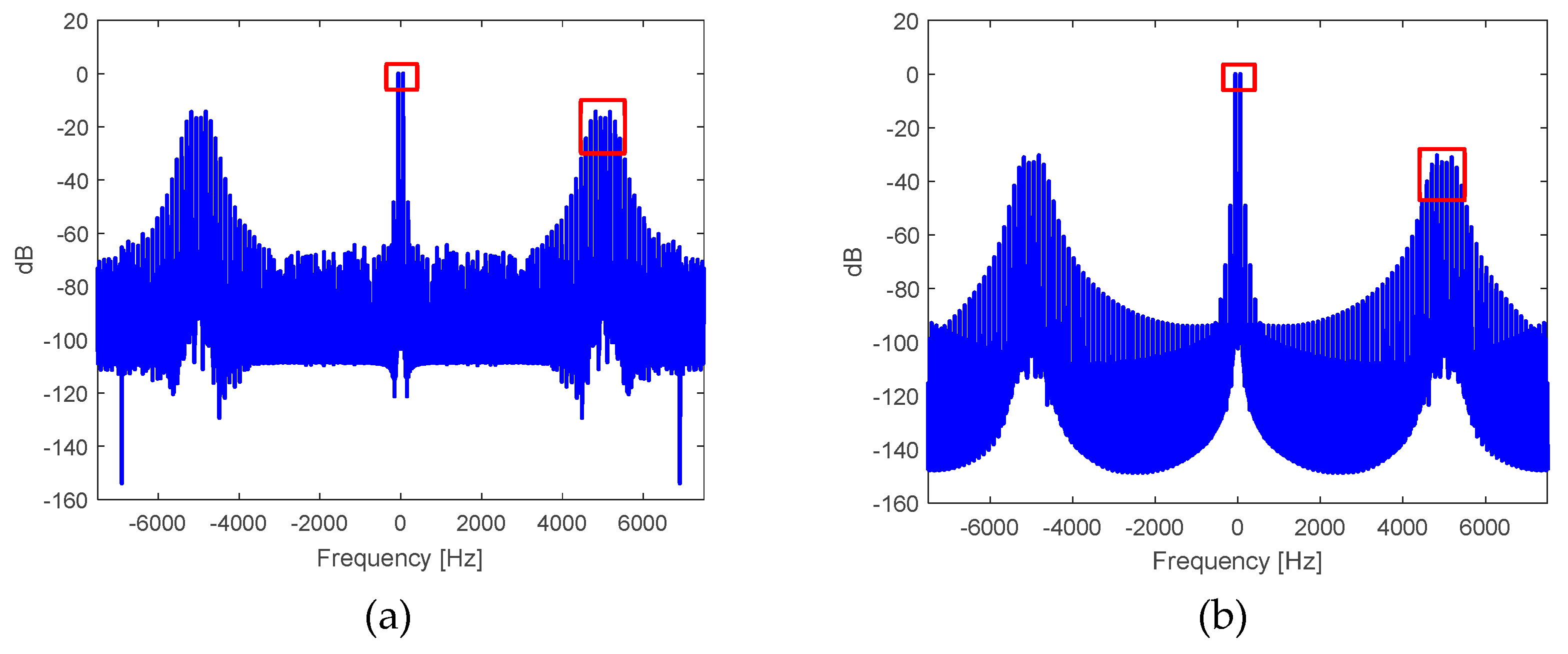
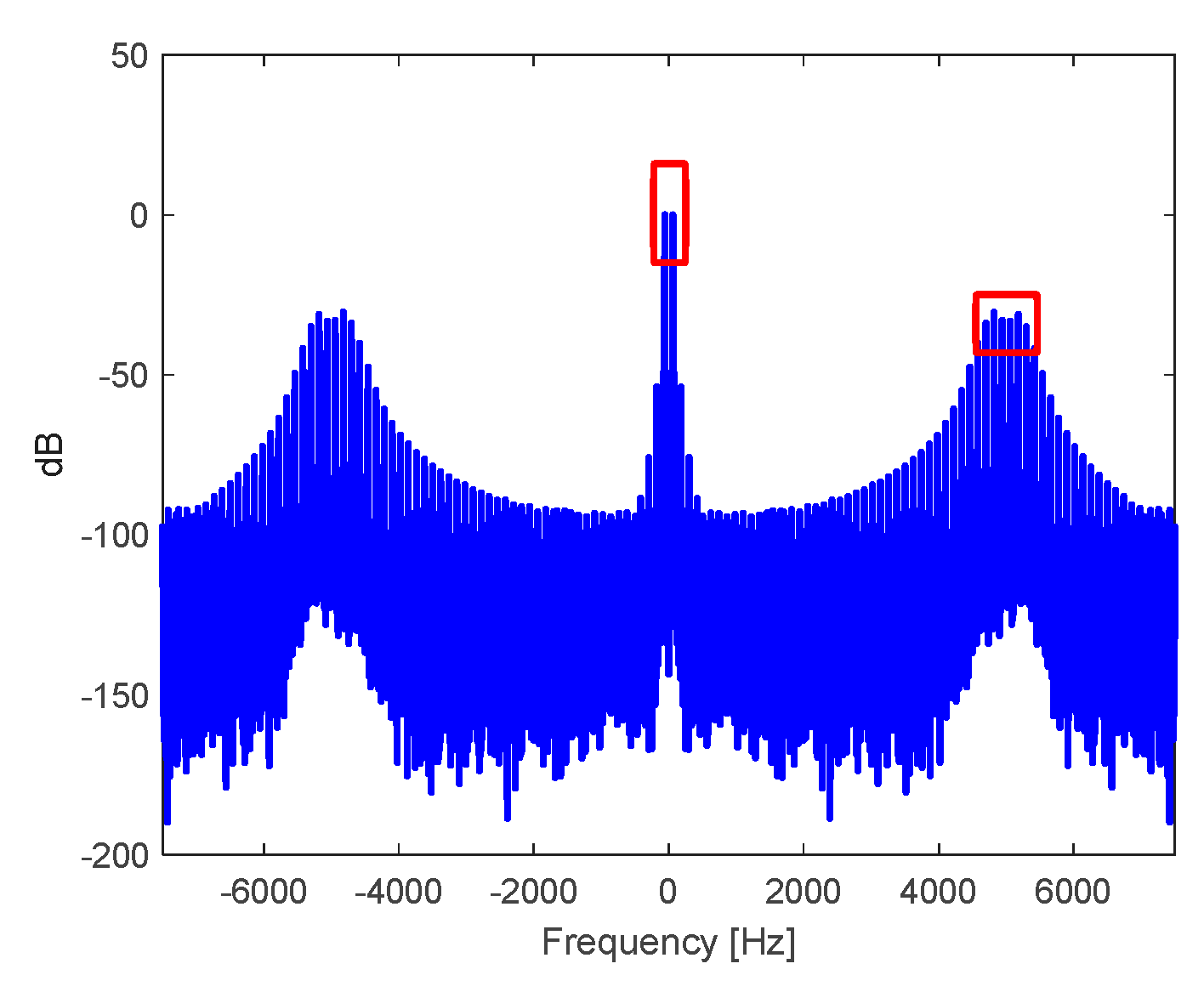
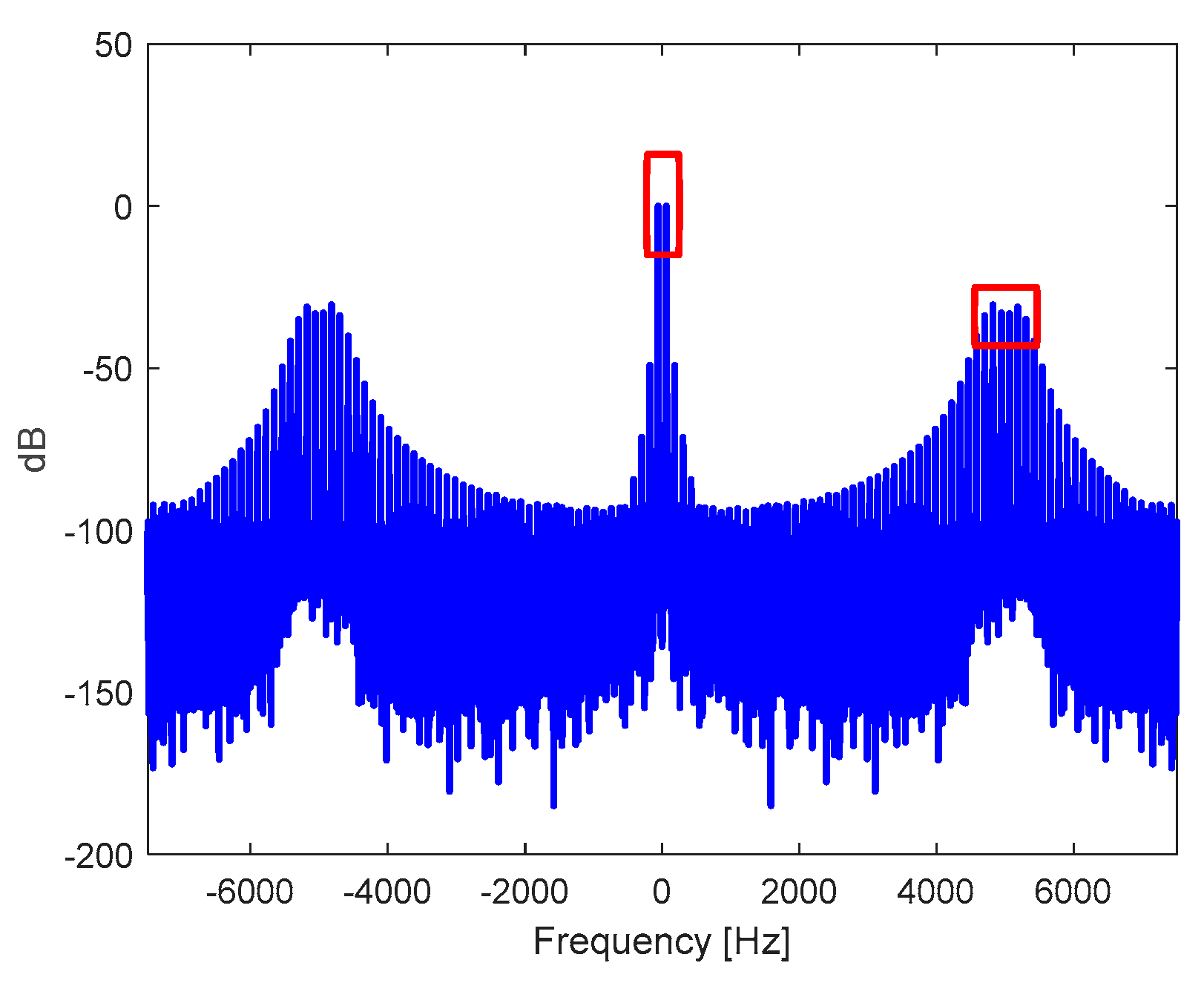
Figure 10.
Spectrum in , normalized with respect to the magnitude at the frequency of the: a) output voltage in the DC-AC inverter stage, and b) voltage at the output of the filtering transformer.
Figure 10.
Spectrum in , normalized with respect to the magnitude at the frequency of the: a) output voltage in the DC-AC inverter stage, and b) voltage at the output of the filtering transformer.
| Parameter |
Mean Value |
|
|
| % Rizo |
% Rizo |
| Output Voltage |
V |
|
|
| Inductor Current |
A |
|
|
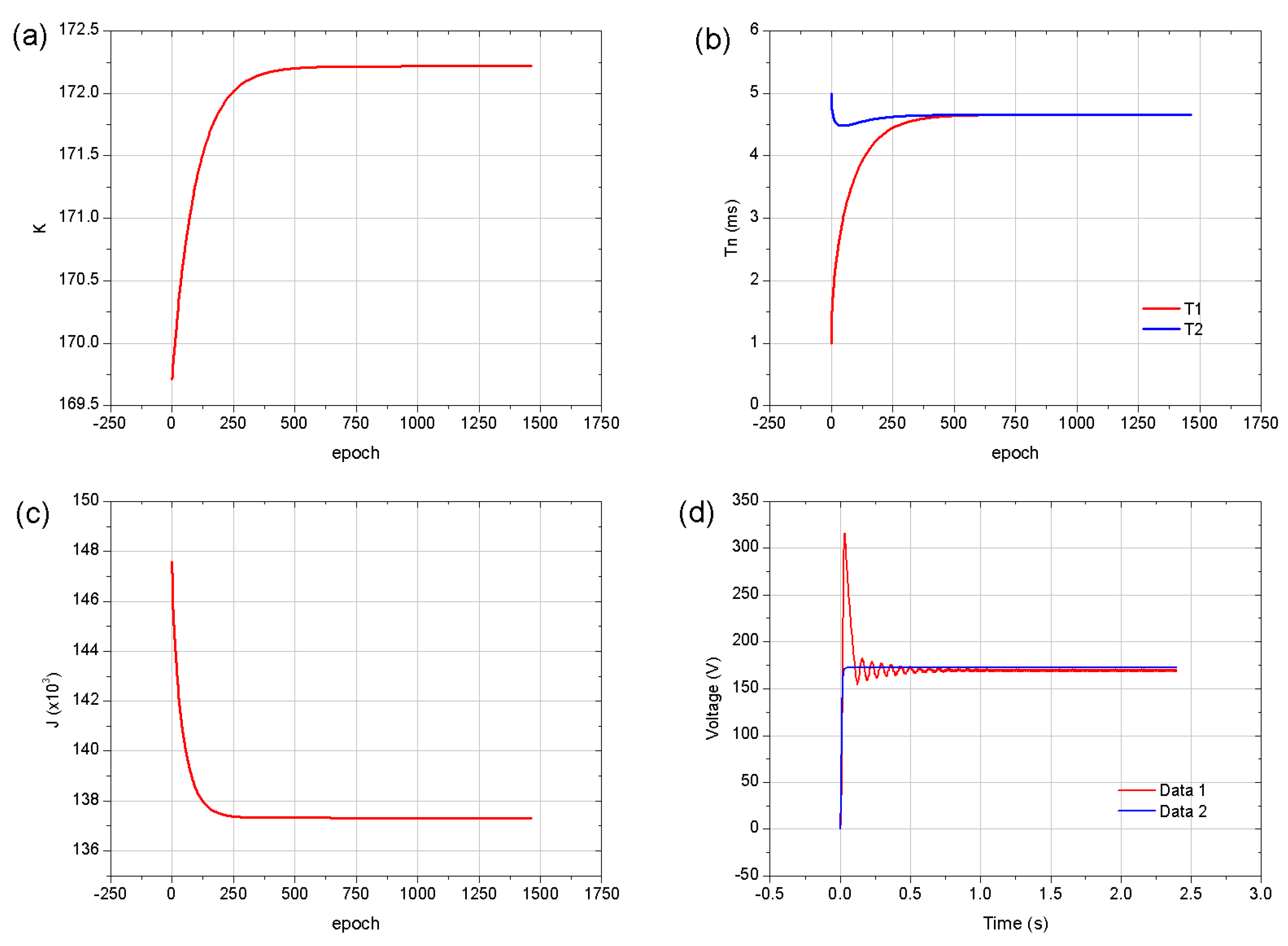
Figure 11.
a) and b) show the evolution of the fitted parameters of the simplified model. c) presents the cost function descending gradient of the optimization process, and d), denotes the time response of the output voltage of the boost converter, where Data 1 represents the simulated dynamics, and Data 2 represents the best fitted second-order system.
Figure 11.
a) and b) show the evolution of the fitted parameters of the simplified model. c) presents the cost function descending gradient of the optimization process, and d), denotes the time response of the output voltage of the boost converter, where Data 1 represents the simulated dynamics, and Data 2 represents the best fitted second-order system.
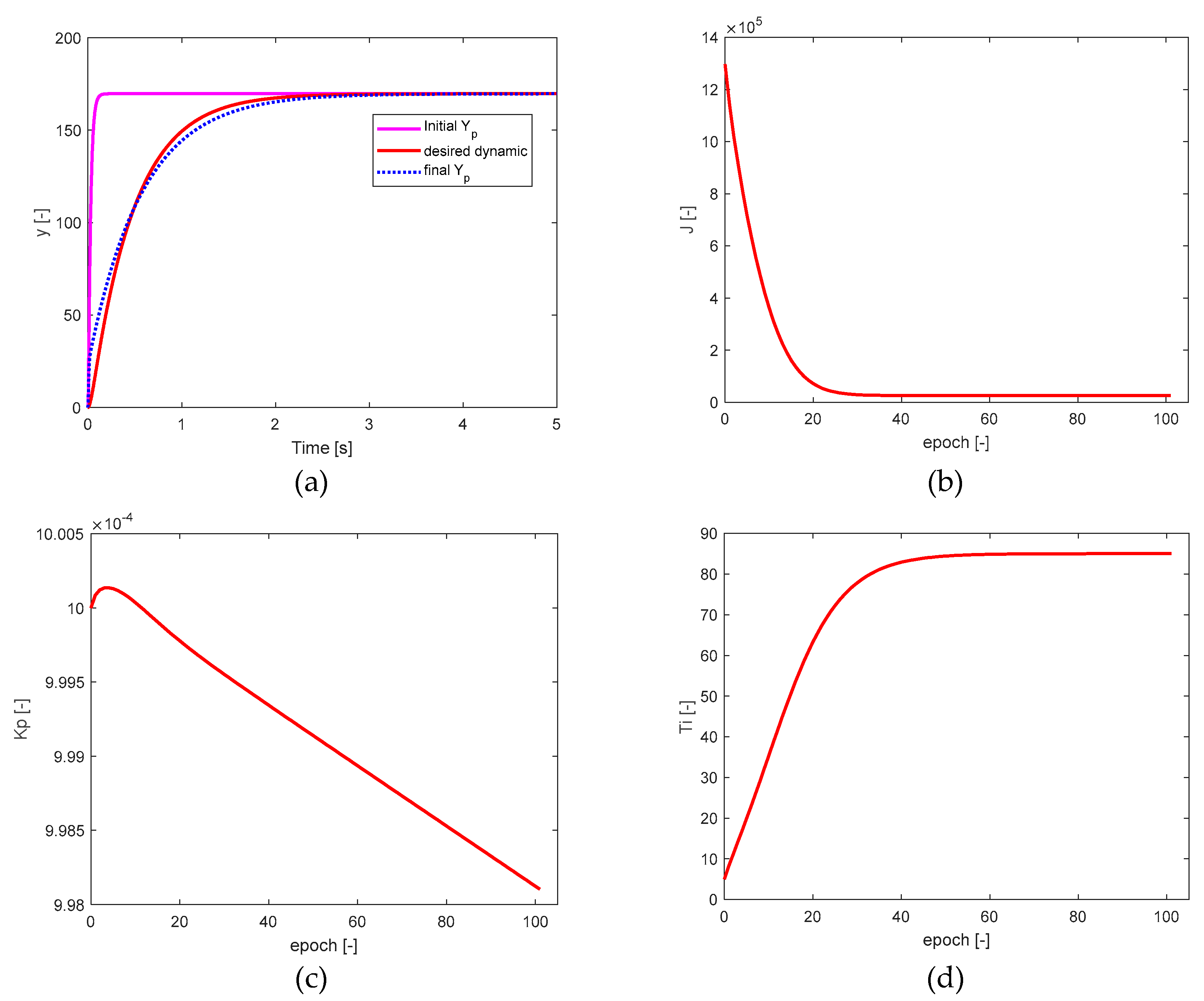
Figure 12.
a) Adjustment of the response of the approximate system with a PI controller, b) optimized cost function, c) evolution of the proportional gain, and d) evolution of the integral time.
Figure 12.
a) Adjustment of the response of the approximate system with a PI controller, b) optimized cost function, c) evolution of the proportional gain, and d) evolution of the integral time.
Figure 13.
a) Control scheme of the fuzzy PI controller with anti-windup effect for voltage regulation of the inverter system from a battery pack.
Figure 13.
a) Control scheme of the fuzzy PI controller with anti-windup effect for voltage regulation of the inverter system from a battery pack.
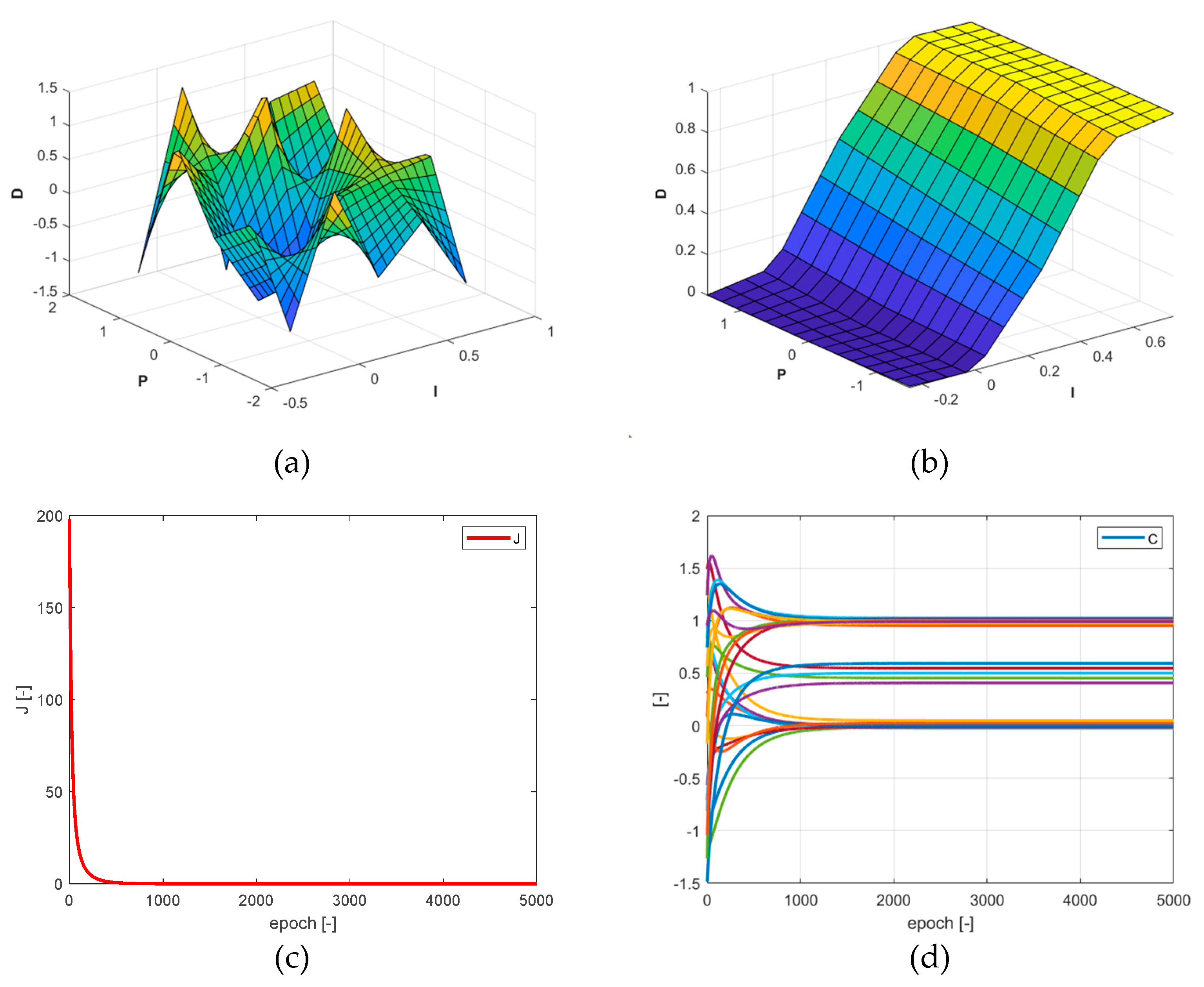
Figure 14.
a) Control output prediction surface defined by randomly adjusted singletons. b) Control output prediction surface after adjusting the weights of the singletons. c) Cost function evolution of training. d) Evolution of the 25 singletons in the fuzzy PI control system training.
Figure 14.
a) Control output prediction surface defined by randomly adjusted singletons. b) Control output prediction surface after adjusting the weights of the singletons. c) Cost function evolution of training. d) Evolution of the 25 singletons in the fuzzy PI control system training.
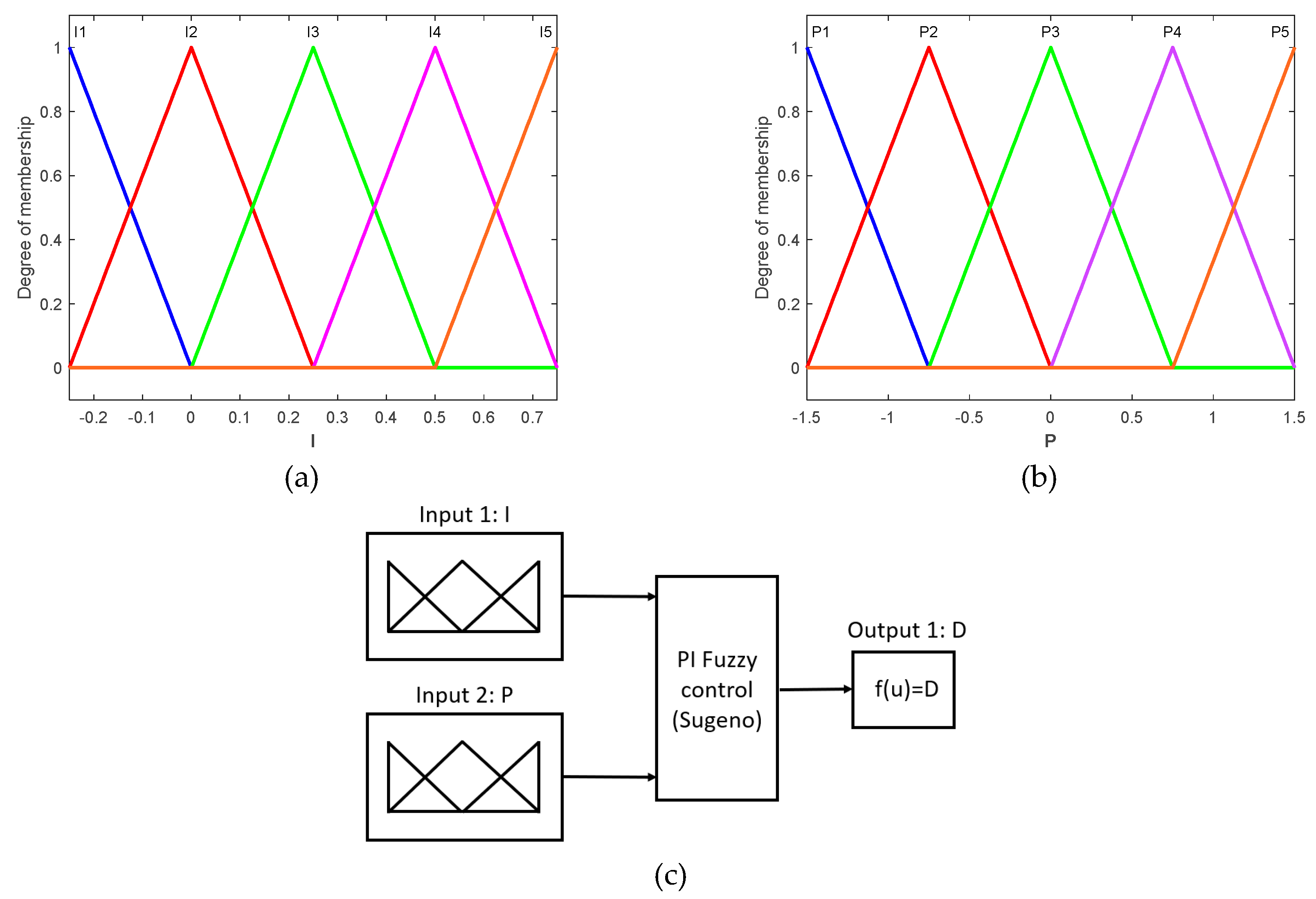
Figure 15.
a) Universe of discourse for the integral effect and its membership functions. b) Universe of discourse for the proportional effect and its membership functions. c) Sugeno-type inference system structure for the implementation of fuzzy PI control.
Figure 15.
a) Universe of discourse for the integral effect and its membership functions. b) Universe of discourse for the proportional effect and its membership functions. c) Sugeno-type inference system structure for the implementation of fuzzy PI control.
| Numeration and order |
Membership functions for the integral effect |
Membership functions for the proportional effect |
| 1 |
-0.5 |
-0.25 |
0 |
-2.25 |
-1.5 |
-0.75 |
| 2 |
-0.25 |
0 |
0.25 |
-1.5 |
-0.75 |
0 |
| 3 |
0 |
0.25 |
0.5 |
-0.75 |
0 |
0.75 |
| 4 |
0.25 |
0.5 |
0.75 |
0 |
0.75 |
1.5 |
| 5 |
0.5 |
0.75 |
1 |
0.75 |
1.5 |
2.25 |
Figure 16.
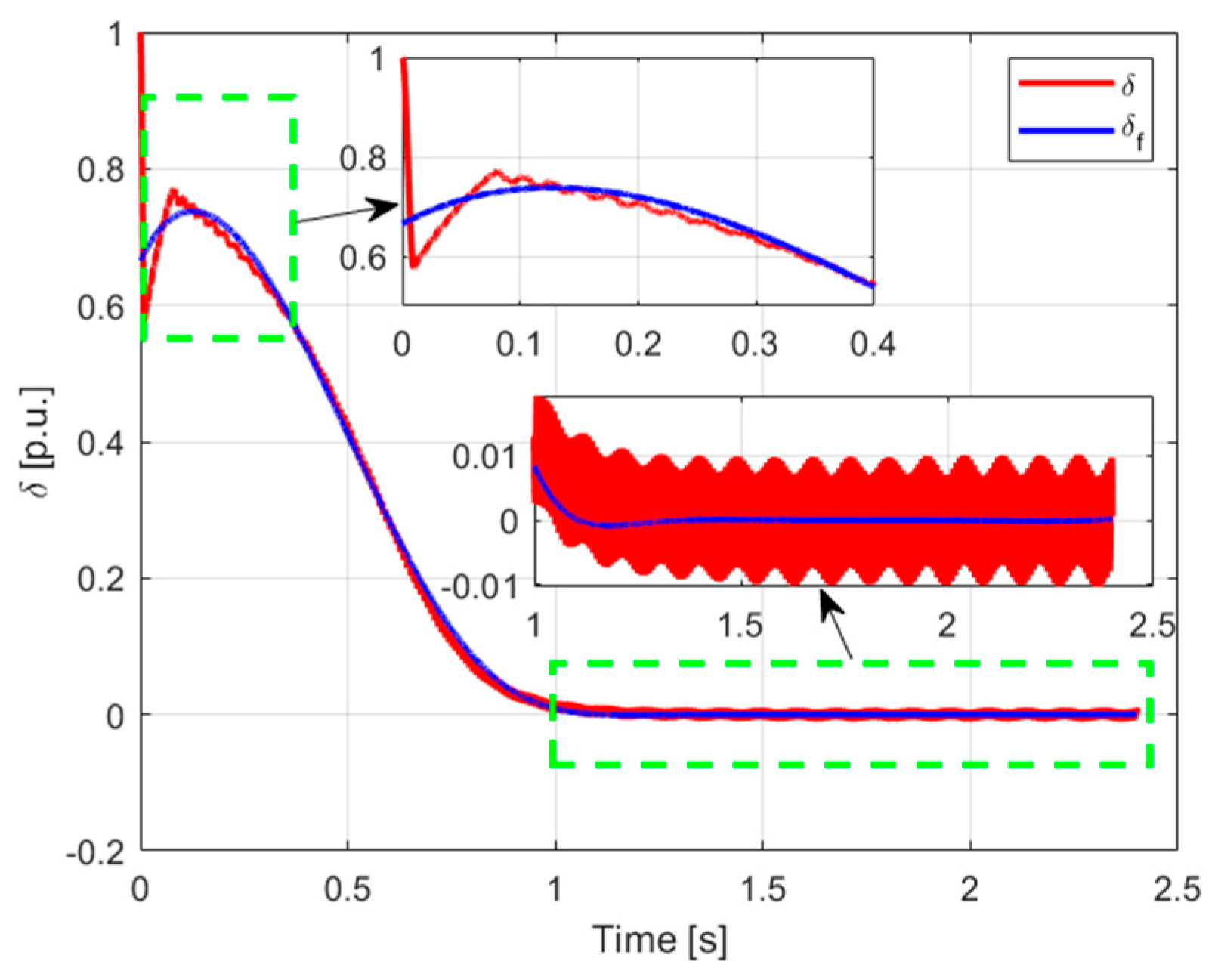
Red path: deviation of the fuzzy control system, Blue path: deviation trend.
Figure 16.
Red path: deviation of the fuzzy control system, Blue path: deviation trend.
Figure 17.
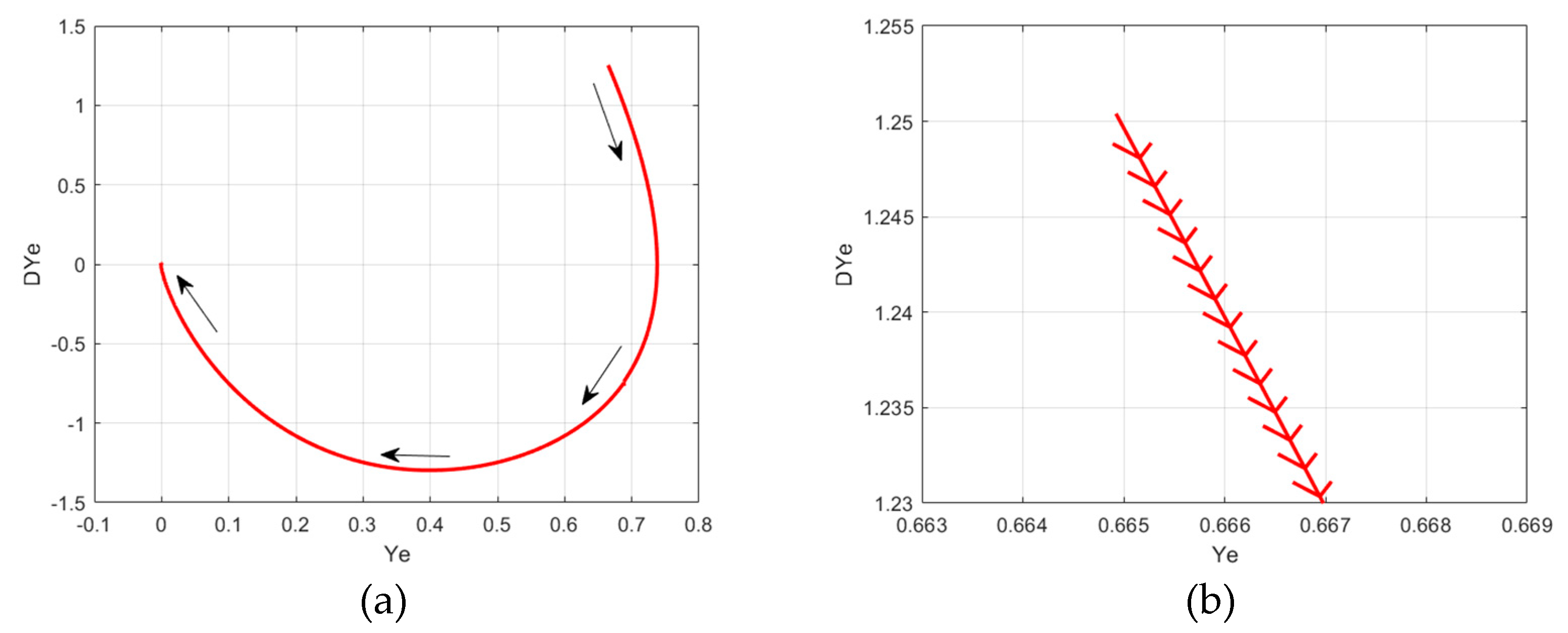
a) Limit cycle of the fuzzy control deviation trend, b) beginning of the limit cycle of the fuzzy control deviation trend, with field lines indicating a clockwise direction for convergence to the stable point of zero deviation and zero deviation gradient change.
Figure 17.
a) Limit cycle of the fuzzy control deviation trend, b) beginning of the limit cycle of the fuzzy control deviation trend, with field lines indicating a clockwise direction for convergence to the stable point of zero deviation and zero deviation gradient change.
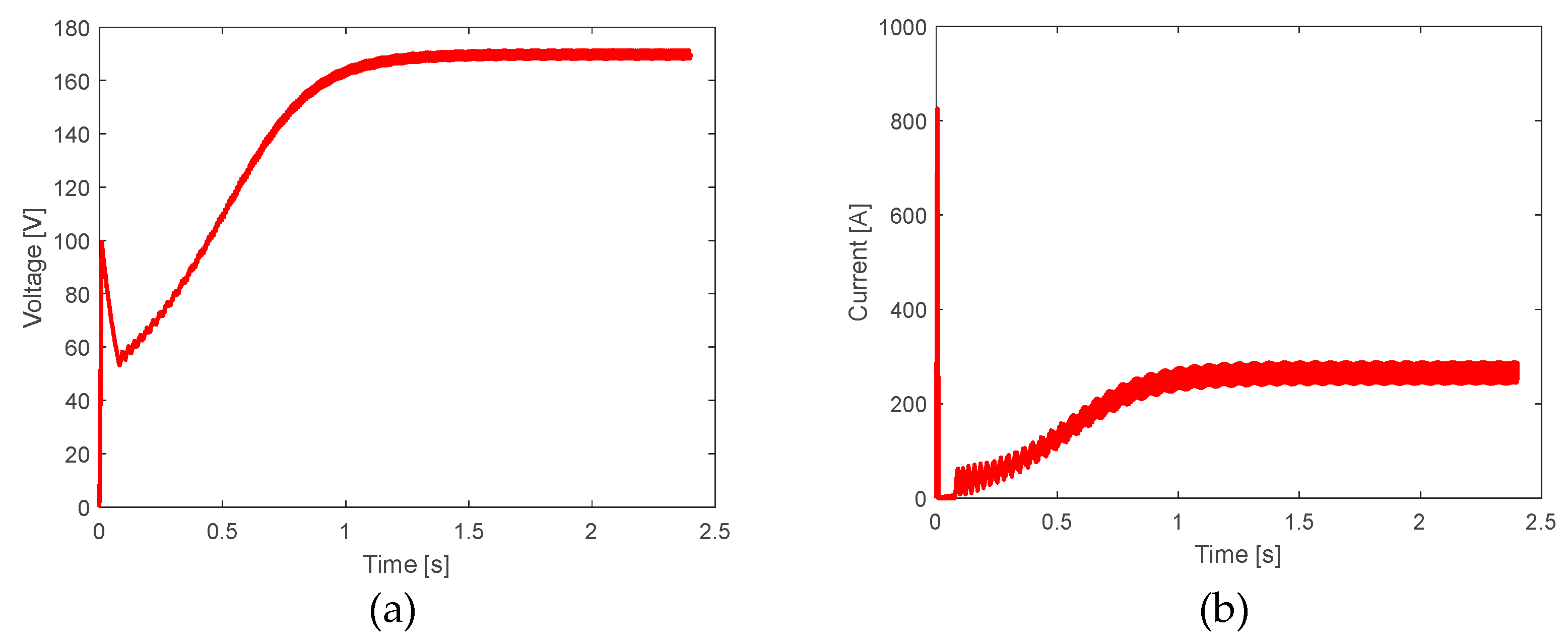
Figure 18.
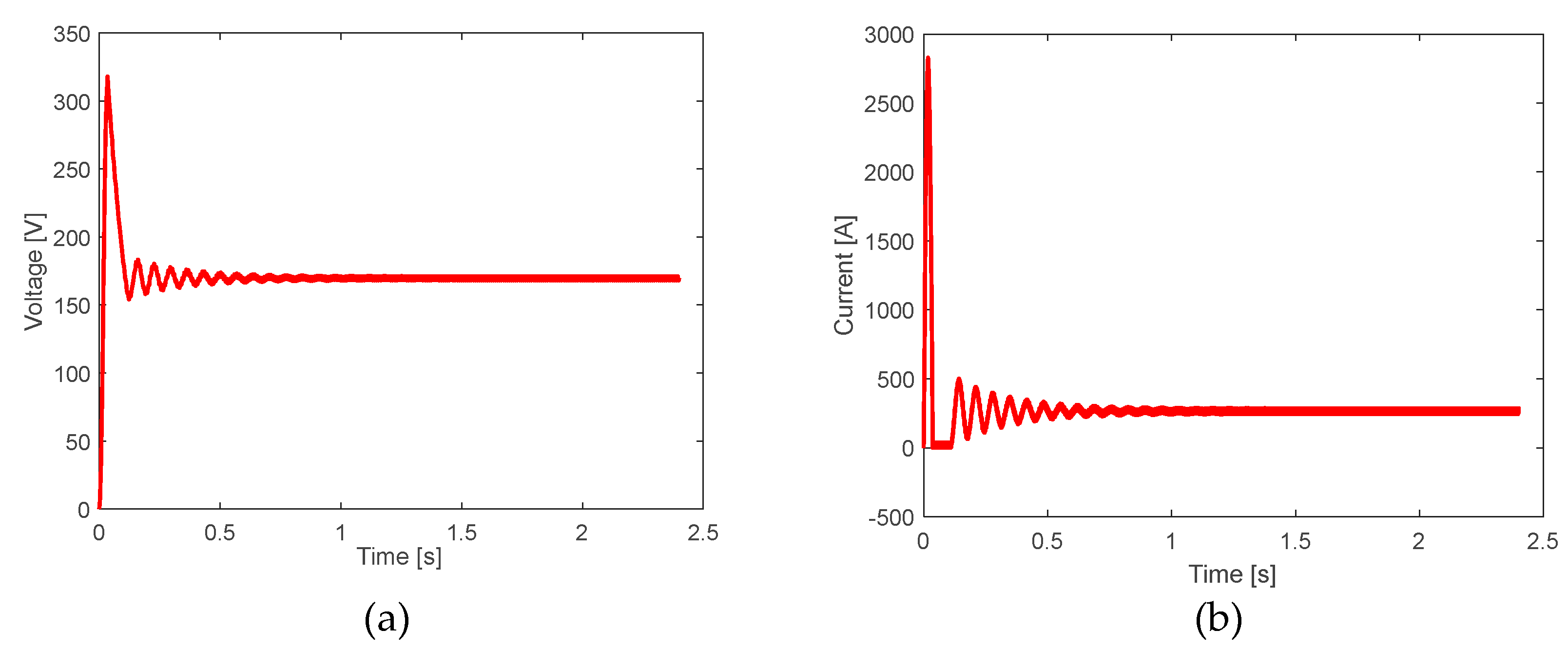
Closed-loop behavior: a) Output voltage of the DC-DC source from to . b) Current measured in the inductor of the DC-DC source.
Figure 18.
Closed-loop behavior: a) Output voltage of the DC-DC source from to . b) Current measured in the inductor of the DC-DC source.
Figure 19.
Spectrums in normalized concerning the magnitude at frequency , of the closed-loop DC-DC converter from to of the: a) voltage at the output capacitor and b) current in the closed-loop inductor.
Figure 19.
Spectrums in normalized concerning the magnitude at frequency , of the closed-loop DC-DC converter from to of the: a) voltage at the output capacitor and b) current in the closed-loop inductor.
Figure 20.
Spectrum in , normalized with respect to the magnitude at the frequency, with the source in closed-loop control using the fuzzy PI controller and in the presence of load variation of the: a) output voltage in the DC-AC inverter stage, and b) voltage at the output of the filtering transformer.
Figure 20.
Spectrum in , normalized with respect to the magnitude at the frequency, with the source in closed-loop control using the fuzzy PI controller and in the presence of load variation of the: a) output voltage in the DC-AC inverter stage, and b) voltage at the output of the filtering transformer.
| Parameter |
Mean value |
|
|
| % Rizo |
% Rizo |
| Output Voltage |
V |
|
|
| Inductor Current |
A |
|
|
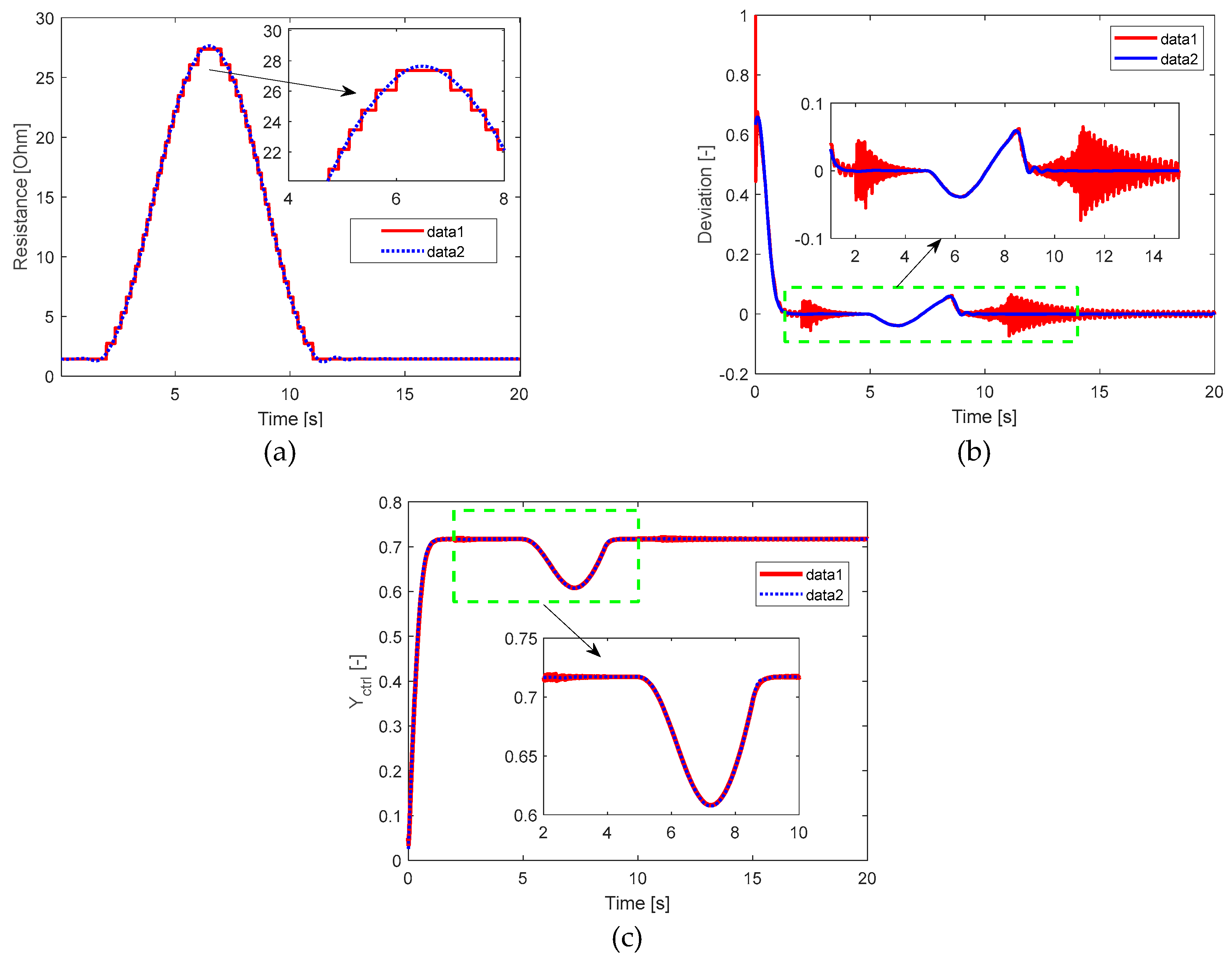
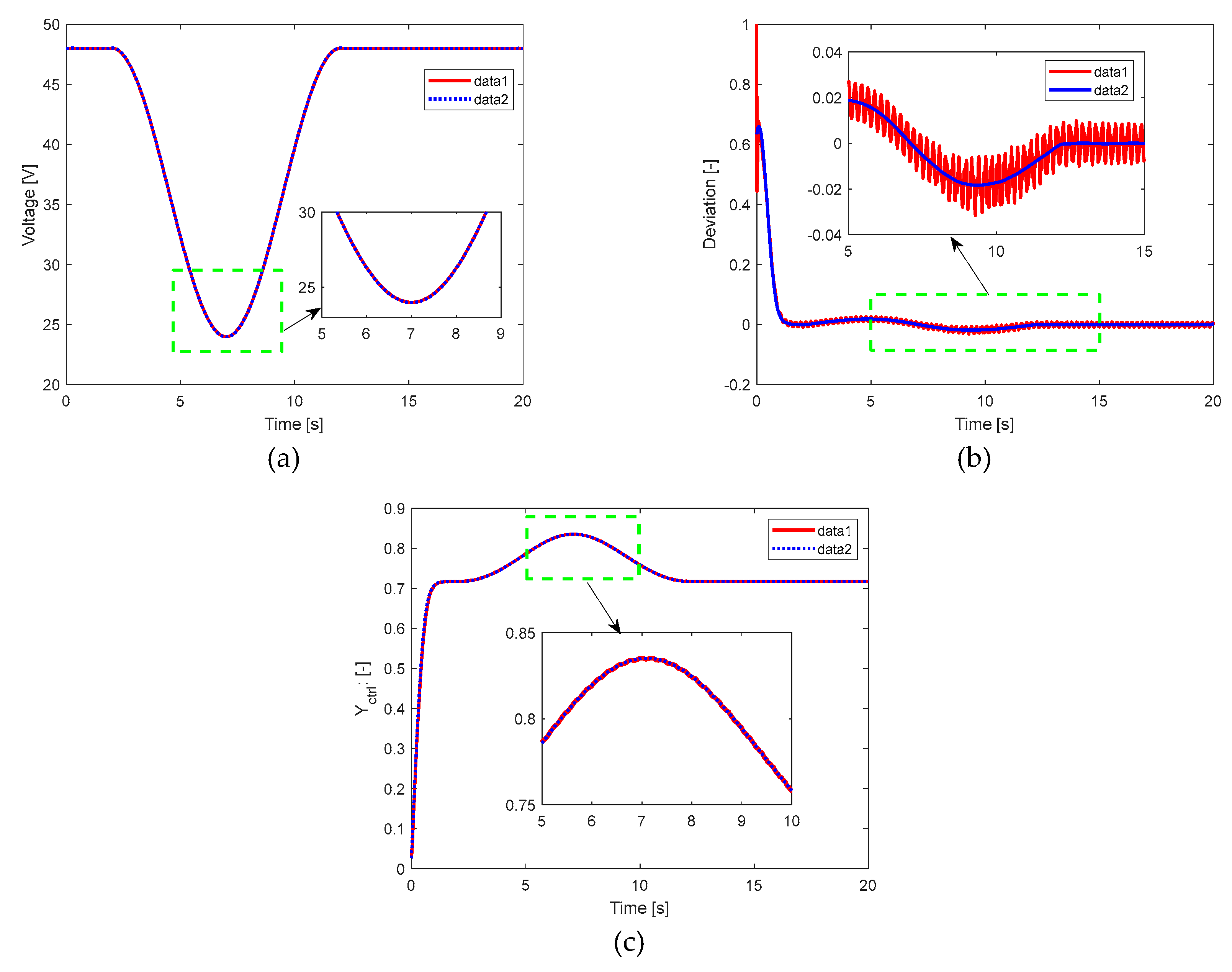
Figure 21.
a) Load variation in b) Deviation of the fuzzy PI control system in per unit (p.u.). c) Output of the fuzzy PI controller. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
Figure 21.
a) Load variation in b) Deviation of the fuzzy PI control system in per unit (p.u.). c) Output of the fuzzy PI controller. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
| Parameter |
THD |
|
| Output Voltage Inverter |
|
|
| Output Voltage Transformer |
0.0632 |
119.82 |
| Parameter |
Mean value |
|
|
| % Rizo |
% Rizo |
| Output Voltage |
V |
|
|
| Inductor Current |
A |
|
|
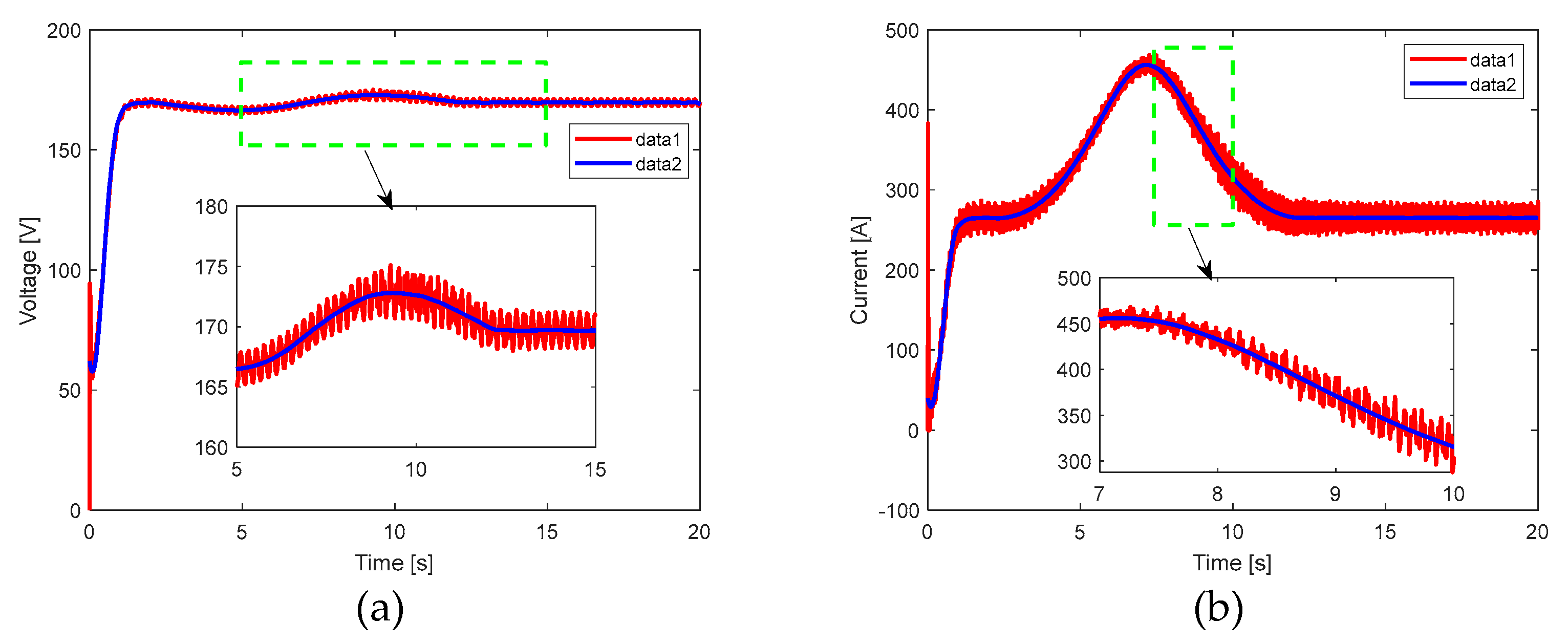
Figure 22.
a) Output voltage of the DC-DC converter from to in response to load variation. b) Current measured in the inductor of the DC-DC converter in response to load variation. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
Figure 22.
a) Output voltage of the DC-DC converter from to in response to load variation. b) Current measured in the inductor of the DC-DC converter in response to load variation. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
| Parameter |
THD |
|
| Output Voltage Inverter |
|
|
| Output Voltage Transformer |
0.0632 |
119.82 |
| Parameter |
Mean value |
|
|
| % Rizo |
% Rizo |
| Output Voltage |
V |
|
|
| Inductor Current |
A |
|
|
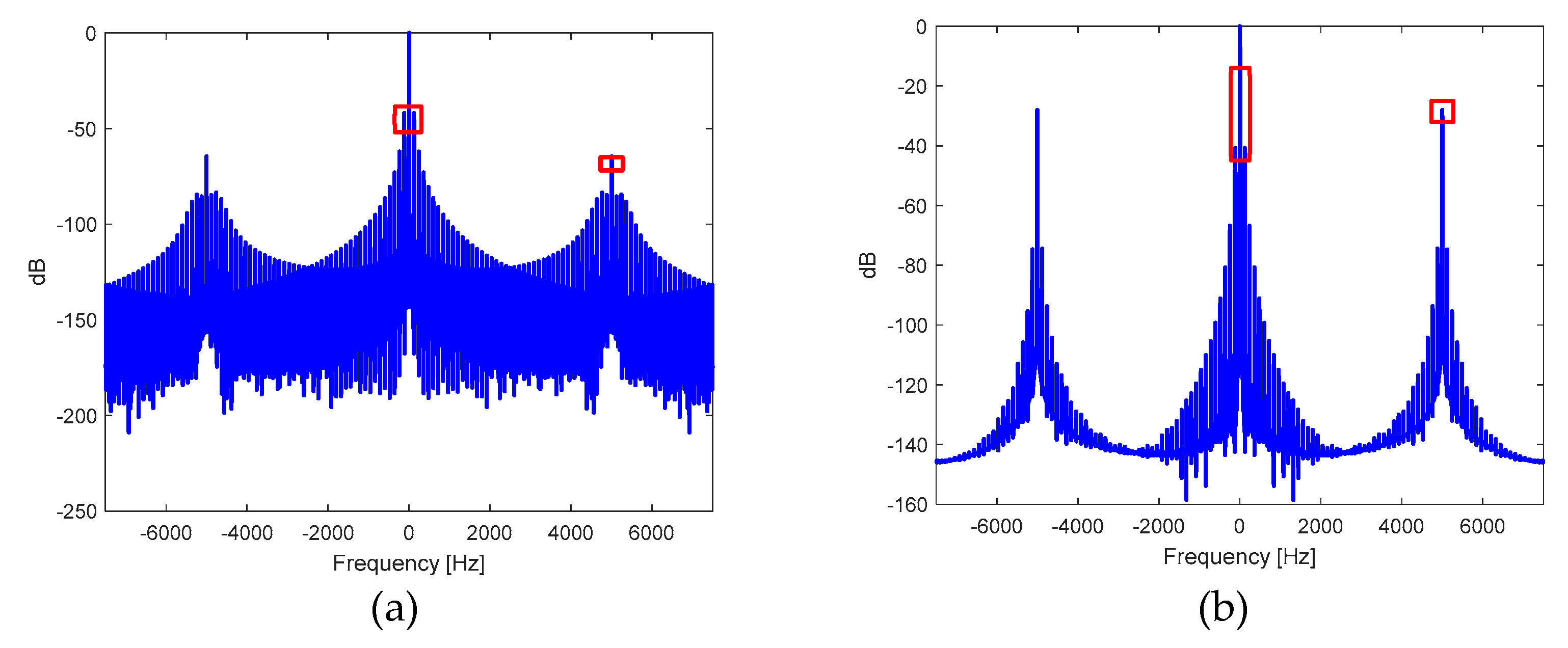
Figure 23.
Spectrum in , normalized with respect to the magnitude at frequency , of the DC-DC converter from to in response to load variation for: a) output voltage and b) inductor current.
Figure 23.
Spectrum in , normalized with respect to the magnitude at frequency , of the DC-DC converter from to in response to load variation for: a) output voltage and b) inductor current.
| Parameter |
THD |
|
| Output Voltage Inverter |
|
|
| Output Voltage Transformer |
0.0632 |
119.82 |
| Parameter |
Mean value |
|
|
| % Rizo |
% Rizo |
| Output Voltage |
V |
|
|
| Inductor Current |
A |
|
|
Figure 24.
Spectrum in , normalized with respect to the magnitude at the frequency, of the voltage at the output of the filtering transformer in response to load variation.
Figure 24.
Spectrum in , normalized with respect to the magnitude at the frequency, of the voltage at the output of the filtering transformer in response to load variation.
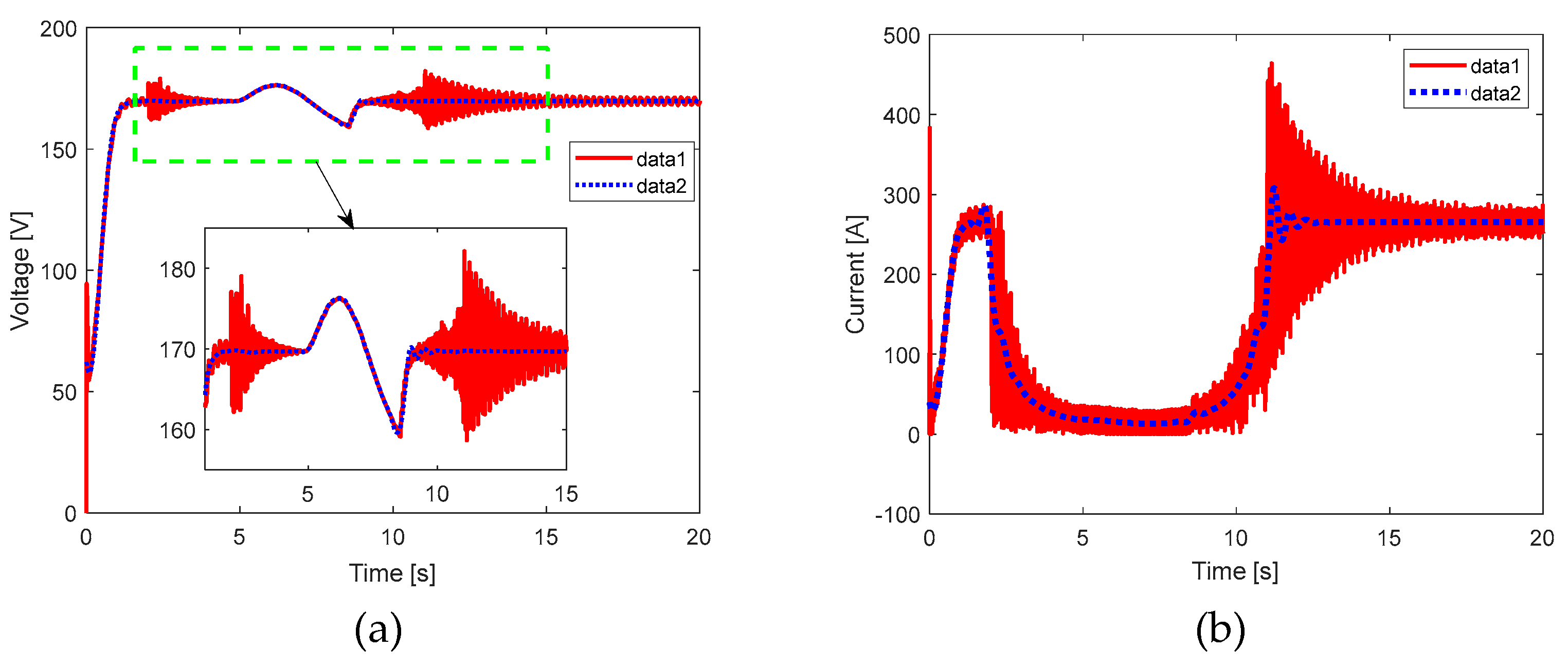
Figure 25.
a) Source voltage variation. b) Deviation of the fuzzy PI control system in per unit (p.u.). c) Output of the fuzzy PI controller. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
Figure 25.
a) Source voltage variation. b) Deviation of the fuzzy PI control system in per unit (p.u.). c) Output of the fuzzy PI controller. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
| THD |
|
|
|
Figure 26.
a) Output voltage of the DC-DC converter from to in response to source voltage variation. b) Current measured in the inductor of the DC-DC converter in response to source voltage variation. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
Figure 26.
a) Output voltage of the DC-DC converter from to in response to source voltage variation. b) Current measured in the inductor of the DC-DC converter in response to source voltage variation. In all cases, data 1 represents the signal at each instant, and data 2 represents the filtered signal or its trend.
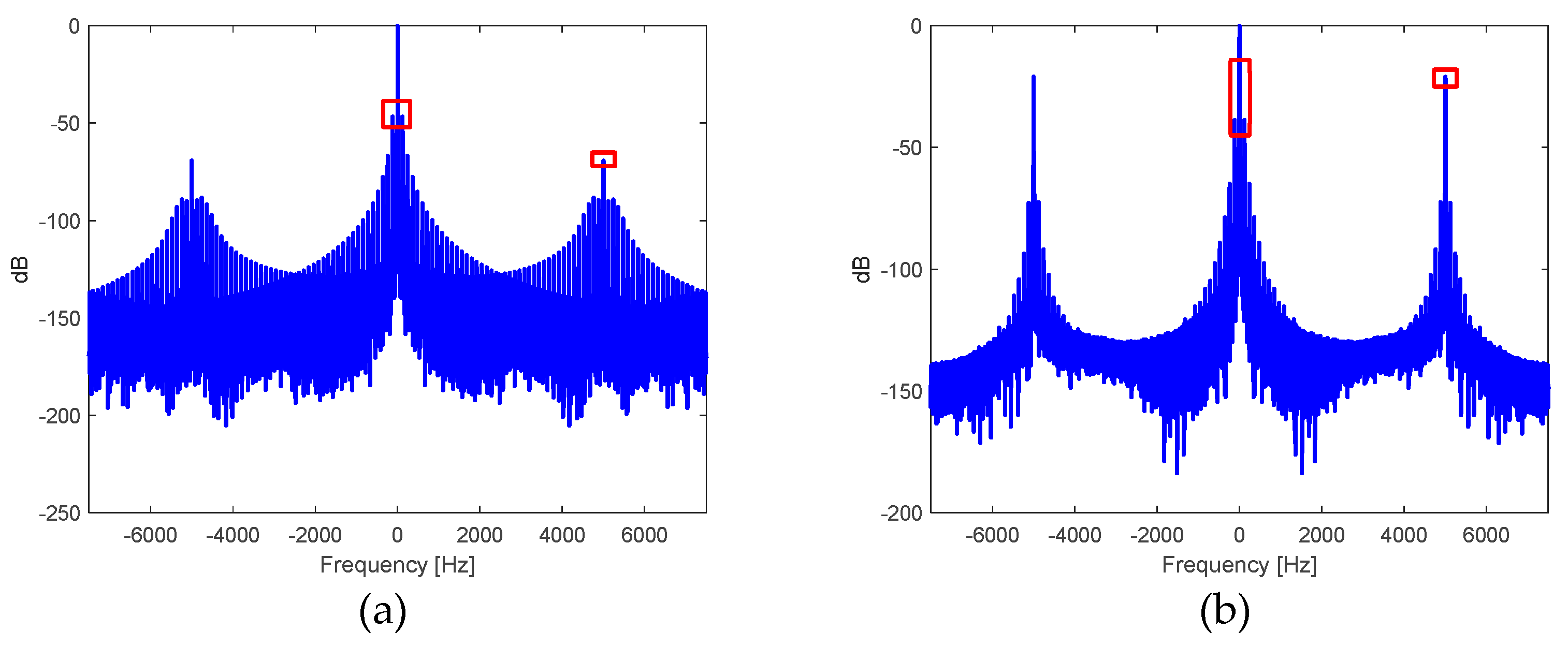
Figure 27.
a) Spectrum in , normalized concerning the magnitude at frequency , of the DC-DC converter from to in response to source voltage variation for the: a) output voltage and b) inductor current at boost stage.
Figure 27.
a) Spectrum in , normalized concerning the magnitude at frequency , of the DC-DC converter from to in response to source voltage variation for the: a) output voltage and b) inductor current at boost stage.
| THD |
|
|
|
Figure 28.
Spectrum in , normalized concerning the magnitude at the frequency of the voltage at the DC-AC inverter stage, when the source in closed-loop using the fuzzy PI controller and in the presence of source voltage variation.
Figure 28.
Spectrum in , normalized concerning the magnitude at the frequency of the voltage at the DC-AC inverter stage, when the source in closed-loop using the fuzzy PI controller and in the presence of source voltage variation.
Table 1.
Percentage Ripple of Output Voltage and Inductor Current at Boost.
Table 1.
Percentage Ripple of Output Voltage and Inductor Current at Boost.
| Parameter |
Mean Value |
|
|
| % Rizo |
% Rizo |
| Output Voltage |
V |
|
|
| Inductor Current |
A |
|
|
Table 2.
THD and Vrms of the sinusoidal PWM signal.
Table 2.
THD and Vrms of the sinusoidal PWM signal.
| Parameter |
THD |
|
| Output Voltage Inverter |
|
|
| Output Voltage Transformer |
0.0322 |
118.57 |
Table 3.
Abcissae values of the Delta membership functions of the controller universes of discourse.
Table 3.
Abcissae values of the Delta membership functions of the controller universes of discourse.
| Numeration and order |
Membership functions for the integral effect |
Membership functions for the proportional effect |
| 1 |
-0.5 |
-0.25 |
0 |
-2.25 |
-1.5 |
-0.75 |
| 2 |
-0.25 |
0 |
0.25 |
-1.5 |
-0.75 |
0 |
| 3 |
0 |
0.25 |
0.5 |
-0.75 |
0 |
0.75 |
| 4 |
0.25 |
0.5 |
0.75 |
0 |
0.75 |
1.5 |
| 5 |
0.5 |
0.75 |
1 |
0.75 |
1.5 |
2.25 |
Table 4.
Structure of the Inference Rules for the Fuzzy PI Control System.
Table 4.
Structure of the Inference Rules for the Fuzzy PI Control System.
| Rule |
Integral Membership Function |
Fuzzy Logic Operation |
Proportional Membership Function |
Implication |
Singleton |
Rule weight |
| Denomination |
Value |
| 1 |
"I==I1 |
& |
P==P1 |
=> |
D=D1 |
0.008823 |
(1)" |
| 2 |
"I==I1 |
& |
P==P2 |
=> |
D=D2 |
0.004411 |
(1)" |
| 3 |
"I==I1 |
& |
P==P3 |
=> |
D=D3 |
0 |
(1)" |
| 4 |
"I==I1 |
& |
P==P4 |
=> |
D=D4 |
0 |
(1)" |
| 5 |
"I==I1 |
& |
P==P5 |
=> |
D=D5 |
0 |
(1)" |
| 6 |
"I==I2 |
& |
P==P1 |
=> |
D=D6 |
0 |
(1)" |
| 7 |
"I==I2 |
& |
P==P2 |
=> |
D=D7 |
0 |
(1)" |
| 8 |
"I==I2 |
& |
P==P3 |
=> |
D=D8 |
0 |
(1)" |
| 9 |
"I==I2 |
& |
P==P4 |
=> |
D=D9 |
0.024193 |
(1)" |
| 10 |
"I==I2 |
& |
P==P5 |
=> |
D=D10 |
0.048387 |
(1)" |
| 11 |
"I==I3 |
& |
P==P1 |
=> |
D=D11 |
0.4068 |
(1)" |
| 12 |
"I==I3 |
& |
P==P2 |
=> |
D=D12 |
0.4534 |
(1)" |
| 13 |
"I==I3 |
& |
P==P3 |
=> |
D=D13 |
0.499999 |
(1)" |
| 14 |
"I==I3 |
& |
P==P4 |
=> |
D=D14 |
0.546599 |
(1)" |
| 15 |
"I==I3 |
& |
P==P5 |
=> |
D=D15 |
0.593199 |
(1)" |
| 16 |
"I==I4 |
& |
P==P1 |
=> |
D=D16 |
0.951612 |
(1)" |
| 17 |
"I==I4 |
& |
P==P2 |
=> |
D=D17 |
0.975806 |
(1)" |
| 18 |
"I==I4 |
& |
P==P3 |
=> |
D=D18 |
1 |
(1)" |
| 19 |
"I==I4 |
& |
P==P4 |
=> |
D=D19 |
1 |
(1)" |
| 20 |
"I==I4 |
& |
P==P5 |
=> |
D=D20 |
1 |
(1)" |
| 21 |
"I==I5 |
& |
P==P1 |
=> |
D=D21 |
1 |
(1)" |
| 22 |
"I==I5 |
& |
P==P2 |
=> |
D=D22 |
1 |
(1)" |
| 23 |
"I==I5 |
& |
P==P3 |
=> |
D=D23 |
0.999999 |
(1)" |
| 24 |
"I==I5 |
& |
P==P4 |
=> |
D=D24 |
0.995588 |
(1)" |
| 25 |
"I==I5 |
& |
P==P5 |
=> |
D=D25 |
0.991176 |
(1)" |
Table 5.
Percentage ripple of output voltage and inductor current at boost in closed-loop operation.
Table 5.
Percentage ripple of output voltage and inductor current at boost in closed-loop operation.
| Parameter |
Mean value |
|
|
| % Rizo |
% Rizo |
| Output Voltage |
V |
|
|
| Inductor Current |
A |
|
|
Table 6.
THD and Vrms of the sinusoidal PWM signal with the source in closed-loop control using the fuzzy PI controller.
Table 6.
THD and Vrms of the sinusoidal PWM signal with the source in closed-loop control using the fuzzy PI controller.
| Parameter |
THD |
|
| Output Voltage Inverter |
|
|
| Output Voltage Transformer |
0.0632 |
119.82 |
Table 7.
Percentage ripple of output voltage and inductor current at boost in closed-loop operation as response to load variations.
Table 7.
Percentage ripple of output voltage and inductor current at boost in closed-loop operation as response to load variations.
| Parameter |
Mean value |
|
|
|
| % Rizo |
% Rizo |
% Rizo |
| Output Voltage |
V |
--- |
|
|
| Inductor Current |
A |
|
|
|
Table 8.
THD and Vrms of the signal at the output of the transformer in response to load variation.
Table 8.
THD and Vrms of the signal at the output of the transformer in response to load variation.
| THD |
|
|
|
Table 9.
Percentage ripple of output voltage and inductor current at boost in closed-loop operation as response to voltage source variations.
Table 9.
Percentage ripple of output voltage and inductor current at boost in closed-loop operation as response to voltage source variations.
| Parameter |
Mean value |
|
|
|
| % Rizo |
% Rizo |
% Rizo |
| Output Voltage |
V |
--- |
|
|
| Inductor Current |
A |
|
|
|
Table 10.
THD and Vrms of the sinusoidal PWM signal with source in closed loop using fuzzy PI controller under source voltage variation.
Table 10.
THD and Vrms of the sinusoidal PWM signal with source in closed loop using fuzzy PI controller under source voltage variation.
| THD |
|
|
|