Prerpints.org logo
Preprint
Article

Differential Diagnosis of Prostate Cancer Grade to Augment Clinical Diagnosis Based on Classifier Models With Tuned Hyperparameters

Altmetrics

Downloads

91

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
We developed a novel machine learning algorithm to augment clinical diagnosis of prostate cancer utilizing first and second-order texture analysis metrics and novel application of machine learning radiomics analysis. We successfully discriminated between significant prostate cancers versus non-tumor regions and provided accurate prediction between Gleason score cohorts with statistical sensitivity of greater than 0.91 sensitivity across three separate cohorts. Tumor heterogeneity and prediction between GS cohorts were quantified using two feature selection approaches and two classifiers with tuned hyperparameters (including grid search and randomized search). There was a total of 71 patients analyzed in this study. Multiparametric MRI, incorporating T2WI and the ADC maps, were used to derive radiomics features. Recursive feature elimination (RFE), the least absolute shrinkage and selection operator (LASSO), and two classification approaches, including a support vector machine (SVM) (with grid search) and random forest (RF) (with randomized search), were utilized to differentiate between non-tumor regions versus significant cancer and prediction among Gleason score groups. In T2WI images, the RFE feature selection approach combined with RF and SVM classifiers outperformed LASSO with SVM and RF classifiers regarding performance. The detection precision of the radiomics framework depending on multiple imaging modalities was lower than the diagnostic accuracy of single imaging modality model with every machine learning approach assessed. The best performance was achieved by combining LASSO and SVM into a model that used both T2WI and ADC. This model had an area under the curve (AUC) of 0.91. Radiomic features computed from ADC and T2WI images were used to predict three groups of Gleason score using two kinds of feature selection methods (RFE and LASSO), RF and SVM classifier models with tuned hyperparameters. Using combined sequences (T2WI and ADC map images) and combined radiomics (1st and GLCM features), LASSO, with a feature selection method with RF, was able to predict G3 with the highest sensitivity at a level AUC of 0.92. To predict G3 for single sequence (T2WI images) using GLCM features, LASSO with SVM achieved the highest sensitivity with an AUC of 0.92.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Prostate cancer is the second most common male tumor globally, with 1,276,106 new cases and 358,989 deaths in 2018 [1,2]. That is 7.1% of new cases and 3.8% of all male cancer mortality in 2018 [3]. Globally, the median age for detection of prostate cancer is 66 years old, and both the recurrence and fatality rates rise with age [4,5]. Early detection of tumors increases the chances of being cured because treatment works even if the cancer is localized.
Multiparametric magnetic resonance imaging (mp-MRI) has been used extensively in prostate cancer (PCa) scanning, identification, and grading throughout the last few decades [6,7]. It is possible to obtain high-resolution anatomical and functional images using the mp-MRI imaging technique [8]. T1 weighted images (T1WI) and T2 weighted images (T2WI) are anatomic sequences used in multiparametric prostate MRI. For example, the zonal structure and tumor foci cannot be identified using T1WI. It is possible to employ T1WI to discover biopsy-associated haemorrhage, which can interfere with the capacity of other PCa MRI techniques to provide accurate diagnoses. T2WI provides the best soft-tissue imaging for malignancies, zonal morphology, seminal vesicle (SV), anterior fibromuscular stroma (AFS), neurovascular bundles, and the capsule [9]. Diffusion-weighted imaging (DWI), Magnetic resonance spectroscopic imaging (MRSI), and Dynamic contrast-enhanced (DCE) are functional MRI sequences [10]. The DWI technique was developed and implemented to detect an acute cerebrovascular stroke. DWI compares water diffusion in soft tissues and free solution to produce image contrast. When a PCa grows, there is a growth in cellularity and degradation of ductal architecture, which limits fluid flow through the prostate [11]. The b-value and Apparent Diffusion Coefficient (ADC) are the two types of images used for analysis in DWI. Tumor diagnostic outcome is improved by utilizing b-values between 1,400 and 2,000 [12,13,14]. Clinical interpretation from DWI is subjective; nevertheless, water molecules’ limitations may be measured quantitatively. Interpretation is performed with ADC maps and ADC measurements (mm2/s). and ADC levels and Gleason scores are proportionally related [15,16]. By using a machine learning approach with clinically relevant radiomics metrics as inputs we aim to improve the interpretation and augment clinical diagnosis.
Radiomics improves image analysis by generating (200+) statistical variables from medical images automatically. Patients can significantly vary in shape and texture depending on the imaging technique used [17] and by utilizing automated or semi-automated radiomics we could improve diagnostic accuracy via statistically analyzing medical images. Textural analysis has been used to extract tissue information from medical images since the 1980s [18,19]. It recognizes that intratumor heterogeneity has significant implications for cancer research, which could be represented by tumors’ texture [20]. Radiomics relies heavily on texture analysis, a necessary part of the process [21]. Radiomics is the technique used to collect essential and extensive data from clinical images and give variables that can be used to assist in detection, prognostic, and treatment response [22]. It aids in the classification of benign and malignant tumors and predicts outcomes in practically every tissue [23,24,25,26,27]. Furthermore, when developing a radiomics model, selecting the best ML model is significant. Different ML approaches may perform differently when applied to different tissues [27,28,29,30,31].
Training is used to derive many of the algorithm parameters used by machine learning, and most contemporary ML algorithms must tune parameters to improve feature identification referred to as Hyperparameters [28,29,30]. The hyperparameters are fine-tuned to optimize an algorithm for a specific learning task [32]. Hyperparameter optimization usually employs Grid and Random Search techniques [33]. Grid Search is a method using all possible permutations of hyperparameters. The training data and the number of layers can be adjusted in a grid search as hyperparameters [34]. In contrast to a grid search, randomized search does not perform a comprehensive investigation of the hyperparameter space. Nonetheless, it permits us to investigate a wider variety of hyperparameter value settings more effectively and affordably. Weerts et al. [35] stated that an increased tuning risk and relative tuning risk were observed from the random forest’s max features and SVM’s gamma and C, suggesting that it is essential to tune these hyperparameters. In the domain of prostate cancer classification and grading, many prior studies have applied machine learning techniques with default hyperparameters, often without extensive hyperparameter optimization. In contrast, our research distinguishes itself by prioritizing hyperparameter tuning. This deliberate optimization process enhances the precision and reliability of our machine-learning models, contributing to more accurate and clinically relevant results. Our work aims to advance the field by systematically refining the parameters that underpin the diagnosis of prostate cancer.
The study aimed to use different classifiers (with tuned hyperparameters) and two feature selection methods (i.e., to find the best for classification and prediction). Multiparametric MRI-derived radiomics features were used (including T2WI and ADC map images). First, to quantify tumor heterogeneity between significant versus non-tumor regions. Second, to predict Gleason scores (i.e., G2 = 3 + 4; G3 = 4 + 3; and G4, Gleason primary pattern of 4 + 4 = 8 G4, 3+5 = 8 (G4), 9 (G5) or 10 (G5)) for significant prostate cancer.

2. Materials and method

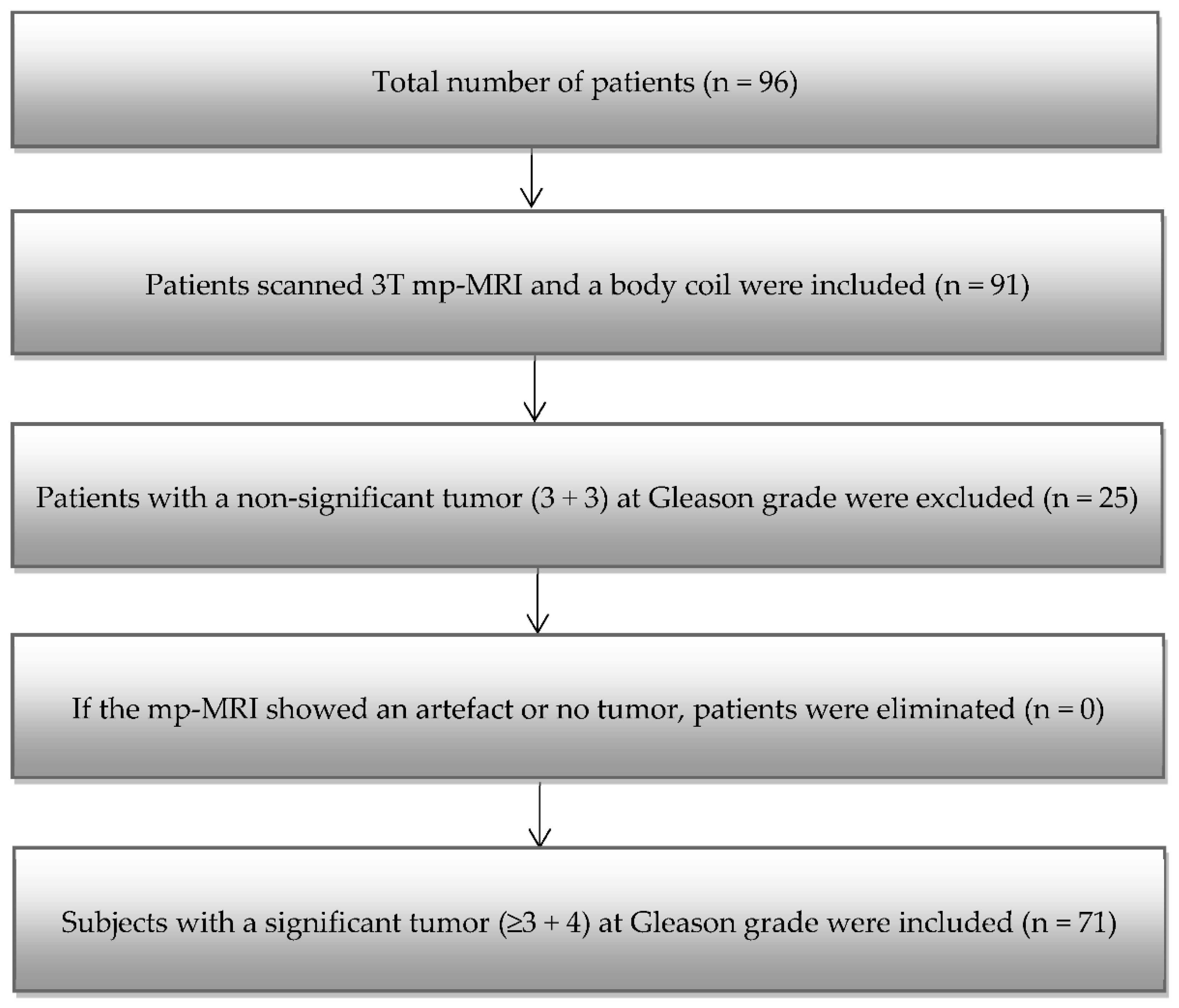
2.1. Patient Group

This study used a dataset from The Cancer Imaging Archive (TCIA) funded through the SPIE, NCI/NIH, AAPM, and Radboud University. The population set used in this work consists of 96 patients, including T2WI and ADC map series from the open-source, freely released SPIE-AAPM-NCI PROSTATEx-2 [34].
Figure 1 illustrates the exclusion and inclusion criteria: (a) the total number of patients (n = 96); (b) patients scanned 3T mp-MRI, and a body coil included (n = 96); (c) patients with a non-significant tumor at (3 + 3) Gleason grade excluded (n = 25); (d) If the mp-MRI showed an artefact or tumour, patients were eliminated (n = 0); and (e) subjects with a significant tumor (≥3 + 4) at Gleason grade included (n = 71).

2.2. Multiparametric Magnetic Resonance Imaging

The images were acquired by Siemens 3T MRI techniques (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany) utilising a pelvic phased-array coil. The axial T2WI and ADC maps were employed for imaging assessment. The current clinical agreement is that T2WI, including at least one or two functional approaches, should be used to identify prostate cancer (from DWI, DCE, and spectroscopic imaging) [5,35,36]. For precise localization, all biopsies were done under MR monitoring. A pathologist then rated biopsy specimens, which served as the ground truth. T2WI was obtained using a turbo spin echo sequence with 0.5 mm resolution and 3.6 mm slice thickness. The DWI images were obtained using a single-shot echo-planar imaging procedure utilizing 2 mm in-plane resolution, 3.6 mm slice thickness, and three-dimensional diffusion encoding gradients. The scanner program generated the ADC map from three b-values (50, 400, and 800 s/mm2). Table 1 contains a description of the mp-MRI acquisition settings. The images were collected with no endorectal coil, According to PI-RADS recommendations regarding prostate MRI images [39].

2.3. Segmentation

ROIs for significant cancer were segmented manually from T2WI, and ADC images predefined ROIs from PROSTATEx-2 Challenge that is available on TCIA [37]. The LIFEx package was used for the segmentation process [16]. Non-tumor regions cancers segmented depending on the same region for significant cancer (in different regions) assessed for every subject’s lesion. Figure 2 illustrates a typical malignancy cancer segmentation on mp-MRI.

2.4. Feature extraction

Pre-processing, including intensity normalization and spatial resampling, was conducted for all mp-MRI images using LIFEx to derive radiomics features. The dimensions were rescaled to 0.5 × 0.5 × 3 mm, preserving the dataset’s in-plane and inter-plane resolutions. The radiomics features uniformity achieved using grey-level discretization defined between 1 and 128 bits/pixel. Absolute resampling between the minimum and maximum fixed bounds for all ROIs used for intensity resizing parameters [20]. Figure 2 demonstrates the analysis procedures. For each ROI, (a) 5 features were computed from the histogram, and (b) Six features were computed from grey-level features co-occurrence, leading to 11 features per ROI for each patient.

2.5. Feature selection

Feature selection refers to the process of selecting essential features in predictive models. Irrelevant features can degrade the prediction model by contributing little to it [6]. Model overfitting challenges arise when there are too numerous features in the algorithm. A significant feature containing fewer numbers, but high precision can be minimised by determining the size of the feature set through the feature selection approach [42]. It is popular to use recursive feature elimination [29,43,44,45,46] and LASSO to select the best features from the dataset. Recursive feature elimination (RFE) and the least absolute shrinkage and selection operator (LASSO) were employed in this study for feature selection due to their high performance and widespread use. The Python environment with scikit-learn (version 1.0.2) was used to implement these feature selection algorithms.

2.5.1. Classification and Prediction

Both SVM with hyperparameter tuning via grid search [43,46,47,48] and RF with hyperparameter tuning via a randomized search [28,49] were used to achieve optimal and robust classification performance for significant cancer versus non-tumor regions and tuning hyper using the scikit-learn library from Python (1.0.2). These classification techniques were selected and assessed because they have been extensively used to identify different organs, as mentioned in previous studies [26,43,45,50]. To differentiate between regions with significant cancer and those without tumors, we employed radiomics parameters. These parameters included statistical features from both the 1st and 2nd order, extracted from the Gray-Level Co-occurrence Matrix (GLCM). Our approach involved utilizing two machine learning classifiers: the Random Forest (RF) classifier and the Support Vector Machine (SVM) classifier. For the RF model, we conducted a randomized search to fine-tune its hyperparameters, which encompassed factors such as the number of estimators, criterion, max depth, and max features. In contrast, for the SVM model, we engaged in a grid search method to optimize hyperparameters such as C, gamma, and the choice of kernel function.
To evaluate the performance and reliability of these models, we conducted a K-fold cross-validation process with K set to 5. This rigorous validation procedure ensured that our models could effectively distinguish between regions with significant cancer and non-tumor regions based on radiomics data.
For prediction among GS cohorts, radiomics parameters, including 1st and 2nd orders looking at GLCM, were entered into an RF classifier via randomized search and an SVM classifier with hyperparameter tuning via grid search to prove their significance. The RF model with a randomized search trained with different hyperparameter settings (including number estimators, criterion, max depth, and max features). The SVM model with grid search trained with different hyperparameter settings (including c, gamma, and kernel). Then the models were computed using starfield K-fold cross-validation (k=5). The RF and SVM-based tuning hyperparameter classifiers were interpreted using a binary classification method, with G2 vs rest, G3 versus rest, and G4 versus rest employed to illustrate the AUC-ROC. Because of class imbalance, a classifier’s performance may suffer if all of the datasets are assigned to the majority class, leading to high accuracy in classification but low specificity or sensitivity. Several ways to deal with this issue are through oversampling [51] and sample weighting [52,53]. G2 was classified from G3 and G4 using ROC-AUC. The G3 and G4 areas under curves were calculated utilizing the same approach (one vs rest). This study used Python’s scikit-learn (1.0.2) library to verify model validity using a five-fold cross-validation approach.

2.6. Statistical analysis

Each radiomics parameter was tested for significance using the Kruskal-Wallis technique. Radiomic features and PCa patients’ significant cancer versus non-tumor regions were correlated using Spearman correlation. Statistical significance was determined using the Holm-Bonferroni method at a p-value of ˂0.05 [54].
Using the Kruskal-Wallis test, each radiomics feature was looked at again to see if it was significant in the GS cohorts. The value of the correlation between radiomics characteristics and the GS groups for prostate cancer subjects was determined using the Spearman correlation, which was employed to measure the correlation value. Statistical significance was determined using the Holm-Bonferroni method at a p-value of ˂0.05 [54].

3. Result

3.1. Patients

This study used 71 prostate cancer subjects from the SPIE, NCI/NIH, and AAPM PROSTATEx-2 Cancer Imaging Archive (TCIA). Epstein et al. [52] identified pathology Gleason Grade Group (GG) numbers for cancer tumors. To better represent clinical management, the patients redefined by GGG: 39 subjects, G2 = 3 + 4; 18 subjects, G3 = 4 + 3; and G4, 14 subjects, Gleason primary pattern of 4+4 = 8, 3+5 = 8, 9 (G5), or 10 (G5).

3.2. Association between radiomic attributes and significant versus non-tumor regions

Each prostate cancer patient’s T2WI and ADC map images were used to extract radiomics features. The Kruskal-Wallis approach was used to ascertain if any feature from radiomics had statistical significance to make a comparison between significant tumor versus non-tumor regions. The radiomics features correlated with significant cancer versus nontumor regions using Spearman correlation.
In the Kruskal-Wallis significance test, eleven features were statistically significant: skewness, kurtosis, entropylog10, entropylog2, uniformity, jointentropylog10, jointentropylog2, correlation, contrast, dissimilarity, and angular second moment after applying the Holm-Bonferroni correction (Table 2). Spearman correlation among radiomics attributes and significant cancer versus non-tumor regions reflects significant strong correlation values of 0.31, 0.30, -0.33, -0.23, 0.37, 0.46, 0.56, 0.56, -0.25, 0.27, 0.26, 0.76, 0.80, and 0.37 for skewness, kurtosis, entropylog10, entropylog2, uniformity, jointentropylog10, jointentropylog2, angular second moment, contrast, dissimilarity, and correlation, respectively (Table 3).

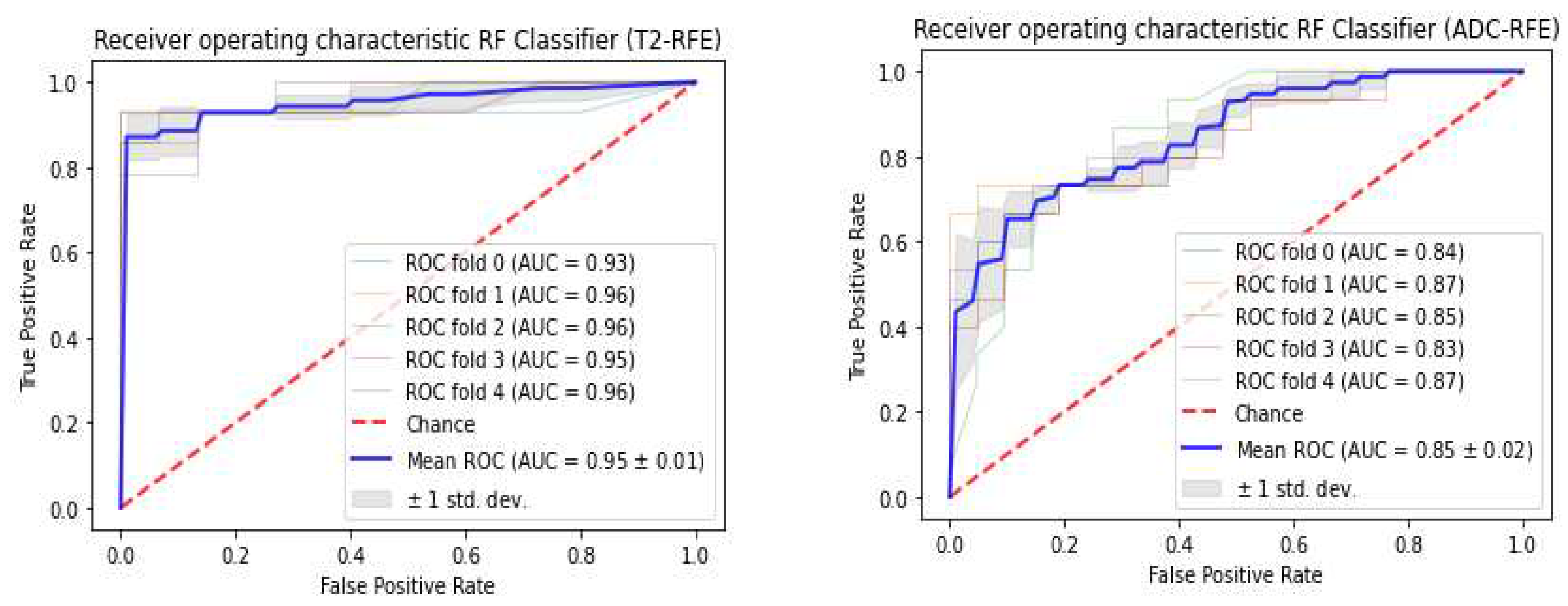
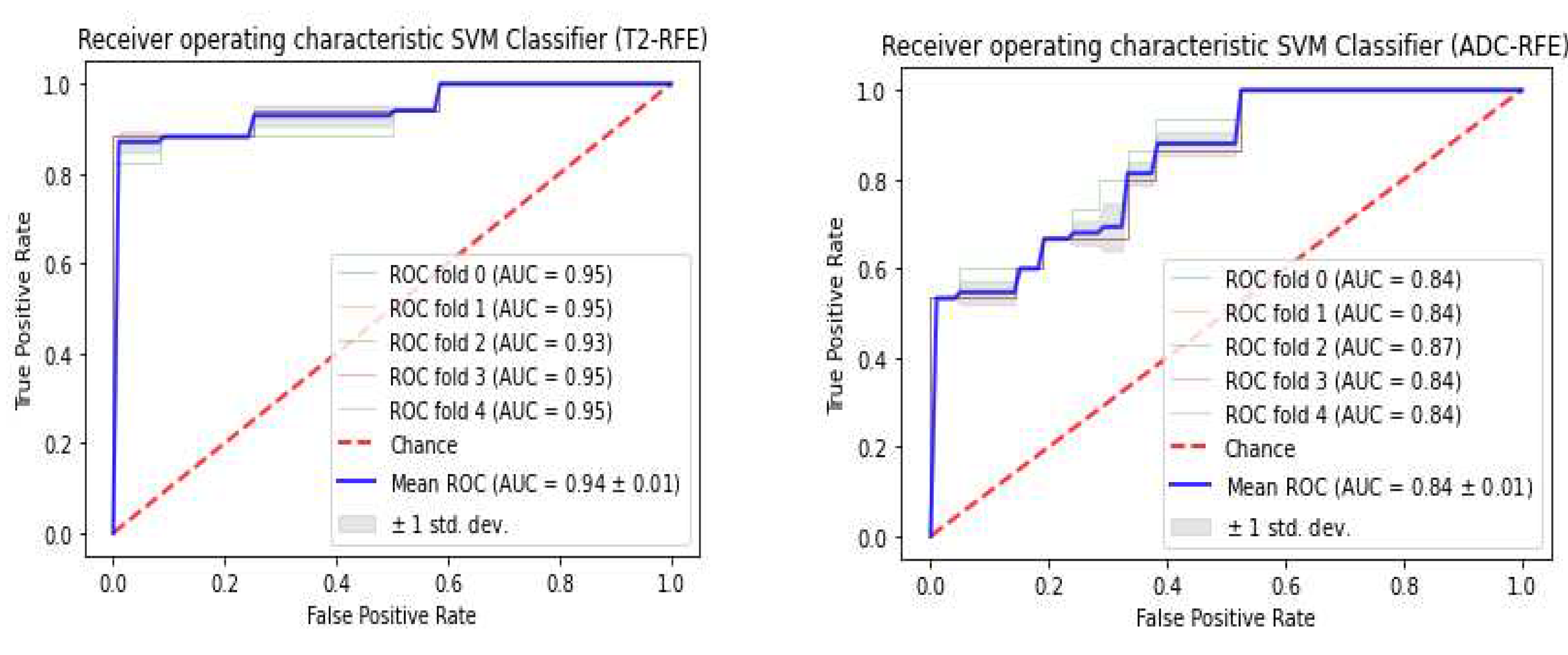
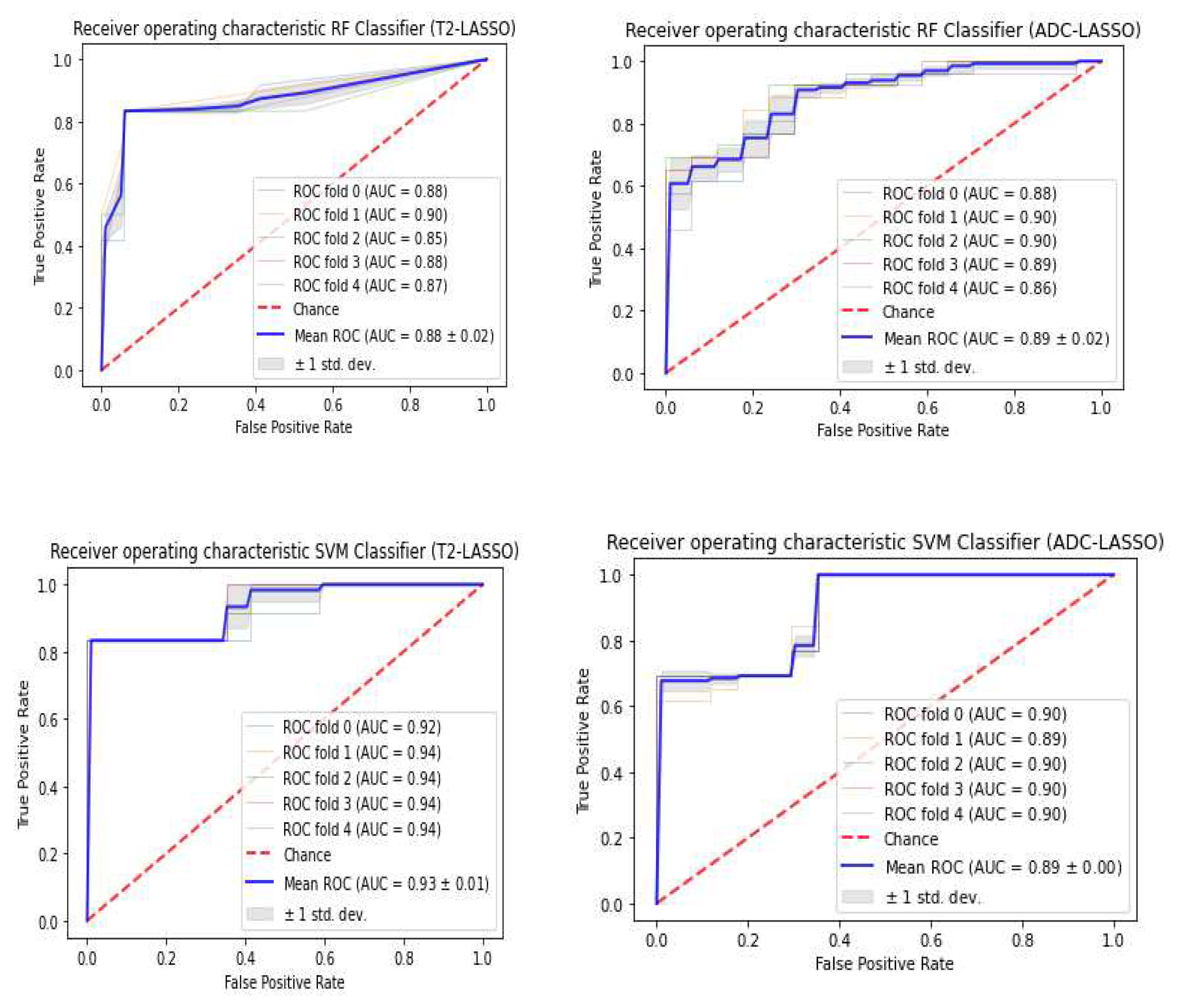
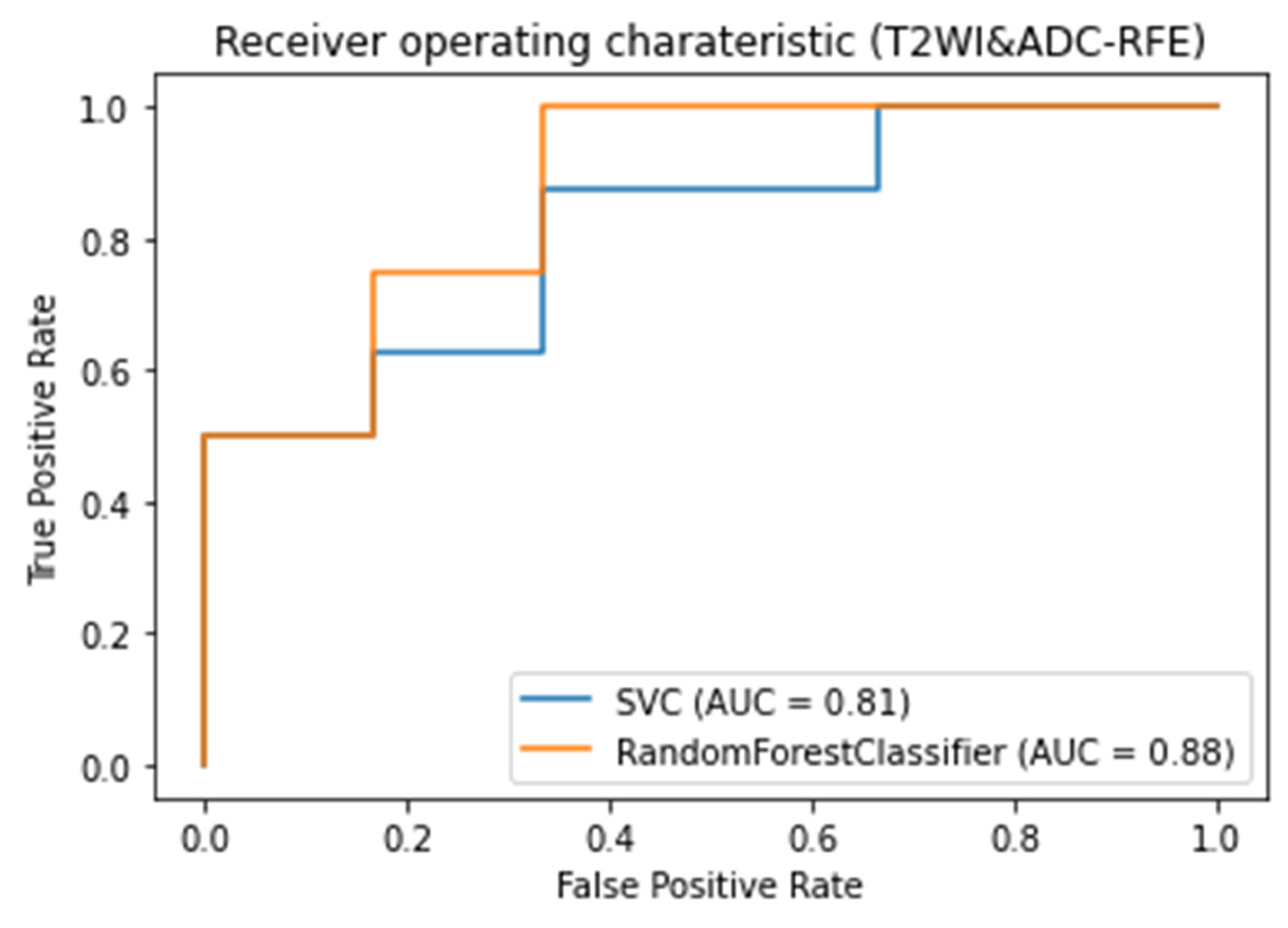
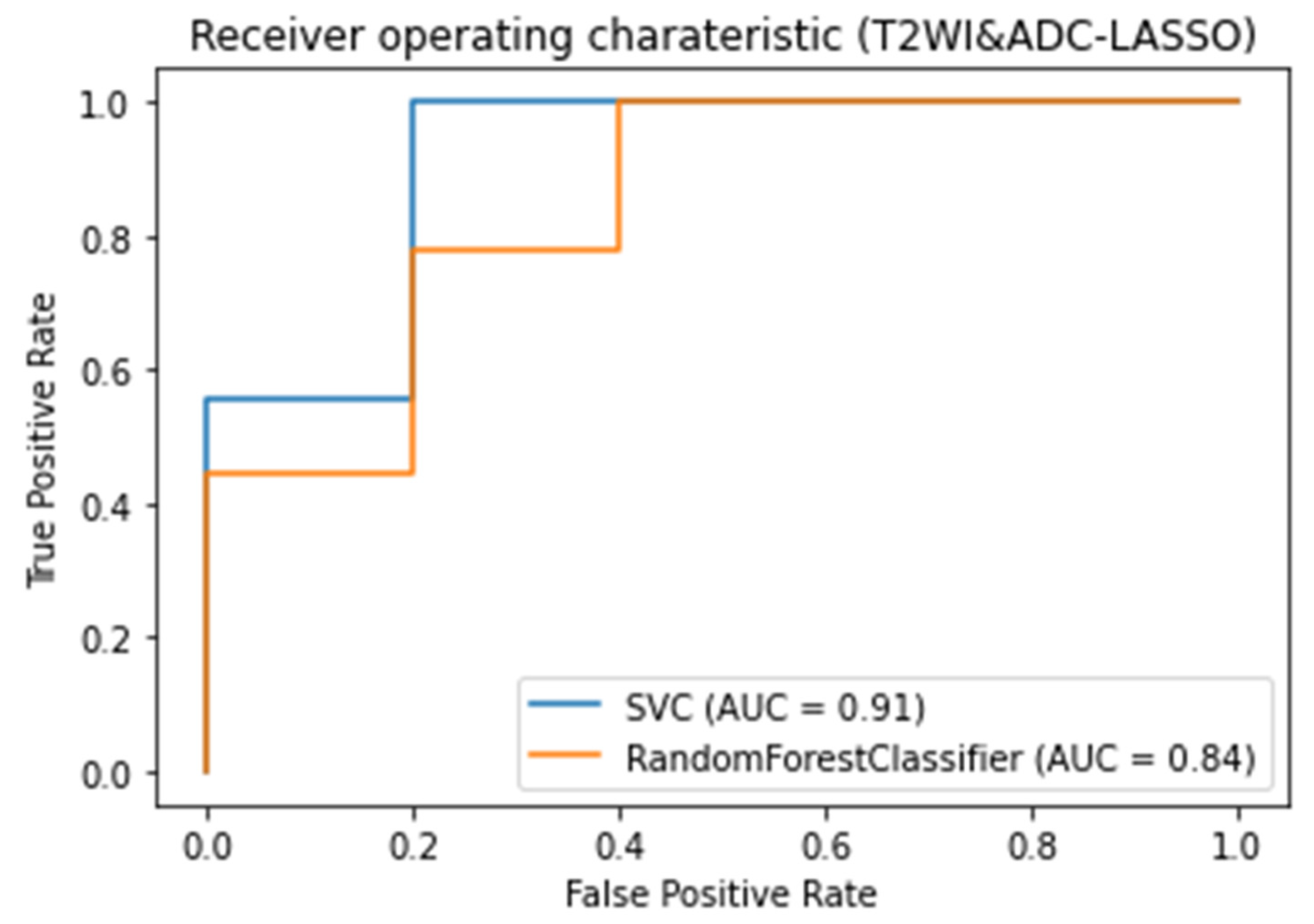
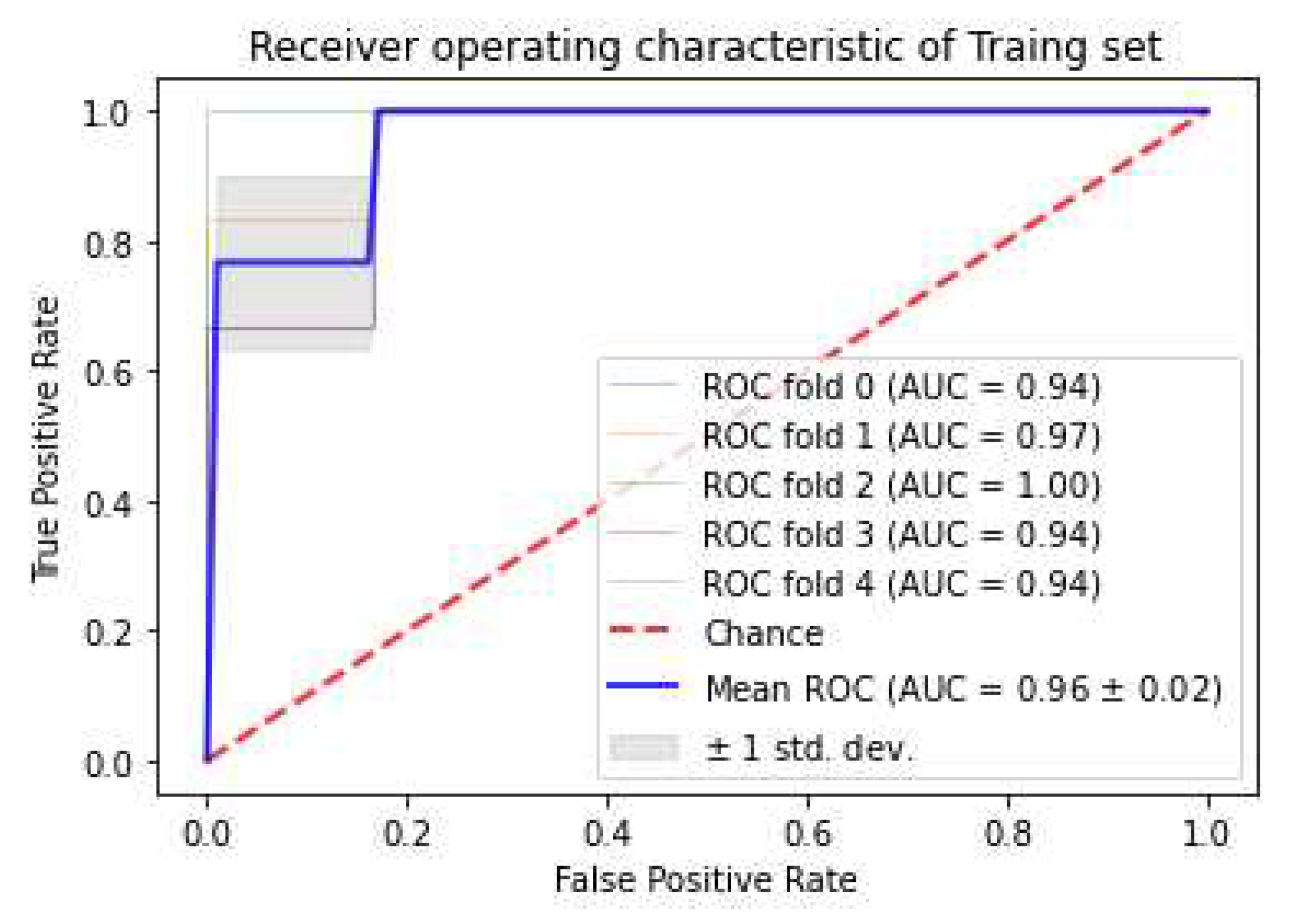
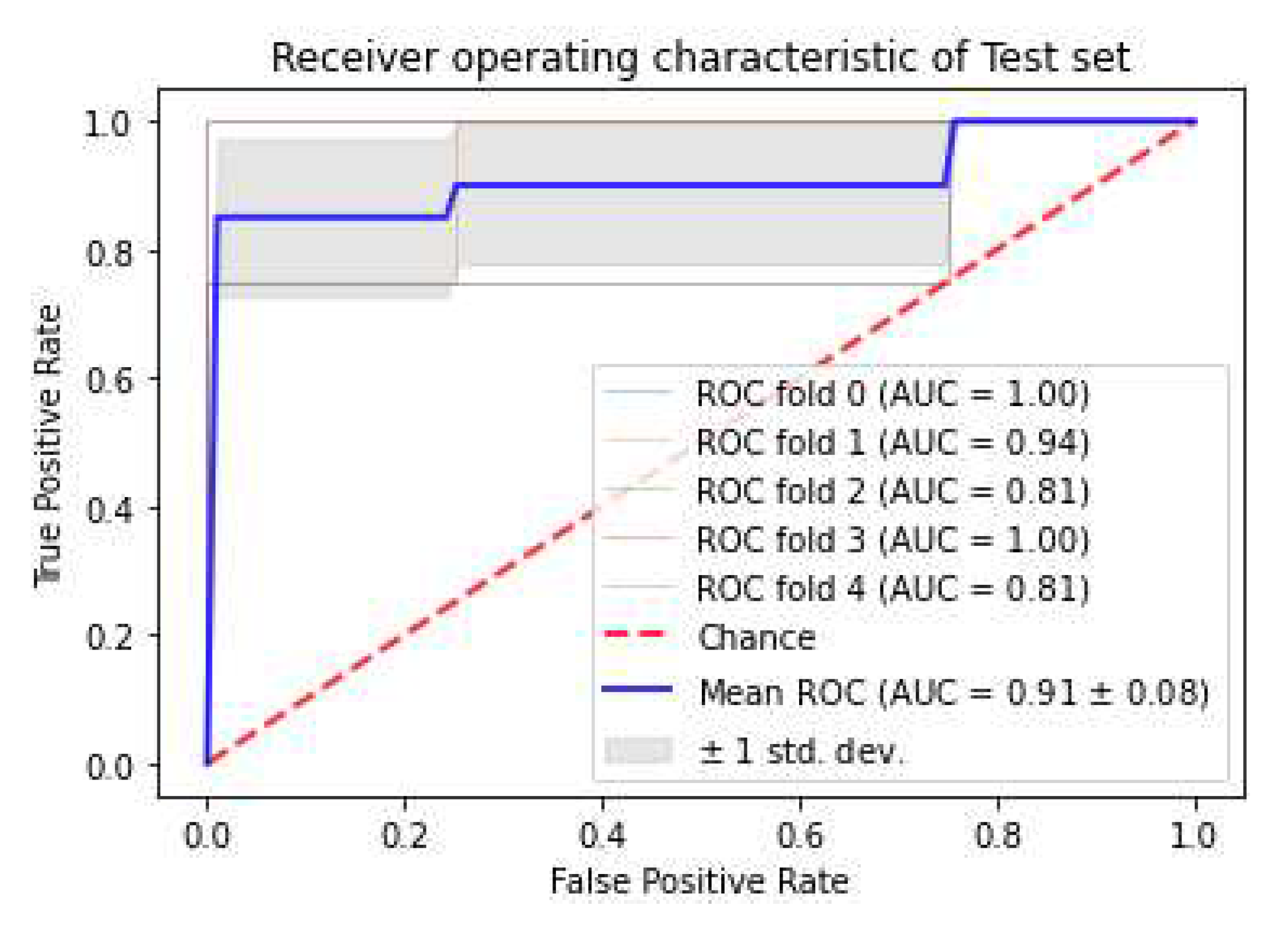
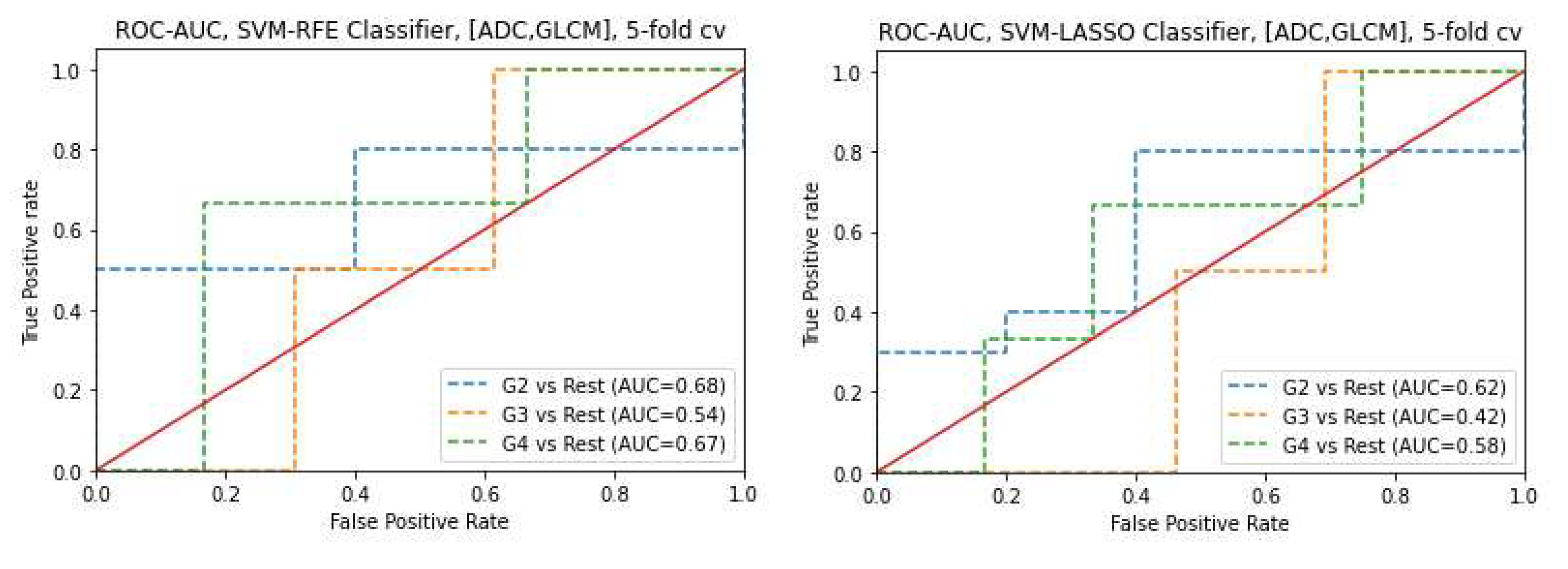
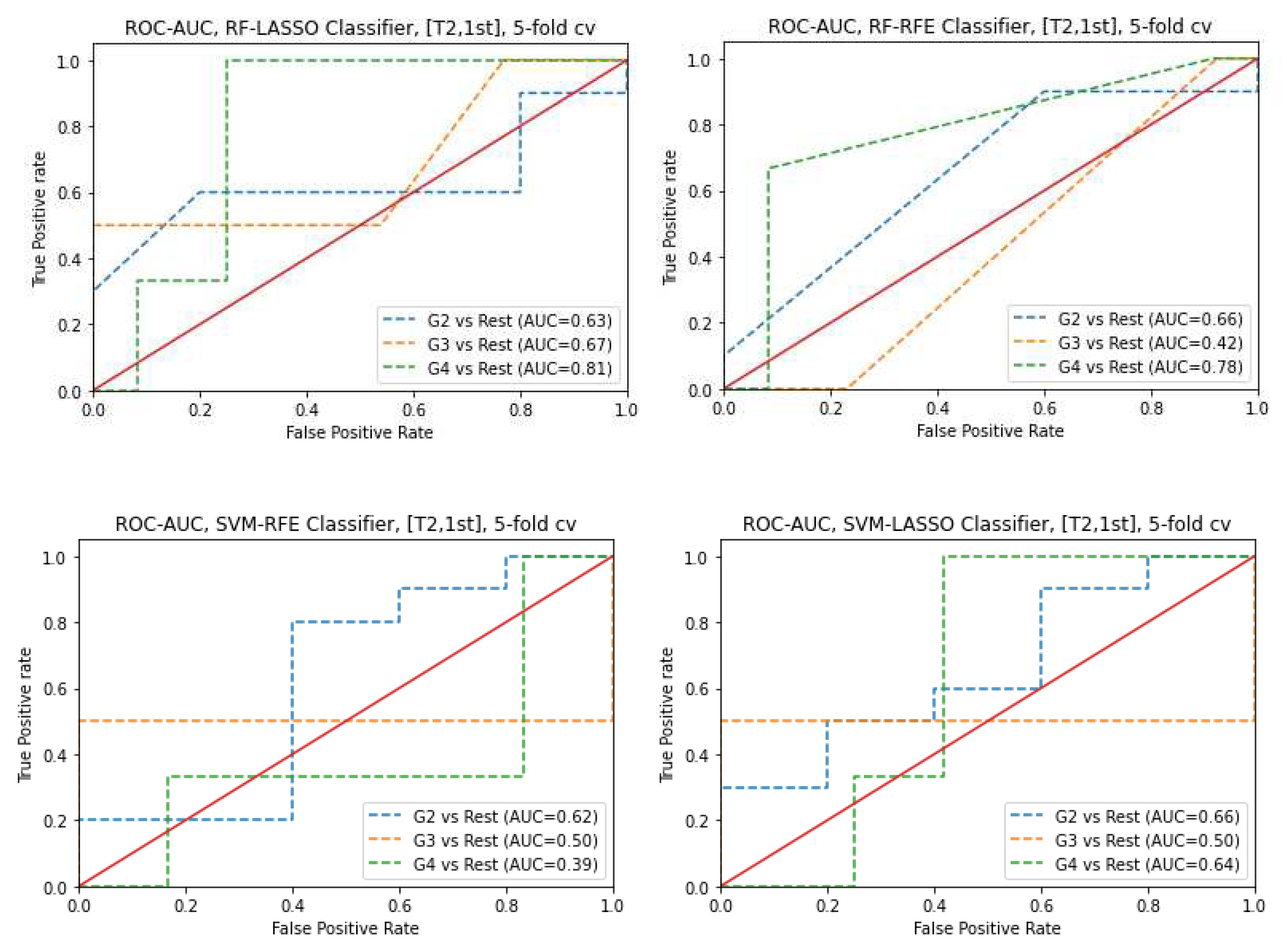
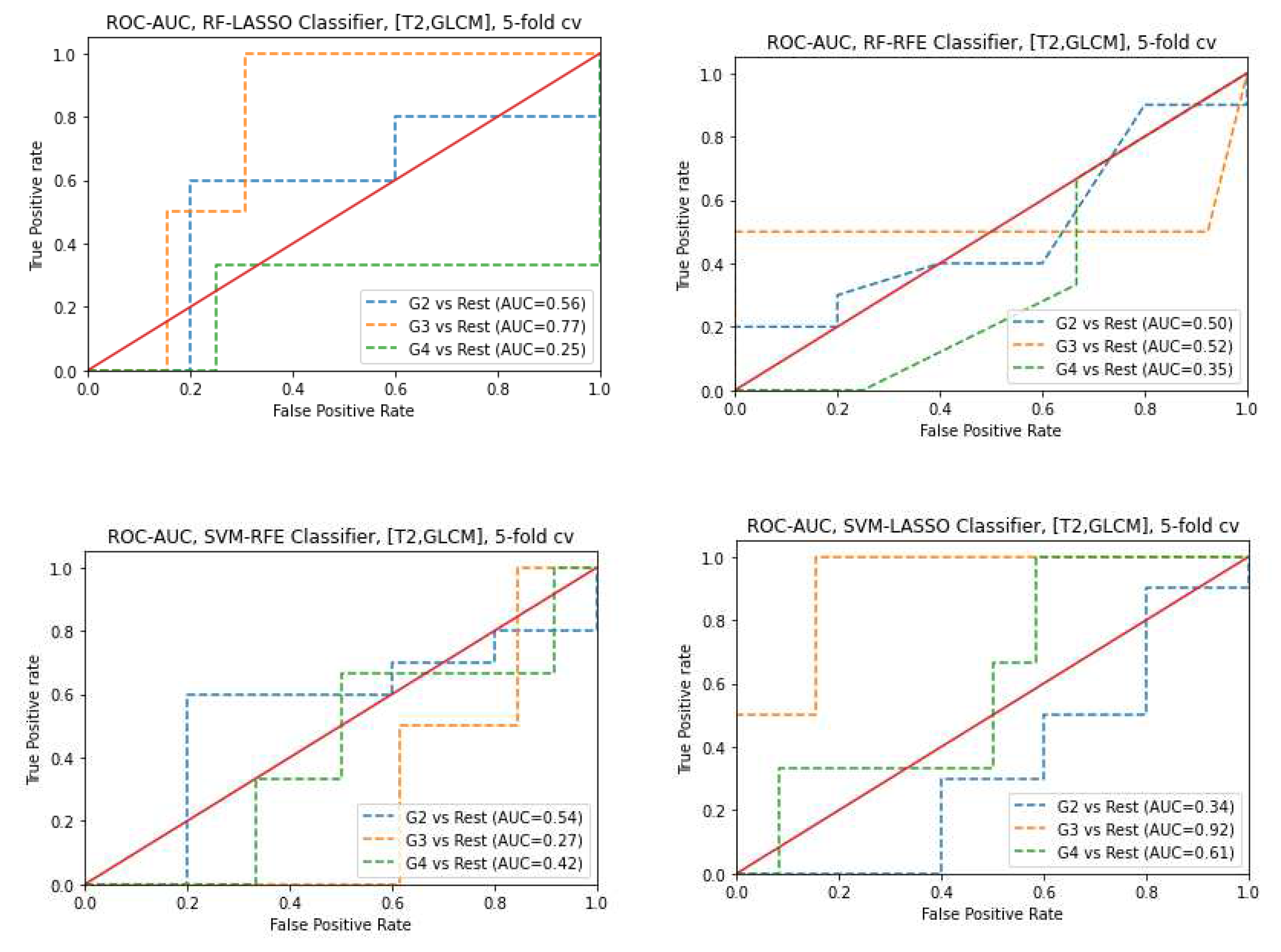
3.3. Classifiers and Feature Selection Performance

The radiomics features were fed into a model that used RF and SVM classifiers with tuned hyperparameters to distinguish between significant cancer versus non-tumor regions in 71 PCa patients. For T2WI images, the RFE combined RF Classification algorithm obtained the maximum AUC of 0.95 ± 0.01 (with 5-fold CV). Furthermore, the RFE with the SVM classification algorithm obtained the second maximum AUC of 0.94 ± 0.01 (with 5-fold cross-validation). Nevertheless, the selection technique LASSO with support vector machine classifier obtained the highest AUC of 0.93 ± 0.01 (with 5-fold cross-validation). Furthermore, the selection technique LASSO with random forest obtained the second-highest AUC of 0.88 ± 0.02 (with 5-fold CV). The LASSO combined SVM Classification algorithm obtained the maximum AUC of 0.89 ± 0.00 (with 5-fold CV) for ADC images.
The selection method LASSO with RF classification algorithm also obtained the second highest AUC of 0.89 ± 0.02 (with 5-fold CV). Nevertheless, the selection approach recursive feature elimination with random forest classification algorithm obtained the highest AUC of 0.85 ± 0.02 (with 5-fold cross-validation). Furthermore, the RFE combined SVM selection technique obtained the second maximum AUC of 0.84 ± 0.01 (with 5-fold CV). In conclusion, we selected the most appropriate feature selection technique and classification algorithm for each sequence. Figure 3 and Figure 4 depict the receiver operating characteristic area under curves (ROC-AUC) for T2WI and ADC map images, respectively.
For combined sequences (T2WI and ADC map images), the LASSO combined SVM Classification algorithm obtained the maximum AUC of 0.91. Furthermore, the RFE with the RF classification algorithm obtained the second maximum AUC of 0.88 (Figure 5 and Figure 6). For combined sequences (T2WI and ADC map images), the RFE combined SVM Classification algorithm obtained an AUC of 0.81 (Figure 5). Furthermore, the LASSO with RF classification algorithm obtained an AUC of 0.84 (Figure 6).

3.4. Model strength and performance variations

Model strength and performance variations were presented in this section to demonstrate how the model performs in different data sets. As illustrated in Figure 7 and Figure 8, the training and test sets performed effectively. Figure 7, illustrates that the AUC for each of the five folds in the training set is 0.94, 0.97, 1.00, 0.94, and 0.94, respectively. The mean AUC is 0.96 ± 0.02 (precision 82%; accuracy 82%; recall 82%; f1-score 82%). Figure 8 shows the receiver operator characteristic area under a curve in the test dataset for the five folds: 1.00, 0.94, 0.81, 1.00, and 0.81, respectively. The mean AUC is 0.91 ± 0.08 (precision 90%; accuracy 87.5.%; recall 88%; f1-score 87%). The model’s performance was tested using the test sets’ mean performance with five-fold cross-validation.

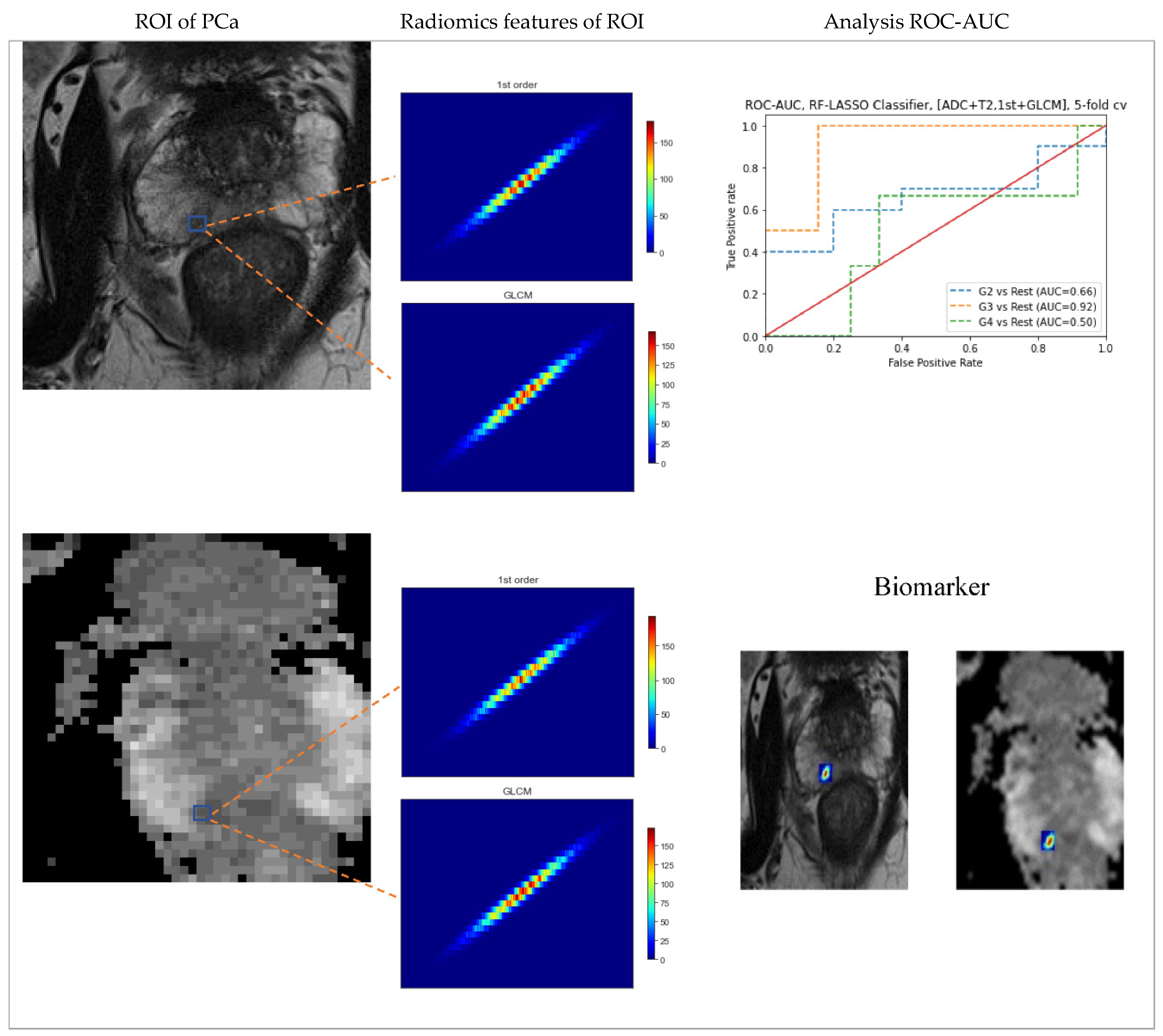
3.5. Association between GS and Radiomics Attributes

The Kruskal-Wallis approach was used to ascertain if any feature from the radiomics aspect had statistical significance to make comparisons between the GS groups after retrieving radiomics features from T2WI and ADC map images of every prostate cancer subject. The radiomics features and GS cohorts were correlated using Spearman’s correlation.
The Kruskal-Wallis test showed that the three GS cohorts (G2, G3, and G4) were statistically different in uniformity (Table 4). After applying the Holm-Bonferroni correction, no other characteristics were significantly different between GS groups. The correlation coefficients for entropylog2, entropylog10, uniformity and the angular second moment are 0.23, 0.23, -0.24, and -0.26. These numbers have a low correlation (Table 5).

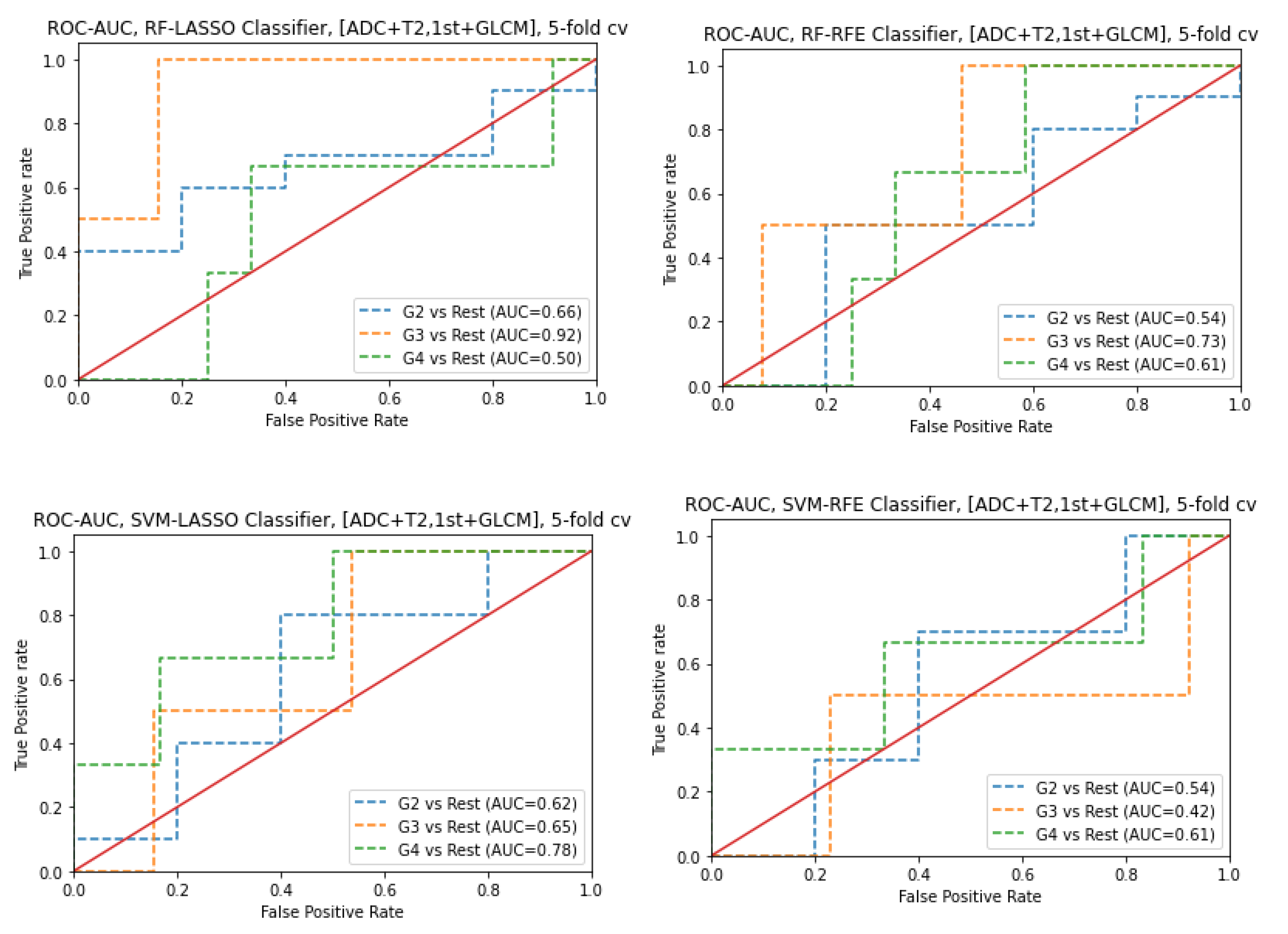
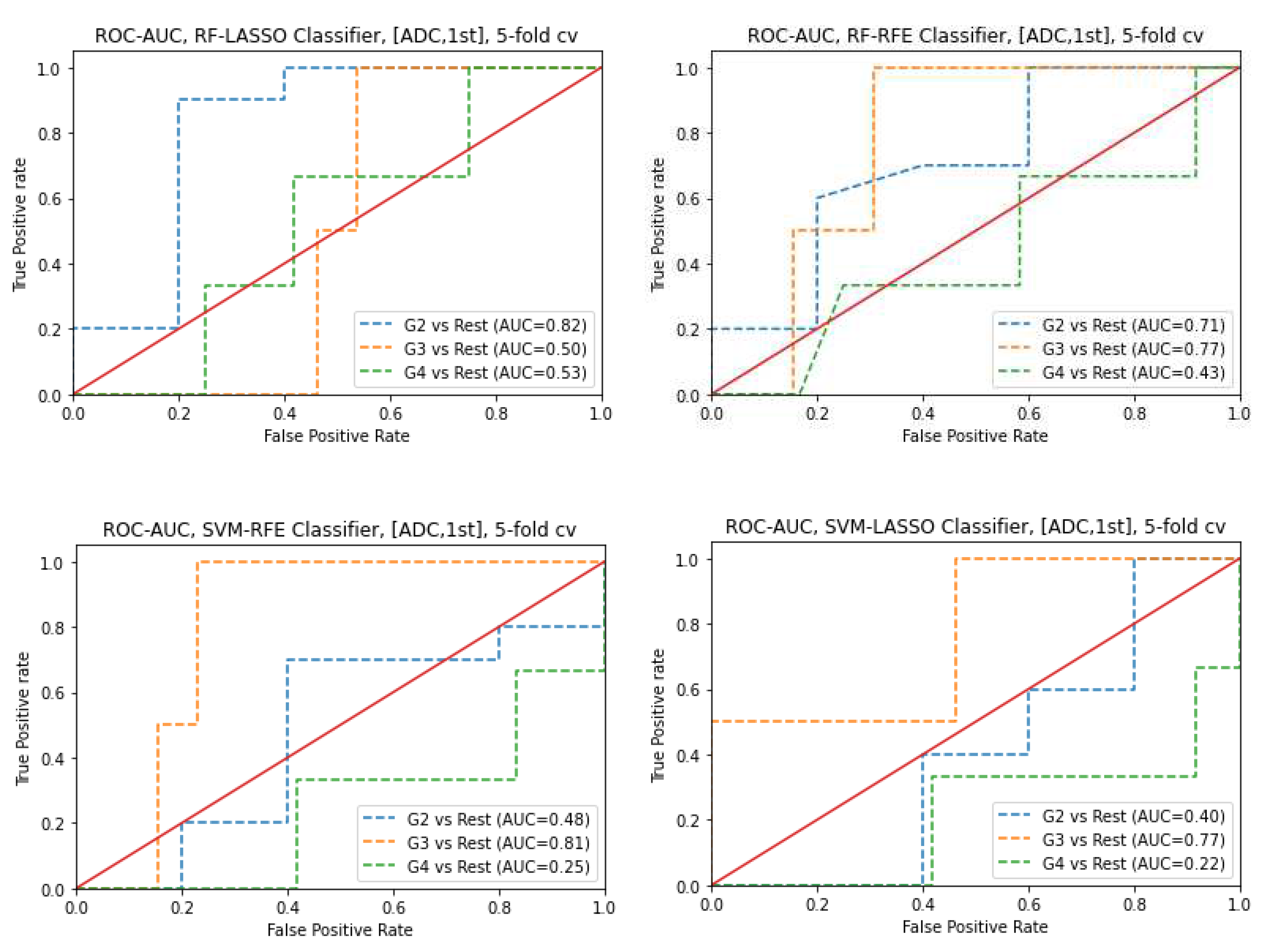
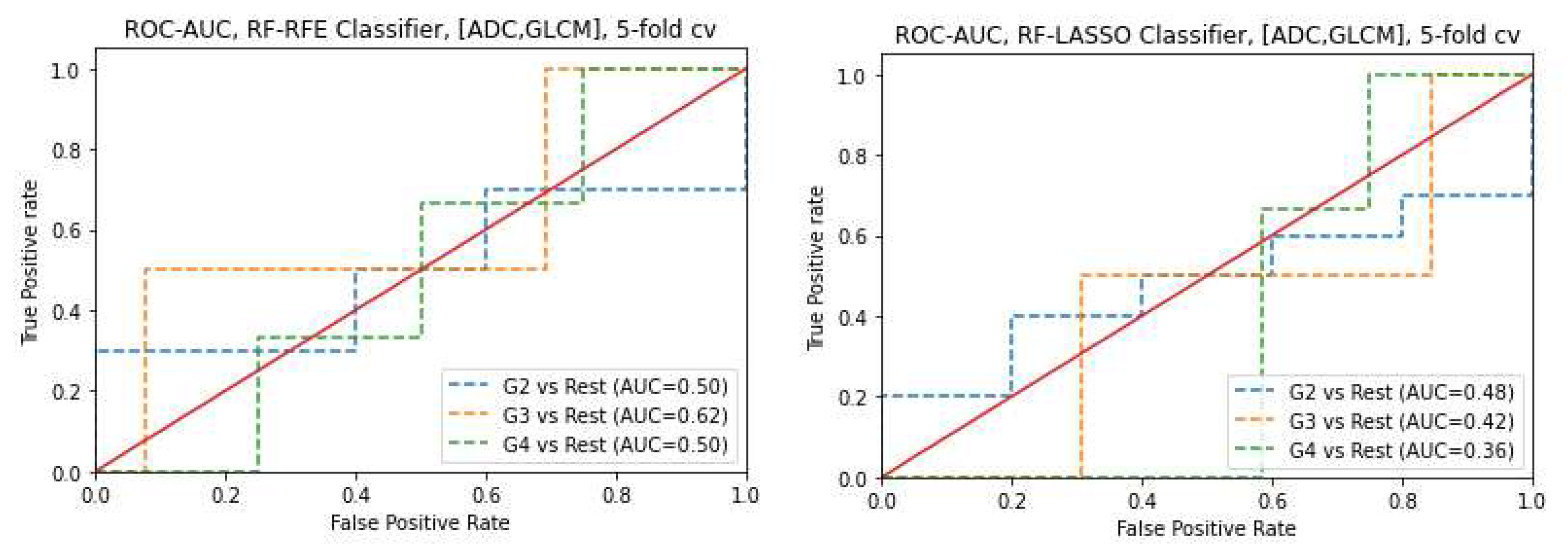
3.6. Prediction of Gleason score

The RF and SVM classifiers with tuning hyperparameters model predicted the GS groups of 71 prostate cancer subjects using all radiomics features. For combined sequences (T2WI and ADC map images) and features (1st order and GLCM), the LASSO combined RF Classification algorithm had an AUC of 0.92 for G3 subjects and 0.66 for G2 and 0.50 for G4 subjects. For combined sequences (T2WI and ADC map images) and features (1st order and GLCM), the RFE combined RF Classification algorithm was AUC of 0.73 for G3 subjects and 0.61 for G4 subjects, respectively and 0.54 for G2 subjects. For combined sequences (T2WI and ADC map images) and features (1st order and GLCM), the LASSO combined SVM classification algorithm was an AUC of 0.78 for G4 subjects, 0.65 for G3, and 0.62 for G2 subjects. For combined sequences (T2WI and ADC map images) and features (1st order and GLCM), the RFE combined SVM Classification algorithm had an AUC of 0.61 for G4 subjects, 0.54 for G2, and 0.42 for G3 subjects. For combined sequences (T2WI and ADC map images), the LASSO with RF classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G4 (SVM-LASSO, AUC = 0,78) and G2 (RF-LASSO, AUC = 0.66) (Figure 9).
For ADC map images, using 1st-order features, the LASSO combined RF Classification algorithm was an AUC of 0.82 for G2 subjects, 0.53 for G4 subjects, and 0.50 for G3 subjects. The RFE combined RF Classification algorithm was an AUC of 0.77 for G3 subjects, 0.71 for G3 subjects, and 0.43 for G4 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.81 for G3 subjects, 0.48 for G2 subjects, and 0.25 for G4 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.77 for G4 subjects, 0.40 for G2 subjects, and 0.22 for G4 subjects. For ADC map images, using 1st order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.82 to predict G2 compared to G3 (SVM-RFE, AUC = 0,81) and G4 (SVM-LASSO, AUC = 0.53) (Figure 10).
However, For ADC map images and GLCM features, the LASSO combined RF Classification algorithm was an AUC of 0.48 for G2 subjects, 0.42 for G3 subjects, and 0.36 for G4 subjects. The RFE combined RF Classification algorithm was an AUC of 0.62 for G3 subjects, 0.50 for G4 subjects, and 0.50 for G2 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.68 for G2 subjects, 0.67 for G4 subjects, and 0.54 for G3 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.62 for G2 subjects, 0.58 for G4 subjects, and 0.42 for G3 subjects. For ADC map images, using GLCM features, the RFE with SVM classification algorithm obtained the highest AUC of 0.68 to predict G2 compared to G4 (SVM-RFE, AUC = 0,67) and G3 (RF-RFE, AUC = 0.62) (Figure 11).
………………………………………………………………………………………………………………………………………………………………………………
For T2WI images, using 1st-order features, the LASSO combined RF Classification algorithm was an AUC of 0.81 for G4 subjects, 0.67 for G3 subjects, and 0.63 for G2 subjects. The RFE combined RF Classification algorithm was an AUC of 0.78 for G4 subjects, 0.66 for G2 subjects, and 0.42 for G3 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.62 for G2 subjects, 0.50 for G3 subjects, and 0.39 for G4 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.66 for G2 subjects, 0.64 for G4 subjects, and 0.50 for G3 subjects. For T2WI images, using 1st order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.81 to predict G4 compared to G2 (SVM-LASSO and RF-RFE, AUC = 0,66, and 0.66 respectively) and G4 (RF-RFE, AUC = 0.78) (Figure 12).
For T2WI images, using GLCM features, the LASSO combined RF Classification algorithm was an AUC of 0.77 for G3 subjects, 0.56 for G2 subjects, and 0.25 for G4 subjects. The RFE combined RF Classification algorithm was an AUC of 0.52 for G3 subjects, 0.50 for G2 subjects, and 0.34 for G4 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.54 for G2 subjects, 0.42 for G4 subjects, and 0.27 for G3 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.92 for G3 subjects, 0.61 for G4 subjects, and 0.34 for G2 subjects. For T2WI images, using GLCM features, the LASSO with SVM classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G2 (RF-LASSO, AUC = 0,56) and G4 (SVM-LASSO, AUC = 0.61) (Figure 13).

4. Discussion

In PCa assessment, mp-MRI has been demonstrated to be a superior technique, allowing for greater accuracy when detecting cancerous growths. That is the only imaging approach with enough spatial resolution and soft tissue contrast to identify prostate cancer effectively [8] without using ionising radiation. Prostate tumor aggressiveness can be evaluated using artificial intelligence, such as radiomics [56]. Consequently, radiomics could be an innovative and effective method for extracting further clinically relevant data [17]. Radiomics can diagnose prostate cancer early, grade it according to Gleason, determine therapy response, and anticipate biochemical recurrence [56].
Different clinical settings may require different ML techniques for discriminating between sacral chordoma and sacral giant cell malignancies; LASSO using a generalised linear model (GLM) significantly outperformed [27]. However, when it came to scoring colon microarray gene expression and identifying meningioma, random forest and eXtreme Gradient Boosting (XGBoost) classification methods achieved the best performance [28,29,30,57]. Wang et al. revealed that the ML approach of recursive elimination features using a support vector machine is better than other feature selection and classification methods [46]. As a result, it is essential and recommended to discover appropriate machine learning approaches in various clinical implementations in future studies. In the context of prostate cancer classification and grading, our research stands out due to its focus on hyperparameter tuning. While many prior studies have applied machine learning techniques with default hyperparameters, we have systematically optimized these parameters to enhance the precision and robustness of our models. This approach has demonstrated its potential to contribute to more accurate and clinically relevant diagnoses, highlighting the critical role of hyperparameter optimization in medical applications of machine learning.
  • Significant cancer versus non-tumor regions
The Kruskal-Wallis test was utilised to examine radiomics characteristics’ relevance in differentiating significant cancer versus non-tumor regions. Then, Spearman correlation was performed to determine the association between radiomics attributes and significant cancer versus non-tumor regions. Two feature selection methods (REF and LASSO) and two classifiers (RF and SVM) with tuned hyperparameters (randomised search and grid search) were used to create an effective ML algorithm. The analysis between radiomics features and the significant versus non-tumor regions revealed eleven radiomics features that are statistically significant (i.e., skewness, kurtosis, entropylog1o, entropylog2, uniformity, jointEntropyLog2, jointEntropyLog10, correlation, contrast, dissimilarity, and angular second moment) with the capacity to discriminate between the significant and non-tumor regions.
Prostate cancer discrimination employing multiparametric MRI radiomics was designed and tested in this study, and the technique consistently performed well in the present study. As this study reveals, classification accuracy varies between ML techniques. For T2WI, RF and SVM classifiers were observed to be very useful when used with REF (AUC = 0.95 ± 0.01, and 0.94 ± 0.01, respectively). The second-best result was observed using LASSO selection with SVM and RF classifiers (AUC = 0.93 ± 0.01 for T2WI, and 0.89 ± 0.00 for ADC map, respectively). That is following previous findings have shown that this system is adequate to other feature selection techniques and classifiers in various organs [29,30,43,53,56,58,59]. With support vector machines and random forests classifiers, the AUC for the T2WI sequence was highest with the selection approach using the REF. Radiomic features can be used to identify the T1-2 and T3-4 stages using an unsupervised clustering algorithm and the supervised LASSO technique, according to Sun et al. [60]. This finding might link to the fact that morphological T2WI depends on the tumor signal for its assessment. The second-highest AUC was achieved using the selection approach of LASSO with SVM and RF. Wang et al. achieved the best result when combining a support vector machine with recursive feature reduction [46].
Nevertheless, the T2WI model performed better than the ADC model (AUCs of 0.95 vs 0.89, respectively). We observed that the AUC of the classification algorithm generated from T2WI images using RF classifiers using the feature selection technique (RFE) was the highest AUC of 0.95 ± 0.01. In addition, the RFE with the SVM classification algorithm obtained the second maximum AUC of 0.94 ± 0.01 (with 5-fold cross-validation). Additionally, T2WI could perform a non-invasive analysis of PCa biological growth, which might assist in classifying patients for adequate treatment. It also provides morphologic data for cancer diagnosis, localisation, and staging [61]. SVM and RF classifiers with LASSO (For LASSO, AUC of 0.89 ± 0.00, 0.89 ± 0.02 for SVM, and RF classifiers, respectively) and RFE (for RFE, AUC of 00.84 ± 0.01, 0.85 ± 0.02 for SVM, and RF classifiers, respectively) for classification between significant cancer versus non-tumor from ADC map images were lower when compared to T2WI images. For combined sequences (T2WI and ADC map images), the LASSO with SVM classification algorithms had an AUC of 0.91. The second-highest AUC was 0.88 for the RFE with the RF classification algorithm. Features from several sequences achieved lower performance compared to single sequence features.
  • GS prediction
The Kruskal-Wallis test assessed radiomics features’ ability to predict GS in prostate cancer patients. Radiomics attributes and GS cohorts were then correlated using Spearman correlation. The ML algorithm was developed using feature selection methods (REF and LASSO) and classifiers (RF and SVM) with tuned hyperparameters (randomised search and grid search). ADC map images revealed one radiomics feature from the uniformity that could distinguish GS cohorts.
For combined sequences (T2WI and ADC map images), the LASSO with RF classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G4 (SVM-LASSO, AUC = 0,78) and G2 (RF-LASSO, AUC = 0.66). In addition, for T2WI images, using GLCM features, the LASSO with SVM classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G2 (RF-LASSO, AUC = 0,56) and G4 (SVM-LASSO, AUC = 0.61). Furthermore, for ADC map images, using the 1st order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.82 to predict G2 compared to G3 (SVM-RFE, AUC = 0,81) and G4 (SVM-LASSO, AUC = 0.53). Additionally, for T2WI images, using First-order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.81 to predict G4 compared to G2 (SVM-LASSO and RF-RFE, AUC = 0,66, and 0.66 respectively) and G4 (RF-RFE, AUC = 0.78).
The results we obtained agree with those of several other studies using texture analysis. It was shown that GLCM texture features are helpful for both PCa detection and GS evaluation [62,63]. Texture features, such as those of the first and second order derived from ADC and T2WI, and sample augmentation, were demonstrated to effectively achieve reasonably accurate classification of Gleason patterns [53]. Our findings align with employing the Gleason score as the primary criterion for differentiating benign from significant prostate tumors.
There were a few limitations identified in this research. As a starting point, we included only 71 patients and additional validation of these findings in a more significant subject cohort is required. Moreover, validation in multiple clinical settings is required to obtain high-level confirmation for its medical use. We agree that there are limitations to this work and that in clinical settings there are compromises made on mismatched resolutions. Ideally all our data and all clinical data would be at the same resolution field strength etc. providing uniformity in data acquisition and this step could be avoided. Due to the nature of clinical MRI time and the time requirement of different sequences employed this mismatch of resolutions will persist for the near future…

5. Conclusion

Within the scope of this study, the classification of prostate cancer and prediction of GS groups using multiparametric MRI-based radiomics has been proposed. This study presents two types of feature selection and two classifier algorithms with tuning hyperparameters. Our study presents a distinct approach to the classification and grading of prostate cancer. By prioritizing hyperparameter tuning, we have significantly improved the precision and reliability of our machine-learning models. This work underscores the importance of meticulous parameter optimization in enhancing the accuracy of medical diagnoses.
Radiomics analysis based on multiparametric MRI showed excellent results in discriminating non-tumor regions from significant prostate cancer results obtained. Findings suggest that recursive feature elimination as a feature selection method with SVM and RF is the best method for classifying significant cancer from non-tumor regions. The second approach we found for classification is LASSO, which combines feature selection methods with SVM and RF. Compared to features taken from a single sequence, the performance of features taken from multiple sequences was lower.
The results of the radiomics analysis, which depended on the multiparametric MRI, demonstrated superior outcomes in predicting between GS groups. This study used combined sequences (ADC and T2WI) and radiomics features to classify three groups of GS utilising RF and SVM classifiers with tuned parameters. When combining sequences (T2WI and ADC map images) and radiomics features (1st and GLCM), LASSO with RF had the highest AUC of 0.92, which enabled it to predict G3. When GLCM features were used, LASSO with SVM achieved the highest AUC (0.92 to predict G3) for single sequence analysis (T2WI images).
Our approach suggests that using multiple features and classifiers with tuning hyperparameters provided a more clinically dependable method of identifying clinically relevant features. It is essential to perform additional prospective studies to verify and establish the significance of our findings.

Author Contributions

Writing—original draft preparation, methodology, analysis, study conception and design, and interpretation of data, S.A.; review, editing, and providing significant comments M.K. supervision, writing review, and editing, study conception and design, interpretation of data, acquisition of data, C.K. &N.C.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted according to the guidelines of the Declaration of Helsinki

Informed Consent Statement

Informed consent was obtained from all the subjects involved in the study.

Data Availability Statement

The code presented in this study is available upon request from the corresponding author. The data is open access.

Acknowledgements

The author wishes to express appreciation to the Northern Border University for their scholarship, and the staff of the University of Galway for all their support.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Johnson, L.M., et al., Multiparametric MRI in prostate cancer management. Nature reviews Clinical oncology, 2014. 11(6): p. 346. [CrossRef]
  2. Zhang, Y., Chen, W., Yue, X., Shen, J., Gao, C., Pang, P., Cui, F. and Xu, M., 2020. Development of a novel, multi-parametric, MRI-based radiomic nomogram for differentiating between clinically significant and insignificant prostate cancer. Frontiers in oncology, 10, p.888. [CrossRef]
  3. Bray, F., et al., Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA: a cancer journal for clinicians, 2018. 68(6): p. 394-424. [CrossRef]
  4. Rawla, P., Epidemiology of prostate cancer. World journal of oncology, 2019. 10(2): p. 63.
  5. Sekhoacha, M., Riet, K., Motloung, P., Gumenku, L., Adegoke, A. and Mashele, S., 2022. Prostate cancer review: Genetics, diagnosis, treatment options, and alternative approaches. Molecules, 27(17), p.5730. [CrossRef]
  6. Wang, J., et al., Machine learning-based analysis of MR radiomics can help to improve the diagnostic performance of PI-RADS v2 in clinically relevant prostate cancer. European radiology, 2017. 27(10): p. 4082-4090. [CrossRef]
  7. Zhu, X., Shao, L., Liu, Z., Liu, Z., He, J., Liu, J., Ping, H. and Lu, J., 2023. MRI-derived radiomics models for diagnosis, aggressiveness, and prognosis evaluation in prostate cancer. Journal of Zhejiang University-SCIENCE B, 24(8), pp.663-681.
  8. Sun, Y., et al., Multiparametric MRI and radiomics in prostate cancer: a review. Australasian physical & engineering sciences in medicine, 2019. 42(1): p. 3-25. [CrossRef]
  9. Turkbey, B. and P.L. Choyke, Multiparametric MRI and prostate cancer diagnosis and risk stratification. Current opinion in urology, 2012. 22(4): p. 310. [CrossRef]
  10. Gibbs, P., M.D. Pickles, and L.W. Turnbull, Diffusion imaging of the prostate at 3.0 tesla. Investigative radiology, 2006. 41(2): p. 185-188. [CrossRef]
  11. Cabarrus, M.C. and A.C. Westphalen, Multiparametric magnetic resonance imaging of the prostate—a basic tutorial. Translational andrology and urology, 2017. 6(3): p. 376. [CrossRef]
  12. Radulescu, E., et al., Abnormalities in fronto-striatal connectivity within language networks relate to differences in grey-matter heterogeneity in Asperger syndrome. Neuroimage Clin, 2013. 2: p. 716-26. [CrossRef]
  13. Katahira, K., et al., Ultra-high-b-value diffusion-weighted MR imaging for the detection of prostate cancer: evaluation in 201 cases with histopathological correlation. European radiology, 2011. 21(1): p. 188-196. [CrossRef]
  14. Rosenkrantz, A.B., et al., Computed diffusion-weighted imaging of the prostate at 3 T: impact on image quality and tumour detection. European radiology, 2013. 23(11): p. 3170-3177. [CrossRef]
  15. Nagarajan, R., et al., Correlation of Gleason scores with diffusion-weighted imaging findings of prostate cancer. Advances in urology, 2012. 2012. [CrossRef]
  16. Hambrock, T., et al., Prostate cancer: computer-aided diagnosis with multiparametric 3-T MR imaging—effect on observer performance. Radiology, 2013. 266(2): p. 521-530. [CrossRef]
  17. Lambin, P., et al., Radiomics: extracting more information from medical images using advanced feature analysis. European journal of cancer, 2012. 48(4): p. 441-446. [CrossRef]
  18. Alic, L., W.J. Niessen, and J.F. Veenland, Quantification of heterogeneity as a biomarker in tumor imaging: a systematic review. PloS one, 2014. 9(10): p. e110300. [CrossRef]
  19. Ghezzo, S., Bezzi, C., Presotto, L., Mapelli, P., Bettinardi, V., Savi, A., Neri, I., Preza, E., Gajate, A.M.S., De Cobelli, F. and Scifo, P., 2022. State of the art of radiomic analysis in the clinical management of prostate cancer: A systematic review. Critical Reviews in Oncology/Hematology, 169, p.103544. [CrossRef]
  20. Nioche, C., et al., LIFEx: a freeware for radiomic feature calculation in multimodality imaging to accelerate advances in the characterization of tumor heterogeneity. Cancer research, 2018. 78(16): p. 4786-4789. [CrossRef]
  21. Fisher, R., L. Pusztai, and C. Swanton, Cancer heterogeneity: implications for targeted therapeutics. British journal of cancer, 2013. 108(3): p. 479-485. [CrossRef]
  22. Gillies, R.J., P.E. Kinahan, and H. Hricak, Radiomics: images are more than pictures, they are data. Radiology, 2016. 278(2): p. 563-577. [CrossRef]
  23. Bi, W.L., et al., Artificial intelligence in cancer imaging: clinical challenges and applications. CA: a cancer journal for clinicians, 2019. 69(2): p. 127-157. [CrossRef]
  24. Van Griethuysen, J.J., et al., Computational radiomics system to decode the radiographic phenotype. Cancer research, 2017. 77(21): p. e104-e107.
  25. De Santi, B., Salvi, M., Giannini, V., Meiburger, K.M., Marzola, F., Russo, F., Bosco, M. and Molinari, F., 2020, July. Comparison of Histogram-based Textural Features between Cancerous and Normal Prostatic Tissue in Multiparametric Magnetic Resonance Images. In 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) (pp. 1671-1674). IEEE.
  26. Woźnicki, P., Westhoff, N., Huber, T., Riffel, P., Froelich, M.F., Gresser, E., von Hardenberg, J., Mühlberg, A., Michel, M.S., Schoenberg, S.O. and Nörenberg, D., 2020. Multiparametric MRI for prostate cancer characterization: Combined use of radiomics model with PI-RADS and clinical parameters. Cancers, 12(7), p.1767. [CrossRef]
  27. Kniep, H.C., et al., Radiomics of brain MRI: utility in prediction of metastatic tumor type. Radiology, 2019. 290(2): p. 479-487. [CrossRef]
  28. Lin, M., et al., Prostate lesion delineation from multiparametric magnetic resonance imaging based on locality alignment discriminant analysis. Medical physics, 2018. 45(10): p. 4607-4618. [CrossRef]
  29. Yin, P., et al., Comparison of radiomics machine-learning classifiers and feature selection for differentiation of sacral chordoma and sacral giant cell tumour based on 3D computed tomography features. European radiology, 2019. 29(4): p. 1841-1847. [CrossRef]
  30. Maniruzzaman, M., et al., Statistical characterization and classification of colon microarray gene expression data using multiple machine learning paradigms. Computer methods and programs in biomedicine, 2019. 176: p. 173-193. [CrossRef]
  31. Zhang, Y., et al., Radiomics analysis for the differentiation of autoimmune pancreatitis and pancreatic ductal adenocarcinoma in 18F-FDG PET/CT. Medical physics, 2019. 46(10): p. 4520-4530. [CrossRef]
  32. Zhang, X., et al., Optimizing a machine learning based glioma grading system using multi-parametric MRI histogram and texture features. Oncotarget, 2017. 8(29): p. 47816. [CrossRef]
  33. Hameed, M., et al., The clinical utility of prostate cancer heterogeneity using texture analysis of multiparametric MRI. International urology and nephrology, 2019. 51(5): p. 817-824. [CrossRef]
  34. Lavesson, N. and P. Davidsson. Quantifying the impact of learning algorithm parameter tuning. in AAAI. 2006.
  35. Mantovani, R.G., et al. To tune or not to tune: recommending when to adjust SVM hyper-parameters via meta-learning. in 2015 International joint conference on neural networks (IJCNN). 2015. Ieee.
  36. Probst, P., B. Bischl, and A.-L. Boulesteix, Tunability: Importance of hyperparameters of machine learning algorithms. arXiv preprint. arXiv:1802.09596, 2018.
  37. Weerts, H.J., A.C. Mueller, and J. Vanschoren, Importance of tuning hyperparameters of machine learning algorithms. arXiv preprint. arXiv:2007.07588, 2020.
  38. Valarmathi, R. and T. Sheela, Heart disease prediction using hyper parameter optimization (HPO) tuning. Biomedical Signal Processing and Control, 2021. 70: p. 103033. [CrossRef]
  39. Montgomery, D.C., Design and analysis of experiments. 2017: John wiley & sons.
  40. Litjens, G., et al., Computer-aided detection of prostate cancer in MRI. IEEE transactions on medical imaging, 2014. 33(5): p. 1083-1092. [CrossRef]
  41. Barentsz, J.O., et al., ESUR prostate MR guidelines 2012. European radiology, 2012. 22(4): p. 746-757. [CrossRef]
  42. Kitajima, K., et al., Prostate cancer detection with 3 T MRI: comparison of diffusion-weighted imaging and dynamic contrast-enhanced MRI in combination with T2-weighted imaging. Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine, 2010. 31(3): p. 625-631. [CrossRef]
  43. Clark, K., et al., The Cancer Imaging Archive (TCIA): maintaining and operating a public information repository. Journal of digital imaging, 2013. 26(6): p. 1045-1057. [CrossRef]
  44. Erickson, B.J., et al., Machine learning for medical imaging. Radiographics, 2017. 37(2): p. 505-515.
  45. Chatterjee, S., D. Dey, and S. Munshi, Integration of morphological preprocessing and fractal based feature extraction with recursive feature elimination for skin lesion types classification. Computer methods and programs in biomedicine, 2019. 178: p. 201-218. [CrossRef]
  46. Fan, M., et al., Integration of dynamic contrast-enhanced magnetic resonance imaging and T2-weighted imaging radiomic features by a canonical correlation analysis-based feature fusion method to predict histological grade in ductal breast carcinoma. Physics in Medicine & Biology, 2019. 64(21): p. 215001. [CrossRef]
  47. Liu, Y., et al., Early prediction of acute xerostomia during radiation therapy for nasopharyngeal cancer based on delta radiomics from CT images. Quantitative imaging in medicine and surgery, 2019. 9(7): p. 1288. [CrossRef]
  48. Wang, X., et al., Classification of pulmonary lesion based on multiparametric MRI: Utility of radiomics and comparison of machine learning methods. European radiology, 2020. 30(8): p. 4595-4605. [CrossRef]
  49. Chen, X., et al., Applying a new quantitative image analysis scheme based on global mammographic features to assist diagnosis of breast cancer. Computer methods and programs in biomedicine, 2019. 179: p. 104995. [CrossRef]
  50. Chen, L., et al., Primary tumor site specificity is preserved in patient-derived tumor xenograft models. Frontiers in genetics, 2019: p. 738. [CrossRef]
  51. Geetha, R., et al., Cervical cancer identification with synthetic minority oversampling technique and PCA analysis using random forest classifier. Journal of medical systems, 2019. 43(9): p. 1-19. [CrossRef]
  52. Peng, Y., et al., Quantitative analysis of multiparametric prostate MR images: differentiation between prostate cancer and normal tissue and correlation with Gleason score—a computer-aided diagnosis development study. Radiology, 2013. 267(3): p. 787-796. [CrossRef]
  53. Chawla, N.V., N. Japkowicz, and A. Kotcz, Special issue on learning from imbalanced data sets. ACM SIGKDD explorations newsletter, 2004. 6(1): p. 1-6.
  54. Weiss, G.M., Mining with rarity: a unifying framework. ACM Sigkdd Explorations Newsletter, 2004. 6(1): p. 7-19.
  55. Fehr, D., et al., Automatic classification of prostate cancer Gleason scores from multiparametric magnetic resonance images. Proceedings of the National Academy of Sciences, 2015. 112(46): p. E6265-E6273. [CrossRef]
  56. Holm, S., A simple sequentially rejective multiple test procedure. Scandinavian journal of statistics, 1979: p. 65-70.
  57. Epstein, J.I., et al., The 2014 International Society of Urological Pathology (ISUP) consensus conference on Gleason grading of prostatic carcinoma. The American journal of surgical pathology, 2016. 40(2): p. 244-252. [CrossRef]
  58. Fan, X., et al., Multiparametric MRI and Machine Learning Based Radiomic Models for Preoperative Prediction of Multiple Biological Characteristics in Prostate Cancer. Frontiers in oncology, 2022. 12. [CrossRef]
  59. Hamerla, G., et al., Comparison of machine learning classifiers for differentiation of grade 1 from higher gradings in meningioma: a multicenter radiomics study. Magnetic resonance imaging, 2019. 63: p. 244-249. [CrossRef]
  60. Larroza, A., et al., Support vector machine classification of brain metastasis and radiation necrosis based on texture analysis in MRI. Journal of magnetic resonance imaging, 2015. 42(5): p. 1362-1368. [CrossRef]
  61. Rustam, Z. and N. Angie. Prostate Cancer Classification Using Random Forest and Support Vector Machines. in Journal of Physics: Conference Series. 2021. IOP Publishing. [CrossRef]
  62. Sun, Y., et al., Radiomic features of pretreatment MRI could identify T stage in patients with rectal cancer: preliminary findings. Journal of Magnetic Resonance Imaging, 2018. 48(3): p. 615-621.
  63. Wang, L., et al., Assessment of biologic aggressiveness of prostate cancer: correlation of MR signal intensity with Gleason grade after radical prostatectomy. Radiology, 2008. 246(1): p. 168-176. [CrossRef]
  64. Wibmer, A., et al., Haralick texture analysis of prostate MRI: utility for differentiating non-cancerous prostate from prostate cancer and differentiating prostate cancers with different Gleason scores. European radiology, 2015. 25(10): p. 2840-2850. [CrossRef]
  65. Qiao, X., Gu, X., Liu, Y., Shu, X., Ai, G., Qian, S., Liu, L., He, X. and Zhang, J., 2023. MRI Radiomics-Based Machine Learning Models for Ki67 Expression and Gleason Grade Group Prediction in Prostate Cancer. Cancers, 15(18), p.4536. [CrossRef]
Preprints 91568 g001
Figure 1. Patient exclusion criteria flowchart.
Figure 1. Patient exclusion criteria flowchart.
Preprints 91568 g001
Preprints 91568 g002
Figure 2. The prostate cancer classification scheme includes: (i) using ROIs that matched where the cancer was on the histology slides and MRI (T2 weighted images and Apparent Diffusion Coefficient map images of 71 subjects with confined histology and magnetic resonance imaging prostate cancer made); (ii) features extraction, including 1st and 2nd orders; (iii) ROC-AUC analysis, including ROC curves.
Figure 2. The prostate cancer classification scheme includes: (i) using ROIs that matched where the cancer was on the histology slides and MRI (T2 weighted images and Apparent Diffusion Coefficient map images of 71 subjects with confined histology and magnetic resonance imaging prostate cancer made); (ii) features extraction, including 1st and 2nd orders; (iii) ROC-AUC analysis, including ROC curves.
Preprints 91568 g002
Preprints 91568 g003aPreprints 91568 g003b
Figure 3. The classification of prostate cancer as significant versus non-tumor regions depends on RFE using mp-MRI within a 5-fold cross-validation.
Figure 3. The classification of prostate cancer as significant versus non-tumor regions depends on RFE using mp-MRI within a 5-fold cross-validation.
Preprints 91568 g003aPreprints 91568 g003b
Preprints 91568 g004
Figure 4. The classification of prostate cancer as significant versus non-tumor regions depends on LASSO using mp-MRI within a 5-fold cross-validation.
Figure 4. The classification of prostate cancer as significant versus non-tumor regions depends on LASSO using mp-MRI within a 5-fold cross-validation.
Preprints 91568 g004
Preprints 91568 g005
Figure 5. The classification of prostate cancer as significant versus non-tumor regions depends on RFE using mp-MRI within a 5-fold cross-validation.
Figure 5. The classification of prostate cancer as significant versus non-tumor regions depends on RFE using mp-MRI within a 5-fold cross-validation.
Preprints 91568 g005
Preprints 91568 g006
Figure 6. The classification of prostate cancer as significant versus non-tumor regions depends on LASSO using mp-MRI within a 5-fold cross-validation.
Figure 6. The classification of prostate cancer as significant versus non-tumor regions depends on LASSO using mp-MRI within a 5-fold cross-validation.
Preprints 91568 g006
Preprints 91568 g007
Figure 7. Accuracy of non-tumor regions and significant tumor discrimination of prostate cancer in the test set.
Figure 7. Accuracy of non-tumor regions and significant tumor discrimination of prostate cancer in the test set.
Preprints 91568 g007
Preprints 91568 g008
Figure 8. Accuracy of non-tumor regions and significant tumor discrimination of prostate cancer in the training set.
Figure 8. Accuracy of non-tumor regions and significant tumor discrimination of prostate cancer in the training set.
Preprints 91568 g008
Preprints 91568 g009
Figure 9. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using 1st order features and GLCM features obtained from T2WI and ADC map images.
Figure 9. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using 1st order features and GLCM features obtained from T2WI and ADC map images.
Preprints 91568 g009
Preprints 91568 g010
Figure 10. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using 1st-order features obtained from ADC map images.
Figure 10. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using 1st-order features obtained from ADC map images.
Preprints 91568 g010
Preprints 91568 g011aPreprints 91568 g011b
Figure 11. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using GLCM features obtained from ADC map images.
Figure 11. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using GLCM features obtained from ADC map images.
Preprints 91568 g011aPreprints 91568 g011b
Preprints 91568 g012
Figure 12. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using 1st-order features obtained from T2WI images.
Figure 12. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using 1st-order features obtained from T2WI images.
Preprints 91568 g012
Preprints 91568 g013
Figure 13. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using GLCM features obtained from T2WI images.
Figure 13. ROC-AUC of predicting Gleason Score of PCa from RF and SVM classifiers (using RFE and LASSO feature selections) using GLCM features obtained from T2WI images.
Preprints 91568 g013
Table 1. Multiparametric MRI sequence parameters.
Table 1. Multiparametric MRI sequence parameters.
Sequence parameter T2WI ADC
Repetition time (ms) 5560 2700
Echo time (ms) 104 63
Flip angle (degrees) 160 90
Bandwidth (Hz/px) 200 1500
Phase FoV % 100 65.625
Slice thickness (mm) 3 3
Slice gap (mm) 3 3
Average 4 8
Phase encoding direction Row Row
Number of acquisitions 1 1
Table 2. Comparisons of radiomics parameters of significant cancer versus non-tumor regions.
Table 2. Comparisons of radiomics parameters of significant cancer versus non-tumor regions.
Feature Median (interquartile 25th,50th, and 75th percentiles) P
Significant cancer nontumor regions
ADC
1st order
Skewness 0.37 (0.02, 0.37, 0.69) 0.03 (-0.29, 0.03, 0.47) 0.001
Kurtosis -0.49 (-0.85, -0.49, 0.29) -0.54 (-0.86, -0.54, -0.12) 0.52
Entropylog1o 1.14 (1.09, 1.14, 1.19) 1.09 (1.05, 1.09, 1.14) ˂ 0.001
Entropylog2 3.80 (3.62, 3.80, 3.97) 3.62 (3.50, 3.62, 3.80) ˂ 0.001
Uniformity 0.07 (0.06, 0.07, 0.08) 0.08 (0.07, 0.08, 0.10) ˂ 0.001
GLCM
JointEntropyLog2 6.18 (5.85, 6.18, 6.45) 6.05(5.83,6.05,6.21) 0.03
JointEntropyLog10 1.86 (1.79, 1.86, 1.94) 1.82(1.75,1.82,1.87) 0.006
Angular Second Moment 0.01 (0.01, 0.1, 0.01) 0.016 (0.014, 0.016, 0.019) 0.006
Contrast 145.64 (107.88, 145.64, 201.96) 84.02 (59.85, 84.02, 122.08) ˂ 0.001
Dissimilarity 9.30 (8.33, 930, 11.36) 7.51 (6.19, 7.51, 8.61) ˂ 0.001
Correlation 0.18 (0.06, 0.18, 0.35) 0.23 (0.09, 0.23, 0.39) 0.37
T2WI
1st order
Skewness 0.07 (-0.20, 0.07, 0.32) 0.15 (-0.20, 0.15, 0.43) 0.50
Kurtosis -0.18 (-0.55, -0.018, 0.43) -0.34 (-0.59, -0.34, 0.11) 0.18
Entropylog1o 1.30 (1.23, 1.30, 1.41) 1.06 (0.97, 1.06, 1.16) ˂ 0.001
Entropylog2 4.34 (4.11, 4.34, 4.69) 3.52 (3.24, 3.52, 3.85) ˂ 0.001
Uniformity 0.05 (0.04, 0.05, 0.06) 0.09 (0.07, 0.09, 0.12) ˂ 0.001
GLCM
JointEntropyLog2 7.50 (6.89, 7.50, 8.16) 6.45 (5.95,6.45,7.12) ˂0.001
JointEntropyLog10 2.31 (2.12, 2.31, 2.50) 1.96 (1.79,1.96,2.14) ˂ 0.001
Angular Second Moment 0.006 (0.004, 0.006, 0.01) 0.01 (0.01, 0.01, 0.02) ˂ 0.001
Contrast 92.42 (64.22, 92.42, 132.48) 13.36 (10.08, 13.36, 20.47) ˂ 0.001
Dissimilarity 7.62 (6.36, 7.62, 9.07) 2.88 (2.46, 2.88, 3.60) ˂ 0.001
Correlation 0.25 (0.13, 0.25, 0.35) 0.38 (0.24, 0.38, 0.50) ˂ 0.001
Table 3. Features associated with the significant malignancy and the non-tumor regions are considered correlated.
Table 3. Features associated with the significant malignancy and the non-tumor regions are considered correlated.
Feature r P
ADC
1st order
Skewness 0.315 ˂0.001
Entropylog1o 0.305 ˂0.001
Entropylog2 0.305 ˂0.001
Uniformity -0.331 ˂0.001
GLCM
Angular Second Moment -0.236 0.005
Contrast 0.376 ˂0.001
Dissimilarity 0.468 ˂0.001
T2WI
1st order
Entropylog1o 0.561 ˂0.001
Entropylog2 0.561 ˂0.001
Uniformity -0.254 0.002
GLCM
JointEntropyLog2 0.270 0.001
JointEntropyLog10 0.269 0.001
Contrast 0.765 ˂0.001
Dissimilarity 0.809 ˂0.001
Correlation 0.370 ˂0.001
Table 4. Comparisons of radiomics parameters of prostate cancer that are associated with the Gleason score groupings.
Table 4. Comparisons of radiomics parameters of prostate cancer that are associated with the Gleason score groupings.
Feature Gleason Score Median (interquartile 25th,50th, and 75th percentiles) P
G2 G3 G4
ADC
1st order
Skewness 0.30 (-0.01, 0.30, 0.58) 0.60 (-0.12, 0.60, 1.24) 0.39 (0.10, 0.39, 0.75) 0.92
Kurtosis -0.49 (-0.87, -0.49, 0.26) -0.38 (-0.78, -0.38, 1.24) -0.34 (-0.90, -0.34, 0.49) 0.81
Entropylog1o 1.12 (1.08, 1.12, 1.16) 1.15 (1.09, 1.15, 1.21) 1.16 (1.09, 1.16, 1.22) 0.03
Entropylog2 3.75(3.61, 3.75, 3.87) 3.83 (3.62, 3.83, 4.03) 3.88 (3.64, 3.88, 3.06) 0.03
Uniformity 0.07(0.07, 0.07, 0.08) 0.07 (0.06, 0.07, 0.08) 0.07 (0.06, 0.07, 0.08) 0.01
GLCM
JointEntropyLog2 6.12 (5.87, 6.12, 6.47) 7.84 (7.42, 7.84, 8.22) 6.28 (6.11, 6.28, 6.60) 0.03
JointEntropyLog10 1.84 (1.76, 1.84, 1.94) 2.36 (2.24, 2.36, 2.54) 1.89 (1.83, 1.89, 1.98) 0.18
Angular Second Moment 0.02 (0.01, 0.02, 0.02) 0.005(0.0037, 0.005, 0.006) 0.01 (0.01, 0.01, 0.01) 0.05
Contrast 132.43 (101.12, 132.43, 182.76) 83.79 (64.25, 83.79, 128.98) 149.88 (107.82, 149.88, 220.89) 0.15
Dissimilarity 9.01 (8.05, 9.01, 10.79) 7.09 (6.25, 7.09, 9.03) 9.84 (8.25, 9.84, 11.96) 0.14
Correlation 0.18 (0.02, 0.18, 0.33) 0.26 (0.14, 0.26, 0.47) 0.20 (0.05, 0.20, 0.41) 0.54
T2WI
1st order
Skewness 0.03 (-0.22, 0.03, 0.29) 0.23 (-0.12, 0.23, 0.47) -0.03 (-0.26, -0.03, 0.23) 0.85
Kurtosis -0.14 (-0.47, -0.14, 0.64) 0.07 (-0.39, 0.07, 0.27) -0.62 (-0.76, -0.62, -0.31) 0.78
Entropylog1o 1.29 (1.23, 1.29, 1.38) 1.33 (1.26, 1.33, 1.44) 1.28 (1.18, 1.28, 1.38) 0.76
Entropylog2 4.31 (4.09, 4.31, 4.61) 4.42 (4.20, 4.42, 4.47) 4.28 (3.92, 4.28, 4.61) 0.76
Uniformity 0.05 (0.04, 0.05, 0.06) 0.05 (0.04, 0.05, 0.06) 0.05 (0.04, 0.05, 0.07) 0.80
GLCM
JointEntropyLog2 7.48 (6.87, 7.48, 8.16) 6.17 (5.75, 6.17, 6.41) 7.12 (6.79, 7.12, 8.23) 0.40
JointEntropyLog10 2.28 (2.11, 2.28, 2.25) 1.88 (1.76, 1.88, 2.01) 2.19 (2.06, 2.19, 2.48) 0.72
Angular Second Moment 0.008 (0.004, 0.01, 0.01) 0.01(0.01, 0.01, 0.02) 0.01(0.01, 001, 0.01) 0.69
Contrast 94.93 (69.61, 94.93, 138.60) 180.96 (126.01, 180.96, 280.64) 101.25 (54.24, 101.25, 125.81) 0.62
Dissimilarity 7.68 (6.58, 7.68, 9.03) 9.71 (8.62, 9.71, 13.23) 7.97 (6.06, 7.97, 9.17) 0.63
Correlation 0.24 (0.10, 0.24, 0.34) 0.24 (0.07, 0.24, 0.33) 0.22 (0.14, 0.22, 0.31) 0.78
Table 5. Features that are associated with the Gleason score groupings regions are considered correlates.
Table 5. Features that are associated with the Gleason score groupings regions are considered correlates.
Feature r P
ADC
1st order
Uniformity -0.30 0.02
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated