Prerpints.org logo
Preprint
Article

Simulation of Pollutants Trajectory in the Black Sea Region Atmosphere with Different Spatial Resolution

Altmetrics

Downloads

147

Views

63

Comments

0

Submitted:

22 November 2023

Posted:

28 November 2023

You are already at the latest version

Alerts
Abstract
As the problem of air pollution becomes more urgent, the precise determination of the characteristics of air pollution and the associated mechanisms of transport of pollutants becomes an increasingly urgent task. The simulation results of the Copernicus Atmospheric Monitoring Service (CAMS) [18] were used as initial data sets. The area of the Crimean Peninsula (within coordinates 44.50 latitude, 33.50 longitude) in 23 - 26 January, 2019 was chosen for the study. That time concentrations of pollutants (aerosol particles with a diameter of 2.5 (PM2.5) and 10 micrometers (PM10)) steadily increased and reached the maximum value. Four kinds of meteorological data sets were used in the work. The first and second data sets were the global NCEP/NCAR and (ERA-5) re-analyses. The third and fourth meteorological data sets were obtained using the Weather tracking and Forecasting model (WRF) as domains on high-resolution grids: 9 km and 2 km. The analysis of meteorological data sets was carried out to analyze the nature of the air masses movement in the studied region. Using the HYSPLIT model simulation was carried out to determine area of the sources of negative impact. The emissions transfer from the supposed sources of negative impact on the Crimea region is analyzed. The sensitivity of simulation the inverse and direct trajectories of air masses transfer was studied based a set of simulation results. On the basis of HYSPLIT model the simulation was carried out separately using meteorological data sets having different spatial and temporal resolutions. In general, the simulation results allowed us to conclude that the HYSPLIT model in combination with high-resolution meteorological input data of the WRF model are good to identify the sources of possible negative effects on atmospheric air located at long distances from the study site.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Intensive socio-economic development, accelerated industrialization and ever-increasing energy consumption are associated with intensive emission into the atmospheric air the solid particles of various nature and size. That can not only reduce visibility in the atmosphere, but also increase mortality and morbidity of respiratory diseases [33]. Studies have shown that air pollution levels in cities and their spatial and temporal distribution are not only related to local emissions, but also depend on interregional transfer from sources to adjacent areas [34].
The increase in anthropogenic load and increasing requirements for environmental quality standards require more accurate assessments of the possible negative impact of sources located at a sufficient distance from the research area.
Various computational models are used to determine the sources of negative impact. Box model, Gaussian, Lagrangian, Eulerian and computational fluid dynamics (CFD) models [10] are used now. Trajectory models based on the Lagrangian and Eulerian approaches have been most used for transport of pollutants simulation over long distances [11,12,13,14]. The HYSPLIT model based on the Langrangian approach has received the greatest use [19]. The basis is the stochastic modeling of a number of single point particles. The trajectory of a single particle is determined by the advector, buoyancy and turbulence.
Meteorology conditions play a crucial role in assessing air quality. The presence of uncertainties in the meteorological profile may negatively affect the results of the assessment. A number of meteorological conditions on a regional scale and prevailing winds affect the trajectories of pollutants and their concentrations in the surface layer. The study of the behavior of air masses in coastal areas is a difficult task. The nature of the movement of air flows is significantly influenced by topographic features and the presence of the land-sea interface.
Currently, various sources of meteorological data are used in research. They are characterized by different spatial and temporal resolution. The analysis of studies shows that the spatial and temporal resolution of meteorological data is an important factor in the accurate assessment of the trajectories of air masses and the formation of concentrations of pollutants dangerous to public health [1, 2, 3].
In [3] Warner, S.; Platt, N. it was shown that improved meteorological data sets with a 0.5 degrees horizontal resolution instead of 2.5 degrees make it possible to more accurately reproduce the processes of mesoscale dispersion of pollutants.
Draxler in 2006 showed that the calculation of variance using ERA-40 data has better convergence with the results of field experiments than using NCEP/NCAR data, and comparable performance with the results when using the data fields of the mesoscale MM5 model. Calculations using MM5 data, which used forecasts for a shorter period, show better convergence with the experiment than NCEP/NCAR data.
According to literature sources, the WRF model can serve as a good tool for providing meteorological input data used in modeling the dispersion of pollutants [6,7]. Many countries are experiencing an acute shortage of meteorological data, as they have meteorological stations in a very small number of places. This data may not be available at a higher time resolution for many meteorological parameters. This limitation can be overcome by using the WRF meteorological model.
To determine the location of emission sources and transport trends, the HYSPLIT model has proven itself well, together with the WRF forecasting model [4,8,9,16]. M. Feyzinejad, as a result of his research, shows that simulation and forecasting using the coupled WRF-HYSPLIT model are in good agreement with the observation results and indicate the reliability of the simulation results [5]. An important role in the joint modeling of WRF-HYSPLIT is played by the assessment of the sensitivity of the results of model variance to meteorological fields [15]. Such studies are carried out using a set of simulations by WRF model for the same case of variance, but with different spatial resolution.
During the study, the HYSPLIT model was integrated with various meteorological fields to determine the location of sources of negative impact on the atmosphere using the analysis of reverse and forward trajectories.
As an example, an episode with a high concentration of suspended particles of 2.5 micrometers (PM2.5) diameter was selected according to simulation data published in the materials of the Copernicus Atmospheric Monitoring Service (CAMS) for the Crimean Peninsula area in January 23 to 26, 2019 [18] within the coordinates 44°50’ lat. and 33°50’ long. The peak concentration estimated during this episode was 27 ug/m3, which is an order of magnitude higher than the normative level recommended by the World Health Organization (WHO) for the average annual PM2.5 level of 10 ug/m3. The present study is an attempt to identify potential sources of emissions that fall on HYSPLIT backscattering trajectories with meteorological data of different spatial resolution.

2. Materials and Methods

2.1. Study Location and Data

Anthropogenic sources of negative impact on atmospheric air (PM2.5 and PM10) are represented by data sets of regional inventories linked to a grid. Data from the European Monitoring and Assessment Program (EMER), the Netherlands Organization for Applied Scientific Research (TNO) for Europe, and the emissions database for Global Atmospheric Research (EDGAR) were used [29,30]. These data were plotted on the map of the studied region Figure 1.
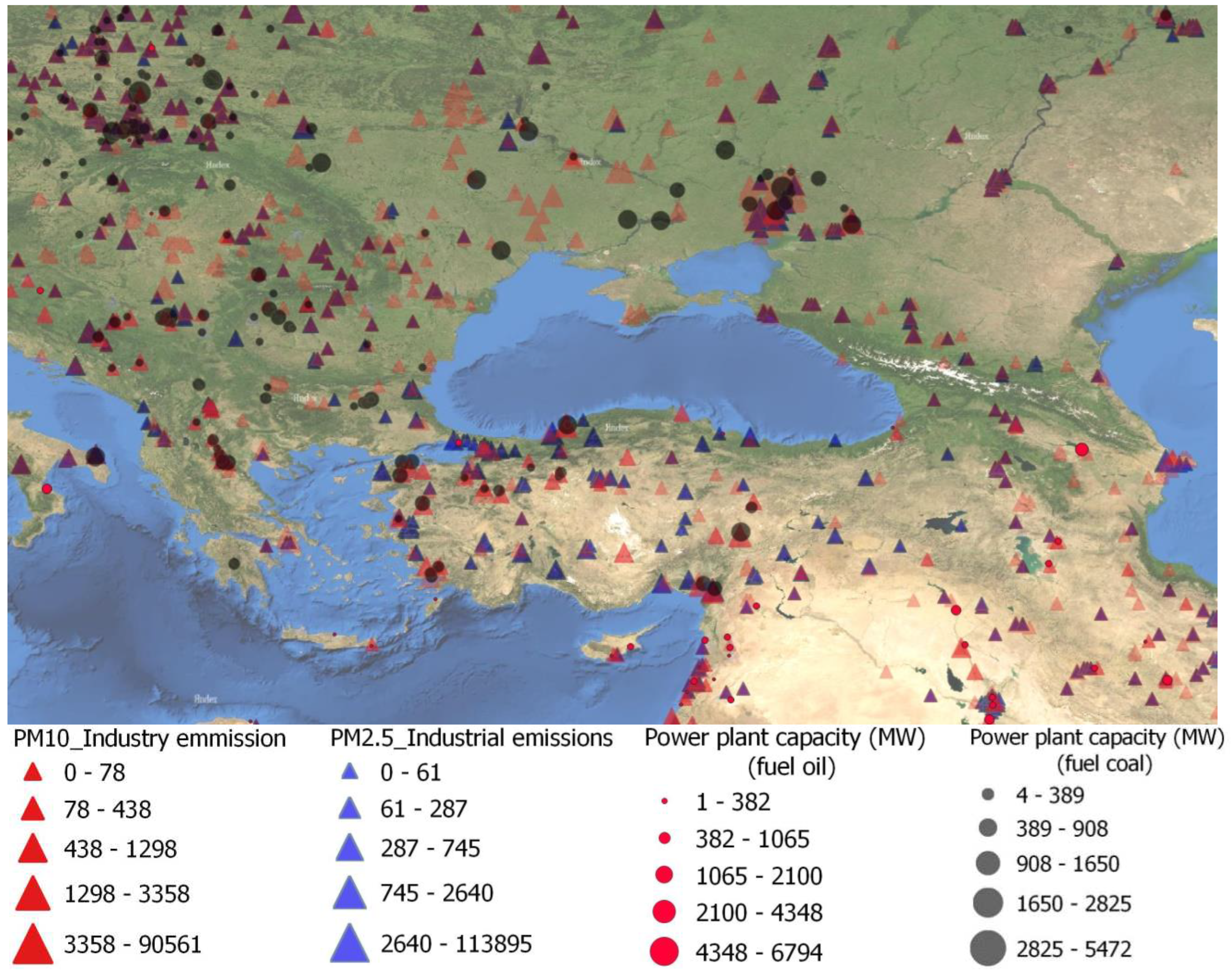
The size of the triangle on the map characterizes the amount of emissions per ton/year. Also, as initial data on the sources of negative impact on the atmosphere of the Crimean peninsula, data from the database of power plants around the world were used [31]. Only power plants using oil (red circles) and coal (black circles) as fuel were selected for the analysis at Figure 1. The size of the circle in Figure 1 corresponds to the capacity of the power plant.

2.2. Meteorological fields

Global reanalyze NCEP/NCAR - Final Analysis (FNL) meteorological data sets with a coarse grid obtained from the National Center for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR) with a spatial resolution of 2.5° × 2.5° and a temporal resolution of 6 hours were used in the work as initial and boundary conditions (information is available online at http://www.cdc.noaa.gov ). The second data set of initial data included the results of a ECMWF re-analysis (ERA5) with a spatial resolution of 0.25° × 0.25° and a time resolution of 1 h obtained from the data server (available online at http://data.ecmwf.int/data ). The simulation was carried out for the period from January 23, 2019 to January 26, 2019.

2.3. Model WRF (ARW)

The WRF (ARW) model was used to calculate high-resolution atmospheric fields over the studied region. It has several variants of spatial discretization, diffusion, lateral boundary conditions and parametrization schemes for physical processes of the subgrid scale. Physics consists of sets of parameters: microphysics, convection, turbulence, planetary boundary layer, parameters of the underlying surface, long-wave and short-wave radiation [17]. To estimate wind flows, simulation results with 9 km and 2 km grid resolution of were used.
In the study, as the physical parameters of the WRF model were used the following: the Kain-Fritsch scheme [22] for parameterization of convection, the Thompson scheme for accurate parameterization of winter precipitation forecast [23], the non-local Yonsei University Scheme (YSU) for the boundary layer [24], the standard five–layer model of the surface layer (5-layer Thermal Diffusion Scheme) [25], Dudhia Shortwave Scheme for shortwave radiation [26] and Rapid Radiative Transfer Model (RRTM) longwave radiation [27] for longwave radiation processes, the scheme of parameters of the surface layer (Revised MM5 Scheme) [28]. 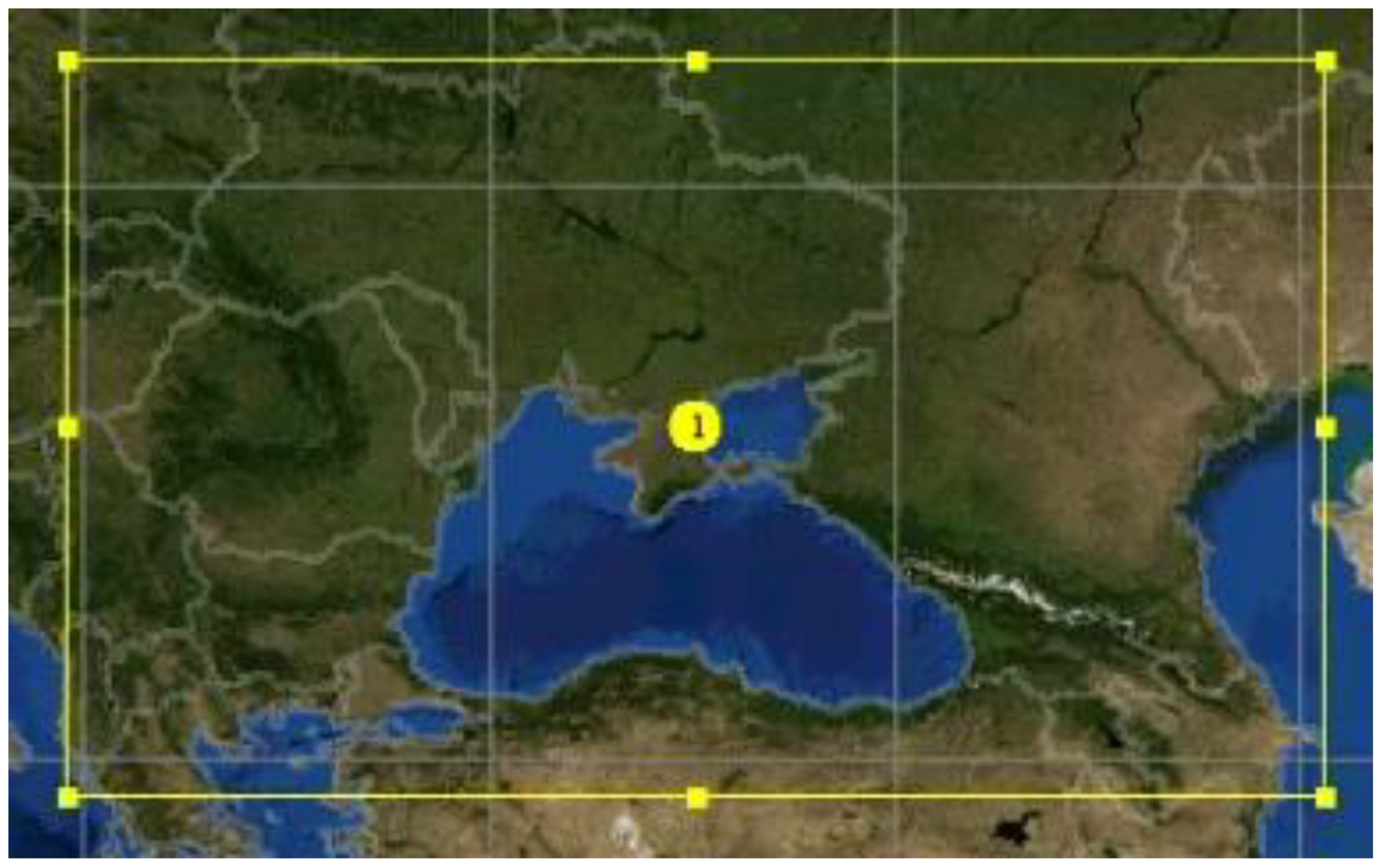WPF and HYSPLIT simulation was done using domain presented at the Figure 2.
The domain is built around the Crimean Peninsula. It has a grid structure with a grid size of 9 km (268 × 175 points). The vertical resolution of the WRF was 38 layers from the ground to 1 GPa at the upper boundary of the domain.2.4. Hybrid Single-Particle Lagrangian

2.4. Integrated Trajectory (HYSPLIT) Model

The HYSPLIT model is a professional system jointly developed by the National Oceanic and Atmospheric Administration and the Bureau of Meteorology of Australia for calculating and analyzing the trajectories of transport and diffusion of atmospheric pollutants [20, 21]. This model is a comprehensive system for calculating the trajectories of air flow, diffusion, chemical transformation, precipitation modeling and various types of pollutant emission sources. The HYSPLIT model has proven itself well in the study of air mass trajectories when the domain under study is within a radius of more than 10 km [19].
In the study, the HYSPLIT model was used to calculate 72-hour forward and reverse air flow trajectories with six vertical levels 10, 25, 50, 100, 200, 500 M. The trajectories began their movement every hour from 00:00 UTC on January 23 to 00:00 UTC on January 26, 2019 in the forward and reverse direction.
Simulation using HYSPLIT model allows us to create ensembles of rerevers and direct trajectories. Instead of creating a single deterministic simulation of air mass trajectories, HYSPLIT includes several approaches for analysis. The approaches can be used to combine several HYSPLIT simulations into a single graph representing a certain change in the probability of trajectory movement [35]. Reverse trajectories were studied to determine the location of the alleged sources of negative impact. The inverse trajectories provide information about the causes of a possible increase in the calculated concentrations and about the synoptic patterns corresponding to this event. Direct trajectories were studied to confirm the fact of the transfer of air masses from the source of negative impact to the Crimean Peninsula. From the group of point sources of negative impact on the atmosphere, those that fell into the area of movement of the reverse trajectories were selected for modeling direct trajectories. Using the HYSPLIT model, modeling was carried out using various sources of meteorological data: 1) NCEP/NCAR analysis; 2) ERA5 analysis; 3) WRF model output with 9 km grid interval domain. In this way, the characteristics of the movement of air flows in the studied zone are analyzed.

3. Results

3.1. Meteorological Fields

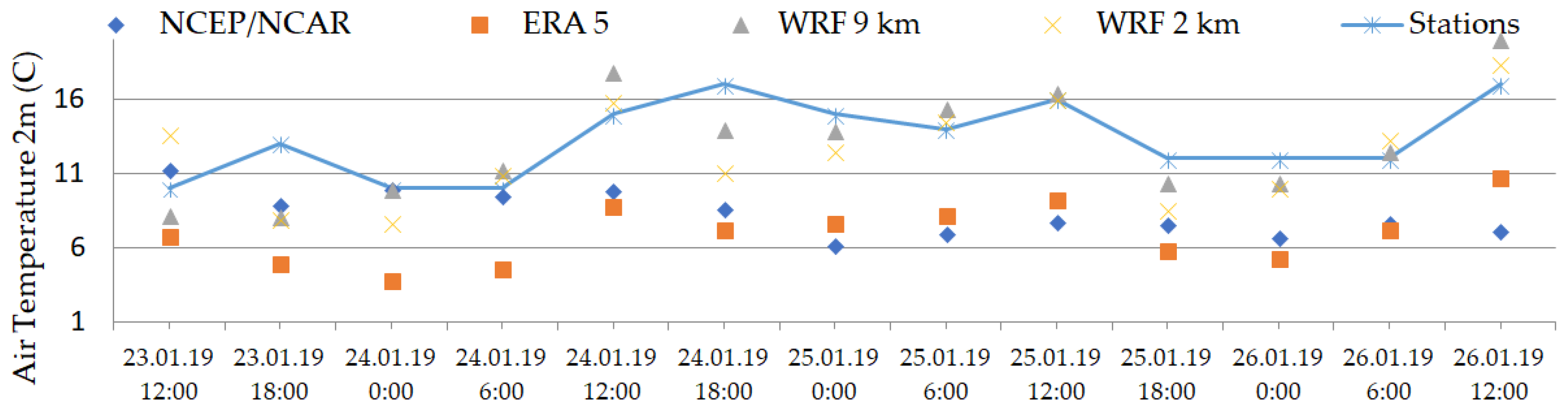
The assessment of the WRF modeling adequacy was carried for two types of grid resolutions (9 km and 2 km) using reanalyses NCEP/NCAR, ERA 5 data sets and the results of observations at meteorological stations. The values of the average daily temperature were analyzed here (Figure 3). The station is located in the Batumi district. The choice of the station is determined by the expected direction of movement of air masses over this territory.
Calculations based on various dispersion models are limited by the nature of the meteorological input data, such as resolution and representation of local terrain features. In this regard, the paper analyzes the surface wind from four sets of input data. Horizontal wind fields from meteorological data sets are shown in Figure 4, Figure 5, Figure 6 and Figure 7. The fields are presented at 00 UTC and 12 UTC, corresponding to night and daytime conditions.
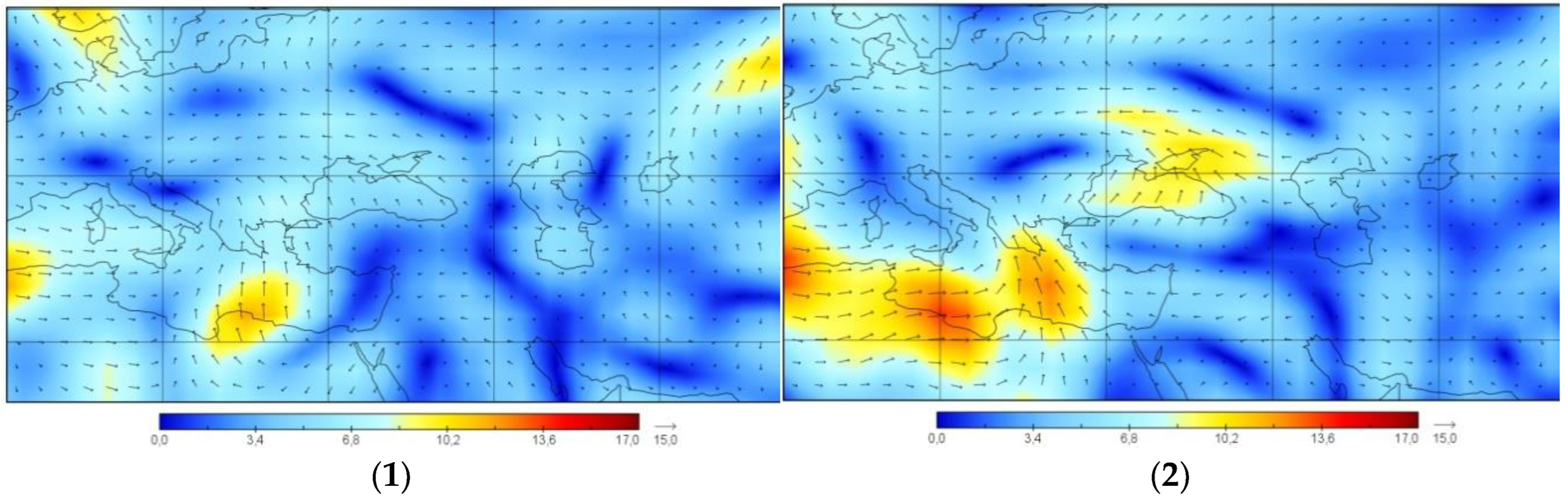
The surface wind in the NCEP/NCAR data sets has a rough resolution. In the analyzed time interval, the southern direction of the air masses movement towards the Crimean Peninsula prevails (Figure 4).
The meteorological data set specified in Figures 4. 1, 2, 3, 4, 5, 6, 7, 8 it reflects well large-scale processes in the near-earth layer of the atmosphere. It needs to note the circulatory activity of air masses, depicted in dark red. However, this permission does not allow to identify regional features of the studied area. That is why a study was conducted with a less resolution of the grid of meteorological data presented at the Figure 5.
The WRF simulations carried out using two grids of resolutions (9 km and 2 km) made it possible to further concretize regional peculiarities. The obtained refined numerical values of meteorological fields confirm the directions of air masses found above.
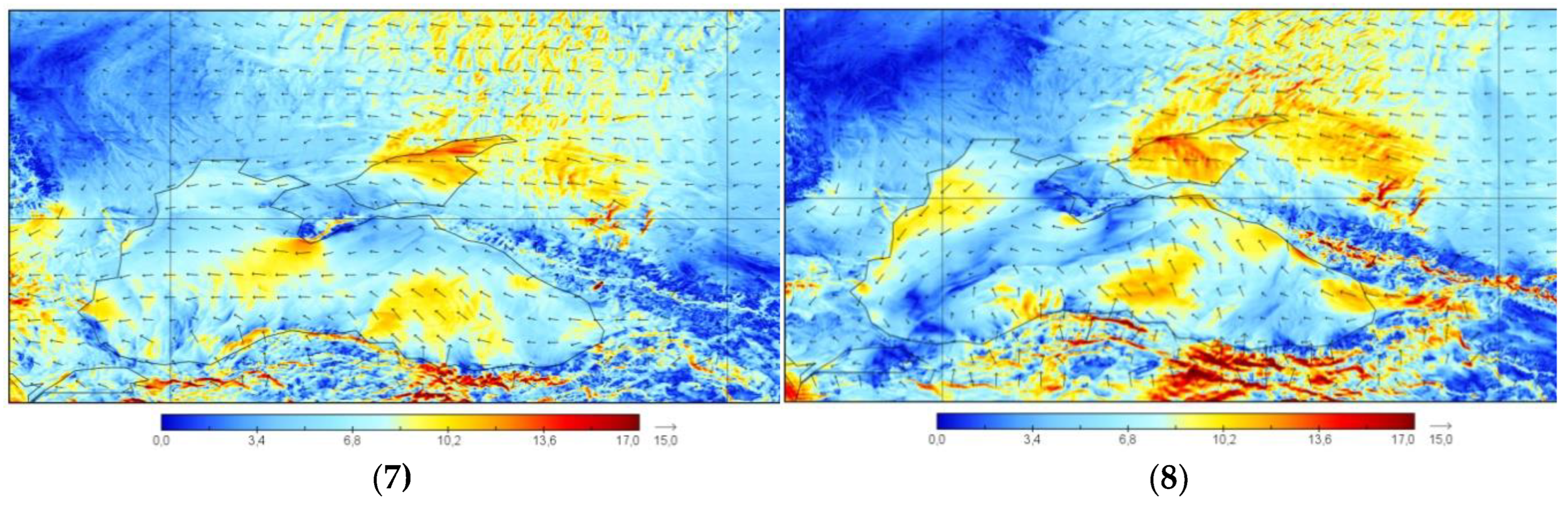
The simulated wind flow by WRF model on a 9 km grid (Figure 6) is well resolved and more clearly reflects the daily wind structure than the NCEP/NCAR and ERA5 data cets. The movements of air masses generally correspond to the topographic features of the Crimean Peninsula and reflect the features of a complex coastline. The wind flow also has a predominantly southern direction, but these calculation results show the separation of the flow and its flow around the Crimean Mountains.
To complete the study, a simulation with an even less grid resolution (2 km) was carried out in order to clarify the dependence of modeling in a dispersed model on a decrease in grid resolution.
As well as clarifying the assessment of the practical significance of using model depending on different resolutions. The results of the WRF model wind flow with an even more detailed grid of 2 km (1200 × 700 points) are presented at Figure 7.
These results practically do not differ from the resolution of the 9 km grid. Therefore, it was concluded that it was inappropriate to use these data for the study.

3.2. Reverse Trajectories

According to literature sources, the transfer of air masses on a regional scale (~ 1000 km) takes 2-3 days [32]. This condition was taken as the basis for determining the duration of the simulation.
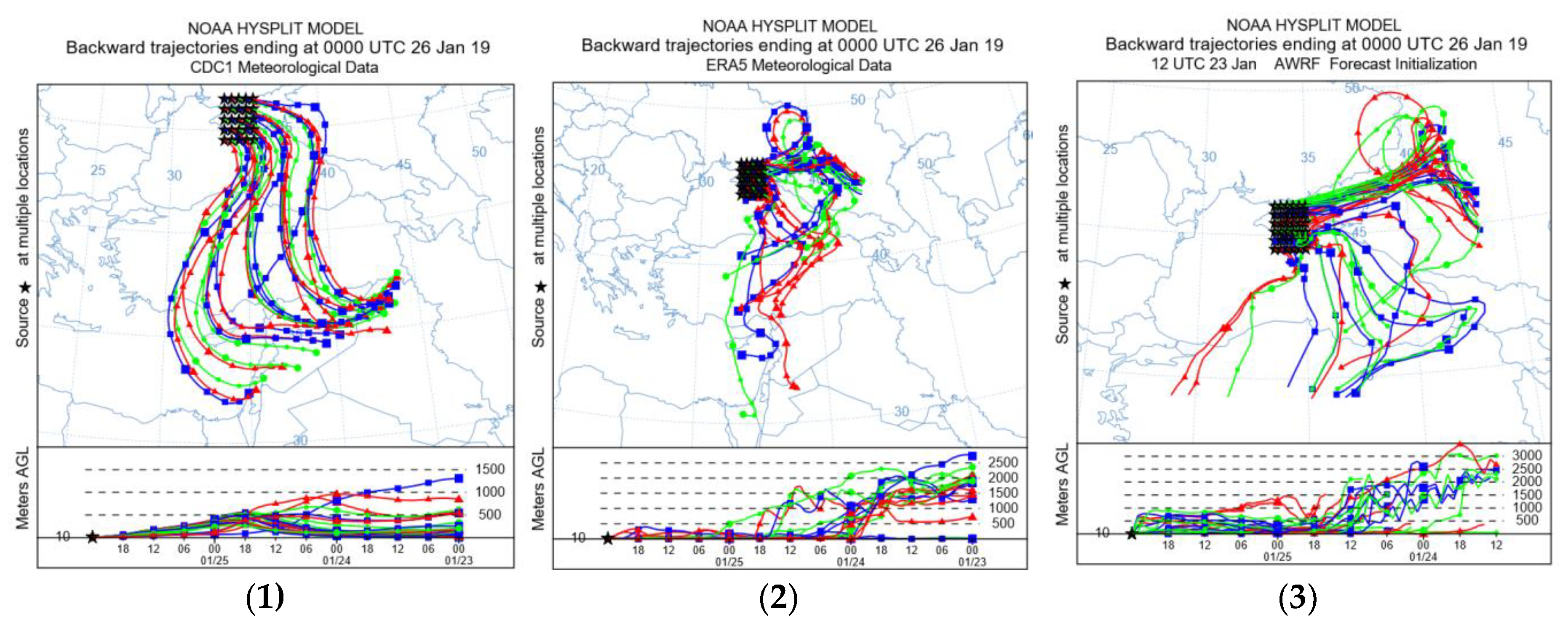
The analysis of the ensemble of resulting trajectories was carried out with the construction of a series of graphs in the rectangle form. Sample cases were obtained by running HYSPLIT using the matrix of trajectories option based on different sets of meteorological data for the period from 00 UTC on January 23 to 00 UTC on January 26, 2019 with six vertical levels (10, 25, 50, 100, 200, 500 m) arrival in the studied area of the Crimean peninsula. The distance between the model grids was 1 degree (latitude/longitude) for NCEP/NCAR and ERA5 and 0.3 degrees for WRF, since this gave a good regional overview of the expected patterns of air mass flow in the boundary layer. The simulation results are presented at Figure 8.
Using a matrix of reverse trajectories (Figure 8), a grid of locations of the arrival points of airborne pollutants within a given meteorological area is modeled to initiate multiple simultaneous trajectories. The result is a grid of trajectories that can provide visualization of the directions of movement of air flows within the domain without the need to launch multiple separate trajectories. This approach allows us to analyze the modeling uncertainties associated with possible variations of the study site.
Analysis of the reverse trajectories matrix shows that there are two predominant directions of air flow over the Crimean Peninsula. These are the southern and north-eastern directions. From the analysis of the arrival heights of the trajectories, it can be seen that the separation is mainly present at altitudes from 10 to 200 meters and when using the NCEP/NCAR and ERA5 data sets. Flows characterize different effects on the movement of air masses. This result is in good agreement with the results of wind flow modeling. The southern direction was chosen for further research. The north-eastern direction is characterized by a low anthropogenic press. This condition does not correspond to the objectives of the study.
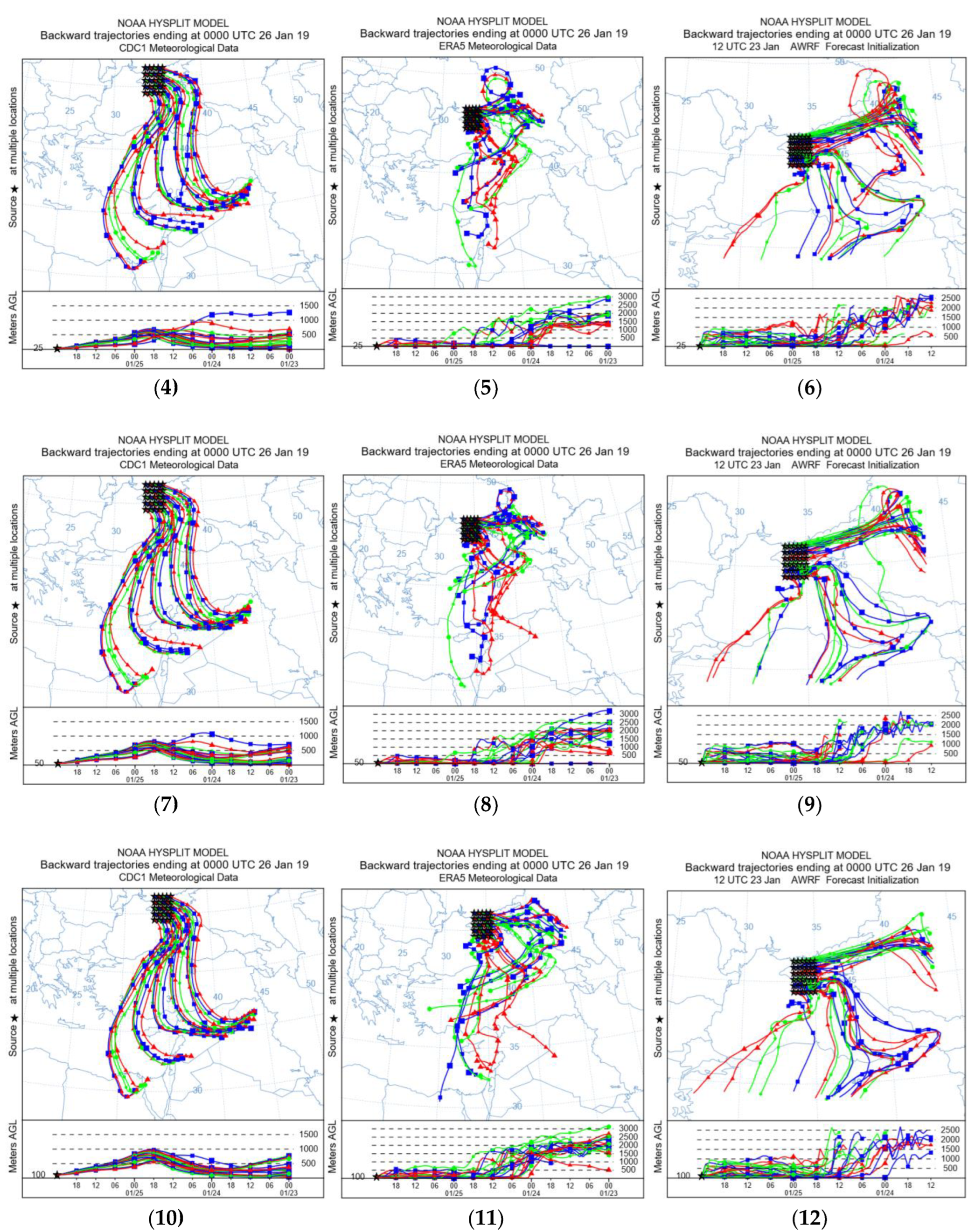
Since the point under study is located in the southern part of the Crimean Peninsula, further studies to identify possible sources of negative effects on atmospheric air affecting the Crimean Peninsula are devoted to the analysis of reverse trajectories arriving in this area (Figure 9).
It is noticed that the modeled reverse trajectories change depending on each case of meteorological data (Figure 9). The trajectories with NCEP/NCAR data are moving in a northeasterly direction, and there is no significant change in the direction of movement or separation of air flows depending on the height of the arrival of air masses.
The trajectories after the ERA 5 and WRF datasets also move in a northeasterly direction, but show a loop to the coast, which indicates the influence of terrain features on the movement of air masses. Trajectories by WRF data show the uniformity of the direction of movement. This is evidence of more accurate modeling using high-resolution meteorological data. A common feature, important for all cases with different meteorological data, is the passage of trajectories over an area with intense anthropogenic impact on the territory of Turkey. In Figure 9, this area is marked with a red oval.

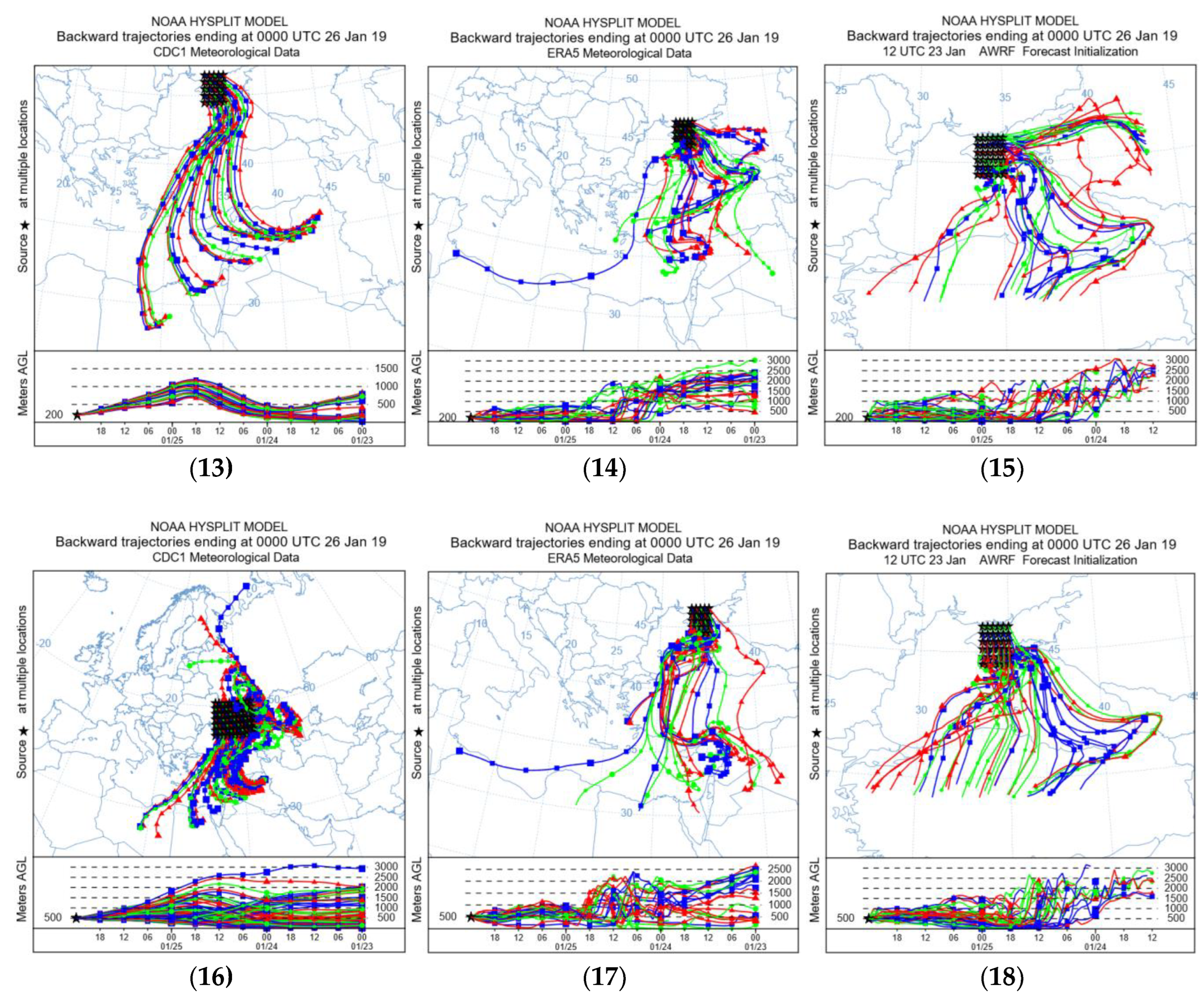
3.3. Frequency Analysis of Trajectories

The analysis of the reverse trajectories showed that they have a wide spatial heterogeneity of the directions of movement (Figure 9). To eliminate this uncertainty, the study used frequency analysis in order to best represent the transfer of pollutants from the intended area of anthropogenic impact. The area is indicated by a red oval (Figure 9.) For modeling, the point with the highest concentration of anthropogenic sources was selected. The point on (Figure 10) is indicated by an asterisk in a red square.
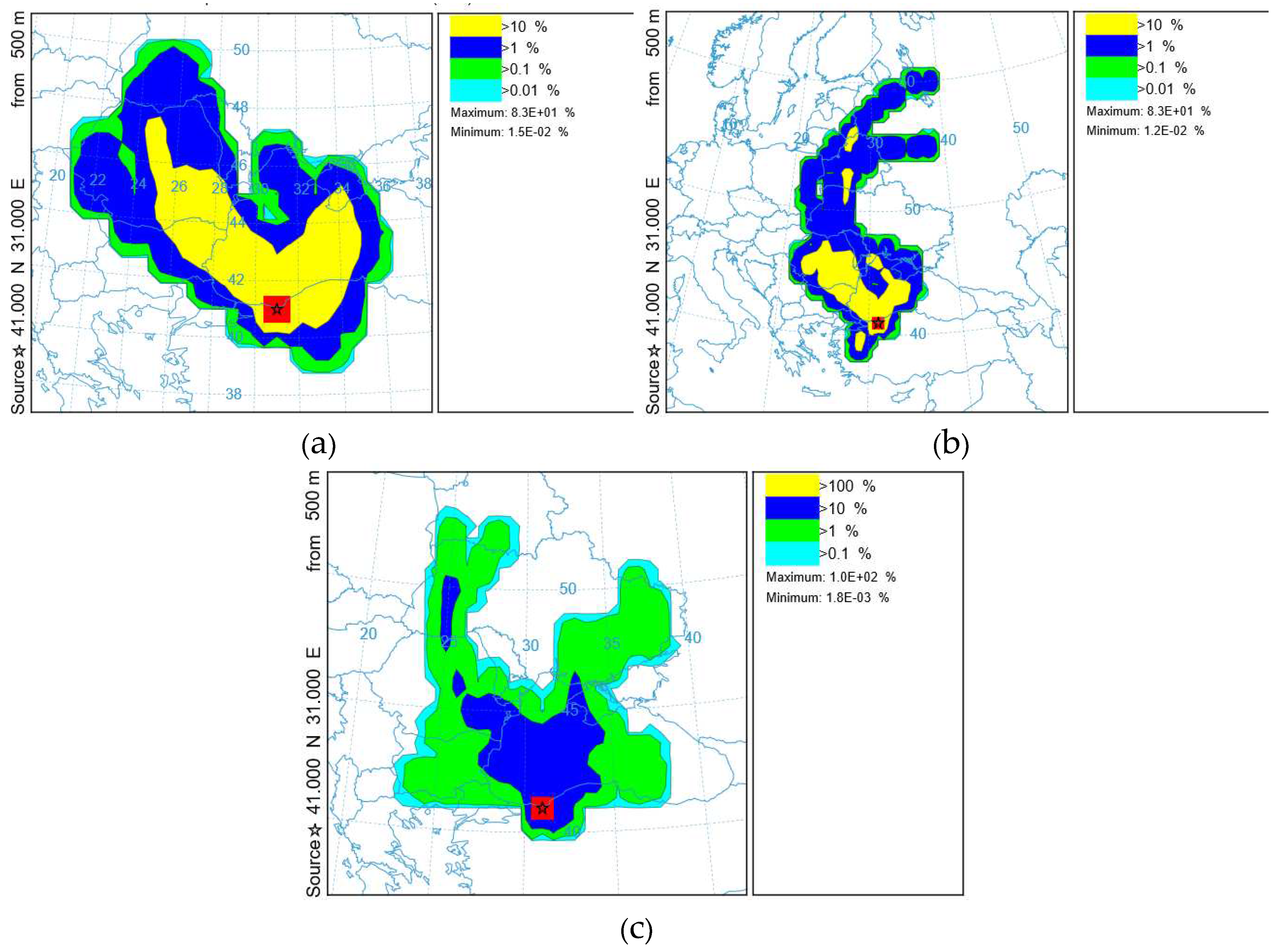
The “Trajectory Frequency” parameter (Figure 10) in the HYSPLIT model starts a trajectory from a single location and altitude at 500 m every 6 hours for 48 hours, and then sums up the number of trajectory passes over each grid cell. The color on Figure 10 shows the percentage of such passes from the total number of trajectories.
The frequency of the HYSPLIT trajectory for the study period with different meteorological grids (Figure 10) shows that air masses arrive in the study area (the Crimean Peninsula). This circumstance indirectly confirms the possibility of increasing the concentration of pollutants.

4. Discussion and Conclusion

Currently, the attention of the scientific community is focused on the so-called climatically significant components of the atmosphere, including not only greenhouse gases and ozone but the aerosol components such as aerosol particles PM2.5 and PM10 [36, 37]. These components change the optical properties. At the same time parameters of atmospheric radiation. high concentrations negatively affect the health of the population [38, 39]. A significant part of the world’s population is affected by this type of pollutants. Emissions of dust and smoke aerosols containing aerosol particles PM2.5 and PM10 can be transported in the atmosphere at distances up to several thousand kilometers [40-46] and can make a significant contribution to the pollution of the urban atmosphere [47].
Concerns related to air quality have given rise to numerous investigations to study issues related to the prediction of such an impact [4-9].
Meteorological data are the cause of uncertainty when predicting concentrations using dispersion models [4-9]. That is why the study analyzed the influence of these meteorological parameters on the results obtained in the calculations of the dispersion model.
The study of surface temperature forecasts based on the WRF model showed that the results are sensitive both to the choice of the parameterization scheme of the surface layer (parameters of turbulence, momentum flows, heat and latent heat of humidity, air density in the surface layer; specific heat capacity at constant pressure and wind velocity coefficient in the lower layer are parameterized) and to the models of the land surface (the land surface temperature is parameterized at various depths) when five-layer model needs to use.
For all conducted numerical experiments with different grid resolution sizes, an insignificant discrepancy of the surface layer temperature values by 2-3°C was obtained.
Probably this situation is caused by the fact that ERA5 reanalysis data sets, which are used as boundary conditions for the regional model, themselves determine the temperature of the surface layer in winter.
As can be seen from (Figure 3), the regional climate model gives closer values of air temperature at the 2 m height, compared with the observed data, than the results of the ERA5 reanalysis and especially the NCEP/NCAR reanalysis. This may be due to the fact that the data in the node of the regular NCEP/NCAR grid, which corresponds to the temperature value, differ in coordinates. The meteorological station is located at a sufficient distance (2.5 km) from the coordinates of the NCEP/NCAR grid.
Among the three cases, the forecasts made on the basis of the WRF model clearly indicate the presence of a specific mesoscale circulation of air masses in the area of the Crimean Peninsula (Figure 6,7). The analysis of ERA5 data to some extent shows these features in contrast to the NCEP/NCAR analysis data. The structure of the movement of air masses according to the NCEP/NCAR analysis corresponded to a large-scale flow. The air flow fields from the WRF model analysis show a better picture of the trajectory distribution than the other two data sets, which may be due to mesoscale model resolution when a 9-kilometer grid over the study area was used.
The study analyzes the impact of using three different meteorological input data on the result of air mass transfer in the atmosphere, calculated using the HYSPLIT model (Figure 8, 9). Modeling using three data sets clearly showed differences in the calculated trajectory of air flow.An assessment of the impact of various scales meteorological data on the result of the analysis of sources of negative impact on the atmosphere of the Crimean Peninsula was carried out. The HYSPLIT model was launched offline using various meteorological data to calculate reverse trajectories on six vertical levels 10, 25, 50, 100, 200, 500 m. Modeling with various meteorological data was carried out and the relationship between a possible increase in the PM2.5 pollutants concentration, PM10 and data with high grid resolution was determined.
The current study outlines the problems associated with the use of NCEP/NCAR and ERA5 reanalyses to represent meteorological changing in an interval of 48 to 72 hours from the start of modeling. Using these data to simulate atmospheric transport and dispersion, it is impossible to accurately represent the displacements in synoptic - regional scale fields. These results indicate the usefulness of the methodology for identifying emission sources using reverse trajectories, as well as the strong influence of the nature of atmospheric flows on the dispersion of pollutants. This study once again emphasizes the need for accurate modeling of atmospheric flow fields with a sufficiently high temporal and spatial resolution.

Author Contributions

All authors contributed to the study conception and design. Conceptualization, E.A. and V.E.; methodology, E.A., formal analysis, E.A. and V.E.; investigation, E.A. and Z.V.; software, V.Yu.Z.; writing—original draft preparation, E.A. and V.E.; writing—review and editing, E.A.; visualization, V.Yu.Z.; supervision, V.E.; project administration, V.E.; funding acquisition, V.E.;. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the state assignment of the Institute of Natural and Technical Systems, project reg. no. 121122300072–3.

Data Availability Statement

Data supporting reported results are available on request.

Acknowledgments

Numeric analysis was carried out using the supercomputer of Shared Research Facilities “Afalina” of Sevastopol State University.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Davis, L.S.; Dacre, H.F. Can dispersion model predictions be improved by increasing the temporal and spatial resolution of the meteorological input data? Weather 2009, 64, 232–237. [Google Scholar] [CrossRef]
  2. Warner, S.; Platt, N.; Heagy, J.F. Comparisons of Transport and Dispersion Model Predictions of the URBAN 2000 Field Experiment. J. Appl. Meteorol. 2004, 43, 829–846. [Google Scholar] [CrossRef]
  3. Nasstrom, J.S. and Pace, J.C. (1998) Evaluation of the effect of meteorological data resolution.
  4. on Lagrangian particle dispersion simulations using ETEX experiment. ATMOSPHERIC.
  5. ENVIRONMENT, 32, No. 24, pp. 4187–4194.
  6. Yerramilli, A.; Dodla, V.B.R.; Challa, V.S.; Myles, L.; Pendergrass, W.R.; Vogel, C.A.; Dasari, H.P.; Tuluri, F.; Baham, J.M.; Hughes, R.L.; et al. An integrated WRF/HYSPLIT modeling approach for the assessment of PM2.5 source regions over the Mississippi Gulf Coast region. Air Qual. Atmosphere Heal. 2011, 5, 401–412. [Google Scholar] [CrossRef] [PubMed]
  7. Feyzinejad, M.; Malakooti, H.; Sadrinasab, M.; Ghader, S. Radiological dose Assessment by Means of a Coupled WRF-HYSPLIT Model under Normal Operation of Bushehr Nuclear Power Plant. Pollution 2019, 5, 429–448. [Google Scholar] [CrossRef]
  8. Appel, K.W.; Roselle, S.J.; Gilliam, R.C.; Pleim, J.E. Sensitivity of the Community Multiscale Air Quality (CMAQ) model v4.7 results for the eastern United States to MM5 and WRF meteorological drivers. Geosci. Model Dev. 2010, 3, 169–188. [Google Scholar] [CrossRef]
  9. Kumar, A.; Patil, R.S.; Dikshit, A.K.; Kumar, R. Application of WRF Model for Air Quality Modelling and AERMOD—A Survey. Aerosol Air Qual. Res. 2017, 17, 1925–1937. [Google Scholar] [CrossRef]
  10. Ngan, F.; Stein, A.; Draxler, R. Inline Coupling of WRF–HYSPLIT: Model Development and Evaluation Using Tracer Experiments. J. Appl. Meteorol. Clim. 2015, 54, 1162–1176. [Google Scholar] [CrossRef]
  11. Chai, T.; Stein, A.; Ngan, F. Weak-constraint inverse modeling using HYSPLIT-4 Lagrangian dispersion model and Cross-Appalachian Tracer Experiment (CAPTEX) observations—effect of including model uncertainties on source term estimation. Geosci. Model Dev. 2018, 11, 5135–5148. [Google Scholar] [CrossRef]
  12. Leelőssy, Á.; Molnár, F.; Izsák, F.; Havasi, Á.; Lagzi, I.; Mészáros, R. Dispersion modeling of air pollutants in the atmosphere: A review. Cent. Eur. J. Geosci. 2014, 6, 257–278. [Google Scholar] [CrossRef]
  13. McGowan, H.; Clark, A. Identification of dust transportpathways from Lake Eyre, Australia using HYSPLIT. Atmos. Environ. 2008, 42, 6915–6925. [Google Scholar] [CrossRef]
  14. Xin, Y.; Wang, G.; Chen, L. Identification of Long-Range Transport Pathways and Potential Sources of PM10 in Tibetan Plateau Uplift Area: Case Study of Xining, China in 2014. Aerosol Air Qual. Res. 2016, 16, 1044–1054. [Google Scholar] [CrossRef]
  15. Zhao, B.; Hu, B.; Li, P.; Li, T.; Li, C.; Jiang, Y.; Meng, Y. Potential Source Area and Transport Route of Atmospheric Particulates in Xi’an, China. Atmosphere 2023, 14, 811. [Google Scholar] [CrossRef]
  16. Khalidy, R.; Salmabadi, H.; Saeedi, M. Numerical Simulation of a Severe Dust Storm over Ahvaz Using the HYSPLIT Model. Int. J. Environ. Res. 2019, 13, 161–174. [Google Scholar] [CrossRef]
  17. Challa, V.S.; Indrcanti, J.; Baham, J.M.; Patrick, C.; Rabarison, M.K.; Young, J.H.; Hughes, R.; Swanier, S.J.; Hardy, M.G.; Yerramilli, A. Sensitivity of atmospheric dispersion simulations by HYSPLIT to the meteorological predictions from a meso-scale model. Environ. Fluid Mech. 2008, 8, 367–387. [Google Scholar] [CrossRef]
  18. Iraji, F.; Memarian, M.H.; Joghataei, M.; Malamiri, H.R.G. Determining the source of dust storms with use of coupling WRF and HYSPLIT models: A case study of Yazd province in central desert of Iran. Dyn. Atmos. Oceans 2020, 93, 101197. [Google Scholar] [CrossRef]
  19. Skamarock, W.C.; et al. (2008) A Description of the Advanced Research WRF Version 3. NCAR Technical Notes, NCAR/TN-4751STR.
  20. Inness, A.; Ades, M.; Agusti-Panareda, A.; Barre, J.; Benedictow, A.; Blechschmidt, A.-M.; Dominguez, J.J.; Engelen, R.; Eskes, H.; Flemming, J.; et al. The CAMS reanalysis of atmospheric composition. Atmospheric Meas. Tech. 2019, 19, 3515–3556. [Google Scholar] [CrossRef]
  21. Draxler, Roland R. and Hess, G.D. “Description of the HYSPLIT4 modeling system”, 1997.
  22. Li, C.; Dai, Z.; Liu, X.; Wu, P. Transport Pathways and Potential Source Region Contributions of PM2.5 in Weifang: Seasonal Variations. Appl. Sci. 2020, 10, 2835. [Google Scholar] [CrossRef]
  23. Escudero, M.; Stein, A.; Draxler, R.R.; Querol, X.; Alastuey, A.; Castillo, S.; Avila, A. Determination of the contribution of northern Africa dust source areas to PM10 concentrations over the central Iberian Peninsula using the Hybrid Single-Particle Lagrangian Integrated Trajectory model (HYSPLIT) model. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
  24. Kain, J.S.; Fritsch, J.M. Convective parameterization for mesoscale models: The Kain-Fritcsh scheme. In The representation of cumulus convection in numerical models; Emanuel, K.A., Raymond, D.J., Eds.; American Meteorological Society: Boston, MA, USA, 1993. [Google Scholar]
  25. Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
  26. Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather. Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
  27. Dudhia, Jimy. (1996). A Multi-layer Soil Temperature Model for MM5.
  28. Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two–dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
  29. Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
  30. Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather. Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
  31. https://edgar.jrc.ec.europa.eu/dataset_ghg70_nuts2 (date of application: 18.08.2023).
  32. https://www.ceip.at/the-emep-grid/gridded-emissions (date of application: 18.08.2023).
  33. Global Energy Observatory, Google, KTH Royal Institute of Technology in Stockholm, Enipedia, World Resources Institute. 2018. Global Power Plant Database. Published on Resource Watch and Google Earth Engine; https://earthengine.google.com/ (date of application: 18.08.2023).
  34. Chen, L.W.A.; Doddridge, B.G.; Dickerson, R.R.; Chow, J.C.; Henry, R.C. Origins of fine aerosol mass in the Baltimore–Washington corridor: Air Qual Atmos Health (2012) 5:401–412 411 implications from observation, factor analysis, and ensemble air parcel back trajectories. Atmos Environ 2002, 36, 4541–4554. [Google Scholar] [CrossRef]
  35. Li, Y.; Dai, Z.; Liu, X. Analysis of Spatial-Temporal Characteristics of the PM2.5 Concentrations in Weifang City, China. Sustainability 2018, 10, 2960. [Google Scholar] [CrossRef]
  36. Wu, X.; Chen, Y.; Guo, J.; Wang, G.; Gong, Y. Spatial concentration, impact factors and prevention-control measures of PM2.5 pollution in China. Nat. Hazards 2016, 86, 393–410. [Google Scholar] [CrossRef]
  37. Ellrod, Gary. (2015). Use of the NOAA ARL HYSPLIT Trajectory Model For the Short Range Prediction of Coastal Stratus and Fog.
Preprints 91212 g001
Figure 1. Sources of emissions of aerosol particles PM2.5, PM10, power plants, depending on their type and capacity.
Figure 1. Sources of emissions of aerosol particles PM2.5, PM10, power plants, depending on their type and capacity.
Preprints 91212 g001
Preprints 91212 g002
Figure 2. The area of the simulation with horizontal resolution of 9 km×9 km in the WRF model system.
Figure 2. The area of the simulation with horizontal resolution of 9 km×9 km in the WRF model system.
Preprints 91212 g002
Preprints 91212 g003
Figure 3. Daily observed at the 2 m height and simulated air temperature (C) for the Batumi station in 12 UTC 23.01.2019 - 00 UTC 26.01.2019.
Figure 3. Daily observed at the 2 m height and simulated air temperature (C) for the Batumi station in 12 UTC 23.01.2019 - 00 UTC 26.01.2019.
Preprints 91212 g003
Preprints 91212 g004aPreprints 91212 g004b
Figure 4. Surface horizontal wind fields in the Crimean Peninsula region from 23 to 26 January 2019. NCEP/NCAR analysis at the following times: (1) 00 UTC 23.01.2019; (2) 12 UTC 23.01.2019; (3) 00 UTC 24.01.2019; (4) 12 UTC 24.01.2019; (5) 00 UTC 25.01.2019; (6) 12 UTC 25.01.2019; (7) 00 UTC 26.01.2019; (8) 12 UTC 26.01.2019. The size of arrow corresponds to the maximum wind speed.
Figure 4. Surface horizontal wind fields in the Crimean Peninsula region from 23 to 26 January 2019. NCEP/NCAR analysis at the following times: (1) 00 UTC 23.01.2019; (2) 12 UTC 23.01.2019; (3) 00 UTC 24.01.2019; (4) 12 UTC 24.01.2019; (5) 00 UTC 25.01.2019; (6) 12 UTC 25.01.2019; (7) 00 UTC 26.01.2019; (8) 12 UTC 26.01.2019. The size of arrow corresponds to the maximum wind speed.
Preprints 91212 g004aPreprints 91212 g004b
Preprints 91212 g005
Figure 5. The surface horizontal wind field in the Crimean Peninsula region in 23 - 26 January 2019 of the ERA5 analysis at the following times: (1) 00 UTC 23.01.2019; (2) 12 UTC 23.01.2019; (3) 00 UTC 24.01.2019; (4) 12 UTC 24.01.2019; (5) 00 UTC 25.01.2019; (6) 12 UTC 25.01.2019; (7) 00 UTC 26.01.2019; (8) 12 UTC 26.01.2019. The size of the arrow corresponds to the maximum wind speed.
Figure 5. The surface horizontal wind field in the Crimean Peninsula region in 23 - 26 January 2019 of the ERA5 analysis at the following times: (1) 00 UTC 23.01.2019; (2) 12 UTC 23.01.2019; (3) 00 UTC 24.01.2019; (4) 12 UTC 24.01.2019; (5) 00 UTC 25.01.2019; (6) 12 UTC 25.01.2019; (7) 00 UTC 26.01.2019; (8) 12 UTC 26.01.2019. The size of the arrow corresponds to the maximum wind speed.
Preprints 91212 g005
Preprints 91212 g006
Figure 6. The surface horizontal wind fields in the Crimean Peninsula region in 23 - 26 January 2019. The output data of the WRF model is a 9 km grid at the following time: (1) 12 UTC 23.01.2019; (2) 00 UTC 24.01.2019; (3) 12 UTC 24.01.2019; (4) 00 UTC 25.01.2019; (5) 12 UTC 25.01.2019; (5) 00 UTC 26.01.2019; (7) 12 UTC 26.01.2019. The size of the arrow corresponds to the maximum wind speed.
Figure 6. The surface horizontal wind fields in the Crimean Peninsula region in 23 - 26 January 2019. The output data of the WRF model is a 9 km grid at the following time: (1) 12 UTC 23.01.2019; (2) 00 UTC 24.01.2019; (3) 12 UTC 24.01.2019; (4) 00 UTC 25.01.2019; (5) 12 UTC 25.01.2019; (5) 00 UTC 26.01.2019; (7) 12 UTC 26.01.2019. The size of the arrow corresponds to the maximum wind speed.
Preprints 91212 g006
Preprints 91212 g007aPreprints 91212 g007b
Figure 7. Surface horizontal wind fields in the Crimean Peninsula region in 23 - 26 January 2019. output data of the WRF model grid 2 km at the following times: (1) 00 UTC 23.01.2019; (2) 12 UTC 23.01.2019; (3) 00 UTC 24.01.2019; (4) 12 UTC 24.01.2019; (5) 00 UTC 25.01.2019; (6) 12 UTC 25.01.2019; (7) 00 UTC 26.01.2019; (8) 12 UTC 26.01.2019. The size of the arrow corresponds to the maximum wind speed.
Figure 7. Surface horizontal wind fields in the Crimean Peninsula region in 23 - 26 January 2019. output data of the WRF model grid 2 km at the following times: (1) 00 UTC 23.01.2019; (2) 12 UTC 23.01.2019; (3) 00 UTC 24.01.2019; (4) 12 UTC 24.01.2019; (5) 00 UTC 25.01.2019; (6) 12 UTC 25.01.2019; (7) 00 UTC 26.01.2019; (8) 12 UTC 26.01.2019. The size of the arrow corresponds to the maximum wind speed.
Preprints 91212 g007aPreprints 91212 g007b
Preprints 91212 g008aPreprints 91212 g008bPreprints 91212 g008c
Figure 8. 72-hour forecast of the HYSPLIT inverse trajectory matrix based on heterogeneous meteorological data and different heights of the arrival air masses in the study area of the Crimean Peninsula, depending on the height of the point of arrival air masses: (1) output data of the NCEP/NCAR model, height 10 m; (2) output data of the ERA5 model, height 10 m; (3) output data of the WRF model grid 9 km, height 10 m; (4) output data of NCEP/NCAR models, height 25 m; (5) output data of the ERA5 model, height 25 m; (6) output data of the WRF model grid 9 km, height 25 m; (7) output data of NCEP/NCAR model, height 50 m; (8) output data of the ERA5 model, height 50 m; (9) output data of the WRF model grid 9 km, height 50 m; (10) output data of the NCEP/NCAR model, height 100 m; (11) output data of the ERA5 model, height 100 m; (12) output data of the WRF model grid 9 km, height 100 m; (13) NCEP/NCAR model output, height 200 m; (14) ERA5 model output, height 200 m; (15) WRF model output grid 9 km, height 200 m; (16) NCEP/NCAR model output, height 500 m; (17) output data of the ERA5 model, height 500 m; (18) the output data of the WRF model is a grid of 9 km, height 500 m (coloring of trajectories in various colors is made to improve the visual perception of information).
Figure 8. 72-hour forecast of the HYSPLIT inverse trajectory matrix based on heterogeneous meteorological data and different heights of the arrival air masses in the study area of the Crimean Peninsula, depending on the height of the point of arrival air masses: (1) output data of the NCEP/NCAR model, height 10 m; (2) output data of the ERA5 model, height 10 m; (3) output data of the WRF model grid 9 km, height 10 m; (4) output data of NCEP/NCAR models, height 25 m; (5) output data of the ERA5 model, height 25 m; (6) output data of the WRF model grid 9 km, height 25 m; (7) output data of NCEP/NCAR model, height 50 m; (8) output data of the ERA5 model, height 50 m; (9) output data of the WRF model grid 9 km, height 50 m; (10) output data of the NCEP/NCAR model, height 100 m; (11) output data of the ERA5 model, height 100 m; (12) output data of the WRF model grid 9 km, height 100 m; (13) NCEP/NCAR model output, height 200 m; (14) ERA5 model output, height 200 m; (15) WRF model output grid 9 km, height 200 m; (16) NCEP/NCAR model output, height 500 m; (17) output data of the ERA5 model, height 500 m; (18) the output data of the WRF model is a grid of 9 km, height 500 m (coloring of trajectories in various colors is made to improve the visual perception of information).
Preprints 91212 g008aPreprints 91212 g008bPreprints 91212 g008c
Preprints 91212 g009
Figure 9. Graph of reverse trajectories depending on meteorological data: analysis: (a) NCEP/NCAR; (b) ERA 5 analysis; (c) WRF model output on 9 km grid/.
Figure 9. Graph of reverse trajectories depending on meteorological data: analysis: (a) NCEP/NCAR; (b) ERA 5 analysis; (c) WRF model output on 9 km grid/.
Preprints 91212 g009
Preprints 91212 g010
Figure 10. Graph of the frequency of straight trajectories for 48 hours from the starting point at an altitude of 500 m above Ground level using heterogeneous meteorological data: (a) NCEP/NCAR analysis; (b) ERA5 analysis; (c) WRF model output 9 km grid. The contours represent a percentage of the number of trajectory endpoints in each grid cell divided by the total number of calculated trajectories.
Figure 10. Graph of the frequency of straight trajectories for 48 hours from the starting point at an altitude of 500 m above Ground level using heterogeneous meteorological data: (a) NCEP/NCAR analysis; (b) ERA5 analysis; (c) WRF model output 9 km grid. The contours represent a percentage of the number of trajectory endpoints in each grid cell divided by the total number of calculated trajectories.
Preprints 91212 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated