Oilfield Reservoir Parameter Inversion Based on Ground Deformation 2D Measurements Acquired by Msbas Time Series InSAR Method

Time series ground deformation monitoring and reservoir parameter inversion are crucial for the dynamic assessment of oilfield resources and sustainable exploitation in an oilfield. As one of the regions with the richest oil reserves in China, the oilfield areas in the western Qaidam Basin are selected as a typical study area. Firstly, we used SAR images collected by the Sentinel-1A satellite from January 2021 to December 2022 and applied the Multidimensional Small Baseline Subset (MSBAS) method to obtain vertical and east-west deformation measurements. On this basis, a nonlinear Bayesian inversion method was applied to model the shallow reservoir in a series of complex deformation areas, based on a single-source model and a multi-source model, respectively. As a result, the ground deformation monitoring results obtained by long time series InSAR clearly reflect the uneven ground deformation caused by the oil extraction and water injection operation process. There is slight subsidence in the Huatugou oilfield, while significant uplift deformation occurred in the Ganchaigou oilfield and the Youshashan oilfield, with a maximum uplift rate of 48 mm/year. Further analysis indicates that the introduction of the 2D deformation field helps to improve the robustness of oilfield reservoir parameter inversion. Moreover, the dual-source model is more suitable than the single-source model for inverting complex deformation reservoir parameters. This study not only fills the blank of InSAR deformation monitoring for the oilfields in the western Qaidam Basin but also provides a theoretical reference for model and method selection of reservoir parameter inversion in other oilfields.

Keywords:

Subject: Environmental and Earth Sciences - Remote Sensing

1. Introduction

oil, as the largest energy source in the world, its extraction and storage are of great significance to national economic development. However, it also brings environmental problems that cannot be ignored [1,2,3]. Oil extraction can cause not only subsidence but also uplift. This is because fluid injection into the reservoir is often carried out to enhance oil recovery, resulting in excessive underground reservoir pressure, which manifests as a ground uplift [4,5]. Whether it is subsidence or uplift, severe ground deformation not only damages oil well production facilities but also affects the safety of surrounding infrastructure such as buildings, railways, and roads. Therefore, ground deformation monitoring and reservoir parameter inversion in oil extraction areas are essential for ensuring the safety of oilfields. The Qaidam Basin, often referred to as China’s “treasure trove, is not only abundant in various mineral resources but also hosts important oil and gas accumulation zones in its western region. By the year 2020, the Qaidam Basin boasts 32 identified oil and gas fields, with a combined proven reserve exceeding 6.4 billion tons [6]. Previous studies on this area mostly described the reservoir characteristics of oilfields from the perspectives of geology, sedimentary petrology, and geochemistry [7,8], there hasn’t been any research on utilizing Interferometric Synthetic Aperture Radar (InSAR) technology for deformation characteristics monitoring and reservoir parameter inversion. Therefore, using InSAR technology to monitor the deformation of the oilfields in the western basin not only provides guidance for sustainable oil extraction but also offers a new approach to understanding the reservoir characteristics in this region.

Conventional monitoring techniques require significant time and effort. However, InSAR technology, due to its benefits of extensive coverage, all-weather capabilities, precision, and efficiency, has found broad application in monitoring urban ground deformation [9,10,11], as well as in the monitoring and early warning of geological disasters such as earthquakes, landslides, and others [12,13,14]. Currently, the most commonly employed InSAR techniques include Permanent Scatterer InSAR (PS-InSAR), Small Baseline Subset InSAR (SBAS-InSAR), and Distributed Scatterer InSAR (DS-InSAR), which can not only effectively overcome the shortcomings of phase decoherence, terrain residual and atmospheric delay, but also quickly obtain the deformation time series in line-of-sight (LOS) direction [15]. Meanwhile, some scholars have also applied InSAR technology to monitor ground deformation in oilfields, geothermal fields, and mines, which is caused by underground reservoir changes, thus exposing the intimate connection between ground deformation characteristics and the state of underground reservoirs [16,17,18]. Sun et al. [19] used multi-track PS-InSAR technology to quantitatively analyze three types of ground subsidence, including oilfields, in the lower Liaohe plain of China. Juncu et al. [20] extracted deformations in a geothermal field by SBAS InSAR technology and found that the primary factor contributing to the subsidence was the observed pressure drawdown. Chen et al. [21] used Differential InSAR (D-InSAR) and SBAS technology to acquire cumulative deformation data within a mining area in China and compared it with the progress of mining operations. However, one-dimensional deformation measurement can not only fail to provide more comprehensive and intuitive information for detecting the ground deformation characters of oilfields but also struggle to reflect the real ground deformation conditions, often leading to deformation interpretation deviations, which is called the LOS fuzzy problem.

In addition, for oilfields, changes in reservoir pore pressure caused by fluid extraction and injection, as well as geometric shapes, positions, volumes, and other physical parameters of the reservoir, greatly influence the ground deformation characteristics. Therefore, using InSAR deformation results to invert reservoir parameters in oilfields can provide a quick and timely understanding of the reservoir state, which is of great significance for oilfield stability evaluation. Klemm et al. [22] monitored an oilfield in the Middle East with PS-InSAR and inverted ground deformations using a geomechanical model. They found that monitoring ground deformations and applying geomechanical inversion can yield valuable insights into the dynamic characteristics of reservoirs. Yang et al. [23] obtained subsidence information of a hydrocarbon reservoir in West Texas, USA, using the SBAS method and simulated ground subsidence based on reservoir parameters. By comparing the InSAR observed deformations with the modeled deformations, they found a high degree of agreement between the two. Ji et al. [24] conducted subsidence monitoring in the Karamay oilfield in Xinjiang by the SBAS method and then inverted its reservoir geometric parameters based on the Okada model. Nevertheless, there is still limited research on applying InSAR deformation results to reservoir parameter inversion in oilfields. The inversion theory is relatively lacking, and most scholars use a single model for the inversion under the assumption that there exists only one source of deformation in the subsurface. There is a lack of comparative studies on joint inversion of multiple-source models for complex deformations. Besides, some scholars have jointly inverted the seismic source parameters with the LOS and azimuthal deformation fields of ascending and descending to improve the inversion efficiency and accuracy by increasing the constraints of nonlinear inversion [25,26], but there are no similar attempts currently in the field of subsurface reservoir parameters inversion, and they all directly utilize the one-dimensional deformation in the inversion.

Based on the 113 ascending and descending Sentinel-1A SAR images from January 2021 to December 2022, Multidimensional Small Baseline Subset (MSBAS) InSAR technology is employed in this study to obtain the vertical and east-west ground deformation of the oilfields in the western Qaidam Basin and then analyze its temporal and spatial characteristics and causes. Afterwards, we combine the obtained two-dimensional deformation measurements for constraints and use a single-source model and a dual-source model to invert the reservoir parameters of the two complex deformation areas in the Youshashan oilfield within the study area, and then comparative analysis and evaluation of the inversion results are conducted. The related results can provide references for the safety maintenance of oilfields in the western and the selection of reservoir parameter inversion models and methods in other areas.

2. Study Area and Datasets

2.1. Background of the Study Area

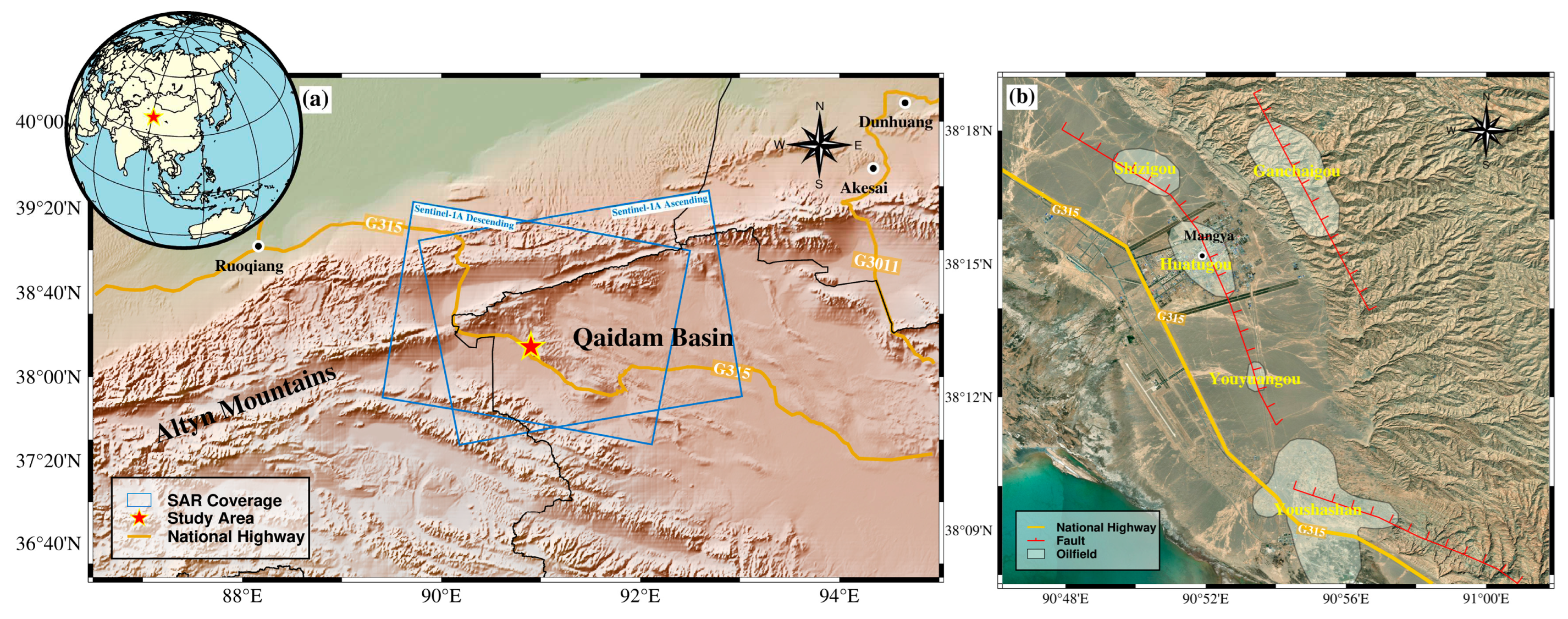
Located in the northern part of the Qinghai-Tibetan Plateau, the Qaidam Basin is one of four major basins in China. It is surrounded by the Kunlun Mountains, Qilian Mountains, Altyn Mountains, and other mountains, covering an expanse of about 240,000 square kilometers. Within the basin, there are not only extensive salt lakes and marshes but also abundant reserves of oil, coal, and various metallic minerals.

The study area is located in the western part of China’s Qaidam Basin. Its eastern region is characterized by hills and mountains and its western region features relatively flat topography, with an average altitude of approximately 3000 meters. The local climate is a typical plateau continental climate, with strong sunshine, cold winters and cool summers, and less rainfall. In this region, the Paleocene and Neocene systems are mainly developed, and the Quaternary is uplifted and thinly deposited. The reservoirs can be broadly categorized into two types: porous clastic rocks and fractured, pore-vug diamictites. In the vertical direction, these two reservoir types are alternately stacked, forming a reservoir distribution characteristic that develops continuously in time and alternately overlaps in space. The unique geological and geographical conditions have fostered abundant oil resources. Following the commencement of development in the Youshashan (YSH) oilfield in 1957, the Huatugou (HTG) oilfield, the Youyuangou (YYG) oilfield, the Shizigou (SZG) oilfield, and the Ganchaigou (GCG) oilfield within the study area were subsequently developed. At the same time, the fluid injection technique was employed to increase oilfield production. By 2014, the total oil production in this region had exceeded 6.5 million tons [27].

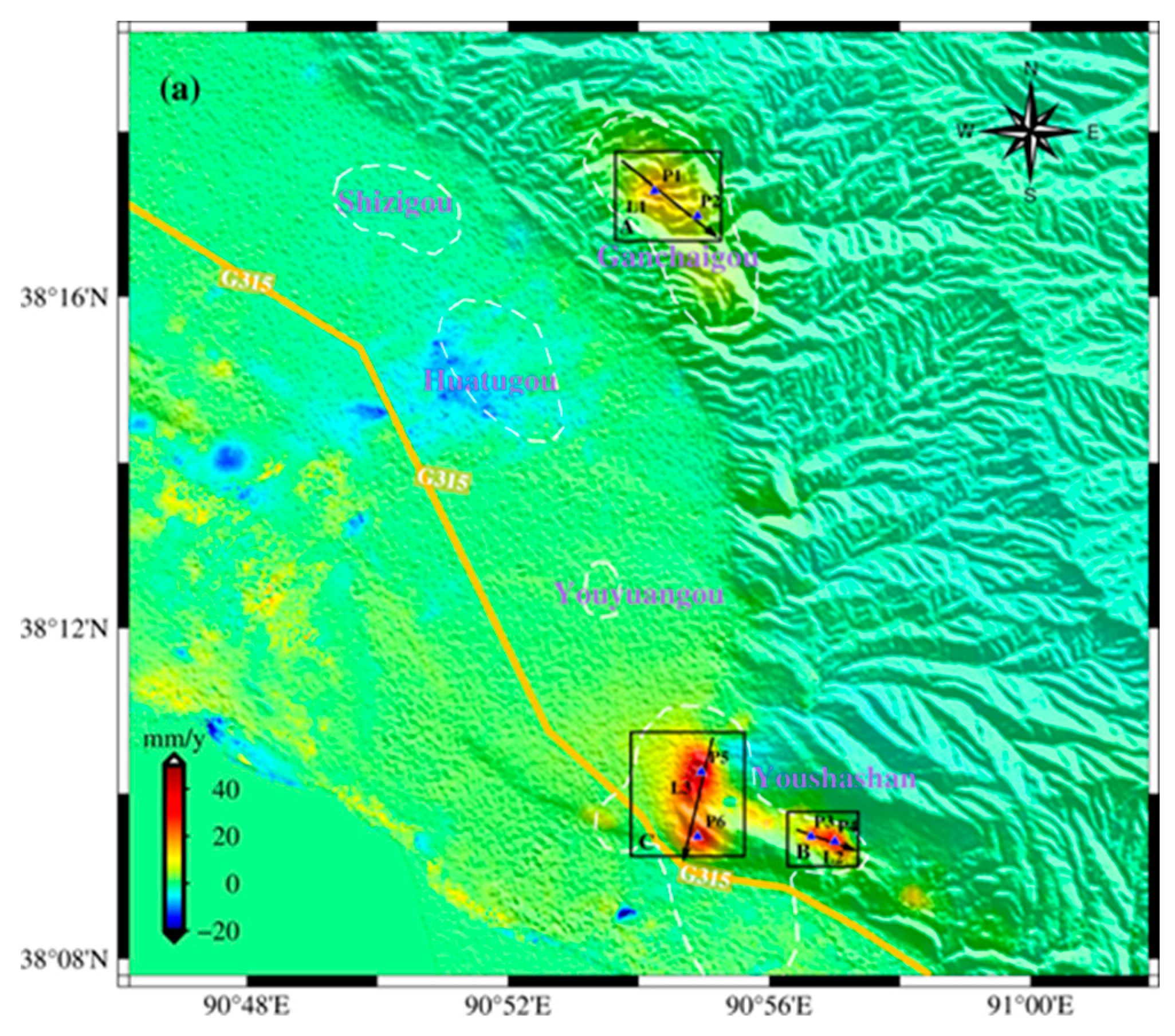
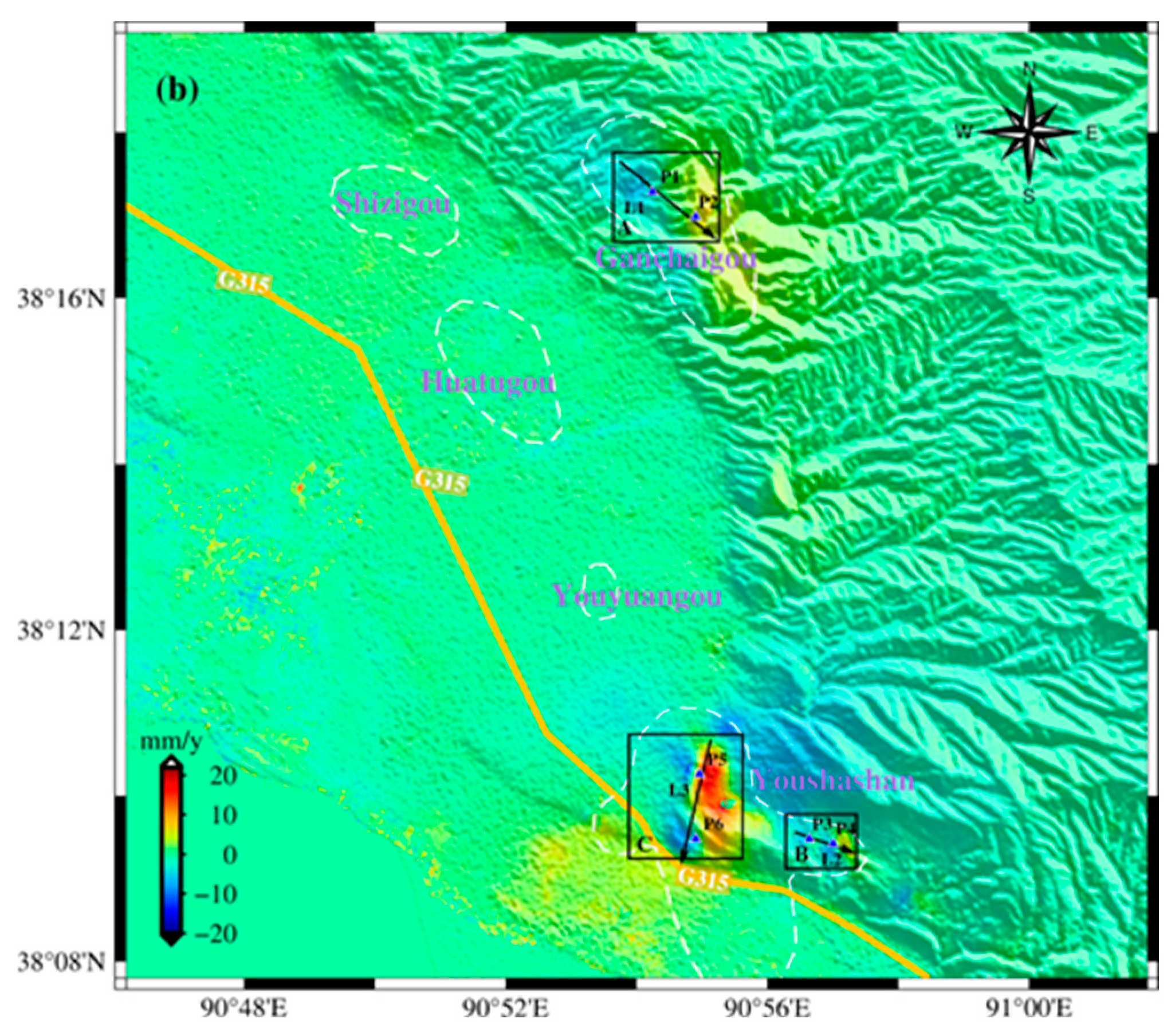
Figure 1. (a) Overview of the western part of Qaidam Basin overlayed on the topography. (b) Detailed satellite image of the study area. The oilfields’ boundary is depicted by the white polygon.

2.2. Data and Processing

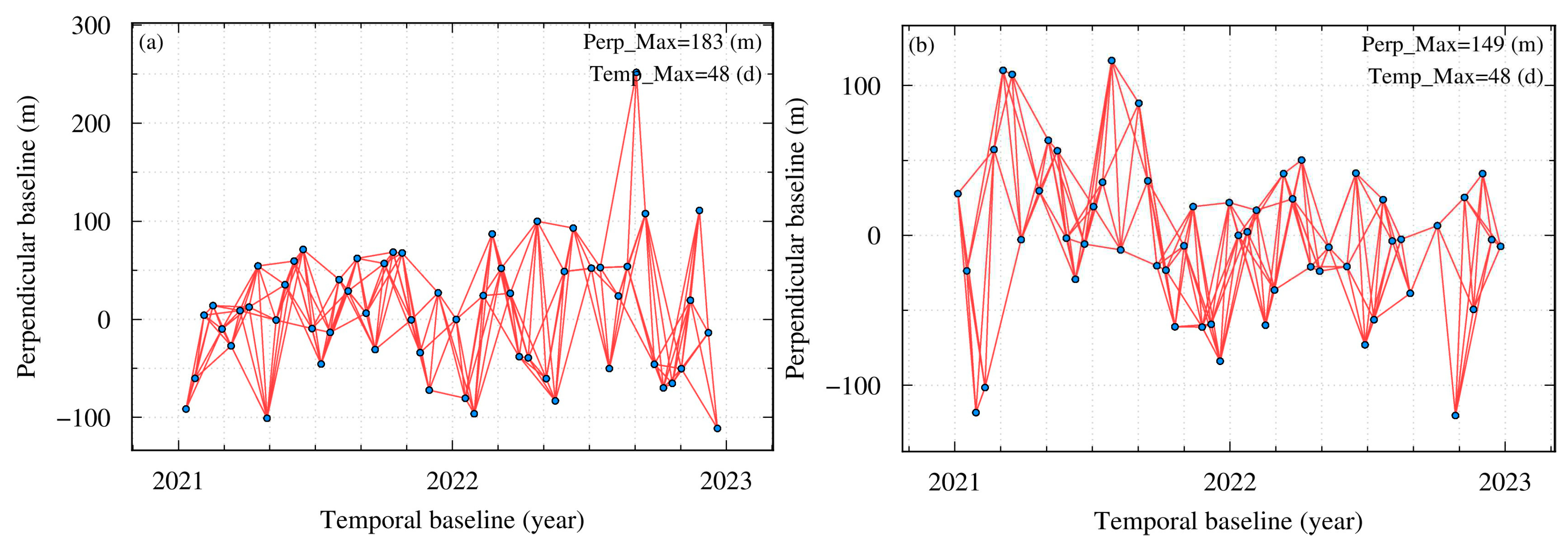
The dataset used in this study is 58 ascending and 56 descending Sentinel-1A SAR images covering the period from January 2021 to December 2022. Sentinel-1A is a satellite equipped with C band synthetic aperture radar with an orbital height of 690 km and a revisit period of 12 days. Strict orbital control technology is adopted to ensure the space baseline is small enough to improve the SAR image interference effect. GAMMA software [28] was used for D-InSAR processing in this study. At the same time, terrain errors are removed by the digital elevation model (DEM) with 30 m resolution, and to remove the atmospheric delay, the Generic Atmospheric Correction Online Service (GACOS) data is also introduced. Finally, to improve the quality of the InSAR result, the interference pairs with spatio-temporal baselines less than 200 meters and 49 days are selected to perform the phase unwrapping by the minimum-cost flow (MCF) method.

Figure 2. Spatio-temporal baseline of the ascending (a) and descending (b) interfering pairs.

Table 1. Main parameters of the SAR data.

Sensor	Wavelength	Azimuth/Range pixel spacing	Orbit direction	Path	Temporal coverage
Sentinel-1A	5.6cm	13.99cm/2.33cm	Ascending	143	2021.01.11-2022.12.20
Sentinel-1A	5.6cm	13.99cm/2.33cm	Descending	48	2021.01.05-2022.12.26

3. Methodology

3.1. MSBAS-InSAR Method

MSBAS technology is improved on the basis of SBAS technology. The result generated by SBAS is the time series of LOS displacement for each pixel in a SAR image. In the case of a single acquisition geometry without supplementary data, it is not possible to fully decompose the LOS solution obtained from SBAS into its three components of ground displacement (vertical, east-west, and north-south directions). However, when the InSAR data come from multiple acquisition geometries, the SBAS method can be adjusted to generate an approximate solution that includes time series of multiple components [27]. Therefore, by simultaneously processing multiple orbit D-InSAR data, MSBAS can obtain the vertical and horizontal east-west deformation time series of the overlapping area [28]. The main steps of the MSBAS method are as follows: firstly, D-InSAR processing is performed on one or more sets of ascending and descending orbit data, followed by resampling the unwrapped and geocoded differential interferograms to a consistent area and grid size. Secondly, a temporal matrix is created and decoherent pixels are removed. Finally, each pixel is solved by singular value decomposition (SVD) [29] to acquire the two- dimensional deformation rate component, and then the deformation time series can be reconstructed by numerically integrating the deformation rate. The use of Tikhonov regularization during the matrix solving process helps solve ill-posed problems in the observation equation. The inversion matrix is:

(\begin{matrix} - \cos θ \sin φ Δ t & \cos φ Δ t \\ λ L \end{matrix}) (\begin{matrix} V_{E} \\ V {}_{U} \end{matrix}) = (\begin{matrix} \hat{ϕ} \\ 0 \end{matrix})

(1)

where

φ, θ

represent the incident and azimuth angle,

Δ t

represents the time interval between adjacent SAR images,

λ

is a regularization parameter, L represents the identity matrix,

V_{E}

and

V_{U}

are the east-west and vertical deformation rate, respectively,

\hat{ϕ}

is the obtained differential interferometry measurements. If we denote the coefficient matrix by C:

C = (\begin{matrix} - \cos θ \sin φ Δ t & \cos φ Δ t \\ λ L \end{matrix})

(2)

Then, we can obtain the east-west and vertical deformation rate by the following formulas:

(\begin{matrix} V_{E} \\ V_{U} \end{matrix}) = {(C^{T} C)}^{- 1} C^{T} (\begin{matrix} \hat{ϕ} \\ 0 \end{matrix})

(3)

3.2. The Source Model and Inversion Method

In 1977, Matsu’Ura [30] inverted the fault properties of the Tango earthquake based on geodetic data and clearly proposed the concept of “geodetic inversion” for the first time. Geodetic inversion mainly consists of three components: geodetic data, geophysical inversion model, and inversion algorithm. In this study, the deformation data obtained through InSAR technology is used as geodetic data, and appropriate inversion models and algorithms will be employed to obtain the underground reservoir parameters of the deformation area in the oilfields. Next, the geophysical inversion models and inversion algorithms used in this study will be introduced.

3.2.1. Finite Prolate Spheroidal Model

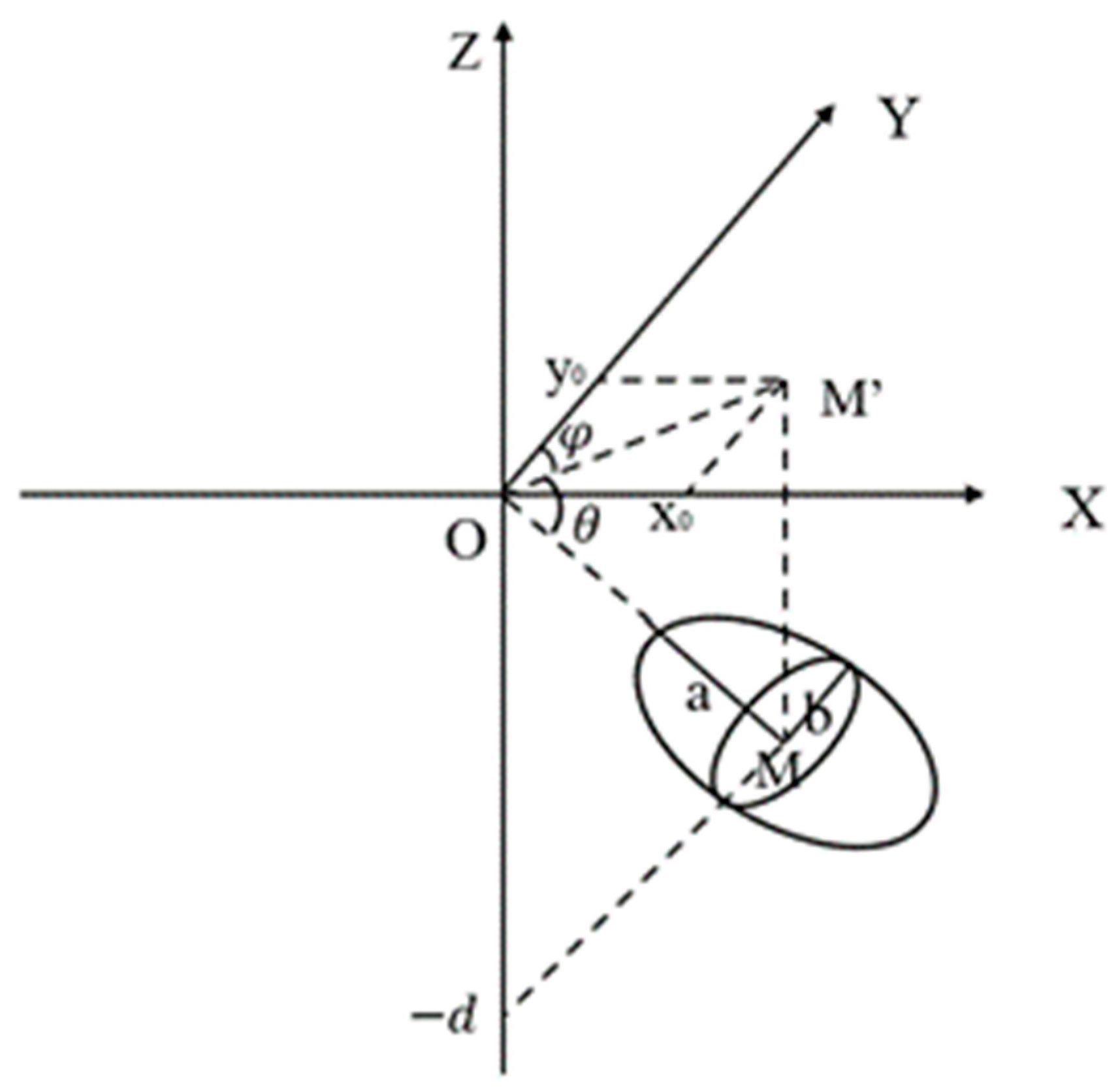
In 1988, Yang et al. [31] derived and calculated the analytical formula for the arbitrary-oriented prolate spheroidal cavity model within a finite-dimensional elastic half-space. They proposed the finite prolate spheroidal model and found that this model has relatively more parameter degrees of freedom compared to the ellipsoidal point source model. The Finite Prolate Spheroidal Model is composed of eight parameters, including the three-dimensional coordinates of the ellipsoid’s center, the long axis, the short axis, pressure variation, as well as the strike and dip of the long axis. A space rectangular coordinate system with O as the origin is established, as shown in Figure 3. M represents the coordinates

(x_{0}, y_{0}, - d)

of the ellipsoid source center, a and b are the major and minor semi-axis of the ellipsoid, respectively,

φ

is the strike, and

θ

is the dip angle.

3.2.2. Dipping Dike with Uniform Opening Model

In 1985, Japanese scholar Yoshimitsu Okada [32] analyzed existing research results on ground deformation caused by elastic half-space faults and proposed a general expression for ground deformation caused by fault dislocations of point sources and finite rectangular surface sources. In 1992, Okada [33] further improved the theory of this fault dislocation model. According to the elastic half-space isotropic dislocation theory, the displacement of a point on the ground due to the dislocation of a rectangular surface within an elastic medium is proportional to the amount of displacement of that surface. The proportionality coefficient is uniquely determined by the relative positions, the geometric dimensions, the inclination, the depth, and the elastic medium of the dislocation surface. If there are multiple dislocation surfaces underground, then the displacement of the point on the ground is the sum of the displacement vectors caused by the respective dislocations of the multiple dislocation surfaces.

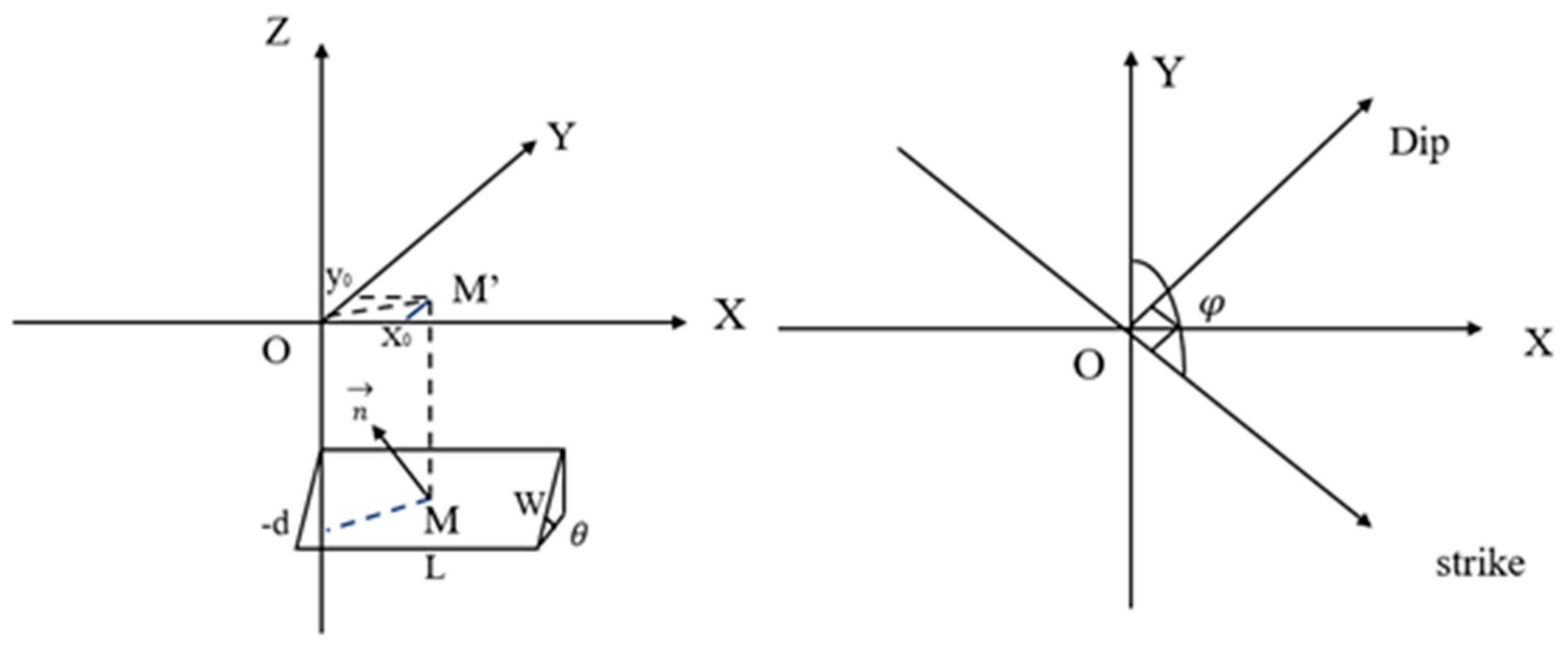
Establish a space rectangular coordinate system with O as the origin, as shown in Figure 4. There are seven main parameters of the dipping dike with uniform opening model, including the length along the strike (L), the width along the inclination (W), the depth of the geometric center of the dislocation surface (d), the inclination angle (

θ

), the strike (

φ

), and the projected coordinates (x₀, y₀) of the geometric center point M on the ground surface.

3.2.3. The Nonlinear Bayesian Inversion Method

Geodetic inversion is a discipline that studies the evolutionary characteristics and laws of ground deformation based on geodetic observation data combined with prior information, and infers the internal and physical parameters of the earth, thereby revealing the internal dynamics of the earth [34]. In the process of geodetic inversion, the functional relationship between observed data and model parameters is as follows:

d = G (m) + ε

(4)

where d denotes the observed data, m represents the model parameters, G is the Green’s function that connects the model parameters and ground deformation, and

ε

is the model error.

Compared with the traditional deterministic inversion algorithm that determines the optimal model parameters by minimizing the error between observation data and model simulation data, the nonlinear Bayesian inversion algorithm in the stochastic inversion algorithm used in this paper [35]. By obtaining the posterior probability density function (PDF) of all model parameters, this algorithm not only can determine the optimal parameter values but also can evaluate the uncertainty of the parameter values well, which is more practical than the traditional algorithms. In addition, this paper proposes to utilize the 2D deformation field measured by MSBAS to constrain and invert the vertical and east-west deformations of the oilfields, so as to obtain more reliable reservoir parameters of the oilfield. At the same time, quadtree sampling is applied to improve inversion efficiency. The likelihood function p(d|m) can be expressed as follows:

p (d | m) = {(2 π)}^{- N / 2} {|\sum_{d}|}^{- \frac{1}{2}} \times \exp [- \frac{1}{2} {(d - G m)}^{T} \sum_{d}^{- 1} (d - G m)]

(5)

where

d = {[d_{u}, d_{e}]}^{T}

represents the vertical and east-west observation data, m represents the model parameters, N refers to the number of data points,

Σ_{d}

refers to the variance-covariance matrix of the data, and

G m = {[G_{u} m, G_{e} m]}^{T}

is the 2D simulated data calculated from the model parameters m through the Green’s function G.

After obtaining the prior information and likelihood function, the PDF

p (m | d)

can be computed by the Bayesian formula. It refers to the probability of the current parameter effectively accounting for the observed data when considering the prior information.

In addition, the Markov Chain Monte Carlo (MCMC) sampling method and the Metropolis-Hastings rule [36,37] will be used to randomly modify the model parameters and calculate new likelihood function values. The newly calculated likelihood function value will be compared with the previously computed value to decide whether the current model parameters are approved or rejected. This process is iterated until the termination condition is met.

4. Results

4.1. 2D Deformation Monitoring and Analysis

The MSBAS method is employed in this research to simultaneously process ascending and descending SAR images, leading to the generation of a vertical average annual deformation rate map and an east-west average annual deformation rate map of the study area, as depicted in Figure 5a and 5b, respectively. It can be observed that from January 2021 to December 2022, the GCG oilfield, HTG oilfield, and YSS oilfield in the study area exhibited varying degrees of ground deformation. Specifically, the GCG oilfield and YSS oilfield experienced notable ground uplift and east-west deformation, with the highest uplift rate reaching 48 mm/year. Only uneven ground subsidence occurred without significant horizontal displacement in the HTG oilfield, with a maximum subsidence rate of about 12 mm/year. Previous studies have indicated that the injection of fluid and gas during oil extraction can cause ground uplift[16]. The study area is characterized by multiple faults and complex structures, posing challenges in oil production. To overcome these challenges and achieve increased and sustained production, water injection methods have been widely adopted in the oilfields. Therefore, the ground uplift in the GCG oilfield and YSS oilfield may be associated with the oilfield’s water injection activities. However, although the HTG oilfield employed the same method to enhance production, its ground didn’t rise but subsided. This may be due to the fact that the HTG oilfield is located in the urban area of Mangya City, where residents predominantly depend on groundwater extraction for their daily water supply. The substantial groundwater and oil extraction as well as city construction has resulted in the compaction of the ground in this area. Considering the complexity of the ground subsidence causes in the HTG oilfield, this study will focus on discussing and analyzing the deformation characteristics of the uplift areas (area A, area B, area C) within the GCG oilfield and the YSS oilfield.

As shown in Figure 5, area A exhibits a maximum uplift rate of 16 mm/year, along with a maximum east-west deformation rate of 8 mm/year. Most of the area B moves westward, and there is an eastward displacement in a small local area. The maximum uplift rate reaches 30 mm/year, and the maximum east-west deformation rate reaches 7 mm/year. The maximum uplift rate of area C is 48 mm/year, and it shows horizontal deformation characteristics with east-west opposing movement centered on the uplift center. The eastern flank of the uplift center is shifting towards the east with a velocity of approximately 15 mm/year, while the western flank of the uplift center is moving in the westward direction at a rate of about 6 mm/year. Moreover, the ground deformation in area C is near China National Highway 315, potentially posing risks to the road and its surrounding infrastructure. Therefore, it is necessary to enhance the supervision and upkeep of this area. The YSS oilfield is located at the high point of the Youshagou in the northwest of the Youshashan structure in the Qaidam Basin. It is a typical abnormally low-pressure reservoir so relying solely on natural energy for development is difficult to achieve satisfactory results. Therefore, water injection development has been conducted in the YSS oilfield since 1996, and it has currently transitioned into the late production stage. The long history of water injection and the large amount of water injection required for production maintenance coincide with the serious ground deformation in area B and area C. However, the GCG oilfield, which just started trial production in 2020, boasts substantial oil and gas resources and has a small amount of water injection, so the ground deformation there is also relatively small.

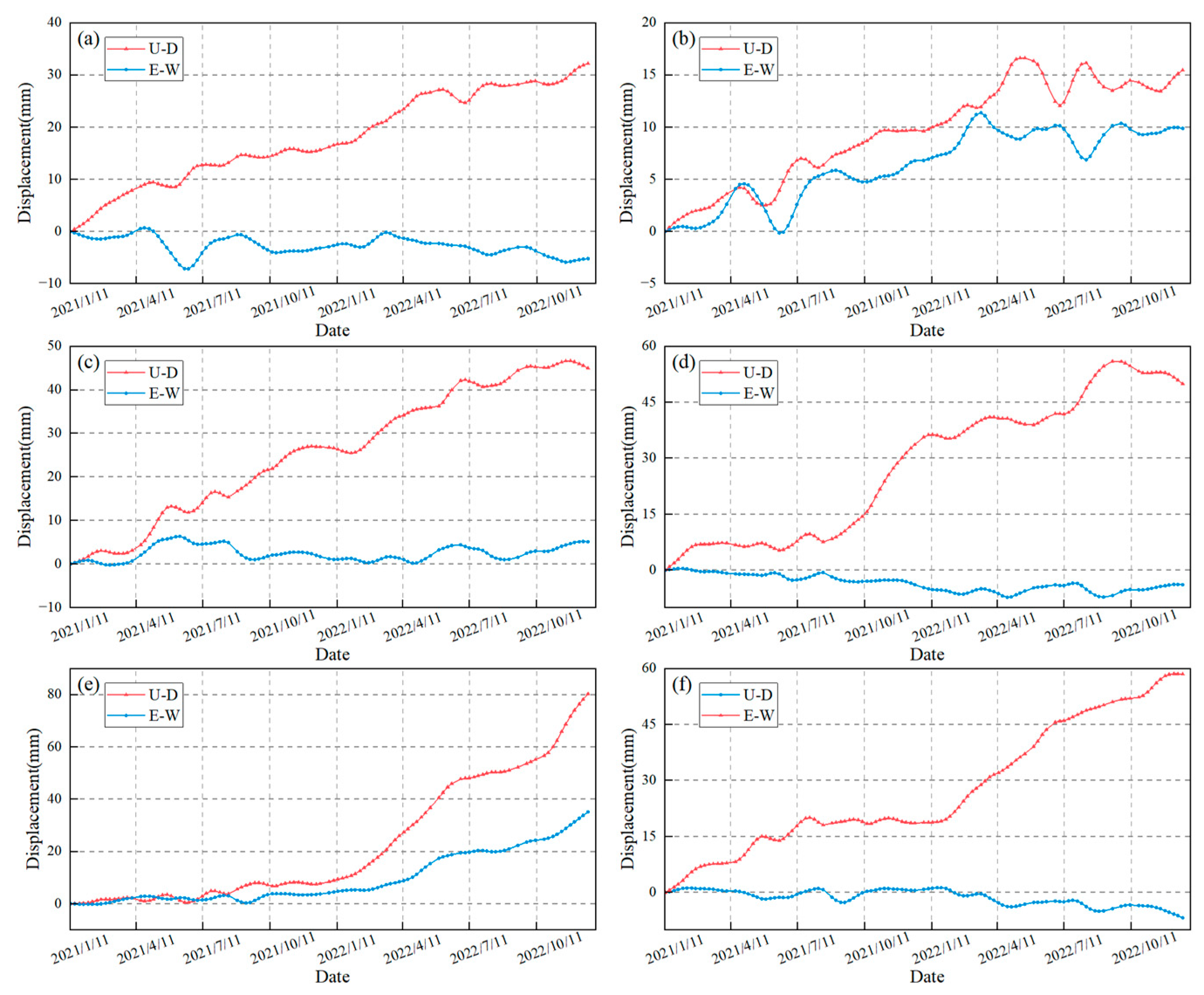
To investigate the spatiotemporal evolution patterns of each uplift in the research area, Figure 6a,b respectively show the time series cumulative vertical and east-west deformation from January 2021 to December 2022. According to Figure 6, area A has been uplifting throughout the observation period, and the uplifted area has gradually expanded southward. As of December 20, 2022, the cumulative uplift reached 34 mm. In the horizontal direction, it moved westward significantly from May 11, 2021, to June 28, 2021, and then resumed its slow movement. Area B exhibited a small relative uplift before September 2021, and a significant increase in relative uplift with time after September 2021, while the east-west deformation always remained relatively stable and slowly increasing. Both the vertical and horizontal deformation rates in area C increased slowly before February 2022 but significantly accelerated thereafter. The maximum vertical displacement was up to 106 mm, and the maximum horizontal displacement was up to 42 mm. Ground deformation is an intuitive reflection of changes in underground reservoir conditions. The greater the intensity of fluid injection into the oil layer, the faster the pore pressure of the reservoir increases. Therefore, we speculate that the variation in ground deformation rate is related to the variation in injection intensity.

Furthermore, we choose the six points’ (P1-P6) (Figure 5) time series InSAR results to specifically analyze the temporal changes in the oilfield ground, as illustrated in Figure 7. P1 and P2 are both located in area A. From their deformation time series, it is observed that although the surface in area A has been uplifted compared to January 2021, there is a brief subsidence followed by a rebound every year from May to August. This may be due to a decrease in reservoir pressure caused by oil extraction during this time period, leading to surface subsidence, but it quickly rebounds due to the injection of fluid. P3 and P4 are situated on the west and east sides of area B, respectively. Unlike the roughly linear deformation trend of P3, the P4 point remained relatively stable before August 2021 but rapidly experienced uplift after August 2021, accompanied by a minor horizontal displacement of less than 5 mm. This may be because the intensity of water injection activities increased in the west side of area B since about August 2021. P5 and P6 are situated on the north and south sides of area C, respectively. They both exhibit a gradual deformation trend before February 2022 and an accelerated deformation trend after February 2022, which is consistent with the increasing injection efforts required for the late-stage production of the oilfield.

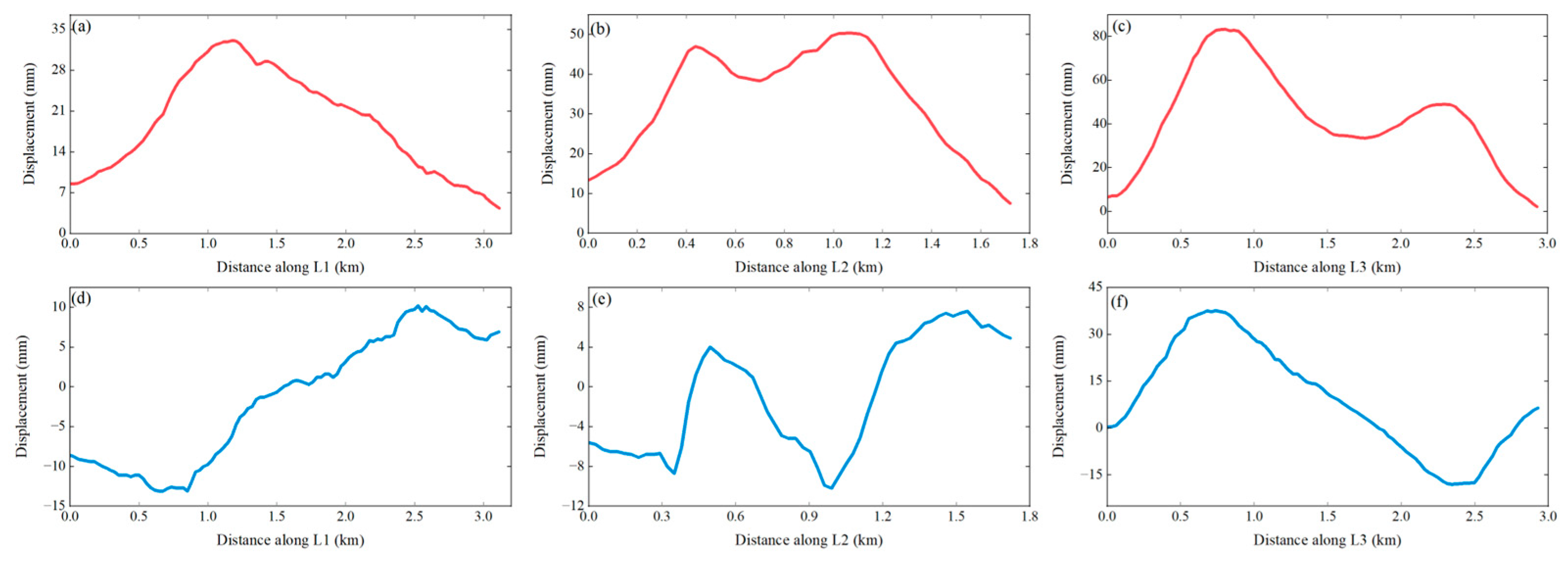
We also plotted three profile lines, L1, L2, and L3, in area A, B, and C respectively. The two-dimensional cumulative deformation along these profile lines is shown in Figure 8. The vertical axis represents the cumulative displacement, and the horizontal axis represents the distance along the direction indicated by the arrows in Figure 5. L1 exhibits an uplift in the vertical direction and reaches its maximum deformation at approximately 1.3 km, after which it gradually decreases. In the horizontal direction, there is a cumulative displacement towards the west before 1.4 km, while there is a cumulative displacement towards the east after 1.4 km. From the analysis above, it can be inferred that there may be a deformation center in area A in the vicinity of 1.3 km to 1.4 km. Unlike the single peak feature of L1, L2 and L3 exhibit two uplift peaks. Combined with their horizontal deformation characteristics, we speculate that the deformation in areas B and C is relatively complex and there is more than one deformation center.

4.2. Reservoir Modeling

Inverting the reservoir parameters based on the deformation information obtained through InSAR technology, combined with corresponding geophysical models allows us to have a deeper understanding of the underground process of injecting fluids and the reservoir’s dynamic behavior. Currently, commonly used geophysical models include the Mogi model [38], the Okada model [33], and the ellipsoid model [39]. The point source model approximates the deformation as a circle, which differs significantly from the observed deformation, while the Okada model and finite ellipsoid model use more adjustable parameters to simulate complex deformation, which is closer to the observed deformation. Therefore, we choose the dipping dike with uniform opening model in the Okada model and the finite prolate spheroidal model to invert the reservoir parameters in area B and area C in this study. Additionally, considering the complex deformation features exhibited in these two areas, this study not only uses the most common single-source model for inversion but also introduces a dual-source model combining a rectangular dislocation surface and a dipping ellipsoid for inversion.

Due to the ambiguity of one-dimensional LOS deformation, it may be difficult for nonlinear inversion to converge quickly. Therefore, we combine InSAR vertical and east-west cumulative ground deformation variables to constrain the inversion, which can increase the robustness of nonlinear inversion. Subsequently, the Bayesian inversion algorithm is used to search for the optimal parameters, and predefined search ranges are set for each parameter. For example, the rectangular length is set from 100 to 1000 m, and the width is set from 10 to 500 m. After 1,000,000 iterations, the parameters reach convergence. In all inversion cases, we typically configure Poisson’s ratio to a value of 0.25.

4.2.1. Inversion Result of Area B

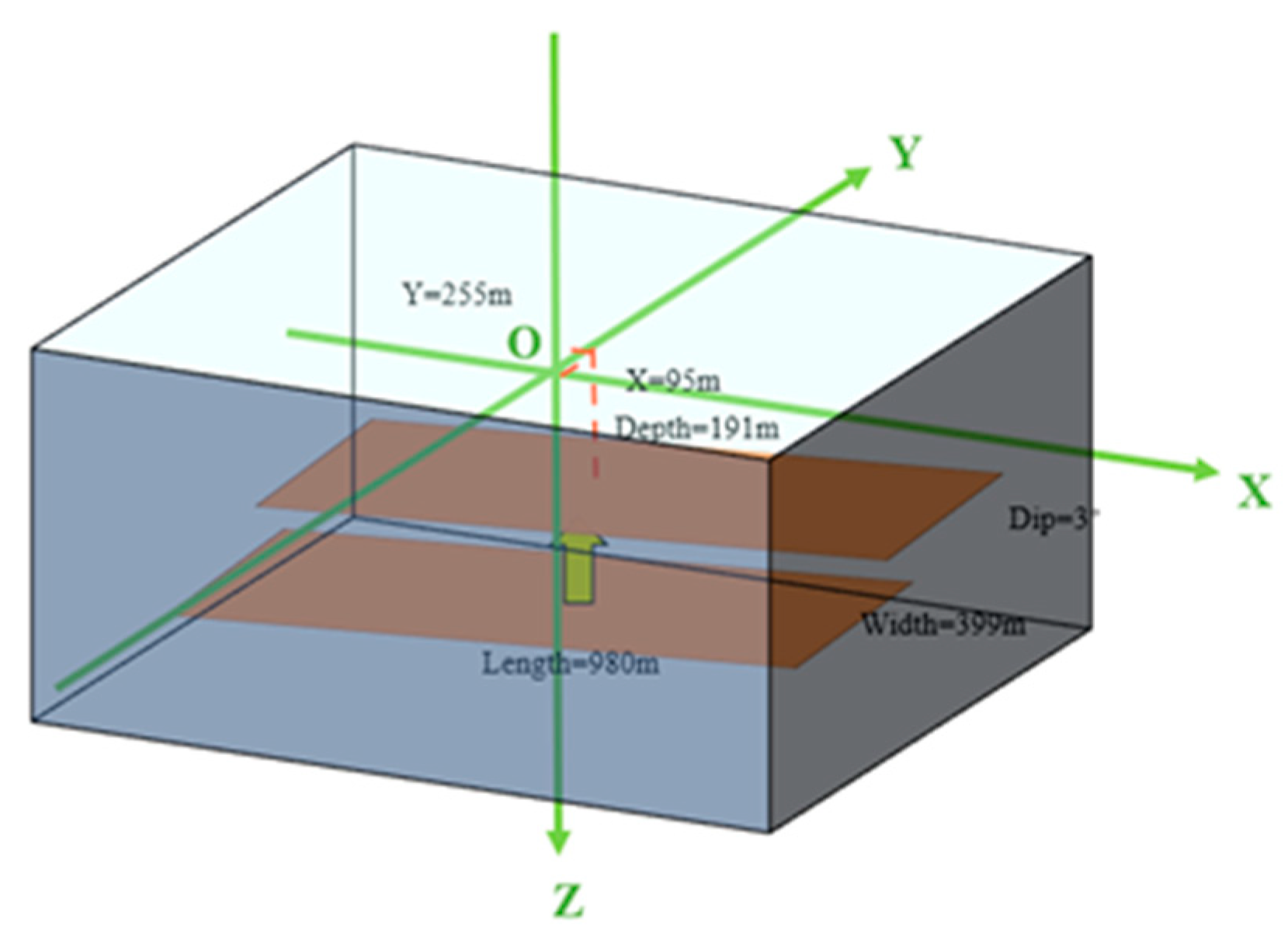
We assume that the ground deformation in area B is the result of a rectangular dislocation source in the shallow reservoir and use the dipping dike with uniform opening model to invert the oilfield reservoir parameters. The optimal parameters acquired through inversion are shown in Table 2. It can be observed that the length and width of the rectangular dislocation surface source are 980.668 m and 399.642 m, respectively. The depth range of the reservoir is 171-227 m, trending from northwest to southeast with an inclination angle of approximately 3°, indicating it is nearly horizontal. The positive value of the opening suggests reservoir expansion. Figure 10 gives the 3D schematic of a rectangular dislocation surface source with optimal parameters in area B.

Figure 9. The observed deformation field in vertical (a) and horizontal (d) directions, the black arrow T1 corresponds to the profile line in Figure 13; The modeled vertical deformation field in vertical (b) and horizontal (c) directions; The residuals in vertical (c) and horizontal (e) directions.

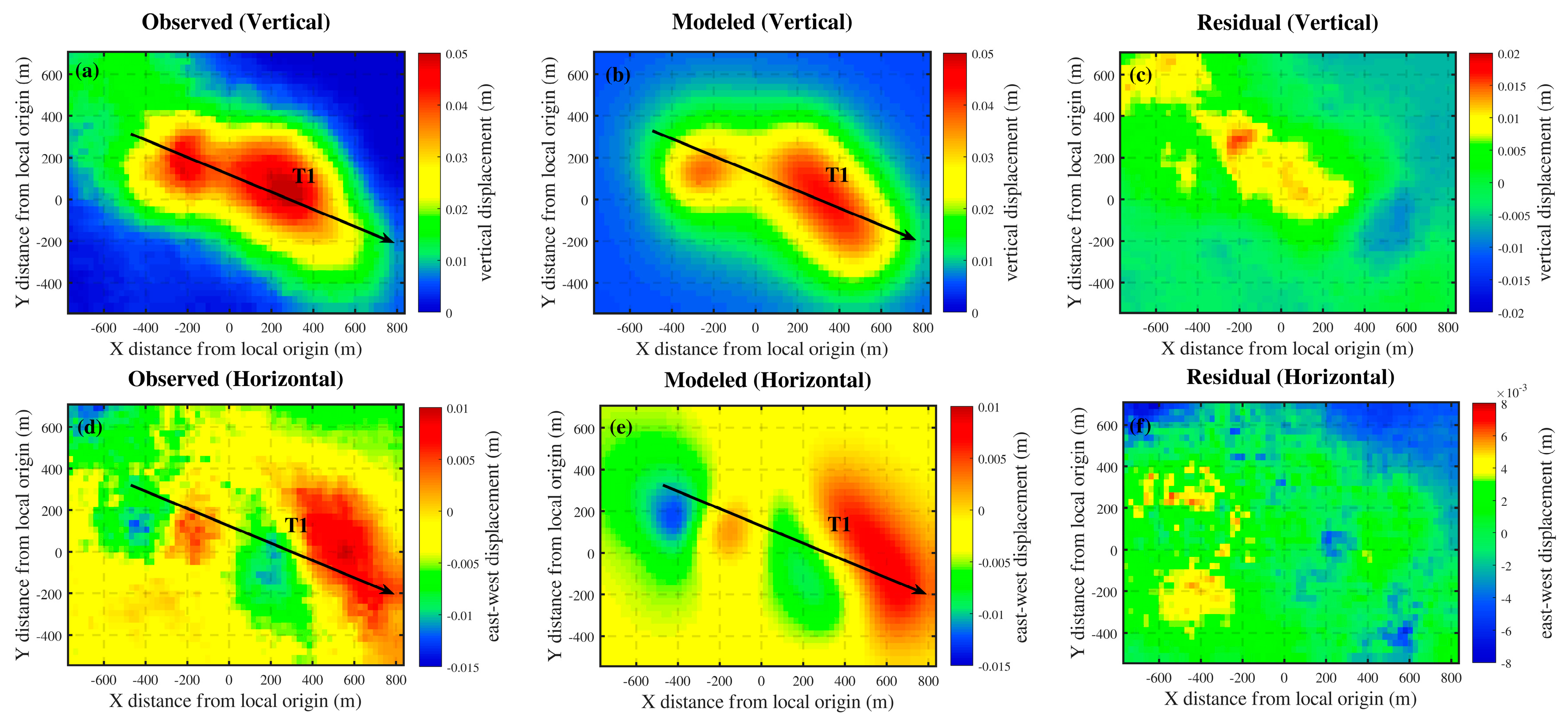
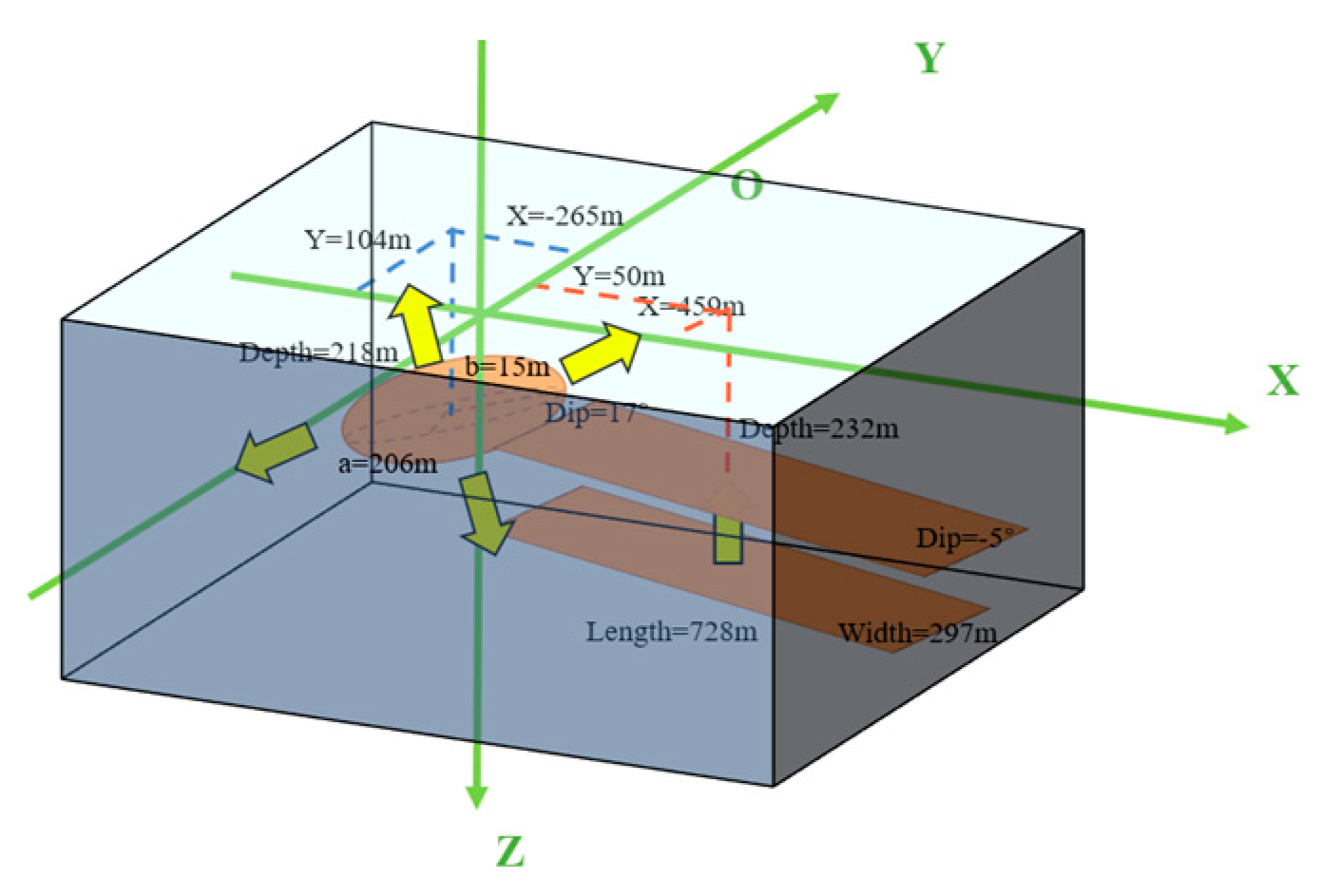
We assume that the ground deformation in area B arises from the combined effect of a dipping ellipsoid source and a rectangular dislocation surface source in the shallow reservoir. Accordingly, we use the finite prolate spheroidal model and the dipping dike with uniform opening model to invert the reservoir parameters of the oilfield. The optimal parameters acquired through inversion are shown in Table 3. For the ellipsoid source, its burial depth is about 218 m. The length of its major and minor semi-axis indicates its morphology as a flat ellipsoid, and its minor axis (30 m) reflects the thickness of the reservoir. The ellipsoid’s strike angle relative to the north direction is 65° (clockwise direction), and the dip angle is 17°. DP/mu stands for the ratio of the pressure change to the shear modulus. For the rectangular surface source, its burial depth is about 232 m and its length and width are 728 m and 297 m, respectively. The strike angle is 39° (counterclockwise) and the dip angle is nearly horizontal. The opening of the dislocation surface is 0.063m. Figure 12 presents the 3D schematic of the two sources in area B.

Figure 11. The observed deformation field in vertical (a) and horizontal (d) directions, the black arrow T1 corresponds to the profile line in Figure 13; The modeled vertical deformation field in vertical (b) and horizontal (c) directions; The residuals in vertical (c) and horizontal (e) directions.

Figure 12. 3D schematic of the two deformation sources in area B.

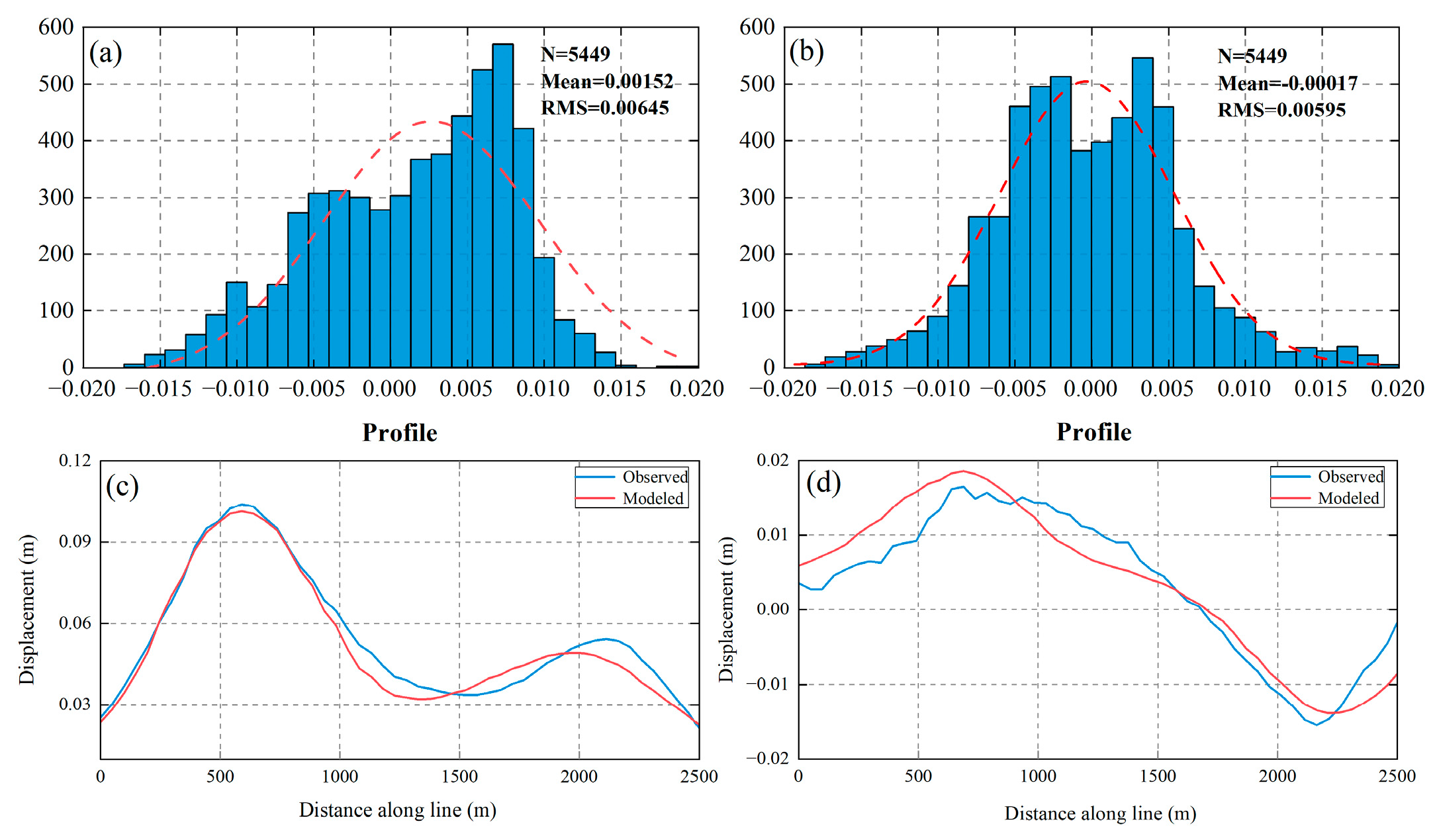
4.2.2. Comparative Analysis of Inversion Results for Area B

The residuals between the observed and simulated deformation fields serve as a reliable indicator of the inversion results quality. From the residual plots in Figure 9 and Figure 11, it can be observed that the residuals in the east-west direction for the single-source model are large and widely distributed, whereas the residuals for the dual-source model are smaller in both two directions and mostly exist in the far-field region, which may be due to the influence of the random noise and topography. Additionally, the models used in this study are based on the assumption that they are modeled in a homogeneous elastic half-space, whereas the area B geology is somewhat inhomogeneous. Considering the inherent limitations of the models themselves (e.g., lack of complete rotational freedom), the presence of some residuals, even in the near-field region, is expected.

Furthermore, to compare and evaluate the inversion effects of the two models more intuitively and quantitatively, we drew the residual histograms and the deformation profiles along T1 between their two-dimensional simulated deformation fields and observed deformation fields, as shown in Figure 13. From the distribution of residuals, it can be seen that the mean and root mean square values of vertical and east-west residuals of the dual-source model are smaller than those of the single-source model. However, compared with the vertical direction, the east-west residuals of both models are smaller and more concentrated towards the zero. This may be due to the fact that the ground uplift caused by the increase of pore pressure is mainly vertical uplift, and the horizontal deformation is smaller and simpler, so the simulation effect of the east-west direction is better than that of the vertical direction. On the other hand, in terms of the fit between the observed and simulated deformations along T1, the simulated curves of the dual-source model are more consistent with the trend of the observed curves, so its degree of fit is higher. In summary, whether from the residual analysis or the fitting degree of deformation, the dual-source model is more suitable for the inversion of reservoir parameters for complex deformations and yields more reliable inversion results than the single-source model.

Figure 13. (a) The distribution of vertical and horizontal residuals for the single-source and dual-source model (b) The distribution of vertical residuals for the dual-source model. (c) The distribution of horizontal residuals for the single-source model. (d) The distribution of horizontal residuals for the dual-source model. (e) The vertical deformation profile alone T1. (f) The horizontal deformation profile along T1. .

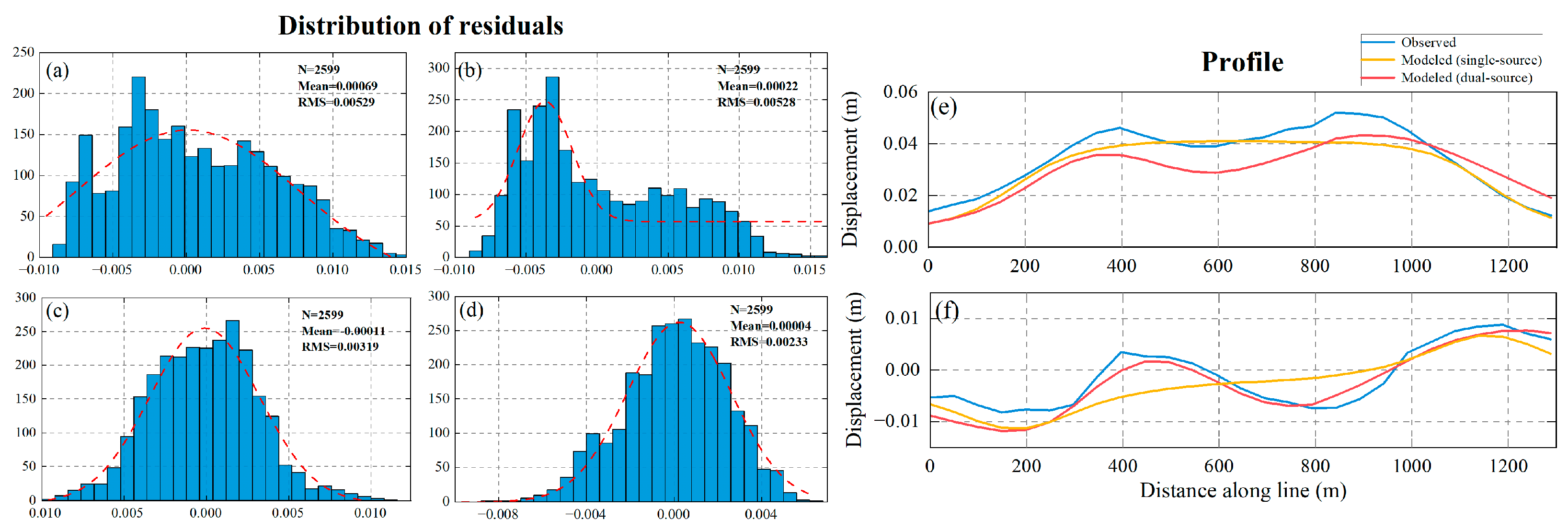
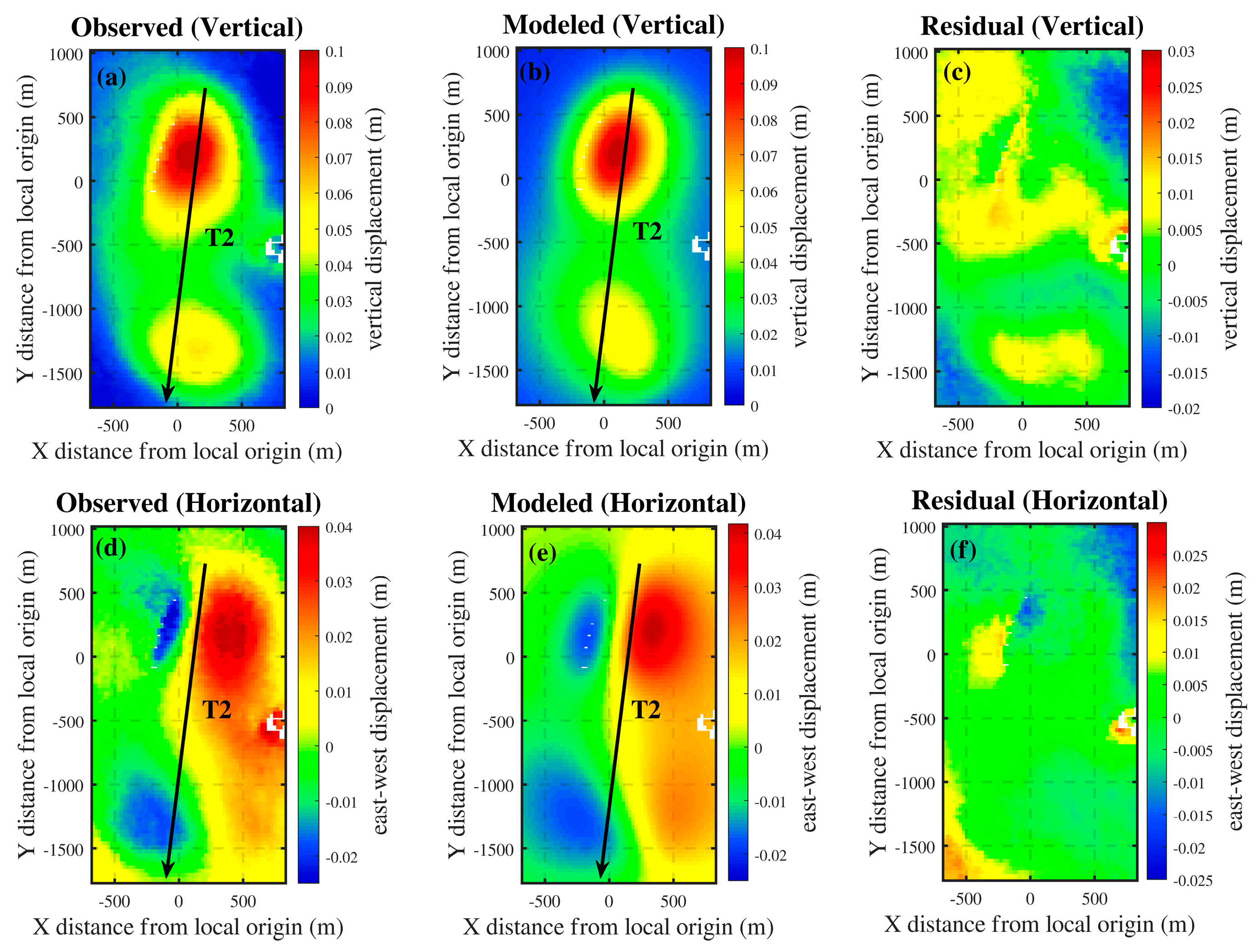
4.2.3. Inversion Results for Area C

The comparative analysis of the inversion results of the single-source model and the dual-source model in area B reveals that the dual-source model is more suitable for inverting the reservoir parameters of complex deformation. Considering the extremely complex deformation in area C, which cannot be reliably inverted using the single-source model, this paper directly applies the dual-source model to invert the complex deformation in area C. 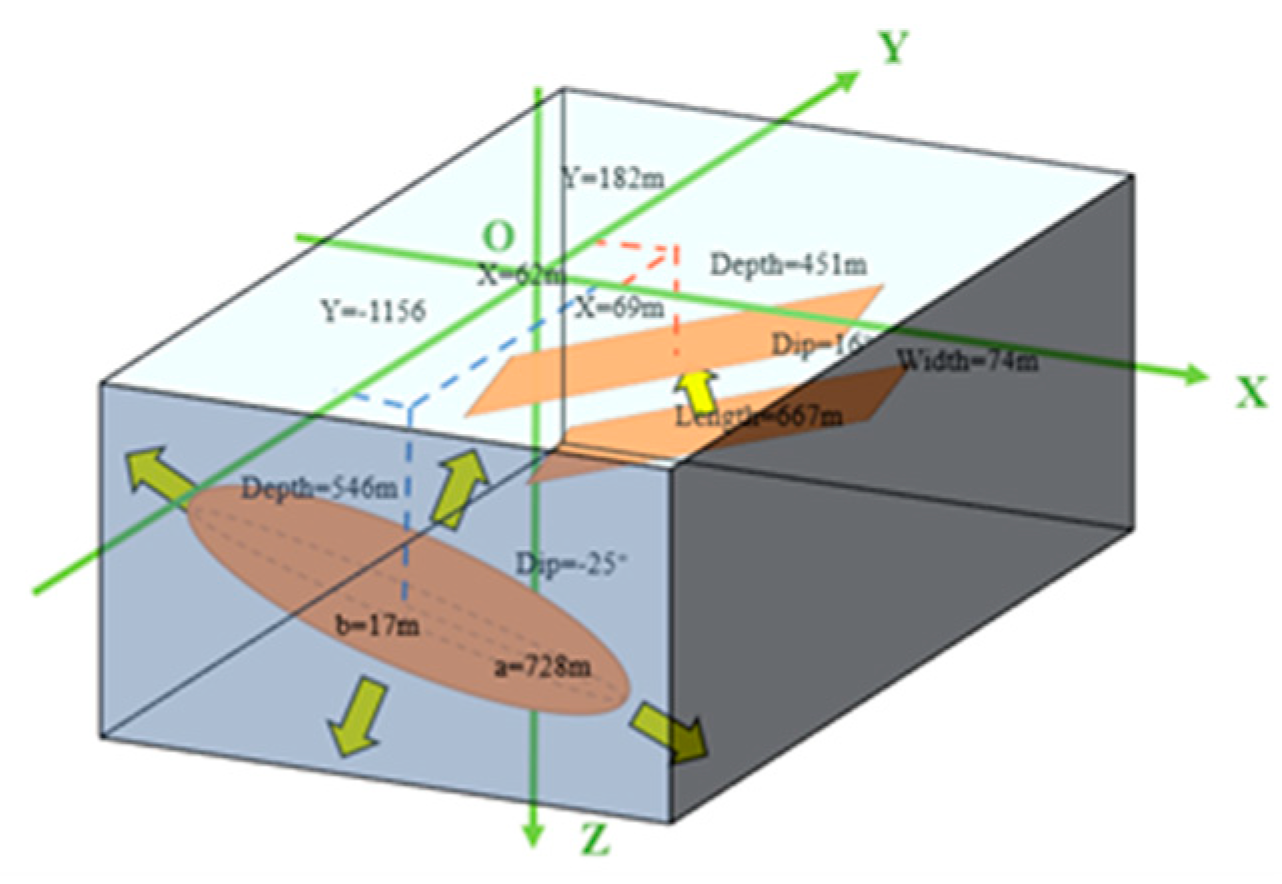The optimal parameters acquired through inversion are shown in Table 4. It can be seen from the inversion results that the ground deformation of area C is caused by a rectangular dislocation surface source on the north side of the shallow reservoir and an inclined ellipsoid source on the south side. For the rectangular fault surface source, its length and width are approximately 667 m and 74 m, respectively, with a burial depth of around 451 m. As for the dipping ellipsoid source, its major semi-axis is approximately 728 m, the minor semi-axis is around 17 m, and the burial depth is 546 m. A 3D schematic of two sources with optimal parameters for area C is given in Figure 15. In Figure 16, the root-mean-square values of the vertical and east-west residuals are 6.45 mm and 5.95 mm, respectively, and the fit between the simulated deformations and the observed deformations along the profile T2 is also high, which indicates that this inversion is effective and the reliability of the obtained parameters is high, and further validates the feasibility of the dual-source model.

Figure 14. The observed deformation field in vertical (a) and horizontal (d) directions, the black arrow T2 corresponds to the profile line in Figure 16 ; The modeled vertical deformation field in vertical (b) and horizontal (c) directions; The residuals in vertical (c) and horizontal (e) directions.

Figure 15. 3D schematic of the two deformation sources in area C.

Figure 16. (a) The distribution of vertical residuals for the dual-source model. (b) The distribution of horizontal residuals for the dual-source model. (c) The vertical deformation profile alone T2. (e) The horizontal deformation profile along T2.

5. Discussion

In this paper, we use the MSBAS method to monitor the ground deformation of the oilfields in the western Qaidam Basin based on Sentinel-1A satellite data. Derived from the SBAS technology, the MSBAS technology inherits the technical advantages of SBAS, which can overcome the influence of interferometric phase decorrelation and correct multiple errors, including terrain residual, orbital errors, and atmospheric delay errors. In addition, regularization or time filtering can remove high-frequency noise and improve the temporal resolution.

Different from only obtaining the one-dimensional deformation field in the line-of-sight direction, we acquired the two-dimensional time series deformation field in vertical and east-west directions by MSBAS technology. A series of results indicate that besides vertical deformation, there is also a significant amount of deformation in the horizontal east-west direction at the ground of the oilfields, with a maximum east-west deformation of 16 mm/year. Unlike the LOS deformation, which is a mixture of vertical and horizontal deformation, independent vertical and east-west deformations can more comprehensively and intuitively reflect the real deformation effects of the oilfields. This provides more reliable support and guidance for oil field development planning and land subsidence management.

Subsequently, based on the acquired two-dimensional cumulative deformation, we perform reservoir modeling for two complex deformation areas using geophysical models. In real work scenarios, the injection and production activities in oilfields are often carried out simultaneously at multiple places, resulting in complex ground deformation. By comparing and analyzing the simulation effects of the single-source model and the dual-source model, this study found that there are often multiple deformation sources underground in areas with complex deformation. The deformation field simulated by the single-source model is relatively simple and cannot effectively reflect the observed deformation field. The dual-source model not only simulates smaller residual mean values and root mean square values than the single-source model but also has a higher fit with the observed deformation field. Therefore, for areas with complex deformation, the reservoir parameters inverted using the dual-source model are more reliable and better represent the mapping relationship between reservoir changes and ground deformation in oilfields. Moreover, the two-dimensional deformation variable used as the model input variable in this study adds nonlinear inversion constraints compared to most current one-dimensional inversion methods, so the inversion efficiency and accuracy are further improved. Unfortunately, due to the lack of water injection and oil production data for the oilfields in the study area, further validation of the inversion results cannot be conducted. In future research on reservoir parameter inversion, efforts should be made to strengthen the collection of such data and the validation of models.

6. Conclusions

This study conducted vertical and east-west deformation monitoring of the oilfields in the western Qaidam Basin by simultaneously processing ascending and descending Sentinel-1A SAR images from 2021 to 2022. Based on this, the reservoir parameters of two deformation areas were inverted using single-source and dual-source models. The main results are as follows:

In the study area, the HTG oilfield exhibited uneven ground subsidence, with a maximum subsidence rate of 12 mm/year. At the same time, the GCG oilfield and YSS oilfield experienced substantial ground uplift, with a maximum rate of 48 mm/year. Along with this uplift process, the east-west deformation rate in this area also reached 16 mm/year. The cause of the ground uplift in the oilfield may be related to increased reservoir pore pressure resulting from water injection. Changes in water injection intensity may lead to changes in deformation rates.

Combining the analysis of inversion results, it can be concluded that the introduction of a two-dimensional deformation field helps improve the non-uniqueness of the inversion results, enhance the robustness of the inversion process, and consequently obtain more reliable oil reservoir parameters. Furthermore, the dual-source model is more suitable for inverting complex deformation reservoir parameters compared to the single-source model.

Author Contributions

Conceptualization, A.L. and R.Z. (Rui Zhang); methodology, A.L.; investigation, Y.Y. and A.S.; data curation, A.L., T.W. (Tianyu Wang) and T.W. (Ting Wang); writing—original draft preparation, A.L.; writing—review and editing, A.L., R.Z. (Rui Zhang) and X.B.; visualization, R.Z. (Runqing Zhan); funding acquisition, R.Z. (Rui Zhang). All authors have read and agreed to the published version of the manuscript.

Funding

This research was jointly funded by the National Natural Science Foundation of China (Grant 42171355 and 42071410); and the Sichuan Science and Technology Program (No.2020JDTD0003 and 2020YJ0322).

Data Availability Statement

The Sentinel-1A SAR images can be downloaded from Alaska Satellite Facility (https://search.asf.alaska.edu/), and the precise orbit data (POD) can be obtained from European Space Agency (http://aux.sentinel1.eo.esa.int/). The digital elevation model (DEM) is from the United States Geological Survey (https://earthexplorer.usgs.gov/). The open-source software MSBAS is available in https://insar.ca/multidimensional-small-baseline-subset-msbas/. The software package GBIS for parameters inversion is from the Centre for Observation and Modelling of Earthquakes, Volcanoes and Tectonics (COMET) (https://comet. nerc.ac.uk/gbis/). We are very grateful for the above support.

Acknowledgments

We appreciate the European Space Agency for providing the Sentinel-1A data freely. We are also grateful to the editor and reviewers for giving us valuable suggestions and comments to help us improve this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

Nasen, L.C.; Noble, B.F.; Johnstone, J.F. Environmental Effects of Oil and Gas Lease Sites in a Grassland Ecosystem. Journal of Environmental Management 2011, 92, 195–204. [Google Scholar] [CrossRef]
Beyer, J.; Trannum, H.C.; Bakke, T.; Hodson, P.V.; Collier, T.K. Environmental Effects of the Deepwater Horizon Oil Spill: A Review. Marine Pollution Bulletin 2016, 110, 28–51. [Google Scholar] [CrossRef]
Weijermars, R. Surface Subsidence and Uplift Resulting from Well Interventions Modeled with Coupled Analytical Solutions: Application to Groningen Gas Extraction (Netherlands) and CO2-EOR in the Kelly-Snyder Oil Field (West Texas). Geoenergy Science and Engineering 2023, 228, 211959. [Google Scholar] [CrossRef]
Comerlati, A. Saving Venice by Seawater. J. Geophys. Res. 2004, 109, F03006. [Google Scholar] [CrossRef]
Khakim, M.Y.N.; Tsuji, T.; Matsuoka, T. Geomechanical Modeling for InSAR-Derived Surface Deformation at Steam-Injection Oil Sand Fields. Journal of Petroleum Science and Engineering 2012, 96–97, 152–161. [Google Scholar] [CrossRef]
Wei, X.; Sha, W.; Shen, X.; Si, D.; Zhang, G.; Ren, S.; Yang, M. Petroleum Exploration History and Enlightenment in Qaidam Basin. Xinjiang Petroleum Geology 2021, 42, 302–311. [Google Scholar] [CrossRef]
Liu, W.; Lin, C.; Wang, G.; Liu, J.; Jiang, Y. Characteristics of Low Permeability Reservoir and Its Origin in Youquanzi Oilfield in the Northwest Part of Qaidam Basin. ACTA PETROLEI SINICA 2009, 30, 417–421. [Google Scholar] [CrossRef]
Yangming, Z.; Huanxin, W.; Aiguo, S.; Digang, L.; Dehua, P. Geochemical Characteristics of Tertiary Saline Lacustrine Oils in the Western Qaidam Basin, Northwest China. Applied Geochemistry 2005, 20, 1875–1889. [Google Scholar] [CrossRef]
Aobpaet, A.; Cuenca, M.C.; Hooper, A.; Trisirisatayawong, I. InSAR Time-Series Analysis of Land Subsidence in Bangkok, Thailand. International Journal of Remote Sensing 2013, 34, 2969–2982. [Google Scholar] [CrossRef]
Liao, M.; Zhang, R.; Lv, J.; Yu, B.; Pang, J.; Li, R.; Xiang, W.; Tao, W. Subsidence Monitoring of Fill Area in Yan’an New District Based on Sentinel-1A Time Series Imagery. Remote Sensing 2021, 13, 3044. [Google Scholar] [CrossRef]
Bao, X.; Zhang, R.; Shama, A.; Li, S.; Xie, L.; Lv, J.; Fu, Y.; Wu, R.; Liu, G. Ground Deformation Pattern Analysis and Evolution Prediction of Shanghai Pudong International Airport Based on PSI Long Time Series Observations. Remote Sensing 2022, 14, 610. [Google Scholar] [CrossRef]
Cai, J.; Zhang, L.; Dong, J.; Dong, X.; Li, M.; Xu, Q.; Liao, M. Detection and Characterization of Slow-Moving Landslides in the 2017 Jiuzhaigou Earthquake Area by Combining Satellite SAR Observations and Airborne Lidar DSM. Engineering Geology 2022, 305, 106730. [Google Scholar] [CrossRef]
Cheaib, A.; Lacroix, P.; Zerathe, S.; Jongmans, D.; Ajorlou, N.; Doin, M.-P.; Hollingsworth, J.; Abdallah, C. Landslides Induced by the 2017 Mw7.3 Sarpol Zahab Earthquake (Iran). Landslides 2022, 19, 603–619. [Google Scholar] [CrossRef]
Zheng, Z.; Xie, C.; He, Y.; Zhu, M.; Huang, W.; Shao, T. Monitoring Potential Geological Hazards with Different InSAR Algorithms: The Case of Western Sichuan. Remote Sensing 2022, 14, 2049. [Google Scholar] [CrossRef]
Wang, T.; Zhang, R.; Zhan, R.; Shama, A.; Liao, M.; Bao, X.; He, L.; Zhan, J. Subsidence Monitoring and Mechanism Analysis of Anju Airport in Suining Based on InSAR and Numerical Simulation. Remote Sensing 2022, 14, 3759. [Google Scholar] [CrossRef]
Shi, J.; Yang, H.; Peng, J.; Wu, L.; Xu, B.; Liu, Y.; Zhao, B. InSAR Monitoring and Analysis of Ground Deformation Due to Fluid or Gas Injection in Fengcheng Oil Field, Xinjiang, China. J Indian Soc Remote Sens 2019, 47, 455–466. [Google Scholar] [CrossRef]
Zhang, Y.; Xiang, W.; Liu, G.; Wang, X.; Zhang, R.; Zhang, X.; Tong, J.; Yuan, H.; Zhang, C. Geodetic Imaging of Ground Deformation and Reservoir Parameters at the Yangbajing Geothermal Field, Tibet, China. Geophysical Journal International 2023, 234, 379–394. [Google Scholar] [CrossRef]
Chen, Y.; Tong, Y.; Tan, K. Coal Mining Deformation Monitoring Using SBAS-InSAR and Offset Tracking: A Case Study of Yu County, China. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2020, 13, 6077–6087. [Google Scholar] [CrossRef]
Sun, H.; Zhang, Q.; Zhao, C.; Yang, C.; Sun, Q.; Chen, W. Monitoring Land Subsidence in the Southern Part of the Lower Liaohe Plain, China with a Multi-Track PS-InSAR Technique. Remote Sensing of Environment 2017, 188, 73–84. [Google Scholar] [CrossRef]
Juncu, D.; Árnadóttir, Th.; Hooper, A.; Gunnarsson, G. Anthropogenic and Natural Ground Deformation in the Hengill Geothermal Area, Iceland. J. Geophys. Res. Solid Earth 2017, 122, 692–709. [Google Scholar] [CrossRef]
Chen, Y.; Yu, S.; Tao, Q.; Liu, G.; Wang, L.; Wang, F. Accuracy Verification and Correction of D-InSAR and SBAS-InSAR in Monitoring Mining Surface Subsidence. Remote Sensing 2021, 13, 4365. [Google Scholar] [CrossRef]
Klemm, H.; Quseimi, I.; Novali, F.; Ferretti, A.; Tamburini, A. Monitoring Horizontal and Vertical Surface Deformation over a Hydrocarbon Reservoir by PSInSAR. First Break 2010, 28. [Google Scholar] [CrossRef]
Yang, Q.; Zhao, W.; Dixon, T.H.; Amelung, F.; Han, W.S.; Li, P. InSAR Monitoring of Ground Deformation Due to CO2 Injection at an Enhanced Oil Recovery Site, West Texas. International Journal of Greenhouse Gas Control 2015, 41, 20–28. [Google Scholar] [CrossRef]
Ji, L.; Zhang, Y.; Wang, Q.; Xin, Y.; Li, J. Detecting Land Uplift Associated with Enhanced Oil Recovery Using InSAR in the Karamay Oil Field, Xinjiang, China. International Journal of Remote Sensing 2016, 37, 1527–1540. [Google Scholar] [CrossRef]
Feng, W.; Li, Z.; Hoey, T.; Zhang, Y.; Wang, R.; Samsonov, S.; Li, Y.; Xu, Z. Patterns and Mechanisms of Coseismic and Postseismic Slips of the 2011 M W 7.1 Van (Turkey) Earthquake Revealed by Multi-Platform Synthetic Aperture Radar Interferometry. Tectonophysics 2014, 632, 188–198. [Google Scholar] [CrossRef]
Wang, Z.; Zhang, R.; Liu, Y. 3D Coseismic Deformation Field and Source Parameters of the 2017 Iran-Iraq Mw7.3 Earthquake Inferred from DInSAR and MAI Measurements. Remote Sensing 2019, 11, 2248. [Google Scholar] [CrossRef]
Samsonov, S.; d’Oreye, N.; Smets, B. Ground Deformation Associated with Post-Mining Activity at the French–German Border Revealed by Novel InSAR Time Series Method. International Journal of Applied Earth Observation and Geoinformation 2013, 23, 142–154. [Google Scholar] [CrossRef]
Samsonov, S.V.; d’Oreye, N. Multidimensional Small Baseline Subset (MSBAS) for Two-Dimensional Deformation Analysis: Case Study Mexico City. Canadian Journal of Remote Sensing 2017, 43, 318–329. [Google Scholar] [CrossRef]
Hansen, P.C. The truncatedSVD as a Method for Regularization. BIT 1987, 27, 534–553. [Google Scholar] [CrossRef]
Matsu’Ura, M. Inversion of Geodetic Data. I. Mathematical Formulation. J,Phys,Earth 1977, 25, 69–90. [Google Scholar] [CrossRef]
Yang, X.-M.; Davis, P.M.; Dieterich, J.H. Deformation from Inflation of a Dipping Finite Prolate Spheroid in an Elastic Half-Space as a Model for Volcanic Stressing. J. Geophys. Res. 1988, 93, 4249–4257. [Google Scholar] [CrossRef]
Okada, Y. Surface Deformation Due to Shear and Tensile Faults in a Half-Space. Bulletin of the Seismological Society of America 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
Okada, Y. Internal Deformation Due to Shear and Tensile Faults in a Half-Space. Bulletin of the Seismological Society of America 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
Du, Z. Theory and Application of Geodesy Inversion Based on Mechanical Models. Acta Geodaetica et Cartographica Sinica 2002, 31, 94. [Google Scholar] [CrossRef]
Bagnardi, M.; Hooper, A. Inversion of Surface Deformation Data for Rapid Estimates of Source Parameters and Uncertainties: A Bayesian Approach. Geochem. Geophys. Geosyst. 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
Mosegaard, K.; Tarantola, A. Monte Carlo Sampling of Solutions to Inverse Problems. Journal of Geophysical Research 1995, 100, 12431–12447. [Google Scholar] [CrossRef]
Mogi, K. Relations between the Eruptions of Various Volcanoes and the Deformations of the Ground Surfaces around Them. Bulletin of the Earthquake Research Institute 1958, 36, 99–134. [Google Scholar]
Yang, X.-M.; Davis, P.M.; Dieterich, J.H. Deformation from Inflation of a Dipping Finite Prolate Spheroid in an Elastic Half-Space as a Model for Volcanic Stressing. J. Geophys. Res. 1988, 93, 4249–4257. [Google Scholar] [CrossRef]

Figure 3. Schematic diagram of Finite Prolate Spheroidal Model.

Figure 4. Schematic diagram of Okada Model.

Figure 5. (a) Vertical deformation rate. Positive and negative values represent uplift and subsidence, respectively. (b) East-west deformation rate. Positive values indicate eastward movement, while negative values signify westward motion.

Figure 6. Time series of vertical (a) and east-west (b) cumulative deformation from January 2021 to December 2022 in the study area.

Figure 7. The time series of the vertical and east-west deformation at points P1-P6, respectively.

Figure 8. The vertical (a-c) and east-west (d-f) displacements along the profile lines L1 to L3, respectively.

Figure 10. 3D schematic of the single deformation source in area B.

Table 2. Inversion result of the rectangular dislocation surface source under area B.

Source	Source parameter	Optimal value	Confidence interval (2.5%)	Confidence interval (97.5%)
Rectangular dislocation surface	Length (m)	980.668	956.542	1016.85
	Width (m)	399.642	372.435	433.755
	X	95.1182	78.7143	117.508
	Y	255.5	232.037	279.799
	Depth (m)	191.863	171.431	227.192
	Strike (°)	-77.5828	-79.791	-74.8579
	Dip (°)	3.20863	-0.540244	-8.16204
	Opening	0.04148	0.03741	0.04697

Table 3. Inversion result of two sources under area B.

Source	Source parameter	Optimal value	Confidence interval (2.5%)	Confidence interval (97.5%)
Dipping ellipsoid	X	-265.211	-288.02	-246.469
	Y	104.859	87.0402	126.723
	Depth (m)	218.904	194.592	246.927
	Major semi-axis (m)	206.595	168.143	252.8
	Minor semi-axis (m)	15.0091	6.77208	55.16096
	Strike (°)	65.0119	46.6214	75.1686
	Dip (°)	17.5249	10.5561	27.3211
	DP/mu	0.03467	0.00378	0.09103
Rectangular dislocation surface	Length (m)	728.471	637.649	777.356
	Width (m)	297.448	204.269	333.208
	X	459.077	413.4	476.708
	Y	50.9312	17.552	80.1817
	Depth (m)	232.529	211.876	286.603
	Strike (°)	-39.4342	-43.6891	-34.872
	Dip (°)	-5.77362	-11.5944	-0.41442
	Opening (m)	0.06292	0.05257	0.09577

Table 4. Inversion result of two sources under area C.

Source	Source parameter	Optimal value	Confidence interval (2.5%)	Confidence interval (97.5%)
Rectangular dislocation surface	Length (m)	667.166	39.456	703.224
	Width (m)	74.3788	35.9698	87.6175
	X	69.8736	44.1824	84.5374
	Y	182.243	170.078	194.093
	Depth (m)	451.511	441.582	468.684
	Strike (°)	15.2082	13.0072	17.5933
	Dip (°)	16.0407	11.3015	19.5505
	Opening (m)	1.15447	1.01517	2.39906
Dipping ellipsoid	X	61.8081	35.3234	151.877
	Y	-1156.77	-1341.57	-1113.89
	Depth (m)	546.16	492.207	598.769
	Major semi-axis (m)	728.4	334.435	792.369
	Minor semi-axis (m)	17.2557	3.82994	55.9840
	Strike (°)	151.538	82.9156	158.568
	Dip (°)	-25.2426	-29.3177	-9.12962
	DP/mu	0.07786	0.01098	0.358436

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer