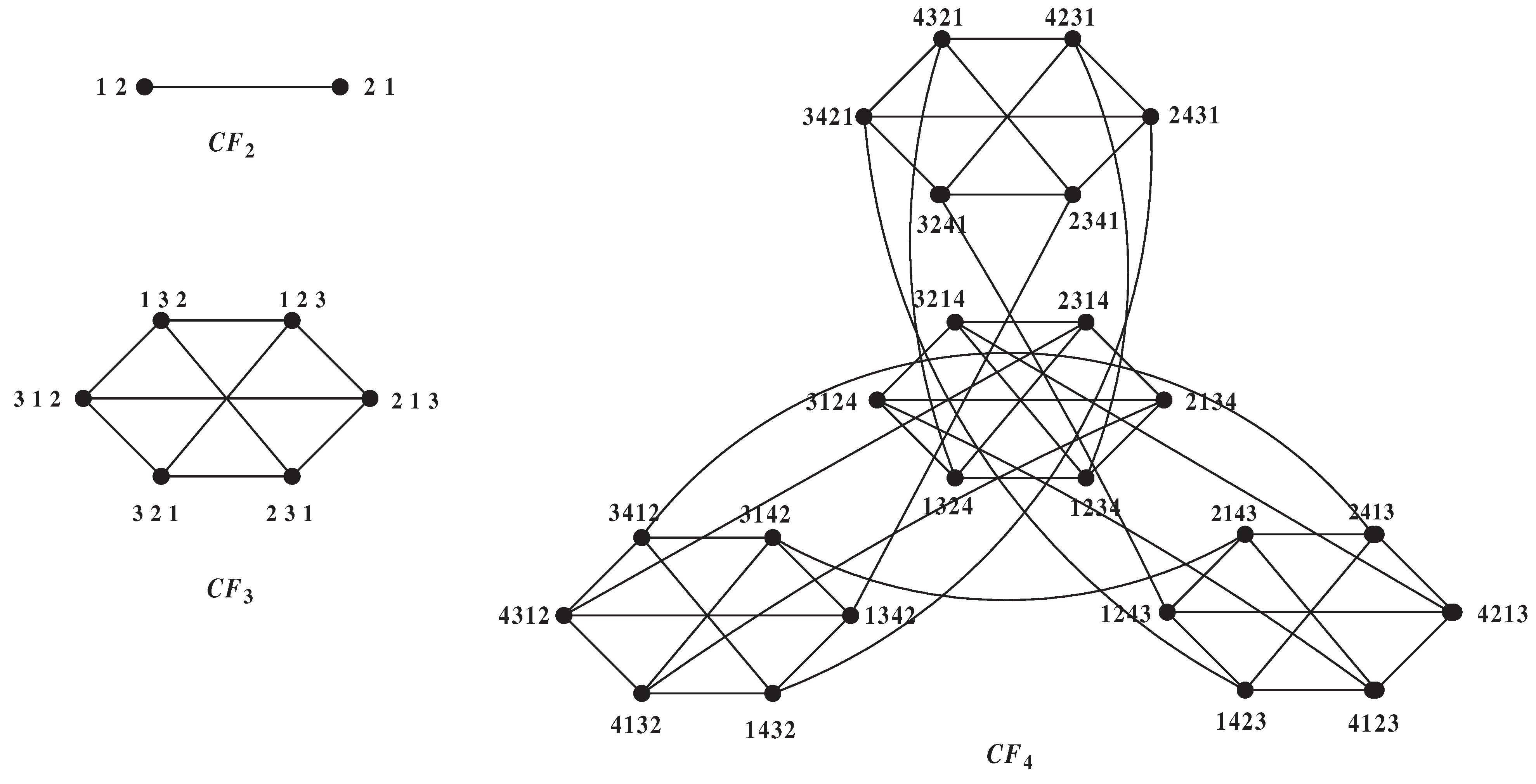
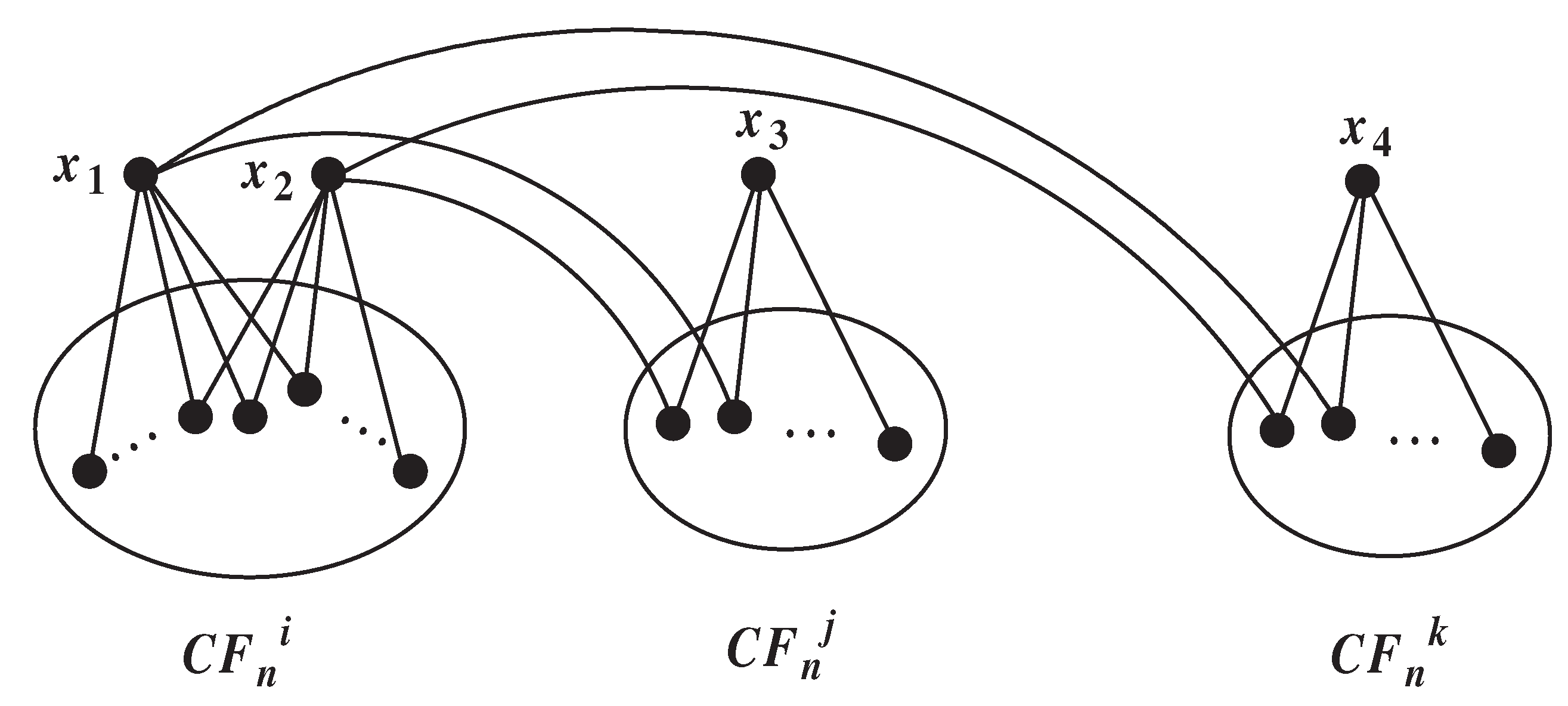
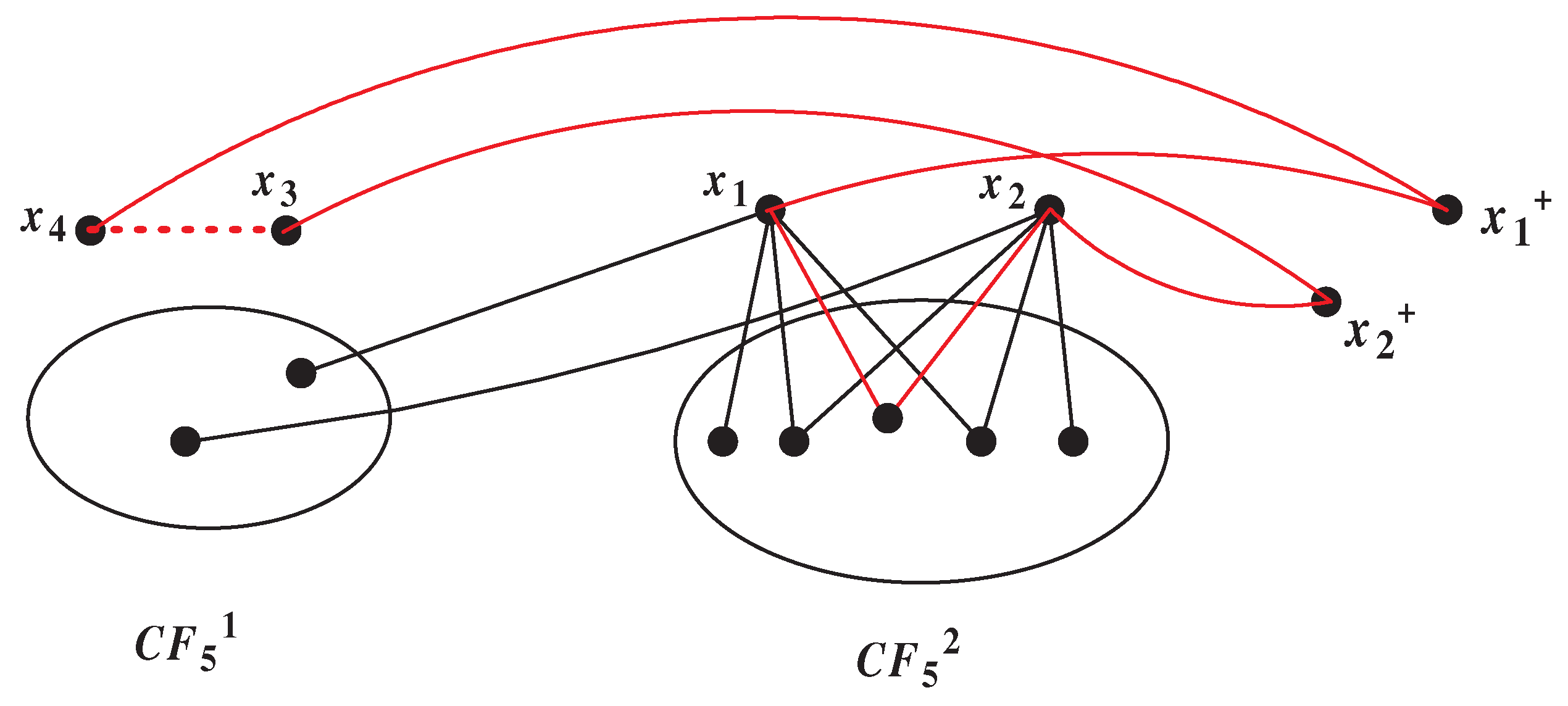
4. The 4-component connectivity of
Lemma 4.1. When , let S is an -set and , .
Proof. Let , since S is an -set, are nonadjacent with each other. Note that , . Next, we will think about the following three cases.
Case 1. belong to the same subgraph .
In this case, since and S is an -set, . By Proposition 2.3, we know the outgoing neighbors of are different. Thus, .
Case 2. belong to two different subgraphs , .
In this case, we can let
,
. Since
and
are nonadjacent, we can get
,
. By the definition of
, we know
only has one outgoing neighbor. If the structure shown in
Figure 2 (a) exists,
. Now we can show that this structure does not exist. As
and
, we assume
, then
or
. Thus
,
, the structure shown in
Figure 2 (a) does not exist. Thus
.
Case 3. belong to three different subgraphs , , are different from each other).
In this case, we can let . By the definition of , we know , thus .
Combining the above three situations, we can get .
Lemma 4.2. When , let S is an -set and , .
Proof. Let , since S is an -set, are nonadjacent with each other. Note that . We think about the following three cases.
Case 1. belong to the same subgraph .
Since , by Lemma 4.1, we can get . By the definition of and Proposition 2.3, we know the outgoing neighbors of are different and every vertex has two different outgoing neighbors. Thus .
Case 2. belong to two different subgraphs , .
In this case, we can let
,
. Since
, by Lemma 3.3, we know that
. By Proposition 2.8, we can get
. By Proposition 2.2, we can get
and
have at most two neighbors which belong to
. In other words, there are at least two neighbors of
and
belong to
. If the structure shown in
Figure 2 (b) exists, then
. Furthermore,
if and only if this structure exists. Now, we can prove this structure does not exist.
Since , and , by Corollary 2.6, we can know that must belong to a common subgraph in . So we can assume , . As the subgraph of is isomorphic to , thus or are different from each other).
If , then , . Since , and one of the two outgoing neighbors of belong to , we can get . Thus . As are adjacent to , so or or . When , , , and is adjacent to . Since , , , . When , , , and is adjacent to . Since , and , , . When , , , and is adjacent to . Since , and , , . So this structure does not exist.
If , then , . Since , and one of the two outgoing neighbors of belong to , we can get . Thus . As are adjacent to , so or or . When , , , and is adjacent to . Since , , , . When , , , and is adjacent to . Since , and , , . When , , , and is adjacent to . Since , and , , .
Thus the structure shown in
Figure 2 (b) does not exist,
.
Case 3. belong to three different subgraphs , , are different from each other).
Without loss of generality, we can let , , . By the definition of , we can get , thus .
Combining the above three situations, we can get .
Lemma 4.3. When n is odd, let is an -set, where , and . Then .
Proof. When
n is odd,
occurs if and only if the structure in
Figure 3 appears. Next, we will prove that these structures can not appear.
Firstly, we prove that the structure shown in
Figure 3 (a) does not exist. Suppose on the contrary, we assume this structure exists and
, then
,
. As
, by the proof process of Lemma 3.3, we can know that
must have three common neighbors in
. Note that
n is odd, then
is even, and
. By Corollary 2.6, we can get
must belong to a common subgraph in
; Otherwise, if
belong to two different subgraphs in
, then
, a contradiction. So
,
,
,
,
. By Corollary 3.2, we know
. As one of the two outgoing neighbors of
and
belong to a common subgraph with
, so
and
. Now we assume
. As one of the two outgoing neighbors of
belongs to
, so
or
. When
,
,
. In this situation,
,
, since
, we have
,
. Thus this structure does not exist. When
, as
are adjacent to
, we can get
,
, this contradicts to the fact
, thus this structure does not exist.
Next we will prove that the structure in
Figure 3 (b) does not exist. Similarly, we know that
,
,
and
. We let
, then
,
. Thus
and
, the structure in
Figure 3 (b) does not exist.
Lemma 4.4. When n is even, let is an -set, where , and . Then .
Proof. When
n is even,
occurs if and only if the structure in
Figure 4 appears. Next, we will prove that this structure does not exist. Note that
,
is odd.
Suppose on the contrary, we assume this structure exists, as , we know must have three common neighbors in by Lemma 3.3. Now, we let , . By Corollary 3.2, we know and . Thus , , and can not belong to a common subgraph in , this contradicts to this structure. Thus .
Lemma 4.5. When , let S is an -set and , then when n is odd, ; when n is even, .
Proof. Let , since S is an -set, are nonadjacent with each other. We proof this result by induction on n. By Lemma and Lemma , we know when , this result holds. Now we assume that and the result holds for . Note that . Next, we think about the following three cases:
Case 1. belong to a same subgraph .
When n is odd, by induction hypothesis, we have . By Proposition 2.3 and the definition of , we know the neighbors of in are different and every vertex has two outgoing neighbors. Thus .
When n is even, by induction hypothesis, we have . By Proposition 2.3 and the definition of , we know the neighbors of in are different and every vertex has only one outgoing neighbor. Thus .
Case 2. belong to two different subgraphs , .
In this case, we can let
,
. By Lemma
, we can get: when
n is odd,
; when
n is even,
. By Proposition 2.8, we know when
n is odd,
; when
n is even,
. When
n is odd, by Proposition 2.2, we know
have at most two outgoing neighbors can belong to
, in another word, there are at least two outgoing neighbors of
can belong to
. So
. By Lemma 4.3, we know
, thus
. When
n is even, if the structure of
Figure 4 exist, then
. By Lemma 4.4, we know this structure does not exist, so
.
Case 3. belong to three different subgraphs , , are different from each other).
Without loss of generality, we can let , , . By Proposition 2.8, we have when n is odd, ; when n is even, . Thus when n is odd, ; when n is even, .
Thus the result holds.
Corollary 4.6. When n is even, let is an -set, if , then belong to a same subgraph in .
Lemma 4.7. For , if , then contains a big component C, which satisfies the result .
Proof. We are not going to think about is connected for the moment, so we assume that is disconnected. Let for with , where . If , then and is connected. By Proposition , we know there exists a vertex in , which has neighbor in . So is connected, a contradiction. Hence we consider . Since , we have , , , , . Firstly, we proof the following Claim is correct.
Claim 1. If for some , then is connected.
Proof of Claim 1. By Proposition , we can get is connected for each . On the other hand, as , we can get , which implies for . Hence is connected.
Since , by Claim 1, we can get is connected. If and are all connected, we know is connected. As , is connected. As , we have is connected. Since is disconnected, at least one of is disconnected, which leads to the following two cases.
Note that if , by Proposition , we can get has a big component and at most two vertices, which has a neighbor in . Thus, if or is connected, then satisfies the condition . If and are all disconnected, then satisfies the condition . Hence we only think about this situation: .
Case 1. Both and are disconnected.
In this case, we know . Since , . Hence , . By Corollary 3.4, we know has a big component and a singleton . By Lemma 1, should consider the following two situations: has two components, one of which is a singleton. has three components, two of which are singletons. For , let is the big component and is the singleton of , since and , by Proposition , we can get is connected. Similarly, we can also get is connected. Thus the result holds. For , let is the big component and , are singletons of . If is nonadjacent to , then are three singletons in . By Lemma , we can get , this contradicts to the fact . If is adjacent to , say , then only has two components; Otherwise, we let has three components, then is a singleton in . By Proposition 2.5, we have , a contradiction. Thus the result holds.
Case 2. Only is disconnected.
Since , . As is disconnected, we have and then . If , then , , a contradiction. Thus . Since , is connected. As , by Corollary , we know has a big component S and at most one singleton. By the same argument as that of Case 1, we can get is connected. Then must satisfies condition .
Case 3. Only is disconnected.
In this case, we have by Proposition and since and . As , we have is connected.
If , by Lemma 1, has a big component S and one single and two singletons. By the same argument as that of Case 1, we can get is connected. Then must be one of conditions and .
Now, we suppose . Then . Let W be the union of components of , whose vertices, which are totally contained in , are not connected with . By Proposition and Proposition , we know , which implies . Thus satisfies or .
Combing the above three cases, we know this result holds.
Lemma 4.8. For , if , then contains a big component C, which satisfies the result .
Proof. Similarly, we do not think about the situation is connected, so we let is disconnected. Let for with , where . If , then and is connected. By Proposition , we can get is connected. So we assume . Since , we have , , , , , . Firstly, we proof the following Claim is correct.
Claim 2. If , then is connected.
Proof of Claim 2. By Proposition , we know is connected for each . On the other hand, since for , we can get . Thus is connected.
By Claim 2, we know is connected. If both and are connected, we can get is connected. As , and is connected, thus is connected. Since is disconnected, at least one of is disconnected, which leads to the following cases.
Case 1. Both and are disconnected.
In this case, we know . By Corollary 3.4, we know that has a big component and one singleton . As . Thus is connected. Similarly, we can get is also connected. Thus the result holds.
Case 2. Only is disconnected.
As is disconnected, we have and then . Since , is connected. Since , by Corollary 3.4, has a big component C and one singleton. Since , we can get is connected. Then must be one of conditions .
Case 3. Only is disconnected.
In this case, , . As , we have is connected.
If , by Lemma , has a big component C with . By the same argument as that of Case 2, we can get is connected. Thus the result holds.
If , then . Let W be the union of components of , whose vertices, which are totally contained in , and are not connected with . By Proposition and Proposition , we have . Thus the result holds.
Lemma 4.9. Let for odd n and for even n, then contains a big component C, which satisfies that .
Proof. By Lemma and Lemma , the result holds for . We proof this result by induction on n. Assume and the result holds for . Now we suppose is disconnected for any with or . Let for with , where .
When n is odd, if , then and is connected, and thus, by Proposition , we can get is connected. Now we assume ; When n is even, if , then and is connected, and thus, by Proposition , we can get is connected. Now we assume .
Claim 3. When n is even, if , then is connected; When n is odd, if , then is connected;
Proof of Claim 3. By Proposition , we know is connected for each . On the other hand, since for is even) and for is odd), we can get . Thus is connected.
Since is even) and is odd), we have for even n and for odd n. By Claim 3, we can get is connected. If and are all connected, as is even) and is odd), then is connected. Similarly, we can also get is connected. So at least one of is disconnected, which leads to the following cases.
Note that, when n is odd, if , by the same argument of Lemma 4.7, we know satisfies condition or . Hence we assume that .
Case 1. Both and are disconnected.
When n is even, we have . By Corollary 3.4, we know and all have a big component and one singleton. As , , Thus is connected, the result holds.
When n is odd, we have .So by Lemma 1, we would consider the following three subcases: Both and have three components, two of which are singletons; Only one of and has three components, two of which are singletons; Both and have two components, one of which is singleton. Now, we just proof the first subcase and the other two subcases could be proved by the same argument. Let (resp., ) be the two singletons and the other big component of (resp., ). Since and , by Proposition , we know is connected. Similarly, we can get is connected.
If are four singletons in , then by Proposition , we know , a contradiction.
If has three singletons, then by Lemma , we can get , this contradicts to the fact . So has two singletons or only one singleton.
Claim 4. If has at least one edge, say , then only has two components.
Proof of Claim 4. Suppose has at least three components. Then is a singleton or . If is a singleton, then , a contradiction. If , then , a contradiction.
Thus, by Claim 4, the result holds.
Case 2. Only is disconnected.
As is disconnected, we have for even n and for odd n, then is even) and is odd). Since is even) and is odd), is connected. Since , when n is even, by Corollary 3.4, we know has a big component C and one singleton; When n is odd, by Lemma 1, we know has a big component C and at most two singletons. By the same argument as that of Case 1, we can get is connected. Then must be one of conditions and .
Case 3. Only is disconnected.
In this case, for even n and for odd n. As is even) and is odd), we have is connected.
When n is even, if , by introduction, we know has a big component C with . By the same argument as that of Case 1, we can get is connected. Thus the result holds. If , then . Let W be the union of components of , whose vertices, which are totally contained in , and are not connected with . By Proposition and Proposition , we have . Thus the result holds.
When n is odd, if , by introduction, has a big component C with . By the same argument as that of Case 1, we can get is connected. Thus the result holds. If , then . Let W be the union of components of , whose vertices, which are totally contained in , and are not connected with . By Proposition , . Then we have . Thus the result holds.
Theorem 2. For , when n is odd, ; when n is even, .
Proof. By Lemma 1, we have . For , by Lemma , we can get when n is odd, ; when n is even, . Next, we will prove that and . For , if we let , then has three singletons: . Thus . For , when n is odd, let , where , , , then and there are three singletons in . Thus when n is odd, . When n is even, let , where , , , then and . As belong to a common subgraph, by Proposition 2.3, we know have different outgoing neighbors. So and are three singletons in . Thus when n is even, .
5. The 5-component connectivity of
Lemma 5.1. For , let S is an -set and , then .
Proof. Let , since S is an -set, are nonadjacent to each other. As , we know can not belong to a same subgraph of . So we need think about the following cases:
Case 1: belong to two different subgraphs of .
In this case, we can divide it into two subcases:
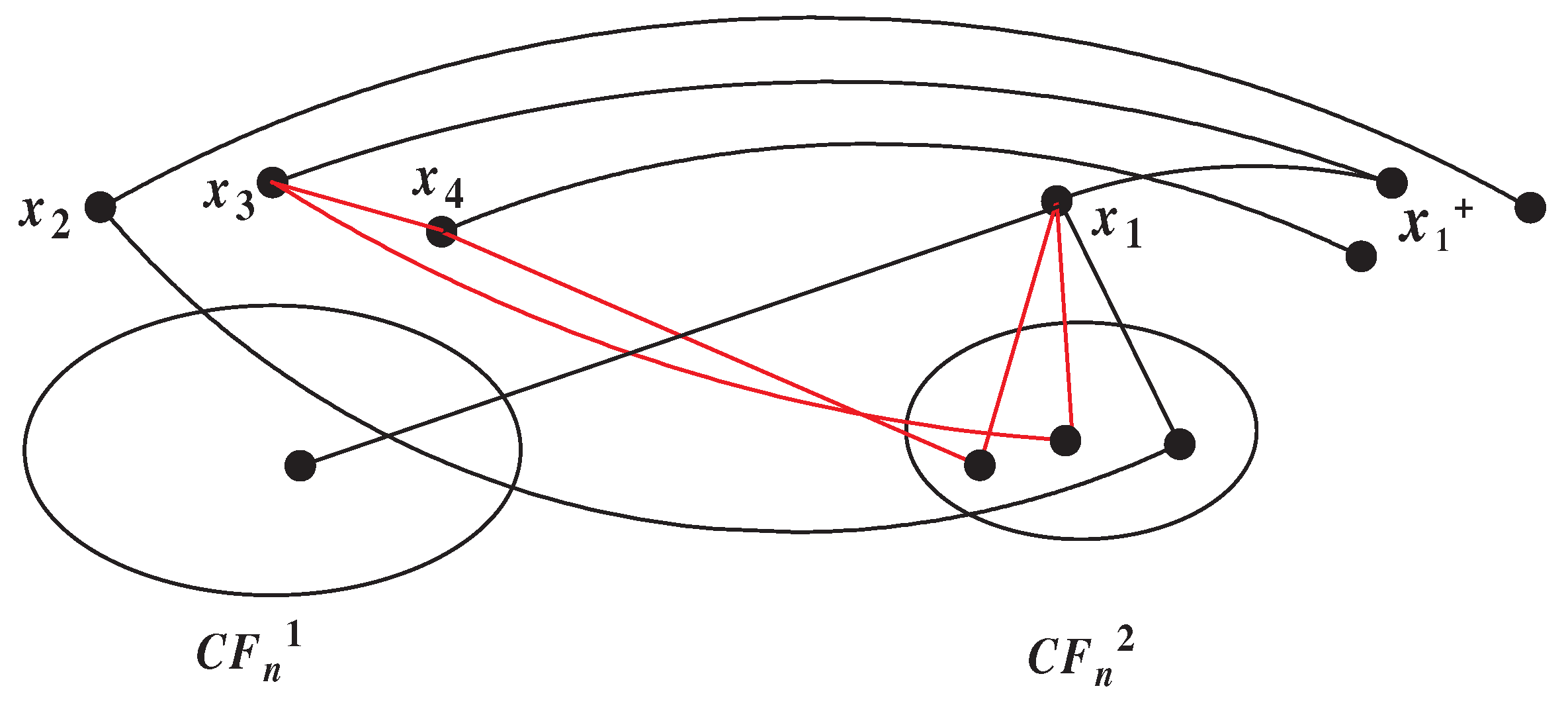
Subcase 1.1: There are two subgraphs of which contain only two vertices of S. Without loss of generality, we can let , . By the definition of , . Now we let , then or . Thus , or . Hence and can not belong to a common subgraph of . Similarly, we know and can not belong to a common subgraph of . If or belong to and adjacent to , meanwhile or belong to and adjacent to , then . Now, we illustrate this structure exists. Let , , then is adjacent to , is adjacent to . Thus .
Subcase 1.2: There is a subgraph of which contains three vertices of S. In this subcase, we can let , . We let , , , then , , . Clearly, , . If and is adjacent to , meanwhile is adjacent to , then . Let , then . Thus is adjacent to and is adjacent to . Thus .
Case 2: belong to three different subgraphs of .
In this case, there exists a subgraph which must contains two vertices of S. Now we can let , , . Then , , .
Case 3: belong to four different subgraphs of .
In this case, we can let , then . Thus .
Combing the above three cases, we have .
Lemma 5.2. When n is odd, let is an -set and , . If , then .
Proof. Since , by the proof process of Lemma 3.3, we know have three common neighbors in . So by Lemma 3.1, we can let , , where and . Then , , , . By Proposition 2.3 and Proposition 2.2, we have , . Then we think about the following three cases:
Case 1: .
In this case, we can easily get .
Case 2: .
In this case, only one of the outgoing neighbors of belong to . So or . We assume , then . If , then . If , one of the outgoing neighbors of must belong to , we assume or belong to , then or . When , then by the proof process of Lemma 3.1, we can let , where and . Thus , , , . Then . Since , . Thus as , , . When , then by the proof process of Lemma 3.1, we can let , where and . Then , , , , . Since , , we know . As and , then , , . Thus .
Case 3: .
In this case, two outgoing neighbors of belong to . Thus and . Now we let , then , where and . If , clearly . If , the proof process is similar to Case 2, we can get . So we let , then one of the outgoing neighbors of and belong to , we assume or . When , we can get , so . By Corollary 3.2, we know and can not have three common neighbors in , so , . Since , and , we have , , , . Thus .
Lemma 5.3. When n is odd, let is an -set and , . If , , then .
Proof. Since , , is even and , by Corollary 4.6, we know must belong to a common subgraph in . So we let , , . Then , , , , , . If , then . Thus we assume , then one of the two outgoing neighbors of must belong to a common subgraph of , we need to think about the following two situations:
Case 1: and .
In this case, we let , then , . If and , then as and , , . If one of the two outgoing neighbors of belong to , we can assume or . If , since , we know are adjacent to , so , , , this contradicts to the fact that are different from each other. So , then , . Hence , , , . Thus .
Case 2: Let , and .
In this case, , , . Then , , , , , . We let , then , . If and , then as , , . If one of the two outgoing neighbors of belong to , we can assume or . When , as are adjacent to , so , , , this contracts to the fact are different from each other. So , , . Then , , , . Thus .
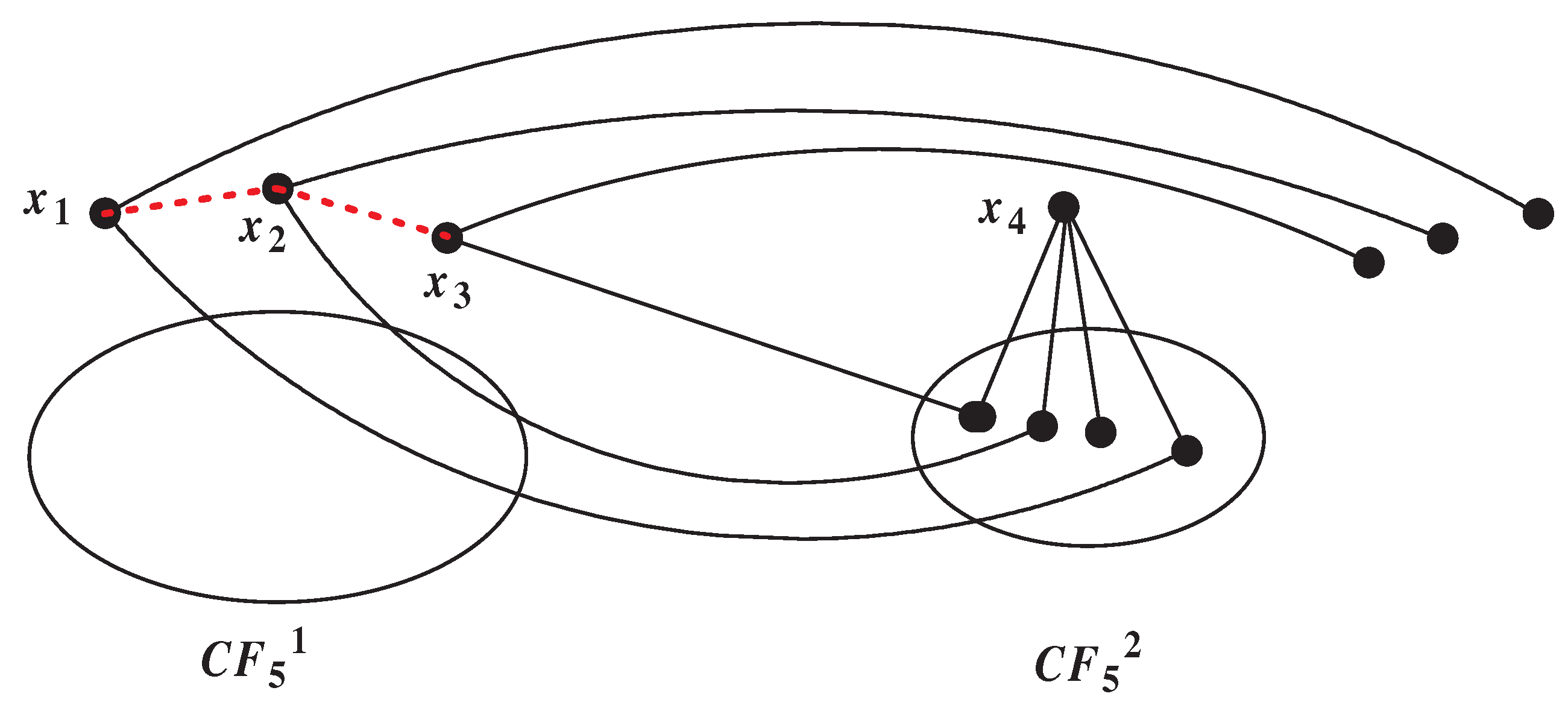
Lemma 5.4. When n is odd, let is an -set and , , are different from each other). If , then .
Proof. If
, the structure in
Figure 5 must exists. Now we can proof this structure does not exist. As
, we can get
must have three common neighbors in
. So we can assume
, then by Lemma 3.1, we can let
, where
and
. Then
,
,
,
. Since
and
,
can not belong to a common subgraph with
or
. Thus the structure in
Figure 5 does not exist,
.
Lemma 5.5. For , let S is an -set and , then .
Proof. Let , since S is an -set, are nonadjacent to each other. Note that . Now we think about the following four cases:
Case 1: belong to a same subgraph .
By Lemma 5.1, we have . By Proposition 2.3, we know . Thus .
Case 2: belong to two different subgraphs , .
In this case, we need to think about the following two situations:
Subcase 2.1: , .
By Lemma 3.3, we can get , . By Lemma 5.2, we have .
Subcase 2.2: , .
By Lemma 4.1, we have , . By Lemma 5.3, we know . Thus .
Case 3: belong to three different subgraphs , , are different from each other).
In this case, there exists a subgraph , which contains two vertices of S, we let . Clearly, , . Thus, by Lemma 5.4, we have .
Case 4: belong to four different subgraphs.
In this case, we can let . Clearly, , thus .
Combing the above four cases, we can get .
Lemma 5.6. For , let S is an -set and , then .
Proof. Let , since S is an -set, are nonadjacent to each other. Note that . Now we think about the following four cases:
Case 1: belong to a same subgraph .
By Lemma , we can get . By the definition of , we know every vertex in has only one outgoing neighbor. Thus .
Case 2: belong to two different subgraphs , .
In this case, we also need to think about the following two situations:
Subcase 2.1: , .
By Lemma 3.3, we can get , . Thus .
Subcase 2.2: , .
By Lemma 4.2, we have , . Thus .
Case 3: belong to three different subgraphs , , are different from each other).
In this case, there exists a subgraph , which contains two vertices of S, we let . Clearly, , . Thus, .
Case 4: belong to four different subgraphs.
In this case, we can let . Clearly, , thus .
Combing the above four cases, we can get .
Lemma 5.7. For , let S is an -set and , then when n is odd, ; when n is even, .
Proof. We proof this result by induction on n. By Lemma 5.5 and Lemma 5.6, we know when , this result holds. Now we assume and the result holds for . Let , since S is an -set, are nonadjacent to each other. Note that . Now we think about the following four cases:
Case 1: belong to a same subgraph .
By induction hypothesis, we know when n is odd, ; when n is even, . By Proposition 2.3, we know when n is odd, ; when n is even, . Thus (n is odd) and (n is even).
Case 2: belong to two different subgraphs , .
In this case, we need to think about two situations:
Subcase 2.1: , .
By Lemma 3.3, we can get when n is odd, , ; when n is even, , . When n is odd, by Lemma 5.2, we have . When n is even, .
Subcase 2.2: , .
When n is odd, by Lemma 4.5, we have . By Lemma 5.3, we know . As , so . When n is even, by Lemma 4.5, we have . As , so .
Case 3: belong to three different subgraphs , , are different from each other).
In this case, there exists a subgraph , which contains two vertices of S, we let . When n is odd, by Lemma 3.3, we have . Clearly, . Thus, by Lemma 5.4, we have . When n is even, by Lemma 3.3, we have . Clearly, . Thus, .
Case 4: belong to four different subgraphs.
In this case, we can let . Clearly, when n is odd, ; when n is even, . Thus when n is odd, ; when n is even, .
Combing the above four cases, we know the result holds.
Lemma 5.8. For , if F satisfies the condition , then contains a big component C with .
Proof. In this Lemma, we do not think about the situation is connected, so we let is disconnected. Let . By Proposition 2.8, we know . Since , we can get there exists at most three vertex set , which can satisfies the condition . Now we think about the following situations:
Case 1: for every .
By Proposition 2.8, we know is connected for . Since , and are connected. Thus we can get is connected, this contradicts to the assumption is disconnected.
Case 2: There exists only one , which can satisfies that .
In this case, we can let , then for . Hence by Proposition 2.8, we can get is connected . Let , similarly to the discussion of Case 1, we know M is connected. Now we think about the following two situations:
Subcase 2.1: .
By the definition of and Proposition 2.3, we know every vertex has two outgoing neighbors, and these outgoing neighbors are different from each other. Thus, if is connected and , there must exists a vertex in such that it has a good neighbor in M. Thus is connected, this contradicts to the assumption is disconnected. If is connected and , the result is certainly true. If is disconnected, we can assume is the vertex set in , which has no good neighbors in M. As , we can get , so the result holds.
Subcase 2.2: .
In this case, if is connected, similar to the case 1, we can get is connected. Now we assume is disconnected. Since , we have , by Lemma 1, we know has a big component and one singleton or two singletons. Since , is connected to M. Thus has a big component C with .
Case 3: There exists two vertex set , , which satisfy that , .
In this case, we can let . Then , . Let , similarly, we can get M is connected. If is connected, by the same argument with Subcase 2.2, we know it connected to M. Thus, if and are all connected, then is connected, this contradicts to the assumption that is disconnected. Hence at least one of is disconnected. Now we think about the following three cases:
Subcase 3.1: .
By Corollary 3.4, we know if is disconnected, then it has a big component and one singleton. Similarly, we can get is connected to M. Thus has a component C with .
Subcase 3.2: .
In this case, we know . By Lemma 1, we can get if is disconnected, then it has a big component and one singleton or two singletons. If , by Corollary 3.4, we can get has a big component and at most one singleton. Similarly, we can also get is connected to M. Thus has a big component C with , the result holds. If , then . By Lemma 1, we know, if is disconnected, it has a big component and one singleton or two singletons. If one of is connected or has only one singleton, then the result holds. Now we consider and are all disconnected and they all have two singletons, we let , . Similarly, we can know that must connected to M, then has a big component C with . Since and (resp.,) are two singletons, must have three common neighbors in (resp., must have three common neighbors in . If are singletons in , then by Lemma 5.2, we can get . Since , we know at least one vertex in must connected to M. Thus has a big component C with . If has at least one edge, we assume , then has a big component C with . Suppose , then are singletons in or . If are singletons in , then , a contradiction. If , then , a contradiction. Thus has a big component C with .
Subcase 3.3: .
In this case, we can get . If , then , , a contradiction. Thus .
If
and
is disconnected, then
has a big component
and one singleton
. Furthermore, we have
. When
, since every vertex in
has two outgoing neighbors, there are at most two vertices in
, which can satisfy that one of the two outgoing neighbors belong to
and the other belongs to
. Thus the result holds. When
,
has at most three vertices, which can satisfy that one of their outgoing neighbors belongs to
and the other belongs to
. We let they are
. If
is connected or has at most two vertices, then the result holds. Now we consider there are three vertices in
, we can get
has a big component
C with
. If
, the structure in
Figure 6 must exists. If there exists one edge between
, then there will be a 5-circle in
, a contradiction. So
are three singletons in
. If
is adjacent to
, then there exists a 3-circle in
. Thus
are four singletons in
. By Lemma 5.3, we know
, this contradicts to the fact
, thus
.
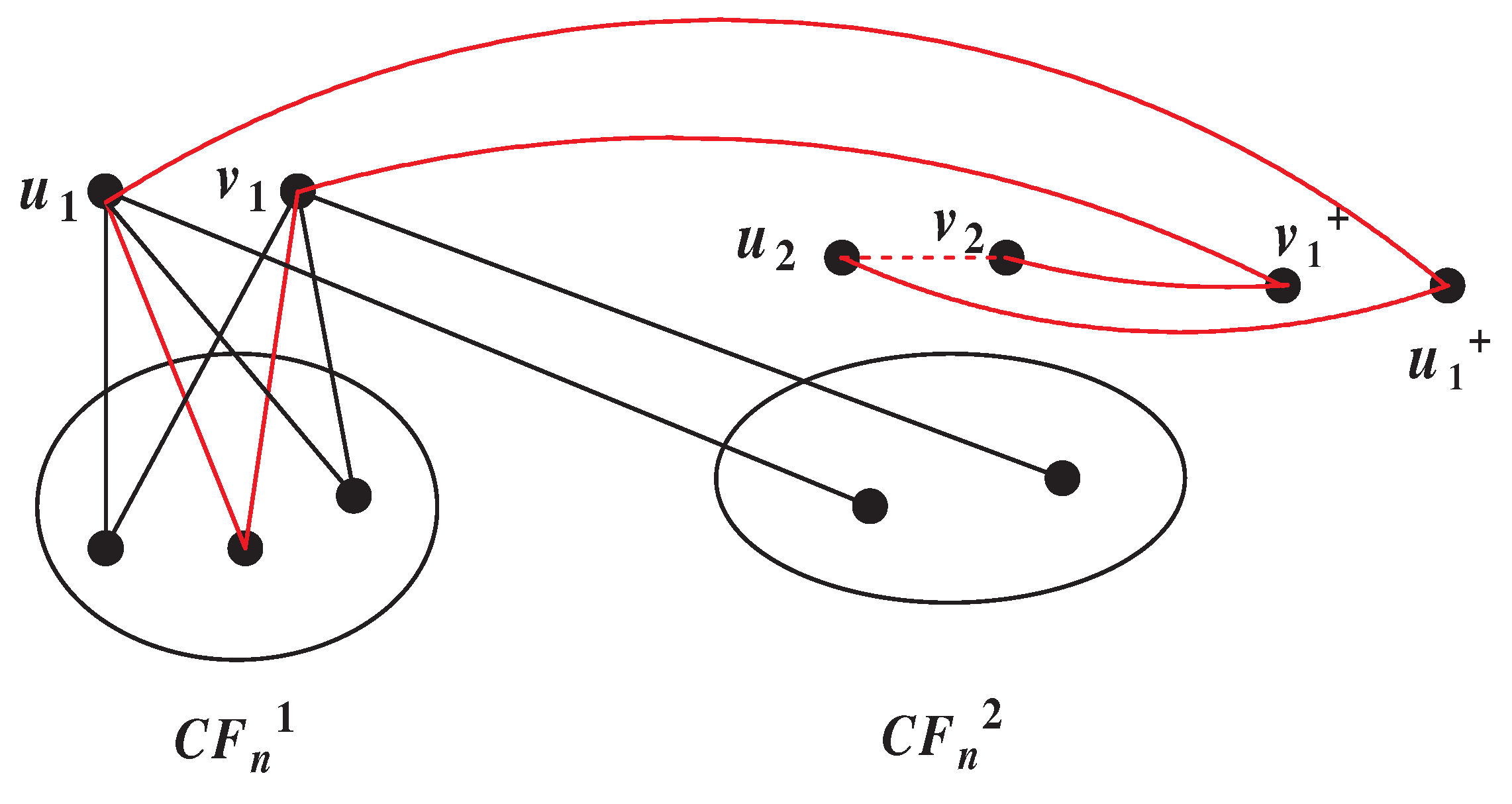
If
, then
. When
,
has a big component and at most two vertices
, where
and they have common outgoing neighbor vertex in
and the other outgoing neighbor vertex belong to
or
, so the result holds. When
, we can get
,
, and if
is disconnected, then it has at most two vertices which has neighbors in
. Thus
has a big component
C with
. Now, we proof
can not exist. Suppose on the contrary, the structure in
Figure 7 exists. Since
, we can get
are two singletons and have three common neighbors in
; Otherwise, if
is adjacent to
, then
, a contradiction. So by Lemma 3.1, we let
and
, where
and
. Then
,
,
,
. Since one of the out neighbor vertices of
belong to
and
,
,
, we have
. Thus
,
. From the structure of
Figure 7, we have
,
. Let
,
, then
,
. Since
,
and
belong to different subgraph in
. As
,
, we know
. Thus
and
have no common neighbors in
. Clearly, we have
is nonadjacent to
; Otherwise, there is a 7-circle in
(as shown in
Figure 7 by read line). Thus,
, this contradicts to the fact
, this structure does not exist. So
has a large component
C with
.
Case 4: There exists three vertex set , , , which can satisfy that , and are different from each other).
In this case, we have . Similarly, we can get , . Let , we can get M is connected. If , and , by Corollary 3.4, we know this result holds. If , and , then by Lemma 1, there are at most two singletons in . Thus has a big component C with . If , then has two singletons and , only has one singleton. Since , and have three common neighbors in . Since , we know belong to a common subgraph with or . By the proof process of Lemma 5.4, we know this situation will not exist. So , has a big component C with . If , , , then , a contradiction. If there are three , , , such that , , , then , a contradiction.
Lemma 5.9. For , if F satisfies the condition , then contains a big component C with .
Proof. In this Lemma, we do not think about is connected, so we assume that is disconnected. Let , note that . By Proposition 2.8, we have . Since , we can get there exists at most two vertex set , which can satisfy . Next we think about the following three cases:
Case 1: for every .
In this case, we know is connected. Since there are cross-edges in different and , is connected, a contradiction.
Case 2: There exists only one vertex set , which can satisfies the condition .
In this case, we know . So is connected. Let , similarly, we can get M is connected. When is connected, since , is connected, this contradicts to the assumption is disconnected. When is disconnected, let S be the set of vertices in , which have no good neighbors in M. If , at most three vertices in such that their out neighbor vertex belong to . Thus . If , then . By Lemma 5.8, we know the result holds.
Case 3: There exists two vertex set , , which can satisfy that and .
In this case, we have . Similarly, we can get . By Lemma 4.7, we know and contain a big component with . If , by Corollary 3.4, we have has a big component with . Thus has a big component C with . If , then . By Corollary 3.4, we can also get has a big component with . Thus has a big component C with .
Lemma 5.10. For , if F satisfies that is odd) and is even), then has a big component C with .
Proof. In this Lemma, we only think about the case is disconnected. Let , we proof this result by induction on n. By Lemma 5.8 and Lemma 5.9, we know this result holds for . Now we assume and the result holds for . Note that . By Proposition 2.8, we know when n is odd, ; when n is even, . Since (n is odd) and (n is even), we can get there exists at most three vertex set , which can satisfy that (n is odd) and (n is even); Otherwise, for , when n is odd, ; when n is even, . Next, we will think about the following situations:
Case 1. When n is odd, for every ; when n is even, for every .
By Proposition 2.8, we can get is connected for . By Proposition 2.1, we know when n is odd, there are cross-edges between and ; when n is even, there are cross-edges between and . Since , and , there are at least one cross-edge between and . Thus is connected, a contradiction.
Case 2. When n is odd, there exists only one vertex set , which satisfies that ; when n is even, there exists only one vertex set , which satisfies that .
In this case, we can assume (n is odd) and (n is even). Then we can get (n is odd) and (n is even) for every . By Proposition 2.8, we know is connected. Let , by the same argument with Case 1, we know M is connected. Now we think about the following two subcases:
Subcase 2.1: When n is odd, ; when n is even, .
By the definition of , we know when n is odd, every vertex in has two outgoing neighbors; when n is even, every vertex in has only one outgoing neighbor. If is connected with , since (n is odd) and (n is even), we can get is connected to M. Thus we can get is connected, this contradicts to the assumption is disconnected. If is connected with , the conclusion is certainly true. If is disconnected, we can let S is the set of vertices in which has no good neighbors in M. Since (n is odd) and (n is even), we can get , the result holds.
Subcase 2.2: When n is odd, ; when n is even, .
In this case, since (n is odd) and (n is even) for , we know if is connected, then is also connected, this contradicts to the assumption is disconnected. Now we assume is disconnected. Since (n is odd) and (n is even), we can get when n is odd, ; when n is even, . Thus by inductive hypothesis, we know has a big component with . Next, we will prove that is connected to M. Clearly, we can get (n is odd) and (n is even). As (n is odd) and (n is even) for , we know must has one vertex which must has a good neighbor in M. So the result holds.
Case 3. When n is odd, there exists two vertex set , , which can satisfies that and ; when n is even, there exists two vertex set , , which can satisfies that and .
In this case, we know is odd) and is even), where . By Proposition 2.8, we know is connected. Let , by the same argument with Case 1, we know M is connected.
Firstly, we think about n is odd. Now we can let , then as , we can get . Now, we think about the following three cases:
Case 3.1: .
In this case, since , , and , we can get if or is connected, then they are connected to M. Hence, if and are all connected, then is connected, this contradicts to the assumption is disconnected. Now we assume is disconnected. Since and , by Corollary 3.4, we know has a big component with . Since for , we know must connected to M. Thus contains a big component C with .
Case 3.2: .
In this case, we can get . If and are all connected, by the similarly discussion with Case 3.1, we can get is connected, this contradicts to the assumption is disconnected. Thus at least one of and is disconnected. Without loss of generality, we let is disconnected. Since , by Lemma 4.9, we can get has a big component with . Similarly, we can get is connected to M. If is connected, we know is connected to M, thus has a big component C with , the result holds. Now we consider is disconnected. If , by Corollary 3.4, we know has a big component and a singleton, the conclusion is certainly true. Now we think about , then . If , we know the vertices in and are all connected to M, thus is connected, a contradiction. If , then has a big component and at most two vertices , where , and they have a common outgoing neighbor in and the other outgoing neighbor of u (resp., v) belong to .
If , then . Since , by Lemma 4.9, we can get and have a big component with . If one of satisfies , the conclusion is certainly true. Now we consider for all , in another word, has a big component and two vertices. Similarly, we can get is connected to M. Since , we know contains two singletons and these two singletons have three common neighbors in ; Otherwise, if is adjacent to , then , a contradiction. Thus has a big component C with . Let . If S is an -set, by Lemma 5.2, we have . Since , can not has a big component and four vertices. Thus has a big component C with . If there exists at least one edge in S, say , then . Suppose on the contrary, we let . If there exists only one edge between S and are singletons in , then , a contradiction. If there exists two edges between S in , then , . Thus , a contradiction.
If
, then
or
. We assume
, then
. By the same argument with the above discussion, we know if one of
satisfies
, the result holds, so we consider
for all
. Hence
has a big component
C with
. If we want
, the structure in
Figure 8 must exists. Now we proof this structure can not exist. Since
,
contains two singletons
and this two singletons have three common neighbors in
. Let
has a big component and two vertices
, then
are nonadjacent; Otherwise, there exists a 7-circle (as shown by the red line in
Figure 8). By Lemma 3.1, we can let
, then
, where
and
. So
,
,
,
. Since
,
and
, we can get
, then
and
. By the structure in
Figure 8, we know
,
. Let
,
, then
,
and
belong to different subgraphs in
. Since
is even and
,
, we know
. Thus
and
have no common neighbors in
. In other words,
and
have no common neighbors in
. So
, this contradicts to the fact that
. Thus this structure does not exist,
has a big component
C with
.
Case 3.3: .
By the same argument with Case 3.2, we know if and are all connected, then is connected, this contradicts to the assumption is disconnected. Thus we assume is disconnected. In this case, we can get , . Thus if is disconnected, then it has a big component and only one singleton; Otherwise, we assume has two vertices . If is adjacent to , then , a contradiction. If is nonadjacent to , then , a contradiction. If is connected, the result is certainly true. Now, we assume is disconnected. If , be the similarly discussion with Case 3.2, the conclusion is certainly true. If , then contains a big component and at most two vertices, which have no neighbors in , the result holds.
When
, we have
and
. Thus we can let
H is the vertex set in
, which are not adjacent to
M, as
, we can get
. Hence
contains a big component
C with
. Furthermore,
if and only if the structure in
Figure 9 exists. Now we can proof this structure does not exist. Let
has a big component and three vertices
and
has a big component and one singleton
. Firstly, we can get
are three singletons in
; Otherwise, there exist a 5-circle in
(as shown by the red line in
Figure 9). Furthermore, we can get
is nonadjacent to
; Otherwise, there exists a 3-circle in
. Thus
is an
-set in
. We let
, then
,
. Since
,
or
must equal to one of the outgoing neighbors of
in
. We assume
, then
. Thus
,
. The neighbors of
in
are follows:
,
…,
,
,
…,
. In these vertices, we need to choose three vertices such that one of their outgoing neighbor belong to
. Then
must belong to
A, where
. Now, we choose a vertex in
A such that one of it’s outgoing neighbors equal to
, we assume this vertex is
,
. As
,
are three singletons, and
, by Corollary 4.6, we can get
must belong to a common subgraph of
. From the choose of
, we know there have not one vertex which belongs to a common subgraph with
in
. Thus this structure does not exist,
has a big component
C with
.
When n is even, we can assume . Then , we think about the following cases:
Case 3.1: .
In this case, since , , and , we can get if or is connected, then it is connected to M. If and are all connected, then is connected, this contradicts to the assumption is disconnected. Thus we assume is disconnected. Since and , by Corollary 3.4, we know contains a big component , which satisfies that . Similarly to the above discussion, we know the big component of is connected to M. Thus contains a big component C, which can satisfies that .
Case 3.2: .
In this case, we know . By the same argument with Case 3.1, we know if and are all connected, then is connected, a contradiction. Thus we assume is disconnected. By Corollary 3.4, we know contains a big component , which can satisfies that . If is connected, the conclusion is certainly true. Now we think about is disconnected. Since , has a big component with . Thus the result holds.
Case 4. When n is odd, there exists three vertex set , , , which can satisfy that , , ; when n is even, there exists three vertex set , , , which can satisfy that , , are different from each other).
In this case, we let .
When n is even, we have , by Corollary 3.4, we know this result holds.
When n is odd, we have . If , , , by Corollary 3.4, we know the result holds. If , and . By Lemma 1, we know there exists one singleton or two singletons in . Thus contains a big component C with . If , then has two singletons and , only has one singleton, meanwhile, these singletons are not connected to M, then . Since , by the proof process of Lemma 5.4, we know can not belong to a common subgraph with and . Thus , this contradicts to the fact . Thus , has a big component C with . If , then , a contradiction. If , then , a contradiction.
Thus, for , if F satisfies the condition is odd) and is even), then has a big component C with .
Theorem 3. For , when n is odd, ; when n is even, .
Proof. By Lemma 5.10, we can get when n is odd, ; when n is even, . Next, we will proof (n is odd) and (n is even). When n is odd, let , , , . Then . Let , then has a big component and four singletons . Thus . When n is even, we let , , , . Then and . In , if we remove , we can get four singletons. From the definition of , we know any two vertices in have different outgoing neighbors. So, if we remove in , we can get a big component and four singletons . Thus .