An Algorithm for Coloring of Picture Fuzzy Graphs Based on Strong and Weak Adjacencies and its Application

Preprint

Article

An Algorithm for Coloring of Picture Fuzzy Graphs Based on Strong and Weak Adjacencies and its Application

Altmetrics

Downloads

140

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 November 2023

Posted:

07 November 2023

You are already at the latest version

Alerts

Abstract

The idea of strong and weak adjacencies between vertices has been generalized into fuzzy graphs and intuitionistic fuzzy graphs (IFGs) and it is an important part of making decisions. However, one or two membership degrees are not always sufficient for making decisions on real-world problems that need an answer of types “yes, neutral, and no". Consequently, in previous work, we generalized the concept into picture fuzzy graphs (PFGs) where each element in the PFG has membership, neutral, and non-membership degrees. Moreover, we constructed the notion of the coloring of PFGs based on strong and weak adjacencies between vertices. In this paper, we investigate some properties of the chromatic number of PFGs based on the concept of strong and weak adjacencies between vertices. According to the properties, we construct an algorithm to find the chromatic number of PFGs. The algorithm is usefull when we work with large PFGs. Further, we improve the method to implement the PFG’s coloring for determining traffic signal phasing at an intersection. A case study has also been done to evaluate the method.

Keywords:

Subject: Computer Science and Mathematics - Computational Mathematics

1. Introduction

The concept of fuzzy graph had been proposed by Rosenfeld [1] to handle indeterminate phenomena on vertices and relation between vertices. Therefore, the vertices and edges have membership degrees to represent the indeterminacy situation. In real-world problems, the degrees of non-membership of elements in a network are needed. For example, in situations that need an answer of types "yes" and "no". To handle this problem, Atanassov [2] proposed an intuitionistic fuzzy set (IFS) and intuitionistic fuzzy graph (IFG). Each element in IFG has membership and non-membership degrees. Numerous studies had been conducted on intuitionistic fuzzy graphs (IFGs), including coloring of IFGs ([3,4]), application of wiener index for IFGs in water pipeline network [5], interval-valued intuitionistic

(S, T)

-fuzzy graphs [6], interval-valued intuitionistic fuzzy competition graph [7], and others.

Two categories of memberships are not always sufficient for making decisions. Therefore, Cuong [8] proposed a picture fuzzy set where each element did not only have membership and non-membership degrees, but also had a neutral membership degree. For instance, in an election problem, the committee must count the number of people who choose or did not choose a candidate and how many abstained (the neutral condition). Further, the concept of a picture fuzzy graph (PFG) was developed in [9] wherein the vertices and edges had membership, neutral, and non-membership degrees.

Researchers recently expanded PFGs in numerous types, such as q-rung PFGs [10], balanced PFGs [11], application of PFGs for selecting best routes in an airlines network [12], picture fuzzy soft graphs [13], complex PFGs [14], regular PFGs [15], and so on. Numerous studies had also been conducted on the use of PFGs in practical issues such as application of balanced PFGs [11], decision making under picture fuzzy soft graphs [13], implementation of regular PFGs in communication networks [15], road map design using picture fuzzy multigraph [16], application of PFGs in social network [17], shortest path algorithm in picture fuzzy digraphs [18], site selection problem using laplacian energy of PFGs [19], application of picture fuzzy tolerance graphs [20], genus of PFGs [21], and multiple attribute decision-making via PFGs [22].

The theory of vertex coloring and edge coloring had been generalized in various types of fuzzy graphs. Some researchers proposed various generalizations of graph coloring such as fuzzy graph coloring based on

δ

-fuzzy independent vertex set [23], fuzzy fractional coloring of fuzzy graphs [24], fuzzy coloring of fuzzy graphs [25], fuzzy colouring of m-polar fuzzy graph [26], the chromatic number and perfectness of fuzzy graph [27], and edge coloring of fuzzy graphs [28]. Several researchers have also proposed the coloring methods through

α

-cut approach and two forms of adjacencies (strong and weak) in fuzzy graphs and IFGs, as seen in [3,4,29,30]. The fact that a PFG is an extension of an IFG, it inspired us to generalize the vertex coloring from IFGs into PFGs in 2021 [31]. We utilized

(α, β, δ)

-cut approach to color PFGs. However, the computation of PFG’s coloring through the cut was complicated since we should use various values of

(α, β, δ)

in determining the cut chromatic numbers. Therefore, we need another approach for coloring the PFGs.

Strong and weak adjacencies—two different forms of adjacencies—between vertices in fuzzy graphs and IFGs are crucial in decision-making issues. Hence, we generalized strong and weak adjacencies into PFGs and proposed a concept to color PFGs based on strong and weak adjacencies [32]. When we work with PFGs with many vertices and edges, we need a computational tool to identify the strong and weak adjacencies and find the chromatic number of PFGs. In this paper, we construct an algorithm to handle the problem. In PFGs, we can classify connections between two movements (two vertices) into one of these three situations, i.e., crossing conflict, merging conflict, and non-conflict. The crowdedness of traffic flows in conflicting movements (crossing or merging conflicts) is a phenomenon that needs an answer of types “yes", “no", and “neutral". The situation at an intersection is usually crowded during peak times (06.30 AM-08.30 AM and 04.00 PM-06.00 PM). However, occasionally it is not congested during non-peak hours (06.00 PM-06.00 AM) or neutral conditions about whether it is crowded or not during 08.30 AM - 03.30 PM. Therefore, we need a PFG to deal with this situation and propose a traffic signal phasing wherein there are no traffic flows from merging conflicts that move simultaneously at the same time. In this article, we improve the method to model traffic flows at an intersection using PFGs and to determine the traffic signal phasing. Moreover, we also evaluate the proposed method through a case study. This is a new finding in view of application of coloring of PFGs.

The following is the structure of this paper: The first section explains an introduction and Section 2 discusses research challenges and gaps. Section 3 presents preliminary materials. Section 4 contains the most important findings in this research and Section 5 provides an experimental result. Finally, the conclusions are given in Section 6.

2. Research Challenges and Gaps

An essential idea that can be used in making decision on various networks of real-world problems is coloring method of fuzzy graphs and IFGs ([3,4,24,33]).
However, one membership degree or two membership degrees of elements in a network are not sufficient for making decision. Therefore, we initiated a coloring method of PFGs based on $(α, β, δ)$ -cut of PFGs [31]. Since the computation of PFG’s coloring through the cuts was complicated in determining the chromatic number, we propose a coloring method of PFGs based on strong and weak adjacencies between vertices in [32].
In this paper, we investigate connection between the cut chromatic numbers and the chromatic number of PFGs based on strong and weak adjacencies. Moreover, we construct an algorithm to find the chromatic number of PFGs and evaluate performance of the algorithm using Python and Matlab R2022b. The algorithm is useful when we deal with large PFGs.
An implementation of coloring method of fuzzy graphs in road networks has been proposed in [33]. However, it did not consider three types of connections between traffic movements and three conditions of crowdedness of traffic flows at an intersection. Sometimes, the traffic flow is crowded during peak times, or sometimes it is not crowded, or a neutral condition about whether it is crowded or not at non peak-times. In this research, we improve the method to implement the PFG’s coloring for determining traffic signal phasing at an intersection and evaluate the method through a case study.

3. Preliminaries

We review some of the key ideas from this study in this part. In the beginning, we are going to discuss intuitionistic fuzzy sets (IFSs) and construction an IFS from a fuzy set.

Given an ordinary finite non-empty set X. An Atanassov IFS in X is a set of the form

A_{I} = {(x_{i}, μ_{A_{I}} (x_{i}), ν_{A_{I}} (x_{i})) | x_{i} \in X}

wherein

μ_{A_{I}}, ν_{A_{I}} : X \to [0, 1]

and

0 \leq μ_{A_{I}} (x_{i}) + ν_{A_{I}} (x_{i}) \leq 1

for each

x_{i} \in X

. Meanwhile, a degree of hesitation of an element x in IFS

A_{I}

is defined as

π_{A_{I}} (x) = 1 - μ_{A_{I}} (x) - ν_{A_{I}} (x)

A method to construct an IFS from a fuzy set is given in Theorem 1 and Corollary 1, which are cited from [34] and [35].

Theorem 1.

Let

F S (X)

be a set of all fuzzy set in X. A fuzzy set

A_{F}

F S (X)

is denoted as

A_{F} = {(x_{i}, μ_{A_{F}} (x_{i})) | x_{i} \in X}

where

μ_{A_{F}} : X \to [0, 1]

. If

π, δ : X \to [0, 1]

are two functions defined on X, then

A_{I} = {(x_{i}, F (μ_{A_{F}} (x_{i}), π (x_{i}), δ (x_{i})) | x_{i} \in X}

is an Atanassov IFS, where the function

F : {[0, 1]}^{2} \times [0, 1] \to L^{*}

with

L^{*} = {(x, y) | (x, y) \in [0, 1] \times [0, 1] & x + y \leq 1}

defined as

F (x, y, δ) = (F_{μ} (x, y, δ), F_{ν} (x, y, δ))

F_{μ} (x, y, δ) = x (1 - δ y)

, and

F_{ν} (x, y, δ) = 1 - x (1 - δ y) - δ y

. The mapping F meets the conditions [34,35]:

If $y_{1} \leq y_{2}$ , then $π (F (x, y_{1}, δ)) \leq π (F (x, y_{2}, δ))$ for $x, δ \in [0, 1]$ ,
$F_{μ} (x, y, δ) \leq x \leq 1 - F_{ν} (x, y, δ)$ for $x \in [0, 1]$ ,
$F (x, 0, δ) = (x, 1 - x)$ ,
$F (0, y, δ) = (0, 1 - δ y)$ ,
$F (x, y, 0) = (x, 1 - x)$ ,
$π F (x, y, δ) = δ y$ .

Corollary 1.

If we choose

δ (x_{i}) = 1

for each

x_{i} \in X

in Theorem 1, then

π (x_{i}) = π (F (μ_{A_{F}} (x_{i}), π (x_{i}), 1)) .

Under the condition in Corollary 1, we get an IFS [34]:

A_{I} = {(x_{i}, μ_{A_{F}} (x_{i}) (1 - π (x_{i})), 1 - μ_{A_{F}} (x_{i}) (1 - π (x_{i})) - π (x_{i}) | x_{i} \in X} .

Furthermore, the notion of a picture fuzzy set (PFS) and construction a PFS from an IFS are discussed.

Definition 1.

A set of the form

\tilde{A} = {(v, μ_{\tilde{A}} (v), η_{\tilde{A}} (v), ν_{\tilde{A}} (v)) | v \in X}

is mentioned as a PFS on X wherein

μ_{\tilde{A}} (v) \in [0, 1]

is a membership degree,

η_{\tilde{A}} (v) \in [0, 1]

is a NeuM degree, and

ν_{\tilde{A}} (v) \in [0, 1]

is a non-membership degree of element v in PFS

\tilde{A}

such that

0 \leq μ_{\tilde{A}} (v) + η_{\tilde{A}} (v) + ν_{\tilde{A}} (v) \leq 1

The value

π_{\tilde{A}} (v) = 1 - (μ_{\tilde{A}} (v) + η_{\tilde{A}} (v) + ν_{\tilde{A}} (v))

is called a refusal degree of membership of v in

\tilde{A}

[8].

A method to construct a PFS from an IFS is given in Theorem 2.

Theorem 2.

A_{I} = {(x, μ_{A_{I}} (x), ν_{A_{I}} (x)) | x \in X}

is an IFS on X and

g : [0, 1] \to [0, 1]

is any function such that

g (0) = 0

and

g (x) \leq x

, then

A_{p} = {(x, F_{μ} (μ_{A_{I}} (x), ν_{A_{I}} (x)), F_{η} (μ_{A_{I}} (x), ν_{A_{I}} (x)), F_{ν} (μ_{A_{I}} (x), ν_{A_{I}} (x)))}

is a PFS on X wherein the mapping

F : [0, 1] \times [0, 1] \to {[0, 1]}^{2} \times [0, 1]

defined by

F (x, y) = (F_{μ} (x, y), F_{η} (x, y), F_{ν} (x, y))

with

F_{μ} (x, y) = x, F_{η} (x, y) = g (1 - x - y),

and

F_{ν} (x, y) = y

The mapping F satisfies the conditions:

$F_{μ} (μ_{A_{I}} (x), ν_{A_{I}} (x)) = μ_{A_{I}} (x)$ ,
$F_{η} (μ_{A_{I}} (x), ν_{A_{I}} (x)) = g (1 - μ_{A_{I}} (x) - ν_{A_{I}} (x))$ , and
$F_{ν} (μ_{A_{I}} (x), ν_{A_{I}} (x)) = ν_{A_{I}} (x) .$

The function g is called a neutral or refusal membership function of PFS

A_{p}

[36].

We present ideas of an empty PFS and a universal PFS in Definition 2 and Definition 3, respectively, which are cited from [37].

Definition 2.

Let

\tilde{A} = {(v, μ_{\tilde{A}} (v), η_{\tilde{A}} (v), ν_{\tilde{A}} (v))}

be a PFS on X. The set

\tilde{A}

is called an empty PFS if

μ_{\tilde{A}} (v) = 0, η_{\tilde{A}} (v) = 0

, and

ν_{\tilde{A}} (v) = 1

for each

v \in X

. The empty PFS is denoted by

\emptyset_{p f s}

[37].

Definition 3.

Let

\tilde{A} = {(y, μ_{\tilde{A}} (y), η_{\tilde{A}} (y), ν_{\tilde{A}} (y))}

be a PFS on X. The set

\tilde{A}

is named a universal PFS if

μ_{\tilde{A}} (y) = 1, η_{\tilde{A}} (y) = 0

, and

ν_{\tilde{A}} (y) = 0

for each

y \in X

[37].

In Definition 4, which is quoted from [8], we provide information on picture fuzzy subset.

Definition 4.

Given two PFSs on X:

\tilde{A} = {(a, μ_{\tilde{A}} (a), η_{\tilde{A}} (a), ν_{\tilde{A}} (a))}

and

\tilde{B} = {(b, μ_{\tilde{B}} (b), η_{\tilde{B}} (b), ν_{\tilde{B}} (b))}

a, b \in X

. The PFS

\tilde{A}

is mentioned as picture fuzzy subset of

\tilde{B}

, denoted by

\tilde{A} \subseteq \tilde{B}

, if

μ_{\tilde{A}} (v) \leq μ_{\tilde{B}} (v), η_{\tilde{A}} (v) \leq η_{\tilde{B}} (v), ν_{\tilde{A}} (v) \geq ν_{\tilde{B}} (v)

for all

v \in X

[8].

The notion of PFS is used as a basis to define a PFG, as described in Definition 5.

Definition 5.

We assume that X is a universal set that contains vertices. We mention a graph

\tilde{G} = (\tilde{V}, \tilde{E})

as a PFG if

\tilde{V} = {(x, μ_{1} (x), η_{1} (x), ν_{1} (x))}

is a picture fuzzy vertex set (PFVS) on X with the membership, neutral, and non-membership functions as follows:

μ_{1}, η_{1}, ν_{1} : X \to [0, 1]

in which

0 \leq μ_{1} (x) + η_{1} (x) + ν_{1} (x) \leq 1

for each

x \in X

Meanwhile,

\tilde{E} = {(x y, μ_{2} (x y), η_{2} (x y), ν_{2} (x y))}

is a picture fuzzy edge set (PFES) on

E \subseteq X \times X

with the membership, neutral membership, and non-membership functions as follows:

μ_{2}, η_{2}, ν_{2} : X \times X \to [0, 1],

such that

μ_{2} (x y) \leq min {μ_{1} (x), μ_{1} (y)}, η_{2} (x y) \leq min {η_{1} (x), η_{1} (y)}, ν_{2} (x y) \leq max {ν_{1} (x), ν_{1} (y)},

and

0 \leq μ_{2} (x y) + η_{2} (x y) + ν_{2} (x y) \leq 1

for each

x y \in E

The value of

μ_{1} (x)

is membership degree that represents the truth of existence of vertex x in X,

η_{1} (x)

is NeuM degree that describes the indeterminacy of existence of x in X, and

ν_{1} (x)

is non-membership degree that represents falsity condition of the existence of vertex x in X. Meanwhile, the values of

μ_{2} (x y), η_{2} (x y), ν_{2} (x y)

represent membership degree that tells the truth of adjacency of x and y, NeuM degree that describes the indeterminacy of adjacency of x and y, and non-membership degree that represents the falsity of adjacency between x and y, respectively [9].

Furthermore, we discuss the concepts of underlying graph, picture fuzzy subgraph, and a complete picture fuzzy graph (CPFG) that will be used in the next section.

Definition 6.

Given a PFG

\tilde{G} = (\tilde{V}, \tilde{E})

on a universal set X. An underlying graph of

\tilde{G}

, symbolized as

G^{*} = (V^{*}, E^{*})

, is a graph wherein

μ_{1} (x) > 0, η_{1} (x) > 0,

and

ν_{1} (x) > 0

for each

x \in V^{*}

[38].

Definition 7.

Let

\tilde{G} = (\tilde{V} (G), \tilde{E} (G))

and

\tilde{H} = (\tilde{V} (H), \tilde{E} (H))

be PFGs on a universal set X. The PFG

\tilde{H}

is said to be a picture fuzzy subgraph of

\tilde{G}

, denoted by

\tilde{H} \subseteq \tilde{G}

, if

\tilde{V} (H) \subseteq \tilde{V} (G)

and

\tilde{E} (H) \subseteq \tilde{E} (G)

[17].

Definition 8.

Given PFG

\tilde{G} = (\tilde{V}, \tilde{E})

where

\tilde{V}

is a PFS on universal set X. We call x and y as neighbor vertices in

\tilde{G}

μ_{\tilde{E}} (x y) > 0, η_{\tilde{E}} (x y) > 0

, and

ν_{\tilde{E}} (x y) > 0 .

Meanwhile, the set

N_{\tilde{E}} (x) = {y \in X | x and y are neighbor vertices}

. In addition,

| N_{\tilde{E}} (v) |

denotes the cardinality of neighbors of vertex v in

\tilde{G}

[15].

Definition 9.

Let

\tilde{G} = (\tilde{V}, \tilde{E})

be a PFG where

\tilde{V}

is a PFS on X. We mention PFG

\tilde{G}

as a CPFG if

\frac{1}{2} min {μ_{1} (u), μ_{1} (v)} = μ_{2} (u v); \frac{1}{2} min {η_{1} (u), η_{1} (v)} = η_{2} (u v); \frac{1}{2} max {ν_{1} (u), ν_{1} (v)} = ν_{2} (u v)

for each pair

u, v \in X

[12].

3.1. Strong and weak adjacencies between vertices in PFGs

The terms “strong adjacency" and “weak adjacency" have been defined in an IFG by [4]. We expand upon these ideas in terms of PFGs in the previous work [32].

Definition 10.

Given a PFG

\tilde{G} = (\tilde{V}, \tilde{E})

where

\tilde{V}

is a PFS on

V .

The vertices

u, v \in V

are mentioned as strongly adjacent vertices if

\frac{1}{2} min {μ_{1} (u), μ_{1} (v)} \leq μ_{2} (u v); \frac{1}{2} min {η_{1} (u), η_{1} (v)} \leq η_{2} (u v); \frac{1}{2} max {ν_{1} (u), ν_{1} (v)} \leq ν_{2} (u v) .

If it is not, we mention u and v as weakly adjacent vertices [32].

3.2. Coloring of PFGs based on strong and weak adjacencies between vertices

In this part, we discuss a coloring of PFGs based on strong and weak adjacencies between vertices.

Definition 11.

Given PFG

\tilde{G} = (\tilde{V}, \tilde{E})

where

\tilde{V}

is a PFS on

V = {v_{1}, v_{2}, \dots, v_{n}}

, i.e.,

\tilde{V} = {(v_{i}, μ_{1} (v_{i}), η_{1} (v_{i}), ν_{1} (v_{i})) | v_{i} \in V}

. Whereas,

\tilde{E} = {(v_{i} v_{j}, μ_{2} (v_{i} v_{j}), η_{2} (v_{i} v_{j}), ν_{2} (v_{i} v_{j})) | i \neq j}

is a PFS on

E \subseteq V \times V .

Let

Γ = {γ_{1}, γ_{2}, \dots, γ_{k}}

be a family of picture fuzzy (PF) subsets of

\tilde{V}

where

γ_{i} = {(v_{j}, μ_{γ_{i}} (v_{j}), η_{γ_{i}} (v_{j}), ν_{γ_{i}} (v_{j}))}

for

1 \leq i \leq k

, and

1 \leq j \leq n

. The family Γ is called as a k-vertex coloring of

\tilde{G}

$⋃_{i = 1}^{k} γ_{i} = \tilde{V}$ , i.e.,

$max {μ_{γ_{i}} (v_{j})} = μ_{1} (v_{j}), max {η_{γ_{i}} (v_{j})} = η_{1} (v_{j}), min {ν_{γ_{i}} (v_{j})} = ν_{1} (v_{j}),$

for $1 \leq i \leq k; 1 \leq j \leq n$ .
$γ_{i} \cap γ_{j} = \emptyset_{p f s}, \forall i \neq j,$ i.e.,

$min {μ_{γ_{i}} (v_{l}), μ_{γ_{j}} (v_{l})} = 0, min {η_{γ_{i}} (v_{l}), η_{γ_{j}} (v_{l})} = 0, max {ν_{γ_{i}} (v_{l}), ν_{γ_{j}} (v_{l})} = 1,$

for $1 \leq i, j \leq k; 1 \leq l \leq n$ .
For every pair of strongly adjacent vertices $u v$ with $u, v \in V$ :

$min {μ_{γ_{i}} (u), μ_{γ_{i}} (v)} = 0, min {η_{γ_{i}} (u), η_{γ_{i}} (v)} = 0, max {ν_{γ_{i}} (u), ν_{γ_{i}} (v)} = 1,$

for $1 \leq i \leq k$ .

The minimum value k for which

\tilde{G}

has k-vertex coloring is referred as the chromatic number of

\tilde{G}

, denoted by

χ^{f} (\tilde{G})

[32].

We describe the coloring of a PFG in Example 1 for more understanding of the concept.

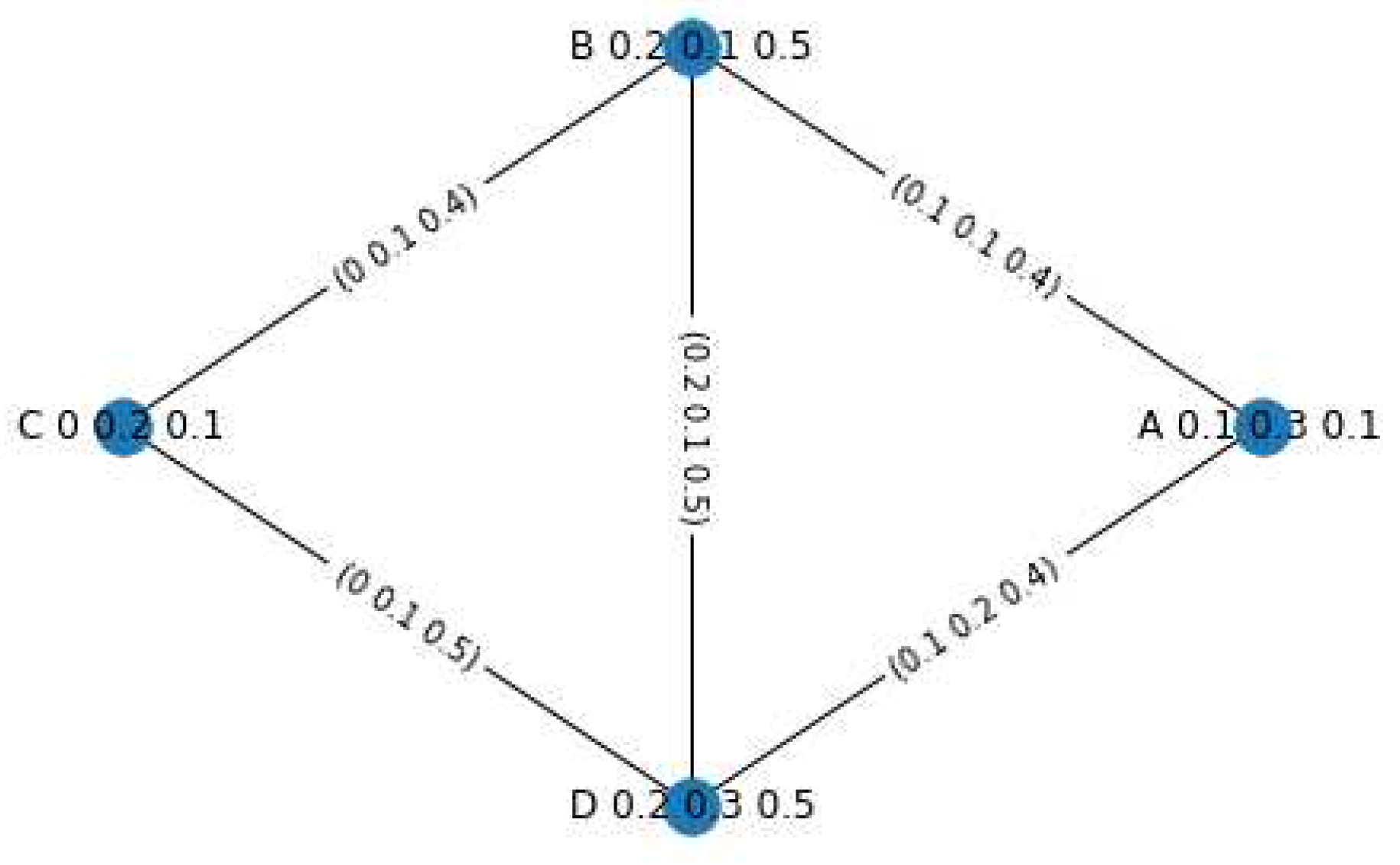
Example 1.

Let us consider PFG

\tilde{G} = (\tilde{V}, \tilde{E})

in Figure 1. The set

\tilde{V}

is a PFVS on universal set

V = {A, B, C, D}

The pairs of strongly adjacent vertices are ${A, B}, {A, D}, {B, C}, {B, D},$ and ${C, D}$ . Meanwhile, $C_{1} = {A, C}, C_{2} = {B}, C_{3} = {D}$ are the sets of weakly adjacent vertices.
Therefore, we get the PF-subsets $γ_{1} = {(A, 0.1, 0.3, 0.1), (C, 0, 0.2, 0.1)}$ , $γ_{2} = {(B, 0.2, 0.1, 0.5)}$ , $γ_{3} = {(D, 0.2, 0.3, 0.5)}$ , and the family $Γ = {γ_{1}, γ_{2}, γ_{3}}$ .
Thus, the chromatic number of $\tilde{G}$ is $χ^{f} (\tilde{G}) = 3$ .

3.3. The chromatic number of PFGs based on $(α, β, δ) -$ cut coloring

In this part, we discuss the concept of

(α, β, δ) -

cut of PFGs and the cut chromatic number as given in [31].

Definition 12.

Given a PFG

\tilde{G} = (\tilde{V}, \tilde{E})

and its underlying graph

G^{*} (V^{*}, E^{*})

. A level set of

\tilde{V}

is defined as a set

L_{\tilde{V}} = {α | μ_{1} (v) = α, v \in V^{*}} \cup {β | η_{1} (v) = β, v \in V^{*}} \cup {δ | ν_{1} (v) = δ, v \in V^{*}}

. Whereas, a level set of

\tilde{E}

is set

L_{\tilde{E}} = {α | μ_{2} (u v) = α, u v \in E^{*}} \cup {β | η_{2} (u v) = β, u v \in E^{*}} \cup {δ | ν_{2} (u v) = δ, u v \in E^{*}}

. Moreover, a level set of

\tilde{G}

is a set

L = L_{\tilde{V}} \cup L_{\tilde{E}}

. An

(α, β, δ) -

cut of

\tilde{G}

is a crisp graph

G_{α, β, δ} = (V_{α, β, δ}, E_{α, β, δ})

where

V_{α, β, δ} = {v \in V^{*} | μ_{1} (v) \geq α & η_{1} (v) \geq β & ν_{1} (v) \leq δ}

and

E_{α, β, δ} = {u v \in E^{*} | μ_{2} (u v) \geq α & η_{2} (u v) \geq β & ν_{2} (u v) \leq δ} .

The

(α, β, δ) -

cut chromatic number, denoted by

χ_{α, β, δ}

, is the chromatic number obtained from crisp coloring of the cut

G_{α, β, δ}

[31].

4. Main Results

In this section, we present some properties of the chromatic number of PFGs and an algorithm to compute the chromatic number.

4.1. Some characteristics of the chromatic number of PFGs

Firstly, we investigate an upper bound for the chromatic number of PFGs in the following theorem.

Theorem 3.

\tilde{G} = (\tilde{V}, \tilde{E})

is a PFG with the underlying graph

G^{*} = (V^{*}, E^{*})

, then

χ^{f} (\tilde{G}) \leq max {| N_{\tilde{E}} (x) | : x \in V^{*}} + 1 .

Proof.

Let

V^{*} = {x_{1}, x_{2}, \dots, x_{n}} .

Assume

Γ = {γ_{1}, γ_{2}, \dots, γ_{k}}

is a family of PF-subsets on

\tilde{V}

where

γ_{i} = {(x_{j}, μ_{γ_{i}} (x_{j}), η_{γ_{i}} (x_{j}), ν_{γ_{i}} (x_{j}))}

1 \leq i \leq k

1 \leq j \leq n

Suppose that

k > max {| N_{\tilde{E}} (x) | : x \in V^{*}} + 1 .

Based on Conditions 1-2 in Definition 11, we have:

$⋃_{i = 1}^{k} γ_{i} = \tilde{V}$ ,
$γ_{i} \cap γ_{j} = \emptyset_{p f s}, \forall i \neq j,$ for $1 \leq i, j \leq k$ .

If all pairs of vertices in

\tilde{G}

are strongly adjacent vertices, then we have

max {N_{\tilde{E}} (x) | : x \in V^{*}} + 1 = n - 1 + 1 = n

(based on third condition in Definition 11). Otherwise,

max {| N_{\tilde{E}} (x) | : x \in V^{*}} + 1 < n - 1 + 1 < n

. It is a contradiction. Thus,

χ^{f} (\tilde{G}) = k \leq max {| N_{\tilde{E}} (x) | : x \in V^{*}} + 1 .

□

We investigate the connection between the chromatic number of PFGs based on strong and weak adjacencies and the

(α, β, δ) -

cut chromatic number in Definition 12.

Definition 13.

Let

\tilde{G} = (\tilde{V}, \tilde{E})

be a PFG. The chromatic number of

\tilde{G}

through the

(α, β, δ) -

cut chromatic number is defined as follows:

χ (\tilde{G}) = max {χ_{α, β, δ} | α, β, δ \in L},

where L is the level set of

\tilde{G}

and

χ_{α, β, δ} = χ (G_{α, β, δ})

When

δ = 0

, Definition 13 becomes the chromatic number of IFGs. In certain conditions, we prove that the chromatic number of the underlying graph of PFG is equal to the chromatic number concept in Definition 13.

Theorem 4.

Given a PFG

\tilde{G} = (\tilde{V}, \tilde{E})

with the underlying graph

G^{*} = (V^{*}, E^{*}) .

α_{1} = min {α | α \in L}

β_{1} = min {β | β \in L},

and

δ_{1} = max {δ | δ \in L},

then the chromatic number of

\tilde{G}

χ (\tilde{G}) = χ (G^{*}) .

Proof.

Since

α_{1} = min {α | α \in L}

β_{1} = min {β | β \in L},

and

δ_{1} = max {δ | δ \in L},

we have

χ (G_{α_{1}, β_{1}, δ_{1}}) = max {χ_{α, β, δ} | α, β, δ \in L} .

Further, all vertices and edges of

\tilde{G}

become elements of the crisp graph

G_{α_{1}, β_{1}, δ_{1}}

. It implies

G_{α_{1}, β_{1}, δ_{1}} = G^{*}

and

χ (G^{*}) = χ (G_{α_{1}, β_{1}, δ_{1}}) = max {χ_{α, β, δ} | α, β, δ \in L} = χ (\tilde{G}) .

□

Theorem 5.

Let

\tilde{G} = (\tilde{V}, \tilde{E})

be a PFG with the underlying graph

G^{*} = (V^{*}, E^{*}) .

If all edges in

\tilde{E}

connect strongly adjacent vertices, then

χ^{f} (\tilde{G}) = χ (G^{*}) .

Proof.

Assume that

χ^{f} (\tilde{G}) = k

. According to Definition 11, we have a family

Γ = {γ_{1}, γ_{2}, \dots, γ_{k}}

of PF-subsets of

\tilde{V}

such that it satisfies 3 conditions in Definition 11:

$⋃_{i = 1}^{k} γ_{i} = \tilde{V}$ ,
$γ_{i} \cap γ_{j} = \emptyset_{p f s}$ , for $1 \leq i, j \leq k$ .
Based on the third condition in Definition 11, we have: $γ_{i} = {(v_{l}, μ_{1} (v_{l}), η_{1} (v_{l}), ν_{1} (v_{l})} \cup {(v_{m}, μ_{1} (v_{m}), η_{1} (v_{m}), ν_{1} (v_{m})}$ where $μ_{2} (v_{l} v_{m}) = 0$ , $η_{2} (v_{l} v_{m}) = 0$ , and $ν_{2} (v_{l} v_{m}) = 1$ (since all edges in $\tilde{E}$ connect strongly adjacent vertices). It shows that each $γ_{i}$ becomes a crisp independent vertex set in $G^{*}$ for $1 \leq i \leq k$ .

Hence, the family

Γ

becomes a partition of

V^{*}

into k-independent vertex set (crisp set). Therefore,

χ^{f} (\tilde{G}) = k = χ (G^{*}) .

□

According to Theorem 5, we obtain the following corollary.

Corollary 2.

\tilde{G} = (\tilde{V}, \tilde{E})

is a complete picture fuzzy graph (CPFG) with n vertices, then

χ^{f} (\tilde{G}) = n

4.2. An algorithm for finding the chromatic number of PFGs

We create an algorithm to compute the chromatic number of PFGs with the exception for CPFG.

Algorithm 1 can also be used for coloring of IFGs when the inputs are intuitionistic fuzzy vertex set and intuitionistic fuzzy edge set.

We show that Algorithm 1 gives the chromatic number

χ^{f} (\tilde{G}) = k

for

k \leq n

and prove correctness of the algorithm by using mathematical induction on the cardinality

| V |

as follows.

Base step

: for

| V | = 2

and

V = {v_{1}, v_{2}}

If the two vertices in V are strongly adjacent vertices, then Steps 1-11 will produce the set

C_{1} = {v_{1}}

and

C_{2} = {v_{2}} .

Further, Steps 12-30 give

γ_{1} = C_{1}, γ_{2} = C_{2}

. In Step 31, we obtain the family

Γ = {γ_{1}, γ_{2}}

and the chromatic number

χ^{f} (\tilde{G}) = 2

in Step 32. If the two vertices in V are weakly adjacent vertices, then Steps 1-30 will produce one PF-subset

γ_{1} = {v_{1}, v_{2}} .

Further, Steps 31-32 give the family

Γ = {γ_{1}}

and

χ^{f} (\tilde{G}) = 1

. The base step is satisfied.

Inductive step

: Assume that Algorithm 1 is correct for cardinality

| V | = n

. Steps 1-11 produce the set of weakly adjacent vertices and the set of strongly adjacent vertices. Furthermore, Steps 12-30 give the PF-subsets:

γ_{11}, γ_{12}, \dots, γ_{1, k 1}; γ_{21}, γ_{22}, \dots, γ_{2, k 2}; \dots; γ_{r 1}, γ_{r 2}, \dots, γ_{r, k r} .

In Steps 31-32, we get

Γ = {γ_{1}, γ_{2}, \dots, γ_{k}}

and the chromatic number

χ^{f} (\tilde{G}) = k

We prove that Algorithm 1 is correct for PFG

\tilde{G}

with cardinality

| V | = n + 1

Suppose that Algorithm 1 gives output “no". In other words, we cannot get the family

Γ = {γ_{1}, γ_{2}, \dots, γ_{k}}

such that

χ^{f} (\tilde{G}) = k

for

k \leq n + 1

. According to Corollary 2 and Theorem 3, if all edges in

\tilde{G}

connect strongly adjacent vertices, then the chromatic number

χ^{f} (\tilde{G}) = k

and

k \leq n + 1

. Otherwise, there exist some pairs of weakly adjacent vertices in

\tilde{G}

. Hence, we can get the the family

Γ = {γ_{1}, γ_{2}, \dots, γ_{k}}

such that the chromatic number

χ^{f} (\tilde{G}) = k

and it should be

k < n + 1 .

It is a contradiction. Thus, Algorithm 1 gives output “yes" and we get the chromatic number

χ^{f} (\tilde{G}) = k

for

k \leq n + 1

. Thus, the inductive step is true and Algorithm 1 is correct.

Example 2 and Example 3 show determination of the chromatic number of PFGs by employing Algorithm 1 and performance of the algorithm is evaluated using Python and Matlab R2022b.

Algorithm 1 To find the chromatic number of PFGs

Input:

The PFG

\tilde{G} = (\tilde{V}, \tilde{E})

with the elements:

Vertex set $V = {v_{i}}$ , $i = 1, 2, \dots, n$ , and edge set $E = {e_{l}}, l = 1, 2, \dots, m$ .
Degree of vertices $W_{V} = {w_{v_{i}}}$ , with $w_{v_{i}} = (μ_{1} (v_{i}), η_{1} (v_{i}), ν_{1} (v_{i}))$ .
Degree of edges $W_{E} = {w_{e_{l}}}$ , where $w_{e_{l}} = (μ_{2} (e_{l}), η_{2} (e_{l}), ν_{2} (e_{l})),$ $e_{l} = v_{i} v_{j}, i \neq j \in {1, \dots, n} .$

Output:

The chromatic number:

χ^{f} (\tilde{G})

1:

for h=1 to n-1 do

2:

for j=1 to n-1 do

3:

Check for all pairs

Q_{h, j + h} = {v_{h} v_{j + h}}

4:

\frac{1}{2} min (μ_{1} (v_{h}), μ_{1} (v_{j + h})) \leq μ_{2} (v_{h} v_{j + h}),

\frac{1}{2} min (η_{1} (v_{h}), η_{1} (v_{j + h})) \leq η_{2} (v_{h} v_{j + h}),

and

\frac{1}{2} max (ν_{1} (v_{h}), ν_{1} (v_{j + h})) \leq ν_{2} (v_{h} v_{j + h})

then

5:

print("

v_{h}

and

v_{j + h}

are strongly adjacent")

6:

else

7:

print("

v_{h}

and

v_{j + h}

are weakly adjacent")

8:

Assign

C_{h} = {v_{h}, v_{j + h}}

9:

end if

10:

end for

11:

end for

12:

Initialization

γ_{11} = C_{1} = {v_{1}, v_{j + 1}}

13:

sc1 = number of elements of

C_{1}

14:

for j=1 to sc1-1 do

15:

{v_{j + 1}, v_{j + 2}} \in C_{2}

then

16:

Assign

γ_{11} = union (C_{1}, {v_{j + 2}})

17:

else

18:

γ_{11} = C_{1}

19:

end if

20:

end for

21:

sc2 = number of elements of

C_{2} = {v_{2}, v_{j + 2}}

22:

for j=1 to sc2-2 do

23:

if elements of

γ_{11}

are not elements of

C_{2} = {v_{2}, v_{j + 2}}

then

24:

Assign

γ_{12} = C_{2} = {v_{2}, v_{j + 2}}

25:

else

26:

γ_{12} = C_{3} = {v_{3}, v_{j + 3}}

27:

end if

28:

end for

29:

Repeat the process in Steps 21-28 so that we get the picture fuzzy (PF) subsets

γ_{11}, γ_{12}, \dots, γ_{1, k 1}

which satisfies

γ_{11} \cup γ_{12} \cup \dots \cup γ_{1, k 1} = V,

γ_{i} \cap γ_{j} = \emptyset

, for

1 \leq i, j \leq k 1

, and every pair of strongly adjacent vertices belongs to different

γ_{1 i}

for

1 \leq i \leq k 1 .

30:

Do the same process in Steps 12-29 with initialization

γ_{21} = C 2

to get the PF-subsets

γ_{21}, γ_{22}, \dots, γ_{2, k 2}

until the subsets

γ_{r 1}, γ_{r 2}, \dots, γ_{r, k r}

with initialization

γ_{r 1} = C_{r}

and

r < n - 1

31:

Choose

k = min {k 1, k 2, \dots, k r}

and obtain the family

Γ = {γ_{1}, γ_{2}, \dots, γ_{k}}

32:

Obtain the chromatic number:

χ^{f} (\tilde{G}) = k

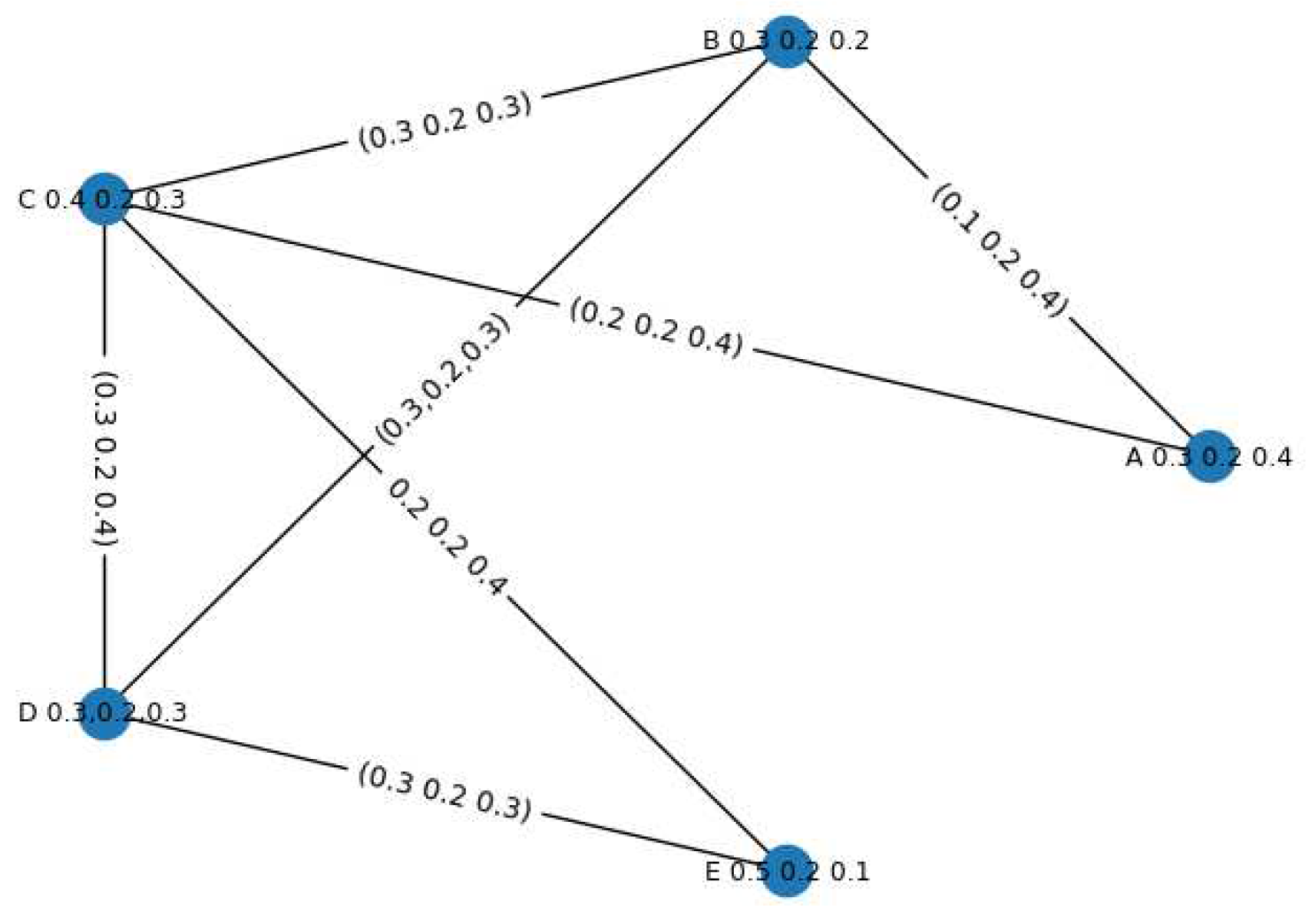
Example 2.

Given PFG

\tilde{G} = (\tilde{V}, \tilde{E})

in Figure 2 with picture fuzzy vertex set

\tilde{V} = {(A, 0.3, 0.2, 0.4), (B, 0.3, 0.2, 0.2), (C, 0.4, 0.2, 0.3), (D, 0.3, 0.2, 0.3), (E, 0.5, 0.2, 0.1)}

and picture fuzzy edge set

\tilde{E} = {(A B, 0.1, 0.2, 0.4), (A C, 0.2, 0.2, 0.4), (B C, 0.3, 0.2, 0.3), (B D, 0.3, 0.2, 0.3), (C D, 0.3, 0.2, 0.4), (C E, 0.2, 0.2, 0.4), (D E, 0.3, 0.2, 0.3)}

The output of Algorithm 1 in determining the chromatic number of

\tilde{G}

is presented in Figure 3.

In Steps 1-11, we obtain the sets of weakly adjacent vertices, i.e., $C_{1} = {A, B}, C_{2} = {A, D}, C_{3} = {A, E}, C_{4} = {B, E}, C_{5} = {C}$ .
In Steps 12-30, we get the PF-subsets $γ_{11} = {(A, 0.3, 0.2, 0.4), (B, 0.3, 0.2, 0.2)}$ , $γ_{12} = {(C, 0.4, 0.2, 0.3)}, γ_{13} = {(D, 0.3, 0.2, 0.3)}, γ_{14} = {(E, 0.5, 0.2, 0.1)},$ with initialization $γ_{11} = C_{1}$ .

Other PF-subsets are $γ_{21} = {(A, 0.3, 0.2, 0.4), (D, 0.3, 0.2, 0.3)}$ , $γ_{22} = {(B, 0.3, 0.2, 0.2), (E, 0.5, 0.2, 0.1)}$ , and $γ_{23} = {(C, 0.4, 0.2, 0.3)}$ with initialization $γ_{21} = C_{2}$ .
In Step 31, we choose $γ_{1} = γ_{21}, γ_{2} = γ_{22}, γ_{3} = γ_{23},$ and get the family $Γ = {γ_{1}, γ_{2}, γ_{3}}$ .
We obtain the chromatic number $χ^{f} (\tilde{G}) = 3$ in Step 32.

Example 3.

Let us consider PFG

\tilde{G} = (\tilde{V}, \tilde{E})

in Figure 4 where

\tilde{V}

is a PFS on

V = {W E, W S, S N, S E, N W, N S, E N, E W}

The output of Algorithm 1 for PFG

\tilde{G}

in Figure 4 is shown in Figure 5. We obtain the family

Γ = {γ_{1}, γ_{2}, γ_{3}, γ_{4}}

and the chromatic number

χ^{f} (\tilde{G}) = 4

5. Experimental Result

In this section, we discuss an implementation of Algorithm 1 in determining traffic signal phasing at an intersection. A phase is defined as any traffic light display that has its own timings and it determines how a specific vehicle or pedestrian will move. Whereas, the term phase set refers to “any distinct combination of concurrent vehicle or pedestrian phases". Conflicting phases are those that cannot both have green indicators at the same time [39]. There are two types of conflicts between traffic movements at an intersection. The first type is crossing conflict that is a collision that occurs when two separate directions of traffic try to cross paths at one spot. The second type is merging conflict, i.e., a conflict happened when vehicles from multiple lanes or directions merge into a single lane traveling in a single direction [40].

Traffic flow is “the number of traffic elements passing an undisturbed point upstream in the approach per unit of time". It is measured by the number of vehicles per hour or passenger car unit (pcu) per hour [40]. In this research, the traffic flow data are presented in pcu per hour where the conversion factors are as follows: 0.2 for motor cycle (MC), 1 for light vehicle (LV) including “passenger cars, pick-up, and micro buses", and 1.3 for heavy vehicle (HV) including “two or three-axle trucks and buses".

5.1. The method to model traffic flows at an intersection using PFGs

We visualize traffic movements from different directions as vertices and connect two vertices with an edge if the two movements are in conflict (crossing conflict or merging conflict). Hence, we get the data of vertex and edge sets V and E, respectively. The degrees of edges and vertices show the following circumstances:

A vertex’s membership degree ( $μ_{1} (x)$ ) indicates the possibility of the crowdedness of traffic flow on the movement x at the intersection. A vertex’s non-membership degree ( $ν_{1} (x)$ ) shows whether the flow of traffic on the movement x is likely to be free of congestion. The NeuM degree of a vertex ( $η_{1} (x)$ ) indicates the possibility of an unknown circumstance about the crowdedness of traffic flow on x. We obtain a PFVS $\tilde{V} = {(x, μ_{1} (x), η_{1} (x), ν_{1} (x))}$ .
Traffic flow on an edge that connects two vertices (traffic movements), is determined through the minimum of traffic flows on both movements. In addition, the membership degree of any edge $u v$ in $\tilde{E}$ , that is $μ_{2} (u v)$ , indicates the possibility of the crowdedness of traffic flows on conflicting movements $u v$ . On the contrary, the non-membership degree $ν_{2} (u v)$ shows the possibility of the non-crowdedness of traffic flows on $u v$ . The NeuM degree $η_{2} (u v)$ represents the possibility of unknown condition of the crowdedness of traffic flows on $u v$ . We get a PFES $\tilde{E} = {(u v, μ_{2} (u v), η_{2} (u v), ν_{2} (u v))}$ .

The degrees of vertices and edges are determined as follows:

The membership degree $μ_{1} (x)$ is calculated through triangular or trapezoidal membership functions. Whereas, the non-membership degree is calculated through Corollary 1, i.e., $μ_{1} (x) = μ_{1} (f_{x}) (1 - π (x))$ and $ν_{1} (x) = 1 - μ_{1} (x) (1 - π (x)) - π (x), x \in V$ by choosing $π (x) = mean {μ_{1} (x) | x \in V},$ where $f_{x}$ stands for traffic flow on movement x.
The NeuM degree $η_{1} (x)$ is determined through Theorem 2:

$η_{1} (x) = g (1 - μ_{1} (x) - ν_{1} (x))$

where the function g is as follows ([35]): $g = \frac{1 - μ_{1} (x) - ν_{1} (x)}{a}$ for $x \in V$ and

$a = \sum_{x \in V} (1 - μ_{1} (x) - ν_{1} (x))$ . The NeuM degree of each edge $η_{2} (u v)$ is defined similarly.
The membership degree $μ_{2} (u v)$ and non-membership degree $ν_{2} (u v)$ are calculated through formulas in Corollary 1: $μ_{2} (u v) = μ_{2} (u v) (1 - π (u v)), u v \in E$ , where

$μ_{2} (u v) = μ_{1} (min {f_{u}, f_{v}})$ ,

$ν_{2} (u v) = 1 - μ_{2} (u v) (1 - π (u v)) - π (u v), u v \in E$ by choosing

$π (u v) = min {μ_{2} (u v) | u v \in E} .$

5.2. Case study

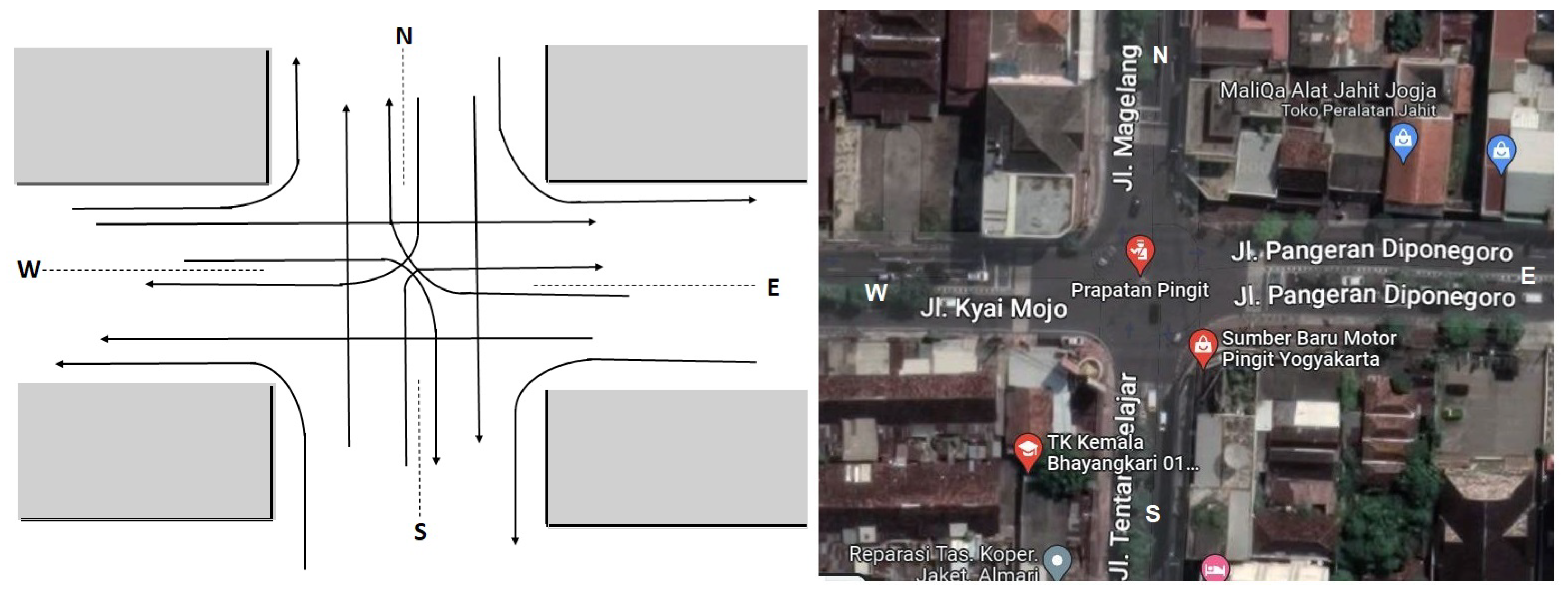
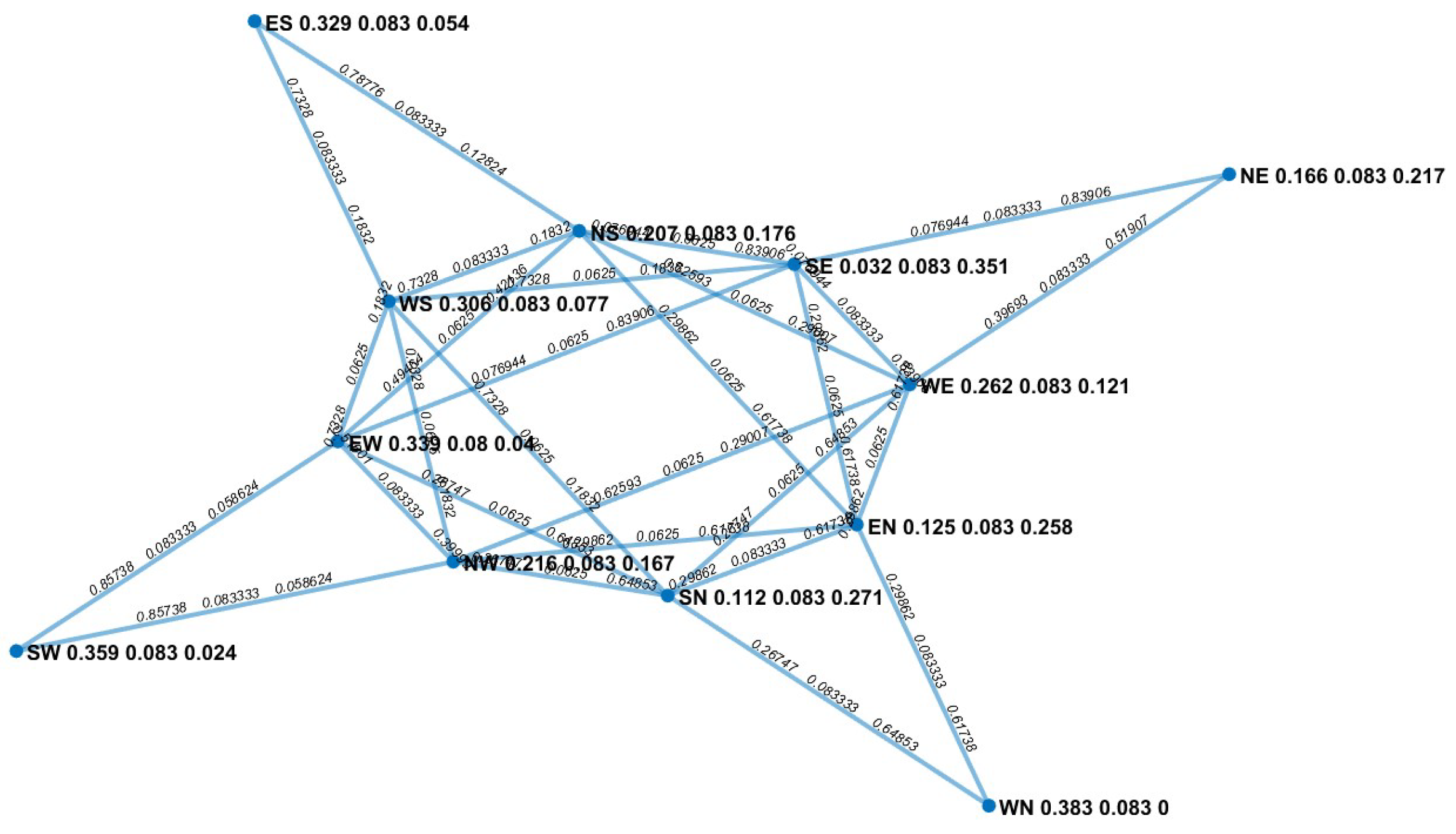
We take a case study at an intersection in Special Region of Yogyakarta, Indonesia, i.e., Pingit intersection. The location of the intersection is depicted in Figure 6 (right side). Tentara Pelajar street is to the South (S) direction, Diponegoro street is to the East (E) direction, Magelang street is to the North (N) direction, and Kyai Mojo street is to the West (W) direction.

Sketch of the intersection is also given in Figure 6 (left side). We collect the data of traffic flows on January 25-27, 2023 in the morning (06.30-07.30 AM) and in the evening (16.30-17.30 PM). There are 12 traffic movements in the intersection, i.e., WN, WE, WS, SN, SW, SE, NE, NW, NS, EN, EW, and ES.

It means that the vertex set V contains 12 vertices.

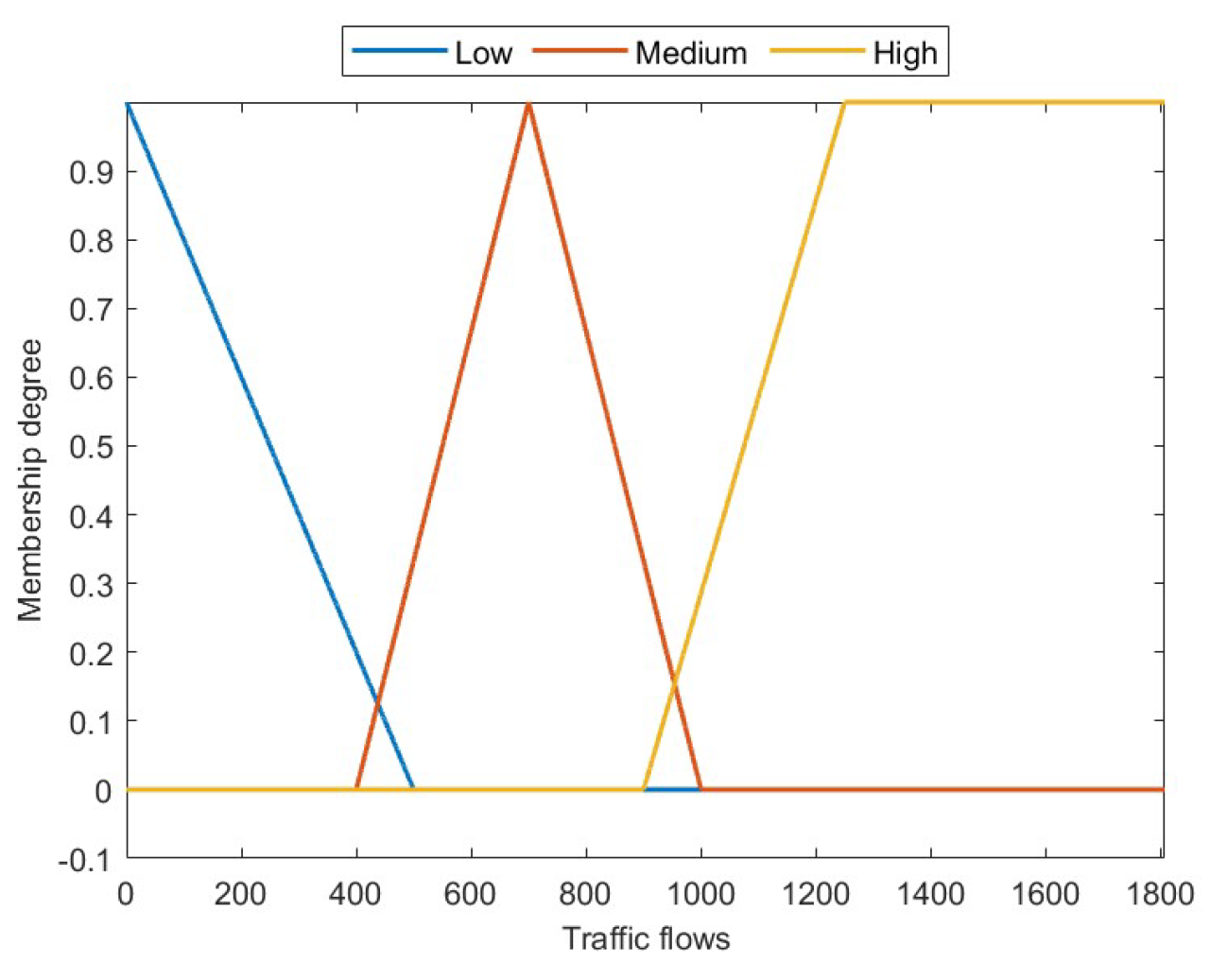
The next step is to transform the traffic flow data into PFVS

\tilde{V}

wherein the membership degree of each element is determined via triangular and trapezoidal membership functions in Figure 7.

The PFVS

\tilde{V}

of traffic flows in the intersection is displayed in Table 1.

It is shown in Table 1 that traffic flows on WN and EW have a high possibility of being crowded compared to traffic flows on other movements. Conversely, traffic flow on SW has a lower possibility of being crowded.

Further, the picture fuzzy edge sets from crossing and merging conflicts in the Pingit intersection are shown in Table 2 and Table 3, respectively. We observe that most of the edges in both tables connect strongly adjacent vertices. Moreover, the traffic flows on edges WS SN, WS SE, WS NW, WS EW, SW NW, SW EW have a high possibility of being crowded.

The PFG model

\tilde{G} = (\tilde{V}, \tilde{E})

of traffic flow data is depicted in Figure 8.

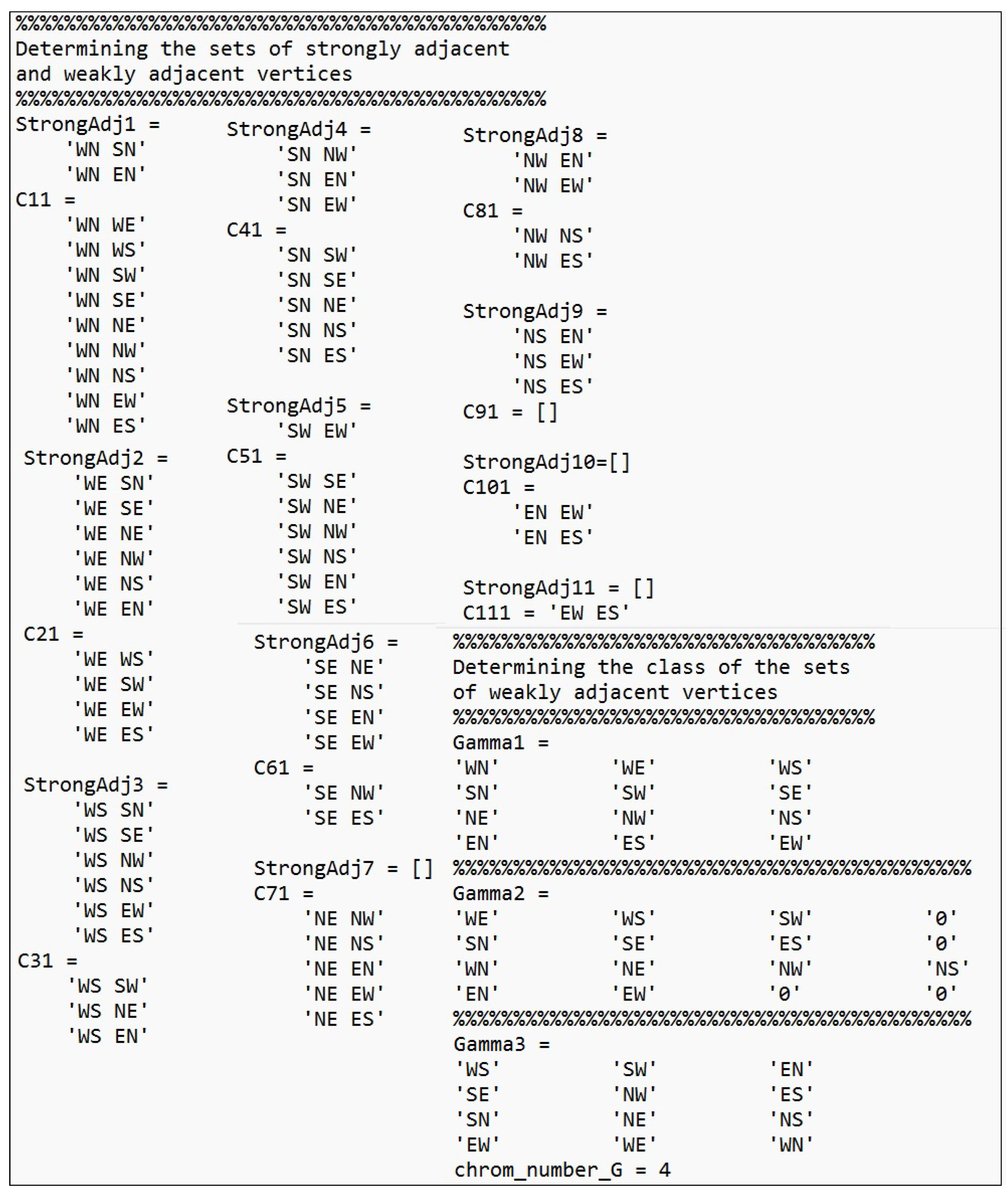
We get the chromatic number

χ (\tilde{G}) = 4

through Algorithm 1, and it has been evaluated in Matlab R2022b, where the output is depicted in Figure 9. The traffic flows can be arranged in 4 phases, and the patterns of traffic signal phasing are presented in Table 4.

5.3. Comparison to the fuzzy graph coloring method

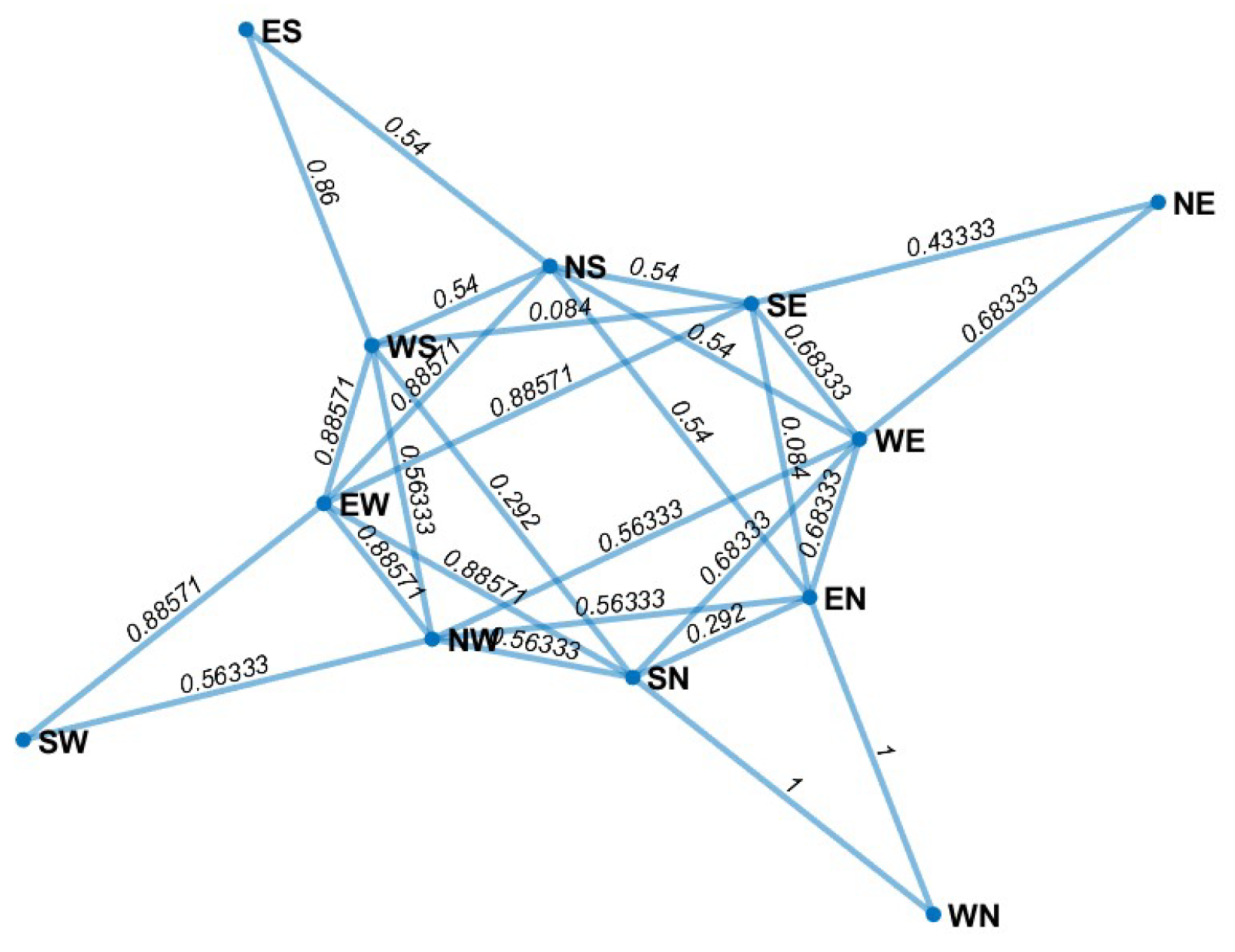
In this part, we compare the result in Table 4 with a traffic signal phasing obtained from the fuzzy graph coloring method based on

δ

-fuzzy independent vertices (

δ \in [0, 1]

) as given in [33]. The fuzzy graph model of traffic flows in the Pingit intersection is depicted in Figure 10.

For

δ = 0.8857

, the sets

{S W, E W, N W}

{E S, W S, N S}

, and

{S E, W E, N E}

are the sets of

δ

-fuzzy independent vertices since

μ (u v) \leq δ

for each pair

u, v

in the above sets. Therefore, we get 4-phase scheduling as follows:

i) S W, E W, N W, W N; i i) S N, N S, E S; i i i) E N, W S, N E; i v) W E, S E .

(1)

We observe that some pairs of vertices in (1) are elements of merging conflict in Table 3. Hence, the traffic signal phasing obtained from PFG coloring in Table 4 is safer than signal phasing from the fuzzy graph coloring in (1) since there are no traffic flows from merging conflict that move simultaneously at the same phase.

6. Conclusions

The concept of strong and weak adjacencies between vertices could be implemented in making decision on real-world problems. Therefore, we generalized the concept from intuitionistic fuzzy graph (IFG) into picture fuzzy graph (PFG) in the previous work. In this research, we investigated some characteristics of the chromatic number of PFGs based on strong and weak adjacencies between vertices and its relation to the

(α, β, δ) -

cut chromatic numbers. Furthermore, we construct an algorithm (Algorithm 1) for determining the chromatic number of PFGs and implement it in Python and Matlab R2022b to assess the algorithm’s performance. The correctness of Algorithm 1 was also proved using mathematical induction.

Additionally, we improve the method to model traffic flows at an intersection using PFGs and to determine an intersection’s traffic light phasing. We took a case study at an intersection in Special Region of Yogyakarta-Indonesia to evaluate the method. The outcome demonstrated that there were no concurrent traffic flows from merging conflict that moved at the same phase. The traffic signal phasing acquired using the PFG coloring method was found to be safer than the signal phasing obtained using the fuzzy graph coloring method.

Further research can be done to improve the method for handling traffic signal phasing at any intersection, such as integrating the algorithm with automatic counting for traffic flow data at the intersection. In the basic theories of PFG’s coloring, we can investigate the chromatic number of certain operations of two PFGs, such as union, join, cartesian product, and composition of two PFGs.

Author Contributions

Conceptualization, I. Rosyida; Methodology, I. Rosyida; Software, I. Rosyida; Validation, I. Rosyida and Ch.R. Indrati; Formal Analysis, I. Rosyida and Ch.R. Indrati; Investigation, I. Rosyida; Resources, I. Rosyida; Data Curation, I. Rosyida; Writing—Original Draft Preparation, I. Rosyida; Writing—Review & Editing, Ch.R. Indrati; Visualization, I. Rosyida; Supervision, Ch.R. Indrati; Project Administration, Ch.R. Indrati; Funding Acquisition, Ch.R. Indrati.

Funding

This research was funded by the Post-doctoral program Universitas Gadjah Mada under grant number 6468/UN1/DITLIT/Dit-Lit/PT.00/2022.

Acknowledgments

The authors express their gratitude to the reviewers for their insightful feedback on how to make the work better.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

IFS	Intuitionistic fuzzy set
IFG	Intuitionistic fuzzy graph
PFS	Picture fuzzy set
PF	Picture fuzzy
PFVS	Picture fuzzy vertex set
PFES	Picture fuzzy edge set
PFG	Picture fuzzy graph
NeuM	Neutral membership
CPFG	Complete picture fuzzy graph

References

Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Zadeh, L.A, Fu, K.S., and Shimura, M. Eds.; Academic Press., 1975; pp. 77–95.
Atanassov, K.T. On intuitionistic fuzzy graphs and intuitionistic fuzzy relations. Proceedings the VI IFSA World Congress, 1995, 551–554.
Prasanna, A., Rifayathali, M.A., and Ismail Mohideen, S. Strong intuitionistic fuzzy graph coloring, Int. J. Latest Eng. Res. Appl., 2017,2(8), 163–169.
Rifayathali, M.A., Prasanna, A., and Ismail Mohideen, S. Intuitionistic fuzzy graph coloring, Int. J. Res. Anal. Rev., 2018 5(3), 734-742.
Dinar, J., Hussain, Z., and Ur Rehman, S. Wiener index for an intuitionistic fuzzy graph and its application in water pipeline network. Ain Shams Eng. J., 2023, 14(1), 1-10. [CrossRef]
Rashmanlou, H. and Borzooei, R.A., New concepts of interval-valued intuitionistic (S,T)-fuzzy graphs, J. Intell. Fuzzy Syst., 2016, 30(4), 1893-1901. [CrossRef]
Talebi, A.A., Rashmanlou, H., and Sadati, S.H., Interval-valued intuitionistic fuzzy competition graph, J. Mult-Valued. Log. S, 2020, 34(3), 335-364.
Cuong, B.C. and Kreinovich, V. Picture fuzzy sets - A new concept for computational intelligence problems, In Proceedings of 2013 Third World Congress on Information and Communication Technologies (WICT), 2013; pp. 1–6.
Al-hawary, T., Mahmood, T., Jan, N., and Ullah, K. On intuitionistic fuzzy graphs and some operations on picture fuzzy graphs. Ital. J. Pure Appl. Math., 2018, 32, 1-15.
Akram, M. and Habib, A. q-Rung picture fuzzy graphs: a creative view on regularity with applications. J. Appl. Math. Comput., 2019, 61, 235–280. [CrossRef]
Amanathulla, S., Bera, B., and Pal, M. Balanced picture fuzzy graph with application. Artif. Intell. Rev., 2021, 54, 5255–5281. [CrossRef]
Amanathulla, S. and Pal, M. An introduction to picture fuzzy graph and its application to select best routes in an airlines network. In Handbook of Research on Advances and Applications of Fuzzy Sets and Logic, 2022, pp. 385-411. [CrossRef]
Chellamani, P.,Ajay, D., Broumi, S., and Ligori, T.A.A. An approach to decision-making via picture fuzzy soft graphs, Granul. Comput., 2022 7, 527–548.
Shoaib, M., Mahmood, W., Xin, Q., Tchier, F., and Tawfiq, F.M.O., Certain operations on complex picture fuzzy graphs, IEEE Access, 2022, 10, 114284-114296. [CrossRef]
Xiao, W., Dey, A., and Son, L.H. A study on regular picture fuzzy graph with applications in communication networks, J. Intell. Fuzzy Syst., 2020, 39(3), 3633–3645. [CrossRef]
Das, S. and Ghorai, G. Analysis of road map design based on multigraph with picture fuzzy information. Int. J. Appl. Comput. Math., 2020, 6(3), 1-17. [CrossRef]
Koczy, L.T., Jan, N., Mahmood, T., and Ullah, K., Analysis of social networks and Wi-Fi networks by using the concept of picture fuzzy graphs. Soft Comput., 2020, 24(21), 16551–16563. [CrossRef]
Mani, P., Vasudevan, B., and Sivaraman, M. Shortest path algorithm of a network via picture fuzzy digraphs and its application. Materials Today: Proceedings, 2021, 45(2), 3014-3018. [CrossRef]
Mahima, P. and Rakesh Kumar, B. On Laplacian energy of picture fuzzy graphs in site selection problem. J. Intell. Fuzzy Syst., 2021, 41(1), 481 – 498. [CrossRef]
Das, S., Ghorai, G., and Pal, M. Picture fuzzy tolerance graphs with application. Complex Intell Syst., 2022, 8(1), 541-554. [CrossRef]
Das, S., Ghorai, G., Pal, M. Genus of graphs under picture fuzzy environment with applications. J. Ambient. Intell. Humaniz. Comput., 2021, 12, 10741–10756. [CrossRef]
Amanathulla, S., Muhiuddin, G., Al-Kadi, D., and Pal, M. Multiple attribute decision-making problem using picture fuzzy graph. Math. Probl. Eng., 2021, 2021, 1-16. [CrossRef]
Rosyida, I., Widodo, Indrati, Ch.R., and K.A. Sugeng, K.A. A new approach for determining fuzzy chromatic number of fuzzy graph. J. Intell. Fuzzy Syst., 2015, 28(5), 2331-2341. [CrossRef]
Mahapatra, T., Ghorai, G., and Pal, M. Fuzzy fractional coloring of fuzzy graph with its application. J. Ambient. Intell. Humaniz. Comput., 2020, 11, 5771-5784. [CrossRef]
Samanta, S., Pramanik, T., and Pal, M. Fuzzy colouring of fuzzy graphs. Afrika Mat., 2016, 27, 37-50. [CrossRef]
Mahapatra, T. and Pal, M. Fuzzy colouring of m-polar fuzzy graph and its application. J. Intell. Fuzzy Syst., 2018, 35(6), 6379-6391. [CrossRef]
Raut, S. and Pal, M. On chromatic number and perfectness of fuzzy graph. Inf. Sci., 2022, 597, 392-411. [CrossRef]
Mahapatra, R., Samanta, S., Pal, M. Applications of edge colouring of fuzzy graphs. Informatica, 2020, 31(2), 313-330. [CrossRef]
Eslahchi, C. and Onagh, B.N. Vertex-strength of fuzzy graphs. Int. J. Math. Math. Sci.. 2006, ID 043614, 1-9.
Munoz, S., Ortuno, M.T., Ramirez, J., and Yanez, J. Coloring fuzzy graphs. Omega, 2005, 33(3), 211-221.
Rosyida, I. and Suryono, S. Coloring picture fuzzy graphs through their cuts and its computation. Int. J. Adv. Intell. Informatics., 2021, 7(1), 63-75.
Rosyida, I., Indrati, Ch.R., and Kalayathankal, S.J. A method based on picture fuzzy graph coloring for determining traffic signal phasing on an intersection. In Proceedings of the INFUS 2023 Conference, 2023, 1, 293-303.
Rosyida, I., Nurhaida, Narendra, A., and Widodo. Matlab algorithms for traffic light assignment using fuzzy graph, fuzzy chromatic number, and fuzzy inference system. MethodsX, 2020, 7, 101-136. [CrossRef]
Jurio, A., Paternain, D., Bustince, H., Guerra, C., and Beliakov, G. A construction method of Atanassov’s intuitionistic fuzzy sets for image processing. In Proceedings of 5th IEEE conference on Intelligent Systems, 2010, pp. 1-6.
Singh, A., Joshi, D.K., and Kumar, S. A novel construction method of intuitionistic fuzzy set from fuzzy set and its application in multi-criteria decision-making problem. Adv. Intell. Syst. Comput., 2019, 702 (2019), 1-9. [CrossRef]
Singh, A. and Kumar, S. Picture fuzzy parameterized soft set and its application in decision making. In Research Square, Retrieved on April 13, 2023, 1-13.
Memis, S. A Study on picture fuzzy sets. In Proceedings of 7th International IFS and Contemporary Mathematics Conference, 2021, pp. 125-132.
Zuo, C., Pal, A., and Dey, A. New concepts of picture fuzzy graphs with application. Mathematics, 2019, 470(7), pp.1-18. [CrossRef]
Buckholz, J.W. Introduction to Traffic Signal Phasing, In CEDengineering.com: An Online Continuing Education Provider for Professional Engineers, Retrieved on February 26, 202, 1-27.
Sumadji, S., Asmoro, D., and Sastrosoegito, S. Urban and semi-urban traffic-facilities. In Indonesian Highway Capacity Manual, Directorate General of Highways, Ministry of Public Works, 1993, pp. 1-76.

Figure 1. The picture fuzzy graph

\tilde{G}

for Example 1.

Figure 1. The picture fuzzy graph

\tilde{G}

for Example 1.

Figure 2. The picture fuzzy graph

\tilde{G}

for Example 2.

Figure 2. The picture fuzzy graph

\tilde{G}

for Example 2.

Figure 3. The output of Algorithm 1 for finding

χ^{f} (\tilde{G})

in Figure 2.

Figure 3. The output of Algorithm 1 for finding

χ^{f} (\tilde{G})

in Figure 2.

Figure 4. The PFG

\tilde{G}

for Example 3.

Figure 4. The PFG

\tilde{G}

for Example 3.

Figure 5. The output of Algorithm 1 for finding

χ^{f} (\tilde{G})

in Figure 4.

Figure 5. The output of Algorithm 1 for finding

χ^{f} (\tilde{G})

in Figure 4.

Figure 6. Location of the Pingit intersection in Special Region of Yogyakarta.

Figure 7. The function to calculate membership degree in the PFVS

\tilde{V}

Figure 7. The function to calculate membership degree in the PFVS

\tilde{V}

Figure 8. The PFG model of traffic flows in the Pingit intersection.

Figure 9. Determination of the chromatic number of PFG model

\tilde{G}

in Figure 8.

Figure 9. Determination of the chromatic number of PFG model

\tilde{G}

in Figure 8.

Figure 10. The fuzzy graph model of traffic flows in the Pingit intersection.

Table 1. The PFVS

\tilde{V}

of traffic flow data in the Pingit intersection.

Table 1. The PFVS

\tilde{V}

of traffic flow data in the Pingit intersection.

Traffic movements	Traffic flows	Clusters	Degree of vertices
(Vertices)
WN	1805	High	(0.383, 0.083,0)
WE	605	Medium	(0.262,0.083,0.121)
WS	100	Low	(0.306,0.083,0.077)
SN	354	Low	(0.112,0.083,0.271)
SW	32	Low	(0.359,0.083,0.024)
SE	458	Low	(0.032,0.083,0.351)
NE	530	Medium	(0.166,0.083,0.217)
NW	831	Medium	(0.216,0.083,0.167)
NS	838	Medium	(0.207,0.083,0.176)
EN	337	Low	(0.125,0.083,0.258)
EW	1210	High	(0.339,0.083,0.044)
ES	742	Medium	(0.329,0.083,0.054)

Table 2. The PFES

\tilde{E}

of crossing conflict in the Pingit intersection

Table 2. The PFES

\tilde{E}

of crossing conflict in the Pingit intersection

Crossing conflict	Degree of conflict	Crossing conflict	Degree of conflict
(Edges)	(Degree of edges)	(Edges)	(Degree of edges)
WE SN	(0.2675,0.0625,0.6485)	SN NW	(0.2675,0.0625,0.6485)
WE NW	(0.6259,0.0625,0.290)	SN EW	(0.2675,0.0625,0.6485)
WE NS	(0.6259,0.0625,0.290)	SE NS	(0.0769,0.0625,0.8390)
WE EN	(0.2986,0.0625,0.6174)	SE EN	(0.2986,0.0625,0.6174)
WS SN	(0.7328,0.0625,0.1832)	SE EW	(0.0769,0.0625,0.839)
WS SE	(0.7328,0.0625,0.1832)	NW EN	(0.2986,0.0625,0.6174)
WS NW	(0.7328,0.0625,0.1832)	NS EN	(0.2986,0.0625,0.6174)
WS EW	(0.7328,0.0625,0.1832)	NS EW	(0.4946,0.0625,0.4214)

Table 3. The PFES

\tilde{E}

of merging conflict.

Table 3. The PFES

\tilde{E}

of merging conflict.

Merging conflict	Degree of conflict	Merging conflict	Degree of conflict
(Edges)	(Degree of edges)	(Edges)	(Degree of edges)
WN SN	(0.2675,0.083,0.6485)	SN EN	(0.2986,0.083,0.6174)
WN EN	(0.2986,0.083,0.6174)	SW NW	(0.8574,0.083,0.0586)
WE SE	(0.0769,0.083,0.839)	SW EW	(0.8574,0.083,0.0586)
WE NE	(0.3969,0.083,0.519)	SE NE	(0.0769,0.083,0.839)
WS NS	(0.7328,0.083,0.1832)	EW NW	(0.516,0.083,0.3999)
WS ES	(0.7328,0.083,0.1832)	NS ES	(0.7877,0.083,0.1282)

Table 4. The traffic signal phasing that can be implemented at the Pingit intersection

Patterns	Phase 1	Phase 2	Phase 3	Phase 4
1	WN, WE, WS	SE, SN, SW	NE, NW, NS	EN, EW, ES
2	WE,WS,SW	SN,SE,ES	WN,NE,NW,NS	EN,EW
3	WS,SW,EN	SE,NW,ES	SN,NE,NS	EW,WE,WN

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Algorithm for Coloring of Picture Fuzzy Graphs Based on Strong and Weak Adjacencies and its Application

Abstract

1. Introduction

2. Research Challenges and Gaps

3. Preliminaries

3.1. Strong and weak adjacencies between vertices in PFGs

3.2. Coloring of PFGs based on strong and weak adjacencies between vertices

3.3. The chromatic number of PFGs based on ( α , β , δ ) − cut coloring

4. Main Results

4.1. Some characteristics of the chromatic number of PFGs

4.2. An algorithm for finding the chromatic number of PFGs

5. Experimental Result

5.1. The method to model traffic flows at an intersection using PFGs

5.2. Case study

5.3. Comparison to the fuzzy graph coloring method

6. Conclusions

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

3.3. The chromatic number of PFGs based on $(α, β, δ) -$ cut coloring