Prerpints.org logo
Preprint
Article

Machine Learning Models for Prediction of Gender Based on Lumbar Vertebral Morphometry

Altmetrics

Downloads

95

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 November 2023

Posted:

02 November 2023

You are already at the latest version

Alerts
Abstract
Identifying skeletal remains has been and will remain a challenge for forensic doctors and forensic anthropologists, especially in disasters with multiple victims or skeletal remains in an advanced stage of decomposition. This study proposes a machine learning method to determine gender starting from morphometric analysis of L1-L5 lumbar vertebrae in a modern Romanian population. The purpose of the present study was to observe whether by using the ML method there is a good predictability of gender in forensic identification based on parameters obtained from the metric analysis of the lumbar spine specific to the Romanian population. This paper offers two models of ML, RF and XGB, each with its own characteristics, and presenting different performance, random forest having the best. For both, we used two metrics (accuracy and roc_auc), the latter being the most used to highlight model performance. The L1-L5 lumbar vertebrae exhibit sexual dimorphism and can be used in gender estimation. Machine learning is more accurate in determining gender than discriminatory function analysis.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Identifying skeletal remains has been and will remain a challenge for forensic doctors and forensic anthropologists, especially in disasters with multiple victims or skeletal remains in an advanced stage of decomposition. In such contexts, forensic doctors must approach knowledge in the field of forensic anthropology, a field which takes interest in the systematic examination of human bones. In order to identify as accurately as possible the bones presented for examination, a first step is to build the biological profile, which involves establishing race, gender, stature and age [1,2].
Gender determination is a fundamental step in estimating biological profile from the examination of skeletal remains in forensic anthropology. Most human bones have been used to establish various methods of estimating gender. Among the human bones, the coxal bone and the bones of the skull are the most accurate for estimating gender, the method used being their simple macroscopic analysis. There are, however, multiple situations in which these two bones are not available, on the contrary even, having to deal with bone fragments or sometimes only with different bones of the human skeleton. In such circumstances, it is important to develop alternative methods that use other skeletal elements to estimate gender [3,4,5].
The literature mentions only a few studies on the involvement of the spine in developing methods for gender estimation. The spine is a part of the human skeleton used in forensic identification, primarily because of its ability to resist mechanical forces, as well as due to the sexual dysmorphism based on the size and shape of certain vertebrae. Regarding the use of the lumbar spine to gender estimation, the literature mentions several studies on the development of discriminatory functions involving only the L1 and L5 lumbar vertebrae[6,7,8].

2. Materials and Methods

Selection of the study lot, criteria for inclusion and exclusion

This study proposes a machine learning method to determine gender starting from morphometric analysis of L1-L5 lumbar vertebrae in a modern Romanian population. A total of 745 lumbar vertebrae (L1-L5) from 149 Romanian individuals (56 men and 93 women) were analyzed by means of MR (magnetic resonance) images in the incidence of T1-FSE (fast spin-echo) of the lumbar vertebral spine. The imaging scans were performed in a Medical Imaging Laboratory in a limited territory in the central region of Romania, with the full consent of the patients according to the working methodology of the Laboratory. The type of study was retrospective.
The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethic Committee of „Grigore T. Popa” Medicine and Pharmacy University.
The inclusion criteria were represented by persons over 17 years of age, who only mainly displayed pain, so that the integrity of the vertebral column was not altered. The exclusion criteria were represented by cases with advanced scoliotic pathology, traumatic injuries (fractures) or surgery of the lumbar vertebral spine.

Recording information in the database

For the cases included in the present study, regarding the retained personal data, we noted exclusively the gender and the age of the person to whom the MR scan was performed.

Working methodology

A total number of 230 cases were examined and analyzed, of which 149 MRI images of the lumbar vertebral spine met the criteria for inclusion.
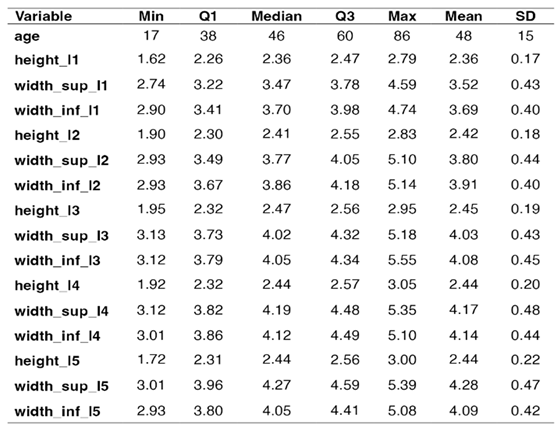
The present study involved performing three measurements on each of the five lumbar vertebrae, totaling 2,235 parameters included in the analysis of gender determination using a machine learning method.
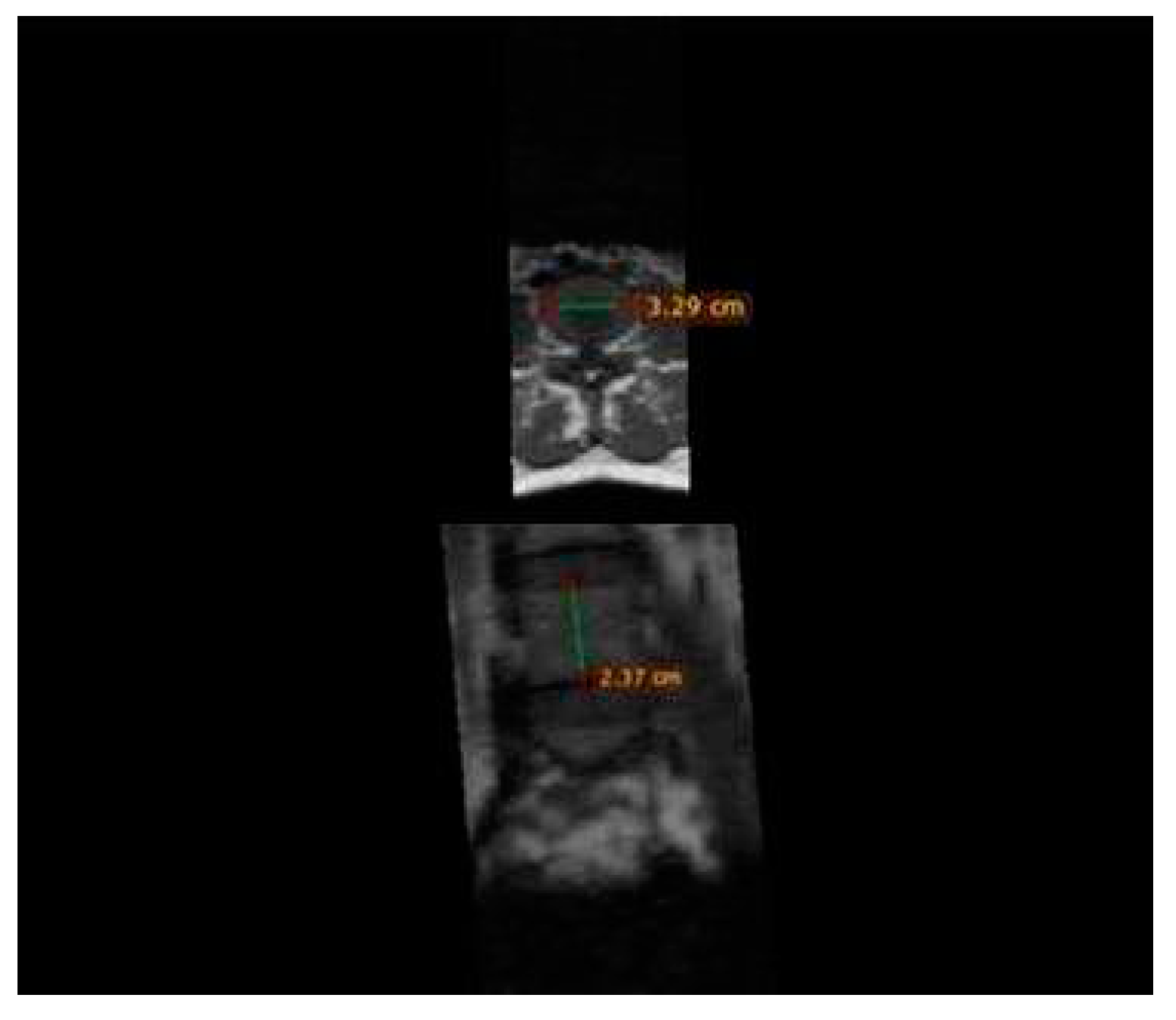
The measurements performed are presented in Table 1 and involve: the posterior height of the vertebral bodies, the width of the upper and, respectively, lower plateau of each vertebral body.
The analysis of MR images and measurements included in the study were performed using the Radiant Dicom Viewer program, using the Ruler function (Figure 1).

Data Analysis and Machine Learning methodology

Distribution of variables was examined with Exploratory Data Analysis techniques [9,10]. In Machine Learning (ML) models the collinearity of the predictors is not such a critical concern as in classical statistical analysis (e.g., liniear or logistic regression). Nevertheless, before building ML models, we removed a series of predictors which recorded large correlations with other predictors.
ML models for classification (the outcome variable was gender) were built and refined with Random Forests (RF) and Extreme Gradient Boosting (XGB), two of the most popular ML algorithms [11,12,13,14,15,16,17].
Both algorithms grow ensembles of classification or regression trees [18,19]. By building trees through split-variable randomization, RF [20] manifest an increased prediction accuracy and a decreased prediction variance [21].
Boosting processed “weak” learners (e.g., stumps or one-level trees) iteratively using a gradient learning strategy and thus resulting “strong” learners [22]. XGB [23] is a regularized implementation of a gradient boosting framework [24] with good performance in both classification and regression [25]. Whereas RF performs better in variance reduction, XGB excels in bias reduction.
Both RF and XGB have hyperparameters (or tuning parameters) that cannot be learned directly from the data, but they need to be refined [26]. Since a larger number of assembled trees does not significantly improve overall performance [27], in this paper the ntrees parameter was fixed to 700; only two parameters were tuned for the RF models: mtry (number of random attributes used for node splitting), and min_n (minimum number of observations in a node as a requirement to continue the tree splitting).
For the XGB models six hyper-parameters were tunned:
  • learn_rate (learning rate),
  • loss_reduction (min reduction in the loss function for continuing the tree split),
  • tree_depth (max tree depth),
  • sample_size (random samples size),
  • min_n and mtry (as for RF models) .
Following the recommendation in [25] the number of trees was not tuned, but fixed at 1000 for all XGB models.
The RF and XGB classification models were tuned by choosing in advance 100 (RF) and 300 (XGB) combinations of values for the selected hyperparameters using random grid search [28]. The best combination of hyperparameters was chosen by the Receiver Operating Characteristic Area Under the Curve (ROC-AUC) metric [29].
Data leakage was avoided by splitting randomly the initial data set into the training subbset (70% of the initial set observations) and the testing subset (30%). Overfitting was reduced by repeated k-fold cross validation [29] of the training subset.
Both algorithms provide the estimated predictors’ contribution to the outcome variation (the variable importance). Among the variable selection methods for RF [30] the permutation-based method was preferred in this study. The importance of variable k is based on the increase of the prediction error in the test set if the variable k’s values are permuted at random. In RF models, through permutation, all correlated predictors are qualified as important if any one of them is important [21]. Of the three scores which generally provide the variable importance in XGB models - gain, cover, and frequency – the xgboost engine focuses on gain [31].
The main interest of this paper was to build a model which properly predicts the gender of a body based solely on the L1-L5 vertebrae measurements. Despite their excelent predictive power, ML algorithms like RF, XGB or neural networks are opaque. Starting with 2016, scholars and professionals in many areas (medicine included) require more transparency and interpretability for the ML models [32,33]. Of the techniques for interpretable machine learning [34,35,36] for this paper we used Variable Importance plots, Partial Dependency Plots and Accumulated Local Effects Plots, as described in literature [37,38].
Partial Dependency Plots (PDPs) and Accumulated Local Effects Plots (ALEs) are two explanatory tools used for visualization and interpretation of effects the analyzed features have on model predictions. The idea behind PDPs is to analyze the behaviour of models predictions based on one or two selected features [37]. A partial dependency profile is calculated as the mean of ceteris-paribus profiles - which is a technique to show dependence between prediction and a feature variable at instance level. The shape of the PDP plot will suggest whether the relationship between the output and predictors is linear, monotonic or complex [38]. These plots provide a simple method to describe the influence a selected feature has on the outcome, but have a major disadvantage when the analyzed features are correlated.
This issue is solved by ALE, which essentialy is the same function of one or two features, but the key difference is how they handle the influence of other features. PDP plots average the predictions and ALE plots use the difference in predictions and accumulate them.
While both PDPs and ALE plots aim to visualize the impact of features on model predictions, ALE plots often provide a more accurate depiction, thus are the way to go when choosing between these two options [38].
Data was imported, prepared, explored, and analyzed using R [39], mainly with the tidyverse ecosystem of packages (dplyr, tidyr, ggplot2, etc.) [40]. Descriptive statistics tables/figures were generated with the gtsummary package [41].
The tidymodels ecosystem of packages (rsample, recipes, parnsip, yardstick, tune, dials, workflows) [42,43] was employed for model building and tuning. The RF models were fitted with the ranger engine [44], whereas the engine used for building the XGB models was xgboost [31].
The model interpretation relied on the DALEX ecosystem [45], mainly the ingredients package [46].

3. Results

This section starts with data exploration, by examining the data distribution and correlation among predictors. Subsequently, some details on model building, assessment and tuning are provided. Finally, models which recorded the best performance are analysed using variable importance and some other techniques related to model interpretation (explainable AI).

3.1. Data distribution. Corrrelation among predictors

Table 2 shows the descriptive statistics for each numerical variable in the data set – the minimal value, the 1st quartile (Q1 or the 25th percentile), the 3rd quartile (Q3 or the 75th percentile), the median (the 50th percentile) and the maximal value. The average value (Mean) is accompanied by the standard deviation (SD).
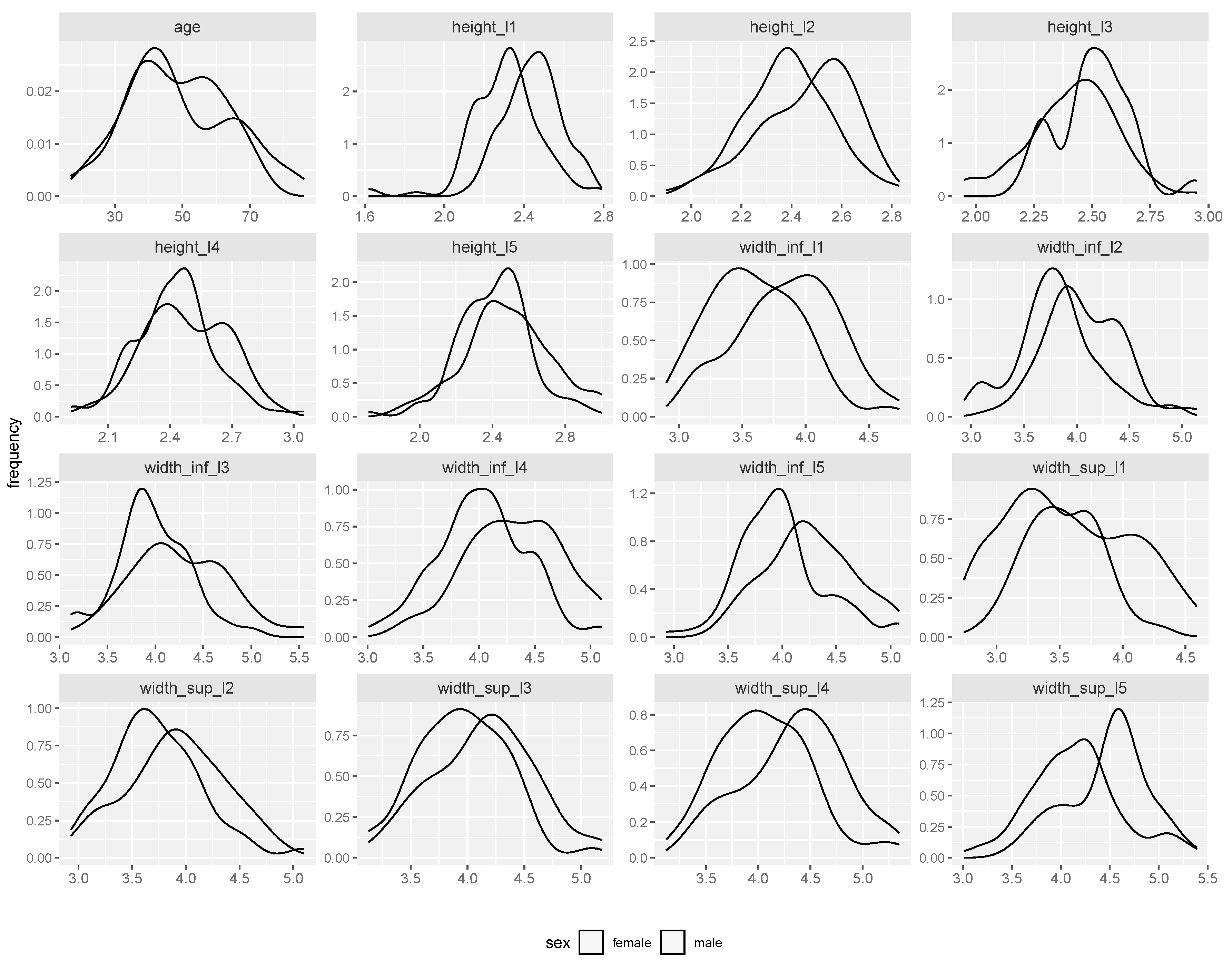
As the main intereset of this paper was to build models for gender estimation based on measurements of the L1-L5 vertebrae, Figure 2 displays the distribution of numeric variables by gender. Despite some differences in between genders, the shape of the distribution is generally similar, with males measurements appearing to exceed the valaues for females. Nevertheless, here we were not interested in the analysis of the statistical differences between genders for the L1-L5 variables.
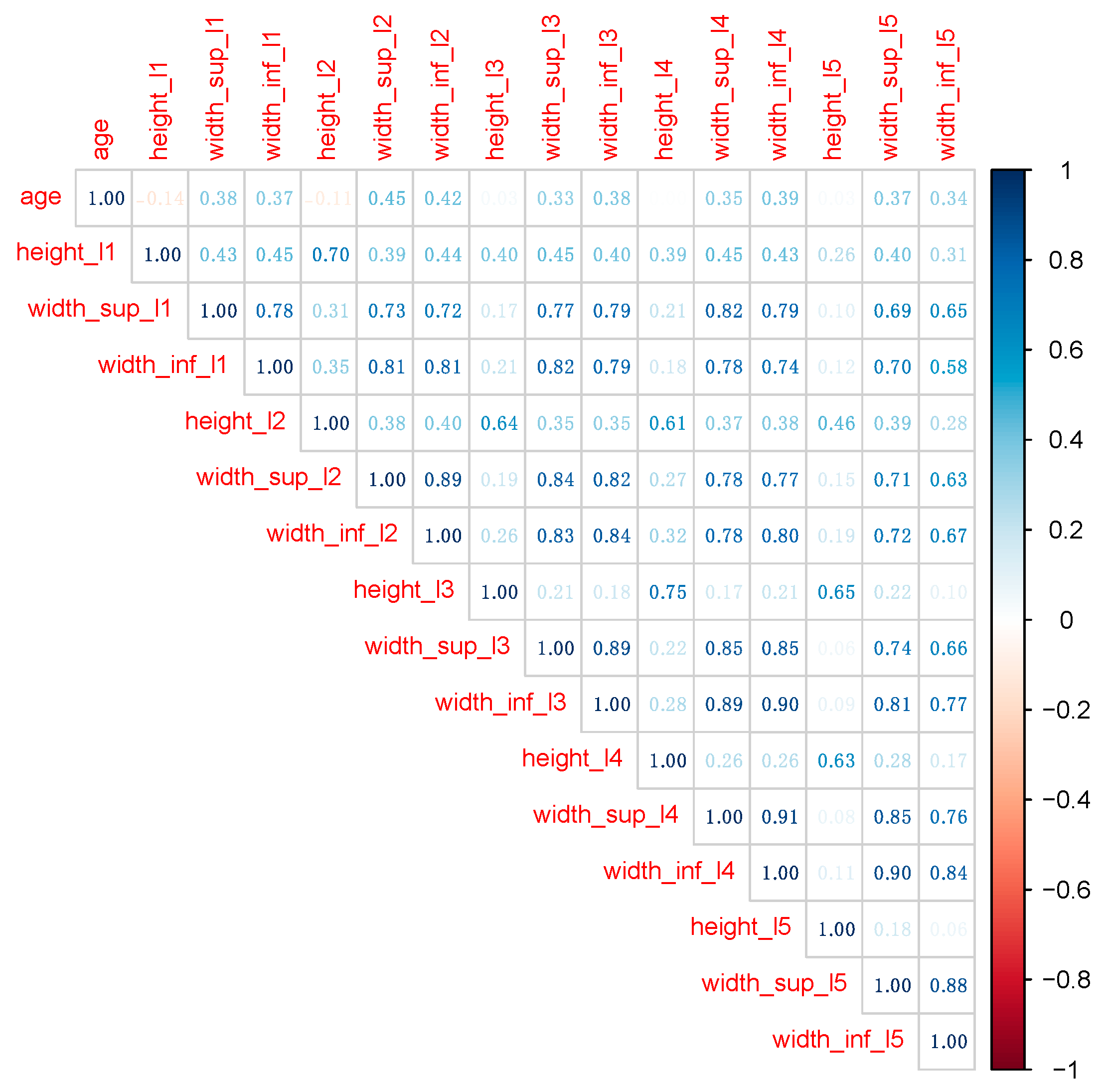
Before building the ML models, predictors collinearity was assessed and fixed. Figure 3 shows the correlation matrix among all numeric variables in the initial data set.
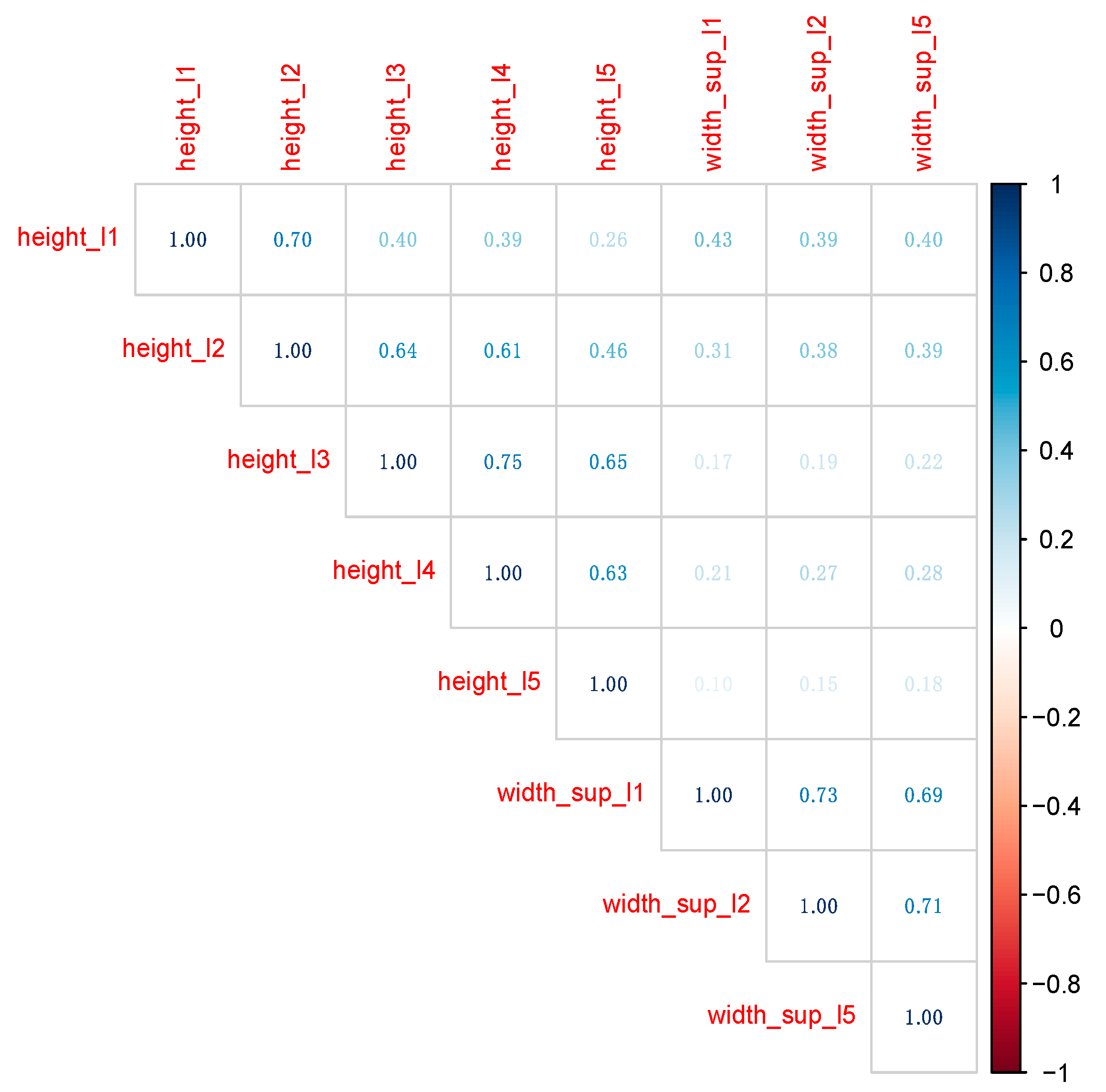
Classical statistical techniques, such as linear and logistic regression, require removing large correlations among predictors, since collinearity usually affects model performance. Even if both RF and XGB models handle collinearity much better, we removed predictors recording correlation coefficients larger than 0.75. The final data set contains predictors in Figure 4.
Also in Figure 4 variable age was removed, since when gender is unknown, also person’s age could not be determined. Consequently, the final dataset on which the ML models were built and tuned contains gender (as the outcome variable) and all variables in Figure 4 (as predictors).

3.2. Model building and refinement

The 149-observation data set was randomly split into the training dataset which contained 111 records (about 75%) and the testing dataset containing 38 records (25%). All further model training, tuning and selection were performed only on the training data set. The testing dataset was used solely for estimating the model performance on new data (data not “seen” during the training steps). This is a basic prerequisite in ML model building.
To reduce overfitting, the training subset was further split randomly into five cross-validation folds. In each training fold, the data was subsequently split into the analysis subset and the validation subset.
For each cross-validation fold, 100 RF models (each model incorporated 700 trees) were built and assessed for each combination of (mtry, min_n) hyper-parameters extracted through random grid search. Figure 5 shows the values of two main performance metrics of classification (accuracy and roc_auc) when mtry (# Randomly Selected Predictors) and min_n (Minimal Node Size) varied within their value range extracted through grid search.
Figure 5 shows that, for both hyper-parameters, larger values generally decrease the model performance and best values of both accuracy and roc_auc for the training data set were recorded during the first half of hyperparameters range. Best models were chosen using the roc_auc metric. For RF, the best peformance along the five cross-validation folds was recorded for mtry = 1 and min = 8.
XGB models were built using the same subsets/folds as for RF. But as the number of hyper-parameters to be tuned was three times higher than in RF models, for the XGB models 300 combination of hyper-parameter value were selected through random grid search (each model incoporated 1000 trees). One of the remarcable features of the tidymodels ecosystem is that the packages managing the grid search (tune and dial) extract automatically the appropriate values of the hyper-parameters, according the the data set characteristics, without any tweaking from the user. This is useful especially for the XGB hyper-parameters such as learning rate, loss reduction, and sample size.
Figure 6 displays the values of accuracy and roc_auc) when varying the XGB hyper-parameters.
For XGB models, the best roc_auc (averaged along the cross-validation folds) was recorded for the following combination: mtry = 2, min_n = 7, learn_rate = 0.0002989344, loss_reduction = 0.0000000001035262, tree_depth = 9, and sample_size = 0.9337572.
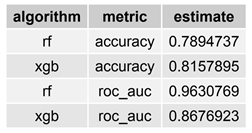
The “moment of truth” for the predictive models is how they perform on new (“unseen”) data. There are models which confound the pattern with the noise, i.e., they found non-existing patterns in data (overfitting). This is the role the testing subset. After identifying the best combination of hyper-parameters, the best RF and XGB models were applied for the testing data. Table 3 displays both accuracy and roc_auc performance metrics for the selected/best RF and XGB models.
Selected models recorded recorded good performance on both metrics. While in terms of accuracy the XGB selected model overperformed the RF selected model (0.816 vs. 0.789), when considering the roc_auc RF performed better (0.963 vs. 0.868). To summarise, in terms of prediction performance, both RF and XGB selected models seem to supply good estimates of the person’s gender based on her/his L1-L5 vertebrae measurements.

3.3. Model interpretation

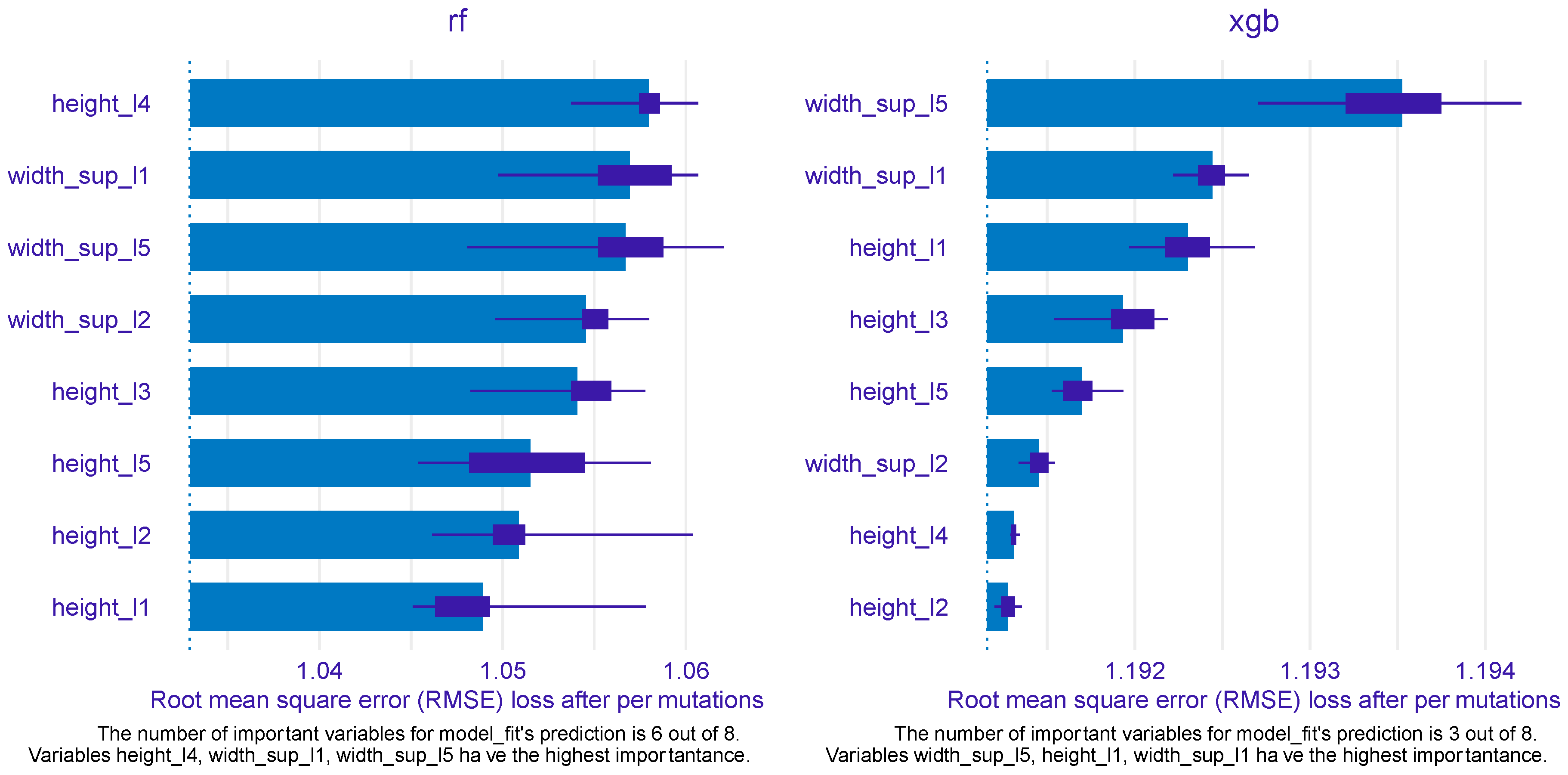
After assessing the predictive power of the ML models built upon RF and XGB, next we were interested in exploring the predictors’ importance in the models, and how the most important predictors were associated with the outcome (gender) within each selected model. Figure 7 mirrors the predictors’ importance for the RF (left) and XGB models (right), as estimated by the ingredients package.
Out of eight predictors, six were found to be particularly important for the RF model, while only three were determined to be important by the XGB model. For RF height_l4 emerged as the most important feature, followed by width_sup_l1 and width_sup_l5 ranking second and third, respectively. These two features also were identified at top important by the XGB model, width_sup_l5 being the most important variable and width_sup_l1 being the second (most) important. The top 3 for XGB was completed by height_l1, which, intriguingly, was the least important in the RF model. The other three variables that were qualified important by the RF model were width_sup_l2, height_l3, and height_l5, filling the fourth, fifth, and sixth positions, respectively.
For PDP and ALE plot analysis (Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12), only the variable importance as estimated by the RF selected model was considered, since its roc_auc metric was the highest on the test set. From the variable importance plot in the left side of the Figure 7, only top 5 most important predictors were selected and examined. For each top predictors, the figure included three charts: the PDP plot, the ALE plot (for checking if the PDP plot is affected by correlation with other predictors), and the density curve (to identify the ranges where models were fitted on a small number of predictor values and thus the interpretation needs extra precaution).
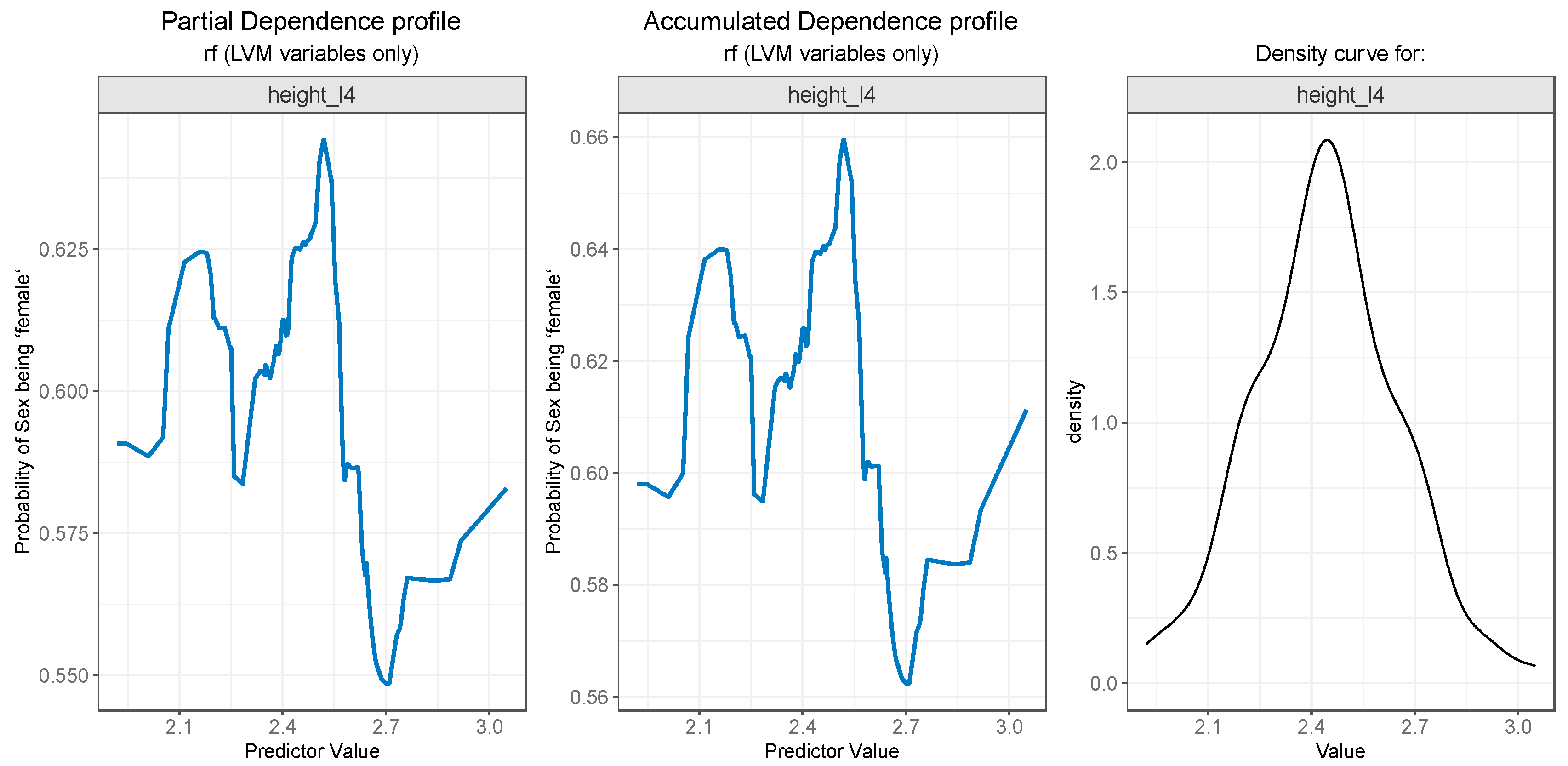
Both PDP (Figure 8 - left) and ALE (Figure 8 - center) plots for height_l4 variable suggest that the probability of gender being predicted as “female” drops after a value of 2.5, i.e., values of height_l4 larger than 2.5 are more likely to be associated with males. The rather weird jumps on the left and right side of the plots can be explained by the low number of values in those regions, as can be seen in the density curve for the variable in Figure 8 (right).
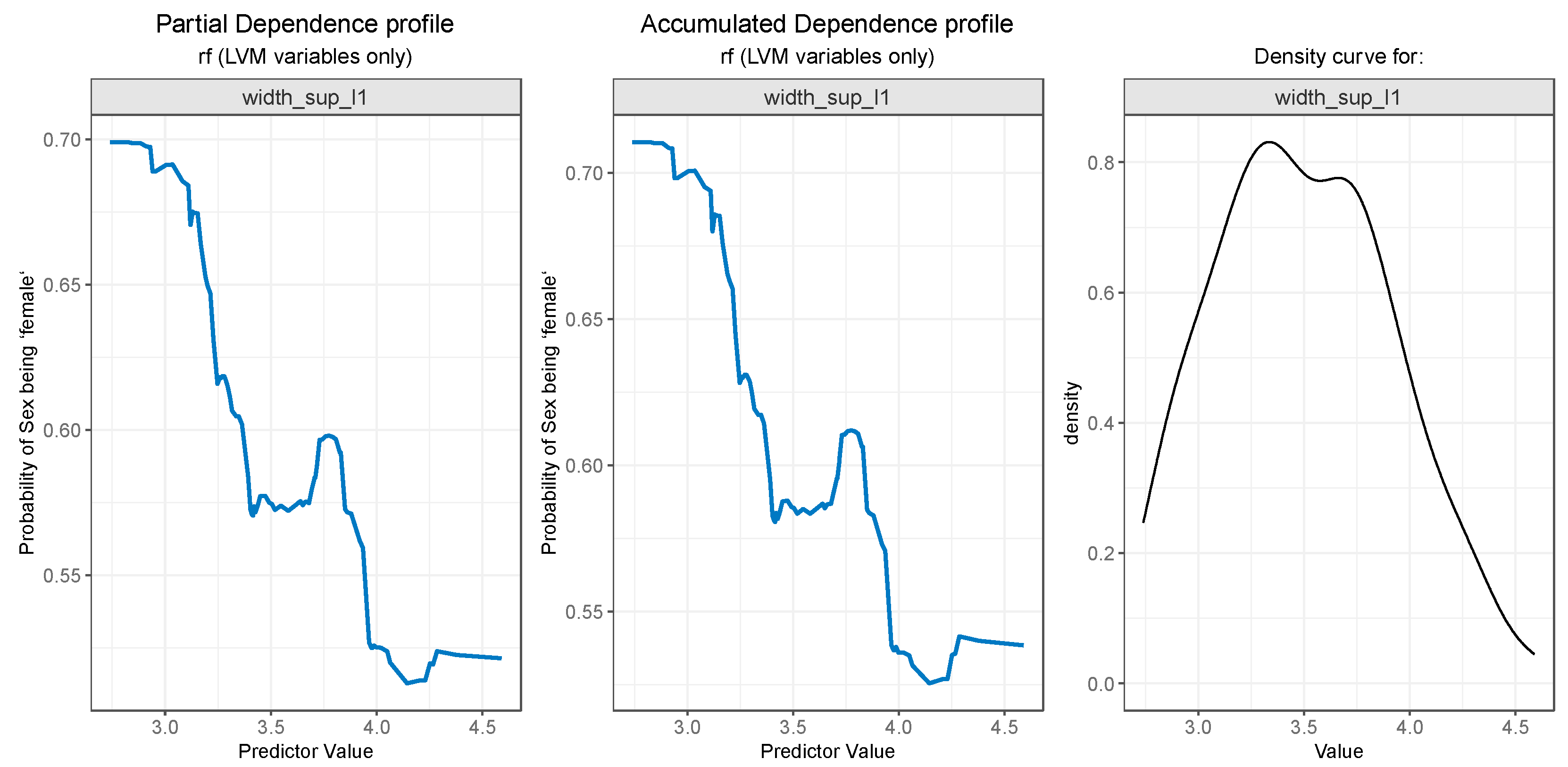
The PDP plot for the second most important feature, width_sup_l1, presented in Figure 9 (left) and the ALE plot (center), follow a similar pattern. Both of them suggest that the probability outcome of gender being “female” is higher while the values for width_sup_l1 are low and slowly decreases as the values rise in value, especially after the 3.6.
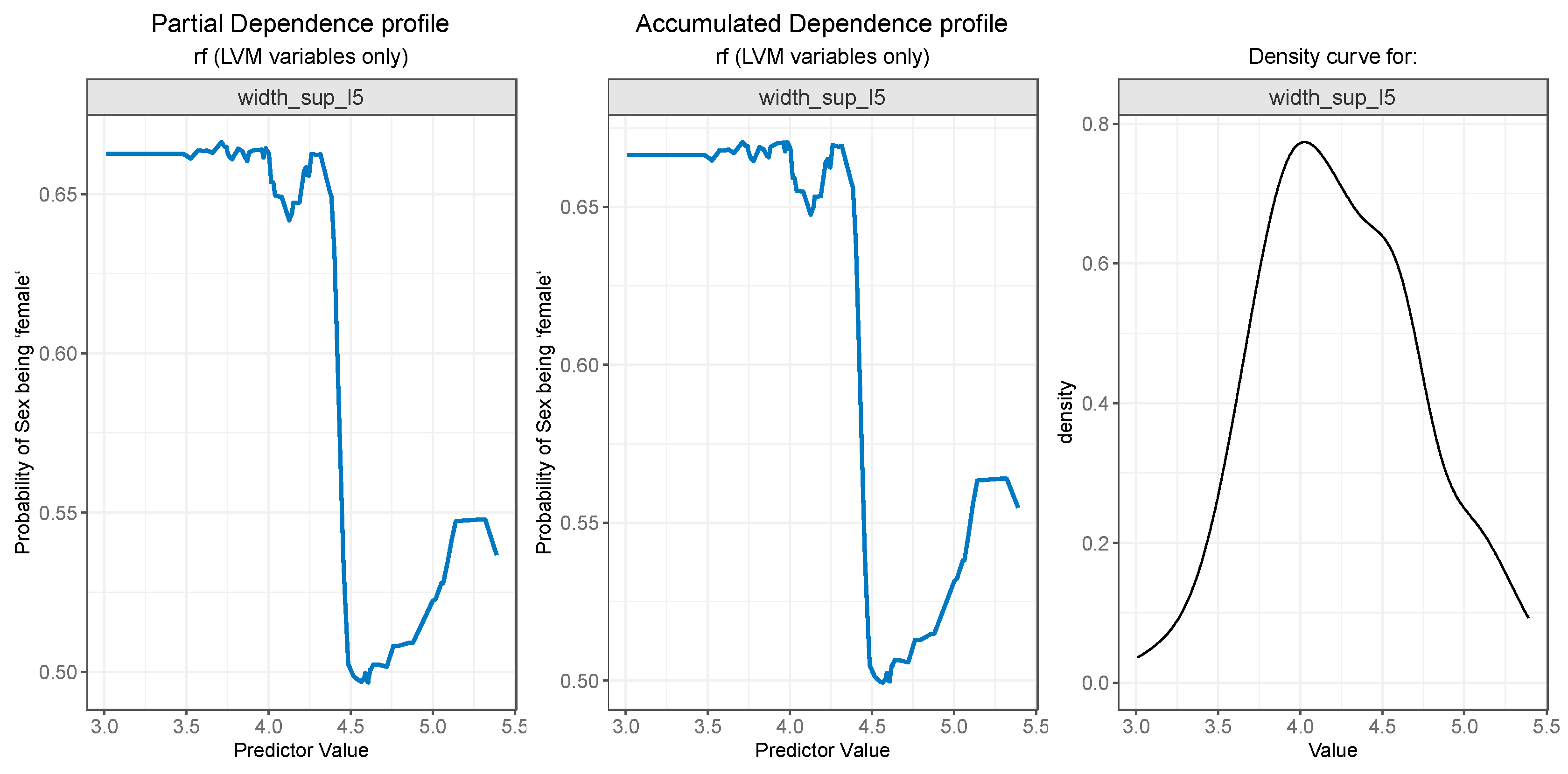
For variable width_sup_l5 both PDP plot (Figure 10 - left) and ALE plot (Figure 10 - center) exhibit similar results. A value below 4.2 is strongly associated with a high probability of the value “female” for the outcome. Notably, the value is also the starting point of a steep decrease in the probability of person being a female. The slight increase after 4.5 can, once again, be explained by the low number of observations in that range, as seen in Figure 10-right.
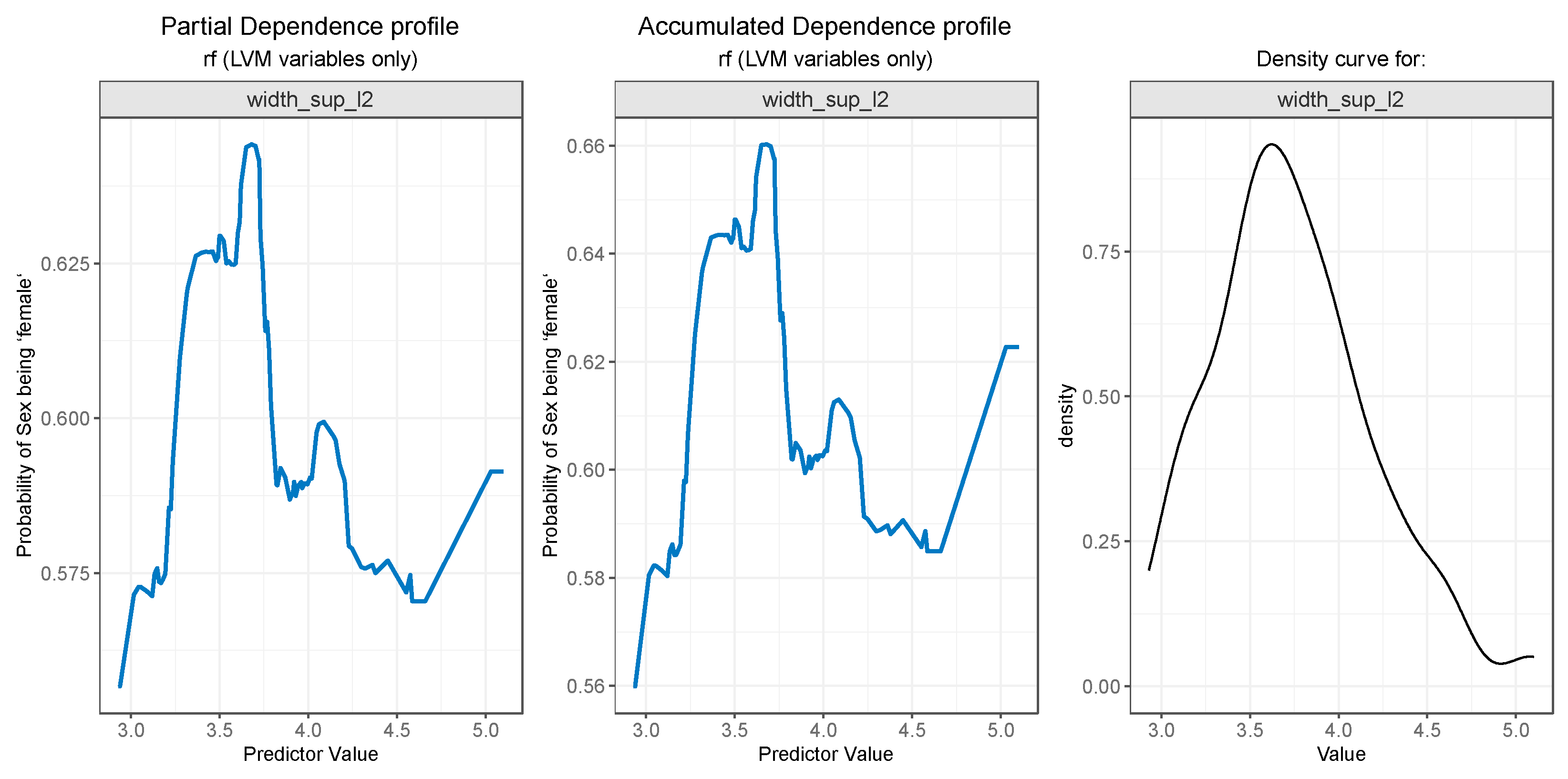
The width_sup_l2 feature os associated with a higher probability of gender being female for values less than 3.6, and the probability starts to lower for values up to 4.6, as can be seen in Figure 11 (left and middle). Marginal intervals contain outliers which result in steep increases or decreases in the plot curves.
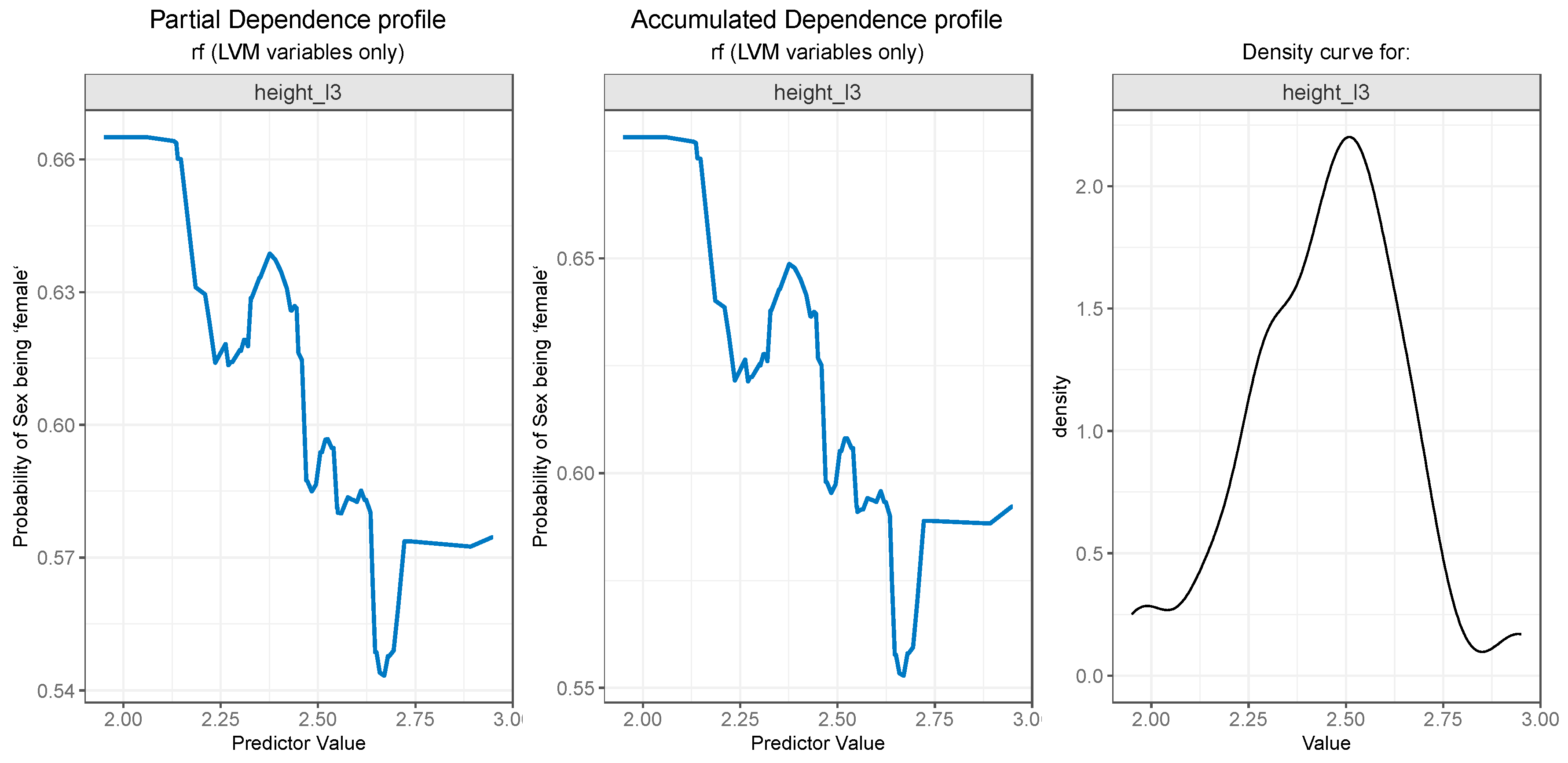
Finally, as seen in Figure 12 (left and center) the height_l3 feature presents a descending curve, meaning that values lower than 2.5 are associated with a higher probability of the outcome being “female”, and values greater than 2.5 decrease the chance of the “gender” being predicted as “female”, but here the outcome probability descends in a more gradual manner.
Generally, larger values of L1-L5 vertebrae measurements are associated with males.

4. Discussion

While artificial intelligence (AI) can be considered an area of research aimed at mimicking human abilities, machine learning is a specific subset of AI that develops a computer’s ability to learn. The interest in ML is due to various factors such as the increasing volume and variety of data available on the internet, cheaper and more powerful computer processing and affordable data storage. Advances in ML have led to the development of the ability to quickly and automatically produce models that can analyze a significant amount of complex data with faster and more accurate results.
The purpose of the present study was to observe whether by using the ML method there is a good predictability of gender in forensic identification based on parameters obtained from the metric analysis of the lumbar spine specific to the Romanian population.
Generating a gender estimation model is based on solving a classification task. Classification is one of the most commonly used exploratory tasks in ML [47].
In this regard, we used MR images, due to their reliability and performance in visualizing the spine, focusing on the lumbar spine, taking into account as parameters the height, width of the upper and lower plateau of each lumbar vertebra L1-L5. Of all the measurements performed, only the heights of the L1-L5 vertebrae, respectively the dimensions of the upper plateaus of the first two vertebrae, L1, L2, and of the fifth lumbar vertebra, L5, were included in the present study. They showed to meet all the characteristics to be entered into the ML classification.
In forensic medicine, and especially in forensic identification, the daily practice of providing the most correct answers both for justice and for humanitarian and ethical reasons, leads to the need to develop and create as many new methods as possible adapted to the new living conditions of humanity. Thus, the involvement of machine learning techniques in determining certain parameters that create the biological profile of an individual, in this case determining gender, is a primary necessity in research in this field.
Sexual dysmorphism can be represented on almost every bone component in the cranial and postcranial skeleton. In the present study, we chose to highlight the sexual dysmorphism provided by the lumbar spine, describing differences in its morphometry between men and women and generating a machine learning model to accurately predict a person’s gender. According to the results, it is observed that the measurements under discussion show higher values in men compared to women for the Romanian population, which also follows the results from the specialized literature for other population groups.
Sexual dimorphism of vertebrae is fundamentally based on size, with male individuals generally being larger than female individuals. Previous studies show different results on statistically significant differences between genders in vertebral regions, but all identify dimorphism in vertebral body measurements [48,49,50,51,52,53,54]. Studies led by Taylor and Twomey [48] suggest that these differences may be due to differential growth rates between males and females during puberty, early growth of vertebrae in female individuals, and greater increase in width in male individuals. In addition, bone size, shape and density are also influenced by physical activity and mechanical stress [55]. The smaller size of the vertebral body in female individuals is associated with greater flexibility of the spine compared to an accentuated lumbar lordosis in response to the biomechanical needs of pregnancy [50,56,57].
The present study proposes a machine learning model in which, for both genders, the selected models performed well, In terms of predictive performance, both selected RF and XGB models appear to estimate the person’s gender based on L1-L5 measurements. In a modern African population study [50]. Significant gender differences were identified in several metric traits of the lumbar vertebrae, and the multiple discriminating functions generated from the analyzed data were able to estimate gender with satisfactory accuracy. Other studies using individual postcranial elements such as femur [58,59,60], tibia [58,61], patella [62,63], humerus [64,65], radius and ulna [66], various hand and foot bones[67,68,69] showed comparable performance to the present study.
This paper offers two models of ML, RF and XGB, each with its own characteristics, and presenting different performance, random forest having the best. For both, we used two metrics (accuracy and roc_auc), the latter being the most used to highlight model performance.
For both metrics the selected models recorded good performance. While in terms of accuracy the XGB selected model overperformes the RF selected models (0.816 vs. 0.789), when considering the roc_auc RF performed better (0.963 vs. 0.868). To summarise, in terms of prediction performance, both RF and XGB selected models seem to estimate the person’s gender based on the L1-L5 measurements.
Because the identity of individuals must be predicted quickly and accurately in events such as war, natural disasters or fires, which profoundly affect society, imaging (virtual forensic) scanning of cadaveric bodies and MLs used in the present study show that prediction time can be minimized and high accuracy can be achieved depending on the situation. Given the high Acc or two-metric percentage found as a result of the RF and XGB algorithm, it is believed that this study will strengthen and contribute to studies related to gender prediction, and beyond.

5. Conclusions

The L1-L5 lumbar vertebrae exhibit sexual dimorphism and can be used in gender estimation. Machine learning is more accurate in determining gender than regression/discriminatory function analysis. In addition, subjectivity and measurement errors are reduced. Finally, this study presented an alternative approach to determining gender from lumbar vertebrae when traditionally used skeletal elements are incomplete or absent.
The perspective of the study is to create a digital interface to be made available to all practitioners of the forensic network in Romania, but not only. This interface would be developed by adding other parameters to be taken into account, on the one hand, and on the other hand, it would be developed by adding other predictions supporting forensic identification, parts of the biological profile, respectively determining the postmortem interval, for example. The proposal of such an interface represents a novelty element in forensic medicine in Romania.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, M.M.D., G.M.T., D.T.; methodology, M.M.D., D.T., G.S.; software, M.F. and N.R.; validation, S.I.D., M.F.; formal analysis, M.F., N.R.; resources, M.M.D., D.T., G.S., A.S..; writing—original draft preparation, M.M.D., T.G.M.,; writing—review and editing, M.M.D., M.F., D.B.I., S.I.D.; supervision, D.B.I., M.H.; project administration, M.H.; funding acquisition, M.M.D., M.H. All authors have read and agreed to the published version of the manuscript.”

Funding

”This article was published with the support of the project „Net4SCIENCE: Applied doctoral and postdoctoral research network in the fields of smart specialization Health and Bioeconomy”, project code POCU/993/6/13/154722”.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethic Committee of „Grigore T. Popa” Medicine and Pharmacy University (protocol code 296/30.04.2023).

Acknowledgments

Data processing and analysis were supported by the Competitiveness Operational Program Romania under project number SMIS 124759 - RaaS-IS (Research as a Service Iasi). This article was published with the support of the project „Net4SCIENCE: Applied doctoral and postdoctoral research network in the fields of smart specialization Health and Bioeconomy”, project code POCU/993/6/13/154722.

Conflicts of Interest

“The authors declare no conflict of interest.”

References

  1. Cattaneo, C. Forensic anthropology: developments of a classical discipline in the new millennium. Forensic Sci Int 2007, 165, 185–193. [Google Scholar] [CrossRef]
  2. Diac, M.M.; Iov, T.; Damian, S.I.; Knieling, A.; Girlesccu, N.; Lucasievici, C.; David, S.; Kranioti, E.F.; Iliescu, D.B. Estimation of stature from tibia length for Romanian adult population. Appl Sci 2021, 11, 11962. [Google Scholar] [CrossRef]
  3. Diac, M.M.; Hunea, I.; Girlescu, N.; Knieling, A.; Damian, S.I.; Iliescu, D.B. Morphometry of the foramen magnum for sex estimation in Romanian adult population. Brain 2020, 11, 231–243. [Google Scholar] [CrossRef]
  4. Blau, S.; Robertson, S.; Johnstone, M. Disaster victim identification: new applications for post-mortem computed tomography. J Forensic Sci 2008, 53, 956–961. [Google Scholar] [CrossRef]
  5. Toy, S.; Secgin, Y.; Oner, Z.; Turan, M.K.; Oner, S.; Senol, D. A study on sex estimation by using machine learning algorithms with parameters obtained from computerized tomography images of the cranium. Sci Reports 2022, 12, 4278. [Google Scholar] [CrossRef]
  6. Cheng, X.G.; Sun, Y.; Boonen, S.; Nicholson, P.H.; Brys, P.; Dequeker, J.; Felsenberg, D. Measurements of vertebral shape by radiographic morphometry: sex differences and relationships with vertebral level and lumbar lordosis. Skeletal Radiology 1998, 27, 380–384. [Google Scholar] [CrossRef]
  7. Decker, S.J.; Foley, R.; Hazelton, J.M.; Ford, J.M. 3D analysis of computed tomography (CT)–derived lumbar spine models for the estimation of sex. International Journal of Legal Medicine 2019, 133, 1497–1506. [Google Scholar] [CrossRef]
  8. Garoufi, N.; Bertsatos, A.; Chovalopoulou, M.E.; Villa, C. Forensic sex estimation using the vertebrae: an evaluation on two European populations. International Journal of Legal Medicine 2020, 134, 2307–2318. [Google Scholar] [CrossRef]
  9. Tukey, J.W. We need both exploratory and confirmatory. American Statistician 1980, 34, 23–25. [Google Scholar] [CrossRef]
  10. Behrens, J.T. Principles and procedures of exploratory data analysis. Psychological methods 1997, 2, 131. [Google Scholar] [CrossRef]
  11. Dettling, M.; Bühlmann, P. Boosting for tumor classification with gene expression data. Bioinformatics 2003, 19, 1061–1069. [Google Scholar] [CrossRef]
  12. Lehmann, C.; Koenig, T.; Jelic, V.; Prichep, L.; John, R.E.; Wahlund, L.O.; Dodge, Y.; Dierks, T. Application and comparison of classification algorithms for recognition of Alzheimer’s disease in electrical brain activity (EEG). J Neurosci Methods 2007, 161, 342–350. [Google Scholar] [CrossRef]
  13. Zaunseder, S.; Huhle, R.; Malberg, H. CinC challenge — Assessing the usability of ECG by ensemble decision trees, in Proc. 2011 Computing in Cardiology, Hangzhou, China, 2011, 277-280.
  14. Austin, P.C.; Lee, D.S.; Steyerberg, E.W.; Tu, J.V. Regression trees for predicting mortality in patients with cardiovascular disease: what improvement is achieved by using ensemble-based methods? Biom J. 2012, 54, 657–673. [Google Scholar] [CrossRef]
  15. Abreu, P.H.; Santos, M.S.; Abreu, M.H.; Andrade, B.; Silva, D.C. Predicting breast cancer recurrence using machine learning techniques: A systematic review. ACM Comput. Surv. 2016, 49, 40. [Google Scholar] [CrossRef]
  16. Lorenzoni, G.; Sabato, S.S.; Lanera, C.; Bottigliengo, D.; Minto, C.; Ocagli, H. Comparison of machine learning techniques for prediction of hospitalization in heart failure patients. J Clin Med 2019, 8, 1298. [Google Scholar] [CrossRef] [PubMed]
  17. Mpanya, D.; Celik, T.; Klug, E.; Ntsinjana, H. Predicting mortality and hospitalization in heart failure using machine learning: A systematic literature review. IJC Heart & Vasculature 2021, 34, 100773. [Google Scholar] [CrossRef]
  18. Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees. Wadsworth/New York: Chapman and Hall, 1984.
  19. Loh, W.Y. Fifty years of classification and regression trees. Int Statist Rev 2014, 82, 329–348. [Google Scholar] [CrossRef]
  20. Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  21. Cutler, A.; Cutler, R.D.; Stevens, J.R. Random forests. Ensemble Machine Learning. Boston, MA: Springer, 2012.
  22. Freund, Y.; Schapire, R. A short introduction to boosting. J Japanese Soc Artif Intellig 1999, 14, 771–780. [Google Scholar]
  23. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System, in Proc. of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ‘16). ACM, New York, NY, USA, 2016, 785–794.
  24. Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors), Ann. Statist. 2000, 28, 337–407. [Google Scholar] [CrossRef]
  25. Bentéjac, C.; Csörgő, A.; Martı́nez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif Intell Rev 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
  26. Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J Machine Learning Research 2019, 20, 5. [Google Scholar]
  27. Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. WIREs Data Mining Knowl Discov 2019, 9, e1301. [Google Scholar] [CrossRef]
  28. Kuhn, M.; Johnson, K. Feature engineering and selection: A practical approach for predictive models., Boca Raton, FL: CRC Press, 2019.
  29. Kuhn, M.; Johnson, K. Applied Predictive Modeling. New York: Springer, 2013.
  30. Degenhardt, F.; Seifert, S.; Szymczak, S. Evaluation of variable selection methods for random forests and omics data sets. Briefings in bioinformatics 2019, 20, 492–503. [Google Scholar] [CrossRef]
  31. Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; Li, M.; Xie, J.; Lin, M.; Geng, Y.; Li, Y. xgboost: Extreme Gradient Boosting, R package version 1.3.2.1, Aug. 10, 2021. Available: https://CRAN.R-project.org/package=xgboost.
  32. Ribeiro, M.T.; Singh, S.; Guestrin, C. Why should I trust you? In Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining; 2016; pp. 1135–1144. [Google Scholar]
  33. Lipton, Z.C. The doctor just won’t accept that! arXiv preprint. arXiv:1711.08037, 2017.
  34. Du, M.; Liu, N.; Hu, X. Techniques for interpretable machine learning. Communications of the ACM 2019, 63, 68–77. [Google Scholar] [CrossRef]
  35. Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Herrera, F. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Information fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
  36. Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G.; Ranjan, R. Explainable AI (XAI): Core ideas, techniques, and solutions. ACM Computing Surveys 2023, 55, 1–33. [Google Scholar] [CrossRef]
  37. Biecek, P.; Burzykowski, T. Explanatory Model Analysis, Publisher: Chapman and Hall/CRC: New York, 2021.
  38. Molnar, C. Interpretable Machine Learning. A Guide for Making Black Box Models Explainable, 2nd ed., independently published, 2022.
  39. R Core Team, R: A Language and Environment for Statistical Computing, Vienna, Austria: R Foundation for Statistical Computing. R version 4.3.0, Aug. 30, 2023. Available: https://www.R-project.org.
  40. Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; D’Agostino McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J. Welcome to the Tidyverse. J Open-Source Software 2019, 4, 1–6. [Google Scholar] [CrossRef]
  41. Sjoberg, D.D.; Whiting, K.; Curry, M.; Lavery, J.A.; Larmarange, J. Reproducible summary tables with the gtsummary package. The R Journal 2021, 13, 570–580. [Google Scholar] [CrossRef]
  42. Kuhn, M.; Wickham, H. Tidymodels: a collection of packages for modeling and machine learning using tidyverse principles, 2022, [Online]. Available: https://www.tidymodels.org, Accessed on: Feb. 1, 2022.
  43. Kuhn, M.; Silge, J. Tidy Modeling with R, Sebastopol, CA: O’Reilly Media, 2022.
  44. Wright, M.N.; Ziegler, A. Ranger: A fast implementation of random forests for high dimensional data in C++ and R. J Statist Soft 2017, 77, 1–17. [Google Scholar] [CrossRef]
  45. Biecek, P. DALEX: Explainers for complex predictive models in R. J Machine Learning Research 2018, 19, 3245–3249. [Google Scholar]
  46. Biecek, P. , Baniecki, H., ingredients: Effects and Importances of Model Ingredients. R package version 2.3.0., 2023, Available: https://CRAN.R-project.org/package=ingredients.
  47. McQueen, R.J.; Holmes, G.; Hunt, L. User satisfaction with machine learning as a data analysis method in agricultural research. N Z J Agric Res 1998, 41, 577–584. [Google Scholar] [CrossRef]
  48. Taylor, J.; Twomey, L. Sexual dimorphism in human vertebral body shape. J Anat 1984, 138, 281–286. [Google Scholar] [PubMed]
  49. Pastor, R.F. Sexual dimorphism in vertebral dimensions at the T12/L1 junction. In: Proceedings of the American Academy of Forensic Sciences 57th Annual Scientific Meeting, New Orleans, LA. 2005.
  50. Ostrofsky, K.R.; Churchill, S.E. Sex determination by discriminant function analysis of lumbar vertebrae. J Forensic Sci 2015, 60, 21–28. [Google Scholar] [CrossRef] [PubMed]
  51. Decker, S.J.; Foley, R.; Hazelton, J.M.; Ford, J.M. 3D analysis of computed tomography (CT)-derived lumbar spine models for the estimation of sex. Int J Legal Med 2019, 133, 1497–1506. [Google Scholar] [CrossRef] [PubMed]
  52. Zheng, W.X.; Cheng, F.B.; Cheng, K.L.; Tian, Y.; Lai, Y.; Zhang, W.S. Sex assessment using measurements of the first lumbar vertebra. Forensic Sci Int 2012, 219, 285.e1-5. [Google Scholar] [CrossRef]
  53. Oura, P.; Karppinen, J.; Niinimäki, J.; Junno, J.A. Sex estimation from dimensions of the fourth lumbar vertebra in Northern Finns of 20, 30, and 46 years of age. Forensic Sci Int 2018, 290, 350.e1-6. [Google Scholar] [CrossRef] [PubMed]
  54. MacLaughlin, S.M.; Oldale, K.N.M. Vertebral body diameters and sex prediction. Ann Hum Biol 1992, 19, 285–292. [Google Scholar] [CrossRef]
  55. Gilsanz, V.; Wren, T.A.L.; Ponrartana, S.; Mora, S.; Rosen, C.J. Sexual dimorphism and the origins of human spinal health. Endocr Rev 2018, 39, 221–239. [Google Scholar] [CrossRef]
  56. Ponrartana, S.; Aggabao, P.C.; Dharmavaram, N.L.; Fisher, C.L.; Friedlich, P.; Devaskar, S.U. Sexual dimorphism in newborn vertebrae and its potential implications. J Pediatr 2015, 167, 416–421. [Google Scholar] [CrossRef] [PubMed]
  57. Steyn, M.; Iscan, M.Y. Sex determination from the femur and tibia in South African whites. Forensic Sci Int 1997, 90, 111–119. [Google Scholar] [CrossRef] [PubMed]
  58. Mall, G.; Graw, M.; Gehring, K.; Hubig, M. Determination of sex from femora. Forensic Sci Int 2000, 113, 315–321. [Google Scholar] [CrossRef] [PubMed]
  59. Asala, S.A.; Bidmos, M.A.; Dayal, M.R. Discriminant function sexing of fragmentary femur of South African blacks. Forensic Sci Int 2004, 145, 25–29. [Google Scholar] [CrossRef] [PubMed]
  60. Iscan, M.Y.; Yoshino, M.; Kato, S. Sex determination from the tibia: standards for contemporary Japan. J Forensic Sci 1994, 39, 785–792. [Google Scholar] [CrossRef] [PubMed]
  61. Dayal, M.R.; Bidmos, M.A. Discriminating sex in South African blacks using patella dimensions. J Forensic Sci 2005, 50, 1294–1297. [Google Scholar] [CrossRef] [PubMed]
  62. Introna, F.; DiVella, G.; Campobasso, C.P. Sex determination by discriminant analysis of patella measurements. Forensic Sci Int 1998, 95, 39–45. [Google Scholar] [CrossRef]
  63. Frutos, L.R. Metric determination of sex from the humerus in a Guatemalan forensic sample. Forensic Sci Int 2005, 147, 153–157. [Google Scholar] [CrossRef] [PubMed]
  64. Kranioti, E.F.; Michalodimitrakis, M. Sexual dimorphism of the humerus in contemporary Cretans – a population-specific study and a review of the literature. J Forensic Sci 2009, 54, 996–1000. [Google Scholar] [CrossRef]
  65. Barrier, I.L.; L’Abbe, E.N. Sex determination from the radius and ulna in a modern South African sample. Forensic Sci Int 2008, 179, 85.e1-e7. [Google Scholar] [CrossRef]
  66. Mastrangelo, P.; Luca, S.D.; Sánchez-Mejorada, G. Sex assessment from carpals bones: discriminant function analysis in a contemporary Mexican sample. Forensic Sci Int 2011, 209, 196.e1-e15. [Google Scholar] [CrossRef] [PubMed]
  67. Barrio, P.A.; Trancho, G.J.; Sánchez, J.A. Metacarpal sexual determination in a Spanish Population. J Forensic Sci 2006, 51, 990–995. [Google Scholar] [CrossRef] [PubMed]
  68. Bidmos, M.A.; Asala, S.A. Sexual dimorphism of the calcaneus of South African blacks. J Forensic Sci 2004, 49, 446–450. [Google Scholar] [CrossRef] [PubMed]
Preprints 89477 g001
Figure 1. Measurements on vertebral column (exemplification of vertebral body height and width of superior endplate).
Figure 1. Measurements on vertebral column (exemplification of vertebral body height and width of superior endplate).
Preprints 89477 g001
Preprints 89477 g002
Figure 2. Distribution of numeric variables, by gender.
Figure 2. Distribution of numeric variables, by gender.
Preprints 89477 g002
Preprints 89477 g003
Figure 3. The correlation plot among numerical variables in the initial data set.
Figure 3. The correlation plot among numerical variables in the initial data set.
Preprints 89477 g003
Preprints 89477 g004
Figure 4. The correlation plot among numeric variables in the final data set.
Figure 4. The correlation plot among numeric variables in the final data set.
Preprints 89477 g004
Preprints 89477 g005
Figure 5. Hyper-parameter tuning for RF models.
Figure 5. Hyper-parameter tuning for RF models.
Preprints 89477 g005
Preprints 89477 g006
Figure 6. Hyper-paramerer tuning for XGB models.
Figure 6. Hyper-paramerer tuning for XGB models.
Preprints 89477 g006
Preprints 89477 g007
Figure 7. Variable importance for the best random forest and xgboost models, as estimated by the ingredients package.
Figure 7. Variable importance for the best random forest and xgboost models, as estimated by the ingredients package.
Preprints 89477 g007
Preprints 89477 g008
Figure 8. Partial Dependence and Accumulated profiles for the most important predictor in RF.
Figure 8. Partial Dependence and Accumulated profiles for the most important predictor in RF.
Preprints 89477 g008
Preprints 89477 g009
Figure 9. Partial Dependence and Accumulated profiles for the 2nd most important predictor in RF.
Figure 9. Partial Dependence and Accumulated profiles for the 2nd most important predictor in RF.
Preprints 89477 g009
Preprints 89477 g010
Figure 10. Partial Dependence and Accumulated profiles for the 3rd most important predictor in RF.
Figure 10. Partial Dependence and Accumulated profiles for the 3rd most important predictor in RF.
Preprints 89477 g010
Preprints 89477 g011
Figure 11. Partial Dependence and Accumulated profiles for the 4th most important predictor in RF.
Figure 11. Partial Dependence and Accumulated profiles for the 4th most important predictor in RF.
Preprints 89477 g011
Preprints 89477 g012
Figure 12. Partial Dependence and Accumulated profiles for the 5th most important predictor in RF.
Figure 12. Partial Dependence and Accumulated profiles for the 5th most important predictor in RF.
Preprints 89477 g012
Table 1. Measurement of the vertebral column L1-L5.
Table 1. Measurement of the vertebral column L1-L5.
Measurement Abbreviation Vertebrae Definition
Width of superior endplate Width_sup_lx L1-L5 Distance between the most lateral edges of the superior plate of the vertebrae
Width of inferior endplate Width_inf_lx L1-L5 Distance between the most lateral edges of the inferior plate of the vertebrae
Posterior height of the vertebral body Heigth_lx L1-L5 Posterior height of the vertebral body from left bisecting plane at the posterior part of the vertebral body at the point, which can get the largest height
Table 2. Descriptive statistics for numerical variables.
Table 2. Descriptive statistics for numerical variables.
Preprints 89477 i001
Table 3. Model performance on new data (the test data subset).
Table 3. Model performance on new data (the test data subset).
Preprints 89477 i002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated