Shaft Wall Damage of High Depth Inclined Ore-Pass under Impact Wear Behavior

Preprint

Article

Shaft Wall Damage of High Depth Inclined Ore-Pass under Impact Wear Behavior

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

31 October 2023

Posted:

31 October 2023

You are already at the latest version

Alerts

Abstract

In order to study the collapse failure of shaft wall of high depth inclined ore-pass under ore impact wear behavior, 25 ore-passes in a deep mine in Yunnan, China were investigated. Considering the ore-pass structural characteristics and the impact wear effect of ore on shaft wall, the shaft wall damage model of high depth inclined ore-pass is constructed based on the contact mechanics theory. Furthermore, No. 1#, 2#, 3# and 9# ore-passes of the mine are taken as examples for analysis, and the three results of theoretical analysis, numerical simulation and engineering case are used for comparison and verification. The shaft wall damage degree is predicted, and the damage mechanism between total shaft wall damage volume Qtol and ore-pass depth H, ore-pass dip angle θ, inclined angle of chute α, shaft diameter D and ore block size P is quantitatively investigated. The results show that the rationality of the proposed model is verified by numerical analysis and field engineering situations. Moreover, the deeper ore-pass depth H, the more shaft wall damage volume Qtol with the increase of collision frequency. Qtol increases exponentially with P and increases gradually with D. With the increase of θ or α, Qtol increases generally first and then decreases. Therefore, Qtol can be effectively reduced by selecting the appropriate structure parameters of ore-pass and adopting the technology of drilling straight ore-pass. This work provides technical support for long period safe operation of high depth inclined ore-pass.

Keywords:

Subject: Engineering - Mining and Mineral Processing

1. Introduction

Deep mining is a future development trend and kilometer-deep metal mines become particularly common [1,2,3,4,5]. High depth inclined ore-pass (depth exceeding 100 m) is regarded as an important project for low-cost downward transportation of deep mining, and it is the throat connecting the middle production levels with haulageways in underground mines [6]. Due to the different geological environment, complex mining conditions, improper structural parameters of ore-pass (i.e. depth and dip angle of ore-pass), the impact wear effect of the extracted ore blocks can cause the shaft wall to sag and wear, even lead to shaft wall damage and collapse accidents. Therefore, the damage degree of shaft wall for high depth inclined ore-pass under impact wear behavior is investigated to ensure long period safety running.

At present, some works have been carried out on the shaft wall damage of ore-pass. Zhao et al. [7] studied the damage characteristics of shaft wall for vertical ore-pass based on the erosion wear theory and Hertz contact theory. Yin et al. [8,9] determined the initial collision position distribution of ore transporting in the vertical ore-pass, and deduced the three-dimensional moving track equation before collision. Deng et al. [10] studied the changes of internal force chain structure of bulk ores under discharge impact at different heights using PFC (Particle Flow Code) numerical simulation. Through the similarity experiments on ore drawing in ore-pass, Liu et al. [11,12] obtained the ore moving track and the shaft wall wear range, and developed a panoramic scanning imaging device of vertical ore-pass; Ren et al. [13] recorded the changes of rock strata using total station observation method, revealing the impact points distribution and its failure rule of ore drawing in the vertical ore-pass with different geological structures. Esmaieli et al. [14,15] analyzed the stress state around the chute using three-dimensional boundary elements to study the shaft wall failure mechanism under impact load and material flow wear. Campbell [16] built lateral pressure theory on the basis of lateral pressure and coefficient of lateral pressure using the micromechanics theory. Kulshrestha et al. [17] proposed an ore-pass scanner based on interferometer synthetic aperture radar (InSAR) time series to monitor potential collapse areas of shaft wall. In addition, scholars also have a preliminary study on the influence factors of shaft wall damage for ore-pass, such as the shape and size of ore [18,19], the size of ore-pass [20], the drawing speed [21], the crack of surrounding rock [22], etc. In general, the relevant researches mainly focus on the damage range of shaft wall and the ore flow rule in the vertical ore-pass, while the shaft wall damage caused by structural parameters of high depth inclined ore-pass and ore block size is rare, which is difficult to meet the requirements of practical engineering.

Based on the field investigation of 25 ore-passes in a deep mine in Yunnan, China, a shaft wall damage model of high depth inclined ore-pass was established, the shaft wall damage volume was calculated using the contact mechanics theory, and the influences of ore block size, shaft diameter, inclined angle of chute, ore-pass depth and dip angle on the shaft wall damage volume were discussed in this paper. Taking No. 1^#, 2^#, 3^# and 9^# ore-passes as examples, the rationality of the proposed model was verified by the numerical simulation and the engineering case. This paper can provide a new approach for the research of damage control and structural parameter optimization of high depth inclined ore-pass under impact wear behavior.

2. Shaft wall damage model of high depth inclined ore-pass

2.1. Basic model

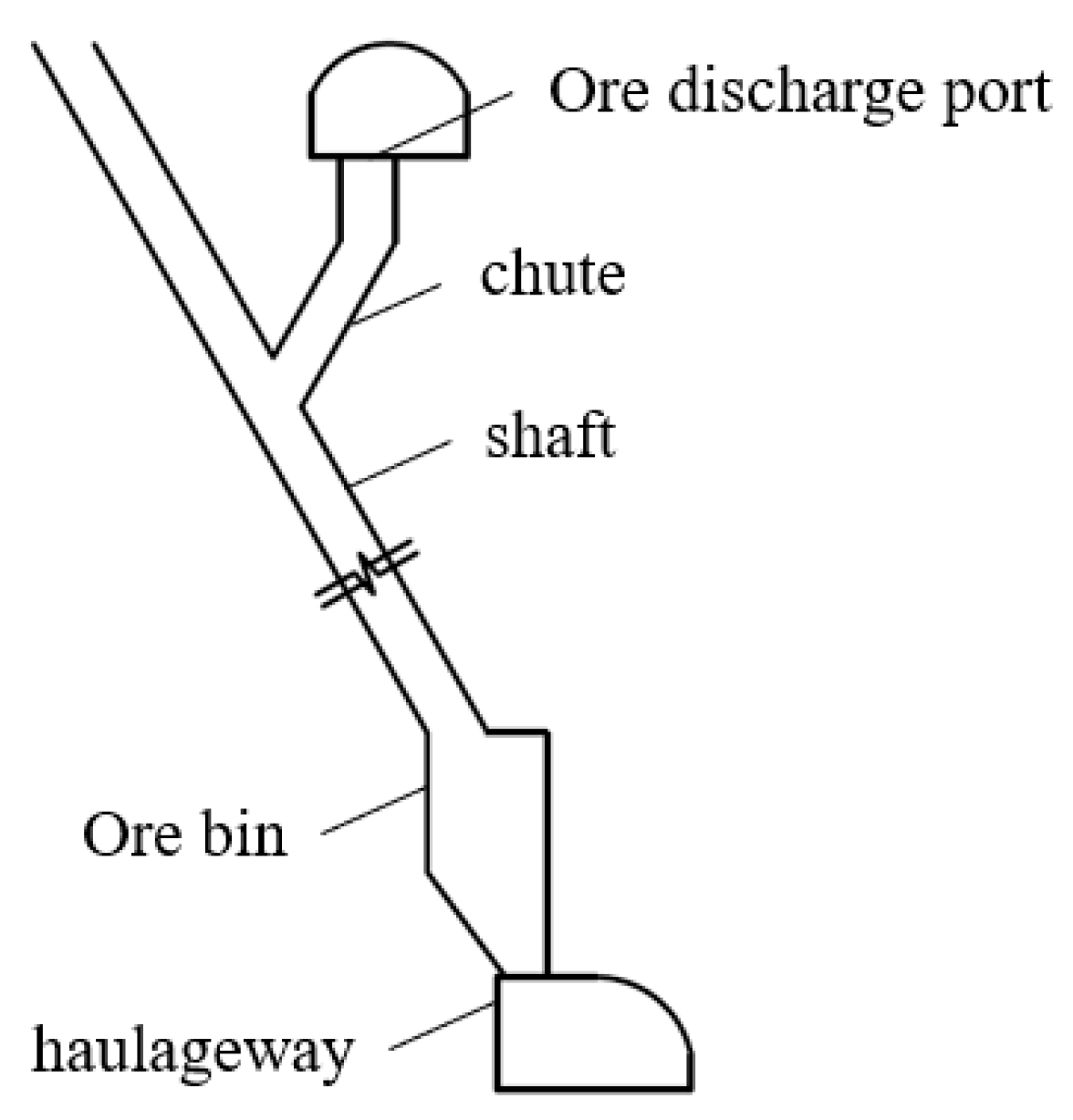
Figure 1 shows the basic structure of high depth inclined ore-pass of a deep mine in Yunnan, China, the extracted ores are discharged to the shaft section from ore discharge port. When the ores collide with shaft wall, problems such as deep depression and large wear range of shaft wall may occur under impact wear effect of ore blocks. In severe cases, it may induce a wide range of shaft wall collapse failure, which is mainly concentrated in the area near the intersection of chute and shaft.

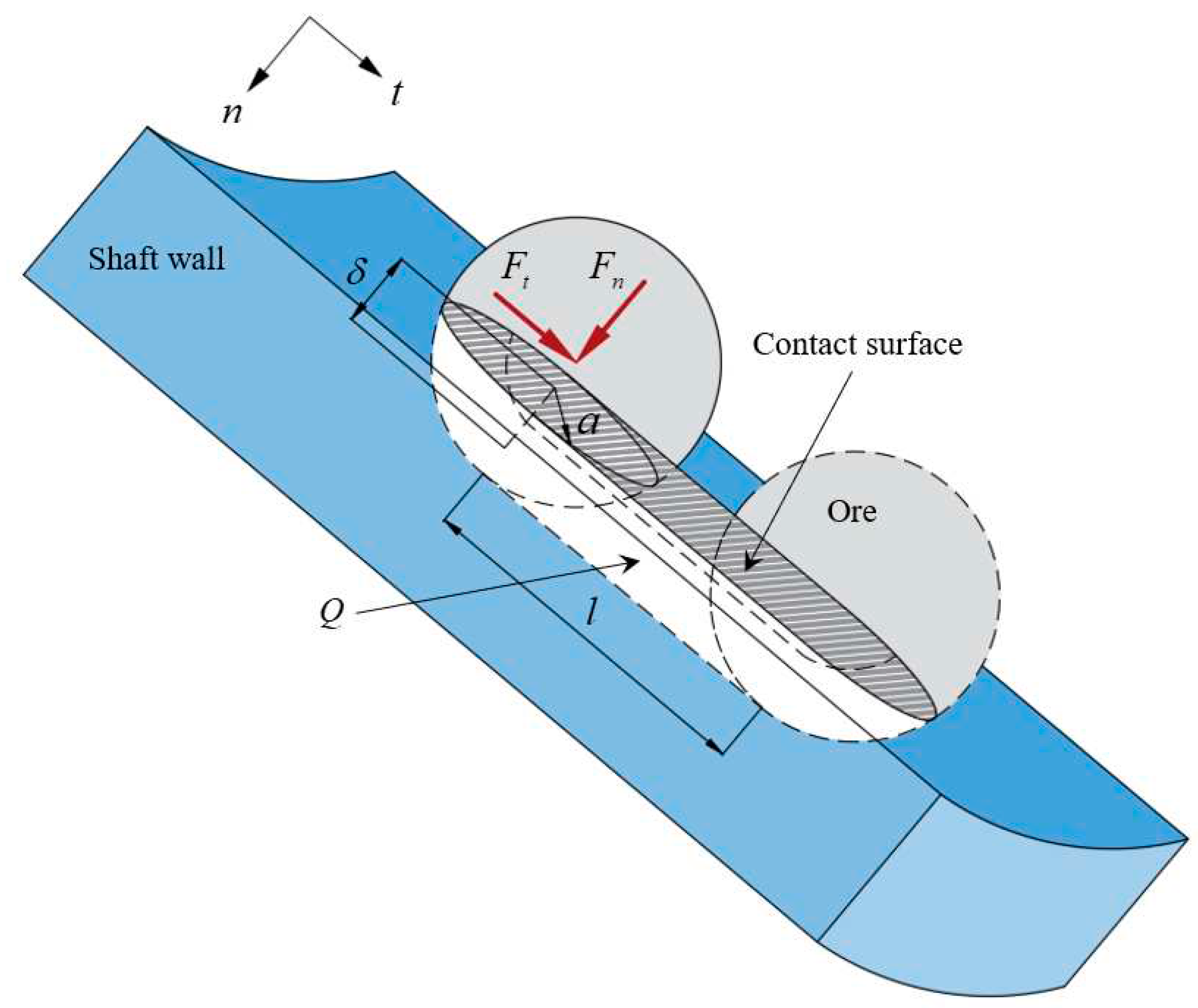
When a large ore block collides with shaft wall, the ore presses into the wall with the normal impact force F_n, and slides relative to shaft wall surface with the tangential impact force F_t, resulting in impact wear on shaft wall.

δ

, l and a are respectively ore indentation depth, wear length and contact radius between ore and shaft wall. As shown in Figure 2, the indentation depth and wear length are coupled together to form the shaft wall damage volume Q.

2.2. Basic Assumptions

In order to simplify the calculation of the shaft wall damage volume, the following assumptions are made.

(1): The extracted ore is assumed to be a sphere of uniform mass, and the moving ore is regarded as a particle. Only the translation of ore is considered, while the rotation of ore is ignored.
(2): The shaft is a flat and inclined cylinder with the same lithology and the rock mass of shaft wall obeys the Mohr-Coulomb criterion.
(3): Only the interaction between ore and shaft wall is considered, while the interaction between ores and the mass loss of ores are ignored.

2.3. Theoretical solution

2.3.1. Ore indentation depth δ

Based on the contact mechanics theory, the deformation process of ore colliding with shaft wall can be roughly divided into two stages: ① the elastic deformation of shaft wall occurs at the initial stage of contact between ore and shaft wall; ② when the deformation of shaft wall exceeds the elastic limit and reaches the initial yield state of shaft wall rock mass, the plastic deformation of shaft wall occurs.

(1) Elastic deformation stage

Due to the low velocity of ore impacting shaft wall, the contact between ore and shaft wall can be regarded as quasi-static contact [23]. Based on the quasi-static contact mechanics theory [24], the normal impact force F_n in elastic deformation can be expressed.

F_{n} = \frac{4}{3} E^{*} R^{\frac{1}{2}} δ^{\frac{3}{2}}

(1)

where R is the radius of spherical ore, P is defined as the ore block size, P = 2R. E^* is the equivalent elastic modulus, satisfying

\frac{1}{E^{*}} = \frac{1 - ν_{1}}{E_{1}} + \frac{1 - ν_{2}}{E_{2}}

(2)

where E₁, ν₁, E₂ and ν₂ are the elastic modulus and the Possion ratio of ore and shaft wall respectively.

By Newton’s second law of motion, it is satisfied that

- m \frac{d^{2} δ}{d t^{2}} = \frac{4}{3} E^{*} R^{\frac{1}{2}} δ^{\frac{3}{2}}

(3)

where m is the mass of spherical ore, m = 4πρR³/3, ρ is the density of ore, d²δ/dt² is the ore normal acceleration at collision. Combined with initial collision conditions, Equation (4) is obtained by integrating Equation (3).

\frac{m}{2} [{v_{n}}^{2} - {(\frac{d δ}{d t})}^{2}] = \frac{8}{15} E^{*} R^{\frac{1}{2}} δ^{\frac{5}{2}}

(4)

where v_n is the ore normal velocity before collision, dδ/dt is the ore normal velocity at collision.

From the general collision process, the ore normal impact velocity decreases continuously from the time when ore starts to contact shaft wall to the time when ore indentation depth reaches the maximum. When dδ/dt = 0, the maximum ore indentation depth δ_m in the elastic stage can be solved.

δ_{m} = {(\frac{15 m {v_{n}}^{2}}{16 E^{*} R^{\frac{1}{2}}})}^{\frac{2}{5}}

(5)

(2) Plastic deformation stage

Based on the elastic-plastic contact mechanics theory [25], when the shaft wall begins to deform plastically, it is satisfied that

σ_{n} = η σ_{q}

(6)

where σ_n is the normal contact stress between ore and shaft wall, σ_q is the initial yield strength of rock mass of shaft wall. η is a dimensionless factor, and η = 1 when the rock mass of shaft wall is initially yielding. From Equation (6), the normal impact force F_n^* in the plastic deformation of shaft wall can be written.

F_{n}^{*} = π a^{* 2} σ_{n}

(7)

where a^* is the contact radius between ore and shaft wall in plastic deformation, and a^* = a_q when the rock mass of shaft wall is initially yielding. The relation between contact radius a and ore indentation depth δ is expressed.

a^{2} = R δ

(8)

Combining Equations (1), (7) and (8), ore indentation depth δ_q at the initial yield can be solved.

δ_{q} = \frac{9 π^{2} {σ_{q}}^{2} R}{16 {E^{*}}^{2}}

(9)

According to the law of conservation of energy, the ore normal impact kinetic energy is transformed into the elastic deformation energy of shaft wall and the energy consumed by the plastic deformation. Thus, it is satisfied that

\frac{1}{2} m {v_{n}}^{2} = U + \int_{δ_{q}}^{δ_{m}^{*}} F_{n}^{*} d δ^{*}

(10)

where δ^* and δ_m^* are respectively ore indentation depth when shaft wall is in plastic deformation and when the plastic deformation reaches the maximum. U is the elastic deformation energy of shaft wall, which can be expressed.

U = \frac{8}{15} E^{*} R^{\frac{1}{2}} δ^{\frac{5}{2}}

(11)

Substituting Equations (7) and (11) into (10), the maximum ore indentation depth δ_m^* can be solved.

δ_{m}^{*} = {(\frac{15 m {v_{n}}^{2} - 16 E^{*} R^{\frac{1}{2}} {δ_{q}}^{\frac{5}{2}}}{15 π R σ_{q}} + {δ_{q}}^{2})}^{\frac{1}{2}}

(12)

The maximum ore normal impact force F_nm^* can be calculated by substituting Equation (12) into (7).

F_{n m}^{*} = {[π R σ_{q} (m {v_{n}}^{2} - \frac{16}{15} E^{*} R^{\frac{1}{2}} {δ_{q}}^{\frac{5}{2}} + π R σ_{q} {δ_{q}}^{2})]}^{\frac{1}{2}}

(13)

2.3.2. Wear length l

Owing to the tangential impact effect of moving ores, the ores have a slight sliding relative to shaft wall, resulting in the wear of shaft wall. Based on the kinetic energy theorem, the change of tangential kinetic energy of ore impacting shaft wall is transformed into friction work, satisfying

- μ F_{n m}^{*} l = \frac{1}{2} m {v_{t}}^{2} (e_{t}^{2} - 1)

(14)

where v_t is the ore tangential velocity before collision, μ is the sliding friction factor, e_n and e_t are respectively normal and tangential collision recovery coefficients. By the quasi-static contact mechanics theory, the collision recovery coefficients are expressed, respectively [26,27].

{\begin{cases} e_{n} = {(\frac{3^{\frac{9}{4}} π^{\frac{5}{4}}}{5 E^{*}})}^{\frac{1}{2}} {(\frac{8 R^{3} {σ_{q}}^{5}}{m})}^{\frac{1}{8}} {v_{n}}^{- \frac{1}{4}} \\ e_{t} = 1 - μ (e_{n} + 1) (\frac{v_{n}}{v_{t}}) \end{cases}

(15)

Combining Equations (14) and (15), the wear length l can be written.

l = \frac{(e_{n} + 1) m v_{n} v_{t}}{2 F_{n m}^{*}}

(16)

2.3.3. Shaft wall damage volume Q

Shaft wall damage volume Q per unit wear length can be expressed [28].

\frac{d Q}{d l} = R^{2} [\arcsin {(\frac{δ_{m}}{4 R})}^{\frac{1}{2}} - {(\frac{δ_{m}}{4 R})}^{\frac{1}{2}} {(1 - \frac{δ_{m}}{4 R})}^{\frac{1}{2}}]

(17)

Combining Equations (13)-(17), shaft wall damage volume Q can be solved.

Q = \frac{λ m v_{n} (2 v_{t} - λ v_{n}) R^{2}}{2 μ F_{n m}^{*}} [\arcsin {(\frac{δ_{m}^{*}}{4 R})}^{\frac{1}{2}} - {(\frac{δ_{m}^{*}}{4 R})}^{\frac{1}{2}} {(1 - \frac{δ_{m}^{*}}{4 R})}^{\frac{1}{2}}]

(18)

where λ is the coefficient, λ = μ(e_n +1).

3. Engineering case

3.1. Reasonableness of the shaft wall damage model of high depth inclined ore-pass

Taking the ore-pass engineering system of a deep mine in Yunnan, China as the research object, the theoretical calculation results of the1 shaft wall damage model are compared with the numerical simulation results and the field engineering situations to verify the rationality of the proposed model of high depth inclined ore-pass.

3.1.1. Engineering survey

The ore body of a deep mine in Yunnan, China mainly occurs in the strata of Baizuo Formation with rock dip angle of 55°-65°, which is like a kind of net-vein ore body. The main mining method is the mechanized panel overhand (underhand) supported mining method with a production capacity of 700,000-750,000 t/a, and the ores produced are mainly primary lead-zinc sulfide ores. At present, the mining depth and middle production level height of the mine are 1614 m and 60 m respectively. After years of mining, paste supporting has been completed in the middle production levels of +1764 m and above, the four middle production levels +1584 m, +1404 m, +1344 m and +1274 m are being stoped, and the middle production levels of +1104 m and below is being developed.

It can be seen from Figure 3 that the mine drills ore-pass by raise-boring machine, and more than 20 ore-passes have been completed. All of these ore-passes are shaft diameter about 2 m, ore-pass dip angle of 50°-80°, ore-pass depth of 60-360 m, and inclined angle of chute of 45°-70°.

3.1.2. Parameter Selection

Four ore-passes, No. 9^#, 2^#, 3^# and 1^#, were selected and labeled respectively as operating conditions 1, 2, 3 and 4 for comparative analysis. According to the geological data of the mine, the physical and mechanical parameters of ore and shaft wall rock mass are reported in Table 1. In addition, based on the engineering design of ore-pass system of the mine, it can be obtained that the vertical height of ore discharge port h₁, chute height h₂ and ore bin height h₃ of the four ore-passes are 4.4 m, 1.0 m and 19.6 m respectively, and other structural parameters are shown in Table 2. The block size of ores in the ore-passes is set at 400 mm.

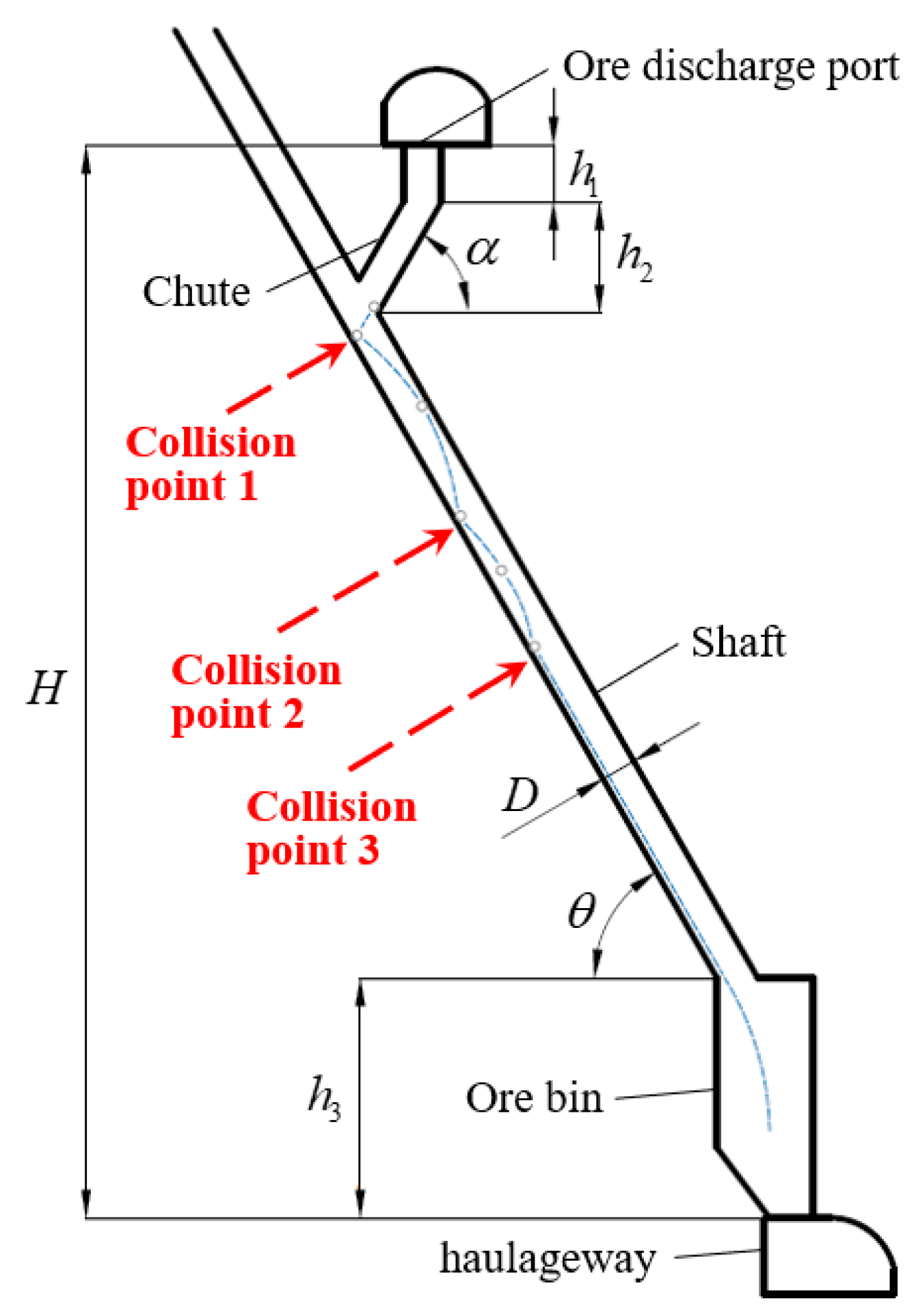
It’s reported that the ore kinetic energy and the shaft wall damage volume decreases greatly with the increase of collision frequency, thus the shaft wall damage volume after more than three collisions is negligible [7,8,9,13]. In this paper, the first three collision positions are taken, and the shaft wall damage volume calculated by Equation (18) is accumulated to obtain the total shaft wall damage volume Q_tol. The collision points in high depth inclined ore-pass of a deep mine are shown in Figure 4.

Considering the structural characteristics of high depth inclined ore-pass, the prerequisite for the k-th collision between ore and shaft wall is as follows.

\sum_{k = 1}^{n} y_{k} < H - (h_{1} + h_{2} + h_{3})

(19)

where k is the number of collision, and y_k is the vertical displacement of ore relative to shaft wall from the (k-1)-th collision to the k-th collision. Based on the kinematic principle and the geometrical structure of the ore-passes, the relation between the ore vertical displacement and the structural parameters of high depth inclined ore-pass can be derived.

y_{k} = {\begin{cases} \frac{D}{\cos θ} + \frac{ξ {v_{0}}^{2} \cos^{2} α \tan θ}{g}, k = 1 \\ \frac{2 v_{(k - 1) n}}{g} [v_{(k - 1) n} \tan^{2} θ + v_{(k - 1) t} \sin^{2} θ \tan θ + v_{(k - 1) t} \sin θ \cos θ], k = 2, 3 \end{cases}

(20)

where ξ is the coefficient, ξ = (tanθ+tanα) –[(tanθ+tanα)²+(2gD)/(v₀²cos²αcosθ)]^1/2. v_kn and v_kt are the normal and tangential velocities before the k-th collision respectively, and they can be derived.

v_{k n} = {\begin{cases} \sqrt{{v_{0}}^{2} \sin^{2} (α + θ) + 2 g D \cos θ}, k = 1 \\ e_{(k - 1) n} v_{(k - 1) n}, k = 2, 3 \end{cases}

(21)

v_{k t} = {\begin{cases} [\sqrt{{v_{0}}^{2} \sin^{2} (α + θ) + 2 g D \cos θ} - v_{0} \sin (α + θ)] \tan θ - v_{0} \cos (α + θ), k = 1 \\ e_{(k - 1) t} v_{(k - 1) t} + 2 e_{(k - 1) n} v_{(k - 1) n} \sin θ (\cos θ + \sin θ \tan θ), k = 2, 3 \end{cases}

(22)

3.1.3. Result analysis

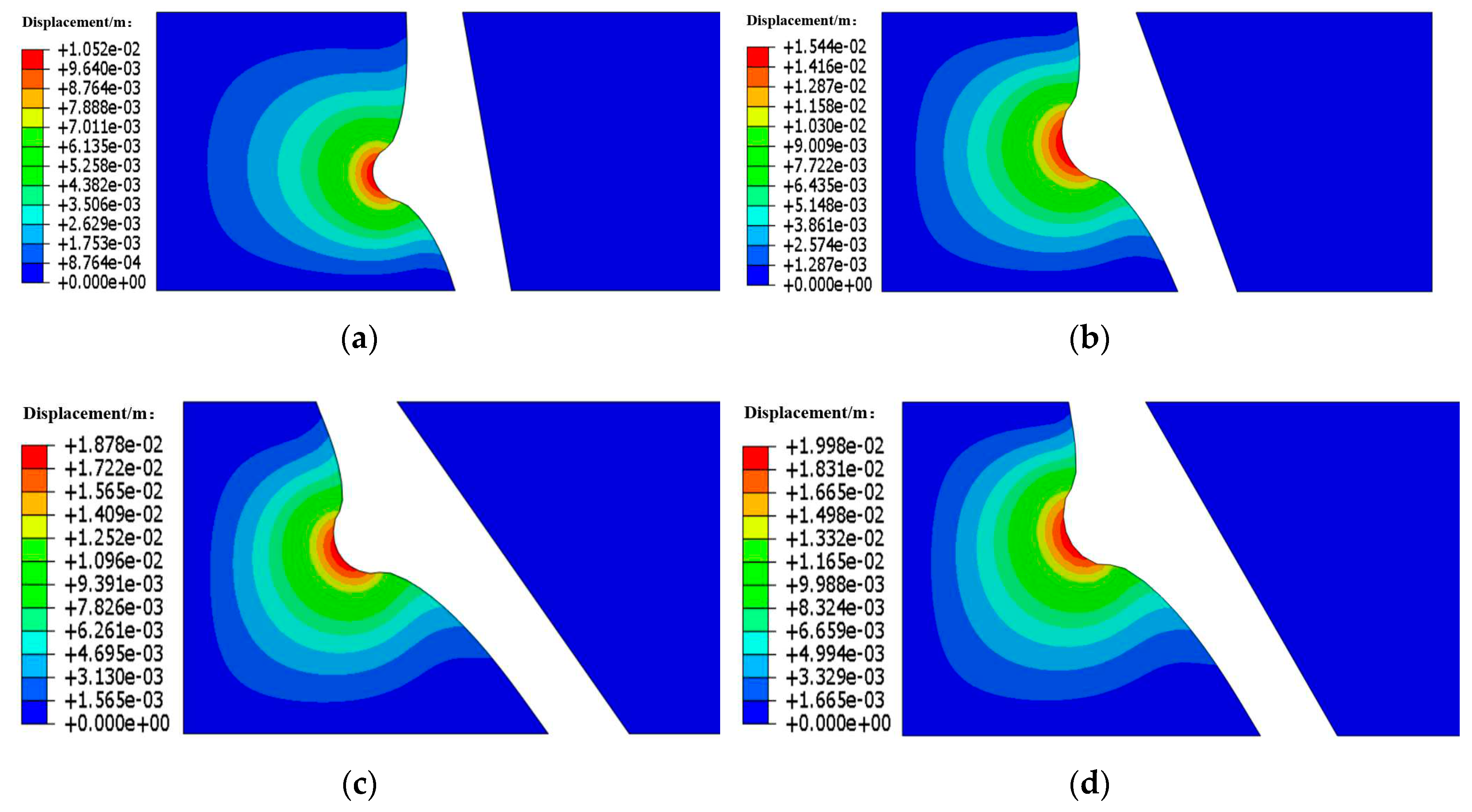
In order to verify the rationality of the theoretical calculation results of the proposed model, the numerical model of shaft wall in operating conditions 1, 2, 3 and 4 was established by ABAQUS software, and the maximum ore indentation depths at the initial collision position obtained by numerical calculation are compared with the theoretical solutions. The boundary of the numerical model was subject to fixed constraints, and the shaft wall rock mass obeyed the Mohr-Coulomb criterion. The numerical simulation results of the four operating conditions are directly presented in Figure 5.

As can be seen from Figure 5, the tendencies of the maximum ore indentation depth of the four operating conditions are distributed radiantly from the collision center to the surrounding areas, and gradually decrease. 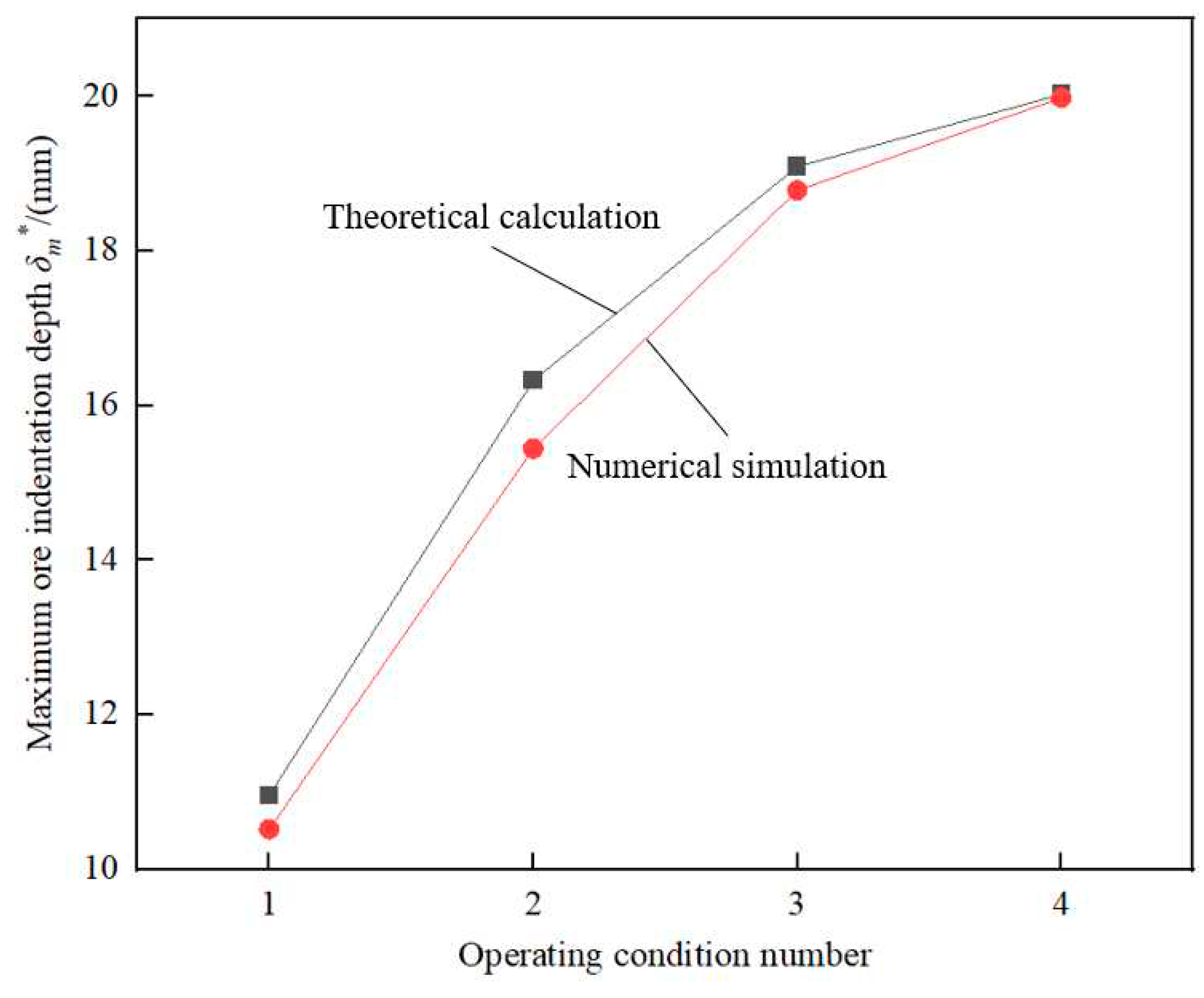The comparison of numerical simulation results and theoretical calculation results of the maximum ore indentation depth at the initial collision position under four operating conditions are presented in Figure 6.

It can be seen from Figure 6 that the theoretical solutions have good agreement with the numerical results. The maximum ore indentation depth in operating conditions 3 and 4 is close and the deepest, and the maximum ore indentation depth in operating condition 1 is the shallowest, which indicates that the damage degree of shaft wall for high depth inclined ore-pass in four operating conditions is successively ranked as working conditions 1, 2, 3 and 4.

Based on the field investigation of the deep mine, the shaft wall of No. 1^# ore-pass (operating condition 4) has collapsed extensively and has stopped operating. The shaft wall of No. 3^# ore-pass (operating condition 3) is seriously damaged, resulting in blockage of ore bin at the bottom of the ore-pass, and it has been scrapped. The damage degree of shaft wall of No. 2^# ore-pass (operating condition 2) is normal, and the entrance of ore bin is occasionally blocked by large chunks of ore. No. 2^# ore-pass can continue operate after rebar bound charge blasting vibration method is used to dredge the blocked position, and residual mineral and rock scattered bodies can be seen at the bottom of the ore-pass (Figure 7). The shaft wall of No. 9^# ore-pass (operating condition 1) has a slight damage, and no shaft wall collapse and ore blocking, it can work normally. Therefore, the results of theoretical calculation, numerical simulation and engineering case are basically consistent, and the rationality of the proposed model is verified.

3.2. Influence of ore-pass depth H

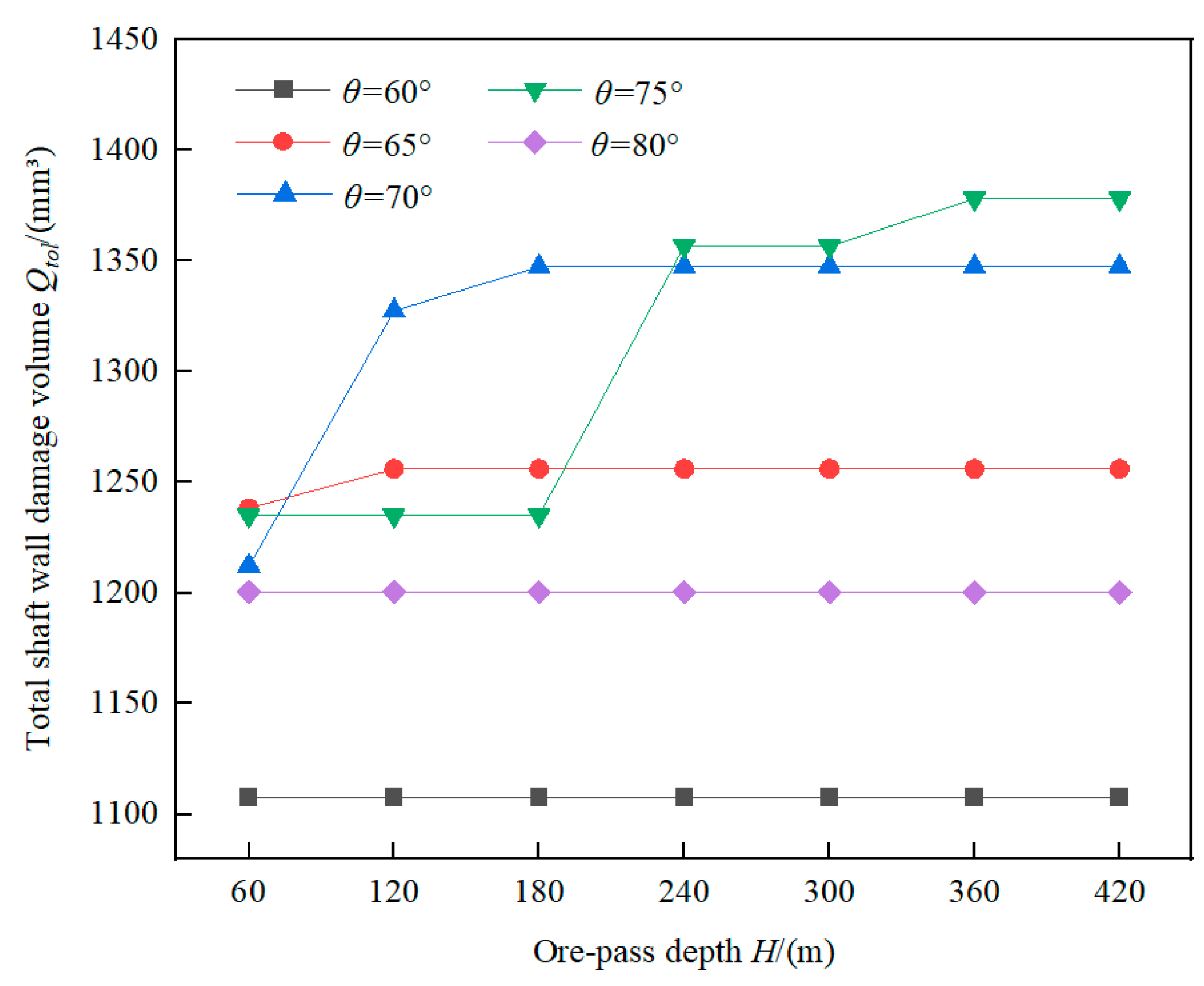
In order to investigate the influence of ore-pass depth on the shaft wall damage volume, the ore block size (P = 400 mm), the shaft diameter (D = 2 m) and the inclined angle of chute (α = 60°) were kept constant, and the ore-pass depth H was set between 60 m and 420 m. The ore-passes were divided into five groups according to ore-pass dip angle θ (60°, 65°, 70°, 75° and 80°). Figure 8 presents the variation of total shaft wall damage volume Q_tol determined from Equation (18) with respect to ore-pass depth H across ore-pass dip angles.

As shown in Figure 8, ore-pass dip angle θ has a significant influence on the Q_tol-H relation curve shape. When θ = 60° and θ = 80°, total shaft wall damage volume Q_tol remains unchanged with the increase of ore-pass depth H. When θ = 65°, θ = 70° and θ = 75°, Q_tol increases at different degrees first and then stabilizes with H.

When θ = 60° and θ = 80°, no matter how ore-pass depth H changes, the number of ore collision with shaft wall remains unchanged, which is 3 times and 1 time respectively, thus casing total shaft wall damage volume Q_tol does not change. When θ = 65°, θ = 70° and θ = 75°, the number of collisions respectively increase from 1 and 2 to 3 with the increase of ore-pass depth H, the total shaft wall damage volume Q_tol increase.

Therefore, controlling ore-pass depth within 240 m can effectively reduce the collision frequency between ore and shaft wall, thereby reducing the damage degree of shaft wall of high depth inclined ore-pass.

3.3. Influence of ore-pass dip angle θ

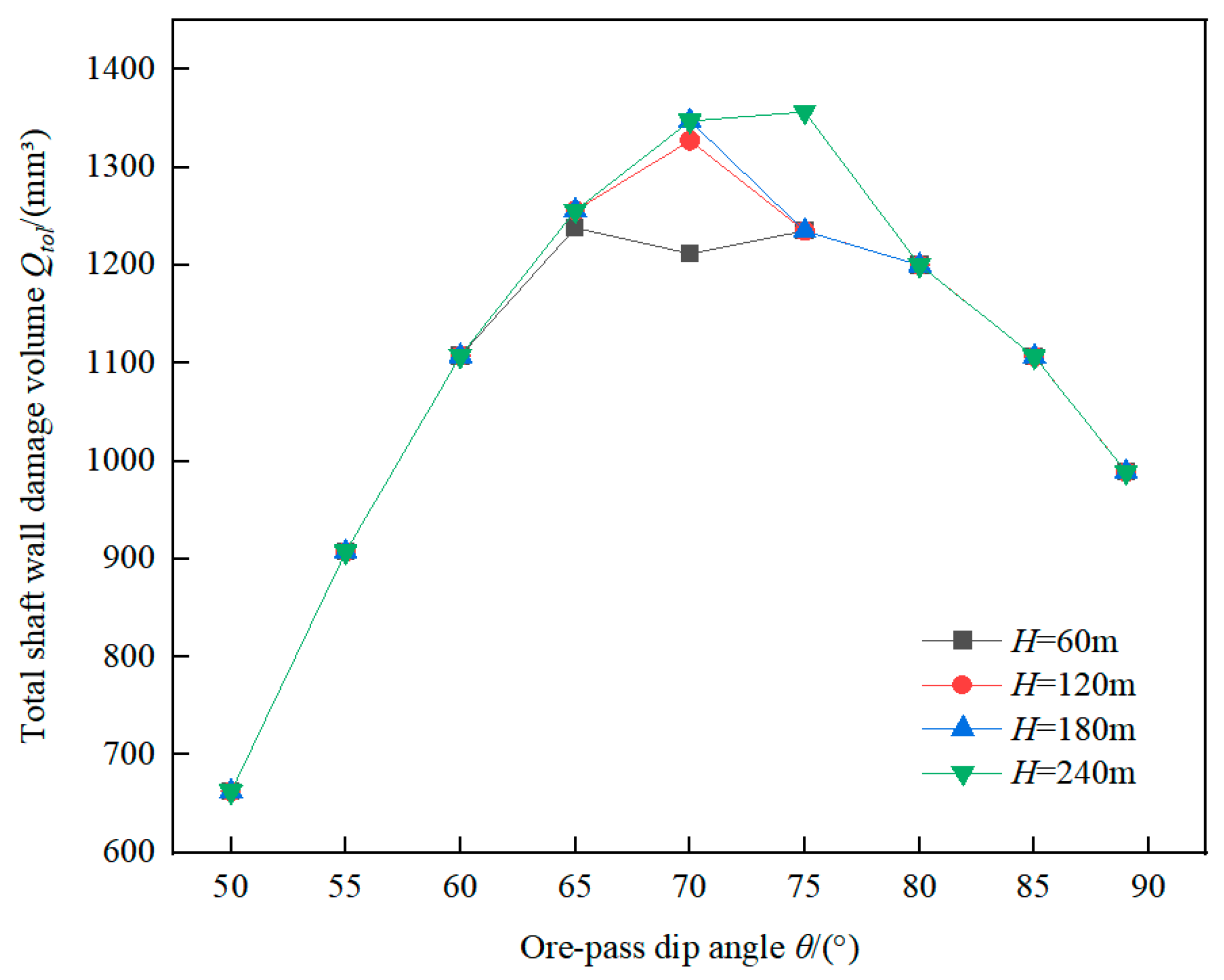
In order to reveal the influence of ore-pass dip angle on the shaft wall damage volume, the ore block size P, the shaft diameter D and the inclined angle of chute α were fixed at 400 mm, 2 m and 60°, respectively, and the ore-pass dip angle θ was set between 50° and 89°. The ore-passes were divided into four groups according to depth H (60, 120, 180 and 240 m). Figure 9 presents the variation of total shaft wall damage volume Q_tol determined from Equation (18) with respect to ore-pass dip angle θ across ore-pass depths.

As shown in Figure 9, the ore-pass depth H has a great influence on the Q_tol-θ relation curve shape. The total shaft wall damage volume Q_tol increases first and then decreases as ore-pass dip angle θ increases, and the maximum point of the curve exists in the range of ore-pass dip angle θ from 60° to 80°. Three curves of H = 120 m, H = 180 m and H = 240 m have a maximum point in this range, and the curve of H = 60 m has two maximum points and one minimum point in the range. Moreover, the greater ore-pass depth H, the greater the maximum value of total shaft wall damage volume Q_tol.

The reason is that when ore-pass dip angle θ gradually increases, the ore indentation depth decreases with the ore normal impact velocity, and the wear length increases with the tangential impact velocity, thus the coupled total shaft wall damage volume Q_tol increases first and then decreases. For the ore-pass with a depth of 60 m, when ore-pass dip angle θ is 65°-80°, the number of collisions between ore and shaft wall gradually decreases from 3 to 1. Since the total shaft wall damage volume Q_tol caused by ore colliding shaft wall is different each time, the curve of Q_tol-θ has two maximum values and one minimum value.

Therefore, on the one hand, it is considered to reduce total shaft wall damage volume by controlling ore-pass dip angle within 60°. On the other hand, the total shaft wall damage volume can be reduced by control the number of collisions between ore and shaft wall, which requires the selection of the ore-pass dip angle greater than 80° or the technology of drilling high depth straight ore-pass.

3.4. Influence of inclined angle of chute α

In order to study the influence of the inclined angle of chute on the shaft wall damage volume, the ore-pass dip angle θ, the shaft diameter D and the ore block size P were fixed at 70°, 2 m and 400 mm, respectively, and the inclined angle of chute α was set between 40° and 90°. The chutes of ore-pass were divided into three groups according to ore-pass depth (60, 120 and 180 m). Figure 10 presents the variation of total shaft wall damage volume determined from Equation (18) with respect to inclined angle of chute α across ore-pass depths.

It can be seen from Figure 10 that the ore-pass depth H plays an important role in the Q_tol-α relation curve shape. As long as ore-pass depth H is deeper, the total shaft wall damage volume Q_tol is greater, and the shaft wall is more vulnerable to damage. It can also be found from Figure 10 that the total shaft wall damage volume Q_tol increases first and then decreases with inclined angle of chute α. When α < 70°, Q_tol increases with α, and the increasing rate of Q_tol-α curve decreases. When α > 70°, Q_tol decreases with α, and the growth rate of this curve increases gradually. The maximum value of Q_tol appears when α = 70°.

The reason is that inclined angle of chute α determines the velocity direction of ore hitting shaft wall. When inclined angle of chute α increases, the ore indentation depth decreases with the decrease of the ore normal impact velocity, the wear length increases with the increase of the tangential impact velocity, thus the total shaft wall damage volume Q_tol increases first and then decreases.

Therefore, on the one hand, the main consideration is to control total shaft wall damage volume by reducing the wear length, which requires that the inclined angle of chute should be less than 50° as far as possible. On the other hand, the total shaft wall damage volume is reduced by controlling ore indentation depth, so inclined angle of chute should be as close as possible to 90°.

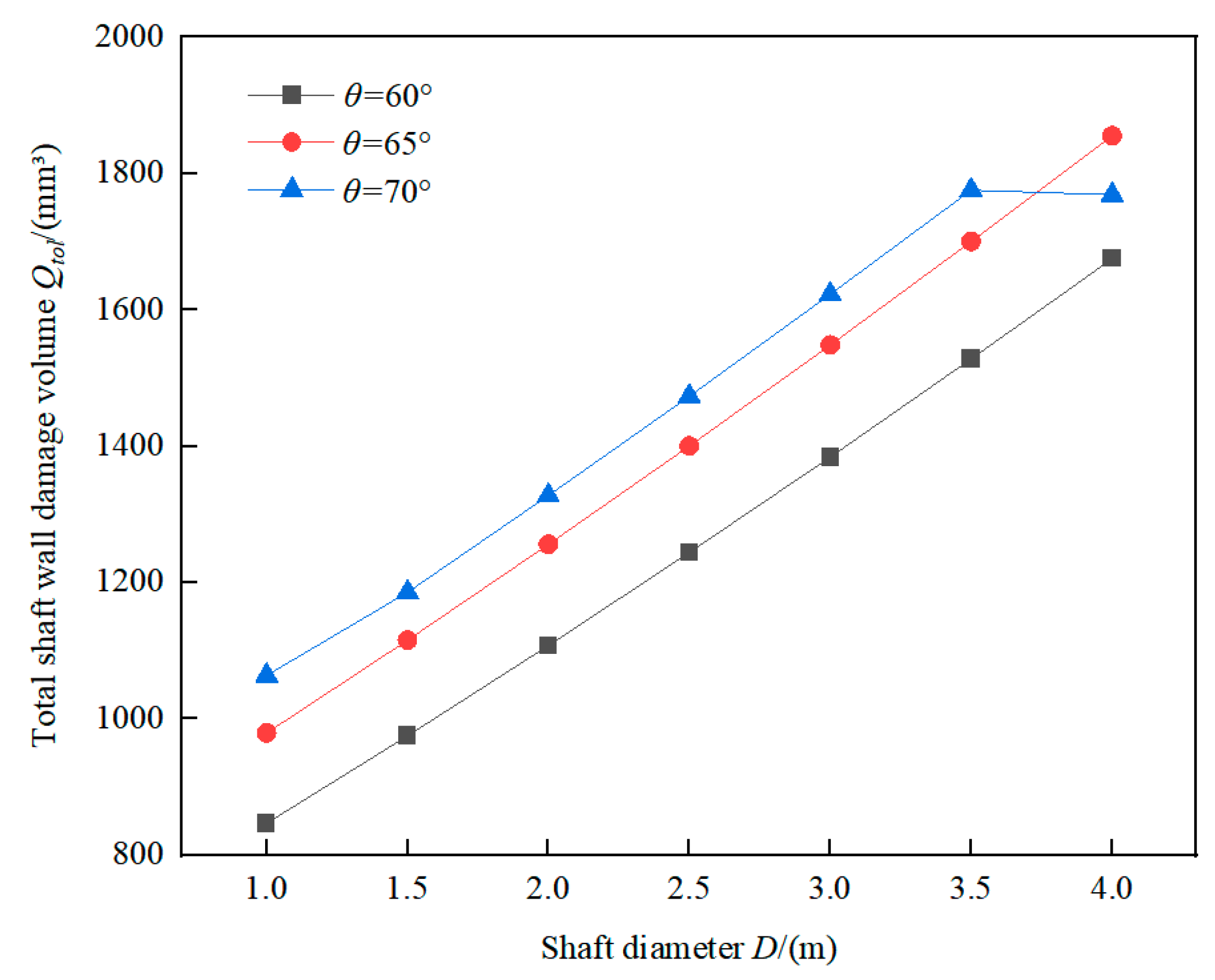
3.5. Influence of shaft diameter D

The influence of shaft diameter on the shaft wall damage volume was evaluated by fixing the inclined angle of chute (α = 60°), the ore-pass depth (H = 120 m) and the ore block size (P = 400 mm). Moreover, the shaft diameter D was set within 1.0-4.0 m, and the ore-passes were divided into three groups according to ore-pass dip angle (60°, 65° and 70°). Figure 11 presents the variation of total shaft wall damage volume determined from Equation (18) with respect to shaft diameter D across ore-pass dip angles.

It can be seen from Figure 11 that ore-pass dip angle θ has an obvious influence on Q_tol-D relation curve shape, and the total shaft wall damage volume Q_tol is positively correlated with shaft diameter D. For the two curves of θ = 60° and θ = 65°, Q_tol increases with D, and the growth rate of Q_tol-D relation curve remains unchanged. For the curve of θ = 70°, when the shaft diameter D is in the range of 1.0-3.5 m, Q_tol increases with D, when the shaft diameter D is greater than 3.5 m, Q_tol decreases slowly with D.

When θ = 60° and θ = 65°, the collision frequency between ore and shaft wall remains unchanged, the increase rate of Q_tol-D relation curve remains relatively stable. When θ = 70°, with the increase of shaft diameter D, the number of ore collision with shaft wall gradually decreases from 3 to 1, thus Q_tol begins to decrease when D = 3.5 m.

In actual engineering project, it is recommended to use raise-boring machine with diameter less than 2 m as far as possible to complete the construction of the shaft, so as to effectively control the total shaft wall damage volume.

Figure 11. Variation of total shaft wall damage volume Q_tol with respect to shaft diameter D across ore-pass dip angles.

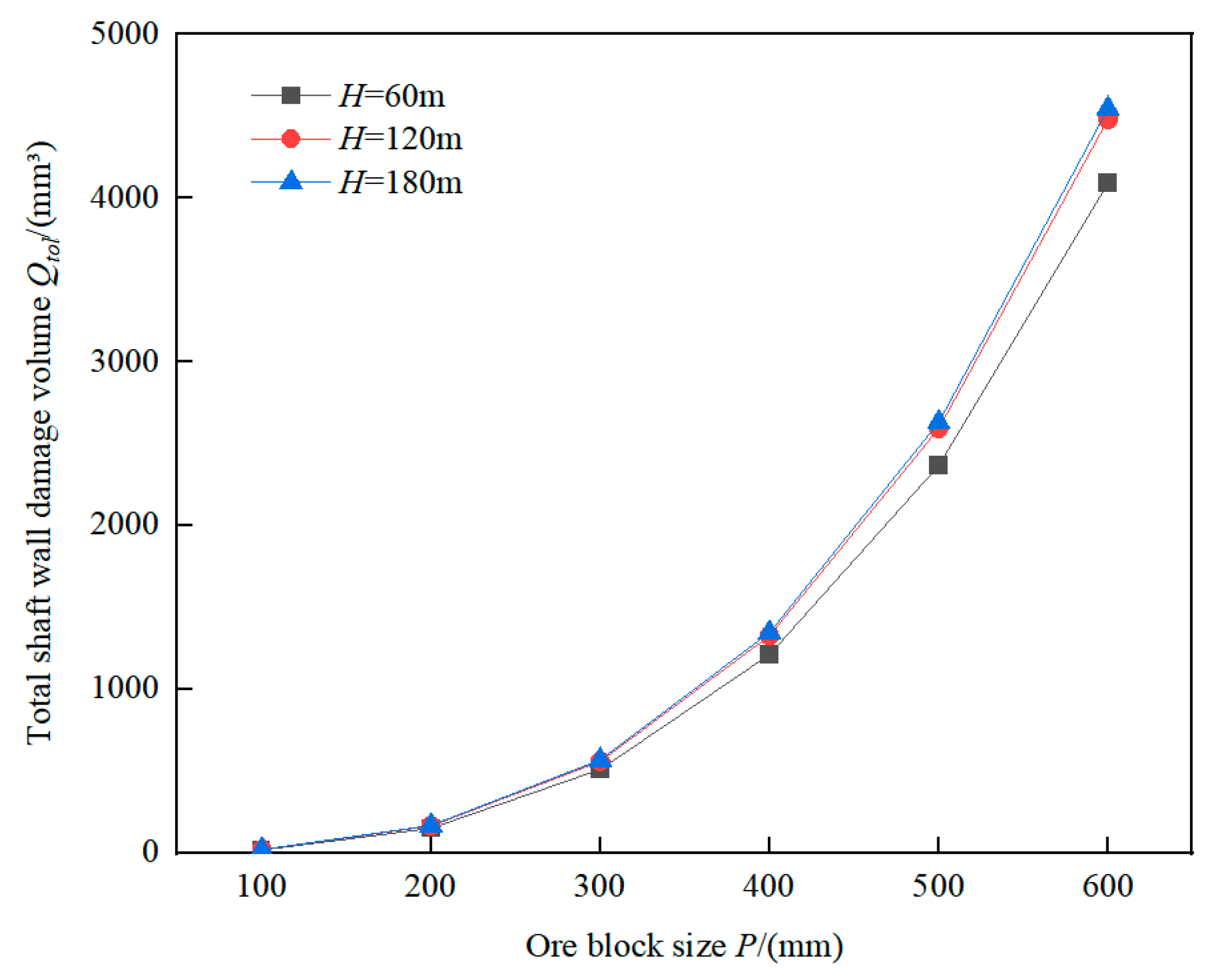
3.6. Influence of ore block size P

The impact of ore block size on the shaft wall damage volume investigated by fixing the inclined angle of chute (α = 60°), the ore-pass dip angle (θ = 70°) and the shaft diameter (D = 2 m). In addition, the ore block size P was set within 100-600 mm, and the ore-passes were divided into three groups according to ore-pass depth (60, 120 and 180 m). Figure 12 shows the variation of shaft wall damage volume determined from Equation (18) with respect to ore block size P across ore-pass depths.

As shown in Figure 12, the ore-pass depth H has a slight influence on the Q_tol-P relation curve shape, and the greater ore-pass depth H, the greater total shaft wall damage volume Q_tol. It can also be found from Figure 12 that Q_tol and P are positively correlated, and Q_tol increases with P. Furthermore, the growth rate of the Q_tol-P relation curve increases continuously, which indicates that the ore block size P greatly affects the total shaft wall damage volume Q_tol.

The reason is that the ore indentation depth and the wear length increase with the increase of ore normal and tangential impact velocity respectively, thus the total shaft wall damage volume increases exponentially.

Therefore, the grate should be installed at ore discharge port to strictly control the ore block size within 300 mm. The total shaft wall damage volume can be reduced by controlling the ore block size, and the large-scale collapse failure caused by the impact wear behavior of large ores on the shaft wall is prevented.

4. Discussion

(1): The moving ore is regarded as a particle without considering its own rotation, and the damage to shaft wall caused by other motion states of ore and gravity of large ore is ignored. In the subsequent research, the oblique impact theory of ball can be considered to study the damage and failure of shaft wall under the action combined various motion states such as translation and rotation.
(2): The analytical solutions of the shaft wall damage volume may exhibit calculation errors as the lithology of rock mass of shaft wall is assumed to be the same. The influence of the lithology of rock mass of shaft wall should be comprehensively considered in future studies.
(3): The interaction between ores and the mass loss of ores in the collision are ignored, which results in an inaccurate calculation result of the shaft wall damage volume. In order to optimize the calculation result, the energy loss caused by ore interaction can be considered from the energy theory.
(4): This paper mainly studies the shaft wall damage of high depth inclined ore-pass under impact wear behavior, calculates the shaft wall damage volume and predicts the damage degree of shaft wall. Considering the influence of ore block size and ore-pass structural parameters on the total shaft wall damage volume, the shaft wall damage degree of ore-pass is controlled actively, which is in line with the actual situation of field engineering.

5. Conclusions

(1): On the basis of field engineering investigation, the shaft wall damage model of high depth inclined ore-pass is constructed by considering the ore-pass structural characteristics and the impact wear behavior of ore on shaft wall. The mathematical expression of the shaft wall damage volume is derived based on the contact mechanics theory, and the damage degree is predicted. The relationship between shaft wall damage volume Q_tol and ore-pass depth H, ore-pass dip angle θ, inclined angle of chute α, shaft diameter D and ore block size P is quantitatively investigated. The rationality of the proposed model is verified by the numerical simulation and the engineering case.
(2): With the increase of ore-pass depth H, the more collisions between ore and shaft wall and the greater shaft wall damage volume Q_tol. This indicates that H has a great influence on Q_tol. Furthermore, Q_tol increases exponentially with P and increases gradually with D, which indicates that P and D significantly affect Q_tol. With the increase of θ and α, Q_tol generally increases first and then decreases, which indicates that θ and α obviously affect Q_tol.
(3): Based on the influence of ore block size and ore-pass structure parameters on the shaft wall damage volume, the damage degree can be reduced from the two aspects. On the one hand, the shaft wall damage volume can be directly reduced by using a raise-boring machine with a diameter less than 2 m to drill ore-pass, controlling the ore block size to less than 300 mm, or selecting an ore-pass dip angle less than 60° and an inclined angle of chute less than 50° or close to 90°. On the other hand, the number of ore and shaft wall collision can be reduced by employing the technology of drilling high depth straight ore-pass, controlling an ore-pass depth within 240 m, or selecting an ore-pass dip angle greater than 80°, thereby the shaft wall damage volume can be effectively reduced.

Author Contributions

Conceptualization, L.J. and H.J.; methodology, L.J. and H.J.; software, L.J. and H.J.; validation, L.J., H.J. and L.X.; formal analysis, L.J., H.J. and L.X.; investigation, L.J., H.J. and L.X.; resources, L.J.; writing—original draft preparation, L.J. and H.J.; writing—review and editing, L.J., H.J. and L.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China (2022YFC2903802).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

Thanks for the support of the National Key Research and Development Program of China (2022YFC2903802) and the great efforts of editors and reviewers.

Conflicts of Interest

The authors declare no conflict of interest.

References

Jiang, L.C.; Jiao, H.Z.; Wang, Y.D.; Wang, G.G. Comprehensive safety factor of roof in goaf underdeep high stress. Journal of Central South University. 2021, 28, 595-603. [CrossRef]
Jiang, L.C.; Zhang, Y.Q. Calculation model of depressurization coefficient for concrete helical pipeline transportation in deep shaft. Journal of Xi’an University of Science and Technology. 2020, 40, 953-959. [CrossRef]
Guo, F.; Zhang, N.; Xie, Z.Z.; Han, C.L.; Zhang, C.H.; Yuan, Y.X.; He, Z.; Liu, J.H. A Three-Dimensional Supporting Technology, Optimization and Inspiration from a Deep Coal Mine in China. Rock Mechanics and Rock Engineering. 2023, 2023, 1-23. [CrossRef]
Xie, J.L.; Ning, S.; Zhu, W.B.; Wang, X.Z.; Hou, T. Influence of Key Strata on the Evolution Law of Mining-Induced Stress in the Working Face under Deep and Large-Scale Mining. Minerals. 2023, 13, 983. [CrossRef]
Zhang, H.; Li, Y.M.; Wang, X.J.; Yu, S.D.; Wang, Y. Study on Stability Control Mechanism of Deep Soft Rock Roadway and Active Support Technology of Bolt-Grouting Flexible Bolt. Minerals. 2023, 13, 409. [CrossRef]
Lu, Z.X.; Ma, C.; Cao, P.; Ma, Q.Y. Study Status and Direction of Orepass Existing Problems in Metal Mine. Metal Mine. 2019, 2019, 1-9. [CrossRef]
Zhao, Y.; Ye, H.W.; Lei, T.; Wang, C.; Wang, Q.Z.; Long, M. Theoretical study of damage characteristics on ore pass wall based on the erosion-wearing theory. Chinese Journal of Rock Mechanics and Engineering. 2017, 36, 4002-4007. [CrossRef]
Yin, Y.; Lu, Z.X.; Ma, C. Mechanism of Deformation and Failure on Orepass Wall under Impact and Wear. Metal Mine. 2020, 2020, 31-36. [CrossRef]
Yin, Y.; Lu, Z.X.; Dong, H.W. Analysis and Verification of 3D Motion Track of Ore or Rock in Main Orepass. Metal Mine. 2019, 2019, 49-53. [CrossRef]
Deng, Z.; Lu, Z.X.; Wang, S.Y.; Ma, Q.Y. Influence and mechanism of upper unloading impact on the pressure distribution of the sidewall in the storage section of the orepass. Nonferrous Metals Science and Engineering. 2023, 14, 257-263. [CrossRef]
Liu, Y.Z.; Zhang, B.T.; Ye, Y.C.; Zou, X.T.; Zhang, Q.; Chen, X.Q.; Pan, S.H. Similarity testing study on characteristics of ore motion and wall damage in mine shaft. Journal of Mining & Safety Engineering. 2018, 35, 545-552. [CrossRef]
Liu, Y.Z.; Wang, Q.F.; Ye, Y.C.; Zhao, W.; Shi, Z.J.; Tu, F.Q. Ore-pass panoramic scanning imaging device and its experiment to monitor ore-pass wall. Rock and Soil Mechanics. 2013, 34, 3329-3334. [CrossRef]
Ren, Z.G.; Ma, H.T.; Wang, S.; Zeng, M.R.; Jin, L.Z. Experimental study on damage laws of ore pass based on similarity simulation. Journal of Safety Science and Technology. 2016, 12, 98-102. [CrossRef]
Esmaieli, K.; Hadjigeorgiou, J.; Grenon, M. Stability Analysis of the 19A Ore Pass at Brunswick Mine Using a Two-Stage Numerical Modeling Approach. Rock mechanics and rock engineering. 2013, 46, 1323-1338. [CrossRef]
Esmaieli, K.; Hadjigeorgiou, J. Selecting ore pass-finger raise configurations in underground mines. Rock mechanics and rock engineering. 2011, 44, 291-303. [CrossRef]
Campbell, C.S. Granular material flows–an overview. Powder Technology. 2006, 162, 208-229. [CrossRef]
Kulshrestha, A.; Chang, L.; Stein, A. Sinkhole scanner: A new method to detect sinkhole-related spatio-temporal patterns in InSAR deformation time series. Remote sensing. 2021, 13, 2906. [CrossRef]
Remennikov, A.M.; Mutton, V.; Nimbalkar, S. Experimental and numerical investigation of high-yield grout ore pass plugs to resist impact loads. International Journal of Rock Mechanics and Mining Sciences. 2014, 70, 1-15. [CrossRef]
Ma, J.Y.; Wei, D.E.; Zhang, Q.S. Experimental study on the probabilities of kinked arches and kinked arch locations in ore passes under the influences of multiple factors. Scientific Reports. 2023, 13, 15364. [CrossRef]
Vo, T.; Yang, H.; Russell, A.R. Cohesion and suction induced hang-up in ore passes. International Journal of Rock Mechanics and Mining Sciences. 2016, 87, 113-128. [CrossRef]
Yang, Y.J.; Deng Z.; Lu Z.X. Effects of ore-rock falling velocity on the stored materials and the force on the shaft wall in a vertical orepass. Mechanics of Advanced Materials and Structures. 2022, 2022, 1-8. [CrossRef]
Xiong, Y.; Yang, S.L.; Kong, D.Z.; Song, G.F.; Ma, Z.Q.; Zuo, Y.J. Analysis on early warning of coal sample failure based on crack development law and strain evolution characteristics. Engineering Failure Analysis. 2023, 148, 107170. [CrossRef]
Hou, T.X.; Yang, X.G.; Huang, C.; Huang, K.X.; Zhou, J.W. A calculation method based on impulse theorem to determine impact force of rockfall on structure. Chinese Journal of Rock Mechanics and Engineering. 2015, 34, 3116-3122. [CrossRef]
Braccesi, C.; Landi, L. A general elastic–plastic approach to impact analisys for stress state limit evaluation in ball screw bearings return system. International Journal of Impact Engineering. 2007, 34, 1272-1285. [CrossRef]
Jackson, R.L.; Green, I.; Marghitu, D.B. Predicting the coefficient of restitution of impacting elastic-perfectly plastic spheres. Nonlinear Dynamics. 2010, 60, 217-229. [CrossRef]
Zhang, G.C.; Tang, H.M.; Xiang, X.; Karakus, M.; Wu, J.P. Theoretical study of rockfall impacts based on logistic curves. International Journal of Rock Mechanics and Mining Sciences. 2015, 78, 133-143. [CrossRef]
Thornton, C. Coefficient of Restitution for Collinear Collisions of Elastic-Perfectly Plastic Spheres. Journal of Applied Mechanics. 1997, 64, 383. [CrossRef]
Benabdallah, S.M.H.; Chalifoux, J.P. Ploughing of soft asperities by a hemispherical slider. Tribology international. 1989, 22, 383-388. [CrossRef]

Figure 1. The basic structure of high depth inclined ore-pass.

Figure 2. Shaft wall damage model of high depth inclined ore-pass.

Figure 3. An ore-pass by raise-boring machine.

Figure 4. Ore collision points in high depth inclined ore-pass of a deep mine.

Figure 5. Numerical simulation results of the maximum ore indentation depth. (a) Operating condition 1; (b) Operating condition 2; (c) Operating condition 3; (d) Operating condition 4.

Figure 6. Comparison of the results of theoretical calculations and numerical simulations.

Figure 7. Bottom of No. 2^# ore-pass of a deep mine.

Figure 8. Variation of total shaft wall damage volume Q_tol with respect to ore-pass depth H across ore-pass dip angles.

Figure 9. Variation of total shaft wall damage volume Q_tol with respect to ore-pass dip angle θ across ore-pass depths.

Figure 10. Variation of total shaft wall damage volume Q_tol with respect to inclined angle of chute α across ore-pass depths.

Figure 12. Variation of total shaft wall damage volume Q_tol with respect to ore block size P across ore-pass depths.

Table 1. Physical and mechanical parameters of ore and shaft wall rock mass.

Type	Elastic modulus E/(GPa)	Poisson ratio ν	Volumetric weight γ/(KN·m^-3)	Initial yield strength σ_q/(MPa)	Friction angle $φ$ /(°)	Cohesion c/(MPa)	Coefficient of sliding friction $μ$
Shaft wall rock mass	16.80	0.26	27.80	59.52	42	10.60	0.40
Ore	14.09	0.25	40.80	—	—	—	0.40

Table 2. Structural parameters of ore-pass.

Operating condition	Ore-pass dip angle $θ$ /(°)	Shaft diameter D/(m)	Ore-pass depth H/(m)	Inclined angle of chute $α$ /(°)
1	80	2	70	70
2	70	2	180	60
3	55	2	60	65
4	60	2	180	45

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Shaft Wall Damage of High Depth Inclined Ore-Pass under Impact Wear Behavior

Abstract

1. Introduction

2. Shaft wall damage model of high depth inclined ore-pass

2.1. Basic model

2.2. Basic Assumptions

2.3. Theoretical solution

2.3.1. Ore indentation depth δ

2.3.2. Wear length l

2.3.3. Shaft wall damage volume Q

3. Engineering case

3.1. Reasonableness of the shaft wall damage model of high depth inclined ore-pass

3.1.1. Engineering survey

3.1.2. Parameter Selection

3.1.3. Result analysis

3.2. Influence of ore-pass depth H

3.3. Influence of ore-pass dip angle θ

3.4. Influence of inclined angle of chute α

3.5. Influence of shaft diameter D

3.6. Influence of ore block size P

4. Discussion

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe