Prerpints.org logo
Preprint
Article

The Significance of the Factors Increasing the Asphalt Pavement Recycling Rate in the Country, Determined by MCDM Methods

Altmetrics

Downloads

68

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 October 2023

Posted:

25 October 2023

You are already at the latest version

Alerts
Abstract
Transport infrastructure’s asphalt pavement deteriorates under the influence of destructive factors. Damages which have been occurred during its exploitation period are repaired, and when their further rehabilitation is economically and technically irrational, the asphalt pavement is recycled. The material from the asphalt pavement layer that has reached its limit state is milled out or broken and crushed and then is repeatedly used in the production of hot-mix asphalt (HMA) or warm-mix asphalt (WMA) mixtures. In this paper, the dynamics of the percentage recycling ratio (RR) of old asphalt pavement material was investigated. RR represents the quantity of reclaimed asphalt pavement (RAP) used in the production of HMA and WMA mixtures in Europe and the USA, divided by the total amount of RAP prepared in the country. Factors and goals affecting it are analyzed. An original system of 10 criteria that increase the RR country has been created. By applying different multiple criteria decision making (MCDM) methods and using the importance given to these criteria by 14 experts, the normalized subjective weights of the criteria were determined. Analytic Hierarchy Process (AHP), rank correlation, Average Rank Transformation into Weight - Linear (ARTIW-L) and Non-linear (ARTIW-N), Direct Percentage Weight (DPW) methods were used in the study. The results display that the RAP recycle rate is close to 100% in countries with a sustainable economic background. In the Baltic countries, it is mostly increased by the adequacy of regulatory documents, the strategy promoting asphalt recycling in the country, and the homogeneity and classifying of RAP. The number and capacity of RAP stocks, the number and productivity of asphalt milling equipment and the wear and tear of the asphalt pavement have the least influence on the increase of RR. The opinions of experts in assessing the significance of all criteria are consistent. The averages of the weights of criteria determined by four MCDM methods (AHP, ARTIW-L, ARTIW-N, DPW) made it possible to obtain more reliable results. These results can be used to make strategic decisions and to create a plan of practical actions to increase the RAP recycling rate in the developing countries.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

Countries where sustainable economy is developed are repeatedly using (recycling) asphalt from the old pavement of the transport infrastructure. Old asphalt grains are properly prepared for the further recycling, called reclaimed asphalt - RA or reclaimed asphalt pavement - RAP. Grains are extracted from asphalt layers by cold milling or breaking them, followed by crushing old pavement blocks and screening. Reclaimed asphalt (RA) is asphalt reclaimed by milling of asphalt road layers, by crushing of slabs ripped up from asphalt pavements or lumps from asphalt slabs and asphalt from surplus production [1].
Used asphalt grains of the determined maximum size (RAP) are dosed at the plant during the production of hot-mix asphalt (HMA) and warm-mix asphalt (WMA) mixtures (hot-mix recycling). In some cases, they are cold-mixed with or without virgin mineral materials and binders and paved in the base layer (cold-mix recycling). In both operations, economic and environmental benefits are targeted as virgin resources and energy are saved, and production waste is not generated. One of the most important goals in the road construction industry is increasing the amount of RAP, i.e., the target is that all or almost all RAP available in the country is reused as rationally as possible.
High quality material milled from a street, aircraft runway and vehicle parking lot pavement the lower or upper asphalt layer course is most beneficial for repeated use in the production of recycled hot and warm asphalt mixtures (RHMA and RWMA). The higher the percentage of RAP is used, the lower the cost of the recycled asphalt mix is [2]. The aim is that the recycled asphalt mixture has no worse properties than a mixture produced only from virgin materials. For this purpose, it is necessary to use homogeneous RAP, to separate the RAP removed from different pavement’s layers, to assess its properties with sufficient accuracy, to be able to choose the mass ratio between it and virgin materials, to choose a suitable renewing material (rejuvenator) or a more liquid bituminous binder, and to accurately dose and mix all materials. It is especially important to produce a recycled mixture of HMA and WMA in an asphalt mixing plant (AMP) that corresponds to its job mix formula (JMF), strictly controlling the required temperature and completely mixing its components. In the process of its production, storage and transportation, it is necessary to reduce segregation, oxidative aging of the bituminous binder and decrease in temperature.
The aim of this paper is to investigate the ratio of the amount of RAP used in the production of HMA and WMA mixtures in individual countries to the total amount of prepared RAP available in the country, to systematize the factors (criteria) that increase this recycling rate and, after using expert assessments, four MCDM methods to determine the weights of these criteria and analyze them.

2. Literature Review

During the service period of the asphalt wearing layer, the deterioration of physical and mechanical properties is most influenced by changes in the bituminous binder due to aging processes.
Due to the influence of temperature and oxygen, a change in the structure and/or composition of the binder occurs, and it turns harder and more brittle [3]. The oils turn to resins, the resins covert to asphaltenes in the result of oxidation process [4]. Oxygen diffusion and oxidative reaction are two main factors in bitumen oxidative aging discovered by experiment, (but the dynamic balance between them could not be easily studied by experimental methods due to its comprehensiveness). A pavement oxidation model for a bituminous binder was used to simulate this process. Oxygen molecules penetrate the bitumen film and react with binder molecules [5]. By decreasing oxygen diffusion, bitumen oxidation can be slowed down, but only works for oxygen diffusion determined cases.
Except binder determination, a numerical model to predict the diffusion and reaction of oxygen in petroleum bitumen film was developed by Herrington [6]. Model parameters for the diffusion-oxidation process was obtained by correlating oxygen uptake of bitumen solutions to changes in carbonyl infrared spectral absorption and viscosity.
The aim of research [7] was to define the effect of oxidative aging on the chemical and rheological properties of neat and styrene-butadiene (SBS) polymer-modified bitumen.
Increasing the amount of RAP in mix asphalt production has been set as target for the industry [8]. This leads to mitigate the impact of tripled binder costs [9]. As the demand for virgin bitumen and virgin mineral aggregates decreases, the use of reclaimed materials is increasing [10].
During rehabilitation RAP is produced milling paved HMA road. HMA recycling is not something unusual as the first site of hot in-place recycling was completed and documented in the 1930s. Invention and development of a big road milling machine and in conjunction with the oil crisis in 1970s leaded the growth of the interest in asphalt recycling [11].
The RAP properties play an initial role in defining the performance of the recycled mixture when high percentage of RAP is used in HMA production. Gradation and the composition of the old asphalt pavement not only define RAP properties as the milling process also has an influence [12].
The asphalt pavement milling machine’s picks wear intensity impacts on the gradation of RAP, the cost of job done, and the utilization of the milling machine [13]. Milled RAP is widely used to in AMP for recycled HMA and WMA mixtures production [14]. In research it was demonstrated that the asphalt mixtures with RAP content performed at least like, or better than, as conventional HMA mixtures [15]. The process of production a recycled HMA or WMA mixtures is more complex than the process of production an asphalt mixture only out of the virgin materials. The storage, transportation, dosing and drying and heating of RAP require additional equipment [14], the design of which depends on whether the heat is transferred to the RAP by conduction or convection.
The HMA mixture production errors of and designed suboptimal mass ratio of constituents have an immediate effect to poor quality of asphalt pavement [16]. The type of asphalt plant and production parameters have an impact on the properties of the recycled asphalt mixture and the degree of mixing of the old and new bituminous binder [17]. New generation asphalt production equipment complying new industry standards replaces outdated design equipment with an insufficient control system to produce high-quality asphalt mixtures [18]. Current HMA’s quality control (QC) methods are work power and time consumptive which makes inefficient processing of information needed to monitor and control the production [19].
Hot recycling in plant is one of the advanced applications adapted for recycling of asphalt pavement materials. Defined in the recipe quantity of RAP, virgin binder and mineral aggregates are added, heated, and mixed to produce the recycled HMA during hot recycling in plant process. Different types of rejuvenators are added [20].
HMA mixtures are stored in heated ready-mix silos before they are ready to be transported to construction sites. The HMA storage time in the silo varies and depends on several factors. Short-term aging of the binder may occur if HMA is exposed to higher temperatures. Blending or diffusion could occur between the RAP and virgin binders in their interaction [21].
The design of individual equipment and the recycling technology plays significant role influencing the process parameters and sequence of hot RAP recycling in an AMP which should be suitable for the application of the most important principles of recycling, which have been systematized and analyzed [22].
Review [23] says that the fundamental thermodynamics and kinematics involved in the plant production of RAP mixtures. This review states that the mixing time, mixture discharge temperature, and silo storage time are fundamental on the mechanical performances of RAP mixtures produced in laboratory or AMP as it was found during experimental studies.
In study [24], thermodynamics and heat transfer principles were used to estimate virgin aggregate temperature. Gradation, moisture content and the mix proportion of virgin aggregates and RAP were the main factors for virgin aggregate temperature estimation in the drum plant.
A numerical model was developed to investigate the RAP grain inside melting potential in asphalt mixing drum based on the thermal properties of asphalt materials [25]. The presented model provides the practice-ready calculation of the minimum time needed for any spherical particle to heat to a required temperature considering the initial temperature, ambient temperature, thermal diffusivity, and particle radius. The resulting equation displays that there may occur conditions where the RAP grain core could not be sufficiently heated in asphalt mixing drum.
The usual method requires a significant amount of energy for production of bituminous binder, drying aggregates, and subsequent production of HMA at AMP. For example, approximately 6 liters of fuel are used for drying and heating one ton of aggregates. Significant amount of greenhouse gases and harmful pollutants are released during the production of tremendous quantities of HMA [26].
Asphalt pavement maintenance and rehabilitation are more frequently performed on porous asphalt (PA) as of its low longevity. This leads to the accumulation of a significant amount of RAP which is not used totally as the use of RAP is not usually allowed in PA [27].
The paper [20] forces to find a solution on the problem of constituent proportioning with the help of a generalized formulation that does require any prefixing of the quantity (or property) of any of the constituents. A linear programming (LP) method has been proposed. An asphalt mixture designer can minimize of the total material cost or maximize of the total RAP quantity to be used in the recycled mixture.
The work [28] presents a method for determining the consumption of the recycled hot-mix asphalt (RHMA) mixture, which allows calculating the maximum allowable percentage of RAP depending on its homogeneity. Getting the established maximum RAP amount as a constant size, the required content of new mineral materials is estimated thus considering bitumen capacities.
Assessing the scale of the blending between virgin and old binders and identifying the key affecting factors are increased during recent years. Viscosity as a function of temperature, exposure time, and film thickness have been mentioned as the main factors controlling the blending between two binders that are in contact [29].
Researchers say [30] that RAP should not be considered a “black rock” because significant blending occurs between the RAP and virgin asphalt binders. In study is recommended that blending charts based on virgin and recovered RAP binder properties be used to account for the RAP contribution to the total binder properties and / or to select a lower grade virgin binder when RAP is used in lower quantities.
The result [31] indicates with short mixing time, RAP tends to work as inert black rock and the complete blending process proceeds towards if the mixing time significantly increased. However, longer RAP and virgin aggregate mixing times could result in recycled HMA higher stiffness modulus and greater homogeneity.
The objective of publication [32] is to provide a methodology to determining the degree of partial blending in high RAP mixtures. When RAP is mixed with virgin aggregates and virgin binder, partial blending of RAP binder with virgin binder develops in the HMA. because As the degree of blending between the RAP and the virgin materials is not known, authorities limit the amount of RAP.
The temperature characteristics of RHMA mixtures were studied through viscosity – temperature dependency of asphalt binders and temperature storage stability of blended mixtures [33]. The characteristics of temperature storage stability would be greatly influenced by the preheated temperatures of various components in asphalt mixtures. The results showed that the control optimization of RHMA mixture could lead to good rheological properties of asphalt binder containing reclaimed (old) and fresh (new) asphalt binder.
The properties of the old bituminous binder are restored in bitumen films, the thickness of which depends on the size (diameter) of the mineral grains. Only the optimal amount of aggregate (old and new) binder allows to obtain the best properties of the regenerated asphalt mixture. Excess and deficiency of aggregate binder deteriorates the properties of RHMA mixture. The design of the bitumen dosing system of the asphalt mixer and its management has a significant influence on the increase in the amount of bituminous binder in the produced asphalt mix from the deviations from the JMF [34].
The average bitumen film thickness (BFT) is not a measured physical property. This parameter is calculated as material’s volumetric characteristics and gradation [35]. Another computational method significantly improves the current conventional method for the asphalt film thickness calculation because grain shape factors and flat surface factors for sieve sizes are considered [35]. The field and laboratory experimental data both show that the bitumen film thickness is a significant factor influencing the rutting performance for asphalt mixtures. The research results [36] show that there is a dependence between the thickness of the bituminous film of the aggregate specific surfaces and the residual deformation.
Mixtures with greater amounts of RAP are enhanced by adding rejuvenator additives. The use of suitable rejuvenators allows to refine the properties of the old binder and the percentage of RAP in recycled asphalt mixture could be increased [9]. Recycled asphalt mixtures can be also produced using a significant amount of different waste materials [37]. The tests performed on the recycled asphalt mixtures containing lard imidazoline confirm the suitability of this agent for paving applications [38].
Rejuvenator is not a commonly used softening agent to be used in recycling of RAP. In study [39] Superpave mixtures containing RAP were designed on a base of rejuvenator and a soft binder. Later mixtures were evaluated in regard of the volumetric result obtained the indirect tensile strength (ITS) of samples and assessing the mixtures for rutting using the asphalt pavement analyzer (APA). All Superpave mixtures wit RAP contents displays same quality properties as the two control virgin mixtures.
Rejuvenator is an oil consistency material which restores RAP binder during hot recycling in plant. Ten potential locations for rejuvenator addition in asphalt plant were ranked and full-scale asphalt mixtures production experiment was performed to compare rejuvenator addition to cold RAP on conveyor belt versus addition to hot RAP in mixer [40,41]. The effects of rejuvenator addition were evaluated to cold RAP before the RAP heating drum as opposed to the more conventional approach to add rejuvenator to hot RAP [40].
The minimum RAP content (min. RAP %) depends on the capability of AMP equipment to provide addition of the RAP accurately and consistently. The maximum amount of RAP (max. RAP %), that can be added to a mixture, depends on several factors including: amount of RAP available; specification limits; capability of the hot-mix plant to dry, heat, and effectively mix the RAP material; gradation of the RAP aggregate, particularly the amount of material passing 0.075-mm sieve (mineral filler); variability of the RAP; properties of the RAP binder and available new binders [42].
The homogeneity of the feedstock shall be determined from the variability of the percentages of coarse and fine aggregates and of fines in the reclaimed asphalt, the binder content of the reclaimed asphalt and either the penetration, the softening point or the viscosity of the binder recovered from the reclaimed asphalt [1,43].
The Literature Review shows that the following are the most important goals of asphalt pavement recycling:
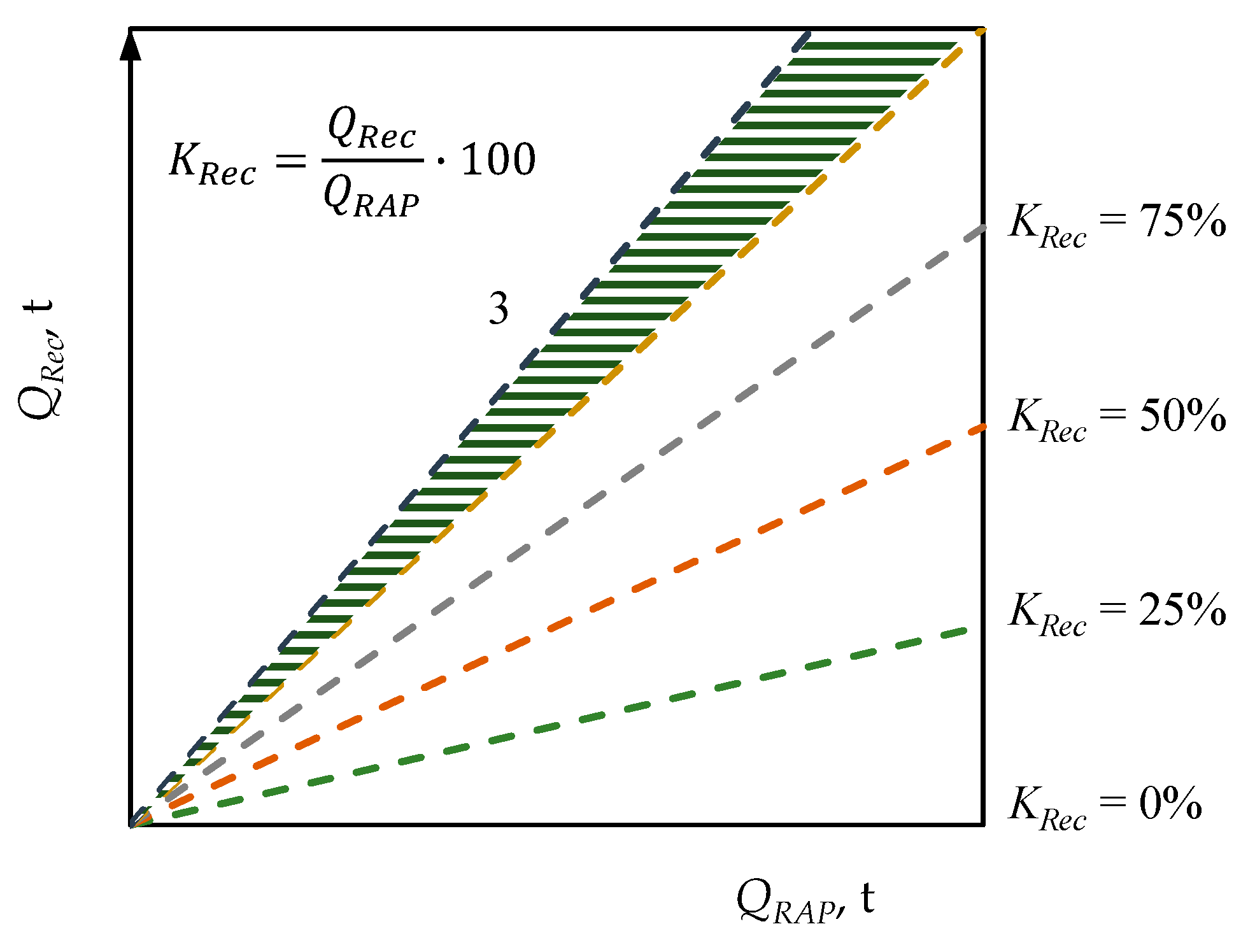
  • All the old asphalt removed from the road, street or other transport infrastructure element should be reused to produce hot and warm mixed asphalt mixtures aim for a recycling ratio K R e c equal to or close to 100%. Factors increasing the relative amount of asphalt pavement recycling in the country and their significance have not been studied.
  • Use as much RAP as possible in the recycled asphalt mixture (RAP percentage in the mix), depending on the design and technological parameters of the recycling equipment and the homogeneity of RAP, because this strategy allows RAP to be used at the highest level of value creation.
  • Aim for the recycled asphalt mixture to be of the same or close quality as the (conventional) mixture made only from new materials. The recycling process is considered complete when the new and old materials are evenly mixed mechanically and when the diffusion mixing of the old and new bituminous binder in the films covering the mineral particles has ended.

3. Asphalt pavement recycling rate in various countries

Worn asphalt pavement layers are recycled in a cold or hot state. The first phase of the recycling process consists of milling or breaking the asphalt pavement layer. During the cold recycling process, the removed asphalt pavement is crushed to a certain size of grains, suitable for their re-use in the production of new (recycled) asphalt mixtures and material mixtures for the construction of road base layers without binders.
The cold milling of asphalt pavement layers should be processed so that the different mixes from the different layers are separated if possible. Selectively milled asphalt pavement can be used at the highest level of the value creation according to its origin (e.g., also for asphalt pavement upper courses construction) [44].
Greater economic benefits can be obtained by increasing the proportion of domestically prepared RAP used in the production of recycled hot-mix and warm-mix asphalt mixtures. The model (Figure 1a) shows that the entire amount of RAP prepared in the country in one year is divided into two parts of its use: for RHMA and RWMA mixtures production (QRec) and for cold road base materials (QMM) production. The amount of RAP prepared in the country QRAP depends on the length of the road network, the degree of wear and tear of the asphalt pavement surface, and investments for the development and maintenance of roads in the country.
The required amount of the virgin materials that improve the gradation of RAP and the properties of the old bituminous binder (mVM) is added to the determined optimal amount of RAP (mRAP) in the design and production process of the recycled asphalt mixture (Figure 1 (b)). The maximum amount of RAP grains m R A P m a x that can be added to the asphalt mixture depends on the homogeneity of the RAP and the method of the heat energy transfer to the RAP granules in AMP, i.e., RHMA mixture production technologies.
Domestical percentage of available RAP re-use in hot and warm mix asphalt production in separate (each) year percentage RR is calculated from formula:
K R e c = Q R e c Q R A P · 100 ,
where K R e c —domestical asphalt pavement recycling rate, %; Q R e c —amount of prepared RAP used in recycled hot and warm asphalt mixtures in the country during the research year, t; Q R A P —amount of prepared all RAP in research year, t.
According to formula above, K R e c is calculated considering the data of Q R e c and Q R A P , using statistical data officially published, for example asphalt pavement associations [45].
Presented model in (Figure 2) displays RAP used in production of HMA and WMA mixture relative amount to the overall RAP amount.
The recycling rate K R e c changes from country to country and varies from 0% to 100%. Conditionally, this variation range can be divided into 4 equal intervals: K R e c = 0 ÷ 25% (small RAP amount is used to produce HMA and WMA); K R e c = 25 ÷ 50% (satisfactory use); K R e c = 50 ÷ 75% (good or sufficient utilization) and K R e c = 75 ÷ 100% (very good utilization). This ratio K R e c shows the actual potential of the restoration of the country’s road infrastructure and the degree of its utilization, to achieve a sustainable economic effect aligned with environmental protection, saving virgin material resources, and reducing the cost of construction. In some case certain amounts of RAP are imported from another country, so its K R e c can be higher than 100% (Figure 2).
European Asphalt Pavement Association (EAPA) Asphalt in Figures [45] statistics provides the percentage of RAP prepared in European countries and the USA, which is used in recycled HMA and WMA mixtures during the last three years. Table 1 displays that the % of available RAP re-use in hot and warm mix asphalt production in 2017‒2019 varies from 100% (Finland) to 0% (Romania). 10 European countries did not provide these results to EAPA, including 3 Baltic countries and Poland. In this research 3 years average was taken because not all countries provided their data each year.
Three years average recycling rate K ¯ R e c (Table 1) shows that it is in the interval from 0 to 25% in five out of nineteen European countries: CZ, IT, SI, TR, RO. K ¯ R e c is found in three European countries: HR, GB, NO in the interval from 25 to 50%. More than half (from 50 to 75%) of RAP is used to produce HMA and WMA mixtures in six European countries: AT, DK, FR, SK, ES, NL. The highest value of K ¯ R e c = 75–100% is presented by five European countries: FI, BE, CH, HU, DE and the United States of America (USA).
The ranks (priorities) assigned to the countries according to K R e c values show that the leaders in Europe are Finland ( K R e c = 100%), Belgium ( K R e c = 91%) and Switzerland ( K R e c = 90%). The USA, which data is provided in report as non-European country, also has a high recycling rate ( K R e c = 94%).
Applying multiple criteria decision making (MCDM) methods can be determined what factors (criteria) identify the K R e c   in the country. For this purpose, a system of criteria with their detailed descriptions is created, MCDM methods are selected, questionnaires are prepared to be answered by road building sector experts (specialists) who are involved in the field of the problems solving of asphalt pavement recycling and experts were selected, then the applied methods and the procedure for filling out the questionnaires are explained to them.

4. Systematized criteria increasing the asphalt recycling rate in the country

4.1. Criteria, increasing asphalt recycling rate

Criteria that increase the relative amount of asphalt pavement recycling (recycling rate) in the country were systematized during discussions with dedicated professionals in the mix design, asphalt production technologies and asphalt mixtures application in the construction process of transport infrastructure, employees of scientific institutions and analyzing scientific publications. The full description and abbreviations of these ten criteria (A, B, C, D, E, F, G, H, I, J) with a detailed explanation of the research object are given below.
Factors which are increasing the recycling rate K R e c of highways, roads, streets, airport runways and taxiways, and other transport infrastructure areas (percentage ratio QRec of the quantity of RAP used in the recycled hot and warm asphalt mixes from the old pavement with the total the amount RAP (QRAP)) in the country:
  • Significant wear and tear of the country’s transport infrastructure’s asphalt pavement up to the limit state: many damages and their rehabilitation sites, a low strength index of the road structure and low residual resource (wear of the asphalt surface).
  • The number of recycling equipment (remixers, recyclers and asphalt plants adapted to recycle RAP) in the country, their innovative design, high productivity and even (proportional to the amount of RA) arrangement (number of recycling equipment and productivity).
  • The large number and cumulative performance of equipment for dismantling, crushing and classifying the used asphalt pavement (road milling machines, crushers, screens), their innovative design (quantity and performance of road milling machines).
  • Relevance of normative documents regulating asphalt recycling technologies, requirements for RAP sorting, storage and quality, design of optimal composition of recycled mixture, testing methods and environmental protection (relevance of the normative documents).
  • Qualification, experience, training system developed in the country of managers, professional specialists and other staff members who intend and can recycle asphalt pavement (personnel qualification and skills).
  • Comprehensible regulation of the ownership of RAP, increasing the economic benefits of their use in the recycled asphalt mix (RAP ownership and economic utility).
  • Classifying and storage of RAP from the upper, bottom, and base layers of different roads and streets in separate stacks, increasing the homogeneity of recycled asphalt and its maximum useable amount (RAP homogeneity and classifying).
  • Sufficient number and large capacity (volume) of stocks (buildings, stacks with roofs) adapted to store prepared RAP) protecting them from precipitation and self-compaction (possible sticking) (number and capacity of RAP stocks).
  • Abundance of rejuvenating materials (additives) for restoring the properties of aged viscous bitumen in RAP on the market, their reasonable price and high efficiency, developed industry of their production in the country (quality of rejuvenating materials).
  • A strategy for the maintenance and development of the country’s transport infrastructure, encouraging energy and material saving by using reclaimed asphalt which quality is not worse than an asphalt mixture made from virgin resources (asphalt recycling strategy).
Each expert received the description of the criteria and the questionnaire in the appropriate form, where he had to give the criteria ranks, percentage weights and scores to fill in the AHP (Analytic Hierarchy Process) pairwise comparison matrix.

4.2. Experts

One of the most important stages of the research was the selection of an expert group of professional specialists in the area under consideration. It was expected that the evaluation of the experts would not be the same, and their slight differences would allow to calculate the significance of the criteria, expressed as average ranks or weights. The opinion of a group of experts is always more accurate than the opinion of a single expert.
A particularly difficult task was to select experts out of potential asphalt professionals, who agreed to participate in the study, range in order properly fill out the questionnaires handed to them. There were 14 experts in the Baltic States, of which 8 were asphalt production and pavement construction professionals, 4 university scientists and 2 researchers working in the road construction and asphalt production companies.

5. Criteria significance research methods

The significance of indexes (criteria), expressed by their subjective normalized weights, can be determined using different methods (algorithms). None of them have a theoretical advantage over other methods. However, the general principle of all these algorithms is the same: the most important criterion must be assigned to the highest weight. The sum of the weight values of all criteria must be equal to one, i.e., they are normalized.
To increase the reliability of the research result, four Multiple Criteria Decision Making (MCDM) methods were chosen. Initially, the rank correlation method presented by Kendall [46] was used. From the ranks of the studied criteria, applying new average rank transformation into weights linear and non-linear (Average Rank Transformation into Weight-Linear - ARTIW-L and Average Rank Transformation into Weight - Non-linear - ARTIW-N) methods [47,48,49], the normalized criteria weights were calculated. The experts also provided percentage importance estimates for the criteria, which were used to calculate all the normalized weights of their subjects using the Direct Percentage Weight (DPW) method. The Analytic Hierarchy Processes AHP method [50] was the most widespread in scientific papers in the world, but it was complicated, because not all experts were able to correctly fill in the pairwise comparison matrix to respect the condition of transitivity and make it consistent.

5.1. Average Rank Transformation into Weight-Linear (ARTIW-L) method

This method calculates the averages of the ranks given by the experts (j = 1, 2, ..., n) participating in the research for each criterion (i = 1, 2, ..., m):
R ¯ i = ∑ j = 1 n R i j n ,
where Rij—the rank assigned to the i-th criterion of the j-th expert; n—number of experts.
The subjective normalized weight of each criterion is calculated using the linear method of transforming rank averages into weights (ARTIW-L) [47].
ω i = m + 1 − R ¯ i ∑ i = 1 m R ¯ i ,
where R ¯ i —i-th criterion average rank; m—the number of criteria describing the research object.
The criteria weights ωi calculated by the ARTIW-L method are linearly correlated with the average ranks of these criteria R ¯ i .
To be able to take the experts group opinions’ average expressed in ranks, scores, or weights, as the result of solving the problem, it is necessary to check whether the opinions of all experts are not contradictory. Only when the assessments of all experts are similar (non-contradictory), the average is a reasonable decision. For this reason, Kendall’s variance concordance coefficient W [46], which shows the compatibility of expert opinions, is calculated and its the numerical value can vary from 0 to 1:
W = 12 S n 2 m 3 − m = 12 S n 2 m m 2 − 1 .
The sum of the squares S of the deviations of the sum of ranks ∑ j = 1 n R i j of each m-th criterion from the average rank R ¯ is calculated from the formula:
S = ∑ i = 1 m ∑ j = 1 n R i j − 1 2 n m + 1 2 ,
where m—criterions number (i = 1, 2, ..., m); n—expert number (j = 1, 2, ..., n).
The calculated value of W is compared with its minimum value Wmin, depending on the chosen significance level α (take α = 0.05 or stricter α = 0.01) and the number of degrees of freedom ν = m − 1 [47]:
W m i n = χ α , ν 2 n m − 1 ,
where χ α , ν 2 —the Pearson’s criterion statistic is found in the Appendix Table of Mathematical Statistics [51].
Whether the opinions of the experts are consistent can be checked by calculating a random variable:
χ 2 = W n m − 1 = 12 S n m m + 1 ,
which is distributed according to the χ 2 (chi-square) distribution with ν = m − 1 degree of freedom. According to the selected significance level α (0.05 or 0.01) from the χ 2 distribution table [52] with ν = m − 1 degree of freedom, the critical value χ α , ν 2 is found. If the value of χ 2 calculated according to formula (7) is greater than χ α , ν 2 , it is considered that the experts’ assessments are consistent (uncontradictory, similar).
How many times the calculated concordance coefficient W is greater than its minimum (critical) value Wmin and how many times χ 2 is greater than its critical value χ α , ν 2 is shown by the new consistency coefficient kc, which is calculated from the formula:
k c = W W m i n = χ 2 χ α , ν 2   .
When the experts’ opinions are aligned, then kc > 1. Otherwise (when kc < 1), the opinions of the expert group differ significantly, i.e., they are not aligned.

5.2. Average Ranks Transformation into Weight-Non-linear (ARTIW-N) method

Criterion-normalized weights ωi can be calculated using another method of transforming the rank average R ¯ i into weights. According to formulas (9) and (10), the criteria weights ωi calculated with the averages of criteria ranks R ¯ i are connected by a non-linear inverse correlation (functional) dependence. Therefore, this method is called the ARTIW-N method by the authors [49].
When applying the ARTIW-N method, the ratio of the most important criterion with the lowest rank average m i n i R ¯ i to the average ranks R ¯ i of all other i-th criteria is calculated at the beginning:
u i = m i n i R ¯ i R ¯ i .
After normalizing the u i values of each criterion, their subjective significances (weights) ωi are calculated:
ω i = u i ∑ i = 1 m u i .

5.3. Direct Percentage Weight (DPW) method

This method is mostly used in practice. The DPW method is as clear and logical as the method of ranking indicators (criteria) (rank correlation), but its accuracy is much higher. When using the direct method of determining percentage weights, the sum of the weights of all evaluations of the research criteria of each expert object must be equal to 100%. With percentage ratings, they are divided by 100. It is easier to evaluate criteria directly in percentages if they were ranked at the beginning: a lower rank corresponds to a higher weight.
The sums of percentage weights pij of all n experts (j = 1, 2, ..., n) of each i-th criterion ∑ j = 1 n p i j and their normalized weights ωi are calculated:
ω i = ∑ j = 1 n p i j 100 n ,
where p i j —expert j-th assigned the weight given to i-th the criterion in percentage; n—expert number.
When assigning percentage weights to the criteria, it is preferable that there are no identical (duplicate) weights. As a result, they can be given to the nearest tenth of a percent.
The weights ωi of the criteria calculated by the DPW method are nonlinearly correlated with the average ranks of these criteria R ¯ i . Most often, non-linearity is determined by the increased significance of the most important criteria.

5.4. Analytic Hierarchy Process (AHP) method

Hierarchy analysis method is usually called Analytic Hierarchy Process (AHP) method. It allows the criteria arranged at the beginning to be compared with each other in terms of importance, giving them a quantitative priority in relation to each other, expressed by the intensity (level) of the mutual importance of the two criteria. The essence of the method consists of the square matrix A of pairwise comparison. The expert compares with each other all the criteria (factors, indicators) Ci and Cj (i,j = 1, 2, ..., m) that make up the object, where m is the compared criteria (factors increasing the relative amount of asphalt pavement recycling (KRec in the country) number. The Saaty scale of five levels of importance (1-3-5-7-9) is used to compare the criteria. Intermediate even estimates (2-4-6-8) can also be used.
The AHP method is convenient because it is easier for the expert to compare the factors that increase the relative amount of asphalt pavement recycling in the KRec country, two at a time, instead of all at once. Such a comparison of criteria is simple and reliable only for an expert who is well versed in the AHP method, and especially in the principles of filling in the pairwise comparison matrix. A matrix indicates how much one of its elements is more important than another element. The method allows the qualitative (linguistic, verbal) assessment of factors (criteria) to be presented in a quantitative (numerical) assessment.
The result of the pairwise comparison of the criteria is the square matrix A = a i j m × m (i,j = 1, 2, ..., m). Comparing the importance of factors Ci and Cj, which increase the relative amount of asphalt pavement recycling KRec in country, it is marked by estimates ω1, ω2, ..., ωm the ratio
a i j = ω i ω j ,   ( i , j   =   1 ,   2 ,   … ,   m )
shows how many times the i-th factor (criterion) Ci is more important than the j-th factor Cj, aij = 1 / aji.
The elements of matrix A (whole and fractional numbers on a nine-point scale) are filled in according to the following requirements. The elements of matrix A aij = 1, when the significance of both compared criteria in relation to the research object (KRec) is the same. In this case, all elements of the main diagonal aij = 1 (i = 1, 2, ..., m) since each criterion is compared with itself. The elements of the matrix A aij = 3, when the criterion Ci is slightly more important than the criterion Cj. The elements of matrix A aij = 5 when the criterion Ci is much more important than the criterion Cj. The elements of the matrix A aij = 7, when the criterion Ci is very much (significantly) more important than the criterion Cj. The elements of the matrix A aij = 9, when the criterion Ci is incomparably (absolutely) more important than the criterion Cj (Table2).
The elements aij of the matrix A can be considered as the ratio of the values of the criteria Ci and Cj after the normalization of these values - as the ratio of the weights of the criteria. The square matrix of the pairwise comparison of the criteria assessed by one expert looks like this (i - rows, j - columns):
A = a 11 a 12 ⋯ a 1 j ⋯ a 1 m a 21 a 22 ⋯ a 2 j ⋯ a 2 m ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ a i 1 a i 2 ⋯ a i j ⋯ a i m ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m j ⋯ a m m = ω 1 ω 1 ω 1 ω 2 ⋯ ω 1 ω j ⋯ ω 1 ω m ω 2 ω 1 ω 2 ω 2 ⋯ ω 2 ω j ⋯ ω 2 ω m ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ω i ω 1 ω i ω 2 ⋯ ω i ω j ⋯ ω i ω m ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ω m ω 1 ω m ω 2 ⋯ ω m ω j ⋯ ω m ω m
The expert, comparing two criteria of the object under investigation, applies the linguistic description of the intensity of mutual importance presented in Table 2 and assigns the corresponding level of importance from 1 to 9. It is convenient to assign ranks to the criteria of the object at the beginning and compare the most important criterion with the second most important, the third most important, etc. t., and at the end - with the last (m-th) according to importance (the line of the most important criterion is filled with integers) [53]. After that, the second most important criterion is compared with all the remaining criteria in the same sequence (the line of the second most important criterion is filled from m-1 integers and one fractional number) and so on.
The most accurate of the approximate algorithms for determining object criteria weights (relative importance) ωi is based on the calculation of geometric averages of the elements aij of the row elements of the pairwise comparison matrix [50,54].
A rational sequence of criteria weight calculation can be the following: 1. A square matrix A = a i j for the pairwise comparison of object criteria is created. 2. The product of the elements of each row of the matrix A is calculated ∏ j = 1 m a i j (i = 1, 2, ..., m). 3. Extract the root of the m-th power of the calculated product ∏ j = 1 m a i j m . 4. The obtained values are normalized, i.e., they are divided by the sum of all their criteria:
ω i = ∏ j = 1 m a i j m ∑ i = 1 m ∏ j = 1 m a i j m .
The calculated true vector ωi corresponds to the significance of the criterion.
In this way, the weights of each criterion are obtained (their sum equals 1.0000), which allows a quantitative comparison of the significance of all criteria for the object under study, determined by one expert.
The compatibility of the pairwise comparison matrix filled by the expert is very important, which shows the non-contradiction of its filling logic despite the transitivity condition. The compatibility of the pairwise comparison matrix A is checked, for which it is necessary to calculate the maximum true value λmax. For this, the sum of the products of each criterion ∑ j = 1 m a i j ω j is divided by the value of the real vector (normalized weight) ωi calculated for the corresponding criterion and the arithmetic mean of all object criteria is obtained:
λ m a x = 1 m × ∑ i = 1 m ∑ j = 1 m a i j ω j ω i .
It was established [50] that the maximum true value of the inverse symmetric matrix of the m-th order is λmax ≥ m. Ideally, when the pairwise comparison matrix A is fully aligned, its column elements are also proportional, λmax = m. The compatibility of the matrix A is shown by the difference λmax ‒ m and the row m × m of the matrix A. Consistency index C.I. is calculated as follows:
C . I . = λ m a x − m m − 1 .
The concordance (inconsistency) of the pairwise comparison matrix completed by each expert is better, the lower the C.I. value: fully matched matrix C.I. close to zero. A matrix whose C.I. = 0 is very rarely obtained in practice, even when the transitivity property of its elements is fully satisfied. Quantitatively, the degree of compatibility of an inverse symmetric matrix can be determined by comparing the calculated compatibility index C.I. of the evaluated matrix with the random index of the inverse symmetric matrix of the same order randomly generated according to the scale 1-3-5-7-9 R.I. [55], presented in Table 3.
The AHP method is best suited for researching an object that consists of 7 criteria. Their number is considered optimal when there are two criteria less or more than 7, i.e., from 5 to 9 [55,56]. The method cannot be applied when there are less than 3 criteria because there are no R.I. meanings. However, it does not limit the number of criteria beyond m = 9, even though the nine-point Saaty scale is used. The greater the number of criteria that make up the research object, the more complex their pairwise comparison matrix is (when m > 9), the more identical elements aij are in it. When the matrix consists of more than 15 criteria, R.I. value is calculated according to the formula [57]:
R . I . = 1.98 m − 2 m .
To increase the reliability of the research result, the arithmetic averages of the weights assigned to the criteria of the expert group are taken, but only if the opinions of individual experts are harmonized. The consistency of expert opinions is determined by the calculated values of W, Wmin, χ2 and χ α , v 2 (formulas 4...7).
The arithmetic mean of the weights of criteria calculated by four MCDM methods is calculated from the formula, without giving preference to any of them:
ω ̿ i = ∑ k = 1 r ω i k r = ω i A R T I W − L + ω i A R T I W − N + ω i D P W + ω ¯ i A H P 4 ,
here ω i k —the weight of the i-th criterion calculated by the k-th MCDM method (k = 1, 2, ..., r); r is the number of methods used in the study (r = 4).
It is likely that ω ̿ i is closer to the population mean that would be obtained by surveying a large number of experts for the values of the criterion weights calculated by any of the four MCDM methods used in the study.
The width of the sample or the width of the data set (range) Δωi of the weights of each criterion determined by different methods is calculated from the formula:
∆ ω i = ω i m a x − ω i m i n ,
where ω i m a x and ω i m i n are, respectively, the maximum and minimum weight of the i-th criterion determined by the (four) different methods used in the study.
The width of the data set Δωi is the simplest characteristic of the variation. It can be used for an approximate but quick estimation of the standard deviation sΔωi [58]:
s Δ ω i = ∆ ω i β = ω i m a x − ω i m i n β ,
here Δ ω i is the range determined according to the formula (19); β - coefficient depending on the number of data r, i.e., number of MCDM methods used in the study. When r = 4, then β = 2.06.
More precisely, the amount of data dispersion can be determined directly by calculating the standard deviation from all data (not from the difference between the maximum ω i m a x and minimum ω i m i n values):
s ω i = ∑ k = 1 r ω i k − ω ̿ i 2 r − 1 ,
here ω i k —the weight of the i-th criterion calculated by the k-th MCDM method (k = 1, 2, ..., r); ω ̿ i —the weighted average calculated by the i-th criterion r methods according to formula (18).
The indicator used to determine the relative degree of variation is the coefficient of variation, which shows the ratio of the standard deviation to the mean and is usually expressed as a percentage:
V w i ' = s ∆ ω i ω ̿ i 100 %
or higher accuracy
V w i = s ω i ω ̿ i 100 % .
According to formulas (22) and (23), the values of the percentage coefficient of variation of the i-th criterion must be similar (close).

6. Results and discussion

Each of the 14 experts participated in the study read the questionnaire and understood the description of the 10 criteria, gave them ranks, percentage weights and filled in the AHP method pairwise comparison matrix using their personal expertise, knowledge, experience, and intuition. The ranks given to the criteria by all experts are presented in Table 4.
For the arithmetic averages R ¯ i (formula 2) of the ranks Rij given by all experts for each criterion to be reasonably taken as the general (collective) opinion of the expert group, the compatibility of their opinions was checked, which is shown by the concordance coefficient W (formula 4).
When calculating W, the sum of squares of deviations S (formula 5) is determined, which consists of ∑ j = 1 n R i j and R ¯ . Average rank (criteria i = 1, 2, ..., m; experts j = 1, 2, ..., n)
R ¯ = 1 2 n m + 1 = 1 2 14 10 + 1 = 77 ,
and sum of squared deviations (Table 4)
S = ∑ j = 1 m   ∑ j = 1 n R i j − 1 2 n m + 1 2 = 6842 .
Concordance coefficient (formula 4)
W = 12 S n 2 m 3 − m = 12 · 6842 14 2 10 3 − 10 = 0.423 .
The smallest value of the concordance coefficient Wmin, when the significance level α = 0.05 and the number of degrees of freedom ν = m − 1 = 10 − 1 = 9.
W m i n = χ ν , α 2 n m − 1 = χ 0.05 ; 9 2 14 10 − 1 = 16.919 126 = 0.134 .
Pearson’s criterion statistic
χ 2 = n m − 1 W = 14 10 − 1 0.423 = 53.3
or for the control
χ 2 = 12 S n m m + 1 = 12 · 6842 14 · 10 10 + 1 = 53.3 .
The fact that the experts’ opinions are aligned is shown by the new compatibility coefficient:
k c = W W m i n = χ 2 χ α , v 2 = 0.423 0.134 = 53.3 16.92 = 3.15 .
Three times higher than the minimum concordance coefficient calculated by kc from the criteria ranks allows us to reasonably assume that the opinions of the 14 expert groups are not contradictory in determining the normalized weights of the 10 criteria using the ARTIW-L, ARTIW-N, DPW and AHP methods.
Criteria weights determined by the ARTIW-L method (formula 3). The weight of the first criterion A is calculated as
ω A = m + 1 − R ¯ i ∑ i = 1 m R ¯ i = 10 + 1 − 7.286 55 = 0.0675 .
The calculated weights of other criterions and the priorities of these criterions are presented in Table 4.
The criteria weights calculated by the ARTIW-N method (formulas 9 and 10) show that the average of the ranks of the most important criterion D is R ¯ D = 2.643 , so its uD = 1, and the other criteria ui are less than 1. The normalized criteria weights ωi and their priorities are given in Table 4.
The first criterion A weight is ω A = 0.3628 5.5416 = 0.0655 . The weights ωi of other criteria were calculated similarly. The criterions priorities calculated by the ARTIW-L and ARTIW-N methods coincide, but the criteria weights ωi differ.
The percentage weights given to the experts’ criteria (Table 5) were used to calculate the normalized weights ωi of these criteria using the DPW method according to formula (11). The sum of percentage weights of the first criterion A is ∑ j = 1 n P A i = 86.3 , and the average of its percentage weights is P ¯ A = 6.1643 . Therefore, the normalized weight of this criterion A is ω A = 0.0616 . The weights ωi and priorities of other criterions (B, C, D, E, F, G, H, I and J) are calculated analogously.
The criteria weights determined by the DPW method are similar to the weights calculated by the ARTIW-L and ARTIW-N methods. However, the difference between the weights of the most important D and the least important C or H criteria is greater as calculated per DPW method accuracy is much higher. The priorities of the criteria are identical, except for criteria C and H.
The criteria’s normalized weights ωi and compatibility ratios C.R. were calculated by the AHP method of the pairwise comparison matrices of the criteria filled out by each expert and presented in Table 6. All matrixes were concordant (C.R. < 0.1) except for E7 expert (C.R. = 0.105). Therefore, with a small margin of error, all matrixes were used to calculate the general opinion about the significance of the criteria for a group of 14 experts. The sums of the weights ∑ j = 1 n ω i j of each i-th criterion were divided by the number of experts n = 14. The averages of the criteria weights ω ¯ i and priorities show a similar trend of their significance as determined by ARTIW-L and ARTIW-N and DPW methods.
However, the significance of the most important criterion D was obtained even higher (ωD = 0.2038), the significance of the least important criterion H was lower (ωH = 0.0376).
The inverse linear (ARTIW-L method) and non-linear (ARTIW-N, DPW, AHP methods) correlation was obtained between the average R ¯ i of the ranks of ten criteria determined by different MCDM methods and the calculated weights ωi of these criteria (Figure 3). The dependence of criteria weights ωi on R ¯ i is shown by regression equations. The coefficients of determination R2 of these equations are equal to 1 (functional association) or very close to it (strong correlation association). Among these variables ( R ¯ i and ωi), the strongest correlation was obtained by the ARTIW-L method (R2 = 1), and the weakest by the DPW method (R2 = 0.9571).
The priorities of the criteria according to their calculated normalized subjective weights ωi are as follows: D > J > G > F > E > I > B > A > C > H (Figure 4). The ωi values of the four most important criteria (D, J, G, F) are greater than 0.1, i.e., for the average weight of the criteria. The ωi of the other six criteria (E, I, B, A, C, H) are lower than 0.1.
The highest weights of almost half of the most important criteria were obtained by the AHP method. The weights of the other half of the less important criteria were the lowest when calculated also by the AHP method. This shows that the AHP method is the most “sensitive” in determining the significance of the criteria, since the difference between the largest and smallest weights determined by the k -th method ( k = 1, 2, ..., r ) ∆ ω k = ω k m a x − ω k m i n is the largest (Figure 5(a)), i.e., it increases the importance of the most important criteria and decreases the importance of the least important criteria.
The research results show that ∆ ω i varies from 0.0135 (criterion F) to 0.0519 (criterion D). The correlation dependence between ω ̿ i and ∆ ω i is shown by the regression curve (Figure 5 (b)) and a sufficiently large coefficient of determination R 2 = 0.9458. The smallest weight difference ∆ ω i is for criteria E and F, that is, those criteria whose average weight ω ̿ i is close to the average weight of all criteria (in the study ω ̿ i =0.1000). As the weight of the criteria ω ̿ i increases to one side and the other from 1.0000, the weight difference ∆ ω i increases unevenly (asymmetrically): the most important criteria G, J, D increase faster.
The average of the weights of each criterion ω ̿ i determined from formula (18) by four MCDM methods is taken as the result of solving the task (Table 7). The priority of criterions weights calculated by ARTIW-L, ARTIW-N, DPW and AHP methods (Table 4, Table 5 and Table 6) coincides with the priority determined from the weight averages ω ̿ i (Table 7). It is likely that the average weight of the criteria ω ̿ i is closer to the average of the population of experts than the weight ω i of the i-th criterion determined by any one method.
The weight of each i-th criterion calculated by the four methods is different. The difference between the weights of the highest ω i m a x and lowest ω i m i n criteria indicate the width of variation (sample width), which is used to calculate the approximate standard deviation s ∆ ω ′ (Table 8).
After dividing the standard deviation of the criteria weights s ∆ ω i ′ , calculated from the sample width and the standard deviation s ω i , calculated from all values of 4 methods, from the weight averages ω ̿ i , the percentage coefficient of variation of the criteria weights V w i ′ and V w i was determined (Table 8). This characteristic showing the relative degree of data variation is calculated from formulas (22) and (23). The dispersion of trait variants is considered low if the coefficient of variation reaches from 0 to 10%, medium - from 10 to 20%, and high - more than 20% [58]. Six out of ten criteria (B, E, F, G, I, J) have low dispersion, and four criteria (A, C, D, H) have medium dispersion. The coefficients of variation V i ′ of almost all criteria are slightly higher (ranging from 6.3% to 20.6%) than the coefficients of variation V i (ranging from 5.6% to 18.1%) and they are linked by a linear positive correlation. Therefore, any of them can be taken with sufficient accuracy for practice to determine the criteria weights of the MCDM methods used in the study.

7. Conclusions

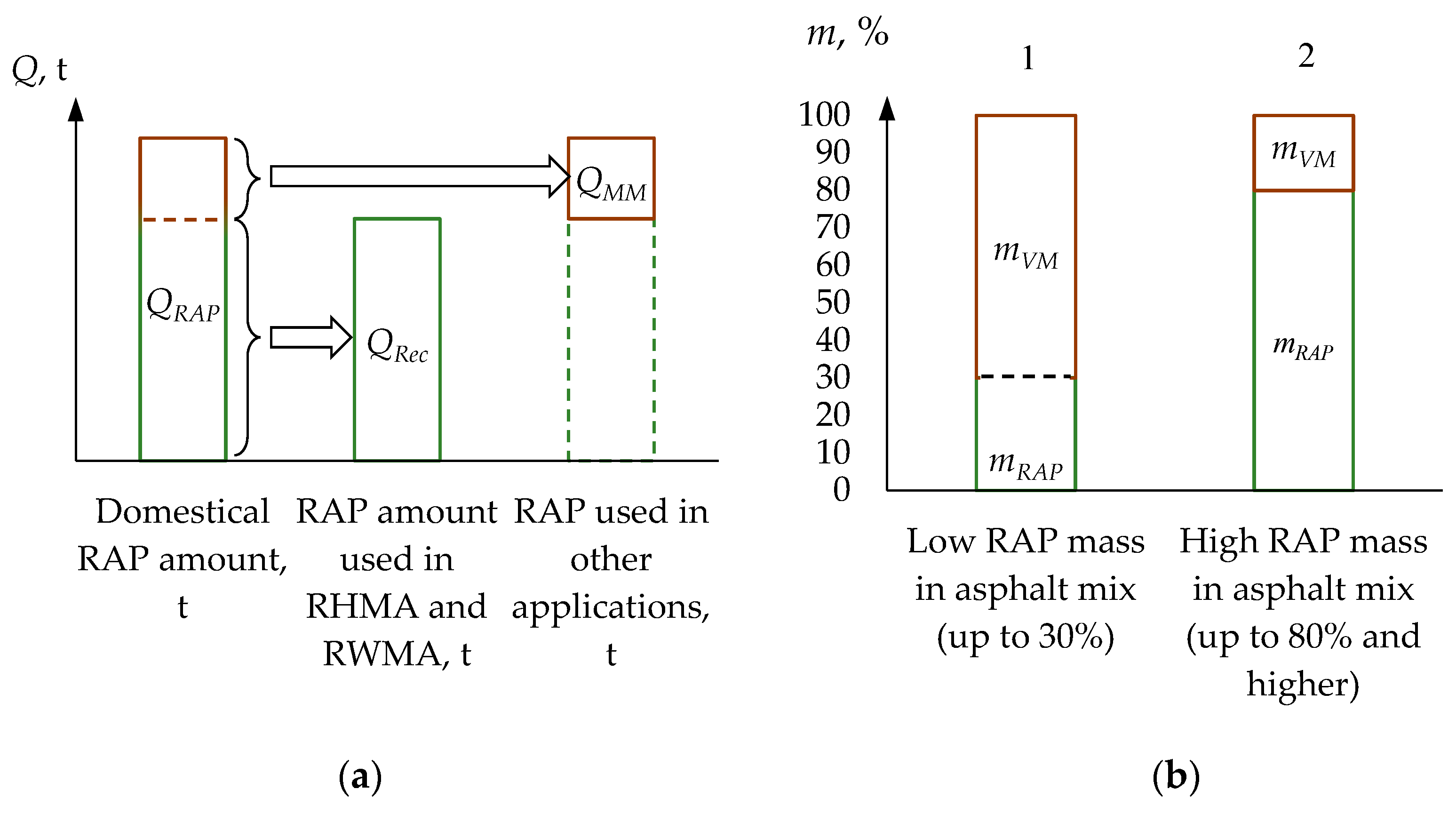
  • The transport infrastructure’s asphalt pavement is recycled applying technological methods, which improve its material characteristics adding virgin mineral and rejuvenating bituminous materials. The milled or broken into flat blocks asphalt pavement layer removed and then crushed to certain asphalt grains size which are intended to be used at the highest level of the value creation. The greatest benefit is achieved using RAP in hot mix (HMA) and warm mix (WMA) asphalt mixes production at an asphalt mixing plant (AMP).
  • European Asphalt Pavement Association (EAPA) data present that different percentages of RAP are used in the production of HMA and WMA mixes in European countries and the USA in 2017‒2019. All (100%) or almost all (75%) domestically prepared RAP in Finland, Belgium, Switzerland, Hungary, Germany and the United States was used in these asphalt mixes. The relative amount of RAP recycling is less than 75% in the other countries. In the Baltic countries, recycling rate (RR) has not been studied. The factors (criteria) increasing RR in the country are not known, as well as their significance.
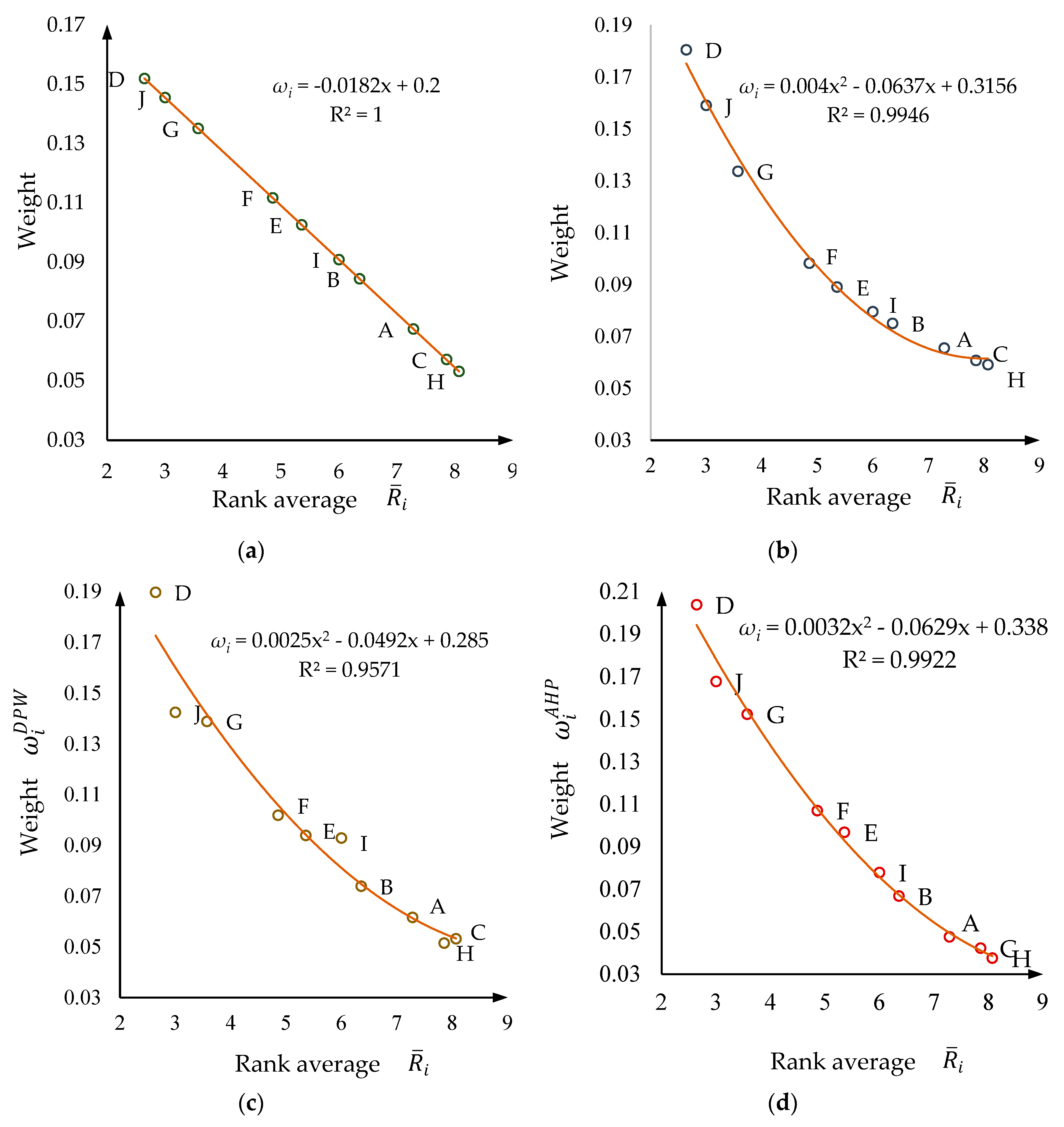
  • The system of ten factors (criteria) created by the authors of this study allowed, with the help of the knowledge, experience, and intuition of 14 asphalt pavement recycling theory and practice professionals to evaluate the criteria that increase the significance of the relative amount of RAP recycling in the Baltic countries using four MCDM methods. In the submitted questionnaire, each expert assigned ranks, percentage weights to the criteria and filled in the pairwise comparison matrix of the AHP method criteria. These primary data were transformed into criterion-normalized subjective weights using the ARTIW-L, ARTIW-N, DPW and AHP methods.
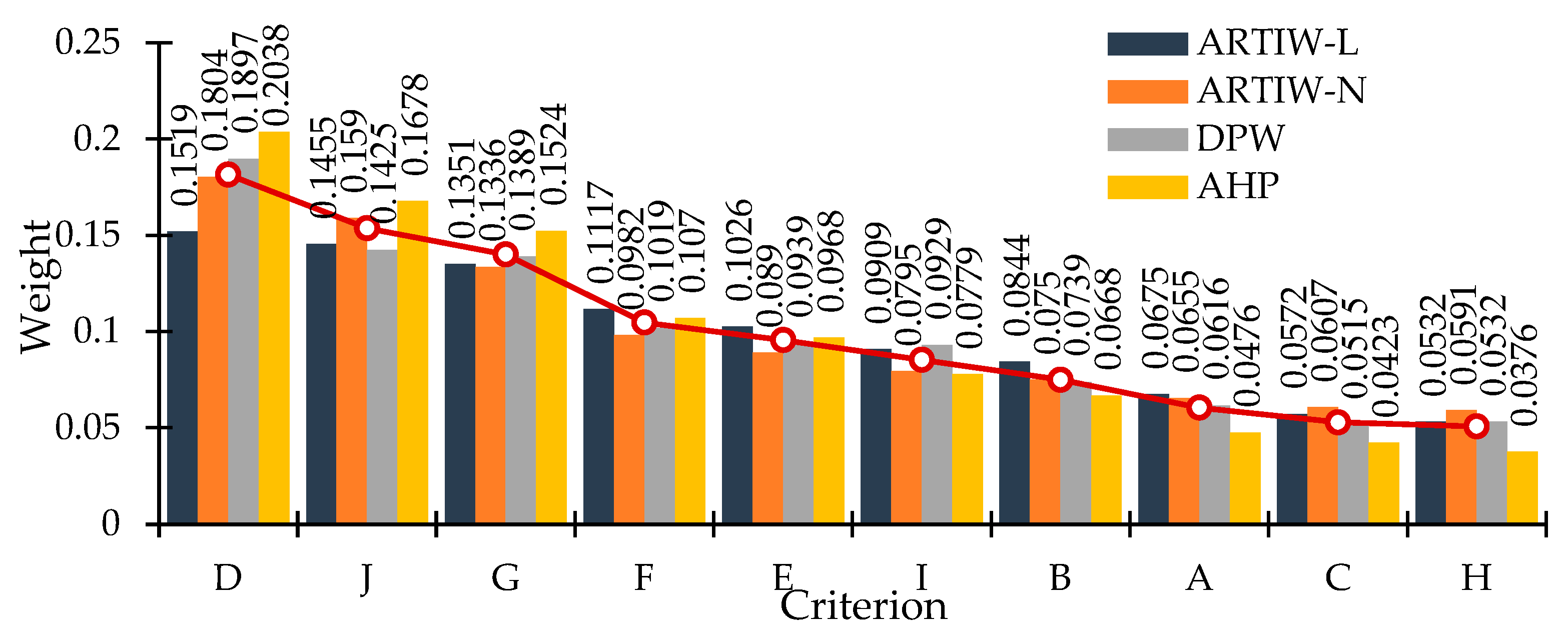
  • The opinions of the 14 experts who participated in the study differed, however were similar. The high degree of concordance of expert opinions, assessed by Kendall’s dispersion coefficient of concordance, allowed the arithmetic averages of numerical estimates of the significance of individual expert opinions (ranks, percentage weights, normalized weights) to be reasonably used as the result of task solving obtained by each of the 4 different MCDM methods. The weights of the 10 criteria determined by the ARTIW-L, ARTIW-N, DPW and AHP methods are different, but their priorities are the same. Arithmetic averages of the percentage weights of the 10 criteria determined by these methods show that the most significant factors (criteria) increasing the RR in the country for experts are the relevance of regulatory documents (18.1%), the asphalt pavement recycling strategy (15.4%), the homogeneity and sorting of RAP (14.0%). Less important are RAP ownership and economic utility (10.5%), personnel qualification and experience (9.6%), quality of renewable materials (8.5%) and number and performance of recycling equipment (7.5%). Experts believe that asphalt pavement wear and tear (6.0%), number and productivity of road milling machines (5.3%) and number and capacity of RAP stocks (5.1%) are the least significant. By improving the most significant criteria in the country, the maximum effectiveness of practical measures that increase of RR is achieved.
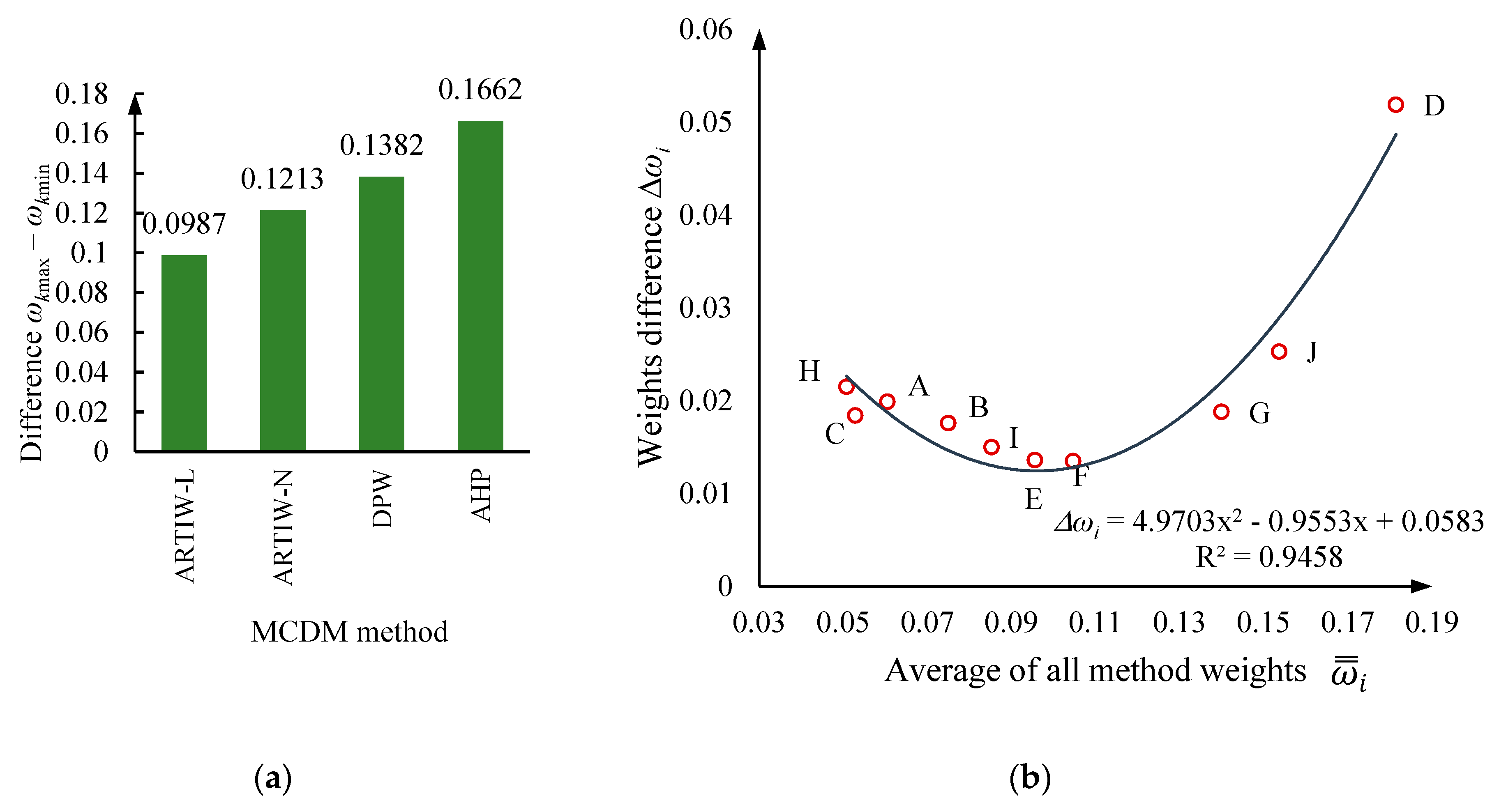
  • The MCDM methods used in the study have different sensitivity, because the difference between the normalized weights of the most important criterion and the least important criterion is not the same. This difference determined by the ARTIW-L method is equal to 0.0987, by the ARTIW-N method – 0.1213, by the DPW method – 0.1382, by the AHP method – 0.1662 (Figure 5(a)). The maximum difference (sample width) of the weight of each criterion calculated by the four methods correlates with the average of the weights of all methods of the criterion. This difference is the smallest for those criteria whose average weight is closest to the average weight of all criteria of 1.000. As the average of criteria weights moves away from one in the decreasing direction, the width of the sample increases slightly, and as it moves away in the increasing direction (of the most important criteria), it increases significantly (Figure 5 (b)). The coefficients of variation of criteria weights, calculated from the sample range varied from 6.3% to 20.5%, and from the standard deviation - from 5.6% to 18.1% (Table 8), i.e., corresponds to a low to medium dispersion of trait (weight) variants the difference is insignificant, suggesting that the MCDM methods used in the study provide a similar result, but the average of the weights of these methods is more reliable than the weights of any of the 4 methods. The difference is insignificant, which allows us to say that the MCDM methods used in the study provide similar results. The averages of the weights of each criterion calculated by these four MCDM methods are more reliable than the criteria weights calculated by any single method.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. LST EN 13108-8. Bituminiai mišiniai. Medžiagų techniniai reikalavimai. 8 dalis. Naudotas asfaltas (Bituminous mixtures-Material specifications. Part 8: Reclaimed asphalt). Vilnius: Lietuvos standartizacijos departamentas, Lithuania.
  2. Zaumanis, M.; Mallick, R.B.; Frank, R. 100% recycled hot mix asphalt: A review and analysis. Resour. Conserv. Recycl. 2014, 92, 230–245. [Google Scholar] [CrossRef]
  3. Papagiannakis, A.T.; Masad, E.A. Pavement Design and Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
  4. Kandahll, P.S.; Rao, S.S.; Watson, D.E.; Young, B. Performance of Recycled Hot Mix Asphalt Mixtures—NCAT Report 95-01; National Center for Asphalt Technology Auburn University: Auburn, USA, 1995. [Google Scholar]
  5. Cui, Y.; Glover, C.J.; Braziunas, J.; Sivilevicius, H. Further exploration of the pavement oxidation model—Diffusion-reaction balance in asphalt. Constr. Build. Mater. 2018, 161, 132–140. [Google Scholar] [CrossRef]
  6. Herrington, P.R. Diffusion and reaction of oxygen in bitumen films. Fuel 2012, 94, 86–92. [Google Scholar] [CrossRef]
  7. Kleizienė, R.; Panasenkienė, M.; Vaitkus, A. Effect of Aging on Chemical Composition and Rheological Properties of Neat and Modified Bitumen. Materials 2019, 12, 4066. [Google Scholar] [CrossRef]
  8. Ržek, L.; Turk, M.R.; Tušar, M. Increasing the rate of reclaimed asphalt in asphalt mixture by using alternative rejuvenator produced by tire pyrolysis. Constr. Build. Mater. 2020, 232, 117–177. [Google Scholar] [CrossRef]
  9. Zaumanis, M.; Malic, R.B.; Poulikakos, L.; Frank, R. Influence of six rejuvenators on th performance properties of reclaimed Asphalt Pavement (RAP) binder and 100% recycled asphalt mixtures. Constr. Build. Mater. 2014, 71, 538–550. [Google Scholar] [CrossRef]
  10. Puccini, M.; Leandri, P.; Tasca, A.L.; Pistonesi, L.; Losa, M. Improving the Environmental Sustainability of Low Noise Pavements: Comparative Life Cycle Assessment of Reclaimed Asphalt and Crumb Rubber Based Warm Mix Technologies. Coatings 2019, 9, 343. [Google Scholar] [CrossRef]
  11. Carter, A.; Stroup-Gardiner, M. Indirect tension relaxation test to evaluate the effect on the addition of RAP to HMA mixes. J. Mater. Civ. Eng. 2007, 19, 219–226. [Google Scholar] [CrossRef]
  12. Zaumanis, M.; Loetscher, D.; Mazor, S.; Stöckli, F.; Poulikakos, L. Impact of milling machine parameters on the properties of reclaimed asphalt pavement. Constr. Build. Mater. 2021, 307, 114–125. [Google Scholar] [CrossRef]
  13. Sivilevičius, H.; Martišius, M. Field investigation and assessment on the wear of asphalt pavement milling machine picks. Transport 2021, 36, 499–509. [Google Scholar] [CrossRef]
  14. Martišius, M.; Sivilevičius, H. Analysis of Design and Technological Processes of Hot Recycling Asphalt Mixture at Batch Asphalt Mixing Plants. In Proceedings of the 11′th International Conference “Environmental Engineering”, Vilnius, Lituania, 21-22 May 2020. [Google Scholar]
  15. Widyatmoko, I. Mechanistic-empirical mixture design for hot mix asphalt pavement recycling. Constr. Build. Mater. 2008, 22, 77–87. [Google Scholar] [CrossRef]
  16. Petkevičius, K.; Sivilevičius, H. Necessary Measures for Ensuring the Quality of Hot Mix Asphalt in Lithuania. Balt. J. Road Bridge Eng. 2008, 3, 29–37. [Google Scholar] [CrossRef]
  17. Mogawer, W.S.; Austerman, A.J.; Bonaquist, R. Determining the influence of plant type and production parameters on performance of plant-produced reclaimed asphalt pavement mixtures. Transp. Res. Rec. 2012, 2268, 71–81. [Google Scholar] [CrossRef]
  18. Sivilevičius, H.; Skrickij, V.; Skačkauskas, P. The Correlation between the Number of Asphalt Mixing Plants and the Production of Asphalt Mixtures in European Countries and the Baltic States. Appl. Sci. 2021, 11, 75–93. [Google Scholar] [CrossRef]
  19. West, R.C. Development of Rapid QC Procedures for Evaluation of HMA Properties during Production; National Center for Asphalt Technology (NCAT). Report 05-01. Auburn: Auburn University. National Center for Asphalt Technology, USA, 2005.
  20. Aravind, K.; Das, A. Preliminary constituent proportioning for central plant hot-mix asphalt recycling. J. Mater. Civ. Eng. 2007, 19, 740–745. [Google Scholar] [CrossRef]
  21. Jacques, C.; Daniel, J.S.; Bennert, T.; Reinke, G.; Norouzi, A.; Ericson, C.; Mogawer, W.; Kim, Y.R. Effect of silo storage time on the characteristics of virgin and reclaimed asphalt pavement mixture. Transp. Res. Rec. 2016, 2573, 76–85. [Google Scholar] [CrossRef]
  22. Sivilevičius, H.; Bražiūnas, J.; Prentkovskis, O. Technologies and principles of hot recycling and investigation of preheated reclaimed asphalt pavement batching process in an asphalt mixing plant. Appl. Sci. 2017, 7, 1104. [Google Scholar] [CrossRef]
  23. Zhang, K.; Huchet, F.; Hobbs, A. A review of thermal processes in the production and their influences on performance of asphalt mixtures with reclaimed asphalt pavement (RAP). Constr. Build. Mater. 2019, 206, 609–619. [Google Scholar] [CrossRef]
  24. Hossain, M.I.; Veginati, V.; Krukow, J. Thermodynamics Between Rap/Ras and Virgin Aggregates During Asphalt Concrete Production—A Literature Review; Illinois Center for Transportation: Rantoul, IL, USA, 2015. [Google Scholar]
  25. DeDene, C.D.; Voller, V.R.; Marasteanu, M.O.; Dave, E.V. Calculation of particle heating times of reclaimed asphalt pavement. Road Mater. Pavement Des. 2014, 15, 721–732. [Google Scholar] [CrossRef]
  26. Harun-Or-Rashid, G.M.; Ahmed, B.; Sobhan, M.A.; Rahman, N. Marshall Characteristics of Bituminous Mixes Using Reclaimed Asphalt Pavement. Am. J. Traffic Transp. Eng. 2018, 3, 57–61. [Google Scholar]
  27. Frigio, F.; Pasquini, E.; Ferrotti, G.; Canestrari, F. Improved durability of recycled porous asphalt. Constr. Build. Mater. 2015, 48, 755–763. [Google Scholar] [CrossRef]
  28. Sivilevičius, H.; Vislavičius, K. Simulation of composition of recycled hot-mix asphalt mixture production in asphalt mixing plant. Constr. Build. Mater. 2019, 214, 17–27. [Google Scholar] [CrossRef]
  29. Rad, F.Y.; Sefidmazgi, N.R.; Bahia, H. Application of Diffusion Mechanism: Degree of Blending Between Fresh and Recycled Asphalt Pavement Binder in Dynamic Shear Rheometer. Transp. Res. Rec. 2014, 2444, 71–77. [Google Scholar] [CrossRef]
  30. McDaniel, R.S.; Soleymani, H.; Anderson, R.M.; Turner, P.; Peterson, R. Recommended Use of Reclaimed Asphalt Pavement in the Superpave Mix Design Method; Asphalt Institute Lexington: Kentucky, USA, 2000. [Google Scholar]
  31. Nguyen, H. Effects of mixing procedures and rap sizes on stiffness distribution of hot recycled asphalt mixtures. Constr. Build. Mater. 2013, 47, 728–742. [Google Scholar] [CrossRef]
  32. Shirodkar, P.; Mehta, Y.; Nolan, A.; Sonpal, K.; Norton, A.; Tomlison, C.; Dubois, F.; Sullivan, P.; Sauber, R. A study to determine the degree of partial blending of reclaimed asphalt pavement (RAP)binder for high RAP hot mix asphalt. Constr. Build. Mater. 2011, 25, 150–155. [Google Scholar] [CrossRef]
  33. Wu, S.; Qiu, J.; Mo, L.; Yu, J.; Zhang, Y.; Li, B. Investigation of temperature characteristics of recycled hot mix asphalt mixtures. Resour. Conserv. Recycl. 2017, 51, 610–620. [Google Scholar] [CrossRef]
  34. Bražiūnas, J.; Sivilevičius, H. The bitumen batching system’s modernization and its effective analysis at the asphalt mixing plant. Transport 2010, 25, 325–335. [Google Scholar] [CrossRef]
  35. Li, X.; Williams, C.R.; Marasteanu, M.O.; Clyne, T.R.; Johnson, E. Investigation of In-Place asphalt film thickness and performance of hot-mix asphalt mixtures. J. Mater. Civ. Eng. 2009, 21, 262–270. [Google Scholar] [CrossRef]
  36. Remišová, E. Effect of Film Thickness on Resistance to Permanent Deformation in Asphalt Mixtures. Balt. J. Road Bridge Eng. 2015, 10, 333–339. [Google Scholar] [CrossRef]
  37. Abreu LP, F.; Oliveira JR, M.; Silva HM, R.D.; Fonseca, P.V. Recycled asphalt mixtures produced with high percentage of different waste materials. Constr. Build. Mater. 2015, 84. [Google Scholar] [CrossRef]
  38. Jurczak, R.; Mieczkowski, P.; Budziński, B. Potential of using imidazoline in recycled asphalt pavement. Balt. J. Road Bridge Eng. 2019, 14, 521–542. [Google Scholar] [CrossRef]
  39. Shen, J.; Amirkhanian, S.; Miller, J.A. Effects of Rejuvenating Agents on Superpave Mixtures Containing Reclaimed Asphalt Pavement. J. Mater. Civ. Eng. 2007, 19, 376–384. [Google Scholar] [CrossRef]
  40. Zaumanis, M.; Boesiger, L.; Kunz, B.; Cavalli, M.C.; Poulikakos, L.D. Determining optimum rejuvenator addition location in asphalt production plant. Constr. Build. Mater. 2019, 198, 368–378. [Google Scholar] [CrossRef]
  41. Zaumanis, M.; Cavalli, M.C.; Poulikakos, L.D. Effect of rejuvenator addition location in plant on mechanical and chemical properties of RAP binder. Int. J. Pavement Eng. 2020, 21, 507–515. [Google Scholar] [CrossRef]
  42. Sterling, V.A. A Manual for Design of Hot Mix Asphalt with Commentary; National Cooperative Highway Research Program (NCHRP) Report 673; Transportation Research Board: Washington, DC, USA, 2011. [Google Scholar]
  43. Vislavičius, K.; Sivilevičius, H. Effect of reclaimed asphalt pavement gradation variation on the homogeneity of recycled hot-mix asphalt. Arch. Civ. Mech. Eng. 2013, 13, 345–353. [Google Scholar] [CrossRef]
  44. R NAG 09. Automobilių kelių naudoto asfalto granulių panaudojimo rekomendacijos. Vilnius: Lietuvos automobilių kelių direkcija prie Susisiekimo ministerijos, Lithuania, 2009.
  45. Asphalt in figures. Brussels: European Asphalt Pavement Association (EAPA), Belgium, 2019.
  46. Kendall, M.; Gibbons, J.D. Rank Correlation Methods, 5th ed.; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
  47. Sivilevičius, H. Application of expert evaluation method to determine the importance of operating asphalt mixing plant quality criteria and rank correlation. Balt. J. Road Bridge Eng. 2011, 6, 48–58. [Google Scholar] [CrossRef]
  48. Šakalys, R.; Sivilevičius, H.; Miliauskaitė, L.; Šakalys, A. Investigation And Evaluation Of Main Indicators Impacting Synchromodality Using Artiw And Ahp Methods. Transport 2019, 34, 300–311. [Google Scholar] [CrossRef]
  49. Maskeliūnaitė, L.; Sivilevičius, H. Identifying the importance of criteria for passenger choice of sustainable travel by train using ARTIW and IHAMCI methods. Appl. Sci. 2021, 11, 11503. [Google Scholar] [CrossRef]
  50. Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
  51. Montgomery, D.C. Statistical Quality Control: A Modern Introduction, 7th ed.; John Wiley & Sons: Arizona, USA, 2013. [Google Scholar]
  52. Čekanavičius, V.; Murauskas, G. Statistika ir jos taikymai. I knyga; Leidykla TEV: Vilnius, Lithuania, 2003. [Google Scholar]
  53. Podvezko, V.; Sivilevičius, H. The use of AHP and rank correlation methods for determining the significance of the interaction between the elements of a transport system having a strong influence on traffic safety. Transport 2013, 28, 389–403. [Google Scholar] [CrossRef]
  54. Liao, M.-S.; Ding, J.-F.; Liang, G.-S.; Lee, K.-L. Key criteria for evaluating the green performance of ports. J. Test. Eval. 2016, 44, 1791–1801. [Google Scholar] [CrossRef]
  55. Saaty, T.L.; Ozdemir, M.S. Why the magic number seven plus or minus two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
  56. Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef] [PubMed]
  57. Taha, H.A. Operations Research: An Introduction, 9th ed.; Pearson: London, UK, 2011. [Google Scholar]
  58. Gonestas, E.; Strielčiūnas, R.R. Taikomoji Statistika; Lietuvos Kūno Kultūros Akademija: Kaunas, Lithuania, 2003. [Google Scholar]
Preprints 88685 g001
Figure 1. Re-use models of old asphalt pavement: (a) Relative recycling rate KRec in the country, (b) RAP percentage mass in the asphalt mixture when heat energy is transferred to it by conduction (1) or convection (2).
Figure 1. Re-use models of old asphalt pavement: (a) Relative recycling rate KRec in the country, (b) RAP percentage mass in the asphalt mixture when heat energy is transferred to it by conduction (1) or convection (2).
Preprints 88685 g001
Preprints 88685 g002
Figure 2. The interface model of percentage recycling rate in the country.
Figure 2. The interface model of percentage recycling rate in the country.
Preprints 88685 g002
Preprints 88685 g003
Figure 3. Correlation of the normalized weights ωi of the criteria calculated by different methods with the rank averages R ¯ i : (a) ARTIW-L; (b) ARTIW-N; (c) DPW, (d) AHP.
Figure 3. Correlation of the normalized weights ωi of the criteria calculated by different methods with the rank averages R ¯ i : (a) ARTIW-L; (b) ARTIW-N; (c) DPW, (d) AHP.
Preprints 88685 g003
Preprints 88685 g004
Figure 4. The importance (weights) of the factors (criteria) increasing the relative amount of asphalt pavement recycling KRec in the country were determined using four different methods.
Figure 4. The importance (weights) of the factors (criteria) increasing the relative amount of asphalt pavement recycling KRec in the country were determined using four different methods.
Preprints 88685 g004
Preprints 88685 g005
Figure 5. Differences in criteria weights ∆ ω k = ω k m a x − ω k m i n calculated by different MCDM methods (a); Correlation between the differences in criteria weights ∆ ω i and weight averages ω ̿ i calculated by four MCDM methods (b).
Figure 5. Differences in criteria weights ∆ ω k = ω k m a x − ω k m i n calculated by different MCDM methods (a); Correlation between the differences in criteria weights ∆ ω i and weight averages ω ̿ i calculated by four MCDM methods (b).
Preprints 88685 g005
Table 1. The relative amount of RAP (recycling rate KRec) used in hot and warm mixed asphalt mixtures in European countries and the USA.
Table 1. The relative amount of RAP (recycling rate KRec) used in hot and warm mixed asphalt mixtures in European countries and the USA.
Country % of available reclaimed asphalt re-use in hot and warm mix asphalt production (KRec) Average   K ¯ R e c , % Rank (priority)
2017 2018 2019
Austria (AT) 60 70 70 67 11
Belgium (BE) 95 100 79 91 2
Croatia (HR) no data no data 35 35 12
Czech Republic (CZ) 14 12 14 13 17
Denmark (DK) 66 68 70 68 10
Finland (FI) 100 100 100 100 1
France (FR) 70 73 75 73 6‒8
Germany (DE) 84 82 82 83 5
Great Britain (GB) half warm 90 30 30 30 14
Hungary (HU) 95 70 98 88 4
Italy (IT) 23 no data 25 24 15‒16
Netherlands (NL) 71 no data no data 71 9
Norway (NO) 30 34 28 31 13
Romania (RO) no data no data 0 0 19
Slovakia (SK) 96 82 40 73 6‒8
Slovenia (SI) 24 24 23 24 15‒16
Spain (ES) 83 76 59.6 73 6‒8
Switzerland (CH) no data no data 90 90 3
Turkey (TR) 9 1 9 6 18
USA 96 90.5 94.1 94 (2)
Table 2. Intensity of criteria mutual interest (Saaty rating scale and its linguistic description).
Table 2. Intensity of criteria mutual interest (Saaty rating scale and its linguistic description).
Importance level Linguistic description
1 Criteria are equally important
3 One criterion is slightly more important than the other
5 One criterion is much more important than the other
7 One criterion is much more important than the other
9 One criterion is incomparably more important than the other
2, 4, 6, 8 Intermediate values
Table 3. Random Index R.I. dependence of values on the order of the matrix (number of compared criteria) m.
Table 3. Random Index R.I. dependence of values on the order of the matrix (number of compared criteria) m.
Matrix row m 3 4 5 6 7 8 9 10 11 12 13 14 15
Random index R.I. 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51 1.48 1.56 1.57 1.59
Table 4. The significance of the factors increasing the relative amount of KRec (the percentage ratio of the amount of old asphalt pavement RAP QRec used in hot and warm asphalt mixtures to the total amount of RAP QRAP) in the country of asphalt pavement recycling in ranks.
Table 4. The significance of the factors increasing the relative amount of KRec (the percentage ratio of the amount of old asphalt pavement RAP QRec used in hot and warm asphalt mixtures to the total amount of RAP QRAP) in the country of asphalt pavement recycling in ranks.
Expert
j = 1, 2, ..., n		 Criterion, (i = 1, 2, ..., m) Sum
A B C D E F G H I J
E1 9 5 8 2 7 4 3 10 6 1 55
E2 6 3 7 9 10 5 1 2 8 4 55
E3 8 6 10 1 3 7 5 9 4 2 55
E4 2 8 9 4 7 3 5 10 6 1 55
E5 6 8 9 1 10 2 4 7 5 3 55
E6 8 9 10 2 5 6 4 7 1 3 55
E7 10 9 8 1 7 3 2 5 4 6 55
E8 10 5 9 1 7 3 4 8 6 2 55
E9 8 6 9 2 3 5 1 10 7 4 55
E10 6 7 8 2 1 9 3 10 4 5 55
E11 8 10 9 2 5 3 4 7 6 1 55
E12 8 5 6 4 2 7 1 9 10 3 55
E13 9 2 1 4 3 8 5 10 7 6 55
E14 4 6 7 2 5 3 8 9 10 1 55
∑ j = 1 n R i j 102 89 110 37 75 68 50 113 84 42 770
R ¯ i 7.286 6.357 7.857 2.643 5.357 4.857 3.571 8.072 6.000 3.000 55.000
∑ j = 1 n R i j − R ¯ 25 12 33 -40 -2 -9 -27 36 7 -35 0
∑ j = 1 n R i j − R ¯ 2 625 144 1089 1600 4 81 729 1296 49 1225 6842
ARTIW-L method ω i = m + 1 − R ¯ i ∑ i = 1 m R ¯ i 0.0675 0.0844 0.0572 0.1519 0.1026 0.1117 0.1351 0.0532 0.0909 0.1455 1.0000
ui 0.3628 0.4158 0.3364 1 0.4934 0.5442 0.7401 0.3274 0.4405 0.8810 5.5416
Priority 8 7 9 1 5 4 3 10 6 2 55
ARTIW-N method ω i = u i ∑ i = 1 m u i 0.0655 0.0750 0.0607 0.1804 0.0890 0.0982 0.1336 0.0591 0.0795 0.1590 1.0000
Priority 8 7 9 1 5 4 3 10 6 2 55
σ = ∑ j = 1 n R i j − R ¯ i 2 n − 1 2.2678 2.3074 2.2823 2.1342 2.7903 2.2138 1.9499 2.3358 2.4179 1.7974 -
Table 5. The significance of the factors increasing the relative amount of KRec in the country of asphalt pavement recycling in percentage weights.
Table 5. The significance of the factors increasing the relative amount of KRec in the country of asphalt pavement recycling in percentage weights.
Expert
j = 1, 2, ..., n		 Criterion, (i = 1, 2, ..., m) Sum
A B C D E F G H I J
E1 3 11 4 17 6 12 15 2 8 22 100
E2 8.5 12 8 7 6 9 20 12.5 7.5 9.5 100
E3 3.8 4.5 2 22 17 4.2 10 3.5 15 18 100
E4 15 6 4 12.5 8 13.5 11 3 9 18 100
E5 4 2 1.5 54 0.5 14 7 3 6 8 100
E6 3 2 1 19 7.5 6.5 17 6 20 18 100
E7 1 2 3 30 4 12 20 10 11 7 100
E8 3.5 11 2.5 18 9 14 12 4 10 16 100
E9 3 7 2 20 12 10 28 1 6 11 100
E10 9 8 7 14 16 6 13 5 12 10 100
E11 7.5 5 6 14 10.5 12.5 11.5 8.5 9.5 15 100
E12 7 10 9 11 15 8 16 6 5 13 100
E13 6 15 16 11 13 7 10 5 8 9 100
E14 12 8 6 16 7 14 4 5 3 25 100
DPW method ∑ j = 1 n P i j 86.3 103.5 72 265.5 131.5 142.7 194.5 74.5 130 199.5 1400
P ¯ i 6.1643 7.3929 5.1429 18.9643 9.3929 10.1929 13.8929 5.3214 9.2857 14.2500 100
ω i 0.0616 0.0739 0.0515 0.1897 0.0939 0.1019 0.1389 0.0532 0.0929 0.1425 1.0000
Priority 8 7 10 1 5 4 3 9 6 2 55
Table 6. The significance of the factors increasing the relative amount of asphalt pavement recycling KRec in the country determined by the AHP method.
Table 6. The significance of the factors increasing the relative amount of asphalt pavement recycling KRec in the country determined by the AHP method.
Expert
j = 1, 2, ..., n		 Criterion, (i = 1, 2, ..., m) C. R.
A B C D E F G H I J
E1 0.0195 0.0791 0.0289 0.1900 0.0413 0.1204 0.1824 0.0128 0.0573 0.2683 0.054
E2 0.0598 0.1491 0.0418 0.0198 0.0150 0.0878 0.2883 0.1765 0.0297 0.1322 0.051
E3 0.0261 0.0458 0.0172 0.2714 0.1849 0.0322 0.0708 0.0187 0.0958 0.2371 0.040
E4 0.2184 0.0255 0.0180 0.1221 0.0391 0.1485 0.0853 0.0128 0.0546 0.2757 0.087
E5 0.0520 0.0232 0.0178 0.3440 0.0107 0.2106 0.1000 0.0339 0.0851 0.1227 0.099
E6 0.0204 0.0152 0.0120 0.2050 0.0718 0.0625 0.1410 0.0417 0.2758 0.1546 0.092
E7 0.0119 0.0168 0.0248 0.3113 0.0347 0.1522 0.2078 0.0863 0.1073 0.0469 0.105
E8 0.0135 0.0950 0.0195 0.2396 0.0404 0.1795 0.1344 0.0254 0.0604 0.1923 0.060
E9 0.0324 0.0588 0.0189 0.2144 0.1539 0.1059 0.2253 0.0135 0.0538 0.1231 0.058
E10 0.0508 0.0374 0.0342 0.2054 0.2498 0.0173 0.1567 0.0109 0.1404 0.0971 0.099
E11 0.0263 0.0149 0.0157 0.2333 0.0833 0.1552 0.1391 0.0386 0.0592 0.2344 0.081
E12 0.0262 0.0658 0.0657 0.1062 0.2322 0.0367 0.3031 0.0191 0.0146 0.1304 0.061
E13 0.0189 0.2621 0.2402 0.1114 0.1513 0.0294 0.0781 0.0142 0.0388 0.0556 0.053
E14 0.0898 0.0473 0.0369 0.2788 0.0473 0.1598 0.0223 0.0214 0.0174 0.2790 0.040
AHP method ∑ j = 1 n ω i j 0.6660 0.9360 0.5916 2.8527 1.3557 1.4980 2.1346 0.5258 1.0902 2.3494 14.0000
ω ¯ i 0.0476 0.0668 0.0423 0.2038 0.0968 0.1070 0.1524 0.0376 0.0779 0.1678 1.0000
Priority 8 7 9 1 5 4 3 10 6 2 55
AHP method ∑ j = 1 n ω i j 0.6660 0.9360 0.5916 2.8527 1.3557 1.4980 2.1346 0.5258 1.0902 2.3494 14.0000
Table 7. The weights ωi, their average ω ̿ i and priority of factors increasing the relative amount of asphalt pavement recycling KRec in the country were determined by different methods.
Table 7. The weights ωi, their average ω ̿ i and priority of factors increasing the relative amount of asphalt pavement recycling KRec in the country were determined by different methods.
Factor (criterion) i = 1, 2, ..., m Method (k = 1, 2, ..., r) and weight Weight   average   of   four   methods   ω ̿ i Priority
ARTIW-L,
ω i A R T I W − L 		ARTIW-N
ω i A R T I W − N 		DPW
ω i D P W 		AHP
ω i A H P
A 0.0675 0.0655 0.0616 0.0476 0.0605 8
B 0.0844 0.0750 0.0739 0.0668 0.0750 7
C 0.0572 0.0607 0.0515 0.0423 0.0529 9
D 0.1519 0.1804 0.1897 0.2038 0.1815 1
E 0.1026 0.0890 0.0939 0.0968 0.0956 5
F 0.1117 0.0982 0.1019 0.1070 0.1047 4
G 0.1351 0.1336 0.1389 0.1524 0.1400 3
H 0.0532 0.0591 0.0532 0.0376 0.0508 10
I 0.0909 0.0795 0.0929 0.0779 0.0853 6
J 0.1455 0.1590 0.1425 0.1678 0.1537 2
Sum 1.0000 1.0000 1.0000 1.0000 1.0000 55
Table 8. Dispersion characteristics of factors increasing the relative amount of asphalt pavement recycling KRec in the country.
Table 8. Dispersion characteristics of factors increasing the relative amount of asphalt pavement recycling KRec in the country.
Factor (criterion) Weight   average   of   four   methods   ω ̿ i Weights ’   difference   ∆ ω i = ω i m a x − ω i m i n Standard deviation Coefficient of variation, %
From   the   sample   width   s ∆ ω i ′ From   all   4   methods   s ω i From   the   sample   width   V w i ′ From   all   4   methods   V w i
A 0.0605 0.0199 0.009660 0.008974 15.97 14.83
B 0.0750 0.0176 0.008544 0.007230 11.39 9.64
C 0.0529 0.0184 0.008932 0.008034 16.88 15.19
D 0.1815 0.0519 0.025194 0.021923 13.88 12.08
E 0.0956 0.0136 0.006602 0.005484 6.91 5.74
F 0.1047 0.0135 0.006553 0.005899 6.26 5.63
G 0.1400 0.0188 0.009126 0.008562 6.52 6.12
H 0.0508 0.0215 0.010437 0.009213 20.55 18.14
I 0.0853 0.0150 0.007282 0.007692 8.54 9.02
J 0.1537 0.0253 0.012281 0.011826 7.99 7.69
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated