Prerpints.org logo
Preprint
Article

Projective Geometry as a Model for Hegel’s Logic

Altmetrics

Downloads

128

Views

122

Comments

2

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

23 October 2023

Posted:

25 October 2023

You are already at the latest version

Alerts
Abstract
Recently, historians have discussed the relevance of the nineteenth-century mathematical discipline of projective geometry for early modern classical logic in relation to possible solutions to semantic problems facing it. In this paper I consider Hegel’s Science of Logic as an attempt to provide a projective geometrical alternative to the implicit Euclidean underpinnings of Aristotle’s syllogistic logic. While this proceeds via Hegel’s acceptance of the role of the three means of Pythagorean music theory in Plato’s cosmology, the relevance of this can be separated from any fanciful “music of the spheres” approach by the fact that common mathematical structures underpin both music theory and projective geometry, as suggested in the name of projective geometry’s principal invariant, the “harmonic cross-ratio”. Here I demonstrate this common structure in terms of the phenomenon of “inverse foreshortening”. As with recent suggestions concerning the relevance of projective geometry for logic, Hegel’s modifications of Aristotle respond to semantic problems of his logic.
Keywords: 
Subject: Arts and Humanities  -   Philosophy

1. Introduction

Modern mathematical logic is standardly thought of as commencing around the middle of the nineteenth century with the work of George Boole and Augustus de Morgan, although, largely unbeknownst to the participants of this movement, a similar attempt to apply algebra to ancient syllogistic logic had been pursued by Leibniz almost two centuries earlier. A few decades after Boole, however, a different approach would be launched with Gottlob Frege’s “classical” logic, later championed and developed by Bertrand Russell. While each movement looked to mathematics, each looked to different branches of the discipline and conceived of the relation of their logics to mathematics in different ways. In contrast to algebra, the Frege-Russell strand looked to analysis and, moreover, conceived of logic not as mathematics but as an autonomous discipline providing its rational foundation. For both Frege and Russell, the new logic showed the foundations of arithmetic, but while for Russell, this indirectly provided a foundation for geometry as well, as geometry, he thought, could be reduced to arithmetic, for Frege, geometry was not so reducible, and so the new logic was conceived as a foundation for arithmetic alone. Within the emerging analytic paradigm of philosophy in the early twentieth century, the Frege-Russell approach would triumph over the earlier “algebra of logic” tradition stemming from Boole1, as well as over traditional Aristotelian forms of logic thought to be ultimately tied to an inadequate “subject-predicate” conception of logical form. One victim in particular would be the logic of Hegel.
Recently, historians of the early years of the modern classicist movement have broadened the mathematical context within which it developed beyond analysis and algebra, with a number of investigators looking to the role of the nineteenth-century discipline of projective geometry—a discipline that had been singled out in the nineteenth thirties of Earnest Nagel [1] as particularly relevant. In fact, before his turn to foundational and logical issues, Frege had worked in projective geometry and the relevance of this discipline has been raised especially in relation to addressing various semantic shortcomings apparent in the early forms of classicism, e.g., [2,3]2. Another example of such a possible role for projective geometry has been suggested by Pablo Acuña [6] (p. 8) with the suggestion that Wittgenstein, in describing the perceptible sign of a proposition as a “projection of a possible state of affairs”, Wittgenstein [7] (§ 3.11) may have had in mind the specific status of projection in projective geometry.
In this paper I explore the idea of the involvement of a form of geometry with many of the features of modern projective geometry in Hegel’s earlier attempts in the nineteenth century to rejuvenate Aristotle’s syllogistic. Within the ancient mathematical culture to which Hegel was appealing, however, this was not identified primarily as a form of geometry, but rather as a mathematical theory of musical harmony.
Projective geometry would be a major area of innovation in nineteenth-century mathematics, but it is not always acknowledged that its roots extended back to antiquity with the work of Pappus of Alexandria (c. 290-350 CE). Pappus, however, had sought to preserve work from earlier times and had taken structures at the heart of projective geometry from Apollonius of Perga (c240-190 BCE), and hints at earlier associations with the Pythagorean music theory can be found in the name that would be eventually given to projective geometry’s principal “invariant”, the “harmonic cross-ratio”3.
Pappus’s early steps in projective geometry had been revived and built on in the seventeenth century by Girard Desargues [8], a French mathematician and engineer and contemporary of Rene Descartes. Although Desargues had a few initial followers, notably the young Blaise Pascal, his work would fall into neglect, swamped by the success of the analytic geometry introduced by Descartes’s Geometrie in 1637. Desargues’s alternative geometry would, however, reemerge in the early nineteenth, an early expression of which—perhaps the earliest—was the book De la Corrélation des Figures de Géométrie by the French military engineer and hero of the French Revolution, Lazare Carnot, a German translation of which Hegel had in his library [9] (p. 673).
It is known that Hegel had become intensely interested in geometry around the time that Carnot’s book was published in 1801, and that his reading of ancient geometry had been influenced by thinkers from the Platonist tradition in antiquity, such as Proclus [10]. Along with this, Hegel’s thinking about astronomy had been strongly influenced by the early seventeenth-century astronomer Johannes Kepler, who, with his theory of optics, had contributed to Desargues’s geometric project and who had, like earlier Neoplatonists, championed Plato’s music-based cosmology. In his 1801 Dissertation completed at Jena [11], Hegel, to the disparagement of many contemporaries, ventured into this “music of the spheres” tradition, and while such an approach to the physical world was, and remains, easy to dismiss, I will argue for its significance via its relation to projective geometry itself. While Hegel may or may not have consciously grasped this link to Plato in Carnot’s work, he would nevertheless attempt to rejuvinate Aristotle’s syllogistic project in ways that reflected something of both Plato’s earlier music-theoretical approach to spatial relations and Carnot’s projective geometry. The result would have surprising consequences for the relation of Hegel’s Science of Logic to the modern science of logic as it continued to develop beyond the form found in Frege and Russell4.
In section 1 below I briefly review the relation of logic to geometry in ancient Greece, against the background of two different approaches to a problem facing Greek mathematics, that of the discovered incommensurability of continuous and discrete magnitudes. Of these, an earlier Pythagorean influenced solution can be seen in Plato, while a later solution more in line with Euclidean geometry can be found in Aristotle. In Section 2, it is argued that while the latter approach would inform Descartes’s analytic geometry in the seventeenth century, the former would inform Desargues’s initially unsuccessful projective alternative to Descartes. Then, in Section 3, a common underlying mathematical structure to both music theory and projective geometry is explored via the phenomenon of “inverse foreshortening”. In Section 4, Desargues’s projective geometry is examined in relation to the type of “science of perspective” that Leibniz had attempted to introduce in the seventeenth century—a science that, like projective geometry, had built upon earlier theories of perspectival representation in painting and architecture that had flourished in the Renaissance. Finally, in Section 5, distinctive features of Hegel’s logic are considered as expressing a projective equivalent of Aristotle’s more “Euclidean” syllogistic.

2. Logic and Geometry in Ancient Greece

The origin of the science of logic within European culture is typically placed around the middle of the fourth century BCE with Aristotle’s development of his system of syllogistic logic as presented in his Prior Analytics [13]. In 367, Aristotle had, as a young man, joined Plato’s Academy in Athens, remaining there some twenty years, and during this time, mathematics had been a major concern of both Plato and many other academicians. This had predominantly taken the form of work on geometry, with the development of approaches that would be later codified around the end of the fourth century by Euclid in the thirteen books of his Elements. Given this prominence, it is not surprising that various authors have speculated about geometry having shaped Aristotle’s logic. John Corcoran [14] (p. 284), for example, has described Aristotle’s logical achievements as “unthinkable without the emphasis on deductive reasoning in geometry that he had found in Plato’s Academy”, while Vangelis Trianatafyllou [15] (p. 10), notes in the light of the “encompassing geometricocentric paradigm” of Greek scientific thinking, “it would indeed make perfect sense for logical methodology to mirror – up to a certain degree – that of geometry”. While Aristotle’s new discipline wasn’t “mathematical” in the modern sense, comments such as these suggest that it had nevertheless been modelled on the extant discipline of geometry.
However, it would seem that what we now know as “Euclidean geometry” had not been the only approach to mathematics during the years between Plato’s founding of the Academy in the mid-380s and Euclid’s codification of that science around 300 BCE. The Greeks did not have an equivalently developed number theory, and what they did have was largely restricted to the theory of musical harmony [16] (p. 72). However, Árpád Szabó [17], has argued for the influence of the music-theoretical approach to ratios and proportions on Euclidean geometry itself.
Book V of Euclid’s Elements containing the theory of ratios and proportions is standardly attributed to Eudoxus of Cnidus, who, while a little older than Aristotle had joined Plato’s Academy about a year before the younger member and about twenty years after Plato’s founding of the school. Eudoxus’s approach to ratios and proportions here are standardly seen as pivotal in the Greek response to a problem that had arisen for Pythagorean mathematicians—that of the incommensurability of ratios of line-lengths with ratios of numbers. It had been grasped that what are now known as the square roots of non-square numbers could not be expressed in ratios of natural numbers. However, Eudoxus, employing a form of reasoning often likened to the way the real numbers would be defined in the later nineteenth century [18,19] (p. 86, n. 14), had shown a way of identifying ratios of lines with ratios of numbers—a solution apparently known to Aristotle. With this, Eudoxus had short-circuited existing Pythagorean attempts to deal with the problem of incommensurability which appealed to a unity of the three “musical means”.
Earlier, ratios (logi) and proportions (analogi) had been discussed in ways appropriate for the three central “proportions” of music theory—numerical relations holding between two “extremes” divided by “middle terms” or “means”, of which there were three, the “geometric”, “arithmetic”, and “harmonic”5. However, the senses of analogos seem to have narrowed between the work of major early Pythagorean music theorist and cosmologist, Archytas of Tarentum, a rough contemporary of Plato, and that of Aristotle. For Archytas and, seemingly, for Plato himself, all three double-ratios, geometric, arithmetic and harmonic, were called proportions [17,20,21]. Archytas had thought of these three ratios as relevant to astronomical study—geometry, arithmetic, astronomy and harmonics being conceived as “sisters” [22] (p. 37).
By the time of Aristotle only the geometric double-ratio or “mean proportional”, defined as an equality of ratios [logi], as in a : b = c : d, was called a proportion. This definition as given by Aristotle [23] (1131a31) and Euclid [24] (Bk. 5, def. 4) effectively coincides with what is known as a proportion today, and Eudoxus’s general theory of ratios and proportions seems to have undercut the earlier appeal to a “unity” existing among the three means, a unity holding despite the incommensurability between the geometric mean, the calculation of which required square roots, and the other two.
With Eudoxus’s innovations the earlier “musical” solution to the problem of incommensurability seemed to have fallen by the wayside, at least for several centuries. Nevertheless, traces of the earlier pre-Eudoxean history of the complex relations between arithmetic, music, and geometry could still be found in a feature of Aristotle’s logic as Aristotle’s technical vocabulary found in Prior Analytics Book 1, involving intervals, extremes and means, had originated in the theory of musical harmony [25,26]. However, given the innovations of Eudoxus, it might be assumed that for Aristotle any continuity with music theory itself had become entirely nominal, such terms by then having shed their specifically musical connotations.
This suspicion is supported by a consideration of the parallel Einarson points to between Aristotle’s account of the first-figure syllogism in the Prior Analytics with a passage from a text on music theory, the Sectio Canonis6, that while usually attributed to Euclid was probably based on some earlier work. Thus, Aristotle has it that: “if A is predicated of every B, and B of every C, it is necessary for A to be predicated of every C” [13] (25b32–26a3), while the author of Sectio Canonis writes: “Let there be an interval BC and let B be a multiple of C; and let it be that as C is to B, so B is to D. I say surely that D is a multiple of C. For since B is a multiple of C, C therefore measures B. Now as C was to B as B was to D, so C also measures D” [27] (p. 239).
It is evident from the Sectio Canonis that here “measure” is being used in the sense of “divide”, since “C measures D” if “D is a multiple of C”, and significantly, in Metaphysics Bk VIII, Aristotle gives a numerical analogy involving division for the relation of concepts within a definition: “For definition is a sort of number; for it is divisible, and into indivisible parts […] and number is also of this nature” [28] (1044b34-35)7. In short, the parallel effectively models the way Aristotle unpacks definitions in inferences, such that concepts will be thought of as contained in other concepts much in the way that numbers are contained as factors in subsequent numbers of a geometric sequence. In short, despite the “musical” analogy, there is no reference to the other two musical means in this model, a fact that sits with Netz’s remark linking the ratios and proportions found in Sectio Canonis to Euclid’s (or Eudoxus’s) treatment of ratios and proportions in Book V of Elements [16] (pp. 65-67).
Plato, who would have been about 60 years old by the time both Aristotle and Eudoxus had become active in the Academy, had clearly adhered to the earlier link between musical and geometrical ratios and proportions as manifest in the dialogue Timaeus. While dismissed by Aristotle as no more than a metaphor [30] (290b12-14), this link would be resurrected in the first century BCE by Neoplatonists [19] (p. 394) and would persist through the Middle Ages, especially in Christianized form via the work of Boethius, and would be revived again in the Renaissance. If, at the turn of the seventeenth century, its continued use by the astronomer Johannes Kepler was starting to look dated, its being broached by Hegel two centuries later would surely have looked distinctly eccentric. However, underlying the Pythagorean-Platonic astronomy was, I will argue, a distinctive and modern non-Euclidean geometry, in which the three “musical means” played a significant role.

3. Projective Geometry from the Greeks to the Seventeenth Century

In Descartes’s “analytic geometry”, the then recent discipline of algebra, a non-Greek form of mathematics derived from Arabic and Indian sources, could be brought to bear on figures of Euclidean geometry by its device of orthogonal “x” and “y” coordinates. This allowed a metric to be applied to continuous geometric magnitudes in a way that couldn’t be envisaged by the Pythagoreans because of the problem of incommensurability. From the perspective of the seventeenth century, however, this Greek problem had resulted by the restriction of Greek numbers to the natural or “counting” numbers, 1, 2, 3, 4, etc., a restriction that had been overcome by the incorporation of new number forms that had by then been adopted. These included fractions or “rational” numbers, zero, negative numbers, and, importantly, the so-called “irrational numbers” such as square roots of non-square numbers such as 2, 3, or 5. Thus, while the Pythagoreans had not been able to give a numerical value to the diagonal of a square of side one unit, this could now be expressed by the new number, √2. From this modern perspective, Eudoxus’s innovations in relation to ratios and proportions could be taken as pointing in this modern direction.
Descartes’s analytic geometry would be spectacularly successful and would largely eclipse the rival geometry contained in Desargues’s treatise, Rough Draft on Conics [31] that had appeared in 1639, just two years after Descartes’s Geometrie8. In contrast to Descartes, Desargues was not so much interested in applying a fixed metric to the figures of Euclidean geometry. As the title of his work suggests, his focus was the “conic sections”, the circle, the ellipse, the hyperbola and the parabola, as conceived by Apollonius in antiquity as produced by sectioning a cone on different angles. Work on the conic sections had been revived a few decades before Desargues by the astronomer Johannes Kepler, who had taken this concept further than Apollonius by treating these seemingly different shapes as different “projections” of a single shape, the circle. That is, ellipses, parabolas and hyperbolas were conceived in the way that so-shaped shadows might be “projected” onto differently inclined flat surfaces by a light source interrupted by an opaque circular disc. In this context, the type of metric introduced by Descartes was not relevant, as now the focus was on the relative relations between points on different projectively linked figures. This, however, would produce a new need within projective geometry.
In Euclidean geometry, line-lengths and the angles between them are fixed or “invariant” but this is no longer the case in projective geometry, and this loss would imply the need for some other source of invariance—some feature that was invariant across different projections. This would be provided by a peculiar double-ratio holding among four points on a line, now known as the “harmonic cross-ratio”, that would be invariant under projection9. Earlier constructions of this object could be found in Pappus and Apollonius.
Another of Kepler’s innovations that would find its way into Desargues’s geometry was the idea of “points at infinity” [31] (pp. 185-188). If ellipses and parabolas were thought of as projections of a circle, there should be some type of correspondence between their respective parts, for example, between the center of a circle and the foci found in ellipses and parabolas. The two foci of an ellipse, for example, might be thought to coincide when the ellipse was squashed into a circle. Similarly, further stretching an ellipse might be thought to further separate the foci, with one eventually coming to exist at an infinite distance from the other. Now, the resulting visualizable figure would be a parabola.
The incorporation of points at infinity into projective geometry would have crucial consequences for this approach. A line can be determined by any two points through which it passes or “joins”, and similarly, a point can be determined by any two lines that intersect or “meet” at it. In projective geometry, however, all points and lines can be so defined, as every pair of lines—including parallel lines—are defined as meeting. This results in a “duality” between points and lines, such that for a theorem concerning a certain structure holding among points, an equivalent theorem exists positing an analogous structure holding among lines.
Points at infinity would also be found within another source of Desargues’s geometry, the various theories of perspective that had developed during the Renaissance in relation to the depiction of perspective in painting and architectural drawing [31] (ch. 2), [32]. Artists of the fifteenth and sixteenth centuries had been principally concerned with the “projection” of three-dimensional objects onto the two-dimensional picture plane and the results of these types of studies are on display in the foreshortening seen in Raphael’s fresco at the Vatican, The School of Athens, painted in 1530 (Figure 1, below). In this, line lengths that are objectively equal, such as the edges of the square floor tiles, become smaller as they are portrayed as receding into the distance, and lines that are objectively parallel appear to converge towards a “vanishing point”. Standardly, the vanishing point had been depicted on, or just above, the horizon, but the horizon is blocked in Raphael’s painting and, as pointed out by Bigelow and Leckey [33], actually converge on and so draw attention to, a book in the hand of the left-most of the two central figures. That figure is meant to portray Plato, and the book he is holding is the Timaeus.
The figure next to Plato is Aristotle, and the foreground figures are clearly divided into two groups. The group on Plato’s side includes Pythagoras (the figure writing in an opened book in the bottom left-hand corner) and that on Aristotle’s side, Euclid (the corresponding figure in the bottom right-hand corner, bending over a slate and holding a compass). The implied association of Plato with Pythagoras (and the corresponding contrast with Aristotle and Euclid) is reinforced by the references within the painting to Neopythagorean music theory. Besides reference to the Timaeus, the work in which Plato had presented his musico-mathematical cosmology, the book in which Pythagoras is writing contains a reference to a sequence of four numbers, 6, 8, 9, and 12 [33] (pp. 419-420), the so-called “harmonia” or “musical tetraktys” structured as a double-ratio in which 6 : 9 is taken as equal to 8 : 12 [34] (p. 200). In the Epinomis, Plato, or one of his followers11, had described this structure as “granted to the human race by the blessed choir of the Muses”, adding that this gift had “bestowed upon us the use of concord and symmetry to promote play in the form of rhythm and harmony” [35] (991b). Later Neoplatonists such as Nicomachus of Gerasa [36] (pp. 284-285), Iamblichus of Chalcis [37] (p. 50) and Proclus [38] (pp. 143-145) would identify this structure with that “most beautiful bond” that Timaeus, the Pythagorean astronomer of Plato’s Timaeus, describes in the dialogue as being responsible for the unity of the parts of the living cosmos [39] (31b–32a). These numbers, 6, 8, 9, and 12, had represented the spacings among the notes of the three fundamental harmonic intervals of Pythagorean music theory: a tonic, here given the value 6, the perfect fourth [diatessaron] above it, that of 8, the perfect fifth [diapente] above it, 9, and the octave, 12.
In the Berlin Lectures on the History of Philosophy, Hegel would claim that Aristotle had based his own formal syllogism on a simplified distortion of the “most beautiful bond” that for Plato had bound the various parts of the living cosmos into a unity [40] (pp. 209-210). Being familiar with the relevant Neoplatonic interpreters of Plato12, Hegel had most likely followed Iamblichus and others in identifying this bond with the musical tetraktys. Further evidence for this association appears in Hegel’s discussion of “ratio” or “proportion” (Verhältnis) in Book 1 of The Science of Logic, where its most developed form, the “power-proportion”, has exactly the features of the inverse double-ratio structure of the harmonic cross-ratio [12] (pp. 70-79).
It seems to have been Archytas who had calculated the musical means such that while the sequence of octaves had been determined as a geometric sequence in which each term doubles its predecessor, the two consonant intervals within the octave, the perfect fourth and perfect fifth, were determined by the harmonic and arithmetic means of the octave’s extremes. We are to understand these different “means” in terms of two fundamentally different numerical sequences, the geometric and arithmetic, which are incommensurable.
In an equally spaced arithmetical sequence of numbers such as 1, 2, 3, 4, 5, …, the middle of three consecutive terms is half the sum of the other two, their “arithmetical mean” (or average). In contrast, the “geometric” mean is the middle term of three consecutive terms of a geometric sequence, such as 1, 2, 4, 8, 16, …, in which each successive term is a constant multiple of its predecessor. Here, the geometric mean will be calculated as the square root of the product of its extremes. As noted above, a sequence of octaves, the foremost consonantal interval, is determined geometrically, but within the octave the most consonant note is the perfect fifth, which is determined by the arithmetic mean of the octave’s extremes. Archytas’s third mean, the harmonic, is the inverse of the arithmetic mean in the context of the underlying geometric sequence, Proclus later summarizing the relation between the three means as such that “the geometric proportion includes the other two and they are reciprocal with one another” [38] (p. 145)13. As its inverse, the harmonic mean of a and b will be calculated as 1 divided by the arithmetic mean of 1 a   a n d   1 b , or ( ( a − 1 + b − 1 2 ) − 1 ) , which reduces to 2 a b a + b 14. For the terms 1 and 2 of a geometric sequence, Archytas had calculated the harmonic mean as the ratio 4:3 and the arithmetic mean as 3:2, and to get a sequence of integers each can be multiplied by 6, resulting in the musical tetraktys, 6, 8, 9, and 12.
Archytas is also attributed with having proved that a pair of “epimoric” (superparticular) numbers, such as 1 and 2, or any multiples of such pairs, could not be “divided” by the mean proportional, that is, divided by the geometric mean [19] (pp. 71-72). That is, without irrational numbers, effectively the only means by which an octaval interval could be divided were the harmonic and arithmetic means15. The two equal ratios 6:9 and 8:12 of the four numbers of the musical tetraktys would provide an instance of the future harmonic cross-ratio, the principal invariant of this form of geometry. The harmonic cross-ratio can seem confusing—Desargues had invented a decidedly non-intuitive “botanical” technical vocabulary with which to describe these relations—but it is based upon a simple idea.
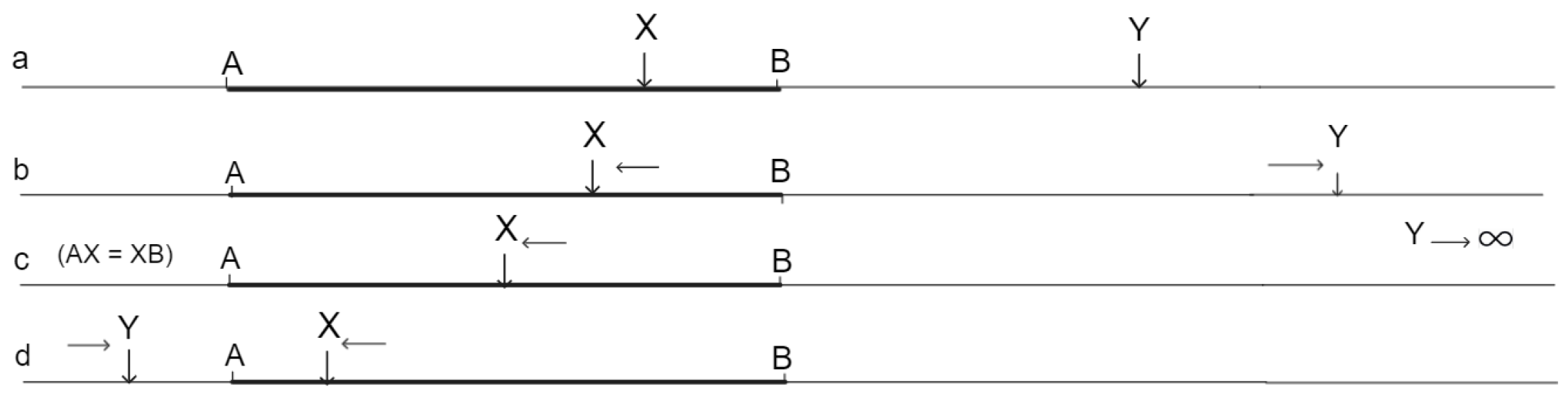
Consider a segment between points A and B on a line, with that segment divided by a variable point X that can move freely within that interval, as in Figure 2 below. The position of X can be said to determine the value of a “division ratio” between the segments AX and XB, i.e., AX:BX, or expressed as a fraction, A X X B 16. It happens that for each point at which X divides AB “internally”, another unique point Y, as displayed in 2b, exists on the line, but outside the interval, dividing the interval “externally”, such that the two division ratios are the same, that is AX:XB = AY:YB (or A X X B = A Y Y B ) [31] (pp. 84-85). The ratio of these two equal division ratios, with the value of 117, is the harmonic cross-ratio18.
This equality of the division ratios in the harmonic cross-ratio has peculiar consequences for relations within the projective plane. As X moves between A and B in a particular direction, for example, away from B and towards A as in Figure 2b, Y will move in the opposite direction away from B. Moreover, as X approaches the point mid-way between A and B, as in Figure 2c, Y will approach a point an infinite distance from the line segment [31] (p. 85)19. If X continues to move past the mid-point in the direction of A, Y will reappear on the line but now on the opposite side of the segment, approaching A from the left as X approaches it from the right.
While in the Euclidean plane, a straight line through points A and B will be thought to extend to infinity in each of the opposed directions from A to B or from B to A, aligning with the idea that the values of ∞ and −∞ are opposed. However, in the projective plane, the point at infinity approached when travelling in the direction from A to B is considered to be the same point that is approached when travelling in the direction of B to A. Again, this was a point made by Kepler in his work on optics [43] (p. 299) and the Platonist heritage of such an idea of an infinite straight line as closed, as typical of a circle, is apparent in the fifteenth-century Platonist Nicholas of Cusa who had proposed the ultimate identity of a straight line and a circle, a “coincidence of opposites” suggestive of this feature of projective geometry [44]20.

4. The role of the Musical Ratios in Projective Geometry

For Plato and the Platonists, the significance of the three Pythagorean means had extended beyond their role in accounting for the consonant musical intervals of octave, perfect fifth and perfect fourth because the “unity” holding among them was seen as addressing the global problem of the incommenensurabilty of continuous and discrete magnitudes. An arithmetical sequence is such that both arithmetic and harmonic means can be expressed in ratios of natural numbers, but the calculation of the geometric mean, involving square roots, meant, as shown in Archytas’s proof, that it could not be calculated21. Facing the need to find approximations for square roots in making actual calculations in the context of astronomy, the Pythagoreans are known to have employed algorithms inherited from earlier Babylonian mathematics22, and the musical tetraktys itself provides such an algorithm23. Taken together, the harmonic and arithmetic means of a pair of extremes provide upper and lower limits for approximate values for the geometric mean of those extremes24. Moreover, taking the harmonic and arithmetic means of those two means provides an even narrower range of approximate values, and so iterated in this way, the harmonic and arithmetic means provide a narrowing range of upper and lower bounds for approximations for √2.
It is such a harmonization of incommensurable opposites like this that Plato seems to refer to in the Timaeus in relation to the bonds required to unify the distinct parts of the cosmos. As Timaeus points out, were the cosmos planar rather than three-dimensional, there would be needed only a single middle term, but as the cosmos is three-dimensional, two are needed [39] (d32a-b). This passage is commonly interpreted as if Plato is referring to the problem of finding two geometric means between extremes, as in finding b and c of the extended geometric proportion a : b :: b : c :: c : d, a well-known problem concerning the calculation cube roots [24] (bk 8, prop. 12), for which Archytas had provided an elaborate geometrically based solution [16] (pp. 66-70)25. Plato does refer to geometric sequences involving squares and cubes in this context [39] (35b), but he also explicitly alludes to the interpolation of harmonic and arithmetic means between the terms of such sequences (36a-b). Moreover, that incommensurables are being united in this double bond seems clear from the way he goes on to describe the ratios in terms of the division of a complex mixture said to combine “the Same” and “the Different”, which is “hard to mix into conformity with the Same” [39] (35a-b). Almost a thousand years later, Proclus would describe this unity achieved in the cosmic soul as one in which “the geometric means binds the substantial totality of the soul, for the essence is a single logos [ratio] running through all things and connecting the first, middle and last” while the “harmonic proportion connects all the Samenesses that has been divided in the case of the soul, establishing a common ratio between the extreme terms and yoking together things that are naturally similar” and “the arithmetic binds together the various Differences in the soul’s procession” [38] (pp. 175-176). As we will see below, a differentiation between objects as grouped in terms of their samenesses, that is, their shared properties, and as distinguished in terms of their differences, will emerge in Hegel’s account of logic in his distinction between the conceptual determinations of “particularity [Besonderheit]” and “singularity [Einzelheit]”—this signaling a major departure from Aristotle’s syllogistic, in which there is no official place for “singular” judgments [46] (p. 1).
Hegel had appealed to Plato’s cosmology in his Dissertation at Jena in 1801, a move treated with derision by many of his contemporaries. However, I suggest that on the basis of his reading of Plato’s own application of the three musical means to the geometry of three-dimensional space, Hegel had been predominantly concerned with a feature of the mathematics underlying both a form of geometry and Pythagorean music theory. Such a feature in relation to projective geometry is not difficult to show, as can be seen by comparing the images in Figure 3 below.
Introductory books in projective geometry typically include diagrams such as images of train tracks receding into the distance as in Figure 3a. While the sleepers on which the tracks rest are of equal length, they appear in the diagram to progressively shrink, while the parallel tracks resting on them appear to converge so as to meet at a vanishing point. But when the neck of a guitar is looked at from a certain angle from the bottom end, as in Figure 3b, while the strings which are (approximately) parallel appear to converge in a similar way to the train tracks, the gaps between the frets do not shrink in the way seen in the railway sleepers. In fact, if the observer gets the angle of viewing right, they actually appear equidistant. This is because objectively, the frets are not evenly spaced like the sleepers as seen in Figure 3c, but get further apart as one moves up the neck from the body of the guitar to the headstock (as in Figure 3d), and thus compensate for the foreshortening. In both phenomena there is a superimposition of an arithmetic sequence, which advances like the sleepers on a railway track, and a geometric sequence, which advances like the sequence of frets of the neck of a guitar. Thus, in receding train tracks, an objective arithmetic sequence is projected onto an apparent geometric one, while on the guitar neck, an objective geometric sequence of fret spacings is projected onto an apparent arithmetic one.
This superimposition of geometric and arithmetic sequences gives to the relations holding among notes on the Pythagorean scale a very specific character. Considered arithmetically if one “adds” a perfect fourth to a perfect fifth a full octave results26. However, when considered as intervals in a geometric sequence, a complete octave results from the multiplication of the two intra-octaval intervals, just as 3 2 × 4 3 = 2 . And this is not peculiar to the Pythagorean scale, as the modern diatonic musical scale effectively extends this same mode of division of the octave into one of 12 equal steps or “semitones”.
In the modern scale, if the pitch of the root note is again given the value 1, that of the first semitone up the scale will have the value 1 × 12√2, the next note 1 ×12√2 × 12√2, and so on. After twelve steps, 12√2 has been multiplied by itself twelve times, giving the value of 2 to the octave above the root note. These ratios correlate with the frequencies of the notes, a concept not possessed by the Greeks, but they coincide with the relative distances between the frets of a guitar—the sorts of distances measured and compared by the Greeks. Here the relation is reversed. If one takes the distance between the twelfth and thirteenth frets as 1 unit, the distance between the eleventh and the twelfth will be 1 × 12√2 unit and so on, along the neck until the distance between the “nut” and the first fret will have the value 2 units. We should not be surprised, then, that the “musical tetraktys” turns out to be an instance of the principal invariant in projective geometry.

5. The Role of the Harmonic Cross-Ratio within Perspectival Representations

In the last quarter of the seventeenth century, Gottfried Leibniz would attempt to develop the types of Renaissance studies of perspective on which Desargues had drawn into a “Scientia perspectiva”, an “art of showing the appearance of an object in the tabula” or “plane of appearance” [47] (p. 48) conceivable as the picture plane on which a painter creates a perspectival representation of an array of objects laid out on some “objective plane”. Like Desargues, Leibniz had aimed to abstract from the three-dimensional relationships of points in space to a type of formal two-dimensional geometry of the “plane of appearance” itself—a type of abstraction manifested, for example, in his dropping reference to any “objective plane” in relation to the tabular or “plane of appearance” [47] (p. 52). This relative disinterpretation to an essentially formal axiomatic geometry would now allow a group of lines intersecting at a point—what geometers call a “pencil of rays”—to receive a variety of interpretations when reapplied to a perspectival representation. For example, such a pencil could represent parallel lines converging on some point at infinity or alternatively they could represent refracted parallel light rays converging at the eye of an observer represented within the picture27. In projective geometry, when rays from a pencil intersect with a line, the relationships among the points of intersection (a “harmonic range”) can be regarded as a projection of the equivalent relationships among the angles between the rays of the pencil (a “harmonic pencil”), allowing determinate structures (“projectivities”and “perspectivities”) to be transmitted across the plane [48] (ch. 1). The various projectively linked pencils of rays and ranges of colinear points could thus allow the idea of correlations among the sightlines or viewpoints of differently located subjects, like those represented in Raphael’s painting, as mediated by the common objects of their vision.
However, these different interpretations could be superimposed, and the points at infinity could also be understood as representing the “viewpoint” of some transcendentally located “viewer”—in the seventeenth-century context, the famed “God’s-eye viewpoint”, the objectivity of which could be contrasted with the subjective and partial perspectival viewpoints of finite subjects located within space and time. Moreover, there is, of course, another viewpoint implied by, if not actually represented within, a typically perspectival painting such as The School of Athens—the point of view at which we viewers are “located” with respect to the portrayed figures, a viewpoint coinciding with that from which the painter had “viewed” the scene being painted28. But while we viewers view the contents of the painting as if from a viewpoint related to those in the scene, in another sense, our viewpoint is understood as akin to a transcendental one at infinity—a type of God’s eye view. This, according to Acuña’s interpretation of Wittgenstein’s account [6] (pp. 10-11, 16-17), is what Wittgenstein had in mind when he had invoked the idea of “projection” in the Tractatus, as “performed in logical space by the trancendental subject” (p. 14)29. The relevance of such ideas for religious thought about the relations of humans to God was clearly not lost on the likes of Pascal and Leibniz.
Pascal had apparently thought that the relations between finite points within the projective plane and its points at infinity might provide an answer to the question of our knowledge of God [49]. Considered in the context of the projective plane, from the perspectives of figures within space, points at infinity are no longer conceived as entirely unreachable or “transcendent”, but rather as infinite points that can enter into determinable relations to finite ones in light of the determinacies of the harmonic cross-ratio30. In his later writings, however, Pascal seems to have changed his mind, and opted for a fundamental incommensurability existing between God and humans, modelled on the incommensurability, or what he described as the “heterogeneity”, between discrete and continuous magnitudes [49] (Section 5).
For Leibniz, clearly his science of perspective was intended to tie into the more general epistemological and metaphysical considerations of the idea of perspective as raised in his Discourse on Metaphysics of 1686 [50]. Being a “rationalist” in theology as elsewhere, he suggested that rational mechanisms were available to a finite subject to lead them, as if climbing “Jacob’s ladder”, to an absolute point of view. In virtue of an individual’s capacity to reflect upon the factors constraining his or her own perceptual knowledge, he or she might ascend rung by rung, moving progressively away from the contingencies shaping experience of a subject within the world. Later, Kant [51] would famously argue against even conceptual possibility here. Human rational thought, he believed, was ultimately tethered to empirical contents by the dependence on the contribution of empirical “intuitions” received by an individual subject located in the world. Thus, Kant’s equivalent “ladder” would take the climber only as far as a view of the world as a totality of objectively justified appearances, the climber being metaphysically cut off from any view of reality “as it is in itself”31.
Leibniz at least knew about Desargues’s projective geometry and certainly was familiar with one of its major theorems—“Pascal’s theorem”—and his proposed perspective science included the idea of points at infinity in the form of the vanishing points of apparently converging parallel lines and similarly to represent the sight-lines of individuals portrayed within a perspectival representation. However, he seems not to have had the one essential element that had allowed Desargues to create a distinct and unified non-Euclidean systematic form of geometry, the harmonic cross-ratio that Pascal had taken as showing how we might understand our links to God. But without this, for Leibniz there was no invariant to ensure that the unity of the space being articulated by variously compounded “projectivities” and “perspectivities”—nothing to rule out the “paradoxical” types of space familiar, for example, within pictures of the Dutch printmaker M. C. Escher with their closed but infinitely ascending staircases32. Nor was he left with any mathematical means for incorporating “points at infinity” into determinate relations with ratios of finite magnitudes.
This type of thinking had formed part of Hegel’s background. He was well aware, for example, of the efforts of the Swiss mathematician Johann Heinrich Lambert to develop Leibniz’s science of perspective, referring to it and criticizing it in The Science of Logic [53] (p. 544)33. In the mid-eighteenth century, Lambert had also been involved in a public dispute with Hegel’s effective logic teacher while he was as student at the Tübingen seminary, Gottfried Ploucquet, over how to develop the diagrammatic, i.e., geometric, dimensions of Leibniz’s logic. The harmonic cross-ratio in the particular form of the musical tetractys from Plato’s Timaeus might suggest a way forward for Leibniz’s intended science. To see how this might work we need to extend this discussion from the geometric to the logical register. One possible way here is to consider Hegel’s logic as standing to Aristotle’s formal logic in a relation analogous to that in which projective geometry stands to its Euclidean counterpart.

6. Hegel’s Logic as Understood as a Projective Equivalent to Aristotle’s Euclidean Syllogistic

We have earlier noted that by the time of Aristotle, any parallel between the structure of the syllogism to the ratios and proportions of music theory had been reduced to the common role played in both by the relation of terms within a geometric sequence, a reduction reflected in Hegel’s comment that Aristotle had employed only one “middle term” in his syllogistic [40] (p. 211)—clearly the geometric—whereas Plato’s middle term had been “broken” or “doubled” into the relation between arithmetic and harmonic means. While for Aristotle, the geometric mean was the principle according to which all logical relations were understood, for Plato and his followers, and eventually Hegel, the geometric mean needed to be divided into the harmonic and arithmetic means, given that, relying on square roots, the geometric mean could often not be given a determinate value and so the common “measure” that it sought to provide could not be found. In the logical context, the need for harmonic and arithmetic means will turn out to be a semantic one necessary to bridge the gap between logical concepts and worldly items to which they apply. Thus, Hegel will distinguish between the conceptual determinations of “particularity” (Besonderheit) and “singularity” (Einzelheit) [53] (pp. 529-549), the former, as alluded to by Proclus [38] (pp. 175-176), relating concrete elements in terms of their “samenesses”—that is, in terms of their common properties—the latter differentiating them in terms of their “differences”.
Elsewhere [12] (chs. 8, 9), I have suggested ways that these Platonic features are translated into the formal syllogism Hegel develops in the “subjective logic” of Book III of The Science of Logic. In relation to the semantic issues, the logic master at the Tübingen seminary during Hegel’s time there, Gottfried Ploucquet, would, from a generally Leibnizian perspective, make essentially the same distinction as Hegel’s particular-singular distinction by reference to two varieties of “particularity”: “comprehensive” and “exclusive” [12] (p. 128). This distinction effectively aligns with the modern modal distinction between proper names and general descriptions, a distinction that had been collapsed in Russell’s version of classical logic, but reintroduced in the second half of the twentieth century as a modally relevant one [54].
Hegel’s distinction fits this modal model. Terms instantiating “particularity” link entities in terms of their common properties: “the particular has one and the same universality as the other particulars to which it is related… It has no other determinateness than that posited by the universal itself” [53] (p. 534). In contrast, “singularity is the concept reflecting itself out of difference into absolute negativity”, “self-referring determinateness is singularity” (pp. 530, 540). That is, considered in its singularity, a thing is considered in the ways that it differentiates itself from other similar things—in Ploucquet’s terms, excludes other instances of the universal it instantiates. An individual human, for example, might be comprehended as “a human”, or “some human”, their humanness being what unites them with others. But cognized as “this human”, or, perhaps, as “Socrates”, the person is grasped in terms of what distinguishes him or her from others such as “that one” or “that one over there”, or, for example, Aristotle or Archytas. In modern modal terms, a particular description such as “the teacher of Alexander the great” picks out whoever fits this description in “all possible worlds”, including ones in which this is someone other than Aristotle, while the proper name “Aristotle” picks out Aristotle in all possible worlds, including those in which he is not the teacher of Alexander34. This is the same play of samenesses and differences that Proclus had linked to the harmonic and arithmetic means respectively. Within an abstractly conceptual hierarchy, singular and particular terms must be inserted like the insertion of arithmetic and harmonic means in a hierarchy of octaves.
Hegel’s singular-particular distinction among the subjects of predication is in turn linked to a similar distinction between the predicates predicated of those subjects and this is expressed in the different ways each receives negation. Hegel thus distinguishes “qualitative” from “reflective” forms of judgment, or “judgments of inherence” from “judgments of subsumption”35, and here, it is the predicates of such judgments that are differentiated as singular or particular.
In the former [53] (p. 557), [56] (§ 166), a predicate is affirmed of some perceptually given concrete singular subject, as when “red” is predicated of some specific observable rose, picked out with the singularly quantified demonstrative “this rose”36. And of course, the red exemplified by this rose will be a specific (i.e., singular) shade of red, opposable to the redness of that rose, over there. Negation as described by Hegel in this type of judgment is what is usually discussed as “internal”, as the negation applies within the judgment and only to the predicate: the rose is not red, but some other colour [53] (p. 565), while that the rose is actually a rose is not brought into question and so is beyond the scope of the negation. However, negation necessarily involves generalization and sets cognition on a path to abstraction. In the original judgment there had also been something singular about the predicate being affirmed, but this specificity is lost in the negative form in which the predicate attributes some non-redness to the rose. While there is a way in which a specific rose is red, there are many ways in which a rose might be not red for there are many non-red colours. For Hegel, negation provides a path for abstraction and takes the judgment from the form of singularity to particularity—from this A to some A or As—and then a second negation takes this abstraction one step further to a type of abstract universality of empirical laws about all As.
In the resulting fully developed “reflective” judgment, it is the whole proposition that becomes negated “externally”. This is seen in the development of particular judgments, in the sense of particularly quantified judgments of the sort, “some As and B” to the universal form “all As are B”37. As Hegel points out (and reflecting the “problem of induction”), such judgments made on an empirical basis will by necessity be about “a mere plurality which is taken for allness”. What such a universal judgment in effect claims is that “if no instance of the contrary can be adduced, a plurality of cases ought to count for an allness” [53] (p. 573)—that is, “All As are B” becomes equivalent to “It is not the case that some As are not B”. In short, a universal reflective judgment has the form of an externally negated particular (and hence itself negative) reflective judgment.
Such external negation is, in fact, the only type of negation operative in modern classical logic, as what is conceived as being affirmed in judgment is a complete proposition with a fixed and so eternal “truth-value”. It is clear, however, from his criticisms of this type of judgment form as found in Leibniz’s characteristica universalis38, that Hegel regards such a judgment type as not properly a judgment at all. Thus, stopping short at this degree of abstraction, we are left with a duality of mutually presupposing qualitative judgments on the one hand and reflective judgments shaping universal empirical laws on the other.
As noted above, in a way that might be thought to anticipate the modern generally “falsificationist” epistemology, Hegel has construed universal empirical laws as meaningful to the degree that they can be refuted, as when the universally quantified “All As and B” is refuted by a judgment asserting the existence of some A (or As) that is (or are) not B. But Hegel’s singular-particular distinction makes the applicability of such a particular judgment about some A or As dependent upon judgments about some specific A, as in “this A”. In short, qualitative judgments, that are clearly “perspectival” or “contextual”, cannot be eliminated in the way they are in Russell’s classical logic. Such “indexical” judgments are sometimes called “self-locating” [57] (p. 128) because they locate the judging subject within the spatio-temporal world as the anchor point of the various indexicals such as “this”, “now”, and “here”. At the same time, however, a singular claim about “this A” must itself coexist with those aperspectival, but clearly fallible, law-like claims about “all As”. This combination of “perspectival” and “aperspectival” judgments conjures up images of perspectival and aperspectival viewpoints within Leibniz’s perspective science, but within Hegel’s projective approach, the meaningfulness of such aperspectival views “from infinity” is dependent on their relation to the limited views from the finite points of view located within space and time. Thus a “duality” of judgment forms is found at the heart of Hegel’s Logic much like that existing between points and lines in projective geometry [58]. Hegel deals with the ultimate mediation of these dual judgment forms in his treatment of syllogisms, which, I have suggested, he models on the role of the harmonic cross-ratio in the projective geometry linking finite and infinite points of view as implicit in Plato’s “musical” cosmology.
The transition of judgment to syllogism is made by Hegel from a distinct form of judgment called the “judgement of the concept”, a type of normative perceptual judgment in which, in its initial “assertoric” form, an evaluation is made about the goodness or otherwise of the way a singular object instantiates its universal: e.g., “this house is bad”, “this act is good” [53] (p. 583). In this context there is no ambiguity about the “exclusive” reading of the subject term and this is consistent with its typically comparative nature: this house is typically judged good in contrast to that one. But value judgments of this sort are “problematic” in that the subjective conditioning of these judgments easily induces disagreement, and so in the face of some counter-assertion, a judge can resort to reason giving. This expands the judgment into an “apodictic” one in which the subject–predicate relation becomes mediated by a “middle term”: “the house, as so and so constituted, is good” [53] (p. 585). Here, the middle term is a particular allowing a general reason to be given for the judgment as it implies that any house so characterized would be good. It is this expanded tripartite judgment with the structure singular–particular–universal (S–P–U) that is implicitly a syllogism: S–P (this house is so and so constituted); P–U (any house so and so constituted is good); therefore, S–U (this house is good). I have suggested that this is essentially a logical translation of the interrelated arithmetic, harmonic, and geometric means as understood by Proclus.
Within Hegel’s structure, the house in question is thus grasped simultaneously in its singularity and its particularity—he says, in its “being” and in its “ought”—so as to express the universal “good”. “That this original division [Teilung], which is the omnipotence of the concept, is equally a turning back into the concept’s unity and the absolute connection of “ought” and “being” to each other, is what makes the actual into a fact; the fact’s inner connection, this concrete identity, constitutes its soul” [53] (p. 586).
Given the structure of Hegel’s logical presentation, his implicitly syllogistic “judgment of the concept” is meant to manifest something universal about all earlier forms of judging and cognition leading up to it. First, to self-consciously judge is to affirm a judgment such that is not only endorsed as true “for oneself” but that it is true in some more general sense and so true for others as well, an assumption motivating reason giving. Thus, when I judge in the simpler mode that “this rose is red”, besides affirming this specific content I commit myself to the more indefinite statement “there is a rose that is red” or “some rose is red” that could be the object of the perception of others. Moreover, I commit myself to the counterfactual that this would be the case even were I not to have experienced it at all. But Hegel clearly does not want to simply reduce the former qualitative and perspectival judgment to the latter reflective aperspectival one, as in the mode of modern classical logic, because this would simply eliminate the underlying incommensurability of “being” and “ought” as instantiations of conceptuality. Both qualitative and reflective judgments must be retained as necessary “moments” of this form of reasoning just as one’s evaluative bodily reactions retain a place in the evaluative “judgments of the concept”.
These aspects of his attitude to judgment, I suggest, show similarities to that found in the modern intuitionist attitude to mathematics and its logic [59] in the intuitionists’ opposition to modern classical logic. Thus, in the manner of the intuitionists one might argue that for every general aperspectival statement known to be true there must exist some qualitative judgment about a specific “witness” that is also held to be true, just as the truth of “houses, as so and so constituted, are good” must presuppose a judgment of the form “this house (the witness) is good”39. For the intuitionist, there exists no independent way to access the truth of “aperspectival” contents—the contents of Hegel’s reflective judgments40. This means that the status of all aperspectival judgments is something like that of being “existential generalizations” from some perspectival judgment. These aperspectival judgments, I suggest, are analogous to those viewpoints “at infinity” that exist for finite viewers in the projective plane despite the fact that they are locations they cannot themselves occupy. This means that singular witness judgments need their abstract equivalents just as much as the latter need the former. In both geometry and logic, these abstract, albeit unoccupiable points of view are required for the coherence of the “space” in question—three-dimensional physical space in one case and the logical space of interconnected assertions about the world on the other41.

7. Conclusions

In the early years of the movement of analytic philosophy Hegel’s logic was thoroughly criticised by Bertrand Russell, the chief early proponent of modern “classical logic”. Russell’s efforts here were largely successful, with Hegel for the most part being eliminated from serious consideration within logic [60] (Intro.). However, the original form of the Frege-Russell logic used to denounce Hegel would itself need modification over the coming decades in ways requiring the incorporation of elements from rival approaches [5]. This need was initially rooted in concerns with the lack of an adequate semantics within classical logic’s original form, a concern motivating investigations into the relevance of projective geometry.
Among the resources of projective geometry deemed significant would be the principle of duality, and it is perhaps not surprising that within the variety of non-classical approaches to logic that would return in the decades after the introduction of classicism, distinctly dual features are apparent which echo some of the fundamental features of Hegel’s “projective” transformation of Aristotle’s syllogistic. For example, Kripke’s rehabilitation of the dual proper name-definite description distinction [54] would overlap with Hegel’s use of the categorial singular-particular distinction in his logic and the same could be said of the duality of modal and nonmodal judgment forms, as found in the tense-logic of Arthur Prior, for example, which reflects Hegel’s non-reductive duality of qualitative and reflective judgments [61]. Elsewhere [12] (chs. 9, 10), I have drawn attention to further ways in which logic over the last century has seemed to reinvent ideas that are easily detectable in Hegel’s logic, but here I want to conclude by drawing attention to a Hegelian analogue of a feature of projective geometry that has been invoked in contrast to the static universalism of Frege’s logic, which is itself seen as underlying many of the semantic problems that faced its initial formulations. This concerns the idea developed by Gunther Edel [2] that logical systems should make possible the reinterpretation of the terms of their initial object languages.
Hegel was keenly aware of the central role of reinterpretation of the concept of number in the history of mathematics from the Greeks to the modern period [12]. He was aware, for example, that the original Greek concept of number had come to be reinterpreted in modern times such that in the seventeenth century there existed numbers, negative numbers, irrationals, etc., which for the Greeks were not recognizable as numbers at all. He was also clearly aware that such conceptual extensions resulted from the dynamic of the development of the sciences themselves. For example, the extension of a numerical metric to Euclidean geometry by Descartes would be bound up with the acceptance of negative numbers because, as continuous magnitudes, lines could be naturally understood as extending in two opposed directions42. For Hegel, such essential reinterpretatibility applied to all scientific concepts, not just mathematical ones, and it is expressed in the methodological shape of the process of laying out the categories of his logic. This conceptual unfolding, as I have argued, follows a process in which some initially meaningful concept is at first disinterpreted because it is found to generate logical paradoxes, allowing it to be reinterpreted in ways that resolve those particular paradoxes [12] (ch. 9).
The variable historical relations between arithmetic and geometry in antiquity had provided the prime example of this for Hegel, and it is therefore not surprising that he would have been attracted to approaches, like that of Leibniz, which signaled a “new relation between algebra and geometry” after which “the evolution of the two fields was henceforth intrinsically linked in a dialectical process” [62] (p. 237). Underlying all this, I have suggested, was a grasp of the relevance of an early precursor to projective geometry for logic. It should not be surprising that an increasing number of parallels can be found between his approach to logic and developments subsequent to the logical revolutions of the late nineteenth century.

References

  1. Nagel, E. The Formation of Modern Conceptions of Formal Logic in the Development of Geometry. Osiris 1939, 7, 142–223. [Google Scholar] [CrossRef]
  2. Eder, G. Frege and the origins of model theory in nineteenth century geometry. Synthese 2021, 198, 5547–5575. [Google Scholar] [CrossRef] [PubMed]
  3. Eder, G. Frege on intuition and objecthood in projective geometry. Synthese 2021, 199, 6523–6561. [Google Scholar] [CrossRef] [PubMed]
  4. Fletcher, S. C. and Nathan L. The introduction of topology into analytic philosophy: two movements and a coda. Synthese 2022, 200, 197. [Google Scholar] [CrossRef]
  5. Brady, G. From Peirce to Skolem. A Neglected Chapter in the History of Logic; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
  6. Acuña, P. 2018. Projective Geometry in Logical Space: Rethinking Tractarian Thoughts. International Journal of Philosophical Studies 2018, 26, 1–23. [Google Scholar] [CrossRef]
  7. Wittgenstein, L. Tractatus Logico-Philosophicus; C. K. Ogden, Trans.; Routledge and Kegan Paul, London, UK, 1922.
  8. Desargues, G. 1987. “The Rough Draft on Conics (1639)”. In The Geometrical Work of Girard Desargues; J. V Field and J. J. Gray Eds.; Springer Verlag: New York, USA, 1987; pp. 69–143. [Google Scholar]
  9. Mense, André. Hegel’s Library: The Works on Mathematics, Mechanics, Optics, and Chemistry. In Hegel and Newtonianism, M. J. Perry, Ed.; Kluwer Dordrecht, The Netherlands, 1993; pp. 669–709.
  10. Paterson, A. Hegel’s Early Geometry. Hegel-Studien 2005, 39/40, 61–124. [Google Scholar]
  11. Hegel, G. W. F. Philosophical Dissertation on the Orbits of the Planets and the Habilitation Theses. In Miscellaneous Writings of G. W. F. Hegel, Stewart, J., Ed.; Northwestern University Press: Evanston, USA, 2002; pp. 163–206. [Google Scholar]
  12. Redding, P. Conceptual Harmonies: The Origin and Significance of Hegel’s Logic; University of Chicago Press: Chicago, USA, 2023. [Google Scholar]
  13. Aristotle. Prior Analytics. In The Complete Works of Aristotle: The Revised Oxford Translation, vol. 1; Barnes, J., Ed.; Princeton University Press: Princeton, USA, 1984; pp. 39–113. [Google Scholar]
  14. Corcoran, J. Aristotle’s Prior Analytics and Boole’s Laws of Thought. History and Philosophy of Logic 2003, 24, 261–288. [Google Scholar] [CrossRef]
  15. Triantafyllou, V. Aristotle’s Syllogistic as a Form of Geometry. History of Philosophy and Logical Analysis 2023, 1–49. [Google Scholar] [CrossRef]
  16. Netz, R. A New History of Greek Mathematics. Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
  17. Szabó, Árpád. The Beginnings of Greek Mathematics. T. Ungar, Trans., Reidel: Dordrecht, The Netherlands, 1978.
  18. Von Fritz. K. The Discovery of Incommensurability by Hippasus of Metapontum. Annals of Mathematics, second series 1945, 46, 242–264. [Google Scholar] [CrossRef]
  19. Netz, Reviel. A New History of Greek Mathematics; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
  20. Knorr, W.R. The Evolution of Euclidean Elements; Reidel: Dordrecht, The Netherlands, 1975. [Google Scholar]
  21. Borzacchini, L. Incommensurability, Music and Continuum: A Cognitive Approach. Arch. for the Hist. Exact Sciences, 2007, 61, 273–302. [Google Scholar] [CrossRef]
  22. Burnyeat, M. Archytas and Optics. Science in Context 2005, 18, 35–53. [Google Scholar] [CrossRef]
  23. Aristotle. Nichomachean Ethics. In The Complete Works of Aristotle: The Revised Oxford Translation, vol. 2; Barnes, J., Ed. Princeton University Press: Princeton, USA, 1984; pp. 1729–1867. [Google Scholar]
  24. Euclid. The Thirteen Books of The Elements, Heath, T. L. Ed,; Dover: New York, USA, 1956. [Google Scholar]
  25. Einarson, B. On Certain Mathematical Terms in Aristotle’s Logic: Parts I and II. Amer. J. Philol. 1936, 57, 33–172. [Google Scholar] [CrossRef]
  26. Smith, R. The Mathematical Origins of Aristotle’s Syllogistic. Arch. Hist. Exact Sci. 1978, 19, 201–210. [Google Scholar] [CrossRef]
  27. Euclid. An Annotated Translation of Euclid’s “Division of a Monochord; Matheisen, T. J. Trans., J. Mus. Theory 1975, 19, 236–258. [Google Scholar] [CrossRef]
  28. Aristotle. Metaphysics. In The Complete Works of Aristotle: The Revised Oxford Translation, vol. 2; Barnes, J., Ed. Princeton University Press: Princeton, USA, 1984; pp. 1552–1728. [Google Scholar]
  29. Leibniz, G. W. Elements of a Calculus (April, 1679). In Leibniz: Logical Papers, Parkinson, G. H. R., Trans. and Ed.; Clarendon Press: Oxford, UK, 1966; pp. 17–24. [Google Scholar]
  30. Aristotle. On the Heavens. In The Complete Works of Aristotle: The Revised Oxford Translation, vol. 1; Barnes, J., Ed. Princeton University Press: Princeton, USA, 1984; pp. 447–511. [Google Scholar]
  31. Desargues, G. The Rough Draft on Conics (1639). In The Geometrical Work of Girard Desargues, Field, J. V., Gray, J. J. Eds.; Springer: New York, USA, 1987; pp. 69–143. [Google Scholar]
  32. Andersen, K. The Geometry of an Art: The History of the Mathematical theory of Perspective from Alberti to Monge; Springer: New York, USA, 2007. [Google Scholar]
  33. Bigelow, J. and Leckey M. Raphael’s Platonic Vision. J. Amer. Philos. Assoc. 2020, 6, 410–430. [Google Scholar] [CrossRef]
  34. Barbera, A. The Consonant Eleventh and the Expansion of the Musical Tetractys: A Study of Ancient Pythagoreanism. J. Mus. Theory 1984, 28, 191–223. [Google Scholar] [CrossRef]
  35. Plato. Epinomis. In Complete Works, Cooper, J. M. Ed., Hackett: Indianapolis, USA, 1997; pp. 1617-1633.
  36. Nicomachus of Gerasa. Introduction to Arithmetic, D’Ooge M. L Trans.; Macmillan Co.: New York, USA, 1926. [Google Scholar]
  37. Iamblichus. The Theology of Arithmetic, Waterfield, R. Trans.; Phanes Press, Grand Rapids, USA, 1988.
  38. Proclus. Commentary on Plato’s Timaeus, Volume IV: Book 3 part II: Proclus on the World Soul, Baltzly, D., Ed. and Trans.; Cambridge University Press, Cambridge, UK, 2009.
  39. Plato. Timaeus. In Complete Works, Cooper, J. M. Ed., Hackett: Indianapolis, USA, 1997; pp. 1224-1291.
  40. Hegel, G. W. F. Lectures on the History of Philosophy, 1825–6, Volume II: Greek Philosophy, Brown, R. F., Ed. and Trans.; Clarendon Press: Oxford, UK, 2006. [Google Scholar]
  41. Barker, A. The Science of Harmonics in Classical Greece. Cambridge University Press: Cambridge, UK, 2007.
  42. Barker, A. Greek Musical Writings. Volume II. Harmonic and Acoustic Theory. Cambridge University Press: Cambridge, UK, 1989.
  43. Kline, M. Mathematical Thought from Ancient to Modern Times. Oxford University Press: Oxford, UK, 1972.
  44. Nicholas of Cusa. On Learned Ignorance. In Selected Spiritual Writings, Bond, H. L., Trans.; Paulist Press: New York, USA, 1997; pp. 85–206. [Google Scholar]
  45. Zellini, P. The Mathematics of the Gods and the Algorithms of Men: A Cultural History; Carnell, S.; Serge, E., Translators; Allen Lane: London, UK, 2020. [Google Scholar]
  46. Łukasiewicz, J. Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic; Oxford University Press: Oxford, UK, 1957. [Google Scholar]
  47. Debuiche, V. , Brancato, M. Scientia Perspectiva. Leibniz and geometric perspective. Historica Mathematica 2023, 63, 47–69. [Google Scholar] [CrossRef]
  48. Coxeter, H. M. S. Projective Geometry, 2nd ed.; Springer: New York, USA, 1987. [Google Scholar]
  49. Cortese, J. F. N. Infinity between mathematics and apologetics: Pascal's notion of infinite distance. Synthese 2015, 192, 2379–2393. [Google Scholar] [CrossRef]
  50. Leibniz, G. W. Discourse on Metaphysics (1686). Philosophical Texts; Woolhouse, R. S., Franks, R. Trans. and Ed., Oxford University Press, Oxford, UK, 1998; pp. 53-93.
  51. Kant, I. Critique of Pure Reason; Guyer, P. , Wood, A. W. Trans. and Ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
  52. Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite; Harvard University Press, Cambridge, USA, 1979.
  53. Hegel, G. W. F. The Science of Logic, di Giovanni, G. Trans. and Ed., Cambridge University Press, Cambridge, UK, 2010.
  54. Kripke, S. A. Naming and Necessity; Harvard University Press: Cambridge, USA, 1980. [Google Scholar]
  55. Tarlazzi, C. Individuals as Universals: Audacious Views in Early Twelfth-Century Realism. J. Hist. Philos. 217, 55, 557-581.
  56. Hegel, G. W. F. Encyclopedia of the Philosophical Sciences in Basic Outline Part I: Science of Logic; Brinkmann, K., Dahlstrom, D. O., Trans., and, Eds.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
  57. Stalnaker, R. Mere Possibilities: Metaphysical Foundations of Modal Semantics; Princeton University Press: Princeton, USA, 2012. [Google Scholar]
  58. Demey, L, Smessaert, H. Duality in Logic and Language. In The Internet Encyclopedia of Philosophy 2022, https://iep.utm.edu/dual-log/ (accessed on 17 October 2023).
  59. Redding, P. Intuitionist and Classical Dimensions of Hegel’s Hybrid Logic. Hist. and Philos. of Logic 2023, 44, 209–224. [Google Scholar] [CrossRef]
  60. Redding, P. Analytic Philosophy and the Return of Hegelian Thought; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  61. Prior, A. N. Past, Present and Future; Clarendon Press: Oxford, UK, 1967. [Google Scholar]
  62. Dorier, J.-L. A General Outline of the Genesis of Vector Space Theory. Hist. math. 1995, 22, 227–261. [Google Scholar] [CrossRef]

Notes:

1
Of course, Boolean logic would continue in the twentieth century in the new discipline of computer science which, developing in the 1920s, predated the actual birth of computers.
2
The role of the related discipline of topology has been similarly discussed in this context. See, for example, [4]. On the need for classicist logic to draw on rival approaches for its development of semantics see [5].
3
This would be called by various names during the history of projective geometry, with the name “harmonic cross-ratio” being coined at the end of the nineteenth century by the English mathematician-philosopher William Kingdon Clifford.
4
In [4] I argue against the common assumption, found in both his supporters and critics, that Hegel’s Science of Logic has nothing to do with logic as it is practiced now.
5
The nature of these musico-mathematical “means” will be explained below.
6
The “canon” was a measuring device attached to a monochord and so the title refers to the proportions in which the device’s string was “sectioned” or divided in experiments.
7
About two thousand years later, Leibniz would also assign numbers to concepts in order to portray inference as a type of transitivity of relations of “inclusion”. “For example, since man is a rational animal, if the number of animal, a, is 2, and of rational, r is 3, then the number of man, h, will be the same as ar: in this example, 2 x 3 or 6” [29] (p. 17).
8
The full title was “Brouillon project d'une atteinte aux événements des rencontres d'un cône avec un plan” [Rough Draft of an Essay on the results of taking plane sections of a cone].
9
The idea of such invariants had also been introduced by Kepler in Astronomica Pars Optica and in the later nineteenth century, when a variety of non-Euclidean geometries had been proposed, they would be classified in terms of the invariants specific to each.
10
Image from Internet Archive, <https://archive.org/details/school-of-athens>, accessed on 17/10/2023.
11
The author of this work, traditionally attributed to Plato, is now thought to be Philip of Opus, a follower of Plato at the Academy. Significantly, Philip had himself authored two works on optics [22] (p. 36).
12
Hegel was familiar with and possessed key works of neo-Platonic authors such as Nicomachus of Gerasa, Iamblichus and Proclus [9].
13
The harmonic mean had, prior to Archytas, been called the “sub-contrary” [hypenantia] [41] (p. 283), which, in the context of Greek geometry, referred to a triangle that was similar to another but inverted, in the sense of as if having been rotated 180° through the third dimension.
14
Archytas describes the harmonic mean as holding when “the part of the third by which the middle term exceeds the third is the same as the part of the first by which the first exceeds the second” [42] (p. 42).
15
While traditionally the problem of incommensurability has been thought to have been a consequence of “Pythagoras’s theorem” concerning squares built on the sides of a right-angle triangle, recent historians have argued that it was more likely to have emerged out of music theory itself [17] (Intro., ch. 1); [41] (pp. 291-292); [21].
16
In Greek style, Desargues talks of ratios and their compoundings, whereas for a modern reader it is more intuitive to talk of fractions and their products.
17
The ratio has the value of 1 when only the absolute value of the lengths is considered as in Desargues’s presentation. In the nineteenth century, the relative directions of the line-segments would be taken into account, in which case the value of the harmonic cross-ratio would be given −1, because the direction of one of the segments will always be opposite to the directions of the other three.
18
A quick calculation shows that the harmonia or musical tetraktys instantiates the harmonic cross-ratio.
19
Desargues had insisted on counting the four points as an instance of the involution despite the fact that the idea of a point at infinity is “incomprehensible” [31] (p. 85). Remember that Desargues had not formulated the harmonic cross-ratio in terms of fractions, but ratios, and so was not faced with the problem of “dividing” by infinity. Later in the nineteenth century, worries about calculating with “infinity” would be bypassed by the introduction of homogeneous coordinates.
20
In fact, the point at infinity as portrayed in figure 2 above will be just one of an infinite number of such points, each being the point of intersecting parallels pointing in different directions. These points will form a single line at infinity which is closed, like a circle.
21
For the Greeks, multiplicative relationships were fundamentally geometrical, in that the multiplication of two numbers was essentially shorthand for the area of a rectangle with sides of lengths equal to those two numbers.
22
For an account of the history of the spread of these algorithms, see [45].
23
It is now known that the Pythagorean musical scale had originated in Mesopotamia.
24
For the interval between 6 and 12, for example, the geometric mean (√72 = ~ 8.48528…) falls between the harmonic mean, 8, and the arithmetic mean, 9.
25
This was known as the “Delian problem” of working out the dimensions of an altar that would be built to twice the volume of an existing one. Arithmetically, the solution involves the calculation of cube roots.
26
This can be appreciated in relation to the fretboard of a modern guitar, where the perfect fourth is equivalent to five steps on the fretboard and the perfect fifth to seven. Adding to the interval of a fifth, say C to G (7 steps), a further fourth (5 steps), results in a full octave (12 steps).
27
Leibniz had, apparently, drawn schematic eyes as located at origins of such rays in his geometric diagrams.
28
Of course, the painter would typically paint their models in the studio from a determinate point of view, which would become that from which the spectator would “view” the characters represented by those models.
29
C.f., “Projections in logical space are always drawn from point P, and that point is the transcendental subject I” [6] (p. 17).
30
In fact, there seem parallels here to Georg Cantor’s attitude to “transfinite” numbers towards the end of the nineteenth century, in that his “actual” infinites had determinable properties for humans, whereas traditionally, knowledge of the infinite had been the exclusive preserve of God. Thus, Cantor had attempted to quieten his Catholic critics by distinguishing between the traditional “absolute infinite” that was the preserve of God and the actual “transfinitum” that could be cognized by humans [52] (pp.144-145).
31
This ladder analogy is clearly on view in Kant’s treatment of “prosyllogistic” forms of inductive inference [51] (A307-8/B364-365; A331-332/B387-389).
32
See, for example, his 1953 lithograph “Relativity” <M.C. Escher's "Relativity" (byu.edu)>).
33
As with Leibniz, there is no evidence that Lambert had grasped the need for a specific invariant in the geometry informing his studies on perspective.
34
Such modal conceptions of individuality in the Renaissance were anticipated by logical conceptions in the Middle Ages. See, for example, [55].
35
Hegel uses “reflective” as the contrary of “qualitative” in discussing judgments, explaining his reluctance to use “quantitative” as this judgment is not purely quantitative [53] (p. 569). This is an odd decision, however, seeing that his qualitative judgments are themselves not entirely qualitative.
36
Hegel often employs “the” rather than the demonstrative “this” in these examples, but that the latter is intended is clear in the Encyclopedia Logic when he notes that “if we say ‘this rose is red’, then it lies in the copula ‘is’ that subject and predicate agree with one another. But now the rose, as something concrete, is not merely red; instead it also has an odour, a determinate form, and many other sorts of determinations that are not contained in the predicate ‘red’” [56] (§ 172 add.) and, “if we say, for example, ‘this rose is red’, we consider the subject in its immediate individuality without relation to another”, (§ 174 add.). This is clearly the form of designation that excludes other instances of the genus “rose” in order to specify what is distinctive of this “singular” one.
37
Here the particular-universal distinction is being applied to the subject term, resulting in the quantities some and all.
38
See Hegel’s account of the “mathematical syllogism” [53] (pp. 602-608). See [12] (ch. 6.3).
39
While not invoking its intuitionist origins, Robert Stalnaker uses this notion to distinguish propositions true in the actual world from those true in a merely possible world [57] (ch. 2.2)
40
This is famously manifest in the intuitionists’ opposition to the classicists’ indirect establishment of truths via proof by contradiction or “reductio ad impossibile”.
41
In the logical context, aperspectival reflective judgments provide the appropriate judgment form that allows properly truth preserving inferences across differently located finite subjects.
42
For his part, Descartes had apparently not extended his coordinates into the territory of negative numbers, but this would happen soon after.
Preprints 88569 g001
Figure 1. The vanishing point of parallels in perspective in Raphael’s The School of Athens10.
Figure 1. The vanishing point of parallels in perspective in Raphael’s The School of Athens10.
Preprints 88569 g001
Preprints 88569 g002
Figure 2. Dividing an interval internally and externally by variable points in the same proportion.
Figure 2. Dividing an interval internally and externally by variable points in the same proportion.
Preprints 88569 g002
Preprints 88569 g003
Figure 3. The inverse foreshortening found in the neck of a guitar.
Figure 3. The inverse foreshortening found in the neck of a guitar.
Preprints 88569 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated