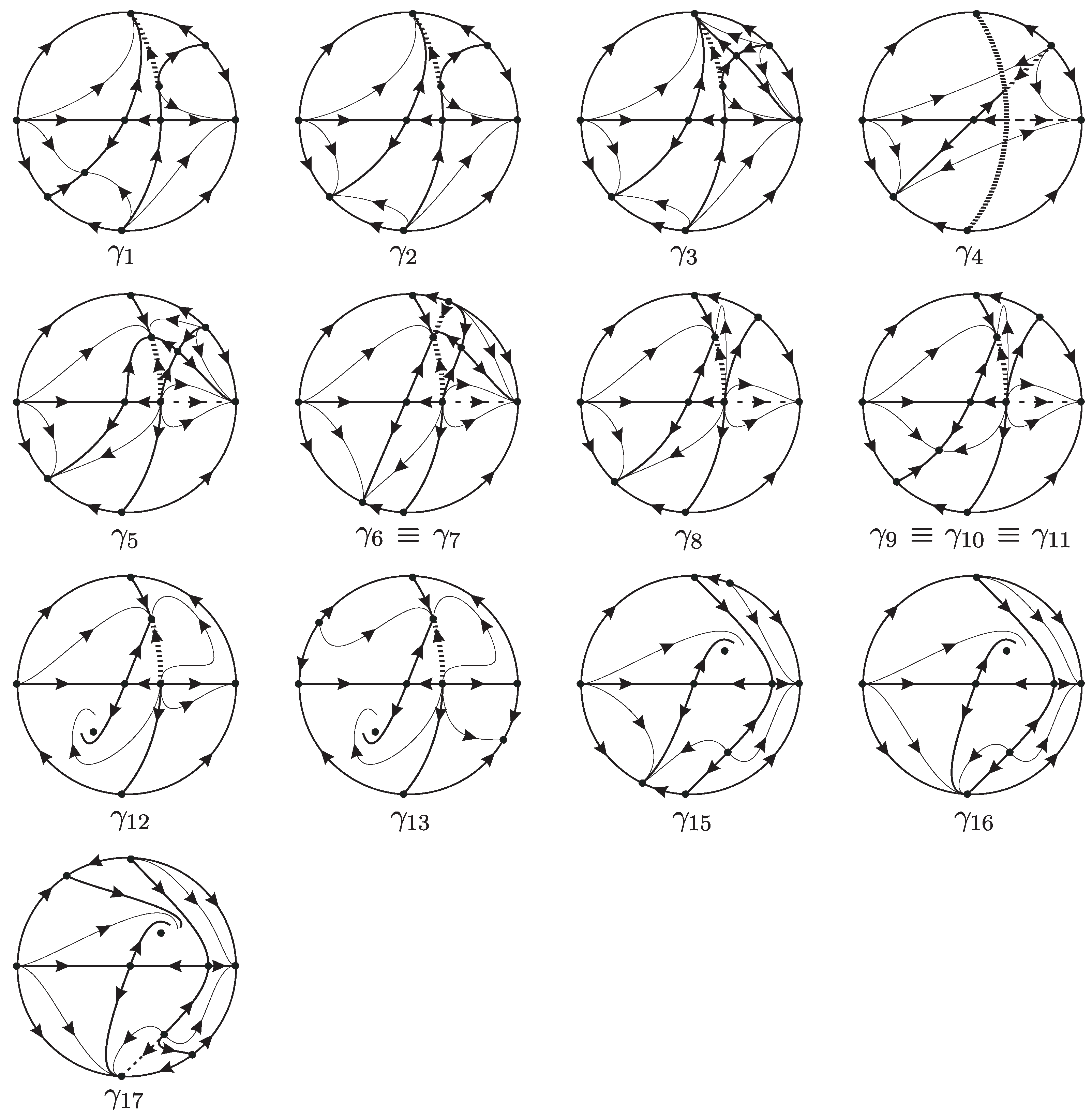Dynamics of the Static Star Differential System from the Mathematical and Physical Point of Views

1. Introduction and the Main Results

The structure equations of a static star in general relativity in the case of the existence of a homologous family of solutions are

$$\begin{array}{c}\dot{x}=y-x,\hfill \\ \dot{y}={\displaystyle \frac{y}{1-2x}}\left(2-\gamma y-{\displaystyle \frac{5\gamma -4}{\gamma -1}}x\right),\hfill \end{array}$$

(1)

where the parameter $\gamma$ varies in the interval $(1,2]$, and the dot denotes derivative with respect to the variable $t=ln(r/R)$ being R the radius of the star. Therefore, from the physical point of view we are interested in the solutions defined in the interval $t\in (-\infty ,0)$. Here $x=m\left(r\right)/r$ where $m\left(r\right)\ge 0$ is the mass inside the sphere of radius r of the star, $y=4\pi r^2\rho$ being $\rho$ the density of the star. For more details on the differential system (4) see [3,4,5,7,8,10].

We remark that from the physical point of view and since $x>0$ and $y>0$ we are mainly interested in the dynamics of the differential system (4) with $\gamma \in (1,2]$ in the set $Q^{*}$ formed by the positive quadrant $Q=\{(x,y)\in {\mathbb{R}}^2:x>0,y>0\}$ of ${\mathbb{R}}^2$ without the straight line $x=1/2$ where the differential system (4) is not defined.

Note that the straight line $y=0$ is invariant because when $y=0$ we have that $\dot{y}=0$. Therefore, since $\dot{x}{|}_{x=0}=y$ the set $Q^{*}$ is positively invariant, i.e. orbits of system (4) can enter in $Q^{*}$ through the positive y-axis but never orbits of the quadrant Q can exit from $Q^{*}$.

Doing the change of the independent variable $t\to s$, where $dt=(1-2x)ds$ the differential system (4) becomes the polynomial differential system

$$\begin{array}{c}\dot{x}=(1-2x)(y-x)=p(x,y),\hfill \\ \dot{y}=y\left(2-\gamma y-{\displaystyle \frac{5\gamma -4}{\gamma -1}}x\right)=q(x,y),\hfill \end{array}$$

(2)

where now the dot denotes derivative with respect to the variable s.

The differential system (2) is a polynomial differential system of degree 2 because the maximum of the degrees of the polynomials $p(x,y)$ and $q(x,y)$ is 2. The polynomial differential systems of degree 2 are called simply quadratic systems and they have been intensively studied, see for instance the books [1,11,13], the paper [5], and the hundreds of references quoted therein.

The domain of definition of the differential system (2) is the whole plane ${\mathbb{R}}^2$. The decomposition of ${\mathbb{R}}^2$ as union of the orbits of system (2) is the phase portrait of the differential system (2). In particular a phase portrait shows where each orbit is born and where each orbit dies, if they are equilibrium points, periodic orbits, ... In summary a phase portrait provides all the qualitative information about the orbits of a differential system. For more information about the phase portraits of the planar differential systems see for instance [6].

The phase portraits of the polynomial differential systems in ${\mathbb{R}}^2$ are usually described in the Poincaré disc. Roughly speaking the Poincaré disc is the unit closed disc ${\mathbb{D}}^2$ whose interior has been identified with the plane ${\mathbb{R}}^2$ and whose boundary, the circle ${\mathbb{S}}^1$ is identified with the infinity of ${\mathbb{R}}^2$. Note that in the plane ${\mathbb{R}}^2$ we can go to infinity in as many directions as points has the circle ${\mathbb{S}}^1$. For more details on the Poincaré disc see Chapter 5 of [6] or the Appendix.

As usual two phase portraits in the Poincaré disc ${\mathbb{D}}^2$ are topologically equivalent if there is a homeomorphism of ${\mathbb{D}}^2$ which sends orbits of the first phase portrait into orbits of the second phase portrait preserving or reversing the sense of all the orbits.

The objective of this paper is double. First we study the phase portraits of the quadratic systems (2) from a mathematical point of view, i.e. for all the values of parameter $\gamma \in \mathbb{R}\setminus \left\{1\right\}$ where the system is defined. These phase portraits are described in the Poincaré disc, in this way we control the orbits which escape or come from the infinity. Second we describe the whole dynamics of the static star in general relativity in the case of the existence of a homologous family of solutions modelled by the differential system (4) for $1<\gamma \le 2$ in the positive quadrant taking into account the orbits which could escape or come from the infinity.

Our main results are described in the next two theorems.

Theorem 1.

The quadratic system (4) when γ varies in $\mathbb{R}\setminus \left\{1\right\}$ has 11 topologically non-equivalent phase portraits in the Poincaré disc. These are the phase portraits ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, ${\gamma }_4$, ${\gamma }_5$, ${\gamma }_8$, ${\gamma }_9$, ${\gamma }_{12}$, ${\gamma }_{13}$, ${\gamma }_{15}$ and ${\gamma }_{16}$ given in Figure 1.

Theorem 1 is proved in Section 2.

In Figure 1 appear other few phase portraits which are needed to complete the bifurcation diagram as it is described in the proof of Theorem 1.

We define $Q_1=Q^{*}\cap \{x<1/2\}$ and $Q_2=Q^{*}\cap \{x>1/2\}$.

Theorem 2.

The static star in general relativity in the case of the existence of a homologous family of solutions modelled by the differential system (4) with $1<\gamma \le 2$ verifies the following statements.

(a) 

The region $Q_1$ is positively invariant, and the region $Q_2$ is invariant, i.e if an orbit of the system has a point in $Q_2$ the whole orbit is contained in $Q_2$.

(b) 

The orbits in $Q_2$ when $r\to 0$ verify that $4\pi r^3\rho \to 0$ and $m\left(r\right)/r\to \infty$.

(c) 

If

$$\frac{m\left(R\right)}{R}=4\pi R^2\rho =-\frac{2\left(\gamma -1\right)}{{\gamma }^2+4\gamma -4},$$

then

$$\frac{m\left(r\right)}{r}=4\pi r^2\rho =-\frac{2\left(\gamma -1\right)}{{\gamma }^2+4\gamma -4},$$

for all $r\in (0,R]$.

(d) 

For every initial condition $\left({\displaystyle \frac{m\left(R\right)}{R}},4\pi R^2\rho \right)$ in $Q_1$ distinct from

$$\left(-\frac{2\left(\gamma -1\right)}{{\gamma }^2+4\gamma -4},-\frac{2\left(\gamma -1\right)}{{\gamma }^2+4\gamma -4}\right),$$

the orbit determined for this condition when r tends to some finite value $r_0<R$ (which depends on the initial condition) satisfies

$$\frac{m\left(r\right)}{r}\to 0and4\pi r^2\rho \to k\ge 0,$$

where k can take any non-negative value when the initial condition varies.

Theorem 2 is proved in Section 3.

The techniques used for studying this 2-dimensional polynomial differential system, can be extended to higher dimensions, see for instance [9].

2. Proof of Theorem 1

Even the study of the bifurcation diagram of this system is not complicate because it has just one parameter, we will make use of the Theory of Invariants developed by the Sibirskii school, and fully developed for quadratic systems in the book [1]. The invariants (and also the comitants) allow to easily determine all the geometric features provided by the system in a methodic and consistent way. These geometric features may even exceed the most simple topological features to which later we will reduce the classification.

Each one of these geometric features is characterized using some of the following 10 invariant polynomials:

$$\left\{{\mu }_0,{\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4,\mathbf{D},W_4,B_1,B_2,B_3,\eta \right\}.$$

(3)

The invariants $B_1$ to $B_3$ can be found in page 14 of [12]. The rest of invariants can be found in pages 121-128 of [1].

Apart from the geometric properties of the singularities, there may also exist bifurcations due to separatrix connections. If these connections are invariant straight lines or polynomial curves, they may also be determined by means of algebraic invariants. But they may also be of non-algebraic nature in which case, only an analytical and numerical study may detect them. Anyway we will not meet any of them in this family.

The first important detail to be remarked of this system is that it is not defined for $\gamma =1$. Thus the bifurcation diagram will show a jump from cases with $\gamma <1$ to cases with $\gamma >1$ and no continuity or coherence must be expected from ones to the others.

Next we detect that for every $\gamma$ the straight lines $y=0$ and $x=1/2$ are invariant. For some values of $\gamma$ we may have more invariant straight lines. It is a known result that quadratic systems having two invariant lines cannot have limit cycles (see [2]), so systems (2) has no limit cycles.

The first relevant invariant is

$${\mu }_0=\frac{4\gamma \left({\gamma }^2+4\gamma -4\right)}{\gamma -1}$$

which if it vanishes (for some $\gamma$), will determine if a finite singularity escapes to infinity. For one of the possible solution of ${\mu }_0=0$ we will have that ${\mu }_1={\mu }_2={\mu }_3={\mu }_4=0$ implying then that the system has an infinite number of finite singularities, see Lemma 5.2 (iii) in [1] .

One usual generic invariant is $\mathbf{D}$ which determines (when it vanishes) that two finite singularities have collided, but for these systems $\mathbf{D}=-\frac{192{\gamma }^6}{{(\gamma -1)}^4}$ and $\gamma =0$ is exactly the value mentioned above for which the systems degenerate. By degenerate system we mean that there is an infinite number of finite singular points (real or complex), which is equivalent to say that the two equations defining the differential system have a non constant common factor.

We will also need the invariant $\eta =\frac{{(\gamma -2)}^2{(7\gamma -6)}^2}{{(\gamma -1)}^2}$ which if equal to zero, determines if two infinite singularities coalesce.

Another interesting geometric feature to capture is whether the system has or not invariant straight lines. Sometimes these lines will not imply a separatrix connection and thus, breaking them will not produce a different phase portrait. However, other times, on these lines we will find separatrix connections and they must be included in the bifurcation diagram. The invariants/comitants that will help us to find those invariant straight lines are $B_1$, $B_2$ and $B_3$. Since $B_1=B_2=0$ for this family we must just concentrate on $B_3$ which is

$$B_3=-\frac{3\gamma {(3\gamma -2)}^2{x}^2{y}^2}{{(\gamma -1)}^2}.$$

We normally add one more invariant in every study which is $W_4$. This invariant detects the transition from a node to a strong focus when the invariant changes its sign. This does not produces a topological change in the phase portrait. Since the fact that an antisaddle is a node or a focus may have some physical interest, we have preferred to include it.

In summary, extracting from the different invariant/comitants the equations that must be solved for obtaining the mentioned qualitative informations are

$$\begin{array}{cc}\hfill \gamma \left({\gamma }^2+4\gamma -4\right)=& 0,\hfill \\ \hfill {(\gamma -2)}^2{(7\gamma -6)}^2=& 0,\hfill \\ \hfill \gamma {(3\gamma -2)}^2=& 0.\hfill \end{array}$$

(4)

Then easy computations determine that the bifurcations points are the values

$$\begin{array}{ccc}{\gamma }_2=-2(1+\sqrt{2}),\hfill & {\gamma }_4=0,\hfill & {\gamma }_6=2/3,\hfill \\ {\gamma }_8=2(\sqrt{2}-1),\hfill & {\gamma }_{12}=6/7,\hfill & {\gamma }_{14}=1,\hfill \\ {\gamma }_{16}=2.\hfill & \hfill \end{array}$$

(5)

We have numerated them with even numbers and leaving some gaps in order to leave space for intermediate generic cases and the values where $W_4=0$. We have also assigned a place for the case $\gamma =1$ even knowing that the differential system is undefined there so to maintain the coherence in the numeration between generic cases (odd) and singular (even).

The invariant

$$W_4=\frac{9{\gamma }^6{(3\gamma -2)}^2\left({\gamma }^2-44\gamma +36\right)}{{(\gamma -1)}^6}$$

only changes sign on the roots of the non multiple component of degree 2. We must solve it. And now we add intermediate values between each singular values. So in order to obtain all the bifurcation diagram of the differential system (2) we must study it for the following values of the parameters:

$$\begin{array}{ccc}{\gamma }_1=-5,\hfill & {\gamma }_2=-2(1+\sqrt{2}),\hfill & {\gamma }_3=-2,\hfill \\ {\gamma }_4=0,\hfill & {\gamma }_5=1/3,\hfill & {\gamma }_6=2/3,\hfill \\ {\gamma }_7=7/10,\hfill & {\gamma }_8=2(\sqrt{2}-1),\hfill & {\gamma }_9=83/100,\hfill \\ {\gamma }_{10}=2(11-4\sqrt{7}),\hfill & {\gamma }_{11}=84/100,\hfill & {\gamma }_{12}=6/7,\hfill \\ {\gamma }_{13}=88/100,\hfill & {\gamma }_{14}=1,\hfill & {\gamma }_{15}=3/2,\hfill \\ {\gamma }_{16}=2,\hfill & {\gamma }_{17}=4,\hfill & {\gamma }_{18}=2(11+4\sqrt{7}),\hfill \\ {\gamma }_{19}=50.\hfill & \hfill \end{array}$$

(6)

Now using the program P4 (see [6]) we obtain a picture of every phase portrait and we describe briefly the bifurcations, explaining what has happened when we move from a case to another one. In fact we additionally have verified that all the local phase portraits of the finite and infinite equilibrium points of the differential system (4) are the ones obtained by the program P4. Thus the local phase portraits of the hyperbolic equilibrium points (i.e. the ones such that the eigenvalues of the linear part of the system evaluated on them have real part non-zero) have been computed with Theorem 2.15 of [6]. The local phase portraits of the semi-hyperbolic or also called semi-elemental equilibrium points (i.e. the ones such that one and only one of the eigenvalues of the linear part of the system evaluated on them is zero) have been computed with Theorem 2.19 of [6]. The local phase portraits of the nilpotent equilibrium points (i.e. the ones such that both eigenvalues of the linear part of the system evaluated on them are zero but the linear part is not identically zero) have been computed with Theorem 3.5 of [6].

Once we now all the local phase portraits of the finite and infinite equilibrium points in order to determine the global phase portraits in the Poincaré disc for the different values of the parameter $\gamma$ we only need to control where start and end the separatrices of the differential system. For the differential systems (4) the separatrices are all the orbits of the infinity, the finite equilibrium points and the separatrices of the hyperbolic sectors of the finite and infinite equilibrium points, for more details see section 1.9 of [6]. The limit cycles, when they exist, also are separatrices but the differential systems (4) has no separatrices for the reason previously explained.

For ${\gamma }_1$ we see two saddles on the x-axis and a finite node. The infinite singularity $N_1=[1:0:0]$ is an elemental node. There is another infinite singularity at $N_2=[0:1:0]$ which is also an elemental node. On these two singularities we have the ends of the finite invariant straight lines. And there is a third equilibrium point at infinity (on first and third quadrant) $N_3$ which is an elemental saddle. The phase portrait is completely determined by the invariant straight line and the distribution of singularities. We draw in wide solid black the separatrices and in thin black the orbits. The parts of the invariant straight lines which are not separatrices, we draw with dashes.

For ${\gamma }_2$ we see that the finite node in the third quadrant has coalesced with the infinite singularity $N_3$ producing a semi-elemental saddle-node $\overline{\left(\genfrac{}{}{0pt}{}{1}{1}\right)}SN$ (see notation in Section 3.7 or Appendix A of [1]).

For ${\gamma }_3$ the infinite singularity $N_3$ ejects a saddle into the first quadrant and remains as a node.

At ${\gamma }_4$ the system degenerates. The invariant straight line $x=1/2$ becomes fulfilled with singularities. While other bifurcations normally need simply the change of one property of the system, this type of bifurcation usually implies several important changes and the next phase portrait needs to be completely described.

At ${\gamma }_5$ the saddle that we had before on the intersection of the two invariant straight lines, now reappears as a node. And the infinite singularity $N_2$ which was before a node, now is a saddle. Again, the strong restrictions produced by the splitting of the phase plane in four regions because of the invariant straight lines makes very simple to complete the phase portrait.

At ${\gamma }_6$ we have that the invariant $B_3=0$ and the system has a new invariant straight line in a different direction from the other two. However, this straight line does not produce any separatrix connection and then the phase portrait is equivalent to the previous case, and it is also equivalent to the case ${\gamma }_7$.

At ${\gamma }_8$ the saddle we had in the first quadrant coalesces back with $N_2$ producing again a semi-elemental saddle-node $\overline{\left(\genfrac{}{}{0pt}{}{1}{1}\right)}SN$

For ${\gamma }_9$ the infinite singularity $N_3$ ejects again a node into the third quadrant.

At ${\gamma }_{10}$ the node in the third quadrant turns into a focus. So the phase portrait is equivalent to the previous one and also to the case ${\gamma }_{11}$.

At ${\gamma }_{12}$ the infinite singularity $N_3$ coalesces with $N_1$ producing a semi-elemental saddle-node $\overline{\left(\genfrac{}{}{0pt}{}{0}{2}\right)}SN$.

For ${\gamma }_{13}$ the infinite singularity breaks. The singularity $N_3$ is now in the second-fourth quadrant as a node. $N_1$ keeps the saddle behavior. It is as if a billiard ball had collided with $N_1$ occupying its position and sending the node in $N_1$ to the fourth quadrant.

For ${\gamma }_{14}$ we have $\gamma =1$ and the system is undefined. No continuity, no coherence may be expected from what we had before and to what we will meet after.

For ${\gamma }_{15}$ we must start describing the phase portrait from zero. We have again two saddles on the x-axis as when $\gamma <{\gamma }_2$. We also have two finite nodes, but different from case ${\gamma }_1$ they are in different relative positions. Moreover, $N_2$ is now a saddle and $N_3$ a node which makes this phase portrait different from the case ${\gamma }_1$.

For ${\gamma }_{16}$ we have again coalescence between infinite singularities. The point $N_3$ coalesces with $N_2$ producing a semi-elemental saddle-node $\overline{\left(\genfrac{}{}{0pt}{}{0}{2}\right)}SN$.

For ${\gamma }_{17}$ the infinite singularity breaks. The singularity $N_3$ is now in the second-fourth quadrant as a saddle. $N_2$ keeps the node behavior that $N_3$ had before. But now one must notice that this phase portrait is topologically equivalent to the case with ${\gamma }_1$.

It must be remarked that this kind of studies must normally be done in a family of systems whose parameter space may be compactified in a projective space. In this way, one can control also what may happen when one parameter escapes to infinity. Somehow, we may even study the phase portrait when one parameter is ∞. Normally there we find some kind of bifurcation which links with both sides (positive and negative of the parameter). Then by confirming the coherence between the phase portrait at ∞ and the largest (and smallest) $\gamma$ of our bifurcation, one may be quiet that one has not forgotten any other large singular value of the bifurcation diagram. In general, one cannot affirm that he has found all possible phase portraits, but one can be certain that the whole set is complete and coherent, and that no new bifurcation value is needed to get the full picture of the diagram. If some other bifurcation occurs, this may not be related with singular points, and whatever occurs, must be undone by another unfound singular bifurcation value. And this may theoretically occur in very small part of the parameter space although we have never found yet such a phenomena.

In the current family it seems that the case $\gamma =\infty$ is not a bifurcation since the phase portrait we obtain for $\gamma >{\gamma }_{17}$ is topologically equivalent to the case $\gamma <{\gamma }_2$. However we have the problem with the undefined case $\gamma =1$ which will produce a similar phenomena as the described case when $\gamma \to \infty$. That is, we have detected the biggest singular value for $\gamma$ lower than 1 and the lowest greater than 1. But in general we cannot know for sure if there are other phantom singular values of $\gamma$ very close to 1.

Anyway, as this family has a two permanent invariant straight line, and there are so few separatrices, it is not hard to see that the phase portrait in every one of the parts that we have divided the straight line, is the corresponding one of Figure 1.

This completes the proof of Theorem 1.

3. Proof of Theorem 2

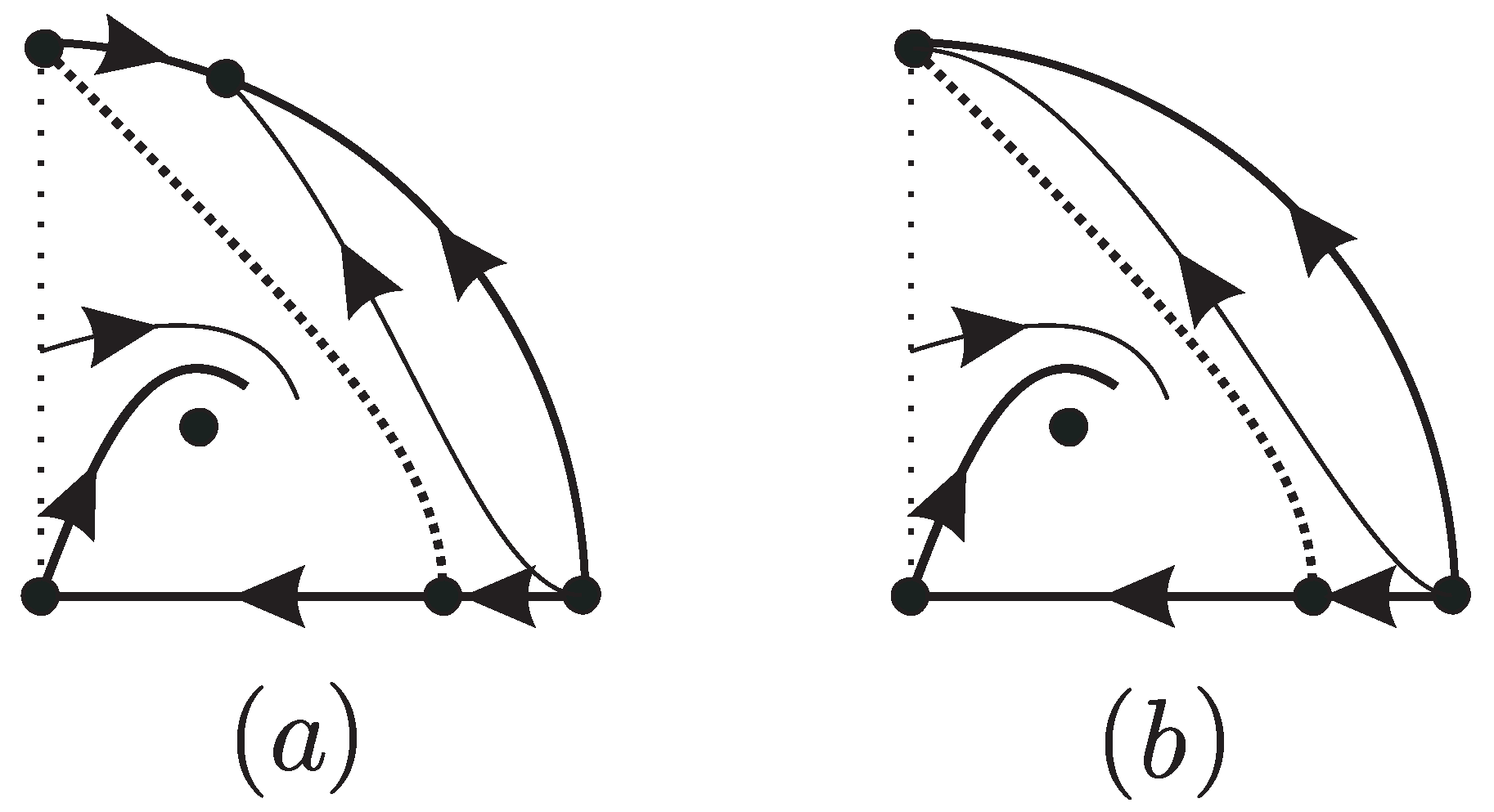
The phase portrait of the differential system (2) when $\gamma \in (1,2)$ is topologically equivalent to the phase portrait ${\gamma }_{15}$, and when $\gamma =2$ is topologically equivalent to the phase portrait ${\gamma }_{16}$. In order to pass from the phase portraits of system (2) to system (4) we must take into account the change in the time $dt=(1-2x)ds$. Then the positive quadrants of the phase portraits ${\gamma }_{15}$ and ${\gamma }_{16}$ of system (2), pass to the positive quadrants of system (4) changing the direction of orbits in the region $x>1/2$, and omitting the straight line $x=1/2$ where system (4) is not defined. In summary, the phase portraits in the positive quadrant Q of system (4) are shown in Figure 2.

Since $t=ln(r/R)$ and r varies on the interval $(0,R]$, t varies in the interval $(-\infty ,0]$. Taking into account that the meaning of the variables x and y are $x=m\left(r\right)/r>0$ and $y=4\pi r^2\rho >0$, from Figure 2 it follows that all the orbits which are in $Q_1$ are positively invariant, and the ones which are in $Q_2$ are invariant. So statement (a) is proved.

From Figure 2 all the orbits which are in $Q_2$ satisfy that

$$\frac{m\left(r\right)}{r}\to \infty \mathrm{and}4\pi r^2\rho \to 0,$$

(7)

when $t\to -\infty$, i.e. when $r\to 0$. This proves statement (b).

In $Q_1$ there is the equilibrium point $P=(2(\gamma -1)/({\gamma }^2+4\gamma -4),2(\gamma -1)/({\gamma }^2+4\gamma -4))$. So if $(m\left(R\right)/R,4\pi R^2\rho )=P$, then for all $r\in (0,R]$ we have that $(m\left(r\right)/r,4\pi r^2\rho )=P$. So statement (c) is proved.

From Figure 2 all the orbits which are in $Q_1$, with the exception of the equilibrium point P, satisfy that

$$\frac{m\left(r\right)}{r}\to 0\mathrm{and}4\pi r^2\rho \to k\ge 0,$$

(8)

for some finite negative value of t, i.e. there is a positive value $r=r_0<R$ for which (8) holds. This completes the proof of statement (d). Hence Theorem 2 is proved.

4. Conclusions

The differential system

$$\frac{dx}{dt}=y-x,\frac{dy}{dt}={\displaystyle \frac{y}{1-2x}}\left(2-\gamma y-{\displaystyle \frac{5\gamma -4}{\gamma -1}}x\right),$$

when the parameter $\gamma \in (1,2]$ models the structure equations of a static star in general relativity in the case of the existence of a homologous family of solutions, being $x=m\left(r\right)/r$ where $m\left(r\right)\ge 0$ is the mass inside the sphere of radius r of the star, $y=4\pi r^2\rho$ where $\rho$ is the density of the star, and $t=ln(r/R)$ where R is the radius of the star. In Theorem 2 we have classified all the possible values of $m\left(r\right)/r$ and $4\pi r^2\rho$ when $r\to 0$.