Finite Difference Scheme and Finite Volume Scheme for Fractional Laplacian Operator and Some Applications

Preprint

Article

Finite Difference Scheme and Finite Volume Scheme for Fractional Laplacian Operator and Some Applications

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Junjie Wang^*,Shoucheng Yuan,Xiao Liu

This version is not peer-reviewed

Submitted:

19 October 2023

Posted:

20 October 2023

You are already at the latest version

Alerts

Abstract

In the paper, we develop some numerical schemes including finite difference scheme and finite volume scheme for the fractional Laplacian operator, and apply the resulted numerical schemes to solve some fractional diffusion equations. First, the fractional Laplacian operator can be characterized as the weak singular integral by a integral operator with zero boundary condition. Second, because of the solution of fractional diffusion equation is usually singular near the boundary, we apply finite difference scheme to discrete fractional Laplacian operator and fractional diffusion equation by fractional interpolation function. Moreover, it is find that the differential matrix of the above scheme is symmetric matrix, and strictly row-wise diagonally dominant in special fractional interpolation function. Third, we show finite volume scheme to discrete fractional diffusion equation by fractional interpolation function, and analyze the properties of differential matrix. Finally, the numerical experiments are given, and verify the correctness of theoretical results and the efficiency of the schemes.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

The fractional Laplacian is a very important fractional order operator that is often used to describe several phenomena such as the thin obstacle problem, optimization, finance, phase transitions, stratified materials, anomalous diffusion etc, and can be defined by the following form [1–3]

\begin{matrix} - {(- Δ)}^{\frac{α}{2}} u (x) = - F^{- 1} {(| ξ |}^{α} F (u (ξ))), \end{matrix}

(1)

where

F

is the Fourier transform. It can also be represented as the hypersingular integral form

\begin{matrix} - {(- Δ)}^{α / 2} u (x) = C_{n, α} P . V . \int_{R^{n}} \frac{u (x) - u (y)}{{| x - y |}^{n + α}} d y, \end{matrix}

(2)

where

C_{n, α} = \frac{α 2^{α 2^{α - 1} Γ (\frac{α + n}{2})}}{π^{n / 2} Γ (\frac{2 - α}{2})}

. In particular, one-dimensional fractional Laplacian can be expressed as the Riesz fractional derivative [4–8]

- {(- Δ)}^{α / 2} u (x) = \frac{\partial^{α}}{{\partial | x |}^{α}} u (x) = - \frac{1}{2 cos \frac{α π}{2}} [_{- \infty} D_{x}^{α} u (x) +_{x} D_{+ \infty}^{α} u (x)],

where

_{- \infty} D_{x}^{α} u (x),_{x} D_{+ \infty}^{α} u (x)

are left and right Riemann-Liouville fractional derivatives of order

α

respectively. When

α = 2

, the fractional Laplacian reduces to classical Laplacian operator. When

α \neq 2

, the fractional Laplacian is a nonlocal generalization of classical Laplacian operator. By investigating the literatures about fractional Laplacian operator, we find that the most of the numerical methods [9–21] for fractional Laplace operator are based on Fourier definition (1). However, the Fourier definition is suitable only for the problems defined either on the whole space or periodic boundary condition. The fractional Laplacian on a bounded domain is of great interest, not only from the mathematical point of view, but also in practical applications. Recently, some studies have been carried out on the fractional Laplacian with zero boundary conditions. First, based on Riesz fractional derivative, some finite difference methods such as fractional centered difference method, weighted and shifted Grünwald difference method, fourth-order compact method and the matrix transform method have been developed to discrete fractional Laplacian. Second, based on fractional Laplacian operator (2), some numerical methods have been proposed in [22–26] to discretize the fractional Laplacian operator, and show corresponding theoretical analysis.

Fractional diffusion equation with fractional Laplacian has been successfully used to simulate some physical phenomena such as the thin obstacle problem, stratified materials, anomalous diffusion etc. It is usually difficult to obtain the analytical solution of the Fractional diffusion equation with fractional Laplacian operator. Therefore, numerical methods have been playing more and more important roles for fractional diffusion equations [4–6]. In fact, some attentions have been paid to theory and numerical methods for the fractional diffusion equations with the fractional Laplacian operator. The main difficulties for dealing with the fraction diffusion equation are: i) the fractional Laplacian operator

{(- Δ)}^{\frac{α}{2}} u (x)

is non-local; ii) the solutions of the fractional diffusion equation is usually singular near the boundary; iii) the fractional Laplacian operator

{(- Δ)}^{\frac{α}{2}} u (x)

is a hypersingular integral. Recently, some attentions have been paid to theory and numerical methods to solve these difficulties. First, in order to deal with hypersingular integral representation of

{(- Δ)}^{α / 2} u (x)

, the main approach is to change the hypersingular integral into weak singular integral. Second, in order to resolve the singularity of non-smooth solutions of fractional diffusion equation, several numerical approaches [27,28] have been developed. In [27], non-uniform refined grids have been employed to solve fractional diffusion equation with non-smooth solutions at the end-points. In [28], an improved algorithm based on finite difference scheme has been employed to solve fractional diffusion equation with non-smooth solutions. In addition, in order to deal with non-smooth solutions of fractional diffusion equation, other numerical methods such as non-uniform refined grids, correction convolution quadrature, and non-polynomial basis functions have also been developed, and display corresponding theoretical analysis. However, in these works only classical interpolation method have been considered. As far as we know, there exist few studies on fractional interpolation function [29] for the differential equations with the fractional Laplacian operator. Because of the solution of fractional diffusion equation is usually singular near the boundary, the fractional interpolation function is more suitable than the classical interpolation function in dealing with the fractional diffusion equation. The main goal of this paper is to construct some numerical schemes for fractional Laplacian operator based on fractional interpolation function with zero boundary condition, and apply the resulted numerical schemes to solve fractional diffusion equation with fractional Laplacian operator.

In this paper, we use mainly finite difference method and finite volume method to discretize the fractional Laplacian and fractional diffusion equation by fractional interpolation function. First, we deal with hypersingular integral representation of

{(- Δ)}^{α / 2} u (x)

as weak singular integral by integral operator

J^{α} (x)

, and show finite difference scheme by linear interpolation function to deal with fractional Laplacian. Second, we use fractional interpolation function in the boundary region to approach fractional Laplacian based on some lemmas, and use classical interpolation function in the inner region. Moreover, applying resulted numerical scheme of fractional Laplacian to the fractional diffusion equation, and we show some corresponding theoretical analysis. Third, we show also finite volume schemes to solve the fractional Laplacian and fractional diffusion equation by fractional interpolation function and classical interpolation function. For simplicity’s sake, we only consider numerical scheme for uniform dissection, but, it is easy to generalize to nonuniform dissection by similar approach.

The outline of the paper is as follows. In Section 2, we present the finite difference scheme to deal with the fractional Laplacian by fractional interpolation function, and apply the resulted numerical schemes to solve some fractional diffusion equation. In Section 3, we present the finite volume scheme to deal with the fractional Laplacian and fractional diffuse equation by fractional interpolation function, and show corresponding theoretical analysis. In Section 4, the numerical experiments are made, and the results verify the efficiency of the schemes. Finally, some conclusion and discussion are given in Section 5.

2. Finite Difference Method for Fractional Laplacian and Fractional Diffusion Equation

Some difference schemes have been designed to discrete fractional Laplacian operator based on Riesz fractional derivative, including shifted Grünwald formula, second-order weighted, shifted Grünwald-Letnikov difference formulas and fractional central difference scheme. However, little attention was paid to approximate the hypersingular integral definition by fractional interpolation function. In this section, we show finite difference scheme for fractional Laplacian and fractional diffusion equation with zero boundary condition by fractional interpolation function. Here, one key idea is to deal with hypersingular integral representation of

{(- Δ)}^{α / 2} u (x)

as weak singular integral.

2.1. Finite Difference Scheme for Fractional Laplacian

Under the zero boundary condition:

u (x) = 0, x \in R / Ω, Ω = [a, b]

, it follows from [12] that the fractional Laplacian can be expressed as

\begin{matrix} {(- Δ)}^{α / 2} u (x) & = C_{1, α} \frac{d}{d x} J^{α} (x), \end{matrix}

(3)

where

\begin{matrix} J^{α} (x) & = \int_{Ω} {| x - y |}^{1 - α} u^{'} (y) d y, 0 < α < 2, α \neq 1, \end{matrix}

(4)

\begin{matrix} = \int_{Ω} ln | x - y | u^{'} (y) d y, α = 1 . \end{matrix}

(5)

For a positive integer N, we set

a = x_{0} < x_{1} < x_{2} < \dots < x_{N} = b

h_{i} = x_{i} - x_{i - 1}, i = 1, 2, \dots, N, I_{j} = (x_{j - 1}, x_{j}), j = 1, 2, \dots, N

. For simplicity’s sake, we only consider numerical scheme for uniform dissection on interval

Ω = [- 1, 1]

. For non-uniform dissection on interval

Ω = [a, b]

, we can also obtain the numerical result by similar approach. Define linear interpolation function of

u (x), x \in [x_{k - 1}, x_{k}]

π_{1, k} u (x)

i.e.

\begin{matrix} π_{1, k} u (x) = \frac{x_{k} - x}{x_{k} - x_{k - 1}} u_{k - 1} + \frac{x - x_{k - 1}}{x_{k} - x_{k - 1}} u_{k}, {(π_{1, k} u (x))}^{'} = δ_{x} u_{k - \frac{1}{2}} = \frac{u_{k} - u_{k - 1}}{x_{k} - x_{k - 1}} . \end{matrix}

(6)

It follows from central difference scheme that fractional Laplacian (3) can be expressed as the following form

\begin{matrix} {(- Δ)}_{h}^{α / 2} u_{i} & = C_{1, α} \frac{J^{α} (x_{i + 1}) - J^{α} (x_{i - 1})}{2 h} + C_{1, α} \frac{{(J^{α})}^{'''} (ξ)}{3} h^{2} . \end{matrix}

(7)

Now, we consider numerical scheme for weak singular integral (4). Let

x = x_{n}

0 < α < 2, α \neq 1

. Then, the integral operator

J^{α} (x_{n})

can be expressed by

\begin{matrix} J^{α} (x_{n}) = \int_{a}^{x_{n}} {(x_{n} - y)}^{1 - α} u^{'} (y) d y + \int_{x_{n}}^{b} {(y - x_{n})}^{1 - α} u^{'} (y) d y . \end{matrix}

(8)

We use

π_{1, k} u (x)

to approximate

u (x)

on every interval

[x_{k - 1}, x_{k}]

, and substituting (6) into (8) can yield

\begin{matrix} J^{α} (x_{n}) \approx J_{h}^{α} (x_{n}) = & \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} {(x_{n} - y)}^{1 - α} {(π_{1, k} u (y))}^{'} d y + \sum_{k = n + 1}^{N} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n})}^{1 - α} {(π_{1, k} u (y))}^{'} d y \\ = & \sum_{k = 1}^{n} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} {(x_{n} - y)}^{1 - α} d y + \sum_{k = n + 1}^{N} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n})}^{1 - α} d y \\ = & \sum_{k = 1}^{N - 1} \frac{b_{n - k}^{2 - α} - b_{n - k - 1}^{2 - α}}{h^{α - 1}} u_{k}, \end{matrix}

(9)

where

\begin{matrix} b_{l}^{2 - α} = \{\begin{matrix} \frac{{(l + 1)}^{2 - α} - {(l)}^{2 - α}}{2 - α}, l \geq 0, \\ \frac{{(- l)}^{2 - α} - {(- l - 1)}^{2 - α}}{2 - α}, l < 0 . \end{matrix} \end{matrix}

When

α = 1

, the integral operator

J^{α} (x_{n})

can be expressed as

\begin{matrix} J^{α} (x_{n}) = \int_{a}^{x_{n}} ln (x_{n} - y) u^{'} (y) d y + \int_{x_{n}}^{b} ln (y - x_{n}) u^{'} (y) d y . \end{matrix}

(10)

Substituting (6) into (10) can yield

\begin{matrix} J^{α} (x_{n}) \approx J_{h}^{α} (x_{n}) = & \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} ln (x_{n} - y) {(π_{1, k} u (y))}^{'} d y + \sum_{k = n + 1}^{N} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n}) {(π_{1, k} u (y))}^{'} d y \\ = & \sum_{k = 1}^{n} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} ln (x_{n} - y) d y + \sum_{k = n + 1}^{N} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n}) d y \\ = & \sum_{k = 1}^{N - 1} \frac{b_{n - k} - b_{n - k - 1}}{h} u_{k}, \end{matrix}

(11)

where

\begin{matrix} b_{l} = \{\begin{matrix} (l + 1) h ln (l + 1) h - l h ln l h - h, l \geq 1, \\ (l + 1) h ln (l + 1) h - h, l = 0, \\ (- l h) ln (- l h) - h, l = - 1, \\ (- l h) ln (- l h) - (- l - 1) h ln (- l - 1) h - h, l < - 1 . \end{matrix} \end{matrix}

It follows from numerical schemes (7), (9) and (11) that fractional Laplacian operator can be approximated by

\begin{matrix} {(- Δ)}_{h}^{α / 2} u (x_{i}) & \approx C_{1, α} \frac{J_{h}^{α} (x_{i + 1}) - J_{h}^{α} (x_{i - 1})}{2 h}, \end{matrix}

\begin{matrix} = C_{1, α} \sum_{k = 1}^{N - 1} \frac{b_{i - k + 1}^{2 - α} - b_{i - k}^{2 - α} - b_{i - k - 1}^{2 - α} + b_{i - k - 2}^{2 - α}}{2 h^{α - 2}} u_{k}, 0 < α < 2, α \neq 1, \end{matrix}

(12)

\begin{matrix} = \frac{1}{π} \sum_{k = 1}^{N - 1} \frac{b_{i - k + 1} - b_{i - k} - b_{i - k - 1} + b_{i - k - 2}}{2 h^{2}} u_{k}, α = 1 . \end{matrix}

(13)

The solution of fractional diffusion equation is usually singular near the boundary. In order to resolve the singularity of non-smooth solution of fractional diffusion equation, some numerical methods have been designed to discrete fractional Laplacian operator based on non-uniform refined grids. However, little attention was paid to fractional interpolation function to deal with fractional problems. In the section, we use fractional interpolation function to discrete fractional Laplacian operator.

Lemma 1.

[30]

Let

0 < α_{1} < α_{2} < \dots α_{n}

. Then, we have

{(x - x_{0})}^{α_{i}}, i = 1, 2, \dots, n

is linearly independent.

Lemma 2.

[30]

Given

n + 1

different interpolation points

x_{0}, x_{1}, \dots, x_{n}

and

0 < α_{1} < α_{2} < \dots α_{n}

. Let

\begin{matrix} D_{i} (x) = |\begin{matrix} {(x - x_{0})}^{α_{1}} & {(x - x_{0})}^{α_{2}} & \dots & {(x - x_{0})}^{α_{i}} & \dots & {(x - x_{0})}^{α_{n}} \\ {(x_{1} - x_{0})}^{α_{1}} & {(x_{1} - x_{0})}^{α_{2}} & \dots & {(x_{1} - x_{0})}^{α_{i}} & \dots & {(x_{1} - x_{0})}^{α_{n}} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋱ & ⋮ \\ {(x_{i - 1} - x_{0})}^{α_{1}} & {(x_{i - 1} - x_{0})}^{α_{2}} & \dots & {(x_{i - 1} - x_{0})}^{α_{i}} & \dots & {(x_{i - 1} - x_{0})}^{α_{n}} \\ {(x_{i + 1} - x_{0})}^{α_{1}} & {(x_{i + 1} - x_{0})}^{α_{2}} & \dots & {(x_{i + 1} - x_{0})}^{α_{i}} & \dots & {(x_{i + 1} - x_{0})}^{α_{n}} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋱ & ⋮ \\ {(x_{n} - x_{0})}^{α_{1}} & {(x_{n} - x_{0})}^{α_{2}} & \dots & {(x_{n} - x_{0})}^{α_{i}} & \dots & {(x_{n} - x_{0})}^{α_{n}} \end{matrix}|, \end{matrix}

and

\begin{matrix} D = |\begin{matrix} {(x_{1} - x_{0})}^{α_{1}} & {(x_{1} - x_{0})}^{α_{2}} & \dots & {(x_{1} - x_{0})}^{α_{n}} \\ {(x_{2} - x_{0})}^{α_{1}} & {(x_{2} - x_{0})}^{α_{2}} & \dots & {(x_{2} - x_{0})}^{α_{n}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ {(x_{n} - x_{0})}^{α_{1}} & {(x_{n} - x_{0})}^{α_{2}} & \dots & {(x_{n} - x_{0})}^{α_{n}} \end{matrix}| . \end{matrix}

Then, the fractional interpolation function

p_{n} (x)

can be expressed as the following form

\begin{matrix} p_{n} (x) = \sum_{i = 0}^{n} l_{i} (x_{i}) f (x_{i}), \end{matrix}

where, fractional interpolation basis function is expressed as

\begin{matrix} l_{i} (x) = \{\begin{matrix} {(- 1)}^{i - 1} \frac{D_{i} (x)}{D}, i \neq 0, \\ 1 - \sum_{i = 1}^{n} l_{i} (x), i = 0 . \end{matrix} \end{matrix}

Because of the solution of fractional diffusion equation is usually singular near the boundary, we use fractional interpolation function

p_{n} (x), x \in [x_{0}, x_{1}] \cup [x_{N - 1}, x_{N}]

and use classical interpolation function

I_{m} (x), x \in [x_{i - 1}, x_{i}], i = 2, 3, \dots, N - 1

\begin{matrix} I_{m} (x) & = \sum_{j = 0}^{m} {\hat{l}}_{j} (x) f (x_{i j}), x \in [x_{i - 1}, x_{i}], 2 \leq i \leq N - 1, \\ p_{n} (x) & = \{\begin{matrix} \sum_{j = 0}^{n} l_{j} (x) f (x_{1 j}), x \in [x_{0}, x_{1}], \\ \sum_{j = 0}^{n} l_{j} (x) f (x_{N j}), x \in [x_{N - 1}, x_{N}], \end{matrix} \end{matrix}

where,

{\hat{l}}_{j} (x)

is classical interpolation basis function, and

\begin{matrix} x_{0} = x_{10} < x_{11} < \dots < x_{1 n} = x_{1}, \\ x_{i - 1} = x_{i 0} < x_{i 1} < \dots < x_{i m} = x_{i}, 2 \leq i \leq N - 1, \\ x_{N - 1} = x_{N 0} < x_{N 1} < \dots < x_{N n} = x_{N} . \end{matrix}

We use fractional interpolation function to approximate

u (x)

x \in [x_{0}, x_{1}] \cup [x_{N - 1}, x_{N}]

, and use classical interpolation function to approximate

u (x)

on every interval

x \in [x_{i - 1}, x_{i}], i = 2, 3, \dots, N - 1

. When

0 < α < 2, α \neq 1

, weak singular integral (8) can be approximated by

\begin{matrix} J^{α} (x_{n}) \approx J_{h}^{α} (x_{n}) = & \int_{x_{0}}^{x_{1}} {(x_{n} - y)}^{1 - α} {(\sum_{j = 0}^{n} l_{j} (x) u (x_{1 j}))}^{'} d y + \sum_{k = 2}^{n} \int_{x_{k - 1}}^{x_{k}} {(x_{n} - y)}^{1 - α} {(\sum_{j = 0}^{m} {\hat{l}}_{j} (x) u (x_{k j}))}^{'} d y \\ + \sum_{k = n + 1}^{N - 1} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n})}^{1 - α} {(\sum_{j = 0}^{m} {\hat{l}}_{j} (x) u (x_{k j}))}^{'} d y + \int_{x_{N - 1}}^{x_{N}} {(y - x_{n})}^{1 - α} {(\sum_{j = 0}^{n} l_{j} (x) u (x_{N j}))}^{'} d y . \end{matrix}

When

α = 1

, weak singular integral (10) can be approximated by

\begin{matrix} J^{α} (x_{n}) \approx J_{h}^{α} (x_{n}) = & \int_{x_{0}}^{x_{1}} ln (x_{n} - y) {(\sum_{j = 0}^{n} l_{j} (x) u (x_{1 j}))}^{'} d y + \sum_{k = 2}^{n} \int_{x_{k - 1}}^{x_{k}} ln (x_{n} - y) {(\sum_{j = 0}^{m} {\hat{l}}_{j} (x) u (x_{k j}))}^{'} d y \\ + \sum_{k = n + 1}^{N - 1} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n}) {(\sum_{j = 0}^{m} {\hat{l}}_{j} (x) u (x_{k j}))}^{'} d y + \int_{x_{N - 1}}^{x_{N}} ln (y - x_{n}) {(\sum_{j = 0}^{n} l_{j} (x) u (x_{N j}))}^{'} d y . \end{matrix}

For simplicity’s sake, we use the following fractional interpolation function and classical interpolation function to approach

u (x)

i.e.

\begin{matrix} π_{α_{1}, 1} u (x) = & \frac{{(x - x_{0})}^{α_{1}}}{h^{α_{1}}} u_{1} + (1 - \frac{{(x - x_{0})}^{α_{1}}}{h^{α_{1}}}) u_{0}, x \in [x_{0}, x_{1}], \end{matrix}

(14)

\begin{matrix} π_{α_{1}, N} u (x) = & \frac{{(x_{N} - x)}^{α_{1}}}{h^{α_{1}}} u_{N - 1} + (1 - \frac{{(x_{N} - x)}^{α_{1}}}{h^{α_{1}}}) u_{N}, x \in [x_{N - 1}, x_{N}], \\ π_{2, k} u (x) = & \frac{(x - x_{k}) (x - x_{k - 1})}{(x_{k - 2} - x_{k}) (x_{k - 2} - x_{k - 1})} u_{k - 2} + \frac{(x - x_{k}) (x - x_{k - 2})}{(x_{k - 1} - x_{k}) (x_{k - 1} - x_{k - 2})} u_{k - 1} \end{matrix}

(15)

\begin{matrix} + \frac{(x - x_{k - 1}) (x - x_{k - 2})}{(x_{k} - x_{k - 1}) (x_{k} - x_{k - 2})} u_{k}, x \in [x_{k - 1}, x_{k}], 2 \leq k \leq N - 1 . \end{matrix}

(16)

It is easy to obtain

\begin{matrix} {(π_{α_{1}, 1} u (x))}^{'} & = α_{1} \frac{{(x - x_{0})}^{α_{1} - 1}}{h^{a_{1} - 1}} δ_{x} u_{N - \frac{1}{2}}, x \in [x_{0}, x_{1}], \end{matrix}

(17)

\begin{matrix} {(π_{α_{1}, N} u (x))}^{'} & = α_{1} \frac{{(x_{N} - x)}^{α_{1} - 1}}{h^{a_{1} - 1}} δ_{x} u_{N - \frac{1}{2}}, x \in [x_{N - 1}, x_{N}], \end{matrix}

(18)

\begin{matrix} {(π_{2, k} u (x))}^{'} & = δ_{x} u_{j - \frac{1}{2}} + δ_{x}^{2} u_{k - 1} (x - x_{k - \frac{1}{2}}), x \in [x_{k - 1}, x_{k}], 2 \leq k \leq N - 1, \end{matrix}

(19)

where

δ_{x}^{2} u_{k} = \frac{1}{x_{k} - x_{k - 1}} (δ_{x} u_{k + \frac{1}{2}} - δ_{x} u_{k - \frac{1}{2}})

Suppose

u (x) \in C^{α_{1}} [x_{0}, x_{1}] \cup [x_{N - 1}, x_{N}]

, we use

π_{α_{1}, 1} u (x), π_{α_{1}, N} u (x)

to approximate

u (x)

on the two small interval

[x_{0}, x_{1}] \cup [x_{N - 1}, x_{N}]

and

π_{2, k} u (x), 2 \leq k \leq N - 1

to approximate

u (x)

on the interval

[x_{k - 1}, x_{k}]

. When

α \neq 1

, substituting (14)-(16) into (8) can yield

\begin{matrix} J^{α} (x_{n}) \approx J_{h}^{α} (x_{n}) = & \int_{x_{0}}^{x_{1}} {(x_{n} - y)}^{1 - α} {(π_{α_{1}, 1} u (y))}^{'} d y + \sum_{k = 2}^{n} \int_{x_{k - 1}}^{x_{k}} {(x_{n} - y)}^{1 - α} {(π_{2, k} u (y))}^{'} d y \\ + \sum_{k = n + 1}^{N - 1} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n})}^{1 - α} {(π_{2, k} u (y))}^{'} d y + \int_{x_{N - 1}}^{x_{N}} {(y - x_{n})}^{1 - α} {(π_{α_{1}, N} u (y))}^{'} d y \\ = & \frac{α_{1}}{h^{a_{1} - 1}} δ_{x} u_{\frac{1}{2}} \int_{x_{0}}^{x_{1}} {(x_{n} - y)}^{1 - α} {(y - x_{0})}^{α_{1} - 1} d y + \frac{α_{1}}{h^{a_{1} - 1}} δ_{x} u_{N - \frac{1}{2}} \int_{x_{N - 1}}^{x_{N}} {(y - x_{n})}^{1 - α} {(y - x_{N})}^{α_{1} - 1} d y \\ + \sum_{k = 2}^{N - 1} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} {(x_{n} - y)}^{1 - α} d y + \sum_{k = n + 1}^{N} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n})}^{1 - α} d y \\ + \sum_{k = 2}^{n} δ_{x}^{2} u_{k - 1} \int_{x_{k - 1}}^{x_{k}} {(x_{n} - y)}^{1 - α} (y - x_{k - \frac{1}{2}}) d y + \sum_{k = n + 1}^{N - 1} δ_{x}^{2} u_{k - 1} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n})}^{1 - α} (y - x_{k - \frac{1}{2}}) d y \\ = & \sum_{k = 1}^{N} {\hat{b}}_{n - k}^{2 - α} \frac{u_{k} - u_{k - 1}}{h^{α - 1}} + \sum_{k = 1}^{N} a_{n - k}^{2 - α} \frac{u_{k} - 2 u_{k - 1} + u_{k - 2}}{h^{α - 1}} \\ = & \sum_{k = 1}^{N - 1} \frac{{\hat{b}}_{n - k}^{2 - α} - {\hat{b}}_{n - k - 1}^{2 - α}}{h^{α - 1}} u_{k} + \sum_{k = 1}^{N} \frac{a_{n - k}^{2 - α} - 2 a_{n - k - 1}^{2 - α} - a_{n - k - 2}^{2 - α}}{h^{α - 1}} u_{k}, \end{matrix}

(20)

where

\begin{matrix} {\hat{b}}_{n - k}^{2 - α} = \{\begin{matrix} \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{0}}^{x_{1}} {(x_{n} - y)}^{1 - α} {(y - x_{0})}^{α_{1} - 1} d y, k = 1, \\ \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{N - 1}}^{x_{N}} {(y - x_{n})}^{1 - α} {(y - x_{N})}^{α_{1} - 1} d y, k = N, \\ b_{n - k}^{2 - α}, 1 < k < N, \end{matrix} \end{matrix}

and

\begin{matrix} a_{l}^{2 - α} = \{\begin{matrix} \frac{l^{3 - α} - {(l + 1)}^{3 - α}}{3 - α} - \frac{(l + \frac{1}{2}) (l^{2 - α} - {(l + 1)}^{2 - α})}{2 - α}, l \geq 0, \\ \frac{{(- l)}^{3 - α} - {(- l - 1)}^{3 - α}}{3 - α} - \frac{(- l - \frac{1}{2}) ({(- l)}^{2 - α} - {(- l - 1)}^{2 - α})}{2 - α}, l < 0 . \end{matrix} \end{matrix}

When

α = 1

, weak singular integrals (10) can be approximated by

\begin{matrix} J^{α} (x_{n}) \approx J_{h}^{α} (x_{n}) = & \int_{x_{0}}^{x_{1}} ln (x_{n} - y) {(π_{α_{1}, 1} u (y))}^{'} d y + \sum_{k = 2}^{n} \int_{x_{k - 1}}^{x_{k}} ln (x_{n} - y) {(π_{2, k} u (y))}^{'} d y \\ + \sum_{k = n + 1}^{N - 1} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n}) {(π_{2, k} u (y))}^{'} d y + \int_{x_{N - 1}}^{x_{N}} ln (y - x_{n}) {(π_{α_{1}, N} u (y))}^{'} d y \\ = & \frac{α_{1}}{h^{a_{1} - 1}} δ_{x} u_{\frac{1}{2}} \int_{x_{0}}^{x_{1}} ln (x_{n} - y) {(y - x_{0})}^{α_{1} - 1} d y + \frac{α_{1}}{h^{a_{1} - 1}} δ_{x} u_{N - \frac{1}{2}} \int_{x_{N - 1}}^{x_{N}} ln (y - x_{n}) {(y - x_{N})}^{α_{1} - 1} d y \\ + \sum_{k = 2}^{N - 1} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} ln (x_{n} - y) d y + \sum_{k = n + 1}^{N} δ_{x} u_{k - \frac{1}{2}} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n}) d y \\ + \sum_{k = 2}^{n} δ_{x}^{2} u_{k - 1} \int_{x_{k - 1}}^{x_{k}} ln (x_{n} - y) (y - x_{k - \frac{1}{2}}) d y + \sum_{k = n + 1}^{N - 1} δ_{x}^{2} u_{k - 1} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n}) (y - x_{k - \frac{1}{2}}) d y \\ = & \sum_{k = 1}^{N} {\hat{b}}_{n - k} \frac{u_{k} - u_{k - 1}}{h} + \sum_{k = 1}^{N} a_{n - k} \frac{u_{k} - 2 u_{k - 1} + u_{k - 2}}{h^{2}} \\ = & \sum_{k = 1}^{N - 1} \frac{{\hat{b}}_{n - k} - {\hat{b}}_{n - k - 1}}{h} u_{k} + \sum_{k = 1}^{N} \frac{a_{n - k} - 2 a_{n - k - 1} - a_{n - k - 2}}{h^{2}} u_{k}, \end{matrix}

(21)

where

\begin{matrix} {\hat{b}}_{n - k} = \{\begin{matrix} \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{0}}^{x_{1}} ln (x_{n} - y) {(y - x_{0})}^{α_{1} - 1} d y, k = 1, \\ \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{N - 1}}^{x_{N}} ln (y - x_{n}) {(y - x_{N})}^{α_{1} - 1} d y, k = N, \\ b_{n - k}, 1 < k < N . \end{matrix} \end{matrix}

and

\begin{matrix} a_{l} = \{\begin{matrix} (l + \frac{1}{2}) [(l + 1) h ln (l + 1) h - l h ln l h - h] + \frac{1}{2} ln l h {(l h)}^{2} - \frac{1}{2} ln (l + 1) h {((l + 1) h)}^{2} + \frac{1}{4} ({((l + 1) h)}^{2} - {(l h)}^{2}), l \geq 1, \\ (l + \frac{1}{2}) [(l + 1) h ln (l + 1) h - h] - \frac{1}{2} ln (l + 1) h {((l + 1) h)}^{2} + \frac{1}{4} {((l + 1) h)}^{2}, l = 0, \\ (l + \frac{1}{2}) [(- l h) ln (- l h) - h] + \frac{1}{2} ln (- l h) {(- l h)}^{2} - \frac{1}{4} {(- l h)}^{2}, l = - 1, \\ (l + \frac{1}{2}) [(- l h) ln (- l h) - (- l - 1) h ln (- l - 1) h - h] \\ + \frac{1}{2} ln (- l h) {(- l h)}^{2} - \frac{1}{2} ln (- l - 1) h {((- l - 1) h)}^{2} + \frac{1}{4} ({((- l - 1) h)}^{2} - {(- l h)}^{2}), l < - 1 . \end{matrix} \end{matrix}

It follows from schemes (7), (20) and (21) that fractional Laplacian operator can be approximated by

\begin{matrix} {(- Δ)}_{h}^{α / 2} u_{i} & = C_{1, α} \frac{J_{h}^{α} (x_{i + 1}) - J_{h}^{α} (x_{i - 1})}{2 h} \end{matrix}

\begin{matrix} = C_{1, α} \sum_{k = 1}^{N - 1} \frac{{\hat{b}}_{i - k + 1}^{2 - α} - {\hat{b}}_{i - k}^{2 - α} - {\hat{b}}_{i - k - 1}^{2 - α} + {\hat{b}}_{i - k - 2}^{2 - α}}{2 h^{α - 2}} u_{k} + C_{1, α} \sum_{k = 1}^{N - 1} \frac{a_{i - k + 1}^{2 - α} - 2 a_{i - k}^{2 - α} + 2 a_{i - k - 2}^{2 - α} - a_{i - k - 3}^{2 - α}}{2 h^{α - 2}} u_{k}, 0 < α < 2, α \neq 1, \end{matrix}

(22)

\begin{matrix} = \frac{1}{π} \sum_{k = 1}^{N - 1} \frac{{\hat{b}}_{i - k + 1} - {\hat{b}}_{i - k} - {\hat{b}}_{i - k - 1} + {\hat{b}}_{i - k - 2}}{2 h^{2}} u_{k} + \frac{1}{π} \sum_{k = 1}^{N - 1} \frac{a_{i - k + 1} - 2 a_{i - k} + 2 a_{i - k - 2} - a_{i - k - 3}}{2 h^{3}} u_{k}, α = 1 . \end{matrix}

(23)

2.2. Finite Difference Scheme for Fractional Diffusion Equation

In the last subsection, we show two numerical schemes of fractional Laplacian operator based on interpolation function (6) and (14)-(16). In the subsection, we apply the numerical schemes to solve the following fractional diffusion equation:

\begin{matrix} μ u (x) + {(- Δ)}^{\frac{α}{2}} u (x) = f (x), x \in Ω, 0 < α < 2, \end{matrix}

(24)

\begin{matrix} u (x) = 0, x \in Ω^{c} . \end{matrix}

(25)

Let

U = [u_{1}, u_{2}, \dots, u_{N - 1}], F = [f (x_{1}), f (x_{2}), \dots, f (x_{N - 1})]

, and I is the unit matrix. First, applying numerical scheme (12)-(13) of fractional Laplacian operator to fractional diffusion Equation (24)-(25), we can obtain the following discrete numerical schemes:

\begin{matrix} μ I U + \frac{C_{1, α}}{2 h^{α - 2}} {\tilde{A}}^{α} U = F, 0 < α < 2, α \neq 1, \end{matrix}

(26)

\begin{matrix} μ I U + \frac{1}{2 π h^{2}} {\tilde{A}}^{α} U = F, α = 1, \end{matrix}

(27)

when

0 < α < 2, α \neq 1

, then

\begin{matrix} {\tilde{A}}_{i j}^{α} = \{\begin{matrix} 2 b_{1}^{2 - α} - 2 b_{0}^{2 - α}, i = j, \\ b_{2}^{2 - α} - b_{1}^{2 - α}, i - j = 1, \\ b_{- 3}^{2 - α} - b_{- 2}^{2 - α}, i - j = - 1, \\ b_{k + 1}^{2 - α} - b_{k}^{2 - α} - b_{k - 1}^{2 - α} + b_{k - 2}^{2 - α}, i - j = k > 1, \\ b_{- k + 1}^{2 - α} - b_{- k}^{2 - α} - b_{- k - 1}^{2 - α} + b_{- k - 2}^{2 - α}, i - j = - k < - 1, \end{matrix} \end{matrix}

when

α = 1

, then

\begin{matrix} {\tilde{A}}_{i j}^{α} = \{\begin{matrix} 2 b_{1} - 2 b_{0}, i = j, \\ b_{2} - b_{1}, i - j = 1, \\ b_{- 3} - b_{- 2}, i - j = - 1, \\ b_{k + 1} - b_{k} - b_{k - 1} + b_{k - 2}, i - j = k > 1, \\ b_{- k + 1} - b_{- k} - b_{- k - 1} + b_{- k - 2}, i - j = - k < - 1 . \end{matrix} \end{matrix}

Second, applying numerical scheme (22)-(23) of fractional Laplacian operator to fractional diffusion Equation (24)-(25), we can obtain the following discrete numerical schemes:

\begin{matrix} μ I U + \frac{C_{1, α}}{2 h^{2 - α}} A^{α} U = F, 0 < α < 2, α \neq 1, \end{matrix}

(28)

\begin{matrix} μ I U + \frac{1}{π} A^{α} U = F, α = 1, \end{matrix}

(29)

when

0 < α < 2, α \neq 1

, then

\begin{matrix} A_{i j}^{α} = \{\begin{matrix} 2 {\hat{b}}_{1}^{2 - α} - 2 {\hat{b}}_{0}^{2 - α} + 2 a_{1}^{2 - α} - 4 a_{0}^{2 - α}, i = j, \\ {\hat{b}}_{2}^{2 - α} - {\hat{b}}_{1}^{2 - α} + a_{2}^{2 - α} - 2 a_{1}^{2 - α} + 3 a_{0}^{2 - α}, i - j = 1, \\ {\hat{b}}_{- 3}^{2 - α} - {\hat{b}}_{- 2}^{2 - α} - 3 a_{- 1}^{2 - α} + 2 a_{- 2}^{2 - α} - a_{- 3}^{2 - α}, i - j = - 1, \\ {\hat{b}}_{k + 1}^{2 - α} - {\hat{b}}_{k}^{2 - α} - {\hat{b}}_{k - 1}^{2 - α} + {\hat{b}}_{k - 2}^{2 - α} + a_{k + 1}^{2 - α} - 2 a_{k}^{2 - α} + 2 a_{k - 1}^{2 - α} - a_{k - 2}^{2 - α}, i - j = k > 1, \\ {\hat{b}}_{- k + 1}^{2 - α} - {\hat{b}}_{- k}^{2 - α} - {\hat{b}}_{- k - 1}^{2 - α} + {\hat{b}}_{- k - 2}^{2 - α} + a_{- k + 1}^{2 - α} - 2 a_{- k}^{2 - α} + 2 a_{- k - 1}^{2 - α} - a_{- k - 2}^{2 - α}, i - j = - k < - 1, \end{matrix} \end{matrix}

when

α = 1

, then

\begin{matrix} A_{i j}^{α} = \{\begin{matrix} \frac{1}{2 h^{2}} (2 {\hat{b}}_{1} - 2 {\hat{b}}_{0}) + \frac{1}{2 h^{3}} (2 a_{1} - 4 a_{0}), i = j, \\ \frac{1}{2 h^{2}} ({\hat{b}}_{2} - {\hat{b}}_{1}) + \frac{1}{2 h^{3}} (a_{2} - 2 a_{1} + 3 a_{0}), i - j = 1, \\ \frac{1}{2 h^{2}} ({\hat{b}}_{- 3} - {\hat{b}}_{- 2}) + \frac{1}{2 h^{3}} (- 3 a_{- 1} + 2 a_{- 2} - a_{- 3}), i - j = - 1, \\ \frac{1}{2 h^{2}} ({\hat{b}}_{k + 1} - {\hat{b}}_{k} - {\hat{b}}_{k - 1} + {\hat{b}}_{k - 2}) + \frac{1}{2 h^{3}} (a_{k + 1} - 2 a_{k} + 2 a_{k - 1} - a_{k - 2}), i - j = k > 1, \\ \frac{1}{2 h^{2}} ({\hat{b}}_{- k + 1} - {\hat{b}}_{- k} - {\hat{b}}_{- k - 1} + {\hat{b}}_{- k - 2}) + \frac{1}{2 h^{3}} (a_{- k + 1} - 2 a_{- k} + 2 a_{- k - 1} - a_{- k - 2}), i - j = - k < - 1 . \end{matrix} \end{matrix}

Theorem 1.

When

α_{1} = 1

0 < α < 2, α \neq 1

, the matrix

A^{α}

is a symmetric matrix, and strictly row-wise diagonally dominant.

Proof: When

l > 0

a_{l}^{2 - α}

satisfy

b_{l}^{2 - α} = b_{- l - 1}^{2 - α}, a_{l}^{2 - α} = - a_{- l - 1}^{2 - α}

. Then, we have

\begin{matrix} b_{2}^{α} - b_{1}^{2 - α} = b_{- 3}^{α} - b_{- 2}^{2 - α}, a_{2}^{2 - α} - 2 a_{1}^{2 - α} + 3 a_{0}^{2 - α} = - 3 a_{- 1}^{2 - α} + 2 a_{- 2}^{2 - α} - a_{- 3}^{2 - α}, \\ b_{k + 1}^{α} - b_{k}^{2 - α} - b_{k - 1}^{2 - α} + b_{k - 2}^{2 - α} = b_{- k + 1}^{α} - b_{- k}^{2 - α} - b_{- k - 1}^{2 - α} + b_{- k - 2}^{2 - α}, \\ a_{k + 1}^{2 - α} - 2 a_{k}^{2 - α} + 2 a_{k - 1}^{2 - α} - a_{k - 2}^{2 - α} = a_{- k + 1}^{2 - α} - 2 a_{- k}^{2 - α} + 2 a_{- k - 1}^{2 - α} - a_{- k - 2}^{2 - α} . \end{matrix}

Thus,

A^{α}

is a symmetric matrix.

Now, we prove the matrix

A^{α}

is a strictly row-wise diagonally dominant. Let

\begin{matrix} {\tilde{c}}_{k} & = a_{k + 1}^{2 - α} - 2 a_{k}^{2 - α} + 2 a_{k - 1}^{2 - α} - a_{k - 2}^{2 - α} = {(k + 2)}^{2 - α} - 2 {(k + 1)}^{2 - α} + 2 {(k - 1)}^{2 - α} - {(k - 2)}^{2 - α}, \\ {\hat{c}}_{k} & = b_{k + 1}^{2 - α} - b_{k}^{2 - α} - b_{k - 1}^{2 - α} + b_{k - 2}^{2 - α} = {(k + 2)}^{2 - α} - {(k + 1)}^{2 - α} - {(k - 1)}^{2 - α} + {(k - 2)}^{2 - α} . \end{matrix}

Then

{\tilde{c}}_{k} = {\tilde{c}}_{- k}, {\hat{c}}_{k} = {\hat{c}}_{- k}

. Let

\begin{matrix} f_{1} (x) & = {(x + 2)}^{2 - α} - 2 {(x + 1)}^{2 - α} + 2 {(x - 1)}^{2 - α} - {(x - 2)}^{2 - α}, \end{matrix}

(30)

\begin{matrix} f_{2} (x) & = {(x + 2)}^{2 - α} - {(x + 1)}^{2 - α} - {(x - 1)}^{2 - α} + {(x - 2)}^{2 - α} . \end{matrix}

(31)

Then

\begin{matrix} f_{1}^{'} (x) & = (2 - α) [{(x + 2)}^{1 - α} - 2 {(x + 1)}^{1 - α} + 2 {(x - 1)}^{1 - α} - {(x - 2)}^{1 - α}] \end{matrix}

\begin{matrix} = (2 - α) [({(x + 2)}^{1 - α} - 2 {(x + 1)}^{1 - α} + x^{1 - α}) - (x^{1 - α} - 2 {(x - 1)}^{1 - α} + {(x - 2)}^{1 - α})], \\ f_{2}^{'} (x) & = (2 - α) [{(x + 2)}^{1 - α} - {(x + 1)}^{1 - α} - {(x - 1)}^{1 - α} + {(x - 2)}^{1 - α}] \end{matrix}

(32)

\begin{matrix} = (2 - α) [({(x + 2)}^{1 - α} - {(x + 1)}^{1 - α}) - ({(x - 1)}^{1 - α} - {(x - 2)}^{1 - α})] . \end{matrix}

(33)

Let

g_{1} (x) = x^{1 - α} - 2 {(x - 1)}^{1 - α} + {(x - 2)}^{1 - α}, g_{2} (x) = {(x - 1)}^{1 - α} + {(x - 2)}^{1 - α}

. Then

f_{1}^{'} (x) = (2 - α) [g_{1} (x + 2) - g_{1} (x)], f_{2}^{'} (x) = (2 - α) [g_{2} (x + 3) - g_{2} (x)] .

It follows from [5] that

g_{1} (x + 1) > g_{1} (x)

. Thus

g_{1} (x + 2) > g_{1} (x)

. It follows from (32) that

\begin{matrix} f_{1}^{'} (x) > 0 . \end{matrix}

(34)

In the same method, we can obtain

f_{2}^{'} (x) > 0

It follows from (30)-(31) that

{\tilde{c}}_{k} = f_{1} (k), {\hat{c}}_{k} = f_{2} (k)

. According to (30)-(31) and (34), we obtain

{\tilde{c}}_{k} > 0, {\tilde{c}}_{k} < {\tilde{c}}_{k + 1}

and

{\hat{c}}_{k} > 0, {\hat{c}}_{k} < {\hat{c}}_{k + 1}

. It follows from Taylor formula that

\begin{matrix} lim_{x \to \infty} (x^{2 - α} - 2 {(x + 1)}^{2 - α} + 2 {(x + 3)}^{2 - α} - {(x + 4)}^{2 - α}) \\ = & lim_{x \to \infty} x^{2 - α} (1 - 2 {(1 + \frac{1}{x})}^{2 - α} + 2 {(1 + \frac{3}{x})}^{2 - α} - {(1 + \frac{4}{x})}^{2 - α}) \\ = & lim_{x \to \infty} x^{2 - α} (1 - 2 (1 + \frac{2 - α}{x} + O (\frac{1}{x^{2}})) + 2 (1 + \frac{3 (2 - α)}{x} + O (\frac{1}{x^{2}})) - (1 + \frac{4 (2 - α)}{x} + O (\frac{1}{x^{2}}))) \\ = & lim_{x \to \infty} x^{2 - α} O (\frac{1}{x^{2}}) = 0, \end{matrix}

and

\begin{matrix} lim_{x \to \infty} (x^{2 - α} - {(x + 1)}^{2 - α} - {(x + 3)}^{2 - α} + {(x + 4)}^{2 - α}) \\ = & lim_{x \to \infty} x^{2 - α} (1 - {(1 + \frac{1}{x})}^{2 - α} - {(1 + \frac{3}{x})}^{2 - α} + {(1 + \frac{4}{x})}^{2 - α}) \\ = & lim_{x \to \infty} x^{2 - α} (1 - (1 + \frac{2 - α}{x} + O (\frac{1}{x^{2}})) - (1 + \frac{3 (2 - α)}{x} + O (\frac{1}{x^{2}})) + (1 + \frac{4 (2 - α)}{x} + O (\frac{1}{x^{2}}))) \\ = & lim_{x \to \infty} x^{2 - α} O (\frac{1}{x^{2}}) = 0 . \end{matrix}

According to (34), we get

lim_{k \to \infty} {\tilde{c}}_{k} = 0, lim_{k \to \infty} {\hat{c}}_{k} = 0

Let

A_{i i} = 2 b_{1} - 2 b_{0} + 2 a_{1} - 4 a_{0}

. Then

\begin{matrix} \sum_{k = 1, k \neq i}^{N - 1} A_{i j} = & \sum_{k = - 1}^{- N + 2} b_{- k + 1} - b_{- k} - b_{- k - 1} + b_{- k - 2} + a_{- k + 1} - 2 a_{- k} + 2 a_{- k - 1} - a_{- k - 2} \\ + \sum_{k = 1}^{N - 2} b_{k + 1} - b_{k} - b_{k - 1} + b_{k - 2} + a_{k + 1} - 2 a_{k} + 2 a_{k - 1} - a_{k - 2} \\ \leq & \sum_{k = - 1}^{- \infty} b_{- k + 1} - b_{- k} - b_{- k - 1} + b_{- k - 2} + a_{- k + 1} - 2 a_{- k} + 2 a_{- k - 1} - a_{- k - 2} \\ + \sum_{k = 1}^{+ \infty} b_{k + 1} - b_{k} - b_{k - 1} + b_{k - 2} + a_{k + 1} - 2 a_{k} + 2 a_{k - 1} - a_{k - 2} \\ \leq & 2 b_{1} - 2 b_{0} + 2 a_{1} - 4 a_{0} = A_{i i} . \end{matrix}

This ends the proof.□

In similar method, the matrix

{\tilde{A}}^{α}

is also a symmetric matrix, and strictly row-wise diagonally dominant.

3. Finite Volume Method for Fractional Diffusion Equation

In this section, we show finite volume method for fractional diffusion equations with zero boundary condition. Here, one key idea is to deal with hypersingular integral representation of

{(- Δ)}^{α / 2} u (x)

as weak singular integral.

3.1. Finite Volume Method Based on a Linear Interpolation Function

We take the integration of fractional diffusion Equation (24) over a control volume

[x_{i - 1 / 2}, x_{i + 1 / 2}]

, which leads to

\begin{matrix} μ \int_{x_{i - 1 / 2}}^{x_{i + 1 / 2}} u (x) d x + C_{1, α} (J^{α} (x_{i + 1 / 2}) - J^{α} (x_{i - 1 / 2})) = \int_{x_{i - 1 / 2}}^{x_{i + 1 / 2}} f (x) d x, 0 < α < 2, α \neq 1, \end{matrix}

(35)

\begin{matrix} μ \int_{x_{i - 1 / 2}}^{x_{i + 1 / 2}} u (x) d x + \frac{1}{π} (J^{α} (x_{i + 1 / 2}) - J^{α} (x_{i - 1 / 2})) = \int_{x_{i - 1 / 2}}^{x_{i + 1 / 2}} f (x) d x, α = 1 . \end{matrix}

(36)

We use

π_{1, k} u (x)

to approximate

u (x)

on the interval

[x_{k - 1}, x_{k}]

. When

0 < α < 2, α \neq 1

, the integral operator

J^{α} (x_{n + 1 / 2})

can be expressed by

\begin{matrix} J^{α} (x_{n + 1 / 2}) \approx J_{h}^{α} (x_{n + 1 / 2}) = & \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} {(x_{n + 1 / 2} - y)}^{1 - α} {(π_{1, k} u (y))}^{'} d y + \sum_{k = n + 2}^{N} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n + 1 / 2})}^{1 - α} {(π_{1, k} u (y))}^{'} d y \\ + \int_{x_{n}}^{x_{n + 1 / 2}} {(y - x_{n + 1 / 2})}^{1 - α} {(π_{1, k} u (y))}^{'} d y + \int_{x_{n + 1 / 2}}^{x_{n + 1}} {(y - x_{n + 1 / 2})}^{1 - α} {(π_{1, k} u (y))}^{'} d y \\ = & \sum_{k = 1}^{N} b_{n - k}^{2 - α} \frac{u_{k} - u_{k - 1}}{h^{α - 1}} \\ = & \sum_{k = 1}^{N - 1} \frac{b_{n - k}^{2 - α} - b_{n - k - 1}^{2 - α}}{h^{α - 1}} u_{k}, \end{matrix}

(37)

where

\begin{matrix} b_{l}^{2 - α} = \{\begin{matrix} \frac{{(l + 1 + \frac{1}{2})}^{2 - α} - {(l + \frac{1}{2})}^{2 - α}}{2 - α}, l \geq 0, \\ \frac{2}{2^{2 - α} (2 - α)}, l = - 1, \\ \frac{{(- l - \frac{1}{2})}^{2 - α} - {(- l - 1 - \frac{1}{2})}^{2 - α}}{2 - α}, l \leq - 2 . \end{matrix} \end{matrix}

When

α = 1

, the integral operator

J^{α} (x_{n + 1 / 2})

can be expressed by

\begin{matrix} J^{α} (x_{n + 1 / 2}) \approx J_{h}^{α} (x_{n + 1 / 2}) = & \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} ln (x_{n + 1 / 2} - y) {(π_{1, k} u (y))}^{'} d y + + \sum_{k = n + 2}^{N} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n + 1 / 2}) {(π_{1, k} u (y))}^{'} d y \\ + \int_{x_{n}}^{x_{n + 1 / 2}} ln (y - x_{n + 1 / 2}) {(π_{1, k} u (y))}^{'} d y + \int_{x_{n + 1 / 2}}^{x_{n + 1}} ln (y - x_{n + 1 / 2}) {(π_{1, k} u (y))}^{'} d y \\ = & \sum_{k = 1}^{N} b_{n - k} \frac{u_{k} - u_{k - 1}}{h} \\ = & \sum_{k = 1}^{N - 1} \frac{b_{n - k} - b_{n - k - 1}}{h} u_{k}, \end{matrix}

(38)

where

\begin{matrix} b_{l} = \{\begin{matrix} (l + 1 + \frac{1}{2}) h ln (l + 1 + \frac{1}{2}) h - (l + \frac{1}{2}) h ln (l + \frac{1}{2}) h - h, l \geq 1, \\ (l + 1 + \frac{1}{2}) h ln (l + 1 + \frac{1}{2}) h - h, l = 0, \\ ((- l - \frac{1}{2}) h) ln ((- l - \frac{1}{2}) h) - h, l = - 1, \\ ((- l - \frac{1}{2}) h) ln (- l h) - (- l - 1) h ln (- l - 1 - \frac{1}{2}) h - h, l < - 1 . \end{matrix} \end{matrix}

Let

U = [u_{1}, u_{2}, \dots, u_{N - 1}], F = [\int_{x_{1 / 2}}^{x_{1 + 1 / 2}} f (x) d x, \int_{x_{1 + 1 / 2}}^{x_{2 + 1 / 2}} f (x) d x, \dots, \int_{x_{N - 3 / 2}}^{x_{N - 1 / 2}} f (x) d x]

. Then, applying numerical scheme (37)-(38) of the integral operator

J^{α} (x_{n + 1 / 2})

to fractional diffusion Equation (24)-(25), we can obtain the following discrete numerical schemes:

\begin{matrix} μ \tilde{B} U + \frac{C_{1, α}}{h^{α - 1}} {\tilde{A}}^{α} U = F, 0 < α < 2, α \neq 1, \end{matrix}

(39)

\begin{matrix} μ \tilde{B} U + \frac{1}{π h} {\tilde{A}}^{α} U = F, α = 1, \end{matrix}

(40)

where

\begin{matrix} \tilde{B} = [\begin{matrix} 6 h / 8 & h / 8 & 0 & \dots & 0 & 0 & 0 \\ h / 8 & 6 h / 8 & h / 8 & \dots & 0 & 0 & 0 \\ 0 & h / 8 & 6 h / 8 & \dots & 0 & 0 & 0 \\ \dots & \dots & \dots & ⋱ & \dots & \dots & \dots \\ 0 & 0 & 0 & \dots & 6 h / 8 & h / 8 & 0 \\ 0 & 0 & 0 & \dots & h / 8 & 6 h / 8 & h / 8 \\ 0 & 0 & 0 & \dots & 0 & 6 h / 8 & h / 8 \end{matrix}] . \end{matrix}

When

0 < α < 2, α \neq 1

, then

\begin{matrix} {\tilde{A}}_{i j}^{α} = \{\begin{matrix} 2 b_{0}^{2 - α} - 2 b_{- 1}^{2 - α}, i = j, \\ b_{1}^{2 - α} - 2 b_{0}^{2 - α} + b_{- 1}^{2 - α}, i - j = 1, \\ b_{- 1}^{2 - α} - 2 b_{- 2}^{2 - α} + b_{- 3}^{2 - α}, i - j = - 1, \\ b_{k}^{2 - α} - 2 b_{k - 1}^{2 - α} + b_{k + 1}^{2 - α}, i - j = k > 1, \\ b_{- k}^{2 - α} - 2 b_{- k - 1}^{2 - α} + b_{- k - 2}^{2 - α}, i - j = - k < - 1 . \end{matrix} \end{matrix}

(41)

When

α = 1

, then

\begin{matrix} {\tilde{A}}_{i j} = \{\begin{matrix} 2 b_{0} - 2 b_{- 1}, i = j, \\ b_{1} - 2 b_{0} + b_{- 1}, i - j = 1, \\ b_{- 1} - 2 b_{- 2} + b_{- 3}, i - j = - 1, \\ b_{k} - 2 b_{k - 1} + b_{k + 1}, i - j = k > 1, \\ b_{- k} - 2 b_{- k - 1} + b_{- k - 2}, i - j = - k < - 1 . \end{matrix} \end{matrix}

(42)

Theorem 2.

For

0 < α < 2, α \neq 1

, the matrix

{\tilde{A}}^{α}

is strictly row-wise diagonally dominant.

Proof: When

l > 0

b_{l}^{2 - α}

satisfy

b_{l}^{2 - α} = b_{- l - 2}^{2 - α}

. Then, we have

\begin{matrix} b_{1}^{α} - 2 b_{0}^{2 - α} + b_{- 1}^{2 - α} = b_{- 1}^{α} - 2 b_{- 2}^{2 - α} + b_{- 3}^{2 - α}, \\ b_{k + 3 / 2}^{α} - b_{k + 1 / 2}^{2 - α} - b_{k - 1 / 2}^{2 - α} - b_{k - 3 / 2}^{2 - α} = b_{- k + 3 / 2}^{α} - b_{- k + 1 / 2}^{2 - α} - b_{- k - 1 / 2}^{2 - α} - b_{- k - 3 / 2}^{2 - α} . \end{matrix}

Thus,

{\tilde{A}}^{α}

is a symmetric matrix.

Now, we prove the matrix

{\tilde{A}}^{α}

is a strictly row-wise diagonally dominant. Let

c_{k} = b_{k + 3 / 2}^{α} - b_{k + 1 / 2}^{2 - α} - b_{k - 1 / 2}^{2 - α} - b_{k - 3 / 2}^{2 - α} = {(k + 3 / 2)}^{2 - α} - 3 {(k + 1 / 2)}^{2 - α} + 3 {(k - 1 / 2)}^{2 - α} - {(k - 3 / 2)}^{2 - α} .

Then

c_{k} = c_{- k}

. Let

\begin{matrix} f (x) = {(x + 2)}^{2 - α} - 3 {(x + 1)}^{2 - α} + 3 {(x)}^{2 - α} - {(x - 1)}^{2 - α} . \end{matrix}

(43)

Then

\begin{matrix} f^{'} (x) & = (2 - α) [{(x + 2)}^{1 - α} - 3 {(x + 1)}^{1 - α} + 3 x^{1 - α} - {(x - 1)}^{1 - α}] \\ = (2 - α) [({(x + 2)}^{1 - α} - 2 {(x + 1)}^{1 - α} + x^{1 - α}) - ({(x + 1)}^{1 - α} - 2 x^{1 - α} + {(x - 1)}^{1 - α})] . \end{matrix}

(44)

Let

g (x) = x^{1 - α} - 2 {(x - 1)}^{1 - α} + {(x - 2)}^{1 - α}

. Then

f^{'} (x) = (2 - α) [g (x + 1) - g (x)] .

It follows from [5] that

g (x + 1) > g (x)

. Thus

g (x + 2) > g (x)

. It follows from (44) that

\begin{matrix} f^{'} (x) > 0 . \end{matrix}

(45)

It follows from (43) that

c_{k} = f (k)

. According to (43) and (45), we obtain

c_{k} < 0, c_{k} < c_{k + 1}

. It follows from Taylor formula that

\begin{matrix} lim_{x \to \infty} (x^{λ} - 3 {(x - 1)}^{λ} + 3 {(x - 2)}^{λ} - {(x - 3)}^{λ}) \\ = & lim_{x \to \infty} x^{λ} (1 - 3 {(1 - \frac{1}{x})}^{λ} + 3 {(1 - \frac{2}{x})}^{λ} - {(1 - \frac{3}{x})}^{λ}) \\ = & lim_{x \to \infty} x^{λ} (1 - 3 (1 + \frac{λ}{x} + O (\frac{1}{x^{2}})) + 3 (1 + \frac{2 λ}{x} + O (\frac{1}{x^{2}})) - (1 + \frac{3 λ}{x} + O (\frac{1}{x^{2}}))) \\ = & lim_{x \to \infty} x^{λ} O (\frac{1}{x^{2}}) = 0 . \end{matrix}

(46)

According to (46), we get

lim_{k \to \infty} c_{k} = 0

When

l > 0

c_{l}

satisfy

c_{l} = c_{- l}

. Thus,

{\tilde{A}}^{α}

is a symmetric matrix. Let

{\tilde{A}}_{i i} = 2 {(3 / 2)}^{2 - α} - 2 {(1 / 2)}^{2 - α}

. Then

\begin{matrix} \sum_{k = 1, k \neq i}^{N - 1} {\tilde{A}}_{i j} & = \sum_{j = - 1}^{- N + 2} c_{k} + \sum_{j = 1}^{N - 2} c_{k} \\ \leq \sum_{j = - 1}^{- \infty} c_{k} + \sum_{j = 1}^{+ \infty} c_{k} \\ \leq 2 {(3 / 2)}^{2 - α} - 2 {(1 / 2)}^{2 - α} = {\tilde{A}}_{i i} . \end{matrix}

This ends the proof.□

3.2. Finite Volume Method Based on Fractional Interpolation Function

In the subsection, in order to resolve the singularity of non-smooth solution of fractional diffusion equation, we use fractional interpolation function to discrete fractional diffusion equation.

Suppose

u (x) \in C^{α_{1}} [x_{0}, x_{1}] \cup [x_{N - 1}, x_{N}]

, we use

π_{α_{1}, 1} u (x), π_{α_{1}, N} u (x)

to approximate

u (x)

on the two small interval

[x_{0}, x_{1}] \cup [x_{N - 1}, x_{N}]

, and

π_{2, k} u (x), 2 \leq k \leq N - 1

to approximate

u (x)

on the interval

[x_{k - 1}, x_{k}]

. Let

x = x_{n + 1 / 2}

0 < α < 2, α \neq 1

, the integral operator

J^{α} (x_{n + 1 / 2})

can be expressed by

\begin{matrix} J^{α} (x_{n + 1 / 2}) \approx J_{h}^{α} (x_{n + 1 / 2}) = & \int_{x_{0}}^{x_{1}} {(x_{n + 1 / 2} - y)}^{1 - α} {(π_{α_{1}, 1} u (y))}^{'} d y + \sum_{k = 2}^{n} \int_{x_{k - 1}}^{x_{k}} {(x_{n + 1 / 2} - y)}^{1 - α} {(π_{2, k} u (y))}^{'} d y \\ + \int_{x_{n}}^{x_{n + 1 / 2}} {(y - x_{n + 1 / 2})}^{1 - α} {(π_{2, k} u (y))}^{'} d y + \int_{x_{n + 1 / 2}}^{x_{n + 1}} {(y - x_{n + 1 / 2})}^{1 - α} {(π_{2, k} u (y))}^{'} d y \\ + \sum_{k = n + 2}^{N - 1} \int_{x_{k - 1}}^{x_{k}} {(y - x_{n + 1 / 2})}^{1 - α} {(π_{2, k} u (y))}^{'} d y + \int_{x_{N - 1}}^{x_{N}} {(y - x_{n + 1 / 2})}^{1 - α} {(π_{α_{1}, N} u (y))}^{'} d y \\ = & \sum_{k = 1}^{N} {\hat{b}}_{n - k}^{2 - α} \frac{u_{k} - u_{k - 1}}{h^{α - 1}} + \sum_{k = 1}^{N} a_{n - k}^{2 - α} \frac{u_{k} - 2 u_{k - 1} + u_{k - 2}}{h^{α - 1}} \\ = & \sum_{k = 1}^{N - 1} \frac{{\hat{b}}_{n - k}^{2 - α} - {\hat{b}}_{n - k - 1}^{2 - α}}{h^{α - 1}} u_{k} + \sum_{k = 1}^{N} \frac{a_{n - k}^{2 - α} - 2 a_{n - k - 1}^{2 - α} + a_{n - k - 2}^{2 - α}}{h^{α - 1}} u_{k}, \end{matrix}

(47)

where

\begin{matrix} {\hat{b}}_{n - k}^{2 - α} = \{\begin{matrix} \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{0}}^{x_{1}} {| x_{n + 1 / 2} - y |}^{1 - α} {(y - x_{0})}^{α_{1} - 1} d y, k = 1, \\ \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{N - 1}}^{x_{N}} {| y - x_{n + 1 / 2} |}^{1 - α} {(y - x_{N})}^{α_{1} - 1} d y, k = N, \\ b_{n - k}^{2 - α}, 1 < k < N, \end{matrix} \end{matrix}

and

\begin{matrix} a_{l}^{2 - α} = \{\begin{matrix} \frac{{(l + \frac{1}{2})}^{3 - α} - {(l + 1 + \frac{1}{2})}^{3 - α}}{3 - α} - \frac{(l + 1) ({(l + \frac{1}{2})}^{2 - α} - {(l + 1 + \frac{1}{2})}^{2 - α})}{2 - α}, l \geq 0, \\ 0, l = - 1, \\ \frac{{(- l - \frac{1}{2})}^{3 - α} - {(- l - 1 - \frac{1}{2})}^{3 - α}}{3 - α} - \frac{(- l - 1) ({(- l - \frac{1}{2})}^{2 - α} - {(- l - 1 - \frac{1}{2})}^{2 - α})}{2 - α}, l \leq - 2 . \end{matrix} \end{matrix}

When

α = 1

, the integral operator

J^{α} (x_{n + 1 / 2})

can be expressed by

\begin{matrix} J^{α} (x_{n + 1 / 2}) \approx J_{h}^{α} (x_{n + 1 / 2}) = & \int_{x_{0}}^{x_{1}} ln (x_{n + 1 / 2} - y) {(π_{1, 1} u (y))}^{'} d y + \sum_{k = 2}^{n} \int_{x_{k - 1}}^{x_{k}} ln (x_{n + 1 / 2} - y) {(π_{2, k} u (y))}^{'} d y \\ + \int_{x_{n}}^{x_{n + 1 / 2}} ln (y - x_{n + 1 / 2}) {(π_{2, k} u (y))}^{'} d y + \int_{x_{n + 1 / 2}}^{x_{n + 1}} ln (y - x_{n + 1 / 2}) {(π_{2, k} u (y))}^{'} d y \\ + \sum_{k = n + 2}^{N - 1} \int_{x_{k - 1}}^{x_{k}} ln (y - x_{n + 1 / 2}) {(π_{2, k} u (y))}^{'} d y + \int_{x_{N - 1}}^{x_{N}} ln (y - x_{n + 1 / 2}) {(π_{1, N} u (y))}^{'} d y \\ = & \sum_{k = 1}^{N} b_{n - k} \frac{u_{k} - u_{k - 1}}{h} + \sum_{k = 1}^{N} a_{n - k}^{2 - α} \frac{u_{k} - 2 u_{k - 1} + u_{k - 2}}{h^{2}} \\ = & \sum_{k = 1}^{N - 1} \frac{b_{n - k} - b_{n - k - 1}}{h} u_{k} + \sum_{k = 1}^{N} \frac{a_{n - k}^{2 - α} - 2 a_{n - k - 1}^{2 - α} + a_{n - k - 2}^{2 - α}}{h^{2}} u_{k}, \end{matrix}

(48)

where

\begin{matrix} {\hat{b}}_{n - k}^{2 - α} = \{\begin{matrix} \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{0}}^{x_{1}} ln | x_{n + 1 / 2} - y | {(y - x_{0})}^{α_{1} - 1} d y, k = 1, \\ \frac{α_{1}}{h^{a_{1} - 1}} \int_{x_{N - 1}}^{x_{N}} ln | y - x_{n + 1 / 2} | {(y - x_{N})}^{α_{1} - 1} d y, k = N, \\ b_{n - k}^{2 - α}, 1 < k < N, \end{matrix} \end{matrix}

and

\begin{matrix} a_{l} = \{\begin{matrix} (l + 1) [(l + 1 + \frac{1}{2}) h ln (l + 1 + \frac{1}{2}) h - (l + + \frac{1}{2}) h ln (l + \frac{1}{2}) h - h] \\ + \frac{1}{2} ln (l + \frac{1}{2}) h {((l + \frac{1}{2}) h)}^{2} - \frac{1}{2} ln (l + 1 + \frac{1}{2}) h {((l + 1 + \frac{1}{2}) h)}^{2} + \frac{1}{4} ({((l + 1 + \frac{1}{2}) h)}^{2} - {((l + \frac{1}{2}) h)}^{2}), l \geq 1, \\ (l + 1) [(l + 1 + \frac{1}{2}) h ln (l + 1 + \frac{1}{2}) h - h] - \frac{1}{2} ln (l + 1 + \frac{1}{2}) h {((l + 1 + \frac{1}{2}) h)}^{2} + \frac{1}{4} {((l + 1 + \frac{1}{2}) h)}^{2}, l = 0, \\ (l + 1) [((- l - \frac{1}{2}) h) ln ((- l - \frac{1}{2}) h) - h] + \frac{1}{2} ln (- l h) {((- l - \frac{1}{2}) h)}^{2} - \frac{1}{4} {((- l - \frac{1}{2}) h)}^{2}, l = - 1, \\ (l + 1) [((- l - \frac{1}{2}) h) ln ((- l - \frac{1}{2}) h) - (- l - 1 - \frac{1}{2}) h ln (- l - 1 - \frac{1}{2}) h - h] \\ + \frac{1}{2} ln ((- l - \frac{1}{2}) h) {((- l - \frac{1}{2}) h)}^{2} - \frac{1}{2} ln (- l - 1 - \frac{1}{2}) h {((- l - 1 - \frac{1}{2}) h)}^{2} + \frac{1}{4} ({((- l - 1 - \frac{1}{2}) h)}^{2} - {((- l - \frac{1}{2}) h)}^{2}), l < - 1 . \end{matrix} \end{matrix}

It follows from (47)-(48) that

\begin{matrix} J_{h}^{α} (x_{n + 1 / 2}) - J_{h}^{α} (x_{n - 1 / 2}) = \sum_{k = 1}^{N - 1} \frac{{\hat{b}}_{n - k}^{2 - α} - 2 {\hat{b}}_{n - k - 1}^{2 - α} + {\hat{b}}_{n - k - 2}^{2 - α}}{h^{α - 1}} u_{k} + \sum_{k = 1}^{N} \frac{a_{n - k}^{2 - α} - 3 a_{n - k - 1}^{2 - α} + 3 a_{n - k - 2}^{2 - α} - a_{n - k - 3}^{2 - α}}{h^{α - 1}} u_{k}, 0 < α < 2, α \neq 1, \\ J_{h}^{α} (x_{n + 1 / 2}) - J_{h}^{α} (x_{n - 1 / 2}) = \sum_{k = 1}^{N - 1} \frac{{\hat{b}}_{n - k} - 2 {\hat{b}}_{n - k - 1} + {\hat{b}}_{n - k - 2}}{h} u_{k} + \sum_{k = 1}^{N} \frac{a_{n - k} - 3 a_{n - k - 1} + 3 a_{n - k - 2} - a_{n - k - 3}}{h^{2}} u_{k}, α = 1 . \end{matrix}

Now, we compute the integral

\int_{x_{i - 1 / 2}}^{x_{i + 1 / 2}} u (x) d x

. When

i = 1

, the integral can be approximated by

\begin{matrix} \int_{x_{1 / 2}}^{x_{3 / 2}} u (x) d x = & \int_{x_{1 / 2}}^{x_{1}} π_{α_{1}, 1} u (x) d x + \int_{x_{1}}^{x_{3 / 2}} π_{2, 2} u (x) d x \\ = & \int_{x_{1 / 2}}^{x_{1}} \frac{{(x - x_{0})}^{α_{1}}}{h^{α_{1}}} u_{1} + (1 - \frac{{(x - x_{0})}^{α_{1}}}{h^{α_{1}}}) u_{0} d x \\ + \int_{x_{1}}^{x_{3 / 2}} \frac{(x - x_{2}) (x - x_{1})}{2 h^{2}} u_{0} + \frac{(x - x_{2}) (x - x_{0})}{- h^{2}} u_{1} + \frac{(x - x_{1}) (x - x_{0})}{2 h^{2}} u_{2} d x \\ = & (\frac{h}{2} - \frac{1}{α_{1} + 1} + \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}}) u_{0} + (\frac{1}{α_{1} + 1} - \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}}) u_{1} - \frac{h}{24} u_{0} + \frac{11 h}{24} u_{1} + \frac{h}{12} u_{2} \\ = & (\frac{h}{2} - \frac{1}{α_{1} + 1} + \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}} - \frac{h}{24}) u_{0} + (\frac{1}{α_{1} + 1} - \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}} + \frac{11 h}{24}) u_{1} + \frac{h}{12} u_{2} \end{matrix}

When

i = N - 1

, the integral can be approximated by

\begin{matrix} \int_{x_{N - 3 / 2}}^{x_{N - 1 / 2}} u (x) d x = & \int_{x_{N - 1}}^{x_{N - 1 / 2}} π_{α_{1}, N} u (x) d x + \int_{x_{N - 3 / 2}}^{x_{N - 1}} π_{2, N - 1} u (x) d x \\ = & \int_{x_{N - 1}}^{x_{N - 1 / 2}} \frac{{(x - x_{N})}^{α_{1}}}{h^{α_{1}}} u_{N - 1} + (1 - \frac{{(x - x_{N})}^{α_{1}}}{h^{α_{1}}}) u_{N} d x \\ + \int_{x_{N - 3 / 2}}^{x_{N - 1}} \frac{(x - x_{N}) (x - x_{N - 1})}{2 h^{2}} u_{N - 2} + \frac{(x - x_{N}) (x - x_{N - 2})}{- h^{2}} u_{N - 1} + \frac{(x - x_{N - 1}) (x - x_{N - 2})}{2 h^{2}} u_{N} d x \\ = & (\frac{h}{2} - \frac{1}{α_{1} + 1} + \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}}) u_{N} + (\frac{1}{α_{1} + 1} - \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}}) u_{N - 1} + \frac{h}{12} u_{N - 2} + \frac{11 h}{24} u_{N - 1} - \frac{h}{24} u_{N} \\ = & (\frac{h}{2} - \frac{1}{α_{1} + 1} + \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}} - \frac{h}{24}) u_{N} + (\frac{1}{α_{1} + 1} - \frac{1}{(α_{1} + 1) 2^{α_{1} + 1}} + \frac{11 h}{24}) u_{N - 1} + \frac{h}{12} u_{N - 2} . \end{matrix}

When

1 < i < N - 1

, the integral can be approximated by

\begin{matrix} \int_{x_{k - 1 / 2}}^{x_{k + 1 / 2}} u (x) d x = & \int_{x_{k - 1 / 2}}^{x_{k + 1 / 2}} π_{2, k} u (x) d x \\ = & \int_{x_{k - 1 / 2}}^{x_{k + 1 / 2}} \frac{(x - x_{k + 1}) (x - x_{k})}{2 h^{2}} u_{k - 1} + \frac{(x - x_{k + 1}) (x - x_{k - 1})}{- h^{2}} u_{k} + \frac{(x - x_{k}) (x - x_{k - 1})}{2 h^{2}} u_{k + 1} d x \\ = & \frac{h}{24} u_{k - 1} + \frac{11 h}{12} u_{k} + \frac{h}{24} u_{k + 1} . \end{matrix}

Applying numerical scheme (47)-(48) of the integral operator

J^{α} (x_{n + 1 / 2})

to fractional diffusion Equation (24)-(25), we can obtain the following discrete numerical schemes:

\begin{matrix} μ B U + \frac{C_{1, α}}{h^{α - 1}} A^{α} U = F, 0 < α < 2, α \neq 1, \end{matrix}

(49)

\begin{matrix} μ B U + \frac{1}{π} A^{α} U = F, α = 1, \end{matrix}

(50)

where

\begin{matrix} B = [\begin{matrix} 5 h / 4 & h / 12 & 0 & \dots & 0 & 0 & 0 \\ h / 12 & 11 h / 12 & h / 12 & \dots & 0 & 0 & 0 \\ 0 & h / 12 & 11 h / 12 & \dots & 0 & 0 & 0 \\ \dots & \dots & \dots & ⋱ & \dots & \dots & \dots \\ 0 & 0 & 0 & \dots & 11 h / 12 & h / 12 & 0 \\ 0 & 0 & 0 & \dots & h / 12 & 11 h / 12 & h / 12 \\ 0 & 0 & 0 & \dots & 0 & h / 12 & 5 h / 4 \end{matrix}] . \end{matrix}

When

0 < α < 2, α \neq 1

, then

\begin{matrix} A_{i j}^{α} = \{\begin{matrix} 2 {\hat{b}}_{0}^{2 - α} - 2 {\hat{b}}_{- 1}^{2 - α} - 2 a_{0}^{2 - α} + a_{1}^{2 - α}, i = j, \\ {\hat{b}}_{1}^{2 - α} - 2 {\hat{b}}_{0}^{2 - α} + {\hat{b}}_{- 1}^{2 - α} + a_{1}^{2 - α} - 2 a_{0}^{2 - α}, i - j = 1, \\ {\hat{b}}_{- 1}^{2 - α} - 2 {\hat{b}}_{- 2}^{2 - α} + {\hat{b}}_{- 3}^{2 - α} + 3 a_{0}^{2 - α} - 3 a_{1}^{2 - α} + a_{2}^{2 - α}, i - j = - 1, \\ {\hat{b}}_{k}^{2 - α} - 2 {\hat{b}}_{k - 1}^{2 - α} + {\hat{b}}_{k + 1}^{2 - α} + a_{k}^{2 - α} - 3 a_{k - 1}^{2 - α} + 3 a_{k - 2}^{2 - α} - a_{k - 3}^{2 - α}, i - j = k > 1, \\ {\hat{b}}_{- k}^{2 - α} - 2 {\hat{b}}_{- k - 1}^{2 - α} + {\hat{b}}_{- k - 2}^{2 - α} + a_{- k}^{2 - α} - 3 a_{- k - 1}^{2 - α} + 3 a_{- k - 2}^{2 - α} - a_{- k - 3}^{2 - α}, i - j = - k < - 1 . \end{matrix} \end{matrix}

(51)

when

α = 1

, then

\begin{matrix} A_{i j} = \{\begin{matrix} \frac{1}{h} (2 {\hat{b}}_{0} - 2 {\hat{b}}_{- 1}) + \frac{1}{h^{2}} (- 2 a_{0} + a_{1}), i = j, \\ \frac{1}{h} ({\hat{b}}_{1} - 2 {\hat{b}}_{0} + {\hat{b}}_{- 1}) + \frac{1}{h^{2}} (a_{1} - 2 a_{0}), i - j = 1, \\ \frac{1}{h} ({\hat{b}}_{- 1} - 2 {\hat{b}}_{- 2} + {\hat{b}}_{- 3}) + \frac{1}{h^{2}} (3 a_{0} - 3 a_{1} + a_{2}), i - j = - 1, \\ \frac{1}{h} ({\hat{b}}_{k} - 2 {\hat{b}}_{k - 1} + {\hat{b}}_{k + 1}) + \frac{1}{h^{2}} (a_{k} - 3 a_{k - 1} + 3 a_{k - 2} - a_{k - 3}), i - j = k > 1, \\ \frac{1}{h} ({\hat{b}}_{- k} - 2 {\hat{b}}_{- k - 1} + {\hat{b}}_{- k - 2}) + \frac{1}{h^{2}} (a_{- k} - 3 a_{- k - 1} + 3 a_{- k - 2} - a_{- k - 3}), i - j = - k < - 1 . \end{matrix} \end{matrix}

(52)

4. Numerical Example

In this section, we use above numerical schemes to solve fractional diffuse equations with fractional Laplacian operator. First, we check the numerical errors of the numerical schemes by fractional diffusion equation. Second, we show the spatial evolution diagram of soliton for fractional Allen-Cahn system with zero boundary condition.

4.1. Example A

In the subsection, we apply our numerical schemes to solve the fractional diffuse Equation (24) with zero boundary conditions. We choose the function

\begin{matrix} f (x) = \frac{2^{α} Γ \frac{α + 1}{2} Γ (s + 1 + \frac{α}{2})}{\sqrt{π} Γ (α + 1)}_{2} F_{1} (\frac{α + 1}{2}, - s; \frac{1}{2}; x^{2}) + {(1 - x^{2})}^{s + \frac{α}{2}}, μ = 1, \end{matrix}

then exact solutions is given by

u (x) = {(1 - x^{2})}^{s + \frac{α}{2}}

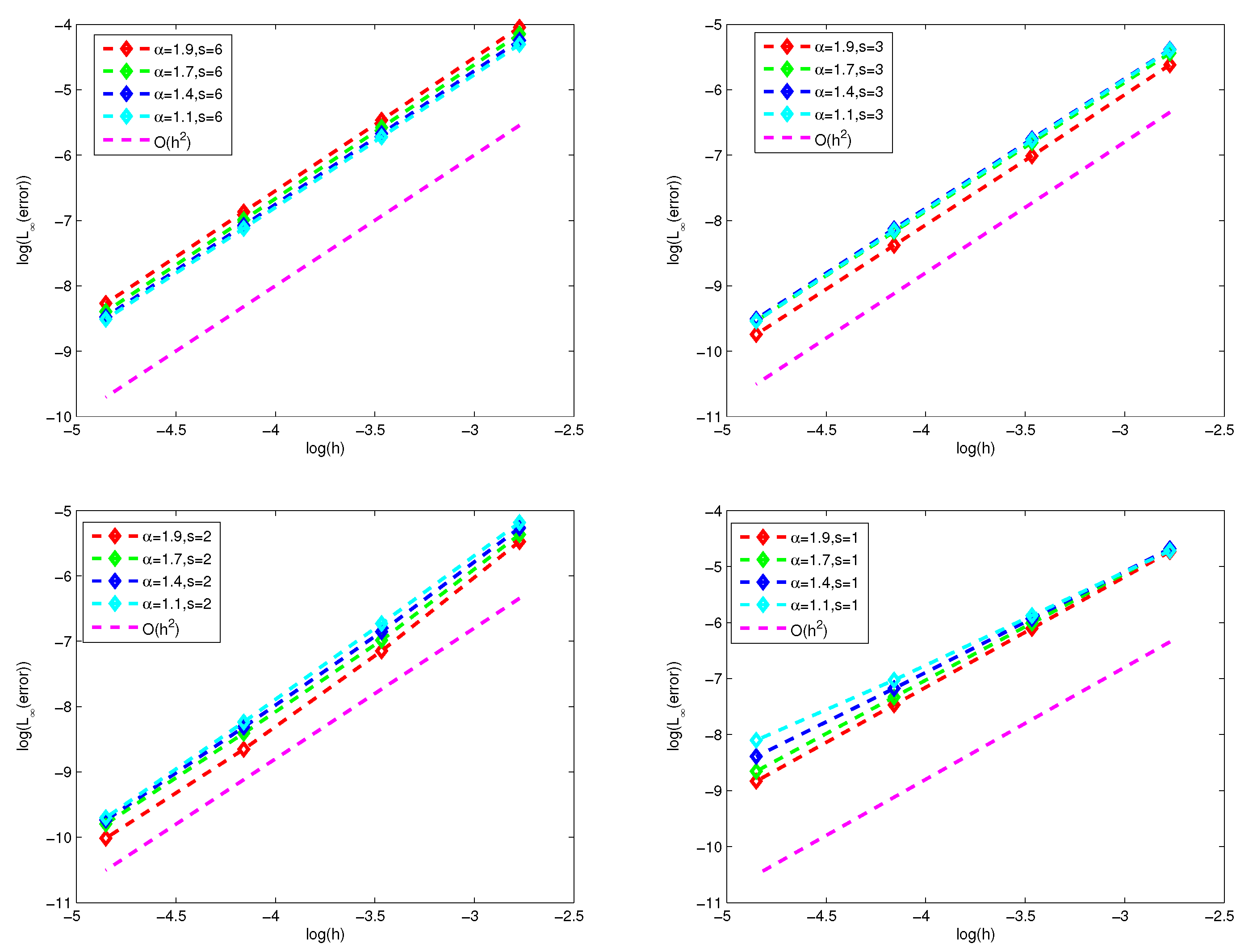
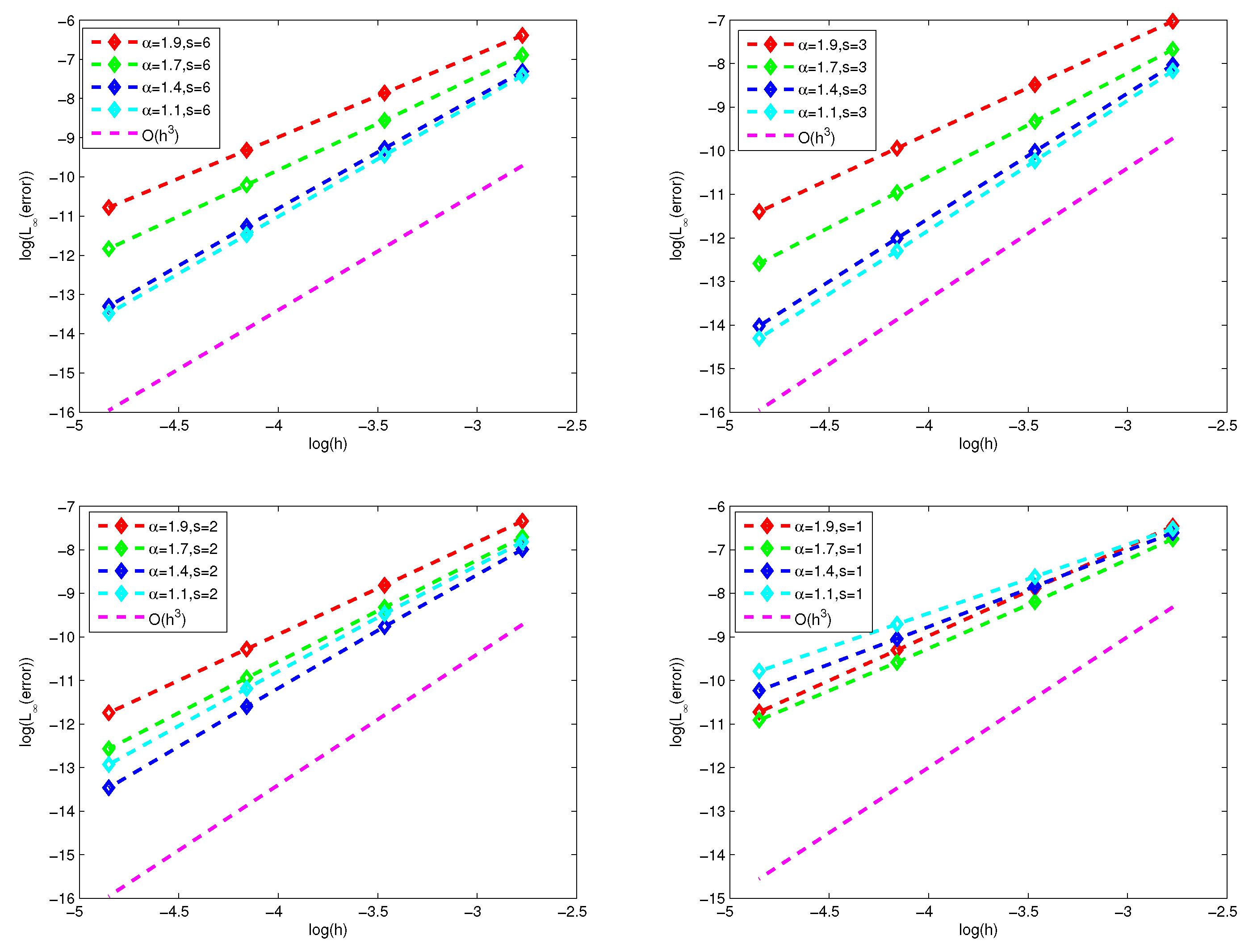
First, we text numerical errors and convergence rates by finite difference scheme and finite volume scheme. Figure 1 and Figure 2 present the numerical errors and convergence rates of the finite difference scheme (26)-(27) and finite volume scheme (39)-(40) for

0 < α < 2, α \neq 1

with

s = 6, 3, 2, 1

respectively. We observe that convergence rates of the finite difference scheme is of second-order for

u \in C^{2} (R)

by Figure 1. From Figure 2, it found that convergence rates of the finite volume scheme is higher than that of finite difference scheme, but has no more than three successive orders. Figure 1 and Figure 2 indicate that convergence rates of the finite difference scheme and finite volume scheme is related to

α

for

u \in C^{1} (R)

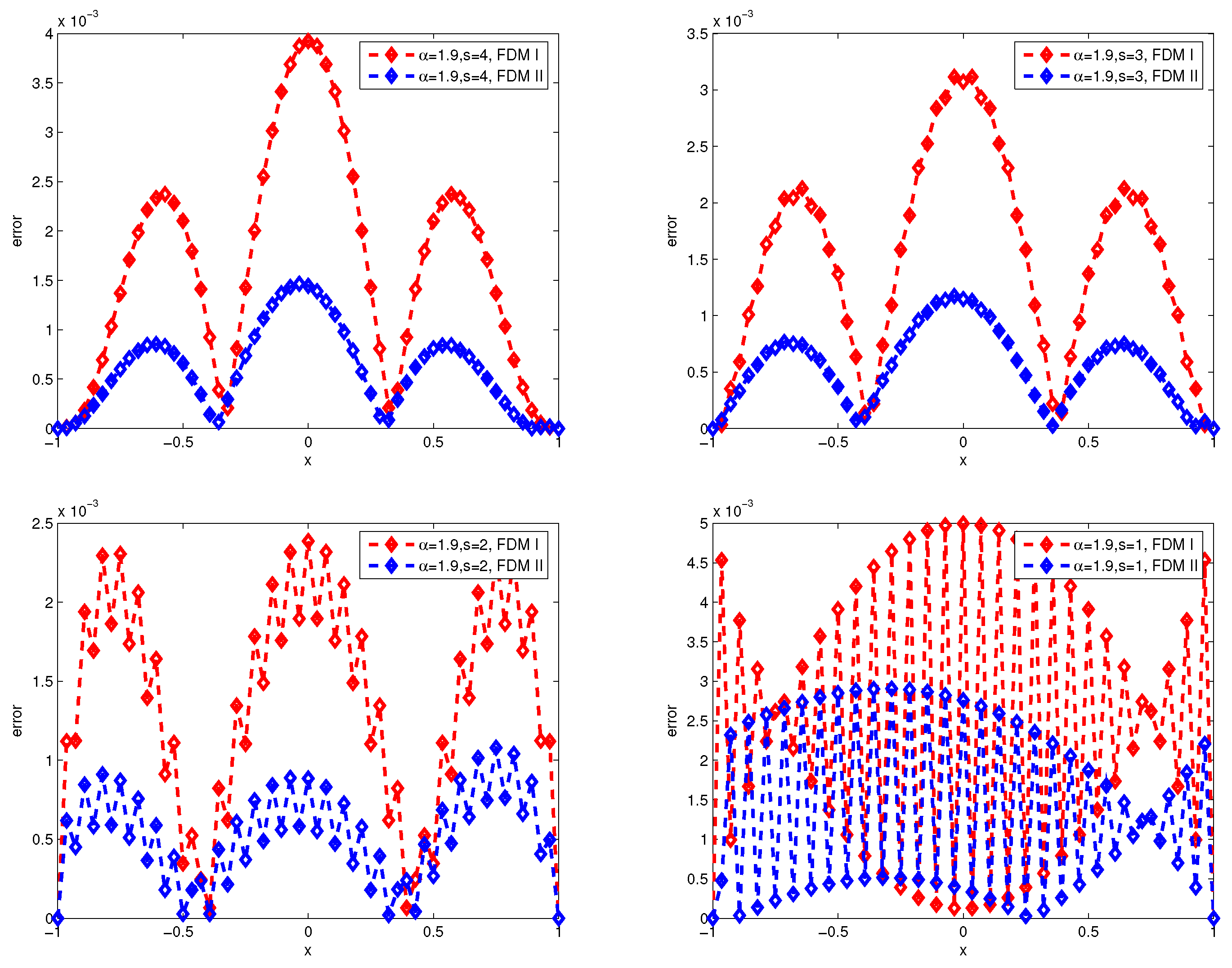
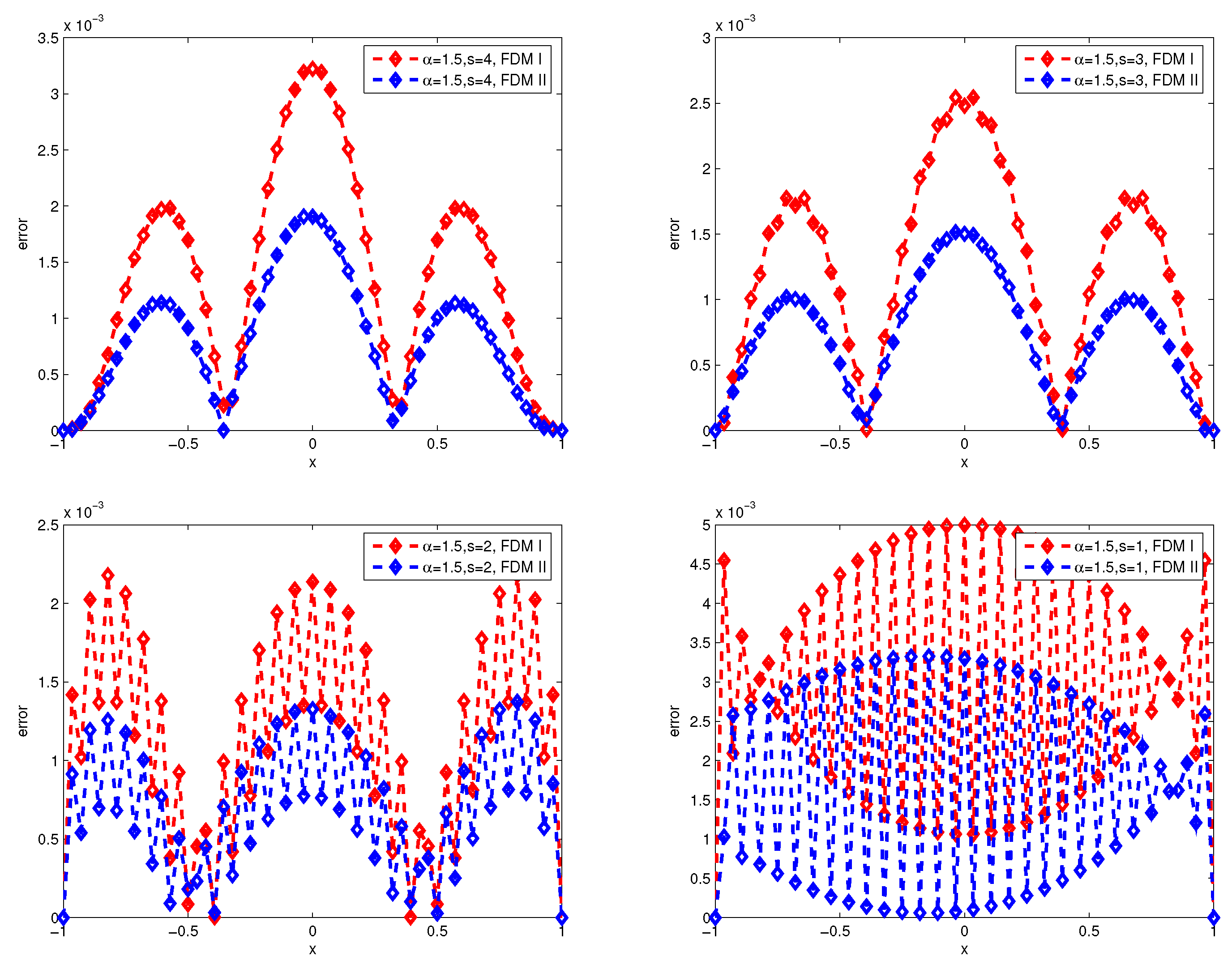
Second, we compare the numerical errors of finite difference method and finite volume method by linear interpolation function and fractional interpolation function (

α_{1} = 0.5

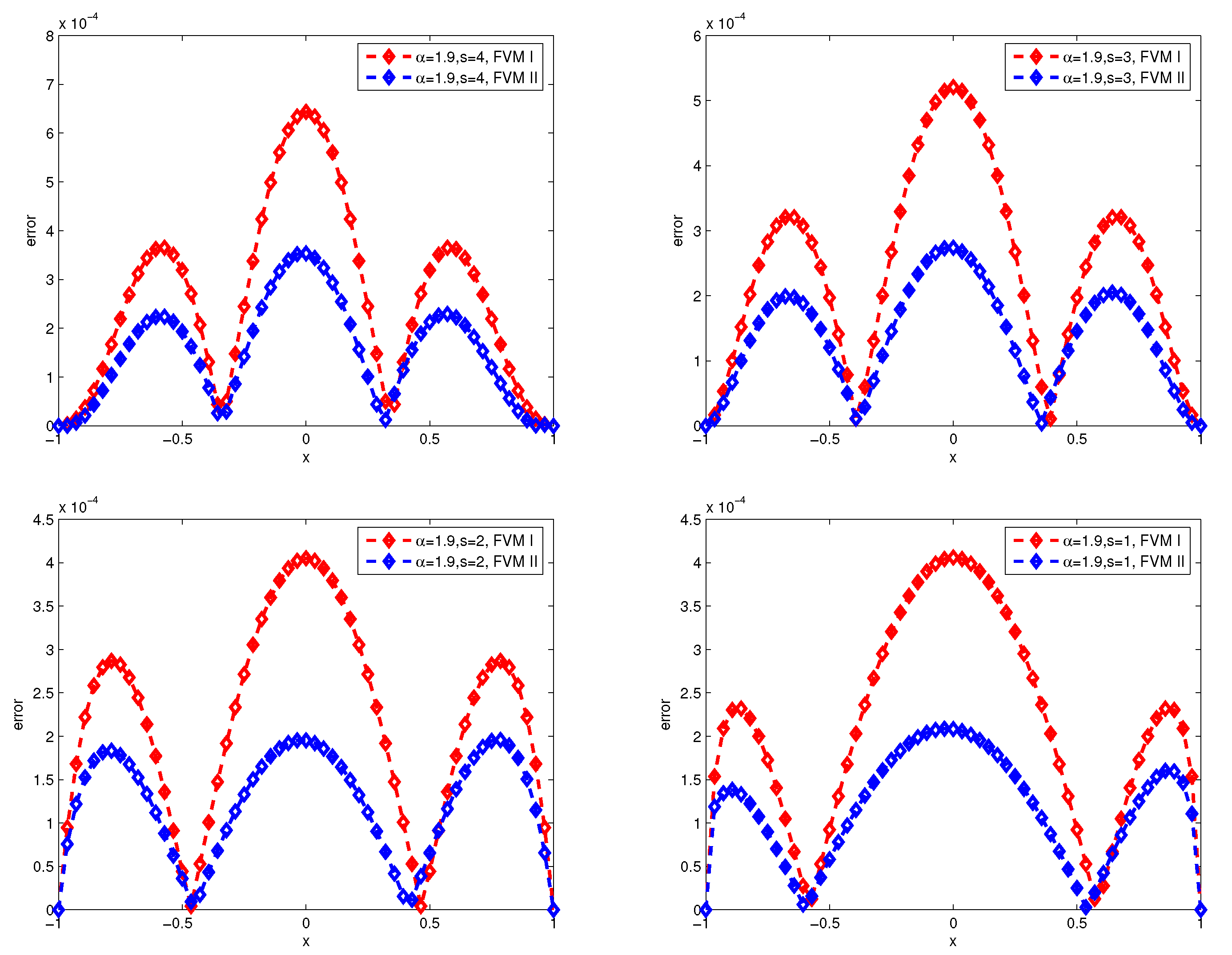
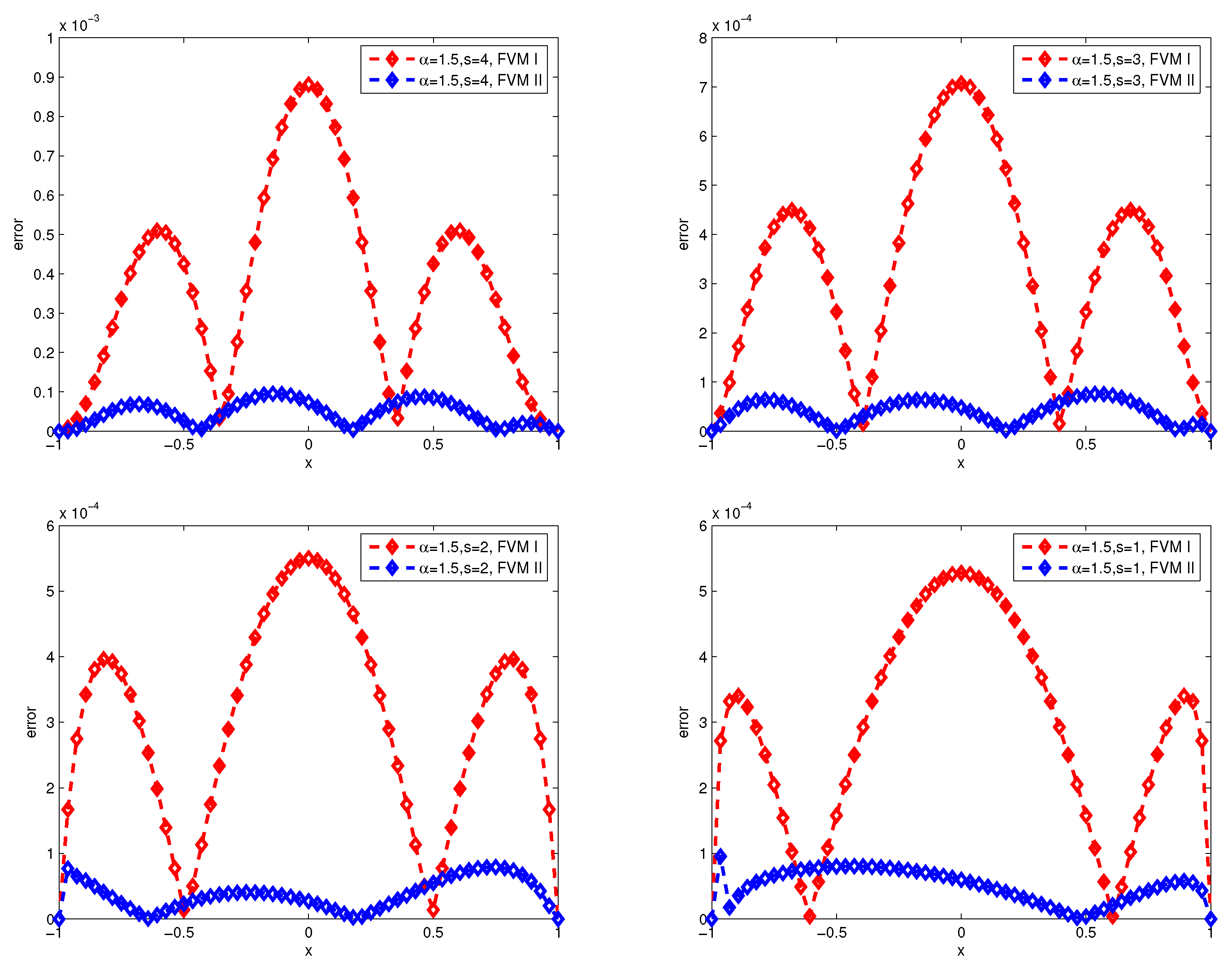
). Figure 3 and Figure 4 present the numerical errors of the finite difference method I (FDM I) and finite difference method II (FDM II) for

0 < α < 2, α \neq 1

with

α = 1.9, 1.5

and

s = 4, 3, 2, 1

respectively, where, FDM I and FDM II represent numerical scheme (26)-(27) and (28)-(29). Figure 5 and Figure 6 present the numerical errors of the finite volume method I (FVM I) and finite volume method II (FVM II) for

0 < α < 2, α \neq 1

with

α = 1.9, 1.5

and

s = 4, 3, 2, 1

respectively, where, FVM I and FVM II represent numerical scheme (39)-(40) and (49)-(50). From Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, we can draw the observations: the accuracy of the finite volume method is higher than that of the finite difference scheme, and the numerical error produces great turbulence for

s = 1, 2

by finite difference scheme.

4.2. Example B

In this subsection, we show the numerical approximations to the space fractional Allen-Cahn equation

\begin{matrix} u_{t} = - ϵ^{2} {(- Δ)}^{α / 2} u - f (u), (x, t) \in (a, b) \times [0, T], \end{matrix}

(53)

\begin{matrix} u (x, 0) = u_{0}, x \in (a, b), \end{matrix}

(54)

\begin{matrix} u (x, t) = 0, (x, t) \in {(a, b)}^{c} \times [0, T], \end{matrix}

(55)

where

f (u) = u^{3} - u .

It follows from numerical scheme (22) that we can obtain the following semi-discrete numerical scheme

\begin{matrix} \frac{d U}{d t} = ϵ^{2} A U + U - U^{3} . \end{matrix}

(56)

Using implicit scheme and Crank-Nicolson scheme to semi-discrete scheme can obtain the following fully-discrete scheme

\begin{matrix} Implicit : & \frac{U^{n + 1} - U^{n}}{Δ t} = U^{n + 1} - {(U^{n + 1})}^{3} + ϵ^{2} A U^{n + 1}, \end{matrix}

(57)

\begin{matrix} Crank - NicolsonI : & \frac{U^{n + 1} - U^{n}}{Δ t} = \frac{U^{n} - {(U^{n})}^{3} + U^{n + 1} - {(U^{n + 1})}^{3}}{2} + ϵ^{2} A \frac{U^{n} + U^{n + 1}}{2}, \end{matrix}

(58)

\begin{matrix} Crank - NicolsonII : & \frac{U^{n + 1} - U^{n}}{Δ t} = \frac{(U^{n} + U^{n + 1})}{2} + \frac{(U^{n} + U^{n + 1}) ({(U^{n})}^{2} + {(U^{n + 1})}^{2})}{4} + ϵ^{2} A \frac{U^{n} + U^{n + 1}}{2} . \end{matrix}

(59)

In this example, we consider fractional Allen-Cahn system (53)-(55), and show the wave form of the implicit scheme and Crank-Nicolson scheme by zero boundary condition. Consider initial value

u_{0} (x) = 1

[- 2, 0]

or zero elsewhere, and we simulate the numerical solution with

[- 10, 10], τ = 0.001, h = 0.1

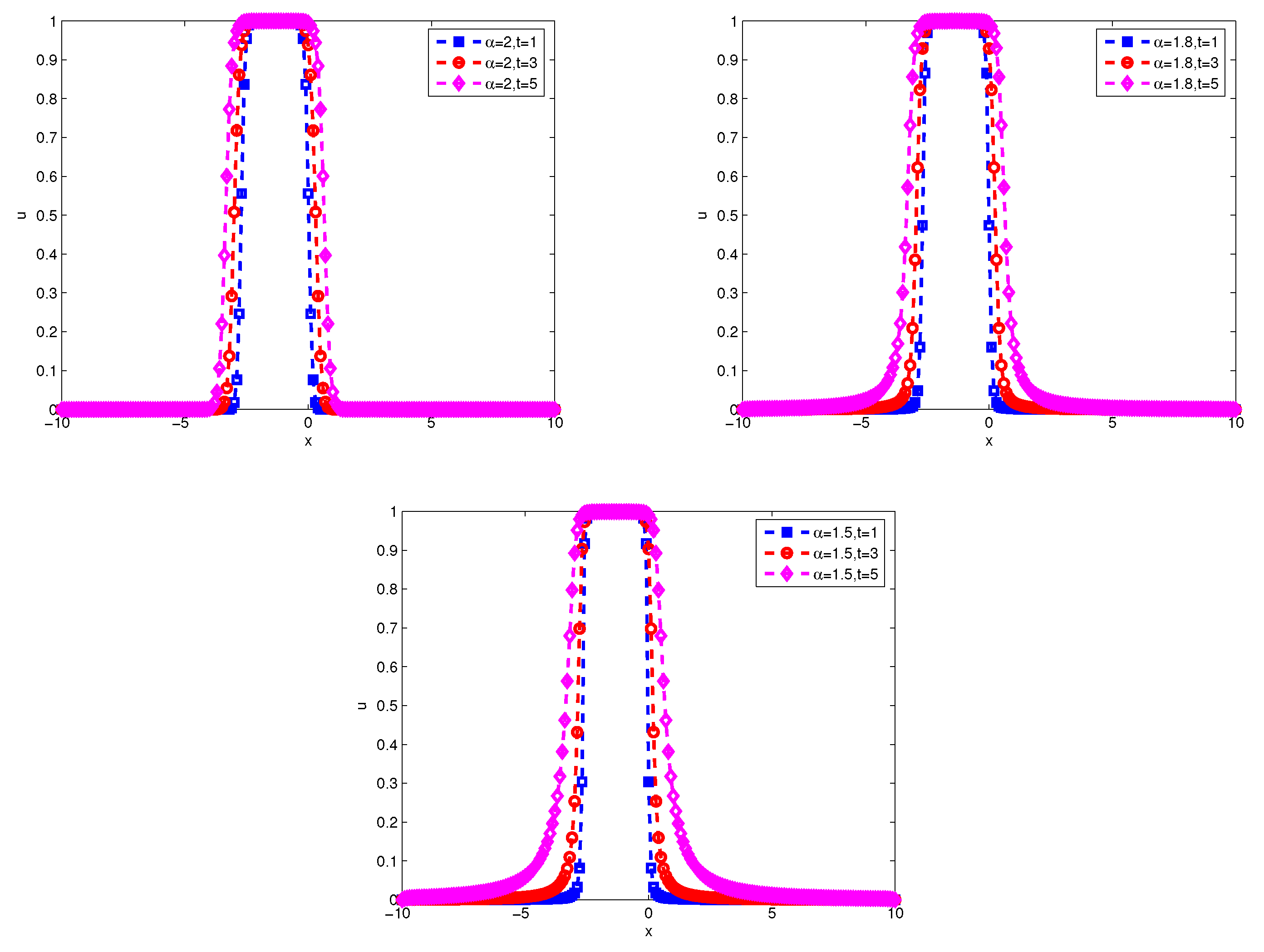
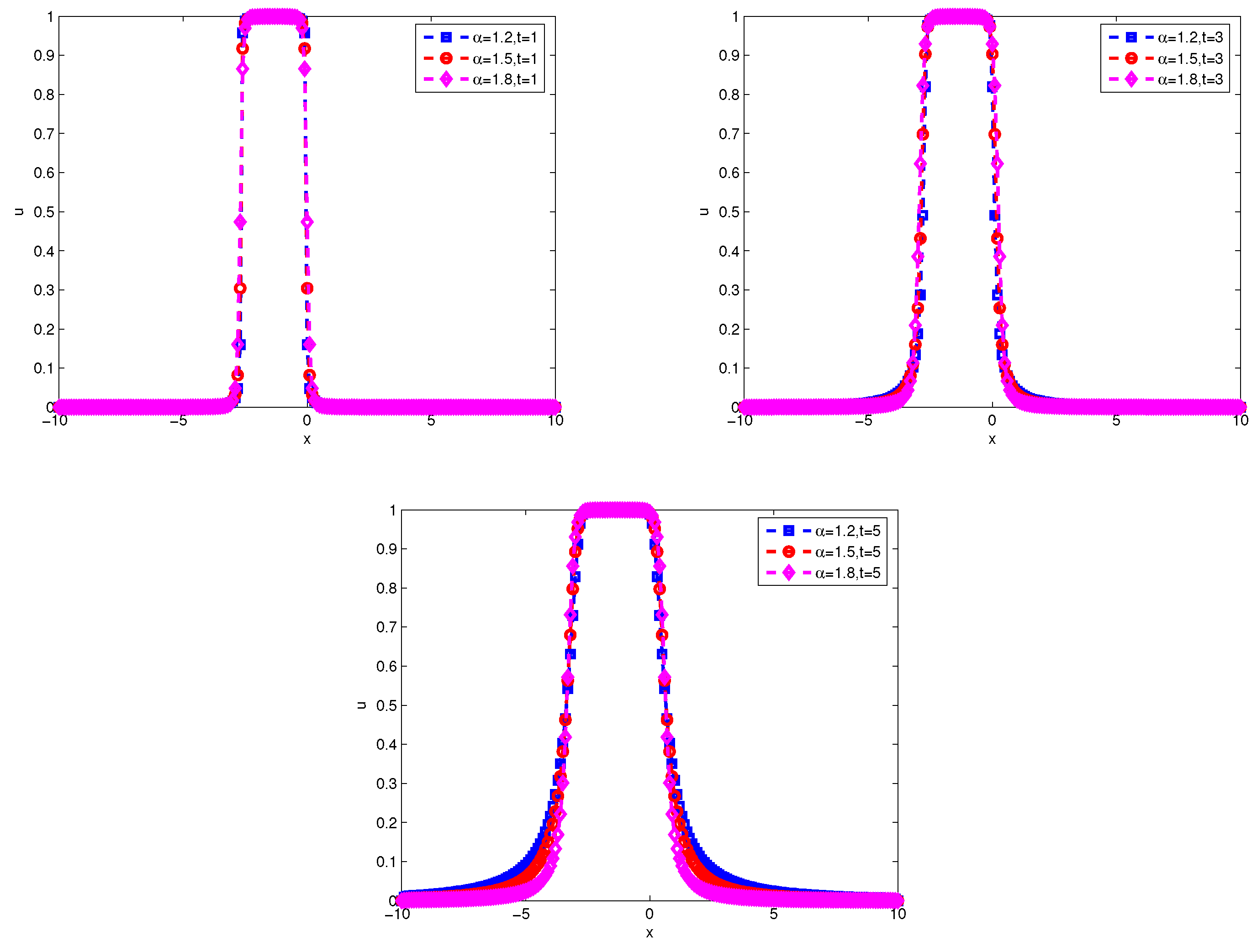
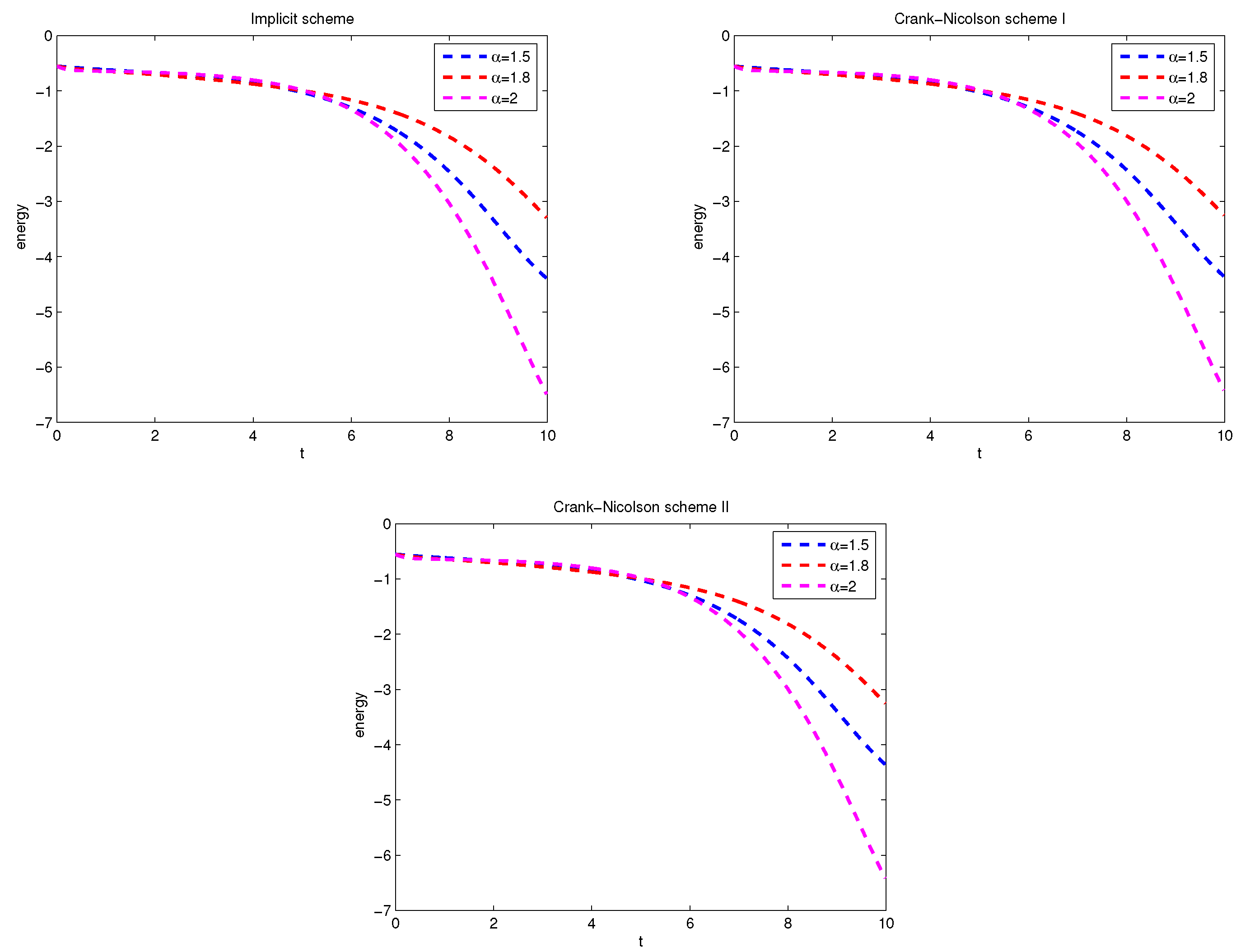
. Figure 7 and Figure 8 display the wave form of numerical solution at the difference

α

and time. Figure 9 displays the the evolution of discrete energy over time by implicit scheme and Crank-Nicolson scheme. They also show that

α

affects the propagation velocity of the solitary wave. For smaller

α

, the propagation of the soliton got slower, thus indicating the presence of the quantum subdiffusion.

5. Conclusions

In the paper, we show the finite difference method and finite volume method for fractional diffuse equation with smooth and non-smooth solutions. The novelty of our method is that we formulated the fractional Laplacian operator as a weak singular integral, so as to avoid directly discretizing the hypersingular integral. Because of the solution of fractional diffusion equation is usually singular near the boundary, we give some numerical schemes including finite difference scheme and finite volume scheme to discrete fractional diffusion equation by fractional interpolation function. Moreover, it is find that the accuracy of the finite volume method is higher than that of the finite difference scheme, and the numerical error produces great turbulence for smaller s by finite difference scheme. Finally, several numerical examples are considered to demonstrate the validity and applicability of the numerical scheme to approximate fractional diffusion equations.

Funding

This work is supported by National Natural Science Foundation of China (No.12161070), Xing dian talent support project (No.XDYC-QNRC-2022-0038), Innovation team of Puer University (CXTD019), Scientific Research Fund Project of Yunnan Education Department (2022J0985).

References

S. Samko, A. Kilbas and O. Marichev, Fractional Integral and Derivatives, Gordon and Breach Science Publishers, Yverdon, 1993. [CrossRef]
S. Zhai, Z. Weng and X. Feng, Fast explicit operator splitting method and time-step adaptivity for fractional non-local Allen-Cahn model, Appl. Math. Model., 40 (2) (2016) 1315-1324. [CrossRef]
N. Landkof, Foundations of Modern Potential Theory, Die Grundlehren der Mathematischen Wissenschaften 180, Springer-Verlag, New York, 1972.
C. Li, F. Zeng, Numerical Methods for Fractional Calculus, Chapman and Hall/CRC, Boca Raton, 2015.
F. Liu, P. Zhuang and Q. Liu, Numerical Methods and Applications of Fractional Partial Differential Equations, Science Press, China, 2015.
Z. Sun and G. Gao, Finite Difference Methods for Fractional-order Differential Equations, Science Press, China, 2015.
V. Tarasov, Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media, Springer, 2011.
B. Guo, Fractional Partial Differential Equations and their Numerical Solutions, Science Press, China, 2011.
S. Duo and Y. Zhang, Mass-conservative Fourier spectral methods for solving the fractional non-linear Schrödinger equation, Comput. Math. Appl., 71 (2016) 2257-2271. [CrossRef]
P. Felmer, A. Quaas and J. Tan, Positive solutions of the nonlinear Schröinger equation with the fractional Laplacian, Proc. Roy. Soc. Edinburgh Sect. A, 142 (06) (2012) 1237-1262. [CrossRef]
C. Celik, M. Duman, Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative, J. Comput. Phys., 231 (2012) 1743-1750. [CrossRef]
G. Acosta, J. Borthagaray, O. Bruno, Regularity theory and high order numerical method for the (1D)-fractinal Laplacian, Math. Comput., 87 (312) (2018) 1821-1857.
M. Li, C. Huang and P. Wang, Galerkin finite element method for nonlinear fractional Schrödinger equations, Numer. Algorithms, 74 (2017) 499-525.
Y. Ran, J. Wang and D. Wang, On HSS-like iteration method for the space fractional coupled nonlinear Schrödinger equations, Appl. Math. Comput., 271 (2015) 482-488.
Y. Ran, J. Wang and D. Wang, On preconditioners based on HSS for the space fractional CNLS equations, East Asian J. Appl. Math., 7 (2017) 70-81.
M. Ran and C. Zhang, A conservative difference scheme for solving the strongly coupled nonlinear fractional Schrödinger equations, Commun. Nonlinear Sci. Numer. Simul., 41 (2016) 64-83.
P. Wang and C. Huang, An energy conservative difference scheme for the nonlinear fractional Schr?dinger equations, J. Comput. Phys., 293 (2015) 238-251.
P. Wang, C. Huang and L. Zhao, Point-wise error estimate of a conservative difference scheme for the fractional Schrödinger equation, J. Comput. Appl. Math., 306 (2016) 231-247.
L. Wang, Y. Ma, L. Kong and Y. Duan, Symplectic Fourier pseudo-spectral schemes for Klein-Gordon-Schrödinger equations, China J. Comput. Phys., 28 (2011) 275-282.
J. Wang and A. Xiao, An efficient conservative difference scheme for fractional Klein-Gordon-Schrödinger equations, Appl. Math. Comput., 320 (2018) 691-709.
D. Wang, A. Xiao and W. Yang, Crank-Nicolson difference scheme for the coupled nonlinear Schr?dinger equations with the Riesz space fractional derivative, J. Comput. Phys. 242, 670- 681 (2013).
H. Yang and A. Oberman,Numerical method for the fractional Laplacinal: a finite difference-quadrature approach, Siam: J.Numer.Anal., 52 (6) 3056-3084.
S. Duo, H. WernervanWyk, Y. Zhang, A novel and accurate finite difference method for the fractional Laplacian and the fractional Poisson problem, J. Comput. Phys., 355 (2018) 233-252.
T. Tang, H. Yuan, T. Zhou, Hermite spectral collocation methods for fractional PDEs in unbounded domains, Commun. Comput. Phys., 24 (4) (2018) 1143-1168 October 2018.
Z. Mao and J. Shen, Hermite spectral methods for fractional PDEs in unbounded domains, to appear in SIAM J. Sci. Comput., 2017.
T. Tang, L. Wang, H. Yuan, T. Zhou, Rational spectral methods for PDEs invoving fractional Laplacian unbounded domains.
Y. Zhang, Z. Sun and H. Liao, Finite difference methods for the time fractional diffusion equation on non-uniform meshes, J. Comput. Phys., 265 (2014) 195-210.
L. Zhao and W. Deng, High order finite difference methods on non-uniform meshes for space fractional operators, Advan. Comput. Math., 42 (2016) 425-468.

Figure 1. The numerical errors and convergence rates of finite difference scheme

Figure 2. The numerical errors and convergence rates of finite volume scheme

Figure 3. The numerical errors of numerical solution for FDM I and FDM II

Figure 4. The numerical errors of numerical solution for FDM I and FDM II

Figure 5. The numerical errors of numerical solution for FVM I and FVM II

Figure 6. The numerical errors of numerical solution for FVM I and FVM II

Figure 7. The wave forms of the numerical solution with

α = 2, 1.8, 1.5

Figure 7. The wave forms of the numerical solution with

α = 2, 1.8, 1.5

Figure 8. The wave forms of the numerical solution with

T = 1, 3, 5

Figure 8. The wave forms of the numerical solution with

T = 1, 3, 5

Figure 9. The evolution of discrete energy over time

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Finite Difference Scheme and Finite Volume Scheme for Fractional Laplacian Operator and Some Applications

Abstract

1. Introduction

2. Finite Difference Method for Fractional Laplacian and Fractional Diffusion Equation

2.1. Finite Difference Scheme for Fractional Laplacian

2.2. Finite Difference Scheme for Fractional Diffusion Equation

3. Finite Volume Method for Fractional Diffusion Equation

3.1. Finite Volume Method Based on a Linear Interpolation Function

3.2. Finite Volume Method Based on Fractional Interpolation Function

4. Numerical Example

4.1. Example A

4.2. Example B

5. Conclusions

Funding

References

MDPI Initiatives

Important Links

Subscribe