Prerpints.org logo
Preprint
Article

An Investigation of Wind Shear Coefficients and Their Impact on Electrical Energy Generation in Coastal Locations of Balochistan, Pakistan

Altmetrics

Downloads

105

Views

81

Comments

0

This version is not peer-reviewed

Submitted:

12 October 2023

Posted:

17 October 2023

You are already at the latest version

Alerts
Abstract
This study examines the wind shear coefficient (WSC) values at three coastal wind sites located in the southern region of Balochistan, Pakistan: Pasni, Ormara, and Jiwani. These WSC values were obtained using 10-minute measured wind speed data at heights of 20, 40, and 60 meters above ground level (AGL). Since wind measurements are typically recorded at lower heights due to cost and resource constraints, extrapolation techniques were employed to estimate wind speeds at higher altitudes. However, using a constant WSC value for extrapolation may lead to significant errors between extrapolated and actual wind speed measurements, impacting the energy output of wind turbines. To evaluate the effect of WSC on energy yield, the study employed power curves and frequency distributions for 2MW and 1.5MW wind turbines. Additionally, wind power density was calculated using air density derived from measured air temperature and surface pressure data, covering two years period from November 2016 to August 2018. The overall mean WSC values were found to be 0.076 at Pasni, 0.094 at Jiwani, and 0.053 at Ormara. The study further investigated the seasonal, monthly, and diurnal variations of WSC. For assessing wind resources at a height of 60m, the study utilized Wind Roses, wind power density, and Weibull parameters. Comparing the actual WSC values presented in this paper with those obtained using the 1/7 power law and measured data at 60m AGL, the energy yield from the wind turbines showed reduced output and capacity factor.
Keywords:Β 
Subject:Β Environmental and Earth SciencesΒ  - Β  Sustainable Science and Technology

1. Introduction

The optimum goal of wind resource assessment is to accurately predict energy performance. For power generation forecasting, information on wind speed near the wind turbine wave height and power curve is required because the external environmental conditions at the wind farm development site directly impact the annual energy production (AEP) calculations [1]. The wind turbine's power curve relative to the external environmental conditions should be calculated as accurately as possible to reduce prediction errors in the energy production calculation process [2]. Environmental factors affecting wind turbines' performance can be broadly classified into terrain influences, surface friction, obstacles, atmospheric conditions, and wakes from nearby wind turbines [3]. Among them, atmospheric conditions can be classified into turbulence intensity (TI), wind shear exponent (WSE), and atmospheric stability. Several studies have been conducted to investigate the effects of these atmospheric conditions on the performance of wind turbines [4,5].
Actual sites mostly present a wide variety of atmospheric conditions. Although the degree of variation may vary within each site, strong diurnal fluctuations caused by solar radiation energy are generally experienced [6,7]. In fact, atmospheric stability shows stable, unstable, as well as neutral states due to thermal factors during the day. This atmospheric stability influences the formation and dissipation of air mixing and Wind shear vertically and horizontally. This effect ultimately flows into the swept area and reflects the wind field affecting the wind power output and the performance of a turbine [8,9]. Therefore, the manufacturer's performance curve (MPC) varies from the performance curve of the wind turbine actually installed on the site which usually leads to errors in the calculation of AEP [10,11].
In most of the data collection stations in the world, wind speed is measured at only one specific height due to which wind shear values are hardly available [12]. Several studies have been conducted to examine wind shear and other related atmospheric conditions to show stable, unstable, and neutral states of stability due to thermal factors in diurnal variation, which influences the production of energy [13]. This difference generally results to show errors in the annual energy production (AEP) calculation [14]. One study was conducted in Jeju Island, South Korea to analyze atmospheric factors, stability, and wind shear exponent on the wind power performance and annual energy production (AEP) of wind turbines, which revealed variation of 1.4-4% due to a difference in Wind shear exponent [15]. The wind shear and its effects on annual energy production for Phagan Island were collected at 65m and 120m above ground level with the help of Weibull parameters, which showed up to 35% difference in Wind energy production due to variation in wind shear coefficient [16]. Another study was conducted in southern Namibia where the hub height and energy yield were found to be dependent on wind shear coefficient. The mean wind shear coefficients were found to be 0.197 and 0.132 with maximum values during winter and minimum in the month of summer while the diurnal values were maximum in night stable hours and minimum in daylight hours [17]. Furthermore, measurement of Wind shear coefficient variability was conducted at three coastal sites of Malaysia at a height of 55m to 70m from ground level by using the Power law equation. The results showed wind shear values larger than the 1/7 power law (0.143) which confirms the variation in wind energy potential with the change in Wind shear coefficient accordingly [10].
Wind data for one year was collected in Balikesir by using power law and Weibull parameters to show the effect of wind shear coefficient on energy production. The difference in wind energy production from collected data at hub height and extrapolated data was up to 49.6% due to wind shear coefficient influence [18]. Another study was conducted in Dhahran Saudi Arabia from the data 20, 30, and 40m above the ground level to find the effect of wind shear coefficient on energy yield from a wind farm of 60MW. Higher values of wind shear coefficient were observed during nighttime and smaller in daylight hours. The energy yield achieved was around 11-12% more for the actual wind shear coefficient compared with the obtained using the 1/7 power law [19]. The wind shear coefficient was also calculated for three coastal locations in southern Italy by using power law for diurnal, monthly, and annual variation. Furthermore, Wind resources were assessed to study the effect and compare it with the energy yield of extrapolated data at 50m from 10m using wind roses, wind speed frequency distribution, and Weibull’s parameters [13]. The wind shear coefficient was determined using wind energy resources for scale-up contribution to renewable energy in rural, pre-urban, and urban areas by using power law and wind velocity profile. The effect of diurnal wind shear resulted to be maximum at nighttime and a minimum in daytime hours, which suggested cooling of the ground surface and air above it [12]. Annual mean wind shear was calculated on 4-year data in a location in the South of Pakistan with elevation of 10m and 30m above ground level. The value of wind shear was reported at about 0.269-0.318[20].
This study utilized the wind measurements made at 20, 40, and 60m above ground level in three different coastal sites Pasni (PS), Jiwani (JW), and Ormara (OR). The power performance of different suitable turbines was analyzed with the variability of vertical and horizontal wind speeds. The site-specific air density was calculated with the help of local temperature and pressure measurements available at ground level. The main aim of the study is to analyze the effect of wind shear on the distribution and measurements of the differences in the power curve and annual energy production with the variation in atmospheric factors.

2. Data Collection and Site Description

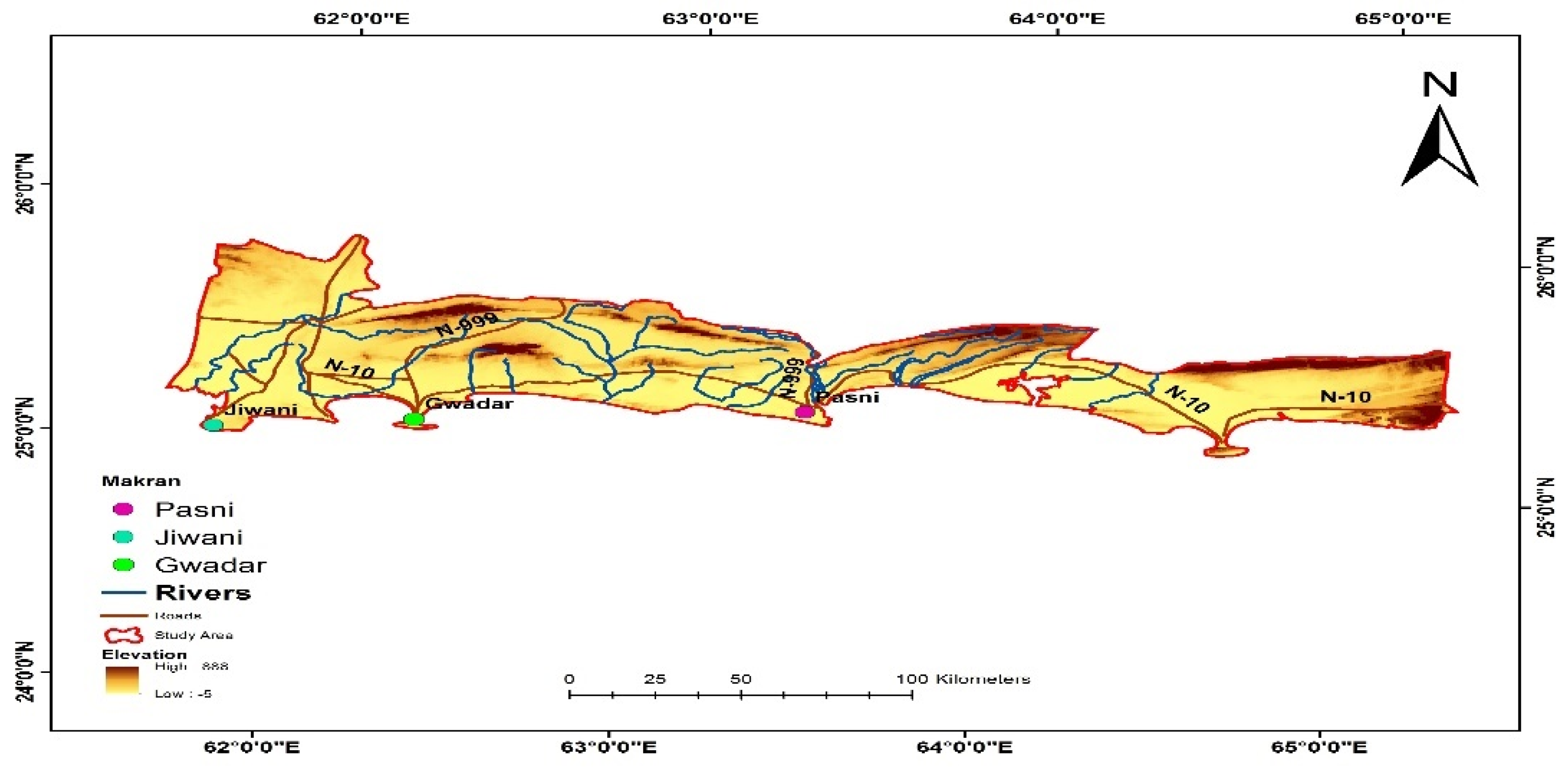
This study was conducted in the coastal area of ​​Mekran in the Balochistan province of Pakistan along a stretch of semi-desert coastline connected with the coast of Iran and the Gulf of Oman, as shown in Figure 1. It stretches west from Sonmiani Bay in the northwest to Karachi (Pakistan's largest city) in the east. Mekran's coastline is about 750 km long and has a dry climate with little rainfall. The main port cities are Ormara, Pasni, Gwadar, Ganz, Pishukan, and Jiwani. Mekran coastline offers great potential for a wind power project in the near future where there are currently no wind turbines installed. Pasni is a city located at 25 Β° 15' 47" N, 63Β° 28' 9" E, 7m (20 ft.), with a hot arid/desert subtropical climate at low latitudes [21]. The average annual temperature is about 25.5 degrees Celsius with an average of 98.2 mm rainfall. Another city, Jiwani is located in the northern hemisphere at a latitude 25Β° 3' 1" N, 61Β° 44' 48"E, 10m above sea level. The annual average temperature of the coast is 27Β°C. Jiwani has a much lower annual rainfall of around 13.66mm and winters here are short, pleasant, and dry, with mostly clear skies of temperature 23Β°C, while summers are relatively warm with temperatures reaching 32Β°C [22]. Jiwani also has an airport with a weather forecast system, just 10 km from the city center. Furthermore, Ormara is also a coastal city in Balochistan, Pakistan at 25Β° 12' 38" North, 64Β° 38' 15", 4m with a hot desert climate [23]. The maximum annual average temperature here is 29Β°C (from 24Β°C in January to 33Β°C in May) with annual precipitation is 75 mm. Like Pasni and Jiwani, Ormara City has also its own domestic airport flight forecast system.
The data used for this research was collected between November 2016 and August 2018 at three stations and is provided by the Meteorological Department of Pakistan. Temperature, barometric pressure, and humidity measurements are taken at 5m AGL, while average wind speeds were recorded at 20m, 40m, and 60m, and wind direction at 58.5m AGL. Each measurement was recorded with duration of ten minutes.
Due to the small population size, it was possible to conduct the study on the whole population. The data collection tools/questionnaires were developed and tested. The questionnaires were distributed to all the individual companies involved in the study. The quantitative data was collected using questionnaires and then collated and fed into MS Excel. The MS Excel generated various statistics, which were used to inform the discussion, conclusion, and recommendations.

3. Materials and Methods

3.1. The Power Law

Wind shear profile is determined by using the power law proposed by Hellmann in 1916, which is used to transfer the recorded data by an anemometer at a certain height for other desired heights [24]:
v 2 = v 1 h 2 h 1 Ξ±
where V1 (m/s) and V2 (m/s) are the wind speeds at height h1 (m) and h2 (m) respectively, Eq (1) and " Ξ± ” is the Hellmann exponent also known as wind shear coefficient (WSC). The exponent is highly dependent and can be expressed as [25,26,27,28,29]:
α = ln ⁑ v 2 / v 1 ln ⁑ h 2 / h 1

3.2. The Logarithmic Law

This is another commonly used method to calculate wind profile (Eq.3) reported by [26,27,28,29,30]:
v 2 / v 1 = h 2 h 1 Ξ±

3.3. Air Density

Air density is known as one of the important parameters when calculating wind energy profile from a site, as it is directly proportional to power density. It depends on ambient air temperature and atmospheric pressure and may be calculated using Eq. 4 reported by [27,28,29]:
ρ = p R T
where ρ (kg/m3) is the air density, p (mbar) is pressure, R is the specific gas constant for air [287.053 J/Kg K], and T is the air temperature [K].

4. Results & Discussion

4.1. Frequency Distribution and Wind Roses

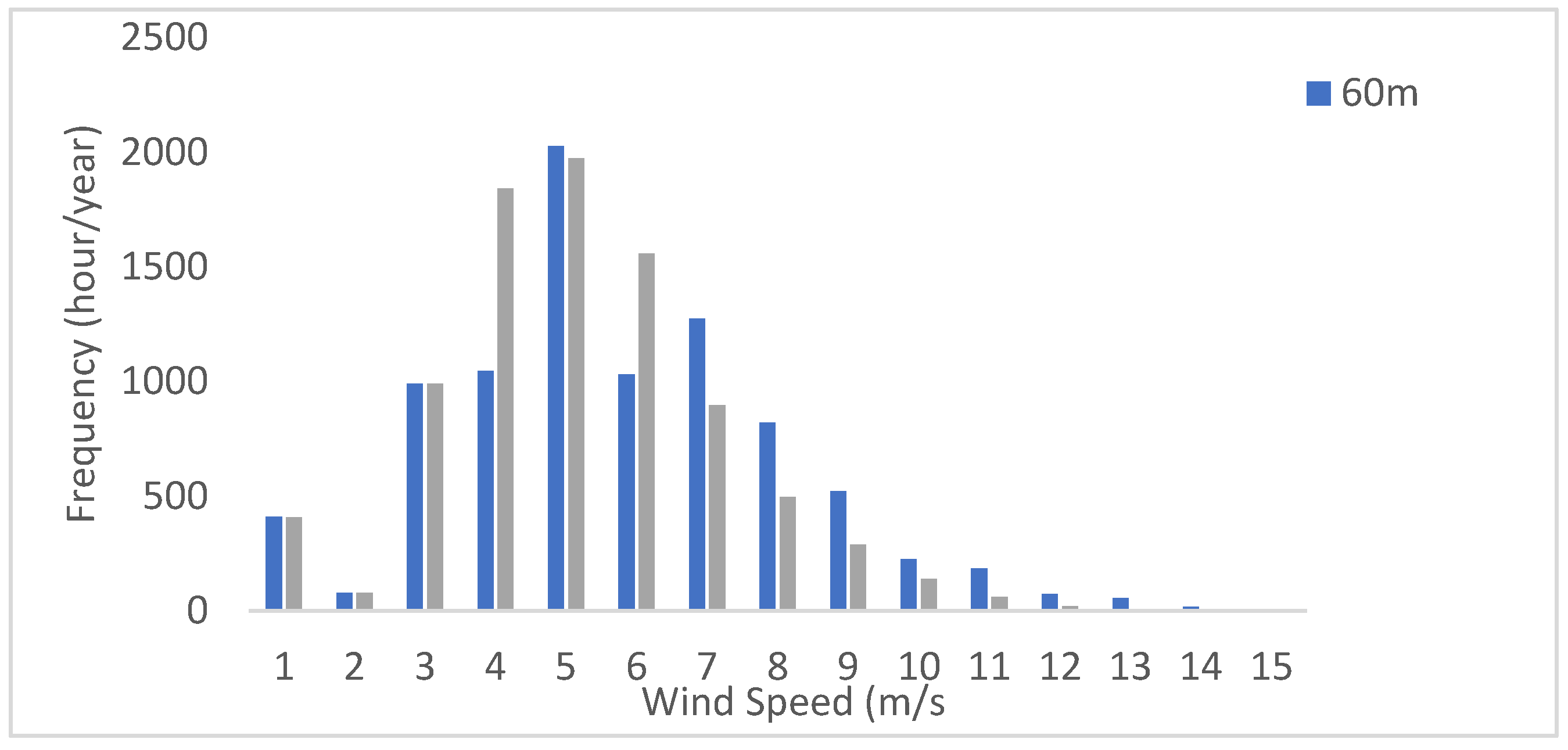
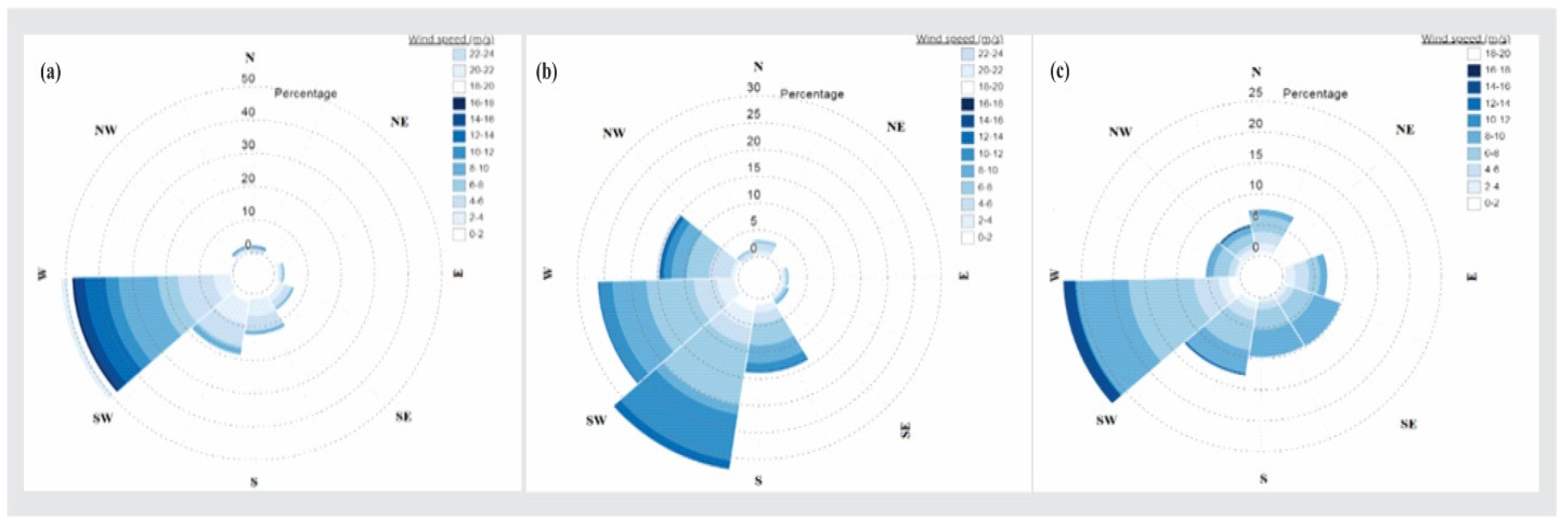
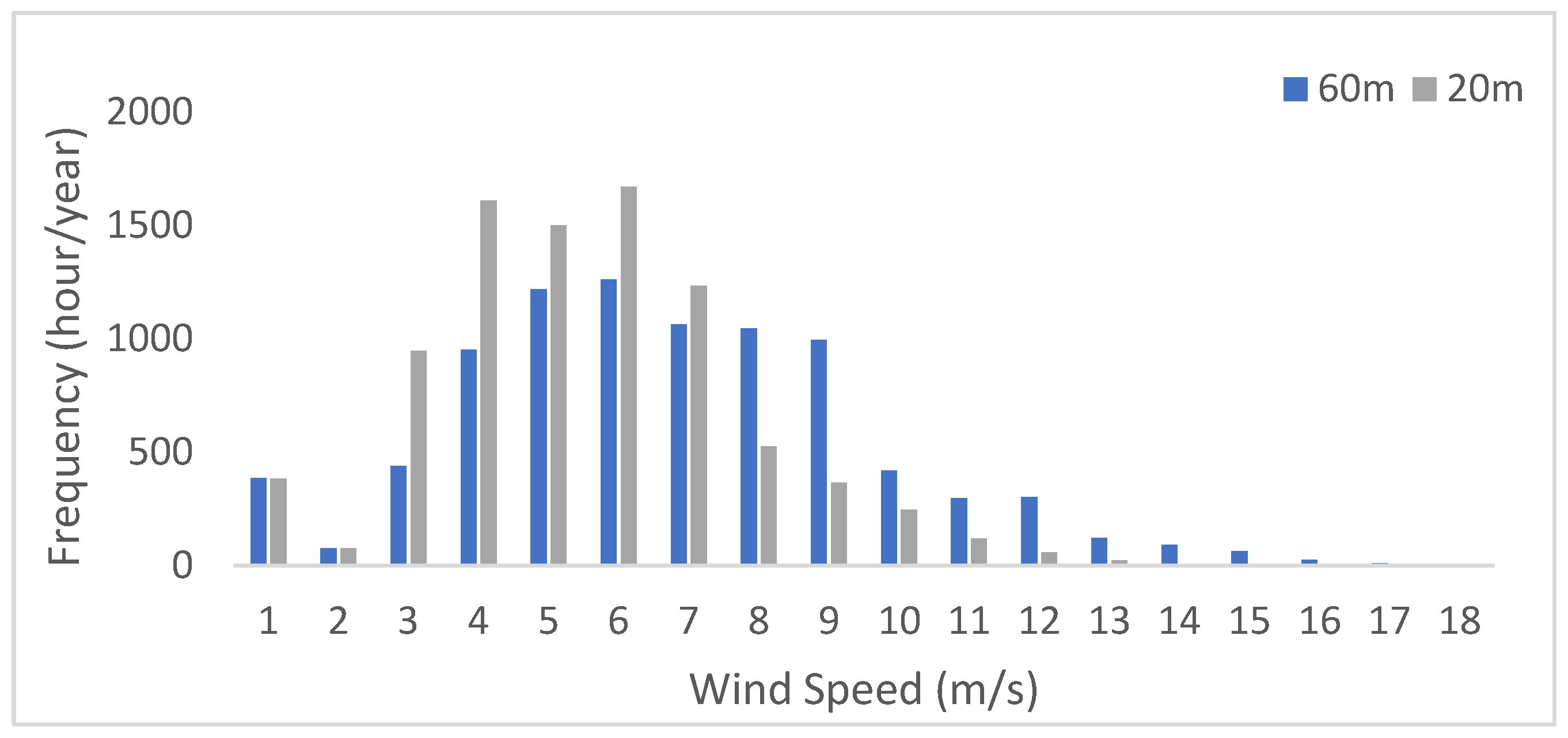
The wind direction was recorded at 57.8m for a period of two years shown in Figure 2 along with annual wind speed frequency distribution at 20m and 60m in Figure 5, Figure 6 and Figure 7 have been studied for all three coastal locations. At the PS site, the annual wind speed frequency distribution in Figure 5 showed wind speeds higher than 4m/s occur about 48% at 20m meanwhile they come up with about 65% at 60m, which is a great increase with an increase in the sensor height. Furthermore, wind direction at the PS site for two years behaved to be appearing from SW and WSW with about 53.9% shown in Figure 2(a) while the strongest winds also appeared from the same directions SW and WSW.
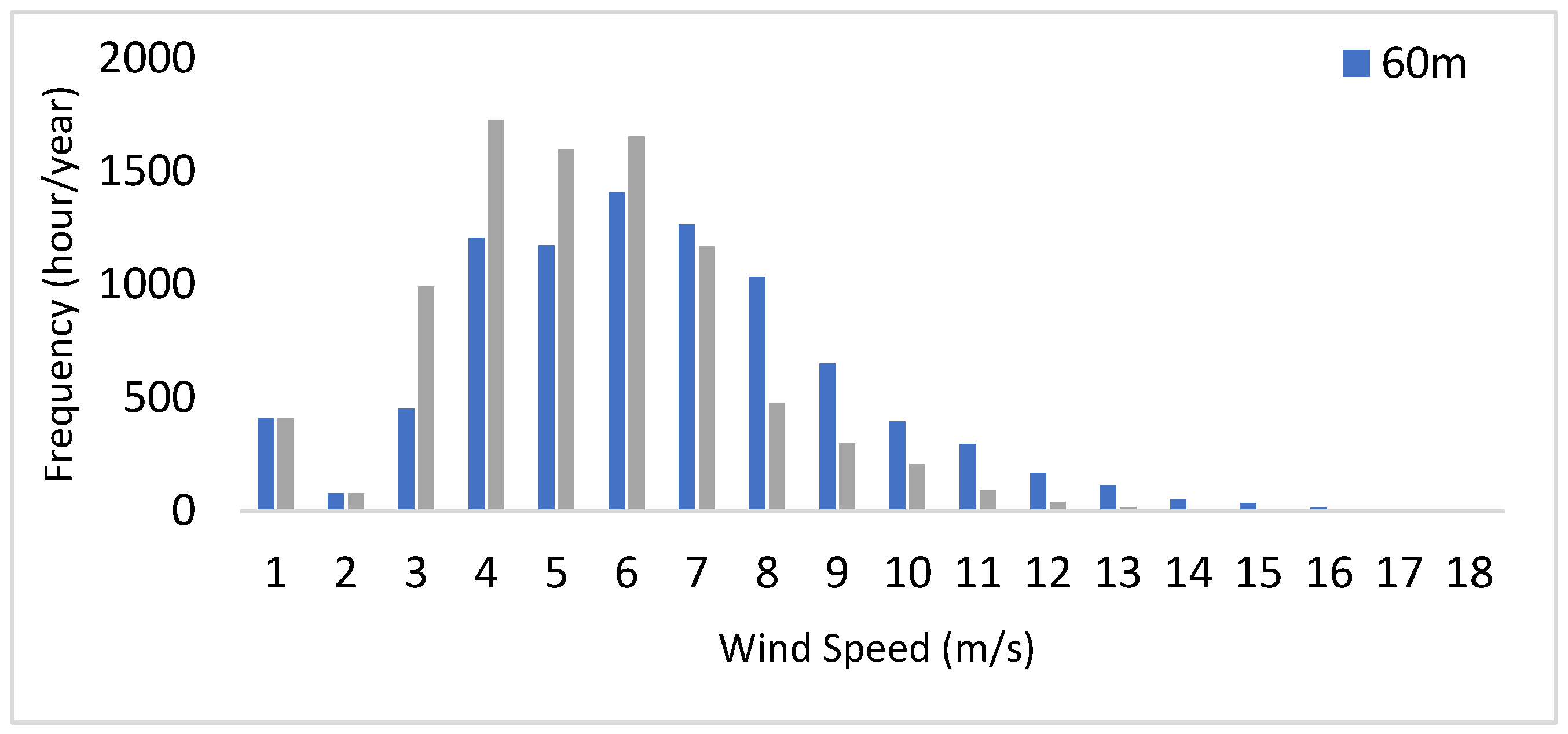
At the JW site, the annual wind speed frequency distribution shown in Figure 6 shows wind speed higher than 4m/s occurred about 45% at 20m while at 60m, it was about 62% which was also a great increase with the increase in the sensor height. The wind direction at the JW site for the selected period behaved to be from WSW, SW, and SSW with 15-33 % in Figure 2(b), while the strongest winds are also from SW and SSW respectively.
At the OR site, the annual wind speed frequency distribution in Figure 7 shows wind speeds higher than 4m/s occurred at about 39.5% at 20m meanwhile at 60m, they come up with about 48% which is a great increase with an increase in the sensor height beside those two stations. Furthermore, wind direction at the OR site behaved to be similar with PS appearing from SW and WSW with a value of about 13-32 % in Figure 2(c). The strongest winds seemed to be emerging from SW.

4.2. Air Density Characteristics

The mean monthly values appear to be higher during winter, and lower in the months of summer, however, the change is negligible. The mean density of the three stations is reported in Table 2. with the values 1.134-1.210kg/m3 at PS, 1.141-1.201kg/m3 at JW, while OR with a range from 1.148-1.203kg/m3. The real value of air density of 1.225 kg/m3 was nearly reached in January and December by all three stations. This monthly density on the coast of Balochistan, Pakistan shows clear agreement with the past literature [12,13].
Table 1. Wind shear coefficient values of various terrains [16].
Table 1. Wind shear coefficient values of various terrains [16].
Terrain Type 𝛂
Lack, ocean and smooth hard ground       0.1
Foot-high grass on level ground       0.15
Tall crops, hedges, and shrubs       0.2
The wooded country with many trees       0.25
Small towns with some trees and shrubs       03
City area with tall buildings       0.4
Table 2. Annual mean air density (kg/m3) variation by all three stations.
Table 2. Annual mean air density (kg/m3) variation by all three stations.
Month Stations
  PS  JW  OR
Jan 1.210 1.201 1.203
Feb 1.200 1.197 1.196
Mar 1.174 1.181 1.180
Apr 1.148 1.160 1.162
May 1.134 1.146 1.148
Jun 1.137 1.141 1.148
Jul 1.141 1.146 1.149
Aug 1.140 1.154 1.159
Sep 1.151 1.162 1.162
Oct 1.151 1.164 1.170
Nov 1.190 1.183 1.183
Dec 1.207 1.199 1.198
Mean 1.166 1.170 1.173

4.3. Wind Shear Characteristics

The wind shear based on 10 min wind speed data measured at different heights from 20, 40, and 60m AGL for three selected sites is calculated using Eq. 2. It is noted that generally height is neglected and wind shear is considered constant using a value from 0.1 up to 0.4 depending upon the terrain, however, it significantly varies with height.
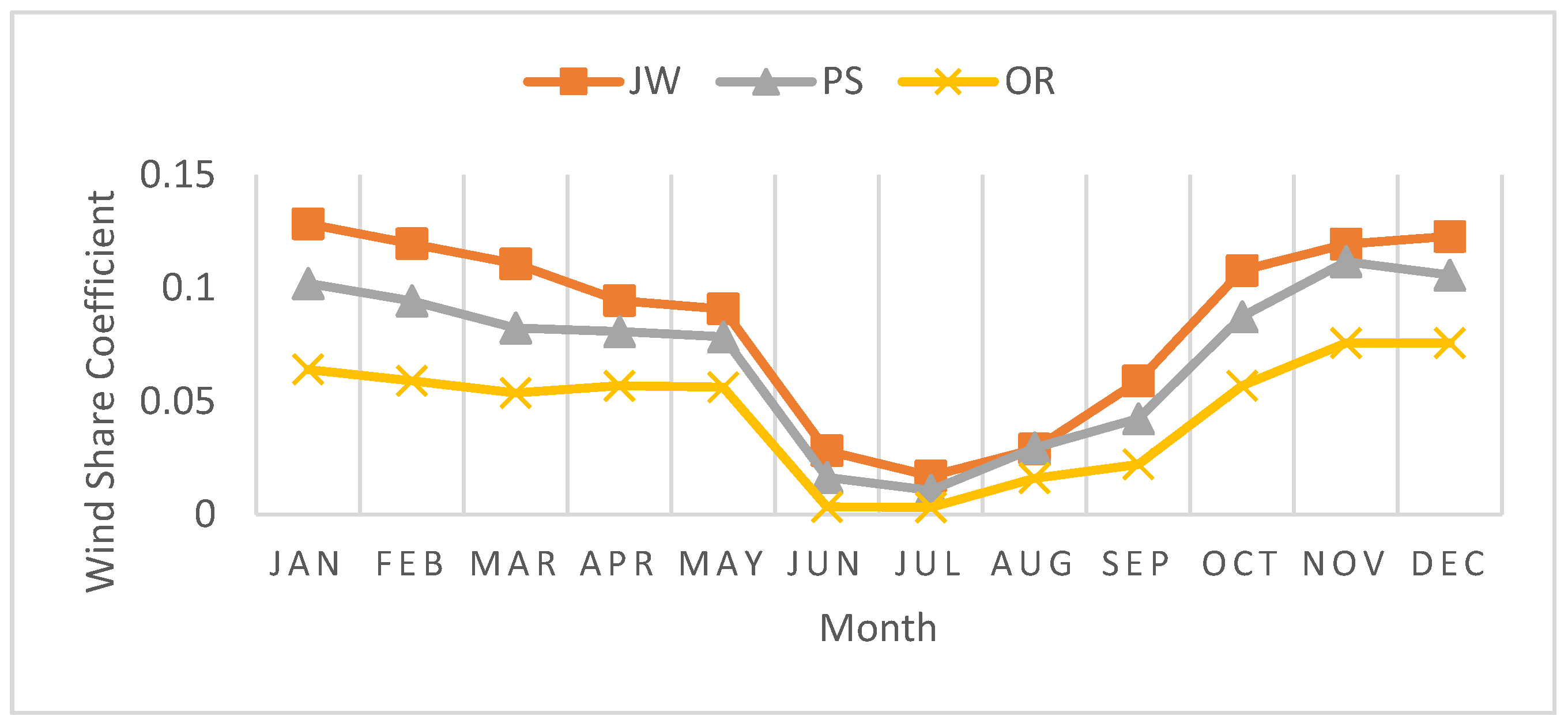
The Annual variation of wind shear Figure 3 generally shows the highest values in winter months (November- January) for all three stations where PS shows winter range 0.102- 0.1110 WSC, JW ranging 0.128 -0.119 and OR representing 0.063-0.075, while the lowest values of WSC occur in summer months (June-August) where for PS, the values range between 0.010-0.029, JW 0.028-0.016 and OR 0.015-0.003 respectively. This is due to higher air mixing above the ground level in the summertime while the ground experiences less air mixing in winter instead, as suggested by different authors [14,17].
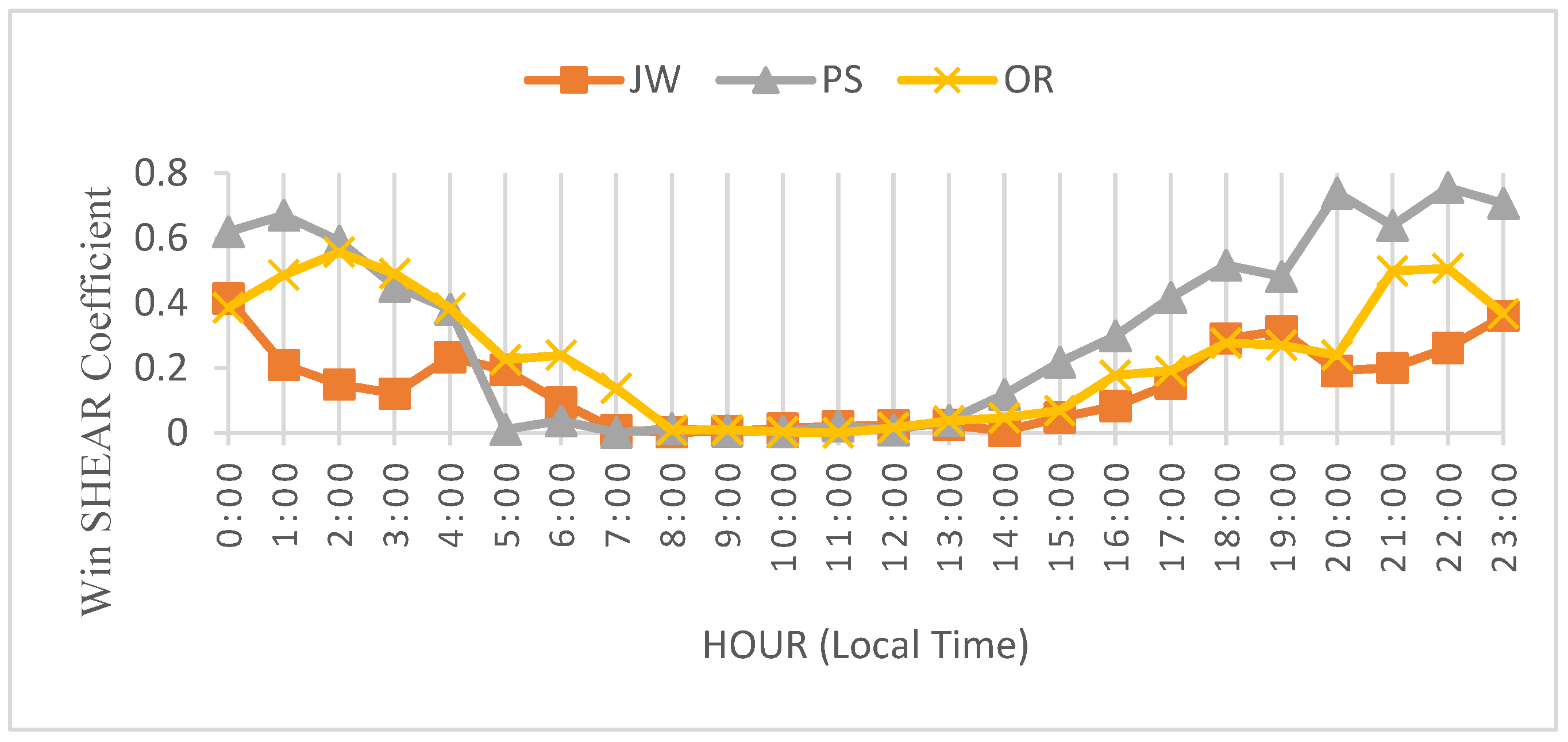
The diurnal WSC variation Figure 4 is significantly correlated with the daily heating/cooling cycle of the air above the ground level where higher values are experienced during the nighttime (00:00-06:00 h) while significantly decreasing after the sun starts heating the air near the ground. These values remain stable and low in the daytime and start to increase from about (16:00) onward, when the air above the ground level starts to cool down resulting gradual turn in stable conditions as suggested by literature [14,18].
Preprints 87661 g003
Figure 3. Annual variation of wind shear coefficient of the three sites PS, JW, OR.
Figure 3. Annual variation of wind shear coefficient of the three sites PS, JW, OR.
Preprints 87661 g003
Preprints 87661 g004
Figure 4. Diurnal variation of wind shear coefficient of the three sites PS, JW, OR.
Figure 4. Diurnal variation of wind shear coefficient of the three sites PS, JW, OR.
Preprints 87661 g004
Preprints 87661 g005
Figure 5. Annual wind speed frequency distribution measured for PS site at 20m and 60m.
Figure 5. Annual wind speed frequency distribution measured for PS site at 20m and 60m.
Preprints 87661 g005
Preprints 87661 g006
Figure 6. Annual wind speed frequency distribution measured for JW site at 20m and 60m.
Figure 6. Annual wind speed frequency distribution measured for JW site at 20m and 60m.
Preprints 87661 g006
Preprints 87661 g007
Figure 7. Annual wind speed frequency distribution measured for the OR site at 20m and 60m.
Figure 7. Annual wind speed frequency distribution measured for the OR site at 20m and 60m.
Preprints 87661 g007

4.4. Wind Energy Yield Estimation and Comparison

The wind shear coefficient has a significant role while measuring wind speed at a given height as mentioned above. Most of the time, wind speed for a higher altitude is extrapolated from lower to obtain the required energy yield assessment using a specific constant value of wind shear coefficient for a site Table 1, however, a slight change in wind shear can affect the wind speed at a height greatly as discussed in literature [13,15]. Based on 60m data, wind resource analysis was carried out for three sites, PS, JW, OR, and results values are summarized in Table 3, Table 4 and Table 5. The aim was to assign a suitable turbine for the sites and compare the different related functions using three composition options (i) measured data at 60m, (ii) extrapolated from 20m using 𝛂= 0.143 and (iii) extrapolated from 20m data using site-specific mean WSC values. Wind resource analysis based on 60m measured data, PS site in Table 3, is classified as a nearly marginal location with mean values of v and power density (P), 5.33 m/s and 142.33 W/m2. Furthermore, site JW is shown to be a poor location with a mean value of wind speed of 4.96 m/s and power density of 115.65 W/m2 in Table 4. The third site OR also indicates to be a poor location with mean v 4.31 m/s and P is 117.49 W/m2 in Table 5.
Wind energy yield parameters were calculated at 60m for the PS site using a single 2-MW Wind power (Vistas-V90) turbine showing CF (24.8%) and AF (89.7%) in Table 3. Comparing 60m measured data with the data extrapolated with 𝛂= 0.143, an underestimation of (10.4%) is detected in the mean V result with 21.5% for CF and AF 2.2%. Similarly, by using the overall mean value of WSC (0.076), an exceptional underestimation occurred with CF (81.9%) and AF (7.2%).
In Table 4, Wind energy yield parameters were calculated at 60m for the JW site using a single 1.5-MW, power (GE15sle) turbine provided a value CF (22.9%) and AF (89.2%). Compared to 60m measured data with the data extrapolated with 𝛂= 0.143, an underestimation of (10.2%) is detected in the mean V result with 23.7% for CF and 3.4% for AF. Moreover, by using the overall mean value of WSC (0.094), a remarkable underestimation occurred with CF (43.1%) and AF (5.7%).
Wind energy parameters were calculated in Table 5 at 60m for OR site using a single 1.5-MW power (GE15sle) turbine showing CF (16.4%) and AF (84.2%). Comparing 60m measured data with the data extrapolated with 𝛂= 0.143, an underestimation of (1.8%) is detected in the mean V result with 3.2% for CF and 1.3% for AF. Furthermore, by using the overall mean value of WSC (0.053), a similar underestimation occurred as in other sites with CF (34.7%) and AF (1.3%). These results showed that the site OR has the lowest values as compared to the other two sites correspondingly.

5. Conclusion

In this study, the Wind shear coefficient and its impact on electrical energy generation was investigated in three coastal locations of Pakistan by estimating the shape and scale factors of the Weibull distribution function using the empirical method. The parameters are used to calculate the wind power density and annual energy yield using two years (2016-2018) wind speed data with ten-minute intervals to predict the behavior of wind more accurately. Different models of wind turbines are proposed for electricity generation considering the possibility of installing wind farms at these locations. Using power law, the wind shear coefficient was calculated using available and extrapolated measurements of wind speed at three different levels, 20m, 40m, and 60m above ground level. The results of this study can be summarized as:
  • The value of wind shear varies with height where higher values appear at lower heights, while lower values are found at higher altitudes.
  • The diurnal WSC was highest in all three sites at nighttime 00:00, for PS 0.620-0.670, JW 0.641, and OR 0.186-0.556 while lower in mid-day 2:00, for PS 0.118, JW 0.006 and 0.016-0.097 for OR, which is certainly due to the heating and cooling cycle of the air during 24 hours of the day, which is shown in the WSC curve.
  • Annual wind variation of WSC was higher in the winter season (November to January) up to 0.105 for PS, 0.122 for JW, and OR 0.063 while lower in summer (May to July) up to 0.010, 0.016, and 0.003 for PS, JW and OR sites respectively.
  • PS site is a marginal location as the mean v is 5.33 m/s for the data measured at 60m AGL with CF (24.8%) and while AF (89.7%) for a suitable 2MW wind power Vistas-V90, where the WSC 𝛂= 0.143 shows a significant effect extrapolated from 20m, an underestimation of (10.4%) is detected in mean V result with 21.5% for CF and AF 2.2%. Similarly, by using the overall value of WSC 𝛂= 0.07, an exceptional underestimation occurred with CF (81.9%) and AF (7.2%).
  • JW site is a poor location where a suitable 1.5MW wind power Vistas-V90 is used with 60m measured data AGL giving a value of the mean v is 4.96 m/s with CF (22.9%) and AF (89.2%). The WSC 𝛂= 0.143 shows an underestimation of (10.2%) in mean v with 23.7% for CF and 3.4% for AF. Moreover, by using the overall mean site suggested value of WSC 𝛂= 0.09, a remarkable underestimation occurred with CF (43.1%) and AF (5.7%).
  • OR site is also a poor location with data measured at 60m AGL, the mean value of v is 4.31 m/s with CF (16.4%) while AF (84.2%) for a suitable 1.5-MW wind powerGE15sle turbine. The value of WSC 𝛂= 0.143 is Compared to 60m measured data, an underestimation of (10.2%) is detected in mean V with 23.7% for CF and 3.4% for AF. Moreover, by using the overall mean value of WSC 𝛂= 0.05, a remarkable underestimation occurred with CF (43.1%) and AF (5.7%).
To conclude, this study confirms that there is a rapid change in wind shear coefficient value even with locations of the same type of terrain. In fact, the default value of 1/7 WSC should be carefully used to extrapolate wind speed values of higher altitudes from lower neglecting which can cause a huge error in the estimation of wind power yield.

Author Contributions

Jan Yasir: Writing – original draft, Writing – review & editing. Ahmed Saeed: Data curation, review & editing. Sydney Mutale: review & editing. Yong Wang: Supervision, review & editing.

Funding

This research received no external funding.

Data Availability Statement

To be made available when requested.

Acknowledgments

We would like to extend our heartfelt appreciation to the Meteorological Department of Pakistan for their necessary support throughout this research endeavor. A special mention goes to Ms. Aleena Younus, Assistant Director, Meteorological Department of Pakistan, Quetta, and Mr. Shafi Muhammad PhD Scholar at China University of Geosciences (Beijing) China, for their critical & scientific review, whose dedication and assistance in providing comprehensive meteorological data have been instrumental in the success of this study. Moreover, the authors are grateful for the generous support received from the School of New Energy at North China Electric Power University (Beijing, China), facilitated and awarded through the Chinese Scholarship Council in 2020. This additional backing has not only facilitated our research but has also helped international collaboration and knowledge exchange. The collective efforts and contributions of these organizations and individuals have significantly elevated the quality and depth of our work, enabling us to advance our understanding of meteorological phenomena.

Conflicts of Interest

None

Abbreviations

List of Variables
MW Mega Watt
P Wind Power (W)
P (V) Wind Turbine’s Power Curve
W/m2 Watt Per Meter Square
C Weibull Scale Parameter
K Weibull Shape Parameter
Km Kilometer
Km2 Kilometer Square
In Natural Logarithm
MWh Megawatt hour
h/yr hour Per Year
KWh Kilo Watt-hour
K Kelvin
J/Kg Joule per Kilogram
Mm Millimeter
M Meter
sec Second
v Wind Velocity (m/s)
ρ Air density
List of Abbreviations
WSC Wind Shear Coefficient
AEP Annual Energy Production
CF Capacity Factor
AF Availability Factor
FLH Full Load Hour
AEY Annual Energy Yield
STDV Standard Deviation
AEP Annual Energy Production

References

  1. Brower M. Wind resource assessment: A practical guide to developing a wind project. John Wiley & Sons; 2012.
  2. Lee, J. C.; Stuart, P.; Clifton, A.; Fields, M. J.; Perr-Sauer, J.; Williams, L.; Housley, P. The Power Curve Working Group's assessment of wind turbine power performance prediction methods. Wind Energy Science. 2020, 5, 199-223. https://wes.copernicus.org/articles/5/199/2020/. [CrossRef]
  3. Landberg, L. Meteorology for wind energy; an introduction. John Wiley & Sons; 2015.
  4. Antoniou, I.; Pedersen, SM.; Enevoldsen, PB. Wind shear and uncertainties in power curve measurement and wind resources. Wind Energy. 2009,33, 449-468. https://journals.sagepub.com/doi/abs/10.1260/03095240 9790291208. [CrossRef]
  5. Dorenkamper, M.; Tambke, J.; Steinfeld, G.; Heinemann, D.; Kuhn, M. Atmospheric impacts on power curves of multi-megawatt offshore wind turbines. In. Journal of Physics. 2014, 555, 12-29. https://ioscience.iop.org/ article/10.1088/1742-6596/555/1/012029/meta. [CrossRef]
  6. Wharton, S.; Lundquist, JK. Assessing atmospheric stability and its impacts on rotor-disk wind characteristics at an onshore wind farm. Wind Energy 2012, 15, 525-546. https://onlinelibrary.wiley.com/doi/abs/10.1002 /we.483. [CrossRef]
  7. Mutale, S.; Banda, A.; Wang, Y.; Yasir, J. Capability of Zambian Industries to Manufacture Grid-Scale Wind Turbine Blades and Towers. 2023. https://www.preprints.org/manuscript/202309.1621/v1. [CrossRef]
  8. Zhang MH. Wind resource assessment and micro-siting. WILEY; 2015.
  9. Sumner, J.; Masson, C. Influence of atmospheric stability on wind turbine power performance curves. J. Solar Energy. 2006, 128, 531-538. [CrossRef]
  10. Wagner, R.; Antoniou, I.; Pedersen, SM.; Courtney, MS.; Jorgensen, HE. The influence of the wind speed profile on wind turbine performance measurements. Wind Energy. 2009,12,348-362. https://onlinelibrary.wiley.com/doi/abs/10.1002/we.297.
  11. Optis, M.; Perr-Sauer, J. The importance of atmospheric turbulence and stability in machine learning models of wind farm power production. Renew. Sustain. Energy Rev. 2019, 112, 27-41.https://www.sciencedirect.com/science/article/pii/S136 4032119303442. [CrossRef]
  12. Azad, A. K.; Alam, M. M.; Saha, M. Effect of wind shear coefficient on wind velocity at coastal sites of Bangladesh. International conference on Mechanical Engineering, Dhaka, Bangladesh. 2011,1-6. https://me.buet.ac.bd/icme/icme2011/Proceedings/PDF/ICME%2011-RE-012.pdf.
  13. Wharton, S.; Lundquist, J. K. Assessing atmospheric stability and its impacts on rotor- disk wind characteristics at an onshore wind farm. Wind Energy. 2012,15, 525-546. https://onlinelibrary.wiley.com/doi/abs/10.1002/we.483. [CrossRef]
  14. St Martin, C. M.; Lundquist, J. K.; Clifton, A.; Poulos, G. S.; Schreck, S. J. Wind turbine power production and annual energy production depend on atmospheric stability and turbulence. Wind Energy Science. 2016,1, 221-236.https://wes.copernicus.org/articles/1/221/2016/. [CrossRef]
  15. Kim, D. Y.; Kim, Y. H.; Kim, B. S. Changes in wind turbine power characteristics and annual energy production due to atmospheric stability, turbulence intensity, and wind shear. Energy. 2021, 214, 119-151. https://www.sciencedirect.com/science/article/abs/pii/S0360544220321587. [CrossRef]
  16. Werapun, W.; Tirawanichakul, Y.; Waewsak, J. Wind shear coefficients and their effect on energy production. Energy Procedia. 2017,138, 1061-1066. https://www.researchgate.net/publication/321122605. [CrossRef]
  17. Okorie, M. E.; Inambao, F.; Chiguvare, Z. Evaluation of wind shear coefficients, surface roughness and energy yields over inland locations in Namibia. Procedia Manufacturing.2017, 7, 630-638. https://www.researchgate.net/publication/312247385. [CrossRef]
  18. FΔ±rtΔ±n, E.; Guler, O.; Akdag, S. A. Investigation of wind shear coefficients and their effect on electrical energy generation. Applied Energy. 2011, 88, 4097-4105. https://www.sciencedirect.com/science/article/abs/pii/S0306261911003205. [CrossRef]
  19. Rehman, S., Al-Abbadi, N. M. Wind shear coefficients and energy yield for Dhahran, Saudi Arabia. Renewable Energy. 2007,32(5), 738-749. https://www.sciencedirect.com/science/ article/abs/pii/ S09601481 06000887. [CrossRef]
  20. Ur Rehman, S.; Shoaib, M.; Siddiqui, I.; Ahmed, F.; Tanveer, M. R.; Jilani, S. U. Effect of wind shear coefficient for the vertical extrapolation of wind speed data and its impact on the viability of wind energy project. Journal of Basic & Applied Sciences. 2015, 11, 90. [CrossRef]
  21. Pasni weather and climate profile. 2023. Available at: http://www.pasnibalochistan.climatemps.com/ (accessed on 13 June 2023).
  22. Ormara weather and tourism. 2023 https://www.triphobo.com/places/ormara-balochistan- pakistan/(accessed on 13 June 2023).
  23. Jiwani overview and climate. 2023 https://en.wikipedia.org/wiki/Jiwani/(accessed on 13 June 2023).
  24. Al-Hinai, A.; Charabi, Y.; Aghay-Kaboli, S. H. Offshore wind energy resource assessment across the territory of Oman: A spatial-temporal data analysis. Sustainability. 2021, 13, 28-62. https://www.mdpi.com/2071-1050/13/5/2862. [CrossRef]
  25. Gualtieri, G.; Secci, S. Wind shear coefficients, roughness length and energy yield over coastal locations in Southern Italy. Renewable Energy. 2011,36, 1081-1094. https://www.sciencedirect.com/science/article/abs/pii/S0960148110004131. [CrossRef]
  26. Ajao, K. R.; Rabiu, A. B.; Gbadeyan, A. A.; Ajibola, G. O.; Olabiyi, A. I. Assessment of wind resource for possibility of small wind turbine installation in Ilorin, Nigeria. 2015,42,298-305. https://ph01.tci- thaijo.org/index.php/easr/article/view/42870.
  27. Albani, A.; Ibrahim, M. Z. Wind energy potential and power law indexes assessment for selected near-coastal sites in Malaysia. Energies. 2017, 10, 307. https://www.mdpi.com/1996- 1073/10/3/307. [CrossRef]
  28. Gualtieri, G. Surface turbulence intensity as a predictor of extrapolated wind resource to the turbine hub height. Renewable Energy. 2015, 78, 68-81. https://www.sciencedirect.com/science/article/abs/pii/S096014811500018X. [CrossRef]
  29. Ayik, A.; Ijumba, N.; Kabiri, C.; Goffin, P. Preliminary wind resource assessment in South Sudan using reanalysis data and statistical methods. Renewable and Sustainable Energy Reviews. 2021, 138, 1106-1121. https://www.sciencedirect.com/science/article/abs/pii/S1364032120309059. [CrossRef]
  30. Ulazia, A.; Saenz, J.; Ibarra-Berastegi, G.; GonzΓ‘lez-Roji, S. J.; Carreno-Madinabeitia, S. Global estimations of wind energy potential considering seasonal air density changes. Energy. 2019, 187, 115-138. https://www.sciencedirect.com/science/article/pii/S0360544219316226. [CrossRef]
Preprints 87661 g001
Figure 1. Location of the three coastal sites of Mekran: PS, JW and OR.
Figure 1. Location of the three coastal sites of Mekran: PS, JW and OR.
Preprints 87661 g001
Preprints 87661 g002
Figure 2. Comparing the two-year wind rose diagram for three cities of Baluchistan (a). Pasni (b) Jiwani (c) Ormara.
Figure 2. Comparing the two-year wind rose diagram for three cities of Baluchistan (a). Pasni (b) Jiwani (c) Ormara.
Preprints 87661 g002
Table 3. Wind resources, energy yield parameters for the PS site calculated at 60m using 2MW rated power Vistas-V90 Table.
Table 3. Wind resources, energy yield parameters for the PS site calculated at 60m using 2MW rated power Vistas-V90 Table.
Parameter       Wind Data
Measured at 60m Extrapolated from 20m using 𝛂 =0.143 Extrapolated from 20m using 𝛂 =0.076
Wind Resources
No. of Valid Data       39906       39790       39790
Valid Data %       95.6       95.3       95.3
Mean       5.33       4.8       4.17
Stdv       2.87       2.64       2.27
C       5.99       5.51       4.7
K       1.95       1.95       1.93
Mean P (W/m2)       142.33       125.80       98.90
Turbine Converted Energy
AEY (MWh/y)       4358.8       3575.4       2387.1
CF (%)       24.8       20.41       13.63
FLH (h/y)       2179.4       1787.7       1193.5
AF (%)       89.77       87.82       83.69
Table 4. Wind resources, energy yield parameters for the JW site calculated at 60m using 1.5MW rated power GE15sle .
Table 4. Wind resources, energy yield parameters for the JW site calculated at 60m using 1.5MW rated power GE15sle .
Parameter       Wind Data
Measured at 60m Extrapolated from 20m using 𝛂 =0.143 Extrapolated from 20m using 𝛂 =0.094
Wind Resources
No. of Valid Data       39786       39790       39790
Valid Data %       95.3       95.3       95.3
Mean       4.96       4.50       4.24
Stdv       2.68       2.43       2.32
C       5.59       5.07       4.78
K       1.95       1.95       1.92
Mean P (W/m2)       124.25       104.73       87.65
Turbine Converted Energy
AEY (MWh/y)       3014.4       2435.3       2105.6
CF (%)       22.94       18.53       16.03
FLH (h/y)       2009.6       1623.5       1403.7
AF (%)       89.28       86.34       84.42
Table 5. Wind resources, energy yield parameters for the OR site calculated at 60m using 1.5MW rated power GE15sle.
Table 5. Wind resources, energy yield parameters for the OR site calculated at 60m using 1.5MW rated power GE15sle.
Parameter       Wind Data
Measured at 60m Extrapolated from 20m using 𝛂 =0.143 Extrapolated from 20m using 𝛂 =0.053
Wind Resources
No. of Valid Data       39786       39790       39790
Valid Data %       95.3       95.3       95.3
Mean       4.31       4.23       3.83
Stdv       2.33       2.28       2.07
C       4.86       4.77       4.32
K       1.95       1.95       1.95
Mean P (W/m2)       115.65       86.78       63.87
Turbine Converted Energy
AEY (MWh/y)       2166.8       2098.6       1607.9
CF (%)       16.49       15.97       12.24
FLH (h/y)       1444.54       1399.12       1071.99
AF (%)       84.24       83.12       83.12
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Β© 2024 MDPI (Basel, Switzerland) unless otherwise stated