Prerpints.org logo
Preprint
Article

The Influences of Micro-Alloying Element Sn and Magnetic Field on the Microstructure Evolution of Al-Bi Immiscible Alloys

Altmetrics

Downloads

70

Views

12

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 October 2023

Posted:

10 October 2023

You are already at the latest version

Alerts
Abstract
Directional solidification experiments were carried out to investigate the effect of micro-alloying element Sn and magnetic field on the solidification of Al-Bi immiscible alloys. Experimental results show that the size distribution of the dispersed particles in the low-speed solidified Al-3.4wt%Bi alloy presents two peaks, while it only shows one peak when solidified at a relatively high speed. The addition of Sn not only can enhance the nucleation rate and the number density of the Bi-rich droplets in the sample, but also decrease the Marangoni migration velocity and the axial resultant velocity of minority phase droplets in front of the solidification interface. Thereby it promotes the formation of Al-Bi alloys with a well-dispersed microstructure. A static magnetic with the strength of 0.2T increase the number density of the dispersed particles and decrease the average size and the size distribution width of the dispersed particles. Under the effect of Sn addition and static magnetic field, the average radius of the dispersed particles <R> and the solidification velocity V_0 satisfy <R>∝〖V_0〗^(-1/3) when the alloy was solidified at a relatively low velocity, <R> and V_0 satisfy <R>∝〖V_0〗^(-1/2) when the alloy is solidified at a high velocity.
Keywords: 
Subject: Chemistry and Materials Science  -   Metals, Alloys and Metallurgy

1. Introduction

Immiscible alloys exhibit a specific type of phase diagram characterized by a miscibility gap in the liquid state [1,2,3,4,5,6]. When cooling into the miscible gap, decomposition will happen, a homogeneous single-phase liquid separates into two liquids that are immiscible with each other and will form distinct phases [7,8,9,10,11,12,13,14]. Immiscible alloys are of particular interest because they can exhibit unique properties that are not found in their individual component metals. Many of them have variety of industrial application potential in the chemical, automotive, machinery, electronic and other fields. For instance, immiscible alloys based on Al-Bi and Al-Pb are potential materials for sliding bearings due to their self-lubricating properties [15,16,17], Cu-Fe alloys are materials with high strength and high conductivity [18,19,20,21]. However, the liquid-liquid decomposition can lead to the formation of phase-segregated microstructure and circumvent their applications. In recent years, Immiscible alloys have been extensively studied due to their unique properties and potential applications, considerable experiments have been conducted under microgravity, rapid solidification, as well as the external fields such as electric current [22]. Models describing the solidification process were established, and the microstructure formation under different conditions was calculated. But so far, little work has been carried out to investigate the effects of micro-alloying elements and magnetic fields on the solidification process and microstructure evolution of immiscible alloys.
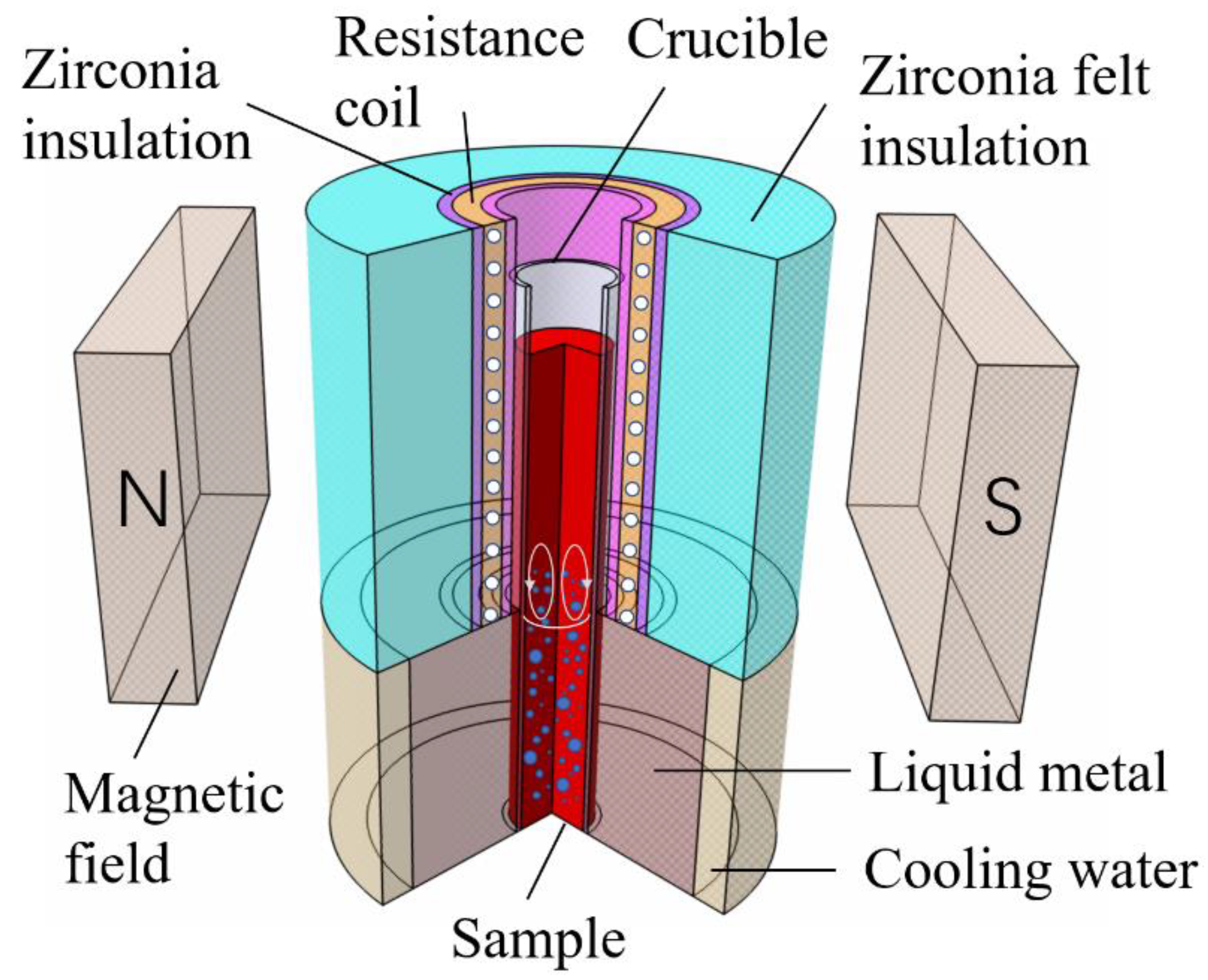
In this study, directional solidification experiments were carried out by a vertical Bridgman type furnace (Figure 1) with a static magnetic field device, the effects of micro-alloying elements Sn and static magnetic field on the solidification of Al-Bi alloys are studied. The solidification behavior of Al-Bi immiscible alloys and the influence mechanism of micro-alloying element Sn and static magnetic field on the microstructure evolution of immiscible alloys are discussed in detail.

2. Experimental Procedure

Directional solidification experiments were carried out by a Bridgman-type solidification apparatus. The Al-3.4wt.%Bi (monotectic composition) and Al-3.4wt.%-0.05wt.%Sn alloys are prepared by pure aluminum (99.99 wt.%), Bi (99.99 wt.%), and Sn (99.99 wt.%), The alloys were then heated in a cylindrical crucible placed in a resistance furnace to a high temperature above their immiscible gap to 973K, stirred and kept at this temperature for 40 minutes to ensure the formation a single-phase liquid. Then, the melt was solidified under the effect of a static magnetic field by withdrawing the crucible into the Ga-In-Sn liquid alloy bath, and the magnetic field was transverse to the alloy growth direction. The cylindrical samples were obtained with the diameter and length were 6 and 120 mm, respectively. The samples were then cut longitudinally along the center plane and polished. The microstructure was examined by scanning electron microscopy (Hitachi S-3400N) in the backscatter mode, and quantitative metallographic analysis was performed using SISC IAS V8.0 software to determine the size distribution and average diameter of the minority phase particles.

3. Results

3.1. The Effect of Micro-Alloying Element Sn on the Microstructure of Al-Bi Samples

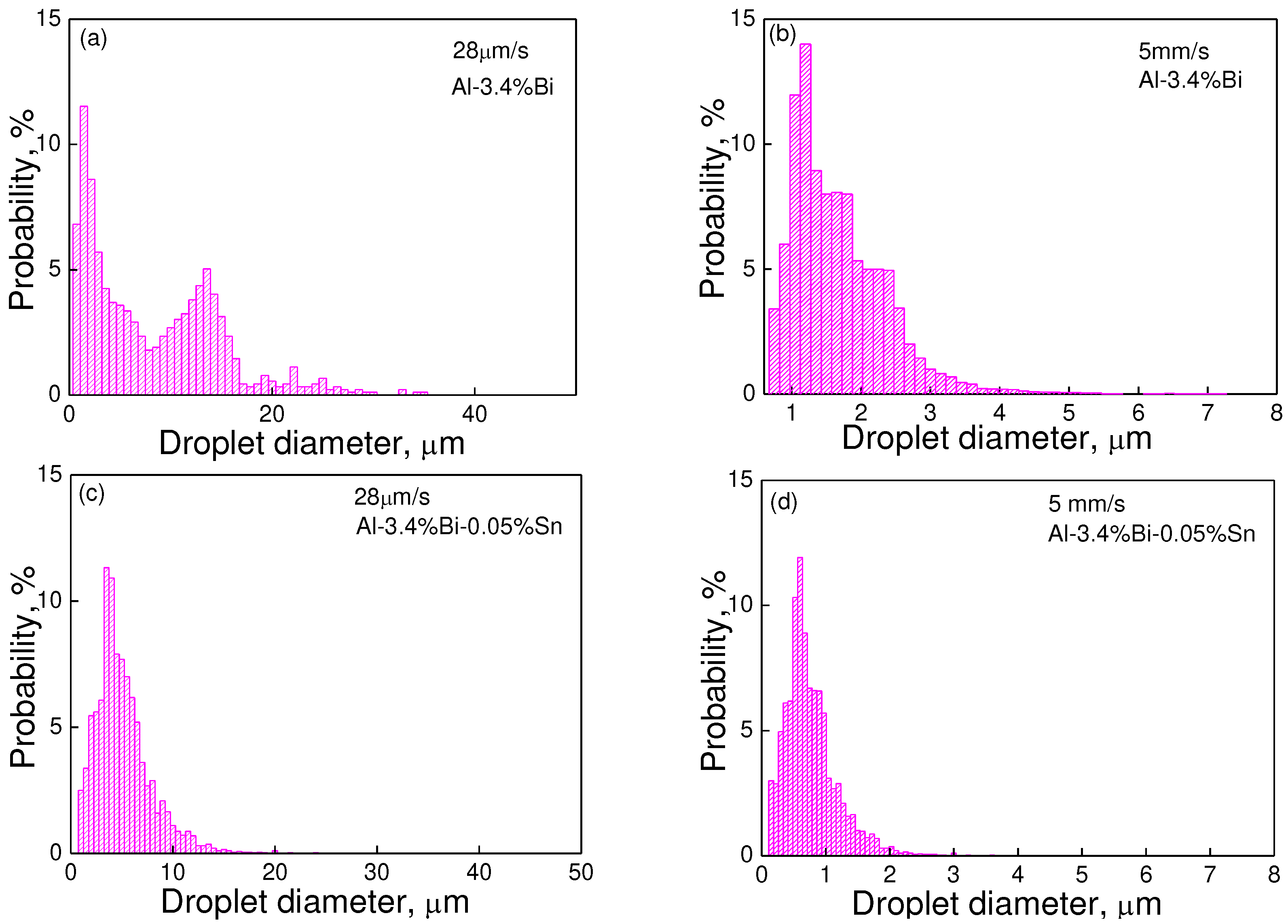
Figure 2 shows the microstructures of Al-3.4wt%Bi alloys (monotectic composition) solidified at different rates under the effect of micro-alloying element Sn. Energy dispersive X-ray spectroscopy (EDS) analysis shows that the dark and white phases are Bi-rich particles and Al-rich matrix phases, respectively. Figure 2 and Figure 3 show the size distributions and the average size of the dispersed particles in the samples. It demonstrates that the Al-3.4wt%Bi alloy exhibits two peaks at a low solidification rate (28 um/s), but only one peak at a relatively high solidification rate (5 mm/s). Moreover, the size distribution of the dispersed phase particles in all Al-3.4wt.%Bi-0.05wt.%Sn samples always has only one peak. Quantitative metallographic analysis indicates that the addition of micro-alloying element Sn can increase the number density of dispersed particles, reduce the average particle size and the width of the size distribution. That is, the addition of micro-alloying element Sn promotes the formation of Al-Bi alloy samples with a well-dispersed microstructure.

3.2. Microstructure Evolution of Al-Bi-(Sn) Samples Solidified under the Effect of Magnetic Field

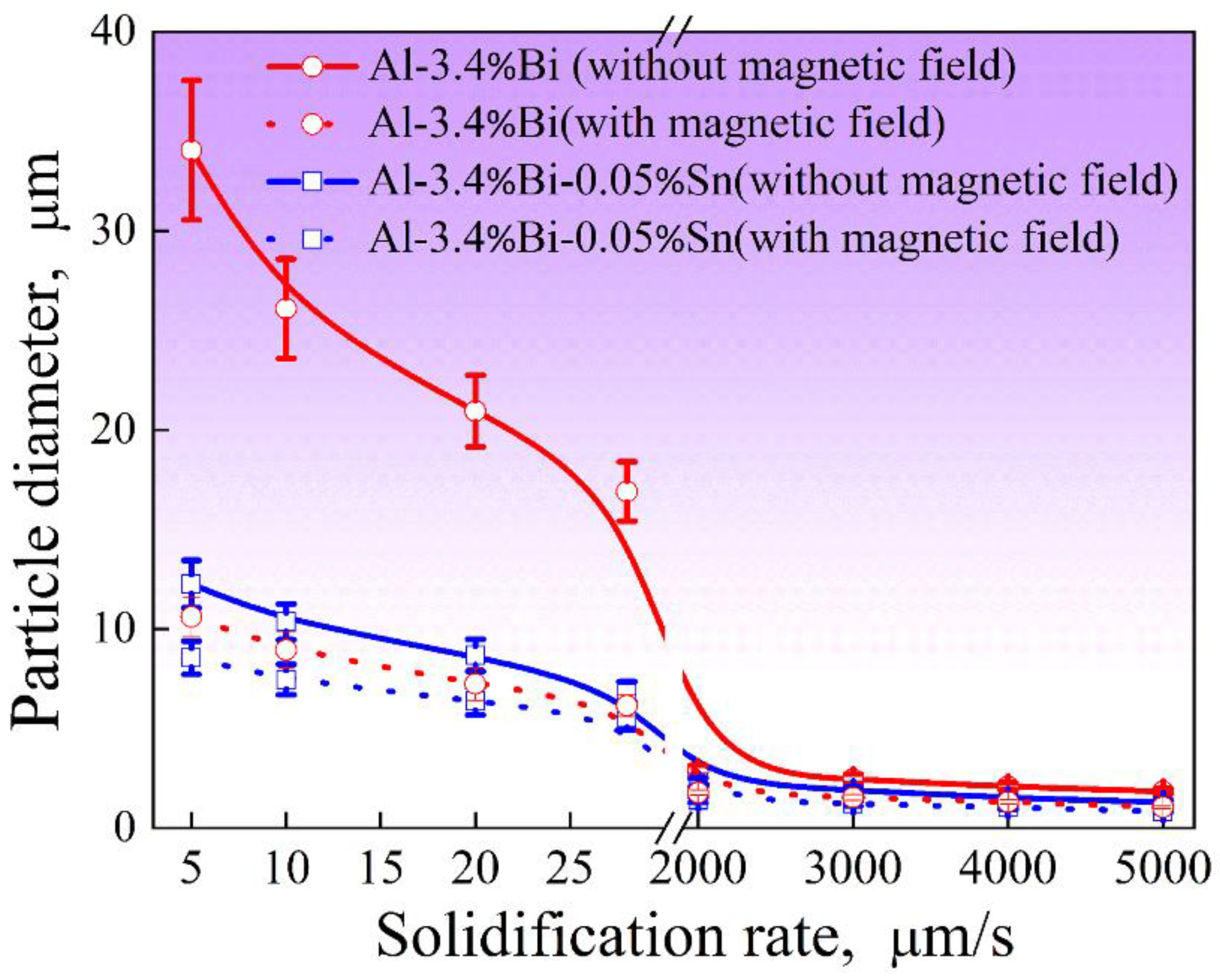
Figure 5 and Figure 6 show the microstructures of Al-3.4%Bi and Al-3.4%Bi-0.05%Sn samples solidified under the effect of 0.2T static magnetic field. It can be demonstrated that, the application of a magnetic field can increase the number density of the dispersed particles. Figure 4 shows the relationship between the average diameter of the dispersed particles in the samples and the solidification velocity. As expected, the size of Bi-rich particle decreases with the solidification rate, and the 0.2 T static magnetic field does not change this general trend, but the static magnetic field can increase the number density of dispersed particles and reduce the average size and size distribution width of dispersed particles. In other words, for Al-3.4%Bi and Al-3.4%Bi-0.05%Sn alloys, the static magnetic field results in the formation of samples with finely dispersed microstructures.

4. Discussions

4.1. Microstructure Evolution of Al-Bi Samples

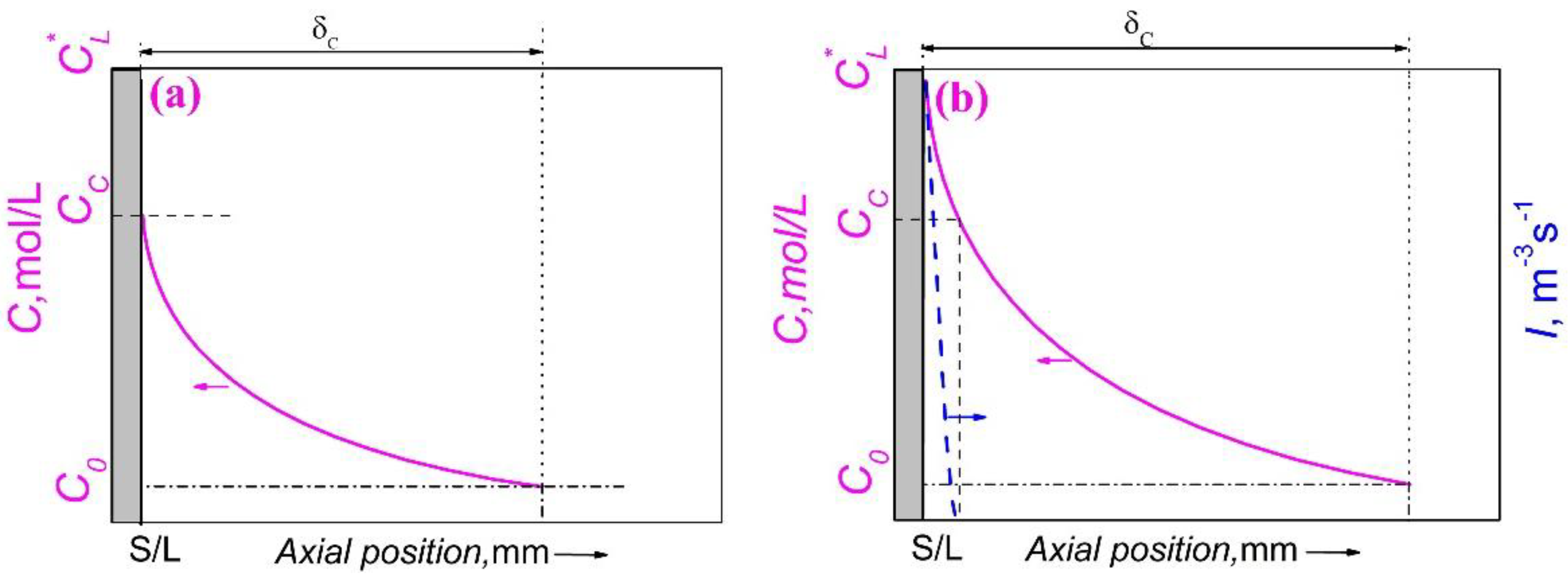
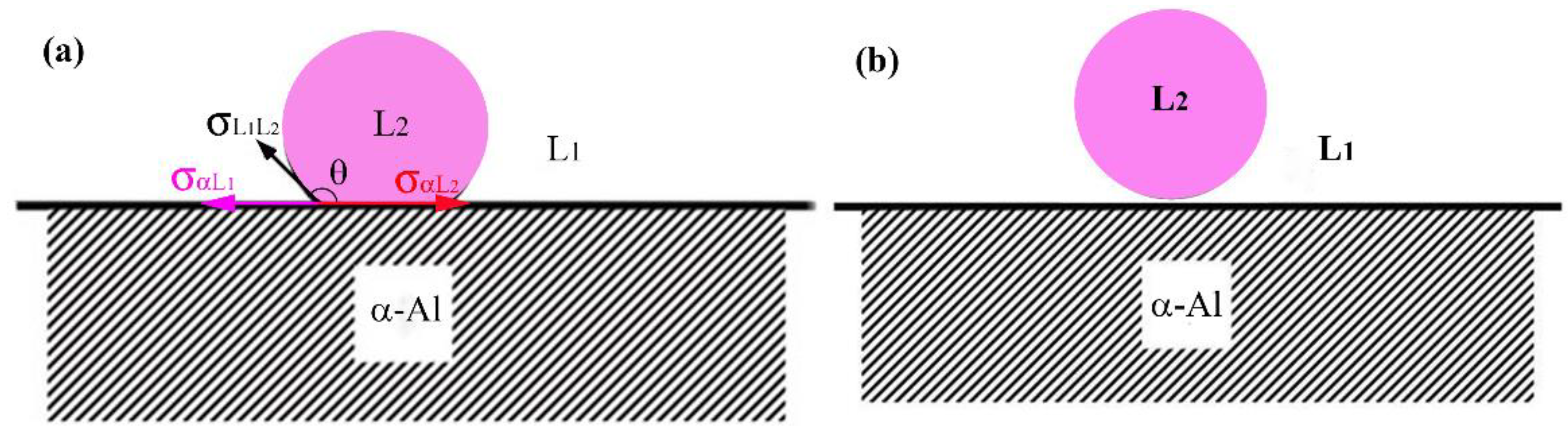
During the solidification of Al-Bi alloy, solute Bi will accumulate in front of the liquid-solid interface and form a Bi-rich boundary layer due to the low solubility in α-Al, as shown in Figure 7. When the concentration of the solute element Bi in the diffusion boundary layer reaches a critical value, the minority phase droplets will precipitate and the nucleation position depends on the interfacial energy between the two liquid phases ( σ L 1 L 2 ), the interfacial energy between the matrix liquid phase and α-Al ( σ α L 1 ), and the interfacial energy between the minority phase droplet and α-Al ( σ α L 2 ). The minority phase droplets nucleate heterogeneously on α-Al surface during the liquid-liquid phase transformation when σ α L 2 < σ α L 1 + σ L 1 L 2 (see Figure 8a), and the minority phase droplets nucleate in the enriched boundary layer during the liquid-liquid phase transformation when σ α L 2 > σ α L 1 + σ L 1 L 2 (see Figure 8b). According to references [23], for Al-Bi alloys, σ L 1 L 2 = 0.0578   J ⋅ m - 2 , σ α L 1 = 0.16   J ⋅ m − 2 , σ α L 2 = 0.23   J ⋅ m − 2 , they satisfy σ α L 2 > σ α L 1 + σ L 1 L 2 , so the minority phase droplets in the Al-Bi alloys nucleate in the enriched boundary layer and the heterogeneous nucleation of minor phase cannot take place on α-Al. The variation of the solute concentration in front of the solid/liquid (S/L) interface is determined by two opposing aspects: the nucleation and growth of minority phase droplets decreases the solute concentration while the solute redistribution increases the solute concentration. In the early stage of nucleation, the nucleation rate and the number density of minority phase droplets are very low and the solute concentration is controlled by the solute redistribution, which leads to an increase in the solute concentration, and causes a rapid increase in the nucleation rate and the number density of the minority phase droplets. As a result, due to the nucleation and growth of the bismuth-rich droplets, the consumption of Bi solute increases, and the composition of the matrix liquid begins to approach a stable composition, as shown in Figure 7.
The nucleated minority phase droplets will move in the melt due to specific gravity differences between phases and the temperature gradient. These movements are called Stokes motion and Marangoni migration, respectively. The migration velocities are expressed as [22]:
u s = − 2 g ρ β − ρ m 3 η m + η β η m 2 η m + 3 η β R 2 e z
u M = − 2 λ m R 2 λ m + λ β 2 η m + 3 η β ∂ σ L 1 L 2 ∂ r ∇ T
where u s and u M are respectively the Stokes motion velocity and Marangoni migration velocity. ρ m and ρ β are the densities of the matrix and the droplets. λ m and λ β are the thermal conductivities of the matrix and the droplets, η m and η β the dynamic viscosities of the liquid matrix and the droplets. e z is the unit vector in the axial direction, ∇ T is the temperature gradient.
The axial resultant velocity of minority phase droplets in front of the solidification interface is approximately given by:
V = u M z − u S − V 0
where V 0 is the solidification rate, u M z is the axial-component of the Marangoni migration velocity of the droplets. When the axial resultant velocity is negative, the minority phase droplets will migrate to the S/L interface. When the axial resultant velocity is positive, the minority phase droplets will migrate backward to the S/L interface.
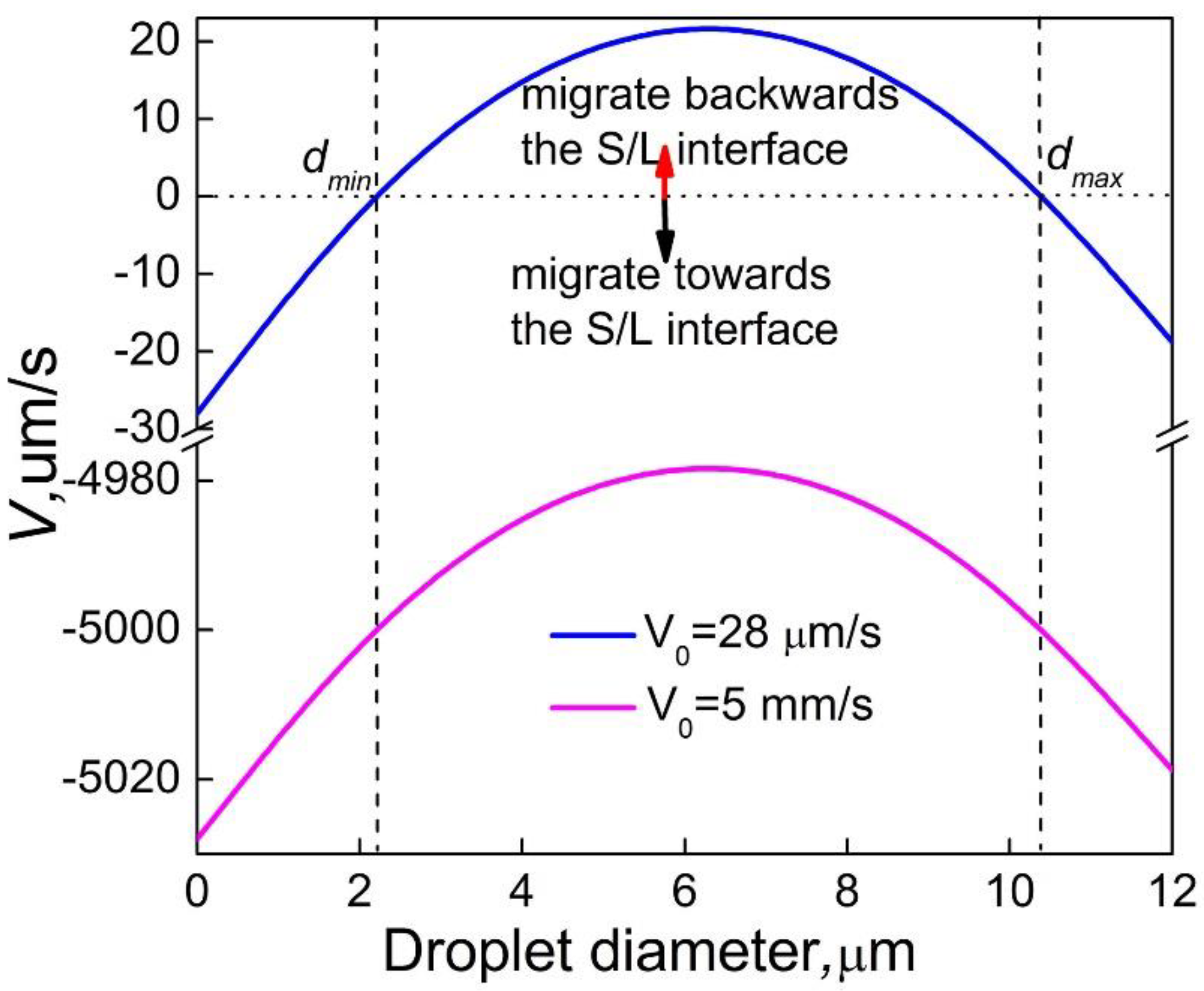
Figure 9 shows the relationship between the resultant velocity of minority phase droplets in front of the solidification interface and the droplet diameter, it indicates that when the alloy is solidified at a high velocity, the minority phase droplets of all sizes at any position in front of the solidification interface migrate to the solidification interface, so the size distribution of the minority phase particles has only one peak. When the alloy is solidified at a relatively lower velocity, the migration of the minority phase droplets is related to the size of the droplets, under the concurrent actions of the Marangoni migration, the Stokes motion of the droplets and the movement of the sample, the minority phase droplets with the size, less than dmin or bigger than dmax, will migrate towards the solidification interface, and the minority phase droplets within a certain size range (from dmin to dmax) may move backwards to the solidification interface, resulting in a size distribution of the minority phase particles with two peaks. After the nucleation, the minority phase droplets will grow and coarse, all of them migrate towards the solidification interface before the size reaches dmin, some of them near the solidification interface can be engulfed, they corresponds to the first peak of the size distribution, while the droplets far away from the solidification interface have more time to grow, their size will exceed dmin before reaching the solidification interface and being engulfed, then they will move backwards to the solidification interface until their size reaches dmax, these droplets corresponds to the second peak of the size distribution. The analytical results are in favorable agreement with the experimental ones, as shown in Figure 3.

4.2. Effect of Sn on the Microstructure Evolution of Al-Bi Samples

Tensioactivity of a component C at the interface in a three-component system A-B-C can be estimated by calculating the adsorption separately from A-rich (L1) and B-rich (L2) liquids [24]. Tensioactivity of component C can be expressed as:
τ L 1 L 2 = K L 1 L 2 τ L 1 + τ L 2 1 + K L 1 L 2
where τ L 1 and τ L 2 represent the changes of energy during adsorption of element C, respectively, from the volume of liquid L 1 and liquid L 2 to the interface. K L 1 L 2 is a partitioning coefficient, which describes the distribution of component C (with concentration XC) between liquid L 1 and liquid L 2 by infinite solution. A negative value of τ L 1 L 2 corresponds to the segregation of component C at the interface between L 1 and L 2 liquid phases. The more negative is τ L 1 L 2 , the more significant is the adsorption, and the more distinctive is the drop of the interfacial tension σ L 1 L 2 . For positive values of τ L 1 L 2 , the solute C will desorb from the interface.
The tensioactivity parameter τ L 1 L 2 for Al-Bi-Sn ternary system was calculated with Equation (4) based on the thermodynamical data in Reference [25]. It is found that τ L 1 L 2 / R T ≈ - 2 for Sn in the Al-Bi-Sn system at 933 K. Thus, the addition of Sn can reduce the interfacial tension between the two liquid phases by the adsorption of Sn at the (L1-L2) interface.
Perepezko [26] and Uebber [27] used the classical nucleation theory to predict the onset of the nucleation in monotectic alloys, and the nucleation rate of the minority phase droplets can be given by [28]:
I = N 0 O Γ Z exp ⁡ ( − 16 π σ L 1 L 2 3 3 k B T Δ G V 2 )
where I is the nucleation rate, N0 is the number density of atoms,  with nc being the number of atoms in a sphere of critical radius R * = 2 σ L 1 L 2 / Δ G v , Δ G v is the gain of volume free energy on nucleation. Γ=6D/λ is the attachment rate, λ is the average jump distance of a solute atom due to diffusion. Z is the Zeldovich factor, kB and T are the Boltzmann’s constant and the absolute temperature, respectively.
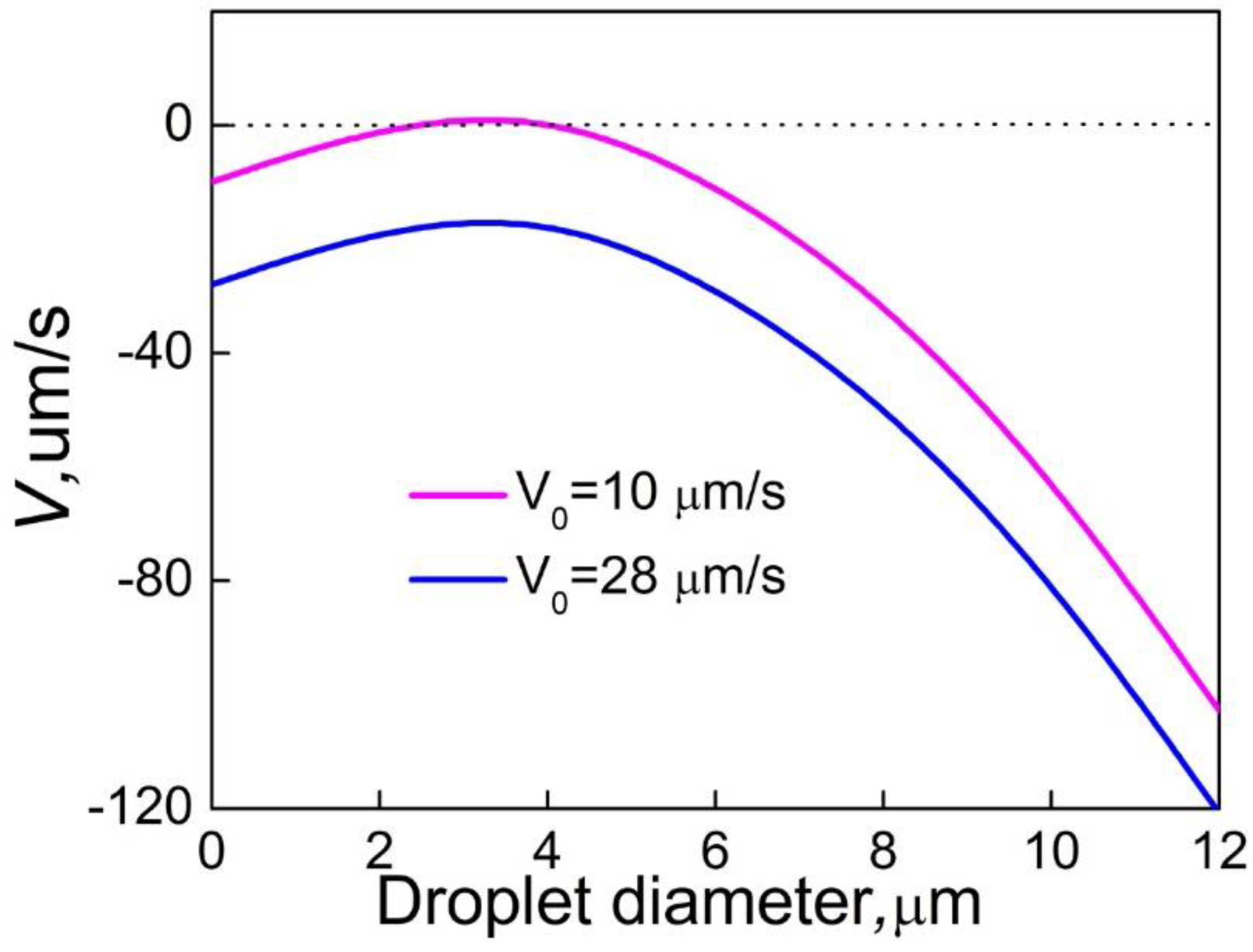
Adding a small amount of Sn (0.01wt.%-0.1wt.%) to the Al-Bi alloy has negligible influence on the phase diagram and the morphology of the S/L interface. Sn mainly affects the microstructure formation through decreasing the interfacial energy between the matrix and the minority phase liquids, which can increase the nucleation rate and number density of the Bi-rich droplets in the sample. This promotes the decrease of the average size of the Bi-rich phase and the formation of Al-Bi alloys with a well-dispersed microstructure. On the other hand, the Marangoni migration velocity and the axial resultant velocity of minority phase droplets in front of the solidification interface will decrease with the decrease of interfacial energy, as shown in Figure 10. When the axial resultant velocity is less than zero, the minority phase droplets of all sizes located at any position in front of the solidification interface will migrate towards the solidification interface, leading to a size distribution of the minority phase particles with only one peak, as shown in Figure 3.

4.3. Effect of static magnetic field on the microstructure evolution

Applying a magnetic field to a substance will change the Gibbs free energy due to magnetization. Considering the magnetic free energy, the gain of volume free energy is expressed as [29]:
Δ G v ′ = Δ G v − 1 2 μ 0 χ L 2 − χ L 1 ⋅ H m 2
where Δ G v is the gain of volume free energy without the magnetic field, μ 0 is the permeability of free space, χ L 1 and χ L 2 are the magnetic susceptibilities of the matrix liquid and the spheres, respectively. When nucleate homogeneously, the ratio of the nucleation rate with and without magnetic field can be given by [29]:
I ′ I = exp ⁡ 16 π σ L 1 L 2 3 3 k B T Δ G ′ v 2 − Δ G v 2 Δ G v 2 Δ G ′ v 2
where kB is the Boltzmann’s constant. In this study, χ L 1 is positive but χ L 2 is negative [29]. It can be concluded from Equation (6) that the inequation Δ G ′ v 2 > Δ G v 2 is satisfied. Therefore, the ratio of the nucleation rate in Equation (7) is large compared to the unit. The static magnetic field can enhance the nucleation of the Bi-rich spheres and promote the refinement of the Bi-rich spheres, as shown in Figures 1, 3, 4 and 5.
Since the Bi-rich sphere and the Al-rich liquid matrix are conductive, the application of the magnetic field results in an inductive drag or magnetic viscosity on the motion of the flow [30]. In general, the effectiveness of the magnetic field in damping convective flows depends on the value of the Hartman number. This inductive drag or magnetic viscosity becomes dominant when the Hartman number, H a = B d σ η m 1 2 , is large compared to the unit [30]. Here, B is the magnetic field strength, d is the characteristic length, and σ is the electrical conductivity. Because the magnetic field is transverse to the alloy growth direction, the diameter of the sample can be taken as the characteristic length. In the present experiment, the magnetic field strength is 0.2T, the Hartmann number is about 70. The magnetic field will increase the effective viscosity in the area in front of the solid/liquid interface, and the movement of the minority phase droplets will be suppressed. As a result, the magnetic field promotes the formation of a well dispersed microstructure.

4.4. Effect of Sn and Static Magnetic Field on the Growth of the Droplets

The nucleated droplets will grow by the diffusional transport of solute in a supersaturated matrix, the growth rate of a droplet is given by [31]:
v = d R d t = D C m − C I C β − C I ⋅ 1 R [ 1 + R ( 4 π N < R > ) 1 / 2 ] ( 1 + 2 3 π η m η m + η β P e ) 1 / 2
where D is the diffusion coefficient of Bi element, R is the droplet radius, <R> is the average radius of the droplet radius, N is the number density of the droplet, η m and η β are the effective viscosities of the matrix melt and the droplets, respectively. Pe is the Peclet number, C m is the mean field concentration in the matrix liquid, C β is the concentration of the liquid within the droplet, and C I is the concentration in the matrix at the interphase boundary. C I depends on R according to the Gibbs-Thomson relation, and it can be written as [23]:
C I = C ∞ ⋅ exp ⁡ α S R ≃ C ∞ ⋅ ( 1 + α S R )
where C ∞   is the equilibrium concentration at a flat interface boundary. α S = 2 Ω d σ L 1 L 2 k β T is the capillary length, Ω d is the atomic volume of the minority phase droplets.
When solidifying the alloy under the effect of Sn addition and static magnetic field, since the average diameter and the volume fraction of the minority phase droplets are both small, and the melt flow is restrained, the effects of the melt flow and the diffusional interactions between droplets can be neglected. Equation (8) can be written as:
v = d R d t = D C m − C I C β − C I ⋅ 1 R
Substituting Equation (9) into Equation (10):
v = D C m − C ∞ − C ∞ ⋅ α S R C β − C ∞ − C ∞ ⋅ α S R · 1 R
For the Al-Bi system, C β ≫ C m ，so ( C β − C ∞ ) ≫ C ∞ ⋅ α S R , if the solidification rate is enough quick, the supersaturation of the melt will be high, it is namely that （ C m − C ∞ ） ≫ C ∞ ⋅ α S R ，then Equation (11) can be written as:
v ≅ α ⋅ 1 R
where α = D C m − C ∞ C β − C ∞
By integrating Equation (12), the following equation can be obtained:
1 2 R 2 = α ⋅ t + β
where β is constant, t is the growth/coarsening time. During cooling the melt, the growth/coarsening time (t) is inversely proportional to the solidification rate ( V 0 ), so the average radius of the droplets can be given by:
< R > ∝ V 0 − 1 / 2
If the solidification rate is very slow, the supersaturation of the melt will be small, Ostwald ripening occurs and the average radius of the droplets can be written by[23]:
< R > 3 = K L S W ⋅ t
Or:
< R > ∝ V 0 − 1 / 3
where K L S W is the Ostwald ripening constant.
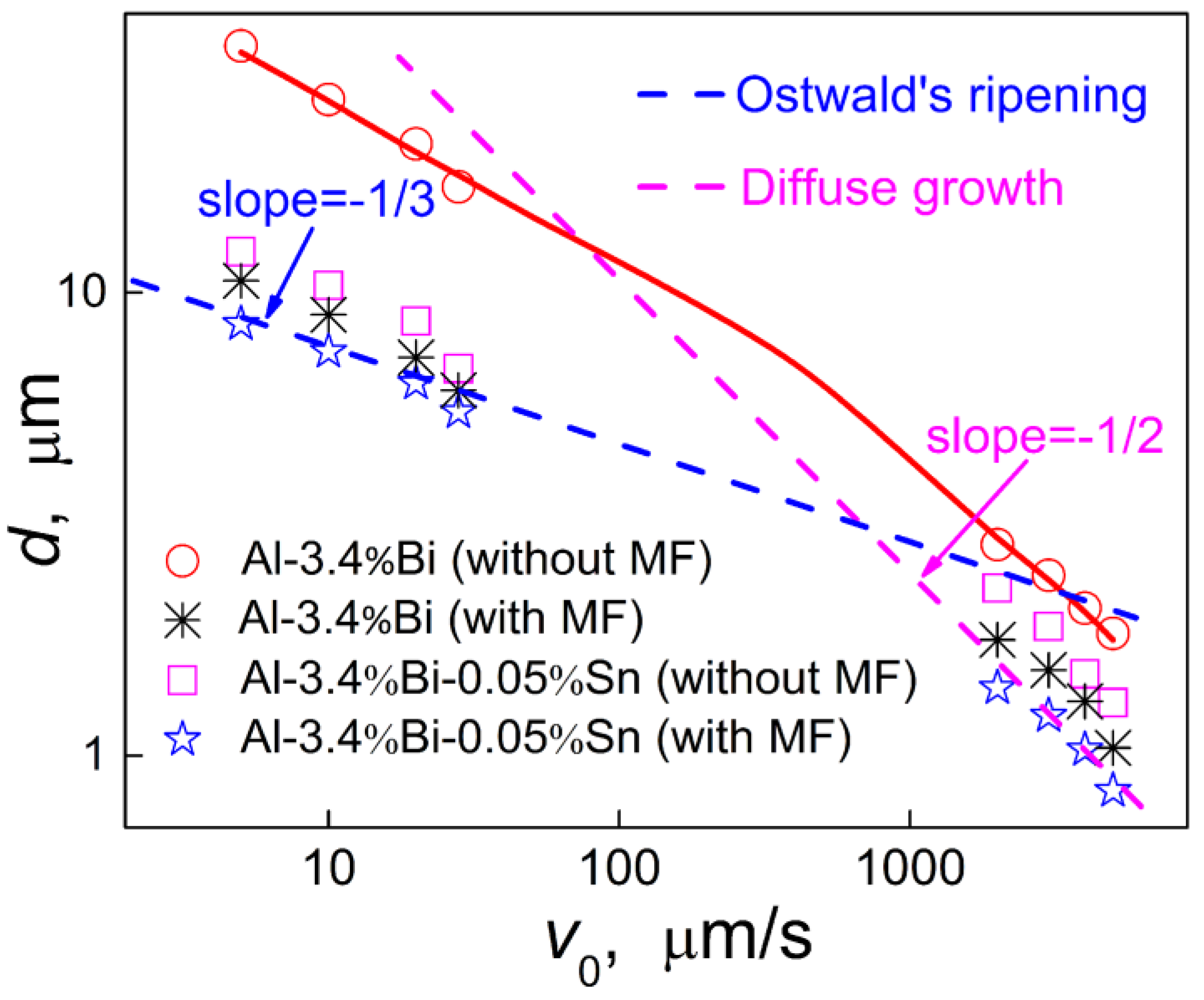
The actual solidification rate is usually between the above two conditions, and the dependence of the average radius of the minority phase particles varies from <R>∝V0-1/3 to <R>∝V0-1/2 with the increase of the solidification rate, as shown in Figure 11. It also demonstrates that when the alloy was solidified at a relatively low velocity, the average radius of the dispersed particles < R > has an exponential relationship with the solidification velocity V 0 , which satisfies to < R > ∝ V 0 − 1 / 3 , and when the alloy is solidified at a high velocity, < R > and V 0 satisfy < R > ∝ V 0 − 1 / 2 .

5. Conclusions

In summary, directional solidification experiments have been carried out to investigate the effect of micro-alloying element Sn and magnetic field on the solidification process of Al-Bi immiscible alloys. The conclusions are as follows:
1)
The size distribution of the dispersed particles in the low-speed solidified Al-3.4wt%Bi alloy shows two peaks, while it only shows one peak when solidified at a relatively high velocity.
2)
The addition of Sn can reduce the interfacial tension between the two liquid phases, it not only can enhance the nucleation rate and the number density of the Bi-rich droplets in the sample, but also decrease the Marangoni migration velocity and the axial resultant velocity of minority phase droplets in front of the solidification interface. It is conducive to the reduction of the average size of the Bi-rich phase and the formation of Al-Bi alloys with a well-dispersed microstructure.
3)
The application of a static magnetic field with 0.2T also can increase the number density of the dispersed particles and decrease the average size and the size distribution width of the dispersed particles.
4)
Under the effect of Sn addition and static magnetic field, the average radius of the dispersed particles < R > well depends on the solidification velocity V 0 exponentially according to < R > ∝ V 0 − 1 / 3 when the alloy was solidified at a relatively low velocity, and the average radius of the dispersed particles < R > well depends on the solidification velocity V 0 exponentially according to < R > ∝ V 0 − 1 / 2 when the alloy is solidified at a high velocity.

Acknowledgments

This work was supported by the National Key Research and Development Program of China [grant number 2021YFA0716303]; the National Natural Science Foundation of China (Grant Numbers 51771210 and 51971227); and the Chinese Academy of Sciences Strategic Priority Program on Space Science (Grant Number XDA15013800).

References

  1. H. X. Jiang, J. He ,J. Z. Zhao, Influence of electric current pulses on the solidification of Cu-Bi-Sn immiscible alloys. Sci. Rep. 2015, 5, 12680.
  2. Q. Sun, H. X. Jiang, J. Z. Zhao ,J. He, Microstructure evolution during the liquid-liquid phase transformation of Al-Bi alloys under the effect of TiC particles. Acta Mater. 2017, 129, 321-330. [CrossRef]
  3. L. Wang, L. Bo, Y. Wang, D. Wu, P. Jia, M. Zuo ,D. Zhao, Effect of solidification rate on the formation of core-shell structure of Al60Bi24Sn16 monotectic alloy. J. Mol. Liq. 2018, 263, 349-356. [CrossRef]
  4. J. Zhao ,H. X. Jiang, Progress in the Solidification of Monotectic Alloys. Acta Metall. Sin. 2018, 54, 682-700. [CrossRef]
  5. T. Zheng, Y. Zhong, J. Wang, Z. Ren, W. Ren, Z. Lei, F. Debray, E. Beaugnon ,X. Wei, Droplet Evolution and Refinement During Liquid–Liquid Decomposition of Zn-6WtPct Bi Immiscible Alloy Under High Static Magnetic Fields. Metall. Mater. Trans. A 2018, 49, 3333-3345.
  6. C. K. Deng, H. X. Jiang, J. Z. Zhao, J. He ,L. Zhao, Study on the Solidification of Ag-Ni Monotectic Alloy. Acta Metall. Sin. 2020, 56, 212-220.
  7. M. Chen, P. Jia, R. Liu, S. Cui ,H. Geng, Solidification of immiscible Al75Bi9Sn16 alloy with different cooling rates. J. Alloys Compd. 2016, 688, 18-22. [CrossRef]
  8. B. W. Dong, J. C. Jie, X. X. Yao, S. C. Liu ,T. J. Li, Effect of Sn addition on morphology evolution of secondary phase in hypo-monotectic Cu-Pb-Sn alloy during solidification. J. Alloys Compd. 2019, 791, 936-946.
  9. S. C. Liu, J. C. Jie, Z. K. Guo, G. M. Yin ,T. M. Wang, Solidification microstructure evolution and its corresponding mechanism of metastable immiscible Cu80Fe20 alloy with different cooling conditions. J. Alloys Compd. 2018, 742, 99-106. [CrossRef]
  10. Q. Sun, H. X. Jiang, J. Z. Zhao ,J. He, Effect of TiC particles on the liquid-liquid decomposition of Al-Pb alloys. Mater. Des. 2016, 91, 361-367. [CrossRef]
  11. W. L. Wang, Y. H. Wu, L. H. Li, N. Yan ,B. Wei, Homogeneous granular microstructures developed by phase separation and rapid solidification of liquid Fe-Sn immiscible alloy. J. Alloys Compd. 2017, 693, 650-657. [CrossRef]
  12. B. Wei, W. L. Wang, S. B. Luo ,Z. Xia, Phase separation and subsequent solidification of peritectic Fe-Cu-Ge alloys subjected to substantial undercooling processing. J. Alloys Compd. 2017, 717, 190-196. [CrossRef]
  13. Y. H. Wu, W. L. Wang, J. Chang ,B. Wei, Evolution kinetics of microgravity facilitated spherical macrosegregation within im-miscible alloys. J. Alloys Compd. 2018, 763, 808-814.
  14. L. Zhang, Y. Gang, X. He, S. Li, W. Ning ,W. Xu, Phase separated characteristics affected by cooling rate of immiscible Cu-Cr alloy by laser surface melting. J. Alloys Compd. 2018, 772, 209-217. [CrossRef]
  15. Cao, Chezheng, Liu, Weiqing, Zhiwei, Xu, Jiaquan, Hwang, Injoo ,De, Scalable manufacturing of immiscible Al-Bi alloy by self-assembled nanoparticles. Mater. Des. 2018, 146, 163-171.
  16. L. Ratke ,S. Diefenbach, Liquid immiscible alloys. Mater. Sci. Eng. R 1995, 15, 263-347. [CrossRef]
  17. Q. Sun, H. X. Jiang ,J. Z. Zhao, Effect of micro-alloying element Bi on solidification and microstructure of Al-Pb alloy. Acta Metall. Sin. 2016, 52, 497-504.
  18. S. Dong, C. Zhang, L. Zhang, J. Cai, P. Lv, Y. Jin ,Q. Guan, Microstructure and properties of Cu-Cr powder metallurgical alloy induced by high-current pulsed electron beam. J. Alloys Compd. 2018, 755, 251-256. [CrossRef]
  19. Hee Ra Jo, Jeong Tae Kim, Sung Hwan Hong, Young Seok Kim, Hae Jin Park, Woo Jin Park, Jin Man Park ,Ki Buem Kim, Effect of silicon on microstructure and mechanical properties of Cu-Fe alloys. J. Alloys Compd. 2017, 707, 184-188. [CrossRef]
  20. X. G. Li, L. F. Cao, J. Y. Zhang, J. Li, J. T. Zhao, X. B. Feng, Y. Q. Wang, K. Wu, P. Zhang ,G. Liu, Tuning the microstructure and mechanical properties of magnetron sputtered Cu-Cr thin films: The optimal Cr addition. Acta Mater. 2018, 151, 87-99. [CrossRef]
  21. S. Sarkar, C. Srivastava ,K. Chattopadhyay, Development of a new class of high strength copper alloy using immiscibility route in Cu-Fe-Si system: Evolution of hierarchical multi-scale microstructure. Mater. Sci. Eng., A 2018, 723, 38-47. [CrossRef]
  22. H. X. Jiang, J. Z. Zhao ,J. He, Solidification Behavior of Immiscible Alloys under the Effect of a Direct Current. J. Mater. Sci. Technol. 2014, 10, 1027-1035. [CrossRef]
  23. Z. Yang, Q. Sun ,J. Zhao, DIRECTIONAL SOLIDIFICATION OF MONOTECTIC COMPOSITION Al-Bi ALLOY. Acta Metall. Sin. 2014, 50(1), 25-31.
  24. D. Chatain, C. Vahlas ,N. Eustathopoulos, Etude des tensions interfaciales liquide-liquide et solide-liquide dans les systemes a monotectique Zn-Pb et Zn-Pb-Sn. Acta Metall. 1984, 32, 227-234.
  25. G. Kaban ,W. Hoyer, Characteristics of liquid-liquid immiscibility in Al-Bi-Cu, Al-Bi-Si, and Al-Bi-Sn monotectic alloys: Dif-ferential scanning calorimetry, interfacial tension, and density difference measurements. Phys. Rev. B 2008, 77, 125426.
  26. J. H. Perepezko, C. Galaup ,K. P. Cooper, Solidification of Undercooled Monotectic Alloys. Mrs Proceedings 1981, 9, 491-501. [CrossRef]
  27. N. Uebber ,L. Ratke, Undercooling and nucleation within the liquid miscibility gap of Zn-Pb alloys. Scripta Metall. Mater. 1991, 25, 1133-1137. [CrossRef]
  28. Z. Lei ,J. Zhao, Microstructure Formation in a Gas-Atomized Drop of Al-Pb-Sn Immiscible Alloy. Metall. Mater. Trans. A 2012, 43, 5019-5028.
  29. H. Jie, J. Zhao, H. Li, X. Zhang ,Q. Zhang, Directional Solidification and Microstructural Refinement of Immiscible Alloys. Metall. Mater. Trans. A 2008, 39, 1174-1182. [CrossRef]
  30. H. Li ,J. Zhao, Directional solidification of an Al-Pb alloy in a static magnetic field. Comp. Mater. Sci. 2009, 46, 1069-1075. [CrossRef]
  31. H. L. Li, J. Z. Zhao, Q. X. Zhang ,J. He, Microstructure Formation in a Directionally Solidified Immiscible Alloy. Metall. Mater. Trans. A 2008, 39, 3308-3316. [CrossRef]
Preprints 87148 g001
Figure 1. Schematic show of the vertical Bridgman type furnace with a static magnetic field device.
Figure 1. Schematic show of the vertical Bridgman type furnace with a static magnetic field device.
Preprints 87148 g001
Preprints 87148 g002
Figure 2. The microstructure of (a,b) Al-3.4wt.%Bi samples and (c,d) Al-3.4wt.%Bi-0.05wt.%Sn samples solidified at the pulling rate of (a,c) 28 um/s and (b,d) 5 mm/s.
Figure 2. The microstructure of (a,b) Al-3.4wt.%Bi samples and (c,d) Al-3.4wt.%Bi-0.05wt.%Sn samples solidified at the pulling rate of (a,c) 28 um/s and (b,d) 5 mm/s.
Preprints 87148 g002
Preprints 87148 g003
Figure 3. Size distributions of the dispersed particles in (a,b) Al-3.4wt.%Bi samples and (c,d) Al-3.4wt.%Bi-0.05wt.%Sn samples solidified at the rate of (a,c) 28 um/s and (b,d) 5 mm/s.
Figure 3. Size distributions of the dispersed particles in (a,b) Al-3.4wt.%Bi samples and (c,d) Al-3.4wt.%Bi-0.05wt.%Sn samples solidified at the rate of (a,c) 28 um/s and (b,d) 5 mm/s.
Preprints 87148 g003
Preprints 87148 g004
Figure 4. Relationship between the average diameter of the dispersed particles in the samples and the solidification velocity.
Figure 4. Relationship between the average diameter of the dispersed particles in the samples and the solidification velocity.
Preprints 87148 g004
Preprints 87148 g005
Figure 5. Microstructures of Al-3.4wt.%Bi samples solidified under the effect of static magnetic field. The magnetic field strength B is 0.2 T. The solidification rates are (a) 10 um/s, (b) 28 um/s, (c) 3 mm/s and (d) 5 mm/s, respectively.
Figure 5. Microstructures of Al-3.4wt.%Bi samples solidified under the effect of static magnetic field. The magnetic field strength B is 0.2 T. The solidification rates are (a) 10 um/s, (b) 28 um/s, (c) 3 mm/s and (d) 5 mm/s, respectively.
Preprints 87148 g005
Preprints 87148 g006
Figure 6. Microstructures of Al-3.4wt.%Bi-0.05wt.%Sn samples solidified under the effect of static magnetic field. The magnetic field strength B is 0.2 T. The solidification rates are (a) 10 um/s, (b) 28 um/s, (c) 3 mm/s and (d) 5 mm/s, respectively.
Figure 6. Microstructures of Al-3.4wt.%Bi-0.05wt.%Sn samples solidified under the effect of static magnetic field. The magnetic field strength B is 0.2 T. The solidification rates are (a) 10 um/s, (b) 28 um/s, (c) 3 mm/s and (d) 5 mm/s, respectively.
Preprints 87148 g006
Preprints 87148 g007
Figure 7. Schematic of solute concentration (solid line) and nucleation rate of the minority phase droplets (dashed line) in front of the solidification interface of a monotectic composition alloy solidified directionally. (a) Solute boundary layer when the melt at the solid/liquid interface arrives at the critical concentration (CC) for the nucleation of the minority phase droplets. (b) Solute boundary layer and nucleation rate of the minority phase droplets when the solidification comes into a stable state.
Figure 7. Schematic of solute concentration (solid line) and nucleation rate of the minority phase droplets (dashed line) in front of the solidification interface of a monotectic composition alloy solidified directionally. (a) Solute boundary layer when the melt at the solid/liquid interface arrives at the critical concentration (CC) for the nucleation of the minority phase droplets. (b) Solute boundary layer and nucleation rate of the minority phase droplets when the solidification comes into a stable state.
Preprints 87148 g007
Preprints 87148 g008
Figure 8. Dependence of the nucleation of the minority phase droplets on the contact angle θ between the droplet and the matrix solid, (a)   0 < θ < π ; (b)   θ = π .
Figure 8. Dependence of the nucleation of the minority phase droplets on the contact angle θ between the droplet and the matrix solid, (a)   0 < θ < π ; (b)   θ = π .
Preprints 87148 g008
Preprints 87148 g009
Figure 9. Relationship between the resultant velocity of minority phase droplets in front of the solidification interface and the droplet diameter for the Al-3.4%Bi sample solidified at different solidification rate.
Figure 9. Relationship between the resultant velocity of minority phase droplets in front of the solidification interface and the droplet diameter for the Al-3.4%Bi sample solidified at different solidification rate.
Preprints 87148 g009
Preprints 87148 g010
Figure 10. Relationship between the resultant velocity of minority phase droplets in front of the solidification interface and the droplet diameter for the Al-3.4%Bi-0.05%Sn sample solidified at different solidification rate.
Figure 10. Relationship between the resultant velocity of minority phase droplets in front of the solidification interface and the droplet diameter for the Al-3.4%Bi-0.05%Sn sample solidified at different solidification rate.
Preprints 87148 g010
Preprints 87148 g011
Figure 11. Relationship between the solidification velocity (V0) and the average diameter (d) of the dispersed particles in the Al-3.4%Bi and Al-3.4%Bi-0.05%Sn samples solidified under the effect of magnetic field.
Figure 11. Relationship between the solidification velocity (V0) and the average diameter (d) of the dispersed particles in the Al-3.4%Bi and Al-3.4%Bi-0.05%Sn samples solidified under the effect of magnetic field.
Preprints 87148 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated