Prerpints.org logo
Preprint
Article

Image Encryption Using Improved Hybrid Chaotic Map and Spiral Transformation

Altmetrics

Downloads

115

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 October 2023

Posted:

06 October 2023

You are already at the latest version

Alerts
Abstract
Image encryption based on chaotic maps is an important way to ensure the secure communication of digital multimedia on the Internet. To improve the encryption performance and security of image encryption systems, a new image encryption algorithm is proposed by employing a compound chaotic map and random cyclic shift. Firstly, an improved Hybrid chaotic system is designed by coupling Logistic, ICMIC, Tent, and Chebyshev maps (HLITC). Comparison tests with previous chaotic maps in terms of chaotic trajectory, Lyapunov exponent, and Kolmogorov entropy illustrate the new hybrid chaotic map has better chaotic performance. Then the proposed HLITC chaotic system is used to develop a new chaotic image encryption scheme with the double cyclic shift. The improved HLITC chaotic system is performed to generate key sequences used in the image scrambling and diffusion stage. The spiral transformation controlled by chaotic sequence is used to scramble the pixels of the plaintext image, while the XOR operation based on a chaotic map is used for pixel diffusion. Extensive experiments of statistical analysis, key sensitivity, and keyspace analysis are conducted. Experimental results show the proposed encryption scheme has good robustness against brute force attacks, statistical attacks, and differential attacks, and is more effective than many existing chaotic image encryption algorithms.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

With the rapid development and wide application of new-generation information technologies such as cloud computing, big data, the Internet of Things, and artificial intelligence [1,2,3,4]. Nowadays, the dissemination of multimedia data such as digital images on the Internet has become increasingly prevalent. At the same time, however, the rapidly developing digital signal processing technology has brought many security problems to the communication and transmission of digital images on the Internet. Secure transmission and access of digital images in the open network environment have attracted more and more attention from researchers [5,6,7,8,9,10,11]. Image encryption transforms a meaningful image into an unrecognized noise-like one, and is an effective method to ensure the security of digital images. Chaos systems have received the researchers’ attention due to their inherent properties of sensitivity to initial conditions, ergodicity, and random behavior [12,13].
In recent years, many chaotic image encryption schemes have been presented. Pareek et al. proposed an image encryption algorithm by employing two logistic maps [14]. In the image encryption scheme, the initial conditions for both logistic maps are derived using an external secret key, and eight different types of operations are exploited to encrypt the image pixels. Given the shortcomings of the small parameter space of the Logistic map, Zhang et al. [15] designed an image encryption algorithm by employing discrete exponential chaotic maps to improve image confusion and diffusion. Zhu and Sun [12] presented a modified skew tent map and its application in image encryption. The proposed modified tent map to generate the plaintext-dependent secret keys set. The diffusion operation with cipher output feedback ensures that the cipher image is dependent on both the initial keys and the plaintext image. In [16], the Camellia block cipher and the logistic chaotic map are used to encrypt images. It scrambles the image using the Cat map and generates the round mask and the post-whitening key with the logistic map. However previous chaos-based image encryption schemes are built on low-dimensional chaotic maps. The low-dimensional chaotic systems have small keyspace, and the generated chaotic sequence has poor randomness. Kumar et al. employed multiple chaotic maps for image encryption [17]. In this scheme, the Logistic map is introduced to shuffle the pixels of the plaintext image, and Arnold's cat map is used in the diffusion process. Those encryption schemes based on low-dimensional chaotic sequences [12,14,15,16,17] cannot effectively resist statistical attacks.
Later, the hyperchaotic maps have been investigated to design more secure image encryption schemes due to their high randomness and ergodicity. Ref. [18] proposed a Lorenz-based image encryption algorithm with a perceptron model. It extended the periodicity of the Lorenz chaotic map by dynamically adjusting the chaotic system’s parameters. The modified Lorenz chaotic map is used to produce three sets of the pseudo-random sequence. Akhshani et al. presented a hierarchy of 2D piecewise chaotic maps with an invariant measure and developed a new image encryption scheme by using significant properties of these chaotic maps such as ergodicity, sensitivity to the initial condition, and random-like behavior [19]. The famous Chen hyperchaotic system is used to generate the shuffling matrix and the diffusing matrix in Ref. [20]. Firstly, the Chen hyper-chaotic system is used to shuffle the position of the image pixels. Hua et al. built a new 2D chaotic system (called 2D-LSM) using the Logistic and Sine maps, and the 2D-LSM chaotic map is further used to devise a new image encryption algorithm based on the image content [21]. To enhance the encryption effectiveness, Ye et al. proposed a chaotic encryption scheme combining a 3D logistic map and the secure hash algorithm-3 (SHA-3) [22]. Wang et al. proposed a color image encryption method by employing 4D chaotic maps and DNA encoding [23]. In the encryption scheme, the rules of DNA encoding are controlled by four chaotic sequences generated by the new 4D chaotic system. Gong et al. designed a new 4D chaotic system with coexisting asymmetric attractors [24]. Theoretical analysis of phase portrait, bifurcation diagram, and Lyapunov exponent, and its applications in random number generator (RNG) and image encryption verified the feasibility of the new 4D chaotic map.
Recently, the compound chaotic system has been an effective approach for image encryption [25,26,27] because it showed better randomness and noise-like behaviors than other chaos. Zhu et al. proposed a 2D composite discrete chaotic system (CDCS) [28]. To obtain a good permutation effect, the new CDCS system is used for the bit-level permutation and the pixel-level diffusion. In 2017, they developed another compound homogeneous hyper-chaotic system (CHHCS) that is employed to permutate the plaintext image [29]. In addition, dynamic LBP operations are used to diffuse each permutated pixel. Hua et al. introduced a cosine-transform-based chaotic system (CTBCS) [30]. The CTBCS is exploited to generate three chaotic maps, one of these maps is used to design an image encryption algorithm where the high-efficiency scrambling is used to separate adjacent pixels and the random order substitution is used to spread a small change in the plaintext image to all pixels of the cipher-image. Gao et al. presented an image encryption algorithm by coupling the sine map and the tent map [31]. The bit rearrangement is used to further improve the composite sine-tent map. Image pixels are encrypted by applying the most significant bit substitution, scrambling, and diffusion. To overcome bandwidth and security issues simultaneously, Yadav et al. devised a joint image compression and encryption scheme using hybrid chaotic maps [32]. The Absolute Moment Truncation Coding approach is used for compression and Arnold’s Cat and Henon maps are applied to the compressed image for encryption. To improve the chaotic characteristics, Zhang and Liu [33] designed a compound Sine-Piecewise Linear Chaotic Map (SPWLCM) and proposed an image encryption algorithm using this SPWLCM chaos and DNA coding. Wang and Du developed two chaotic systems: 1D Logistic-Chebyshev map (1DLCM) and Logistic-Chebyshev coupled map lattices (LCDCML) [34]. LCDCML uses 1DLCM as the dynamic coupling coefficient and further proposes a pixel-level and bit-level image encryption algorithm using these two new chaotic systems. In the encryption scheme, the image scrambling and diffusion are implemented with chaotic sequences generated by the LCDCML map. Basha et al. presented a bit-level color image encryption scheme using Logistic-Sine-Tent-Chebyshev (LSTC) map [35]. The LSTC map, cyclic shifts, and the XOR operation are used for the mutual diffusion of two color components. The binary element is exchanged and transformed into another binary bit plane by using the LSTC map.
To obtain better randomness and ergodicity, we constructed a new hybrid chaotic map by coupling multiple chaotic maps and designed a new image encryption application for this compound chaotic map. The main contributions of this paper are summarized as follows: (1) Developed a new hybrid chaotic map by coupling Logistic, ICMIC, Tent, and Chebyshev maps (called HLITC). Performance evaluations by chaotic trajectory, Lyapunov exponent, and Kolmogorov entropy testify the new hybrid chaotic map has better key sensitivity to the initial value and larger control parameter space. (2) Proposed a chaotic image encryption algorithm using the presented HLITC system. In the encryption, key sequences generated by the HLITC map are used for image scrambling and diffusion stages. The spiral transformation controlled by the HLITC map is employed to scramble the pixels of the plaintext image, and the XOR operation dependent on the chaotic map is used for image diffusion. (3) The experiments demonstrate that the proposed encryption algorithm has high resistance to statistical attacks, differential attacks, and brute-force attacks, and it can achieve higher security than several previous chaotic image encryption algorithms.
The rest of the paper is organized as follows. Section 2 introduces the classic chaotic maps and the new hybrid chaotic map. The new image encryption algorithm based on the HLITC system is presented in Section 3. We discuss the experimental results in Section 4 and conclude in Section 5.

2. Construction of the Hybrid Chaotic Map

This section presents the new hybrid chaotic system by coupling Logistic, ICMIC, Tent, and Chebyshev maps (HLITC), and their properties. To prove the superiority of the HLITC system, a comparison between three sample chaotic maps is conducted in terms of chaotic trajectory, Lyapunov exponent, and Kolmogorov entropy.

2.1. Classic Chaotic Maps

2.1.1. Logistic Map

The Logistic map is a quadratic polynomial map, which is one of the typical maps representing complex nonlinear behavior. The mathematical expression is written as follows.
x n + 1 = μ x n 1 − x n ,   μ ∈ 0,4 , x n ∈ 0,1
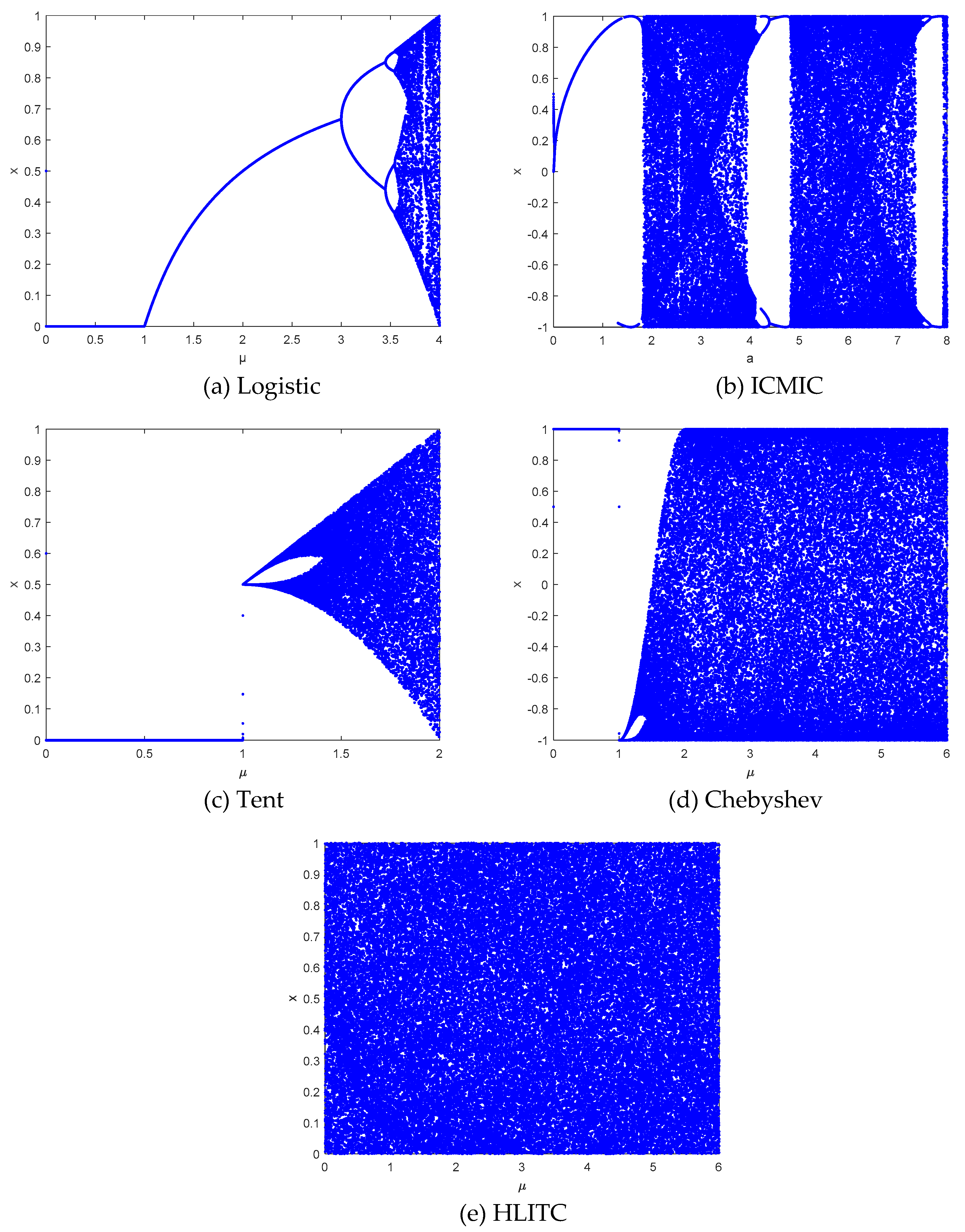
where μ is the bifurcation parameter, only when 3.5699456< μ ≤ 4, the Logistic map falls into the chaotic state. The bifurcation diagram of the Logistic map is shown in Figure 1(a).

2.1.2. ICMIC Map

He et al. proposed a 1D iterative chaotic map with infinite collapses (ICMIC) [36]. Compared with the Logistic map and Tent map, the ICMIC map has the advantages of uniform traversal and fast convergence. It can be expressed as
x n + 1 = s i n α / x n , α ∈ 0 , ∞ , x n ∈ − 1,0 ) , ] ∪ ( 0,1
Figure 1(b) shows the corresponding bifurcation diagram.

2.1.3. Tent Map

Tent map is a piecewise linear map with a relatively uniform distribution. The bifurcation diagram for the tent map is represented in Figure 1(c). It has been widely used in chaotic cryptography. Its mathematical expression is as follows.
x n + 1 = μ x n ,                                     x n ∈ 0,0.5 μ 1 − x n ,             x n ∈ [ 0.5,1 )
where the control parameter μ ∈ 0,2 .

2.1.4. Chebyshev Map

Chebyshev map is one of 1D chaotic maps with good nonlinear dynamic characteristics. Figure 1(d) is the bifurcation diagram for the Chebyshev map. When the control parameter μ is greater than 1, chaos phenomenon begins to occur. When greater than 2, The map is in a chaotic state. It can be defined as follows.
x n + 1 = c o s μ · a r c c o s x n , x n ∈ − 1,1

2.2. Proposed HLITC Chaotic System

To enhance the randomness of chaotic systems, we design a new chaotic system by combining the Logistic map, ICMIC map, Tent map, and Chebyshev map. The main process of building the chaotic system is as follows:
First, compound ICMIC map and Logistic map, we have
x n + 1 = s i n μ π μ x n 1 − x n  
To further skip blank windows, we change the parameter μ to μ 4 + 3.6 . The compound ICMIC map can be rewritten as
x n + 1 = s i n μ 4 + 3.6 π μ x n 1 − x n  
Then compound the Chebyshev map and the Tent map, and modify control parameter μ by μ + 2 to avoid falling into blank areas. The compounded Chebyshev chaotic map is expressed as
x n + 1 = c o s μ + 2 a r c c o s 4 μ x n ,                                           x n ∈ 0,0.5 c o s μ + 2 a r c c o s 4 μ 1 − x n ,               x n ∈ [ 0.5,1 )
Finally, to improve the randomness of the chaotic system, the modular function is used to integrate the compound Chebyshev map and the improved ICMIC map, and the hybrid HLITC chaotic system is produced. Its mathematical definition is as follows.
x n + 1 = m o d s i n μ 4 + 3.6 μ x n 1 − x n   + c o s μ + 2 a r c c o s μ + 3.6 x n , 1 ,                     x n ∈ 0,0.5 m o d s i n μ 4 + 3.6 x n   + c o s μ + 2 a r c c o s μ + 3.6 1 − x n , 1 ,   x n ∈ [ 0.5,1 )
The improved HLITC map makes the chaotic sequence distribution more uniform and has a large parameter space range from μ ∈ [ 0 , ∞ ) . It can avoid the stability window and the blank area. Its bifurcation diagram is illustrated in Figure 1(e). From Figure 1, it can be seen that the HLITC map has a larger parameter space and better randomness than the traditional chaotic maps.

2.3. Chaotic Behaviours

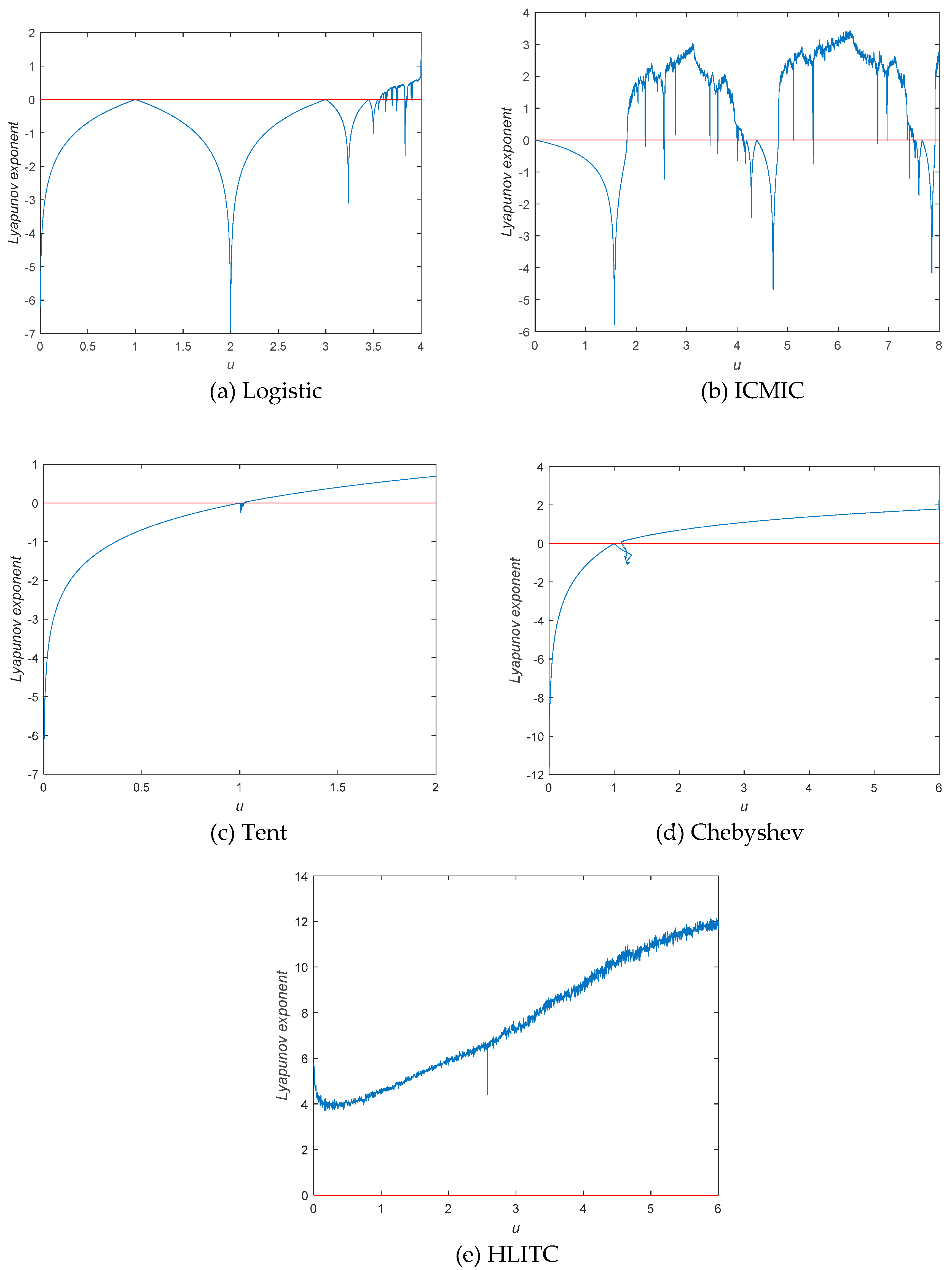
In this section, Lyapunov Exponent (LE), and information entropy are further used to analyze the dynamics of the HLITC chaotic system. Figure 2 shows the comparison between Logistic, ICMIC, Tent, Chebyshev, and HLITC for the parameter Lyapunov Exponent. From Figure 2, It can be found that all the LE values of the HLTIC map for all control parameter values are greater than 0. So, the HLITC map has more chaotic behaviors than the classic chaotic maps in terms of LE.
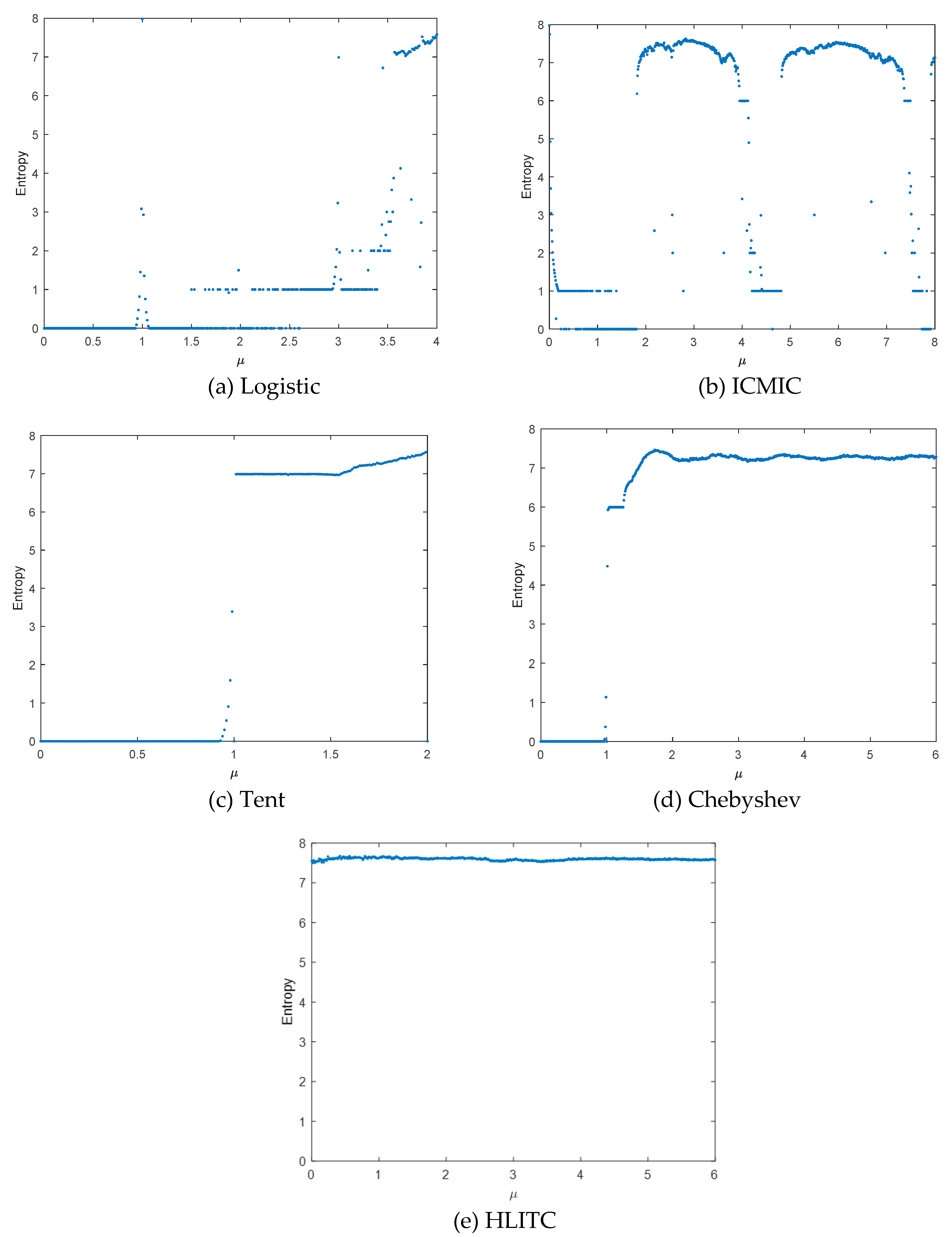
Information entropy is usually used to measure the uncertainty of a variable. The greater the uncertainty of variables, the higher the information entropy, and it is defined as
H X = ∑ i = 0 L − 1 p x i l o g 1 p x i
where X = x i x i ∈ 0,255 , p x i is the probability of x i , and L = 256 for gray-scale images. The maximum value of information entropy is 8 for the grayscale images.
Figure 3 shows the information entropy diagrams of different chaotic maps. It can be seen that the entropy values of output sequences generated by the proposed HLITC map are close to the ideal value 8, which indicates the HTLITC map has better unpredictability than the above-mentioned traditional chaotic maps.

2.4. Randomness Test

To further test the randomness of the HLITC map, the NIST SP800 test is performed on the chaotic sequences generated by the HTLITC system. The NIST randomness testing has 15 performance tests which are accessed by P-value. If the P-value is less than 0.01, the randomness of the tested sequence is poor, and if the P-value is greater than or equal to 0.01, the randomness of the tested sequence is good.
In the testing, the chaotic sequence generated by the HLITC map is first converted into a binary sequence and then the NIST randomness testing is performed. The test results are listed in Table 1. From Table 1, it can be seen that the chaotic sequence produced by the new HLITC system has good randomness among all 15 indicators tested by NIST, and all P-values are greater than 0.01, indicating that the generated chaotic sequence has good randomness.

3. Image Encryption Based on Hybrid HLITC Map

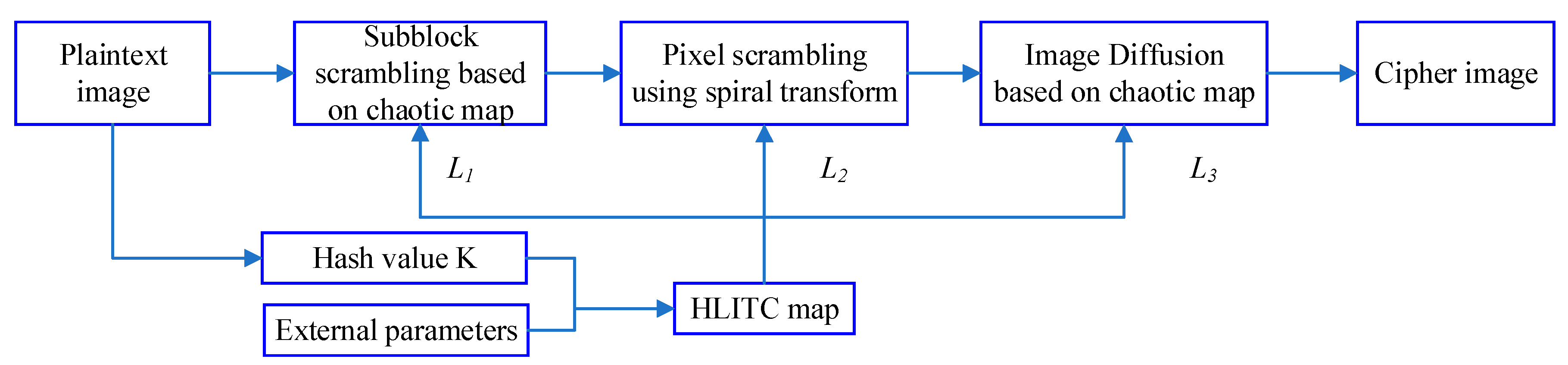
This section introduces the proposed image encryption algorithms based on spiral transformation and chaos maps. The proposed image encryption algorithm based on the HLITC map is composed of three stages, i.e., key generation, image scrambling, and image diffusion process as illustrated in Figure 4.

3.1. Key Generation

To enhance the security and enlarge the key space, the hash value of the plaintext image and external parameters are employed to produce the control parameters and initial values of the proposed HLITC map. Assume that the original image is denoted as I m × n . The detailed process of key generation is illustrated as follows.
Step 1: Obtain the hash value K of the plaintext image by applying the SHA-256 hash function.
Step 2: Divide the hash value K into 32 segments with each of one byte. Thus, K can be expressed as K = k 1 , k 2 , … , k i , … , k 32 , where i=1,2,…,…,32, and k i is an integer in the interval [0, 255].
Step 3: Set the secret keys λ i , i=1,2,3 as the external parameters, and generate the initial values x i   and control parameters μ i .
x i = m o d k 6 i − 1 + 1 ⊗ k 6 i − 1 + 2 ⊗ k 6 i − 1 + 3 ⊗ k 6 i − 1 + 4 ⊗ k 6 i − 1 + 5 ⊗ k 6 i ⊗ k 31 + λ i , 256 256 μ i = m o d ∑ j = 1 5 k 6 i + 2 + j + k 32 + λ i + 3 , 256                                                                                                
Step 4: Iterate the HLITC map for n 0 + n u m times using x i and μ i as the initial values and the control parameters, and generate 3 chaotic sequences y 1 , y 2 , y 3 . Their length n u m is N b , N b , and m × n , respectively. To minimize the nonperiodic effect, the first   n 0 values are discarded, where m × n is the size of the original image.
Step 5: Produce 3 random integer sequences L 1 ,   L 2 ,   a n d   L 3 for image scrambling and image diffsion.
L 1 = m o d r o u n d y 1 × 10 15 , N b + 1
L 2 = m o d r o u n d y 2 × 10 15 , B + 1
L 3 = m o d r o u n d y 3 × 10 15 , 256
where B is the number of elements of an image subblock, N b is the number of image subblocks.
N b = m × n B

3.2. Image encryption

In this method, to enhance the pseudo-randomness of image scrambling, the arbitrary points spiral transformation based on a chaotic map is used for image scrambling, and the XOR operation of chaotic control is introduced in the pixel diffusion process to further improve the encryption effect.

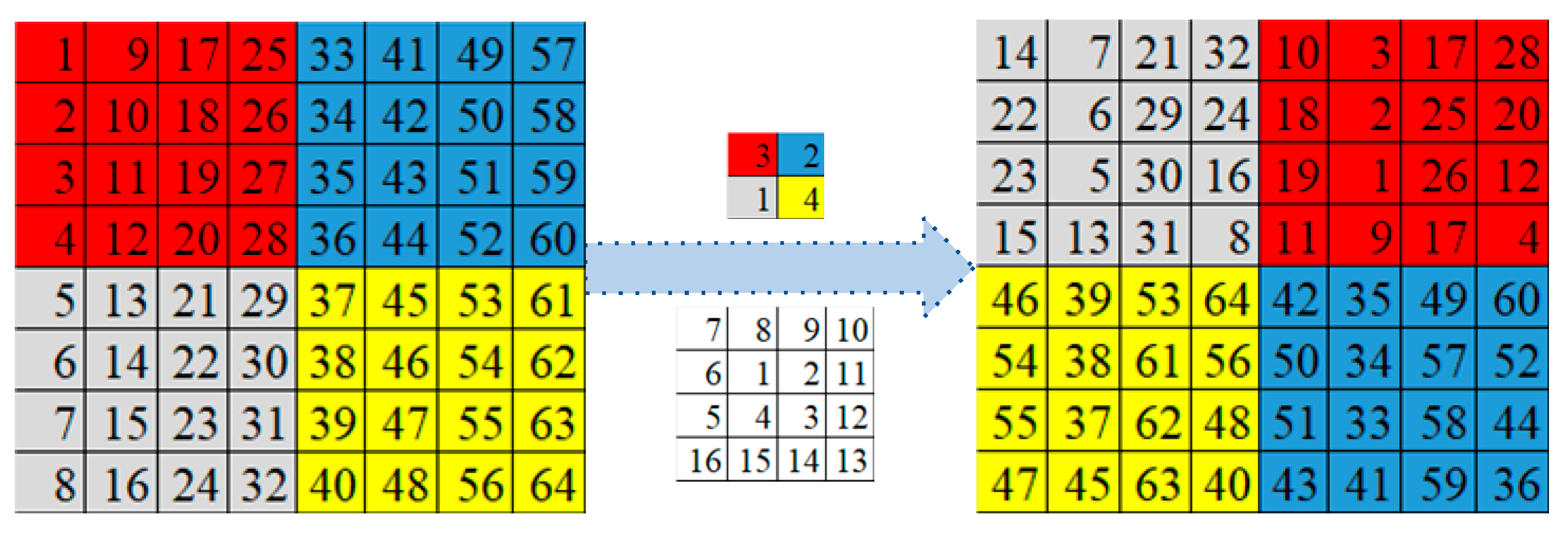
3.2.1. Image scrambling based on a spiral transformation

The image scrambling process consists of image sub-block scrambling based on chaos control and pixel scrambling based on arbitrary points spiral transformation. The detailed scrambling process is as follows.
Step 1: Divide the plaintext image I m × n into subblock of size s × s , i.e. B = s × s .
Step 2: Use a chaotic sequence L 1 of length N b to scramble each image subblock I b i , and so the scrambled image I ' is obtained.
Step 3: Generate a chaotic sequence L 2 by utilizing the average of each image subblock I b i .
Step 4: According to the random starting point L 2 i , we perform the spiral transformation on all the pixels within each image subblock to obtain the scrambled image I ' ' .
Figure 5 shows an example of image scrambling based on spiral transformation.

3.2.2. Image diffusion based on chaotic map

Step 1: Read scrambled image data P from the scrambled image I ' ' .
Step 2: Reshape matrix P to sequence P ' of length m × n .
Step 3: Perform XOR operation for image diffusion, the detailed process is written as follows.
E i = P ' i ⨂ L 3 i ⨂ E 1 ,               i = 1   P ' i ⨂ L 3 i ⨂ E i − 1 ,   i > 1
Where E 1 = m o d r o u n d ∑ i = 1 32 k i 32 × 10 15 , 256 Step 4: Reshape sequence E to a matrix of size m × n to obtain the final encrypted image I e .
The proposed image encryption system is symmetric, and the decryption algorithm is the inverse process of the encryption algorithm.

4. Experimental Results

In the experiment, some grayscale images of size 512×512 are used to evaluate encryption performance. Figure 6 illustrates the results of image encryption and decryption using the proposed encryption algorithm. From Figure 6, it can be seen that the ciphertext image is an irregular noise signal image, and it is hard to observe the relevant information from the ciphertext image. However, the decrypted image is consistent with the plaintext image, indicating that the proposed encryption method has good encryption performance.

4.1. Histogram analysis

The image histogram is the probability statistics of image pixels, and the ideal distribution of encrypted image pixels should be uniform. Figure 7 shows the comparison of image histograms before and after encryption.
From Figure 7, it can be observed that the histogram distribution of plaintext images is uneven, while the histogram of ciphertext images is uniformly distributed, indicating that the proposed method has good resistance to statistical attacks. In addition, the histogram variance is used to quantitatively measure the uniformity of pixel distribution in ciphertext images. The smaller the value of the histogram variance, the more uniform the distribution of ciphertext images is, and the higher the security of the encryption method. The corresponding results of the histogram variance test for ciphertext images are shown in Table 2. From Table 2, it can be seen that the histogram variance of the ciphertext image obtained by our encryption method is smaller than that of the existing encryption methods, indicating that it has good security.

4.2. Correlation analysis

There exist rich relationships and dependencies between adjacent pixels in original images, resulting in high correlation. Therefore, eliminating the correlation between adjacent pixels is one of the key requirements for ensuring the security of image encryption methods. Cipher images with low correlation in the horizontal, vertical, and diagonal directions are considered to be effective in resisting statistical attacks. The visual results of the correlation before and after encryption are shown in Figure 8. From Figure 8, it can be seen that the scatter points related to adjacent pixels in the plaintext image are relatively concentrated, while the ciphertext image is uniformly distributed, indicating that the encryption algorithm effectively eliminates the correlation in all directions of plaintext images.

4.3. Analysis for differential attack

A differential attack means that an attacker finds the corresponding relationship between the plaintext image and the ciphertext image by comparing the differences between the corresponding ciphertext before and after slightly changing the plaintext. The ability of algorithms to resist differential attacks is generally evaluated using two indicators: Number of Pixels Change Rate (NPCR) and Unified Average Change Intensity (UACI).
C i , j = 0 ,     i f   I 1 i , j = I 2 i , j 1 ,     e l s e                                                        
N P C R = ∑ i = 1 m ∑ j = 1 n C i , j m × n × 100 %
U C A I = ∑ i = 1 m ∑ j = 1 n I 1 i , j − I 2 i , j m × n × 255
In the Lena plaintext image, randomly select a pixel and increase its value by 1. Use the algorithm in this paper to encrypt and calculate the NPCR and UACI values. The results are shown in Table 3.
From Table 3, it can be seen that the NPCR and UACI values of the encrypted images using our algorithm all exceed 99.66 and 33.60 respectively. Compared with other chaotic image encryption algorithms, our algorithm has slightly higher average NPCR and UCAI values, indicating that it can more effectively resist differential attacks.

4.4. Information entropy analysis

Information entropy reflects the uncertainty of image information. Generally, the larger the entropy, the greater the amount of information, and the less detectable information For 256-level grayscale images, the theoretical value of information entropy is 8. Table 4 records the information entropy before and after image encryption, and compares it with other algorithms The results show that the encrypted image proposed in this paper can effectively conceal information.

5. Conclusions

This paper designs a composite Chebyshev chaotic map (HLITC), and random testing shows that the composite HLITC map has good randomness. Subsequently, a new image encryption algorithm is proposed by combining the HLITC map with the spiral transformation. Firstly, the initial values of the compound HLITC chaotic system are generated using the SHA-256 hash function and plaintext images and used for the generation of chaotic sequences. Then, a random starting point spiral transformation is introduced to eliminate the periodicity of chaotic systems. The spiral transformation is used for the scrambling, and the image diffusion is achieved by combining chaos and XOR operation. The experimental results show that the proposed algorithm can effectively hide plaintext information, has strong key sensitivity, and can resist differential attacks and other attack methods.

Author Contributions

Conceptualization, M.J.; Methodology, M.J. and H.Y.; Investigation, M.J.; Writing—original draft, M.J.; Writing—review and editing, H.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China under Grant 61872408, the Natural Science Foundation of Changsha under Grant 2022199, and the Social Science Foundation of Hunan Province under Grant 19YBA098.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sandryhaila, A.; Moura, J. Big data analysis with signal processing on graphs: Representation and processing of massive data sets with irregular structure. IEEE Signal Processing Magazine 2014, 31, 80–90. [Google Scholar] [CrossRef]
  2. Chen; JG; KL; Tang; Bilal; Weng; CL; KQ. A parallel random forest algorithm for big data in a spark cloud computing environment. IEEE Transactions On Parallel And Distributed Systems 2017, 28, 919–933. [Google Scholar] [CrossRef]
  3. Furini, M.; Gaggi, O.; Mirri, S.; Montangero, M.; Pelle, E.; Poggi, F.; Prandi, C. Digital twins and artificial intelligence as Pillars of personalized learning models. Communications of the ACM 2022, 65, 98–104. [Google Scholar] [CrossRef]
  4. Wu, X.; Zhang, Y.; Wang, A.; Shi, M.; Wang, H.; Liu, L. MNSSp3: Medical big data privacy protection platform based on Internet of things. Neural computing & applications 2022, 11491–11505. [Google Scholar]
  5. Yang, H.; Yin, J.; Yang, Y. Robust image hashing scheme based on low-rank decomposition and path integral LBP. IEEE Access 2019, 7, 51656–51664. [Google Scholar] [CrossRef]
  6. Hua, Z.; Zhang, K.; Li, Y.; Zhou, Y. Visually secure image encryption using adaptive-thresholding sparsification and parallel compressive sensing. Signal Processing 2021, 183, 107998. [Google Scholar] [CrossRef]
  7. Elshoush, H.T.; Mahmoud, M.M.; Altigani, A. A new high capacity and secure image realization steganography based on ASCII code matching. Multimedia tools and applications 2022, 81, 5191–5237. [Google Scholar] [CrossRef]
  8. Fagbohungbe, O.; Reza, S.R.; Dong, X.; Qian, L. Efficient privacy preserving edge intelligent computing framework for image classification in IoT. IEEE Transactions on Emerging Topics in Computational Intelligence 2022, 6, 941–956. [Google Scholar] [CrossRef]
  9. Sharma, S.; Gupta, V.; Juneja, M. A novel unsupervised multiple feature hashing for image retrieval and indexing (MFHIRI). Journal of Visual Communication and Image Representation 2022, 84, 103467. [Google Scholar] [CrossRef]
  10. Singh, C.; Sunitha, C.A. Chaotic and Paillier secure image data sharing based on blockchain and cloud security. Expert Systems with Applications 2022, 198, 116874. [Google Scholar] [CrossRef]
  11. Mai, H.E.; Envelope, E.R.; Envelope, I.E.; Envelope, E.S. Proposed hybrid encryption algorithm for robust 3D image communication over wireless channels. Optik 2023, 273, 170205. [Google Scholar]
  12. Zhu, C.; Sun, K. Chaotic image encryption algorithm by correlating keys with plaintext. China Communications 2012, 9, 73–79. [Google Scholar]
  13. Tang, Z.; Yang, Y.; Xu, S.; Yu, C.; Zhang, X. Image encryption with double spiral scans and chaotic maps. Security and Communication Networks 2019, 2019, 8694678. [Google Scholar] [CrossRef]
  14. Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image and Vision Computing 2006, 24, 926–934. [Google Scholar] [CrossRef]
  15. Zhang, L.; Liao, X.; Wang, X. An image encryption approach based on chaotic maps. Chaos Solitons & Fractals 2005, 24, 759–765. [Google Scholar]
  16. Elpeltagy, M.S.; Abdelwahab, M.M.; Sayed, M.S. Image encryption using Camellia and chaotic maps. In Proceedings of the 2015 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Abu Dhabi, United Arab Emirates, 2015, 7-10 Dec. 2015; pp. 209–214. [Google Scholar]
  17. Kumar, K.; Roy, S.; Rawat, U.; Malhotra, S. IEHC: An efficient image encryption technique using hybrid chaotic map. Chaos, Solitons & Fractals 2022, 158, 111994. [Google Scholar] [CrossRef]
  18. Wang, X.Y.; Lei, Y.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dynamics 2010, 62, 615–621. [Google Scholar] [CrossRef]
  19. Akhshani, A.; Behnia, S.; Akhavan, A.; Hassan, H.A.; Hassan, Z. A novel scheme for image encryption based on 2D piecewise chaotic maps. Optics Communications 2010, 283, 3259–3266. [Google Scholar] [CrossRef]
  20. Chen, Z.; Li, H.; Dong, E.; Du, Y. A hyper-chaos based image encryption algorithm. In Proceedings of the 2010 Second International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanjing, China, 2010, 26-28 Aug. 2010; pp. 188–191. [Google Scholar]
  21. Hua, Z.; Zhou, B.; Zhou, Y. Image content-based encryption algorithm using high-dimensional chaotic system. In Proceedings of the 2015 International Symposium on Nonlinear Theory and its Applications (NOLTA2015), Hong Kong, China, 2015, 2015, December 1-4; pp. 554–557.
  22. Wang, S.; Peng, Q.; Du, B. Chaotic color image encryption based on 4D chaotic maps and DNA sequence. Optics & Laser Technology 2022, 148, 107753. [Google Scholar] [CrossRef]
  23. Ye, G.; Jiao, K.; Pan, C.; Huang, X. An effective framework for chaotic image encryption based on 3D logistic map. Security and Communication Networks 2018, 2018, 8402578. [Google Scholar] [CrossRef]
  24. Gong, L.; Luo, H.; Wu, R.; Zhou, N. New 4D chaotic system with hidden attractors and self-excited attractors and its application in image encryption based on RNG. Physica A: Statistical Mechanics and its Applications 2022, 591, 126793. [Google Scholar] [CrossRef]
  25. Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Information Sciences 2016, 339, 237–253. [Google Scholar] [CrossRef]
  26. Wang, X.; Yang, J. A privacy image encryption algorithm based on piecewise coupled map lattice with multi dynamic coupling coefficient. Information Sciences 2021, 569, 217–240. [Google Scholar] [CrossRef]
  27. Zhu, H.; Zhao, Y.; Song, Y. 2D Logistic-Modulated-Sine-Coupling-Logistic Chaotic Map for Image Encryption. IEEE Access 2019, 7, 14081–14098. [Google Scholar] [CrossRef]
  28. Zhu, H.; Zhang, X.; Yu, H.; Zhao, C.; Zhu, Z. A Novel Image Encryption Scheme Using the Composite Discrete Chaotic System. Entropy 2016, 18, 276. [Google Scholar] [CrossRef]
  29. Zhu, H.; Zhang, X.; Yu, H.; Zhao, C.; Zhu, Z. An image encryption algorithm based on compound homogeneous hyper-chaotic system. Nonlinear Dynamics 2017, 89, 61–79. [Google Scholar] [CrossRef]
  30. Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Information Sciences 2019, 480, 403–419. [Google Scholar] [CrossRef]
  31. Gao, Z.; Liu, Z.; Wang, L. An Image Encryption Algorithm Based on the Improved Sine-Tent Map. Discrete Dynamics in Nature and Society 2021, 2021, 9187619. [Google Scholar] [CrossRef]
  32. Yadav, A.; Saini, B.; Verma, V.K.; Pal, V. A joint medical image compression and encryption using AMBTC and hybrid chaotic system. Journal of Discrete Mathematical Sciences and Cryptography 2021, 24, 2233–2244. [Google Scholar] [CrossRef]
  33. Zhang, S.; Liu, L. A novel image encryption algorithm based on SPWLCM and DNA coding. Mathematics and Computers in Simulation 2021, 190, 723–744. [Google Scholar] [CrossRef]
  34. Wang, X.; Du, X. Pixel-level and bit-level image encryption method based on Logistic-Chebyshev dynamic coupled map lattices. Chaos, Solitons & Fractals 2022, 155, 111629. [Google Scholar] [CrossRef]
  35. Basha, S.M.; Mathivanan, P.; Ganesh, A.B. Bit level color image encryption using Logistic-Sine-Tent-Chebyshev (LSTC) map. Optik 2022, 259, 168956. [Google Scholar] [CrossRef]
  36. Di, H.; Chen, H.; Lingge, J.; Hongwen, Z.; Guangrui, H. Chaotic characteristics of a one-dimensional iterative map with infinite collapses. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications 2001, 48, 900–906. [Google Scholar] [CrossRef]
  37. Diab, H. An efficient chaotic image cryptosystem based on simultaneous permutation and diffusion operations. IEEE Access 2018, 6, 42227–42244. [Google Scholar] [CrossRef]
  38. Shahna, K.U.; Mohamed, A. A novel image encryption scheme using both pixel level and bit level permutation with chaotic map. Applied Soft Computing 2020, 90, 106162. [Google Scholar] [CrossRef]
Preprints 87077 g001
Figure 1. Dynamics comparison with Bifurcation diagrams: (a) Logistic, (b) ICMIC, (c) Tent, (d) Chebyshev and (e) HLITC.
Figure 1. Dynamics comparison with Bifurcation diagrams: (a) Logistic, (b) ICMIC, (c) Tent, (d) Chebyshev and (e) HLITC.
Preprints 87077 g001
Preprints 87077 g002
Figure 2. Lyapunov exponent diagrams of different chaotic maps: (a) Logistic, (b) ICMIC, (c) Tent, (d) Chebyshev, and (e) HLITC.
Figure 2. Lyapunov exponent diagrams of different chaotic maps: (a) Logistic, (b) ICMIC, (c) Tent, (d) Chebyshev, and (e) HLITC.
Preprints 87077 g002
Preprints 87077 g003
Figure 3. Dynamics comparison of different chaotic maps in terms of information entropy.
Figure 3. Dynamics comparison of different chaotic maps in terms of information entropy.
Preprints 87077 g003
Preprints 87077 g004
Figure 4. The image encryption process.
Figure 4. The image encryption process.
Preprints 87077 g004
Preprints 87077 g005
Figure 5. Image scrambling based on a spiral transformation.
Figure 5. Image scrambling based on a spiral transformation.
Preprints 87077 g005
Preprints 87077 g006
Figure 6. Results of image encryption and decryption. left column: plaintext image, center column: cipher image, and right column: decipher image (top to down: Lena, Peppers, Man, and Baboon).
Figure 6. Results of image encryption and decryption. left column: plaintext image, center column: cipher image, and right column: decipher image (top to down: Lena, Peppers, Man, and Baboon).
Preprints 87077 g006
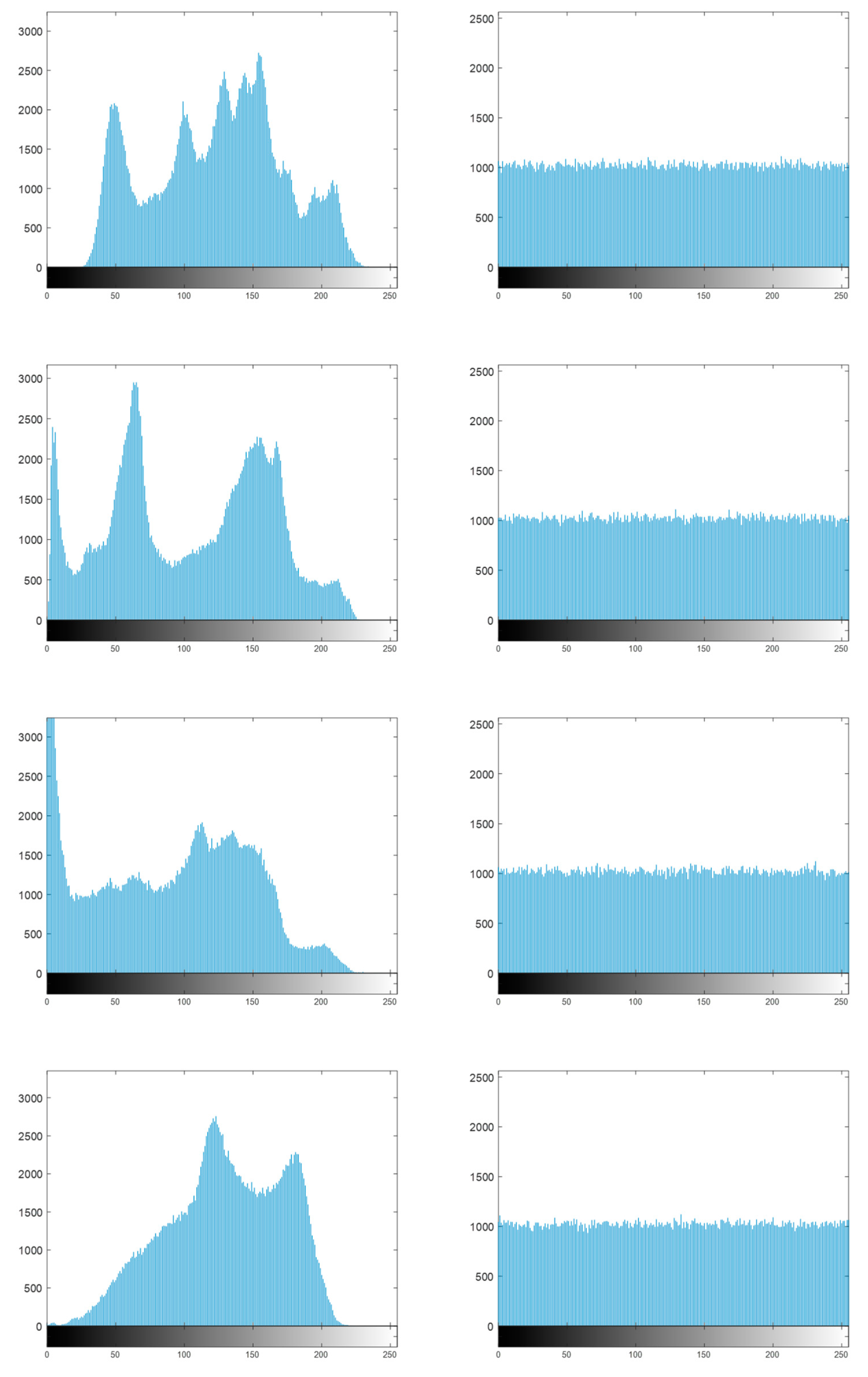
Preprints 87077 g007
Figure 7. Histogram analysis (top to down: Lena, Peppers, Man and Baboon).
Figure 7. Histogram analysis (top to down: Lena, Peppers, Man and Baboon).
Preprints 87077 g007
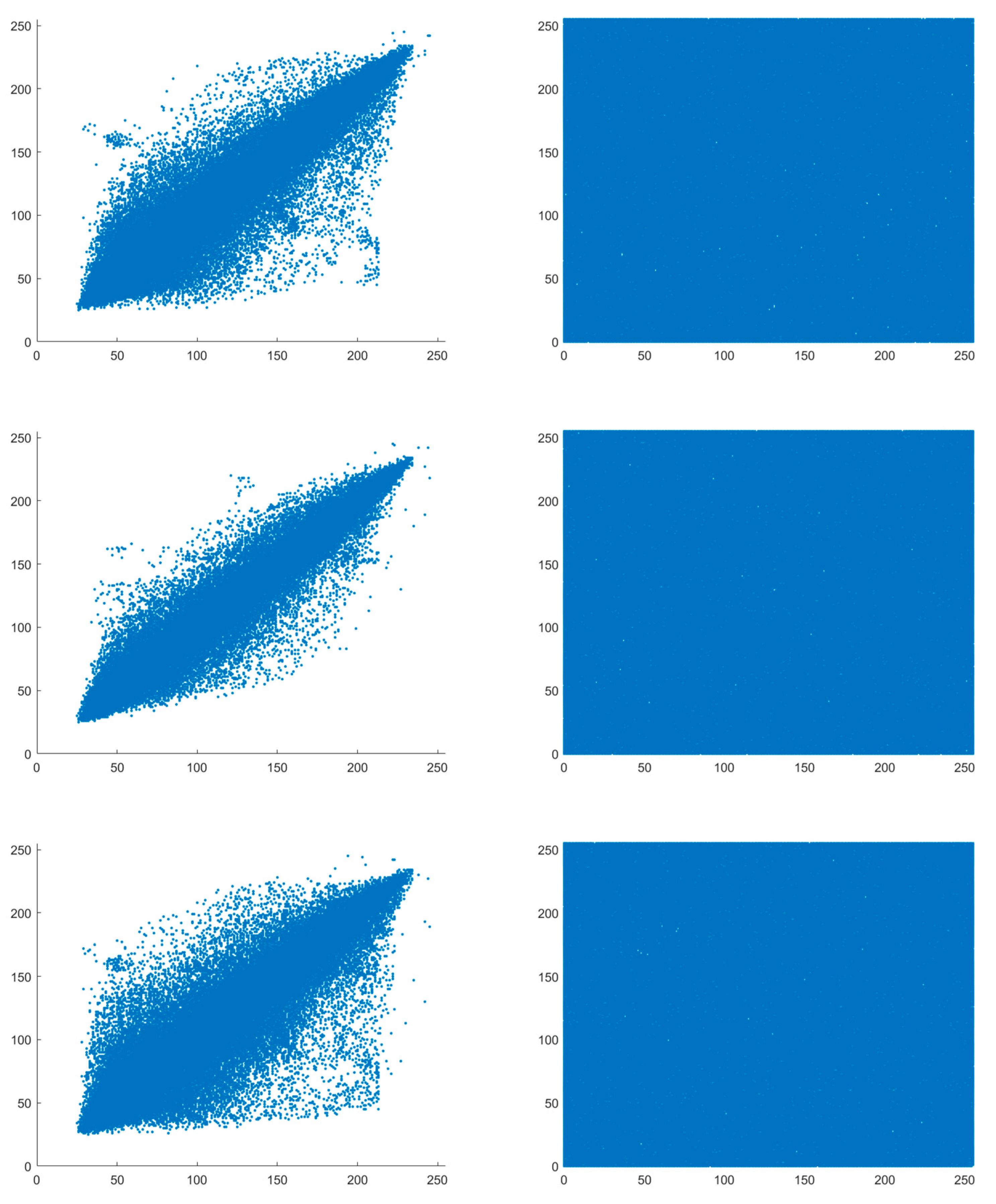
Preprints 87077 g008
Figure 8. Pixel correlation between Lena image and its ciphertext image in various directions (Left: plaintext image Right: ciphertext image, top to down: Horizontal, Vertical, and Diagonal).
Figure 8. Pixel correlation between Lena image and its ciphertext image in various directions (Left: plaintext image Right: ciphertext image, top to down: Horizontal, Vertical, and Diagonal).
Preprints 87077 g008
Table 1. Results of NIST randomness test for HLITC.
Table 1. Results of NIST randomness test for HLITC.
Test Name P-value Results
Approximate entropy test 0.9548 Success
Block frequency test 0.0383 Success
Cumulative sums (forward) test 0.2631 Success
FFT test 0.2789 Success
Frequency test 0.2919 Success
Linear complexity test 0.8934 Success
Longest runs of ones test 0.4398 Success
Nonoverlapping template matching test 0.9961 Success
Overlapping template matching test 0.4771 Success
Binary matrix rank test 0.9562 Success
Runs test 0.3959 Success
Serial test 0.0297 Success
Maurer's universal statistical test 0.4439 Success
Random excursions test 0.3061 Success
Random excursions variant test 0.0527 Success
Table 2. Histogram variance analysis of ciphertext image.
Table 2. Histogram variance analysis of ciphertext image.
Encryption method (ciphertext image) Histogram variance
[37] (Lena) 242.4651
[38] (Lena) 124.6218
[34] (Lena) 68.9023
Our method (Lena) 31.5731
Our method (Peppers) 29.7752
Our method (Man) 32.6184
Our method (Baboon) 30.2543
Table 3. Comparison of NPCR and UCAI results.
Table 3. Comparison of NPCR and UCAI results.
Metrics Our method [37] [38]
NPCR 99.6627 99.6134 99.6283
UCAI 33.64 33.28 33.53
Table 4. Information entropy comparison.
Table 4. Information entropy comparison.
Plaintext image Cipher text image [37] [38]
7.4455 7.9986 7.9935 7.9926
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated