Submitted:
02 October 2023
Posted:
04 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- We propose a novel variational pixel-wise regularization model for image restoration.
- We devise an algorithm capable of effectively and efficiently solving the proposed model.
- Through numerical experiments, we demonstrate that the proposed approach can proficiently eliminate noise and blur in smooth areas of an image while preserving its edges.
2. Materials and Methods
| Algorithm 1 Input: , , , Output: |
|
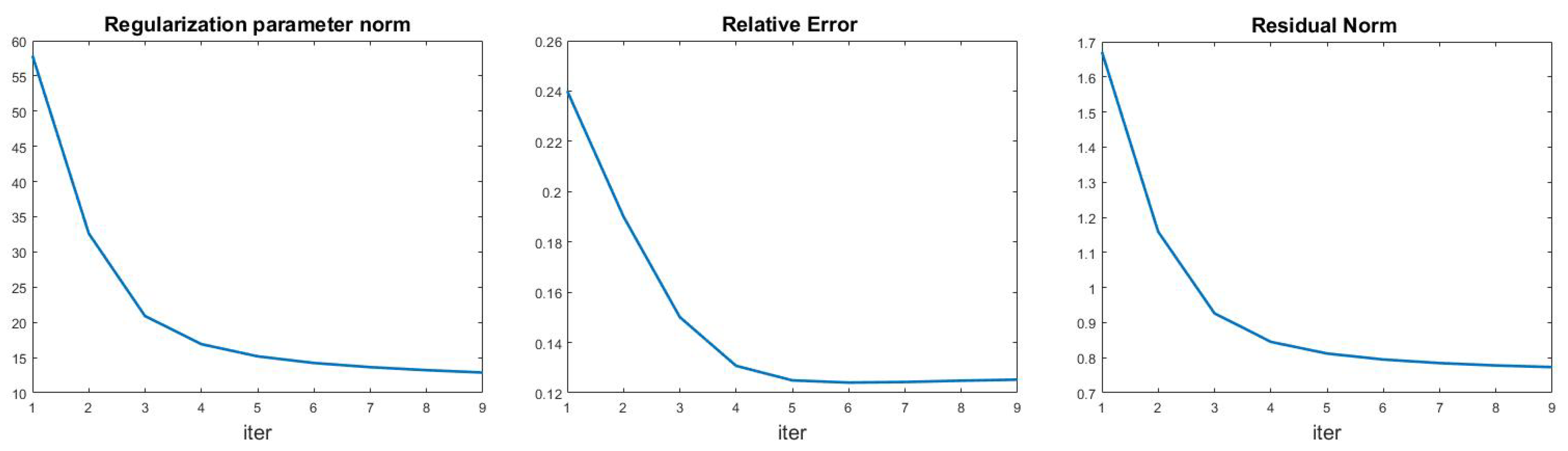
3. Numerical Experiments
4. Conclusions
Acknowledgments
References
- Hansen, P.C.; Nagy, J.G.; O’leary, D.P. Deblurring Images: Matrices, Spectra, and Filtering; SIAM: 2006.
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imaging Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Lu, S.; Pereverzev, S.V. Multi-parameter regularization and its numerical realization. Numer. Math. 2011, 118, 1–31. [Google Scholar] [CrossRef]
- Lu, S.; Pereverzev, S.V.; Shao, Y.; Tautenhahn, U. Discrepancy Curves for Multi-Parameter Regularization; 2010. [Google Scholar]
- Belge, M.; Kilmer, M.E.; Miller, E.L. Efficient determination of multiple regularization parameters in a generalized L-curve framework. Inverse Probl. 2002, 18, 1161. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zaglia, M.; Rodriguez, G.; Seatzu, S. Multi-parameter regularization techniques for ill-conditioned linear systems. Numer. Math. 2003, 94, 203–228. [Google Scholar] [CrossRef]
- Gazzola, S.; Reichel, L. A new framework for multi-parameter regularization. BIT Numer. Math. 2016, 56, 919–949. [Google Scholar] [CrossRef]
- Fornasier, M.; Naumova, V.; Pereverzyev, S.V. Parameter choice strategies for multipenalty regularization. SIAM J. Numer. Anal. 2014, 52, 1770–1794. [Google Scholar] [CrossRef]
- Kereta, Z.; Maly, J.; Naumova, V. Linear convergence and support recovery for non-convex multi-penalty regularization. CoRR 2019. [Google Scholar]
- Naumova, V.; Peter, S. Minimization of multi-penalty functionals by alternating iterative thresholding and optimal parameter choices. Inverse Probl. 2014, 30, 125003. [Google Scholar] [CrossRef]
- Kereta, Ž.; Maly, J.; Naumova, V. Computational approaches to non-convex, sparsity-inducing multi-penalty regularization. Inverse Probl. 2021, 37, 055008. [Google Scholar] [CrossRef]
- Naumova, V.; Pereverzyev, S.V. Multi-penalty regularization with a component-wise penalization. Inverse Probl. 2013, 29, 075002. [Google Scholar] [CrossRef]
- Grasmair, M.; Klock, T.; Naumova, V. Adaptive multi-penalty regularization based on a generalized lasso path. Appl. Comput. Harmon. Anal. 2020, 49, 30–55. [Google Scholar] [CrossRef]
- Wang, W.; Lu, S.; Mao, H.; Cheng, J. Multi-parameter Tikhonov regularization with the ℓ0 sparsity constraint. Inverse Probl. 2013, 29, 065018. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, J.; Wu, C.; He, Z.; Zeng, T.; Jin, Q. Edge adaptive hybrid regularization model for image deblurring. Inverse Probl. 2022, 38, 065010. [Google Scholar] [CrossRef]
- Calatroni, L.; Lanza, A.; Pragliola, M.; Sgallari, F. A flexible space-variant anisotropic regularization for image restoration with automated parameter selection. SIAM J. Imaging Sci. 2019, 12, 1001–1037. [Google Scholar] [CrossRef]
- Bortolotti, V.; Landi, G.; Zama, F. Uniform multi-penalty regularization for linear ill-posed inverse problems. arXiv 2023, arXiv:2309.14163. [Google Scholar]
- Landi, G.; Loli Piccolomini, E. An improved Newton projection method for nonnegative deblurring of Poisson-corrupted images with Tikhonov regularization. Numer. Algorithms 2012, 60, 169–188. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Projected Newton methods for optimization problems with simple constraints. SIAM J. Control. Optim. 1982, 20, 221–246. [Google Scholar] [CrossRef]
- Wang, S.; Rehman, A.; Wang, Z.; Ma, S.; Gao, W. SSIM-motivated rate-distortion optimization for video coding. IEEE Trans. Circuits Syst. Video Technol. 2011, 22, 516–529. [Google Scholar] [CrossRef]
- di Serafino, D.; Landi, G.; Viola, M. Directional TGV-based image restoration under Poisson noise. J. Imaging 2021, 7, 99. [Google Scholar] [CrossRef]

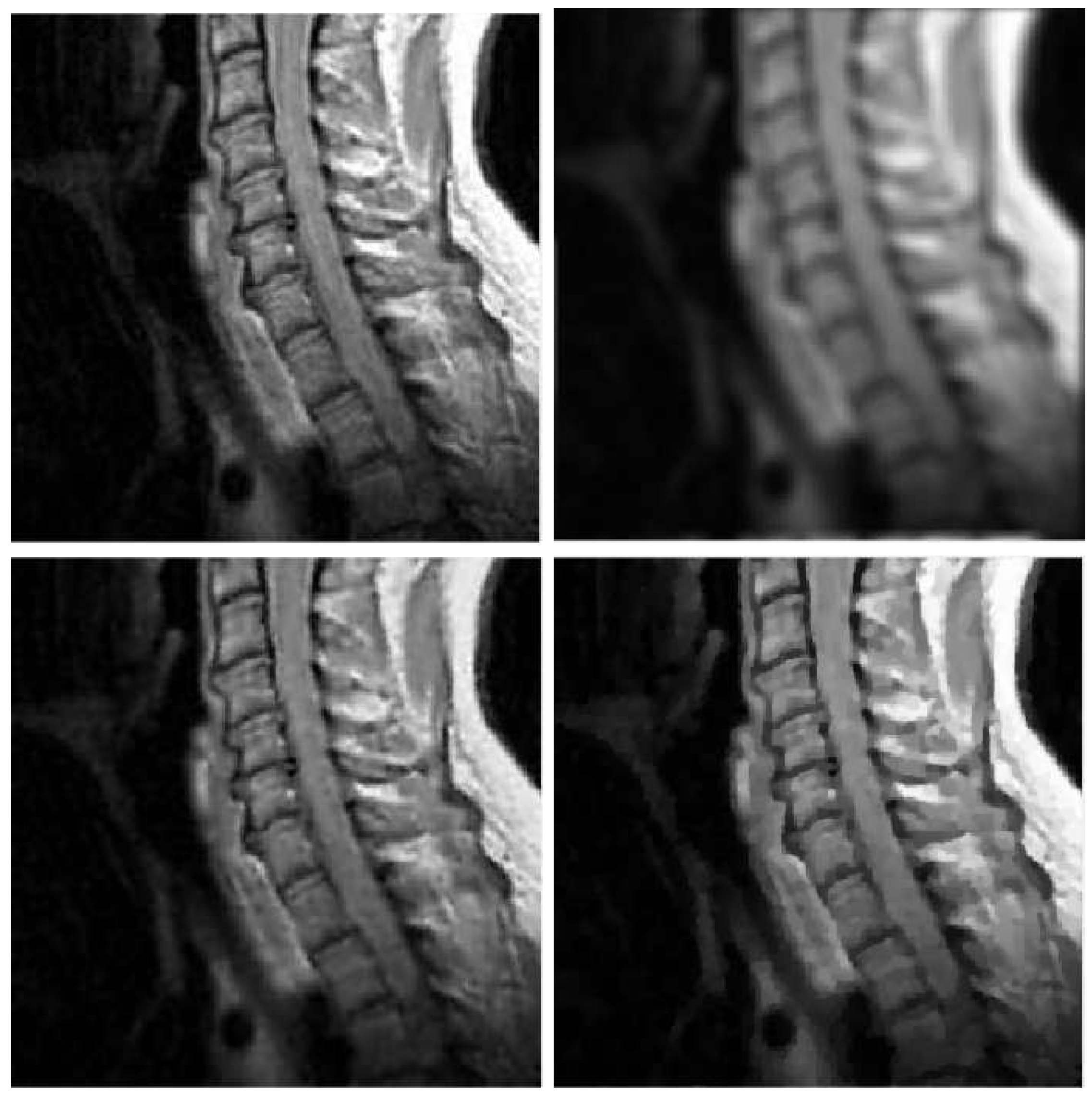




| Test Problem | Blur | |||
|---|---|---|---|---|
| Galaxy | Out-of-focus | 0.5e-3 | 0.25e-3 | 0.1e-3 |
| Gaussian | 0.5e-3 | 0.25e-3 | 0.1e-3 | |
| mri | Out-of-focus | 1.5e-3 | 1e-3 | 0.5e-3 |
| Gaussian | 1.5e-3 | 1e-3 | 0.5e-3 | |
| leopard | Out-of-focus | 2.5e-3 | 1.5e-3 | 1.e-3 |
| Gaussian | 2.5e-3 | 0.1e-3 | 0.5e-4 | |
| Elaine | Out-of-focus | 1e-3 | 1e-3 | 1e-3 |
| Gaussian | 1e-3 | 0.5e-3 | 0.5e-3 |
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 9.5953e-02 | 7.2175e+00 | 9.1418e-01 | 226 | 3.0000e+02 | |
| TV | 1.0268e-01 | 6.6291e+00 | 8.7089e-01 | 278 | 1.0000e-04 | ||
| TIKH | 1.3864e-01 | 4.0211e+00 | 8.3486e-01 | 200 | 1.1000e-02 | ||
| MULTI | 8.2096e-02 | 8.5722e+00 | 9.3431e-01 | 4(857) | 8.4116e+00 | ||
| TGV | 7.1519e-02 | 9.7292e+00 | 9.5015e-01 | 302 | 7.5000e+02 | ||
| TV | 6.7196e-02 | 1.0271e+01 | 9.4744e-01 | 259 | 5.0000e-05 | ||
| TIKH | 1.0943e-01 | 6.0351e+00 | 8.5965e-01 | 200 | 3.0000e-03 | ||
| MULTI | 6.2660e-02 | 1.0878e+01 | 9.5843e-01 | 7(1061) | 2.1493e+00 | ||
| TGV | 6.1028e-02 | 1.1102e+01 | 9.6274e-01 | 323 | 1.0000e+03 | ||
| TV | 6.3776e-02 | 1.0719e+01 | 9.4229e-01 | 303 | 1.0000e-05 | ||
| TIKH | 9.1181e-02 | 7.6143e+00 | 8.7665e-01 | 200 | 1.0000e-03 | ||
| MULTI | 4.8955e-02 | 1.3017e+01 | 9.7150e-01 | 9(1013) | 1.0491e+00 | ||
| Gaussian | TGV | 9.6150e-02 | 4.5854e+00 | 9.3328e-01 | 198 | 2.5000e+02 | |
| TV | 8.8306e-02 | 5.3246e+00 | 9.2702e-01 | 224 | 1.0000e-04 | ||
| TIKH | 1.0047e-01 | 4.2032e+00 | 9.0136e-01 | 200 | 5.0000e-03 | ||
| MULTI | 7.3686e-02 | 6.8966e+00 | 9.5114e-01 | 4(699) | 8.3317e+00 | ||
| TGV | 8.5737e-02 | 5.5019e+00 | 9.4922e-01 | 246 | 1.0000e+03 | ||
| TV | 7.7929e-02 | 6.3312e+00 | 9.3945e-01 | 223 | 1.0000e-05 | ||
| TIKH | 8.4284e-02 | 5.6503e+00 | 9.2110e-01 | 200 | 1.0000e-03 | ||
| MULTI | 6.0402e-02 | 8.5442e+00 | 9.6606e-01 | 5(437) | 2.3968e+00 | ||
| TGV | 8.0734e-02 | 6.0131e+00 | 9.5637e-01 | 280 | 2.5000e+03 | ||
| TV | 7.3912e-02 | 6.7800e+00 | 9.5186e-01 | 214 | 1.0000e-06 | ||
| TIKH | 7.3620e-02 | 6.8143e+00 | 9.4621e-01 | 200 | 5.0000e-04 | ||
| MULTI | 5.7592e-02 | 8.9471e+00 | 9.7129e-01 | 6(383) | 1.3106e+00 |
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 8.6404e-02 | 6.8531e+00 | 8.3691e-01 | 185 | 9.0000e+01 | |
| TV | 8.7052e-02 | 6.7882e+00 | 8.3805e-01 | 212 | 5.0000e-04 | ||
| TIKH | 1.1476e-01 | 4.3882e+00 | 7.4472e-01 | 200 | 1.0000e-02 | ||
| MULTI | 7.9139e-02 | 7.6160e+00 | 8.5073e-01 | 4(1403) | 1.0098e+01 | ||
| TGV | 6.6508e-02 | 9.0670e+00 | 8.9245e-01 | 180 | 2.5000e+02 | ||
| TV | 6.7875e-02 | 8.8903e+00 | 8.9272e-01 | 232 | 1.0000e-04 | ||
| TIKH | 9.4934e-02 | 5.9760e+00 | 8.2645e-01 | 200 | 5.0000e-03 | ||
| MULTI | 5.4634e-02 | 1.0775e+01 | 9.1681e-01 | 5(1456) | 1.7962e+00 | ||
| TGV | 5.3582e-02 | 1.0936e+01 | 9.2644e-01 | 292 | 1.0000e+03 | ||
| TV | 6.2557e-02 | 9.5905e+00 | 8.9043e-01 | 283 | 1.0000e-05 | ||
| TIKH | 7.8021e-02 | 7.6717e+00 | 8.2844e-01 | 200 | 1.0000e-03 | ||
| MULTI | 4.6590e-02 | 1.2150e+01 | 9.4086e-01 | 7(2483) | 5.8348e-01 | ||
| Gaussian | TGV | 7.4295e-02 | 5.1521e+00 | 8.8489e-01 | 212 | 5.0000e+01 | |
| TV | 7.2950e-02 | 5.3107e+00 | 8.9032e-01 | 214 | 5.0000e-04 | ||
| TIKH | 8.0602e-02 | 4.4444e+00 | 8.6998e-01 | 200 | 7.5000e-03 | ||
| MULTI | 5.8445e-02 | 7.2363e+00 | 9.0902e-01 | 4(650) | 9.6213e+00 | ||
| TGV | 6.3055e-02 | 6.4566e+00 | 9.1791e-01 | 204 | 1.7500e+02 | ||
| TV | 6.1079e-02 | 6.7331e+00 | 9.3336e-01 | 173 | 8.0000e-05 | ||
| TIKH | 6.7156e-02 | 5.9092e+00 | 9.1910e-01 | 200 | 2.5000e-03 | ||
| MULTI | 4.6651e-02 | 9.0737e+00 | 9.4174e-01 | 3(462) | 1.9888e+00 | ||
| TGV | 5.6288e-02 | 7.4254e+00 | 9.3696e-01 | 222 | 1.0000e+03 | ||
| TV | 5.7295e-02 | 7.2713e+00 | 9.5196e-01 | 155 | 5.0000e-05 | ||
| TIKH | 5.8965e-02 | 7.0219e+00 | 9.3828e-01 | 200 | 7.5000e-04 | ||
| MULTI | 4.0354e-02 | 1.0316e+01 | 9.5758e-01 | 4(1075) | 8.1542e-01 |
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 1.6971e-01 | 6.0610e+00 | 7.5515e-01 | 221 | 1.2500e+02 | |
| TV | 1.7345e-01 | 5.8714e+00 | 7.5114e-01 | 276 | 5.0000e-04 | ||
| TIKH | 2.0715e-01 | 4.3292e+00 | 5.8731e-01 | 200 | 5.0000e-03 | ||
| MULTI | 1.6854e-01 | 6.1211e+00 | 7.4807e-01 | 3(325) | 4.4885e+00 | ||
| TGV | 1.3874e-01 | 7.7949e+00 | 8.0408e-01 | 250 | 3.0000e+02 | ||
| TV | 1.3360e-01 | 8.1228e+00 | 8.0757e-01 | 371 | 1.0000e-04 | ||
| TIKH | 1.6784e-01 | 6.1411e+00 | 6.6137e-01 | 200 | 1.5000e-03 | ||
| MULTI | 1.2572e-01 | 8.6512e+00 | 8.1534e-01 | 10(9141) | 1.2627e+01 | ||
| TGV | 1.1579e-01 | 9.3633e+00 | 8.3657e-01 | 353 | 7.5000e+02 | ||
| TV | 1.1976e-01 | 9.0706e+00 | 8.2166e-01 | 411 | 2.5000e-05 | ||
| TIKH | 1.3891e-01 | 7.7821e+00 | 7.1537e-01 | 200 | 5.0000e-04 | ||
| MULTI | 1.1057e-01 | 9.7643e+00 | 8.1755e-01 | 19(18607) | 2.7656e+00 | ||
| Gaussian | TGV | 1.6936e-01 | 3.7549e+00 | 7.7259e-01 | 261 | 1.0000e+02 | |
| TV | 1.6515e-01 | 3.9736e+00 | 7.7529e-01 | 314 | 4.0000e-04 | ||
| TIKH | 1.7150e-01 | 3.6456e+00 | 6.8620e-01 | 200 | 2.5000e-03 | ||
| MULTI | 1.6298e-01 | 4.0884e+00 | 7.7539e-01 | 3(241) | 4.5599e+00 | ||
| TGV | 1.5058e-01 | 4.7470e+00 | 8.0108e-01 | 339 | 1.0000e+03 | ||
| TV | 1.4747e-01 | 4.9279e+00 | 8.0458e-01 | 281 | 5.0000e-05 | ||
| TIKH | 1.5280e-01 | 4.6194e+00 | 7.2992e-01 | 200 | 5.0000e-04 | ||
| MULTI | 1.4385e-01 | 5.1440e+00 | 8.0937e-01 | 4(375) | 1.0924e+00 | ||
| TGV | 1.4220e-01 | 5.2400e+00 | 8.1688e-01 | 500 | 1.0000e+04 | ||
| TV | 1.4489e-01 | 5.0775e+00 | 8.0509e-01 | 309 | 1.0000e-06 | ||
| TIKH | 1.4156e-01 | 5.2795e+00 | 7.7128e-01 | 200 | 1.0000e-04 | ||
| MULTI | 1.3314e-01 | 5.8118e+00 | 8.2728e-01 | 5(513) | 3.6611e-01 |
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 5.2937e-02 | 4.2620e+00 | 7.0502e-01 | 117 | 2.5000e+01 | |
| TV | 5.3390e-02 | 4.1879e+00 | 7.0068e-01 | 79 | 2.5000e-03 | ||
| TIKH | 6.7772e-02 | 2.1162e+00 | 6.4440e-01 | 200 | 2.5000e-02 | ||
| MULTI | 5.2967e-02 | 4.2571e+00 | 7.0941e-01 | 6(789) | 9.2884e+01 | ||
| TGV | 4.7522e-02 | 4.8898e+00 | 7.2933e-01 | 111 | 1.0000e+02 | ||
| TV | 4.7884e-02 | 4.8238e+00 | 7.3036e-01 | 86 | 5.0000e-04 | ||
| TIKH | 5.6612e-02 | 3.3695e+00 | 6.9381e-01 | 200 | 1.0000e-02 | ||
| MULTI | 4.6498e-02 | 5.0791e+00 | 7.3630e-01 | 4(426) | 2.6005e+01 | ||
| TGV | 4.4345e-02 | 5.4451e+00 | 7.4655e-01 | 123 | 2.0000e+02 | ||
| TV | 4.6262e-02 | 5.0776e+00 | 7.4001e-01 | 80 | 5.0000e-04 | ||
| TIKH | 5.0669e-02 | 4.2873e+00 | 7.3213e-01 | 200 | 5.0000e-03 | ||
| MULTI | 4.3129e-02 | 5.6867e+00 | 7.5707e-01 | 4(201) | 5.5324e+00 >> | ||
| Gaussian | TGV | 4.8945e-02 | 2.5540e+00 | 7.2618e-01 | 98 | 1.5000e+01 | |
| TV | 4.8877e-02 | 2.5660e+00 | 7.2428e-01 | 78 | 2.5000e-03 | ||
| TIKH | 6.0527e-02 | 7.0909e-01 | 7.1350e-01 | 200 | 3.0000e-02 | ||
| MULTI | 4.7693e-02 | 2.7791e+00 | 7.3403e-01 | 5(537) | 8.6631e+01 | ||
| TGV | 4.5610e-02 | 2.6121e+00 | 7.4550e-01 | 100 | 1.0000e+02 | ||
| TV | 4.5903e-02 | 2.5566e+00 | 7.4522e-01 | 75 | 8.0000e-04 | ||
| TIKH | 4.9219e-02 | 1.9508e+00 | 7.3947e-01 | 200 | 7.5000e-03 | ||
| MULTI | 4.4332e-02 | 2.8590e+00 | 7.5318e-01 | 3(135) | 1.2558e+01 | ||
| TGV | 4.3903e-02 | 2.8586e+00 | 7.5594e-01 | 112 | 2.5000e+02 | ||
| TV | 4.4699e-02 | 2.7025e+00 | 7.5904e-01 | 68 | 2.5000e-04 | ||
| TIKH | 4.6376e-02 | 2.3826e+00 | 7.5546e-01 | 200 | 2.5000e-03 | ||
| MULTI | 4.2950e-02 | 3.0493e+00 | 7.6433e-01 | 2(56) | 2.9785e+00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





