Prerpints.org logo
Preprint
Article

Effects of the Use of a Passive Lumbar Exoskeleton in Muscle under Laboratory Conditions

Altmetrics

Downloads

102

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 September 2023

Posted:

28 September 2023

You are already at the latest version

Alerts
Abstract
The introduction of exoskeletons in the industry has focused on improving worker safety. Exoskeletons have the objective of decreasing the risk of injury or fatigue when performing physically demanding tasks. The exoskeleton’s effects on the muscles is one of the most common focus in the assessments. The present study aims to analyse the muscle interactions generated by using a passive lumbar exoskeleton during load-handling tasks in laboratory conditions with and without an exoskeleton. Electromyographic data of the muscles involved in the task were recorded from twelve participants performing load-handling tasks. Correlation Coefficient, Coherence Coefficient, Mutual Information, and Multivariate Sample Entropy were calculated to determine if there were significant differences in muscle interactions between the two test conditions. Results showed statistically significant differences for all pairs of muscles and indicated that the use of the exoskeleton implied more constant values throughout the exercise. The Directed Conditional Granger Causality was obtained to study the directionality of the interactions, with significant differences in two muscle pairs Gluteus-Quadriceps and Gluteus-Lumbar in the gravity-positive direction in both cases. In conclusion, EMG parameters chosen appear to be appropriate measurements for studying the exoskeleton effects over muscle couplings.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Exoskeletons have become a popular technology in recent years due to their potential to enhance human performance and protect against musculoskeletal injuries. These wearable devices are designed to improve or replace the function of the human musculoskeletal system by providing external support, assistance, or resistance. However, the use of exoskeletons could also have additional consequences, such as changes in muscle activation patterns that are yet to be studied and described.
In the last years, numerous studies have evaluated the impact of industrial exoskeletons on ergonomics in the workplace [1,2]. These studies have generally focused on assessing the effect of exoskeletons on the physical strain and discomfort experienced by workers during tasks that involve repetitive or heavy lifting, bending, or reaching. The results of these studies have been controversial, with some suggesting that exoskeletons can effectively reduce muscle activity, joint forces, and fatigue , while others indicating no significant effect or even negative outcomes [3]. Previous works concerning the study of the effects of industrial passive exoskeleton over the users, included the assessment of muscles through EMG [4]. Those studies addressed the quantification of muscular activity and fatigue focusing only on the effects over each muscle individually.
The study of the effects over individual muscles carried out by other authors start with the selection of objective muscles. In the case of the passive lumbar exoskeleton, the lumbar muscle is selected for being the objective muscle of the device, and it should be the potentially most benefited one. The authors [5,6,7] agreed finding a reduction in the lumbar activity when assessing the same exoskeleton, but this reduction was also observed in studies using different back support exoskeletons used in the present study [8,9,10,11]. Besides, reductions in the lumbar fatigue were also found in numerous works [5,12,13]. On the other hand, the quadriceps was also a muscle chosen to be studied, for being potentially affected by compensating for reduced lumbar muscle activity. Iranzo et al. [5], showed reduced activity but no significant changes in fatigue [5,14].
The interaction between exoskeletons and the human body is complex, and understanding the underlying mechanisms is critical to optimize the design and effectiveness of these devices. One important factor to consider is the interaction between muscles, which refers to the coordinated activation of different muscles to produce a desired movement or force [15]. Muscles interactions play a crucial role in human movement and could be potentially affected by exoskeleton use.
One of the most common ways to study the muscle couplings in the literature consists of the calculation of certain parameters, such as the Correlation Coefficient, the Coherence Coefficient, the Mutual Information, and the Multivariate Sample Entropy. These variables have been proposed in the literature to evaluate the muscular coupling, in smooth and striated muscles, although for different muscles and applications to the ones studied in the present work.
The Correlation Coefficient can reflect the linear correlation between two signals in the time domain. It was used in the literature to characterize pairs of uterine muscle synchronizations prior to labour [16,17], finding a significant increase in its value as the delivery approaches. Also, King [18] calculated it to find correlations during movement compared to static poses, obtaining also differences between conditions with higher values in dynamic versus static. The Coherence Coefficient, can reflect also the linear correlations between time series in the frequency domain, and it is also widely used in bibliography. De Marchis et al. [19] calculated this variable to study the intermuscular synchronization in a free pedalling task, finding peak values of coherence in the pair of muscles Soleous and Gastrocneminus Medialis. Coherence was additionally assessed for labor prediction [16], getting greater values with the approach of the delivery. Coherence was computed to study the after stroke muscle interactions in Deltoid and Triceps [20], the values of coherence were lower for patients than for control.
Mutual Information coefficient (MI) represents a general method to detect both linear and nonlinear statistical dependencies between time series. This variable was also assessed in the above mentioned work of uterine muscles synchronizations [16,17] with higher results of MI with the delivery advancing. Furthermore, Wu et al. [21] propose a methodology based on MI to analyze intermuscular coupling during the movement of upper limbs, getting higher values for the pair Triceps Brachii and Posterior Deltoid compared to statatic states. MI was also was utilized to measure the inter-muscular coupling between Biceps and Triceps with aging [22], obtaining decreased values of MI with aging. Svendsen et al. [23] used MI to reflect the inter-muscular coupling of four forearm muscles during static and dynamic tracking tasks with greater values for static states.
The Multivariate Sample Entropy (MSE) measures the structural complexity of real-world multichannel data by examining nonlinear correlations within and between channels. It provides a robust relative complexity measure for multivariate data and has been validated on real world multivariate gait, physiological, or in wind data [24]. It has been also used for study uterine muscles in during delivery progression [16] obtaining very lower values with the approaching of delivery. Muscle relations between dynamic and resting 85 states were also addressed by MSE computation [18], finding lower values, and therefore stronger couplings in the pair of muscles External Oblique and Transverse. In a different study, the authors calculated the MSE for pairs of muscles in different conditions of speed of gait and running [25].
Finally, besides the approach of studying the described parameters for finding interactions between pairs, the causal relation between pairs is found to be of great relevance. The Conditional Granger Causality (CG-Causality) analyzes the directed functional coordination between pairs of muscles. Ye-Lin et al. [26] used the conditional CG-Causality from surface electromyography signals to examine the directed functional coordination of various swallowing muscles during the ingestion of different liquids in both healthy and dysphagic subjects. Zhou et al. [27] in their work implemented a method of PCA based CG-Causality to detect brain networks connectivity. As a step further, the parameter Directed Conditional Granger Causality (DCG-Causality) adds information about the direction of the causality. This calculus was performed in the study of the uterine muscles synchronization to see the direction in which the signals propagated, finding that the majority of signals propagated downward to expulse the fetus [1].
The aim of the present paper is to investigate the couplings and synchronization between pairs muscles when using an exoskeleton. To achieve this goal, we performed EMG recordings, process them, and obtained of the above mentioned four parameters to assess correlations and couplings between pairs of signals: correlation coefficient, the coherence coefficient, the mutual information, and the multivariate sample entropy. And also, the parameter, DCG-Causality to study the direction of the causality. Overall, this paper aims to contribute to a better understanding of the complex interplay between exoskeletons and the human body, and provide insights into how to optimize the design and use of these devices for different applications.

2. Materials and Methods

To participate in the study, individuals of both genders had to meet following criteria: being between 30 to 45 years old, having a body mass index (BMI) within the range of 18.5 k g / m 2 to 25.5 k g / m 2 . Individuals with a history of musculoskeletal lesions or respiratory or cardiovascular pathologies were excluded. Specifically, the study involved 8 volunteers, consisting of 4 women and 4 men, who visited the Instituto de Biomecánica de Valencia (IBV) facilities and provided written consent for the use and publication of their data for the study. The average weight, and height of the participants were 67.9 ± 7.8 kg and, 175.6 ± 4.6 cm, respectively, with standard deviations indicated.

2.1. Setup design

The aim of task design was to replicate a common manual handling task in industrial and warehouse settings, which typically involves a high physical load and adheres to ergonomic requirements. Although the designed tasks may not encompass all possible postures involved in carrying heavy objects, they simulate a depalletizing job that involves musculoskeletal risks from forced postures. The selected tasks recreate a stationary workstation with limited dynamic movements that may necessitate minimal support, what happens in the workstations that use passive exoskeletons. The task design is based on ergonomic risk factors, and all the details can be found in the work of the authors [5].
In summary, it consisted on depalletizing a block of four rows of four boxes. In Figure 1 appears the type of box over the destination table, and a schematic drawing in white of the initial configuration of the 16 boxes pallet.
To ensure consistency across users, a predetermined pattern is followed when moving the boxes from the pallet to the destination. 16 boxes are numbered in sequence from top row (boxes 1 to 4) to the bottom (boxes 13 to 16). The users performed the depalletizing task six times. The first three repetitions were performed without the exoskeleton, handling weights of 7kg, 8kg, and 9kg respectively. The second three were performed with the exoskeleton, 7kg, 8kg, and 9kg weights in each repetition. Therefore, under the condition of no exoskeleton there were 48 boxes moved in total, and then 48 boxes with exoskeleton. The use of the exoskeleton for the second round of 48 boxes responds to ensure the worst case possible from the point of view of fatigue. Finally, the rhythm is indicated by a metronome sound every 6 seconds (frequency of manipulation).

2.2. Equipment

The exoskeleton used was the commercial passive lumbar LaevoTM V2 exoskeleton [6,28,29].
EMG signals were measured using a Noraxon wireless electromyography system (UltiumTM EMG) to monitor the muscular activity of the right side muscles: erector spinae, gluteus medius, quadriceps femoris, and semitendinosus; from now on: lumbar, gluteus, quadriceps and semitendinosus. The signals were sampled at 2000 H z . A clinical evaluator followed the SENIAM guidelines [30] to place the bipolar electrodes.
The XsensTM MVN Analyze system in whole-body configuration was used for motion capture; These data were collected to track the postures of the users in order to perform the segmentation of the EMG signals at the desired positions. Both systems, EMG and MoCap were synchronized using the Noraxon Myosync channel.

2.3. Data analysis

2.3.1. Signal preprocessing

The EMG signals pre-processing consisted of two stages. First, a filtering stage with the objective of cleaning and preparing the signals. Once the EMG signals were obtained, a zero-phase bandpass Butterworth filter of order 10 was utilized for pre-processing. The cut-off frequencies of 20 and 200 Hz were applied to eliminate movement noise and limit the study’s bandwidth.
And secondly, a segmentation task for selecting the fragments of muscular signal activation when the user was holding the box, from lifting to downloading, common to all muscle channels was carried out. In total, 48 fragments (three exercises of 16 boxes each) for each muscle in both, with and without exoskeleton condition. The extended details of the segmentation methodology can be find in a previous work [5].

2.3.2. Feature extraction

The interaction among muscles were analyzed by using pairs of EMG signals. A series of parameters were calculated from each 48 common fragments of both conditions with and without exoskeleton. Four of the parameters: Correlation Coefficient, Coherence Coefficient, Mutual Information, and the Multivariate Sample Entropy, correspond to non directional parameters. Besides, the parameter of Granger Causality is a directional parameter.

2.3.2.1. Correlation Coefficient

The correlation coefficient (CC) expresses the linear correlation between a pair of EMG signals in the time domain. The CC of two signals X and Y is defined as:
C O R R X , Y = C o v X , Y S X S Y
where S X and S Y is the standard deviation of X and Y, and C o v X , Y is the covariance of X and Y. C C X , Y represents the Pearson correlation coefficient of X and Y. There would be a higher correlation between X and Y with higher values of CC. CC goes from − 1 to 1 and equals 0 when there is no linear correlation between X and Y. With the use of the exoskeleton, the values could be expected to be higher in specific pair of muscles, because due to the design of the exoskeleton some muscles will be forced to be coupled.

2.3.2.2. Coherence Coefficient

The coherence expresses the linear correlation between a pair of EMG signals in the frequency domain. It is an extension of Pearson’s correlation coefficient in the frequency domain. Taking two signals X and Y, the coherence is calculated as:
C O H X , Y f = P x , y f 2 P x x f P y y f
where P x x and P y y are power spectral density estimates of X and Y, and P x , y is the cross spectral density estimate of X and Y. In this paper the maximum value of this function is considered. The values of COH go from 0 to 1, closer the coefficient is to 1, the more lineal is the relation between both signals. The closer to 0, the more unrelated the signals are. Like in the case of CORR, the use of the exoskeleton, the values could be expected to be higher.

2.3.2.3. Mutual information

The Mutual information (MI) measures the amount of information that one random variable contributes to another variable. This variable is defined in the following way [31,32]:
M I X , Y = ∑ x ∈ X ∑ y ∈ Y p x , y l o g p x , y p x p y
where X and Y are EMG signals, p ( x , y ) is the joint probability distribution of X and Y, and p ( x ) and p ( y ) are the marginal probability distributions of X and Y. The higher correlation between X and Y, the higher value of MI; MI being zero when X and Y are statistically independent. The behaviour of this parameter can be comparable with parameters CORR and COH,the higher the M I the higher the muscle couplings.

2.3.2.4. Multivariate Sample Entropy

The sample entropy characterizes the likelihood that similar patterns in a time series will remain similar in time [33]. The multivariate sample entropy characterizes potential correlations among multichannel data. The algorithm consists of implementing a multivariate vector of the analyzed signal. This vector embeds the information of the signal with whom the correlations are studied. All signals are firstly normalized with Z-score, then the multivariate embedded vector is build. If we define a time series with lag τ and dimension m:
X m i = x i , x i + 1 , . . . , x i + τ m − 1
Then, with p being the number of EMG signals:
X m ( i ) = [ x 1 ( i ) , x 1 ( i + τ 1 ) , . . . , x 1 ( i + τ 1 m 1 − 1 ) x 2 ( i ) , x 2 ( i + τ 2 ) , . . . , x 2 ( i + τ 2 m 2 − 1 ) x p ( i ) , x p ( i + τ p ) , . . . , x p ( i + τ p m p − 1 ) ]
M = [ m 1 , m 2 , . . . , m p ] is the embedding vector, and T = [ τ 1 , τ 2 , . . . , τ p ] , the time delay vector. In the present case we have chosen, p = 2 , M = [ 2 , 2 , 2 ] . and T = [ 1 , 1 , 1 ] as in [16].
For given multivariate delay vectors X m ( i ) , and X m ( j ) , and a threshold r and , i = 1 , 2 , . . . , N the number of instances is defined as Φ m ( i , r ) , where d is the distance between them:
d X m ( i ) , X m ( j ) ≤ r , i ≠ j
where d expresses the maximum norm. The frequency of occurrence can be express as [33]:
Φ m r = 1 N − τ ( m − 1 ) + 1 ) ∑ i = 1 N − τ ( m − 1 ) + 1 Φ m ( i , r )
If the dimension of the multivariate delay composite vector is extended from m to m + 1 , the frequency of occurrence can be obtained for X m + 1 i . Finally, the MSE can be calculated as:
M S E ( m , τ , r , N ) = − l n Φ m + 1 ( r ) Φ m ( r )
The lower this value is, the most correlated both signals are. In this case, oppositely to CORR, COHM, and MI, the MSE values are expected to be lower for higher degree of coupling.

2.3.2.5. Directional Conditional Granger Causality

The Conditional Granger Causality (CG-Causality) is defined as the level of prediction that the past of a signal Y makes over a signal X, besides the prediction of X that its own past, and the past of a conditioning variable Z make [34]. In the case of EMG signals, CG-Causality allows to detect interactions between muscles, and out of common causal influences [34]. If we take the universe U of known recorded variables can split it in three inter-dependent multivariate processes:
U = X t Y t Z t
The factor introduced by the Z is needed to be isolated from the CG-Causality from Y to X. So we can consider the full regression, where A x x , k are the coefficients of the dependence of X on the past of Y and Z respectively [26]:
X t = ∑ k = 1 p A x x , k · X t − k + ∑ k = 1 p A x y , k · Y t − k + ∑ k = 1 p A x z , k · Z t − k + ε x , t
The dependence of X on the past of Y is included in the coefficients A x y , k . So if A x y , 1 = A x y , 2 = . . . = A x y , p = 0 , there is no dependence of X on the past of Y, so this leads to the reduced regression:
X t = ∑ k = 1 p A x x , k ′ · X t − k + ∑ k = 1 p A x z , k ′ · Z t − k + ε x , t ′
And then, the null hypothesis to be tested is the CG-Causality of Y to X conditioned by Z:
F Y → X ∣ Z ≡ l n ∑ x x ′ ∑ x x
So, in the present case, the CG-causality will be calculated for each pair of muscles E M G i → E M G j [34].
D C G i , j ( E M G ) ≡ F E M G j → E M G i ∣ E M G i j
For each pair of muscles the Directional Conditional Granger Causality (DCG-Causality) is implemented G i , j ( E M G ) ≠ G j , i ( E M G ) .
D C G C X → Y | Z = G i , j ( E M G ) − G j , i ( E M G )
Details of the algorithm can be found in the original work by Barnett and Seth [34]. The optimal order of the vector autoregresssive model to achieve a compromise between the model’s precision and complexity was determined with the Akaike information criterion [35]. This parameter express directionality, and so, the effect of the exoskeleton will depend on the pair of muscles studied. The results will talk about in which degree the effect of the device makes one muscle "director" of another, in a different way as their relationship was in absence of it.
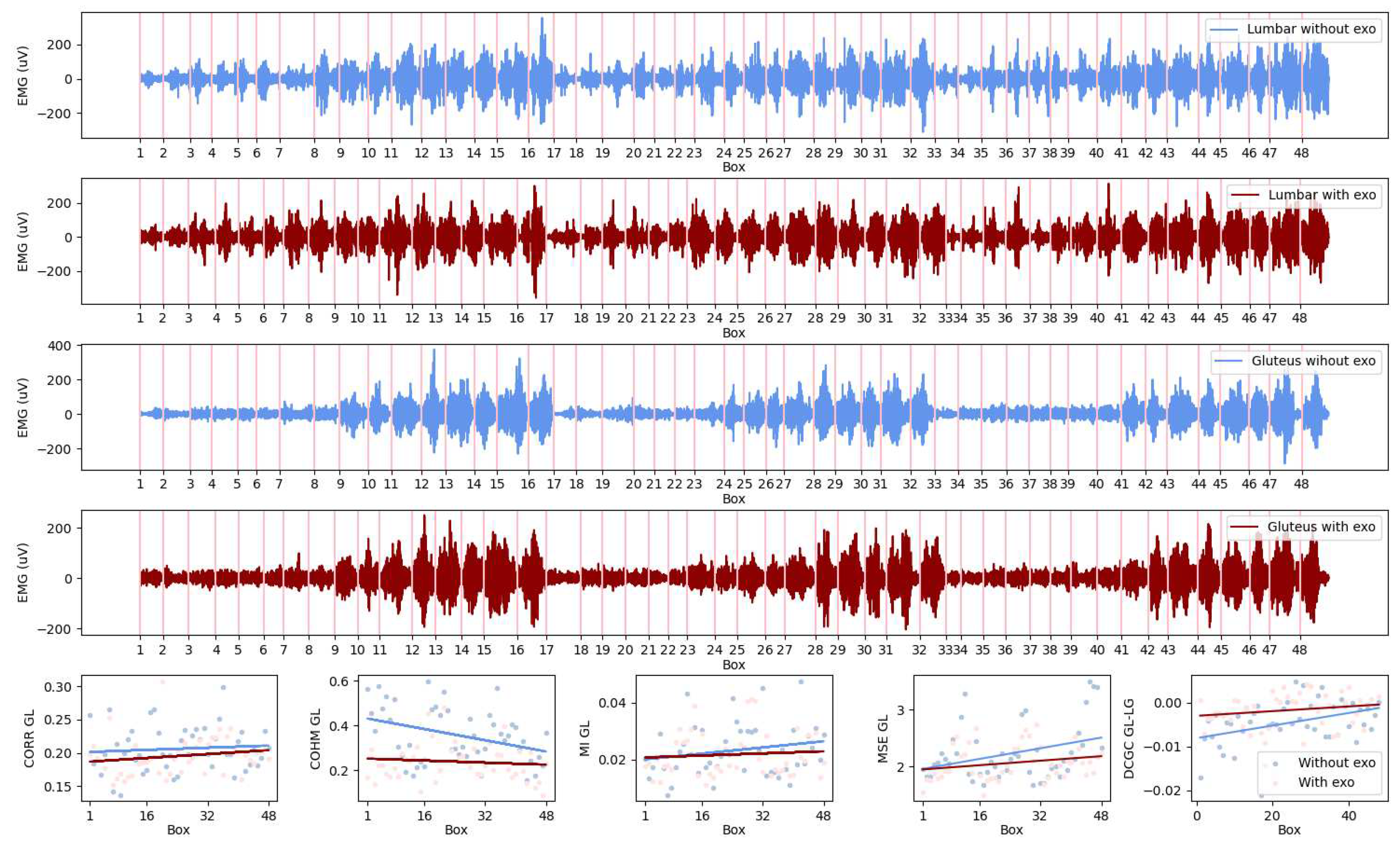
Figure 2 shows an example of signals and parameters of a specific user. It is also depicted the corresponding EMG coupling parameters por this muscle pair in the conditions with and without exoskeleton.
The four subplots at the top contain the EMG signal fragments that belong to each of the raised boxes. In the four subplots, the two pairs of measurements for the Lumbar and Gluteus muscles can be observed, each pair contains a signal in red, belonging to recordings in which the exoskeleton is used, and blue, without an exoskeleton.
In the last row, the series of plots corresponding to the calculated values of the parameters for each of the fragments for the pair of muscles is shown. In red, the lines of trend corresponding to the condition with exo, and in blue without exo. With the purpose to analyse the parameters obtained of all users, a mixed model is build to calculate the trend lines for the whole set. In the following section, the mixed model is described, together with the post-hoc analysis carried out to obtain the slopes and intercepts for each pair of muscles.

2.3.3. Mixed model

The data treatment and posterior statitistical analysis performed had the objective of finding the evidence of changes of values and patterns of muscle synergies between the conditions with and without exoskeleton. The interactions per fragment are characterized by the feature calculated for each muscle pair, as shown in the Figure 2 first row.
The main hypothesis is that the exoskeleton could affect muscle couplings, and muscle couplings could also be affected by fatigue components.For this reason, the data will be analysed to find the significant differences ( p < 0.05 ), on the one hand, on the values of the parameters of one condition, and the other. And, on the other hand, to find significant differences in the evolution of the parameters throughout the exercise and how the fatigue that appears through the time affects the possible changes in the couplings.
Fatigue component could be reflected on the trend of the parameters, therefore the order, understood as the position of the box (1 to 48) has been considered as a numerical factor. Besides, interaction between the use of the exo and the order has been considered in the model. User has been introduced as random factor in the model (15).
y ( f e a t u r e , m u s c l e p a i r ) ∼ e x o * o r d e r + ( 1 | u s e r )
This calculus was carried out for each y ( f e a t u r e , m u s c l e p a i r ) , five features and six muscle combinations. The mixed model was built in R using the R package lme4 [36].

2.3.4. Statistical analysis

A post-hoc analysis was performed adjusted by holm-method using the phia package in R [37,38].
Once obtained the cases with significant differences ( p < 0.05 ), the values of slopes and intercepts were extracted from the model. With the slopes and intercepts, it is possible to appreciate if the trend of the parameter values were increasing or decreasing for each case, and compare between conditions with and without exoskeleton.

3. Results

In Figure 3 there is a matrix of representations of the calculated trends for the conditions with and without exoskeleton. The graphical representation of the trends was build using the obtained slopes and intercepts with x-axis values from one to 48 representing each of the 48 order positions of each box handled (16 of 7kg, followed by 16 of 8kg, and followed of 16 of 9kg) for each condition. 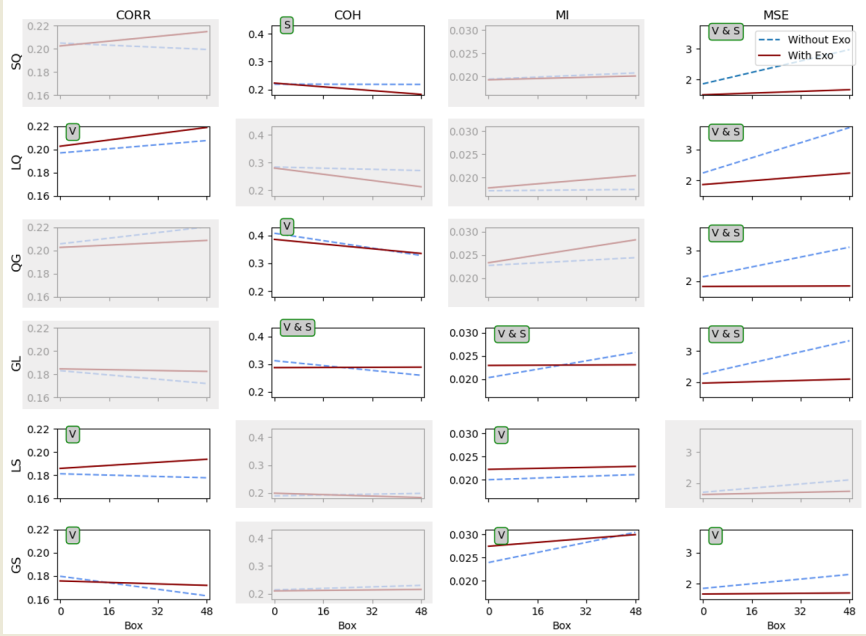The slopes and intercepts used to build the lines represented are obtained from the mixed model (15). The blue dashed lines represent the condition without exoskeleton, and the red solid lines, the condition with exoskeleton. In the columns each of the four coupling parameters: Correlation Coefficient (CORR), and Coherence Coefficient (COH), Mutual Information (MI), and Multivariate Sample Entropy (MSE); In the rows, each of the six muscle combinations: Semitendinosus - Quadriceps (SQ), Lumbar - Quadriceps (LQ), Quadriceps - Gluteus (QG), Gluteus-Lumbar (GL), Lumbar - Semitendinosus (LS), and Gluteus - Semitendinosus (GS).
In this matrix, the plots without grey shadowing are the ones that show significant differences. Over each plot in the Figure 3, there is a tag with the type of significant differences found. An "V" corresponds to the differences found between the conditions with and without exoskeleton, meaning that the condition produces a significant change in the values of the interactions found. And an "S" corresponding to the differences found in the slope between the conditions, meaning that the conditions changes significantly the way that the coupling evolve throughout the whole exercise (48 boxes). "V S" corresponds to significant differences for both value and slope. In Table 1 there are included the p-values corresponding to each pair of muscles and variable.
For all the pair of muscles there are significant differences found between conditions in two or more parameters.
Observing the parameters MSE and MI, in all cases the evolution remains near to constant throughout all the positions and boxes when using the exoskeleton. Also, in all cases an upward trend is observed when task is carried out without exoskeleton. This observation is significant for both parameters in the pair GL and also for the pairs SQ, LQ and QG, which considers the iteraction of quadriceps with other muscles regarding MSE. The MI has, throughout almost all the exercise, higher values when no exo is used, and lower with the use of the exo; and the MSE has exactly the opposite, in a more markedly way. By definition of the variables, this result is consistent with the theoretical expectation. Because the higher values of the MI, the higher the coupling between the pair muscle. On the contrary, the lower the values for MSE the higher the coupling.
It is also noticeable that MI values for LS muscle pair, the exoskeleton used reinforces the mutual information for all boxes for this muscle pair, with very subtle variations throughout the exercise. This could be as a way of "release" efforts from Lumbar to Semitendinosus muscle. MI for GS behaves in a similar way. For GL it is remarkable that the use of exoskeleton tends to maintain a constant coupling between muscles.
The correlation and the coherence parameters show statistically significant differences in several combinations of muscles, although none of the pairs are in common. In the case of the CORR, the differences are significant in terms of the values, and for all significant pairs, the values between conditions agree with the ones obtained for the parameter MI. For LQ and LS the values of CORR are higher when wearing the exoskeleton, which point out a higher coupling, in terms of linear correlation, between lumbar and Semintendionosus and Quadriceps muscle when using the exoskeleton, maybe due to the transfer of efforts that the exoskeleton causes. In the case of GS, the exoskeleton maintains the coupling, regarding linear correlation, between Gluteus and Semitendinosus almost constant, with similar values to those of at the beginning of the exercise without exoskeleton. This effect is also present at the COH parameter for the pairs QG, and GL. Moreover, a significant difference is found for the slope of the COH parameter for the GL pair, in agreement with the differences found in MI and MSE for the same pair of muscles, almost constant when wearing the exoskeleton.
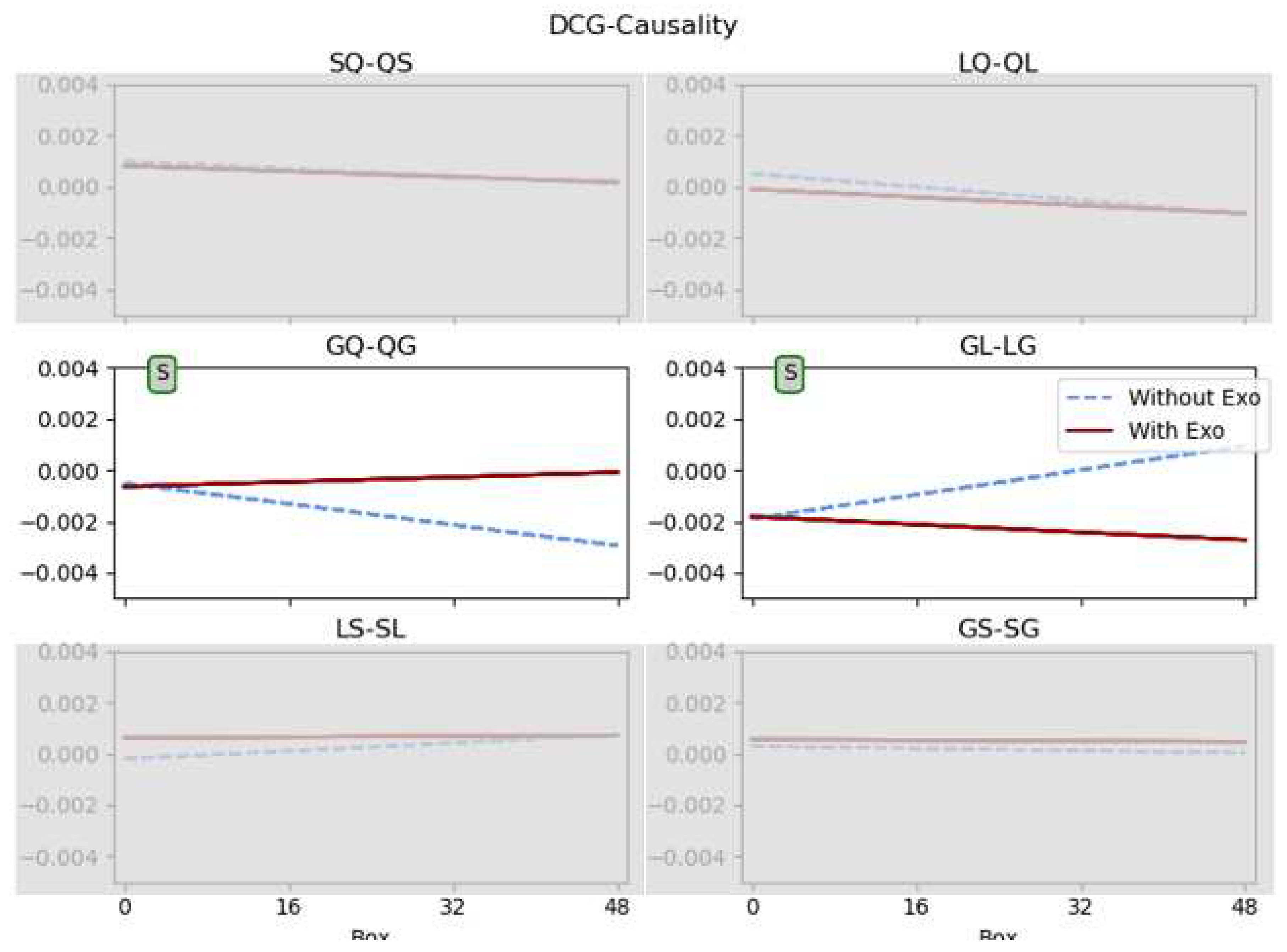
In the Figure 4 there are represented the results of the mixed model for the Directional Conditional Granger Causality feature. This parameter is represented individually due to the characteristic of expressing directionality, not applicable to the other parameters. In this case, each combination of muscles appears indicated in each plot, and the type of significant difference is annotated in the plots where they were found in the same way as in the Figure 3. In Table 2 there are included the the p-values of the significant differences found in Figure 3. Here also the dashed line represents the without exo condition, and the solid line, the with exo condition.
For this variable, there were found statistically significant differences in the slope in the pair of muscles of Semitendinosus-Quadriceps and Gluteus-Lumbar. That is to say, in the way that the parameter of the DCG-Causality evolves throughout the exercise. In both cases the values of the condition with exoskeleton evolve in a more steadily way (like observed in MSE, MI, and CORR), so the values of SQ-QS and GL-LG are more constant. In the case of no exo condition, those values change more either to a negative value (SQ-QS) or to positive values (GL-LG). GC values presented downward trend and negative values for GQ -QG and upward trend with positive values for GL-LG. Which manifests that the exoskeleton tends to soften the evolution of the muscles interactions during the exercise.

4. Discussion

Encountering situations where there are no other papers to compare results can be both challenging and thought-provoking. This circumstance has arisen when exploring topics with limited prior research. In the present case, the approach, the effect of the exoskeleton over the users performing repetitive tasks have been studied previously, but performing different approaches. Approaches such as studying the effects over the muscles independently, studying the kinematic restrictions, or the effects over joint tensions [1].
The study of the interactions between muscles in the research field of the exoskeleton has focused its interest in the case of the synergies approach and the active exoskeletons. These devices intend to react actively and sometimes in real time to muscular needs, and are widely used for therapy. Muscle synergies were extracted with Non-Negative Matrix Factorization (NNMF) and compared to obtain a gait symmetry index over therapy sessions with no differences between groups [39]. Other authors studied the influence of the exoskeletons on synergies, while participants are performing different tasks such as walking. At this respect, for some authors muscle synergies during walk are not affected by the use of an exoskeleton[40]. Other authors found that synergies depend on the control introduced by the exoskeleton [41]. Tan et al. [42] in an exoskeleton for back pain. Their results indicate that muscle coordination changes were dominated by changes in timing coefficients, with minimal change in muscle synergy vectors.
In this study, we aimed to assess how the use of the exoskeleton affects the coupling and synchronization (with and without directionality) between a set of muscles involved in the task. It is a new approach, therefore, no papers have been found making specific comparisons helping in the interpretation of results.
The CORR differences in values between muscles, depics lower linear coupling (LQ, LS, and GS) with the absence of the exo. This could indicate that the exoskeleton increases the involvement of the semitendinosus carrying out the movements, which is consistent with previous results that pointed to an increase in fatigue of the semitendinosus with an exoskeleton [5].
Variables COH, MI, and MSE reveal that the exoskeleton tends to maintain the degree of coupling throughout the exercise.
This leads us to corroborate that the use of the exoskeleton implies restrictions in the degrees of freedom of movement and a harmonization of the redistribution of loads. It implies that some muscles that fatigued without an exoskeleton do not do so with the use of an exo. The displacement of the spectrum towards low frequencies no longer occurs, therefore reducing the coherence (the linear similarity of their spectra decreases).
MSE seems to have great consistency among almost all pairs of muscles. It is evident that, the multivariate entropy presents from high variations when the exoskeleton is not used to slight ones when used, with a very flat slope during the performance of the exercises (trying to maintain the muscular relationship with the exoskeleton). Like other studies that used this parameter for characterizing muscle pairs synchronization [16,17,18], the lower values are related to a higher degree of coupling, and in the present case, it is caused by the action of the exoskeleton. The results obtained for the MSE demonstrate is suitability for the study of couplings between pair of muscles in this application.
The Directed Conditional Granger Causality results, like the case of the MSE, express that the exoskeleton tends to maintain the directionality of the causal relationships between muscles and with lower slopes of the causal differences throughout the exercises. The observation could lead interpret that the exoskeleton directionality of muscle information “flows” in the positive gravity direction. Although this premise should be validated in a future research.
This study stands as an initial approach to characterize the phenomena of couplings differences between wearing and not wearing an exoskeleton. Further studies would be required for a deeper understanding, involving designing the methodology specifically for the study of couplings with more superficial muscles and by pairs of antagonists. Also, the study of synergies through the NNMF would be of great interest.

5. Conclusions

The findings indicate that employing a lumbar exoskeleton do have effects over the synchronizations that occur between the pairs of muscles monitored.
A reduction in the values (and in general in the slope) of the MSE parameter is observed with significant differences in all the muscle pairs analyzed except LS, which points to an increase in synchronization with the use of the exo. This is corroborated by the increase in MI values, with statistically significant differences in GL. The results are not so evident for CORR and COH that only assess the linear relationships between muscle pairs in the temporal and spectral domain.
The consequences of these differences found, whether if they imply advantages or drawbacks are still to be studied. There is still ample room for further investigation, over the long-term health effects of the users.
It is important to note that the study focused on objectively evaluating tasks with short durations and limited types of movements. To comprehensively assess acceptance and long-term effects, a longitudinal study incorporating a broader range of tasks will be conducted.
Companies should recognize that using this equipment may offer a viable solution when other technical or organizational measures are impractical or ineffective in reducing physical strain at the workplace. The primary approach to improving a job should always involve an ergonomic evaluation and job redesign, informed by the evaluation results. Exoskeletons can be considered as a supplementary measure when efforts have been exhausted, and the desired improvements have not been attained.

Author Contributions

Conceptualization, S.I., J.-L. M.-d.-J., J.-M.B.-L. and G.P.; methodology, S.I., and J.-M. B.-L.; validation, S.I., and J.-M. B.-L.; formal analysis, S.I., G.P., J.-L. M.-d.-J., and J.-M. B.-L.; investigation, S.I., G.P., J.-L. M.-d.-J., and J.-M. B.-L.; data curation, S.I., G.P., J.-L. M.-d.-J., and J.-M. B.-L.; writing—original draft preparation, S.I., G.P., J.-L. M.-d.-J., and J.-M. B.-L.; writing—review and editing, S.I., G.P., J.-L. M.-d.-J., and J.-M. B.-L.; visualization, M.S.; supervision, J.-M. B.-L..; All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by Fundación Prevent.

Institutional Review Board Statement

The study was conducted in accordance with The European Code of Conduct for Research Integrity, and approved by the Research Ethics Committee of the Polytechnic University of Valencia (protocol code P 18 _31_10_19 and date of approval November 16th of 2019).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pesenti, M.; Antonietti, A.; Gandolla, M.; Pedrocchi, A. Towards a Functional Performance Validation Standard for Industrial Low-Back Exoskeletons: State of the Art Review. Sensors 2021, 21. [Google Scholar] [CrossRef]
  2. Ashta, G.; Finco, S.; Battini, D.; Persona, A. Passive Exoskeletons to Enhance Workforce Sustainability: Literature Review and Future Research Agenda. Sustainability 2023, 15. [Google Scholar] [CrossRef]
  3. Kermavnar, T.; de Vries, A.W.; de Looze, M.P.; O’Sullivan, L.W. Effects of industrial back-support exoskeletons on body loading and user experience: an updated systematic review. Ergonomics 2021, 64, 685–711. [Google Scholar] [CrossRef] [PubMed]
  4. Di Natali, C.; Chini, G.; Toxiri, S.; Monica, L.; Anastasi, S.; Draicchio, F.; Caldwell, D.G.; Ortiz, J. Equivalent Weight: Connecting Exoskeleton Effectiveness with Ergonomic Risk during Manual Material Handling. International Journal of Environmental Research and Public Health 2021, 18. [Google Scholar] [CrossRef] [PubMed]
  5. Iranzo, S.; Piedrabuena, A.; García-Torres, F.; Martinez-de Juan, J.L.; Prats-Boluda, G.; Sanchis, M.; Belda-Lois, J.M. Assessment of a Passive Lumbar Exoskeleton in Material Manual Handling Tasks under Laboratory Conditions. Sensors 2022, 22. [Google Scholar] [CrossRef]
  6. Koopman, A.S.; Kingma, I.; Faber, G.S.; de Looze, M.P.; van Dieën, J.H. Effects of a passive exoskeleton on the mechanical loading of the low back in static holding tasks. Journal of Biomechanics 2019, 83, 97–103. [Google Scholar] [CrossRef]
  7. Bosch, T.; van Eck, J.; Knitel, K.; de Looze, M. The effects of a passive exoskeleton on muscle activity, discomfort and endurance time in forward bending work. Applied Ergonomics 2016, 54, 212–217. [Google Scholar] [CrossRef] [PubMed]
  8. Kim, H.K.; Hussain, M.; Park, J.; Lee, J.; Lee, J.W. Analysis of Active Back-Support Exoskeleton During Manual Load-Lifting Tasks. Journal of Medical and Biological Engineering 2021, 41, 704–714. [Google Scholar] [CrossRef]
  9. Lazzaroni, M.; Poliero, T.; Sposito, M.; Toxiri, S.; Caldwell, D.G.; Di Natali, C.; Ortiz, J. Back-Support Exoskeleton Control Strategy for Pulling Activities: Design and Preliminary Evaluation. Designs 2021, 5, 39. [Google Scholar] [CrossRef]
  10. Antwi-Afari, M.F.; Li, H.; Anwer, S.; Li, D.; Yu, Y.; Mi, H.Y.; Wuni, I.Y. Assessment of a passive exoskeleton system on spinal biomechanics and subjective responses during manual repetitive handling tasks among construction workers. Safety Science 2021, 142, 105382. [Google Scholar] [CrossRef]
  11. Di Natali, C.; Chini, G.; Toxiri, S.; Monica, L.; Anastasi, S.; Draicchio, F.; Caldwell, D.G.; Ortiz, J. Equivalent Weight: Connecting Exoskeleton Effectiveness with Ergonomic Risk during Manual Material Handling. International Journal of Environmental Research and Public Health 2021, 18, 2677. [Google Scholar] [CrossRef] [PubMed]
  12. Lotz, C.A.; Agnew, M.J.; Godwin, A.A.; Stevenson, J.M. The effect of an on-body personal lift assist device (PLAD) on fatigue during a repetitive lifting task. Journal of Electromyography and Kinesiology 2009, 19, 331–340. [Google Scholar] [CrossRef]
  13. Godwin, A.A.; Stevenson, J.M.; Agnew, M.J.; Twiddy, A.L.; Abdoli-Eramaki, M.; Lotz, C.A. Testing the efficacy of an ergonomic lifting aid at diminishing muscular fatigue in women over a prolonged period of lifting. International Journal of Industrial Ergonomics 2009, 39, 121–126. [Google Scholar] [CrossRef]
  14. Glinski, A.v.; Yilmaz, E.; Mrotzek, S.; Marek, E.; Jettkant, B.; Brinkemper, A.; Fisahn, C.; Schildhauer, T.A.; Geßmann, J. Effectiveness of an on-body lifting aid (HAL® for care support) to reduce lower back muscle activity during repetitive lifting tasks. Journal of Clinical Neuroscience 2019, 63, 249–255. [Google Scholar] [CrossRef] [PubMed]
  15. Bizzi, E.; Cheung, V.; d’Avella, A.; Saltiel, P.; Tresch, M. Combining modules for movement. Brain Research Reviews 2008, 57, 125–133. [Google Scholar] [CrossRef]
  16. Zhang, Y.; Hao, D.; Yang, L.; Zhou, X.; Ye-Lin, Y.; Yang, Y. Assessment of Features between Multichannel Electrohysterogram for Differentiation of Labors. Sensors 2022, 22. [Google Scholar] [CrossRef]
  17. Mas-Cabo, J.; Ye-Lin, Y.; Garcia-Casado, J.; Alberola-Rubio, J.; Perales, A.; Prats-Boluda, G. Uterine contractile efficiency indexes for labor prediction: A bivariate approach from multichannel electrohysterographic records. Biomedical Signal Processing and Control 2018, 46, 238–248. [Google Scholar] [CrossRef]
  18. King, A.C. The effect of movement and load on the dynamic coupling of abdominal electromyography. Neuroscience Letters 2018, 675, 64–67. [Google Scholar] [CrossRef]
  19. De Marchis, C.; Severini, G.; Castronovo, A.M.; Schmid, M.; Conforto, S. Intermuscular coherence contributions in synergistic muscles during pedaling. Experimental Brain Research 2015, 233, 1907–1919. [Google Scholar] [CrossRef]
  20. Kisiel-Sajewicz, K.; Fang, Y.; Hrovat, K.; Yue, G.H.; Siemionow, V.; Sun, C.K.; Jaskólska, A.; Jaskólski, A.; Sahgal, V.; Daly, J.J. Weakening of Synergist Muscle Coupling During Reaching Movement in Stroke Patients. Neurorehabilitation and Neural Repair 2011, 25, 359–368. [Google Scholar] [CrossRef]
  21. Wu, Y.; She, Q.; Wang, H.; Ma, Y.; Sun, M.; Shen, T. R-Vine Copula Mutual Information for Intermuscular Coupling Analysis. Proceedings of the 11th International Conference on Computer Engineering and Networks; Liu, Q., Liu, X., Chen, B., Zhang, Y., Peng, J., Eds.; Springer Nature: Singapore, 2022. [Google Scholar] [CrossRef]
  22. Sun, W.; Liang, J.; Yang, Y.; Wu, Y.; Yan, T.; Song, R. Investigating Aging-Related Changes in the Coordination of Agonist and Antagonist Muscles Using Fuzzy Entropy and Mutual Information. Entropy 2016, 18, 229. [Google Scholar] [CrossRef]
  23. Svendsen, J.H.; Samani, A.; Mayntzhusen, K.; Madeleine, P. Muscle coordination and force variability during static and dynamic tracking tasks. Human Movement Science 2011, 30, 1039–1051. [Google Scholar] [CrossRef] [PubMed]
  24. Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef]
  25. Estrada, L.; Torres, A.; Sarlabous, L.; Jané, R. Influence of Parameter Selection in Fixed Sample Entropy of Surface Diaphragm Electromyography for Estimating Respiratory Activity. Entropy 2017, 19, 460. [Google Scholar] [CrossRef]
  26. Ye-Lin, Y.; Prats-Boluda, G.; Galiano-Botella, M.; Roldan-Vasco, S.; Orozco-Duque, A.; Garcia-Casado, J. Directed Functional Coordination Analysis of Swallowing Muscles in Healthy and Dysphagic Subjects by Surface Electromyography. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
  27. Zhou, Z.; Chen, Y.; Ding, M.; Wright, P.; Lu, Z.; Liu, Y. Analyzing brain networks with PCA and conditional Granger causality. Human Brain Mapping 2009, 30, 2197–2206. [Google Scholar] [CrossRef]
  28. Settembre, N.; Maurice, P.; Paysant, J.; Theurel, J.; Claudon, L.; Kimmoun, A.; Levy, B.; Hani, H.; Chenuel, B.; Ivaldi, S. The use of exoskeletons to help with prone positioning in the intensive care unit during COVID-19. Annals of Physical and Rehabilitation Medicine 2020, 63, 379–382. [Google Scholar] [CrossRef]
  29. Flor, R.; Gaspar, J.; Fujao, C. How Workers Perceive LAEVO Exoskeleton Use in Non-cyclic Tasks. Advances in Human Factors and System Interactions; Nunes, I.L., Ed.; Springer International Publishing: Cham, 2021; pp. 147–154. [Google Scholar]
  30. Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of recommendations for SEMG sensors and sensor placement procedures. Journal of Electromyography and Kinesiology 2000, 10, 361–374. [Google Scholar] [CrossRef]
  31. Ross, B.C. Mutual Information between Discrete and Continuous Data Sets. PLOS ONE 2014, 9, e87357. [Google Scholar] [CrossRef]
  32. Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Physical Review E 2004, 69, 066138. [Google Scholar] [CrossRef]
  33. Looney, D.; Adjei, T.; Mandic, D.P. A Novel Multivariate Sample Entropy Algorithm for Modeling Time Series Synchronization. Entropy 2018, 20. [Google Scholar] [CrossRef]
  34. Barnett, L.; Seth, A.K. The MVGC multivariate Granger causality toolbox: A new approach to Granger-causal inference. Journal of Neuroscience Methods 2014, 223, 50–68. [Google Scholar] [CrossRef] [PubMed]
  35. McQuarrie, A.D.R.; Tsai, C.L. Regression and Time Series Model Selection; World Scientific, 1998. Google-Books-ID: K0NqDQAAQBAJ.
  36. Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software 2015, 67, 1–48. [Google Scholar] [CrossRef]
  37. De Rosario-Martinez, H.; Fox, J.; Team, R.C. phia: post-hoc interaction analysis, 2015. R package version 0.2-1.
  38. de Rosario, H. Analysing interactions of fitted models. 2012.
  39. Tan, C.K.; Kadone, H.; Watanabe, H.; Marushima, A.; Hada, Y.; Yamazaki, M.; Sankai, Y.; Matsumura, A.; Suzuki, K. Differences in Muscle Synergy Symmetry Between Subacute Post-stroke Patients With Bioelectrically-Controlled Exoskeleton Gait Training and Conventional Gait Training. Frontiers in Bioengineering and Biotechnology 2020, 8. [Google Scholar] [CrossRef] [PubMed]
  40. Afzal, T.; Zhu, F.; Tseng, S.C.; Lincoln, J.A.; Francisco, G.E.; Su, H.; Chang, S.H. Evaluation of Muscle Synergy During Exoskeleton-Assisted Walking in Persons With Multiple Sclerosis. IEEE Transactions on Biomedical Engineering 2022, 69, 3265–3274. [Google Scholar] [CrossRef]
  41. Escalona, M.J.; Bourbonnais, D.; Le Flem, D.; Goyette, M.; Duclos, C.; Gagnon, D.H. Effects of robotic exoskeleton control options on lower limb muscle synergies during overground walking: An exploratory study among able-bodied adults. Neurophysiologie Clinique 2020, 50, 495–505. [Google Scholar] [CrossRef] [PubMed]
  42. Tan, C.K.; Kadone, H.; Miura, K.; Abe, T.; Koda, M.; Yamazaki, M.; Sankai, Y.; Suzuki, K. Muscle Synergies During Repetitive Stoop Lifting With a Bioelectrically-Controlled Lumbar Support Exoskeleton. Frontiers in Human Neuroscience 2019, 13. [Google Scholar] [CrossRef]
Preprints 86298 g001
Figure 1. Picture of the laboratory configuration, showing the box over the destination table, and a schematic drawing in white of the initial configuration of the 16 boxes pallet.
Figure 1. Picture of the laboratory configuration, showing the box over the destination table, and a schematic drawing in white of the initial configuration of the 16 boxes pallet.
Preprints 86298 g001
Preprints 86298 g002
Figure 2. Subplots containing the example of a user’s signals and parameters calculated for the pair of muscles Lumbar (L) and Gluteus (GL). In the first four rows, the concatenated 48 fragments of the EMG signals of Lumbar and Gluteus in red with exoskeleton, and in blue, without. In the last row, each of the five parameters calculated for the EMG segments of the pair GL, in light red dots with exoskeleton, and in light blue, without. Over the dots, the lines of the trends have been represented (red with exoskeleton, blue without).
Figure 2. Subplots containing the example of a user’s signals and parameters calculated for the pair of muscles Lumbar (L) and Gluteus (GL). In the first four rows, the concatenated 48 fragments of the EMG signals of Lumbar and Gluteus in red with exoskeleton, and in blue, without. In the last row, each of the five parameters calculated for the EMG segments of the pair GL, in light red dots with exoskeleton, and in light blue, without. Over the dots, the lines of the trends have been represented (red with exoskeleton, blue without).
Preprints 86298 g002
Preprints 86298 g003
Figure 3. Plots of the trends for the conditions with (solid red lines) and without exoskeleton (dashed blue lines). In the columns each of the four parameters: CORR, COH, MI, and MSE; In the rows, each of the six muscle combinations: SQ, LQ, QG, GL,LS, and GS. "V": significant differences in the values between conditions, "S": in the slope between conditions, and "V & S": in both values and slope.
Figure 3. Plots of the trends for the conditions with (solid red lines) and without exoskeleton (dashed blue lines). In the columns each of the four parameters: CORR, COH, MI, and MSE; In the rows, each of the six muscle combinations: SQ, LQ, QG, GL,LS, and GS. "V": significant differences in the values between conditions, "S": in the slope between conditions, and "V & S": in both values and slope.
Preprints 86298 g003
Preprints 86298 g004
Figure 4. Matrix of representations of the calculated slopes for the conditions with (solid red line) and without (dashed blue line) exoskeleton of DCG-Causality parameter. In the columns, each of the six muscle combinations : Semitendinosus to Quadriceps minus Quadriceps to Semitendinosus: SQ-QS, and the same for the other five subplots LQ-QL, QG-GQ, GL-LG, LS-SL, and GS-SG. "V": significant differences in the values between conditions, "S": in the slope between conditions, and "V & S": in both values and slope
Figure 4. Matrix of representations of the calculated slopes for the conditions with (solid red line) and without (dashed blue line) exoskeleton of DCG-Causality parameter. In the columns, each of the six muscle combinations : Semitendinosus to Quadriceps minus Quadriceps to Semitendinosus: SQ-QS, and the same for the other five subplots LQ-QL, QG-GQ, GL-LG, LS-SL, and GS-SG. "V": significant differences in the values between conditions, "S": in the slope between conditions, and "V & S": in both values and slope
Preprints 86298 g004
Table 1. Matrix of p-values corresponding to the plots in Figure 3. Only included significant differences, values of p ≤ 0.05 .
Table 1. Matrix of p-values corresponding to the plots in Figure 3. Only included significant differences, values of p ≤ 0.05 .
CORR COH MI MSE
V S V S V S V S
SQ - - - 0.02 - - 0.000003 0.00004
LQ 0.04 - - - - - 0.00002 0.00002
QG - - 0.012 - - - 0.000003 0.000009
GL - - 0.001 0.04 0.00003 0.016 0.00002 0.000014
LS 0.03 - 0.05 - 0.00002 - - -
GS 0.05 - - - 0.00004 - 0.005 0.06
Table 2. matrix of p-values corresponding to the plots in Figure 4, only included significant differences, values of p ≤ 0.05 .
Table 2. matrix of p-values corresponding to the plots in Figure 4, only included significant differences, values of p ≤ 0.05 .
DCG-Causality
V S
SQ-QS - -
LQ-QL - -
QG-GQ - 0.04
GL-LG - 0.03
LS-SL - -
GS-SG - -
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated