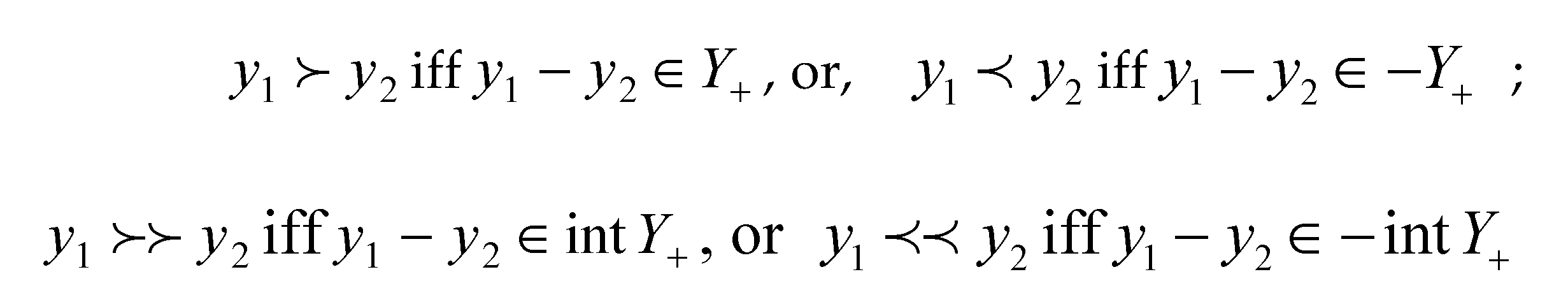Prerpints.org logo
Preprint
Article

Constraint Qualifications for Vector Optimization Problemsin Real Topological Spaces

Altmetrics

Downloads

70

Views

9

Comments

0

This version is not peer-reviewed

Submitted:

15 September 2023

Posted:

20 September 2023

You are already at the latest version

Alerts
Abstract
. In this paper, we introduce a series of definitions of generalized affine functions for vector-valued functions. We prove that our generalized affine functions have some similar properties with generalized convex functions. We present examples to show that our generalized affinenesses are different from one another, and also provide an example to show that our definition of presubaffinelikeness is non-trivial; presubaffinelikeness is the weakest generalized affineness introduced in this article. We work with optimization problems that are defined and taking values in linear topological spaces. We devote to the study of constraint qualifications, and derive some optimality conditions as well as a strong duality theorem. Our optimization problems have inequality constraints, equality constrains and abstract constraints; our inequality constraints are generalized convex functions and equality constraints are generalized affine functions.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction and Preliminary

The theory of vector optimization is at the crossroads of many subjects. The terms “minimum,” “maximum,” and “optimum” are in line with a mathematical tradition while words such as “efficient” or “non-dominated” find a larger use in business-related topics. Historically, linear programs were the focus in the optimization community, and initially, it was thought that the major divide was between linear and nonlinear optimization problems; later people discovered that some nonlinear problems were much harder than others, and the “right” divide was between convex and nonconvex problems. The author finds out that the affineness and generalized affinenesses are also very useful for the subject “optimization”.
Suppose X, Y are a real linear topological space [1].
A subset B ⊆ X is called a linear set if B is a vector subspace of X (i.e., B is nonempty, and α x 1 + β x 2 ∈ A whenever x 1 , x 2 ∈ B and α , β ∈ R ).
A subset B ⊆ X is called an affine set if the line passing through any two points of B is entirely contained in B (i.e., α x 1 + ( 1 − α ) x 2 ∈ B whenever x 1 , x 2 ∈ B and α ∈ R );
A subset B ⊆ X is called a convex set if any segment with endpoints in B is contained in B (i.e., α x 1 + ( 1 − α ) x 2 ∈ B whenever x 1 , x 2 ∈ B and α ∈ [ 0 , 1 ] ).
Each linear set is affine, and each affine set is convex. Moreover, any translate of an affine (convex, respectively) set is affine (convex, resp.). It is known that a set B is linear if and only if B is affine and contains the zero point 0 X of X; a set B is affine if and only if B is a translate of a linear set.
A subset Y+ of Y is said to be a cone if λ y ∈ Y + for all y ∈ Y + and λ ≥ 0 . We denote by 0 Y the zero element in the topological vector space Y and simply by 0 if there is no confusion. A convex cone is one for which λ 1 y 1 + λ 2 y 2 ∈ Y + for all y 1 , y 2 ∈ Y + and λ 1 , λ 2 ≥ 0 . A pointed cone is one for which Y + ∩ ( − Y + ) = { 0 } . Let Y be a real topological vector space with pointed convex cone Y+. We denote the partial order induced by Y+ as follows:
Preprints 85282 i002
where intY+ denotes the topological interior of a set Y+.
A function f: X → Y is said to be linear if
f ( α x 1 + β x 2 ) = α f ( x 1 ) + β f ( x 2 )
whenever x 1 , x 2 ∈ X and α , β ∈ R ; f is said to be affine if
f ( α x 1 + ( 1 − α ) x 2 ) = α f ( x 1 ) + ( 1 − α ) f ( x 2 )
whenever x 1 , x 2 ∈ D , α ∈ R ; and f is said to be convex if
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ f ( α x 1 + ( 1 − α ) x 2 )
whenever x 1 , x 2 ∈ D , α ∈ [ 0 , 1 ] .
In the next section, we generalize the definition of affine function, prove that our generalized affine functions have some similar properties with generalized convex functions, and present some examples which show that our generalized affinenesses are not equivalent to one another.
In Section 3, we recall some existing definitions of generalized convexities, which are very comparable with the definitions of generalized affinenesses introduced in this article.
Section 4 works with optimization problems that are defined and taking values in linear topological spaces, devotes to the study of constraint qualifications, and derive some optimality conditions as well as a strong duality theorem.

2. Generalized Affinenesses

A function f: D ⊆ X → Y is said to be affine on D if ∀ x 1 , x 2 ∈ D , ∀ α ∈ R , there holds
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( α x 1 + ( 1 − α ) x 2 ) .
We introduce here the following definitions of generalized affine functions.
Definition 2.1 A function f : D ⊆ X → Y is said to be affinelike on D if ∀ x 1 , x 2 ∈ D , ∀ α ∈ R , ∃ x 3 ∈ D such that
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) .
Definition 2.2 A function f: D ⊆ X → Y is said to be preaffinelike on D if ∀ x 1 , x 2 ∈ D , ∀ α ∈ R , ∃ x 3 ∈ D , ∃ τ ∈ R \ { 0 } such that
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = τ f ( x 3 ) .
In the following Definition 2.3 and 2.4, we assume that B ⊆ Y is any given linear set.
Definition 2.3 A function f : D ⊆ X → Y is said to be B-subaffinelike on D if ∀ x 1 , x 2 ∈ D , ∀ α ∈ R , ∃ u ∈ B , ∃ x 3 ∈ D such that
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) .
Definition 2.4 A function f : D ⊆ X → Y is said to be B-presubaffinelike on D if ∀ x 1 , x 2 ∈ D , ∀ α ∈ R , ∃ u ∈ B , ∃ x 3 ∈ D , ∃ τ ∈ R \ { 0 } such that
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = τ f ( x 3 ) .
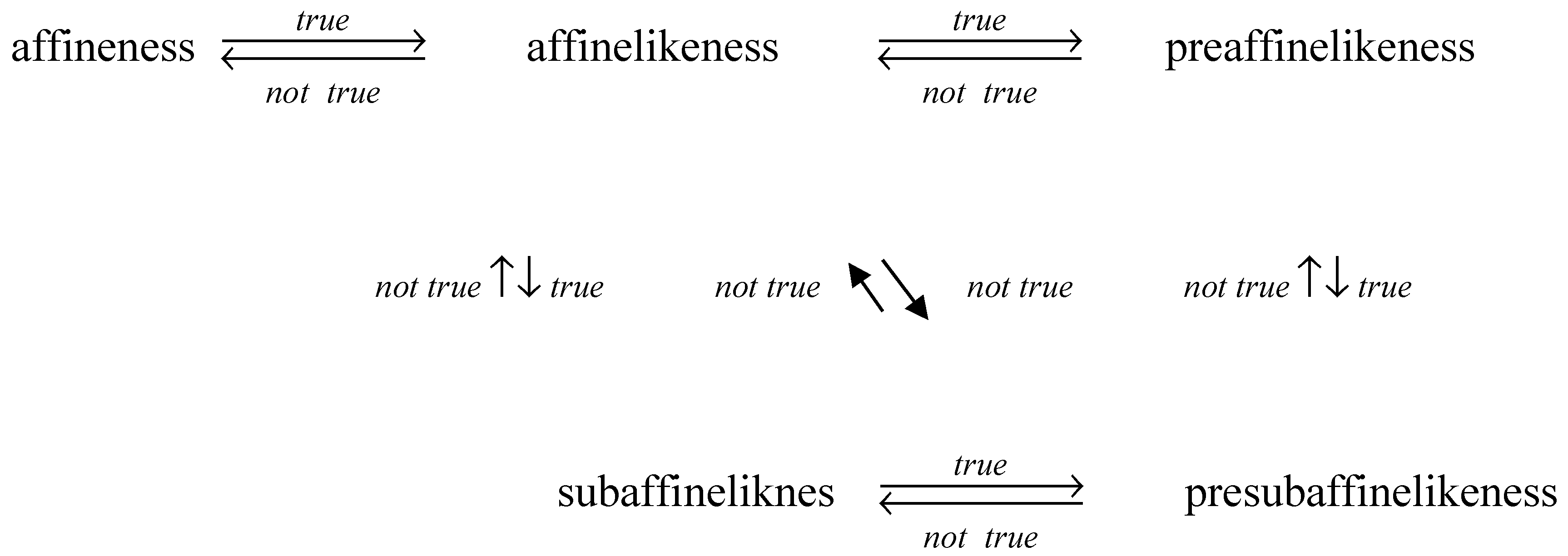
For any linear set B, since 0 ∈ B , we may take u = 0. So, affinelikeness implies subaffinelikeness, and preaffinelikeness implies presubaffinelikeness.
It is obviously that affineness implies preaffineness, and the following Example 2.1 shows that the converse is not true.
Example 2.1 An example of an affinelike function which is not an affine function.
It is known that, a function is an affine function if and only it is in the form of f ( x ) = a x + b , therefore
f ( x ) = x 3 , x ∈ R
is not an affine function.
However, f is affinelike. ∀ x 1 , x 2 ∈ R , ∀ α ∈ R ,
taking
x 3 = [ α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ] 1 / 3
then
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) .
Similarly, affinelikesness implies preaffinelikeness ( τ = 1 ), presubaffinelikeness implies subaffinelikeness. The following Example 1.2 shows that a preaffinelike function is not necessary to be an affinelike function.
Example 2.2 An example of preaffinelike function which is not an affinelike function.
Consider the function f ( x ) = x 2 , x ∈ R .
Take x 1 = 0 , x 2 = 1 , α = 2 , then α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = − 1 ; but
∀ x 3 ∈ R , f ( x 3 ) = x 3 2 ≥ 0 ;
therefore
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≠ f ( x 3 ) , ∀ x 3 ∈ R .
So f is not affinelike.
But f is an preaffinelike function. For ∀ x 1 , x 2 ∈ R , ∀ α ∈ R , taking τ = 1 if α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≥ 0 , τ = − 1 if α f ( x 1 ) + ( 1 − α ) f ( x 2 ) < 0 , then
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = τ f ( x 3 ) ,
where x 3 = | α f ( x 1 ) + ( 1 − α ) f ( x 2 ) | 1 / 2 .
Example 2.3 An example of subaffinelike function which is not an affinelike function.
Consider the function f ( x ) = x 3 + 8 , x ∈ D = [ 0 , 1 ] , and the linear set B = R .
∀ x 1 , x 2 ∈ D = [ 0 , 1 ] , ∀ α ∈ R , take x 3 = 1 ∈ D , u = 8 − [ α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ] ∈ B , then
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) ,
therefore f ( x ) = x 3 + 8 , x ∈ [ 0 , 1 ] is B-subaffinelike on D = [ 0 , 1 ] .
f ( x ) = x 3 + 8 , x ∈ [ 0 , 1 ] is not affinelike on D = [ 0 , 1 ] . Actually, for α = − 8 ∈ R , x 1 = 1 ∈ D , x 2 = 0 ∈ D = [ 0 , 1 ] , one has α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = 0 , but
f ( x 3 ) = x 3 3 + 8 ≠ 0 , ∀ x ∈ [ 0 , 1 ] ,
hence
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≠ f ( x 3 ) .
Example 2.4 An example of presubaffinelike function which is not a preaffinelike function.
Actually, the function in Example 2.3 is subaffinelike, therefore it is presubaffinelike on D.
However, for α = 9 ∈ R , x 1 = 0 ∈ D , x 2 = 1 ∈ D , one has
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = 0 ,
but
f ( x 3 ) = x 3 3 − 8 ≠ 0 , ∀ x ∈ [ 0 , 1 ] .
Hence
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≠ τ f ( x 3 ) .
This shows that the function f is not preaffinelike on D.
Example 2.5 An example of presubaffinelike function which is not a subaffinelike function.
Consider the function f ( x , y ) = ( x 2 , y 2 ) , x , y ∈ R .
Take the 2-dimensional linear set B = { ( x , y ) : y = − x , x ∈ R } .
Take α = 3 , ( x 1 , y 1 ) = ( 0 , 0 ) , ( x 2 , y 2 ) = ( 1 , 1 ) , then
α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = ( − 2 , − 2 ) .
Either x − 2 or − x − 2
must be negative; but x 3 2 ≥ 0 , y 3 2 ≥ 0 , ∀ u = ( x , − x ) ∈ B , therefore
u + α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = ( x − 2 , − x − 2 ) ≠ f ( x 3 , y 3 ) = ( x 3 2 , y 3 2 ) .
And so, f ( x , y ) = ( x 2 , y 2 ) is not B-subaffinelike.
However, f ( x , y ) = ( x 2 , y 2 ) is B-presubaffinelike.
∀ x 1 , x 2 ∈ [ 0 , 1 ] , ∀ α ∈ R ,
α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = ( α x 1 2 + ( 1 − α ) x 2 2 , α y 1 2 + ( 1 − α ) y 2 2 ) .
Case 1 . If both of α x 1 2 + ( 1 − α ) x 2 2 , α y 1 2 + ( 1 − α ) y 2 2 are positive, we take u = ( 0 , 0 ) , τ = 1 , x 3 = | α x 1 2 + ( 1 − α ) x 2 2 | 1 / 2 , y 3 = | α y 1 2 + ( 1 − α ) y 2 2 | 1 / 2 , then
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = τ f ( x 3 ) .
Case 2 . If both of α x 1 2 + ( 1 − α ) x 2 2 , α y 1 2 + ( 1 − α ) y 2 2 are negative, we take u = ( 0 , 0 ) , τ = − 1 , x 3 = | α x 1 2 + ( 1 − α ) x 2 2 | 1 / 2 , y 3 = | α y 1 2 + ( 1 − α ) y 2 2 | 1 / 2 , then
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = τ f ( x 3 ) .
Case 3 . If one of α x 1 2 + ( 1 − α ) x 2 2 , α y 1 2 + ( 1 − α ) y 2 2 is negative, and the other is non-negative, we take
x = [ ( α y 1 2 + ( 1 − α ) y 2 2 ) − ( α x 1 2 + ( 1 − α ) x 2 2 ) ] / 2 ,
Then
x + α x 1 2 + ( 1 − α ) x 2 2 = − x + α y 1 2 + ( 1 − α ) y 2 2 = [ α x 1 2 + ( 1 − α ) x 2 2 + α y 1 2 + ( 1 − α ) y 2 2 ] / 2.
And so x + α x 1 2 + ( 1 − α ) x 2 2 , − x + α y 1 2 + ( 1 − α ) y 2 2 are both non-negative or both negative, take τ = 1 or τ = − 1 , respectively, one has
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = τ f ( x 3 ) .
Where
x 3 = | x + α x 1 2 + ( 1 − α ) x 2 2 | 1 / 2 , y 3 = | − x + α y 1 2 + ( 1 − α ) y 2 2 | 1 / 2 .
Therefore f ( x , y ) = ( x 2 , y 2 ) is B-presubaffinelike.
Example 2.6 An example of subaffinelike function which is not a preaffinelike function.
Consider the function f ( x , y ) = ( x 2 , y 2 ) , x , y ∈ R .
Take the 2-dimensional linear set B = { ( x , y ) : y = x , x ∈ R } .
Take x 1 = 0 , x 2 = 1 , α = 2 , then
α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = ( α x 1 2 + ( 1 − α ) x 2 2 , α y 1 2 + ( 1 − α ) y 2 2 ) = ( − 2 , 3 ) ≠ τ f ( x 3 , y 3 ) = ( τ x 3 2 , τ y 3 2 ) .
In the above inequality, we note that either τ x 3 2 ≥ 0 , τ y 3 2 ≥ 0 or τ x 3 2 ≤ 0 , τ y 3 2 ≤ 0 , ∀ τ ≠ 0 .
Therefore, f ( x , y ) = ( x 2 , y 2 ) is not preaffinelike.
However, f ( x , y ) = ( x 2 , y 2 ) , x , y ∈ R is B-subaffinelike.
In fact, ∀ x 1 , x 2 ∈ R , ∀ α ∈ R , we may choose u = ( x , x ) ∈ B with x large enough such that
u + α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = ( x + α x 1 2 + ( 1 − α ) x 2 2 , x + α y 1 2 + ( 1 − α ) y 2 2 ) ≻ 0 .
Then,
u + α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = f ( x 3 , y 3 ) ,
where
x 3 = ( x + α x 1 2 + ( 1 − α ) x 2 2 ) 1 / 2 .
Example 2.7 An example preaffinelike function which is not a subaffinelike function.
Consider the function f ( x , y ) = ( x 2 , − x 2 ) , x , y ∈ R .
Take the 2-dimensional linear set B = { ( x , y ) : y = x , x ∈ R } .
Take x 1 = 0 , x 2 = 1 , α = 2 , then
α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = ( α x 1 2 + ( 1 − α ) x 2 2 , − ( α x 1 2 + ( 1 − α ) x 2 2 ) ) = ( − 1 , 1 ) .
So, ∀ u = ( x , x ) ∈ B ,
u + α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = = ( x + 1 , x − 1 ) .
However, for f ( x 3 , y 3 ) = ( x 3 2 , − x 3 2 ) , ∀ x 3 ∈ R ,
( x 3 2 , − x 3 2 ) ≠ ( x − 1 , x + 1 ) , ∀ x , x 3 ∈ R .
Actually, if x = 0, it is obviously that ( x 3 2 , − x 3 2 ) ≠ ( − 1 , 1 ) ; if x ≠ 0 , the right side of (1) implies that x 3 2 + ( − x 3 2 ) = 0 , and the left side of (1) is ( x − 1 ) + ( x + 1 ) = 2 x ≠ 0 . This proves that the inequality (1) must be true. Consequently,
u + α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) ≠ f ( x 3 , y 3 ) , ∀ α ∈ R , ∀ x 1 , x 2 , x 3 , y , 1 y 2 , y 3 ∈ R .
So f ( x , y ) = ( x 2 , − x 2 ) , x , y ∈ R is not B-subaffinelike.
On the other hand, ∀ x 1 , x 2 ∈ R , ∀ α ∈ R , we may take τ = 1 if α x 1 2 + ( 1 − α ) x 2 2 ≥ 0 or τ = − 1 if α x 1 2 + ( 1 − α ) x 2 2 ≤ 0 , then
α f ( x 1 , y 1 ) + ( 1 − α ) f ( x 2 , y 2 ) = ( α x 1 2 + ( 1 − α ) x 2 2 , − ( α x 1 2 + ( 1 − α ) x 2 2 ) ) = τ ( x 3 2 , − x 3 2 ) = τ f ( x 3 , y 3 )
where x 3 = | α x 1 2 + ( 1 − α ) x 2 2 | 1 / 2 .
Therefore, f ( x , y ) = ( x 2 , − x 2 ) , x , y ∈ R is preaffinelike.
So far, we have showed the following relationships (where subaffinelikeness and presubaffinelikeness are related to “a given linear set B”).
Preprints 85282 i001
The following Proposition 2.1 is very similar to the corresponding results for generalized convexities (see Proposition 3.1).
Proposition 2.1 Suppose f: D ⊆ X → Y is a function, B ⊆ Y given linear set, and t is any real scalar.
a) f is affinelike on D if and only if f (D) is an affine set;
b) f is preaffinelike on D if and only if ∪ t ∈ R \ { 0 } t f ( D ) is an affine set;
c) f is B-subaffinelike on D if and only if f (D) + B is an affine set;
d) f is B-presubaffinelike on D if and only if ∪ t ∈ R \ { 0 } t f ( D ) + B is an affine set.
Proof. a) If f is affinelike on D, ∀ f ( x 1 ) , f ( x 2 ) ∈ f ( D ) , ∀ α ∈ R , ∃ x 3 ∈ D such that
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) .
Therefore f (D) is an affine set.
On the other hand, assume that f (D) is an affine set. ∀ x 1 , x 2 ∈ D , ∀ α ∈ R , we have
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) .
Therefore ∃ x 3 ∈ D such that
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) .
And hence f is affinelike on D.
b) Assume f is a preaffinelike function.
∀ y 1 , y 2 ∈ ∪ t ∈ R \ { 0 } t f ( D ) , ∀ α ∈ R , ∃ x 1 , x 2 ∈ D , ∃ t 1 , t 2 ∈ R \ { 0 } for ∃ x 3 ∈ D ,
∃ t ∈ R \ { 0 }
such that
α y 1 + ( 1 − α ) y 2 = α t 1 f ( x 1 ) + ( 1 − α ) t 2 f ( x 2 ) = ( α t 1 + ( 1 − α ) t 2 ) [ α t 1 α t 1 + ( 1 − α ) t 2 f ( x 1 ) + ( 1 − α ) t 2 α t 1 + ( 1 − α ) t 2 f ( x 2 ) ] .
Since f is preaffinelike, ∃ x 3 ∈ D , ∃ t ∈ R \ { 0 } such that
α t 1 α t 1 + ( 1 − α ) t 2 f ( x 1 ) + ( 1 − α ) t 2 α t 1 + ( 1 − α ) t 2 f ( x 2 ) = t f ( x 3 ) .
Therefore
α y 1 + ( 1 − α ) y 2 = α t 1 f ( x 1 ) + ( 1 − α ) t 2 f ( x 2 ) = ( α t 1 + ( 1 − α ) t 2 ) [ α t 1 α t 1 + ( 1 − α ) t 2 f ( x 1 ) + ( 1 − α ) t 2 α t 1 + ( 1 − α ) t 2 f ( x 2 ) ] = ( α t 1 + ( 1 − α ) t 2 ) t f ( x 3 ) = τ f ( x 3 ) ∈ ∪ t ∈ R \ { 0 } t f ( D )
where τ = ( α t 1 + ( 1 − α ) t 2 ) t . Consequently, ∪ t ∈ R \ { 0 } t f ( D ) is an affine set.
On the other hand, suppose that ∪ t ∈ R \ { 0 } t f ( D ) is an affine set. Then ∀ x 1 , x 2 ∈ D , ∀ α ∈ R , since f ( x 1 ) , f ( x 2 ) ∈ ∪ t ∈ R \ { 0 } t f ( D ) ,
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) .
Therefore ∃ x 3 ∈ D , ∃ τ ≠ 0 such that
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = τ f ( x 3 ) .
Then f is an affinelike function.
c) Assume that f is B-subaffinelike.
∀ y 1 , y 2 ∈ f ( D ) + B , ∃ x 1 , x 2 ∈ D , ∃ b 1 , b 2 ∈ B , such that y 1 = f ( x 1 ) + b 1 and y 2 = f ( x 2 ) + b 2 . The subaffinelikeness of f implies that ∀ α ∈ R , ∃ x 3 ∈ D , and ∃ v ∈ B such that
v + ,
i.e.,
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) − v .
Therefore
α y 1 + ( 1 − α ) y 2 = α ( f ( x 1 ) + b 1 ) + ( 1 − α ) ( f ( x 2 ) + b 2 ) = f ( x 3 ) − v + α b 1 + ( 1 − α ) b 2 = f ( x 3 ) + u ∈ f ( D ) + B ,
Where u = − v + α b 1 + ( 1 − α ) b 2 ∈ B Then, f (D) + B is an affine set.
On the other hand, assume that f (D) + B is an affine set.
∀ x 1 , x 2 ∈ D , ∀ α ∈ R , ∃ b 1 , b 2 , b 3 ∈ B , ∃ x 3 ∈ D , such that
α ( f ( x 1 ) + b 1 ) + ( 1 − α ) ( f ( x 2 ) + b 2 ) = f ( x 3 ) + b 3 ,
i.e.,
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = f ( x 3 ) ,
where α b 1 + ( 1 − α ) b 2 − b 3 ∈ B . And hence f is B-subaffinelike.
d) Suppose f is a B-presubaffinelike function.
∀ y 1 , y 2 ∈ ∪ t ∈ R \ { 0 } t f ( D ) + B , similar to the proof of (b), ∀ α ∈ R , ∃ x 1 , x 2 , x 3 ∈ D , ∃ b 1 , b 2 , b 3 , u ∈ B , ∃ t 1 , t 2 , t 3 ∈ R \ { 0 } , for which y 1 = t 1 f ( x 1 ) + b 1 , y 2 = t 2 f ( x 2 ) + b 2 , and
α y 1 + ( 1 − α ) y 2 = α t 1 f ( x 1 ) + ( 1 − α ) t 2 f ( x 2 ) + α b 1 + ( 1 − α ) b 2 = ( α t 1 + ( 1 − α ) t 2 ) [ t 3 f ( x 3 ) + b 3 − u ] + α b 1 + ( 1 − α ) b 2 = ( α t 1 + ( 1 − α ) t 2 ) t 3 f ( x 3 ) + α b 1 + ( 1 − α ) b 2 + ( α t 1 + ( 1 − α ) t 2 ) ( b 3 − u ) ∈ t f ( D ) + B ⊆ ∪ t ∈ R \ { 0 } t f ( D ) + B ,
where t = ( α t 1 + ( 1 − α ) t 2 ) t 3 . This proves that ∪ t ∈ R \ { 0 } t f ( D ) + B is an affine set.
On the other hand, assume that ∪ t ∈ R \ { 0 } t f ( D ) + B is an affine set.
∀ x 1 , x 2 ∈ D , ∀ b 1 , b 2 ∈ B , ∀ α ∈ R , since f ( x 1 ) + b 1 , f ( x 2 ) + b 2 ∈ ∪ t ∈ R \ { 0 } t f ( D ) + B , ∃ x 3 ∈ D , ∃ b 3 ∈ B , ∃ t ∈ R \ { 0 } such that
α ( f ( x 1 ) + b 1 ) + ( 1 − α ) ( f ( x 2 ) + b 2 ) = t f ( x 3 ) + b 3 .
Therefore
α b 1 + ( 1 − α ) b 2 − b 3 + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = t f ( x 3 ) ,
i.e.,
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) = t f ( x 3 ) ,
where u = α b 1 + ( 1 − α ) b 2 − b 3 ∈ B . And so f is B-presubaffinelike.
The presubaffineness is the weakest one in the series of the generalized affinenesses introduced here. The following example shows that our definition of presubaffinelikeness is not trivial.
Example 2.8 An example of non-presubaffinelike function.
Consider the function f ( x , y , z ) = ( x 2 , y 2 , z 2 ) , x , y , z ∈ R .
Take the linear set B = { ( x , − x , 0 ) : x ∈ R } .
Take α = 5 , ( x 1 , y 1 , z 1 ) = ( 0 , 0 , 1 ) , ( x 2 , y 2 , z 2 ) = ( 1 , 1 , 0 ) , then
α f ( x 1 , y 1 , z 1 ) + ( 1 − α ) f ( x 2 , y 2 , z 2 ) = ( − 4 , − 4 , 5 ) .
Either x − 4 or − x − 4 must be negative, but x 3 2 ≥ 0 , y 3 2 ≥ 0 hold for ∀ u = ( x , − x , 0 ) ∈ B , therefore, for any scalar τ ≠ 0
u + α f ( x 1 , y 1 , z 1 ) + ( 1 − α ) f ( x 2 , y 2 , z 2 ) = ( x − 4 , − x − 4 , 5 ) ≠ τ f ( x 3 , y 3 , z 3 ) = τ ( x 3 2 , y 3 2 , z 3 2 )
(Actually, ∀ τ < 0 , one has τ z 3 2 ≤ 0 < 5 ; and ∀ τ > 0 , either τ ( x − 4 ) < 0 or τ ( − x − 4 ) < 0 , then, either τ ( x − 4 ) < 0 ≤ τ x 3 2 or τ ( − x − 4 ) < 0 ≤ τ y 3 2 ).
And so, f ( x , y ) = ( x 2 , y 2 ) is not B-presubaffinelike.

3. Generalized Convexities

In this section, we recall some existing definitions of generalized convexities, which are very comparable with the definitions of generalized affinenesses introduced in this article.
Let Y be a topological vector space and D ⊆ X be a nonempty set and Y+ be a convex cone in Y and int Y + ≠ ∅ .
It is known that, a function f : D → Y is said to be Y+-convex on D if for all x 1 , x 2 ∈ D , α ∈ [ 0 , 1 ] , there holds
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ f ( α x 1 + ( 1 − α ) x 2 ) . The following Definition 3.1 was introduced in Fan [2].
Definition 3.1 A function f : D → Y is said to be Y+-convexlike on D if ∀ ,
∀ α ∈ [ 0 , 1 ] , ∃ x 3 ∈ D such that
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ f ( x 3 ) . We may define Y+-preconvexlike functions as follows.
Definition 3.2 A function f : D → Y is said to be Y+-preconvexlike on D if ∀ x 1 , x 2 ∈ D , ∀ α ∈ [ 0 , 1 ] , ∃ x 3 ∈ D , ∃ τ > 0 such that
α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ τ f ( x 3 ) . Definition 3.3 was introduced by Jeyakumar [3].
Definition 3.3 A function f : D → Y is said to be Y+-subconvexlike on D if ∀ u ∈ int Y + , ∀ x 1 , x 2 ∈ D , ∀ α ∈ [ 0 , 1 ] , ∃ x 3 ∈ D such that
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ f ( x 3 ) . In fact, in Jeyakumar [3], the definition of subconvexlike was introduced as the following form Definition 3.3*.
Definition 3.3* A function f : D → Y is said to be Y+-subconvexlike on D if ∃ u ∈ int Y + , ∀ ε > 0 , ∀ x 1 , x 2 ∈ D , ∀ α ∈ [ 0 , 1 ] , ∃ x 3 ∈ D such that
ε u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ f ( x 3 ) . Li and Wang ([4], Lemma 2.3) proved that: A function f : D → Y is Y+-subconvexlike on D by Definition 3.3* if and only if ∀ u ∈ int Y + , ∀ x 1 , x 2 ∈ D , ∀ α ∈ [ 0 , 1 ] , ∃ x 3 ∈ D such that
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ f ( x 3 ) . From the definitions above, one may introduce the following definition of presubconvexlike functions.
Definition 3.4 A function f : D → Y is said to be Y+-presubconvexlike on D if ∀ u ∈ int Y + , ∀ x 1 , x 2 ∈ D , ∀ α ∈ [ 0 , 1 ] , ∃ x 3 ∈ D , ∃ τ > 0 such that
u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ τ f ( x 3 ) . And, similar to ([4], Lemma 2.3), one can prove that, a function f : D → Y is Y+-presubconvexlike on D if and only if ∃ u ∈ int Y + , ∀ ε > 0 , ∀ x 1 , x 2 ∈ D , ∀ α ∈ [ 0 , 1 ] , ∃ x 3 ∈ D , ∃ τ > 0 such that
ε u + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ τ f ( x 3 ) . Our Definitions 3.3 and 3.4 are more comparable with our definitions of generalized affineness.
Similar to the proof of the above Proposition 2.1, one has the following Proposition 3.1.
Some examples of generalized convexities were given in [5,6].
Proposition 3.1 Let f : X → Y be function, and t > 0 be any positive scalar, then
a) f is Y+-convexlike on D if and only if f ( D ) + Y + is convex;
b) f is Y+-subconvexlike on D if and only if f ( D ) + int Y + is convex;
c) f is Y+-preconvexlike on D if and only if ∪ t > 0 t f ( D ) + Y + is convex;
d) f is Y+-presubconvexlike on D if and only if ∪ t > 0 t f ( D ) + int Y + is convex.

4. Constraint Qualifications

Consider the following vector optimization problem:
Y + − min f ( x ) g i ( x ) ≺ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , m ; h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , n ; x ∈ D ,
where f : X → Y , g i : X → Z i , h j : X → W j , Y+, Zi+ are closed convex cones in Y and Zi, respectively, and D is a nonempty subset of X.
Throughout this paper, the following assumptions will be used ( τ i , t j are real scalars).
(A1) ∀ x 1 , x 2 ∈ D , ∀ α ∈ [ 0 , 1 ] , ∃ u 0 ∈ int Y + , ∃ u i ∈ int Z i + ( i = 1 , 2 , ⋅ ⋅ ⋅ , n ) , ∃ x 3 ∈ D , ∃ τ i > 0 ( i = 0 , 1 , 2 , ⋅ ⋅ ⋅ , m ) , ∃ t j ≠ 0 ( j = 1 , 2 , ⋅ ⋅ ⋅ , n ) such that
u 0 + α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≺ τ 0 f ( x 3 ) u i + α g i ( x 1 ) + ( 1 − α ) g ( x 2 ) i ≺ τ i g i ( x 3 ) α h j ( x 1 ) + ( 1 − α ) h ( x 2 ) j = t j h j ( x 3 ) ;
(A2) int h j ( D ) ≠ ∅ , (j = 1, 2, …, n);
(A3)Wj (j = 1, 2, …, n) are finite dimensional spaces.
Remark 4.1 We note that the condition (A1) says that f and g i ( i = 1 , 2 , ⋅ ⋅ ⋅ , m ) are presubconvexlike, and h j (j = 1, 2, …, n) are preaffinelike.
Let F be the feasible set of (VP), i.e.
F : = { x ∈ D : g i ( x ) ≺ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , m ; h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , n } . The following is the well-known definition of weakly efficient solution.
Definition 4.1 A point x ¯ ∈ F
is said to be a weakly efficient solution of (VP) with a weakly efficient value y ¯ ∈ f ( x ¯ ) if for every x ∈ F , there exists no y ∈ f ( x ) satisfying y ¯ ≻ ≻ y .
We first introduce the following constraint qualification which is similar to the constraint qualification in the differentiate form from nonlinear programming (see e.g. [9]).
Definition 4.2 Let x ¯ ∈ F . We say that (VP) satisfies the No Nonzero Abnormal Multiplier Constraint Qualification (NNAMCQ) at x ¯ if there is no nonzero vector ( η , ς ) ∈ Π i = 1 m Z i * × Π j = 1 n W j * satisfying the system
min x ∈ D ∩ U ( x ¯ ) [ ∑ i = 1 m η i g i ( x ) + ∑ j = 1 n ς j h j ( x ) ] = 0 ∑ i = 1 m η i g i ( x ¯ ) = 0 ,
where U ( x ¯ ) is some neighborhood of x ¯ .
It is obvious that NNAMCQ holds at x ¯ ∈ F with U ( x ¯ ) being the whole space X if and only if for all ( η , ς ) ∈ ( Π i = 1 m Z i * × Π j = 1 n W ) j * \ { 0 } satisfying min ∑ i = 1 m η i g i ( x ¯ � = 0 , there exists x ∈ D such that
( ∑ i = 1 m η i g i ( x ) + ∑ j = 1 n ς j h j ( x ) ) ≺ ≺ 0
Hence NNAMCQ is weaker than ([7], (CQ1)) (in [7], CQ1 was for set-valued optimization problems) in the constraint min ∑ i = 1 m η i g i ( x ¯ � = 0 , which means that only the binding constraints are considered. Under the NNAMCQ, the following Kuhn-Tucker type necessary optimality condition holds.
Theorem 4.1 Assume that the generalized convexity assumption (A1) is satisfied and either (A2) or (A3) holds. If x ¯ ∈ F is a weakly efficient solution of (VP) with y ¯ ∈ f ( x ¯ ) , then exists a vector ( ξ , η , ς ) ∈ Y * × Π i = 1 m Z i * × Π j = 1 n W j * with ξ ≠ 0 such that
ξ ( y ¯ ) = min x ∈ D ∩ U ( x ¯ ) [ ξ ( f ( x ) ) + ∑ i = 1 m η i ( g i ( x ) ) + ∑ j = 1 n ς j ( h j ( x ) ) ] ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0 ,
for a neighbourhood U ( x ¯ ) of x ¯ .
Proof. Since x ¯ is a weakly efficient solution of (VP) with y ¯ ∈ f ( x ¯ ) there exists a nonzero vector ( ξ , η , ς ) ∈ Y * × Π i = 1 m Z i * × Π j = 1 n W j * such that (2) holds. Since NNAMCQ holds at x ¯ , ξ must be nonzero. Otherwise if ξ = 0 then ( η , ς ) must be a nonzero solution of
0 = min x ∈ D ∩ U ( x ¯ ) [ ∑ i = 1 m η i ( g i ( x ) ) + ∑ j = 1 n ς j ( h j ( x ) ) ] ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0.
But this is impossible since the NNAMCQ holds at x ¯ .
Similar to ([7], (CQ2)) which is slightly stronger than ([7], (CQ1)), we define the following constraint qualification which is stronger than the NNAMCQ.
Definition 4.2 (SNNAMCQ) Let x ¯ ∈ F .We say that (VP) satisfies the No Nonzero Abnormal Multiplier Constraint Qualification (NNAMCQ) at x ¯ provided that
∀ η ∈ Π i = 1 m Z i * \ { 0 } satisfying ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0 ,
∃ x ∈ D , s.t. h j ( x ) = 0 , η i ( g i ( x ) ) ≺ ≺ 0 ;
∀ ς ∈ Π j = 1 n W j * \ { 0 } , ∃ x ∈ D , s.t. ς j ( h j ( x ) ) ≺ ≺ 0 for all j = 1 , 2 , ⋅ ⋅ ⋅ , n .
We now quote the Slater condition introduced in ([10], (CQ3)).
Definition 4.3 (Slater Condition CQ) Let x ¯ ∈ F . We say that (VP) satisfies the Slater condition at x ¯ if the following conditions hold:
∃ x ∈ D , s.t. h j ( x ) = 0 , g i ( x ) ≺ ≺ 0 ;
0 ∈ int h j ( D ) for all j.
Similar to ([7], Proposition 2) (again, in [7], discussions are made for set-valued optimization problems), we have the following relationship between the constraint qualifications.
Proposition 4.1 The following statements are true:
(i) Slater CQ ⇒ SNNAMCQ ⇒ NNAMCQ with U ( x ¯ ) being the whole space X;
(ii) Assume that (A1) and (A2) (or (A1) and (A3)) hold and the NNAMCQ with U ( x ¯ ) being the whole space X without the restriction of ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0 at x ¯ , Then the Slater condition (CQ) holds.
Proof. The proof of (i) is similar to ([7], Proposition 2). Now we prove (ii). By the assumption (A1), the following sets C1 and C2 are convex:
C 1 = { ( z , w ) ∈ Π i = 1 m Z i * × Π j = 1 n W : j * ∃ x ∈ D , τ i , t j > 0 , s . t . z i ∈ τ i g i ( x ) + int Z i + , w j ∈ t j h j ( x ) } C 2 = ∪ t > 0 t h ( D ) .
Suppose to the contrary that Slater condition does not hold. Then 0 ∉ C 1 or 0 ∉ C 2 . If the former 0 ∉ C 1 holds, then by the separation theorem [1], there exists a nonzero vector ( η , ς ) ∈ Π i = 1 m Z i * × Π j = 1 n W j * such that
∑ i = 1 m η i ( τ i z i + z i 0 ) + ∑ j = 1 n ς j ( t j w j ) ≥ 0
for all x ∈ D , τ i , t j > 0 , z i = g i ( x ) , z i 0 ∈ int Z i + , w j = h j ( x ) . Since int Z i + are convex cones, consequently we have
∑ i = 1 m η i ( τ i z i + s i z i 0 ) + ∑ j = 1 n ς j ( t j w j ) ≥ 0
for all x ∈ D , τ i , t j � s i > 0 , z i ∈ g i ( x ) , z i 0 ∈ int Z i + , w j ∈ h j ( x ) } and take s → i 0 in (3), we have
∑ i = 1 m η i ( z i ) + ∑ j = 1 n ς j ( w j ) ≥ 0 , x ∈ D , z i ∈ g i ( x ) , w j = h j ( x ) ,
which contradicts the NNAMCQ. Similarly if the latter 0 ∉ int h j ( D ) holds then there exists ς ∈ Π j = 1 n W \ j * { 0 } such that ς j ( h j ( x ) ) ≥ 0 , ∀ x ∈ D , which contradicts NNAMCQ.
Definition 4.4 (Calmness Condition) Let x ¯ ∈ F . Let Z : = ∑ i = 1 m Z i and W : = ∑ j = 1 n W j . We say that (VP) satisfies the calmness condition at x ¯ provided that there exist U ( x ¯ , 0 Z , 0 W ) , a neighborhood of ( x ¯ , 0 Z , 0 W ) , and a map ψ ( p , q ) : Z × W → Y + with ψ ( 0 Z , 0 ) W = 0 Y such that for each
( x , p , q ) ∈ U ( x ¯ , 0 Z , 0 W ) \ { ( x ¯ , 0 Z , 0 W ) }
Satisfying
( g i ( x ) + p i ) ≺ 0 , q j = h j ( x ) ) , x ∈ D ,
there is no y ∈ f ( x ) ) such that
y ¯ ∈ y + ψ ( p , q ) + int Y +
Theorem 4.2 Assume that (A1) is satisfied and either (A2) or (A3) holds. If x ¯ ∈ F is a weakly efficient solution of (VP) with y ¯ = f ( x ¯ ) , and the calmness condition holds at x ¯ , then there exists U ( x ¯ ) , a neighborhood of x ¯ and a vector ( ξ , η , ς ) ∈ Y + * × Z + * × W * with ξ ≠ 0 such that
ξ ( y ¯ ) = min x ∈ D ∩ U ( x ¯ ) [ ξ ( f ( x ) ) + ∑ i = 1 m η i ( g i ( x ) ) + ∑ j = 1 n ς j ( h j ( x ) ) ] ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0 ,
Proof. It is easy to see that under the calmness condition, x ¯ being a weakly efficient solution of (VP) implies that ( x ¯ , 0 Z , 0 W ) is a weakly efficient solution of the perturbed problem:
VP(p,q) Y + − min f ( x ) + ψ ( p , q ) s . t . ( g i ( x ) + p i ) ≺ 0 , q j = h j ( x ) , x ∈ D , ( x , p , q ) ∈ U ( x ¯ , 0 Z , 0 W ) . By assumption, the above optimization problem satisfies the generalized convexity assumption (A1). Now we prove that the NNAMCQ holds naturally at ( x ¯ , 0 Z , 0 W ) . Suppose that ( η , ς ) ∈ Z + * × W * satisfies the system:
min x ∈ D ( x , p , q ) ∈ U ( x ¯ , 0 Z , 0 W ) [ ∑ i = 1 m η i ( g i ( x ) + p i ) + ∑ j = 1 n ς j ( − q j + h j ( x ) ) ] ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0.
If ς ≠ 0 , then there exists q j ∈ W j small enough such that ∑ j = 1 n ς j ( − q j ) < 0 . Since x ¯ ∈ F , 0 ∈ h j ( x ¯ ) and there exists z i x ∈ g i ( x ) ∩ ( − Z i + ) which implies that η ( z i x ) ≤ 0 and hence
∑ i = 1 m η i ( z i x ) + ∑ j = 1 n ς j ( − q j ) < 0
which contradicts (5). Hence ς = 0 and (5) becomes
min x ∈ D , ( x , p , q ) ∈ U ( x ¯ , 0 Z , 0 W ) ∑ i = 1 m η i ( g i ( x ) + p i ) ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0.
If η ≠ 0 then there exists p small enough such that ∑ i = 1 m η i ( p i ) < 0 . Let z i x = g i ( x ) , then
∑ i = 1 m η i ( z i x ) ≤ 0
and hence
∑ i = 1 m η i ( z i x + p i ) = ∑ i = 1 m η i ( z i x ) + ∑ i = 1 m η i ( p i ) < 0
which is impossible. Consequently, η = 0 as well. Hence there exists ( ξ , η , ς ) ∈ Y * × Z + * × W + * with ξ ≠ 0 such that
min x ∈ D , ( x , p , q ) ∈ U ( x ¯ , 0 Z , 0 W ) [ ξ ( f ( x ) + ψ ( p , q ) ) + ∑ i = 1 m η i ( g i ( x ) + p i ) + ∑ j = 1 n ς j ( − q j + h j ( x ) ) ] ∑ i = 1 m η i ( g i ( x ¯ ) ) = 0.
It is obvious that (6) implies (4) and hence the proof of the theorem is complete.
Definition 4.5 Let Z i ( i = 1 , 2 , ⋅ ⋅ ⋅ , m ) , W ( j = 1 , 2 , ⋅ ⋅ ⋅ , n ) j be normed spaces. We say that (VP) satisfies the error bound constraint qualification at a feasible point x ¯ if there exist positive constants λ � δ and ε such that
d ( x ¯ , Σ ( 0 Z , 0 W ) ) ≤ λ | | ( p , q ) | | , ∀ ( p , q ) ∈ ε B X , x ∈ Σ ( p , q ) ∩ U δ ( x ¯ ) ,
where BX is the unit ball of X, and
Σ ( p , q ) : = { x ∈ D : ( g i ( x ) + p i ) ∩ ( − Z i + ) ) ≠ ∅ , q j ∈ h j ( x ) }
Remark 4.2 Note that the error bound constraint qualification is satisfied at a feasible point x ¯ if and only if the function Σ ( p , q ) is pseudo upper-Lipschitz continuous around ( 0 Z , 0 W , x ¯ ) in the terminology of ([8], Definition 2.8) (which is referred to as being calm at x ¯ in [9]). Hence Σ ( p , q ) being either pseudo-Lipschitz continuous around ( 0 Z , 0 W , x ¯ ) . in the terminology of [10] or upper-Lipschitz continuous at x ¯ in the terminology of [11] implies that the error bound constraint qualification holds at x ¯ . Recall that a function F ( x ) : R n → R m is called a polyhedral multifunction if its graph is a union of finitely many polyhedral convex sets. This class of function is closed under (finite) addition, scalar multiplication, and (finite) composition. By ([12], Proposition 1), a polyhedral multifunction is upper-Lipschitz. Hence the following result provides a sufficient condition for the error bound constraint qualification.
Proposition 4.2 Let X = Rn and W = Rm. Suppose that D is polyhedral and h is a polyhedral multifunction. Then the error bound constraint qualification always holds at any feasible point x ¯ ∈ F : = { x ∈ D : 0 = h ( x ) } .
Proof. Since D is polyhedral and h is a polyhedral multifunction, its inverse map S ( q ) = { x ∈ R n : q ∈ h ( x ) } is a polyhedral multifunction. That is, the graph of S is a union of polyhedral convex sets. Since
g p h Σ ( p , q ) : = { ( q , x ) ∈ R m × D : q ∈ h ( x ) } = g p h S ∩ ( R m × D )
which is also a union of polyhedral convex sets, Σ is also a polyhedral multifunction and hence upper-Lipschitz at any point of x ¯ ∈ R n by ([12], Proposition 1). Therefore the error bound constraint qualification holds at x ¯ .
Definition 4.6 Let X be a normed space, f ( x ) : X → Y be a function and x ¯ ∈ X . f is said to be Lipschitz near x ¯ if there exist U ( x ¯ ) , a neighbourhood of x ¯ and a constant L f > 0 such that for all x 1 , x 2 ∈ U ( x ¯ ) ,
f ( x 1 ) ⊆ f ( x 2 ) + L f | | x 1 − x 2 | | B Y
Where BY is the unit ball of Y.
Definition 4.7 Let X be a normed space, f ( x ) : X → Y be a function and x ¯ ∈ X . f is said to be strongly Lipschitz on S ⊆ X if there exist a constant Lf > 0 such that for all x 1 , x 2 ∈ S y 1 = f ( x 1 ) , y 2 = f ( x 2 ) and e ∈ B Y ∩ Y + ,
y 1 ≺ y 2 + L f | | x 1 − x 2 | | e
The following result generalizes the exact penalization ([9], Theorem 2.4.5).
Proposition 4.3 Let X be a normed space, f ( x ) : X → Y be a function which is strongly Lipschitz of rank Lf on a set S ⊆ X . Let C ⊆ X and suppose that x ¯ is a weakly efficient solution of
Y + − min x ∈ S f ( x )
with y ¯ = f ( x ¯ ) . Then for all K ≥ L f , x ¯ is a weakly efficient solution of the exact penalized optimization problem
Y + − min x ∈ S f ( x ) + K d C ( x ) B Y ∩ Y +
where d C ( x ) : = min { | x − c | , c ∈ C } .
Proof. Let us prove the assertion by supposing the contrary. Then there is a point S ⊆ X , y = f ( x ) and e ∈ B Y ∩ Y + satisfying y + K d C ( x ) e ≺ y ¯ . Let ε > 0 and c ∈ C be a point such that | | x − c | | ≤ d C ( x ) + ε . Then for any c * ∈ f ( c ) ,
c * ≺ y + K | | x − c | | e ≺ y + K ( d C ( x ) + ε ) e ≺ y ¯ + K ε e .
Since ε > 0 is arbitrary it contradicts the fact that x ¯ is a weakly efficient solution of
Y + − min x ∈ S f ( x ) .
Proposition 4.4 Suppose X × Z × W is a normed space and f is strongly Lipschitz on D. If x ¯ is a weakly efficient solution of (VP) and the error bound constraint qualification is satisfied at x ¯ , then (VP) satisfies the calmness condition at x ¯ .
Proof. By the exact penalization principle in Proposition 3.3, x ¯ is a weakly efficient solution of the penalized problem
Y + − min x ∈ D f ( x ) + K d Σ ( 0 , 0 ) ( x ) B Y ∩ Y + .
The results then follow from the definitions of the calmness and the error bound constraint qualification.
Theorem 4.3 Assume that the generalized convexity assumption (A1) is satisfied with f replaced by f + K d C ( x ) B Y ∩ Y + and either (A2) or (A3) holds. Suppose X × Z × W is a normed space and f is strongly Lipschitz on D. If x ¯ is a weakly efficient solution of (VP) and the error bound constraint qualification is satisfied at x ¯ , then there exist U ( x ¯ ) , a neighborhood of x ¯ and a vector ( ξ , η , ς ) ∈ Y + * × Z + * × W * with ξ ≠ 0 such that (4) holds.
Using Proposition 4.2, Theorem 4.3 has the following easy corollary.
Corollary 4.1 Suppose Y is a normed space, X = Rn, W = Rm and D is polyhedral and f is strongly Lipschitz on D. Assume that the generalized convexity assumption (A1) is satisfied with f replaced by f + K d C ( x ) B Y ∩ Y + and either (A2) or (A3) holds. If x ¯ is a weakly efficient solution of (VP) without the inequality constraint g ( x ) ≻ 0 ; and h is a polyhedral multifunction, then there exist U ( x ¯ ) , a neighborhood of x ¯ a vector ( ξ , ς ) ∈ Y + * × W * with ξ ≠ 0 such that
ξ ( y ¯ ) = min x ∈ D ∩ U ( x ¯ ) [ ξ ( f ( x ) ) + ς j ( h j ( x ) ) ]
Our last result Theorem 4.4 is a strong duality theorem, which generalizes a result in Fang, Li, and Ng [13].
For two topological vector spaces Z and Y, let B(Z; Y ) be the set of continuous linear transformations from Z to Y and
B + ( Z , Y ) : = { S ∈ B ( Z , Y ) : S ( Z ) + ⊆ Y + }
The Lagrangian map for (VP) is the function
L : X × Π i = 1 m B + ( Z i , Y ) × Π j = 1 n B + ( W j , Y ) → Y
defined by
L ( x , S , T ) : = f ( x ) + ∑ i = 1 m S i ( g i ( x ) ) + ∑ j = 1 n T j ( h j ( x ) )
Given ( S , T ) ∈ Π i = 1 m B + ( Z i , Y ) × Π j = 1 n B + ( W j , Y ) , consider the vector minimization problem induced by (VP):
Y + − min L ( x , S , T ) s . t . x ∈ D ,
and denote by Φ ( S , T ) the set of weakly efficient value of the problem (VPST). The Lagrange dual problem associated with the primal problem (VP) is
Y + − max Φ ( S , T ) s . t . ( S , T ) ∈ Π ( VD ) i = 1 m B + ( Z i , Y ) + Π j = 1 n B + ( W j , Y ) .
The following strong duality result holds which extends the strong duality theorem in ([7], Theorem 7) (which was for set-valued optimization problems), to allow weaker convexity assumptions. We omit the proof since it is similar to [7].
Theorem 4.4 Assume that (A1) is satisfied, either (A2) or (A3) is satisfied, and a constraint qualification such as NNAMCQ is satisfied. If x ¯ is a weakly efficient solution of (VP), then there exists
( S ¯ , T ¯ ) ∈ Π i = 1 m B + ( Z i , Y ) × Π j = 1 n B + ( W j , Y )
such that
Φ ( S ¯ , T ¯ ) ∩ f ( x ) ≠ ∅

5. Conclusions

We introduce the following definitions of generalized affine functions: affinelikeness, preaffinelikeness, subaffinelikeness, and presubaffinelikeness. Examples 2.1 to 2.7 show that definitions of affine, affinelike, preaffinelike, subaffinelike, and presubaffinelike functions are all different. Example 2.8 is an example of non-presubaffinelike function; presubaffineness is the weakest one in the series. Proposition 2.1 demonstrates that our generalized affine functions have some similar properties with generalized convex functions.
And then, we work with vector optimization problems in real linear topological spaces, and obtain necessary conditions, sufficient conditions, or necessary and sufficient conditions for weakly efficient solutions, which generalize the corresponding classical results in [14,15] and some recent results in [7,9,16,17,18]. We note that the constraint qualifications in [15,17,18] are in the differentiation form. Comparing with the results in [19] and ([20], pp.297) in discussions of convex constraints, we only required weakened convexities for constraint qualifications in this article. We note that, [17] works with semi-definite programming. In [17], two groups of functions gi(x) ≥ 0, i ∈ I and hj(x) = 0, j ∈ J can be just considered as two topological spaces (I and J do not have to be finite sets). We also note that f is supposed to be “proper convex” in [18]; and in [18], functions are required to be “quasiconvex”.
Generalized affine functions and generalized convex functions can be used for other discussions of optimization problems, e.g., dualities, scalarizations, as well as saddle points, etc.

References

  1. Deimling, K., Nonlinear Functional Analysis, Springer-Verlag, Berlin, 1985.
  2. Fan, K. Minimax Theorems. Proceedings of the National Academy of Sciences of the USA 1953, 39, 42–47. [Google Scholar] [CrossRef]
  3. Jeyakumar, V. Convexlike Alternative Theorems and Mathematical Programming. Optimization 1985, 16, 643–652. [Google Scholar] [CrossRef]
  4. Li, Z. F., and Wang S. Y., Lagrange Multipliers and Saddle Points in Multiobjective Programming. J. Optim. Theo. Appl. 1994, 1, 63–80.
  5. Zeng, R. Generalized Gordan Alternative Theorem with Weakened Convexity and its Applications. Optimization 2002, 51, 709–717. [Google Scholar] [CrossRef]
  6. Zeng, R., and Caron, R. J., Generalized Motzkin Theorem of the Alternative and Vector Optimization Problems. J. Optim. Theo. Appl. 2006, 131, 281–299. [CrossRef]
  7. Li, Z.-F., and Chen, G.-Y., Lagrangian Multipliers, Saddle Points and Duality in Vector Optimization of Set-Valued Maps. J. of Math. Anal. Appl. 1997, 215, 297–315. [CrossRef]
  8. Ye, J. J., and Ye, X. Y., Necessary Optimality Conditions for Optimization Problems with Variational Inequality Constriants. Math. Oper. Res. 1997, 22, 977–997. [CrossRef]
  9. Rockafellar, R. T., and Wets, R. J.-B., Variational Analysis, Springer-Verlag, Berlin, 1998.
  10. Aubin, J.-P. Lipschitz Behavior of Solutions to Convex Minimization Problems. Math. Oper. Res. 1984, 9, 87–111. [Google Scholar] [CrossRef]
  11. Robinson, S. M. Stability Theory for Systems of Inequalities. Part I: Linear Systems. SIAM J. Numer. Anal., 1975, 12, 754–769. [Google Scholar] [CrossRef]
  12. Robinson, S. M. , Some Continuity Properties of Polyhedral Multifunctions, Math. Programming Stud. 1981, 14, 206–214. [Google Scholar]
  13. Fang, D. H., Li, C., and Ng, K. F., Constraint Qualifications for Optimality Conditions and Total Lagrange Dualities in Convex Infinite Programming. Nonlinear Analysis 2010, 73, 1143–1159. [CrossRef]
  14. Luc, D. T., Theory of Vector Optimization. Springer-Verlag, Berlin, 1989.
  15. Clarke, F. H., Optimization and Nonsmooth Analysis, Wiley-Interscience, New York, 1983.
  16. Nguyen, M.-H., and Luu, D. V., On Constraint Qualifications with Generalized Convexity and Optimality Conditions, Cahiers de la Maison des Sciences Economiques 2006.20 - ISSN 1624-0340. 2006.
  17. Kanzi, N., and Nobakhtian, S., Nonsmooth Semi-Infinite Programming Problems with Mixed Constraints. J. Math. Anal. Appl. 2009, 351, 170–181. [CrossRef]
  18. Zhao, X. P. Constraint Qualification for Quasiconvex Inequality System with Applications in Constraint Optimization. J. Nonlinear. Convex Anal. 2016, 17, 879–889. [Google Scholar]
  19. Khazayel, B., Farajzadeh A. On the Optimality Conditions for DC Vector Optimization Problems. Optimization 2022, 71, 2033–2045. [CrossRef]
  20. Ansari, Q. H.; Yao J.-C., Recent Developments in Vector Optimization, Springer Link, 2012.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated