Anisotropic Fractional Cosmology: K-Essence Theory

1. Introduction

Fractional cosmology is a new line of research born approximately twenty years ago based on fractional calculus (FC). The FC is a non-local natural generalization to the arbitrary order of derivatives and integrals. Non-local effects occur in space and time. In the time domain, a non-local description becomes manifest as a memory effect, and in the space domain, it manifests as non-homogeneous similarity structures [1,2,3]. During the last decades, FC has been the subject of intense theoretical and applied research, almost in all areas of the sciences and engineering, from the point of view of the classical and quantum systems [4,5,6,7,8,9,10,11,12,13,14], recently new studies on FC have been made [15,16,17,18]. This is because, the FC describes more accurately the complex physical systems and at the same time, investigates more about simple dynamical systems [19,20]. The general relativity could not be the exception, in [21,22,23,24,25,26,27,28,29,30,31] the importance of FC and its potential applications in cosmology was introduced. In [32] the FRW universe was presented in the context of the variational principle of fractional action. In this new cosmological formulation, the accelerated expansion of the universe can be attributed to the fractional dissipative force without the need to introduce any kind of matter or scalar fields, similar results are obtained in [33,34]. In [35], the concept of fractional action cosmology was applied to massive gravity, where fractional graviton masses are introduced.

Unlike the previously described formalism to obtain fractional cosmology, in [36] it is mentioned that by quantifying different epochs of the K-essence theory, a fractional Wheeler-DeWitt equation in the scalar field component is naturally obtained. Recently, such an equation was solved for some epochs in the FRW model and communicated in [37]. In this work we present the continuation of our previous investigation, in this case, we will analyze the Bianchi type I, which is the anisotropic generalization of the flat FRW cosmological model. In the quantum scheme, we introduce the factor ordering problem in the variables $(\Omega ,\varphi )$ and its corresponding momenta (${\Pi }_{\Omega },{\Pi }_{\varphi }$), obtaining a fractional differential equation with variable coefficients in the scalar field equation. The solution is found using a fractional series expansion [38,39], generalizing our previous work [37].

This paper is organized in such a way: in Section 1, we give a brief review of fractional calculus and the main ideas of the K-essence formalism; in Section 2, we construct the Lagrangian and Hamiltonian densities for the anisotropic Bianchi type I cosmological model, considering a barotropic perfect fluid for the scale field in the variable X. We found the classical solution in the usual gauge N obtained in the Hamiltonian formalism, and without a gauge. In the last case, the general solution is presented in a transformed time $T\left(\tau \right)$, however in the dust era we found a closed solution in the gauge time $\tau$; in Section 3, the quantization of the model for any era in our universe is done and present particular scenarios, too. In this section, we introduce the factor ordering in both variables; finally, in Section 4, the conclusions are given.

2. Brief review on fractional calculus and K-essence theory

2.1. Brief review on fractional calculus

In the theory of fractional calculus, there are some definitions of fractional derivatives; Rieman-Liouville, Caputo, Caputo-Fabrizio, Atangana-Baleanu, to name a few, each with its advantages and disadvantages [40,41,42]. In this work, we use the Caputo fractional derivative of order $\gamma$, defined by using the Riemann-Liouville fractional integral [1]

$$I^{\gamma }f\left(t\right)=\frac{1}{\Gamma \left(\gamma \right)}{\int }_0^t\frac{f\left(\tau \right)}{{(t-\tau )}^{1-\gamma }}d\tau ,\gamma >0,$$

(1)

recovering ordinary integral, when $\gamma \to 1$. The Caputo fractional derivative of order $\gamma \ge 0$ of a function $f\left(t\right)$, then, is defined as the fractional order integral (1) of the integer order derivative

$${}_0^C{D}_t^{\gamma }f\left(t\right)=I^{(n-\gamma )}{}_0{D}_t^{n}f\left(t\right)=\frac{1}{\Gamma (n-\gamma )}{\int }_0^t\frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\gamma -n+1}}d\tau ,$$

(2)

with $n-1<\gamma \le n\in \mathbb{N}=1,2,...$, and $\gamma \in \mathbb{R}$ is the order of the fractional derivative and $f^{\left(n\right)}$ are the ordinary integer derivatives, and $\Gamma \left(x\right)={\int }_0^{\infty }{e}^{-t}{t}^{x-1}dt$, is the gamma function. The Caputo derivative satisfies the following relations

$$\begin{array}{ccc}\hfill {}_0^C{D}^{\gamma }(f\left(t\right)+g\left(t\right)]& =& {}_0^C{D}^{\gamma }f\left(t\right)+{}_0^C{D}^{\gamma }g\left(t\right).\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill {}_0^C{D}^{\gamma }c& =& 0,\mathrm{where}c\mathrm{is}\mathrm{a}\mathrm{constant}.\hfill \end{array}$$

(4)

The Laplace transform of the function $f\left(t\right)$ defined in the ordinary case is given by

$$\mathbb{L}\left[f\left(t\right)\right]={\int }_0^{\infty }f\left(t\right)e^{-st}dt\equiv F\left(s\right),$$

(5)

then, the Laplace transform of the Caputo fractional derivative (2) has the form

$$\mathbb{L}{[}_0^C{D}^{\gamma }f\left(t\right)]=s^{\gamma }F\left(s\right)-\sum _{k=0}^{n-1}{s}^{\gamma -k-1}{f}^{\left(k\right)}\left(0\right),$$

(6)

where $f^{\left(k\right)}$ is the ordinary derivative. Another definition which will be used is the Mittag-Leffler function [43,44,45],

$${\mathbb{E}}_{\chi ,\sigma }\left(z\right)=\sum _{n=0}^{\infty }\frac{z^n}{\Gamma (n\chi +\sigma )}(\chi ,\sigma >0),$$

(7)

for $\sigma =1$, we have one parameter Mittag-Leffler function

$${\mathbb{E}}_{\chi }\left(z\right)={\mathbb{E}}_{\chi ,1}\left(z\right)=\sum _{n=0}^{\infty }\frac{z^n}{\Gamma (n\chi +1)}(\chi >0).$$

(8)

Another special cases are in [44,45]

$$\begin{array}{ccc}\hfill {\mathbb{E}}_1(\pm z)& =& e^{\pm z},{\mathbb{E}}_2\left(z\right)=cosh\sqrt{z},{\mathbb{E}}_{2,1}(-z^2)=cosz,\hfill \\ \hfill {\mathbb{E}}_{2,2}\left(z^2\right)& =& \frac{sinhz}{z},{\mathbb{E}}_{2,2}(-z^2)=\frac{sinz}{z}.\hfill \end{array}$$

(9)

Laplace transform (5) of the Mittage-Leffler function is given by the formula

$${\int }_0^{\infty }{e}^{-st}{t}^{\chi m+\sigma -1}{\mathbb{E}}_{\chi ,\sigma }^{\left(m\right)}(\pm a{t}^{\chi })dt=\frac{m!s^{\chi -\sigma }}{{(s^{\chi }\mp a)}^{m+1}}.$$

(10)

Consequently, the inverse Laplace transform is

$${\mathbb{L}}^{-1}\left[\frac{m!s^{\chi -\sigma }}{{(s^{\chi }\mp a)}^{m+1}}\right]=t^{\chi m+\sigma -1}{\mathbb{E}}_{\chi ,\sigma }^{\left(m\right)}(\pm a{t}^{\chi }).$$

(11)

This expression will be very useful to obtain analytical solutions of fractional differential equations using the Laplace transform.

2.2. K-essence fractional in the Bianchi I scenario.

One of the fundamental problems of cosmology is to find an explanation consistent with experiments for the accelerated expansion of the universe. Many proposals to tackle this task suggest modifying the general relativity theory. A recent proposal suggests unifying the description of dark matter, dark energy and inflation, employing a scalar field with a nonstandard kinetic term, known as K-essence theory. Usually, the action of the K-essence models [46,47,48,49,50,51] can be written as

$$S=\int d^{4}x\sqrt{-g}\left(\frac{1}{2}\mathcal{R}+f\left(\varphi \right)\mathcal{G}\left(X\right)+{\mathcal{L}}_{matter}\right),$$

(12)

g being the determinant of the metric, $\mathcal{R}$ the scalar curvature, $f\left(\varphi \right)$ an arbitrary function of the dimensionless scalar field $\varphi$, $X=-\frac{1}{2}{g}^{\mu \nu }{\nabla }_{\mu }\varphi {\nabla }_{\nu }\varphi$ the canonical kinetic energy and ${\mathcal{L}}_{matter}$ is the corresponding Lagrangian density of ordinary matter. So, performing the variation of the action (12) with respect to the metric $g_{\mu \nu }$ and X, the field equations are obtained

$$\begin{array}{ccc}\hfill G_{\mu \nu }-f\left(\varphi \right)\left[{\mathcal{G}}_X{\nabla }_{\mu }\varphi {\nabla }_{\nu }\varphi +\mathcal{G}{g}_{\mu \nu }\right]& =& T_{\mu \nu },\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill f\left(\varphi \right)\left[{\mathcal{G}}_X{\nabla }^{\mu }{\nabla }_{\mu }\varphi +{\mathcal{G}}_{XX}{\nabla }_{\mu }X{\nabla }^{\mu }\varphi \right]+\frac{df}{d\varphi }\left[\mathcal{G}-2X{\mathcal{G}}_X\right]& =& 0,\hfill \end{array}$$

(14)

where, we have assumed that $8\pi G=1$ and a subscript X denotes differentiation with respect to X. K-essence was originally proposed as a model for inflation; and then, as a model for dark energy, along with explorations of unifying dark energy and dark matter [52,53].

Last set of field equations (13) and (14) are the results of considering the scalar field $X\left(\varphi \right)$ as part of the matter content, i.e. ${\mathcal{L}}_{X,\varphi }=f\left(\varphi \right)\mathcal{G}\left(X\right)$, with the corresponding energy-momentum tensor

$${\mathcal{T}}_{\mu \nu }^{\left(\varphi \right)}=f\left(\varphi \right)\left[{\mathcal{G}}_X{\nabla }_{\mu }\varphi {\nabla }_{\nu }\varphi +\mathcal{G}\left(X\right)g_{\mu \nu }\right].$$

(15)

Also, considering the energy-momentum tensor of a barotropic perfect fluid,

$$T_{\mu \nu }^{\left(\varphi \right)}=({\rho }_{\varphi }+P_{\varphi })u_{\mu }{u}_{\nu }+P_{\varphi }{g}_{\mu \nu },$$

(16)

with $u_{\mu }$ being the four-velocity satisfying the relation $u_{\mu }{u}^{\mu }=-1$, ${\rho }_{\varphi }$ the energy density and $P_{\varphi }$ the pressure of the fluid. To simplify, we are going to consider a comoving perfect fluid, whose pressure and energy density corresponding to the energy moment tensor of the field X are

$$P_{\varphi }\left(X\right)=f\left(\varphi \right)\mathcal{G},{\rho }_{\varphi }\left(X\right)=f\left(\varphi \right)\left[2X{\mathcal{G}}_X-\mathcal{G}\right],$$

(17)

thus the barotropic parameter ${\omega }_X=\frac{P_{\varphi }\left(X\right)}{{\rho }_{\varphi }\left(X\right)}$ for the equivalent fluid is

$${\omega }_X=\frac{\mathcal{G}}{2X{\mathcal{G}}_X-\mathcal{G}}.$$

(18)

Notice that the case of a constant barotropic index ${\omega }_X$ (with the exception ${\omega }_X=0$) can be obtained by the $\mathcal{G}$ function

$$\mathcal{G}=X^{\frac{1+{\omega }_X}{2{\omega }_X}}.$$

(19)

At this point we can choose

$$\mathcal{G}=X^{\alpha },\alpha =\frac{1+{\omega }_X}{2{\omega }_X}\to {\omega }_X=\frac{1}{2\alpha -1}.$$

(20)

With this, we can write the states in the evolution of the universe resumed in the Table 1.

We are interested in the four-dimensional fractional cosmology in the scenario of k-essence within the anisotropic background, precisely the Bianchi type I, whose metric has the line element $g_{\alpha \beta }$, which can be read as

$$d{s}^2=-N^2\left(t\right)d{t}^2+A^2\left(t\right)d{x}^2+B^2\left(t\right)d{y}^2+C^2\left(t\right)d{z}^2,$$

(21)

where $N\left(t\right)$ is the lapse function, the functions $A\left(t\right)$, $B\left(t\right)$ and $C\left(t\right)$ are the corresponding scale factors in the $(x,y,z)$ directions, respectively. Moreover, in the Misner’s parametrization, the radii for this anisotropic background have the explicit form

$$A=e^{\Omega +{\beta }_{+}+\sqrt{3}{\beta }_{-}},B=e^{\Omega +{\beta }_{+}-\sqrt{3}{\beta }_{-}},C=e^{\Omega -2{\beta }_{+}},$$

(22)

where the functions in the radii are dependent on time, $\Omega =\Omega \left(t\right)$ and ${\beta }_{\pm }={\beta }_{\pm }\left(t\right)$. In this point, we notice that the line element (21), in the time $d\tau =Ndt$ reads as

$$d{s}^2=-d{\tau }^2+e^{2(\Omega \left(\tau \right)+{\beta }_{+}\left(\tau \right)+\sqrt{3}{\beta }_{-}\left(\tau \right))}d{x}^2+e^{2(\Omega \left(\tau \right)+{\beta }_{+}\left(\tau \right)-\sqrt{3}{\beta }_{-}\left(\tau \right))}d{y}^2+e^{2\Omega \left(\tau \right)-4{\beta }_{+}\left(\tau \right)}d{z}^2,$$

(23)

and employing the form of the functional $\mathcal{G}=X^{\alpha }$, and the following quantities

$$\begin{array}{ccc}& & \prime =\frac{d}{d\tau }=\frac{d}{Ndt},g_{\tau \tau }=g^{\tau \tau }-1,{\mathcal{G}}_X=\alpha X^{\alpha -1},{\mathcal{G}}_{XX}=\alpha (\alpha -1)X^{\alpha -2},\hfill \\ & & {\varphi }_{;\mu }^{,\mu }=g^{\mu \nu }\left({\varphi }_{,\mu \nu }-{\Gamma }_{\mu \nu }^{\theta }{\varphi }_{,\theta }\right)=-\left({\varphi }^{\prime \prime }+3{\Omega }^{\prime }{\varphi }^{\prime }\right),X_{;\mu }{\varphi }^{,\mu }=g^{\mu \nu }{\varphi }_{,\nu }{X}_{;\mu }=-X^{\prime }{\varphi }^{\prime },\hfill \\ & & X=\frac{1}{2}{\left({\varphi }^{\prime }\right)}^2,{\left({\varphi }^{\prime }\right)}^2=2X,X^{\prime }={\varphi }^{\prime }{\varphi }^{\prime \prime },{\varphi }^{\prime \prime }=\frac{X^{\prime }}{{\varphi }^{\prime }},\hfill \end{array}$$

then the Equation (14) is written as ,

$$\alpha X^{\alpha -1}\left({\varphi }^{\prime \prime }+3{\Omega }^{\prime }{\varphi }^{\prime }\right)+\alpha (\alpha -1)X^{\alpha -2}{X}^{\prime }{\varphi }^{\prime }+(2\alpha -1)X^{\alpha }\frac{d}{d\varphi }Lnf=0,$$

(24)

which can be transformed into

$$\frac{d}{d\tau }\left(LnX+\frac{6\Omega }{2\alpha -1}+Ln{f}^{\frac{1}{\alpha }}\right)=0,$$

(25)

and in turn integrated, resulting

$$\int f^{\frac{1}{2\alpha }}\left(\varphi \right)d\varphi =\sqrt{2\lambda }\int e^{-\frac{3\Omega \left(\tau \right)}{2\alpha -1}}d\tau ,$$

(26)

where $\lambda$ is an integration constant and has the same sign as $f\left(\varphi \right)$. In the gauge $N=24e^{\frac{3\Omega }{2\alpha -1}}$ the right side is

$$\int f^{\frac{1}{2\alpha }}\left(\varphi \right)d\varphi =24\sqrt{2\lambda }(t-t_i),$$

(27)

where $t_i$ is the initial time for the $\alpha$ scenario in the universe. At this point, we can introduce some structure for the function $f\left(\varphi \right)$ and solve the integral.

When we consider the particular mathematical structure for the function $f\left(\varphi \right)=p{\varphi }^m$ or $f\left(\varphi \right)=p{e}^{m\varphi }$ with p and m constants, the classical solutions for the field $\varphi$ in quadratures are

$$\varphi \left(\tau \right)=\varphi \left({\tau }_i\right)+\left\{\begin{array}{cc}\hfill ll{\left[\frac{(2\alpha +m)}{2\alpha }{p}^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\int e^{-\frac{3\Omega \left(\tau \right)}{2\alpha -1}}d\tau \right]}^{\frac{2\alpha }{2\alpha +m}},& f\left(\varphi \right)=p{\varphi }^m,m\ne -2\alpha \\ \hfill Exp\left[p^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\int e^{-\frac{3\Omega \left(\tau \right)}{2\alpha -1}}d\tau \right],& f\left(\varphi \right)=p{\varphi }^{-2\alpha },m=-2\alpha \\ \hfill \frac{2\alpha }{m}Ln\left[\frac{m}{2\alpha }{p}^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\int e^{-\frac{3\Omega \left(\tau \right)}{2\alpha -1}}d\tau \right],& f\left(\varphi \right)=p{e}^{m\varphi },m\ne 0,\\ \hfill p^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\int e^{-\frac{3\Omega \left(\tau \right)}{2\alpha -1}}d\tau & f\left(\varphi \right)=p,m=0.\end{array}\right.$$

(28)

The complete solution to the scalar field $\varphi$ depends strongly on the mathematical structure of the scale factor $\Omega \left(\tau \right)$ in the $\alpha$ scenario in our universe. In the gauge $N=24e^{\frac{3\Omega }{2\alpha -1}}$, these solutions are

$$\varphi \left(t\right)=\varphi \left(t_i\right)+\left\{\begin{array}{cc}\hfill ll{\left[\frac{12(2\alpha +m)}{\alpha }{p}^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\left(t-t_i\right)\right]}^{\frac{2\alpha }{2\alpha +m}},& f\left(\varphi \right)=p{\varphi }^m,m\ne -2\alpha \\ \hfill Exp\left[24p^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\left(t-t_i\right)\right],& f\left(\varphi \right)=p{\varphi }^{-2\alpha },m=-2\alpha \\ \hfill \frac{2\alpha }{m}Ln\left[\frac{12m}{\alpha }{p}^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\left(t-t_i\right)\right],& f\left(\varphi \right)=p{e}^{m\varphi },m\ne 0,\\ \hfill 24p^{-\frac{1}{2\alpha }}\sqrt{2\lambda }\left(t-t_i\right)& f\left(\varphi \right)=p,m=0,\end{array}\right.$$

(29)

where $t_i$ and $\varphi \left(t_i\right)$ are the initial time and the scalar field in this time for the $\alpha$ scenario in the universe. In what follows, we do the calculations to obtain the scale factor in some cases.

3. Lagrange and Hamilton formalism

Introducing the line element (21) of the anisotropic Bianchi type I cosmological model into the Lagrangian (12), we have

$${\mathcal{L}}_I=e^{3\Omega }\left\{6\frac{{\dot{\Omega }}^2}{N}-6\frac{{\dot{\beta }}_{+}^2}{N}-6\frac{{\dot{\beta }}_{-}^2}{N}-f\left(\varphi \right){\left(\frac{1}{2}\right)}^{\alpha }{\left(\dot{\varphi }\right)}^{2\alpha }{N}^{-2\alpha +1}\right\}.$$

(30)

Using the standard definition of the momenta ${\Pi }_{q^{\mu }}=\frac{\partial \mathcal{L}}{\partial {\dot{q}}^{\mu }}$, where $q^{\mu }$ are the coordinate fields $q^{\mu }=(\Omega ,{\beta }_{\pm },\varphi )$, we obtain the momenta associated with each field

$$\begin{array}{cccc}\hfill {\Pi }_{\Omega }& =\frac{12}{N}{e}^{3\Omega }\dot{\Omega },\hfill & \hfill \dot{\Omega }& =e^{-3\Omega }\frac{N{\Pi }_{\Omega }}{12},\hfill \\ \hfill {\Pi }_{\pm }& =-\frac{12}{N}{e}^{3\Omega }{\dot{\beta }}_{\pm },\hfill & \hfill \dot{{\beta }_{\pm }}& =-e^{-3\Omega }\frac{N{\Pi }_{\pm }}{12},,\hfill \\ \hfill {\Pi }_{\varphi }& =-f\left(\varphi \right){\left(\frac{1}{2}\right)}^{\alpha }\frac{2\alpha }{N^{2\alpha -1}}{e}^{3\Omega }{\dot{\varphi }}^{2\alpha -1},\hfill & \hfill \dot{\varphi }& =-N{e}^{-\frac{3\Omega }{2\alpha -1}}{\left[\frac{2^{\alpha }}{2\alpha }\frac{{\Pi }_{\varphi }}{f\left(\varphi \right)}\right]}^{\frac{1}{2\alpha -1}},\hfill \end{array}$$

(31)

and introducing them into the Lagrangian density, we obtain the canonical Lagrangian as ${\mathcal{L}}_{canonical}={\Pi }_{q^{\mu }}{\dot{q}}^{\mu }-N\mathcal{H}={\Pi }_{q^{\mu }}{\dot{q}}^{\mu }-H$. When we perform the variation of this canonical Lagrangian with respect to N, $\frac{\delta {\mathcal{L}}_{canonical}}{\delta N}=0$, we obtain the constraint $\mathcal{H}=0$. In our model, this is the only constraint corresponding to the Hamiltonian density, which is weakly zero. So, the Hamiltonian is

$$H=\frac{N}{24}{e}^{-\frac{3}{2\alpha -1}\Omega }\left\{e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }\left[{\Pi }_{\Omega }^2-{\Pi }_{+}^2-{\Pi }_{-}^2\right]-\frac{12(2\alpha -1)}{\alpha }{\left(\frac{2^{\alpha -1}}{\alpha f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\Pi }_{\varphi }^{\frac{2\alpha }{2\alpha -1}}\right\}.$$

(32)

3.1. Exact solution in the gauge $N=24e^{\frac{3}{2\alpha -1}\Omega }$.

Using the Hamilton equations for the momenta ${\dot{\Pi }}_{\mu }=-\frac{\partial H}{\partial q^{\mu }}$ and coordinates ${\dot{q}}^{\mu }=\frac{\partial H}{\partial {\Pi }_{\mu }}$, we have

$$\begin{array}{ccc}\hfill \dot{\Omega }& =& 2e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }{\Pi }_{\Omega }\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill \dot{{\beta }_{+}}& =& -2e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }{\Pi }_{+},\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill \dot{{\beta }_{-}}& =& -2e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }{\Pi }_{-},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill \dot{\varphi }& =& -24{\left(\frac{2^{\alpha -1}}{\alpha f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\Pi }_{\varphi }^{\frac{1}{2\alpha -1}},\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill {\dot{\Pi }}_{\Omega }& =& \frac{6(\alpha -1)}{2\alpha -1}{e}^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }\left[{\Pi }_{\Omega }^2-{\Pi }_{+}^2-{\Pi }_{-}^2\right],\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill {\dot{\Pi }}_{\pm }& =& 0,\Rightarrow {\Pi }_{\pm }=p_{\pm }=constant,\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {\dot{\Pi }}_{\varphi }& =& -\frac{12}{\alpha }{\left(\frac{2^{\alpha -1}}{\alpha }\right)}^{\frac{1}{2\alpha -1}}{\Pi }_{\varphi }^{\frac{2\alpha }{2\alpha -1}}{f}^{-\frac{2\alpha }{2\alpha -1}}\frac{\dot{f}}{\dot{\varphi }},\hfill \end{array}$$

(39)

solving the equation (39) using (36), we have ${\Pi }_{\varphi }=p_{\varphi }{f}^{\frac{1}{2\alpha }}$, with $p_{\varphi }$ an integration constant. With this result and taking into account the equation (36), we get

$$\int f^{\frac{1}{2\alpha }}d\varphi =-24{\left(\frac{p_{\varphi }{2}^{\alpha -1}}{\alpha }\right)}^{\frac{1}{2\alpha -1}}\left(t-t_i\right),$$

(40)

that is, similar to (27), previously obtained, when was solved a Klein-Gordon like equation, directly. Using the Hamiltonian constraint and the solution to equation (39) found previously, we have

$$e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }\left[{\Pi }_{\Omega }^2-{\Pi }_{+}^2-{\Pi }_{-}^2\right]=\frac{12(2\alpha -1)}{\alpha }{\left(\frac{p_{\varphi }^{2\alpha }{2}^{\alpha -1}}{\alpha }\right)}^{\frac{1}{2\alpha -1}},$$

(41)

then, the solution for the momenta becomes

$${\Pi }_{\Omega }={\eta }_{\alpha }t+p_0,$$

(42)

where the constant ${\eta }_{\alpha }=\frac{72(\alpha -1)}{\alpha }{\left(\frac{p_{\varphi }^{2\alpha }{2}^{\alpha -1}}{\alpha }\right)}^{\frac{1}{2\alpha -1}}$, and $p_0$ are constants of integration, that introducing in the equation for $\Omega$, we get the equation for the $\Omega$ function

$$\frac{d\Omega }{dt}=2e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }\left({\eta }_{\alpha }t+p_0\right),e^{\frac{6(\alpha -1)}{2\alpha -1}\Omega }=\frac{6(\alpha -1)}{2\alpha -1}\left({\eta }_{\alpha }{t}^2+2p_{0}t+p_1\right),$$

(43)

whose solution becomes

$$\Omega =\frac{2\alpha -1}{6(\alpha -1)}ln\left[\frac{6(\alpha -1)}{2\alpha -1}\left({\eta }_{\alpha }{t}^2+2p_{0}t+p_1\right)\right],$$

(44)

and the solution for the scalar field is given by the equations (29). The solutions for the anisotropic function ${\beta }_{\pm }$ are given by

$${\beta }_{\pm }\left(t\right)=b_{\pm }-\frac{(2\alpha -1)p_{\pm }}{24(\alpha -1){\eta }_{\alpha }\sqrt{p_0^2-{\eta }_{\alpha }{p}_1}}ln\left[\frac{{\eta }_{\alpha }t+p_0-\sqrt{p_0^2-{\eta }_{\alpha }{p}_1}}{{\eta }_{\alpha }t+p_0+\sqrt{p_0^2-{\eta }_{\alpha }{p}_1}}\right],$$

(45)

$${\beta }_{\pm }=b_{\pm }-\left(\frac{2\alpha -1}{24(\alpha -1)}\right)\frac{p_{\pm }}{{\eta }_{\alpha }\sqrt{{\lambda }_{\alpha }}}ln\left(\frac{{\Sigma }_{-}\left(t\right)}{{\Sigma }_{+}\left(t\right)}\right),$$

(46)

where

$${\Sigma }_{\pm }\left(t\right)={\eta }_{\alpha }t+p_0\pm \sqrt{{\lambda }_{\alpha }},\mathrm{and}{\lambda }_{\alpha }=p_0^2-{\eta }_{\alpha }{p}_1>0.$$

According to the last expressions, the radii associated with the Bianchi I have the following behaviour

$$\begin{array}{cc}\hfill A\left(t\right)& =e^{\Omega +{\beta }_{+}+\sqrt{3}{\beta }_{-}}=A_0{\left[\frac{6(\alpha -1)}{2\alpha -1}{\left(\frac{{\Sigma }_{+}\left(t\right)}{{\Sigma }_{-}\left(t\right)}\right)}^{\frac{p_{+}+\sqrt{3}{p}_{-}}{4{\eta }_{\alpha }\sqrt{{\lambda }_{\alpha }}}}({\eta }_{\alpha }{t}^2+2p_{0}t+p_1)\right]}^{\frac{2\alpha -1}{6(\alpha -1)}},\hfill \end{array}$$

(47a)

$$\begin{array}{cc}\hfill B\left(t\right)& =e^{\Omega +{\beta }_{+}-\sqrt{3}{\beta }_{-}}=B_0{\left[\frac{6(\alpha -1)}{2\alpha -1}{\left(\frac{{\Sigma }_{+}\left(t\right)}{{\Sigma }_{-}\left(t\right)}\right)}^{\frac{p_{+}-\sqrt{3}{p}_{-}}{4{\eta }_{\alpha }\sqrt{{\lambda }_{\alpha }}}}({\eta }_{\alpha }{t}^2+2p_{0}t+p_1)\right]}^{\frac{2\alpha -1}{6(\alpha -1)}},\hfill \end{array}$$

(47b)

$$\begin{array}{cc}\hfill C\left(t\right)& =e^{\Omega -2{\beta }_{+}}=C_0\left[\frac{6(\alpha -1)}{2\alpha -1}\right(\frac{{\Sigma }_{-}\left(t\right)}{{\Sigma }_{+}\left(t\right)}{\left){}^{\frac{p_{+}}{2{\eta }_{\alpha }\sqrt{{\lambda }_{\alpha }}}}({\eta }_{\alpha }{t}^2+2p_{0}t+p_1)\right]}^{\frac{2\alpha -1}{6(\alpha -1}},\hfill \end{array}$$

(47c)

and the volume of this universe $V\left(t\right)=ABC=e^{3\Omega }$ being,

$$V\left(t\right)=V_0{\left[\frac{6(\alpha -1)}{2\alpha -1}({\eta }_{\alpha }{t}^2+2p_{0}t+p_1)\right]}^{\frac{2\alpha -1}{2(\alpha -1)}}.$$

(48)

Figure 1. Volume of the universe into the radiation and Dust age, respectively, according to the Table 1, we choose $p_{\varphi }=2$ and $p_1=1$.

Figure 1. Volume of the universe into the radiation and Dust age, respectively, according to the Table 1, we choose $p_{\varphi }=2$ and $p_1=1$.

Where we have graphed on different time scales in each scenario, in both cases the volume is increasing.

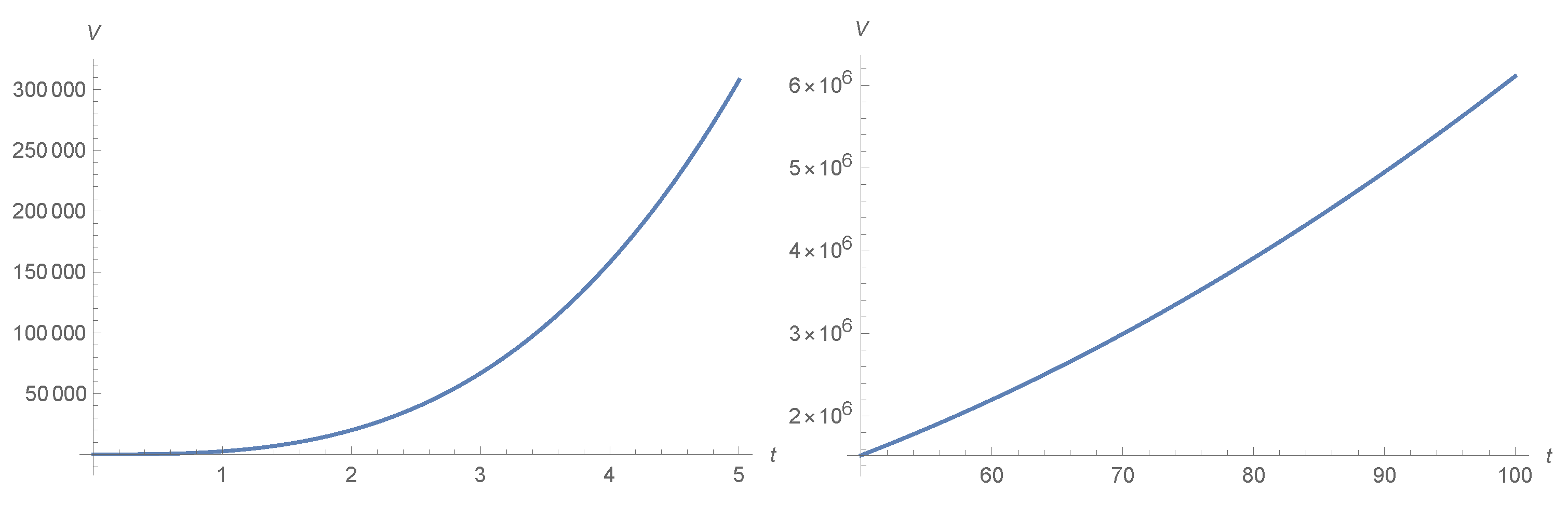
3.2. Exact solution without gauge N in the time $\tau$

For this case, the Hamilton procedure is not adequate, then we shall use the Hamilton-Jacobi procedure in order to find the solutions for the remaining minisuperspace variables, which arises by making the identification $\frac{\partial S(\Omega ,{\beta }_{\pm },\varphi )}{\partial q_{\mu }}={\Pi }_{\mu }$ in the Hamiltonian constraint (32), $H=0$, taking $S(\Omega ,{\beta }_{\pm },\varphi )=S_{\Omega }\left(\Omega \right)+S_{+}\left({\beta }_{+}\right)+S_{-}\left({\beta }_{-}\right)+S_{\varphi }\left(\varphi \right)$ which results in

$$e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }\left[{\left(\frac{d{S}_{\Omega }}{d\Omega }\right)}^2-{\left(\frac{d{S}_{+}}{d{\beta }_{+}}\right)}^2-{\left(\frac{d{S}_{-}}{d{\beta }_{-}}\right)}^2\right]-A_{\alpha }{\left(\frac{1}{f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\left(\frac{d{S}_{\varphi }}{d\varphi }\right)}^{\frac{2\alpha }{2\alpha -1}}=0.$$

(49)

Separating this equation, we have

$$e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }\left[{\left(\frac{d{S}_{\Omega }}{d\Omega }\right)}^2-{\left(\frac{d{S}_{+}}{d{\beta }_{+}}\right)}^2-{\left(\frac{d{S}_{-}}{d{\beta }_{-}}\right)}^2\right]=A_{\alpha }{\left(\frac{1}{f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\left(\frac{d{S}_{\varphi }}{d\varphi }\right)}^{\frac{2\alpha }{2\alpha -1}}={\ell }_{\varphi }^2.$$

(50)

with ${\ell }_{\varphi }$ a separation constant. The solution in the variable $\varphi$ is,

$${\Pi }_{\varphi }=\frac{d{S}_{\varphi }}{d\varphi }={\left[\frac{{\ell }_{\varphi }^2}{A_{\alpha }}\right]}^{\frac{2\alpha -1}{2\alpha }}{f}^{\frac{1}{2\alpha }}\left(\varphi \right)=p_{\varphi }{f}^{\frac{1}{2\alpha }}\left(\varphi \right),$$

(51)

where $S\left(\varphi \right)=p_{\varphi }\int f^{\frac{1}{2\alpha }}\left(\varphi \right)d\varphi$, obtaining similar results in the Hamilton procedure.

The specific values of the constants are $p_{\varphi }={\left[\frac{{\ell }_{\varphi }^2}{A_{\alpha }}\right]}^{\frac{2\alpha -1}{2\alpha }}$ and $A_{\alpha }=\frac{12(2\alpha -1)}{\alpha }{\left(\frac{2^{\alpha -1}}{\alpha }\right)}^{\frac{1}{2\alpha -1}}$, in terms of the $\alpha$ parameter.

The other equations are read as

$$\begin{array}{ccc}\hfill {\left(\frac{d{S}_{\Omega }}{d\Omega }\right)}^2& =& {\ell }_{+}^2+{\ell }_{-}^2+{\ell }_{\varphi }^2{e}^{\frac{6(\alpha -1}{2\alpha -1}},\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill {\left(\frac{d{S}_{+}}{d{\beta }_{+}}\right)}^2& =& {\ell }_{+}^2,S_{+}=s_{+}\pm {\ell }_{+}{\beta }_{+},\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill {\left(\frac{d{S}_{-}}{d{\beta }_{-}}\right)}^2& =& {\ell }_{-}^2,S_{-}=s_{-}\pm {\ell }_{-}{\beta }_{-},\hfill \end{array}$$

(54)

where ${\ell }_i^2$ are separation constants and $s_{\pm }$ integration constants. On the other side, recalling the expressions for the momenta we can obtain solutions for equations (52), (53) and (54) in quadrature; for the variable $\Omega$ and for $\alpha \ne 1$,

3.3. Case for $\alpha \ne 1$

In this particular case, we have

$$d\tau =12\frac{e^{3\Omega }d\Omega }{\sqrt{{\ell }^2+{\ell }_{\varphi }^2{e}^{\frac{6(\alpha -1)}{2\alpha -1}\Omega }}},{\ell }^2={\ell }_{+}^2+{\ell }_{-}^2,$$

(55)

and for the anisotropic variables,

$$\Delta {\beta }_{\pm }=\mp \frac{{\ell }_{\pm }}{12}\int e^{-3\Omega \left(\tau \right)}d\tau .$$

(56)

For solving equation (55), we employ the transformation in the time variable $d\tau =e^{\frac{3}{2\alpha -1}\Omega }dT$ and $\mathcal{U}={\ell }^2+{\ell }_{\varphi }^2{e}^{\frac{6(\alpha -1)}{2\alpha -1}\Omega }$, so, $d\mathcal{U}={\ell }_{\varphi }^2\frac{6(\alpha -1)}{2\alpha -1}{e}^{\frac{6(\alpha -1)}{2\alpha -1}\Omega }d\Omega$, resulting

$$dT=12\frac{e^{\frac{6(\alpha -1)}{2\alpha -1}\Omega }d\Omega }{\sqrt{\mathcal{U}}}=\frac{2(2\alpha -1)}{(\alpha -1){\ell }_{\varphi }^2}\frac{d\mathcal{U}}{\sqrt{\mathcal{U}}},$$

and the solution is

$$T-T_0=\frac{4(2\alpha -1)}{(\alpha -1){\ell }_{\varphi }^2}\left(\sqrt{\mathcal{U}}-\sqrt{{\mathcal{U}}_0}\right),$$

then for the $\Omega$ variable, we have

$$\Omega \left(T\right)=Ln{\left[{\left(\frac{{\ell }_{\varphi }(\alpha -1)}{4(2\alpha -1)}(T-T_0)+\sqrt{\frac{{\mathcal{U}}_0}{{\ell }_{\varphi }^2}}\right)}^2-{\left(\frac{\ell }{{\ell }_{\varphi }}\right)}^2\right]}^{\frac{2\alpha -1}{6(\alpha -1)}},$$

(57)

and the time transformation becomes

$$d\tau ={\left[{\left(\frac{{\ell }_{\varphi }(\alpha -1)}{4(2\alpha -1)}(T-T_0)+\sqrt{\frac{{\mathcal{U}}_0}{{\ell }_{\varphi }^2}}\right)}^2-{\left(\frac{\ell }{{\ell }_{\varphi }}\right)}^2\right]}^{\frac{1}{2(\alpha -1)}}dT.$$

(58)

To obtain the solutions in the time T, for the anisotropic functions ${\beta }_{\pm }\left(T\right)$, we solve the integral

$$\begin{array}{ccc}\hfill \int e^{-3\Omega \left(\tau \right)}d\tau & =& \int e^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega \left(T\right)}dT=\int \frac{dT}{{\left(\frac{{\ell }_{\varphi }(\alpha -1)}{4(2\alpha -1)}(T-T_0)+\sqrt{\frac{{\mathcal{U}}_0}{{\ell }_{\varphi }^2}}\right)}^2-{\left(\frac{\ell }{{\ell }_{\varphi }}\right)}^2}\hfill \\ & =& \frac{4(2\alpha -1)}{\ell (\alpha -1)}Ln\left[\frac{\frac{{\ell }_{\varphi }^2(\alpha -1)}{4(2\alpha -1))}(T-T_0)+\sqrt{{\mu }_0}-\ell }{\frac{{\ell }_{\varphi }^2(\alpha -1)}{4(2\alpha -1))}(T-T_0)+\sqrt{{\mu }_0}+\ell }\right],\hfill \end{array}$$

(59)

then, the anisotropic functions (56) become

$${\beta }_{\pm }\left(T\right)={\beta }_{\pm }\left(T_i\right)\mp \frac{{\ell }_{\pm }}{3}\frac{(2\alpha -1)}{\ell (\alpha -1)}Ln\left[\frac{\frac{{\ell }_{\varphi }^2(\alpha -1)}{4(2\alpha -1))}(T-T_0)+\sqrt{{\mu }_0}-\ell }{\frac{{\ell }_{\varphi }^2(\alpha -1)}{4(2\alpha -1))}(T-T_0)+\sqrt{{\mu }_0}+\ell }\right].$$

(60)

and the scalar field (28), takes the form

$$\varphi \left(T\right)=\varphi \left(T_i\right)+\left\{\begin{array}{cc}\hfill ll{\left[\frac{(2\alpha +m)}{2\alpha }{p}^{-\frac{1}{2\alpha }}\sqrt{2\lambda }(T-T_i)\right]}^{\frac{2\alpha }{2\alpha +m}},& f\left(\varphi \right)=p{\varphi }^m,m\ne -2\alpha ,\\ \hfill Exp\left[p^{-\frac{1}{2\alpha }}\sqrt{2\lambda }(T-T_i)\right],& f\left(\varphi \right)=p{\varphi }^{-2\alpha },m=-2\alpha ,\\ \hfill \frac{2\alpha }{m}Ln\left[\frac{m}{2\alpha }{p}^{-\frac{1}{2\alpha }}\sqrt{2\lambda }(T-T_i)\right],& f\left(\varphi \right)=p{e}^{m\varphi },m\ne 0,\\ \hfill p^{-\frac{1}{2\alpha }}\sqrt{2\lambda }(T-T_i),& f\left(\varphi \right)=p,m=0,\end{array}\right.$$

(61)

On the other side, the only state when the time $\tau =T$, corresponds to the scenario, $\alpha \to \infty$, which is calculated below.

3.3.1. Dust scenario, $\alpha \to \infty$

For this particular case, we have

$$\Omega \left(\tau \right)=Ln{\left[{\left(\frac{{\ell }_{\varphi }}{8}(\tau -{\tau }_0)+\sqrt{\frac{{\mathcal{U}}_0}{{\ell }_{\varphi }^2}}\right)}^2-{\left(\frac{\ell }{{\ell }_{\varphi }}\right)}^2\right]}^{\frac{1}{3}},$$

(62)

then the volume function becomes

$$V\left(\tau \right)=V_0\left\{{\left(\frac{{\ell }_{\varphi }}{8}(\tau -{\tau }_0)+\sqrt{\frac{{\mathcal{U}}_0}{{\ell }_{\varphi }^2}}\right)}^2-{\left(\frac{\ell }{{\ell }_{\varphi }}\right)}^2\right\},$$

(63)

and the anisotropic functions are

$${\beta }_{\pm }\left(\tau \right)={\beta }_{\pm }\left({\tau }_0\right)\mp \frac{{\ell }_{\pm }}{3}\frac{2}{\ell }Ln\left[\frac{\frac{{\ell }_{\varphi }^2}{8}(\tau -{\tau }_0)+\sqrt{{\mu }_0}-\ell }{\frac{{\ell }_{\varphi }^2}{8}(\tau -{\tau }_0)+\sqrt{{\mu }_0}+\ell }\right].$$

(64)

We can see that the scalar field constant ${\ell }_{\varphi }$ is huge, the anisotropic function goes to constant, and the anisotropic model can be isotropic one. We rewrite the corresponding solutions in the scalar field (28), for this scenario

$$\varphi \left(\tau \right)=\varphi \left({\tau }_0\right)+\left\{\begin{array}{cc}\hfill ll\left[\sqrt{2\lambda }(\tau -{\tau }_0)\right],& f\left(\varphi \right)=p{\varphi }^m,m\ne -2\alpha ,\\ \hfill Exp\left[\sqrt{2\lambda }(\tau -{\tau }_0)\right],& f\left(\varphi \right)=,m=-2\alpha ,\\ \hfill Ln\left[\sqrt{2\lambda }(\tau -{\tau }_i)\right],& f\left(\varphi \right)=p{e}^{2\alpha \varphi },\\ \hfill \sqrt{2\lambda }(\tau -{\tau }_0),& f\left(\varphi \right)=p,m=0.\end{array}\right.$$

(65)

4. Quantum Regime

The WDW equation for these models is obtained by making the usual substitution ${\Pi }_{q^{\mu }}=-i\hslash {\partial }_{q^{\mu }}$ in (32), and promoting the classical Hamiltonian density in the differential operator applied to the wave function $\Psi (\Omega ,{\beta }_{\pm },\varphi )$, $\widehat{\mathcal{H}}\Psi =0$; we have

$${\hslash }^2{e}^{-\frac{6(\alpha -1)}{2\alpha -1}\Omega }\left[-\frac{{\partial }^2\Psi }{\partial {\Omega }^2}+\frac{{\partial }^2\Psi }{\partial {\beta }_{+}^2}+\frac{{\partial }^2\Psi }{\partial {\beta }_{-}^2}\right]-\frac{12(2\alpha -1)}{\alpha }{\left(\frac{2^{\alpha -1}}{\alpha f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\hslash }^{\frac{2\alpha }{2\alpha -1}}\frac{{\partial }^{\frac{2\alpha }{2\alpha -1}}}{\partial {\varphi }^{\frac{2\alpha }{2\alpha -1}}}\Psi =0.$$

(66)

This fractional differential equation of degree $\beta =\frac{2\alpha }{2\alpha -1}$, belongs to different intervals, depending on the value of the barotropic parameter [37]. We can write this equation in terms of the $\beta$ parameter, we have

$${\hslash }^2{e}^{-3(2-\beta )\Omega }\left[-\frac{{\partial }^2\Psi }{\partial {\Omega }^2}+\frac{{\partial }^2\Psi }{\partial {\beta }_{+}^2}+\frac{{\partial }^2\Psi }{\partial {\beta }_{-}^2}\right]-\frac{24}{\beta }{\left(\frac{2^{\alpha -1}}{\alpha f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\hslash }^{\beta }\frac{{\partial }^{\beta }}{\partial {\varphi }^{\beta }}\Psi =0.$$

(67)

For simplicity, the factor $e^{-3(2-\beta )\Omega }$ may be the factor ordered with ${\widehat{\Pi }}_{\Omega }$ and $f^{-\frac{1}{2\alpha -1}}\left(\varphi \right)$ may be the factor ordered with $\frac{{\partial }^{\beta }}{\partial {\varphi }^{\beta }}$ in many ways, we employ it might be called a semi-general factor ordering, which, in this case, would order the terms $e^{-3(2-\beta )\Omega }{\widehat{\Pi }}_{\Omega }^2$ as $-e^{-\left(3\right(2-\beta )-Q)\Omega }{\partial }_{\Omega }{e}^{-Q\Omega }{\partial }_{\Omega }=-e^{-3(2-\beta )\Omega }{\partial }_{\Omega }^2+Q{e}^{-3(2-\beta )\Omega }{\partial }_{\Omega },$ where Q is any real constant that measures the ambiguity in the factor ordering in the variables $\Omega$ and its corresponding momenta. For the other factor ordering, we make the following calculation which, in this case, would order the terms $\frac{g\left(\varphi \right)}{f^{\frac{1}{2\alpha -1}}\left(\varphi \right)}\frac{{\partial }^{\beta }}{\partial {\varphi }^{\beta }}$, where in the particular case we choose $g\left(\varphi \right)={\varphi }^s$, similarly to $f\left(\varphi \right)$ in the classical case, that is

$$f^{-\frac{1}{2\alpha -1}}\left(\varphi \right){\varphi }^{-s}\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}{\varphi }^s\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}=f^{-\frac{1}{2\alpha -1}}\left(\varphi \right)\frac{{\partial }^{\beta }}{\partial {\varphi }^{\beta }}+f^{-\frac{1}{2\alpha -1}}\left(\varphi \right){\varphi }^{-s}\left[\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}{\varphi }^s\right]\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}},$$

(68)

where the Caputo fractional derivative of $\left[\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}{\varphi }^s\right]$ becomes [1],

$${}_0^c{D}_x^{\beta /2}{\varphi }^s=\frac{\Gamma (s+1)}{\Gamma (s-\beta /2+1)}{\varphi }^{s-\beta /2}.$$

(69)

Thus, the equation (68) is rewritten as

$$\begin{array}{ccc}\hfill f^{-\frac{1}{2\alpha -1}}\left(\varphi \right){\varphi }^{-s}\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}{\varphi }^s\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}& =& f^{-\frac{1}{2\alpha -1}}\left(\varphi \right)\frac{{\partial }^{\beta }}{\partial {\varphi }^{\beta }}+f^{-\frac{1}{2\alpha -1}}\left(\varphi \right){\varphi }^{-s}\frac{\Gamma (s+1)}{\Gamma (s+1-\beta /2)}{\varphi }^{s-\beta /2}\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}\hfill \\ & =& f^{-\frac{1}{2\alpha -1}}\left(\varphi \right)\frac{{\partial }^{\beta }}{\partial {\varphi }^{\beta }}+f^{-\frac{1}{2\alpha -1}}\left(\varphi \right)\frac{\Gamma (s+1)}{\Gamma (s+1-\beta /2)}{\varphi }^{-\beta /2}\frac{{\partial }^{\beta /2}}{\partial {\varphi }^{\beta /2}}\hfill \end{array}$$

(70)

Assuming this factor ordering for the Wheeler-DeWitt equation, we get

$$\begin{array}{ccc}& & e^{-3(2-\beta )\Omega }\left[-\frac{{\partial }^2\Psi }{\partial {\Omega }^2}+Q\frac{\partial \Psi }{\partial \Omega }+\frac{{\partial }^2\Psi }{\partial {\beta }_{+}^2}+\frac{{\partial }^2\Psi }{\partial {\beta }_{-}^2}\right]\hfill \\ & & -\frac{24}{\beta }{\left(\frac{2^{\alpha -1}}{\alpha f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\hslash }^{\beta }\frac{{\partial }^{\beta }}{\partial {\varphi }^{\beta }}\Psi -\frac{24}{\beta }{\left(\frac{2^{\alpha -1}}{\alpha f\left(\varphi \right)}\right)}^{\frac{1}{2\alpha -1}}{\hslash }^{\beta }{\varphi }^{-s}\frac{\Gamma (s+1)}{\Gamma (s+1-\mu )}\frac{{\partial }^{\frac{\beta }{2}}}{\partial {\varphi }^{\frac{\beta }{2}}}\Psi =0.\hfill \end{array}$$

(71)

Using the ansatz for the wave function $\Psi (\Omega ,{\beta }_{+},{\beta }_{-},\varphi )=\mathcal{A}\left(\Omega \right){\mathcal{B}}_{+}\left({\beta }_{+}\right){\mathcal{B}}_{-}\left({\beta }_{-}\right)\mathcal{C}\left(\varphi \right)$, we obtain the following differential equations on the corresponding variables

$$\begin{array}{ccc}\hfill \frac{d^2\mathcal{A}}{d{\Omega }^2}-Q\frac{d\mathcal{A}}{d\Omega }-\left[\pm {\left(\frac{\rho }{\hslash }\right)}^2{e}^{3(2-\beta )\Omega }+{\rho }_1^2\right]\mathcal{A}& =& 0,\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill \frac{d^2{\mathcal{B}}_{+}}{d{\beta }_{+}^2}-{\rho }_2^2{\mathcal{B}}_{+}& =& 0,\hfill \end{array}$$

(73)

$$\begin{array}{ccc}\hfill \frac{d^2{\mathcal{B}}_{-}}{d{\beta }_{-}^2}-{\rho }_3^2{\mathcal{B}}_{-}& =& 0,{\rho }_3^2={\rho }_2^2-{\rho }_1^2\hfill \end{array}$$

(74)

$$\begin{array}{ccc}\hfill {\varphi }^{\gamma }\frac{d^{2\gamma }\mathcal{C}}{d{\varphi }^{2\gamma }}+\frac{\Gamma (s+1)}{\Gamma (s+1-\gamma )}\frac{d^{\gamma }\mathcal{C}}{d{\varphi }^{\gamma }}\pm {\left(\frac{p_{\varphi }\alpha }{2^{\alpha -1}}\right)}^{\frac{1}{2\alpha -1}}\frac{\gamma {\rho }^2}{12{\hslash }^{2\gamma }}\mathcal{C}& =& 0,\beta =2\gamma ,0<\gamma \le 1.\hfill \end{array}$$

(75)

Figure 2. Probability density (80) of the universe dominated by Dust era, in this stage of the universe shows that the probability density has a decay, both in $\Omega$ and $\varphi$. Both are plotting with $\rho =0.5$, $\gamma =\frac{1}{2}$, ${\rho }_1=0.1$.

Figure 2. Probability density (80) of the universe dominated by Dust era, in this stage of the universe shows that the probability density has a decay, both in $\Omega$ and $\varphi$. Both are plotting with $\rho =0.5$, $\gamma =\frac{1}{2}$, ${\rho }_1=0.1$.

We can see that the fractional differential equation (75) has variable coefficients, so to solve it we can use the fractional power series [38,39], also $f\left(\varphi \right)=p_{\varphi }{\varphi }^m$, with $p_{\varphi }$ a constant and choosing $\frac{m}{2\alpha -1}=-\gamma$, as particular case, which implies that the parameter $m=-\alpha$ in sense that $\gamma$ parameter is in accordance with its original definition (see equation (75) and definition of the $\beta$ parameter, or the equation in the text after equation (76)).

Following the book of Polyanin [54] (page 179.10), we find the solution for the first equation, considering different values in the factor ordering parameter, (we take the corresponding sign minus in the constant ${\rho }^2$)

$$\mathcal{A}\left(\Omega \right)=e^{\frac{Q\Omega }{2}}\left[C_1{K}_{\nu }\left(\frac{\rho }{3\hslash (1-\gamma )}{e}^{3(1-\gamma )\Omega }\right)+C_2{I}_{\nu }\left(\frac{\rho }{3\hslash (1-\gamma )}{e}^{3(1-\gamma )\Omega }\right)\right],$$

(76)

where $K_{\nu }\left(z\right)$ and $I_{\nu }\left(z\right)$ are the modified Bessel functions, and order $\nu =\frac{\sqrt{Q^2+4{\rho }_1^2}}{6(1-\gamma )}$ with $\gamma =\frac{\beta }{2}=\frac{\alpha }{2\alpha -1}$ the new order in the fractional derivative. However, for physical conditions we will only take the modified Bessel $K_{\nu }$.

The corresponding quantum solution for equations (73) and (74) are

$$\begin{array}{c}\hfill {\mathcal{B}}_{+}=a_0{e}^{{\rho }_2{\beta }_{+}}+a_1{e}^{-{\rho }_2{\beta }_{+}},\end{array}$$

(77)

$$\begin{array}{c}\hfill {\mathcal{B}}_{-}=b_0{e}^{{\rho }_3{\beta }_{-}}+b_1{e}^{-{\rho }_3{\beta }_{-}}.\end{array}$$

(78)

with ${\rho }^2$ and ${\rho }_i^2$ are separation constants.

The solution of the equation (75) with positive sign and $f\left(\varphi \right)=p_{\varphi }=constant$, with zero factor ordering, may be obtained by applying direct and inverse Laplace transform [20,37], providing

$${\mathcal{C}}_{+}(\varphi ,\gamma )={\mathbb{E}}_{2\gamma }\left(-z^2\right),z={\left(\frac{p_{\varphi }\alpha }{2^{\alpha -1}}\right)}^{\frac{1}{2(2\alpha -)}}\frac{\sqrt{\gamma }\rho }{2\sqrt{3}{\hslash }^{\gamma }}{\varphi }^{\gamma },0<\gamma \le 1,$$

(79)

where ${\mathbb{E}}_{2\gamma }$ is the Mittag-Leffler function (7), then, the probability density of the wave function for this particular case becomes

$${\left|\Psi \right|}^2={\psi }_0^2{e}^{Q\Omega \pm 2{\rho }_2{\beta }_{+}\pm 2{\rho }_3{\beta }_{-}}{K}_{\nu }^2\left[\frac{\rho }{3\hslash (1-\gamma )}{e}^{3(1-\gamma )\Omega }\right]{\mathbb{E}}_{2\gamma }^2(-z^2),$$

(80)

and its corresponding plot for two values in the ordering parameter Q.

Table II shows the differential equations obtained from (75), depending on the values of ${\omega }_X$, $\alpha$ and $\gamma$

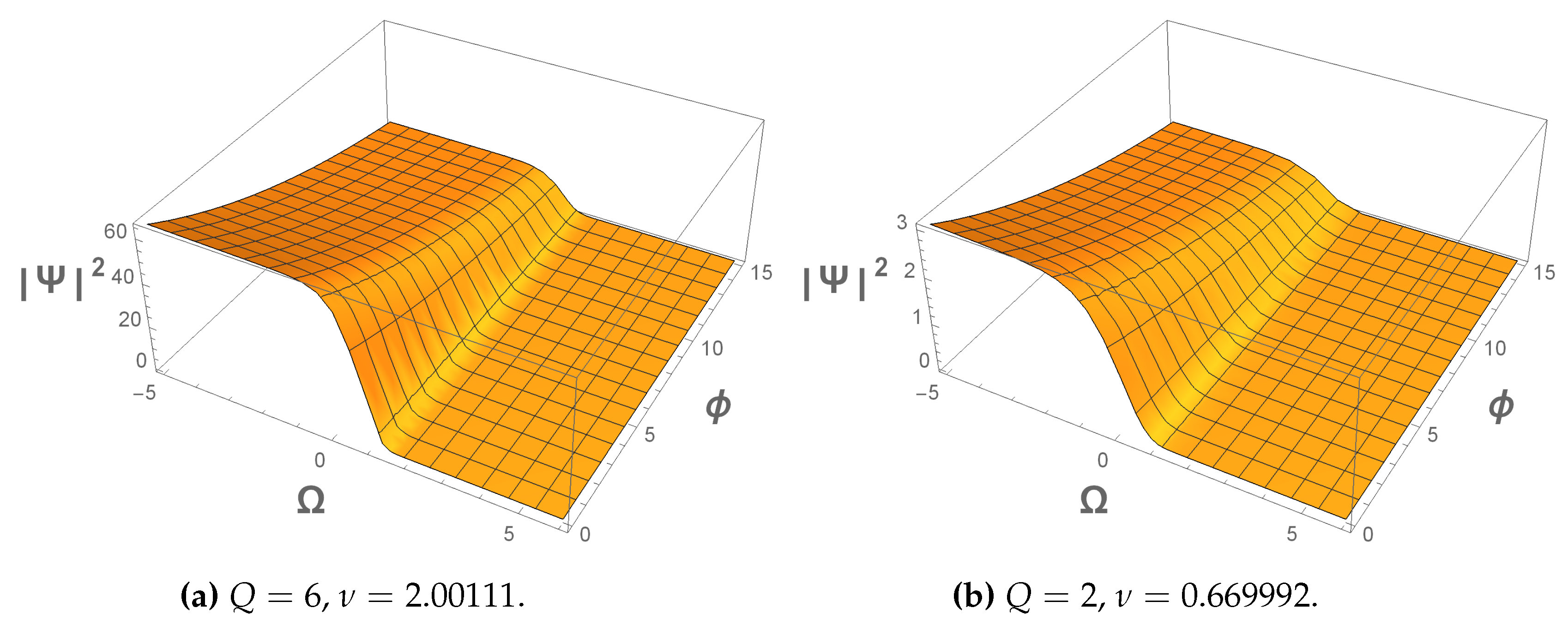
4.1. Solution to FDE associated with the different state evolutions

We write the fractional differential equation (75) as follows,

$${\varphi }^{\gamma }\frac{d^{2\gamma }\mathcal{C}}{d{\varphi }^{2\gamma }}+A\frac{d^{\gamma }\mathcal{C}}{d{\varphi }^{\gamma }}+B\mathcal{C}=0,0<\gamma \le 1,$$

(81)

where we have made the simplifications $A=\frac{\Gamma (s+1)}{\Gamma (s+1-\gamma )}$ and $B_{(\alpha ,\gamma )}=\pm {\left(\frac{p_{\varphi }\alpha }{2^{\alpha -1}}\right)}^{\frac{1}{2\alpha -1}}\frac{\gamma {\mu }^2}{12{\hslash }^{2\gamma }}$. The last linear fractional differential equation (81), will be solved using the fractional power series [38,39]

$$\mathcal{C}=\sum _{n=0}^{\infty }{a}_n{\varphi }^{n\gamma }.$$

(82)

Then, the fractional derivatives are

$$\begin{array}{cc}\hfill \frac{d^{\gamma }\mathcal{C}}{d^{\gamma }\varphi }& =\sum _{n=1}^{\infty }{a}_n\frac{\Gamma [n\gamma +1]}{\Gamma \left[\right(n-1)\gamma +1]}{\varphi }^{(n-1)\gamma },\hfill \end{array}$$

(83a)

$$\begin{array}{cc}\hfill \frac{d^{2\gamma }\mathcal{C}}{d^{2\gamma }\varphi }& =\sum _{n=2}^{\infty }{a}_n\frac{\Gamma [n\gamma +1]\Gamma \left[\right(n-1)\gamma +1]}{\Gamma \left[\right(n-1)\gamma +1]\Gamma \left[\right(n-2)\gamma +1]}{\varphi }^{(n-2)\gamma }.\hfill \end{array}$$

(83b)

Replacing the expressions (Section 4.1) into (81), we get

$$\sum _{n=2}^{\infty }{a}_n\frac{\Gamma [n\gamma +1]}{\Gamma \left[\right(n-2)\gamma +1]}{\varphi }^{(n-1)\gamma }+A\sum _{n=1}^{\infty }{a}_n\frac{\Gamma [n\gamma +1]}{\Gamma \left[\right(n-1)\gamma +1]}{\varphi }^{(n-1)\gamma }+B_{(\alpha ,\gamma )}\sum _{n=0}^{\infty }{a}_n{\varphi }^{n\gamma }=0.$$

(84)

Now, taking $\ell =n-1$ into the first and second terms, and $n=\ell$ into the third term of (84), we have

$$\sum _{\ell =1}^{\infty }{a}_{\ell +1}\frac{\Gamma \left[\right(\ell +1)\gamma +1]}{\Gamma \left[\right(\ell -1)\gamma +1]}{\varphi }^{\ell \gamma }+A\sum _{\ell =0}^{\infty }{a}_{\ell +1}\frac{\Gamma \left[\right(\ell +1)\gamma +1]}{\Gamma [\ell \gamma +1]}{\varphi }^{\ell \gamma }+B_{(\alpha ,\gamma )}\sum _{\ell =0}^{\infty }{a}_{\ell }{\varphi }^{\ell \gamma }=0.$$

(85)

Shifting one place in the second and third summations, we have

$$\begin{array}{cc}\hfill \sum _{\ell =1}^{\infty }{a}_{\ell +1}\frac{\Gamma \left[\right(\ell +1)\gamma +1]}{\Gamma \left[\right(\ell -1)\gamma +1]}{\varphi }^{\ell \gamma }+& A\frac{\Gamma [\gamma +1]}{\Gamma \left[1\right]}{a}_1+A\sum _{\ell =1}^{\infty }{a}_{\ell +1}\frac{\Gamma \left[\right(\ell +1)\gamma +1]}{\Gamma [\ell \gamma +1]}{\varphi }^{\ell \gamma }\hfill \\ \hfill & +B_{(\alpha ,\gamma )}{a}_0+B_{(\alpha ,\gamma )}\sum _{\ell =1}^{\infty }{a}_{\ell }{\varphi }^{\ell \gamma }=0.\hfill \end{array}$$

(86)

From last expression (86), we get $(s\ne 0)$

$$a_1=-\frac{B_{(\alpha ,\gamma )}}{A\Gamma (\gamma +1)}=-\frac{\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}}{\Gamma [s+1]\Gamma [\gamma +1]}{a}_0,$$

(87)

and the recurrence relationships between the parameters $a_{\ell }$, is

$$a_{\ell +1}=-\frac{\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}\Gamma [\ell \gamma +1]\Gamma [(\ell -1)\gamma +1]}{\Gamma [(\ell +1)\gamma +1]\left\{\Gamma [s+1-\gamma ]\Gamma [\ell \gamma +1]+\Gamma [s+1]\Gamma \left[\right(\ell -1)\gamma +1]\right\}}{a}_{\ell },\forall \ell \ge 1.$$

(88)

Some terms of this relation are

$$\begin{array}{cc}\hfill a_1& =-\frac{\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}}{\Gamma [s+1]\Gamma [\gamma +1]}{a}_0,\hfill \\ \hfill a_2& =\frac{{\left(\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}\right)}^2}{\Gamma [s+1]\Gamma [2\gamma +1]\left(\Gamma [s+1]+\Gamma [s+1-\gamma ]\Gamma [\gamma +1]\right)}{a}_0,\hfill \\ \hfill a_3& =-\frac{\Gamma [\gamma +1]}{\Gamma [s+1]\Gamma [3\gamma +1]\left(\Gamma [s+1-\gamma ]\Gamma [2\gamma +1]+\Gamma [s+1]\Gamma [\gamma +1]\right)}\times \hfill \\ \hfill & \left(\frac{{\left(\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}\right)}^3}{\left(\Gamma [s+1]+\Gamma [s+1-\gamma ]\Gamma [\gamma +1]\right)}\right)a_0,\hfill \\ \hfill a_4& =\frac{\Gamma [\gamma +1]\Gamma [2\gamma +1]}{\Gamma [s+1]\Gamma [4\gamma +1]\left(\Gamma [s+1-\gamma ]\Gamma [3\gamma +1]+\Gamma [s+1]\Gamma [2\gamma +1]\right)}\times \hfill \\ \hfill & \left(\frac{{\left(\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}\right)}^4}{\left(\Gamma [s+1\gamma ]\Gamma [2\gamma +1]+\Gamma [s+1]\Gamma [\gamma +1]\right)\left(\Gamma [s+1]+\Gamma [s+1-\gamma ]\Gamma [\gamma +1]\right)}\right)a_0,\hfill \\ \hfill ⋮\end{array}$$

(89)

Then, the solution of the fractional equation (81) has the form

$$\begin{array}{ccc}\hfill {\mathcal{C}}_{s,\alpha ,\gamma }& =& a_0\left[1-\frac{\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}}{\Gamma [s+1]\Gamma [\gamma +1]}{\varphi }^{\gamma }\right.\hfill \\ & & \left.+\frac{{\left(\Gamma [s+1-\gamma ]B_{(\alpha ,\gamma )}\right)}^2}{\Gamma [s+1]\Gamma [2\gamma +1]\left(\Gamma [s+1]+\Gamma [s+1-\gamma ]\Gamma [\gamma +1]\right)}{\varphi }^{2\gamma }+\dots \right].\hfill \end{array}$$

(90)

For the Dust-like scenario (see Table 2), $\alpha \to \infty$ and $\gamma =\frac{1}{2}$, then $B_{(\infty ,\frac{1}{2})}=\frac{{\mu }^2}{24\hslash }$. The solution associated with this fractional differential equation is given in fractional series form by,

$$\begin{array}{ccc}\hfill {\mathcal{C}}_{s,\to \infty ,\frac{1}{2}}& =& a_0\left[1-\frac{2\Gamma [s+\frac{1}{2}]B_{(\infty ,\frac{1}{2})}}{\Gamma [s+1]\sqrt{\pi }}{\varphi }^{\frac{1}{2}}+\frac{2{\left(\Gamma [s+\frac{1}{2}]B_{(\infty ,\frac{1}{2})}\right)}^2}{\Gamma [s+1](2\Gamma [s+1]+\Gamma [s+\frac{1}{2}]\sqrt{\pi })}\varphi \right.\hfill \\ & & \left.-\frac{2{\left(2\Gamma [s+\frac{1}{2}]B_{(\infty ,\frac{1}{2})}\right)}^3}{3\sqrt{\pi }\Gamma [s+1](2\Gamma [s+\frac{1}{2}]+\Gamma [s+1]\sqrt{\pi })(2\Gamma [s+1]+\Gamma [s+\frac{1}{2}]\sqrt{\pi })}{\varphi }^{\frac{3}{2}}+\cdots \right],\hfill \end{array}$$

(91)

where we employed $\Gamma \left[\frac{3}{2}\right]=\frac{\sqrt{\pi }}{2}$ and $\Gamma \left[\frac{5}{2}\right]=\frac{3\sqrt{\pi }}{4}$.

For the radiation stage, $\alpha =2$ and $\gamma =\frac{2}{3}$, then $B_{(2,\frac{2}{3})}=\frac{\sqrt[3]{p_{\varphi }}{\mu }^2}{18{\hslash }^{\frac{4}{3}}}$, the solution for the fractional differential equation is

$$\begin{array}{ccc}\hfill {\mathcal{C}}_{s,2,\frac{2}{3}}& =& a_0\left[1-\frac{3\Gamma [s+\frac{1}{3}]B_{(2,\frac{2}{3})}}{2\Gamma [s+1]\Gamma \left[\frac{2}{3}\right]}{\varphi }^{\frac{2}{3}}+\frac{{\left(3\Gamma [s+\frac{1}{3}]B_{(2,\frac{2}{3})}\right)}^2}{4\Gamma [s+1]\Gamma \left[\frac{4}{3}\right]\left(3\Gamma [s+1]+2\Gamma [s+\frac{1}{3}]\Gamma \left[\frac{2}{3}\right]\right)}{\varphi }^{\frac{4}{3}}\right.\hfill \\ & & \left.-\frac{\frac{2}{3}\Gamma \left[\frac{2}{3}\right]{\left(3\Gamma [s+\frac{1}{3}]B_{(2,\frac{2}{3})}\right)}^3}{2\Gamma [s+1]\left(2\Gamma [s+\frac{1}{3}]\Gamma \left[\frac{4}{3}\right]+\Gamma [s+1]\Gamma \left[\frac{2}{3}\right]\right)\left(3\Gamma [s+1]+2\Gamma [s+\frac{1}{3}]\Gamma \left[\frac{2}{3}\right]\right)}{\varphi }^{\frac{8}{3}}+\cdots \right],\hfill \end{array}$$

(92)

with $\Gamma \left[\frac{2}{3}\right]=1.35412$ and $\Gamma \left[\frac{4}{3}\right]=0.89298$.

We are going to present the graphical behaviour of the wave function for the Dust-like case, in which the solution is constrained to the variables $\Omega$ and $\varphi$. This means we are going to shrink the directions ${\beta }_{+}$ and ${\beta }_{-}$. So, the wave function takes the form

$$\begin{array}{cc}\hfill \Psi (\Omega ,{\beta }_{+},{\beta }_{-},\varphi )& =e^{\frac{Q\Omega }{2}}\left[C_1{K}_{\nu }\left(\frac{\rho }{3\hslash (1-\gamma )}{e}^{3(1-\gamma )\Omega }\right)\right]\times \hfill \\ \hfill & \left[1-a_1{\varphi }^{\frac{1}{2}}+a_2\varphi -a_3{\varphi }^{\frac{3}{2}}+a_4{\varphi }^2-a_5{\varphi }^{\frac{5}{2}}+a_6{\varphi }^3-a_7{\varphi }^{\frac{7}{2}}+a_8{\varphi }^4+\dots \right].\hfill \end{array}$$

(93)

By restraining ourselves to the values of $\nu =\frac{\sqrt{Q^2+4{\rho }_1^2}}{6(1-\gamma ))}$, $Q=10,6,2,1.6$, $\rho =\frac{1}{2}$, $\gamma =\frac{1}{2}$, $s=1$, ${\rho }_1=0.1$ and $C_1=1$, we see that the wave function ((93)) can be rewritten as

$$\begin{array}{ccc}\hfill {\Psi }^2(\Omega ,\varphi )& =& e^{Q\Omega }{K}_{\nu }^2\left(\frac{2}{3}{e}^{\frac{3\Omega }{2}}\right)\left[1-\frac{1}{24}{\varphi }^{1/2}+\frac{\sqrt{\pi }}{576(4+\pi )}\varphi -\frac{2\sqrt{\pi }}{41472(4+\pi )}{\varphi }^{3/2}\right.\hfill \\ & & +\frac{{\pi }^{\frac{3}{2}}}{663552(8+3\pi )(4+\pi )}{\varphi }^2-\frac{{\pi }^{\frac{3}{2}}}{69672960(8+3\pi )(4+\pi )}{\varphi }^{\frac{5}{2}}\hfill \\ & & +\frac{{\pi }^{\frac{5}{2}}}{334430208(8+3\pi )(4+\pi )(32+15\pi )}{\varphi }^3\hfill \\ & & -\frac{{\pi }^{\frac{5}{2}}}{45649723392(8+3\pi )(4+\pi )(32+15\pi )}{\varphi }^{\frac{7}{2}}\hfill \\ & & {\left.+\frac{5{\pi }^{\frac{7}{2}}}{208684449792(8+3\pi )(4+\pi )(32+15\pi )(192+105\pi )}{\varphi }^4\right]}^2,\hfill \end{array}$$

(94)

where we have taken the cut-off order in ${\varphi }^4$ and the a’s parameter are read from (89). In the following, we present some plots of the probability density of the wave function, including the factor ordering parameter Q and particular values in the parameter $\rho$, ${\rho }_1$ and the particular value to the ordering parameter s=1. In all of them we observe that for any value of Q, the probability density decays with respect to the scale factor, but has a different evolution in the scalar field. For small Q’s, the quantum universe has considerable existence in the evolution with respect to the scale factor and then decays. On the other hand, for large Q’s, this interval is small. What we can say about the evolution of the scalar field is that at small Q’s, the scalar field appears faster than for large Q’s, which enters late, but has existed forever.

Figure 3. Probability density (94) of the universe dominated by Dust era, in this stage of the universe shows that the probability density has a decay in $\Omega$ and exhibits considerable growth for certain values of $\varphi$. The plots have the parameters $\rho =0.5$, $\gamma =\frac{1}{2}$, ${\rho }_1=0.1$.

Figure 3. Probability density (94) of the universe dominated by Dust era, in this stage of the universe shows that the probability density has a decay in $\Omega$ and exhibits considerable growth for certain values of $\varphi$. The plots have the parameters $\rho =0.5$, $\gamma =\frac{1}{2}$, ${\rho }_1=0.1$.

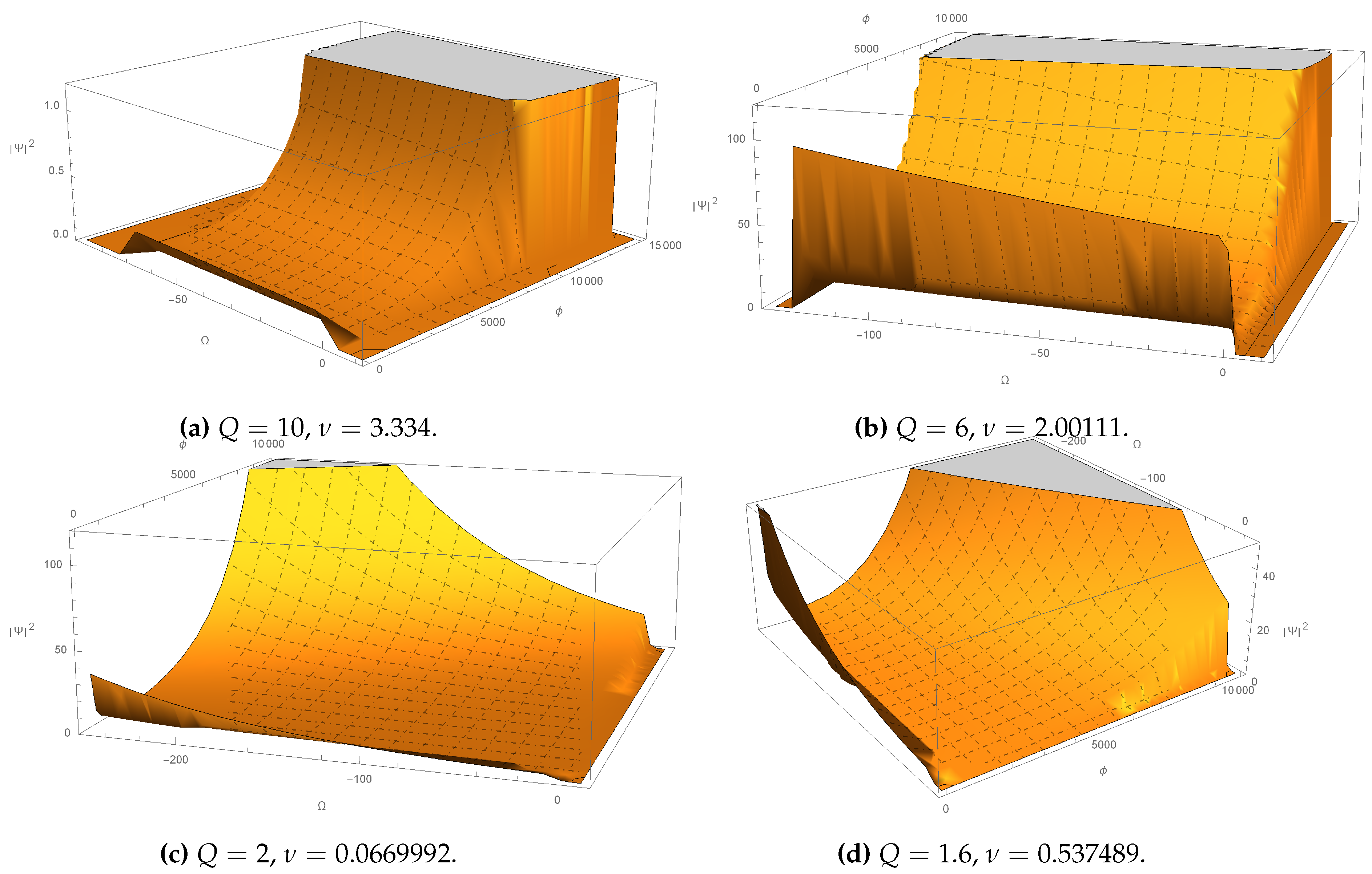
5. Conclusions

Unlike the previous work [37], in the present paper we employed a barotropic equation with perfect fluid for energy-momentum tensor in the K-essence scalar field into the Lagrangian and Hamiltonian formalism, obtaining the momentum of a scalar field with fractional numbers, while the momentum of the scale factor appears in the usual way. We obtained the classical solutions for different scenarios in the universe, employing different times $(t,T(\tau ),\tau )$. In the quantum scheme, we include the factor ordering problem, and we find a fractional differential equation for the scalar field with variable coefficients, which was solved using the fractional series expansion. With this in mind, we visualize two alternatives in our analysis; the first one is within the traditional expectation over the behaviour of the probability density, that the best candidates for quantum solutions are those that have a damping behaviour with respect to the scale factor, appearing in all scenarios under our study, without saying anything about the scalar field. The other scenario is when we keep the scale factor, and we consider the values of the scalar field as significant in the quantum regime, appearing in various scenarios in the behaviour of the universe; mainly in those where the universe has a huge behaviour, for example, in the actual epoch, where the scalar field appears as background.

In other words, the interpretation of the probability density of the the unnormalized wave function is given, when we demand that $\Psi$ does not diverge when the scale factor A (or $\Omega$) goes to infinity, and the scalar field is arbitrary. However, the evolution with the scalar field is important in this class of theory and others, as it appears in some stages of the evolution of our Universe.

We briefly illustrate the main results of this work.

• Using the K-essence formalism in a general way, applied to anisotropic Bianchi type I cosmological model, we found the Hamiltonian density in the scalar field momenta raised to power with non-integers, which produces in the quantum scheme a fractional differential equation in a natural way. We include the factor ordering problem in both variables $(\Omega ,\varphi )$ and its momenta $({\Pi }_{\Omega },{\Pi }_{\varphi })$, with the order $\beta =\frac{2\alpha }{2\alpha -1}$, where $\alpha \in (-1,\infty )$, and it was solved in a general way, we include two particular scenarios of our Universe.
• We found the solution in the classical scheme employing two gauge, $N=24e^{3\Omega }$, for two forms of the function $f\left(\varphi \right)$ in the time t; however, when we let the Lagrange multiplier N, we need to employ a transformed time $T\left(\tau \right)$ for solving the classical equation, and only in the dust era, we recover the gauge time $\tau$.
• In the quantum regime, when we include the factor ordering problem, the fractional differential equation in the scalar field appears with variable coefficients, and it was necessary to use the fractional series expansion to solve it in a general way.
• In one of our analysis presented on the probability density, we consider the values of the scalar field as significant in the quantum regime, appearing in various scenarios in the behaviour of the universe; mainly in those where the universe has a huge behaviour, for example, in the actual epoch, where the scalar field appears as a background, the quantum regime appears with big values, but it presents a moderate development in other scenarios with different ordering parameters Q and s.