Prerpints.org logo
Preprint
Article

Classification of Skin Lesion Images Using Artificial Intelligence Methodologies through Radial FourierMellin, Hilbert Transforms Signatures

Altmetrics

Downloads

95

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts
Abstract
Eight lesions were analyzed using some algorithms of Intelligence Artificial: basal cell carcinoma (BCC), squamous cell carcinoma (SCC), melanoma (MEL), actinic keratosis (AK), benign keratosis (BKL), dermatofibromas (DF), melanocytic nevi (NV), and vascular lesions (VASC). This manuscript presents the possibility of using concatenated signatures (instead of images) obtained from different integral transforms, such as Fourier, Mellin, and Hilbert, to classify skin lesions. Eleven other Artificial Intelligence models were applied so that eight skin lesions could be classified by analyzing the particular signatures of each lesion. The database was randomly divided into 80%–20% for the training and test datasets images, respectively. The metrics that are being reported are accuracy, sensitivity, specificity, and precision. Each case was repeated 30 times to avoid bias, according to the central limit theorem in this work, and the average and ±standard deviation were reported. Although all the results were very satisfactory, the best average mark for the eight lesions analyzed was obtained using the Subspace KNN model, where the metrics for the test were 99.98% accuracy, 99.96% sensitivity, 99.99% specificity, and 99.95% precision.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The skin is the largest organ in the body. It covers and protects the body externally. Its condition and appearance show the state of health and well-being of a person; however, due to exposure to the environment, specific skin injuries can occur, which vary in size and shape. Different types of skin diseases vary according to the symptoms. The presence of any mild condition can lead to severe complications and even death. Skin cancer is a serious disease, one of the most common carcinomas. It is mainly classified into basal cell carcinoma (BCC), squamous cell carcinoma or epidermoid carcinoma (SCC), and melanoma (MEL) [1,2,3,4]. BCC is the most frequent skin cancer in the population worldwide, and its growth is slow. It can grow and destroy the skin. It is generally observed as a flat or raised lesion; its color is reddish [1,5,6,7]. The SSC is a malignant tumor that appears in red spots, with raised growths like warts; it is the second most common skin cancer [1,2]. Melanoma is the most aggressive skin cancer, appearing as a pigmented lesion, usually beginning on normal skin as a new, small, pigmented growth [2]. Other common diseases are actinic keratosis (AK), benign keratosis (BKL), dermatofibromas (DF), melanocytic nevi (NV), and vascular lesions (VASC), among others.
Actinic keratosis occurs due to frequent exposure to ultraviolet rays from the sun or tanning beds; it usually appears as small rough spots and presents color variations. Some areas are generally malignant, causing squamous cell carcinoma [7,8,9]. Seborrheic keratoses or benign keratoses are benign tumors that frequently occur in the geriatric population. This type of tumor consists of a brown or brown spot or lesion. In some cases, it is often confused with basal cell carcinoma or melanoma [10,11]. Dermatofibroma is a benign skin lesion; it appears as a slow-growing papule, and its color varies from light to dark brown, purple to red, or yellowish. Its clinical diagnosis is simple; however, sometimes it is difficult to differentiate it from other tumors, such as malignant melanoma [12,13]. Melanocytic nevi or moles are the most common benign lesions with smooth, flat, or palpable surfaces. They form as a brown spot or freckle that varies in size and thickness [14,15]. Vascular lesions are disorders of the blood vessels. They become evident on the skin’s surface, forming red structures, dark spots, or scars so that they present an aesthetic problem. Some VASCs develop over time due to environmental changes, temperature, poor blood circulation, or sensitive skin [16,17]. The skin can warn of a health problem; its care is critical in the physical and emotional aspects. Different conditions can affect the skin; some are present at birth, and others are acquired throughout life. Some lesions may have similar characteristics, making differentiating them from the most common malignant neoplasms difficult. Skin diseases are a significant health problem. New digital tools and technologies based on Artificial Intelligence (AI) have been developed for detecting and treating diseases due to the ability to analyze large amounts of data. The latest developments based on Artificial Intelligence tools help identify health problems in the early stages. These developments are also based on image processing, where the recognition of visual patterns through images represents a potential in the face of the failure of the human eye. Applying algorithms based on Artificial Intelligence allows the development of non-invasive tools in the health area.
In recent decades, Machine Learning (ML) techniques have been reached impressive applications in many research areas and still growing. Since many studies about medical imaging are focused on automating skin lesion identification from dermatological images to provide an adequate diagnosis and treatment to patients, ML techniques can be a powerful tool to detect melanoma automatically, quickly, and reliably.
Some ML techniques, such as convolutional neural networks (CNNs), are the most popular due to represent the closest technique to the learning process of human vision. The CNNs are based on the mathematical operator of the convolution between the image and filters to extract information. Even though CNNs have provided successful results for image classification, their high computational cost, as well the non-invariance property under rotation, scale, and translation of the convolution operation, makes the CNNs an ineffective tool in practice to implement in the identification or classification of some images, especially for those corresponding to skin lesions where vital information could be lost due to low contrast that exists, on many occasions, between the lesion and healthy skin and therefore during the segmentation carried out by some filters, information on the lesion is not extracted correctly [18,19]. In this context, other ML techniques, such as Support Vector Machine (SVM), k--nearest neighbors (KNN), or ensemble classifiers, have shown acceptable performance [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56].
The KNN method classifies the data X by finding the closet neighbor among the training data points X ’ . It has been used in other works for skin lesion classification: In reference [20] used KNN, SVM, decision trees, Naïve Bayes, ensemble tree, and single hidden layer extreme learning machine (ELM), for cancer classification. In reference [21] evaluated KNN, SVM, and other machine-learning methods for the multiclass classification of skin lesions. In reference [22] implemented KNN, SVM, and other methods for skin cancer lesions by using prism- and segmentation-based fractal signatures. In reference [23] worked with KNN on a descriptor made by skin surface fractal dimension and relevant color area features. In reference [24] used KNN alongside a proposed optimal feature selection through an entropy-controlled approach. In reference [25] used KNN and SVM with the Stacking Ensemble Method based on the Meta-Learning algorithm to classify skin lesions as melanoma, dysplastic and benign. In reference [26] classified ten skin lesions and compared hierarchical KNN and deep net classifiers. In reference [27] implemented KNN and SVM and a decision tree for classification. They also worked with the Dull Razor algorithm [28] and median filtering for hair removal. In reference [29] worked with texture features based on fractional Poisson to classify melanocytic and non-melanocytic lesions. In reference [30] used KNN, SVM, and decision trees to pre-classify the skin lesions as normal, abnormal, and melanoma. In reference [31] implemented KNN and SVM to classify skin lesion asymmetry. In reference [32] used hierarchical KNN to organize ten classes of skin lesions. In reference [33] compared KNN, SVM, and a feed feed-forward backpropagation Neural Network using 19 features, which include area, perimeter, circularity, border irregularity, principal axis, minor axis, color variegation, mean intensities of RGB plane separately, entropy, energy, contrast, homogeneity, correlation, eccentricity, and area difference. In reference [34] reviewed the procedures for classifying pigmented skin lesions from macroscopic images. In reference [35] used hierarchical KNN for non-melanoma classification. In reference [36] designed a system to run on a mobile device with a camera.
The SVM method aims to find the optimal separating hyperplane that separates various classes. It has been widely used for skin lesion classification: In reference [27] classified ten different skin lesions. In reference [38] classified melanoma and non-melanoma. In reference [39] identified melanoma, seborrheic keratosis, and lupus Erythematosus using modified ABCD features. In reference [40] evaluated the SVM classifier and two convolutional neural networks. In reference [41] used SVM alongside morphological preprocessing and fractal-based feature extraction. In reference [42] applied the SVM classifier with the saliency-based segmentation method and feature selection by the entropy method after extraction of deep color and PHOG (Pyramid Histogram of Oriented Gradients) features to classify skin lesions. In reference [43] implemented SVM for multiclass classification using a saliency map constructed from the 2D blue channel. In reference [44] used the Aujol decomposition model for structure and texture identification, k-means segmentation, and four feature extraction methods to classify with SVM. In reference [45] used SVM alongside probabilistic distribution-based segmentation and entropy-based feature selection. In reference [46] implemented the color, texture, and Histogram of Oriented Gradients (HOG) feature and the Dull Razor hair removal method. In reference [47] combined the SVM classifier with segmentation-based image decomposition into texture and geometrical components. In reference [48] used SVM to classify Basal cell carcinoma and the benign nevus. In reference [49] implemented SVM for the classification step in a system that considers the estimated depth of skin lesions with a 3-D reconstruction. In reference [50] compared polynomial SVM, Radial Basis Function, and backpropagation Multy-layer Perceptron for the classification of Tinea Corporis, Pityriasis Versicolor, and Herpes Zoster. In reference [51] used SVM and a segmentation-based image decomposition into texture and geometrical components. In reference [52] used the Dull razor hair removal algorithm alongside active contours and watersheds for segmentation. In reference [53] implemented SVM to classify feature vectors in a 6D Riemannian manifold.
In reference [54] identify lesion feature vectors in a 4D Riemannian manifold. In reference [55] used SVM and proposed a set of high-level intuitive features (HLIF) to describe border irregularity from skin lesions.
Ensemble classifiers combine multiple classifiers to achieve a better performance than working with the classifiers individually. This method has also been used for skin lesion classification. As mentioned in reference [20] used ensemble trees alongside KNN, SVM, decision trees, Naïve Bayes, and a single hidden layer extreme learning machine (ELM). In reference [56] implemented KNN and SVN and ensemble classification using fractal-deep learning features. In [57] used the ensemble method to search optimal wavelet bases to maximize the classification quality.
Although SVM, KNN, and Ensemble classifiers were successfully implemented to classify skin lesions, a digital image under rotation, scaling, or translation was not considered. The application of the Fractional Radial Fourier Transform in pattern recognition for digital images is invariant to translation, scale, and rotation, and the results obtained to classify phytoplankton species showed a high level of confidence (greater than 90%) [58]. In this paper, we implemented the Hilbert mask on the Module of the Fourier-Mellin Transform to obtain the unique signature of the skin lesion called the Radial Fourier-Mellin signature. Also, we included as a signature the extraction of the Local Binary Pattern (LBP) image features. The classification task was obtained using KNN, SVM, and ensemble classifiers. Section 2 contains the description and image dataset pre-processing procedure and methods used to achieve its skin lesion classification. Section 3 presents the results using these supervised machine learning methods. In Section 4, we discuss the obtained results, and in Section 5, we incorporate the discussion of our research.

2. Materials and Methods

2.1. Image dataset

The images used in our study were obtained from the 2019 challenge Training data of the “International Skin Imaging Collaboration” (ISIC) [59]. This dataset consists of 25,331 digital images of 8 types of skin lesions. 3323 basal cell carcinoma (BCC) digital images, 628 digital images of squamous cell carcinoma (SCC), 4522 melanoma (MEL) digital images, 867 actinic keratosis (AK) skin lesion digital images, 2624 benign keratosis (BKL) skin lesion images as solar lentigo, seborrheic keratosis and lichen planus-like keratosis, 239 dermatofibroma (DF) digital skin lesion images, 12875 melanocytic nevus (NV) digital images and 253 images of vascular skin lesion (VASC). However, we proceeded to eliminate the skin lesions images that contained noise, such as hair, measurement artifacts, and other noise types that made it difficult to segment lesions. The image dataset debugged reduced the data to 9067 dermatologic skin lesions, where 6747 images are for NV, 1032 for MEL, 512 for BCC, 471 for BKL, 130 for VASC, 67 for DF, 62 for SCC, and 46 for AK. This dramatic reduction motivated us to include a data augmentation procedure resulting in 362,680 dermatologic skin lesion images, and we randomly selected images to classify using SVM, KNN, and ensemble classifiers machine-learning methodologies. To avoid classification bias, we homogenize the classes in the database using 1840 images for each type of skin lesion. Each of these 14,720 randomly selected image datasets was transformed into its Radial Fourier signatures and texture descriptors using the Hilbert transform.
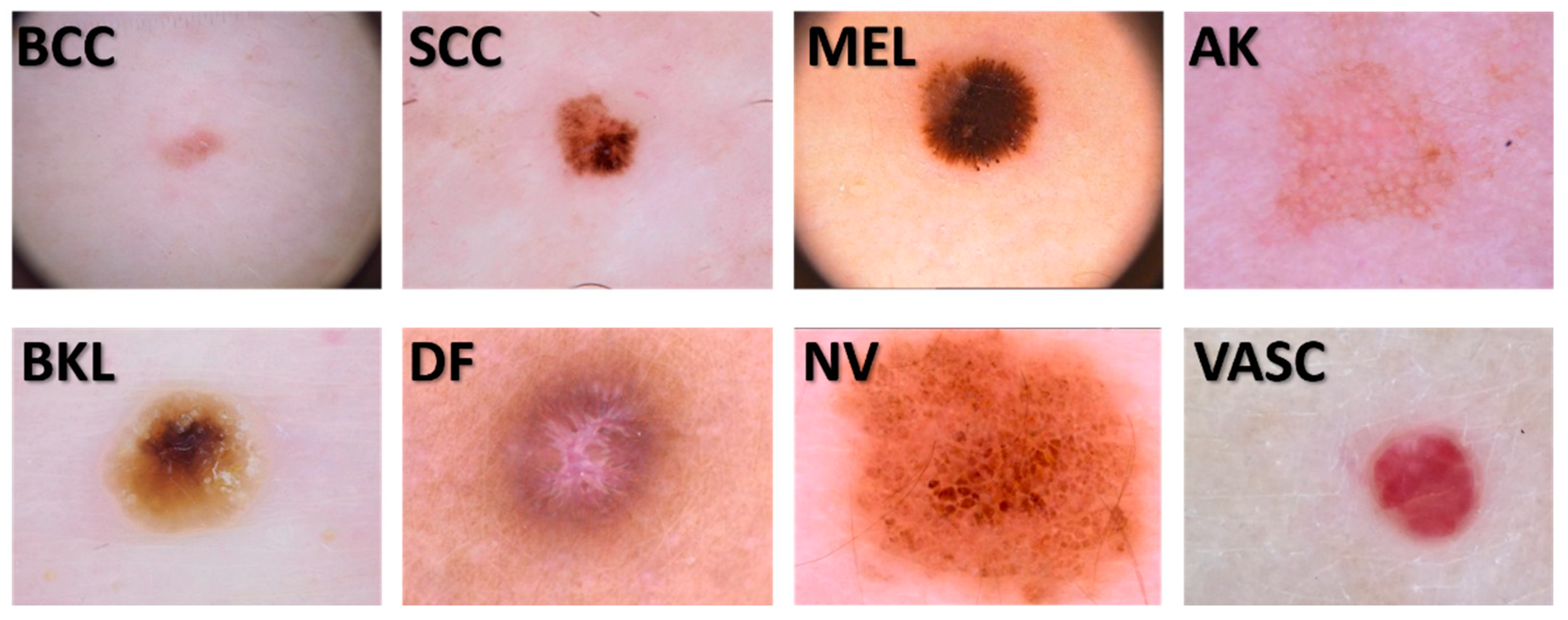
Preprints 85294 g001
Figure 1. Some digital skin lesion images of our dataset.
Figure 1. Some digital skin lesion images of our dataset.
Preprints 85294 g001

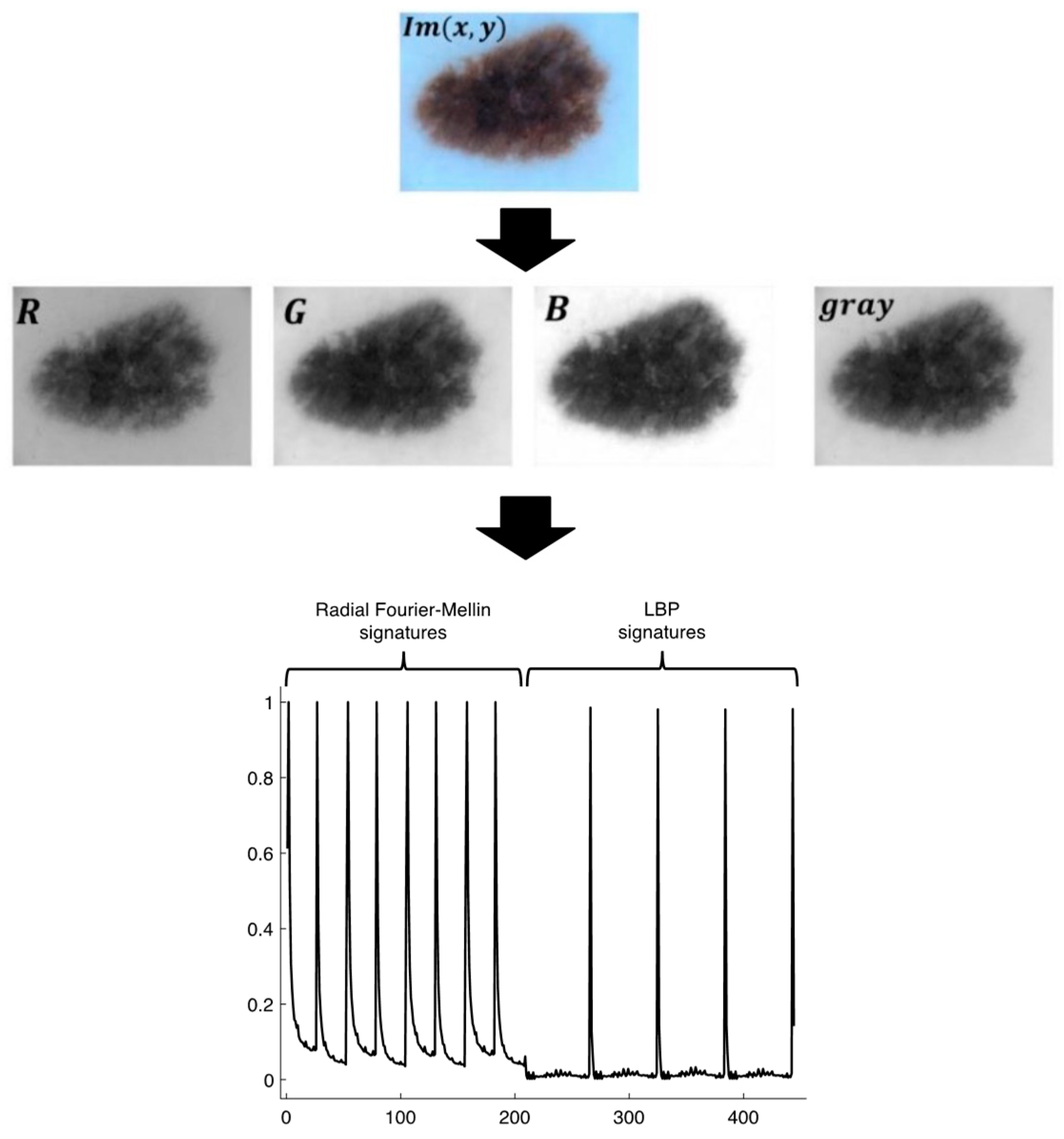
2.2. The signatures

We generated several signature vectors of each RGB channel and grayscale image using our data set (362,680) obtained through data augmentation. The data augmentation procedure considered five image scale percentages (100%, 95%, 90%, 85%, and 80%) and eight rotation angle values (45°, 90°, 135°, 180°, 225°, 270°, 315°, and 360°). These signatures or descriptors use invariance properties to the translation and scale of the modules of the Fourier Transform and the Mellin Transform, respectively. To include the invariant object rotation property, we used the Hilbert Transform. To calculate the unique signatures of the image, we sum the pixel value of each ring obtained after using the Hilbert masks as a filter. We incorporate the texture signatures or descriptors on the radial Fourier signatures previously generated. The process to obtain this one-dimensional skin lesion digital image representation or signature is shown in Figure 2. The original image ( I m ( x , y ) ) contains 3 matrix channels in RGB (Red, Green, and Blue channels). Thus, the picture was segmented into these three primary color channels to apply the Radial Fourier-Mellin method and the LBP image features extraction. Also, we considered the grayscale skin lesion digital image obtained by a weighted sum of RGB values defined by: 0.299R+0.587G+0.114B.

2.3. Radial Fourier-Mellin signatures through Hilbert transform

To generate the Radial Fourier signatures, first, the module of the Fourier-Mellin (FM) Transform of the RGB image channels and gray-scale skin digital image, named I m ( x , y ) , was obtained using the next equation [60,61].
| F M s , t | = ∬ 0 ∞ | F T [ I m ( x , y ) ] | x s − 1 y t − 1 d x d y = M | F T [ I m ( x , y ) ] |
where | F M s , t | is the module of the Mellin transform which give us a scale invariance of an object in the image necessary due that the skin lesion digital images were obtained from different distance lesion-camera. Thus, the lesion region is small for far lesion-camera distances, or the image contains a large lesion region for oppositive. The ( s , t ) represents the 2D coordinates transformed of x , y , pixel coordinates, on Mellin’s plane. Notice that these pixels coordinates x , y , are the corresponding to the module Fourier transform of the image ( | F T [ I m ( x , y ) ] | ) taking advantage of its translation invariance, so at this moment, the object (skin lesion) in the image is invariant to translation and scale.
Now, using the Hilbert Transform, also we achieve that the skin lesion in the image be invariant to rotation. The Hilbert Transform of the image is given by [58,62,63,64,65]:
F H r [ I m ( x , y ) ] = e i p θ F T I m x , y = e i p θ F u , v
where p is the order of the radial Hilbert transform, θ is the angle on frequency domain/space of the pixel coordinates in the image ( x , y ) after being transformed to Fourier plane coordinates as ( u , v ) . Therefore, this angle is determined by θ = a c o s ⁡ ( u / u 2 + v 2 ) . Then, using the Euler’s formula, we calculated the binary ring masks of the RGB channels and gray-scale skin lesion digital image, using both, the real ( H R ) and imaginary ( H I ) part of the radial Hilbert transform of the image as follows [58,62,63,64,65].
H R = R e [ H r u , v ] = 1 ,   i f   s i n ⁡ = p θ > 0       0 ,     o t h e r w i s e
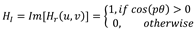
Preprints 85294 i001
The binary ring masks obtained above were applied to filter the skin lesion digital image processed previously (using the module of the Fourier-Mellin transform). The results require the sum of the values in the pixels of each ring, obtaining two unique signatures of each skin gray-scale lesion image ( S g r a y H R   a n d   S g r a y H I ) and its RGB channels given by: S R H R , S R H I , S G H R , S G H I , S B H R and S B H I . To include texture descriptor, we used the extractLBPFeatures MATLAB’s function to obtain the LBP of image features of each RGB and gray-scale image LPBR, LPBG, LPBB and LPBgray. We concatenate these signatures to get 444 components of one-dimensional objects/signatures.

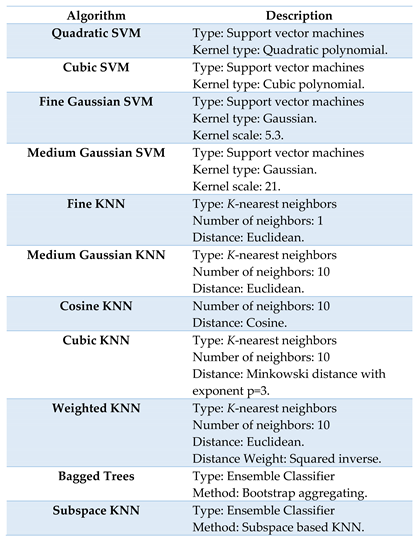
2.4. Signature Classification

We generated radial Fourier and texture signature vectors of each RGB channel and gray-scale dermatological digital image in our dataset. These descriptors are invariant to scale, rotation, illumination, and noise on the image to analyze, so a data augmentation procedure considering scale and rotation was included. To homogenize the classes in the database, we used 1840 images for each type of skin lesion. The signature classification was performed with support vector machines (SVM), K-nearest neighbors (KNN), and ensemble classifiers.
Variations of these methods were implemented. In the case of SVM, four different Kernels were used [66]: Quadratic SVM works by implementing a polynomial of degree=2 as Kernel, while the Cubic SVM method uses a polynomial of degree=3. The Fine Gaussian SVM method uses a Gaussian Kernel with a Kernel scale=5.3. The Medium Gaussian SVM works with a wider Gaussian Kernel using a Kernel scale=21.
Also, five KNN variations were explored [67,68]: Fine KNN works using the Euclidean distance and a k=1 neighbor. The Medium KNN algorithm also uses Euclidean distance, but the number of neighbors is k=10. The Cosine KNN algorithm implements the Cosine distance with k=10 neighbors. The Minkowski distance with exponent p=3 is used for the Cubic KNN method. For the Weighted KNN, the same length and number of neighbors were used as in the Medium KKN, but for this case, the neighbors are weighted based on the square inverse of the distance.
Finally, two Ensemble Classifiers were used. These classifiers aggregate the predictions of a group of predictors to get better forecasts than the best individual predictor [69]. The Bagged Trees method implements decision trees using bootstrap aggregation (Bagging) [70]. The Subspace KNN method uses the Random Subspace Method for KNN classification [71,72].
In total 11 algorithms were explored, shown in Table 1.
MATLAB 2022b was used to carry out the classification process, using the same data set for all 11 algorithms. The data set was balanced by selecting 1840 signatures from each skin lesion. Therefore, the data set consists of 14,720 Signatures.

3. Results

To measure the performance of each algorithm, the data set was split by selecting randomly 80% of the data as the training set and 20% as the test set. This process was performed 30 times, and the mean ±standard deviation was calculated for accuracy, sensitivity, specificity, and precision [69] for each class C i , which are given by
a c c u r a c y C i = T P i + T N i T P i + T N i + F P i + F N i
s e n s i t i v i t y C i = T P i T P i + F N i      
s p e c i f i c i t y C i = T N i T N i + F P i    
p r e c i s i o n C i = T P i T P i + F P i    
where
T P i : true positives for class i .
T N i : true negatives for class i .
F P i : false positives for class i .
F N i : false negatives for class i .
Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12 show the results for each algorithm.

4. Discussion

The results obtained from this new methodology for classifying skin lesions using eleven artificial intelligence algorithms using concatenated signatures were promising. This methodology proposes using several integral transforms: Fourier, Mellin, and Hilbert, along with the LBP method of texture features, to obtain a series of concatenated signatures for each lesion. The concatenation of the signatures has been carried out using the three-color spaces (RGB) and the grayscale image to extract as much information as possible. This methodology works quite well for those images of skin lesions that lack noise. It is important to note that the concatenation of the signatures was achieved using the three-color spaces (RGB) and the gray image to extract as much information as possible. This allows the artificial intelligence algorithms to detect the most subtle differences between the lesions. The eleven tables show excellent results in the accuracy, sensitivity, specificity, and precision metrics of the method, both for the training set and the test set. The group of lesions used to test this methodology was absent in the set of images used to train the various artificial intelligence algorithms. For both the training and test sets, the algorithms were run 30 times, thus obtaining an average and a ±standard deviation for each case. When comparing the best classifier of the eleven presented in this work for this class of images, it is observed that the classifier with the best performance was that of Subspace KNN when the best results for the test set were analyzed. The same happens when we compare the metrics regarding the training of the various classifiers. The other ten remaining classifiers also performed well. Using these classifiers where the input is concatenated signatures is an excellent contribution to this work. This work aligns with previous studies on the classification of skin lesions using artificial intelligence algorithms. For example, [73] presented a dataset of 2241 histopathological images from 2008 to 2018. They employed two deep learning architectures, VGG19 and ResNet50. The results showed a high accuracy in distinguishing melanoma from nevi, with an average F1 score of 0.89, sensitivity of 0.92, specificity of 0.94, and AUC of 0.98. In reference [74] presented an automated skin lesion detection and classification technique utilizing an optimized stacked sparse autoencoder (OSSAE) based feature extractor with backpropagation neural network (BPNN), named the OSSAE-BPNN technique, reaching a testing accuracy of 0.947, a sensitivity of 0.824, a specificity of 0.974 and a precision of 0.830. These studies demonstrate the potential of artificial intelligence algorithms for the classification of skin lesions, and this work furthers our understanding of how to achieve the best results. This methodology is a breakthrough in classifying skin lesions using artificial intelligence algorithms and concatenated signatures. It is a promising development in medical diagnosis and has the potential to revolutionize the way medical professionals diagnose and treat skin lesions. It is worth mentioning that concatenated signatures are not just for classifying skin lesions; they can be used for other medical imaging tasks, such as identifying tumors or categorizing brain scans. Furthermore, this technique can be applied to other areas, such as facial recognition or the categorization of satellite images.

Author Contributions

Methodology, L.F.L.-A, E.G.-R., J.A.-B. and E. G.-F.; Software, L.F.L.-A, E.G.-R., J. A.-B. and E.G.-F.; Validation, J.A.-B., E. G.-F., L.F. L.-A. and C.A.V.-B.; Data curation, E. G.-R. and C. A. V.-B.; Visualization, E.G.-R. and J.A.-B.; Supervision, J.A.-B.; Project administration, J.A.-B.; Funding acquisition, J.A.-B.; All authors have read and agreed to be published version of the manuscript.

Funding

This research was funded by Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE), Baja California, grant number F0F181.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

Luis Felipe López-Ávila hold a postdoc in Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE) supported by CONAHCYT with postdoc application number 4553917, CVU 693156, Clave: BP-PA-20230502163027674-4553917. Claudia Andrea Vidales-Basurto hold a postdoc in Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE) supported by CONAHCYT with postdoc application number 2340213, CVU 395914, Clave: BP-PA-20220621205655995-2340213.

Conflicts of Interest

The authors declare no conflict of interest related to this study.

References

  1. Lomas, A.; Leonardi-Bee, J.; Bath-Hextall, F. A systematic review of worldwide incidence of nonmelanoma skin cancer. Br J Dermatol. 2012, 166, 1069–1080. [Google Scholar] [CrossRef] [PubMed]
  2. Gordon, R. Skin cancer: an overview of epidemiology and risk factors. Semin Oncol Nurs. 2013, 29, 160–169. [Google Scholar] [CrossRef]
  3. Cameron, M.C.; Lee, E.; Hibler, B.P.; Barker, C.A.; Mori, S.; Cordova, M.; Nehal, K.S.; Rossi, A.M. Basal cell carcinoma: epidemiology; pathophysiology; clinical and histological subtypes; and disease associations. J Am Acad Dermatol. 2019, 80, 303–317. [Google Scholar] [CrossRef]
  4. Zhang, W.; Zeng, W.; Jiang, A.; He, Z.; Shen, X.; Dong, X.; Feng, J.; Lu, H. Global, regional and national incidence, mortality and disability-adjusted life-years of skin cancers and trend analysis from 1990 to 2019: An analysis of the Global Burden of Disease Study 2019. Cancer Med. 2021, 10, 4905–4922. [Google Scholar] [CrossRef] [PubMed]
  5. Born, L.J. , Khachemoune, A. Basal cell carcinosarcoma: a systematic review and reappraisal of its challenges and the role of Mohs surgery. Arch Dermatol Res, 2023, 315, 2195–2205. [Google Scholar] [CrossRef]
  6. Naik, P.P.; Desai, M.B. Basal Cell Carcinoma: A Narrative Review on Contemporary Diagnosis and Management. Oncol Ther, 2022, 10, 317–335. [Google Scholar] [CrossRef]
  7. Reinehr, C.P.H.; Bakos, R.M. Actinic keratoses: review of clinical, dermoscopic, and therapeutic aspects. An Bras Dermatol. 2019, 94, 637–657. [Google Scholar] [CrossRef]
  8. Del Regno, L.; Catapano, S.; Di Stefani, A.; Cappilli, S.; Peris, K. A Review of Existing Therapies for Actinic Keratosis: Current Status and Future Directions. Am J Clin Dermatol, 2022, 23, 339–352. [Google Scholar] [CrossRef]
  9. Casari, A.; Chester, J.; Pellacani, G. Actinic Keratosis and Non-Invasive Diagnostic Techniques: An Update. Biomedicines, 2018, 6, 1–12. [Google Scholar] [CrossRef]
  10. Opoko, U.; Sabr, A.; Raiteb, M.; Maadane, A.; Slimani, F. Seborrheic keratosis of the cheek simulating squamous cell carcinoma. Int J Surg Case Rep. 2021, 84. [Google Scholar] [CrossRef]
  11. Moscarella, E.; Brancaccio, G.; Briatico, G.; Ronchi, A.; Piana, S. Argenziano G. Differential Diagnosis and Management on Seborrheic Keratosis in Elderly Patients. Clin Cosmet Investig Dermatol. 2021, 14, 395–406. [Google Scholar] [CrossRef]
  12. Jiahua, Xing.; Yi, Chen.; Liwu, Zheng.; Yan, Shao.; Yichi, Xu.; Lingli, Guo. Innovative combined therapy for multiple keloidal dermatofibromas of the chest wall: A novel case report. CJPRS, 2022, 4, 182–186. [CrossRef]
  13. Sofia, Endzhievskaya.; Chao-Kai, Hsu.; Hsing-San, Yang.; Hsin-Yu, Huang.; Yu-Chen, Lin.; Yi-Kai, Hong.; John, Y.W. Lee.; Alexandros, Onoufriadis.; Takuya, Takeichi,.; Julia, Yu-Yun, Lee.; Tanya, J. Shaw.; John, A.McGrath.; Maddy, Parsons. Loss of RhoE Function in Dermatofibroma Promotes Disorganized Dermal Fibroblast Extracellular Matrix and Increased Integrin Activation. JID 2023, 143, 1487–1497. [CrossRef]
  14. Park, S.; Yun, S.J. Acral Melanocytic Neoplasms: A Comprehensive Review of Acral Nevus and Acral Melanoma in Asian Perspective. Dermatopathology 2022, 9, 292–303. [Google Scholar] [CrossRef]
  15. Frischhut, N.; Zelger, B.; Andre, F.; Zelger, B.G. The spectrum of melanocytic nevi and their clinical implications. J Dtsch Dermatol Ges. 2022, 20, 483–504. [Google Scholar] [CrossRef]
  16. Hu, K.; Li, Y.; Ke, Z.; Yang, H.; Lu, C.; Li, Y.; Guo, Y.; Wang, W. History, progress and future challenges of artificial blood vessels: a narrative review. Biomater Transl. 2022, 28, 81–98. [Google Scholar] [CrossRef]
  17. Liu, C.; Dai, J.; Wang, X.; Hu, X. The Influence of Textile Structure Characteristics on the Performance of Artificial Blood Vessels. Polymers. 2023, 15, 1–24. [Google Scholar] [CrossRef]
  18. Folland, G.B. Fourier Analysis and Its Applications; American Mathematical Society: Providence, RI, USA, 2000; pp. 314–318. [Google Scholar]
  19. Al-masni, M.A.; Al-antari, M.A.; Choi, M.T.; Han, S.M.; Kim, T.S. Skin lesion segmentation in dermoscopy images via deep full resolution convolutional networks. Comput. Meth. Prog. Biomed. 2018, 162, 221–231. [Google Scholar] [CrossRef]
  20. Afza, F.; Sharif, M.; Khan, M.A.; Tariq, U.; Yong, H.-S.; Cha, J. Multiclass Skin Lesion Classification Using Hybrid Deep Features Selection and Extreme Learning Machine. Sensors. 2022, 22, 799. [Google Scholar] [CrossRef] [PubMed]
  21. Shetty, B.; Fernandes, R.; Rodrigues, A. P.; Chengoden, R.; Bhattacharya, S.; Lakshmanna, K. Skin lesion classification of dermoscopic images using machine learning and convolutional neural network. Scientific reports. 2022, 12, 1–11. [Google Scholar] [CrossRef]
  22. Camacho-Gutiérrez, J. A.; Solorza-Calderón, S.; Álvarez-Borrego, J. Multi-class skin lesion classification using prism- and segmentation-based fractal signatures. Expert Syst. Appl. 2022, 197. [Google Scholar] [CrossRef]
  23. Moldovanu, S.; Damian Michis, F.A.; Biswas, K.C.; Culea-Florescu, A.; Moraru, L. Skin Lesion Classification Based on Surface Fractal Dimensions and Statistical Color Cluster Features Using an Ensemble of Machine Learning Techniques. Cancers 2021, 13. [Google Scholar] [CrossRef]
  24. Afza, F.; Khan, M.A.; Sharif, M.; Saba, T.; Rehman, A.; Javed, M.Y. Skin Lesion Classification: An Optimized Framework of Optimal Color Features Selection. 2020 2nd International Conference on Computer and Information Sciences (ICCIS), Sakaka, Saudi Arabia, 2020. [CrossRef]
  25. Ghalejoogh, G.S.; Kordy, H.M.; Ebrahimi, F. A hierarchical structure based on Stacking approach for skin lesion classification. Expert Syst. Appl. 2020, 145. [Google Scholar] [CrossRef]
  26. Fisher, R.; Rees, J.; Bertrand, A. Classification of Ten Skin Lesion Classes: Hierarchical KNN versus Deep Net. in Medical Image Understanding and Analysis: 23rd Conference, MIUA 2019, Liverpool, UK, July 24-26, 2019, Proceedings. Communications in Computer and Information Science (CCIS), Springer 2020. 24 July. [CrossRef]
  27. Lynn, N. C.; Kyu, Z. M. Segmentation and Classification of Skin Cancer Melanoma from Skin Lesion Images. 18th International Conference on Parallel and Distributed Computing, Applications and Technologies (PDCAT), 2017. [CrossRef]
  28. DermWeb. Available online: http://www.dermweb.com/dull_razor/ (accessed on 7 April 1997).
  29. Al-abayechi, A.A.; Jalab, H.A.; Ibrahim, R.W. A classification of skin lesion using fractional poisson for texture feature extraction. Proceedings of the Second International Conference on Internet of things, Data and Cloud Computing 2017. [CrossRef]
  30. Ozkan, I.A.; Koklu, M. Skin Lesion Classification using Machine Learning Algorithms. IJISAE. 2017, 5, 285–289. [Google Scholar] [CrossRef]
  31. Chakravorty, R.; Liang, S.; Abedini, M.; Garnavi, R. Dermatologist-like feature extraction from skin lesion for improved asymmetry classification in PH2 database. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016. [Google Scholar] [CrossRef]
  32. Leo, C.D.; Bevilacqua, V.; Ballerini, L.; Fisher, R.B.; Aldridge, B.; Rees, J. Hierarchical Classification of Ten Skin Lesion Classes. In Proceedings of the SICSA Dundee Medical Image Analysis Workshop, Dundee, UK, 27 March 2015. [Google Scholar]
  33. Patil, P. P.; Patil, S. A.; Udupi, V. Detection and classification of skin lesion in dermoscopy images. Int. J. Appl. Eng. Res. 2014, 9, 27719–27731. [Google Scholar]
  34. Cavalcanti, P. G.; Scharcanski, J. Macroscopic pigmented skin lesion segmentation and its influence on lesion classification and diagnosis. In Color Medical Image Analysis. Lecture Notes in Computational Vision and Biomechanics; Celebi, M., Schaefer, G., Eds.; Dordrecht: Springer Netherlands, 2013; Volume 6, pp. 15–39. [Google Scholar] [CrossRef]
  35. Ballerini, L.; Fisher, R. B.; Aldridge, B.; Rees, J. Non-melanoma skin lesion classification using colour image data in a hierarchical k-nn classifier. In Proceedings of the 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), Barcelona, Spain, 05 May 2012. [Google Scholar] [CrossRef]
  36. Ramlakhan, K.; Shang, Y. A mobile automated skin lesion classification system. In Proceedings of the 2011 IEEE 23rd International Conference on Tools with Artificial Intelligence, Boca Raton, FL, USA, 7–9 November 2011. [Google Scholar] [CrossRef]
  37. Mohanty, N.; Pradhan, M.; Reddy, A. V. N.; Kumar, S.; Alkhayyat, A. Integrated Design of Optimized Weighted Deep Feature Fusion Strategies for Skin Lesion Image Classification. Cancers. 2022, 14, 2–25. [Google Scholar] [CrossRef] [PubMed]
  38. Benyahia, S.; Meftah, B.; Lézoray, O. Multi-features extraction based on deep learning for skin lesion classification. Tissue Cell. 2022, 74, 101701. [Google Scholar] [CrossRef] [PubMed]
  39. Melbin, K.; Raj, Y.J.V. Integration of modified ABCD features and support vector machine for skin lesion types classification. Multimed. Tools. Appl. 2021, 80, 8909–8929. [Google Scholar] [CrossRef]
  40. Guha, S.R.; Rafizul Haque, S.M. Performance Comparison of Machine Learning-Based Classification of Skin Diseases from Skin Lesion Images. In International Conference on Communication, Computing and Electronics Systems. Lecture Notes in Electrical Engineering; Bindhu, V., Chen, J., Tavares, J., Eds.; Springer: Singapore, 2020; Volume 637, pp. 15–25. [Google Scholar] [CrossRef]
  41. Chatterjee, S.; Dey, D.; Munshi, S. Integration of morphological preprocessing and fractal based feature extraction with recursive feature elimination for skin lesion types classification. Comput. Methods. Program.s Biomed. 2019, 178, 201–218. [Google Scholar] [CrossRef] [PubMed]
  42. Javed, R.; Saba, T.; Shafry, M.; Rahim, M. An Intelligent Saliency Segmentation Technique and Classification of Low Contrast Skin Lesion Dermoscopic Images Based on Histogram Decision. In Proceedings of the 2019 12th International Conference on Developments in eSystems Engineering (DeSE), Kazan, Russia, 7–10 October 2019. [Google Scholar] [CrossRef]
  43. Khan, M.A.; Akram, T.; Sharif, M.; Saba, T.; Javed, K.; Lali, I.U.; Tanik, U.J. Rehman, A. Construction of saliency map and hybrid set of features for efficient segmentation and classification of skin lesion. Microsc. Res. Tech. 2019, 82, 741–763. [Google Scholar] [CrossRef]
  44. Filali, Y.; Abdelouahed, S.; Aarab, A. An Improved Segmentation Approach for Skin Lesion Classification. Stat. Optim. Inf. Comput. 2019, 7, 456–467. [Google Scholar] [CrossRef]
  45. Akram, T.; Khan, M.A.; Sharif, M.; Yasmin, M. Skin lesion segmentation and recognition using multichannel saliency estimation and M-SVM on selected serially fused features. J. Ambient. Intell. Human. Comput. 2018, 1–20. [Google Scholar] [CrossRef]
  46. Nasir, M.; Attique Khan, M.; Sharif, M.; Lali, I. U.; Saba, T.; Iqbal, T. An improved strategy for skin lesion detection and classification using uniform segmentation and feature selection based approach. Microsc. Res. Tech. 2018, 81, 528–543. [Google Scholar] [CrossRef]
  47. Wahba, M.A.; Ashour, A.S.; Guo, Y.; Napoleon, S.A.; Abd-Elnaby, M.M. A novel cumulative level difference mean based GLDM and modified ABCD features ranked using eigenvector centrality approach for four skin lesion types classification. Comput. Methods. Programs. Biomed. 2018, 165, 163–174. [Google Scholar] [CrossRef]
  48. Wahba, M. A.; Ashour, A. S.; Napoleon, S. A.; Abd Elnaby, M. M.; Guo, Y. Combined empirical mode decomposition and texture features for skin lesion classification using quadratic support vector machine. Health. Inf. Sci. Syst. 2017, 5, 1–13. [Google Scholar] [CrossRef]
  49. Satheesha, T. Y.; Satyanarayana, D.; Prasad, M. N. G.; Dhruve, K. D. Melanoma Is Skin Deep: A 3D Reconstruction Technique for Computerized Dermoscopic Skin Lesion Classification. IEEE J. Transl. Eng. Health. Med. 2017, 5, 1–17. [Google Scholar] [CrossRef]
  50. Danpakdee, N.; Songpan, W. Classification Model for Skin Lesion Image. In Information Science and Applications 2017. ICISA 2017. Lecture Notes in Electrical Engineering, Kim, K., Joukov, N., Eds.; Springer: Singapore, 2017; Volume 424, pp. 553–561. [Google Scholar] [CrossRef]
  51. Filali, Y.; Ennouni, A.; Sabri, M. A.; Aarab, A. Multiscale approach for skin lesion analysis and classification. In Proceedings of the 2017 International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Fez, Morocco, 22–24 May 2017. [Google Scholar] [CrossRef]
  52. Farooq, M.A.; Azhar, M.A.; Raza, R.H. Automatic Lesion Detection System (ALDS) for Skin Cancer Classification Using SVM and Neural Classifiers. In Proceedings of the 2016 IEEE 16th International Conference on Bioinformatics and Bioengineering (BIBE), Taichung, Taiwan, 31 October 2016–02 November 2016. [Google Scholar] [CrossRef]
  53. Sirakov, N.M.; Ou, YL.; Mete, M. Skin lesion feature vectors classification in models of a Riemannian manifold. Ann. Math. Artif. Intell. 2015, 75, 217–229. [Google Scholar] [CrossRef]
  54. Mete, M.; Ou, YL.; Sirakov, N.M. Skin Lesion Feature Vector Space with a Metric to Model Geometric Structures of Malignancy for Classification. In Combinatorial Image Analaysis. IWCIA 2012. Lecture Notes in Computer Science, Barneva, R.P., Brimkov, V.E., Aggarwal, J.K., Eds.; Springer, Berlin, Heidelberg, Germany, 2012; Volume 7655, pp. 285–297. [CrossRef]
  55. Amelard, R.; Wong, A.; Clausi, D. A. Extracting morphological high-level intuitive features (HLIF) for enhancing skin lesion classification. In 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August 2012 - 01 September 2012. 28 August. [CrossRef]
  56. Molina-Molina, E.O.; Solorza-Calderón, S.; Álvarez-Borrego, J. Classification of Dermoscopy Skin Lesion Color-Images Using Fractal-Deep Learning Features. Appl. Sci. 2020, 10, 5954. [Google Scholar] [CrossRef]
  57. Surówka, G; Ogorzalek, M. On optimal wavelet bases for classification of skin lesion images through ensemble learning. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 06-11 July 2014. [CrossRef]
  58. López-Ávila, L. F.; Álvarez-Borrego, J.; Solorza-Calderón, S. Fractional Fourier-Radial Transform for Digital Image Recognition. J. Sign. Process. Syst. 2021, pp. 49–66 (2021). [CrossRef]
  59. ISICCHALLENGE. Available online: https://challenge.isic-archive.com/data/#2019.
  60. Casasent, D. , Psaltis, D. Scale invariant optical correlation using Mellin transforms. Opt. Commun. 1976, 17, 59–63. [Google Scholar] [CrossRef]
  61. Derrode, S. , Ghorbel, F. Robust and efficient Fourier– Mellin transform approximations for gray-level image reconstruction and complete invariant description. Comput. Vis. Image. Underst. 2001, 83, 57–78. [Google Scholar] [CrossRef]
  62. Alcaraz-Ubach, D.F. Reconocimiento de patrones en imágenes digitales usando máscaras de Hilbert Binarias de anillos concéntricos. Bachelor thesis, Science Faculty, UABC, Ensenada, Baja California, México, 2015.
  63. Davis, J. A., McNamara, D. E., Cottrell, D. M., Campos, J. Image processing with the radial Hilbert transform: Theory and experiments. Opt. Lett. 2000, 25, 99–101. [Google Scholar] [CrossRef] [PubMed]
  64. Pei, S.C., Ding, J.J. The generalized radial Hilbert transform and its applications to 2D edge detection (any direction or specified directions). In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal, Hong Kong China, 06-10 April 2003. Speech, and Signal, Hong Kong China, 6–10 April 2003. [CrossRef]
  65. King, F. W. Hilbert transforms; Cambridge University Press. UK, 2009; pp. 1–858. [CrossRef]
  66. Rogers, S.; Girolami, M. A first course in machine learning, 2nd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2017; pp. 185–195. [Google Scholar]
  67. K-nearest neighbor. Available online: http://scholarpedia.org/article/K-nearest_neighbor (accessed on 16 August 2023).
  68. Mucherino, A., Papajorgji, P. J., Pardalos, P. M., Mucherino, A., Papajorgji, P. J., Pardalos, P. M. K-nearest neighbor classification. In Data mining in agriculture. Springer Optimization and Its Applications, 2nd ed.; Springer: New York, NY, USA, 2009; Volume 34, pp. 83–106. [Google Scholar] [CrossRef]
  69. Gerón, A. Hands-On Machine Learnign with Scikit-Learn, Keras & TensorFlow, 2nd ed.; O’Reily: Sebastopol, CA, USA, 2019; pp. 189–212. [Google Scholar]
  70. Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
  71. Ho, T. K. The random subspace method for constructing decision forests. IEEE Transactions on Pattern Analysis and Machine Intelligence 1998, 20, 832–844. [Google Scholar] [CrossRef]
  72. X. Ma, T. Yang, J. Chen and Z. Liu, k-Nearest Neighbor algorithm based on feature subspace, In Proceedings of the 2021 International Conference on Big Data Analysis and Computer Science (BDACS), Kunming, China, 25-27 June 2021. 27 June. [CrossRef]
  73. Xie, P., Zuo, K., Zhang, Y., Li, F., Yin, M., Lu, K. Interpretable classification from skin cancer histology slides using deep learning: A retrospective multicenter study. ArXiv 2019, preprint arXiv:1904.06156. arXiv:1904.06156. [CrossRef]
  74. Ogudo, K. A., Surendran, R., Khalaf, O. I. Optimal Artificial Intelligence Based Automated Skin Lesion Detection and Classification Model. Comput. Syst. Sci. Eng. 2023, 44, 693–707. [Google Scholar] [CrossRef]
Preprints 85294 g002
Figure 2. Signatures of an image. The presentation of the graphic on the vertical log scale allows the visualization of the two types of descriptors.
Figure 2. Signatures of an image. The presentation of the graphic on the vertical log scale allows the visualization of the two types of descriptors.
Preprints 85294 g002
Table 1. This table shows a description of the 11 algorithms implemented.
Table 1. This table shows a description of the 11 algorithms implemented.
Preprints 85294 i002
Table 2. Results for Quadratic SVM.
Table 2. Results for Quadratic SVM.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.997713 0.000435 0.992518 0.001918 0.998454 0.000441 0.989201 0.003089
SCC 0.994121 0.000502 0.989432 0.002688 0.994789 0.000394 0.96442 0.002662
MEL 0.995564 0.000634 0.978523 0.00349 0.997998 0.000466 0.985882 0.003276
AK 0.994141 0.00064 0.969387 0.004028 0.997692 0.000405 0.983691 0.002828
BKL 0.994707 0.000585 0.982108 0.003661 0.9965 0.000433 0.975644 0.002831
DF 0.996077 0.00053 0.975942 0.003758 0.998964 0.0003 0.992662 0.00211
NV 0.995768 0.000637 0.987118 0.003555 0.996996 0.00054 0.979067 0.003622
VASC 0.998452 0.000227 0.991186 0.001829 0.999489 0.000202 0.996405 0.001409
MEAN±1SD 0.995818 0.001585 0.983277 0.008205 0.99761 0.001502 0.983371 0.01024
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.998902 0.000771 0.995155 0.003451 0.999443 0.000747 0.996129 0.005223
SCC 0.996671 0.001348 0.994984 0.006641 0.99692 0.001477 0.978896 0.009978
MEL 0.997328 0.001484 0.984985 0.011026 0.999095 0.000836 0.993616 0.005861
AK 0.996467 0.001355 0.981774 0.008303 0.998527 0.001044 0.989513 0.007158
BKL 0.99692 0.001044 0.99105 0.006158 0.997775 0.001073 0.984501 0.00745
DF 0.997656 0.00109 0.984903 0.008138 0.999431 0.000583 0.995944 0.004108
NV 0.997464 0.001555 0.99428 0.006072 0.99791 0.00166 0.98595 0.010578
VASC 0.998913 0.000538 0.993741 0.004151 0.999651 0.000327 0.997529 0.002344
MEAN±1SD 0.99754 0.000933 0.990109 0.005392 0.998594 0.000981 0.99026 0.006679
Table 3. Results for Cubic SVM.
Table 3. Results for Cubic SVM.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.997931 0.000475 0.991772 0.002502 0.998815 0.0004 0.99175 0.002773
SCC 0.998225 0.000515 0.9958 0.00246 0.998571 0.000366 0.990031 0.002564
MEL 0.998585 0.000376 0.995069 0.002159 0.999085 0.000309 0.993581 0.002148
AK 0.997857 0.000469 0.98977 0.002736 0.99901 0.000418 0.993046 0.002911
BKL 0.997951 0.000604 0.99258 0.003565 0.998719 0.000419 0.991067 0.002932
DF 0.998488 0.00042 0.993297 0.003042 0.99923 0.000292 0.994617 0.002015
NV 0.998321 0.000412 0.99141 0.002184 0.999311 0.000323 0.995173 0.002237
VASC 0.999768 0.000158 0.998817 0.001053 0.999903 0.000108 0.99932 0.000756
MEAN±1SD 0.998391 0.000617 0.993565 0.002882 0.99908 0.000417 0.993573 0.002906
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.999241 0.000701 0.997109 0.004113 0.999535 0.000714 0.996713 0.005081
SCC 0.999411 0.000667 0.998569 0.003459 0.999534 0.000685 0.996772 0.00483
MEL 0.999468 0.000548 0.998491 0.003087 0.999611 0.000568 0.997317 0.003941
AK 0.999207 0.000769 0.996019 0.004335 0.999665 0.000615 0.997598 0.004424
BKL 0.999343 0.000807 0.997474 0.005446 0.999612 0.000638 0.997301 0.004364
DF 0.999683 0.000527 0.999094 0.002063 0.999767 0.000507 0.998393 0.003469
NV 0.999162 0.000816 0.995287 0.00487 0.999716 0.000584 0.997986 0.004132
VASC 1 0 1 0 1 0 1 0
MEAN±1SD 0.99944 0.000281 0.997755 0.001587 0.99968 0.000153 0.99776 0.001067
Table 4. Results for Fine Gaussian SVM.
Table 4. Results for Fine Gaussian SVM.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.990617 0.001202 0.938094 0.009789 0.998108 0.000634 0.986097 0.004562
SCC 0.991729 0.000776 0.9374 0.006256 0.999511 0.000248 0.996384 0.001816
MEL 0.990704 0.000929 0.948301 0.004959 0.99677 0.000679 0.976802 0.004607
AK 0.964331 0.002284 0.992258 0.002383 0.960355 0.002588 0.781032 0.01118
BKL 0.988485 0.000888 0.915523 0.006838 0.998884 0.000384 0.991531 0.002881
DF 0.993657 0.000814 0.963894 0.006035 0.997907 0.000437 0.985045 0.003063
NV 0.987007 0.000943 0.955562 0.006548 0.991504 0.000797 0.941491 0.00538
VASC 0.993679 0.000848 0.949736 0.006868 0.999951 7.96E-05 0.999643 0.000587
MEAN±1SD 0.987526 0.009651 0.950096 0.022366 0.992874 0.013403 0.957253 0.073477
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.994792 0.001981 0.963688 0.014052 0.999249 0.000668 0.994572 0.004833
SCC 0.996071 0.000904 0.968772 0.007678 0.999922 0.000214 0.999446 0.001521
MEL 0.996535 0.001641 0.980529 0.012471 0.998837 0.00096 0.991698 0.006806
AK 0.982756 0.002737 0.994899 0.00495 0.980997 0.002822 0.883549 0.015957
BKL 0.99435 0.001641 0.960839 0.010733 0.999222 0.000671 0.994451 0.004731
DF 0.997226 0.001441 0.983665 0.008772 0.999148 0.00091 0.993885 0.006639
NV 0.994124 0.001773 0.982219 0.008845 0.995812 0.001428 0.970819 0.010054
VASC 0.997271 0.001331 0.978214 0.010582 1 0 1 0
MEAN±1SD 0.994141 0.004764 0.976603 0.011407 0.996649 0.006459 0.978552 0.039459
Table 5. Results for Medium Gaussian SVM.
Table 5. Results for Medium Gaussian SVM.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.970352 0.001239 0.904254 0.007983 0.979737 0.001104 0.863793 0.006639
SCC 0.973061 0.001097 0.893946 0.007351 0.984325 0.00116 0.890457 0.006616
MEL 0.970867 0.000961 0.829685 0.006684 0.991048 0.000499 0.929828 0.003744
AK 0.977499 0.000898 0.897616 0.006106 0.988921 0.00103 0.920629 0.006421
BKL 0.972529 0.000865 0.865436 0.00704 0.987814 0.000886 0.910286 0.005526
DF 0.985904 0.000616 0.921273 0.004687 0.995152 0.000607 0.96458 0.004144
NV 0.959978 0.000896 0.944947 0.003669 0.96213 0.001128 0.781547 0.004489
VASC 0.991525 0.000697 0.949302 0.005961 0.997563 0.000433 0.982402 0.002982
MEAN±1SD 0.975214 0.009798 0.900808 0.039817 0.985836 0.011125 0.90544 0.062767
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.977502 0.003381 0.93541 0.015774 0.98365 0.003091 0.89323 0.018677
SCC 0.979337 0.002892 0.921498 0.020366 0.987716 0.0027 0.915755 0.017457
MEL 0.976551 0.003395 0.858984 0.024565 0.993301 0.00136 0.947996 0.010845
AK 0.983243 0.002995 0.913926 0.013777 0.993147 0.002206 0.949931 0.015829
BKL 0.978023 0.003674 0.893106 0.022957 0.990187 0.001856 0.928795 0.012963
DF 0.991078 0.001802 0.947692 0.011963 0.997261 0.001098 0.979965 0.008013
NV 0.966044 0.004155 0.952837 0.010116 0.967897 0.005143 0.807599 0.024077
VASC 0.993671 0.001883 0.959445 0.013131 0.998526 0.000779 0.989305 0.005602
MEAN±1SD 0.980681 0.008731 0.922862 0.033929 0.988961 0.009796 0.926572 0.057544
Table 6. Results for Fine KNN.
Table 6. Results for Fine KNN.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.996612 0.000647 0.988253 0.003377 0.997809 0.000452 0.984767 0.003143
SCC 0.996459 0.000687 0.992086 0.00247 0.997082 0.000661 0.979832 0.004407
MEL 0.991981 0.000865 0.967874 0.005457 0.995412 0.00063 0.967787 0.004308
AK 0.997019 0.000537 0.98884 0.00308 0.998188 0.000476 0.98736 0.003258
BKL 0.993662 0.000735 0.968304 0.005179 0.997277 0.000491 0.980674 0.003422
DF 0.995847 0.00054 0.984048 0.003433 0.997534 0.000475 0.9828 0.003276
NV 0.9906 0.000995 0.962863 0.005059 0.994565 0.000698 0.962032 0.004756
VASC 0.997852 0.000516 0.987744 0.003771 0.999295 0.000296 0.995033 0.002071
MEAN±1SD 0.995004 0.002616 0.980001 0.011626 0.997145 0.001511 0.980036 0.010578
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.998562 0.000776 0.995856 0.00456 0.998941 0.00065 0.992512 0.004646
SCC 0.998709 0.000954 0.997816 0.002984 0.998835 0.000948 0.991932 0.006699
MEL 0.996581 0.001444 0.98485 0.010675 0.998316 0.001431 0.988392 0.009868
AK 0.998913 0.001019 0.996475 0.005015 0.999275 0.000801 0.994956 0.005579
BKL 0.997101 0.001219 0.984999 0.007762 0.998836 0.001008 0.991779 0.007134
DF 0.998358 0.000953 0.995091 0.004975 0.998823 0.000948 0.991805 0.006562
NV 0.995811 0.001733 0.983651 0.008814 0.997541 0.001488 0.982872 0.010041
VASC 0.999026 0.000761 0.993904 0.006181 0.999754 0.00033 0.998266 0.002323
MEAN±1SD 0.997883 0.001215 0.99158 0.00598 0.99879 0.000652 0.991564 0.004523
Table 7. Results for Medium Gaussian KNN.
Table 7. Results for Medium Gaussian KNN.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.968962 0.001612 0.902908 0.008807 0.978419 0.001602 0.857063 0.008559
SCC 0.964886 0.001417 0.886476 0.009336 0.976084 0.001643 0.841252 0.008924
MEL 0.956256 0.001899 0.817315 0.011059 0.976133 0.001703 0.830625 0.009523
AK 0.966205 0.001226 0.862392 0.009765 0.98104 0.001444 0.866847 0.008002
BKL 0.963505 0.00187 0.84941 0.00938 0.979755 0.002278 0.856939 0.013198
DF 0.969574 0.001417 0.849535 0.010333 0.986664 0.001288 0.900786 0.008433
NV 0.951404 0.001651 0.834493 0.010815 0.968077 0.001882 0.788632 0.009132
VASC 0.985493 0.001017 0.902211 0.007839 0.997421 0.000526 0.980456 0.003871
MEAN±1SD 0.965786 0.010118 0.863092 0.031504 0.980449 0.008639 0.865325 0.056466
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.977899 0.002878 0.946323 0.014022 0.982366 0.003188 0.884054 0.017584
SCC 0.975928 0.003423 0.906904 0.021586 0.985793 0.00251 0.901248 0.016761
MEL 0.965308 0.004586 0.879849 0.023875 0.977466 0.003912 0.847469 0.023878
AK 0.97474 0.003065 0.891863 0.016402 0.986582 0.002767 0.904245 0.020062
BKL 0.971558 0.00339 0.897429 0.017104 0.982317 0.002985 0.879933 0.018989
DF 0.977219 0.002996 0.877022 0.024321 0.991761 0.002146 0.939128 0.015253
NV 0.960462 0.004176 0.85456 0.025912 0.975699 0.004218 0.83514 0.02571
VASC 0.988055 0.00234 0.912879 0.018859 0.998694 0.000701 0.990039 0.005171
MEAN±1SD 0.973896 0.008384 0.895854 0.027499 0.985085 0.0075 0.897657 0.049623
Table 8. Results for Cosine KNN.
Table 8. Results for Cosine KNN.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.96834 0.00108 0.851159 0.010441 0.985047 0.001385 0.890453 0.008299
SCC 0.963689 0.001617 0.849973 0.013445 0.979887 0.001611 0.857745 0.009328
MEL 0.954031 0.001684 0.798347 0.012674 0.976334 0.002385 0.828959 0.012168
AK 0.965667 0.001554 0.867501 0.009935 0.9797 0.002158 0.859622 0.011847
BKL 0.959197 0.001785 0.813381 0.012224 0.979997 0.001902 0.853189 0.010953
DF 0.969908 0.001379 0.833521 0.010051 0.989456 0.001226 0.918975 0.008551
NV 0.941463 0.002009 0.890112 0.013375 0.94879 0.00315 0.71319 0.010549
VASC 0.981986 0.001287 0.91312 0.008143 0.991796 0.001024 0.940725 0.006908
MEAN±1SD 0.963035 0.01197 0.852139 0.038069 0.978876 0.013264 0.857857 0.069131
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.977434 0.002263 0.911182 0.014176 0.986988 0.002337 0.909599 0.016076
SCC 0.972271 0.003538 0.871525 0.020069 0.986818 0.002835 0.904842 0.020734
MEL 0.9643 0.00416 0.853384 0.026301 0.979937 0.0029 0.857077 0.018503
AK 0.973607 0.003901 0.895428 0.016813 0.98474 0.003515 0.893324 0.023071
BKL 0.967969 0.004153 0.871239 0.02185 0.981898 0.003421 0.873844 0.020752
DF 0.974411 0.00296 0.85076 0.016279 0.99186 0.002333 0.936737 0.016802
NV 0.95608 0.003435 0.912351 0.018579 0.962345 0.004294 0.7758 0.022732
VASC 0.985847 0.00222 0.921673 0.014345 0.995114 0.001557 0.964687 0.010787
MEAN±1SD 0.97149 0.008917 0.885943 0.027834 0.983713 0.009942 0.889489 0.057024
Table 9. Results for Cubic KNN.
Table 9. Results for Cubic KNN.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.967544 0.001553 0.892731 0.011109 0.978245 0.00162 0.85463 0.008652
SCC 0.958837 0.002056 0.87173 0.011594 0.971249 0.002404 0.812395 0.011305
MEL 0.951254 0.001966 0.792743 0.016617 0.973954 0.002412 0.813743 0.012396
AK 0.961603 0.001413 0.843246 0.008752 0.978504 0.001808 0.84871 0.010153
BKL 0.958948 0.001545 0.83026 0.009622 0.977347 0.001845 0.839881 0.010704
DF 0.965498 0.001278 0.833468 0.010531 0.984356 0.001613 0.884018 0.009842
NV 0.950286 0.001692 0.834216 0.013508 0.966907 0.002334 0.783326 0.010768
VASC 0.984078 0.000932 0.893935 0.007509 0.996871 0.000587 0.975965 0.004312
MEAN±1SD 0.962256 0.010704 0.849041 0.034759 0.978429 0.009109 0.851583 0.058924
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.977231 0.002806 0.950159 0.012809 0.98111 0.003381 0.876928 0.021674
SCC 0.970211 0.003376 0.883554 0.021992 0.982757 0.003779 0.880785 0.024607
MEL 0.962183 0.00427 0.867746 0.025005 0.975543 0.003754 0.83374 0.023414
AK 0.970652 0.003369 0.869158 0.015176 0.985198 0.003215 0.893751 0.021674
BKL 0.966769 0.003754 0.882164 0.019933 0.978868 0.003254 0.856108 0.020597
DF 0.972883 0.003797 0.859058 0.019839 0.989167 0.002575 0.919144 0.017968
NV 0.960417 0.003748 0.849669 0.027438 0.976155 0.004667 0.834863 0.027576
VASC 0.986458 0.002753 0.907463 0.018557 0.998054 0.000889 0.985479 0.006777
MEAN±1SD 0.97085 0.008363 0.883622 0.032105 0.983357 0.00748 0.8851 0.049853
Table 10. Results for Weighted KNN.
Table 10. Results for Weighted KNN.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.99101 0.000853 0.966399 0.004479 0.99452 0.000799 0.961846 0.005073
SCC 0.990489 0.000854 0.973897 0.005359 0.992855 0.000691 0.951129 0.004412
MEL 0.98292 0.001179 0.929858 0.006006 0.990501 0.000993 0.933329 0.006406
AK 0.990648 0.000956 0.961649 0.00594 0.994779 0.000829 0.963376 0.005514
BKL 0.987704 0.001124 0.94218 0.007959 0.994208 0.000832 0.958831 0.005584
DF 0.991358 0.000866 0.961126 0.005819 0.995669 0.000647 0.969407 0.004409
NV 0.978637 0.001198 0.930944 0.008927 0.985455 0.001282 0.901657 0.006904
VASC 0.994882 0.000687 0.964408 0.004778 0.999236 0.000312 0.994494 0.002249
MEAN±1SD 0.988456 0.005248 0.953808 0.016992 0.993403 0.00405 0.954259 0.02732
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.995143 0.001416 0.980286 0.006849 0.997283 0.001247 0.980993 0.008724
SCC 0.995709 0.001617 0.989698 0.008021 0.996571 0.001178 0.976347 0.008376
MEL 0.989232 0.002362 0.953552 0.012095 0.994358 0.001925 0.960311 0.013101
AK 0.995822 0.001604 0.982016 0.008189 0.997812 0.001377 0.984743 0.009674
BKL 0.993795 0.002086 0.967452 0.010927 0.997569 0.001363 0.982643 0.009614
DF 0.995958 0.001499 0.984228 0.007814 0.997658 0.001094 0.983658 0.007641
NV 0.985892 0.002686 0.957146 0.013847 0.989976 0.00227 0.931492 0.013995
VASC 0.997543 0.001159 0.982462 0.007462 0.99969 0.000459 0.997759 0.003378
MEAN±1SD 0.993637 0.003989 0.974605 0.013462 0.996365 0.002976 0.974743 0.020327
Table 11. Results for Bagged Trees.
Table 11. Results for Bagged Trees.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.998053 0.000557 0.991325 0.003305 0.999013 0.000478 0.993097 0.003319
SCC 0.996912 0.000734 0.985676 0.004545 0.998515 0.000531 0.989579 0.003716
MEL 0.997727 0.000607 0.990838 0.002973 0.998709 0.000528 0.990981 0.003639
AK 0.996932 0.000557 0.991146 0.00306 0.997758 0.00052 0.984448 0.003544
BKL 0.995689 0.00073 0.98531 0.004189 0.997167 0.00062 0.980236 0.004258
DF 0.997554 0.000714 0.987148 0.003966 0.999039 0.000378 0.993235 0.002618
NV 0.997815 0.000605 0.991293 0.003389 0.998745 0.000487 0.991221 0.003352
VASC 0.99912 0.000359 0.996388 0.001829 0.999511 0.000323 0.996589 0.00225
MEAN±1SD 0.997475 0.001002 0.98989 0.003684 0.998557 0.000754 0.989923 0.00524
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.999241 0.000712 0.996774 0.003976 0.999586 0.000548 0.997078 0.00388
SCC 0.998992 0.001031 0.994303 0.007762 0.999665 0.000483 0.997583 0.003562
MEL 0.999479 0.000826 0.998582 0.002601 0.999611 0.000737 0.997366 0.004978
AK 0.999253 0.000693 0.997617 0.003347 0.999483 0.00057 0.996359 0.003996
BKL 0.998471 0.001062 0.996698 0.003667 0.998732 0.001071 0.991193 0.00753
DF 0.999377 0.000606 0.99615 0.003906 0.999844 0.000283 0.998946 0.001909
NV 0.999298 0.000719 0.997054 0.004332 0.999625 0.000591 0.997368 0.004074
VASC 0.999841 0.000365 0.998721 0.002971 1 0 1 0
MEAN±1SD 0.999244 0.000395 0.996987 0.001413 0.999568 0.000375 0.996987 0.002606
Table 12. Results for Subspace KNN.
Table 12. Results for Subspace KNN.
TRAIN SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.999462 0.000296 0.997958 0.001851 0.999677 0.000245 0.997737 0.0017
SCC 0.999038 0.000615 0.995829 0.002757 0.999496 0.000445 0.99646 0.003122
MEL 0.998709 0.000469 0.995324 0.003062 0.999194 0.000339 0.994398 0.002311
AK 0.998958 0.000546 0.995273 0.003405 0.999485 0.000285 0.996408 0.00199
BKL 0.999128 0.000355 0.997912 0.001905 0.999301 0.00039 0.995139 0.0027
DF 0.999176 0.000554 0.99656 0.002521 0.99955 0.000403 0.996853 0.002832
NV 0.998814 0.000494 0.99408 0.003025 0.999486 0.000315 0.996381 0.002206
VASC 0.999853 0.00013 0.999591 0.000708 0.99989 0.000134 0.999234 0.000934
MEAN±1SD 0.999142 0.000368 0.996566 0.001806 0.99951 0.000213 0.996576 0.001482
TEST SET
ACCURACY SENSITIVITY SPECIFICITY PRECISION
LESION MEAN ±1SD MEAN ±1SD MEAN ±1SD MEAN ±1SD
BCC 0.999955 0.000248 1 0 0.999948 0.000284 0.999642 0.001963
SCC 0.999774 0.000515 0.998957 0.003181 0.999896 0.000394 0.999284 0.002726
MEL 0.999909 0.000345 1 0 0.999897 0.000393 0.999268 0.002791
AK 0.999909 0.000345 0.999643 0.001958 0.999948 0.000283 0.999637 0.00199
BKL 0.999864 0.000415 1 0 0.999845 0.000473 0.998915 0.003311
DF 0.999864 0.000415 0.998952 0.0032 1 0 1 0
NV 0.999909 0.000345 0.999282 0.002732 1 0 1 0
VASC 1 0 1 0 1 0 1 0
MEAN±1SD 0.999898 6.74E-05 0.999604 0.000475 0.999942 5.82E-05 0.999593 0.000407
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated