Submitted:
29 August 2023
Posted:
18 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Convergence Theory
Lax’s equivalence theorem [24]
3. Consistency and Stability Analysis
4. Numerical Results
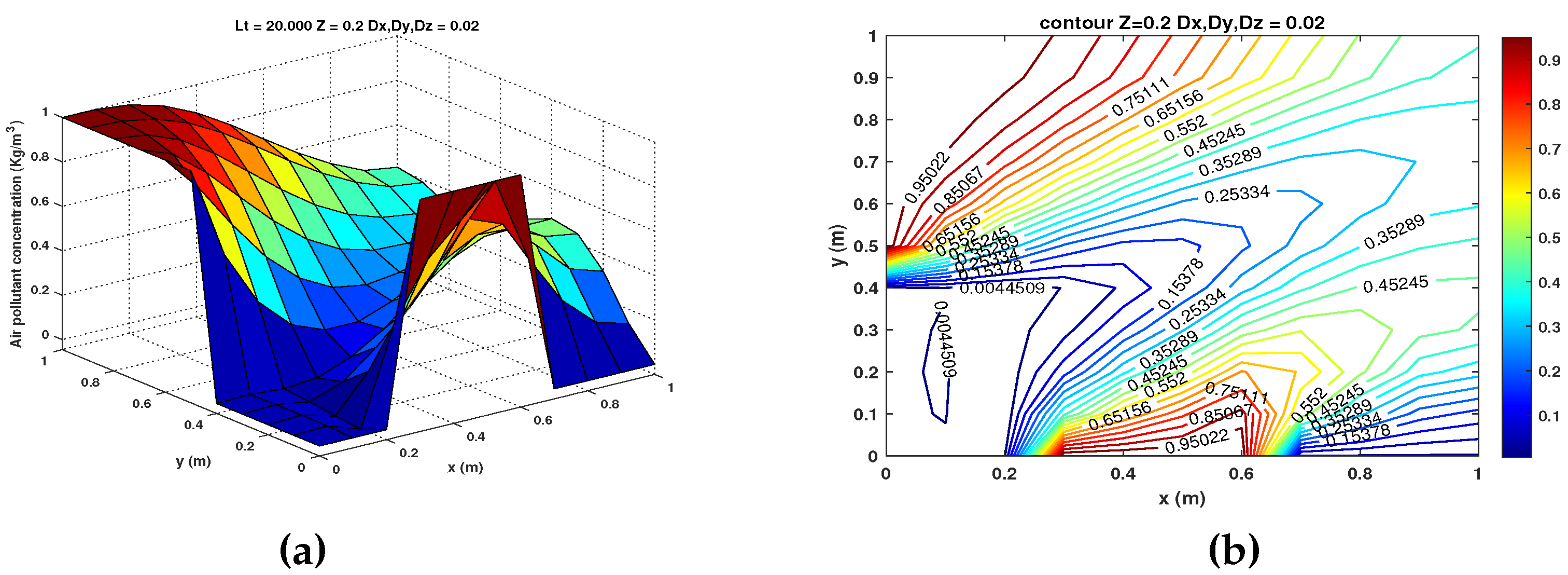
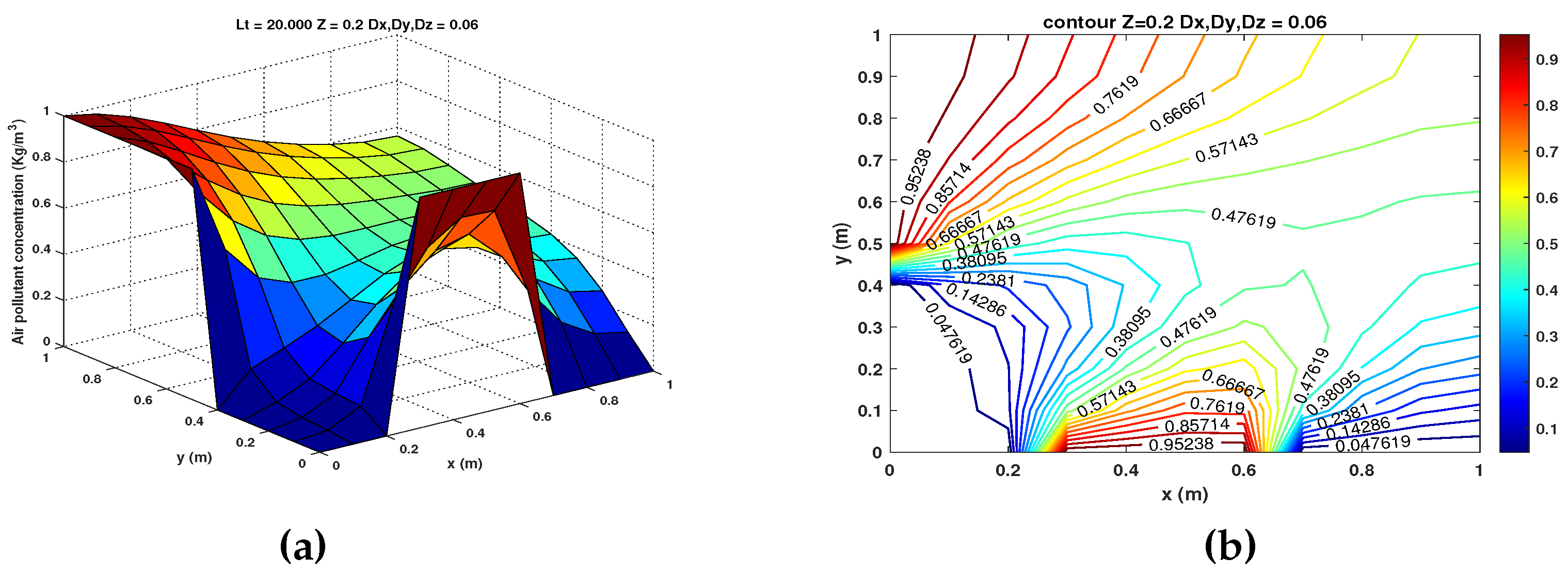
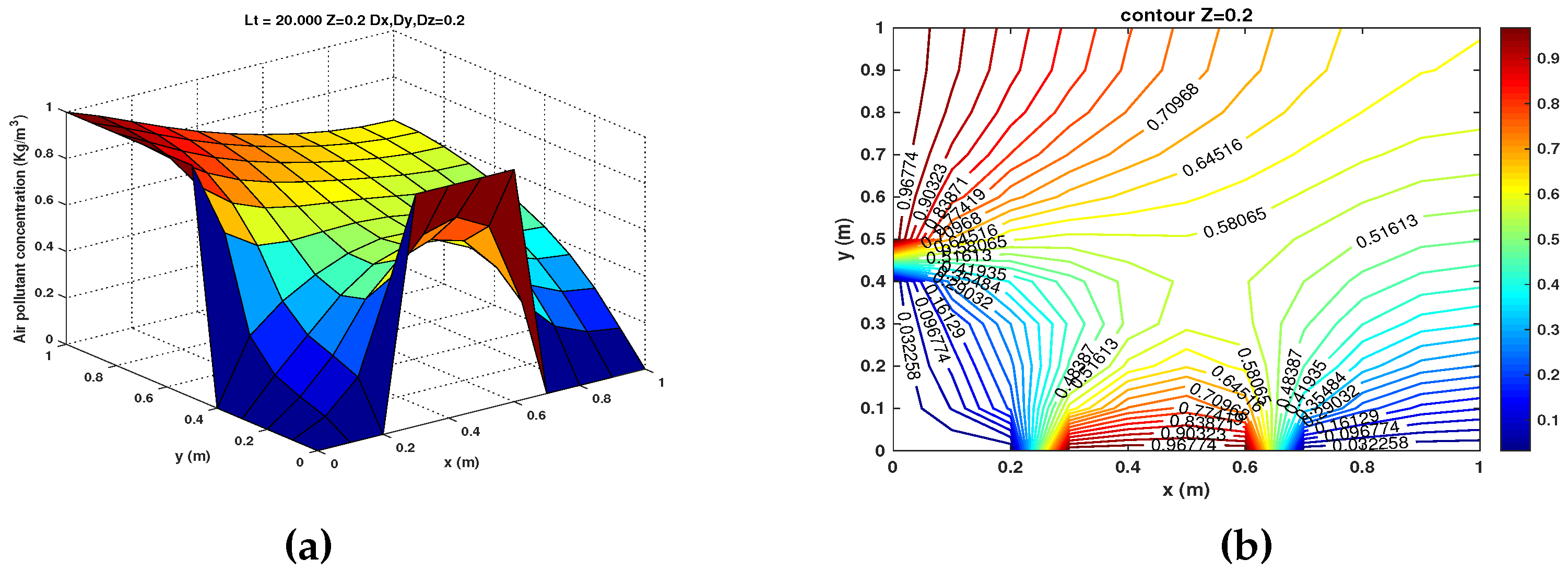
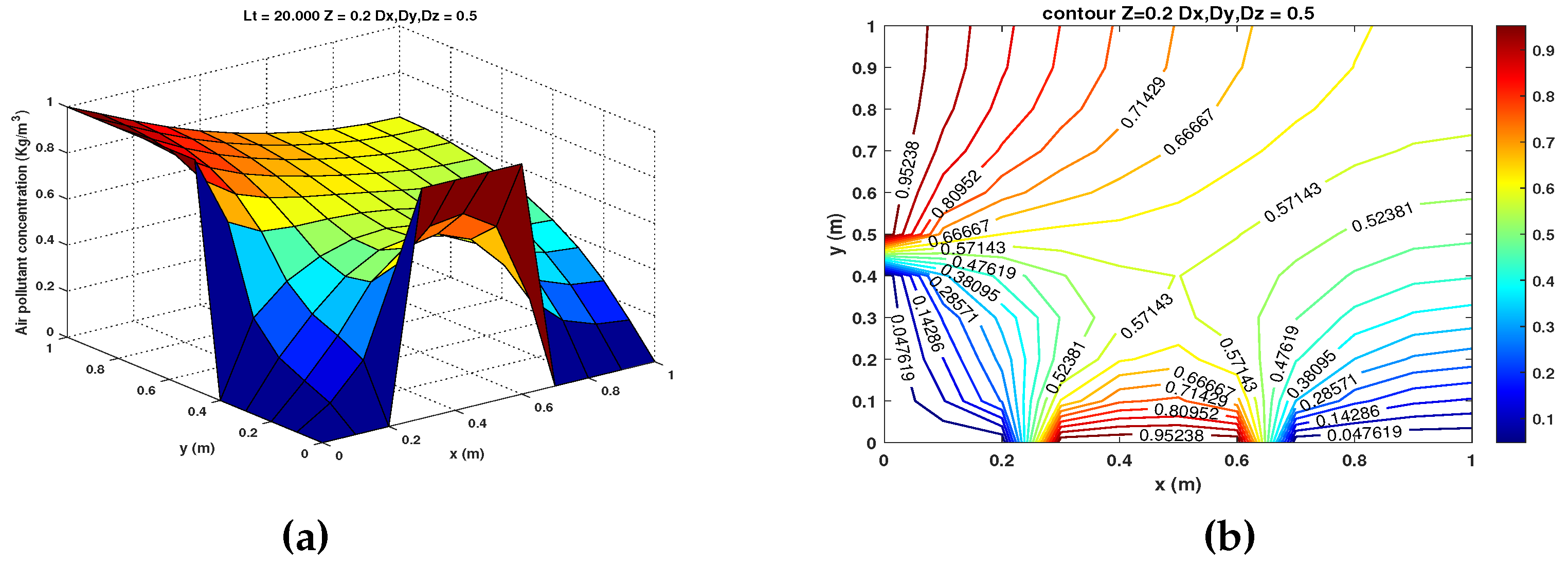
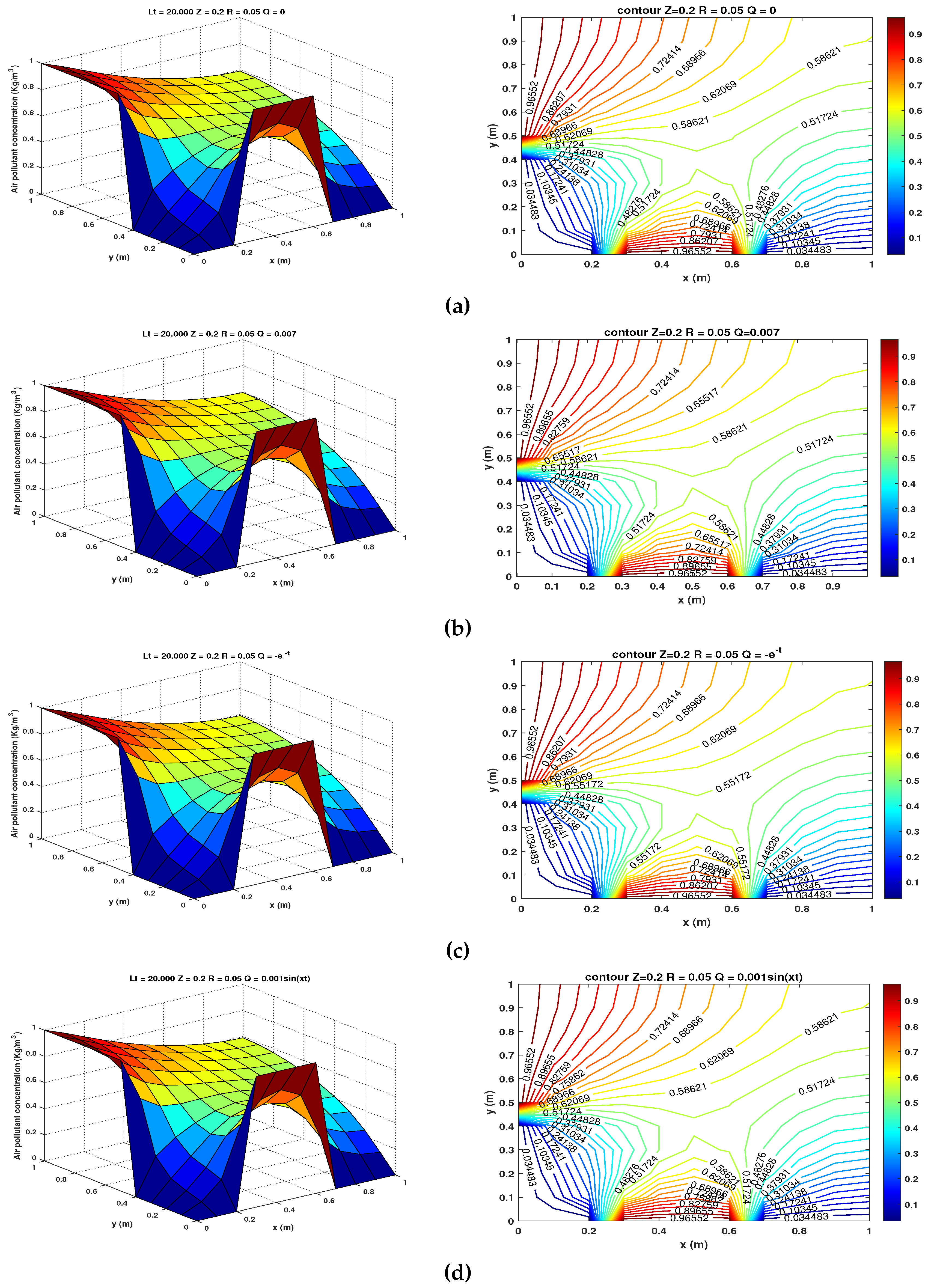
- and . The results for this case are shown in Figure 5 (a) - (d) at a height meters for and , respectively.
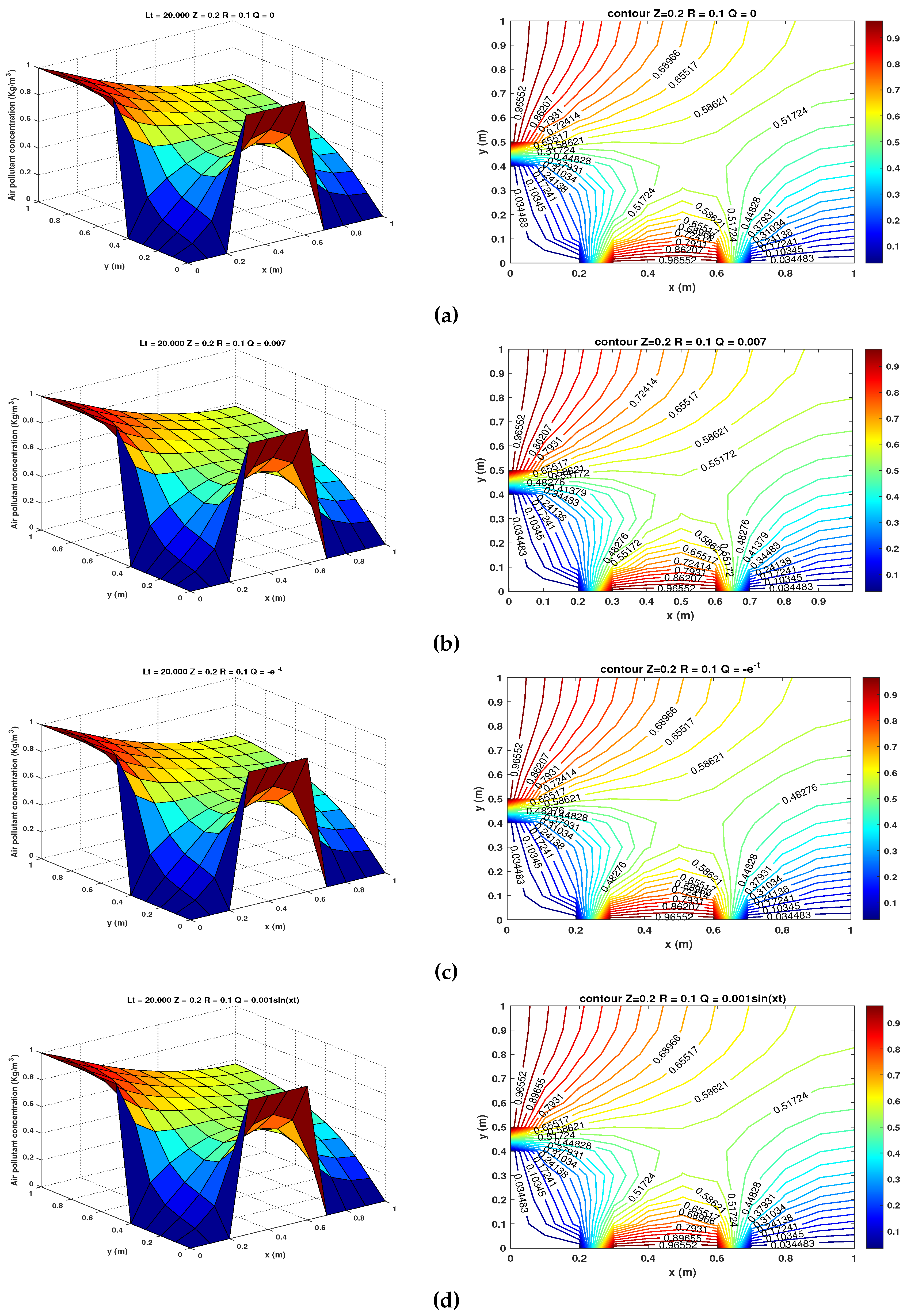
- and . The results for this case are shown in Figure 6 (a) - (d) at a height meters for and , respectively.
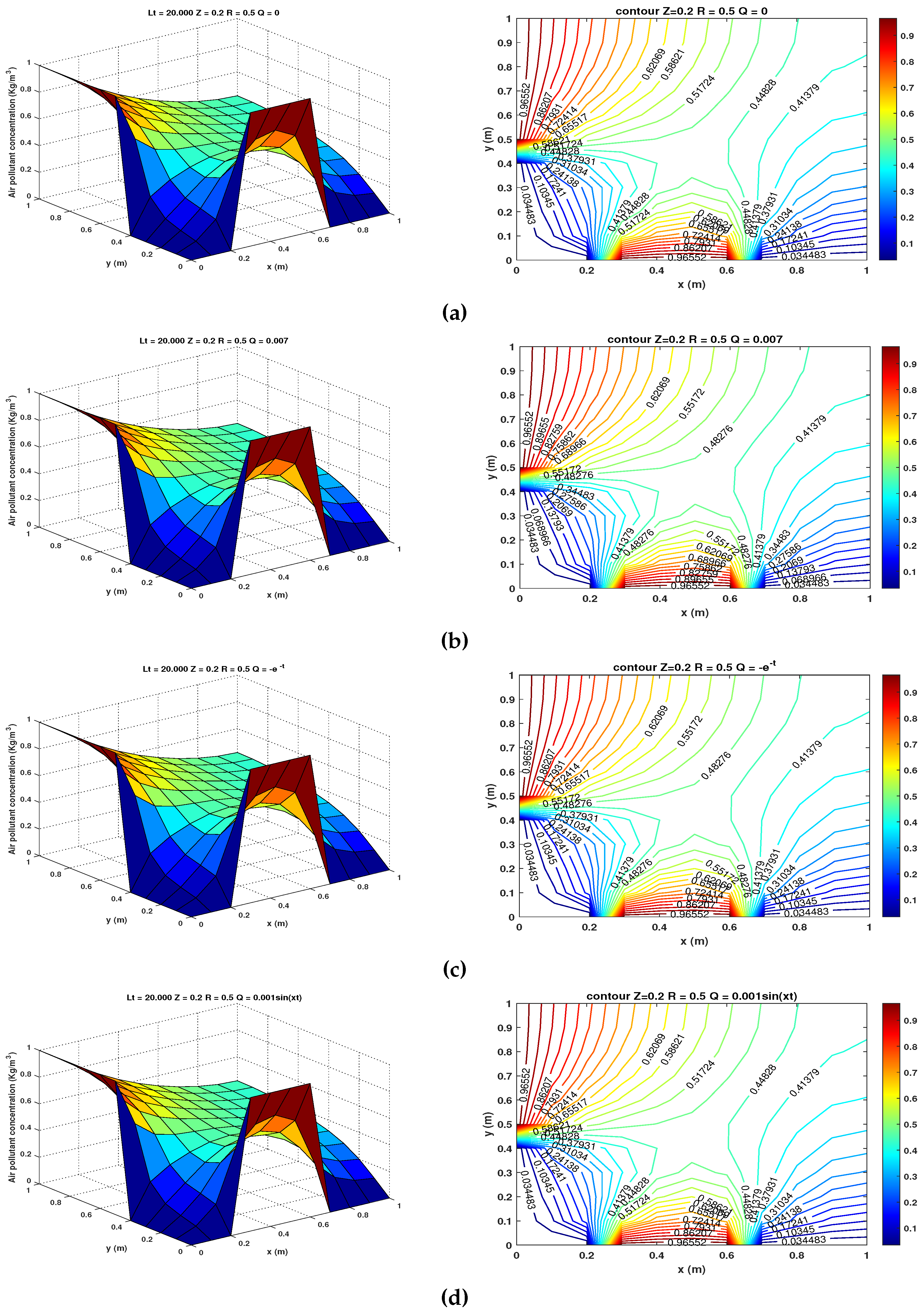
- and . The results for this case are shown in Figure 7 (a) - (d) at a height meters for and , respectively.
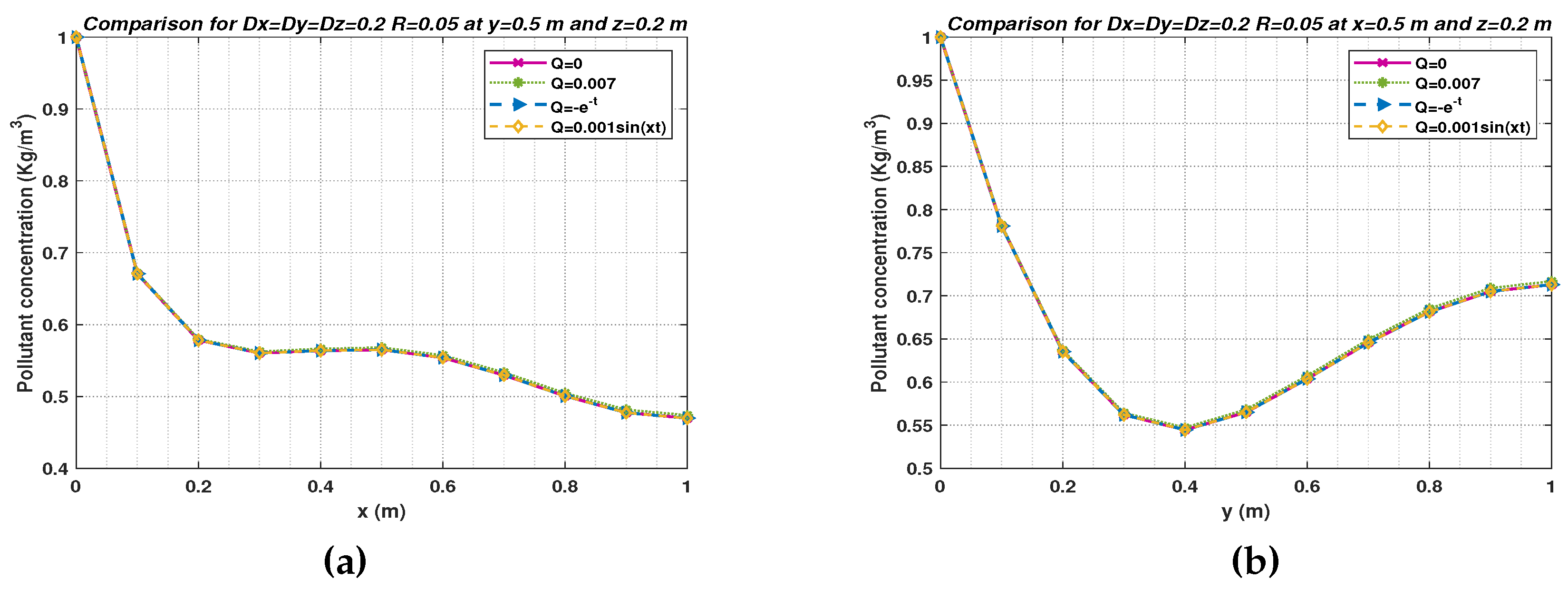
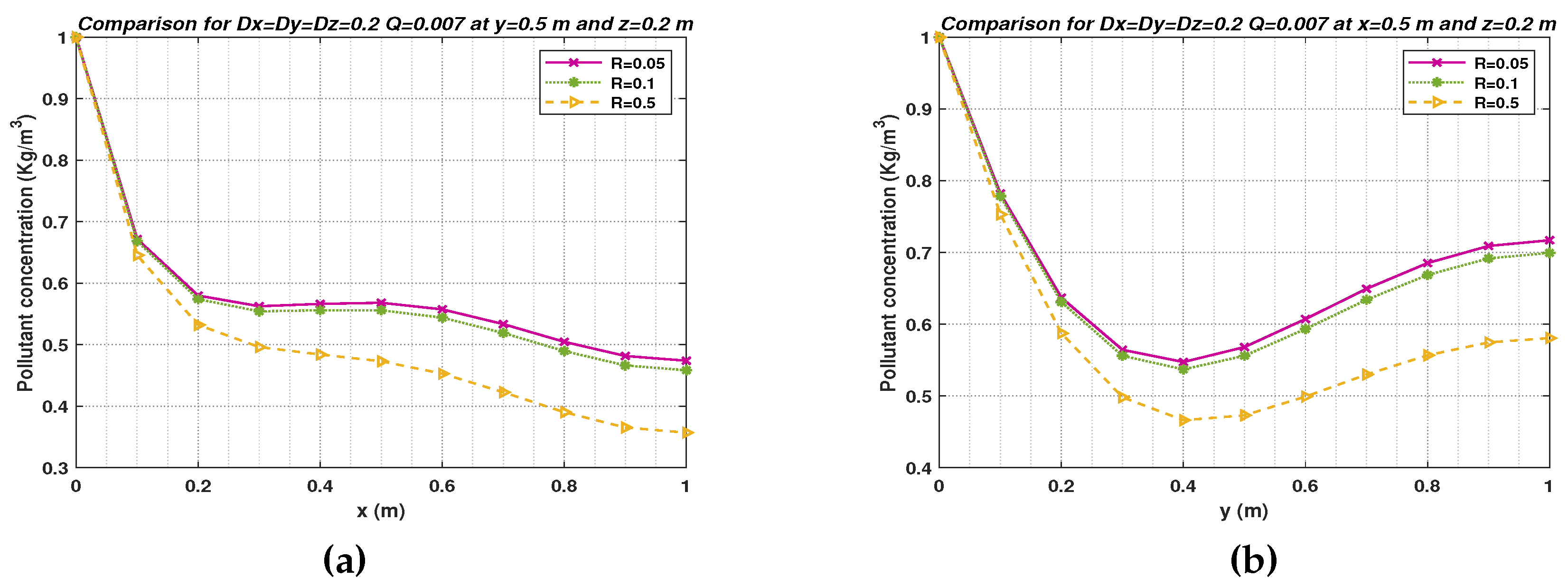
- m for and . The results for this case are shown in Figure 8 (a) at m and (b) at m.
- m for and . The results for this case are shown in Figure 9 (a) at m and (b) at m.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Di Pietro, D.A.; Ern, A. Mathematical Aspects of Discontinuous Galerkin Methods 2012.
- Savović, S.; Djordjevich, A. Finite difference solution of the one-dimensional advection–diffusion equation with variable coefficients in semi-infinite media. International Journal of Heat and Mass Transfer 2012, 55, 4291–4294. [Google Scholar] [CrossRef]
- Appadu, A.R.; Gidey, H. Time-splitting procedures for the numerical solution of the 2D advection-diffusion equation. Mathematical Problems in Engineering 2013, 2013. [Google Scholar] [CrossRef]
- Bause, M.; Schwegler, K. Higher order finite element approximation of systems of convection–diffusion–reaction equations with small diffusion. Journal of computational and applied mathematics 2013, 246, 52–64. [Google Scholar] [CrossRef]
- Mojtabi, A.; Deville, M.O. One-dimensional linear advection–diffusion equation: Analytical and finite element solutions. Computers & Fluids 2015, 107, 189–195. [Google Scholar]
- Gharehbaghi, A. Explicit and implicit forms of differential quadrature method for advection–diffusion equation with variable coefficients in semi-infinite domain. Journal of Hydrology 2016, 541, 935–940. [Google Scholar] [CrossRef]
- Gyrya, V.; Lipnikov, K. The arbitrary order mimetic finite difference method for a diffusion equation with a non-symmetric diffusion tensor. Journal of Computational Physics 2017, 348, 549–566. [Google Scholar] [CrossRef]
- Bahar, E.; Gürarslan, G. Numerical solution of advection-diffusion equation using operator splitting method. International Journal of Engineering and Applied Sciences 2017, 9, 76–88. [Google Scholar] [CrossRef]
- Oyjinda, P.; Pochai, N. Numerical Simulation to Air Pollution Emission Control near an Industrial Zone. Advances in Mathematical Physics 2017, 2017. [Google Scholar] [CrossRef]
- Suebyat, K.; Pochai, N. Numerical Simulation for a Three-Dimensional Air Pollution Measurement Model in a Heavy Traffic Area under the Bangkok Sky Train Platform. Abstract and Applied Analysis. Hindawi, 2018, Vol. 2018.
- Al-Jawary, M.A.; Azeez, M.M.; Radhi, G.H. Analytical and numerical solutions for the nonlinear Burgers and advection–diffusion equations by using a semi-analytical iterative method. Computers & Mathematics with Applications 2018, 76, 155–171. [Google Scholar]
- Kusuma, J.; Ribal, A.; Mahie, A.G. On FTCS Approach for Box Model of Three-Dimension Advection-Diffusion Equation. International Journal of Differential Equations 2018, 2018. [Google Scholar] [CrossRef]
- Lou, J.; Li, L.; Luo, H.; Nishikawa, H. Reconstructed discontinuous Galerkin methods for linear advection–diffusion equations based on first-order hyperbolic system. Journal of Computational Physics 2018, 369, 103–124. [Google Scholar] [CrossRef]
- Bhatt, H.; Khaliq, A.; Wade, B. Efficient Krylov-based exponential time differencing method in application to 3D advection-diffusion-reaction systems. Applied Mathematics and Computation 2018, 338, 260–273. [Google Scholar] [CrossRef]
- Pananu, K.; Sungnul, S.; Sirisubtawee, S.; Phongthanapanich, S. Convergence and Applications of the Implicit Finite Difference Method for Advection-Diffusion-Reaction Equations. IAENG International Journal of Computer Science 2020, 47, 645–663. [Google Scholar]
- Cheng, H.; Zheng, G. Analyzing 3D advection-diffusion problems by using the improved element-free Galerkin method. Mathematical Problems in Engineering 2020, 2020. [Google Scholar] [CrossRef]
- Cruz-Quintero, E.; Jurado, F. Boundary Control for a Certain Class of Reaction-Advection-Diffusion System. Mathematics 2020, 8, 1854. [Google Scholar] [CrossRef]
- Para, K.; Jitsom, B.; Eymard, R.; Sungnul, S.; Sirisubtawee, S.; Phongthanapanich, S. An accuracy comparison of piecewise linear reconstruction techniques for the characteristic finite volume method for two-dimensional convection-diffusion equation. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik 2021, 101, e201900245. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Y.; Lin, J.; Zhang, Y. A space-time backward substitution method for three-dimensional advection-diffusion equations. Computers & Mathematics with Applications 2021, 97, 77–85. [Google Scholar]
- Hidayat, M.I.P. Meshless finite difference method with B-splines for numerical solution of coupled advection-diffusion-reaction problems. International Journal of Thermal Sciences 2021, 165, 106933. [Google Scholar] [CrossRef]
- Shahid, N.; Rehman, M.A.u.; Khalid, A.; Fatima, U.; Shaikh, T.S.; Ahmed, N.; Alotaibi, H.; Rafiq, M.; Khan, I.; Nisar, K.S. Mathematical analysis and numerical investigation of advection-reaction-diffusion computer virus model. Results in Physics 2021, 26, 104294. [Google Scholar] [CrossRef]
- Murillo-García, O.F.; Jurado, F. Adaptive Boundary Control for a Certain Class of Reaction–Advection–Diffusion System. Mathematics 2021, 9, 2224. [Google Scholar] [CrossRef]
- Para, K.; Sungnul, S.; Sirisubtawee, S.; Phongthanapanich, S. A Comparison of Numerical Solutions for Advection-Diffusion-Reaction Equations between Finite Volume and Finite Difference Methods. Engineering Letters 2022, 30. [Google Scholar]
- Tannehill, J.C.; Anderson, D.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer, 2nd ed.; Taylor & Francis, 1997. [Google Scholar]
- Thongmoon, M.; McKibbin, R.; Tangmanee, S. Numerical solution of a 3-D advection-dispersion model for pollutant transport. Thai Journal of Mathematics 2012, 5, 91–108. [Google Scholar]
| Boundary | Boundary condition | Value |
|---|---|---|
| Entrance gate : | 0 | |
| Entrance gate : | 1 | |
| Exit gate : | 0 | |
| Right side wall : | 0 | |
| Right side wall : | 1 | |
| Right side wall : | 0 | |
| Left side wall : | 0 | |
| Ground : | 0 | |
| Ceiling : | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





