1. A sufficient and necessary condition for proof of Goldbach conjecture
The square of a natural square number greater than 2 is equal to the square of a natural square number greater or equal to 0 and a Goldbach partition semiprime.
Let
m be a natural number greater or equal to 2. Let
n be a natural number greater or equal to zero. Let
sg be a Goldbach partition semiprime. Gold- bach partition semiprimes contain prime factors of the same parity. The above condition means that:
1.1. Proof
The above mathematical statement implies that for every natural number m ≥ 2 there exists a Goldbach partition semiprime sg ≤ m subject to condition (1).
Let
p and
q be the prime factors of the semiprime
sg such that
In which case, by (1),
and
This also implies that
and
Thus the above condition is sufficient for the proof of the Binary Goldbach conjecture.
We can now proceed on to prove the Binary Goldbach conjecture assuming the condition (1) above.
2. Proof of Binary Goldach conjecture
The above partition (1) also implies that the prime factors of
sg are
m +
n and
m − n. By (1):
Substituting (2) into the first factor of (3) we obtain the formulation given by(4) that generates prime numbers.
Substituting (2) into the second factor of (3) we obtain the formulation given by (5) that generates the first prime factor of
sg.
Adding together equations (4) and (5) we obtain the Goldbach partition formu- lation of even numbers greater or equal to 4 given by formulation (6) below.
by (1)
Thus all composite even numbers have a Goldbach partition given by any of the formulae (6) and (10) above.
The gap between primes in a Goldbach partition is given by
Thus given the zeta function (11):
Then the equation (12) below is holds true:
When a sum series is presented in the form (12) above then n would represent half the gap between consecutive primes and sg would represent product of consecutive primes. The sum series (12) is exactly in accordance to distribution of prime numbers. The above findings are in agreement with the Riemann’s hypothesis.
3. Results
Example 1. work out the Goldbach partition pairs of 100 using equaton (1) and (10)
The partition pairs are (3, 97), (11, 89), (17,83), (29, 71), (41, 59) and (47, 53).
Example 2 Use formula (11) to determine the gaps between primes of the Goldbach partition of 40.
3.1. Conclusion on the Binary Goldbach conjecture
The binary Goldbach conjecture is true. A necessary neccessary and sufficient condition it’s for proof exists.
The binary Goldbach conjecture qualifies to be a theorem.
The findings from this proof method furnishes the tools for the proof of An- drica conjecture.
4. Proof of Andrica Conjecture
The conjecture asserts that the inequality
holds for all
n where
pn is the
nth prime.
In this research, consecutive primes share are common Goldbach partition semiprime. Thus if
then
If The Andrica conjecture is true then:
The above inequality simplifies to
If
gn represents the gap between the primes, then also
We can afford to omit 1 on the left side of the inequality.This also means that
Since the smallest gap is 1 then the above inequality also implies that:
m represents the average of the two consecutive primes. The gap beween two consecutive primes is less that average of the two primes. Thus Andrica conjec- ture is true and qualifies to be a theorem.
The findings from the proof method used in resolving the Andrica conjecture can be used to prove Legendre conjecture.
5. Proof of Legendre conjecture
The Legendre conjecture proposes that exist prime numbers in between two consecutive square integers.
5.1. proof method
Let
r and
t be positive integers that fit the conditions of the equation (24) below.
The equation (24) can thus be considered to be an Andrica theorem problem. Thus is we set
where n is an integer, then by (24)
It should be clarified in the above form n has no bearing with gap between consecutive primes. The Andrica theorem equation (24) rather implies primes pn, pn+j lie in between consecutive square integers n2 and (n + 1)2. Thus Andrica theorem implies that Legendre conjecture is true.
5.2. Additional notes. On the Riemann zeta function as viewed through the Andrica theorem equation
For the purpose of analysis of the zeta function in sum series, the pn of equation (25) will be taken as the nth prime in which case the maximum integer value of rn is +1.
Thus for
p1 = 2,
r1 = +1. For
p2 = 3,
r2 = +1, and so on. If
s is a complex number given by equation (12) we note that:
Thus in equation (27)
n represents the number of primes. Thus
This also means from Euler product that
When we permit
s =
k where then
k is an integer then
Again we can also use the formulation below for relating
pn and
n:
where
zn is an integer greater or equal to zero. This means that
Thus the
nth integer is connected to the
nth prime by the above relationship. Thus
and
where:
On the other hand if:
then:
in which case:
Now know from complex analysis that −1 =
eiπ and
i =
eiπ The followingcomplex numbers fit with the s of the Riemann zeta function.
Also
Where k is a positive real number, rational or irrational, not equal to 1. There are other formulations of s given by the formulations:
Here
N is permitted to take fractional values. The above values of
s form the source of non trivial zeroes outside the critical strip.
5.3. The Riemann zeta function
The Riemman zeta function is a function of the complex variable s. Where ℜ(
s)
> 1 the function it is defined in the half absolutely by the convergent series
In the whole complex plane it is defined by analytical continuation through the functional equation
It should be noted that Riemann does not speak of analytical continuation of the function Σ
n−s beyond the half plane ℜ(
s)
> 1 but speaks rather of finding a formula for it which “remains valid for all s”[
3]. The view of analytic continuation in terms of chains of disks and power series convergent in each disk descends from Weierstrass and is quite antithetical to Riemann’s basic philosophy that analytic functions should be dealt with globally, not locally in terms of power series[
3]. Riemann introduced a function of a complex variable t defined by
with
s = +
it He then shows that is an entire even function of t whose zero have imaginary parts between −
and
.
He further states, sketching a proof of the number of zeroes in range between 0 and T. Riemann then continues: “Man findet nun in der That etwa so viel reelle Wurzeln innerhalb dieser Grenzen, und es ist sehr wahrscheinlich, dass alle Wurzeln reell sind.”, which can be translated as “Indeed, one finds between those limits about that many real zeros, and it is very likely that all zeros are real.” The statement that all zeros of the function
ξ(
t) are real is the Riemann hypothesis [
2].
When the complex numbers (54) to (58) are used in the ξ(t) even function (61) non trivial zeros are generated outside the critical line on which ℜ(s) = . The zeroes of the ξ(t) function will then have imaginary parts between between − and . Indeed the critical strip when N is permitted to be fractional. The Riemann hypothesis does not permit non trivial zeroes to be generated outside the critical line
6. Solution of the Riemann zeta equation
When the Riemann zeta function is equated to zero it becomes an equation with infinite number of solutions or zeroes. The complex number proposed in
Riemann hypothesis can be generalized to
where
logk is the unknown. Now the general Riemann zeta equation is given by
The solution of the above equation is finding the infinite logk values for a given N and use the same values of logk to determine the complex number s given by (62) above. These solutions can be computer generated.
Infinite number of solitions have been found for the case N = 2. The Riemman hypothesis proposes that the above Riemann equation has infinite number of solutions only for the case N = 2.This is false.
A preliminary test using N ≤ , that is, the real part of s ≥ 100 and k = 2 shows that infinite number of zeroes are generated. These results falsify the Riemann hypothesis.
This non-trivial zero is outside the critical strip and critical line ℜ(s) = . This result alone disproves the Riemann hypothesis.
7. A further examination of gaps between two consecutive primes
In equation (7)
n represents half the gap between primes of Goldbach partition. For the purpose of our present analysis, as applied to consecutive primes we will rewrite it to the form (65) below.
where
pn is
nth prime number,
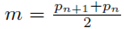
,
sg =
pn+1pn,
α is a positive integer. This means that means that the gap between consecutive primes is given by:
In determining gaps between primes using (67) rather than (71) it should be noted that 1.75 ≤
α ≤
pn − 1. Formula (67) suggests that the gap between the primes
pn and
pn+1 ranges from 2 to 2
floor 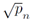
.
8. Conclusion
The binary Goldbach conjecture is true and qualifies to be a theorem. Each composite even number has at least one Goldbach partition semiprime for its Goldbach partition.
Andrica conjecture is true. Andrica conjecture qualifies to be a theorem. Andrica theorem implies that Goldbach conjecture is true.
The Riemman hypothesis is not true. non trivial zeroes can be generated outside the critical strip.
References
- Samuel B. B; Bezaleel J.N; Proofs of weak and Binary Goldbach conjectures.
- E. Bombieri;Problems of the millennium: The Riemann hypothesis.
- Edwards H.M; Riemann’s Zeta function.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
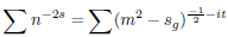
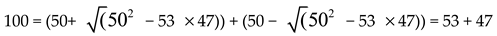
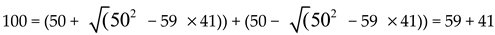
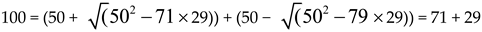
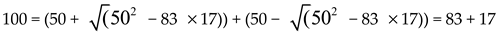
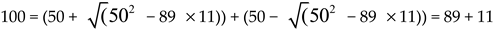
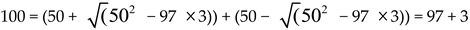
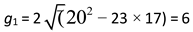

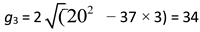
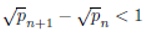
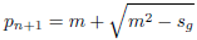
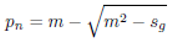

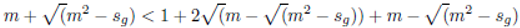
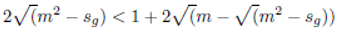
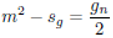
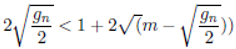
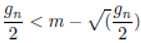
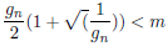
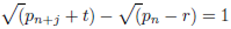
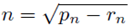
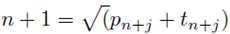
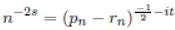
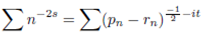
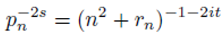
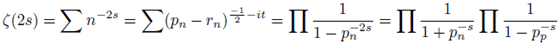
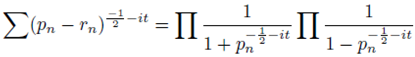
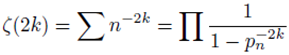
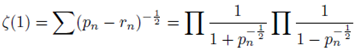
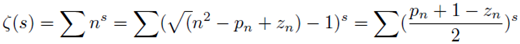
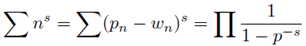
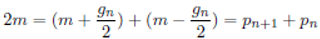
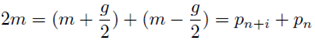
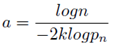
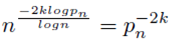
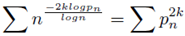
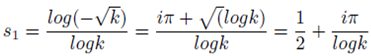
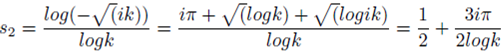
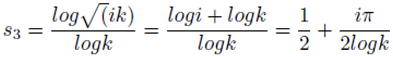
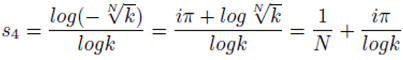
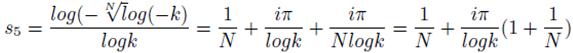
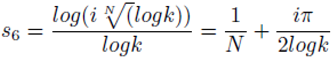
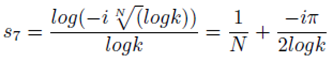
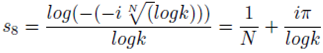
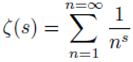
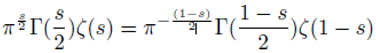
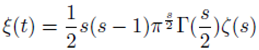
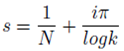
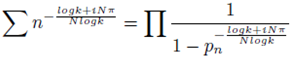
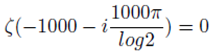
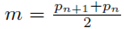 , sg = pn+1pn, α is a positive integer. This means that means that the gap between consecutive primes is given by:
, sg = pn+1pn, α is a positive integer. This means that means that the gap between consecutive primes is given by:
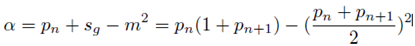
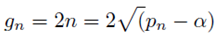
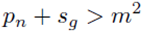
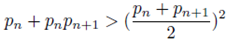
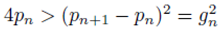
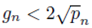
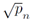 .
.


