An Order-Theoretic Study on Formal Concept Analysis

Preprint

Article

An Order-Theoretic Study on Formal Concept Analysis

Altmetrics

Downloads

105

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 September 2023

Posted:

13 September 2023

You are already at the latest version

Alerts

Abstract

In this paper, we study properties of formal concepts from an order-theoretic perspective. We first establish a natural correspondence between formal contexts and preorders as well as their induced posets. Then, based on the poset induced from a formal context, we provide characterization for join-irreducible or meet-irreducible elements of finite concept lattices. In addition, we introduce the notion of rough conceptual approximations based on topological closure and interior operators. In contrast with the conventional definition of equivalence class of an object used in Pawlakian approximation spaces, we instead utilize the extent of an object concept. We show that rough conceptual approximations are equivalent to approximation operators in the generalized approximation space associated with the preorder corresponding to a formal context. We also illustrate these theoretical results with examples and discuss their potential applications.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Formal concept analysis (FCA) and rough set theory (RST), which were respectively introduced by Rudolf Wille [1] and Zdzislaw Pawlak [2], are two mathematical theories that have been developed with the primary objective of facilitating data analysis and knowledge processing. These theories have proved to be extremely effective in extracting knowledge from data and have become powerful tools for knowledge acquisition.

FCA is initiated by a formal context (or simply context)

(G, M, I)

, where G and M are nonempty sets comprising objects and attributes respectively, and

I \subseteq G \times M

is a binary incidence relation connecting objects and attributes. Specifically,

(g, m) \in I

indicates that object g has attribute m.

Given a formal context

(G, M, I)

, we have two basic operators1,

{(\cdot)}^{↑} : ℘ (G) ⟶ ℘ (M)

and

{(\cdot)}^{↓} : ℘ (M) ⟶ ℘ (G)

defined by

A^{↑} = {m \in M ∣ \forall g \in A, (g, m) \in I}, and

B^{↓} = {g \in G ∣ \forall m \in B, (g, m) \in I},

for any

A \subseteq G

and

B \subseteq M

. Intuitively,

A^{↑}

is the maximal set of attributes shared by all objects in A and

B^{↓}

is the maximal set of objects that possess all attributes in B.

In a context, a formal concept is a pair

(A, B) \subseteq ℘ (G) \times ℘ (M)

such that

A^{↑} = B and B^{↓} = A,

(1.1)

where A and B are called the extent and the intent of the formal concept respectively. For a given

g \in G

and

m \in M

{g}^{↑}

and

{m}^{↓}

are called the object intent of g and the attribute extent of m respectively. The concept

({(g^{↑})}^{↓}

g^{↑})

(respectively,

(m^{↓}, {(m^{↓})}^{↑})

) is the object (respectively, attribute) concept associated with g (respectively, m).

The formal concepts of

(G, M, I)

are partially ordered based on the inclusion between extents or, equivalently, the inverse inclusion between intents. Formally,

(A_{1}, B_{1}) \leq (A_{2}, B_{2}) : ⟺ A_{1} \subseteq A_{2} (⟺ B_{1} \supseteq B_{2}) .

(1.2)

Equipped with this partial order ≤, the set

B (G, M, I)

consisting of all formal concepts of

(G, M, I)

forms a complete lattice2, referred to as the concept lattice of

(G, M, I)

[3].

According to [3], every formal concept

(A, B)

of a context

(G, M, I)

is the supremum (respectively, infimum) of some object (respectively, attribute) concepts. That is, in the concept lattice

B (G, M, I)

, all join-irreducible (respectively, meet-irreducible) elements are object (respectively, attribute) concepts, but not all object (respectively, attribute) concepts are join-irreducible (respectively, meet-irreducible). This motivates us to characterize join-irreducible (respectively, meet-irreducible) elements in terms of object intents (respectively, attribute extents) of the formal context.

The notion of formal contexts can also serve as a unifying framework for both RST and FCA [4]. The fundamental principle of rough set philosophy lies in considering objects as indiscernible when they possess the same attributes. Mathematically, the indiscernibility relation forms an equivalence relation that identifies all indiscernible objects. For a set X of objects, the lower approximation of X consists of objects whose equivalence classes are subsets of X, while the upper approximation of X comprises objects whose equivalence classes have a nonempty intersection with X. These lower and upper approximations are analogous to the interior and closure in topology, and the induced topology is Alexandroff. In other words, it is a topology where arbitrary intersections of open sets are open, or equivalently, every object has a smallest open neighborhood [5]. However, it should be noted, as Yamaguchi et al. [6] pointed out, that these approximations do not establish a direct relationship between an object and its corresponding attributes.

As the extent and intent of a formal concept can uniquely determine each other, FCA enables the analysis of both the data objects and their attributes. Kent [7] combined RST with FCA to explore the rough approximation of conceptual structures. However, as Saquer and Deogun [23] highlighted, Kent’s approach relies on the existence of an expert-provided equivalence relation on the set of objects, which gives rise to different results depending on the chosen equivalence relation.

To address this limitation, Saquer and Deogun [8] proposed an approach for approximating concepts within the framework of FCA. In a given formal context

(G, M, I)

, they introduced an equivalence relation on G, where two objects are considered equivalent if they share the same set of attributes. They presented a novel method for concept approximation using RST. It is worth noting that the equivalence relation employed by Saquer and Deogun [8] aligns precisely with the indiscernibility relation from the RST standpoint. In this regard, we also introduce the notion of lower and upper conceptual approximations for a set of objects. The notion arises from the topological study of a formal context and is related with preorder induced from it.

The paper is structured as follows. Section 2 provides essential background information on preorders, equivalence relations, posets, lattices, FCA, including the Basic Theorem on Concept Lattices, and RST. In Section 3, we establish necessary and sufficient conditions for a concept lattice to be finite. We also discuss conditions related to the irreducibility of object and attribute concepts. In addition, we introduce rough conceptual approximations. To illustrate the obtained results, we present two examples and potential applications in Section 4. Finally, Section 5 concludes the paper with several insightful remarks.

2. Preliminaries

If U is a finite set, the number of its elements is symbolically denoted by

| U |

. Let

R \subseteq U \times V

be a binary relation from a set U to another set V. Then, following Norris [9], for any

u \in U

and

v \in V

, we use the notation

u R = {v \in V ∣ u R v}, R v = {u \in U ∣ u R v} .

(2.3)

2.1. Preorders, partial orders and equivalence relations

A (binary) relation R on a set U, i.e.

R \subseteq U \times U

, is called a preorder if it is reflexive and transitive. A symmetric (respectively, anti-symmetric) preorder is called an equivalence relation (respectively, a partial order).

We will use the symbol ≤ to denote a partial order on a set U, and call

(U, \leq)

a partially ordered set, or a poset. We write

x < y

for “

x \leq y

and

x \neq y

”. The relation ≥ on U defined by

y \geq x

if and only if (shortened iff)

x \leq y

is the inverse relation of ≤.

For elements x and y of a given poset

(U, \leq)

, we say x is covered by y or y covers x, written

x ≺ y

y ≻ x

, if

x < y

and there exists no element

z \in U

such that

x < z < y

. In this case, x is called a lower cover of y and y is an upper cover of x.

If R is an equivalence relation on a set U and

u \in U

, then the R-equivalence class of u, denoted

{[u]}_{R}

, is the set of all elements

u^{'} \in U

such that

(u, u^{'}) \in R

. The set of all distinct R-equivalence classes, denoted

U / R

, is called the quotient set of U modulo R.

Lemma 1.

[10]A preorder ⊑ on a set U determines a topology

T

whose basis is the family of all sets

N_{u} = {v ∣ u ⊑ v}

for any

u \in U

. In addition,

(U, T)

is an Alexandroff space.

Lemma 2.

[11]If f is a function with domain U, then the relation ∼ on U defined by

x \sim y

iff

f (x) = f (y)

, is an equivalence relation on U, called the kernel relation of f.

2.2. Lattices

A poset

(L, \leq)

is called a lattice if every pair of elements x and y in L has both a meet (greatest lower bound)

x \land y

, and a join (least upper bound)

x \lor y

If a lattice has a least (respectively, largest) element, then it is unique. It’s called the bottom (respectively, top) element of the lattice. We are specially interested in finite lattices. The bottom and top elements exist for every nonempty finite lattice.

Let

(L, \leq)

be a nonempty finite lattice with ⊥ and ⊤ representing its bottom and top elements. An atom of

(L, \leq)

is an element covering ⊥. Dually, a coatom is an element covered by ⊤. An element

j \in L ∖ {⊥}

is join-irreducible, if whenever

j = x \lor y

for

x, y \in L

, then

j = x

j = y

. Dually, an element

m \in L ∖ {⊤}

is meet-irreducible if whenever

m = x \land y

for

x, y \in L

, then

m = x

m = y

Proposition 1.

[3]An element of a nonempty finite lattice is join-irreducible, iff it has exactly one lower cover, and meet-irreducible, iff it has exactly one upper cover.

Corollary 1.

In a nonempty finite concept lattice, every atom (respectively, coatom) is join-irreducible (respectively, meet-irreducible).

2.3. Formal concept analysis

In a formal context

(G, M, I)

{(^{↑})}^{↓} : ℘ (G) ⟶ ℘ (G)

and

{(^{↓})}^{↑} : ℘ (M) ⟶ ℘ (M)

are respectively closure operators3 on G and M. Also, as can be easily seen from [12], for each

g \in G

and

m \in M

{({g}^{↑})}^{↓} = {(g I)}^{↓} = {g^{'} \in G ∣ g^{'} I \supseteq g I},

(2.4)

{({m}^{↓})}^{↑} = {(I m)}^{↑} = {m^{'} \in M ∣ I m^{'} \supseteq I m} .

(2.5)

Denote by

Ext (G, M, I)

the set of all concept extents of

(G, M, I)

. We then have

Ext (G, M, I) = {A \subseteq G ∣ A = {(A^{↑})}^{↓}} = {{(X^{↑})}^{↓} ∣ X \subseteq G}

(2.6)

Since

{(^{↑})}^{↓} : ℘ (G) ⟶ ℘ (G)

is extensive and isotonic, it follows that for

X \subseteq G

\begin{matrix} X \subseteq A \in Ext (G, M, I) & ⟹ & X \subseteq {(X^{↑})}^{↓} \subseteq {(A^{↑})}^{↓} \\ ⟹ & {(X^{↑})}^{↓} \subseteq A \end{matrix}

(2.7)

This gives:

Lemma 3.

Let

(G, M, I)

be a formal context. Then

(1): For each $X \subseteq G$ , ${(X^{↑})}^{↓}$ is the smallest extent containing X.
(2): For each $g \in G$ and $A \in Ext (G, M, I)$ ,

$g \in A ⟹ {({g}}}^{↑})^{↓} \subseteq A$

(2.8)

Let us recall the Basic Theorem of Formal Concept Analysis.

Theorem 1.

(The Basic Theorem on Concept Lattices [3]). Let

(G, M, I)

be a formal context. Then

(B (G, M, I), \leq)

is a complete lattice in which the infimum and supremum of a family of formal concepts

(A_{t}, B_{t})

t \in T

, are respectively given by

\underset{t \in T}{⋀} (A_{t}, B_{t}) = (⋂_{t \in T} A_{t}, {({(⋃_{t \in T} B_{t})}^{↓})}^{↑}),

(2.9)

\underset{t \in T}{⋁} (A_{t}, B_{t}) = ({({(⋃_{t \in T} A_{t})}^{↑})}^{↓}, ⋂_{t \in T} B_{t}) .

(2.10)

In addition, for any formal concept

(A, B) \in B (G, M, I)

, we have

\underset{g \in A}{⋁} ({({g}^{↑})}^{↓}, {g}^{↑}) = (A, B) = \underset{m \in B}{⋀} ({m}^{↓}, {({m}^{↓})}^{↑}) .

(2.11)

2.4. Rough set theory

The basic construct of RST is the (Pawlakian) approximation space

(U, R)

, where U is a finite set of objects and R is an equivalence relation on U. For any

X \subseteq U

, its lower and upper approximations,

\underset{̲}{R} X

and

\bar{R} X

, in the approximation space are respectively defined as

\underset{̲}{R} X : = {u ∣ {[u]}_{R} \subseteq X},

(2.12)

\bar{R} X : = {u ∣ {[u]}_{R} \cap X \neq \emptyset} .

(2.13)

The R-equivalence classes are called elementary sets. A set

X \subseteq U

is called R-definable, iff it is a finite union of elementary sets. In this case,

\underset{̲}{R} X = \bar{R} X

While the Pawlakian approximation space is based on the equivalence relation, there has been extensive work on generalized approximation space defined as

(U, R)

, where R is an arbitrary binary relation on U. For such a generalized approximation space, the lower and upper approximations of a subset

X \subseteq U

are

\underset{̲}{R} X : = {u ∣ u R \subseteq X},

(2.14)

\bar{R} X : = {u ∣ u R \cap X \neq \emptyset} .

(2.15)

As RST provides an effective tool for data analysis, an approximation space is usually induced from a data table formally defined as an information system [2].

Definition 1.

An information system is a quadruple

(U, A, {V_{i} ∣ i \in A}, {f_{i} ∣ i \in A}),

where

U is a finite set, called the universe,
A is a finite set of attributes,
for each $i \in A$ , $V_{i}$ is the domain of values for i, and
for each $i \in A$ , $f_{i} : U ⟶ V_{i}$ is a total function.

Given an information system

I = (U, A, {V_{i} ∣ i \in A}, {f_{i} ∣ i \in A})

and a subset of attributes

B \subseteq A

, the indiscernibility relation with respect to B, denoted by

i n d (B)

, is a binary relation on U defined by

(x, y) \in i n d (B) ⟺ f_{i} (x) = f_{i} (y) \forall i \in B .

Sometimes, we also write

i n d (I)

to denote the indiscernibility relation with respect to all attributes

i n d (A)

. Obviously,

i n d (B)

is an equivalence relation on U and so

(U, i n d (B))

is an approximation space.

A straightforward connection between FCA and RST is that a formal context can be regarded as a special kind of information system. Formally, the incidence matrix of the binary relation I in a formal context

(G, M, I)

is simply a two-valued information system

(U, A, {V_{i} ∣ i \in A}, {f_{i} ∣ i \in A})

such that

U = G, A = M, V_{a} = {0, 1}

for all

a \in M

, and

f_{a} (x) = 1

iff

(x, a) \in I

for all

x \in G

and

a \in M

. With this viewpoint, the set of objects G and the indiscernibility relation

i n d (M)

form an approximation space. Dually, the transposed incidence matrix of I is also a two-valued information system with rows and columns of the above-mentioned information system being exchanged. Then,

(M, i n d (G))

is also an approximation space. Hence, rough set approximations can be defined for subsets of objects or attributes in a formal context. This is exactly the approach of formal rough concept analysis proposed in [8].

3. Ordered Sets from Formal Contexts

Analogous to the relationship between approximation spaces and information systems, in this section, we show the correspondence between pre-ordered sets and formal contexts. The correspondence can be constructed from the perspective of objects or attributes. Here, we only consider the perspective of objects as all results can be easily dualized to the attribute case.

On one hand, observing from (2.4), we can define a pre-order

⊑_{C}

on G for a formal context

C = (G, M, I)

as follows:

g ⊑_{C} g^{'} : ⟺ g I \subseteq g^{'} I (⟺ {({g^{'}}^{↑})}^{↓} \subseteq {({g}^{↑})}^{↓}) .

(3.16)

On the other hand, given a pre-ordered set

P = (G, ⊑)

, we can define a canonical formal context

C_{P} = (G, G, ⊒)

. In other words, it is a special kind of formal context

(G, M, I)

, where

M = G

and

g I g^{'}

iff

g^{'} ⊑ g

. Then, it is easy to show that

⊑_{C_{P}} = ⊑

For a pre-ordered set

P = (G, ⊑)

, the binary relation ≡ defined by

x \equiv y

iff

x ⊑ y \land y ⊑ x

is an equivalence relation. In fact, ≡ is a congruence relation with respect to ⊑. Hence, a pre-ordered set

(G, ⊑)

naturally determine a poset

(G / \equiv, \leq)

, where ≤ is defined by

{[x]}_{\equiv} \leq {[y]}_{\equiv}

iff

x ⊑ y

Based on the viewpoint of formal contexts as information systems mentioned in Section 2.4, it is easy to verify that the equivalence relation

\equiv_{C}

induced from

⊑_{C}

is exactly the indiscernibility relation

i n d (C)

. In addition, the poset determined by

⊑_{C}

is isomorphic to

({g I ∣ g \in G}, \subseteq)

Next, we study properties of a formal context based on its induced poset and pre-order. For the simplicity of presentation, we will fix a formal context

C

and omit the subscript of orders induced from

C

. For example, we will write the pre-order

⊑_{C}

simply as ⊑. Moreover, because we are especially interested in properties of finite concept lattices, we will first prove main results on the characterization about finiteness of concept lattices.

3.1. Characterization about the finiteness of concept lattices

In a formal context

(G, M, I)

, the set of its object concepts is

O (G, M, I)

. Similarly,

A (G, M, I)

denotes the set of its attribute concepts. We denote

Int (G, M, I)

the set of concept intents of

(G, M, I)

. It is clear from (1.1) that either the extent or intent of a formal concept can uniquely identifies the formal concept. As a consequence, we obtain

B (G, M, I) = {(B^{↓}, B) ∣ B \in Int (G, M, I)}

(3.17)

Using (2.3), we have

{g}^{↑} = g I for each g \in G

(3.18)

That is,

g I

is the object intent of g and so, by (2.11),

Int (G, M, I) = {⋂_{g I \in C} g I ∣ C \subseteq {g I ∣ g \in G}}

(3.19)

From (1.1) and (3.18), we have for any

g, g^{'} \in G

{({g^{'}}^{↑})}^{↓} = {({g}^{↑})}^{↓} ⟺ g^{'} I = g I

(3.20)

Dually, we have

{m}^{↓} = I m for each m \in M,

(3.21)

and for any

m, m^{'} \in M

{({m^{'}}^{↓})}^{↑} = {({m}^{↓})}^{↑} ⟺ I m^{'} = I m

(3.22)

Denote by

R_{M}

the kernel relation of the function

g ⟼ g I

on G. That is,

R_{M}

is the indiscernibility relation

i n d (M)

if we regard

(G, M, I)

as an information system. We then have

{({g}^{↑})}^{↓} = ⋃ {{[g^{'}]}_{R_{M}} ∣ g^{'} I \supseteq g I} for each g \in G,

(3.23)

and therefore, we have

{[g]}_{R_{M}} \subseteq {({g}^{↑})}^{↓} for each g \in G,

(3.24)

This, together with (2.8), implies that every extent of

(G, M, I)

is a definable set in the approximation space

(U, R_{M})

. In other words,

\underset{̲}{R_{M}} (A) = A = \bar{R_{M}} (A) for each A \in Ext (G, M, I) .

(3.25)

Dually, let

R_{G}

be the kernel relation of the function

m ⟼ I m

on M. Then we have

{({m^{'}}^{↓})}^{↑} = ⋃ {{[m^{'}]}_{R_{G}} ∣ I m^{'} \supseteq I m} for each m \in M,

(3.26)

{[m]}_{R_{G}} \subseteq {({m}^{↓})}^{↑} for each m \in M

(3.27)

According to (2.11), an intent (respectively, extent) is the intersection of some object intents (respectively, attribute extents). Therefore, from (3.20) and (3.22), we obtain

Lemma 4.

For a formal context

(G, M, I)

, the following statements are equivalent:

(1): $B (G, M, I)$ is a finite lattice.
(2): The set ${{g}^{↑} ∣ g \in G} = {g I ∣ g \in G}$ of object intents is a finite set.
(3): $O (G, M, I)$ is a finite set.
(4): The set ${{m}^{↓} ∣ m \in M} = {I m ∣ m \in M}$ of attribute extents is a finite set.
(5): $A (G, M, I)$ is a finite set.

This gives necessary and sufficient conditions for a concept lattice to be finite.

3.2. Join-irreducibles and meet-irreducibles of finite concept lattices

Recall that two posets

(P, \leq_{P})

and

(Q, \leq_{Q})

are isomorphic (respectively, dual isomorphic) if there exists a function f from P onto Q such that

x \leq_{P} y

iff

f (x) \leq_{Q} f (y)

(respectively,

f (y) \leq_{Q} f (x)

). In this case, f is bijective and is called an order isomorphism (respectively, a dual order isomorphism).

In a formal context

(G, M, I)

, it is clear from (1.1), (1.2) and Theorem 1 that

Ext (G, M, I)

and

Int (G, M, I)

are lattices under inclusion.

O (G, M, I)

and

A (G, M, I)

are posets under the order ≤ from the concept lattice. Therefore, from (1.2) and (3.18), we obtain the following

Lemma 5.

Let

(G, M, I)

be a formal context. Then

(1): $(Ext (G, M, I), \subseteq)$ is a lattice isomorphic to the concept lattice $(B (G, M, I), \leq)$ .
(2): $(Int (G, M, I), \subseteq)$ is a lattice dual isomorphic to the concept lattice $(B (G, M, I), \leq)$ .
(3): The posets $(O (G, M, I), \leq)$ and $({g I ∣ g \in G}, \subseteq)$ are dual isomorphic.
(4): The posets $(A (G, M, I), \leq)$ and $({I m ∣ m \in M}, \subseteq)$ are isomorphic.

In the remainder of this section, we assume that

(G, M, I)

is a formal context whose concept lattice

B (G, M, I)

is finite. From (2.10) and the principle of vacuous truth, the extent of the top element ⊤ is (always) the object set G. Dually, the intent of the bottom element ⊥ is the attribute set M. Using (2.3), we have

G^{↑} = ⋂_{g \in G} g I

and

M^{↓} = ⋂_{m \in M} I m

. It follws that

⊥ = (⋂_{m \in M} I m, M), ⊤ = (G, ⋂_{g \in G} g I)

(3.28)

Notice that the intent

G^{↑}

of ⊤ can be empty, if

⋂_{g \in G} g I = \emptyset

. Dually, the extent

M^{↓}

of ⊥ can be empty, if no such object has been specified.

Denote by

J

the set of join-irreducible elements of

B (G, M, I)

. From (2.11), we have

J \subseteq O (G, M, I)

(3.29)

This, together with (3.28), Corollary 1 and Theorem 1, leads to the following:

Lemma 6.

Let

(G, M, I)

be a formal context whose concept lattice

B (G, M, I)

is a finite lattice. An atom of

B (G, M, I)

can be characterized in any of the following ways:

It has the bottom element of $B (G, M, I)$ as its lower cover.
It is an object concept whose intent is covered by M in the lattice $(Int (G, M, I), \subseteq)$ .
It is an object concept whose intent is a maximal element within the poset

$({g I ∣ g \in G} ∖ {M}, \subseteq)$ .
It is an object concept whose intent is covered by M within the poset

$({g I ∣ g \in G} \cup {M}, \subseteq)$ .

This gives characterizations of atoms of finite concept lattices in terms of object intents. Clearly, the dual of Lemma 6 also holds in a finite concept lattice. As a consequence, we obtain the following result.

Lemma 7.

Let

(G, M, I)

be a formal context whose concept lattice

B (G, M, I)

is a finite lattice. An coatom of

B (G, M, I)

can be characterized in any of the following ways:

(1): It has the top element of $B (G, M, I)$ as its upper cover.
(2): It is an attribute concept whose extent is covered by G within the lattice

$(Ext (G, M, I), \subseteq)$ .
(3): It is an attribute concept whose extent is a maximal element within the poset

$({I m ∣ m \in M} ∖ {G}, \subseteq)$ .
(4): It is an attribute concept whose extent is covered by G within the poset

$({I m ∣ m \in M} \cup {G}, \subseteq)$ .

Within the poset

({g I ∣ g \in G}, \subseteq)

, if an object intent

\tilde{g} I

of the formal context

(G, M, I)

has exactly one upper cover, say

{\tilde{g}}^{*} I

. Then for any nonempty

F \subseteq {g I ∣ g \in G}

\begin{matrix} \tilde{g} I \subset ⋂_{g I \in F} g I & ⟹ & \tilde{g} I \subset {\tilde{g}}^{*} I \subseteq g I for every g I \in F \\ ⟹ & \tilde{g} I \subset {\tilde{g}}^{*} I \subseteq ⋂_{g I \in F} g I \end{matrix}

(3.30)

This, together with Lemma 6, implies that an object intent has exactly one upper cover within the lattice

(Int (G, M, I), \subseteq)

iff it has exactly one upper cover within the poset

({g I ∣ g \in G} \cup {M}, \subseteq)

. Since the lattice

(Int (G, M, I), \subseteq)

and the concept lattice are dual isomorphic, and since the posets

(O (G, M, I), \leq)

and

({g I ∣ g \in G}, \subseteq)

are dual isomorphic, we obtain the following:

Proposition 2.

Let

(G, M, I)

be a formal context whose concept lattice

B (G, M, I)

is a finite lattice. A formal concept is join-irreducible iff it is an object concept whose intent having exactly one upper cover within the poset

({g I ∣ g \in G} \cup {M}, \subseteq)

Dually, we have the following:

Proposition 3.

Let

(G, M, I)

be a formal context whose concept lattice

B (G, M, I)

is a finite lattice. A formal concept is meet-irreducible iff it is an attribute concept whose attribute extent having exactly one upper cover within the poset

({I m ∣ m \in M} \cup {G}, \subseteq)

Proposition 2 and Proposition 3 provide conditions for determining the join-irreducibility of an object concept and the meet-irreducibility of an attribute concept, respectively. These propositions offer insights into the structure of the concept lattice in a formal context. By examining the upper covers within the appropriate posets, we can identify the specific characteristics of join-irreducible object concepts and meet-irreducible attribute concepts within the lattice. These propositions serve as powerful tools for understanding and analyzing the concept lattice, enabling us to identify and study important concepts that possess unique properties within the context.

3.3. Rough conceptual approximations

Let

R_{M}

and ⊑ be respectively the indiscernibility relation and pre-order associated with the formal context

(G, M, I)

. Then,

(G, R_{M})

and

(G, ⊑)

are a Pawlakian and generalized approximation space respectively. Hence, it is natural to define lower and upper approximations in these two spaces based on RST. Indeed, rough set approximations for FCA have been defined with these two kinds of approximation spaces in [8] and [12] respectively.

On the other hand, by Lemma 1, ⊑ determines an Alexandroff topology

T

on G in which for each

g \in G

N_{g} = {g^{'} ∣ g ⊑ g^{'}} = {g^{'} ∣ g I \subseteq g^{'} I} = {({g}^{↑})}^{↓}

is the smallest open neighborhood of g. It is easily seen that the binary neighborhood system [13]

B N : U ⟶ ℘ (U)

on U defined by

B N (g) = {({g}^{↑})}^{↓}

is equivalent to the topological neighborhood system of the Alexandroff space

(G, T)

. Therefore, the topological closure and interior operators of

(G, T)

will send any

X \subseteq G

{g \in G ∣ {({g}^{↑})}^{↓} \cap X \neq \emptyset}

and

{g \in G ∣ {({g}^{↑})}^{↓} \subseteq X}

respectively. This observation motivates us to introduce the notion of rough conceptual approximations:

Definition 2.

Let

(G, M, I)

be a formal context. For any

X \subseteq G

, the lower conceptual approximation of X, denoted by

{I_{M}}_{*} (X)

, and upper conceptual approximation of X, denoted by

{I_{M}}^{*} (X)

, are respectively defined as follows:

{I_{M}}_{*} (X) = {g \in G ∣ {({g}^{↑})}^{↓} \subseteq X},

(3.31)

{I_{M}}^{*} (X) = {g \in G ∣ {({g}^{↑})}^{↓} \cap X \neq \emptyset} .

(3.32)

Using (3.23), (3.31) and (3.32) can be rewritten as

{I_{M}}_{*} (X) = ⋃_{g \in G : {({g}^{↑})}^{↓} \subseteq X} {[g]}_{R_{M}}

(3.33)

{I_{M}}^{*} (X) = ⋃_{g \in G : {({g}^{↑})}^{↓} \cap X \neq \emptyset} {[g]}_{R_{M}} .

(3.34)

From the definition, we can derive the following theorem.

Theorem 2.

(G, M, I)

is a formal context

(G, M, I)

, then

the lower and upper conceptual approximations

${I_{M}}_{*} : G ⟶ ℘ (G) and {I_{M}}^{*} : G ⟶ ℘ (G)$

are respectively toplogical interior and closure operators on $G;$
the set $T = {A \subseteq G ∣ {I_{M}}_{*} (A) = A}$ is an Alexandroff topology on $G;$
for each $g \in G$ , ${({g}^{↑})}^{↓}$ is the smallest open neighborhood of g in the Alexandroff space $(G, T)$ .

According to Theorem 2, we have

{I_{M}}_{*} (X) \subseteq X

for any

X \subseteq G

. This, together with (2.8) and (3.31), leads to the following:

Corollary 2.

(G, M, I)

is a formal context

(G, M, I)

, then

{I_{M}}_{*} (A) = A for each A \in Ext (G, M, I)

(3.35)

Combining (3.25) and (3.35), we obtain

{I_{M}}_{*} (A) = \underset{̲}{R_{M}} (A) = A = \bar{R_{M}} (A) for each A \in Ext (G, M, I)

(3.36)

In addition, by the definition of

N_{g}

in the topology, it is easy to see that the topology-inspired definition of rough conceptual approximations is equivalent to the standard definition of rough set approximations in the space

(G, ⊑)

. Formally, we have

{I_{M}}_{*} (X) = \underset{̲}{⊑} (X)

and

{I_{M}}^{*} (X) = \bar{⊑} (X)

. As

R_{M}

is a sub-relation of ⊑, the following relationship holds.

Proposition 4.

For a formal context

(G, M, I)

and any

X \subseteq G

{I_{M}}_{*} (X) \subseteq \underset{̲}{R_{M}} (X) \subseteq X \subseteq \bar{R_{M}} (X) \subseteq {I_{M}}^{*} (X)

(3.37)

4. Examples and Applications

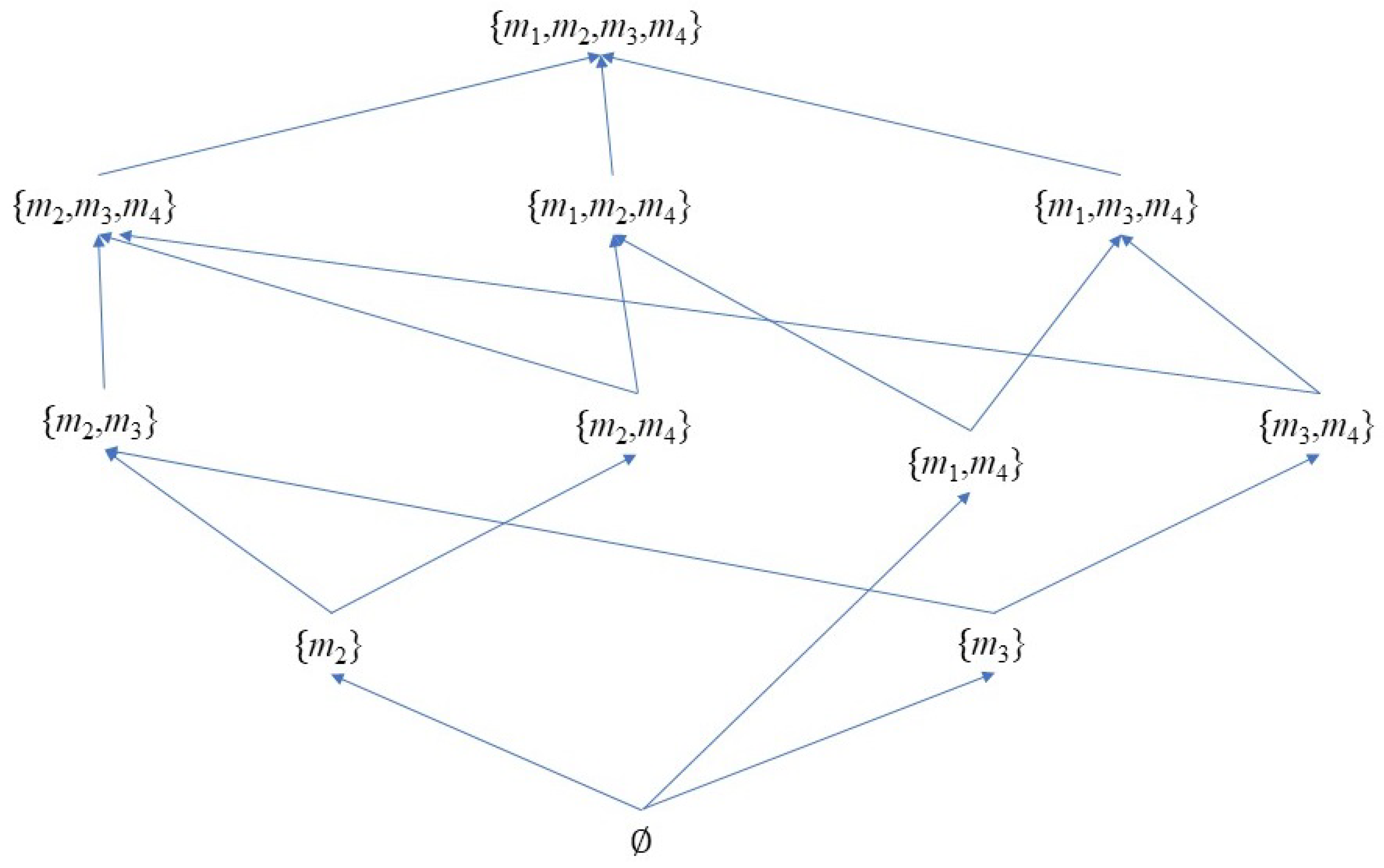
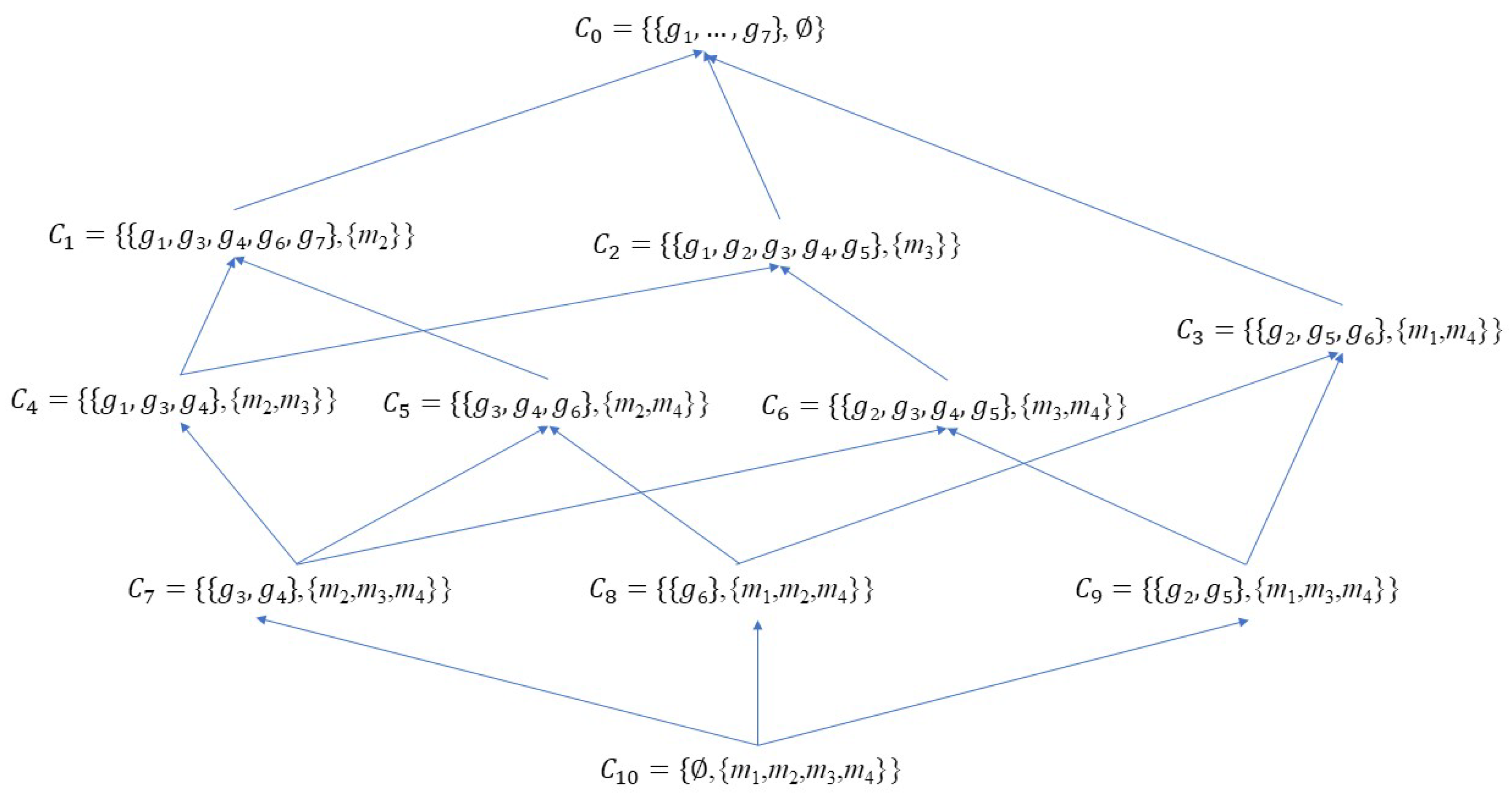
4.1. Illustrative examples

We present in this section two examples of a formal context to demonstrate and verify the obtained results.

Example 1.

Let us consider a formal context

(G, M, I)

, where

G = {g_{1}, \dots, g_{7}}

M = {m_{1}, \dots, m_{4}}

and the incidence relation I are described in Table 1. A

` ` 1^{''}

in row

g_{i}

and column

m_{j}

means that the object

g_{i}

has the attribute

m_{j}

and

` ` 0^{''}

means that

(g_{i}, m_{j}) \notin I

From Table 1, we have

\begin{matrix} g_{1} I = {m_{2}, m_{3}}, g_{2} I = g_{5} I = {m_{1}, m_{3}, m_{4}}, \\ g_{3} I = g_{4} I = {m_{2}, m_{3}, m_{4}}, \\ g_{6} I = {m_{1}, m_{2}, m_{4}}, g_{7} I = {m_{2}} . \end{matrix}

(4.38)

Using (2.10), (2.11) and (4.38), the concept intents of

(G, M, I)

can be computed as given in Figure 1.

From (3.17) and Figure 1, the formal concepts of

(G, M, I)

can be computed as given in Figure 2.

First, observe from Figure 2 that the object concepts

C_{7} = ({g_{3}, g_{4}}, {m_{2}, m_{3}, m_{4}})

C_{8} = ({g_{6}}, {m_{1}, m_{2}, m_{4}})

and

C_{9} = ({g_{2}, g_{5}}, {m_{1}, m_{3}, m_{4}})

are the atoms of the concept lattice. We can observe from (4.38) and Figure 1, the intents

{m_{2}, m_{3}, m_{4}}

{m_{1}, m_{2}, m_{4}}

and

{m_{1}, m_{3}, m_{4}}

C_{7}

C_{8}

and

C_{9}

, respectively, are

the elements covered by M in the lattice $(Int (G, M, I), \subseteq)$ .
the maximal elements of the poset $({g_{j} I ∣ g_{j} \in G} ∖ {M}, \subseteq)$ .
the elements covered by M within the poset $({g_{j} I ∣ g_{j} \in G} \cup {M}, \subseteq)$ .

These observations verify Lemma 6.

In the concept lattice, we have the following observations from Figure 2:

$C_{4}$ and $C_{5}$ are the lower covers of $C_{1}$ .
$C_{4}$ and $C_{6}$ are the lower covers of $C_{2}$ .
$C_{8}$ and $C_{9}$ are the lower covers of $C_{3}$ .
$C_{4} = ({g_{1}, g_{3}, g_{4}}, {m_{2}, m_{3}})$ has $C_{7} = ({g_{3}, g_{4}}, {m_{2}, m_{3}, m_{4}})$ as its only lower cover.
$C_{7}$ and $C_{8}$ are the lower covers of $C_{5}$ .
$C_{7}$ and $C_{9}$ are the lower covers of $C_{6}$ .

It follows that except for the atoms, the object concep

C_{4}

is the only element having exactly one lower cover in the concept lattice. We can observe from (4.38) that except for the intents of the atoms, the object intent

{m_{2}, m_{3}}

C_{4}

is the only object intent having exactly one upper cover within the poset

({g_{j} I ∣ g_{j} \in G} \cup {M}, \subseteq)

In this example, we first examine Lemma 6 which gives characterizations of atoms of finite concept lattices in terms of object intents. We then examine proposition 2 which states that a formal concept of a formal context

(G, M, I)

with finite concept lattice is join-irreducible iff it is an object concept and its object intent has only one element above it within the poset

({g I ∣ g \in G} \cup {M}, \subseteq)

Example 2.

Let us continue with Example 1. According to (4.38),

U / R_{M} = {{g_{1}}, {g_{2}, g_{5}}, {g_{3}, g_{4}}, {g_{6}}, {g_{7}}} .

(4.39)

Using (2.4), (4.38) and (4.39), we can compute

{({g}^{↑})}^{↓}

and

{[g]}_{R_{M}}

for each object

g \in G

as given in Table 2.

We can observe from Table 2 that

{[g_{j}]}_{R_{M}} \subseteq {({g_{j}}^{↑})}^{↓}

for every

g_{j} \in G

. These observations verify (3.24).

Let us approximate the rough set and rough conceptual approximations of the extent

A = {g_{1}, g_{3}, g_{4}}

and the set

X = {g_{1}, g_{2}, g_{3}, g_{5}} \notin Ext (G, M, I)

. According to (2.12), (2.13) and Table 2, we have

\underset{̲}{R_{M}} (A) = {g_{1}, g_{3}, g_{4}}, \bar{R_{M}} (A) = {g_{1}, g_{3}, g_{4}}

(4.40)

\underset{̲}{R_{M}} (X) = {g_{1}, g_{2}, g_{5}}, \bar{R_{M}} (X) = {g_{1}, g_{2}, g_{3}, g_{4}, g_{5}}

(4.41)

According to (3.31), (3.32) and Table 2, we have

{I_{M}}_{*} (A) = {g_{1}, g_{3}, g_{4}}, {I_{M}}^{*} (A) = {g_{1}, g_{3}, g_{4}, g_{7}}

(4.42)

{I_{M}}_{*} (X) = {g_{2}, g_{5}}, {I_{M}}^{*} (X) = {g_{1}, g_{2}, g_{3}, g_{4}, g_{5}, g_{7}}

(4.43)

Combining (4.40) and (4.42) , we obtain

{I_{M}}_{*} (A) = \underset{̲}{R_{M}} (A) = A = \bar{R_{M}} (A)

Combining (4.41) and (4.43), we obtain

\begin{matrix} {I_{M}}_{*} (X) = {g_{2}, g_{5}} \subseteq \underset{̲}{R_{M}} (X) = {g_{1}, g_{2}, g_{5}} \subseteq X = {g_{1}, g_{2}, g_{3}, g_{5}} \\ \subseteq & \bar{R_{M}} (X) = {g_{1}, g_{2}, g_{3}, g_{4}, g_{5}} \subseteq {I_{M}}^{*} (X) = {g_{1}, g_{2}, g_{3}, g_{4}, g_{5}, g_{7}} . \end{matrix}

This validates (3.36) and Proposition 4.

Table 2.

{({g}^{↑})}^{↓}

and

{[g]}_{R_{M}}

for every

g \in G

Table 2.

{({g}^{↑})}^{↓}

and

{[g]}_{R_{M}}

for every

g \in G

$Object g$	${({g}^{↑})}^{↓}$	${[g]}_{R_{M}}$
$g_{1}$	${g_{1}, g_{3}, g_{4}}$	${g_{1}}$
$g_{2}$	${g_{2}, g_{5}}$	${g_{2}, g_{5}}$
$g_{3}$	${g_{3}, g_{4}}$	${g_{3}, g_{4}}$
$g_{4}$	${g_{3}, g_{4}}$	${g_{3}, g_{4}}$
$g_{5}$	${g_{2}, g_{5}}$	${g_{2}, g_{5}}$
$g_{6}$	${g_{6}}$	${g_{6}}$
$g_{7}$	${g_{1}, g_{3}, g_{4}, g_{6}, g_{7}}$	${g_{7}}$

4.2. Applications

We have seen that there are mainly two approaches to rough set approximations in formal contexts based on equivalence classes

{[g]}_{R_{M}}

and extents of object concepts

{({g}^{↑})}^{↓}

respectively. Intuitively,

{[g]}_{R_{M}}

contains all objects that have exactly the same attributes of g and

{({g}^{↑})}^{↓}

represents objects that posses all attributes of g but possibly with more attributes than g.

In real-world applications, customer behavior analysis for targeted marketing campaigns can be described by formal contexts. By leveraging the object-attribute links in a formal context, businesses can identify distinct customer segments based on their shared attributes. These segments, corresponding to

{[g]}_{R_{M}}

{({g}^{↑})}^{↓}

, can provide valuable insights into customer behavior and preferences, enabling businesses to create more effective marketing strategies. Here are some potential applications based on the identified customer segments [14,15,16,17,18]:

Personalized Product Recommendations: AI algorithms can utilize collaborative filtering or content-based recommendation techniques to identify products or services that are likely to appeal to a customer segment. By providing personalized recommendations based on their shared attributes, businesses can enhance the customer experience and increase conversion rates.
Churn Prediction and Retention: Leveraging machine learning algorithms, businesses can analyze historical data of different segments and predict which groups of customers are at a higher risk of churn (i.e., discontinuing their association with the business). By proactively identifying these customers, companies can take targeted retention measures such as offering discounts, loyalty rewards, or personalized incentives to prevent churn.
Cross-Selling and Upselling Opportunities: AI-based recommender systems can analyze the purchase history and behavior of a customer segment to identify potential cross-selling or upselling opportunities. By suggesting complementary products or premium upgrades based on their shared attributes, businesses can increase their average order value and revenue.
Customer Segmentation: Using clustering algorithms such as k-means or hierarchical clustering, businesses can group customers into distinct segments based on their shared attributes. The segments derived from the formal context can serve as initial cluster assignments. AI algorithms can then refine these segments and uncover hidden patterns or subgroups within each segment. This kind of information can be used to develop targeted marketing campaigns tailored to the specific needs and preferences of each customer segment.

By applying AI techniques to analyze the extended formal context and the identified equivalence classes or extents, businesses can gain valuable insights into customer behavior, improve customer satisfaction, optimize marketing efforts, and ultimately drive revenue growth. The power of AI lies in its ability to uncover patterns and trends within vast amounts of data, enabling businesses to make data-driven decisions and deliver personalized experiences to their customers.

In all these applications, the success of AI techniques depends on an appropriate choice of customer segmentation. As mentioned above, we have at least two possibilities to form a group containing a given customer. In general, by taking the equivalence class

{[g]}_{R_{M}}

as a customer segment, the business can reach a target customer more precisely with a lower cost. On the other hand, choosing

{({g}^{↑})}^{↓}

as the customer segment enables the business to reach a broader scope of potential customers. Hence, the choice between these two approaches should depend on the goal that the business would like to achieve.

5. Conclusion

FCA and RST are two powerful mathematical theories that have been used extensively for data analysis and knowledge processing. FCA starts by defining a formal context using a triple

(G, M, I)

, where objects and attributes are linked through a binary relation. Formal concepts are sets that capture the maximal commonalities between objects and attributes, and the collection of all formal concepts forms a complete lattice known as the concept lattice. In contrast, RST employs equivalence relations to partition a set and reduce the number of attributes. The resulting partitions form the basis of the approximation space, which is used to derive the lower and upper approximations of a set. The use of these theories has led to significant advances in knowledge acquisition from data, with applications across diverse domains.

In this paper, we provide criteria to determine atoms and coatoms of finite concept lattices. In addition, we establish conditions under which certain formal concepts are join-irreducible or meet-irreducible. These properties are fundamental to understanding how the lattice of all concepts in a formal context is constructed and analyzed. Our findings have implications that extend beyond the theory of FCA, as they can be applied to various domains. Furthermore, we establish the relationship between the pre-order relation and the smallest open neighborhoods of elements in G. We show that the binary neighborhood system is equivalent to the topological neighborhood system of the Alexandroff space

(G, T)

. The closure and interior operators induced by the binary neighborhood system form a pair of topological closure and interior operators on

(G, T)

. Inspired by this, we introduce the notion of rough conceptual approximations and show that it is equivalent to rough approximations based on the pre-order relation. Overall, these findings contribute to the understanding of topological properties and rough approximations in FCA.

In summary, our contributions advance the theory of FCA and will enable us to gain deeper insights into the structures and relationships of complex data sets, making it easier to extract meaningful knowledge from them.

Author Contributions

All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Taiwan’s NSTC grant numbers 112-2221-E-150-032 (Y.R. Syau) and 110-2221-E-001-022-MY3 (C.J. Liau).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Wille, R. Restructuring lattice theory. In Ordered Sets; Rival, I., Ed.; Reidel, 1982; Volume 83, pp. 445–470. [Google Scholar]
Pawlak, Z. Rough sets. International Journal of Computer and Information Science. 1982; 11: 341-356. [CrossRef]
Ganter, B. , Wille R. Formal Concept Analysis: Mathematical Foundations. Springer-Verlag, 1999.
Shen, L. , Zhang, D. The concept lattice functors. International Journal of Approximate Reasoning. 2013; 54(1): 166-183. [CrossRef]
Arenas, F.G. Alexandroff spaces. Acta Mathematica Universitatis Comenianae. 1999; 68: 68 17-25.
Yamaguchi, D. , Murata, A., Li, G.D., Nagai, M. Rough Set Approximations in Formal Concept Analysis, in: Peters J.F. et al. (Eds.) Transactions on Rough Sets XII. Lecture Notes in Computer Science, vol 6190. Springer, Berlin, Heidelberg, 2010, pp. 226-235.
Kent, R.E. Rough concept analysis: a synthesis of rough sets and formal concept analysis. Fundamenta Informaticae. 1996; 27: 169-181.
Saquer, J. , Deogun, J.S. Formal rough concept analysis, in: Proceedings of the International Workshop on Rough Sets, Fuzzy Sets, Data Mining, and Granular-Soft Computing, 1999, pp. 91-99.
Norris, E. An algorithm for computing the maximal rectangles in a binary relation. Revue Roumaine des Mathematiques Pures et Appliquees. 1978; 23: 476-481.
May, J.P. Finite topological spaces. Notes for REU (2008). Available at http://www.math.uchicago.edu/ may/MISC/FiniteSpaces.pdf.
Hein, James L. Discrete Mathematics. 2nd Edition, Jones and Bartlett Publishers, Inc., 2003.
Hu, K. , Sui, Y., Lu, Y. Wang, J., Shi, C. Concept approximation in concept lattice, in: Hu K. et al. (Eds.) Advances in Knowledge Discovery and Data Mining. PAKDD 2001. Lecture Notes in Computer Science, vol 2035. Springer, Berlin, Heidelberg, 2001, pp. 167-173.
Lin, T.Y. Granular computing on binary relations I: data mining and neighborhood systems, in: Skowron A., Polkowski L. (Eds.) Rough Sets and Knowledge Discovery, Physica -Verlag, 1998, 107-121.
Banu, J. F. , Neelakandan, S., Geetha, B. T., Selvalakshmi, V., Umadevi, A., and Martinson, E. O., Artificial Intelligence Based Customer- Churn Prediction Model for Business Markets, Comput Intell Neurosci, 2022. [CrossRef]
Davenport, T. , Guha, A., Grewal, D., Bressgott, T., How artificial intelligence will change the future of marketing, Journal of Academy of Marketing Science, 2020; 48:24-42. [CrossRef]
Habil, S. , El-Deeb, S., and El-Bassiouny, N., AI-Based Recommendation Systems: The Ultimate Solution for Market Prediction and Targeting, The Palgrave Handbook of Interactive Marketing, C. L. Wang (ed.), 683-704.
Murray, P. W. , Agard, B., Barajas, M. A., Market segmentation through data mining: A method to extract behaviors from a noisy data set, Computers & Industrial Engineering, 2017: 109: 233-252.
Suh, Y. , Machine learning based customer churn prediction in home appliance rental business, J Big Data. 2023; 10(1): 41. [CrossRef]
Babin, M.A. , Kuznetsov, S.O. Dualization in lattices given by ordered sets of irreducubles. Theoretical Computer Science. 2017; 658: 316 -326. [CrossRef]
Birkhoff, G. Lattice Theory. American Mathematical Society, Providence, 3rd edition, 1967.
Day, M.M. Convergence, closure, and neighborhoods, Duke Mathematical Journal. 1944; 11:181-199.
Ganter, B. , Obiedkov, S. Conceptual Exploration. Springer-Verlag, Berlin Heidelberg, 2016.
Kent, R.E. Rough Concept Analysis. CoRR abs/1810.06986 (2018).
Markowsky, G. The Factorization and Representation of Lattices. Transactions of the American Mathematical Society. 1975; 203: 185-200.
Pawlak, Z. Rough sets: theoretical aspects of reasoning about data, Dordrecht: Kluwer Academic Publishers, 1991.
Pawlak, Z. Reasoning about data - a rough set perspective, in: Polkowski L., Skowron A. (Eds.) Rough Sets and Current Trends in Computing. RSCTC 1998. Lecture Notes in Computer Science, vol 1424. Springer, Berlin, Heidelberg, 1998, pp. 25-34.
Priss, U. Formal concept analysis in information science. Annual Review of Information Science and Technology. 2006; 40(1): 521-543.

1	In this paper, we use $℘ (X)$ to denote the powerset of a set X.
2	A complete lattice is a partially ordered set in which every subset has an infimum and a supremum.
3	A closure operator on a set U is a function from the power set of U into itself which is extensive, isotonic (order-preserving) and idempotent.

Figure 1. Concepts intents in Table 1.

Figure 2. Formal concepts in Table 1.

Table 1. Exemplary formal Context.

I	$m_{1}$	$m_{2}$	$m_{3}$	$m_{4}$
$g_{1}$	0	1	1	0
$g_{2}$	1	0	1	1
$g_{3}$	0	1	1	1
$g_{4}$	0	1	1	1
$g_{5}$	1	0	1	1
$g_{6}$	1	1	0	1
$g_{7}$	0	1	0	0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Order-Theoretic Study on Formal Concept Analysis

Abstract

1. Introduction

2. Preliminaries

2.1. Preorders, partial orders and equivalence relations

2.2. Lattices

2.3. Formal concept analysis

2.4. Rough set theory

3. Ordered Sets from Formal Contexts

3.1. Characterization about the finiteness of concept lattices

3.2. Join-irreducibles and meet-irreducibles of finite concept lattices

3.3. Rough conceptual approximations

4. Examples and Applications

4.1. Illustrative examples

4.2. Applications

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe