1. Introduction

2. Constitutive modelling

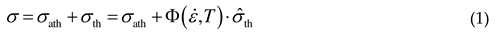
2.1. Thermal stress

The thermal stress is closely related to the microstructural features of the material, as it utilizes the thermal vibrations of the crystal lattice to assist dislocations in overcoming weak barriers (such as forest dislocations and Peierls barriers). This facilitates the diffusion or glide of dislocations, resulting in material deformation.

2.1.1. Thermal activation effect in fixed structures

In the mechanism of thermally activated dislocation motion, the average waiting time of dislocations before encountering short-range barriers can be expressed in a modified form of Arrhenius equation [17]:

where, v₀ represents the vibration frequency (~ 10¹¹ s^-1) of the dislocation before encountering barriers [23], k_B is the Boltzmann constant, T is the temperature, and ΔG is the thermal activation free energy (Gibbs free energy) required for dislocations to overcome the barriers, which is a function associated with the shape of the barrier (e.g., rectangular, square, triangular, parabolic, exponential) as well as stress. The modified form indicates that the waiting time for dislocations in a continuous slip system (ΔG = 0) is zero.

Kocks and Ashby proposed a general expression for activation energy:

where, G₀ is the reference free energy at 0 K (=g₀μ₀b³, g₀ is the normalized free energy, μ₀ is the shear modulus (=μ(0K)), b is the magnitude of Burgers vector). p and q are a pair of parameters that characterize the shape of the barrier. q corresponds to the shape of the short-range barrier, where for a quasi-parabolic barrier, the range is 1 ≤ q ≤ 2. p describes the rate of decay of the field at longer distances, with a value of 0 < p ≤ 1. A value of p = 1 indicates no decay, while smaller values indicate faster decay of the activation energy at longer distances.

During the thermal activation stage, the time required for dislocations to overcome barriers is primarily determined by the waiting time of t_w. According to Orowan's law (γ=N_mb·Δl), the equivalent true strain rate can be expressed as follows:

where, Δl represents the average distance traveled by dislocations between barriers, N_m denotes the mobile dislocation density. In the high strain rate regime, the mobile dislocation density dominates the total dislocation density, that is N_m = N_tot [2,24]. M is the Taylor factor, where σ=Mτ, ε=γ/M, τ and γ represent the shear stress and strain, respectively. The reference strain rate is defined as ${\dot{\epsilon }}_0$ = N_mb·Δlv₀/M with general order of 10⁷ s^-1 [10]。

By substituting Eq.(4) into Eq.(3), and considering the relationship of $\mathsf{\Phi }(\dot{\epsilon },T)={\mathsf{\sigma }}_{\mathrm{th}}{\hat{\mathsf{\sigma }}}_{\mathrm{th}}$, the following expression is obtained:

when the temperature exceeds the critical temperature T_cr, the thermal activation stress term disappears, and the flow stress is solely determined by the athermal stress component, that is σ=σ_ath. The expression for the critical temperature is given by:

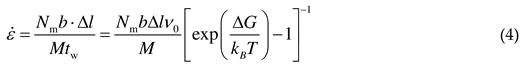
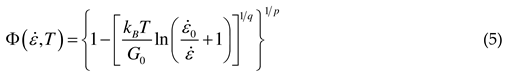
2.1.2. Microstructural evolution

Based on the analysis of microstructural evolution in deformation processing experiments, one of the key features of metal deformation is the variation of cell size with strain. Sevillano's experimental results demonstrate that the cell size decreases with increasing equivalent plastic strain. For certain metals, the ratio of the average cell size δ to its saturated size δ_s is a function of equivalent plastic strain, and the data points cluster around a curve that is independent of the metal type [26]. The normalized cell size $\tilde{\delta }$, defined as the ratio of the average cell size to its initial value ${\delta }_0(\tilde{\delta }=\delta /{\delta }_0\le 1)$, can be described by the following evolution equation:

where, δ_r is a dimensionless coefficient that represents the rate of cell refinement, while ${\tilde{\delta }}_s$ denotes the normalized saturated cell size (=δ_s/δ₀). Both are functions related to strain rate and temperature. It is worth noting that this study is consistent with the theoretical framework proposed by Molinari and Ravichandran [20], which suggests that δ is a generalized characteristic length of the microstructure and does not have a direct relationship with geometric dimensions. Therefore, the use of dimensionless size $\tilde{\delta }$ captures the essential trends in simulating microstructural evolution, where specific cell sizes of δ, δ₀, and δ_s become less important, and there is no need to precisely capture quantitative results regarding the microstructure.

The integral Eq.(7) yields the normalized cell size $\tilde{\delta }$, denoted as:

The coefficients ${\tilde{\delta }}_s$ and δ_r can be expressed using the following empirical relationships [16]:

where, T_r and ${\dot{\epsilon }}_r$ represent the reference temperature and strain rate, respectively. a_s and a_r are non-negative constants, and ξ_s, ν_s, ξ_r, ν_r are constant values ranging from 0 to 1, controlling the dependence of ${\tilde{\delta }}_s$ and δ_r on strain rate and temperature. ${\tilde{\delta }}_{s0}$ represents the maximum reference saturated cell size δ_s0 in comparison to its initial size (${\tilde{\delta }}_s\le {\tilde{\delta }}_{s0}<1$), while δ_r0 is the minimum reference refinement rate (δ_r0≤δ_r). The normalized saturated cell size ${\tilde{\delta }}_s$ decreases with increasing deformation rate and increases with elevated temperature. Conversely, the cell refinement rate δ_r accelerates with higher deformation rates and decelerates with increasing temperature. The evolution of these two parameters indicates that under low-temperature and high-strain-rate conditions, the dynamic cell refinement rate is faster, resulting in smaller achievable saturated sizes. In Eq.(9), a modification is made to the temperature term, suggesting that the evolution of cell size becomes insensitive to temperature when it is lower than T_r.

Staker and Holt proposed a simple relationship between the average cell size δ and the average total dislocation density N_tot, which can be expressed as follows:

where, K_c is a material constant, with a value of 16 for OFHC.

Therefore, the square root of the normalized dislocation density is inversely proportional to the normalized cell size $\tilde{\delta }$:

By substituting the saturation value into equation (11), the normalized initial saturated cell size ${\tilde{\delta }}_{s0}$ = √N₀/N_s0 can be obtained, where N_s0 represents the minimum reference value (~ 10¹⁴ m^-2 [28]) of the saturated dislocation density.

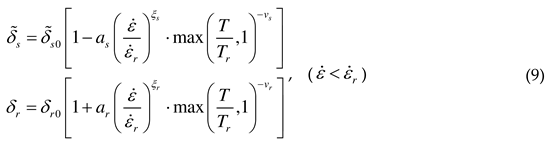
2.1.3. Threshold stress and thermal stress

In the theory of MTS, the threshold stress associated with thermal activation is related to microstructural evolution and can be expressed in combination with Eq.(11) as:

where, $\hat{\alpha }$ represents the intensity of dislocation interaction (< 1), and μ(T) is the temperature-dependent shear modulus. ${\hat{\sigma }}_0=M\hat{\alpha }{\mu }_{0}b\sqrt{N_0}$ represents a constant threshold stress value associated with the initial microstructure state at 0 K.

By substituting Eq.(8) into Eq.(12) and combining it with Eq.(5), the thermal activation stress can be expressed as:

here, $\tilde{\mu }$ is the normalized shear modulus (=μ(T)/μ₀). The thermal activation stress consists of two components: the structural evolution (threshold stress) part and the strain rate and temperature response of the material under fixed structure. The structural evolution (normalized cell size) is related to strain rate and temperature. Therefore, the strain rate sensitivity of the thermal activation stress can be divided into two parts: the rate sensitivity of material strain hardening caused by structural evolution and the instantaneous rate sensitivity of stress [12,29].

Eq.(13) can also be written in the standard Voce-Kocks format [30]:

where, ${\sigma }_{\mathrm{th}}^{\epsilon =\infty }$ and ${\sigma }_{\mathrm{th}}^{\epsilon =0}$ represent the saturation and initial thermal activation stresses, respectively, with the following dependencies on strain rate and temperature:

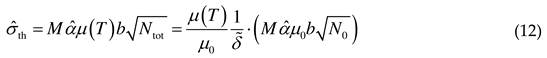
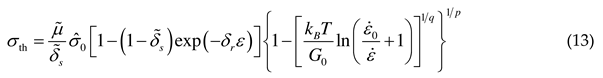
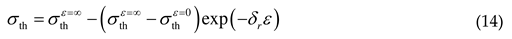
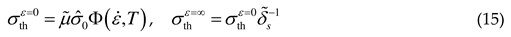
2.2. Athermal stress

The athermal stress is a result of the interaction between dislocations and long-range obstacles, known as the Hall-Petch strengthening effect [12]. The long-range obstacles mainly include thermally independent grain boundaries and far-field forest dislocations. As the grain size decreases (~ μm), the number of grain boundaries increases, or the density of far-field forest dislocations increases with increasing deformation. These long-range obstacles hinder dislocation motion and capture more dislocations, thereby enhancing the material strength [31,32].

The Hall-Petch strengthening effect caused by the grain size effect can be expressed as follows [32,33]:

where, σ₀ represents the friction stress required for the motion of dislocations, which is typically negligible for FCC metals. k_s is the strengthening coefficient, and D₀ is the initial grain size.

The density of far-field forest dislocations N_f can be calculated using the rate-independent dislocation density evolution equation proposed by Klepaczko [12], where the effective forest dislocation density ${\overline{N}}_f$ is represented as:

where, M_II and k_a0 are constants representing the proliferation rate and annihilation rate of dislocations, respectively. As the strain increases, the effective dislocation density approaches a saturation value, which is ${\overline{N}}_{\mathit{fs}}=M_{\mathrm{II}}/k_{a0}$.

The athermal stress can be expressed as [1,29]:

here, B represents the stress at the saturation dislocation density at 0 K, denoted as B = α_dμ₀b$\sqrt{{\overline{N}}_{\mathit{fs}}}$, and α_d is a material constant (< 1). The athermal stress indirectly achieves the thermal softening effect of the material through the relationship between the shear modulus (elastic field) and temperature. It realizes strain hardening of the material through the generation and storage of dislocations during deformation, while the deformation rate does not affect the evolution of non-thermal stress.

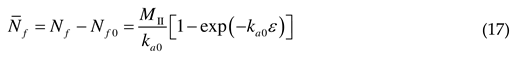
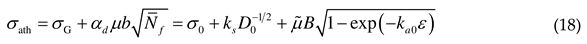
2.3. Flow stress and hardening rate

Finally, combining Eq.(13) and Eq.(18), the constitutive relationship for the flow stress of FCC metals is obtained as:

The strain hardening rate with respect to stress is given by:

where, the first term represents the strain hardening rate induced by the evolution of long-range obstacles in the microstructure, such as grain size and grain boundaries. The hardening rate initially decreases inversely proportional to the athermal stress and follows a linear function with a constant slope k_a0 at higher stresses. The second term accounts for the strain hardening rate due to thermal stress arising from the evolution of short-range obstacles, such as line defects represented by dislocation spacing. Under stable loading conditions, the hardening rate decreases linearly as the thermal stress increases, where δ_r is a constant.

Observing the model's behavior under constant loading conditions (stable strain rate and temperature), the overall strain hardening rate exhibits a rapid decrease as the deformation intensifies due to the inverse proportional function, reflecting the hardening characteristics of FCC metals at stage III [11,26]. Once the material reaches a certain level of strengthening, the overall strain hardening rate gradually decreases linearly until it approaches zero, with a slope approximately equal to −(k_a0 + δ_r). This behavior is consistent with the hardening characteristics of stage IV [26,34]. Since k_a0 is a material constant, the sensitivity of the hardening rate to strain rate and temperature primarily depends on the microstructural refinement rate δ_r.

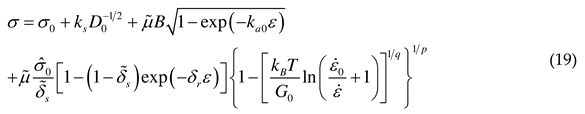
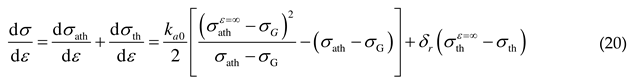
2.4. Shear modulus

The Nadal-Le Poac (NP) shear modulus model replaces the empirical temperature dependence of the shear modulus in the SCG model with an equation based on the Lindemann melting theory. This modification enhances the robustness of the model when applied under high-temperature and high-pressure conditions. Moreover, the NP model mitigates the instantaneous decrease of the shear modulus at the melting point. The zero-pressure form of the NP shear modulus model can be expressed as:

where, ρ_m represents the material's standard density, T_m denotes the melting point of the material under standard conditions, $\tilde{C}$ is a material constant related to the Lindemann constant, m_u signifies the atomic mass, Γ(T/T_m) controls its nonlinear behavior when T/T_m ≈ 1, and ζ_m << 1 serves as a fitting parameter that governs the overall fit quality.

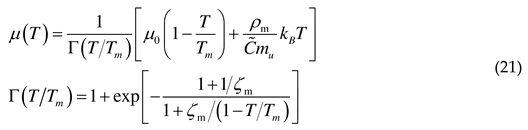
2.5. Adiabatic temperature rise

During metal deformation process, experimentally found that the majority of the energy supplied to effect plastic deformation converted to heat, contributing to an increase in temperature [36,37]. The conversion coefficient β generally falls within the range of 0.9 to 1.0 for high deformation rates (> 1 s^-1) in adiabatic processes [37,38]. If adiabatic shear banding (ASB) occurs under high strain rates, the heat generated during plastic deformation can lead to a rapid increase in temperature within the localized region of the adiabatic shear band. The equation connecting temperature raising and plastic work is presented in an integral format [39]:

where, T₀ is the initial temperature, C_p is the specific heat of the material at constant pressure. In the calculation of flow stress during adiabatic processes, it is necessary to update the temperature state variable at each incremental strain step.

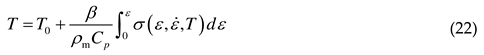
3. Application

3.1. Parameter calibration

The physical constants of annealed OFHC and the parameters in the NP shear modulus model at zero hydrostatic pressure are shown in Table 1.

Table 1. Parameters in the NP shear modulus model and temperature evolution model of OFHC.

Table 1. Parameters in the NP shear modulus model and temperature evolution model of OFHC.

ρm (kg/m3)	Cp (J/kg/K)	β	μ0 (GPa)	Tm (K)	ζm	$\tilde{C}$	mu (amu)
8930	382	0.9	50.7	1356	0.04	0.057	63.55

In the component of athermal stress, Meyers et al. conducted a study and found that the value of k_s for OFHC decreases linearly with increasing strain under low strain rates, ranging from (56 − 260) MPa√μm. However, at high strain rates, the value remains approximately constant. This behavior is taken into account in the ZA model [14], where an intermediate value is employed. The coefficients for the athermal stress in the model are provided in Table 2.

Table 2. Material coefficients in the athermal stress component.

Table 2. Material coefficients in the athermal stress component.

σG (MPa)	ks (MPa√μm)	D0 (μm)	B (MPa)	ka0
20.6	158 [14]	62	230 [2]	0.64 [2]

The material parameters for the thermal stress component are described in the following two tables. Table 3 provides the parameters that are independent of microstructural evolution, calculated ${\hat{\sigma }}_0$ as 50.2 MPa based on the data.

Table 3. Material parameters in the thermal stress component that are independent of microstructure.

Table 3. Material parameters in the thermal stress component that are independent of microstructure.

N0 (m-2)	M	$\hat{\alpha }$	b (nm)	kB/G0 (K-1)	p	q	${\dot{\epsilon }}_0$ (s-1)
1013 [39]	3.06 [40]	0.4 [41]	0.256 [26]	4.9×10-5 [15]	2/3 [10]	1 [10]	107 [10]

The parameters for the normalized cell size evolution model are proposed by Molinari and Ravichandran and illustrated in Table 4. By utilizing the data in the table and Eq.(11), the minimum value of the reference saturated dislocation density is approximately 7×10¹⁴ m^-2, which consistent with the actual physical laws.

Table 4. Parameters of the evolution equation for normalized cell size.

Table 4. Parameters of the evolution equation for normalized cell size.

${\tilde{\delta }}_{s0}$	as	ξs	vs	δr0	ar	ξr	vr	${\dot{\epsilon }}_r$ (s-1)	Tr (K)
0.12	0.377	0.24	0.5	4.3	50	0.8	0	107	298

3.2. Simulation results

The experimental values for comparison with the model calculations can be found in Appendix A. In Fig. 1, the relationships between flow stress, normalized cell size, and strain rate for OFHC at fixed strains and room temperature are depicted. It is noteworthy that the sensitivity of flow stress to strain rate undergoes a sudden change at 10⁴ s^-1, which aligns with the evolution pattern of the normalized reciprocal cell size ${\tilde{\delta }}^{-1}$. This observation suggests that the sensitivity of flow stress to strain rate is dominated by the microstructural evolution law. Specifically, when $\dot{\epsilon }$<10⁴ s^-1, the normalized reciprocal cell size lines are horizontally parallel with fixed strains. This behavior arises from the fact that the saturation size and refinement rate, as controlled by Eq.(9), remain approximately constant, indicating that the microstructure exhibits low sensitivity to changes in strain rate. Additionally, the sensitivity of flow stress to strain rate is influenced by the term Φ($\dot{\epsilon }$,T). At extremely low strain rates ($\dot{\epsilon }$<10^-3 s^-1), the value of Φ($\dot{\epsilon }$,T) exhibits minimal variation with strain rate, implying that the flow stress is predominantly determined by the deformation level and temperature.

Figure 1. Relationship between flow Stress, normalized cell size, and strain rate of annealed OFHC at fixed strain and room temperature.

Figure 1. Relationship between flow Stress, normalized cell size, and strain rate of annealed OFHC at fixed strain and room temperature.

Fig. 2 and Fig. 3 present the relationship between flow stress and strain within a wide range of strain rates at room temperature and a wide range of temperatures at a fixed strain rate for OFHC, respectively. The results demonstrate a strong agreement between the model's predicted values and the experimental data, which will be further analyzed in the subsequent section to quantify the error. In Fig. 2, when the strain exceeds ε₁ (≈ 0.2), a distinct change in the surface occurs near 1 s^-1 for a fixed strain. Within a narrow range of strain rates, an intriguing phenomenon emerges as the flow stress decreases with increasing strain rate. This intriguing behavior can be attributed to the consideration of temperature increase induced by plastic deformation when $\dot{\epsilon }$ > 1 s^-1, where the thermal softening effect of the material surpasses the strengthening effect associated with strain rate.

Figure 2. Flow stress-strain curved surface of annealed OFHC over a wide strain rate range at room temperature.

Figure 2. Flow stress-strain curved surface of annealed OFHC over a wide strain rate range at room temperature.

Figure 3. Flow stress-strain curved surface of annealed OFHC over a wide temperature range with $\dot{\epsilon }$ = 4000 s^-1

Figure 3. Flow stress-strain curved surface of annealed OFHC over a wide temperature range with $\dot{\epsilon }$ = 4000 s^-1

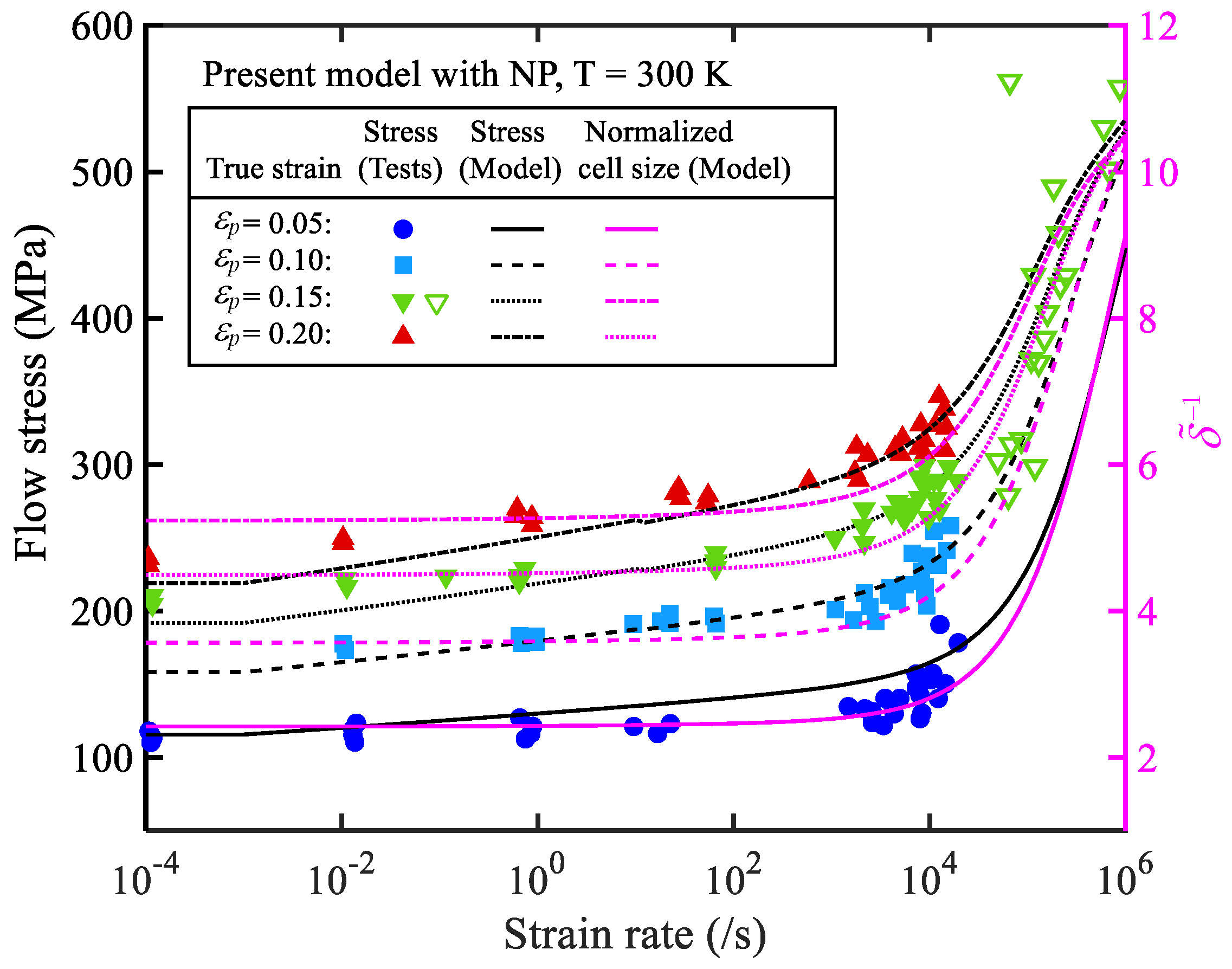
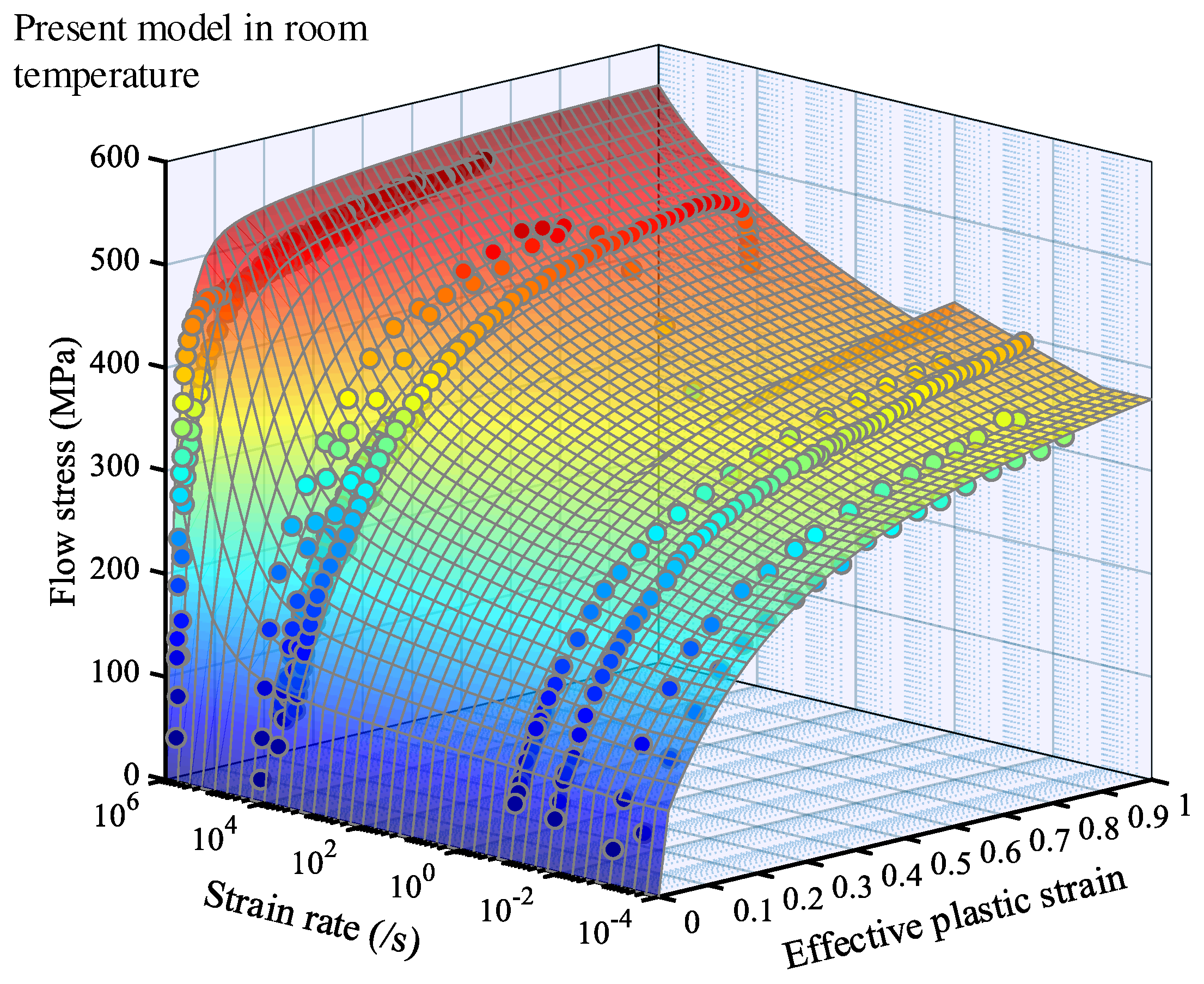
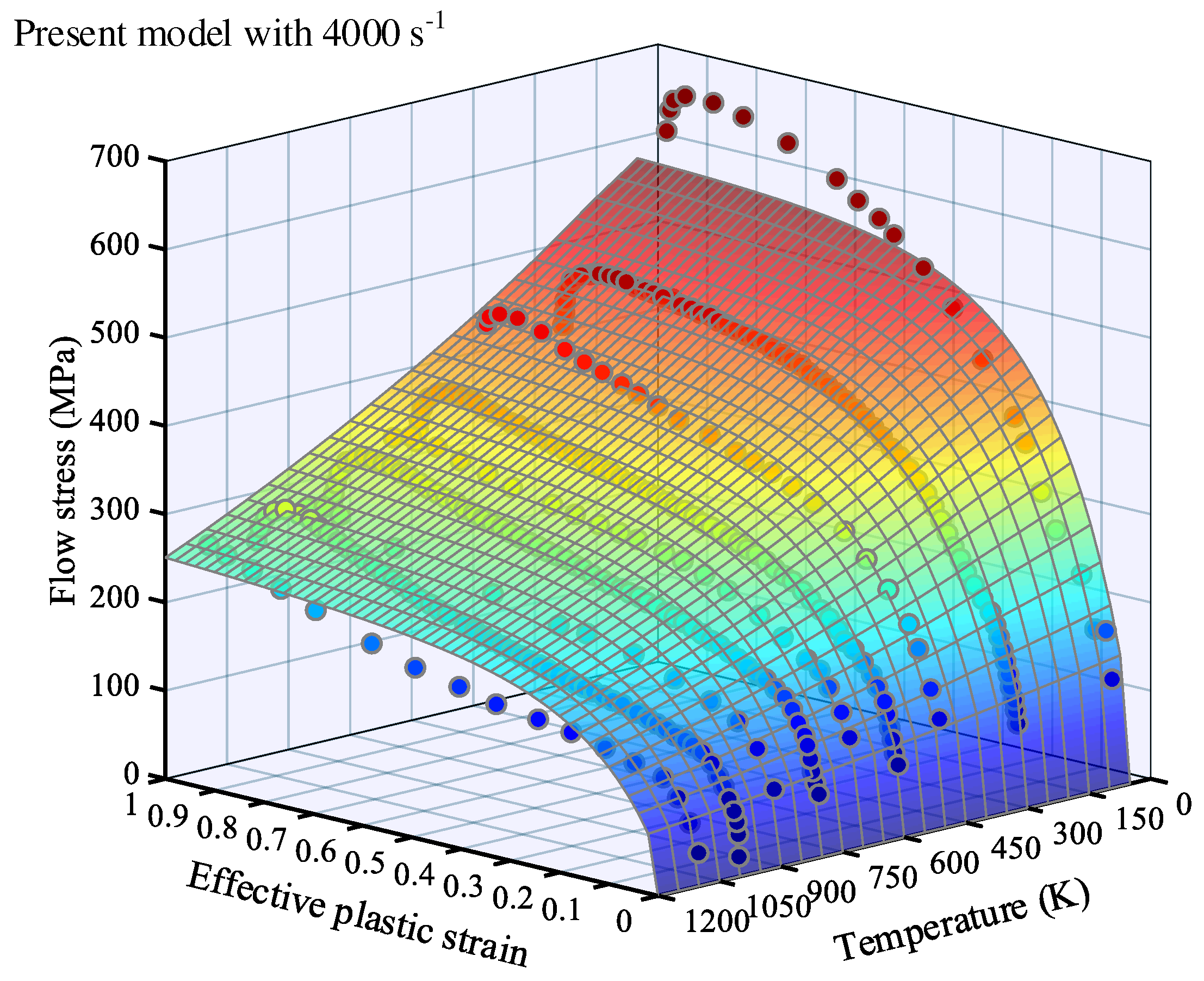
4. Result analysis and discussion

4.1. Relative error analysis

Based on the experimental results of OFHC across a wide range of strain rates and deformation temperatures, Biswajit Banerjee conducted a meticulous evaluation in their research [42,43]. They identified the hierarchical order of the model's evaluation errors: PTW, MTS, ZA, JC, SCGL (Steinberg-Cochran-Guinan-Lund [44]). Notably, the present model's microstructure evolution is predicated upon the MR model, while the validation experiments predominantly stem from Nemat-Nasser and Li [15]. To enhance the understanding of the predictive accuracy of the constitutive models, the paper undertakes a thorough analysis of errors and evaluated the performance of not only the present model but also five alternative constitutive models: MTS, PTW, JC, NNL, and MR. This comprehensive assessment encompassed a total of six distinct models, providing valuable insights into their respective prediction capabilities.

The relative error values E_i,j are computed using Eq.(23):

where, ${\sigma }_{i,j}^{\mathrm{pre}}$ denotes the model-predicted flow stress and ${\sigma }_{i,j}^{\exp }$ represents the experimental flow stress. The subscripts 'i' and 'j' signify the relative error for the i-th data point under the j-th deformation condition.

Fig. 4 and Fig. 5 showcase the error curves representing the disparities between the predicted flow stress of OFHC using six distinct models and the corresponding experimental results. The order in which these models are presented is as follows: (a) Present, (b) MTS, (c) NNL, (d) PTW, (e) JC, and (d) MR. Models (a) to (d) encompass constitutive models that incorporate microstructure evolution, while model (e) is an empirical model and (f) is a semi-empirical physical model.

As shown in Fig. 4(a), the present model exhibits relatively larger relative errors (between ±20%) in predicting results at room temperature and strain rates of 8000 s^-1 and 13000 s^-1. However, under other strain rate conditions, the relative errors of the model are mainly within ±10%. Notably, the relative error curves of the other five models at the above two strain rates exhibit similar trends to that of the present model. Therefore, it is plausible that these significant discrepancies may stem from experimental errors at these two strain rates. Regarding extremely high strain rates (6.4×10⁵ s^-1), the present model, PTW, and MR demonstrate relatively accurate prediction results, while the MTS model exhibits a slightly higher values compared to the present. Both NNL and JC models significantly underestimate the experimental results at low strains, with relative errors approaching -40%. Nevertheless, the accuracy of NNL predictions notably improves as the strain increases, while the JC model still remains approximately -20%. Moreover, under all other strain rate conditions, the JC model overestimates material flow stress at low strains with relative errors exceeding +20%. Excluding the JC model, the other models exhibit satisfactory consistency with the experimental results across the range of 0.001 − 8500 s^-1. However, at an extremely low strain rate of 4×10^-4 s^-1, all models predict higher values than the experimental results. Generally speaking, the predictions of the present model outperform those of the other models. This discrepancy can be attributed to the fact that the dislocation slip velocity is slower at relatively low strain rates, resulting in prolonged interaction time between dislocations and internal defects or barriers within the material. Consequently, dislocation diffusion or dispersion mechanisms may become the dominant deformation mechanisms, leading to a decrease in material strength and causing the model to predict higher flow stress values compared to the experimental data [45,14].

Figure 4. The relative error curve between the predicted values of models and the experimental results over a wide range of strain rates at room temperature.

Figure 4. The relative error curve between the predicted values of models and the experimental results over a wide range of strain rates at room temperature.

The relative error curves of Fig. 5 (a), (b), and (f) exhibit a high degree of similarity. These error curves demonstrate a consistent pattern, where the curves gradually shift upwards as the temperature increases, indicating that the predicted values are higher compared to the experimental results at high temperatures. Furthermore, for model (c) NNL, its predicted values are consistently higher than the experimental values at both high and low temperatures. This behavior can be attributed to the fact that, under high-temperature, the solid-state diffusion rate in the crystal significantly increases, promoting grain growth. Larger grains may contain more structural defects or dislocations, resulting in a decrease in material strength. Since these models does not account for microstructural coarsening, the predicted results at high temperatures tend to be higher than the experimental ones. On the other hand, PTW and JC models underestimate the material's flow stress at higher temperatures, and as the strain increases, their predictions deviate even further from the experimental results. From the perspective of the error curves, the MTS model exhibits the best predictive performance, while there is still room for improvement in the present model's predictions at higher temperatures (> 0.7 T_m).

Figure 5. The relative error curve between the predicted values of models and the experimental results over a wide range of temperatures at strain rate of 4000 s^-1.

Figure 5. The relative error curve between the predicted values of models and the experimental results over a wide range of temperatures at strain rate of 4000 s^-1.

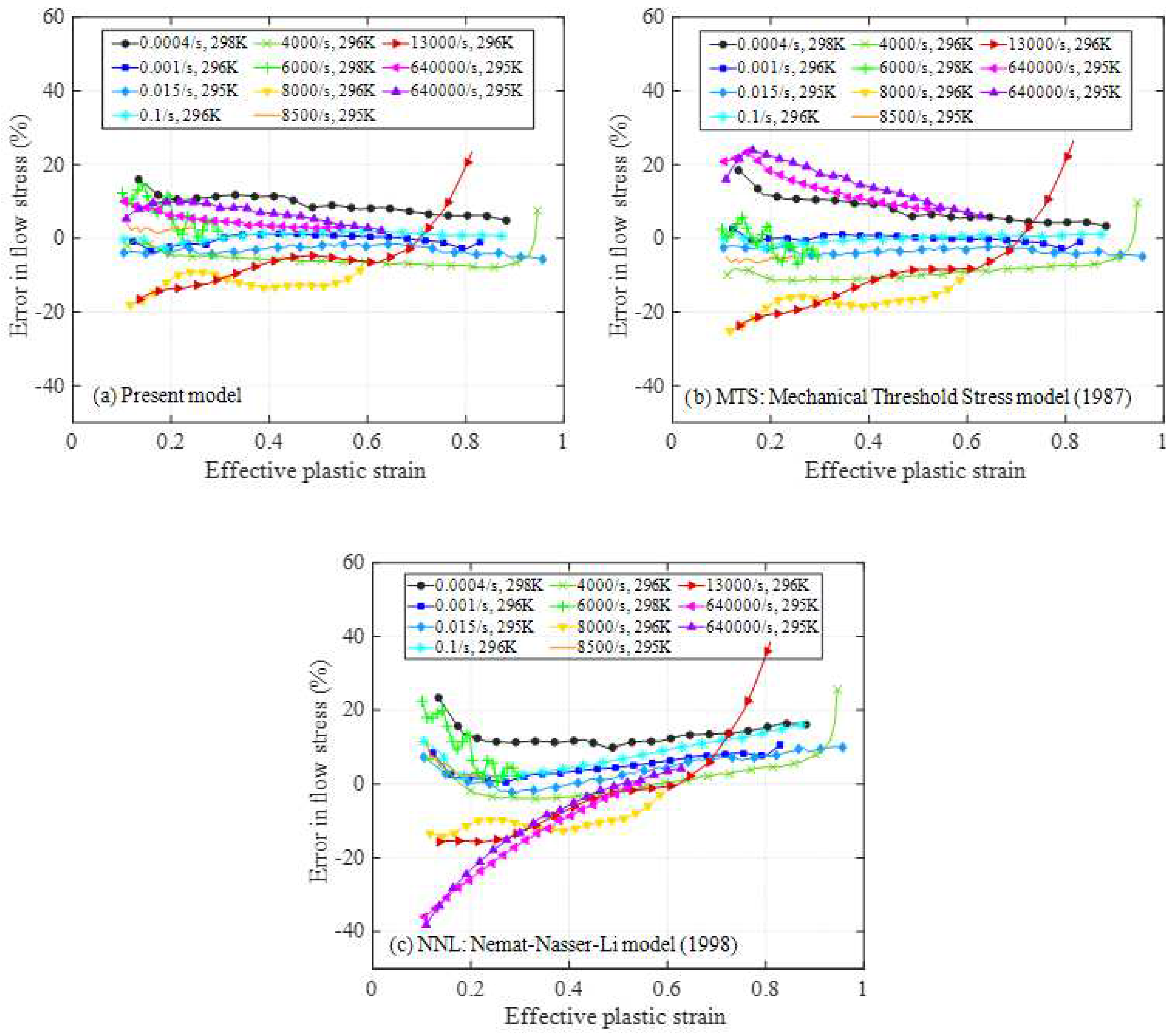
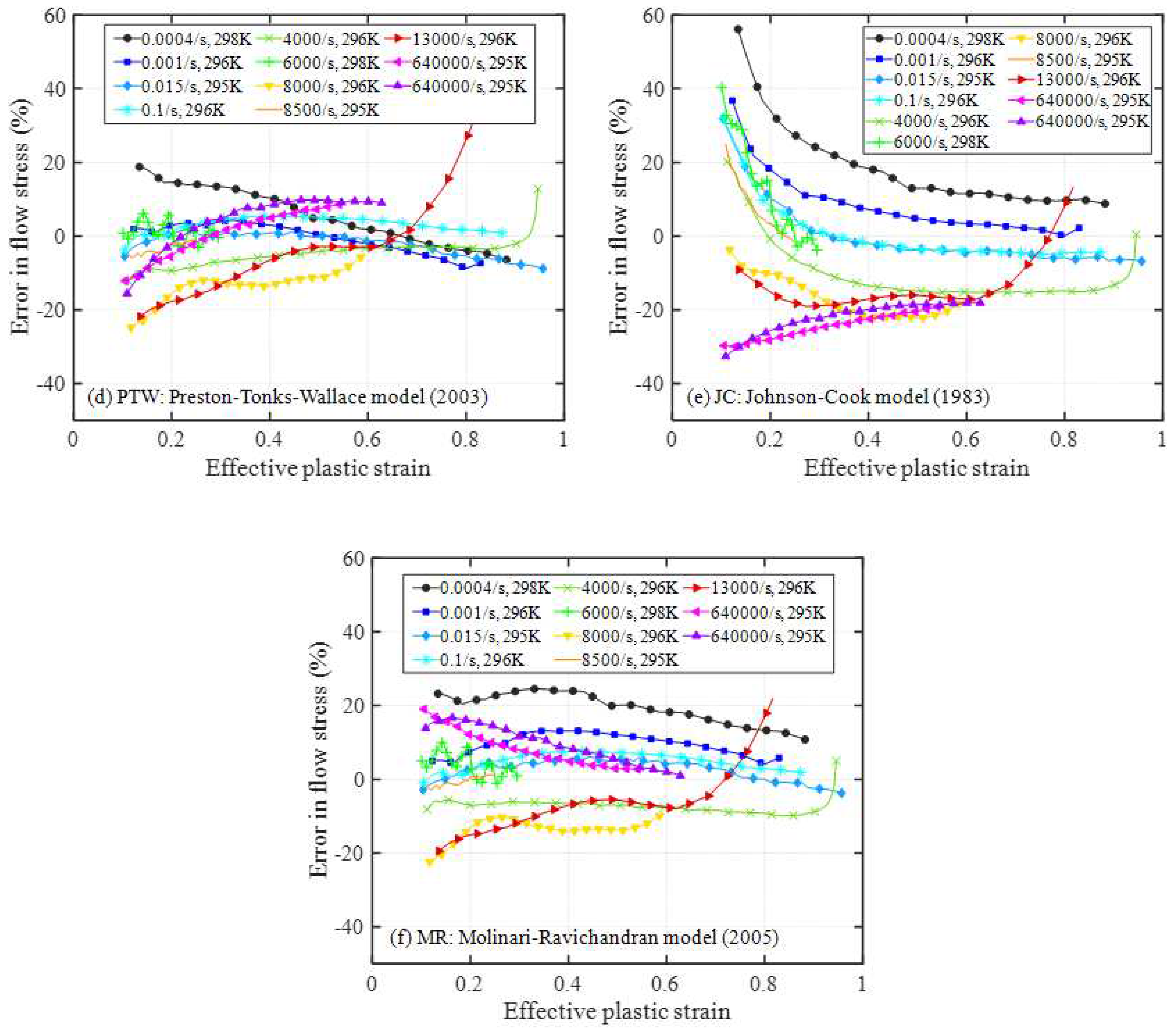
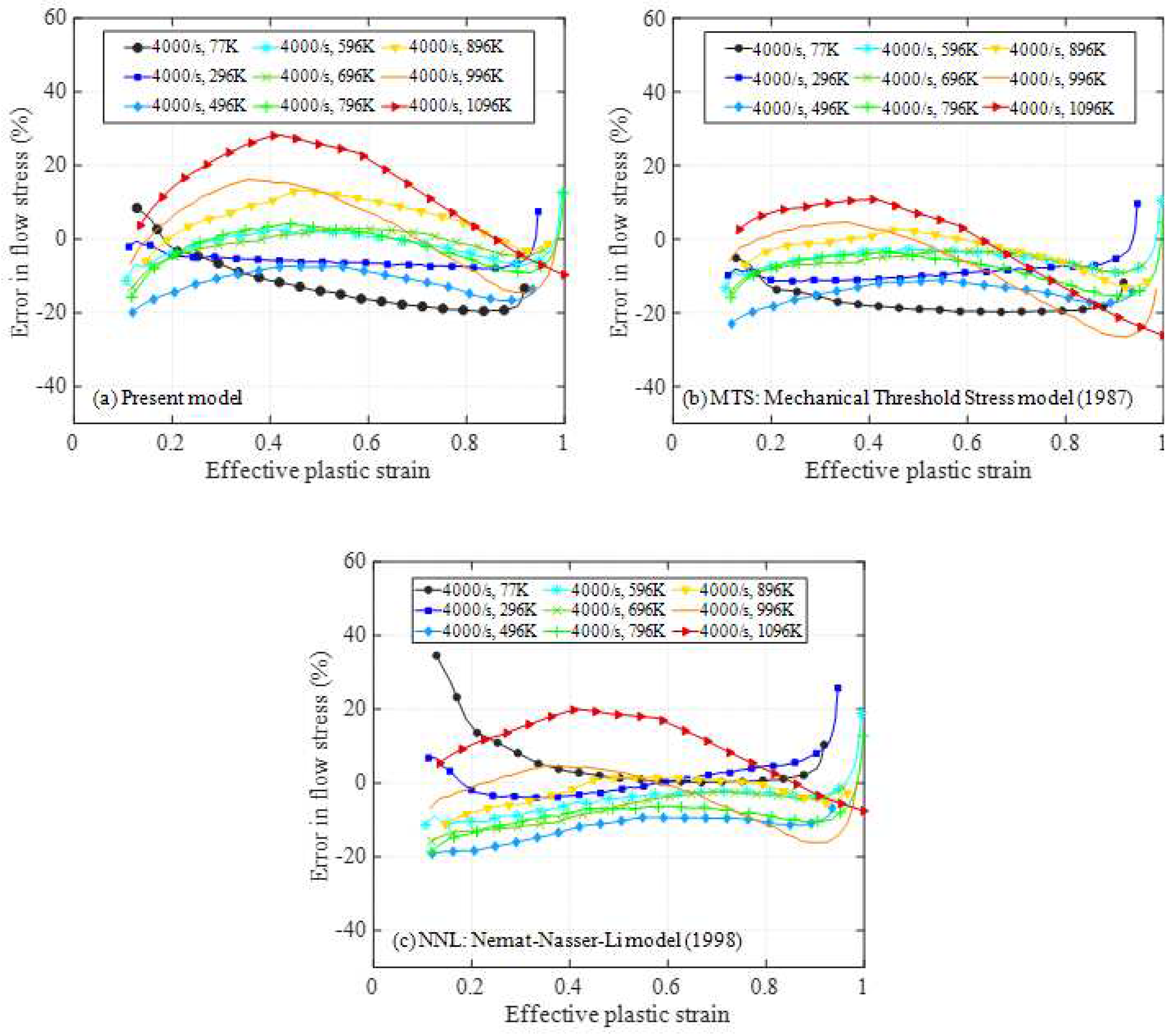
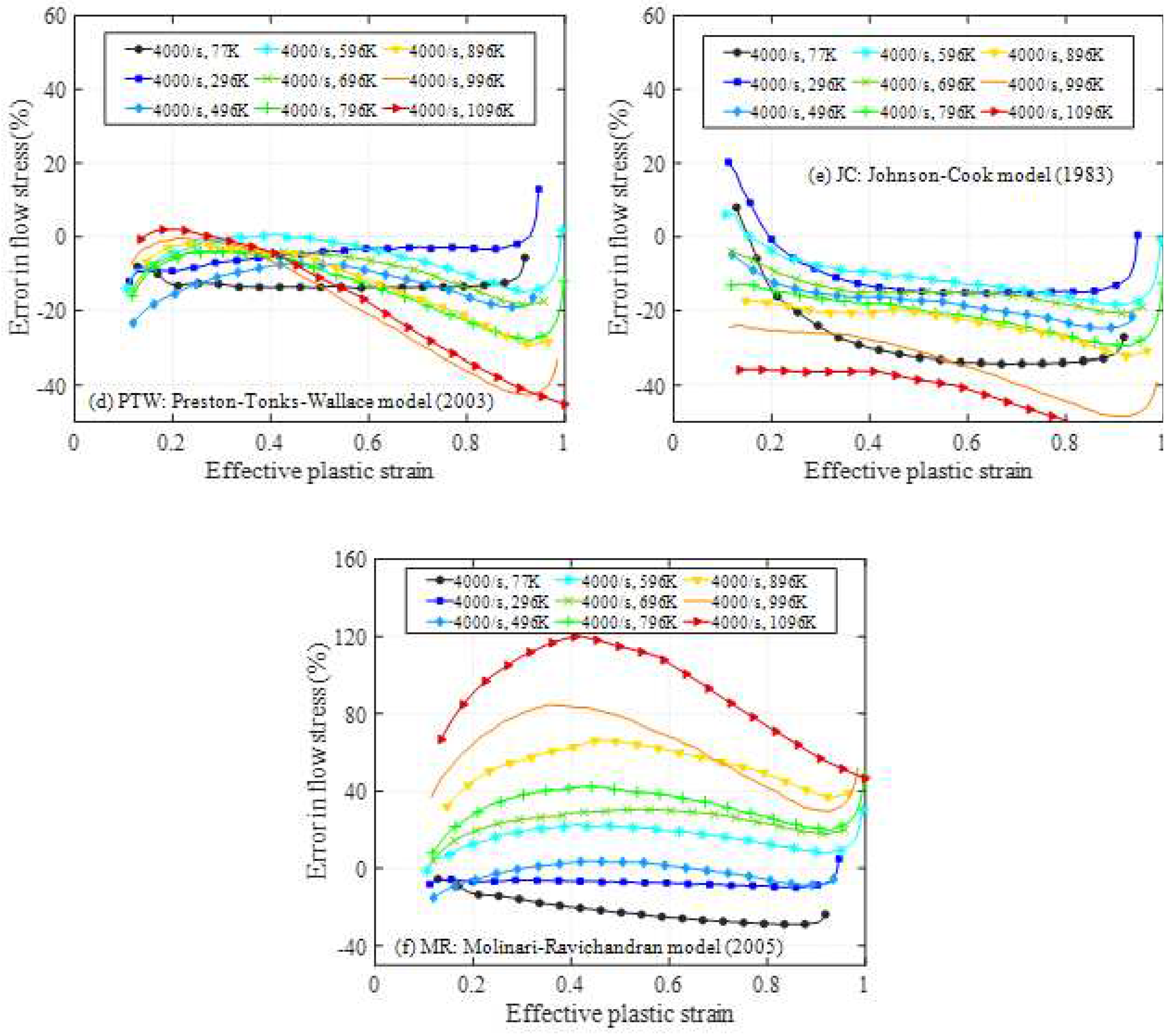
4.2. Comprehensive error analysis

To provide a more comprehensive assessment of the predictive capabilities of the abovementioned six constitutive models for the flow stress of OFHC, three statistical average errors were employed to evaluate the model predictions. These include the mean absolute relative error of plastic work (MARE-P.WK, ${\overline{E}}_{\mathrm{AR}.\mathrm{W}}$), the mean absolute relative error of flow stress (MARE-F.S, ${\overline{E}}_{\mathrm{AR}.\mathrm{Y}}$), and the mean maximum absolute error of flow stress (MMAE-F.S, ${\overline{E}}_{\mathrm{MA}.\mathrm{Y}}$). The calculation formulas for these metrics are as follows:

where, I_j represents the total number of data points with the deformation condition of index j, ${\overline{E}}_j$ denotes the average value of the relative error curve j. and J refers to the total number of experimental data that satisfy the statistical criteria. For example, there are four sets of experimental data with $\dot{\epsilon }$ ≤ 10³ s^-1 at room temperature, that is J = 4.

The statistical average errors for the predictions of the six models under different strain rate gradients at room temperature are presented in Fig. 6. It is observed that the majority of the models perform well in accurately capturing the flow stress behavior of the material at low strain rates, with the exception of the JC model which exhibits a higher MMAE-F.S value. The strain rate sensitivity of the flow stress undergoes a notable transition within the range of 10³ s^-1 – 10⁴ s^-1. Specifically, the present model, MTS, and NNL models exhibit relatively low statistical average errors of approximately 10% within this range, while the JC and MR models demonstrate larger errors exceeding >20%. This finding indicates that the abrupt change in flow stress sensitivity of OFHC is significantly influenced by microstructural evolution. Moreover, at extremely high strain rates, the values of MMAE-F.S for the MTS, NNL, and JC models exceed 20%, suggesting that these three models may not yield accurate results under such extreme high-strain-rate conditions.

Figure 6. Three statistical average errors of model predictions within different strain rate ranges: MARE-P.WK, MARE-F.S, and MMAE-F.S.

Figure 6. Three statistical average errors of model predictions within different strain rate ranges: MARE-P.WK, MARE-F.S, and MMAE-F.S.

The statistical average errors for the predictions of the six models under different temperature gradients at a strain rate of 4000 s^-1 are shown in Fig. 7. It is observed that the present model, MTS, and NNL models consistently demonstrate relatively small statistical average errors across all temperature ranges (maximum value is approximately 10%). The PTW and MR models demonstrate statistical average errors below 10% at temperatures below 0.4 T_m. However, as the temperature increases, the statistical average errors increase as well. Notably, the MR model exhibits statistical average errors exceeding 20% within the intermediate temperature range and even surpass 60% at high temperatures. Therefore, the MR and PTW models are deemed unsuitable for high-temperature conditions. Moreover, throughout the entire temperature range, the JC model displays statistical average errors ranging from 15% to 30%. This indicates that the standard JC model is not suitable for simulations involving strain rates equal to or greater than 4000 s^-1.

Figure 7. Three statistical average errors of model predictions within different temperature ranges: MARE-P.WK, MARE-F.S, and MMAE-F.S.

Figure 7. Three statistical average errors of model predictions within different temperature ranges: MARE-P.WK, MARE-F.S, and MMAE-F.S.

The statistical average errors in model predictions across all strain rates and temperature ranges are comprehensively evaluated and presented in Fig. 8. The enclosed triangle area formed by the lines serves as a measure of the model's prediction accuracy, with a smaller area indicating higher precision. When considering different strain rates, the sizes of the triangles formed by the three statistical average errors follow the order: Present ≈ PTW < MTS < MR < NNL < JC. Similarly, for varying temperatures, the triangle sizes adhere to the sequence: Present ≈ NNL < MTS < PTW < JC < MR. From the results, it is evident that the proposed model demonstrates favorable simulation outcomes across a broad range of strain rates and temperatures.

Figure 8. Comprehensive evaluation of three statistical average errors in model prediction results.

Figure 8. Comprehensive evaluation of three statistical average errors in model prediction results.

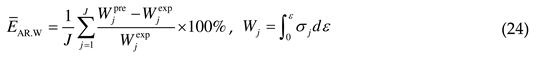
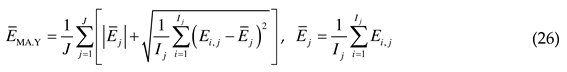
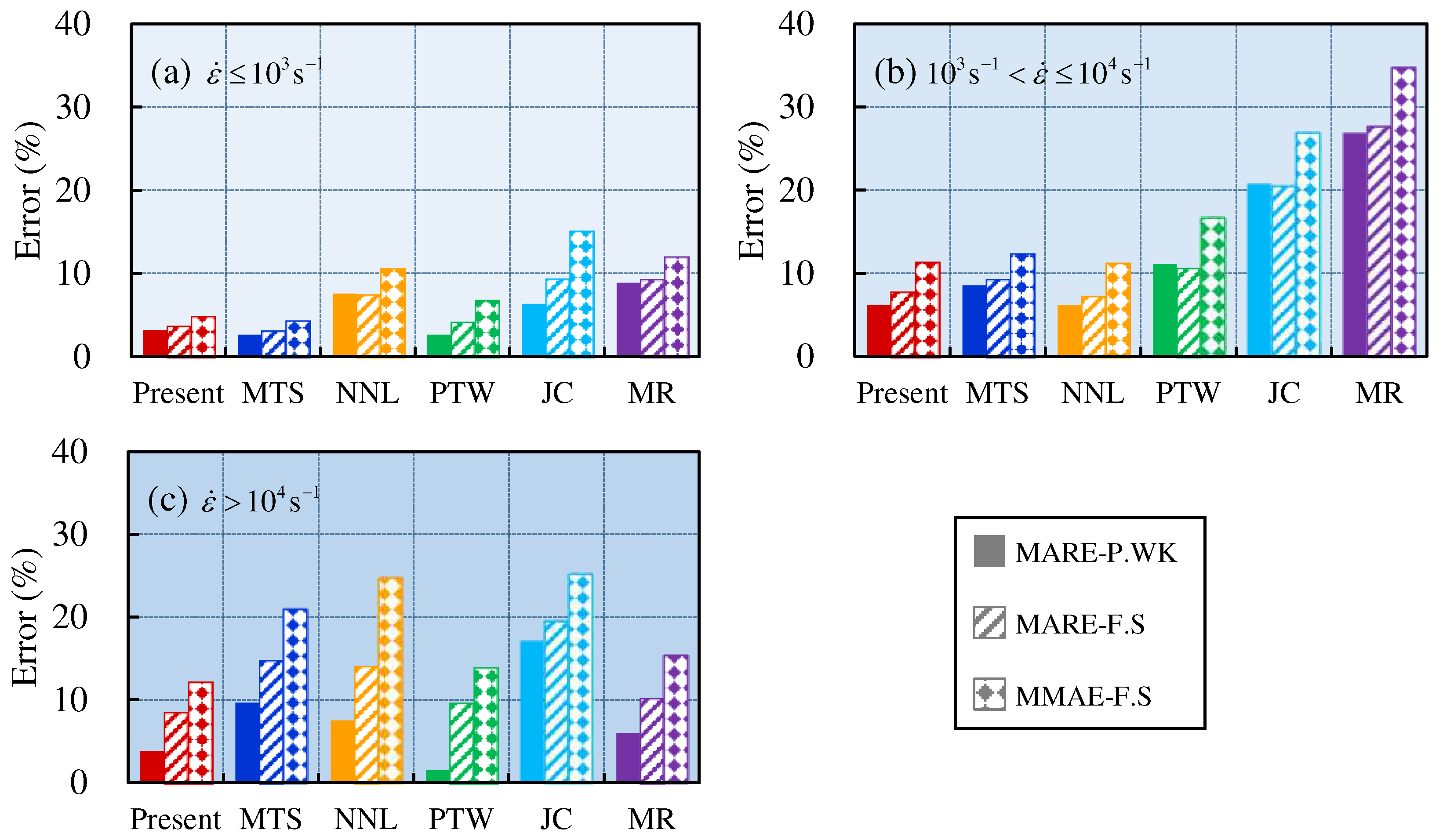
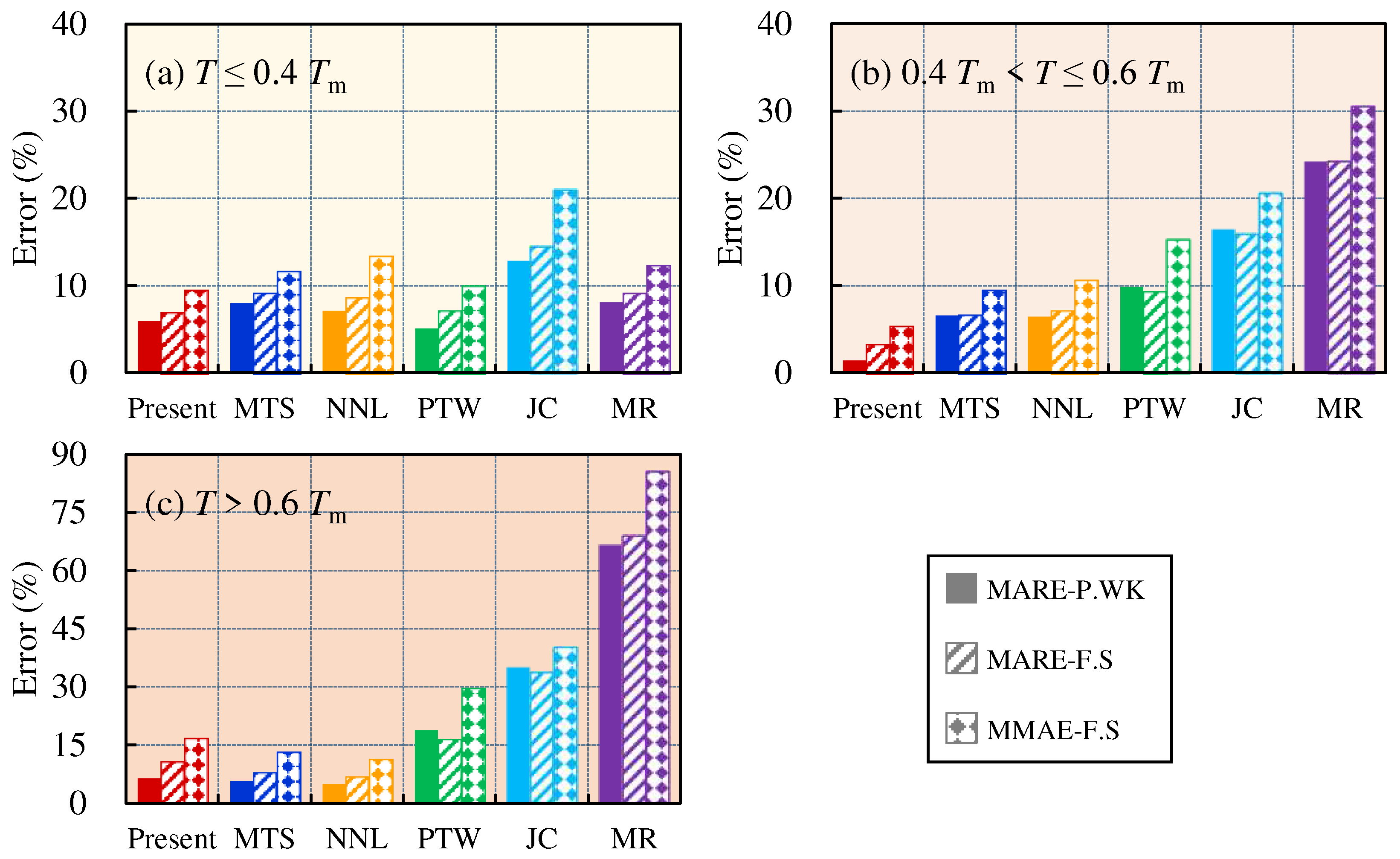
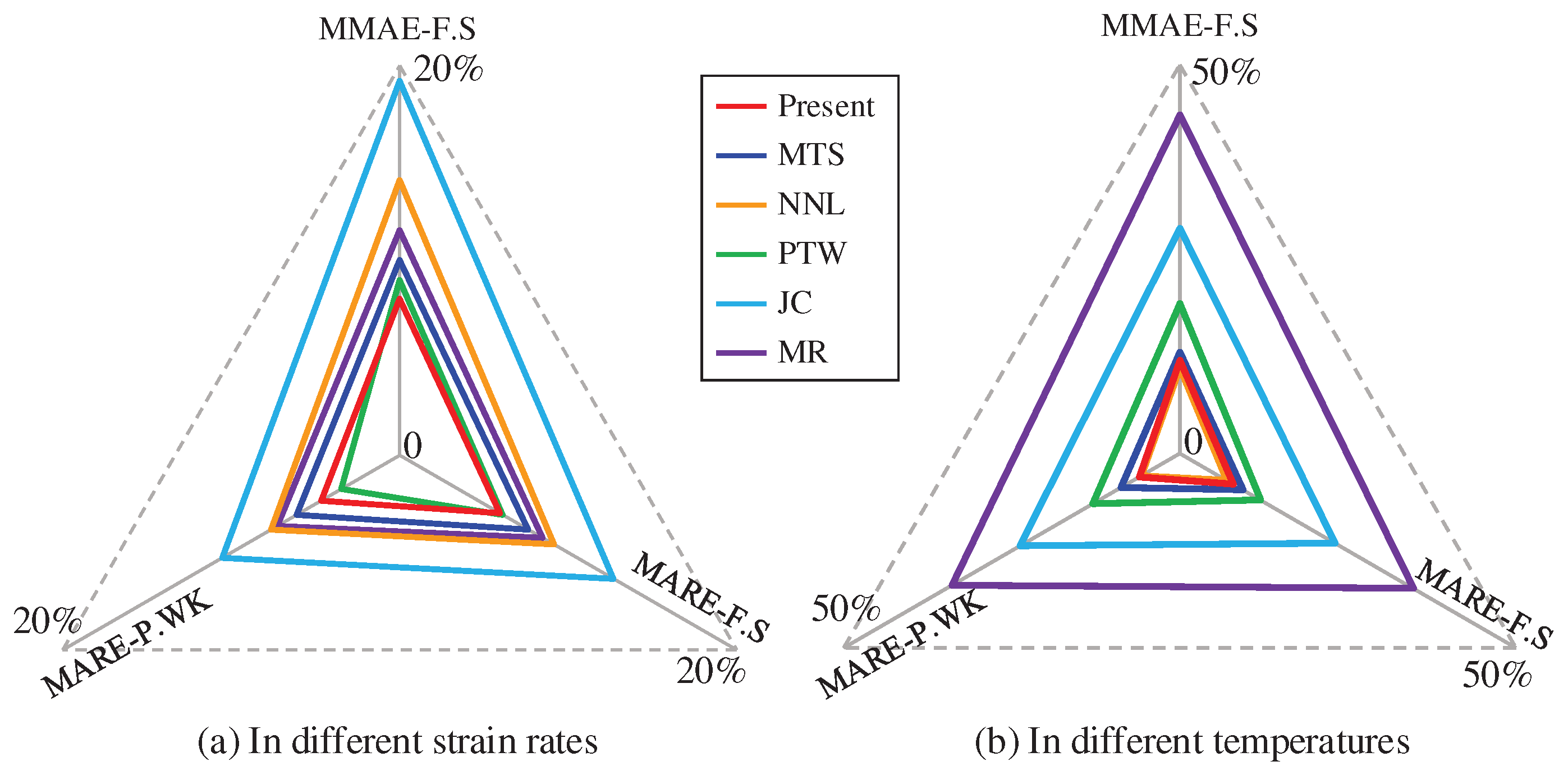
5. Conclusion

References

1. Armstrong RW, Walley SM. High strain rate properties of metals and alloys. International Materials Reviews 2008;53:105–28. [CrossRef]
2. Gao CY, Zhang LC. Constitutive modelling of plasticity of fcc metals under extremely high strain rates. International Journal of Plasticity 2012;32–33:121–33. [CrossRef]
3. Salvado F, Teixeira-Dias F, Walley SM, Lea L, Cardoso J. A review on the strain rate dependency of the dynamic viscoplastic response of FCC metals. Progress in Materials Science 2017;88. [CrossRef]
4. Jia X, Hao K, Luo Z, Fan Z. Plastic Deformation Behavior of Metal Materials: A Review of Constitutive Models. METALS 2022;12. [CrossRef]
5. Johnson GR, Cook WH. A constitutive model and data for materials subjected to large strains, Proceedings 7th International Symposium on Ballistics, The Hague: 1983, p. 541–7.
6. Rule WK, Jones SE. A revised form for the Johnson–Cook strength model. International Journal of Impact Engineering 1998;21:609–24. [CrossRef]
7. Wang J, Guo W-G, Li P, Zhou P. Modified Johnson-Cook description of wide temperature and strain rate measurements made on a nickel-base superalloy. Materials at High Temperatures 2017;34:157–65. [CrossRef]
8. Wang Y, Zeng X, Chen H, Yang X, Wang F, Zeng L. Modified Johnson-Cook constitutive model of metallic materials under a wide range of temperatures and strain rates. Results in Physics 2021;27:104498. [CrossRef]
9. Kumar Reddy Sirigiri V, Yadav Gudiga V, Shankar Gattu U, Suneesh G, Mohan Buddaraju K. A review on Johnson Cook material model. Materials Today: Proceedings 2022;62:3450–6. [CrossRef]
10. Follansbee PS, Kocks UF. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable. Acta Metallurgica 1988;36:81–93. [CrossRef]
11. Mecking H, Kocks UF. Kinetics of flow and strain-hardening. Acta Metallurgica 1981;29:1865–75. [CrossRef]
12. Klepaczko, JR. Physical-state variables — the key to constitutive modeling in dynamic plasticity. Nuclear Engineering and Design 1991;127:103–15. [CrossRef]
13. Mohamadnejad S, Basti A, Ansari R. Analyses of Dislocation Effects on Plastic Deformation. Multiscale Sci Eng 2020;2:69–89. [CrossRef]
14. Zerilli FJ, Armstrong RW. Dislocation-mechanics-based constitutive relations for material dynamics calculations. Journal of Applied Physics 1987;61:1816–25. [CrossRef]
15. Nemat-Nasser S, Li Y. Flow stress of f.c.c. polycrystals with application to OFHC Cu. Acta Materialia 1998;46:565–77. [CrossRef]
16. Gao CY, Zhang LC. A constitutive model for dynamic plasticity of FCC metals. Materials Science and Engineering: A 2010;527:3138–43. [CrossRef]
17. Austin RA, McDowell D. A dislocation-based constitutive model for viscoplastic deformation of fcc metals at very high strain rates. International Journal of Plasticity 2011;27:1–24. [CrossRef]
18. Austin RA, McDowell DL. Parameterization of a rate-dependent model of shock-induced plasticity for copper, nickel, and aluminum. International Journal of Plasticity 2012;32–33:134–54. [CrossRef]
19. Preston D, Tonks D, Wallace D. Model of plastic deformation for extreme loading conditions. Journal of Applied Physics 2003;93. [CrossRef]
20. Molinari A, Ravichandran G. Constitutive modeling of high-strain-rate deformation in metals based on the evolution of an effective microstructural length. Mechanics of Materials 2005;37:737–52. [CrossRef]
21. Durrenberger L, Molinari A, Rusinek A. Internal variable modeling of the high strain-rate behavior of metals with applications to multiphase steels. Materials Science and Engineering: A 2008;478:297–304. [CrossRef]
22. Durrenberger L, Molinari A. Modeling of Temperature and Strain-Rate Effects in Metals Using an Internal Variable Model. Experimental Mechanics 2009;49:247–55. [CrossRef]
23. Kocks UF, Argon AS, Ashby MF. Thermodynamics and kinetics of slip. Progress in Materials Science 1975;19:141–5.
24. Wang ZQ, Beyerlein IJ, LeSar R. Slip band formation and mobile dislocation density generation in high rate deformation of single fcc crystals. Philosophical Magazine 2008;88:1321–43. [CrossRef]
25. Gil Sevillano J, van Houtte P, Aernoudt E. Large strain work hardening and textures. Progress in Materials Science 1980;25:69–134. [CrossRef]
26. Nes, E. Modelling of work hardening and stress saturation in FCC metals. Progress in Materials Science 1997;41:129–93. [CrossRef]
27. Staker MR, Holt DL. The dislocation cell size and dislocation density in copper deformed at temperatures between 25 and 700°C. Acta Metallurgica 1972;20:569–79. [CrossRef]
28. Estrin Y, Kubin LP. Local strain hardening and nonuniformity of plastic deformation. Acta Metallurgica 1986;34:2455–64. [CrossRef]
29. Voce, E. The relationship between stress and strain for homogeneous deformations 1948.
30. Hall, EO. The Deformation and Ageing of Mild Steel: III Discussion of Results. Proc Phys Soc B 1951;64:747. [CrossRef]
31. Armstrong, RW. The (cleavage) strength of pre-cracked polycrystals. Engineering Fracture Mechanics 1987;28:529–38. [CrossRef]
32. Meyers MA, Andrade UR, Chokshi AH. The effect of grain size on the high-strain, high-strain-rate behavior of copper. Metall Mater Trans A 1995;26:2881–93. [CrossRef]
33. Yan S, Yang H, Li H, Yao X. A unified model for coupling constitutive behavior and micro-defects evolution of aluminum alloys under high-strain-rate deformation. International Journal of Plasticity 2016;85:203–29. [CrossRef]
34. Kocks F, Mecking H. Physics and phenomenology of strain hardening: The FCC case. Progress in Materials Science 2003;48:171–273. [CrossRef]
35. Nadal M-H, Le Poac P. Continuous model for the shear modulus as a function of pressure and temperature up to the melting point: Analysis and ultrasonic validation. Journal of Applied Physics 2003;93:2472–80. [CrossRef]
36. Klepaczko J, Rusinek A, Rodríguez-Martínez JA, Pęcherski R, Arias A. Modelling of thermo-viscoplastic behaviour of DH36 and Weldox 460-E structural steels at wide ranges of strain rates and temperatures, comparison of constitutive relations for impact problems. Mechanics of Materials - MECH MATER 2009;41:599–621. [CrossRef]
37. Baig M, Khan AS, Choi S-H, Jeong A. Shear and multiaxial responses of oxygen free high conductivity (OFHC) copper over wide range of strain-rates and temperatures and constitutive modeling. International Journal of Plasticity 2013;40:65–80. [CrossRef]
38. Mason JJ, Rosakis AJ, Ravichandran G. On the strain and strain rate dependence of the fraction of plastic work converted to heat: an experimental study using high speed infrared detectors and the Kolsky bar. Mechanics of Materials 1994;17:135–45. [CrossRef]
39. Voyiadjis GZ, Abed FH. Effect of dislocation density evolution on the thermomechanical response of metals with different crystal structures at low and high strain rates and temperatures. Archives of Mechanics 2005;57:299–343. [CrossRef]
40. Humphreys FJ, Hatherly M. Recrystallization and related annealing phenomena. 2nd ed. Amsterdam ; Boston : Elsevier; 2004.
41. Huang M, Rivera-Díaz-del-Castillo PEJ, Bouaziz O, van der Zwaag S. A constitutive model for high strain rate deformation in FCC metals based on irreversible thermodynamics. Mechanics of Materials 2009;41:982–8. [CrossRef]
42. Banerjee, B. Taylor impact tests: Detailed report 2005.
43. Banerjee, B. An evaluation of plastic flow stress models for the simulation of high-temperature and high-strain-rate deformation of metals. 2005. [CrossRef]
44. Steinberg DJ, Lund CM. A constitutive model for strain rates from 10−4 to 106 s−1. Journal of Applied Physics 1989;65:1528–33. [CrossRef]
45. Nix WD, Gibeling JC, Hughes DA. Time-dependent deformation of metals. Metallurgical Transactions A 1985;16:2215–26. [CrossRef]