Ultrasonic Non-Contact Air-Coupled Technique For Assessment Of Sandwich Composites Plates Using Antisymmetric Lamb Waves

This paper describes the design and implementation of an ultrasonic non-contact air-coupled technique (UNCACT) using antisymmetric Lamb waves (ALW) for NDT assessment in novel composite sandwich plates of the car body shell. This technique is complemented with a C-Scan image implementation using this kind of guided waves. The finite element method using Comsol 6.1 is developed for the interpretation of the several wave modes presented in the experiments, including the ALW mode. The phase velocity method (PVM) is applied for the verification of the ALW mode in the portion of the RF signal necessary in the C-Scan image.

Keywords:

Subject: Engineering - Other

1. Introduction

One of the must sustainable transportation methods is the train. To achieve this, the maintenance of the railway vehicle plays a central role. This should include a fast automatic testing method for the car body structure in order to find possible flaws in its plate shell, as a consequence of possible impacts from the external environment. The problem is that this vehicle is introducing novel composite materials, likes the sandwich plates made of two layers of anisotropic CFRP of a few mm that covers a central Foam layer.

The testing of car body composite sandwich material is very complex because of the anisotropic presented in the CFRP, a greater attenuation of the Foam and its plane geometry. Classical high ultrasonic techniques in MHz ranges are not possible to apply in practical implementations. One possible solution is to use low ultrasound frequencies, which could induce antisymmetric Lamb wave (ALW) mode and, using two air-coupled ultrasonic transducers, emitter (T_x) and receiver (R_x).

The ultrasonic non-contact air-coupled technique (UNCACT) is considered as an emerging NDT method [1,2]. It is the objective of this paper the implementation of this technique based on the ALW mode, induced only on the upper CFRP layer of the sandwich material. This target is improved with a C-Scan image output presentation, according to a mechanical scanning performance of the transducers T_x and R_x, moving as a whole at a fixed distance, over the sample. Two images were obtained, on both sides of a single sandwich plate, a sample that was made specifically for this work. This one includes induced defects with different sizes and positions in both CFRP layers.

The use of the upper CFRP layer, with the ALW mode, is related to the idea of evaluating possible defects in the upper side of the car body shell induced by accidental impacts as expressed above. The ALW mode, which propagate in the upper CFRP plate, is justified because it is assumed that any defect in this layer, changes its amplitude. As a consequence, it produces a color change in the C-Scan image. Then, part of the objective of this paper includes the identification and selection of this ALW mode. This should be done on the RF signal received at R_x, as a consequence of the multiple modes induced by the emitter T_x. For these purposes, the phase velocity method (PVM) was included for helping the identification of the Lamb mode, as a part of the RF signal.

Theoretical models were also developed, using finite element method on Comsol software for the wave propagation in the sandwich plate. In these models, the CFRP were considered as orthotropic material [7] and the Foam as isotropic. The idea of these models is to describe and identify the several propagation modes in the RF ultrasonic signal components. Analytical dispersion curves were also implemented for the single CFRP plate.

2. Theoretical models

2.1. Analytical Dispersion curve of orthotropic materials.

In the case of Lamb waves, there are the dispersion phenomena. These are relations between the phase (and group velocity) with the frequency (or with the ratio of the thickness and wavelength). These relations are known as dispersion curves and in the case of isotropic material are obtained from the classic Lame equations [8] [9]. In [10] Castaing presents the basic formulation of a single orthotropic CFRP layer with similar results as the previous case.

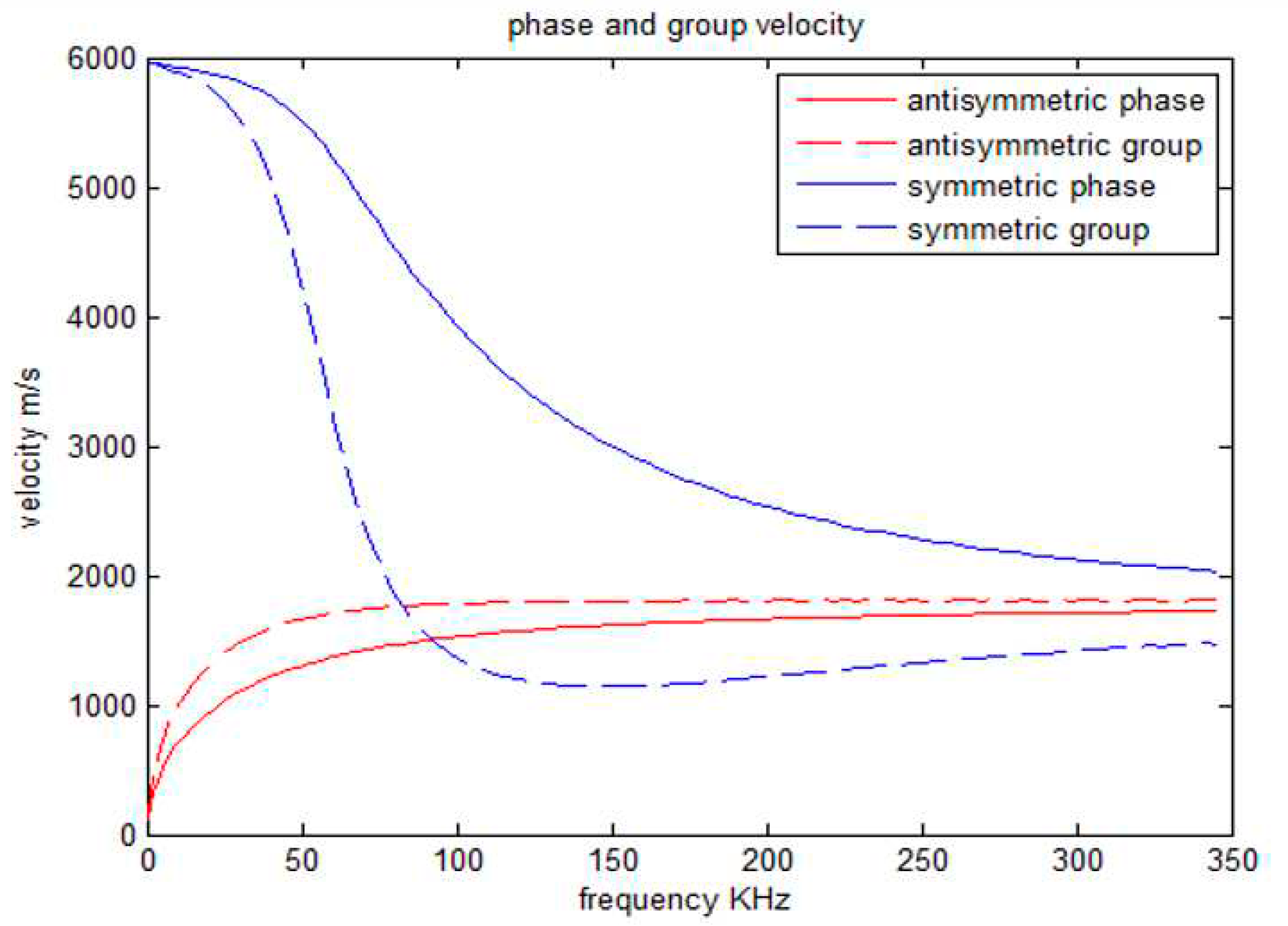
Figure 1 shows the results of an example for the dispersion curves for a CFRP plate with a thickness of 5 mm using values of elastic constants obtained from a previous paper [7] (Table 1). As it is well known, these curves do not consider neither excitation nor pulse propagation.

2.2. Excitation of Lamb wave mode by the Non-contact air-coupled transducers

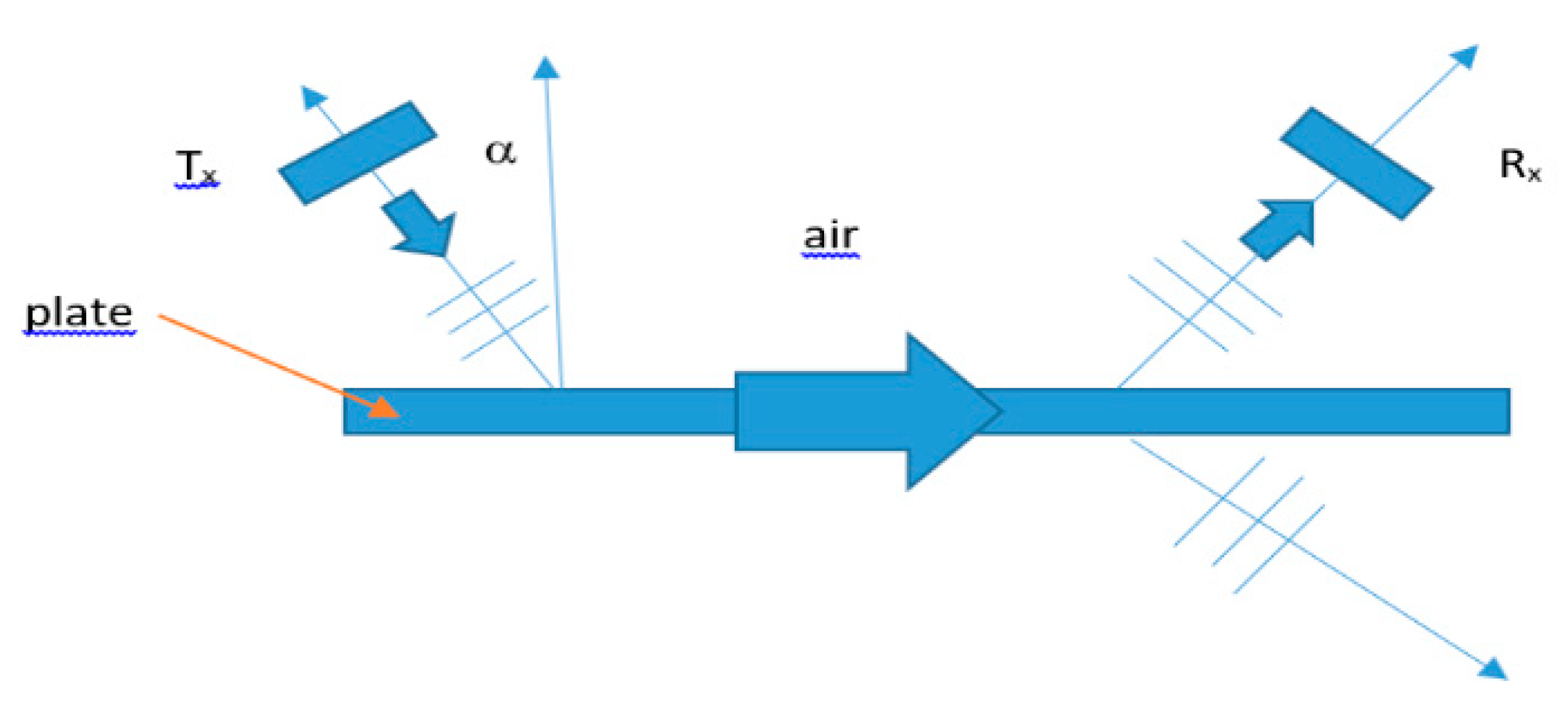
Figure 2 shows a diagram for the generation and detection of an ALW mode in a single plate, as a first theoretical model. There are displayed two air-coupled transducers (transmitter T_x and Receiver Rx) with the same angle. In the case of T_x. A first simple model, for the incident angle, could be obtained from the Snell law (1), assuming a refracted critical angle of 90°. In (1) the c_air corresponds to the velocity of longitudinal waves in air (360 m/s) and c corresponds to the desired Lamb mode, at a specific frequency, from the dispersion curve of Figure 1.

s i n (α) = \frac{C_{a i r}}{C}

(1)

In the same Figure 2, a second air transducer (R_x), located close to the T_x, is used to receive a complex RF signal. This should be composed by the air leakage from the ALW propagation and a possible air reverberation between both transducers. The air leakage in the reception, formally it is not considered in the previous dispersion curves. Nevertheless, these last ones could be used according to the low acoustic impedance of the air. For the leakage Lamb waves, there are some references of its use in NDT testing [12,13,14], but they assume a plate immersed in a fluid, generally water [15], that is not our air case.

The equation (1) shows also a minimum condition for the phase velocity c. This value should be greater than the velocity of longitudinal waves in the air (360 m/s). Then for a frequency of 250 KHz i.e., it is possible to induce the ALW mode, because the phase velocity is still higher than air velocity according to the dispersion curves (Figure 1). This mode is not possible to obtain, for instance, in an acrylic or rexolite wedge with its longitudinal velocity greater than 2000 m/s. An estimated angle, in this case, should be in an interval from 10⁰ to 15⁰ approximately.

In the use of (1) for angle calculations, it was assumed a dispersion curve of a single homogeneous and orthotropic plate. So this is a first approach of the complex sandwich case where it is only considered the upper CFRP plate for the ALW mode propagation. To describe the wave propagation in this complex material, with two CFRP layers covering a Foam plate, it is necessary to develop models based on the Finite Element Method (FEM). These models include both air wedges, with T_x and R_x transducers respectively. Finally, the pulse propagation is included, which it is not possible to consider in the previous single model plate.

2.3. Finite Element Method Models.

As expressed before, for describing the pulse propagation in the sandwich case with the UNCACT method, several FEM models were developed with Comsol 6.1. These models allow getting more insight the physics of the wave propagation in the sandwich plate.

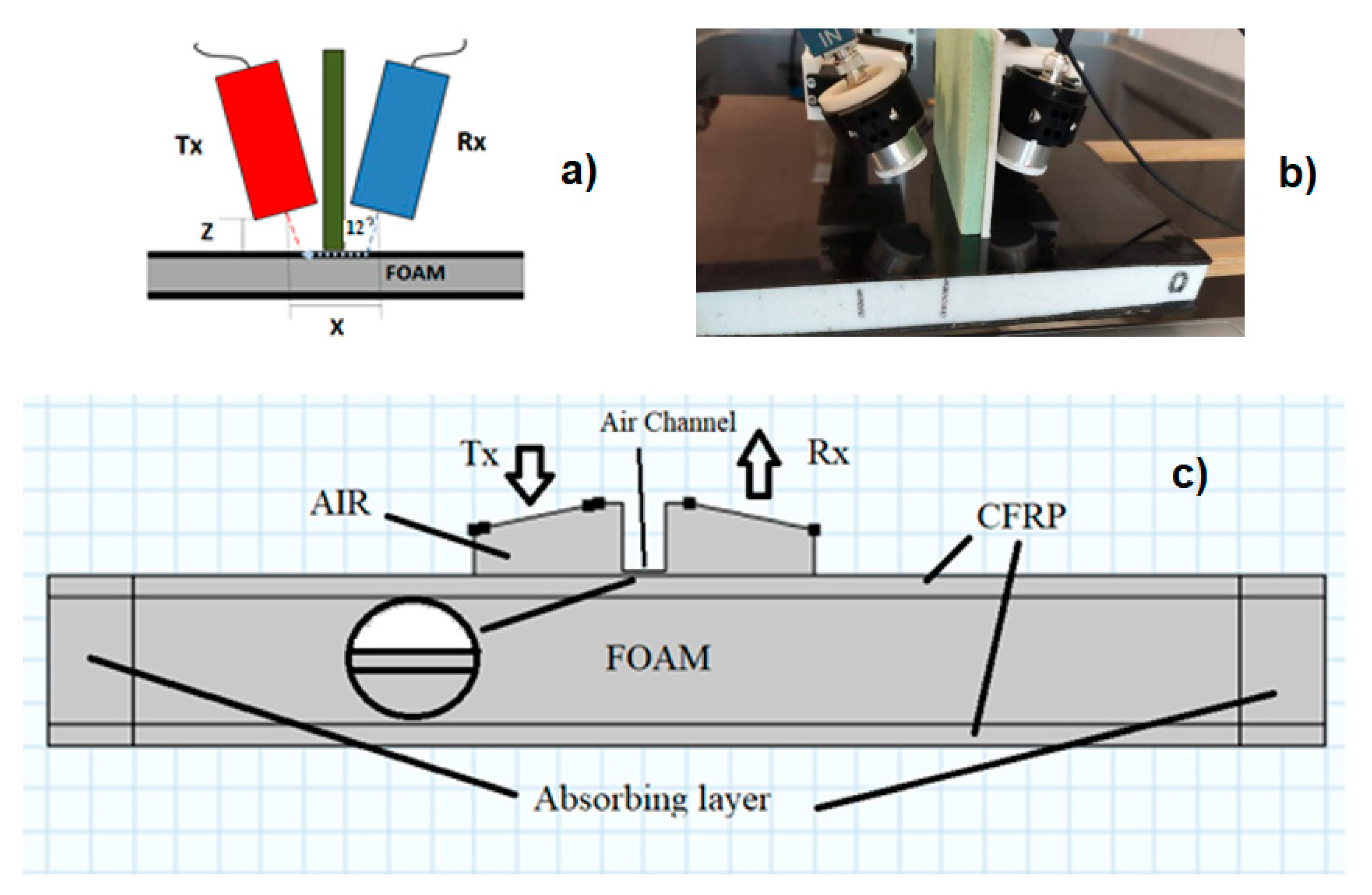
In this case, the material components were considered as solids. Figure 3c shows the Comsol domain, compared with a diagram (Figure 3a) and a photo (Figure 3b) of the experimental configuration. The transducer T_x and R_x are represented as boundary conditions in the two air wedges respectively. Additionally, there is an acoustic isolation barrier, which separates both wedges with the exception of small air layer in the lower part.

The models included in the Comsol Multiphysics 6.1 were the following:

Elastic Wave, Time Explicit (denominated by elte, in Comsol)
Pressure Acoustic, Time Explicit (denominated by pate in Comsol)

These two models are running together based on the discontinuous Galerkin method (dG-FEM) that uses a time explicit solver. The advantage of the dG-FEM method is that it solves the time wave propagation with a greater efficiency. Hence, the mesh the maximum element size (MES) could be defined according to the following expression:

MES=

(2)

The expression (2) represents and advantage added by the dG-FEM compared with the classic FEM, because it generates a lower density mesh. In (2) λ should be evaluated for each component material in the sandwich plate.

In the dG-FEM, lower freedom degrees are generated compared with the classic FEM. This represents an improvement of the computing performance.

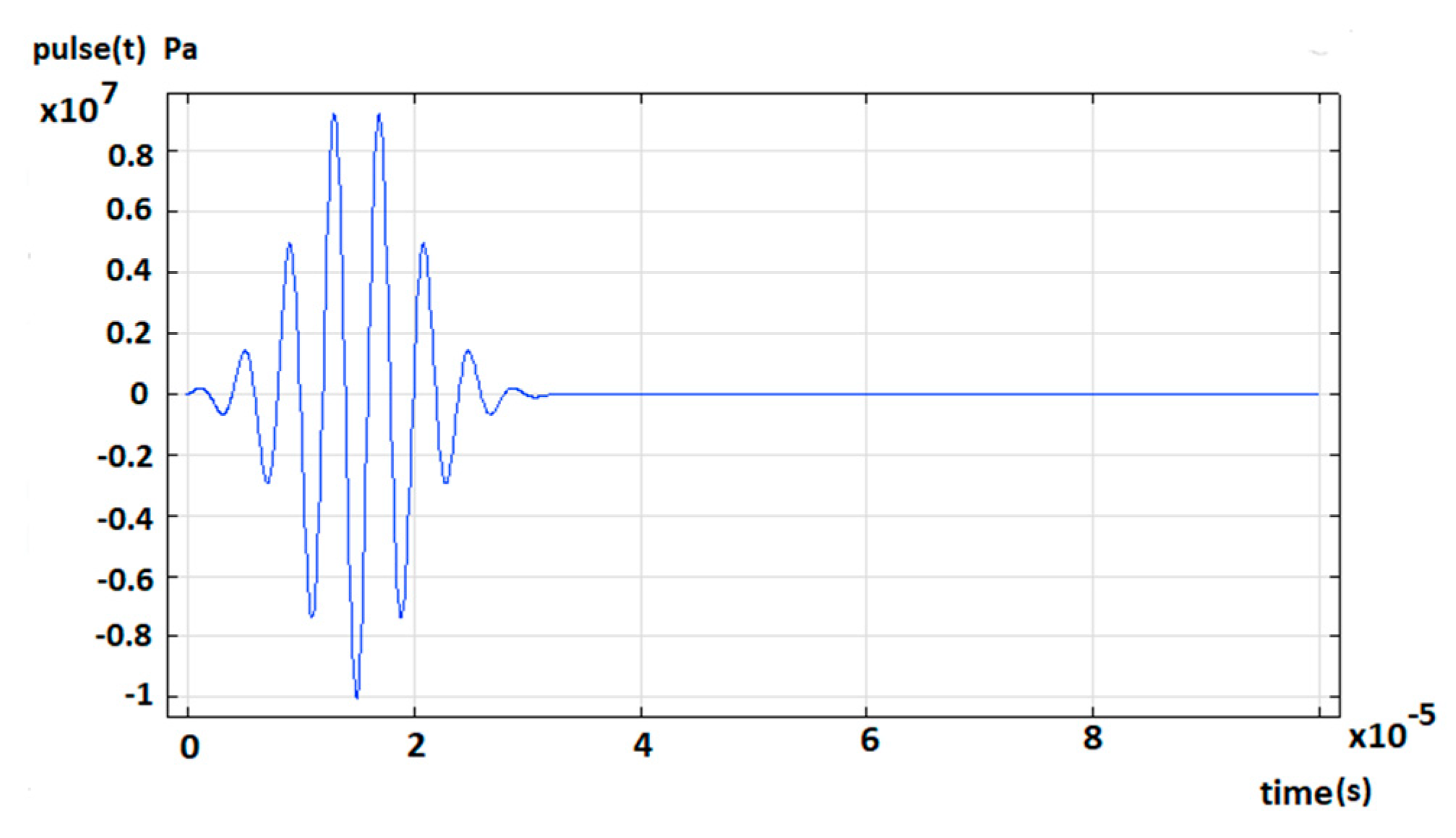
In Figure 4, it is shown the excitation pulse applied to the boundary T_x (Figure 3). The frequency was 250 KHz for both domain cases. The function used was a sinus function with a Gaussian envelope. The angle 𝜶 of the “air wedge” was 12^°, according to a previous evaluation using (1). This value was evaluated according to an approximately c phase velocity of 1800 m/s, obtained from dispersion curves of Figure 1 (using Table 1) as expressed above. With this specific angle, the model should describe an ALW mode propagation over the upper CFRP plate of the sandwich plate.

According to the domain in Figure 3, it is expected that the FEM models could also describe additional wave propagation modes that arrive to the boundary R_x. An average operator (Non-local Coupling in Comsol) was defined for this boundary. This allows the acquisition and display of a complex RF signal detected by this R_x transducer.

Although the transducers separation X is fixed, for a basic first simulation model for the C-Scan images, it was considered also a distance change between the transducers. This was done, in order to evaluate by FEM the PVM as it will be explained later on.

3. Material and methods

3.1. The sandwich sample.

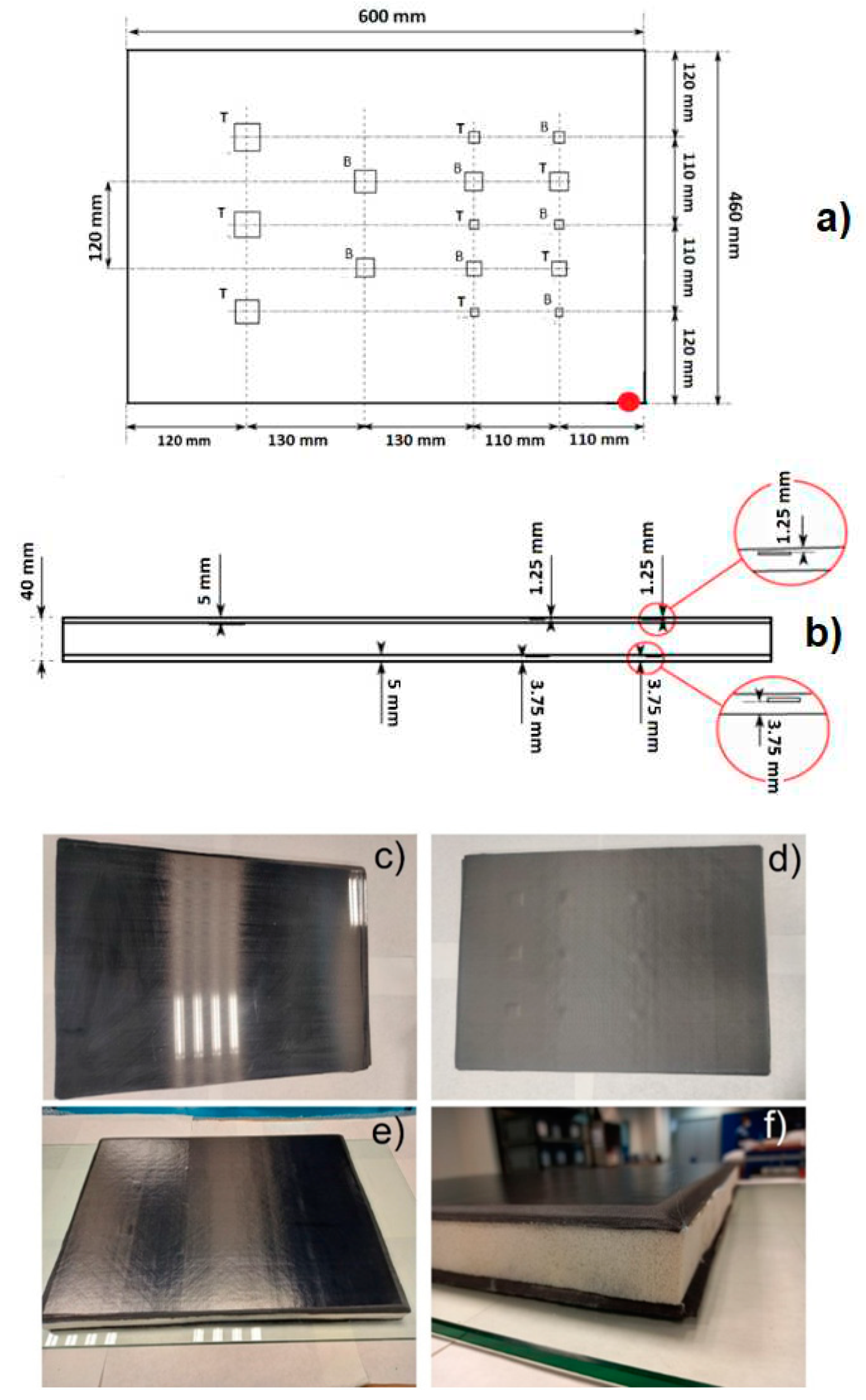
A flat coupon was selected to reproduce the sandwich based car body panels at lab scale. This geometry was chosen to simplify measurements and comparisons with railway car body demonstrator. The sandwich sample was manufactured with unidirectional epoxy/CF (epoxy-carbon fiber) pre-preg (pre-impregnated fabric) (TORAY P707AG-15) as material for the skins and a 30 mm thick sheet of PET Foam (supplied by DIAB, www.diabgroup.com) as the core material. Artificial defects were created introducing small square-shaped pieces of PTFE film located between pre-preg plies and between the core and the skin of sandwich structure. Schematic representation of the distribution of defects and of the laminate is shown in Figure 5a and b respectively. For the manufacturing of the skins, these pre-pregs plies were sequentially piled up with a quasi-isotropic stacking sequences [0, 90, +45, -45], until reaching a thickness of 10 mm. This way the resulting structure had homogeneous strength and stiffness. Afterwards, the core material was placed and then the upper skin laminate was positioned on top to form the sandwich structure. The laminate was manufactured by curing the thermoset material in an oven with temperature and pressure using a flat glass as a tool. The curing cycle followed was: 1) 6h at 40ºC, 2) ramps up to 1ºC/min up to 80ºC, 3) 5h at 80ºC, 4) ramps up to 132ºC, 5) 2h at 132ºC, 6) cool down to room temperature and 7) demoulding when the coupon temperature was below 50ºC.

The surface of the laminate in contact with the glass tool had a smoother surface after manufacturing, see Figure 5c. The other side, displayed in Figure 5d, presents a rougher texture since this surface was in contact with the vacuum bag consumables (the peel ply left a rough surface after manufacturing). Bumps originated by the presence of defects can be clearly observed in this picture. The cross section and surface of sandwich laminate is shown in image of Figure 5e, where both components of this type of structure are clearly distinguished: carbon fiber-based skins and PET Foam core. The porous core can be detailed observed in Figure 5f. The Table 2 shows a resume of the characteristic of the sample used in this paper. For the Foam =232 kg/m³, Young modulus=0.9e8 Pa and Poisson ratio=0.33.

3.2. Ultrasonic Instruments and experiments methods.

The Airscope system (DASEL [16]) was used as ultrasonic equipment for experiments. Two air-coupled transducers, made also by Dasel, were used working in an emitter-receiver configuration of longitudinal waves. Figure 3a,b shows diagram details and a photo of the air-coupled transducers over the sandwich sample. An acoustic isolation perpendicular barrier is also shown. With this configuration, two kinds of experiments were performed, where an excitation pulse of 250 KHz with 5 cycles is applied to the T_x by the Airscope and the received RF signal arriving to R_x is collected according to the specific experiment.

3.2.1. Phase velocity method (PVM).

In the first experiment, one dimensional case (1D), the receiver R_x was displaced lineally away from the transmitter T_x, at step 5 mm, from 55 to 115 mm approximately (black arrow of Figure 6 left) in a line-region without defects. At each position of R_x, the RF signal is registered. This signal is composed of several consecutive pulses. The problem is to identify, which part correspond to the ALW necessary for the C-Scan image conforming. For this purpose, the PVM is used [7].

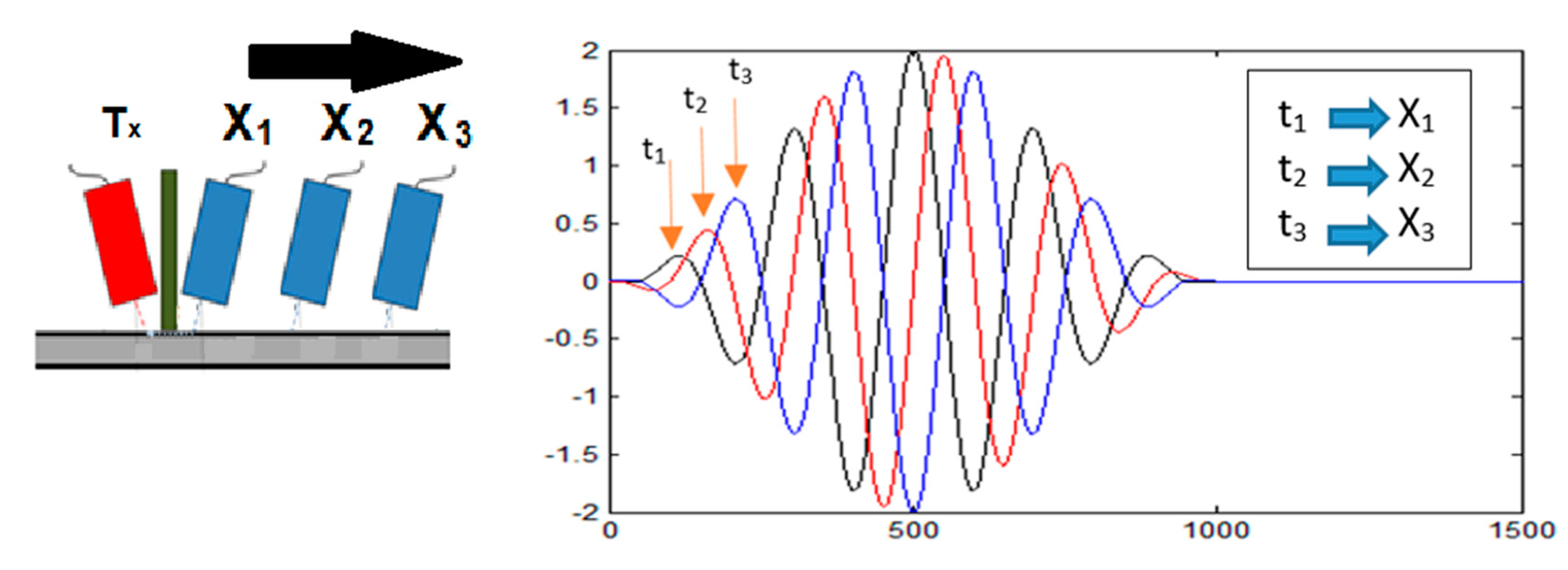
Figure 6 shows a diagram of the PVM. At left, it is represented a plate with three R_x transducer positions with the corresponding RF signal portion at right. Each red arrow shows the same constant phase point with a relative displacement over the RF signal.

At the points X₁, X₂ and X₃, the respectively time values of T₁, T₂ and T₃, of the constant phase value, are collected. With a linear time-space diagram [7], it is possible from the slope, to evaluate the phase velocity. It this way it is completed the identification of the ALW. The PVM could be also applied to the RF signals obtained from FEM simulations as well from the experimental results.

3.2.2. C-Scan image formation.

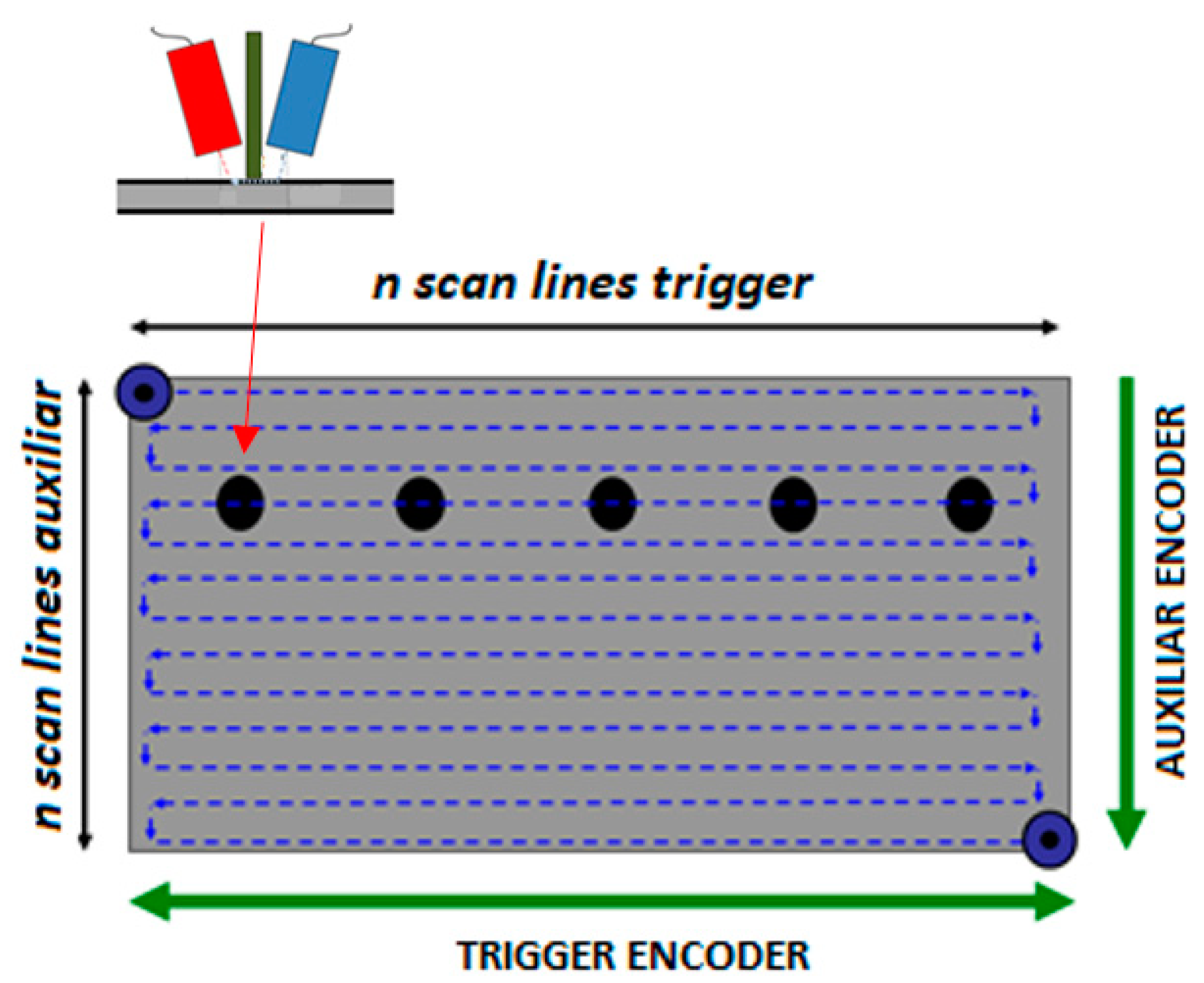
The second, two dimensional (2D) scanner experiments were performed for obtaining a C-Scan image, from a portion selected of the RF signals. This means the ALW mode. In this case, both transducers move as a whole, keeping fixed the distances X=50 mm and Z=10 mm over the sample plate as expressed in Figure 3a,b. In Figure 7, it is shown, the 2D scanner strategy, where the transducers move first in a horizontal line capturing RF signals at each 2 mm position defined by the Trigger Encoder. Afterwards the complete line acquisition, both transducers move to a second line at a 2 mm distance from the previous line defined by the Auxiliary Encoder. This process is repeated to complete all the area of the sample plate, where several RF signals are obtained.

4. Results and Discussion.

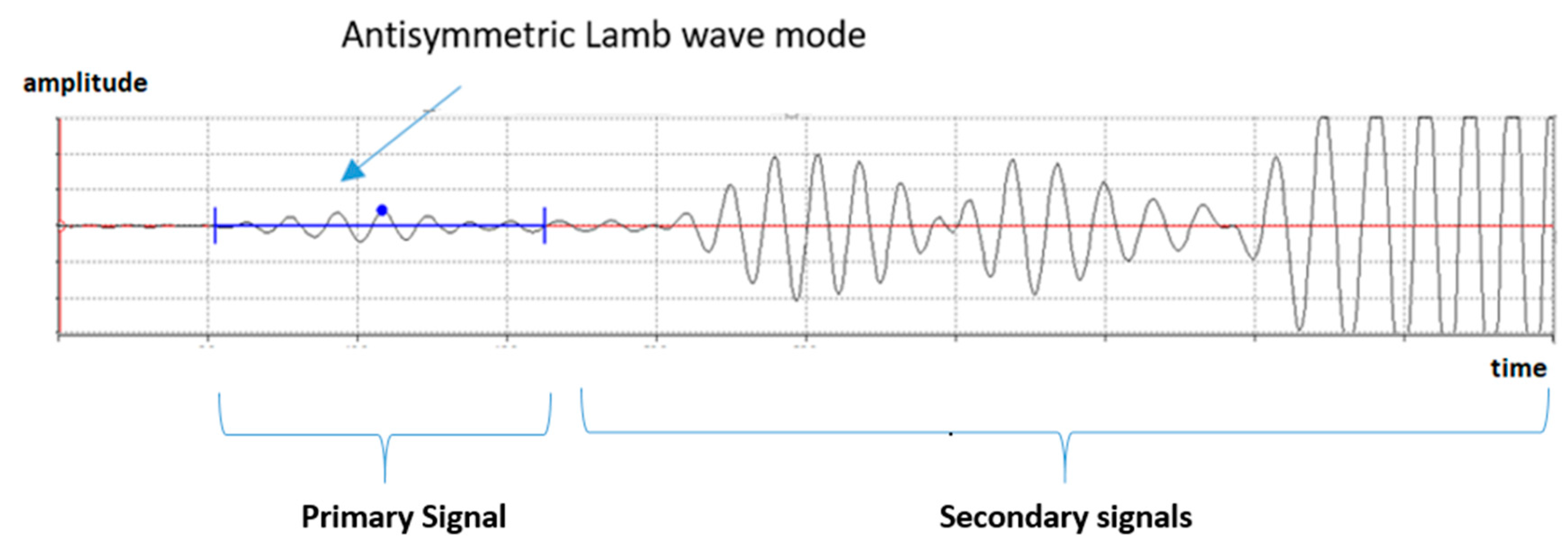
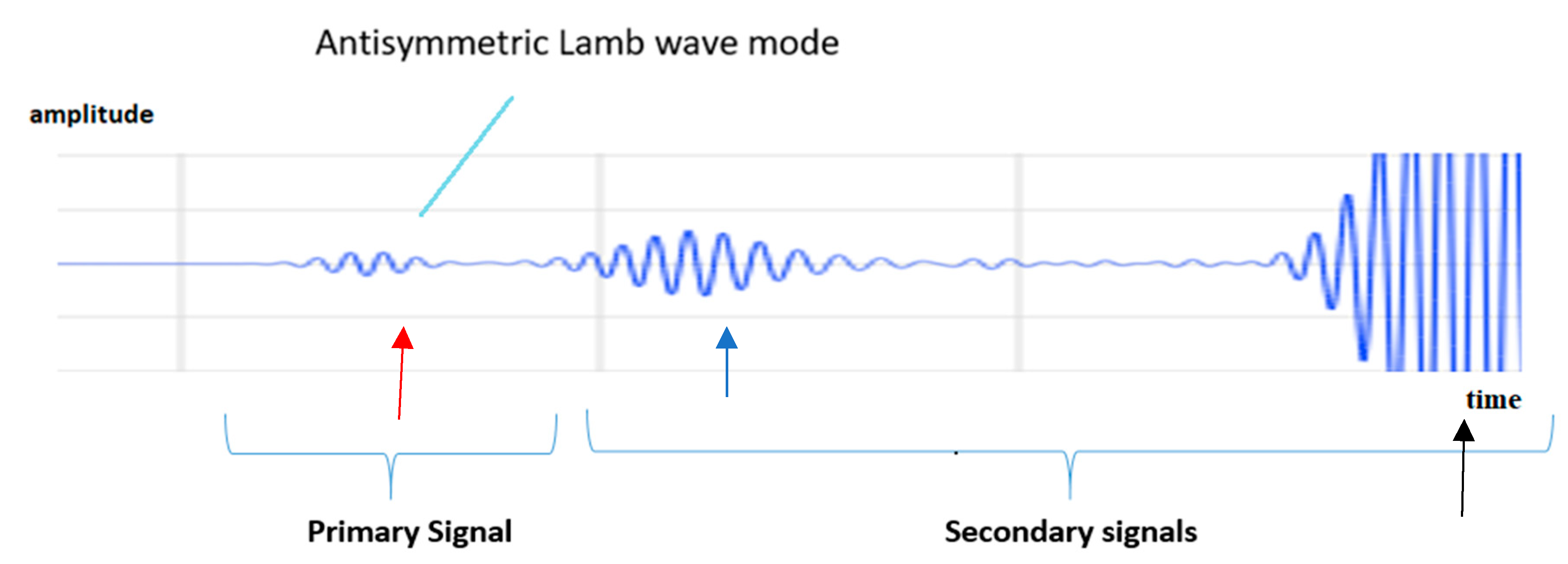
The next Figure 8 shows an experimental example of an RF signal obtained in the sandwich sample at 250 KHz. The blue gate, on the figure, expresses the primary portion of the signal that is selected for the C-Scan imaging. This corresponds to the ALW mode, which was probed using the PVM. Secondary signals are rejected, for the C-Scan, as a consequence of the multiple reflections in the experimental setup. However, all these signals, primary and secondary should be evaluated with the FEM models as it will be shown later on.

4.1. FEM Simulation results of RF signals and wave propagation. Relation to the dispersion curve and the PVM method

Figure 9 displays the simulation of the RF signal according to the FEM model of the Figure 3. If it is compared with the previous Figure 8, it shows similar characteristics.

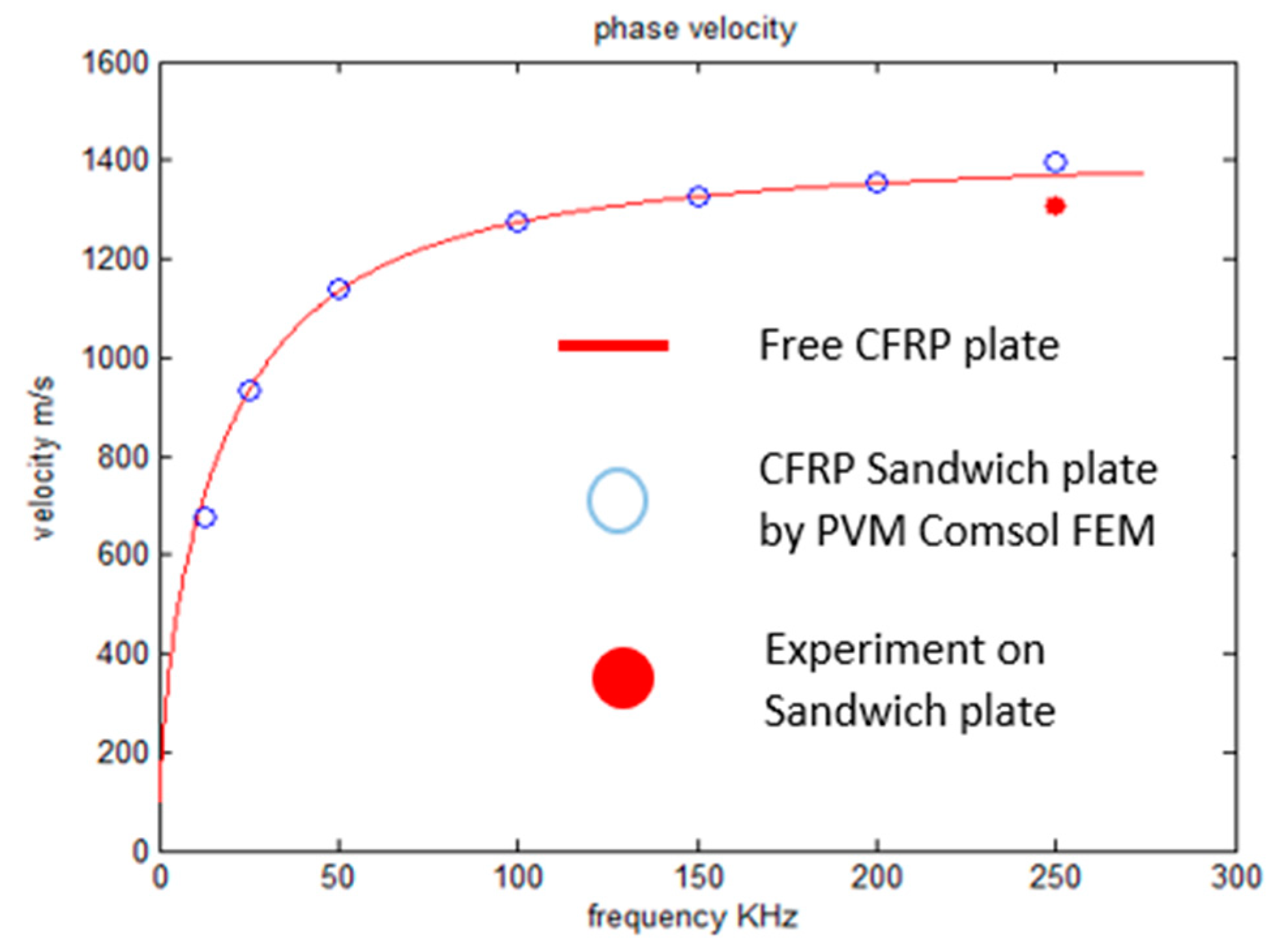
As in the experimental case, the first part of the RF signal named as Primary signal, was identified as the ALW mode using the PVM Figure 10 shows a resume of the results with the dispersion curve (continuous red line) [7]. Also, it resumes the experimental point obtained at 250 KHz with the same PVM method (Figure 8). The experimental phase velocity value obtained and its correspondence with the theoretical models, confirm that the primary signal is the ALW mode.

From Figure 10, it is clear that it is not possible to detect, a difference from a single CFRP plate with the same CFRP plate in the sandwich structure. In this last case, it is expected a leakage conversion from the ALW in the upper CFRP to the Foam plate component of the sandwich. Hence, the phase velocity in the upper CFRP plate is not affected by the leakage into the Foam.

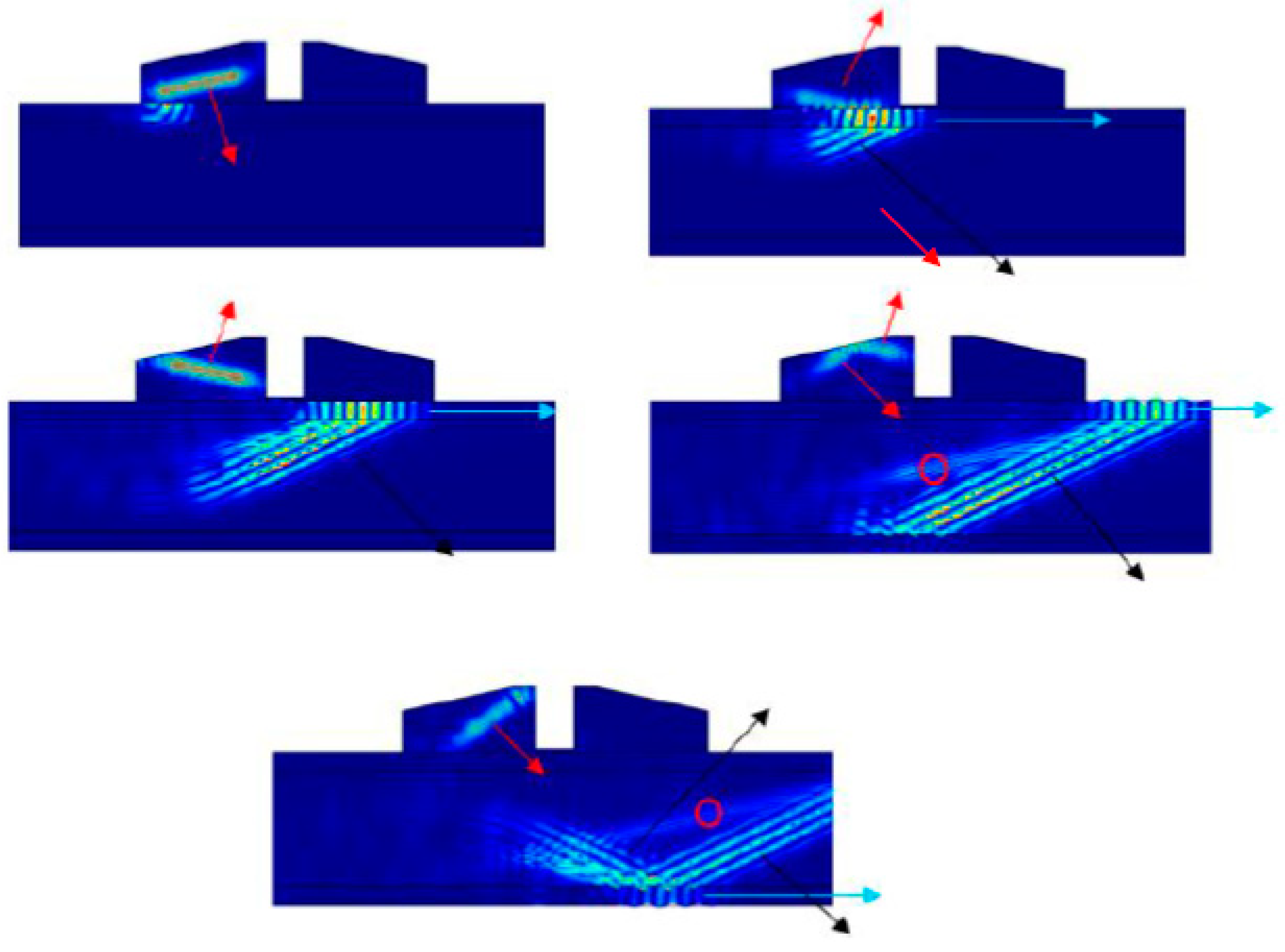
In Figure 11, it is displayed a time evolution of the wave propagation obtained from FEM simulations. In this sequence, it is possible to observe the conversion of longitudinal waves (red arrow) into the ALW in the upper CFRP layer (blue arrow). In parallel, the ALW mode produces a leakage (longitudinal wave, black arrow) that converts again in a second ALW mode on the lower CFRP layer.

Some important details emerge from the previous figure. First, for the incident angle (12^o), FEM simulation confirms the ALW mode. Second, the longitudinal wave, inside the air wedge in T_x, shows multiple reflections. Comparing the 4 seg with the 12 seg frame, there is a second longitudinal incident wave with an angle greater to 12⁰. Although this has no consequence with another mode in the CFRP plate, it is important for the origin of the secondary signals as it will be next shown. In this sequence, it is not possible to observe any mode inside the second R_x wedge, as a consequence of the range of the color scale. Finally, the red circle, in the last two frames of the time sequence, shows another refracted wave that should be a shear type according to its minor angle.

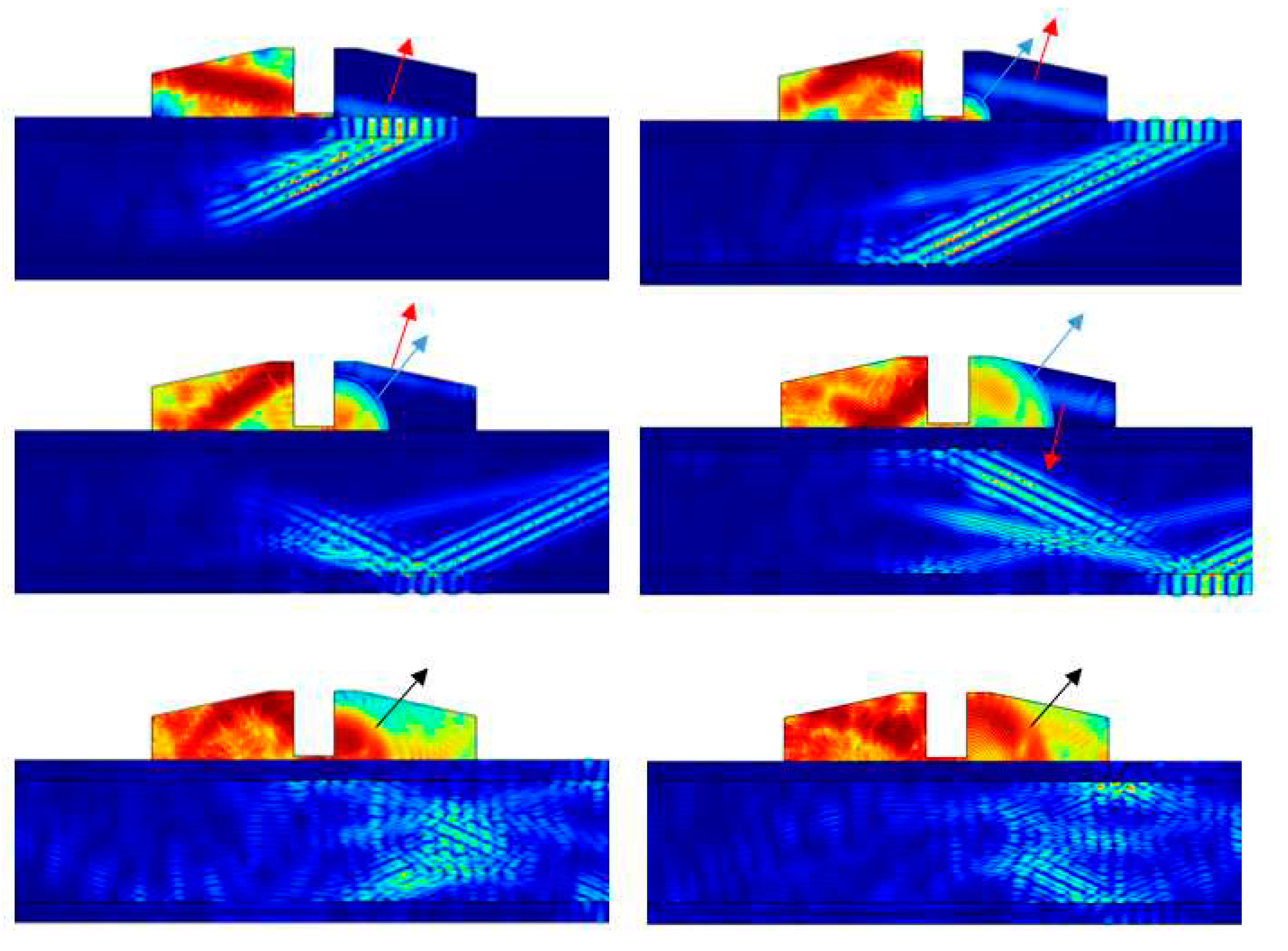
Figure 12 shows a similar sequence at 8, 10, 12, 14, 18 and 20 seg. In this case, a logarithm scale was used in order to improve the details of the signals on the R_x air wedge. The red arrow shows the signal obtained as a consequence of the ALW mode leakage. Following the sequence of Figure 12, then arrives a pulse (blue arrow) that corresponds to the longitudinal signal, which propagates through the gap between the sandwich surface and the acoustic barrier. This means that the acoustic barrier that is not good enough for a complete isolation. Finally, as a consequence of the multiple reflection in the T_x air-wedge (Figure 11 and Figure 12 μseg), a third signal arrives (black arrow). This signal has a higher amplitude than the previous signal. This is a consequence of a complex process of dependence of the amplitude with a different incident angle, which is beyond the scope of this paper. These amplitude increment was also observed in the experimental signal (Figure 8).

The results obtained show the convenient of simulation using FEM models, which allows to understand the complex signal components obtained in the experiments. Of course, the experimental RF signal has another component in the secondary signal zone. This could be explained with another complex FEM model that includes the structure of the UT transducers itself with its internal components.

4.2. C-Scan Image Mode Method.

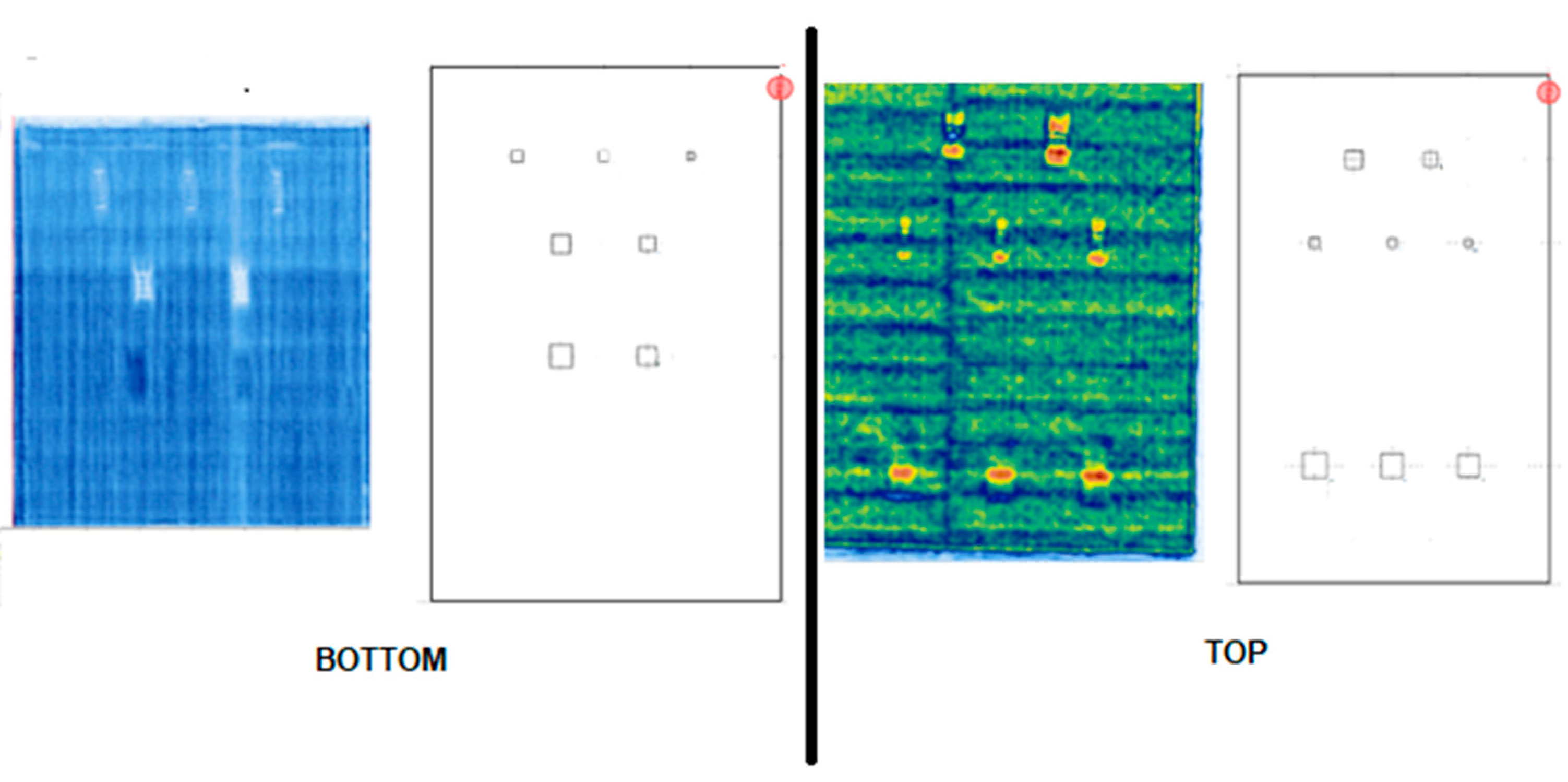
In Figure 13, it is shown two C-Scan images, at both sides of the sandwich plate. For these images, the AWL mode pulse, previously identified in the RF signal, was selected according to Figure 8. Then, the flaws associated with the upper part of the CFRP plate, disbonds and delaminations, are detected. This is a consequence that the principal objective is related to the external sandwich layer, which could be exposed at several impact accidents.

In this figure, it is shown that the images from the defect are rectangular and not square according the sample design. This is a consequence of the scanner strategy shown in Figure 7 and also the transducer configuration (Figure 3a). This could be corrected by an additional image processing algorithm.

The defects, at the previous Figure 13, depend on the change of the amplitude of the ALW pulse selected by a gate (Figure 8). It is expected that the amplitude increases with a disbond, in the boundary of the CFRP with the Foam. This could be explained by the interruption of the leakage. If the disbond are separated, from this boundary, then the amplitude decreases. This could be explained by the change in the phase velocity according to the thickness decrement of the disbond plate and the dispersion curves [7]. This change demands a new angle according to the Snell Law, which is not accomplished in the experiments. 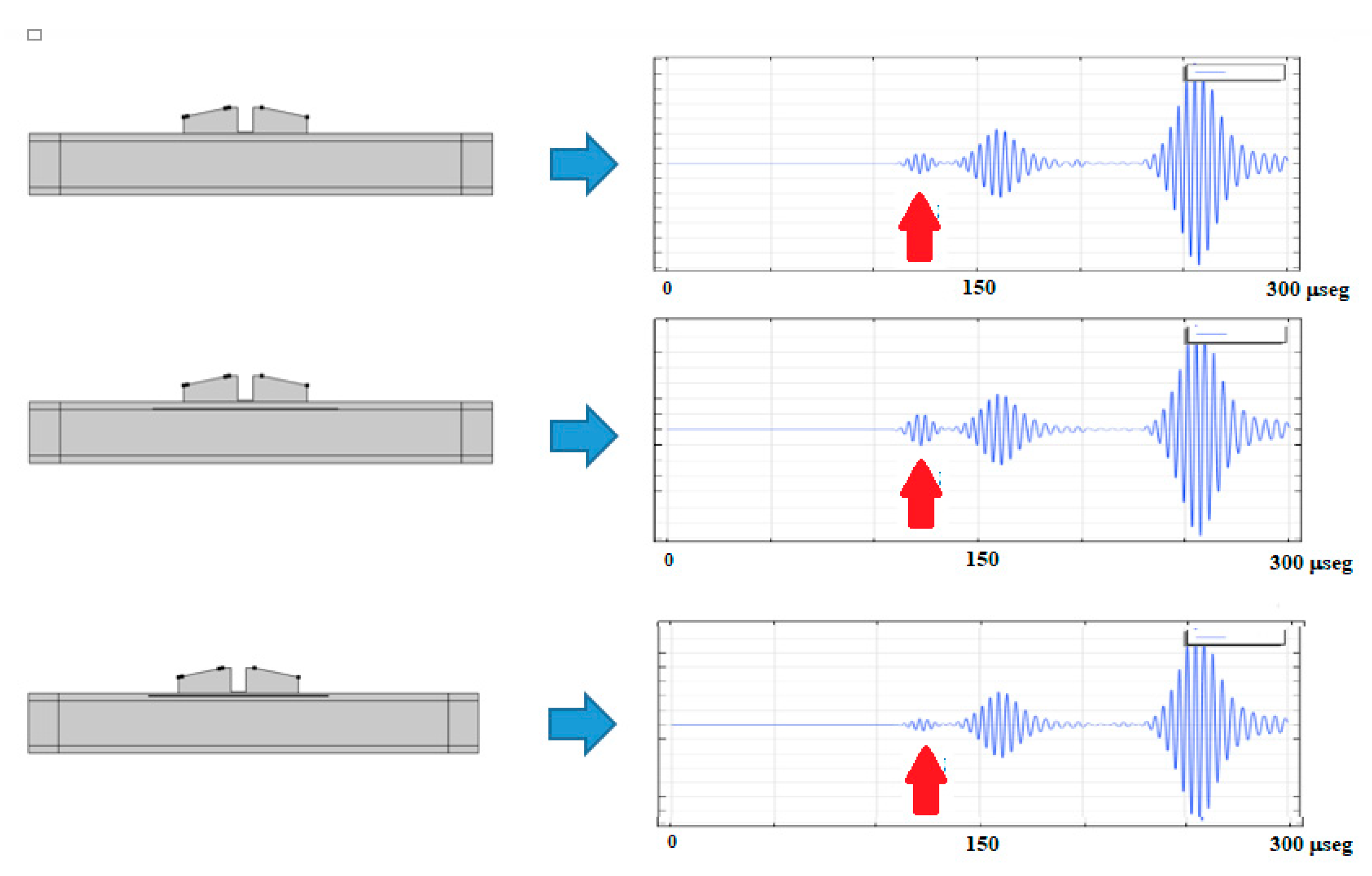The next Figure 14 shows the development of FEM models for these two disbond situations compared with the flawless case.

However, the models developed for the disbond situations do not explain the C-Scan images obtained. This could be a consequence that the artificial defects, in the sample, were created introducing small square-shaped pieces of PTFE film. This material does not represent a real disbond condition.

At the end, the FEM models could help to understand a possible disbond in a real future impact situations of the car body. The fundamental idea is that the models explain the change in amplitude of the ALW mode. The rest of signals are not affected by the defects. Then only the ALW mode should be used for a CS-Scan formation.

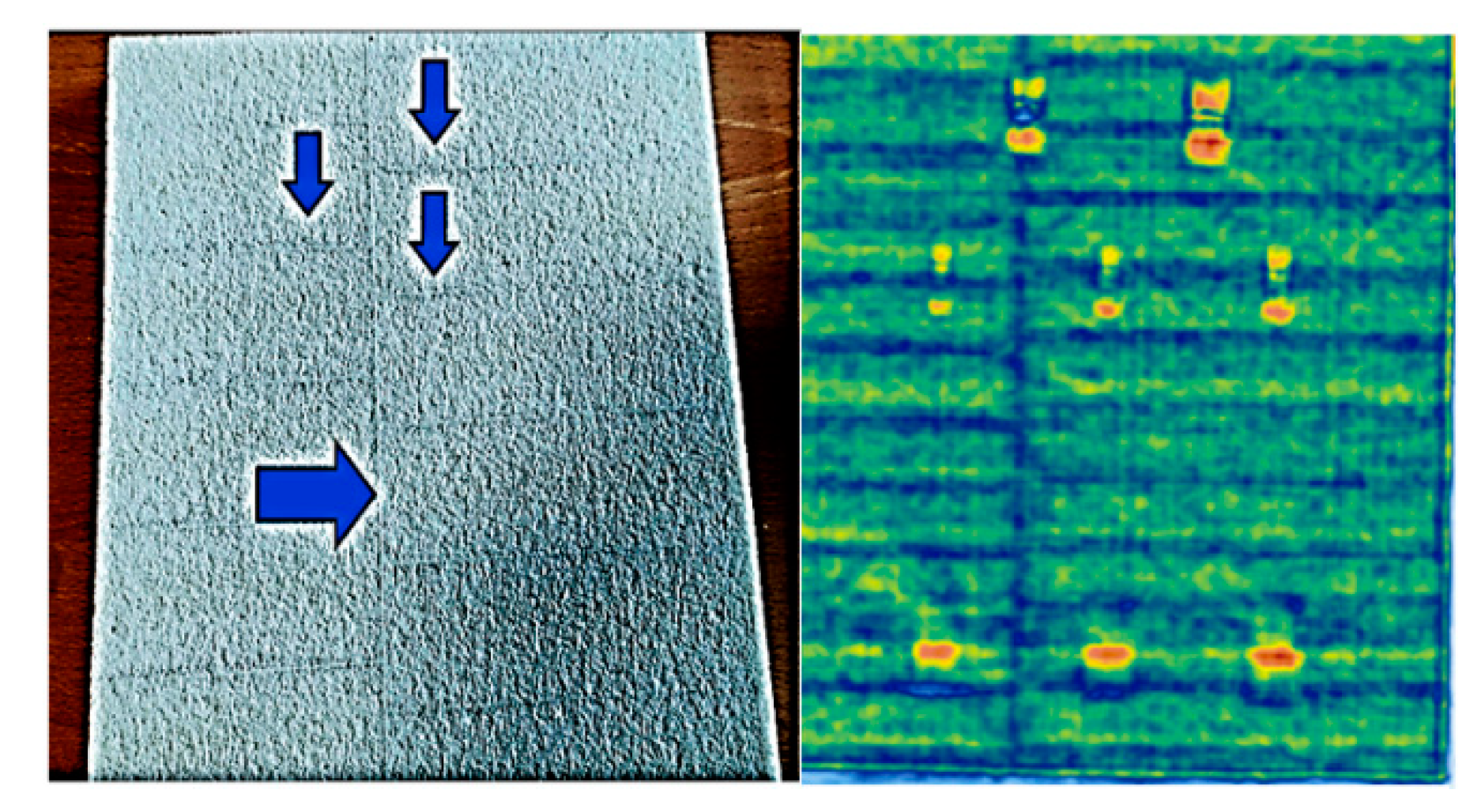
Finally, Figure 15 shows an interesting detail. Both sides of the C-Scan, shows several horizontal lines and one vertical line. This is associated with the Foam structure that was made by several blocks glued together as shown in the figure. The arrows show some examples of the boundaries of these blocks. The impedance of the epoxy resin is higher than the Foam, and then a change is the ALW amplitude makes the contrast in the C-Scan.

5. Conclusions

For sandwich structure plane elements in the car body shell, it is possible to use the UNCACT for flaw detection over the upper CFRP layer. The excitation using air transducer allows the generation of the antisymmetric Lamb wave (ALW) on the upper CFRP layer, which it is not possible using conventional plastic wedge transducers i.e. This mode was obtained by a specific angle according to the phase velocity from the analytical dispersion curves of the single CFRP plate in despite its sandwich structure.

The ALW mode propagating on the upper CFRP plate was identified as a part of a complex RF signal obtained at each T_x/R_x transducer position. The PVM was used to corroborate this mode. The mechanical scanning of these transducers, at a fixed distance, was used for obtaining C-Scan images, according to the maximum amplitude of the ALW mode. The artificial flaws were detected in the sandwich sample plate at both faces.

Several FEM models were developed for the sandwich sample with the air coupling transducers, which include and acoustic barrier. The reverberation in the T_x transducer, of longitudinal waves, introduces pulses under the barrier with several RF signals at the receiver. This was observed experimentally and described by the FEM models.

In the sandwich structure, the FEM model shows, that the ALW mode propagating on the upper CFRP plate, produces a leakage to the Foam structure. Others FEM models were complemented with two kinds of disbond according to its position in the CFRP layer. In this case, the models do not correspond exactly with the models. This could be explained, as a consequence of the technology used for the induced of defect in the sandwich sample. The idea is to show the potential of the FEM models for the interpretation of the several signals obtained with the ultrasonic technique.

The C-Scan images made with the ALW were obtained only in the upper layer of the sandwich plate. This is important according to the objective of using the UNCACT method to detect defect induced by an accident impact in the upside part of the car body shell. The use of air transducers help to obtain images faster than others UT-NDT methods with a good resolution.

The evaluation of the lower second CFRP layer of the composite sandwich plate is yet a real challenge. In the propagation of the ALW in the first CFRP layer, a possible leakage into the Foam material is considered.

Acknowledgment

This paper was supported by Gearbodies project, No. 101013296 from the European Horizon 2020 program.

References

Essig, W.; Bernhardt, Y.; Döring, D.; Solodov, I.; Gautzsch, T.; Gaal, M.; Hufschläger, D.; Sommerhubee, R.; Brauns, M.; Marhenke, T.; Hasener, J. Air-coupled Ultrasound – Emerging NDT Method. ZfP-Zeitung 2021, 173, 32–43. [Google Scholar]
Castaings, M.; Hosten, B. The use of electrostatic, ultrasonic, air-coupled transducers to generate and receive Lamb waves in anisotropic viscoelastic plates. Ultrasonics 1998, 36, 361–365. [Google Scholar] [CrossRef]
Martincek, G.; Kadlecik, T. The use of wave propagation method in evaluations of road pavements stiffness. Proceddings of the international Symposium of Bearing Capacity of Road and Airfields, Trondheim, Norway, 1982; pp. 119–127. [Google Scholar]
Moreno, E.; Acevedo, P. Thickness measurement in composite material using Lamb wave. Ultrasonic 1998, 35, 581–586. [Google Scholar] [CrossRef]
Cruz, M.; Hernandez, V.; Estrada, J.; Moreno, E.; Mansur, A. Numerical Solution of the wave propagation in a plate. Journal of Theoretical and Computational Acoustics 2021. [Google Scholar]
Moreno, E.; Acevedo, P.; Castillo, M. Pulse propagation in plate elements. European Journal of Mechanics A/Solids 2003, 23, 283–294. [Google Scholar] [CrossRef]
Moreno, E.; Galarza, N.; Rubio, B.; Otero, J.A. Phase velocity method for guided wave measurements in composite. Physics Procedia 2015, 63, 54–60. [Google Scholar] [CrossRef]
Rose, Guided wave, Elsevier, 2015.
Auld, Acoustic field and waves in solids, Krieger Pub Co, 1990.
Castaings, M.; Predoi, M.; Hosten, B. Ultrasound propagation in viscoelastic material guides. In Proceedings of the COMSOL Multiphysics User's Conference 2005 Paris; 2005. [Google Scholar]
Martincek, G. Theory and methods of dynamic nondestructive testing of plane elements (in Slovak), Brastislava: Veda, 1975.
Chimenti, D. Leaky Lamb waves in fibrous composite laminates. Journal of Applied Physics 1985, 58. [Google Scholar] [CrossRef]
Dayal, V.; Kinhra, V. Leaky Lamb waves in an anisotropic plate. II: Nondestructive evaluation of matrix cracks in fiber-reinforced composites. The Journal of the Acoustical Society of America 1991, 89, 1590. [Google Scholar] [CrossRef]
Bar-Cohen, Y.; Lih, S.-S. NDE of Composites Using Leaky Lamb Waves (LLW). ndt.net 2001, 6. [Google Scholar] [CrossRef]
Dayal, V.; Kinhra, V. Leaky Lamb waves in an anisotropic plate. I: An exact solution and experiments. The Journal of the Acoustical Society of America 1989, 85, 2268. [Google Scholar] [CrossRef]
https://www.daselsistemas.com/en/.

Figure 1. Analytical dispersion curves for the fundamental symmetric and antisymmetric mode for a single CFRP plate of 5 mm thickness. Phase=phase velocity, Group=group velocity. It is assumed free boundary conditions [7].

Figure 2. Description of the propagation modes that includes the incident longitudinal wave in the air. Longitudinal leakage waves are produced on both sides of the air surrounding a single plate, where the Lamb wave is propagating. T_x and R_x are transmitter and receiver air transducers. Both are situated at the same angle .

Figure 3. (a) Transducer configuration. Z=10 mm, X=50 mm. (b) Photo of the transducers used in the experiments over the sandwich plate. c) Comsol domain. Both transducers are simulated by a boundary condition over an air wedge (T_x and R_x). The air wedges are connected by a small air channel below of 1 mm high (zoom circle).

Figure 4. Excitation pulse applied to the boundary T_x.

Figure 5. Diagram and manufacturing details of the sandwich plate used in experiments and simulation models. Two defects are presented: delaminations in CFRP skin and disbonds between Foam and CFRP skins. T and B represent the Top and Bottom flaws relative to each CFRP skin respectively.

Figure 6. Phase Velocity Method (PVM). Left, a sample plate with three space reference points X_i. Right, the RF signal associated with the previous reference points at the plate. The scales in the RF are relative displacement vertical amplitude vs. time. In the RF signals, the red arrows show a constant phase point relative to the first maximum.

Figure 7. The 2D scanner diagram for obtaining the C-Scan image. The black point represents both transducers T_x and R_x, which moves as a whole with fixed distances. Two encoders, at each axis, are used to control the displacements in these experiments.

Figure 8. Example of an RF signal. The blue gate selects the antisymmetric Lamb wave mode (ALW). At this gate the maximum amplitude at the blue point is used in the C-Scan image.

Figure 9. FEM simulation of the RF signal at a fixed distance X=10 and Z=50 mm. The red arrow shows the ALW mode. The blue arrow shows the first secondary signal, and the black arrow shows the second secondary signal.

Figure 10. Phase Velocity Method. Left, Analytical dispersion curve for single CFRP plate (Free CFRP plate), the CFRP Sandwich plate by PVM Comsol FEM and a sandwich experimental point at 250 KHz.

Figure 11. Time sequence (4, 6, 8, 10 and 12 seg) of emission of longitudinal wave from T_x (red arrow), and conversion to ALW (green arrow) and longitudinal leakage (black arrow). The red circle shows shear wave.

Figure 12. A time sequence of wave propagation at 8, 10, 12, 14, 18 and 20 μseg. A logarithmic scale was used to improve the R_x air-wedge color scale. The red arrow shows the AWL mode leakage. The blue arrow and the back arrows, the first and the second respectively longitudinal wave that travels under the acoustic barrier. All these are related to the RF signals of Figure 9.

Figure 13. Two C-Scam images for both sides of the sandwich plate obtained with the ALW mode selected. The right represents the Top case and the left the Bottom case respectively according to Figure 5a. Each includes two diagrams of the flaws relative to the upper CFRP plate according to its orientation. These diagrams were extracted from Figure 5a, the T (Top) and B (Bottom) cases.

Figure 14. The red arrows show the ALW mode used for C-Scan images. The two disbond situations (middle and bottom) are compared with the flawless case (up).

Figure 15. The Foam structure observed in the C-Scan image. The dimension scales are a little different from the photo (left) to the C-Scan case.

Table 1. Elastic constants used for a CFRP plate.

C₁₁ (GPa)	C₂₂ (GPa)	C₁₂ (GPa)	C₆₆ (GPa)
38,4	7,7	3	2,6

Table 2. Characteristic sample used for UT testing.

Sample	Dimensions	Fiber orientation
Sandwich plate made by two layers of CFRP and a Foam core. Defects were included.	600 x 460 x 5 (each skin) 600 x 460 x 30 (core)	0/90/+45/-45

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer