Tensor-Train Decomposition Based Hybrid Beamforming for Millimeter-Wave Massive MIMO/FSO in UAV with RIS Networks

Preprint

Article

Tensor-Train Decomposition Based Hybrid Beamforming for Millimeter-Wave Massive MIMO/FSO in UAV with RIS Networks

Altmetrics

Downloads

141

Views

Comments

A peer-reviewed article of this preprint also exists.

Xiaoping Zhou^*,Pengyan Feng,

Jiehui Li^*,Jiajia Chen,Yang Wang

Xiaoping Zhou^*,Pengyan Feng,

Jiehui Li^*,Jiajia Chen,Yang Wang

This version is not peer-reviewed

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts

Abstract

UAV (Unmanned aerial vehicle) communication offers the possibility to establish the new net-works. To overcome the PE (pointing error) and beam misalignment of millimeter-wave massive MIMO (Multiple-in multiple-out)/FSO (Free Space Optical) caused by UAV jitter, a Tensor-train decomposition based hybrid beamforming for millimeter-wave massive MIMO/FSO in UAV with RIS (Reconfigurable Intelligence Surface) networks is investigated to improve the system spectral efficiency. Firstly, the high-dimensional channels of the RIS-assisted millimeter-wave massive MIMO/FSO in UAV are represented as the low-dimensional channels by Tensor-train decomposition. Secondly, the FSO PE caused by UAV jitter can be effectively solved by BIGRU (Bidirectional Gated Recurrent Unit)-attention neural network model. The fast-fading channels and Doppler shifts are estimated by the FCTPM (Fast Circulant Tensor Power Method) based on the Tensor-train decomposition. Finally, the RIS phase shift matrix is optimized by the SVD (Singular Value Decomposition). The Hybrid beamforming and RIS phase shift matrix are esti-mated by the low-complexity PE-AltMin (Phase Extraction Alternating Minimization) method to solve the beam misalignment. Simulation experiments demonstrate that the proposed method has higher spectrum utilization than other methods.

Keywords:

Subject: Computer Science and Mathematics - Signal Processing

1. Introduction

UAV (Unmanned aerial vehicle) combined with cellular networks can support communications in a cost-effective and highly mobile manner. UAV communication offers the possibility to establish new dedicated terrestrial networks [1-3]. In areas with dense traffic hotspots in cities, the coverage of traditional cellular base stations cannot meet the demand. UAV can quickly provide coverage and service triage to hotspots based on their high flexibility and easy deployment and have a wide range of application scenarios. Compared with terrestrial base stations, the ABS (Aerial Base Station) is more adaptable to environmental changes [4]. Therefore, UAV can also be deployed to provide emergency communication connections in areas without infrastructure coverage. Ground base stations are often destroyed during natural disasters such as earthquakes, tsunamis, and flash floods. The communication infrastructure in the disaster area is damaged and cannot provide communication services. This implements rescue operations more hindered.

To improve the transmission performance of UAV communication, RA-FSO-RF (Relay-Assisted Free Space Optical-Radio Frequency) was introduced relaying into the communication system [5-6]. The LDPC-MIMO/FSO (Low-Density Parity-Check Coded Multiple-Input Multiple-Output/Free Space Optical) method investigates the performance evaluation of power-series based málaga distributed MIMO/FSO links with m-QAM and pointing error (PE) [7]. DHPL-ML (Dynamic Hybrid Precoding with Manifold Learning) method proposes a manifold learning inspired dynamic hybrid precoding dual hop hybrid FSO-RF system based on antenna partitioning algorithm [8]. Similarly, MIMO techniques were used to eliminate the effects of atmospheric turbulence (AT) and pointing errors on link performance in FSO systems [9]. The bit error rate (BER) and the channel capacity of MIMO system employing an optical space scheme ware investigated under the combined effect of AT and PE [10]. The communication environment in UAV was greatly affected by atmospheric turbulence. It can have a significant impact on the performance of laser communication. The UAV communication mainly includes visual axis errors and jitter errors. At present, the jitter influence of free-space laser links was studied [11]. However, the existing algorithms have rarely reported the bit error rate performance of UAV under the influence of turbulence. Meantime, these previous studies on FSO-RF systems have focused on the FSO link or relay selection problem [12-15]. The problems of the PE and beam misalignment of millimeter-wave massive MIMO/FSO in UAV communication RF links are ignored.

The coverage performance of UAV base stations is affected by the dynamic movement of UAV and obstacles [16]. In addition, the issues of beam misalignment and Doppler frequency shift caused by obstacle interference and wind speed is needed to consider [17]. To improve UAV communication performance, the beamforming of UAV antenna arrays can help overcome the problems of beam misalignment and Doppler shift. Beamforming was designed for UAV communication with random blockages [18-19]. The 3D location of the UAV base station with a certain number of indoor users and obstacles was determined. UAV can perceive user and obstacle locations to maximize the total coverage of base stations. The ZF-HBF (Zero Forcing-Hybrid beamforming) method was explored for multi-user orthogonal frequency division multiplexing systems over downlink [20-23]. The zero forcing method is used to achieve beamforming according to the system's SE (Spectrum Effectiveness) up to the maximum upper bound. To enable fast beamforming training and tracking, a hierarchical structure of beamforming codebooks and design of hierarchical codebooks with different beam widths via sub-array techniques was investigated [24]. The Doppler effect as a result of UAV movement was examined and found that the Doppler effect may be catastrophic when low gain beamforming is used. A hybrid beamforming for millimeter-wave massive MIMO with channel estimation was proposed [25-27]. By exploiting the angular sparsity of mmWave channels, the continuously distributed angle of arrivals/departures (AoAs/AoDs) can be jointly estimated for hybrid beamforming. A Hy-BD (Hybrid Block Diagonalization) method on phase beamforming with a combiner was obtained [28]. The digital block diagonalization of massive array gain was used to process equivalent baseband channels. However, in the case of high-speed motion, the currently available beamforming techniques are limited in terms of performance improvement. The RIS (Reconfigurable Intelligent Surface) for beamforming in wireless communication [29] was considered for UAV communication systems. The RIS is needed to further consider the altitude, transmission distance, and multipath channel of the UAV to plan its path. The REHS (RIS for nonlinear energy harvesting algorithm) method was investigated to improve the UAV communication performance by optimizing the phase of the RIS reflective elements and the parameters of the nonlinear energy harvesting circuit [30-32]. However, the indoor wireless network coverage lacks adaptivity due to the mobility of UAV and the time-varying channel. The RBOP (RIS-Based optimization and passive beamforming algorithm) was investigated to maximize the signal received power of the UAV communication system [33]. The RBOP aims at joint trajectory design and passive beamforming in UAV communication. The system performance will degrade if the hybrid beamforming is targeted for partial connections. Multi-user beamforming for millimeter-wave massive MIMO in UAV leads to high-dimensional operations[34-37]. To maximize the spectral efficiency of the system, it is necessary to jointly design its RIS reflection coefficient and hybrid beamforming. These algorithms require high computational costs, leading to degraded energy efficiency.

To overcome the light PE and beam misalignment of millimeter-wave massive MIMO/FSO caused by UAV jitter, a Tensor-train decomposition based hybrid beamforming for FSO and millimeter-wave massive MIMO of UAV with RIS is investigated. Firstly, the RIS-assisted millimeter-wave massive MIMO/FSO in UAV channel model is established, and the high-dimensional channels of the RIS-assisted millimeter-wave massive MIMO/FSO of UAV is represented as the low-dimensional channels by Tensor-train decomposition. Secondly, the problem of maximizing the system spectral efficiency is decomposed into two sub-problems optimizing the light PE of FSO and the hybrid beamforming matrix. The FSO PE caused by UAV jitter can be effectively solved by BIGRU (Bidirectional Gated Recurrent Unit)-attention neural network model. The fast-fading channels and Doppler shift are estimated by the FCTPM (Fast Circulant Tensor Power Method) [38-39] based on the Tensor-train decomposition. Finally, the RIS phase shift matrix is optimized by the SVD (Singular Value Decomposition). The Hybrid beamforming and RIS phase shift matrix are estimated by the low-complexity PE-AltMin (Phase Extraction Alternating Minimization) method to solve the beam misalignment. Simulation experiments demonstrate that the proposed method has higher spectrum utilization than other methods.

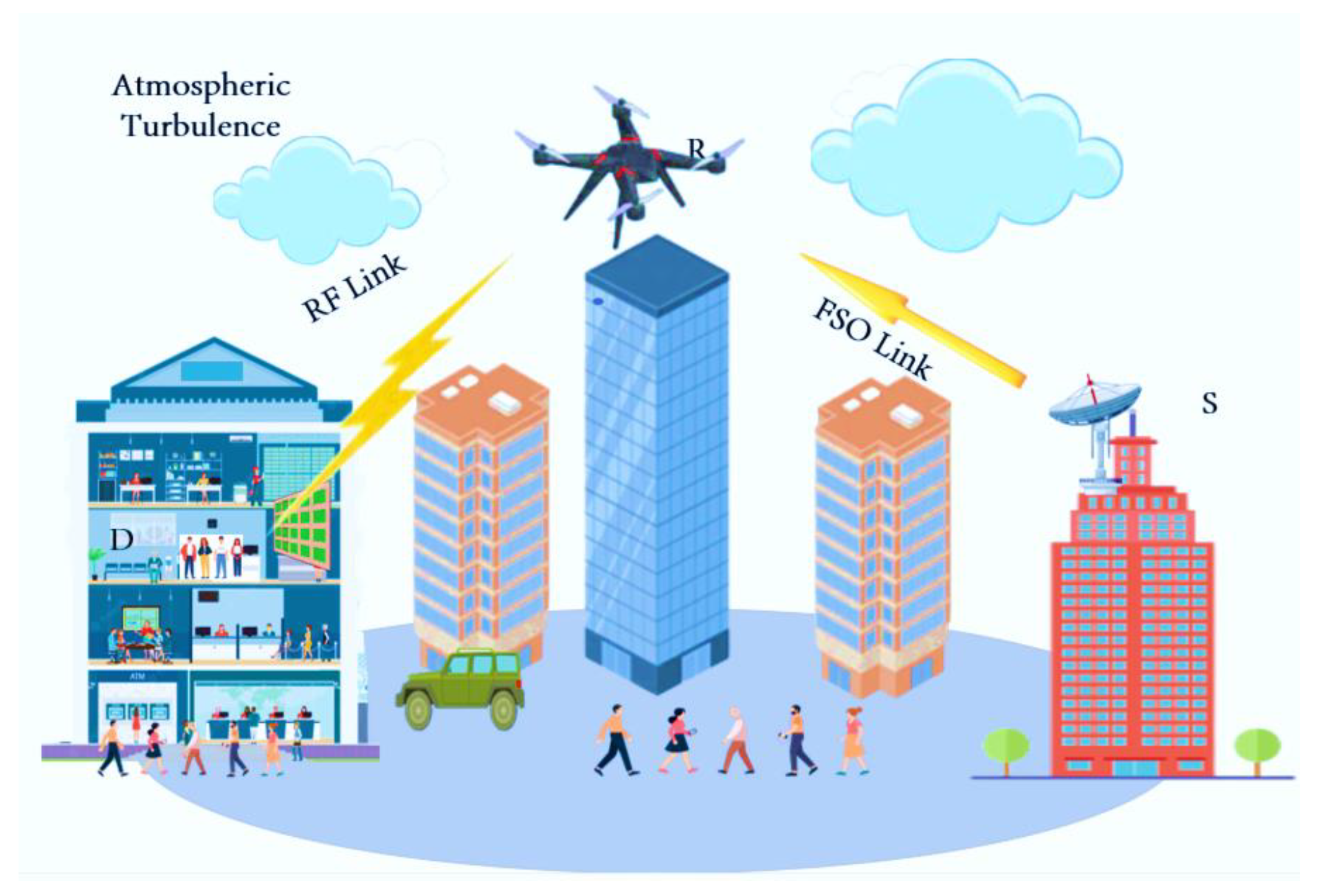
2. System model

This paper considers a RIS-assisted multi-user millimeter-wave massive MIMO /FSO UAV communication system, as shown in Figure 1. Covering densely indoors can affect the connectivity of signal transmission, and the window of RIS components is small. When the UAV experiences shaking, it can cause beam misalignment during signal transmission. The multi-user millimeter-wave massive MIMO in UAV, in turn, leads to high dimensional operations in the beamforming process. To maximize the spectral efficiency of the system, it is necessary to jointly design its RIS reflection coefficient and hybrid beamforming. However, due to the non-convexity of the problem, it is decomposed into two independent optimization subproblems. The block diagram of a mixed FSO-RF system is presented in Figure 1 in which the source node (S) communicates with the destination node (D) through a decode-and-forward (DF) relay node (R). The S-R link is equipped with a single antenna, and the R-D link is a millimeter wave massive MIMO system model. Node R has both optical and RF signal processing capabilities. We employ non-coherent intensity modulation with direct detection (IM/DD) receiver at R. After converting the incoming optical signal to an electrical signal, node R utilizes a power splitter to separate the alternating current (AC) and direct current (DC) components. The unsolicited DC component (which is normally filtered out at the receiver) is applied to the energy harvesting unit which supplies the harvested power to the RF transmitter. The information-bearing AC component is given to the decoder circuit which decodes the information and demodulates using an RF modulation scheme before forwarding it through the RF transmitter.

2.1. FSO system model

The FSO channel between S and R is modelled as Gamma-Gamma distribution with pointing error [40]. The statistical behavior of the received optical irradiance is characterized by means of Gamma-Gamma turbulence model which has been widely used to model the FSO channel in the recent literature depending on its doubly stochastic scintillation model. The probability distribution function (PDF) of channel coefficient

h_{F S O}

is given as

f_{h_{F S O}} (h_{F S O}) = \frac{ς^{2}}{h_{F S O} Γ (α) Γ (β)} G_{1,3}^{3,0} (α β \frac{h_{F S O}}{I_{F S O} M_{o}} |_{ς^{2}, α, β}^{ς^{2} + 1})

(1)

Where

Γ (

.) is the well-known Gamma function,

G_{p, q}^{m, n} ({x|}_{b_{1}, \dots, b_{q}}^{a_{1}, \dots, a_{p}})

is the Meijer’s G-function. The atmospheric turbulence induced fading channel gains of FSO links, denoted as

I_{F S O}

deled with s and path loss. It is assumed that the elements of

I

are modeled as independent and identically distributed random variables

ς = {\bar{ω}}_{e} / 2 σ_{s}

is the ratio of equivalent beam radius and zero boresight displacement standard deviation at the photo-detector (PD), the constant term

M_{o}

is the power fraction that the detector receives when there is no, and

1 / α

and

1 / β

 are the variances of the large and small turbulence eddies, respectively. The FSO system is modeled as shown in Figure 2.

The parameters

α

and

β

are the distance-dependent fading variables which corresponds to atmospheric turbulence conditions as

α = {\{e x p [\frac{0.49 σ_{R}^{2}}{{(1 + 1.11 σ_{R}^{\frac{12}{5}})}^{\frac{7}{6}}}] - 1\}}^{- 1}

(2)

and

β = {\{e x p [\frac{0.51 σ_{R}^{2}}{{(1 + 0.69 σ_{R}^{\frac{12}{5}})}^{\frac{5}{6}}}] - 1\}}^{- 1}

(3)

Where

σ_{R}^{2} = 1.23 C_{n}^{2} v^{7 / 6} d_{S R}^{11 / 6}

denoting the Rytov variance,

C_{n}^{2}

v

and

d_{S R}

represent the refractive index structure constant, wave number, and the link length, respectively.

C_{n}^{2}

usually takes values in the range

10^{- 17} - 10^{- 13}

for weak up to strong turbulence conditions.

2.2. DF transmission protocol

The communication between S and D is accomplished in two time slots

T_{1}

and

T_{2}

for the first and second hop, respectively. The relay harvests energy during

T_{1}

only as simultaneous harvesting and discharging of power increases the complexity at the node. The S employs sub-carrier intensity modulation (SIM) to convert RF signal vector

r

with electrical power

ρ

to an optical signal. A DC bias

A \in [A_{m i n}, A_{m a x}]

(where

A_{m i n}

and

A_{m a x}

are minimum and maximum values of DC bias, respectively) is added to the RF signal to ensure a non-negative optical signal. Let

P_{s}

represents the electrical power of S for transmitting the optical signal vector

s_{1}

, then we can write:

s_{1} = \sqrt{P_{S}} [δ r + A]

(4)

Where

δ

is electrical to optical conversion coefficient. To prevent clipping due to non-linearity of laser diode such that it operates in linear region,

δ

should satisfy the following constraint [26]

δ \leq m i n (\frac{A - A_{m i n}}{ρ}, \frac{A_{m a x} - A}{ρ})

(5)

The electrical signal at the output of the PD, can be expressed as

y_{F S O} = h_{F S O} s + n_{F S O}

(6)

Where

h_{F S O} = (P_{S}^{2} η^{2} / σ_{F S O}^{2}) I_{F S O}

is the channel coefficient of S-D link, where

η

is optical to electrical conversion coefficient. The noise

η_{F S O}

is due to circuit noise as well as high-intensity background illumination and is conventionally modeled as being zero mean additive white Gaussian noise.

σ_{F S O}^{2}

is the variance of additive white Gaussian noise with zero mean.

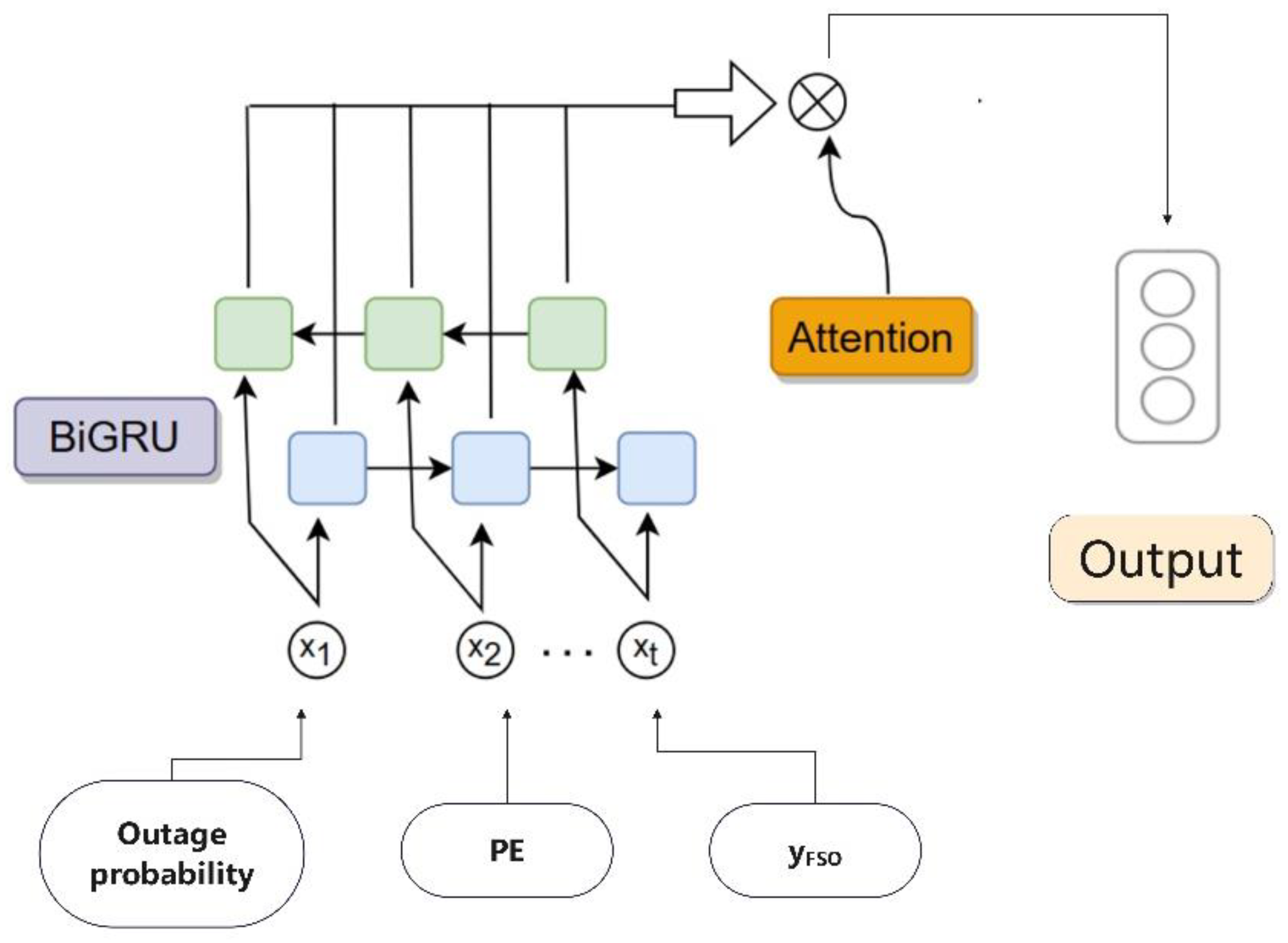
2.3. Mathematical modeling of the PE tracking system

The received electrical SNR with the slow fading channel can be expressed by the following equation:

S N R (h_{F S O}) = \frac{2 P_{t}^{2} h^{2} R^{2}}{σ_{n}^{2}}

(7)

Where

h_{F S O} = h_{p} h_{d}

, it comprises the impact of PE

h_{p}

which is an independent random variable, and

h_{d}

，the path loss component due to other atmospheric attenuation. The path loss component can be determined by the Beer-lambert's law as [33]

h_{d} = e x p (- α_{a t m o} z)

(8)

Where

z

is the propagation distance and

α_{a t m o}

is the attenuation coefficient due to atmospheric conditions. The received power collected by the detector in the presence of geometric spread and PE can be expressed by the following equation:

h_{p} \approx A_{0} e x p (\frac{- 2 r^{2}}{w_{z e q}^{2}})

(9)

Where

A_{0} = [e r f (v)]^{2}

is the power collected at radial displacement of

r = 0

and

w_{z e q}^{2} \hat{=} w_{z}^{2} ((\sqrt{π} e r f (v)) / (2 v e x p (- v^{2})

is the equivalent beamwidth.

v = \sqrt{π} a / \sqrt{2} w_{z}

is the beamwidth at distance

z

a

is the radius of the detection aperture. Performance of FSO communication under PE can be evaluated based on the outage probability.

The performance of the proposed FSO system is provided in terms of outage probability due to s. The outage 0ccurs when the channel capacity,

C (h)

is not sufficient to support the data rate

R_{0}

and it can be expressed by the following equation:

P_{o u t} (R_{0}) = P_{r} (C ({S N R}_{R x} (h)) < R_{0})

P_{o u t} (R_{0}) = P_{r} ({S N R}_{R x} (h) < C^{- 1} (R_{0}))

(10)

= P_{r} (\frac{2 P_{t}^{2} h^{2} R^{2}}{σ_{n}^{2}} < C^{- 1} (R_{0})) .

(11)

The outage probability can be expressed by the following equation:

P_{o u t} = P_{r} (h < h_{0})

(12)

Where

h_{0} = (((C^{- 1} (R_{0}) σ_{n}^{2}) / (2 P_{t}^{2} R^{2})))^{1 / 2}

. The outage probability is the cumulative density function of

h

evaluated

h_{0}

and it can be expressed by the following equation:

P_{o u t} = \int_{0}^{h_{0}} f_{h_{p}} (h_{p}) d h_{p} = k^{'} \int_{0}^{h_{0}} {(l n (\frac{A_{0}}{h_{p}}))}^{m - 1} (h_{p})^{ζ - 1} d h_{p} .

(13)

On substitution

x = l n (A_{0} / h_{p})

P_{o u t} = k^{'} A_{0}^{ζ} \int_{\infty}^{\ln (\frac{A_{0}}{h_{0}})} x^{m - 1} e x p (- x ζ) d x

(14)

Where

k^{'} = \frac{ζ^{m}}{Γ (m) A_{0}^{ζ^{m}}}

(15)

Using the approximation of

\int_{u}^{\infty} x^{v - 1} e x p (- μ x) d x = μ^{- v} Γ (v, u μ)

(16)

P_{o u t} = k^{'} A_{0}^{ζ} ζ^{- m} Γ (m, ζ l n (\frac{A_{0}}{h_{0}}))

(17)

2.4. Estimation of FSO PE with BIGRU-Attention model

When the distance of airborne laser communication is long, the requirements for the pointing of the airborne laser communication terminal are higher. Large s cause large deviations from the laser beam. The application of BiGRU-Attention neural network model in FSO system can effectively solve the problem of light PE caused by UAV jitter. The structure of BiGRU-Attention model is shown in Figure 3. The

y_{F S O}

in Equation (6), PE in Equation (9) and outage probability in Equation (17) are inputted into the neural network as parameters corresponding to

x_{1}

x_{2}

and

x_{3}

, respectively. After the BiGRU-Attention layer, the BiGRU network extracts the time-varying information of the

y_{F S O}

, PE and outage probability parameters. The attention mechanism will assign different attention weights to

y_{F S O}

, PE and outage probability parameters. Different weights can distinguish the importance level of different parameters and improve the accuracy of classification. Finally, the classification result is obtained, so that the problems in FSO can be solved effectively.

The BiGRU network is a bi-directional recurrent neural network that simultaneously reads the inputs from both ends of the

y_{F S O}

, PE, and outrage probability parameter time series This allows the BiGRU network to capture the temporal information of the above three parameter sequences of the inputs, which helps in extracting the feature information of the entire parameter. The attention mechanism network selects the most critical part of the

y_{F S O}

, PE, outrage probability parameter time series by learning the attention distribution. This distribution indicates that the network should enhance the critical parameter feature information while decoding. The BiGRU-Attention model proposed in this paper enters the network through the input and output signals

y_{F S O}

, PE and outage probability as parameters. Firstly, the BiGRU network learns the parameter time series information. Secondly, the importance of key parameter features is emphasized by the Attention network. Finally, the BiGRU-Attention network effectively solves the pointing error problem in the FSO system.

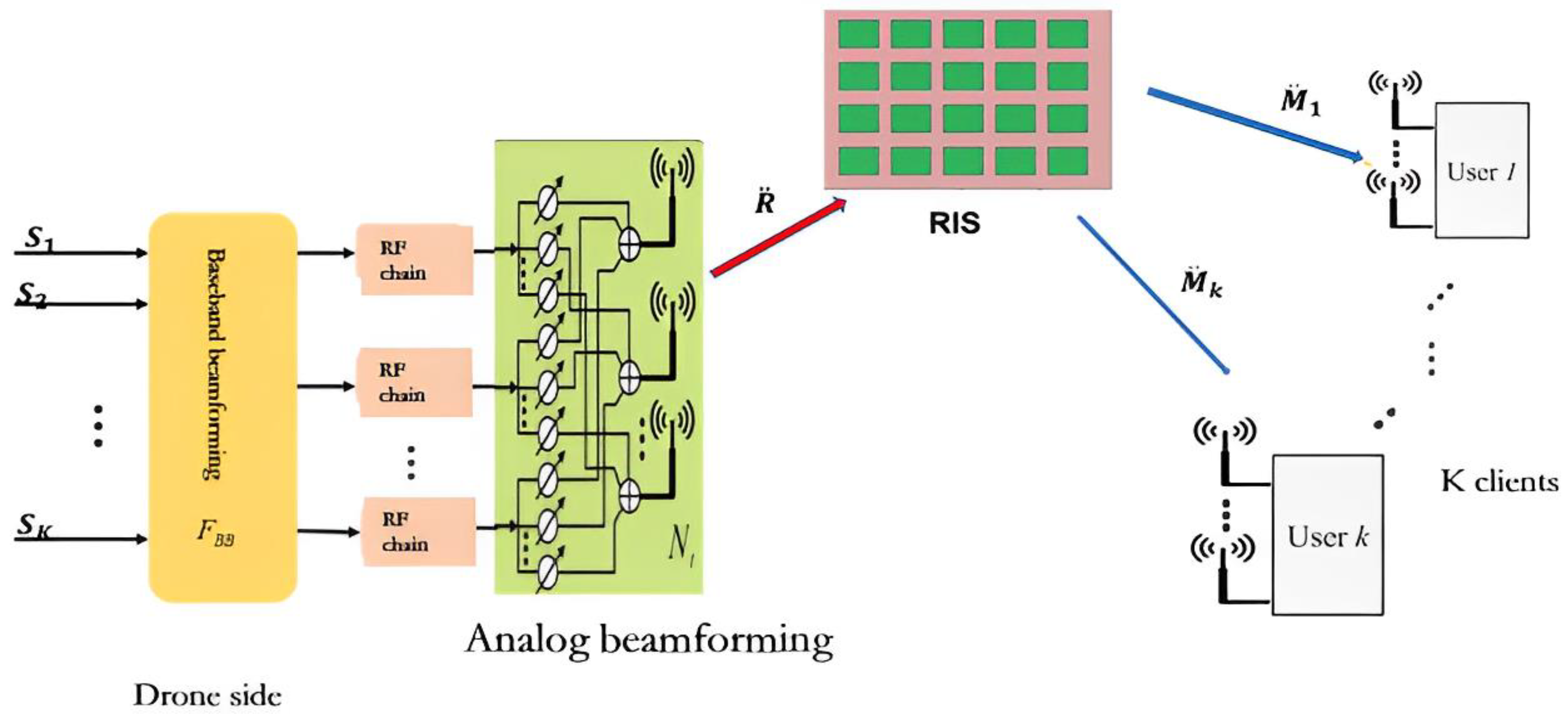
2.5. Multi-user UAV communication channel model with RIS

Firstly, the total number of users is K, and the number of data streams is

N_{s, K}

. The UAV communication transmitter is equipped with

N_{T}

two transmitting antennas with

N_{T}^{R F}

RF chains, where the

N_{s, K} \leq N_{T}^{R F} \leq N_{T}

. The RIS then consists of

T^{‘}

reflective elements, where the set of reflective elements

T^{‘}

\{1, \dots, T^{‘}\}

. In general, the RIS can communicate with the UAV using a specific link to exchange information about the channel status of the system, while allowing for better coordination of downlink transmissions to multipleuser sides. The reflection coefficient of the RIS is

ϱ_{t^{‘}} = e^{j θ_{t^{‘}}}, \forall t^{‘} ϵ T^{‘}

θ_{t^{‘}} ϵ [0,2 π ）

denotes the first

t^{‘}

phase shift of the first RIS reflection element. The RIS reflection matrix is expressed as

Φ = d i a g \{ϱ_{1^{‘}}, \dots, ϱ_{T^{‘}}\}

, and that

|ϱ_{t^{‘}}| = 1, \forall t^{‘} ϵ T^{‘}

. Similarly, the phase shifts of the RIS reflection elements have discrete values satisfying

θ_{t^{‘}} ϵ I ≜ \{\frac{2 π \overset{⃑}{i}}{2^{\overset{⃑}{I}}} | \overset{⃑}{i} = 0,1, \dots, 2^{\overset{⃑}{I}} - 1\}

, and

I

denotes the resolution of each reflecting element.

Let

s_{1} = \sqrt{P_{R}} y_{F S O}

denotes the signal forwarded by the node R. For this system, for K terrestrial users, the signal is first passed through a baseband beamforming matrix

F_{B B}

into a digital signal vector. Then the simulated beamforming matrix

F_{R F}

gets the UAV transmit signal as:

x = \sum_{k = 1}^{K} F_{R F} F_{B B, k} {s_{1}}_{k}

(18)

Where

F_{R F} ϵ C^{N_{T} \times N_{R F}^{T}}

F_{B B, k} = [F_{B B, 1}, \dots F_{B B, K}] ϵ C^{N_{R F}^{T} \times N_{s, k}}

N_{s, k} = \sum_{k = 1}^{K} N_{s, k}

{s_{1}}_{k} = {[s_{1}^{T}, \dots, s_{K}^{T}]}^{T} ϵ C^{N_{s} \times 1}

denotes

k

the concatenation of the parallel data streams of the individual users, and

s_{k} ϵ C^{N_{S, k} \times 1}

denotes the first

k

Gaussian encoded data stream vector for the first user satisfying

E [s_{k} s_{k}^{H}] = I_{N_{s, k}}

. The maximum signal transmission power

P

satisfies

{‖F_{R F} F_{B B}‖}_{F}^{2} \leq P

The UAV transmits a communication signal to the RIS and the RIS passes the communication signal to theuser. Theuser is equipped with

N_{R}

a receiving antenna with

N_{R}^{R F}

an RF chain, where

{N_{S, k} \leq N}_{R}^{R F} \leq N_{R}

. For signal accuracy, an analogue combiner matrix is designed

W_{R F, k}

and a digital combiner matrix

W_{B B, k} （ W_{R F, k} ϵ C^{N_{R} \times N_{R F}^{R}}

and

W_{B B, k} ϵ C^{N_{R F}^{R} \times N_{s, k}}

). Therefore, the received signal

y_{k} \in C^{Ν_{s, k} \times 1}

at the kth terrestrial user can be expressed by the following equation:

y_{k} (t) = W_{B B, k}^{H} W_{R F, k}^{H} （ {\ddot{M}}_{k} (t) {Φ \ddot{R} (t) ） F}_{R F} F_{B B, k} s_{k}

+ W_{B B, k}^{H} W_{R F, k}^{H} {({\ddot{M}}_{k} (t) Φ \ddot{R} (t)) \sum_{j \neq k, j ϵ K} W_{B B, k}^{H} W_{R F, k}^{H} {F_{R F} F}_{B B, k} s_{k} + W_{B B, k}^{H} W_{R F, k}^{H} n}_{k} (t)

(19)

Where

W_{B B, k}^{H} W_{R F, k}^{H} （ {\ddot{M}}_{k} (t) {Φ \ddot{R} (t) ） F}_{R F} F_{B B, k} s_{k}

represents the received signal excluding other interference,

W_{B B, k}^{H} W_{R F, k}^{H} {({\ddot{M}}_{k} (t) Φ \ddot{R} (t)) \sum_{j \neq k, j ϵ K} W_{B B, k}^{H} W_{R F, k}^{H} {F_{R F} F}_{B B, k} s_{k}}_{}

is the interference signal and

W_{B B, k}^{H} W_{R F, k}^{H} n_{k}

represents the total noise.

F_{B B, k} ϵ C^{N_{R F}^{T} \times N_{s, k}}

and

F_{R F} ϵ C^{N_{T} \times N_{R F}^{T}}

represent the baseband beamforming matrix and the analogue beamforming matrix, respectively.

n_{k} ~ C N (0, δ^{2} I)

is the

k

additive Gaussian white noise at theuser.

{\ddot{M}}_{k} (t)

is the millimeter wave large-scale channel matrix from the RIS to theuser, and

\ddot{R} (t)

is the millimeter-wave large-scale channel matrix from the UAV to the RIS.

{\ddot{M}}_{k} (t)

and

\ddot{R} (t)

are defined as follows, respectively:

{\ddot{M}}_{k} (t) = \sqrt{\frac{{T^{‘} N}_{R}}{Q_{{\ddot{M}}_{k}}}} \sum_{q = 1}^{Q_{{\ddot{M}}_{k}}} {\overset{̿}{κ}}_{k m, q} (t) {\overset{̿}{α}}_{R} ({φ_{k m, q}}^{R} (t)) {\overset{̿}{α}}_{P_{1}}^{H} ({φ_{k m, q}}^{T} (t), {η_{k m, q}}^{T} (t)) ϵ C^{N_{R} \times T^{‘}}

(20)

\ddot{R} (t) = \sqrt{\frac{{T^{‘} N}_{T}}{Q_{\ddot{R}}}} \sum_{q = 1}^{Q_{\ddot{R}}} {\overset{̿}{κ}}_{r, q} (t) {\overset{̿}{α}}_{P_{2}} ({φ_{r, q}}^{R} (t), {η_{r, q}}^{R} (t)) {\overset{̿}{α}}_{T}^{H} ({ν_{r, q}}^{T} (t)) ϵ C^{T^{‘} \times N_{T}}

(21)

The UAV and theuser are equipped with uniform linear arrays. RIS is equipped with a uniform planar array of size

{T^{‘}}_{y} \times {T^{‘}}_{z}

Q_{{\ddot{M}}_{k}}

and

Q_{\ddot{R}}

are the numbers of channel paths from the RIS to the

k

user and the number of channel paths between the UAV and the RIS.

{\overset{̿}{κ}}_{k m, q} (t)

denotes the path gain from the RIS to the

k

user , the path gain between

{\overset{̿}{κ}}_{r, q} (t)

denotes the fast fading path gain between the UAV and the RIS.

{\overset{̿}{α}}_{R} （ {φ_{k m, q}}^{R} (t))

{\overset{̿}{α}}_{T} （ {ν_{r, q}}^{T} (t)

{\overset{̿}{α}}_{P_{1}} （ {φ_{k m, q}}^{T} (t)

{η_{k m, q}}^{T} (t)

and

{\overset{̿}{α}}_{P_{2}} （ {φ_{r, q}}^{R} (t), {η_{r, q}}^{R} (t) ）

are the steering vectors corresponding to the uniform linear array and the uniform planar array, which can be defined, respectively:

{\overset{̿}{α}}_{R} ({φ_{k m, q}}^{R} (t)) = \frac{1}{\sqrt{N_{R}}} [1, \dots, e^{j (N_{R} - 1) d \sin ({φ_{k m, q}}^{R} (t)) \frac{2 π}{λ}}]

(22)

{\overset{̿}{α}}_{T} ({ν_{r, q}}^{T} (t)) = \frac{1}{\sqrt{N_{T}}} [1, \dots, e^{j (N_{T} - 1) d \sin ({φ_{k m, q}}^{T} (t)) \frac{2 π}{λ}}]

(23)

{\overset{̿}{α}}_{P_{1}} ({φ_{k m, q}}^{T} (t), {η_{k m, q}}^{T} (t)) = \frac{1}{\sqrt{M_{y} M_{z}}} [1, \dots, e^{j d \sin ((M_{y} - 1) \sin ({φ_{k m, q}}^{T} (t)) \sin ({η_{k m, q}}^{T} (t)) + (M_{z} - 1) \cos ({φ_{k m, q}}^{T} (t))) \frac{2 π}{λ}}]

(24)

{\overset{̿}{α}}_{P_{2}} ({φ_{r, q}}^{R} (t), {η_{r, q}}^{R} (t)) = \frac{1}{\sqrt{M_{y} M_{z}}} [1, \dots, e^{j d \sin ((M_{y} - 1) \sin ({φ_{r, q}}^{R} (t)) \sin ({η_{r, q}}^{R} (t)) + (M_{z} - 1) \cos ({η_{r, q}}^{R} (t))) \frac{2 π}{λ}}]

(25)

where

d = \frac{λ}{2}

is the antenna spacing and

λ

is the signal wavelength.

3. Power fading factor and Doppler shift estimation for fast fading channels based on Tensor-train Decomposition

3.1. Tensor-train Decomposition

Tensor-train is a higher-order tensor decomposition, which represents a higher-order tensor as a product of several lower-order tensor. Tensor-train decomposition is an effective method for compressed representation of high-dimensional data, which can reduce the number of dimensions and simplify the computation, while maintaining the main structure of the data. It is very useful in dealing with large-scale high-dimensional data. The main benefit of the Tensor-train method is the ability to obtain a low-dimensional representation of the high-dimensional signal by Tensor-train decomposition, which simplifies the dimensionality and improves the robustness. Thus Tensor-train helps to improve the accuracy of parameter estimation for power fading and Doppler shift.

X

is an nth order tensor of size

I_{1} \times \dots \times I_{N}

. Its Tensor-train representation uses N tensor cores

G_{1}, G_{2}, \dots, G_{N}

where the size of each tensor core is

R_{n - 1} \times I_{n} \times R_{n}

R_{0} = R_{N} = 1

X = \sum_{r_{1} = 1}^{R_{1}} \sum_{r_{2} = 2}^{R_{2}} \dots \sum_{r_{N - 1} = 1}^{R_{N - 1}} G_{1} (:, r_{1}) \circ G_{2} (r_{1}, :, r_{2}) \circ \dots \circ G_{N - 2} (r_{N - 2}, :, r_{N - 1}) \circ G_{N} (r_{N - 1}, :)

(26)

A Tensor-train

Y = G_{1} \circ G_{2} \cdot \dots \circ G_{N}

of rank

(R_{0}, R_{1}, \dots R_{N})

has rank

R_{1} R_{2} \dots R_{N - 1}

, and the equivalent Kruskal tensor is denoted as

Y = ⟦A^{(1)}, A^{(2)}, \dots A^{(N)}⟧

, where

A^{(n)}

is given by the following equation:

A^{(n)} = {[G_{n}]}_{(2)} (I_{R > n}^{T} ⨂ I_{R_{n - 1} R_{n}} ⨂ I_{R < n - 1}^{T})

(27)

Where

R_{< n} = R_{0} R_{1} \dots R_{n - 1}

，

R_{> n} = R_{n + 1} \dots R_{N - 1} R_{N}

3.2. Estimation of Power Fading Factor and Doppler Shift for Fast Fading Channels using Tensor-Train Decomposition

The received signal at the single-user of a millimeter-wave MIMO in UAV can be expressed as the following equation:

y_{k} (t) = W_{B B, k}^{H} W_{R F, k}^{H} \sqrt{\frac{{T^{‘} N}_{R}}{Q_{{\ddot{M}}_{k}}}} \sum_{q = 1}^{Q_{{\ddot{M}}_{k}}} {\overset{̿}{κ}}_{k m, q} (t) {\overset{̿}{α}}_{R} ({φ_{k m, q}}^{R} (t)) {\overset{̿}{α}}_{P_{1}}^{H} ({φ_{k m, q}}^{T} (t), {η_{k m, q}}^{T} (t)) F_{R F} F_{B B, k} s_{k}

+ {(W_{R F} W_{B B})}^{H} \overset{\leftarrow}{N} (t)

(28)

Set the conversion again as follows:

\sqrt{\frac{N_{T} N_{R}}{Q}}

is a constant, namely

\sqrt{\frac{N_{T} N_{R}}{Q}} = 1

{\tilde{α}}_{R} ({φ_{k m, q}}^{R} (t)) = W_{B B, k}^{H} W_{R F, k}^{H} {\overset{̿}{α}}_{R} ({φ_{k m, q}}^{R} (t)) ϵ C^{N_{R F}^{R} \times 1}

(29)

{\tilde{α}}_{P} ({η_{k m, q}}^{T} (t)) = {\overset{̿}{α}}_{P_{1}}^{H} ({φ_{k m, q}}^{T} (t), {η_{k m, q}}^{T} (t)) {\ddot{Φ R} (t) F}_{R F} F_{B B, k} s_{k} ϵ C^{N_{R F}^{T} \times 1}

(30)

Where

{\tilde{α}}_{R} ({φ_{k m, q}}^{R} (t))

and

{\tilde{α}}_{P} ({η_{k m, q}}^{T} (t))

represent the receive vector and the send vector respectively. Equation (28) is expressed as the following equation:

Y (t) = \sum_{q = 1}^{Q_{{\ddot{M}}_{k}}} {\overset{̿}{κ}}_{k m, q} (t) {\tilde{α}}_{R} ({φ_{k m, q}}^{R} (t)) {\tilde{α}}_{P} ({η_{k m, q}}^{T} (t)) + {(W_{R F} W_{B B})}^{H} \overset{\leftarrow}{N} (t)

(31)

The received signal tensor for T consecutive time slots as a rank one vector accumulation pattern is expressed as the following equation:

Y = \sum_{q = 1}^{Q} T {\tilde{α}}_{R} ({β_{q}}^{R} (t)) \cdot {\tilde{α}}_{T} ({γ_{q}}^{T} (t)) \cdot {\tilde{κ}}_{q} (t) + N

(32)

Where

T

is the weight of the multiplication of the rank one factors,

Y ϵ C^{N_{R F}^{R} \times N_{R F}^{T} \times T}

is the received signal tensor,

{\tilde{κ}}_{q} (t) = {[κ_{q} (1), \dots, κ_{q} (T)]}^{T} ϵ C^{T \times 1}

is the vector containing the fast fading coefficients from T consecutive time slots, and

N ϵ C^{N_{R F}^{R} \times N_{R F}^{T} \times T}

is the noise tensor. Meanwhile, equations (32) can continue to be expressed as a Tensor-train decomposition of the

K

r u s k a l

form:

Y = T; U_{1}, U_{2}, U_{3} + N

(33)

U_{1} = [{\tilde{α}}_{R} ({β_{1}}^{R} (t)), \dots, {\tilde{α}}_{R} ({β_{Q}}^{R} (t))] \in C^{N_{R F}^{R} \times Q}

(34)

U_{2} = [{\tilde{κ}}_{1} (t), \dots {\tilde{κ}}_{Q} (t)] \in C^{N_{R F}^{T} \times Q}

(35)

U_{3} = [{\tilde{α}}_{T} ({γ_{1}}^{T} (t)), \dots {\tilde{α}}_{T} ({γ_{Q}}^{T} (t))] \in C^{T \times Q}

(36)

The FCTPM based on tensor decomposition is utilized the PM (Power Method) for the auxiliary unfolding matrix decomposition. FCTPM is based on a combination of Tensor-train decomposition and power. The FCTPM approximates the most dominant rank-negative-one tensor of the input tensor by the Tensor-train decomposition, and each unfolding matrix is also decomposed using a rank-negative-one matrix decomposition. This property allows each unfolding matrix to ignore the concatenation between other unfolding matrices. Therefore, a cyclic update method is proposed to consider the connectivity between the unfolding matrices. After all the left singular vectors have been computed, the order of the update steps for the right singular vectors needs to be changed. The FCTPM utilizes the PM for the auxiliary unfolding matrix decomposition. Therefore, the PM ensures the convergence of the decomposition factors. The cyclic updating method enhances the connectivity between the decomposition factors.

The FCTPM then consists of two main components, namely the rank-negative-one tensor approximated by the Tensor-train decomposition of the auxiliary expansion matrix, and the PM of determining the left and right singular vectors obtained from the randomly initialized vectors. The core tensor in the Tensor-train decomposition

G^{(n)}

calculation is based on the N-dimensional input tensor

Y \in R^{I_{1} \times \dots I_{N}}

the low-rank approximation of the auxiliary matrix of

R_{N}

denotes the received signal tensor

Y

the Tensor-train rank in Tensor-train decomposition. In FCTPM, a rank-negative-one approximation is made to the high-dimensional input tensor using the Tensor-train decomposition. The received signal at theuser is compressed into a low-order core tensor

G^{(1)}

, and

G^{(2)}

, and

G^{(3)}

of the concatenation. The received signal tensor

Y

is written in the following form:

Y = \sum_{r_{1} = 1}^{R_{1}} \dots \sum_{r_{2} = 1}^{R_{2}} G_{r_{0}, ∶, r_{1}}^{(1)} \circ G_{r_{1}, ∶, r_{2}}^{(2)} \circ G_{r_{2}, ∶, r_{3}}^{(3)} + N

= G_{1, ∶, 1}^{(1)} \circ G_{1, ∶, 1}^{(2)} \circ G_{1, ∶, 1}^{(3)} + N

= g^{(1)} \circ g^{(2)} \circ g^{(3)} + N

(37)

Where

G^{(n)}

denotes the core tensor of size

R_{n - 1} \times I_{n} \times R_{n}

of the core tensor of the rank-negative-one Tensor-train with all elements of the Tensor-train rank being 1, then

G^{(n)}

size become

1 \times I_{n} \times 1

the core tensor of the rank-negative-one Tensor-train. Furthermore, if the core tensor

G^{(n)}

of dimensionality is compressed, the core tensor can be regarded as factored vector data

g^{(n)} ϵ R^{I_{n}}

that

g^{(n)}

is the rank-negative-one Tensor-train core tensor

G_{1, ∶, 1}^{(n)}

of the first-order factor vector.

To solve for the factor vector

g^{(n)}

, equation (32) is expressed as the following equation (38):

\min_{g^{(1)}, g^{(2)}, g^{(3)}} {‖Y - d g^{(1)} \circ g^{(2)} \circ g^{(3)}‖}^{2}

s_{.} t_{.} d > 0, {g^{(n)}}^{T} g^{(n)} = 1 (n = 1,2, 3)

(38)

Where

d

is the principal singular value of the approximate rank-negative-one tensor. According to the FCTPM, the higher order tensor is decomposed in the Tensor-train decomposition by a low-rank decomposition of the auxiliary expansion matrix of the input tensor.

The solution to the factor vector

g^{(n)}

can be solved in a uniform manner by expressing:

\min_{g^{(N - 1)}, g^{(N)}} {‖Y_{〈N - 1〉} - d^{(N - 1)} g^{(N - 1)} {g^{(N)}}^{T}‖}_{F}^{2}

s_{.} t_{.} d > 0, {g^{(N - 1)}}^{T} g^{(N - 1)} = 1, {g^{(N)}}^{T} g^{(N)} = 1

(39)

Where

Y_{〈N - 1〉} = r e s h a p e (v^{(N - 2)}, [I_{N - 1}, I_{N}]) ， d^{(N - 1)}

is the principal singular value after reshaping the matrix. The principal singular value of the rank-negative-one tensor can be calculated as

d = \prod_{i = 1}^{N - 1} d^{(i)}

that is the corresponding factor vector.

g^{(N - 1)}

and

g^{(N)}

is the corresponding factor vector, from which the factor vector can then be composed to derive the corresponding factor matrix. The solution process is repeated until the right singular vector in the decomposition process

v^{(N - 1)}

is the last factor vector

g^{(N)}

. Therefore, the first factor vector

g^{(1)}

can be expressed as follows:

\min_{g^{(1)}, v} {‖Y_{〈1〉} - d^{(1)} g^{(1)} {v^{(1)}}^{T}‖}_{F}^{2}

s_{.} t_{.} d^{(1)} > 0, {g^{(1)}}^{T} g^{(1)} = 1, {v^{(1)}}^{T} v^{(1)} = 1

(40)

Where

Y_{〈1〉}

is the modulo 1 expansion matrix,

d^{(1)}

is the

Y_{〈1〉}

the principal singular values of

g^{(1)}

represents the first factor vector of the rank-negative-one Tensor-train decomposition, and

v^{(1)}

is the right singular vector of

Y_{〈1〉}

. After obtaining

g^{(1)}

v^{(1)}

is expressed as the modulo 2 expansion matrix form of the received signal tensor

Y

. The second factor vector

g^{(2)}

is calculated as:

Y_{〈2〉} = r e s h a p e (v^{(1)}, [I_{2}, \prod_{j = 3}^{N} I_{j}])

(41)

Y_{〈2〉}

the rank-negative-one matrix decomposition is expressed as the following equation:

\min_{g^{(2)}, v^{(2)}} {‖Y_{〈2〉} - d^{(2)} g^{(2)} {v^{(2)}}^{T}‖}_{F}^{2}

s_{.} t_{.} d^{(2)} > 0, {g^{(2)}}^{T} g^{(2)} = 1, {v^{(2)}}^{T} v^{(2)} = 1

(42)

Where

d^{(2)}

is the principal singular value of the tensor

Y

modulo 2 matrix

Y_{〈2〉}

, and

g^{(2)}

represents the second factor vector of the rank-negative-one Tensor-train decomposition. Similarly, the third factor vector can be obtained. This computation can be performed repeatedly until the right singularity vector of the decomposition process is the last factor vector. To ensure convergence of the factorization, a matrix factorization method PM is incorporated. In solving the first factor matrix, the PM method initializes the factor vector

g^{(1)}

to a random unit vector satisfying

{‖g^{(1)}‖}_{2} = 1

. After that, the vector matrix operation is performed iteratively until the factor vectors satisfy the pre-set specific termination conditions, as shown below:

v^{(1)} = \frac{Y_{〈1〉}^{T} g^{(1)}}{{‖Y_{〈1〉}^{T} g^{(1)}‖}_{2}} ϵ R^{\prod_{j = 2}^{N} I_{j}}

(43)

g^{(1)} = \frac{Y_{〈1〉} v^{(1)}}{{‖Y_{〈1〉} v^{(1)}‖}_{2}} ϵ R^{I_{1}}

(44)

Where

g^{(1)}

and

v^{(1)}

are

Y_{〈1〉}

the left and right singular vectors, respectively. The main singular values

d^{(1)}

associated with it can be expressed as

d^{(1)} = {g^{(1)}}^{T} Y_{〈1〉} v^{(1)}

. The left singular vector calculation follows immediately after the right singular vector calculation. Assuming the existence of an orthogonal basis

\bar{U} ϵ R^{I_{1} \times R}

and

\bar{V} ϵ R^{I_{2} \dots I_{N} \times R}

, the unfolding matrix

Y_{〈1〉}

satisfies the following equation:

Y_{〈1〉} = \sum_{j = 1}^{R} d_{j} {\bar{U}}_{:, j} {\bar{V}}_{:, j}^{T}

(45)

Where

d_{j}

Y_{〈1〉}

the singular values in corresponding to the singular vectors. After several iterations, the

v^{(1)}

and

g^{(1)}

can be defined as the following equation, respectively:

v^{(1)} = δ_{v^{(1)}} \sum_{j = 1}^{R} d_{j}^{2 k + 1} {\bar{V}}_{:, j} {\bar{U}}_{:, j}^{T} g^{(1)}

(46)

g^{(1)} = δ_{g^{(1)}} \sum_{j = 1}^{R} d_{j}^{2 k} {\bar{U}}_{:, j} {\bar{U}}_{:, j}^{T} g^{(1)}

(47)

Where

δ_{g^{(1)}}

and

δ_{v^{(1)}}

are the corresponding normalisation factors. Thus, after several iterations of PM,

v^{(1)}

and

g^{(1)}

satisfy

\frac{{‖v^{(1)}‖}_{2}^{2}}{{‖g^{(1)}‖}_{2}^{2}} = 1

by the convergence property, the

\frac{δ_{v^{(1)}}}{δ_{g^{(1)}}}

converges to the maximum singular value

d_{1}

, at

Y_{〈1〉}^{T} g^{(1)} = (\frac{δ_{v^{(1)}}}{δ_{g^{(1)}}}) v^{(1)}

{‖Y_{〈1〉}^{T} g^{(1)} - d_{1} v^{(1)}‖}_{2} = 0

From the previous rank-negative-one Tensor-train decomposition, the nth factor vector

g^{(n)}

depends on the previously computed right singular vector

v^{(n - 1)}

, while

v^{(n - 1)}

is obtained from n-1 factor vector

g^{(n - 1)}

computed. Because the matrix decomposition of each factor vector is performed independently. These properties can lead to problems with local optimization, resulting in a loss of critical performance in FCTPM. To enhance the connectivity between the decomposition factors, a circular update method is proposed, which changes the order in which the left singular vectors are computed is sufficient. According to the decomposition method of Tensor-train of rank-negative-one and the nature of PM,

v^{(n)}

can be obtained from

g^{(n + 1)}

and

v^{(n + 1)}

which are reshaped to form

v^{(n)}

. The relationship

g^{(n)}

is updated by the following way:

v^{(n)} \approx {\hat{v}}^{(n)} = r e s h a p e (d^{(n + 1)} g^{(n + 1)} {v^{(n + 1)}}^{T}, [I_{n + 1} \dots I_{N}])

g^{(n)} = \frac{Y_{〈n〉} {\hat{v}}^{(n)}}{{‖Y_{〈n〉} {\hat{v}}^{(n)}‖}_{2}}

(48)

The updated factor vector

g^{(2)}

can be derived as

g^{(2)} = \frac{Y_{〈2〉} {\hat{v}}^{(2)}}{{‖Y_{〈2〉} {\hat{v}}^{(2)}‖}_{2}}

Channel parameter is estimated for UAV with millimeter wave massive MIMO based on the FCTPM. The number of factor matrix time slots is associated with the structure of the transmission frame, using a downlink transmission frame structure. It consists of an AOA/AOD estimation phase (

T_{1}

time slot), a fast-fading factor estimation phase (

T_{2}

time slot) and the data transmission phase (

T_{3}

time slot). Using equation (32) and equation (33), the received signal at the terrestrial user is represented as the following equation:

Y^{T_{2}} = T; U_{1}, U_{2}, U_{3} + N^{T_{2}}

(49)

Matrix

\{U_{1}, U_{2}, U_{3}\}

is the received signal at the user.

Y

is corresponding to the matrix of three factors.

U_{2}

is the corresponding fast fading factor matrix. From the Tensor-train decomposition's

K r u s k a l

representation,

U_{n}

and

G_{n}

the correspondence can be expressed by the following equation:

U_{n} = {[G_{n}]}_{(2)} (1_{R_{> (n)}}^{T} ⨂ Ι_{R_{n - 1}} R_{n} ⨂ 1_{R_{< n - 1}}^{T}), n = 1,2, 3

= {[g^{(n)}]}_{(2)} (1_{R_{> (n)}}^{T} ⨂ Ι_{R_{n - 1}} R_{n} ⨂ 1_{R_{< n - 1}}^{T}), n = 1,2, 3

(50)

The factor matrix

U_{2} = {[g^{(n)}]}_{(2)} (1_{R_{> (2)}}^{T} ⨂ Ι_{R_{1}} R_{n} ⨂ 1_{R_{1}}^{T})

. From equation (35), we can find that the factor matrix

U_{2}

has the fast fading channel power fading factor associated with the Doppler shift in its elements. We can derive the fast fading channel power factor. We can obtain

U_{2} = [{\tilde{κ}}_{1}, \dots {\tilde{κ}}_{Q}] ϵ C^{T_{2} \times Q}

{\tilde{κ}}_{Q} = {[{\tilde{κ}}_{1} (1), \dots {\tilde{κ}}_{Q} (T_{2})]}^{T} ϵ C^{T_{2} \times 1}

. According to the correlation scheme, the Doppler shift on the

q

path is solved as follows:

{\hat{f}}_{q} = \underset{f_{q}}{argmax} \frac{|[{\hat{U}}_{2}]_{:, q}^{H} κ (f_{q})|}{{‖[{\hat{U}}_{2}]_{:, q}‖}_{2} {‖κ (f_{q})‖}_{2}} . 1 \leq q \leq Q . {\hat{f}}_{q} \in [0, f_{m a x}]

(51)

f_{m a x} = \frac{f_{c} v^{'}}{c} κ_{q} (t) = b_{q} e^{j 2 π f_{q} t}

(52)

Where

f_{m a x}

is the maximum Doppler shift,

f_{c}

is the carrier frequency,

v^{'}

is the speed of the drone, and

c

is the speed of light. The path gain is then estimated from the estimated Doppler shift, i.e:

{\hat{b}}_{q} = [κ ({\hat{f}}_{q})]^{↑} [{\hat{U}}_{2}]_{:, q}

(53)

Finally, all parameters of the time-varying channel of the millimeter-wave MIMO in UAV are estimated and the channel matrix can be recovered from (51).

4. Hybrid beamforming and RIS phase shift matrix design

4.1. Hybrid beamforming and RIS phase shift matrix design based on Tensor-train decomposition

Define

\sqrt{\frac{{T^{‘} N}_{R}}{Q_{{\ddot{M}}_{k}}}}

and

\sqrt{\frac{{T^{‘} N}_{T}}{Q_{\ddot{R}}}}

as constants and set it to 1. The millimeter-wave massive channel from the RIS to the user side

{\ddot{M}}_{k}

and the millimeter wave massive channel from the UAV side to the RIS

\ddot{R}

can be written with Tensor-train decomposition form as follows, respectively :

{\ddot{M}}_{k} = \sum_{q = 1}^{Q_{{\ddot{M}}_{k}}} T {\overset{̿}{κ}}_{k m, q} \cdot {\overset{̿}{α}}_{R} ({φ_{k m, q}}^{R} (t)) \cdot {\overset{̿}{α}}_{P_{1}}^{H} ({φ_{k m, q}}^{T} (t), {η_{k m, q}}^{T} (t))

= T; {\overset{̿}{A}}_{R, k m}, {\overset{̿}{Λ}}_{k m, q}, {\overset{̿}{A}}_{P_{1}, k m}^{H}

= {\overset{̿}{g}}_{R, k m}^{(1)} \circ {\overset{̿}{g}}_{k m, q}^{(2)} \circ {\overset{̿}{g}}_{P_{1}, k m}^{H (3)}

(54)

\ddot{R} = \sum_{q = 1}^{Q_{\ddot{R}}} {T \overset{̿}{κ}}_{r, q} (t) \cdot {\overset{̿}{α}}_{P_{2}} ({φ_{r, q}}^{R} (t), {η_{r, q}}^{R} (t)) \cdot {\overset{̿}{α}}_{T}^{H} ({ν_{r, q}}^{T} (t))

= T; {\overset{̿}{A}}_{P_{2}, r}, {\overset{̿}{Λ}}_{r, q}, {\overset{̿}{A}}_{T, r}^{H}

= {\overset{̿}{g}}_{P_{2}, r}^{(1)} \circ {\overset{̿}{g}}_{r, q}^{(2)} \circ {\overset{̿}{g}}_{T, r}^{H (3)}

(55)

Where

{\overset{̿}{κ}}_{k m, q} (t) = {[κ_{k m, q} (1), \dots, κ_{k m, q} (T)]}^{T} ϵ C^{T \times 1}

{\overset{̿}{κ}}_{r, q} (t) = {[κ_{r, q} (1), \dots, κ_{r, q} (T)]}^{T} ϵ C^{T \times 1}

. The three factor matrices obtained by tensor decomposition of

{\ddot{M}}_{k}

are the receive antenna array response matrix

{\overset{̿}{A}}_{R, k m}

, the path gain factor matrix

Λ_{k m, q}

, the RIS reflector antenna array response matrix

{\overset{̿}{A}}_{P_{1}, k m}^{H}

. The three factor matrices are defined as follows, respectively :

{\overset{̿}{A}}_{R, k m} = {\overset{̿}{g}}_{R, k m}^{(1)} (1_{R_{> (2)}}^{T} ⨂ Ι_{R_{1}} R_{R, k m} ⨂ 1_{R_{1}}^{T})

= [{\overset{̿}{α}}_{R} （ {φ_{k m, 1}}^{R} (t) ）, \dots, {\overset{̿}{α}}_{R} （ {φ_{k m, Q_{{\ddot{M}}_{k}}}}^{R} (t) ）] ϵ C^{N_{R} \times Q_{{\ddot{M}}_{k}}}

(56)

Λ_{k m, q} = {\overset{̿}{g}}_{k m, q}^{(2)} (1_{R_{> (2)}}^{T} ⨂ Ι_{R_{1}} R_{k m, q} ⨂ 1_{R_{1}}^{T})

= [{\overset{̿}{κ}}_{k m, 1} (t), \dots, {\overset{̿}{κ}}_{k m, Q_{{\ddot{M}}_{k}}} (t)] ϵ C^{T \times Q_{{\ddot{M}}_{k}}}

(57)

{\overset{̿}{A}}_{P_{1}, k m}^{H} = {\overset{̿}{g}}_{P_{1}, k m}^{H (3)} (1_{R_{> (2)}}^{T} ⨂ Ι_{R_{1}} R_{k m, q} ⨂ 1_{R_{1}}^{T})

= [{\overset{̿}{α}}_{P_{1}} ({φ_{k m, 1}}^{T} (t), {η_{k m, 1}}^{T} (t)), \dots, {\overset{̿}{α}}_{P_{1}} ({φ_{k m, Q_{{\ddot{M}}_{k}}}}^{T} (t), {η_{k m, Q_{{\ddot{M}}_{k}}}}^{T} (t))] ϵ C^{T^{‘} \times Q_{{\ddot{M}}_{k}}}

(58)

Where

{\ddot{R}}_{k}

is also obtained by tensor decomposition to obtain the RIS receive antenna array response factor matrix

{\overset{̿}{A}}_{P, r}

, the fast-fading factor matrix

{\overset{̿}{Λ}}_{r, q}

, and the UAV end transmit antenna factor matrix

{\overset{̿}{A}}_{T, r}^{H}

. The three factor matrices are defined respectively as follows:

{\overset{̿}{A}}_{P, r} = {\overset{̿}{g}}_{P, r}^{(1)} (1_{R_{> (2)}}^{T} ⨂ Ι_{R_{1}} R_{P, r} ⨂ 1_{R_{1}}^{T})

= [{\overset{̿}{α}}_{P} ({φ_{r, 1}}^{R} (t), {η_{r, 1}}^{R} (t)), \dots, {\overset{̿}{α}}_{P} ({φ_{r, Q_{\ddot{R}}}}^{R} (t), {η_{r, Q_{\ddot{R}}}}^{R} (t))] ϵ C^{T^{‘} \times Q_{\ddot{R}}}

(59)

{\overset{̿}{Λ}}_{r, q} = {\overset{̿}{g}}_{r, q}^{(2)} (1_{R_{> (2)}}^{T} ⨂ Ι_{R_{1}} R_{r, q} ⨂ 1_{R_{1}}^{T})

= [{\overset{̿}{κ}}_{k m, 1} (t), \dots, {\overset{̿}{κ}}_{k m, Q_{\ddot{R}}} (t)] ϵ C^{T \times Q_{\ddot{R}}}

(60)

{\overset{̿}{A}}_{T, r}^{H} = {\overset{̿}{g}}_{T, r}^{H (3)} (1_{R_{> (2)}}^{T} ⨂ Ι_{R_{1}} R_{T, r} ⨂ 1_{R_{1}}^{T})

= [{\overset{̿}{α}}_{P} ({ν_{r, 1}}^{T} (t)), \dots, {\overset{̿}{α}}_{P} ({ν_{r, Q_{\ddot{R}}}}^{T} (t))] ϵ C^{N_{T} \times Q_{\ddot{R}}}

(61)

According to the existing tensor form

{\ddot{M}}_{k}

and tensor form

\ddot{R}

, the received signal

Y_{k}

The tensor form of k is expressed as:

Y_{k} = W_{B B, k}^{H} W_{R F, k}^{H} \cdot {\ddot{M}}_{k} Φ \ddot{R} \cdot F_{R F}^{T} F_{B B, k}^{T} s_{k} + \sum_{j \neq k}^{K} W_{B B, k}^{H} W_{R F, k}^{H} \cdot {\ddot{M}}_{k} Φ \ddot{R} {\cdot W}_{B B, k}^{H} W_{R F, k}^{H} \cdot F_{R F}^{T} F_{B B, j}^{T} s_{j} + N_{k}

= T; W_{B B, k}^{H} W_{R F, k}^{H}, {\overset{̿}{A}}_{R, k m}, {\overset{̿}{Λ}}_{k m, q}, {\overset{̿}{A}}_{P, k m}^{H}, Φ, T; {\overset{̿}{A}}_{P, r}, {\overset{̿}{Λ}}_{r, q}, {\overset{̿}{A}}_{T, r}^{H}, F_{R F}^{T} F_{B B, k}^{T} s_{k} +

\sum_{j \neq k}^{K} T; W_{B B, k}^{H} W_{R F, k}^{H}, {\overset{̿}{A}}_{R, k m}, {\overset{̿}{Λ}}_{k m, q}, {\overset{̿}{A}}_{P, k m}^{H}, Φ, T; {\overset{̿}{A}}_{P, r}, {\overset{̿}{Λ}}_{r, q}, {\overset{̿}{A}}_{T, r}^{H}, F_{R F}^{T} F_{B B, j}^{T} s_{j} + N_{k}

(62)

Where

Y_{k} \in C^{N_{s} \times k N_{s, k} \times T}

is the received signal tensor of the kth terrestrial user, and

N_{k} \in C^{N_{s} \times k N_{s, k} \times T}

is the noise tensor of the kth terrestrial user.

By utilizing RIS assisted millimeter wave massive MIMO of UAV communication, the spectral efficiency

R_{k}

of hybrid beamforming can be expressed as:

R_{k} = \sum_{k = 1}^{K} \log_{2} |I_{k N_{s}} + \frac{p^{‘}}{k N_{s}} R_{k n}^{- 1} W_{B B, k}^{H} W_{R F, k}^{H} {\ddot{M}}_{k} Φ {{\ddot{R}}_{k} F}_{R F} F_{B B, k} {(W_{B B, k}^{H} W_{R F, k}^{H} {\ddot{M}}_{k} Φ {\ddot{R}}_{k} F_{R F} F_{B B, k})}^{H}|

(63)

Where

R_{k n} = σ_{n}^{2} W_{B B, k}^{H} W_{R F, k}^{H} W_{R F, k} W_{B B, k}

denotes the

k

noise covariance matrix at the received user, and

p^{‘}

denotes the transmit power. So the maximum spectral efficiency problem can be expressed as the following equation:

\max_{F_{RF}, F_{BB, k}, W_{RF, k} {, W}_{BB, k}, Φ} R_{k}

s_{.} {t_{.} ‖F_{R F} F_{B B, k}‖}_{F}^{2} = {k N}_{s, k}

θ_{t^{‘}} ϵ I, \forall t^{‘}

(64)

This is a non-convex NP-hard problem. It decomposes the original optimization problem into two independent optimization subproblems, namely

Φ

the optimization problem and (

F_{R F}, F_{B B, k}, W_{R F, k} W_{B B, k} ）

of the optimization problem. Setting up the hybrid channel

H_{k c} = {\ddot{M}}_{k} Φ {\ddot{R}}_{k}

. Next, it is necessary to calibrate the RIS phase shift matrix

Φ

Perform optimization solutions.

4.2. RIS phase shift matrix design

To simplify the problem, we consider the use of a fully digital beamforming matrix

F_{k}^{f} ϵ C^{N_{T} \times N_{s}}

and a fully digital combination matrix

W_{k}^{f} ϵ C^{N_{R} \times N_{s}}

to replace the hybrid beamforming matrix

F_{R F}

, the

F_{B B, k}

and the hybrid combiner matrix

W_{R F, k} W_{B B, k}

. The previous optimization problem can be expressed as follows:

\max_{F, W, Φ} \log_{2} d e t (I_{k N_{s}} + \frac{ρ^{‘}}{k N_{s} σ_{n}^{2}} {W_{k}^{f}}^{- 1} {\ddot{M}}_{k}^{H} Φ \times {\ddot{R}}_{k} F_{k}^{f} {F_{k}^{f}}^{H} {\ddot{R}}_{k}^{H} Φ^{H} {\ddot{M}}_{k} W_{k}^{f})

s_{.} {t_{.} ‖F_{k}^{f}‖}_{F}^{2} = {k N}_{s, k}

θ_{t^{‘}} ϵ I, \forall t^{‘}

(65)

RIS reflection matrix

Φ

is set as fixed. The mixed channel matrix is constructed as

H_{k c} = {\ddot{M}}_{k} Φ {\ddot{R}}_{k}

. By decomposing the effective mixed channel matrix

H_{k c}

performing a singular value decomposition, the optimal

F_{k}^{f}

and

W_{k}^{f}

can be obtained.

H_{k c} = {\overset{⏞}{Q}}_{k c} {\tilde{Σ}}_{k c} {\overset{̿}{Γ}}_{k c}^{'}^{H}

. Where

{\overset{⏞}{Q}}_{k c} ϵ C^{N_{R} \times N_{R}}

{\overset{̿}{Γ}}_{k c}^{'} ϵ C^{N_{T} \times N_{T}}

, and

{\tilde{Σ}}_{k c}

is a rectangular diagonal matrix composed of singular values in descending order. Due to the sparsity of the UAV channel for millimeter wave massive MIMO, the mixed channel matrix

H_{k c}

usually has a low rank.

H_{k c}

approximation can be obtained as

H_{k c} \approx {\overset{⏞}{Q}}_{k c 1} {\tilde{Σ}}_{k c 1} {\overset{̿}{Γ}}_{k c 1}^{'}^{H}

. It simultaneously satisfies

{\overset{⏞}{Q}}_{k c 1} ≜ {\overset{⏞}{Q}}_{k c} (:, 1 : N_{s, k})

{\tilde{Σ}}_{k c 1} ≜ \tilde{Σ} (1 : N_{s, k}, 1 : N_{s, k})

and

{\overset{̿}{Γ}}_{k c 1}^{'} ≜ {\overset{̿}{Γ}}_{k c}^{'} (:, 1 : N_{s, k})

. Afterwards, with a fixed RIS reflection matrix, the channel matrix

H_{k c}

of the optimal unconstrained beamforming matrix is

{F_{k}^{f}}_{o p t} = {\overset{̿}{Γ}}_{k c 1}^{'}

{W_{k}^{f}}_{o p t}

{\overset{⏞}{Q}}_{k c 1}

. Substituting this into equation (65), a simplified optimization problem can be obtained as follows:

\max_{Φ} \log_{2} d e t (I_{k N_{s}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {\tilde{Σ}}_{k c 1}^{2})

s_{.} t_{.} θ_{t^{‘}} ϵ I, \forall t^{‘}

(66)

This optimization problem remains intractable due to the determinant operation of the objective function and the non-convex constraint of the RIS reflection. To simplify the problem, an upper bound on the above objective is first derived to eliminate the determinant function as follows:

\log_{2} d e t (I_{k N_{s}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {\tilde{Σ}}_{k c 1}^{2}) \begin{matrix} (a) \\ \leq \end{matrix} N_{s, k} \log_{2} (1 + \frac{ρ^{‘}}{k {N_{s, k}}^{2} σ_{n}^{2}} T r ({\tilde{Σ}}_{k c 1}^{2}))

\begin{matrix} (b) \\ \leq \end{matrix} N_{s, k} \log_{2} (1 + \frac{ρ^{‘}}{k {N_{s, k}}^{2} σ_{n}^{2}} T r (H_{k c} H_{k c}^{H}))

(67)

Where

(a)

according to Jensen's inequality holds. When

(b)

holds,

T r (H_{k c} H_{k c}^{H}) = \sum_{i = 1}^{\tilde{Q}} λ_{i}^{2} \geq \sum_{i = 1}^{N_{s}} λ_{i}^{2} = T r ({\tilde{Σ}}_{k c 1}^{2})

, at t

r a n k ({\tilde{Σ}}_{k c}) = N_{s}

the equal sign holds,

{\tilde{λ}}_{k c i}

denotes

\tilde{Σ}

the first

i

diagonal element. The reflection design is then used to maximize this upper bound, as in the following equation:

\max_{Φ} T r (H_{k c} H_{k c}^{H})

= \max_{Φ} T r ({\ddot{M}}_{k}^{H} Φ {\ddot{R}}_{k} {\ddot{R}}_{k}^{H} Φ^{H} {\ddot{M}}_{k})

\begin{matrix} (a) \\ = \end{matrix} \underset{Φ}{m a x} \sum_{i = 1}^{N_{R}} {\ddot{m}}_{k}_{i}^{H} Φ {\ddot{R}}_{k} {\ddot{R}}_{k}^{H} Φ^{H} {\ddot{m}}_{k i}

\begin{matrix} (b) \\ = \end{matrix} \underset{Φ}{m a x} \sum_{i = 1}^{N_{R}} {\overset{̿}{Γ}}_{k c}^{'}^{H} \ddot{T} {\overset{̿}{Γ}}_{k c}^{'}

(68)

When

(a)

holds,

{\ddot{m}}_{k}_{i} （ \forall i = 1, \dots, N_{R}

) is the channel matrix

{\ddot{M}}_{k}

of the

i

column. When

(b)

holds, the matrix

\ddot{T}

is defined

\ddot{T} ≜ \sum_{i = 1}^{N_{R}} d i a g ({\ddot{m}}_{k}_{i}^{H}) {\ddot{R}}_{k} {\ddot{R}}_{k}^{H} d i a g ({\ddot{m}}_{k}_{i})

To solve this problem efficiently, we use other fixed other phase shifts to optimize each reflection element in turn in an iterative manner until convergence is reached. Specifically, for the

t^{‘}

reflection matrix

Φ

element, the corresponding objective function is designed to be linear as follows:

2 R \{e^{j ϕ_{t^{‘}}} I_{t^{‘}}\} + \sum_{n \neq t^{‘}}^{T^{‘}} \sum_{i \neq t^{‘}}^{T^{‘}} \ddot{T} (n, i) e^{j (ϕ_{n}^{'} - ϕ_{i}^{'})} + \ddot{T} (t^{‘}, t^{‘})

(69)

Where

I_{t^{‘}} = \sum_{n \neq t^{‘}}^{T^{‘}} \ddot{T} (t^{‘}, n) e^{- j ϕ_{n}} = |I_{t^{‘}}| e^{- j φ_{t^{‘}}}

, the last two terms in the above equation are constants with fixed other reflective elements. The question of the

t^{‘}

element can be written as follows:

\underset{ϕ_{t^{‘}}}{m a x} R \{e^{j ϕ_{t^{‘}}} I_{t^{‘}}\} = \underset{θ_{t^{‘}}}{m a x} R \{{|I_{t^{‘}}| e}^{j (ϕ_{t^{‘}} - φ_{t^{‘}})}\} = \underset{θ_{t^{‘}}}{m i n} |ϕ_{t^{‘}} - φ_{t^{‘}}|

(70)

Where the closed-form solution of the above equation is

{ϕ_{t^{‘}}}^{*} = [\frac{φ_{t^{‘}}}{∆ θ}] \times ∆ ϕ

∆ ϕ = \frac{2 π}{2^{I}}

is the angular resolution. The phase shift of each reflection element can be designed in turn.

5. Low-complexity hybrid beamforming

5.1. Hybrid beamforming based on spectral efficiency maximization

When the computation of the RIS reflection matrix

Φ

is complete, we will next solve the optimization problem of (

F_{R F}, F_{B B, k}, W_{R F, k} W_{B B, k})

. The computational complexity becomes high if the joint optimization is performed at both (

F_{R F}, F_{B B, k}, W_{R F, k} W_{B B, k} ）

transceivers at the same time. Because of the constant mode constraints of

F_{R F, k}

and

W_{R F, k}

, this optimization problem will be nonconvex, further increasing the complexity of the problem. To facilitate the solution, we decouple the transceiver and the transmitter, while considering the design of the hybrid beamforming matrix at the transmitter side only. The problem in this section is translated into designing the optimal hybrid beamforming matrix

（F_{R F}, F_{B B, k}） .

This maximizes the system spectral efficiency. After designing the RIS reflection matrix

Φ

, the channel

H_{k c} = {\ddot{M}}_{k} Φ {\ddot{R}}_{k}

. The channel

H_{k c}

perform a singular value decomposition as the following equation:

H_{k c} = {G'}_{k c} {Σ'}_{k c} {V'}_{k c}^{H}

(71)

Where

{Σ'}_{k c} = [\begin{matrix} {Σ'}_{k c, 1} & 0 \\ 0 & {Σ'}_{k c, 2} \end{matrix}]

{V'}_{k c} = [\begin{matrix} {V'}_{k c, 1}, & {V'}_{k c, 2} \end{matrix}]

{Σ'}_{k c, 1}

represents a stream of information to be processed, and

{V'}_{k c, 1} ϵ C^{N_{T} \times N_{s, k}}

represents the product between the information stream to be processed and the number of transmitting antennas. It is assumed that the beamforming matrix received at the receiving end is perfect, that is

{G'}_{k c} = W_{R F, k} W_{B B, k}

. By referring to the noise covariance matrix of the receiving user above, we can express

R_{n}

as:

R_{n} = σ_{n}^{2} W_{B B, k}^{H} W_{R F, k}^{H} W_{R F, k} W_{B B, k}

= σ_{n}^{2} {G'}_{k c}^{H} {G'}_{k c}

= σ_{n}^{2} I_{{k N}_{s, k}}

(72)

Combined with the hybrid channel

H_{k c}

, we can express the spectral efficiency of the system through equation (63) as:

R = \log_{2} (⌈\begin{matrix} I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k}} R_{n}^{- 1} W_{B B, k}^{H} W_{R F, k}^{H} ({G'}_{k R} {Σ'}_{k R} {V'}_{k c}^{H}) \\ \times F_{R F} F_{B B, k} {(W_{B B, k}^{H} W_{R F, k}^{H} ({G'}_{k R} {Σ'}_{k R} {V'}_{k R}^{H}) F_{R F} F_{B B, k})}^{H} \end{matrix}⌉) = \log_{2} (⌈I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} ({Σ'}_{k R}^{2}) {{V'}_{k R}^{H} F}_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k R}⌉)

(73)

From the above, it is clear that

{V'}_{k R, 1} ϵ C^{N_{T} \times N_{s}}

. Then the best unconstrained digital beamforming matrix in the system can be

F_{o p t} = {V'}_{k R, 1}

. Because of the constant mode constraint, the

F_{o p t}

is not possible to use

F_{R F, k} F_{B B, k}

be represented. Assume that

{V'}_{1 c}^{H} F_{R F, k} F_{B B, k} \approx I_{k N_{s}}

{V'}_{2 c}^{H} F_{R F, k} F_{B B, k} \approx 0

, the precoding matrix is expressed as:

{{V'}_{k c}^{H} F}_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c}

= [\begin{matrix} {V'}_{k c, 1}^{H} F_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c, 1} & {V'}_{k c, 1}^{H} F_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c, 2} \\ {V'}_{k c, 2}^{H} F_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c, 1} & {V'}_{k c, 2}^{H} F_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c, 2} \end{matrix}]

\approx [\begin{matrix} \bar{Q} & 0 \\ 0 & 0 \end{matrix}]

(74)

The spectral efficiency can then be approximated by deducing as follows:

R = \log_{2} (|I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} ({Σ'}_{k c}^{2}) {{V'}_{k c}^{H} F}_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c}|) \approx \log_{2} (|I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} [\begin{matrix} {Σ'}_{k c, 1}^{2} & 0 \\ 0 & {Σ'}_{k c, 2}^{2} \end{matrix}] [\begin{matrix} \bar{Q} & 0 \\ 0 & 0 \end{matrix}]|) = \log_{2} (|I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2} \bar{Q}|) = \log_{2} (|I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2} \bar{Q}|) = \log_{2} (|I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2}|) + \log_{2} (|I_{k N_{s, k}} - {(I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2})}^{- 1} \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2} (I_{k N_{s, k}} - \bar{Q})|) \begin{matrix} a \\ \approx \end{matrix} \log_{2} (|I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2}|) - t r (I_{k N_{s, k}} - {V'}_{k c, 1}^{H} F_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c, 1}) = \log_{2} (|I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2}|) - (k N_{s, k} - {‖{V'}_{k c, 1}^{H} F_{R F} F_{B B, k}‖}_{F}^{2})

(75)

Where

\begin{matrix} a \\ \approx \end{matrix}

denotes the two approximations

{(I_{k N_{s, k}} + \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2})}^{- 1} \frac{ρ^{‘}}{k N_{s, k} σ_{n}^{2}} {Σ'}_{k c, 1}^{2} \approx I_{k N_{s, k}}

. When the

\ddot{Y}

values are not very large,

{l o g}_{2} |I_{k N_{s}} - \ddot{Y}| \approx {l o g}_{2} (1 - t r (\ddot{Y})) \approx - t r (\ddot{Y})

\bar{Q} = {V'}_{k c, 1}^{H} F_{R F} F_{B B, k} {F_{R F}}^{H} {F_{B B, k}}^{H} {V'}_{k c, 1}

, and

\ddot{Y} = {l o g}_{2} |I_{k N_{s, k}} - \bar{Q}|

The system spectral efficiency is maximizing

{‖{V'}_{k c, 1}^{H} F_{R F} F_{B B, k}‖}_{F}

, which represents the optimal beamforming matrix

F_{o p t} = {V'}_{k c, 1}

and

F_{R F} F_{B B, k}

the chord distance in the Grassmann manifold. The problem can be expressed as

{‖F_{o p t} - F_{R F} F_{B B, k}‖}_{F}

. The beamforming optimization problem for a millimeter wave massive MIMO UAV is expressed as follows:

(F_{R F}^{o p t}, F_{B B}^{o p t}) = a r g \min_{F_{RF} {, F}_{BB}} {‖F_{o p t} - F_{R F} F_{B B, k}‖}_{F}

s_{.} t_{.} F_{R F} ϵ F_{R F}

{‖F_{R F} F_{B B, k}‖}_{F}^{2} = {k N}_{s}

(76)

Because the constraint

F_{R F} ϵ F_{R F}

, that is

F_{R F}

the constant mode constraint on the column elements makes the problem non-convex and difficult to find an optimal solution. There is a need to improve the performance of the system while reducing the complexity and solving the non-convex optimization problem, so a hybrid beamforming optimization method based on PE-AltMin is introduced.

5.2. Digital and analogue beamforming matrix solutions

This section proposes an alternating minimization method to solve the above problem, and such methods have been successful in solving optimization problems on two variables. The optimization equation (76) is decoupled by keeping one variable fixed and optimizing iteratively the other variable. The optimization equation (76) is rewritten as the following equation:

\min_{F_{BB}} {‖F_{o p t} - F_{R F} F_{B B, k}‖}_{F}

\min_{F_{RF}} {‖F_{o p t} - F_{R F} F_{B B, k}‖}_{F}^{2}

s_{.} t_{.} |{(F_{R F})}_{i, j}| = 1, \forall i, j

(77)

Two sets of alternating minimization methods (AltMin, Alternating Minimization) are defined in the literature [35]. One of them is a method for high complexity manifold optimization. In this case, the above problem can be solved iteratively by defining a Riemannian manifold. We first use the conjugate line-step gradient method to determine the analog beamformer under the constraints, after which we use the least squares method to find the digital beamformer. The first using the conjugate line step gradient method to determine the analogue beamformer under constraints, and the later using the least squares method to find the digital beamformer. The least-squares method is used to find the digital beamformer. The MO-AltMin (Manifold Optimization Alternating Minimization) method offers better performance as it optimizes both variables simultaneously. However, the complexity of the MO-AltMin method is relatively high in that the update of the simulated beamformer in each iteration involves a line search method, the conjugate gradient method. Therefore, the nested loops in the MO-AltMin method slow down the overall solution process. This requires the study of a hybrid beamforming method with low computational complexity and low performance loss. A low-complexity PE-AltMin is designed on the basis.

The constraint that the columns about the digital beamformer should be orthogonal is expressed as:

F_{B B, k}^{H} F_{B B, k} = α F_{D D, k}^{H} α F_{D D, k} = α^{2} I_{{k N}_{s}}

(78)

Where

F_{D D, k}

is a matrix with the same dimension as

F_{B B, k}

.Your matrix with the same dimension. The orthogonality constraint provides the possibility that the analogue beamformer can discard the product form with

F_{B B, k}

product form, which will help to greatly simplify the design of the analogue beamformer. The objective function in (77) greatly simplifies the design of the analog beamformer when the AltMin method is applied. Since the matrix F_RF removes the product form of

F_{B B, k}

, the

F_{R F}

closed form solution is expressed as:

a r g (F_{R F}) = a r g (F_{o p t} F_{D D, k}^{H})

(79)

Where

a r g (F_{R F})

generates a new matrix containing the phase of the

F_{R F}

matrix. The results show that the

F_{R F}

the phase can be extracted from the equivalent beamformer

F_{o p t} F_{D D, k}^{H}

. This closed form of the solution can also be seen as

F_{o p t} F_{D D, k}^{H}

on the feasible set of the simulated beamformer

F_{R F}

on the Euclidean projection. However, this does not affect the complexity of the digital beamformer and modifies equation (77) to (80):

(80)

Based on the low-complexity PE-AltMin method, we reduce the search range of the digital beamformer. Equation (77) is expressed as:

F_{D D, k} F_{R F} = F_{o p t}

(81)

In equation (80), since the combined optimization problem eliminates the need for

F_{D D, k}

the other solutions, the complexity of the PE-AltMin method can be better reduced. Furthermore, instead of randomly selecting the phase during the initialisation of the PE-AltMin method, equation (79) is used to select

F_{R F}

. Finally, the final solution of the digital beamformer can be obtained by the least squares correction given in Equation (82).

F_{D D, k} = {(F_{R F}^{H} F_{R F})}^{- 1} F_{R F}^{H} F_{o p t}

(82)

In millimeter-wave massive MIMO of UAV, the number of antennas at the transmitting would be large, where

F_{D D, k} ϵ C^{N_{R F}^{T} \times N_{S, k}}

F_{R F} ϵ C^{N_{T} \times N_{R F}^{T}}

F_{o p t} ϵ C^{N_{T} \times N_{S, k}}

. The time consumed and the corresponding complexity of the matrix

F_{o p t} F_{R F}

performing SVD gradually increases. So the projection approximation subspace tracking method with lower complexity and better real-time is designed to estimate only

F_{o p t} F_{R F}

of the right singular matrix

\overset{⏞}{S}

. This avoids the need for SVD to obtain the entire left and right singular matrices and the computation of the singular value matrix.

In the projection approximation subspace tracking method, the

F_{o p t} F_{R F}

as the data sample.

F_{o p t} F_{R F}

is selected a row in the data sample vector

\overset{⏞}{x}

. When inputting the

\overset{⏞}{j} (1 \leq \overset{⏞}{j} \leq N_{T})

row

{\overset{⏞}{x}}_{\overset{⏞}{j}}

is entered, it is possible to obtain

F_{o p t} F_{R F}

\overset{⏞}{s}

\leq \overset{⏞}{s} \leq \overset{⏞}{S}

) column

{\overset{⏞}{B}}_{j} (:, \overset{⏞}{s})

{\overset{⏞}{B}}_{j} (:, \overset{⏞}{s})

can be expressed as the following equation:

{\overset{⏞}{B}}_{\overset{⏞}{j}} (:, \overset{⏞}{s}) = {\overset{⏞}{B}}_{\overset{⏞}{j} - 1} (:, \overset{⏞}{s}) + \frac{1}{d_{\overset{⏞}{j}} (\overset{⏞}{s})} [x_{\overset{⏞}{j}} - {\overset{⏞}{B}}_{\overset{⏞}{j} - 1} (:, \overset{⏞}{s}) \overset{⏞}{y}] {\overset{⏞}{y}}^{*}

(83)

Where

\overset{⏞}{y} = {\overset{⏞}{B}}_{\overset{⏞}{j} - 1}^{H} (:, \overset{⏞}{s}) {\overset{⏞}{x}}_{\overset{⏞}{j}}

is the intermediate variable, and

{\overset{⏞}{y}}^{*}

denotes the

\overset{⏞}{y}

the conjugate.

{d'}_{\overset{⏞}{j}} (\overset{⏞}{s}) = {d'}_{\overset{⏞}{j} - 1} (\overset{⏞}{s}) + {|{\overset{⏞}{y}}_{\overset{⏞}{j}}|}^{2}

is the step size used for the correction. For the method steps can be described as follows:

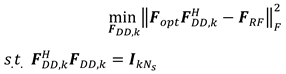
Algorithm 1: Projection Approximation Subspace Algorithm

Applying the above method to the improved hybrid beamforming optimization method of finding PE-AltMin for

F_{o p t}^{H} F_{R F}^{(\overset{`}{k})}

the SVD calculation, then the specific method based on PE-AltMin can be expressed as follows:

Algorithm 2: Improved hybrid beamforming optimization algorithm based on PE-AltMin

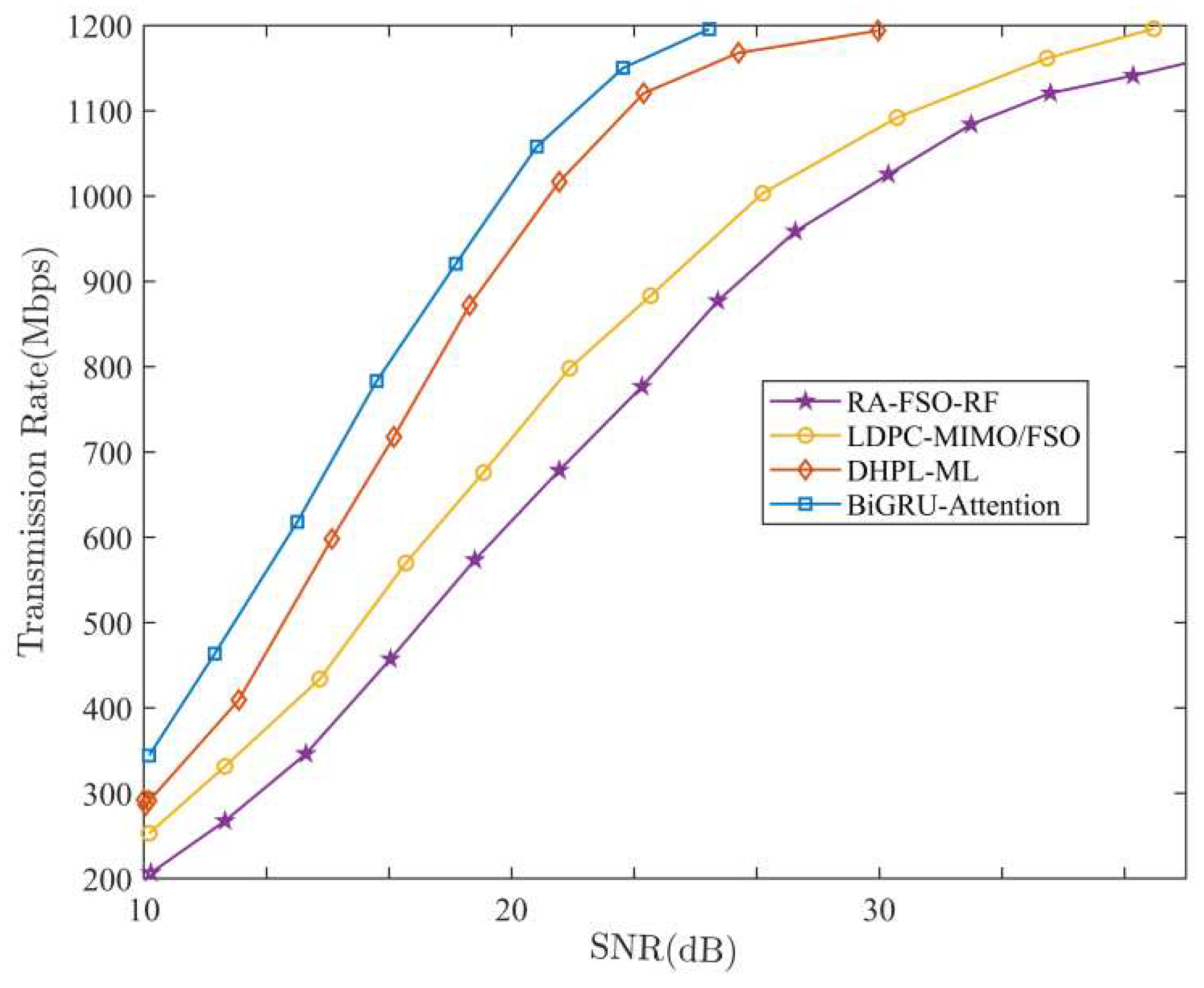
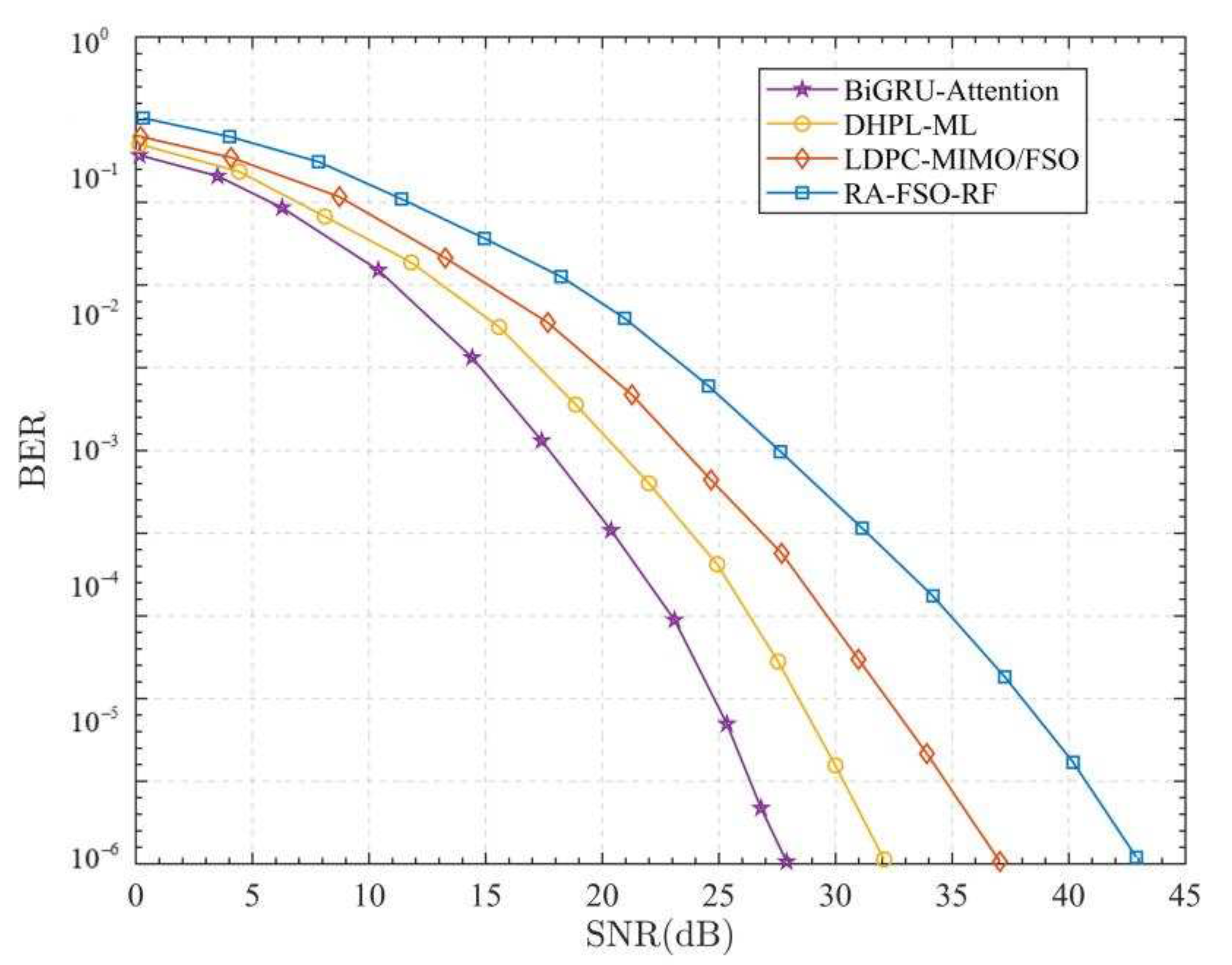
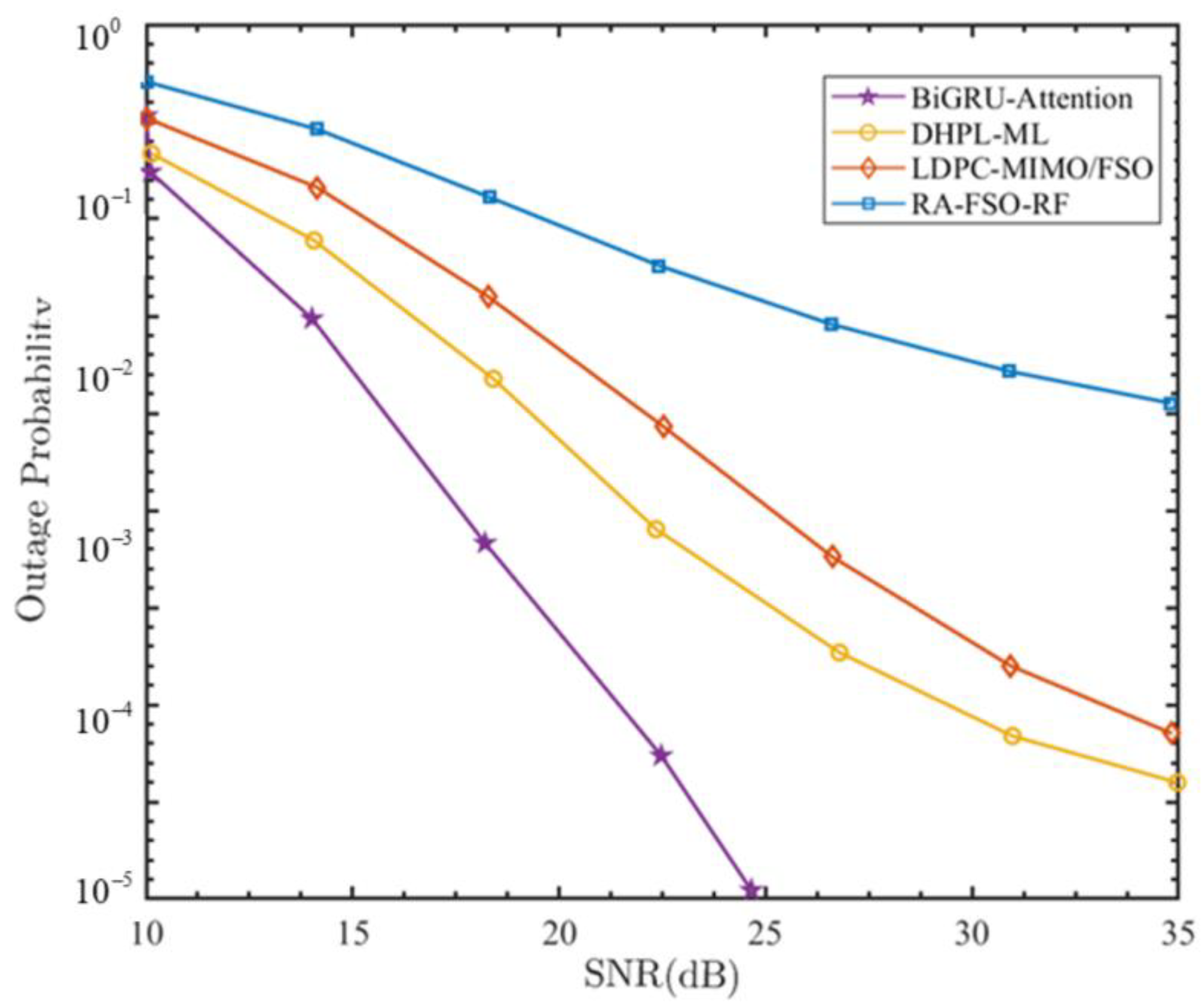
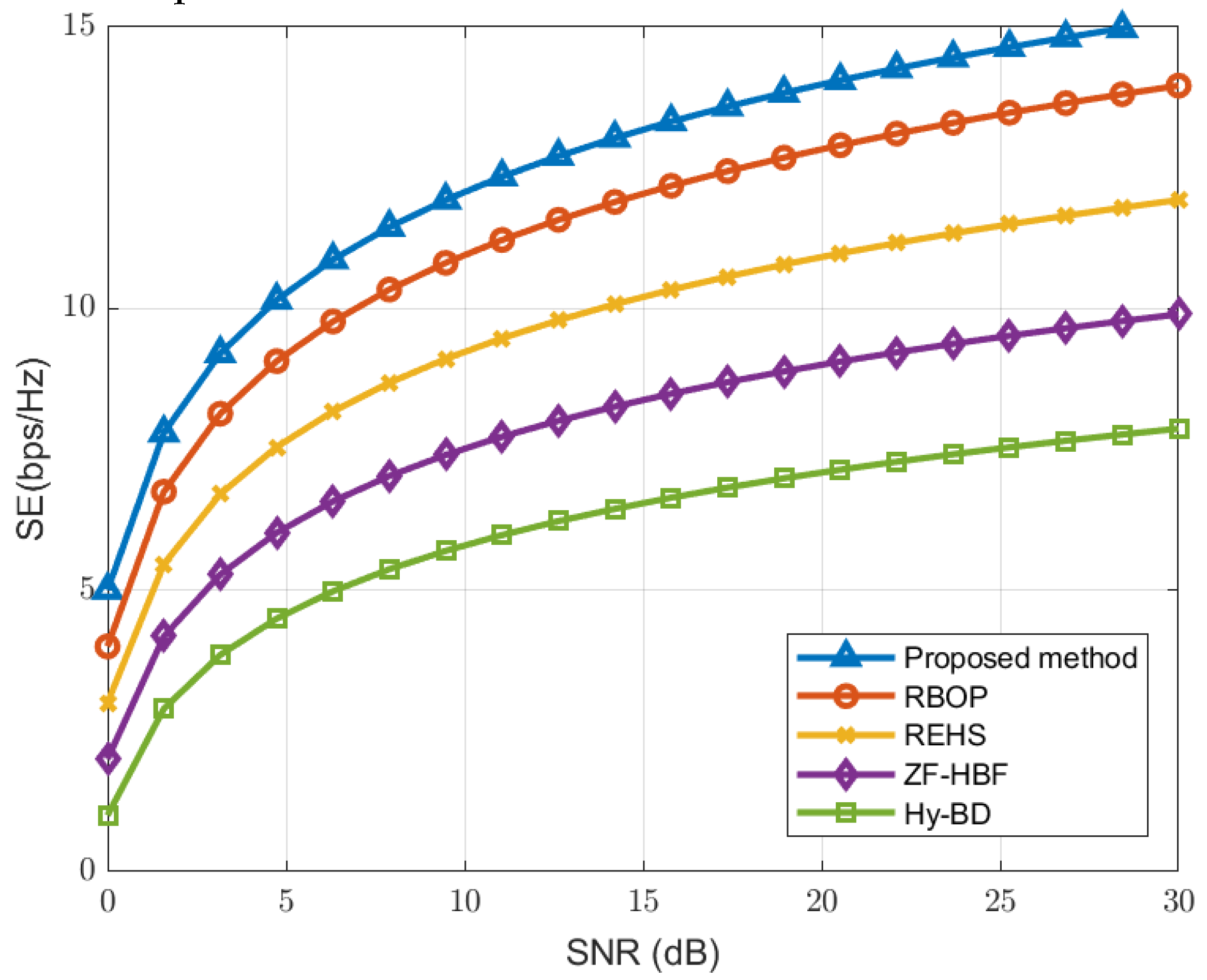
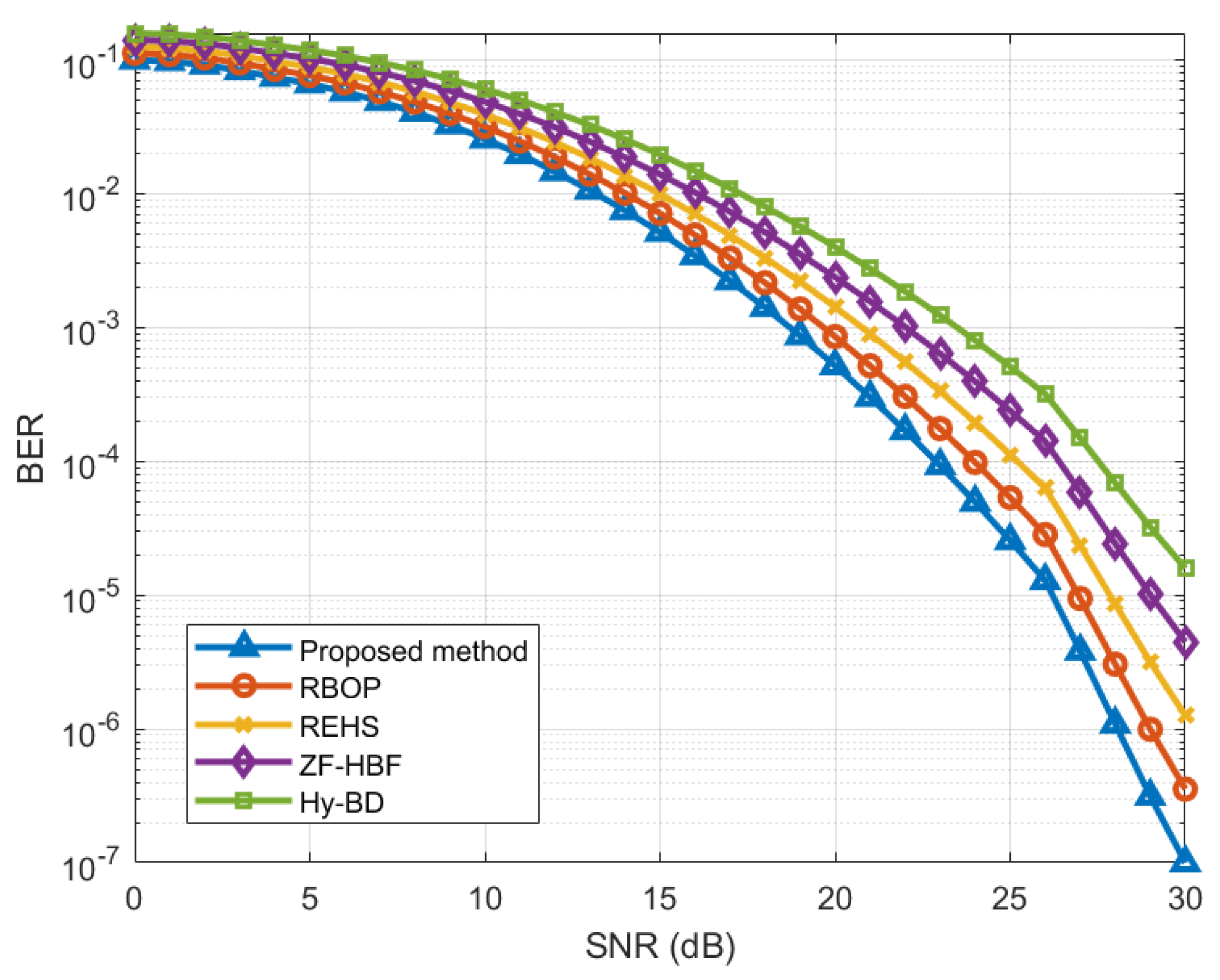
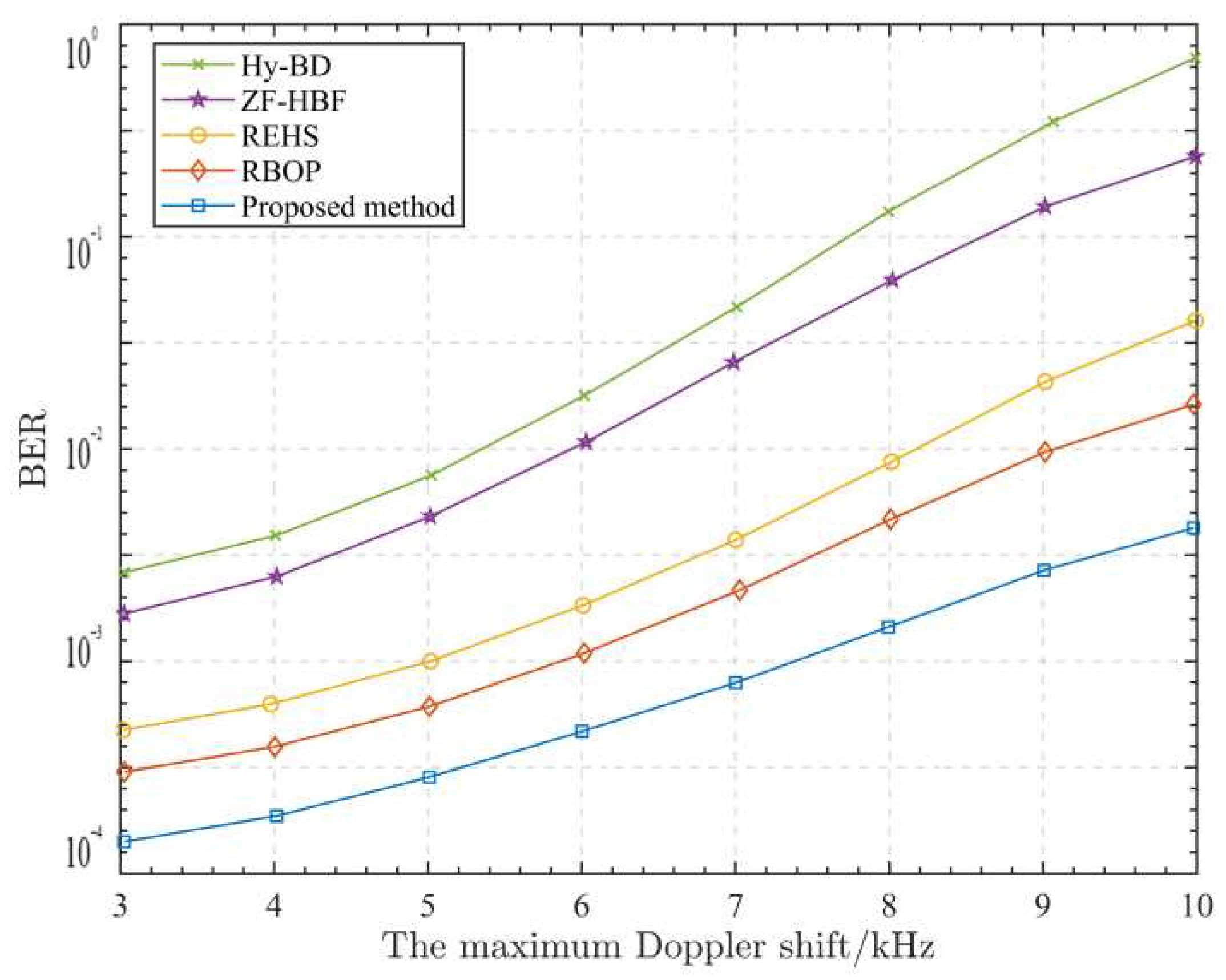
6. Simulation results and analysis

For evaluation, we perform Monte-Carlo simulations. We present numerical results forOutage probability, the transmission rate and BER (Bit Error Rate) performance of FSO links for various numbers of transmit/receive apertures and correlation values. We consider a FSO system with a receive aperture of size

D_{0}

= 5cm and the wavelength of

λ

= 1.55μm. The link distance is assumed to be

L

= 2km. The correlation length can be therefore approximated as

d_{0}

≈

\sqrt{λ L}

= 5.5cm. To validate the performance of these models millimete-wave massive MIMO/FSO in UAV system, the carrier frequency is 78GHz. The grid size of the dictionary matrix is set to

G_{R} = 2 N_{R} = 64

G_{T} = 2 N_{T} = 128

. The maximum number of channel paths is set to

Q_{m a x} = 5

. The UAV speed is 0-80 km/h.

We compared the performance of four methods in terms of FSO transmission rate, as shown in Figure 5. As can be seen, the dual-hop FSO in UAV system with BiGRU-Attention neural network method offers the best performance in terms of the average FSO transmission rate. For instance, at SNR=20dB, using BiGRU-Attention network results in the average FSO transmission rate of 1050Mbps, 900Mbps, 700Mbps, 600Mbps, compared with the DHPL-ML, LDPC-MIMO/FSO, and RA-FSO-RF, respectively. The results indicate that the application of BiGRU-Attention neural network model in FSO system can effectively solve the optical PE problem caused by UAV jitter. Although other methods can improve optical communication performance, the ability of FSO PE to handle complex jitter in FSO environments is limited.

We compared the BER of four methods. As shown in Figure 6, the dual-hop FSO in UAV system with BiGRU-Attention neural network method offers the best performance in terms of the average BER. When the SNR=25dB, using BiGRU-Attention network results in a decrease in the average BER of

10^{- 5}

10^{- 5}

10^{- 5}

10^{- 5}

, compared with the DHPL-ML, LDPC-MIMO/FSO, and RA-FSO-RF, respectively. Obviously, the BiGRU-Attention network model achieves lower BER compared to other methods. In addition, all considered methods exhibit a trend of decreasing error rate with increasing SNR. This also reveals the significant impact of PE of UAV in these systems.

We investigate the performance of the system under consideration based on the probability of interruption. Figure 7 shows the relationship between interruption probability and SNR ratio under different methods. Under the same SNR ratio conditions, the BiGRU-Attention network performs the best. For instance, at SNR=20dB, using BiGRU-Attention network results in outage probability of

10^{- 4}

10^{- 4}

10^{- 4}

10^{- 1}

, compared with the DHPL-ML, LDPC-MIMO/FSO, and RA-FSO-RF, respectively.

According to the simulation results shown in Figure 10, the spectral efficiency of the proposed method in this paper reaches 14bps/Hz with SNR=20 dB, which is the best performance. In comparison, the spectral efficiency of the RBOP method is 12.5 bps/Hz, the REHS method is 11 bps/Hz, the ZF-HBF method is 8 bps/Hz, and the Hy-BD method has a spectral efficiency of only 6 bps/Hz, which is the worst performer.

We compared the BER of five methods, as shown in Figure 11. When the SNR=25dB, the bit error rate of the proposed method is

10^{- 5}

, which is better than other methods. The bit error rate of the RBOP method is

{0.5 \times 10}^{- 4}

, the bit error rate of the REHS method is

{0.7 \times 10}^{- 4}

, the bit error rate of the ZF-HBF method is

{1.2 \times 10}^{- 4}

, and the bit error rate of the Hy-BD method is the highest, reaching

{5 \times 10}^{- 4}

Figure 12 shows that when the maximum Doppler shift is 8kHz, the BER of the proposed method reaches

10^{- 3}

, which is the best performance. The BER of the RBOP method is

5.5 \times 10^{- 3}

, because the RBOP method has high channel requirements and cannot effectively suppress multipath interference, which affects the improvement of system performance. The REHS method has BER of

10^{- 2}

. The REHS method requires a lot of computation and processing, which reduces the performance of the system. The BER of the ZF-HBF method is

5.5 \times 10^{- 2}

. The Hy-BD method has the highest BER of

10^{- 1}

. The Hy-BD method performed the worst.

7. Summary

In this paper, a Tensor-train decomposition based hybrid beamforming for millimeter-wave massive MIMO/FSO in UAV with RIS Networks is investigated. Firstly, the system channel model of millimeter-wave massive MIMO/FSO in UAV with RIS is established. The application of BIGRU (Bidirectional Gated Recurrent Unit)-Attention neural net-work model in an FSO system can effectively solve the problem of light PE caused by UAV jitter. The multidimensional received signal of millimeter-wave massive MIMO in UAV with RIS is represented as a low-rank tensor signal by Tensor-train decomposition. The problem of maximizing the system spectral efficiency is decomposed into two subproblems of optimizing the RIS phase shift matrix and solving the hybrid beamforming matrix. The hybrid channel matrix is decomposed by SVD. The RIS phase shift matrix is optimized. Finally, the hybrid beamforming matrix is solved by decoupling the transceiver and transmitter using an improved hybrid beamforming method based on PE-AltMin.

Author Contributions

Conceptualization, X.Z. and P.F.; methodology, X.Z.; software, P.F. and J.L.; validation, X.Z. and J.C.; formal analysis, X.Z. and P.F.; investigation, X.Z. and J.C.; resources, X.Z. and J.L.; data curation, J.L.; writing—original draft preparation, P.F.; writing—review and editing, Y.W.; visualization, J.L.; supervision, X.Z.; project administration, X.Z. and Y.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Shanghai Capacity Building Projects in Local Institutions, grant number 19070502900, Science and Technology Commission of Shanghai Municipality, grant number 22142201900.

References

Wang, Y.; Zhang, Y.; Liu, Y. A survey on UAV communication: Channel modeling and performance evaluation. IEEE Communication Surveys Tuts. 2018, 20, 2804–2831. [Google Scholar]
Zhou,F. ; Hu,R. Q.; Li, Z. and Wang,Y. Mobile Edge Computing in Unmanned Aerial Vehicle Networks, IEEE Wireless Communications 2020, 27, 140–146.
Cao, X.; Xu, J. and Zhang, R. Mobile Edge Computing for Cellular-Connected UAV: Computation Offloading and Trajectory, Proc. IEEE Int. Wksp. Signal Process. Advances in Wireless Commun, June 2018.
Liu, Y.; & Chen, Y.; & Chen, Y. UAV-assisted communication for 5G and beyond: Challenges and opportunities. IEEE Wireless Communications 2019, 26, 56–63. [Google Scholar]
Nguyen,T. V.; Le, H. D.; Dang, N. T. and A. T. Pham, On the Design of Rate Adaptation for Relay-Assisted Satellite Hybrid FSO/RF Systems. IEEE Photonics Journal 2022, 14, 1–11. [Google Scholar]
Safari, M.; Uysal, M. ; & Uysal, M. Relay-Assisted Free-Space Optical Communication. Conference Record of the Forty-First Asilomar Conference on Signals. Systems and Computers 2007, 1891–1895. [Google Scholar]
Anandkumar, D.; Sangeetha, R. G. Performance Evaluation of LDPC-Coded Power Series Based Málaga (Ḿ) Distributed MIMO/FSO Link With M-QAM and Pointing Error. IEEE Access 2022, 10, 62037–62055. [Google Scholar] [CrossRef]
Zhou, X.; Tian, X. , Tong, L.; & Wang, Y. Manifold Learning Inspired Dynamic Hybrid Precoding with Antenna Partitioning Algorithm for Dual-Hop Hybrid FSO-RF Systems. IEEE Access 2022, 10, 133385–133401. [Google Scholar]
Jaiswal, A.; Abaza, M.; Bhatnagar, M. R.; Jain, V. K. An Investigation of Performance and Diversity Property of Optical Space Shift Keying-Based FSO-MIMO System. IEEE Transactions on Communications 2018, 66, 4028–4042. [Google Scholar] [CrossRef]
AnandKumar, D. and Sangeetha, R. G. Performance Analysis of Power Series based MIMO/FSO Link with Pointing Errors and Atmospheric Turbulence, International Conference on Communication Systems & Networks (COMSNETS), Bangalore, India, 2021, 78-81.
Chen, J. , et al. A Novel Energy Harvesting Scheme for Mixed FSO-RF Relaying Systems. IEEE Transactions on Vehicular Technology 2019, 68, 8259–8263. [Google Scholar] [CrossRef]
Ansari, I. S.; Yilmaz, F.; & Alouini, M. S. Performance Analysis of FSO Links over Unified Gamma-Gamma Turbulence Channels. In 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), 2015, 1-5.
Tokgoz, S. C. , Althunibat, S., Yarkan, S., & Qaraqe, K. A. Physical Layer Security of Hybrid FSO-mm-Wave Communications in Presence of Correlated Wiretap Channels. IEEE International Conference on Communications. Montreal, QC, Canada, 2021, 1-7.
Sun, Q.; Zhang, Z.; Zhang, Y.; López-Benítez, M.; Zhang, J. Performance Analysis of Dual-Hop Wireless Systems Over Mixed FSO/RF Fading Channel. IEEE Access 2021, 9, 85529–85542. [Google Scholar] [CrossRef]
Xu, Z.; Xu, G.; Zheng, Z. BER and Channel Capacity Performance of an FSO Communication System over Atmospheric Turbulence with Different Types of Noise. Sensors 2021, 21, 3454. [Google Scholar] [CrossRef] [PubMed]
Zhou, L.; Yang, Z.; Zhou, S. and Zhang, W. Coverage Probability Analysis of UAV Cellular Networks in Urban Environments, IEEE International Conference on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 2018, 1-6.
Shi, Y.; Zhang, Y.; Liu, Y. Beamforming design for UAV communication with random blockages. IEEE Transactions on Vehicular Technology 2020, 69, 7863–7871. [Google Scholar]
Tokgoz,S. C.; Althunibat, S.; Yarkan, S. and Qaraqe, K. A. Physical Layer Security of Hybrid FSO-mm Wave Communications in Presence of Correlated Wiretap Channels, IEEE International Conference on Communications, Montreal, QC, Canada, 2021, 1-7.
Sun, Q.; Zhang, Z.; Zhang, Y.; López-Benítez, M.; Zhang, J. Performance Analysis of Dual-Hop Wireless Systems Over Mixed FSO/RF Fading Channel. IEEE Access 2021, 9, 85529–85542. [Google Scholar] [CrossRef]
Yu, H.; Tuan, H. D.; Dutkiewicz, E.; Poor, H. V. and Hanzo, L. Regularized Zero-Forcing Aided Hybrid Beamforming for Millimeter-Wave Multiuser MIMO Systems. IEEE Transactions on Wireless Communications 2023, 22, 3280–3295. [Google Scholar] [CrossRef]
Zhou, R.; Zhang, C. and Zhang, G. Generalized Space-Time Adaptive Monopulse Angle Estimation Approach, International Conference on Control, Automation and Information Sciences, Chengdu, China, 2019, 1-5.
Wang, Z.; Li, Y.; Wang, C.; Ouyang, D. and Huang, Y. A-OMP: An Adaptive OMP Algorithm for Underwater Acoustic OFDM Channel Estimation. IEEE Wireless Communications Letters 2021, 10, 1761–1765. [Google Scholar] [CrossRef]
Wu, F. Y.; Yang, K.; Tian, T.; Huang, C.; Zhu, Y. and Tong, F. Estimation of Doubly Spread Underwater Acoustic Channel via Gram-Schmidt Matching Pursuit, OCEANS- Marseille, Marseille, France, 2019, 1-5.
Liao, A.; Gao, Z.; Wu, Y.; Wang, H.; Alouini, M. S. 2D Unitary ESPRIT Based Super-Resolution Channel Estimation for Millimeter-Wave Massive MIMO with Hybrid Precoding. IEEE Access 2017, 5, 24747–24757. [Google Scholar] [CrossRef]
Li, S.; Chai, Y.; Guo, M. and Liu, Y. Research on Detection Method of UAV Based on micro-Doppler Effect, 39th Chinese Control Conference (CCC), Shenyang, China, 2020, 3118-3122.
Beom-Seok, Oh; Guo, Xin; and Wan, Fangyuan. MicroDoppler Mini-UAV Classification Using Empirical-Mode Decomposition Features. IEEE Geosocience and Remote Sensing Letters 2018, 15, 227–231. [Google Scholar] [CrossRef]
Wu, Q.; Zhang, R.; Zhang, Y. Multi-Antenna Techniques for UAV Communication: A Survey. IEEE Communications Surveys & Tutorials 2019, 21, 2702–2724. [Google Scholar]
Chauhan, A.; Sharma, S.E. and Budhiraja, R. Hybrid Block Diagonalization for Massive MIMO Two-Way Half-Duplex AF Hybrid Relay, International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 2018, 367-371.
Sharma, N. and Gautam, S. Optimizing RIS-assisted Wireless Communication Systems with Non-Linear Energy Harvesting, 5th International Conference on Energy, Power and Environment: Towards Flexible Green Energy Technologies (ICEPE), Shillong, India, 2023, 1-5.
Zhang, T.; He, Y.; Huang, J. Intelligent Reflecting Surface Assisted UAV Wireless Communication with Nonlinear Energy Harvesting. IEEE Transactions on Wireless Communications 2020, 19, 4375–4386. [Google Scholar]
Hu, H.; You, X.; Huang, Y.; Chen, J. Robust intelligent reflecting surface aided multiuser beamforming optimization. IEEE Journal on Selected Areas in Communications 2019, 11, 1. [Google Scholar]
Ma, J.; Chen, X.; Liu, G.; Zhang, W. Adaptive Beamforming for UAV Communications via Intelligent Reflecting Surface. IEEE Transactions on Communications 2021, 69, 573–584. [Google Scholar]
Feng, K.; Chen, Y.; Han, Y.; Li, X. and Jin, S. Passive Beamforming Design for Reconfigurable Intelligent Surface-aided OFDM: A Fractional Programming Based Approach, IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 2021, 1-6.
Cheng, M.; Wang, K.; Liu, A. Joint Beamforming and Power Control in RIS-Aided Communications: A Rotation-Invariant Design. IEEE Transactions on Vehicular Technology 2020, 69, 8324–8328. [Google Scholar]
Renzo, M. Di et al. Smart Radio Environments Empowered by Reconfigurable Intelligent Surfaces: How It Works, State of Research, and The Road Ahead. IEEE Journal on Selected Areas in Communications 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
Jiang, W.; Chen, B.; Zhao, J.; Xiong, Z. and Ding, Z. Joint Active and Passive Beamforming Design for the IRS-Assisted MIMOME-OFDM Secure Communications. IEEE Transactions on Vehicular Technology 2021, 70, 10369–10381. [Google Scholar] [CrossRef]
Shi, J.; Xu, Y.; Wang, L.; Zeng, Y.; Liang, Y. Joint Trajectory Design and Passive Beamforming for UAV Communication via Intelligent Reflecting Surface. IEEE Wireless Communications Letters 2020, 9, 1256–1260. [Google Scholar]
Kim,T. and Choe, Y. Fast Circulant Tensor Power Method for High-Order Principal Component Analysis. in IEEE Access 2021, 9, 62478–62492. [Google Scholar] [CrossRef]
Yu, X.; Shen, J.C.; Zhang, J.; Letaief, K. B. Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems. IEEE Journal of Selected Topics in Signal Processing 2016, 10, 485–500. [Google Scholar] [CrossRef]
Bhatnagar, M. R.; Ghassemlooy, Z. Performance Analysis of Gamma–Gamma Fading FSO MIMO Links with Pointing Errors. Journal of Lightwave Technology 2016, 34, 2158–2169. [Google Scholar] [CrossRef]

Figure 1. RIS-assisted multi-user UAV communication system model.

Figure 2. FSO system model.

Figure 3. BIGRU-Attention model.

Figure 4. RIS-assisted multi-user UAV communication system model

Figure 5. FSO transmission rate comparison of other methods with the proposed method

Figure 6. BER comparison of other methods with the proposed method.

Figure 7. Outage probability for different distributions of PE.

Figure 10. Comparison of the spectral efficiency of the proposed method with other methods

Figure 11. Comparison of the proposed method with other methods for BER.

Figure 12. The effect of the maximum Doppler shift on the performance of different systems.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Tensor-Train Decomposition Based Hybrid Beamforming for Millimeter-Wave Massive MIMO/FSO in UAV with RIS Networks

Abstract

1. Introduction

2. System model

2.1. FSO system model

2.2. DF transmission protocol

2.3. Mathematical modeling of the PE tracking system

2.4. Estimation of FSO PE with BIGRU-Attention model

2.5. Multi-user UAV communication channel model with RIS

3. Power fading factor and Doppler shift estimation for fast fading channels based on Tensor-train Decomposition

3.1. Tensor-train Decomposition

3.2. Estimation of Power Fading Factor and Doppler Shift for Fast Fading Channels using Tensor-Train Decomposition

4. Hybrid beamforming and RIS phase shift matrix design

4.1. Hybrid beamforming and RIS phase shift matrix design based on Tensor-train decomposition

4.2. RIS phase shift matrix design

5. Low-complexity hybrid beamforming

5.1. Hybrid beamforming based on spectral efficiency maximization

5.2. Digital and analogue beamforming matrix solutions

6. Simulation results and analysis

7. Summary

Author Contributions

Funding

References

MDPI Initiatives

Important Links

Subscribe