Enhancing the Convergence Order from p to p+3 in Iterative Methods for Solving Nonlinear Systems of Equations without the Use of Jacobian Matrices

Preprint

Article

Enhancing the Convergence Order from p to p+3 in Iterative Methods for Solving Nonlinear Systems of Equations without the Use of Jacobian Matrices

Altmetrics

Downloads

128

Views

Comments

A peer-reviewed article of this preprint also exists.

Alicia Cordero^*

Miguel Leonardo–Sepúlveda

Juan Torregrosa

,María P. Vassileva

Alicia Cordero^*

Miguel Leonardo–Sepúlveda

Juan Torregrosa

,María P. Vassileva

This version is not peer-reviewed

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts

Abstract

In this paper, we present an innovative technique that improves the convergence order of iterative schemes that do not require the evaluation of Jacobian matrices. Using this procedure, we achieve a remarkable increase in the order of convergence, raising it from p to p + 3 units, which results in a remarkable improvement in the overall performance. We have conducted comprehensive numerical tests in various scenarios to validate the theoretical results, showing the efficiency and effectiveness of the new Jacobian-free schemes.

Keywords:

Subject: Computer Science and Mathematics - Computational Mathematics

1. Introduction

Let us consider the system of nonlinear equations

F (x) = 0

, where

F : Ω \subseteq R^{n} ⟶ R^{n}

and

f_{i}, i = 1, 2, \dots, n

, are the coordinate functions of F, with

F (x) =

{(f_{1} (x), f_{2} (x), \dots, f_{n} (x))}^{T}

. Solving nonlinear systems is a challenging task, typically requiring either linearization of certain nonlinear problems or the application of a fixed-point function

G : Ω \subseteq R^{n} ⟶ R^{n}

, which leads to a fixed-point iteration scheme. Additionally, these schemes can be applied in different areas of knowledge, including engineering, chemistry, fluid dynamics, among others, making them valuable tools for solving nonlinear and nondifferentiable problems. Tackling such systems often involves employing linearization techniques to approximate solutions or employing fixed-point iteration methods based on a function G. These strategies provide valuable insights and approximated solutions of the nonlinear systems.

In many of these methods, the evaluation of Jacobian matrices at one or more points per iteration is required. However, a significant challenge arises from the computation of the Jacobian matrix, especially in cases where it may not exist or, for high-dimensional scenarios, its computation becomes excessively costly or even infeasible. As a result, certain authors have attempted to overcome this issue by eliminating the dependence on the Jacobian matrix and replacing it with alternative techniques.

There are numerous methods for solving systems of nonlinear equations. Among them, Steffensen’s method which was presented by Samanskii in [1]. This stands out as one of the most renowned techniques in the literature on iterative methods without Jacobian, its iterative scheme is given by the expression,

x^{(k + 1)} = x^{(k)} - {[w^{(k)}, x^{(k)}; F]}^{- 1} F (x^{(k)}), k = 0, 1, 2, \dots,

where

w^{(k)} = x^{(k)} + F (x^{(k)})

, being

[\cdot, \cdot; F] : Ω \times Ω \subset R^{n} \times R^{n} ⟶ L (R^{n})

the divided difference operator of F on

R^{n}

defined as (see [2]).

\begin{matrix} [x, y; F] (x - y) = F (x) - F (y), for any x, y \in Ω . \end{matrix}

(1)

In this work, we explore innovative iterative methods for the resolution of nonlinear systems of equations without the need to compute Jacobian matrices. Different researchers in this field have made significant contributions to the development of these strategies.

Cordero et al. in [3] developed memory-based methods that also utilize the Kurchatov divided difference to enhance the efficiency of known methods. Additionally, as part of our strategy, we adopted the m-th-order vectorial divided differences proposed by Amiri et al. in [4]. These strategies, found in the literature, circumvent the complexity and costs associated with Jacobian matrices, making them particularly valuable for large-scale systems. Among the most commonly used approaches are the finite difference method, as well as polynomial interpolators, divided differences, and other clever techniques that have also been employed in the literature to avoid the direct evaluation of derivatives. These additional techniques further expand the tools available for tackling derivative-related problems in complex systems.

The advances made by these and other researchers in the field allow us to envision more effective solutions in a wide range of disciplines that require advanced numerical methods. Effective solutions in a wide range of disciplines that require advanced numerical methods. In addition to the above, other authors have worked on non-Jacobian methods, which can be found in the following references [3,5,6,7,8].

In this research, we present an approach that improves the convergence order from p to

p + 3

, applicable to Jacobian-free schemes. We replace the traditional Jacobian matrix of F with

[x^{(k)} + H (x^{(k)}), x^{(k)}; F]

, a concept introduced by Amiri et al. in [4], where

H : Ω \subseteq R^{n} ⟶ R^{n}

with

H (x^{(k)}) = {(f_{1}^{m} (x^{(k)}), f_{2}^{m} (x^{(k)}), \dots, f_{n}^{m} (x^{(k)}))}^{T}

, provides a remarkable approximation of the Jacobian matrix for the function

F (x)

at any given point. By leveraging this approach with

m = 2

, we achieve a convergence order of

p + 3

This novel approach not only circumvents the complexities associated with traditional Jacobian matrix computations, but also opens new avenues for improving the convergence rate of numerical methods, making it a valuable contribution to the field of numerical analysis and optimization.

The work is developed as follows: first, in Section 1, we introduce the basic concepts necessary for the development of the paper. Then, in Section 2, we prove in a general way that the scheme has a convergence order of

p + 3

. To illustrate this, in Section 3 we solve some academic problems to confirm the reliability of the modified methods without Jacobian matrices. Finally, we address the solution of the problem entitled Modeling of nutrient diffusion in a biological substrate, which is formulated through a nonlinear non-differentiable second-order elliptic nonlinear partial differential equation. To address this question, we proceed to discretize the equation by means of the finite difference method, transforming it into a system of nonlinear equations. We then employ the modified Traub method with increased order of convergence, which we denote as Traub-M2, to solve the resulting system. We conclude by presenting the matrix representing the approximate solution of this system of equations.

1.1. Preliminary concepts

First, we introduce a number of necessary concepts, in order to develop the proposed Taylor series scheme and prove the order of convergence of the proposed iterative scheme.

Definition 1.

Let

{\{x^{(k)}\}}_{k \geq 0}

be a sequence in

R^{n}, n \geq 1

, convergent to ξ. Then, convergence is said to

linear, if there exists $M, 0 < M < 1$ for $M \in R$ , and $k_{0} \in N$ , such that

$∥x^{(k + 1)} - ξ∥ \leq M ∥x^{(k)} - ξ∥, \forall k \geq k_{0} .$
Sequence ${\{x^{(k)}\}}_{k \geq 0}$ converges to ξ woth order $p, p > 1$ , if there exists $M, M > 0$ for $M \in R$ and $k_{0} \in N$ such that

$∥x^{(k + 1)} - ξ∥ \leq M {∥x^{(k)} - ξ∥}^{p} \forall k \geq k_{0} .$

Let

F : Ω \subseteq R^{n} ⟶ R^{n}

sufficiently differentiable in

Ω

. The q-th derivative of F in

u \in R^{n}, q \geq 1

, is the q-linear function

F^{(q)} (u) : R^{n} \times \dots \times R^{n} ⟶

R^{n}

such that

F^{(q)} (u) (ω_{1}, \dots, ω_{q}) \in R^{n}

. It is easy to see that

$F^{(q)} (u) (ω_{1}, ω_{2}, \dots, ω_{q - 1}, \cdot)$ is a linear operator that maps $R^{n}$ to $L (R^{n})$ .
$F^{(q)} (u) (ω_{τ (1)}, \dots, ω_{τ (q)}) = F^{(q)} (u) (ω_{1}, \dots, ω_{q})$ , for every permutation $τ$ of ${1, 2, \dots, q}$ .

From the above properties we define the following notation:

$a)$: $F^{(q)} (u) (ω_{1}, \dots, ω_{q}) = F^{(q)} (u) ω_{1} \dots ω_{q}$ ,
$b)$: $F^{(q)} (u) ω^{q - 1} F^{(p)} ω^{p} = F^{(q)} (u) F^{(p)} (u) ω^{q + p - 1}$ .

On the other hand, for

ξ + h \in R^{n}

which lies in a vicinity of a solution

ξ

F (x) = 0

, we can apply the Taylor expansion and if the Jacobian matrix

F^{'} (ξ)

is not singular, can express

F (ξ + h) = F^{'} (ξ) [h + \sum_{j = 2}^{p - 1} C_{j} h^{j}] + O (h^{p})

(2)

where

C_{j} = (\frac{1}{j!}) {[F^{'} (ξ)]}^{- 1} F^{(j)} (ξ), j \geq 2

. We observe that

C_{j} h^{j} \in R^{n}

since In addition, we can express

F^{'} (ξ + h)

F^{'} (ξ + h) = F^{'} (ξ) [I + \sum_{j = 2}^{p - 1} j C_{j} h^{j - 1}] + O (h^{p})

(3)

where I is the identity matrix. Therefore,

j C_{j} h^{j - 1} \in L (R^{n})

. From (3), we can obtain

{[F^{'} (ξ + h)]}^{- 1} = [I - X_{2} h + X_{3} h^{2} - X_{4} h^{3} + \dots] {[F^{'} (ξ)]}^{- 1} + O (h^{p}),

(4)

where

\begin{matrix} X_{2} & = & 2 C_{2}, \\ X_{3} & = & 4 C_{2}^{2} - 3 C_{3}, \\ X_{4} & = & 8 C_{2}^{3} - 6 C_{2} C_{3} - 6 C_{3} C_{2} + 4 C_{4}, \\ ⋮ \end{matrix}

On the other hand, we denote by

e^{(k)} = x^{(k)} - ξ

the error in the k-th iteration. The equation

e^{(k + 1)} = M e^{{(k)}^{p}} + O (e^{{(k)}^{p + 1}}),

where M is a p-linear function

M \in L (R^{n} \times \dots \times R^{n}, R^{n})

, is called the error equations and p is the order of convergence of the sequence

x^{(k)}

generated by the iterative process. Observe that

e^{{(k)}^{p}}

(e^{(k)}, e^{(k)}, \dots, e^{(k)})

To estimate the convergence order, Cordero and Torregrosa presented in [9] the following definition the so-called Approximated Computational Order of Convergence (ACOC).

Definition 2.

Let ξ be a zero of function F and suppose that

x^{(k - 1)}, x^{(k)}

and

x^{(k + 1)}

are three consecutive iterations close to ξ. Then, the order of convergence p can be approximated using the formula

p \approx A C O C = \frac{ln (∥x^{(k + 1)} - x^{(k)}∥ / ∥x^{(k)} - x^{(k - 1)}∥)}{ln (∥x^{(k)} - x^{(k - 1)}∥ / ∥x^{(k - 1)} - x^{(k - 2)}∥)} .

(5)

To compare the different methods obtained by applying the results proposed in this work, we employ Ostrowski’s efficiency index

I = p^{1 / d}

(see [10]), where p is the order of convergence and d is the total number of functional evaluations required by the method (per iteration). This is the most commonly used index, but not the only one. In his book [11], Traub uses an operational index that is defined as

C = p^{1 / o p}

, where

o p

is the number of operations per iteration. Recall that the number of products and quotients needed to solve r linear systems with the same coefficient matrix, using the factorization

L U

, is calculated as follows.

\frac{1}{3} n^{3} + r n^{2} - \frac{1}{3} n,

We will use both this index and a combination of both,

C E = p^{1 / (d + o p)}

, which Cordero et al. in [12], and which is called the computational efficiency index.

The formula of Gennochi-Hermite (see [2])

[x + h, x; F] = \int_{0}^{1} F^{'} (x + t h) d t, \forall x, h \in Ω \subset R^{n},

allows us to calculate the Taylor expansion of the divided difference operator in terms of the successive derivatives of F,

[x + h, x; F] = \sum_{j = 0}^{p} \frac{1}{(j + 1)!} F^{(j + 1)} (x) h^{j} + O (h^{p + 1}), \forall x, h \in Ω

By denoting

y = x + h

and using the error at both points,

e = x - ξ, e_{y} = y - ξ

, the Taylor expansion of the divided difference (1) can be written as

\begin{matrix} [y, x; F] = F^{'} (ξ) [I + C_{2} (e_{y} + e) + C_{3} (e_{y}^{2} + e_{y} e + e^{2}) + C_{4} (e_{y}^{3} + e_{y}^{2} e + e_{y} e^{2} + e^{3}) + \dots] . \end{matrix}

(6)

Now, we use these expressions to prove the following result.

In order to perform the Taylor development of

H (x^{(k)})

we use the following result, presented in the work of Amiri et al. in [4].

Theorem 1.

Let H be a nonlinear operator

H : Ω \subseteq R^{n} ⟶ R^{n}

with coordinate functions

h_{i}, i = 1, 2, \dots, n

and

m \in N

such that

m \geq 1

. Let us consider the divided difference operator

[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]

where,

H (x^{(k)}) = {(h_{1}^{m} (x^{(k)}), h_{2}^{m} (x^{(k)}), \dots, h_{n}^{m} (x^{(k)}))}^{T}

and

λ \in R

, then the order of the divided difference

[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]

as an approximation of the Jacobian matrix

F^{'} (x^{(k)})

is m.

Proof.

Let

h_{i} (x), i = 0, 1, 2, \dots,

be the coordinate functions of

H (x)

. Let us consider the Taylor expansion of

h_{i} (x)

around

ξ

\begin{matrix} h_{i} (x) = & h_{i} (ξ) + \sum_{j_{1} = 1}^{n} \frac{\partial h_{i} (ξ)}{\partial x_{j_{1}}} e_{j_{1}} + \sum_{j_{2} = 1}^{n} \sum_{j_{1} = 1}^{n} \frac{\partial^{2} h_{i} (ξ)}{\partial x_{j_{2}} \partial x_{j_{1}}} e_{j_{1}} e_{j_{2}} + \sum_{j_{3} = 1}^{n} \sum_{j_{2} = 1}^{n} \sum_{j_{1} = 1}^{n} \frac{\partial^{3} h_{i} (ξ)}{\partial x_{j_{3}} \partial x_{j_{2}} \partial x_{j_{1}}} e_{j_{1}} e_{j_{2}} e_{j_{3}} \\ + \dots + \sum_{j_{l} = 1}^{n} \dots \sum_{j_{2} = 1}^{n} \sum_{j_{1} = 1}^{n} \frac{\partial^{r} h_{i} (ξ)}{\partial x_{j_{1}}^{r_{1}} \partial x_{j_{2}}^{r_{2}} \dots \partial x_{j_{l}}^{r_{l}}} e_{j_{1}}^{r_{1}} e_{j_{2}}^{r_{2}} \dots e_{j_{l}}^{r_{l}} + \dots, \end{matrix}

(7)

where

r_{s} \in {1, 2, \dots, r}

for

s = 1, 2, \dots, l

and

r = r_{1} + r_{2} + \dots + r_{l}, e = x - ξ

and

e_{j_{s}} = x_{j_{s}} - ξ_{j_{s}}

, for

s = 1, 2, \dots, l

is the

j_{s}

th coordinate of error e. We can write (7), as

\begin{matrix} h_{i} (x^{(k)}) = A_{1}^{i} e^{(k)} + A_{2}^{i} e^{{(k)}^{2}} + \dots + A_{m - 1}^{i} e^{{(k)}^{m - 1}} + A_{m}^{i} e^{{(k)}^{m}} + A_{m + 1}^{i} e^{{(k)}^{m + 1}} + \dots, \end{matrix}

(8)

with

A_{t}^{i} \in L (R^{n}, R^{n})

for

t = 1, 2, \dots

, since

\frac{\partial^{r} h_{i} (ξ)}{\partial x_{j_{1}}^{r_{1}} \partial x_{j_{2}}^{r_{2}} \dots \partial x_{j_{l}}^{r_{l}}} = m (m - 1) \dots (m - r + 1) h_{i}^{m - r} (ξ) \frac{\partial^{r} h_{i} (ξ)}{\partial x_{j_{1}}^{r_{1}} \partial x_{j_{2}}^{r_{2}}} = 0, for all r < m,

A_{t}^{i} = 0

for

t = 1, 2, \dots, m - 1

and we have

h_{i} (x^{(k)}) = A_{m}^{i} e^{{(k)}^{m}} + A_{m + 1}^{i} e^{{(k)}^{m + 1}} + O (e^{{(k)}^{m + 2}}) .

By introducing the multilinear operator

A_{t} = [A_{t}^{1}, A_{t}^{2}, \dots, A_{t}^{n}]

for

t = 1, 2, \dots

, we can express the Taylor series of

H (x^{(k)})

around

ξ

as follows:

H (x^{(k)}) = A_{m} e^{{(k)}^{m}} + A_{m + 1} e^{{(k)}^{m + 1}} + O (e^{{(k)}^{m + 2}}),

(9)

so we define the error at

w = x + λ H (x)

e_{w} = w - ξ = x + λ H (x) - ξ = e + H (x) .

Now let

F (x) = F^{'} (ξ) [e + C_{2} e^{2} + C_{3} e^{3} + C_{4} e^{4} + C_{5} e^{5} + C_{6} e^{6} + C_{7} e^{7}] + O (e^{8}) .

Let us consider the Taylor expansion of

F (x)

around

ξ

. When we apply the Gennochi-Hermite formula (6), we obtain:

\begin{matrix} [w, x; F] = & F^{'} (ξ) [I + C_{2} (e_{w} + e) + C_{3} (e_{w}^{2} + e_{w} e + e^{2}) + C_{4} (e_{w}^{3} + e_{w}^{2} e + e_{w} e^{2} + e^{3}) + \dots] \\ = & F^{'} (ξ) [I + 2 C_{2} e + 3 C_{3} e^{2} + \dots + m C_{m} e^{m - 1} + (C_{2} A_{m} + (m + 1) C_{m + 1}) e^{m} \\ + (C_{2} A_{m + 1} + C_{3} A_{m} + (m + 2) C_{m + 2}) e^{m + 1} + \dots] . \end{matrix}

Since the Taylor expansions of

F^{'} (x)

and

[w, x; F]

around

ξ

coincide for the first m terms, the order of the divided difference

[w, x; F]

is exactly m. □

2. Main Result

In the following, we present a technique that allows increasing the order of convergence from p to

p + 3

units in Jacobian-free methods. To achieve this goal, it is necessary to introduce a second arbitrary scheme or class of two-step iterative methods whose predictor step must be Newton’s scheme, a second generic step

φ (x^{(k)}, y^{(k)})

of order p . Adding a third corrector step

x^{(k + 1)}

, which depends on real numbers

α

β

and

γ

, such that guarantee that any scheme with such conditions will reach converge order

p + 3

, for which we state the following result.

In the following section, we introduce an iterative scheme that utilizes a Steffensen-type method as a predictor. This concept is inspired by the work of researchers Cordero and Torregrosa, who introduced in their paper [5] the idea of using divided differences

f [w_{k}, x_{k}] \approx f^{'} (x_{k}) = \frac{f (w_{k}) - f (x_{k})}{w_{k} - x_{k}}

with

w_{k} = x_{k} + λ f {(x_{k})}^{m}

to adapt various families of derivative-dependent iterative methods. This adaptation ensures consistent convergence orders when substituting derivatives with divided differences for different values of m, especially in the scalar case.

For the scalar case, the iterative expression of a Steffensen-type method is defined as:

x_{k + 1} = x_{k} - \frac{f (x_{k})}{f [w_{k}, x_{k}]}, w_{k} = x_{k} + λ f (x_{k}), k = 0, 1, 2, \dots .

(1)

By applying a similar concept and replacing Jacobian matrices with divided differences in the vectorial case, we create a generic scheme with an undetermined number of steps, where the first step is an extension of the Steffensen scheme (1) to systems. This extension enables an increase in the convergence order from p to

p + 3

units.

In a more general way, we represent the scheme as follows:

\begin{matrix} y^{(k)} & = & x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (x^{(k)}), \\ z^{(k)} & = & φ (x^{(k)}, y^{(k)}), \\ x^{(k + 1)} & = & z^{(k)} - [α I + G (x^{(k)}, y^{(k)}) (β I + γ G (x^{(k)}, y^{(k)}))] {[x^{(k)} + H (x^{(k)}), x^{(k)}; F]}^{- 1} F (z^{(k)}), \end{matrix}

(2)

where

G (x^{(k)}, y^{(k)}) = {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [z^{(k)}, y^{(k)}; F]

, and

Theorem 2.

Let

F : Ω \subseteq R^{n} \to R^{n}

be a sufficiently differentiable function at each point in a neighborhood of an open convex set Ω containing

ξ \in R^{n}

, such that

F (ξ) = 0

is a solution of the system. Let

x^{(0)}

be an initial estimate sufficiently close to ξ, and suppose that the Jacobian matrix

F^{'} (x)

is continuous and nonsingular at ξ.

Then, the method defined by (2) has a convergence order of

p + 3

, where p is the order of the arbitrary scheme

z^{(k)}

, whose first step is Steffensen-type method, for

α = \frac{13}{4}, β = - \frac{7}{2}

, and

γ = \frac{5}{4}

and its error equation is as follows:

e^{(k + 1)} = \frac{1}{2} [2 C_{2} (C_{2} A_{2} - A_{2} C_{2}) - 3 (C_{3} + C_{2}^{2}) C_{2} + C_{2} C_{3}] M_{p} e^{{(k)}^{p + 3}} + O [e^{{(k)}^{p + 4}}],

(3)

Proof.

To perform a Taylor series expansion of the divided difference, we need to develop the Taylor series of

F (x^{(k)})

F^{'} (x^{(k)})

, and

F^{''} (x^{(k)})

around

ξ

F (x^{(k)}) = F^{'} (ξ) [e^{(k)} + C_{2} e^{{(k)}^{2}} + C_{3} e^{{(k)}^{3}}] + O [e^{{(k)}^{4}}],

(4)

where

C_{j} = (\frac{1}{j!}) {[F^{'} (ξ)]}^{- 1} [F^{(j)} (ξ)], j \geq 2 with x^{(k)} - ξ = e^{(k)} .

The derivative

F^{'} (x^{(k)})

is:

F^{'} (x^{(k)}) = F^{'} (ξ) [I + 2 C_{2} e^{(k)} + 3 C_{3} e^{{(k)}^{2}} + 4 C_{4} e^{{(k)}^{3}}] + O [e^{{(k)}^{4}}],

(5)

F^{''} (x^{(k)}) = F^{'} (ξ) [2 C_{2} + 6 C_{3} e^{(k)} + 12 C_{4} e^{{(k)}^{2}}] + O [e^{{(k)}^{3}}] .

(6)

According to Theorem 1,

[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]

for

m = 2

is a second-order approximation of the Jacobian matrix

F^{'} (x^{(k)})

. Using (5) and (6), its Taylor series expansion is as follows:

\begin{matrix} [x^{(k)} + λ H (x^{(k)}), x^{(k)}; F] = & F^{'} (ξ) [I + 2 C_{2} e^{(k)} + 3 C_{3} e^{{(k)}^{2}} + 4 C_{4} e^{{(k)}^{3}}] \\ + \frac{1}{2} F^{'} (ξ) [2 C_{2} + 6 C_{3} e^{(k)} + 12 C_{4} e^{{(k)}^{2}}] (λ H (x^{(k)})) \\ = & F^{'} (ξ) [I + 2 C_{2} e^{(k)} + (3 C_{3} + λ C_{2} A_{2}) e^{{(k)}^{2}} + (4 C_{4} + λ C_{2} A_{3} + 3 λ C_{3} A_{2}) e^{{(k)}^{3}}] \\ + O [e^{{(k)}^{4}}] . \end{matrix}

(7)

Let us now calculate the Taylor’s series development of

{[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1}

. Forcing that equality

{[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [x^{(k)} + λ H (x^{(k)}), x^{(k)}; F] = I

must be satisfied, we conjecture

\begin{matrix} {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} = [I + X_{2} e^{(k)} + X_{3} e^{{(k)}^{2}} + X_{4} e^{{(k)}^{3}}] {[F^{'} (ξ)]}^{- 1} + O [e^{{(k)}^{4}}], \end{matrix}

(8)

and consequently,

\begin{matrix} I = [I + X_{2} e^{(k)} + X_{3} e^{{(k)}^{2}} + X_{4} e^{{(k)}^{3}}] [I + 2 C_{2} e^{(k)} + (3 C_{3} + λ C_{2} A_{2}) e^{{(k)}^{2}} + (4 C_{4} + λ C_{2} A_{3} + 3 λ C_{3} A_{2}) e^{{(k)}^{3}}] . \end{matrix}

(9)

So,

\{\begin{matrix} X_{2} = - 2 C_{2}, \\ X_{3} = 4 C_{2}^{2} - 3 C_{3} - λ C_{2} A_{2}, \\ X_{4} = - λ C_{2} A_{3} + λ (4 C_{2}^{2} - 3 C_{3}) A_{2} - 8 C_{2}^{3} + 6 C_{2} C_{3} + 6 C_{3} C_{2} - 4 C_{4} . \end{matrix}

Let us calculate the error equation for the first step of the scheme, as

\begin{matrix} y^{(k)} & = x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [F (x^{(k)})], \end{matrix}

it follows that

\begin{matrix} y^{(k)} - ξ & = C_{2} e^{{(k)}^{2}} + (- X_{2} C_{2} - X_{3} - C_{3}) e^{{(k)}^{3}} + O [e^{{(k)}^{4}}] . \end{matrix}

We denote

B_{3} = - X_{2} C_{2} - X_{3} - C_{3} .

Now, let us suppose that the error of the second step

φ (x^{(k)}, y^{(k)})

is of order p then, the error in the k-th iterate

z^{(k)}

is:

\begin{matrix} z^{(k)} - ξ = M_{p} e^{{(k)}^{p}} + M_{p + 1} e^{{(k)}^{p + 1}} + M_{p + 2} e^{{(k)}^{p + 2}} + M_{p + 3} e^{{(k)}^{p + 3}} + O [e^{{(k)}^{p + 4}}], \end{matrix}

(10)

and therefore the Taylor development of

F (z^{(k)})

around

ξ

\begin{matrix} F (z^{(k)}) = & F^{'} (ξ) [M_{p} e^{{(k)}^{p}} + M_{p + 1} e^{{(k)}^{p + 1}} + M_{p + 2} e^{{(k)}^{p + 2}} + M_{p + 3} e^{{(k)}^{p + 3}} + C_{2} M_{p}^{2} e^{{(k)}^{2 p}}] \\ + O [e^{{(k)}^{p + 4}}] . \end{matrix}

(11)

Thus, the Taylor series expansion of the Jacobian matrix

F^{'} (y^{(k)})

using the divided difference

[z^{(k)}, y^{(k)}; F]

is as follows:

\begin{matrix} [z^{(k)}, y^{(k)}; F] = & F^{'} (ξ) [I + C_{2}^{2} e^{{(k)}^{2}} + C_{2} B_{3} e^{{(k)}^{3}} + C_{2} M_{p} e^{{(k)}^{p}} + C_{2} M_{p + 1} e^{{(k)}^{p + 1}} \\ + C_{2} M_{p + 2} e^{{(k)}^{p + 2}} + C_{2} M_{p + 3} e^{{(k)}^{p + 3}}] + O [e^{{(k)}^{p + 4}}] . \end{matrix}

(12)

In order to calculate the error equation at the last step, we first calculate the product

\begin{matrix} G (x^{(k)}, y^{(k)}) = & {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [z^{(k)}, y^{(k)}; F] \\ = & I + X_{2} e^{(k)} + D_{2} e^{{(k)}^{2}} + D_{3} e^{{(k)}^{3}} + D_{4} e^{{(k)}^{p}} \\ + D_{5} e^{{(k)}^{p + 1}} + D_{6} e^{{(k)}^{p + 2}} + D_{7} e^{{(k)}^{p + 3}} + O [e^{{(k)}^{p + 4}}], \end{matrix}

(13)

where

\begin{matrix} \{\begin{matrix} D_{2} = X_{3} + C_{2}^{2}, \\ D_{3} = X_{4} + C_{2} B_{3} + X_{2} C_{2}^{2}, \\ D_{4} = C_{2} M_{p}, \\ D_{5} = C_{2} M_{p + 1} + X_{2} C_{2} M_{p}, \\ D_{6} = C_{2} M_{p + 2} + X_{2} C_{2} M_{p + 1} + X_{3} C_{2} M_{p}, \\ D_{7} = C_{2} M_{p + 3} + X_{2} C_{2} M_{p + 2} + X_{3} C_{2} M_{p + 1} + X_{4} C_{2} M_{p} . \end{matrix} \end{matrix}

(14)

In addition,

\begin{matrix} {(G (x^{(k)}, y^{(k)}))}^{2} = & {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [z^{(k)}, y^{(k)}; F] {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [z^{(k)}, y^{(k)}; F] \\ = & I + 2 X_{2} e^{(k)} + E_{2} e^{{(k)}^{2}} + E_{3} e^{{(k)}^{3}} + E_{4} e^{{(k)}^{p}} \\ + E_{5} e^{{(k)}^{p + 1}} + E_{6} e^{{(k)}^{p + 2}} + E_{7} e^{{(k)}^{p + 3}} + O [e^{{(k)}^{p + 4}}], \end{matrix}

(15)

where

\begin{matrix} \{\begin{matrix} E_{2} = 2 D_{2} + X_{2}^{2}, \\ E_{3} = 2 D_{3} + X_{2} D_{2} + D_{2} X_{2}, \\ E_{4} = 2 D_{4}, \\ E_{5} = 2 D_{5} + X_{2} D_{4} + D_{4} X_{2}, \\ E_{6} = 2 D_{6} + X_{2} D_{5} + D_{4} D_{2} + D_{5} X_{2} + D_{2} D_{4}, \\ E_{7} = 2 D_{7} + X_{2} D_{6} + D_{2} D_{5} + D_{3} D_{4} + D_{4} D_{3} + D_{5} D_{2} + D_{6} X_{2} . \end{matrix} \end{matrix}

(16)

Finally, we calculate the product

{[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [F (z^{(k)})]

, using (8) and (11):

\begin{matrix} {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [F (z^{(k)})] = & M_{p} e^{{(n)}^{p}} + (M_{p + 1} + X_{2} M_{p}) e^{{(k)}^{p + 1}} \\ + (M_{p + 2} + X_{2} M_{p + 1} + X_{3} M_{p}) e^{{(k)}^{p + 2}} \\ + (M_{p + 3} + X_{2} M_{p + 2} + X_{3} M_{p + 1} + X_{4} M_{p}) e^{{(k)}^{p + 3}} + O [e^{{(k)}^{p + 4}}] . \end{matrix}

(17)

Therefore, the error in the third step

x^{(k + 1)}

is calculated by using (10), (13), (15) and (17) therefore.

\begin{matrix} x^{(k + 1)} = & z^{(k)} - [α I + G (x^{(k)}, y^{(k)}) (β I + γ G (x^{(k)}, y^{(k)}))] {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [F (z^{(k)})], \\ e^{(k + 1)} = & M_{p} e^{{(k)}^{p}} + M_{p + 1} e^{{(k)}^{p + 1}} + M_{p + 2} e^{{(k)}^{p + 2}} + M_{p + 3} e^{{(k)}^{p + 3}} \\ - [(α + β + γ) I + (β + 2 γ) X_{2} e^{(k)} + (β D_{2} + γ E_{2}) e^{{(k)}^{2}} + (β D_{3} + γ E_{3}) e^{{(k)}^{3}} \\ + (β D_{4} + γ E_{4}) e^{{(k)}^{p}} + (β D_{5} + γ E_{5}) e^{{(k)}^{p + 1}} + (β D_{6} + γ E_{6}) e^{{(k)}^{p + 2}} \\ + (β D_{7} + γ E_{7}) e^{{(k)}^{p + 3}}] \cdot [M_{p} e^{{(k)}^{p}} + (M_{p + 1} + X_{2} M_{p}) e^{{(k)}^{p + 1}} \\ + (M_{p + 2} + X_{2} M_{p + 1} + X_{3} M_{p}) e^{{(k)}^{p + 2}} + (M_{p + 3} + X_{2} M_{p + 2} + X_{3} M_{p + 1}) e^{{(k)}^{p + 3}}] \\ + O [e^{{(k)}^{4}}], \\ = & (1 - α - β - γ) M_{p} e^{{(k)}^{p}} + [(1 - α - β - γ) M_{p + 1} - (α + 2 β + 3 γ) X_{2} M_{p}] e^{{(k)}^{p + 1}} \\ + [(1 - α - β - γ) M_{p + 2} + (α + 2 β + 3 γ) X_{2} M_{p + 1} - (α + 2 β + 3 γ) X_{3} M_{p} \\ - (5 β + 14 γ) C_{2}^{2} M_{p}] e^{{(k)}^{p + 2}} + [(1 - α - β - γ) M_{p + 3} - (α + 2 β + 3 γ) X_{2} M_{p + 2} \\ - (α + 2 β + 3 γ) X_{3} M_{p + 1} - (α + 2 β + 3 γ) X_{4} M_{p}] e^{{(k)}^{p + 3}} \\ + [- (5 β + 14 γ) C_{2}^{2} M_{p + 1} + (3 β + 8 γ) C_{2} X_{3} M_{p} - (β + 3 γ) X_{3} X_{2} M_{p} \\ + (2 β + 10 γ) C_{2}^{3} M_{p} + (β + 2 γ) C_{2} C_{3} M_{p}] e^{{(k)}^{p + 3}} . \end{matrix}

(18)

From (18), we derive the system,

\{\begin{matrix} 1 - α - β - γ & = & 0, \\ α + 2 β + 3 γ & = & 0, \\ 5 β + 14 γ & = & 0, \end{matrix}

whose solution is

α = \frac{13}{4}

β = - \frac{7}{2}

and

γ = \frac{5}{4}

. Simplifying the resulting error equation, we get

\begin{matrix} e^{(k + 1)} = \frac{1}{2} [2 C_{2} (C_{2} A_{2} - A_{2} C_{2}) - 3 (C_{3} + C_{2}^{2}) C_{2} + C_{2} C_{3}] M_{p} e^{{(k)}^{p + 3}} + O [e^{{(k)}^{p + 4}}], \end{matrix}

showing that the order of convergence will be

p + 3

. This ends our proof. □

3. Numerical results

Below, we present several systems of nonlinear equations that we solve to confirm the reliability of the methods based on the conditions stated in Theorem 2. Specifically, methods that do not require the evaluation of Jacobian matrices.

Each table displays the initial approximation

x^{(0)}

used to find the solutions. Additionally, we indicate the number of iterations (Iter) required for the schemes to converge, the approximate computational order of convergence (ACOC) for each method, and the approximate computational time (e-time) required (in seconds).

The calculations have been performed with MATLAB programming software, using variable precision arithmetics with 2000 digits of mantissa and an error tolerance of

ϵ = 10^{- 8}

. In addition, the expression (5) is used to calculate the approximated computational order of convergence ACOC. Each table includes the CPU time used by each method to obtain the solution. It is important to note that the computer used for these calculations has the following software and hardware specifications: macOS Ventura operating system version 13.4.1, Intel Core i7 quad-core processor Chip M1 Pro, 16 GB Ram Memory LPDDR5 and year of manufacture 2021. In addition, we applied the following stopping criteria:

∥x^{(k + 1)} - x^{(k)}∥ + ∥F (x^{(k + 1)})∥ < ϵ .

3.1. Computational Efficiency

Now, we present five classes of iterative methods that we use to apply our technique and perform various numerical tests in relation to specific academic problems. Then, we apply the third step of our approach to each of these methods. In a first step, we compute the computational efficiency index of each of these methods, in order to be able to compare the methods of order p with the schemes modified to

p + 3

among the different classes of approaches.

The first scheme to be used to increase its convergence order and check its efficiency is a modification of the method presented by Cordero et al. in [13], where we have eliminated the Jacobian matrix. For simplicity we denote it as

M E T_{1, λ, 4}

, where

λ

represents the parameter selected in that scheme, 4 is the order of the method and

m = 2

\begin{matrix} M E T_{1, λ, 4} : \{\begin{matrix} y^{(k)} = x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (x^{(k)}), \\ x^{(k + 1)} = x^{(k)} - [(\frac{β}{6} G^{3} + 2 G^{2} + G + 1)] {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (x^{(k)}), \end{matrix} \\ for β = 1, G (x^{(k)}, y^{(k)}) = 1 - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [x^{(k)}, y^{(k)}; F], \end{matrix}

where

k = 0, 1, 2 \dots .

The second test scheme we employ in this paper is Traub’s method, which is introduced by Traub in [14]. The system-transferred version of this method, where the Jacobian was also replaced by the split difference and

m = 2

, is represented by the following expression:

\begin{matrix} M E T_{2, λ, 3} : \{\begin{matrix} y^{(k)} = x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (x^{(k)}), \\ x^{(k + 1)} = x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [F (x^{(k)}) + F (y^{(k)})], \end{matrix} \end{matrix}

where

k = 0, 1, 2 \dots .

Chun’s method was initially introduced in [15]. Now, we present a modification of this scheme, in which we replace the Jacobian matrix with the divided difference for

m = 2

\begin{matrix} M E T_{3, λ, 4} : \{\begin{matrix} y^{(k)} = x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (x^{(k)}), \\ x^{(k + 1)} = y^{(k)} - (3 - 2 Γ (k)) {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (y^{(k)}), \end{matrix} \end{matrix}

being

Γ^{(k)} = {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} [x^{(k)}, y^{(k)}; F],

where

k = 0, 1, 2 \dots .

Ostrowski’s method presented in [10] and transferred to systems by Grau et al. in [16], as in the previous cases we modify this method by replacing the Jacobian matrix by the split difference proposed in this work for

m = 2

\begin{matrix} M E T_{4, λ, 4} : \{\begin{matrix} y^{(k)} = x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (x^{(k)}), \\ x^{(k + 1)} = y^{(k)} - {[2 [x^{(k)}, y^{(k)}; F] - [x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]]}^{- 1} F (y^{(k)}), \end{matrix} \end{matrix}

where

k = 0, 1, 2 \dots .

Finally, we employ the family of iterative methods proposed by Cordero et al. in [17]. This class, characterized by having convergence order

p = 6

in three steps, allows us to apply our new technique, stated in Theorem 2, resulting in a transformation of the scheme into a four-step method, achieving an increase in its convergence order up to

p = 9

units. The adoption of this advanced technique promises to offer a level of accuracy and efficiency in the results obtained. This scheme takes its new form after replacing the Jacobian matrix by the proposed divided difference for

m = 2

, its iterative expression in three steps is as follows:

\begin{matrix} M E T_{5, λ, 6} : \{\begin{matrix} y^{(k)} = x^{(k)} - {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (x^{(k)}), \\ z^{(k)} = y^{(k)} - {(2 [x^{(k)}, y^{(k)}; F] - [x^{(k)} + λ H (x^{(k)}), x^{(k)}; F])}^{- 1} F (y^{(k)}), \\ x^{(k + 1)} = z^{(k)} - Λ^{(k)} F (z^{(k)}) - (1 + γ) [I - Γ^{(k)}] {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} F (z^{(k)}), \end{matrix} \end{matrix}

for

Λ^{(k)} = [γ {[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]}^{- 1} + (1 - γ) {[x^{(k)}, y^{(k)}; F]}^{- 1}]

and Note that in each method we use the value

λ = 0.001

. After several numerical tests, we found that the iterative schemes converge faster to the solution when

λ

is near to zero.

We apply to each of them the conditions of Theorem 2 in order to increase their orders of convergence from p to

p + 3

In Table 1, we present information on the order of convergence, the number of scalar functional evaluations per iteration, the number of products/quotients per iteration, and the computational efficiency index (CI) for each method, both before and after applying our proposed third step. It is important to remember that in order to evaluate the function in one iteration, the computation of scalar functions is required. The number of scalar function evaluations is

n^{2} - n

for any split-difference evaluation

[x^{(k)}, y^{(k)}; F]

and

n^{2} - 2 n

for the expression

[x^{(k)} + λ H (x^{(k)}), x^{(k)}; F]

. Furthermore, to each iterative class presented after applying our scheme, we refer to them as

M E T_{1, λ, p}

through

M E T_{5, λ, p}

respectively, where p represents the convergence order of each modified method.

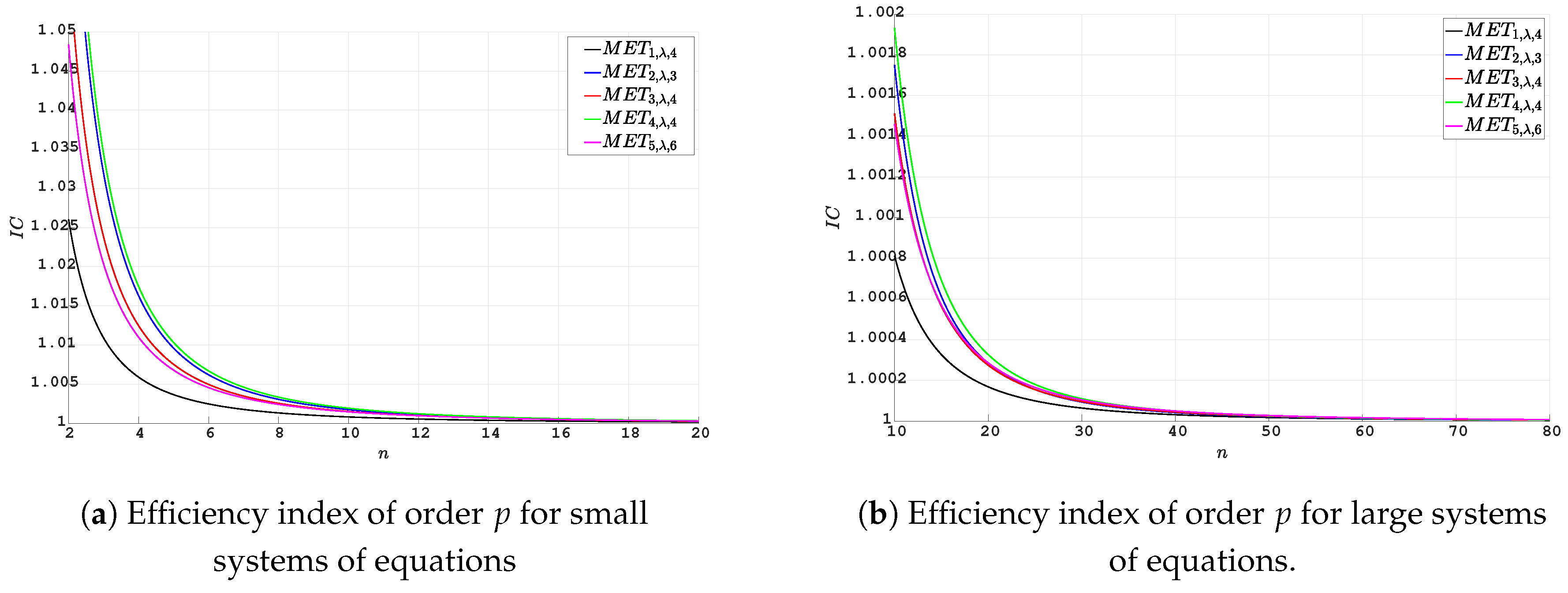
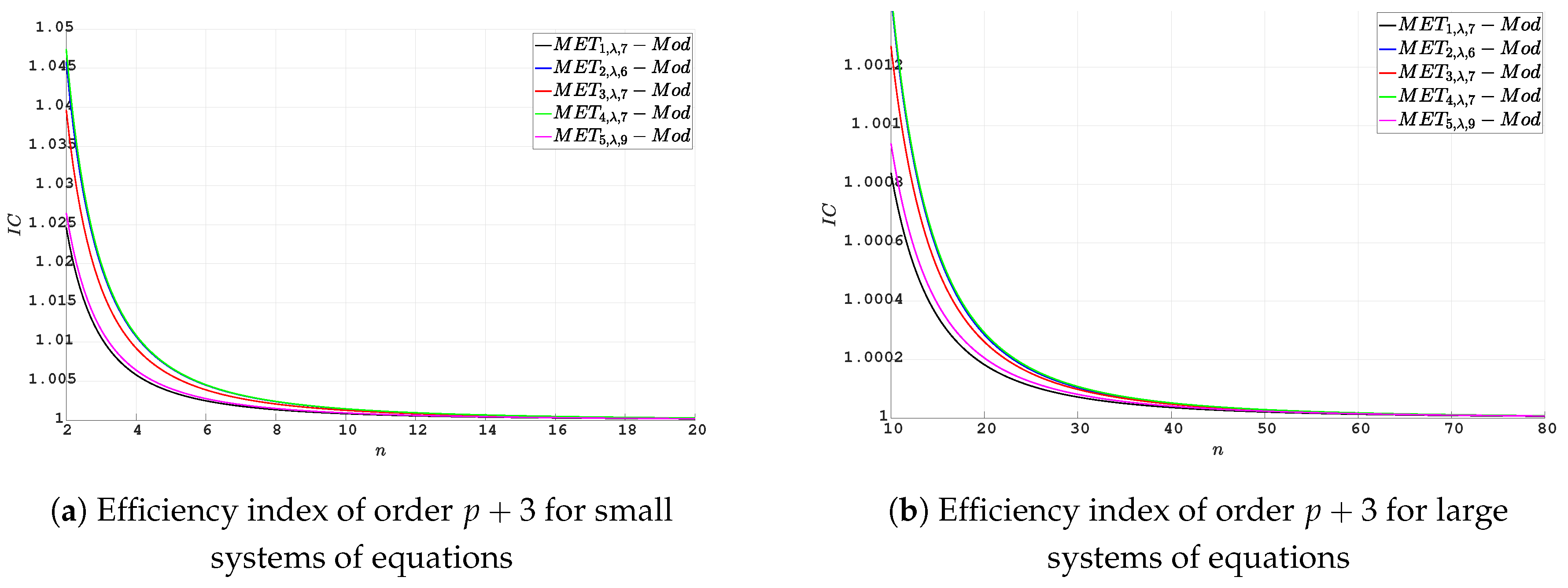
In Figure 1 and Figure 2, we can observe the computational efficiency behavior of our technique, both for the methods

M E T_{1, λ, p}

through

M E T_{5, λ, p}

and for the modified methods by incorporating our third step when applied to small and large systems.

3.2. Some academical problems

Example 1.

The first case we present is a system of equations of size

n = 20

(2 x_{j}^{2} + 1) - 2 (\sum_{m = 1}^{20} x_{m}^{2}) + arctan x_{j} = 0, j = 1, 2, \dots n .

(1)

The solution of system (1) is given by

ξ \approx {(0.175768, \dots, 0.175768)}^{T}

and the initial estimate used is

x^{(0)} = {(\frac{1}{2}, \frac{1}{2}, \dots, \frac{1}{2})}^{T}

Example 2.

The second case presented is a system of size

n = 30

x_{j} - cos (2 x_{j} - \sum_{m = 1}^{30} x_{m}) = 0, j = 1, 2, \dots, n .

(2)

The solution of system (2) is

ξ \approx {(0.486743, \dots, 0.486743)}^{T}

and the initial estimate used is

x^{(0)} = {(\frac{1}{2}, \frac{1}{2} \dots, \frac{1}{2})}^{T}

Example 3.

The third case presented is a system of size

n = 30

\begin{matrix} \{\begin{matrix} x_{j}^{2} x_{j + 1} - 1 & = & 0 j = 1, 2, \dots, n - 1; \\ x_{n}^{2} x_{1} - 1 & = & 0, \end{matrix} \end{matrix}

(3)

whose the exact solution is

ξ = {(1, 1, \dots, 1)}^{T}

, and initial estimate is

x^{(0)} = {(\frac{3}{2}, \frac{3}{2}, \dots, \frac{3}{2})}^{T}

Example 4.

The fourth system presented has size

n = 40

, the expression representing this system is given by:

\begin{matrix} \{\begin{matrix} x_{j} x_{j + 1} - 1 & = & 0, j = 1, 2, \dots, n - 1, \\ x_{n} x_{1} - 1 & = & 0 . \end{matrix} \end{matrix}

(4)

The exact solution of the system (4) is

ξ = {(1, 1, \dots, 1)}^{T}

, for which we use the initial estimate

x^{(0)} = {(\frac{3}{2}, \frac{3}{2}, \dots, \frac{3}{2})}^{T}

Example 5.

Finally, we consider the system

\begin{matrix} \{\begin{matrix} x_{j} sin (x_{j + 1}) - 1 & = & 0, j = 1, 2, \dots, n - 1, \\ x_{n} sin (x_{1}) - 1 & = & 0 . \end{matrix} \end{matrix}

(5)

A system of size

n = 40

, and we select the initial estimation

x^{(0)} = {(\frac{3}{4}, \frac{3}{4}, \dots, \frac{3}{4})}^{T}

to approximate the solution

ξ \approx {(1.1141, 1.1141 \dots, 1.1141)}^{T} .

The Table 2, Table 3, Table 4, Table 5 and Table 6 provide strong confirmation of our theoretical findings as the application of the proposed scheme to each class yielded a convergence order of

p + 3

. Remarkably, the

M E T_{2, λ}

class exhibited outstanding efficiency, particularly in terms of computational time, when compared to alternative approaches that do not utilize Jacobian matrices. This observation reinforces the practical viability of our technique and its potential to significantly accelerate numerical computations, supporting its relevance in academic problem-solving.

3.3. Application of the finite difference method on a model of nutrient diffusion in a biological substrate

Now, we focus on the detailed study of a nonlinear elliptic initial value and contour problem, which has been previously treated in [18]. To enrich and improve the analysis, we have introduced an additional term in the equation, namely

| u |

, which makes the problem non-differentiable.The proposed partial differential equation has the ability to model a wide range of nonlinear phenomena in physical, chemical and biological systems.

In the following, we delve into an applied problem concerning the modeling of nutrient diffusion in a biological substrate. We will state the problem and discuss the potential implications that solving it could have for researchers in various fields and for farmers, as well as the interpretation of its solution.

In the context of agriculture and biotechnology, let us consider a two-dimensional biological substrate that represents a cultivation area or a growth medium for microorganisms. We aim to understand how nutrients diffuse and distribute within this substrate, impacting the growth and health of the organisms present,

\begin{matrix} \{\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} = u {(x, y)}^{3} + | u (x, y) |, with Ω = \{(x, y) \in R^{2} : x, y \in [0, 1]\}, \\ u (x, 0) = 2 x^{2} - x + 1, u (x, 1) = 2, 0 \leq x \leq 1, \\ u (0, y) = 2 y^{2} - y + 1, u (1, y) = 2, 0 \leq y \leq 1 . \end{matrix} \end{matrix}

(6)

In this scenario,

u (x, y)

represents the concentration of nutrients at each point

(x, y)

within the substrate. The equation reflects how nutrients diffuse within the substrate, while the term

u {(x, y)}^{3} + | u (x, y) |

incorporates the interaction between nutrient concentration and the biochemical processes present in the substrate.

The boundary conditions are derived from the conditions at the edges of the cultivation area. The conditions at the lateral edges (

x = 0

and

x = 1

) could reflect the initial nutrient concentration or the constant input of nutrients into the substrate. The conditions at the upper and lower edges (

y = 0

and

y = 1

) could represent nutrient absorption by plant roots or interaction with microorganisms on the surface.

Solving this problem would enable researchers and farmers to understand how nutrients are distributed within the substrate and how they impact the growth and health of the organisms present, providing valuable insights for optimizing agricultural practices and enhancing biological yields.

As an illustrative example, we solve this equation for a small system, employing a block-wise approach to represent it as follows.

We create a mesh for discretizing the problem

h = \frac{1}{n + 1}

k = \frac{1}{m + 1}

, we have the mesh point

(x_{i}, y_{j})

with

x_{i} = i h

i = 0, \dots, n + 1

and

y_{i} = j k

j = 0, \dots, m + 1,

such that :

u_{x x} (x_{i}, y_{j}) + u_{y y} (x_{i}, y_{j}) = u {(x_{i}, y_{j})}^{3} + |u (x_{i}, y_{j})|,

So, by approximating the partial derivatives by central divided differences, we have

\frac{u (x_{i + 1}, y_{j}) - 2 u (x_{i}, y_{j}) + u (x_{i - 1}, y_{j})}{h^{2}} + \frac{u (x_{i}, y_{j + 1}) - 2 u (x_{i}, y_{j}) + u (x_{i}, y_{j - 1})}{k^{2}} = u {(x_{i}, y_{j})}^{3} + | u (x_{i}, y_{j}) |,

for

i = 1, \dots, n and j = 1, \dots, m .

Now, we denote

u (x_{i}, y_{j}) = u_{i, j}

simplifying the notation we obtain:

2 (λ^{2} + 1) u_{i, j} - λ^{2} (u_{i, j + 1} + λ^{2} u_{i, j - 1}) - (u_{i + 1, j} + u_{i - 1, j}) + h^{2} (u_{i j}^{3} + |u_{i j}|) = 0,

(7)

with

λ = \frac{h}{k},

i = 1, \dots, n

and

j = 1, \dots, m .

The equations (7) together with the boundary and initial conditions form a nonlinear system of size

(n m) \times (n m)

given by:

τ u (x, y) + h^{2} ν (u (x, y)) = W,

where

τ = (\begin{matrix} A & B & 0 & \dots & 0 \\ B & A & B & ⋱ & ⋮ \\ 0 & ⋱ & ⋱ & ⋱ & 0 \\ ⋮ & ⋱ & ⋱ & ⋱ & B \\ 0 & \dots & 0 & B & A \end{matrix}), A = (\begin{matrix} 2 (λ^{2} + 1) & - 1 & 0 & \dots & 0 \\ - 1 & 2 (λ^{2} + 1) & - 1 & ⋱ & ⋮ \\ 0 & ⋱ & ⋱ & ⋱ & 0 \\ ⋮ & ⋱ & ⋱ & ⋱ & - 1 \\ 0 & \dots & 0 & - 1 & 2 (λ^{2} + 1) \end{matrix}),

B = - λ^{2} \cdot I_{n \times n}, u = {(u_{1}, \dots, u_{d})}^{T}, ν (u) = {(u_{1}^{3}, \dots, u_{d}^{3})}^{T} + {(|u_{1}|, \dots, |u_{d}|)}^{T},

with

d = n m

. in addition, W denotes a vector containing the boundary conditions. We can set the nonlinear system as follows,

P (u) = τ u (x, y) + h^{2} v (u (x, y)) - W = 0 .

(8)

Let us define the differentiable part as

F (u) = h^{2} (u_{1}, \dots, u_{d}) + h^{2} {(u_{1}^{3}, \dots, u_{d}^{3})}^{T} - W

, and the non-differentiable part as

G (u) = h^{2} {(|u_{1}|, \dots, |u_{d}|)}^{T}

, so that the equation

F (u) + G (u) = 0

holds.

To solve the equation (8), we employ the iterative method

M E T_{2, λ, 6} - M o d

. We generate an initial approximation

u^{(0)} = (1, 1, \dots, 1)

of the exact solution

u (x, y)

. During the execution of the iterative process, we use variable precision arithmetics with a precision of 100 digits. We define the stopping criterion as the difference between two consecutive iterations, such that

∥u^{(n + 1)} - u^{(n)}∥ < 10^{- 8}

and also

∥P (u^{(k)})∥ \leq 10^{- 8}

. The technical specifications of the computer used to solve this case are identical to those employed in solving academical problems. In this instance, we select

n = m = 25

Solving the system associated with this PDE, we write the solution of the system represented in the following matrix.

\begin{matrix} u (x_{i}, y_{j}) = (\begin{matrix} 1 & 0.96449704 & \dots & 0.911242 & 0.89349112 & \dots & 1.78106509 & 1.88757396 & 2 \\ 0.96449704 & 0.94077958 & \dots & 0.89904994 & 0.88363618 & \dots & 1.18118983 & 0.86468611 & 2 \\ 0.93491124 & 0.91837384 & \dots & 0.8853521 & 0.87175486 & \dots & 0.80447293 & 0.49872502 & 2 \\ 0.9112426 & 0.89904994 & \dots & 0.87168096 & 0.85914444 & \dots & 0.57490717 & 0.3266623 & 2 \\ 0.89349112 & 0.88363618 & \dots & 0.85914444 & 0.8468333 & \dots & 0.43058144 & 0.23355179 & 2 \\ 0.8816568 & 0.87257659 & \dots & 0.84851767 & 0.83559769 & \dots & 0.33553995 & 0.17732774 & 2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0.93491124 & 0.90648025 & \dots & 0.84363755 & 0.8109766 & \dots & 0.1225449 & 0.06200892 & 2 \\ 0.96449704 & 0.9290334 & \dots & 0.85300742 & 0.81435483 & \dots & 0.10830767 & 0.05468412 & 2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 1.49704142 & 1.27264469 & \dots & 0.89476719 & 0.75181019 & \dots & 0.03252994 & 0.01627615 & 2 \\ 1.58579882 & 1.29317295 & \dots & 0.83884556 & 0.68304563 & \dots & 0.02596847 & 0.012988 & 2 \\ 1.68047337 & 1.27872037 & \dots & 0.73904355 & 0.5790819 & \dots & 0.01945358 & 0.00972662 & 2 \\ 1.78106509 & 1.18118983 & \dots & 0.57490717 & 0.43058144 & \dots & 0.01296163 & 0.00647928 & 2 \\ 1.88757396 & 0.86468611 & \dots & 0.3266623 & 0.23355179 & \dots & 0.00647928 & 0.00323844 & 2 \\ 2 & 2 & \dots & 2 & 2 & \dots & 2 & 2 & 2 \end{matrix}), \end{matrix}

After 3 iterations, the obtained solution satisfies

∥u^{(3)} - u^{(2)}∥ < 5.34 \times 10^{- 5}

, and the norm of the nonlinear operator

P (u)

evaluated at the last iteration is such that

∥P (u^{(3)})∥ \leq 7.035 e \times 10^{- 34}

. The approximate solution in

R^{625}

, resized to a

25 \times 25

matrix for

i, j = 1, \dots, 25

, and then embedded in the solution matrix within the grid bounded by the boundary conditions, is presented in the matrix above.

We can affirm that the values

u (x_{i}, y_{j})

obtained fall within the range

0 < u (x_{i}, y_{j}) < 1.3

. In the context of the posed problem, involving the diffusion of nutrients in a two-dimensional biological substrate, these observations take on fundamental significance. The concentration of nutrients

u (x_{i}, y_{j})

demonstrates a trend in which values are bounded between 0 and

1.3

. This limitation in concentration implies a biological equilibrium in the system, where absorption, diffusion, and biochemical reactions harmonize. This characteristic suggests that the system is stable and well-regulated in terms of nutrient availability.

The coherence between the obtained values and the initial and boundary conditions of the problem reinforces the validity of the solution. This indicates that the nutrient distribution aligns with the influences of the boundary conditions, thus supporting the biological interpretation of the model.

The influence of the differential equation

u {(x, y)}^{3} + | u (x, y) |

is reflected in the limited concentration range. This implies that biochemical interactions between nutrients and present species are influencing nutrient distribution in the substrate.

In summary, the observation that the internal values of the solution matrix

u (x_{i}, y_{j})

lie within the range 0 to

1.3

suggests a balanced, stable, and regulated biological system in terms of nutrient concentration. The alignment with the conditions of the problem and the influence of biochemical interactions endorse the validity of the obtained results and their interpretation in the context of agriculture and biotechnology.

4. Conclusions

In this paper, we have presented an innovative proposal that shows an ability to increase the order of convergence from p to

p + 3

, without relying on Jacobian matrices. Our validation is solidly supported by consistently obtaining this three-unit increase, as evidenced in various academic problems. This approach has generated equally significant results, translating into an increase of the order of convergence by

p + 3

units in each of the iterative classes we use to perform our numerical tests as we already assumed. Finally, we have successfully tackled the resolution of a problem modeled by a nonlinear partial differential equation describing the phenomenon of nutrient diffusion in a biological substrate.

Author Contributions

Conceptualization, A.C.; methodology, M.P.V.; software, M.A.L.; validation, J.R.T; formal analysis, M.A.L.; writing—original draft preparation, M.A.L.; writing—review and editing, A.C., J.R.T., M.P.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

Samanskii, V. On a modification of the Newton method. Ukrainian Mathematical Journal 1967, 19, 133–138. [Google Scholar]
Ortega, J.M.; Rheinboldt, W.C. Iterative solution of nonlinear equations in several variables; SIAM, 2000. [Google Scholar]
Cordero, A.; Garrido, N.; Torregrosa, J.R.; Triguero-Navarro, P. Design of iterative methods with memory for solving nonlinear systems. Mathematical Methods in the Applied Sciences 2022. [Google Scholar] [CrossRef]
Amiri, A.; Cordero, A.; Darvishi, M.T.; Torregrosa, J.R. Preserving the order of convergence: Low-complexity Jacobian-free iterative schemes for solving nonlinear systems. Journal of Computational and Applied Mathematics 2018, 337, 87–97. [Google Scholar] [CrossRef]
Cordero, A.; Torregrosa, J.R. Low-complexity root-finding iteration functions with no derivatives of any order of convergence. Journal of Computational and Applied Mathematics 2015, 275, 502–515. [Google Scholar] [CrossRef]
Džunić, J. On efficient two-parameter methods for solving nonlinear equations. Numerical algorithms 2013, 63, 549–569. [Google Scholar] [CrossRef]
Soleymani, F. An optimally convergent three-step class of derivative-free methods. World Applied Sciences Journal 2011, 13, 2515–2521. [Google Scholar]
Lotfi, T.; Tavakoli, E.; others. On a new efficient Steffensen-like iterative class by applying a suitable self-accelerator parameter. The Scientific World Journal 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Applied Mathematics and Computation 2007, 190, 686–698. [Google Scholar] [CrossRef]
Ostrowski, A. Solution of equations and systems of equations; Acad. Press: New York, 1966. [Google Scholar]
Traub, J.F. Iterative methods for the solution of equations. American Mathematical Soc. 1982, 312. [Google Scholar] [CrossRef]
Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. A modified Newton-Jarratt’s composition. Numerical Algorithms 2010, 55, 87–99. [Google Scholar] [CrossRef]
Cordero, A.; Leonardo Sepúlveda, M.A.; Torregrosa, J.R. Dynamics and Stability on a Family of Optimal Fourth-Order Iterative Methods. Algorithms 2022, 15, 387. [Google Scholar] [CrossRef]
Traub, J. Iterative Methods for the Solution of Equations. Prentice-Hall.: Englewood Cliffs, New Jersey, 1964. [Google Scholar]
Chun, C. Construction of Newton-like iterative methods for solving nonlinear equations. Numer. Math 2006, 104, 297–315. [Google Scholar] [CrossRef]
Grau-Sánchez, M.; Grau, Á.; Noguera, M. Ostrowski type methods for solving systems of nonlinear equations. Applied Mathematics and Computation 2011, 218, 2377–2385. [Google Scholar] [CrossRef]
Cordero, A.G.; Maimó, J.; Rodríguez-Cabral, A.; Torregrosa, J.R. Convergence and Stability of a New Parametric Class of Iterative Processes for Nonlinear Systems. Algorithms 2023, 16, 163. [Google Scholar] [CrossRef]
Villalba, E.G.; Hernandez, M.; Hueso, J.L.; Martínez, E. Using decomposition of the nonlinear operator for solving non-differentiable problems. Mathematical Methods in the Applied Sciences 2022. [Google Scholar] [CrossRef]

Figure 1. Efficiency index for methods of order p.

Figure 2. Efficiency index for methods of order

p + 3

Figure 2. Efficiency index for methods of order

p + 3

Table 1. Computational efficiency index of order p and

p + 3

Table 1. Computational efficiency index of order p and

p + 3

Original methods
Scheme	C. Order	d	Op	CI
$M E T_{1, λ, 4}$	4	$2 n^{2} - 2 n$	$\frac{1}{3} n^{3} + 12 n^{2} - \frac{1}{3} n$	$4^{1 / ((1 / 3) n^{3} + 14 n^{2} - (7 / 3) n)}$
$M E T_{2, λ, 3}$	3	$n^{2}$	$\frac{1}{3} n^{3} + 2 n^{2} - \frac{1}{3} n$	$3^{1 / ((1 / 3) n^{3} + 3 n^{2} - (1 / 3) n)}$
$M E T_{3, λ, 4}$	4	$2 n^{2} - n$	$\frac{1}{3} n^{3} + 4 n^{2} - \frac{1}{3} n$	$4^{1 / ((1 / 3) n^{3} + 6 n^{2} - (4 / 3) n)}$
$M E T_{4, λ, 4}$	4	$2 n^{2} - n$	$\frac{1}{3} n^{3} + 2 n^{2} - \frac{1}{3} n$	$4^{1 / ((1 / 3) n^{3} + 4 n^{2} - (4 / 3) n)}$
$M E T_{5, λ, 6}$	6	$2 n^{2}$	$\frac{1}{3} n^{3} + 6 n^{2} - \frac{1}{3} n$	$6^{1 / ((1 / 3) n^{3} + 9 n^{2} - (1 / 3) n)}$
Schemes with modified order
$M E T_{1, λ, 7} - M o d$	7	$2 n^{2} - n$	$\frac{1}{3} n^{3} + 18 n^{2} - \frac{1}{3} n$	$7^{1 / ((1 / 3) n^{3} + 20 n^{2} - (4 / 3) n)}$
$M E T_{2, λ, 6} - M o d$	6	$n^{2} + n$	$\frac{1}{3} n^{3} + 8 n^{2} - \frac{1}{3} n$	$6^{1 / ((1 / 3) n^{3} + 9 n^{2} + (2 / 3) n)}$
$M E T_{3, λ, 7} - M o d$	7	$2 n^{2}$	$\frac{1}{3} n^{3} + 10 n^{2} - \frac{1}{3} n$	$7^{1 / ((1 / 3) n^{3} + 12 n^{2} - (1 / 3) n)}$
$M E T_{4, λ, 7} - M o d$	7	$2 n^{2}$	$\frac{1}{3} n^{3} + 8 n^{2} - \frac{1}{3} n$	$7^{1 / ((1 / 3) n^{3} + 10 n^{2} - (1 / 3) n)}$
$M E T_{5, λ, 9} - M o d$	9	$2 n^{2} + n$	$\frac{1}{3} n^{3} + 12 n^{2} - \frac{1}{3} n$	$9^{1 / ((1 / 3) n^{3} + 20 n^{2} + (2 / 3) n)}$

Table 2. Numerical results for Example 1.

$x^{(0)}$	Schemes	$∥x^{(k + 1)} - x^{(k)}∥$	$∥F (x^{(k + 1)})∥$	Iter	ACOC	e-time
$[\begin{matrix} \frac{1}{2} \\ ⋮ \\ \frac{1}{2} \end{matrix}]$	${MET}_{1, 0.0001, 7}$	$5.97084 \times 10^{- 9}$	$2.28557 \times 10^{- 56}$	3	7	36.042129
	${MET}_{2, 0.0001, 6}$	$1.49472 \times 10^{- 37}$	$5.57149 \times 10^{- 220}$	4	6	29.970914
	${MET}_{3, 0.0001, 7}$	$6.24761 \times 10^{- 9}$	$3.19194 \times 10^{- 56}$	3	7	35.809333
	${MET}_{4, 0.0001, 7}$	$3.21705 \times 10^{- 11}$	$6.09164 \times 10^{- 73}$	3	7	32.057150
	${MET}_{5, 0.0001, 9}$	$2.59355 \times 10^{- 16}$	$2.57919 \times 10^{- 139}$	3	9	35.072059

Table 3. Numerical results for Example 2.

$x^{(0)}$	Schemes	$∥x^{(k + 1)} - x^{(k)}∥$	$∥F (x^{(k + 1)})∥$	Iter	ACOC	e-time
$[\begin{matrix} \frac{1}{2} \\ ⋮ \\ \frac{1}{2} \end{matrix}]$	${MET}_{1, . 0001, 7}$	$4.79372 \times 10^{- 43}$	$1.05769 \times 10^{- 292}$	3	7	62.517649
	${MET}_{2, 0.0001, 6}$	$4.0445 \times 10^{- 34}$	$1.62857 \times 10^{- 197}$	3	6	41.767678
	${MET}_{3, 0.0001, 7}$	$4.99649 \times 10^{- 43}$	$1.43001 \times 10^{- 292}$	3	7	60.174395
	${MET}_{4, 0.0001, 7}$	$3.79676 \times 10^{- 44}$	$9.34063 \times 10^{- 301}$	3	7	59.730706
	${MET}_{5, 0.0001, 9}$	$8.03053 \times 10^{- 69}$	$1.7569 \times 10^{- 608}$	3	9	61.974947

Table 4. Numerical results for Example 3.

$x^{(0)}$	Schemes	$∥x^{(k + 1)} - x^{(k)}∥$	$∥F (x^{(k + 1)})∥$	Iter	ACOC	e-time
$[\begin{matrix} \frac{3}{2} \\ ⋮ \\ \frac{3}{2} \end{matrix}]$	${MET}_{1, 0.0001, 7}$	$4.29798 \times 10^{- 13}$	$1.74729 \times 10^{- 89}$	3	7	49.968165
	${MET}_{2, 0.0001, 6}$	$7.04681 \times 10^{- 10}$	$1.88785 \times 10^{- 57}$	3	6	33.644034
	${MET}_{3, 0.0001, 7}$	$4.59589 \times 10^{- 13}$	$2.84399 \times 10^{- 89}$	3	7	47.877513
	${MET}_{4, 0.0001, 7}$	$7.00027 \times 10^{- 17}$	$7.71875 \times 10^{- 117}$	3	7	48.574717
	${MET}_{5, 0.0001, 9}$	$3.93811 \times 10^{- 25}$	$4.0315 \times 10^{- 224}$	3	9	47.829303

Table 5. Numerical results for Example 4.

$x^{(0)}$	Schemes	$∥x^{(k + 1)} - x^{(k)}∥$	$∥F (x^{(k + 1)})∥$	Iter	ACOC	e-time
$[\begin{matrix} \frac{3}{2} \\ ⋮ \\ \frac{3}{2} \end{matrix}]$	${MET}_{1, 0.0001, 7}$	$3.42900 \times 10^{- 23}$	$1.73936 \times 10^{- 162}$	3	7	85.570920
	${MET}_{2, 0.0001, 6}$	$2.12985 \times 10^{- 17}$	$1.49899 \times 10^{- 104}$	3	6	56.147216
	${MET}_{3, 0.0001, 7}$	$3.23467 \times 10^{- 23}$	$2.78702 \times 10^{- 162}$	3	7	83.842336
	${MET}_{4, 0.0001, 7}$	$4.28905 \times 10^{- 27}$	$1.69352 \times 10^{- 190}$	3	7	81.009858
	${MET}_{5, 0.0001, 9}$	$6.93376 \times 10^{- 42}$	$8.80969 \times 10^{- 378}$	3	9	81.163539

Table 6. Numerical results for Example 5.

$x^{(0)}$	Schemes	$∥x^{(k + 1)} - x^{(k)}∥$	$∥F (x^{(k + 1)})∥$	Iter	ACOC	e-time
$[\begin{matrix} \frac{3}{4} \\ ⋮ \\ \frac{3}{4} \end{matrix}]$	${MET}_{1, 0.0001, 7}$	$6.85093 \times 10^{- 36}$	$4.40923 \times 10^{- 255}$	3	7	88.183026
	${MET}_{2, 0.0001, 6}$	$7.36696 \times 10^{- 31}$	$1.36910 \times 10^{- 189}$	3	6	57.656010
	${MET}_{3, 0.0001, 7}$	$7.34097 \times 10^{- 36}$	$7.15417 \times 10^{- 255}$	3	7	84.166798
	${MET}_{4, 0.0001, 7}$	$2.15009 \times 10^{- 37}$	$1.29829 \times 10^{- 265}$	3	7	82.999383
	${MET}_{5, 0.0001, 9}$	$3.52145 \times 10^{- 57}$	$4.99971 \times 10^{- 519}$	3	9	83.408546

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Enhancing the Convergence Order from p to p+3 in Iterative Methods for Solving Nonlinear Systems of Equations without the Use of Jacobian Matrices

Abstract

1. Introduction

1.1. Preliminary concepts

2. Main Result

3. Numerical results

3.1. Computational Efficiency

3.2. Some academical problems

3.3. Application of the finite difference method on a model of nutrient diffusion in a biological substrate

4. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe