Prerpints.org logo
Preprint
Article

Bipartisan/Range Voting in Two Rounds Reaches a Promising Balance between Efficiency and Strategy-Resistance

Altmetrics

Downloads

117

Views

30

Comments

0

This version is not peer-reviewed

Submitted:

05 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts
Abstract
In the quest to develop a more effective and representative electoral system that offers a higher global satisfaction while also resisting strategic voting, this paper introduces the Bipartisan/Range method. This electoral system operates in two separate rounds: a first round where voters rank candidates, and if no Condorcet winner emerges, a second round where voters score candidates within a small head set known as the bipartisan set. The proposed method takes inspiration from randomized Condorcet voting system, probably the most strategy-resistant Condorcet methods, but eliminates the non-determinism while improving efficiency in the case of paradoxes. By introducing an unpredictable second round spaced in time and prohibiting predictive surveys, voters face difficulties in anticipating paradoxes, and insincere votes carry inherent risks. Furthermore, the Bipartisan set's limited size mitigates the range voting problem of exaggerated votes. Thus, the method has the potential to be both efficient in reflecting voters' preferences and resistant to strategic voting, exceeding expectations from Arrow's theorem. The method's versatility allows for extensions to multiple candidates, enhancing its applicability across various electoral contexts. Additionally, we have developed BipartiVox, an online platform specifically designed to conduct elections using the Bipartisan/Range method, making it accessible to a wider audience. In conclusion, the Bipartisan/Range method represents a substantial contribution to the field of voting systems, providing a practical, strategy-resistant, and efficient alternative that aligns closely with genuine voter preferences.
Keywords: 
Subject: Social Sciences  -   Decision Sciences

1. Introduction

The design of voting systems is pivotal in shaping the outcomes of elections, which in turn have a profound influence on society. In democratic systems, such as presidential elections or decisions within associations or companies, it is imperative to devise methods that accurately reflect voters’ preferences while curtailing opportunities for strategic manipulation, which can misrepresent collective opinion.
One of the earliest attempts to devise a fair voting method was proposed by Condorcet in the 18th century. He introduced the notion of a Condorcet winner – a choice that is favored over any other by the majority of voters. However, the existence of a Condorcet winner is not always assured, as demonstrated by the Condorcet paradox where the majority prefers x to y, y to z, and z to x. This paradox has spurred the development of several alternative methods to resolve the Condorcet paradox, such as the Schulze method [1], the Tideman method [2] (also known as the "Ranked Pairs" method), the Copeland method [3,4], and the essential set method [5].
The limitations of these methods are underscored by several impossibility theorems, including Arrow’s theorem [6], Campbell and Kelly’s theorem [7], and Gibbard’s theorem [8]. Arrow’s theorem famously posits the impossibility of a "fair" aggregation of individual preferences into a group preference. Campbell and Kelly’s theorem illustrates the impossibility of combining the Condorcet principle with strategy-proofness for deterministic social choice rules that select one or two alternatives. Gibbard’s theorem asserts that a random dictatorship is the only strategy-proof, anonymous, neutral, and unanimous voting system, assuming voters’ preferences comply with the von Neumann and Morgenstern axioms.
In light of these impossibility theorems, it is crucial to develop voting methods that strike a balance between representing voter preferences and minimizing strategic manipulation incentives. The Randomized Condorcet (RC) method [5,9,10], also known as "Essential set" or "Bipartisan Set", is one such approach that abandons determinism to improve resistance to strategic manipulation. This method is primarily a Condorcet method in that if a Condorcet winner exists, it is chosen. However, in the case of a paradox, it introduces randomness in the choice of alternatives, thereby significantly reducing incentives for strategic voting that would aim to create or resolve a paradox for a more favorable outcome. However, this element of randomness can be perceived unfavorably by some voters, and it does not necessarily provide the best possible average satisfaction.
In this paper, we propose a novel approach that combines the advantages of the RC method while addressing voters’ concerns about the use of randomness. Our approach involves implementing organizational or legislative measures, such as conducting a second round of voting and prohibiting opinion polls. These measures can instill a sense of uncertainty in voters during the first round, making the randomness of the RC method more acceptable. In the event that there is no Condorcet winner in the first round, we determine the Bipartisan Set and propose to use normalized range voting [11] within this set. Normalized range voting is a relatively intuitive method already known to the population, quite efficient in these dilemmas, with limited and relatively fair tactical voting possibilities. This two-round method, which can be conventionally named Bipartisan/Range Voting, offers a way to subtly bypass the efficiency/strategy-resistance trade-off imposed on deterministic methods.
This paper first presents the existing methods before introducing the Bipartisan/Range Method. In the final part, we present BipartiVox, an online platform we develop to test the Bipartisan/Range method.

2. Related existing methods and their current limitations

2.1. Voting Methods

Voting systems, or electoral systems, are methods by which voters make a choice between options, often in an election or on a policy referendum. An example is the two-round system (also known as runoff voting) used in French presidential elections. This system is known to have several limitations [12]. For instance, even if a candidate is preferred by a majority of voters over any other candidate, they may not advance to the second round if another candidate with similar views splits the vote.
This system often compels people to vote strategically, instead of by their true preferences. Tactical voting may include casting a useful vote (where a voter insincerely ranks or rates an alternative higher in the hope of getting it elected because their preferred choice has no chance), or burying (where a voter insincerely ranks or rates an alternative lower in the hope of getting it defeated because it has a high chance to win).
Moreover, this system is highly sensitive to cloning [13]: if an alternative B is very similar to another A, but B is not preferred to A by the majority, then B risks splitting the votes of A in the first round, thus reducing A’s chances of advancing to the second round and being elected.
There are many better methods, such as Condorcet methods, Approval voting [14], and Score Then Automatic Runoff (STAR) [15]. Despite their improved efficiency and often better properties of strategic voting resistance, they often have their own limitations, many of which are dictated by various voting impossibility theorems.

2.2. Approval Voting and Range voting

Approval voting is a system where each voter can vote for as many candidates as they like [14]. In other words, they approve or disapprove of each candidate. Each vote counts equally, and the candidate with the most votes or approvals wins. This system is simple and easy to understand. However, it has a potential drawback: a voter who knows the likely outcome from opinion polls and slightly prefers the second-place candidate (on the overall list) B to the first-place candidate A might choose to either (i) insincerely approve B even if they sincerely disapprove both A and B (this is called “compromising”) or (ii) conversely, insincerely disapprove A even if they sincerely approve both A and B (this is called a “bullet voting” for B). However, unlike other systems, this system does not encourage voters to change the order of their preferences: for example, it is immune to push-over (A voter ranks a perceived weak alternative above their preferred candidate, in order to actually elect the preferred candidate and not the weak candidate which is very paradoxal in some voting system) and burying strategies (A voter insincerely ranks an alternative lower in the hopes of defeating it).
A natural extension is range voting (also called normalized score voting), where voters can express partial approval, allowing more freedom of expression for voters. Range voting is a simple method which strikes a good balance between efficiency and resistance to tactical voting. [11] Like approval voting, it allows for bullet voting and compromising, while it is immune to push-over and burying.
The main limitation of range voting could be when there are many candidates and then the consideration of strategic votes is particularly important. For example, if a voter has approximately linear preferences over 6 candidates (i.e., approvals are A:1, B:0.8, C:0.6, D:0.4, E:0.2, F:0) and if the top two candidates on the overall list are B and C, this voter should set A:1, B:1, C:0, D:0, E:0, F:0. In doing so, they have 5 times more influence in electing B over C than if they rated sincerely. With a higher number of candidates, this ratio generally increases, and thus this system can be considered better when the number of alternatives is low.

2.3. Condorcet Methods

In Condorcet methods, voters rank candidates according to their preferences. In most cases, there is a Condorcet winner: a candidate who would prevail in a one-on-one contest against each of the other candidates. However, situations can arise where no Condorcet winner exists due to cyclical preferences among the voters, leading to what is known as a Condorcet paradox. For example, if two voters prefer A≻B≻C, two others prefer B≻C≻A, and one other prefers C≻A≻B. In this case, A is preferred over B (3 votes to 2), B is preferred over C (4 votes to 1), and C is preferred over A (3 votes to 2).
Several methods have been proposed to choose a candidate when a paradox occurs, including the Schulze [1], Tideman [2], Minimax [16], Kemeny-Young [17], Dodgson [18], and Copeland [3,4] methods. Condorcet methods are generally effective and resistant to vote dilution (spread of votes between close candidates, reducing each candidate’s chance of winning). However, in all deterministic methods, there may be an incentive for voters to manipulate their preferences to create or resolve a paradox. Manipulations within the same paradox are also possible.

2.4. Randomized Condorcet Voting Method

The Randomized Condorcet (RC) voting method [5,9,10], also referred to as the essential set or the Bipartisan Set method, is primarily a Condorcet method. If a Condorcet winner exists, they are chosen.
In the event of a paradox, a subset of candidates, known as the Bipartisan Set, is identified. A winner is then be randomly selected from this set according to a specific distribution. This distribution depends solely on the duel graph, irrespective of the margin by which each duel is won. The method for determining the Bipartisan Set and the distribution for each candidate mirrors the one used for the rock-paper-scissors game and its variants with more options. The min-max strategy, which cannot be beaten by an adaptive adversary, is determined. This optimal strategy is a Nash equilibrium. For implementation, the optimal strategy can be obtained through a simplex algorithm in polynomial time [19].
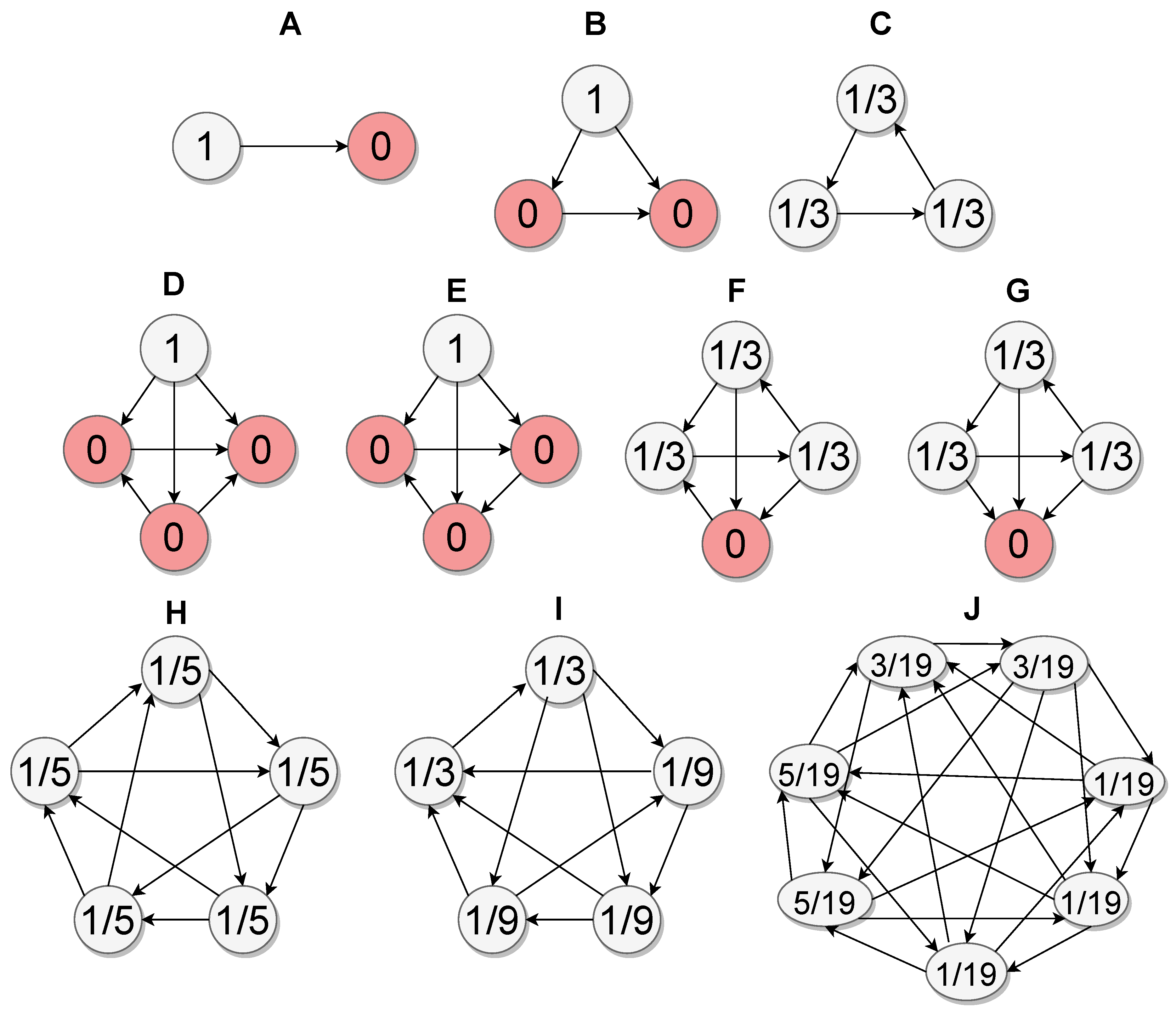
For instance, in the most probable case of a paradox where A≻B, B≻C, and C≻A, and A, B, and C each beat any other candidate in a head-to-head contest, the probabilities would be P A = P B = P C = 1 / 3 . Adding candidate D, who beats C but loses to A and B, there would be no cases where it is better to choose D over B (every duel won by D is also won by B, and B wins against D). Thus, the optimal strategy remains P A = P B = P C = 1 / 3 , and D will not be in the Bipartisan Set. The number of candidates in the set is always odd, and with at least five candidates, it is not necessary for all probabilities in the Bipartisan Set to be equal (e.g., Figure 1).
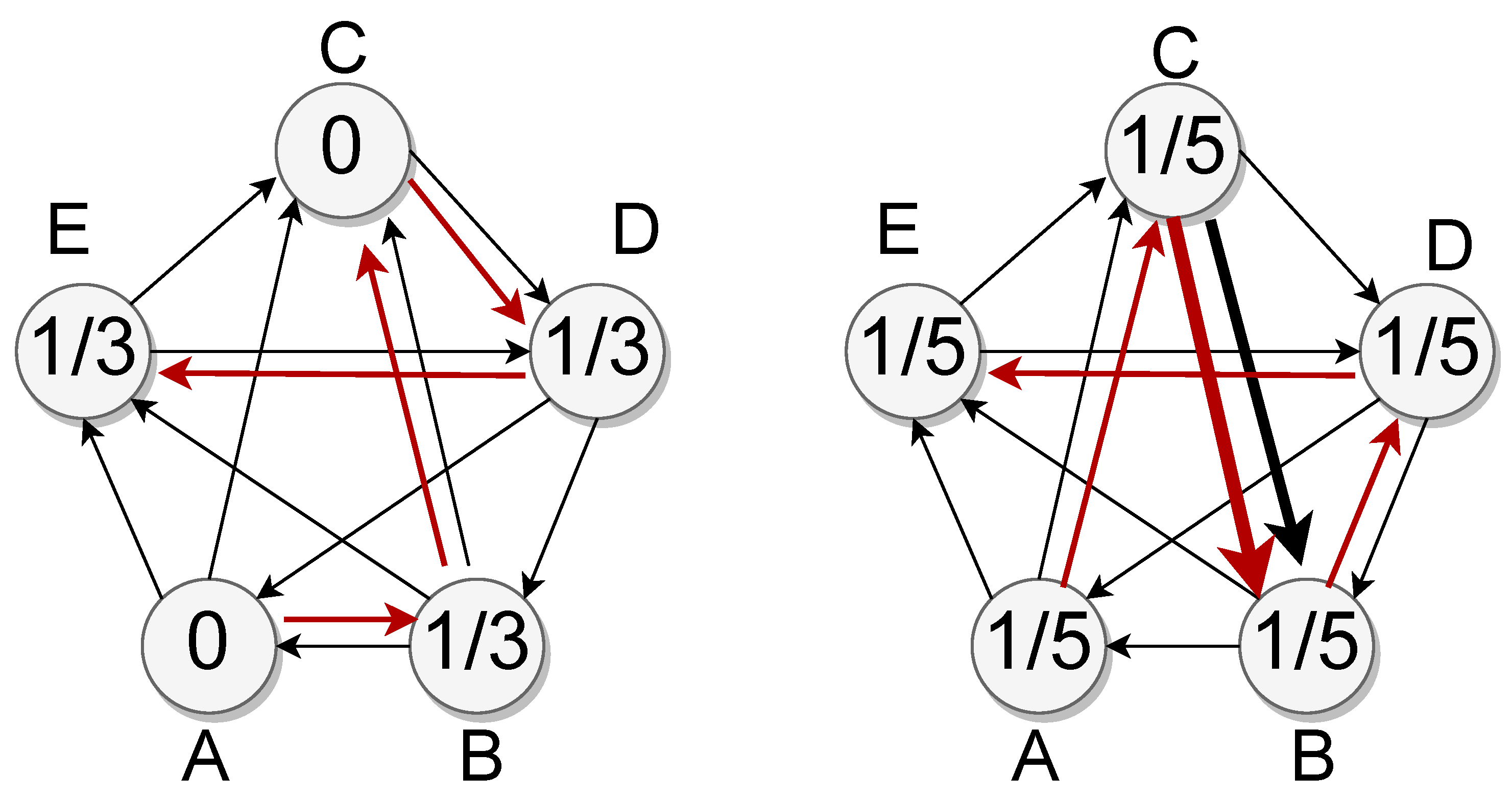
The RC method is considered to be particularly resistant to strategic voting. Lê Nguyên Hoang demonstrated that if we assume that preferences are "linear" (i.e., if a voter E1 prefers A≻B≻C, having B or having the lottery {A,B,C} with a probability of 1/3 is equivalent for them), then the Condorcet winners, if there are any (which is true in the vast majority of cases), will be elected [10]. Under this assumption, there is no incentive to manipulate one’s vote. However, this assumption is not realistic because there can be situations where a voter considers that A is slightly better than B and B is significantly better than C (i.e., the preferences are not linear). In such cases, the resistance to strategic voting falls. Nevertheless, there remains a property that could be qualified as "strategy-risked". If a voter changes their vote, they can obtain a chance of getting a more favorable alternative, but thus also obtain a chance of getting a less favorable alternative. This property remains true regardless of the non-zero probabilities on the Bipartisan Set and is not specific to the probabilities attributed by the RC method. For RC, this property is stronger since if a voter changes their vote, they can obtain a chance of getting a more favorable alternative, but thus also obtain “the same” chance of getting a less favorable alternative.
Moreover, Figure 2 illustrates a case where the RC method is not resistant to strategic voting. This is a complicated case which is a bit unsatisfying intellectually, but it is difficult to imagine that there will be such strategic votes in practice.
There is also one property which is desirable: the independence of clones. If candidate A is an under-clone of B, i.e. each other candidate that A beats is also beaten by B, and B beats A, then there is no interest in "playing" A and thus P A = 0 in the bipartisan strategy. The remaining probabilities will be unchanged compared to the case where A is not present in the graph.
One can note that in voting system theory the definition of independence of clones may vary. Here, we consider an extended definition: a candidate B is a ’clone’ of A if he does not beat any candidate that A already beats, he does not tie any candidate that A already ties or beats, and he his beaten by A.
Another small drawback is that the distribution depends only on the duel graph and not how much a duel is won. In an extreme case, if voters vote A≻B≻C at 49%, B≻C≻A at 2%, and C≻A≻B at 49%, we are in the case of a paradox and therefore the winning lottery is (1/3,1/3,1/3). A is first for 49% of voters and last for only 2% of voters, B is first for 2% of voters and last for 49%. A has the same probability as B even though A beats B with 98%, B beats C with 51%, and C beats A with 51%. Therefore, one might intuitively feel that A deserves a better probability than B or C.
The major drawback is probably the fact that the method is not deterministic. Even if it corresponds to cases where no candidate is truly legitimate, this is probably something that is difficult to be accepted.

2.4.1. Smith set and bipartisan set

A set of Condorcet method can be build if we consider the Smith set (also known as the top cycle) which is defined as the smallest non-empty set of candidates in a particular election such that each member defeats every candidate outside the set in a pairwise election [20]. Voting systems that always elect a candidate from the Smith set pass the Smith criterion and are said to be ’Smith-efficient’. For example, Schulze and Ranked Pairs are Smith efficient. Being Smith efficient implies being a Condorcet method since if there is a Condorcet winner, the Smith set is reduced to this winner.
Any voting method can be made Smith-efficient by first eliminating everyone outside the Smith set and then running the voting method. For example we can define the Smith/IRV [21] by applying Instant Runoff Voting (IRV) on the Smith set. Other examples are Smith/minimax and Smith/range [22]. Such constructed methods also have the desirable property of being independent to irrelevant alternatives since if we add an alternative not pairwise beats anyone, it will not be in the Smith set and the winner will be the same as without these added alternatives.
In this paper we propose to use instead the bipartisan set which is included in the Smith set. Figure 1.F is an example of a Bipartisan set being smaller than the Smith set since the bottom alternative beating the left alternative is in the Smith set but is not in the bipartisan set. Thus any method which is applied to select inside the bipartisan is said to be bipartisan-efficient and is then Smith-efficient and Condorcet-efficient. Advantages are discussed in the next section.

3. The proposed method

3.1. Introduction to Bipartisan/Range Voting

In this paper, we put forward the utilization of Bipartisan/Range Voting. The system is in two rounds. In the first round, voters rank the candidates according to their preference. If a Condorcet winner emerges, the election concludes. However, if a paradox arises, we determine the bipartisan set and proceed to a second round.
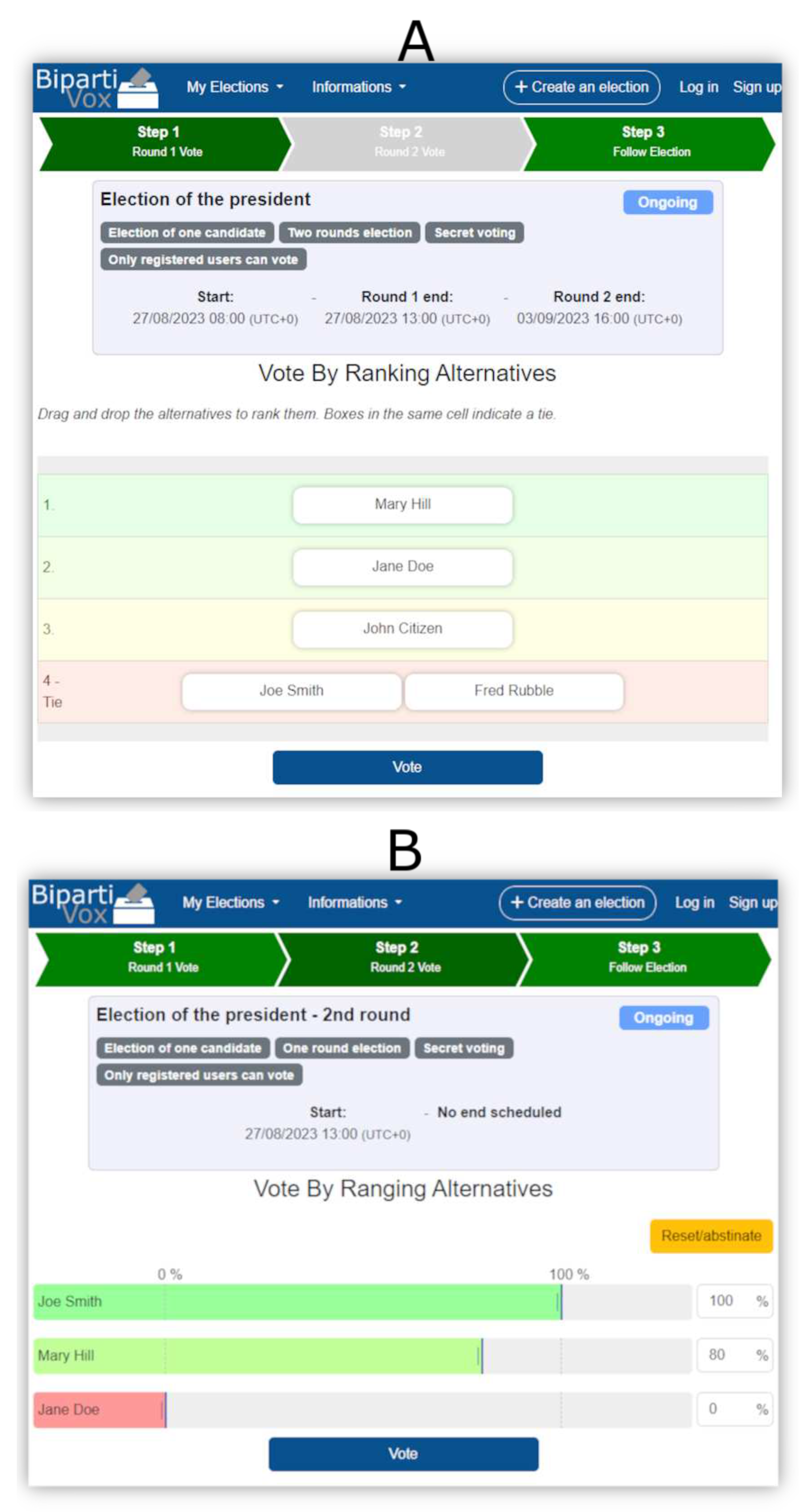
In the second round, contrary to RC where the winner is chosen randomly, we opt to a deterministic solution: voters assign approval percentages for each candidate within that bipartisan set. Ballots are then min-max normalized: the top candidate necessarily has a 100% approval rating, while the least preferred one is necessarily at 0%. Figure 3 showcases the voting ballot for both rounds.

3.2. Second Round: Distinct vs. Instantaneous

In most scenarios, given genuine voter preferences, a Condorcet winner will emerge. However, the cases of paradoxes may be concerning since coordinated actions by a group can provoke a paradox if it provides a more beneficial choice for the group. Thus, the probability of paradox may increase in case of strategic voters. It is essential, therefore, to introduce uncertainty concerning the aftermath of a paradox so that strategic voting becomes risky.
As discussed earlier, the RC method is likely the best solution for introducing this uncertainty. The essence isn’t the actual randomness in the face of a paradox, but the voters’ perception of such randomness.
To fully leverage this method, it is essential to conduct it in two distinct and time-separated rounds, similar to the runoff voting used in many countries. Thus, the perception of unpredictability of the final elected candidate is instilled in voters during the first round, even if the global method is deterministic. Should a voter misrepresent their true feelings in the first round for tactical reasons based on predicting surveys, forecasting the second round’s result with certainty becomes challenging, and thus the first round can be considered as "strategy-risked" (see Section 2.4). For the efficiency of this approach, stringent measures, like banning second-round polling, are recommended. Moreover, the uncertainty about the second round’s result, perceived during the first round, becomes more significant when rounds are spaced out, allowing candidates to campaign in between. This can considerably shift voter preferences, making predictions based on first-round data difficult.
Instantaneous second rounds may be nonetheless possible, for low-stakes election or for elections of several candidates (see Section 3.4). It consists of asking voters to score each alternative at the first round instead of just ranking the alternatives. If there should be a second round, votes of each voter are deduced by min-max normalization of the scores in the bipartisan set. Manipulation remains complex unless accurate predictive surveys are available; nonetheless, we still recommend distinct second round when possible for better strategic resistance.
Another advantage of having two separate rounds is to simplify the ballots. Scoring candidates accurately may be complicated when there are many, particularly due to the min-max normalization in Range voting. For example, initial ratings of A:100% B:99% C:90% D:0% change significantly to A:100% B:91% C:90% D:0%, if the bipartisan set is {A,B,C}, even though the difference may appear small on the global ballot.

3.3. Advantages

As explained earlier, the Bipartisan/Range method has first the advantage of being a Condorcet method. It also has the advantage of being simple even if the bipartisan set on complicated cases is not so obvious. Compared to RC, it has the huge advantage of being deterministic and the first round offers some resistance to tactical voting due to the risk of changing preference order which can lead to adverse outcomes and due to the difficulty to know which paradox could be created.
To speak about the second round, tactical voting methods, such as "bullet voting" and "compromising", remain a concern for range voting. However, such second rounds would typically be rare and in the rare cases it happens, it will be probably limited to three candidates. As explained in Section 2.2, strategies become more significant with more than three candidates. This is one of the reasons the bipartisan set is chosen over the Smith Set: it typically yields the smallest set (the Bipartisan set is included in the Smith Set). Globally, range voting ensures that voters aren’t tempted to change their order of preferences, and with a small number of candidates, the tactics that can be used in the range voting, are less worrisome than those in some other existing systems like push-over and burying strategies.
Every voter who prefers A≻B≻C must question what’s more crucial: having A win, regardless of whether B or C loses, or ensuring C is eliminated at all costs. Without survey knowledge, it’s typically hard to gauge if A stands no chance, and we can assume that the voted approvals will be close to the real preferences. Thus, another advantage of range voting is its efficiency, capturing satisfaction and not just preference.
Lastly, the bipartisan set has the attractive property "Freedom from influence by clones", with the extended definition of clone (Section 2.4). This makes the overall Bipartisan/Range method free from clone influence since clones are eliminated from in the first rounds. Thus, a candidate B close to another candidate A but not preferred to is not incentivized to withdraw its candidacy from the election nor he will not increase the chance of A.

3.4. Extensions of the Bipartisan/Range method

Should the goal of the election not be exclusively to elect one individual but rather to rank or select multiple winners, two natural methodologies can be considered:
  • The n candidates of the bipartisan set are designated as the head set. If this set consists of more than one candidate, they are arranged based on a second round of range voting. Subsequently, these candidates are excluded, and a new bipartisan set is identified from the leftover candidates. This process continues until all candidates are accounted for. This method meshes well with the two-round process since all second-round voting for each bipartisan set can occur concurrently. However, once the first is elected, there may be a Condorcet winner for the second place candidate and it is not necessarily the one that will be chosen with this method. Thus, we suggest the second solution:
  • The primary winner is determined via the entire, two-round bipartisan/range method, and this entire process is reiterated for the second winner, and so on. This can necessitate several second rounds successively, instead of all at the same time and this is not very realistic. In this case it may be better to realize instantaneous second rounds with the process described in section 3.b.
As another extension, both the bipartisan set and range voting systems allow for incomplete voting (i.e. each voter rate only a small part of candidates). Indeed, in elections with a large number of candidates, it’s challenging to require every voter to provide a precise assessment of their preference for each candidate. Nonetheless, if many voters abstain from ranking, the results could be unpredictably biased, possibly not reflecting the majority’s true opinion. A preliminary round using the bipartisan/range method (or potentially another method) could narrow down to a selection of n candidates. Since the operation of determining the bipartisan set is idempotent (i.e. the bipartisan set of the bipartisan set is the bipartisan set), conducting this additional round doesn’t inherently change the usual winner, but it helps mitigate the bias from voters not evaluating certain candidates.

3.5. Limitations and challenges

Like all voting systems, the method isn’t devoid of manipulative possibilities, albeit they are constrained, challenging, and fraught with risks. Introducing a time-spaced second round is a non-mathematical approach to navigate the constraints set by impossibility theorems but some strategic voting remains possible.
Another limitation is that if a majority has a slight preference for Candidate A over B, while a minority strongly favors B over A, this isn’t captured, potentially leading to sub-optimal satisfaction levels.
Lastly, a limitation arises in dynamic ranking scenarios – for instance, continuous updates on a site ranking movies. Once the second round concludes, subsequent voters can more easily manipulate their preferences to a degree to create a favorable Condorcet paradox or to exaggerate their votes if there is a range voting. Indeed they already know the final outcome and the “strategy-risked” property may be lost. Nonetheless, if the graph of duels is not publicly shared, the manipulation of order remains difficult. Thus, the Bipartisan/range remains a possible solution for dynamic ranking.
One can also note that the computation is fast as long as the Smith set is not too important and if it is, the simplex algorithm (Section 3.6) in this form may have difficulty to converge. To have an idea, if the Smith set is 40 candidates and the total number of candidates is 20,000 the computation time is 0.5s on a high-end laptop computer with a Matlab program. Some optimisation should be possible.
This kind of vote can be realized by paper ballot but requires more extensive logistic organization for vote counting. This should not be a problem for electronic voting. However, since electronic voting is still challenging to secure, particularly against coercion, vote buying, targeted reminders, user authentication, malware on personal computers, paper ballots may still be a better solution for large scale elections.
This solution requires that the voters know each candidate if they have to rank them or score them. This is not always the case when there is a long list of candidates and if voters vote too much at random, this risks creating significant paradoxes, potentially causing the method to fail in finding satisfactory results. In this case the traditional approval voting is probably better.
Also if the rank has not so much importance than the score on itself, as an example to rate a video, a method like median voting may be better. Nonetheless, sometimes there can be a mixing in the stakes and the bipartisan/range method may be a good choice to order the firsts options which will be prominently displayed and then use median voting for the remaining options.

3.6. Computation of the Bipartisan Set

The bipartisan set can be determined in polynomial time using the simplex method [10,19]. The main idea to formulate the problem mathematically is to discern a strategy { P i } , ( P i being the probability to play option i) which cannot be beaten by any other strategy. We have thus the constraint P i ≥ 0 , ∑ i P i = 1 and DP ≤ 0 with D the matrix of duels such that:
D i , j = 1 if candidate i wins against candidate j − 1 if candidate i loses against candidate j
It can thus be transformed in an linear optimisation problem solvable by the simplex method from an initial solution P i = 0 , S = 1 , with S being a variable introduced to transform the problem in an optimisation problem.
max ∑ i P i subject to P i ≥ 0 , S ≥ 0 , DP ≤ 0 , S + ∑ i P i ≤ 1
For heightened computation efficiency when dealing with thousands of candidates, one can first compute the smith set based on the described algorithm in [16], and then determine the bipartisan set only within the smith set. We have shared a Matlab program to determine the bipartisan set at https://github.com/utsb-fmm/bipartisan-set-matlab.

4. BipartiVox - an online website to test Bipartisan/Range method

4.1. Presentation

To advocate for this voting method, we have developed a website for conducting elections using the Bipartisan/Range system: BipartiVox available at https://www.bipartivox.com. We tried to provide a modern, responsive and user-friendly interface and we are committed to its continuous improvement. Primarily aimed at small-scale elections, such as associations, class representatives, and enterprise committees, the access is entirely free. Figure 4 displays the ballot interface as seen on a desktop computer.

4.2. Features

Here’s a rundown of the platform’s current features:
  • Ability to conduct an election for a single candidate in two distinct rounds: an initial round to rank candidates (Figure 4.A) and a subsequent round to score them (Figure 4.B).
  • Ability to organize an election for a single candidate with an instantaneous second round, utilizing the scoring candidate ballot and which implements min-max normalization within the bipartisan set if a Condorcet paradox arises in this round.
  • Ability to conduct an election for n>1 candidates, or for ranking candidates using the method described in Section 3.5.ii, paired with an instantaneous second round.
  • Voters can participate using a token sent to their email by the platform (no account creation required). The election manager inputs the voter list.
  • While votes remain confidential, voters can view the list of invitees and participants, with identities censored or pseudonymized (e.g. f*****g.n*****h@gmail.com or a pseudonym specified by the election manager.)
  • Voters can modify their vote anytime before the voting round concludes. An email notification is dispatched with each vote change. Post closure, voters can still view their ballot.
  • Upon the election’s conclusion, voters can inspect the duel matrix including the vote count each candidate receives in every duel. They can also view the Bipartisan set and the average (min-max-normalized) approval each candidate receives within the Bipartisan set (or within each respective Bipartisan set when multiple candidates are elected).
This platform is still in beta testing and may have bugs and vulnerabilities. It does not yet offer end-to-end encryption, and the platform manager has access to the votes (though only for technical reasons, as outlined in the terms and conditions). Also, without a failover server for high availability, it does not yet adhere to several recommended secure electronic voting guidelines. Constructing a secured electronic voting system remains a daunting task. There are unresolved challenges related to non-technical auditability, coercion, vote purchasing, targeted reminders, identity verification, and personal computer malware, among others. Owing to these constraints, we have capped the voter count at 300 per election and we are striving to gradually bolster our security measures.

5. Conclusion

The Bipartisan/Range method introduced in this paper offers a concrete advancement in electoral systems, providing an approach that is both efficient and resistant to strategic voting.
Indeed, the first round ensures that the Condorcet winners are chosen, and having a separate second round creates a risk for voters who attempt strategic voting, potentially leading to a less favorable outcome for them. Remaining possible strategic voting are difficult to elaborate on since they require anticipation of possible Condorcet paradoxes. Therefore, the incentives for strategic voting are highly reduced.
In the second round, in the case of paradoxes, normalized range voting is particularly effective if sincere voting is assumed. Limiting the candidate pool in the second round curtails the impact of exaggerated voting, and the unpredictability of the final outcome also encourages sincere voting.
Other advantages include the fact that the method is deterministic, it remains simple and understandable (except maybe for very rare cases with paradoxes involving more than 3 candidates), and it possesses the attractive property of freedom from influence by clones, using an extended definition of clones.
The method can also be employed when multiple candidates are to be elected, or a general ranking is required. In this case, we recommend an instantaneous second round. The voter scores each candidate, and the ballots for both rounds can then be generated from these scores.
A challenging area for future research is the rating of a large number of options, such as YouTube videos [23]. Current limitations include computation time, stability, sparse vote biases, and dynamic ranking. Additionally, ranking is less meaningful for lower-tier candidates.
We propose the BipartiVox platform, a responsive and free web-based interface, currently in the testing phase, to conduct elections using the Bipartisan/Range method. The platform is user-friendly, responsive, and has a modern interface. We plan further enhancements in security and educational resources, such as explanatory videos.
Among the immediate prospects for BipartiVox is the implementation of a sandbox for (i) easier testing and (ii) simplified organization of secure paper ballots with ease in vote counting. Continuous development, refinement, and assessment of the platform, alongside understanding voters’ and the scientific community’s perceptions, will be crucial in enhancing the method’s applicability and reach.
In conclusion, the Bipartisan/Range method and the BipartiVox platform represent a significant innovation in electoral systems. By fostering genuine voter preferences and offering a reliable, user-friendly platform, they pave the way for a more transparent and representative democratic process.

References

  1. Schulze, M. A New Monotonic, Clone-Independent, Reversal Symmetric, and Condorcet-Consistent Single-Winner Election Method. Soc Choice Welf 2011, 36, 267–303. [Google Scholar] [CrossRef]
  2. Munger, C.T. The Best Condorcet-compatible Election Method: Ranked Pairs. Const Polit Econ 2023, 34, 434–444. [Google Scholar] [CrossRef]
  3. Saari, D.G.; Merlin, V.R. The Copeland Method, I: Relationships and the Dictionary. Econ Theory 1996, 8, 51–76. [Google Scholar] [CrossRef]
  4. Merlin, V.R.; Saari, D.G. Copeland Method II: Manipulation, Monotonicity, and Paradoxes. Journal of Economic Theory 1997, 72, 148–172. [Google Scholar] [CrossRef]
  5. Brandt, F.; Fischer, F. Computing the Minimal Covering Set. Mathematical Social Sciences 2008, 56, 254–268. [Google Scholar] [CrossRef]
  6. Arrow, K.J. Social Choice and Individual Values, third edition ed.; Yale University Press, 2012.
  7. Campbell, D.E.; Kelly, J.S. Incompatibility of Strategy-Proofness and the Condorcet Principle. Social Choice and Welfare 1998, 15, 583–592. [Google Scholar] [CrossRef]
  8. Gibbard, A. Manipulation of Voting Schemes: A General Result. Econometrica 1973, 41, 587–601. [Google Scholar] [CrossRef]
  9. Laffond, G.; Laslier, J.F.; Le Breton, M. The Bipartisan Set of a Tournament Game. Games and Economic Behavior 1993, 5, 182–201. [Google Scholar] [CrossRef]
  10. Lê Nguyên, H. Strategy-Proofness of the Randomized Condorcet Voting System. Social Choice and Welfare 2017, pp. 1–23.
  11. Smith, W.D. Range Voting. Technical report, 2000.
  12. Bouton, L. A Theory of Strategic Voting in Runoff Elections. American Economic Review 2013, 103, 1248–1288. [Google Scholar] [CrossRef]
  13. Tideman, T.N. Independence of Clones as a Criterion for Voting Rules. Soc Choice Welfare 1987, 4, 185–206. [Google Scholar] [CrossRef]
  14. Brams, S.; Fishburn, P.C. Approval Voting. The American Political Science Review 1978, 72, 831–847. [Google Scholar] [CrossRef]
  15. Wolk, S.; Quinn, J.; Ogren, M. STAR Voting, Equality of Voice, and Voter Satisfaction: Considerations for Voting Method Reform. Const Polit Econ 2023, 34, 310–334. [Google Scholar] [CrossRef]
  16. Darlington, R. Are Condorcet and Minimax Voting Systems the Best? 2019.
  17. Young, P. Optimal Voting Rules. Journal of Economic Perspectives 1995, 9, 51–64. [Google Scholar] [CrossRef]
  18. Brandt, F. Some Remarks on Dodgson’s Voting Rule. Mathematical Logic Quarterly 2009, 55, 460–463. [Google Scholar] [CrossRef]
  19. Fisher, D.C.; Ryan, J. Optimal Strategies for a Generalized" Scissors, Paper, and Stone" Game. American Mathematical Monthly 1992, pp. 935–942.
  20. Smith, J.H. Aggregation of Preferences with Variable Electorate. Econometrica 1973, 41, 1027–1041. [Google Scholar] [CrossRef]
  21. Woodall, D.R. Monotonicity of Single-Seat Preferential Election Rules. Discrete Applied Mathematics 1997, 77, 81–98. [Google Scholar] [CrossRef]
  22. Electowiki. Smith//Score. Available online: https://electowiki.org/wiki/Smith//Score.
  23. Hoang, L.N.; Faucon, L.; Jungo, A.; Volodin, S.; Papuc, D.; Liossatos, O.; Crulis, B.; Tighanimine, M.; Constantin, I.; Kucherenko, A.; et al. Tournesol: A Quest for a Large, Secure and Trustworthy Database of Reliable Human Judgments, 2021. arXiv:2107.07334. [CrossRef]
Preprints 84346 g001
Figure 1. Examples of graphs of duels with the associated distribution given by the randomized Condorcet method. An arrow from candidate C1 to candidate C2 indicates that C1 defeats C2 in a head-to-head duel. The probability of each candidate winning in the optimal lottery is indicated in each circle. The red candidates have probabilities of zeros and are thus outside the bipartisan set. On graphs A, B, D, E, there is a Condorcet winner. C is the simplest possible paradox with 3 alternatives. On G, an irrelevant alternative is added to C which does not change the distribution. On F, the bottom candidate can be considered as a clone of the top and thus it has a zero probability. H, I, J are some more complicated cases. One can check that for each alternative A the sum of probabilities of alternatives that beat A is inferior or equal to the sum of probabilities of alternatives beaten by A.
Figure 1. Examples of graphs of duels with the associated distribution given by the randomized Condorcet method. An arrow from candidate C1 to candidate C2 indicates that C1 defeats C2 in a head-to-head duel. The probability of each candidate winning in the optimal lottery is indicated in each circle. The red candidates have probabilities of zeros and are thus outside the bipartisan set. On graphs A, B, D, E, there is a Condorcet winner. C is the simplest possible paradox with 3 alternatives. On G, an irrelevant alternative is added to C which does not change the distribution. On F, the bottom candidate can be considered as a clone of the top and thus it has a zero probability. H, I, J are some more complicated cases. One can check that for each alternative A the sum of probabilities of alternatives that beat A is inferior or equal to the sum of probabilities of alternatives beaten by A.
Preprints 84346 g001
Preprints 84346 g002
Figure 2. Example of a case where there is no Condorcet winner and, with the randomized Condorcet method, a voter has an incentive to insincerely change its order of preferences. The voter prefers A≻B≻C≻D≻E (indicated by red arrows in the left graph) and the expected winning lottery is P B = P D = P E = 1 / 3 . By altering its ballot to A≻C≻B≻D≻E (indicated by red arrows in the right graph), he can reach a more favorable lottery P A = P B = P C = P D = P E = 1 / 5 .
Figure 2. Example of a case where there is no Condorcet winner and, with the randomized Condorcet method, a voter has an incentive to insincerely change its order of preferences. The voter prefers A≻B≻C≻D≻E (indicated by red arrows in the left graph) and the expected winning lottery is P B = P D = P E = 1 / 3 . By altering its ballot to A≻C≻B≻D≻E (indicated by red arrows in the right graph), he can reach a more favorable lottery P A = P B = P C = P D = P E = 1 / 5 .
Preprints 84346 g002
Preprints 84346 g003
Figure 3. Example of ballots for the two rounds: A. The ballot for the rank voting in the the first round; B. the ballot for the range voting in the second round.
Figure 3. Example of ballots for the two rounds: A. The ballot for the rank voting in the the first round; B. the ballot for the range voting in the second round.
Preprints 84346 g003
Preprints 84346 g004
Figure 4. Screenshots of BipartiVox’s two ballot pages: (a) the rank candidate ballot where users can drag and drop candidates into positions, and (b) the score candidate ballot.
Figure 4. Screenshots of BipartiVox’s two ballot pages: (a) the rank candidate ballot where users can drag and drop candidates into positions, and (b) the score candidate ballot.
Preprints 84346 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated