The Structure of Semiconic Idempotent Commutative Residuated Lattices

Preprint

Article

The Structure of Semiconic Idempotent Commutative Residuated Lattices

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Wei Chen^*

This version is not peer-reviewed

Submitted:

04 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts

Abstract

In this paper, we study semiconic idempotent commutative residuated lattices. After giving some properties of such residuated lattices, we obtain a structure theorem for semiconic idempotent com- mutative residuated lattices. As an application, we make use of the structure theorem to prove that the variety of strongly semiconic idempotent commutative residuated lattices has the amalgamation property.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Introduction

A commutative residuated lattice is defined as an algebra

(L, \land, \lor, \cdot, \to, e)

of type

(2, 2, 2, 2, 0)

satisfying the following conditions:

(R L 1)

(L, \land, \lor)

is a lattice;

(R L 2)

(L, \cdot, e)

is a commutative monoid with identity e; and

(R L 3)

(\forall x, y, z \in L) x \cdot y \leq z ⟺ y \leq x \to z

, where ≤ is the lattice ordering.

Some time, commutative residuated lattices are also called commutative residuated lattice-ordered monoids and abbreviated by CRLs. It is well known that

(R L 3)

holds if and only if ≤ is compatible with · and for all

a, b \in L,

{p \in L : a \cdot p \leq b}

contains a greatest element (denoted by

a \to b)

A CRL

L

is called idempotent if for all

a \in L

a \cdot a = a

; is called integral if for all

a \in L

a \leq e

; is called totally ordered if for all

a, b \in L

a \leq b

a \geq b

; is called semilinear when it is a subdirect product of totally ordered CRLs; is called conic if for all

a \in L

a \leq e

a \geq e

(see [4,9,12]). A semilinear idempotent CRL is said to be an odd Sugihara monoid if for all

a \in L

(a \to e) \to e = a

. An integral idempotent CRL is said to be a Brouwerian algebra if for all

a, b \in L

a b = a \land b

. As in [12], a CRL

L

is called semiconic when it is a subdirect product of conic CRLs.

Idempotent CRLs form an important tool both in algebra and logic ( see [10]). Among them, semiconic ones make a valuable contribution, because they include several important algebraic counterparts of substructural logics (see [19]). Recently, algebra properties for semiconic CRLs have been given by many authors ( see [4,5,7,8,9,10,12,13,14,15,16,17,18,19,20,21]). In [20], the authors obtain a structure theorem for semilinear idempotent CRLs. In this paper, we will investigated algebraic structure properties of semiconic idempotent CRLs. Idempotent CRLs are indeed ordered semigroups (for ordered semigroups, see [1]). The natural partial order play an important role in investigation of semigroups (see [16]). We will make use of the natural partial order to obtain some important properties and then establish a structure theorem of semiconic idempotent CRLs, which generalizes the main result of [20].

We proceed as follows: in Section 2, we present some definitions and facts used in the sequel. In Section 3, we obtain some properties of semiconic idempotent CRLs. In Section 4, we give a structure theorem for semiconic idempotent CRLs, which generalizes the main result of [20]. In Section 5, we prove that the variety of strongly semiconic idempotent CRLs has the amalgamation property, which generalizes the main result of [11].

2. Preliminaries

In this section, we will list some facts about CRLs.

A monoid

(M, \cdot, e)

is said to be a po-monoid when it is also a poset

(M, \leq)

, and in which ≤ is compatible with ·, in the sense that

(\forall a, b, c \in M) a \leq b ⟹ c \cdot a \leq c b, a \cdot c \leq b c

. A po-monoid

(M, \cdot, e, \leq)

is said to be a lattice-ordered monoid when

(M, \leq)

is a lattice. A lattice-ordered monoid

(M, \cdot, e, \leq)

is said to be idempotent if for all

a \in M

a \cdot a = a

; is said to be commutative when the monoid reduct

(M, \cdot, e)

is a commutative monoid; is said to be conic, if for all

a \in M

a \leq e

a \geq e

. For convenience, we simply write

a \cdot b

a b

for

a, b \in M

. The reader is referred to reference [1] for detailed information on lattice-ordered monoids.

We need the following results.

Lemma 1.

[21]Let

(M, \cdot, e, \leq)

be an idempotent lattice-ordered monoid with identity e, and

a, b \in M

(1)

a \land b \leq a b \leq a \lor b

(2)

a, b \geq e

, then

a b = a \lor b

(3)

a, b \leq e

, then

a b = a \land b

(4)

a \leq e \leq a b

, then

a b = b

(5)

a b \leq e \leq a

, then

a b = b

Let

(L, \land, \lor, \cdot, \to, e)

be a CRL and ≤ shall always denote the lattice order of

L

in this paper.

Lemma 2.

[10,14]Let

(L, \land, \lor, \cdot, \to, e)

be a

C R L

and

a, b, c \in L

(1)

a (b \lor c) = a b \lor a c

(2)

a \to (b \land c) = (a \to b) \land (a \to c)

(3)

(b \lor c) \to a = (b \to a) \land (c \to a)

(4)

b (b \to a) \leq a

(5)

e \leq a \to a

(6)

((a \to b) \to b) \to b = a \to b .

(7)

a \to (b \to c) = (a b) \to c

From now on, we denote

a \to e

and

(a \to e) \to e

a^{*}

and

a^{* *}

, respectively. Next, we shall present some known facts on conic idempotent

C R L

s used in later proofs. More details on semiconic residuated lattices can be found in [4,12,13].

Lemma 3.

[12]Let

L

be a conic idempotent

C R L

, and

a, b \in L

(1)

If a and b are incomparable, then

a^{*} = b^{*} .

(2)

The elements a and

b^{*}

are comparable.

(3)

a ≰ b

if and only if

a \to b < e .

(4)

a \leq e (a > e)

, then

a^{*} = a \to a \geq e (a^{*} < e) .

(5)

{a^{*} : a \in L}

is a chain in

(L, \land, \lor) .

3. Some Properties

To begin with, we obtain some properties of conic idempotent commutative lattice-ordered monoids.

Now let

(L, \cdot, e, \leq)

be a conic idempotent commutative lattice-ordered monoid. Since the monoid reduct of

L

is an idempotent commutative monoid, we define the natural partial order on

L

as follows: for

a, b \in L

a \leq_{n} b if and only if a b = a .

It is clear that

(L, \leq_{n})

is a semilattice. For

a, b \in L

a ‖ b

[resp.

{a ‖}_{n} b

] means that a and b are incomparable under ≤ [resp.

\leq_{n}

];

a ≺ b

[resp.

a ≺_{n} b

] means that

a < b

[resp.

a <_{n} b

] and for any

c \in L

a \leq c \leq b

[resp.

a \leq_{n} c \leq_{n} b

] implies either

a = c

b = c

. Let

a \land_{n} b = max {c \in L : c \leq_{n} a, b}

and

a \lor_{n} b = min {c \in L : a, b \leq_{n} c}

if it exists in

(L, \leq_{n})

Proposition 1.

Let

(L, \cdot, e, \leq)

be a conic idempotent commutative lattice-ordered monoid. The following statements are true for

a, b \in L

(1): If $a, b \leq e$ , then $a \leq_{n} b$ if and only if $a \leq b$ .
(2): If $a, b \geq e$ , then $a \leq_{n} b$ if and only if $a \geq b$ .
(3): $a ‖ b$ if and only if ${a ‖}_{n} b$ .
(4): If $a ‖ b$ and $a < e$ , then $a \land_{n} b = a \land b$ .
(5): If $a ‖ b$ and $a > e$ , then $a \land_{n} b = a \lor b$ .

Proof.

(1)

Let

a, b \in L

be such that

a, b \leq e

. Then by Lemma 1(3),

a \leq_{n} b ⟺ a b = a ⟺ a \land b = a ⟺ a \leq b .

(2)

: is similar to

(1)

(3)

a ‖ b

, then since

L

is conic,

a, b \leq e

a, b \geq e

. If

a, b \leq e

, then by

(1)

a ∦_{n} b

is impossible. Thus

{a ‖}_{n} b

. Similarly, if

a, b \geq e

, then

{a ‖}_{n} b

. Conversely, let

a, b \in L

such that

{a ‖}_{n} b

. Suppose that

a \leq e \leq b

b \leq e \leq a

. Then since

L

is conic, by Lemma 1(4,5),

a b = a

a b = b

, which implies that

a \leq_{n} b

b \leq_{n} a

, a contradiction. Hence

a, b \leq e

e \leq a, b

. Thus, by (1) and (2),

a ‖ b

(4)

Let

a, b \in L

such that

a ‖ b

and

a < e

. Then by Lemma 1(3),

a \land b = a b

. Let

c \in L

such that

c \leq_{n} a

and

c \leq_{n} b

. Then

c a = c

and

c b = c

, so

c a b = c b = c

. Thus

c \leq_{n} a b

. Since

a b \leq_{n} a

and

a b \leq_{n} b

a \land b = a b = a \land_{n} b .

(5)

Let

a, b \in L

such that

a ‖ b

and

a > e

. Then by Lemma 1(2),

a b = a \lor b > a, b > e

. So by (2),

a \lor b \leq_{n} a

and

a \lor b \leq_{n} b

. Let

c \in L

such that

c \leq_{n} a

and

c \leq_{n} b

. Then

c a = c

and

c b = c

, so

c a b = c b = c

. Thus

c \leq_{n} a b = a \lor b

. Therefore

a \land_{n} b = a \lor b

. □

Secondly, we obtain some properties of conic idempotent CRLs.

Proposition 2.

Let

L

be a conic idempotent

C R L

. The following statements are true for

a, b \in L

(1): If $a < e$ , then $a <_{n} a^{*}$ and $a^{*} ∦_{n} b$ .
(2): If $a < e$ and $a <_{n} b <_{n} a^{*}$ , then $b < e$ .
(3): If $a > e$ , then $a^{*} <_{n} a$ and $a^{*} ∦_{n} b$ .
(4): If $a > e$ and $a^{*} <_{n} b <_{n} a$ , then $b > e$ .
(5): If $a ‖ b$ and $a < e$ , then $a \lor_{n} b = a \lor b$ and ${(a \land b)}^{*} = a^{*} .$

Proof.

(1)

Let

a, b \in L

such that

a < e

. Then

a e = a < e

and so

a < e \leq a \to e = a^{*}

. Since

a (a \to e) \leq e

by Lemma 2(4),

a (a \to e) = a

by Lemma 1(5), which implies that

a <_{n} a \to e = a^{*} .

Since by Lemma 3(2),

a^{*} ∦ b

, by Proposition 1(3),

a^{*} ∦_{n} b

(2)

Let

a \in L

such that

a < e

and

a <_{n} b <_{n} a^{*} = a \to e

. Then

a b = a < e

and so

b \leq a \to e = a^{*}

. Suppose that

b \geq e

. Then since by Lemma 3(4),

a^{*} \geq e

, by Proposition 1(2),

a^{*} \leq_{n} b

, contrary to

b <_{n} a^{*}

. Thus

b < e .

(3)

: is similar to

(1)

(4)

: is similar to

(2)

(5)

Let

a, b \in L

such that

a, b < e

and

a ‖ b

. Since

a, b \leq a \lor b \leq e

, by (1),

a \leq_{n} a \lor b

and

b \leq_{n} a \lor b .

Let

d \in L

such that

a \leq_{n} d

and

b \leq_{n} d

. Then

a d = a

and

b d = b

, so

d (a \lor b) = d a \lor d b = a \lor b

by Lemma 2(1). Thus

a \lor b \leq_{n} d

. Therefore

a \lor_{n} b = a \lor b .

Because

a \land b \leq a < e

a^{*} = a \to e \leq (a \land b) \to e = {(a \land b)}^{*}

by Lemma 2(3). Suppose that

a^{*} < {(a \land b)}^{*} .

Then

a \land b < a < a^{*} < {(a \land b)}^{*}

, so by

(2)

a^{*} < e

. But since

a < e

a^{*} \geq e

by Lemma 3(4), a contradiction. Thus

a^{*} = {(a \land b)}^{*}

. □

Proposition 3.

[4]Let

L

be a conic idempotent

C R L

, and let

a, b \in L

such that

a \leq e

. If

b < a

a ‖ b

, then

a \to b = b

a \to b ‖ a .

Let

(L, \leq)

be a join-semilattice, and let

L_{⊥} = L \cup {⊥}

such that

⊥ \leq a

for all

a \in L

L

is said to be an upper pre-lattice when

L

isn’t a lattice and

(L_{⊥}, \leq)

is a lattice. Let

L

be a lattice and

C \subseteq L

C

is said to be an upper pre-sublattice of

L

C

is an upper pre-lattice and there exists

a \in L

such that

(C \cup {a}, \leq)

is a sublattice of

L

. Similarly, we can define lower pre-lattice and lower pre-sublattice.

Let

L

be a conic idempotent CRL. We define the following sets:

L^{+} = {a \in L : a > e}

L^{-} = {b \in L : b \leq e}

L^{*} = {j \in L : (\exists a \in L) j = a^{*}}

L^{* -} = {j \in L^{*} : j \leq e}

L^{* +} = {j \in L^{*} : j > e} = {j \in L^{*} : (\exists i \in L^{* -}) j = i^{*}}

. For every

j \in L^{*}

, let

L_{j} = {c \in L : c^{* *} = j}

. By Lemma 3(4),

L_{j} \subseteq L^{+}

for all

j \in L^{* +}

. Since

a^{*} <_{n} a^{* *} \leq_{n} a <_{n} e

for all

a > e

by Proposition 2(1,3) and Lemma 3(4),

a^{* *} > e

by Proposition 2(4). It follows that

L_{i} \subseteq L^{-}

for all

i \in L^{* -}

. Because

L^{* -} \subseteq L^{*}

and

(L^{*}, \leq)

is a chain by Lemma 3(5),

(L^{* -}, \leq)

is a chain. It is clear that

L^{*} = L^{* -} \cup L^{* +}

We have the following result, which generalizes [7].

Theorem 1.

Let

L

be a conic idempotent

C R L

(1)

a \in L

, then

a \in L^{*}

if and only if

a^{* *} = a

(2)

i, l \in L^{* -}

, then

i = l

if and only if

i^{*} = l^{*}

. In addition,

i ≺_{n} i^{*}

for all

i \in L^{* -} ∖ {e}

(3)

j, s \in L^{*}

such that

j \neq s

, then

L_{j} \cap L_{s} = \emptyset

(4)

i \in L^{* -}

, then

L_{i}

is a sublattice of

(L, \land, \lor)

and

(L_{i}, \land, \lor, \cdot, \to^{L_{i}}, i)

is a Brouwerian algebra, where

\to^{L_{i}}

is given by

x \to^{L_{i}} y = (x \to y) \land i

for all

x, y \in L_{i}

(5)

j = i^{*} \in L^{* +}

, then

L_{j}

has a greatest element j and is either a sublattice of

L

or an upper pre-sublattice of

L

(6)

i, l \in L^{* -}

such that

i \neq l

a \in L_{i}, b \in L_{l}

and

c \in L_{i^{*}}, d \in L_{l^{*}}

then

i < l ⟺ a < b ⟺ c > d

(7)

i \in L^{* -}

and

j = i^{*}

such that

L_{j}

is an upper pre-sublattice of

L

, then there exists

l \in L^{* -}

such that

i ≺ l

L^{* -}

and

(L_{j} \cup {l^{*}}, \leq)

is a sublattice of

L

with a least element

l^{*}

(8)

L

satisfies that

{(x \land y)}^{*} = x^{*} \lor y^{*}

, then

L_{i}

is a sublattice of

L

for all

i \in L^{* +}

(9)

i \in L^{* -}, l \in L^{* +}

and

a \in L_{i}, b \in L_{l}

, then

i <_{n} l ⟺ a <_{n} b

(10)

L

is finitely subdirectly irreducible if and only if

L_{e}

is a finitely subdirectly irreducible Brouwerian algebra.

(11)

L^{*}

is a totally ordered odd Sugihara monoid and subalgebra of

L

, that we call its skeleton.

Proof.

(1)

We only need to verify the necessity because the sufficiency is clear. Suppose that

a \in L^{*}

. Then there exists

c \in L

such that

c^{*} = a

. Thus by Lemma 2(6),

a = c^{*} = c^{* * *} = a^{* *}

(2)

We only need to prove the sufficiency because the necessity is obvious. Suppose that

i^{*} = l^{*}

. Since

i, l \in L^{* -}

by assumption,

i = i^{* *} = l^{* *} = l

(1)

. Let

i \in L^{* -} ∖ {e}

. Then by Proposition 2(1),

i <_{n} i^{*}

. Let

a \in L

such that

i \leq_{n} a \leq_{n} i^{*}

. Suppose that

i <_{n} a <_{n} i^{*}

. If

a \geq e

, then by Proposition 2(2),

a < e

, a contradiction. If

a < e

, then since

i = i^{* *} <_{n} a <_{n} i^{*}

a > e

by Proposition 2(4), a contradiction. Consequently,

i ≺_{n} i^{*}

(3)

It is obvious.

(4)

Let

i \in L^{* -}

and let

x, y \in L_{i}

. Then

x^{* *} = y^{* *} = i

which together with

{(x \lor y)}^{*} = x^{*} \land y^{*} \in {x^{*}, y^{*}}

by Lemmas 2(3) and 3(5), derives that

{(x \lor y)}^{* *} = i

, whence

x \lor y \in L_{i}

. If

x \leq y

y < x

, then

{(x y)}^{*} = {(x \land y)}^{*} = x^{*}

{(x y)}^{*} = {(x \land y)}^{*} = y^{*}

, and so

{(x y)}^{* *} = {(x \land y)}^{* *} = i

, which implies that

x y = x \land y \in L_{i}

. If

x ‖ y,

then by Proposition 2(5),

{(x y)}^{*} = {(x \land y)}^{*} = x^{*}

and so

{(x y)}^{* *} = {(x \land y)}^{* *} = i

, which implies that

x y = x \land y \in L_{i}

. Thus

L_{i}

is a sublattice of

(L, \land, \lor)

. By (1),

i \in L_{i}

. Let

c \in L_{i}

. Then

c \leq (c \to e) \to e = c^{*} \to e = c^{* *} = i

. Thus i is the greatest element of

L_{i}

and so

(L_{i}, \cdot, i, \leq)

is an integral idempotent commutative lattice-ordered monoid with an identity i. We can claim that

max {z \in L_{i} : x z \leq y} = (x \to y) \land i

for all

x, y \in L_{i}

. To prove this, we consider the following cases:

If $x \leq y$ , then $i \leq e \leq x \to y$ by Lemma 3(3) and so $max {z \in L_{i} : x z \leq y} = i = (x \to y) \land i$ .
If $x > y$ or $x ‖ y$ , then by Proposition 3, $x \to y = y$ or $x \to y ‖ x$ . So ${(x \to y)}^{* *} = y^{* *} = i$ or ${(x \to y)}^{* *} = x^{* *} = i$ by Lemma 3(1). Thus $x \to y \in L_{i}$ , whence $max {z \in L_{i} : x z \leq y} = x \to y = (x \to y) \land i$

We define

x \to^{L_{i}} y = (x \to y) \land i

for all

x, y \in L_{i}

. Thus

(L_{i}, \land, \lor, \cdot, \to^{L_{i}}, i)

is a Brouwerian algebra.

(5)

Let

j = i^{*} \in L^{* +}

. By similar arguments as in the proof of

(4)

, j is the greatest element of

L_{j}

and

b \lor c \in L_{j}

for all

b, c \in L_{j}

, so

L_{j}

is a join-semilattice with a greatest element j. Suppose that

L_{j}

isn’t a sublattice of

L

. Then there exist

b, b^{'} \in L_{j}

such that

b ‖ b^{'}

and

d = b \land b^{'} \notin L_{j} .

Hence

e \leq d < b

and

d^{* *} < b^{* *} = j

by Lemma 2(3). Let

c \in L_{j}

. Suppose that

c ‖ d

. Then

d^{* *} = c^{* *} = j

by Lemma 3(1), which is contrary to

d^{* *} < j

. Assume that

c < d

. Then

d^{* *} > c^{* *} = b^{* *} = j

by Lemma 2(3), which is contrary to

d^{* *} < j

. Thus for all

c \in L_{j}

d < c .

Similarly, if

g, g^{'} \in L_{j}

such that

g \land g^{'} \notin L_{j},

then for all

c \in L_{j}

g \land g^{'} < c .

It follows that

d = g \land g^{'}

. Therefore

(L_{j} \cup {d}, \leq)

is a sublattice of

L

. Consequently,

L_{j}

is an upper pre-sublattice.

(6)

Let

i, l \in L^{* -}

such that

i \neq l

and let

a \in L_{i}

b \in L_{l}

. If

i < l

, then by

(4)

a \leq i < l

and

b \leq l

. Suppose that

b \leq i

. Then

b^{* *} \leq i^{* *} = i < j

, which is contrary to

b^{* *} = j

. Thus

i < b

by Lemma 3(2), whence

a < b

. Conversely, if

a < b

, then

a \leq i

and

a < b \leq l

. Suppose that

l < i

. Then

a^{* *} \leq l^{* *} = l < i

, which is contrary to

a^{* *} = i

. Thus

i < l

. Similarly,

i < l ⟺ c > d

(7)

Let

i \in L^{* -}

and

j = i^{*}

such that

L_{j}

is an upper pre-sublattice of

L

. Then there exist

b, b^{'} \in L_{j}

such that

b ‖ b^{'}

and

d = b \land b^{'} \notin L_{j} .

Let

l = d^{*}

. Then

d \in L_{l^{*}}

. Since

d < b

i < l

(6)

. Let

k \in L^{* -}

such that

i \leq k \leq l

. Suppose that

i < k < l

. Then by

(6)

d < k^{*} < b, b^{'}

, contrary to

d = b \land b^{'}

. Thus

i ≺ l

L^{*}

. We have

d l = d d^{*} = d (d \to e) \leq e ⟹ d \leq d^{*} \to e = d^{* *} = l^{*}

. We claim that

l^{*} = d

. Otherwise, if

d < l^{*}

, then since

i < l

j = i^{*} > l^{*}

by (6) and so

l^{*} < b, b^{'}

. It follows that

l^{*} \leq b \land b^{'} = d

. It’s a contradiction. Thus

l^{*} = d^{* *} = d = a \land b

. Consequently,

(L_{j} \cup {l^{*}}, \leq)

is a sublattice of

L

with a least element

l^{*}

(8)

Let

i \in L^{* +}

and

a, b \in L_{i}

. Then

{(a \land b)}^{* *} = {(a^{*} \lor b^{*})}^{*} = a^{* *} \land b^{* *} = i

and so

a \land b \in L_{i}

. It follows that

L_{i}

is a sublattice of

L

(9)

Since

a \in L_{i}

and

b \in L_{l}

a \leq i \leq e < b \leq l

(4 - 5)

and

i^{*} \neq e

. Then

a \leq_{n} i

and

l \leq_{n} b

by Proposition 1(1-2). Suppose that

i <_{n} l

. Then

a <_{n} b

. Conversely, assume that

a <_{n} b

. We claim that

a^{*} \neq e

. Otherwise if

a^{*} = e

, then

a <_{n} b ⟹ a b = a \leq e ⟹ b \leq a \to e = a^{*} = e

, which contrary to

b > e

. Consequently,

a^{*} > e

by Lemma 3(4). By Proposition 2(1,3),

a \leq_{n} i = a^{* *} <_{n} a^{*}

and

b^{*} <_{n} l = b^{* *} \leq_{n} b

. Suppose that

l <_{n} i .

a <_{n} l

, then

a <_{n} l <_{n} i = a^{* *} <_{n} a^{*}

, and so by Proposition 2(2),

l < e

, which contrary to

l > e

. If

l <_{n} a

, then

b^{*} <_{n} l = b^{* *} <_{n} a <_{n} b

, and so by Proposition 2(4),

a > e

, which contrary to

a \leq e

. Consequently,

i <_{n} l

(10)

Suppose that

L

is finitely subdirectly irreducible, then e is join-irreducible in L. Since

L_{e}

is a sublattice of

L

, e is join-irreducible in

L_{e}

, which implies that

L_{e}

is finitely subdirectly irreducible. Conversely,

L_{e}

is finitely subdirectly irreducible. Then e is join-irreducible in

L_{e}

. By (6), we have that

b < a

for all

a \in L_{e}

and

b \in L_{i}

such that

i \in L^{* -} ∖ {e}

, which implies that e is join-irreducible in

L .

Thus

L

is finitely subdirectly irreducible.

(11)

By Lemma 3(5),

(L^{*}, \leq)

is a totally ordered set, which implies that

L^{*}

is a sublattice of

L

. Let

a^{*}, b^{*} \in L^{*}

. If

a^{*}, b^{*} \leq e

, then

a^{*} b^{*} = a^{*} \land b^{*} \in L^{*}

. If

a^{*}, b^{*} \geq e

, then

a^{*} b^{*} = a^{*} \lor b^{*} \in L^{*}

. If

a^{*} \leq e, b^{*} > e

a^{*} > e, b^{*} \leq e

, then by Lemma 1(4,5),

a^{*} b^{*} \in {a^{*}, b^{*}} \subseteq L^{*}

. Thus

L^{*}

is closed with respect to multiplication. By Lemma 2(7), we have

a^{*} \to b^{*} = a^{*} \to (b \to e) = (a^{*} b) \to e \in L^{*}

. Consequently,

L^{*}

is a subalgebra of

L

. By Lemma 2(6),

(a^{*} \to e) \to e = ((a \to e) \to e) \to e = a \to e = a^{*}

. It follows that

L^{*}

is a totally ordered odd Sugihara monoid. □

Theorem 2.

Let

L, K

be conic idempotent

C R L

s, and

f : L \to K

be a homomorphism between conic idempotent

C R L

(1)

f (L^{*}) \subseteq K^{*}

and

f (L_{i}) \subseteq K_{f (i)}

for all

i \in L^{*}

(2)

i \in L^{*}

such that

L_{i}

is an upper pre-sublattice of

L

and

f (i) \neq e

, then

K_{f (i)}

is an upper pre-sublattice of

K

and there exists

j \in L^{*}

such that

j ≺ i

L^{*}

and

f (j) ≺ f (i)

K^{*}

Proof.

(1)

Let

a \in L^{*}

. Then there exists

b \in L

such that

a = b^{*}

. Since f is a homomorphism,

f (a) = f (b^{*}) = f {(b)}^{*} \in K^{*}

, which implies that

f (L^{*}) \subseteq K^{*}

. Let

i \in L^{*}

and

a \in L_{i}

. Then

a^{* *} = i

and so

f {(a)}^{* *} = f (a^{* *}) = f (i)

, which implies that

f (a) \in K_{f (i)}

. It follows that

f (L_{i}) \subseteq K_{f (i)}

(2)

Since

L_{i}

is an upper pre-sublattice of

L

i > e

by Theorem 1(4) and there exist

a, b \in L_{i}

such that

a \land b \notin L_{i}

. Let

j = a \land b

. By the proof of Theorem 1(7),

e \leq a \land b = j ≺ i

L^{*}

and so

j < i

in L. Hence

i^{*} < j^{*}

by Theorem 1(6). It follows that

i <_{n} j

and

i^{*} <_{n} j^{*}

by Theorem 1(2). We claim that

i <_{n} j^{*}

. Otherwise if

j^{*} <_{n} i

, then

i^{*} <_{n} j^{*} <_{n} i

and so by Proposition 2(4),

j^{*} > e

, which contrary to

j^{*} = {(a \land b)}^{*} \leq e

. Thus

i <_{n} j^{*}

. We have

f (a), f (b) \in K_{f (i)}

and

f (a) \land f (b) = f (a \land b) = f (j) \in K_{f (j)}

by (1). Suppose that

f (j) = f (i)

. Then

f (j) = f (i) = f (i j^{*}) = f (i) f (j^{*}) = f (j) f {(j)}^{*} = f {(j)}^{*}

and so by Proposition 2(1,3),

f (i) = f (j) = e

which contrary to

f (i) \neq e

. Consequently,

f (j) \neq f (i)

. It follows that

K_{f (i)}

is an upper pre-sublattice of

K

and by the proof of Theorem 1(7),

f (j) = f (a \land b) = f (a) \land f (b) ≺ f (i)

K^{*}

. □

4. The Construction Theorem

In this section we shall show how to construct a conic idempotent

C R L

and then prove that any conic idempotent

C R L

is isomorphic to some conic idempotent

C R L

constructed in this way.

To start with, we introduce some new concepts.

Definition 1.

Let

(I, \leq)

be a chain with a greatest element e. Let

I^{+} = {i^{+} : i \in I ∖ {e}}

such that

I \cap I^{+} = \emptyset

and

i^{+} \neq l^{+}

for every pair

i, l \in I ∖ {e}

such that

i \neq l

. Let

J = I \cup I^{+}

. Let

A = {(A_{j}, \leq_{A_{j}}) : j \in J}

be a family of pairwise disjoint nonempty poset indexed by J.

(I, I^{+}, J; A)

is called a chain expansion-system (abbreviated by

C E

-system) if the following conditions hold:

(CE1): If $i \in I$ , then $(A_{i}, \leq_{A_{i}})$ is a Brouwerian algebra with a greatest element i.
(CE2): If $i^{+} \in I^{+}$ , then $(A_{i^{+}}, \leq_{A_{i^{+}}})$ is either a lattice with a greatest element $i^{+}$ or an upper pre-lattice with a greatest element $i^{+}$ .
(CE3): If $i^{+} \in I^{+}$ such that $(A_{i^{+}}, \leq_{A_{i^{+}}})$ is an upper pre-lattice, then there exists $j \in I$ such that $i ≺ j$ in I.

Given a

C E

-system

(I, I^{+}, J; A)

, put

L = ⋃_{j \in J} A_{j}

. Define a binary relation ≤ on the set L as follows. Let

a \in A_{j}, b \in A_{k}

a \leq b

in L if one of the following conditions is satisfied:

(P1): $j = k \in J$ and $a \leq_{A_{j}} b$ .
(P2): $j, k \in I$ and $j < k$ .
(P3): $j = i_{1}^{+} \in I^{+}$ , $k = i_{2}^{+} \in I^{+}$ and $i_{2} < i_{1}$ in I.
(P4): $j \in I$ and $k \in I^{+}$ .

Lemma 4.

(L, \leq)

is a lattice.

Proof.

Firstly, we will prove that

(L, \leq)

is a poset. Obviously, ≤ is reflexive. Next we prove that ≤ is antisymmetric. To see this, let

a \in A_{j}, b \in A_{k}

such that

a \leq b

and

b \leq a

.We consider four cases:

If $j = k \in J$ , then by $(P 1)$ , $a \leq_{A_{j}} b$ and $b \leq_{A_{j}} a$ . Since $(A_{j}, \leq_{A_{j}})$ is a poset, $a = b$ .
Suppose $j \neq k$ and $j, k \in I$ . Then since $a \leq b$ and $b \leq a$ , $j < k$ and $k < j$ , a contradiction. Thus $j \neq k$ and $j, k \in I$ is impossible.
By similar arguments as in the previous case, $j \neq k$ and $j, k \in I^{+}$ is impossible.
Similarly, either $j \in I, k \in I^{+}$ or $k \in I, j \in I^{+}$ is impossible.

Next, we prove that ≤ is transitive. Let

a \in A_{j}, b \in A_{k}, c \in A_{s}

be such that

a \leq b

and

b \leq c

. We consider four cases:

$j = k = s \in J$ . Then by $(P 1)$ , $a \leq_{A_{j}} b$ and $b \leq_{A_{j}} c$ . Since $(A_{j}, \leq_{A_{j}})$ is a poset, $a \leq_{A_{j}} c$ . Thus by $(P 1)$ , $a \leq c$ .
$j = k \neq s$ . If $k, s \in I$ and $k < s$ , then $j < s$ and so by $(P 2)$ , $a \leq c$ . If $k = i_{1}^{+}, s = i_{2}^{+} \in I^{+}$ such that $i_{2} < i_{1}$ in I, then $j = i_{1}^{+}$ and so by $(P 3)$ , $a \leq c$ . If $k \in I$ and $s \in I^{+}$ , then $j \in I$ and so by $(P 4)$ , $a \leq c$ .
$j \neq k = s$ . Then by similar arguments as in the prior case , $a \leq c$ .
$j \neq k$ and $k \neq s$ . If $j, k, s \in I$ , then $j < k$ and $k < s$ , and so $j < s$ , which implies that $a \leq c$ by $(P 2)$ . If $j \in I$ and $s \in I^{+}$ , then by $(P 4)$ , $a \leq c$ . If $j, k, s \in I^{+}$ such that $j = i_{1}^{+}, k = i_{2}^{+}, s = i_{3}^{+}$ , then $i_{3} < i_{2}$ and $i_{2} < i_{1}$ in I by $(P 3)$ . Since $(I, \leq)$ is a chain, $i_{3} < i_{2}$ and so by $(P 3)$ , $a \leq c$ .

We conclude

a \leq c

, and whence ≤ is transitive.

Finally, we will prove that for all

a, b \in L

a \lor b

and

a \land b

exist in L. Let

a \in A_{j}, b \in A_{k}

. We consider three cases:

If $a \leq b$ , then $a \lor b = b$ and $a \land b = a$ in L.
If $b \leq a$ , then $a \lor b = a$ and $a \land b = b$ in L.
If $a ‖ b$ , then by the definition of ≤, $j = k$ . If $j, k \in I$ , then since $(A_{j}, \leq_{A_{j}})$ is a Brouwerian algebra, $a \lor^{A_{j}} b$ exist in $A_{j}$ . Let $c \in A_{s}$ such that $a, b \leq c$ . If $s = j$ , then by $(P 1)$ , $a \leq_{A_{j}} c$ and $b \leq_{A_{j}} c$ , and so $a \lor^{A_{j}} b \leq_{A_{j}} c$ . Thus by $(P 1)$ , $a \lor^{A_{j}} b \leq c$ . If $s \neq j$ , then since $a \leq c$ , either $s \in I$ and $j < s$ or $s \in I^{+}$ , which together with $a \lor^{A_{j}} b \in A_{j}$ , derives that $a \lor^{A_{j}} b \leq c$ . It follows that $a \lor b = a \lor^{A_{j}} b$ in L. Similarly, $a \land b = a \land^{A_{j}} b$ in L. If $j = k = i^{+} \in I^{+}$ , then $(A_{i^{+}}, \leq_{A_{i^{+}}})$ is either a lattice or a pre-lattice by (CE2). If $(A_{i^{+}}, \leq_{A_{i^{+}}})$ is a lattice or an upper pre-lattice and $a \land^{A_{i^{+}}} b$ exists, then by similar arguments as in the prior case, $a \lor b = a \lor^{A_{i^{+}}} b$ and $a \land b = a \land^{A_{i^{+}}} b$ in L. If $(A_{i^{+}}, \leq_{A_{i^{+}}})$ is an upper pre-lattice and $a \land^{A_{i^{+}}} b$ doesn’t exist, then by similar arguments in the prior case, $a \lor b = a \lor^{A_{i^{+}}} b$ in L. By (CE3), there exists $t \in I$ such that $i ≺ t$ in I. We claim that $t^{+} = a \land b$ in L. Because $t^{+}$ is the greatest element of $(A_{t^{+}}, \leq_{A_{t^{+}}})$ by $(C E 2)$ , $t^{+} \leq a, b$ by $(P 3)$ . Let $c \in A_{s}$ such that $c \leq a, b$ . Since $(A_{i^{+}}, \leq_{A_{i^{+}}})$ is an upper pre-lattice and $a \land^{A_{i^{+}}} b$ doesn’t exist, $c \notin A_{i^{+}}$ , and so by $(P 3 - 4)$ , either $s \in I$ or there exists $l \in I$ such that $s = l^{+}$ and $i < l$ in I, which implies that either $s \in I$ or $s = l^{+}$ such that $t \leq l$ . It follows that $c \leq t^{+}$ by $(P 3 - 4)$ . Thus $a \land b = t^{+}$ in L.

□

We define a multiplication ∘ on L in the following ways: for

a \in A_{j}, b \in A_{k}

a \circ b = \{\begin{matrix} a \land b & if j, k \in I, \\ a \lor b & if j, k \in I^{+}, \\ a & if j = i^{+} \in I^{+}, k \in I, i < k or j \in I, k = l^{+} \in I^{+}, j \leq l, \\ b & if j = i^{+} \in I^{+}, k \in I, i \geq k or j \in I, k = l^{+} \in I^{+}, j > l . \end{matrix}

Lemma 5.

(L, \land, \lor, \circ, e)

is a conic lattice-ordered idempotent commutative monoid with identity e.

Proof.

It is clear that

a \circ a = a

and

a \circ b = b \circ a

for

a, b \in L

Let

a \in A_{j}

. If

j \in I

, then since e is the greatest of I,

j \leq e

which together with e is the greatest element of

A_{e}

(C E 1)

, derives that

a \leq e

and

a \circ e = a

. If

j = i^{+} \in I^{+}

, then

i < e

, so

a > e

and

a \circ e = a

. Now, we will show that ∘ satisfies the associative law. Let

a \in A_{j}, b \in A_{k}, c \in A_{s}

. We consider the following cases:

If $j, k, s \in I,$ then $(a \circ b) \circ c = (a \land b) \circ c = a \land b \land c$ and $a \circ (b \circ c) = a \circ (b \land c) = a \land b \land c,$ whence $a \circ (b \circ c) = (a \circ b) \circ c$ .
If $j, k \in I$ and $s = i^{+} \in I^{+}$ , then

$(a \circ b) \circ c = (a \land b) \circ c = \{\begin{matrix} a \land b & if j \land k \leq i, \\ c & if i < j \land k; \end{matrix}$

and

$\begin{matrix} a \circ (b \circ c) & = & \{\begin{matrix} a \circ b = a \land b & if k \leq i, \\ a \circ c = a = a \land b & if j \leq i < k, \\ c & if i < j \land k; \end{matrix} \\ = & \{\begin{matrix} a \land b & if j \land k \leq i, \\ c & if i < j \land k . \end{matrix} \end{matrix}$

It follows that $a \circ (b \circ c) = (a \circ b) \circ c$ .
If $j \in I, k = i^{+}, s = l^{+} \in I^{+},$ then

$\begin{matrix} (a \circ b) \circ c & = & \{\begin{matrix} a \circ c = a & if j \leq i \land l, \\ b \circ c = b \lor c & if i < j, \\ a \circ c = c & if l < j \leq i; \end{matrix} \\ = & \{\begin{matrix} a & if j \leq i \land l, \\ b \lor c & if j > i \land l; \end{matrix} \end{matrix}$

and

$a \circ (b \circ c) = a \circ (b \lor c) = \{\begin{matrix} a & if j \leq i \land l, \\ b \lor c & if j > i \land l . \end{matrix}$

However, $a \circ (b \circ c) = (a \circ b) \circ c$ .
If $j, k, s \in I^{+}$ then $(a \circ b) \circ c = (a \lor b) \circ c = a \lor b \lor c$ and $a \circ (b \circ c) = a \circ (b \lor c) = a \lor b \lor c,$ whence $a \circ (b \circ c) = (a \circ b) \circ c$ .

Finally, we will show that ≤ is compatible with ∘. Let

a, b \in L

be such that

a \leq b

. We need only to prove that

a \circ c \leq b \circ c

for every

c \in L

. Suppose that

a \in A_{j}, b \in A_{k}, c \in A_{s}

. We need to consider the following cases:

(1)

j, k, s \in I

, then by the definition of ∘,

a \circ c = a \land c

and

b \circ c = b \land c

. Since

a \leq b

a \circ c \leq b \circ c

(2)

j, k \in I

and

s = i^{+} \in I^{+}

, then

a \leq b < c

and

j \leq k

. The following subcases need be considered:

If $i < j$ , then $i < k$ and so by the definition of ∘, $a \circ c = c$ and $b \circ c = c$ , whence $a \circ c \leq b \circ c$ .
If $j \leq i$ , then by the definition of ∘, $a \circ c = a$ and $b \circ c \in {b, c}$ . It follows that $a \circ c \leq b \circ c$ .

(3)

j, s \in I

and

k \in I^{+}

, then by the definition of ∘,

a \circ c = a \land c \leq c < b

and

b \circ c \in {b, c}

, whence

a \circ c \leq b \circ c

(4)

j \in I

and

k, s \in I^{+}

, then

a < b \leq b \lor c

, so by the definition of ∘,

a \circ c \in {a, c}

and

b \circ c = b \lor c

, whence

a \circ c \leq b \circ c

(5)

j = i^{+}, k = l^{+} \in I^{+}

and

s \in I

, then since

a \leq b

l \leq i

in I by

(P 3)

. The following subcases need be considered:

If $s \leq l$ , then by the definition of ∘, $a \circ c = c$ and $b \circ c = c$ , whence $a \circ c \leq b \circ c$ .
If $s > l$ , then by the definition of ∘, $a \circ c \in {a, c}$ and $b \circ c = b$ . It follows that $a \circ c \leq b \circ c$ .

(6)

j, k, s \in I^{+}

, then by the definition of ∘,

a \circ c = a \lor c

and

b \circ c = b \lor c

, whence

a \circ c \leq b \circ c

. □

We may define a binary operation → on L in the following way: for

a, b \in L

such that

a \in A_{j}, b \in A_{k}

a \to b = \{\begin{matrix} j^{+} & if j, k \in I and a \leq b, or j \in I, k = i^{+} \in I^{+} and j \leq i, \\ b & if j, k \in I and j > k, or j \in I, k = i^{+} \in I^{+} and j > i, \\ a \to^{A_{j}} b & if j = k \in I such that a ‖ b or a > b, \\ b & if j, k \in I^{+} and a \leq b, or j = i^{+} \in I^{+}, k \in I and i \geq k, \\ i & if j = i^{+}, k \in I^{+} and a ≰ b, or j = i^{+} \in I^{+}, k \in I and i < k . \end{matrix}

We denote by

J ⨂ A

the above

(L, \land, \lor, \circ, \to, e)

Theorem 3.

L = J ⨂ A

is a conic idempotentCRL .

Proof.

We need only to prove that for all

a, b \in L, a \to b = max {c : a \circ c \leq b}

. Suppose that

a \in A_{j}, b \in A_{k}

. We need to consider the following cases:

Case 1.

j, k \in I

and

a \leq b

, or

j \in I, k = i^{+} \in I^{+}

and

j \leq i

. We need only to check the following subcases:

(1)

j, k \in I

and

a \leq b

, then by the definition of ∘,

a \circ (a \to b) = a \circ j^{+} = a \leq b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. If

s \in I

, then by

(P 4)

c \leq j^{+} = a \to b

. If

s = l^{+} \in I^{+}

, then

b < c

(P 4)

, and by the definition of ∘,

a \circ c \in {a, c}

, which together with

a \circ c \leq b

, derives that

a \circ c = a

. Thus

j \leq l

, whence

c \leq j^{+} = a \to b

(2)

j \in I, k = i^{+} \in I^{+}

and

j \leq i

, then by the definition of ∘ and

(P 4)

a \circ (a \to b) = a \circ j^{+} = a \leq b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. If

s \in I

, then by

(P 4)

c \leq j^{+} = a \to b

. If

s = l^{+} \in I^{+}

, then by the definition of ∘,

a \circ c \in {a, c}

. Assume that

a \circ c = c

. Then by the definition of ∘,

l < j \leq i

, so

b < c = a \circ c

(P 3)

, which is contrary to

a \circ c \leq b

. Thus

a \circ c = a

, which implies that

j \leq l

and so

c \leq j^{+}

(P 1)

and

(P 3)

Case 2.

j, k \in I

and

j > k

, or

j \in I, k = i^{+} \in I^{+}

and

j > i

. We need only to check the following subcases:

(1)

j, k \in I

and

j > k

, then

a > b

(P 2)

, and so by the definition of ∘,

a \circ (a \to b) = a \circ b = a \land b = b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. Suppose that

s \in I^{+}

. Then

c > b

(P 4)

, and by the definition of ∘,

a \circ c \in {a, c}

, which implies that

a \circ c > b

, a contradiction. Suppose that

s \in I

such that

s \geq j

. Then

a \circ c = a \land c \in A_{j}

, which implies that

a \circ c > b

, a contradiction. Thus

s \in I

and

s < j

, whence

c = a \land c = a \circ c \leq b = a \to b .

(2)

j \in I, k = i^{+} \in I^{+}

and

j > i

, then by the definition of ∘,

a \circ (a \to b) = a \circ b = b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. If

s \in I

, then

c \leq b = a \to b

(P 4)

. If

s = l^{+} \in I^{+}

such that

l \geq j

, then

l > i

and so

c \leq b = a \to b

(P 3)

. If

s = l^{+} \in I^{+}

such that

l < j

, then by the definition of ∘,

c = a \circ c \leq b = a \to b

Case 3.

j = k \in I

such that

a ‖ b

a > b

. Then by the definition of ∘ and

(C E 1)

a \circ (a \to b) = a \circ (a \to^{A_{j}} b) = a \land (a \to^{A_{j}} b) = a \land^{A_{j}} (a \to^{A_{j}} b) \leq_{A_{j}} b

, which implies that

a \circ (a \to b) \leq b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. Suppose that

s \in I^{+}

s \in I

such that

s > j

. Then

c > b

(P 2, 4)

, and by the definition of ∘,

a \circ c \in {a, c}

, which implies that

a \circ c ≰ b

, a contradiction. If

s \in I

such that

s < j

, then

c \leq a \to^{A_{j}} b = a \to b

(P 2)

. If

s \in I

such that

s = j

, then by the definition of ∘,

a \land^{A_{j}} c = a \land c = a \circ c \leq b

, which implies that

a \land^{A_{j}} c \leq_{A_{j}} b

, so

c \leq_{A_{j}} a \to^{A_{j}} b

(C E 1)

. Thus

c \leq a \to^{A_{j}} b = a \to b

Case 4.

j, k \in I^{+}

and

a \leq b

, or

j = i^{+} \in I^{+}, k \in I

and

i \geq k

. We need only to check the following subcases:

(1)

j, k \in I^{+}

and

a \leq b

, then by the definition of ∘,

a \circ (a \to b) = a \circ b = a \lor b = b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. If

s \in I

, then by

(P 4), c \leq b

. If

s \in I^{+}

, then by the definition of ∘,

c \leq a \lor c = a \circ c \leq b = a \to b

(2)

j = i^{+} \in I^{+}, k \in I

and

i \geq k

, then by the definition of ∘,

a \circ (a \to b) = a \circ b = b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. Suppose that

s \in I^{+}

. Then by the definition of ∘,

a \circ c = a \lor c > b

, a contradiction. If

s \in I

, then by the definition of ∘,

a \circ c \in {a, c}

, which together with

a > b

, derives that

c = a \circ c \leq b = a \to b

Case 5.

j = i^{+}, k \in I^{+}

and

a ≰ b

, or

j = i^{+} \in I^{+}, k \in I

and

i < k

. We need only to check the following subcases:

(1)

j = i^{+}, k \in I^{+}

and

a ≰ b

, then by the definition of ∘ and

(P 4)

a \circ (a \to b) = a \circ i = i \leq b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. Suppose that

s \in I^{+}

. Then

a \circ c = a \lor c ≰ b

, a contradiction. If

s \in I

, then by the definition of ∘,

a \circ c \in {a, c}

, which together with

a ≰ b

, derives that

c = a \circ c \leq b

(2)

j = i^{+} \in I^{+}, k \in I

and

i < k

, then by the definition of ∘ and

(P 2)

a \circ (a \to b) = a \circ i = i \leq b

. Let

c \in A_{s} \subseteq L

such that

a \circ c \leq b

. Suppose that

s \in I^{+}

. Then by the definition of ∘,

a \circ c = a \lor c > b

, a contradiction. If

s \in I

, then by the definition of ∘,

a \circ c \in {a, c}

, which together with

a > b

, derives that

a \circ c = c

. Thus

s \leq i

, whence

c \leq i

. □

Next we shall prove that any conic idempotent CRL is isomorphic to some

J ⨂ A

. Suppose that

L = (L, \land, \lor, \cdot, \to, e)

is a conic idempotent CRL. Let

L^{*} = {j \in L : (\exists a \in L) j = a^{*}}

I = {i \in L^{*} : i \leq e} = L^{* -}

and

I^{*} = {i^{*} : i \in I ∖ {e}} = L^{* +}

. Let

Y = {(L_{j}, \leq) : j \in L^{*}}

. By Proposition 2, for all

i \in I ∖ {e}

i^{*} > e

, so

I^{*} \cap I = \emptyset

. If

i, l \in I

such that

i \neq l

, then there exist

a, b \in L

such that

a^{*} = i

and

b^{*} = l

, so

i^{* *} = a^{* * *} = a^{*} = i \neq l = b^{*} = b^{* * *} = l^{* *}

. Thus

i^{*} \neq l^{*}

Lemma 6.

(I, I^{*}, L^{*}; Y)

is a

C E

-system.

Proof.

By Theorem 1(1-5,7),

(I, I^{*}, L^{*}; Y)

is a

C E

-system. □

Theorem 4.

L

is equal to

L^{*} ⨂ Y

Proof.

For convenience, we denote by

\leq_{1}

the imposed ordering on

L^{*} ⨂ Y

. We need only to prove that for all

a, b \in L, \leq = \leq_{1}

and

a \cdot b = a \circ b

We now prove

\leq = \leq_{1}

. Let

a, b \in L

. Assume that

a \leq b

. We need to consider three cases:

(1)

a \leq e, b \leq e

, then

a^{* *}, b^{* *} \in I

by Lemma 3(4) and by Theorem 1(6),

a^{* *} \leq b^{* *}

, which together with

a \in L_{a^{* *}}

and

b \in L_{b^{* *}}

, derives that

a \leq_{1} b

(P 1 - 2)

(2)

a \geq e, b \geq e,

then

a^{*}, b^{*} \in I

, which together with

a \in L_{a^{* *}}

and

b \in L_{b^{* *}}

, derives that

a^{*} \geq b^{*}

by Theorem 1(6). Thus by

(P 3)

a \leq_{1} b

(3)

a \leq e

and

b > e,

then by Lemma 3(4),

a^{* *} \leq e

and

b^{* *} > e

, so

a^{* *} \in I

and

b^{* *} \in I^{*}

, whence by

(P 4)

a \leq_{1} b .

Thus

\leq \subseteq \leq_{1} .

Suppose that

a \leq_{1} b

. We need to consider four cases:

(1)

a^{* *} = b^{* *} \in I

, then

a \leq b

(P 1)

(2)

a^{* *}, b^{* *} \in I

such that

a^{* *} < b^{* *}

, then by Theorem 1(6),

a \leq b

(3)

a^{* *}, b^{* *} \in I^{*}

such that

a^{*} > b^{*}

, then by Theorem 1(6),

a \leq b

(4)

a^{* *} \in I

and

b^{* *} \in I^{*}

, then by Lemma 3(4),

a \leq e

and

b > e

, so

a \leq b

Thus

\leq_{1} \subseteq \leq,

whence

\leq_{1} = \leq

It remains to verify

a \cdot b = a \circ b

for all

a, b \in L

. For this, we need to consider three cases:

(1)

a \leq e, b \leq e

, then by Lemma 1(3),

a \cdot b = a \land b .

On the other hand, by the definition of ∘ and

\leq = \leq_{1}

a \circ b = a \land b

, whence

a \cdot b = a \circ b

(2)

a > e, b > e,

then by similar arguments as in (1),

a \cdot b = a \circ b .

(3)

a > e

and

b \leq e

If $b \leq a^{*}$ , then $a^{*}, b^{* *} \in I$ by Lemma 3(4) and $b^{* *} \leq a^{* * *} = a^{*}$ by Lemma 2(3), which together with $a \in L_{{(a^{*})}^{*}}$ and $b \in L_{b^{* *}}$ derives $a \circ b = b$ by the definition of ∘. On the other hand, $a \cdot b = a \cdot a^{*} \cdot b = a^{*} \cdot b = b$ by Proposition 2(3). Hence $a \cdot b = b = a \circ b$ .
If $b > a^{*}$ , then $a^{*}, b^{* *} \in I$ by Lemma 3(4) and $b^{* *} \geq b > a^{* * *} = a^{*}$ by Theorem 1(4), which together with $a \in L_{{(a^{*})}^{*}}$ and $b \in L_{b^{* *}}$ derives $a \circ b = a$ by the definition of $\circ .$ Suppose that $a \cdot b = b$ . Then $a^{*} <_{n} b <_{n} a$ , so by Proposition 2(4), $b > e$ , a contradiction. Thus $a \cdot b = a$ by Lemma 1(4,5). Hence $a \cdot b = a = a \circ b$ .

□

By Theorem 4, we have the following result, which generalizes [20].

Theorem 5.

Let

L = (L, \land, \lor, \cdot, \to, e)

be aCRL. The following conditions are equivalent:

(I): $L$ is a subdirectly irreducible idempotent semiconicCRL .
(II): There exists a $C E$ -system $(I, I^{+}, J; A)$ such that

$(1)$ $A_{e}$ is a nontrivial subdirectly irreducible Brouwerian algebra or $A_{e} = {e}$ and there exists $i \in I$ such that $i ≺ e$ in I;

$(2)$ $L ≅ J ⨂ A$ .

Proof.

Let

L

be a subdirectly irreducible semiconic idempotent CRL. Then since semiconic idempotent CRL is the variety generated by conic idempotent CRLs,

L

is conic. By Theorem 4,

L ≅ L^{*} ⨂ Y

, where

(I, I^{*}, L^{*}; Y)

is a

C E

-system. Because

L

is a subdirectly irreducible CRL, the set

{a \in L : a < e}

has a greatest element. Let

i = max {a \in L : a < e}

. If

i \in L_{e}

, then

i = max {a \in L_{e} : a < e}

, so by Theorem 1(4),

L_{e}

is a nontrivial subdirectly irreducible Brouwerian algebra. If

i \notin L_{e}

, then since

L_{e} \subseteq L^{-}

L_{e} = {e}

and

i ≺ e

, so

i^{* *} < e

, which implies that

i^{* *} \leq i

. On the other hand, by Proposition 2(1),

i i^{*} = i \leq e

, so

i \leq i^{*} \to e = i^{* *}

. Thus

i = i^{* *}

, whence

i \in I

by Theorem 1(1).

Conversely, let

(I, I^{+}, J; A)

be a

C E

-system such that

(1)

and

(2)

. Then by Theorem 3,

L

is a conic idempotent CRL. If

A_{e}

is a nontrivial subdirectly irreducible Brouwerian algebra, then

max {a \in A_{e} : a < e}

exists and so

max {a \in A_{e} : a < e} = max {a \in L : a < e}

, which implies that

L

is a subdirectly irreducible semiconic idempotent CRL. If

A_{e} = {e}

and there exists

i \in I

such that

i ≺ e

, then by

(P 1, 2)

max {a \in L : a < e} = i

, which implies that

L

is a subdirectly irreducible semiconic idempotent CRL. □

5. The Amalgamation Property

In this section we will use the structure theorem of conic idempotent CRLs to give some new result about the amalgamation property of the variety of semiconic idempotent CRLs, which generalize the main results of [11].

Let

K

be a class of algebras. A span is a pair of embeddings

〈 i_{1} : A ↪ B, i_{2} : A ↪ C 〉

between algebras

A, B, C \in K

. The class K is said to have the amalgamation property if for every span of K, there exist an amalgam

D \in K

and embeddings

j_{1} : B ↪ D

and

j_{2} : C ↪ D

such that

j_{1} \circ i_{1} = j_{2} \circ i_{2}

Example 1.

Let

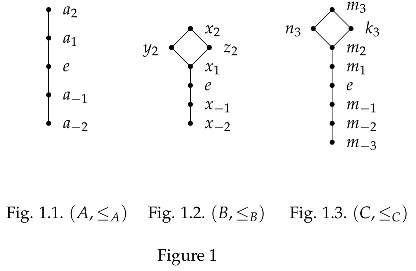
A = {a_{2}, a_{1}, e, a_{- 1}, a_{- 2}}

. We define an order relation

\leq_{A}

on A by

a_{- 2} <_{A} a_{- 1} <_{A} e <_{A} a_{1} <_{A} a_{2}

, see Figure 1.1. We can define a multiplication operation on A by for all

i, j \in {1, 2, - 1, - 2}

a_{i} a_{j} = a_{j} a_{i} = \{\begin{matrix} a_{i} & if | j | < | i |, \\ a_{i} & if i = j, \\ a_{i} & if i = - j < 0; \end{matrix}

and

a e = e a = a

for all

a \in A

. Let

B = {x_{- 2}, x_{- 1}, e, x_{1}, y_{2}, z_{2}, x_{2}}

. We define an order relation

\leq_{B}

on B by

x_{- 2} <_{B} x_{- 1} <_{B} e <_{B} x_{1} <_{B} y_{2}, z_{2} <_{B} x_{2}

, see Figure 1.2. We can define a multiplication operation on B by for all

i, j \in {1, 2, - 1, - 2}

and

b \in {y, z}

x_{i} x_{j} = x_{j} x_{i} = \{\begin{matrix} x_{i} & if | j | < | i |, \\ x_{i} & if i = j, \\ x_{i} & if i = - j < 0; \end{matrix}

x_{i} b_{2} = b_{2} x_{i} = \{\begin{matrix} b_{2} & if | i | < 2, \\ x_{i} & if | i | = 2; \end{matrix}

y_{2} z_{2} = z_{2} y_{2} = x_{2}

and

c e = e c = c

for all

c \in B

. Let

C = {m_{- 3}, m_{- 2}, m_{- 1}, e, m_{1}, m_{2}, n_{3}, k_{3}, m_{3}}

. We define an order relation

\leq_{C}

on C by

m_{- 3} <_{C} m_{- 2} <_{C} m_{- 1} <_{C} e <_{C} m_{1} <_{C} m_{2} <_{C} n_{3}, k_{3} <_{C} m_{3}

, see Figure 1.3. We can define a multiplication operation on C by for all

i, j \in {1, 2, 3, - 1, - 2, - 3}

and

b \in {n, k}

m_{i} m_{j} = m_{j} m_{i} = \{\begin{matrix} m_{i} & if | j | < | i |, \\ m_{i} & if i = j, \\ m_{i} & if i = - j < 0; \end{matrix}

m_{i} b_{3} = b_{3} m_{i} = \{\begin{matrix} b_{3} & if | i | < 3, \\ m_{i} & if | i | = 3; \end{matrix}

n_{3} k_{3} = k_{3} n_{3} = m_{3}

and

c e = e c = c

for all

c \in C

. We define a division operation on P by

a \to b = max {p \in P ∣ a p \leq b}

for all

a, b \in P

, where

P \in {A, B, C}

. It’s easy to see that

A, B

and

C

are subdirectly irreducible semiconic idempotentCRLs. We define two maps as follows:

φ_{1} : A ⟶ B

;

e \mapsto e

and

a_{i} \mapsto x_{i}

for

i \in {- 2, - 1, 1, 2}

;

φ_{2} : A ⟶ C

;

e \mapsto e

a_{i} \mapsto m_{i}

for

i \in {- 1, 1}; a_{2} \mapsto m_{3}

and

a_{- 2} \mapsto m_{- 3}

. It’s clear that

φ_{1}

φ_{2}

are embeddings of

A

into

B, C,

respectively. We claim that there doesn’t an amalgam in

K

where

K

is the class of all conic idempotentCRLs. Suppose that there exist an amalgam

D \in K

and embeddings

ψ_{1} : B ↪ D

and

ψ_{2} : C ↪ D

such that

ψ_{1} φ_{1} = ψ_{2} φ_{2}

. Then

ψ_{1} (x_{1}) = ψ_{1} φ_{1} (a_{1}) = ψ_{2} φ_{2} (a_{1}) = ψ_{2} (m_{1})

and

ψ_{1} (x_{2}) = ψ_{1} φ_{1} (a_{2}) = ψ_{2} φ_{2} (a_{2}) = ψ_{2} (m_{3})

. Hence by Theorem 2,

ψ_{2} (m_{1}) = ψ_{1} (x_{1}) ≺ ψ_{1} (x_{2}) = ψ_{2} (m_{3})

D^{*}

. But

ψ_{2} (m_{1}) < ψ_{2} (m_{2}) < ψ_{2} (m_{3})

D^{*}

. It’s a contradiction. We conclude that the span

〈 φ_{1} : A ⟶ B, φ_{2} : A ⟶ C 〉

hasn’t an amalgam in

K

a_{- 2}

a_{- 1}

a_{1}

a_{2}

Fig. 1.1.

(A, \leq_{A})

x_{- 2}

x_{- 1}

x_{1}

x_{2}

y_{2}

z_{2}

Fig. 1.2.

(B, \leq_{B})

m_{- 3}

m_{- 2}

m_{- 1}

m_{1}

m_{2}

n_{3}

k_{3}

m_{3}

Fig. 1.3.

(C, \leq_{C})

Figure 1

By Example 1, we have the following result.

Proposition 4.

The class of all conic idempotentCRLs and the class of subdirectly irreducible semiconic idempotentCRLs haven’t the amalgamation property.

Definition 2.

The variety of strongly semiconic idempotentCRLs consists of the semiconic idempotentCRLs that satisfy

{(x \land y)}^{*} = x^{*} \lor y^{*} .

Proposition 5.

A conic idempotentCRL

L

is a strongly semiconic idempotentCRLif and only if

L_{i}

is a lattice for all

i \in L^{*}

Let

L

be a CRL. A lattice filter F of

L

is called normal if it contains e and it’s closed under multiplication. A normal filter F of

L

is said to be prime if it is prime in the usual lattice-theoretic sense; that is, whenever

x \lor y \in F

, then

x \in F

y \in F .

Let F and

Θ

be a normal filter and a congruence of

L

respectively. It’s well known that

Θ_{F} = {(x, y) \in L^{2} ∣ (x \to y) \land (y \to x) \in F}

is a congruence of

L

and the upper set

F_{Θ} {= ↑ [e]}_{Θ}

of the equivalence class

{[e]}_{Θ}

is a normal filter. Moreover:

Lemma 7.

[2]The lattice

NF (L)

of normal filters of aCRL

L

is isomorphic to its congruence lattice

C o n (L)

. The isomorphism is given by the mutually inverse maps

F \mapsto Θ_{F}

and

{Θ \mapsto ↑ [e]}_{Θ}

Lemma 8.

[2]Let

L

be aCRLand let F be a normal filter of

L

. Then

{[e]}_{Θ_{F}} = {x ∣ x \land (x \to e) \land e \in F} = {x ∣ \exists a \in F^{-}, a \leq x \leq a \to e}

In what follows, if F is a normal filter of

L

L / F

shall always denote the quotient algebra

L / Θ_{F}

. Given a element

x \in L

, we write

{[x]}_{F}

[x]

if no confusion for the equivalence class of x in

L / F

Lemma 9.

Let

L

be a semiconicCRL, and let F be a normal filter of

L

. Then the following statements are equivalent

(1): F is prime.
(2): For all $a, b \in L^{-}$ , whenever $a \lor b \in F$ , then $a \in F$ or $b \in F$ .
(3): $L / F$ is a finitely subdirectly irreducible conicCRL .

Proof.

(1) \Rightarrow (2)

By specialization.

(2) \Rightarrow (3)

Suppose that

(2)

holds, and let

a \in L

. Since

L

is semiconic,

(a \land e) \lor (a \to e \land e) = e \in F

. It follows that either

a \land e \in F

a \to e \land e \in F

. If

a \land e \in F

, then by Lemma 8,

[a \land e] = [e] ⟹ [a] \land [e] = [e] ⟹ [a] \geq [e]

. If

a \to e \land e \in F

, then

[a \to e \land e] = [e] ⟹ [a] \to [e] \land [e] = [e] ⟹ [a] \to [e] \geq [e] ⟹ [a] \leq [e] .

Thus

L / F

is a conic CRL. Let

a, b \in L

such that

[a] \lor [b] = [e]

. Then since

L

is conic,

([a] \lor [b]) \land [e] = [e] ⟹ ([a] \land [e]) \lor ([b] \land [e]) = [e] ⟹ [(a \land e) \lor (b \land e)] = [e]

, which implies that

(a \land e) \lor (b \land e) \in F

. Hence

a \land e \in F

b \land e \in F

, which derives that

[a \land e] = [e]

[b \land e] = [e]

. Since

[a \lor b] = [e], [a] \leq [e]

and

[b] \leq [e]

. It follows that

[a] = [a] \land [e] = [a \land e] = [e]

[b] = [b] \land [e] = [b \land e] = [e]

. Consequently,

L / F

is a finitely subdirectly irreducible conic CRL.

(3) \Rightarrow (1)

Assume that

(3)

holds, and let

a, b \in L

such that

a \lor b \in F

. Then

(a \lor b) \land e = (a \land e) \lor (b \land e) \in F

. It follows that

[(a \land e) \lor (b \land e)] = [e] ⟹ [a \land e] \lor [b \land e] = [e] ⟹ [a \land e] = [e]

[b \land e] = [e] ⟹ a \land e \in F

b \land e \in F ⟹ a \in F

b \in F

. Thus F is prime. □

Lemma 10.

[2]Let

L

be a residuated lattice and

{a_{i} ∣ 1 \leq i \leq n}

{b_{j} ∣ 1 \leq j \leq m} \subseteq L^{-}

finite subsets of the negative cone of

L

with the property that

a_{i} \lor b_{j} = e

, for any i and j. Then

(\prod_{i = 1}^{n} a_{i}) \lor (\prod_{j = 1}^{m} b_{j}) = e .

Lemma 11.

[15]Let

U

be a subclass of a variety

V

satisfying the following conditions:

(i): Every subdirectly irreducible member of $V$ is in $U$ .
(ii): $U$ is closed under isomorphisms and subalgebras.
(iii): For any algebra $B \in V$ and subalgebra $A$ of $B$ , if $Θ \in C o n (A)$ and $A / Θ \in U$ , then there exists $Φ \in C o n (B)$ such that $Φ ⋂ A^{2} = Θ$ and $B / Φ \in U$ .
(iV): Every span in $U$ has an amalgam in $V$ .

Then

V

has the amalgamation property.

We have the following result, which generalizes [15] in the commutative case.

Theorem 6.

Let

V

be a variety of semiconicCRLs, and suppose that the class of finitely subdirectly irreducible conicCRLs in

V

has the amalgamation property. Then

V

has the amalgamation property.

Proof.

It is well known that every subdirectly irreducible semiconic CRL is a finitely subdirectly irreducible conic CRL. It is clear that the class of finitely subdirectly irreducible conic CRL is closed under isomorphisms and subalgebras. By Lemma 11, we need only to prove that for any

B \in V

, any subalgebra

A

B

, and

P \in NF (A)

such that

A / P

is a finitely subdirectly irreducible conic CRL, there is

Q \in NF (B)

such that

Q \cap A = P

and

B / Q

is a finitely subdirectly irreducible conic CRL. Since

V

has the congruence extension property, there is a normal filter F of

B

, such that

P = F \cap A

. Let

X

denote the poset, under set-inclusion, of all set-inclusion, of all normal filters of

B

whose intersection with A is P. Since

F \in X

X \neq \emptyset

. By Zorn’s lemma, element Q. Next, we shall show that Q is a prime normal filter of

B

. Suppose otherwise, and let

x, y \in B^{-}

be such that

x \lor y \in Q

but

x \notin Q

and

y \notin Q

. Let

Q_{x}

and

Q_{y}

be the normal filters of

B

generated by

Q \cup {x}

and

Q \cup {y}

, respectively. Then, by the maximality of Q, P is a proper subset of the normal filters

Q_{x} \cap A

and

Q_{y} \cap A

A

and so there exist elements

c, d \in A ∖ P

q, r \in Q^{-}

and

n, m \in Z^{+}

such that

q x^{n} \leq c \leq e

, and

r y^{m} \leq d \leq e

. Hence by Lemma 8,

{[q]}_{Q} = {[r]}_{Q} = {[e]}_{Q}

and

x \lor y \in Q \cap B^{-} ⟹ {[x \lor y]}_{Q} = {[e]}_{Q}

. Thus by Lemma 10,

{[e]}_{Q} = {[x^{n}]}_{Q} \lor {[y^{m}]}_{Q} = {[q]}_{Q} {[x^{n}]}_{Q} \lor {[r]}_{Q} {[y^{m}]}_{Q} = {[q x^{n}]}_{Q} \lor {[r y^{m}]}_{Q} = {[q x^{n} \lor r y^{m}]}_{Q} \leq {[c \lor d]}_{Q} \leq {[e]}_{Q}

. It follows that

{[c \lor d]}_{Q} = {[e]}_{Q}

. Since

P = Q \cap A

, the map

φ : A / P \to B / Q

is an embedding, which together with

c \lor d \in A

derives that

{[c]}_{P} \lor {[d]}_{P} = {[c \lor d]}_{P} = {[e]}_{P}

. Because

A / P

is a finitely subdirectly irreducible conic CRL,

{[c]}_{P} = {[e]}_{P}

{[d]}_{P} = {[e]}_{P}

. Then by Lemma 8,

c \in P

, or

d \in P

. But

c, d \notin P

, which is a contradiction. Thus Q is a prime normal filter of

B

, and by Lemma 9,

B / Q

is a finitely subdirectly irreducible conic CRL. The proof of the theorem is complete. □

Lemma 12.

[11]The class of totally ordered Sugihara monoids has the amalgamation property.

The following result is essentially due to Maksimova (see [6]).

Lemma 13.(Maksimova) The variety all Brouwerian algebras has the amalgamation property and the class of finitely subdirectly irreducible Brouwerian algebras has the amalgamation property.

Theorem 7.

The class of finitely subdirectly irreducible strongly conic idempotentCRLs has the amalgamation property.

Proof.

Let

〈 i_{1} : A ↪ B, i_{2} : A ↪ C 〉

be a span of finitely subdirectly irreducible strongly conic idempotent CRLs, assuming without loss of generality that

i_{1}

and

i_{2}

are inclusion maps and that

B \cap C = A .

Then using Theorem 1(11), we also have inclusions between their skeletons

A^{*} ↪ B^{*}

and

A^{*} ↪ C^{*}

. Since by Theorem 1(11), these skeletons are totally ordered odd Sugihara monoids, Lemma 12 yields an amalgam J for this span that is also a totally ordered odd Sugihara monoid. Moreover, we may assume that

J = B^{*} \cup C^{*}

. Let

J^{-} = {j \in J ∣ j \leq e}

and

J^{+} = {j \in J ∣ j > e}

Consider

i \in A^{*}

. Recalling that

A_{i} = {x \in A ∣ x^{* *} = i}

, clearly

A_{i} \subseteq B_{i} = {x \in B ∣ x^{* *} = i}

and

A_{i} \subseteq C_{i} = {x \in C ∣ x^{* *} = i}

. If

i = e

, then by Theorem 1(10),

A_{e}

B_{e}

and

C_{e}

are finitely subdirectly irreducible Brouwerian algebras and by Theorem 2,

A_{e}

is a subalgebra of

B_{e}

and

C_{e}

. Hence by Lemma 13, there exists a finitely subdirectly irreducible Brouwerian algebra

D_{e}

as an amalgam with

D_{e} = B_{e} \cup C_{e}

. If

i < e

, then by Lemma 13, there exists a Brouwerian algebra

D_{i}

as an amalgam with

D_{i} = B_{i} \cup C_{i}

. If

i > e

, then by Proposition 5, each of

B_{i}

and

C_{i}

is a lattice. It is well known that class of lattices has the amalgamation property. It follows that there exists a lattice

D_{i}

as an amalgam with

D_{i} = B_{i} \cup C_{i}

. Since i is the greatest element of

A_{i}, B_{i}

and

C_{i}

, it is also the greatest element of

D_{i}

. Now, for all

j \in B^{*} ∖ A^{*}

and

k \in C^{*} ∖ A^{*}

, let

D_{j} = B_{j}

and

D_{k} = C_{k}

. Let

X = {(D_{j}, \leq_{D_{j}}) ∣ j \in J}

. By construction,

(J^{-}, J^{+}, J; X)

is a

C E

-system. Thus

D = J ⨂ X

is a conic idempotent CRL. Since

D_{e}

is a finitely subdirectly irreducible Brouwerian algebra,

D = J ⨂ X

is a finitely subdirectly irreducible conic idempotent CRL. By Proposition 5,

D = J ⨂ X

is strongly finitely subdirectly irreducible conic idempotent CRL. To show that

D

is an amalgam of the original span, it suffices to check that

B

and

C

are subalgebras of

D

. Consider

x, y \in B

with

x \in B_{i}, y \in B_{j}

. Then

i, j \in J

. If

i < j

B^{*} \subseteq J

, then

x \leq_{B} y

and

x \leq_{D} y

, so

x \lor^{D} y = y = x \lor^{B} y

and

x \land^{D} y = x = x \land^{B} y

. If

i = j \in B^{* +} \subseteq J^{+}

, then since

D_{i}

is a lattice and

B_{i}

is a sublattice of

D_{i}

x \lor^{D} y = x \lor^{D_{i}} y = x \lor^{B_{i}} y = x \lor^{B} y

and

x \land^{D} y = x \land^{D_{i}} y = x \land^{B_{i}} y = x \land^{B} y \in B

. If

i = j \in B^{* -} \subseteq J^{-}

, then since

D_{i}

is a Brouwerian algebra and

B_{i}

is a subalgebra of

D_{i}

x \lor^{D} y = x \lor^{D_{i}} y = x \lor^{B_{i}} y = x \lor^{B} y

and

x \land^{D} y = x \land^{D_{i}} y = x \land^{B_{i}} y = x \land^{B} y

. Thus

B

is a sublattice of

D

. By the definition of

D

, we have

x \circ^{B} y = \{\begin{matrix} x \land^{B} y & if i, j \in B^{* -} \subseteq J^{-}, \\ x \lor^{B} y & if i, j \in B^{* +} \subseteq J^{+}, \\ x & if i \in B^{* +} \subseteq J^{+}, j \in B^{* -} \subseteq J^{-}, i^{*} <_{B^{*}} j or i \in B^{* -} \subseteq J^{-}, j \in B^{* +} \subseteq J^{+}, i \leq_{B^{*}} j^{*}, \\ y & if i \in B^{* +} \subseteq J^{+}, j \in B^{* -} \subseteq J^{-}, i^{*} \geq_{B^{*}} j or i \in B^{* -} \subseteq J^{-}, j \in B^{* +} \subseteq J^{+}, i >_{B^{*}} j^{*} . \end{matrix}

and

x \circ^{D} y = \{\begin{matrix} x \land^{D} y & if i, j \in J^{-}, \\ x \lor^{D} y & if i, j \in J^{+}, \\ x & if i \in J^{+}, j \in J^{-}, i^{*} <_{J} j or i \in J^{-}, j \in J^{+}, i \leq_{J} j^{*}, \\ y & if i \in J^{+}, j \in J^{-}, i^{*} \geq_{J} j or i \in J^{-}, j \in J^{+}, i >_{J} j^{*} . \end{matrix}

Thus

x \circ^{D} y = x \circ^{B} y

By the similar arguments, we have

x \to^{D} y = x \to^{B} y

The proof that

C

is a subalgebra of

D

is symmetrical. □

Since every variety of commutative residuated lattices has the congruence extension property, by Theorem 6, we have the following result ,which generalizes [11, Theorem 5.6].

Theorem 8.

The variety of strongly semiconic idempotentCRLs has the amalgamation property.

Funding

This research was funded by the NSF of China grant number 11571158 and the NSF of Fujian Province grant number 2020J01799.

Data Availability Statement

This paper contains no data.

Conflicts of Interest

The author declares no conflict of interest.

References

Birkhoff, G. : Lattice Theory; Amer. Math. Soc.: Providence, 1967. [Google Scholar]
Blount, K. , Tsinakis, C.: The structure of residuated lattices. Internat. J. Algebra Comput. 2003, 13(4), 437–461. [Google Scholar] [CrossRef]
Chen, W. : On semiconic idempotent commutative residuated lattices. Algebra Univers. 2020, 81, 36. [Google Scholar] [CrossRef]
Chen, W. , Chen, Y.: Variety generated by conical residuated lattice-ordered idempotent monoids. Semigroup Forum 2019, 98, 431–455. [Google Scholar] [CrossRef]
Chen, W. , Zhao, X.: The structure of idempotent residuated chains. Czechoslovak Mathematical Journal 2009, 59(134), 453–479. [Google Scholar] [CrossRef]
Gabbay, D. M. , Maksimova, L.: Interpolation and definability: Modal and intuitionistic logics; Oxford Logic Guides, vol. 46, The Clarendon Press Oxford University Press: Oxford, 2005. [Google Scholar]
Galatos, N. , Raftery, J.G.: Idempotent residuated structures: some category equivalences and their applications. Trans. Amer. Math. Soc. 2015, 367, 3189–3223. [Google Scholar] [CrossRef]
Galatos, N. , Raftery, J.G.: A category equivalence for odd Sugihara monoids and its applications. J. Pure Appl. Algebra 2012, 216, 2177–2192. [Google Scholar] [CrossRef]
Galatos, N. , Olson,J., Raftery, J.G.: Irreducible residuated semilattices and finitely based varieties. Rep. Math. Logic 2008, 43, 85–108. [Google Scholar]
Galatos, N. , Jipsen, P., Kowalski, T., Ono, H.: Residuated Lattices: an algebraic glimpse at substructural logics; Studies in Logics and the Foundations of Mathematics, Elsevier, 2007.
Gil-Férez, J. , Jipsen, P., Metcalfe, G.: Structure theorems for idempotent residuated lattices. Algebra Univers. 2020, 81, 28. [Google Scholar] [CrossRef]
Hsieh, A. , Raftery, J.G.: Semiconic idempotent residuated structures. Algebra Univers. 2009, 61, 413–430. [Google Scholar] [CrossRef]
Hsieh, A. : Some locally tabular logics with contraction and mingle. Reports on Mathematical Logic 2010, 45, 143–159. [Google Scholar]
Jipsen, P. , Tsinakis, C., A survey of residuated lattices, in: Ordered Algebraic Structures; J. Martinez ed., Kluwer Academic Publishers, Dordrecht, 2002; 19-56.
Metcalfe, G. , Montagna, F., Tsinakis, C.: Amalgamation and interpolation in ordered algebras. Journal of Algebra 2014, 402, 21–82. [Google Scholar] [CrossRef]
Mitsch, H. : A natural partial order for semigroups. Proceedings of the American Mathematical Society 1986, 97(3), 384–384. [Google Scholar] [CrossRef]
Olson, J.S. : The subvariety lattice for representable idempotent commutative residuated lattices. Algebra Univers. 2012, 67, 43–58. [Google Scholar] [CrossRef]
Olson, J.S. : Free representable idempotent commutative residuated lattices. Internat. J. Algebra Comput. 2008, 18, 1365–1394. [Google Scholar] [CrossRef]
Olson, J.S. , Raftery, J.G.: Positive Sugihara monoids. Algebra Univers. 2007, 57, 75–99. [Google Scholar] [CrossRef]
Raftery, J.G. : Representable idempotent commutative residuated lattices. Trans. Amer. Math. Soc. 2007, 359, 4405–4427. [Google Scholar] [CrossRef]
Stanovský, D. : Commutative idempotent residuated lattices. Czechoslovak Math. J. 2007, 57(132), 191–200. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Structure of Semiconic Idempotent Commutative Residuated Lattices

Abstract

1. Introduction

2. Preliminaries

3. Some Properties

4. The Construction Theorem

5. The Amalgamation Property

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe