1. Introduction

2. Materials and Methods

3. Results and discussion

3.1. Dilatometry analysis

The axial strain during the sintering cycle of monolayer and bilayer samples is plotted as a function of the time and temperature in Figure 1a. It is found that curves show at first a dilation until the sintering is activated at 680 °C. Then, the slope of the curve changes to be negative, which indicates a shrinkage of the compacts that has an exponential behavior until the end of the isothermal stage. Finally, the stage of cooling added a small shrinkage due to the thermal contraction of samples. It is found that the final strain is larger for the porous sample, and the one obtained for the bilayer is in the middle between the porous and dense monolayer samples. It can also be noted that the shrinkage of the bilayer with the porous core with a ratio with the dense shell of 50/50 is larger than the one with a ratio of 85/15. This behavior indicates that densification is due to a combination of both layers. This can be confirmed by the strain rate of the bilayer samples that increases as the diameter of porous core does it, see Figure 1b. High strain rate is reached in the porous sample because the macroscopic deformation is due to the sintering effects; necks formation and growing, and by the deformation of large pores due to the sintering stresses developed by the densification.

The sintered relative density of all samples is listed in Table 1, and as it was expected, the values of the bilayer samples are in between of the monolayer sample. However, in order to establish if the relative density of samples corresponds to the volume of each layer, the rule of mixtures is used to estimate the relative density. The rule of mixture can be written as follows:

$$D_b=f_c{D}_c+f_s{D}_s$$

(1)

In where, the D_b, D_c and D_s means the relative density of the bilayer, core and shell samples, respectively. D_c and D_s will be assumed to be the relative density of the monolayer samples obtained at the same fabrication conditions of the bilayer samples. And fc and fs mean the volume fraction of the core and shell samples, respectively. The volume fractions of the porous core and dense shell layers correspond to 15, 50 % and 85, 50 %, respectively. It is found that all the relative densities estimated by the rule of mixtures are higher than the ones measured. This suggests that more interparticle porosity is obtained, which is generated by the stresses generated at the interface of both layers. Although this difference can be as high as 10 times from the porous to the dense samples, delamination of the core layer was not observed [30,33,34]. The larger ratios of the DR-M/D (see Table 1) found in bilayer 85/15 samples indicate that the dense layer should be more affected for this effect. Therefore, the relative density of bilayers is lower than the one predicted by the rule of mixtures.

Figure 1. Dilatometry of the bilayer layers of Ti64 samples a) axial strain and b) strain rate.

Figure 1. Dilatometry of the bilayer layers of Ti64 samples a) axial strain and b) strain rate.

Table 1. Relative density measured and estimated by the rule of mixtures (R-M).

Table 1. Relative density measured and estimated by the rule of mixtures (R-M).

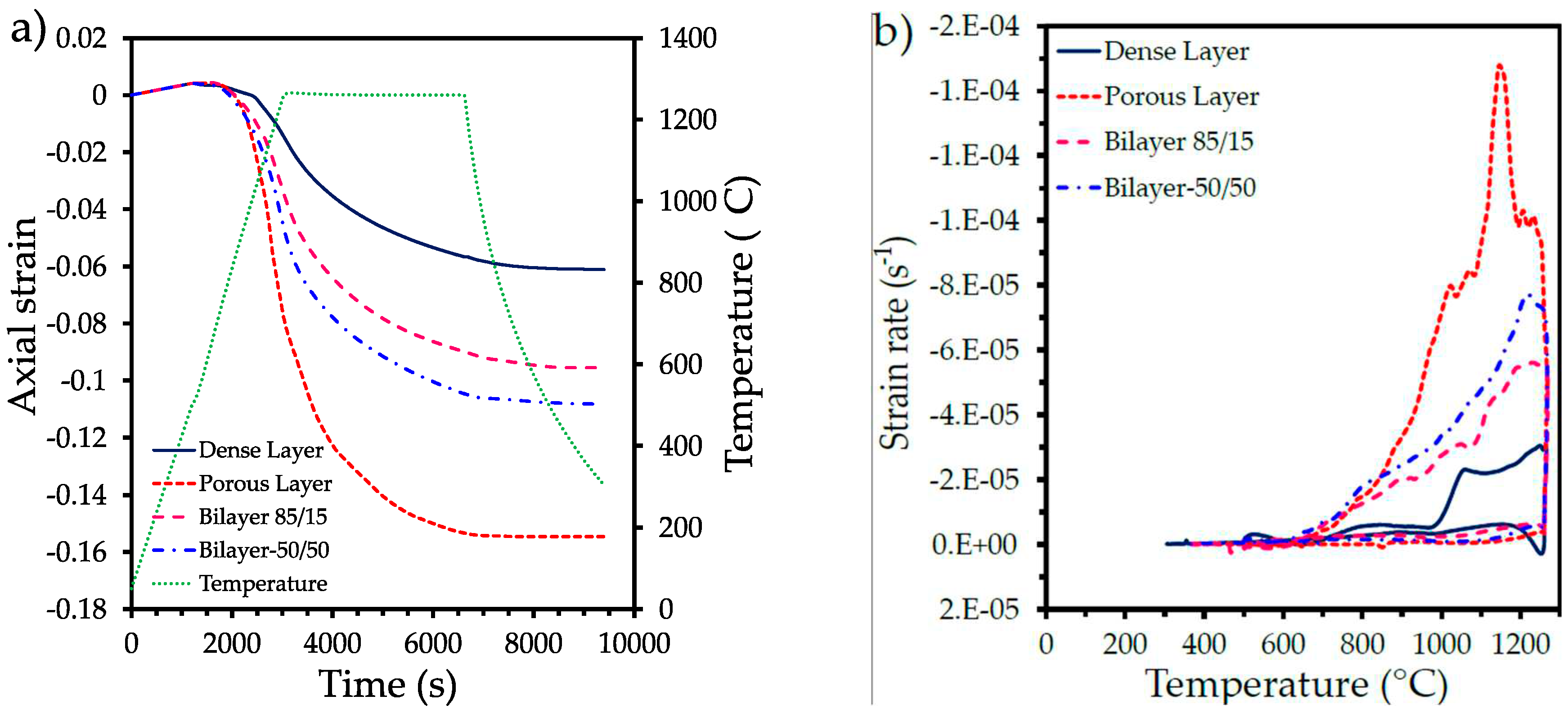
Sample	Relative density (D)	Relative density (R-M)	Ratio DR-M/D
Ti6Al4V P0	0.9633	--
Ti6Al4V P30	0.5436	--
Ti6Al4V P40	0.3972	--
Ti6Al4V P50	0.3378	--
Bilayer 85/15 P30	0.7706	0.9043	1.17
Bilayer 85/15 P40	0.7544	0.8837	1.17
Bilayer 85/15 P50	0.7238	0.8753	1.20
Bilayer 50/50 P30	0.6557	0.7532	1.14
Bilayer 50/50 P40	0.6026	0.6800	1.12
Bilayer 50/50 P50	0.5827	0.6502	1.11

3.2. Tomography analysis

Virtual 2D slices of bilayer samples showing the distribution of large pores illustrate the interface between the porous core and the dense shell, Figure 2. Large pores are well located in the middle of the samples and two different diameters can be distinguished. Because of the voxel resolution of the 3D images; is not possible to observe the interparticle porosity remaining after sintering. Nevertheless, this analysis is more focused on the location of the large pores and, to confirm that no fissures or delamination are found at the interface. It can also be qualitative noticed that the strut size in the porous core is reduced as the pore volume increased. A 3D rendering of the bilayer samples fabricated with 30 and 50 vol.% of salts and 85/15 and 50/50 diameter ratio of the core are shown in Figure 3a-3b and 3c-3d, respectively. It can be notice that the core has a cylindrical shape that goes from the top to the bottom. Also, the connectivity of pores is illustrated by a color code that indicates if large pores are connected to each other. As it can be observed, the porosity created is fully interconnected, which is according to that found for monolithic porous samples in [12].

The pore volume fraction in the porous core in bilayer samples shows an increment with respect to the volume fraction of pore formers used, see Table 2. This is mainly because the interaction of the pore formers particles induces additional interparticle porosity. The pore size distribution of the porous core in bilayer samples was estimated from the 3D images and it is very similar no matter the quantity of pore formers used, Figure 4a. This suggests that salts particles are randomly distributed without big agglomerates that could form larger pores. A wide pore size distribution from 50 to 580 µm is found (see Table 2), which corresponds to the size of pore formers. The pore size (d₅₀) measured range was from 168 to 184 µm (see Table 2), which indicates that pore formers particles were surrounded by the Ti64 particles. On the contrary, the median strut size shows a reduction as the pore volume of pore formers increases from 97 to 61 µm, see Table 2. This represents a reduction of 38 % for an increment in the pore volume of 44 % indicating a linear behavior for the strut size with respect to the pore volume fraction. The pore and strut size are lower than those obtained in scaffolds fabricated for additive manufacturing (AM), which ranged between 350 to 1400 µm for pores and 466 to 941 µm for struts depending on the AM technique used [35,36,37]. However, the pore size distribution is suitable to allow the cell adhesion and the formation of mineralization tissues that lead to the bone ingrowth [38,39,40].

Figure 2. 2D virtual slices of bilayer samples, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

Figure 2. 2D virtual slices of bilayer samples, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

Figure 3. Rendering 3D of bilayer samples and simulated flow paths in the porous core; a), b) and e) porous core 30% of pore formers and c), d) and f) porous core 50% of pore formers.

Figure 3. Rendering 3D of bilayer samples and simulated flow paths in the porous core; a), b) and e) porous core 30% of pore formers and c), d) and f) porous core 50% of pore formers.

Permeability was estimated from numerical simulations on the 3D microstructure issue from the porous core and the values are listed in Table 2. As expected, the permeability increases as the volume fraction does. The behavior corresponds to a cubic power law with respect to the pore volume fraction as it is shown in Figure 4b. This is consistent with different models proposed to estimate the permeability based on the Kozeny-Carman model [41,42]. It can also be noted from the flow lines a more tortuous path for the samples with 30 vol.% of pore formers in comparison to the ones with 50 vol.% of pore formers, Figure 3e and 3f. This confirms the reduction in the tortuosity measured from the 3D images and listed in Table 2. The permeability values also are in the range of that reported for human bones. For example, it is 3.10−11 to 5.10−10 m² for human proximal femur and 10-8 to 10-9 m² for human vertebral body, according to Nauman et al. [27].

Figure 4. Pore and strut size distributions a) and b) permeability as a function of the pore volume fraction of the porous core layer with different volume fractions of bilayer samples.

Figure 4. Pore and strut size distributions a) and b) permeability as a function of the pore volume fraction of the porous core layer with different volume fractions of bilayer samples.

Table 2. Pore characteristics of the porous core layers fabricated with different quantities of pore formers.

Table 2. Pore characteristics of the porous core layers fabricated with different quantities of pore formers.

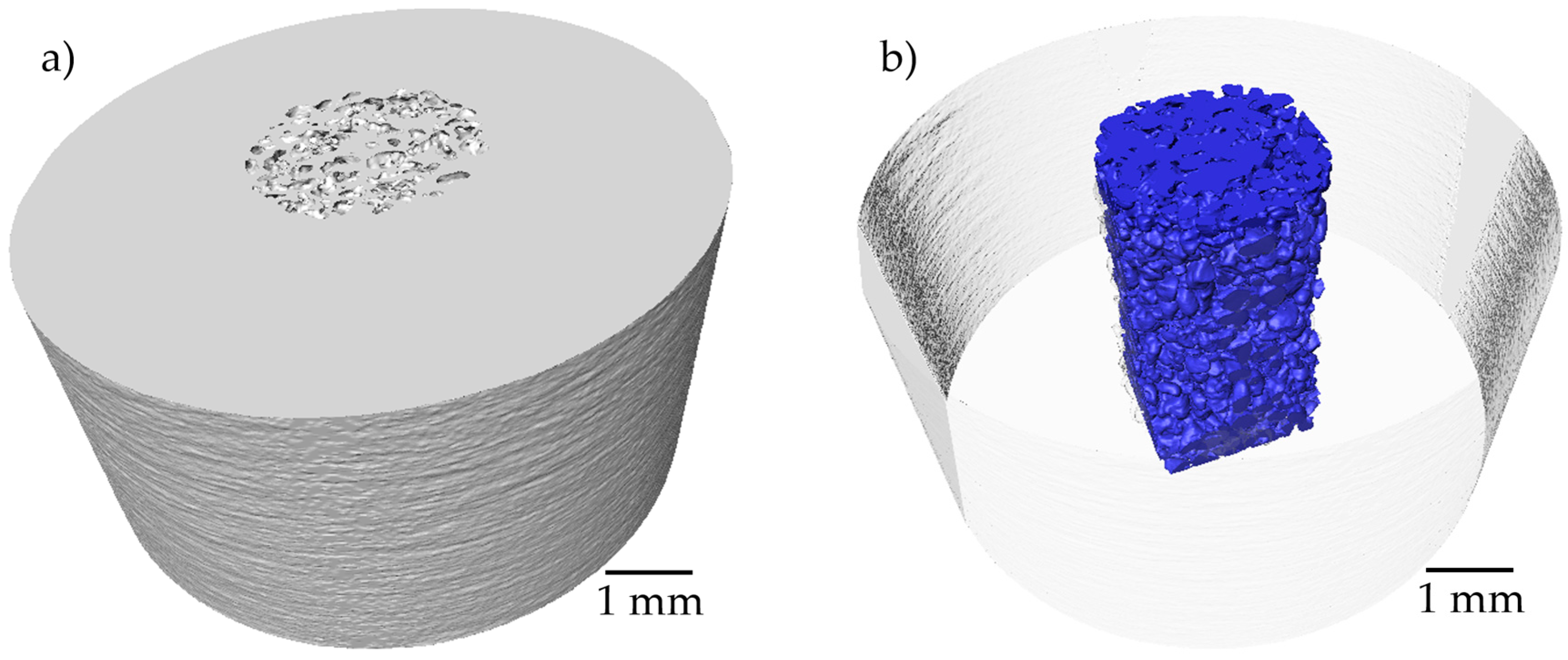
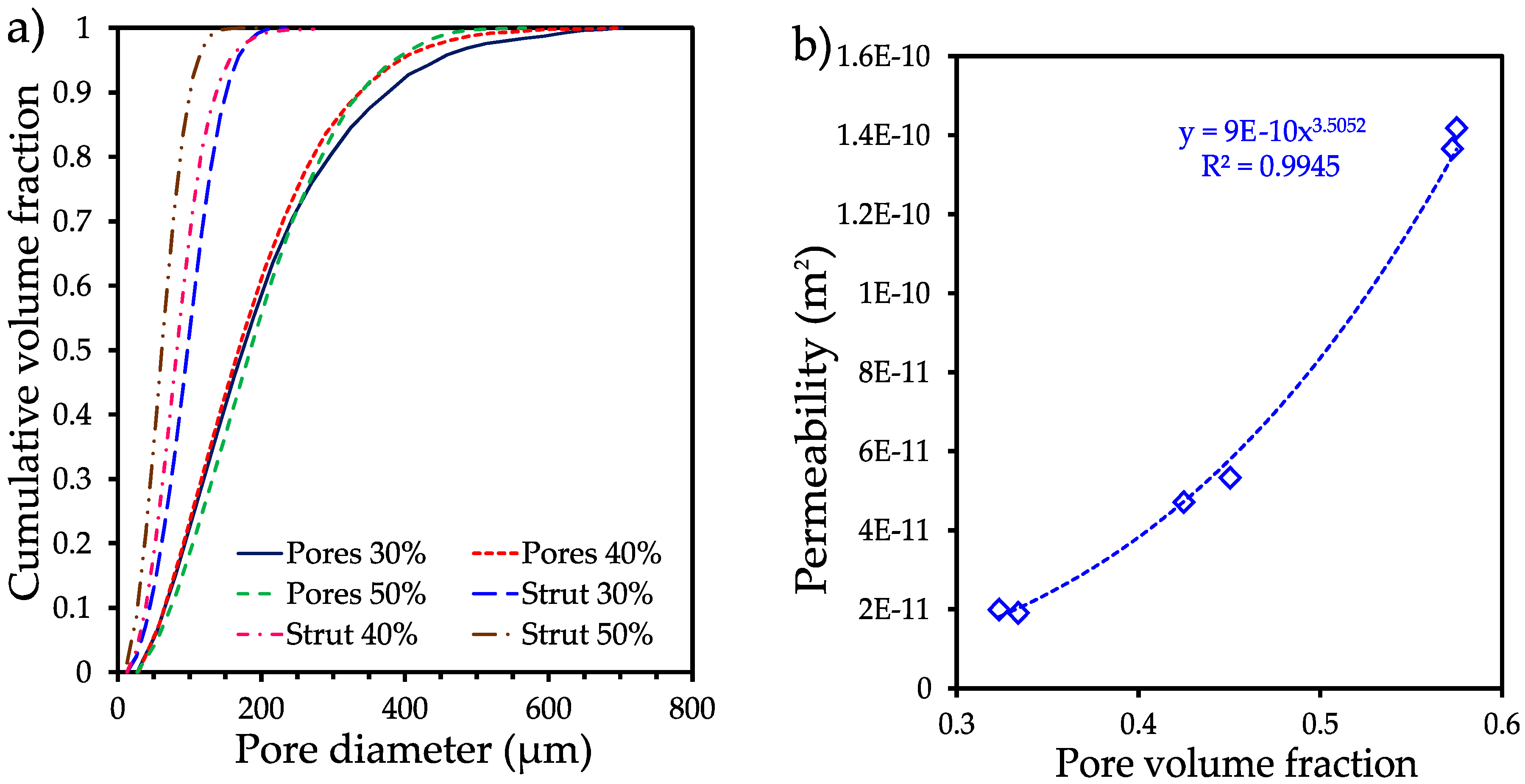
Volume fraction of pore formers (%)	Pore volume fraction (%)	Median pore size (d50 µm)	Median strut size (d50 µm)	Permeability (m2 E-10)	Tortuosity
30	32.32	174.10	97.12	0.19	1.82
40	42.50	168.36	82.26	0.47	1.58
50	57.26	184.79	61.27	1.36	1.37

3.3. Mechanical strength analysis

The compression behavior of bilayer samples is shown in the stress-strain curves in Figure 5a. As a reference, the monolithically samples are also plotted. As expected, the strength decreases as the pore formers and the core diameter increase. It can also be noticed that ductility is reduce because the strain of bilayers is reduced by the effect of the dense shell. The elastic modulus (E) and the yield stress (σy) were estimated from the elastic part of the curves in Figure 5a and the values are listed in Table 3. Monolithically samples show a high reduction as the pore volume increases showing the lowest value of E, 0.32 GPa and σy, 9.7 MPa. Although, the values of E deduced from the stress–strain curves should be taken with caution because they are frequently underestimated in comparison to the ones reported by ultrasonic method [33,43]. The E values of the bilayer samples also show a reduction that shows an exponential behavior as a function of the ratio between the surface of the porous core and the dense shell, Figure 5b. This behavior is different to the lineal one reported by Ahmadi and Sadrnezhaad [33], whose values are also plotted in Figure 5b as a comparison. It can be noticed that lower values were obtained in this work for similar porous core diameter, which is due to the quantity of pores generated by the pore formers. The E value was calculated using the rule of mixture, as it was done above for the density, with the aim to understand the behavior of the samples under compression. The rule of mixture can be re-written as follows:

$$E_b=f_c{E}_c+f_s{E}_s$$

(2)

In where, the Eb, Ec and Es means the elastic modulus of the bilayer, core and shell samples, respectively. Ec and Es will be assumed to be the E of the monolayer samples obtained at the same fabrication conditions of the bilayer samples. And fc and fs mean the volume fraction of the core and shell samples, respectively. The ER-M values are higher than those measured from the stress-strain curves, see Table 3. This is consistent with the values of the relative density estimated from the rule of mixtures, however the ER-M/E the ratio is larger than that obtained from the density.

Figure 5. Stress-strain compression curves of bilayer samples with different ratio of porous core diameter.

Figure 5. Stress-strain compression curves of bilayer samples with different ratio of porous core diameter.

On the other hand, the σy values of bilayer samples also show a reduction as the core diameter increases, as expected. Nevertheless, the behavior is close to be linear, instead of exponential as found for E. The σy was also estimated by the rule of mixture as it was made for the E:

$${\sigma }_{yb}=f_c{\sigma }_{yc}+f_s{\sigma }_{ys}$$

(3)

In where, the σ_yb, σ_yc and σ_ys mean the yield stress of the bilayer, core and shell samples, respectively. σ_yc and σ_ys will be assumed to be the σ_y of the monolayer samples listed in Table 3. It was also found that the rule of mixture overestimates the σ_y measured, however, σ_y R-M/ σ_y the ratio is close to one. This indicates that the σ_y follows a linear trend since the rule of mixture is a linear equation. In addition, the admissible strain (σy/E), which should be as high as possible to improve the mechanical behavior of a bone implant, as suggested in [44], is also shown in Table 3. The values go from 10 E^-3 to 43 E^-3, the highest being for the Bilayer 50/50 P50. These values are in the range reported for human bones (from 0.011 for compact bone to 0.035 for trabecular vertebra [1].

Table 3. Mechanical properties of monolayer and bilayer samples.

Table 3. Mechanical properties of monolayer and bilayer samples.

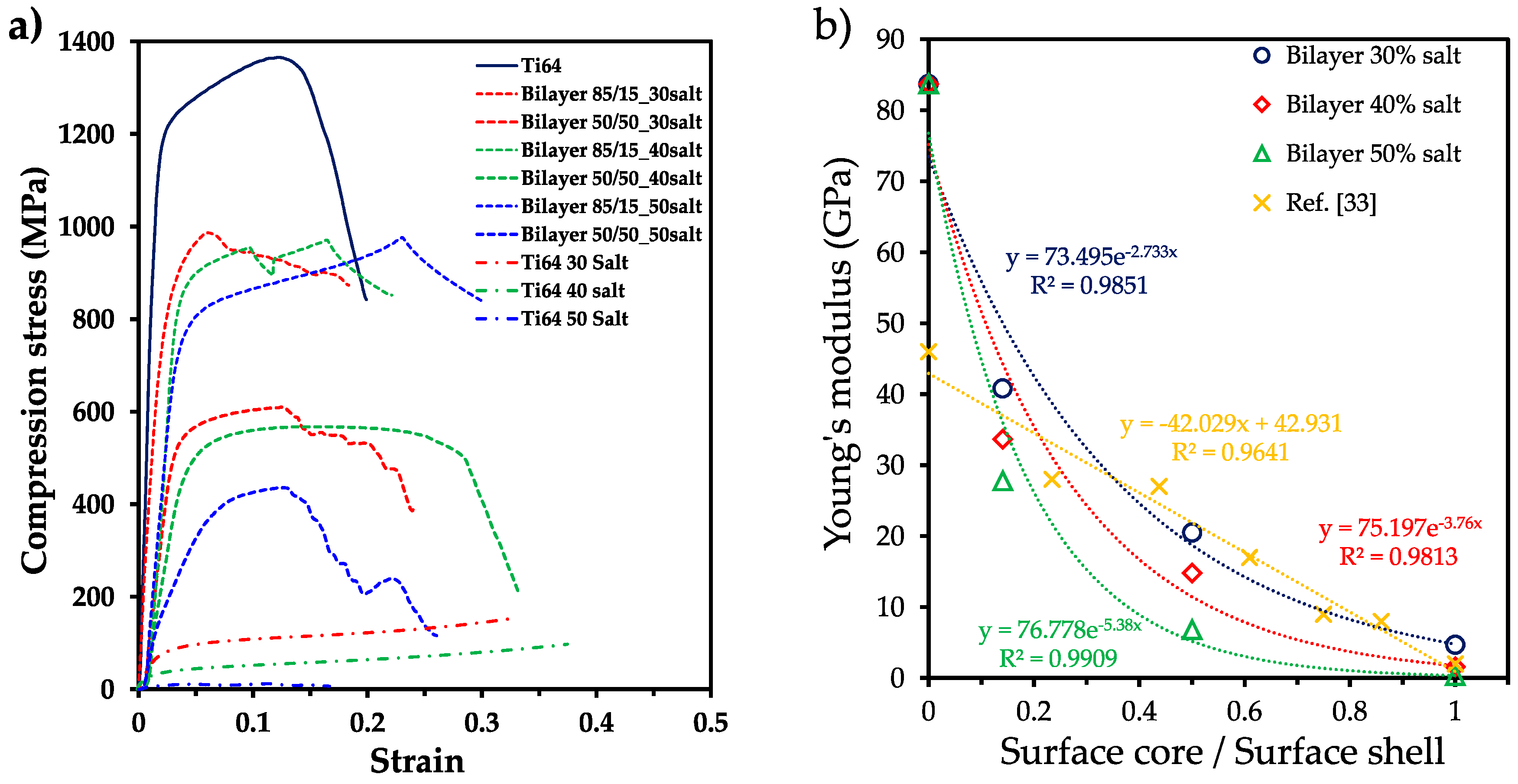
Sample	E (GPa)	ER-M (GPa)	ER-M/E	σy (MPa)	σy R-M (MPa)	σy R-M/ σy	σy/E (10-3)
Ti6Al4V P0	83.7	--		846.5			10.11
Ti6Al4V P30	4.7	--		58			12.34
Ti6Al4V P40	1.6	--		31.3			19.56
Ti6Al4V P50	0.32	--		9.7			30.31
Bilayer 85/15 P30	40.8	72.59	1.77	643.9	735.61	1.14	15.78
Bilayer 85/15 P40	33.7	44.15	2.15	445.5	451.81	1.01	21.73
Bilayer 85/15 P50	27.8	72.15	2.14	615.5	731.86	1.18	18.26
Bilayer 50/50 P30	20.5	42.60	2.87	399.8	438.44	1.09	27.01
Bilayer 50/50 P40	14.8	71.97	2.58	608.5	728.82	1.19	21.88
Bilayer 50/50 P50	6.83	42.60	6.23	299	438.44	1.46	43.77

Different models have been proposed to predict the elastic modulus of porous materials as a function of pore volume fraction [15,45,46,47]. Some of them are considering the pore shape by introducing shape factors that are generally measured from 2D postmortem images, which makes difficult to englobe the different porous materials. Cabezas et al. [12] found that the Gibson and Ashby [15] power law can accurately predict the E values by fitting the exponent of the power law to be 4 instead of the original 2 proposed, resulting in:

$$E=E_{0}D^4$$

(4)

where E₀ is the elastic modulus of the fully dense materials. Thus, the E values of monolayer and bilayer samples are depicted in Figure 6a, and it is found a good accuracy with the model to predict the E values by considering the relative density. This could suggest that stiffness on the bilayer samples is driven by the porosity in the samples. This can be confirmed from the fractured images shown in Figure 7, in where pores in the core layer are closed during the deformation process can be noted. It can also notice that the fracture shows a 45° angle, which is formed at the shell, Figure 7a and 7c, no matter the core diameter, nor the pore volume fraction.

On the contrary, the values of the σ_y for the bilayer samples does not follow the behavior estimated for the same power law proposed in [12]. These values are much higher, which suggests that σ_y is more depending on the dense shell. This could confirm that stiffness and strength in bilayer samples cannot be simply estimated by the rule of mixtures since the interaction of both layers play a role in the mechanical behavior. In where, the deformation of pores gives a more elasticity, as it can be noticed from the fractured images in Figure 7b and 7d. Meanwhile, the dense shell gives a high resistance as suggested by the fracture path in Figure 7a and 7c.

From the results obtained and discussed above, it can be said that bilayer samples with a volume ratio of core to shell of 50/50 and beyond, can be used for bone implants since their microstructure, permeability and mechanical characteristics can better mimic the human bones values.

Figure 6. a) Young’s modulus and b) yield stress as a function of the relative density.

Figure 6. a) Young’s modulus and b) yield stress as a function of the relative density.

Figure 7. SEM images of the fractured samples after compression tests, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

Figure 7. SEM images of the fractured samples after compression tests, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

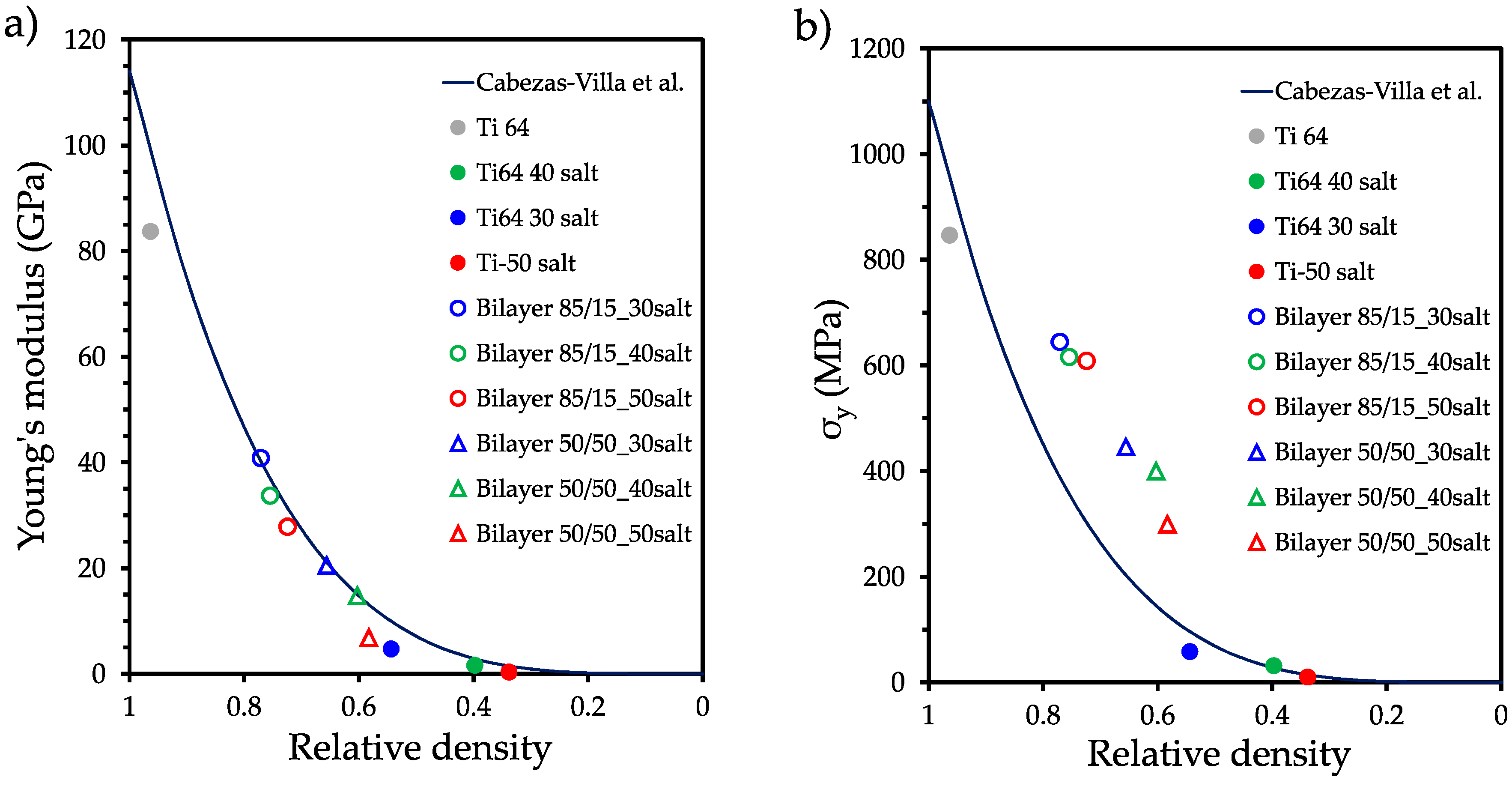
4. Conclusions

References

1. Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review. Biomaterials 2016, 83, 127-141. https://doi.org/10.1016/j.biomaterials.2016.01.012. [CrossRef]
2. Murr, L. E., Gaytan, S. M., Martinez, E., Medina, F., Wicker, R. B. Next generation orthopaedic implants by additive manufacturing using electron beam melting. Int. J. Biomater., 2012, 2012. https://doi.org/10.1155/2012/245727. [CrossRef]
3. Chen, Q. Z., Thompson, I. D., Boccaccini, A. R. 45S5 Bioglass®-derived glass–ceramic scaffolds for bone tissue engineering. Biomaterials, 2006, 27(11), 2414-2425. https://doi.org/10.1016/j.biomaterials.2005.11.025. [CrossRef]
4. Russell Levive, B., Spoere, S., Poggie, R. A., Della Valle, C. J., Jacobs, J. J. Experimental and clinical performance of porous tantalum in orthopaedic surgery. J Biomaterials, 2006, 27(27), 4671-81. https://doi.org/10.1016/j.biomaterials.2006.04.041. [CrossRef]
5. España, F. A., Balla, V. K., Bose, S., Bandyopadhyay, A. (2010). Design and fabrication of CoCrMo alloy based novel structures for load bearing implants using laser engineered net shaping. Mater. Sci. Eng. C, 2010, 30(1), 50-57. https://doi.org/10.1016/j.msec.2009.08.006. [CrossRef]
6. Bansiddhi, A., Sargeant, T. D., Stupp, S. I., Dunand, D. C. Porous NiTi for bone implants: a review. Acta Biomater., 2008, 4(4), 773-782. https://doi.org/10.1016/j.actbio.2008.02.009. [CrossRef]
7. Ballarre, J., Manjubala, I., Schreiner, W. H., Orellano, J. C., Fratzl, P., Ceré, S. Improving the osteointegration and bone–implant interface by incorporation of bioactive particles in sol–gel coatings of stainless-steel implants. Acta Biomater., 2010, 6(4), 1601-1609. https://doi.org/10.1016/j.actbio.2009.10.015. [CrossRef]
8. Shirazi, S. F. S., Gharehkhani, S., Mehrali, M., Yarmand, H., Metselaar, H. S. C., Kadri, N. A., Osman, N. A. A. A review on powder-based additive manufacturing for tissue engineering: selective laser sintering and inkjet 3D printing. Sci. Technol. Adv., 2015, 16(3), 033502. https://doi.org/10.1088/1468-6996/16/3/033502. [CrossRef]
9. Arifvianto, B., Zhou, J. Fabrication of metallic biomedical scaffolds with the space holder method: a review. Mater, 2014, 7(5), 3588-3622. https://doi.org/10.3390/ma7053588. [CrossRef]
10. Reig, L., Amigó, V., Busquets, D. J., Calero, J. A. Development of porous Ti6Al4V samples by microsphere sintering. Mater. Process. Technol, 2012, 212(1), 3-7. https://doi.org/10.1016/j.jmatprotec.2011.06.026. [CrossRef]
11. Torres, Y., Rodríguez, J. A., Arias, S., Echeverry, M., Robledo, S., Amigo, V., Pavón, J. J. Processing, characterization and biological testing of porous titanium obtained by space-holder technique. J. Mater. Sci., 2012, 47, 6565-6576. https://doi.org/10.1007/s10853-012-6586-9. [CrossRef]
12. Cabezas-Villa, J. L., Olmos, L., Bouvard, D., Lemus-Ruiz, J., Jiménez, O. Processing and properties of highly porous Ti6Al4V mimicking human bones. Mater. Res., 2018, 33(6), 650-661. https://doi.org/10.1557/jmr.2018.35. [CrossRef]
13. Jakubowicz, J., Adamek, G., Dewidar, M. Titanium foam made with saccharose as a space holder. J. Porous Mater, 2013, 20, 1137-1141. https://doi.org/10.1007/s10934-013-9696-0. [CrossRef]
14. Bahraminasab, M., Sahari, B. B., Edwards, K. L., Farahmand, F., Arumugam, M., Hong, T. S. Aseptic loosening of femoral components–a review of current and future trends in materials used. Mater. Des., 2012, 42, 459-470. https://doi.org/10.1016/j.matdes.2012.05.046. [CrossRef]
15. Gibson, L. J., & Ashby, M. F. Cellular Solids: Structure and Properties. Cambridge Univ Press. Cambridge, UK, 1999, 175, 2^nd ed.
16. Phani, K. K., & Niyogi, S. K. Young’s modulus of porous brittle solids. J. Mater. Sci., 1987, 22, 257-263. https://doi.org/10.1007/BF01160581. [CrossRef]
17. Nielsen, L. F. Elasticity and damping of porous materials and impregnated materials. J. Am. Ceram. Soc., 1984, 67(2), 93-98. https://doi.org/10.1111/j.1151-2916.1984.tb09622.x. [CrossRef]
18. Breme, J., Wadewitz, V. Comparison of titanium-tantalum and titanium-niobium alloys for application as dental implants. The Int J Oral Maxillofac. Implants, 1989, 4(2), 113-118.
19. Woodard, J. R., Hilldore, A. J., Lan, S. K., Park, C. J., Morgan, A. W., Eurell, J. A. C., Clark, S. G., Wheeler, M. B., Jamison, R. D. Johnson, A. J. W. The mechanical properties and osteoconductivity of hydroxyapatite bone scaffolds with multi-scale porosity. Biomaterials, 2007, 28(1), 45-54. https://doi.org/10.1016/j.biomaterials.2006.08.021. [CrossRef]
20. Takemoto, M., Fujibayashi, S., Neo, M., Suzuki, J., Kokubo, T., Nakamura, T. Mechanical properties and osteoconductivity of porous bioactive titanium. Biomaterials, 2005, 26(30), 6014-6023. https://doi.org/10.1016/j.biomaterials.2005.03.019. [CrossRef]
21. Dabrowski, B., Swieszkowski, W., Godlinski, D., Kurzydlowski, K. J. Highly porous titanium scaffolds for orthopaedic applications. ACS Appl. Bio Mater. B, 2010, 95(1), 53-61. https://doi.org/10.1002/jbm.b.31682. [CrossRef]
22. Wang, C. A., Le, H., & Huang, Y. Rapid assembly processes of ordered inorganic/organic nanocomposites. Biomimetics: Learning From Nature, 2010, 1-24.
23. Kienapfel, H., Sprey, C., Wilke, A., Griss, P. Implant fixation by bone ingrowth. J. Arthroplasty, 1999, 14(3), 355-368. https://doi.org/10.1016/S0883-5403(99)90063-3. [CrossRef]
24. Singh, R., Lee, P. D., Lindley, T. C., Dashwood, R. J., Ferrie, E., Imwinkelried, T. (2009). Characterization of the structure and permeability of titanium foams for spinal fusion devices. Acta Biomater., 2009, 5(1), 477-487. https://doi.org/10.1016/j.actbio.2008.06.014. [CrossRef]
25. Varley, M. C., Neelakantan, S., Clyne, T. W., Dean, J., Brooks, R. A., Markaki, A. E. Cell structure, stiffness and permeability of freeze-dried collagen scaffolds in dry and hydrated states. Acta Biomater., 2016, 33, 166-175. https://doi.org/10.1016/j.actbio.2016.01.041. [CrossRef]
26. Olmos, L., Bouvard, D., Cabezas-Villa, J. L., Lemus-Ruiz, J., Jiménez, O., Arteaga, D. Analysis of compression and permeability behavior of porous Ti6Al4V by computed microtomography. Met. Mater. Int., 2019, 25(3), 669-682. https://doi.org/10.1007/s12540-018-00223-w. [CrossRef]
27. Nauman, E. A., Fong, K. E., Keaveny, T. M. Dependence of intertrabecular permeability on flow direction and anatomic site. Ann. Biomed. Eng., 1999, 27, 517-524. https://doi.org/10.1114/1.195. [CrossRef]
28. Dewidar, M. M., Lim, J. K. Properties of solid core and porous surface Ti–6Al–4V implants manufactured by powder metallurgy. J. Alloys Compd, 2008, 454(1-2), 442-446. https://doi.org/10.1016/j.jallcom.2006.12.143. [CrossRef]
29. Lee, J. H., Park, H. J., Hong, S. H., Kim, J. T., Lee, W. H., Park, J. M., Kim, K. B. Characterization and deformation behavior of Ti hybrid compacts with solid-to-porous gradient structure. Mater. Des., 2014, 60, 66-71. https://doi.org/10.1016/j.matdes.2014.03.051. [CrossRef]
30. Ahmadi, S., & Sadrnezhaad, S. K. A novel method for production of foamy core@ compact shell Ti6Al4V bone-like composite. J. Alloys Compd, 2016, 656, 416-422. https://doi.org/10.1016/j.jallcom.2015.09.248. [CrossRef]
31. Olmos, L., Mihalcea, E., Vergara-Hernández, H. J., Bouvard, D., Jimenez, O., Chávez, J., Camacho, N., Macías, R. Design of architectured Ti6Al4V-based materials for biomedical applications fabricated via powder metallurgy. Mater. Today Commun., 2021, 29, 102937. https://doi.org/10.1016/j.mtcomm.2021.102937. [CrossRef]
32. Okuma, G., Kadowaki, D., Shinoda, Y., Akatsu, T., Guillon, O., Wakai, F. Determination of the size of representative volume element for viscous sintering. JCS-Japan, 2016, 124(4), 421-425. https://doi.org/10.2109/jcersj2.15275. [CrossRef]
33. Trueba, P., Chicardi, E., Rodríguez-Ortiz, J. A., Torres, Y. Development and implementation of a sequential compaction device to obtain radial graded porosity cylinders. J. Manuf. Process, 2020, 50, 142-153. https://doi.org/10.1016/j.jmapro.2019.12.011. [CrossRef]
34. Cocks, A. C. Constitutive modelling of powder compaction and sintering. Prog. Mater. Sci., 2001, 46(3-4), 201-22. https://doi.org/10.1016/S0079-6425(00)00017-7. [CrossRef]
35. Parthasarathy, J., Starly, B., Raman, S., Christensen, A. Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting (EBM). Mech Behav Biomed Mater, 2010, 3(3), 249-259. https://doi.org/10.1016/j.jmbbm.2009.10.006. [CrossRef]
36. Sallica-Leva, E., Jardini, A. L., Fogagnolo, J. B. Microstructure and mechanical behavior of porous Ti–6Al–4V parts obtained by selective laser melting. Mech Behav Biomed Mater, 2013, 26, 98-108. https://doi.org/10.1016/j.jmbbm.2013.05.011. [CrossRef]
37. Coffigniez, M., Gremillard, L., Balvay, S., Lachambre, J., Adrien, J., Boulnat, X. Direct-ink writing of strong and biocompatible titanium scaffolds with bimodal interconnected porosity. Addit. Manuf, 2021, 39, 101859. https://doi.org/10.1016/j.addma.2021.101859. [CrossRef]
38. Itälä, A. I., Ylänen, H. O., Ekholm, C., Karlsson, K. H., Aro, H. T. (2001). Pore diameter of more than 100 μm is not requisite for bone ingrowth in rabbits. J. Biomed. Mater. Res, 2001, 58(6), 679-683. https://doi.org/10.1002/jbm.1069. [CrossRef]
39. Taniguchi, N., Fujibayashi, S., Takemoto, M., Sasaki, K., Otsuki, B., Nakamura, T., Matsuda, T., Kokubo, T., Matsuda, S. Effect of pore size on bone ingrowth into porous titanium implants fabricated by additive manufacturing: an in vivo experiment. Mater. Sci. Eng. C, 2016, 59, 690-701. https://doi.org/10.1016/j.msec.2015.10.069. [CrossRef]
40. Bohner, M., Baroud, G., Bernstein, A., Doebelin, N., Galea, L., Hesse, B., ... & Seeherman, H. Characterization and distribution of mechanically competent mineralized tissue in micropores of β-tricalcium phosphate bone substitutes. Today Commun., 2017, 20(3), 106-115. https://doi.org/10.1016/j.mattod.2017.02.002. [CrossRef]
41. Kaviany, M., Principles of Heat Transfer in Porous Media, 1995, Springer-Verlag, New York.
42. Katz, A. J., & Thompson, A. H. Quantitative prediction of permeability in porous rock. Phys. Rev. B, 1986, 34(11), 8179. https://doi.org/10.1103/PhysRevB.34.8179. [CrossRef]
43. Torres, Y., Lascano, S., Bris, J., Pavón, J., & Rodriguez, J. A. Development of porous titanium for biomedical applications: A comparison between loose sintering and space-holder techniques. Mater. Sci. Eng. C, 2014, 37, 148-155. https://doi.org/10.1016/j.msec.2013.11.036. [CrossRef]
44. Song, Y., Xu, D. S., Yang, R., Li, D., Wu, W. T., & Guo, Z. X. (1999). Theoretical study of the effects of alloying elements on the strength and modulus of β-type bio-titanium alloys. Mater. Sci. Eng. A, 1999, 260(1-2), 269-274. https://doi.org/10.1016/S0921-5093(98)00886-7. [CrossRef]
45. Kováčik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett, 1999, 18(13), 1007-1010.
46. Nielsen, L. F. Elasticity and damping of porous materials and impregnated materials. J. Am. Ceram. Soc., 1984, 67(2), 93-98. https://doi.org/10.1111/j.1151-2916.1984.tb09622.x. [CrossRef]
47. Phani, K. K., & Niyogi, S. K. Young’s modulus of porous brittle solids. J. Mater. Sci., 1987, 22(1), 257-263. https://doi.org/10.1007/BF01160581. [CrossRef]