1. Introduction
Currently, greenhouse effect problems have been concerned by scientists. The main reason leading to those problems is that the process of economic and social development of humans has directly polluted the environment by creating industrial emissions. And one of those causes is the exhaust gas caused by refrigerant leakage of air-conditioning systems as well as industrial and commercial refrigeration systems. Therefore, research to find environmentally friendly refrigerants is the goal of experts. Experts have found and considered CO2 (known as R744) as a refrigerant that has the potential to replace traditional refrigerants which many advantages such as having the low Global Warming Potential (GWP=1) and Ozone Depletion Potential (ODP=0) in current refrigerants and not being able to cause fire or explosion when a leak occurs. Based on the above advantages, many previous studies have been conducted to experimentally evaluate systems operating under subcritical and transcritical of CO2 refrigeration systems.
Recently the R744 transcritical cycle has been widely researched to find optimal working points as well as optimal designs to improve compressor energy efficiency. Related to this field, Zhang et al. [
1] conducted simulations based on the R744 transcritical cycle involving a few performance parameters and using CFD (Computational Fluid Mechanics) models for tubular and wing air cooling condenser. The simulation results indicated that the approaching temperature decreases with the increasing of the air inlet velocity. Moreover, the model was compared and confirmed with experimental measurements and literature correlation. The simulation and experiment results in [2-4] were analyzed with an R744 transcritical cycle operating in heat pump mode with auxiliary thermoelectric cooling equipments. These studies show the effects of coolant flow rate and temperature, auxiliary cooling capacity, compressor discharge pressure on the COP (Coefficient of Performance) and the heating efficiency factor. Deng et al. [
5] theoretically analyzed an ejector refrigeration cycle operating on a transcritical cycle. Using an expansion device and controlling the suction rate, the ejector ensures the amount of vapour returning to the compressor and the amount of liquid at the evaporator. The COP was studied in a variety of injection ratios while simultaneously comparing it with conventional vapor-compressed refrigeration cycles. Zhang et al. [
6,
7] experimentally compared the R744/R290 subcritical cycle in the cascade system to the R744 transcritical cycle. The results of the analysis of the transition discharge pressure, the mass ratio between R744 and R290 and the outlet temperature of the gas cooler show that using IHX for the subcritical cycle was less effective than the transcritical cycle. Gullo et al. [
8] evaluated the aspects related to the R744 transcritical cycle in a refrigeration plant in supermarkets. The study concluded that R744 can be well applied at supermarkets, especially suitable for areas with high ambient temperatures. Hazarika et al. [
9] conducted an experimental study and numerical simulation of an R744 transcritical air conditioning system. Not only variations in the heat transfer area of the evaporator were proposed to study the system COP further but also evaluation of the effect of air velocity and pressure at the air cooler. However, the studies in [1-9] did not mention CO
2 air conditioning systems with throttling inlet temperatures below the critical point.
In the field of R744 applications research, some studies have applied the operating cycle under the critical point to reduce the condensation pressure and increase the overall refrigeration performance. Sanz-Kock et al. [
10] conducted an experimental evaluation of the energy efficiency of a cascade refrigeration system using R134a/CO
2, where they used semi-hermetic compressors in subcritical cycles. Parameters such as compressor efficiency, temperature difference at the cascade heat exchanger, and compressor discharge temperature are evaluated under conditions of various evaporation temperature and condensation temperature. Zhang et al. [
11] proposed a cascade refrigeration system with R1270/CO
2. Particularly, R1270 was used in the high temperature cycle while CO
2 was used as a refrigerant in the low temperature cycle. They focused on evaluating the system's COP and the isentropic efficiency of the R1270 compressor when the evaporation temperature changes from -7
oC to -19
oC. The results showed that R1270 replaces R290 and R717 better at the high-stage cycle. Llopis et al. [
12] implemented an experimental evaluation of welded plate heat exchangers in subcritical cycles using R744 with water cooling evaporative condenser and semi-hermetic compressors. Within the study limits, the evaporation temperature and the condensation temperature were changing while the operating frequency of the compressor was kept at a fixed value. The assessments given include the COP and the cooling capacity. In addition, the influence of the internal heat exchanger in the cascade cycle was analyzed theoretically. The results indicate that welded plate heat exchangers for subcritical cycles had less impact on energy efficiency but were suitable for energy improvements in the cascade cycles. Nicola et al. [
13] analyzed the thermal efficiency of the cascade refrigeration cycle, in which the low-layer substance R744 was mixed with other refrigerants such as R170, R290, R1150, and R717, respectively. Based on the Carnahane Starlinge DeSantis equation, the COP results indicated that R744 should only be used in its monocomponent, in combination with other refrigerants would reduce cooling capacity and low energy efficiency. The experimental results in [
14,
15] discussed the operating parameters and energy efficiency in a cascade cycle using the R717/R744. Dopazo et al. [
14] performed a comparison with a two-stage cycle using R717 under the same operating conditions with evaporation temperatures and condensation temperatures corresponding to cascade cycles ranging from -17.5
oC to -7.5
oC. In addition, Lee et al. [
15] were given further exploitation of the evaporation temperature, condensation temperature, and temperature difference in the cascade heat exchanger. From [10-15], most of the research in the subcritical cycle focused on experimental research to find suitable refrigerants in the high-temperature cycle, find out the relationship between COP and operating parameters, and determine the optimal operation regime. They used the cascade refrigeration system and did not use the single-stage subcritical refrigeration system.
From the research in recent years mentioned above, the studies mainly have focused on exploiting the influence of parameters such as evaporation temperature, condensation temperature, condensation pressure, different ways of configuring equipment, adjusting design parameters as well as replacing refrigerants to find the most suitable ones in each specific application. While there are fewer of the R744 subcritical cycle applications that use evaporative condensers by water and air, especially with the condensing mini tubes that are flooded in the cooling water tank. Therefore, the numerical simulation and experimental investigation for this application are potential directions, which should be developed especially in the conditions of tropical countries.
2. Methodology
2.1. Calculation Design
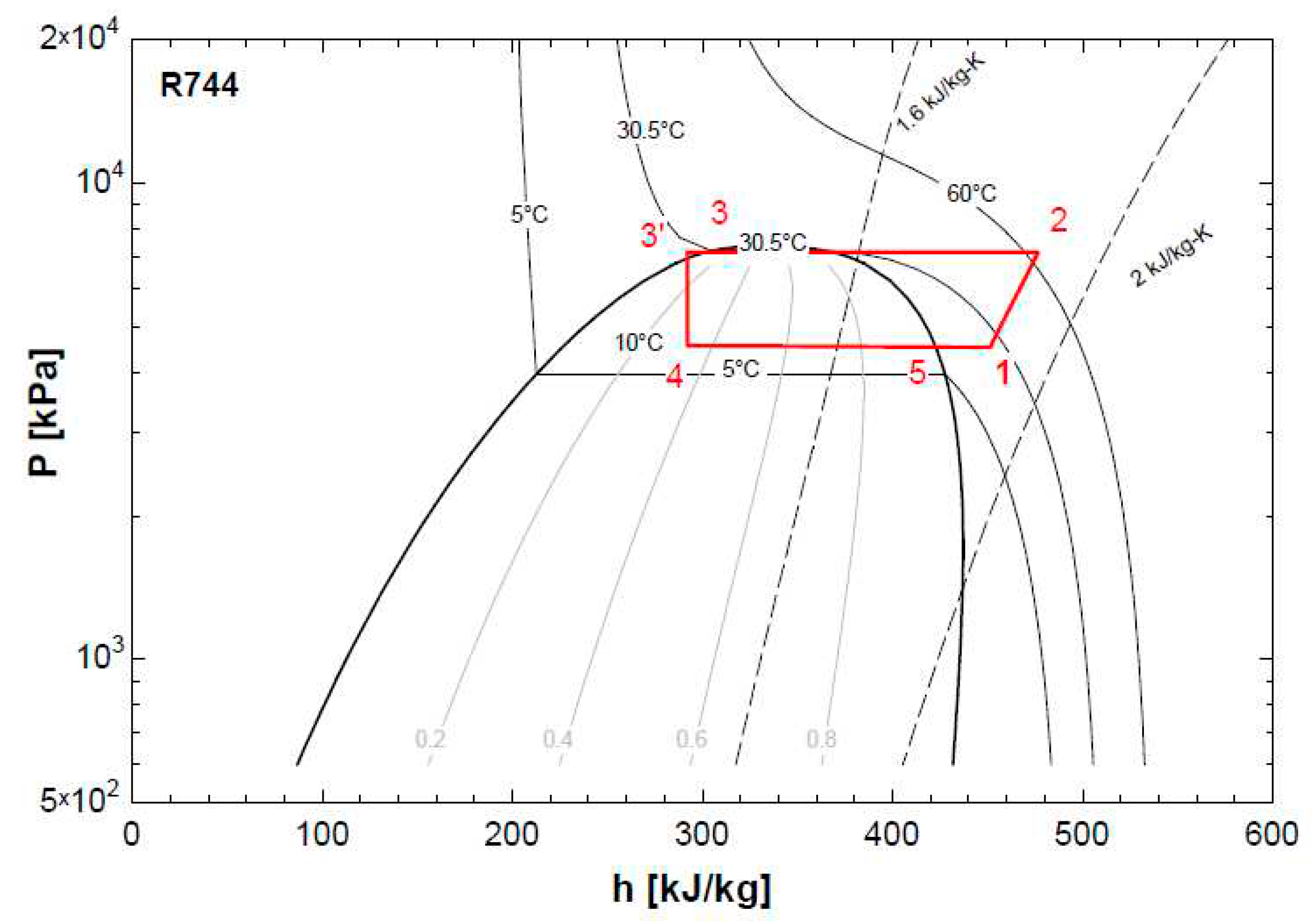
With the initial design data for an R744 air conditioning system, the testing cycle has a cooling capacity of 1000W, an evaporation temperature of 10
oC, and a condensation temperature of 30.5
oC. Design parameters are calculated and expressed according to
Figure 1 and
Table 1.
In this study, the key components of a testing cycle were designed based on the computational theory of [
16] with the following equations:
The cooling capacity was calculated as:
The condensing capacity for G kg was calculated as:
The work of adiabatic compression was determined by:
The Coefficiency of Performance of the cycle was calculated as:
The overall heat transfer rate was calculated as:
Where is the heat transfer area (m2)
is condensing capacity (W)
is the overall heat transfer coefficient (W/m2.K)
is Log mean temperature difference (oC)
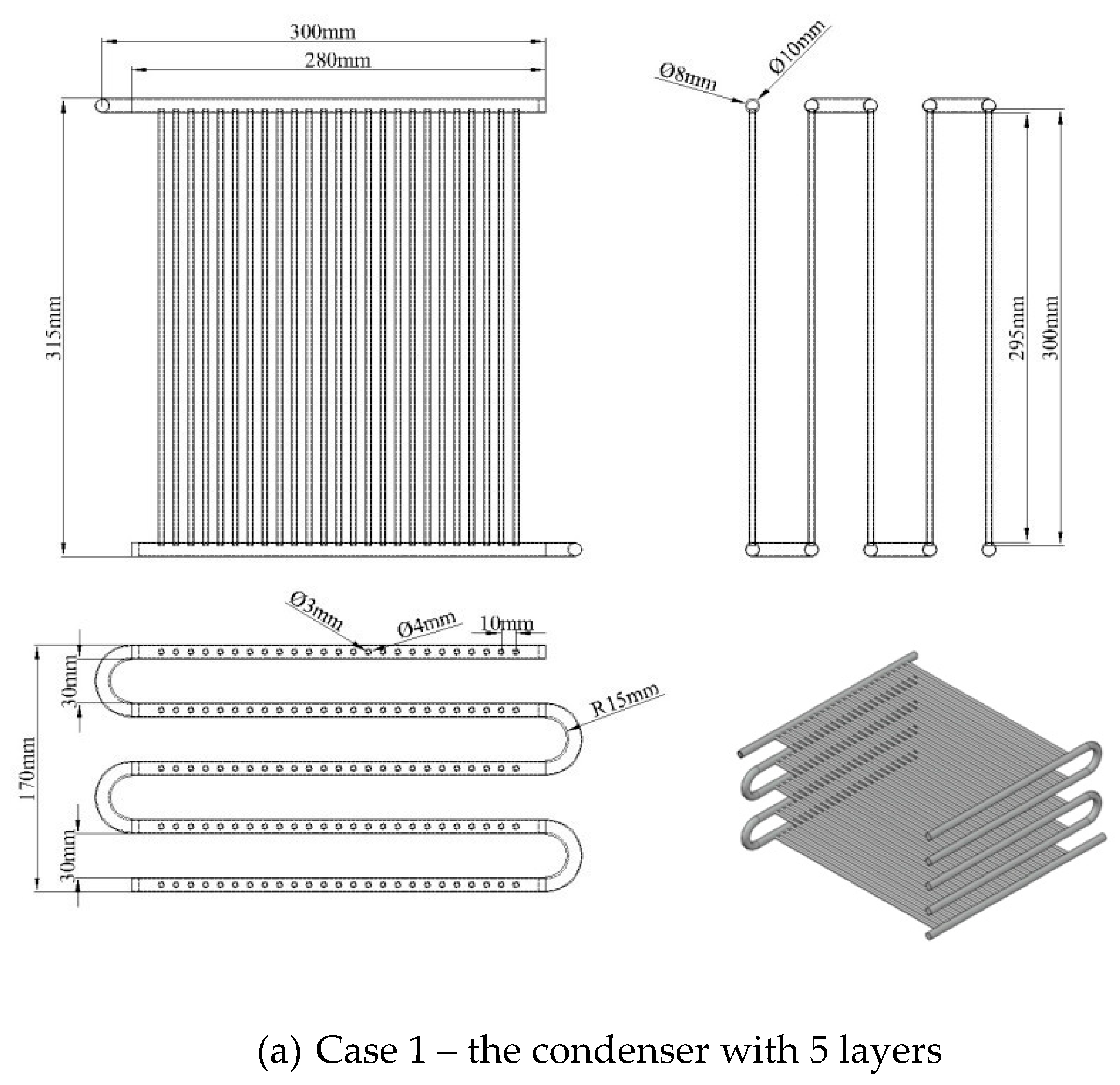
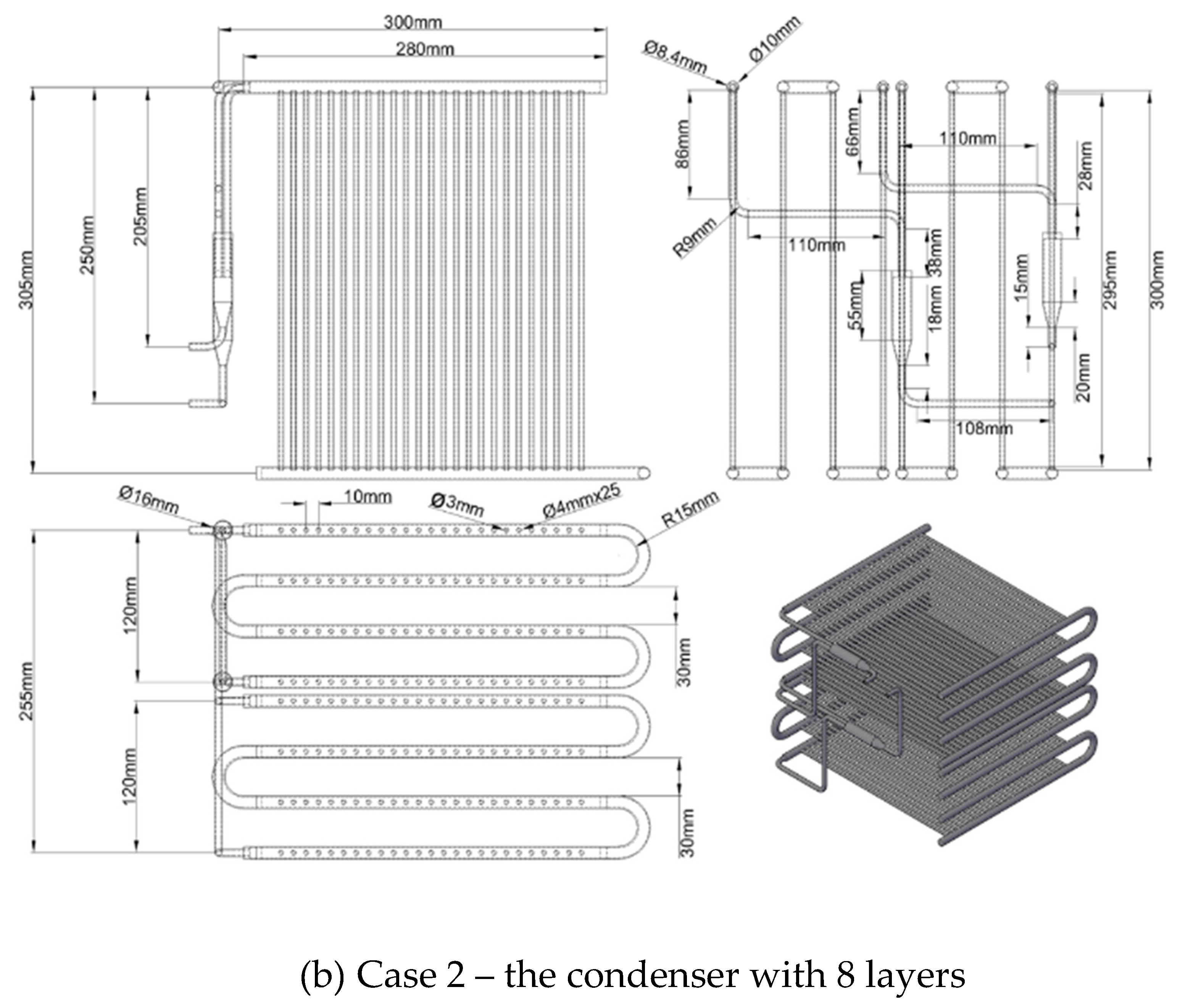
Based on the same overall heat transfer coefficient, this study offers two design configurations for the condenser consisting of Case 1 (5 layers of copper tube) and Case 2 (8 layers of copper tube) with dimensions and parameters shown in
Figure 2 and
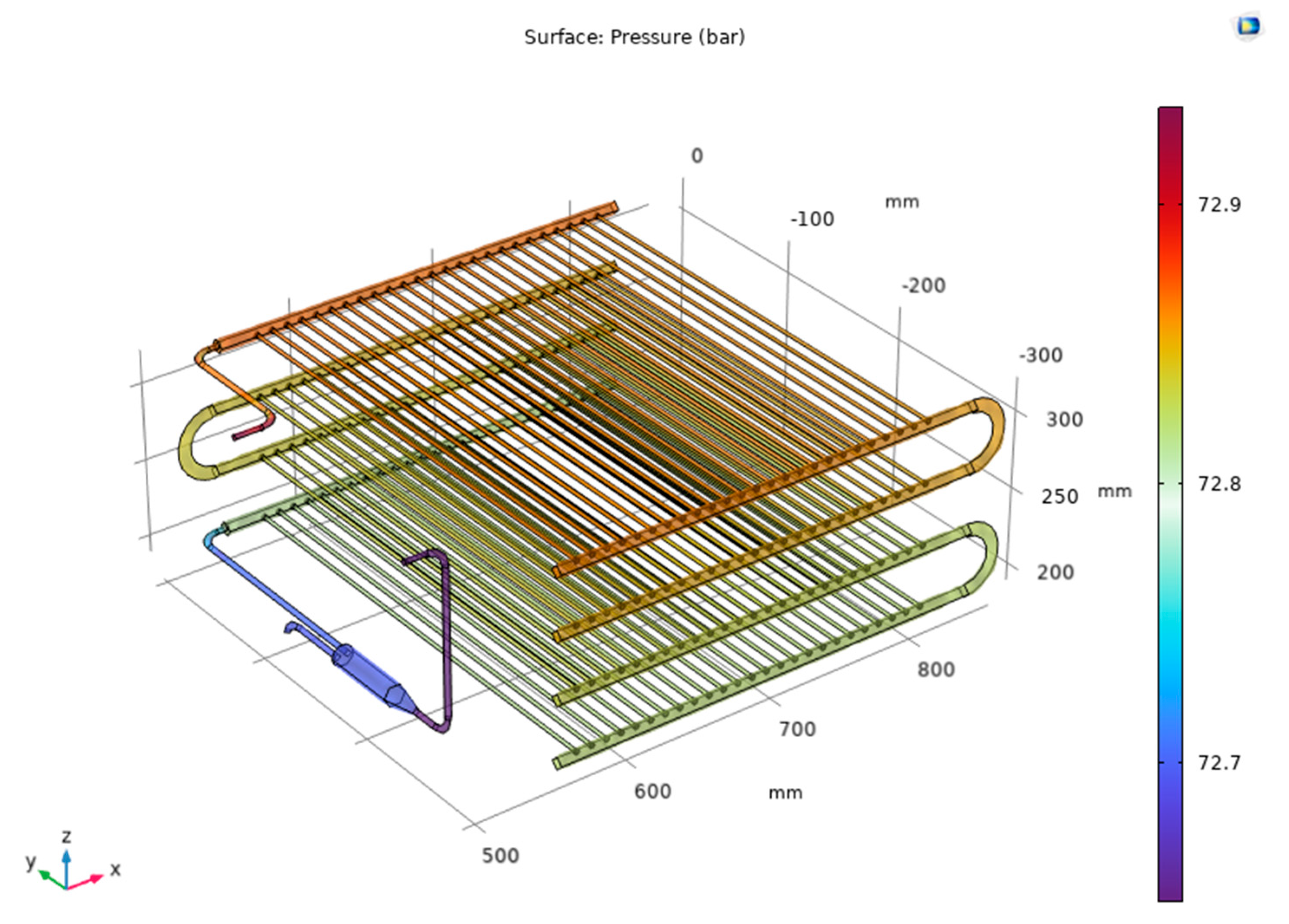
Table 2. These condensers use mini-size tubes. For Case 2, there are two tube sets (banks) arranged in parallel; each set has four tube layers (or four passes). Each layer has 25 tubes with the outer and the inner diameters are 4 mm and 3 mm, respectively. The actual image is shown in Figure 3. The condensing mini tubes are flooded in the cooling water tank.
Figure 2.
The design parameters of two condensers using mini tubes.
Figure 2.
The design parameters of two condensers using mini tubes.
Figure 3.
The actual photo of the condenser with 8 layers using mini tubes.
Figure 3.
The actual photo of the condenser with 8 layers using mini tubes.
2.2. Numerical Simulation
This model was solved based on Conjugate Heat Transfer model, which formed of two models: (1) Heat transfer in Solid and Fluid and (2) Turbulent flow.
For Heat transfer in the Solids and Fluids model, the assuming equations are expressed by:
For the Turbulent flow model, the assuming equations are expressed by:
The transport equation for k reads by:
The transport equation for ε is as follows:
The momentum formulation is as follows:
Where is the turbulence viscosity (Pa.s)
is velocity of fluid (m/s)
is density of fluid (kg/m3)
is thermal conductivity (W/m.K)
The simulation focuses on a water-cooled condenser using COMSOL Multiphysics 6.1 software using a heat transfer model in the Conjugate Heat Transfer synthesis consisting of 2 models: the Turbulent Flow model, Low Renold k- combined with the Heat transfer in Solids and Fluids model.
To simplify the simulation model, there is an even division of rows of pipes between 2 sets, the R744 entering the condenser is evenly divided. Therefore, the simulation model uses a symmetrical method with a lower number of elements, saving time, improving convergence, and increasing accuracy.
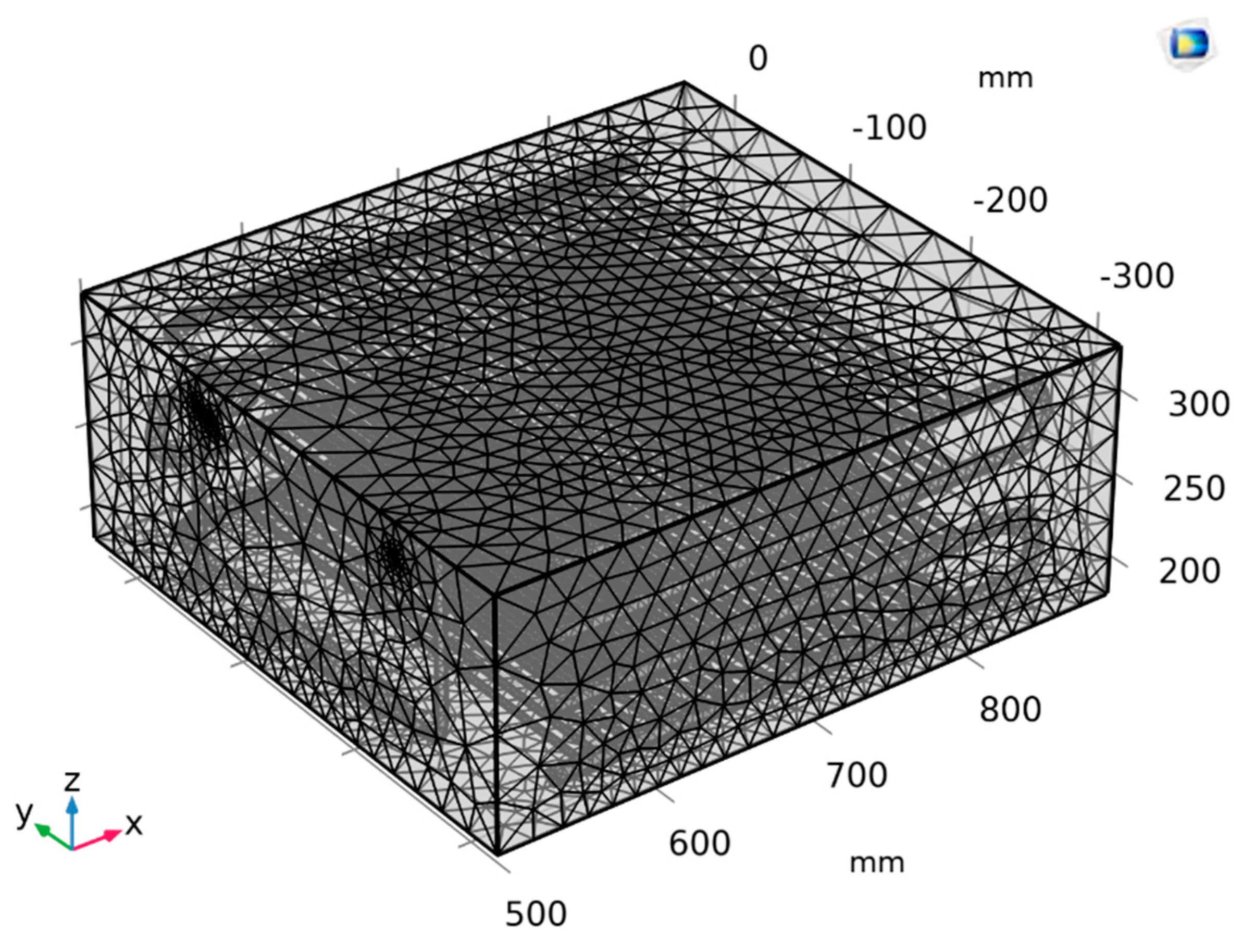
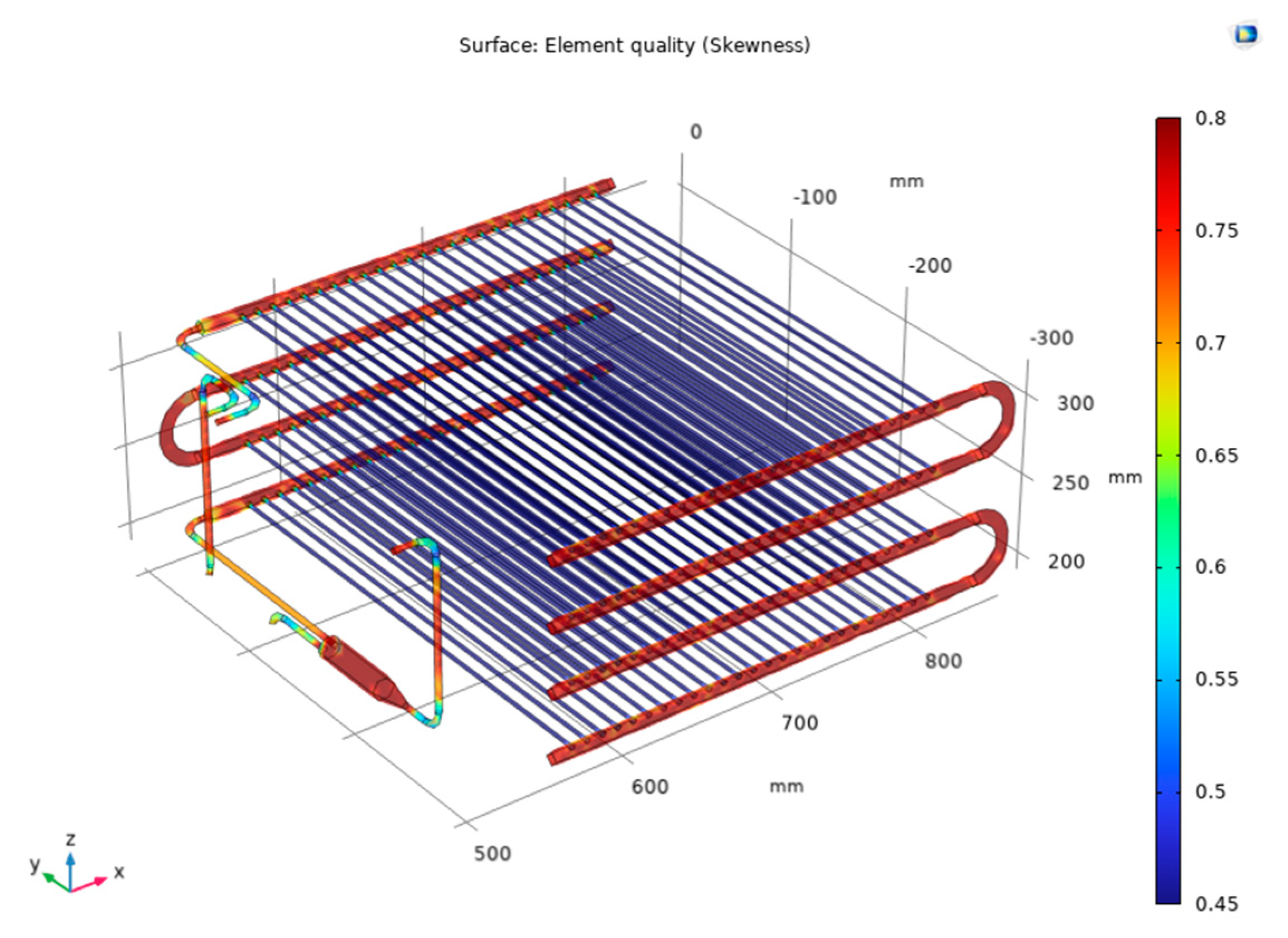
Complete mesh consists of 692399 domain elements, 134042 boundary elements, and 24441 edge elements as shown in Figure 3. With the quality of the simulation mesh supporting a faster simulation process, the average Skewness acceptable index in the rows of pipes at the condenser ranges from 0.5 – 0.7 inside the tube bank and range from 0.75 – 0.8 at the manifolds as shown in
Figure 4.
For heat transfer variables, the GMRES (Generalized Minimal Residual Method) iterative solver was used. This method produces an approximate solution to the linear system after a finite number of steps. These methods are useful for large systems of equations where it is reasonable to trade-off precision for a shorter run time. Iterative methods use the coefficient matrix only indirectly, through a matrix-vector product or an abstract linear operator. Iterative methods can be used with any matrix, but they are typically applied to large sparse matrices for which direct solves are slow. Besides, for turbulence variables, the PARDISO (Parallel Sparse Direct Solver) was used to improve sequential and parallel sparse numerical factorization performance, they exploit pipelining parallelism with a combination of left-looking and right-looking supernode techniques. PARDISO is multithreaded on platforms that support multithreading for saving solving time.
Figure 3.
Meshing for the test sample.
Figure 3.
Meshing for the test sample.
Figure 4.
Skewness index for simulation model.
Figure 4.
Skewness index for simulation model.
2.3. Experiment Set Up
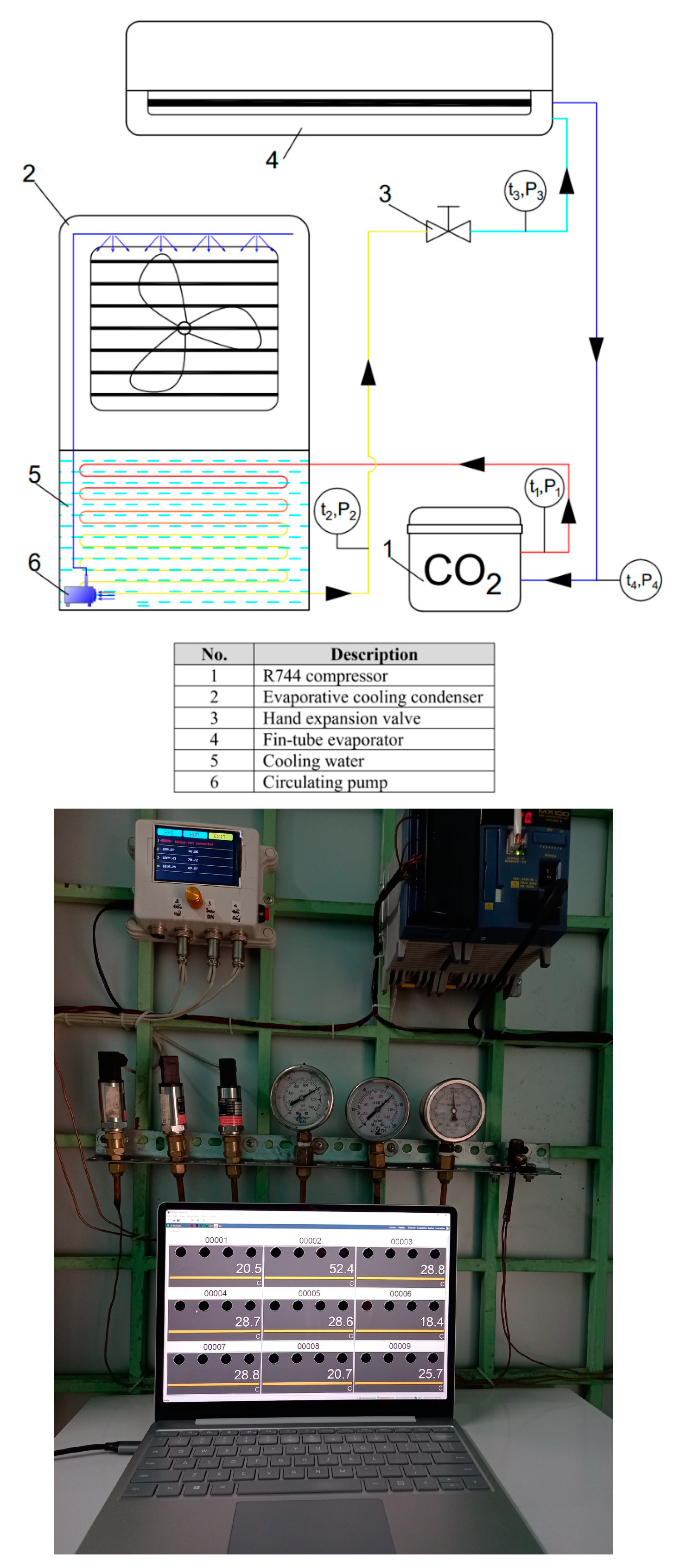
The diagram for the testing system is shown in
Figure 5. The experimental system is designed with a completely R744 air conditioning cycle, which cooled by the evaporative cooling method, operating in the Vietnam climatic conditions. For this testing system, the low-pressure, low-temperature superheated vapor coming from the evaporator enters the compressor to perform the process of isotropy adiabatic compression that consumes an external work into high-pressure, high-temperature superheated vapor. The superheated vapor continues enter to the condenser, releasing heat to water, performing complete liquefied isobaric condensation. The liquid refrigerant goes to the hand throttle valve, the enthalpy isometric throttle becomes a wet saturated vapor of low pressure, low temperature enters the evaporator receiving heat from the ambient that performs isobaric evaporation becomes dry saturated vapor, which leaves the evaporator then return to the compressor to complete a closed cycle.
Besides, measuring devices such as flowmeters, temperature and pressure at cycle’s state points are set at specified locations to collect data to determine operating parameters. The types of measuring devices and their accuracies are shown in
Table 3.
3. Results and discussion
3.1. Temperature Field at R744 Side in Numerical Simulation
The simulation model is solved with the boundary conditions as shown in
Table 4. For example, the inlet temperature of the condenser for the R744 side is 63.3 °C and the mass flow rate of R744 is 3.28 g/s. These values were verified by the experimental data.
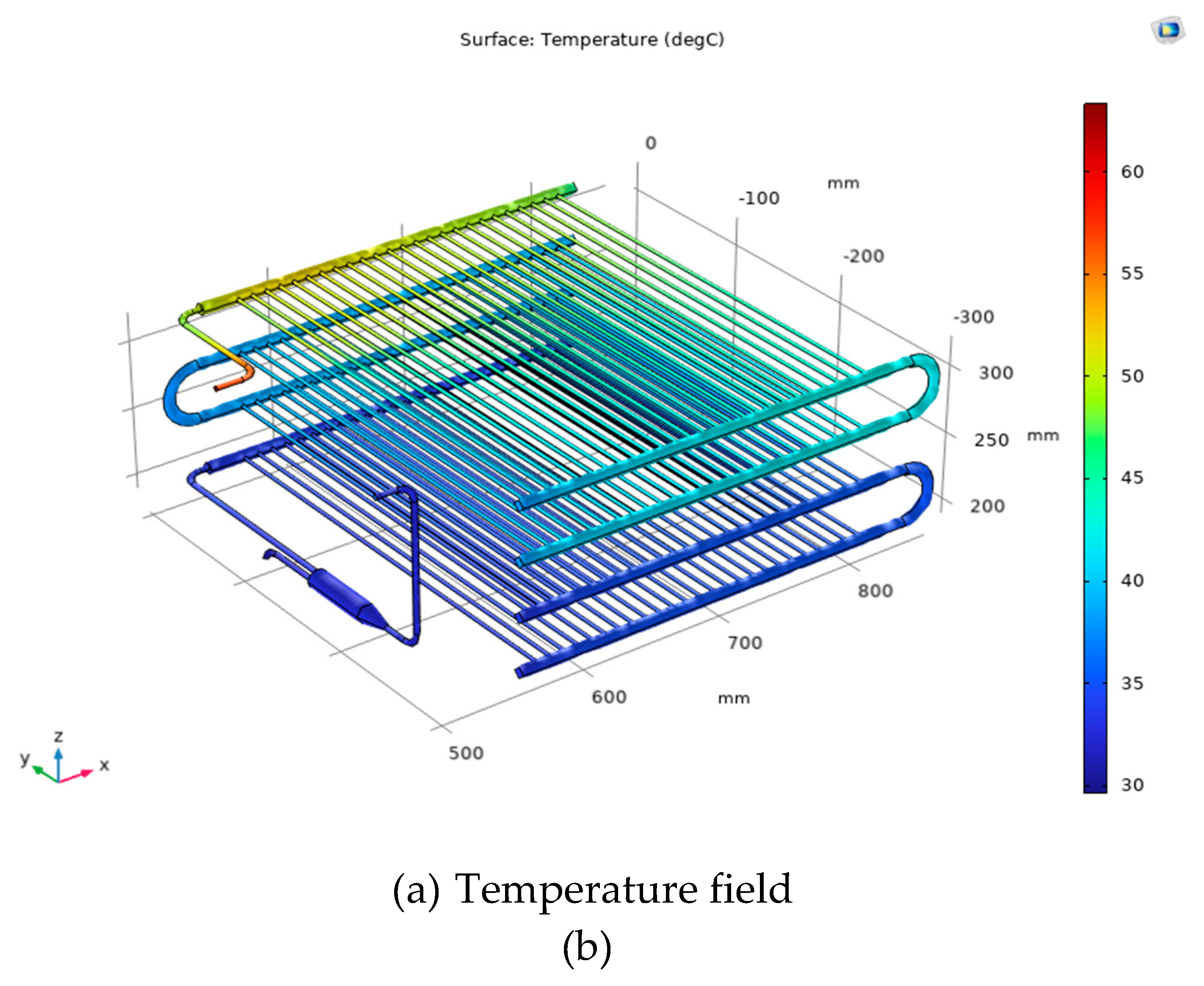
Figure 6a shows the temperature field of R744 in the condenser. Based on 3D images and temperature scales (Celsius), under current simulation conditions, the system operates under a pressure of 72.6 bar, superheated vapors enter the condenser at a temperature of 63.3
oC. It is observed that the temperature distribution through the unit has changed with the input temperature of R744 is 63.3
oC after exchanging heat with temperature water of 26.4
oC and the average velocity of water is 0.003 m/s. The temperature field of the R744 at the inlet decreases gradually through each layer until the end of the condenser the outlet temperature of 27.8
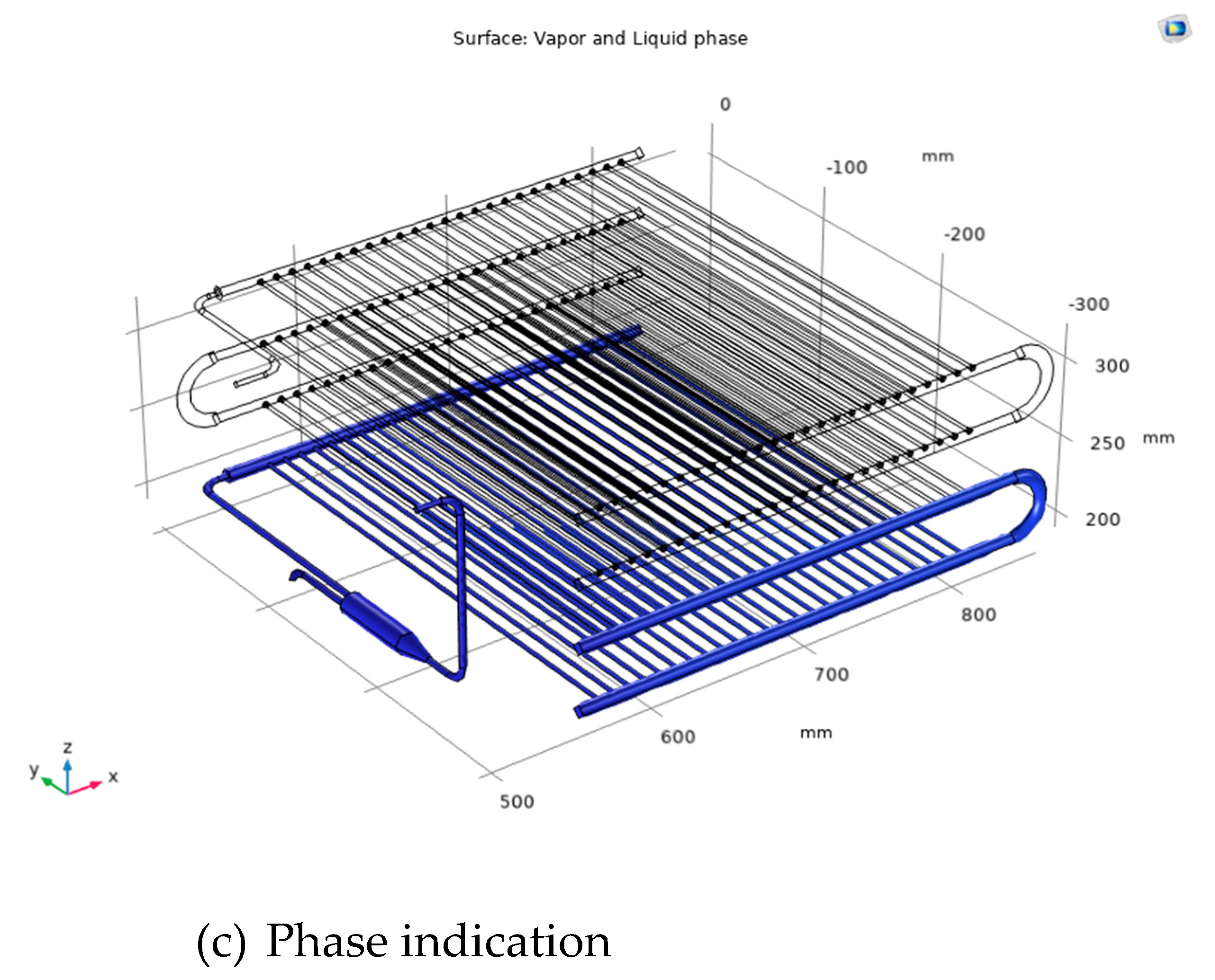
oC. Besides,
Figure 6b indicates phase of R744, the vapor phase is indicated transparent while the liquid phase is indicated on a blue scale. At the operating pressure and temperature obtained from the numerical simulation, it is figured out that R744 is completely liquid in the last two layers. This is the peculiarity that numerical simulation can show while the experiment is difficult to observe.
3.2. The Effect of the Inlet and Outlet R744 Temperatures of Condenser
In this study, the evaporation temperature is adjusted in an ascending trend by adjusting the opening of the throttle valve, which gradually increased the evaporation pressure in the range from 43.38 bar to 50 bar as well as the evaporation temperature range from 9.2
oC to 16.2
oC with the mass flow rate of R744 through the condenser increased from 14.34 kg/h to 46.08 kg/h. The boundary conditions for the simulation are shown in
Table 5.
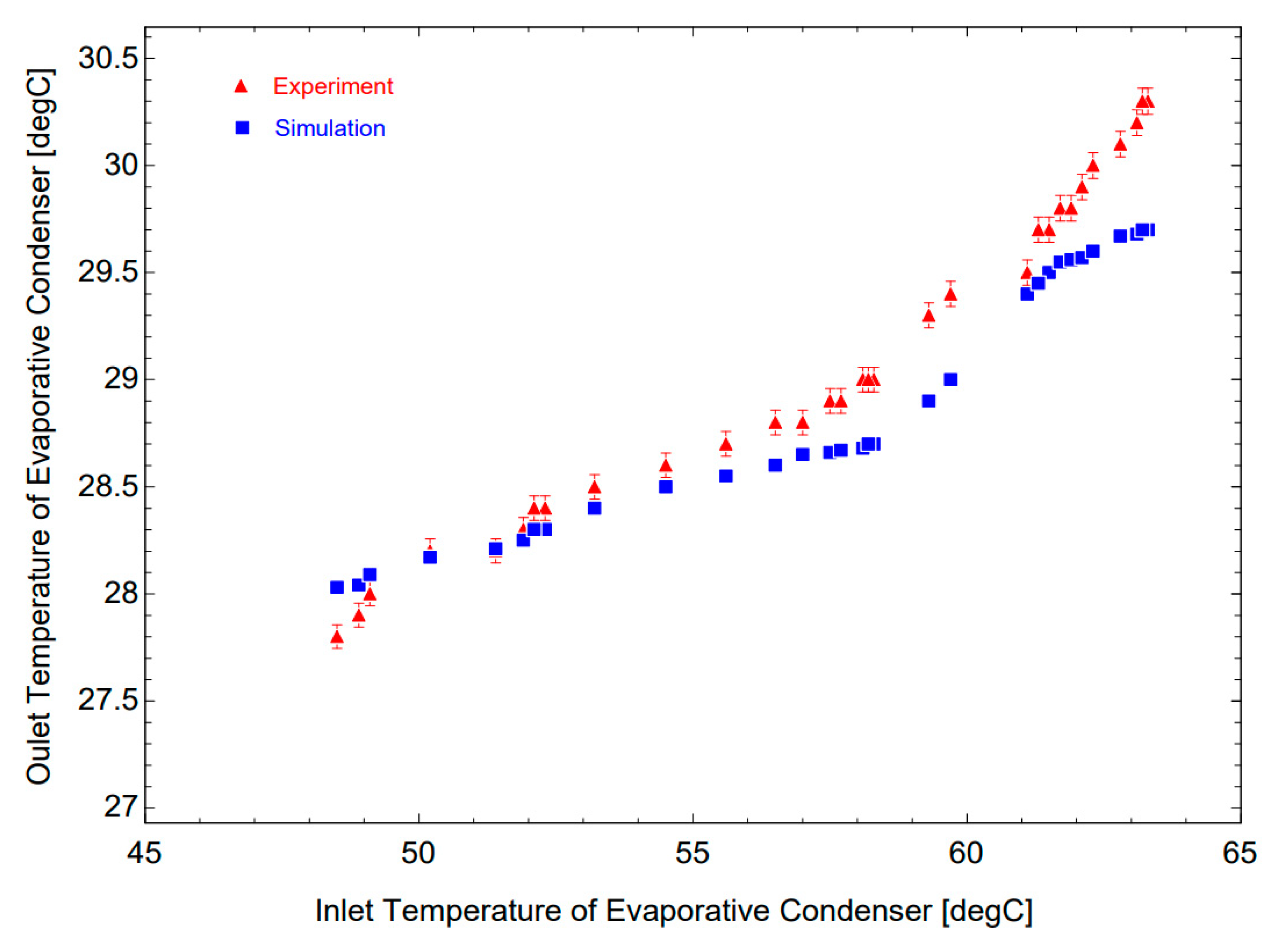
The data obtained from the experiments and the predictions from the simulation are shown in
Figure 7. In the case studies, which indicates that the temperature obtained at the outlet of the condenser gradually decreases from 29.7
oC to 28.03
oC in the simulation, compare with the experimental data the outlet temperature decreases from 30.3
oC to 27.8
oC respectively. Here the similarity is quite high between the simulation and the experiment results with the largest error of 1.9%.
3.3. Pressure Distribution at R744 side in Numerical Simulation
Figure 8 shows the pressure distribution at the R744 side. The pressure distribution result shows that the pressure value has an uneven decrease. However, the result is quite evenly distributed between the 2 layers of staging, the pressure drop is uniform on the small rows of pipes inside, when passing through large manifolds creating vortex zones that increase pressure loss at the manifolds. The pressure at the inlet of the unit is 72.83 bar and fall to the outlet with the value of 72.6 bar. The above results show that the pressure drop between the inlet and outlet of the unit is 0.23 bar.
3.4. The Effect of the Mass Flow Rate on the Pressure Drop
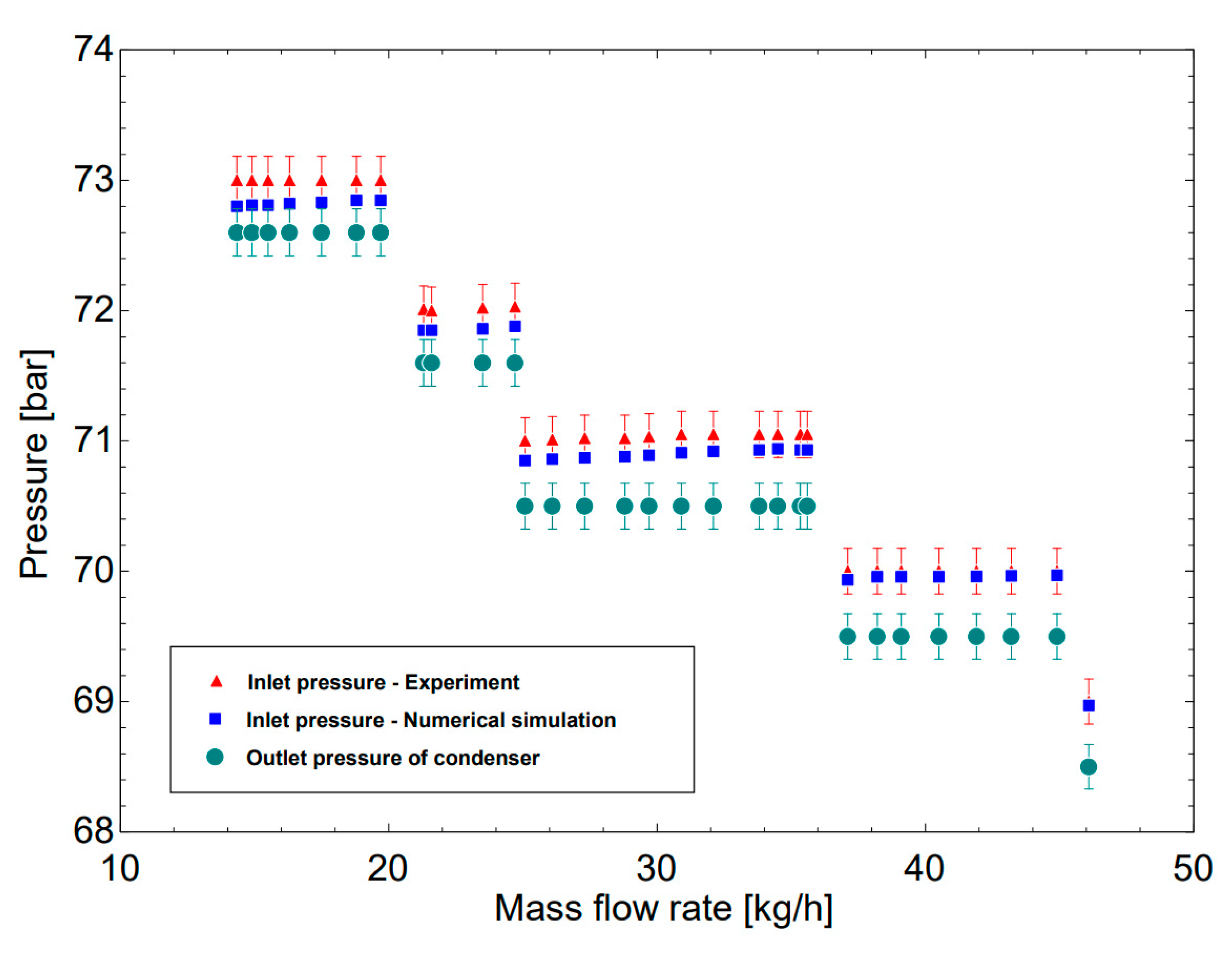
Figure 9 shows the relationship between the inlet pressure of the condenser and the mass flow rate of R744 according to simulation and experiment. The study included 30 steady states to figure out pressure drop when R744 passes through the condenser while outlet pressure is kept at constant (Green color point), the inlet pressure is collected and verified with experimental data sets. It is observed that at low evaporation temperature values corresponding to the mass flow rate range from 14.34 to 21.6 kg/h, the pressure drop is relatively stable at 0.4 bar (the inlet of 73 bar and the outlet of 72.6 bar) in experiment and increase negligibly according to the simulation results from 0.23 bar to 0.25 bar. However, when increasing the mass flow rate from 25.08 to 46.08 kg/h, the pressure drop from experiment is relatively stable at 0.5 bar while it achieves in the range of 0.3 bar to 0.47 bar in simulation. This phenomenon is caused by the fact that the flowmeter in experiment is quite high error at low flow values, when the flow increases, the accuracy of the measuring device is improved. To sum up, the numerical simulation can predict the pressure drop with greater accuracy at high value of the mass flow rate.
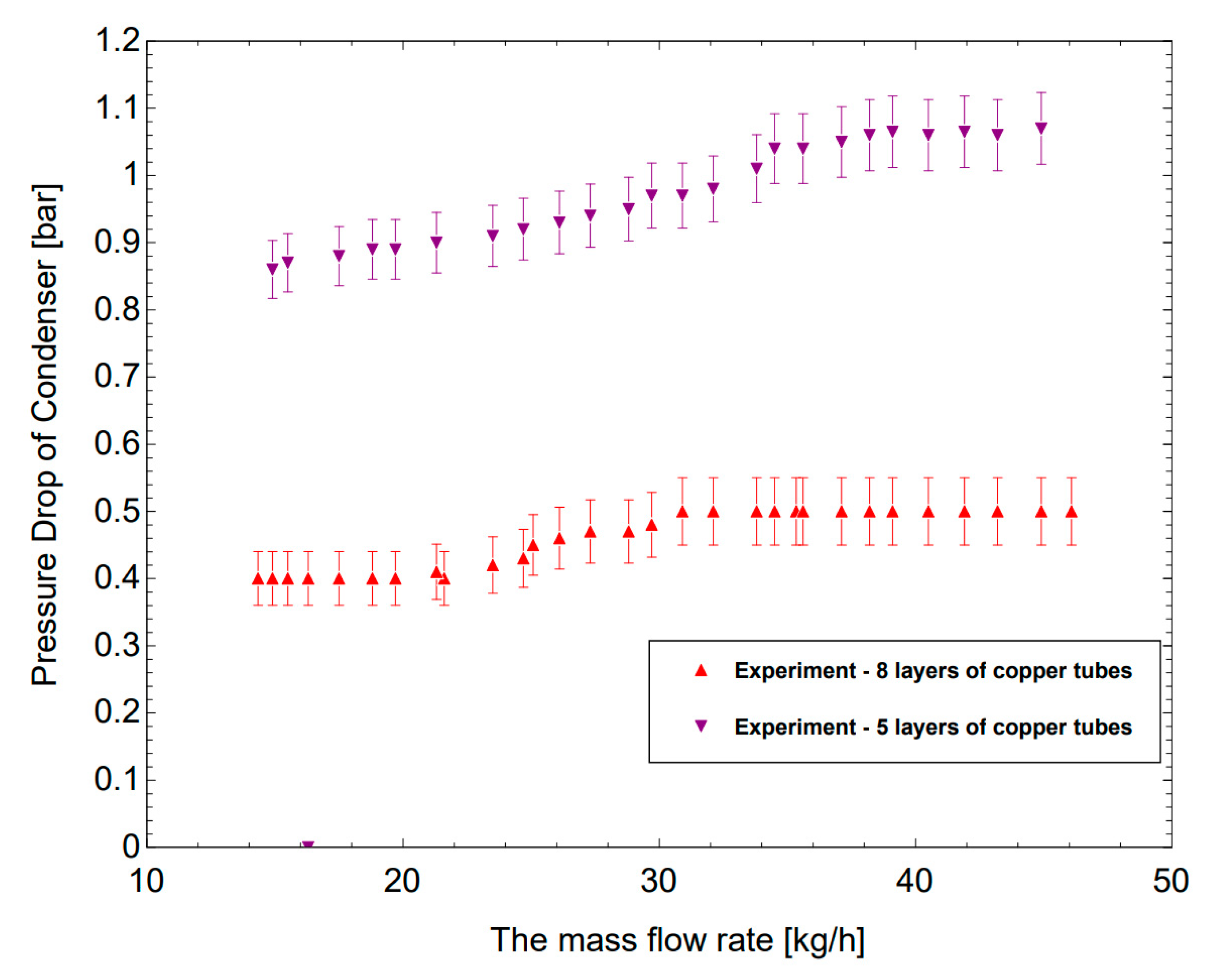
Figure 10 shows a comparison pressure drop between Case 1 and Case 2 in the experiment. In the Case 1 with 5 layers (passes), the mass flow rates are range from 14.9 to 44.9 kg/h while the lowest pressure drop of 0.86 bar and the highest of 1.07 bar, much higher than in the Case 2 of the 8-layer configuration from 0.4 bar to 0.5 bar. This phenomenon is caused by the flowing path of the R744 is longer with more passes than in the case of 8 layers divided into 2 sets (only 4 passes). The local pressure drop and the friction pressure drop generated are larger thus causing an increasing the overall pressure drop.
3.5. The Comparison to Figure out the Optimal Design between 2-Case Studies
In a typical case, the thermodynamic parameters when operating at the same cooling capacity of 960W are given in
Table 6 for comparing of 2-case studies.
Based on the data obtained for Case 1 (5 layers), it is observed that the pressure drop is 1.07 bar which is quite large compared to the Case 2 (8 layers) pressure drop with a value of 0.4 bar; so, this causes increasing the adiabatic compression. At the same time, the log mean temperature difference of 8.56oC in Case 1 is compared to 14.7oC of Case 2, demonstrating for the heat transfer efficiency. In addition, the efficiency of the system expressed at a COP value of 4.34 in Case 2 is quite high compared to 2.72 in Case 1. Thus, the configuration of 8 layers divided into 2 sets is more optimal in the distribution of R744 to ensure low pressure drop, increasing the efficiency factor of the system.
From the results above, the evaporative condensers using mini tubes that are flooded in the cooling water tank are suitable for the subcritical R744 air conditioning system. The method could decrease the inlet temperature of the throttle valve and increase the system efficiency.
3.6. Validation
The R744 temperature data released from the condenser collected from the simulation were compared experimentally to verify the reliability of the simulation under the same conditions.
Table 7 presents comparative data between simulation and experiment under typical operating conditions for the condensers: the evaporation temperature of 9.2
oC, the mass flow rate of 14.34 kg/h, the inlet pressure is 72.6 bar, inlet temperature is 63.3
oC. It is observed that the deviation number is quite small (1.9% with temperature and 0.3% with pressure), that demonstrates the predictive simulation is very good and reliable when compared to the experiment for studying on the evaporative condenser.
4. Conclusion
Two evaporative condensers using mini tubes were simulated by the numerical metho via the Comsol Multiphysics 6.1 software. The study has achieved some of the following results:
The study simulated the temperature field under specific operating conditions, the outlet temperature at the end of the condenser reached from 28.7 oC to 30.3 oC, combined with the operating pressure from 72.6 bar to 68.5 bar showed the state of fully liquefied of R744.
The mass flow rate plays an important role in deciding the pressure drop of the condenser. Within the study limits, the mass flow rate increases from 14.34 kg/h to 46.08 kg/h, the pressure drop also increases from 0.23 bar to 0.47 bar for the simulation and 0.4 bar to 0.5 bar for the experiment, respectively. Increase of turbulent flow increases the local pressure drop at manifold sites, which in turn affects pressure drop throughout the evaporative condenser.
For the design of condensers, it is essential to arrange the number of tube layers accordingly to achieve heat transfer efficiency while reducing pressure drop. This study indicates that a 5-layers of copper tube configuration causes a higher pressure drop of 0.86 bar to 1.07 bar when compared to an 8-layers of copper tubes that split into 2 sets for smaller pressure drop.
The evaporative condensers using mini tubes that are flooded in the cooling water tank are suitable for the subcritical R744 air conditioning system. The method could decrease the inlet temperature of the throttle valve and increase the system efficiency.
The numerical results are in good agreement with those obtained from the experimental results, with the maximum percentage errors are less than 5%.
Acknowledgments
The supports of this work by the project No. T2022-107 (sponsored by the HCMC University of Technology and Education, Vietnam) are deeply appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
|
the absolute temperature (K) |
|
cooling capacity (W) |
|
the fluid velocity (m/s) |
|
condensing capacity (W) |
|
pressure (Pa) |
|
enthalpy of fluid (kJ/kg) |
|
the turbulence viscosity (Pa.s) |
|
work of adiabatic compression (W) |
|
external forces (N/m3) |
|
mass flow rate of fluid (kg/s) |
|
the density of fluid (kg/m3), |
|
heat transfer area (m2) |
|
the specific heat (J/(kg·K)) |
|
overall heat transfer area (m2) |
|
additional heat sources (W/m3) |
|
log mean temperature difference (oC) |
|
external heat flux (W/m2) |
|
|
|
thermal conductivity (W/m.K) |
|
|
References
- Xinyu Zhang, Yunting Ge, Jining Sun, Liang Li, Savvas A. Tassou, "CFD Modelling of Finned-tube CO2 Gas Cooler for Refrigeration Systems", Energy Procedia, vol. 161, 2019, pp. 275-282. [CrossRef]
- Sánchez, Daniel, Jesús Catalán-Gil, Ramón Cabello, Daniel Calleja-Anta, Rodrigo Llopis, and Laura Nebot-Andrés, "Experimental Analysis and Optimization of an R744 Transcritical Cycle Working with a Mechanical Subcooling System", Energies 13, no. 12: 3204, 2020. [CrossRef]
- Yang, Junlan, Linxiu Wang, Yifei Han, Xin Zhang, and Yufan Du, "Simulation and Experimental Study of CO2 Transcritical Heat Pump System with Thermoelectric Subcooling" Designs 6, no. 6: 115, 2022. [CrossRef]
- Yinhai Zhu, Yulei Huang, Conghui Li, Fuzhen Zhang, Pei-Xue Jiang, "Experimental investigation on the performance of transcritical CO2 ejector–expansion heat pump water heater system", Energy Conversion and Management, vol. 167, pp. 147-155, 2018. [CrossRef]
- Jian-qiang Deng, Pei-xue Jiang, Tao Lu, Wei Lu, "Particular characteristics of transcritical CO2 refrigeration cycle with an ejector", Applied Thermal Engineering, vol. 27, pp. 381-388, 2007. [CrossRef]
- F.Z. Zhang, P.X. Jiang, Y.S. Lin, Y.W. Zhang, "Efficiencies of subcritical and transcritical CO2 inverse cycles with and without an internal heat exchanger", Applied Thermal Engineering, vol. 31, pp. 432-438, 2011. [CrossRef]
- X.P. Zhang, F. Wang, X.W. Fan, X.L. Wei, F.K. Wang, “Determination of the optimum heat rejection pressure in transcritical cycles working with R744/R290 mixture”, Applied Thermal Engineering, vol. 54, pp. 176-184, 2013. [CrossRef]
- Paride Gullo, Armin Hafner, Krzysztof Banasiak, "Transcritical R744 refrigeration systems for supermarket applications: Current status and future perspectives", International Journal of Refrigeration, vol. 93, pp. 269-310, 2018. [CrossRef]
- Mihir M. Hazarika, Maddali Ramgopal, Souvik Bhattacharyya, "Studies on a transcritical R744 based summer air-conditioning unit: Impact of refrigerant charge on system performance", International Journal of Refrigeration, vol. 89, pp. 22-39, 2018. [CrossRef]
- Carlos Sanz-Kock, Rodrigo Llopis, Daniel Sánchez, Ramón Cabello, Enrique Torrella, "Experimental evaluation of a R134a/CO2 cascade refrigeration plant", Applied Thermal Engineering, vol. 73, pp. 41-50, 2014. [CrossRef]
- Yeqiang Zhang, Yongning He, Yanling Wang, Xuehong Wu, Mingzheng Jia, Yi Gong, "Experimental investigation of the performance of an R1270/CO2 cascade refrigerant system", International Journal of Refrigeration, vol. 114, pp. 175-180, 2020. [CrossRef]
- Rodrigo Llopis, Carlos Sanz-Kock, Ramón Cabello, Daniel Sánchez, Enrique Torrella, "Experimental evaluation of an internal heat exchanger in a CO2 subcritical refrigeration cycle with gas-cooler", Applied Thermal Engineering, vol. 80, pp. 31-41, 2015. [CrossRef]
- Giovanni Di Nicola, Fabio Polonara, Roman Stryjek, Alessia Arteconi, "Performance of cascade cycles working with blends of CO2 + natural refrigerants", International Journal of Refrigeration, vol. 34, pp. 1436-1445, 2011. [CrossRef]
- J. Alberto Dopazo, José Fernández-Seara, "Experimental evaluation of a cascade refrigeration system prototype with CO2 and NH3 for freezing process applications", International Journal of Refrigeration, vol. 34, pp. 257-267, 2011. [CrossRef]
- Tzong-Shing Lee, Cheng-Hao Liu, Tung-Wei Chen, "Thermodynamic analysis of optimal condensing temperature of cascade-condenser in CO2/NH3 cascade refrigeration systems", International Journal of Refrigeration, vol. 29, pp. 1100-1108, 2006. [CrossRef]
- Bejan et al., Heat Transfer Handbook, John Wiley & Sons, 2003.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).