Prerpints.org logo
Preprint
Article

Response Analysis of the Three-degree-of-freedom Vibroimpact System with an Uncertain Parameter

Altmetrics

Downloads

90

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 August 2023

Posted:

18 August 2023

You are already at the latest version

Alerts
Abstract
The inherent non-smoothness of vibroimpact system leads to complex behaviors as well as strong sensitive dependence on parameter changes. Unfortunately, uncertainties and errors in system parameters are inevitable in mechanical engineering. Therefore, the investigations of dynamical behaviors for vibroimpact systems with stochastic parameters are highly essential. The present study aims to analyze the dynamical characteristics of the three-degree-of-freedom vibroimpact system with an uncertain parameter by means of the Chebyshev polynomial approximation method. Specifically, the vibroimpact system model considered is one with unilateral constraint. Firstly, the three-degree-of-freedom vibroimpact system with an uncertain parameter is transformed into an equivalent deterministic form by the Chebyshev orthogonal approximation. Then, the ensemble means responses of the stochastic vibroimpact system are derived. Numerical simulations are performed to verify the effectiveness of the approximation method. Furthermore, the periodic and chaos motions under different system parameters are investigated, and the bifurcations of the vibroimpact system are analyzed by the Poincaré map. The results demonstrate that both the restitution coefficient and the random factor can induce the appearance of the periodic bifurcation. It is worth noting that the bifurcations fundamentally differ between the stochastic and deterministic systems. The former has a bifurcation interval, while the latter occurs at a critical point.
Keywords: 
Subject: Physical Sciences  -   Other

1. Introduction

Collisions and impacts are common physical phenomena in complex engineering structures and systems, which can significantly affect their stability, reliability, and even cause irreversible damage to mechanical equipment. Such systems, referred to as vibroimpact systems, are typically described by differential equations with constraints due to the non-smooth nature of collisions and impacts [1-3]. This inherent non-smoothness introduces strong nonlinearity into the system dynamics, leading to complex behaviors and high sensitivity to parameter changes [4,5]. Moreover, engineering structures are inevitably influenced by random factors, such as air temperature variations, humidity changes, and ground vibrations [6-9]. These factors can introduce randomization characteristics to the system parameters, making the analysis of dynamic properties even more challenging. Thus, studying the stochastic dynamics of vibroimpact systems is not only interesting but also crucial, albeit facing significant challenges.
Due to the non-smoothness and nonlinearity, closed-form solutions for vibroimpact systems are generally unavailable [10]. Numerical simulations play a crucial role in understanding and analyzing the dynamics of these systems [11-13]. By employing a mapping that relates conditions at subsequent impacts，Shaw and Holmes[14-16] discussed the dynamical behaviors of harmonically excited impact systems, including periodic motions, harmonic and subharmonic motions, chaotic motions, and global bifurcations. Mason [17] analyzed codimension-one, -two and -three bifurcations in a periodically-forced impact oscillator with two discontinuity surfaces using discontinuity-geometry methodology. Li [18] investigated the effects of various system parameters on the stochastic P-bifurcation phenomenon in a vibro-impact system using path integration and the generalized cell mapping method. Liu [19] studied the crises in the Duffing vibro-impact oscillator with non-viscously damping by the composite cell coordinate system method. Qian [20] utilized the radial basis function neural networks method to analyze typical randomly excited Vibroimpact systems. Ding [21] established a six-dimensional Poincaré map to explore the double Neimark–Sacker bifurcation, torus T2 of a three-degree-of-freedom vibro-impact system. As research on vibroimpact systems deepens, unique dynamic phenomena have been discovered, including grazing bifurcations [22-24], stick-slip motion [25,26], chattering [27,28], and corner point bifurcation [29,30].
As the study of vibroimpact systems progresses, it becomes evident that these systems exhibit strong parameter sensitivity dependencies [31-34]. This implies that even small variations or adjustments in the system parameters can have a significant impact on the system’s dynamic behavior. Unfortunately, uncertainties and errors are inevitable in various stages such as modeling, measurement, and manufacturing. Even minor deviations can result in fundamental alterations in the dynamic characteristics of the system. Consequently, studying vibro-impact systems with stochastic parameters becomes highly essential. Feng [35] studied the period doubling phenomenon of a single-degree-of-freedom vibroimpact system with an uncertain parameter by means of Chebyshev polynomial approximation method. However, research on vibroimpact systems with multiple degrees of freedom and uncertain parameters is limited. Although extensive studies have been conducted on single-degree-of-freedom vibroimpact systems, extending the analysis to multiple degrees of freedom introduces additional complexities and challenges. The presence of uncertain parameters further exacerbates the complexity of system dynamics.
In this paper, we aim to analyze the dynamic response of a three-degree-of-freedom vibroimpact system with an uncertain parameter using polynomial approximation methods. Section 2 presents the model of a three-degree-of-freedom vibroimpact system with an uncertain parameter. In Section 3, the Chebyshev polynomial approximation is utilized to transform the vibroimpact system with an uncertain parameter into an equivalent deterministic system. Section 4 provides numerical results to demonstrate the effectiveness of our method and analyzes the influence of system parameters on the dynamic behavior of the system. Finally, the paper concludes with key findings.

2. Model of the Three-degree-of-freedom Vibroimpact System with an Uncertain Parameter

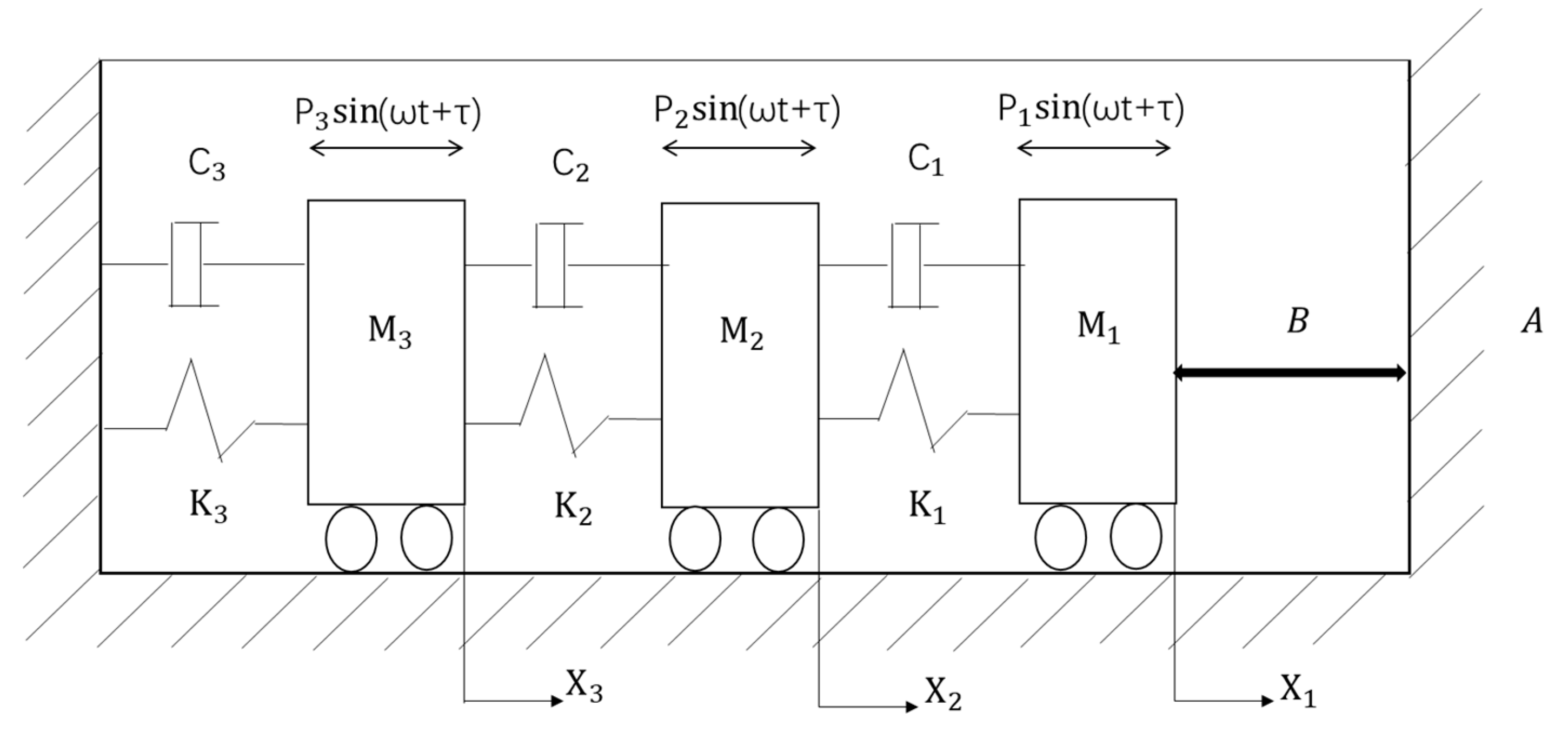
Vibroimpact systems often involve multiple impacts with rigid barriers, and the model represented by differential equations with constraints is referred to as the classical impact model. A schematic of the three-degree-of-freedom vibroimpact system with unilateral rigid constrain [36] is shown in Figure 1. The stiffness coefficients of the three springs are K 1 , K 2 , K 3 . Three masses M 1 , M 2 , M 3 are attached to the wall by these three springs. Simultaneously, three linear dampers with damping coefficients C 1 , C 2 , C 3 are connected to the masses at the same time. Above every mass, there is a harmonic excitation force P i sin ( ω t + τ ) { i = 1 , 2 , 3 } , respectively. When the first mass M 1 moves the distance of B , it will impact with the rigid barrier A . The energy loss during the impact is determined by the restitution coefficient.
The dimensionless form of the system motion differential equation can be written as
M X ¨ + 2 C X ˙ + K X = P sin ( ω t + τ ) ,   ( x 1 < b )
x ˙ 1 A + = − r x ˙ 1 A − ,   ( x 1 = b )
where, X → = ( x 1 , x 2 , x 3 ) T , P → = ( p 1 , p 2 , p 3 ) T , M → = [ m 1 0 0 0 m 2 0 0 0 m 3 ] ,
K → = [ k 1 − k 1 0 − k 1 k 1 + k 2 − k 2 0 − k 2 k 2 + k 3 ] , C → = [ ζ 1 − ζ 1 0 − ζ 1 ζ 1 + ζ 2 − ζ 2 0 − ζ 2 ζ 2 + ζ 3 ]
During the dimensionless form transformation, some assumptions have been done such as M 1 ≠ 0 , K 1 ≠ 0 and P 0 = P 1 2 + P 2 2 + P 3 2 , and the dimensionless quantities are m i = M i M 1 , k i = K i K 1 , p i = P i P 1 , ζ i = C i 2 K 1 M 1 , ω = Ω M 1 K 1 , t = T K 1 M 1 , b = B K 1 P 0 , x i = X i K 1 P 0 , i = 1 , 2 , 3 .
Note that the linear damper C i is considered to be the random parameter of the system, thus ζ i can be reduced to the form of ζ i = ζ ¯ i + δ i u , in which ζ ¯ i and δ i 2 are the mean value and variance of m i respectively, and u is the random variable whose probability density function defined on [ − 1 , 1 ] following the arch distribution. x i represents the dimensionless displacement of each mass block relative to its initial position. When the mass M 1 arrives at the position of the rigid barrier A , its velocity will change abruptly, and r is Newton’s restitution coefficient used to characterize the magnitude of energy loss during the impact instant. x ˙ 1 A + and x ˙ 1 A − represent the velocity before and after the impact, respectively.

3. The Approximation of the Vibroimpact System with an Uncertain Parameter

3.1. Chebyshev polynomial Approximation

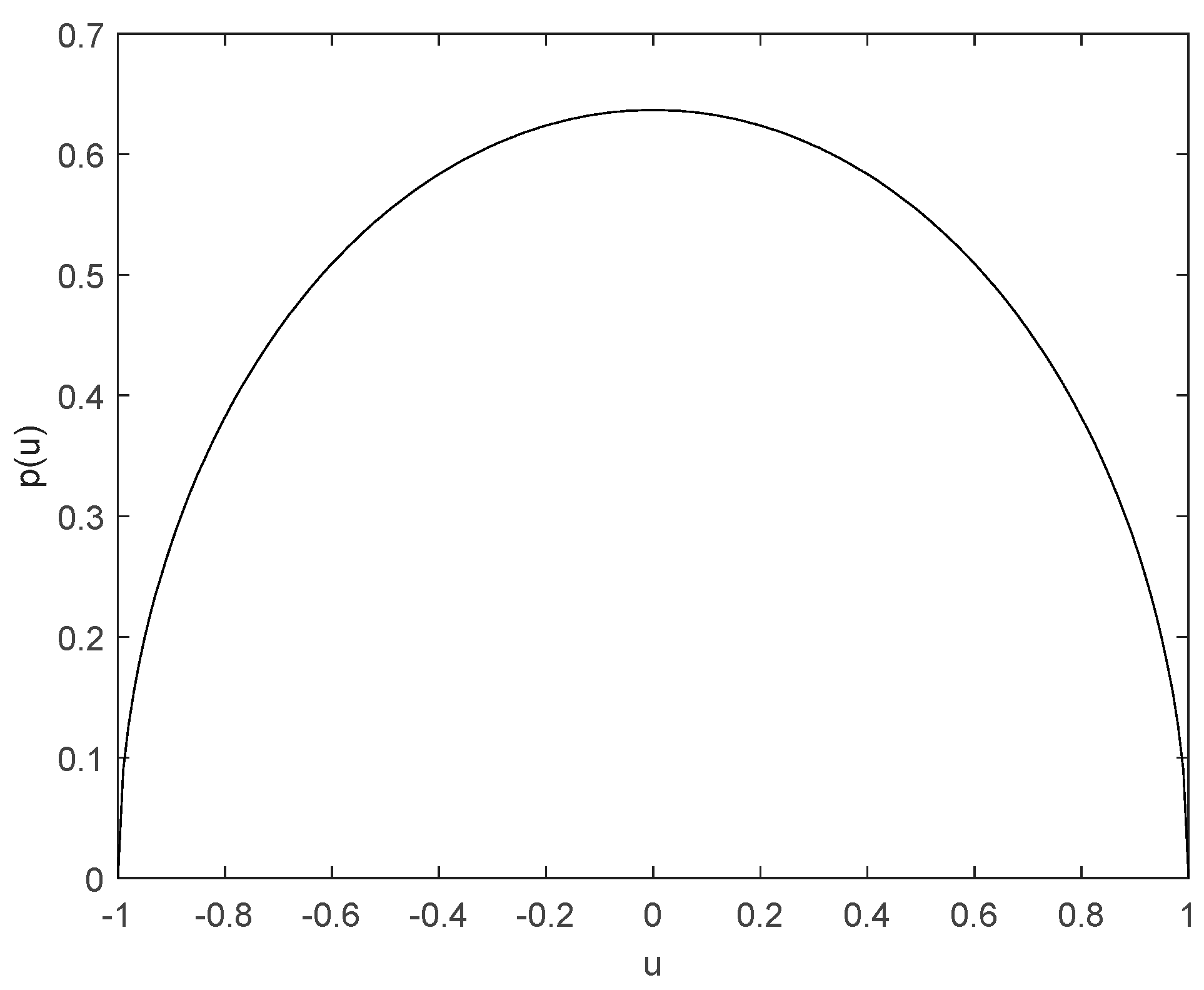
Orthogonal polynomial approximation is an effective method to solve complex nonlinear equations. However, the selection of a polynomial basis must be consistent with the probability density function satisfied by the random parameters in the equation. Though the normal distribution corresponding to Hermite polynomials will provide us useful procedure to deal with the case that system parameter obeys Gaussian distribution, the value range of normal distribution random variable is from negative infinity to positive infinity, which is contrary to the actual situation. Therefore, the random parameter is considered as the random variable subject to arch distribution, which not only meets the implementation situation, but also will not cause the phenomenon of system instability. The probability density function of random variables satisfying the arch distribution is as follow:
p ( u ) = { 2 π 1 − u 2 | u | ≤ 1 , 0 | u | > 1.
The curve of p ( u ) is shown in Figure 2. It is easy to see from the figure that the random parameter is bounded, which is more reasonable in mechanical engineering.
The corresponding polynomial of arch distribution is the Chebyshev polynomial of the second kind, and its general expression is
U n ( u ) = ∑ i = 0 n 2 ( − 1 ) i ( n − i ) ! i ! ( n − 2 i ) ! ( 2 u ) n − 2 i .
Applying Eq. (4), we have
U 0 ( u ) = 1 U 1 ( u ) = 2 u U 2 ( u ) = 4 u 2 − 1 U 3 ( u ) = 8 u 3 − 4 u U 4 ( u ) = 16 u 4 − 12 u 2 + 1 ...
Besides, the second kind of Chebyshev polynomials also have a recursive formula
u U i ( u ) = 1 2 [ U i − 1 ( u ) + U i + 1 ( u ) ] .
The second type of Chebyshev polynomials has orthogonality, whose weighted orthogonality can be expressed as
∫ − 1 1 2 π 1 − u 2 U i ( u ) U j ( u ) d u = { 1   ( i = j ) , 0   ( i ≠ j ) .
Eq. (7) represents the weighted orthogonal relation of polynomials. Although u is a random variable between − 1 and + 1 , since the weight function is the same as the probability density function of the random variable u , the left side of Eq. (7) can be considered as the expectation of the random function U i ( u ) U j ( u ) . According to the nature of function of random variable, the randomness does not affect the orthogonality of polynomial. And because of the orthogonality of the second kind of Chebyshev polynomials, any measurable function f ( u ) of random variable u can be expanded into the following series:
f ( u ) = ∑ i = 0 ∞ c i U i ( u ) ,
in which,
c i = ∫ − ∞ ∞ p ( u ) f ( u ) U i ( u ) d u ∫ − ∞ ∞ p ( u ) U i ( u ) U i ( u ) d u = ∫ − 1 1 p ( u ) f ( u ) U i ( u ) d u .
This expansion method based on the generalized Fourier series is called the orthogonal decomposition of random function f ( u ) , and this approximation method is the best mean square approximation.

3.2. Equivalent Deterministic System

In this section, Eq. (1) will be approximated by orthogonal polynomial. Under unconstrained conditions, the response of the system can be expressed as a function of time t and random variable u , and can be expanded into the following series form:
X → ( t , u ) = ∑ t = 0 ∞ X → i ( t ) U → i ( u ) .
When i only takes a finite number N , Eq. (9) can be approximately expressed as
X → ( t , u ) ≈ ∑ t = 0 N X → i ( t ) U → i ( u ) .
Where, U → i ( u ) represents the three-dimensional vector composed of the i − t h Chebyshev polynomial. We also have X i ( t ) = ∫ − 1 1 p ( u ) X ( t , u ) U i ( u ) d u , in which X i ( t ) = ( X 1 i , X 2 i , X 3 i ) T .
When the impact factor is not taken into account, substituting Eq. (10) is into Eq. (1) yields the following result
M → d 2 ∑ i = 0 N X → i ( t ) U → i ( u ) d t 2 + 2 C → d ∑ i = 0 N X → i ( t ) U → i ( u ) d t + K → ∑ i = 0 N X → i ( t ) U → i ( u ) = P → sin ( ω t + τ ) .
By dividing the vector form of Eq. (11) into scalar form, three equations can be obtained
( m 1 d 2 d t 2 + k 1 ) ∑ i = 0 N X 1 i ( t ) U i ( u ) − k 1 ∑ i = 0 N X 2 i ( t ) U i ( u ) − 2 ζ 1 ¯ d d t ∑ i = 0 N X 1 i ( t ) U i ( u ) + 2 δ 1 u d d t ∑ i = 0 N X 1 i ( t ) U i ( u ) − 2 ζ 1 ¯ d d t ∑ i = 0 N X 2 i ( t ) U i ( u ) − 2 δ 1 u d d t ∑ i = 0 N X 2 i ( t ) U i ( u ) = p 1 sin ( ω t + τ )
( m 2 d 2 d t 2 + k 1 + k 2 ) ∑ i = 0 N X 2 i ( t ) U i ( u ) − k 1 ∑ i = 0 N X 1 i ( t ) U i ( u ) − k 2 ∑ i = 0 N X 3 i ( t ) U i ( u ) + 2 ( ζ 1 ¯ + ζ 2 ¯ ) d d t ∑ i = 0 N X 2 i ( t ) U i ( u ) − 2 ζ 1 ¯ d d t ∑ i = 0 N X 1 i ( t ) U i ( u ) − 2 ζ 2 ¯ d d t ∑ i = 0 N X 3 i ( t ) U i ( u ) + 2 ( δ 1 + δ 2 ) u d d t ∑ i = 0 N X 2 i ( t ) U i ( u ) − 2 δ 1 u d d t ∑ i = 0 N X 1 i ( t ) U i ( u ) − 2 δ 2 u d d t ∑ i = 0 N X 3 i ( t ) U i ( u ) = p 2 sin ( ω t + τ )
( m 3 d 2 d t 2 + k 2 + k 3 ) ∑ i = 0 N X 3 i ( t ) U i ( u ) − k 2 ∑ i = 0 N X 2 i ( t ) U i ( u ) − 2 ζ 2 ¯ d d t ∑ i = 0 N X 2 i ( t ) U i ( u ) + 2 ( ζ 2 ¯ + ζ 3 ¯ ) d d t ∑ i = 0 N X 3 i ( t ) U i ( u ) + 2 ( δ 2 + δ 3 ) u d d t ∑ i = 0 N X 3 i ( t ) U i ( u ) − 2 δ 2 u d d t ∑ i = 0 N X 2 i ( t ) U i ( u ) = p 3 sin ( ω t + τ )
The recursive relation Eq. (6) of Chebyshev polynomial can be obtained as
u ∑ i = 0 N X i ( t ) U i ( u ) = 1 2 ∑ i = 0 N X i ( t ) [ U i − 1 ( u ) + U i + 1 ( u ) ] = 1 2 ∑ i = 0 N U i ( u ) [ X i − 1 ( t ) + X i + 1 ( t ) ] .
Due to the approximation of Eq. (10), X − 1 and X N + 1 are set to zero. By substituting Eq. (13) into each of the expressions in Eq. (12), and then multiplying both ends of each of the resulting equations by U i ( u ) ( i = 0 , ... , N ) , and finally taking the expectation with regard to the random variable u , the following result is obtained.
{ ( m 1 d 2 d t 2 + k 1 ) X 10 ( t ) − k 1 X 20 ( t ) + 2 ζ 1 ¯ d d t X 10 ( t ) + δ 2 d d t X 11 ( t ) = p 1 sin ( ω t + τ ) ( m 2 d 2 d t 2 + k 1 + k 2 ) X 20 ( t ) − k 1 X 10 ( t ) − k 3 X 30 ( t ) + 2 ( ζ 1 ¯ + ζ 2 ¯ ) d d t X 20 ( t ) − 2 ζ 1 ¯ d d t X 10 ( t ) − 2 ζ 2 ¯ d d t X 30 ( t ) + ( δ 1 + δ 2 ) d d t X 21 ( t ) − δ 1 d d t X 11 ( t ) − δ 2 d d t X 31 ( t ) = p 2 sin ( ω t + τ ) ( m 3 d 2 d t 2 + k 1 + k 2 ) X 30 ( t ) − k 2 X 20 ( t ) + 2 ( ζ 3 ¯ + ζ 2 ¯ ) d d t X 30 ( t ) − 2 ζ 2 ¯ d d t X 20 ( t ) + ( δ 3 + δ 2 ) d d t X 31 ( t ) − δ 2 d d t X 21 ( t ) = p 3 sin ( ω t + τ ) ( m 1 d 2 d t 2 + k 1 ) X 1 i ( t ) U i ( u ) − k 1 X 2 i ( t ) + 2 ζ 1 ¯ d d t X 1 i ( t ) − 2 ζ 1 ¯ d d t X 2 i ( t ) + δ 1 d d t ( X 1 i − 1 ( t ) + X 1 i + 1 ( t ) ) − δ 1 d d t ( X 2 i − 1 ( t ) + X 2 i + 1 ( t ) ) = 0 ( m 2 d 2 d t 2 + k 1 + k 2 ) X 2 i ( t ) − k 1 X 1 i ( t ) − k 2 X 3 i ( t ) + 2 ( ζ 1 ¯ + ζ 2 ¯ ) d d t X 2 i ( t ) U i ( u ) − 2 ζ 1 ¯ d d t X 1 i ( t ) − 2 ζ 2 ¯ d d t X 3 i ( t ) U i ( u ) + ( δ 1 + δ 2 ) d d t ( X 2 i − 1 ( t ) + X 2 i + 1 ( t ) ) − δ 1 d d t ( X 1 i − 1 ( t ) + X 1 i + 1 ( t ) ) − δ 2 d d t ( X 3 i − 1 ( t ) + X 3 i + 1 ( t ) ) = 0 ( m 3 d 2 d t 2 + k 2 + k 3 ) X 3 i ( t ) U i ( u ) − k 2 X 2 i ( t ) − 2 ζ 2 ¯ d d t X 2 i ( t ) + 2 ( ζ 3 ¯ + ζ 2 ¯ ) d d t X 3 i ( t ) + ( δ 3 + δ 2 ) d d t ( X 3 i − 1 ( t ) + X 3 i + 1 ( t ) ) U i ( u ) − δ 2 d d t ( X 2 i − 1 ( t ) + X 2 i + 1 ( t ) ) = 0   ( i = 1 , ... , N )
Therefore, the unconstrained three-degree-of-freedom unilateral rigid constraint vibroimpact system Eq. (1) is reduced to an equivalent deterministic system Eq. (14).
According to the approximation of Eq. (10), the ensemble mean response of the system can be approximated as
E [ X → ( t , u ) ] = E [ ∑ i = 0 N X → i ( t ) U → i ( u ) ] = ∑ i = 0 N X → i ( t ) E [ U → i ( u ) ] = X 0 ,
where, X 0 → = ( x 10 , x 20 , x 30 ) T .
Note that the random variable u takes a random value of { u i } on the interval [ − 1 , 1 ] , there exists a certain time t in the constrained case in which some orbits of the sample system have impacted with the constraint plane ∑ ( b ) (the virtual constraint plane here), while some have not reached the constraint plane ∑ ( b ) due to the influence of random factors. Therefore, it is necessary to average the constraint conditions.
According to Eq. (15), the average response can be obtained. The average constraint surface is:
∑ ¯ = { ( X → , X ˙ → ) | X 0 → = b → } .
The average constraint condition is:
E [ X → ( t , u ) ] = X 0 → < b → .
The average jump equation:
X ˙ 0 + → = − r X ˙ 0 − → .
Based on the above Chebyshev polynomial approximation, the introduced average constraint conditions Eq. (17) and the average jump Eq. (18), the stochastic three-degree-of-freedom vibroimpact system is transformed into an equivalent deterministic system. When N → ∞ , the solution ∑ i = 0 N X → i ( t ) U → i ( u ) approximates X → ( t , u ) in the sense of the best square error. The value of N determines the accuracy of the solution. In this paper, N = 2 is taken to obtain an equivalent deterministic unilateral constraint system.

4. Reponses of the Three-degree-of-freedom Vibroimpact System

4.1. Period-doubling Bifurcation

Through the analysis of Eq. (1) and Eq. (10), three systems can be obtained: one is the deterministic three-degree-of-freedom vibroimpact system in which the amplitude of the random response δ = 0 ; one is the original stochastic three-degree-of-freedom vibroimpact system; and the last one is the equivalent deterministic system. The corresponding responses of the three systems are deterministic system response (DSR), stochastic system response (SSR) and equivalent system response (ESR), respectively. The response of the original stochastic system is obtained by random simulation using ARM algorithm and Monte Carlo method. While responses of DSR and ESR are obtained by using numerical simulation methods of deterministic systems. The phase orbit diagrams of the responses of the three systems are compared by numerical simulation to study the dynamical behaviors of the stochastic three-degree-of-freedom vibroimpact system. The maximum Lyapunov exponent is a state quantity that can effectively judge the chaotic state of the system. At present, the Lyapunov exponent method for smooth system has been relatively mature. For vibroimpact systems, the Jacobian matrix discontinuity caused by impact factors exists in the model, the calculation method of smooth system cannot be directly applied to the system. In this paper, a Lyapunov exponent calculation method for non-smooth systems based on discontinuous mapping is used to calculate the Lyapunov exponent.
In order to investigate the effect of the frequency of resonant forces, some parameters of the system are taken as follows: the amplitude of random parameter δ = 0.01 , the restitution coefficient r = 0.7 , and the impact boundary r = 0.7 , resonant forces P = ( 1 , 0 , 0 ) T , m 2 = m 3 = 1.5 , k 2 = k 3 = 4 . Since δ is a small quantity, the initial values of both the stochastic system and the deterministic system can be taken as X → = ( 1 , 5 , 0 ) T and X ˙ → = ( 1 , 0 , 0 ) T . For the parameter ω = 2.25 , the system has a steady-state periodic response, and period is 1 T for this case, where T = 2 π ω . This is the so-called 1 − 1 periodic motion in which n − p represents periodic motion, n represents the number of cycles and p represents the number of impacts with the constraint surface. The time history diagram and phase orbit diagram are shown in Figure 3(a) and 3(b), respectively. The corresponding results for the parameter ω = 2.2 are shown in Figure 3(c) and 3(d), respectively. It is easy to see that 1 − 1 motion in Figure 3(b) becomes a stable period 2 − 2 motion with the frequency change. That is the period-doubling bifurcation has occurred.
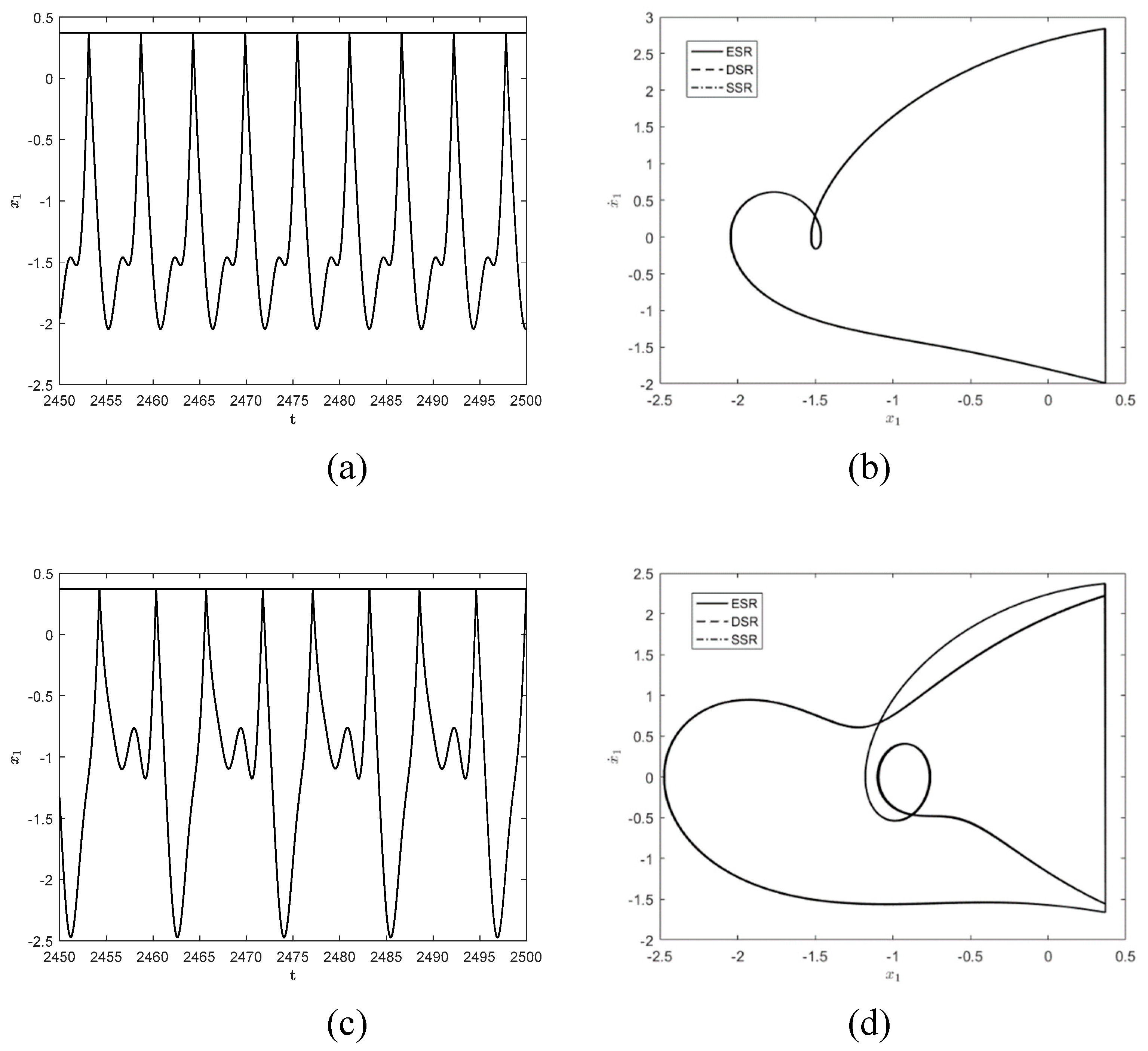
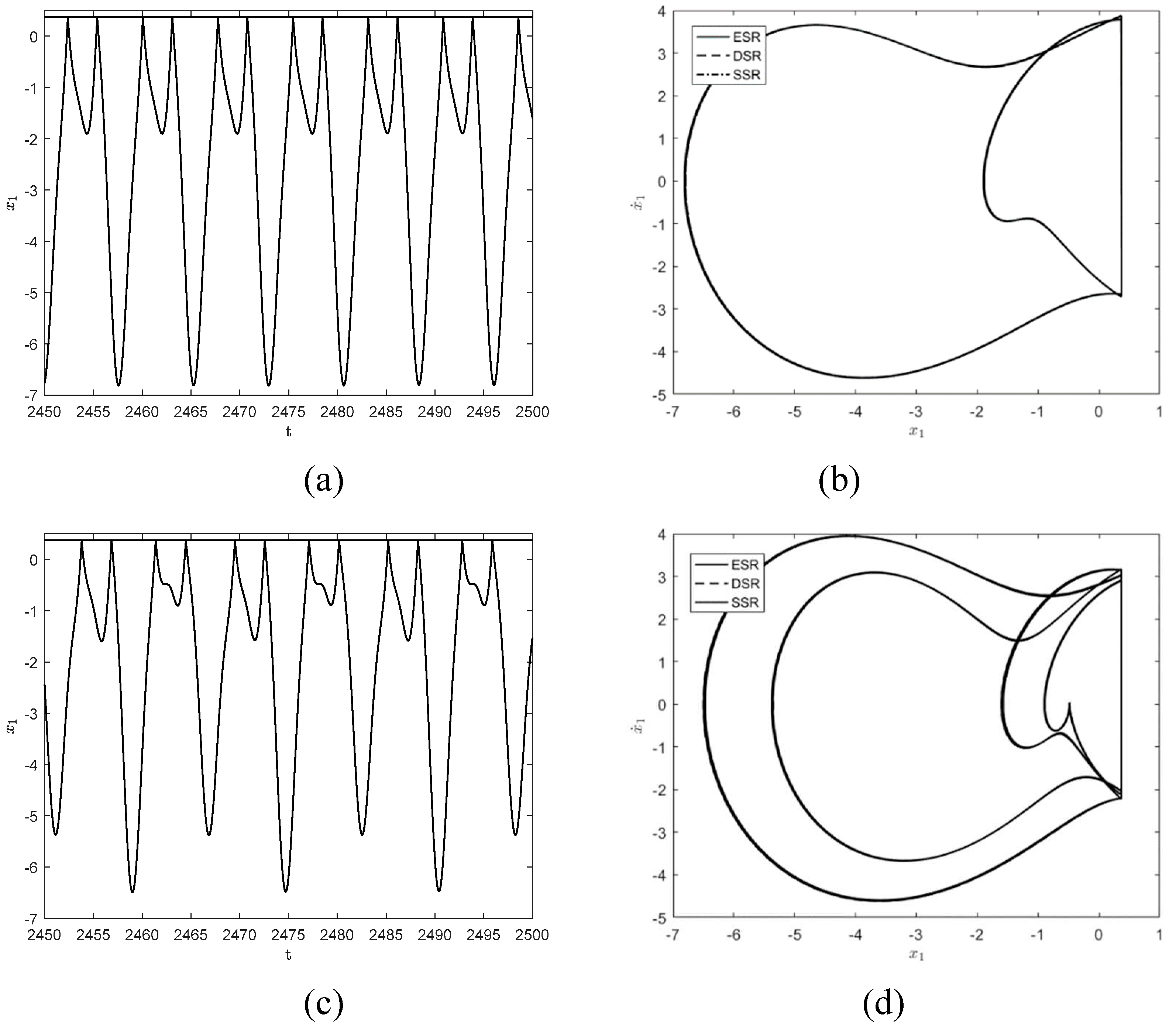
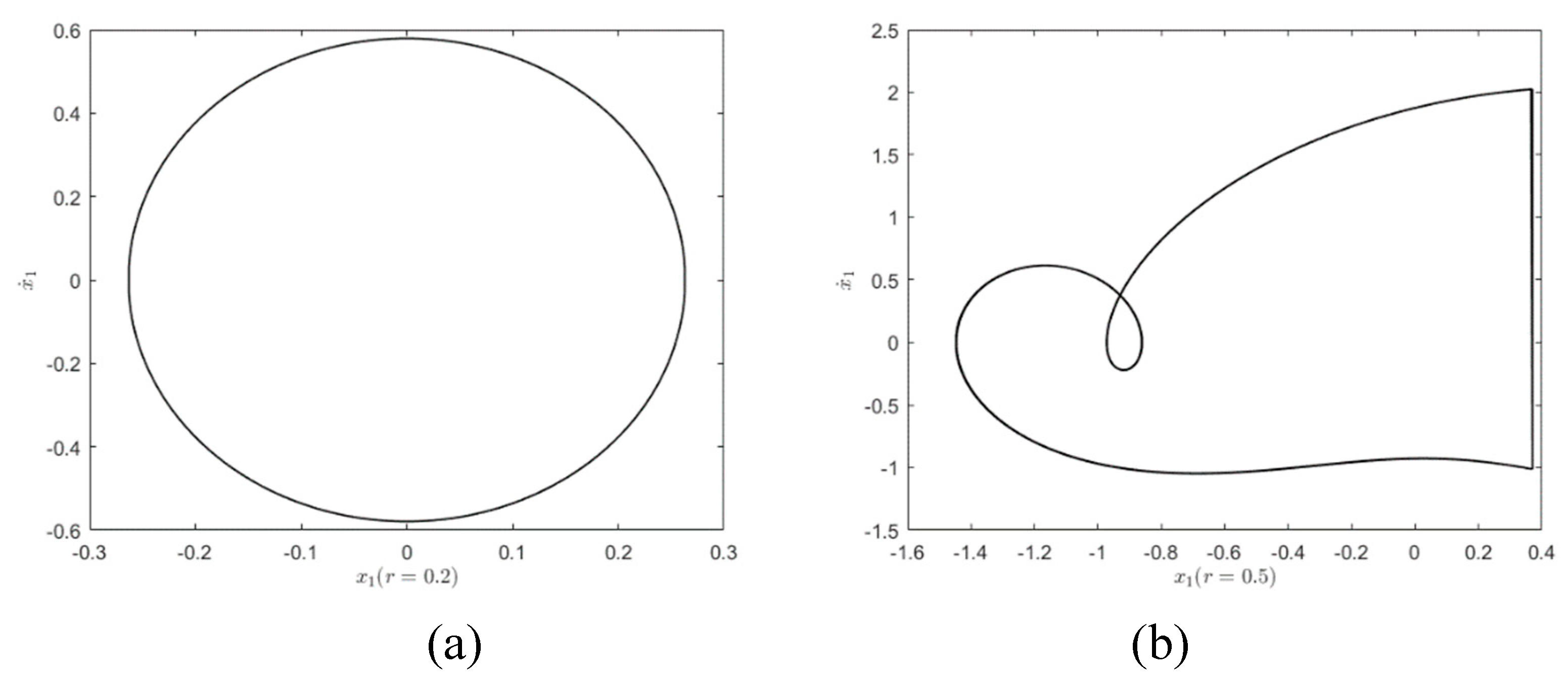
To further observe the dynamical behaviors of the three systems, Figure 4 show the responses when ω = 1.65 and ω = 1.787 . As shown in Figure 4(a) and (b), the system exhibits a stable 1 − 1 symmetric motion at ω = 1.65 , which is close to the motion form of simple harmonic motion. when ω = 1.787 , 1 − 1 motion has period-doubling bifurcation and becomes a stable period 2 − 2 motion, as shown in Figure 4(c) and (d).
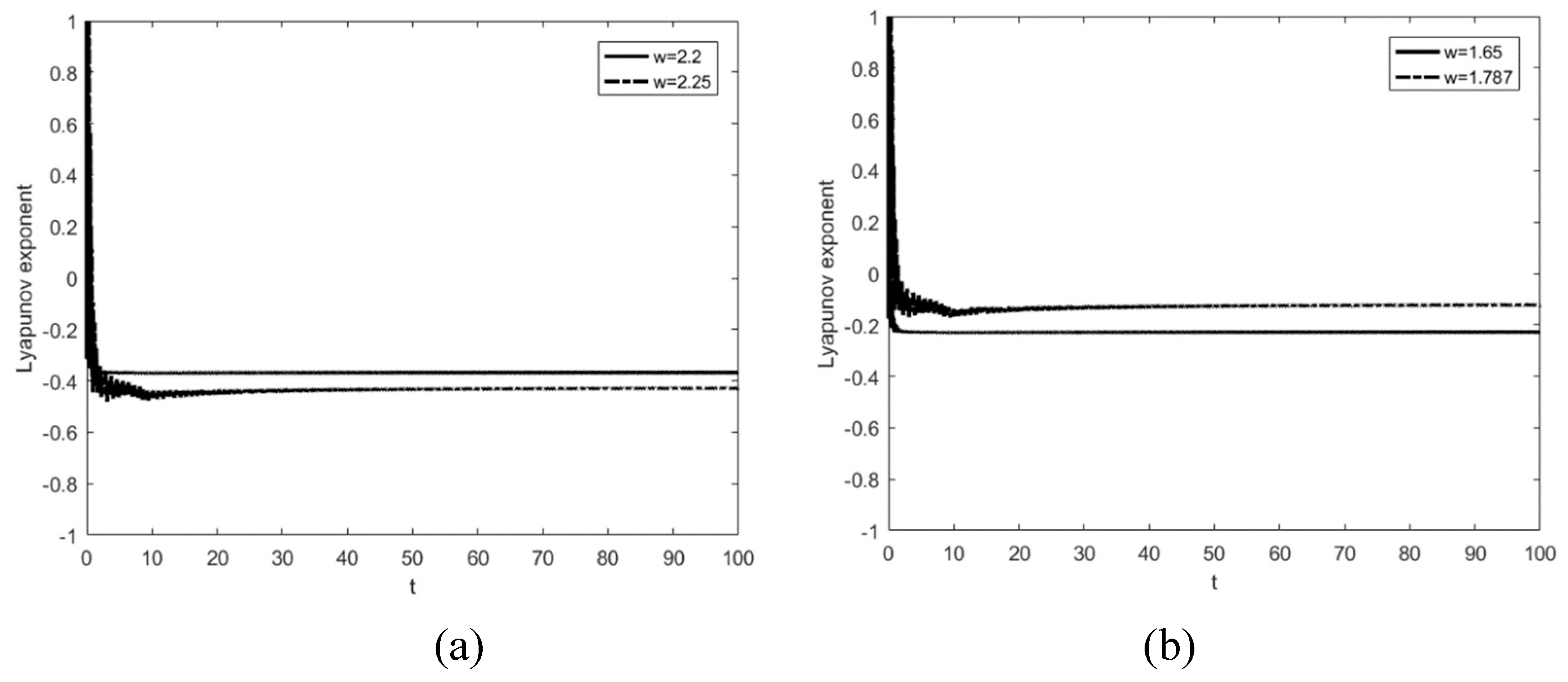
In Figure 5, the curve of the maximum Lyapunov exponent is given for different frequencies in Figure 3 and Figure 4. As can be seen from the figure, the maximum Lyapunov exponent at all four positions is stable and less than 0, which means that the system is indeed in a stable state, matching with the phase orbit diagrams. However, with the appearance of period-doubling bifurcation, the maximum Lyapunov exponent also becomes larger in response, which means that the degree of chaos of the system increases.

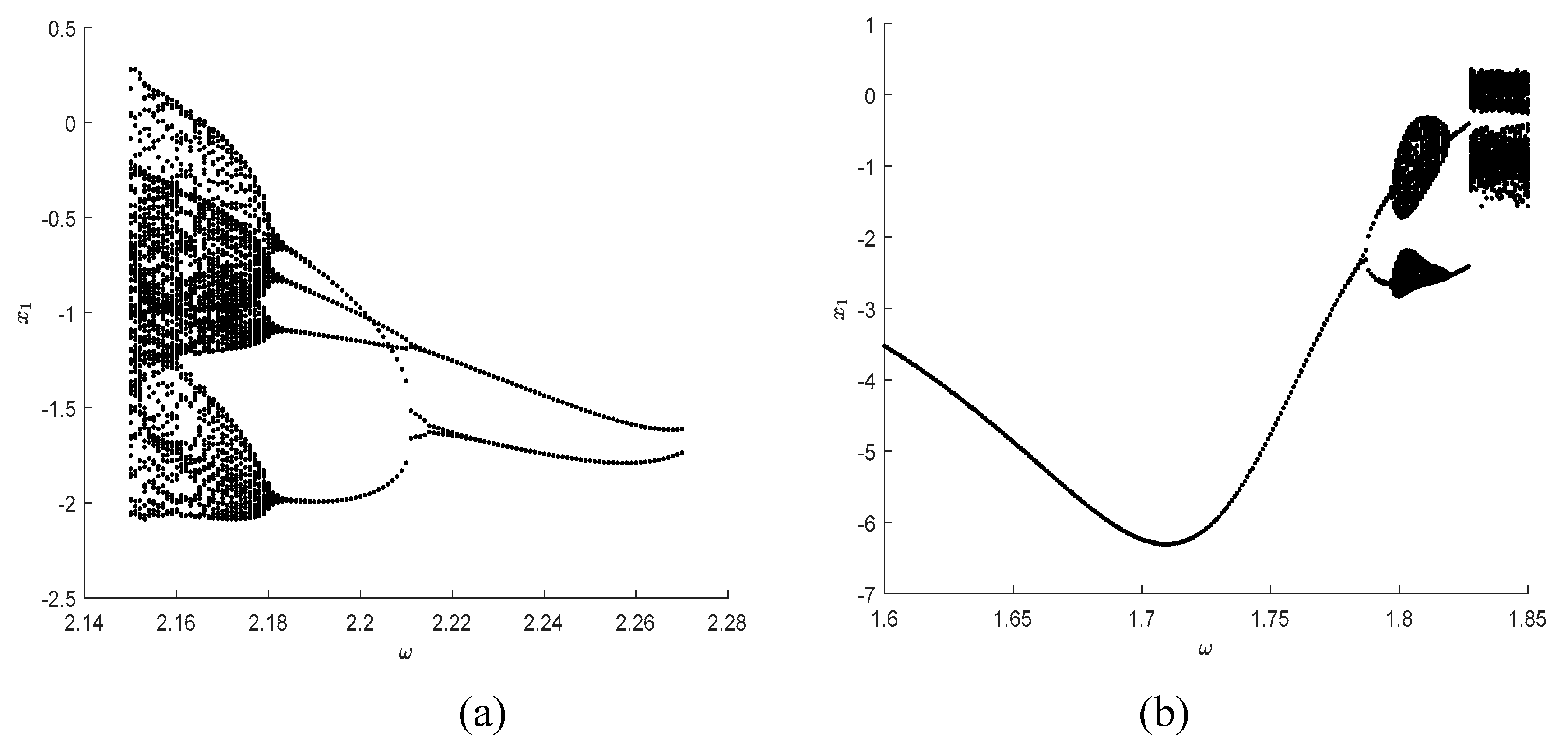
4.2. From Period-doubling Bifurcation to Chaos

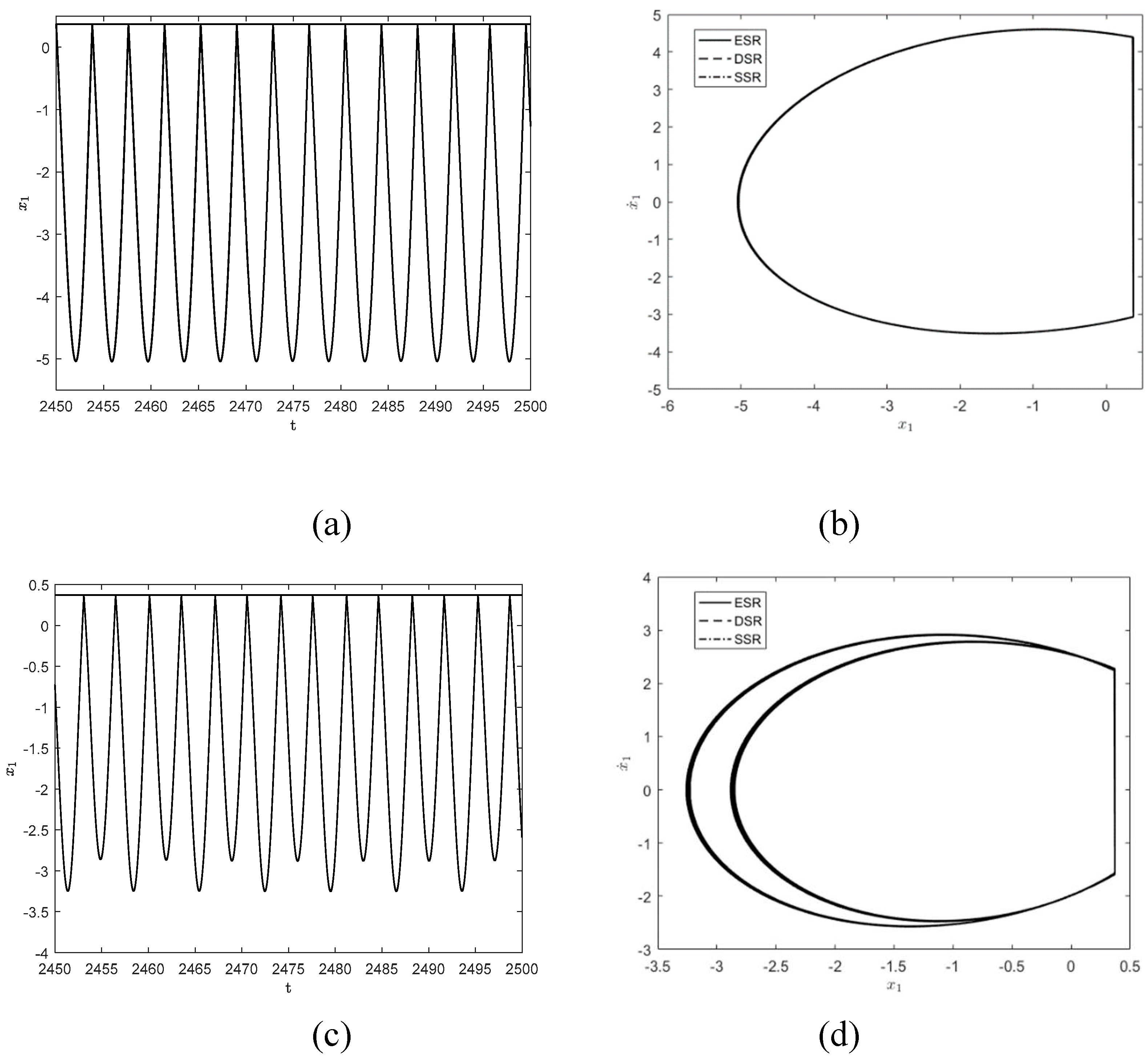
Considering the system parameter P = ( 3 , 0 , 0 ) T , m 2 = m 3 = 2 . The influence on the system responses for different frequency values is investigated. The time history diagram and phase orbit diagram of the system responses are shown in Figure 6. When ω = 2.45 , the system has periodic response, and the system motion mode is 1 − 1 , as shown in Figure 6(a) and 6(b). 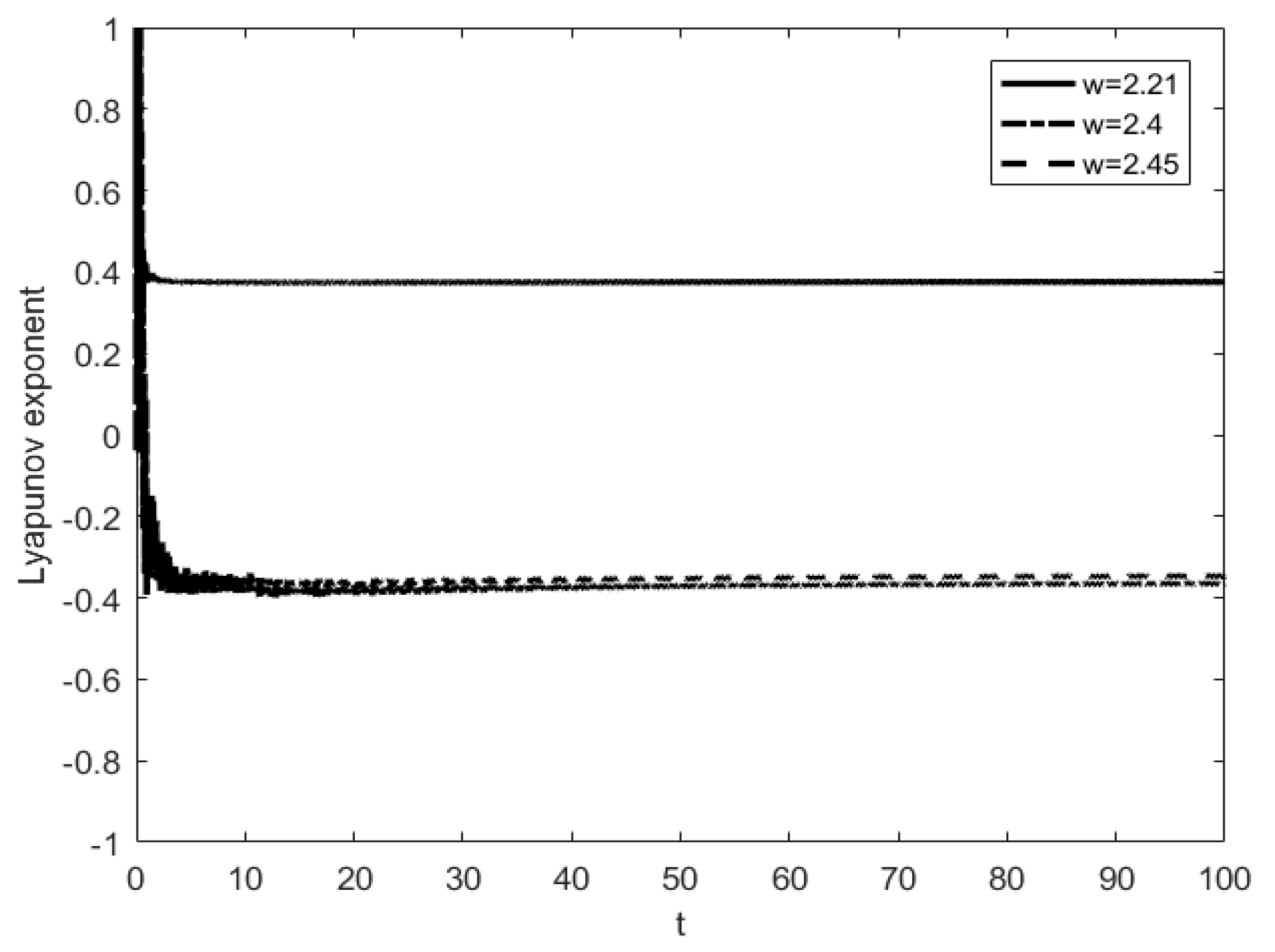As the angular frequency of the harmonic excitation P decreases to 1 − 1 , the system motion mode changes to 2 − 2 after period-doubling bifurcation, as shown in Figure 6(c) and 6(d). The successive occurrence of such period-doubling bifurcations indicates the arrival of chaos. It can be seen from the maximum Lyapunov exponent shown in Figure 7 that the maximum Lyapunov exponent changes as the parameters change. When the angular frequency of harmonic excitation P decreases to ω = 2.21 . 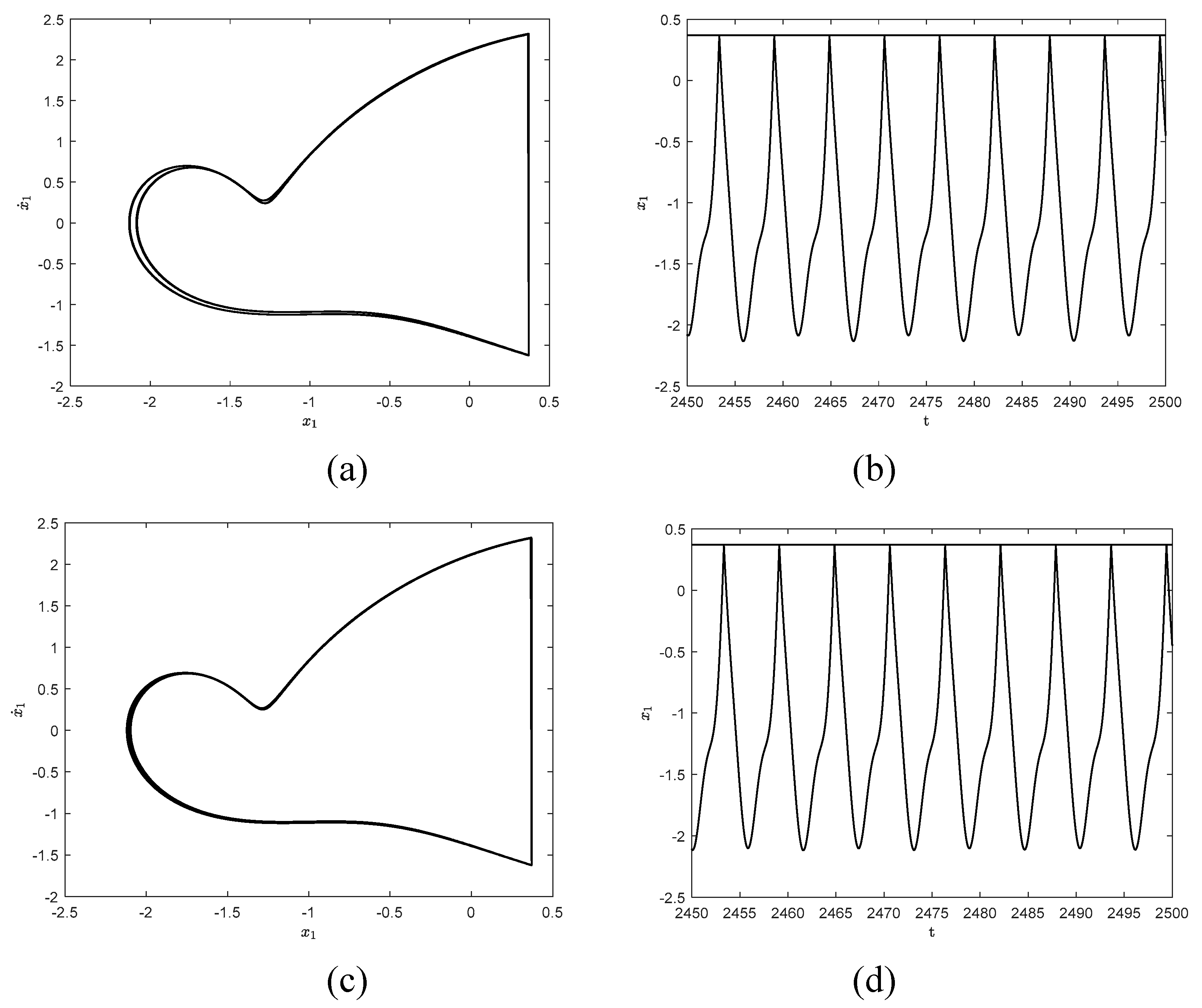The maximum Lyapunov exponent becomes a positive number, which means the system appears chaotic, as shown in Figure 8.
As can be seen from Figure 7 and Figure 8, when other parameters have been determined, as the angular frequency keeps decreasing, the system responses produce abundant period-doubling bifurcation phenomenon in the process from ω = 2.45 to ω = 2.21 , and finally lead to chaos. The numerical simulation results show that the phase diagrams of the three systems agree well with each other in the path from period-doubling bifurcation to chaos, which reflects the evolution process of the system.

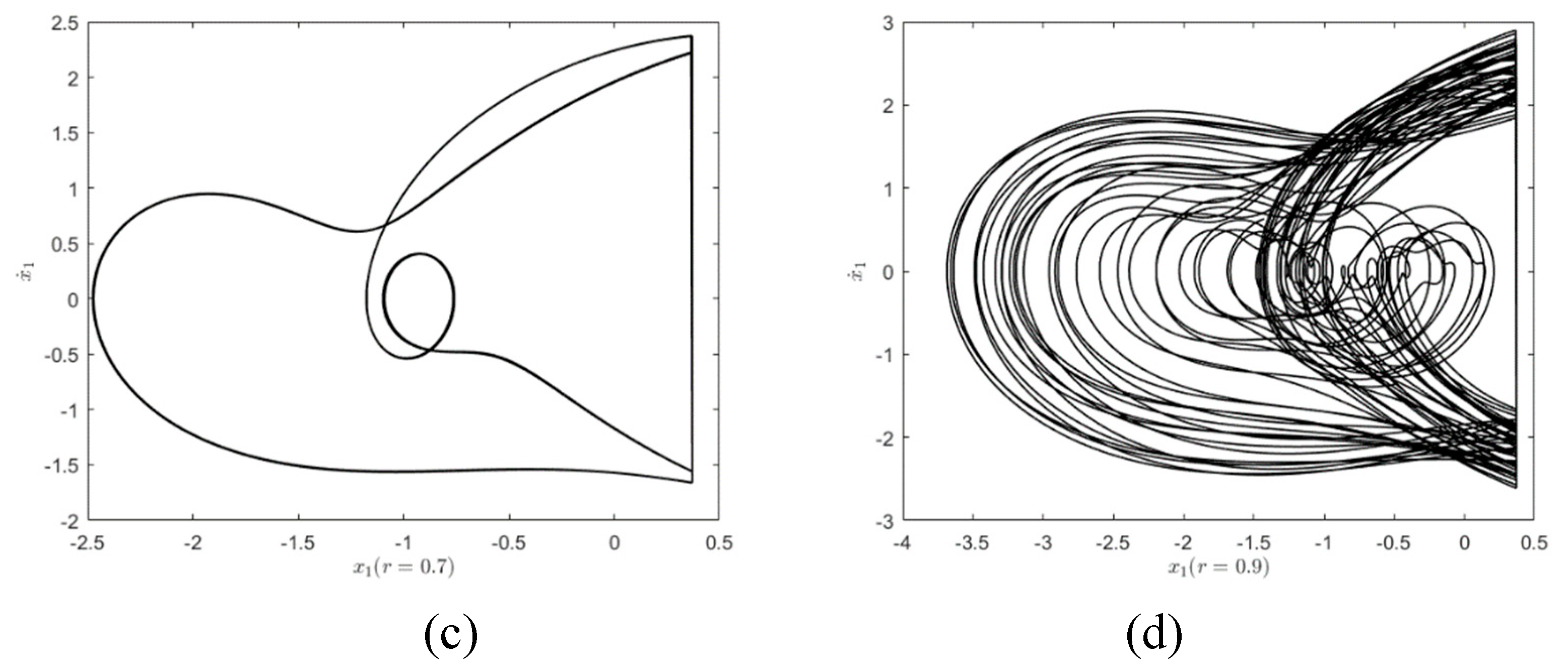
4.3. Influence of the Restitution Coefficient

In the stochastic three-degree-of-freedom vibroimpact system Eq. (1) and Eq. (2), The restitution coefficient r represents the energy loss in the impact process, which will further affect the periodic phenomenon of the system and lead to bifurcation. The parameters are considered as: P = ( 1 , 0 , 0 ) T , m 2 = m 3 = 1.5 , and k 2 = k 3 = 4 . Bifurcation diagram with respect to restitution coefficient r for deterministic three-degree-of-freedom vibroimpact system is shown in Figure 9. It is obvious that the system response experienced two period doubling bifurcations, and then leading to chaos.
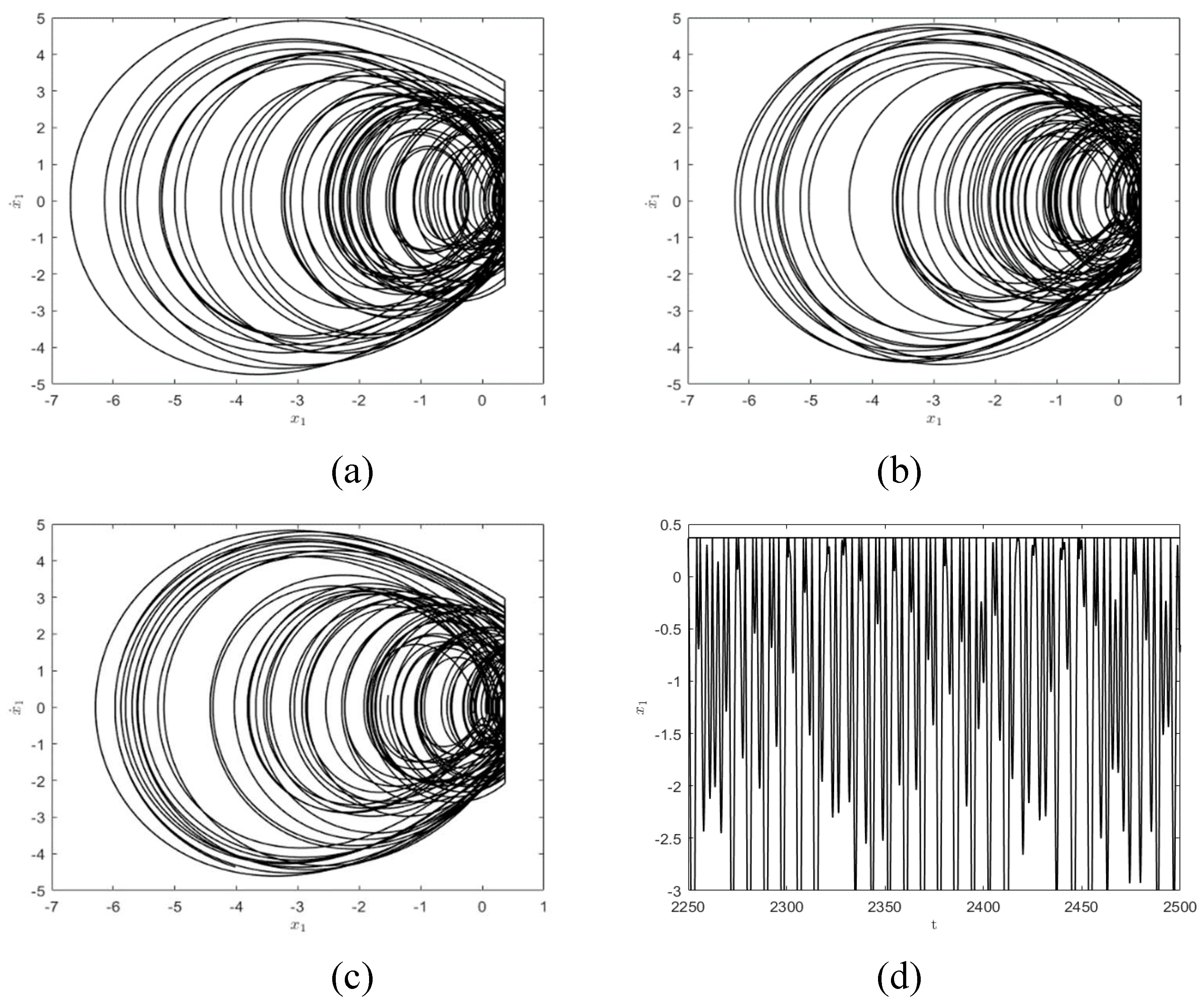
To clearly show the influence on the system responses for different restitution coefficients, the phase diagrams are presented in Figure 10. It is easy to see that the larger the restitution coefficient r is, the smaller the energy loss during the impact of the system is. That is the greater the energy available when the system is stable. Thus, different stable phase orbital diagrams may be generated. As shown in Figure 10(a), when r < 0.295 , the energy left by the system is no longer enough to reach the impact surface, so a motion state similar to simple harmonic motion will be formed. When 0.295 < r < 0.613 , the first block has the energy to reach the constraint surface, so the impact phenomenon occurs shown in Figure 10(b). When 0.613 < r < 0.776 , the system energy further increases and the period-doubling bifurcation occurs, as shown in Figure 10(c). When r > 0.776 , the system enters a chaotic state, as shown in Figure 10(d).

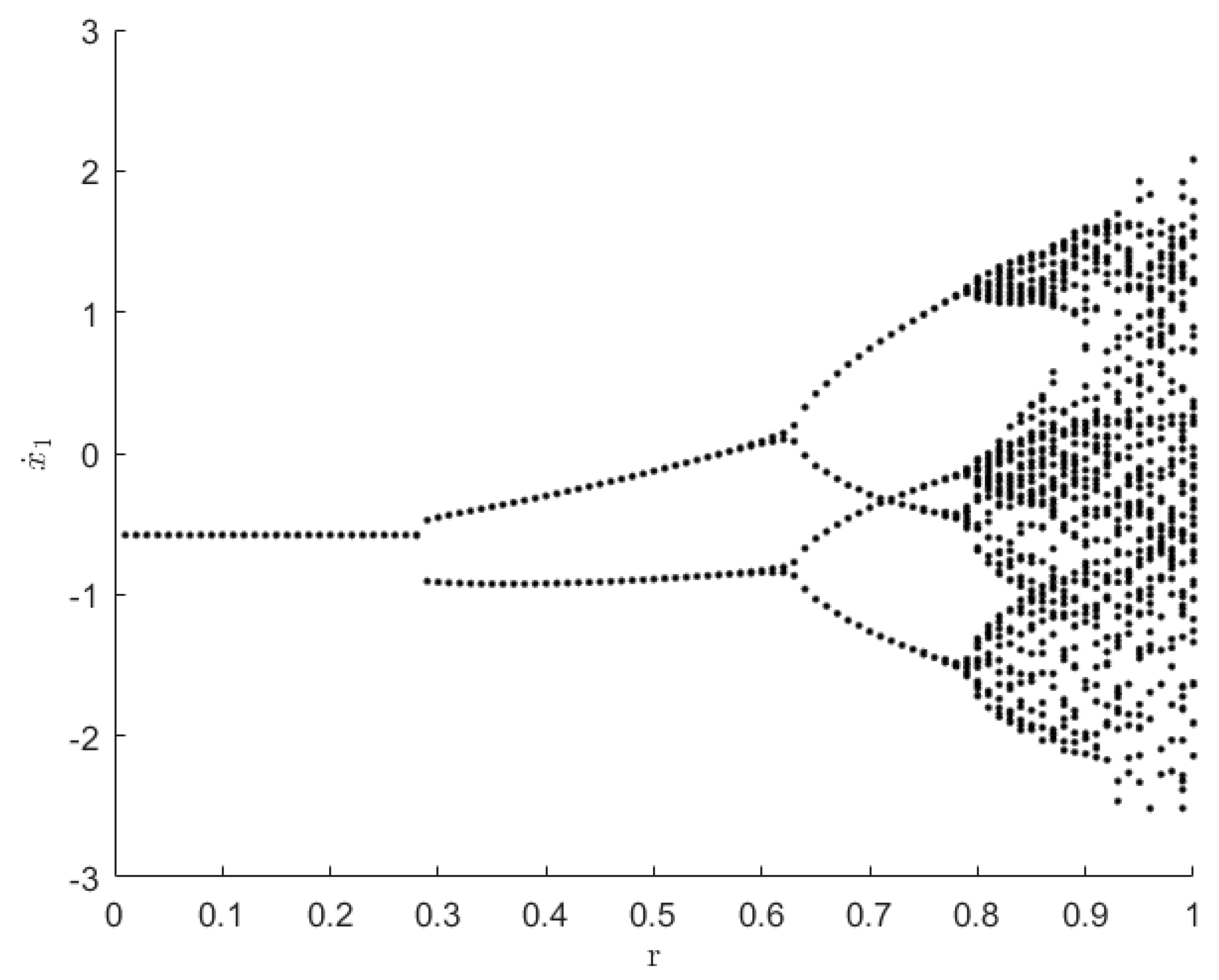
4.4. Influence of the Uncertain Parameter

For the stochastic three-degree-of-freedom vibroimpact system, When the random variable u randomly takes a series of values { u i } in the interval [ − 1 , 1 ] , each value of u i corresponds to a certain non-smooth sample system ∏ u i . If there is a period-doubling bifurcation in the system, a deterministic bifurcation must occur at a critical point. However, a series of sample systems of a stochastic system may not present bifurcation at the same critical point. There must be an interval in which the period-doubling bifurcation may or may not have occurred in the samples of the random system. When the bifurcation parameters pass through this transition interval, almost all samples have bifurcations, and the period-doubling bifurcation of the random system is considered to be completed.
Take system parameters as P = ( 1 , 0 , 0 ) T , m 2 = m 3 = 1.5 , k 2 = k 3 = 4 . When bifurcation parameters change from ω = 2.14 to ω = 2.28 , the deterministic three-degree-of-freedom vibroimpact system presents reverse period-doubling bifurcation, as depicted in Figure 11(a). Meanwhile, when bifurcation parameters change from ω = 1.6 to ω = 1.85 , period-doubling bifurcation to chaos from Figure 11(b) will also occur.
It can be seen from Figure 12 that, when ω = 2.135 , the phase orbit diagrams of the deterministic system and the random system will be greatly different. The deterministic system has not yet had bifurcation, but the random system has already had bifurcation. Therefore, under the same initial values and parameters, the bifurcation interval of the stochastic system is indeed different from the bifurcation point of the deterministic system. In this bifurcation interval, the phase orbit diagrams of the stochastic vibroimapct system and the deterministic system are quite different. The period doubling bifurcation has occurred in the former, but not yet in the latter.

5. Conclusion

This paper establishes a model of three-degree-of-freedom unilateral rigid restraint vibroimpact system with an uncertain parameter. The damping coefficient is considered as the uncertain parameter and approximated by the arch distribution. The vibroimpact system with the uncertain parameter is firstly transformed to a deterministic system by Chebyshev polynomial approximation method. Then the numerical method of the deterministic system is used to study the bifurcation behavior of the system under asymmetric constraint. The result from Monte Carlo method and the response of the deterministic system are compared, the period-doubling bifurcation behavior of the system is studied, and the bifurcation behavior of the system is analyzed. The results show that Chebyshev polynomial approximation is an effective method for solving multi-degree-of-freedom systems with uncertain parameter. At the same time, the results of numerical simulations show that the asymmetry of the constraint conditions makes the period-doubling bifurcation of the stochastic constraint system more sensitive to the change of the bifurcation coefficient. The general period response will not change much under the influence of weak random factors. However, at the nodes where period doubling bifurcation occurs, even small random vibrations can have a significant impact. Besides, the method may be further generalized to more general vibroimpact systems with uncertain parameters in future research.

Funding Statement

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12172291, 12272283), the Fundamental Research Funds for the Central Universities (Grant No. ZYTS23053).

Author Contributions

Conceptualization, Zichen Deng; Formal analysis, Zicheng Lin; Methodology, Guidong Yang and Lin Du; Project administration, Zichen Deng; Validation, Zicheng Lin; Writing – original draft, Guidong Yang; Writing – review & editing, Zichen Deng and Lin Du.

Conflicts of Interest

The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. Dimentberg, M. F., Iourtchenko, D. V. (2004). Random vibrations with impacts: a review. Nonlinear Dynamics, 36, 229-254. [CrossRef]
  2. Guo, Y., Yin, X., Yu, B., Hao, Q., Xiao, X. et al. (2023). Experimental analysis of dynamic behavior of elastic visco-plastic beam under repeated mass impacts. International Journal of Impact Engineering, 171, 104371. [CrossRef]
  3. Wang, L., Wang, B., Peng, J., Yue, X., Xu, W. (2021). Stochastic response of a vibro-impact system via a new impact-to-impact mapping. International Journal of Bifurcation and Chaos, 31(08), 2150139. [CrossRef]
  4. Chen, L., Zhu, H., Sun, J. Q. (2019). Novel method for random vibration analysis of single-degree-of-freedom vibroimpact systems with bilateral barriers. Applied Mathematics and Mechanics, 40(12), 1759-1776. [CrossRef]
  5. Yue, Y., Xie, J. H. (2008). Symmetry and bifurcations of a two-degree-of-freedom vibro-impact system. Journal of Sound and Vibration, 314(1-2), 228-245. [CrossRef]
  6. Xu, Y., Liu, Q., Guo, G., Xu, C., Liu, D. (2017). Dynamical responses of airfoil models with harmonic excitation under uncertain disturbance. Nonlinear Dynamics, 89, 1579-1590. [CrossRef]
  7. Huang, D., Han, J., Zhou, S., Han, Q., Yang, G., Yurchenko, D. (2022). Stochastic and deterministic responses of an asymmetric quad-stable energy harvester. Mechanical Systems and Signal Processing, 168, 108672. [CrossRef]
  8. Deng, H., Ye, J., Li, W., Huang, D. (2023). Theoretical Analysis of the Galloping Energy Harvesters under Bounded Random Parameter Excitation. CMES-COMPUTER MODELING IN ENGINEERING & SCIENCES. [CrossRef]
  9. Zhu, W., Cai, G. (2002). Nonlinear stochastic dynamics: A survey of recent developments. Acta Mechanica Sinica, 18(6), 551-566. [CrossRef]
  10. Ibrahim, R. A. (2009). Vibro-impact dynamics: modeling, mapping and applications (Vol. 43). Springer Science & Business Media.
  11. Whiston, G. S. (1992). Singularities in vibro-impact dynamics. Journal of Sound and Vibration, 152(3), 427-460. [CrossRef]
  12. Knudsen, J., Massih, A. R. (2000). Vibro-impact dynamics of a periodically forced beam. J. Pressure Vessel Technol., 122(2), 210-221. [CrossRef]
  13. Iourtchenko, D. V., Song, L. (2006). Numerical investigation of a response probability density function of stochastic vibroimpact systems with inelastic impacts. International Journal of Non-Linear Mechanics, 41(3), 447-455. [CrossRef]
  14. Shaw, S. W., Holmes, P. J. (1983). A periodically forced impact oscillator with large dissipation. Journal of Applied Mechanics, 50(4a), 849-857. [CrossRef]
  15. Shaw, S. W. (1985). The dynamics of a harmonically excited system having rigid amplitude constraints, Part 1: Subharmonic motions and local bifurcations. Journal of Applied Mechanics, 52(2), 453-458. [CrossRef]
  16. Shaw, S. W. (1985). The dynamics of a harmonically excited system having rigid amplitude constraints, Part 2: Chaotic motions and Glocal bifurcations. Journal of Applied Mechanics, 52(2), 459-464. [CrossRef]
  17. Mason, J. F., Humphries, N., Piiroinen, P. T. (2014). Numerical analysis of codimension-one,-two and-three bifurcations in a periodically-forced impact oscillator with two discontinuity surfaces. Mathematics and Computers in Simulation, 95, 98-110. [CrossRef]
  18. Li, C., Xu, W., Yue, X. (2014). Stochastic response of a vibro-impact system by path integration based on generalized cell mapping method. International Journal of Bifurcation and Chaos, 24(10), 1450129. [CrossRef]
  19. Liu, L., Xu, W., Yue, X. L., Han, Q. (2013). Global analysis of crises in a Duffing vibro-impact oscillator with non-viscously damping. Wuli Xuebao, 62(20), 200501-200501. [CrossRef]
  20. Qian, J., Chen, L., Sun, J. Q. (2023). Random vibration analysis of vibro-impact systems: RBF neural network method. International Journal of Non-Linear Mechanics, 148, 104261. [CrossRef]
  21. Ding, W., Li, G., Luo, G., Xie, J. (2012). Torus T2 and its locking, doubling, chaos of a vibro-impact system. Journal of the Franklin Institute, 349(1), 337-348. [CrossRef]
  22. Chin, W., Ott, E., Nusse, H. E., Grebogi, C. (1994). Grazing bifurcations in impact oscillators. Physical Review E, 50(6), 4427. [CrossRef]
  23. Nordmark, A. B. (2001). Existence of periodic orbits in grazing bifurcations of impacting mechanical oscillators. Nonlinearity, 14(6), 1517. [CrossRef]
  24. Budd, C. J. (1996). Non-smooth dynamical systems and the grazing bifurcation. Nonlinear mathematics and its applications, 219-235.
  25. Wagg, D. J. (2005). Periodic sticking motion in a two-degree-of-freedom impact oscillator. International Journal of Non-Linear Mechanics, 40(8), 1076-1087. [CrossRef]
  26. Li, X., Yao, Z., Wu, R. (2015). Modeling and sticking motion analysis of a vibro-impact system in linear ultrasonic motors. International Journal of Mechanical Sciences, 100, 23-31. [CrossRef]
  27. Dankowicz, H., Fotsch, E. (2017). On the analysis of chatter in mechanical systems with impacts. Procedia IUTAM, 20, 18-25. [CrossRef]
  28. Wagg, D. J., Bishop, S. R. (2001). Chatter, sticking and chaotic impacting motion in a two-degree of freedom impact oscillator. International Journal of Bifurcation and Chaos, 11(01), 57-71. [CrossRef]
  29. Budd, C. J., Piiroinen, P. T. (2006). Corner bifurcations in non-smoothly forced impact oscillators. Physica D: Nonlinear Phenomena, 220(2), 127-145. [CrossRef]
  30. di Bernardo, M., Budd, C. J., Champneys, A. R. (2001). Corner collision implies border-collision bifurcation. Physica D: Nonlinear Phenomena, 154(3-4), 171-194. [CrossRef]
  31. Xu,W., Yang, G., Yue, X. (2016). P-bifurcations of a Duffing-Rayleigh vibroimpact system under stochastic parametric excitation. Acta Physica Sinica, 65(21). [CrossRef]
  32. Zhu, H. (2014). Stochastic response of vibro-impact Duffing oscillators under external and parametric Gaussian white noises. Journal of Sound and Vibration, 333(3), 954-961. [CrossRef]
  33. Yang, G., Xu, W., Feng, J., Gu, X. (2015). Response analysis of Rayleigh–Van der Pol vibroimpact system with inelastic impact under two parametric white-noise excitations. Nonlinear Dynamics, 82, 1797-1810. [CrossRef]
  34. Liu, L., Xu, W., Yang, G., & Huang, D. (2020). Reliability and control of strongly nonlinear vibro-impact system under external and parametric Gaussian noises. Science China Technological Sciences, 63(9), 1837-1845. [CrossRef]
  35. Feng, J. , Xu, W., Wang, R. (2006). Period-doubling bifurcation of stochastic Duffing one-sided constraint system. Acta Physica Sinica, 55(11), 5733-5739. [CrossRef]
  36. Zhang, Y., Zhang, J., Gu, SH. (2006). Periodic motions and bifurcations of a three-degree-of-freedom vibration system with a rigid constrain. Journal of Lanzhou Jiaotong University, 25(1),39-43.
Preprints 82740 g001
Figure 1. A schematic of the three-degree-of-freedom vibroimpact system with unilateral rigid constrain.
Figure 1. A schematic of the three-degree-of-freedom vibroimpact system with unilateral rigid constrain.
Preprints 82740 g001
Preprints 82740 g002
Figure 2. The probability density function curve of the arch distribution.
Figure 2. The probability density function curve of the arch distribution.
Preprints 82740 g002
Preprints 82740 g003
Figure 3. The time history diagram and phase orbit diagram of the response for different excitation frequency: (a) time history diagram of deterministic system for ω = 2.25 ; (b) the corresponding 1 − 1 cycles of the three systems for ω = 2.25 ; (c) time history diagram of deterministic system for ω = 2.2 ; (d) the corresponding 2 − 2 cycles of the three systems for ω = 2.2 .
Figure 3. The time history diagram and phase orbit diagram of the response for different excitation frequency: (a) time history diagram of deterministic system for ω = 2.25 ; (b) the corresponding 1 − 1 cycles of the three systems for ω = 2.25 ; (c) time history diagram of deterministic system for ω = 2.2 ; (d) the corresponding 2 − 2 cycles of the three systems for ω = 2.2 .
Preprints 82740 g003
Preprints 82740 g004
Figure 4. The time history diagram and phase orbit diagram of the system responses: (a) the time history diagram of the deterministic system for ω = 1.65 ; (b) the phase orbit diagram of the three systems in 1 − 1 cycles for ω = 1.65 ; (c) the time history diagram of the deterministic system for ω = 1.787 ; (d) the phase orbit diagram of the three systems in 2 − 2 cycles for ω = 1.787 .
Figure 4. The time history diagram and phase orbit diagram of the system responses: (a) the time history diagram of the deterministic system for ω = 1.65 ; (b) the phase orbit diagram of the three systems in 1 − 1 cycles for ω = 1.65 ; (c) the time history diagram of the deterministic system for ω = 1.787 ; (d) the phase orbit diagram of the three systems in 2 − 2 cycles for ω = 1.787 .
Preprints 82740 g004
Preprints 82740 g005
Figure 5. The image of the maximum Lyapunov exponent changing with time.
Figure 5. The image of the maximum Lyapunov exponent changing with time.
Preprints 82740 g005
Preprints 82740 g006
Figure 6. The time history diagram and phase orbit diagram of the system responses: (a) the time history diagram of the deterministic system for ω = 2 . 45 ; (b) the phase orbit diagram of the three systems in 1 − 1 cycles for ω = 2 . 45 ; (c) the time history diagram of the deterministic system for ω = 2 . 4 ; (d) the phase orbit diagram of the three systems in 2 − 2 cycles for ω = 2 . 4 .
Figure 6. The time history diagram and phase orbit diagram of the system responses: (a) the time history diagram of the deterministic system for ω = 2 . 45 ; (b) the phase orbit diagram of the three systems in 1 − 1 cycles for ω = 2 . 45 ; (c) the time history diagram of the deterministic system for ω = 2 . 4 ; (d) the phase orbit diagram of the three systems in 2 − 2 cycles for ω = 2 . 4 .
Preprints 82740 g006
Preprints 82740 g007
Figure 7. The maximum Lyapunov exponent of period-fold bifurcation to chaos varying with time.
Figure 7. The maximum Lyapunov exponent of period-fold bifurcation to chaos varying with time.
Preprints 82740 g007
Preprints 82740 g008
Figure 8. Chaotic phase orbit diagram and time history diagram: (a) phase orbit diagram of equivalent deterministic system; (b) phase orbit diagram of deterministic system; (c) phase orbit diagram of original stochastic vibroimpact system; (d) time history diagram of deterministic vibroimpact system.
Figure 8. Chaotic phase orbit diagram and time history diagram: (a) phase orbit diagram of equivalent deterministic system; (b) phase orbit diagram of deterministic system; (c) phase orbit diagram of original stochastic vibroimpact system; (d) time history diagram of deterministic vibroimpact system.
Preprints 82740 g008
Preprints 82740 g009
Figure 9. Bifurcation diagram with respect to r for Deterministic three-degree-of-freedom unilateral rigid restraint vibroimpact system.
Figure 9. Bifurcation diagram with respect to r for Deterministic three-degree-of-freedom unilateral rigid restraint vibroimpact system.
Preprints 82740 g009
Preprints 82740 g010aPreprints 82740 g010b
Figure 10. Phase orbital diagram of the system with respect to r : (a) r = 0.2 ; (b) r = 0.5 ;(c) r = 0.7 ;(d) r = 0.9. .
Figure 10. Phase orbital diagram of the system with respect to r : (a) r = 0.2 ; (b) r = 0.5 ;(c) r = 0.7 ;(d) r = 0.9. .
Preprints 82740 g010aPreprints 82740 g010b
Preprints 82740 g011
Figure 11. Bifurcation diagram with respect to ω for Deterministic three-degree-of-freedom vibroimpact system: (a) ω = 2.14 to ω = 2.28 ; (b) ω = 1.6 to ω = 1.85 .
Figure 11. Bifurcation diagram with respect to ω for Deterministic three-degree-of-freedom vibroimpact system: (a) ω = 2.14 to ω = 2.28 ; (b) ω = 1.6 to ω = 1.85 .
Preprints 82740 g011
Preprints 82740 g012
Figure 12. Time history and phase orbit diagrams of stochastic and deterministic systems with ω = 2.135 : (a) phase orbit diagram of original stochastic vibroimpact system; (b) time history diagram of original stochastic vibroimpact system; (c) phase orbit diagram of the deterministic system; (d) time history diagram of the deterministic system.
Figure 12. Time history and phase orbit diagrams of stochastic and deterministic systems with ω = 2.135 : (a) phase orbit diagram of original stochastic vibroimpact system; (b) time history diagram of original stochastic vibroimpact system; (c) phase orbit diagram of the deterministic system; (d) time history diagram of the deterministic system.
Preprints 82740 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated