Prerpints.org logo
Preprint
Article

Benchmarking Maintenance Practices for Allocating Features Affecting Hydraulic Systems Maintenance: A West-Balkan Perspective

Altmetrics

Downloads

108

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (349.31KB )

This version is not peer-reviewed

Submitted:

11 August 2023

Posted:

14 August 2023

You are already at the latest version

Alerts
Abstract
As a consequence of applying advanced maintenance practices, the theoretical probability of failures is relatively low. However, observation of low market intelligence and maintenance management has been reported. The experimental investigation is supported by findings from a survey targeting asset-intensive companies applying hydraulic power systems. Next, the study incorporates multidimensional data analysis using CA-AHC (Correspondance Analysis with Agglomerative Hierarchical Clustering) approach. The non-parametric machine learning models are used from generated feature subspace to extract features affecting maintenance performance indicators. The results support empirical evidence that equipment age increases the probability of failures. However, the novel findings show that number of maintenance personnel, equipment size measured by nominal working energy consumption, and activities dedicated to maintaining fluid cleanliness impact regression results of companies utilising hydraulic applications.
Keywords: 
Subject: Engineering  -   Industrial and Manufacturing Engineering

MSC:  90B25

1. Introduction

1.1. Background and Rationale

Companies have always been aware of the risk associated with their operational and production processes. Although there are many risk factors, the maintenance function is mainly related to operational performance and overall equipment effectiveness [1]. Although usually perceived as a “necessary evil” nowadays, many consider maintenance a strategic move for gaining a competitive advantage [2]. However, uncoordinated investments and poor management severely affect RAM (Reliability, Availability and Maintainability) [3], which is why many companies face difficulties in implementing advanced data-driven and sustainable practices [4]. Such issues are mainly attributed to problems of selecting appropriate Maintenance Practice (MP), implementation suitability [5], industrial environment [6], asset management risks [7], and other technological issues.
Consequently, the Maintenance Strategy Selection (MSS) domain emerged for dealing with these multiple interrelated issues. Although the MSS provided a “bright avenue” for dealing with disruptive market demands, problems associated with complex applications, lack of personnel, and around-the-clock industrial requirements led to human factor deficiencies and poor decision-making [7].
The problem is that maintenance managers have preconceived notions about “good” or “bad” maintenance strategies. Thus, many believe that adopting PdM (Predictive Maintenance) will significantly reduce their downtime and improve production flows, which is a misconception. This is especially an issue in companies adopting PdM as a cost-cutting and time-reducing practice [8], believing that AI (Artificial Intelligence) will significantly advance their performance [9], which ultimately fails to fulfill the expectations [10].

1.2. Literature review

With the expansion of PdM 4.0 [11], the performance and competitiveness of manufacturing companies strongly depend on the reliability and availability of manufacturing assets. Recent studies acknowledge that lacking maintenance knowledge and skills will have practical/financial implications [12]. Although issues are constantly assessed in smaller companies, there is a lack of evidence considering large-scale applications. Some argue that the efficiency of maintenance play a pivotal role in securing profit [13,14]. Most, however, argue that OEE (Overall Equipment Effectiveness), is one of the driving factors fothe r selection of MSS. Although there is an extensive literature on MPIs (Maintenance Performance Indicators), the availability [6], with MTBF (Mean-Time-Between-Failure) and MTTR (Mean-Time-To-Repair) as cores [7], are mostly highlighted as most important MPIs [15]. As noticed, the indicators do not include qualitative data (e.g., maintenance activities) that usually exist in practice. This is primarily because such information is hard to collect, process and maintain over time.
As many studies incorporate machine and deep learning techniques in diagnosis and prognosis [16,17], while also for reliability modelling and optimisation [18], there is a lack of use machine learning and multidimensional data analysis from a strategic and tactical standpoint [19]. This is especially the case in asset-intensive industries with heavy-duty machinery such as hydraulic power systems. Moreover, existing body-of-knowledge within the sphere of hydraulic system maintenance is mostly concerned with diagnostic and prognostic aspect [20], there is a lack of empricial evidence on the issues affecting maintenance performance from a management perspective. As such, there is lack of evidence regarding the impact of latent factors affecting output maintenance performance metrics (e.g., MTBF, MTTR).
Nevertheless, entering digitalisation and cloud computing era, many companies incorporate visual analytics [21] for assessing business issues by relying on MDA (Multivariate Data Analysis) [22]. The benefits of using MDA is in its ability to incorporate multidimensional data: unstructured text, categorical data, numerical data, logs, binary data, etc., and project such data in a lower-dimensional subspace for investigating latent indicators [23] that impact production performance. Although there has not been much engagement in maintenance management, visual analytics with MDA are landscaping other fields, such as business management, disaster management, and many other fields [24]. As such, the study intent is to use MDA for allocating features impacting maintenance performance that can be considered for improvement of higher-level maintenance decision-making.

1.3. Aims and objectives

With the idea of using textual and numerical data, performed experimental analysis is done by surveying companies utilising hydraulic systems. By conducting longitudinal study over the course of three years, the evidence gathered helped us gain insights into potential relationships between applied MPs and output results. Namely, using MDA, we extrapolate feature subspace through Correspondance Analysis (CA). Using CA, the aim of the study is to generate components by combining MPs with associated CFT (Component Failure Types) and RCF (Root Causes of Failure) for benchmarking MPs in terms of output performance. Next, the goal is to extract most important features impacting maintenance performance (e.g., MTBF, MTTR) using machine learning algorithms.
The rest of the study is structured as follows. The methodology describes survey design, synthesis and processing data with an in-detail description of the analysis. The third chapter provides descriptive statistics and research results. The fourth chapter includes discussion of research results and post hoc analysis considering MMPs. The last chapter provides concluding remarks, implications and future research directions.

2. Methodology

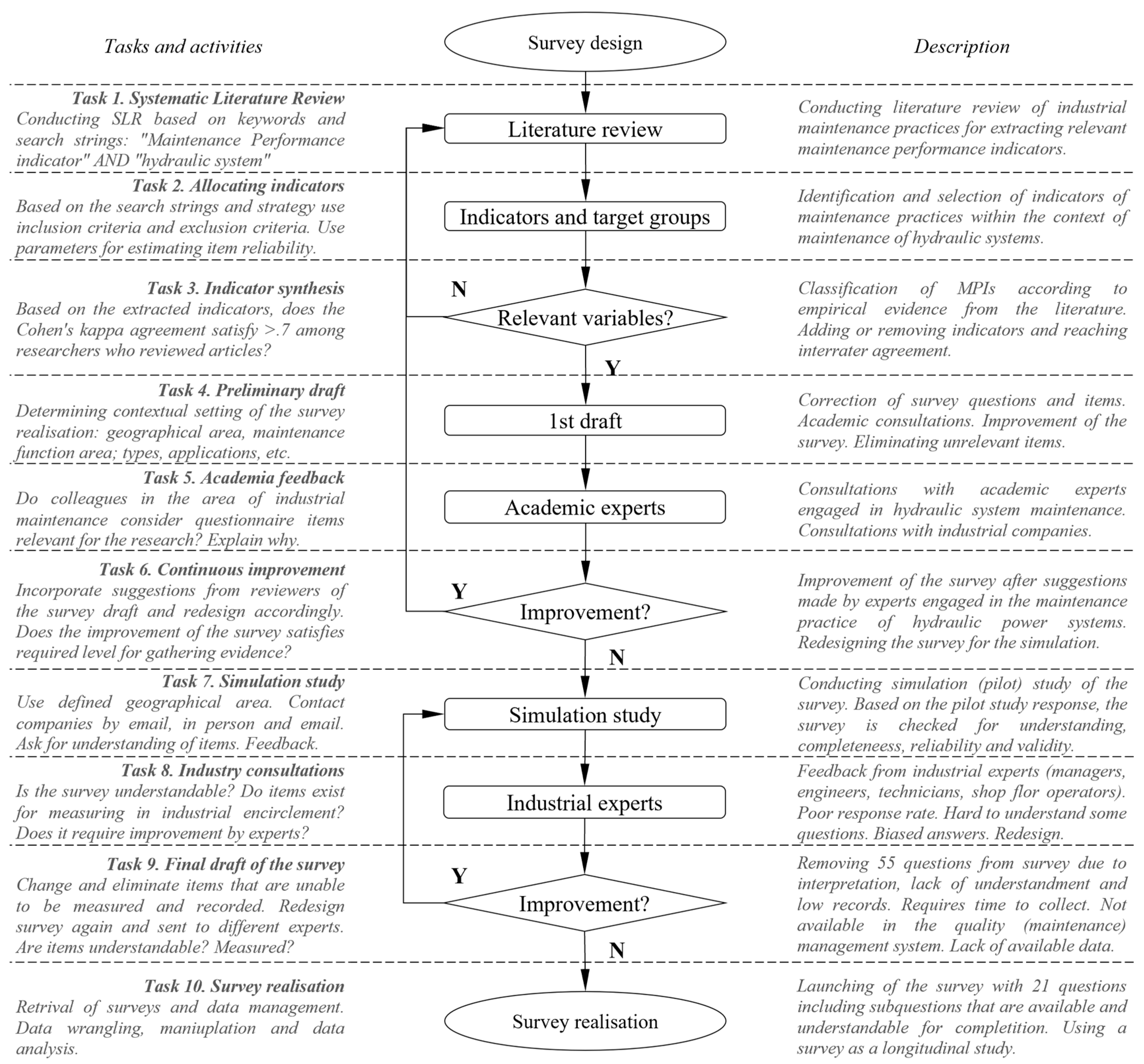
2.1. Study design

The study workflow consists of three parts: (a) survey design and realisation; (b) survey data processing and wrangling; and (c) feature subspace extraction and data analysis. The design of the survey is performed in several iterations consistsing of the organisational, maintenance management and performance characterstics. After data was obtained the CA and Agglomerative Hierarchical Clustering (AHC) are used to generate a feature subspace. Finally, selected MPs are used in conjunction with output performance metrics to isolate the features, including programs, factors and activities using machine learning (ML) algorithms.

2.2. Survey design and realisation

Design of survey items started with a systematic review of the literature (Task 1) regarding keywords and search strings: “maintenance performance indicators” AND “hydraulic system”. After the review, the authors individually synthesised indicators (Task 2) from the literature and extracted the most important ones (Task 3) while respecting interrater agreement using Cohens’ K = 0.89. The first draft is used to target companies utilising hydraulic applications in West Balkan Penninsula (Task 4). Consultations with experts helped eliminate unnecessary indicators and modify the survey (Task 5). After redesigning the first draft (Task 6), the simulation is performed within the sample of 5 companies (Task 7). The feedback from experts (Task 8) helped eliminate most survey items due to time, understanding of metics, and lack of records. In the final version of the survey (Task 9) all three companies agreed to 22 questions (with 5 sub-questions). The first realisation phase started on September 2019 (Task 10). In the first run, a total of 81 samples were collected. In the second run (September 2020 - June 2021), 100 companies participated. In the final run, 115 companies participated and shared the data. The survey is available in Supplementary Material 1.

2.3. Survey items and data extraction

The survey design (Figure 1) started in February 2019 and lasted until June 2019. Segmentation of survey questions include three facets, namely: (i) organisational characteristics; (ii) characteristics of maintenance functions; and (iii) output data as performance metrics. The organisational facet includes questions regarding organisational structure and asset characteristics. The maintenance characteristics include department size and staff; qualifications; condition monitoring (e.g., sensors, instruments); preventive/corrective activities (e.g., filter replacement time). The output performance metrics measured include MTBF; MTTR (Mean-time-to-repair); CFT; RCF; and WOMM (wasted oil per month-machine).
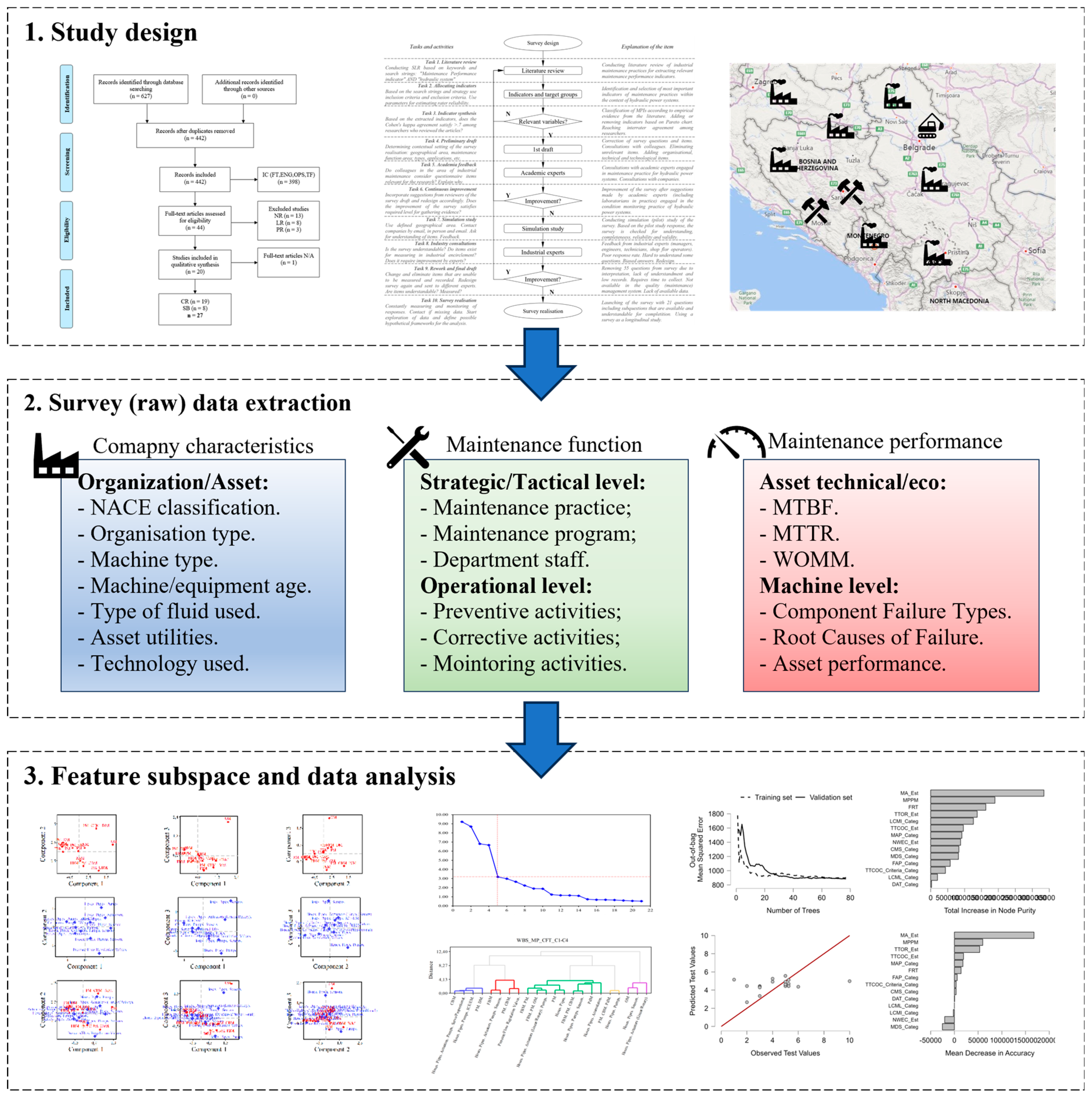
Preprints 82189 g001a
Figure 1. Study design and data wrangling process.
Figure 1. Study design and data wrangling process.
Preprints 82189 g001a
Preprints 82189 g001
Figure 1. Survey design workflow.
Figure 1. Survey design workflow.
Preprints 82189 g001

2.4. Correspondence analysis

Since survey contains mostly categorical data, the contingency tables is formed and χ2 distance metrics is used for CA. The contingency table(s) considers i categories (rows) of variable V1, where i = 1, 2… I, and j categories (columns) of variable V2 where j = 1, 2…J. The value xi,j corresponds to the values of variable with i rows and j columns, with n instances. Using contingency tables, we first calculate probabilities as follows:
f i j = x i j n   ,
where the sum of rows equals marginal probability:
f . j = ∑ i = 1 I f i j ,
and for the sum of columns, the marginal probability:
f i . = ∑ j = 1 J f i j .  
The relationship between selected variables measured by the χ2-distance:
χ o b s 2 = ∑ i = 1 I ∑ j = 1 J n f i j − n f i . f . j 2 n f i . f . j ,
where nfij is observed probability and nfi.f.j is the theoretical probability, and factoring out n out of eq. 4, we get total inertia Φ2:
χ o b s 2 = ∑ i = 1 I ∑ j = 1 J n f i j − f i . f . j 2 f i . f . j = n Φ 2 .
The CA is described as point clouds proposed by [25], alongside mathematical formulations [26,27]. Considering row profiles i, we obtain a cloud of profiles NI. With generated point cloud, we add GI point, depicted as the centre of gravity with coordinate f.j. The GI can be considered a centre of gravity if we associate each point i with the weight proportional to its marginal value (fi.). The space then compares profile i with the GI by distance measure. As stated, distance between i and i’ is defined:
d χ 2 2 i , i ′ = ∑ j = 1 J 1 f . j f i j f i . − f i ' j f i ' . 2 .
Although it can suggest Euclidian distance, the χ2 compares the sum of differences where each dimension J is associated with the weight 1/f.j. Therefore, the centre of the gravity GI corresponds to the mean profile as:
d χ 2 2 i , G I = ∑ j = 1 J 1 f . j f i j f i . − f . j 2 .
The same principles are used for estimating the distances in the column profile. A column profile is a set of I values in ℝI dimensional space. The coordinate of the jth point is fij/f.j, and j points together to form the Nj cloud. The central point, i.e., the centre of gravity GJ, is added with coordinate fi. in the Ith dimension. The GI is the centre of gravity as long as we assign a column profile j a weight corresponding to its marginal probability f.j. Same as row profiles, we estimate the distances between points j and j’ with χ2 distance as:
d χ 2 2 j , j ′ = ∑ i = 1 I 1 f i . f i j f . j − f i j ' f . j ' 2 ,
and the centre of gravity GJ is estimated as:
d χ 2 2 j , G J = ∑ i = 1 I 1 f i . f i j f . j − f i . 2 .
If independence exists, the conditional probability equals marginal probability for all i (f.j = fij/fi.), meaning that all profiles are the same as the mean, i.e., NI becomes GI. As such, we measure the inertia by the eq. 5 as:
Inertia N I G I = ∑ i = 1 I ∑ j = 1 J f i j − f i . f . j 2 f i . f . j = χ 2 n = Φ 2 .
The same holds for NJ, Inertia(NJ/GJ) = Inertia(NI/GI). Therefore, Φ2 presents the strength of the link. The CA proceeds, as all components (i.e., factors), by projecting NI to axes C1 and C2, forming a plane P. Finding a plane P is determined by the criteria of maximum inertia, such that:
∑ i = 1 I f i . O H i 2 ,
is maximal and is used to determine the Mi point that corresponds to the Ith profile on the plane P, where OHi represents the distance to the origin GI = O. The plane P is the sum of the inertia such that projected Hi overall i is maximal. The C1 and C2 axes (components) represent maximal inertia such that C2⊥C1, and as a result, we get plane P. The inertia λs of the sth axis is then:
∑ i = 1 I f i . O H i s 2 = λ s ,
and λs represents the eigenvalue of the Cs. Calculating fi. on Cs (same for column) over the total inertia of the λs is:
C o n t r i b u t i o n f i . ,   λ s = f i . O H i s 2 λ s ,
where summation leads to the inertia of Cs, and we determine the quality (Qual) of the representation as:
Q u a l s = ∑ i = 1 I f i . O H i s 2 ∑ i = 1 I f i . O M i 2 = λ s ∑ k = 1 K λ k ,
where OMi is the distance of Mi point to origin O. The numerator represents the inertia of NI on the axis Cs, and the denominator is the total Inertia(NI) = Φ2. Calculating position on the plot of rows and columns, we use transitional formulas for determining coordinates of i row on the sth axis (Fs) as:
F s i = 1 λ s ∑ j = 1 J f i j f i . G s j   ,
where Gs(j) is the coordinate of the column j on the sth axis, and λs is the inertia of the sth axis. Permuting Gs and Fs, we get the same outcome for the different barycentre. Intuitively, the number axes is S ≤ min(J – 1, I – 1) that contain non-zero inertia. Estimating Φ2 of points axes gives us:
Φ 2 = ∑ k = 1 min I − 1 , J − 1 λ k ≤ min I − 1 , J − 1 .

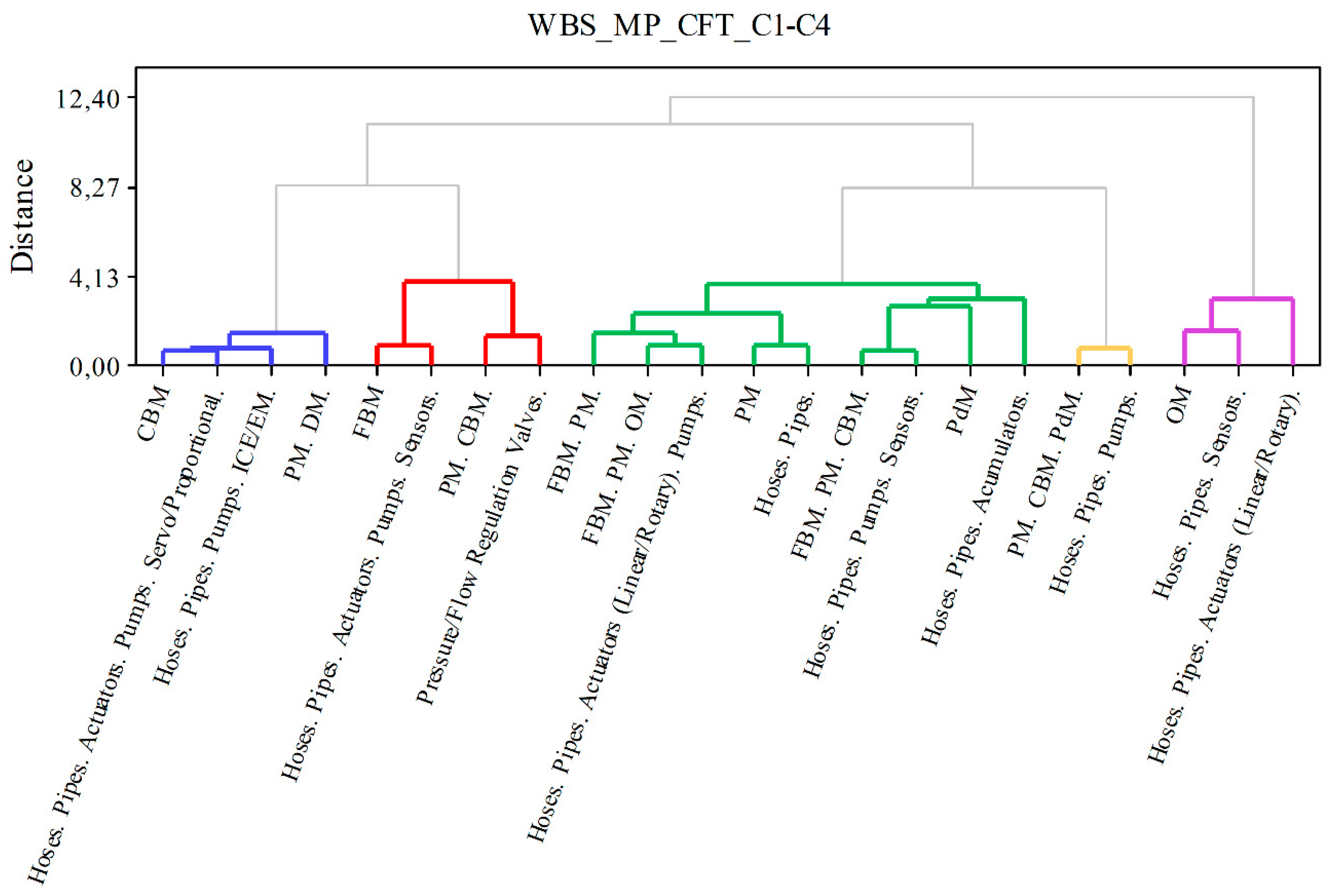
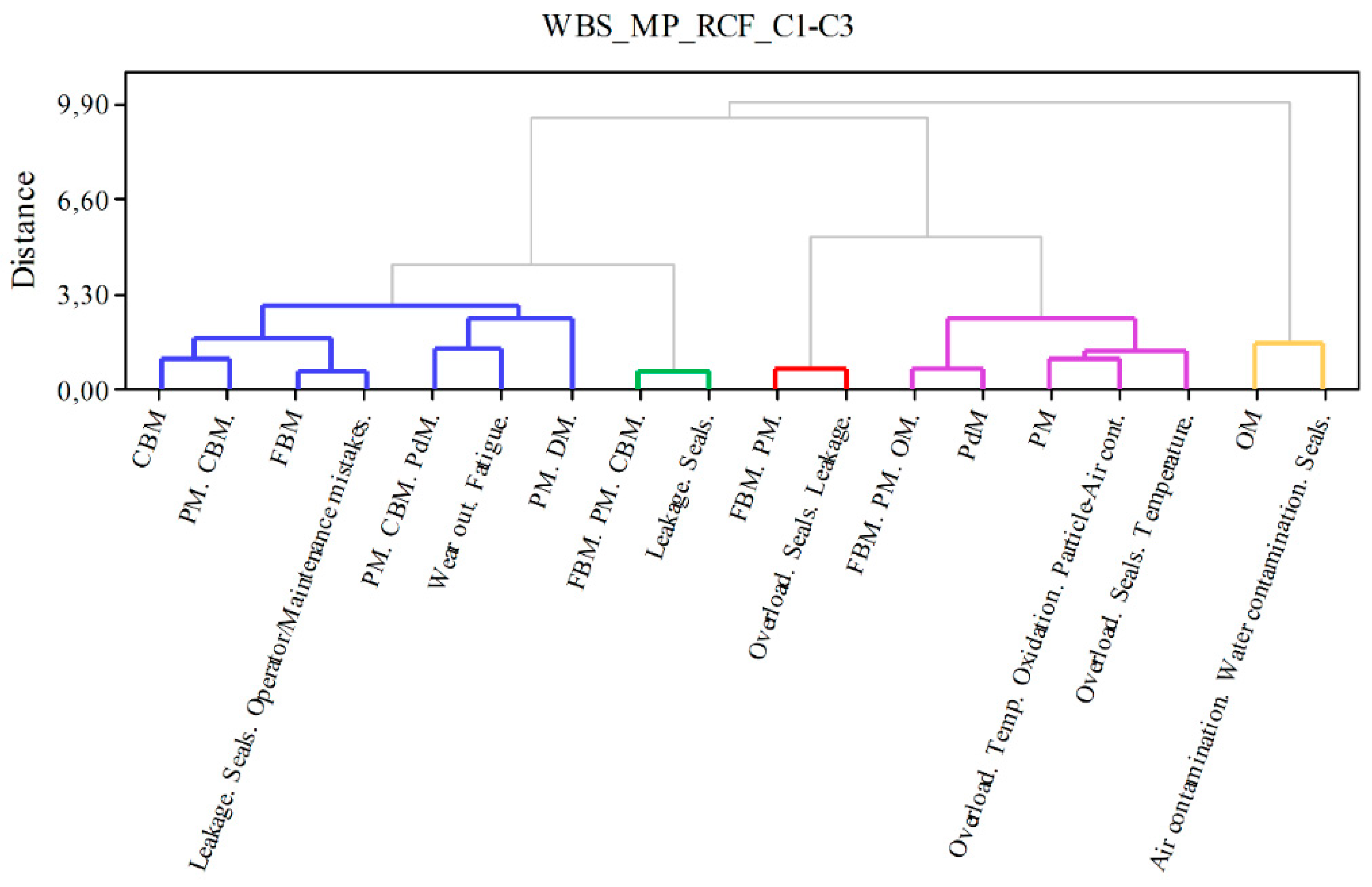
2.5. Clustering CA-components using AHC

Agglomerative Hierarchical Clustering (AHC) is added to replace the inability of CA to project data in more than three dimensions. The two important measures of the AHC is distance and linkage. The AHC assumes that each point x is a singleton [28]. The algorithm creates a collection of higher-level clusters ci by merging the point(s) (singletons) into a new cluster ci’. For measuring distances between points, the Euclidian distance is used [29]:
E D p , q = ∑ i n p i − q i 2 = x c − x c ′   ,
where p and q are coordinates of c. For the cluster linkage we use Ward’s method [30]. The method is imputed by the Lance-Williams algorithm [29] and calculated as:
d g i , g j = i j i + j g i − g j 2 ,
where agglomeration factors are estimated by the Lance-Williams dissimilarity:
α i = i + k i + j + k ;   β = − k i + j + k ;   γ = 0   ,
such that ǀiǀ represents the number of objects in cluster i, g represents the centre coordinates estimated as:
g = i g i + j g j i + j .
After obtaining the distance metrics the clustering of principal components, the CA-AHC is performed.

3. Research results

3.1. Survey insights and descriptives

From the sample of 297 companies, the 7.41% (22 companies) of respondents strictly underlined that they were unwilling to participate in the study. The 19.53% (58 companies) of respondents were willing to participate in the survey; however, the results were not obtained even after contacting three times. Next 34.3% of respondents (102 companies) did not respond. The final dataset comprises 115 companies (38.72% response rate).
The samples consists of large (51.3%), medium (37.4%), and small (11.3%) companies. According to NACE (Nomenclature of Economic Activities), respondents comprise of: 8.7% AFF (Agriculture, forestry, and fishing), 19.1% CON (Construction), 47.0% MAN (Manufacturing) and 25.2% M&Q (Mining and Quarrying). Considering the asset characteristics, the HMA (Hydraulic Machinery Age) shows average distribution across classes (Table 1). The NoM (Number of Machines) is the largest in M&Q. The MPPM (Maintenance Personnel per Machine) is highest in MAN (0.75), and lowest in CON (0.45).
The CFT (Component Failure Types) item is used to construct categories based on the text mining. Hence, the most reported failures include “hoses OR pipes” 85.65%; pumps in 71.3%; “actuators OR cylinders” OR “linear OR rotary” 53.05%; sensors 23.48%; “servo OR proportional” 21.6%; “pressure OR flow OR check OR regulation valves” 4.35%; accumulators 3.48%; “ice OR internal combustion engine” OR “em OR electrical motor” 3.48%; and other 3.4%. The categories are devised into ten categories for the analysis. Considering RCF (Root Causes of Failure), most reported RCFs relate to seals (92.2%); leakage (64.35%); overload (42.61%); temperature (24.35%); technician and operator mistakes (23.48%); air and water contamination (10.43%); “wear OR fatigue” (4.35%), particle contamination (3.48%), and other stoppages (27.83%) failures.
The reader should note that most companies do not use a single but a combination of different MPs, and for the sake of understanding we use curly brackets for reporting cases where companies utilise MP variants. For instance, in cases where a company is utilising OM, CBM and PdM practice, they are noted as “{OM. CBM. PdM.}”.

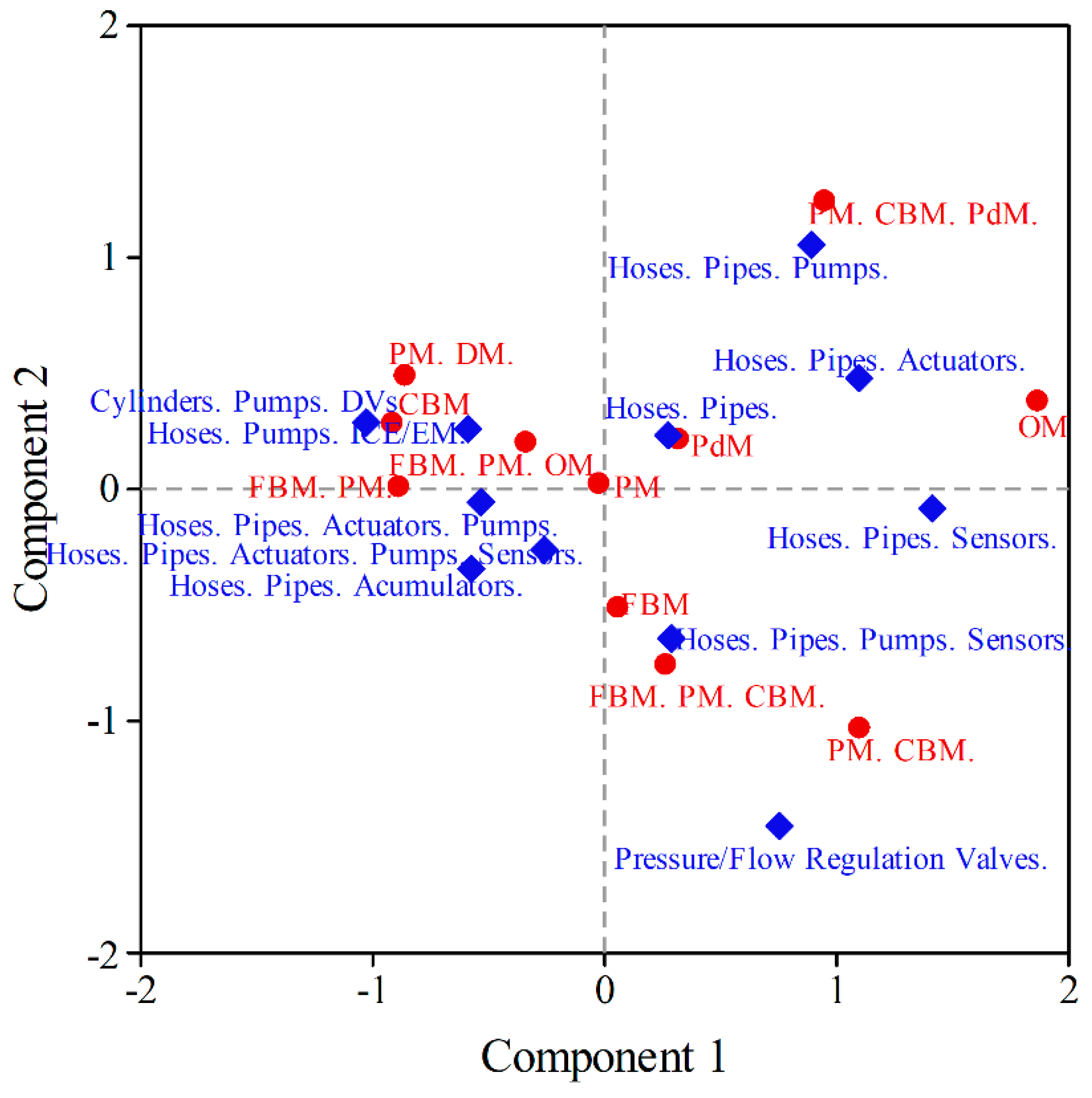
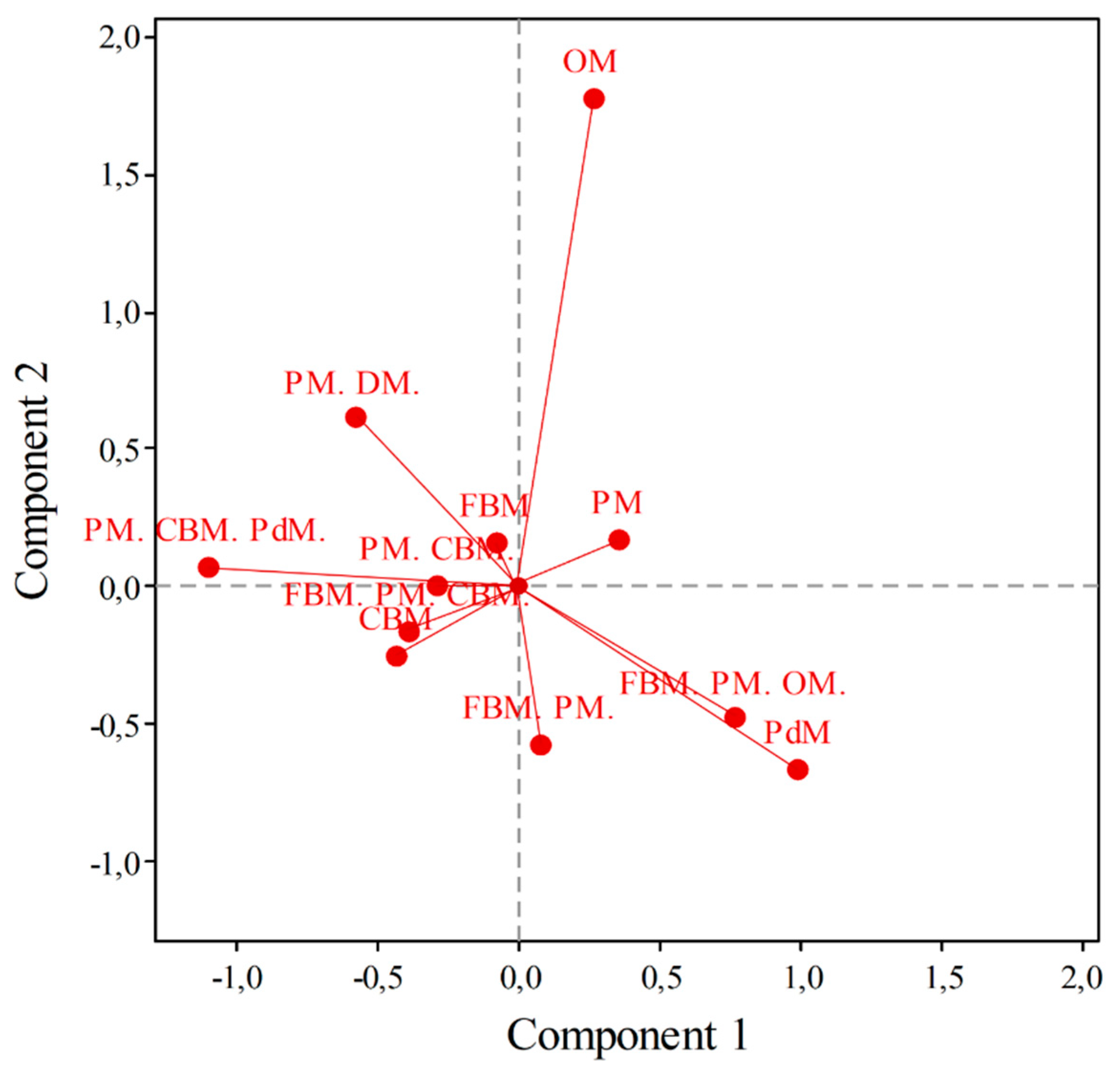
3.2. Relationship between MP and CFT using CA-AHC

Obtained results show that the total inertia is Φ2 = 1.435, out of which first two components account for 50% of the total inertia (Table 2). Out of the mentioned MPs, only {OM} and {PM. CBM. PdM.} account > 0.95 of the quality (Table 3). On the other hand, we can see that {PdM} accounts significantly less to the inertia λPdM = 0.05; however, with the proposed three axes, the Qual{PdM} = 0.568, shows high interpretability.
The analysis from CA (Figure 2), interpreting and making conclusions solely on biplot can be insufficient. For instance, points on the left ({PM. DM.}; {CBM}; {FBM. PM. OM.}; {FBM. PM.}) clusters, while same can be said for ({FBM}; {FBM.PM.CBM.}; {PM. CBM.}). However, looking at points one cannot confirm that {FBM} and {PM. CBM.} cluster even when similarity might suggest association within the two. Looking at {PM. CBM.} and {PM. CBM. PdM.}, the results imply no association between the two. However, interpreting results in the Table 2, coordinates of C1{PM. CBM.};coord = 1.092 and C3{PM. CBM.};coord = -0.343 are closely associated with C1{PM. CBM. PdM.};coord = 0.945 and C3{PM. CBM. PdM.};coord = -0.760.
Observing column profiles, the results show that {Hoses. Pipes. Pumps.} λHPP = 0.236; followed by {Hoses. Pipes. Sensors.} λHPS = 0.211; and {Pressure. Flow. Contr.-Reg.} valves λPFCR = 0.181 account for most of the explained inertia. However, {Hoses. Pipes. Actuators.} suggest higher quality QualHPA = 0.851 > QualPFCR = 0.686.
Looking at the left side of the C1 (Figure 3), we can assume poor effectiveness based on frequency and variety of failures, while on the right side of the C1-axis (positive), there is an increase in sensor failures. This is a valuable insight for detecting association with MPs and a better interpretation of the biplot.
Although CA (Figure 4) provides different ways to interpret the association between categories, the post hoc analysis can be misleading if one neglects the quality of visualisations. Looking at the row profile (Table 3) and column profile (Table 4) tables, we see that only 8/20 components show quality of representation > 0.70. Therefore, at least 80.8% of inertia must be preserved, consequently the fourth component is added.
The results (Figure 5) show that the first cluster (blue) consisting of {CBM} and {PM. DM.} report variety of failures, alongside the second (red) where {FBM} and {PM. CBM.} report reduced variety of failures. The third cluster (green) implies higher association among MPs. The fourth cluster (yellow) shows the smallest distance between {PM. CBM. PdM.} and failures {Hoses. Pipes. Pumps.}, suggesting the higher performance within applications. Finally, the last cluster (purple) shows small distances between {OM} and ({Hoses. Pipes. Sensors.} and {Hoses. Pipes. Actuators}).

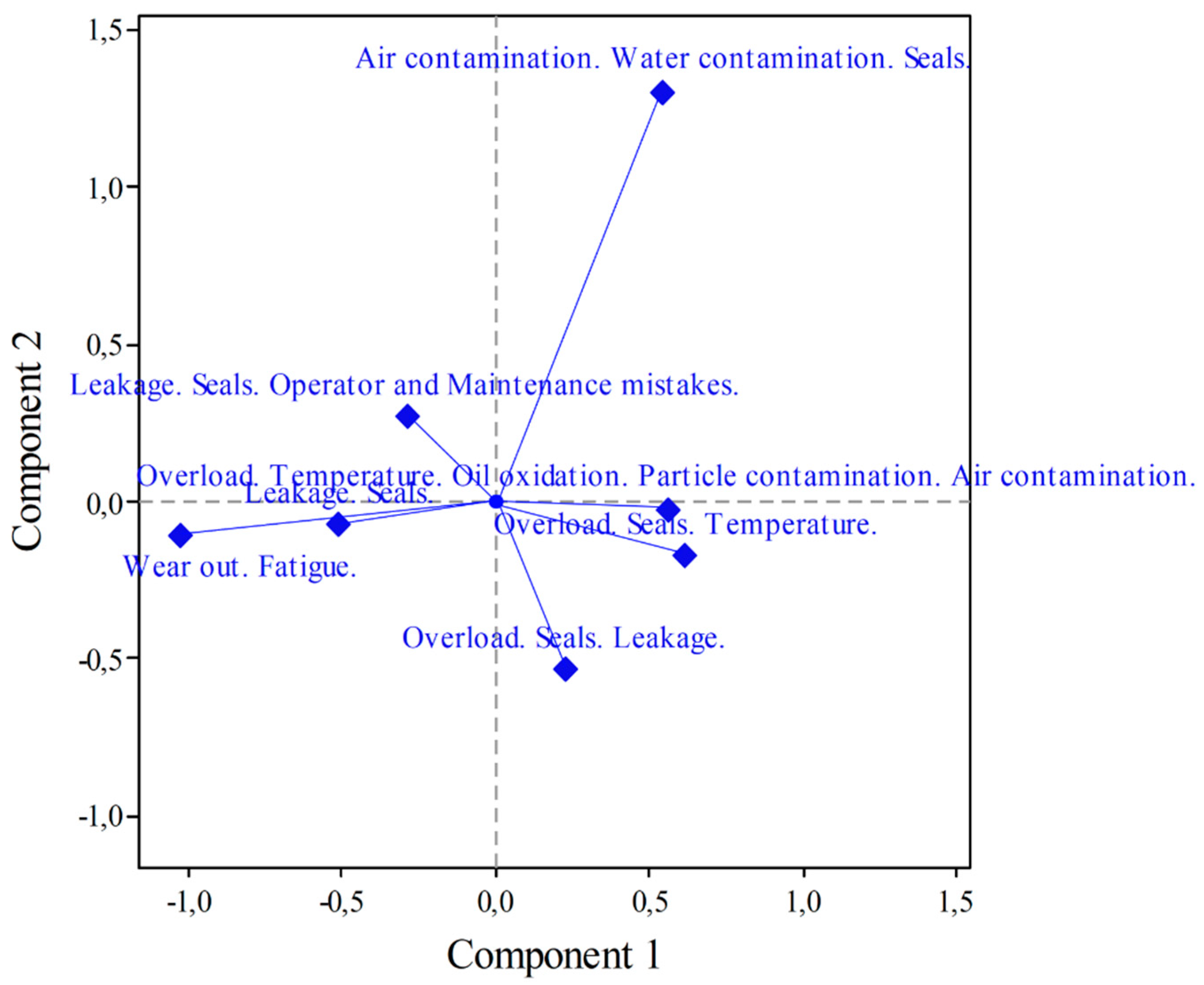
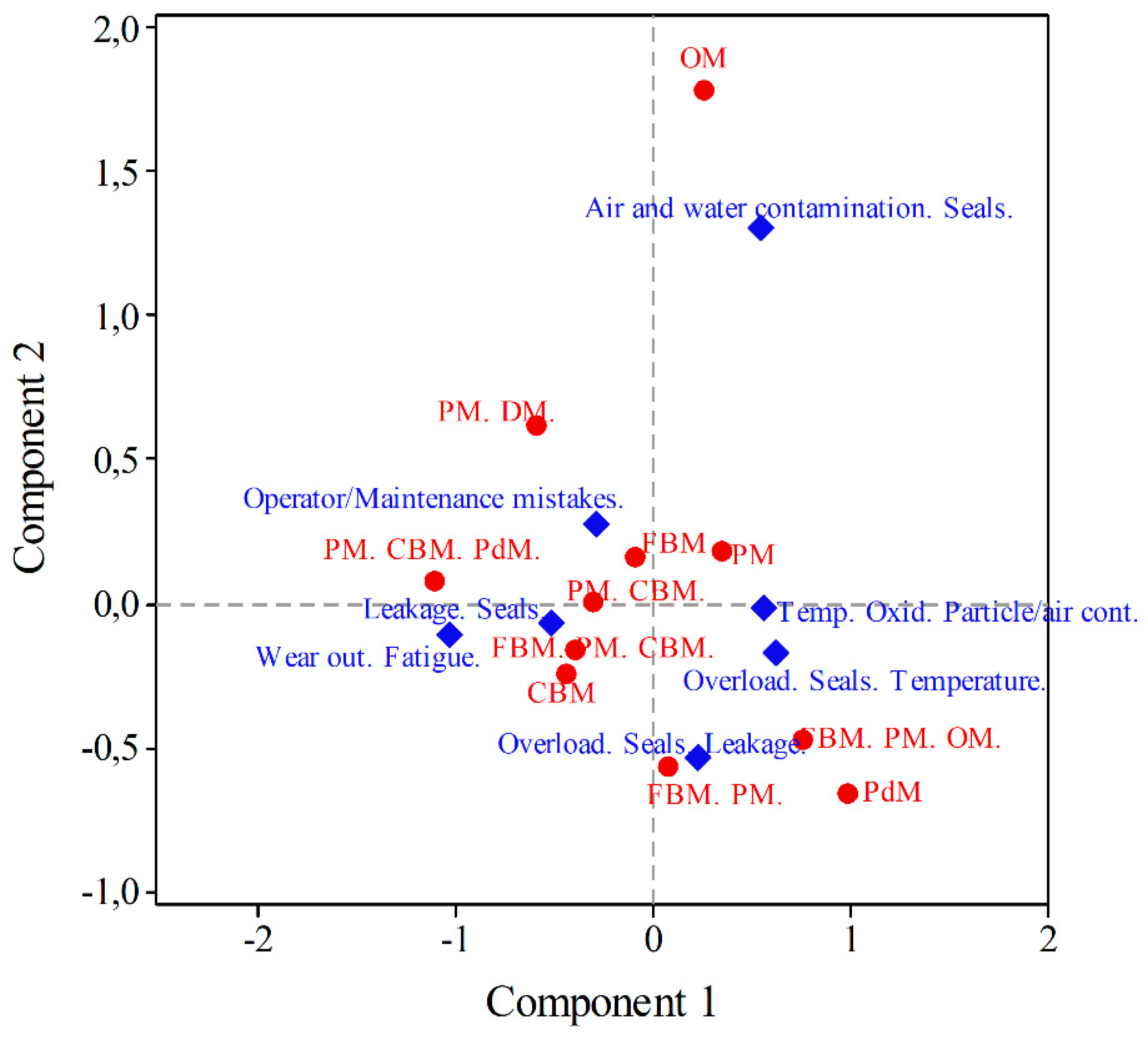
3.3. Relationship between MP and CFT using CA-AHC

Considering the RCF variable, the category of {Leakage. Seals. Operator and Maintenance mistakes.} is the most dominant. The frequency of reported root causes, the highest frequency fij association is among {PdM} and OST {Overload. Seals. Temperature.} (fPdM.OST =.667). Aside from failures associated with leakage and seals, operator/maintenance personnel mistakes are dominant in {PM. DM.} and {OM}.
The results show a statistically significant value (Table 5) of χ2 = 85.769 (p = 0.016), which suggests existance of the relationship between categories. Comparing to the previous case, the total inertia of Φ2 = 0.746 with components C1-3 (75.7%) suggests better interpretability than MP and CFT (69.3%).
Observing the row profiles’ inertia (Table 6), selected components (dimensions) show that {OM} provides the highest percentage of variation λOM = 0.127 (17%), followed by {PM. CBM. PdM.} λPM.CBM.PdM = 0.116 (15.6%), and {FBM. PM.} λFBM.PM = 0.095 (12.7%). Looking at the Qual of interpretation, we can see that for the suggested categories of row profiles, the selected components contribute highly (Qual > 0.80) to the inertia.
Looking at the inertia by individual components (Figure 6), {OM} seems not to be associated with previous points. Although {PM. CBM. PdM.} and {PdM} closely associate in the previous analysis; the points here repel on C1. The biplot (Figure 6) provides significant insights without the explicit use of data.
The data (Table 7) suggests that within dimensions (C1-3) {AWCS} has the highest inertia λAWCS = 0.149, followed by {OST} λAWCS = 0.136 and {LS} λAWCS = 0.120. The Qual metric suggests that AWCS {Air contamination. Water contamination. Seals.} contains enough information for visualisation (QualAWCS = 0.950).
The graph (Figure 7) shows that C1 (positive side) suggests that failures are associated with contamination, while the left side of C1 (negative) associate with failures of operator/maintenance mistakes. Results from the biplot (Figure 8) suggests high association between {OM} and {Air/Water contamination. Seals.}. The positive side of C1-C2 components suggest association among practices that report failures due to contamination, whilst centre and negative side report variety of failures.
Considering of 75.7% of inertia, representation shows Qual > 0.70 holds 12/18 categories while the extension on the fourth component all except {PM. DM.} have Qual > 0.70. Thus, interpretation only on three components (75.7% inertia) was enough. The first cluster (blue) on dendrogram (Figure 9) has the largest association among MPs and failures associated with {Leakage. Seals. Operator and Maintenance Mistakes}, especially {FBM}. The second cluster (green) shows the smallest distance between {FBM. PM. CBM.} and {Leakage. Seals.}. The third (red) cluster shows similarity between {FBM. PM.} and {Overload. Seals. Leakage.}. The forth (purple) cluster shows similarity across different applied MPs and failures regarding overload and temperature. Finally, the last cluster (yellow) shows similarity {OM} and {Air contamination. Water contamination. Seals.}.

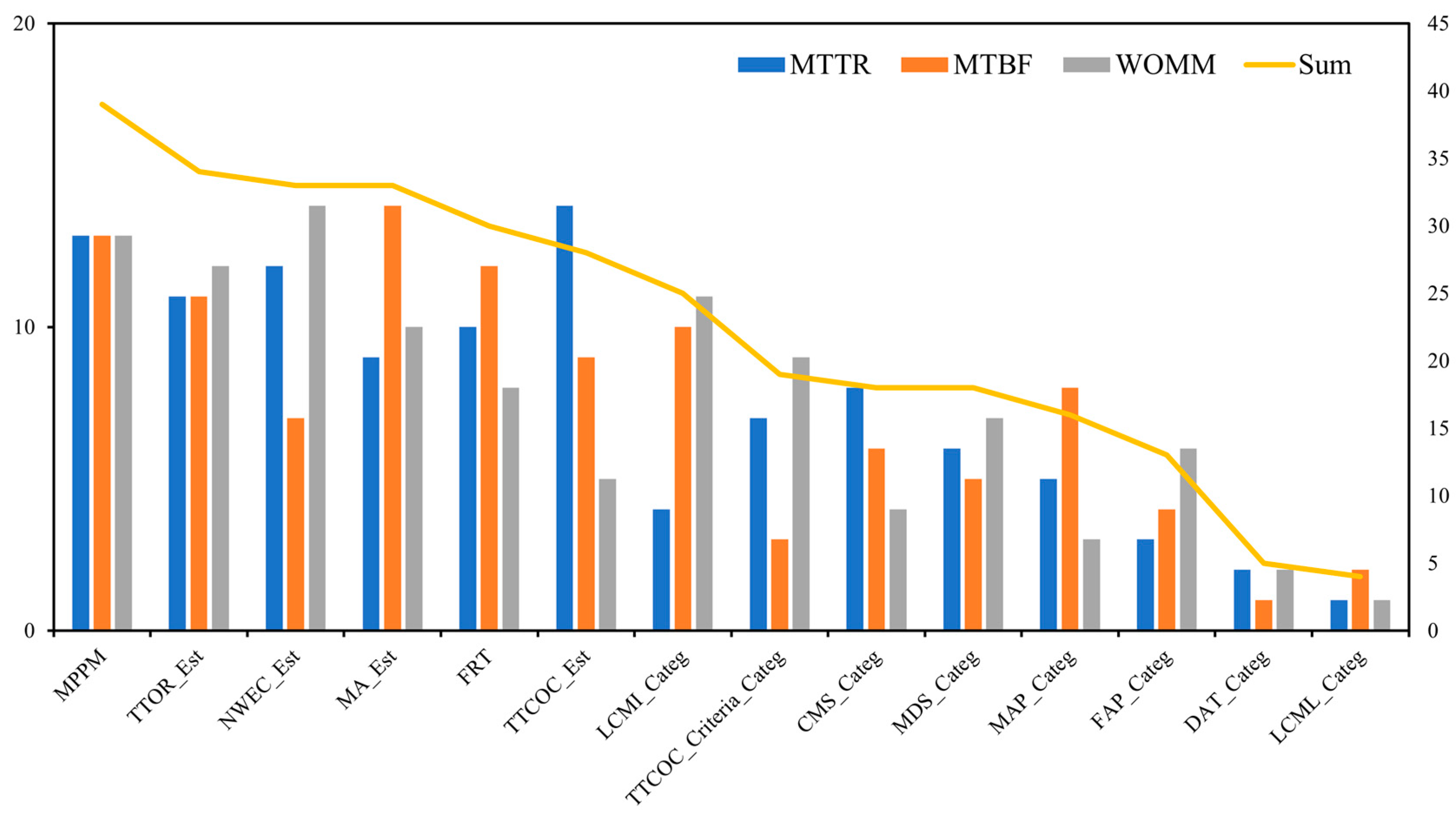
3.4. Clusters and performance metrics

The obtained clusters (MP-CFT and MP-RCF) are benchmarked against performance metrics, including both technical (i.e., MTTR, MTBF) and sustainable (e.g., WOMM). Although there is no significant variation among MTTR considering clusters, the MTBF metric show difference amongst metrics. Namely, in both cases clusters 2, 3, and 4, outperform other clusters, where the second cluster shows the best performance considering mean value of MTBF. Considering WOMM metric, the result suggests that 2nd, 3rd and 4th cluster show lower average WOMM. Note: The cluster 0* (n = 21) considers respondents that were not clustered and were left out of the analysis.
Table 8. MP-CFT clusters and performance metrics.
Table 8. MP-CFT clusters and performance metrics.
Metric MTTR MTBF WOMM
Cluster 0* 1 2 3 4 5 0* 1 2 3 4 5 0* 1 2 3 4 5
Med 5 3 5.1 5 5 4 950 550 1950 1500 1650 945.5 26.3 40.7 22.7 23.4 9.6 30.3
Mean 5.1 4.1 5.3 5.2 4.7 4 1196 907.1 1558 1495 1616 1010.2 39.8 39.8 41.2 27.9 30.1 30.3
Stdev 2.3 2.7 1.5 3.1 1.8 1.1 706.6 673.6 1157.7 735.5 728.8 655.5 45.6 19.1 50.2 26.1 26.7 1.1
Min 1 2 3 2 2 3 200 350 150 100 250 450 2.22 16.1 2.5 1.25 7.2 29.4
Max 12 10 7.5 15 8 5 2650 2500 2950 3500 2500 1700 250 71.43 136.3 142.9 62.5 31.2
Table 9. MP-RCF clusters and performance metrics.
Table 9. MP-RCF clusters and performance metrics.
Metric MTTR MTBF WOMM
Cluster 0* 1 2 3 4 5 0* 1 2 3 4 5 0* 1 2 3 4 5
Med 5 5 3 5.5 4 3 1250 950 1995.5 950 1575 1570.5 26 36.5 19.4 11.9 31.3 29.4
Mean 5 5.1 3.5 6.9 4.7 3 1290.8 1087.5 2023.5 1341.7 1418.7 1570.5 36.1 41.3 19.2 29.5 27.6 29.4
Stdev 2.8 2 1.3 3.3 2.6 0 710.5 805.6 1096.3 651.5 745.4 183.1 40.3 28.9 5.9 39.3 19.5 0
Min 1 2 2 3.5 1 3 150 150 850 950 100 1441 2.2 2.5 12.2 7.1 1.3 29.4
Max 15 10 5.3 12 12 3 2950 2500 3500 2500 2750 1700 250 129.4 26.8 108.3 71.4 29.4

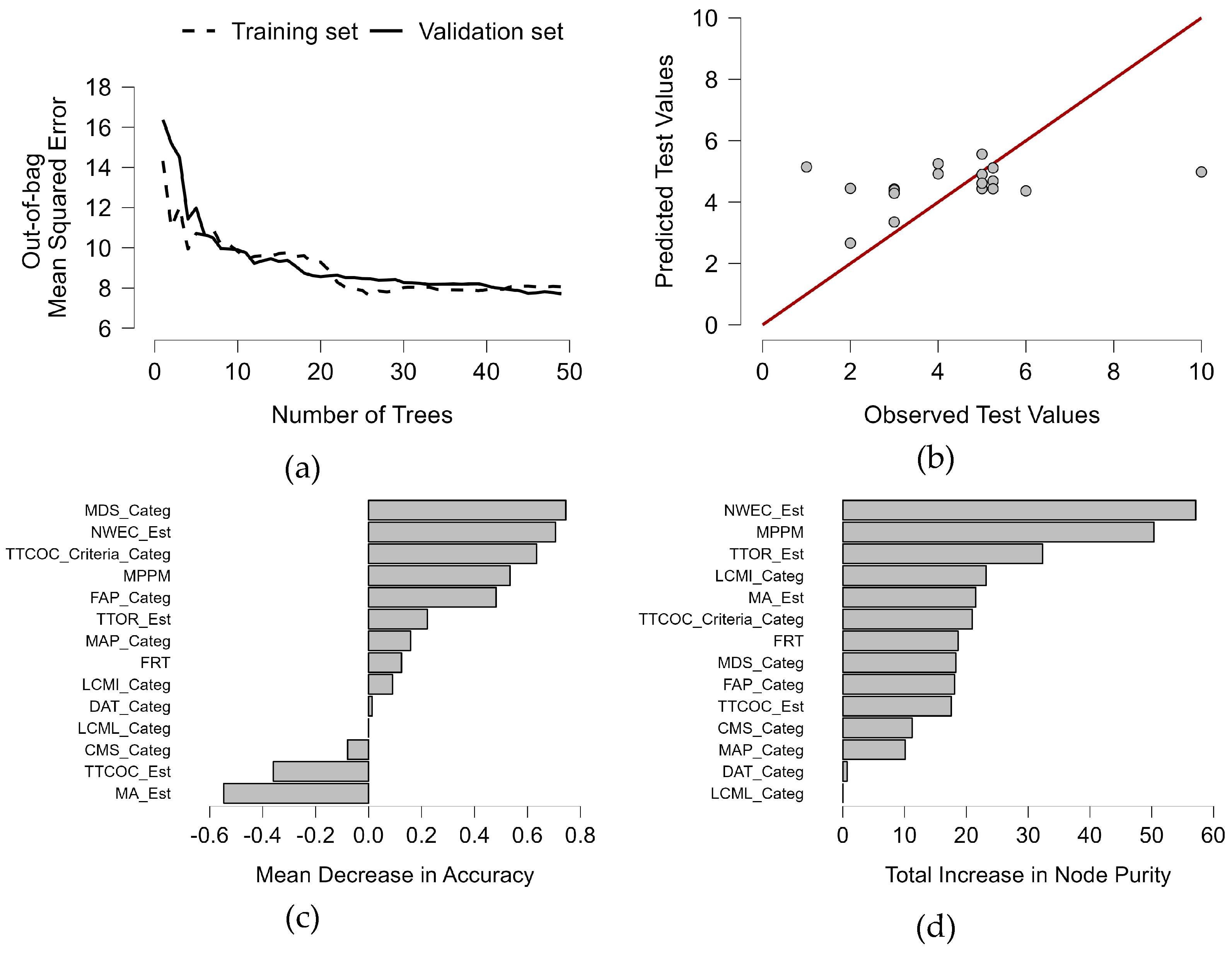
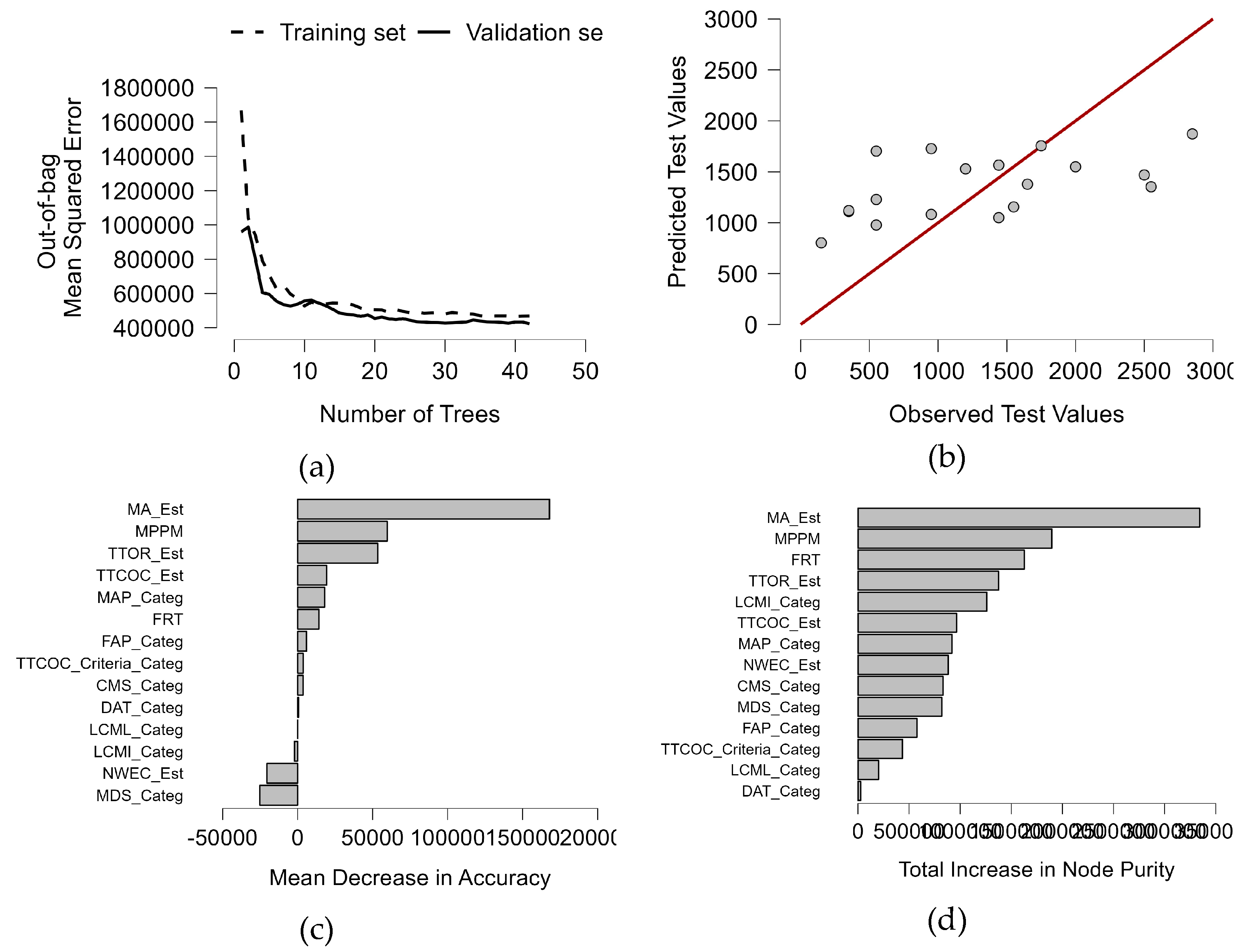
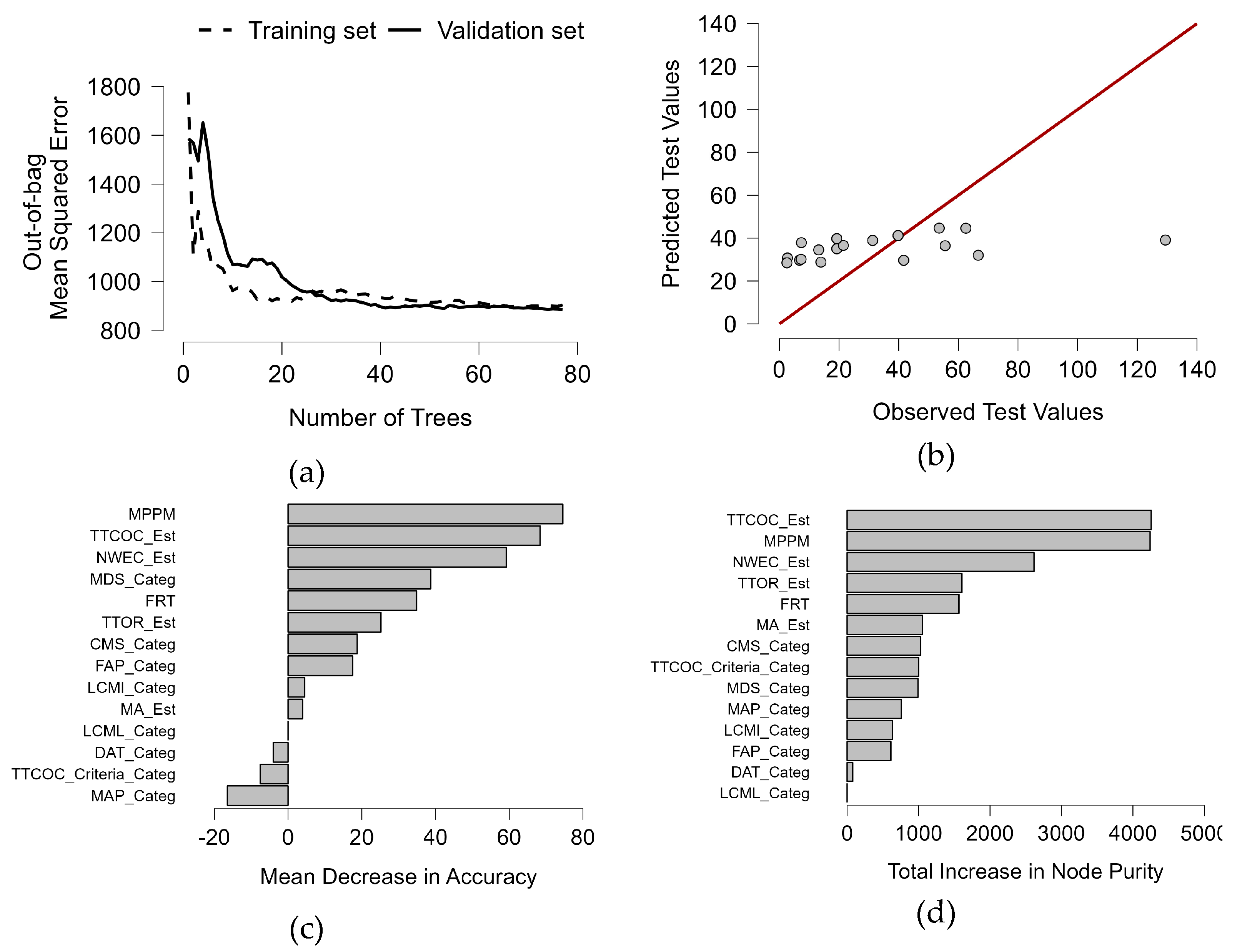
3.5. Machine learning feature importance

For the selection of machine learning algorithms, we check normality of data using Shapiro-Wilk test. The test shows that normality assumption is violated, thus we used non-parametric ML algorithms that consists of: RF (Random Forest), SVM (Support Vector Machine), kNN (k-Neirest Neighboor) and DT (Decision Tree). Also, the decision for selecting these non-parametric regression algorithms is that they can be used with continuous and categorical predictors. Finally, from obtained results we use feature importance for allocating most important predictors.
Table 10. Performance results of MTTR.
Table 10. Performance results of MTTR.
ML RF SVM kNN DT
MSE 3.412 1.009 4.846 877137.904
RMSE 1.847 1.004 2.201 936.556
MAE/MAD 1.314 0.627 1.694 767.94
R2 0.125 0.002 0.033 0.009
Table 11. Performance results of MTBF.
Table 11. Performance results of MTBF.
ML RF SVM kNN DT
MSE 463982.999 833283.033 648621.198 877137.904
RMSE 681.163 912.843 805.37 936.556
MAE/MAD 584.637 712.324 633.333 767.94
R2 0.304 0.059 0.156 0.058
Table 12. Performance results of WOMM.
Table 12. Performance results of WOMM.
ML RF SVM kNN DT
MSE 853.157 991.228 1560.16 979.015
RMSE 29.209 31.484 39.499 31.289
MAE/MAD 22.789 23.051 27.713 20.396
R2 0.222 0.03 0.02 0.056
Based on the obtained results considering performance indicators, in all cases RF outperforms other ML models. Hence, we use feature importance of RF algorithm to investigate the most relevant features impacting the regression. The results from out-of-bag MSE shows that within each observation MSE does not change significantly (Figure 10), as with all cases, approximately up to 10 trees was enough to reduce the descrepancy between training and testing. However, there exist a significant error in all cases due to low prediction accuracy of such complex data. The regression plot (Figure 10) shows significant variation in validation (predicted vs observed values). Conducting feature perturbations to measure mean descrease in accuracy, i.e., increase of MSE, shows that MDS (Maintenance Department Staff), NWEC (Nominal Working Energy Consumption), TTCOC (Time To Complete Oil Change), MPPM, and FAP are most important maintenance features (Figure 10). On the other side, looking at increase in node purity (Figure 10) it shows that NWEC, MPPM, and TTOR (Time To Oil Refilling) mostly contribute to the homogeneity of the output, i.e., reduction of variance. In addition, negative features such as CMS (Condition Monitoring Sensors), TTCOC, and MA, suggests noise and/or overfitting, which questions their suitability for modeling since they do not seem to positively contribute to the prediction.
Considering the MTBF (Figure 11) metric, evidence suggest that highest impact on MTBF is the machine age. This is also supported with empirical evidence [19], as equipment age significantly contributes to the reduction of MTBF. Also, MPPM, TTOR, TTCOC, MAP (Maintenance Analysis Program) and FRT (Filter Replacement Time) are the most important indicators of MTBF. This suggests that hydraulic fluid condition significantly affects the MTBF of hydraulic machinery. Observing the sustainability metric of WOMM, it shows that MPPM, TTCOC, NWEC, MDS, and FRT are the most impactful factors when it comes to fluid waste (Figure 12), considering both reduction in MSE and decrease in variance. For the sake of understanding, we use ranking of feature importance to establish most important features (Figure 13). From the ranking, it can be seen that number of maintenance personnel per machine plays an important role in hydraulic system’s maintenance, followed by time to oil refilling, the equipment size measured by nominal working energy consumption, machinery age, filter replacement time, etc. Surprisingly, although only 9.6% of companies apply data analysis tools in hydraulic machine maintenance, only slight improvement is noticable considering the output metrics. This also stands for laboratorial analysis of hydraulic oil, which shows that there is no significant impact on improving the output metrics.

4. Discussion

4.1. Research results from the analysis of MP and CFT

The results show a high association between investigated variables of MP and CFT, χ2 = 165.021, with a p-value < 0.001. Looking at the categories of MP, the {PM} is reported as the most applied MP, while CFT suggest that {Hoses. Pipes. Actuators. Pumps. Servo/Proportional valves.} is the most report category of component failures.
The results obtained show that the first cluster {CBM} and {Pipes. Actuators. Pumps. DV (Servo/Proportional) valves.} with {Hoses. Pipes. Pumps. ICE/EM.}, suggests poor performance of MPs. Namely, filtering {CBM} by using different items it turns out that companies reporting using strictly {CBM} had the lowest MTBFCBM = 835h, and in that sense had the worst performance considering this metric. The results show that maintenance activities behind {CBM} mostly consider visual inspection (56%) while up to 75% of the cases using condition monitoring instruments like PFT (Pressure/Flow/Temperature) are not used for maintenance decision-making. Considering data analysis, the results show that only 7% of {CBM} respondents report using data analysis tools. This also poses a question whether maintenance practitioners trully apply CBM and at what level. The second (red) and third (green) cluster show mixed MPs and variety of failures reported, although with less severity and variation unlike the first one. The fourth (yellow) and fifth (purple) cluster show presumably better performance in terms of reducing severity of failures of main components.
Taking a practical standpoint regarding the association between MPs and CFT using CA-AHC analysis, the results suggests advanced maintenance practices, such as CBM and PdM, seem to report a smaller variety of failures while at the same time an increased frequency of sensor failures. This can be attributed to the fact that some serious failures can be avoided with the use of sophisticated monitoring technology and instruments. On the other hand, applying traditional practices – FBM and PM – stoppages are mostly associated with failures associated with actuators and power units. This can suggest poor maintenance skills and lack competences for preventing this types of failures. The absence of such abilities leads to severe type of failures and productivity drop.

4.2. Results from the analysis of MP and RCF

The results show an existence of relationship between the MP and RCF, χ2 = 85.769 (p < 0.05). As {PM} is reported as the most applied practice, {Leakage. Seals. Operator and Maintenance personnel mistakes.} is the most reported category of RCF, while leakage and seals are most reported root causes of failure across categories.
From the CA-AHC analysis the obtained clusters suggest the following. The first (blue) cluster (Figure 9) show similarity mostly between {CBM}; {PM. CBM.}; {FBM} and failures associated with {Leakage. Seals. Operator and Maintenance mistakes.} on one side, while at the higher distance among categories at the same cluster {PM. CBM. PdM.} and {PM. DM.} show association with {Wear out. Fatigue.} of hydraulic components. Comparing with other items from the survey considering quantitative data, the {Wear out. Fatigue.} indeed report highest MTBF{Wear out. Fatigue} = 2080 h.
Looking at qualitative items, 60% of cases show the utilisation of Pressure/Flow/Temperature/Contamination sensors, suggesting that failures were avoided using an effective maintenance program. The second (green) cluster reports failures mainly {Leakage. Seals.} and similarity with {FBM. PM. CBM.}. Looking at the analysis of MP and CFT, this type of practice shows small distance to {Hoses. Pipes. Pumps. Sensors}, suggesting CM practice, however, the leakage/seals was unable to be prevented. The third (red) and fourth (purple) clusters show similarity to failures associated with overload, unlike previous cases. This also justifies failures associated with the temperature since overload leads to dissipation and transformation of power into heat. Finally, the last (yellow) cluster shows similarity between {OM} and {Air/Water contamination. Seals.} suggesting that these failures are associated with constant inspections and activities (e.g., filter replacements, oil refilling). Indeed, looking at quantitive data, MTTR{AirWater cont.} = 6.13h, which is second to highest (operator/maintenance mistakes being the top) suggests long time to repair leaves the system exposed to the environment. The time to complete oil change shows 3995h on average, when usual practice and equipment manufacturers suggest approx. 2000h. Also, looking at the activity of TTOR, which is usual maintenance activity applied to “refresh” the oil properties, is 191.7h. Such practice of trying to compensate the loss of fluid properties (e.g., viscosity), consequently system response, by constantly adding the fluid into the system is associated with oxidation and particle/air contamination.
Taking altogether, we derive several remarks. Firstly, component failures and root causes of failures in hydraulic system can be clustered into three categories: (1) Random events – typically include failures of components such as pipes and hoses. This can also be said for failures associated with leakage and seals, since over 90% of companies report these failures. (2) Non-random events – usually include degradational events under advanced maintenance practices. For instance, pumps and actuators’ failures for which the usage of indicators of pressure, flow and temperature can explain or indicate degradational behavior. Looking at RCF, non-random effects include failures associated with contamination in which instruments (e.g., particle counters) can be implemented to monitor and reduce the severity of wear. (3) Human-related events – the obtained evidence suggest lack of industrial maintenance personnel, especially considering advanced data analytics and specialist in the domain of hydraulic system maintenance.

4.3. Feature importance considering performance metrics

Generated CA-AHC feature subspace of devised categories are used with RF to extract relevant predictors, i.e., features considering performance metrics. From the asset and machine perspective equipment size (i.e., NWEC) and machine age are the most important predictors. Introducing the variable of NWEC for measuring the maintenance performance prooved to be significant and not available in the literature, by authors knowledge. From maintenance perspective, number of maintenance personnel per machine, i.e., MPPM has the highest impact on prediction properties of the RF regression, overall. This is also an important remark, since by authors knowledge no empirical evidence exists in the literature.
Also, considering maintenance activities TTOR, FRT, TTCOC, TTCOC criteria, are the most important features. Hence, considering statements that fluid contamination is one of the common causes of failure, the constant refilling of hydraulic oil and complete oil change in the system, pressumably by overhaul, does in fact reduce the probability of failure, increasing MTBF and at the same time reducing MTTR of hydraulic machinery. From a technological perspective, LCMI (Lubricant Condition Monitoring Instruments) is the most important feature overall; however, it is questionable the impact on MTTR, unlike MTBF and WOMM where it has significant impact. Also, the CMS and LCML (Lubricant Condition Monitoring Laboratory) analysis show poor or negative prediction properties considering performance metrics.
Finally, the features that show negative or poor contribution to the regression model suggest that existing maintenance of hydraulic systems show low technological and digital readiness level. Namely, the fact that 45.2% of MDS consists only of operators and technicians’ questions whether companies perceive maintenance as a “strategic move” or still as a “neccesary evil”. Rhetorically, companies utilising advanced PdM solutions face difficulties in managing assets, and report high amount of failures. This prooved to be a business opportunity for companies and maintenance experts in engaging and providing outsourced maintenance services with in-door solutions, which is why many engage with MaaS (Maintenance as a Service) concepts [31]. Also, the results show that 13.1% of companies outsource their maintenance activities, while 50.4% of rely on external experts or companies to perform failure analysis of their equipment. Moreover, confounding statistics regarding application of data analysis show that only 9.6% companies apply some statistical or data analysis tools in hydraulic machine maintenance, which is why no actual contribution to the prediction properties was observed.

5. Conclusions

The study presents an extensive and in-depth study of features affecting the maintenance performance of companies utilising hydraulic machines. The study uses empirical evidence and data synthesised from questionnaire-based survey disseminated on the territory of West-Balkan countries. Since extensive amount of data is gathered, the study uses correspondance analysis in combination with agglomerative hierarchical clustering for generating feature subspace, afterwhich components are used to allocate predictors impacting maintenance performance metrics, such as MTBF, MTTR and WOMM. Obtained evidence show that maintenance personnel, machine age, equipment size measured by nominal working energy consumption level, filter replacement time and time to complete oil change are the highest ranked predictors, which was established by using random forest algorithm.
Although obtained evidence show significant contributions to the body of knowledge regarding hydraulic system maintenance, there are limitations of the study. Namely, obtained results include variety of companies under different NACE classifications, thus environmental conditions and working regimes can differ. Next, obtained results performed via non-parametric ML algorithms due to violation of normality needed to be further verified with a larger sample size. Also, further analysis needs to be conducted to verify and validate the impact of features on operational performance.
In the future, we plan to to conduct study regarding the impact of maintenance features on maintenance performance metrics, considering both categorical and numerical data. Specifically, we will include measuring the impact of outsourced versus in-door maintenance and the impact of data analysis tools in hydraulic machine maintenance. The underlying reason is that there is an obvious barriers in transitioning between preventive and predictive maintenance, which also supported by evidence showing lack of success with implemented advanced maintenance practices in this domain.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1: title; Table S1: title; Video S1: title.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, M.O. and D.Š.; methodology, M.O. and D.Š.; formal analysis, M.O.; investigation, M.O. and D.Š; data curation, M.O. and D.Š.; writing—original draft preparation, M.O. and D.Š.; writing—review and editing, M.O. and D.Š.; visualization, M.O.; supervision, D.Š. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data is available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Orošnjak, M.; Jocanović, M.; Čavić, M.; Karanović, V.; Penčić, M. Industrial Maintenance 4(.0) Horizon Europe: Consequences of the Iron Curtain and Energy-Based Maintenance. J Clean Prod 2021, 314, 128034. [Google Scholar] [CrossRef]
  2. Simões, J.M.; Gomes, C.F.; Yasin, M.M. A Literature Review of Maintenance Performance Measurement: A Conceptual Framework and Directions for Future Research. J Qual Maint Eng 2011, 17, 116–137. [Google Scholar] [CrossRef]
  3. Van Horenbeek, A.; Pintelon, L. Development of a Maintenance Performance Measurement Framework-Using the Analytic Network Process (ANP) for Maintenance Performance Indicator Selection. Omega (United Kingdom) 2014, 42, 33–46. [Google Scholar] [CrossRef]
  4. Orošnjak, M.; Brkljač, N.; Šević, D.; Čavić, M.; Oros, D.; Penčić, M. From Predictive to Energy-Based Maintenance Paradigm: Achieving Cleaner Production through Functional-Productiveness. J Clean Prod 2023, 408, 137177. [Google Scholar] [CrossRef]
  5. Ding, S.H.; Kamaruddin, S.; Azid, I.A. Maintenance Policy Selection Model - A Case Study in the Palm Oil Industry. Journal of Manufacturing Technology Management 2014, 25, 415–435. [Google Scholar] [CrossRef]
  6. Muchiri, P.N.; Pintelon, L.; Martin, H.; De Meyer, A.-M. Empirical Analysis of Maintenance Performance Measurement in Belgian Industries. Int J Prod Res 2010, 48, 5905–5924. [Google Scholar] [CrossRef]
  7. Piechnicki, F.; Dos Santos, C.F.; De Freitas Rocha Loures, E.; Dos Santos, E.A.P. Data Fusion Framework for Decision-Making Support in Reliability-Centered Maintenance. Journal of Industrial and Production Engineering 2021, 38, 1–17. [Google Scholar] [CrossRef]
  8. Wang, J.; Wang, Y.; Fu, Y. Joint Optimization of Condition-Based Maintenance and Performance Control for Linear Multi-State Consecutively Connected Systems. Mathematics 2023, 11, 2724. [Google Scholar] [CrossRef]
  9. Chui, M.; Henke, N.; Miremadi, M. Most of AI’s Business Uses Will Be in Two Areas. Available online: https://hbr.org/2018/07/most-of-ais-business-uses-will-be-in-two-areas (accessed on 8 February 2023).
  10. Orosnjak, M. Maintenance Practice Performance Assessment of Hydraulic Machinery: West Balkan Meta-Statistics and Energy-Based Maintenance Paradigm. In Proceedings of the 2021 5th International Conference on System Reliability and Safety (ICSRS); IEEE, November 24 2021; pp. 108–114. [Google Scholar]
  11. Cachada, A.; Moreira, P.M.; Romero, L.; Barbosa, J.; Leitno, P.; Gcraldcs, C.A.S.; Deusdado, L.; Costa, J.; Teixeira, C.; Teixeira, J.; et al. Maintenance 4.0: Intelligent and Predictive Maintenance System Architecture. In In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA); IEEE, September 2018; pp. 139–146. [Google Scholar]
  12. Nunes, P.; Santos, J.; Rocha, E. Challenges in Predictive Maintenance – A Review. CIRP J Manuf Sci Technol 2023, 40, 53–67. [Google Scholar] [CrossRef]
  13. Parida, A.; Kumar, U. Maintenance Performance Measurement (MPM): Issues and Challenges. J Qual Maint Eng 2006, 12, 239–251. [Google Scholar] [CrossRef]
  14. Dui, H.; Zhang, Y.; Zhang, Y.-A. Grouping Maintenance Policy for Improving Reliability of Wind Turbine Systems Considering Variable Cost. Mathematics 2023, 11, 1954. [Google Scholar] [CrossRef]
  15. Parida, A.; Chattopadhyay, G. Development of a Multi-Criteria Hierarchical Framework for Maintenance Performance Measurement (MPM). J Qual Maint Eng 2007, 13, 241–258. [Google Scholar] [CrossRef]
  16. Roosefert Mohan, T.; Preetha Roselyn, J.; Annie Uthra, R.; Devaraj, D.; Umachandran, K. Intelligent Machine Learning Based Total Productive Maintenance Approach for Achieving Zero Downtime in Industrial Machinery. Comput Ind Eng 2021, 157, 107267. [Google Scholar] [CrossRef]
  17. Dalzochio, J.; Kunst, R.; Pignaton, E.; Binotto, A.; Sanyal, S.; Favilla, J.; Barbosa, J. Machine Learning and Reasoning for Predictive Maintenance in Industry 4.0: Current Status and Challenges. Comput Ind 2020, 123. [Google Scholar] [CrossRef]
  18. He, Y.; Su, H.; Zio, E.; Peng, S.; Fan, L.; Yang, Z.; Yang, Z.; Zhang, J. A Systematic Method of Remaining Useful Life Estimation Based on Physics-Informed Graph Neural Networks with Multisensor Data. Reliab Eng Syst Saf 2023, 237. [Google Scholar] [CrossRef]
  19. Orošnjak, M.; Delić, M.; Ramos, S. Influence of Maintenance Practice on MTBF of Industrial and Mobile Hydraulic Failures: A West Balkan Study. In Proceedings of the International Conference on Machine and Industrial Design in Mechanical Engineering; Rackov, M., Mitrović, R., Čavić, M., Eds.; SpringerLink, 2022; pp. 617–625. [Google Scholar]
  20. Wang, S.; Xiang, J. A Minimum Entropy Deconvolution-Enhanced Convolutional Neural Networks for Fault Diagnosis of Axial Piston Pumps. Soft comput 2020, 24, 2983–2997. [Google Scholar] [CrossRef]
  21. Cheng, X.; Chaw, J.K.; Goh, K.M.; Ting, T.T.; Sahrani, S.; Ahmad, M.N.; Abdul Kadir, R.; Ang, M.C. Systematic Literature Review on Visual Analytics of Predictive Maintenance in the Manufacturing Industry. Sensors 2022, 22, 1–16. [Google Scholar] [CrossRef]
  22. Zhang, X.; Fujiwara, T.; Chandrasegaran, S.; Brundage, M.P.; Sexton, T.; Dima, A.; Ma, K.-L. A Visual Analytics Approach for the Diagnosis of Heterogeneous and Multidimensional Machine Maintenance Data. In Proceedings of the 2021 IEEE 14th Pacific Visualization Symposium (PacificVis); IEEE, April 2021; Vol. 2021-April; pp. 196–205. [Google Scholar]
  23. Navinchandran, M.; Sharp, M.E.; Brundage, M.P.; Sexton, T.B. Discovering Critical KPI Factors from Natural Language in Maintenance Work Orders. J Intell Manuf 2022, 33, 1859–1877. [Google Scholar] [CrossRef]
  24. Lu, Y.; Garcia, R.; Hansen, B.; Gleicher, M.; Maciejewski, R. The State-of-the-Art in Predictive Visual Analytics. Computer Graphics Forum 2017, 36, 539–562. [Google Scholar] [CrossRef]
  25. Husson, F.; Houee-Bigot, M. Correspondence Analysis Available online:. Available online: https://husson.github.io/MOOC_GB/CA_course_slides.pdf (accessed on 30 December 2022).
  26. Husson, F.; Lê, S.; Pagès, J. Computer Science and Data Analysis Series: Exploratory Multivariate Analysis by Example Using R; CRC Press. Taylor & Francis Group, 2017; ISBN 9781138196346. [Google Scholar]
  27. Le, S.; Josse, J.; Husson, F. FactoMineR: An R Package for Multivariate Analysis. Journal of Statistical Software2 2008, 25, 1–18. [Google Scholar]
  28. Nielsen, F. Hierarchical Clustering. In Introduction to HPC with MPI for Data Science; Undergraduate Topics in Computer Science; Springer International Publishing: Cham, 2016; pp. 223–239. ISBN 978-3-319-21902-8. [Google Scholar]
  29. Murtagh, F.; Contreras, P. Algorithms for Hierarchical Clustering: An Overview. Wiley Interdiscip Rev Data Min Knowl Discov 2012, 2, 86–97. [Google Scholar] [CrossRef]
  30. Murtagh, F.; Contreras, P. Methods of Hierarchical Clustering. 2011; 1–21. [Google Scholar]
  31. Mourtzis, D.; Zogopoulos, V.; Vlachou, E. Augmented Reality Application to Support Remote Maintenance as a Service in the Robotics Industry. Procedia CIRP 2017, 63, 46–51. [Google Scholar] [CrossRef]
Preprints 82189 g002
Figure 2. MP biplot of C1 and C2.
Figure 2. MP biplot of C1 and C2.
Preprints 82189 g002
Preprints 82189 g003
Figure 3. CFT biplot of C1 and C2.
Figure 3. CFT biplot of C1 and C2.
Preprints 82189 g003
Preprints 82189 g004
Figure 4. MP and CFT biplot.
Figure 4. MP and CFT biplot.
Preprints 82189 g004
Preprints 82189 g005
Figure 5. Dendrogram of MP and CFT.
Figure 5. Dendrogram of MP and CFT.
Preprints 82189 g005
Preprints 82189 g006
Figure 6. MP biplot of C1 and C2.
Figure 6. MP biplot of C1 and C2.
Preprints 82189 g006
Preprints 82189 g007
Figure 7. RCF biplot of C1 and C2.
Figure 7. RCF biplot of C1 and C2.
Preprints 82189 g007
Preprints 82189 g008
Figure 8. MP and RCF biplot.
Figure 8. MP and RCF biplot.
Preprints 82189 g008
Preprints 82189 g009
Figure 9. Dendrogram of MP and RCF.
Figure 9. Dendrogram of MP and RCF.
Preprints 82189 g009
Preprints 82189 g010
Figure 10. Results of clusters considering MTTR metric via (a) OOB-MSE error; (b) predicted versus observed test value; (c) mean decrease in accuracy; and (d) total increase in node purity of features.
Figure 10. Results of clusters considering MTTR metric via (a) OOB-MSE error; (b) predicted versus observed test value; (c) mean decrease in accuracy; and (d) total increase in node purity of features.
Preprints 82189 g010
Preprints 82189 g011
Figure 11. Results of clusters considering MTBF metric via (a) OOB-MSE error; (b) predicted versus observed test value; (c) mean decrease in accuracy; and (d) total increase in node purity of features.
Figure 11. Results of clusters considering MTBF metric via (a) OOB-MSE error; (b) predicted versus observed test value; (c) mean decrease in accuracy; and (d) total increase in node purity of features.
Preprints 82189 g011
Preprints 82189 g012
Figure 12. Results of clusters considering WOMM metric via (a) OOB-MSE error; (b) predicted versus observed values; (c) mean decrease in accuracy; and (d) total increase in node purity of features.
Figure 12. Results of clusters considering WOMM metric via (a) OOB-MSE error; (b) predicted versus observed values; (c) mean decrease in accuracy; and (d) total increase in node purity of features.
Preprints 82189 g012
Preprints 82189 g013
Figure 13. RF-Feature Importance scores summarised by rankings in respect to the performance metrics of MTTR, MTBF and WOMM.
Figure 13. RF-Feature Importance scores summarised by rankings in respect to the performance metrics of MTTR, MTBF and WOMM.
Preprints 82189 g013
Table 1. Descriptive statistics of survey results.
Table 1. Descriptive statistics of survey results.
Feature AFF1 CON1 MAN1 M&Q1
HMA 10.5 10.25 11.80 10.54
NoM 62.4 41.86 52.94 85.2
MPPM 0.55 0.37 1.09 0.62
1AFF=Agriculture, forestry, and fishing; CON=Construction; MAN=Manufacturing; M&Q=Mining and quarrying;
Table 2. The quality of interpretation of MP and CFT.
Table 2. The quality of interpretation of MP and CFT.
Dimension SV* Inertia Chi2 Sig. Proportion of Inertia Confidence SV
Accounted Cumulative St. dev Corr. C2 Corr. C3
C1 .673 .452 .315 .315 .051 .159 .417
C2 .526 .277 .193 .508 .083 .160
C3 .515 .265 .185 .693 .099
C4 .406 .165 .115 .808
C5 .355 .126 .088 .896
C6 .267 .071 .050 .946
C7 .187 .035 .024 .970
C8 .156 .024 .017 .987
C9 .130 .017 .012 .999
C10 .040 .002 .001 1.00
Total 1.435 165.021 .000 1.00 1.00
Table 3. Overview of row components of MP and CFT.
Table 3. Overview of row components of MP and CFT.
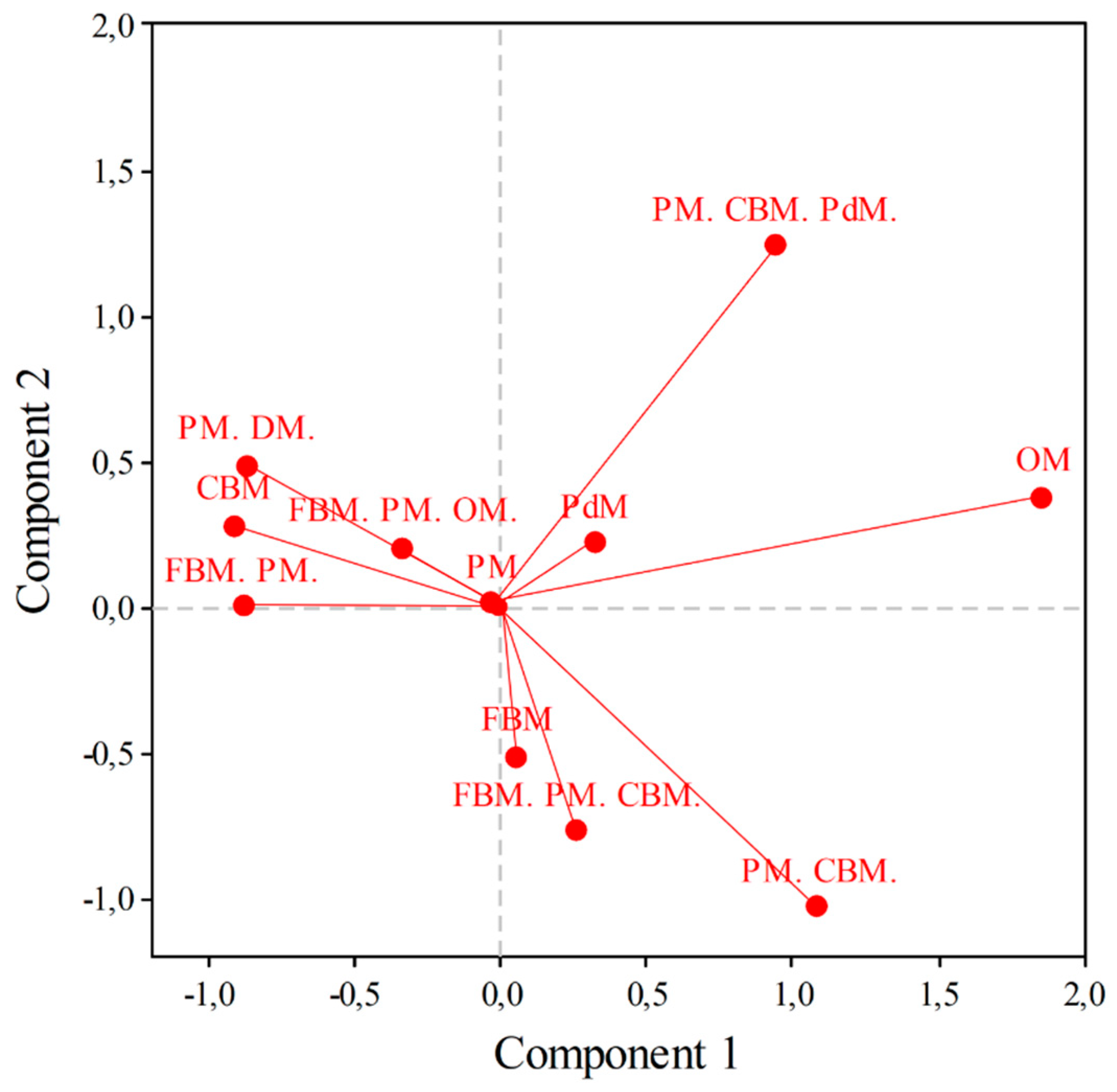
MP Mass Coordinates λ Correlation Contribution
C1 C2 C3 C1 C2 C3 C1 C2 C3 Qual
CBM .113 -.915 .288 .338 .160 .209 .034 .049 .591 .058 .081 .731
FBM .096 .055 -.508 -.021 .105 .001 .089 .000 .003 .234 .000 .238
FBM. PM. .104 -.885 .012 .143 .160 .181 .000 .008 .510 .000 .013 .523
FBM. PM. CBM. .096 .259 -.760 -.319 .114 .014 .200 .037 .056 .483 .085 .624
FBM. PM. OM. .061 -.339 .208 -.324 .044 .015 .009 .024 .158 .059 .145 .362
OM .035 1.861 .382 2.115 .290 .266 .018 .586 .415 .018 .536 .969
PdM .026 .321 .224 -.964 .050 .006 .005 .091 .054 .026 .488 .568
PM .330 -.031 .022 .075 .061 .001 .001 .007 .005 .003 .031 .038
PM. CBM. .052 1.092 -1.023 -.343 .175 .138 .197 .023 .356 .313 .035 .704
PM. CBM. PdM. .078 .945 1.246 -.760 .244 .155 .439 .170 .286 .497 .185 .968
PM. DM. .009 -.869 .489 .360 .031 .015 .008 .004 .210 .066 .036 .312
Total 1.00 1.435 1.00 1.00 1.00
Table 4. Overview of column components of MP and CFT.
Table 4. Overview of column components of MP and CFT.
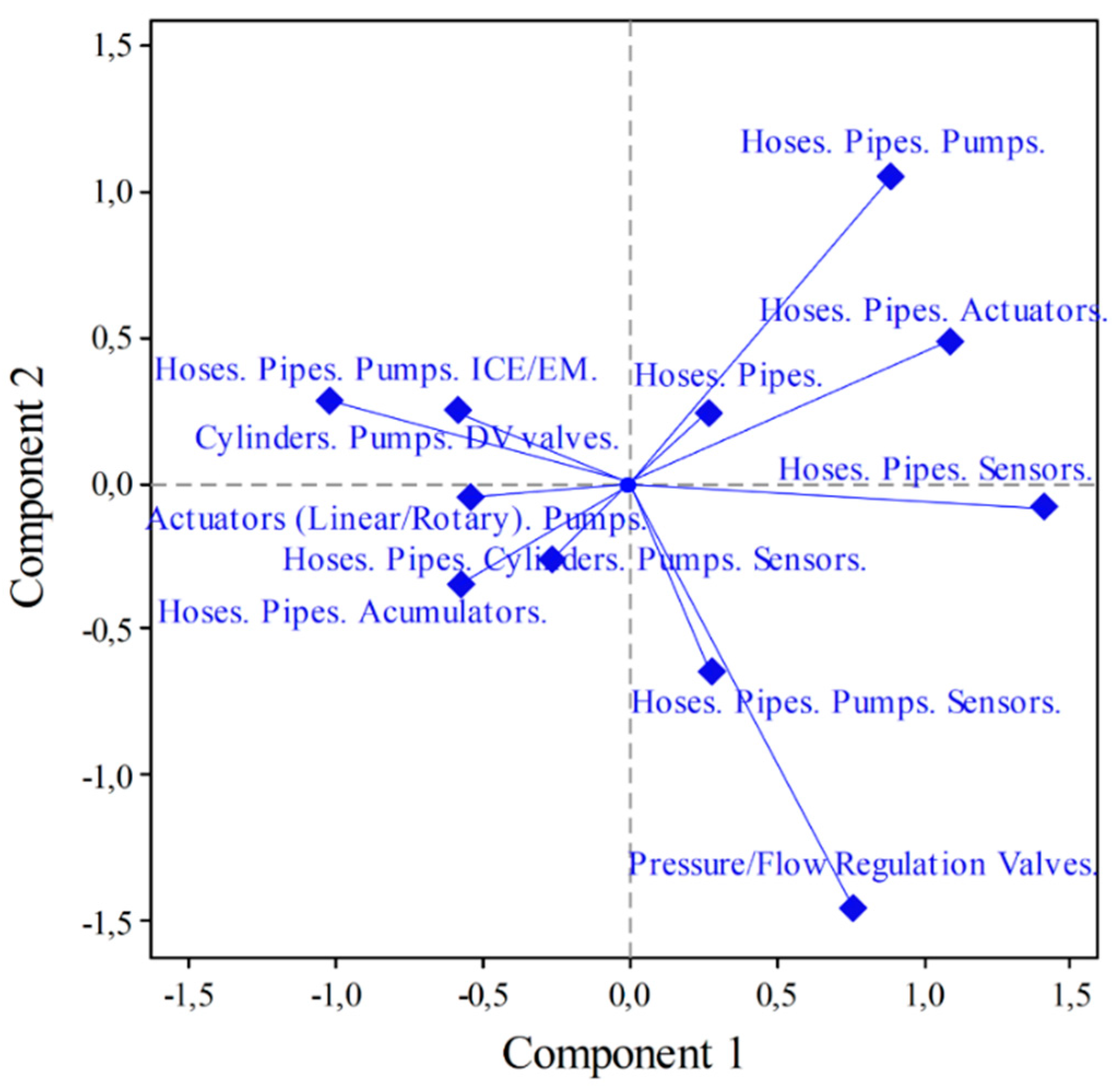
CFT Mass C1 C2 C3 λ Correlation Contribution
C1 C2 C3 C1 C2 C3 Qual
Hoses. Pipes. .096 .269 .239 -.236 .079 .015 .020 .020 .088 .069 .068 .225
Hoses. Pipes. Actuators. .070 1.090 .483 .611 .147 .183 .059 .098 .563 .111 .177 .851
Hoses. Pipes. Actuators. Pumps. .200 -.537 -.052 -.024 .104 .127 .002 .000 .556 .005 .001 .562
Hoses. Pipes. Accumulators. .035 -.573 -.340 .021 .078 .025 .015 .000 .147 .052 .000 .199
Hoses. Pipes. Act. Pumps. S-PV. .217 -.585 .257 .185 .130 .164 .052 .028 .569 .110 .057 .737
Hoses. Pipes. Act. Pumps. Sensors. .043 -.258 -.260 .174 .066 .006 .011 .005 .044 .045 .020 .109
Hoses. Pipes. Pumps. .070 .897 1.05 -1.12 .236 .124 .277 .326 .237 .324 .366 .927
Hoses. Pipes. Pumps. ICE/EM. .035 -1.02 .289 .435 .070 .080 .011 .025 .521 .042 .094 .657
Hoses. Pipes. Pumps. Sensors. .148 .289 -.645 -.350 .134 .027 .222 .068 .092 .458 .135 .684
Hoses. Pipes. Sensors. .043 1.414 -.081 1.57 .211 .192 .001 .402 .412 .001 .506 .920
Pressure/Flow Control-Reg. .043 .759 -1.45 -.406 .181 .055 .332 .027 .139 .508 .040 .686
Total 1.00 1.435 1.00 1.00 1.00
Table 5. The quality of interpretation of MP and RCF.
Table 5. The quality of interpretation of MP and RCF.
Component Inertia Chi2 Sig. Proportion of Inertia Confidence Singular Value
Accounted Cumulative C1 C2 C3
1 .245 .329 .329 .064 .044 -.450
2 .196 .262 .591 .090 .144
3 .124 .166 .757 .081
4 .113 .151 .909
5 .052 .070 .979
6 .016 .021 1.00
Total .746 85.769 0.016 1.00 1.00
Table 6. Row profiles inertia of MP and RCF.
Table 6. Row profiles inertia of MP and RCF.
MP Mass C1 C2 C3 λ Correlation Contribution
C1 C2 C3 C1 C2 C3 Qual
CBM .113 -.436 .245 .135 .065 .088 .035 .016 .329 .104 .031 .465
FBM .096 -.085 -.166 .309 .024 .003 .013 .074 .029 .111 .386 .525
FBM. PM. .104 .072 .570 .707 .095 .002 .173 .420 .006 .357 .549 .911
FBM. PM. CBM. .096 -.400 .157 -.60 .063 .062 .012 .275 .242 .037 .541 .820
FBM. PM. OM. .061 .760 .476 -.10 .067 .143 .071 .005 .526 .206 .010 .742
OM .035 .259 -1.78 .532 .127 .010 .566 .079 .018 .870 .077 .966
PdM .026 .985 .658 -.22 .045 .103 .058 .010 .558 .249 .027 .834
PM .330 .347 -.177 -.18 .075 .163 .053 .083 .532 .139 .137 .809
PM. CBM. .052 -.296 -.008 -.15 .040 .019 .000 .010 .114 .000 .030 .145
PM. CBM. PdM. .078 -1.11 -.077 -.08 .116 .395 .002 .005 .835 .004 .005 .844
PM. DM. .009 -.588 -.615 .569 .028 .012 .017 .023 .106 .116 .099 .321
Total 1.00 .746 1.00 1.00 1.00
Table 7. Column profiles inertia of MP and RCF.
Table 7. Column profiles inertia of MP and RCF.
MP Mass C1 C2 C3 Inertia Correlation for column Contribution
C1 C2 C3 C1 C2 C3 Qual
AWCS .070 .548 -1.306 .175 .149 .085 .607 .017 .140 .796 .014 .950
LS .226 -.509 .073 -.415 .120 .239 .006 .313 .489 .010 .324 .823
LSOMM .235 -.291 -.272 .200 .067 .081 .089 .076 .299 .261 .141 .701
OSL .183 .227 .533 .472 .115 .038 .265 .328 .082 .451 .354 .887
OST .209 .618 .170 -.351 .136 .325 .031 .207 .584 .044 .188 .817
OTOPAW .035 .562 .021 .126 .045 .045 .000 .004 .243 .000 .012 .256
WFF .043 -1.024 .110 .395 .114 .186 .003 .055 .401 .005 .060 .466
Total 1.00 .746 1.00 1.00 1.00
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated