Dual Neighborhoods Search for Solving The Minimum Dominating Tree Problem

Preprint

Article

Dual Neighborhoods Search for Solving The Minimum Dominating Tree Problem

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Ze Pan,

Xinyun Wu^*,Caiquan Xiong

Ze Pan,

Xinyun Wu^*,Caiquan Xiong

This version is not peer-reviewed

Submitted:

11 August 2023

Posted:

14 August 2023

You are already at the latest version

Alerts

Abstract

The minimum dominating tree (MDT) problem consists of finding a minimum weight sub-graph from an undirected graph, such that each vertex not in this sub-graph is adjacent to at least one of the vertices in it, and the sub-graph is connected without any ring structures. This paper presents a Dual Neighborhoods Search (DNS) algorithm for solving the MDT problem, which integrates several distinguishing features, such as two neighborhoods collaboratively working for optimizing the objective function, a fast neighborhood evaluation method to boost the searching effectiveness, and several diversification techniques to help the searching process jump out of the local optimum trap thus obtaining better solutions. DNS improves the previous best-known results for 4 public benchmark instances while providing competitive results for the remaining ones. Several ingredients of DNS are investigated to demonstrate the importance of the proposed ideas and techniques.

Keywords:

Subject: Computer Science and Mathematics - Data Structures, Algorithms and Complexity

1. Introduction

The minimum dominating tree problem for weighted undirected graphs is to find a dominating tree in a weighted undirected graph such that all vertices in this weighted undirected graph are either in or adjacent to this tree, and the sum of the edge weights of this tree is minimized [1]. Adjacent means that there is an edge between this vertex and at least one vertex in the tree. The minimum dominating tree is a concept in graph theory and one of the important classes of tree structures in graph theory.

A highly related problem, the Minimum Connected Dominating Set (MCDS), has been extensively studied for building routing backbone wireless sensor networks (WSNs) [2,3]. One of the goals of introducing MCDS in WSNs is to minimize energy consumption; if two devices are too far away from each other, they may consume too much power to communicate [4,5]. Using a routing backbone to transmit messages will greatly reduce energy consumption, which increases dramatically as the transmission distance becomes longer [6]. However, some directly connected vertices in MCDS may still be far away from each other because MCDS does not account for distance [7]. Therefore, considering each edge in the routing backbone is more in line with energy consumption purposes [8]. The Minimum Dominating Tree (MDT) problem was first proposed by Zhang et al. [9] for generating a routing backbone that is well adapted to broadcast protocols.

Shin et al. [1] proved that MDT is NP-hard and introduced an approximate framework for solving it. They also provided heuristic algorithms and mixed integer programming (MIP) formulations for the MDT problem. Adasme et al. [10] introduced two other MIP formulations, one based on a tree formulation in the bidirectional counterpart of the input graph, and the other obtained from a generalized spanning tree polyhedron. Adasme et al. [11] proposed a primal dyadic model for the minimum cost dominated tree problem and an effective inequality to improve the linear relaxation. Álvarez-Miranda et al. [12] proposed an precise solution framework that combines a primal-dual heuristic algorithm with a branch-and-cut approach to transform the problem into a Steiner tree problem with additional constraints. Their framework solves most instances in the literature within three hours and proves its optimality.

In recent years, efficient heuristic algorithms for MDT problems have flourished. Sundar and Singh [13] proposed two meta-heuristic algorithms, the Artificial Bee Colony (ABC-DT) algorithm and the Ant Colony Optimization (ACO-DT) algorithm, for the MDT problem. These two algorithms are the first meta-heuristics for the MDT problem and provide better performance than previous algorithms. They also provided 54 randomly generated instances in their work, which are considered challenging instances of the MDT problem and are widely used to evaluate the performance of algorithms for the MDT problem. Based on the latter work, Chaurasia and Singh [14] proposed an evolutionary algorithm with guided mutation (EA/G-MP) for MDT problems. Dražic et al. [15] proposed a variable neighborhood search algorithm for MDT problems. Singh and Sundar [16] proposed another artificial bee colony (ABC-DTP) algorithm for the MDT problem. This new ABC-DTP method differs from ABC-DT in the way it generates initial solutions and in the strategy for determining neighboring solutions. Their experiments show that for the MDT problem, ABC-DTP outperforms all existing problem-specific heuristics and meta-heuristics available in the literature. Hu et al. [17] proposed a hybrid algorithm combining genetic algorithms (GAITLS) and iterative local search to solve the dominated tree problem. Experimental results on classical instances show that the method outperforms existing algorithms. Xiong et al. [18] present a two-level meta-heuristic (TLMH) algorithm for solving the MDT problem with a solution sampling phase and two local search based procedures nested in a hierarchical structure. The results demonstrate the efficiency of the proposed algorithm in terms of solution quality compared with the existing meta-heuristics.

Metaheuristics have been shown to be very effective in solving many challenging real-world problems [19]. However, for some problems, due to the complexity of the problem structure and the large search space, the classical metaheuristic framework fails to produce the desired results [20]. Many researchers have relied on composite neighborhood structures. If properly designed, most composite neighborhood structures have proven successful [21]. These methods include Variable Depth Search (VDS), which searches a large search space through a series of successive simple neighborhood search operations. Although understanding of the basic concepts of VDS algorithms dates back to the 1970s [22], researchers have maintained a sustained enthusiasm for the term [23,24]. For a more detailed survey of VDS, we refer to Ahuja et al. [25,26,27]. Another idea for dealing with complex structural problems is to use a hierarchical meta-trial approach, where several trials are combined in a nested structure. Wu et al. [28] successfully implemented a two-level iterative local search for a network design problem with traffic sparing. According to their analysis, hierarchical metaheuristics must be carefully designed to balance the complexity of the algorithm and its performance. In particular, for the outer framework, keeping it as simple as possible makes the algorithm converge faster. Pop et al. [29] proposed a two-level solution to the generalized minimum spanning tree problem. Carrabs et al. [30] introduced a meta-heuristic algorithm implementing a two-level structure to solve the shortest path problem for all colors. Contreras Bolton and Parada [31] proposed an iterative local search method to solve the generalized minimum spanning tree problem using a two-level solution.

In this paper, we design a meta-heuristic algorithm for two-neighborhood search to solve the MDT problem that uses two neighborhood moves to perform the search and combines a taboo search to escape local optima. The DNS algorithm is described in detail in Section II, the experimental results of the DNS algorithm and comparison with other algorithms are given in Section III, and some comparative experiments within the DNS algorithm are done in Section IV.

2. Dual Neighborhood Search

2.1. Main Framework

The basic idea of our proposed DNS algorithm is to tackle the MDT problem by optimizing the candidate dominating tree weight using a neighborhood search based meta-heuristic with two neighborhood move operators. The search space of DNS consists of all the minimum spanning trees of all the possible dominating sets of the instance graph. The proposed NDS algorithm optimizes the following objective function:

f (T) = α f_{1} (X) + f_{2} (E^{'})

(1)

Where

T = (X, E^{'})

stands for the current configuration, i.e., the candidate dominating tree; Notations X and

E^{'}

represents the vertex and edge sets of T respectively. Function

f_{1} (X)

calculates the number of vertices not dominated by T. Function

f_{2} (E^{'})

calculates the weights of the minimum spanning tree of T. And

α

is a constant parameter to balance the importance between

f_{1}

and

f_{2}

. T is a feasible solution to the minimum dominating tree problem if and only if

f_{1} (X) = 0

The algorithm primarily comprises several key steps. Firstly, an initial solution is generated, followed by a neighborhood evaluation. Subsequently, the best neighborhood move is selected and executed iteratively. During the iteration, the ever best configuration is recorded. The framework of the algorithm can be represented in pseudo-code as follows:

In Algorithm 1,

T_{i}

represents the initial configuration,

T_{b}

represents the recorded ever best solution, and

T_{c}

represents the current configuration. In each iteration, the sub-procedure Do_NeighborEvaluate evaluates all the neighborhood moves in the current configuration. The following two sub-procedure select and execute the best move. The termination condition can be the time or iteration limits.

2.2. Initial Solution Generation

The proposed DNS algorithm uses a feasible dominating tree as the initial configuration. The sub-procedure Generate_InitialSolution generates this initial dominating tree. It first find the minimum spanning tree for the whole graph, and try to trim the tree by removing leaves iteratively until removing one more leave will break the dominancy of the tree. The pseudo-code of this procedure is defined in Algorithm 2.

The procedure starts from the minimum spanning tree

T_{i}

generated by Kruskal’s algorithm. Then it tries to delete the leaf with the largest edge weight. The process terminates if no more leaf can be deleted. The algorithm returns a feasible dominating tree as the initial configuration. In the following sections, we focus on the meta-heuristic part of the proposed DNS algorithm, i.e., the neighborhood structure as well as its evaluation.

2.3. Definition

For better description, we first define some important concepts and notations used in the proposed DNS algorithm.

X : the set of vertices in the current dominator tree.
$X_{p l u s}$ : the set of vertices dominated by X and not in X.
$A_{1}$ : An array of the number of un-dominated vertices, the length of the array is the number of graph vertices.

$A_{1} [i] = | {j \in V ∖ (X \cup X_{p l u s}) : (i, j) \in E, \forall k \in (X \cup X_{p l u s}), (k, j) \notin E} |$

(2)

$A_{1} [i]$ denotes the number of vertices not dominated by the new X if move i from X to $X_{p l u s}$ (or from $X_{p l u s}$ to X).
$A_{2}$ : array of minimum spanning tree weights for X. The length of the array is the number of graph vertices.

$A_{2} [i] = \{\begin{matrix} w (M S T (G [X ∖ {i}])) & if i \in X \\ w (M S T (G [X \cup {i}])) & if i \in X_{p l u s} \end{matrix}$

(3)

$A_{2} [i]$ denotes the weight of the new minimum spanning tree of X if move i from X to $X_{p l u s}$ (or from $X_{p l u s}$ to X).

The following example illustrates how

A_{1}

and

A_{2}

are calculated.

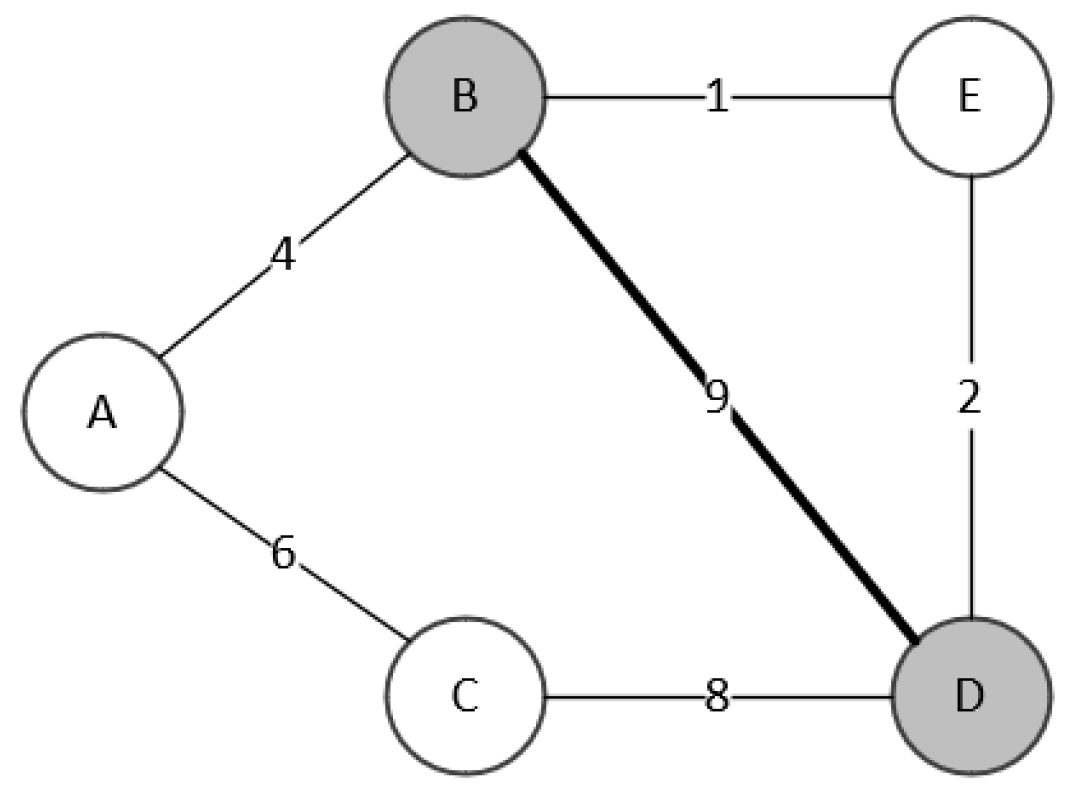
As shown in the Figure 1, the current dominating tree is

T_{< B, D >}

containing two vertices, B and D. Therefore,

X = B, D

. The vertices dominated by X are A, C, and E. Thus,

X_{p l u s} = A, C, E

. We correspond the vertices A, B, C, D, and E to the array subscripts 0, 1, 2, 3, and 4, respectively. To evaluate the neighborhood moves, the algorithm takes vertex A out and puts it in the set of the other side. The number of vertices that are not dominated by the new X after this move is 0, thus

A_{1} [0]

is assigned to 0. The weight of the new minimum spanning tree of X is 13, thus

A_{2} [0]

is assigned to 13. After evaluating all the neighborhood moves, the resulting arrays are

A_{1} = [0, 1, 0, 1, 0]

and

A_{2} = [13, 0, 17, 0, 3]

A_{1}

and

A_{2}

are used to evaluate the neighborhood moves.

2.4. Neighborhood move and Evaluation

There are two kinds of neighborhood moves in DNS algorithm, one is to take out one vertex in X and put it into

X_{p l u s}

, and the other one is to take out one vertex in

X_{p l u s}

and put it into X. In each iteration, the best neighborhood move is selected and performed among all the two kinds of neighborhood moves. There are two criteria to evaluate the quality of the moves, one is the dominance and the other is the weight of the dominating tree. The pseudo-code for neighborhood evaluation is described in Algorithm 3.

The evaluation is done by trying to move each vertex to the other set, then calculate the

A_{1}

and

A_{2}

values. Based on these two arrays, the best move is selected as described in Algorithm 4.

Procedure Select_BestMove picks the move with the smallest

A_{1}

and

A_{2}

, higher priority for

A_{1}

. Then, the best move selected is performed by Algorithm 5.

Procedure Execute_BestMove moves the selected vertex to

X_{p l u s}

if it is in X, and vice versa. After the move, the minimum spanning tree of

G (X)

is calculated using Kruskal’s algorithm and assigned to

T_{c}

. The following example illustrates how the best move is evaluated and performed.

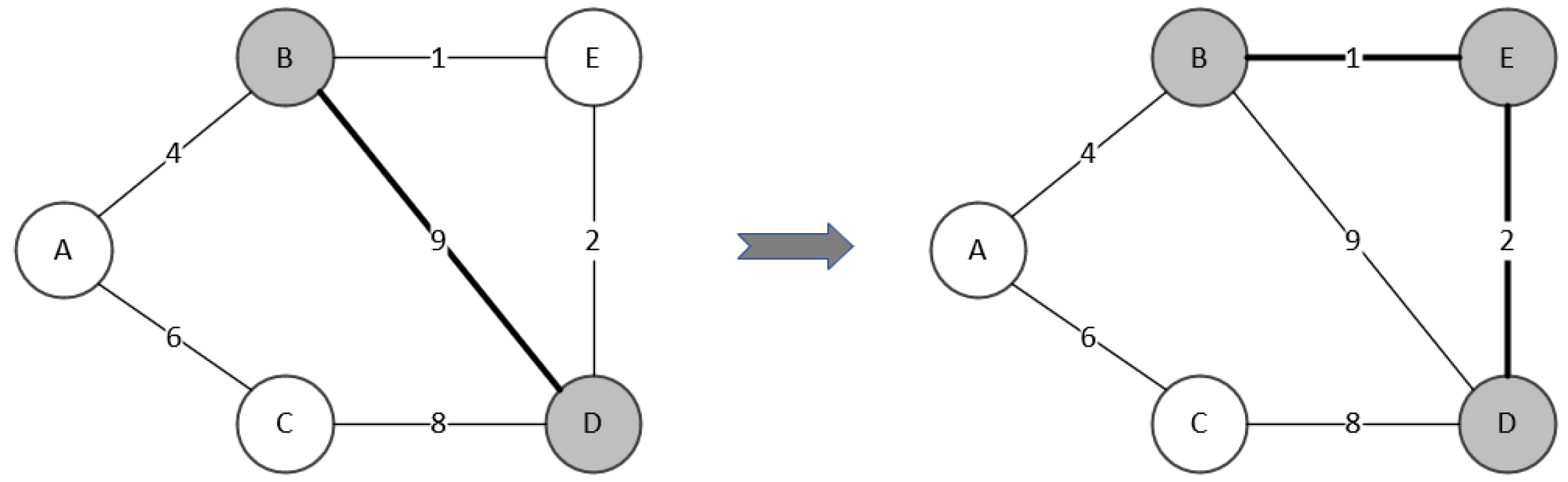
As shown in Figure 2, the current domination tree is

T_{< B, D >}

X = {B, D}

X_{p l u s} = {A, C, E}

. To evaluate vertex A, we first move it from

X_{p l u s}

to X, then X becomes

{A, B, D}

. The number of vertices that are not dominated by the new X at this point is 0, thus

A_{1} [A] = 0

. The minimum spanning tree weight of

X = {A, B, D}

is 13, thus

A_{2} [A] = 13

. We then move A back to its original set. The evaluation for A is done. The B, C, D, and E are evaluated sequentially by the same process. After the evaluation for each vertex,

A_{1} = [0, 1, 0, 1, 0]

and

A_{2} = [13, 0, 17, 0, 3]

Then we pick the best neighborhood move, finding the minimum value from

A_{1}

and

A_{2}

, prior to

A_{1}

. There are 3 minimum values in

A_{1}

, corresponding to A, C, and E. Then we compare the value of these three vertices in

A_{2}

, the minimum value is 3, corresponding to vertex E. Therefore, the best vertex is E, and the best neighboring move is to move E. After the move, the new

X = {B, D, E}

. We calculate the minimum spanning tree of the new X. The new minimum spanning tree is

T_{< B, D, E >}

with a weight of 3.

2.5. Fast Neighborhood Evaluation

In order to improve the efficiency of the algorithm, this paper proposes a method to dynamically update the neighborhood evaluation matrices

A_{1}

A_{2}

2.5.1. Fast evaluation for $A_{1}$

The number of un-dominated vertices may increase or remain unchanged when vertices are removed from X to

X_{p l u s}

. The newly added un-dominated vertices must be originally in the

X_{p l u s}

set and connected to the moved vertex. Since the number of un-dominated vertices is zero throughout the algorithm, we can count the newly introduced un-dominated vertices by counting the vertices in

X_{p l u s}

, which the moved vertex is its only connection to X.

When we move vertices from

X_{p l u s}

to X, the number of un-dominated vertices may decrease or remain the same. Because X is dominated throughout the algorithm, the number of un-dominated vertices after this kind of moves is still 0. The above observation can be utilized to dynamically compute

A_{1}

without having to traverse the entire graph. The formula is as follows:

A_{1} [i] = \{\begin{matrix} | {j \in X_{p l u s} : (i, j) \in E} | & if i \in X \\ 0 & if i \in X_{p l u s} \end{matrix}

(4)

2.5.2. Fast evaluation for $A_{2}$

For

A_{2}

, we use a dynamic Kruskal’s algorithm. The algorithm dynamically maintains a set

R o a d s

, which is the set of edges contained in the subgraph

G (X)

, i.e., the set of edges whose two vertices are in X. The

R o a d s

set is sorted from smallest to largest by the weights of the edges. When a X to

X_{p l u s}

move is performed, the edges connecting to the moved vertex and X are deleted from the

R o a d s

set. Similarly, when a

X_{p l u s}

to X move is performed, the edges connecting to the moved vertex and X are inserted to the

R o a d s

set. Note that, edges should be inserted into the appropriate position in

R o a d s

to guarantee that it is sorted. The dynamic Kruskal’s algorithm then assumes that the edges before the deletion or insertion position are sure to be in the new minimum spanning tree, then start the normal procedure from that position. The pseudo-code for dynamic Kruskal’s algorithm is described in Algorithm 6 and 7.

In Algorithm 6, The notate

E (a, b)

represents the edge connecting vertices a and b,

T_{c}

is the original minimum spanning tree, i.e., the entire algorithm of the current solution. The main job for this procedure is to update the

R o a d s

set. And the Algorithm 7 calculates the spanning tree dynamically according to

R o a d s

The following example illustrates the above procedures:

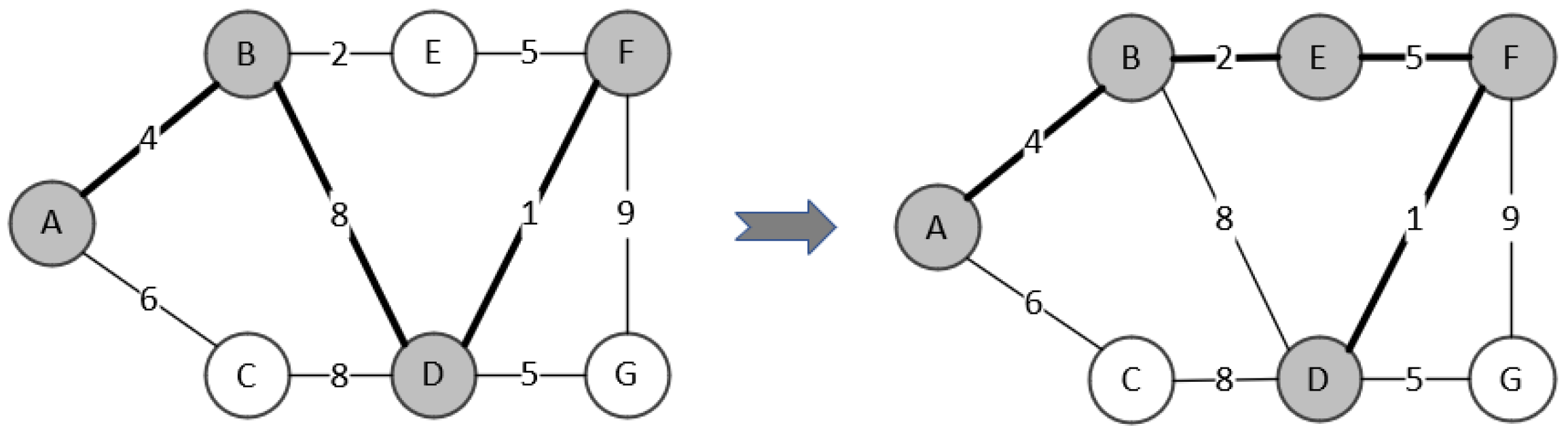
As shown in Figure 3, the original tree is

T_{< A, B, D, F >}

, currently,

X = {A, B, D, F}

X_{p l u s} = {C, E, G}

R o a d s = {< D, F >, < A, B >, < B, D >}

, and the weights of the edges

w (R o a d s) = {1, 4, 8}

. Let’s evaluate the move of vertex E from

X_{p l u s}

to X. After the move

X = {A, B, D, E, F}

X_{p l u s} = {C, G}

. Since E was originally in

X_{p l u s}

A_{1} [E] = 0

. The new edge added after the move is the edge

{< B, E >, < E, F >}

with weights

{2, 5}

. Then we insert these two edges into the appropriate position in

R o a d s

according to their weights from smallest to largest in

w (R o a d s) = {1, 2, 4, 5, 8}

, and the corresponding

R o a d s = {< D, F >, < B, E >, < A, B >, < E, F >, < B, D >}

. We only need to start from position of

< B, E >

to determine the new minimum spanning tree. The edges before

< B, E >

must be in the new minimum spanning tree. The evaluated minimum spanning tree is

T_{< A, B, D, E, F >} = {< D, F >, < B, E >, < A, B >, < E, F >}

with weight 12, thus

A_{2} [E] = 12

2.6. Tabu strategy and aspiration mechanism

The proposed DNS algorithm implements tabu strategy. The vertex is prohibited to be moved again within a tenure once it is moved. The tabu strategy is implemented to both kinds of moves in the algorithm. Since there is no intersection of X and

X_{p l u s}

, only one taboo table is needed. We denote the tabu tenure of the move from

X_{p l u s}

to X as

T a b u L e n g t h_{1}

and the move from X to

X_{p l u s}

T a b u L e n g t h_{2}

. These two tabu tenures are set to the number of vertices in X and

X_{p l u s}

, respectively, thus implementing dynamic tabu tenures in this way. This tabu strategy improves the accuracy and efficiency makes the algorithm to jump out of the local optimum more easily.

In order to avoid missing some good solutions, an aspiration strategy is introduced. If one tabu move may improve the ever best solution, the searching process breaks its tabu status and selects it as a candidate best move.

Note that we do not describe the details of how the tabu and aspiration is implemented in the previous pseudo-codes to give a clearer layout for better understanding. For more details of tabu we recommend readers to the literature [32].

2.7. Perturbation Strategy

In order to further improve the quality of the solution, the proposed DNS algorithm implements a perturbation strategy. The specific perturbation is to move some vertices from

X_{p l u s}

to X randomly. The algorithm set a parameter as the perturbation period. When the number of iterations reaches the perturbation period a perturbation will be triggered, and the number of iterations will be cleared to zero if the ever best solution is updated within this period. There are another two parameters, the perturbation amplitude and the perturbation tabu tenure. The perturbation amplitude is the number of vertices taken out from

X_{p l u s}

in the perturbation. The perturbation tabu tenure is the tabu tenure used during the perturbation period. In addition, after a certain number of small perturbations, a larger perturbation needs to be triggered to give a larger spatial span to the search process. The larger perturbation is implemented by moving one-third of the vertices from

X_{p l u s}

to X randomly.

3. Algorithm Experimentation

3.1. Datasets and Experimental Protocols

The experiments are carried out on the following two data sets:

The DTP dataset is a dataset proposed by Dražic et al. [15], with the number of vertices ranging from 150 to 1000.
The Range dataset is a dataset proposed by Sundar and Singh [13], with the number of vertices ranging from 50 to 500 and a transmission range of 100 to 150 meters.

Both datasets are randomly generated and can be downloaded online or obtained from the authors. The DNS algorithm is implemented in Java (JDK17) and tested on a desktop computer equipped with an Intel® Xeon® W-2235 CPU @3.80GHz, with 16.0GB of RAM.

3.2. Calibration

This section we conduct experiments to fix the value of key parameters of DNS algorithm:

Parameter $D i s t u r b P e r i o d$ , the first perturbation period. Values from 14 to 17 are tested.
Parameter $D i s t u r b L e v e l$ , the perturbation amplitude. Values from 7 to 12 are tested.
Parameter $D i s t u r b T L_{1}$ , The tabu length of the neighborhood move of taking a vertex from $X_{p l u s}$ and putting it into X during perturbation. Values from 1 to 2 are tested.
Parameter $D i s t u r b T L_{2}$ , The tabu length of the neighborhood move of taking a vertex from X and putting it into $X_{p l u s}$ during perturbation. Values from 3 to 8 are tested.

We select 13 representative instances to tackle the calibration experiments. Representatives are instances 200-400-1, 200-600-1, 300-600-1 and 300-1000-1 In DTP; instances 300-1, 400-1 and 500-1 respectively in Range100, Range125 and Range150. The experiment is done as following steps: First, roughly experiment with parameter combinations to select better parameter combinations. Then for each set of parameters, run these 13 instances in sequence. Each instance is run five times with different random seeds for 300 seconds each time. We compare the gap rates for each parameter setting. The gap is calculated as:

g a p = \frac{n 1 - n 2}{n 2}

(5)

, where

n_{1}

is the average result obtained and

n_{2}

is the known best objective. Table 1 shows the result for the calibration experiment.

According to the experimental data, the minimum total

g a p

rate is 0.075, corresponding to

D i s t u r b P e r i o d

of 15,

D i s t u r b L e v e l

of 8,

D i s t u r b T L_{1}

of 1, and

D i s t u r b T L_{2}

of 4. In the following experiment, we set the parameters of the algorithm to this setting. Note that this experiment does not guarantee the optimal values of the parameters and the optimal scheme may vary from one benchmark to another. It can also be seen that for different parameter combinations, the

g a p

rate is small, indicating the robustness of the algorithm.

3.3. Comparison on DTP Data Set

In this section, we compare the proposed DNS algorithm with other methods in the literature on DTP data set. There are two DTP datasets: dtp_large and dtp_small. Since all algorithms can obtain the best results for dtp_small with little difference in speed, only the experimental results for dtp_large are shown here. The compared algorithms are TLMH, VNS, and GAITLS algorithms. For each instance, 10 runs with different random seeds are made, each lasting 1000 seconds. The best, average objective values, and average time are recorded for each instance. The experimental results and comparisons are shown in Table 2. Bolded numbers represent that the current best value has been obtained and the results are not worse than other algorithms. The start marks represent that DNS algorithm updates the best objective in the literature.

From Table 2, it can be seen that this algorithm runs most instances to the best value, and those that do not reach the optimal value are also very close to it. The overall best values are slightly worse than the TLMH algorithm but better than the VNS and GAITLS algorithms. The overall average of this algorithm outperforms other algorithms, demonstrating its stability and faster speed. It also improves the best solution for two instances.

3.4. Range Dataset Experiments

In this section, the widely used Range dataset with 54 instances is tested and compared with the TLMH, ACO-DT, EA/G-MP, and ABC-DTP algorithms. The experimental results of these algorithms compared in this paper are the best results obtained using the best parameters in the original literature. In this section, this algorithm is run 10 times for each dataset with the previously measured best parameters and different random seeds. Each run lasts 1000 seconds and the best, average objective values, and average time are calculated. The results and comparisons are shown in Table 3, Table 4 and Table 5:

==layoutwidth=297mm,layoutheight=210 mm, left=2.7cm,right=2.7cm,top=1.8cm,bottom=1.5cm, includehead,includefoot [LO,RE]0cm [RO,LE]0cm

==This algorithm obtains best solutions for most instances in the Range dataset, and those that are not optimal are close to the optimal solution. It updates the best solution for two instances and outperforms the TLMH algorithm in speed.

4. Analysis and Discussion

4.1. The Importance of the Initial Solution

A procedure for generating the initial solution was proposed in the previous chapter. To see the effect of this procedure, experiments were conducted on it in this section, where 18 instances of Range150 were tested. The objective value obtained by this procedure were compared with both the minimum spanning tree weights and the known best objective value to see how much this procedure improves on the initial solution and how close this initial solution is to the minimum domination tree. The experimental results are shown in Table 6.

In Table 6,

T_{m}

represents the minimum spanning tree,

T_{i}

represents the objective value obtained from the initialization procedure,

T_{b}

represents the known best objective value. From the results, it can be seen that using the initialization procedure to obtain a domination tree as the initial solution improves significantly over using the minimum spanning tree as the initial solution. The weight of this initial domination tree is relatively close to that of the minimum domination tree, allowing the algorithm to converge quickly to a near-optimal solution at the very beginning. To verify this improvement, this paper also uses the minimum spanning tree of graph

G (V, E)

as an initial solution and conducts experiments on Range150 for comparison. This method is denoted as DNS-ms. The experimental results are in Table 7.

The experimental results show that DNS outperforms the DNS-ms algorithm in terms of best, average objective values, and speed, indicating that the initial solution proposed in this paper improves the efficiency of the algorithm. It can also be seen that there is not much difference between the best and average values obtained by DNS and DNS-ms, demonstrating the robustness of the local search procedure of DNS algorithm.

4.2. The Importance of the Fast Neighborhood Evaluation

The proposed DNS algorithm uses a fast neighborhood evaluation technique. To verify its effectiveness, an experiment was conducted to test the time taken to reach the same result for 18 instances of Range150 with and without fast neighborhood evaluation. In this experiment, the perturbation is disabled while only tabu mechanism is enabled. The best objective value that can be reached at complete convergence is tested in advance for each instance and used as the target result. The random seed is fixed for each instance because the difference in speed is only due to using fast neighborhood evaluation. The program runs until it reaches the target result, and the time taken by each instance to reach the target result under these two methods is recorded separately. The results are shown in Table 8, where Method 1 represents the version without fast neighborhood evaluation and Method 2 represents the version with fast neighborhood evaluation:

From Table 8, it can be seen that the version using fast neighborhood evaluation significantly improves speed compared to the version without it, verifying the effectiveness of fast neighborhood evaluation. To observe the convergence of these two methods, scatter plots are generated by outputting the weights and corresponding times after each update. The convergence curves of some instances are shown in Figure 4, where NDNU represents the method without fast neighborhood evaluation and DNU represents the method with the fast neighborhood evaluation.

From Figure 4, it can be seen that the version using fast neighborhood evaluation converges to the target value more quickly. For the version without the fast neighborhood evaluation, the curve is slower and takes longer to converge to the same objective value.

4.3. Importance of the Perturbation

The proposed DNS algorithm also implements a perturbation strategy. In this section the effectiveness of this strategy is verified through experiments by testing the version with and without this strategy, for 18 instances in Range150. Each instance is run 5 times with different random seeds, with a time limit of 1000 seconds, and the results of the experiments are shown in Table 9:

From Table 9, it can be seen that better solutions can be obtained by the version using the perturbation strategy, especially in some larger instances, verifying the effectiveness of this strategy.

5. Conclusion

In this paper, a dual-neighborhood search algorithm is proposed to solve the minimum dominating tree problem. In order to improve the efficiency of the algorithm, a fast neighborhood evaluation method is proposed, in which the method of dynamically generating the minimum spanning tree from the sub-graph deduced from the dominating set. The tabu and the perturbation mechanisms help the algorithm jump out of the local optimum trap, thus obtaining better solutions. The DNS algorithm is demonstrated to be highly effective in tests on a collection of widely used benchmark instances where it is compared with the algorithms in the literature. Out of 72 public instances, DNS improves the best result on 4 problems while being competitive on the remaining ones with less computational time. Although the techniques proposed in this paper are specific to the minimum dominating tree problem, most of these ideas can be applied to other combinatorial optimization problems. For example, the dynamic spanning tree calculation used in the fast neighborhood evaluation can be used in problems with spanning tree structures. And the collaboration of two neighborhood structures can be also introduced to other relevant optimization problems. Finally, it is interesting to test the proposed ideas in other meta-heuristic frameworks with other optimization problems.

References

Shin, I.; Shen, Y.; Thai, M.T. On approximation of dominating tree in wireless sensor networks. Optimization Letters 2010, 4, 393–403. [Google Scholar] [CrossRef]
Wu, X.; Lü, Z.; Galinier, P. Restricted swap-based neighborhood search for the minimum connected dominating set problem. Networks 2017, 69, 222–236. [Google Scholar] [CrossRef]
Li, R.; Hu, S.; Gao, J.; Zhou, Y.; Wang, Y.; Yin, M. GRASP for connected dominating set problems. Neural Computing and Applications 2017, 28, 1059–1067. [Google Scholar] [CrossRef]
Li, R.; Hu, S.; Liu, H.; Li, R.; Ouyang, D.; Yin, M. Multi-start local search algorithm for the minimum connected dominating set problems. Mathematics 2019, 7, 1173. [Google Scholar] [CrossRef]
Bouamama, S.; Blum, C.; Fages, J.G. An algorithm based on ant colony optimization for the minimum connected dominating set problem. Applied Soft Computing 2019, 80, 672–686. [Google Scholar] [CrossRef]
Chinnasamy, A.; Sivakumar, B.; Selvakumari, P.; Suresh, A. Minimum connected dominating set based RSU allocation for smartCloud vehicles in VANET. Cluster Computing 2019, 22, 12795–12804. [Google Scholar] [CrossRef]
Hedar, A.R.; Ismail, R.; El-Sayed, G.A.; Khayyat, K.M.J. Two meta-heuristics designed to solve the minimum connected dominating set problem for wireless networks design and management. Journal of Network and Systems Management 2019, 27, 647–687. [Google Scholar] [CrossRef]
Li, B.; Zhang, X.; Cai, S.; Lin, J.; Wang, Y.; Blum, C. Nucds: An efficient local search algorithm for minimum connected dominating set. In Proceedings of the Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, 2021; pp. 1503–1510.
Zhang, N.; Shin, I.; Li, B.; Boyaci, C.; Tiwari, R.; Thai, M.T. New approximation for minimum-weight routing backbone in wireless sensor network. In Proceedings of the Wireless Algorithms, Systems and Applications: Third International Conference, WASA 2008, Dallas, TX, USA, October 26-28, 2008. Proceedings 3. Springer, 2008; pp. 96–108.
Adasme, P.; Andrade, R.; Leung, J.; Lisser, A. Models for minimum cost dominating trees. Electronic Notes in Discrete Mathematics 2016, 52, 101–107. [Google Scholar] [CrossRef]
Adasme, P.; Andrade, R.; Leung, J.; Lisser, A. Improved solution strategies for dominating trees. Expert Systems with Applications 2018, 100, 30–40. [Google Scholar] [CrossRef]
Álvarez-Miranda, E.; Luipersbeck, M.; Sinnl, M. An exact solution framework for the minimum cost dominating tree problem. Optimization Letters 2018, 12, 1669–1681. [Google Scholar] [CrossRef]
Sundar, S.; Singh, A. New heuristic approaches for the dominating tree problem. Applied Soft Computing 2013, 13, 4695–4703. [Google Scholar] [CrossRef]
Chaurasia, S.N.; Singh, A. A hybrid heuristic for dominating tree problem. Soft Computing 2016, 20, 377–397. [Google Scholar] [CrossRef]
Dražić, Z.; Čangalović, M.; Kovačević-Vujčić, V. A metaheuristic approach to the dominating tree problem. Optimization Letters 2017, 11, 1155–1167. [Google Scholar] [CrossRef]
Singh, K.; Sundar, S. Two new heuristics for the dominating tree problem. Applied Intelligence 2018, 48, 2247–2267. [Google Scholar] [CrossRef]
Hu, S.; Liu, H.; Wu, X.; Li, R.; Zhou, J.; Wang, J. A hybrid framework combining genetic algorithm with iterated local search for the dominating tree problem. Mathematics 2019, 7, 359. [Google Scholar] [CrossRef]
Xiong, C.; Liu, H.; Wu, X.; Deng, N. A two-level meta-heuristic approach for the minimum dominating tree problem. Frontiers of Computer Science 2023, 17, 171406. [Google Scholar] [CrossRef]
Yang, W.; Ke, L. An improved fireworks algorithm for the capacitated vehicle routing problem. Frontiers of Computer Science 2019, 13, 552–564. [Google Scholar] [CrossRef]
Hou, N.; He, F.; Zhou, Y.; Chen, Y. An efficient GPU-based parallel tabu search algorithm for hardware/software co-design. Frontiers of Computer Science 2020, 14, 1–18. [Google Scholar] [CrossRef]
Hao, X.; Liu, J.; Zhang, Y.; Sanga, G. Mathematical model and simulated annealing algorithm for Chinese high school timetabling problems under the new curriculum innovation. Frontiers of Computer Science 2021, 15, 1–11. [Google Scholar] [CrossRef]
Lin, S.; Kernighan, B.W. An effective heuristic algorithm for the traveling-salesman problem. Operations research 1973, 21, 498–516. [Google Scholar] [CrossRef]
Glover, F. Ejection chains, reference structures and alternating path methods for traveling salesman problems. Discrete Applied Mathematics 1996, 65, 223–253. [Google Scholar] [CrossRef]
Yagiura, M.; Yamaguchi, T.; Ibaraki, T. A variable depth search algorithm with branching search for the generalized assignment problem. Optimization Methods and Software 1998, 10, 419–441. [Google Scholar] [CrossRef]
Ahuja, R.K.; Ergun, Ö.; Orlin, J.B.; Punnen, A.P. A survey of very large-scale neighborhood search techniques. Discrete Applied Mathematics 2002, 123, 75–102. [Google Scholar] [CrossRef]
Santos, L.F.M.; Iwayama, R.S.; Cavalcanti, L.B.; Turi, L.M.; de Souza Morais, F.E.; Mormilho, G.; Cunha, C.B. A variable neighborhood search algorithm for the bin packing problem with compatible categories. Expert Systems with Applications 2019, 124, 209–225. [Google Scholar] [CrossRef]
Wu, X.; Xiong, C.; Deng, N.; Xia, D. A variable depth neighborhood search algorithm for the Min–Max Arc Crossing Problem. Computers & Operations Research 2021, 134, 105403. [Google Scholar]
Wu, X.; Lü, Z.; Guo, Q.; Ye, T. Two-level iterated local search for WDM network design problem with traffic grooming. Applied Soft Computing 2015, 37, 715–724. [Google Scholar] [CrossRef]
Pop, P.C.; Matei, O.; Sabo, C.; Petrovan, A. A two-level solution approach for solving the generalized minimum spanning tree problem. European Journal of Operational Research 2018, 265, 478–487. [Google Scholar] [CrossRef]
Carrabs, F.; Cerulli, R.; Pentangelo, R.; Raiconi, A. A two-level metaheuristic for the all colors shortest path problem. Computational Optimization and Applications 2018, 71, 525–551. [Google Scholar] [CrossRef]
Contreras-Bolton, C.; Parada, V. An effective two-level solution approach for the prize-collecting generalized minimum spanning tree problem by iterated local search. International Transactions in Operational Research 2021, 28, 1190–1212. [Google Scholar] [CrossRef]
Glover, F.; Laguna, M. Tabu search; Springer, 1998.

Figure 1.

T_{< B, D >}

Figure 1.

T_{< B, D >}

Figure 2. Move

T_{< B, D >}

T_{< B, D, E >}

Figure 2. Move

T_{< B, D >}

T_{< B, D, E >}

Figure 3.

T_{< A, B, D, F >}

T_{< A, B, D, E, F >}

Figure 3.

T_{< A, B, D, F >}

T_{< A, B, D, E, F >}

Figure 4. Fast neighborhood evaluation scatter plot

Table 1. Experimental results of parameter testing for DNS

DisturbPeriod	DisturbLevel	DisturbTL_1	DisturbTL_2	TotalGap	AverageTime
14	7	1	3	0.083	1959
14	7	1	4	0.082	1696
14	7	1	5	0.083	1806
14	8	1	3	0.093	1803
14	8	1	4	0.077	1776
14	8	1	5	0.080	1733
14	9	1	3	0.093	1910
14	9	1	4	0.090	1985
14	9	1	5	0.095	2084
15	8	1	4	0.075	1822
15	8	1	5	0.086	1768
15	8	1	6	0.083	1854
15	9	1	4	0.096	1956
15	9	1	5	0.095	1772
15	9	1	6	0.107	1835
15	10	1	4	0.077	1945
15	10	1	5	0.093	1955
15	10	1	6	0.096	1906
16	9	2	5	0.097	1930
16	9	2	6	0.110	1932
16	9	2	7	0.094	2168
16	10	2	5	0.087	1919
16	10	2	6	0.089	2025
16	10	2	7	0.101	2054
16	11	2	5	0.101	2013
16	11	2	6	0.093	1769
16	11	2	7	0.093	1895
17	10	2	6	0.106	1662
17	10	2	7	0.106	1781
17	10	2	8	0.111	1968
17	11	2	6	0.108	1835
17	11	2	7	0.117	1863
17	11	2	8	0.108	1896
17	12	2	6	0.113	1942
17	12	2	7	0.114	1892
17	12	2	8	0.110	1707

Table 2. Computational results of DNS and comparisons on DTP-large

	DNS			TLMH			VNS		GAITLS
instance	best	average	time	best	average	time	best	average	best	average
100-150-0	152.57	152.57	14	152.57	152.57	2	152.57	154.61	152.57	152.57
100-150-1	192.21	192.21	6	192.21	192.21	11	192.21	194.22	192.21	192.21
100-150-2	146.34	146.34	<1	146.34	146.34	87	146.34	148.35	146.34	146.34
100-200-0	135.04	135.04	<1	135.04	135.04	60	135.04	136.41	135.04	135.04
100-200-1	91.88	91.88	<1	91.88	91.88	13	91.88	92.03	91.88	91.88
100-200-2	115.93	115.93	17	115.93	115.93	9	115.93	117.11	115.93	115.93
200-400-0	257.09	257.52	376	257.09	257.23	370	306.06	343.95	257.09	257.09
200-400-1	258.77	258.88	181	258.77	258.88	486	303.53	331.10	258.93	258.93
200-400-2	241.07	241.42	6	238.27	241.72	370	274.37	389.51	238.29	238.29
200-600-0	121.62	122.94	307	121.62	127.73	460	132.49	150.39	121.62	121.62
200-600-1	135.08	137.63	293	135.08	145.20	441	162.92	198.21	135.08	135.08
200-600-2	123.70	124.04	166	123.31	123.70	264	139.08	154.36	123.31	123.31
300-600-0	352.32	353.36	297	348.03	351.22	529	471.69	494.62	348.03	348.03
300-600-1	416.23	416.99	157	413.93	416.64	753	494.91	542.46	415.32	415.32
300-600-2	354.35	356.52	57	352.15	353.77	760	500.72	535.30	385.53	385.53
300-1000-0	148.86	151.05	331	148.63	150.10	629	257.72	264.33	149.57	149.57
300-1000-1	*164.65	165.77	404	165.21	165.91	477	242.79	325.16	165.19	165.19
300-1000-2	*154.59	158.90	434	154.64	169.39	595	233.18	251.41	154.61	154.61
average	197.91	198.83	169	197.26	199.75	351	241.86	267.97	199.25	199.25

Table 3. Computational results of DNS and comparisons on Range-100

	DNS			TLMH			ACO-DT		EA/G-MP		ABC-DTP
instance	best	average	time	best	average	time	best	average	best	average	best	average
50-1	1204.41	1204.41	29	1204.41	1204.41	1	1204.41	1204.41	1204.41	1204.41	1204.41	1204.41
50-2	1340.44	1340.44	25	1340.44	1340.44	<1	1340.44	1340.44	1340.44	1340.44	1340.44	1340.69
50-3	1316.39	1316.39	6	1316.39	1316.39	<1	1316.39	1316.39	1316.39	1316.39	1316.39	1316.39
100-1	1217.47	1217.47	<1	1217.47	1217.47	17	1217.47	1217.47	1217.47	1217.61	1217.47	1218.59
100-2	1128.40	1128.40	7	1128.40	1128.40	44	1152.85	1152.85	1128.40	1128.54	1128.40	1136.50
100-3	1252.99	1252.99	20	1252.99	1253.41	202	1253.49	1253.49	1253.49	1257.37	1252.99	1253.30
200-1	1206.79	1206.79	23	1206.79	1206.80	515	1206.79	1207.61	1206.79	1208.26	1206.79	1210.25
200-2	1213.24	1213.24	170	1213.24	1213.27	395	1216.23	1217.73	1216.41	1222.23	1216.41	1219.38
200-3	1247.25	1247.25	114	1247.25	1247.41	313	1247.25	1248.94	1247.63	1250.78	1247.73	1252.15
300-1	1217.59	1224.32	587	1215.48	1217.40	564	1228.24	1243.70	1225.22	1230.48	1215.48	1220.39
300-2	1170.85	1171.53	441	1170.85	1171.08	341	1176.45	1193.95	1170.85	1171.30	1170.85	1171.15
300-3	1247.51	1254.16	453	1247.51	1249.51	348	1261.18	1276.75	1252.14	1260.83	1249.54	1254.67
400-1	1211.33	1216.45	426	1211.33	1213.51	502	1220.62	1237.45	1211.72	1220.79	1212.51	1214.36
400-2	1201.74	1205.34	425	1197.66	1198.99	432	1209.69	1246.14	1199.92	1202.82	1199.23	1202.90
400-3	1257.52	1262.98	487	1245.31	1248.47	633	1254.10	1270.34	1248.29	1268.38	1246.94	1258.76
500-1	1202.12	1209.06	482	1197.26	1202.81	678	1219.66	1240.05	1206.07	1222.12	1200.06	1208.73
500-2	*1220.47	1233.98	624	1221.76	1226.81	570	1273.86	1295.51	1226.78	1240.62	1220.68	1230.07
500-3	*1231.81	1244.93	381	1231.84	1236.64	583	1232.71	1259.08	1232.15	1250.48	1231.95	1236.33
average	1227.13	1230.56	261	1225.91	1227.32	348	1235.10	1245.68	1228.03	1234.10	1226.57	1230.57

Table 4. Computational results of DNS and comparisons on Range-125

	DNS			TLMH			ACO-DT		EA/G-MP		ABC-DTP
instance	best	average	time	best	average	time	best	average	best	average	best	average
50-1	802.95	802.95	10	802.95	802.95	1	802.95	803.26	802.95	802.95	802.95	802.95
50-2	1055.10	1055.10	19	1055.10	1055.10	2	1055.10	1055.10	1055.10	1055.10	1055.10	1055.10
50-3	877.77	877.77	3	877.77	877.77	4	877.77	877.77	877.77	877.77	877.77	877.83
100-1	943.01	943.01	3	943.01	943.01	102	943.01	946.37	943.01	943.01	943.01	943.01
100-2	917.00	917.00	126	917.00	917.23	281	935.71	938.71	917.95	917.95	917.00	917.38
100-3	998.18	998.18	5	998.18	998.18	44	998.18	1006.11	998.18	998.18	998.18	999.91
200-1	910.17	910.17	11	910.17	910.17	195	910.17	910.50	910.17	910.17	910.17	911.66
200-2	921.76	921.76	79	921.76	921.76	184	928.84	942.72	921.76	923.03	921.76	925.38
200-3	939.58	939.58	452	939.60	939.61	333	951.36	959.63	939.58	949.18	939.58	943.20
300-1	977.65	978.33	412	977.65	977.65	416	978.91	980.11	977.65	981.04	979.81	981.85
300-2	913.01	913.01	228	913.01	913.01	402	918.40	949.05	913.01	914.08	913.01	913.88
300-3	974.85	974.94	383	974.78	974.78	315	981.15	981.33	974.85	979.34	974.78	978.35
400-1	965.99	966.08	292	966.01	966.03	225	968.66	980.60	965.99	966.59	965.99	966.71
400-2	938.54	942.45	643	934.17	937.88	506	941.52	961.71	941.02	943.53	941.02	942.59
400-3	1002.61	1003.13	579	1002.61	1002.67	525	1002.61	1009.07	1002.97	1003.62	1002.61	1003.33
500-1	963.89	964.10	484	963.89	965.91	272	986.49	991.85	963.89	963.89	963.89	964.80
500-2	950.18	956.48	539	948.57	949.57	457	953.77	996.85	948.57	952.96	948.96	950.12
500-3	982.02	988.86	514	980.67	982.73	553	1006.23	1007.36	980.67	992.64	981.90	986.01
average	946.35	947.38	265	945.94	946.45	283	952.27	961.01	946.39	948.61	946.53	948.00

Table 5. Computational results of DNS and comparisons on Range-150

	DNS			TLMH			ACO-DT		EA/G-MP		ABC-DTP
instance	best	average	time	best	average	time	best	average	best	average	best	average
50-1	647.75	647.75	<1	647.75	647.75	1	647.75	647.75	647.75	647.75	647.75	647.75
50-2	863.69	863.69	<1	863.69	863.69	2	863.69	863.69	863.69	863.69	863.69	864.04
50-3	743.94	743.94	<1	743.94	743.94	2	743.94	743.94	743.94	743.94	743.94	745.68
100-1	876.69	876.69	7	876.69	876.79	297	881.37	885.36	876.69	876.69	876.69	877.02
100-2	657.35	657.35	<1	657.35	657.35	11	657.35	657.35	657.35	657.53	657.35	657.53
100-3	722.87	722.87	<1	722.87	722.87	2	722.87	722.87	722.87	722.87	722.87	722.87
200-1	809.90	809.90	23	809.90	809.90	138	809.90	810.87	809.90	810.49	809.90	809.90
200-2	736.23	736.23	2	736.23	736.23	354	736.23	736.23	736.23	736.23	736.23	736.23
200-3	792.71	792.71	17	792.71	792.71	97	792.71	793.73	792.71	795.65	792.71	793.48
300-1	796.15	796.60	288	796.15	796.15	283	796.70	797.17	796.15	798.12	796.29	796.99
300-2	741.02	741.72	257	741.02	741.03	298	748.94	752.33	741.02	743.05	741.02	742.88
300-3	819.76	819.76	171	819.76	819.78	129	826.48	826.56	819.76	821.67	819.76	820.45
400-1	796.70	797.42	435	795.53	795.88	445	796.70	798.24	795.53	798.82	795.53	797.92
400-2	779.63	780.64	477	779.67	779.67	388	782.91	787.66	779.63	783.14	779.63	781.40
400-3	814.14	816.62	589	814.14	814.18	388	826.48	831.32	814.14	817.38	814.14	815.35
500-1	792.32	793.49	469	792.21	792.31	357	794.47	797.13	792.21	793.59	793.98	796.16
500-2	779.35	779.92	465	779.38	779.41	274	779.35	791.20	779.35	781.28	779.35	780.04
500-3	808.64	810.00	538	808.37	808.39	281	808.50	811.35	808.50	810.27	808.50	808.50
average	776.60	777.07	207	776.52	776.56	208	778.69	780.82	776.52	777.90	776.53	777.46

Table 6. Experimental results of the initial dominating tree algorithm

instance	$T_{m}$	$T_{i}$	$T_{b}$
50-1	2368.21	1145.40	647.75
50-2	2521.75	1222.31	863.69
50-3	2461.33	1103.13	743.94
100-1	3313.79	1324.04	876.69
100-2	3155.53	1212.55	657.35
100-3	3354.60	1043.87	722.87
200-1	4618.79	1327.49	809.90
200-2	4704.18	1322.38	736.23
200-3	4720.93	1353.97	792.71
300-1	5685.14	1559.49	796.15
300-2	5718.30	1269.55	741.02
300-3	5839.22	1516.01	819.76
400-1	6599.33	1730.84	795.53
400-2	6618.89	1833.34	779.63
400-3	6524.29	1638.08	814.14
500-1	7356.76	1375.03	792.21
500-2	7342.62	1334.51	779.35
500-3	7305.09	2111.56	808.37

Table 7. Computational results of initial solution experiment on Range-150

	DNS			DNS-ms
instance	best	average	time	best	average	time
50-1	647.75	647.75	<1	647.75	647.75	<1
50-2	863.69	863.69	<1	863.69	863.69	<1
50-3	743.94	743.94	<1	743.94	743.94	<1
100-1	876.69	876.69	7	876.69	876.69	10
100-2	657.35	657.35	<1	657.35	657.35	<1
100-3	722.87	722.87	<1	722.87	722.87	<1
200-1	809.90	809.90	23	809.90	809.90	20
200-2	736.23	736.23	2	736.23	736.23	7
200-3	792.71	792.71	17	792.71	792.71	32
300-1	796.15	796.60	288	796.65	796.69	282
300-2	741.02	741.72	257	741.02	741.02	273
300-3	819.76	819.76	171	819.76	819.84	484
400-1	796.70	797.42	435	796.70	797.34	500
400-2	779.63	780.64	477	779.63	780.40	525
400-3	814.14	816.62	589	815.03	817.09	567
500-1	792.32	793.49	469	792.21	793.73	808
500-2	779.35	779.92	465	779.35	780.31	652
500-3	808.64	810.00	538	809.69	810.34	670
average	776.60	777.07	207	776.73	777.11	268

Table 8. Comparison of fast neighborhood evaluation experiments

instance	Target results	Method 1 time	Method 2 time
50-1	647.75	<1	<1
50-2	903.37	<1	<1
50-3	751.24	<1	<1
100-1	876.69	13	3
100-2	657.35	1	<1
100-3	722.87	1	<1
200-1	809.90	10	1
200-2	736.23	10	1
200-3	797.11	85	15
300-1	798.18	136	22
300-2	745.29	28	3
300-3	827.56	447	77
400-1	803.07	288	36
400-2	785.63	411	61
400-3	825.07	448	72
500-1	801.36	200	23
500-2	780.03	372	56
500-3	818.49	315	20
average	782.62	153	21

Table 9. Comparison of Disturbance Strategy Experiments

	Using Perturbation		Without Perturbation
instance	best	average	best	average
50-1	647.75	647.75	647.75	647.75
50-2	863.69	863.69	903.37	903.37
50-3	743.94	743.94	751.24	751.24
100-1	876.69	876.69	876.69	876.69
100-2	657.35	657.35	657.35	657.35
100-3	722.87	722.87	722.87	722.87
200-1	809.90	809.90	809.90	809.90
200-2	736.23	736.23	736.23	736.23
200-3	792.71	792.71	792.71	794.27
300-1	796.29	796.62	796.70	799.93
300-2	741.02	741.02	743.99	744.87
300-3	819.76	819.76	822.70	828.09
400-1	796.70	797.84	802.80	805.29
400-2	779.63	781.21	782.98	786.56
400-3	814.14	816.47	824.31	825.71
500-1	792.65	793.55	799.82	806.55
500-2	779.35	779.65	780.03	784.35
500-3	808.64	809.92	811.63	817.03
average	776.63	777.07	781.28	783.23

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dual Neighborhoods Search for Solving The Minimum Dominating Tree Problem

Abstract

1. Introduction

2. Dual Neighborhood Search

2.1. Main Framework

2.2. Initial Solution Generation

2.3. Definition

2.4. Neighborhood move and Evaluation

2.5. Fast Neighborhood Evaluation

2.5.1. Fast evaluation for A 1

2.5.2. Fast evaluation for A 2

2.6. Tabu strategy and aspiration mechanism

2.7. Perturbation Strategy

3. Algorithm Experimentation

3.1. Datasets and Experimental Protocols

3.2. Calibration

3.3. Comparison on DTP Data Set

3.4. Range Dataset Experiments

4. Analysis and Discussion

4.1. The Importance of the Initial Solution

4.2. The Importance of the Fast Neighborhood Evaluation

4.3. Importance of the Perturbation

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

2.5.1. Fast evaluation for $A_{1}$

2.5.2. Fast evaluation for $A_{2}$