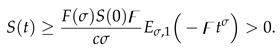1. Introduction
Whooping cough is a highly contagious disease that is caused by a bacterium called Bordetella pertussis. Many outbreaks of the disease have occurred in different parts of the world. The history of the disease dates back to late fifteenth century [
1]. However, the first recorded outbreak was witnessed in France in 1578. In 1947, a major whooping cough epidemic occurred in Cape Town that registered 107 deaths [
2]. In early 2010, a outbreak occurred in USA, Ireland and Israel. More than 10,000 whooping cough cases were reported in California in 2014 and it was declared as the worst outbreak since 1947. According to a report that published in 2014, there were around 24.1 million cases of whooping cough with 160,700 deaths in younger children around the world [
3,
8]. According to WHO, there were more than 151,000 pertussis cases worldwide in 2018 [
3].
Whooping cough is an extremely infectious disease that has become a serious threat to people of all ages specially dangerous to children younger than 5 years. The disease spreads from one infected person to another susceptible person through the droplets released by sneezing or coughing. The symptoms of whooping cough appear gradually and can stay for few weeks to months. Once a person is caught by infection, the first disease symptoms appear within 7 to 10 days. Early stage common symptoms are minor fever, stuffed or runny nose and cough. At this level, it is not easy to apart it from common cold. After early stage symptoms, the coughing fits start that gradually turns into hacking cough, which is followed by whooping. Sickness, vomiting and difficulty in breathing are the other symptoms of disease. The people who contract infection become infectious up to three weeks. Quarantining such people may help to restrict the spread of disease. The risk of complications and the spread of the virus to others can be reduced with early whooping cough diagnosis and treatment. Whooping cough vaccines also provide the highest level of protection against this highly infectious disease.
Whooping cough is still one of the leading causes of death and illness especially in infants around the world. The disease is on the rise again in many parts of the world, including the USA, Australia and the Great Britain. There is no definite explanation for this rise, but it’s thought to be caused by the vaccine losing its effectiveness, the bacterium becoming more aggressive, and improved diagnostics that have resulted in more cases being diagnosed. It is therefore necessary to develop mathematical models that can be used to forecast dynamics of the whooping cough disease and also to propose strategies for eliminating the disease in the most effective manner. In the existing literature, there are very few mathematical models that have been designed for whooping cough to study its dynamics and to propose effective control strategies. In [
4], an effective numerical scheme was presented to simulate second order whooping cough model. In 2018, the authors conducted a study on the cost-effectiveness of maternal vaccination for whooping cough in Australia [
5]. Whooping cough model with optimal vaccination control was studied in [
6]. A whooping cough model was proposed in [
7] to analyze the disease transmission in Nebraska. An implicit numerical integration method was established in [
8] to ensure a consistent dynamic convergence of the SEIR model for the whooping cough epidemic. In [
9], ABC fractional derivative is employed to model phytoplankton nutrient and whooping cough epidemics. The authors, in this article, used homotopy perturbation Elzaki transform method for numerical solutions and proved that the implemented method is an effective technique to handle such fractional models. In all of the above articles, no one has used fractional modeling for whooping cough with optimal control analysis.
Mathematical modeling is a powerful tool for predicting the dynamics of communicable disease with prevention measures. The differential equations for the epidemiological compartmental models have symmetry in the sense that these are constructed on the principle that the rate of change of individuals in a particular compartment is equal to the incoming individuals minus the outgoing individuals. In recent years, many scientists have begun to use fractional models with different fractional operators to include memory effects for better epidemiological disease analysis [
10,
11,
12,
13,
14,
15,
16,
17,
18]. Fractional operators have a wide range of uses in modern mathematics, including the complex and significant study of symmetric systems. Furthermore, fractional models work better and are more consistent with the real data. In this study, we develop a new Atangana-Baleanu-Caputo (ABC) fractional whooping cough model, SVEIQR, with an aim to evaluate the effectiveness of different disease control strategies, including vaccination of susceptible and the isolation of infected individuals, and to observe the influence of fractional order on disease dynamics. The reason of choosing ABC operator for the proposed model is due to its non-local and non-singular kernel. In addition to this, the operator has the ability to capture higher susceptibilities and less infections as compared to other fractional operators, such as Caputo and Caputo-Fabrizo [
19]. First of all, we will examine validity of the proposed model by proving basic properties of the model, such as existence of positive and bounded unique solution, local and global stability analysis at equilibrium points. In addition, this article contributes to the development of a fractional optimal control problem to identify optimal vaccination and quarantine rates that will help to limit the spread of whooping cough infection. Symmetry analysis is a robust tool to come up with numerical solutions for a certain fractional differential equations. In this study, we implement Toufik-Atangana type numerical scheme for numerical simulations of state and adjoint equations.
The other sections are organized as follows: In
Section 2, we describe the formulation of a
fractional model to express dynamics of whooping cough disease. The formulation is given with the help of the Atangana-Baleanu fractional derivative. Theoretical aspects of the proposed fractional model are discussed in
Section 3, including the existence and uniqueness of the solution, the positivity and boundedness of the solutions, the calculation of equilibrium points and the determination of fundamental reproduction number
, the analysis of local and global stability at equilibrium points. In
Section 4, Toufik-Atangana type numerical scheme is established and implemented to observe the impact of fractional order on disease dynamics. The effect of vaccination and quarantine rates on disease transmission is also simulated here. In
Section 5, we provide sensitivity analysis to identify extremely sensitive parameters for reproduction number
. In
Section 6, the model is further modified with time dependent controls to form an optimal control problem. The associated optimality conditions arising from Pontryagin’s principle are then numerically solved by applying the Toufik-Atangana numerical scheme for determining the best time-dependent vaccination and quarantine rates for whooping cough control. The results of this study are concluded in
Section 7.
2. Model formulation
Mathematical models of infectious diseases play a vital role in understanding disease flow patterns and in designing appropriate disease control strategies. Therefore, while developing a mathematical models for infectious diseases, it is very important to focus on procedures needed in formulating the epidemiology of the disease and to identify the most important and controllable parameters disease control. A variety of epidemiological models have been developed on the basis of disease transmission mechanism and are available in literature, see [
20,
21,
22,
23,
24,
25,
26,
27]. These models have played a significant role in formulating and designing control strategies for different diseases.
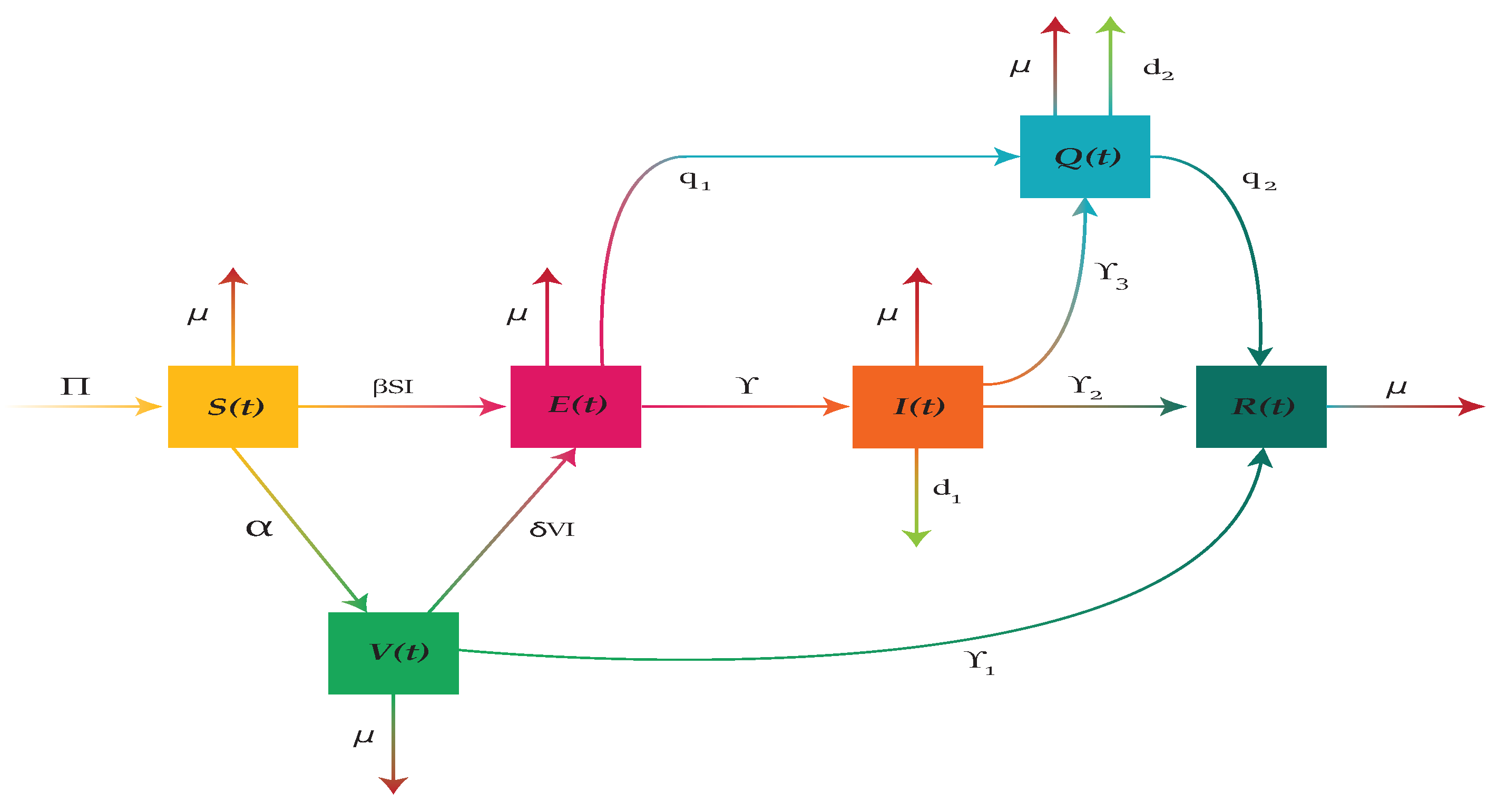
In this study, we develop a new SVEIQR model for whooping cough infectious disease. The aim is to study the disease dynamics comprehensively and to formulate the most suitable control strategies to restrict spread of the disease. We divide the total human population
into six compartments: susceptible
, vaccinated
, exposed
, infected
, quarantined
and recovered
. The humans specified by
are those who are at the risk of getting virus after having contact with an infectious person. Thus, the susceptible who caught by virus move to exposed class
and those who are vaccinated at the rate
move to
. The vaccinated individuals may either move to recovered class
at the rate
or to exposed class
after getting infection as a result of having contact with an infectious person. The exposed individuals who become infectious move to infected class
at the rate
. To restrict the spread of disease, we introduce an isolation compartment
in the model. The individuals from exposed and infected classes are transferred to quarantined class
at rates
and
respectively. The individuals of
and
classes who recovered either by medication or by their natural immunity move to recovered class
respectively at the rates
and
. The rates at which infected and quarantined die due to disease are
and
. Thus, the whole human population at any time
t is given by
The whooping cough disease flow pattern given in
Figure 1 is governed by a mathematical model consisting of the following nonlinear system of coupled ordinary differential equations:
subject to the conditions:
2.1. Fractional model
Generally, classical integer order models are neither robust nor more useful for understanding the dynamic behavior of an infectious disease. On the other hand, fractional order models work more appropriately with the real data. Hence, to generalize the system (2) for whooping cough, we use fractional Atangana-Baleanu derivative
, defined in (
3), in place of the classical integer order time derivative
. This fractional order formulation will allow us to observe memory impacts and gain further insight into disease dynamics. For the fractional formulation, we first consider some basics related to Atangana-Baleanu fractional derivatives [
28].
Definition 1.
[28] If the differentiable function is defined on such that , and , then the Atangana-Baleanu derivative of Φ in Caputo sense is defined as:
where is a well-known one parameter Mittag-Leffler function and is a normalizing function such that .
Definition 2.
[28,29] An ABC fractional integral with non-local kernal is defined by
For
and
, the proposed nonlinear fractional order model for whooping cough in the sense of ABC-fractional operator is given as:
with conditions:
The system (5) is an autonomous, hence it can be written in the following compact form:
along with
where
and
are vector valued functions given as:
3. Theoretical analysis of the proposed model
This section is devoted for a comprehensive theoretical analysis of the proposed fractional model (6) where we investigate some key characteristics of the model and show that the model is well-posed for numerical approximations.
3.1. Existence and uniqueness of solution
First of all, we prove that the solution of model (6) exists and is unique. We make use of some basic definitions and theorems stated in [
30] to prove the existence and uniqueness of solution of the proposed fractional model.
Theorem 1. [30] Every contractive sequence is a Cauchy sequence, and therefore convergent in complete metric space.
Theorem 2.
[31] Let and be a continuously differentiable mapping, . Then, Ψ satisfies a Lipschitz condition on each convex compact subset of B with Lipchitz constant L. Where is the supremum of the derivative of Ψ on , i.e.,
Theorem 3. The function in equation (6) is Lipschitz continuous.
Proof. Let
be a convex compact subset of
Let
, then by mean value theorem ∃
such that
or
Since
, hence over convex compact set
, ∃ a constant
such that
hence,
Thus, is Lipschitz. □
Theorem 4.
Suppose that the function satisfies the Lipschitz condition
then the problem (6) has a unique solution for
Proof. We shall prove that the function
satisfies equation (6) if and only if it satisfies the relation
Let
satisfies equation (6). We apply Atangana-Beleanu fractional integral (
4) to both sides of (6) to get
Simplification yields us the integral equation:
Now for converse, we suppose that
is a sequence of solutions that converges to the solution (
7) with Picard successive iteration, i.e.
First of all we show that the sequence (
8) is contractive if
where
and
.
Using Lipchitz property of function
, we get the following expression:
where
This implies that
Thus from equation (
9), sequence (
8) is contractive, hence Theorem 1 implies it is a Cauchy sequence. Now for
and
,
Right hand side is a geometric series which is always convergent for
.
Since
,
. Therefore, we infer that sequence
is Cauchy and hence by a theorem from [
30] it is convergent. Let
, then equation (
8) gives
which is the required solution.
Uniqueness For uniqueness of the solution, we assume on contrary that the sequence
converges to two limits
and
such that
. Then, there exist
such that,
Let
. Then,
which implies,
Hence, it is proved that the solution (
10) is a unique solution of (6) or equivalently of the system (5). □
3.2. Boundedness and positivity of the solutions
Next, we prove another property of the model, i.e. we prove that the model (5) has a positive and bounded solution for .
Theorem 5. The solution of the model (5) is bounded.
Proof. Applying Atangana-Baleanu-Caputo derivative operator
to (
1), we have
Since
, so
We apply Laplace transform on both sides of the above inequality to obtain:
and
where
represents the initial value of the total population.
Inequality (
11) is solved to get:
where
.
Application of inverse Laplace transform on both sides of (
12) gives us:
Since the Mittag-Leffler function
is bounded for all
, so possess an asymptotic behavior [
32]. It is obvious from (
13) that
as
. Thus,
and all other variables of the model (5) are bounded. □
Theorem 6. The solution space of the system (5) will remain positive forever with any positive initial conditions.
Proof. Let us consider equation (26a) of the model (5).
We have proved that the solutions of model (5) are bounded, so we can take
as a constant. Then,
Now, applying the Laplace transform on both sides of (
14), we obtain
This can be solved to get
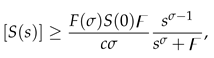
where
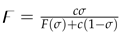
.
Now applying inverse Laplace transform in the above inequality and using property of Mittage-Laffler function, we obtain
Thus, the solution variable for all . Similarly, it can be proved that other state variables are also positive for all corresponding to any non-negative initial data. Thus, the solutions in remain positive forever. □
On the basis of above results, the feasible invariant region is defined as
with non-negative initial conditions in
.
3.3. Equilibrium points and threshold parameter
Equilibrium points represent the steady-state prevalence of the disease, where the number of new infections is balanced by the number of recoveries and deaths. We find equilibrium points of the model (5) by solving corresponding steady state equations. To find steady state equations, we put
in system (5).
3.3.1. Disease free equilibrium point
When no one is infected, the state is known as disease-free state and the corresponding equilibrium point is called disease free equilibrium (DFE) point. So to get DFE point, we put
in steady state equations of model (5) and solve them to get following DFE point.
It is to be noted that .
3.3.2. Reproduction number
The reproduction number is a mathematical term used to describe contagiousness of an infectious disease. Specifically, it represents the average number of new infections that will occur as a result of each infected individual. If the reproduction number is high, it means that the disease is very contagious and will likely require significant interventions to restrict its spread.
We implement the next-generation matrix method [
33] to find
. The recruitment of new infections, and the inside and outside transmission terms of infected compartments are respectively represented by the following matrices
and
, i.e.
The jacobian of
and
evaluated at
are respectively given as:
Reproduction number
is computed as the spectral radius of the matrix
. Thus,
where
,
,
,
. The disease is contiguous and spreading in population if
.
3.3.3. Endemic equilibrium
The other equilibrium point where disease is constantly present in the system is called the endemic equilibrium (EE) point. With the consideration that
, the steady state equations of model (5) are solved to get following EE point.
where
3.4. Stability analysis
Now, we discuss local and global stabilities of model (5) at equilibrium points
and
. For local stability, we check signs of eigenvalues of the Jacobian matrix computed at equilibrium points whereas for global stability, we implement the Lyapunov theory with LaSalle invariance principle [
34] and the Castillo-Chavez theory [
35].
3.4.1. Local stability
In epidemiological models, local stability at equilibrium points is an important concept for understanding the behavior of infectious diseases and how they spread through a population. This section investigates the local stability of the whooping cough model (5) at the DFE point and EE point .
Theorem 7. If model (5) is locally asymptotically stable at and unstable if .
Proof. The model (5) at disease-free equilibrium
corresponds to the following jacobian matrix:
Eigenvalues of the Jacobian matrix
are given as:
Here,
for
when
. Therefore, the system (5) is locally asymptotically stable at the point
. If
, the eigenvalue
with a positive sign demonstrate the model’s local instability at
. □
Theorem 8. If model (5) is locally asymptotically stable at and unstable if .
Proof. The model (5) at endemic equilibrium
corresponds to the following jacobian matrix:
We determine following eigenvalues of the jacobian matrix
.
After plugging in the values of parameters and endemic equilibrium point, the eigenvalue is approximated to give , a negative eigenvalue. Hence, all of the eigenvalues for are less than zero for . Therefore, at the endemic equilibrium point , the system (5) is locally asymptotically stable. □
3.4.2. Global stability
To demonstrate that the model (5) at DFE state is globally stable, the Castillo-Chavez [
35] approach is applied. Using the technique introduced by Castillo-Chavez et. al., we reproduce our model in the form of following equations.
Where the number of persons who are not affected is indicated by
and
indicates the number of individuals having infection. The last equation of the model is ignored since it is independent to the rest. Here,
is the disease free equilibrium point. To verify that the DFE point is globally asymptotically stable (GAS) by the Castillo-Chavez technique, following two requirements must be fulfilled.
where
is an M-matrix, and
represents the model’s feasible region. Thus according to Castillo-Chavez et. al., when the system of equation (
18) satisfies the conditions (C1) and (C2) the following theorem holds valid.
Theorem 9. The DFE point is GAS if in the region Ξ and the conditions (C1) and (C2) are satisfied.
Proof. Suppose
represents uninfected individuals, while
symbolize the states haveing infection, and
is the DFE. Then,
At
, we get
where
. Thus,
is GAS.
Now,
where
Matrix
is clearly a M-matrix. As at DFE point
and
, therefore
. Consequently, DFE point
is GAS. □
Theorem 10. The endemic equilibrium (EE) point is globally stable if and unstable if .
Proof. Assume that the basic reproductive number
so that the endemic equilibrium point exist’s. We now develop a Volterra type Lyapunov functional
givrn as
Applying
on both sides, we get
Equations from the model (5) are used to obtain
After rearranging the terms, we obtain
It is now easier to write it as:
where
Since all of the parameters in model are non-negative, we have
when
and
iff
. The later case implies that
,
,
,
,
, and
. Thus, by LaSalle’s invariance principle, the EE point
is GAS. □
4. Numerical investigations and implementations
To approximate solution of the proposed ABC fractional model for whooping cough, we use the Toufik-Atangana scheme [
36,
37] with MATLAB code. We employ the technique to investigate the dynamical behaviour of the whooping cough pandemic over time t for various fractional order values
.
4.1. Toufik-Atangana discretizations
In this section, we present a brief overview of the numerical scheme that will be used to approximate solution of the fractional model (5). Derivation of the scheme is based on the Toufik-Atangana scheme [
36] for fractional differential equations with ABC-derivative operator. Finally, we discretize each differential equation of the model (5).
Application of fundamental theorem of fractional calculus to model (6) gives us:
and in discrete form:
where
.
This can be equivalently put in the form:
We use interpolation polynomial to approximate the function
to get
We substitute approximation of
in (
24) to obtain
The integrals in (
25) are evaluated to get following numerical scheme for the equations of type (6).
Thus, the model (5) in discrete form is given as:
For numerical simulations, we shall consider days as time unit. The model parameters are assigned following appropriate numerical values: where is natural death rate, and are disease induced death rates respectively of infected and quarantined individuals.
4.1.1. Fractional order effect on disease dynamics
We employ the aforementioned approximations to present a graphical representation of the proposed fractional model and investigate the influence of order on solution curves.
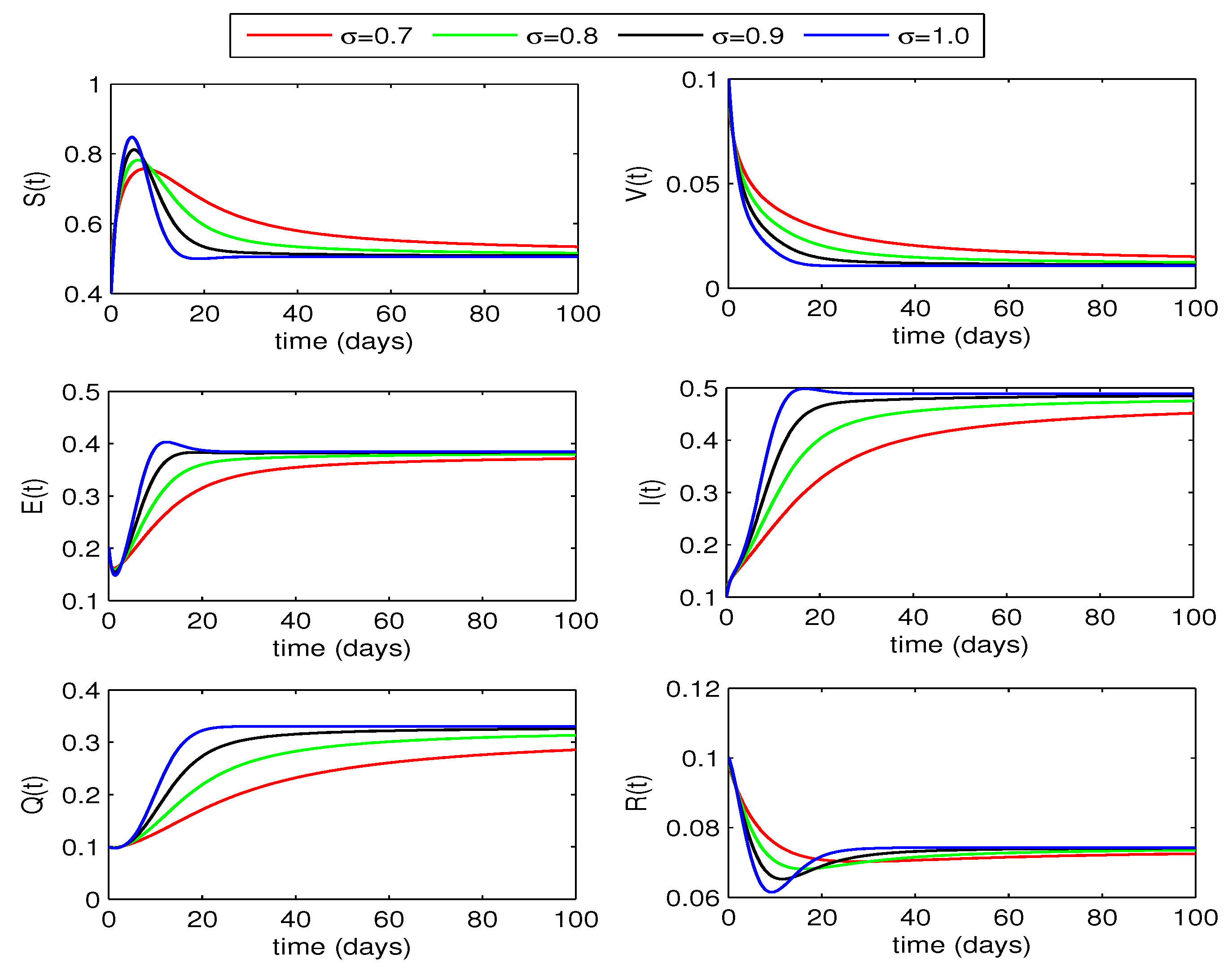
From graphical curves of the state variables shown in
Figure 2, we observe a decrease in exposed, infected and quarantined individuals with decrease in the fractional order of the differential equations. However, the susceptible increase with decrease of fractional order. Thus, reduction in fractional order values will help to reduce the whooping cough infection in humans.
4.2. Quarantining effects on disease dynamics
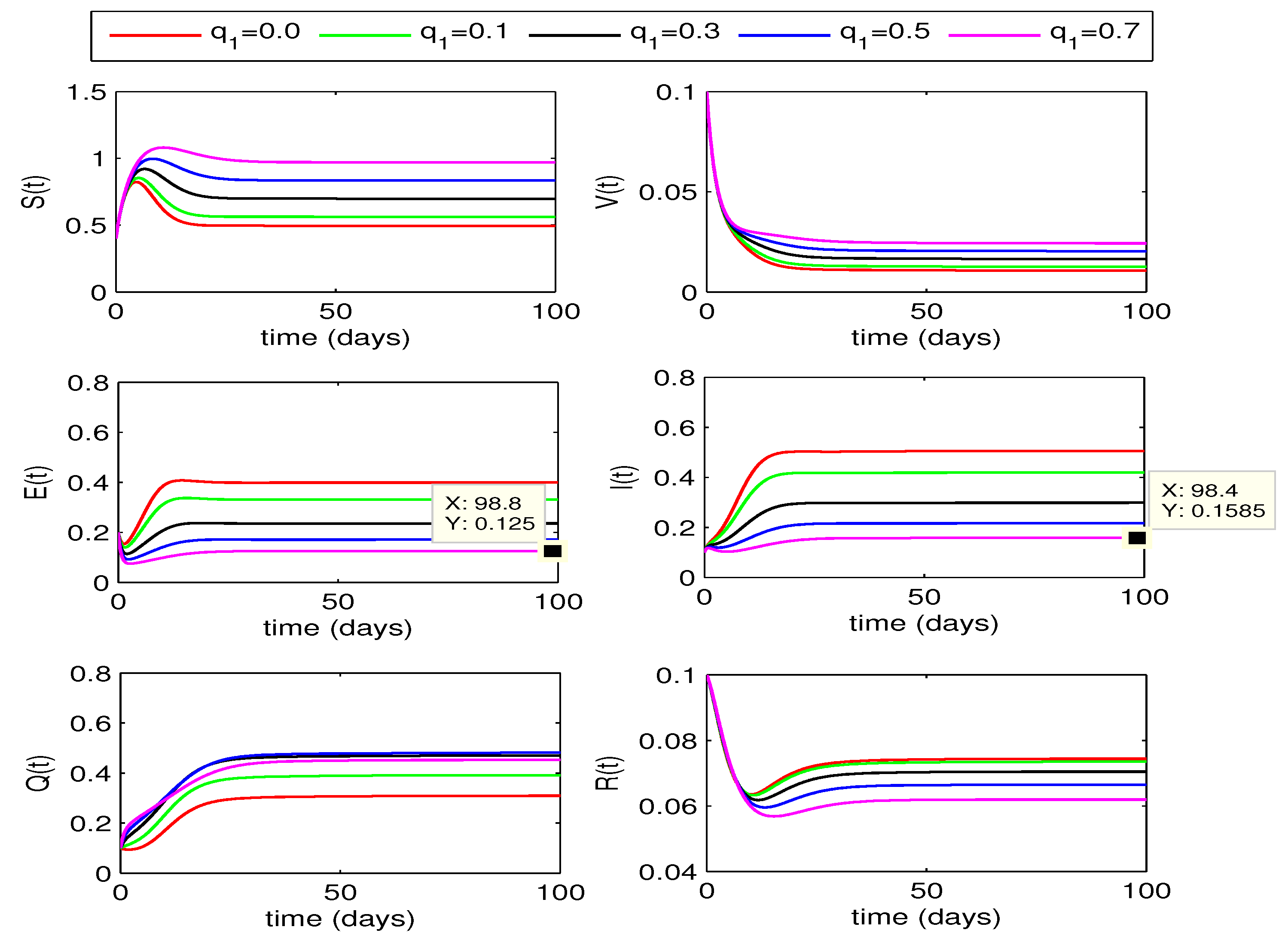
In model formulation, we had considered quarantining both of the exposed and infected individuals respectively at rates and . So in this section, we study the effect of both of the rates on disease control for two different values of fractional order, i.e. for and .
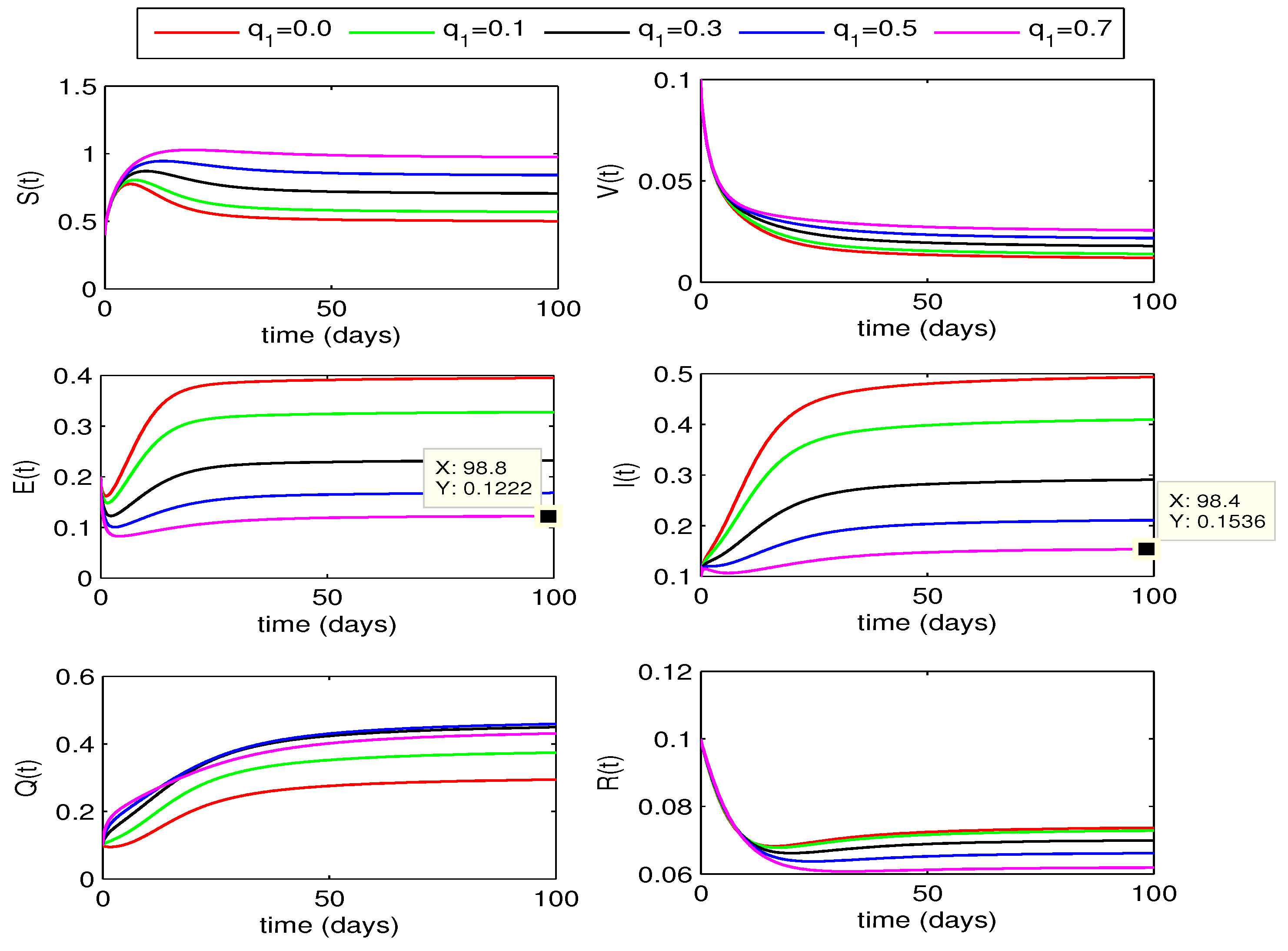
4.2.1. Effect of
The impact of quarantining exposed individuals on disease dynamics can bee seen in
Figure 3 and
Figure 4. The curves for exposed and infected individuals decrease with increase in the quarantine rate
from 0 to 0.7. In this case, the recovered individuals also decrease but susceptible rise with increase in the value of
. We also observe that for
, the decline in infection is more as compared to the corresponding curves for fractional order
.
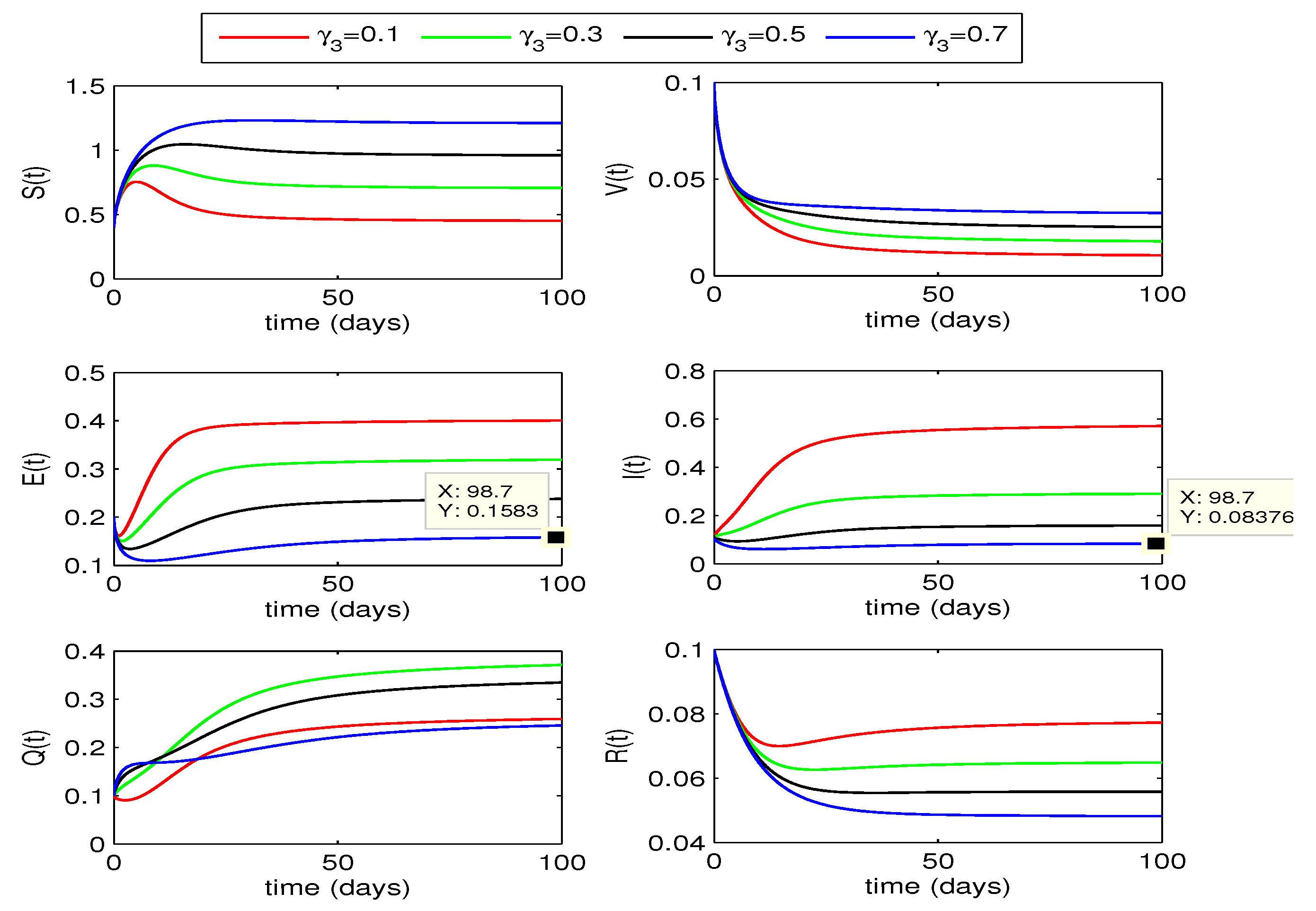
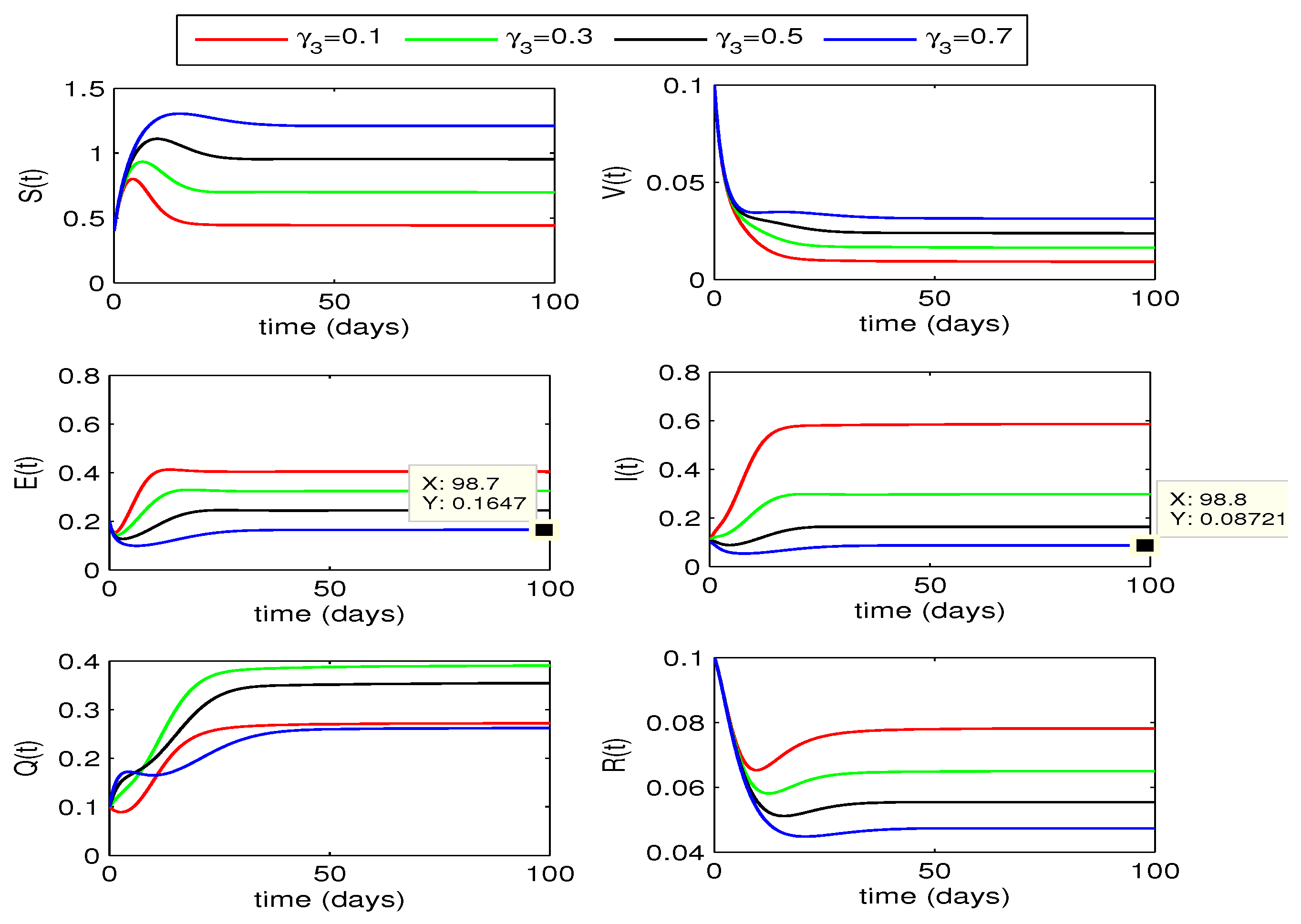
4.2.2. Effect of
The impact of quarantining infected individuals,
, on disease dynamics can be seen in
Figure 5 and
Figure 6. If the quarantining rate
is gradually increased up to 0.7, the curves for exposed and infected individuals gradually decrease. From this declining behavior, we may conclude that the disease may move to disease free state if the quarantining rate is increased further. Decline in infection for for fractional order
is more as compared to the case for
.
From the above two quarantining studies, we observe that the quarantine rate has more effect in reduction of exposed cases, whereas the impact of quarantine rate is more on infected individuals.
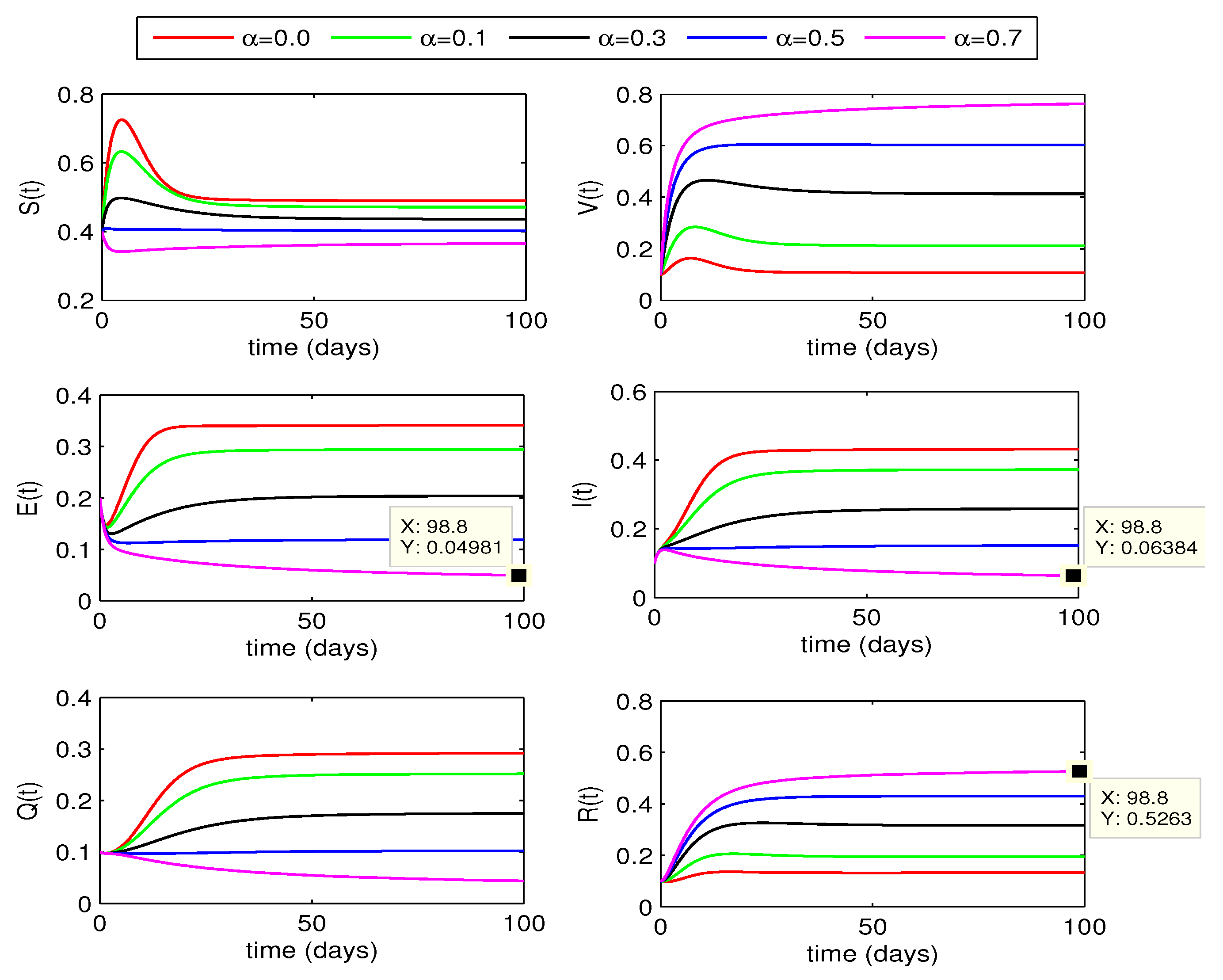
4.3. Vaccination effect on disease dynamics
In this section, we look at how varying vaccination rates affect the dynamics of the whooping cough model quantitatively. From
Figure 7 and
Figure 8, we observe that the infection in population decreases as the vaccination rates increase from 0 to 0.7. If the rates are increased further, the curves for infected classes may further decline to move to disease free state. We also notice a remarkable rise in the recovered individuals in this case. The curves for exposed and infected individuals slightly decline more with increase of fractional order
.
5. Sensitivity analysis
In this section, we find sensitivity index for each parameter of the reproduction number . One the basis of these indices we determine the sensitivity of the parameter to . A parameter with high index value is more sensitive to . The sensitivity analysis may be helpful in designing optimal control strategies for disease control. Parameters having high sensitivity indices may be considered as control variables for the control problem.
We implement the approach given in [
38] to compute sensitivity indices of the parameters of
. The approach is to use the following formula to compute sensitivity index of a parameter
of
.
Evaluated sensitivity indices for each parameter of
are listed in
Table 1. Other than
and
, transmission rate
has the highest sensitivity index. Thus, this parameter is highly sensitive to
. A unit change in
will produce a change of
in
. Other parameters having comparatively high sensitivity index are
and
. Since
is a controllable parameter, it will be considered as one of the control variable for disease control strategy.
6. Optimization of the whooping cough model
In this section, we construct an optimal control problem with an objective to determine optimal quarantine and vaccination rates to restrict the spread of whooping cough infection. For this, we first update the disease model (5) to adjust time dependent controls and then define objective functional. We formulate Hamiltonain function by introducing adjoint variables and develop optimality conditions by implementing Pontryagin’s principle [
39,
40,
41]. The conditions will be evaluated by following steps of an algorithm to produce optimal solutions of the control problem.
6.1. Optimal control problem and optimality conditions
The objective of defining an optimal control problem is to optimally investigate the effect of quarantining and vaccination on the spread of whooping cough disease. To achieve this objective, we formulate a control strategy for the minimization of exposed and infected individuals at a lowest cost.
First of all, we update model (5) by considering vaccination rate
and quarantining rates
,
as time dependent controls respectively represented by
and
. With these controls, the updated whooping cough model is given below:
along with conditions:
The objective functional consisting of infected states and controls is defined as:
where
is the terminal time,
represent state variables,
represent control variables,
are non-negative weights associated with state variables and
are cost of controls.
Our aim is to determine optimal control variable
that minimizes the objective functional
, i.e.,
where
is an appropriate space of control variables.
Now, we define a Hamiltonian function and implement Pontryagin’s maximum principle to derive the optimality conditions which are necessary for the solution of optimal control problem (
28).
where
is a vector of state variables,
are adjoint variables associated with the state equations of system (26).
Theorem 11.
[18] Let be the optimal solution for model (26) corresponding to optimal control variable for the control problem (28). Then, there exists a system of linear adjoint equations given as:
along with the conditions:
and the control variable characterized by
Evaluation and simplification of equations (
30a)-(30f) lead us to the following system of linear adjoint equations:
along with the conditions
Differentiation of Hamiltonian with respect to controls give us the expressions for controls, i.e.,
and the optimal characterizations for controls are given as:
To approximate solutions of the state model (26), we employ the Toufik-Atangana method described in sub
Section 4.1, and for the corresponding adjoint system (31), we implement Toufik-Atangana scheme backward in time, together with the conditions (
31g).
6.2. Solution algorithm
Optimality conditions for the control problem (
28) are approximated for optimal solutions by following steps of the algorithm given below.
|
Algorithm 1:Algorithm to find minimizer of the control problem (28) |
- (1)
Make an initial guess for control for . - (2)
Use values of control to approximate solutions of state system (26) and adjoint system (31). - (3)
Determine from (32). - (4)
Refine control by using . - (5)
-
Stop iterations when for ,
otherwise and jump back to step 2.
|
Where represents each of the state variables, adjoint variables and control variables and is the tolerance set as per accuracy requirements.
6.3. Optimal solutions
Simulation results of the optimal control problem (
28) are presented and discussed in this section. To obtain these results, we implemented steps of the Algorithm 1 through MATLAB code. We discretize the domain
into
discrete points
where
and approximate the state and adjoint equations using the approximating scheme, explained in
Section 4.1. We use Simpson’s rule to approximate the cost functional (
27) at the discrete points. Results are simulated for different values of fractional order, i.e., for
.
The objective of this study is to determine the optimal quarantine rates , and the vaccination rate that will not only minimize the cost functional but will also reduce the whooping cough infection in the society. For detailed analysis, we discuss here three different cases. In the first case, we keep quarantine rates , fix in time and determine the optimal vaccination rate for disease control. In second case, we determine the best quarantine rates , that will reduce the spread of whooping cough infection. In this case, vaccination rate will be considered as time independent. In the last strategy, we deal with time-dependent vaccination rate and quarantine rates together to determine their optimal profiles that will help to reduce the cost functional to its minimum and to curtail the whooping cough disease infection.
6.3.1. Optimal vaccination rate
In the first case, we consider optimization of the problem (
28) by considering only vaccination rate
as the time dependent control variable.
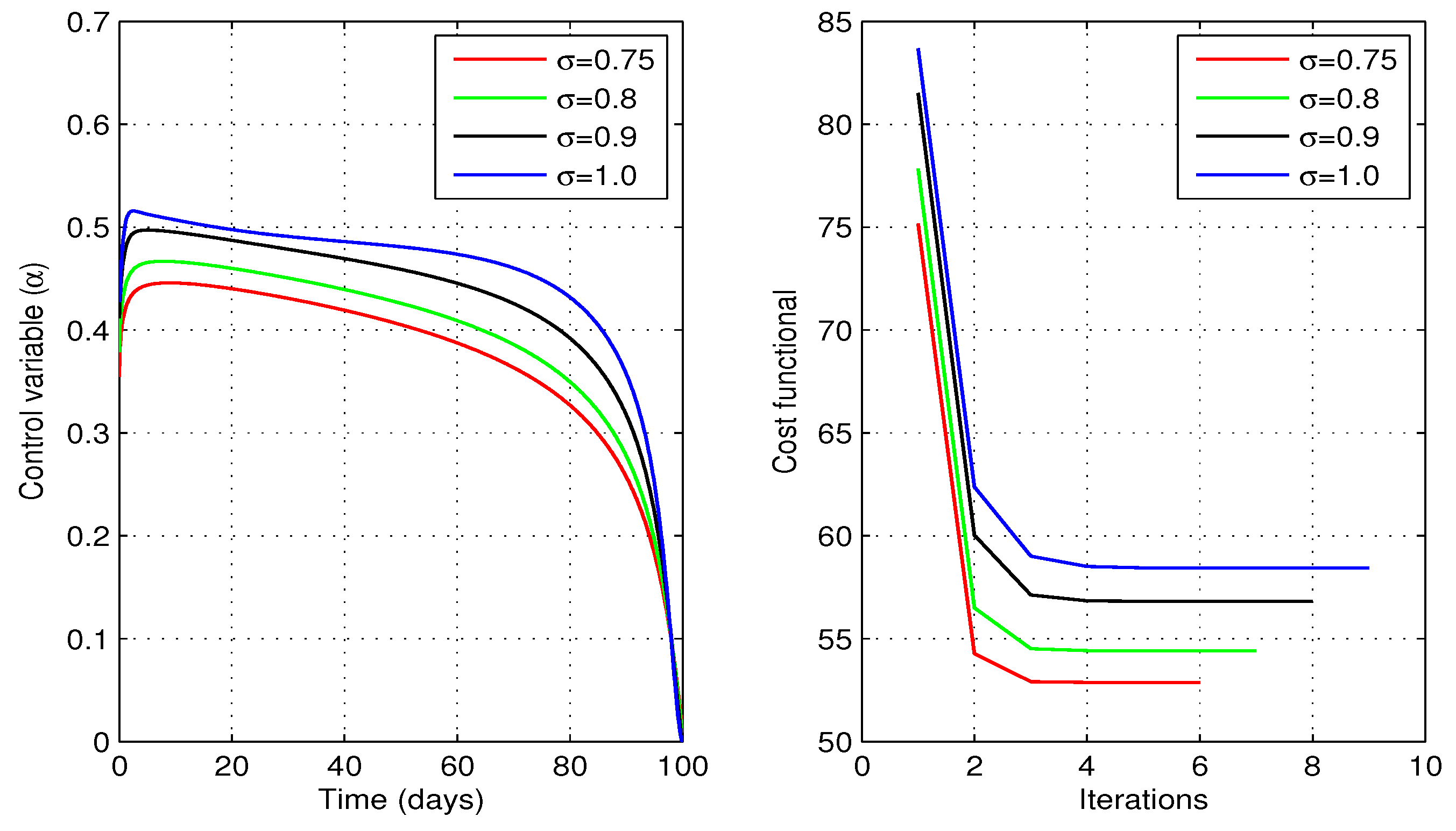
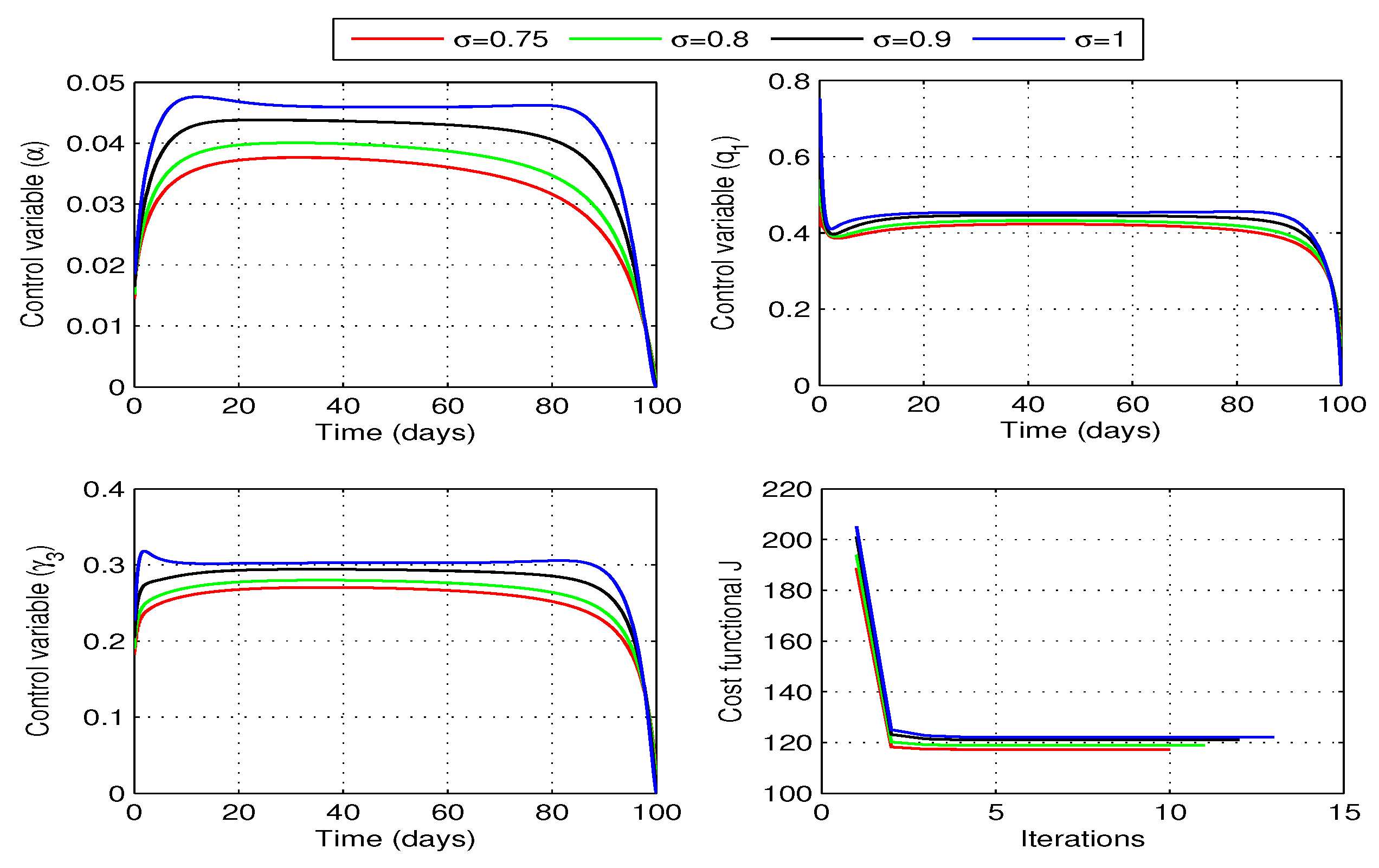
Figure 9 shows profiles of the optimal vaccination rate
and the associated cost functional
J for different values of fractional order
. We observe that the cost functional has attained its minimum for each value of the considered fractional order
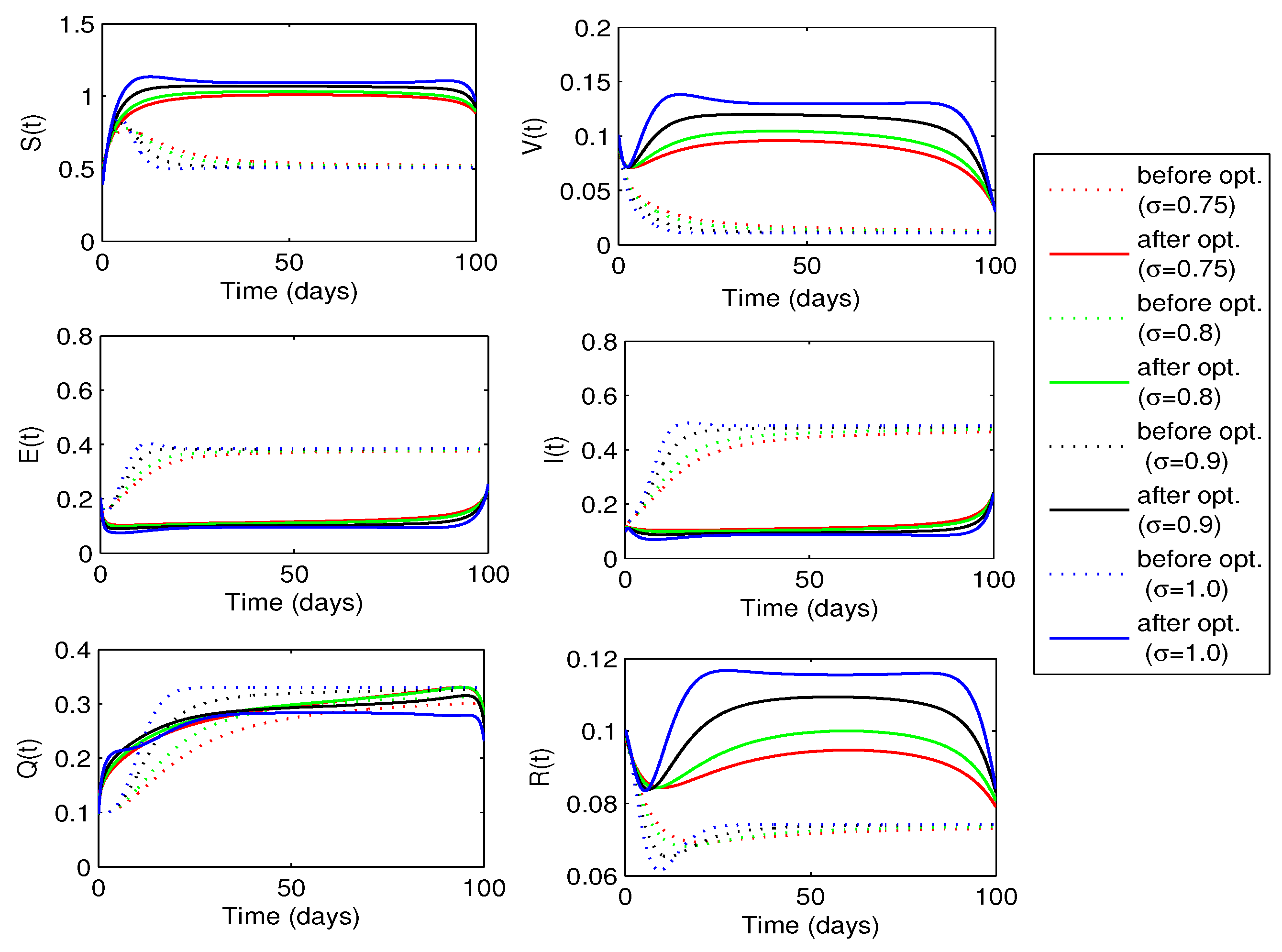
. The behaviors of state variables before and after optimization for each value of the fractional order
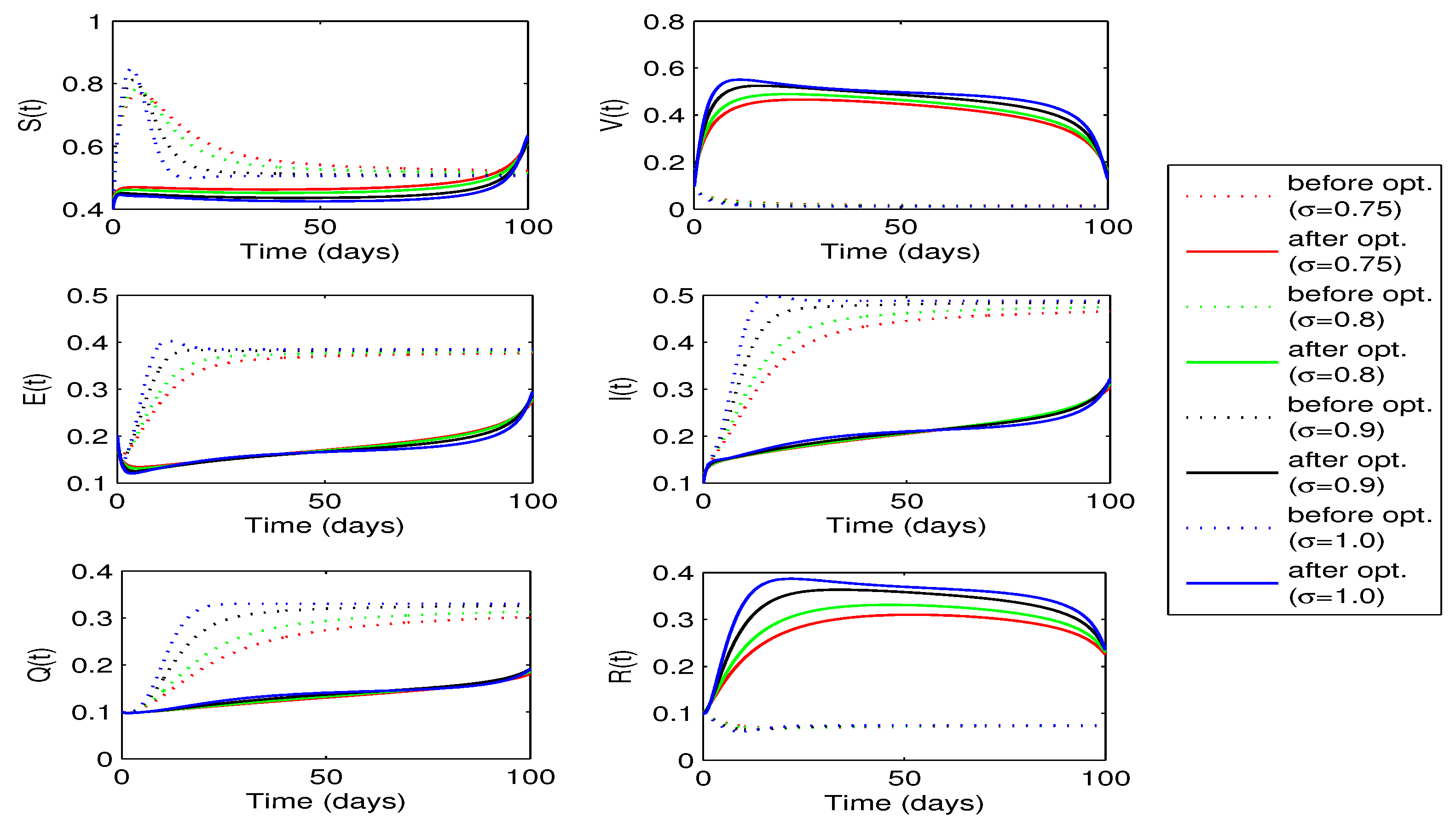
are shown in
Figure 10. A sufficient decrease in the exposed and infected individuals is noticed in this figure, however, there is a significant rise in the recovered individuals. Thus, the strategy is successful in reducing the disease infection and increasing the recovered individuals.
6.3.2. Optimal quarantine rates
Now, we take quarantine rates
and
as the time dependent control variables for the problem (
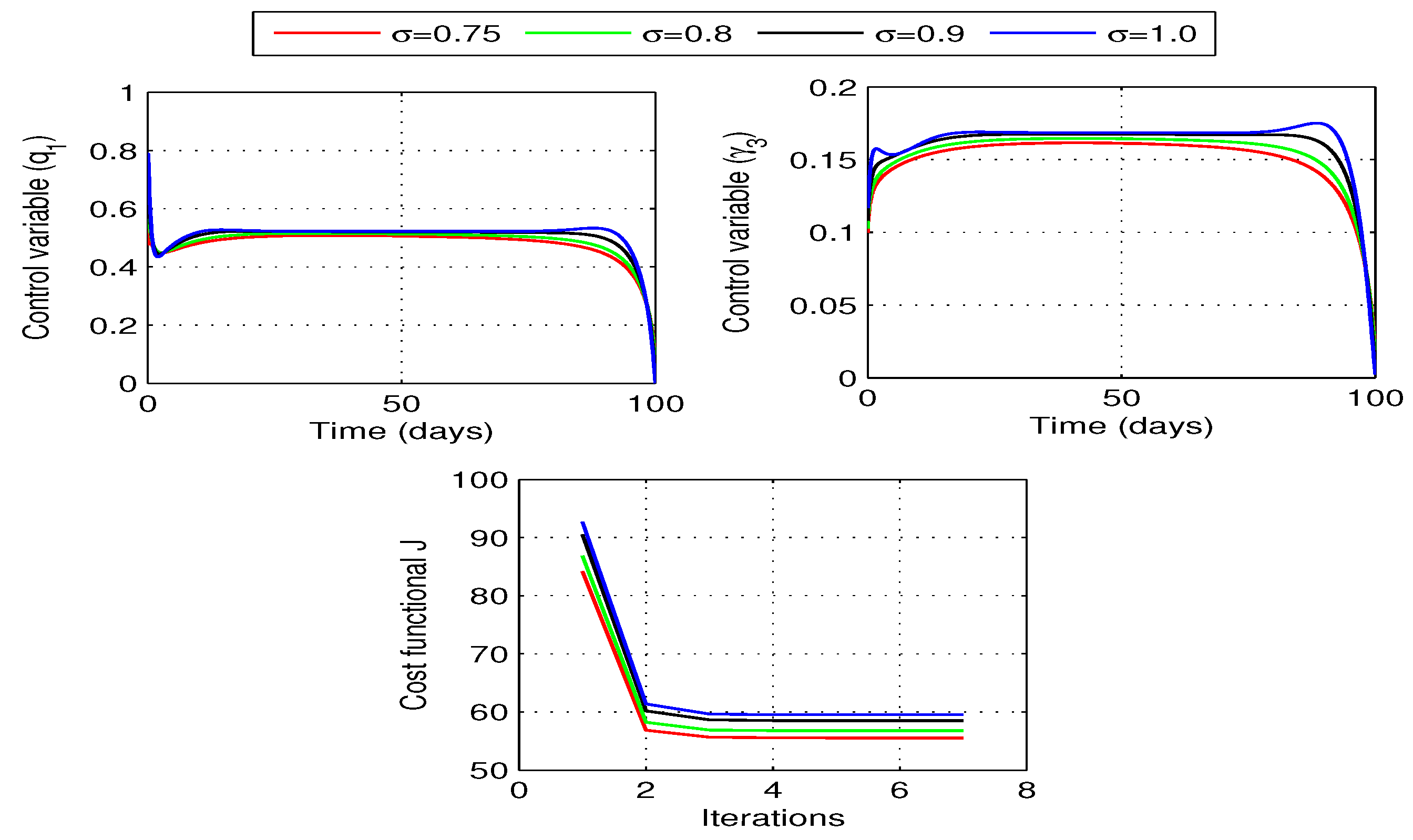
28). Optimal curves for the control variables and the corresponding behavior of cost functional for different values of fractional order are shown in the
Figure 11. In each case, the curves for cost functional reaches to their minimum in seven iterations.
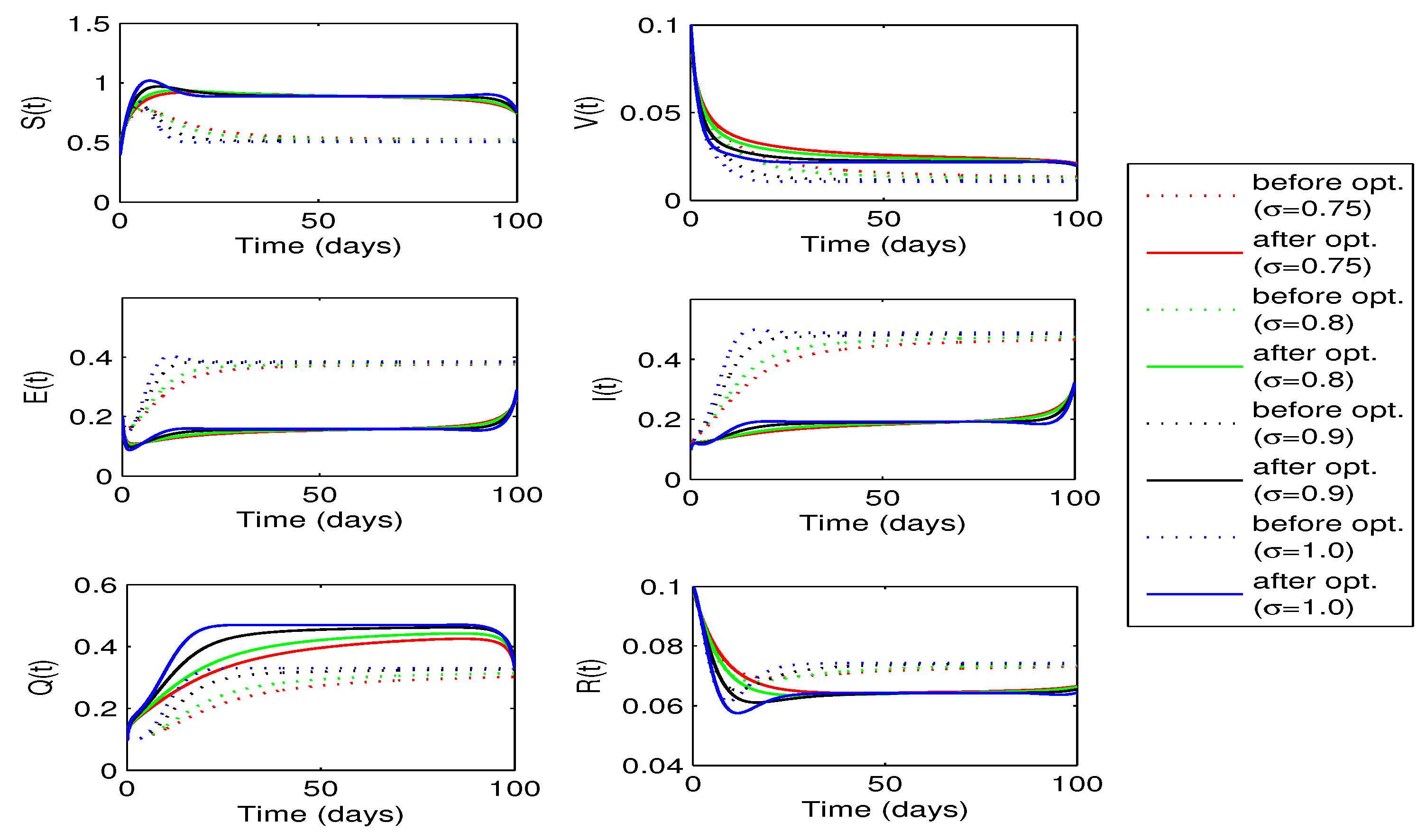
Figure 12 shows the curves for state variables before and after optimization. Once again we observe a decrease in the number of exposed and infected individuals in this case. However, decrease in this case is slightly more as compared to the when only vaccination rate
is considered as a single control variable. We also notice a decrease in the number of recovered individuals but increase in the susceptibles for each value of fractional order
.
6.3.3. Optimal vaccination and quarantine rates
In the last case, we consider vaccination rate
and the quarantine rates
as control variables for the optimal control problem (
28). For this case, optimal behavior of the control variables and minimization of the related objective functional
J are shown in
Figure 13. In this case, the cost functional reduces to its minimum in different number of iterations for different values of fractional order
. However, cost functional takes more iterations to reach minimum value as compared to the last two considerations. Profiles of state variables before and after optimization are shown in
Figure 14. Number of exposed and infected individuals decrease more in this case as compared to the previous two optimal cases. We also notice a sufficient rise in the susceptible and recovered curves for each given value of the fractional order
.
The analysis of the three cases reveals that considering all the three controls together is more effective in reducing the infection of whooping cough disease. However, implementation of this strategy requires more resources and infrastructure as compared to the first two cases.
7. Conclusions
In this work, we formulated a new ABC fractional disease model for whooping cough infection to analyze dynamics of the disease and to suggest optimal control strategies for minimizing effect of the disease. First of all, we analyzed the model theoretically by establishing biologically significant aspects of the model. We proved that the proposed model has a unique solution which is positive and bounded. It is also verified that the equilibrium points are locally and globally stable with restriction to threshold parameter . These results concluded that the proposed model is well-posed for further numerical investigations. Through sensitivity analysis, we determined that the disease transmission rates and , and the quarantine parameter are the most sensitive parameters to . Due to their significant impact on , the parameters may be considered as control variable for optimal control analysis.
Another objective of this study was to suggest an optimal control strategy to restrict the spread of whooping cough infection. For this, we considered vaccination rate and quarantine rates to , to as control variables and studied their impact on disease control. First of all, we took different levels (0 to 0.7) of these parameters and explored impact of each on disease control. We determined that the disease can be controlled significantly by increasing values of these parameters. However, it is concluded that vaccination of susceptible is more effective as compared to quarantining the exposed or infected individuals. The impact of memory index (fractional order) on disease dynamics was also investigated here. We visualized a decrease in the infection cases with a decrease in the memory index.
For optimal control analysis, we considered the parameters and as time dependent controls and formulated an optimal control problem by defining a cost functional. The aim was to determine optimal values of the control variables that minimize the cost functional. By implementing Pontryagin’s principle, we derived necessary optimality conditions for optimal solution of the problem. In this study, we discussed three different optimal control approaches. In the first case, we determined optimal solutions by considering only vaccination rate as the control variable. In the second approach, we considered quarantine rates as the time-dependent controls and determined optimal solutions for the given problem. In the last case, all the three parameters were taken as time-dependent controls for optimal solutions. Graphical results show that each of the considered strategy is very much effective in reducing the exposed and infected individuals and hence may be implemented to reduce the whooping cough infection from the society. The graphical results also revealed that the case where we have considered all the three controls together is more effective in reducing the spread of whooping cough infection. However, implementation of this approach requires more resources and infrastructure as compared to the other two cases. It is also concluded that the simulation results through time-dependent controls are more cost-effective as compared to the results produced by time-independent controls. In future, a Covid-19 and whooping cough co-infection model may be developed and explored for various optimal control strategies with cost-effective analysis.
Funding
Funding is not available so far.
Sample Availability
The data is given with in the article.
References
- H. Bokhari, F. Said, M. A. Syed, A. Mughal, Y. F. Kazi, K. Heuvelman and F. R. Mooi, Whooping cough in Pakistan- Bordetella Pertussis vs Bordetella Parapertussis in 2005-2009, Scandanavian Journal of Infectious Disease 47, No. 2 (2011) 01-03.
- H. R. Joshi, S. Lenhart, M. Y. Li and L. Wang, Optimal control methods applied to disease models in the mathematical studies on human disease dynamics, Contemporary Mathematics 410, (2006) 187-207.
- CDC report on Pertussis (Whooping Cough) in Other Countries, https://www.cdc.gov/pertussis/countries/index.html. Available online: https://www.cdc.gov/pertussis/countries/index.html.
- S. Obaidat, M.R.A. Elrish, S. Mesloub, A second order scheme for the numerical solution of a whooping cough model, Journal of Computational and Theoretical Nanoscience, 14(9):4352-4360, 2017.
- L.A. Van Bellinghen, A. Dimitroff, M. Haberl et.al., Is adding maternal vaccination to prevent whooping cough cost effective in Australia? Human Vaccines and Immunotherapeutics, 14(9), 2263-2277, 2018, doi: 10.1080/21645515.2018.1474315. [CrossRef]
- M. Suleman, An optimal control of vaccination applied to whooping cough model, Journal of Mathematics, 51:121-136, 2019.
- K. Ameri, K.D. Cooper, A Network-Based compartmental model for the spread of whooping cough in Nebraska, AMIA Summits on Translational Science Proceedings, Vol. 388, 2019.
- M.M. Algarni, Arooj Nasir, M.A. Alyami, A. Raza, et. al., A SEIR epidemic model of whooping cough-like infections and its dynamically consistent approximation, Hindawi Complexity, Volume 2022, Article ID:3642444.
- R.M. Jena, S. Chakraverty, S. K. Jena, Analysis of the dynamics of phytoplankton nutrient and whooping cough models with nonsingular kernel arising in the biological system, Chaos, Solitons and Fractals, 141, 2020, 110373,https://doi.org/10.1016/j.chaos.2020.110373. [CrossRef]
- K. Diethelm, A fractional calculus based model for the simulation of an outbreak of dengue fever, Nonlinear Dynam., 71 (2013), 613–619. https://doi.org/10.1007/s11071-012-0475-2. [CrossRef]
- M. A. Khan, S. Ullah, M. Farooq, A new fractional model for tuberculosis with relapse via Atangana-Baleanu derivative, Chaos Soliton. Fract., 116 (2018), 227–238. https://doi.org/10.1016/j.chaos.2018.09.039. [CrossRef]
- S. Ullah, M. A. Khan, M. Farooq, A fractional model for the dynamics of tuberculosis virus, Chaos Soliton. Fract., 116 (2018), 63–71. https://doi.org/10.1016/j.chaos.2018.09.001. [CrossRef]
- H. W. Berhe, S. Qureshi, A. A. Shaikh, Deterministic modeling of dysentery diarrhea epidemic under fractional Caputo differential operator via real statistical analysis, Chaos Soliton. Fract., 131 (2020), 109536, https://doi.org/10.1016/j.chaos.2019.109536. [CrossRef]
- S. Qureshi, Z. N. Memon, Monotonically decreasing behavior of measles epidemic well captured by Atangana-Baleanu-Caputo fractional operator under real measles data of Pakistan, Chaos Soliton. Fract., 131 (2020), 109478,https://doi.org/10.1016/j.chaos.2019.109478. [CrossRef]
- A. I. K. Butt, W. Ahmad, M. Rafiq, D. Baleanu, Numerical analysis of Atangana-Baleanu fractional model to understand the propagation of a novel corona virus pandemic, Alexandria Engineering Journal. (2022) 61, 7007-7027.
- A.I.K. Butt, M. Imran, S. Batool, M. AL Nuwairan, Theoretical Analysis of a COVID-19 CF-Fractional Model to Optimally Control the Spread of Pandemic, Symmetry. (2023), 15, 380. https:// doi.org/10.3390/sym15020380. [CrossRef]
- Asma Hanif, A.I.K. Butt, W. Ahmad, Numerical approach to solve Caputo-Fabrizio fractional model of corona pandemic with optimal control design and analysis, Mathematical Methods in the Applied Sciences. (2023) 1-32, https://doi.org/10.1002/mma.9085. [CrossRef]
- Asma Hanif, A.I.K. Butt, Atangana-Baleanu fractional dynamics of dengue fever with optimal control strategies, AIMS Mathematics. (2023), 8(7): 15499–15535, doi: 10.3934/math.2023791. [CrossRef]
- J. K. K. Asamoah, Fractal fractional model and numerical scheme based on Newton polynomial for Q fever disease under Atangana-Baleanu derivative, Results Phys., 34 (2022). https://doi.org/10.1016/j.rinp.2022.105189. [CrossRef]
- D. Baleanu, A. Jajarmi, H. Mohammadi, S. Rezapour, A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative, Chaos, Solitons & Fractals. 134 (2020) 109705.
- D. Baleanu, F. Akhavan Ghassabzade, J.J. Nieto, A. Jajarmi, On a new and generalized fractional model for a real cholera outbreak, Alexandria Engineering Journal. 61(11) (2022) 9175-9186.
- Ali, I., Khan, S.U, Threshold of Stochastic SIRS Epidemic Model from Infectious to Susceptible Class with Saturated Incidence Rate Using Spectral Method, Symmetry. (2022), 14, 1838. https://doi.org/10.3390/sym14091838. [CrossRef]
- Ishtiaq Ali, Sami Ullah Khan, Dynamics and simulations of stochastic COVID-19 epidemic model using Legendre spectral collocation method, AIMS Mathematics. (2023), Volume 8, Issue 2: 4220-4236. doi: 10.3934/math.2023210. [CrossRef]
- A.I.K. Butt, S. Batool, M. Imran, M. AL Nuwairan, Design and analysis of a new COVID-19 model with comparative study of control strategies, Mathematics. (2023) 11(9) 1978; https://doi.org/10.3390/ math11091978. [CrossRef]
- A.I.K. Butt, D.B.D. Chamaleen, S. Batool, M. AL Nuwairan, A new design and analysis of optimal control problems arising from COVID-19 outbreak, Math Meth Appl Sci. (2023), https://doi.org/10.1002/mma.9482. [CrossRef]
- A.I.K. Butt, M. Rafiq, W. Ahmad, N. Ahmad, Implementation of a computationally efficient numerical approach to analyze a Covid-19 pandemic model, Alexandria Engineering Journal. 69(2023), 341-362, 2023. https://doi.org/10.1016/j.aej.2023.01.052. [CrossRef]
- Begum, Razia; Tunç, Osman; Khan, Hasib; Gulzar, Haseena; Khan, Aziz A fractional order Zika virus model with Mittag-Leffler kernel, Chaos Solitons Fractals. 146 (2021), Paper No. 110898, 11 pp.
- A. Atangana, D. Baleanu, New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model, Thermal Science, 2016; 20(2):763-9.
- A. Atangana, I. Koca, Chaos in a simple nonlinear system with Atangana-Baleanu derivative with fractional order, Chaos Solitons and Fractals, vol. 89, pp:447-454, 2016.
- E. Kreyszig, Introductry functional analysis with application, John Wiley and Sons, New York, 1993.
- V. I. Arnold, Ordinary differential equations, MIT Press, London, UK, 1998.
- A. Atangana, D. Baleanu, New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model, Therm. Sci., 20 (2016), 763–769. https://doi.org/10.2298/TSCI160111018A. [CrossRef]
- O. Diekmann, J. A. P. Heesterbeek, and J. A. Metz, On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations, J. Math. Biol. 28 (1990), 365–382.
- W. Ahmad, M. Rafiq, M. Abbas, Mathematical analysis to control the spread of Ebola virus epidemic through voluntary vaccination, European Physical Journal Plus. (2020), vol. 135, Issue 10, Article no. 775, pp: 1-34.
- Castillo-Chavez, C., Feng, Z., Huanz, W., Driessche, P.V.D., Kirschner, D.E. On the computation of R0 and its role in global stability, In Mathematical Approaches for Emerging and Reemerging Infectious Diseases: An Introduction; Springer: Berlin/Heidelberg, Germany (2002).
- M. Toufik, A. Atangana, New numerical approximation of fractional derivative with nonlocal and non-singular kernel: Application to chaotic models, Eur. Phys. J. Plus, 132 (2017). https://doi.org/10.1140/epjp/i2017-11717-0. [CrossRef]
- M. A. Khan, A. Atangana, Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative, Alex. Eng. J., 59 (2020), 2379–2389. https://doi.org/10.1016/j.aej.2020.02.033. [CrossRef]
- Pauline Van Den Drissche, Reproduction numbers of infectious disease models, Infectious Disease Modelling. (2017) 2,288-303.
- R. Kamocki, Pontryagin maximum principle for fractional ordinary optimal control problems, Math. Method. Appl. Sci., 37 (2014), 1668–1686. https://doi.org/10.1002/mma.2928. [CrossRef]
- S. Lenhart, J. T. Workman, Optimal control applied to biological models, CRC Press, 2007.
- H. M. Ali, F. L. Pereira, S. M. Gama, A new approach to the Pontryagin maximum principle for nonlinear fractional optimal control problems, Math. Method. Appl. Sci., 39 (2016). https://doi.org/10.1002/mma.3811. [CrossRef]
Figure 1.
Flow diagram of whooping cough disease transmission.
Figure 1.
Flow diagram of whooping cough disease transmission.
Figure 2.
Dynamics of the state variables of whooping cough epidemic model for different values of fractional order .
Figure 2.
Dynamics of the state variables of whooping cough epidemic model for different values of fractional order .
Figure 3.
Effect of quarantine rate on state variables with .
Figure 3.
Effect of quarantine rate on state variables with .
Figure 4.
Effect of quarantine rate on state variables with .
Figure 4.
Effect of quarantine rate on state variables with .
Figure 5.
Effect of quarantine rate on state variables with .
Figure 5.
Effect of quarantine rate on state variables with .
Figure 6.
Effect of quarantine rate on state variables with .
Figure 6.
Effect of quarantine rate on state variables with .
Figure 7.
Effect of vaccination rate on state variables with .
Figure 7.
Effect of vaccination rate on state variables with .
Figure 8.
Effect of vaccination rate on state variables with .
Figure 8.
Effect of vaccination rate on state variables with .
Figure 9.
Optimal vaccination rate and the cost functional J for different values of fractional order .
Figure 9.
Optimal vaccination rate and the cost functional J for different values of fractional order .
Figure 10.
State variables before and after optimization with vaccination rate as control variable.
Figure 10.
State variables before and after optimization with vaccination rate as control variable.
Figure 11.
Optimal quarantine rates to , to and the cost functional J for different values of fractional order .
Figure 11.
Optimal quarantine rates to , to and the cost functional J for different values of fractional order .
Figure 12.
State variables before and after optimization with quarantine rates as control variables.
Figure 12.
State variables before and after optimization with quarantine rates as control variables.
Figure 13.
Optimal vaccination rate , quarantine rates to , to and the cost functional J for different values of fractional order .
Figure 13.
Optimal vaccination rate , quarantine rates to , to and the cost functional J for different values of fractional order .
Figure 14.
State variables before and after optimization with vaccination and quarantine rates as control variables.
Figure 14.
State variables before and after optimization with vaccination and quarantine rates as control variables.
Table 1.
Sensitivity indices for each parameter of
Table 1.
Sensitivity indices for each parameter of
| Parameter |
Sensitivity Index |
Parameter |
Sensitivity Index |
|
1.0000 |
|
-1.8150 |
|
-0.0388 |
|
0.9953 |
|
0.0046 |
|
0.3243 |
|
-0.0018 |
|
-0.0507 |
|
-0.3807 |
|
-0.0270 |
|
-0.0101 |
|
0.0000 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
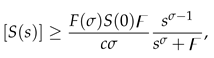 where
where 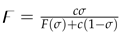 .
.