Prerpints.org logo
Preprint
Article

The Double-Nozzle Technique Equipped with RF-Only Funnel and RF-Buncher for the Ion Beam Extraction into Vacuum

Altmetrics

Downloads

74

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 August 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
This paper is a further development of our “Proposal of a new double-nozzle technique for in-gas-jet laser resonance ionization spectroscopy” published in journal Atoms earlier in this year. Here, we propose to equip the proposed double-nozzle technique with the RF-only funnel and RF-buncher placed in the gas-jet chamber at 70 mm distance downstream the double-nozzle exit. It allows for highly effective extraction into vacuum heavy ion beams, produced in two-steps laser resonance ionization in the argon supersonic jet. We explored the operation of this new full version of the double-nozzle technique through detailed gas dynamic and then Monte Carlo trajectory simulations, which results are presented and discussed. In particularly, we have shown by calculations that more than 80% of all nobelium-254 neutral atoms, extracted by argon flow from the gas stopping cell through the double-nozzle into the supersonic jet can be extracted into vacuum in a form of pulsed ion beam having low transverse and longitudinal emittance.s dynamic and Monte Carlo simulations
Keywords: 
Subject: Physical Sciences  -   Atomic and Molecular Physics

1. Introduction

Recently, in the work [1] we have proposed a new double-nozzle technique for its use in-gas-jet laser resonance ionization spectroscopy. The operation of this original technique we explored by means of computer experiments, which were consisted in detailed gas dynamic simulations of the buffer gas flow (inside the gas stopping cell, double-nozzle and supersonic argon gas jet) and atom-trajectory Monte Carlo simulations. The results of these computer simulations presented and discussed in [1]. In addition, the work [1] presents and discuss results of similar computer simulations for JetRIS project (see, e.g., [2,3]) that is under development at GSI and which is a typical representative of the conventional in-gas-jet technique that is in use or under development nowadays.
In total, the calculation results presented in [1} show that the proposed double-nozzle technique has many advantages compared with the one used in the JetRIS setup for future high-resolution laser spectroscopic study of heaviest elements.
The detailed description of the double-nozzle technique as well as the conventional in-gas-jet technique readers can easily find elsewhere, for example, in [1] and many links within it.
Shortly, the both experimental techniques for the laser resonance ionization spectroscopy (the proposed double-nozzle and convention one-nozzle techniques) consists in the following.
The ions of interest after their thermal evaporation as neutral atoms from the hot filament placed inside the gas stopping cell in front of the nozzle are transported by the buffer gas flow through the converging-diverging nozzle (or through the double-nozzle device, as it is in case of new technique proposed in [1]) into the gas-jet chamber.
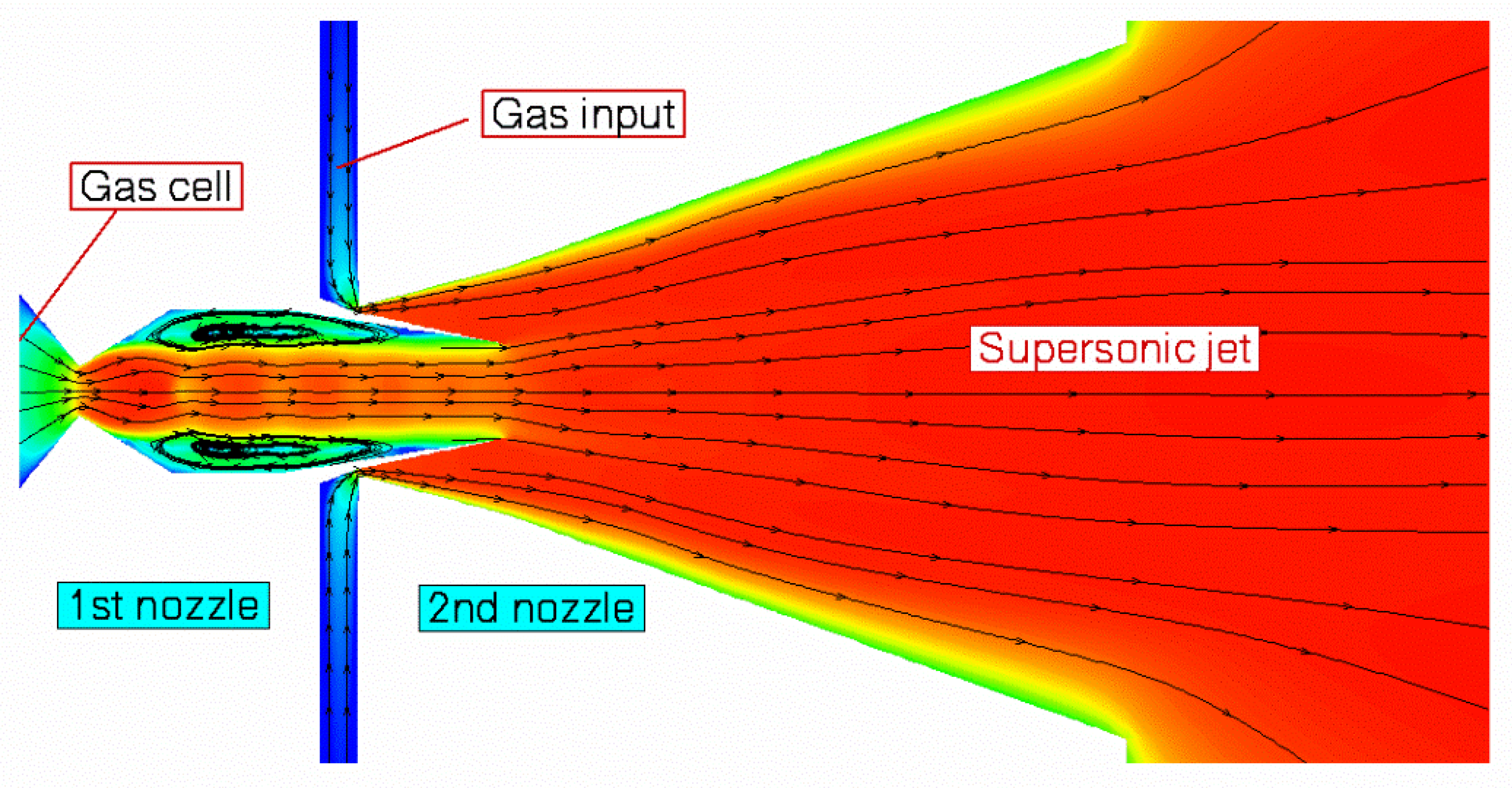
Schematic view of the double-nozzle design combined with results of the gas dynamic simulation for argon velocity flow field shown in Figure 1 for illustration.
Two lasers in cross-beam geometry perform the excitation and ionization of the extracted into the gas-jet chamber neutral atomic beam. (In all Monte Carlo simulations in this article, we will use nobelium-254, as a representative of the heavy atoms extracted from the gas cell via argon gas flow). One laser beam (we will refer to as a Laser-1) directed along the axis upstream of the gas jet direction excites atoms of interest, and the second one (we will refer to as Laser-2) directed perpendicular to the gas jet ionizes these excited atoms. The ionized by the Laser-2 atoms are transported by the gas jet through the gas-jet chamber to the entrance of the bent RFQ (e.g., S-shaped [4] or bend 90 degrees [2,3,4]) placed on the axis downstream at 50-70 mm distance from the nozzle exit.
E.g., the description of the segmented 90° bent RFQ ion guide one can find in the section 9.1 of the detailed and of good quality work [4]. This bent RFQ placed in the gas-jet chamber, which 3D schematic view shown in Figure 17a [4], allows for the Laser-1 beam up to 8 mm in diameter to be inserted through the RFQ segments into the region of laser ionization.
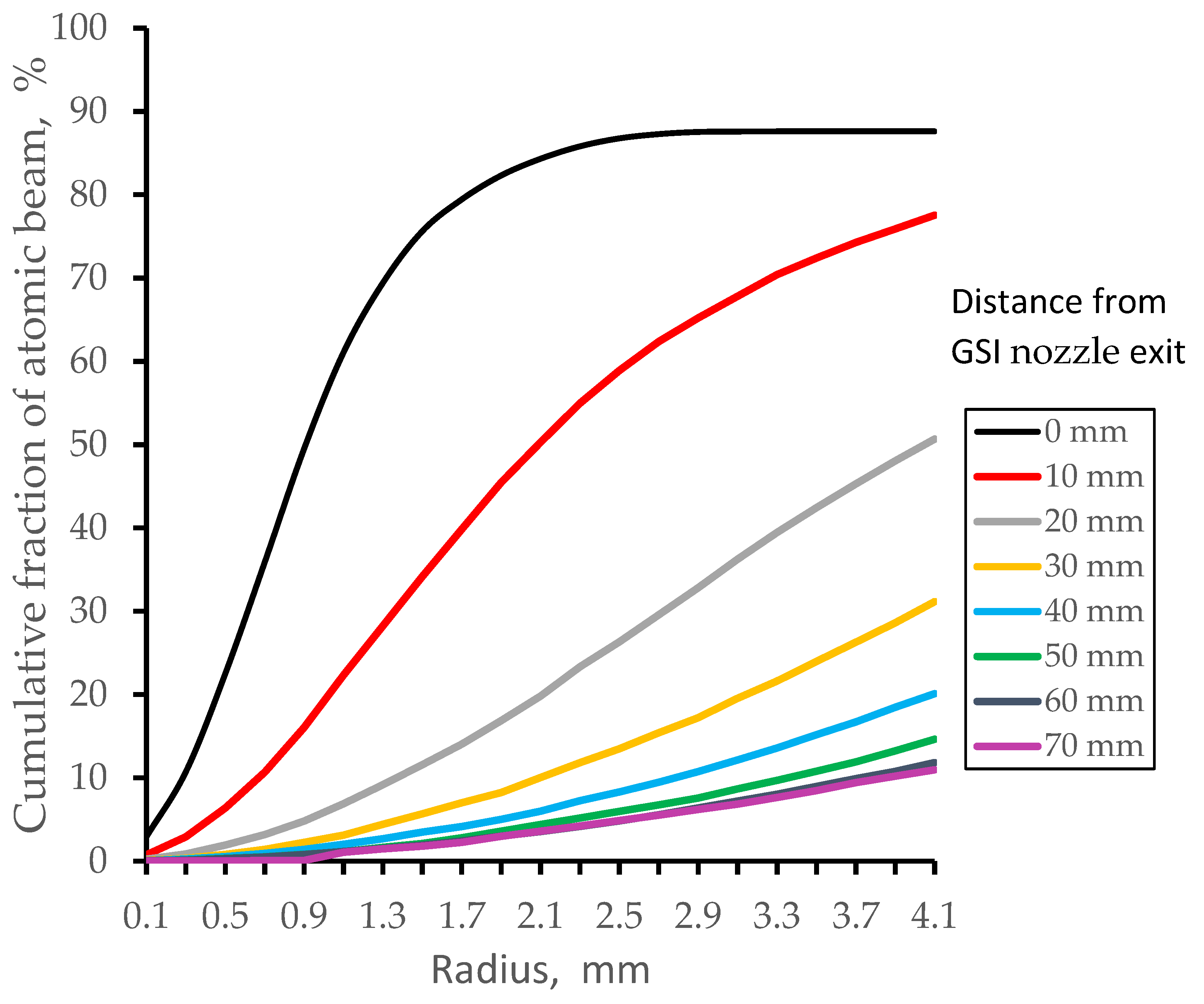
Results of our simulations (Gas dynamic + Monte Carlo) for cumulative fractions of nobelium-254 atomic beam inside the region of 8 mm in diameter (Laser -1 beam diameter) presented in Figure 2 for different downstream distances from the GSI nozzle (In this article, we will use the same definitions as the work [1], e.g., “GSI nozzle” and “double-nozzle”). It corresponds to the JetRIS setup operation at the stagnation gas cell pressure Pcell = 100 mbar and pumping capacity of the turbo molecular pump of 1300 l/s.
To be sure, that the Laser-2 pulsed beam having repetition rate of 10 kHz will ionize all nobelium atoms in a free supersonic jet, the length of the ionization zone has to be not less than 55–60 mm [2,3,4].
Due to the argon supersonic jet expansion (one can see it in Figure 4 of Ref. [1]), only nobelium atoms which are inside the axial region of 8 mm in diameter can be excited by this Laser-1. After the data of Figure 2 averaging along the ionization region of 60 mm in length, one get that only 41.9% of the total atomic beam can be ionized in the two-steps laser resonance ionization process. Notice, the diffusion atomic beam losses inside the nozzle have automatically included here, as well.
In the case of the double-nozzle technique proposed in [1], the corresponding fraction of nobelium atomic beam that can be excited with the use of Laser-1 beam of 8 mm in diameter is 49.0 %. It corresponds to results of Monte Carlo simulations presented in Figure 9 below.
Unfortunately, we could not find in literature quantitate data nether on the focusing efficiency of laser-ionized heavy atom beams into the curved RFQ, nether on the transmission efficiencies of these ions, first through this curved RFQ and then through the extraction RFQ placed behind the curved RFQ in the vacuum chamber (see Figure 17b in Ref. [4]).
This work is devoted to the further development of the double-nozzle technique [1]. To do so, we suggest replacing the conventional bent RFQ in the gas-jet chamber by a simple RF-only funnel placed on the axis of the gas-jet chamber at 70 mm distance downstream the 2nd nozzle exit. In addition, we recommend replacing the conventional extraction RFQ (e.g., see Figure 3 in Ref. [4]) by an original compact and simple cylindrical RF- buncher. It will allow for the fast and highly efficient ion beam extraction into vacuum and its bunching.
The idea of the RF-only funnel for ion beam extraction into vacuum we have suggested for the first time in 2001 [5]. Later it has been further developed and experimentally tested at Stanford University [6,7], ETH, Zürich [8,9], Technical University, Darmstadt [10].
The original, very compact and effective RF-buncher we have proposed and numerically investigated for the first time in [11,12].
A detailed description of the RF-only funnel and RF-buncher technique readers can find in our recent review [13].
In Section 3 and Section 4, we present results of detailed computer simulations for the full version of the double-nozzle technique, which includes the ion beam extraction using of RF-only funnel and RF-buncher. For this purpose, we used the same software that we have used in our work [1].
Section 5 describes the numerical investigations of the possible using the GSI nozzle combined with RF-only funnel and RF-buncher in the JetRIS project at GSI.

2. General description and main design parameters

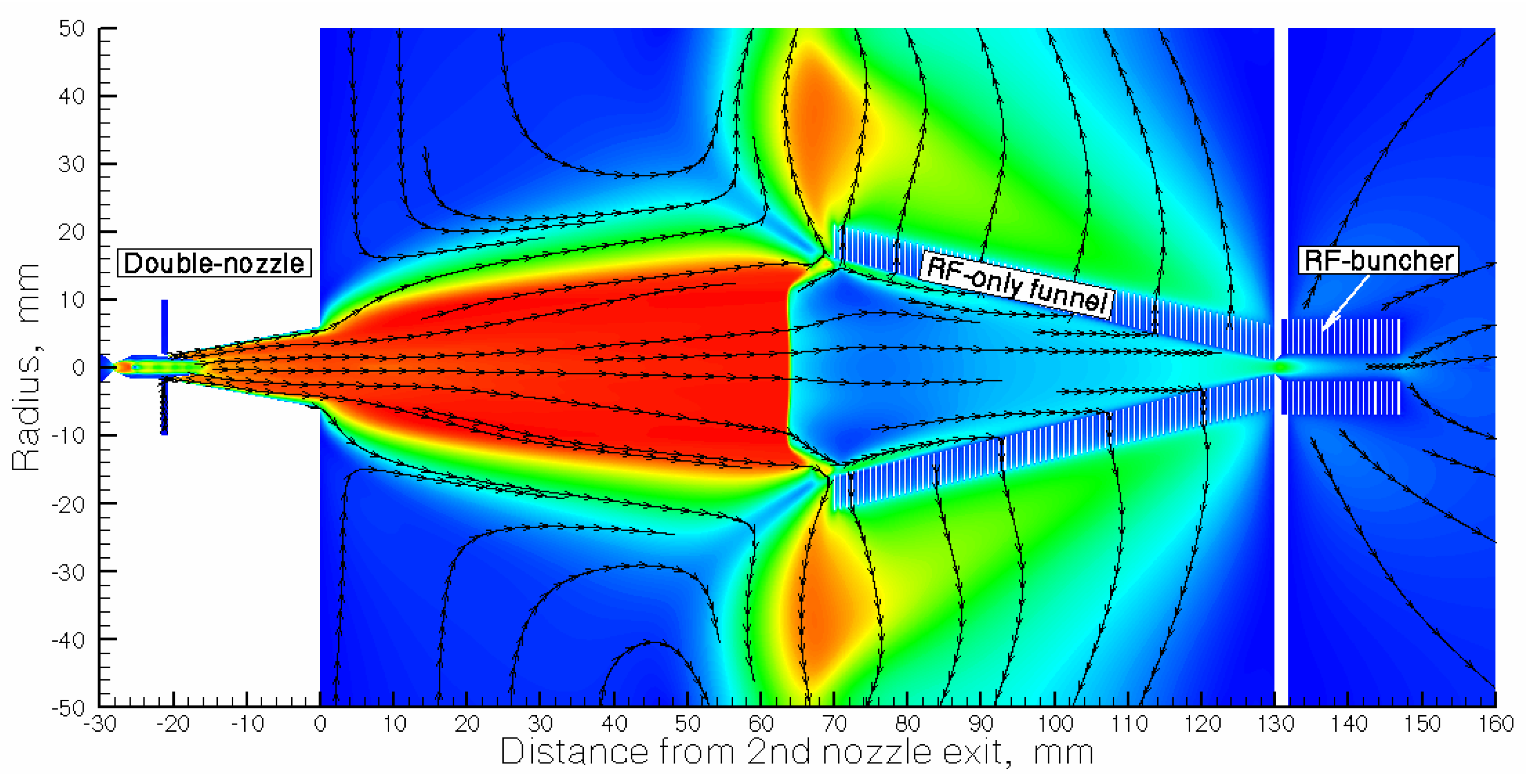
Schematic view of the full version of double-nozzle technique shown in Figure 3. We skip a detailed description of the design of the double nozzle shown above in Figure 1 because its exact geometry listed in Table 1 of Ref. [1].
The RF-only funnel and the RF-buncher installed at the jet axis have the length of 60 mm and 16 mm, correspondingly. The distance between the exit of the 2nd nozzle and the funnel entrance is 70 mm. Stainless steel funnel electrodes of 0.2 mm thickness have a shape of rings with decreasing diameters in direction to the funnel exit, but all ring-electrodes have the same width of 5 mm (it is the difference between outer and inner ring's radius). Electrodes of the RF-buncher are similar to electrodes of the RF-only funnel, but have the cylindrical geometry, when all electrodes have a constant inner diameter of 4 mm.
Each ring-electrode has two supporting legs of about 3 ÷ 6 mm width for their assembling into the funnel and buncher stacks on the supporting rods. The assembly of electrodes into the funnel and buncher can be done similarly as it is described in detail in [10], in particular, shown there in the photographs of Figure 4.
Main design parameters of the RF-only funnel and RF-buncher listed in Table 1.
Table 1. Main design parameters of the RF-only funnel and RF-buncher.
Table 1. Main design parameters of the RF-only funnel and RF-buncher.
Rf-only funnel RF-buncher
Entrance aperture diameter (mm) 32 4
Exit aperture diameter (mm) 2 4
Electrode thickness (mm) 0.2 0,2
Inter-electrode spacing (mm) 0.6 0.6
Number of electrodes 75 20
Taking into account that the exit aperture of the RF-only funnel has a diameter of 2 mm, the Laser-1 beam inserted through this aperture into the gas-jet chamber must have some small divergence in order to cover the nobelium atoms inside the supersonic jet in the region of their ionization. It can be realized by optics, when the Laser-1 beam has focus at about 2 mm distance downstream the RF-buncher exit and then diverge and pass through the RF-buncher and RF-only funnel with a half-divergence angle of 3.2°. In this case, the Laser-1 beam will have the diameter of 12 mm at 40 mm downstream distance from the 2nd nozzle exit. The results of Monte Carlo simulations presented below in the Section 3 definitely show that this Laser-1 beam geometry suits well for excitation of nobelium atomic beam in the supersonic jet.
The extracted from the RF-buncher into vacuum of 10-3 – 10-4 mbar pulsed ion beam having low transverse and longitudinal emittance can be easily 90° bent by the use of a standard Quadrupole deflector, e.g., as it shown in the Figure 1 in Ref. [6].

3. Results of gas dynamic simulations

The results of gas dynamic simulations for 8 combinations of gas stagnation pressures in the gas cell (Pcell) and in the double-nozzle (Pnoz) listed in Table 2.
Results of the gas dynamic simulation of argon gas density, temperature, Mach number and velocity flow fields presented in the next four Figures for the calculation variant #7 (see Table 2).
Figure 8 demonstrates the detailed structure of the supersonic jet in the region of the RF-only funnel entrance. It is a close up view of the calculation result shown in the Figure 7.
Of course, we could present pictures with results of gas dynamic simulations for each calculation variant listed in Table 2, but we decide not to overload the text of this paper by many similar, in principle, graphic figures.
In the Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 one can clear see the effect of a strong interaction of the supersonic gas jet with the RF-only funnel, when the supersonic gas flow passing through the direct shockwave (or how it sometime calls - a Mach disk) are converted into subsonic gas flow. In a sense, we can say that this RF-only funnel works as a "killer" of the supersonic gas jet.

4. Results of Monte Carlo trajectory simulations

Results of simulations for the atomic beam radius (90% level) for different distances from the 2nd nozzle exit and for 8 calculation variants listed in Table 3.
As an illustration of the data in the Table 3, Figure 9 shows calculated cumulative radial distributions of the nobelium-254 atomic beam at different downstream distances from the 2nd nozzle exit for the calculation variant #7.
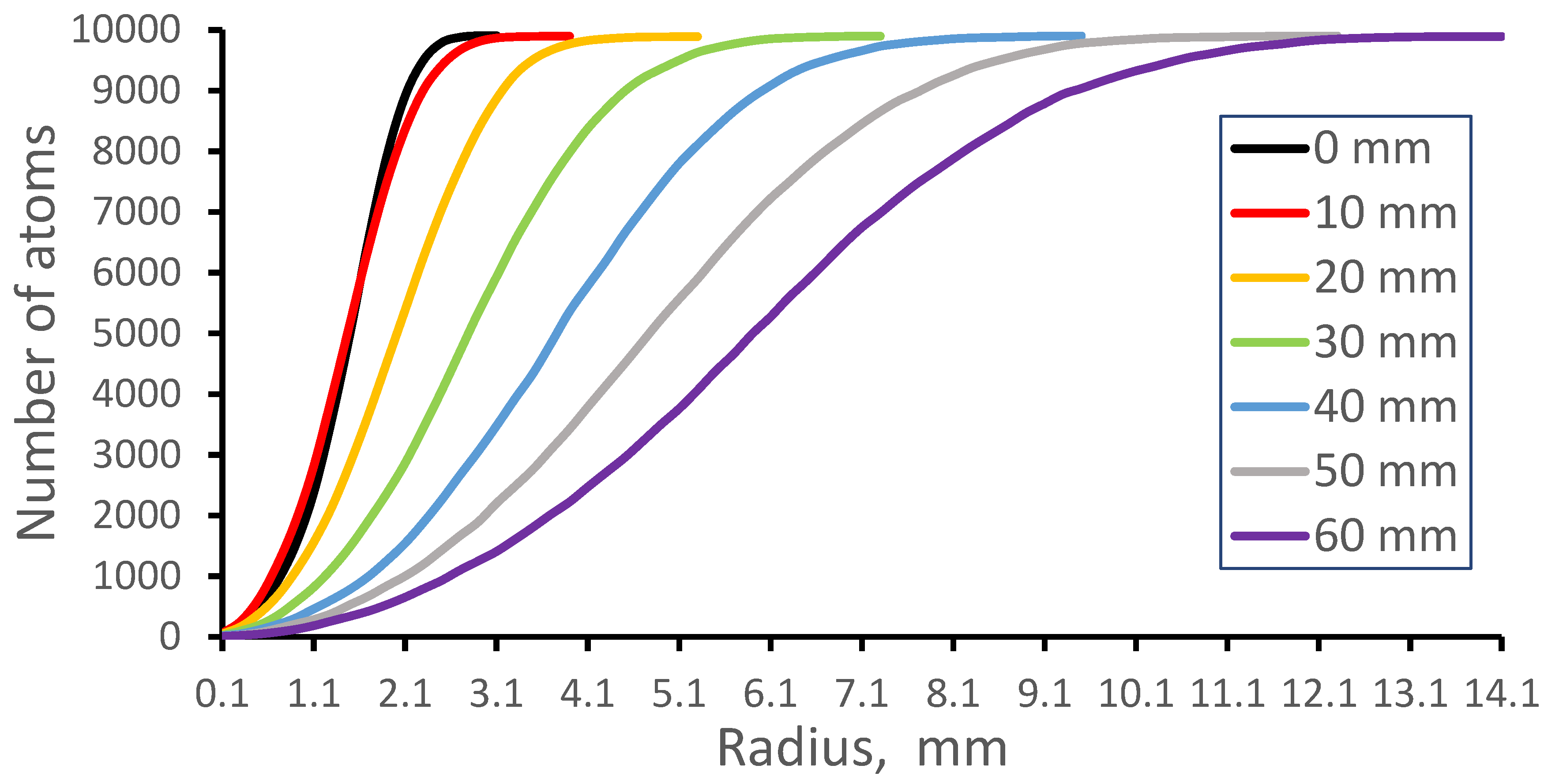
The diverging Laser-1 beam has a radius of 6 mm at 40 mm distance from the 2nd nozzle exit. Therefore, by using the data in Figure 9 we conclude that the Laser-1 beam overlaps 87.3 % of all atoms extracted from the gas stopping cell by the gas flow and, as a result, they can be ionized in the process of two-step resonance laser ionization.
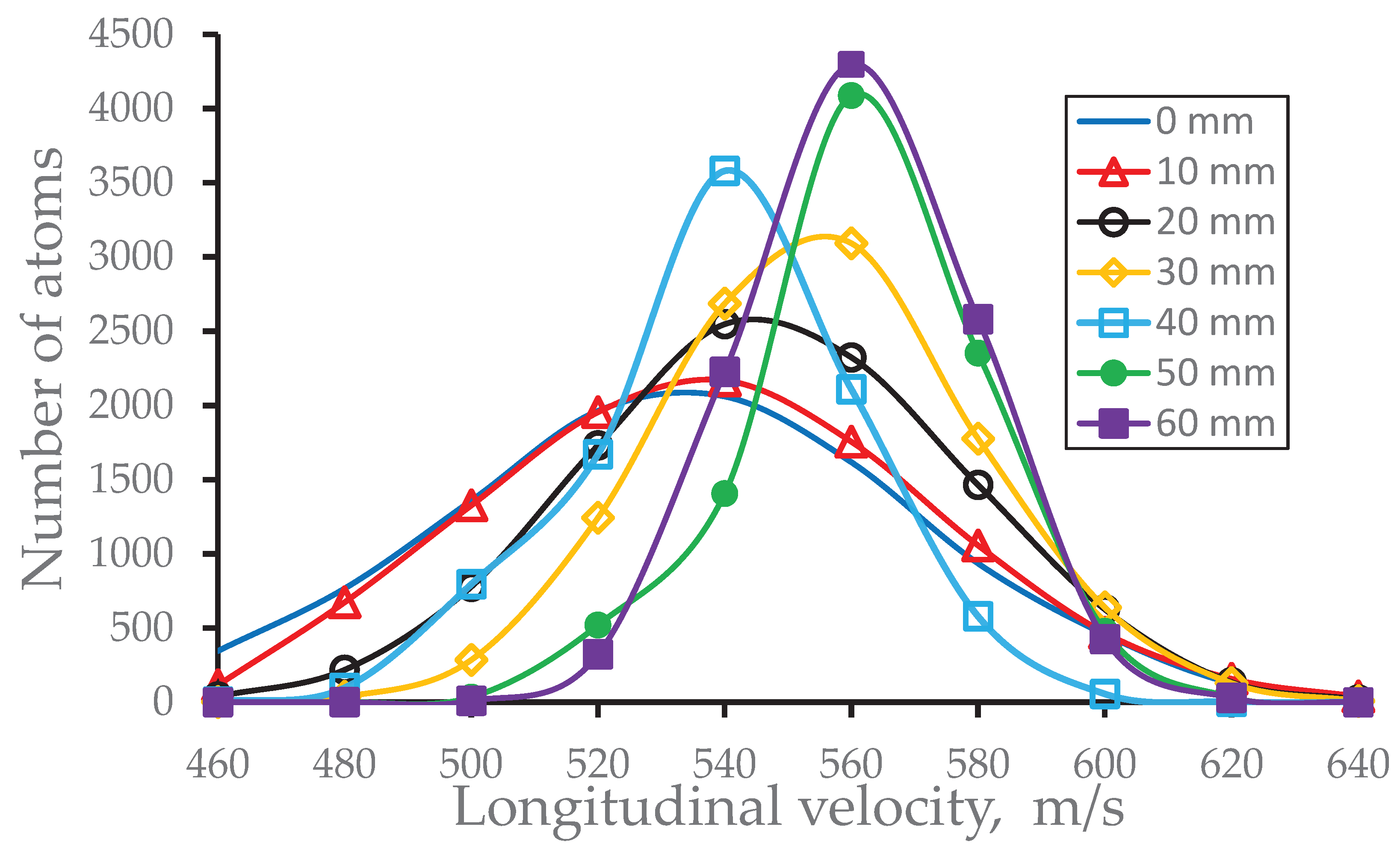
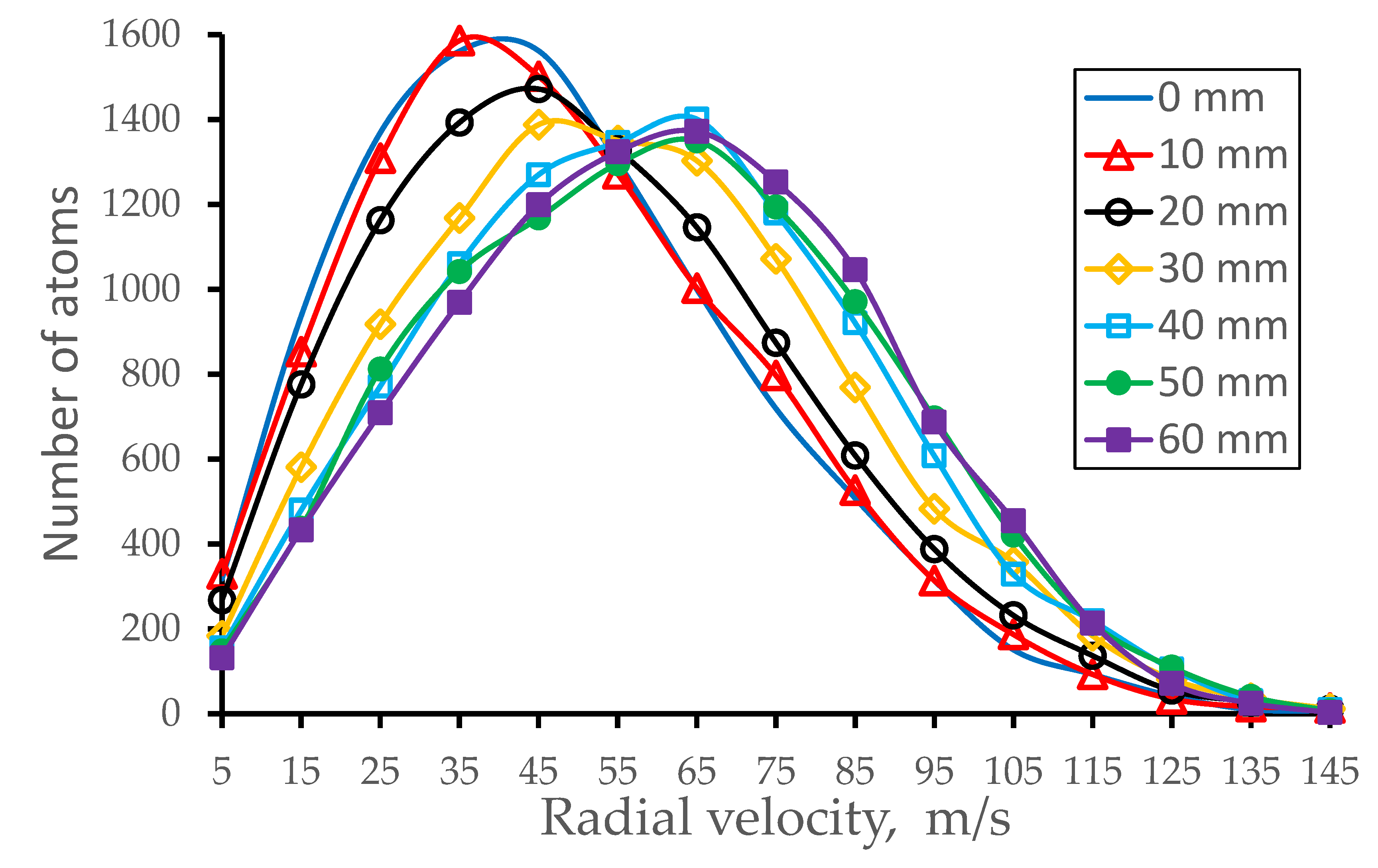
Results of Monte Carlo simulations for atomic beam longitudinal and radial velocity spreads (FWHM) as a function of the distance downstream from the 2nd nozzle exit are listed in Table 4 and Table 5, correspondingly. As an illustration of the data in Table 4 and Table 5, Figure 10 and Figure 11 show calculated longitudinal and radial velocity distributions of the nobelium-254 atomic beam for the calculation variant #7.
Table 6 presents results of Monte Carlo simulations for atomic beam time of flight (µsec) starting from the gas cell nozzle throat as a function of the downstream distance from the 2nd nozzle exit for 8 calculation variants. It is clear that the length of the ionization zone of 60 mm is enough to ionize all excited by the Laser-1 nobelium atoms by the pulsed Laser-2 beam having the repetition rate of 10 kHz and enough size of diameter.
The RF frequency and voltages applied to the RF-only funnel and RF-buncher electrodes, which we used in Monte Carlo simulations, listed in Table 7.
E.g. the calculated capacitance ot this RF-only funnel is equal to 0.235 nF that corresponds to a capacitive reactance of 135 Ώ at operating frequency of 5 MHz.
Main calculated characteristics of the extracted pulsed nobelium ion beam listed in Table 8 and Table 9.
We would like to emphasize that the values of total ion beam extraction efficiency into vacuum in Table 8 include the both diffusion losses of atoms inside the double-nozzle and ions losses inside the RF-only funnel. The transmission efficiency of ions through the RF-buncher is close to 100% for all calculation variants. In other words, the total ion beam extraction efficiencies here are the ratio of the number of extracted into vacuum nobelium ions, obtained as a result of two-stage resonant laser ionization, to the number of neutral nobelium atoms extracted by the gas flow from the gas cell.

5. Perspectives of the using the RF-only funnel and RF-buncher for the JetRIS project at GSI

To check an efficiency of the possible using the described above RF-only funnel and RF-buncher in the JetRIS project with the GSI nozzle, we performed gas dynamic and Monte Carlo simulations, which are similar to presented above for the double-nozzle technique.
The design parameters and operation conditions of RF-only funnel and RF-buncher used in these simulations are the same as listed in Table 1 and Table 7, correspondingly.

5.1. Results of gas dynamic simulations

Results of gas dynamic simulations for the GSI nozzle at two gas cell stagnation pressures listed in Table 10.
Figure 12 shows the result of gas dynamic simulation for the gas velocity flow field in the region of the RF-only funnel entrance for boundary conditions listed in Table 10 for the stagnation gas pressure Pcell = 300 mbar. This figure demonstrates a clear difference in detailed structure of the supersonic jet flowing out of the GSI nozzle compared to that one for the case of the double-nozzle operation shown in Figure 8 for the calculation variant #7 (see Table 2).

5.2. Results of Monte Carlo simulations

Table 11 and 12 present results of Monte Carlo simulations for nobelium-254 atomic beam parameters for different downstream distances from the GSI nozzle exit.
Table 11. Results of simulations for nobelium-254 atomic beam parameters for different downstream distances from the GSI nozzle exit. Stagnation pressure Pcell = 200 mbar, background pressure Pbg = 0.0179 mbar, the nozzle temperature T0 =296 K. Number of calculated ions is 10000 for each distance.
Table 11. Results of simulations for nobelium-254 atomic beam parameters for different downstream distances from the GSI nozzle exit. Stagnation pressure Pcell = 200 mbar, background pressure Pbg = 0.0179 mbar, the nozzle temperature T0 =296 K. Number of calculated ions is 10000 for each distance.
Distance from GSI nozzle exit (mm) 0 10 20 30 40 50 60
Beam radius (90%) (mm) 1.68 3.8 6.68 9.27 11.06 12.4 13.12
Longitudinal velocity spread (FWHM) (m/s) 91.2 59.0 43.3 40.2 40.6 44.1 56.0
Radial velocity spread (FWHM) (m/s) 65.1 99.8 99.2 85.0 58.0 51.0 59.4
Time of flight (µs) 44 60 80 96 116 132 152
Table 12. Results of simulations for nobelium-254 atomic beam parameters for different downstream distances from the GSI nozzle exit. Stagnation pressure Pcell = 300 mbar, background pressure Pbg = 0.0268 mbar, the nozzle temperature T0 =296 K. Number of calculated ions is 10000 for each distance.
Table 12. Results of simulations for nobelium-254 atomic beam parameters for different downstream distances from the GSI nozzle exit. Stagnation pressure Pcell = 300 mbar, background pressure Pbg = 0.0268 mbar, the nozzle temperature T0 =296 K. Number of calculated ions is 10000 for each distance.
Distance from GSI nozzle exit (mm) 0 10 20 30 40 50 60
Beam radius (90%) (mm) 1.67 3.6 6.1 8.4 10.3 11.8 11.8
Longitudinal velocity spread (FWHM) (m/s) 84.3 55.1 51.4 47.8 38.1 40.0 43,6
Radial velocity spread (FWHM) (m/s) 56.9 95,9 97.2 80.5 71.3 50.7 44.0
Time of flight (µs) 44 60 80 96 116 132 152
Table 13 presents results of Monte Carlo simulations for total nobelium-254 ion beam extraction efficiencies into vacuum for different stagnation gas cell pressures Pcell.
Important note. If participants of the JetRIS project will decide, if they do ever, experimentally test the functionality of the described RF-only funnel and RF-buncher installed into their present setup with GSI nozzle, they should not be surprised, if at Pcell = 100 mbar they would not see any ions extracted from RF-buncher into vacuum.
The point is that at this stagnation pressure in the gas cell, the supersonic free jet is not powerful enough, and the viscous subsonic gas flow transporting ions is almost completely "killed"(or strongly decelerated) inside the RF-only funnel. Thus, most of the ions are lost, the gas flow rate into the RF-buncher turns out to be less than 0.01 mbar l/s, and this is insufficient for efficient ion beam bunching. We made the simulations for this pressure (Pcell = 100 mbar) as well, but we have decided not include these results in the article.

6. Discussion and Outlook

In Section 2 of the article, we present the description of the suggested here full version of the double-nozzle technique, which schematic view shown in Figure 3. Main design parameters of the RF-only funnel and RF-buncher listed in Table 1. The compact RF-only funnel of 60 mm length and RF-buncher of 16 mm length have a simple design, can be easily manufactured and installed on the axis of the gas-jet chamber at 70 mm downstream distance from the exit of the double-nozzle.
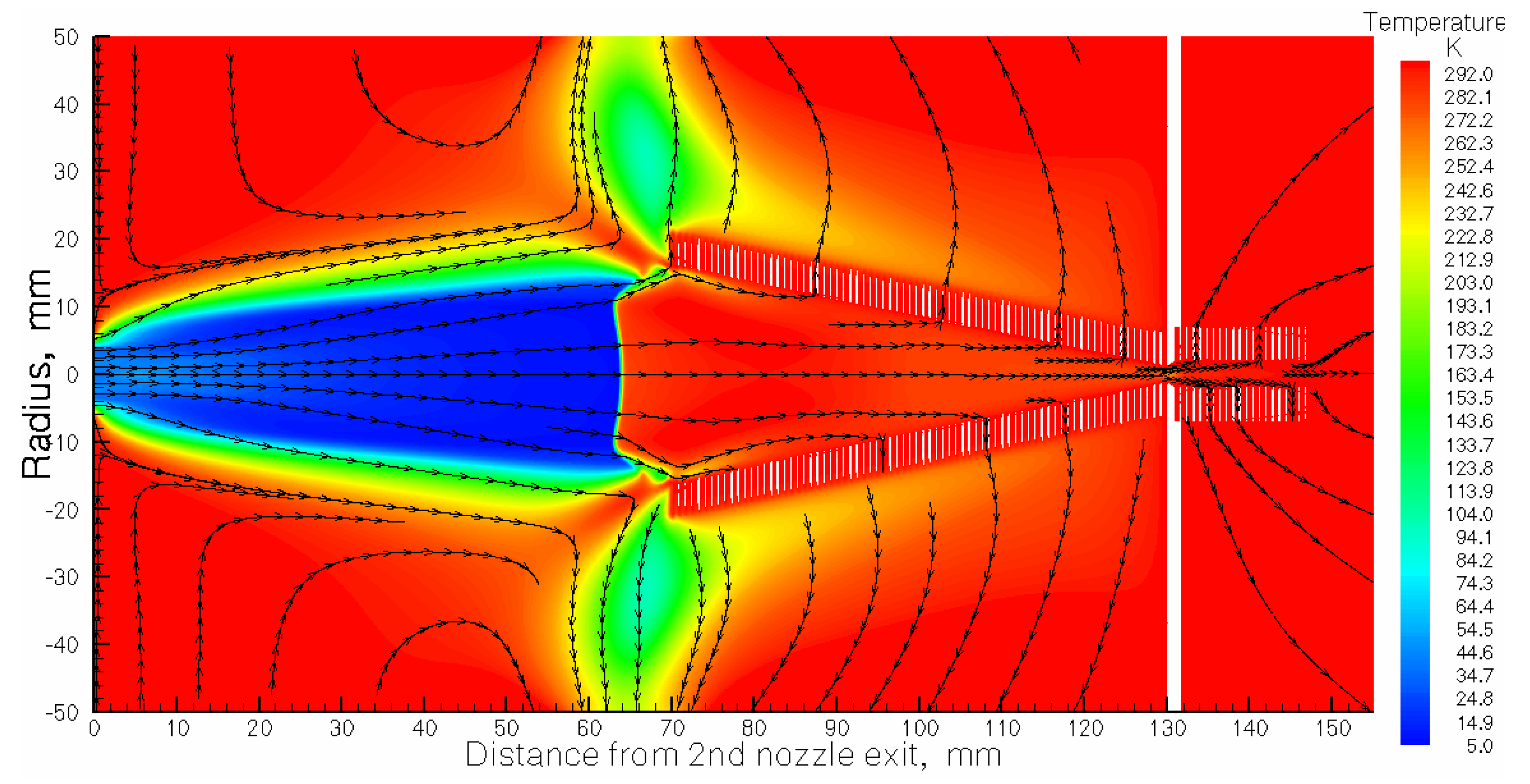
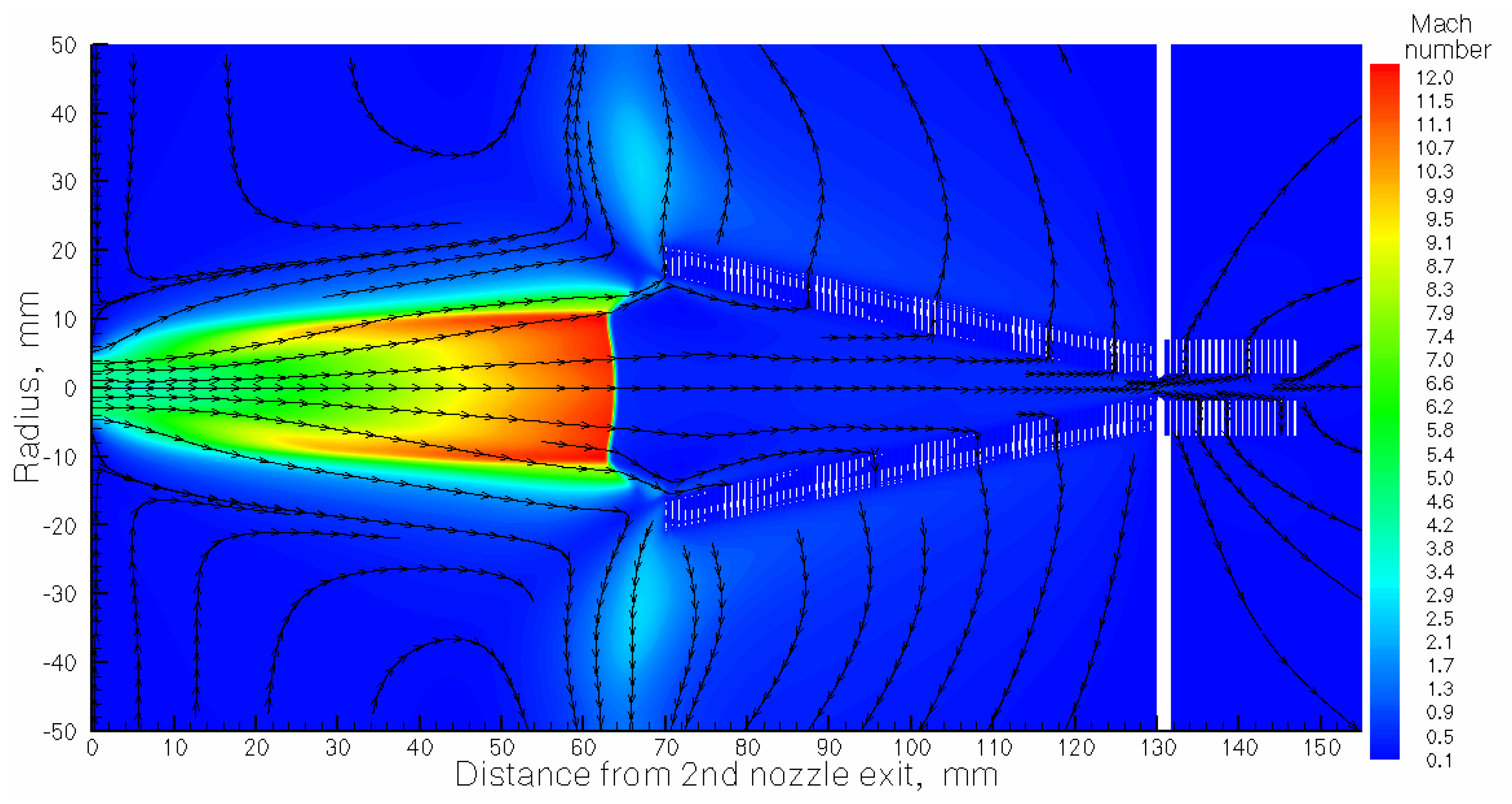
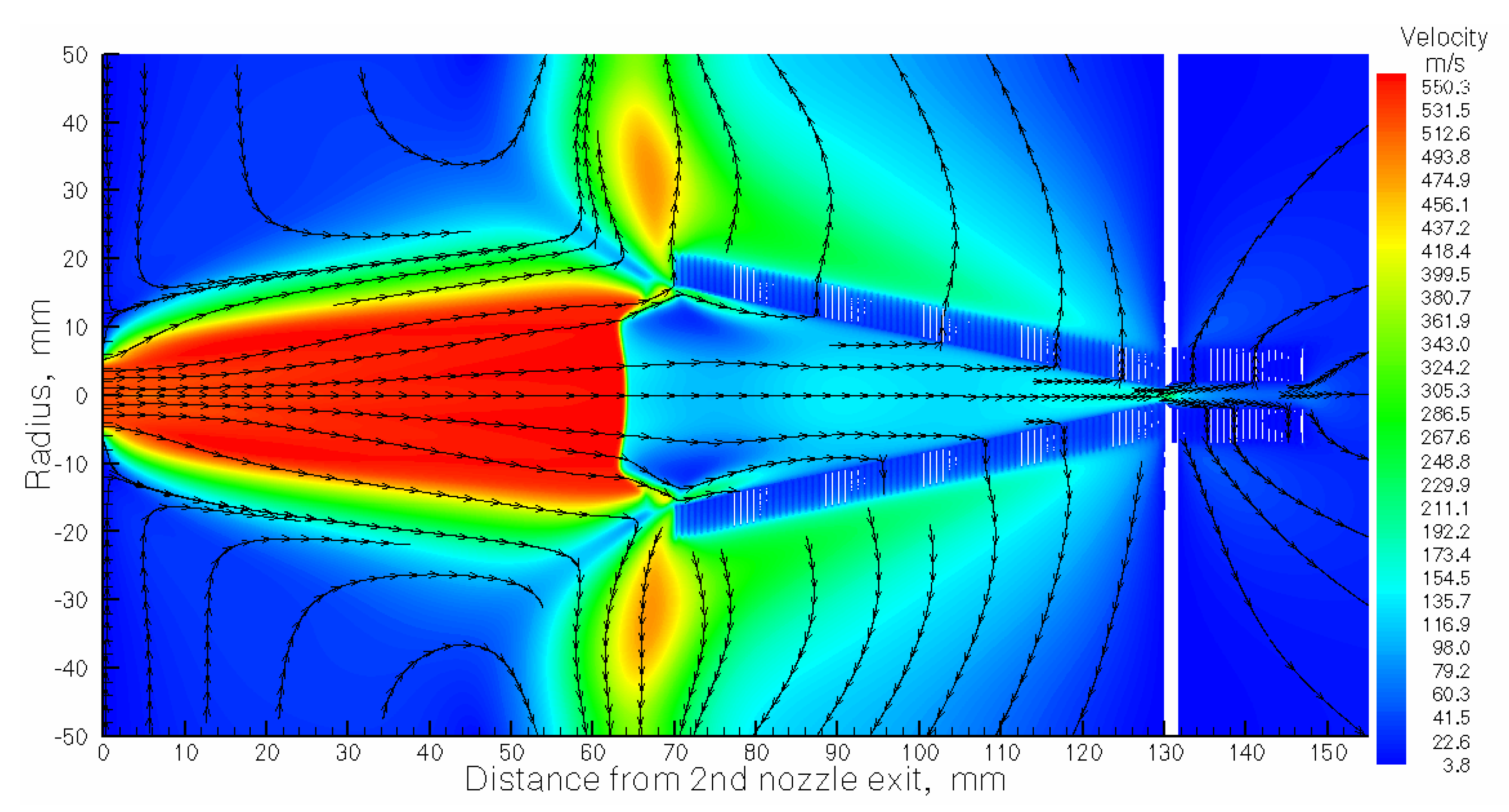
Results of the gas dynamic simulations for 8 combinations of gas stagnation pressures in the gas cell (Pcell) and in the double-nozzle (Pnoz) presented in Section 3. 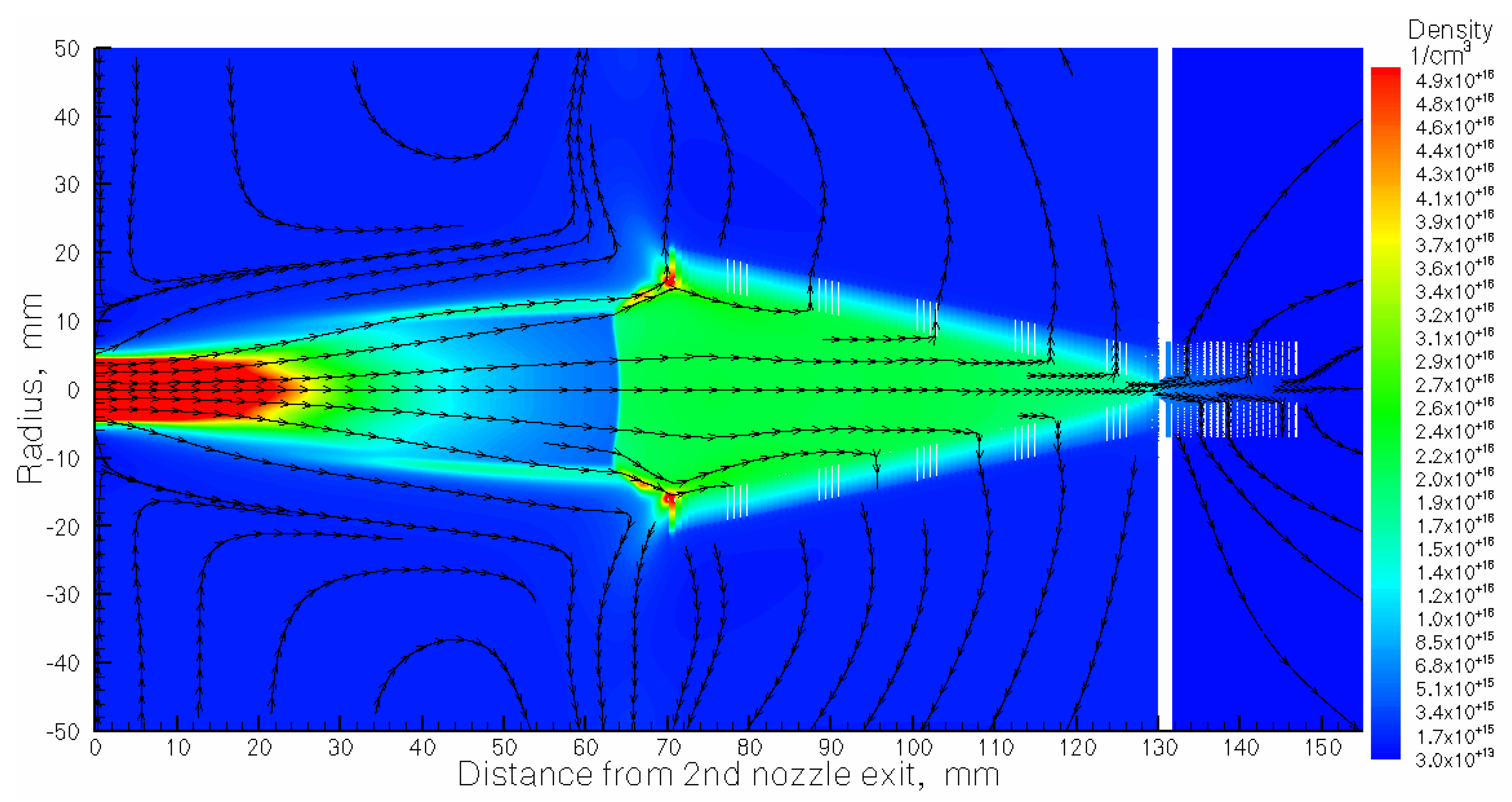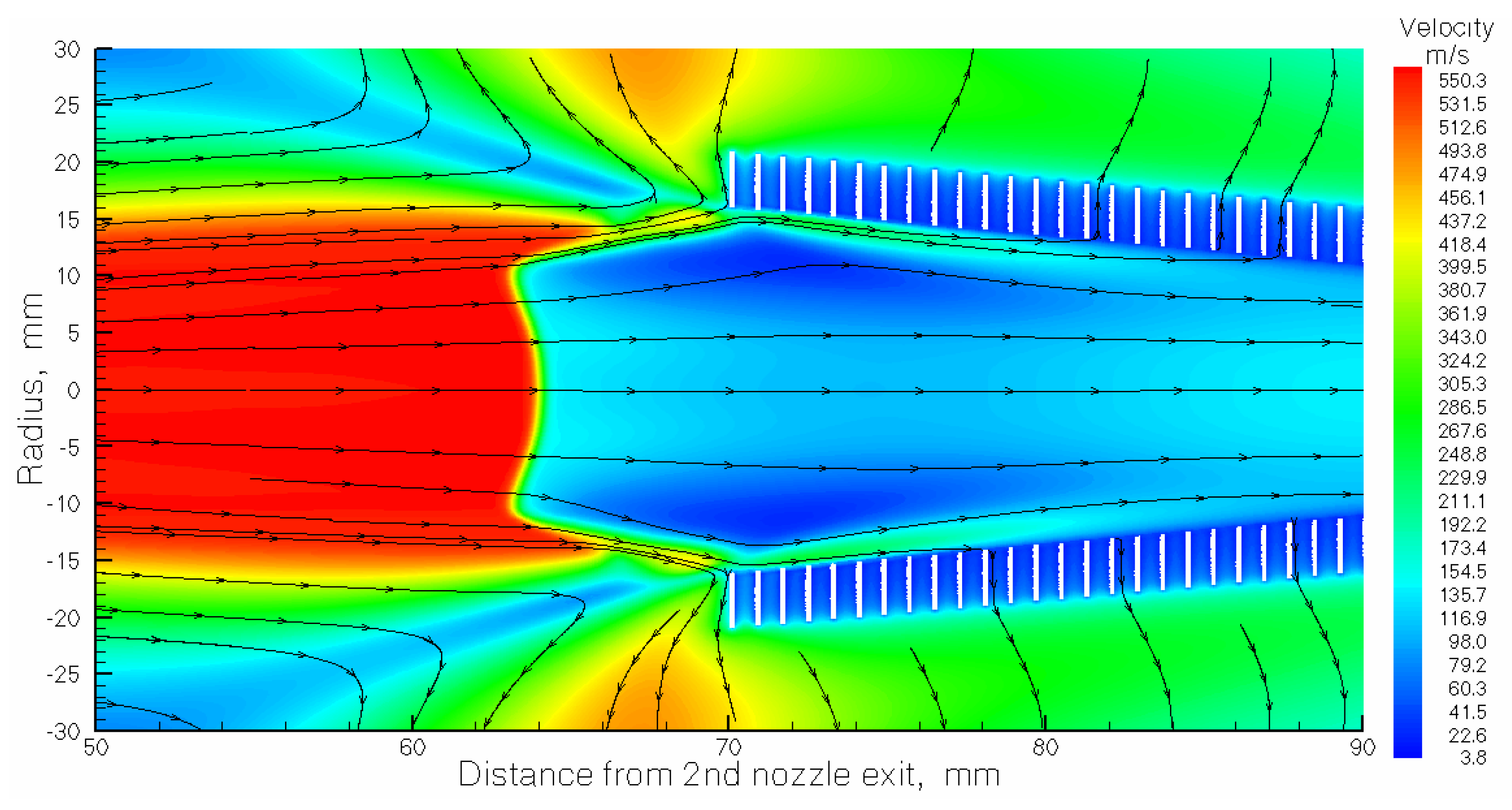The graphic description of the supersonic and subsonic gas flow structure (flow fields of gas density, temperature, Mach number and velocity) shown for the calculation variant #7 (see Table 2) in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Here one can clear see in the jet a direct shock wave having about 20 mm in diameter, that appears in front of the RF-only funnel due to a strong interaction of the supersonic gas jet with this funnel. The supersonic gas jet passing through this direct shockwave are converted into subsonic gas flow, and it helps a lot to dramatically decrease the gas load into the vacuum chamber with the RF-buncher (for details, see Qvac values in Table 2).
Results of many Monte Carlo simulations presented in Section 4 in form of tables and graphics. In particularly, the values of total ion beam extraction efficiency into vacuum listed in Table 8 for all 8 calculation variants. Main parameters of the extracted bunched nobelium ion beam, including values of longitudinal and normalized transverse emittance, for 8 calculation variants one can find in Table 9.
In order to find out how effective the use of the RF-only funnel and RF-buncher can be even in case of their use for conventional technology of in-gas-jet laser resonance spectroscopy (e.g., in the setup of the JetRIS project at GSI) we made similar gas dynamic + Monte Carlo simulations. These results presented in Section 5 for the GSI nozzle operation at Pcell values of 200 mbar and 300 mbar and at the pumping speed of 1300 l/s.
There is an impressive difference between gas flow structure shown in Figure 12 and that one shown in Figure 7 for the double-nozzle technique (variant #7 in Table 2).
It is also interesting to note that the gas flow rate through funnel exit into vacuum is Qvac = 0.05 mbar l/s for the case of Pcell = 200 mbar (see Table 10) in a factor of 5.4 less than this value for the case of Pcell = 300 mbar. At first glance, this looks great, because with such a small gas load into the vacuum chamber, where the RF-buncher is located, it is enough to use a vacuum pump with a capacity of 100 l/s to maintain a vacuum in this chamber at a level of 5 × 10−4 mbar. On the other hand, the total efficiency of ion beam extraction into vacuum at Pcell = 200 mbar turns out to be only 16.8% (see it in Table 13), which is 2.1 times less than this value for the case of Pcell = 300 mbar. That is why the variant of Pcell = 300 mbar is, in our opinion, more preferable for experiments with radioactive elements. E.g., the authors of the work [2], who write in the abstract of their article, share the same opinion: “In view of the low production rates of the heaviest elements, a high total efficiency is a crucial requirement for any experimental setup to be used in on-line experiments”.
In this respect, our double-nozzle technique also has great advantages over the conventional in-gas-get laser resonance ionization technique [2,3,4], even when they both use the RF-only funnel and RF-buncher. This assertion is confirmed by the results of our presented above calculations, because the total extraction efficiency of the nobedium-254 ions into vacuum is 81.2% (see variant # 7 in Table 8), which is 2.3 times higher than that one for the Pcell = 300 mbar variant in Table 13.
By the way, there are no in the literature quantitative data (which are even a little bit similar to that one’s presented in Table 8, Table 9, Table 11, Table 12 and Table 13) about characteristics of heavy ion beams extracted into vacuum after two-steps laser resonance ionization of their neutral atoms in the supersonic gas jet. At least, we do not know about it.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Varentsov, V. Proposal of a New Double-Nozzle Technique for In-Gas-Jet Laser Resonance Ionization Spectroscopy. Atoms 2023, 11, 88. [Google Scholar] [CrossRef]
  2. Raeder, S.; Block, M.; Chhetri, P.; Ferrer, R.; Kraemer, S.; Kron, T.; Laatiaoui, M.; Nothhelfer, S.; Schneider, F.; Van Duppen, P.; et al. A gas-jet apparatus for high-resolution laser spectroscopy on the heaviest elements at SHIP. Nucl. Instrum. Methods Phys. Res. B 2020, 463, 272–276. [Google Scholar] [CrossRef]
  3. Münzberg, D.; Block, M.; Claessens, A.; Ferrer, R.; Laatiaoui, M.; Lantis, J.; Nothhelfer, S.; Raeder, S.; Van Duppen, P. Resolution Characterizations of JetRIS in Mainz Using 164Dy. Atoms 2022, 10, 57. [Google Scholar] [CrossRef]
  4. Kudryavtsev, Y.; Ferrer, R.; Huyse, M.; Van den Bergh, P.; Van Duppen, P. The in-gas-jet laser ion source: Resonance ionization spectroscopy of radioactive atoms in supersonic gas jets. Nucl. Instrum. Methods Phys. Res. B 2013, 297, 7–22 https://. [Google Scholar] [CrossRef]
  5. V. Varentsov. A New Approach to the Extraction System Design, SHIPTRAP Collaboration Meeting, Mainz, March 19, 2001. 19 March. [CrossRef]
  6. T. Brunner, D. Fudenberg, A. Sabourov, V.L. Varentsov, G. Gratta, D. Sinclair, for the EXO collaboration, A setup for Ba-ion extraction from high pressure Xe gas for double-beta decay studies with EXO, Nuclear Instruments and Methods in Physics Research Section A, 317 Part B (2013) 473. [CrossRef]
  7. Brunner, T.; Fudenberg, D.; Varentsov, V.; Sabourov, A.; Gratta, G.; Dilling, J.; nEXO Collaboration. An RF-only ion-funnel for extraction from high-pressure gases. Int. J. Mass Spectrom. 2015, 379, 110–120. [Google Scholar] [CrossRef]
  8. R. Dietiker, T. Egorova, D. Günther, B. Hattendorf, V. Varentsov, Laser-ablation ion source with ion funnel, WO Patent App. PCT/EP2011/003,256 (Jan. 12 2012). www.google.com/patents/WO2012003946A1?cl=en.
  9. Querci, L.; Varentsov, V.; Günther, D.; Hattendorf, B. An RF-only ion funnel interface for ion cooling in laser ablation time of flight mass spectrometry. Spectrochim. Acta B 2018, 146, 57–68. [Google Scholar] [CrossRef]
  10. Ratajczyk, T.; Bollinger, P.; Lellinger, T.; Varentsov, V.; Nörtershäuser, W. Towards a He-buffered laser ablation ion source for collinear laser spectroscopy. Hyperfine Interact 2020, 241, 52. [Google Scholar] [CrossRef]
  11. Varentsov, V. Proposal of an RF-Only Double-Funnel System for Ions Extraction from a Cryogenic Stopping Cell for the Super-FRS at FAIR. GSI Sci. Rep. 2015, 1, 503–504. [Google Scholar] [CrossRef]
  12. Varentsov, V. Proposal of a new Laser ablation ion source for LaSpec and MATS testing. In Proceedings of the NUSTAR Collaboration Meeting, Darmstadt, Germany, 29 February–4 March 2016. [Google Scholar] [CrossRef]
  13. Varentsov, V. Review of Gas Dynamic RF-Only Funnel Technique for Ion Beams Cooling and Extraction into Vacuum; FAIR: Darmstadt, Germany, 2022. [Google Scholar] [CrossRef]
DisclAimer/PuBlisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Preprints 81161 g001
Figure 1. Schematic view of the double-nozzle design combined with the gas dynamic simulation results for argon velocity flow field. Black arrowed lines show the gas flow directions. For details, of the design see Table 1 in [1].
Figure 1. Schematic view of the double-nozzle design combined with the gas dynamic simulation results for argon velocity flow field. Black arrowed lines show the gas flow directions. For details, of the design see Table 1 in [1].
Preprints 81161 g001
Preprints 81161 g002
Figure 2. Simulation results for cumulative fractions of nobelium-254 atomic beam inside the diameter of 8 mm (it is the Laser-1 beam diameter) for different downstream distances from the GSI nozzle exit. Stagnation gas cell pressure Pcell = 100 mbar, pumping capacity of the turbo molecular pump for the gas-jet chamber is 1300 l/s.
Figure 2. Simulation results for cumulative fractions of nobelium-254 atomic beam inside the diameter of 8 mm (it is the Laser-1 beam diameter) for different downstream distances from the GSI nozzle exit. Stagnation gas cell pressure Pcell = 100 mbar, pumping capacity of the turbo molecular pump for the gas-jet chamber is 1300 l/s.
Preprints 81161 g002
Preprints 81161 g003
Figure 3. Schematic view of the full version of double-nozzle technique combined with the gas dynamic simulation results for argon velocity flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background pressure in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Figure 3. Schematic view of the full version of double-nozzle technique combined with the gas dynamic simulation results for argon velocity flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background pressure in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Preprints 81161 g003
Preprints 81161 g004
Figure 4. Result of the gas dynamic simulation for argon density flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Figure 4. Result of the gas dynamic simulation for argon density flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Preprints 81161 g004
Preprints 81161 g005
Figure 5. Result of the gas dynamic simulation for argon temperature flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Figure 5. Result of the gas dynamic simulation for argon temperature flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Preprints 81161 g005
Preprints 81161 g006
Figure 6. Result of the gas dynamic simulation for argon Mach number flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Figure 6. Result of the gas dynamic simulation for argon Mach number flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Preprints 81161 g006
Preprints 81161 g007
Figure 7. Result of the gas dynamic simulation for argon velocity flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Figure 7. Result of the gas dynamic simulation for argon velocity flow field. The stagnation gas cell pressure Pcell = 300 mbar, gas input (stagnation) pressure Pnoz = 200 mbar, background presses in the gas-jet chamber Pbg = 5.1 × 10−2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and nozzles is 296 K. Black arrowed lines show the gas flow direction.
Preprints 81161 g007
Preprints 81161 g008
Figure 8. Result of the gas dynamic simulation for argon velocity flow field in the region of the RF-only funnel entrance. It is a part of Figure 7, shown in close up view.
Figure 8. Result of the gas dynamic simulation for argon velocity flow field in the region of the RF-only funnel entrance. It is a part of Figure 7, shown in close up view.
Preprints 81161 g008
Preprints 81161 g009
Figure 9. Results of Monte-Carlo trajectory simulations for cumulative radial distributions of the nobelium-254 atomic beam at different downstream distances from the 2nd nozzle exit for the calculation variant #7. The number of calculated atoms is 10,000 for each distance.
Figure 9. Results of Monte-Carlo trajectory simulations for cumulative radial distributions of the nobelium-254 atomic beam at different downstream distances from the 2nd nozzle exit for the calculation variant #7. The number of calculated atoms is 10,000 for each distance.
Preprints 81161 g009
Preprints 81161 g010
Figure 10. Results of Monte-Carlo trajectory simulations for atomic beam longitudinal velocity distributions for different distances from the 2nd nozzle exit for the calculation variant #7. The data averaged in the radial plane for the total beam. Number of calculated atoms is 10,000 for each distance.
Figure 10. Results of Monte-Carlo trajectory simulations for atomic beam longitudinal velocity distributions for different distances from the 2nd nozzle exit for the calculation variant #7. The data averaged in the radial plane for the total beam. Number of calculated atoms is 10,000 for each distance.
Preprints 81161 g010
Preprints 81161 g011
Figure 11. Results of Monte-Carlo trajectory simulations for atomic beam radial velocity distributions for different distances from the 2nd nozzle exit for the calculation variant #7. The data averaged in the radial plane for the total beam. Number of calculated atoms is 10,000 for each distance.
Figure 11. Results of Monte-Carlo trajectory simulations for atomic beam radial velocity distributions for different distances from the 2nd nozzle exit for the calculation variant #7. The data averaged in the radial plane for the total beam. Number of calculated atoms is 10,000 for each distance.
Preprints 81161 g011
Preprints 81161 g012
Figure 12. Results of the gas dynamic simulation for argon velocity flow field in the region of the RF-only funnel entrance for the GSI nozzle operating at Pcell = 300 mbar and pumping capacity in the gas-jet chamber of 1300 l/s.
Figure 12. Results of the gas dynamic simulation for argon velocity flow field in the region of the RF-only funnel entrance for the GSI nozzle operating at Pcell = 300 mbar and pumping capacity in the gas-jet chamber of 1300 l/s.
Preprints 81161 g012
Table 2. Results of gas dynamic simulations for the gas flow rates through the nozzles at pumping capacity of the gas-jet chamber of 1300 l/s.
Table 2. Results of gas dynamic simulations for the gas flow rates through the nozzles at pumping capacity of the gas-jet chamber of 1300 l/s.
Calculation variant #1 #2 #3 #4 #5 #6 #7 #8
Stagnation pressure Pcell (mbar) 100 100 200 200 200 300 300 300
Stagnation pressure Pnoz (mbar) 200 300 100 200 300 100 200 300
Background pressure in gas-jet chamber Pbg (mbar) 0,033 0,045 0,03 0,042 0,054 0,039 0,051 0,063
Total gas flow rate Qtot (mbar l/s) 42.8 58.4 38.8 54.4 70 50.4 66 81.6
Gas flow rate through funnel exit into vacuum Qvac (mbar l/s) 0.154 0.435 0.053 0.172 0.538 0.11 0.245 0.432
Flow rate ratio Qtot / Qvac 278 134 732 316 112 458 269 189
Table 3. Results of Monte Carlo simulations for the atomic beam radius (90% level) at different downstream distances from the 2nd nozzle exit for 8 calculation variants. Number of calculated atoms is 10,000 for each variant.
Table 3. Results of Monte Carlo simulations for the atomic beam radius (90% level) at different downstream distances from the 2nd nozzle exit for 8 calculation variants. Number of calculated atoms is 10,000 for each variant.
Calculation variant #1 #2 #3 #4 #5 #6 #7 #8
0 mm 2.0 2.0 2.14 2.17 2.08 2.2 2.2 2,23
10 mm 2.25 2.35 2.6 2.36 2.29 2.62 2.36 2.33
20 mm 2.84 4.35 3.91 3.1 2.74 4.09 3.22 2.89
30 mm 3.83 4.95 5.6 4.36 3.69 5.99 4.54 3.98
40 mm 5.1 6.6 7.6 5.69 4.84 7.99 6.02 5.26
50 mm 6.4 8.15 9.5 7.32 6.07 9.98 7.7 6.57
60 mm 7.8 10.5 11.4 8.78 7.32 11.8 9.35 7.96
Table 4. Results of Monte Carlo trajectory simulations for atomic beam longitudinal velocity spread (FWHM) in [m/s] as a function of the downstream distance from the 2nd nozzle exit for different calculation variants. The data averaged in the radial plane for the total beam. Number of calculated atoms is 10,000 for each calculation variant.
Table 4. Results of Monte Carlo trajectory simulations for atomic beam longitudinal velocity spread (FWHM) in [m/s] as a function of the downstream distance from the 2nd nozzle exit for different calculation variants. The data averaged in the radial plane for the total beam. Number of calculated atoms is 10,000 for each calculation variant.
Calculation variant #1 #2 #3 #4 #5 #6 #7 #8
0 mm 97.6 95.7 94.5 90.8 91.2 93.6 95.0 86.1
10 mm 88.7 89.4 78.0 87.3 87.6 90.4 85.0 81.2
20 mm 60.1 65.0 65.5 73.4 77.6 66.5 71.4 73.7
30 mm 64.0 59.9 56.6 62.9 64.4 54.2 57.1 63.7
40 mm 55.0 50.8 52.4 54.5 54.2 47.2 51.1 59.4
50 mm 50.7 47.7 44.6 47.0 48.5 43.5 45.0 45.5
60 mm 46.8 47.8 43.2 41.6 44.6 41.3 43.4 42.6
Table 5. Results of Monte Carlo trajectory simulations for atomic beam radial velocity spread (FWHM) in [m/s] as a function of the downstream distance from the 2nd nozzle exit for different calculation variants. The data averaged in the radial plane for the total beam diameter. Number of calculated atoms is 10,000 for each calculation variant.
Table 5. Results of Monte Carlo trajectory simulations for atomic beam radial velocity spread (FWHM) in [m/s] as a function of the downstream distance from the 2nd nozzle exit for different calculation variants. The data averaged in the radial plane for the total beam diameter. Number of calculated atoms is 10,000 for each calculation variant.
Calculation variant #1 #2 #3 #4 #5 #6 #7 #8
0 mm 63.7 45.2 52.5 61.5 63.2 64.6 59.3 53.5
10 mm 70.9 49.1 72.4 60.7 57.2 69.1 68.1 58.6
20 mm 59.4 53.2 72.2 65.1 61.1 78.3 64.0 60.9
30 mm 62.3 57.3 86.0 67.7 61.2 83.3 64.5 62.0
40 mm 69.3 55.5 78.0 71.2 64.2 69.4 66.3 63.3
50 mm 66.3 55.2 81.6 67.9 64.9 70.6 60.0 62.6
60 mm 67.0 52.3 82.7 73.3 63.0 71.0 56.2 64.6
Table 6. Results of Monte Carlo trajectory simulations for the atomic beam time of flight in [µsec] starting from the gas cell nozzle throat as a function of the downstream distance from the 2nd nozzle exit for 8 calculation variants. The data averaged in the radial plane for the total beam diameter. Number of calculated atoms is 10000 for each calculation variant.
Table 6. Results of Monte Carlo trajectory simulations for the atomic beam time of flight in [µsec] starting from the gas cell nozzle throat as a function of the downstream distance from the 2nd nozzle exit for 8 calculation variants. The data averaged in the radial plane for the total beam diameter. Number of calculated atoms is 10000 for each calculation variant.
Calculation variant #1 #2 #3 #4 #5 #6 #7 #8
0 mm 68 68 64 64 64 63 63 63
10 mm 88 88 86 84 84 82 82 82
20 mm 108 108 104 103 102 101 101 101
30 mm 125 124 124 121 121 120 120 120
40 mm 144 142 142 140 140 138 138 138
50 mm 162 162 162 158 157 157 155 155
60 mm 180 180 180 176 176 175 174 174
Table 7. RF frequency and RF amplitude (peak-to-peak) applied to the extraction RF-only funnel and RF-buncher. Extraction DC field = – 10 V/cm.
Table 7. RF frequency and RF amplitude (peak-to-peak) applied to the extraction RF-only funnel and RF-buncher. Extraction DC field = – 10 V/cm.
RF-only funnel RF-buncher
RF-amplitude [Vpp] 100 100
RF-frequency [MHz] 5 5
Rf-funnel-RFbuncher DC bias - -0.8 V
DC potential gradient - -0.08 V
Table 8. Results of Monte Carlo simulations for fraction of ions in nobelium-254 beam at RF-only funnel entrance and total ion beam extraction efficiency into vacuum for 8 calculation variants. The number of calculated ions is 10,000 for each variant.
Table 8. Results of Monte Carlo simulations for fraction of ions in nobelium-254 beam at RF-only funnel entrance and total ion beam extraction efficiency into vacuum for 8 calculation variants. The number of calculated ions is 10,000 for each variant.
Calculation variant #1 #2 #3 #4 #5 #6 #7 #8
Fraction of ions in nobelium beam at RF-only funnel entrance (%) 89.6 82.3 76.9 85.7 91.0 74.9 83.5 88.2
Total ion beam extraction efficiency into vacuum (%) 69.7 52.6 46.8 79.5 89.0 66.1 81.2 87.4
Table 9. Results of Monte Carlo trajectory simulations for main parameters of the extracted pulsed nobelium ion beam for 8 calculation variants. Number of calculated ions is 10000 for each variant.
Table 9. Results of Monte Carlo trajectory simulations for main parameters of the extracted pulsed nobelium ion beam for 8 calculation variants. Number of calculated ions is 10000 for each variant.
Calculation variant #1 #2 #3 #4 #5 #6 #7 #8
Longitudinal (90%) energy spread (eV) 0.29 1.1 0.43 0.42 0.62 0.46 0.45 0.59
Bunch time (90%) width (µs) 9 9 9 9 9 9 9 9.4
Longitudinal emittance (90%) (eV µs) 2.6 9.9 3.8 3.8 5.6 4.1 4.0 5.6
Beam radius (90%) (mm) 1.85 1.93 1.90 1.88 1.88 1.90 1.92 1.95
Transverse (90%) energy spread (eV) 0.12 0.21 0.18 0.18 0.17 0.23 0.16 0.17
Normalized transverse emittance (90%) (π∙mm∙mrad ∙[eV]1/2) 224 156.1 292 289 309.8 321 336 310
Table 10. Results of gas dynamic simulations for the gas flow rates through the GSI nozzle at pumping capacity of the gas-jet chamber of 1300 l/s.
Table 10. Results of gas dynamic simulations for the gas flow rates through the GSI nozzle at pumping capacity of the gas-jet chamber of 1300 l/s.
Stagnation pressure Pcell 200 mbar 300 mbar
Background pressure in gas-jet chamber Pbg (mbar) 0,0178 0,0267
Total gas flow rate Qtot (mbar l/s) 23.2 34.8
Gas flow rate through funnel exit into vacuum Qvac (mbar l/s) 0.05 0.271
Flow rate ratio Qtot / Qvac 464 128
Table 13. Results of Monte Carlo simulations for total nobelium-254 ion beam extraction efficiencies for different stagnation gas pressures Pcell. The number of calculated ions is 10,000 for each variant.
Table 13. Results of Monte Carlo simulations for total nobelium-254 ion beam extraction efficiencies for different stagnation gas pressures Pcell. The number of calculated ions is 10,000 for each variant.
Stagnation pressure Pcell 200 mbar 300 mbar
Fraction of ions in nobelium beam at FR-only funnel entrance (%) 64.2 64.9
Total ion beam extraction efficiency into vacuum (%) 16.8 35.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated