Research on Differentiated Dynamic Reactive Power Compensation Scheme considering the Suppression of Transient Voltage Dips

In order to reduce the risk of grid transient voltage instability brought about by the new energy and system dynamic loads and the increasing proportion of new energy access, this paper proposes a differentiated dynamic reactive power compensation configuration method for suppressing transient voltage dip instability. The method first establishes a dynamic reactive power device configuration index system based on a multi-binary table, and then establishes a differentiated dynamic reactive power compensation device configuration model based on the node instability risk characteristics by combining with the regional division of system transient voltage instability risk. The model takes the investment cost and suppression effect as the optimization objectives, and realizes differentiated dynamic reactive power compensation by flexibly adjusting the optimization weights of economic benefits and reactive power compensation effects in the configuration process; Compared with the traditional compensation methods, differentiated compensation can significantly improve the economic benefits of reactive power compensation configuration. Finally, taking the IEEE39 node test system as an example, the improved TLBO algorithm is used to solve the model, which verifies the accuracy and effectiveness of the method proposed in this paper.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The rapid development of modern power network, with the gradual construction of new power system, DC transmission system, the wide application of power electronic equipment, new energy access and induction motor loads accounted for an increasing proportion of the power system voltage regulation ability to weaken, the risk of transient voltage instability increases, especially transient reactive power support ability to decline the problem is increasingly serious.

Dynamic reactive power compensation device can react quickly when the grid fault occurs, provide a large amount of reactive power, inhibit transient voltage dips, thus avoiding system transient voltage instability [1]. Dynamic reactive power compensation technology is an important and effective means to improve the reliability of power system operation and to increase the stability margin. Reasonable planning of location, selection of device types according to different device characteristics and determination of installation capacity are necessary prerequisites for dynamic reactive power compensation devices to give full play to the reactive power compensation effect [2].

The disadvantage of dynamic reactive power compensation is that it is expensive, with high configuration and maintenance costs, and it is not practical to universally configure it in practical engineering applications, so it is necessary to consider a reasonable arrangement of the distribution points and capacity of dynamic reactive power compensation devices in the planning stage [3]. At present, the research on the optimal configuration of dynamic reactive power compensation mainly focuses on the selection of reasonable installation locations, and the methods used are generally the analysis methods of static voltage stability, such as the pilot node method, the U-Q curve method, and the participation factor method, etc. [4]. However, the main purpose of the dynamic reactive power compensation device should be to improve the transient voltage stability of the system rather than to improve the static voltage stability margin, so it is more appropriate to use the analysis method of transient voltage stability to determine the installation location and capacity of the dynamic reactive power compensation device. Literature [5] determines the transient voltage stability by comparing the magnitude of motor slip before and after the fault and the magnitude of electromagnetic torque and mechanical torque when the voltage reaches the extreme value. However, only comparing the slip or torque can not accurately reflect whether the motor is unstable or not, and it is difficult to be used in engineering practice. Another criterion is to judge the transient voltage stability according to the time when the voltage is lower than a certain threshold in the transient process, and the literature [6] stipulates that in the transient process, the load bus voltage can be restored to more than 0.80p.u. within 10s after the fault. Literature [7] stipulates that the time for the pivot point bus voltage to remain below 0.75 p.u. is not more than 1s, and that the pivot point bus voltage at 220KV and above voltage levels is not less than 0.9 p.u. after the end of the transient process. Literature [8] defines this kind of criterion as transient voltage drop acceptability, and this kind of criterion usually can only qualitatively judge the stability of transient voltage, without considering the influence of voltage drop, and cannot quantitatively analyze the voltage stability.

In addition, the research on the capacity configuration of dynamic reactive power compensation devices is still relatively few and lacks differentiated analysis of the characteristics of the compensation nodes, which can easily lead to over-compensation of the nodes and make it difficult to improve the economy. Literature [9] used the mean-variance mapping algorithm to optimize the STATCOM capacity of compensation node configuration using the short-circuit ratio as a constraint; Literature [10] regarded the capacity of each dynamic reactive power compensation device as a fixed value, and calculated the compensation effect indexes of all the candidate deployment locations through the cyclic deployment method to determine the compensation capacity. However, this method does not take the characteristics of the compensation nodes into account and cannot realize the fine planning of the compensation capacity.

Based on the above research status and existing problems, this paper proposes a differentiated dynamic reactive power compensation configuration method based on transient voltage assessment indexes, which is based on multiple-two-element notation for suppressing transient voltage dips, and by differentiating compensation according to the characteristics of the device type and flexibly considering the weight of the optimization objective to minimize the configuration cost and improve the practicability. Section 2 of this paper analyzes the mechanism of voltage multi-binary table, proposes the safety margin index of transient voltage dips for buses and systems, determines the set of the most serious fault scenarios, and divides the risk regions of transient voltage instability of different grades; Section 3 establishes the model of node-differentiated dynamic reactive power compensation device according to the division of the risk regions of instability, reasonably adjusts the optimization weights of nodes with different risk regions, and makes use of the Improved multi-objective genetic algorithm in IEEE39 node system using PSD-BPA and MATLAB joint simulation of the proposed method in Section 2 and Section 3 for calculation and model solving, which verifies the effectiveness of the proposed method.

2. Dynamic reactive device configuration index system based on Multiple-two-element notation

2.1. Multiple-two-element notation criterion

At present, the engineering empirical criterion is usually adopted internationally for the system transient voltage instability, i.e., to roughly judge whether the system voltage is in a stable state or not by identifying the depth of the voltage drop and the corresponding duration of each busbar after the fault disturbance. It should be noted that the practical criterion can only judge whether the voltage is stable or not, but not the degree of stability [11]. On the other hand, the multi-binary tables criterion can accurately judge the transient voltage stability margin by integrating the transient voltage response curve and quantitatively analyzing the predetermined threshold depth and duration of the voltage deviation. Among the transient voltage quantization methods, the transient voltage stability margin index based on the multiple-two-element notation criterion has a significant advantage, and can quantitatively evaluate the improvement effect of dynamic reactive power compensation on transient voltage [12].

The core idea of the multiple-two-element notation criterion is that by inelectrical force system setting n voltage two-element notations {[V_cr¹,T_cr¹], [V_cr²,T_cr²],…,[V_crⁿ,T_crⁿ]}in the system for transient voltage stability judgment. For any single electric voltage two-element notation, the maximum duration for which the voltage of a bus is below the preset threshold cannot exceed the specified time, when the voltage of a bus meets this condition, the transient voltage of the bus is considered to be stable, otherwise the transient voltage is destabilized. According to the voltage perturbation trajectory using the basic principle of curve integration, according to the idea of giving different weights to different levels of dips, the impact of voltage dip level on system stability is refined, as shown in Figure 1.

For bus i, define the safety margin for transient voltage dips as follow.

η_{V_{i}} = 1 - \sum_{k = 1}^{n - 1} K_{k} \int_{t_{k}}^{t_{k + 1}} [V_{i N} - V_{i} (t)] d t - K_{n} \int_{t_{n}}^{t_{n}^{'}} [V_{i N} - V_{i} (t)] d t - \sum_{k = 1}^{n - 1} K_{k} \int_{t_{k + 1}^{'}}^{t_{k}^{'}} [V_{i N} - V_{i} (t)] d t

(1)

t_k and t_k′ represent the system transient process, bus i transient voltage V_i(t) twice through the V_cr^k moment; K_k corresponds to the kth two-element notation [V_cr^k, T_cr^k] weight coefficients; V_iN is the rated voltage of the bus i, the value of which can be set according to relevant standards, buses need to meet the (0.75p.u.,1s) and (0.8p.u.,10s) standard requirements[13]. When η_Vi > 0, the system transient voltage is stable; conversely, when η_Vi < 0, the transient voltage is unstable.

In the dynamic process, when the system state is critically stable, it satisfies η_Vi= 0. The weight coefficients are solved as follows.

\{\begin{cases} K_{1} (V_{iN} - V_{cr}^{1}) T_{cr}^{1} = 1 \\ K_{1} (V_{iN} - V_{cr}^{1}) T_{cr}^{2} + K_{2} (V_{iN} - V_{cr}^{2}) T_{cr}^{2} = 1 \\ ⋮ \\ K_{1} (V_{iN} - V_{cr}^{1}) T_{cr}^{2} + K_{2} (V_{iN} - V_{cr}^{2}) T_{cr}^{n} + \dots + K_{n} (V_{iN} - V_{cr}^{n}) T_{cr}^{n} = 1 \end{cases}

(2)

For equation (2) the deeper the voltage dip, the shorter its maximum acceptable duration, generally having V_crⁱ < V_cr^j when T_crⁱ < T_cr^j, the larger the corresponding weighting coefficients; conversely, the shallower the dip, the smaller the corresponding weighting coefficients.

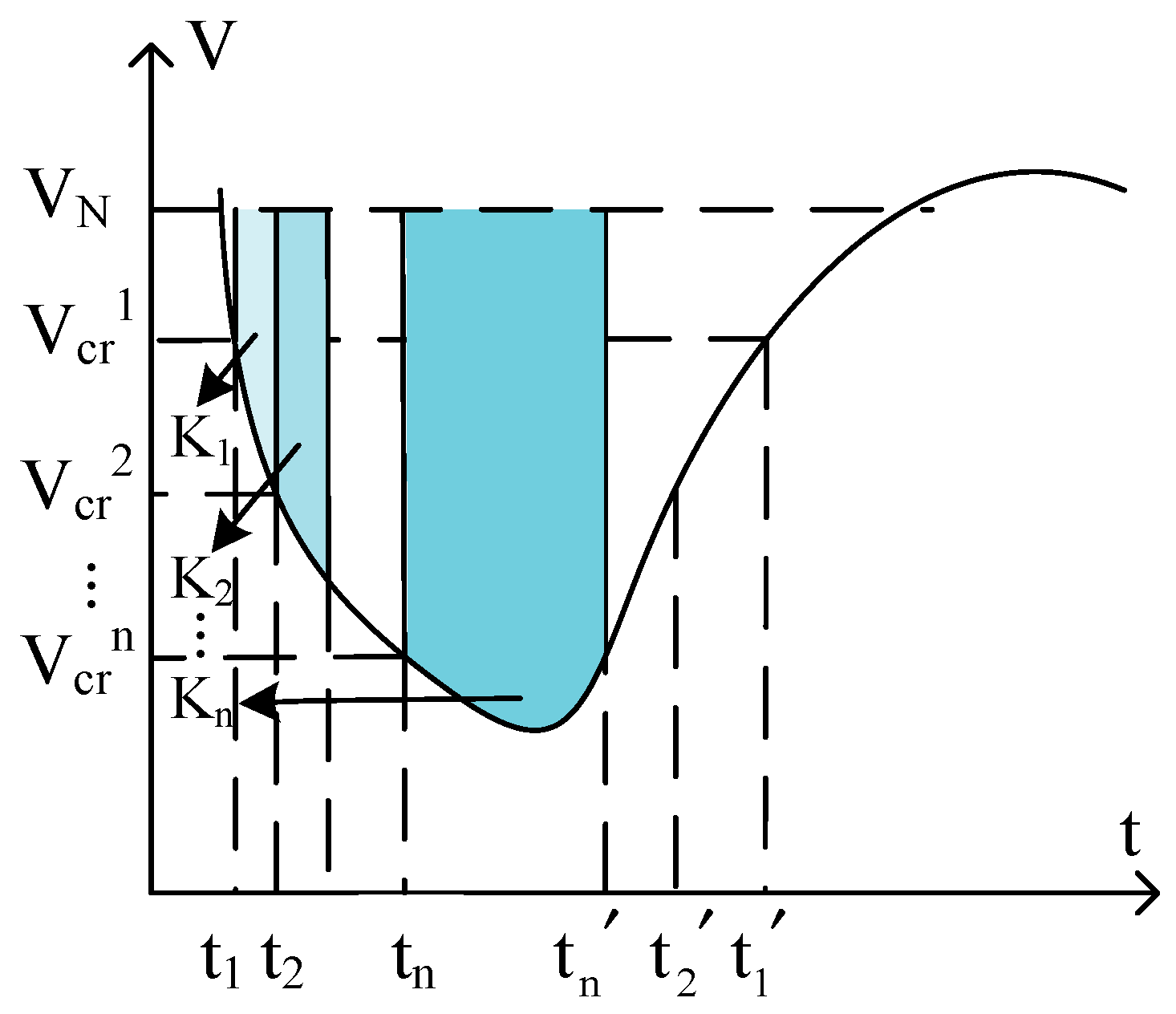
2.2. Indicator of safety margin for integrated transient voltage dips of the system

The selection of the optimal node for reactive power compensation should be able to take into account the improvement effect of the configured reactive power compensation device on the overall voltage stability of the system. Based on the transient voltage dip safety margin index of the node in Equation (1), the comprehensive transient voltage dip safety margin index Γ of the regional system is proposed, and its calculation method is as follows:

Γ = \sum_{l = 1}^{N_{l}} δ_{l} \sum_{i = 1}^{n} W_{i} η_{V_{i, l}}

(3)

N₁ is the total number of faults considered, δ_l denotes the probability of the lth fault, (l=1,2,…,N₁); W_i denotes the weight of the ith node within the system, and η_Vi,l denotes the transient voltage dip safety margin indicator of node i under the fault l scenario. It can be seen that Γ has the same incremental and decremental nature as the indicator η_V, and the larger Γ is, the higher the transient voltage stabilization margin of the system and the better the safety.

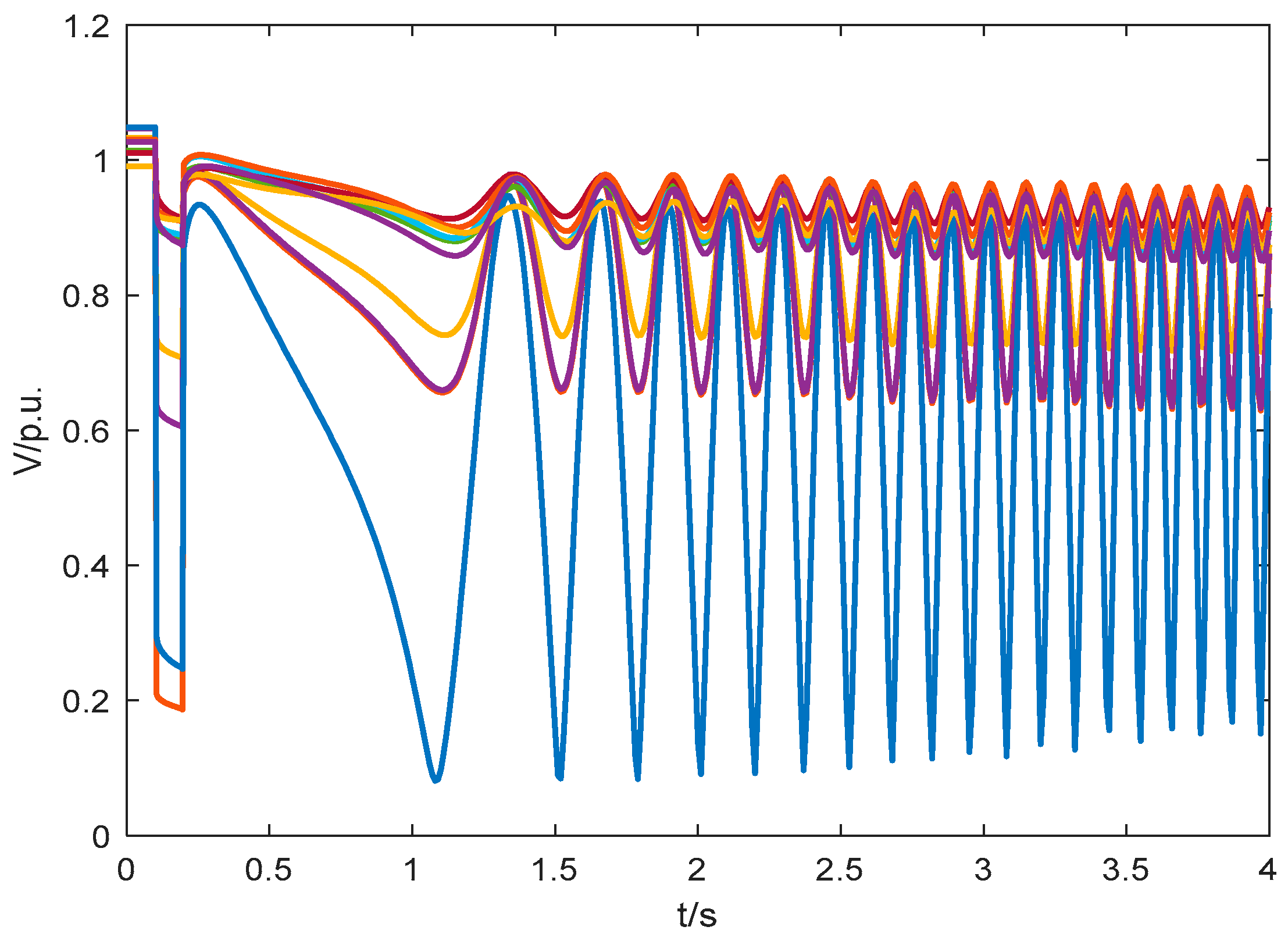
2.3. Set of worst failures

Before selecting configuration nodes for reactive power devices, the most severe fault set affecting the safe and stable operation of the system should be selected based on the baseline scenario for reactive power planning , which is selected on the basis of:

D_{Γ, l} = δ_{l} \sum_{i = 1}^{n} λ_{i} η_{i}^{risk}

(4)

D_Γ,l is the voltage destabilization risk index of the system when fault l occurs in the system, δ_l denotes the probability that the lth fault occurs in the system, λ_i is the weighting factor of bus i, and η_i^risk is the voltage destabilization risk factor of bus i.

λ_{i} = \frac{χ_{1} N_{i} + χ_{2} \frac{S_{i}}{S_{b a s e}}}{\sum_{i = 1}^{N} (χ_{1} N_{i} + χ_{2} \frac{S_{i}}{S_{b a s e}})}

(5)

N_i is the degree of bus i, reflecting the number of edges associated with bus i; χ_1, χ₂ are the weight coefficients, which satisfy χ₁ + χ₂= 1 In this paper, χ₁ =χ₂= 0.5; S_i is the apparent power injected into bus i; S_base is the power base value, which is taken as 100MV∙A in this paper; S_i/ S_base represents the magnitude of the power that is transmitted or distributed by bus i in the system. The larger its value, the more power the bus transmits and distributes in the system, and the more important it is to the system.

η_{i}^{r i s k} = 1 - η_{V_{i}}

(6)

η_i^risk is defined as the voltage destabilization risk factor of bus i. The larger its value, the higher the destabilization risk of bus i is.

ξ = {l |s o r t {D_{Γ, l}}, | l \in {1, 2, \dots, N_{l}}}

(7)

D_Γ,l is the voltage destabilization risk index of the system when a fault l occurs in the system; ξ is the set of the worst faults based on the benchmark scenario of reactive power planning; and srot{D_Γ,l} denotes the set formed by arranging the buses in descending order according to the magnitude of the D_Γ,l value.

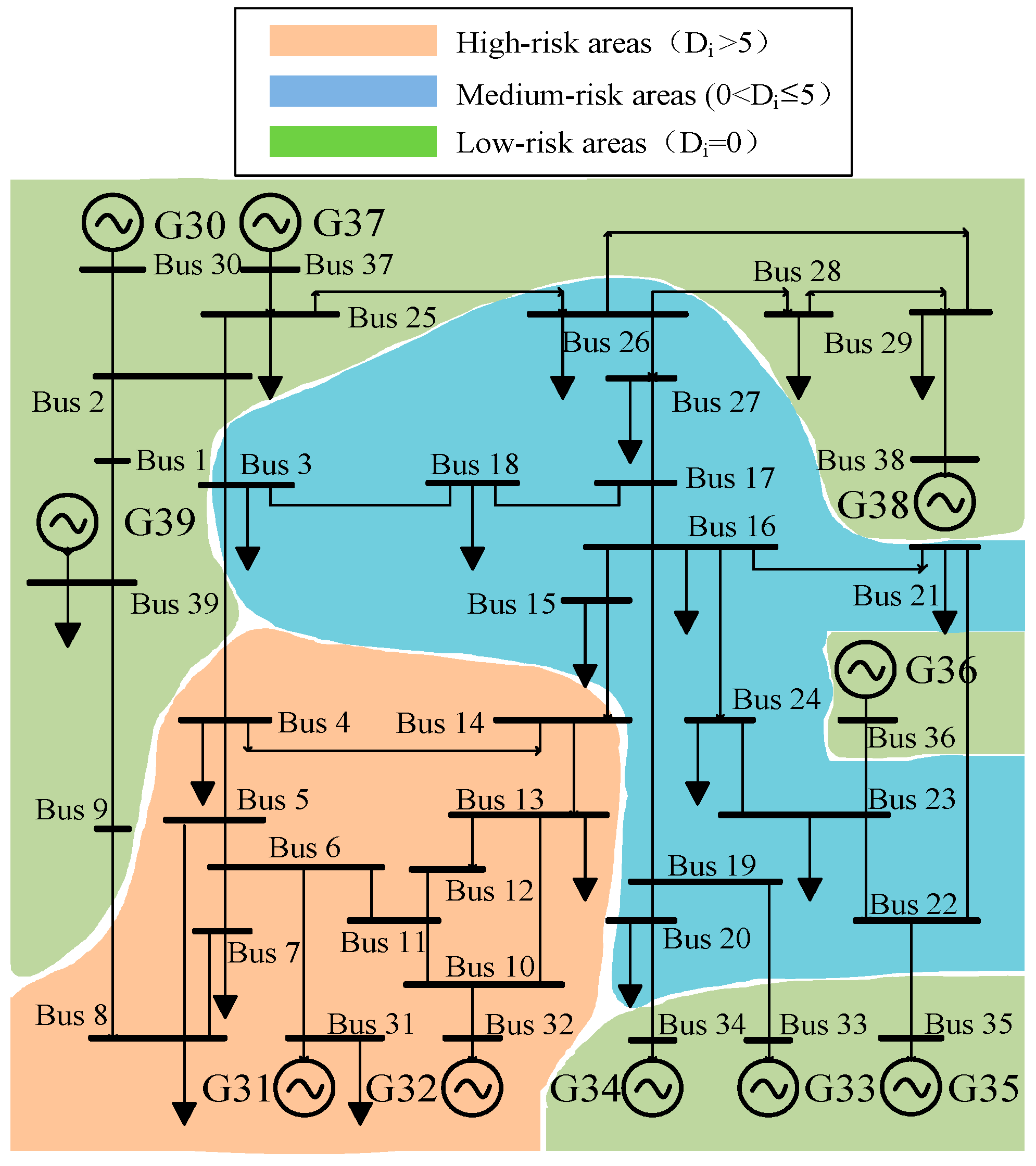
2.4. Regional classification of the risk of transient voltage destabilization

In order to determine the buses with higher risk of transient voltage destabilization in the system and to divide the destabilization risk areas of different levels, so as to carry out differentiated dynamic reactive power compensation according to the different risk level areas belonging to the buses to be compensated, this section defines the buses transient voltage destabilization risk index D_i as based on the most serious fault set ξ affecting the safe and stable operation of the system and the bus transient voltage dip safety margin η_Vi:

D_{i} = \sum_{l = 1}^{N_{l}} N_{u, i, l} \sum_{l = 1}^{N_{l}} δ_{l} λ_{i} η_{i}^{risk}

(8)

D_i is the voltage destabilization risk index of the system when fault l occurs in the system, δ_l denotes the probability that the lth fault occurs in the system, λ_i is the weight coefficient of bus i, η_i^risk is the transient voltage dip safety margin of bus i. N_u,I,l is used to determine whether bus voltage i is destabilized or not in the scenario of the system with the occurrence of fault l. If it is destabilized, N_u,I,l=1; otherwise, N_u,I,l=0.

When D_i>0, it indicates that transient voltage destabilization of bus i occurs under the set of critical fault scenarios, and the larger D_i is, the larger the degree of transient voltage drop of bus i is, the more serious the destabilization is, and the risk of destabilization is higher. On the contrary, D_i=0 indicates that bus i does not experience transient voltage destabilization and its destabilization risk is low.

According to “Code on security and stability for power system of China”, the criterion for transient voltage stabilization is that the load bus voltage can be restored to the specified operating voltage level or above during the transient and dynamic processes after the power system is disturbed. This defines the area where the node of is located as a low-risk area for transient voltage destabilization, and the area where the node of is located as a medium-high risk area for transient voltage.

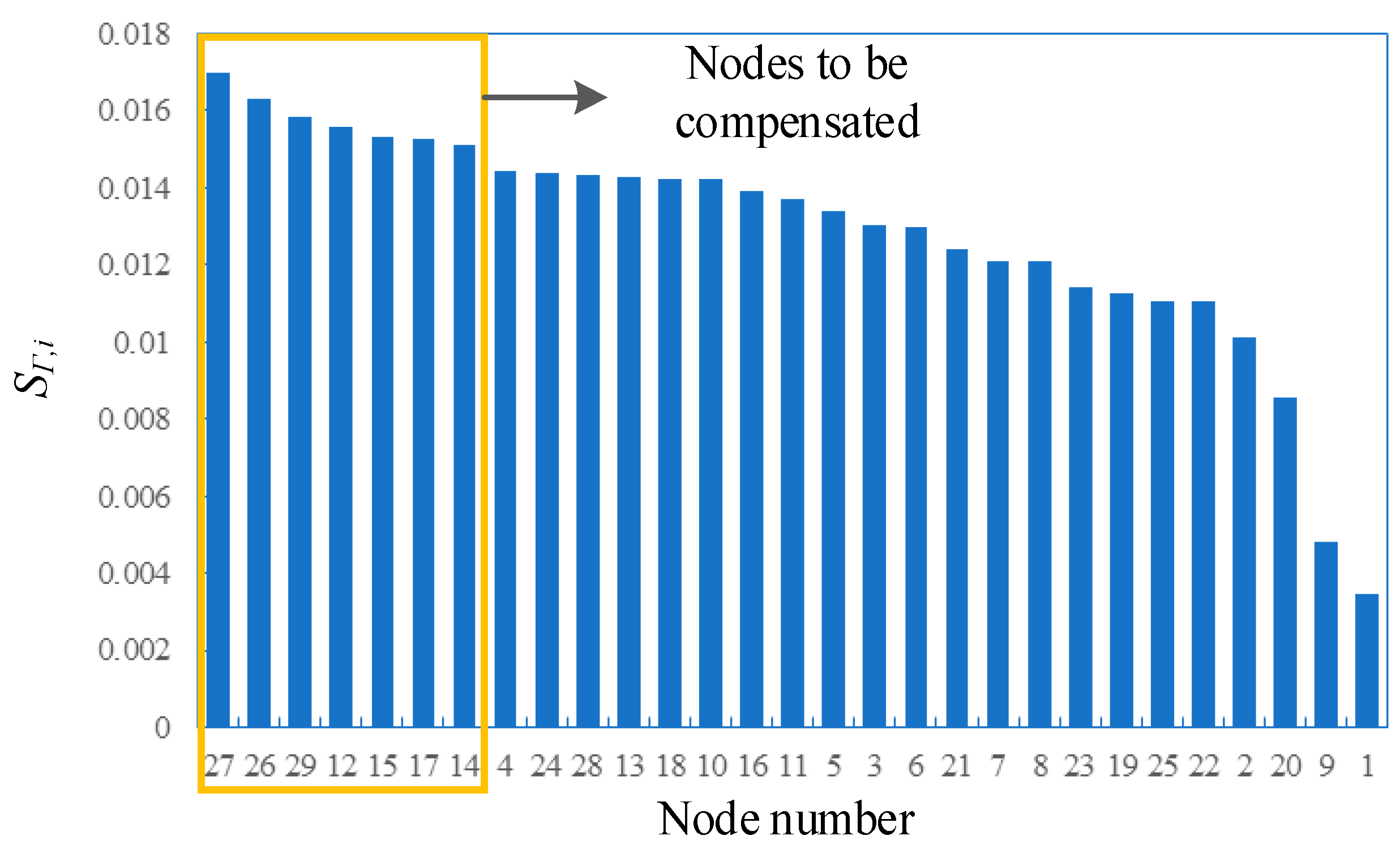
2.5. Sensitivity index

Configure reactive power compensation devices in the initial candidate nodes within the regional system, calculate the increment of the integrated transient voltage dip safety margin index Γ of the system after configuration, and take the ratio of it to the configured capacity of the reactive power compensation equipment as the key index for selecting the optimal installation node.

S_{Γ, i} = \frac{Γ (Q_{c o m p, i}) - Γ (Q_{0, i})}{S_{c o m p}}

(9)

Γ(Q_0,i) is the safety margin index value of comprehensive transient voltage dips when the system is not configured with reactive power compensation device; S_comp is the capacity of reactive power compensation device configured at node i; Γ(Q_comp,i) is the safety margin index of comprehensive transient voltage dips of the system after configuring reactive power compensation device with capacity S_comp at node i.

The sensitivity index reflects the compensation effect of reactive power compensation device on system transient voltage dips, and the larger its value, the better the compensation effect. Usually, the faster the response speed of the dynamic reactive power compensation device, the better the improvement of the system voltage in the short term. If only the voltage binary table with low time threshold is utilized to constrain, the sensitivity index can also reflect the speed of the reactive power compensation device response.

After calculating the reactive power compensation sensitivity index at each node, the node with larger sensitivity is selected as the optimal installation node for reactive power compensation. The set of buses to be compensated is constructed as:

C_{b u s}^{} = \{i |s o r t {S_{Γ, i}}, i \in {1, 2, \dots, N}\}

(10)

the set of candidate buses for C_bus; sort{S_Γ,i} denotes the set composed by sorting the buses in descending order according to the size of the S_Γ,i values.

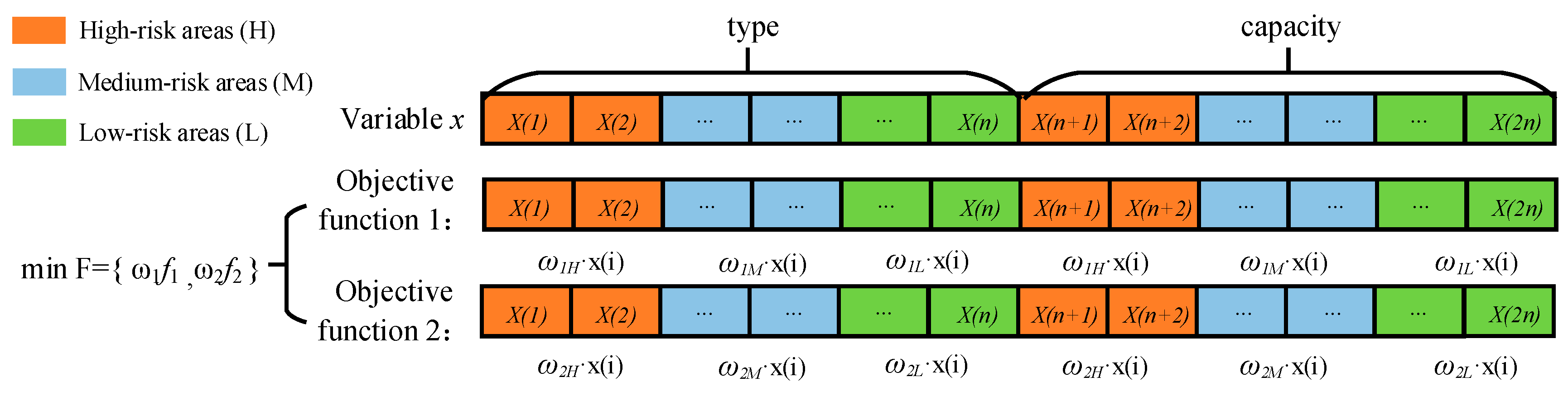
2.6. Dynamic reactive power compensation configuration index system

This chapter defines the index system for the optimal configuration of dynamic reactive power compensation devices based on the multiple binary table criterion, η_Vi and Γ are used to judge the transient voltage dip safety margins of the bus and the system, respectively, which can subsequently be used as the compensation effect objective function for the optimal configuration; and by defining the system instability risk indicator D_Γ,l, the system is scanned in N-1, and the most severe fault set of the reactive planning scenarios is obtained; then the The worst fault set and the transient voltage instability risk indicator D_i are used to partition the transient voltage instability risk characteristics, and the differentiated compensation is performed by judging the level of the transient voltage instability risk region to which the reactive power compensation candidate nodes obtained by the sensitivity indicator S_Γ,i belong. By flexibly adjusting the optimization weights of the two sub-objectives of economic efficiency and reactive power compensation effect of the optimal configuration of dynamic reactive power compensation, the differentiated reactive power compensation can reduce the wastage of reactive power resources and economic costs due to over-compensation on the basis of maintaining the reactive power compensation effect, which effectively improves the economy and practicability of the configuration of dynamic reactive power compensation devices.

Figure 2. Dynamic reactive device configuration index system.

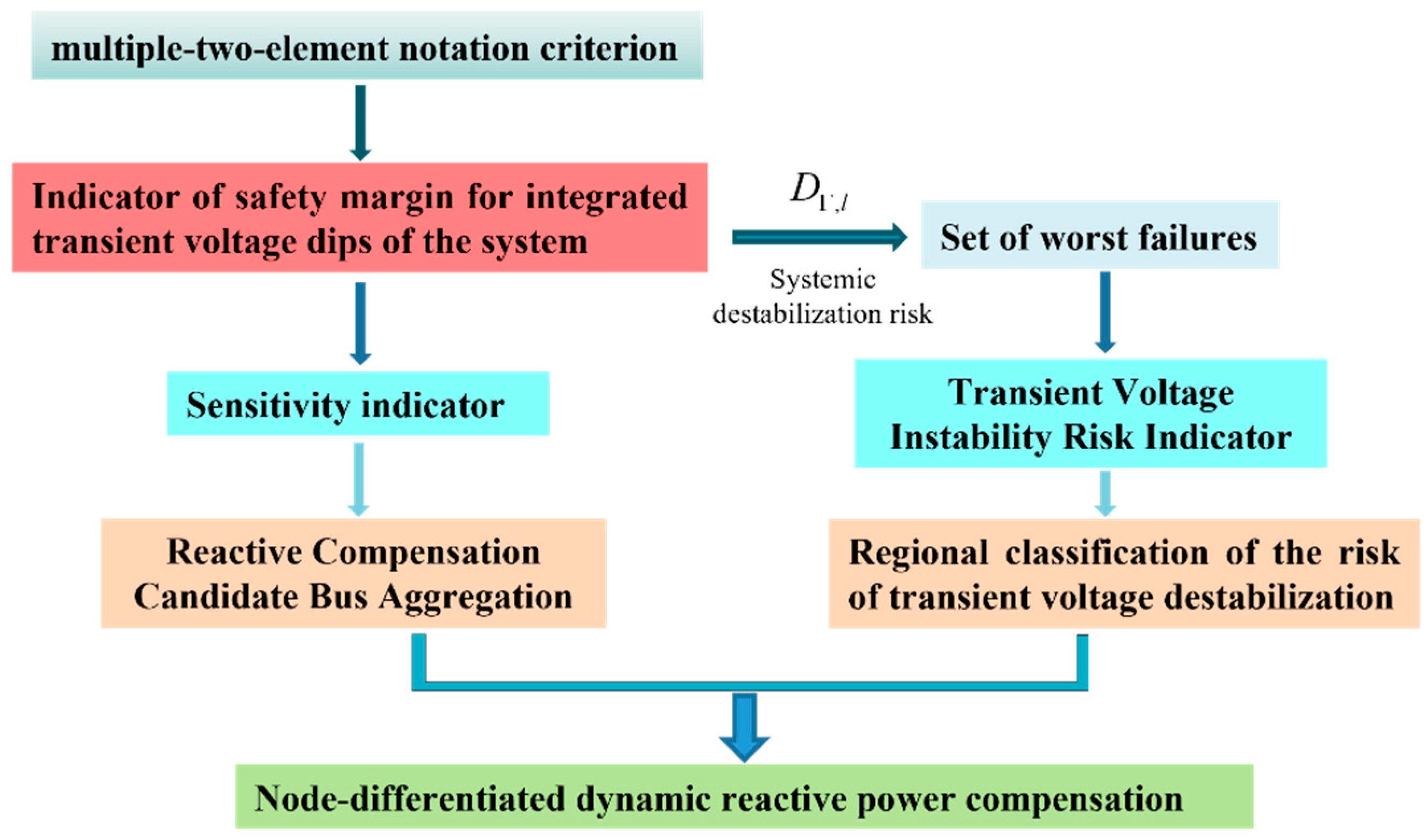
3. Node-differentiated dynamic reactive power compensation models

3.1. Device selection

SVC and STATCOM are two kinds of dynamic reactive power compensation devices which are widely used in current power system, SVC has the features of continuous adjustment of reactive power, fast response speed, etc., but SVC is easily affected by bus voltage, and the output reactive current will drop proportionally with the system bus voltage when serious fault occurs [14]. STATCOM is a new generation of reactive power compensation equipment after SVC, and its output reactive current is not affected by AC bus voltage, but the project cost is higher, and the overall economy is not as good as that of SVC [15].

In order to visualize the performance difference between SVC and STATCOM in suppressing the effect of transient voltage dips, a three-phase non-metallic short-circuit fault is set up in a power grid at 0.1s, and the fault lasts for 0.3s before it is removed. In the fault bus near the node were configured 300Mvar SVC and STATCOM, the observation of its reactive power response characteristics and fault bus voltage shown in Figure 3.

It can be seen that both SVC and STATCOM can quickly send out a large amount of reactive power during faults to support the bus transient voltage, so that the voltage can be restored to normal operation as soon as possible, and the transient voltage dips can be suppressed. At the same time, it can also be seen from the figure that in the short term, STATCOM responds to more reactive power than SVC, with faster speed, better reactive power compensation effect, more stable output, and significantly better performance than SVC.

3.2. Configuration model

The configuration problem of dynamic reactive power compensation device is essentially a multi-objective optimization problem, and cost and reactive power compensation effect are the 2 sub-objective functions of this optimization problem. The node differentiated compensation is mainly reflected in the flexible adjustment of the optimization weights of the 2 sub-objectives according to the transient voltage instability risk characteristics of the compensation node, in order to achieve differentiated compensation and avoid the cost waste caused by over-compensation. Since STATCOM has a faster response speed, better reactive power compensation effect and more stable output than SVC, it can make the system obtain the best compensation effect in the pre-transient process. The nodes with high risk of transient voltage instability should focus more on the reactive power compensation effect, give priority to the configuration of STATCOM, increase the safety margin of comprehensive transient voltage dips of the system, and improve the transient stabilization capability of the system. And SVC has significant economic advantages, which can maximize the economic cost savings. Considering the high installation and operation cost of dynamic reactive power device, for nodes with low risk of transient voltage instability, the economic consideration should be improved appropriately, and SVC is preferred to be configured to maximize the economic benefit of the compensation scheme under the premise of meeting the reactive power demand of the system.

1) Objective function

f_{1} = \sum_{i = 1}^{m} (C_{i n s - x} + C_{p e r - x} Q_{i - x})

(11)

f_{2} = - Γ

(12)

m i n F = {w_{1} f_{1}, w_{2} f_{2}}

(13)

f₁, f₂ are the two sub-objective functions of the multi-objective optimization function F, f₁ is the cost objective function, f₂ is the reactive power compensation effect objective function, the smaller the value of f₂ indicates the better the reactive power compensation effect; w₁, w₂ are the optimization weights of the sub-objective functions f₁, f₂, respectively; x is the control variable, including the type and the capacity, the The coding is shown in Figure 4, where different weights are taken to optimize the n candidate compensation nodes at different risks of transient voltage instability, and the first n bits are used to store the dynamic reactive power compensation device type judgment variables (0 means no dynamic reactive power compensation device is installed, 1 means that SVC is installed, 2 means that STATCOM), and the last n bits are used to store the configured capacity; the number of dynamic reactive power compensation devices installed is m, C_ins-x is the installation cost, C_per-x is the reactive power compensation unit price, and Q_i-x is the reactive power compensation capacity.

In order to reflect the principle of differentiation, the high-risk region can highlight the weight of reactive power compensation, so that w₁:w₂=1:2, i.e., w₁=0.33, w₂=0.67; the medium-risk region can be optimized with equal weights, so that w₁:w₂=1:1, i.e., w₁=0.5, w₂=0.5; the low-risk region should highlight the weight of cost, so that w₁:w₂=2:1, i.e., w₁=0.67, w₂=0.33. Then, when solving the differentiated capacity model, different optimization weights should be taken on the control variable x corresponding to different transient voltage instability level compensation nodes according to the idea of differentiated compensation, respectively.

2) Constraints

Power balance constraints:

\{\begin{array}{l} U_{i} \sum_{j = 1}^{n_{b}} U_{j} (G_{i j} \cos δ_{i j} + B_{i j} \sin δ_{i j}) = P_{G i} - P_{L i} \\ U_{i} \sum_{j = 1}^{n_{b}} U_{j} (G_{i j} \sin δ_{i j} - B_{i j} \cos δ_{i j}) = Q_{G i} - Q_{L i} \end{array}

(14)

P_Gi, Q_Gi, P_Li, Q_Li are the active and reactive power input and output at the nodes, respectively; U_i is the voltage at the nodes; G_ij is the conductance between branches i-j, B_ij is the conductance between branches i-j, and δ_ij denotes the difference in phase angle between branches i-j; n_b is the total number of nodes; and the reactive and active power inflow and outflow at the nodes in the system should be balanced at all times.

Generator output, nodal voltage and reactive power capacity constraints:

\{\begin{array}{l} P_{G i}^{\min} \leq P_{G i} \leq P_{G i}^{\max}, i = 1, 2, \dots, N \\ Q_{G i}^{\min} \leq Q_{G i} \leq Q_{G i}^{\max}, i = 1, 2, \dots, N \\ U_{i}^{\min} \leq U_{i} \leq U_{i}^{\max}, i = 1, 2, \dots, N \\ Q_{i}^{\min} \leq Q_{i} \leq Q_{i}^{\max}, i = 1, 2, \dots, n \end{array}

(15)

P_{G i}^{\max}

P_{G i}^{\min}

and

Q_{G i}^{\max}

Q_{G i}^{\min}

denote the upper and lower limits of the node input active and reactive power, respectively;

U_{i}^{\max}

U_{i}^{\min}

and

Q_{i}^{\max}

Q_{i}^{\min}

are the upper and lower limits of the voltage and reactive power compensation capacity, respectively.

The above equation constrains the limits of generator active reactive power output, reactive power compensation output and nodal voltage in each node to prevent the occurrence of relevant power and voltage overruns, respectively.

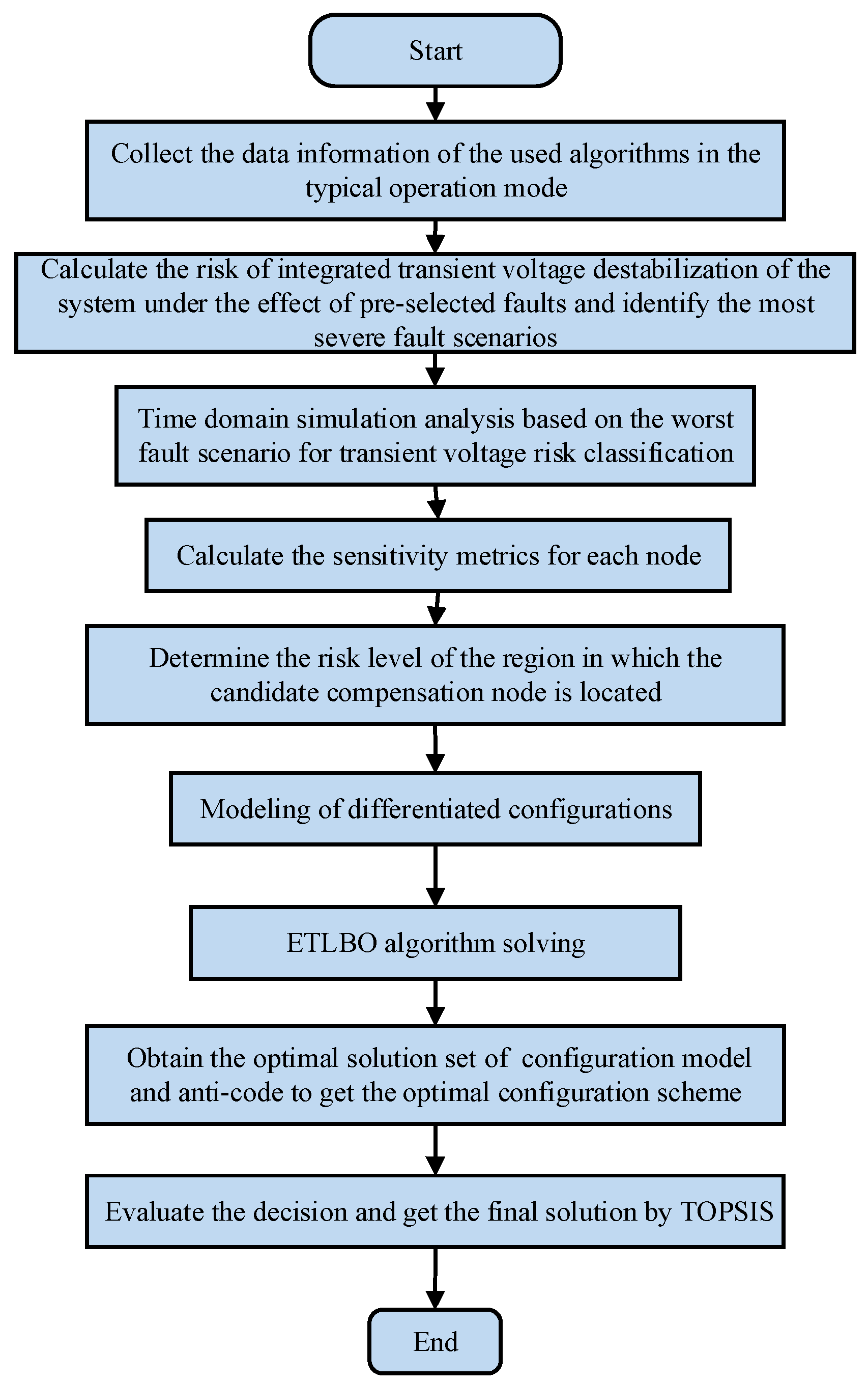
4. Solving Algorithm and Process

4.1. ETLBO optimization algorithm

TLBO algorithm is a new type of intelligent algorithm that simulates the class teaching process. It has the advantages of few parameters, easy to implement, and fast convergence speed, but also has the disadvantages such as easy to fall into the local optimum, and the convergence speed slows down dramatically with the increase of the number of dimensions [16]. The improved ETLBO (Elitist Teaching-Learning-Based Optimization) algorithm adds elite strategies to the basic TLBO algorithm to accelerate the convergence of the algorithm and greatly reduce the risk of falling into a local optimum, and its main process is similar to the TLBO algorithm, which can be better applied to the optimal allocation of the dynamic reactive power compensation [17]. The main processes are as follows:

a. Initialization

First set the number of iterations, the number of students in the class and the number of subjects to randomly initialize the class students to generate a class population as follows:

[\begin{matrix} X_{1} & f (X_{1}) \\ X_{2} & f (X_{2}) \\ ⋮ & ⋮ \\ X_{N} & f (X_{N}) \end{matrix}] = [\begin{matrix} x_{11} & x_{12} & \dots & x_{1 d} & f (X_{1}) \\ x_{21} & x_{22} & \dots & x_{2 d} & f (X_{2}) \\ \dots & \dots & \dots & \dots & \dots \\ x_{N 1} & x_{N 2} & \dots & x_{N d} & f (X_{N}) \end{matrix}]

(16)

f(X_i) is the value of the objective function for individual X_i; N is the population size, i.e., the number of individuals in the class. X_i denotes the ith individual, X_i=(x_i1, x_i2,…, x_id,), where d is the dimension of each individual student.

b "Teaching" process

In the "teaching" process, the "difference" between the teacher and the learner is calculated to promote the learner to approach the teacher to improve the learner's knowledge, as shown in Equation (17):

X_{i}^{'} = X_{i} + D = X_{i} + r (X_{t e a c h e r} - T_{F} X_{M e a n})

(17)

X_i^′ is the new trainee generated by trainee X_i after the "teaching" process; X_teacher is the teacher, X_Mean is the average value of the trainees in the class; r is a random number with the value ranging from 0 to 1. T_F stands for Teaching Factor, whose value is taken as 1 or 2. After the "teaching" process, the "grades" of the old and new learners are compared and the one with better grades is retained.

c "Self-learning" process

This process ensures population diversity through mutual learning between individual participants in the form of communication, group discussion, etc., with the formula:

X_{i}^{'} = \{\begin{array}{l} X_{i} + r (X_{i} - X_{i}) & f (X_{i}) < f (X_{i}) \\ X_{i} - r (X_{i} - X_{j}) & f (X_{i}) > f (X_{j}) \end{array}

(18)

X_i^′ is the new learner generated by learner X_i after the "self-study" process; X_j is a randomly selected other learner; r is a random number with a value ranging from 0 to 1. Similarly, after the "self-study" process, the better of the old and new trainees are retained.

4.2. TOPSIS Evaluation Method

The optimal solution of the objective function by the ETLBO algorithm results in a set of non-inferior solution sets located on the Pareto front. In order to select the optimal configuration scheme from them, the optimization results also need to be evaluated and ranked. TOPSIS (Technique For Order Preference By Similarity To Ideal Solution) target decision-making method, also known as the ideal solution approximation method, is a kind of relative merits and demerits based on the proximity of the existing objects to the idealized target Evaluation of multi-attribute decision-making method [18], which is calculated as follows:

Let there are m evaluation objectives D_i={D₁, D₂,···, D_m} in the multi-objective optimization problem, and each evaluation objective contains n evaluation indexes x_j={x₁, x₂,···, x_n}, then we can establish the feature matrix of the evaluation objectives D, in which D_i(x_j)=x_ij. The elements in the feature matrix are uniformly normalized as shown in Equation (19).

r_{i j} = \frac{x_{i j}}{\sqrt{\sum_{i = 1}^{m} x_{i j}^{2}}}

(19)

Establish the normalization matrix v_ij as shown in Equation (20), where w_j is the weight of the jth indicator in the normalization matrix v_ij.

v_{i j} = w_{j} r_{i j}, i = 1, 2, \dots, m, j = 1, 2, \dots, n

(20)

Ideal solution A and negative ideal solution A can be represented by the normalized matrix v_ij with weights, J₁ and J₂ are the highest value and the lowest value of weights on the ith evaluation objective, respectively.

\begin{array}{l} A^{+} = {v_{1}^{+}, v_{2}^{+}, \dots, v_{m}^{+}}, v_{j}^{+} = {\max_{i} v_{i j}, j \in J_{1}; \min_{i} v_{i j}, j \in J_{2}} \\ A^{-} = {v_{1}^{-}, v_{2}^{-}, \dots, v_{m}^{-}}, v_{j}^{-} = {\min_{i} v_{i j}, j \in J_{1}; \max_{i} v_{i j}, j \in J_{2}} \end{array}

(21)

The smaller the distance between the solution to be evaluated and the ideal solution, i.e., the larger the distance between the solution and the negative ideal solution, the more optimal the solution is. Calculate the distance between each program to be evaluated and the positive and negative ideal solutions and solve for the closeness P_i, the program with the largest closeness value is the optimal program sought.

\{\begin{matrix} P_{i} = \frac{S_{i}^{-}}{S_{i}^{+} + S_{i}^{-}} \\ S_{i}^{+} = \sqrt{\sum_{j = 1}^{n} {(v_{j}^{+} - v_{i j})}^{2}} \\ S_{i}^{-} = \sqrt{\sum_{j = 1}^{n} {(v_{j}^{-} - v_{i j})}^{2}} \end{matrix}

(22)

4.3. Solution Steps

The configuration steps of the dynamic reactive power compensation device are as follows.

1) Perform the trend calculation of the algorithm by PSD-BPA, collect the trend information of the system, and calculate the weight coefficients of each bus.

2) Perform N-1 fault scanning on the system, calculate the integrated transient voltage instability risk D_Γ,l of the system under the action of pre-selected faults, and rank them to determine the reactive power planning benchmark scenario for the most severe faults.

3) Based on the most severe fault of the reactive power planning benchmark scenario, the time domain simulation analysis is carried out to calculate the transient voltage instability risk index D_i of each node, and divide the three kinds of regions with high, medium and low risk of transient voltage instability.

4) Based on the scenario of the most serious fault, the dynamic reactive power compensation devices of the same type and capacity are connected at each node of the system in turn, and the time domain simulation analysis is performed. The sensitivity index S_Γ,i of each node is calculated, and the set of candidate nodes based on S_Γ,i is constructed.

5) Based on the location of the determined candidate nodes for reactive power compensation, determine the transient voltage instability risk region to which they belong, and combine the optimization weights of each selected reactive power compensation node, encode the type and capacity of the dynamic reactive power compensation device, and use the optimization algorithm to differentially solve the problem, and obtain a set of candidate solutions.

6) The TOPSIS evaluation decision method is used to evaluate the to-be-configured scenarios of dynamic reactive power compensation devices under the resulting baseline scenario and select the final scenario.

The corresponding general flow of dynamic reactive power device configuration is shown in Figure 5

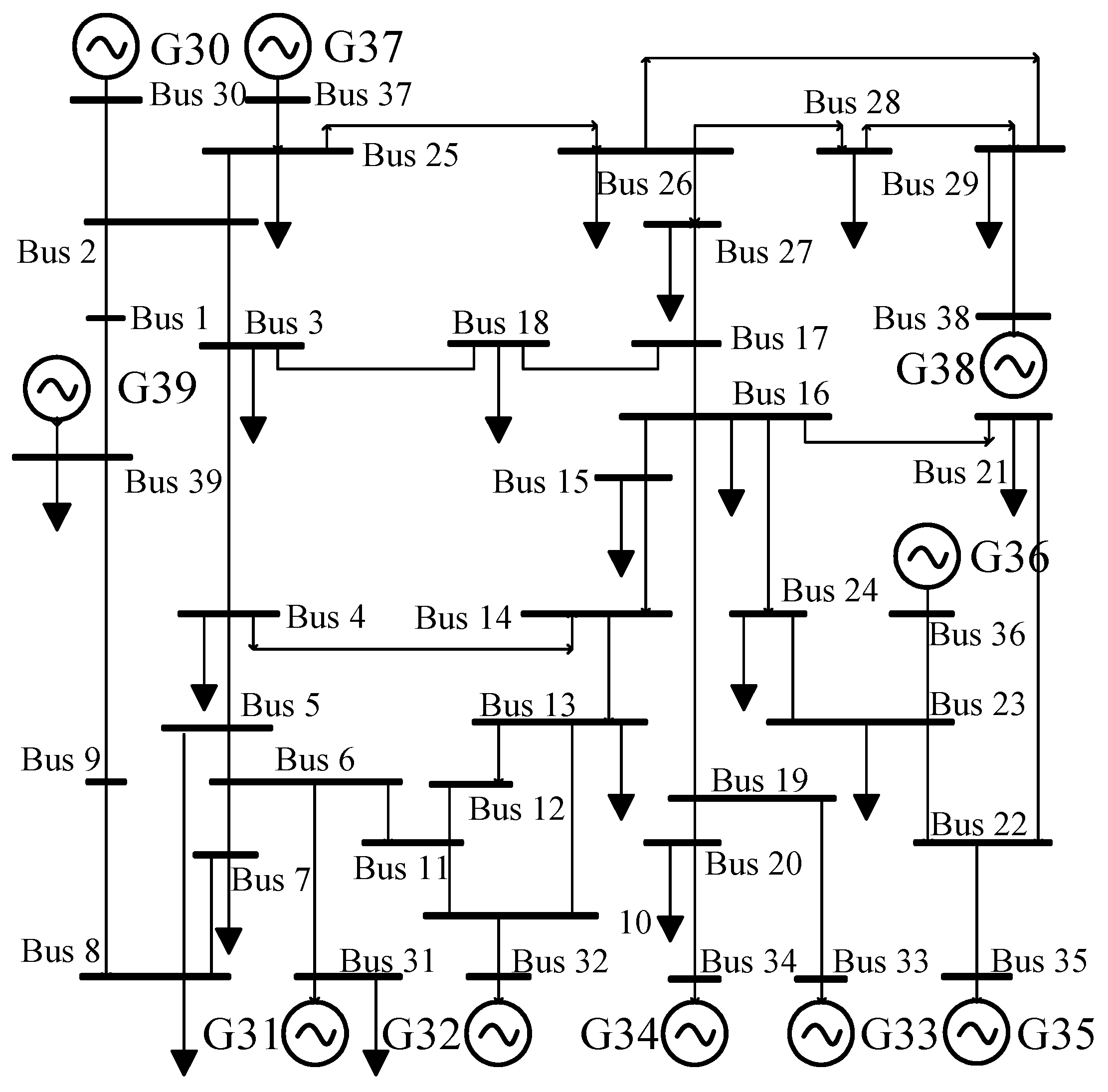
5. Example analysis

In this section, the IEEE39 node system is used as an example for simulation and analysis, and the system wiring diagram is shown in Figure 6. The branch, node, transformer and generator parameters of the system are shown in the literature [19] and are simulated by applying Matlab and PSD-BPA software. All the loads are configured in the ratio of 50% constant impedance and 50% induction motor, and the load model parameters are referred to literature [20]. Considering the typicality of the algorithm and the computational volume, this paper considers the installation of dynamic reactive power compensation devices at 6 nodes, i.e., the dimension of the type variable n = 6 and the total dimension of the decision variable 2n = 12.

5.1. Candidate compensation nodes

1) Filtering the set of worst failures

The problem of dynamic reactive power compensation device placement and capacity setting is an integer nonlinear programming problem, and in order to reduce the amount of computation, it is necessary to determine in advance the severe faults that may occur in the system. In order to simplify the processing, this algorithm examines the three-phase short-circuit fault situation, and sets the probability of faults occurring in each line to be equal, with a total of 46 fault scenarios for N-1 scanning. A three-phase short-circuit is set to occur on the line at the moment of t=0.1s, and the duration of the fault is set to be 0.1s. The fault is set to be a three-phase short-circuit grounding of all transmission lines within the sub-district at the 50% position of the line in sequence, and the fault disappears after 0.1s. The time interval included in the index calculation is 0.1~2.0s, i.e., within 1.9s after the fault appears, the sampling interval of voltage magnitude is 0.02s, and the weights of each moment are all 1. According to the simulation results, the system voltage instability risk index D_Γ,l is calculated by Equation (4) for each fault, and it can be seen from the analysis in Section 2.3 that the bigger D_Γ,l is, the more likely that the system will be voltage instability, and the results are as follows in Table 1:

As can be seen from Table 1, the risk of system transient voltage destabilization is different for faults occurring in different lines, and the impact of three-phase short-circuit faults occurring in some lines on the system transient voltage is small, such as fault 2 and so on. In this paper, the eight most serious faults are selected as the most serious fault set, i.e., faults numbered 34, 9, 12, 21, 16, 17, 18, and 35, which correspond to the actual faults of bus-28 and bus-29 lines, bus-05 and bus-06 lines, bus-06 and bus-11 lines, bus-10 and bus-11 lines, bus-16 and bus-17 lines, bus-10 and bus-13 lines, bus-13 and bus-14 lines, and bus-11 and bus-12 lines at the midpoint of the three-phase ground short circuit. Taking the three-phase short circuit of bus-28 and bus-29 lines as an example, some of the bus voltages of the system are shown in Figure 7:

2) Candidate nodes

Similarly, the pre-selection of candidate installation nodes for reactive power compensation devices will greatly reduce the calculation amount of the example and improve the practicality of the project. Dynamic reactive power compensation devices are generally not installed at the bus where the synchronous generators are located, so this paper only considers installing reactive power devices at nodes where the non-generators are located. In order to determine the effect of installing reactive power devices of the same capacity at different nodes on suppressing transient voltage instability, a 50 Mvar STATCOM device is configured at each node of the system respectively as an example, and the integrated transient voltage dip safety margin index Γ of the system after compensation at each node is computed under the most severe fault set scenario, and the corresponding sensitivity index is derived, as shown in Table 2:

The corresponding sensitivity index S_Γ,i for each node is shown in Figure 8:

From Figure 8, it can be seen that the effects of installing reactive power compensation devices with the same capacity at different nodes on reducing the risk of transient voltage instability are different, and the installation of reactive power compensation devices at some nodes can more significantly inhibit the occurrence of transient voltage instability. In this paper, six nodes with the largest sensitivity indexes are selected as the candidate nodes for dynamic reactive power compensation device installation, which are nodes 27, 26, 29, 12, 15 and 17.

5.2. System transient voltage instability risk partitioning

Once the candidate compensation nodes of the system are known, the instability risk of the selected reactive power compensation nodes can be determined for the region in which they are located in the system, and their optimization weights can be determined to achieve differentiated dynamic reactive power compensation. Also based on the worst fault set scenario, the transient voltage instability risk indicator D_i is calculated for each node of the system and the number of instabilities of the node is counted.

Table 3. Indicators of risk of node destabilization.

Nodal	D_i	Number of instabilities	Nodal	D_i	Number of instabilities	Nodal	D_i	Number of instabilities
1	0.0000	0	14	16.7118	6	27	1.7394	1
2	0.0000	0	15	4.2450	3	28	0.0000	1
3	0.5803	1	16	2.5523	1	29	0.0000	1
4	11.7646	6	17	2.3568	1	30	0.0000	0
5	10.3804	6	18	2.0995	1	31	7.3380	5
6	10.6489	6	19	1.5516	1	32	7.4773	5
7	9.9658	5	20	1.4768	1	33	0.0000	0
8	9.5830	5	21	2.1258	1	34	0.0000	0
9	0.0000	0	22	1.6480	1	35	0.0000	0
10	11.2007	6	23	1.7070	1	36	0.0000	0
11	11.5400	6	24	2.6959	1	37	0.0000	0
12	11.2962	6	25	0.0000	0	38	0.0000	0
13	10.8595	6	26	0.3354	2	39	0.0000	0

In all the worst fault set scenarios nodes with D_i≥5 have at least 5 transient voltage destabilizations; nodes with 0<D_i≤5 have at most 3 voltage destabilizations, and most of them have only 1 destabilization; and nodes with D_i≥5 have transient voltages that remain stable. Based on this, the nodes with D_i=0 are located in low-risk areas; nodes with 0<D_i≤5 are located in medium-risk areas; and nodes with D_i≥5 are located in high-risk areas.The risk zoning of transient voltage instability in the IEEE39 system is shown in Figure 9 below:

From the figure it can be seen that most of the nodes containing generators are located in low-risk areas, and the risk of instability of nodes that are electrically distant from generators is generally relatively high, which is closely related to the ability of generators to quickly provide voltage support and maintain system stability.

In order to reflect the principle of differentiation, the high-risk region can highlight the proportion of reactive power compensation, so that ω₁:ω₂=1:2, i.e., ω₁=0.33, ω₂=0.67; medium-risk region can be optimized with equal proportion, so that ω₁:ω₂=1:1, i.e., ω₁=0.5, ω₂=0.5; low-risk regions should be highlighted with cost weighting, so that ω₁:ω₂=2:1, i.e., ω₁=0.67, and ω₂=0.33. Then, when solving the differentiated fixed capacity model, the compensation nodes corresponding to different transient voltage instability risk levels on the control variable x should be calculated by taking different optimization weights according to the idea of differentiated compensation, respectively.

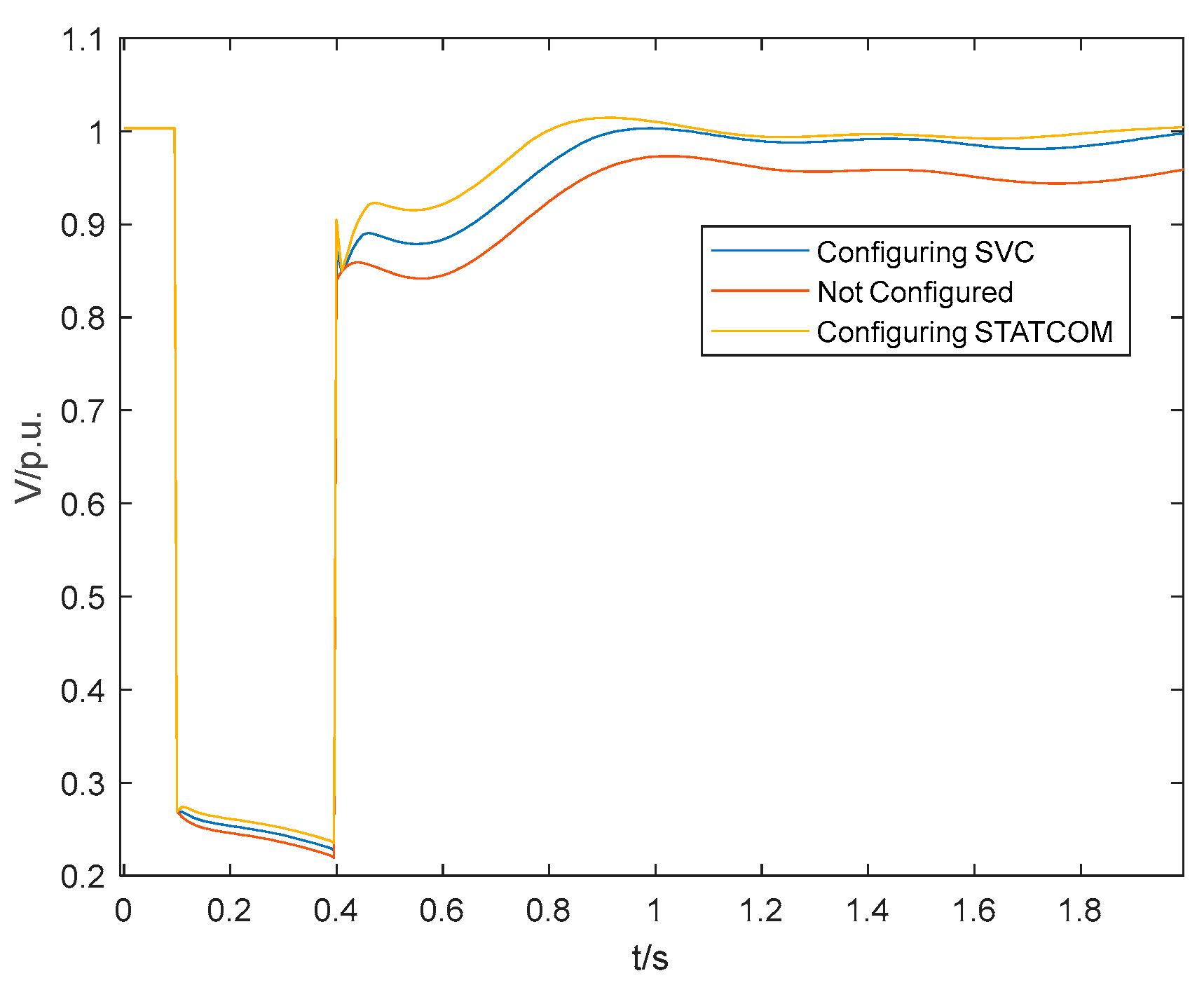
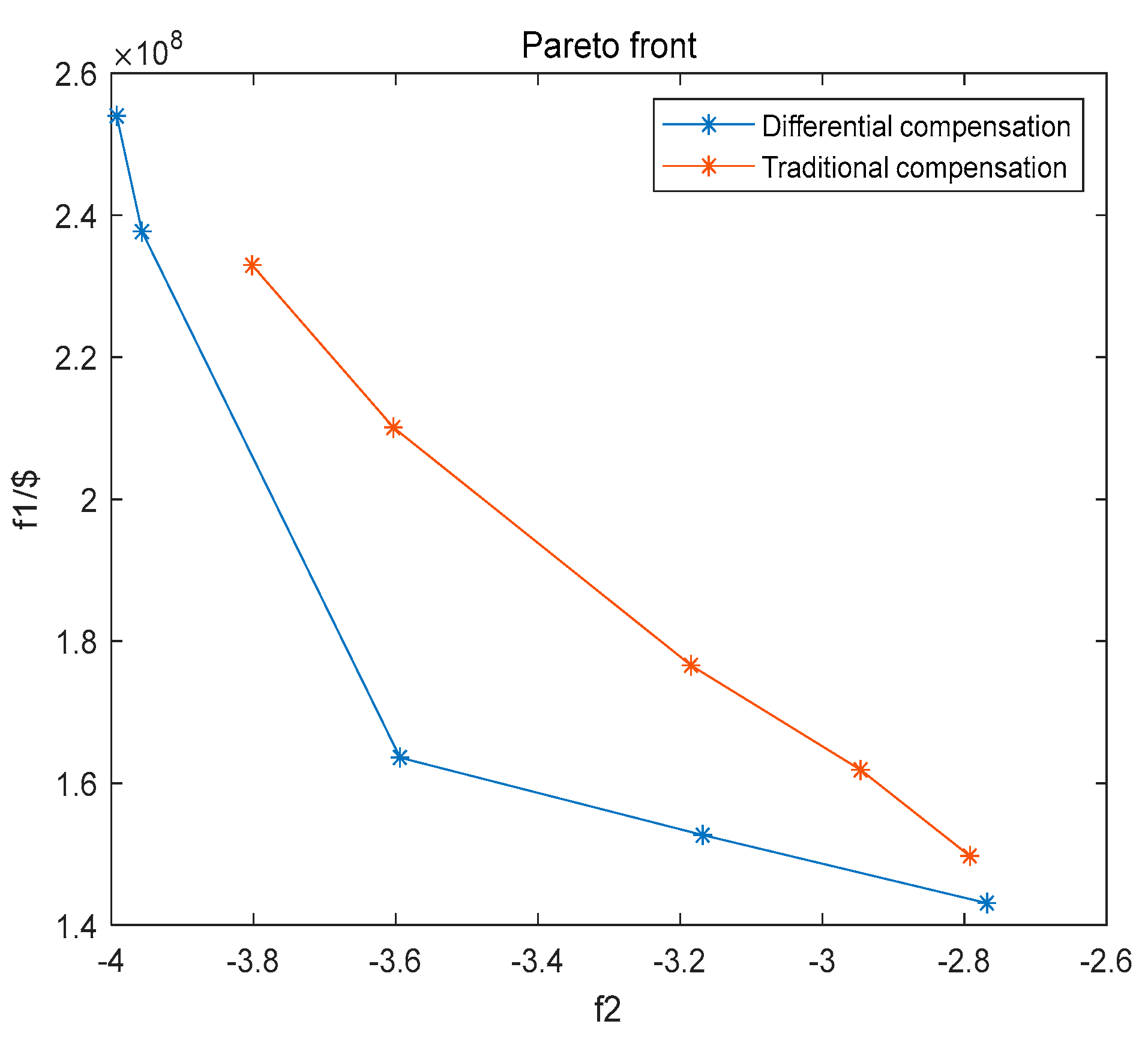
5.3. Configuration results

As can be seen from Figure 8, the proposed compensation nodes for the six selected dynamic reactive power compensation devices are nodes 27, 26, 29, 12, 15, 17. Combined with Figure 9, the six compensation nodes are classified into risk areas: nodes 12 and 15 are in the high-risk area, and nodes 27, 26 and 17 are in the medium-risk area. Node 29 is in the low risk region.

The candidate types of dynamic reactive power compensation devices are SVC and STATCOM, and the parameters are set according to the parameters of the equipment actually put into the project, and the fixed installation costs and compensation unit prices of SVC and STATCOM devices are shown in Table 4. The dynamic reactive power compensation device selection and capacity fixing are carried out at the selected compensation nodes according to the traditional method and the improved differentiated compensation method in this paper, respectively, and the results obtained by the multi-objective optimization algorithm solution are shown in Figure 10.

First, from the overall view of the figure, the configuration cost of the dynamic reactive power compensation device is positively correlated with the reactive power compensation effect, and increasing the configured capacity can effectively improve the compensation effect of the dynamic reactive power compensation device, but at the same time, it also requires a higher cost. Secondly, in terms of the specific curve, the results obtained from the differentiated dynamic reactive power compensation method proposed in this paper are significantly better than the traditional compensation method in terms of overall economy. Due to the optimization weight of node differentiation, the optimization weight of reactive power compensation effect index is appropriately lowered for the nodes in the medium and low-risk correlation area, and the cost index is considered in a balanced manner, so that while satisfying the system reactive power compensation needs, the cost economy of the configuration of the dynamic reactive power compensation device is satisfied to a greater extent. Finally, from the curve trend, it can be found that there is a certain saturation between reactive power compensation effect and cost. When the capacity of the dynamic reactive power compensation device is increased to a certain degree, the enhancement effect on reactive power compensation effect is not obvious, but will increase the cost burden. Therefore, it is necessary to carry out a comprehensive assessment of the configuration results obtained by multi-objective optimization to select the most reasonable configuration scheme to achieve the balanced optimization of economy and reactive power compensation effect.

The inverse coding of the optimization solution set using the differentiated dynamic reactive power compensation method yields the capacity configuration scheme and evaluation of the dynamic reactive power compensation device as shown in Table 5 and Table 6.

From Table 5 dynamic reactive power compensation device type selection and capacity configuration, it can be seen that for economic considerations, the number of compensation nodes ready to install SVC is significantly more than STATCOM, and the single node installation capacity of STATCOM is always lower than that of SVC, which indicates that STATCOM can issue a large amount of reactive power for compensation with smaller compensation capacity, and the reactive power support capability is better than that of SVC. In addition, the compensation nodes ready to install STATCOM are all in the transient voltage instability high-risk area, which also confirms that the differentiated compensation method proposed in this paper can meet the required reactive power compensation effect based on the risk characteristics of nodes and improve the overall economy of the system at the same time.

The evaluation results of each candidate scheme of Table 5 using TOPSIS method are listed in Table 6. Among them, Scheme 5 has the best reactive power compensation effect but also the highest cost; Scheme 3 achieves the optimal economy but its reactive power compensation effect is unsatisfactory. Therefore, Scheme 2 with the highest closeness index should be selected as the final configuration scheme.

According to the optimization results obtained from the traditional dynamic reactive power compensation method and the differentiated dynamic reactive power compensation method used in this paper, respectively, the corresponding types and capacities of dynamic reactive power compensation devices are installed in the selected compensation nodes under the most serious fault scenarios, and the integrated transient voltage drop safety margin indexes of the system before and after the dynamic reactive power compensation are calculated Γ and the node instability, and the results are shown in Table 7.

As can be seen from Table 7, in the worst fault scenario, compared with the original example (without any reactive power compensation), the installation of dynamic reactive power compensation device can significantly reduce the number of transient voltage instability of the system and improve the stability of the system, which indicates that the dynamic reactive power compensation methods proposed in the paper are all able to achieve the purpose of effective suppression of the risk of transient voltage instability of the system. From the comparison of the results of the two dynamic reactive power compensation methods, the differentiated dynamic reactive power compensation method based on node characteristics is comparable to the traditional method in terms of the improvement of system stability and the suppression of the risk of transient voltage instability, but there is a very obvious improvement in the economy, which can save a lot of investment costs and obtain high economic benefits in the practical engineering application.

6. Conclusions

Based on the voltage multiple-two-element notation criterion, this paper proposes a differentiated dynamic reactive power compensation device configuration scheme to maximize the economic performance of reactive power compensation and the risk suppression effect of transient voltage instability. The conclusions are as follows:

(1) A dynamic reactive power device configuration index system based on multiple-two-element notation is proposed, and a corresponding differentiated dynamic reactive power compensation model is established under this system. For the compensation nodes located in different risk regions, the optimization weights of economic benefits and reactive power compensation effects in the configuration process are flexibly adjusted to achieve differentiated compensation, reduce the investment cost of reactive power compensation and increase economic benefits.

2) Taking economy and suppression effect as the optimization objectives, the improved algorithm of ETLBO is used to optimize the model and obtain the configuration scheme that satisfies the optimization objectives. The TOPSIS evaluation method is used for evaluation, and the optimal scheme with the highest score is selected as the final scheme (the scheme with the highest score is selected for the final configuration scheme, Scheme 2). The correctness and effectiveness of the method proposed in this paper are verified in the IEEE39 system.

Author Contributions

The authors confirm their contributions as follows: J.D. and F.T. proposed the innovations and wrote the paper; J.W. reviewed the simulation results and revised the manuscript; X.Y. and H.D. approved the final version. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by State Grid Central China Branch Science and Technology Program.

Conflicts of Interest

The authors declare no conflict of interest.

References

Sami, M.; Gheorghe, S.; Toma, L. Transient stability improvement and voltage regulation in power system hosting Renewables by SVC. In Proceedings of the International Conference on Electrical, Computer and Energy Technologies (ICECET); 2022; pp. 1–7. [Google Scholar]
Opana, S.; Charles, J.K.; Nabaala, A. STATCOM Application for Grid Dynamic Voltage Regulation: A Kenyan Case Study. In Proceedings of the 2020 IEEE PES/IAS PowerAfrica 2020; pp. 1–5.
Zhang, J. Research on Dynamic Reactive Power Compensation Configuration of High Proportion New Energy Grid. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE) 2020; pp. 2002–2006.
Zhang, Y.; Zhang, Y.; Jian, W.; Tang, F. Optimal Configuration Method of Dynamic Reactive Power Compensation Device Considering Reducing Commutation Failure Risk of Multi-infeed DC System. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2) 2020; pp. 3233–3237.
Cui, J. Research on transient voltage characterization and control of AC and DC power grids. Master's Thesis (M.A.), North China Electric Power University, Beijing, China, 2020. [Google Scholar]
National Energy Administration. Technical specification for power system safety and stability calculation; China Electric Power Press: Beijing, China, 2013; p. 15. [Google Scholar]
China Southern Power Grid Co. Guidelines for calculation and analysis of safety and stability of the Southern Power Grid; Guangzhou, China, 2009; p. 8.
Overbye, T.J.; Klump, R.P. Effective Calculation of Power System Low-Voltage Solutions. IEEE Trans 1996, 11, 75–82. [Google Scholar]
Wildenhues, S.; Rueda, J.L.; Erlich, I. Optimal allocation and sizing of dynamic var sources using heuristic optimization. IEEE Transactions on Power Systems 2015, 30, 2538–2546. [Google Scholar] [CrossRef]
Zhou, Q.; Zhang, Y.; He, H. A practical site selection method for dynamic reactive power compensation in multi-infeed DC power grid. Power System Technology 2014, 38, 1753–1757. [Google Scholar]
Xue, A.; Zhou, J.; Liu, R. Research on practical transient voltage stability margin index using multiple binary table criterion. Chinese Journal of Electrical Engineering 2018, 38, 4117–4125+4317. [Google Scholar]
Liu, Z.; Zhang, Q.; Wang, Y. Research on reactive power compensation measures to improve the safety and stability level of 750kV sending end power grid in Northwest New Ganqing. Chinese Journal of Electrical Engineering 2015, 35, 1015–1022. [Google Scholar]
Xu, Y.; Jiang, W.; Sun, S. Quantitative assessment method of transient voltage in distribution network containing high penetration wind power. China Electric Power 2022, 55, 152–162. [Google Scholar]
Eltamaly, A.M.; El-Sayed, A.-H.M.; Mohamed, Y.S.; Elghaffar, A.N.A. A Modified Techniques of Transmission System by Static Var Compensation (SVC) for Voltage Control. In Proceedings of the 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO) 2019; pp. 1–5.
Yarlagadda, V.; Garikapati, A.K.; Gadupudi, L.; Kapoor, R.; Veeresham, K. Comparative Analysis of STATCOM and SVC on Power System Dynamic Response and Stability Margins with time and frequency responses using Modelling. In Proceedings of the 2022 International Conference on Smart Technologies and Systems for Next Generation Computing (ICSTSN) 2022; pp. 1–8.
Mourad, A.; Youcef, Z. Wheeled Mobile Robot Path Planning and Path Tracking in a static environment using TLBO AND PID- TLBO control. In Proceedings of the 2022 IEEE 21st international Ccnference on Sciences and Techniques of Automatic Control and Computer Engineering (STA) 2022; pp. 116–121.
Valluru, H.V.; Khandavilli, S.; Sela, N.V.S.K.C.; Thota, P.R.; Muktevi, L.N.V. Modified TLBO Technique for Economic Dispatch Problem. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS) 2018; pp. 1970–1973.
Arif, Y.M.; Nugroho, S.M.S.; Hariadi, M. Selection of Tourism Destinations Priority using 6AsTD Framework and TOPSIS. In Proceedings of the 2019 International Seminar on Research of Information Technology and Intelligent Systems (ISRITI) 2019; pp. 346–351.
Zhou, S.; Zhu, L.; Guo, X. Power system voltage stability and its control; China Electric Power Press: Beijing, China, 2004. [Google Scholar]
Xia, C.; Yang, Z.; Zhou, B. Analysis of commutation failure in multi-infeed HVDC system under different load models. Power System Protection and Control 2015, 43, 76–81. [Google Scholar] [CrossRef]

Figure 1. Weighted quantitative analysis based on multiple-two-element notation.

Figure 3. Comparison curve of the effect of reactive power compensation.

Figure 4. Schematic diagram of the operation of the differentiation operation on the control variable x.

Figure 5. General flow of dynamic reactive device configuration.

Figure 6. IEEE39 New England System Wiring Diagrams.

Figure 7. Partial bus voltage waveforms under the worst fault.

Figure 8. sensitivity index.

Figure 9. IEEE39 System Transient Voltage Instability Risk Partitioning.

Figure 10. Pareto solution set.

Table 1. D_Γ,l under the set of failures.

Failure Number	D_Γ,l	Failure Number	D_Γ,l	Failure Number	D_Γ,l
1	0.0909	17	0.9490	33	0.2714
2	0.0796	18	0.9148	34	1.7133
3	0.4212	19	0.7055	35	0.8796
4	0.4380	20	0.8705	36	0.3278
5	0.6902	21	0.9528	37	0.5423
6	0.4949	22	0.6184	38	0.6378
7	0.8572	23	0.6772	39	0.3311
8	0.8787	24	0.8356	40	0.2553
9	0.9739	25	0.6696	41	0.3781
10	0.8299	26	0.4717	42	0.2440
11	0.8614	27	0.5254	43	0.1699
12	0.9562	28	0.5051	44	0.2006
13	0.7955	29	0.3624	45	0.2976
14	0.3163	30	0.3121	46	0.3557
15	0.0928	31	0.3784
16	0.9501	32	0.2797

Table 2. Comparison of metrics for candidate compensation nodes.

Nodal	Γ	S_Γ,i	Nodal	Γ	S_Γ,i
1	-5.48855	0.003469	16	-4.96675	0.013905
2	-5.15575	0.010125	17	-4.8989	0.015262
3	-5.0114	0.013012	18	-4.9498	0.014244
4	-4.9407	0.014426	19	-5.09815	0.011277
5	-4.99185	0.013403	20	-5.23305	0.008579
6	-5.0139	0.012962	21	-5.04085	0.012423
7	-5.05725	0.012095	22	-5.10995	0.011041
8	-5.05815	0.012077	23	-5.0916	0.011408
9	-5.4201	0.004838	24	-4.94405	0.014359
10	-4.9501	0.014238	25	-5.1098	0.011044
11	-4.97635	0.013713	26	-4.84815	0.016277
12	-4.8839	0.015562	27	-4.8134	0.016972
13	-4.947	0.0143	28	-4.9461	0.014318
14	-4.9066	0.015108	29	-4.8698	0.015844
15	-4.89625	0.015315

Table 4. Economic parameters and investment cost of dynamic reactive power compensation devices.

Device type	Operational life / a	Installation costs / $	Reimbursement unit price / [$∙Mvar^-1]
SVC	10	1.3×10⁷	3×10⁴
STATCOM	10	2.6×10⁷	9×10⁴

Table 5. configuration scheme.

Compensation nodal	Scheme 1		Scheme 2		Scheme 3		Scheme 4		Scheme 5
Compensation nodal	Capacity /Mvar	Type	Capacity /Mvar	Type	Capacity /Mvar	Type	Capacity /Mvar	Type	Capacity /Mvar	Type
Bus-12	463	SVC	372	STATCOM	438	SVC	306	STATCOM	433	SVC
Bus-15	453	STATCOM	255	SVC	225	SVC	206	SVC	460	STATCOM
Bus-17	478	SVC	456	SVC	114	SVC	300	SVC	418	STATCOM
Bus-26	238	STATCOM	310	SVC	363	SVC	240	SVC	91	SVC
Bus-27	406	SVC	402	SVC	395	SVC	397	SVC	454	SVC
Bus-29	201	STATCOM	115	SVC	85	SVC	195	SVC	318	STATCOM

Table 6. Evaluation on configuration scheme.

Scheme	Cost /$	Γ	Closeness value
1	2.3769×10⁸	3.9567	0.4179
2	1.6360×10⁸	3.5939	0.7707
3	1.4310×10⁸	2.7685	0.6202
4	1.5268×10⁸	3.1681	0.6894
5	2.5398×10⁸	3.9922	0.3798

Table 7. Comparison of Costs and Effectiveness of Compensation Methods.

Method of compensation	Cost/$	Γ	Total number of instabilities
Uncompensated	0	-5.6620	106
Traditional compensation method	2.1008×10⁸	3.6032	78
Differentiated compensation method	1.6360×10⁸	3.5939	79

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer