1. Introduction
Natural convection in a porous medium with non-Newtonian Casson fluid has gained significant attention due to its application in various industrial and environmental processes. The study of entropy generation in such systems plays a crucial role in understanding the irreversibilities and inefficiencies inherent in the heat transfer process [
1,
2]. In this context, the Finite Element Method (FEM) emerges as a powerful numerical tool for conducting detailed analyses. This study performs the entropy generation analysis of natural convection in a porous medium with Casson fluid and highlights the importance of employing FEM as a computational technique for studying the intricate interplay of fluid dynamics and heat transfer in complex systems. By investigating entropy generation, researchers gain valuable insights into optimizing energy transfer and enhancing the overall efficiency of natural convection processes with profound implications for a wide range of engineering and environmental applications.
Casson fluid are shear thinning fluid which return to their original form when applied shear stress is release. These type of fluids are been categorize as viscoelastic. The rheological model has been successfully applied to various fields, including food processing, pharmaceuticals, cosmetics, and oil drilling, so as to understand and predict the flow behavior of non-Newtonian materials. However, its utilization in the context of natural convection and entropy generation within the Darcy-Forchheimer model remains relatively unexplored. Pop et al. [
3] in a pioneering study, investigated the heat transfer systems of Casson fluid inside a square enclosure subjected to temperature differences. The results provided insights into the convective heat transfer characteristics and can be utilized to optimize systems involving Casson fluids subjected to thermal radiation and viscous dissipation effects. Hamid et al. [
4] investigated the fluid flow phenomena inside a trapezoidal enclosure containing a Casson fluid. Furthermore, Aneja et al. [
5] examined Casson fluid in a buoyancy induced convective phenomena inside a porous hollow that is partially heated. The findings have implications for various engineering applications and non-Newtonian fluids such as energy systems, environmental engineering, and materials processing. Aghighi et al. [
6] investigated double-diffusive natural convection, which involves the simultaneous transport of heat and mass within a fluid due to density differences. The findings of the study revealed the impact of double diffusion and Casson fluid behavior on the flow and temperature distributions within the enclosure. Shah et al. [
7] analysed the behavior of Casson fluids in a curved corrugated cavity and the influence of convective heat and mass transport.
Entropy generation can be found in all heat transfer process due to its irreversibility natural process as stated on the second law of thermodynamics. It is the qualitative representation of lost of energy in most systems. Entropy quantifies the rate at which the useful energy in a system degrades into less useful forms, such as thermal energy dissipation. By analyzing entropy generation, valuable insights can be gained regarding the performance and efficiency of convective heat transfer systems. Additionally, the study of entropy generation in natural convection provides valuable insights into the irreversibility’s and energy losses associated with convective heat transfer processes. Gireesha et al. [
8] focused on the analysis of entropy generation and heat transmission in the flow of Casson fluids within an inclined porous microchannel, considering the effects of viscous and Joule heating. Kotha et al. [
9] investigated the behavior of a Casson fluid on a convectively heated surface and analyze the entropy generation characteristics. They consider the influence of viscous dissipation, which arises due to the internal friction of the fluid and leads to the conversion of mechanical energy into heat. Consequently, Sohail et al. [
10] examined the behavior of a Casson fluid and analyze the entropy generation characteristics. The behavior of Casson fluids in an enclosure and analysis of convection and thermal radiation characteristics was also studied by Alzahrani et al. [
11]. The authors considered the generation of entropy, which quantifies the irreversibility and dissipation of energy within the system. Hossain et al. [
12] focused on Casson fluids in a staggered cavity and entropy generation on double diffusive free convection. They consider magnetic effect, which can alter the transfer of heat movements, and the generation of entropy, which represents the irreversible energy loss and dissipation within the system.
In porous media, where fluid flow occurs through a solid matrix with interconnected void spaces, the Brinkman-Forchheimer model is commonly employed to characterise the behaviour of fluid flow. This model accounts for both viscous and inertial effects in porous media flow and has proven to be effective in capturing the flow characteristics in such systems. The Darcy-Forchheimer model provides a valuable framework for analyzing natural convection in porous media, where the convective flow is significantly influenced by the porous structure. It is important to consider that many fluids encountered in practical applications exhibit non-Newtonian behavior, deviating from the classical Newtonian viscosity assumption. Non-Newtonian fluids display complex flow characteristics due to factors such as shear-thinning or shear-thickening behavior, yield stress, and viscoelasticity. Seth et al. [
13] investigated the behavior of Casson fluid for a rotating system within a porous enclosure. The presence of the Darcy-Forchheimer porous medium is also considered. Fluid rotation and porosity interaction was observed to affect the flow characteristics. Qawasmeh et al. [
14] focused on buoyancy-driven convective heat transmission of the Casson fluid in Darcy-Forchheimer porous media. Furthermore, Farooq et al. [
15] considered the non-Darcy model to show the flow of the Casson fluid in an enclosure. Darcy-Forchheimer Casson fluid flow over a stretching sheets was investigated by Zhang et al. [
16]. Consequently, Li et al. [
17] investigated the effects of activation energy on a Darcy-Forchheimer flow of a Casson fluid through a channel.
The finite element method (FEM) will be employed as a numerical tool to solved the governing equations, accounting for the non-Newtonian behavior of the Casson fluid. This study will contribute to the understanding of the impact of Casson fluid properties, such as yield stress and flow behavior index, on the convective flow patterns, heat transfer characteristics, and entropy generation rates. Finite element analysis (FEA) discretizes the domain into smaller finite elements to approximate the solutions. In the past decades, researchers have explore the use of FEM to analyse fluid flow interaction in complex situation. Among which includes, Raju et al. [
18] used FEM to investigate the free convective flow of the Casson fluid on a vertically inclined plate which indicates that the plate is oriented at an angle relative to the horizontal direction. Reddy et al. [
19] studied dissipation effect on fluid flow behavior and can significantly affect the temperature distribution of the fluid. Consequently, Goud et al. [
20] considered the flow of the Casson fluid in a vertical plate (oscillating) in a porous enclosure. The plate undergoes oscillatory motion, which introduces time-dependent behavior into the flow. Rehman et al. [
21] employed finite element analysis as a numerical technique to understand the thermal behavior with Casson liquid suspension. Shahzad et al. [
22] examined Casson fluid in a bifurcated channel, which is a channel that splits into two or more branches. The channel contains a stenosis, which refers to a constriction in the channel geometry.
Natural convection is the process of heat transfer driven by density differences in a fluid cause by temperature gradients. The phenomena plays an important role in numerous engineering and environmental systems. Understanding the characteristics of buoyancy-induced convection is essential for optimizing heat transfer and energy efficiency in various applications, including geothermal systems, solar collectors, building ventilation, and electronic cooling. Recent research of significance have focus on natural convection. This is evident by contribution registered in the field of buoyancy driven convection. Khan et al. [
23] investigated the effects of various factors on natural convection with the used of Casson fluid flow over a plate imbedded with porosity. Alwawi et al. [
24] focused on the natural convection of a Casson nanofluid in an enclosure. Consequently, Devi et al. [
25] sudied Casson viscoplastic natural convection of fluid flows. Casson fluid under changeable wall circumstances was explored by Anwar et al. [
26] taking into account thermal radiative flux and heat injection process with natural convection.
This study will advance the understanding of the thermodynamic efficiency of convective heat transfer systems involving Casson fluids. The findings from this research can guide the design and optimization of various engineering and environmental systems, leading to enhanced energy efficiency and sustainability as well as entropy generation.
2. Mathematical formulation and physical representation
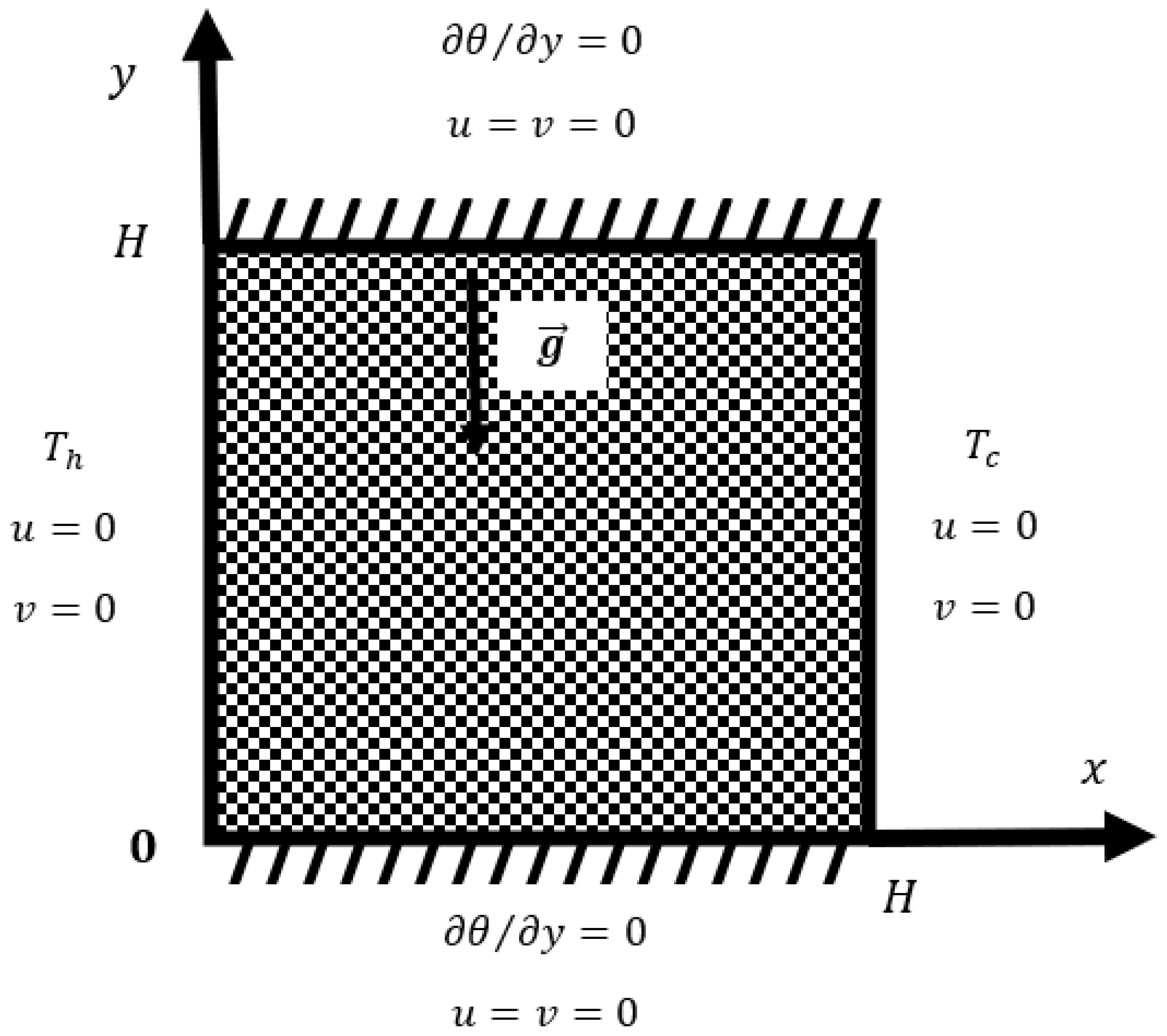
The current study focused on analyzing the behavior of buoyant convective unsteady laminar flow in a square two-dimensional cavity with length . The hallow is filled with a type of liquid called Casson liquid through a porous medium. In this study, the left wall of the cavity maintains a constant higher temperature , while the right wall maintains a constant lower temperature . The horizontal walls of the enclosure are considered adiabatic. Gravity applied to the y-momentum equation, and thermal radiation is considered in the energy equation. The thermal properties of the liquid remain constant, except for the density term in the buoyancy equation, which follows the Boussinesq approximation. The density of the liquid is defined using the thermal expansion coefficient.
The following are the governing equations for the above problem stated
Figure 1.
The schematic representation problem statement.
Figure 1.
The schematic representation problem statement.
The parameters from Eq.(
1)-(
4) are specified clearly as
which is considered dimensional velocity related to components along the
cartesian coordinate.
p is the pressure,
T is the local temperature. The density, dynamic viscosity, specific heat, time, casson fluid parameter and thermal conduction are represented as
and
k respectively.
is considered as permeability of the porous system, where
d is the mean particle diameter, the porosity
is classified as the fraction of entire volume in void space.
is the form drag constant, the constant
is the Forchheimer number. The norm of the velocity vector
, and
g represents gravitational acceleration. From Roseland approximate thermal radiation,
can be express as
,where
denotes the absorption coefficient and
the Stefan-Boltzmann constant. Using expansion of Taylor series on
about
and dropping high order terms we have
where the viscous dissipation is given as
Eq.(
6) represents the dimensionless variables
we transform Eq.(
1) to Eq.(
5) by using Eq.(
6) to obtained Eq.(
7) to Eq.(
10)
where
is the Forchheimer number,
is Grashof number,
is Prandtl number, where
is the kinematic viscosity,
is the Rayleigh number,
is the inverse Darcy number. The Darcy number is represented as
,
is the radiation parameter, and
is the Eckert number.
The Nusselt number signifies the enhancement of convective heat transfer compared to purely conductive heat transfer. A high Nusselt number indicates efficient heat transfer, while a low Nusselt number indicates poor heat transfer.
The average Nusselt number
is used when there are variations in the Nusselt number along the surface. It represents the average convective heat transfer coefficient over the entire surface. It is calculated by integrating the local Nusselt number over the surface and dividing it by the surface area:
2.1. Boundary condition
The dimensionless variables for the conditions stated for initial and boundary are
6. Conclusion
In conclusion, this study has successfully investigated the entropy generation characteristics during natural convection in a porous medium with Casson fluid, utilizing the Finite Element Method which provides accurate modeling and simulation capabilities, enabling a detailed analysis of the complex fluid flow and heat transfer phenomena. The analysis has provided valuable insights into the complex interplay between fluid flow, heat transfer, and entropy generation in such systems. Through numerical simulations and analysis, the study revealed the significant influence of the Casson fluid parameter, Darcy number, Prandtl number, and Rayleigh number on the entropy generation rate. The Casson fluid parameter, which consider the non-Newtonian behavior of the fluid, was observed to have an important impact on the flow and heat transfer characteristics. The Darcy number and Rayleigh number controlled the intensity of natural convection, while the Prandtl number determined the relative significance of the heat transfer as compared to viscous effects.
The findings of this study contribute to the advancement of fundamental knowledge in heat transfer, fluid dynamics, and entropy generation. The use of a porous medium will enhanced and ensure the realism of the model, accounting for its significant influence on the system behavior.
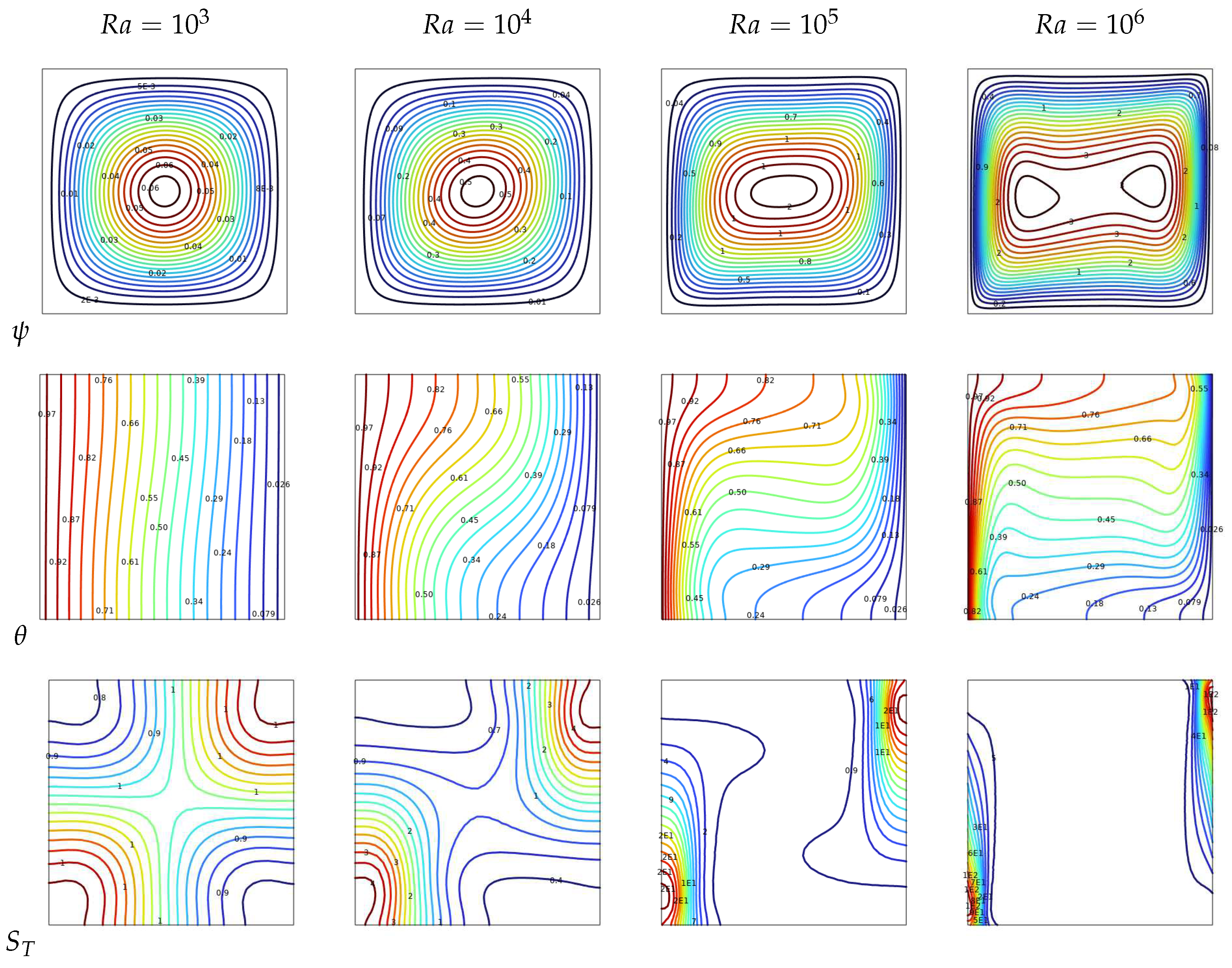
Figure 2.
Streamline , isotherms , total entropy isolines at, ,, , , and for various .
Figure 2.
Streamline , isotherms , total entropy isolines at, ,, , , and for various .
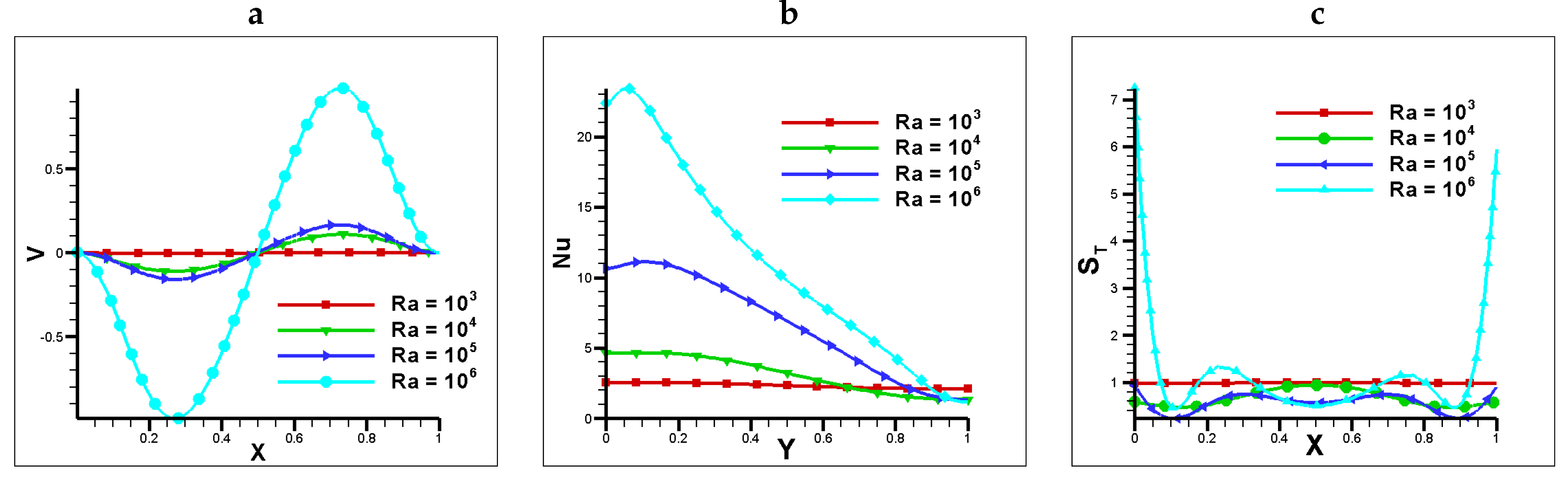
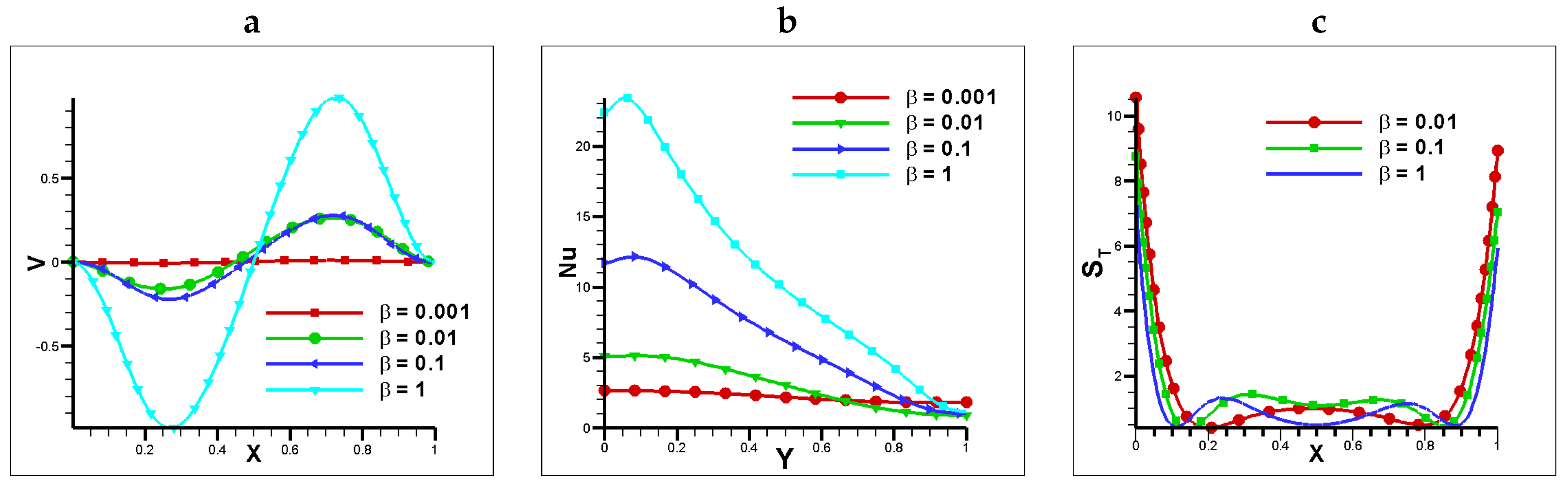
Figure 3.
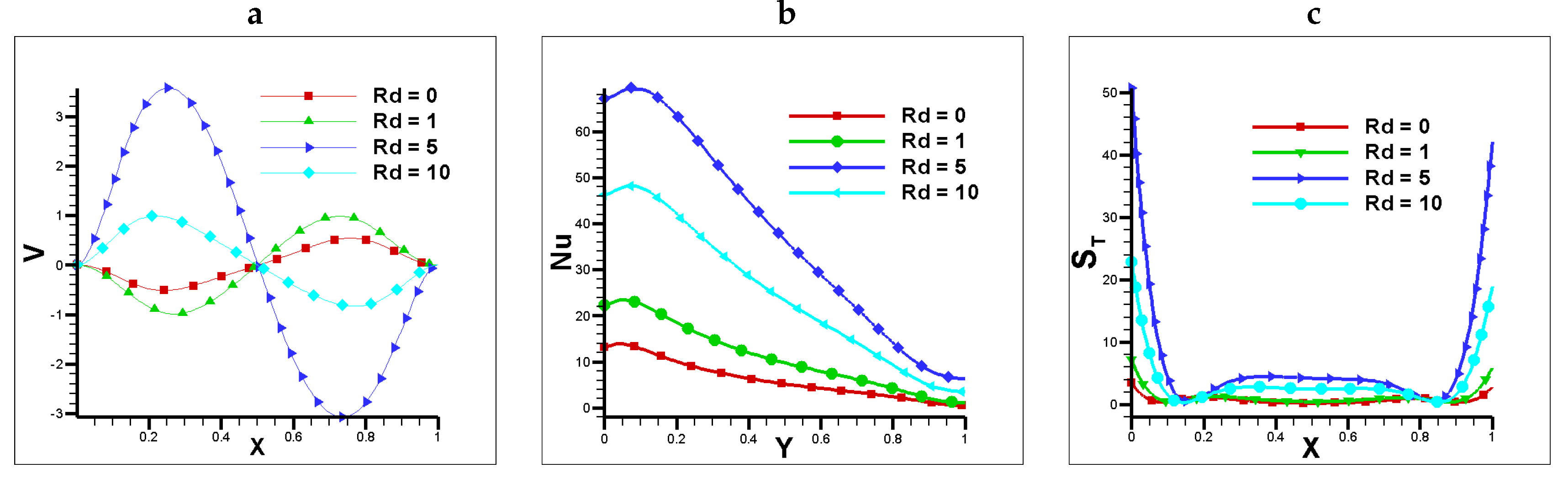
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for .
Figure 3.
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for .
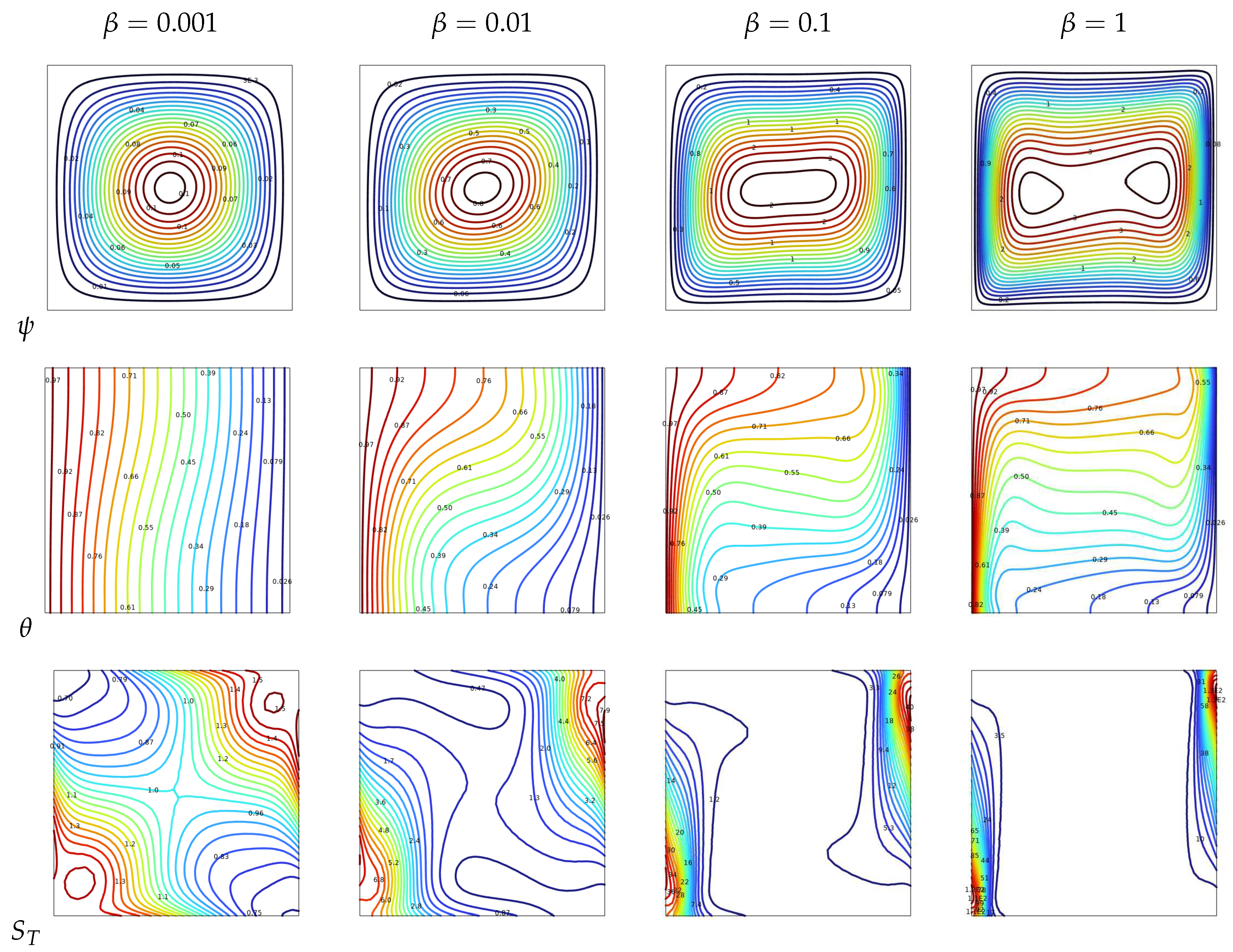
Figure 4.
Streamline , isotherms , total entropy isolines at, , , , , and for different .
Figure 4.
Streamline , isotherms , total entropy isolines at, , , , , and for different .
Figure 5.
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for different Radiation parameters with fixed parameters , , , , and .
Figure 5.
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for different Radiation parameters with fixed parameters , , , , and .
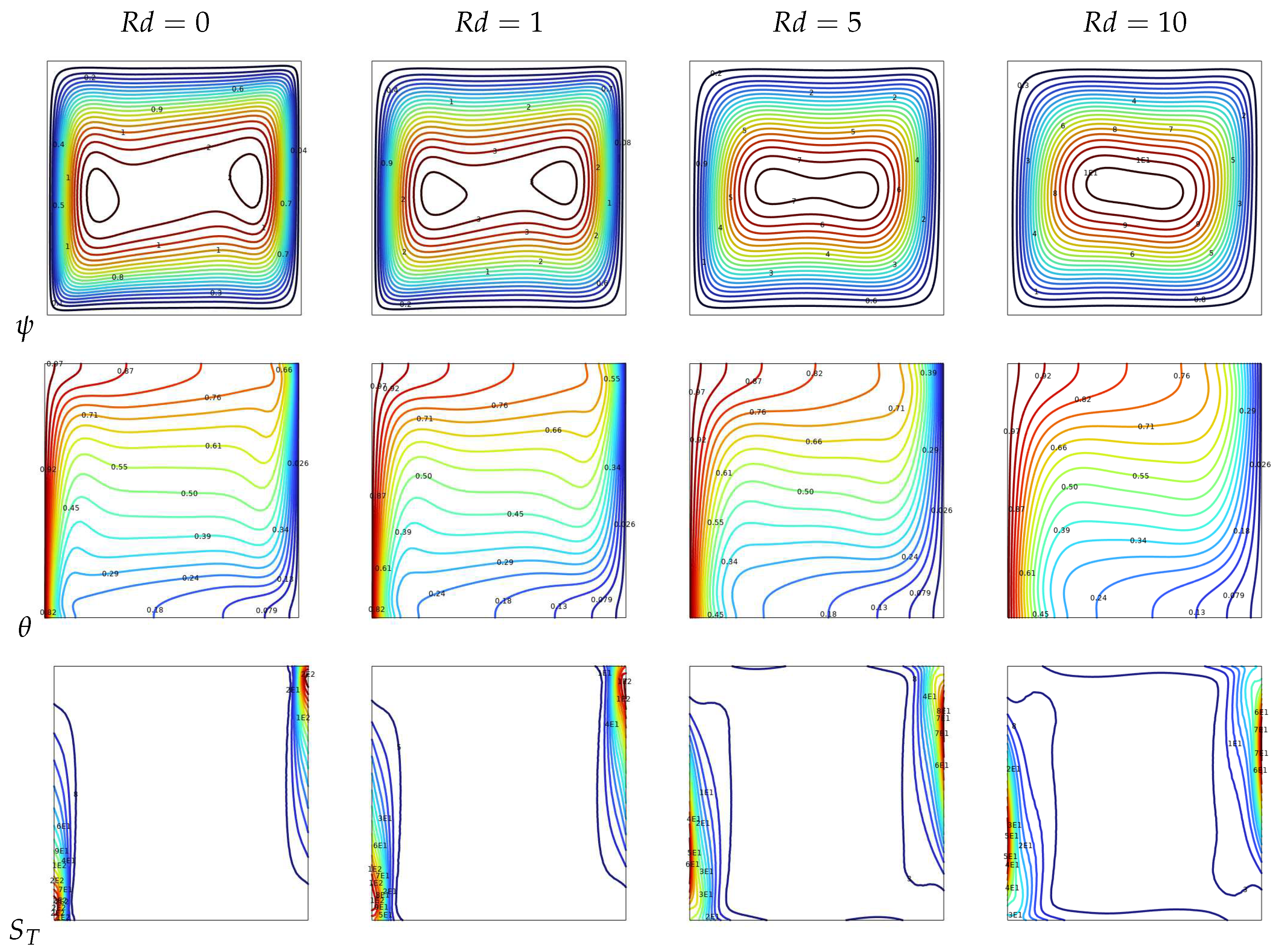
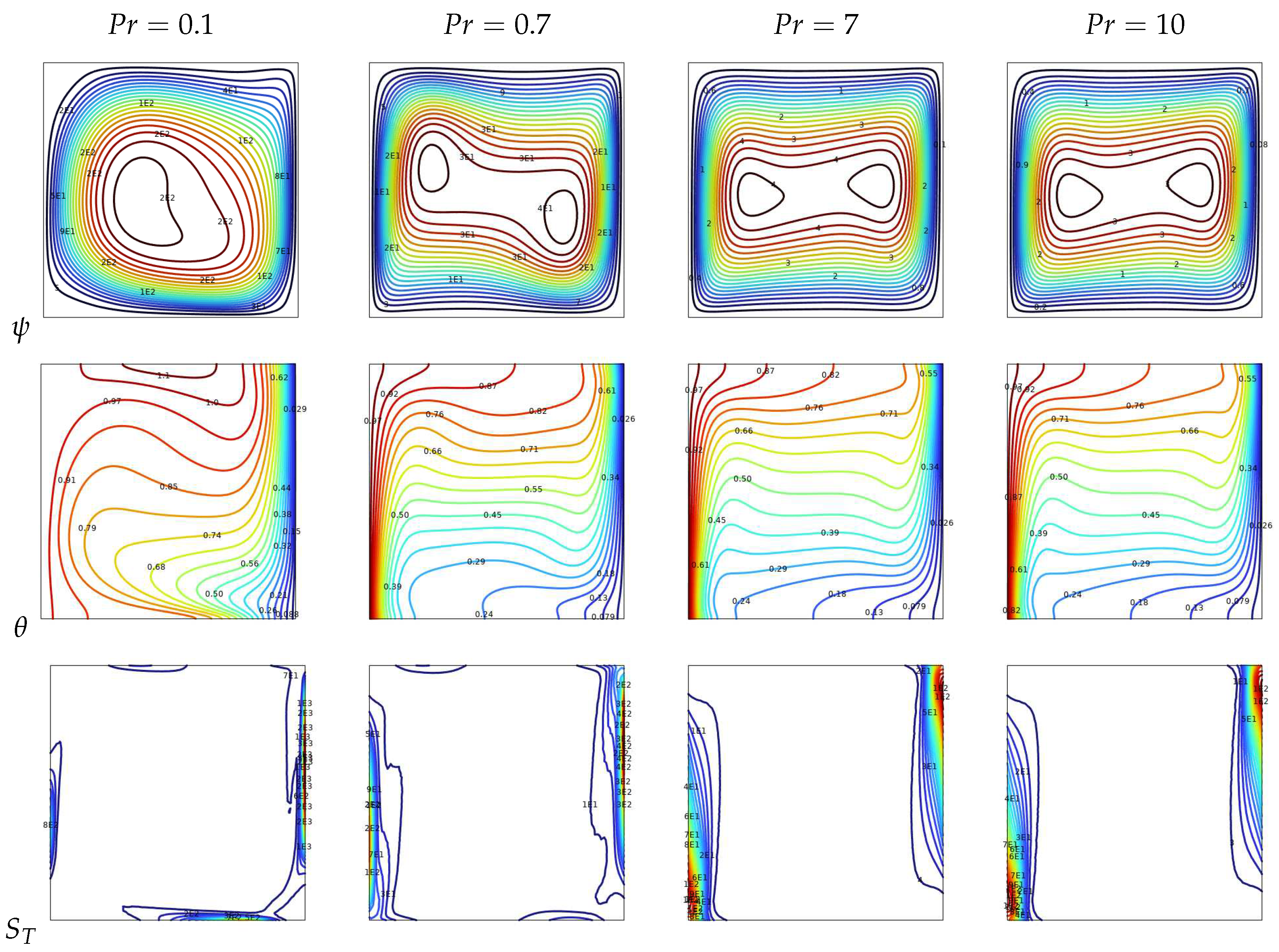
Figure 6.
Streamline , isotherms , total entropy isolines at, , , , , and for various .
Figure 6.
Streamline , isotherms , total entropy isolines at, , , , , and for various .
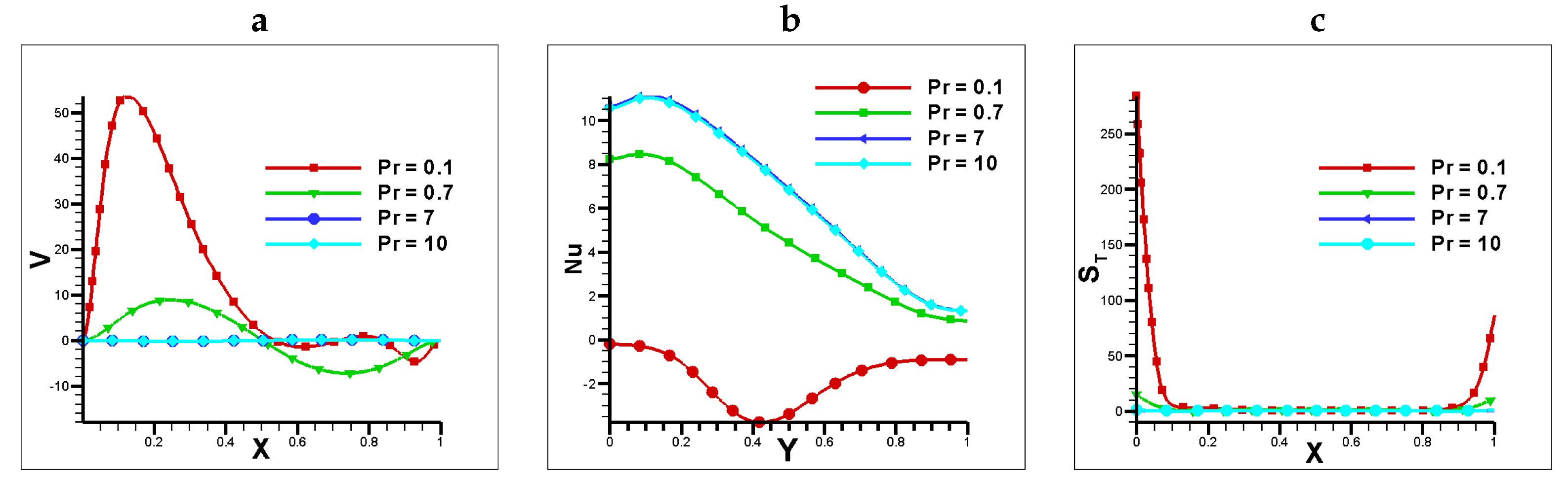
Figure 7.
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for different Prandtl numbers at , , , , and .
Figure 7.
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for different Prandtl numbers at , , , , and .
Figure 8.
Streamline , isotherms , total entropy isolines at, ,, , , and for various .
Figure 8.
Streamline , isotherms , total entropy isolines at, ,, , , and for various .
Figure 9.
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for for different Casson fluid parameters at , , , , and .
Figure 9.
a) Vertical velocity at vertical mid plane, b) Nusselt number at horizontal mid plane c) Total Entropy at vertical mid plane for for different Casson fluid parameters at , , , , and .
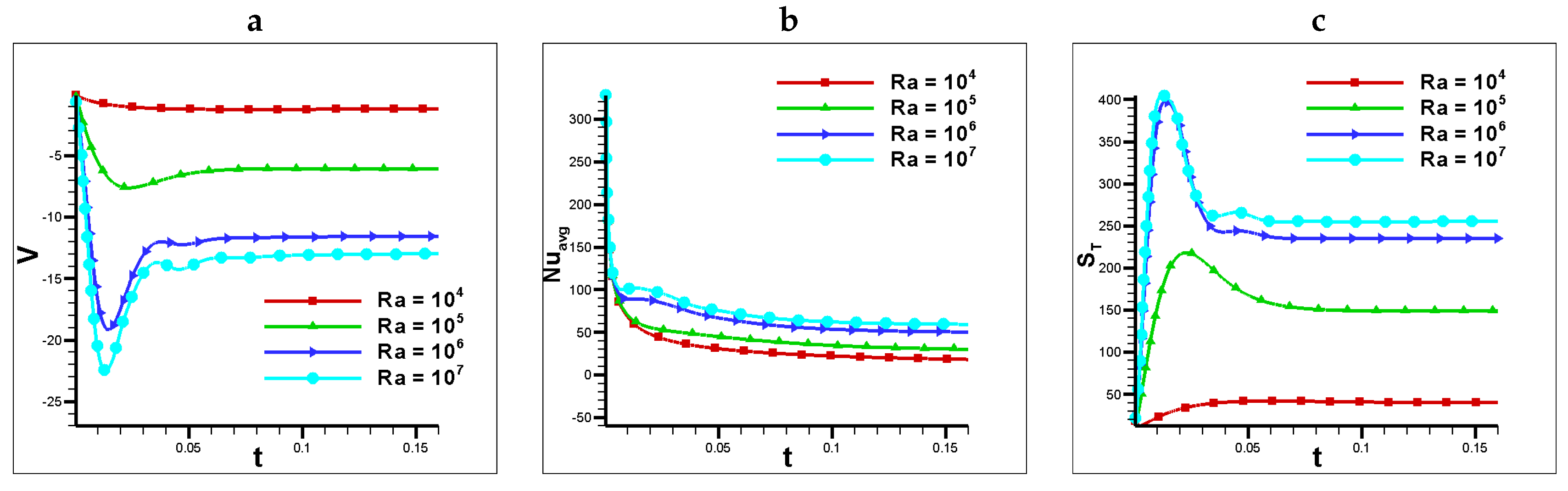
Figure 10.
a) Velocity with time , b) Average Nusselt number with time c) Total Entropy with time at , , , , and .
Figure 10.
a) Velocity with time , b) Average Nusselt number with time c) Total Entropy with time at , , , , and .
Table 1.
Average Nusselt number comparison for .
Table 1.
Average Nusselt number comparison for .
| |
|
|
|
|
|
[11] |
[27] |
[28] |
Present |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|