Prerpints.org logo
Preprint
Article

Dark Current Analysis on GeSn p-i-n Photodetectors

Altmetrics

Downloads

231

Views

63

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 July 2023

Posted:

27 July 2023

You are already at the latest version

Alerts
Abstract
Group IV alloys of GeSn have been extensively investigated as a competing material alternative in short-wave to mid-infrared photodetectors (PDs). The relatively large defect densities present in GeSn alloys are the major challenge in developing practical devices, owing to the low-temperature growth and lattice mismatch with Si or Ge substrates. In this paper, we comprehensively analyze the impact of defects on the performance of GeSn p-i-n homojunction PDs. We first present our theoretical models to calculate various contributing components of the dark current including minority carrier diffusion in p- and n-regions, carrier generation-recombination in the active intrinsic region, as well as the tunneling effect. We then analyze the effect of defect density in the GeSn active region on carrier mobilities, scattering times and the dark current. A higher defect density increases the dark current, resulting in reduction in detectivity of GeSn p-i-n PDs. In addition, at low Sn concentrations, defect-related dark current density is dominant, while the generation dark current becomes dominant at a higher Sn content. These results point to the importance of minimizing defect densities in the GeSn material growth and device processing, particularly for higher Sn compositions necessary to expand the cutoff wavelength to mid- and long-wave infrared regime. The study provides more of realistic expectations and guidelines for evaluating GeSn p-i-n PDs as a competitor to the III-V and II-VI-based infrared PDs currently on the commercial market.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Infrared (IR) photodetectors (PDs) are important optical sensors for wide range applications, such as fiber-optic communications, Lidar, gas-sensing, and thermal version. The III-V and II-VI based photodetectors have gained a strong traction in IR commercial market due to their high detectivity in short-wave IR (SWIR) (λ = 1-3µm) and mid-IR (MIR) regions (λ = 3-5 µm) at room temperature (T = 300 K) as well as 77 K [1-12]. However, their incompatibility with the Si-based complementary metal-oxide-semiconductor (CMOS) processing technology makes them expensive and complex to integrate with Si readout circuits, restricting their application scope. On the other hand, the group IV semiconductors, i.e. Si- and Ge-based devices have attracted attention because of their CMOS compatibility, monolithic integrability on the same Si or silicon-on-insulator (SOI) chips and lower fabrication cost with respect to the III-V and II-VI-based devices. However, the limited cut-off wavelengths ~1.1 µm and 1.5 µm of the Si and Ge-based PDs, respectively, make them unsuitable for the recent telecommunication window (1.55 µm) as well as MIR applications [13-15].
The successful development of both strained and unstrained high-quality group-IV Ge1-xSnx alloy on Si or SOI substrates via a suitable buffer layer using either low-temperature chemical vapor deposition (CVD) or molecular beam epitaxy (MBE) growth techniques has changed the prospect dramatically in last two decades [16-18]. The incorporation of Sn, another group-IV element, into Ge reduces the direct bandgap faster than the indirect bandgap of the alloy, leading to direct-bandgap GeSn alloys when the Sn concentrations reach beyond a certain critical value (~6-8%) [19]. In addition, Ge1-xSnx alloys also provide a wide range of bandgap tunability, large absorption coefficient [20], high carrier mobility [21] and high carrier saturation velocity [22]. These noteworthy features have made Ge1-xSnx alloy a promising material for PDs that can cover the entire SWIR range and a good portion of the MIR region up to 3.7 μm [22-29]. Furthermore, the presence of the L-valley in the conduction band enables a special momentum-space carrier separation scheme in favor of high-performance photodetection [30]. Recently, a theoretical analysis of the defect-free GeSnp-i-n PDs in the MIR region indicates that their achievable performance can indeed compete with the existing III-V and II-VI-based PDs, showing great promises for eventual, low-cost MIR photodetection [19]. However, the reported GeSn-based PDs to date usually suffer from relatively high levels of defect densities owing to the low-temperature growth and lattice mismatch with the Si or Ge substrates. Despite the continuous advances in material growth, defects are not likely to disappear in GeSn alloys in the near future, significantly impacting the dark current which is one of the most critical parameters of IR PDs. Although there have been numerous reports about the dark current densities of GeSn-based PDs [31-40], very little has been done to clarify the various contributors to the dark current density GeSn PDs with different Sn concentrations and the effect of defect density, limiting the optimization of GeSn PDs to achieve uncooled and high-performance MIR photodetection. A few recent experimental studies have shed light on the contributing components of dark currents such as minority carrier diffusion, Shockley-Read-Hall (SRH) generation-recombination (GR) and trap-assisted tunneling (TAT), providing evidence that the dark current of GeSn PDs is lower with lower defect densities [41-43]. This work is intended to further study the effect of defect density on the PD performance by establishing a theoretical model upon which material and device developers can form realistic expectations in developing GeSn PD architectures for various applications.
In this work, for the first time, we present a comprehensive theoretical study of device performance of GeSn PDs in terms of Sn concentrations and defect density. Starting from analyzing the impact of defect densities on the carriers’ mobility and scattering time, we examine different components contributing to the dark current including minority carrier diffusion, carrier generation-recombination and tunneling. We then calculate the responsivity and detectivity, and discuss the dependences of defect density and Sn composition on detectivity.
The rest of the paper is organized as follows: the envisioned structure of the GeSn p-i-n PD is described in Section 2; the analytical modeling of mobility and scattering time under different defect densities are discussed in Section 3; the theoretical model of the dark current is presented in Section 4; the performance analysis on such envisioned architecture is discussed in Section 5 and 6; and finally the conclusion is summarized in Section 7.

2. Device Structure of GeSn p-i-n PDs

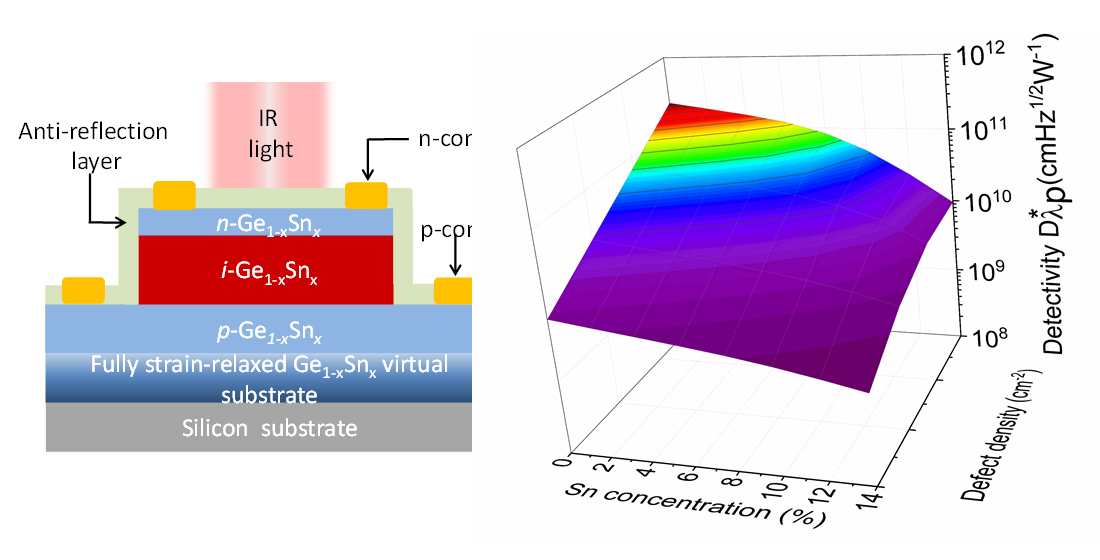
The conceptual structure of the homojunction Ge1-xSnx p-i-n PD is shown in Fig. 1(a). A composition-graded fully-strain-relaxed Ge1-xSnx buffer layer is first grown on a Si (001) substrate. Then a lattice-matched strain-free Ge1-xSnx p-i-n structure is grown, where an intrinsic Ge1-xSnx layer with a thickness of ti=3000 nm is sandwiched between two heavily doped (Na = Nd = 1×1019 cm-3) n-type Ge1-xSnx layer with a thickness of tn=100 nm and a p-type Ge1-xSnx layer with a thickness of tp=500 nm. Compositional fraction, x, is presumed the same in all layers. Similar GeSn p-i-n PD structures on silicon substrates via a GeSn buffer has been experimentally demonstrated [42]. An anti-reflection coating (ARC) is deposited on top of the PD to minimize the reflection of the incident light in order to increase the light absorption. The defect density in the Ge1-xSnx p-i-n PD is assumed to be Ndef. With different Sn concentrations, the Ge1-xSnx can be an indirect-bandgap (Fig. 1(c)) and a direct bandgap material. Here we consider the GeSn PD operates at zero bias conditions, so the dark current density is minimal and the detectivity is maximal. Using junction theory, the built-in electric field across the i-GeSn region is estimated as F~6 kV/cm.
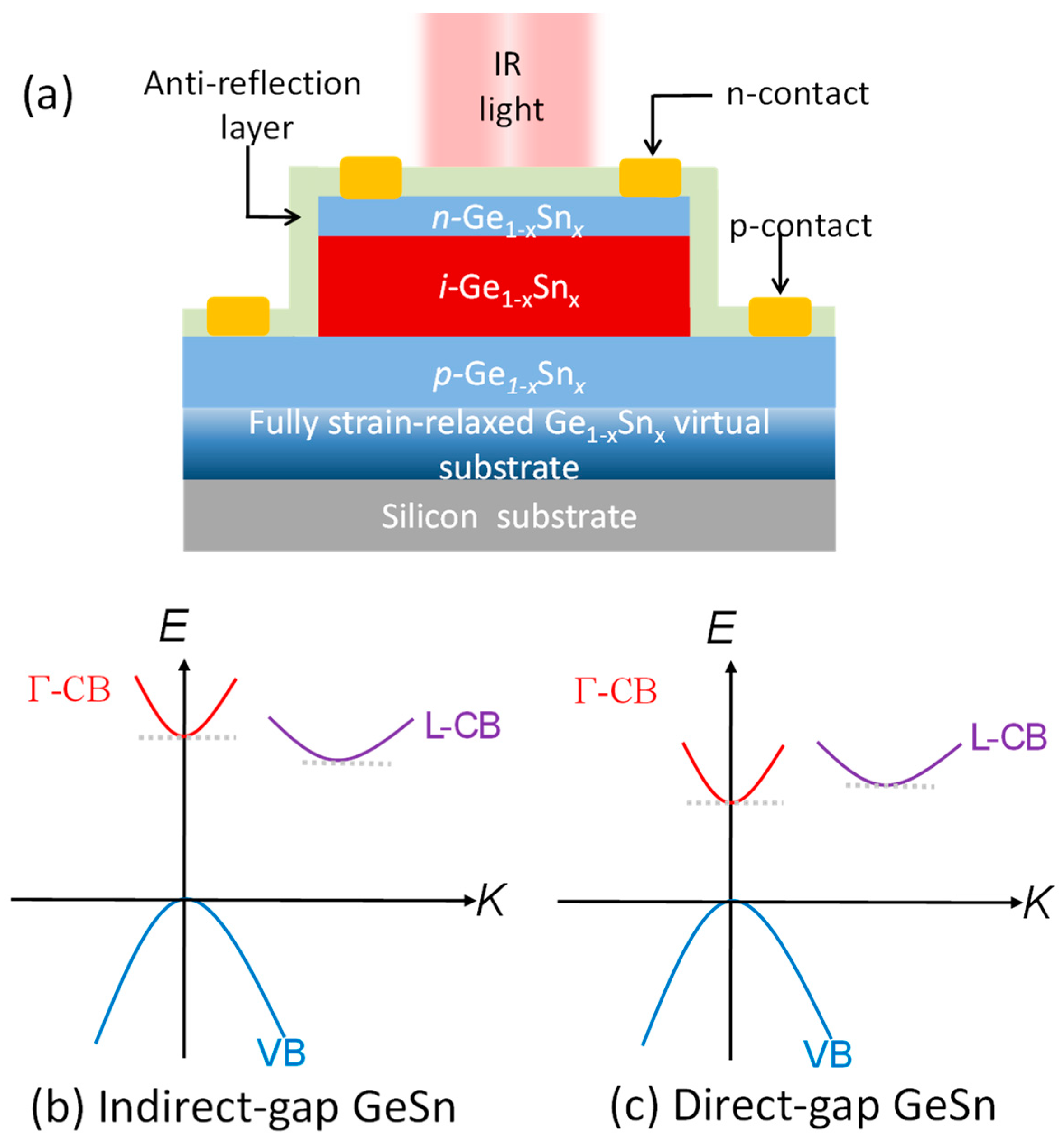
Preprints 80568 g001
Figure 1. (a). Schematic diagram of the lattice-matched, strain-free Ge1-xSnxp-i-n PD on a Si (001) substrate via a fully strain-relaxed, lattice-matched, compositionally-graded Ge1-xSnx buffer layer (not to scale). Schematic band structures of (b) indirect-bandgap GeSn and (c) direct-bandgap GeSn layers.
Figure 1. (a). Schematic diagram of the lattice-matched, strain-free Ge1-xSnxp-i-n PD on a Si (001) substrate via a fully strain-relaxed, lattice-matched, compositionally-graded Ge1-xSnx buffer layer (not to scale). Schematic band structures of (b) indirect-bandgap GeSn and (c) direct-bandgap GeSn layers.
Preprints 80568 g001

3. Mobilities and Scattering Times

In this section, we formulate and calculate the carriers’ mobility and scattering time of Ge1-xSnx alloys in the presence of defect density.
Dislocation densities in the intrinsic region have been considered as the predominant defect centers that obstruct a carriers’ movement, resulting in reduction of carrier mobilityand scattering times. We consider three different mobilities: electrons in Γ-valley conduction band (Γ-CB) and L-valley CB (L-CB) and holes in the valence band (VB). In the presence of defects, they can all be expressed as [44,45]
μ e = 30 2 π ε 2 d 2 ( k B T ) 3 / 2 N def q 3 f def 2 L d m c e *
μ h = 30 2 π ε 2 d 2 ( k B T ) 3 / 2 N def q 3 ( 1 − f def ) 2 L d m c h *
where ε is permittivity of the Ge1-xSnx, q is the electronic charge, kB the Boltzmann constant, T is the temperature, d is the distance between the defect centers (can be estimated from the defect density via N def ( cm − 2 ) = 10 14 / ( π d 2 ) [46]), fdef is the Fermi occupation factor of ionized defect centers (approximated as ~0.5, assuming they are situated near the center of the bandgap of the intrinsic region), and m c e * and m c h * denote the conductivity effective masses of electron and hole, respectively, that depends on the Sn composition of GeSn alloys taken from the 30-band full-zone k·p model [47]. The Debye screening length is L d [ = ( ε k B T / q 2 n i ) 1 / 2 ] [45] where ni is the intrinsic carrier concentration that depends on the GeSn alloy bandgap governed by the Sn concentration.
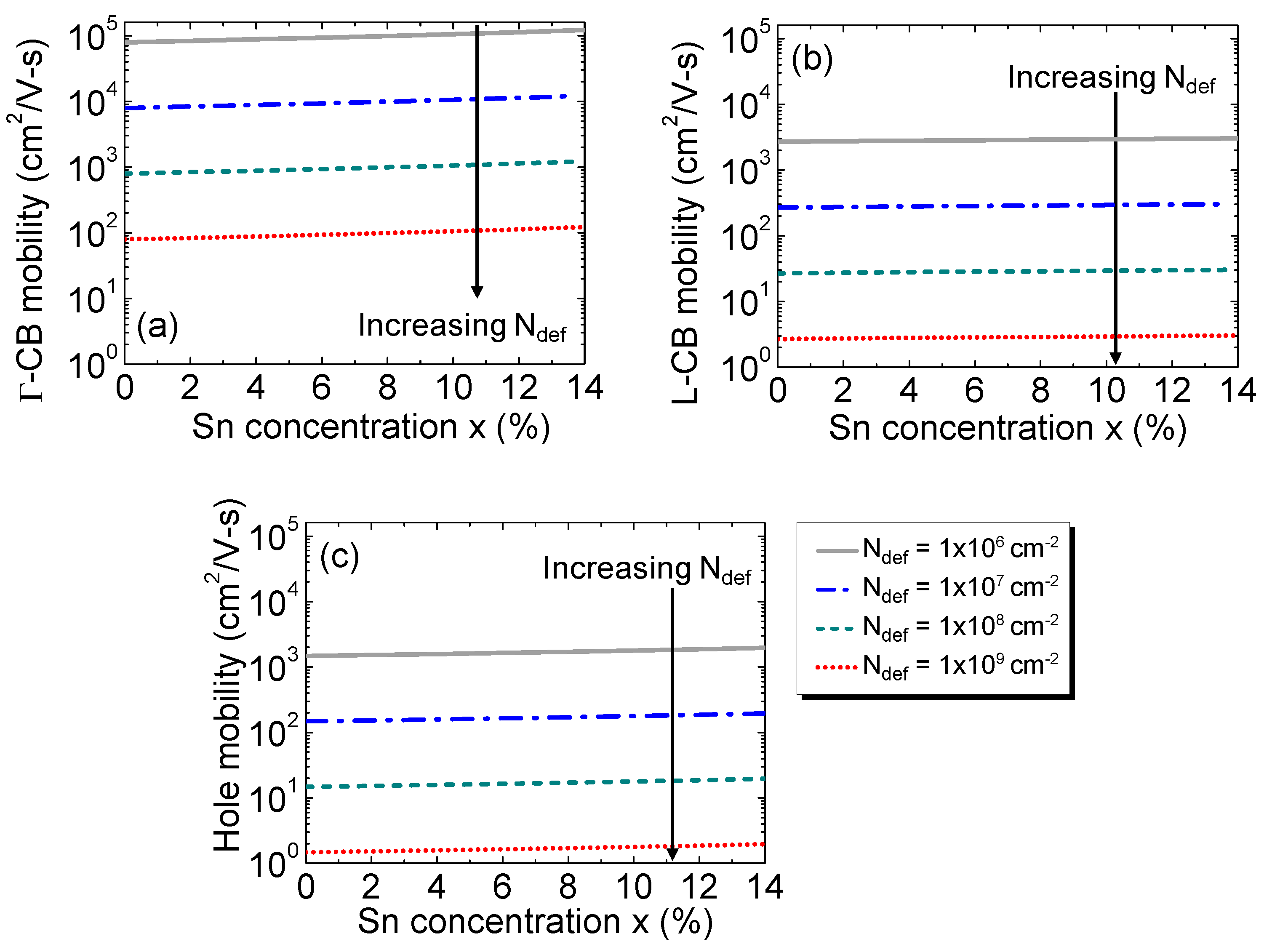
Preprints 80568 g002
Figure 2. Mobility of the electrons in (a) Γ-CB and (b) L-CB and (c) holes, as a function of Sn concentration for different defect densities.
Figure 2. Mobility of the electrons in (a) Γ-CB and (b) L-CB and (c) holes, as a function of Sn concentration for different defect densities.
Preprints 80568 g002
The calculated electron mobilities at Γ-CB and L-CB and hole mobility as a function of Sn concentration with various defect densities are shown in Fig. 2. The results show that the mobilities significantly decrease with increasing defect density. Concomitantly, mobility increases modestly with increasing Sn concentration because of the reduction in the conductivity mass m c e * and the Debye length as a result of the increased intrinsic carrier concentration.
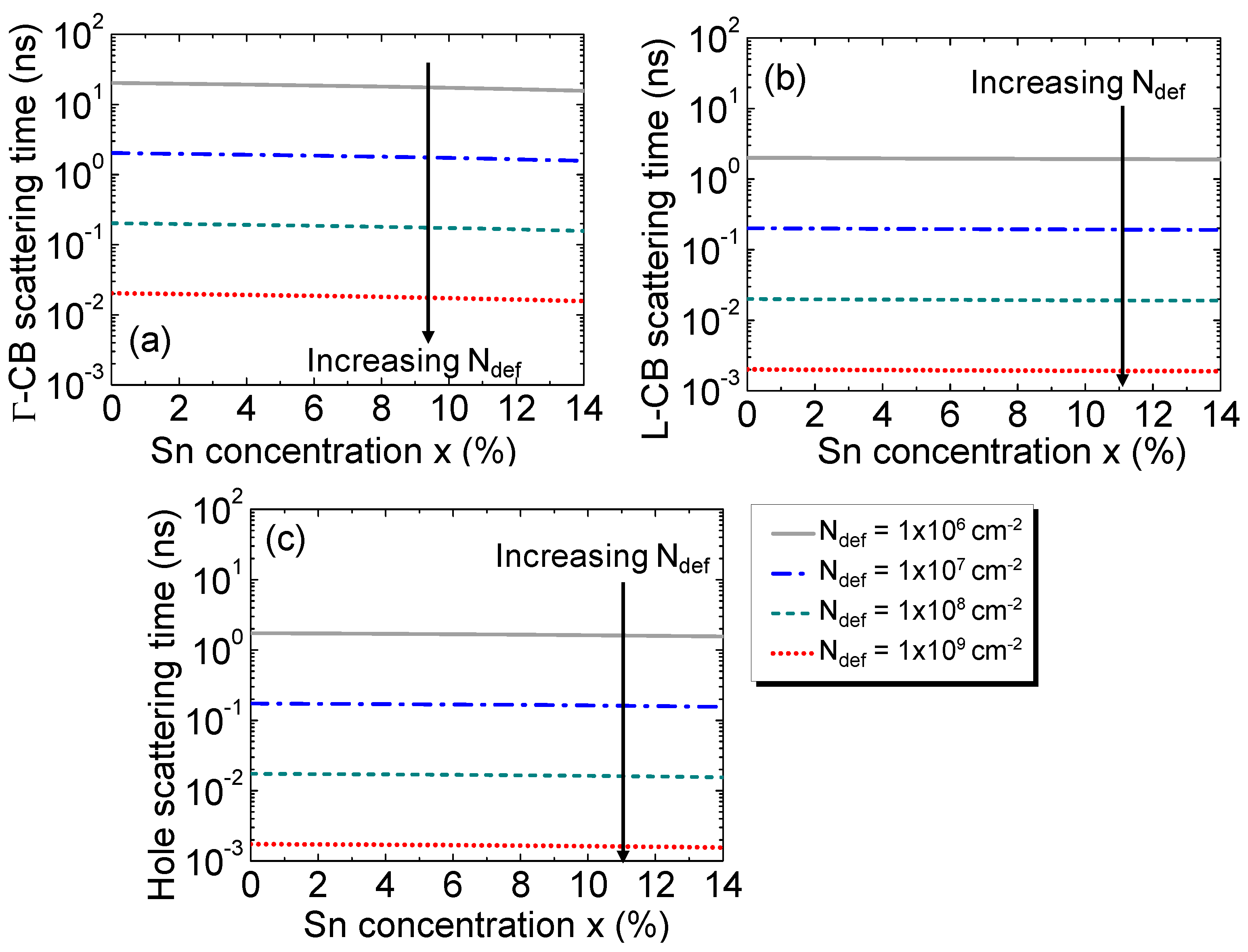
The carrier scattering time is related to the mobility as [45]
τ = m c * μ q
Their dependences on Sn concentration are shown for Γ-CB and L-CB electrons and holes in Fig. 3(a), (b) and (c), respectively, for several defect densities. In addition to the rapid reduction in the scattering time as the defect density increases, the increase of the Sn concentration, on the other hand, results in a small increase of the scattering time because of the reduction in the conductivity mass and the Debye length that tends to compensate each other at a fixed defect density.
Preprints 80568 g003
Figure 3. Scattering times of the electrons in (a) Γ-CB and (b) L-CB and (c) holes, as a function of Sn concentration for various defect densities.
Figure 3. Scattering times of the electrons in (a) Γ-CB and (b) L-CB and (c) holes, as a function of Sn concentration for various defect densities.
Preprints 80568 g003

4. Dark Current Analysis

Dark current density is an important parameter of the PD andseveral mechanisms contribute to the dark current density, including diffusion of the minority carriers towards the intrinsic region from the heavily doped contact layers (Jdiff), the generation-recombination (GR) current due to the presence of defect states acting as the GR centers inside the intrinsic region, as well as carrier tunneling. The GR current density consists of (a) SRH (JSRH) or trap-assisted, (b) interband generation (Jgen), and (c) Auger or three-carrier processes (JAug). The tunneling component generally occurs due to the tunneling of the carriers and is of two types: TAT (JTAT) and band-to-band tunneling (BTBT). The thicker intrinsic region (~3000 nm) in the GeSn PDs under consideration prevents the BTBT. Therefore, the reverse saturation current density (J0) can be expressed as the summation of these contributing mechanisms as,
J 0 = J diff + J SRH + J gen + J Aug + J TAT
Next, we show our theoretical models for different dark current components and present the calculation results. The material parameters of GeSn alloys are obtained from the linear interpolation of those of Ge and Sn taken from Ref. [48].

4.1. Diffusion Dark Current Density

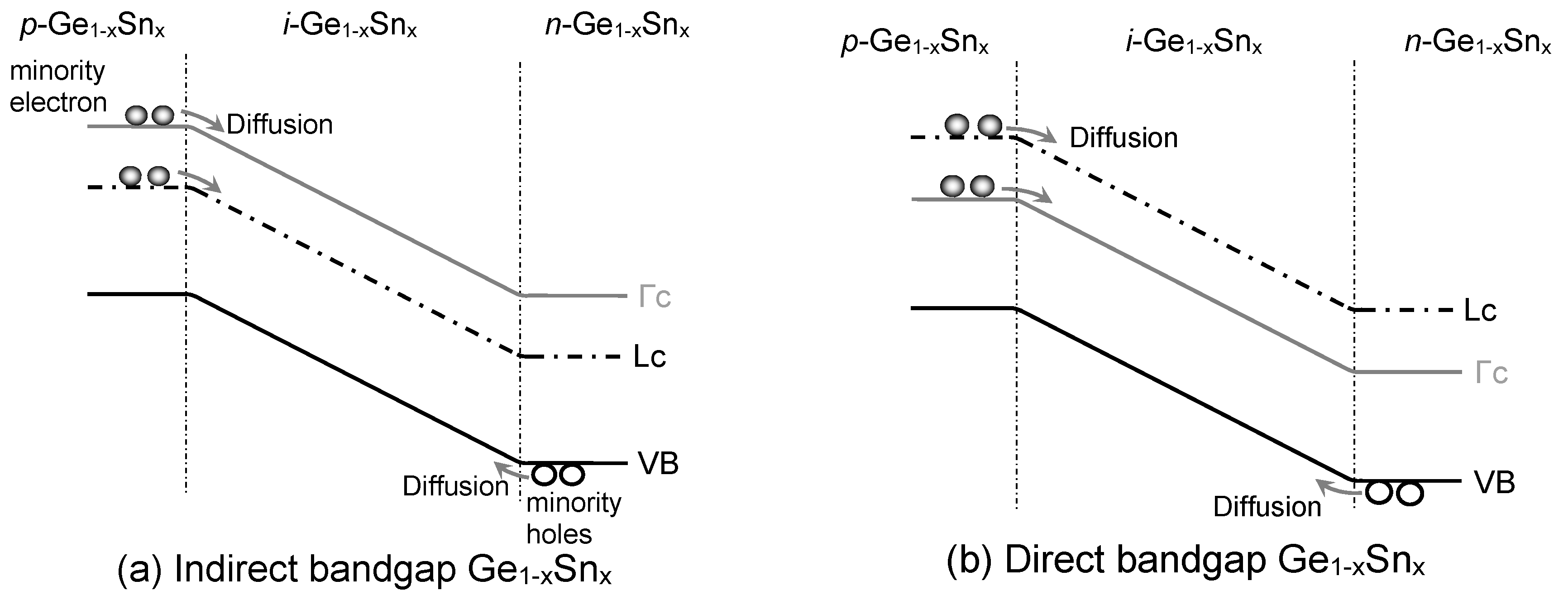
Figure 4 depicts the generation of diffusion dark current due to the diffusion of minority holes (electrons in Γ-CB and L-CB) towards i-Ge1-xSnx layer from heavily doped n-Ge1-xSnx (p-Ge1-xSnx) layer. The minority carriers’ diffusion current density under the short-base approximation can be calculated as [19]
J diff = q [ D n Γ t p n p 0 Γ + D n L t p n p 0 L + D p t n p n 0 ]
where D n L , D n Γ and D p are the diffusion coefficients of electrons in L-CB and Γ-CB and holes, respectively, which are related to the mobility via D = μ k B T / q and obviously they are also a function of defect density. tp and tn denote the thickness of the heavily doped p- and n-type Ge1-xSnx layer. The minority concentrations are related to doping concentrations and the intrinsic carrier concentration (ni) by ( n p 0 Γ + n p 0 Γ ) = n i 2 / N a , and p n 0 = n i 2 / N d .The intrinsic carrier concentration in GeSn alloy can be expressed as the sum of contributions from Γ- ( n i Γ ) and L-CB ( n i L ) as [19]
n i 2 = ( n i Γ + n i L ) 2 = N C Γ N V exp ( − E g Γ k B T ) + N C L N V exp ( − E g L k B T )
N C Γ = 2 ( 2 π m Γ * k B T ℏ 2 ) 3 2
N C L = 2 ( 2 π m L * k B T ℏ 2 ) 3 2
N V = 2 ( 2 π m h * k B T ℏ 2 ) 3 2
where ħ is the reduced Planck’s constant, E g Γ and E g L represent the direct- and indirect-bandgap energies of the Ge1-xSnx alloy, respectively, taken from Ref. [19]; N C Γ , N C L and N V are the effective density-of-state (DOS) for electrons in Γ-CB, L-CB and holes in the VB, respectively [19], m Γ * , m L * and m h * are the DOS effective masses of electrons in Γ-CB, L-CB and holes, respectively, with their values taken from the 30-band full-zone k·p model [47].
The diffusion dark current density along with its various contributing components is shown in Figure 5(a) for Ndef= 1×106 cm-2. The increase of Sn concentration not only shrinks the bandgap of the alloy but also increases the intrinsic carrier concentration [19]. As a result, the minority carrier diffusion into the i-GeSn region increases and thereby increases the diffusion current density. For lower Sn concentrations, the L-CB sits below the Γ-CB, so the GeSn is still an indirect bandgap material. 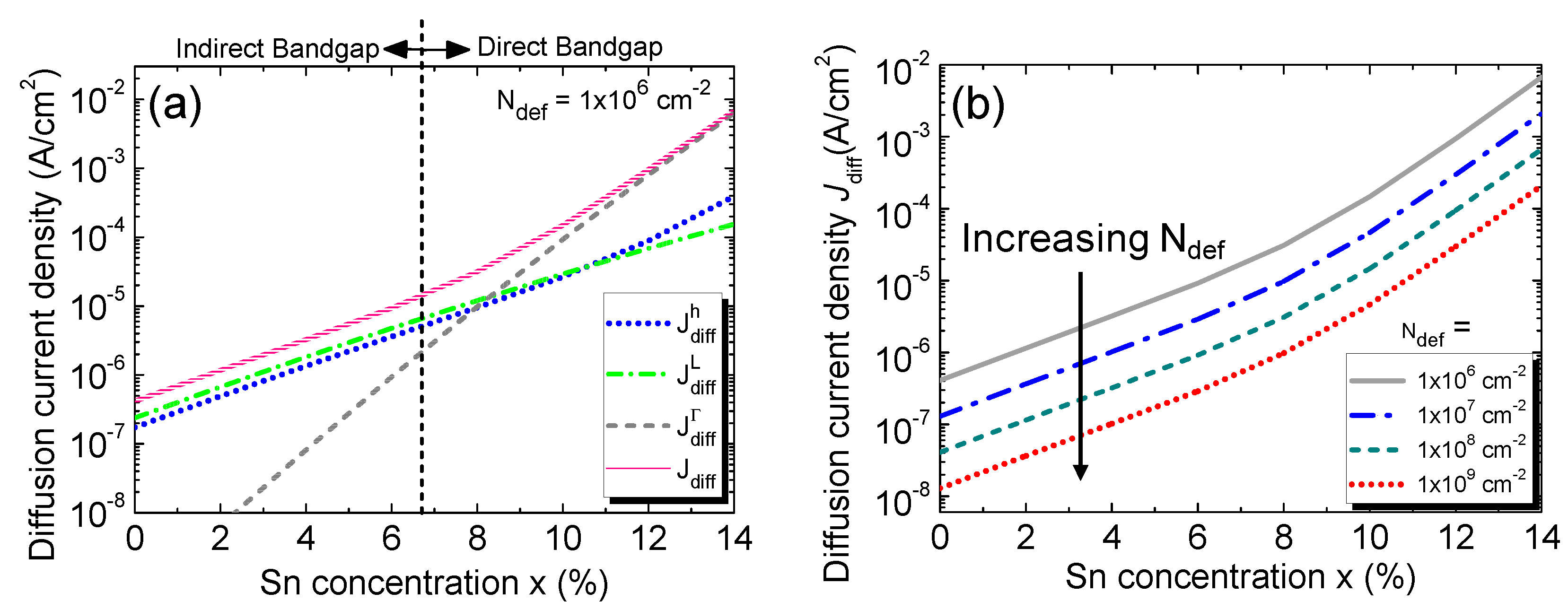Thus, more electrons reside in L-CB than in Γ-CB in the p-doped region, so the L-CB-component is more dominant. On the other hand, beyond the indirect-to-direct transition, Γ-CB becomes lower than L-CB, the Γ-CB component increases sharply and ultimately cross the L-CB component after reaching a Sn composition of ~8% and becomes dominating. The hole component is always lower than that of electrons because of its lower mobility.
Next, we show the calculated diffusion current density as a function of Sn concentration with various defect densities in Fig. 5(b). At a fixed defect density, the diffusion current increases with increasing Sn concentration owing the increased intrinsic carrier density. As the defect density increases, the carriers’ scattering time, mobility, and diffusion coefficients decrease, resulting in reduction of minority carrier diffusion current density.

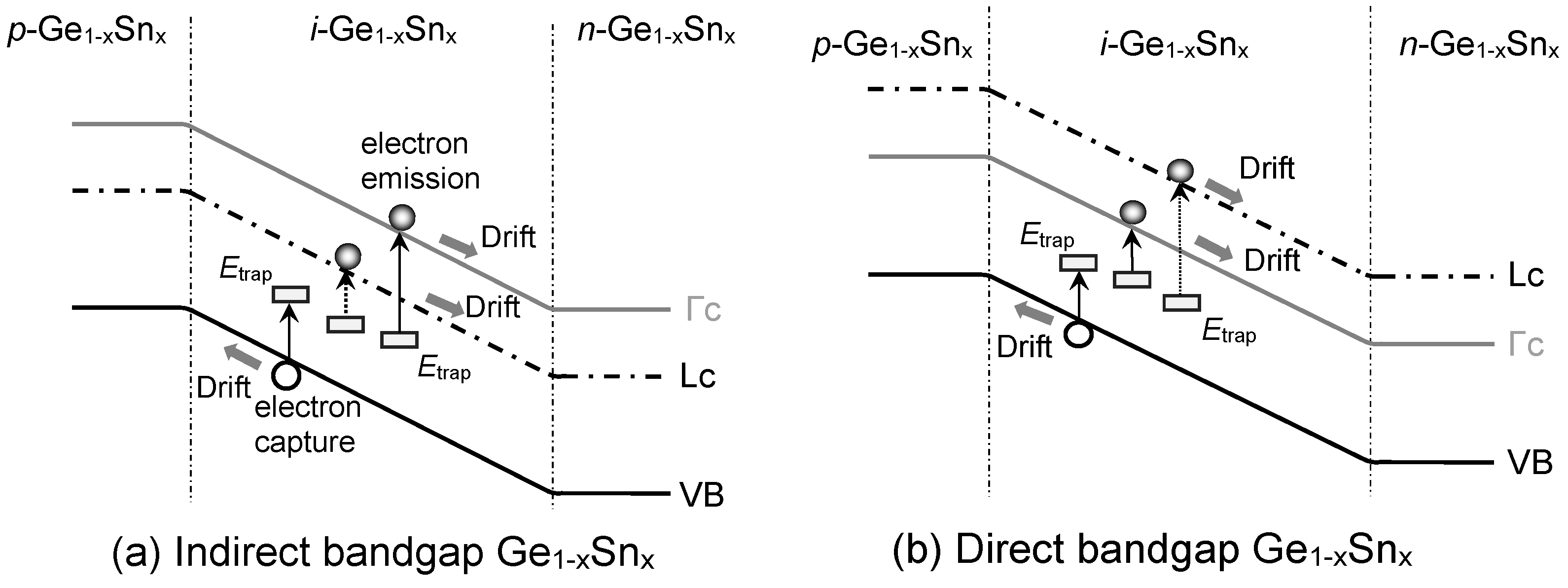
4.2. SRH Dark Current Density

The dark current density induced by either capturing an electron from the VB while leaving a hole or emitting an electron to the CB by the defect states (Etrap) situated in bandgap, is SRH or trap assisted current. Figure 6 illustrates the SRH current inside the i-Ge1-xSnx layer for both direct- and indirect-bandap Ge1-xSnx PDs in which contributions from both Γ-CB and L-CB as well as VB are accounted for by [49]
J SRH = J SRH Γ + J SRH L + J SRH h = q [ A e Γ n i Γ + A e L n i L + A h n i ] × t i
where the SRH coefficients of electrons in the Γ-CB ( A e Γ ) and L-CB ( A e L ), and holes in the VB ( A h ) are [49]
A e Γ = σ e v th Γ N def N TD
A e L = σ e v th L N def N TD
A h = σ h v th h N def N TD
where σe (σh) is the electron (hole) capture cross-sectional area; v th = 3 k B T / m c * is the thermal velocity of the carriers, and NTD is the number of traps per unit length of defect. The capture cross-sectional area of electron at room temperature are approximated as these of pure Ge (σe = 7×10-16 cm2 [50]) owing to the lack of experimental data of GeSn alloys. For holes we have considered the value of capture cross-sectional area of GeSn alloy from Gupta et al. work as σh = 1.5×10-19 cm2 [51].
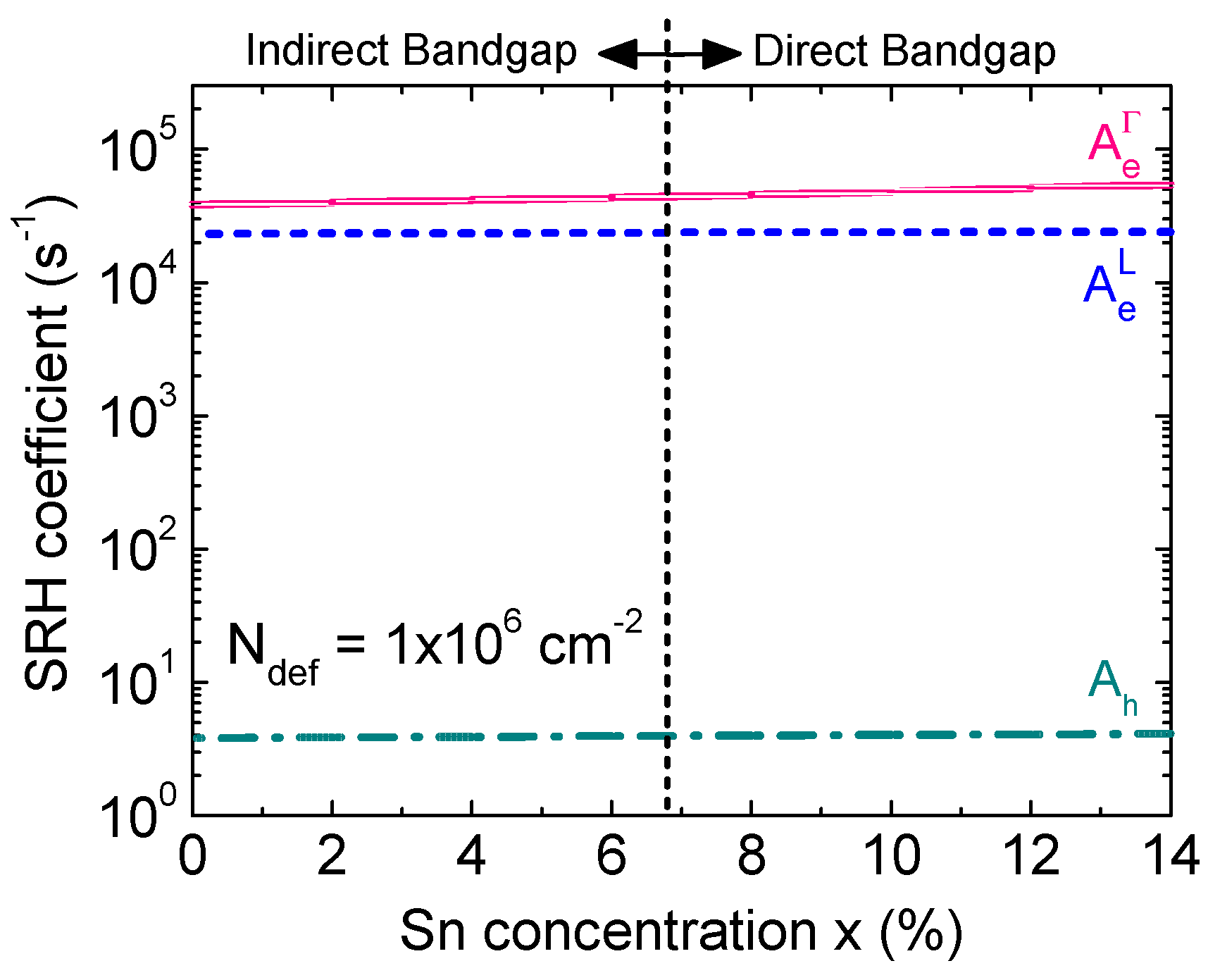
Figure 7 shows the calculated SRH coefficients as a function of Sn concentration for Ndef = 1×106 cm-2. Because the lowest effective mass of electron belongs to the Γ-CB its thermal velocity is much higher than these of electron in L-CB and hole. Thus, the SRH recombination coefficient of electron inΓ-CB is the highest among them. The thermal velocity increases with the increase of Sn concentration due to the reduction of effective masses. Therefore, the SRH recombination coefficient shows an increasing trend with the increase of Sn concentration.
Figure 8(a) depicts the calculated SRH current density against the Sn concentration with a fixed defect density of Ndef = 1×106 cm-2. The increase of Sn concentration reduces both the direct and indirect bandgap of the GeSn alloy as well as increases the intrinsic carrier concentration [19]. As a result, more electron-hole pairs (EHPs) are generated due to the capture and emission of electrons by the defect states present inside the intrinsic Ge1-xSnx region at higher Sn concentrations. Thus, the SRH current density increases with increasing Sn concentration. With low Sn concentrations, more electrons emitted by the defect states land in L-CB, producing a larger L-CB component than that of Γ-CB. As Ge1-xSnx becomes a direct-bandgapmaterial at higher Sn concentrations, the Γ-CB component increases rapidly and eventually surpasses the L-CB component when the Sn concentration is higher than ~10%. Since electrons have higher thermal velocity than holes, electron SRH current density of either Γ-CB or L-CB is always higher than the hole one. Figure 8(b) shows the SRH current density as a function of Sn concentration for various defect densities. The increase of defect density increases the GR rate of the carriers by the defect states. Thus, the SRH current density increases rapidly with increasing defect density.

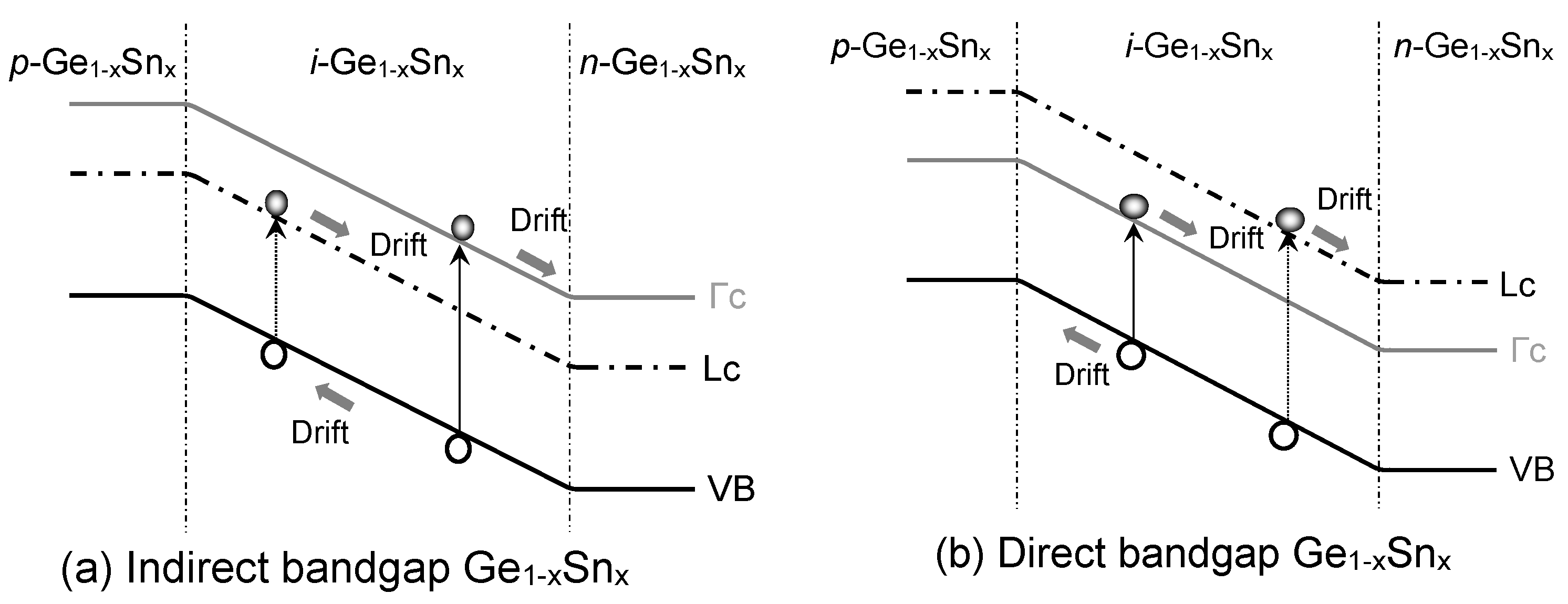
4.3. Generation Dark Current Density

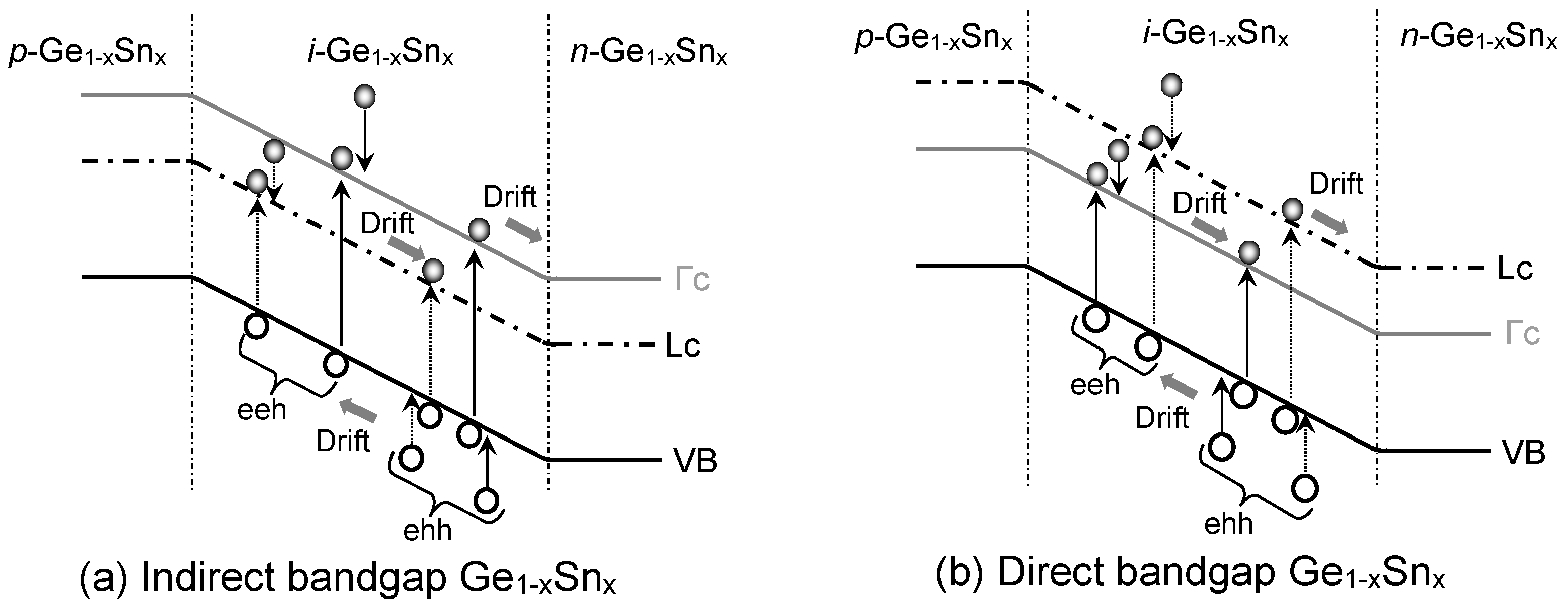
Figure 9 illuminates the mechanisms ofgeneration dark current in GeSn PDs, where the band-to-band interband transitions in the i-Ge1-xSnx region also contributes to the dark current. EHPs are created thermally in the intrinsic Ge1-xSnx layer, then swept by the built-in electric field to form dark currents.
To calculate the generation dark current in the GeSn active region, we start with the calculation of absorption coefficient of Ge1-xSnx alloy. In Ge1-xSnx, the photon absorption can take place via direct-gap transition (VB→Γ-CB) and indirect-gap (VB→L-CB) interband transitions. The absorption coefficient (αdir) for direct transition can be calculated using the Fermi’s golden rule considering Lorentzian lineshape function and the nonparabolicity effect as [52,53]
α dir ( E ) = π ℏ q 2 n r c ε 0 m 0 2 E ∑ m ∫ 2 d k ( 2 π ) 3 | q ^ . p C V | 2 × γ / 2 π [ E C Γ ( k ) − E m ( k ) − E ] 2 + ( γ / 2 ) 2
where nr represents the refractive index of the active medium; c is the velocity of light in vacuum; ɛ0 is the free space permittivity; m0 is the rest mass of electron; ω denotes the angular frequency of incident light; E is the incident photon energy; | q ^ . p C V | 2 = m 0 E P / 6 ndicates the momentum matrix with E p denoting the optical energy parameter; γ is the full-width-at-half-maximum (FWHM) of the Lorentzian lineshape function; ECΓ(k) and Em(k) denote the electron and hole energy in the Γ-CB and VB, respectively, which can be calculated using a multi-band k·p method [52,53] and the summation is over all interband transitions from VB (both heavy hole and light hole) to Γ-CB.
The indirect absorption coefficient (αindir), on the other hand, can be calculated by considering acoustic phonon absorption and emission processes using the following empirical expression [22]
α indir ( E ) = A p ( E − E g L + E a p ) 2 + A p ( E − E g L − E a p ) 2
where the first term is associated with acoustic phonon absorption ( E > E g L − E a p ) and the second term is associated with acoustic phonon emission ( E > E g L + E a p ) , and Eap is the energy of acoustic phonon. Experimental data on Ap and Eapare not currently available for Ge1-xSnx. Because of the similarity of band structures between Ge1-xSnx and Ge, the values for Ge1-xSnx are approximated to those of Ge (Ap= 2717 cm-1 and Eap= 27.7 meV at room temperature [22]). The total optical absorption coefficient (α) can then be calculated as
α ( E ) = α dir ( E ) + α indir ( E )
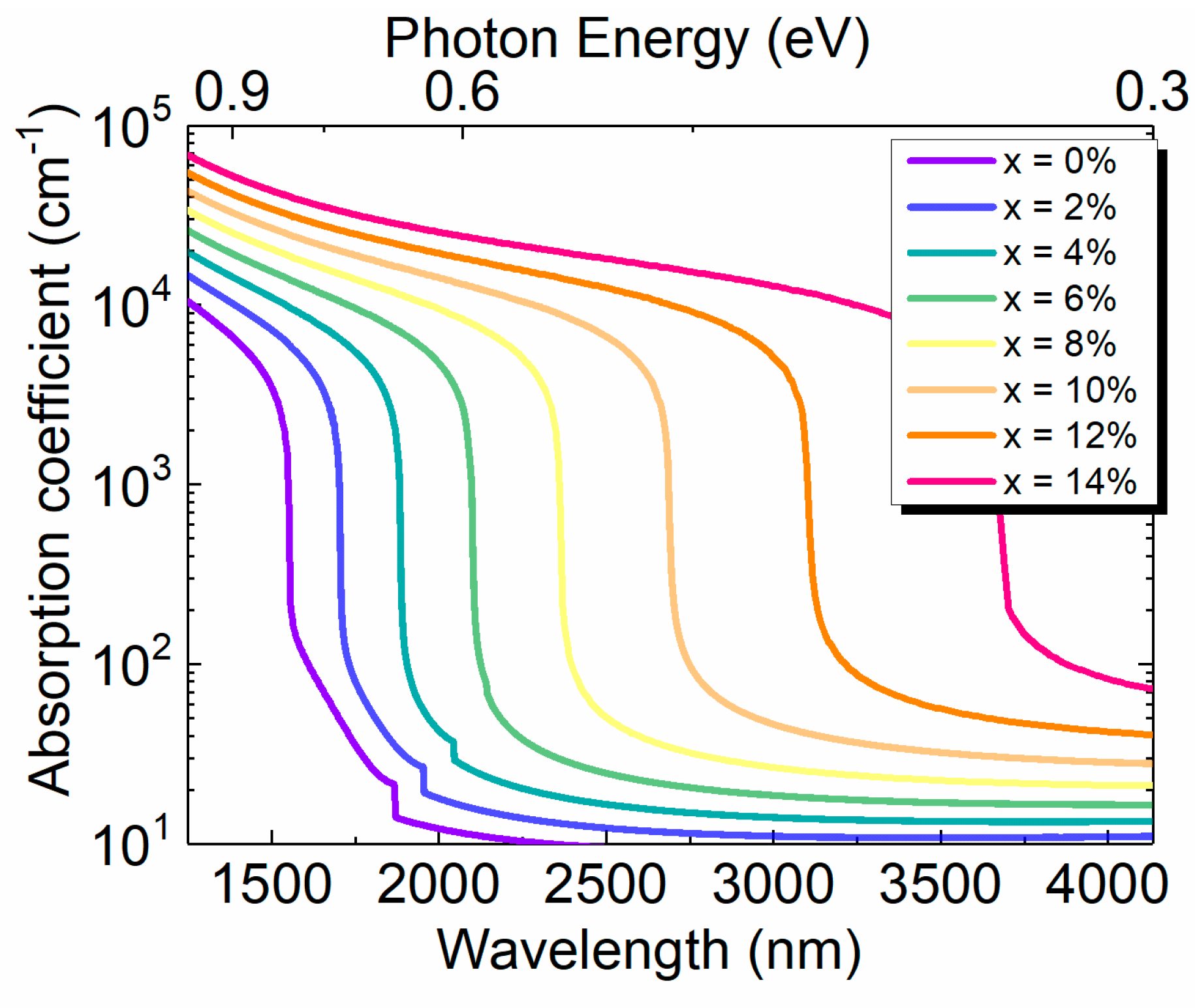
The calculated result of optical absorption coefficient spectra is shown in Fig. 10 for a range of Sn concentrations. It can be noted that for a particular Sn concentration, the absorption coefficient decreases with increase of the wavelength, followed by a sharp decrease near the direct bandgap energy. With the increase of Sn concentration, the bandgap energy decreases, causing redshift of the cutoff wavelength of Ge1-xSnx PDs.
Preprints 80568 g010
Figure 10. Calculated total absorption coefficient spectra for different Sn concentrations.
Figure 10. Calculated total absorption coefficient spectra for different Sn concentrations.
Preprints 80568 g010
The direct-gap ( R 0 Γ ) and indirect-gap absorption rate per unit volume ( R 0 L ) can be calculated according to van Roosbroeck-Schokley model as [54,55]
R 0 Γ ( E ) = ∫ 0 ∞ n r 2 π 2 ℏ 3 c 2 α dir ( E ) E 2 exp [ ( E − q φ ) / k B T ] − 1 d E
R 0 L ( E ) = ∫ 0 ∞ n r 2 π 2 ℏ 3 c 2 α indir ( E ) E 2 exp [ ( E − q φ ) / k B T ] − 1 d E
where qϕ denotes the energy difference between the quasi-fermi levels of n- and p-GeSn regions. Under equilibrium condition, the direct-gap ( B e h Γ ) and indirect-gap bimolecular recombination coefficients ( B e h L ) can be calculated as [54]
B e h Γ = R 0 Γ ( E ) N C Γ N V exp ( − E g Γ k B T )
B e h L = R 0 L ( E ) N C L N V exp ( − E g L k B T )
The generation current density in Ge1-xSnx can then be calculated as [52]
J gen = J gen Γ + J gen L = q [ B e h Γ n i Γ n i + B e h L n i L n i ] × t i
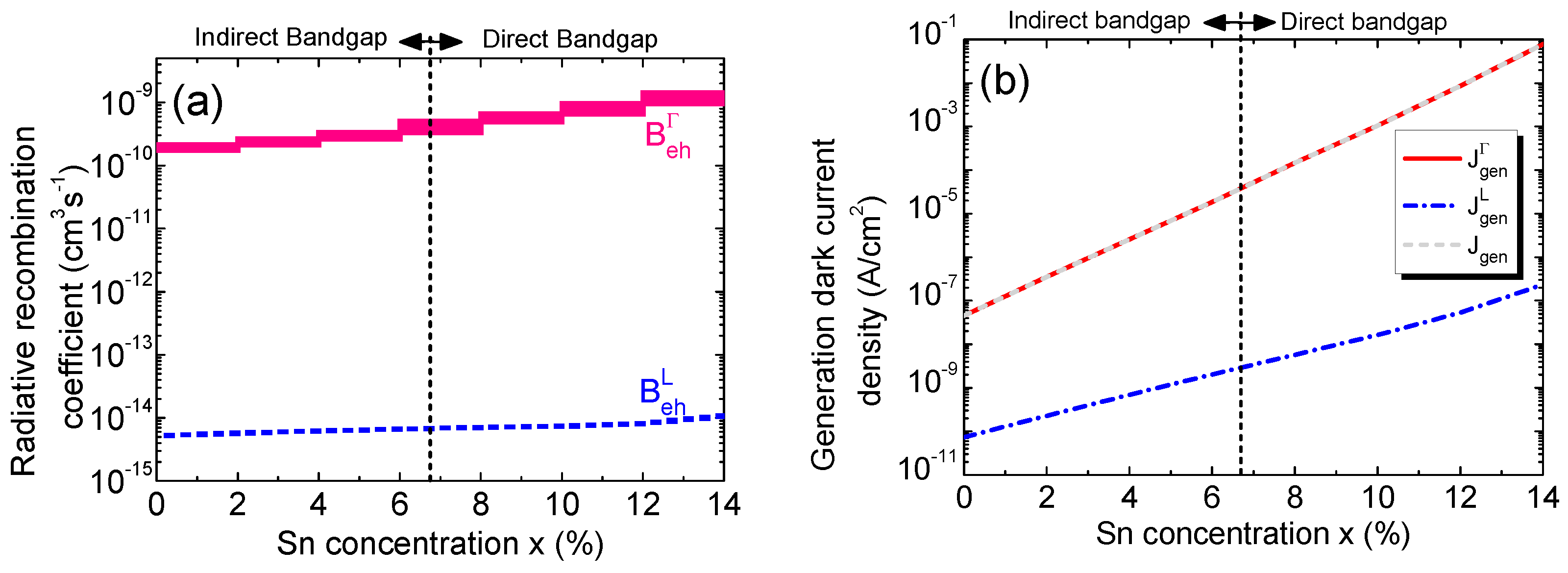
To validate the calculation results, we firstly compare our calculation for Ge1-xSnx at x = 0 (i.e., pure Ge) with the reported experimental data for Ge [56], as shown in Table 1. A good agreement is found. Figure 11(a) depicts the calculated direct and indirect radiative recombination coefficients calculated as a function of Sn concentration. As the Sn concentration increases, so does the absorption coefficient, which in turn leads to the increase of recombination coefficients in the infrared region. Because the Γ-CB bandgap drops down faster than the L-CB with increasing Sn concentration, the Γ-valley radiative recombination coefficient increases more rapidly than the L-valley one.
Figure 11(b) depicts the calculated generation dark current density along with its contributing components. The increase of Sn concentration causes the bandgaps to decrease and intrinsic carrier concentration to increase, which in turn leads to increase of both direct and indirect generation rates. As a result, the total generation dark current density increases significantly with the increase of Sn concentration. In addition, it is not difficult to see from Fig. 11(b) that the direct-gap generation dark current dominates over its indirect counterpart because L-CB electrons require phonon participation to induce interband transitions which are far less efficient process than that of Γ-CB. The difference becomes more pronounced with higher Sn concentrations, particularly when Ge1-xSnx becomes direct-gap materials.

4.4. Auger Dark Current Density

Auger or three-carrier GR is another important contributor to the dark current especially when the carrier concentrations are high. Such a process takes place when an electron or hole relaxes from higher energy level to lower energy level while transferring its energy to create an EHP as illustrated in Fig. 12. Those generated EHPs can then produce Auger dark current. Depending on the participating carriers, Auger process can be designated as either electron-electron-hole (eeh) or electron-hole-hole (ehh). It is needless to say Auger current is significant only at higher carrier concentrations. Here, we shall illustrate the calculation of eeh Auger coefficient. The ehh Auger coefficient can be calculated similarly. The Auger coefficient involving eeh process can be calculated as [57]
C e e h = m e * α c 2 | M a | 2 4 π 4 ℏ 3 ( 1 + 2 m r ) 3 / 2 I 0 N C 2 N V exp ( − E T − E g k B T )
m r = m e * / m h *
α c = ( m h * + m e * ) / ( m h * + 2 m e * )
where m e * is the DOS effective mass of electrons in CB, E T ( = E g / α c ) is the threshold energy required for the second electron to participate in the Auger process, | M a | 2 is the matrix elements of coulomb interaction between two electrons at threshold energy with k T = ( 2 m e * / ℏ 2 ) E T and I0 is expressed as [57]
I 0 = ∫ 0 ∞ k 2 ( k + k T ) 2 ( k + 2 k T ) 2 × exp [ − ℏ 2 2 m e * k B T k ( k + 2 k T ) ] d k
Because of the close proximity between Γ-CB and L-CB, both contribute to the Auger current density which can be calculated as
J Aug = J Aug Γ + J Aug L + J Aug h = q [ C e e h Γ ( n i Γ ) 2 n i + C e e h L ( n i L ) 2 n i + C e h h n i 3 ] × t i
Preprints 80568 g012
Figure 12. Illustration of Auger dark current due to eeh and ehh processes in (a) indirect-banfgap and (b) direct-bandgap Ge1-xSnx alloys.
Figure 12. Illustration of Auger dark current due to eeh and ehh processes in (a) indirect-banfgap and (b) direct-bandgap Ge1-xSnx alloys.
Preprints 80568 g012
Table 2. Auger Generation-Recombination Coefficients.
Table 2. Auger Generation-Recombination Coefficients.
Auger Generation-Recombination Coefficients (cm6s-1) Pure Ge [56] This work
Γ-valley eeh ( C e e h Γ ) - 2.62×10-33
L-valley eeh ( C e e h L ) ehh ( C e h h ) 3.0×10-327.0×10-32 3.15×10-327.31×10-32
To validate our model, we first calculate the Auger coefficients for pure Ge (x = 0%) and compare our results with the experiment data in the literature [56]. The comparison is shown in Table II where excellent agreement is found. Next, we calculate the Auger coefficients as a function of Sn concentration for eeh and ehh processes involving either L-CB or Γ-CB electrons and the results are shown in Fig. 13(a). From Eq. (16) it can be observed that the Auger coefficients are dependent on bandgap energy as well as the effective DOS in the energy bands. Auger coefficients increase with increasing Sn concentration because of the reduction of both bandgap and effective DOS. Moreover, the direct-bandgap Ge1-xSnx at higher Sn concentration produces larger Auger coefficient than that of the indirect-bandgap Ge1-xSnx, thus dominating the Auger process. 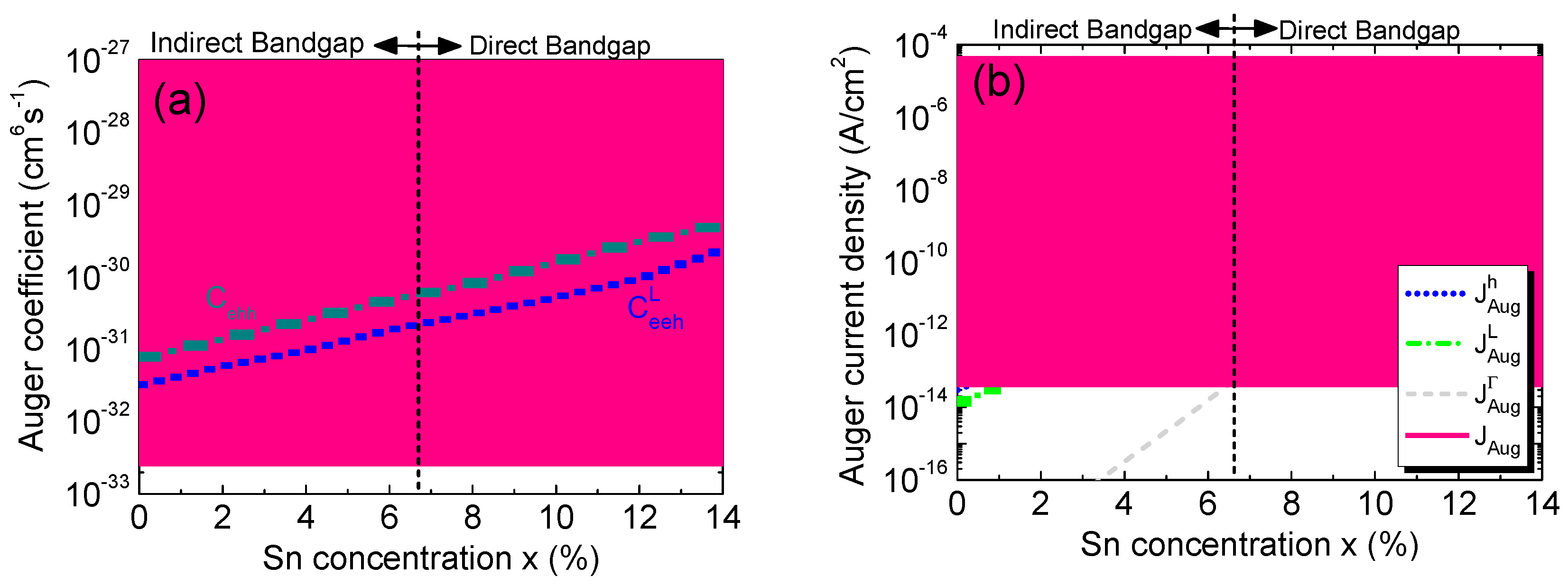Figure 13(b) shows our calculated Auger current density along with its contributing components as a function of Sn concentration. A higher Sn concentration leads to higher intrinsic carrier concentration [19], thereby producing a larger Auger current. At lower Sn concentration when Ge1-xSnx is indirect, most electrons reside in L-CB. As a result, L-CB Auger dark current dominates over the Γ-CB component. However, as the Sn concentration increases, more and more electrons reside in the Γ-CB, the trend becomes reversed, so the Γ-CB Auger process eventually surpasses both L-CB and ehh Auger components and becomes dominant.

4.5. Tunneling Dark Current Density

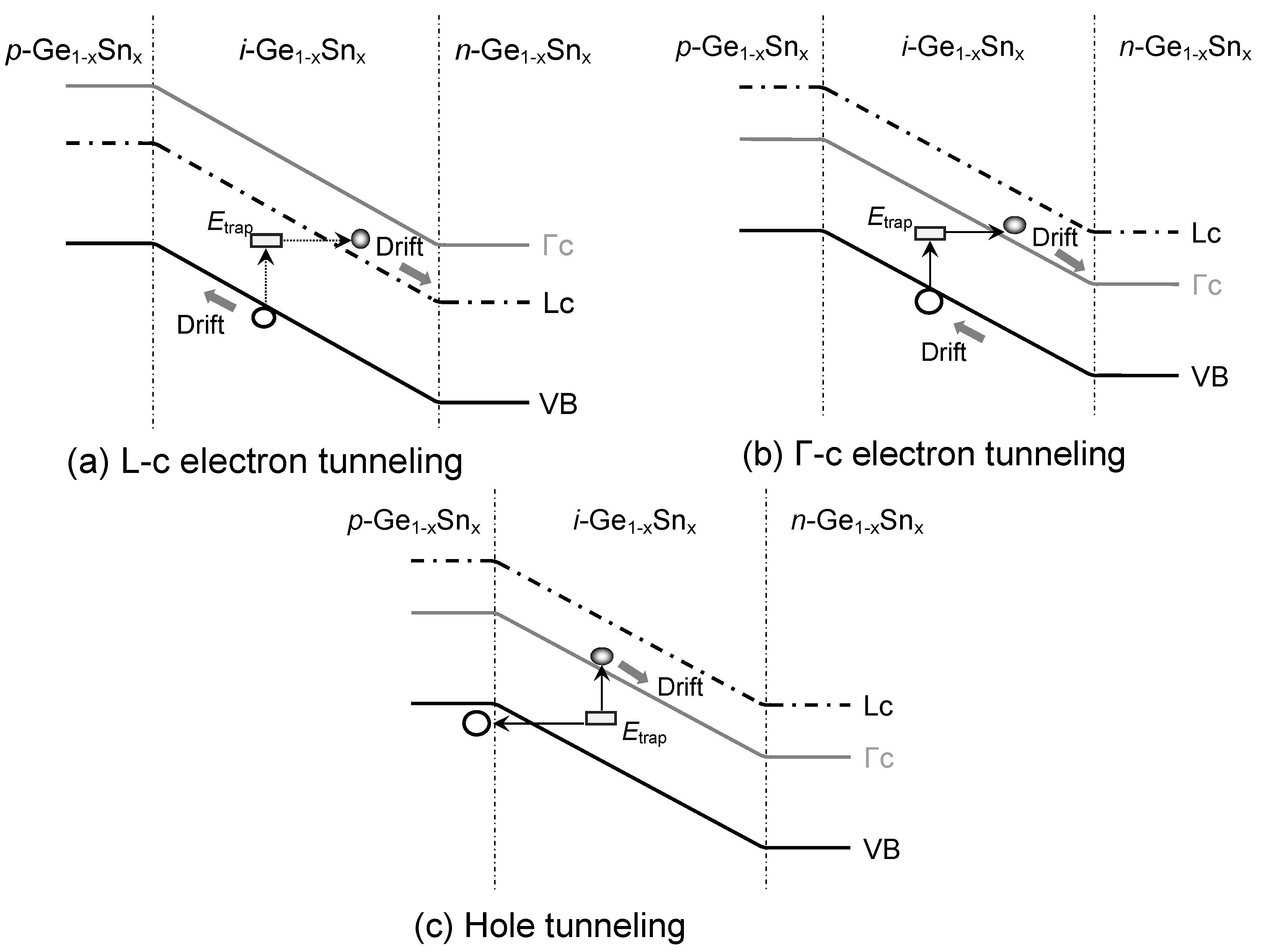
Figure 14 illustrates the mechanisms of tunneling dark currents in GeSn PDs. The presence of defect states inside the Ge1-xSnx active layer introduces trap-assisted tunneling (TAT) of the carriers that is the source of the TAT-related-dark current which depends on tunneling effective mass, defect states energy and electric field in the depletion region [58]. Because of the close proximity of Γ-CB and L-CB in energy, electrons residing in both Γ-CB and L-CB participate in TAT to contribute to dark current. According to Hurkx model, the TAT-related dark current can be evaluated using [59]
J TAT = J TAT Γ + J TAT L + J TAT h = q [ A e Γ G e Γ n i Γ + A e L G e L n i L + A h G h n i ] × t i
where G e Γ , G e L and G h are the corresponding TAT enhancement factors, which can be calculated as [59]
G e ( h ) = Δ E e ( h ) k B T ∫ 0 1 exp [ Δ E e ( h ) k B T u − K e ( h ) u 3 / 2 ] d u
K e ( h ) = 4 3 2 m c e ( h ) * Δ E e ( h ) 3 q ℏ | F |
where Δ E e ( h ) is the energy difference between the defect state and CB minima (VB maxima) and F is the local electric field.
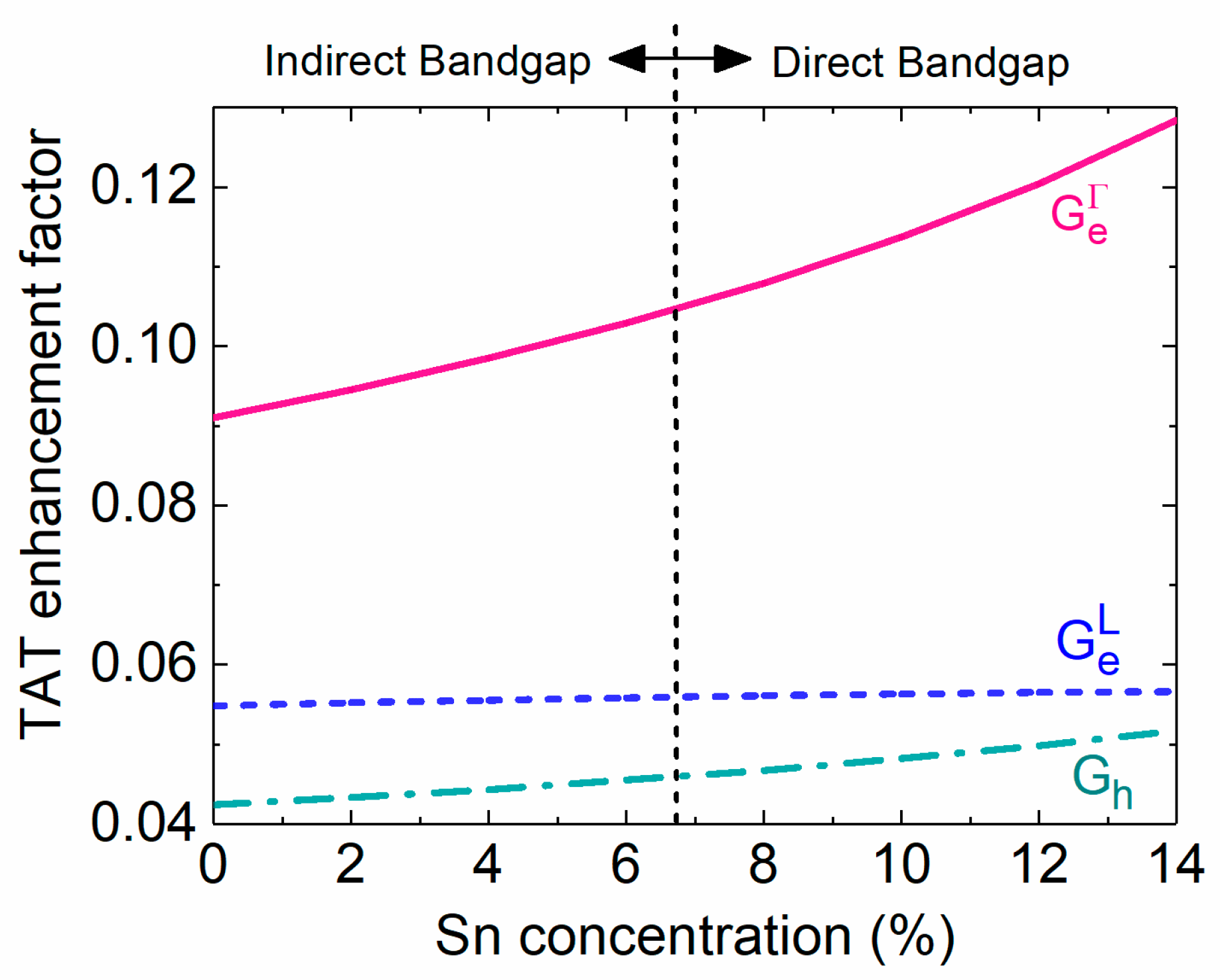
Figure 15 depicts the calculated TAT enhancement factors as a function of Sn concentration. Because zero-bias condition is considered in this analysis, TAT tunneling occurs due to the presence of built-in electric field. The tunneling effective masses reduce with the increase of Sn concentration, resulting in increase of TAT enhancement factors. Because Γ-CB electrons have much smaller effective mass (0.045 – 0.166x + 0.043x2) than L-CB electrons (0.566 – 0.449x + 1.401x2 [47]), they are more likely to be captured by defect states, yielding higher TAT enhancement factors. On the other hand, the holes in the VB have large effective mass, leading to low TAT enhancement factors.
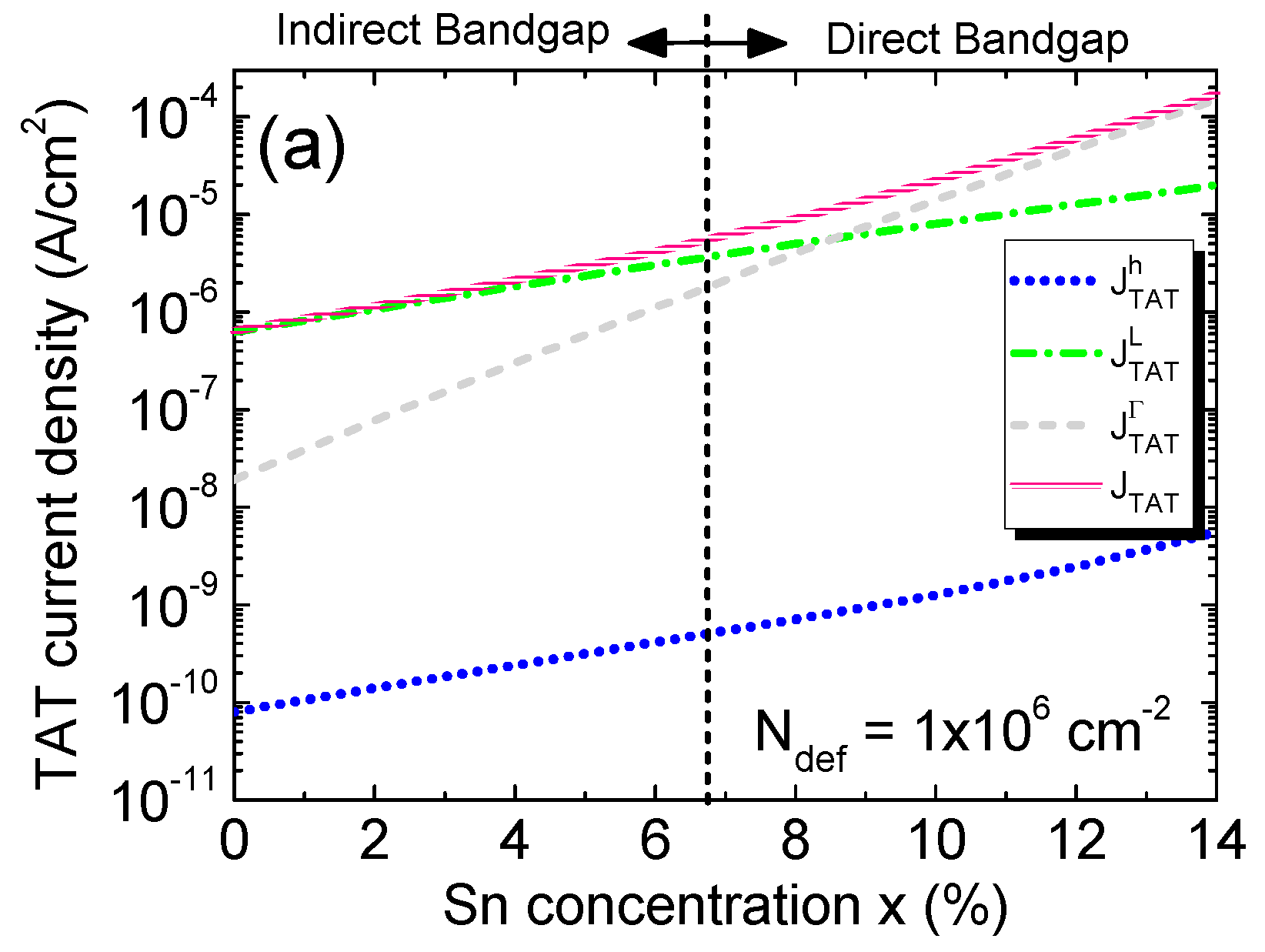
Figure 16 (a) shows the calculated TAT current density with its contributing component calculated defect density of Ndef= 1×106 cm-2 against Sn concentration. Due to their lower effective mass, the electrons can tunnel with faster rates through the defect states than holes. For lower Sn concentrations, Γ-CB sits above L-CB, so most electrons reside in L-CB. As a result, L-CB component is therefore higher than Γ-CB component. Furthermore, TAT dark current density increases with increasing Sn concentration because of reduction in bandgap energy that lowers the tunneling barrier, thereby increasing tunneling probability and current. For higher Sn concentrations where Ge1-xSnx becomes direct-bandgap materials and Γ-CB sits lower than L-CB, more and more electrons populate in the Γ-CB. Together with the small effective mass of Γ-CB electrons, the Γ-CB tunneling current goes up. 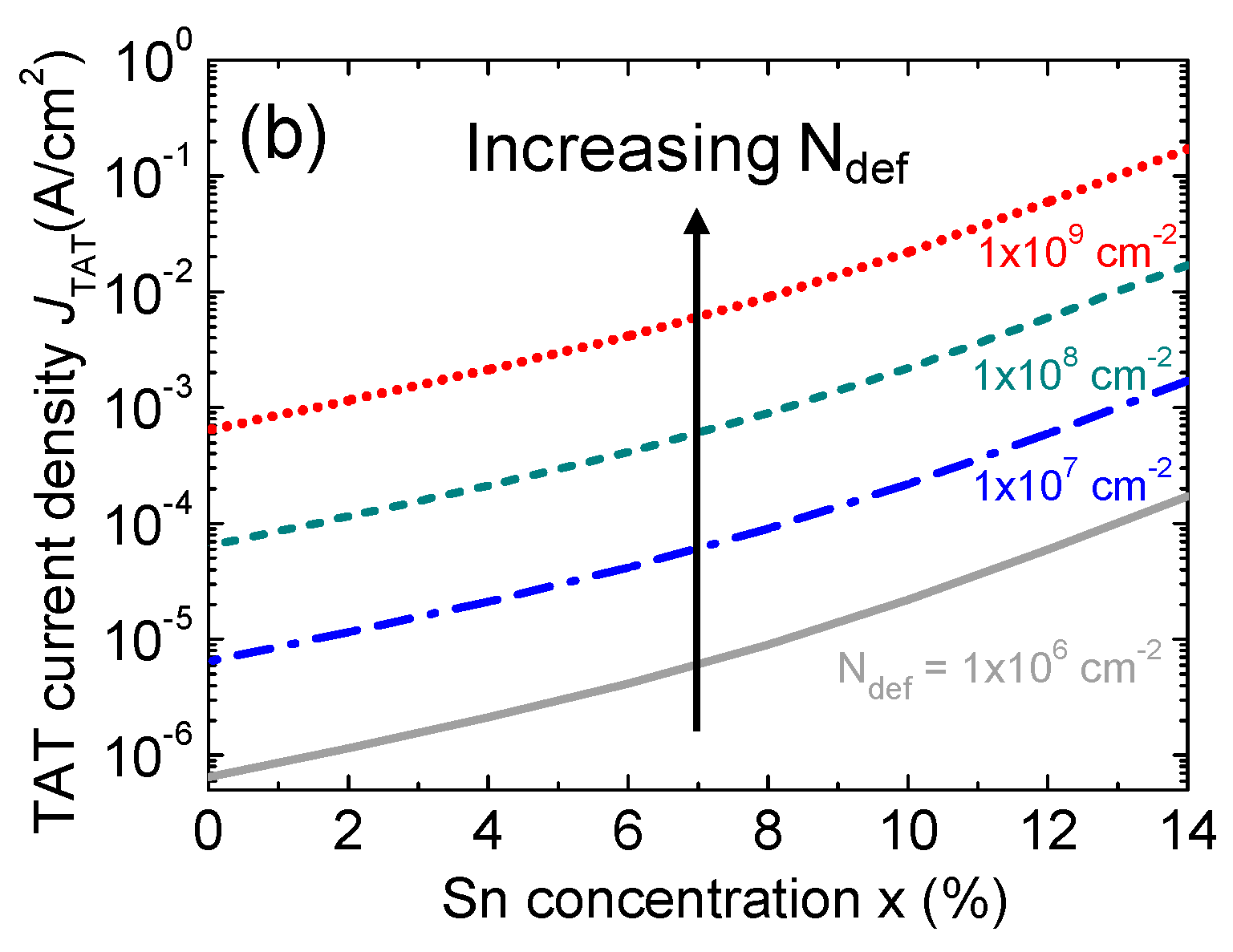Figure 16 (b) shows the total TAT dark current density as a function of Sn concentration for defect densities ranging from 1×106 to 1×109 cm-2. The TAT dark current density increases rapidly with increasing defect density that causes the tunneling rate to go up.

4.6. Total Dark Current

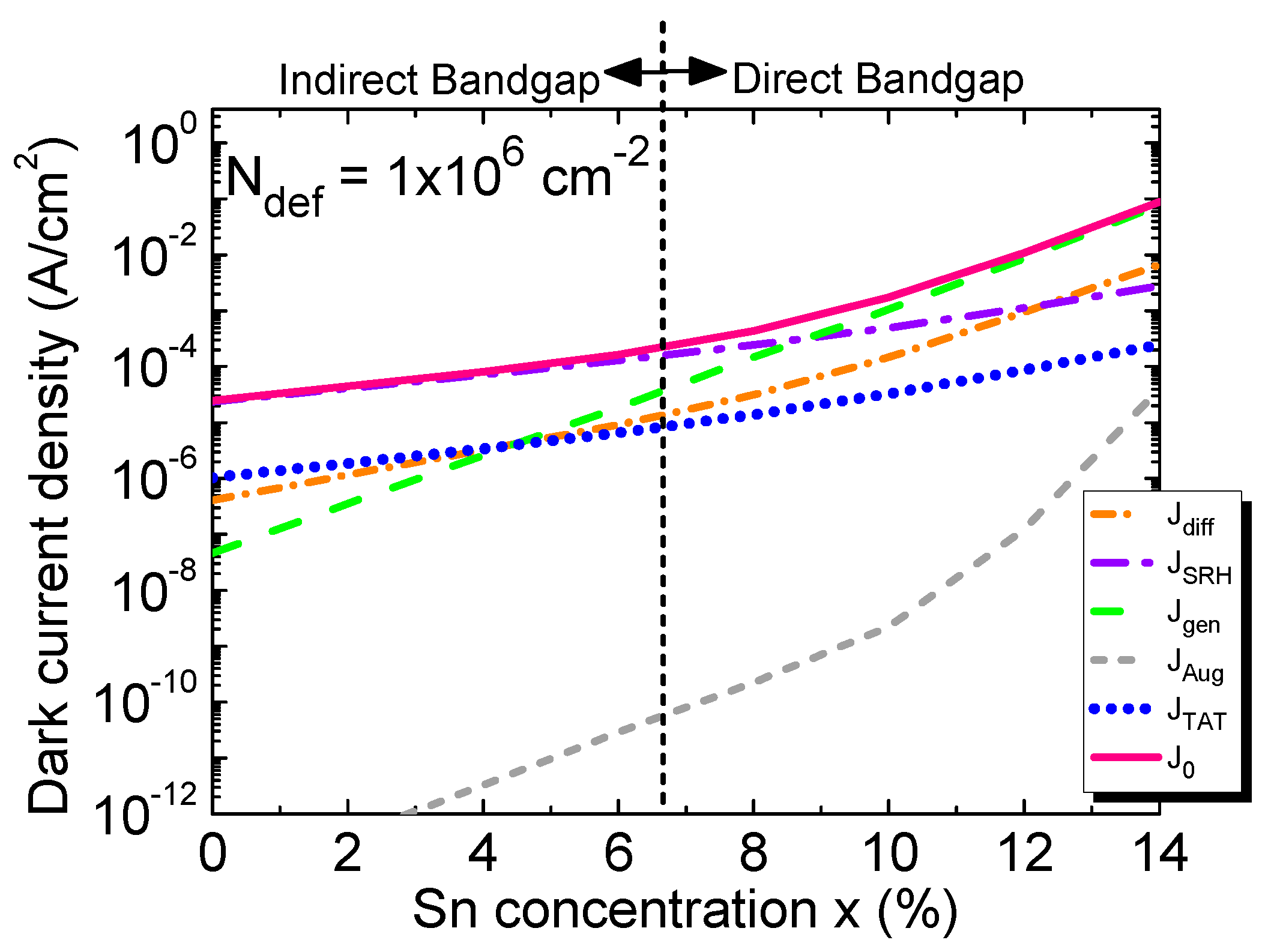
Following the above analysis of various dark current components, we are in the position to calculate the total dark current density. Figure 17 shows the calculated total dark current and its contributing components as a function of Sn concentration at a fixed defect density of Ndef=1×106 cm-2. In the case of pure Ge (x = 0%), the SRH and TAT components are the main contributors of the dark current which is a good agreement with the reported result [58].The total dark current density along its contributing components all increases with increasing Sn concentration. At lower Sn concentration (x< 5%), SRH, TAT and diffusion components dominate the dark current. At higher Sn concentrations, however, as Ge1-xSnx becomes a direct-bandgap material, the interband generation component takes over rapidly in dominating the total dark current. Meanwhile, in the absence of incident photon signal, the carrier concentration remains low in i-Ge1-xSnx region, the Auger contribution is therefore weak with respect to the other components throughout the Sn-concentration range of interest. Under the zero-bias condition, the electric field inside the intrinsic region is very small (~6 kV/cm), so the TAT current is therefore relatively insignificant in comparison with the SRH component.
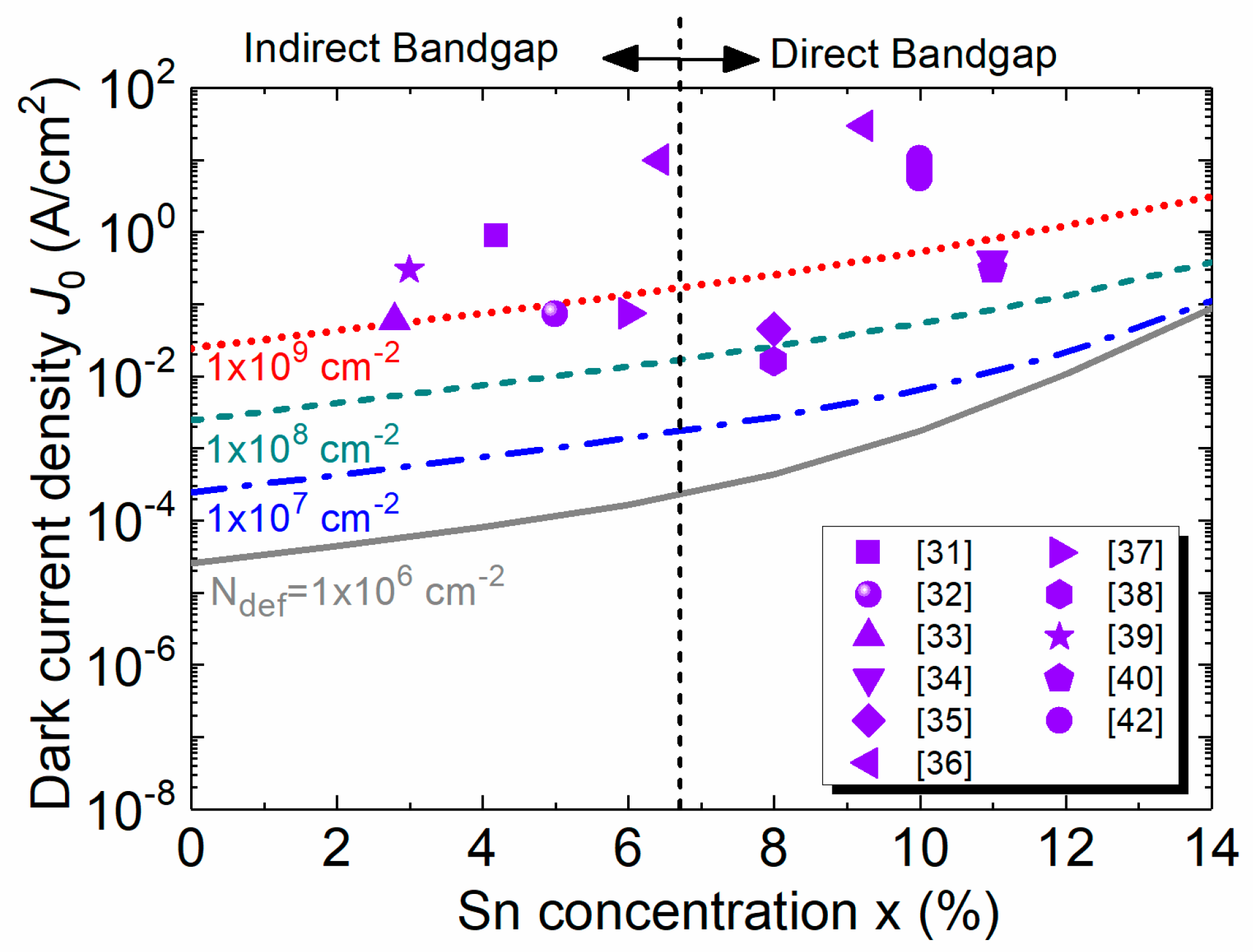
We next study the effect of higher defect densities on the dark current density. Figure 18 shows the calculated total dark current density as a function of Sn concentration for defect densities ranging from 1×106to 1×109 cm-2and compares with the previously reported experimental data [31-40,42]. For a fixed Sn concentration, the increase of defect density increases the GR centers inside the i-Ge1-xSnxregion, thereby increasing in the dark current. Because the dark current density is dominated by its SRH component at lower Sn concentrations (< 8%), the total dark current increases sharply with the increase of defect density. These results suggest that for Ge1-xSnx PDs with lower Sn concentrations, it is crucial to lower defect density as much as possible in order to minimize the dark current. At higher Sn concentrations, however, as the i-Ge1-xSnxlayer becomes a direct-bandgap material, the intrinsic carrier concentration increases rapidly with the bandgap reduction and more of these carriers reside in Γ-CB, so the interband generation current becomes dominant. Thus, at higher Sn concentrations, the dark current density depends mostly on the material intrinsic properties and becomes less sensitive to defect density. The analysis implies that significant improvement in dark current is less likely to be obtained with further reducing the defect density to less than 107 cm-².In addition, from the experimental data measured from the Ge1-xSnx PDs, it can be found that some experimental data fall in the range of calculated dark current density between Ndef=1×106 and 1×109 cm-2, and some are higher than the calculated dark current density for Ndef=1×109 cm-2. This discrepancy is attributed to the much thinner GeSn active layer of the reported GeSn PDs (typically 100-500 nm) which leads to much higher TAT currents. The results suggest that further optimization of GeSn PDs is necessary to minimize the dark current density of GeSn PDs.

5. Optical Responsivity Analysis

The optical responsivity of Ge1-xSnx p-i-n PD under normal incidence can be calculated as [28]
R λ = q λ h c η i ( 1 − R ) [ 1 − exp ( − α t i ) ]
where λ is the wavelength, h is the Planck’s constant, ηi is the internal quantum efficiency, and R is the reflectivity of the anti-reflection coating of the top surface. To obtain the highest achievable responsivity of GeSn PDs, we assume that the internal quantum efficiency is 100% and that the reflectivity of the ARC layer is almost zero. (It should be noted that in reality the quantum efficiency of GeSn PDs may be lower and the reflectivity may not be zero, so the responsivity would be lower.)
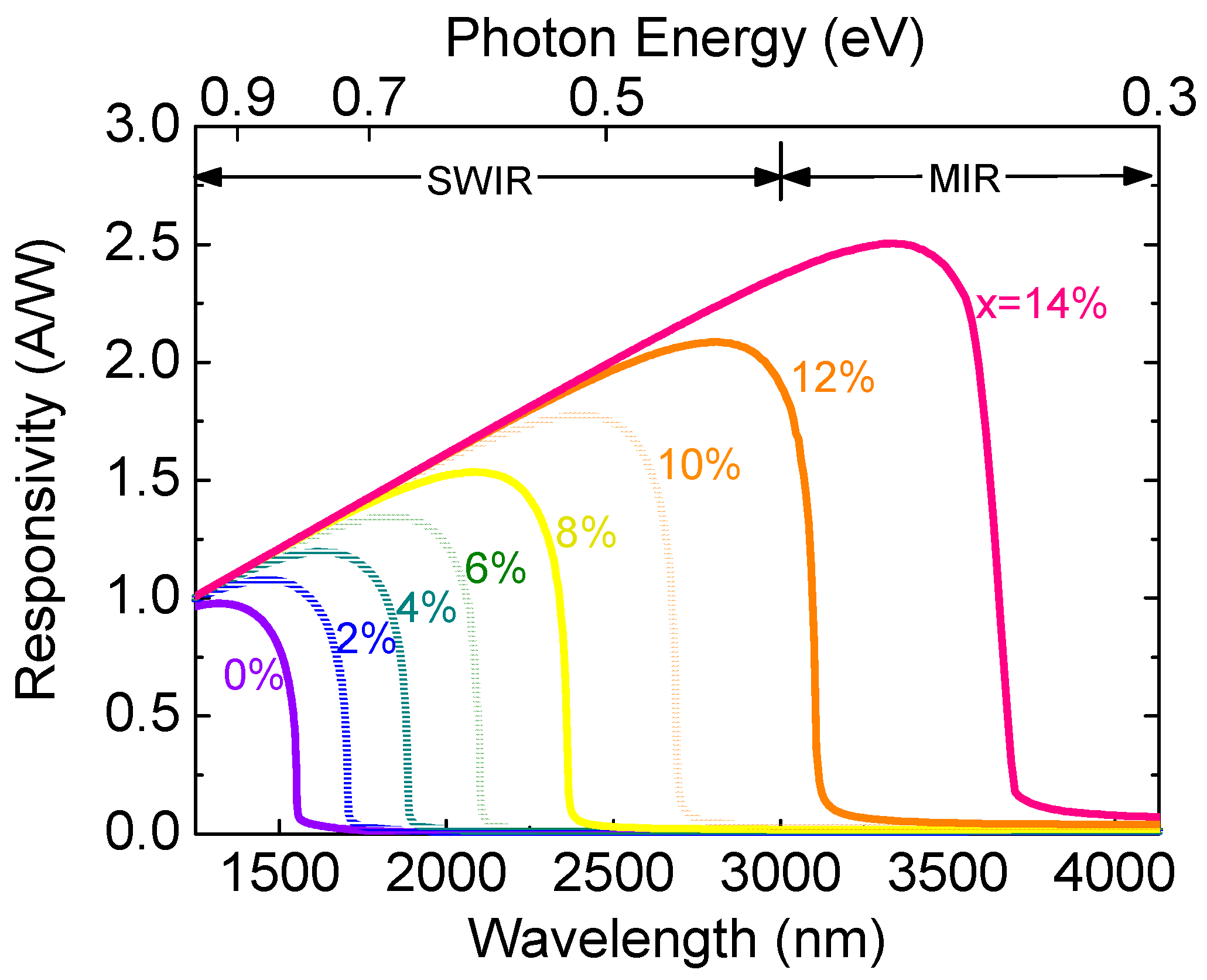
Figure 19 sows the calculated optical responsivity spectra of the GeSn PD for different Sn concentrations. For a fixed Sn concentration, the optical responsivity increases with increasing wavelength, and sharply decreases at the direct-bandgap energy. As the Sn concentration increases, the cutoff wavelength redshifts owing to the reduced direct-bandgap energy. As a result, the optical responses of the GeSn PDs can cover the MIR region.

6. Detectivity Analysis

Finally, with the calculated total dark current density and optical responsivity, we then study one of the most important figure-of-merit for PDs, detectivity (D*). The detectivity of the Ge1-xSnx PD can be expressed as [60]
D * = R λ A d Δ f 〈 i n 2 〉
where Ad is the detection area, Δf denotes the bandwidth and i n is the thermal noise. Under dark condition, i n can be evaluated using [19]
〈 i n 2 〉 = 4 k B T Δ f R 0
where R0 is the differential zero-bias resistance [52,60]. Combining Eqns. (23) and (24) with the dark current in Eq. (4), the detectivity of the Ge1-xSnx p-i-n PD can be expressed as
D * = R λ 2 q J 0
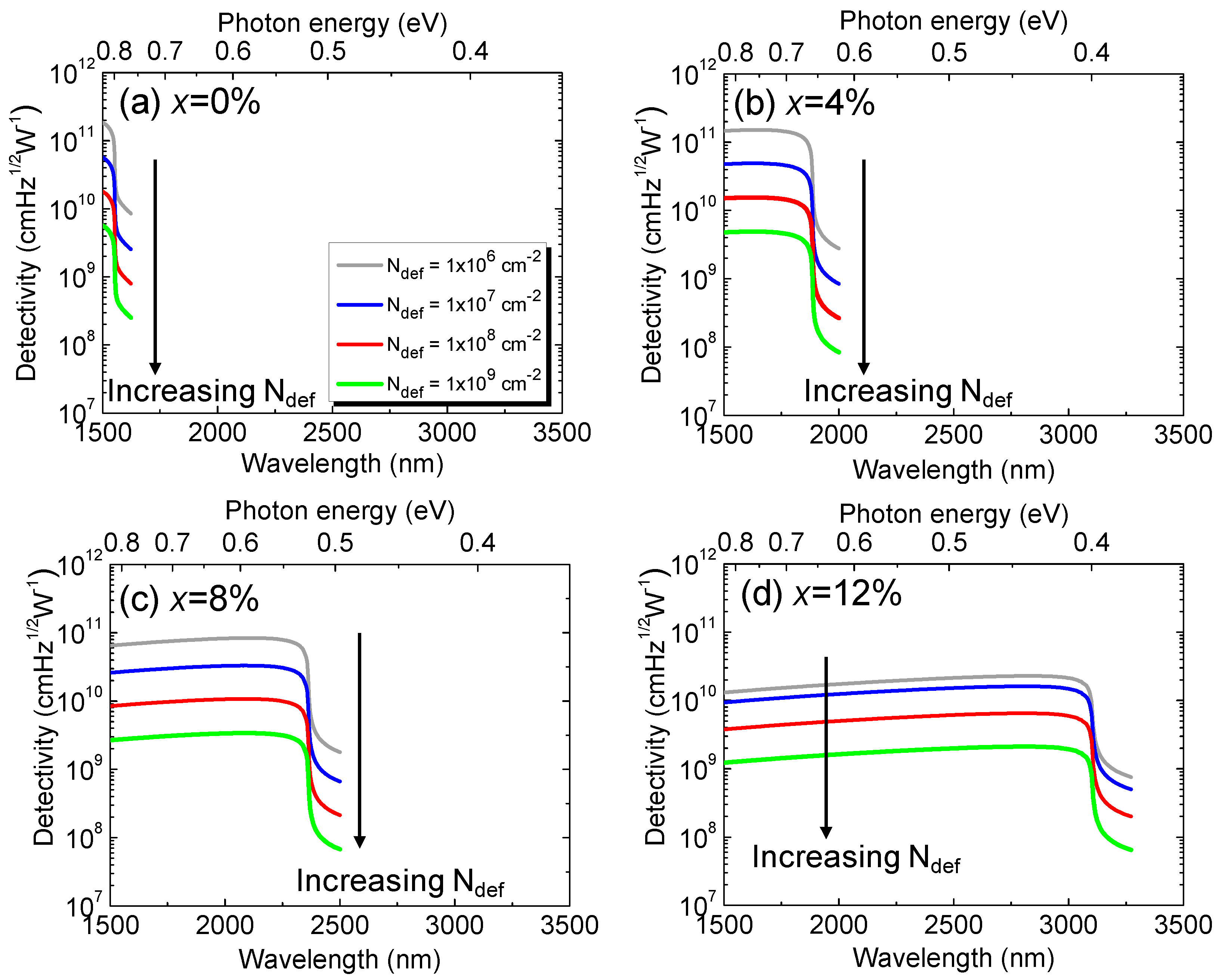
Figure 20 shows the calculated detectivity of the Ge1-xSnx p-i-n PD under zero-bias condition in the presence of various defect densities. For a fixed defect density and Sn concentration, the detectivity is higher at longer wavelengths, and then rapidly decreases when reaching its cutoff wavelength. When the defect density increases, the detectivity drops owing to the increased dark current density. 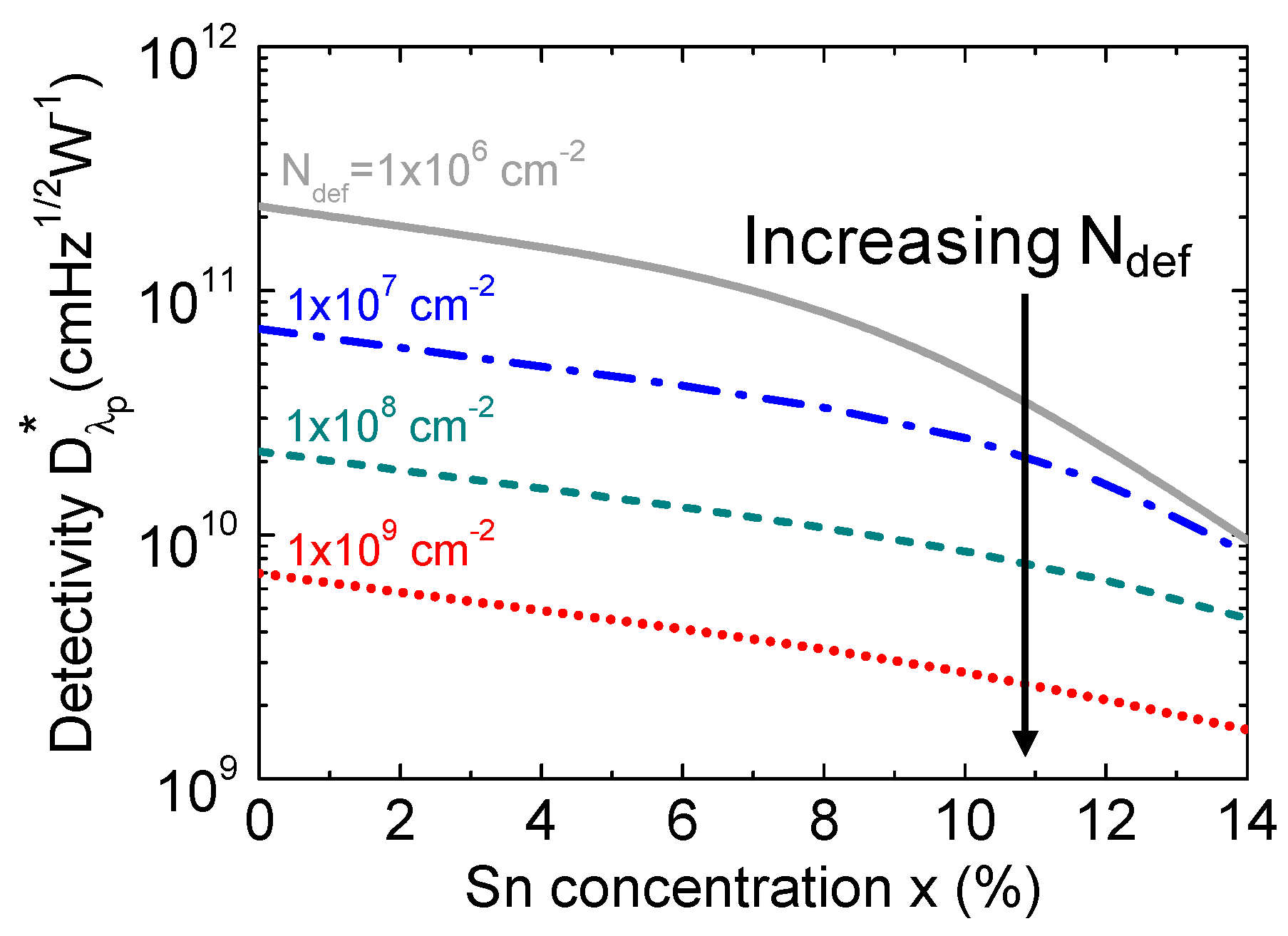From calculated detectivity spectra, we extracted the peak detectivity (which is defined as the detectivity at a wavelength of λp=0.9×λc) as a function of Sn concentration with various defect densities, and the results are depicted in Fig. 21.The presence of higher defect states inside the intrinsic region acting as the GR centers produces higher dark current. As a result, the detectivity decreases with increasing defect density. Reducing defect density can certainly improve detectivity. However, the degree to which the improvement can be obtained depends on the Sn concentration. It can be seen that, for smaller Sn concentrations (<8%), the significant improvement in detectivity can be achieved by reducing defect density. However, when Ge1-xSnxbecomes a direct-bandgap material at higher Sn concentrations, and payoff on detectivity by reducing defect density to less than ~1×107 cm-2 is not as impressive because generation dark current becomes the dominant component. These results highlight the dependences of defect density and Sn composition on the detectivity and photodetection range of GeSn PDs, providing useful guidelines for device and system developers to optimize GeSn PDs to achieve desired performance for practical application.

7. Conclusion

In this paper, to illuminate practical applications, we have theoretically studied the achievable performance of the homojunction Ge1-xSnx p-i-n PD at room temperature owing to different sources of dark current including minority carrier diffusion, various GR techniques and tunneling of carriers. The presence of defect states produces GR centers that significantly impact the dark current. The calculation results show that the defect density significantly increases the dark current at low Sn concentrations, so improving the material quality is necessary and effective to suppress the dark current density and thus enhance the detectivity. On the other hand, when the Sn concentration is high enough to transfer the GeSn layers into a direct-bandgap material, the significantly reduced bandgap energy leads to a high intrinsic carrier density, so the generation dark current density dominates the dark current density. Thus, the detectivity is less sensitive to the defect density. These results provide insights into the dark current density in terms of defect density and Sn concentration of GeSn PDs, establishing important guidelines for device developers to improve the performance of GeSn PDs for practical applications.

Author Contributions

Conceptualization, G. E. C., S. G., and G. S.; methodology, G. E. C. and S. G.; software, S. G.; validation, S. G., G. E. C., T. A. M., G. T. F. and G. S.; formal analysis, S. G., G. E. C., T. A. M., G. T. F. and G. S.; investigation, S. G., and G. E. C.; resources, G. E. C. and G. S.; data curation, , S. G., G. E. C., T. A. M., G. T. F. and G. S.; writing—original draft preparation, S. G.; writing—review and editing, , S. G., G. E. C., T. A. M., G. T. F. and G. S.; supervision, G. E. C. and G. S.; project administration, G. E. C. and G. S.; funding acquisition, G. E. C. and G. S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Science and Technology Council of Taiwan (NSTC) under Grant Nos. MOST 111-2636-E-194-002, NSTC112-2636-E-194-001 and NSTC 112-2923-M-002-004.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to commercial privacy policy.

Acknowledgments

G.S. acknowledges support from Air Force Office of Scientific Research (FA9550-19-1-0341). T.A.M. and G.T.F. acknowledge support from Office of Naval Research Code 312 and the Naval Innovative Science & Engineering program.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hoogeveen, R. W. M.; van der A, R. J.; and Goede, A. P. H. Extended wavelength InGaAs infrared (1.0–2.4 μm) detector arrays on SCIAMACHY for space-based spectrometry of the Earth atmosphere. Infr. Phys. Technol., 2001, 42, 1–16. [Google Scholar] [CrossRef]
  2. Arslan, Y.; Oguz, F.; Besikci, C. Extended wavelength SWIR InGaAs focal plane array: Characteristics and limitations. Infrared Phys. Technol. 2015, 70, 134–137. [Google Scholar] [CrossRef]
  3. Long, M.; Gao, A.; Wang, P.; Xia, H.; Ott, C.; Pan, C.; Fu, Y.; Liu, E.; Chen, X.; Lu, W.; et al. Room temperature high-detectivity mid-infrared photodetectors based on black arsenic phosphorus. Sci. Adv. 2017, 3, e1700589–1700589. [Google Scholar] [CrossRef]
  4. Deng, G.; Yang, W.; Gong, X.; Zhang, Y. High-performance uncooled InAsSb-based pCBn mid-infrared photodetectors. Infr. Phys. Technol., 2020, 105, 103260. [Google Scholar] [CrossRef]
  5. Kimukin, I.; Biyikli, N.; Kartaloglu, T.; Aytur, O.; Ozbay, E. High-Speed InSb Photodetectors on GaAs for Mid-IR Applications. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 766–770. [Google Scholar] [CrossRef]
  6. Martin, J.M.; Hernández, J.L.; Adell, L.; Rodriguez, A.; López, F. Arrays of thermally evaporated PbSe infrared photodetectors deposited on Si substrates operating at room temperature. Semicond. Sci. Technol. 1996, 11, 1740–1744. [Google Scholar] [CrossRef]
  7. Muñoz, A.; Meléndez, J.; Torquemada, M.; Rodrigo, M.; Cebrián, J.; de Castro, A.; Meneses, J.; Ugarte, M.; López, F.; Vergara, G.; et al. PbSe photodetector arrays for IR sensors. Thin Solid Films 1998, 317, 425–428. [Google Scholar] [CrossRef]
  8. Su, Y. K.; Juang, F. –S.; Chang, S. –M.; Chiang, C. –D.; Cherng, Y. –T. 1/f noise and specific detectivity of HgCdTe photodiodes passivated with ZnS-CdS films. IEEE J. Quantum Electron. 1999, 35, 751–756. [CrossRef]
  9. Kasiyan, V.; Dashevsky, Z.; Schwarz, C.M.; Shatkhin, M.; Flitsiyan, E.; Chernyak, L.; Khokhlov, D. Infrared detectors based on semiconductor p-n junction of PbSe. J. Appl. Phys. 2012, 112, 086101. [Google Scholar] [CrossRef]
  10. Bansal, S.; Das, A.; Jain, P.; Prakash, K.; Sharma, K.; Kumar, N.; Sardana, N.; Gupta, N.; Kumar, S.; Singh, A. K. Enhanced Optoelectronic Properties of Bilayer Graphene/HgCdTe-Based Single- and Dual-Junction Photodetectors in Long Infrared Regime. IEEE Trans. Nanotechnol., 2019, 18, 781–789. [Google Scholar] [CrossRef]
  11. Wang, J.; Xing, Y.; Wan, F.; Fu, C.; Xu, C. –H.; Liang, F. –X.; and Luo, L. –B. Progress in ultraviolet photodetectors based on II-VI group compound semiconductors. J. Mater. Chem. C, 2022, 10, 12929–12946. [CrossRef]
  12. Wang, Y.; Gu, Y.; Cui, A.; Li, Q.; He, T.; Zhang, K.; Wang, Z.; Li, Z.; Zhang, Z.; Wu, P.; et al. Fast Uncooled Mid-Wavelength Infrared Photodetectors with Heterostructures of van der Waals on Epitaxial HgCdTe. Adv. Mater. 2021, 34, 2107772. [Google Scholar] [CrossRef]
  13. Soref, R. Silicon-based silicon-germanium-tin heterostructure photonics. Philos. Trans. R. Soc. London, Ser. A, 2014, 372, 20130113. [Google Scholar] [CrossRef] [PubMed]
  14. Deen, M.J.; Basu, P.K. Silicon Photonics: Fundamentals and Devices; Willey: Hoboken, NJ, USA, 2012. [Google Scholar]
  15. Michel, J.; Liu, J.; Kimerling, L.C. High-performance Ge-on-Si photodetectors. Nat. Photon- 2010, 4, 527–534. [Google Scholar] [CrossRef]
  16. Gupta, J.P.; Bhargava, N.; Kim, S.; Adam, T.; Kolodzey, J. Infrared electroluminescence from GeSn heterojunction diodes grown by molecular beam epitaxy. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
  17. Bauer, M.; Taraci, J.; Tolle, J.; Chizmeshya, A.V.G.; Zollner, S.; Smith, D.J.; Menendez, J.; Hu, C.; Kouvetakis, J. Ge–Sn semiconductors for band-gap and lattice engineering. Appl. Phys. Lett. 2002, 81, 2992–2994. [Google Scholar] [CrossRef]
  18. Chizmeshy, A.V.G.; Ritter, C.; Tolle, J.; Cook, C.; Menendez, J.; Kuovetakis, J. Fundamental studies of P(GeH3)3, As(GeH3)3, and Sb(GeH3)3: Practical n-dopants for New Group IV Semiconductors. Chem. Mater. 2006, 18, 6266–6277. [Google Scholar] [CrossRef]
  19. Chang, G. -E.; Yu, S. -Q.; Liu, J.; Cheng, H. H.; Soref, R. A.; Sun, G. Achievable performance of uncooled homojunction GeSn mid-infrared photodetectors. IEEE J. Sel. Quantum Electron. 2022, 28, 3800611.
  20. Chang, G.E.; Basu, R.; Mukhopadhyay, B.; Basu, P.K. Design and Modeling of GeSn-based Heterojucntion Phototransistors for Communication Applications. IEEE J. Sel. Quantum Electron. 2016, 22, 8200409. [Google Scholar] [CrossRef]
  21. Soref, R. Mid-Infrared Photonics. In Optical Fiber Communication Conference (OFC); 2015, W4A.4. [Google Scholar]
  22. Ghosh, S.; Bansal, R.; Sun, G.; Soref, R. A.; Cheng, H. –H.; and Chang, G. –E. Design and Optimization of GeSn Waveguide Photodetectors for 2-μm Band Silicon Photonics. Sensors 2022, 22, 3978. [CrossRef]
  23. Tseng, H.H.; Li, H.; Mashanov, V.; Yang, Y.J.; Cheng, H.H.; Chang, G.-E.; Soref, R. A.; Sun, G. GeSn-based p-i-n photodiodes with strained active layer on a Si wafer. Appl. Phys. Lett., 2013, 103, 231907. [Google Scholar] [CrossRef]
  24. Pham, T.; Du, W.; Tran, H.; Margetis, J.; Tolle, J.; Sun, G.; Soref, R. A.; Naseem, H. A.; Li, B.; Yu, S.-Q. Systematic study of Si-based GeSn photodiodes 2.6 µm detector cutoff for short-wave infrared detection. Opt. Express, 2016, 24, 4519–4531. [Google Scholar] [CrossRef]
  25. Xu, S.; Huang, Y.-C.; Lee, K.H.; Wang, W.; Dong, Y.; Lei, D.; Masudy-Panah, S.; Tan, C.S.; Gong, X.; Yeo, Y.-C. GeSn lateral p-i-n photodetector on insulating substrate. Opt. Express 2018, 26, 17312–17321. [Google Scholar] [CrossRef]
  26. Tran, H.; Pham, T.; Margetis, J.; Zhou, Y.; Dou, W.; Grant, P.C.; Grant, J.M.; Alkabi, S.; Sun, G.; Soref, R.A.; et al. Study of High Performance GeSn Photodetectors with Cutoff Wavelength up to 3.7 µm for Low-Cost Infrared Imaging. In Proceedings of the CLEO: Science and Innovations 2019, San Jose, CA, USA, 5–10 May 2019. [CrossRef]
  27. Tran, H.; Pham, T. Tran, H.; Pham, T.; Margetis, J;. Zhou, Y.; Dou, W.; Grant, P. C.; Grant, J. M.; Al-Kabi, S.; Sun, G.; Soref, R. A.; Tolle, J.; Zhang, Y. -H.; Du, W.; Li, B.; Mortazavi, M.; and Yu, S. -Q. Si-Based GeSn Photodetectors toward Mid-Infrared Imaging Applications. ACS Photonics 2019, 6, 2807–2815. [Google Scholar] [CrossRef]
  28. Ghosh, S.; Mukhopadhyay, B.; Sen, G.; Basu, P. Performance analysis of GeSn/SiGeSn quantum well infrared photodetector in terahertz wavelength region. Phys. E: Low-dimensional Syst. Nanostructures 2019, 115, 113692. [Google Scholar] [CrossRef]
  29. Ghosh, S.; Bhattacharyya, A.; Sen, G.; Mukhopadhyay, B. Optimization of different structural parameters of GeSn/SiGeSn Quantum Well Infrared Photodetectors (QWIPs) for low dark current and high responsivity. J. Comput. Electron. 2021, 20, 1224–1233. [Google Scholar] [CrossRef]
  30. McCarthy, T. T.; Ju, Z.; Schaefer, S.; Yu, S. –Q.; and Zhang, Y. –H. Momentum (k)-space carrier separation using SiGeSn alloys for photodetector applications. J. Appl. Phys. 2021, 130, 223102. [CrossRef]
  31. Oehme, M. GeSn-on-Si normal incidence photodetectors with bandwidths more than 40 GHz. Opt. Express, 2014, 22, 839–846. [Google Scholar] [CrossRef]
  32. Dong, Y.; Wang, W.; Lei, D.; Gong, X.; Zhou, Q.; Lee, S.Y.; Loke, W.K.; Yoon, S.-F.; Tok, E.S.; Liang, G.; et al. Suppression of dark current in germanium-tin on silicon p-i-n photodiode by a silicon surface passivation technique. Opt. Express 2015, 23, 18611–18619. [Google Scholar] [CrossRef]
  33. Huang, Y. Huang, Y. –H. et al. Sn-based waveguide p-i-n photodetector with strained GeSn/Ge multiple-quantum-well active layer. Opt. Lett., 2017, 42, 1652–1655. [Google Scholar] [CrossRef]
  34. Tran, H. High performance Ge0.89Sn0.11 photodiodes for lowcost shortwave infrared imaging. J. Appl. Phys., 2018, 124, 013101. [Google Scholar] [CrossRef]
  35. Xu, S.; Wang, W.; Huang, Y.-C.; Dong, Y.; Masudy-Panah, S.; Wang, H.; Gong, X.; Yeo, Y.-C. High-speed photo detection at two-micron-wavelength: technology enablement by GeSn/Ge multiple-quantum-well photodiode on 300 mm Si substrate. Opt. Express 2019, 27, 5798–5813. [Google Scholar] [CrossRef]
  36. Tran, H.; Littlejohns, C.G.; Thomson, D.J.; Pham, T.; Ghetmiri, A.; Mosleh, A.; Margetis, J.; Tolle, J.; Mashanovich, G.Z.; Du, W.; et al. Study of GeSn Mid-infrared Photodetectors for High Frequency Applications. Front. Mater. 2019, 6. [Google Scholar] [CrossRef]
  37. Zhao, Y. High performance silicon-based GeSn p–i–n photodetectors for short-wave infrared application. Chin. Phys. B, 2019, 28, 128501. [Google Scholar] [CrossRef]
  38. Zhou, H.; Xu, S.; Wu, S.; Huang, Y.-C.; Zhao, P.; Tong, J.; Son, B.; Guo, X.; Zhang, D.; Gong, X.; et al. Photo detection and modulation from 1,550 to 2,000 nm realized by a GeSn/Ge multiple-quantum-well photodiode on a 300-mm Si substrate. Opt. Express 2020, 28, 34772–34786. [Google Scholar] [CrossRef]
  39. Wang, N.; Xue, C.; Wan, F.; Zhao, Y.; Xu, G.; Liu, Z.; Zheng, J.; Zuo, Y.; Cheng, B.; Wang, Q. High-Performance GeSn Photodetector Covering All Telecommunication Bands. IEEE Photon- J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
  40. Li, M.; Zheng, J.; Liu, X.; Zhu, Y.; Niu, C.; Pang, Y.; Liu, Z.; Zuo, Y.; Cheng, B. Sn composition graded GeSn photodetectors on Si substrate with cutoff wavelength of 3.3 μm for mid-infrared Si photonics. Appl. Phys. Lett. 2022, 120, 121103. [Google Scholar] [CrossRef]
  41. Nawwar, M. A.; Ghazala, M. S. A.; El-Deen, L. M. S.; El-Shaer, A.; Anis, B.; and Kashyout, A. E. H. B. Toward white light random lasing emission based on strained nanopoly germanium doped with tin via metal-induced crystallization (MIC). Cryst. Growth Des., 2022, 23, 751–768. [Google Scholar] [CrossRef]
  42. Atalla, M.R.M.; Assali, S.; Koelling, S.; Attiaoui, A.; Moutanabbir, O. Dark current in monolithic extended-SWIR GeSn PIN photodetectors. Appl. Phys. Lett. 2023, 122, 031103. [Google Scholar] [CrossRef]
  43. Nawwar, M. A.; Ghazala, M. S.; El-Deen, L. M. S.; Anis, B.; El-Shaer, A.; Elseman, A. M.; Rashad, M. M.; and Kashyout, A. E. H. B. ; Controlling barrier height and spectral responsivity of p-i-n based GeSn photodetectors via arsenic incorporation. RSC Adv., 2023, 13, 9154–9167. [Google Scholar] [CrossRef]
  44. Karthik, R.; Sathyakam P., U.; Mallick, P. S. ; Effect of dislocation scattering on electron mobility in GaN,”. Natural Science 2011, 3, 812–815. [Google Scholar]
  45. Ghosh, S.; Leonhardt, D.; Han, S.M. Effect of threading dislocation density and dielectric layer on temperature-dependent electrical characteristics of high-hole-mobility metal semiconductor field effect transistors fabricated from wafer-scale epitaxially grown p-type germanium on silicon substrates. J. Appl. Phys. 2014, 115, 094507. [Google Scholar] [CrossRef]
  46. Wang, Z.; Liu, J.; Wang, W.; Chen, H.; Liu, Z.; Yu, Q.; Zeng, H.; Sun, L. Aqueous phase preparation of graphene with low defect density and adjustable layers. Chem. Commun. 2013, 49, 10835–10837. [Google Scholar] [CrossRef]
  47. Song, Z.; Fan, W.; Tan, C. S.; Wang, Q.; Nam, D.; and Sun, G. Band structure of Ge1-xSnx alloy: a full-zone 30-band k·p model. New J. Phys., 2020, 21, 073037. [Google Scholar] [CrossRef]
  48. Chang, G. -E.; Chang, S. -W.; Chuang, S. L. Strain-Balanced GezSn1-z-SixGeySn1-x-y Multiple-Quantum-Well Lasers. IEEE J. Quantum Electron. 2010, 46, 1813–1820.
  49. Giovane, L. M.; Luan, H. –C. ; Agarwal, A. M.; and Kimerling, L. C. Correlation between leakage current density and threading dislocation density in SiGe p-i-n diodes grown on relaxed graded buffer layers. Appl. Phys. Lett., 2001, 78, 541. [Google Scholar]
  50. Scajev, P.; Soriute, V.; Kreiza, G.; Malinauskas, T.; Stanionyte, S.; Onufrijevs, P.; Medvids, A.; and Cheng, H. –H. Temperature dependent carrier lifetime, diffusion coefficient, and diffusion length in Ge0.95Sn0.05 epilayer. J. Appl. Phys., 2020, 128, 115103. [CrossRef]
  51. Gupta, S.; Simoen, E.; Loo, R.; Shimura, Y.; Porret, C.; Gencarelli, F.; Paredis, K.; Bender, H.; Lauwaert, J.; Vrielinck, H.; et al. Electrical properties of extended defects in strain relaxed GeSn. Appl. Phys. Lett. 2018, 113, 022102. [Google Scholar] [CrossRef]
  52. Chuang, S.L. Physics of Photonic Devices, 2nd ed.; Willey: Hoboken, NJ, USA, 2012. [Google Scholar]
  53. Ghosh, S.; Lin, K. –C.; Tsai, C. –H.; Kumar, H.; Chen, Q.; Zhang, L.; Son, B.; Tan, C. S.; Kim, M.; Mukhopadhyay, B.; Chang, G. –E. Metal-Semiconductor-Metal GeSn Photodetectors on Silicon for Short-Wave Infrared Applications. Micromachines 2020, 11, 795. [CrossRef]
  54. Schubert, E. F. Light-Emitting Diodes, 2nd ed; Cambridge University Press: UK, 2006. [Google Scholar]
  55. Grzybowski, G.; Roucka, R.; Mathews, J.; Jiang, L.; Beeler, R.T.; Kouvetakis, J.; Menéndez, J. Direct versus indirect optical recombination in Ge films grown on Si substrates. Phys. Rev. B 2011, 84, 205307. [Google Scholar] [CrossRef]
  56. Liu, J.; Sun, X.; Pan, D.; Wang, X.; Kimerling, L.C.; Koch, T.L.; Michel, J. Tensile-strained, n-type Ge as a gain medium for monolithic laser integration on Si. Opt. Express 2007, 15, 11272–11277. [Google Scholar] [CrossRef] [PubMed]
  57. Sun, G.; Soref R. A.; and Cheng, H. –H. Design of an electrically pumped SiGeSn/GeSn/SiGeSn double-heterostructure midinfrared laser. J. Appl. Phys., 2010, 108, 033107. [CrossRef]
  58. Son, B.; Lin, Y.; Lee, K.H.; Chen, Q.; Tan, C.S. Dark current analysis of germanium-on-insulator vertical p-i-n photodetectors with varying threading dislocation density. J. Appl. Phys. 2020, 127, 203105. [Google Scholar] [CrossRef]
  59. Hurkx, G.A.M.; Klaassen, D.B.M.; Knuvers, M.P.G. A new recombination model for device simulation including tunneling. IEEE Trans. Electron Devices 1992, 39, 331–338. [Google Scholar] [CrossRef]
  60. Ghosh, S.; Bhattacharyya, A.; Sen, G.; Mukhopadhyay, B. Optimization of different structural parameters of GeSn/SiGeSn Quantum Well Infrared Photodetectors (QWIPs) for low dark current and high responsivity. J. Comput. Electron. 2021, 20, 1224–1233. [Google Scholar] [CrossRef]
Preprints 80568 g004
Figure 4. Illustration of dark current due to diffusion of minority carriers in homojunction GeSn PD with (a) indirect-bandgap and (b) direct-bandgap GeSn layers.
Figure 4. Illustration of dark current due to diffusion of minority carriers in homojunction GeSn PD with (a) indirect-bandgap and (b) direct-bandgap GeSn layers.
Preprints 80568 g004
Preprints 80568 g005
Figure 5. (a) Minority carrier diffusion current density and its different contributing components as a function of Sn concentration with a defect density of 106 cm-2. (b) Minority carrier diffusion current density as a function of Sn concentration with various defect densities.
Figure 5. (a) Minority carrier diffusion current density and its different contributing components as a function of Sn concentration with a defect density of 106 cm-2. (b) Minority carrier diffusion current density as a function of Sn concentration with various defect densities.
Preprints 80568 g005
Preprints 80568 g006
Figure 6. Illustration of SRH dark currents in GeSn PD with (a) indirect-bandgap and (b) direct-bandgap GeSn layers.
Figure 6. Illustration of SRH dark currents in GeSn PD with (a) indirect-bandgap and (b) direct-bandgap GeSn layers.
Preprints 80568 g006
Preprints 80568 g007
Figure 7. SRH coefficients for electrons and holes of GeSn alloys as a function of Sn concentration.
Figure 7. SRH coefficients for electrons and holes of GeSn alloys as a function of Sn concentration.
Preprints 80568 g007
Preprints 80568 g008
Figure 8. (a) SRH current density along with its contributing components as a function of Sn concentration at a fixed defect density of 1×106 cm-2. (b) SRH current density as a function of Sn concentration for various defect densities.
Figure 8. (a) SRH current density along with its contributing components as a function of Sn concentration at a fixed defect density of 1×106 cm-2. (b) SRH current density as a function of Sn concentration for various defect densities.
Preprints 80568 g008
Preprints 80568 g009
Figure 9. Illustration of dark current due to generation of EHPs in homojunction GeSn PD with (a) indirect-bandgap and (b) direct-bandgap Ge1-xSnx layers.
Figure 9. Illustration of dark current due to generation of EHPs in homojunction GeSn PD with (a) indirect-bandgap and (b) direct-bandgap Ge1-xSnx layers.
Preprints 80568 g009
Preprints 80568 g011
Figure 11. (a) Radiative recombination coefficients as a function of Sn concentration. (b) Different contributors and total interband generation dark current density as a function of Sn concentration.
Figure 11. (a) Radiative recombination coefficients as a function of Sn concentration. (b) Different contributors and total interband generation dark current density as a function of Sn concentration.
Preprints 80568 g011
Preprints 80568 g013
Figure 13. (a) Auger coefficients as a function of Sn concentration. (b) Auger current density and its contributing components as a function of Sn concentration.
Figure 13. (a) Auger coefficients as a function of Sn concentration. (b) Auger current density and its contributing components as a function of Sn concentration.
Preprints 80568 g013
Preprints 80568 g014
Figure 14. Illustration of TAT-related electron tunneling in Ge1-xSnxPD with (a) indirect-bandgap and (b) direct-bandgap GeSn alloys, and (c) hole tunneling.
Figure 14. Illustration of TAT-related electron tunneling in Ge1-xSnxPD with (a) indirect-bandgap and (b) direct-bandgap GeSn alloys, and (c) hole tunneling.
Preprints 80568 g014
Preprints 80568 g015
Figure 15. TAT enhancement factors as a function of Sn concentration.
Figure 15. TAT enhancement factors as a function of Sn concentration.
Preprints 80568 g015
Preprints 80568 g016aPreprints 80568 g016b
Figure 16. (a) Different contributors and total TAT current density as a function of Sn concentration with a defect density of 1×106 cm-2. (b) Total TAT current density as a function of Sn concentration for different defect densities.
Figure 16. (a) Different contributors and total TAT current density as a function of Sn concentration with a defect density of 1×106 cm-2. (b) Total TAT current density as a function of Sn concentration for different defect densities.
Preprints 80568 g016aPreprints 80568 g016b
Preprints 80568 g017
Figure 17. Total dark current density and its components as a function of Sn concentration.
Figure 17. Total dark current density and its components as a function of Sn concentration.
Preprints 80568 g017
Preprints 80568 g018
Figure 18. Calculated dark current density as a function of Sn concentration for different defect densities (lines) compared with reported experimental results (scatters) at -1V bias voltage [31-40,42].
Figure 18. Calculated dark current density as a function of Sn concentration for different defect densities (lines) compared with reported experimental results (scatters) at -1V bias voltage [31-40,42].
Preprints 80568 g018
Preprints 80568 g019
Figure 19. Optical responsivity spectra of GeSn PDs with different Sn concentrations.
Figure 19. Optical responsivity spectra of GeSn PDs with different Sn concentrations.
Preprints 80568 g019
Preprints 80568 g020
Figure 20. Calculated detectivity spectra of Ge1-xSnx PDs for (a) x=0%, (b) x=4%, (c) x=8%, and (d) x=12% with various defect densities.
Figure 20. Calculated detectivity spectra of Ge1-xSnx PDs for (a) x=0%, (b) x=4%, (c) x=8%, and (d) x=12% with various defect densities.
Preprints 80568 g020
Preprints 80568 g021
Figure 21. Variation of calculated detectivity as a function of Sn concentration for different defect densities at a specified wavelength (λp = 0.9×λc).
Figure 21. Variation of calculated detectivity as a function of Sn concentration for different defect densities at a specified wavelength (λp = 0.9×λc).
Preprints 80568 g021
Table 1. Direct and Indirect-band Radiative Recombination Coefficients of Ge.
Table 1. Direct and Indirect-band Radiative Recombination Coefficients of Ge.
Radiative Recombination Coefficients (cm3s-1) Pure Ge [56] This work
Direct-Bandgap ( B e h Γ ) 1.3×10-10 1.75×10-10
Indirect-Bandgap ( B e h L ) 5.1×10-15 5.2×10-15
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated