Prerpints.org logo
Preprint
Article

Shannon Entropy of Ramsey Graphs

This version is not peer-reviewed.

Submitted:

24 July 2023

Posted:

25 July 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Shannon entropy quantifying bi-colored Ramsey complete graphs is introduced. Complete graphs in which vertices are connected with two types of links, labeled as α-links and β-links are considered. Shannon-entropy is introduced according to the classical Shannon formula considering the fractions of monochromatic convex α-colored polygons with n α-sides or edges, and the fraction of monochromatic β-colored convex polygons with m β-sides in the given complete graph. Introduced Shannon entropy is insensitive to the exact shape of the graph, but it is sensitive to the distribution of monochromatic polygons in a given graph. The introduced Shannon Entropies Sα and Sβ are interpreted as follows: Sα is interpreted as an average uncertainty to find the green α-polygon in the given graph, Sβ is, in turn, an average uncertainty to find the red β-polygon in the same graph. The re-shaping of the Ramsey theorem in terms of the Shannon Entropy is suggested. Various measures quantifying the Shannon Entropy of the entire complete bi-colored graphs are suggested. Physical interpretations of the suggested Shannon Entropies are discussed.
Keywords: 
Complete graph
;  
Shannon Entropy
;  
bi-colored graph
;  
Ramsey Theorem
;  
Ramsey Number
;  
Voronoi tessellation.
Subject: 
Computer Science and Mathematics  -   Discrete Mathematics and Combinatorics

1. Introduction

The intriguing history of the birth and development of the Ramsey theory is surveyed in detail in ref. 1. Frank Plumpton Ramsey was a British logician, mathematician, and thinker who made major contributions to various fields of knowledge before his death at the age of 26. His brother Michael once said about Frank Ramsey: He was interested in almost everything [1]. In our paper we address the sub-field of the graph theory, which is known as the “Ramsey theory”, which deals with the specific kind of graphs, namely: complete graphs. A complete graph is a graph in which each pair of graph vertices is connected by an edge/link. The classical problem considered by the Ramsey theory is the so-called “party problem”, which predicts the minimum number of guests R m , n that must be invited so that at least m of the guests will be acquainted with each other, or at least n of them will not be familiar with each other [2,3,4,5,6,7]. In this case R m , n is known as a Ramsey number [7,8,9,10,11]. A classical result in Ramsey theory states that if some mathematical structure/graph is separated into finitely many sub-parts, then one of the sub-parts necessarily must contain a substructure/graph of the given type.
Let us discuss first the Infinite Ramsey Theorem in a rigorous way: let's think about all the positive integers, and imagine joining every pair with a line. Every pair of positive integers is joined by a line. Let us denote the emerging graph as K ∞ . Now we color each line either red or green. The infinite Ramsey Theorem States that: no matter how we two-color the edges in K ∞ , it will always be possible to find infinitely many points that are all connected by the same color. The finite Ramsey theorem states that there exists R(m) which is the smallest n such that, for all bi-colorings of K n , there is a homogeneous set of size m. In its graph-theory form Ramsey's theorem, states that there exist monochromatic cliques in any edge labelling (with colors) of a sufficiently large complete graph [7,8,9,10,11]. A clique in graph theory is a subset of vertices of a graph (undirected) such that every two distinct vertices in the clique are adjacent; that is, its induced subgraph is complete
In the graph theory a complete graph is a simple undirected graph in which every pair of different vertices is connected by a unique edge [7,8,9,10,11]. Complete graphs emerge in a various fields of economic science, physics and engineering. For example, cyclic molecules may be seen as a system of particles interconnected with springs of various kinds [12]. Sets of thermodynamic states form complete graphs [13]. Interacting particles/dipoles may be seen as complete graphs [14]. Ramsey theory was successfully applied for the theory of communication and decision making [15]. Thus, numerous applications of the Ramsey theory are foreseen.
The present paper is devoted to quantitative characterization of bi-colored Ramsey graphs. We propose to carry out this quantification with the Shannon entropy, successfully applied for characterization of Voronoi tessellations [16,17,18,19]. Voronoi tessellation is a partitioning of an infinite plane into regions based on the distance to a specified discrete set of points (called seeds or nuclei) [16,17,18,19]. Voronoi tessellation divides a plane into polygons, known as cells, which surround each point/seed, consisting of the region of the plane nearer to that point than any other. It is noteworthy that the Voronoi tessellation actually was introduced first be Descartes [19]. Shannon Entropy, as applied to Voronoi tessellations may be seen as a measure of “ordering” in a given tessellation [17,18,19,20,21,22]. For any given set of points corresponding to the Voronoi tessellation diagram, the Shannon Entropy (also known as the Shannon Measure of Information), denoted S, is defined by Equation 1:
S = − ∑ n P n l n P n ,
where P n is the fraction of polygons with n sides or edges in a given Voronoi tessellation [16,17,18,19,20,21,22]. We demonstrate how the Shannon Entropy may be introduced for Ramsey bi-colored complete graphs [23,24].

2. Shannon Entropy of Ramsey graphs

2.1. Shannon Entropy of Complete Bi-Color Graphs Built of Three Vertices

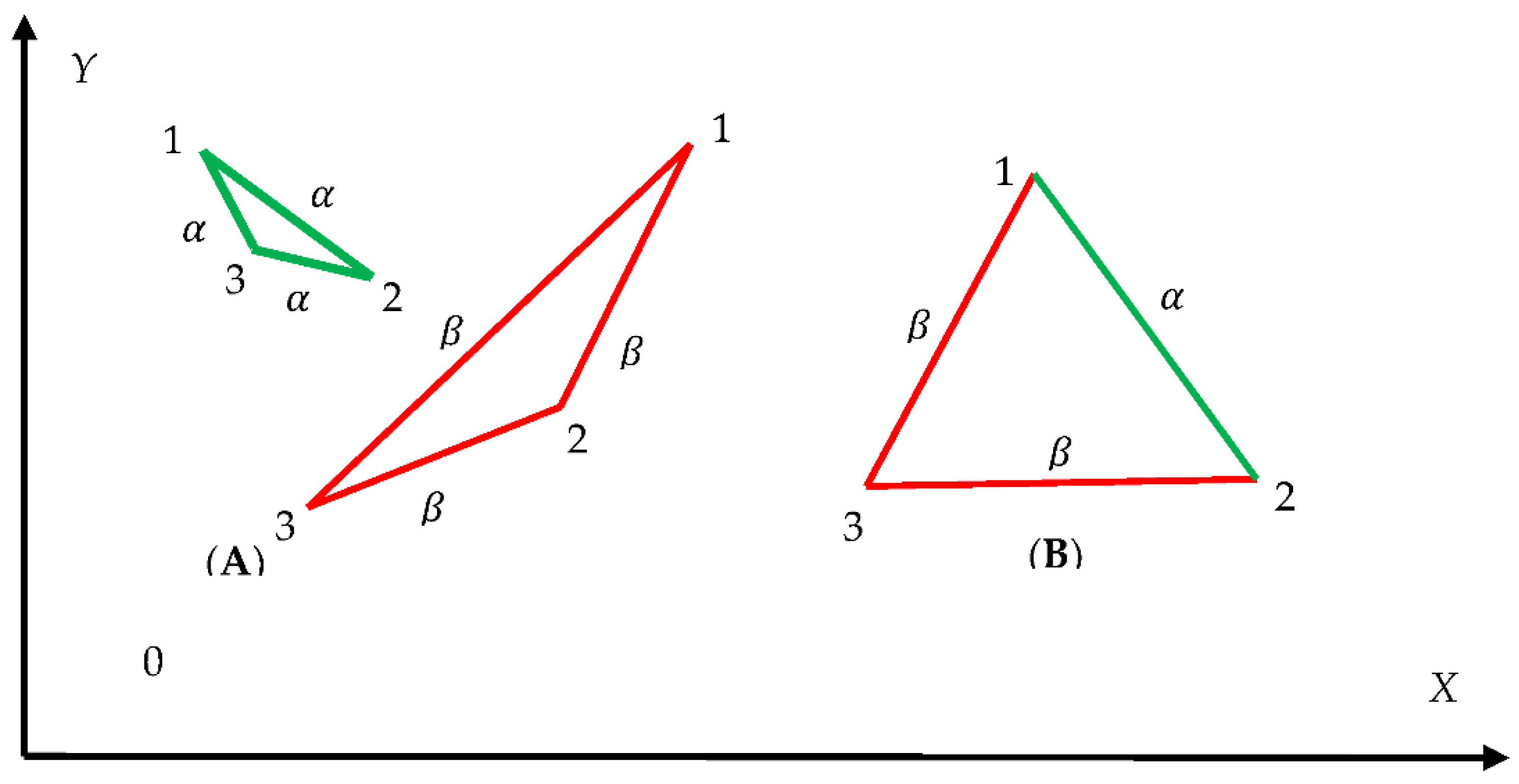
We start from the simplest complete graphs forming triangles depicted in Figure 1. Vertices of the graphs are denoted “123”. Vertices are connected with two kinds of links (edges) labeled α − l i n k s and β − l i n k s ; α − l i n k s are colored with green and β − l i n k s are colored with red (see Figure 1). Thus, complete, bi-colored or mono-colored graphs, addressed by the Ramsey theory emerge. Two situations are possible, the graphs are built of edges of the same kind as depicted in inset A of Figure 1, and graphs built of the edges of different kinds as shown in inset B of Figure 2.
Let us introduce the Shannon entropies of the graphs according to Eq. 2:
S α = − ∑ n P n α l n P n a , n ≥ 3
S β = − ∑ i P i β l n P i β ,   i ≥ 3
where P n α is the fraction of monochromatic α -colored polygons with n α-sides or edges (green edges), and P i β is the fraction of monochromatic β − c o l o r e d polygons with i  β -sides or edges (red edges) in a given complete graph. Sampling of polygons is carried out separately from the green and red subsets of convex polygons. Thus, a pair of Shannon entropies S α , S β corresponds to any complete bi- or mono-colored complete graph. Let us illustrate this idea with the simplest triangle complete graphs, presented in Figure 1. We start from the green monochromatic triangle shown in inset A of Figure 1. For this graph, we derive: P 3 α = 1 , P n α = 0 f o r n ≠ 3 ; P i β = 0 f o r a n y i ≥ 3 . Thus, according to Eq. 1, the both of the Shannon entropies S α and S β equal zero. Now we introduce the following notation: S α = 0 , S β = 0 ~ . This notation enables distinguishing between zero Shannon entropies emerging from the situations when P n = 0 and P n = 1 appearing in Eq. 1, namely S = 0 , w h e n P n = 1 for a given n>3, and S = 0 ~ , w h e n P n = 0 for any n > 3 . This distinguishing is useful for separating between various mathematical/physical cases, illustrated with Figure 1, arising from essentially different coloring of the graph [23]. Thus, for the green monochromatic triangles shown in insert A of Figure 1, we derive:
S α , S β = 0 , 0 ~
In turn, for the red monochromatic triangles, depicted in Figure 1 we obtain:
S α , S β = 0 ~ , 0
Graph depicted in inset B of Figure 1 demonstrate the bi-chromatic triangle. In this graph P n α = 0   f o r a n y   n ≥ 3 , P i β = 0   f o r a n y   i ≥ 3 . Thus, according to the introduced notation, the Shannon entropy corresponding to this graph is given by Eq. 5.
S α , S β = 0 ~ , 0 ~
Thus, the suggested notation enables exact quantification of various graphs, shown in Figure 1. Moreover, the introduced notation will enable elegant re-shaping of the Ramsey theory in the terms, at will be demonstrated below.

2.2. Shannon Entropy of Complete Bi-Color Graphs Built of Four and Five Vertices

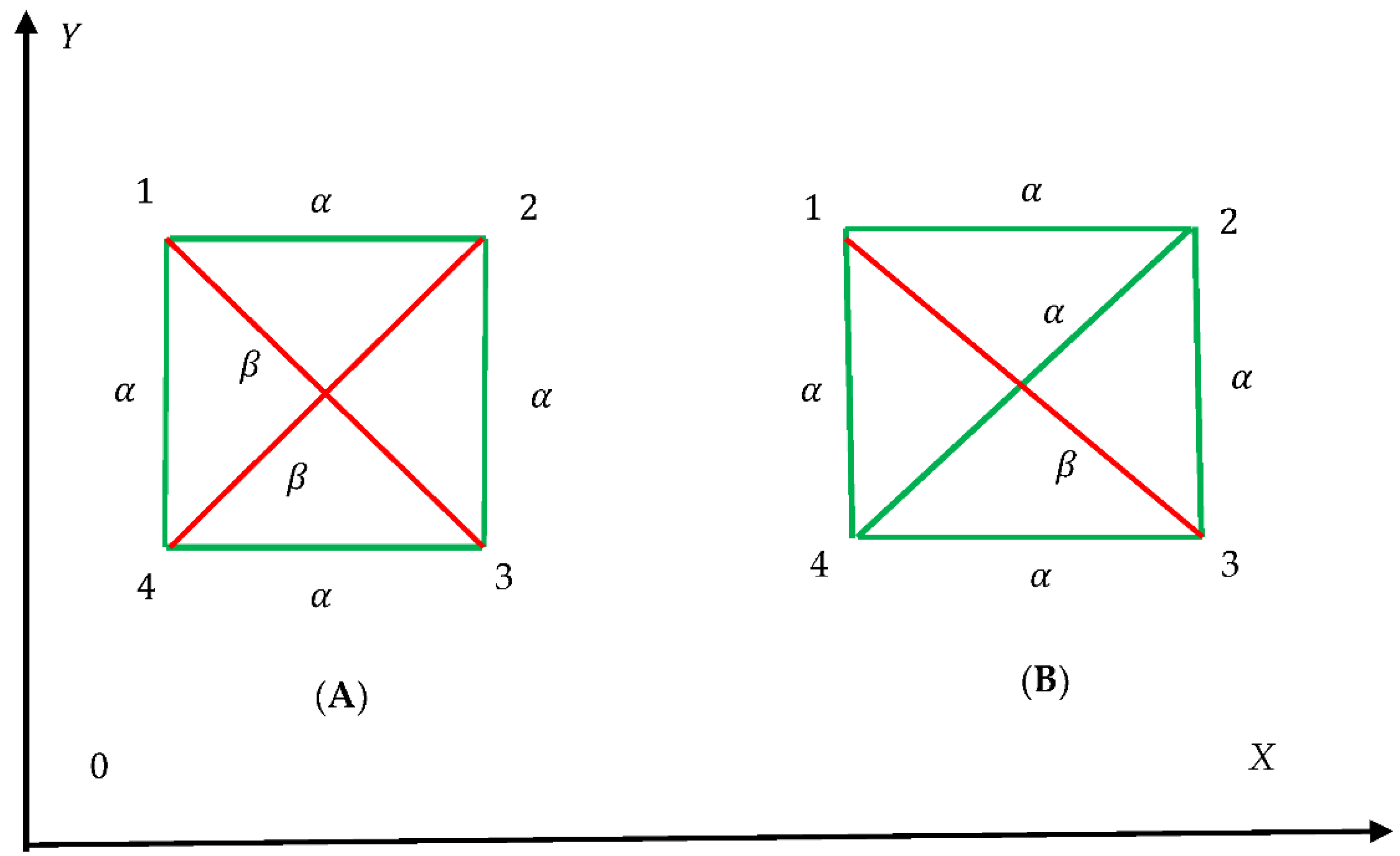
Now consider the complete bi-color graph, built of four vertices and six edges, depicted in inset A of Figure 2. Again α − l i n k s (green) and β – links (red) are present in the graph. We recognize the single monochromatic green quadrangle in the graph. Thus, P 4 α = 1 , P n α = 0 , n ≠ 4 . Thus, we calculate with Eq. 2a: S α = 0 . There is no monochromatic red polygon in inset A of Figure 2, hence S β = 0 ~ . Finally, the pair of Shannon entropies of the complete bicolor graph, shown in inset A of Figure 2 is given by: S α , S β = 0 , 0 ~ . Now we address the complete bi-color graph, depicted in inset B of Figure 2. We recognize one monochromatic, green quadrangle “1234” and two monochromatic green triangles “124” and ”234”. No monochromatic red polygons are recognized. Thus, we calculate: P 4 α = 1 3 , P 3 a = 2 3 . According to Eq. 2a we obtain: S α = − 1 3 l n 1 3 + 2 3 l n 2 3 = 0.64 . Obviously S β = 0 ~ takes place for this graph. Finally, the Shannon entropies for the graph shown in inset B of Figure 2 are given by: S α , S β = 0.64 , 0 ~ . What is the meaning of the calculated values? We keep the interpretation of the Shannon entropy, suggested in ref. 23. According to this interpretation S α is an average uncertainty to find the green α − polygon in the given graph, S β is, in turn, an average uncertainty to find the red β − polygon in the same graph.
The total Shannon Entropy of the given bi-colored complete graph may be introduced with Eq. 6, exploiting Eq. 2a and Eq. 2b.
S t o t = S α + S β = − ∑ n P n α l n P n a − ∑ m P m β l n P m β
Again, sampling of polygons is carried out separately from the green and red subsets of convex polygons. The total Shannon Entropy of the graph depicted in inset A of Figure 2 is zero; whereas, the total entropy of the graph shown in inset B of Figure 2 is S t o t = 0.64 . What is the meaning of these values? An average uncertainty to find the mono-colored polygon (of any color) in inset A is zero; whereas, an average uncertainty to find the mono-colored polygon (of any color) in inset B equals 0.64. In other words S t o t quantifies the average unlikelihood, or unexpectedness to find the mono-colored polygon in the given graph [23]. S t o t also may be referred as a measure of the amount of information contained in the given bi-colored graph, associated with a given probability distribution of finding mono-colored polygons within a given graph, when sampling of polygons is performed separately from the green and red subsets of polygons [23]. It was demonstrated that the Shannon entropy S t o t is a measure of information associated with the entire distributions of monochromatic polygons, not with the individual probabilities [23].
Two peculiarities of the Shannon Entropy defined for the Ramsey graphs with Eqs. 2a-2b and Eq. 6 are noteworthy:
i)
The Shannon Entropies are insensitive to the exact shapes of the graphs, as illustrated in Figure 3. The graphs depicted in insets (A) a (B) of Figure 2 are quantified with the same values of the Shannon Entropies introduced with Eqs. 2a-2b and Eq. 6. Only the polygon types distribution influences the values of the Shannon entropies.
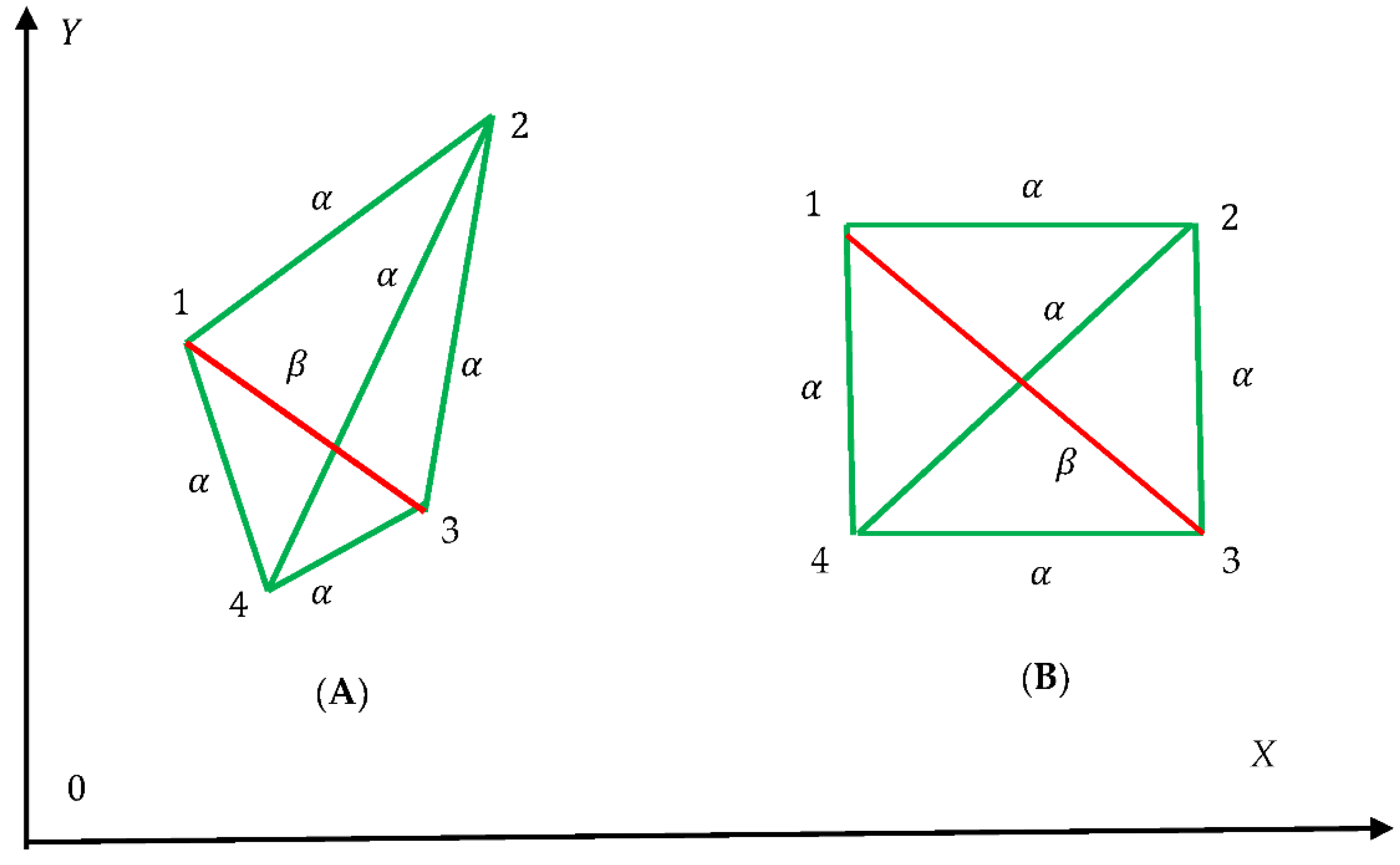
ii)
Consider now the patterns built of N bicolored graphs, presented in Figure 3. The entire Shannon Entropy of the patterns will be equal to that of the single graph, namely S t o t = 0.64 , and is independent on the number of the elementary cells/Ramsey graphs. Thus, the Shannon Entropy is the intensive property of the pattern in contrast to the well-known Boltzmann entropy.
It will be also instructive to calculate the Shannon Entropy of the mono-colored complete graph built of four vertices such as those depicted in Figure 2 and Figure 3. Consider complete graph built of four vertices forming a convex quadrangle, connected with green links only. The complete graph in this case comprise for triangles and one quadrangle. Thus, the Shannon energy is calculated with Eq. 2a as S α = − 1 5 l n 1 5 + 4 5 l n 4 5 = 0.496 . Finally, the Shannon entropies mono-colored complete graph, forming a convex quadrangle is given by: S α , S β = 0.496 , 0 ~ , S t o t = 0.496 . The minimal possible Shannon Entropy quantifying graphs built of four vertices corresponds to the graph, depicted in inset A of Figure 2 , S α , S β = 0 , 0 ~ , S t o t = 0 .
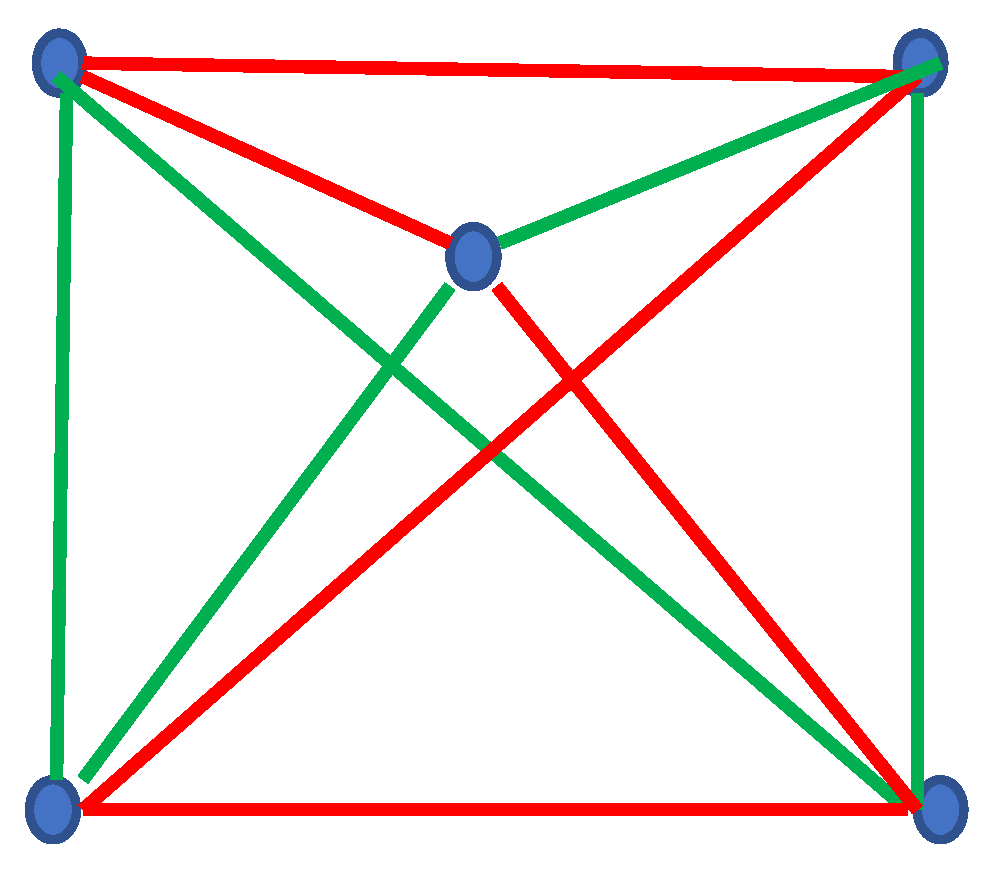
Now consider the Shannon Entropy of the complete bi-colored graph built of five vertices depicted in Figure 4. This graph does not contain any mono-colored triangle or polygon. And this is possible according to the Ramsey Theorem, indeed, the Ramsey number R 3,3 = 6 . Thus, the Shannon Entropies of this graph are zero; according to the introduced notation: S α , S β = 0 ~ , 0 ~ , S t o t = 0 .

2.3. Shannon Entropy of Complete Bi-Color Graphs Built of Four and Five Vertices

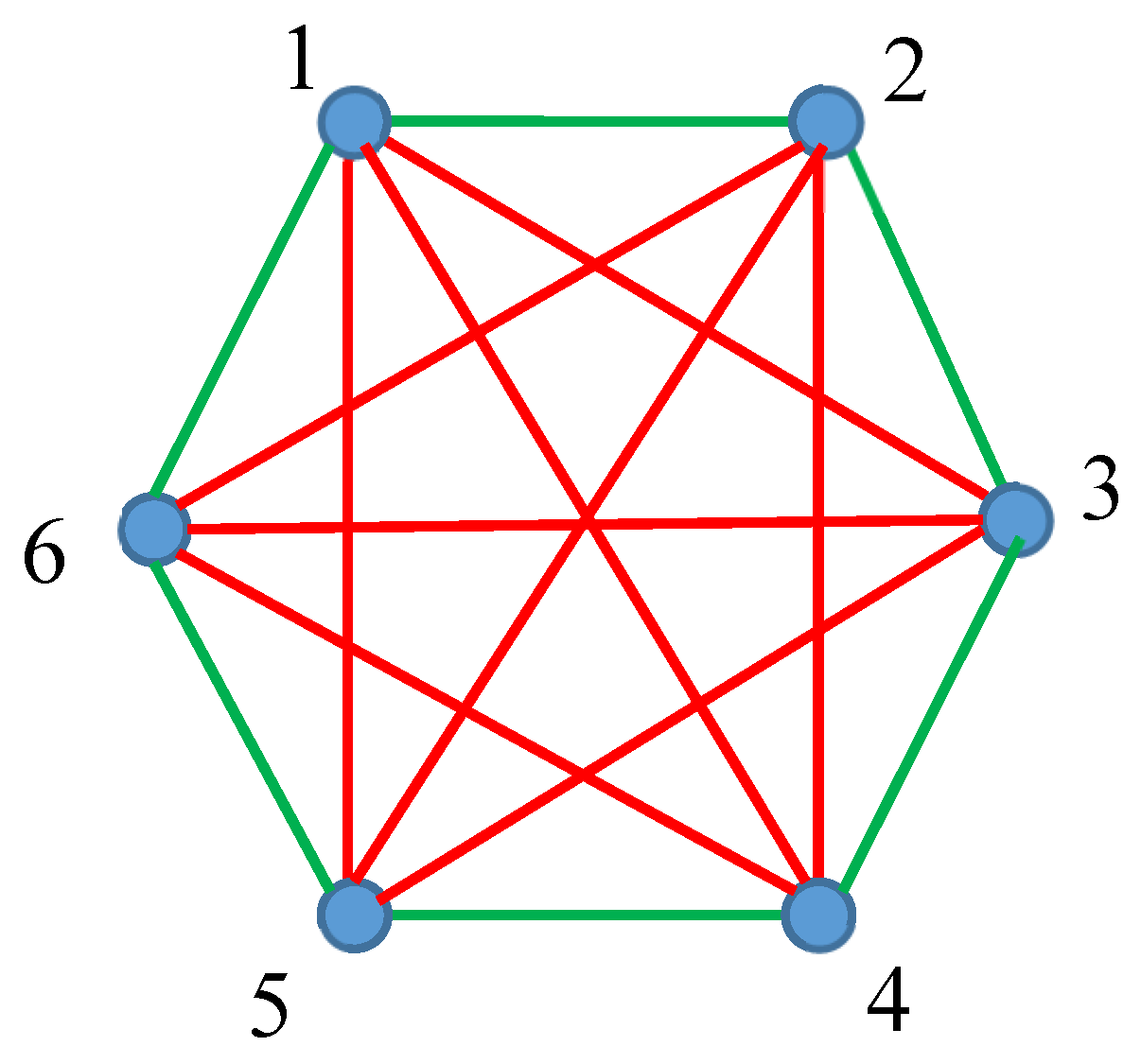
Consider the complete bi-colored graph built of six vertices depicted in Figure 5. One green α -hexagon and two red β triangles (namely “135” and “246” red triangles are recognized in the graph. Thus, the pair of Shannon Entropies of the graph is given by S α , S β = 0,0 . In other words the average uncertainties to find green or red polygons within the graph, shown in Figure 5 are zero.
The introduced Shannon Entropy of the complete bi-colored graphs enables re-shaping of the Ramsey Theorem for the graphs built of six vertices. The Ramsey number R 3,3 = 6 , this means at least one monochromatic triangle will be inevitably present in any bicolored graph built of six vertices. In other words, the complete bi-colored graph, built of six vertices, for which S α , S β = 0 ~ , 0 ~ takes place does not exist. The total Shannon Entropy of the graph calculated with Eq. 6 is zero. Thus, we come to the re-shaping of the Ramsey theorem in the terms of the Shannon Entropy.
Theorem:
Consider a complete bi-colored graph built of six vertices. The graph is built of two kinds of links, labeled correspondingly the α- and β-links. The Shannon Entropies of the graphs are defined according to S α = − ∑ n P n α l n P n a , n ≥ 3 ; S β = − ∑ i P i β l n P i β , i ≥ 3 , where P n α is the fraction of monochromatic α -colored polygons with n α-sides or edges, and P i β is the fraction of monochromatic β − c o l o r e d polygons with i  β -sides or edges. Assume: S α = 0 for the graphs for which, P n α = 1 is true for a given n > 3 , and S α = 0 ~ for the graphs for which P n α = 0 for any n > 3 takes place. Correspondingly, S β = 0 , for the graphs for which, P i β = 1 is true for a given i > 3 , and S β = 0 ~ for the graphs for which P i β = 0 for any i > 3 is assumed. No bi-coloring of the graph exists for which S α , S β = 0 ~ , 0 ~ is true.
Now we demonstrate one more, alternative possibility to introduce the total Shannon Entropy of the bi-colored Ramsey complete graph, labeled S ^ and introduced with Eq. 7:
S ^ = − ∑ k P k l n P k , k ≥ 3
where P k is the fraction of monochromatic polygons (whatever red or green ones) in the given complete graph. Now sampling takes place over the entire set of monochromatic polygons, whatever are their colors. Let us calculate S ^ for the graph depicted in Figure 5. This graph comprises three monochromatic polygons, namely two red triangles and one green hexagon. Thus, S ^ for this graph is calculated as follows: S ^ = − 1 3 l n 1 3 + 2 3 l n 2 3 = 0.64 . What is the meaning of S ^ ?   S ^ is adequately interpreted as the average uncertainty to find the monochromatic polygon (whatever its color) within the given complete bi-colored graph. Consider the graphs shown in Figure 1, Figure 2 and Figure 3. S ^ = 0 for all of the graphs, shown in Figure 1. We recognize a single green quadrangle for the graph shown in inset A of Figure 2; thus, in this case S ^ = 0 . For the graph, shown in inset B of Figure 2 we calculate: S ^ = − 1 3 l n 1 3 + 2 3 l n 2 3 = 0.64 . The total Shannon Entropy introduced with Eq. 7 is also insensitive to the shapes of the graphs. S ^ = 0.64 for both of graphs, depicted in Figure 3. S ^ = 0 for the graph presented in Figure 4, indeed, no monochromatic polygon is recognized in the graph.

3. Discussion

The paper presents the synthesis of three mathematical ideas, namely: Ramsey graphs, Voronoi tessellations and the Shannon Measure of information. We demonstrate the Shannon Entropy may be introduced for the bi-colored graphs in a way similar to that in which it is defined for the Voronoi diagrams. For p-colored graphs a set Shannon Entropies S 1 , S 2 … S r … S p , should be introduced where S r is given by:
S r = − ∑ n P n r l n P n r , n ≥ 3 ; 1 ≤ r ≤ p
   ,
where P n r is the fraction of monochromatic r-colored polygons with n edges. Thus, the matrix of probabilities P n r emerges. Obviously 0 ≤ P n r ≤ 1 , n ≥ 3 ; 1 ≤ r ≤ p is true.
Graphs depicted in Figure 1, Figure 2 and Figure 3 are embedded into XOZ coordinate frames. In our recent paper we suggested coloring of the graphs dependent on the orientation of the coordinate axes [25]. Thus, the introduced Shannon Entropies will be also dependent of the orientation of the coordinate axes. We plan to study this dependence in our future investigations.
Let us discuss the physical/chemical meaning of the introduced Shannon Entropies S α , S β . The complete bi-colored graph, presented in Figure 5, may be interpreted as a scheme of a cyclic molecule, in which two kinds of chemical bonds depicted with green ( α ) links and red β links/edges are present [12]. In this case, the Shannon Entropies S α , S β are seen as an averaged uncertainties to find α or β cyclic sub-structures within the molecule. The presence of cyclic structures will influence the vibrational spectrum of the molecule [12].
Another physical interpretation of the graph, shown in Figure 5, emerges, when the vertices of the graph are treated as interacting particles. In this case α-links may correspond to the attraction between the particles, and β-links may correspond, in turn, to repulsion between interacting entities (for example, electric or magnetic dipoles) [14]. In this situation, the Shannon Entropies S α , S β are interpreted as an averaged uncertainties to find α or β sub-structures, in which the entities interact only by attraction or repulsive forces within an entire set of particles. This reasoning may be important for predicting of the elementary cell of crystals built of electric or magnetic dipoles [14].
We do not suggest the algorithm enabling the calculation of the introduced Shannon Entropies S α , S β for a given Ramsey graph, and this fact stipulates weakness of proposed approach. The algorithmic calculation of Ramsey Numbers also remains the unsolved problem, in spite of the progress in this field reported recently [26,27].

4. Conclusions

We conclude that the Shannon Entropy/Measure of Information may be successfully introduced for the Ramsey complete bi-colored graphs. We addressed the complete bi-colored graphs. Shannon-entropy is introduced according to the classical Shannon formula considering the fractions of monochromatic convex α -colored polygons with n α-sides or edges, and the fraction of monochromatic β − c o l o r e d convex polygons with m β-sides in the given complete graph. The introduced Shannon Entropies S α   and S β are interpreted as follows, S α is seen as an average uncertainty to find the green α − polygon in subset of α   polygons of the given graph, S β is, in turn, an average uncertainty to find the red β − polygon in the subset of β-polygons of the same graph. Sampling of polygons is carried out separately from the green (α) and red (β) subsets of convex polygons. The introduced Shannon Entropies resemble the Shannon Entropy of Voronoi diagrams, in which the fractions of n-sided polygons in a given Voronoi tessellation yield the Shannon Entropy of the entire diagram. Introduced Shannon Entropy is insensitive to the exact shape of the graph, being sensitive to the distribution of monochromatic polygons in a given graph. Re-shaping of the Ramsey Theorem in terms of the Shannon Entropy is presented. The alternative ways of defining of the total Shannon Entropy of bi-colored graphs are suggested. The generalization of the suggested approach for multi-colored complete graphs is introduced.
The complete bi-colored graphs, may be interpreted as schemes of a cyclic molecules, in which two kinds of chemical bonds are present. In this case, the introduced Shannon Entropies S α , S β are seen as an averaged uncertainties to find α or β cyclic sub-structures within the molecule. Another interpretation of the complete bi-colored graphs emerges, when the vertices of the graph are treated as interacting physical entities. In this case, α-links may correspond to the attraction between the particles, and β-links may correspond, in turn, to repulsion between the interacting entities (electric or magnetic dipoles). Thus, the Shannon Entropies S α , S β are interpreted as an averaged uncertainties to find α or β sub-structures, in which the aforementioned entities interact only by attraction or repulsion within an entire set of particles.

Author Contributions

Conceptualization, M.F., S.S. and E.B..; methodology, M.F., S.S. and E.B; formal analysis, M.F., S.S. and E.B; investigation, M.F., S.S. and E.B; writing—original draft preparation, E.B.; writing—review and editing, M.F., S.S. and E.B.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data are contained within the article.

Acknowledgments

The authors are thankful to Professor Nir Shvalb for extremely useful discussions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chartrand, G.; Zhang, P. New directions in Ramsey theory. Discrete Math. Lett. 2021, 6, 84–96. [Google Scholar]
  2. Ramsey, F. P. On a Problem of Formal Logic. In Classic Papers in Combinatorics. Modern Birkhäuser Classics; Gessel, I., Rota, GC., Eds.; Birkhäuser Boston: Boston, USA, 2009; pp. 264–286. [Google Scholar] [CrossRef]
  3. Ali, A.; Chartrand, G.; Zhang, P. Irregularity in Graphs, Springer Briefs in Mathematic, Springer Nature, Cham, Switzerland AG 2021.
  4. Gerencsér, L.; Gyárfás, A. On Ramsey-type problems, Ann. Univ. Sci. Budapest. Eötvös Sect. Math 1967, 10, 167–170. [Google Scholar]
  5. Erdős, P. , Gyárfás, A. A variant of the classical Ramsey problem. Combinatorica. 1997, 17, 459–467. [Google Scholar] [CrossRef]
  6. P Erdős: Solved and unsolved problems in combinatorics and combinatorial number theory,Congressus Numerantium, 1981, 32, 49–62.
  7. Katz, M.; Reimann, J. An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2018; Volume 87, pp. 1–34. [Google Scholar]
  8. Graham, R. L.; Spencer, J. H. Ramsey Theory. Sci. Am. 1990, 7, 112–117. [Google Scholar] [CrossRef]
  9. Graham, R.; Butler, S. Rudiments of Ramsey Theory (2nd ed.). American Mathematical Society: Providence, Rhode Island, USA, 2015; pp. 7–46.
  10. Graph Theory and Applications, Proceedings of the Conference at Western Michigan University, May 10 - 13, 1972, in the series Lecture Notes in Mathematics, eds. Alavi, V; Lick, D. R.; White, A. T. Springer, Berlin, Ge., 1972.
  11. Graham, R.L.; Rothschild, B. L.; Spencer, J. H. Ramsey theory, 2nd ed.; Wiley-Interscience Series in Discrete Mathematics and Optimization; John Wiley & Sons, Inc. A Wiley-Interscience Publication: New York, USA, 1990; pp. 10–110. [Google Scholar]
  12. Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds, Dynamics 2023, 3, 272-281. [CrossRef]
  13. Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Ramsey theory and thermodynamics. Heliyon 2023, 9, e13561. [Google Scholar] [CrossRef] [PubMed]
  14. Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Universe as a Graph (Ramsey Approach to Analysis of Physical Systems). World J. Phys. 2023, 1, 1–24. [Google Scholar] [CrossRef]
  15. Roberts, F.S. Applications of Ramsey theory. Discret. Appl. Math. 1984, 9, 251–261. [Google Scholar] [CrossRef]
  16. Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Re-cherches sur les paralléloèdres primitifs. J. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
  17. Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
  18. Weaire, D.; Rivier, N. Soap, cells and statistics—Random patterns in two dimensions. Contemp. Phys. 1984, 25, 59–99. [Google Scholar] [CrossRef]
  19. Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.A.; Aktaev, N.E.; Dombrovsky, L.A.; Nosonovsky, M. Characterization of self-assembled 2D patterns with Voronoi Entropy. Entropy 2018, 20, 956. [Google Scholar] [CrossRef]
  20. Ljaz, A.; Topcu, G.; Miko, A.; Demirel, A. L. Synergistic control of breath figures on Styrene-Butadiene-Styrene films by poly-2-ethyl-2-oxazoline capped CaCl2 loaded mesoporous silica particles, Colloids & Surfaces A, 2023, 672, 131740.
  21. Zhong, T,; Meng, J. ; Andrews, M. P. Insights into Permanent Encodings of Macroscopic Spike Patterns by Magnetic-Field-Directed Evaporative Self-Assembly from Ferrofluids, Langmuir. 2023, 39, 8186–8195. [CrossRef]
  22. Bormashenko, Ed.; Legchenkova, I.; Frenkel, M.; Shvalb, N. ; Voronoi Tessellations and the Shannon Entropy of the Pentagonal Tilings, Entropy 2023, 25, 92.
  23. Ben-Naim, A. Entropy, Shannon’s Measure of Information and Boltzmann’s H-Theorem, Entropy 2017, 19(2), 48.
  24. Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Chicago, IL, USA, 1949. [Google Scholar]
  25. Frenkel, M,; Shoval, Sh.; Bormashenko, Ed. Ramsey Theory and Transformations of Coordinate Systems,Preprints, 2023. [CrossRef]
  26. Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332. [Google Scholar] [CrossRef]
  27. Radziszowski, S. Small Ramsey numbers, The Electronic Journal of Combinatorics, 2021, 1000, MR1670625.
Preprints 80388 g001
Figure 1. Simplest mono-colored and bi-colored graphs built of three vertices and three edges are depicted. A- monochromatic triangles built of the green α − links, and red β -links are shown. B. Bi-color graph is depicted.
Figure 1. Simplest mono-colored and bi-colored graphs built of three vertices and three edges are depicted. A- monochromatic triangles built of the green α − links, and red β -links are shown. B. Bi-color graph is depicted.
Preprints 80388 g001
Preprints 80388 g002
Figure 2. Complete bi-colored graphs, built of four vertices and six edges are depicted. α links are depicted in green; β links are shown in red. A. The single green quadrangle is recognized. S t o t = 0 B. One monochromatic, green quadrangle “1234” and two monochromatic green triangles “124” and ”234” are recognized. S t o t = 0.64 .
Figure 2. Complete bi-colored graphs, built of four vertices and six edges are depicted. α links are depicted in green; β links are shown in red. A. The single green quadrangle is recognized. S t o t = 0 B. One monochromatic, green quadrangle “1234” and two monochromatic green triangles “124” and ”234” are recognized. S t o t = 0.64 .
Preprints 80388 g002
Preprints 80388 g003
Figure 3. Insensitivity of the Ramsey bi-colored complete graphs to their shapes is demonstrated. Graphs depicted in insets (A) a (B) are characterized by the same values of the Shannon Entropies introduced with Eqs. 2a-2b and Eq. 6. Only the polygon types distribution impacts the values of the Shannon entropies. S t o t = 0.64 for both graphs.
Figure 3. Insensitivity of the Ramsey bi-colored complete graphs to their shapes is demonstrated. Graphs depicted in insets (A) a (B) are characterized by the same values of the Shannon Entropies introduced with Eqs. 2a-2b and Eq. 6. Only the polygon types distribution impacts the values of the Shannon entropies. S t o t = 0.64 for both graphs.
Preprints 80388 g003
Preprints 80388 g004
Figure 4. Complete bi-colored graph built of five vertices is shown. No monochromatic triangle or polygons are recognized in the graph. The Shannon Entropies of this graph are zero, according to the introduced notation: S α , S β = 0 ~ , 0 ~ , S t o t = 0 .
Figure 4. Complete bi-colored graph built of five vertices is shown. No monochromatic triangle or polygons are recognized in the graph. The Shannon Entropies of this graph are zero, according to the introduced notation: S α , S β = 0 ~ , 0 ~ , S t o t = 0 .
Preprints 80388 g004
Preprints 80388 g005
Figure 5. Complete Ramsey bi-colored graph built of six vertices is shown. One green hexagon and two red triangles (“135 and “246”) are recognized in the graph. S α , S β = 0,0 is true for the graph.
Figure 5. Complete Ramsey bi-colored graph built of six vertices is shown. One green hexagon and two red triangles (“135 and “246”) are recognized in the graph. S α , S β = 0,0 is true for the graph.
Preprints 80388 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

129

Views

30

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated