Nonlinear thermal transport of non-Newtonian polymer flows is an increasingly important area in materials engineering. Motivated by new developments in this area which entail more re-fined and mathematical frameworks, the present analysis investigates the boundary layer ap-proximation and heat transfer persuaded by a symmetrical cylindrical surface positioned hori-zontally. To simulate thermal relaxation impacts the bioconvection cross nanofluid flow Buongiorno model is deployed. The impact of the magnetic field applied on the nanofluid using the heat generation and melting phenomena are inspected. The nonlinear effect of thermosolutal buoyant forces is incorporated into the proposed model. The novel mathematical equations comprise thermophoresis and Brownian diffusion effects. Via robust transformation techniques, the primitive resulting partial equations for momentum, energy, concentration, and motile living microorganism are rendered into nonlinear ordinary equations with convective boundary postulates. An explicit and efficient numerical solver procedure in Mathematica 11.0 programming platform is developed to engage the nonlinear equations. The consequence of multiple governing parameters on dimensionless fluid profiles is inspected through plotted visuals and tables. Finally, outcomes declared on the surface drag force, heat, and mass transfer coefficients are exhibited through 3D visuals via different influential parameters.

Keywords:

Subject: Physical Sciences - Fluids and Plasmas Physics

1. Introduction

Several researchers have conducted investigations on the thermophysical importance of nanoparticles. Nanofluids are formed by mixing nanomaterials and a base liquid, where the suspensions consist of various metals or nonmetals such as aluminum, copper, silver, graphite, and base liquids which include water, glycerol, and ethylene glycol. Nanofluids play an important role in various processes such as polymer, wire coating, and biomedical processes. These applications include heat transportation, nuclear reactors, and electronic devices, as well as medical applications such as the diagnosis and treatment of several diseases. Ferrofluids, which are a special type of magnetized fluid, have significant applications in various engineering processes such as micro-fluid pumps, ferrofluid lubrication of bearings, lithographic design, electromechanical and chemical devices, electrical engines, medicine, and magnet therapy for treating migraines and arthritis, among others [1,2,3,4,5].

Buongiorno nanofluid model [6] describes two unusual processes to enhance the rate of heat transfer. Venkatadri et al. [7] examined the melting heat exchange between an electrically conductive flow of nanofluid across an exponentially expanding permeable channel with Cattaneo-Christov heat flux in the presence of an external magnetic field.

Mondal et al. [8] explored the effects of MHD flow and heat exchange on the flow of stagnation point nanofluids over an extended surface with chemical reaction and thermal radiation effect. Ying et al. [9] explored the radiative heat transfers of molten salt-based nanofluids over cooling coils with non-uniform heat flow. Zainal et al. [10] monitored the MHD hybrid nanofluid stream to a porous expanding/shrinking channel with the emergence of quadratic momentum. Eid et al. [11] studied the variable thermal conductivity effect and heat transfer phenomena on an MHD flow nanofluid across a porous channel with velocity slip. Many researchers have used the Buongiorno model to study nanofluids, as evidenced by references [12,13,14,15,16,17,18,19]. Kamal et al. [20] conducted an analytical investigation of a viscoelastic nanofluid with a twofold diffusion problem resulting from the stagnation point flow induced by heat transfer in a space environment. Anuar et al. [21] investigated the numerical outcome of the stagnation point flow of radiative Maxwell nanofluids and heat transfer analysis over a nonlinear stretching channel with a hybrid nanofluid. Rizwana et al. [22] examined the slip effects on radiative oblique stagnation point nanofluid with convective heat transfer effect in the presence of the inclined magnetic field. In their research, Giri et al. [23] investigated the nanoparticle diameter effect and interfacial layer on MHD flow nanofluid and melting flow of heat inside the rotating plates channel positioned horizontally. Meanwhile, Sharma et al. [24] studied the impact of varying thickness and melting on heat exchange in MHD nanofluids through the slender elongated surface. Bioconvection is a phenomenon where microorganisms swim upwards in less dense fluids than water, resulting in an increased concentration of microorganisms at the upper layer, leading to breakdowns due to the frailty of the substances. Microorganisms like bacteria or algae use this up-swimming technique for their growth and development. The bioconvection process has various applications in biochemistry and bioengineering, including diesel fuel products, bioreactors, and fuel cell engineering, making it an important field in biomedical engineering. The discovery of the bioconvection phenomenon is attributed to Platt [25], while Kuznetsov [26] is believed to have been the first to use the term "nanofluid bioconvection." Kuznetsov [27] further developed this concept by focusing on the role of gyrotactic motile microorganisms in nanofluids and demonstrating that the large-scale fluid movement generated by these self-propelled microorganisms improves mixing and prevents nanomaterial buildup in nanofluids. In their study, Haq et al. [28] considered the flow properties of the natural bioconvective process of nanofluid flow with living gyrotactic microbes under the influence of a uniform magnetic field and the Arrhenius activation energy effect. Ahmad et al. [29] explored the bioconvection nanofluid flow of gyrotactic motile bacteria with chemical reactions in a porous medium over a stretched surface. Finally, Elanchezhian et al. [30] studied the heat and mass transfer of an Oldroyd-B mixed bioconvection flow of nanofluid by a stratified medium with swimming microorganisms and nanoparticles under the influence of an inclined magnetic field. In a study by Bhatti et al. [31], a theoretical investigation was carried out on living microbes in a blood base nanofluid flow through anisotropically tapered arteries. Khan et al. [32] studied important aspects of activation energy and effective Prandtl number in Jeffrey nanofluid flow with gyrotactic living microorganisms. Shafiq et al. [33] investigated heat and mass flow in second-grade bio-convective flow with buoyancy effect and first-order chemical reaction. Kotnurkar et al. [34] studied the bio-convective peristaltic flow of a nanofluid with microorganisms in the presence of Cu-blood nanoparticles across a permeable channel. Muhammad et al. [35] established the impact of time-dependent bioconvection magnetized Carreau fluid flow under the velocity slip effect in the presence of motile microorganisms. Farooq et al. [36] introduced the effect of thermally radioactive bio-convection flow of Carreau fluid with Cattaneo-Christov heat flux and exponential space-based heat source over a stretching cylinder under the influence of magnetic effect. Hosseinzadeh et al. [37] investigated cross-fluid flow containing living microbes and tiny particles through a 3D stretching cylinder. The heat transfer analysis in non-Newtonian fluids is more prominent in terms of the applications like drug delivery, heat optimization [38,39]. This concept is also more attractive in the case of the nanofluids/hybrid nanofluids to enhance the heat transfer rate of traditional fluids [40,41].

Other important theoretical and experimental studies recently carried out on bio-convection-containing living microorganisms were explored analytically by various researchers and can be viewed in the following citations [42–54].

The studies cite that no survey is yet offered for 2D bio-convectional cross nanofluid with the impact of living motile microbes through cylindrical surface positioned horizontally subject to milting heat rheology and convective boundary conditions. The present analysis aims to introduce an effective mathematical description of the cross-flow of nanofluid through the cylindrical channel. The impact of Brownian diffusion and thermophoresis phenomenon are invoked simultaneously to make more efficient the considered problem. Following are the precise goals of this numerical evaluation have remained undone, and goals are:

To study time subservient 2D bio-convectional cross nanofluid flow resulting from the cylindrical surface with the impression of living microbes, thermal conductivity, and melting phenomenon.
The mathematical model of the nonlinear governing PDEs comprises momentum, temperature gradient, mass balances, and swimming microorganism.
To engage numerical techniques for attaining the computational outcomes. Also, to render a convergence and stability analysis for optimizing flow fields.
To unveil the graphical outlines of diversified emerging parameters on flow fields together with 3D visuals of skin friction, heat transfer, and mass flow coefficients.

2. Flow analysis and mathematical setup

In this mathematical model, we include the influence of thermal conductivity on the viscous 2D bio-convectional flow of a cross nanofluid bounded by a symmetrical cylindrical surface with the melting phenomenon and motile living microbes. Aspects of nonlinear thermal radiation and convective boundary conditions are invoked. The impact of Brownian diffusion and thermophoresis deposition processes are retained in the proposed model. The ambient temperature, nanoparticle volume fraction, and motile micro-organisms are signified as

T_{\infty}^{*}, C_{\infty}^{*}, a n d N_{\infty}^{*}

. The implications of the induced magnetic field and external electric field are ignored due to the small Reynolds number. One can see the physical scenario in Figure 1a.

Under the above conditions, the boundary-layer approximation yields the following governing equations [33,34]:

τ = - p I + μ A_{1}, μ = μ_{\infty} + (μ_{0} + μ_{\infty}) / (1 + {(Γ \bar{γ})}^{n})

(1)

where

A_{1} = g r a d V + {(g r a d V)}^{t}, \bar{γ} = \sqrt{0.5 {(t r A_{1})}^{2}}

Herein,

V

is the velocity, and the shear rate is zero at infinity, accordingly Eq. (1) may rewrite as:

μ = μ_{0} (1 / 1 + {(Γ \bar{γ})}^{n})

(2)

For 2D unsteady flow, the momentum, temperature gradient, concentration balance, and living microbes are:

V = (u^{*}, v^{*}), T^{*} = T^{*} (r^{*}, x^{*}, t^{*}), C^{*} = C^{*} (r^{*}, x^{*}, t^{*})

(3)

Substituting Eq. (3) in Eqs. (1)–(2), one get the resulting equations as [44]:

r^{*} \frac{\partial u^{*}}{\partial x^{*}} + r^{*} \frac{\partial v^{*}}{\partial r^{*}} = 0

(4)

\begin{array}{l} \frac{\partial u^{*}}{\partial t^{*}} + u^{*} \frac{\partial u^{*}}{\partial x^{*}} + v^{*} \frac{\partial u^{*}}{\partial r^{*}} = \frac{\partial U_{e}}{\partial t^{*}} + U_{e} \frac{\partial}{\partial z^{*}} U_{e} + \frac{ν}{r^{*}} \frac{\partial u^{*}}{\partial r^{*}} (\frac{1}{1 + {(Γ \frac{\partial u^{*}}{\partial r^{*}})}^{n}}) + ν \frac{\partial}{\partial t^{*}} (\frac{\frac{\partial u^{*}}{\partial r^{*}}}{1 + {(Γ \frac{\partial u^{*}}{\partial r^{*}})}^{n}}) - \\ \frac{1}{ρ f} σ B^{2} (t^{*}) (u^{*} - U_{e}) + β^{*} g (1 - C_{f}^{*}) (T^{*} - T_{\infty}^{*}) - \frac{g}{ρ_{f}} (ρ_{p} - ρ_{f}) (C^{*} - C_{\infty}^{*}) \\ - \frac{g \bar{\bar{γ}}}{ρ_{f}} (ρ_{m} - ρ_{f}) (N^{*} - N_{\infty}^{*}) \end{array}

(5)

\begin{array}{l} \frac{\partial T^{*}}{\partial t^{*}} + u^{*} (\frac{\partial T^{*}}{\partial x^{*}}) + v^{*} (\frac{\partial T^{*}}{\partial r^{*}}) = \frac{1}{r^{*} {(ρ c)}_{f}} \frac{\partial}{\partial r^{*}} (r^{*} K (T^{*}) \frac{\partial T^{*}}{\partial r^{*}}) + \frac{1}{r^{*} {(ρ c)}_{f}} \frac{\partial}{\partial r^{*}} (α r^{*} \frac{\partial T^{*}}{\partial r^{*}}) + \\ τ (D_{B} \frac{\partial C^{*}}{\partial r^{*}} \frac{\partial T^{*}}{\partial r^{*}} + \frac{D_{T}}{T_{\infty}^{*}} {(\frac{\partial T^{*}}{\partial r^{*}})}^{2}) - \frac{\partial}{\partial r^{*}} (\frac{1}{{(ρ c)}_{f}} \frac{16 σ^{*}}{3 k^{*}} T^{* 3} \frac{\partial T^{*}}{\partial r^{*}}) \end{array}

(6)

K (T^{*}) = (1 + \in \frac{T^{*} - T_{\infty}^{*}}{Δ T^{*}}) k_{\infty}

(7)

\frac{\partial C^{*}}{\partial t^{*}} + u^{*} \frac{\partial C^{*}}{\partial x^{*}} + v^{*} \frac{\partial C^{*}}{\partial r^{*}} = \frac{1}{{(ρ c)}_{f}} \frac{\partial}{\partial r^{*}} [D (T^{*}) \frac{\partial C^{*}}{\partial r^{*}}] + \frac{D_{B}}{r^{*}} \frac{\partial}{\partial r^{*}} [r^{*} \frac{\partial C^{*}}{\partial r^{*}}] + \frac{D_{T^{*}}}{T_{\infty}^{*}} \frac{1}{r^{*}} \frac{\partial}{\partial r^{*}} [r^{*} \frac{\partial T^{*}}{\partial r^{*}}]

(8)

D (C^{*}) = (1 + \in_{1} \frac{C^{*} - C_{\infty}^{*}}{Δ C^{*}}) D_{\infty}

(9)

\frac{\partial N^{*}}{\partial t^{*}} + u^{*} (\frac{\partial N^{*}}{\partial x^{*}}) + v^{*} (\frac{\partial C^{*}}{\partial r^{*}}) = D_{m} (\frac{\partial^{2} N^{*}}{\partial r^{*}^{2}}) - (\frac{b W_{c}}{C_{w}^{*} - C_{\infty}^{*}}) \frac{\partial}{\partial r^{*}} (N^{*} \frac{\partial C^{*}}{\partial r^{*}})

(10)

The corresponding boundary postulates for the proposed problem as given beneath [44]:

\begin{array}{l} u^{*} = u_{w} (x^{*}, t^{*}), v^{*} = 0, - k_{f} \frac{\partial T^{*}}{\partial r^{*}} = h_{f} (T^{*} - T_{w}^{*}), D_{B} \frac{\partial C^{*}}{\partial r^{*}} + \frac{D_{T^{*}}}{T_{\infty}^{*}} \frac{\partial T^{*}}{\partial r^{*}} = 0, N^{*} = N_{w}^{*} a t r^{*} = R \\ u^{*} \to 0, T^{*} \to T_{\infty}^{*}, C^{*} \to C_{\infty}^{*}, N^{*} \to N_{\infty}^{*} a t r^{*} \to \infty \end{array}

(11)

Additionally, the melting heat phenomenon is:

k_{f} \frac{\partial T^{*}}{\partial r^{*}} = ρ_{f} (λ^{*} + {(C_{p})}_{s} (T_{w}^{*} - T_{0}^{*}) u^{*})

(12)

For solving the resulting Eqs. (5)- (11) the dimensionless quantities are implemented as:

\begin{array}{l} ψ = \sqrt{u_{w} ν x^{*}} R u_{0}^{*} (ξ), ξ = \sqrt{\frac{u_{w}}{ν x^{*}}} (\frac{r^{* 2} - R^{2}}{2 R}), g (ξ) = \frac{T^{*} - T_{\infty}^{*}}{T_{w}^{*} - T_{\infty}^{*}}, h (ξ) = \frac{C^{*} - C_{\infty}^{*}}{C_{w}^{*} - C_{\infty}^{*}}, \\ Χ (ξ) = \frac{N^{*} - N_{\infty}^{*}}{N_{w}^{*} - N_{\infty}^{*}} \end{array}

(13)

Thus, the dimensionless forms are achieved as:

\begin{array}{l} (1 + (1 + n) + {(W e u_{0}^{''})}^{n}) (1 + 2 α ξ) u_{0}^{'''} + 2 α u_{0}^{''} ((1 + {(W e u_{0}^{''})}^{n} (1 - \frac{n}{2}))) {(1 + {(W e u_{0}^{''})}^{n})}^{2} \times \\ (Re (u_{0} u_{0}^{''} + u_{0}^{'' 2} + 1)) - A (u_{0}^{'} + \frac{ξ}{2} u_{0} u_{0}^{''}) - M^{2} Re (u_{0}^{'} - 1) + λ (g - N r h - N c Χ) = 0 \end{array}

(14)

\begin{array}{l} \frac{1}{\Pr} (1 + 2 α ξ) (1 + \in g) g^{''} + \in ξ {(g^{''})}^{2} + g^{'} (2 α + u_{0}) - \frac{1}{2} A ξ g^{'} + N b (1 + 2 α ξ) (g^{'} h^{'} + \frac{N t}{N b} g^{'}) + \\ \frac{2}{3 \Pr R} ({(1 + (θ_{w} - 1) g)}^{3} (2 α g^{'} + 2 g^{''} (1 + 2 α ξ)) + 6 {(1 + (θ_{w} - 1) g)}^{2}) \times \\ (θ_{w} - 1) {(g^{''})}^{2} (1 + 2 α ξ) = 0 \end{array}

(15)

(1 + 2 α ξ) (1 + \in_{2} g) h^{'''} + \in_{2} {(h^{'})}^{2} + 2 α h^{'} + \Pr L e (u_{0} h^{'} + \frac{N t}{N b} ((1 + 2 α ξ) g^{''} + 2 α g^{'}) - \frac{1}{2} ξ h^{'}) = 0

(16)

(1 + 2 α ξ) Χ^{''} + (2 α + L b u_{0}) Χ^{'} - P e ((δ_{1} + Χ) h^{''} + h^{'} Χ^{'}) = 0

(17)

The transformed boundary postulates in dimensionless form as:

\begin{array}{l} u_{0}^{'} = 1, g^{'} = - B i (1 - g), h^{'} + (\frac{N t}{N b}) g^{'} = 0, Χ = 1 a t ξ = 0 \\ u_{0}^{'} = 0, g = 0, h = 0, Χ = 1 a t ξ = \infty \end{array}

(18)

where,

\begin{array}{l} α = \frac{1}{R} \sqrt{\frac{ν l}{U_{0}}}; M = \frac{σ B_{0}^{2}}{ρ C_{p}}; A = \frac{c}{a}; N r = \frac{(ρ_{p} - ρ_{f}) (C_{w}^{*} - C_{\infty}^{*})}{β^{*} (1 - C_{\infty}^{*}) (T_{w}^{*} - T_{\infty}^{*})}; N c = (\frac{ρ_{m} - ρ_{f}}{β}) \frac{(N_{w}^{*} - N_{\infty}^{*})}{(T_{w}^{*} - T_{\infty}^{*}) (1 - C_{\infty}^{*})} γ^{* *}; \\ λ = \frac{g ν (1 - C_{\infty}^{*}) (T_{w}^{*} - T_{\infty}^{*}) β^{*}}{u_{w}}; W e = \frac{u_{w} r^{*} Γ^{2} g (1 - C_{\infty}^{*}) (T_{w}^{*} - T_{\infty}^{*}) β^{*}}{{(1 - c t^{*})}^{3} υ}; \Pr = \frac{ν_{f}}{α}; R = \frac{k k^{*}}{4 σ^{*} T_{\infty}^{* 3}}; \\ N b = D_{B} E \frac{(C_{w}^{*} - C_{\infty}^{*})}{α}; N t = D_{T} E \frac{(T_{w}^{*} - T_{\infty}^{*})}{T_{\infty}^{*} α}; θ_{w} = \frac{T_{w}^{*}}{T_{\infty}^{*}}; L e = \frac{α}{D_{B}}; L b = \frac{ν}{D_{m}}; P e = \frac{b W_{c}}{D_{m}}; \\ M a = \frac{c_{p} (T_{w}^{*} - T_{\infty}^{*})}{λ + c_{s} (T_{w}^{*} - T_{0}^{*})}; B i = \frac{h_{f}}{k} \sqrt{\frac{ν_{f}}{a}} \end{array}

are curvature parameter, magnetic parameter, time-dependent parameter, buoyancy parameter, Rayleigh number, convection parameter, Weissenberg number, Prandtl number, radiation parameter, Brownian factor, thermophoretic force, ratio parameter, Lewis number, bio-convection Lewis number, Peclet number, melting heat phenomenon, and Biot number, respectively.

Melting phenomenon in dimensionless form is:

\Pr u_{0} (0) + M a g^{'} (0) = 0

(19)

The skin fraction, heat transfer coefficient, mass flow rate, and living microbe’s gradients are defined as:

C f = \frac{τ_{x^{*} r^{*}}}{ρ_{f} U^{2}}, N u = \frac{x^{*} q_{w}}{k (T_{w}^{*} - T_{\infty}^{*})}, S h = \frac{x^{*} q_{m}}{- D_{B} (C_{w}^{*} - C_{\infty}^{*})}, N h = \frac{x^{*} q_{j}}{- D_{B} (N_{w}^{*} - N_{\infty}^{*})}

(20)

whereas

τ_{x^{*} r^{*}}

elucidates shear stress,

q_{w}

heat flux,

q_{m}

mass flux, and

q_{j}

mass of living microbes are characterized underneath:

{\begin{array}{l} τ_{x^{*} r^{*}} = μ_{0} \frac{\partial u^{*}}{\partial r^{*}} (\frac{1}{1 + {(Γ \frac{\partial u^{*}}{\partial r^{*}})}^{n}}) \\ q_{w} = - k (T^{*}) \frac{\partial T^{*}}{\partial r^{*}} \\ q_{m} = - D_{B} \frac{\partial C^{*}}{\partial r^{*}} \\ q_{j} = - D_{B} \frac{\partial N^{*}}{\partial r^{*}} \end{array}\}}_{r^{*} = R}

(21)

Replacing Eq. (21) in Eq. (20), we get the dimensionless form in Eq. (22):

\begin{array}{l} \sqrt{{Re}_{x}} C f_{x} = u_{0}^{''} (0) (\frac{1}{{(1 + (W e) u_{0}^{''} (0))}^{n}}) \\ \frac{N u_{x}}{\sqrt{{Re}_{x}}} = - g^{'} (0) (1 + \frac{1}{N_{R}} ({(1 + (θ_{w} - 1) g^{'} (0))}^{3})) \\ \frac{S h_{x}}{\sqrt{{Re}_{x}}} = - h^{'} (0) \\ \frac{N h_{x}}{\sqrt{{Re}_{x}}} = - Χ^{'} (0) \end{array}\}

(22)

Here

{Re}_{x} = \frac{x^{*} u_{w}}{ν}

is the local Reynolds number.

1.: Computational procedure.

In this section, the solution of nonlinear differential Eqs. (14)– (17) subject to boundary conditions represented in Eq. (18). The physical system is engaged numerically through a built-in algorithm/shooting technique (RKF-45) via Mathematica 11.0 programming platform. The nonlinear coupled equations are first diminished towards a system of first-order initial value differential equations using suitable transformation variables [38,46]. The entire nonlinear computational framework of the shooting technique is described below in Figure 1.

Figure 1. b) Computational flow chat.

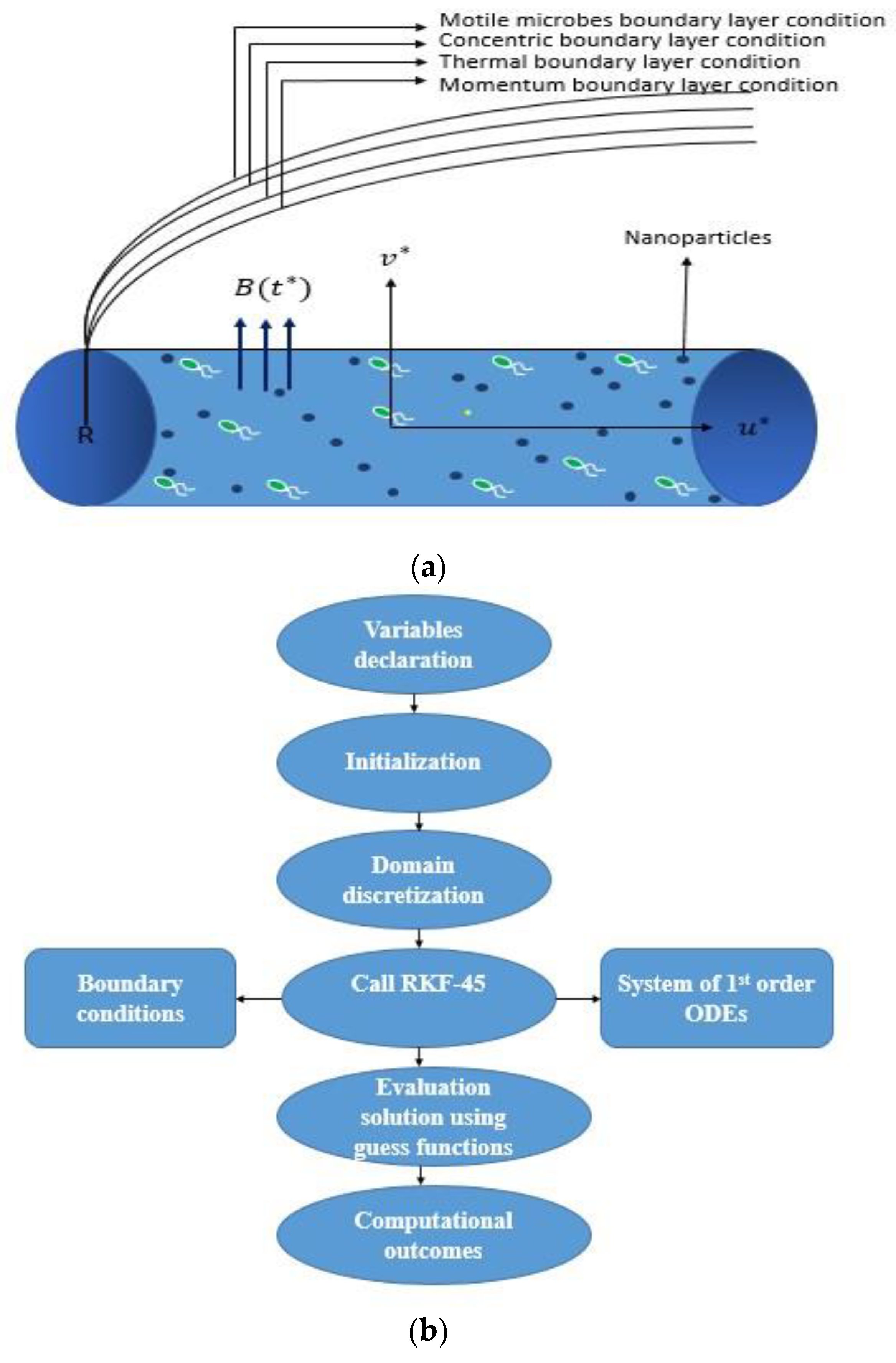
2.: Graphical outcomes

The present segment deals to inspect the physical insight of the cross nanofluid problem from a numerical solution, a computational framework through a built-in algorithm is obtained by the use of a shooting procedure. The action of important parameters via different flow fields such as flow stream, temperature gradient, concentration, the concentration of microprobes, skin friction, heat transfer coefficient, and mass flow rate characteristics. The set of nonlinear computational outcomes for fluid velocity profile, temperature gradient, mass concentration, and living microbes within the boundary layer for varying values of dimensionless flow parameter have been computed by Mathematica 11.0 programming software. The involved assorted parameters are exhibited in graphical representation via Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21.

Figure 2a explains the effects of varying nature of

Re

via

u_{0}^{'} (ζ)

outlines. On increasing data of

Re

result as the reduction is witnessed in the

u_{0}^{'} (ζ)

curves. Figure 2b elucidates the role of

(α)

against

u_{0}^{'} (ζ)

field. The higher estimation of the

(α)

decline the flow stream as well as the boundary layer thickness. Figure 3 sketches the impact of

(M a)

u_{0}^{'} (ζ)

. The velocity boundary layer leads to upsurges subjected to increasing data of the

(M a)

parameter. The outlines of

(λ)

u_{0}^{'} (ζ)

profile is explained in Figure 3. The velocity outlines are increased with incrementing values of

(λ)

. Figure 4 demonstrations effects of

(M)

for various stream of fluid. Physically, this figure describes that the incrementing data of

(M)

causes obstruction in the fluid flow profile. This retardation in velocity field due the Lorentz forces that are resistive in nature included in the magnetic parameter and reacts as retarding force. As the magnetic effect boost up, the Lorentz force developed which acts against the flow of fluid and consequently the velocity patterns decline. On the other hands Figure 4 displays the effective correlation between the flow profile and the

(N c)

parameter. One can observe that the incrementing values of the

(N c)

parameter, the velocity field of nanofluid decreases. Figure 5 presented the influence of

(W e)

at velocity function. The velocity distribution diminished due to increment of

(W e)

. Physically, the velocity function dwindled for different values of

(W e)

because increment of

(W e)

means increment in internal forces which decreased fluid flow within the channel. The impacts of the

(N r)

u_{0}^{'} (ζ)

profile are established through Figure 5, it can be detected that with the incrementing data of

(N r)

parameter, the

u_{0}^{'} (ζ)

field is declined, and the maximum velocity is attained at

(N r = 0.1)

and minimum velocity curved is achieved at maximum value

(N r = 1.3)

of buoyancy ratio parameter. From Figure 6, it can be discerned that the energy gradient

g (ζ)

upturns by increasing the

(N t)

. In reality, this phenomenon is occurred due to the fact that high energetic worm nano-particles are drawn away from heated stretching surface and towards the colder regions by the thermophoretic diffusion effect, triggering an upsurge in the internal heating inside the thermal boundary layer curves. Figure 6 explains the result of the

(θ_{w})

on energy gradient

g (ζ)

of the fluid profile. It is countersigned that an improvement in

(θ_{w})

rises the thermal field distribution. Figure 7 describes the implication of the

(B i)

on energy outline

g (ζ)

. As witnessed that higher estimation of the

(B i)

results in high convective transfer of heat in the fluid nanoparticles. Consequently, the energy fields curves increases due to increment in

(B i)

results in massive convective heat transfer observed. Physically, the

(B i)

is related to the coefficient of heat transfer. Therefore,

g (ζ)

increases and associated layer thickness. The outcomes of the increasing values of the conductivity factor

(ε)

via energy

g (ζ)

profile is characterized through Figure 7. Here the energy gradient of the fluid intensifies for increasing data of the

(ε)

. Physically, extra heat is added to nanofluid for increased values of

(ε)

. Figures 8a,b designates the outlines of melting parameter

(M a)

and

(α)

fluid temperature gradient. It can be seen that from these profiles that the increasing values of these parameters increases the internal energy of the fluid. Inconsequently,

g (ζ)

increases. The consequences of

(\Pr)

on fluid energy gradient

g (ζ)

distribution is illustrated through Figure 9. Here one can admit that the energy profile

g (ζ)

diminishes for greater estimations

(\Pr)

. Physically,

(\Pr)

is designated as the ratio of thermal conductivity to thermal diffusivity of a fluid. For expending nature of

(\Pr)

causes minimum thermal diffusivity behavior of the nanofluid. Consequently,

g (ζ)

and related thermal layer thickness deteriorates. Effects of

(λ)

on energy profile

g (ζ)

is plotted through Figure 9. As witnessed the energy profile of the nanofluid diminishing through higher estimation of

(λ)

values. Figure 10 reveals

(N t)

parameter impact on

h (ς)

. As exhibited, the nanoparticles concentration profile increase through higher

(N t)

estimations. From physical perspective, an increase in thermophoretic diffusion force is perceived via incrementing values of

(N t)

which often moves the fluid molecules higher temperature region towards lower one. Figure 10 describes the impression of the

(L e)

number on

h (ς)

profile by keeping the default parameters fixed. For diversified data of

(L e)

number,

L e

designate the decay of

h (ς)

profiles. Physically, leading values declines the diffusivity rapidly. Thus,

h (ς)

profiles decreased. Figure 11 explains Brownian parameter effect on

h (ς)

. Evidently an increment in the

(N b)

magnitude increases the velocity through which fluid particles move with various speed in different directions owing to

(N b)

aspect. Subsequently, larger Brownian estimations creates a decline in

h (ς)

and associated concentration layer thickness. Figure 11 portrayed the upshot of

(\in_{1})

h (ς)

. Here, nanoparticles concentration profile increases with incrementing values of

(\in_{1})

. Figure 12a,b illustrated the result of

(M a)

and

(α)

h (ς)

profiles. As established, nanoparticles’ concentration enhances by increasing the values of

(M a)

. Thus, the effect of the melting parameter on

h (ς)

depends on some factors, including the nanoparticle size, shape, and surface chemistry visualized through Figure 12. The concentration profile of the nanoparticles is improved for greater values of

(α)

shown in Figure 12.

Figure 13 illustrates how the distribution of motile swimming microbes, denoted as

Χ (ς)

, is affected by the

(L b)

number. As witnessed

(L b)

increases, the thickness of the

Χ (ς)

profile declines for both the shear thickening and shear thinning cases. On the other hand, Figure 13 displays the outline of the

(P e)

number on the distribution of living microbes profile. When the dimensionless parameter uplift, the motile swimming outlook

Χ (ς)

declining subject to increasing the values of

(P e)

number. The motile swimming microbes profile

Χ (ς)

is depicted in Figure 14a,b to exemplify the characteristics of the

(α)

and

(M a)

parameters. It can be viewed that the motility of the living microbes enhances as

(α)

parameter intensifies. Furthermore, it is revealed that the swimming profiles increase as the

(M a)

parameter becomes larger.

Figure 15 and Figure 16 are offered to elucidate the role of the drag force coefficient for various physical parameters which includes the

(N r)

(N r)

(α)

(A)

, and

(M a)

respectively. From these visuals, it is witnessed that the surface drag force coefficient enhances through higher estimation of these parameters, whereas decreasing with the increasing values of

(λ)

. Figure 17 and Figure 18 explain the impact of important physical constraints via the heat transfer rate coefficient. The heat flow rate enhances with the expanding nature of the physical parameters. Figure 19 and Figure 20 exhibits variation of mass flow rate coefficient via different parameters. It is witnessed an increment in the response of the flow rate of mass when

(\Pr)

number and

(N t)

parameter increased from low-level to high-level values. While the mass flow coefficient is decreased significantly from low level to higher level values

(L e)

number,

(N b)

, and

(α)

are highlighted through these visuals. Displayed here is the local microorganism number through Figure 21correspondingly. From this visual, one can be clearly noticed that the microorganism number enhances with the higher estimation of the involved data of

(M a)

(L b)

number, and

(P e)

number.

Figure 2. (a,b):

u_{0}^{'}

impacts for various

Re a n d α

Figure 2. (a,b):

u_{0}^{'}

impacts for various

Re a n d α

Figure 3. (a,b):

u_{0}^{'}

impacts for various

M a a n d λ

Figure 3. (a,b):

u_{0}^{'}

impacts for various

M a a n d λ

Figure 4. (a,b):

u_{0}^{'}

impacts for various

M a n d N c

Figure 4. (a,b):

u_{0}^{'}

impacts for various

M a n d N c

Figure 5. (a,b):

u_{0}^{'}

impacts for various

W e a n d N r

Figure 5. (a,b):

u_{0}^{'}

impacts for various

W e a n d N r

Figure 6. (a,b):

g (ς)

impacts for various

N t a n d θ_{w}

Figure 6. (a,b):

g (ς)

impacts for various

N t a n d θ_{w}

Figure 7. (a,b):

g (ς)

impacts for various

B i a n d ε

Figure 7. (a,b):

g (ς)

impacts for various

B i a n d ε

Figure 8. (a,b):

g (ς)

impacts for various

M a a n d α

Figure 8. (a,b):

g (ς)

impacts for various

M a a n d α

Figure 9. (a,b):

g (ς)

impacts for various

\Pr a n d λ

Figure 9. (a,b):

g (ς)

impacts for various

\Pr a n d λ

Figure 10. (a,b):

h (ς)

impacts for various

N t a n d L e

Figure 10. (a,b):

h (ς)

impacts for various

N t a n d L e

Figure 11. (a,b):

h (ς)

impacts for various

N t a n d \in_{1}

Figure 11. (a,b):

h (ς)

impacts for various

N t a n d \in_{1}

Figure 12. (a,b):

h (ς)

impacts for various

M a a n d α

Figure 12. (a,b):

h (ς)

impacts for various

M a a n d α

Figure 13. (a,b):

Υ (ς)

impacts for various

L b a n d P e

Figure 13. (a,b):

Υ (ς)

impacts for various

L b a n d P e

Figure 14. (a,b):

Υ (ς)

impacts for various

M a a n d α

Figure 14. (a,b):

Υ (ς)

impacts for various

M a a n d α

Figure 15. Skin friction estimation via different physical parameters.

Figure 16. Skin friction estimation via different physical parameters.

Figure 17. Heat transfer estimation via different physical parameters.

Figure 18. Heat transfer estimation via different physical parameters.

Figure 19. Mass flow rate estimation via different physical parameters.

Figure 20. Mass flow rate estimation via different physical parameters.

Figure 21. Microorganism estimation via different physical parameters.

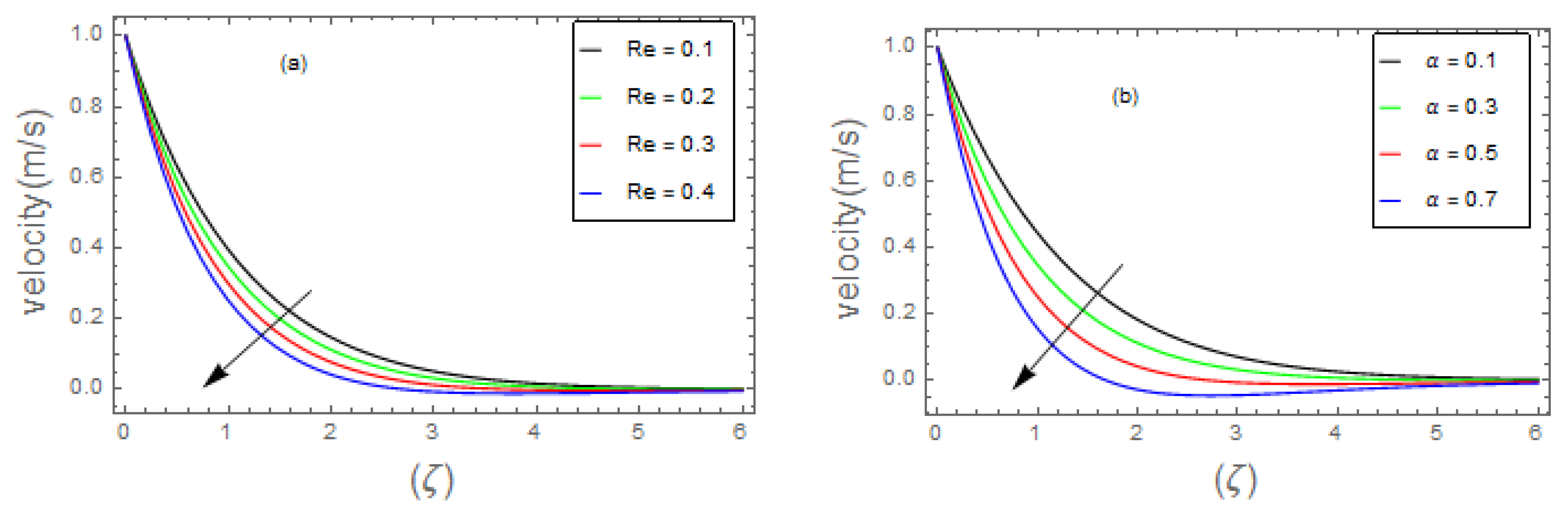
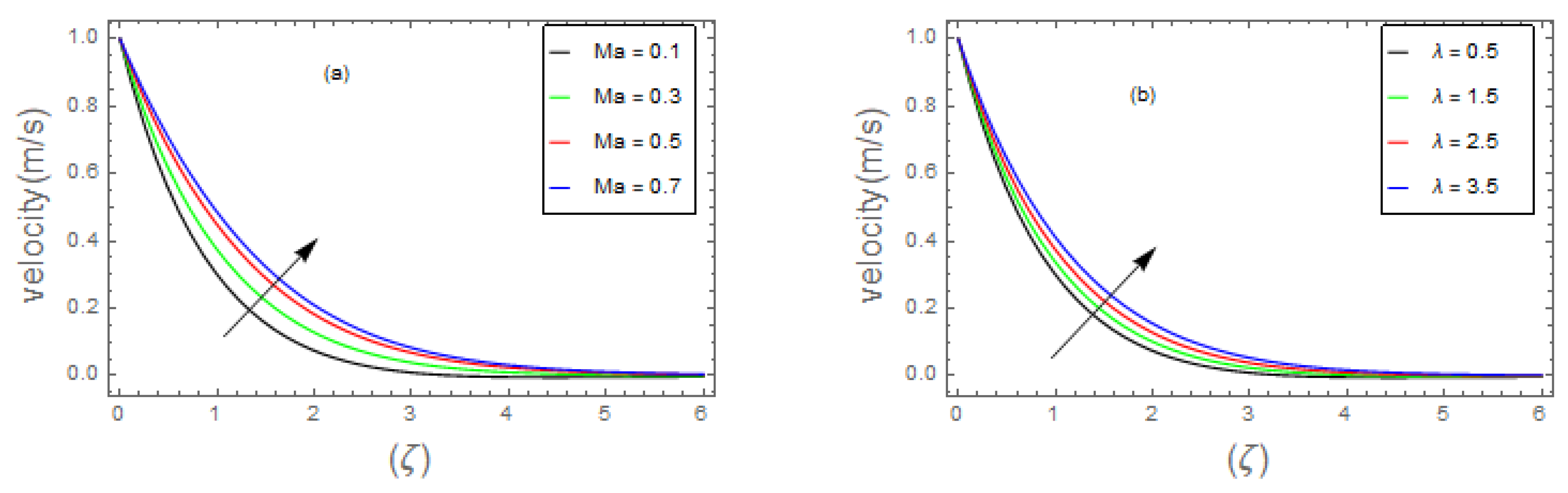
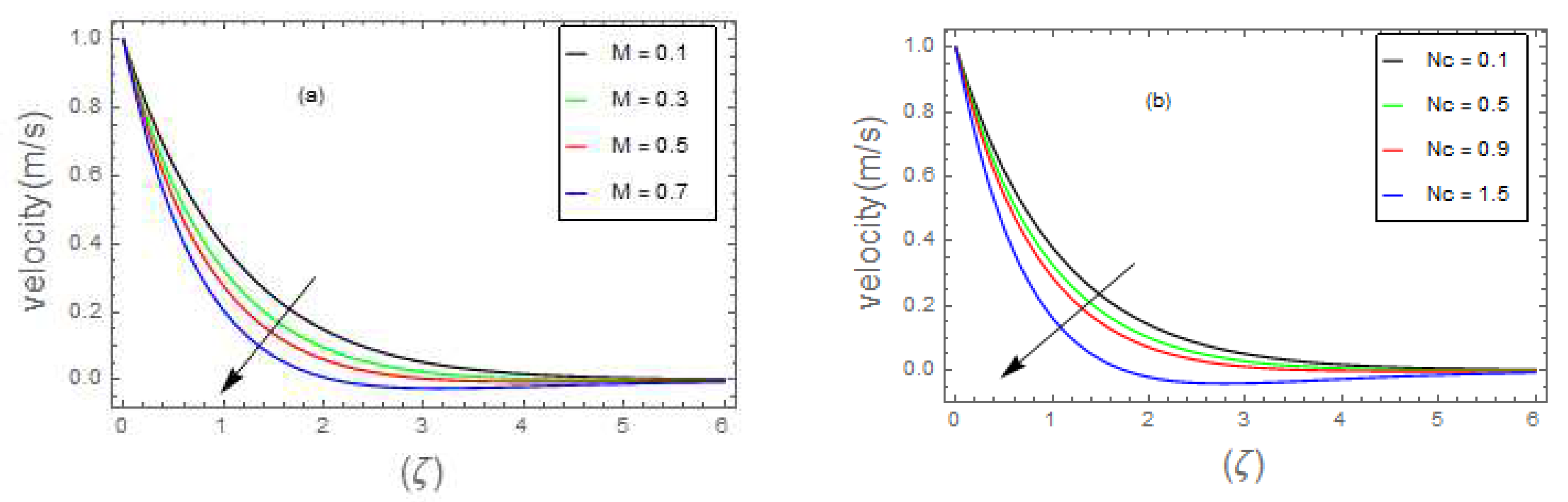
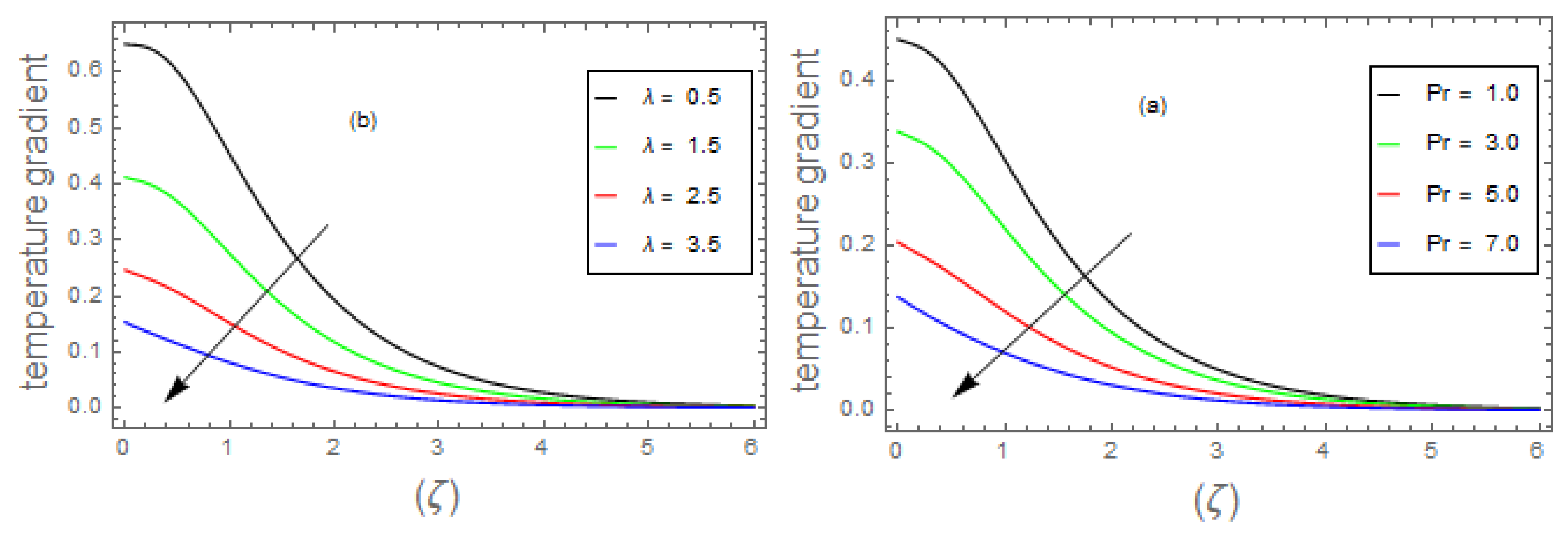
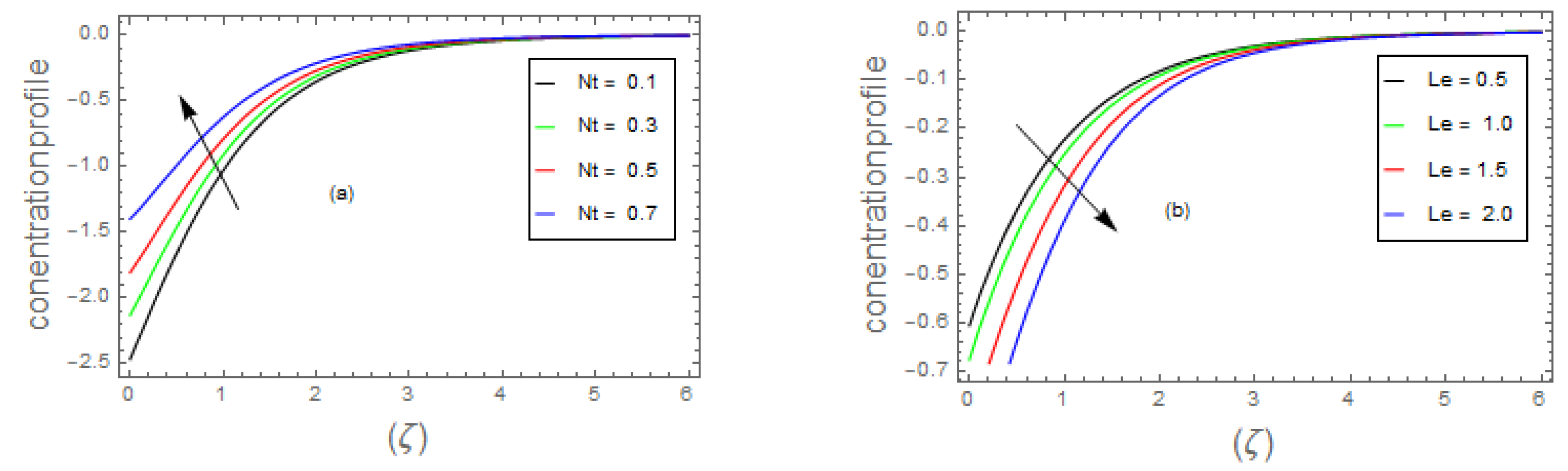
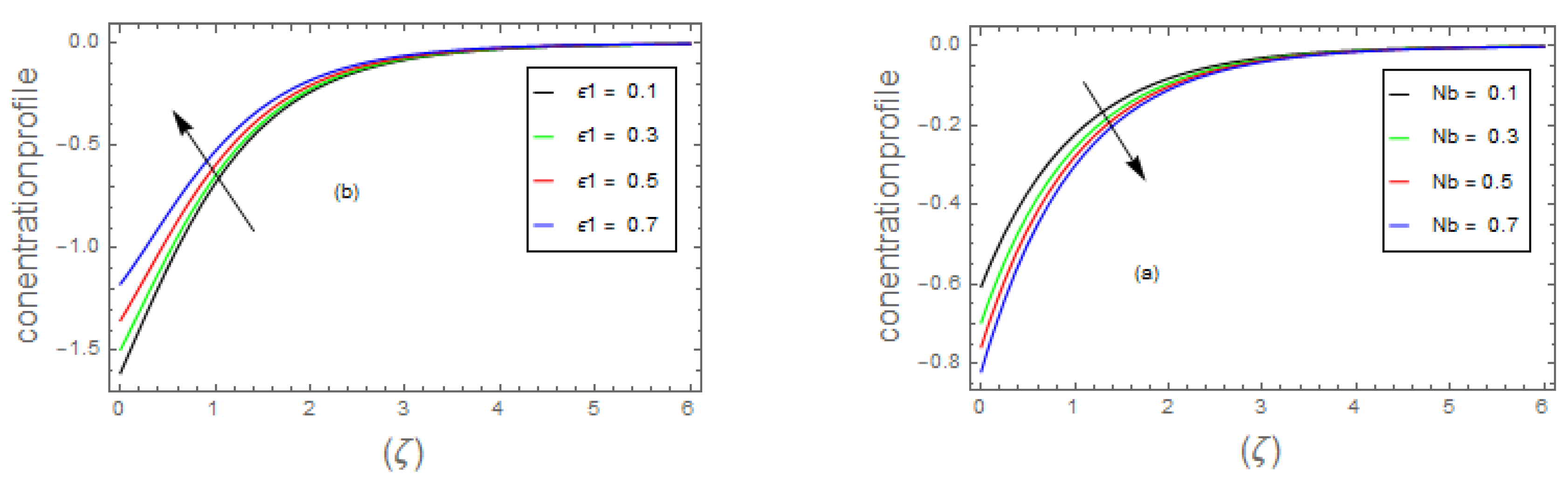
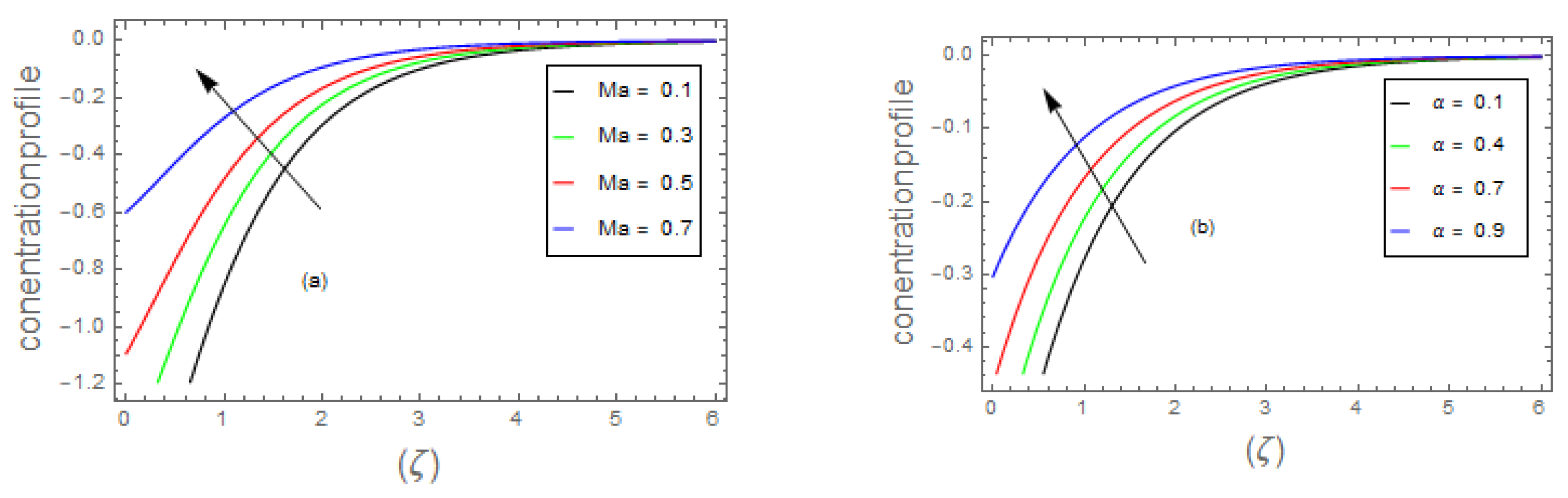
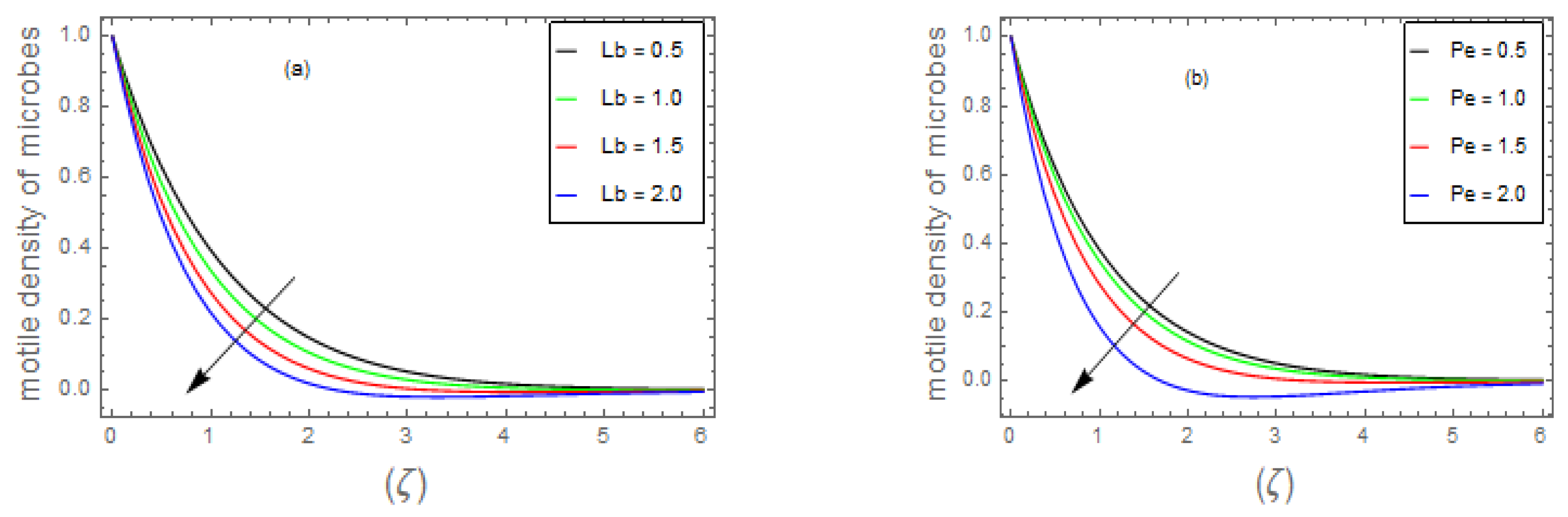
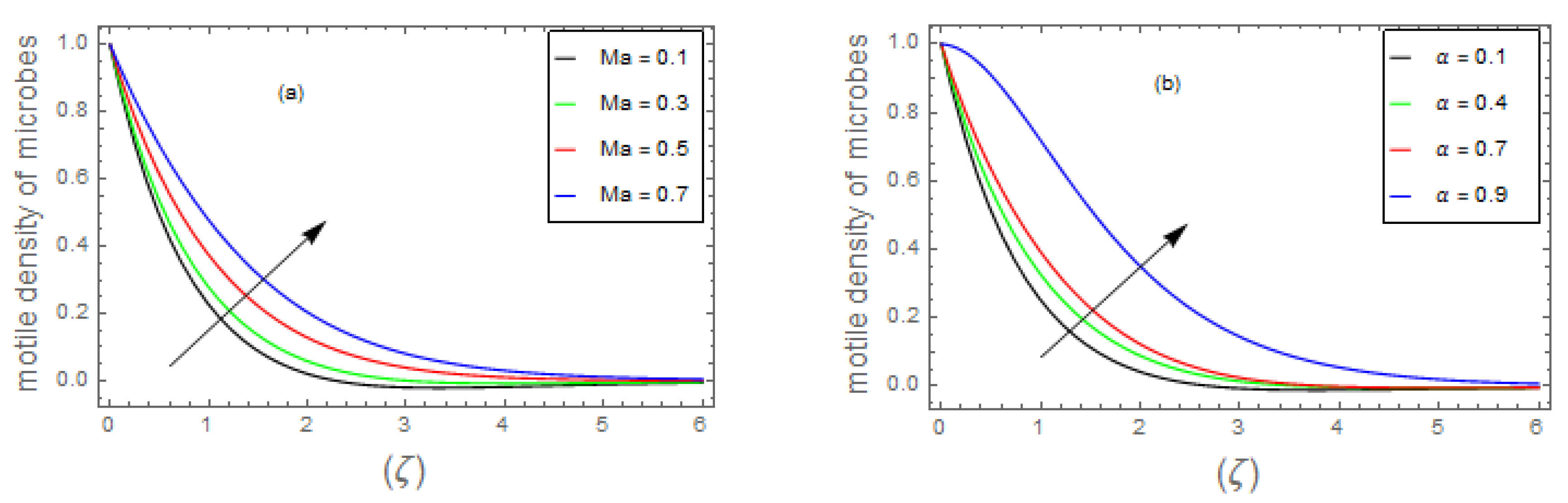
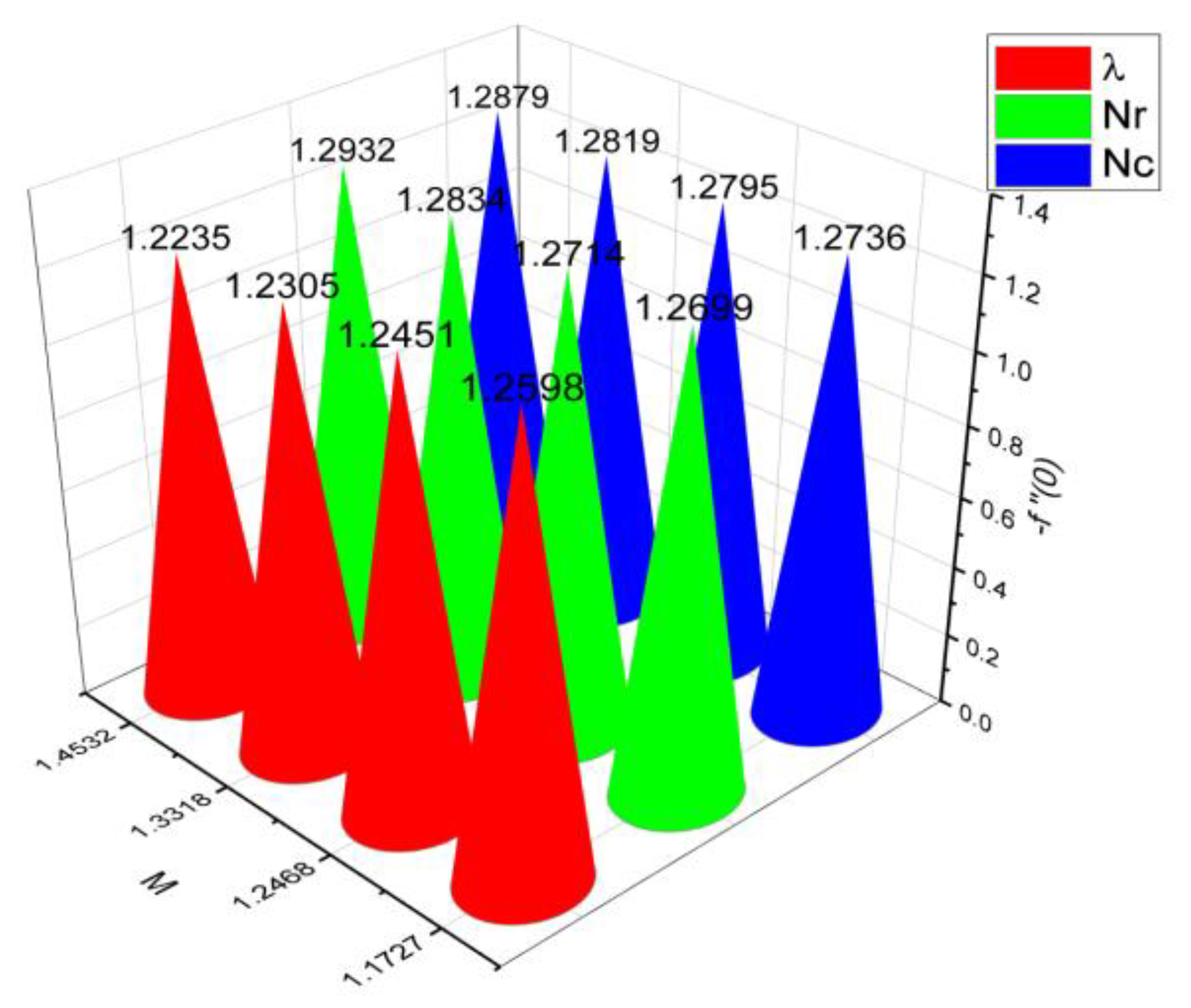
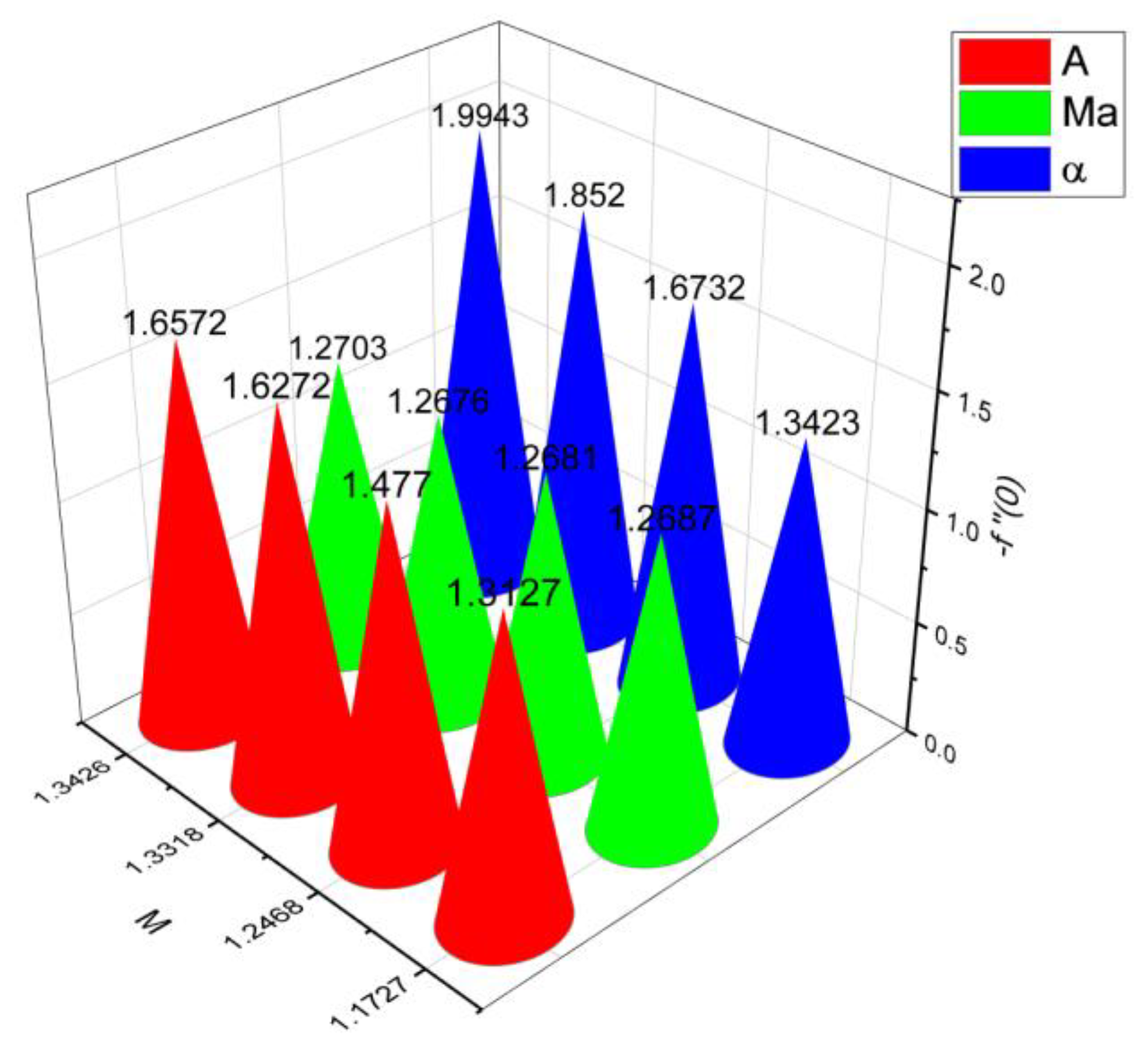
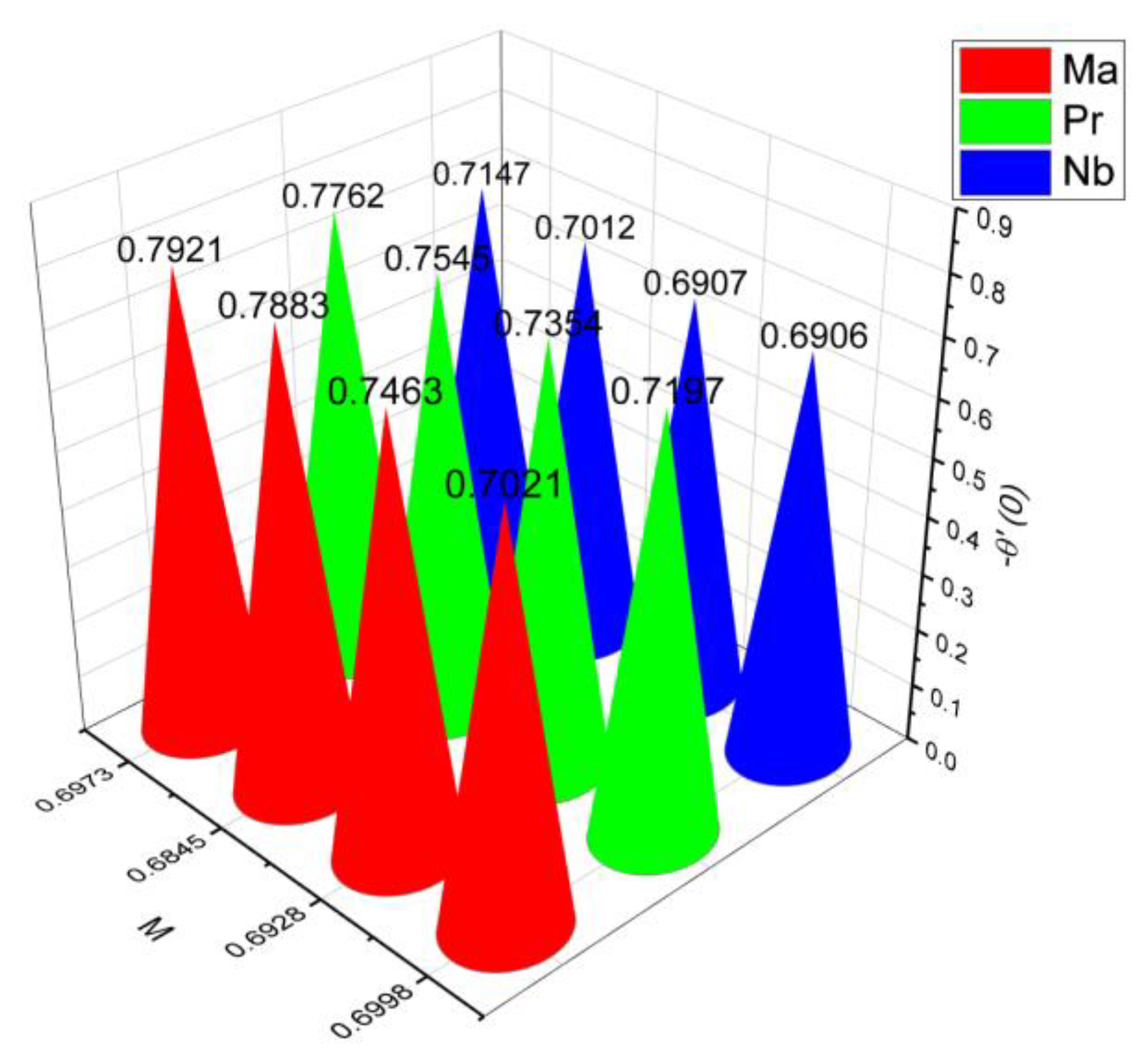
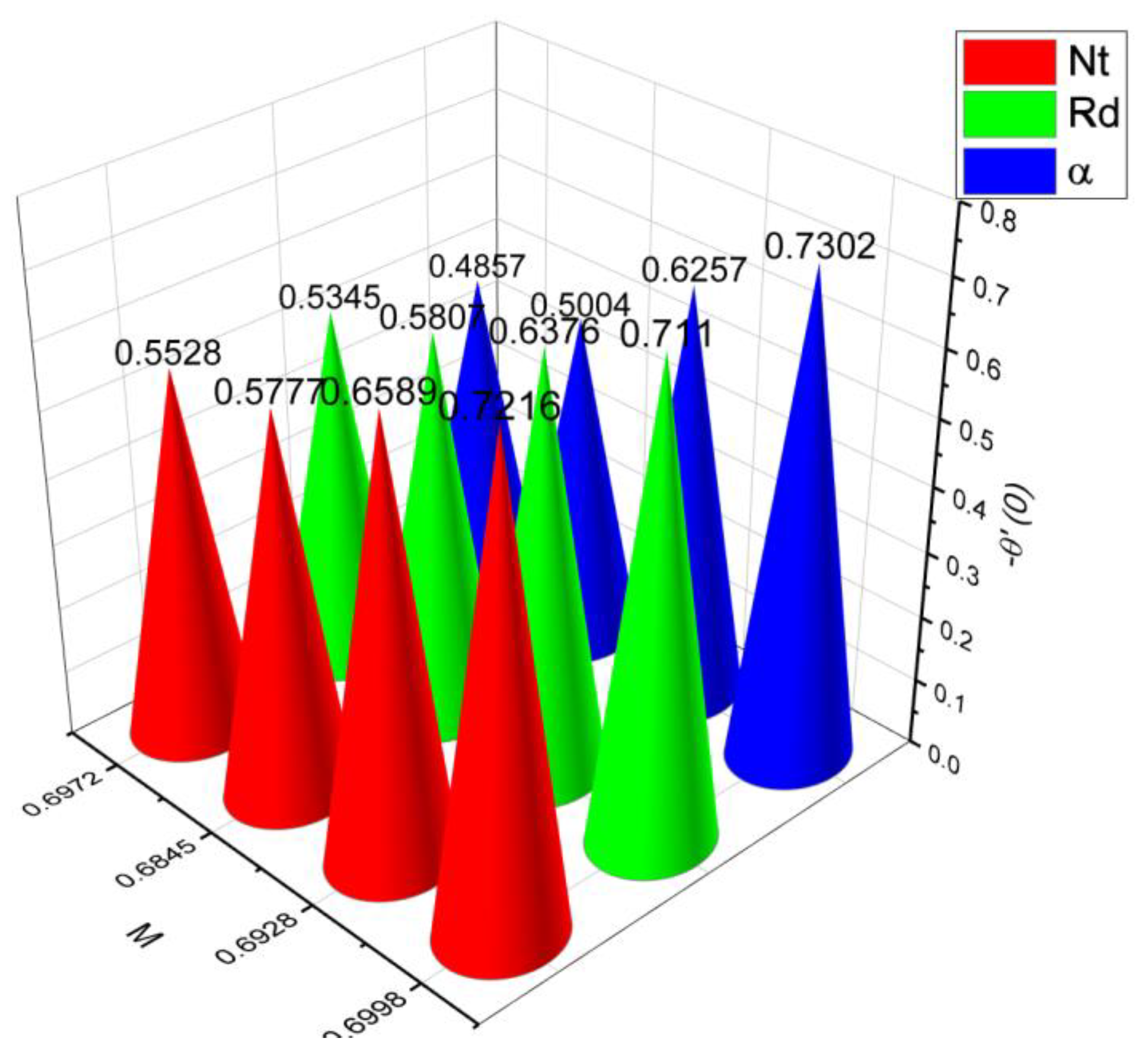
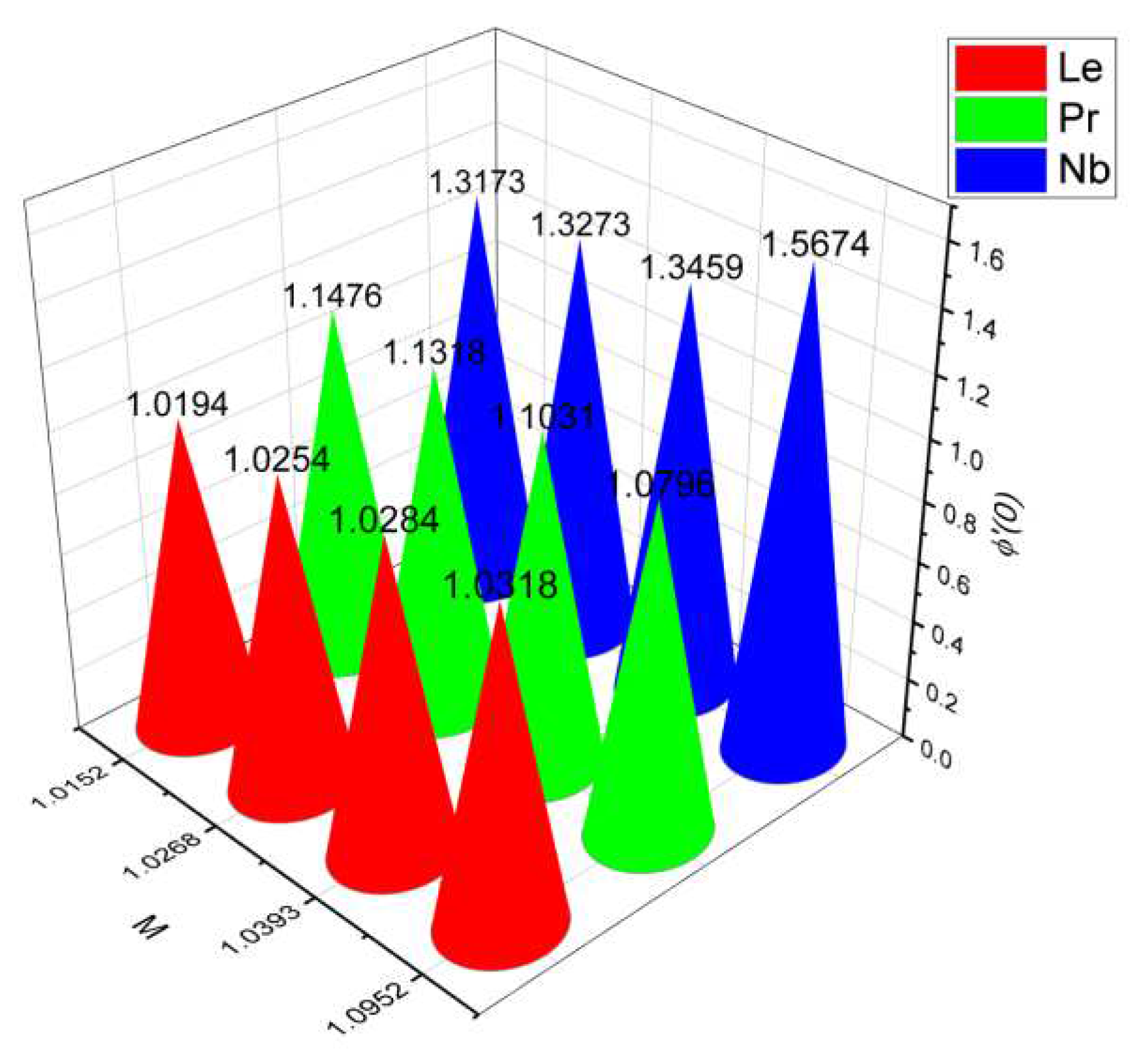
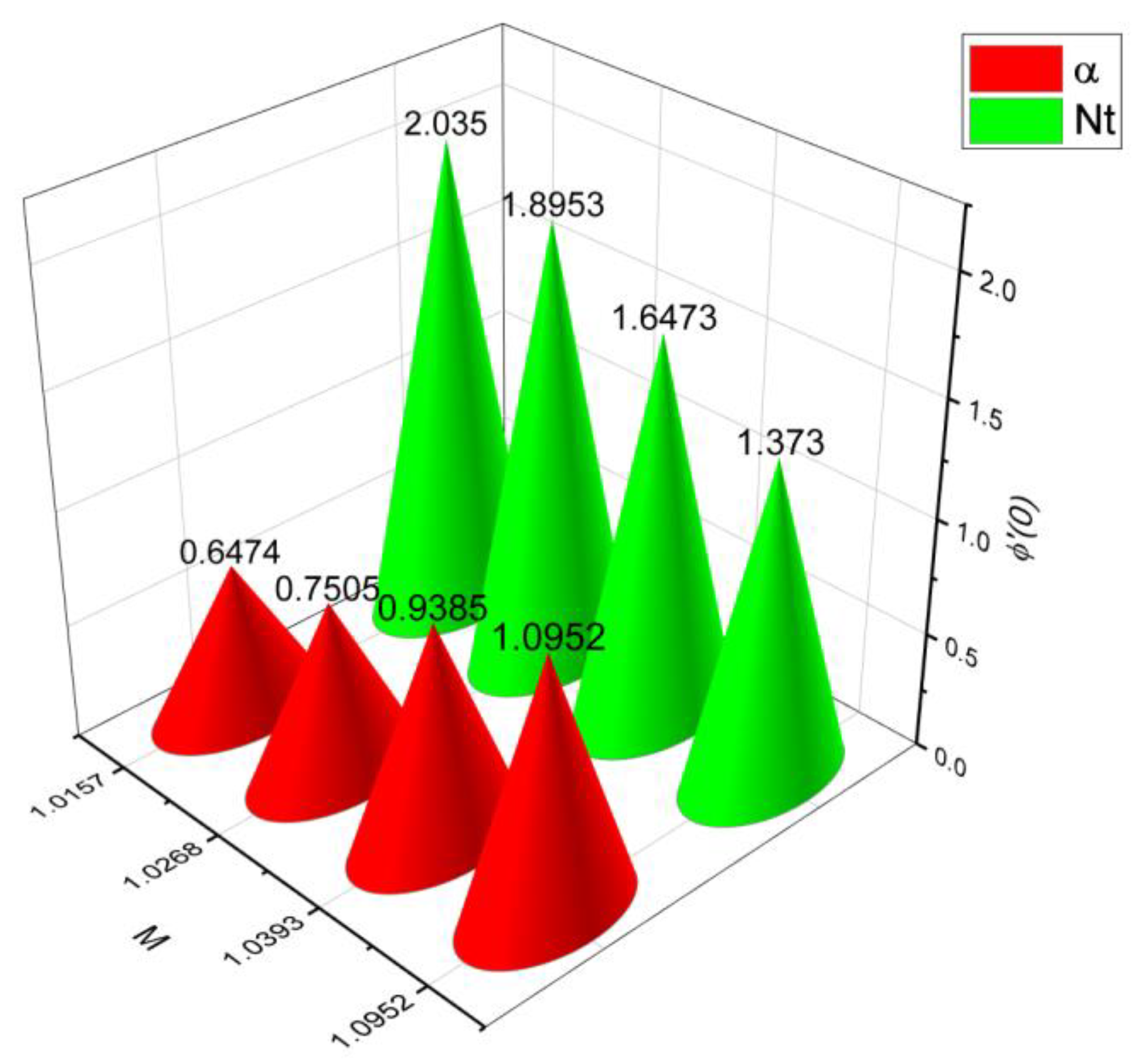
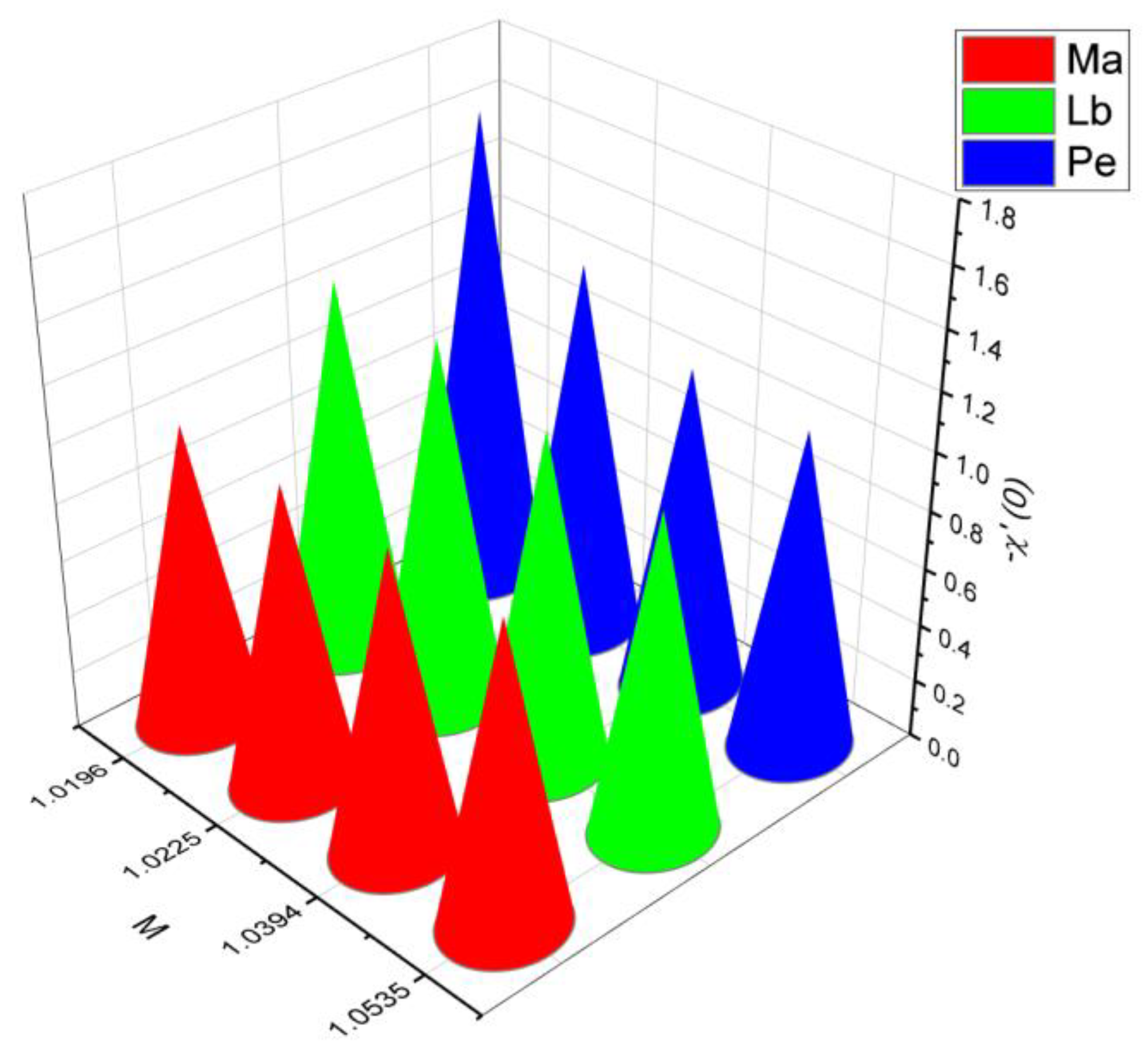
3.: Closing points

This study investigates, the characteristics of MHD bioconvection flow of nanofluid under the melting heat transfer rheology and is analyzed by implementing the swimming microbes model for heat and mass flow rate. Additionally, a homotopic scheme is engaged to get the nonlinear computational outcomes of the ODEs acquired through similarity transformations of the resulting PDEs. The computational results so acquired were correlated to the published work done, and a reasonable degree of agreement was established, hence authenticating the nonlinear solution. The leading outcomes of the existing survey are shortened as underneath:

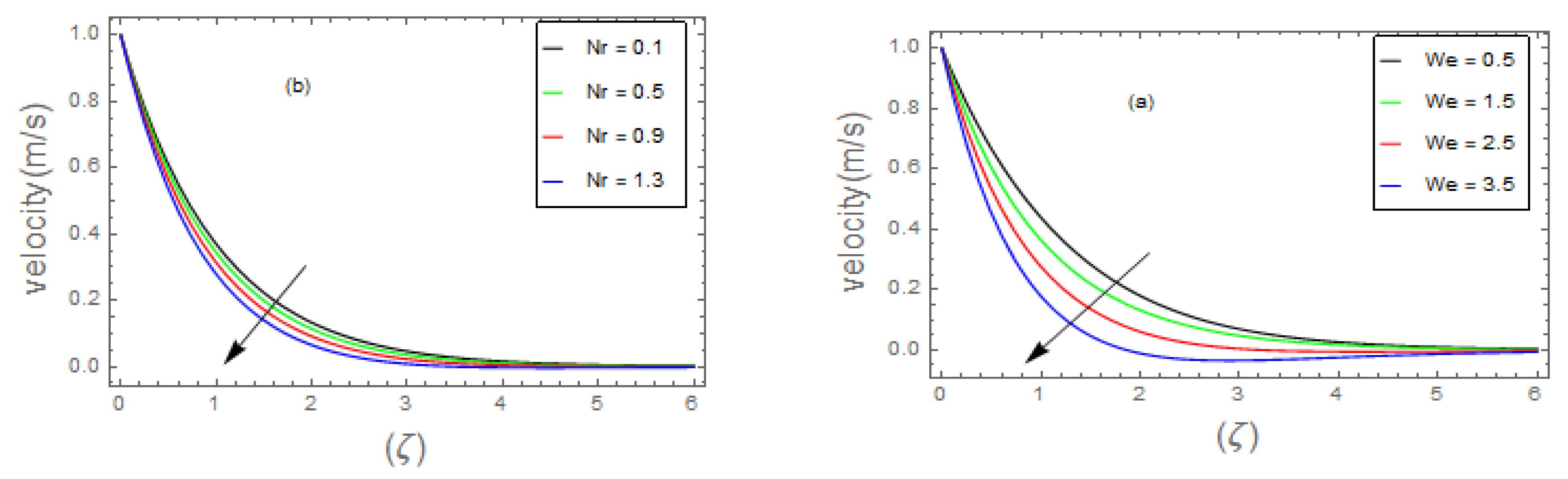
The velocity field of bio-nanofluid flow rises as the values of $(α)$ and $(M a)$ parameter is increased, however, the velocity profile reduces with the expanding values of $(W e)$ , $(M)$ and $(α)$ parameters.
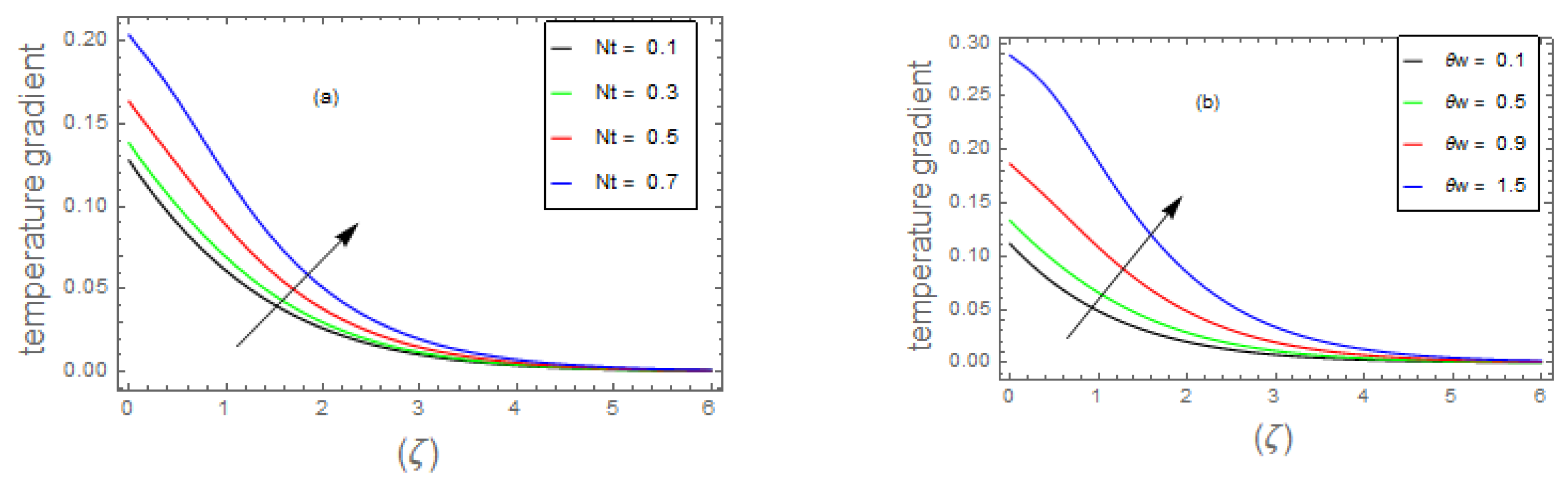
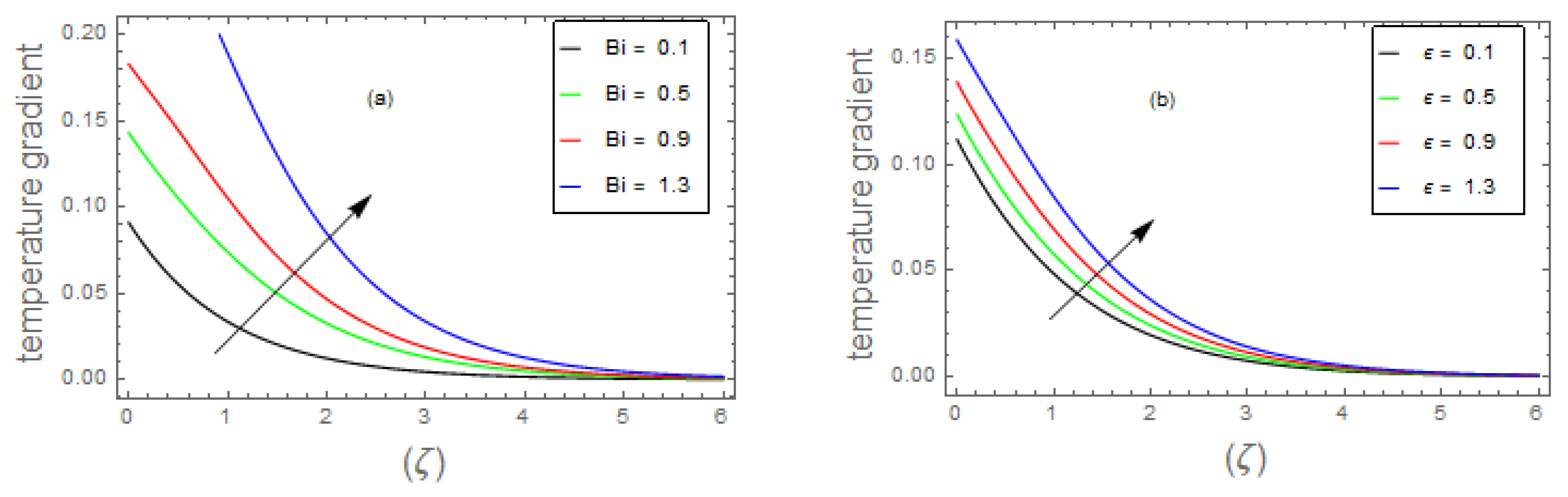
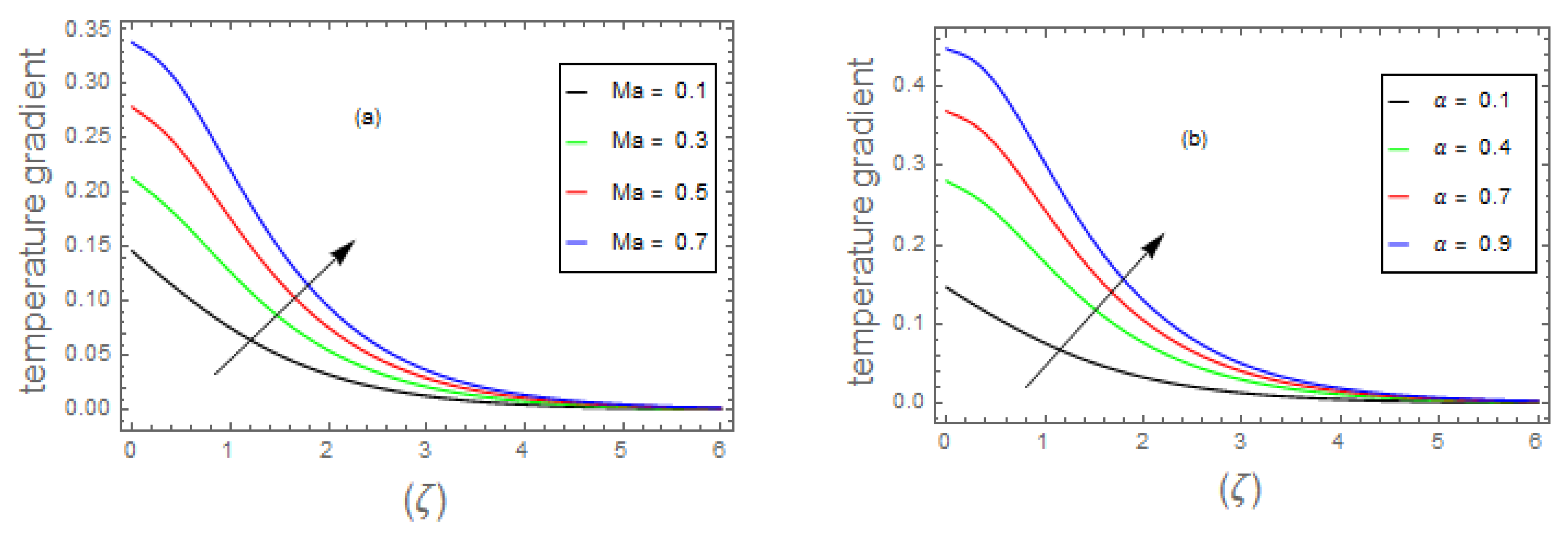
The fluid energy profile decremented with the mounting data of $(α)$ parameter and $(L e)$ number but increases by $(M a)$ , $(N t)$ , and thermal $(B i)$ number.
Due to the increment in the magnitude of $(N t)$ parameter, $(ε)$ , and $(α)$ the concentric layer thickness increases. On the contrary, for growing data on the $(L e)$ and $(N b)$ dispersion effect the concentration profile decreases.
It has been observed that the increasing trends of $(L b)$ and $(P e)$ numbers suppresses considerably the density profile of living microbes, whereas the $(α)$ and $(M a)$ parameters boost the motile density of microorganism profile.
The surface drag force coefficient decays via higher estimation of $(λ)$ but it increments when $(N c)$ and $(α)$ parameter are increased.
It is observed that the mass flow rate increase when $(\Pr)$ number as well as $(N t)$ the parameter increased. On the contrary, it decreases when $(N b)$ parameter and $(L e)$ number increase.

Funding

Project number (RSPD2023R576), King Saud University, Riyadh, Saudi Arabia,.

Acknowledgments

Researchers Supporting Project number (RSPD2023R576), King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest

The authors don't have any conflict of interest.

References

S.U.S. Choi, Enhancing thermal conductivity of fluids with nanoparticles, development and applications of non-Newtonian flows, in: D.A. Siginer, H.P. Wang(Eds.), ASME MD, vol. 231, 1995, pp. 99–110.
G. Narsimulu, D. Gopal, Rama Udaikumar, Numerical approach for enhanced mass transfer of Bio-convection on Magneto-hydrodynamic Carreau fluid flow through a nonlinear stretching surface, Materials Today: Proceedings, 49, Part 5, 2022, 2267-2275. [CrossRef]
Muhammad Imran, Tahir Kamran, Shan Ali Khan, Taseer Muhammad, Hassan Waqas, Physical attributes of bio-convection in nanofluid flow through a paraboloid of revolution on horizontal surface with motile microorganisms, International Communications in Heat and Mass Transfer, 133, 2022. [CrossRef]
Hassan Waqas, Shan Ali Khan, Sami Ullah Khan, M. Ijaz Khan, Seifedine Kadry, Yu-Ming Chu, Falkner-Skan time-dependent bioconvrction flow of cross nanofluid with nonlinear thermal radiation, activation energy and melting process, International Communications in Heat and Mass Transfer, 120, 2021. [CrossRef]
Asmat Ullah Yahya, Nadeem Salamat, Danial Habib, Bagh Ali, Sajjad Hussain, Sohaib Abdal, Implication of Bio-convection and Cattaneo-Christov heat flux on Williamson Sutterby nanofluid transportation caused by a stretching surface with convective boundary, Chinese Journal of Physics, 73, 2021, 706-718. [CrossRef]
J. Buongiorno, Convective transport in nanofluid, J.Heat Transfer 128 (3) (2006) 240–250. [CrossRef]
K. Venkatadri, S. Abdul Gaffar, P. Rajarajeswari, V.R. Prasad, B.O. Anwar, K.B.M. Hidayathulla, Melting heat transfer analysis of electrically conducting nanofluid flow over an exponentially shrinking/stretching porous sheet with radiative heat flux under a magnetic field, Heat Transfer (2020). [CrossRef]
H. Mondal, S. Bharti, Spectral Quasi-linearization for MHD nanofluid stagnation boundary layer flow due to a stretching/shrinking surface, Journal of Applied and Computational Mechanics 6 (4) (2020) 1058–1068. [CrossRef]
Z. Ying, B. He, L. Su, Y. Kuang, D. He, C. Lin, Convective heat transfer of molten salt-based nanofluid in a receiver tube with non-uniform heat flux, Appl. Therm. Eng. 181 (2020), 115922. [CrossRef]
N.A. Zainal, R. Nazar, K. Naganthran, I. Pop, Stability analysis of MHD hybrid nanofluid flow over a stretching/shrinking sheet with quadratic velocity, Alexandria Engineering Journal (2020). [CrossRef]
M.R. Eid, M.A. Nafe, Thermal Conductivity Variation and Heat Generation Effects on Magneto-Hybrid Nanofluid Flow in a Porous Medium with Slip Condition. Waves in Random and Complex Media, 2020, pp. 1–25. [CrossRef]
H. Eshgarf, R. Kalbasi, A. Maleki, M.S. Shadloo, A review on the properties, preparation, models and stability of hybrid nanofluids to optimize energy consumption, J. Therm. Anal. Calorim. (2020) 1–25. [CrossRef]
N. Khan, M.S. Hashmi, S.U. Khan, F. Chaudhry, I. Tlili, M.S. Shadloo, Effects of homogeneous and heterogeneous chemical features on Oldroyd-B fluid flow between stretching disks with velocity and temperature boundary assumptions, Math. Probl Eng. (2020). [CrossRef]
I. Tlili, M. Rabeti, M.S. Shadloo, Z. Abdelmalek, Forced convection heat transfer of nanofluids from a horizontal plate with convective boundary condition and a line heat source embedded in porous media, J. Therm. Anal. Calorim. (2020) 1–14. [CrossRef]
F.S. Al-Mubaddel, U. Farooq, K. Al-Khaled, S. Hussain, S.U. Khan, M.O. Aijaz, H. Waqas, Double stratified analysis for bioconvection radiative flow of Sisko nanofluid with generalized heat/mass fluxes, Phys. Scripta 96 (5) (2021), 055004. [CrossRef]
H. Waqas, U. Farooq, R. Naseem, S. Hussain, M. Alghamdi, Impact of MHD radiative flow of hybrid nanofluid over a rotating disk, Case Studies in Thermal Engineering 26 (2021), 101015. [CrossRef]
H. Eshgarf, R. Kalbasi, A. Maleki, M.S. Shadloo, A review on the properties, preparation, models and stability of hybrid nanofluids to optimize energy consumption, J. Therm. Anal. Calorim. (2020) 1–25. [CrossRef]
M. Imran, U. Farooq, T. Muhammad, S.U. Khan, H. Waqas, Bioconvection transport of Carreau nanofluid with magnetic dipole and nonlinear thermal radiation, Case Stud. Ther. Eng. (2021) 101129. [CrossRef]
I. Tlili, M. Rabeti, M.S. Shadloo, Z. Abdelmalek, Forced convection heat transfer of nanofluids from a horizontal plate with convective boundary condition and a line heat source embedded in porous media, J. Therm. Anal. Calorim. (2020) 1–14. [CrossRef]
M.H.A. Kamal, A. Ali, S. Shafie, N.A. Rawi, M.R. Ilias, G-Jitter effect on heat and mass transfer of 3-D stagnation point nanofluid flow with heat generation, Ain Shams Engineering Journal (2020). [CrossRef]
N.S. Anuar, N. Bachok, N.M. Arifin, H. Rosali, Numerical solution of stagnation point flow and heat transfer over a non-linear stretching/shrinking sheet in hybrid nanofluid: stability analysis, Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 76 (2) (2020) 85–98. [CrossRef]
R. Rizwana, A. Hussain, S. Nadeem, Slip Effects on Unsteady Oblique Stagnation Point Flow of Nanofluid in a View of Inclined Magnetic Field, Mathematical Problems in Engineering, 2020. [CrossRef]
S.S. Giri, K. Das, P.K. Kundu, Influence of nanoparticle diameter and interfacial layer on magnetohydrodynamic nanofluid flow with melting heat transfer inside rotating channel, Math. Methods Appl. Sci. (2020). [CrossRef]
R.P. Sharma, N. Acharya, K. Das, On the Impact of Variable Thickness and Melting Transfer of Heat on Magnetohydrodynamics Nanofluid Flow Past a Slandering Stretching Sheet, 2020.
J.R. Platt, Bioconvection patterns’ in cultures of free swimming organisms, Science 133 (1961) 1766–1767. [CrossRef]
A.V. Kuznetsov, Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: oscillatory instability, Nanoscale Res. Lett. 6 (2011) 100. [CrossRef]
A.V. Kuznetsov, Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth, Eur. J. Mech. B Fluid 30 (2010) 156–165. [CrossRef]
F. Haq, M. Saleem, M. Ur Rahman, Investigation of natural bio-convective flow of Cross nanofluid containing gyrotactic microorganisms subject to activation energy and magnetic field, Phys. Scripta 95 (10) (2020), 105219. [CrossRef]
S. Ahmad, M. Ashraf, K. Ali, Nanofluid flow comprising gyrotactic microorganisms through a porous medium, J. Appl. Fluid Mech. 13 (5) (2020). [CrossRef]
E. Elanchezhian, R. Nirmalkumar, M. Balamurugan, K. Mohana, K.M. Prabu, A. Viloria, Heat and mass transmission of an Oldroyd-B nanofluid flow through a stratified medium with swimming of motile gyrotactic microorganisms and nanoparticles, J. Therm. Anal. Calorim. 141 (2020) 2613–2623. [CrossRef]
M.M. Bhatti, M. Marin, A. Zeeshan, R. Ellahi, S.I. Abdelsalam, Swimming of motile gyrotactic microorganisms and nanoparticles in blood flow through anisotropically tapered arteries, Frontiers in Physics 8 (2020) 95. [CrossRef]
S.U. Khan, I. Tlili, Significance of activation energy and effective Prandtl number in accelerated flow of Jeffrey nanoparticles with gyrotactic microorganisms, J. Energy Resour. Technol. 142 (11) (2020). [CrossRef]
A. Shafiq, G. Rasool, C.M. Khalique, S. Aslam, Second grade bioconvective nanofluid flow with buoyancy effect and chemical reaction, Symmetry 12 (4) (2020) 621. [CrossRef]
A.S. Kotnurkar, D.C. Katagi, Bioconvective Peristaltic Flow of a Third-Grade Nanofluid Embodying Gyrotactic Microorganisms in the Presence of Cu-Blood Nanoparticles with Permeable Walls. Multidiscipline Modeling in Materials and Structures, 2020. [CrossRef]
T. Muhammad, S.Z. Alamri, H. Waqas, D. Habib, R. Ellahi, Bioconvection flow of magnetized Carreau nanofluid under the influence of slip over a wedge with motile microorganisms, J. Therm. Anal. Calorim. (2020) 1–13. [CrossRef]
U. Farooq, H. Waqas, M.I. Khan, S.U. Khan, Y.M. Chu, S. Kadry, Thermally radioactive bioconvection flow of Carreau nanofluid with modified Cattaneo-Christov expressions and exponential space-based heat source, Alexandria Engineering Journal 60 (3) (2021) 3073–3086. [CrossRef]
K. Hosseinzadeh, S. Roghani, A.R. Mogharrebi, A. Asadi, M. Waqas, D.D. Ganji, Investigation of cross-fluid flow containing motile gyrotactic microorganisms and nanoparticles over a three-dimensional cylinder, Alexandria Engineering Journal (2020). [CrossRef]
Algehyne, E. A., Ahammad, N. A., Elnair, M. E., Zidan, M., Alhusayni, Y. Y., El-Bashir, B. O., ... & Alzahrani, F. (2023). Enhancing Heat Transfer in Blood Hybrid Nanofluid Flow with A g–T i O 2 Nanoparticles and Electrical Field in a Tilted Cylindrical W-Shape Stenosis Artery: A Finite Difference Approach. Symmetry, 15(6), 1242. [CrossRef]
Loganathan, K., Eswaramoorthi, S., Chinnasamy, P., Jain, R., Sivasakthivel, R., Ali, R., & Devi, N. N. (2023). Heat and Mass Transport in Casson Nanofluid Flow over a 3-D Riga Plate with Cattaneo-Christov Double Flux: A Computational Modeling through Analytical Method. Symmetry, 15(3), 725. [CrossRef]
Awwad, F. A., Ismail, E. A., & Gul, T. (2023). Heat and Mass Transfer Gravity Driven Fluid Flow over a Symmetrically-Vertical Plane through Neural Networks. Symmetry, 15(6), 1288. [CrossRef]
Sindhu, R., Alessa, N., Eswaramoorthi, S., & Loganathan, K. (2023). Comparative Analysis of Darcy–Forchheimer Radiative Flow of a Water-Based Al2O3-Ag/TiO2 Hybrid Nanofluid over a Riga Plate with Heat Sink/Source. Symmetry, 15(1), 199. [CrossRef]
T.A. Yusuf, F. Mabood, B.C. Prasannakumara, I.E. Sarris, Magneto-bioconvection flow of williamson nanofluid over an inclined plate with gyrotactic microorganisms and entropy generation, Fluid 6 (3) (2021) 109. [CrossRef]
B.J. Gireesha, B.M. Shankaralingappa, B.C. Prasannakumar, B. Nagaraja, MHD flow and melting heat transfer of dusty Casson fluid over a stretching sheet with Cattaneo–Christov heat flux model, Int. J. Ambient Energy (2020) 1–9. [CrossRef]
M.A. Alazwari, M.R. Safaei, Combination effect of baffle arrangement and hybrid nanofluid on thermal performance of a shell and tube heat exchanger using 3-D homogeneous mixture model, Mathematics 9 (8) (2021) 881. [CrossRef]
W.A. Khan, M. Ali, M. Shahzad, F. Sultan, M. Irfan, Z. Asghar, A note on activation energy and magnetic dipole aspects for Cross nanofluid subjected to cylindrical surface, Appl. Nanosci. 10 (8) (2020) 3235–3244. [CrossRef]
Rasheed, HU, Zeeshan, Islam, S, Ali, B, Shah, Q, Ali, R. Implementation of shooting technique for Buongiorno nanofluid model driven by a continuous permeable surface. Heat Transfer. 2023; 52: 3119-3134. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.