Prerpints.org logo
Preprint
Review

Metastability Demystified — the Foundational Past, the Pragmatic Present, and the Potential Future

Altmetrics

Downloads

1090

Views

1726

Comments

0

supplementary.pdf (1.03MB )

Submitted:

20 July 2023

Posted:

21 July 2023

You are already at the latest version

Alerts
Abstract
Healthy brain functioning depends on balancing stable integration between brain areas for effective coordinated functioning, with bursts of desynchronisation to allow subsystems to reconfigure and express functional specialisation. Metastability, a concept originated in statistical physics and dynamical systems theory, has been proposed as a key signature that characterises this balance. Building on this principle, the neuroscience literature has employed markers of metastability to investigate various aspects of brain function including cognitive performance, healthy ageing, meditation, sleep, responses to pharmacological challenges, and to characterise psychiatric conditions or disorders of consciousness. However, this body of work often uses the notion of metastability heuristically, and sometimes inaccurately, making it hard for the uninitiated to navigate the vast literature, interpret findings, and foster further development of theoretical and experimental methodologies. In this paper we provide a comprehensive review of metastability and its applications in neuroscience, covering its scientific and historical foundations and the practical estimators used to estimate it in empirical data. We also provide a critical analysis of recent theoretical developments, clarifying common misconceptions and paving the road for future developments.
Keywords: 
Subject: Biology and Life Sciences  -   Neuroscience and Neurology

Introduction

The notion of “metastability” has been increasingly employed in neuroscience investigations.1 Metastability has been associated with coexisting tendencies in neuronal populations (e.g., brain regions) to work collectively by coordinating the activity across multiple brain regions while also exhibiting segregated activity to allow the performance of specialised functions. Thus, metastability is said to reflect a mixture of cooperation and relative independence between brain areas in response to inputs from the environment; it is considered to be a fundamental signature of high brain functions [1,2,3].
Metastability is commonly invoked in neuroscience literature, but, unfortunately, its empirical and theoretical origins are sometimes lost in the process — thus depriving the wider neuroscience community of an understanding of its empirical and physics-based foundations. In effect, the plethora of successful studies of metastability using quite heterogeneous methodologies can make it challenging for neuroscientists to build a fundamental understanding about what metastability actually is, and how different applications relate to each other. An unfortunate consequence of this rich landscape is that unfamiliar readers could easily misinterpret applications of different signatures of metastability as conflicting definitions [4]. The aim of this paper is to provide a comprehensive account of metastability and its applications in neurosciences, while clarifying common misconceptions and paving the road for future developments.
For this purpose, we first provide a phenomenological account of the origin of metastable states and metastability in physical systems before considering evidence for their existence in coordination dynamics [5], and the brain [6,7]. We then explore how a number of signatures of metastability have been measured in both empirical and computational modelling studies. Next we review a number of “dynamical routes” to metastability (i.e., different types of dynamical scenarios that give rise to metastability) that have originated from various computational models [6,8,9,10,11]. We differentiate these dynamical routes using associated metrics that have been proposed to capture metastable dynamics. These are not alternative definitions, but aim to capture some key signatures — a distinction that helps to dispel much of the current confusion. Finally, we provide suggestions for future avenues of study of metastability.

The past

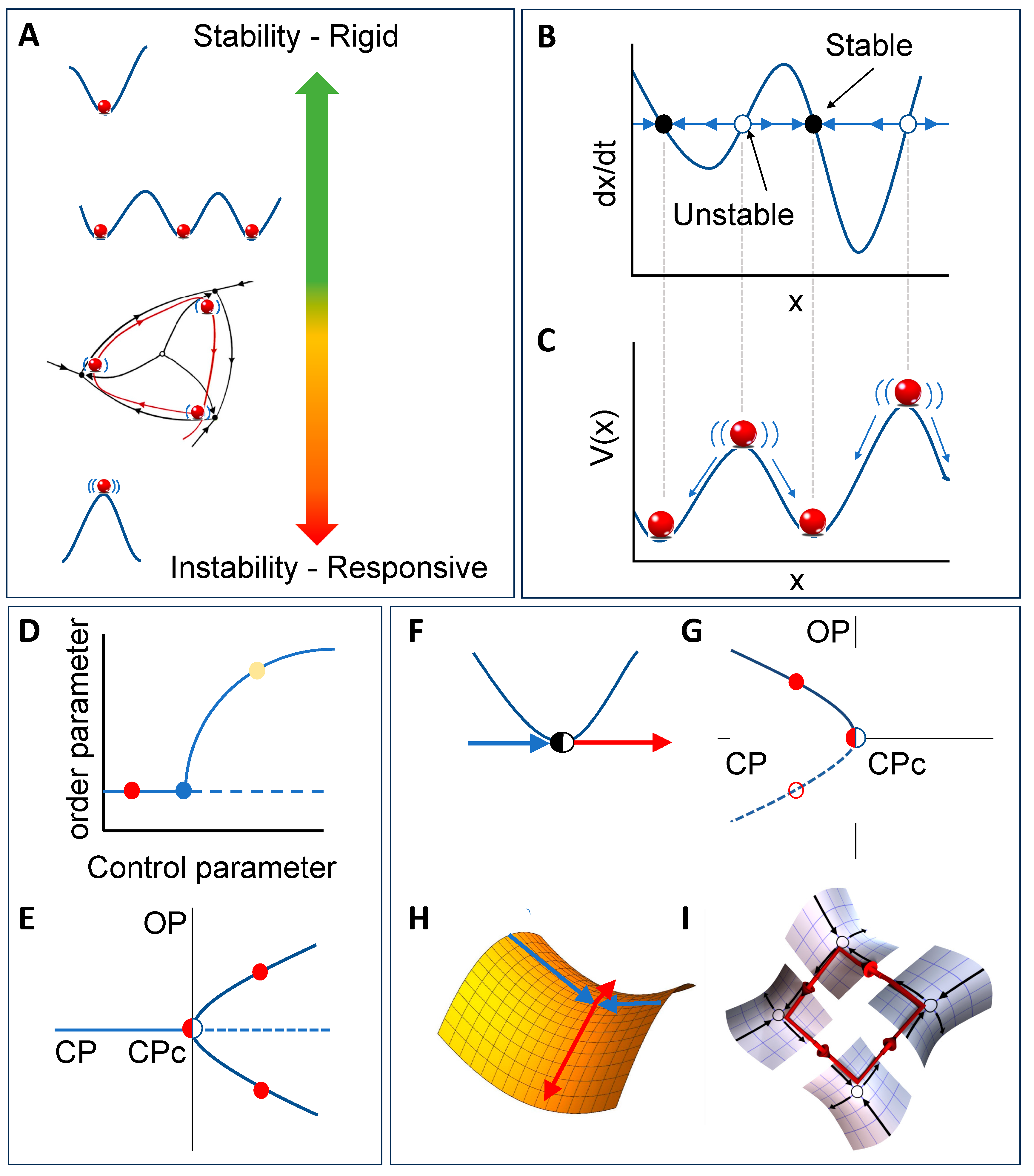
A phenomenological account of metastability

A useful way to think about metastability is to compare it with other types of stability described by dynamical systems theory (see Figure 1). The simplest type of stability is monostability, which corresponds to the case when the system has a single attractor (i.e., when there is one stable solution to the differential equation describing its dynamics). A slightly richer type of dynamics can be observed on systems that exhibit bistability, which have two attractors — the system will settle into one of the attractors depending on the initial conditions, but if the system is perturbed then trajectories can switch from one to the other. More generally, a system is said to exhibit multistability when there are multiple stable solutions to the differential or difference equation, and hence also multiple attractors of the corresponding dynamics. Finally, the notion of metastability (which literally means “beyond stability”) describes dynamics that have more structure than a system with no persistent dynamics and are as rich, if not richer, as dynamics than multistable systems. Any given system can exhibit all of these stability solutions depending on control parameters.
More specifically, a system is said to exhibit metastability when it exhibits “unstable attraction” — i.e., regions of phase space that attract in some directions but repel in others, pulling the system into it then pushing it away. A metastable system approaches successive saddle-like regions, dwells at them for a period, and spontaneously escapes to visit another. Hence, in contrast to standard attractors, which tend to pull and trap trajectories, metastability works a bit like a children’s slide: when the slide is nearly flat, the dynamics slow down giving the impression of nearly stopping (“attraction”), before being released, setting the system free to continue its trajectory. Therefore, while in multistable systems a trajectory can only escape from an attractor due to “external’ (i.e., noise or external control) means, in metastable systems trajectories transition between attracting and repelling regions by construction.
An important consequence of the previous argumentation is that metastability refers to a specific type of dynamics that may take place in a system characterised by patterns that recur either in repeatable sequences (pattern) [10,12] or flexible alternation (no pattern) [11,13] As such, metastability is more flexible than multistability but more structured than mere randomness [1]. Therefore, metastability corresponds to a specific type of collective “behaviour” — i.e., something certain systems do — and not a specific mechanism — i.e., how these systems do it [14]. In fact, metastability can be realised by several different mechanisms, as we will discuss in the sequel.

A brief history of metastability

The mechanistic origins of metastability and associated phase transitions in human movement [1] can be traced back half a century ago to the fledgling study of complex systems [15], and over thirty years for its application to studying the brain [6,7,16]. Here we provide a brief description of the initial steps in the development of this concept before it was developed in neuroscience (which is covered in a later subsection).
At the turn of the 19th century, a chemical system (supersaturated solution of sodium nitrate) in a “metastable condition” was reported, such that its transition time to a stable or ground state exceeded the relaxation time of the elementary microscopic processes [17]. Another example of this long transient behaviour is supercooled water, which remains liquid after being cooled below zero degrees to then freeze abruptly [18]. In physical systems, this behaviour is referred to as metastability “en route” to a ground configuration [19]. When more than one metastable condition or configuration is possible, repeatable metastable transitions between these configurations characterises metastability in complex biological or chemical systems.
Metastability first became associated with brain function in the context of motor coordination in animals and humans. By studying the movements of the fish Labrus, Erich von Holst observed that the movements of the fins were not always synchronous – they could move at slightly different frequencies, but spending more time in specific phase relations where they were almost in sync [20]. Von Holst termed this type of behaviour “relative coordination”, where occasional slippages between coordinating components are balanced by an intrinsic attraction to certain preferred phase relations. Similar patterns were later observed in experiments related to human coordination, where participants were required to flex their index finger in synchronisation or out-of-synchronisation (syncopation) with or without a metronome [21,22,23]. When starting in syncopation, participants spontaneously switched to synchronisation when the metronome frequency exceeded a critical value. However, in synchronisation, their movements were not fully in-phase with the metronome. With further increased metronome frequency, the participants maintained their intrinsically preferred phase relationship with the metronome only for some time, before eventually losing this entrainment, and then modifying their movement until the preferred phase relationship was once more established. This cyclic behaviour of dwelling almost-in-sync before escaping through desynchronisation was considered “metastable” where tendencies for integration (intrinsic preferred phase relations to maintain synchronisation or ‘integration’ between movement and sensory stimuli) coexisted with tendencies for segregation (loss of entrainment) [1,5,21,23] and the cycle of relative coordination between bursts of desynchronisation was described as “metastability” [1]. Similar behaviour was observed in the signal dynamics when the experiment was repeated simultaneously with superconducting quantum interference device acquisition (SQUID) [6,24]. The relative coordination observed in both behaviour and brain signals was interpreted theoretically in terms of intermittent dynamics [25] in the vicinity of the “remnant” or “ghost” of a fixed point that disappeared as the system passed a saddle-node bifurcation [5]. Independent of these studies, experimental and theoretical evidence was reported to support the hypothesis that phase transitions and metastability existed in the brain [7,26].

The present

Practical signatures of metastability

Measuring metastability in neurophysiological and modelled data presents a methodological challenge. In effect, although metastability is well defined mathematically, it is often hard to evaluate in experimental data — as a thorough evaluation requires a full reconstruction of the attractor landscape of the neural dynamics. This difficulty has motivated the search for heuristic signatures of metastability that could be more easily estimated from data. This section reviews several markers of metastability, which allow tractable computation and have led to interesting findings and insights. Despite the success of some of these measures, it is crucial to remark that these measures are not alternative definitions of metastability but rather aim to capture some of its key signatures.
While reviewing these markers, it is important to keep in mind that metastability is a property of a dynamical system (i.e., a mathematical or theoretical model aimed at capturing empirically observed phenomena.) and not of data. Neuroscientists can use techniques to study the likelihood of neuronal activity being generated by a specific type of dynamical system. As usually we have no certainty of what the actual underlying dynamical system is, it is hence inappropriate to conclude that the data — by itself — shows metastability. Instead, what one can conclude is that some data is consistent with metastability as quantified by a particular signature.

Entropy of the spectral density

An early attempt to characterise metastability in brain activity used a model of coupled chaotic oscillators, where groups of oscillators were connected via excitatory and inhibitory connections, and the groups were linked with only excitatory connections [9,27]. The metastability of this system was estimated by calculating the entropy of the spectral density time series, which led to the following measure:
H = l o g ⁡ ( 2 π e m   d e t C o v g ( w , t ) / 2 ,
where m is the number of oscillators, ω is the frequency of each oscillator, Cov{g( ω ,t)} is the covariance matrix of the spectral density, and det is the determinant. The main intuition behind this proposal relates to the dynamic modulation of frequencies as observed say, in self-paced movement [28] — similar to what was found by Niebur [29,30]. It was expected that the spectral density of the model would change over time, and the changeability (as captured by the entropy) of the spectral density was therefore proposed as a marker of metastability. However, for this measure to be of practical use, the frequency range in a experimental modality should match the frequency range in the model, which is not always the case for example, in the case of functional MRI data.

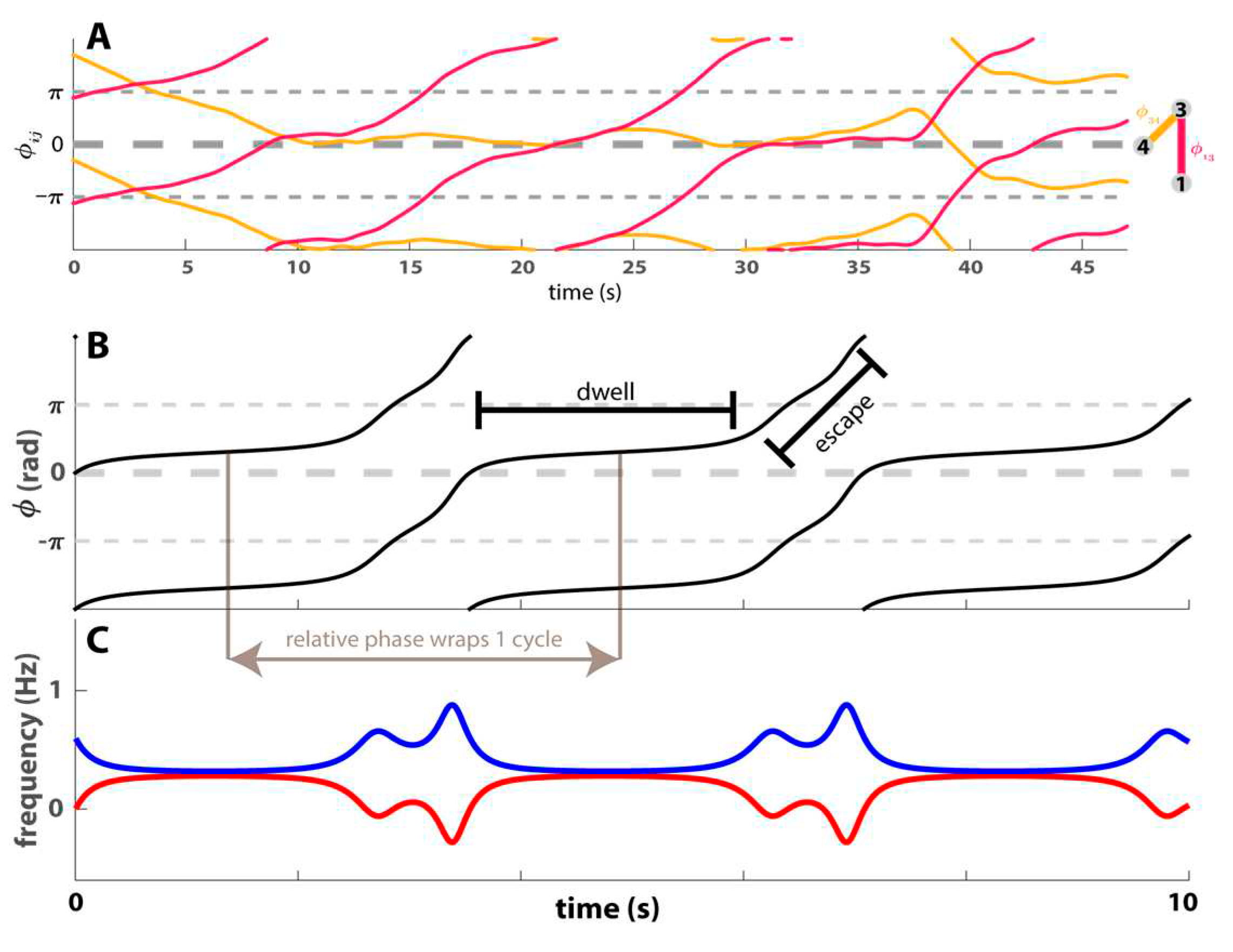
Ratio between dwell and escape time

A second signature of metastability builds on a posited relationship between metastability and the timescales associated with dynamic patterns of dwelling and escaping from quasi phase-locked states, hypothesized to represent the balance between integration and segregation. This measure is based on the concepts of dwell and escape times — dwell time is the time the relative phase remains relatively constant, and escape time is the time to ‘escape’ a dwell period and move to another dwell period, i.e., it is the time between successive dwellings. Then, the tendency of the system towards integration is identified by its average dwell time, and its tendency for segregation with its escape time. A marker of metastability may then be built via via the ratio of these two quantities [31]:
k = dwell time / escape time.
Clearly, as this ratio gets greater and greater, the system stays longer and longer near a phase-locked, highly integrated state (and consequently, as the ratio gets smaller the greater the likelihood for total independence or segregated activity).

Variance or standard deviation of the Kuramoto order parameter

A third signature of metastability, derived from classical measures of synchrony in a population of oscillators [32] captures the temporal variability of phase relationships in a system. This approach is built on the Kuramoto model of weakly coupled oscillators, for which its instantaneous phase synchrony (iPS) at time t, Π t is defined as the absolute value of the complex-valued Kuramoto order parameter (KOP) (see Appendix C).
Π t = 1 N ∑ j   e i ∅ j ( t )   = 〈 e i ∅ j ( t ) 〉 ,
where ∅ j ( t ) denotes the phase of oscillator j at time t. The iPS is bound between 0 for a fully desynchronized state and 1 for a completely synchronised state. Building on this order parameter, a signature of metastability can be then defined as the temporal variance of iPS within a community, σ met(c) [33]
σ m e t c = 1 T − 1 ∑ t ≤ T ( i P S c t − i P S c T ) 2 ,
which captures the heterogeneity of phase patterns exhibited by the system over its temporal evolution. See Supplementary video 1 for the behaviour of the Kuramoto model and the signatures of metastability, replicated from [33].
This signature of metastability has found extensive applications, spanning both computational models and empirical studies [34,35,36,37,38,39,40,41,42,43,44]. However, one should keep in mind that this marker only captures the variability of the mean phase of synchronous system states, while being insensitive to potentially relevant anti-phase synchrony (discussed in the subsequent section).

Standard deviation of the average spatial coherence

A fourth signature of metastability is a variation of the previous one but adapted for cases such as fMRI data, where the number of time points is often insufficient to properly measure phase synchrony as in [33] or signal coherence using methods such as wavelet coherence as in [45]. In such scenarios, one first considers the spatial coherence of the system, i.e., how the signal changes as a function of distance [46]. This can be denoted as V(t) and calculated via
V t = 1 N ∑ i = 1 N S ( t ) i − S ¯ ( t )   ,
where S i is the signal for an individual region, and S ¯ is the spatial mean.
Then, a signature of metastability is defined as the standard deviation of V across time. V is actually a measure of chimerality [33] and the reciprocal of mean V across time is used as a proxy for synchrony.

Variance of functional connectivity

Interpreting metastability as the repertoire of configurations visited by a system over time, the variance of the temporal evolution of functional connectivity has been proposed as a signature of metastability [47]. When functional connectivity is calculated with Pearson correlation, the time evolution of “global cohesion” or mean functional connectivity is obtained through windowing the time series. The variance of this time series provides a signature of metastability. If functional connectivity is calculated with instantaneous phase differences, then the first eigenvalue of the instantaneous functional connectivity matrix, the “spectral radius”, provides a measure of the total amount of variance in the first eigenvector. The variance of the temporal evolution of the spectral radius has been proposed as a signature of metastability [48].

Fluctuation of relative frequency

Another signature of metastability was proposed in the context of a “human firefly” experiment, where a broad range of movement frequencies was explored in the setting of social coordination [49]. This signature measures the amplitude of frequency fluctuations caused by the dwell-escape dynamics of the relative phase (see Supplementary video 2). This measure was based on the observation that in a metastable regime, whenever the order parameter (the relative phase ∅ i j ) , wraps around one cycle (goes through 2 Π ), the relative instantaneous frequency (proportional to the time derivative of the relative phase) will fluctuate (dwell and escape) at least once near the remnant of the in-phase attractor (whether it fluctuates at the antiphase remnant depends on other parameters), since by definition a dwell (escape) is characterised by an decrease (increase) of the relative instantaneous frequency (Figure 2 B-C). Thus, the relative frequency should fluctuate at the rate of relative phase wrapping, which can be assessed by the Fourier transform of the relative frequency time series. This gives rise to the following definition of the metastability index (MI) [49]:
M I = P Δ F i j w i n d ( ∅ i j ) T ,
where 𝑃[Δ𝐹𝑖𝑗] is the power spectrum of Δ𝐹𝑖𝑗, the relative instantaneous frequency between participant i and j (e.g., difference between two curves in Figure 2C), w i n d ∅ i j = | ϕ ( T ) − ϕ ( 0 ) |     2 π is the winding number, w i n d ( ∅ i j ) T is the rate at which relative phase is wrapping, ∅ is the unwrapped relative phase, that is, appropriate multiples of 2𝜋 are added to each phase measurement to reconstruct the original phase, and T is the length of the trial over which the metastability index is being calculated. In essence, MI measures the amplitude of frequency fluctuations caused by the dwell-escape dynamics of the relative phase. A higher MI indicates a more pronounced differentiation between dwells and escapes, interpreted as stronger metastability.

Variance of the Leading Eigenvectors

There have been several studies simultaneously investigating the relationship between time-varying functional connectivity and metastability [37,42,52], where the former is assessed via a phase-based correlation function (usually c o s ( ∅ m − ∅ n ) ), and the latter is estimated using the Kuramoto order parameter. However, it is not straightforward to align the nature of time-varying functional connectivity based on relative phase on the one hand, and metastability based on average phase on the other.
In an effort to overcome this methodological limitation, a new signature based on relative phase, VAR, was proposed [53]. Rather than using instantaneous phase synchrony, iPS, as in [33], this new signature leverages the cosine of the phase difference between brain areas, bound between [-1 +1] in the form of instantaneous phase-locking, iPL [37,42,54,55]. A signature of metastability was then defined as the mean temporal variance of iPL within a community,
V A R c = σ V 1 c ,
Where,
σ V 1 c = 1 T − 1 ∑ t ≤ T ( V 1 c t − V 1 c T ) 2 ,
Details for its calculation can be found in Appendix D. This signature of metastability was proposed as a candidate neuromechanistic biomarker of schizophrenia pathology.

Variance of the phase difference differential

The Phase Difference Differential (PDD) was created to identify instances of phase desynchronization in high-dimensional systems of chaotic attractors (PDD) [56]. Instantaneous phase was extracted with the Hilbert transform, and instantaneous phase differences were calculated. Phase desynchronisation occurs when these phase relations change, and the PDD captures the speed of these changes, that is the derivative exceeds a threshold ≈ 0. High values of PDD indicate rapid desynchronisation. Similar to [49,53] the variable of interest is relative phase, in this case the derivative rather than the cosine or the relative phase itself. Therefore, analogue to VAR, the variance of the PDD could be a valid signature of metastability in high-dimensional systems of chaotic attractors (See Technical Appendix).
In summary, we have seen that there are many ways to define and attempt to quantify proxies for signatures of metastability. The most popularly used indicator based on the Kuramoto order parameter, can be credited with facilitating numerous important empirical findings, computational modelling insights, and popularising the study of metastability in the general neuroscientific community. Recent signatures embed the notion of relative phase, rather than mean phase, in their definition, returning to the origins of metastable coordination dynamics and in congruence with chaotic itinerancy.

Metastability in computational neuroscience

Metastability has been explicitly, and sometimes implicitly investigated in a wide range of computational models related to the brain. In this section we review a selection of computational studies, highlighting the dynamical route to metastability and resulting characteristics found in the studies. We also identify instances where terminology may have caused confusion for non-experts. For those readers wishing to understand the different routes to metastability at a deeper level, we provide an accompanying Technical Appendix.

Metastability in Coordination Dynamics

Metastability in coordination dynamics appears as relatively long periods of phase entrainment where phases are ‘almost in-sync’, a behaviour called ‘relative coordination’, interrupted by rapid bursts of phase desynchronisation. The Synergetics (see Technical Appendix) framework was used to develop a mathematical model, the Haken-Kelso-Bunz [HKB: 57] which captured these, and other dynamics. As observed in experiments on human bimanual coordination [22] at certain frequencies the model exhibited bistability, while only monostability remained beyond a critical frequency [57]. Extensions to the original model showed that ‘critical fluctuations’ initiated the transition from symmetric to anti-symmetric rhythms at a critical frequency value [58]. A further extension, to take account of symmetry breaking when a metronome provided the rhythm frequency, discovered the metastable behaviour of epochs of relative coordination interspersed with loss of entrainment in the absence of noise. This behaviour was found when the control parameter, that is the frequency of the metronome, had a value just beyond the critical value which corresponded to a saddle-node bifurcation. Although the original fixed point no longer existed, trajectories remained attracted to where it once was exhibiting bifurcation memory or a ghost [23]. The original model and its extensions are described in Technical Appendix, and the resulting dynamics are illustrated in Figure 3.
When the metronome experiment was repeated simultaneously with superconducting quantum interference device acquisition (SQUID) and the dominant spatial dynamics investigated [6], the signal dynamics observed in the brain closely resembled a model of chaos [60], where the actual trajectories of the main spatial pattern displayed the geometry of homoclinic loops [61].

Noise-driven metastability with time delays

One of the earliest reports of metastability is related to investigations of the effect of finite transmission speed in a neural network represented by nonlinearly coupled oscillators [29,30]. The studied system consisted of oscillators with different intrinsic frequencies, time-delayed nearest-neighbour coupling, and noise were simulated on a 128x128 square lattice. While at small delay times the system exhibited a decrease in the collective frequency, larger delay or coupling values lead to metastable frequency-synchronised states were found, characterised by a zero relative phase between the oscillators. Increases in noise level triggered transitions destabilising the synchronisation, which was accompanied by discrete increases in the relative phase by odd integer values of pi/2.
Although the noise-induced switching exhibited by this system is reminiscent of multistable switching, the stationary solutions (calculated analytically) showed that only the absolute stable state was the one representing the final collective frequency, while all other solutions were metastable. It is, therefore, reasonable to explain the metastability exhibited by this system as being noise-driven.

Hidden faces of metastability

Hansel et al. (1993) investigated a model of weakly coupled Hodgkin–Huxley neurons [62] with noise [63]. This Hansel-Mato-Meunier model exhibits pairs of unstable 2-cluster states at saddles connected through a heteroclinic loop. However, before stabilising into this two-cluster state, the transient dynamics displays limited spontaneous switching between the 2 clusters. While the time between switching increased following each switch, the switching state stabilised (exhibiting slow switching) under the presence of a small noise factor. See Supplementary video 3 for the behaviour of the model. Kori and Kuramoto (2000) [64] showed that this behaviour was also present in a Hindmarsh-Rose model of neuronal bursting [65] also with time delayed coupling, and demonstrated that the slow switching could be invoked when the time delays were randomly distributed or the uniformity of the coupling was broken [64].
Although these two studies simulated heteroclinic cycles between saddles (see Figure 1), the saddles were not associated with metastable states, nor were the heteroclinic cycles associated with metastability in the original publications. As neither of the models look at the dynamics among the basic elements i.e., neuronal ensembles, it is not possible to investigate the dynamical origin of the saddles. However, later studies on extensions of the original Hansel-Mato-Meunier model found repeated sequential visits to metastable clusters facilitated by a heteroclinic network [66]. We revisit both the Hansel et al. and the Kori & Kuramoto models in a later section.

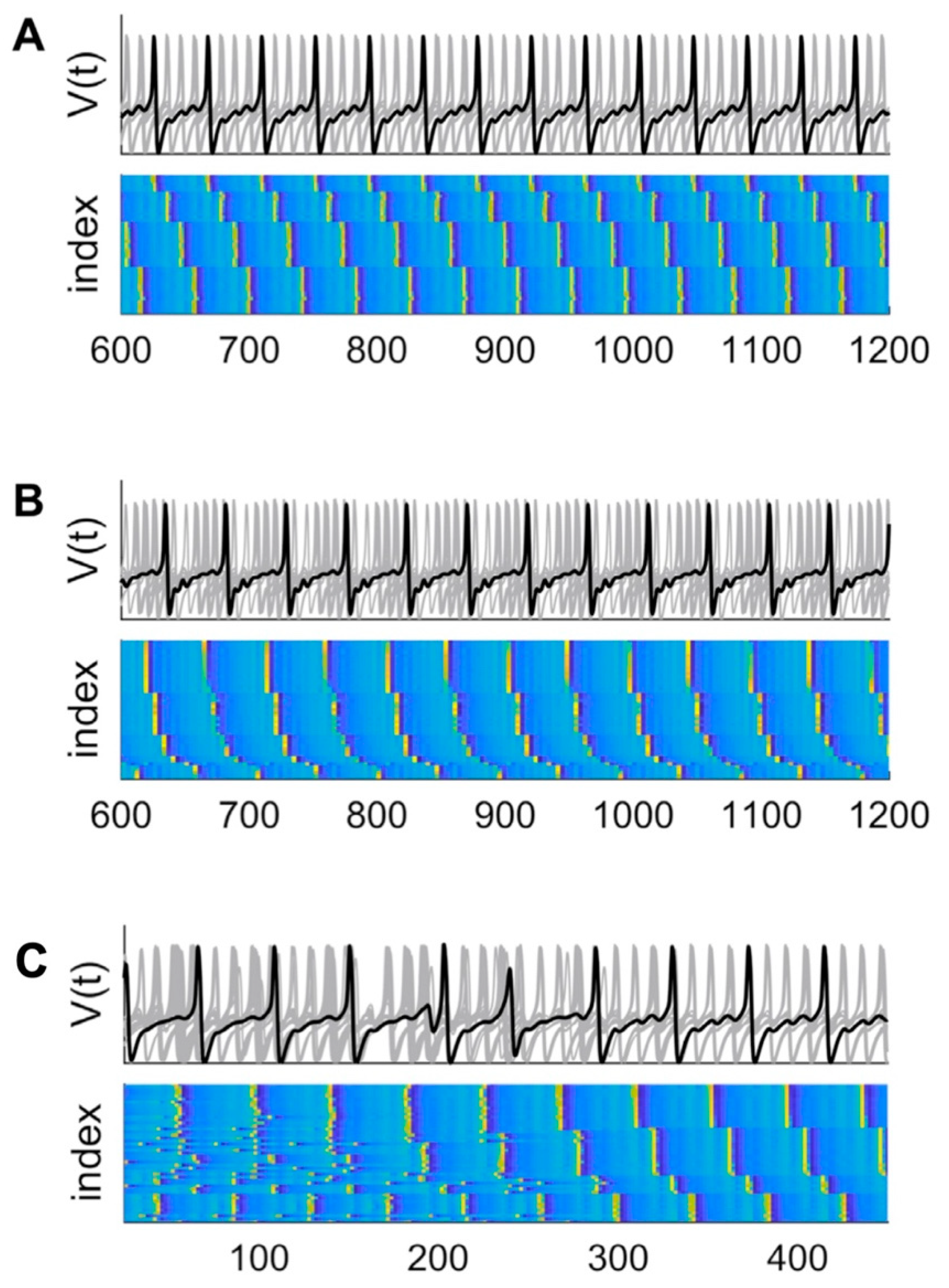
Metastability in neural mass models

Complex dynamics suggestive of metastability have been found with chaotic attractors in local [67] and whole brain neural mass models (NMM) [68]. These dynamics include the appearance of phase-shifted synchronised clusters and alliance switching among these clusters in a conductance based model [69] parameterised to exhibit chaotic behaviour.
Phase-shifted synchronised clusters are internally synchronised but have a phase-offset to other clusters. Clustering in high-dimensional chaotic systems has been proposed to arise due to competition between local chaos (sensitivity to initial conditions leading to divergence of orbits and desynchronisation) and global averaging (global coupling leading to synchronisation) [70]. In the reduced NMM, subsystems with the most similar parameter values were found to synchronise into clusters of various sizes [67]. In the whole-brain NMM created with the CoCoMAC connectivity diagram of the macaque brain [71], different ranks of clusters were found which depended on parameter settings for internode coupling c, and time delays t [68] as illustrated in Figure 4A-B.
The formation and subsequent spontaneous desynchronisation of large clusters was observed in the reduced NMM with 12 nodes and C=0.09 [67]. When clusters merge the dimension of the synchronisation block (synchronisation manifold with dimensionality equal to the number of clusters) decreases, but the dimensions of the transverse blocks increases [72] which could explain the observation above. Additionally, all clusters in the reduced NMM with c=0.12 desynchronised and synchronised on perturbation of a single node, and synchronisation could be induced by selectively increasing coupling between subsystems [67]. Subsequently, a quantitative measure for measuring phase synchronous dynamics and desynchronisation bursts in both the temporal and spatial domains, the phase desynchronisation derivative (PDD), was developed which demonstrated phase-clustering and desynchronisation in human scalp-recorded EEG from 40 subjects [56]. Additionally, nodes were found to change their cluster alliance in the whole-brain NMM for weak coupling and/or shorter time delays (c=0.45, t = 5 ms). See Figure 4C. These two studies are congruent with the mechanism of metastability realised through “chaotic itinerancy” (see Technical Appendix).

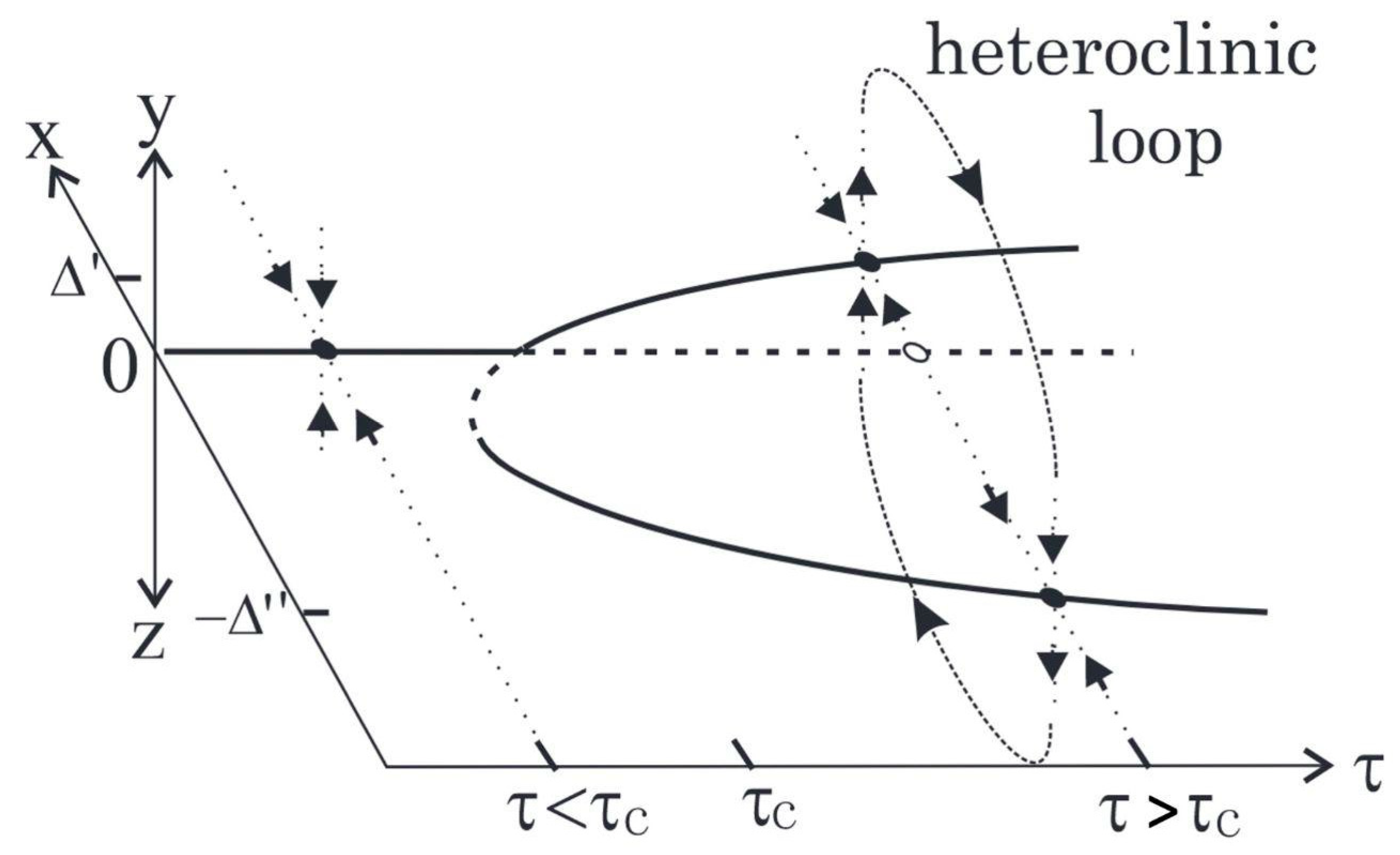
Metastability with saddles — Winnerless Competition

The role of saddles in escaping from metastable states is well acknowledged in statistical physics [73]. Saddles play a central role in a mathematical model for metastability where metastable states are saddles linked through their unstable manifolds, where noise induces transitions through a heteroclinic sequence confined within a stable heteroclinic channel (SHC) [10,74,75]. SHC have been shown to be repeatable and robust to noise while remaining sensitive to informational input, and have been proposed to support cognitive and emotional processes [76]. The underlying model of neuronal activity is based on the winnerless competition principle [74]. Cognitive modes, consisting of specific collections of neuronal groups, are in constant competition for dominance, where each mode becomes the winner periodically. It has been proposed that sequential switching among saddles reflects this principle. Using a generalised Lotka-Volterra model which is the canonical model for Winnerless Competition (WLC) in the evolution of species, reproducible robust transient sequential activity within a SHC with 3 competing modes was demonstrated [10]. This model can be used to explain how such dynamics can be robust to noise and reproducible, while the nature of the saddles ensures flexibility. Metastability may be seen as a delicate balance between robustness and flexibility. Although clusters are not considered specifically in SHCs, they have been demonstrated in stable heteroclinic cycles in a WLC model [77].

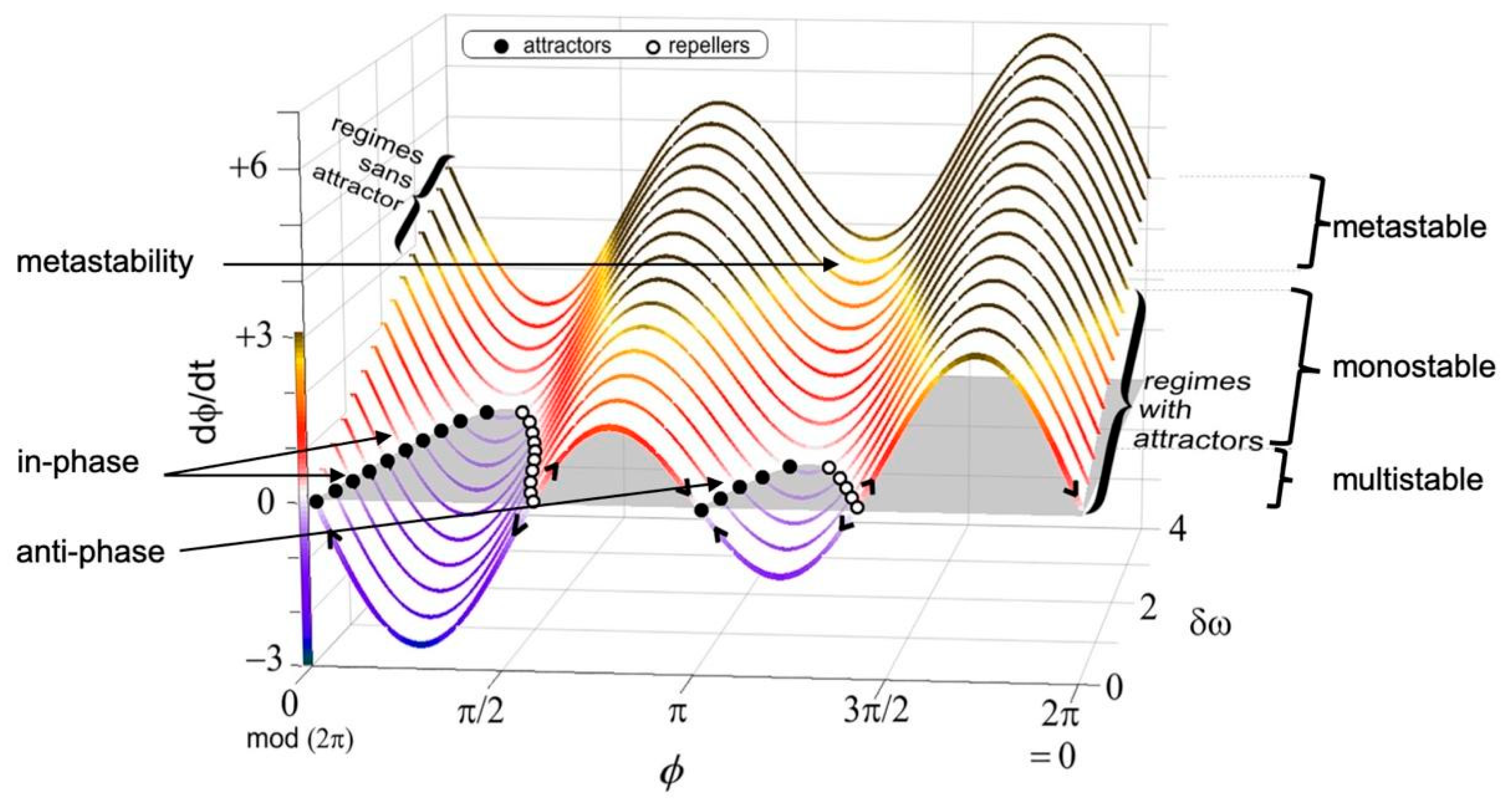
Metastability in models of coupled oscillators

Metastable “chimera” states [78], where synchronisation and desynchronisation coexisted, were found in a Kuramoto model with symmetrically coupled identical phase-lagged oscillators — which we call the Shanahan model [33].
This computational model was developed to investigate the mechanisms of conscious and unconscious processing in the brain [79]. Building on the global workspace theory, conscious processing is posited to entail competition between coalitions of specialist processes to access the global workspace and disseminate or broadcast their influence throughout the brain [80,81]. Membership of a coalition is dynamic, competitive, and variable, and coalition formation is open-ended and combinatorially large (coalitions that are not in competition may co-exist). As a proof of concept of these ideas, the Shanahan model (2010) exhibited dynamics of coalition formation and competitive queuing or a “winner takes all” principle. In the framework of chaotic itinerancy [79], coalitions are determined by clusters found in the partially ordered phase between the ordered and turbulent phases [82]. The same cluster may have different successors on different occasions, which allows rapid parallel searching of the cluster repertoire to either revisit a previous cluster or generate a new successor. Combinatorial possibilities of clusters or coalitions have been considered to be constrained by the maintenance of a balance between functional segregation and dynamic integration, the extent of which is described as being a key signature of dynamical complexity [3,79,83,84].
Whilst the Shanahan model produced metastable chimeras, these metastable states arose only from in-phase synchronisation and transitions proceeded from disorder to partial order. Interestingly, previous modelling [68] demonstrated the coexistence of both in-phase and antiphase clusters in chaotic itinerancy as shown in Figure 4A-B, and exhibited transitions from disorder to partial order as illustrated in Figure 4D. This discrepancy can be accounted for by the form of the Shanahan model, which did not include any harmonic components. This point will be discussed in a later section. Additionally, the measure for quantifying metastability is based on average phase which subsumes antiphase relations into its calculation, and thus misses the contribution of antiphase coalitions. Thus, the measure for metastability based on the Kuramoto order parameter is indicative of metastability which facilitates flexible alternations between metastable states. This theoretical limitation has not reduced its comprehensive and successful application in empirical and computational modelling studies which we will visit in a later section.

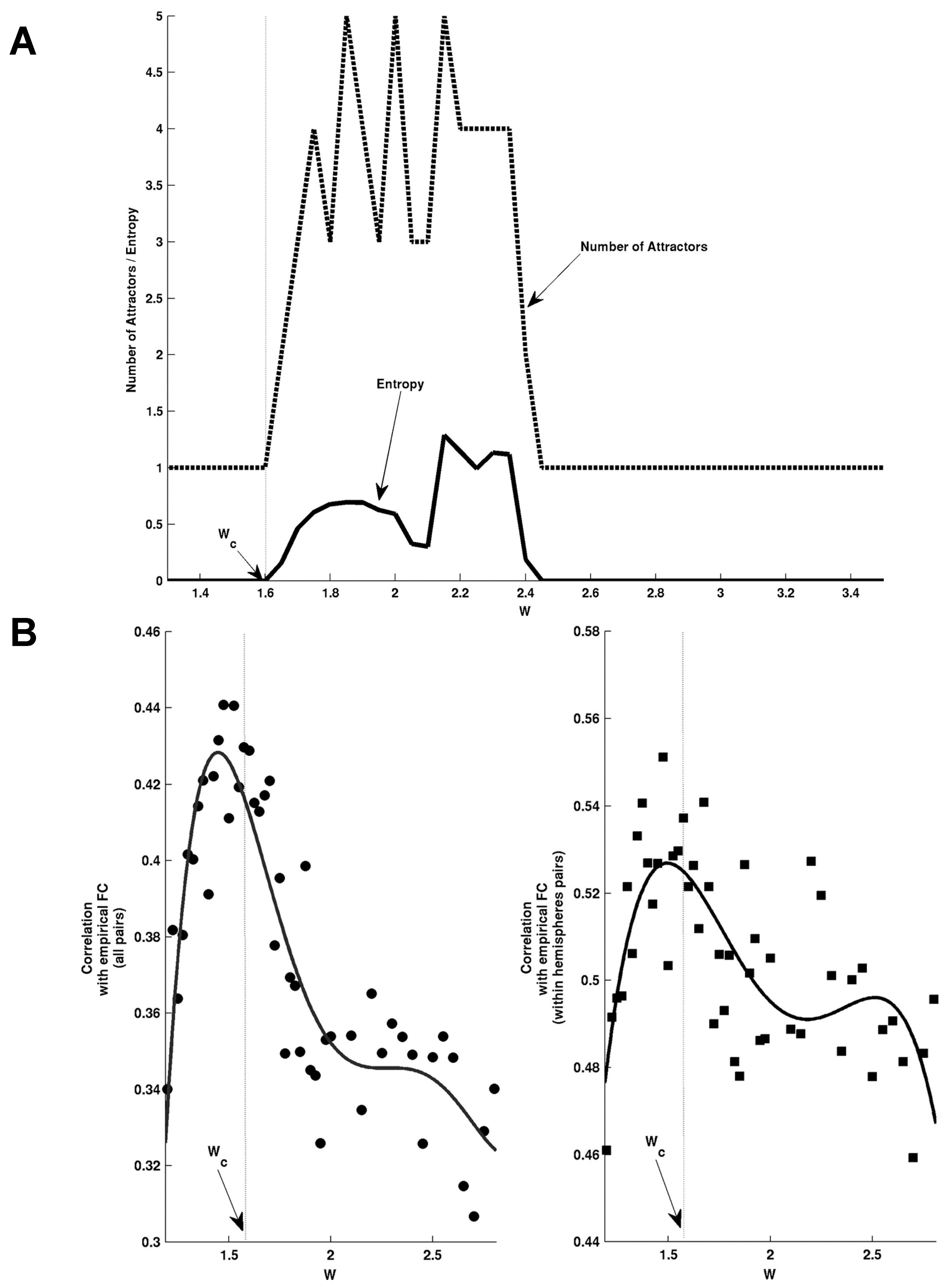
Multistable ghost attractors

Resting state functional connectivity, as observed e.g., in human fMRI data, has been proposed to be the result of fluctuations — i.e., noise-driven explorations — from one of many multistable states or attractors in a corticothalamic model [85] and a whole-brain model of neuronal activity [86]. Using a detailed physiological model for brain dynamics, a whole-brain global spiking attractor network model incorporating structural connectivity was fitted to empirical fMRI data [87]. Multistable attractors were extracted through iteration of the associated mean-field reduced spiking rate equations, to find fixed points (aka attractors) for different values of the global (inter-areal) coupling strength. The simulations suggested that a bifurcation occurred at a critical coupling value, at which the system went from 1 to many attractors (Figure 5A).
At the same critical value the best fit between empirical fMRI FC and simulated FC (estimated via the Balloon-Windkessel model [88]) was found with a Pearson correlation of around 0.52. These results suggested that rsFC was influenced by latent or “ghost attractors” (Figure 5B). That is, the multistable attractors beyond the bifurcation point induced structure in the noise-driven explorations or fluctuations at the brink of the bifurcation. Although the dynamics giving rise to the ghost attractors were considered to be due to Milnor attractors and chaotic itinerancy [89], they were referred to as ghosts which normally arise due to bifurcation memory.
The dynamics reported in this study [87] have on many occasions been associated with metastability [8,90], perhaps due to the unfortunate labelling of latent attractors (attractors not yet existing) as ghosts — a term that has been associated with metastability in human sensorimotor coordination where the attractors (coordinated states) have disappeared but trajectories remain attracted to where these attractors once resided – that is their ghosts [2,31,91,92,93]. Additionally, while the term “ghost attractor” may be a useful metaphor, it has to be noted that a ghost does not conform to the mathematical definition of an attractor [94]. It should also be noted that when the study was repeated with slightly different parameters and model reductions, the best fit with empirical FC was found for small fluctuations around the spontaneous state rather than fluctuations structured by the ghosts of multistable attractors [95].

Role of antiphase synchronisation

When markers of metastability are used to fit computational models to empirical data, the fitting may be biased to in-phase synchronisation, which risks ignoring the importance and relevance of anti-phase synchronisation. Indeed, it has been reported that anti-phase synchronisation in both models and experimental data sets, is a common phase relationship between separated cortical regions, and so congruent with large-scale cortical networks [96]. It may also be indicative of wave-like behaviour which has been found in computational models elsewhere [97]. Indeed, the subject of antiphase in neuronal networks has been the subject of investigation in rat cortex slice cultures [98] and computational models [96,99,100]. We can align several determinants of metastability with the findings of these studies. Starting with structural connectivity, a combination of resonance pairs, i.e., mutually coupled neuronal ensembles, and frustrated motifs, i.e., triads of coupled neuronal ensembles where 2 ensembles are in antiphase and 1 is in-phase, was shown to be required for metastability [96]. Antiphase synchrony was shown to arise from excitatory coupling, in-phase synchrony from inhibitory coupling, and inhibition suppressed antiphase patterns [98,100,101]. Moving on to propagation delays, antiphase synchrony was found to occur when time delays within an ensemble were shorter than between ensembles [100], and finally, coupling strength i.e., connectivity densities were found to stabilise antiphase synchrony [100]. Antiphase synchrony was considered necessary to distinguish coherent activity in one ensemble from another [100].

Identifying the determinants and moderators of metastability

In the effort to better understand what are the physiological aspects driving metastability in the brain, research have proposed several determinants and moderators of metastability, including connectivity-derived propagation delays [102], dynamic frustration caused by time-delayed interactions [96], global time-delays [64], network topology [33], heterogeneous intrinsic frequencies of neuronal ensembles [41,44,103,104], structural connectivity [35,38,105], and global coupling strength [103,106,107]. In the following sections, we look at the relationship between these determinants and moderators with differences in metastability signatures in three brain disorders and link them to disease symptoms. References to empirical studies are prefixed with the metastability signature investigated.
In a combined empirical and computational study of Traumatic Brain Injury, damage to structural connectivity was found to be associated with reduced metastability, and reduced cognitive flexibility and information processing [std spatial coherence: ,38]. Similarly, using connectomes derived from patients with Alzheimer’s Disease (AD) and Mild Cognitive Impairment (MCI), metastability was found to be reduced in both with concomitant reductions in cognitive performance, with larger impairment in AD relative to MCI [std KOP: ,35]. Congruent with these findings, an empirical study also found similar reductions in metastability for patients with AD, MCI, and Subjective Cognitive Impairment (SCI) (std KOP: ,[108]). These results confirm the role of structural connectivity in the determination and moderation of metastability and concomitant disease symptoms.
In contrast to AD, functional alterations reported in a study of patients with schizophrenia [107] were replicated in a computational model when global coupling strength was reduced [109], reflecting an overall reduction in the strength of white matter connectivity [110]. In agreement with these findings, global reductions in structural connectivity strength and topological changes in brain networks were reported for patients with schizophrenia [111]. Weak global coupling has been linked to reduced integration and increased segregation in a computational whole-brain model [112]. In a recent empirical study, both early psychosis and chronic schizophrenia patients showed reduced integration and increased segregation and metastability relative to healthy controls [VAR: 53]. Taken together, these results suggest that coupling strength, a determinant and moderator for metastability in computational models, reflects impaired white matter connectivity which leads to reduced global integration in patients with schizophrenia.
Although several studies investigated differences in metastability associated with pharmacological challenges [std KOP: ,42,std KOP: ,105] and sleep-wake states [std KOP 39], disentangling the relationship of the determinants and modulators of metastability with biophysical events such as neuromodulatory-invoked changes in coupling strength or topology, has not yet warranted scientific attention, although related studies may contribute to this understanding [113,114,115].
Understanding the biological underpinnings of metastability in psychiatric illnesses could help in treatment decisions, or the early identification of treatment resistance in depression or psychosis, and so transform signatures of metastability from theoretical curiosities to valuable candidate neuromechanistic biomarkers for psychiatric disorders.

The future

Here we describe potential lines for future developments related to metastability in neuroscience. First, we discuss avenues for theoretical improvements, and we then focus on possible empirical work.

Beyond metastability — Turbulence

Turbulence, when a smooth flow breaks up into whorls and eddies, has been found to provide a fundamental principle governing optimal mixing and efficient transfer of energy/information over space and time [116].
Preprints 80060 i001 “Big whorls have little whorls
Which feed on their velocity,
And little whorls have lesser whorls
And so on to viscosity.”

[117]
Recent research has shown how the brain is turbulent and how the scale-free nature of turbulence provides a dynamical regime where hierarchical information cascades allow the brain to function optimally despite its relative slowness [118,119,120]. Turbulence has been demonstrated in fast local field potentials in local brain regions [121] as well as in whole-brain dynamics measured with magnetoencephalography [122].
A key insight relating metastability and turbulence comes from Kuramoto's pioneering research, which showed that models of coupled oscillators can be used to capture turbulence in many other systems [32]. He showed that the Kuramoto order parameter can be extended to include information about space to provide a measure of spatiotemporal metastability, as the variability across spacetime of the local Kuramoto order parameter R [123]. Specifically, Rn(t), is defined as the modulus of the local order parameter for a given brain node as a function of time:
R n t e i v n t = ∑ p C n p ∑ q C n q e i ϕ p ( t ) ,
Where ϕ p ( t ) are the phases of the timeseries and Cnp is the anatomical distance rule connectivity matrix
C n p = e − λ ( r ( n , p ) ,
and r(n,p) is the Euclidean distance between regions n and p, and λ the decay.
In other words, Rn defines local levels of synchronisation at a given scale, λ , as function of space and time. This measure captures what could be called brain vortex space, Rn, over time, inspired by the rotational vortices found in fluid dynamics, but of course not identical.
As such, the level of amplitude turbulence D can be defined as the standard deviation of the modulus of Kuramoto local order parameter and can be applied to the empirical data of any physical system. The amplitude turbulence [124], D, corresponds to the standard deviation across time and space of R:
D = R 2 − R 2 ,
where the brackets < > denotes averages across space and time. This measure has been used to show turbulence in relatively slow neuroimaging fMRI data using a parcellation of 1000 regions (Cruzat et al., 2022; Deco, Kemp, et al., 2021; Deco, Sanz Perl, et al., 2021; Escrichs et al., 2022).
In other words, local metastability is measuring the local vorticity and is in essence an extension of the concept of global metastability (Kawamura et al., 2007), introduced in neuroscience to measure the variability across time of the global level of synchronisation of the whole system described here (Cabral et al., 2014; Kitzbichler, Smith, Christensen, & Bullmore, 2009; Kuramoto, 1984; Shanahan, 2010; Tognoli & Kelso, 2014; Wildie & Shanahan, 2012).
However, in order to show turbulence in fast neuronal dynamics of magnetoencephalography which has less good spatial resolution, a new edge metastability measure was introduced (Deco et al., 2023). This metric captures phase difference rather than mean phase and is defined as the standard deviation of the edge centred matrix E. In this matrix, each column corresponds to a time point t, where the column is defined as a vector combining all pairwise combinations of the differences of the phases’ state at time t. With N parcels this results in N(N-1)/2 pairs. The difference of the phase state at a given time point t for the different pairs is given by:
E i , j t = ( c o s ⁡ ( ϕ i t ) − c o s ⁡ ( ϕ j t ) ) 2 + ( s i n ⁡ ( ϕ i t ) − s i n ⁡ ( ϕ j t ) ) 2 ,
Where i,j are the parcels in a given parcellation. The edge metastability is thus the standard deviation across space and time of the edge-centric measure.
As such, the concepts of local and edge metastability in brain dynamics provide a way of generalising vorticity in fluid dynamics of the brain.

Beyond first order coupling in the Kuramoto model

The Kuramoto model [32] consists of a population of N coupled phase oscillators φ i (t) with natural frequencies ω i , whose dynamics are governed by the following equation:
d φ i / d t = ω i + ε N ∑ j = 1 N s i n ⁡ ( φ i − φ j )     ,
As discussed in the previous section, the variance of the instantaneous phase synchrony (i.e., the variance of the modulus of the complex-valued Kuramoto order parameter) is one of the most popular signatures of metastability [33]. However, by construction, the corresponding order parameter is a mean-field value for in-phase synchrony — in other words, this measure of metastability only takes into account mean phase synchronisation, and other types of patterns (e.g., anti-phase) are neglected [53,125]. Therefore, the switching within the metastable regime considered by this signature only includes changes between disorder and partial order where in-phase cluster synchronisation and desynchronisation coexist, and ignores partial order where in-phase and antiphase clusters coexist with low desynchronised activity [68,82]. We will see in the next section that it is necessary to expand the Kuramoto model used in [33] to allow for antiphase cluster synchronisation.

Kuramoto model with 2 Fourier modes

In the Hansel-Mato-Meunier model [63], the canonical Kuramoto model was extended to include the 2nd Fourier mode in a model of weakly excitatory, synaptically coupled Hodgkin–Huxley neurons with phase lag. A similar modification was applied in a Hindmarsh-Rose model of neuronal bursting with-time delayed coupling [64]. The general form of the extended model is:
d φ i d t = ω + g 1 N ∑ j = 1 N Γ φ i − φ j + η i ( t ) ,
A coupling function of the form:
Γ ( θ ) = − s i n ( θ + α ) + r s i n ( 2 θ )
was used by Hansel et al. (1993), where θ = ( φ i − φ j ) is relative phase, α de-phases the relative position of the two modes which is similar to introducing a time delay, r modifies the contribution of the second order antiphase locking term, and the positive sign serves to destabilise the antiphase attractor. Three types of dynamics were found in the model: a fully synchronised state with one cluster, a totally incoherent state, and pairs of two-cluster saddle states linked by heteroclinic loops. Switching between in-phase and anti-phase synchrony in a 2-cluster state was observed in the transient dynamics before the system stabilised into 2-phase-locked clusters with a fixed phase-offset. The switching behaviour was dependent on the control parameter α which controlled the phase lag, or equivalently the time delay of the oscillators. Adding a small noise term led to a slow periodic switching between the two-cluster states, where the frequency of oscillations was proportional to the logarithm of the noise intensity (see Supplementary Video 3).
Building on the work of Hansel [63], Kori & Kuramoto [64] developed a second phase reduced model based on the Hindmarsh-Rose oscillator model of neuronal bursting [65,126] which included a time-delay as a phase shift [64]. The coupling function of the phase-reduced model was determined numerically. In this model, when the oscillators clustered non-symmetrically, a saddle-node bifurcation transferred stability to the unstable dimension of the saddle-node. A heteroclinic loop then linked these two solutions (Figure 6). They also found that slow switching could be induced by randomly distributing the time delay and/or breaking the uniformity in the coupling.

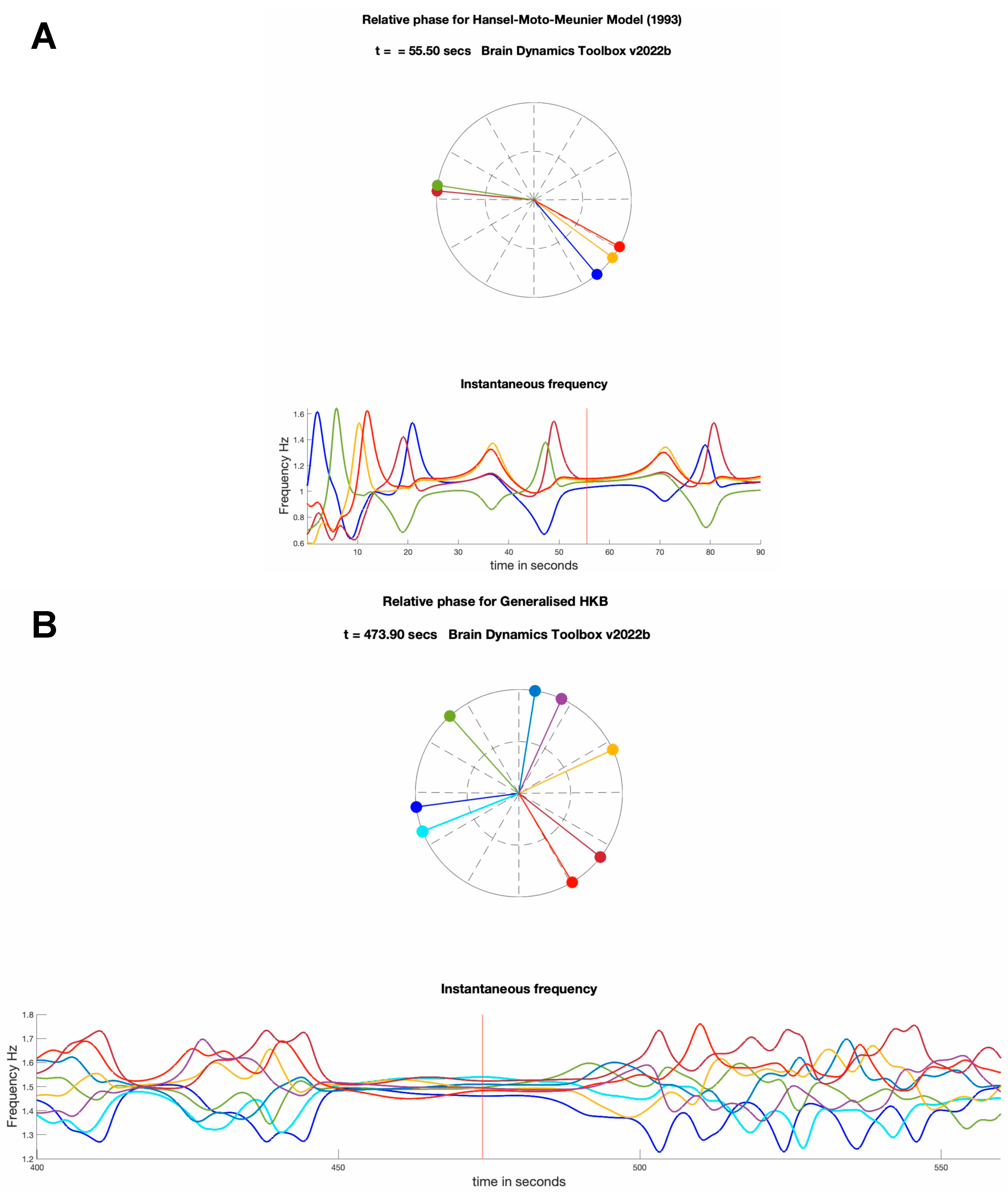
Generalised Haken-Kelso-Bunz model

Finally, we return to the roots of metastability in human movement coordination. The extended HKB model [23,127] was initially developed to model metastable coordination between two oscillatory components (for a review see [128]). More recently, driven by experimental observations of in-phase and antiphase coordination and metastability in multiagent interaction [49], a N-dimensional generalisation of the extended HKB model was developed [50,125], here referred to as the generalised HKB model. The equation of motion for the generalised HKB model has a coupling function that includes the first two Fourier modes:
φ i ˙ = ω i   − a ∑ j = 1 N s i n ϕ i j − b     ∑ j = 1 N s i n 2 ϕ i j  
where φ i is the phase of the i-th oscillator, ω i is the natural frequency of the i-th oscillator, ϕ i j = φ i − φ j is relative phase, and a and b are the first and second coupling parameter, respectively. The model was initially developed as a phase-oscillator model in the form above [50]. Later theoretical work confirmed that this phase-oscillator model can be derived from the N-dimensional van der Pol-Rayleigh oscillators model via phase reduction, thus consistent with the initial derivation of the dyadic HKB models [129]. Note that the second order coupling is negative (c.f. [63]), which stabilises the antiphase attractor. Adding the second order coupling was key to capture all experimental observations, which the canonical Kuramoto model could not (compare Supplementary videos 1 (Shanahan model) and 2 (generalised HKB model)). See the Technical Appendix for additional discussion of this model.
There is an assumption that the phenomenon of ghosts in dyadic interactions holds for higher dimensional interactions. The metastability in the Hansel et al., and Kori and Kuramoto models, was dynamically realised with heteroclinic cycles where the system slows down progressively as it approaches a saddle for longer periods between cycling. Interestingly, the intermittent converging behaviour of the General HKB model is not dissimilar from the Hansel et al. model, suggesting a similarity in the dynamics (see Figure 7).

Avenues for future empirical work

Metastability has been proposed as a principle of brain function that reflects the simultaneous tendencies for global integration and functional segregation. It would be interesting to see how signatures of metastability correlate with these tendencies in clinical groups, pharmacological challenge studies, and studies in disorders of consciousness.
Although many questions are still open on the nature of metastability, an interesting dilemma relates to the saddle-type feature that facilitates metastable dynamics in the brain - is it a ghost left after a saddle-node bifurcation, a destabilised Milnor attractor, or a conventional saddle, or even all three, when viewed from different levels of observation? [9]. Perhaps extending the Kuramoto model to include a second term to account for antiphase synchronisation provides a modelling framework where this dilemma could potentially be investigated.
Markers of metastability in empirical data tend to be time-averaged measures, and the underlying system has been shown to contain mono-, multi- and metastable regimes and transitions between them. Perhaps it would make sense to calculate these markers over windows of brain activity and compare the values with changes in similar windowed spatiotemporal patterns of activity, such as in time-varying functional connectivity. Investigating a time-varying marker of metastability at local, i.e., community level, and comparing across all communities, could identify if any particular community leads the transitions between mono-, multi- and metastability, if such regimes exist in the data.
The catchphrase terms of metastability and multistability are often used interchangeably and indiscriminately, as noted by [4,68] and [31] respectively. Before describing some observation as metastable, it would be helpful to provide the rationale for this description. For example, in [97], the brain waves found in a computational model were classified as metastable as they appeared and changed without any perturbation or added noise to the system, and transitions among metastable waves were identified through a interhemispheric cross-correlation function. Whilst a visual confirmation of metastability is possible with a limited number of oscillatory components as in [49], this solution is not tractable for whole-brain models with a large number of parcellated brain regions. However, it would be interesting to investigate the dynamics of the generalised HKB model [50,125] to look for evidence of ghosts or heteroclinic cycles, and subsequently develop a large-scale brain model using a network of coupled neural masses as in [97] to investigate if the dynamics are similar at larger scales (see [130]).
There are also many open questions about the relationship between metastability and biophysical properties of the brain. With the release of NeuroMaps [131], differences in local metastability could be mapped to myelination, metabolism, receptor and transmitter density, developmental expansion, or genomics. This could potentially provide insights into the biophysical underpinnings of metastability as it differs across psychiatric conditions, throughout healthy ageing, across disorders of consciousness and within development.
Specifically, we would like to establish the molecular, metabolic, physiological and cellular determinants of metastability, keeping in mind that one would expect these neurobiological factors to display not only reciprocal interaction but also bilateral relations with higher functions and environmental stimuli [132]. For example, pronounced propagation delays have been posited to hinder information integration [133]. Reduced integration has been found to strongly correlate with increased metastability [53]. Propagation delays are dependent on myelination, which in turn is linked to metabolism, and in particular oxygen tension [134]. Higher oxygen tension appears to favour the growth of neurons and oligodendrocytes, and a reduction in partial pressure results in thinner myelin sheaths [135]. Reduced myelination in left temporal white matter was found in patients with recent onset psychosis [136], and numerical density of oligodendrocytes was found to be significantly reduced in post-mortem studies, together with signs of compromised energy and redox metabolisms [137]. However, myelin plasticity [138] is modulated by astrocytes and microglia, and so one possible research question is to what extent glia contribute to metastability.
Another cellular question relates to the role of parvalbumin-expressing GABAergic interneurons in the generation of gamma-band oscillations which are altered in schizophrenia [139,140,141,142] and which drive neurovascular coupling [143]. The E/I ratio reflects a homeostatic plasticity that keeps the relative levels of excitatory and inhibitory drive within a narrow range for healthy functioning [144]. Alterations in the E/I ratio have been consistently found in schizophrenia [145,146,147,148,149], and the E/I ratio is posited to be dependent on continual adaptation of the synaptic strength of PV GABA interneurons [150,151,152]. The high metabolic demand required to maintain gamma oscillations puts strains on PV GABA interneurons making them susceptible to neuroinflammation and oxidative stress [134,151]. Immune gene expression analysis identified an immune fingerprint that could discriminate early psychosis from chronic schizophrenia and health controls [153], and both reduced antioxidant status and a pro-inflammatory imbalance were found with first-episode psychosis [154]. Brain metabolism in schizophrenia patients was modified with clozapine with concomitant improvements in symptoms. Metabolic activity measured with [18F]Fluoro-deoxy-glucose PET was found to be reduced in the prefrontal, motor, and basal ganglia, and promoted in the visual cortex with improvements in disorganisation, negative and positive symptoms [155]. Establishing whether any or all of the above cellular, molecular, and metabolic disease markers are determinants of metastability, could lead to improved understanding of the pathophysiology of schizophrenia, and potentially lead to new treatment targets.
Ultimately, the future of metastability as a theoretical construct rests upon demonstrating its causal roles in behaviour, cognition, and neuropsychiatric disorders, and the potential to leverage them in clinical settings. In the study of human movement coordination, metastability was often induced via causal manipulation of the control parameters, instrumentalized as, for example, pacing metronomes [49,156]. However, applications of the concept of metastability to common measures of neural activities have largely been observational, that is, without the causal manipulation of a control parameter guided by specific theoretical assumptions about the route to metastability (e.g., phase lag, delay, frequency differences). Developing methods to causally induce metastability in simultaneously measured brain activities in a theoretically predictable manner would further provide the opportunity to reveal the causal relationships between network specific metastability and cognitive functions and psychiatric symptoms. Notably, non-invasive brain stimulation, such as transcranial magnetic stimulation (TMS) and transcranial alternating current stimulation (tACS), has become an increasingly important tool for probing the causal roles of different brain oscillations in cognition and psychiatric disorders, with applications in clinical treatments (e.g., the use of alpha frequency stimulation to reduce depressive symptoms [157,158,159,160]). Currently, rhythmic brain stimulations are primarily designed to engage or entrain endogenous brain oscillations at their natural frequency rather than to induce metastability. However, existing techniques in non-invasive brain stimulation are fully equipped to control delay in coupling and frequency differences between the stimulator and endogenous oscillations, which provides promising grounds for inducing metastability. How to control the metastable interaction between existing endogenous oscillations using one or more external stimulators remains an open theoretical question.
In summary, the aim of future research in this area should strive to predict the behaviour of metastability with computational models, and then, supported with biological understanding, look for ways to return metastability to a healthy regime through appropriate pharmacological, psychotherapeutic, or non-invasive brain stimulation control strategies.

Concluding remarks

This paper provides a broad overview of the concept of metastability, reviewing its past and present, and exploring some possibilities for its future. Specifically, we have traced the historical foundations of metastability from the concepts of Synergetics and Coordination Dynamics and looked at alternative routes to metastability including bifurcation memory, chaotic itinerancy, and stable heteroclinic channels in computational models of brain activity. Moreover, we have explored a range of signatures of metastability, reviewing in detail the ones that have led to most of the important and insightful empirical and computational results in the last decade.
In principle, metastability offers a conceptual framework to think rigorously about phenomena that result from underlying heterogeneity related to structural connectivity, anatomical distance, and/or intrinsic neuronal ensemble frequencies. Metastability has been found to be associated with many forms of neural brain complexity [37], but cannot be reduced to any of them — in particular, metastability is not the same as criticality, as signatures of the former provide measures of time-averaged variability in an order parameter or variable of interest, whereas signatures of criticality are temporally variable and intermittently peak at second-order phase transitions [161,162].
Metastability is a fascinating dynamical phenomenon that has been pursued from the perspective of low-, medium-, and high-dimensional systems. Dynamical phenomena consistent with signatures of metastability guide computational model-fitting and offer potential biomarkers for neuropsychiatric disorders. We have brought together seemingly diverse accounts of the concept of metastability in brain activity to collectively contribute to a community-level understanding of the concept, and so encourage further research and collaboration across interest groups.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Glossary

Dynamical systems theory
A branch of mathematics that studies how the state of systems evolve over time based on either an analytical (pencil and paper), or a geometric (shapes), or a numeric (approximations using a computer) study of deterministic evolution equations.
The state of a dynamical system
A vector representation that fully determines the value of its variables (e.g., the position and velocity of a given particle). The temporal evolution of the state of a dynamical system can be mathematically described by a difference (i.e., discrete) or differential (i.e., continuous) equation.
Phase space
The set of all possible states, and hence contains all the allowed combinations of values of the system’s variables (also known as state variables).
Trajectory of the system
A sequence of states within the phase space that satisfy the dynamics of the system as defined by its differential equation.
A phase portrait
A geometric representation of the trajectories of a dynamical system.
Potential landscape
The state space of some dynamical systems can be illustrated by a potential landscape, where valleys/dwells represent stable fixed points which correspond to attractors, peaks represent unstable fixed points which correspond to repellers, and balls represent the states of the system.
Manifold
A geometric model that can represent a broad range of shapes. While at each point of a manifold it looks like a flat, n-dimensional (euclidian) space, their overall structure can be highly non-trivial. The dimensionality of the manifold, n, is the same for all its points.
Equilibria or fixed points
Points in the state space where the rate of change of the system with respect to time is equal to zero, corresponding to states at which the system remains unchanged unless perturbed.
Attractor
When many trajectories converge to a set of states, that set is called an attractor.
Chaotic attractor
An attractor that holds dynamics that are highly sensitive to their initial conditions.
Basin of attraction
All the points in phase space that flow onto the attractor.
Repeller
A set of states from which many trajectories migrate.
Saddle Point
A fixed point that is stable in one direction but unstable in another, that is it behaves as an attractor for some trajectories and as a repellor for others.
Heteroclinic orbit or cycle
A path in phase space that links saddles
Homoclinic cycle (or loop)
A path that links a saddle back onto itself.
Control parameters
A parameter that modifies the system of differential or difference equations, hence deforming the corresponding flows through phase space.
Critical point
The value of a control parameter at which a bifurcation occurs.
Order parameter
A single variable that captures the collective or macro behaviour of a system composed of microscopic elements.
Saddle-node bifurcation
When a stable and an unstable fixed point collide and annihilate each other.
Bifurcation
A qualitative change in dynamics produced by varying a control parameter in a dynamical system.
Bifurcation diagram
A diagram follows how the landscape changes with the control parameter showing the location of attractors and repellers.
Phase transition
A concept originated from statistical physics. In general, a system is said to undergo a phase transition when a small change in a control parameter (e.g., temperature) causes a large collective change (e.g., the system going from liquid state to solid).
Non-equilibrium phase transition
A phase transition that occurs in a physical system—like the brain—that is far from equilibrium.
Synchronisation manifold
A smooth surface onto which the orbits of synchronised chaotic attractors converge.
Metastability
A specific type of dynamics that may take place in a system characterised by patterns that recur either in repeatable sequences (pattern) or flexible alternation (no pattern).
Global cohesion
Mean functional connectivity computed using Pearson’s correlation.
Spectral radius
The maximum of the absolute values of its eigenvalues for a square matrix.
Relative coordination
Where occasional slippages between coordinating components are balanced by an intrinsic attraction to certain preferred phase relations.
Critical fluctuations
As a control parameter approaches a critical point, fluctuations increase, and this enhancement of fluctuations signals an upcoming phase transition.
Bifurcation memory
Fixed points disappear after a saddle-node bifurcation, but the “memory” of the fixed point remains attractive for the system and the dynamics become very slow due to a bifurcation delay.
Ghost
Fixed points disappear after a saddle-node bifurcation, but the “memory” of the fixed point remains attractive for the system and the dynamics become very slow due to a bifurcation delay.
Chaos
A form of dynamical behaviour that can arise from time-invariant nonlinear system. Chaos is characterized by sustained aperiodic (nonrepeating) oscillations, leading to extreme sensitivity of future states to small changes in present values of the system.
Chaotic itinerancy
The behaviour of complicated systems with weakly attracting sets, where destabilised attractors allow the system to leave its basin of attraction for another through heteroclinic orbits.
Milnor attractor
An attractor that has lost asymptotic stability, that is, there exists a number of repelling sets.
Stable heteroclinic channel
A sequence of successive metastable (saddle) states in the phase space
Chimera state
A state that represents the co-existence of coherent and incoherent dynamics
Edge centric matrix
A matrix that contains the pairwise phase difference between brain regions stored in upper triangle format.

References

  1. Kelso, J.A.S. Dynamic patterns: The self-organization of brain and behavior; Dynamic patterns: The self-organization of brain and behavior; The MIT Press: Cambridge, MA, US, 1995; pp. xvii, 334; ISBN 978-0-262-11200-0. [Google Scholar]
  2. Kelso, J.A.S.; Tognoli, E. Toward a Complementary Neuroscience: Metastable Coordination Dynamics of the Brain. In Neurodynamics of Cognition and Consciousness; Perlovsky, L.I., Kozma, R., Eds.; Understanding Complex Systems; Springer: Berlin, Heidelberg, 2007; pp. 39–59. ISBN 978-3-540-73267-9. [Google Scholar]
  3. Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. 1994, 91, 5033–5037. [Google Scholar] [CrossRef]
  4. Cocchi, L.; Gollo, L.L.; Zalesky, A.; Breakspear, M. Criticality in the brain: A synthesis of neurobiology, models and cognition. Prog. Neurobiol. 2017, 158, 132–152. [Google Scholar] [CrossRef]
  5. Kelso, J.A.S. Coordination Dynamics of Human Brain and Behavior. In Proceedings of the Evolution of Dynamical Structures in Complex Systems; Friedrich, R., Wunderlin, A., Eds.; Springer: Berlin, Heidelberg, 1992; pp. 223–234. [Google Scholar]
  6. Fuchs, A.; Kelso, J.A.S.; Haken, H. Phase transitions in the human brain: spatial mode dynamics. Int. J. Bifurc. Chaos 1992, 02, 917–939. [Google Scholar] [CrossRef]
  7. Kryukov, V. The metastable and unstable states in the brain. Neural Netw. 1988, 1, 264. [Google Scholar] [CrossRef]
  8. Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
  9. Friston, K.J. Transients, Metastability, and Neuronal Dynamics. NeuroImage 1997, 5, 164–171. [Google Scholar] [CrossRef] [PubMed]
  10. Rabinovich, M.I.; Huerta, R.; Varona, P.; Afraimovich, V.S. Transient Cognitive Dynamics, Metastability, and Decision Making. PLOS Comput. Biol. 2008, 4, e1000072. [Google Scholar] [CrossRef]
  11. Tsuda, I. Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems. Behav. Brain Sci. 2001, 24, 793–810. [Google Scholar] [CrossRef]
  12. Ashwin, P.; Postlethwaite, C. On designing heteroclinic networks from graphs. Phys. Nonlinear Phenom. 2013, 265, 26–39. [Google Scholar] [CrossRef]
  13. Tsuda, I. Chaotic itinerancy and its roles in cognitive neurodynamics. Curr. Opin. Neurobiol. 2015, 31, 67–71. [Google Scholar] [CrossRef]
  14. Rosas, F.E.; Mediano, P.A.M.; Luppi, A.I.; Varley, T.F.; Lizier, J.T.; Stramaglia, S.; Jensen, H.J.; Marinazzo, D. Disentangling high-order mechanisms and high-order behaviours in complex systems. Nat. Phys. 2022, 18, 476–477. [Google Scholar] [CrossRef]
  15. Haken, H. Cooperative phenomena in systems far from thermal equilibrium and in nonphysical systems. Rev. Mod. Phys. 1975, 47, 67–121. [Google Scholar] [CrossRef]
  16. Kelso, J.A.S.; Bressler, S.L.; Buchanan, S.; Ding, M.; Fuchs, A.; Holroyd, T. Cooperative and critical phenomena in the human brain revealed by multiple SQUIDS. In Measuring Chaos in The Human Brain; Duke, D.W., Pritchard, W.S., Eds.; WORLD SCIENTIFIC, 1991; pp. 1–266 ISBN 978-981-02-0701-4.
  17. Miets, H.A.; Chevalier, J. On the crystallization of sodium nitrate. Mineral. Mag. J. Mineral. Soc. 1906, 14, 123–133. [Google Scholar] [CrossRef]
  18. Shlosman, S. Metastable States. In Encyclopedia of Mathematical Physics; Françoise, J.-P., Naber, G.L., Tsun, T.S., Eds.; Academic Press: Oxford, 2006; pp. 417–420. ISBN 978-0-12-512666-3. [Google Scholar]
  19. Brinkman, B.A.W.; Yan, H.; Maffei, A.; Park, I.M.; Fontanini, A.; Wang, J.; La Camera, G. Metastable dynamics of neural circuits and networks. Appl. Phys. Rev. 2022, 9, 011313. [Google Scholar] [CrossRef] [PubMed]
  20. Holst, E.R.M. von The behavioural physiology of animals and man; : The collected papers of Erich von Holst; University of Miami Press: Coral Gables, Fla, 1973; ISBN 978-0-87024-261-8. [Google Scholar]
  21. DeGuzman; Kelso, J.A.S. The Flexible Dynamics of Biologial Coordination: Living in the Niche between Order and Disorder. In Principles Of Organization In Organisms; Mittenthal, J.E., Ed.; Addison-Wesley, 1992 ISBN 978-0-429-97218-8.
  22. Kelso, J.A.S. Phase transitions and critical behavior in human bimanual coordination. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1984, 246, R1000–R1004. [Google Scholar] [CrossRef]
  23. Kelso, J.A.S.; Del Colle, J.D.; Schöner, G. Action-perception as a pattern formation process. In Attention and performance 13: Motor representation and control; Lawrence Erlbaum Associates, Inc: Hillsdale, NJ, US, 1990; pp. 139–169. ISBN 978-0-8058-0565-9. [Google Scholar]
  24. Kelso, J.A.S.; Bressler, S.L.; Buchanan, S.; DeGuzman, G.C.; Ding, M.; Fuchs, A.; Holroyd, T. A phase transition in human brain and behavior. Phys. Lett. A 1992, 169, 134–144. [Google Scholar] [CrossRef]
  25. Pomeau, Y.; Manneville, P. Intermittent transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 1980, 74, 189–197. [Google Scholar] [CrossRef]
  26. Holden, A.V.; Kryukov, V.I. Neural Networks: theory and architecture. Manchester University Press; 1990.
  27. Friston, K.J.; Tononi, G.; Sporns, O.; Edelman, G.M. Characterising the complexity of neuronal interactions. Hum. Brain Mapp. 1995, 3, 302–314. [Google Scholar] [CrossRef]
  28. Pfurtscheller, G.; Aranibar, A. Evaluation of event-related desynchronization (ERD) preceding and following voluntary self-paced movement. Electroencephalogr. Clin. Neurophysiol. 1979, 46, 138–146. [Google Scholar] [CrossRef]
  29. Niebur, E.; Schuster, H.G.; Kammen, D.M. Collective frequencies and metastability in networks of limit-cycle oscillators with time delay. Phys. Rev. Lett. 1991, 67, 2753–2756. [Google Scholar] [CrossRef]
  30. Niebur, E.; Schuster, H.G.; Kammen, D.M. Systems of Relaxation Oscillators with Time-Delayed Coupling. In Neural Network Dynamics; Taylor, J.G., Caianiello, E.R., Cotterill, R.M.J., Clark, J.W., Eds.; Perspectives in Neural Computing; Springer London: London, 1992; pp. 226–233. ISBN 978-3-540-19771-3. [Google Scholar]
  31. Kelso, J.A.S. An Essay on Understanding the Mind. Ecol. Psychol. Publ. Int. Soc. Ecol. Psychol. 2008, 20, 180–208. [Google Scholar] [CrossRef] [PubMed]
  32. Kuramoto, Y. Mutual Entrainment. In Chemical Oscillations, Waves, and Turbulence; Springer Series in Synergetics; Springer Berlin Heidelberg: Berlin, Heidelberg, 1984; Vol. 19, pp. 60–88. ISBN 978-3-642-69691-6. [Google Scholar]
  33. Shanahan, M. Metastable chimera states in community-structured oscillator networks. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 013108. [Google Scholar] [CrossRef] [PubMed]
  34. Abeysuriya, R.G.; Hadida, J.; Sotiropoulos, S.N.; Jbabdi, S.; Becker, R.; Hunt, B.A.E.; Brookes, M.J.; Woolrich, M.W. A biophysical model of dynamic balancing of excitation and inhibition in fast oscillatory large-scale networks. PLOS Comput. Biol. 2018, 14, e1006007. [Google Scholar] [CrossRef] [PubMed]
  35. Alderson, T.H.; Bokde, A.L.W.; Kelso, J.A.S.; Maguire, L.; Coyle, D. Metastable neural dynamics in Alzheimer’s disease are disrupted by lesions to the structural connectome. NeuroImage 2018, 183, 438–455. [Google Scholar] [CrossRef] [PubMed]
  36. Deco, G.; Kringelbach, M.L.; Jirsa, V.K.; Ritter, P. The dynamics of resting fluctuations in the brain: metastability and its dynamical cortical core. Sci. Rep. 2017, 7, 3095. [Google Scholar] [CrossRef]
  37. Hancock, F.; Cabral, J.; Luppi, A.I.; Rosas, F.E.; Mediano, P.A.M.; Dipasquale, O.; Turkheimer, F.E. Metastability, fractal scaling, and synergistic information processing: What phase relationships reveal about intrinsic brain activity. NeuroImage 2022, 259, 119433. [Google Scholar] [CrossRef]
  38. Hellyer, P.J.; Scott, G.; Shanahan, M.; Sharp, D.J.; Leech, R. Cognitive Flexibility through Metastable Neural Dynamics Is Disrupted by Damage to the Structural Connectome. J. Neurosci. 2015, 35, 9050–9063. [Google Scholar] [CrossRef]
  39. Jobst, B.M.; Hindriks, R.; Laufs, H.; Tagliazucchi, E.; Hahn, G.; Ponce-Alvarez, A.; Stevner, A.B.A.; Kringelbach, M.L.; Deco, G. Increased Stability and Breakdown of Brain Effective Connectivity During Slow-Wave Sleep: Mechanistic Insights from Whole-Brain Computational Modelling. Sci. Rep. 2017, 7, 4634. [Google Scholar] [CrossRef]
  40. Lee, W.H.; Doucet, G.E.; Leibu, E.; Frangou, S. Resting-state network connectivity and metastability predict clinical symptoms in schizophrenia. Schizophr. Res. 2018, 201, 208–216. [Google Scholar] [CrossRef]
  41. Lee, W.H.; Frangou, S. Emergence of metastable dynamics in functional brain organization via spontaneous fMRI signal and whole-brain computational modeling. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC); 2017; pp. 4471–4474. [Google Scholar]
  42. Lord, L.-D.; Expert, P.; Atasoy, S.; Roseman, L.; Rapuano, K.; Lambiotte, R.; Nutt, D.J.; Deco, G.; Carhart-Harris, R.L.; Kringelbach, M.L.; et al. Dynamical exploration of the repertoire of brain networks at rest is modulated by psilocybin. NeuroImage 2019, 199, 127–142. [Google Scholar] [CrossRef]
  43. Mediano, P.A.M.; Rosas, F.E.; Farah, J.C.; Shanahan, M.; Bor, D.; Barrett, A.B. Integrated information as a common signature of dynamical and information-processing complexity. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 013115. [Google Scholar] [CrossRef] [PubMed]
  44. Váša, F.; Shanahan, M.; Hellyer, P.J.; Scott, G.; Cabral, J.; Leech, R. Effects of lesions on synchrony and metastability in cortical networks. NeuroImage 2015, 118, 456–467. [Google Scholar] [CrossRef] [PubMed]
  45. Chang, C.; Glover, G.H. Time–frequency dynamics of resting-state brain connectivity measured with fMRI. NeuroImage 2010, 50, 81–98. [Google Scholar] [CrossRef] [PubMed]
  46. Hellyer, P.J.; Shanahan, M.; Scott, G.; Wise, R.J.S.; Sharp, D.J.; Leech, R. The Control of Global Brain Dynamics: Opposing Actions of Frontoparietal Control and Default Mode Networks on Attention. J. Neurosci. 2014, 34, 451–461. [Google Scholar] [CrossRef] [PubMed]
  47. Tagliazucchi, E. The signatures of conscious access and its phenomenology are consistent with large-scale brain communication at criticality. Conscious. Cogn. 2017, 55, 136–147. [Google Scholar] [CrossRef]
  48. Alteriis, G. de; MacNicol, E.; Hancock, F.; Cash, D.; Expert, P.; Turkheimer, F.E. EiDA: A Lossless Approach for the Dynamic Analysis of Connectivity Patterns in Signals; Application to Resting State fMRI of a Model of Ageing. bioRxiv 2023. [Google Scholar] [CrossRef]
  49. Zhang, M.; Kelso, J.A.S.; Tognoli, E. Critical diversity: Divided or united states of social coordination. PLOS ONE 2018, 13, e0193843. [Google Scholar] [CrossRef]
  50. Zhang, M.; Beetle, C.; Kelso, J.A.S.; Tognoli, E. Connecting empirical phenomena and theoretical models of biological coordination across scales. J. R. Soc. Interface 2019, 16, 20190360. [Google Scholar] [CrossRef]
  51. Zhang, M.; Kalies, W.D.; Kelso, J.A.S.; Tognoli, E. Topological portraits of multiscale coordination dynamics. J. Neurosci. Methods 2020, 108672. [Google Scholar] [CrossRef]
  52. Alonso Martínez, S.; Deco, G.; Ter Horst, G.J.; Cabral, J. The Dynamics of Functional Brain Networks Associated With Depressive Symptoms in a Nonclinical Sample. Front. Neural Circuits 2020, 14, 570583. [Google Scholar] [CrossRef]
  53. Hancock, F.; Rosas, F.E.; McCutcheon, R.A.; Cabral, J.; Dipasquale, O.; Turkheimer, F.E. Metastability as a candidate neuromechanistic biomarker of schizophrenia pathology. PLOS ONE 2023, 18, e0282707. [Google Scholar] [CrossRef]
  54. Cabral, J.; Vidaurre, D.; Marques, P.; Magalhães, R.; Silva Moreira, P.; Miguel Soares, J.; Deco, G.; Sousa, N.; Kringelbach, M.L. Cognitive performance in healthy older adults relates to spontaneous switching between states of functional connectivity during rest. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
  55. Vohryzek, J.; Deco, G.; Cessac, B.; Kringelbach, M.L.; Cabral, J. Ghost Attractors in Spontaneous Brain Activity: Recurrent Excursions Into Functionally-Relevant BOLD Phase-Locking States. Front. Syst. Neurosci. 2020, 14, 20. [Google Scholar] [CrossRef] [PubMed]
  56. Breakspear, M.; Williams, L.M.; Stam, C.J. A Novel Method for the Topographic Analysis of Neural Activity Reveals Formation and Dissolution of ‘Dynamic Cell Assemblies.’. J. Comput. Neurosci. 2004, 16, 49–68. [Google Scholar] [CrossRef] [PubMed]
  57. Haken, H.; Kelso, J.A.S.; Bunz, H. A theoretical model of phase transitions in human hand movements. Biol. Cybern. 1985, 51, 347–356. [Google Scholar] [CrossRef] [PubMed]
  58. Schöner, G.; Haken, H.; Kelso, J.A.S. A stochastic theory of phase transitions in human hand movement. Biol. Cybern. 1986, 53, 247–257. [Google Scholar] [CrossRef] [PubMed]
  59. Tognoli, E.; Zhang, M.; Fuchs, A.; Beetle, C.; Kelso, J.A.S. Coordination Dynamics: A Foundation for Understanding Social Behavior. Front. Hum. Neurosci. 2020, 14, 317. [Google Scholar] [CrossRef]
  60. Coullet, P.; Tresser, C.; Arnéodo, A. Transition to stochasticity for a class of forced oscillators. Phys. Lett. A 1979, 72, 268–270. [Google Scholar] [CrossRef]
  61. Kelso, J.A.S.; Fuchs, A. Self-organizing dynamics of the human brain: Critical instabilities and Sil’nikov chaos. Chaos Woodbury N 1995, 5, 64–69. [Google Scholar] [CrossRef]
  62. Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
  63. Hansel, D.; Mato, G.; Meunier, C. Clustering and slow switching in globally coupled phase oscillators. Phys. Rev. E 1993, 48, 3470–3477. [Google Scholar] [CrossRef] [PubMed]
  64. Kori, H.; Kuramoto, Y. Slow Switching in Globally Coupled Oscillators: Robustness and Occurrence through Delayed Coupling. Phys. Rev. E 2000, 63. [Google Scholar] [CrossRef] [PubMed]
  65. Hindmarsh, J.L.; Rose, R.M.; Huxley, A.F. A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. Lond. B Biol. Sci. 1984, 221, 87–102. [Google Scholar] [CrossRef] [PubMed]
  66. Ashwin, P.; Orosz, G.; Wordsworth, J.; Townley, S. Dynamics on Networks of Cluster States for Globally Coupled Phase Oscillators. SIAM J. Appl. Dyn. Syst. 2007, 6, 728–758. [Google Scholar] [CrossRef]
  67. Breakspear, M.; Terry, J.R.; Friston, K.J. Modulation of excitatory synaptic coupling facilitates synchronization and complex dynamics in a biophysical model of neuronal dynamics. Netw. Comput. Neural Syst. 2003, 14, 703–732. [Google Scholar] [CrossRef]
  68. Heitmann, S.; Breakspear, M. Putting the “dynamic” back into dynamic functional connectivity. Netw. Neurosci. 2018, 2, 150–174. [Google Scholar] [CrossRef]
  69. Morris, C.; Lecar, H. Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 1981, 35, 193–213. [Google Scholar] [CrossRef]
  70. Kaneko, K.; Tsuda, I. Networks of Chaotic Elements. In Complex Systems: Chaos and Beyond: A Constructive Approach with Applications in Life Sciences; Kaneko, K., Tsuda, I., Eds.; Springer: Berlin, Heidelberg, 2001; pp. 107–161. ISBN 978-3-642-56861-9. [Google Scholar]
  71. Stephan, K.E.; Kamper, L.; Bozkurt, A.; Burns, G.A.P.C.; Young, M.P.; Kötter, R. Advanced database methodology for the Collation of Connectivity data on the Macaque brain (CoCoMac). Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2001, 356, 1159–1186. [Google Scholar] [CrossRef]
  72. Sorrentino, F.; Pecora, L.M.; Hagerstrom, A.M.; Murphy, T.E.; Roy, R. Complete characterization of the stability of cluster synchronization in complex dynamical networks. Sci. Adv. 2016, 2, e1501737. [Google Scholar] [CrossRef]
  73. Hanggi, P. Escape from a metastable state. J. Stat. Phys. 1986, 42, 105–148. [Google Scholar] [CrossRef]
  74. Afraimovich, V.; Rabinovich, M.; Varona, P. Heteroclinic Contours in Neural Ensembles and the Winnerless Competition Principle. Int. J. Bifurc. Chaos 2003, 14. [Google Scholar] [CrossRef]
  75. Afraimovich, V.; Zhigulin, V.P.; Rabinovich, M.I. On the origin of reproducible sequential activity in neural circuits. Chaos Woodbury N 2004, 14, 1123–1129. [Google Scholar] [CrossRef]
  76. Afraimovich, V.; Muezzinoglu, M.K.; Rabinovich, M.I. Metastability and Transients in Brain Dynamics: Problems and Rigorous Results. In Long-range Interactions, Stochasticity and Fractional Dynamics: Dedicated to George M. Zaslavsky (1935–2008); Luo, A.C.J., Afraimovich, V., Eds.; Nonlinear Physical Science; Springer: Berlin, Heidelberg, 2010; pp. 133–175. ISBN 978-3-642-12343-6. [Google Scholar]
  77. Ashwin, P.; Karabacak, Ö.; Nowotny, T. Criteria for robustness of heteroclinic cycles in neural microcircuits. J. Math. Neurosci. 2011, 1, 13. [Google Scholar] [CrossRef] [PubMed]
  78. Kuramoto, Y.; Battogtokh, D. Coexistence of Coherence and Incoherence in Nonlocally Coupled Phase Oscillators. In Nonlinear Phenomena in Complex Systems; Haken, H., Ed.; 5; 2002; Vol. 4, pp. 380–385.
  79. Shanahan, M. Embodiment and the inner life: Cognition and Consciousness in the Space of Possible Minds; Oxford University Press: Oxford, New York, 2010; ISBN 978-0-19-922655-9. [Google Scholar]
  80. Baars, B.J. A Cognitive Theory of Consciousness; New York: Cambridge University Press, 1988. [Google Scholar]
  81. Dehaene, S.; Kerszberg, M.; Changeux, J.-P. A neuronal model of a global workspace in effortful cognitive tasks. Proc. Natl. Acad. Sci. 1998, 95, 14529–14534. [Google Scholar] [CrossRef] [PubMed]
  82. Kaneko, K. Clustering, coding, switching, hierarchical ordering, and control in a network of chaotic elements. Phys. Nonlinear Phenom. 1990, 41, 137–172. [Google Scholar] [CrossRef]
  83. Seth, A.K.; Izhikevich, E.; Reeke, G.N.; Edelman, G.M. Theories and measures of consciousness: An extended framework. Proc. Natl. Acad. Sci. 2006, 103, 10799–10804. [Google Scholar] [CrossRef] [PubMed]
  84. Shanahan, M. Dynamical complexity in small-world networks of spiking neurons. Phys. Rev. E 2008, 78, 041924. [Google Scholar] [CrossRef]
  85. Freyer, F.; Roberts, J.A.; Becker, R.; Robinson, P.A.; Ritter, P.; Breakspear, M. Biophysical Mechanisms of Multistability in Resting-State Cortical Rhythms. J. Neurosci. 2011, 31, 6353–6361. [Google Scholar] [CrossRef]
  86. Ghosh, A.; Rho, Y.; McIntosh, A.R.; Kötter, R.; Jirsa, V.K. Noise during Rest Enables the Exploration of the Brain’s Dynamic Repertoire. PLOS Comput. Biol. 2008, 4, e1000196. [Google Scholar] [CrossRef]
  87. Deco, G.; Jirsa, V.K. Ongoing Cortical Activity at Rest: Criticality, Multistability, and Ghost Attractors. J. Neurosci. 2012, 32, 3366–3375. [Google Scholar] [CrossRef]
  88. Friston, K.J.; Mechelli, A.; Turner, R.; Price, C.J. Nonlinear Responses in fMRI: The Balloon Model, Volterra Kernels, and Other Hemodynamics. NeuroImage 2000, 12, 466–477. [Google Scholar] [CrossRef] [PubMed]
  89. Deco, G.; Senden, M.; Jirsa, V. How anatomy shapes dynamics: a semi-analytical study of the brain at rest by a simple spin model. Front. Comput. Neurosci. 2012, 6. [Google Scholar] [CrossRef] [PubMed]
  90. Cabral, J.; Kringelbach, M.L.; Deco, G. Functional connectivity dynamically evolves on multiple time-scales over a static structural connectome: Models and mechanisms. NeuroImage 2017, 160, 84–96. [Google Scholar] [CrossRef] [PubMed]
  91. Kelso, J.A.S. Metastable Coordination Dynamics of Brain and Behavior. Brain Neural Netw. 2001, 8, 125–130. [Google Scholar] [CrossRef]
  92. Kelso, J.A.S. Multistability and metastability: understanding dynamic coordination in the brain. Philos. Trans. Biol. Sci. 2012, 367, 906–918. [Google Scholar] [CrossRef]
  93. Kelso, J.A.S.; DeGuzman, G.C.; Holroyd, T. Synergetic Dynamics of Biological Coordination with Special Reference to Phase Attraction and Intermittency. In Proceedings of the Rhythms in Physiological Systems; Haken, H., Koepchen, H.P., Eds.; Springer: Berlin, Heidelberg, 1991; pp. 195–213. [Google Scholar]
  94. Izhikevich, E.M. Dynamical systems in neuroscience: the geometry of excitability and bursting; Computational neuroscience; MIT Press: Cambridge, Mass, 2007; ISBN 978-0-262-09043-8. [Google Scholar]
  95. Deco, G.; Ponce-Alvarez, A.; Mantini, D.; Romani, G.L.; Hagmann, P.; Corbetta, M. Resting-State Functional Connectivity Emerges from Structurally and Dynamically Shaped Slow Linear Fluctuations. J. Neurosci. 2013, 33, 11239–11252. [Google Scholar] [CrossRef]
  96. Gollo, L.L.; Breakspear, M. The frustrated brain: from dynamics on motifs to communities and networks. Philos. Trans. R. Soc. B Biol. Sci. 2014, 369, 20130532. [Google Scholar] [CrossRef]
  97. Roberts, J.A.; Gollo, L.L.; Abeysuriya, R.G.; Roberts, G.; Mitchell, P.B.; Woolrich, M.W.; Breakspear, M. Metastable brain waves. Nat. Commun. 2019, 10, 1–17. [Google Scholar] [CrossRef]
  98. Yang, H.; Shew, W.L.; Roy, R.; Plenz, D. Maximal Variability of Phase Synchrony in Cortical Networks with Neuronal Avalanches. J. Neurosci. 2012, 32, 1061–1072. [Google Scholar] [CrossRef]
  99. Kanamaru, T. Analysis of synchronization between two modules of pulse neural networks with excitatory and inhibitory connections. Neural Comput. 2006, 18, 1111–1131. [Google Scholar] [CrossRef]
  100. Li, D.; Zhou, C. Organization of Anti-Phase Synchronization Pattern in Neural Networks: What are the Key Factors? Front. Syst. Neurosci. 2011, 5. [Google Scholar] [CrossRef] [PubMed]
  101. Neltner, L.; Hansel, D. On synchrony of weakly coupled neurons at low firing rate. Neural Comput. 2001, 13, 765–774. [Google Scholar] [CrossRef] [PubMed]
  102. Cabral, J.; Hugues, E.; Sporns, O.; Deco, G. Role of local network oscillations in resting-state functional connectivity. NeuroImage 2011, 57, 130–139. [Google Scholar] [CrossRef]
  103. Pang, J.C.; Gollo, L.L.; Roberts, J.A. Stochastic synchronization of dynamics on the human connectome. NeuroImage 2021, 229, 117738. [Google Scholar] [CrossRef]
  104. Ponce-Alvarez, A.; Deco, G.; Hagmann, P.; Romani, G.L.; Mantini, D.; Corbetta, M. Resting-State Temporal Synchronization Networks Emerge from Connectivity Topology and Heterogeneity. PLOS Comput. Biol. 2015, 11, e1004100. [Google Scholar] [CrossRef] [PubMed]
  105. López-González, A.; Panda, R.; Ponce-Alvarez, A.; Zamora-López, G.; Escrichs, A.; Martial, C.; Thibaut, A.; Gosseries, O.; Kringelbach, M.L.; Annen, J.; et al. Loss of consciousness reduces the stability of brain hubs and the heterogeneity of brain dynamics. Commun. Biol. 2021, 4, 1–15. [Google Scholar] [CrossRef]
  106. Deco, G.; Jirsa, V.; McIntosh, A.R.; Sporns, O.; Kötter, R. Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. 2009, 106, 10302–10307. [Google Scholar] [CrossRef]
  107. Lynall, M.-E.; Bassett, D.S.; Kerwin, R.; McKenna, P.J.; Kitzbichler, M.; Muller, U.; Bullmore, E. Functional Connectivity and Brain Networks in Schizophrenia. J. Neurosci. 2010, 30, 9477–9487. [Google Scholar] [CrossRef]
  108. Córdova-Palomera, A.; Kaufmann, T.; Persson, K.; Alnæs, D.; Doan, N.T.; Moberget, T.; Lund, M.J.; Barca, M.L.; Engvig, A.; Brækhus, A.; et al. Disrupted global metastability and static and dynamic brain connectivity across individuals in the Alzheimer’s disease continuum. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef]
  109. Cabral, J.; Fernandes, H.M.; Van Hartevelt, T.J.; James, A.C.; Kringelbach, M.L.; Deco, G. Structural connectivity in schizophrenia and its impact on the dynamics of spontaneous functional networks. Chaos Woodbury N 2013, 23, 046111. [Google Scholar] [CrossRef]
  110. Kelly, S.; Jahanshad, N.; Zalesky, A.; Kochunov, P.; Agartz, I.; Alloza, C.; Andreassen, O.A.; Arango, C.; Banaj, N.; Bouix, S.; et al. Widespread white matter microstructural differences in schizophrenia across 4322 individuals: results from the ENIGMA Schizophrenia DTI Working Group. Mol. Psychiatry 2018, 23, 1261–1269. [Google Scholar] [CrossRef] [PubMed]
  111. van den Heuvel, M.P.; Fornito, A. Brain Networks in Schizophrenia. Neuropsychol. Rev. 2014, 24, 32–48. [Google Scholar] [CrossRef]
  112. Deco, G.; Tononi, G.; Boly, M.; Kringelbach, M.L. Rethinking segregation and integration: contributions of whole-brain modelling. Nat. Rev. Neurosci. 2015, 16, 430–439. [Google Scholar] [CrossRef] [PubMed]
  113. Deco, G.; Cruzat, J.; Cabral, J.; Knudsen, G.M.; Carhart-Harris, R.L.; Whybrow, P.C.; Logothetis, N.K.; Kringelbach, M.L. Whole-Brain Multimodal Neuroimaging Model Using Serotonin Receptor Maps Explains Non-linear Functional Effects of LSD. Curr. Biol. 2018, 28, 3065-3074.e6. [CrossRef]
  114. Kringelbach, M.L.; Cruzat, J.; Cabral, J.; Knudsen, G.M.; Carhart-Harris, R.; Whybrow, P.C.; Logothetis, N.K.; Deco, G. Dynamic coupling of whole-brain neuronal and neurotransmitter systems. Proc. Natl. Acad. Sci. 2020, 201921475. [Google Scholar] [CrossRef]
  115. Luppi, A.I.; Carhart-Harris, R.L.; Roseman, L.; Pappas, I.; Menon, D.K.; Stamatakis, E.A. LSD alters dynamic integration and segregation in the human brain. NeuroImage 2021, 227, 117653. [Google Scholar] [CrossRef]
  116. Frisch, U. Turbulence: The Legacy of A.N. Kolmogorov; 1995; ISBN 978-0-521-45103-1.
  117. Richardson, L.F. Weather Prediction by Numerical Process | Numerical analysis; University Press, 1922.
  118. Deco, G.; Kemp, M.; Kringelbach, M.L. Leonardo da Vinci and the search for order in neuroscience. Curr. Biol. 2021, 31, R704–R709. [Google Scholar] [CrossRef] [PubMed]
  119. Deco, G.; Kringelbach, M.L. Turbulent-like Dynamics in the Human Brain. Cell Rep. 2020, 33, 108471. [Google Scholar] [CrossRef]
  120. Deco, G.; Sanz Perl, Y.; Vuust, P.; Tagliazucchi, E.; Kennedy, H.; Kringelbach, M.L. Rare long-range cortical connections enhance human information processing. Curr. Biol. 2021, 31, 4436–4448.e5. [Google Scholar] [CrossRef]
  121. Sheremet, A.; Qin, Y.; Kennedy, J.P.; Zhou, Y.; Maurer, A.P. Wave Turbulence and Energy Cascade in the Hippocampus. Front. Syst. Neurosci. 2019, 12. [Google Scholar] [CrossRef]
  122. Deco, G.; Liebana Garcia, S.; Sanz Perl, Y.; Sporns, O.; Kringelbach, M.L. The effect of turbulence in brain dynamics information transfer measured with magnetoencephalography. Commun. Phys. 2023, 6, 1–8. [Google Scholar] [CrossRef]
  123. Kawamura, Y.; Nakao, H.; Kuramoto, Y. Noise-induced turbulence in nonlocally coupled oscillators. Phys. Rev. E 2007, 75, 036209. [Google Scholar] [CrossRef] [PubMed]
  124. Shraiman, B.I.; Pumir, A.; van Saarloos, W.; Hohenberg, P.C.; Chaté, H.; Holen, M. Spatiotemporal chaos in the one-dimensional complex Ginzburg-Landau equation. Phys. Nonlinear Phenom. 1992, 57, 241–248. [Google Scholar] [CrossRef]
  125. Kelso, J.A.S. Unifying Large- and Small-Scale Theories of Coordination. Entropy 2021, 23, 537. [Google Scholar] [CrossRef] [PubMed]
  126. Hindmarsh, J.L.; Rose, R.M. A model of the nerve impulse using two first-order differential equations. Nature 1982, 296, 162–164. [Google Scholar] [CrossRef]
  127. Fuchs, A.; Jirsa, V.K.; Haken, H.; Kelso, J.A.S. Extending the HKB model of coordinated movement to oscillators with different eigenfrequencies. Biol. Cybern. 1996, 74, 21–30. [Google Scholar] [CrossRef]
  128. Kelso, J.A.S. The Haken–Kelso–Bunz (HKB) model: from matter to movement to mind. Biol. Cybern. 2021, 115, 305–322. [Google Scholar] [CrossRef]
  129. McKinley, J.; Zhang, M.; Wead, A.; Williams, C.; Tognoli, E.; Beetle, C. Third party stabilization of unstable coordination in systems of coupled oscillators. J. Phys. Conf. Ser. 2021, 2090. [Google Scholar] [CrossRef]
  130. Zhang, M.; Sun, Y.; Saggar, M. Cross-attractor repertoire provides new perspective on structure-function relationship in the brain. NeuroImage 2022, 259, 119401. [Google Scholar] [CrossRef]
  131. Markello, R.D.; Hansen, J.Y.; Liu, Z.-Q.; Bazinet, V.; Shafiei, G.; Suárez, L.E.; Blostein, N.; Seidlitz, J.; Baillet, S.; Satterthwaite, T.D.; et al. neuromaps: structural and functional interpretation of brain maps. Nat. Methods 2022, 19, 1472–1479. [Google Scholar] [CrossRef]
  132. Turkheimer, F.E.; Veronese, M.; Mondelli, V.; Cash, D.; Pariante, C.M. Sickness behaviour and depression: An updated model of peripheral-central immunity interactions. Brain. Behav. Immun. 2023, 111, 202–210. [Google Scholar] [CrossRef]
  133. Kutchko, K.M.; Fröhlich, F. Emergence of Metastable State Dynamics in Interconnected Cortical Networks with Propagation Delays. PLoS Comput. Biol. 2013, 9, e1003304. [Google Scholar] [CrossRef] [PubMed]
  134. Luppi, A.I.; Rosas, F.E.; Noonan, M.P.; Mediano, P.A.M.; Kringelbach, M.L.; Carhart-Harris, R.L.; Stamatakis, E.A.; Vernon, A.C.; Turkheimer, F.E. Oxygen and the Spark of Human Brain Evolution: Complex Interactions of Metabolism and Cortical Expansion across Development and Evolution. The Neuroscientist 2022, 10738584221138032. [Google Scholar] [CrossRef] [PubMed]
  135. Burt, J.B.; Demirtaş, M.; Eckner, W.J.; Navejar, N.M.; Ji, J.L.; Martin, W.J.; Bernacchia, A.; Anticevic, A.; Murray, J.D. Hierarchy of transcriptomic specialization across human cortex captured by structural neuroimaging topography. Nat. Neurosci. 2018, 21, 1251–1259. [Google Scholar] [CrossRef] [PubMed]
  136. Vanes, L.D.; Mouchlianitis, E.; Barry, E.; Patel, K.; Wong, K.; Shergill, S.S. Cognitive correlates of abnormal myelination in psychosis. Sci. Rep. 2019, 9, 5162. [Google Scholar] [CrossRef]
  137. Valdés-Tovar, M.; Rodríguez-Ramírez, A.M.; Rodríguez-Cárdenas, L.; Sotelo-Ramírez, C.E.; Camarena, B.; Sanabrais-Jiménez, M.A.; Solís-Chagoyán, H.; Argueta, J.; López-Riquelme, G.O. Insights into myelin dysfunction in schizophrenia and bipolar disorder. World J. Psychiatry 2022, 12, 264–285. [Google Scholar] [CrossRef]
  138. Kaller, M.S.; Lazari, A.; Blanco-Duque, C.; Sampaio-Baptista, C.; Johansen-Berg, H. Myelin plasticity and behaviour—connecting the dots. Curr. Opin. Neurobiol. 2017, 47, 86–92. [Google Scholar] [CrossRef]
  139. Uhlhaas, P.J. High-Frequency Oscillations in Schizophrenia. Clin. EEG Neurosci. 2011, 42, 77–82. [Google Scholar] [CrossRef]
  140. Uhlhaas, P.J. Dysconnectivity, large-scale networks and neuronal dynamics in schizophrenia. Curr. Opin. Neurobiol. 2013, 23, 283–290. [Google Scholar] [CrossRef]
  141. Uhlhaas, P.J.; Singer, W. Abnormal neural oscillations and synchrony in schizophrenia. Nat. Rev. Neurosci. 2010, 11, 100. [Google Scholar] [CrossRef]
  142. Uhlhaas, P.J.; Singer, W. High-frequency oscillations and the neurobiology of schizophrenia. Dialogues Clin. Neurosci. 2013, 15, 301–313. [Google Scholar] [CrossRef]
  143. Sumiyoshi, A.; Suzuki, H.; Ogawa, T.; Riera, J.J.; Shimokawa, H.; Kawashima, R. Coupling between gamma oscillation and fMRI signal in the rat somatosensory cortex: its dependence on systemic physiological parameters. NeuroImage 2012, 60, 738–746. [Google Scholar] [CrossRef] [PubMed]
  144. Haider, B.; Duque, A.; Hasenstaub, A.R.; McCormick, D.A. Neocortical Network Activity In Vivo Is Generated through a Dynamic Balance of Excitation and Inhibition. J. Neurosci. 2006, 26, 4535–4545. [Google Scholar] [CrossRef] [PubMed]
  145. Gandal, M.J.; Sisti, J.; Klook, K.; Ortinski, P.I.; Leitman, V.; Liang, Y.; Thieu, T.; Anderson, R.; Pierce, R.C.; Jonak, G.; et al. GABA B -mediated rescue of altered excitatory–inhibitory balance, gamma synchrony and behavioral deficits following constitutive NMDAR-hypofunction. Transl. Psychiatry 2012, 2, e142–e142. [Google Scholar] [CrossRef] [PubMed]
  146. Lewis, D.A.; Curley, A.A.; Glausier, J.R.; Volk, D.W. Cortical parvalbumin interneurons and cognitive dysfunction in schizophrenia. Trends Neurosci. 2012, 35, 57–67. [Google Scholar] [CrossRef]
  147. Mikanmaa, E.; Grent-’t-Jong, T.; Hua, L.; Recasens, M.; Thune, H.; Uhlhaas, P.J. Towards a neurodynamical understanding of the prodrome in schizophrenia. NeuroImage 2019, 190, 144–153. [Google Scholar] [CrossRef]
  148. Tatti, R.; Haley, M.S.; Swanson, O.K.; Tselha, T.; Maffei, A. Neurophysiology and Regulation of the Balance Between Excitation and Inhibition in Neocortical Circuits. Biol. Psychiatry 2017, 81, 821–831. [Google Scholar] [CrossRef]
  149. Thune, H.E.A. Auditory neural oscillations and excitation/inhibition balance in emerging psychosis. PhD, University of Glasgow, 2019.
  150. Hellyer, P.J.; Jachs, B.; Clopath, C.; Leech, R. Local inhibitory plasticity tunes macroscopic brain dynamics and allows the emergence of functional brain networks. NeuroImage 2016, 124, 85–95. [Google Scholar] [CrossRef]
  151. Turkheimer, F.E.; Leech, R.; Expert, P.; Lord, L.-D.; Vernon, A.C. The brain’s code and its canonical computational motifs. From sensory cortex to the default mode network: A multi-scale model of brain function in health and disease. Neurosci. Biobehav. Rev. 2015, 55, 211–222. [Google Scholar] [CrossRef]
  152. Xue, M.; Atallah, B.V.; Scanziani, M. Equalizing excitation–inhibition ratios across visual cortical neurons. Nature 2014, 511, 596–600. [Google Scholar] [CrossRef]
  153. Enrico, P.; Delvecchio, G.; Turtulici, N.; Pigoni, A.; Villa, F.M.; Perlini, C.; Rossetti, M.G.; Bellani, M.; Lasalvia, A.; Bonetto, C.; et al. Classification of Psychoses Based on Immunological Features: A Machine Learning Study in a Large Cohort of First-Episode and Chronic Patients. Schizophr. Bull. 2021, 47, 1141–1155. [Google Scholar] [CrossRef]
  154. Fraguas, D.; Díaz-Caneja, C.M.; Ayora, M.; Hernández-Álvarez, F.; Rodríguez-Quiroga, A.; Recio, S.; Leza, J.C.; Arango, C. Oxidative Stress and Inflammation in First-Episode Psychosis: A Systematic Review and Meta-analysis. Schizophr. Bull. 2019, 45, 742–751. [Google Scholar] [CrossRef] [PubMed]
  155. Molina, V.; Gispert, J.D.; Reig, S.; Sanz, J.; Pascau, J.; Santos, A.; Desco, M.; Palomo, T. Cerebral metabolic changes induced by clozapine in schizophrenia and related to clinical improvement. Psychopharmacology (Berl.) 2005, 178, 17–26. [Google Scholar] [CrossRef] [PubMed]
  156. Tognoli, E.; Kelso, J.A.S. The Metastable Brain. Neuron 2014, 81, 35–48. [Google Scholar] [CrossRef]
  157. Alexander, M.L.; Alagapan, S.; Lugo, C.E.; Mellin, J.M.; Lustenberger, C.; Rubinow, D.R.; Fröhlich, F. Double-blind, randomized pilot clinical trial targeting alpha oscillations with transcranial alternating current stimulation (tACS) for the treatment of major depressive disorder (MDD). Transl. Psychiatry 2019, 9, 106. [Google Scholar] [CrossRef] [PubMed]
  158. Avery, D.H.; Holtzheimer, P.E.; Fawaz, W.; Russo, J.; Neumaier, J.; Dunner, D.L.; Haynor, D.R.; Claypoole, K.H.; Wajdik, C.; Roy-Byrne, P. A Controlled Study of Repetitive Transcranial Magnetic Stimulation in Medication-Resistant Major Depression. Biol. Psychiatry 2006, 59, 187–194. [Google Scholar] [CrossRef]
  159. O’Reardon, J.P.; Solvason, H.B.; Janicak, P.G.; Sampson, S.; Isenberg, K.E.; Nahas, Z.; McDonald, W.M.; Avery, D.; Fitzgerald, P.B.; Loo, C.; et al. Efficacy and Safety of Transcranial Magnetic Stimulation in the Acute Treatment of Major Depression: A Multisite Randomized Controlled Trial. Biol. Psychiatry 2007, 62, 1208–1216. [Google Scholar] [CrossRef]
  160. Zhang, M.; Force, R.B.; Walker, C.; Ahn, S.; Jarskog, L.F.; Frohlich, F. Alpha transcranial alternating current stimulation reduces depressive symptoms in people with schizophrenia and auditory hallucinations: a double-blind, randomized pilot clinical trial. Schizophrenia 2022, 8, 1–17. [Google Scholar] [CrossRef]
  161. Expert, P.; Lambiotte, R.; Chialvo, D.R.; Christensen, K.; Jensen, H.J.; Sharp, D.J.; Turkheimer, F. Self-similar correlation function in brain resting-state functional magnetic resonance imaging. J. R. Soc. Interface 2011, 8, 472–479. [Google Scholar] [CrossRef]
  162. Plenz, D.; Ribeiro, T.L.; Miller, S.R.; Kells, P.A.; Vakili, A.; Capek, E.L. Self-Organized Criticality in the Brain. Front. Phys. 2021, 9. [Google Scholar] [CrossRef]
Preprints 80060 g001
Figure 1. Different types of stability in dynamical systems. A) From top to bottom, monostability, multistability, metastability, instability. B) Phase portrait of a 1-dimensional dynamical system. The horizontal line presents a 1-dimensional state space (x). Horizontal blue arrows indicate the direction of the flow in the phase space determined by the differential equation (dx/dt), which is plotted in black as a function of x. Where dx/dt is above (resp. below) the horizontal line, the trajectories in the state space flow to the right (resp. left) corresponding to a positive (resp. negative) change of the state variable. Where the function intersects with the horizontal axis, there is no change to the state, making that value of x a fixed point. The slope of the function at the equilibrium point indicates its stability: a negative slope implies an attractor (i.e., a stable fixed point, as seen by nearby flows pointing towards the equilibrium), whilst a positive slope indicates a repeller (i.e., an unstable fixed point, as seen by nearby flows pointing away from the equilibrium). By convention, stable attracting points are represented by a filled circle, while repelling unstable points corresponding to empty circles. C) Potential landscape of the same system. Valleys in this landscape represent stable fixed points, which may also be attractors. In contrast, peaks represent unstable fixed points which in this case are repellers. D) A bifurcation diagram of a bistable system. Stable solutions, the red and yellow points, away from the critical blue point, exist for different values of the control parameter. E) A pitchfork bifurcation where at a critical value of a control parameter, a stable fixed point transfers its stability resulting in 2 new fixed points. The system may reside in either of the two states marked with red circles. F) In a 1-dimensional system, the saddle is represented as a dual-coloured circle. The blue line shows the flow towards the saddle fixed point and the red line shows the flow away from the saddle. G) A saddle-node bifurcation where a stable and unstable fixed point collide and annihilate each other. The saddle-node is stable in one direction and unstable in the other. H) In a 3-D picture, it is easier to see how this fixed point got the name of a saddle node. I) A heteroclinic cycle linking 4 saddles though their unstable directions. Metastability in part A adapted with permission from [4]. Part I reproduced with permission from Alexander Steele Kernbaum https://www.researchgate.net/profile/Alexander-Kernbaum-2/research.
Figure 1. Different types of stability in dynamical systems. A) From top to bottom, monostability, multistability, metastability, instability. B) Phase portrait of a 1-dimensional dynamical system. The horizontal line presents a 1-dimensional state space (x). Horizontal blue arrows indicate the direction of the flow in the phase space determined by the differential equation (dx/dt), which is plotted in black as a function of x. Where dx/dt is above (resp. below) the horizontal line, the trajectories in the state space flow to the right (resp. left) corresponding to a positive (resp. negative) change of the state variable. Where the function intersects with the horizontal axis, there is no change to the state, making that value of x a fixed point. The slope of the function at the equilibrium point indicates its stability: a negative slope implies an attractor (i.e., a stable fixed point, as seen by nearby flows pointing towards the equilibrium), whilst a positive slope indicates a repeller (i.e., an unstable fixed point, as seen by nearby flows pointing away from the equilibrium). By convention, stable attracting points are represented by a filled circle, while repelling unstable points corresponding to empty circles. C) Potential landscape of the same system. Valleys in this landscape represent stable fixed points, which may also be attractors. In contrast, peaks represent unstable fixed points which in this case are repellers. D) A bifurcation diagram of a bistable system. Stable solutions, the red and yellow points, away from the critical blue point, exist for different values of the control parameter. E) A pitchfork bifurcation where at a critical value of a control parameter, a stable fixed point transfers its stability resulting in 2 new fixed points. The system may reside in either of the two states marked with red circles. F) In a 1-dimensional system, the saddle is represented as a dual-coloured circle. The blue line shows the flow towards the saddle fixed point and the red line shows the flow away from the saddle. G) A saddle-node bifurcation where a stable and unstable fixed point collide and annihilate each other. The saddle-node is stable in one direction and unstable in the other. H) In a 3-D picture, it is easier to see how this fixed point got the name of a saddle node. I) A heteroclinic cycle linking 4 saddles though their unstable directions. Metastability in part A adapted with permission from [4]. Part I reproduced with permission from Alexander Steele Kernbaum https://www.researchgate.net/profile/Alexander-Kernbaum-2/research.
Preprints 80060 g001
Preprints 80060 g002
Figure 2. Metastability in multiagent social coordination and the relation between metastability and frequency fluctuations. A) Experimental observation of the coordination dynamics between 3 persons (agent 1,3,4) in terms of relative phase ( ϕ 13, ϕ 34; y-coordinates) as a function of time (x-coordinates). ϕ 34 (yellow) persisted at in-phase for a long time (10–37 s trajectory flattened near ϕ ij = 0) before switching to anti-phase (40 s; in-phase and anti-phase are labelled with thick and thin dashed lines, respectively, throughout this figure). ϕ 13 (red) dwelt at in-phase intermittently (flattening of trajectory around 10, 20, and 35 s). Reproduced with permission from [50]. B-C) A short segment of simulated metastable coordination between two oscillators using the generalised HKB model in terms of the relative phase ϕ between the two oscillators (B) and the instantaneous frequencies of each of the two oscillators, shown in different colours (C). Adapted with permission from [51]. As the relative phase wraps for one cycle ( 2 π ), the difference between the two oscillators’ instantaneous frequency shows one large fluctuation. Thus, the fundamental rate of frequency fluctuation is the same as the rate of relative phase wrapping.
Figure 2. Metastability in multiagent social coordination and the relation between metastability and frequency fluctuations. A) Experimental observation of the coordination dynamics between 3 persons (agent 1,3,4) in terms of relative phase ( ϕ 13, ϕ 34; y-coordinates) as a function of time (x-coordinates). ϕ 34 (yellow) persisted at in-phase for a long time (10–37 s trajectory flattened near ϕ ij = 0) before switching to anti-phase (40 s; in-phase and anti-phase are labelled with thick and thin dashed lines, respectively, throughout this figure). ϕ 13 (red) dwelt at in-phase intermittently (flattening of trajectory around 10, 20, and 35 s). Reproduced with permission from [50]. B-C) A short segment of simulated metastable coordination between two oscillators using the generalised HKB model in terms of the relative phase ϕ between the two oscillators (B) and the instantaneous frequencies of each of the two oscillators, shown in different colours (C). Adapted with permission from [51]. As the relative phase wraps for one cycle ( 2 π ), the difference between the two oscillators’ instantaneous frequency shows one large fluctuation. Thus, the fundamental rate of frequency fluctuation is the same as the rate of relative phase wrapping.
Preprints 80060 g002
Preprints 80060 g003
Figure 3. The rich dynamics in the HKB model illustrated in a phase portrait. A) The phase portrait of ∅ in the “extended” HKB model [23] for various values of a diversity (control) parameter δ ω . This graph carries regimes of coordination with attractors in the front of the figure (for modest diversity δ ω ) and those without attractors (large diversity of the parts, shown in the back of the figure). Multi-, mono-, and metastable regimes are indicated to the right of the figure. Examples of anti-phase and in-phase attractors, and the absence of attractors in metastability, are shown on the left of the figure. Adapted with permission from [59].
Figure 3. The rich dynamics in the HKB model illustrated in a phase portrait. A) The phase portrait of ∅ in the “extended” HKB model [23] for various values of a diversity (control) parameter δ ω . This graph carries regimes of coordination with attractors in the front of the figure (for modest diversity δ ω ) and those without attractors (large diversity of the parts, shown in the back of the figure). Multi-, mono-, and metastable regimes are indicated to the right of the figure. Examples of anti-phase and in-phase attractors, and the absence of attractors in metastability, are shown on the left of the figure. Adapted with permission from [59].
Preprints 80060 g003
Preprints 80060 g004
Figure 4. Complex dynamics in large ensembles. A) Stable partitioning of ensemble dynamics into four phase-coupled clusters with time delay t = 10 ms and internode coupling c = 0.75. B) Partitioning of ensemble dynamics into six phase-coupled clusters with t = 6 ms and coupling c = 0.75. C) Alliance switching. With weaker coupling and/or shorter time delays (τ =5.5 ms, c = 0.45), there are brief phase slips, leading to a reorganisation of the cluster configuration. Reproduced with permission from [68].
Figure 4. Complex dynamics in large ensembles. A) Stable partitioning of ensemble dynamics into four phase-coupled clusters with time delay t = 10 ms and internode coupling c = 0.75. B) Partitioning of ensemble dynamics into six phase-coupled clusters with t = 6 ms and coupling c = 0.75. C) Alliance switching. With weaker coupling and/or shorter time delays (τ =5.5 ms, c = 0.45), there are brief phase slips, leading to a reorganisation of the cluster configuration. Reproduced with permission from [68].
Preprints 80060 g004
Preprints 80060 g005
Figure 5. Mean-field analyses of the attractor landscape of the cortical spiking network as a function of the global inter-areal coupling strength. A) Mean-field analyses of the attractor landscape of the cortical spiking network as a function of the global inter-areal coupling strength Wc. The dashed line plots the number of stable attractors, whereas the continued line shows the entropy of the attractors. B) Fitting of empirical data as measured by the correlation between simulated and empirical functional connectivity as a function of the global coupling parameter W. The best fit is achieved at the edge of the bifurcation, Wc. Reproduced with permission from [87].
Figure 5. Mean-field analyses of the attractor landscape of the cortical spiking network as a function of the global inter-areal coupling strength. A) Mean-field analyses of the attractor landscape of the cortical spiking network as a function of the global inter-areal coupling strength Wc. The dashed line plots the number of stable attractors, whereas the continued line shows the entropy of the attractors. B) Fitting of empirical data as measured by the correlation between simulated and empirical functional connectivity as a function of the global coupling parameter W. The best fit is achieved at the edge of the bifurcation, Wc. Reproduced with permission from [87].
Preprints 80060 g005
Preprints 80060 g006
Figure 6. Schematic representation of the bifurcation structure. The trivial solution x = 0 loses its stability at τ = τ   c . Two solid lines existing for τ > τ c correspond to (p, ∆′) and (1 − p, ∆′′) respectively, each being unstable with respect to the y- or z-direction alternately. P is the number of oscillators in one cluster, and 1-p the number of oscillators in the second cluster. A heteroclinic loop is formed between these two solutions. Reproduced with permission from [64].
Figure 6. Schematic representation of the bifurcation structure. The trivial solution x = 0 loses its stability at τ = τ   c . Two solid lines existing for τ > τ c correspond to (p, ∆′) and (1 − p, ∆′′) respectively, each being unstable with respect to the y- or z-direction alternately. P is the number of oscillators in one cluster, and 1-p the number of oscillators in the second cluster. A heteroclinic loop is formed between these two solutions. Reproduced with permission from [64].
Preprints 80060 g006
Preprints 80060 g007
Figure 7. Hansel-Mato-Meunier and Generalised Haken-Kelso-Bunz models. A) Intermittent convergence and progressive slowing down before switching in the Hansel-Mato-Meunier model [63]. The relative phase relations remain constant for approximately 5 seconds between approximately 25-30 seconds reflecting phase clustering before switching occurs. The next epoch of clustering lasts around 11 seconds occurring between approximately 55-66 seconds. B) Intermittent convergence and progressive slowing down in the generalised HKB model [50]. The duration of the phase clustering between approximately 400-470 seconds is considerably longer than that between approximately 420-423 seconds.
Figure 7. Hansel-Mato-Meunier and Generalised Haken-Kelso-Bunz models. A) Intermittent convergence and progressive slowing down before switching in the Hansel-Mato-Meunier model [63]. The relative phase relations remain constant for approximately 5 seconds between approximately 25-30 seconds reflecting phase clustering before switching occurs. The next epoch of clustering lasts around 11 seconds occurring between approximately 55-66 seconds. B) Intermittent convergence and progressive slowing down in the generalised HKB model [50]. The duration of the phase clustering between approximately 400-470 seconds is considerably longer than that between approximately 420-423 seconds.
Preprints 80060 g007
1
In preparing this paper, the authors found over 300 published neuroscience-related articles since 1988 that contained the word ‘metastability’.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated