Prerpints.org logo
Preprint
Article

Hotel Comment Emotion Classification Based on the MF-DFA and Partial Differential Equation Classifier

Altmetrics

Downloads

107

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 July 2023

Posted:

19 July 2023

You are already at the latest version

Alerts
Abstract
In this paper, we propose a partial differential equation model based on phase-field for sentiment analysis in the field of hotel comment texts. The comment texts are converted into word vectors using the Word2Vec tool, and then we utilize the multifractal detrended fluctuation analysis (MF-DFA) model to extract the generalized Hurst exponent of the word vector time series to achieve dimensionality reduction of the word vector data. The dimensionality reduced data is represented in a two-dimensional computational domain, and the modified Allen-Cahn (AC) function is used to evolve the phase values of the data to obtain a stable nonlinear boundary, thereby achieving automatic classification of hotel comment texts. The experimental results show that the proposed method can effectively classify positive and negative samples and achieve excellent results in classification indicators. We compared our proposed classifier with traditional machine learning models and the results indicate that our method possesses a better performance.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Natural Language Processing (NLP) is an important direction in computer science and artificial intelligence, aiming to explore various theories and methods that can realize effective communication between humans and computers in natural language [1,2]. NLP has been used by many scholars to excavate emotional bias in texts, especially company press releases and consumer online comments [3,4,5,6]. For the detailed development of NLP, please refer to the review [7,8]. Online reviews provide the customers’ feelings to the companies and other customers. In order to obtain valuable knowledge about customers, it is significant to collect and analyze the online reviews. Sann and Lai [9] adopted NLP to the hotel complaints about the synthesize specific service failure items, which can help hotels improve service. Jiao and Qu [10] proposed a computerized method which can extract Kansei knowledge from online reviews. Sharma et al. [11] exhibited a hybrid 3-layer NLP framework based on genetic algorithm and ontology, which owned excellent performance of opinion mining patent. Guerrero-Rodriguez et al. [12] proved that online travel reviews can help tourists determine which places are positive and negative. As well, the double language representation model based on NLP has developed rapidly. However, the model can not handle the absence of information. Therefore, a concept of interval-probabilistic two-hierarchy language set combining EDAS was proposed by Wang et al. [13].
Multifractal theories have strong nonlinear processing ability, which has attracted much attention. Therefore, multifractal theories has been widely adopted in the analysis of markets and prices in economics and finance [14,15]. The complexity and uncertainty of the market can be obtained by analyzing the multifractal characteristics of financial time series. Meanwhile, multifractal theories can be used to investigate the volatility of stock prices and risk management, which can help develop effective risk management strategies [16,17]. In addition, mutifractal theory owns excellent dimensionality reduction capability, which has been widely applied to feature extraction [18,19]. In general, Hurst exponent is used to characterize the multifractal features. As well, multifractal method is used in conjunction with other methods to improve classification accuracy. Hurst exponent, Lempel-Ziv information and Shannon entropy were combined as feature vectors into the support vector machine to determine normal and noisy heart sounds [20]. Abbasi et al. [21] extracted Hurst exponent and autoregressive moving average features from EEG signals and put the feature vector into long short-term memory classifier, the accuracy of which was high.
Phase field model is a model in materials science and physics that describes the relationship between the microstructure and macroscopic behavior of a material, and is a mathematical model that can be used to solve the two-phase interface. In 1979, Allen and Cahn first applied the Allen-Cahn (AC) equation in [22] to describe the process of phase separation in a binary alloy, and it has been one of the most widely studied phase field models. In the field of volume reconstruction, Li et al. [23] developed a computational method for weighted 3D volume reconstruction from a series of slice data based on the modified AC equation with a fidelity term. Liu et al. [24] proposed a novel variational model by integrating the AC term with a local binary fitting energy term, aiming to segment images with intensity inhomogeneity and noise. In terms of theoretical research, to ensure unconditional stability of proposed AC equation with logarithmic free energy, Park et al. [25] employed interpolation and finite difference methods to solve the splitting terms. Choi and Kim [26] introduced a novel conservative AC equation with new Lagrange multipliers, and provided corresponding numerical methods that maintain the maximum principle and ensure unconditional stability. Zhang and Yang [27] presented a numerical method for solving the spatial fractional Allen-Cahn equation. Their approach involved utilizing the Crank-Nicolson method for time discretization and employing the second-order weighted and shifted Grünwald difference formula for spatial discretization. Based on the characteristics of phase field phase separation, phase field model can form a interface like hyperplane and the exciting thing is that the interface is nonlinear. Therefore, based on phase field model, novel classifiers were constructed by Wang et al. [28,29], which owned excellent classification performance.
The remainder of the paper is structured as follows. We introduce the methodology in Section 2. Section 3 present the data information. Section 4 contains the empirical results. Section 5 reports the conclusion.

2. Methodology

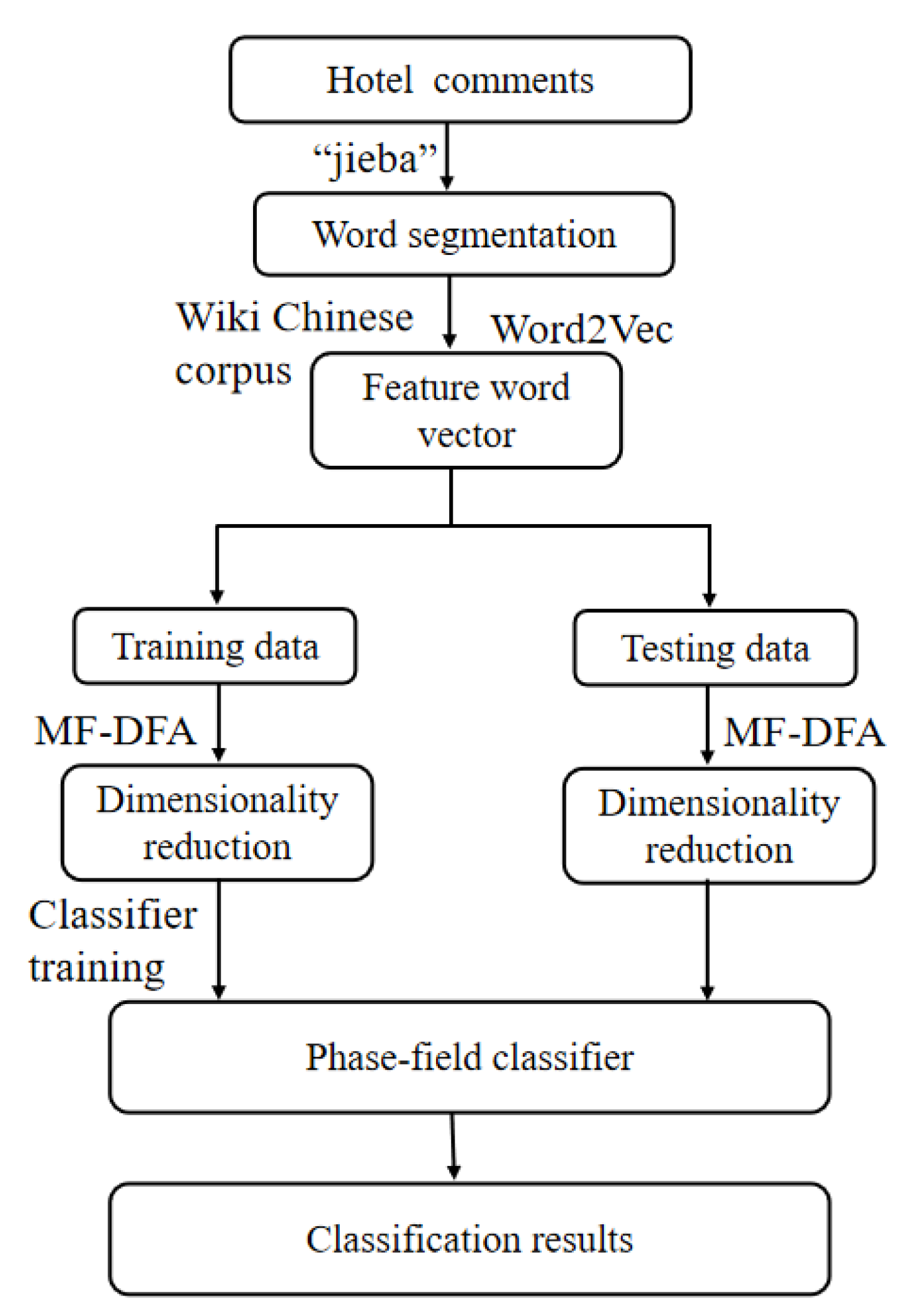
This study proposes a hotel comment sentiment analysis model in Figure 1 based on the characteristics of hotel comment text. The proposed algorithm mainly includes the modules such as the preprocessing, word vector acquisition, word vector feature extraction, and phase-field classification. Subsequently, we describe the two main methods used in this article.

2.1. MF-DFA

MF-DFA is adopted to explore the fractal characteristic of the time series, which has been widely applied in finance [30,31], medicine [32,33], etc. The detailed calculation about MF-DFA is presented as follows.
Firstly, construct a mean-removed sum series T ( i ) for the time series t k , the length of which is N:
T ( i ) = ∑ k = 1 i ( t k − t ¯ ) , i = 1 , 2 , ⋯ , N .
where t ¯ is the mean of the series t k .
Next, divide the new series T ( i ) into N disjoint intervals of length s, which aims to change the time scale. Here, N is rounded to N / s . In order to reduce the loss of the information in the process of dividing the sum series T ( i ) , T ( i ) needs to be divided once according to i from small to large and from large to small, so that a total of 2 N s intervals can be obtained.
The following step is performing a polynomial fitting of the series between each interval and the polynomial fitting adopted is the least square method, designed to remove the trend of the series segment:
y v ( i ) = α 1 i m + α 2 i m − 1 + ⋯ + α m i + α m + 1 , i = 1 , 2 , ⋯ , s ; m = i , 2 , ⋯ .
where v is the number of the points in each interval.
Then, calculate the mean square error f 2 ( s , v ) of the each interval. When v = 1 , 2 , ⋯ , N s ,
f 2 ( s , v ) = 1 s ∑ i = 1 s T [ ( v − 1 ) s + i ] − y v ( i ) 2 .
When v = N s + 1 , N s + 2 , ⋯ , 2 N s ,
f 2 ( s , v ) = 1 s ∑ i = 1 s T [ N − ( v − N s ) s + i ] − y v ( i ) 2 .
Average the f 2 ( s , v ) obtained from all the segment and the q − th wave function F can be obtained as follows:
F ( s ) = 1 2 N s ∑ v = 1 2 N s [ f 2 ( s , v ) ] q / 2 1 / q , q ≠ 0 , e x p 1 2 N s ∑ v = 1 2 N s l n [ f 2 ( s , v ) ] , q = 0 .
F ( s ) is the function of the dividing length s and the fractal order q. Here, F ( s ) ∝ H ( q ) , where H ( q ) is called the generalized Hurst exponents. When q equals 2, H ( q ) , that is, H ( 2 ) is the standard Hurst exponent and F ( s ) is the standard DFA.

2.2. Phase-Field Model

Based on the energy minimization theory, to handle binary classification problems using the modified Allen-Cahn equation, we minimize the following energy equation:
E ( s ( x , t ) ) = ∫ Ω ∑ k = 1 2 H s k ( x , t ) ϵ 2 + 2 | ∇ s k ( x , t ) | 2 + 2 s k ( x , t ) − h k ( x ) 2 d x ,
where x = ( x , y ) represents the spatial coordinates, H ( s k ) = 0.25 s k 2 ( s k − 1 ) 2 denotes the double-well potential energy function, ϵ represents the interface energy parameter, and λ is a fidelity parameter. In this paper, h k ( x ) represents a fitting term that conforms to the given data while satisfying the constraint ∑ k = 1 2 h k ( x ) = 1 . The vector s = ( s 1 , s 2 ) abides by the constraint ∑ k = 1 2 s k ( x , t ) = 1 , where H ′ ( s ) = ( H ′ ( s 1 ) , H ′ ( s 2 ) ) and h = ( h 1 , h 2 ) . After minimizing the free energy functional Equation (6), we can obtain the following modified Allen-Cahn equation in the sense of L 2 , which can be used for binary classification, by employing the gradient flow for k = 1 , 2 :
∂ s k ( x , t ) ∂ t = − H ′ ( s k ( x , t ) ) ϵ 2 + Δ s k ( x , t ) − λ ( s k ( x , t ) − h k ( x ) ) − ζ ( s ( x , t ) ) ,
where ζ ( s ( x , t ) ) = − ∑ k = 1 2 H ′ ( s k ( x , t ) ) / ( 2 ϵ 2 ) . Due to s 1 ( x , t ) + s 2 ( x , t ) = 1 , we utilize zero Neumann boundary conditions to obtain n · ∇ s k ( x , t ) = 0 , for x ∈ ∂ Ω , t > 0 , where n is the unit outward normal vector to ∂ Ω . In the two-dimensional space Ω = ( L x , R x ) × ( L y , R y ) , we discretize it to obtain the following discrete computational domain Ω h = { ( x i , y j ) | x i = L x + ( i − 0.5 ) h , y j = L y + ( j − 0.5 ) h , 1 ≤ i ≤ N x , 1 ≤ j ≤ N y } , where N x and N y are positive integers and h is the uniform mesh size. Let s k ( i j ) n denote the numerical approximations of s k ( x i , y j , n Δ t ) with a time step of Δ t . We divide the modified Allen-Cahn equation into the following two equations for k = 1 , 2 :
∂ s k ( x , t ) ∂ t = − H ′ ( s k ( x , t ) ) ϵ 2 + Δ s k ( x , t ) − ζ ( s ( x , t ) ) ,
∂ s k ( x , t ) ∂ t = λ [ h k ( x ) − s k ( x , t ) ] .
To solve Equation (8) using numerical methods, we employ the explicit Euler method:
s k ( i j ) n + 2 − s k ( i j ) n Δ t = − H ′ ( s k ( i j ) n ) ϵ 2 + Δ h s k ( i j ) n + ∑ k = 1 2 2 ϵ 2 ,
where Δ h s k ( i j ) n represents the Laplace operator. Next, we solve the fidelity equation Equation (9) for s k ( i j ) n + 1 2 using the implicit Euler method and we can rewrite it as follows:
s k ( i j ) n + 1 = s k ( i j ) n + 1 2 + 1 + λ Δ t h k ( i j ) 1 + λ Δ t .
This scheme is explicit, which means we do not need to solve a system of discrete equations implicitly, resulting in faster computations. However, to ensure the stability of the scheme, we have the constraint Δ t < 0.25 h 2 [34].

3. Data Collection

The public sentiment dictionary of hotel comment emotion analysis corpus in this article comes from Tan et al. [35]. Among them, 728 are positive ratings and 772 are negative comments. We take 80 % of these samples as the training set and the rest are the test set.
Firstly, we preprocess the hotel text and use the precise word segmentation function “lcut()" from the jieba library in Python to segment the text. In the jieba word segmentation mode, the precise word segmentation mode can accurately separate the text without redundancy. Then, the preprocessed hotel comments are used as a training set, and a given length word vector time series can be trained through the Word2Vec tool. Next, we use the MF-DFA method to extract the generalized Hurst exponents of the word vector time series, and finally utilize the generalized Hurst exponents in the Phase-field classifier model for sentiment classification of hotel texts.

4. Experimental Results

The experimental environment is based on Python 3.8 with the computer by Intel(R) Core(TM) i5-4430 CPU 3.00GHz processor, using the windows 10 operating system.
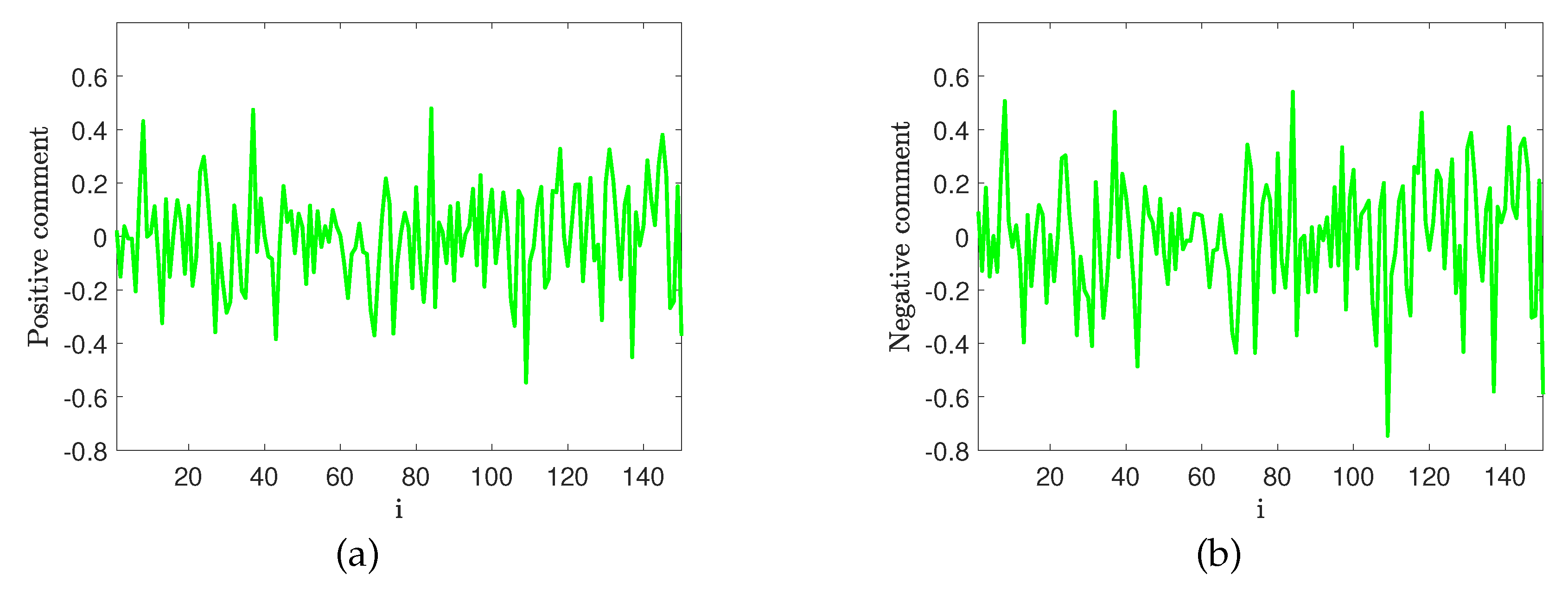
We first convert 1500 hotel comment texts into 1500 word vectors using Word2Vec model. Figure 2 represent a positive hotel comment word vector time series and a negative word vector sequence, respectively. Both sequences are unstable fluctuation sequences, with a large amount of noise in the data. From the sequence perspective, there is no significant difference between the two types of texts. Therefore, we use the MF-DFA method to extract features from time series to reduce data dimensions and improve classification accuracy.
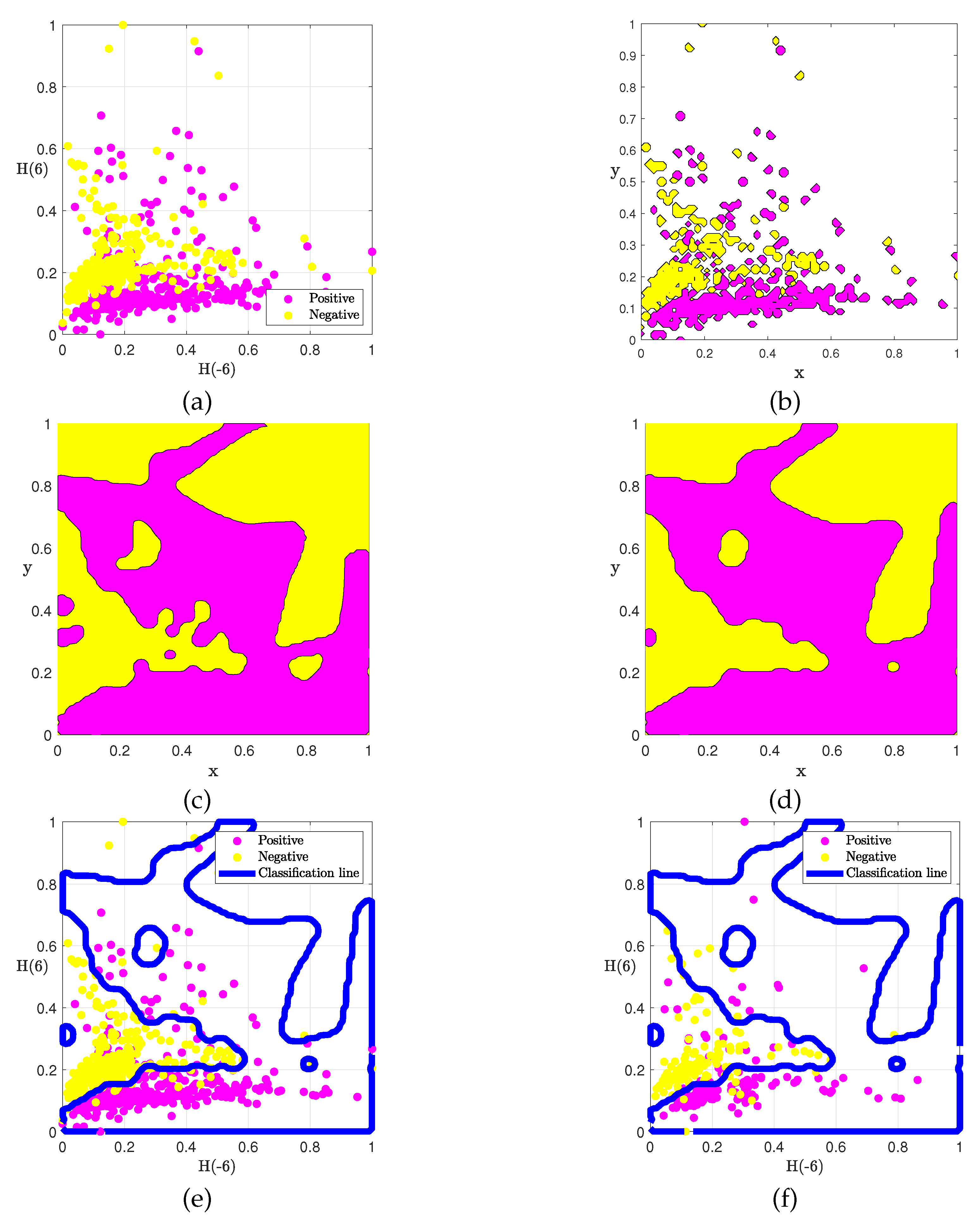
We reduce the dimensionality of the data to three dimensions and extracted generalized Hurst exponents H ( − 6 ) , H ( 0 ) , and H ( 6 ) . For ease of representation, we characterize these three feature values in pairs on a two-dimensional plane and regularize the data within the computational domain of Ω = ( 0 , 1 ) 2 . Next, we first use the Phase-field model classifier to train the training set, and get a nonlinear dividing line suitable for the data distribution characteristics. The parameter settings here are: N x = N y = 100 , h = 1 / N x , ϵ = h / ( 2 2 a t a n h ( 0.9 ) ) , λ = 4500 , α = 0.12 , Δ t = α h 2 .
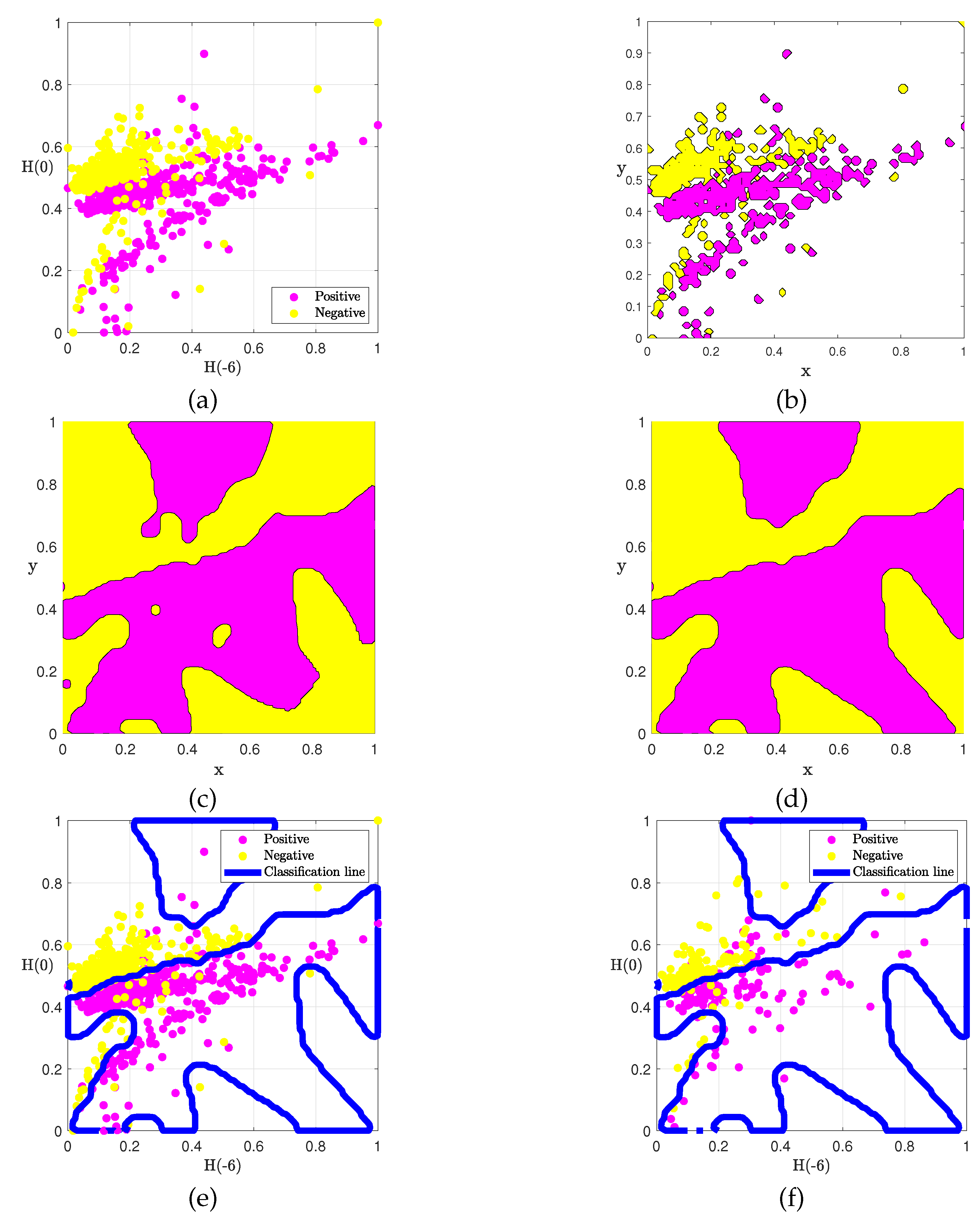
We first investigate the formation of the classification interface under the phase-field model when the Hurst exponent combination is H ( − 6 ) and H ( 0 ) . As shown in Figure 3, the classifier model has strong adaptability to the distribution of initial data. Figure 3(a) shows the data distribution of positive and negative samples of hotel comments, and Figs Figure 3(b)-(d) show the evolution process of the phase of the data points in Figure 3(a) over time, ultimately forming a stable state in Figure 3(d). It can be seen from Figure 3(e) that the dividing line under the phase-field model is nonlinear and can effectively classify texts belonging to different types. However, traditional machine learning models such as DNN and SVM have a linear classification interface, which makes it easy for text data with unclear boundaries to be misclassified.
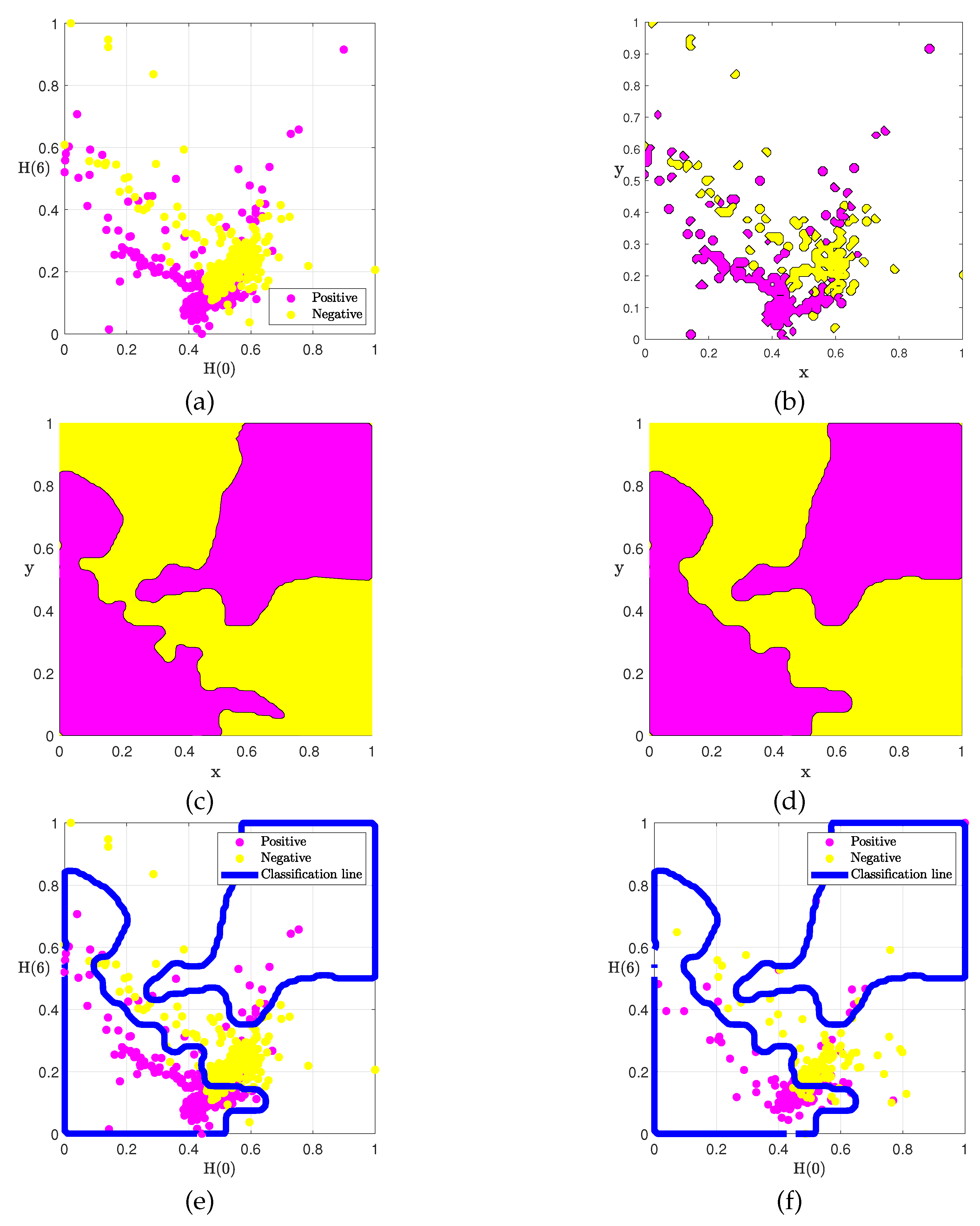
Next, we change the Hurst expponent combination to H ( 0 ) and H ( 6 ) , and use the same parameters as before. As shown in Figure 4, the classifier model can still effectively classify the hotel comment data. Due to differences in the distribution of the initial data compared to Figure 3, the classification interface formed here has also changed.
Finally, we also observed the phase-field evolution process under the combination of H ( − 6 ) and H ( 6 ) , and the classification process is shown in Figure 5.
Next, we adopt the calculation of classification metrics to evaluate the classification effectiveness in the above three scenarios. Accuracy, Precision, Recall, and F 1 Score ars used as the indicators to evaluate the classification results in this study, and the calculation formulas are as follows:
A c c u r a c y = T P + T N T P + F N + F P + T N ,
P r e c i s i o n = T P T P + F P ,
R e c a l l = T P T P + F N ,
F 1 = 2 × P r e c i s i o n × R e c a l l ( P r e c i s i o n + R e c a l l ) ,
For a binary classification problem, where instances are divided into positive or negative classes, the following four situations may occur in actual classification:
I. If an instance is positive and predicted to be positive, it is the true class TP (True Positive).
II. If an instance is positive but predicted to be negative, it is called a false negative class FN (False Negative).
III. If an instance is negative but predicted to be positive, it is a false positive FP (False Positive).
IV. If an instance is negative and predicted to be negative, it is true negative class TN (True Negative).
The classification metrics in Table 1 show that there is no significant difference in the classification results of our model under the combination of three different Hurst exponents. This further indicates that the three Hurst indices extracted by MF-DFA retain the main features of the original word vector, and the feature values are all efficient. Excellent results have been achieved on all the indicators of Accuracy, Precision, Recall, and F 1 Score.
In order to demonstrate the nonlinear interface formed by our proposed model in hotel comment text classification and achieve the advantage of high accuracy, we compared the model with DNN and SVM classifiers which have linear classification interfaces. As shown in Table 2, the classification indicators of hotel comment texts under the phase-field classifier are superior to the traditional two classifier models. However, our model needs a large number of grids because of the discretization in the required space. Therefore, it is suitable for data classification in low dimensions. For high-dimensional data and is prone to Curse of dimensionality for high-dimensional data.

5. Conclusions

This paper mainly studied the emotional classification problem of hotel comment texts. Firstly, the original text data were preprocessed, and the texts were segmented using the jieba tool. Then, the text was processed into a time series type word vector using Word2Vec. For these unstable sequences with weak features, we adopted the MF-DFA method for feature extraction, reducing the dimensionality of the word vector sequence with a length of 150 to a length of 3. Then, we combine the three reduced featiure values in pair in the two-dimensional computing domain. Then we used the phase-field model to evolve the data based phase values, and finally get a nonlinear classification interface that can adapt to the distribution characteristics of data in the computing domain. Through experimental verification on the test set, the results showed that in all three classification scenarios, the classifier can effectively form and classify the positive and negative emotions of hotel comment texts in the test set. In order to demonstrate the advantages of the nonlinear classification interface, we calculated the classification indicators for the same data using DNN and SVM, and the calculation results exhibited that our model was more efficient. Since the phase-field model needs to assign phase values on the discrete grid in space, the data dimensions used for calculation cannot be too large, and the equation discretization in the phase-field model is difficult to occur in a space larger than 3 dimensions. In our future research, our main focus will be on improving the robustness of the classification algorithm in high-dimensional data, improving the accuracy of classifier classification, and enhancing the applicability of the classification algorithm in other fields of network commentary.

Acknowledgments

The author Jian Wang expresses thanks for the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant Nos. 22KJB110020).

Conflicts of Interest

The authors declare that there is no conflict of interests regarding the publication of this article.

References

  1. Hirschberg, J., & Manning. Advances in natural language processing. Science 2015, 349(6245), 261–266. [Google Scholar] [CrossRef] [PubMed]
  2. Lu, Y. (2019). Artificial intelligence: A survey on evolution, models, applications and future trends. Journal of Management Analytics, 6(1), 1–29.
  3. Hu, M., Dang. Search and learning at a daily deals website. Marketing Science 2019, 38(4), 609–642. [Google Scholar] [CrossRef]
  4. Bansal, N., Sharma. Fuzzy AHP approach for legal judgement summarization. Journal of Management Analytics 2019, 6(3), 323–340. [Google Scholar] [CrossRef]
  5. He, W. , Tian, X., Tao, R., Zhang, W., Yan, G., & Akula, V. (2017). Application of social media analytics: A case of analyzing online hotel reviews. Online Information Review, 41(7), 921-935. [CrossRef]
  6. Gaur, L. , Afaq, A., Solanki, A., Singh, G., Sharma, S., Jhanjhi, N. Z.,... &amp; Le, D. N. (2021). Capitalizing on big data and revolutionary 5G technology: Extracting and visualizing ratings and reviews of global chain hotels. Computers and Electrical Engineering, 95, 107374. [Google Scholar] [CrossRef]
  7. Kang, Y. , Cai, Z., Tan, C. W., Huang, Q., & Liu, H. (2020). Natural language processing (NLP) in management research: A literature review. Journal of Management Analytics, 7(2), 139-172. [CrossRef]
  8. Alshemali, B. , &amp; Kalita, J. (2020). Improving the reliability of deep neural networks in NLP: A review. Knowledge-Based Systems, 191, 105210. [Google Scholar] [CrossRef]
  9. Sann, R. , &amp; Lai, P. C. (2020). Understanding homophily of service failure within the hotel guest cycle: Applying NLP-aspect-based sentiment analysis to the hospitality industry. International Journal of Hospitality Management, 91, 102678. [Google Scholar] [CrossRef]
  10. Jiao, Y., & Qu. A proposal for Kansei knowledge extraction method based on natural language processing technology and online product reviews. Computers in Industry 2019, 108, 1–11. [Google Scholar] [CrossRef]
  11. Sharma, M., Singh, G., & Singh, R. Design of GA and ontology based NLP frameworks for online opinion mining. Recent Patents on Engineering. 2019, 13(2), 159–165. [CrossRef]
  12. Guerrero-Rodriguez, R. , Álvarez-Carmona, M. Á., Aranda, R., & López-Monroy, A. P. (2023). Studying online travel reviews related to tourist attractions using nlp methods: The case of guanajuato, mexico. Current issues in tourism, 26(2), 289-304. [CrossRef]
  13. Wang, X. , Xu, Z. ( 2022). The Interval probabilistic double hierarchy linguistic EDAS method based on natural language processing basic techniques and its application to hotel online reviews. International Journal of Machine Learning and Cybernetics, 1–18. [CrossRef]
  14. Jiang, Z. Q. , Xie, W. J., Zhou, W. X., &amp; Sornette, D. (2019). Multifractal analysis of financial markets: A review. Reports on Progress in Physics, 82(12), 125901. [Google Scholar] [CrossRef]
  15. Fernandes, L. H. , Silva, J. W., de Araujo, F. H., & Tabak, B. M. (2023). Multifractal cross-correlations between green bonds and financial assets. Finance Research Letters, 53, 103603. [CrossRef]
  16. Yao, C. Z. , Liu, C., &amp; Ju, W. J. (2020). Multifractal analysis of the WTI crude oil market, US stock market and EPU. Physica A: Statistical Mechanics and its Applications, 550, 124096. [Google Scholar] [CrossRef]
  17. Mensi, W. Vo, X. V., & Kang, S. H. (2022). Upward/downward multifractality and efficiency in metals futures markets: The impacts of financial and oil crises. Resources Policy, 76, 102645. [CrossRef]
  18. Li, N. , Wu, S. B., Yu, Z. H., & Gong, X. Y. (2023). Feature Extraction with Multi-fractal Spectrum for Coal and Gangue Recognition Based on Texture Energy Field. Natural Resources Research, 1-17. [CrossRef]
  19. Joseph, A. J. , & Pournami, P. N. (2021). Multifractal theory based breast tissue characterization for early detection of breast cancer. Chaos, Solitons & Fractals, 152, 111301. [CrossRef]
  20. Lahmiri, S. , & Bekiros, S. (2022). Complexity measures of high oscillations in phonocardiogram as biomarkers to distinguish between normal heart sound and pathological murmur. Chaos, Solitons & Fractals, 154, 111610. [CrossRef]
  21. Abbasi, M. U. , Rashad, A., Basalamah, A., & Tariq, M. (2019). Detection of epilepsy seizures in neo-natal EEG using LSTM architecture. IEEE Access, 7, 179074-179085.
  22. Allen, S. M. , & Cahn, J. W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta metallurgica 1979, 27(6), 1085–1095. [Google Scholar]
  23. Li, Y. , Song, X., Kwak, S., & Kim, J. (2022). Weighted 3D volume reconstruction from series of slice data using a modified Allen–Cahn equation. Pattern Recognition, 132, 108914. [CrossRef]
  24. Liu, C. , Qiao, Z., & Zhang, Q. (2022). Two-Phase Segmentation for Intensity Inhomogeneous Images by the Allen–Cahn Local Binary Fitting Model. SIAM Journal on Scientific Computing, 44(1), B177-B196. [CrossRef]
  25. Park, J. , Lee, C., Choi, Y., Lee, H. G., Kwak, S., Hwang, Y., & Kim, J. (2022). An unconditionally stable splitting method for the Allen–Cahn equation with logarithmic free energy. Journal of Engineering Mathematics, 132(1), 18. [CrossRef]
  26. Choi, Y. , & Kim, J. (2023). Maximum principle preserving and unconditionally stable scheme for a conservative Allen–Cahn equation. Engineering Analysis with Boundary Elements, 150, 111-119. [CrossRef]
  27. Zhang, B. , & Yang, Y. (2023). A new linearized maximum principle preserving and energy stability scheme for the space fractional Allen-Cahn equation. Numerical Algorithms, 93(1), 179-202. [CrossRef]
  28. Wang, J. , Han, Z., Jiang, W., & Kim, J. (2023). A novel classification method combining Phase-Field and DNN. Pattern Recognition, 109723. [CrossRef]
  29. Wang, J. , Xu, H., Jiang, W., Han, Z., & Kim, J. (2023). A novel MF-DFA-Phase-Field hybrid MRIs classification system. Expert Systems with Applications, 225, 120071. [CrossRef]
  30. Miloş, L. R. , Haţiegan, C., Miloş, M. C., Barna, F. M., Boțoc, C. (2020). Multifractal detrended fluctuation analysis (MF-DFA) of stock market indexes. Empirical evidence from seven central and eastern European markets. Sustainability, 12(2), 535. [CrossRef]
  31. Aslam, F. , Aziz, S., Nguyen, D. K., Mughal, K. S., Khan, M. (2020). On the efficiency of foreign exchange markets in times of the COVID-19 pandemic. Technological forecasting and social change, 161, 120261. [CrossRef]
  32. Wang, J. , Shao, W., Kim, J. (2021). Ecg classification comparison between mf-dfa and mf-dxa. Fractals, 29(02), 2150029. [CrossRef]
  33. Wang, F. , Wang, H., Zhou, X., Fu, R. (2022). Study on the effect of judgment excitation mode to relieve driving fatigue based on MF-DFA. Brain sciences, 12(9), 1199. [CrossRef]
  34. J.W. Thomas, Numerical Partial Differential Equations: Finite Difference Methods, Springer Science & Business Media, 22 (2013) New York.
  35. Tan S, Zhang J. An empirical study of sentiment analysis for Chinese documents. Expert Syst. Appl. (2008);34(4):2622–2629. [CrossRef]
Preprints 79927 g001
Figure 1. Flowchart of hotel comment emotional analysis model.
Figure 1. Flowchart of hotel comment emotional analysis model.
Preprints 79927 g001
Preprints 79927 g002
Figure 2. Word vector sequence of (a) positive hotel comment, and (b) negative hotel comment.
Figure 2. Word vector sequence of (a) positive hotel comment, and (b) negative hotel comment.
Preprints 79927 g002
Preprints 79927 g003
Figure 3. Classification process of Hurst exponent group H ( − 6 ) and H(0) of (a) initial training data, (b) phase evolution at t = 0 , (c) phase evolution at t = 50 Δ t , (d) phase evolution at t = 350 Δ t , (e) classification interface under training set, and (f) classification results under the test set.
Figure 3. Classification process of Hurst exponent group H ( − 6 ) and H(0) of (a) initial training data, (b) phase evolution at t = 0 , (c) phase evolution at t = 50 Δ t , (d) phase evolution at t = 350 Δ t , (e) classification interface under training set, and (f) classification results under the test set.
Preprints 79927 g003
Preprints 79927 g004
Figure 4. Classification process of Hurst exponent group H ( 0 ) and H(6) of (a) initial training data, (b) phase evolution at t = 0 , (c) phase evolution at t = 50 Δ t , (d) phase evolution at t = 350 Δ t , (e) classification interface under training set, and (f) classification results under the test set.
Figure 4. Classification process of Hurst exponent group H ( 0 ) and H(6) of (a) initial training data, (b) phase evolution at t = 0 , (c) phase evolution at t = 50 Δ t , (d) phase evolution at t = 350 Δ t , (e) classification interface under training set, and (f) classification results under the test set.
Preprints 79927 g004
Preprints 79927 g005
Figure 5. Classification process of Hurst exponent group H ( − 6 ) and H(6) of (a) initial training data, (b) phase evolution at t = 0 , (c) phase evolution at t = 50 Δ t , (d) phase evolution at t = 350 Δ t , (e) classification interface under training set, and (f) classification results under the test set.
Figure 5. Classification process of Hurst exponent group H ( − 6 ) and H(6) of (a) initial training data, (b) phase evolution at t = 0 , (c) phase evolution at t = 50 Δ t , (d) phase evolution at t = 350 Δ t , (e) classification interface under training set, and (f) classification results under the test set.
Preprints 79927 g005
Table 1. Classification metrics according to different Hurst exponents group.
Table 1. Classification metrics according to different Hurst exponents group.
Group TP TN FP FN Accuracy Precision Recall F 1
H(-6) & H(0) 115 149 10 26 0.88 0.92 0.82 0.87
H(0) & H(6) 118 145 14 23 0.88 0.89 0.84 0.86
H(-6) & H(6) 120 146 13 21 0.89 0.90 0.85 0.87
Table 2. Comparisons between other classifiers and ours.
Table 2. Comparisons between other classifiers and ours.
Method Accuracy Precision Recall F 1
DNN 0.80 0.79 0.77 0.78
SVM 0.82 0.83 0.79 0.81
Ours 0.89 0.90 0.85 0.87
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated