Prerpints.org logo
Preprint
Article

Closed Form Solutions to a Class of Pursuit Problems Using Geometric Analogies

Altmetrics

Downloads

184

Views

44

Comments

0

This version is not peer-reviewed

Submitted:

19 July 2023

Posted:

19 July 2023

Read the latest preprint version here

Alerts
Abstract
This article studies a class of pursuit problems admitting both a simple geometric solution as well as a more general analytic treatment. The results are specialized to demonstrate solutions to certain elementary problems typically posed to high schoolers, although a full analytic treatment, requiring some more comfort with geometry and calculus, is typically avoided at that stage.
Keywords: 
Subject: Physical Sciences  -   Other

1. Introduction

Pursuit problems are of critical importance in several engineering and science applications today, including navigation, warfare, and so on. The study of these problems were first motivated by the problems of navigating ships in the age of exploration [1,3]. The Apollonius pursuit problem was defined as that of finding whether a ship leaving from a point A with a constant velocity v A will intercept another ship leaving from point B with a constant velocity v B . The situation of adaptive pursuit, where the pursuer maneuvers their “ship” adaptively according to position of the pursuee, was first studied by Bouguer [5], who derived the so-called “radiodrome” as the curve of best pursuit.
More recently, this problem has been generalized in various ways, for example, allowing for variable speeds of the pursuer and the pursued, adaptive strategies for the pursued, energy constraints on the pursuer and pursued, as well as errors in observation and imperfect information. For a detailed survey on these various generalizations and constraints, we refer the reader to [2,7,10,13] and references therein.
In this work, we look at a class of pursuit problems admitting a simple geometrical argument for establishing the locus and further generalize the result using analytic arguments. We demonstrate that certain popular challenge problems typically posed to senior high school or freshmen undergraduate students in physics admit simple solutions as special cases of these results.

2. Problem Setup and Main Results

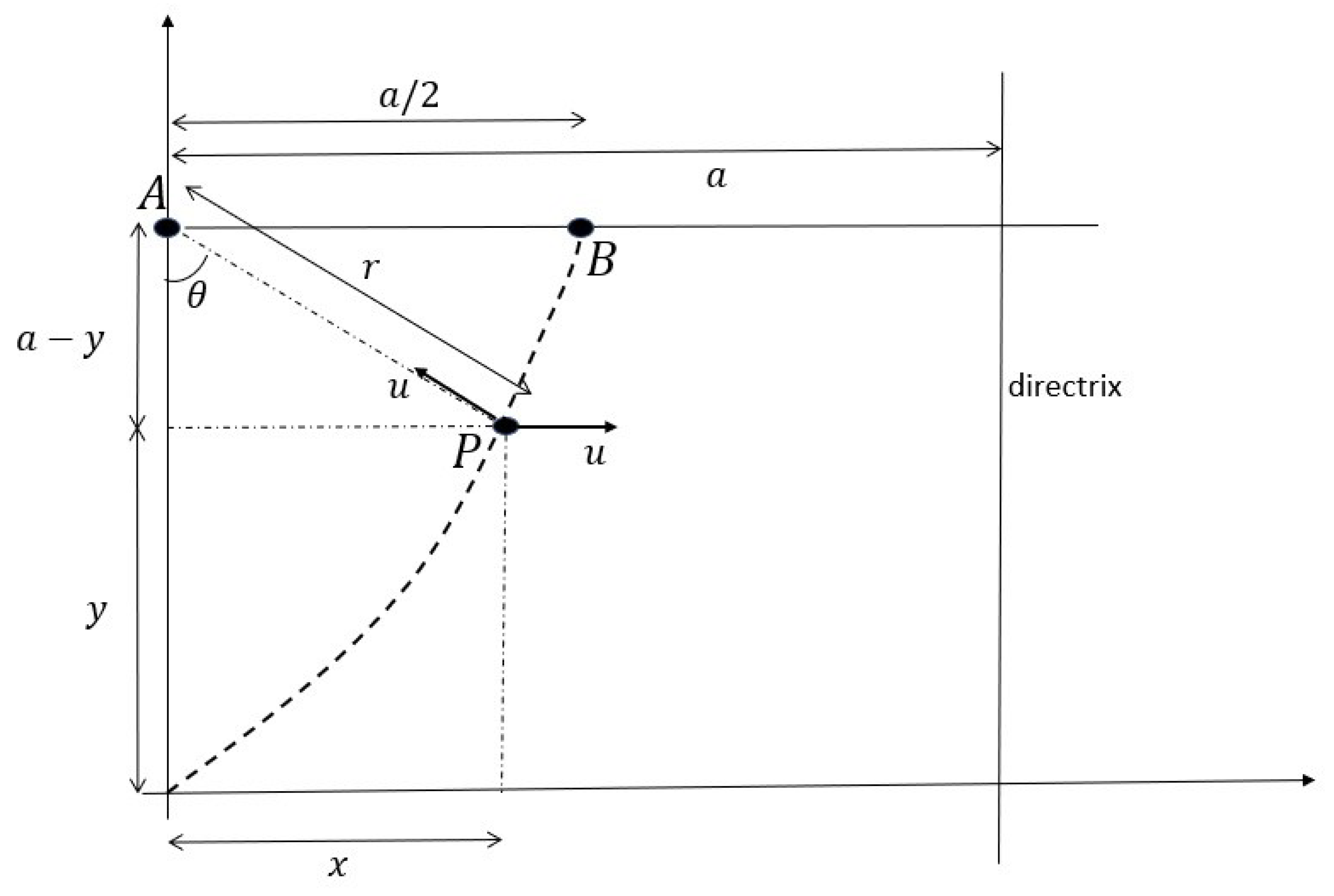
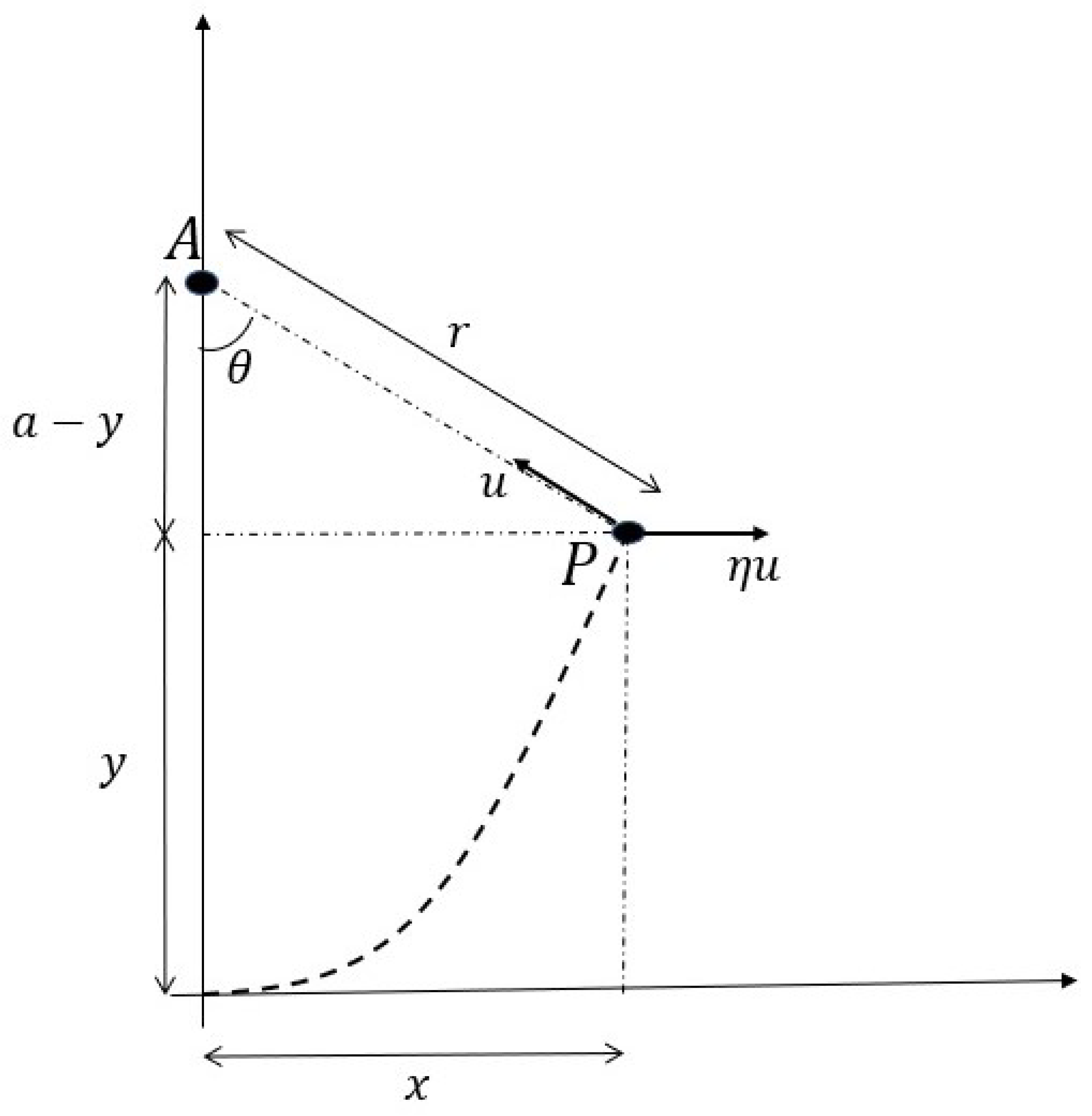
The main setup of our problem is illustrated in Figure 1 and Figure 2. A pursuer P wishes to catch a stationary “prey” A by always approaching A with speed η u pointing towards A , while drifting in the x direction with constant speed η u . The problem now is to find the trajectory of P and decide if P will ever be able to catch A .
The general solution to this problem for η ∈ R in presented in Theorem 1 and requires an analytic treatment; however, for the special case η = 1 , it can be argued geometrically that the trajectory is a conic section, without delving into any analytic derivation. The critical observation that makes this argument possible is that for this case (see Figure 1), the component of the velocity of P along the x axis remains identical to the component of the velocity of P in the instantaneous direction of A , each being equal to u ( 1 − sin θ ) . Therefore, the total amount of drift in the x direction till any time t is equal to the reduction in the distance between P and A till t . This observation immediately enables us to prove the following lemma.
Lemma 1. 
Suppose a point P , starting from the origin ( 0 , 0 ) , wishes to reach the point A ( 0 , a ) by always trying to approach A at speed u , as shown in Figure 1. However, there is a constant “current” of the same speed u towards the positive x direction, which causes the path of P to drift. Then, the resultant locus of P is a parabola with focus at A , given by the equation
x = a 2 1 − a − y a 2
for y ∈ [ 0 , a ] .
Geometric proof of Lemma 1. 
Consider a line parallel to the y-axis, at a distance a (i.e., the line satisfying y = a ). By the previous arguments, the distance of the man from this line remains equal to his distance from A . This leads us immediately to conclude, from elementary geometry, that the locus of the path is a parabola with focus at A and directrix given by the line y = a . Moreover, the final point B lies on the perpendicular drawn from the focus to the directrix and is therefore the vertex. The length of the latus rectum is then given by 2 a , and the parabola “opens” in the negative x direction with vertex at ( a / 2 , a ) . The equation of the path is then given by
( a − y ) 2 x − a 2 = − 2 a i . e . , x = a 2 − ( a − y ) 2 2 a i . e . , x = a 2 1 − a − y a 2 .
□
Finding the time dependence of the motion, however, requires some additional effort. To that end, note that since the positive y component of the velocity is given by u cos θ = u ( a − y ) / x 2 + ( a − y ) 2 , we have
d t = x 2 + ( a − y ) 2 u ( a − y ) d y = ( 2 a − y ) 2 y 2 4 a 2 + ( a − y ) 2 u ( a − y ) d y .
Setting z : = ( a − y ) / a , we then have
u d t a = − 1 + ( 1 + z ) 2 ( 1 − z ) 2 4 z 2 d z = − 1 + z 2 2 z d z .
The integrated equation of motion is then given by
2 u t a = ∫ 1 − y a 1 ( z − 1 + z ) d z .
Integrating Equation 2 and re-arranging leads to
t = a 4 u 1 − a − y a 2 − 2 log a − y a .
We now tackle the general case where the speed of the current is given by η u for η ∈ R . As a first step, we present the following elementary result, which is a popular problem posed in elementary kinematics (see, for example, [14] prob. 1.13, p. 13).
Lemma 2. 
For | η | < 1 , the pursuer reaches the point A, as depicted in Figure 2, at time t f = a / u ( 1 − η 2 ) .
Proof. 
From Figure 2, we have x ˙ = η u − u sin θ and r ˙ = η u sin θ − u . Eliminating θ between these relations leads to η x ˙ + r ˙ + ( 1 − η 2 ) u = 0 . Integrating this equation with the initial conditions x ( 0 ) = 0 , r ( 0 ) = a leads to
r = a − η x − ( 1 − η 2 ) u t .
Setting r ( t f ) = x ( t f ) = 0 in (4) leads to the result. □
Remark 1. 
We note that eqn (4) holds in general for any η . However, t f is finite only for | η | < 1 .
Remark 2. 
We can use eqn (4) to provide a second proof of Lemma 1 as follows. Setting η = 1 in (4) leads to
r = a − x i . e . , x 2 + ( a − y ) 2 = ( a − x ) 2 i . e . , 2 a x = a 2 − ( a − y ) 2 ,
which yields eqn (1) on dividing both sides by 2 a .
We now establish the most general result of this section.
Theorem 1. 
The equation of path of the pursuer, with x , y , r , and θ as depicted in Figure 2, is given by
x = a 2 a − y a 1 − η − a − y a 1 + η .
Further, the time dependence of the path is given by
t = a 2 u 2 1 − η 2 − 1 1 − η a − y a 1 − η − 1 1 + η a − y a 1 + η , | η | ≠ 1 a 4 u 1 − a − y a 2 − 2 log a − y a , | η | = 1 .
The path equation (5) holds for y ∈ [ 0 , a ] for | η | ≤ 1 and y ∈ [ 0 , a ) for | η | > 1 , while (6) holds for y ∈ [ 0 , a ] for | η | < 1 and y ∈ [ 0 , a ) for | η | ≥ 1 .
Corollary 1. 
We note here that Theorem 1 immediately recovers the result of Lemma 1 by setting η = 1 . In addition, setting y = a in (6) (for | η | < 1 ) leads to
t f = a u ( 1 − η 2 ) ,
which recovers the result of Lemma 2.
Proof of Theorem 1. 
We start from eqn (4). Setting x = r sin θ in (4) and solving for r leads to
r = a + ( η 2 − 1 ) u t 1 + η sin θ .
Now, going back to Figure 2, we note that the θ component of the velocity is given by η u cos θ , whence, we have
r θ ˙ = η u cos θ .
Eliminating r between (7) and (8) lets us write down a linear differential equation in θ and t , as
θ ˙ = η u cos θ ( 1 + η sin θ ) a + ( η 2 − 1 ) u t
Integrating (9) leads to
∫ 0 t d τ a + ( η 2 − 1 ) u τ = ∫ 0 θ d ϕ η u cos ϕ ( 1 + η sin ϕ ) .
The LHS of (9) equals
1 ( η 2 − 1 ) u log a + ( η 2 − 1 ) u t a ,
while the RHS, with the substitution z = sin ϕ , can be written as
∫ 0 sin θ d z η u ( 1 − z 2 ) ( 1 + η z ) = ( a ) 1 η u A ∫ 0 sin θ d z 1 − z + B ∫ 0 sin θ d z 1 + z + C ∫ 0 sin θ d z 1 + η z = 1 η u − A log ( 1 − sin θ ) + B log ( 1 + sin θ ) + ( C / η ) log ( 1 + η sin θ ) .
Here, ( a ) is obtained through a standard partial fraction decomposition (see, for example, [18] Sec. IV.5) and the constants A ,   B , and C are obtained as
A = lim z → 1 1 ( 1 + z ) ( 1 + η z ) = 1 2 ( 1 + η ) ,
B = lim z → − 1 1 ( 1 − z ) ( 1 + η z ) = 1 2 ( 1 − η ) ,
C = lim z → − 1 / η 1 1 − z 2 = η 2 η 2 − 1 .
Substituting (12), (13), (14), and (11) into (10) leads to
a + ( η 2 − 1 ) u t a = ( 1 − sin θ ) − 1 2 ( 1 + η ) ( 1 + sin θ ) 1 2 ( 1 − η ) ( 1 + η sin θ ) η 2 η 2 − 1 η 2 − 1 η = ( 1 + η sin θ ) ( 1 − sin θ ) 1 − η 2 η ( 1 + sin θ ) − 1 + η 2 η .
Rearranging leads to
a + ( η 2 − 1 ) u t 1 + η sin θ = a ( 1 − sin θ ) 1 − η 2 η ( 1 + sin θ ) − 1 + η 2 η = a ( 1 − sin 2 θ ) 1 − η 2 η ( 1 + sin θ ) − 1 / η = a ( cos θ ) 1 η − 1 ( 1 + sin θ ) − 1 / η .
Now, from Figure 2, we have cos θ = ( a − y ) / r and sin θ = x / r . Therefore, continuing (15), we have
a + ( η 2 − 1 ) u t 1 + η sin θ = a r ( a − y ) 1 η − 1 ( r + x ) − 1 / η .
Now, using (7) leads to
( r + x ) 1 / η = a ( a − y ) 1 η − 1 ,
which simplifies to
r = a η ( a − y ) 1 − η − x .
Squaring (16) and using r 2 = x 2 + ( a − y ) 2 yields
a − y = a 2 η ( a − y ) 1 − 2 η − 2 x a a − y η .
Finally, solving for x yields
x = ( a − y ) a 2 η ( a − y ) − 2 η − 1 2 a a − y η = a 2 a − y a 1 − η − a − y a 1 + η ,
which establishes the equation of the path. Using this equation of path in (16) yields
r = a 2 2 a − y a 1 − η − a − y a 1 − η + a − y a 1 + η = a 2 a − y a 1 − η + a − y a 1 + η .
Now, using (7), we have, for | η | ≠ 1 ,
( η 2 − 1 ) u t = r ( 1 + η sin θ ) − a = ( a ) r + η x − a = ( b ) a 2 ( 1 + η ) a − y a 1 − η + ( 1 − η ) a − y a 1 + η − 2 ,
which simplifies to
t = a 2 u 2 1 − η 2 − 1 1 − η a − y a 1 − η − 1 1 + η a − y a 1 + η ,
establishing the time dependence for | η | ≠ 1 . Here, ( a ) follows by using x = r sin θ , and ( b ) follows by substituting the expressions for r and x from (18) and (17), respectively. Note that the time dependence for the case η = 1 was already established in (3). We demonstrate here an additional sanity check that seems to corroborate this result. We have, for z > 0 ,
lim η → 1 2 1 − η 2 − 1 1 − η z 1 − η − 1 1 + η z 1 + η = lim η → 1 1 − z 1 − η 1 − η + 1 − z 1 + η 1 + η = 1 − z 2 2 − log z .
Setting z = ( a − y ) / a recovers the time dependence expression for η = 1 . □
Remark 3. 
Note that the analysis leading to (19) is merely asanity checkand not a rigorous proof, since we did not argue that t has to be continuous in η for each y . This can, however, be argued fairly easily from elementary results on ordinary differential equations; we point the interested reader to [16] and references therein.

3. Other Pursuit Problems

In this section, we briefly comment on a class of pursuit problems which are commonly stated in the following form. Referring again to Figure 2, suppose the point A moves horizontally with speed η u and the pursuer P always points their velocity vector towards A , but there is no “current”. Clearly, the problem is equivalent to the setting in Theorem 1, but observed from a frame moving in the x direction with velocity η u . Accordingly, for the scenario where A moves in the positive x direction, the x coordinate of P will be given by − ( x − η u t ) , according to the notation used in Section 2, and t ( y ) will remain unchanged. Thus, for this problem, we have, using (5) and (6),
x = a 2 1 1 + η a − y a 1 + η − 1 1 − η a − y a 1 − η + 2 η 1 − η 2 , | η | ≠ 1 , a 4 a − y a 2 − 2 log a − y a − 1 , η = 1 , a 4 1 − a − y a 2 + 2 log a − y a , η = − 1 .
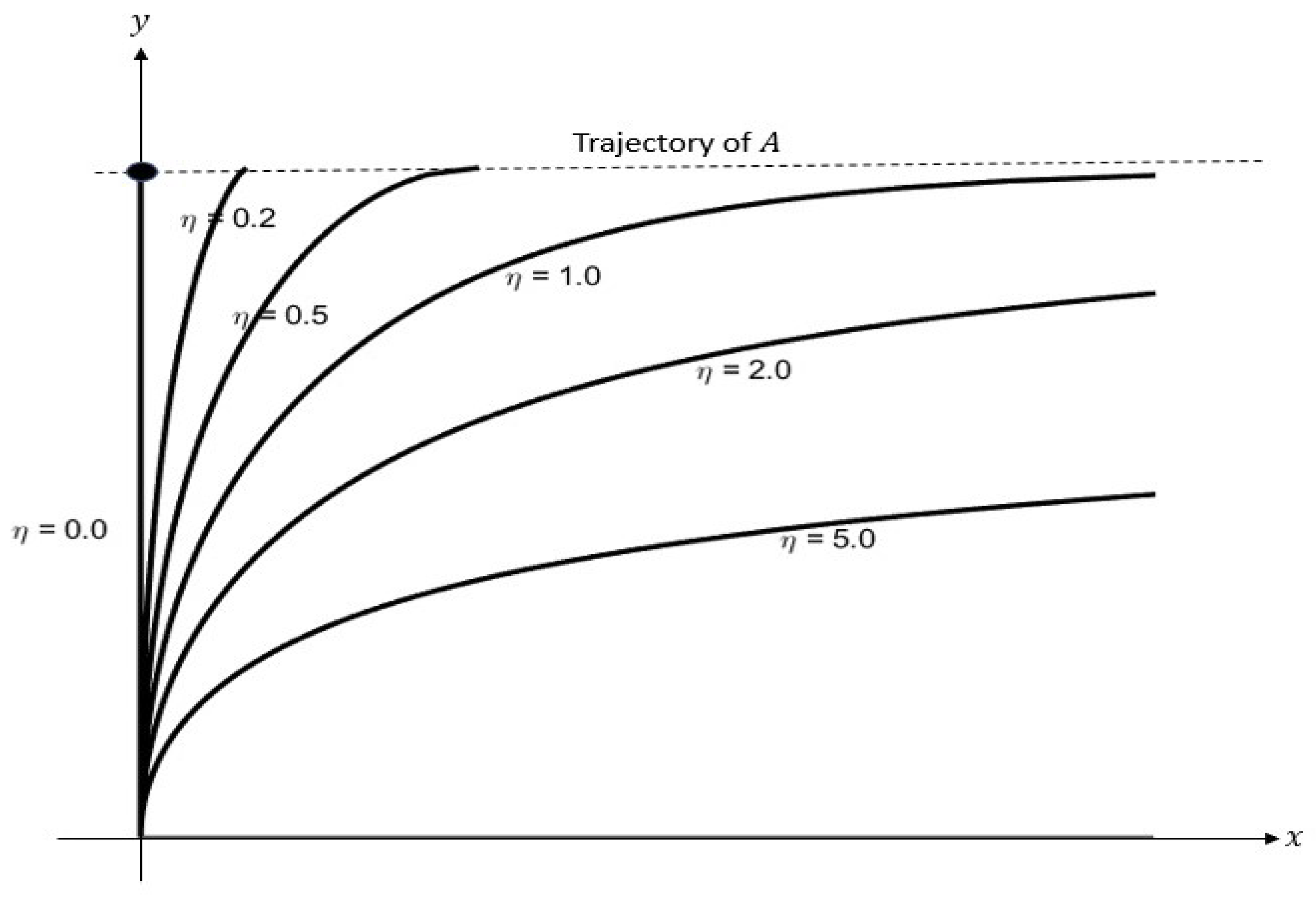
Figure 3 plots the pursuit trajectories (20) for various values of η . For | η | ≥ 1 , the trajectory approaches the trajectory of A asymptotically, while for | η | < 1 , the pursuer “catches” the prey at x = a η / ( 1 − η 2 ) .
Remark 4. 
This problem illustrates an interesting kinematic phenomenon: the trajectory in the first problem (Theorem 1) for η = 1 is a finite segment of a parabola with no asymtotes, while the trajectory for the same problem observed from a different frame has an asymptote ( y = a ) and “looks” quite different (cf. Figure 3), even though the frames move with uniform velocity with respect to one another.

4. Discussions

The settings explored in this work can be generalized to include various scenarios, as allued to in the introduction. A geometric solution, while it may not be feasible in a general setting, might still provide a useful starting point and provide insights critical to solving many such problems. Bernhart [20] and others [7,9,23] have performed in-depth treatment specifically of the geometric properties and aspects of pursuit curves.

References

  1. E. Kasner and F. Supnick, “The Apollonian packing of circles”, Proceedings of the National Academy of Sciences USA 29(11), pp. 378–384, 1943.
  2. N. Ghaddar, S. Ganguly, L. Wang, and Y.-H. Kim, “A Lego-Brick Approach to Coding for Asymmetric Channels and Channels with State”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1367–1372, 2021.
  3. Isaac Weintraub, Eloy Garcia, and Meir E. Pachter, “Optimal guidance strategy for the defense of a non-manoeuverable target in 3-dimensions”, IET Control Theory & Applications 14(11), pp. 1531–1538, 2020.
  4. S. Ganguly and Y.-H. Kim, “Capacity Scaling for Cloud Radio Access Networks with Limited Orthogonal Fronthaul”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1472–1476, 2019.
  5. Pierre Bouguer, “Sur de nouvelles courbes auxquelles on peut donner le nom de lignes de poursuite”, Mémoires de mathématique et de physique tirés des registres de l’Académie royale des sciences, pp. 1–15, 1732.
  6. N. Ghaddar, S. Ganguly, L. Wang, and Y.-H. Kim, “A Lego-Brick Approach to Coding for Network Communication”, arXiv:2211.07208v3 [cs.IT], 2022.
  7. J. C. Barton and C. J. Eliezer, “On Pursuit Curves”, The Journal of the Australian Mathematical Society B41: Applied Mathematics (3), pp. 358–371, 2000.
  8. S. Ganguly and S. Pal, “Bounds on the Density of States and the Spectral Gap in CFT–2”, Phys. Rev. D 101(14):106022, pp. 1–4, May 2020.
  9. S. Ganguly, L. Wang, and Y.-H. Kim, “A Functional Construction of Codes for Multiple Access and Broadcast Channels”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1581–1586, 2020.
  10. C. Hoenselaers, “Chasing Relativistic Rabbits”, General Relativity and Gravitation (4), pp. 351–360, 1995.
  11. S. Ganguly and L. Wang, “Sliding-Window Gelfand–Pinsker Coding: General K-User Broadcast Channels”, Proceedings of the IEEE Information Theory Workshop (ITW), pp. 1–5, 2020.
  12. Richard P. Feynman, Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics, Vol. 1 (Addison-Wesley, 1964), p. 3–10.
  13. S. Ganguly and Y.-H. Kim, “On the Capacity of Cloud Radio Access Networks”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 2063–2067, 2017.
  14. I. E. Irodov, Problems in General Physics (Mir Publishers, 1988).
  15. S. Ganguly, S.-E. Hong, and Y.-H. Kim, “On the Capacity Regions of Cloud Radio Access Networks with Limited Orthogonal Fronthaul”, IEEE Trans. Inf. Theory 67(5), pp. 2958–2988, May 2021.
  16. Erwin Kreyszig, Advanced Engineering Mathematics (3rd ed.) (New York: Wiley, 1972).
  17. S. Ganguly, K. Sahasranand, and V. Sharma, “A New Algorithm for Distributed Nonparametric Sequential Detection”, Proceedings of the IEEE International Conference on Communications (ICC), pp. 1409–1415, 2014.
  18. Richard Courant, Differential and Integral Calculus, Vol. 1 (London: Blacktie & Son Limited, 1961).
  19. J. Ryu, S. Ganguly, Y.-H. Kim, Y.-K. Noh, and D. D. Lee, “Nearest Neighbor Density Functional Estimation based on Inverse Laplace Transform”, IEEE Trans. Inf. Theory 68(6), pp. 3511–3551, June 2022.
  20. Arthur Bernhart, “Curves of general pursuit”, Scripta Mathematica 24, 1959.
  21. S. Ganguly, K. Sahasranand, and V. Sharma, “A New Algorithm for Nonparametric Sequential Detection”, Proceedings of the National Conference on Communications (NCC), India, pp. 1–6, 2014.
  22. N. Ghaddar, S. Ganguly, L. Wang, and Y.-H. Kim, “A Lego-Brick Approach to Lossy Source Coding”, Proceedings of the 17th Canadian Workshop on Information Theory (CWIT), pp. 45–50, 2022.
  23. A. Guha and S. K. Biswas, “On Leonardo da Vinci’s cat and mouse problem”, Bulletin of the Institute of Mathematics and its Applications 30(1, 2), pp. 12–15, 1994.
Preprints 79926 g001
Figure 1. Schematic description of problem setup for Lemma 1.
Figure 1. Schematic description of problem setup for Lemma 1.
Preprints 79926 g001
Preprints 79926 g002
Figure 2. Schematic description of problem setup for Theorem 1.
Figure 2. Schematic description of problem setup for Theorem 1.
Preprints 79926 g002
Preprints 79926 g003
Figure 3. Pursuit curves.
Figure 3. Pursuit curves.
Preprints 79926 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated