Prerpints.org logo
Preprint
Article

Is PNP Theory Valid for a Black Hole Solution in Modified Gravity?

Altmetrics

Downloads

90

Views

38

Comments

0

This version is not peer-reviewed

Submitted:

14 July 2023

Posted:

17 July 2023

You are already at the latest version

Alerts
Abstract
In this work, we investigated whether the Pseudo-Newtonian theory (PNP) is applicable to black hole solution in modified gravity. In this regard, as an example, a static spherically symmetric 4D AdS Schwarzschild Yang-Mills black hole in EinsteinGauss-Bonnet gravity is considered. Also, a brief discussion on the structure and horizons of this black hole spacetime is presented. We calculated angular momentum and energy in the framework of the general theory of relativity as well as in PNP theory. In both of these framework, a graphical comparison of angular momentum has been studied
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

As is well-known, a Pseudo-Newtonian potential (abbreviated as PNP) is a mathematical construction used in theoretical astrophysics to approximate the effects of general relativity in the motion of a massive particle near a black hole. In other words, most of the theoretical analysis of general theory of relativity in astronomy are studied by a Newtonian or pseudo-Newtonian method. It is called "Pseudo-Newtonian" because it has a form similar to the gravitational potential in Newtonian mechanics but it include additional terms that account for the curvature of spacetime in general relativity. PNP’s are commonly used in studying the accretion of matter onto black holes and the dynamics of relativistic systems. To avoid the complication of full general relativistic equations, it is easier to use non-relativistic treatment but with the domination of corresponding (pseudo) potential which can simulate some relativistic effects consequent to the geometry of spacetime. Using this potential one can obtain the approximate solutions of the hydrodynamical equations. In 2002, Ghosh et al. introduced such a Pseudo-Newtonian potential for a rotating Kerr black hole which is useful enough to reproduce the scenario of the classical mechanics [6]. PNP can replicate all the properties of an accretion disk near a black hole [6,7,8,9]. Chakraborty et al., a few years back, introduced a general formalism of the trajectory of test particles around a general spherically symmetric non-rotating black hole [10] and as an example they considered non-rotating charged Reissner-Nordström black hole. It is worth mentioning that the general formulation of the trajectory is not only limited to standard general relativity but this formulation can also be extendable and applicable for any black hole solution in modified gravity theory. They did not extend the analysis considering the modified theories of gravity. This extended study was carried out by Surajit considering a static black hole in f ( R ) gravity [11]. It is interesting to generalize the results to other gravity models like Einstein-Gauss-Bonnet gravity and Lee-Wick gravity. Here in the present study, in order to generalize the previous result [11], we have extended this analysis considering other modified gravity and as an example we have considered a static and spherically symmetric 4 D AdS Schwarzschild Yang-Mills Black Hole in Einstein-Gauss-Bonnet gravity.
In theoretical physics, theory of general relativity (henceforth GR) by Einstein is one of the most successful theories. Despite its prominenat achievements, there are still some unsolved challenging problems in the universe such as the cosmological constant problem, the hierarchy problem and the late time accelerated expansion of the Universe. This gleams that GR is not the ultimate theory and require further generalization. Addition of the higher curvature terms in the standard Einstein-Hilbert action is one of the possible generalization. Lovelock gravities can provided the higher curvature corrections of natural candidates and are the unique theories that execute generally covariant field equations [12]. Gauss-Bonnet gravity, also familiar as Einstein-Gauss-Bonnet (henceforth EGB), is the normal extension of the standard Einstein-Hilbert action to comprise higher curvature Lovelock terms. In string theory, a Gauss-Bonnet term arrives naturally in the low energy effective action [13]. Recently, Glavan and Lin formulated the EGB gravity in four dimensions as of higher dimensional field equation by rescalling the Gauss-Bonnet coupling constant α by α D − 4 [14]. Examples of some other higher order gravity theory are scalar-tensor theories [15,16,17,18,19,20], Brane world cosmology [21,22,23] and regular black holes [24,25,26]. Moreover, the charged AdS solution of EGB theory can be found in Ref. [27]. For a complete study on 4D GB gravity, see Refs. [28]. Some of the other static and spherically symmetric black hole solutions and their phase transition, thermodynamics in 4D or higher dimensions EGB gravity can be found in Refs. [29,30,31,32,33,34,35].
The consistent theory of 4 D EGB gravity was studied in [36,37]. Singh et al. have studied on 4 D AdS Einstein-Gauss-Bonnet black hole with Yang-Mills field and its thermodynamics [38]. AdS charged black holes in Einstein–Yang–Mills gravity’s rainbow: thermal stability and P − V criticality was studied by Hendi et al. [39]. Naeimipour et al. studied on Yang-Mills black holes in Quasitopological gravity [40]. Rotating Einstein-Yang-Mills black holes and black hole solution of Einstein-Born-Infeld-Yang-Mills theory can be found in [41,42]. P-V criticality of a specific black hole in f ( R ) gravity coupled with Yang-Mills field was studied by Övgün [43] and Aounallah et al. have studied five-dimensional Yang–Mills black holes in massive gravity’s rainbow [44].
The paper is organized in six parts. A brief study regarding the structure of AdS Schwarzschild Yang-Mills black hole spacetime in EGB gravity is presented in Section 2. The horizon and graphical analysis of the lapse function (metric function) with respect to radial coordinate r of this black hole are studied in Section 3. The calculation of the energy and general relativistic angular momentum is presented in Section 4 and also calculated the energy and angular momentum in the framework of PNP theory in Section 5. In this section, to verify PNP theory, we compare both the GR and PNP angular momentum graphically. Finally, we make our conclusion and final remarks in Section 6.

2. Spacetime structure of 4D AdS Schwarzschild Yang-Mills black hole for EGB gravity

In this section, we introduce the metric tensor of a static spherically symmetric black hole of the EGB gravity with the Yang-Mills field. The original theory of EGB gravity by Glavin and Lin [45] has been shown to not be self-consistent. The issue was resolved by Fernandes et.al. in [46] and by Hennigar et.al. in [47]. The D-dimensional EGB gravity in the presence of the Yang-Mills field is given by the following action,
A = 1 2 ∫ d D x − g R − 2 Λ + α D − 4 G − L Y M ,
where α is the Gauss-Bonnet coupling coefficient α ≥ 0 ; G is the Lagrangian density for EGB gravity (called Gauss-Bonnet invariant), given by,
G = R μ ν ρ σ R μ ν ρ σ − 4 R μ ν R μ ν + R 2
and Yang-Mills Lagrangian,
L Y M = − F μ ν ( a ) F ( a ) μ ν ,
which is given in terms of the Faraday–Maxwell tensor or electromagnetic field tensor F μ ν described by F μ ν ( a ) = ∇ ν A μ ( a ) − ∇ μ A ν ( a ) with ∇ ν representing the covariant derivative, and A μ ( a ) , the electromagnetic gauge field.
The equation of motion for the metric tensor ( g μ ν ) and the electromagnetic potential A μ ( a ) are given by respectively,
G μ ν + Λ g μ ν + H μ ν = T μ ν Y M
and
D μ F ( a ) μ ν = 0 ,
where G μ ν and H μ ν , are the Einstein tensor and the Lanczos tensor with the following expressions:
G μ ν ≡ R μ ν − 1 2 g μ ν R ,
H μ ν = − α 2 [ 8 R ρ σ R μ ρ ν σ − 4 R μ ρ σ R μ ρ σ λ − 4 R R μ ν + 8 R μ λ R ν λ + g μ ν ( R ρ σ γ δ R ρ σ γ δ − 4 R ρ σ R ρ σ + R 2 ) ] ,
with R, R μ ν and R μ ν γ δ represents the D = d + 1 dimensional Ricci scalar, Ricci tensor and Riemann tensor respectively. On the other hand, the energy-momentum tensor due to the effect of Yang-Mills field is given by,
T μ ν Y M = − 1 2 g μ ν F ρ σ ( a ) F ( a ) ρ σ + 2 F μ σ ( a ) F ν ( a ) σ .
Now in order to get static spherically symmetric black hole solution for the EGB gravity with Yang-Mills field, we write the line element as,
d s 2 = − f ( r ) d t 2 + d r 2 f ( r ) + r 2 d Ω D − 2 ,
where d Ω D − 2 denotes the metric of a ( D − 2 )-dimensional sphere. The two branch solutions of metric potential for D → 4 has the following form [38]:
f ± ( r ) = 1 + r 2 2 α 1 ± 1 + 4 α 2 M r 3 − ν 2 r 4 − 1 l 2 ,
where naturally adopted Λ in terms of scale length l as, Λ = − 3 l 2 for AdS solution. Since +ve signature of Eq. 10 is completely unphysical as it converted to Reissner-Nordström black hole having negative mass and imaginary charge. Hence we bound ourselves to the -ve branch of solution of Eq. 10, because the -ve signature reduces to the Schwarzschild solution for α → 0 , ν → 0 and l → ∞ . Also, from the above solution, in the limit of ν → 0 and l → ∞ we can be recovered the solution by Glavan and Lin [45]. Finally in α → 0 , the metric function for AdS Schwarzschild Yang-Mills black hole becomes
f ( r ) = 1 − 2 M r + ν 2 r 2 + r 2 l 2 .
Here, M is an integration constant related to the black hole mass and ν is called Yang-Mills charge. However this solution reduces to the Schwarzschild black hole solution for ν = 0 and l → ∞ .
Here, we should note that the Yang-Mills case considered here corroborates with the case of an electrically charged black hole [48] because both yield the same metric function 10. However, AdS Schwarzschild Yang-Mills black hole corroborates with the Reissner-Nordström-AdS black hole [48]. Therefore, our study will be equally valid for Reissner-Nordström-AdS black hole case also.

3. Horizons of spacetime for 4D AdS Schwarzschild Yang-Mills black hole

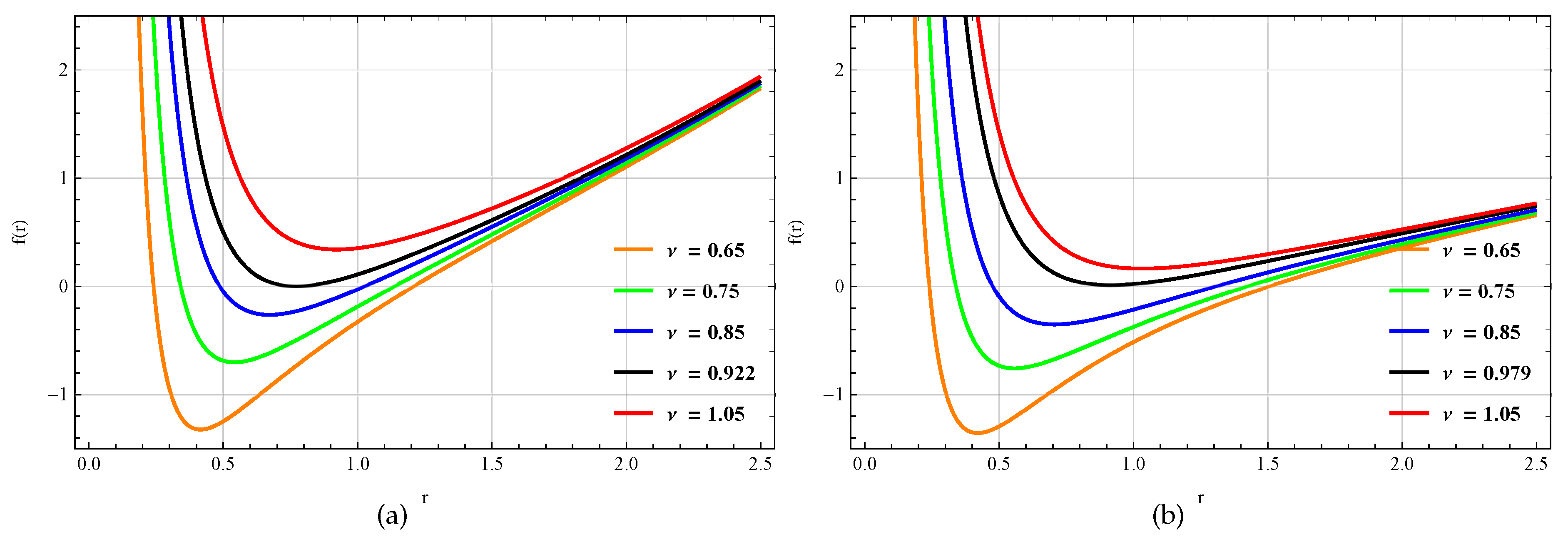
The horizon of the AdS Schwarzschild Yang-Mills black hole 11 is given by setting f ( r ) = 0 . Now, we can plot the graph to estimate the horizons as shown in Figure 1. Figure 1 depicts the profile of metric function f ( r ) with radial coordinate r for five different values of Yang-Mills charge ν , when scale length is l = 2 (left) and l = 4 (right). It is evident from the figure that the radius of the outer horizon increases when the Yang-Mills charge ν decreases. In particular, all the plots are scaled with ν taking values of order 1.
By doing elementary analysis of the zeros of f ( r ) , Figure 1 shows that it has no zeros for ν > ν c , one double zero if ν = ν c and two simple zeros for ν < ν c . It is evident, from the figure that the two horizons coincide at the critical radius,
r c = l 2 1 + 12 ν 2 l 2 − l 2 6 .
It is also evident that r c depends upon the parameters ν and l.

4. Relativistic theory: energy and angular momentum

The basic relativistic theory of energy, angular momentum, and effective potential for a general static non-rotating black hole can be found in Refs. [10,11]. Now, the energy and relativistic conserved angular momentum for circular orbits are respectively
E c = r ( 1 − 2 M r + ν 2 r 2 + r 2 l 2 ) r 2 − 3 M r + 2 ν 2
and
L c = r M r l 2 − ν 2 l 2 + r 4 l r 2 − 3 M r + 2 ν 2 .
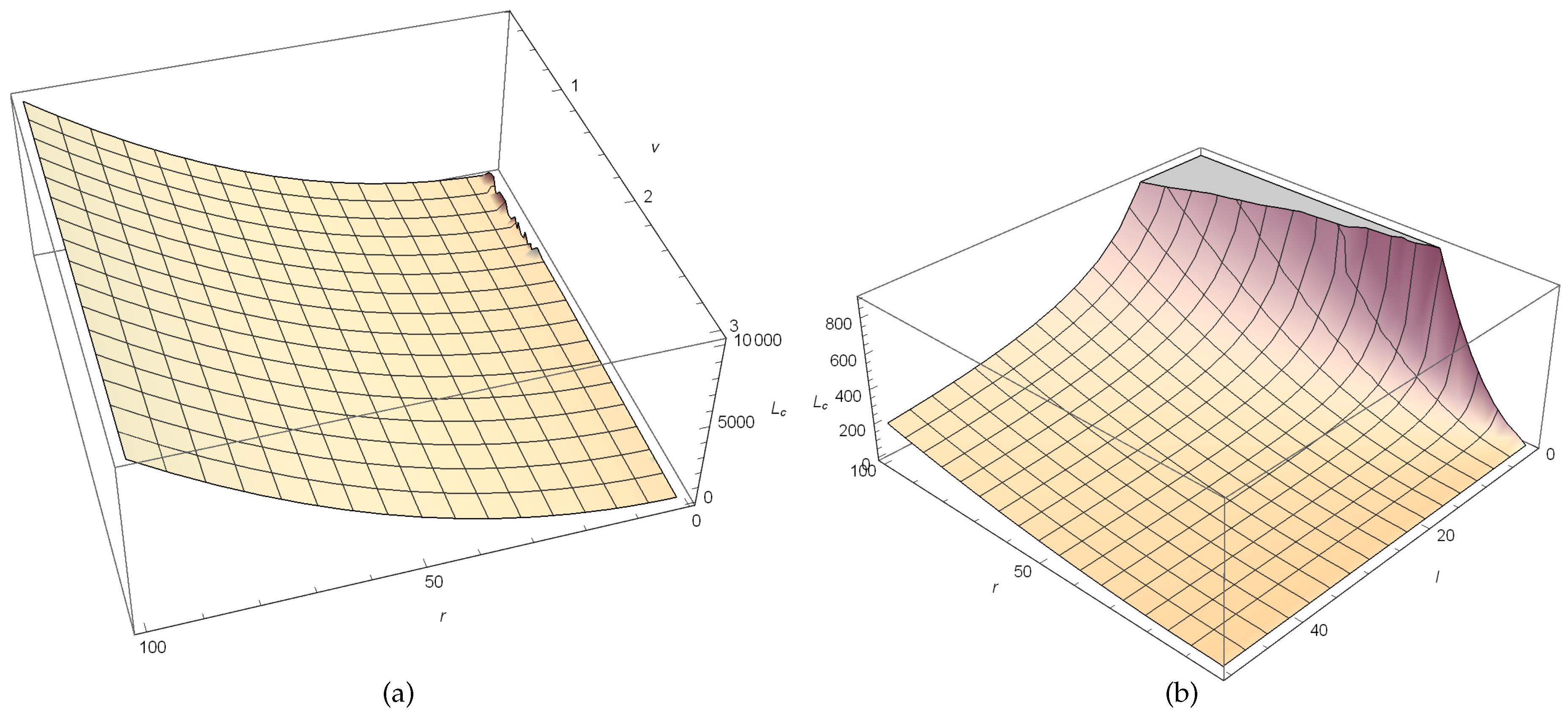
It is notified that both E c and L c depend on various parameters like Yang-Mills charge ν , scale length l, radial coordinate r and mass M of the AdS Schwarzschild Yang-Mills black hole. Figure 2a depicts the variation of relativistic angular momentum L c with respect to changing r and ν , for a fixed l and Figure 2b depicts, the variation of relativistic angular momentum L c with respect to changing r and l for a fixed ν . 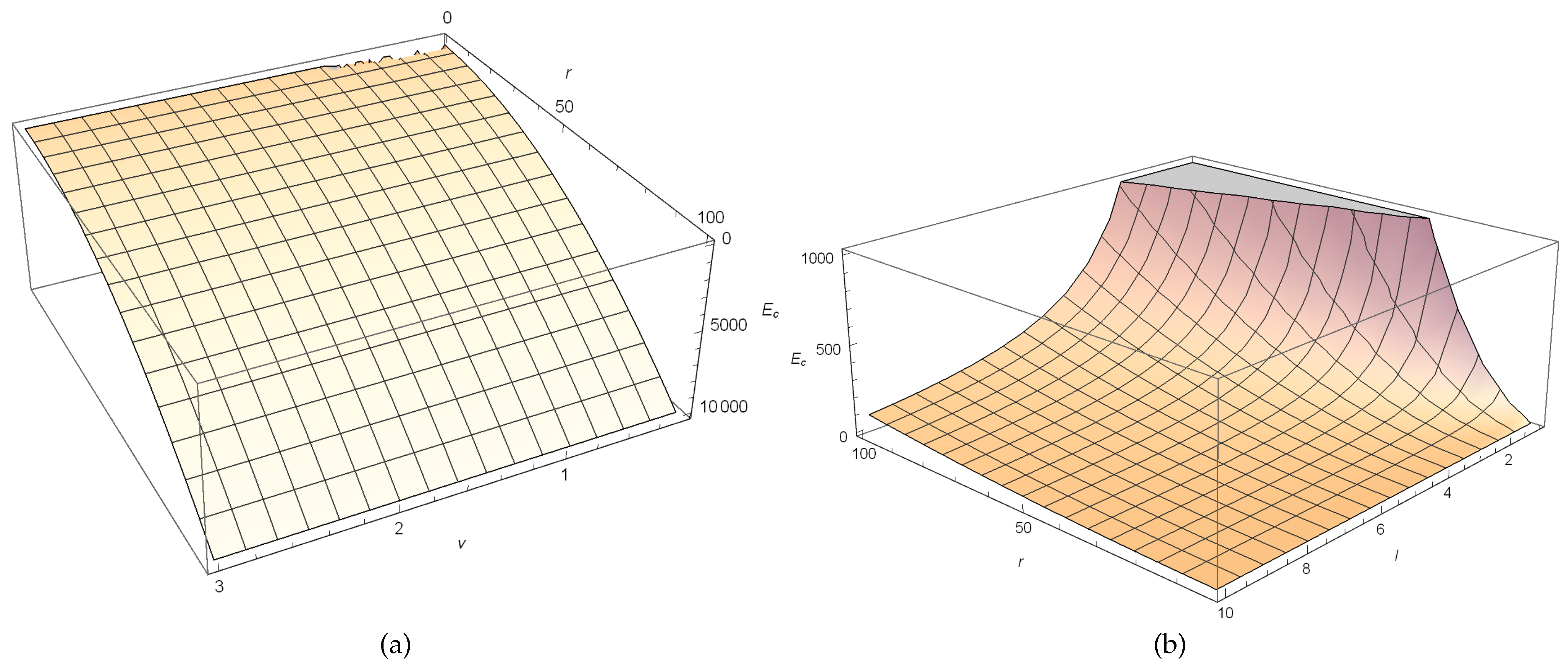However, in Figure 3a, the variation of energy E c with respect to changing r and ν for a fixed l and in Figure 3b, the variation of energy E c with respect to changing r and l for a fixed ν are depicted.
Now, relativistic specific angular momentum l c ( = L c E c ) can be calculated as
l c = M r l 2 − ν 2 l 2 + r 4 l ( 1 − 2 M r + ν 2 r 2 + r 2 l 2 ) .
Effective potential V e f f can be estimated as
V e f f = 1 − 2 M r + ν 2 r 2 + r 2 l 2 1 + h 2 r 2 .
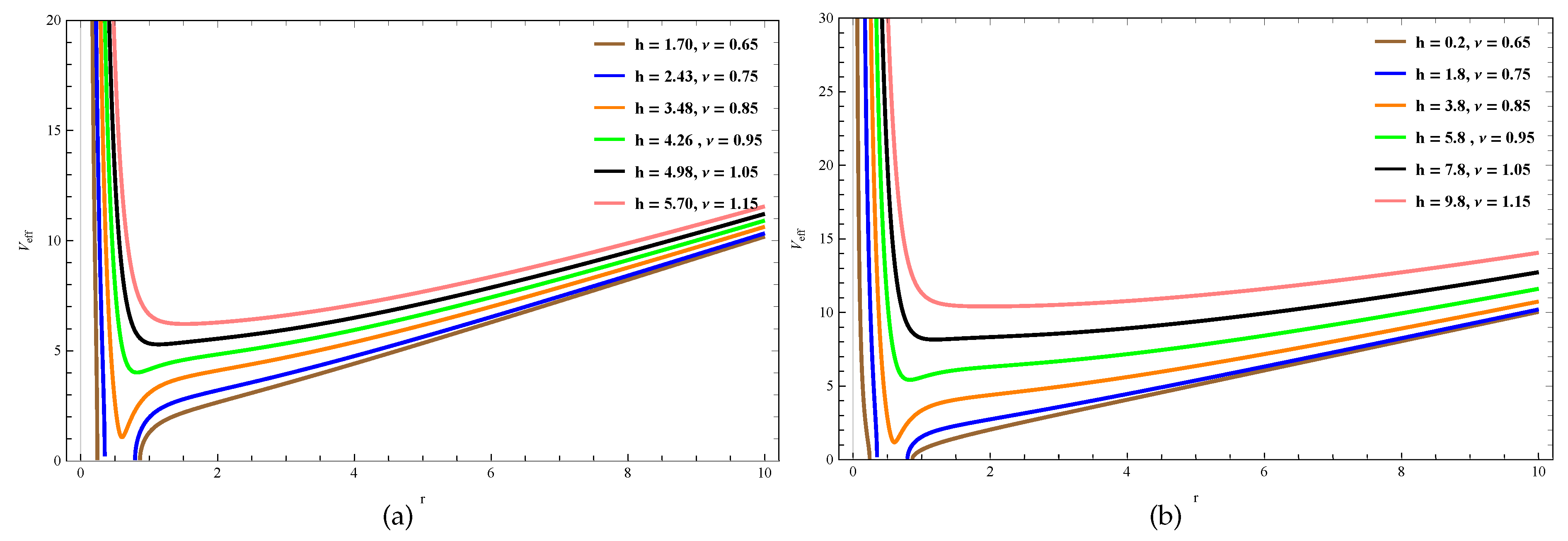
The nature of V e f f versus r by varying h, ν for fixed l is plotted in Figure 4. In both plots, V e f f increases for increasing ν .

5. Pseudo-Newtonian theory: potential, energy and angular momentum

The basic PNP theory for a general static non-rotating and spherically symmetric black hole was studied in Refs. [10,11]. The PNP and effective potentials, respectively, are,
ψ = r 4 − 2 M r l 2 + ν 2 l 2 2 r 4 − 2 M r l 2 + ν 2 l 2 + r 2 l 2
and
V e f f = ψ + l 2 2 r 2 = 1 2 r 4 − 2 M r l 2 + ν 2 l 2 r 4 − 2 M r l 2 + ν 2 l 2 + r 2 l 2 + l 2 r 2 .
It can be easily observed by analyzing the boundary behavior of PNP ψ that when we approach spatial infinity,
lim r → ∞ ψ = 1 2
This is presented in Figure 5 and Figure 6.
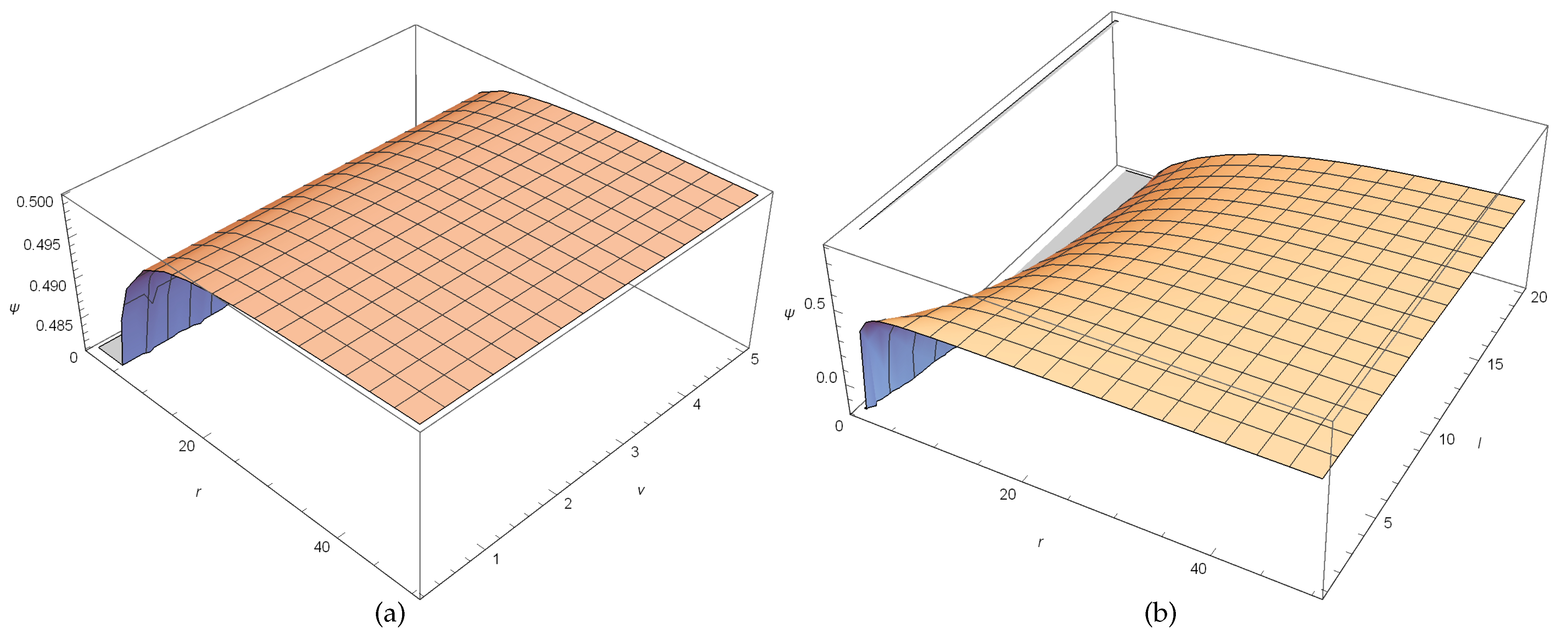
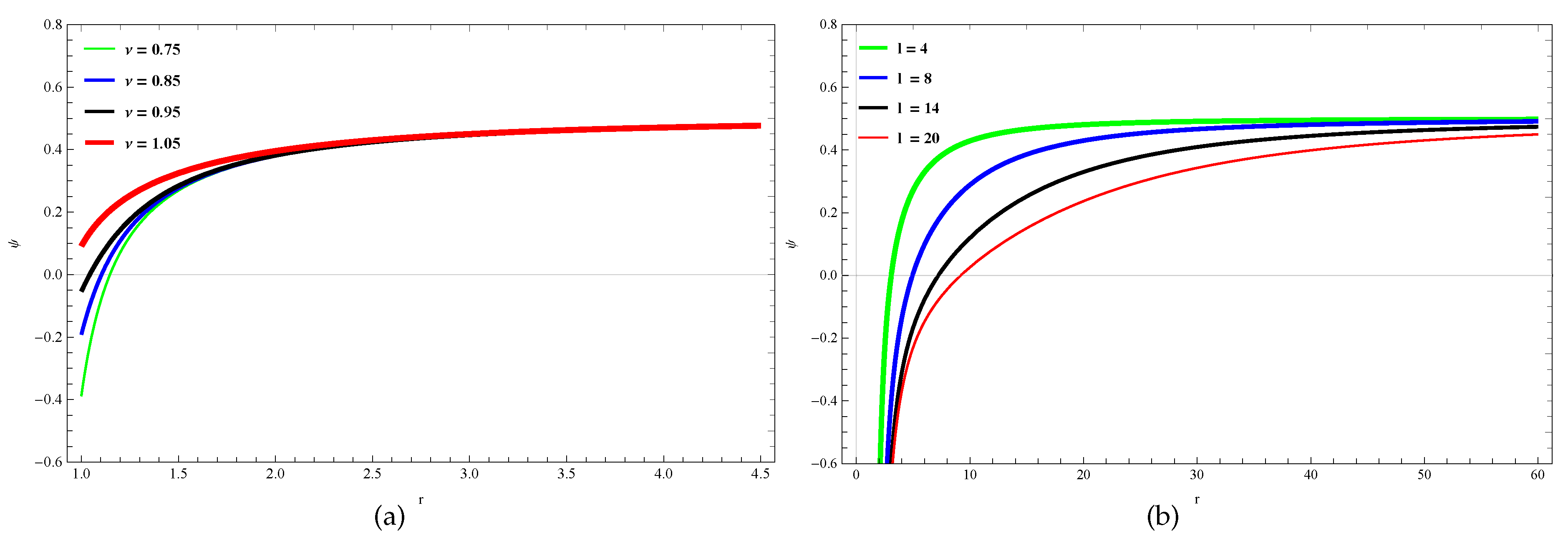
In Figure 5a, we plot PNP ψ for variation of both r and ν with l = 1 . In Figure 5b, the variation of PNP ψ for varying both r and l with ν = 0.75 is plotted. Moreover, in Figure 6, we present the behavior of PNP with r for different values of ν (left figure) and l (right figure). Figure 6a shows that for lower values of r, PNP ψ will be increased when Yang-Mills charge ν will take larger values. On the other hand, from Figure 6b, it is clear that for lower r PNP ψ will be decreases for increasing values of scale length l. Both plots of Figure 5 and Figure 6 also reveal that in the limit r → ∞ , ψ clearly approaches to 1 2 .
We obtain pseudo-Newtonian angular momentum as following:
l c = M r l 2 − ν 2 l 2 + r 4 l ( 1 − 2 M r + ν 2 r 2 + r 2 l 2 ) .
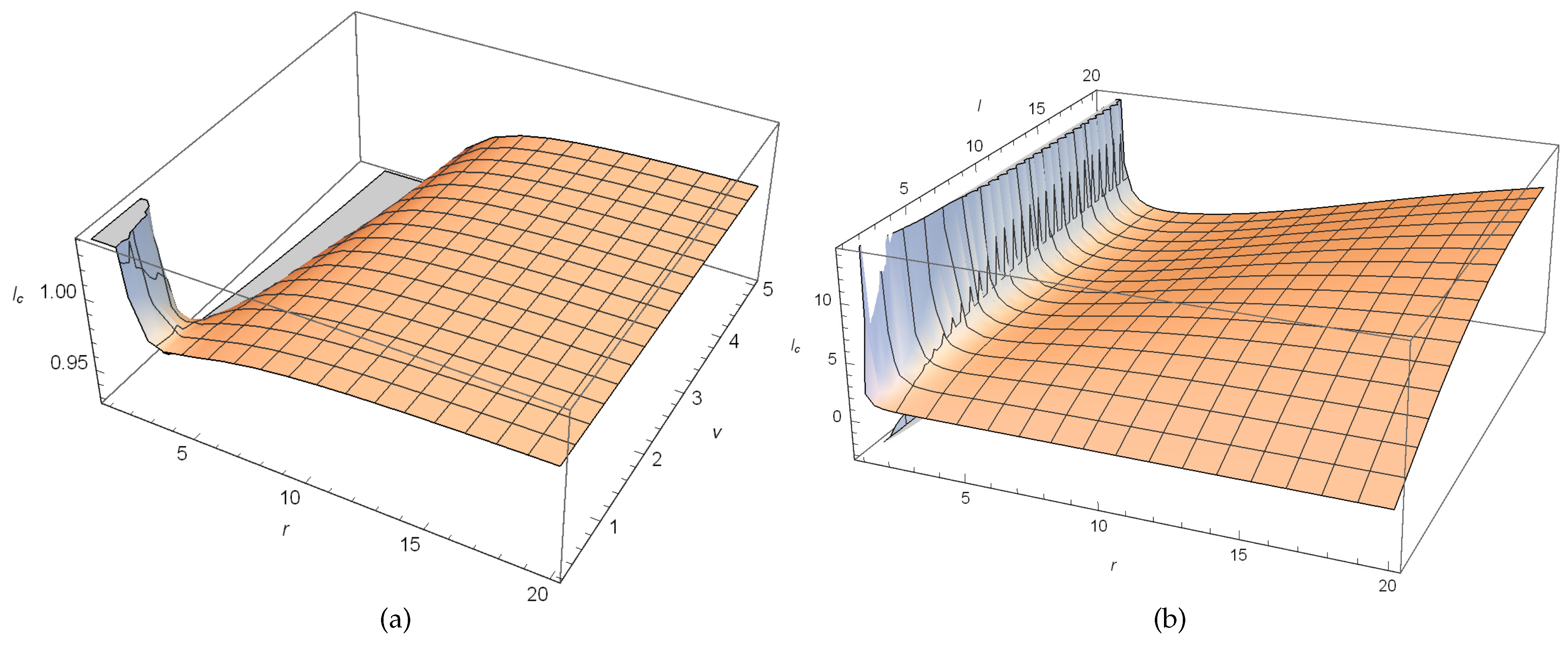
Figure 7a shows the variation of l c for the variation of both r and ν with fixed l and Figure 7a shows the variation of l c for the variation of both r and l with fixed ν .
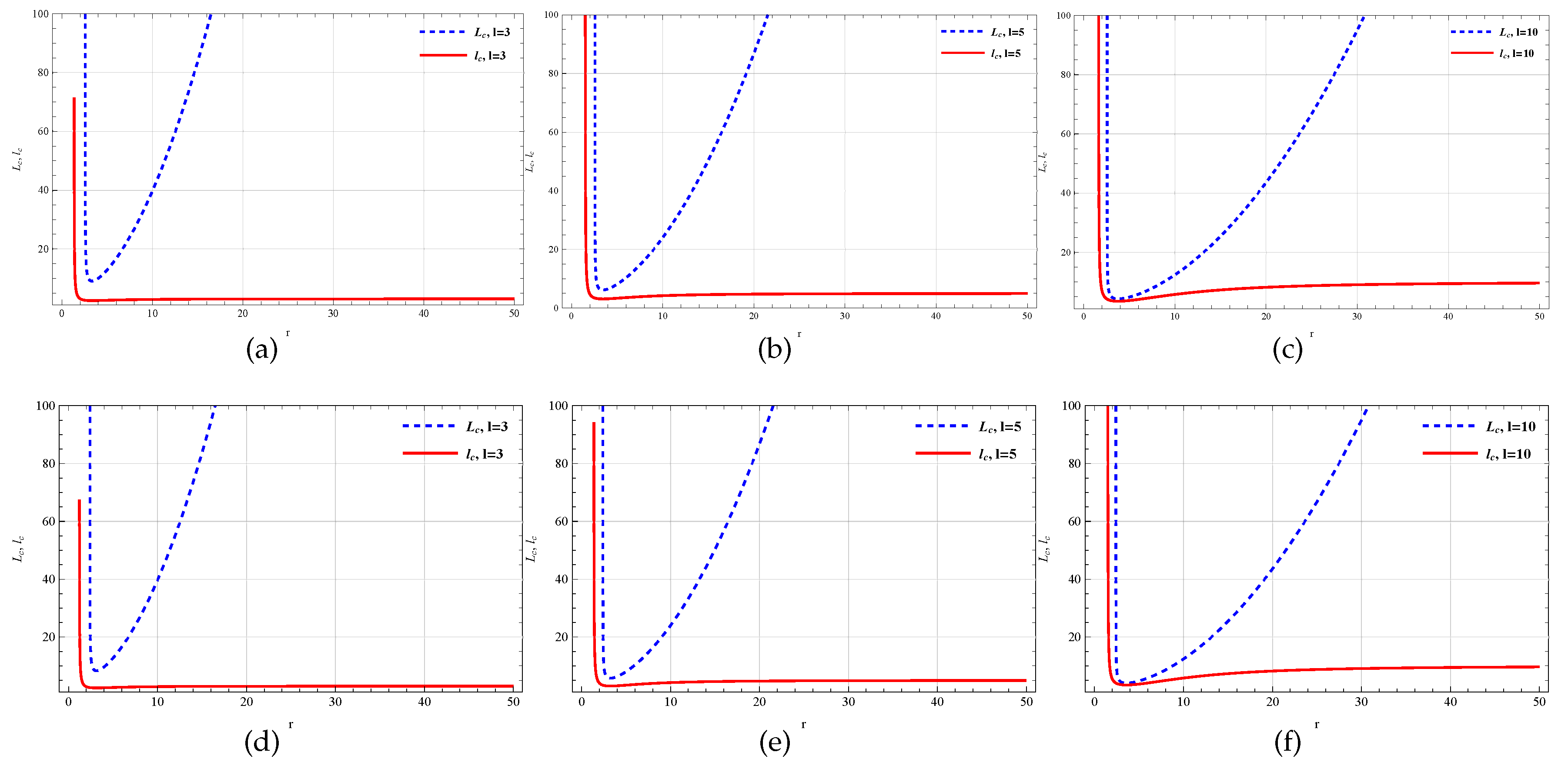
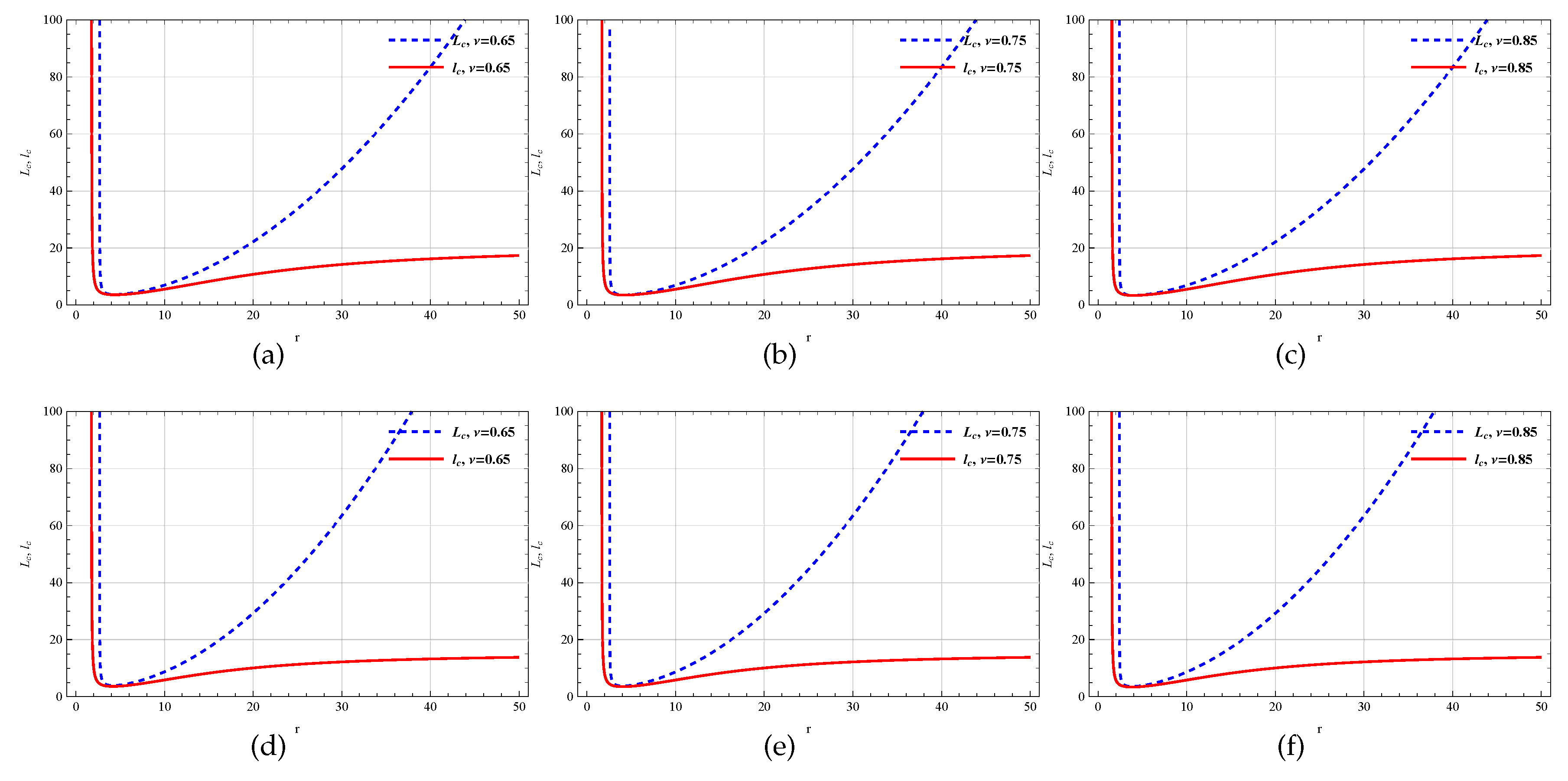
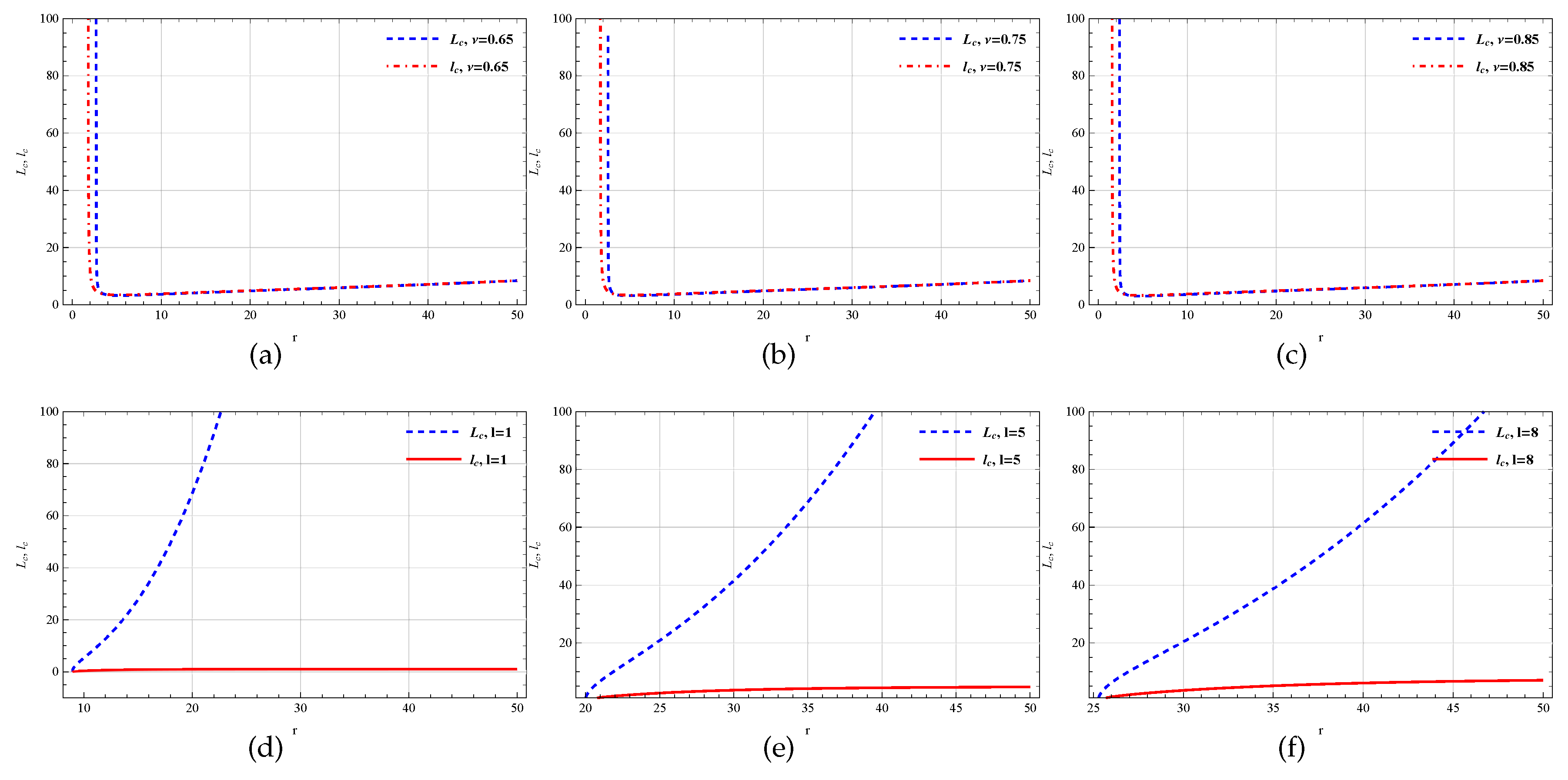
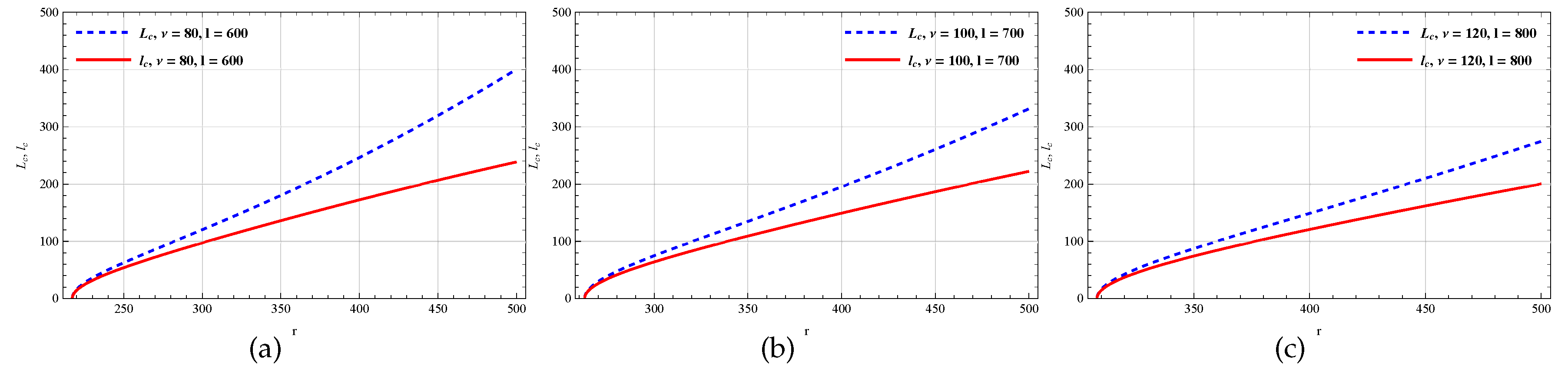
Now a comparative plot of L c (from Eq.(14)) and l c (from Eq.(18)) has been presented in Figure 8, Figure 9, Figure 10 and Figure 11 for different values of ν and l. In Figure 8 and Figure 9, ν and l are taken very small (up to the order of unity). On the other hand Figure 10 is for higher l, lower ν (top panel) and lower l, higher ν (bottom panel) while Figure 11 is for both higher l and higher ν . The solid curve (red) is for Pseudo-Newtonian angular momentum l c and the dashed curve (blue) is for General Relativistic angular momentum L c . From Figure 8 and Figure 9, it is visible that for lower values of r, both the curves become asymptotical to L c , l c axis and for higher values of r the L c curve is increasing whereas l c curve become asymptotical to the radial coordinate axis. So it can be easily understood that l c and L c curve takes the same form for the lower values of r, however, both curve no longer matches for higher values of r. Interestingly Figure 10 (top panel) shows that for higher scale length l, both curves take the same form for all values of r whereas the bottom panel depicts that both curves have different behavior i.e., L c curve is an increasing function of r while l c curve is asymptotic to r - axis. Both of the curves of Figure 11, for higher l and higher ν , also take the same form.
It is worth mentioning that, PNP theory for 4 D AdS Schwarzschild Yang-Mills black hole can reproduce the scenario of GR theory when both the scale length parameter l and Yang-Mills charge ν are taken low (valid for low ranges of r, but for higher ranges of r it does not reproduce the result any more) and also can simulate the GR theory when both of these parameters are taken high (for all values of r). However, for higher l and lower ν , we get the case of a Schwarzschild black hole. Finally, all results are verified for 4 D AdS Schwarzschild Yang-Mills black hole solution in EGB gravity. The above result generalizes that the above analysis is not only restricted to Einstein’s gravity but it can also be extendable to black hole solution in any modified gravity theory.
Moreover, the expression for e c is given by [10,11],
e c = 1 2 r 8 − 4 M r 5 l 2 + 2 r 6 l 2 + 2 r 4 ν 2 l 2 + 4 M 2 r 2 l 4 − M r 3 l 4 − 4 M r ν 2 l 4 + ν 4 l 4 r 4 − 2 M r l 2 + ν 2 l 2 + r 2 l 2 2 .
The positive roots of the following equation give marginally stable circular orbits:
8 l 2 r 6 − 4 ( 3 M l 2 + M ) r 5 + 10 ν 2 l 2 r 4 + 2 ( 3 M l 4 − 2 M l 2 ) r 3 + ( 8 M 2 l 2 − 13 M 2 l 4 ) r 2 + 4 ( 2 M ν 2 l 4 − M ν 2 l 2 ) r − ν 4 l 4 = 0 .
Finally, to get stable circular orbit we have the following condition:
8 l 2 r 6 − 4 ( 3 M l 2 + M ) r 5 + 10 ν 2 l 2 r 4 + 2 ( 3 M l 4 − 2 M l 2 ) r 3 + ( 8 M 2 l 2 − 13 M 2 l 4 ) r 2 + 4 ( 2 M ν 2 l 4 − M ν 2 l 2 ) r − ν 4 l 4 > 0 .

6. Conclusion and final remarks

Now we summarize and conclude our work here. In this paper, we outline spacetime structure in EGB gravity and to get a deeper insight about the horizon, we plot lapse function with respect to the radial coordinate r. Using GR treatment, we calculate energy and angular momentum. Here we noticed that the energy and angular momentum depend on various parameters like scale length, Yang-Mills charge and mass of the black hole. To check the dependency of energy and angular momentum on these parameters we make a graphical analysis. Moreover, we determined the effective potential and graphical analysis shows that effective potential increases when Yang-Mills charge increases.
Within the context of PN theory, we determined PNP, angular momentum, and energy. Here it is also notified that PNP, energy, and angular momentum also depend on various parameters like scale length, Yang-Mills charge, and mass of the black hole. In this framework, we also made a graphical analysis of the energy and angular momentum. The graph of PNP for different values of ν and l shows that for lower values of r, PNP will be increased when Yang-Mills charge will take larger values and PNP will decrease for increasing values of scale length. Interestingly, in the limit r → ∞ , PNP clearly approaches to 1 2 . More importantly, we have presented a comparative plot of relativistic angular momentum L c and PN angular momentum l c for different values of scale length and Yang-Mills charge. The graph for lower values of Yang-Mills charge and scale length demonstrated that in both, the GR treatment and PN treatment, the angular momentum curve takes the same form only for lower ranges of r while both curves no longer match for higher ranges of r. These plots justify the PNP theory for 4 D Schwarzschild Yang-Mills black hole for some lower values of r. The graph for both higher l and higher ν can justify the PNP theory for 4 D Schwarzschild Yang-Mills black hole for the entire ranges of r. While the graph for higher values of scale length parameter and lower values of Yang-Mills charge demonstrated that both angular momentum curves take the same form for all ranges of r. These plots justify the PNP theory for Schwarzschild black hole.
We also noticed that a marginally stable circular orbit depends on the parameters like scale length, Yang-Mills charge, and mass of the black hole. It is important to note that, the general formulation of the general gravity theory was used very well to a black hole solution in EGB gravity. Our result generalizes that this analysis is not only restricted to Einstein’s gravity but it can also be extendable and applicable to black hole solution in any modified theories of gravity.
Furthermore, this analysis can also be applicable and extendable for any black hole in higher dimensions. For example, the metric for a N-dimensional black hole can be written as,
d s 2 = − f ( r ) d t 2 + d r 2 f ( r ) + r 2 d Ω N − 2 2 ,
where d Ω N − 2 2 represents the metric on unit ( N − 2 ) sphere, given by,
d Ω 1 2 = d ϕ
and
d Ω k + 1 2 = d θ k 2 + S i n 2 θ k d Ω k 2 , k ≥ 1 .
In our analysis, the motion of a test particle (massive or photon) should be restricted to the equatorial plane ( θ k = π 2 , k ≥ 1 ), because of the fact that we have considered only spherical symmetry of the spacetime. Therefore, in future work, an extension of the above approach for non-spherical system (especially axisymmetric) would be interesting.

Acknowledgement

The author is thankful to Dr. Sudhaker Upadhyay, Department of Physics, K. L. S. College, Nawada, Bihar 805110, India, for various suggestions which developed the presentation of the paper.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data Availibility

Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.

Conflict of Interest

The authors declare no conflict of interest.

References

  1. Einstein, A. Relativity: The Special and General Theory (Methuen, London) 1920.
  2. Schwarzchild, K. Sitzungsber. Dtsch. Akad. Wiss. Berl., Kl. Math., Phys. Tech., 1923 (1923) 189.
  3. Einstein, A. The Meaning of Relativity (Methuen, London) 1951.
  4. Einstein, A. Sitzungsber. Preuss. Akad. Wiss. Berlin, 1917 (1917) 142.
  5. Einstein, A. Sitzungsber. Preuss. Akad. Wiss. Berlin, 1915 (1915) 778; 799; 831; 844.
  6. Ghosh Shubhrangshu and Mukhopadhyay Banibrata, Astrophys. J., 667 (2007) 367.
  7. Sarkar Siddhartha Sankar and Biswas Ritabrata, Eur. Phys. J. C, 79 (2019) 380.
  8. Vanov R. I. and Prodanov E. M., arXiv:grqc/0504025v1.
  9. Mukhopadhyay, B. Astrophys. J., 581 (2002) 427.
  10. Sumanta Chakraborty and Subenoy Chakraborty, Can. J. Phys., 89 (2011) 686.
  11. Surajit Mandal 2022 EPL 140 69001.
  12. Lovelock, D. J. Math. Phys. 12 (1971) 498.
  13. B. Zwiebach, Phys. Lett. B 156 (1985) 315.
  14. D. Glavan and C. Lin, Phys. Rev. Lett. 124 (2020) 081301.
  15. C. Barrabes and G. F. Bressange. “Singular hypersurfaces in scalar - tensor theories of gravity”. In: Class. Quant. Grav. 14 (1997), pp. 805–824. arXiv: gr-qc/9701026. [CrossRef]
  16. S. Capozziello and Antonio Troisi. “PPN-limit of fourth order gravity inspired by scalar-tensor gravity”. In: Phys. Rev. D 72 (2005), p. 044022. arXiv: astro-ph/0507545.
  17. J. W. Moffat. “Scalar-tensor-vector gravity theory”. In: JCAP 03 (2006), p. 004. arXiv: grqc/0506021. [CrossRef]
  18. Thomas P. Sotiriou. “f(R) gravity and scalar-tensor theory”. In: Class. Quant. Grav. 23 (2006), pp. 5117–5128. arXiv: gr-qc/0604028. [CrossRef]
  19. Valerio Faraoni. “de Sitter space and the equivalence between f(R) and scalar-tensor gravity”. In: Phys. Rev. D 75 (2007), p. 067302. arXiv: gr-qc/0703044. [CrossRef]
  20. Rong-Gen Cai and Y. S. Myung. “Black holes in the Brans-Dicke-Maxwell theory”. In: Phys. Rev. D 56 (1997), pp. 3466–3470. arXiv: gr-qc/9702037. [CrossRef]
  21. James M. Cline and Hassan Firouzjahi. “Brane world cosmology of modulus stabilization with a bulk scalar field”. In: Phys. Rev. D 64 (2001), p. 023505. arXiv: hep-ph/0005235. [CrossRef]
  22. Takeshi Nihei, Nobuchika Okada, and Osamu Seto. “Neutralino dark matter in brane world cosmology”. In: Phys. Rev. D 71 (2005), p. 063535. arXiv: hep-ph/0409219. [CrossRef]
  23. Michal Demetrian. “False vacuum decay in a brane world cosmological model”. In: Gen. Rel. Grav. 38 (2006), pp. 953–962. arXiv: gr-qc/0506028. [CrossRef]
  24. Takol Tangphati et al. “Anisotropic stars in 4D Einstein–Gauss–Bonnet gravity”. In: Physics of the Dark Universe 33 (2021), p. 100877. [CrossRef]
  25. Takol Tangphati et al. “Anisotropic quark stars in Einstein-Gauss-Bonnet theory”. In: Physics Letters B 819 (2021), p. 136423. [CrossRef]
  26. J.M.Z. Pretel, A. Banerjee, and A. Pradhan. “Electrically charged quark stars in 4D Einstein–Gauss–Bonnet gravity”. In: Eur. Phys. J. C 82 (2022), p. 180. [CrossRef]
  27. Pedro GS Fernandes. “Charged black holes in AdS spaces in 4D Einstein Gauss-Bonnet gravity”. In: Physics Letters B 805 (2020), p. 135468. [CrossRef]
  28. Pedro G. S. Fernandes et al. “The 4D Einstein–Gauss–Bonnet theory of gravity: a review”. In: Class. Quant. Grav. 39.6 (2022), p. 063001. arXiv:2202.13908 [gr-qc]. [CrossRef]
  29. Kartheek Hegde et al. “Thermodynamics, Phase Transition and Joule Thomson Expansion of novel 4-D Gauss Bonnet AdS Black Hole”. In: (Mar. 2020). arXiv:2003.08778 [gr-qc]. [CrossRef]
  30. Dharm Veer Singh, Sushant G. Ghosh, and Sunil D. Maharaj. “Clouds of strings in 4D Einstein–Gauss–Bonnet black holes”. In: Phys. Dark Univ. 30 (2020), p. 100730. arXiv:2003.14136 [gr-qc]. [CrossRef]
  31. B. Eslam Panah, Kh. Jafarzade, and S. H. Hendi. “Charged 4D Einstein-Gauss-Bonnet-AdS black holes: Shadow, energy emission, deflection angle and heat engine”. In: Nucl. Phys. B 961 (2020), p. 115269. arXiv:2004.04058 [hep-th]. [CrossRef]
  32. Nisha Godani, Dharm Veer Singh, and Gauranga C. Samanta. “Stability of thin-shell wormhole in 4D Einstein–Gauss–Bonnet gravity”. In: Phys. Dark Univ. 35 (2022), p. 100952. [CrossRef]
  33. Dharm Veer Singh and Sanjay Siwach. “Thermodynamics and P-v criticality of Bardeen-AdS Black Hole in 4D Einstein-Gauss-Bonnet Gravity”. In: Phys. Lett. B 808 (2020), p. 135658. arXiv:2003.11754 [gr-qc]. [CrossRef]
  34. Yuan-Yuan Wang, Bing-Yu Su, and Nan Li. “Hawking–Page phase transitions in four-dimensional Einstein–Gauss–Bonnet gravity”. In: Phys. Dark Univ. 31 (2021), p. 100769. arXiv:2008.01985 [gr-qc]. [CrossRef]
  35. Shao-Wen Wei and Yu-Xiao Liu. “Extended thermodynamics and microstructures of four-dimensional charged Gauss-Bonnet black hole in AdS space”. In: Phys. Rev. D 101.10 (2020), p. 104018. arXiv:2003.14275 [gr-qc]. [CrossRef]
  36. K. Aolki, M. A. Gorji and S. Mukohyama, JCAP 2009 (2020) 014.
  37. K. Aolki, M. A. Gorji and S. Mukohyama, Phys. Lett. B 810 (2020) 135843.
  38. Dharm Veer Singh, Benoy Kumar Singh, Sudhaker Upadhyay, 4D AdS Einstein-Gauss-Bonnet black hole with Yang–Mills field and its thermodynamics, Annals of Physics, Volume 434, 2021, 168642, ISSN 0003-4916. [CrossRef]
  39. Seyed Hossein Hendi, Mehrab Momennia, AdS charged black holes in Einstein-Yang-Mills gravity’s rainbow: Thermal stability and P-V criticality, Physics Letters B, Volume 777, 2018, Pages 222-234, ISSN 0370-2693. [CrossRef]
  40. Naeimipour, F., Mirza, B. & Masoumi Jahromi, F. Yang–Mills black holes in quasitopological gravity. Eur. Phys. J. C 81, 455 (2021). [CrossRef]
  41. Burkhard Kleihaus, Jutta Kunz, and Francisco Navarro-Lerida Phys. Rev. D 66, 104001.
  42. Kun Meng, Da-Bao Yang, Zhan-Ning Hu, “Black Hole Solution of Einstein-Born-Infeld-Yang-Mills Theory”, Advances in High Energy Physics, vol. 2017, Article ID 2038202, 7 pages, 2017. [CrossRef]
  43. Ali O¨vgu¨n, “P-v Criticality of a Specific Black Hole in f(R) Gravity Coupled with Yang-Mills Field”, Advances in High Energy Physics, vol. 2018, Article ID 8153721, 7 pages, 2018. [CrossRef]
  44. Aounallah, H., Pourhassan, B., Hendi, S.H. et al. Five-dimensional Yang–Mills black holes in massive gravity’s rainbow. Eur. Phys. J. C 82, 351 (2022). [CrossRef]
  45. D. Glavan and C. Lin, Phys. Rev. Lett. 124 (2020) 081301.
  46. Pedro G. S. Fernandes, Pedro Carrilho, Timothy Clifton, David J. Mulryne, “Derivation of Regularized Field Equations for the Einstein-Gauss-Bonnet Theory in Four Dimensions”. [CrossRef]
  47. Hennigar, R.A., Kubizňák, D., Mann, R.B. et al. On taking the D→4 limit of Gauss-Bonnet gravity: theory and solutions. J. High Energ. Phys. 2020, 27 (2020). [CrossRef]
  48. Pedro, G.S. Fernandes, Charged black holes in AdS spaces in 4D Einstein Gauss-Bonnet gravity, Physics Letters B, Volume 805, 2020, 135468, ISSN 0370-2693. [CrossRef]
  49. R. Saffari and S. Rahvar, Phys. Rev. D 77, 104028 (2008).
  50. S. Soroushfar, R. Saffari, J. Kunz and C. Lammerzahl, Phys. Rev. D 92, 044010 (2015).
  51. Z. Stuchlik, and S. Hledik, Phys.Rev. D 60 (1999) 044006.
  52. Z. Stuchlik, Bulletin of the Astronomical Institute of Czechoslovakia 34, 129 (1983).
  53. Z. Roupas, Universe 5(1), 12 (2019).
  54. I. Arraut, Universe 3(2), 45 (2017).
  55. S. Bhattacharya, K. F. Dialektopoulos, A. E. Romano, C. Skordis and T. N. Tomaras, JCAP 7, 018 (2017).
  56. V. Faraoni, Physics of the Dark Universe 11, 11 (2016).
  57. Z. Stuchlk, S. Hledk and J. Novotn, Phys. Rev. D 94, 103513(2016).
  58. Z. Stuchlk and J. Schee, JCAP 2011, 18 (2011).
Preprints 79480 g001
Figure 1. The behavior of f ( r ) versus r by changing ν for a fixed l = 2 , (a). In (b), the behavior of f ( r ) versus r by changing ν for a fixed l = 4 is shown. Taking M = 1 .
Figure 1. The behavior of f ( r ) versus r by changing ν for a fixed l = 2 , (a). In (b), the behavior of f ( r ) versus r by changing ν for a fixed l = 4 is shown. Taking M = 1 .
Preprints 79480 g001
Preprints 79480 g002
Figure 2. (a) is the variation of relativistic angular momentum L c with respect to changing r and ν for a fixed l = 1. In (b), it is shown, the variation of relativistic angular momentum L c with respect to changing r and l for a fixed ν = 0.75. Here, M = 1 .
Figure 2. (a) is the variation of relativistic angular momentum L c with respect to changing r and ν for a fixed l = 1. In (b), it is shown, the variation of relativistic angular momentum L c with respect to changing r and l for a fixed ν = 0.75. Here, M = 1 .
Preprints 79480 g002
Preprints 79480 g003
Figure 3. In (a), the variation of energy E c with respect to changing r and ν for a fixed l = 1 is shown. In (b), the variation of energy E c with respect to changing r and l for a fixed ν = 0.75, taking M = 1 .
Figure 3. In (a), the variation of energy E c with respect to changing r and ν for a fixed l = 1 is shown. In (b), the variation of energy E c with respect to changing r and l for a fixed ν = 0.75, taking M = 1 .
Preprints 79480 g003
Preprints 79480 g004
Figure 4. In (a) and (b), the behavior of V e f f with r by varying h, ν for constant l = 1 is shown. M = 1 .
Figure 4. In (a) and (b), the behavior of V e f f with r by varying h, ν for constant l = 1 is shown. M = 1 .
Preprints 79480 g004
Preprints 79480 g005
Figure 5. (a) is the variation of PNP ψ with respect to changing r and ν for a fixed l = 1 . In (b), the variation of PNP ψ with respect to changing r and l for a fixed ν = 0.75 is plotted. Here, M = 1 .
Figure 5. (a) is the variation of PNP ψ with respect to changing r and ν for a fixed l = 1 . In (b), the variation of PNP ψ with respect to changing r and l for a fixed ν = 0.75 is plotted. Here, M = 1 .
Preprints 79480 g005
Preprints 79480 g006
Figure 6. In (a), the variation of PNP ψ with respect to r for changing ν for a fixed l = 1 is shown. In (b), the variation of PNP ψ with respect to r for changing l for a fixed ν = 0.75 is shown. Taking M = 1 .
Figure 6. In (a), the variation of PNP ψ with respect to r for changing ν for a fixed l = 1 is shown. In (b), the variation of PNP ψ with respect to r for changing l for a fixed ν = 0.75 is shown. Taking M = 1 .
Preprints 79480 g006
Preprints 79480 g007
Figure 7. In (a), plot of l c with respect to r and ν for fixed l = 1 . In (b), plot of l c with respect to r and l for fixed ν = 0.75, taking M = 1 .
Figure 7. In (a), plot of l c with respect to r and ν for fixed l = 1 . In (b), plot of l c with respect to r and l for fixed ν = 0.75, taking M = 1 .
Preprints 79480 g007
Preprints 79480 g008
Figure 8. (a-c) are the variation of L c and l c with respect to r for changing l = 3 , 5 , 10 but fixed ν = 0.75 while (d-f) is the plot of the variation of L c and l c with respect to r for changing l = 3 , 5 , 10 but fixed ν = 0.85 . Here, M = 1 .
Figure 8. (a-c) are the variation of L c and l c with respect to r for changing l = 3 , 5 , 10 but fixed ν = 0.75 while (d-f) is the plot of the variation of L c and l c with respect to r for changing l = 3 , 5 , 10 but fixed ν = 0.85 . Here, M = 1 .
Preprints 79480 g008
Preprints 79480 g009
Figure 9. (a-c) are the variation of L c and l c with respect to r for changing ν = 0.65 , 0.75 , 0.85 , but fixed l = 20 . In (d-f), the variation of L c and l c with respect to r for changing ν = 0.65 , 0.75 , 0.85 but fixed l = 15 is shown. Here, M = 1 .
Figure 9. (a-c) are the variation of L c and l c with respect to r for changing ν = 0.65 , 0.75 , 0.85 , but fixed l = 20 . In (d-f), the variation of L c and l c with respect to r for changing ν = 0.65 , 0.75 , 0.85 but fixed l = 15 is shown. Here, M = 1 .
Preprints 79480 g009
Preprints 79480 g010
Figure 10. In (a-c), the variation of L c and l c with respect to r for changing ν = 0.65 , 0.75 , 0.85 but fixed l = 600 (high). In (d-f), the variation of L c and l c with respect to r for changing l = 1 , 5 , 8 but fixed ν = 80 (high). Here, M = 1 .
Figure 10. In (a-c), the variation of L c and l c with respect to r for changing ν = 0.65 , 0.75 , 0.85 but fixed l = 600 (high). In (d-f), the variation of L c and l c with respect to r for changing l = 1 , 5 , 8 but fixed ν = 80 (high). Here, M = 1 .
Preprints 79480 g010
Preprints 79480 g011
Figure 11. The variation of L c and l c with r for changing ν = 80 , l = 600 [a], ν = 100 , l = 700 [b] and ν = 120 , l = 800 [c] along with M = 1 .
Figure 11. The variation of L c and l c with r for changing ν = 80 , l = 600 [a], ν = 100 , l = 700 [b] and ν = 120 , l = 800 [c] along with M = 1 .
Preprints 79480 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated