1. Introduction
Music information retrieval is one of the core research areas of computer vision and audition[
1,
2], which mainly provides technical support for music education, music theory, music composition, and other related fields through understanding and analyzing music content. Among them, the staff is an extremely important way to record auditory music in an image way and also an important source of digital music. Semantic understanding of optical staff aims to encode pictorial music into playable digital code. Because of the multitude of scores recorded in staff, this technology is and will continue to have a huge impact on musical applications in the deluge of digital information[
3,
4].
Semantic understanding of optical staff is closely related to optical music recognition (OMR)[
5,
6,
7]. This area has been an important application in machine learning since the middle of the last century. The extent to which optical music recognition can be achieved has been varying according to technology development and different needs. In the nadir of deep learning, OMR went from separating and extracting symbolic primitives (lines, heads, stems, tails, beams, etc.) to using correlations between primitives and related rules of musical notation and recognizing notes[
8,
9].With the gradual improvement of deep learning ecology, various researches based on deep learning provide new ideas for OMR and put forward new recognition requirements. Pacha et al.[
10] proposed a Region-based convolutional neural networks for staff symbol detection tasks and used the Faster R-CNN[
11] neural network model to locate and classify single-line staff symbols. Both the semantic segmentation methods to staff symbols, where one is the U-Net[
12] neural network model applied by Hajič jr. et al.[
13] and the other is deep-water detector algorithm proposed by Tuggener et al.[
14], fail to detect pitch and duration. Huang et al.[
15] proposed an end-to-end network model for staff symbol recognition by modifying the YOLOv3[
16] to detect pitch and duration separately. OMR algorithms based on sequence modeling mainly target monophonic music sheet, and cannot completely understand the meaning of all symbols, e.g. Van der Wel et al.[
17] used a sequence-to-sequence[
18] model; Baró et al.[
19] used convolutional recurrent neural network which consists of CNN and LSTM[
20]. In summary, as so far deep learning algorithms are able to detect and recognize the locations and classes of some symbols in staff images with low complexities (i.e., low symbol density, small span, and few varieties) and achieve partial semantic understanding.
This paper aims to achieve codes of pitch and duration of the notes in a complex staff image during the performance, so an end-to-end optical staff semantic understanding system is designed. The system consists of the YOLOv5 as the Low-level Semantic Understanding Stage (LSNS) and the Note Encoding Reconstruction Algorithm (NERA) as the High-level Semantic Understanding Stage (HSNS). In the LSNS, the whole optical staff is the input of the system. The model is then trained with the self-constructed SUSN dataset to output digital codes for the pitch and duration of the main note under the natural scales and other symbols that affect the pitch and duration of the main note. The NERA which takes the output of the LSNS of the staff as the input and applies music theory and MIDI encoding rules[
21] , resolves the natural scale and other symbol semantics and their mutual logical, spatial, and temporal relationships which results in the output of the staff symbol relationship structure of the given symbols, and realizes the HSNS of the main notes through calculation, outputs the pitch-duration codes of the main notes during the performance and provides an end-to-end optical staff symbol semantic understanding encoding for notation recognition through listening, intelligent score flipping and music information retrieval.
2. Materials and Methods
2.1. Dataset
Since YOLO[
22,
23,
24] is based on an end-to-end object detection algorithm, the datasets which are applicable to the YOLO should be those with the detected target as the object, while datasets that does not consider the relationship between symbols’ spacial locations in the staff (e.g., DeepScoresV2[
25], MUSCIMA++[
26]) cannot be applied to this algorithm. In this paper, the overall goal of the Semantic Understanding of Staff Notation (SUSN) dataset
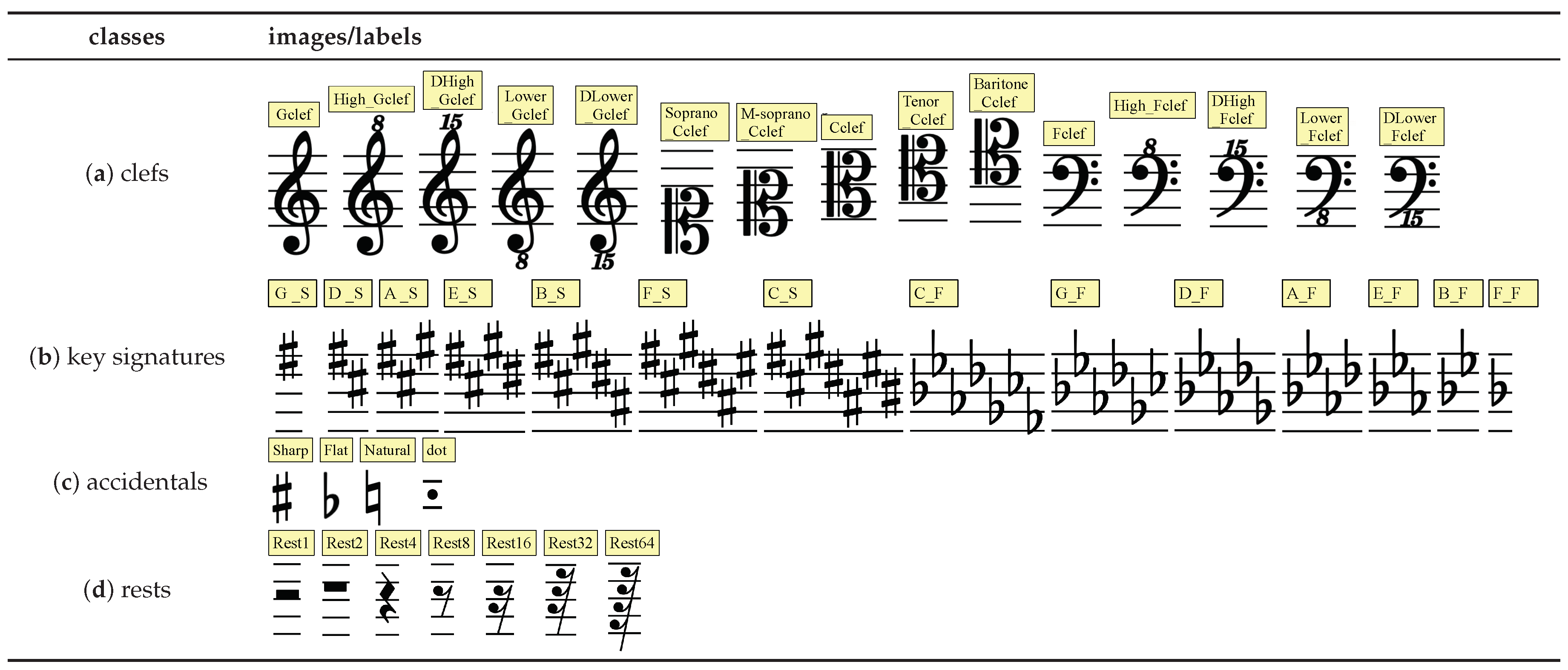
1 self-constructed is to encode the pitch and duration of the main notes during the performance. In addition to single notes, there are numerous other forms of notes in the score, such as appoggiaturas, overtones and harmonies. Aurally, appoggiaturas (shown in
Figure 1(
h)) and overtones increase the richness of musical frequencies, but do not change the fundamental frequency of the main melody; generally, all the notes in harmony except the first one are weak-sounding. Therefore, we define single notes and the first note of the harmony in the score as the main note. When labeling the dataset, the notes are only labeled with the category of the main note and its related information. In this context, the annotated information and the method of labeling used for this dataset are as follows:
The main notes are labeling with information about the note position and pitch and duration in the natural scale. The labeling method has two steps. Firstly, draw the bounding box: the bounding box should contain the complete notes (head, stem and tail) and the specific spatial information of the head. In other words, the bounding box is supposed to contain the 0th line to 5th line of the staff and position of the head. Then, annotate the object: the format of the label is the ’duration_pitch’ code under the natural scale. As shown in
Figure 1f,g.
Label the categories of symbols that affect the pitch and duration of the main notes as well as position information. In the score, the clef, key signature, dot and pitch-shifting notation (sharp, flat and natural) are the main control symbols that affect the pitch and duration of the main note, and
Table 1a–c list the control symbols identified and understood in this paper. Each of all these kinds of symbols is labeled with a minimum external bounding box containing the whole symbol and category information, as shown in
Figure 1a–c,e.
Label the categories and position of the symbols of the rest. The rest is used in a score to express stopping performance for a specified duration. The symbol of the rest is labeled with a minimum external bounding box that contains the rest entirely as well as information of its category and duration. The rests identified and understood in this paper are listed in
Table 1d, while the rests in the staff are labeled as shown in
Figure 1d.
In this paper, the system trained by the SUSN dataset achieves a great result. This proves that it meets the requirements of the system in this paper.
2.2. Low-level Semantic Understanding Stage
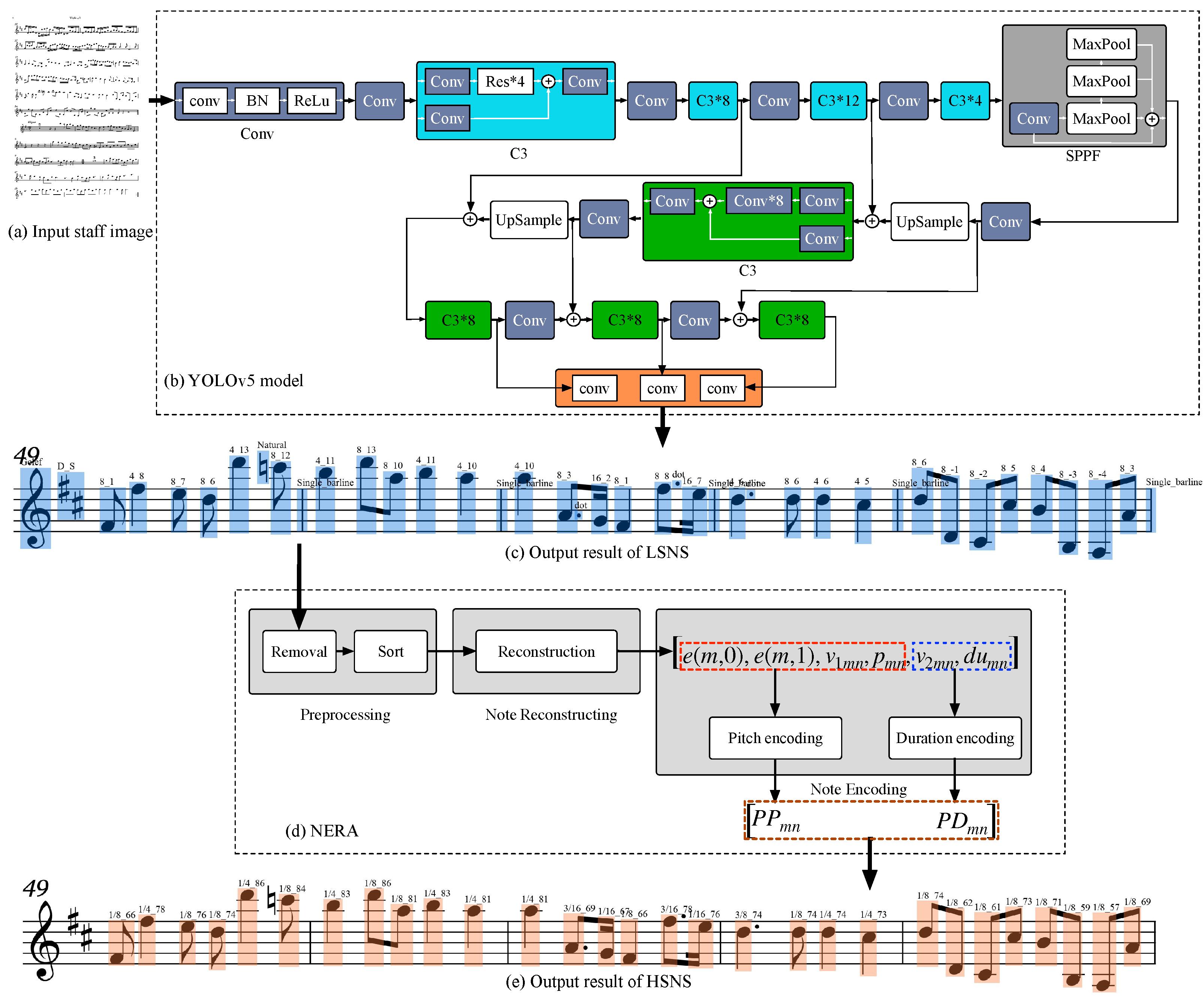
The YOLOv5 is used to implement the LSNS of the staff notation. The symbols in the staff images belong to the category of small object graphics in image recognition, and the multi-scale (1×1, 2×2, 3×3) convolutional neural network is used as the backbone network structure for feature extraction. The multi-scale convolutional network uses convolutional kernels of different sizes to obtain different types of features at different scales, thus can extract richer symbolic features to address the small object, multiple poses and complexity of the staff symbols. The backbone network is composed of the convolutional layers, the C3 modules and an SPPF module[
27]. The C3 module of the backbone network, mainly composed of a convolutional layer and X ResNet blocks, is the main module for learning the residual features of the staff, which divides the feature mapping into two parts: one goes through multiple stacked residual modules and a convolutional layer; and the other goes through one convolutional layer. They were then merged through a cross-stage hierarchy to reduce the computational effort while ensuring the accuracy. The SPPF module passes the staff symbol feature map sequentially through three maximum pooling layers each with a 5 x 5 network structure, which extracts spatial features of different sizes and improves the model’s computational speed and robustness to the spatial layout.
The neck network uses a pathway aggregation network[
28] for feature fusion. The neck network is composed of the convolutional layers, the upsampling layers, the connection layers and the C3 modules without the residual structure. The staff features generated by the feature extraction network contains more symbol location information in the bottom features and more symbol semantic information in the top features. The FPN[
29] is introduced to communicate symbolic semantic features from top to bottom. Path Enhancement is achieved by the bottom-up feature pyramid structure to convey the localized features. The entire feature hierarchy is enhanced by using the localized information at the lower levels, which has also shortened the information path between the bottom-level and top-level features.
The LSNS implements the mapping
of the input staff image
to the output set
of digital codes corresponding to the symbols. Where
denotes all symbols in the staff, each symbol
(
) has positional coordinates and semantic information. The overall structure of the model is shown in
Figure 3 for the YOLOv5.
2.3. High-level Semantic Understanding Stage
The NERA is designed to convey music theory and the method of staff notation into a system model. Using this algorithm, the resulting set is preprocessed to construct a structure of notation relations for the given symbols, and using music theory and MIDI encoding rules, the pitch and duration of each note are parsed to achieve the HSNS of the optical staff notation. The general rules of the music theory targeted by the NERA are as follows:
The clefs are the symbols used to determine the exact pitch position of a natural scale in the staff. It is recorded at the leftmost end of each staff, and also a flag that indicates the m-th line in the staff. Meanwhile, it is also the first symbol considered by the NERA when encoding the pitch;
The key signature located after clef is the symbol used to mark the ascending or descending the pitch of the corresponding notes and expressed as a value in the NERA. The clefs and key signatures are effective within one line of staff notation;
In accidentals, the pitch-shifting notations change the pitch. It raises, lowers or restores the pitch of the note on which it is applied. The dot extends the original duration of the note by half.
2.3.1. Data Preprocessing
Data preprocessing using the preprocessing part of the NERA for numeric encoding set has the purpose and function as follows:
Removal of invalid symbols. The task of this paper is to implement the encoding of the pitch and duration of staff notes during the performance. Among the numerous symbols that affect the pitch and duration of notes are the clefs, the key signatures, the accidentals and the natural scales, while other symbols are considered as invalid symbols within this article. In the preprocessing stage, invalid symbols are removed and valid symbols are retained. We define the set of valid symbols as
. The relationships among clefs, key signatures, accidentals, natural scales, valid symbol set and dataset are shown in equation (
1):
where clef, key signature, accidental and natural scale are denoted by
,
,
and set
, respectively. Specifically, the
P is the space spanned by the natural scale
, and the
spanned by the duration
. What’s more, the element 0 in set
means there is no key signature and implys that the signature in this line is C major. Each natural scale
s has two pieces of information which indicate the pitch and duration respectively;
Sort of valid symbols. The YOLOv5 algorithm in the LSNS outputs the objects, and each object is unordered with the information , where denotes the symbol’s class, and denote the Cartesian coordinate values of the center point of the object bounding box, and denote the width and height. The clef is the first element of each row in the staff. Let its center point coordinate is . Denote , where D is the distance between two adjacent clefs’ center points. If the symbol with , then it goes to the same line. Next, the symbols in the same row are sorted in order of X from small to large. By this method, all valid symbols are rearranged in a new order which is the exact order of the symbols when reading the staff.
After the preprocessing, the digital information of the staff with
M lines are represented as
M vectors, and each vector has
elements. The specific implementation of the preprocessing part is shown in Algorithm 1.
|
Algorithm 1:Algorithm of the NERA Preprocessing Part |
- 1:
Initialize:;//
- 2:
whiledo
- 3:
- 4:
if then
- 5:
;//To determine whether the current symbol is a valid symbol. - 6:
end if
- 7:
if then
- 8:
; - 9:
;//If the input symbol belongs to the clefs, a new vector is created. - 10:
else
- 11:
;//If the valid symbols are not clefs, then continue. - 12:
end if
- 13:
end whilereturn Output
|
2.3.2. Note Reconstructing
In the process of constructing the staff symbol relationship structure, the understanding of the semantic information of the symbols and the interrelationship between the symbols are what we should focus on. We define as the semantics of the element j in the m-th vector, . As the symbol acts directly or indirectly on the natural scale, it affects the played pitch and duration. Then as for the entire staff image, we define the global variables and for the m-th line, where , . In addition, we define the local variables and that effect on the n-th note in the m-th line. The variable indicates whether the note is transposed or not and how to be transposed, i.e. sharp, flat and natural. The variable means whether the note’s duration is extended to its 1.5 times.
In this context, when the YOLOv5 outputs the symbol class as a note, the duration and pitch information of the symbol is expressed as . Thus, the note information in line m is represented as , where vectors and , is the number of notes in each line and its value varies depending on the line; the control information for pitch and duration is expressed as , where vectors and .
The variables
and
are calculated as shown in equation (
2) and equation (
3):
In equation (
2),
is the update of the note index. If
is natural, the corresponding note performs the opposite control of the key signature, e.g. ’F’ in G major has been raised a semitone, but when there is a natural before an ’F’,
controls the note to perform a descending semitone operation. In equation (
3), if the
is a dot, the duration of the corresponding note is extended by 1/2 of the original duration, otherwise it is not extended. The specific implementation of the note reconstructing part is shown in Algorithm 2.
|
Algorithm 2 Algorithm of NERA Notation Reconstructing Part |
- 1:
Initialize:;);//Maximum value of the line index according to the clef number,Initializes the row index and symbolic index. - 2:
whiledo
- 3:
;//Initializes index j for symbols and index n for notes - 4:
;//Gets the value of the line clef and key signature. - 5:
whiledo
- 6:
;//Loop through all valid symbols in the m-th line. - 7:
ifthen
- 8:
;//Assign pitch-shifting notation to the of the next note. - 9:
else - 10:
ifthen
- 11:
;;//If it is a note, then calculate its value of pitch and duration. - 12:
;//Assign the note duration. - 13:
;//Assign the pitch of the next note. - 14:
else - 15:
;//If it is a dot. - 16:
end if - 17:
end if - 18:
end while - 19:
end whilereturn Output - 20:
return Output
|
2.3.3. Note Encoding
In note encoding part, the encoding strategy is as follows:
-
Pitch Encoding
According to the clef, key signature and the MIDI encoding rules, the pitch code
of the nature scale is converted to a code that includes the function of clef
and key signature
in
m-th line one by one. We define
as the mapping of this strategy, and obtain the converted code
. The encoding process is shown in
Figure 2. Then, the pitch encoding part obtains the pitch code
for each note played with using the MIDI encoding rules after scanning the note control vector
. As shown in equation (
4):
-
Duration Encoding
Scan each duration control vector
and corresponding note duration vector
, define the individual performance style coefficient as
, apply MIDI encoding rule, then duration encoding strategy is shown in equation (
5):
where,
is varying according to the different performers.
means that the performers’ characteristics are not considered.
2.4. System Structure
The structure of the optical staff symbol semantic understanding system is shown in
Figure 3. The system consists of two parts: the LSNS (shown in
Figure 3b) and the HSNS (shown in
Figure 3d). The LSNS is the YOLOv5. The model outputs information of the object
expressed as
when it feeds with a staff image, and the visualization image of its results is shown in
Figure 3c. The HSNS has three steps to achieve the code of pitch and duration during the performing. To begin with, data preprocessing removes invalid symbols from the disordered
, then sorts the valid symbols. Besides, the staff symbol structure vector set is obtained by using note reconstructing. Last but not least, the note encoding part outputs the final results according to the encoding strategies of pitch and duration, as shown in
Figure 3e.
Figure 3.
Structure of the optical staff symbol semantic understanding system. The system comprises two parts: the LSNS (b) and the HSNS (d). Natual scale (c) is the response of the (b) modual when the optical staff image (a) is the system’s excitation. (c) then acts as the excitation of the module (d) which eventually outputs the performance code (e).
Figure 3.
Structure of the optical staff symbol semantic understanding system. The system comprises two parts: the LSNS (b) and the HSNS (d). Natual scale (c) is the response of the (b) modual when the optical staff image (a) is the system’s excitation. (c) then acts as the excitation of the module (d) which eventually outputs the performance code (e).
3. Results
3.1. Data
The dataset used in this article includes a self-built SUSN dataset and an independent test set. The SUSN dataset contains 130k labeled samples. In training, a random partitioning strategy is adopted – – with 90% of the dataset divided into training set and the remaining 10% as validation set. The test set contains 47 pages of staff images from ten different tracks with varying complexities (see Appendix A) for a comprehensive evaluation of the system’s performance. Among them, the complexities of the staff image of a track are defined by attributes. The key attributes in this paper are the number of symbol types, interval span, symbol density, external-note density, and image resolution.
3.2. Trainning
The hardware platform used for training is a workstation which CPU is AMD 32-Core Processor with 80GB of memory and an NVIDIA RTX 3090 graphics card. The system model is built on PyCharm platform using PyTorch framework. In training, the system adopted Stochastic Gradient Descent (SGD) algorithm to optimize the loss function. In the experiments, each training epochs was 300, and the first 3 epochs contained linear warm-up, which linearly increases the learning rate from 0 to the initial learning rate. Cosine Annealing algorithm was adopted to update the learning rate. After 11 times of training, we determine the initial learning rate as 0.01 by the maximum mAP.
3.3. Evaluation Metrics
In this paper, the precision and the recall are used to evaluate the performance of the model and recognition effect. The precision reflects the ability of the model to accurately classify symbols:
The recall shows the ability of the model to recognize symbols:
where
is the number of symbols whose categories are correctly identified,
is the number of incorrectly identified symbols, and
is the number of symbols that are not identified.
3.4. Experiment and analysis
3.4.1. Experiment of LSNS
In this paper, the type of symbols, the span of the interval, the density of symbols, the density of external-notes and the resolution of staff images are defined as staff complexity variables.
Table 2 statistics the complexity properties of the test set of ten track staves, and calculates the precision and recall after LSNS.
The following analysis is from three perspectives:
(1) Evaluation metrics
The average precision of the test set is 0.989, the recall is 0.972. It is verified that the model has good generalization and robustness to the LSNS of staff with different complexity. The recall of the model is lower than the precision for all staff images, which shows that the model misses a lot of symbols, especially the external-note. For the semantic understanding of the line notation, both missed and wrong checks affect the pitch and duration of the corresponding notes, especially the clef and key signature which determine the pitch and duration of all the notes in a line.
Table 3 shows the precision and recall of all the clefs and key signatures in the test set.
(2) Complexity variables
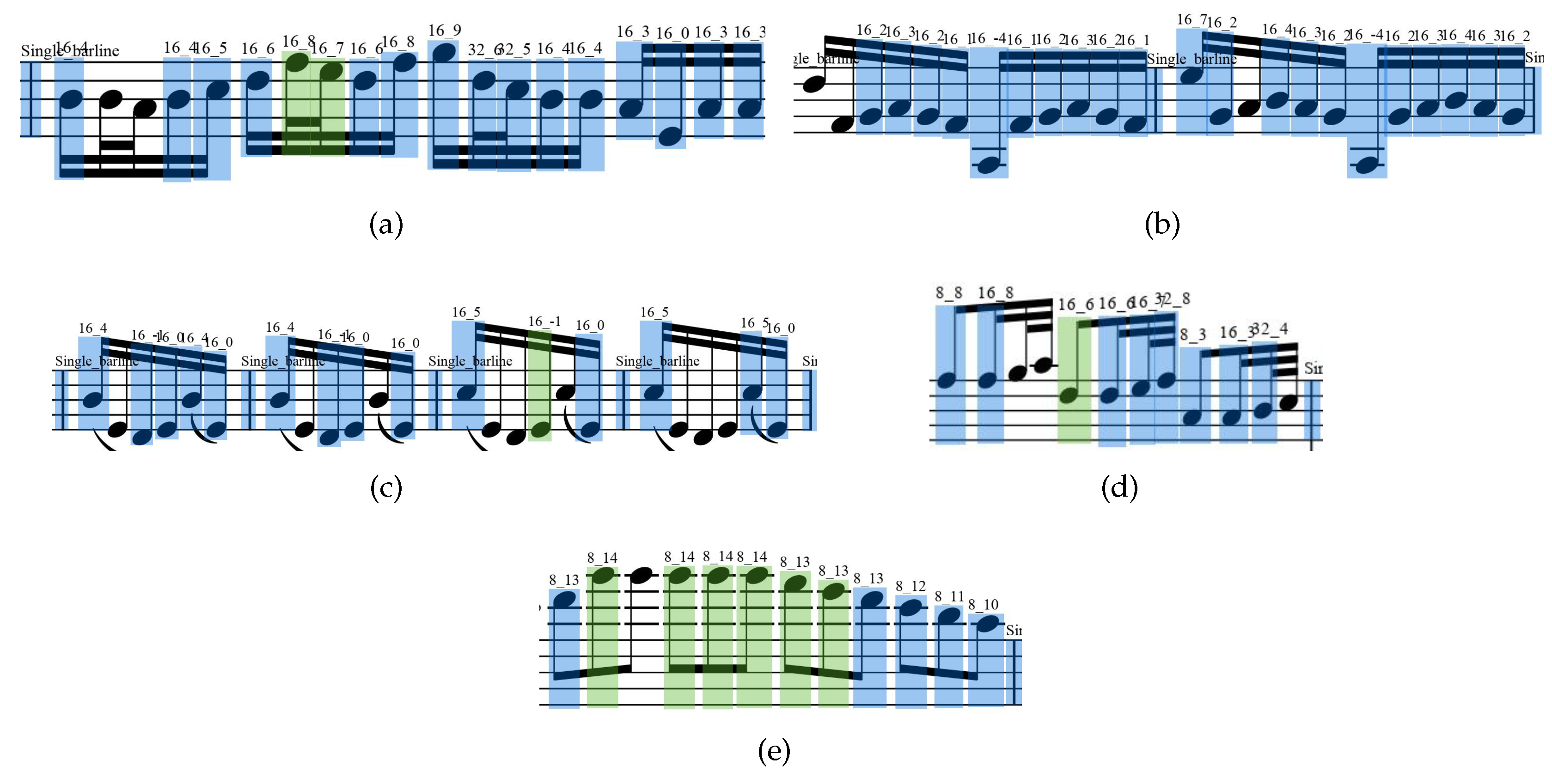
In the test set of this paper, the error and omission of symbols at the LSNS are mainly caused by the following:
In staff 1, many cumbersome note beams along with the high density of symbols result in relative high rates of error and omission. As shown in
Figure 4a;
Staff 2 has the highest density of symbols and its recall is relatively low. As shown in
Figure 4b;
Staff 3 has lower complexity of each item and its performance evaluation is better;
The error and omission of notes in staff 4 are mostly concentrated in the notes with longer note stem. As shown in
Figure 4c;
Staff 5 has higher complexity of each item and very low image resolution, and its evaluation are worse than others;
Staff 6 has lower image resolution. Similar to staff 1, its notes with common note beams are tedious. As shown in
Figure 4d;
Staff 7 has a lower image resolution, but its performance evaluation is better due to the lower complexities of other attributes;
In staff 9, the error detection notes are those located in the higher plus line on the staff, as shown in
Figure 4e.
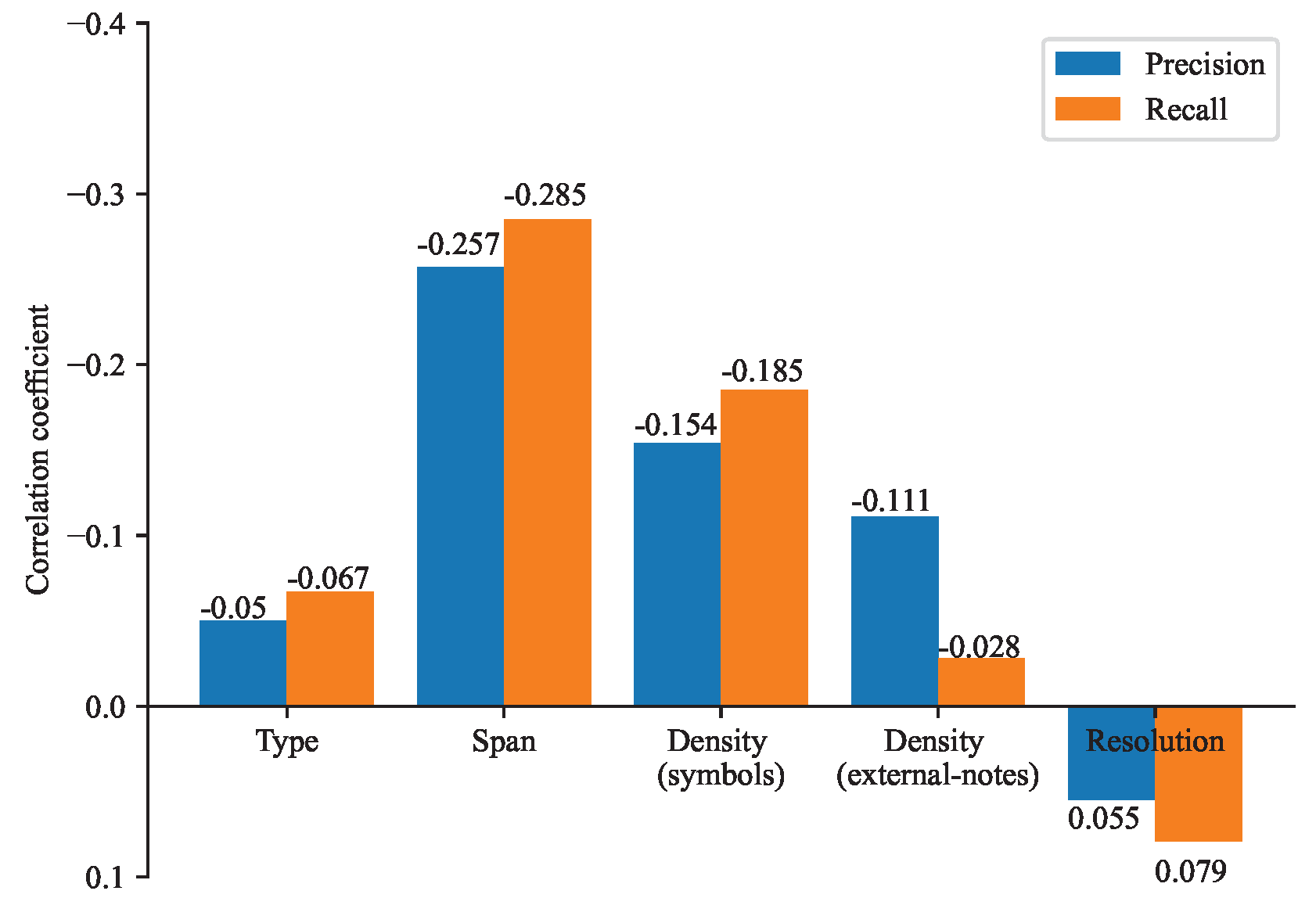
(3) Correlation analysis
The different complexity of staves is a factor that affects the accuracy of symbol recognition. Using the Pearson correlation coefficient to calculate the correlation between the precision and recall of each of the complexity variables can eliminate the magnitude of the complexity variables and provide a more direct observation of the correlation between performance evaluation and complexity. The Pearson correlation coefficient is calculated as shown in equation (
8).
where, by calculating covariance
, the strength of linear correlation between complexity variable
X and the precision and recall
Y is obtained. By calculating the standard deviation
of each complexity variable, and the standard deviation
of recall and precision, we ensure that the calculation of correlation coefficients is not affected by the scale of each variable. The computed complexity variable correlation coefficients are shown in
Figure 5.
As seen in
Figure 5, the type of symbols, the span of interval, the density of symbols and the density of external-notes have a negative correlation with the performance evaluation of the recognition model, and the resolution of images has a positive correlation with the model ability. Take the example for staff 3 and staff 10, with a high similarity in other complexity variables, staff 10 has more types of symbols and their performance evaluation is lower than staff 3. Staff 6 has a higher image resolution results in higher performance evaluation compared with staff 4.
The visualization of the output results at the LSNS is shown in
Figure 6.
3.4.2. Experiment of HSNS
The accuracy of the HSNS is related to the accuracy of the output of the LSNS and the stability and accuracy of the NERA. To verify the accuracy of the NERA, using the ideal data (manual annotation) and the practical data (the output of the LSNS) as inputs —-named ideal input and practical input respectively, the error rate and the omission rate of the output results are calculated:
When the input is ideal, the error rate and the omission rate of the output result are the performance indexes of the NERA.
The error rate and the omission rate are the performance indexes of the whole system when the output is practical.
Tests were conducted by the test set and the experimental results are shown in
Table 4. The specific analysis is as follows:
(1) HSNS output error
As shown in Table 4, the ideal data as the input of HSNS has a zero omission rate, which indicates that the NERA has performed the HSNS for each note input, and proving its stability. The error is mainly caused by the deviation of the range of accidentals. The accidentals are defined in the music theory to work for the notes with the same height within a bar, but in this paper, the note reconstruction does not extend the effective range of accidentals to other symbols within the bar, which leads to the error in the HSNS. As shown in
Figure 7.
(2) Scope of application of NERA
The NERA proposed in this paper can only be applied to the general rules of staff notation whose expression is notation, i.e., the rules described in
Section 2.3. And due to the ambiguous restriction that the author may want to express the content using symbols, there will be some special rules of note expressions[
5], then the output of HSNS will be very different from what the author expresses, as the example shown in
Figure 8.
(3) LSNS as input
The average error rate of the HSNS is 0.031 and the omission rate is 0.021 when the input is system’s practical data. Among numerous replicate experiments, we found that despite the high overall accuracy of the system output, some errors with very low probability still occur. After analysis, we found that these errors are caused by LSNS errors, as shown in
Figure 9, mainly as follows:
Misidentification of the pitch and duration of natural scales can lead to errors during HSNS;
Misidentification or omission of accidentals (sharp, flat, natural, dot) acting on natural scales can lead to errors during HSNS;
Omission of a note affects the HSNS of the note or the preceding and following notes. There are three cases: When the note is preceded and followed by separate notes, the omission of the note does not affect the semantics of the preceding and following notes; when a note is preceded by a pitch-shifting notation (sharp, flat, natural) and followed by another note, the omission of the note will cause the pitch-shifting notation originally used for the note to be applied on the latter note, resulting in a pitch error at the HSNS of understanding of the latter note; when the note is preceded by a note and followed by a dot, the omission of the note will cause the appendage originally used for the note to act on the preceding note, thus the HSNS of the preceding note will be incorrectly timed;
Misidentification or omission of key signature will result in a pitch error in the HSNS for some notes in this line. There are three cases: when the key signature is missed, the pitch of the note in the key signature range is incorrect at the HSNS; When the key signature is misidentified as a key with the same mode of action, i.e., when both modes of action are the same, making the natural scale ascending (or descending) but with a different range of action, the HSNS of some of the notes will be wrong in terms of pitch; When the key signature is incorrectly identified as a key with a different mode of action, the pitch will be incorrect when the note is semantically understood;
When the clef is missed, all natural scales in this row are affected by the clef of the previous line. When the clef is incorrectly identified, an error occurs at the HSNS of all natural scales in this row;
The pitch and duration codes of the played notes output by the staff notation semantic understanding system after the HSNS are shown in
Figure 10.
4. Conclusions and Outlooks
4.1. Conclusions
This paper aims to solve the problem of semantic understanding of the main notes of the optical staff as the pitch and duration during performances in the field of music information retrieval. The SUSN dataset is constructed using the basic properties of the staff as a starting point, and the YOLO object detection algorithm is used to achieve LSNS of the pitch and duration of the natural scale and other symbols (such as clefs, key signatures, accidentals, etc.) that affect the natural scale. Experimental results of LSNS show that the precision is 0.989 and the recall is 0.972. We analyze the causes of error and omission at the LSNS due to the difference in the complexity of the staff.
The HSNS is based on the NERA proposed by the music theory, which parses the low-level semantic information according to the semantics of each symbol and its logical, spatial, and temporal relationships with each other, constructs the staff symbol relationship structure of the given symbols, and calculates the pitch and duration of each note played. The NERA has limitations in modeling the staff image system, and can only realize the encoding of the pitch and duration of the notes whose staff symbols are defined according to a version of the rules of notation. The accuracy of notes in the process of HSNS depends on the accuracy of LSNS, and once there is symbol error and omission, it will lead to wrong pitch and duration encoding of corresponding notes in the process of HSNS. In this paper, we summarize the different cases of HSNS errors caused by the symbol errors and omissions of different symbols of the staff scale during the LSNS.The optical staff notation semantic understanding system implements the input staff images and outputs the encoding of the pitch and duration of each note when it is played.
4.2. Outlooks
The main problems of LSNS are as follows:
The staff notation in this paper is mainly related to the pitch and duration of musical melodies. The recognition of other symbols, such as dynamics, staccatos, trills and characters related to the information of the staff is one of the future tasks to be solved;
The accurate recognition of complex natural scales such as chords is a priority;
The recognition of symbols in more complex staff images, e.g., those with larger intervals, denser symbols and more noise in the image.
For the HSNS, the following problems still need to be solved:
It is important to improve the scope of accidentals, so that they can be combined with bar lines and repetition lines, etc;
The semantic understanding of notes is based on the LSNS, and after solving the problem of the types of symbols recognized by the model, each note can be given richer expression information;
In this paper, rests are recognized, but the information is not utilized in semantic understanding. In the future, this information and the semantic relationships of other symbols can be used to generate a complete code of the staff during performances.
The system provides an accurate semantic understanding of optical staff symbols for multimodal music artificial intelligence applications such as notation recognition through listening, intelligent score flipping and automatic performance.
Author Contributions
Conceptualization, F.L. and Y.L.; methodology, F.L. and Y.L.; software, F.L.; validation, F.L.; formal analysis, F.L. and Y.L.; data curation, F.L. and G.W.; writing—original draft preparation, F.L.; writing—review and editing, F.L., Y.L. and G.W.; visualization, F.L.; supervision, Y.L.; project administration, F.L.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LSNS |
Low-level semantic understanding stage |
| HSNS |
High-level semantic understanding stage |
| NERA |
Note encoding reconstruction algorithm |
Appendix A
The ten staves selected for the test set are shown below:
Staff 1: Canon and Gigue in D major (Pachelbel, Johann)
Staff 2: Oboe String Quartet in C Minor,Violino concertato (JS BACH BWV 1060)
Staff 3: Sechs ländlerische Tänze für 2 Violinen und Bass (Woo15),Violino 1 (Beethoven, Ludwig van)
Staff 4: Violin Concerto RV 226,Violino principale (A. Vivaldi)
Staff 5: String Duo no. 1 in G for violin and viola KV 423 (Wolfgang Amadeus Mozart)
Staff 6: Partia à Cembalo solo (G. Ph. Telemann)
Staff 7: Canon in D,Piano Solo (Johann Pachelbel)
Staff 8: Für Elise in A Minor Wo0 59 (Ludwig van Beethoven)
Staff 9: Passacaglia (Handel Halvorsen)
Staff 10: Prélude n°1 Do Majeur (J.S. Bach)
References
- Downie, J.S. Music information retrieval. Annu. Rev. Inf. Sci. Technol. 2003, 37, 295–340. [Google Scholar]
- Casey, M.A.; Veltkamp, R.; Goto, M.; Leman, M.; Rhodes, C.; Slaney, M. Content-Based Music Information Retrieval: Current Directions and Future Challenges. Proc. IEEE 2008, 96, 668–696. [Google Scholar] [CrossRef]
- Moysis, L.; Iliadis, L.A.; Sotiroudis, S.P.; Boursianis, A.D.; Papadopoulou, M.S.; Kokkinidis, K.-I.D.; Volos, C.; Sarigiannidis, P.; Nikolaidis, S.; Goudos, S.K. Music Deep Learning: Deep Learning Methods for Music Signal Processing-A Review of the State-of-the-Art. IEEE Access 2023, 11, 17031–17052. [Google Scholar] [CrossRef]
- Tardon, L.J.; Barbancho, I.; Barbancho, A.M.; Peinado, A.; Serafin, S.; Avanzini, F. 16th Sound and Music Computing Conference SMC 2019 (28–31 May 2019, Malaga, Spain). Applied Sciences-Basel 2019, 9, 2492. [Google Scholar] [CrossRef]
- Calvo-Zaragoza, J.; Hajič, J., Jr.; Pacha, A. Understanding Optical Music Recognition. ACM Comput. Surv. 2020, 53, 7499. [Google Scholar] [CrossRef]
- Rebelo, A.; Fujinaga, I.; Paszkiewicz, F.; Marcal, A.R.S.; Guedes, C.; Cardoso, J.S. Optical music recognition: state-of-the-art and open issues. Int. J. Multimed. Inf. Retr. 2012, 1, 173–190. [Google Scholar] [CrossRef]
- Calvo-Zaragoza, J.; Barbancho, I.; Tardon, L.J.; Barbancho, A.M. Avoiding staff removal stage in optical music recognition: application to scores written in white mensural notation. Pattern Anal. Appl. 2015, 18, 933–943. [Google Scholar] [CrossRef]
- Rebelo, A.; Capela, G.; Cardoso, J.S. Optical recognition of music symbols. Int. J. Doc. Anal. Recognit. (IJDAR) 2010, 13, 19–31. [Google Scholar] [CrossRef]
- Baró, A.; Riba, P.; Fornés, A. Towards the Recognition of Compound Music Notes in Handwritten Music Scores. In Proceedings of the 2016 15th International Conference on Frontiers in Handwriting Recognition (ICFHR), Shenzhen, China, 23–26 October 2016; pp. 465–470. [Google Scholar]
- Pacha, A.; Choi, K.Y.; Coüasnon, B.; Ricquebourg, Y.; Zanibbi, R.; Eidenberger, H. Handwritten Music Object Detection: Open Issues and Baseline Results. In Proceedings of the 2018 13th IAPR International Workshop on Document Analysis Systems (DAS), Vienna, Austria, 24–27 April 2018; pp. 163–168. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 Dcember 2015. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Hajič jr., J.; Dorfer, M.; Widmer, G.; Pecina, P. Towards Full-Pipeline Handwritten OMR with Musical Symbol Detection by U-Nets. In Proceedings of the 19th International Society for Music Information Retrieval Conference, Paris, France, 23–27 September 2018; pp. 225–232. [Google Scholar]
- Tuggener, L.; Elezi, I.; Schmidhuber, J.; Stadelmann, T. Deep Watershed Detector for Music Object Recognition. arXiv 2018, arXiv:1805.10548. [Google Scholar]
- Huang, Z.; Jia, X.; Guo, Y. State-of-the-Art Model for Music Object Recognition with Deep Learning. Appl. Sci. 2019, 9, 2645. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Van der Wel, E.; Ullrich, K. Optical Music Recognition with Convolutional Sequence-to-Sequence Models. arXiv 2017, arXiv:1707.04877. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 Dcember 2014. [Google Scholar]
- Baró, A.; Riba, P.; Calvo-Zaragoza, J.; Fornés, A. From Optical Music Recognition to Handwritten Music Recognition: A baseline. Pattern Recognit. Lett. 2019, 123, 1–8. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.D. The MIDI Manual: A Practical Guide to MIDI in the Project Studio; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Tuggener, L.; Satyawan, Y.P.; Pacha, A.; Schmidhuber, J.; Stadelmann, T. The DeepScoresV2 Dataset and Benchmark for Music Object Detection. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 Jauary 2021; pp. 9188–9195. [Google Scholar]
- Hajič, J., Jr.; Pecina, P. The MUSCIMA++ Dataset for Handwritten Optical Music Recognition. In Proceedings of the 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), Kyoto, Japan, 9–15 November 2017; pp. 39–46. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path Aggregation Network for Instance Segmentation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8759–8768. [Google Scholar]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 936–944. [Google Scholar]
| 1 |
The staff images in the dataset are the open-licence staffs provided by the International Music Score Library Project (IMSLP). No copyright issues are involved. |
Figure 1.
Dataset labeling method. (a) Labeling of the treble clef: the yellow minimum external bounding box labeled as ’Gclef’; (b) Labeling of the D major: the blue minimum external bounding box labeled as ’D_S’; (c) Labeling of the dot: the red minimum external bounding box labeled as ’dot’; (d) Labeling of the quarter rest: the gray minimum external bounding box labeled as ’Rest4’; (e) Labeling of the sharp symbol: the orange minimum external bounding box labeled as ’Sharp’; (f) Labeling of the single note ’C’ in the main note: purple bounding box from the note head (including the lower plus 1 line) to the 5th line labeled as ’16_-1’. (g) Harmony in the main note: the rose minimum external bounding box, labeled only the first note and annotated as ’8_5’; (h) Appoggiatura: appoggiatura’s size is smaller than main note’s in the staff.
Figure 1.
Dataset labeling method. (a) Labeling of the treble clef: the yellow minimum external bounding box labeled as ’Gclef’; (b) Labeling of the D major: the blue minimum external bounding box labeled as ’D_S’; (c) Labeling of the dot: the red minimum external bounding box labeled as ’dot’; (d) Labeling of the quarter rest: the gray minimum external bounding box labeled as ’Rest4’; (e) Labeling of the sharp symbol: the orange minimum external bounding box labeled as ’Sharp’; (f) Labeling of the single note ’C’ in the main note: purple bounding box from the note head (including the lower plus 1 line) to the 5th line labeled as ’16_-1’. (g) Harmony in the main note: the rose minimum external bounding box, labeled only the first note and annotated as ’8_5’; (h) Appoggiatura: appoggiatura’s size is smaller than main note’s in the staff.
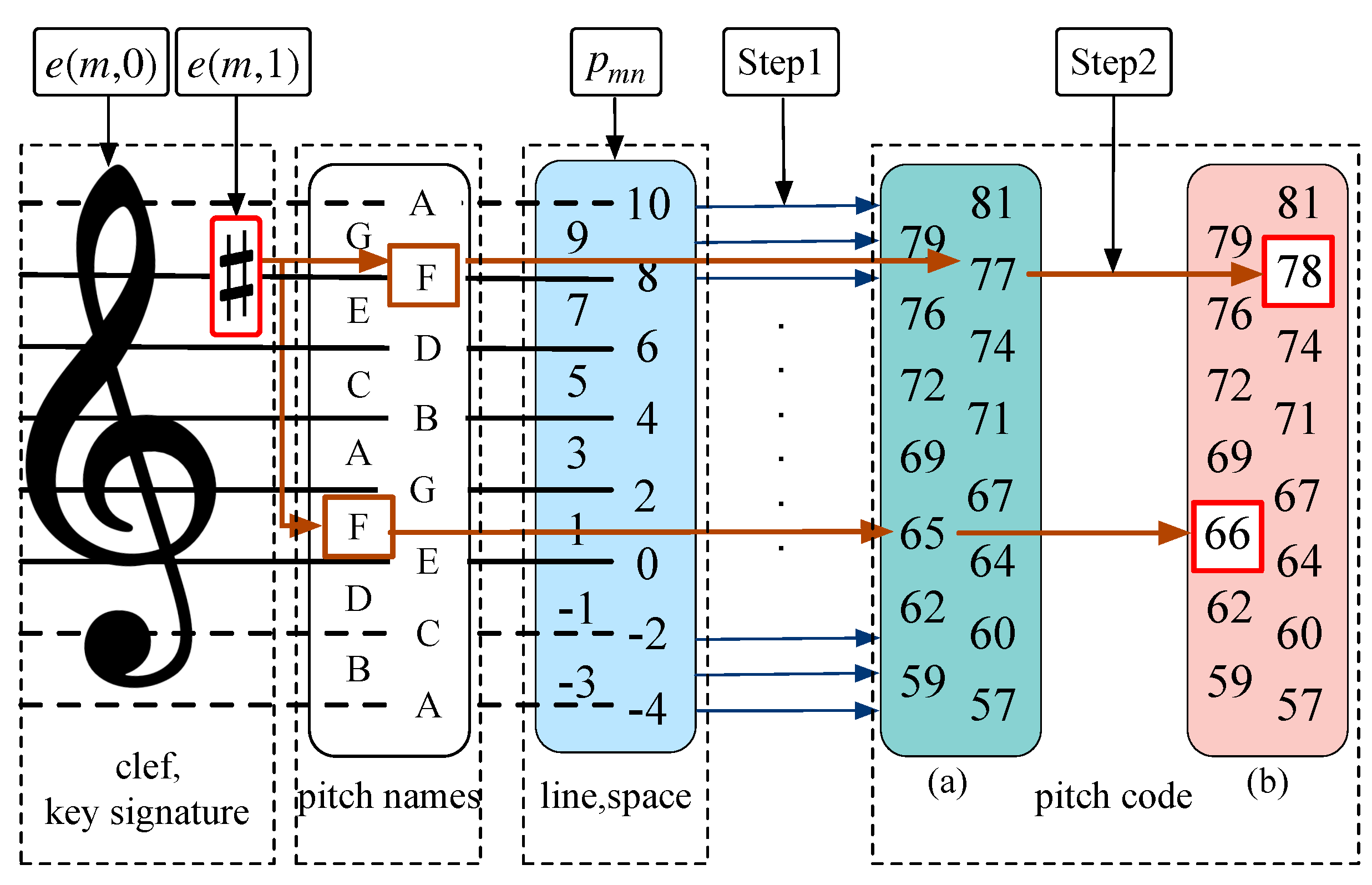
Figure 2.
The mapping between the clef, key signature and the pitch code. In the diagram, the clef is a treble clef. Step1 means the clef’s mapping and the MIDI encoding rules. After passing Step1, is converted to (a). The key signature is G major. Each note in the m-th line is raised a half tone correspondingly, i.e. the upper is 78, and the lower is 66. Then, (a) is converted to (b). The mapping relationship is shown in Step2 in the figure.
Figure 2.
The mapping between the clef, key signature and the pitch code. In the diagram, the clef is a treble clef. Step1 means the clef’s mapping and the MIDI encoding rules. After passing Step1, is converted to (a). The key signature is G major. Each note in the m-th line is raised a half tone correspondingly, i.e. the upper is 78, and the lower is 66. Then, (a) is converted to (b). The mapping relationship is shown in Step2 in the figure.
Figure 4.
The partial error causes of LSNS. The blue boxes are the correctly identified symbols, the green boxes are the incorrectly identified symbols, the characters on the boxes are the identification results, and the symbols without boxes are the missed notes.
Figure 4.
The partial error causes of LSNS. The blue boxes are the correctly identified symbols, the green boxes are the incorrectly identified symbols, the characters on the boxes are the identification results, and the symbols without boxes are the missed notes.
Figure 5.
Complexity variable correlation coefficient.
Figure 5.
Complexity variable correlation coefficient.
Figure 6.
For LSNS visualization, the diagram shows the staff of Oboe String Quartet in C Minor, Violino concertato (JS BACH BWV 1060), page 5, lines 1 and 2. The characters on each box indicate the semantics of the corresponding symbol. In the diagram, green boxes indicate incorrectly identified symbols and the symbols without boxes are the missed notes.
Figure 6.
For LSNS visualization, the diagram shows the staff of Oboe String Quartet in C Minor, Violino concertato (JS BACH BWV 1060), page 5, lines 1 and 2. The characters on each box indicate the semantics of the corresponding symbol. In the diagram, green boxes indicate incorrectly identified symbols and the symbols without boxes are the missed notes.
Figure 7.
The pitch-shifting notation leads to HSNS errors. The sharp should be applied to notes of the same height in the bar, but the NERA only applies to the first note after the sharp.
Figure 7.
The pitch-shifting notation leads to HSNS errors. The sharp should be applied to notes of the same height in the bar, but the NERA only applies to the first note after the sharp.
Figure 8.
This excerpt from Beethoven’s Piano Sonata illustrates some of the characteristics that distinguish musical notation from ordinary notation. The chord in the lower left contains a mixture of half- and quarter-notes of the mixed note head, yet the musical intent is that the two quarter notes in the middle of the chord are actually played as eighth notes, adding the thickness of the first beat. (Excerpted from
Understanding Optical Music Recognition by Calvo.J et al.[
5]).
Figure 8.
This excerpt from Beethoven’s Piano Sonata illustrates some of the characteristics that distinguish musical notation from ordinary notation. The chord in the lower left contains a mixture of half- and quarter-notes of the mixed note head, yet the musical intent is that the two quarter notes in the middle of the chord are actually played as eighth notes, adding the thickness of the first beat. (Excerpted from
Understanding Optical Music Recognition by Calvo.J et al.[
5]).
Figure 9.
Impact on HSNS in case of symbolic errors or omissions at LSNS. (a) indicates the meaning of the corresponding symbol in the figure below. (b) has a wrong note pitch identification of 12, then the HSNS has a pitch error. (c) missed a sharp, then the note pitch of the action is wrong. (d) omission of the dot, then the note duration of the action is wrong. (e) has a note omission which does not affect the semantics of the preceding and following notes. (f) however has an omission of a note which causes the flat to act on the pitch of the next note, and the pitch of the next note is incorrect. (g) has an omission of a note which causes the dot to act on the duration of the preceding note, and duration of the preceding note is incorrect. (h) has missed the key signature of D major, and the notes in the natural scale roll call of "Do" and "Fa" will not be raised. (i) has incorrectly indentified the D major as G major, and the pitches of the notes in the range of action are raised (D major acts on natural scales with the with a roll call of "Fa" and "Do", while G major acts on natural scales with the roll call of "Fa "), when performing the HSNS, natural scales with a roll call of "Fa" in this line of the staff are not subject to error, while natural scales with a roll call of "Do" are subject to error. (j) has recognized D major as F major, and the mode of action is different, which causes the pitch of all the notes in the range to be incorrect. (k) missed the bass clef, and the pitch of all the notes in this line of the staff is determined by the clef of the previous line. (l) identified the alto clef incorrectly as the treble clef, and all the pitches in this line of the pitch are incorrect.
Figure 9.
Impact on HSNS in case of symbolic errors or omissions at LSNS. (a) indicates the meaning of the corresponding symbol in the figure below. (b) has a wrong note pitch identification of 12, then the HSNS has a pitch error. (c) missed a sharp, then the note pitch of the action is wrong. (d) omission of the dot, then the note duration of the action is wrong. (e) has a note omission which does not affect the semantics of the preceding and following notes. (f) however has an omission of a note which causes the flat to act on the pitch of the next note, and the pitch of the next note is incorrect. (g) has an omission of a note which causes the dot to act on the duration of the preceding note, and duration of the preceding note is incorrect. (h) has missed the key signature of D major, and the notes in the natural scale roll call of "Do" and "Fa" will not be raised. (i) has incorrectly indentified the D major as G major, and the pitches of the notes in the range of action are raised (D major acts on natural scales with the with a roll call of "Fa" and "Do", while G major acts on natural scales with the roll call of "Fa "), when performing the HSNS, natural scales with a roll call of "Fa" in this line of the staff are not subject to error, while natural scales with a roll call of "Do" are subject to error. (j) has recognized D major as F major, and the mode of action is different, which causes the pitch of all the notes in the range to be incorrect. (k) missed the bass clef, and the pitch of all the notes in this line of the staff is determined by the clef of the previous line. (l) identified the alto clef incorrectly as the treble clef, and all the pitches in this line of the pitch are incorrect.
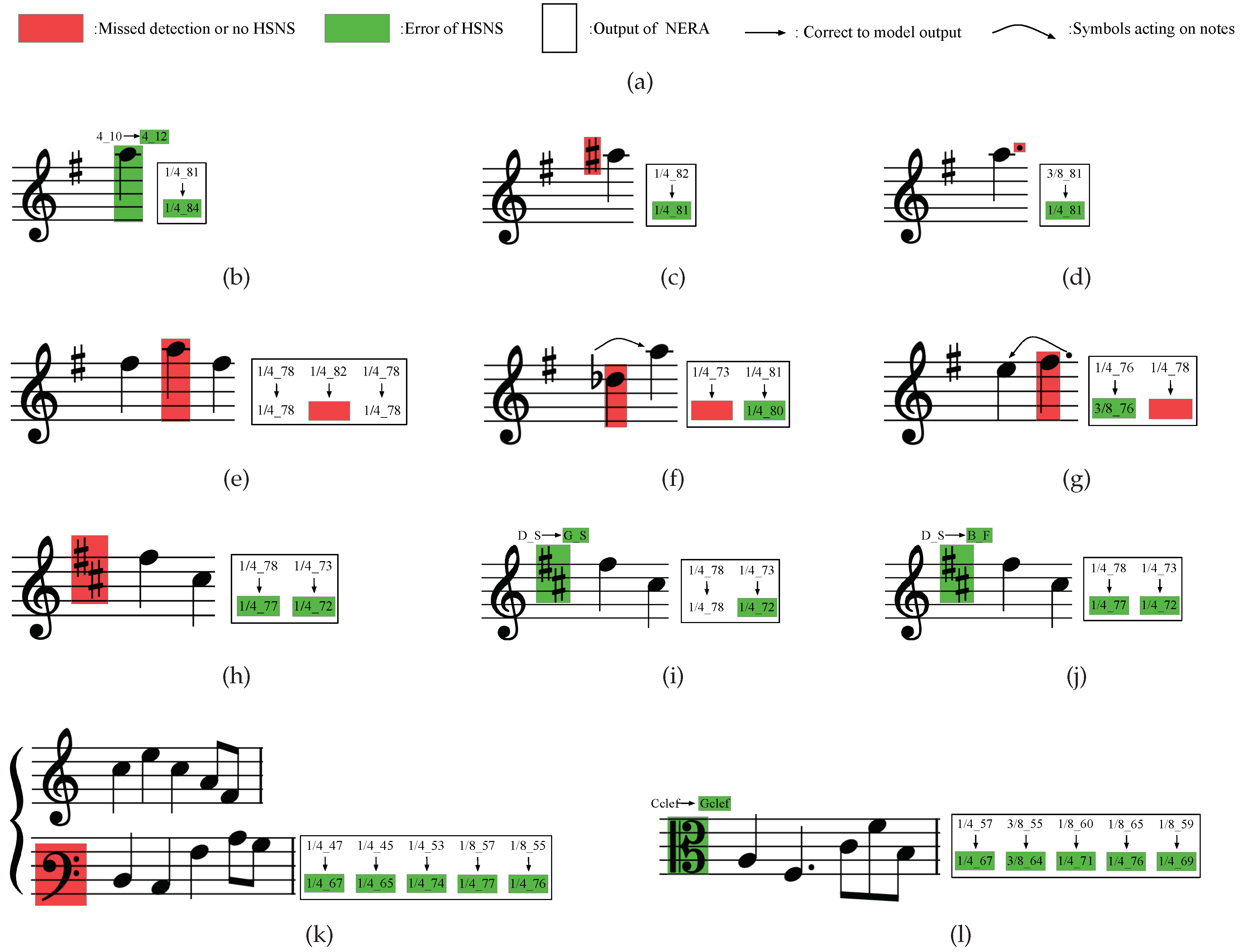
Figure 10.
Visualization of the results of HSNS.
Figure 10.
Visualization of the results of HSNS.
Table 1.
Images with labels of the note control symbols and rests.
Table 1.
Images with labels of the note control symbols and rests.
Table 2.
Performance evaluation of LSNS with different complexity quintiles.
Table 2.
Performance evaluation of LSNS with different complexity quintiles.
| Staff |
|
Complexity Variables |
|
Evaluation |
| name |
page |
|
Type |
Span |
Density (symbols) |
Density (external-notes) |
Resolution |
|
Precision |
Recall |
| Staff 1 |
2 |
|
16 |
19 |
484 |
78 |
1741 |
|
0.968 |
0.930 |
| Staff 2 |
5 |
|
17 |
19 |
679 |
146 |
2232 |
|
0.996 |
0.988 |
| Staff 3 |
3 |
|
13 |
19 |
319 |
95 |
1673 |
|
0.997 |
0.992 |
| Staff 4 |
12 |
|
20 |
20 |
478 |
80 |
1741 |
|
0.994 |
0.981 |
| Staff 5 |
7 |
|
19 |
24 |
530 |
145 |
200 |
|
0.980 |
0.958 |
| Staff 6 |
5 |
|
19 |
20 |
367 |
63 |
435 |
|
0.992 |
0.970 |
| Staff 7 |
5 |
|
15 |
19 |
350 |
62 |
854 |
|
0.996 |
0.993 |
| Staff 8 |
3 |
|
13 |
20 |
441 |
40 |
1536 |
|
0.990 |
0.969 |
| Staff 9 |
3 |
|
11 |
20 |
424 |
160 |
2389 |
|
0.986 |
0.966 |
| Staff 10 |
2 |
|
17 |
18 |
315 |
86 |
1780 |
|
0.987 |
0.976 |
Table 3.
Precision and Recall of clef and key signature.
Table 3.
Precision and Recall of clef and key signature.
| |
Precision |
Recall |
| clef |
1.0 00 |
0.993 |
| key signature |
0.992 |
0.990 |
Table 4.
Experimental results of HSNS.
Table 4.
Experimental results of HSNS.
| Staff |
|
Ideal input |
|
Practical input |
| |
|
Error rate |
Omission rate |
|
Error rate |
Omission rate |
| Staff 1 |
|
0.006 |
0.000 |
|
0.052 |
0.044 |
| Staff 2 |
|
0.011 |
0.000 |
|
0.016 |
0.010 |
| Staff 3 |
|
0.010 |
0.000 |
|
0.020 |
0.006 |
| Staff 4 |
|
0.019 |
0.000 |
|
0.027 |
0.020 |
| Staff 5 |
|
0.013 |
0.000 |
|
0.044 |
0.014 |
| Staff 6 |
|
0.005 |
0.000 |
|
0.020 |
0.008 |
| Staff 7 |
|
0.000 |
0.000 |
|
0.004 |
0.010 |
| Staff 8 |
|
0.020 |
0.000 |
|
0.055 |
0.053 |
| Staff 9 |
|
0.022 |
0.000 |
|
0.037 |
0.021 |
| Staff 10 |
|
0.000 |
0.000 |
|
0.036 |
0.019 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).