Prerpints.org logo
Preprint
Article

Multi-scale Friction Simulation of Carbon Nanotube-Reinforced Nitrile Butadiene Rubber Composites Based on Molecular Dynamics and Finite Element Analysis

Altmetrics

Downloads

148

Views

63

Comments

0

This version is not peer-reviewed

Submitted:

07 July 2023

Posted:

10 July 2023

You are already at the latest version

Alerts
Abstract
Nitrile butadiene rubber (NBR) and its various composites are extensively studied as matrix materials for oil-free lubricated mechanical friction surfaces. While numerous macroscopic friction experiments can compare the frictional performance of different NBR composites, the complex material preparation and low experimental efficiency pose challenges. Nanoscale molecular dynamics (MD) simulations can help develop materials with improved friction properties, but they cannot directly provide the friction coefficients of actual macroscopic friction surfaces. Therefore, it is important to integrate the advantages of macroscopic and nanoscale friction studies and perform a synergistic analysis to modify the friction properties of composite materials. In this study, a multi-scale approach is proposed to simulate the frictional characteristics of carbon nanotube (CNT)-reinforced NBR by combining the MD friction simulation， micromechanical bridging model, and macroscopic finite element analysis (FEA) methods. The results of the multi-scale friction simulation of copper (Cu)-CNT/NBR composites show that the addition of CNTs significantly improves the frictional properties of NBR, and the extent of the improvement is related to the mass fraction of CNTs. As the mass fraction of CNTs increases (0%, 1.25%, 2.5%, 5%), the coefficient of friction decreases from 0.50 to 0.38. The results are validated by ring-block friction experiments at the same scale as the simulations.
Keywords: 
Subject: Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

NBR is widely used in mechanical industries such as sealing and bearing systems due to its excellent mechanical properties, aging resistance, heat resistance, electrical insulation, and wear resistance [1,2,3,4]. To further improve the mechanical and frictional properties of NBR and meet the requirements of various components, various fillers are used to modify NBR composites. Various reinforcing or lubricating fillers such as graphene, alumina, silica, and carbon black improve the mechanical and frictional properties of the composites to varying degrees [5,6,7,8,9]. It is important to effectively predict the frictional properties of NBR composites and develop suitable composites.
Traditional methods for studying the friction characteristics of NBR composites involve directly preparing the materials and conducting macroscopic friction experiments. Water-lubricated friction and wear experiments have shown that the addition of graphene and CNTs can effectively reduce the friction coefficient of NBR. Compared to graphene, CNTs exhibit better performance in reducing surface cracks and improving the wear resistance of NBR [10]. Under water-lubricated conditions, X. Yang et al. [11] utilized an ionic liquid-assisted method to prepare NBR composites with uniformly dispersed graphene. The friction coefficient and volume wear rate of the composites were reduced by 31.52% and 51.9%, respectively, compared to pure NBR. Dry friction experiments and scanning electron microscopy (SEM) observations have revealed that short carbon fiber (SCF)-reinforced NBR composites and Fe3O4 particle-reinforced NBR composites exhibit superior friction and wear properties compared to pure NBR [12,13]. The friction performance of hydrogenated NBR composites filled with 35% carbon black or silica was compared by E. Padenko et al. [14], and the experimental results demonstrated a more pronounced advantage of carbon black over silica as a filler. In addition to the type of filler, the filler loading also influences the friction performance of NBR. Y. Jia et al. [15] prepared NBR composites with different alumina doping levels using mechanical blending, and corresponding friction and wear experiments revealed that the composite with 5 g of alumina exhibited the best friction and wear resistance. Similarly, Q. He et al. [16] prepared NBR nanocomposites with varying contents of WS2 using mechanical blending. The experimental results showed that the composite with 10 parts of nano WS2 exhibited the lowest friction coefficient. Furthermore, the size and dispersion of the nanofillers are also critical factors influencing the performance of NBR composites. W. Yang et al. [17] prepared hydrogenated NBR reinforced with nano-sized Al2O3 particles of different sizes. Comparative experiments on mechanical and frictional properties revealed that as the particle size of nano Al2O3 decreased, the mechanical performance of the hydrogenated NBR composite gradually improved, accompanied by a reduction in dry friction coefficient and wear rate.In a study by X. Liu et al. [18], the influence of silica particle size and dispersion on the frictional properties of NBR was investigated under water-lubricated and constant temperature conditions. The experimental results demonstrated that smaller-sized nano silica exhibited better dispersion within the NBR matrix, leading to superior frictional characteristics of the composite material. Furthermore, modified fillers can exhibit different frictional performances in composite materials. Y. R. Liang et al. [19] employed cetyltrimethylammonium bromide (CTAB), silane coupling agent (KH570), and polyethylene glycol (PEG) to modify the surface properties of molybdenum disulfide (MoS2). Friction test results of MoS2/ NBR composites with different modified fillers indicated that CTAB-modified MoS2 exhibited the most significant enhancement in the frictional performance of NBR.
Despite the comparative analysis provided by traditional frictional experiments on the frictional characteristics of NBR composites, accurately predicting their frictional properties before material preparation remains challenging. The intricate process of material preparation and the substantial number of repetitive experiments contribute to the inefficiency of studying frictional characteristics. To facilitate the efficient selection of appropriate fillers and guide the frictional modification of materials, a reliable friction model is required for predicting the frictional properties of composite materials.
In recent years, with the rapid development of computer hardware performance, the utilization of molecular dynamics (MD) methods to investigate the mechanical and frictional properties of NBR composites at the nanoscale has become a focus of research. Y. Li et al. [20] employed MD simulations to study the atomic motion in the contact frictional region between iron atoms and CNT-reinforced NBR. The simulation results revealed that the incorporation of CNTs led to a maximum increase of 60% in the shear modulus of the composite material and significantly improved its frictional performance. Building upon these findings, Y. Li's research team further conducted MD simulations to explore the frictional properties of NBR composites filled with defective CNTs and functionalized CNTs. These simulations provided a series of insights at the nanoscale to comprehend the mechanisms by which carbon nanotubes enhance the frictional performance of composite materials [21,22,23,24]. In addition to CNTs, molecular-level simulations can also be employed to investigate the frictional properties of NBR composites reinforced with other nanofillers. X. Liu et al. [25,26] conducted studies on the mechanical and tribological properties of NBR composites reinforced with silica nanoparticles at the nanoscale. The simulation results demonstrated significant improvements in frictional performance and wear resistance of the NBR composites filled with silica compared to pure NBR under both dry friction and water lubrication conditions. J. Cui et al. [27] employed MD simulations to study the functionalized graphene-reinforced nitrile rubber composites with hydroxyl, carboxyl, and ester groups. The results indicated that carboxyl -functionalized graphene exhibited the best enhancement in the mechanical and frictional properties of NBR. Furthermore, MD simulations of zinc oxide nanoparticle-reinforced NBR revealed a reduction of 30% in the friction coefficient of the NBR matrix after the incorporation of zinc oxide particles [28].
Despite the ability of MD simulations to predict the frictional performance of composites at the nanoscale and provide new insights for frictional modification, it is challenging to validate the simulation results through nanoscale friction experiments. Moreover, there exists a significant disparity in spatial and temporal scales between MD and the actual frictional motion of contacting components, making it difficult to effectively predict macroscopic friction behavior based solely on MD simulations. Therefore, it is of great significance to employ a multi-scale modeling approach that combines nanoscale MD simulations with macroscopic friction models for synergistic analysis. This approach enables the accurate prediction of the friction coefficient of real components and provides guidance for the frictional modification of composite materials.
Since its discovery in 1991 [29], CNTs have been considered an ideal filler for improving the friction and wear performance of polymers due to their exceptional mechanical properties, self-lubricating nature, and high wear resistance [30,31,32].
To effectively predict the frictional performance of actual CNT-reinforced NBR composite materials and guide the modification of their frictional characteristics, this study proposes a multi-scale friction model that combines MD and macroscopic FEA methods, utilizing the bridging model from micromechanics [33,34] as a key component. At the nanoscale, MD simulations are employed to obtain the mechanical properties of isotropic pure NBR and transversely isotropic representative volume elements (RVE) of CNT/NBR composites, as well as the friction coefficients at different pressures. By homogenizing the mechanical parameters from MD simulations using the micromechanical bridging model, the macroscopic mechanical properties of NBR composites with different mass fractions of CNTs can be obtained at a macroscopic (micrometer-level) scale. These macroscopic mechanical properties are then incorporated into a macroscopic finite element (FE) contact friction model to obtain the pressure distribution at the contact interface. Subsequently, the MD-derived friction coefficients are applied to the entire contact interface and integrated to predict the macroscopic friction coefficient. Finally, the multi-scale model is validated through friction tests on actual CNT-reinforced NBR blocks in contact with copper rings of the same size. This study represents the first attempt at multi-scale friction simulation for CNT-reinforced NBR, providing a new approach for predicting the friction coefficient of composite materials at the actual scale and guiding friction modification.

2. Methods

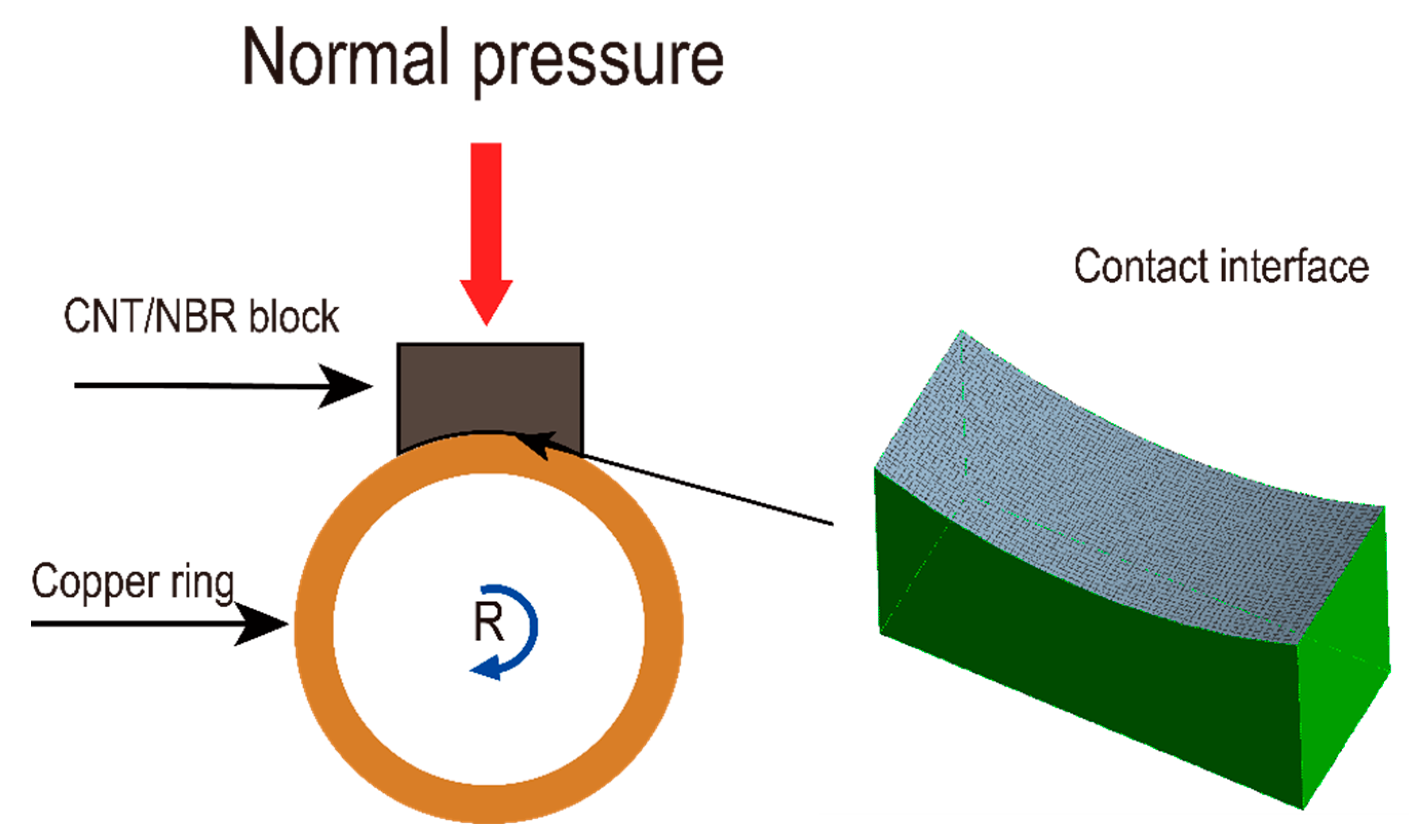
As this is the first attempt to perform multi-scale friction simulation for CNT/NBR composites, this study focuses on investigating the elastic deformation stage and dry friction characteristics of the material. Considering the unique structure of carbon nanotubes CNTs, the mechanical and frictional properties of the CNT/NBR representative volume element (RVE) are analyzed in both axial and radial directions during the molecular simulation. Given the potential application of the composite material in oil-free lubricated rotating machinery, the target of this multi-scale simulation is the friction pair of a copper ring and a CNT/NBR block. Using the multi-scale friction model, the frictional characteristics of four CNT/NBR composite materials with CNT mass fractions of 0% (pure NBR), 1.25%, 2.5%, and 5% are predicted under the conditions of 0.5 MPa normal pressure, 30 rpm rotational speed, and room temperature. The effectiveness of the multi-scale model is validated through friction experiments conducted on copper ring-CNT/NBR block pairs with identical dimensions and operating conditions.

2.1. MD Simulations

At the nanoscale, the elastic and frictional properties of pure NBR and the CNT/NBR RVE are simulated. The obtained elastic mechanical parameters and dry friction coefficients from the MD serve as the foundation for the latter part of the multi-scale model. Taking advantage of the capabilities of various MD simulation software, the model construction is performed using the Materials Studio (MS) commercial software (2019 edition), and system optimization and MD simulation are carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [35]. The CAMPASS force field [36] is employed for the MD simulation in this study.

2.1.1. Modeling and Mechanical Simulations of Pure NBR and CNT/NBR RVE

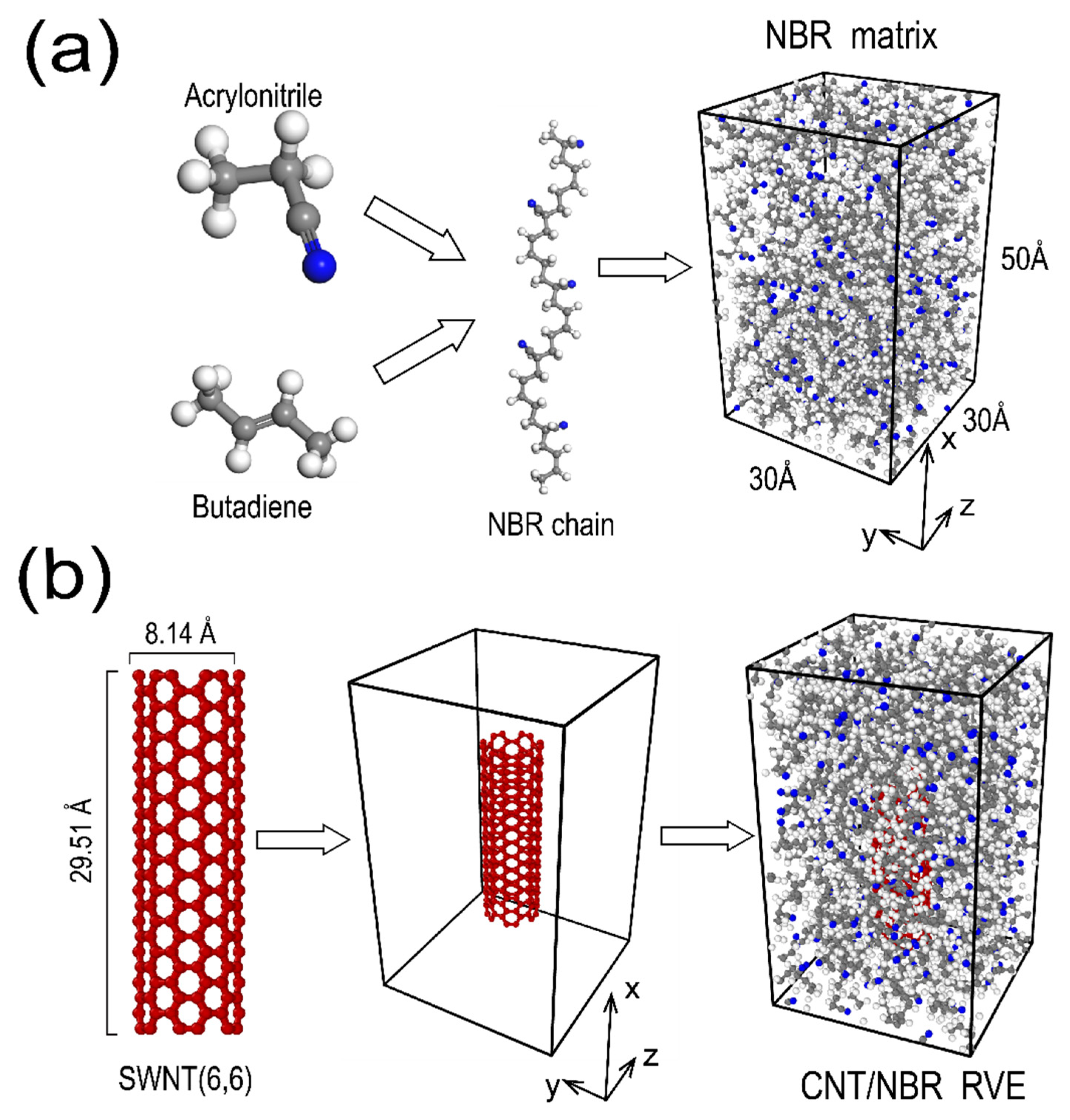
First, pure NBR is molecularly modeled. NBR is a copolymer composed of acrylonitrile and butadiene monomers. In this simulation, the NBR polymer chains are constructed based on a 1:1 ratio of butadiene and acrylonitrile monomers. The polymerization degree of the NBR chains is set to 20. A periodic box with dimensions of 50 Å × 30 Å × 30 Å is constructed in the MS software. Using the Monte Carlo method [37], multiple NBR polymer chains are placed in the periodic box until the box density reaches the actual density of NBR, which is 1.0 g/cm3. The constructed pure NBR unit cell is shown in Figure 1(a). This is followed by the modeling of the CNT/NBR RVE. An armchair single-walled CNT was placed in the center of a 50 Å × 30 Å × 30 Å periodic box such that the axial direction of the CNT was parallel to the x-direction of the box. The same Monte Carlo method was used to fill the box with NBR molecular chains such that the mass fraction of carbon nanotubes was 10%. The generated CNT/NBR RVE density is 1.03 g/cm3. The structure and size of carbon nanotubes and the filling process are shown in Figure 1(b)
The pure NBR and CNT/NBR RVE periodic unit cells were imported into LAMMPS using the msi2lmp module in the MS software for system optimization and simulation. The initially established amorphous unit cell had high total energy and exhibited highly unstable internal states. To achieve energy minimization, the conjugate gradient method was applied to the entire molecular system. The energy convergence threshold was set to 10-5 kcal/mol, and the force convergence criterion was set to 10-4 kcal/mol/Å. To eliminate peculiar connections between polymer chains and molecules, a 1 ns molecular dynamics equilibration was performed in the NPT (constant-pressure, constant-temperature) ensemble at a temperature of 300 K and a pressure of 0.1 MPa (atmospheric pressure). Subsequently, the equilibrated unit cell was subjected to an annealing process with a temperature range of 250 K to 500 K and a temperature step size of 50 K, repeated for 10 cycles. The repeated high-temperature to low-temperature annealing cycles allowed for better relaxation and optimization of the molecular structure within the system. A subsequent 1 ns molecular dynamics equilibration was performed in the NVT (canonical ensemble) ensemble. The optimized total energy of the system reached its lowest level at a temperature of 300 K, and the pressures in all directions were reduced to zero.
The molecular models of the optimized systems were subjected to elastic mechanics simulations. Before the mechanical simulations, it is necessary to discuss the independent elastic parameters of pure NBR and CNT/NBR RVE. The principles of elastic mechanics describe the constitutive relationship between stress and strain during the elastic deformation stage, which can be expressed as follows:
{ ε i } = [ S i j ] { σ i }
{ σ i } = [ C i j ] { ε i }
where [ S i j ] and [ C i j ] are the flexibility tensor and the stiffness tensor, respectively.
Since pure NBR is an isotropic material, its flexibility tensor [ S M ] can be expressed as:
[ S M ] = [ 1 E − ν E − ν E 0 0 0 − ν E 1 E − ν E 0 0 0 − ν E − ν E 1 E 0 0 0 0 0 0 1 G 0 0 0 0 0 0 1 G 0 0 0 0 0 0 1 G   ]
where Young's modulus E and Poisson's ratio ν are independent parameters, and the relationship between shear modulus G and them is satisfied as follows:
G = E 2 ( 1 + ν )
For CNT/NBR RVE, the filling of the CNT leads to transverse isotropy in mechanical properties, and the flexibility tensor [ S R ] can be expressed as:
[ S R ] = [ 1 E 11 − ν 12 E 11 − ν 12 E 11 0 0 0 − ν 12 E 11 1 E 22 − ν 23 E 0 0 0 − ν 12 E 11 − ν 23 E 1 E 22 0 0 0 0 0 0 1 G 12 0 0 0 0 0 0 1 G 12 0 0 0 0 0 0 1 G 23   ]
where E 11 is the axial (x-direction) Young's modulus, E 22 is the transverse elastic modulus ( E 22 = E 33 ), ν 12 is the axial Poisson's ratio ( ν 12 = ν 13 ), ν 23 is the transverse Poisson's ratio, and G 12 is the axial shear modulus. Since in the 2-3 plane, CNT/NBR RVE behaves isotropically, the transverse shear modulus G 23 can be expressed as:
G 23 = E 22 2 ( 1 + ν 23 )
After determining the independent elastic parameters to be obtained, the mechanical properties were simulated for pure NBR as well as CNT/NBR RVE. To obtain Young's modulus E and Poisson's ratio ν of the pure NBR, continuous strains were applied in the x(11) direction with strain steps of 0.0025 until a minimum strain of 0.05 was reached. For the transverse isotropic CNT/NBR RVE, three simulation actions (axial tension, axial shear, and transverse tension) were designed to obtain its five elastic parameters ( E 11 , E 22 , ν 12 , ν 23 , G 12 ).

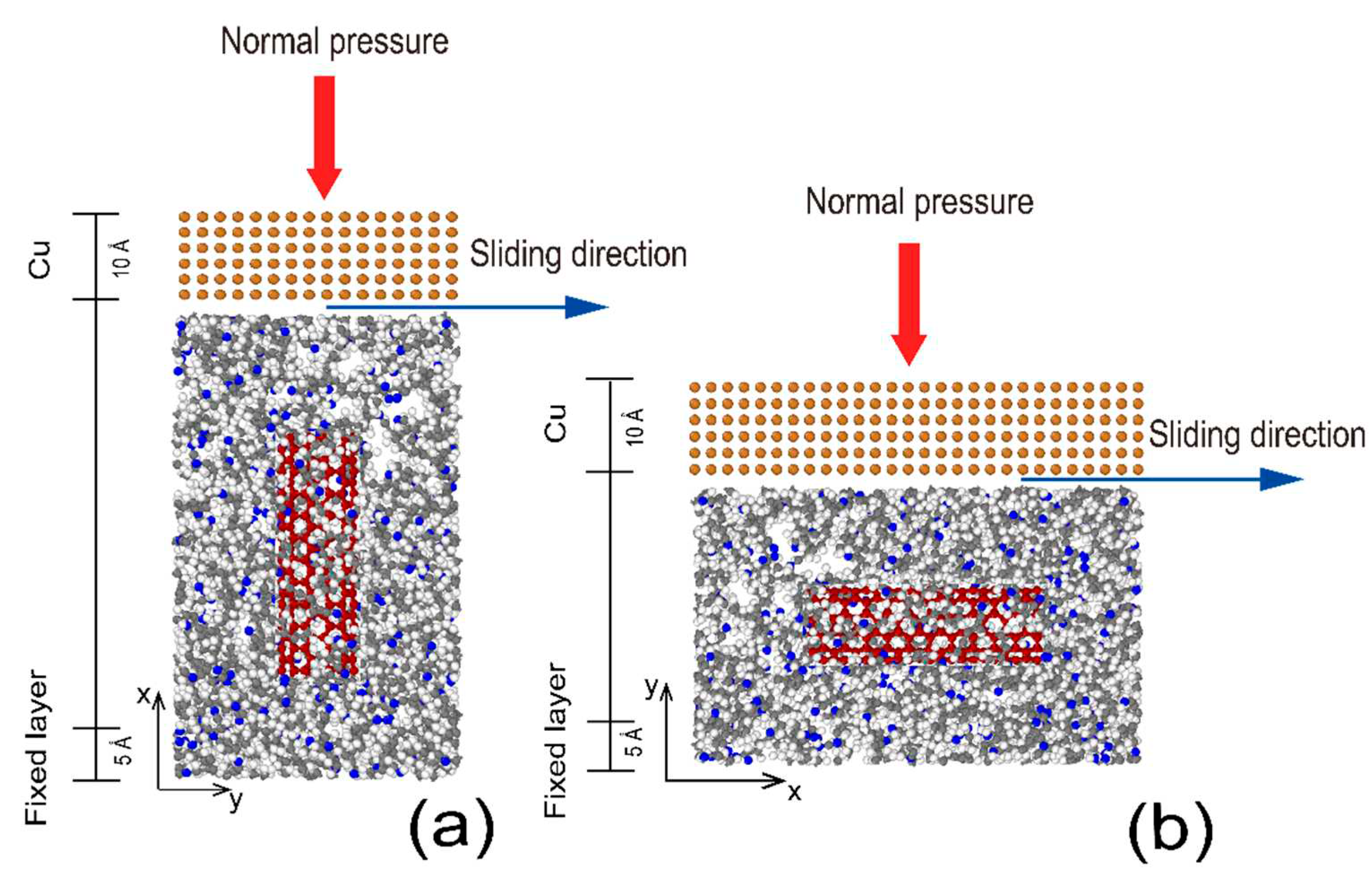
2.1.2. Friction Simulations of Cu-NBR and Cu-CNT/NBR RVE

In order to simulate the frictional behavior of pure NBR and CNT/NBR RVE, we selected copper (Cu) as the counterpart material for the frictional contact. A Cu crystal box with a thickness of 10 Å was placed on top of the pure NBR box, where the bottom region of the NBR box with a thickness of 5 Å was fixed as the stationary layer, while the remaining part served as the sliding layer. A normal pressure ranging from 0.05 to 0.90 MPa (corresponding to the contact load distribution at the interface analyzed by finite element analysis) was applied to the Cu atom layer, and a tangential sliding velocity of 0.055 m/s (equivalent to 30 rpm) was imposed to simulate the dry friction motion. The friction coefficient was obtained by calculating the ratio of the total tangential force acting on the Cu atoms to the normal pressure. Each friction simulation was conducted for a duration of 300 ps with a time step of 1 fs. The average value of the friction coefficient over the stable state of 150 ps was considered the effective value, and three replicates were performed to ensure the reproducibility of the results.
The friction simulation process for CNT/NBR RVE is similar to that of pure NBR. Due to the transversely isotropic nature of CNT/NBR, the frictional characteristics in the Y and Z directions are essentially the same [38]. Taking into account the influence of the CNT orientation on the frictional performance of CNT/NBR, simulations were conducted in both the X and Y directions as shown in Figure 2. The simulation settings were the same as those for pure NBR.

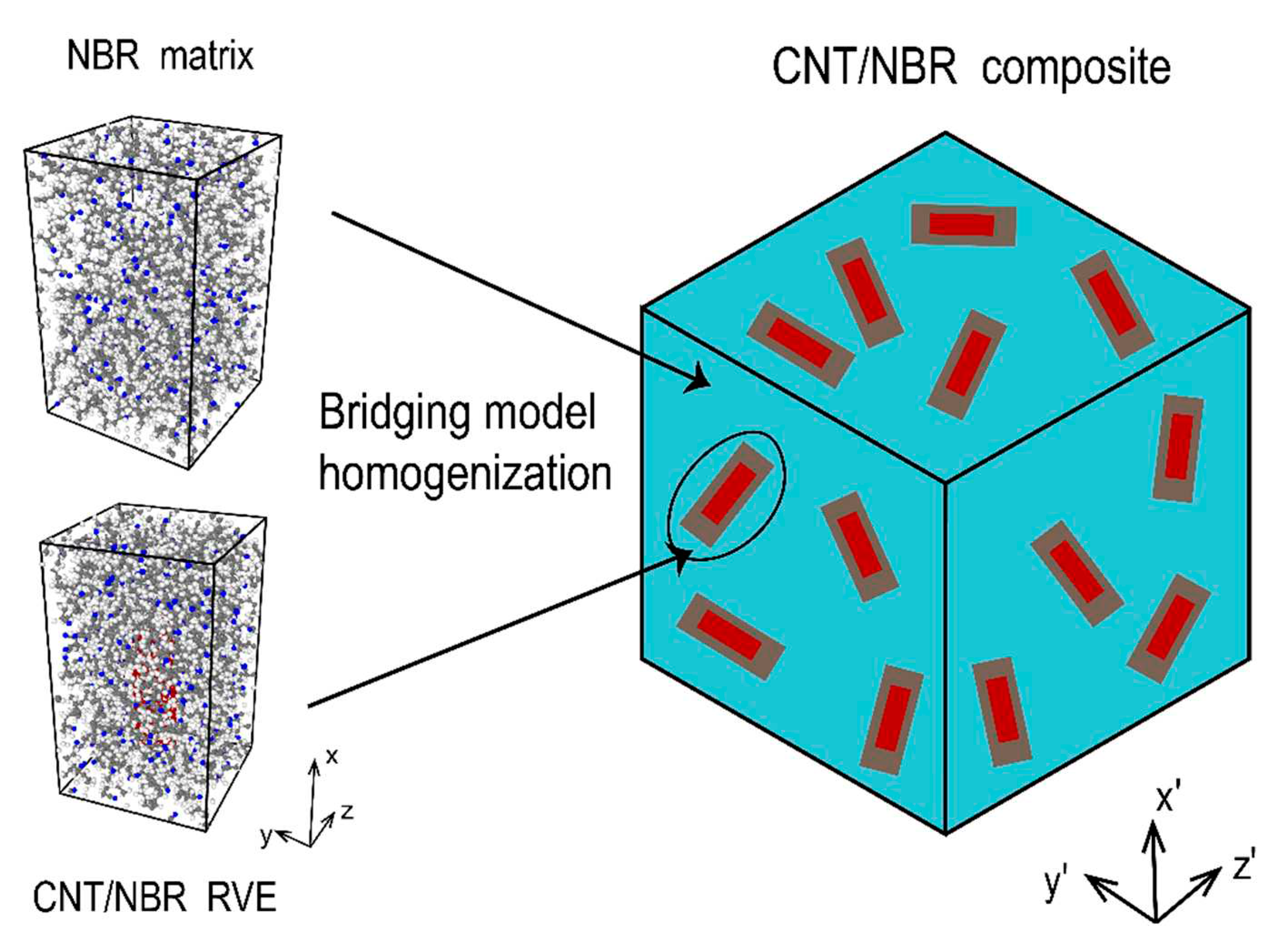
2.2. Bridging Model Homogenization

Given the known mechanical properties of the matrix (pure NBR) and the reinforcing fibers (CNT/NBR RVE), the macroscopic mechanical properties of the resulting composite material can be determined using the homogenization method in micromechanics. In this section, the homogenization approach based on the micromechanical bridging model is employed to calculate the macroscopic mechanical properties of the CNT/NBR composite material, which is a crucial step in establishing the multi-scale friction model, as illustrated in Figure 3.
Assuming that the stresses and displacements of the matrix and fibers satisfy the continuity boundary condition at the common interface, their stresses and strains satisfy the following relationship:
{ σ i } = V R { σ i R } + V M { σ i M }
{ ε i } = V R { ε i R } + V M { ε i M }
Here V R and V M are the respective volume fractions of CNT/NBR RVE fibers and pure NBR matrix, and i = 1 , 2 , ⋅ ⋅ ⋅ , 6 is the six principal directions of stress-strain.
Since the internal stresses of the fiber and matrix are equal at the common interface, the mean internal stresses of the fiber and matrix must have a non-singular matrix leading to the following relationship:
{ σ i M } = [ A ] { σ i R }
Here [ A ] is called bridging tensor. The effective flexibility tensor [ S ] of CNT/NBR composite can be expressed as.
[ S ] = ( V R [ S R ] + V M [ S M ] [ A ] ) ( V R [ I ] + V M [ A ] ) − 1
where [ S M ] and [ S R ] are the flexibility tensor of the NBR matrix and CNT/NBR RVE fibers, and their respective component parameters are determined from the MD simulations in Section 2.1.1; [ I ] is the unit tensor. in the bridging tensor model, each of the independent variables in the bridging tensor is more than a function of both types of parameters, and always expands Taylor series on them:
A 11 = 1 + λ 11 ( 1 − E M / E 11 R ) + ⋅ ⋅ ⋅
A 21 = λ 21 ( 1 − ν M / ν 12 R ) + ⋅ ⋅ ⋅
A 22 = A 33 = 1 + λ 31 ( 1 − E M / E 22 R ) + ⋅ ⋅ ⋅
A 32 = λ 41 ( 1 − ν M / ν 23 R ) + ⋅ ⋅ ⋅
A 55 = A 66 = 1 + λ 51 ( 1 − G M / G 12 R ) + ⋅ ⋅ ⋅
The subsequent expansion terms of the above series are omitted, where λ i j ( i = 1 , 2 , ⋅ ⋅ ⋅ , 6 ; j = 1 , 2 , ⋅ ⋅ ⋅ , ∞ ) is the expansion coefficient [34].
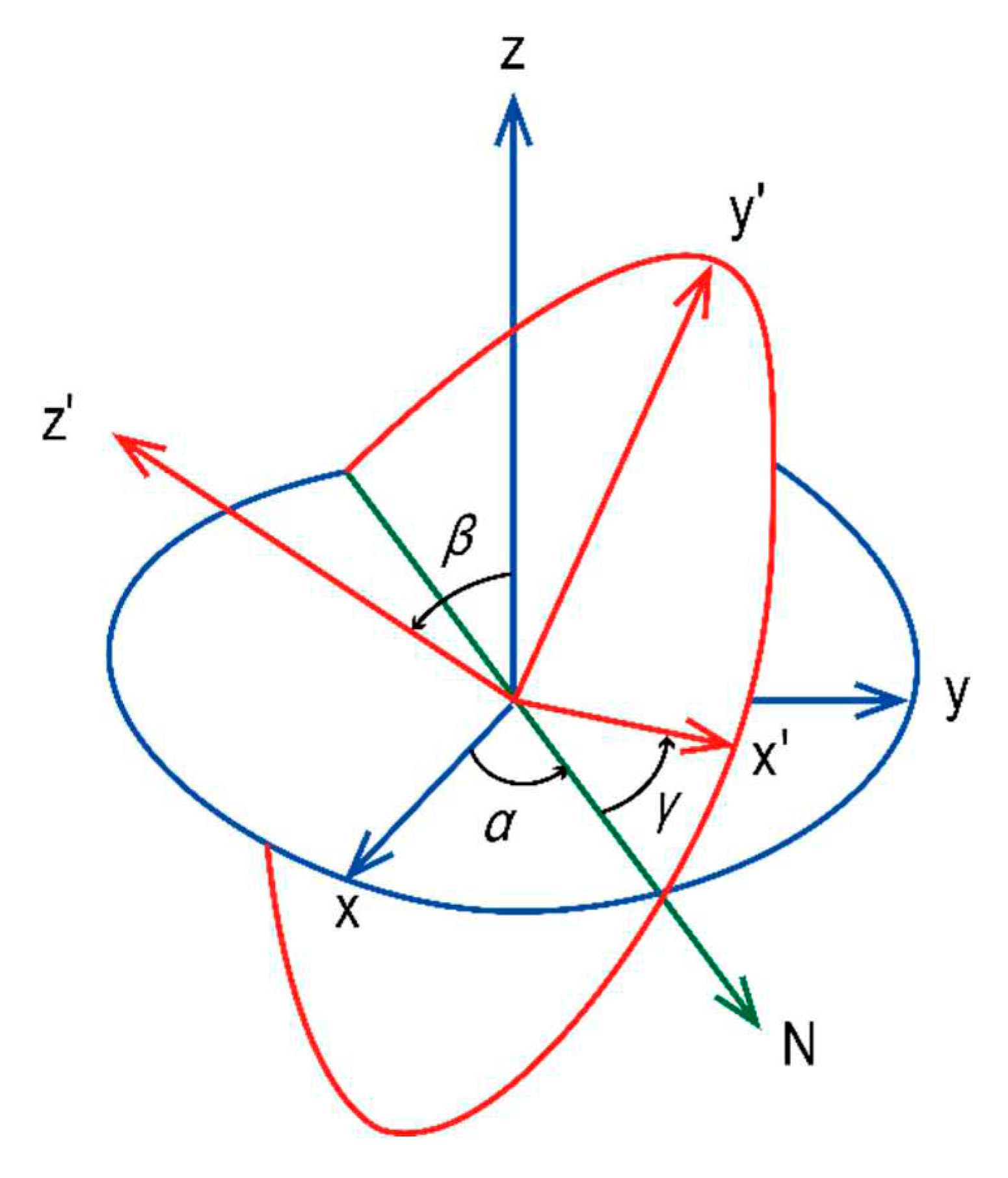
Considering the directional randomness of CNT/NBR RVE mixed into the matrix, the bridging tensor needs to be transformed from the local coordinate system ( x   y   z ) to the global coordinate system (   x   ′   y   ′   z   ′ ). The bridging tensor [ A ′ ] after coordinate transformation can be expressed as:
[ A ′ ] = [ R ] [ A ]
Here [ R ] is the rotation operator matrix:
[ R ] = [ cos α cos γ − sin α cos β sin γ sin α cos γ + cos α cos β sin γ sin γ sin β − cos α sin γ − sin α cos β cos γ − sin α sin γ + cos α cos β cos γ sin β cos γ sin α sin β − cos α sin β cos β ]
Where α , γ , β are Euler angles as shown in Figure 4. Averaging over [ A ′ ] yields [ A ¯ ] [39]:
[ A ¯ ] = ∫ − π π ∫ 0 π ∫ 0 π / 2 [ A ′ ] ( α , β , γ ) sin β d α d β d γ ∫ − π π ∫ 0 π ∫ 0 π / 2 sin β d α d β d γ
Based on the elastic parameters from MD simulations, the macroscopic mechanical properties of three CNT/NBR composites with CNTs mass fractions of 1.25%, 2.5%, and 5%, respectively, were obtained in this section using a bridging model homogenization method.

2.3. Finite Element Simulations

A FE friction model was constructed, which was consistent with the dimensions of the actual copper ring-CNT/NBR sample block. The elastic parameters obtained from the homogenization of the CNT/NBR material using the bridging model were incorporated into the FE model. The material structure was divided into numerous elements and nodes through finite element meshing, and the overall mechanical response was obtained by solving the stress-strain transfer between the nodes. The Arbitrary Lagrangian-Eulerian method [40] was employed to solve the rolling contact problem in this study. The structure of the FE friction model is shown in Figure 5, and Table 1 provides the statistical parameters for the dimensions of the copper ring and CNT/NBR block.

2.3.1. Effect of Contact Interface Meshing on Pressure Distribution

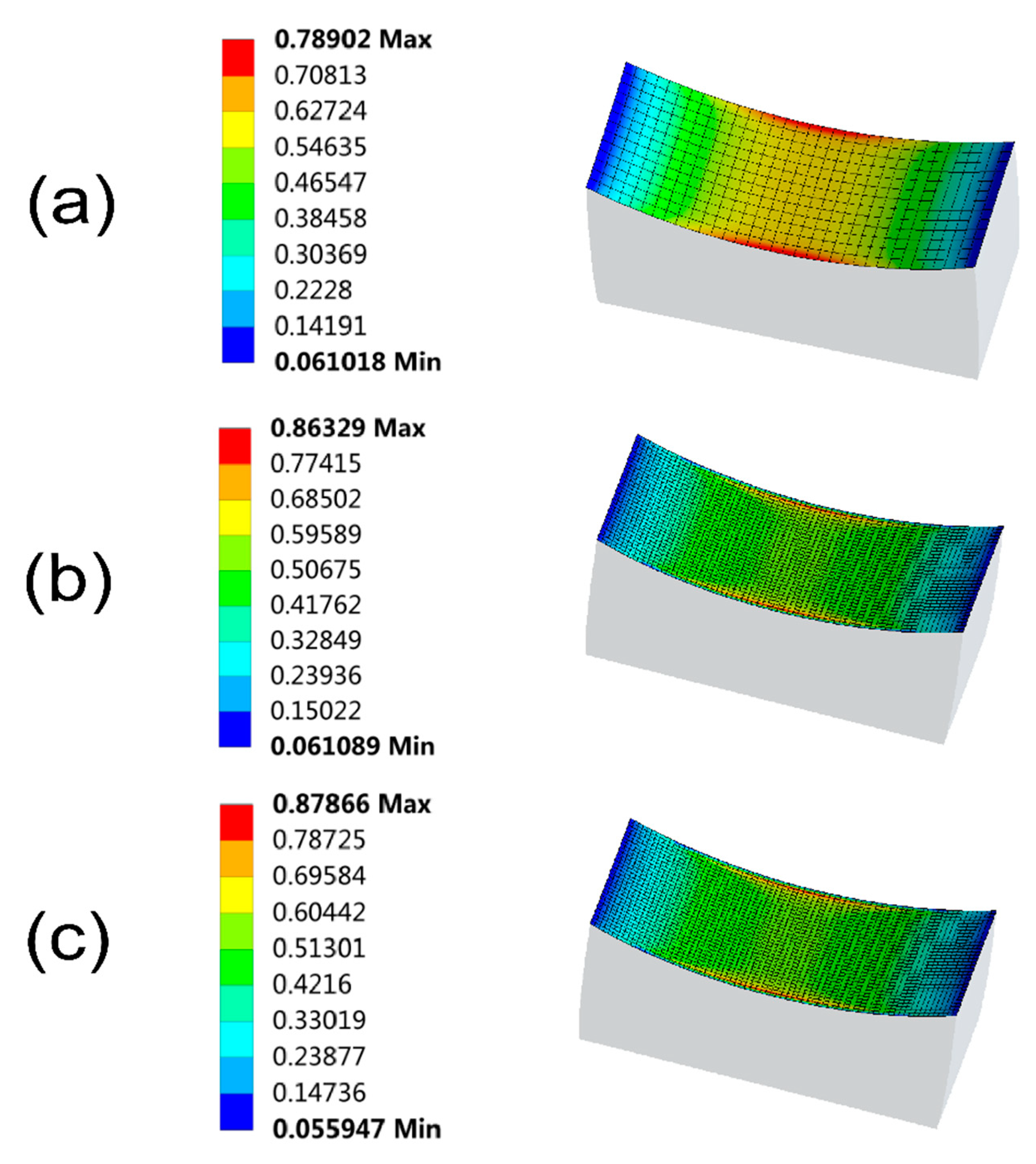
The quality of mesh partitioning plays a key role in influencing the results of FEA. In the present ring-block friction model, the contact interface is a critical region for transmitting contact pressure and frictional stress, necessitating an analysis of the mesh partitioning accuracy at the contact interface. Considering the actual dimensions of the copper ring and CNT/NBR block, as well as the hardware capabilities of the computer, an initial choice of a global mesh accuracy of 1 mm and a local mesh accuracy of 0.5 mm was made. An external normal pressure of 0.5 MPa was applied to calculate the pressure distribution at the contact interface. Based on the results obtained with a local mesh accuracy of 0.5 mm, the local mesh accuracy was further refined to 0.3 mm and then to 0.2 mm. The pressure distribution at the contact interface of the CNT/NBR composite with a 5% mass fraction of CNTs under the three kinds mesh accuracies is shown in Figure 6.
Comparing the pressure distribution resulting from the three different mesh accuracies in Figure 6, it can be observed that the local maximum pressure in all three cases occurs at the edge of the CNT/NBR block, which is attributed to the greater thickness of the copper ring compared to the CNT/NBR block. Furthermore, when refining the local mesh accuracy from 0.3 mm to 0.2 mm, the difference in the local maximum pressure is only 1.7%. Therefore, a local mesh accuracy of 0.2 mm is determined for the subsequent finite element analysis.

2.3.2. Calculation of Friction Coefficient

When the contact interface pressure distribution is known, the friction coefficient μ i of each cell at the contact interface is a function of the cell pressure p i and the sliding velocity v [41]:
μ i = f ( p i , v )
By overlaying the friction coefficients at different pressures from the MD simulations in section 2.1.2 to each contact unit, the friction coefficient of the entire contact interface can be expressed as:
μ = 1 p A c ∑ i = 1 N ( μ i p i A i )
Here, p is the overall external pressure, A c is the area of the overall contact area, and A i is the area of each contact unit.
FE simulations were conducted to investigate the frictional behavior of four CNT/NBR composite materials with CNT mass fractions of 0% (pure NBR), 1.25%, 2.5%, and 5%, under normal pressure of 0.5 MPa and a relative sliding velocity of 30 rpm (corresponding to 0.055 m/s). The simulations were performed for a duration of 5 seconds, and the average friction coefficient during the stable state of 2.5 seconds was taken as the representative value. Each material was subjected to three repeated simulations for statistical analysis.

2.4. Experimental Setup

Frictional properties of four CNT/NBR composite materials with CNT mass fractions of 0% (pure NBR), 1.25%, 2.5%, and 5% were tested using the UMT-type friction tester manufactured by Bruker Corporation, as shown in Figure 7. The CNT/NBR composite materials required for the experiments were prepared by physically blending different mass fractions of carbon nanotubes with nitrile butadiene rubber. Considering the potential application of CNT/NBR composite materials in oil-free lubricated rotating mechanical components, the ring-block friction module was selected for the tests. The dimensions of the copper ring and CNT/NBR block in the experiments were identical to those in Section 2.3 simulations. A normal pressure of 0.5 MPa and a sliding velocity of 30 rpm were applied during the tests. Each friction test lasted for 1 minute, and the average friction coefficient during the stable stage of 30 seconds was taken as the representative value. Three repeated experiments were conducted for each material to ensure reliability and reproducibility.

3. Results and Discussion

3.1. Subsection

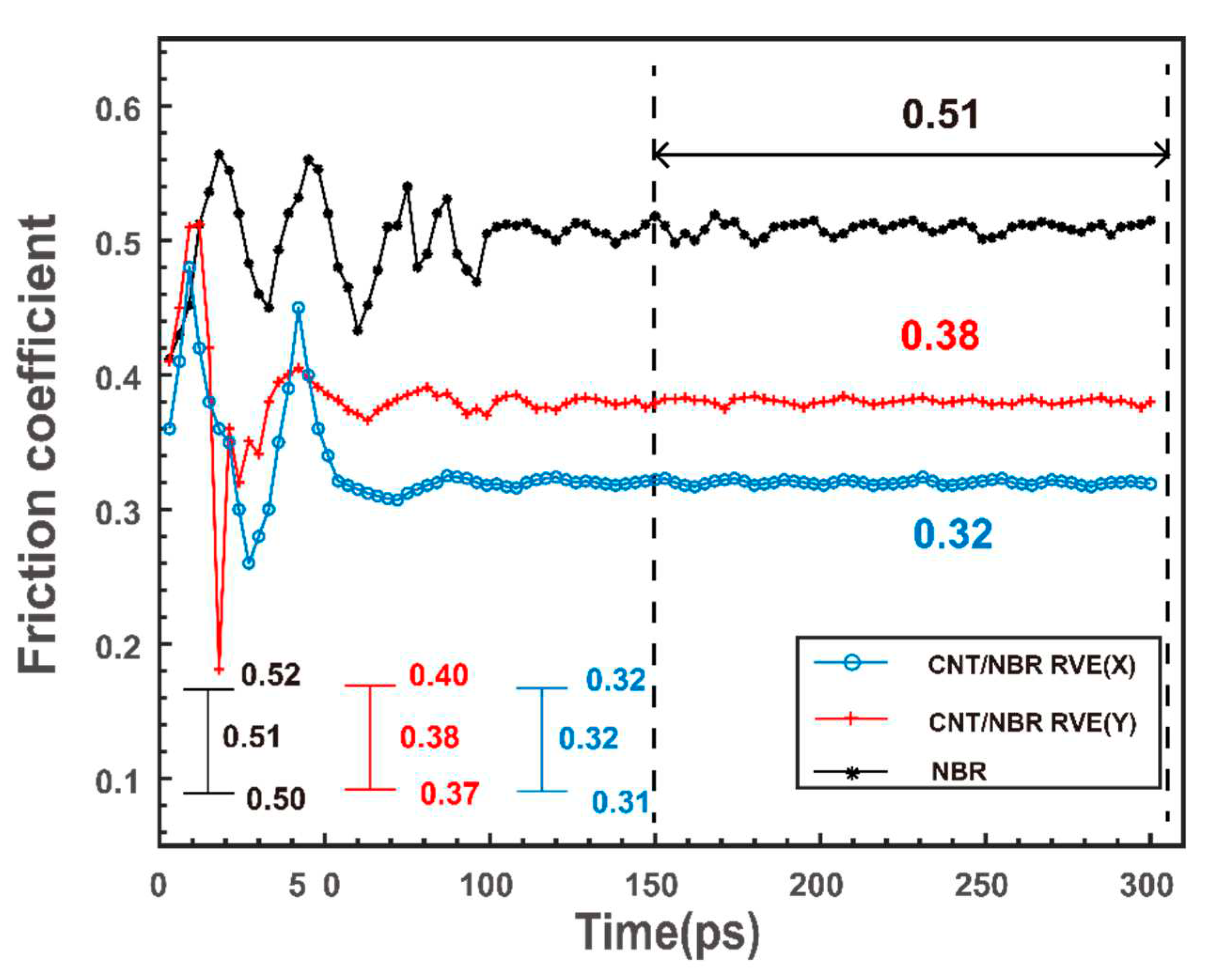
MD simulations were conducted at the nanoscale to simulate the sliding process of Cu-NBR and Cu-CNT/NBR RVE under dry friction conditions, and the friction coefficients were calculated. The trend of friction coefficient variation and the error bars of repeated simulations at a normal pressure of 0.5 MPa and a relative sliding velocity of 0.055 m/s are shown in Figure 8.
From Figure 8, it can be observed that after the introduction of carbon CNTs, the friction coefficients of CNT/NBR along the CNT axis (X-direction) and radial direction (Y-direction) significantly decreased by 34.2% and 37.3% compared to pure NBR. This molecular-level observation indicates that CNTs, as effective lubricating fillers, can improve the friction performance of NBR. The improvement in friction performance can be attributed to the intermolecular interactions. Upon the addition of CNTs into NBR, a large number of NBR polymer chains are adsorbed around the CNTs due to strong van der Waals forces. Moreover, NBR chains originally adsorbed on the Cu surface also migrate towards the vicinity of the CNTs, resulting in a reduction of the overall adhesion force at the Cu-NBR interface and subsequently decreasing the tangential friction force. It is worth noting that the orientation of CNTs also influences the friction performance of NBR, with lower friction coefficients observed along the X-direction compared to the Y-direction. This is attributed to the unique structure of CNTs with a higher aspect ratio, leading to a significantly higher carbon atom density along the axial direction compared to the radial direction. The denser arrangement of carbon atoms along the axial direction enhances the interaction with NBR polymer chains, resulting in reduced adhesion between Cu atoms and CNT/NBR along the axial direction and, consequently, better friction performance.
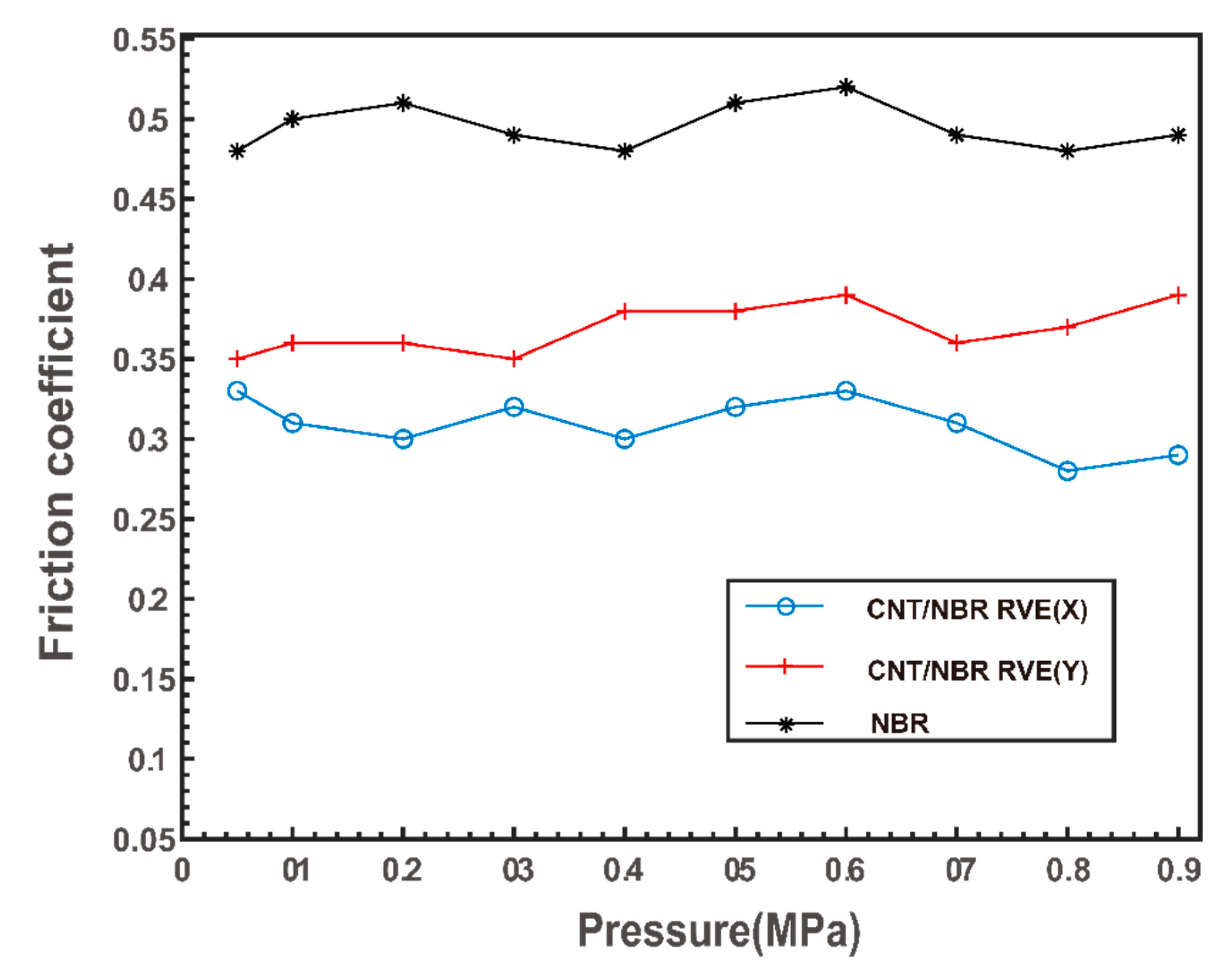
Furthermore, based on the FE analysis, the pressure distribution range at the contact interface of the CNT/NBR block (0.055-0.878 MPa) was obtained. Friction simulations were conducted for Cu-NBR and Cu-CNT/NBR RVE at different pressure levels, and Figure 9 summarizes the corresponding friction coefficients.

3.2. Finite Element Simulation Results

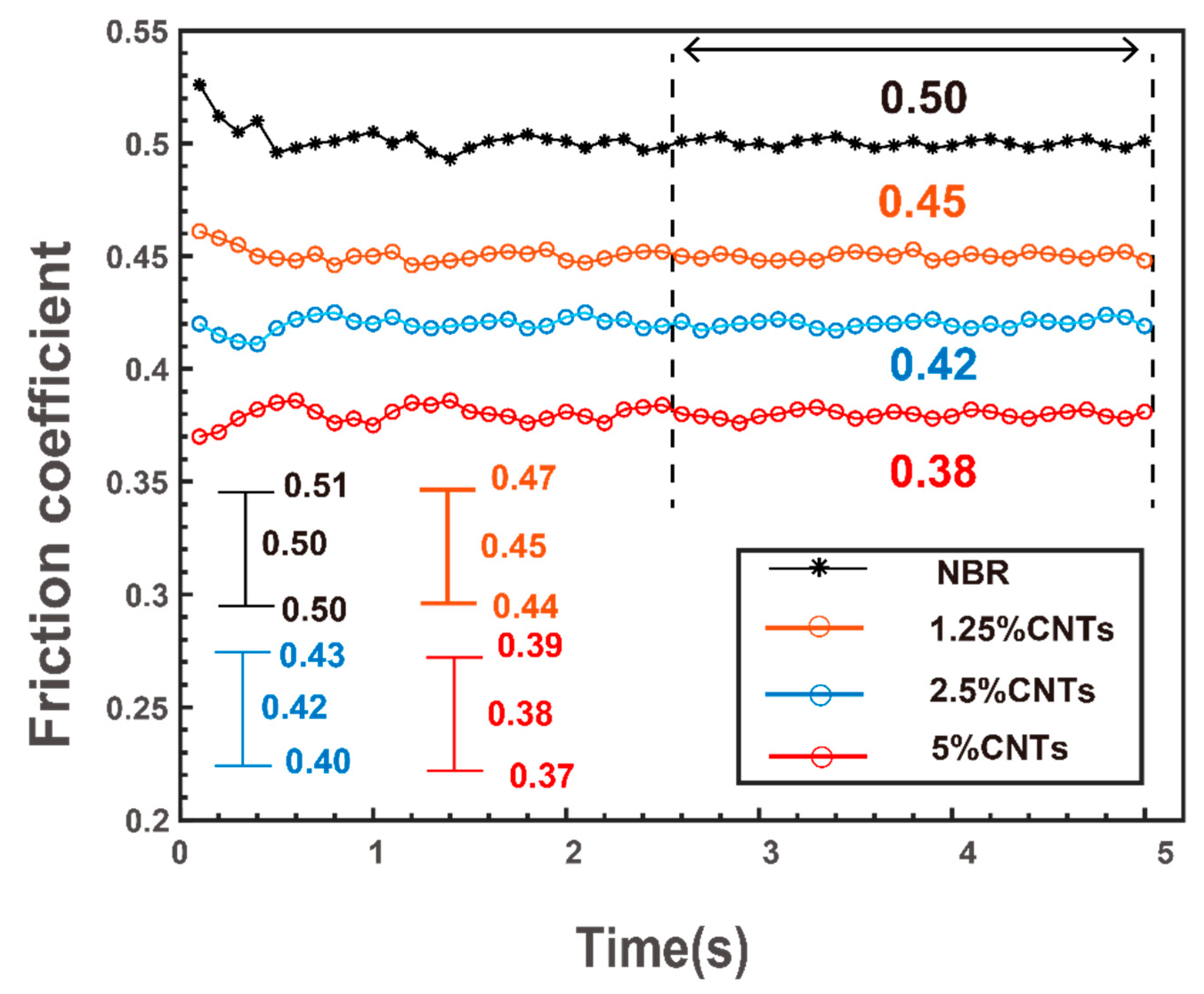
Based on the MD simulations and the homogenization of the bridging model, FE simulations were conducted to simulate the friction process of the macroscopic-scale Cu-CNT/NBR composite material. Under a normal pressure of 0.5 MPa and a relative sliding velocity of 30 rpm, the variations in friction coefficients for the four different CNTs mass fractions in the CNT/NBR composites, as well as the error bars representing the repeatability of the simulations, are shown in Figure 10.
From Figure 10, it is evident that the addition of carbon nanotubes CNTs leads to a reduction in the dry friction coefficient of NBR, highlighting the excellent lubricating properties of CNTs as fillers at the macroscopic scale. The comparative simulations with different CNT mass fractions demonstrate that the CNT content is a key factor influencing the friction performance of the filled composite material. The trend depicted in Figure 10 indicates a continuous decrease in the friction coefficient of the CNT/NBR composite material as the CNT mass fraction increases (0%, 1.25%, 2.5%, 5%), ranging from 0.50 to 0.38. This trend can be utilized to guide the design of NBR friction modification, enabling the preparation of tailored CNT/NBR composite materials for specific friction applications.

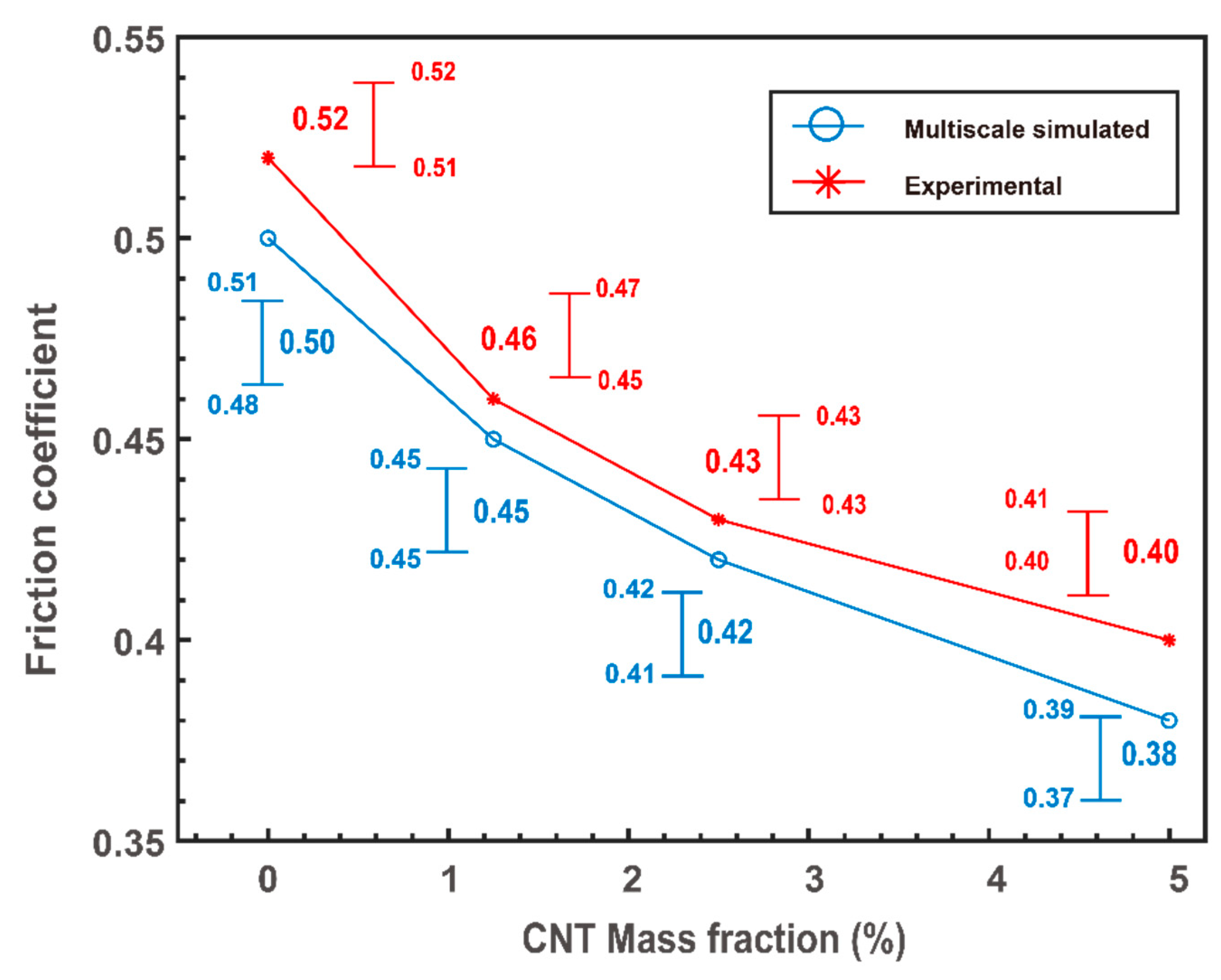
3.3. Comparison of Experimental Results and Multi-scale Simulation

To evaluate the effectiveness of the proposed multiscale friction model, friction testing experiments were conducted on copper ring-CNT/NBR samples of the same size. The experimental results of the four different CNT mass fractions in the CNT/NBR composite materials, along with the corresponding multiscale simulation results, are compared in Figure 11 under the conditions of 0.5 MPa normal pressure and 30 rpm relative sliding velocity.
From Figure 11, it can be observed that as the mass fraction of CNTs increases, the experimental friction coefficients decrease, which is consistent with the trend predicted by the multi-scale simulation. Although the consistency in the trend of friction coefficients validates the effectiveness of the proposed multi-scale friction model to some extent, there still exist discrepancies between the multi-scale model and the experimental results. Several factors contribute to these discrepancies, including the dispersion of CNTs in NBR, temperature variations during the dry friction testing process, and surface wear of the materials, among others. In the next step of model optimization, a detailed investigation of these error factors can be conducted.

4. Conclusions

This paper presents a novel multi-scale friction simulation method for predicting the friction characteristics of CNT-reinforced NBR composites. By bridging the nanoscale molecular dynamics friction simulation and the macroscale finite element analysis through a mesoscale mechanics homogenization model, a multi-scale friction model is developed. The multi-scale model reveals the underlying mechanism of how carbon nanotubes enhance the friction properties of NBR composite materials at the molecular chain level and predicts the friction coefficients of actual Cu-CNT/NBR friction pairs at the macroscopic scale. The multi-scale friction simulation results demonstrate that the friction coefficients of CNT/NBR composite materials decrease continuously with increasing mass fraction of carbon nanotubes (0%, 1.25%, 2.5%, 5%), ranging from 0.50 to 0.38. The corresponding friction experiments on Cu ring-CNT/NBR blocks validate the reliability of the predicted trend by the multi-scale simulation. Although the simulation cannot precisely predict the experimental results, the multi-scale friction simulation provides a new approach for studying the friction characteristics of CNT/NBR composite materials and guiding their friction modification.

Author Contributions

Conceptualization, C.L. and X.Y.; methodology, C.L.; software, C.L.; validation, C.L., C.S. and X.Y.; formal analysis, C.S.; investigation, C.S.; resources, C.S.; data curation, C.L.; writing—original draft preparation, C.L.; writing—review and editing, X.Y.; visualization, C.L.; supervision, C.S.; project administration, C.S.; funding acquisition, C.S. All authors have read and agreed to the published version of the manuscript.

Funding

Please add: This research was funded by the Defense Foundation Enhancement Program, grant number [2020-XXJQ-ZD-20X].

Institutional Review Board Statement

All authors have read and consented to the publication of the final draft.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author, upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Akhmedgoraeva, A.R.; Sultanov, A.A.; Galimzyanova, R.Yu.; Khakimullin, Yu.N. Nonhardening Sealants Based on Modified Nitrile Butadiene Rubber. Polym. Sci. Ser. D 2022, 15, 379–383. [Google Scholar] [CrossRef]
  2. Porter, C.; Zaman, B.; Pazur, R. A Critical Examination of the Shelf Life of Nitrile Rubber O-Rings Used in Aerospace Sealing Applications. Polymer Degradation and Stability 2022, 206, 110199. [Google Scholar] [CrossRef]
  3. Zhou, G.; Wu, K.; Pu, W.; Li, P.; Han, Y. Tribological Modification of Hydrogenated Nitrile Rubber Nanocomposites for Water-Lubricated Bearing of Ship Stern Shaft. Wear 2022, 504–505, 204432. [Google Scholar] [CrossRef]
  4. Jin, D.; Xiao, K.; Han, Y.; Xiang, G.; Zhou, Z.; Wang, J. A Preparation Method of Porous Surface Nitrile Butadiene Rubber with Low Friction Coefficient under Water Lubrication Condition by Salt Leaching. J Appl Polym Sci 2021, 138, 50555. [Google Scholar] [CrossRef]
  5. Guezzout, Z.; Boublia, A.; Haddaoui, N. Enhancing Thermal and Mechanical Properties of Polypropylene-Nitrile Butadiene Rubber Nanocomposites through Graphene Oxide Functionalization. J Polym Res 2023, 30, 207. [Google Scholar] [CrossRef]
  6. Jia, Y.; Zhao, Y.; Yan, C.; Wang, G.; Xu, Z.; He, Q. Effects of Alumina Doping on Mechanical and Tribological Properties of Nitrile Butadiene Rubber. Fibers Polym 2021, 22, 3106–3119. [Google Scholar] [CrossRef]
  7. Hussain, M.; Yasin, S.; Ali, A.; Li, Z.; Fan, X.; Song, Y.; Zheng, Q.; Wang, W. Synergistic Impact of Ionic Liquid on Interfacial Interaction and Viscoelastic Behaviors of Silica Filled Nitrile Butadiene Rubber Nanocomposites. Composites Part A: Applied Science and Manufacturing 2022, 163, 107202. [Google Scholar] [CrossRef]
  8. Zainal Abidin, Z.; Mamauod, S.N.L.; Romli, A.Z.; Sarkawi, S.S.; Zainal, N.H. Synergistic Effect of Partial Replacement of Carbon Black by Palm Kernel Shell Biochar in Carboxylated Nitrile Butadiene Rubber Composites. Polymers 2023, 15, 943. [Google Scholar] [CrossRef]
  9. Li, X.; Li, Y.; Qian, C.; Zhao, J.; Wang, S. Molecular Dynamics Study of the Mechanical and Tribological Properties of Graphene Oxide-Reinforced Polyamide 66/Nitrile Butadiene Rubber Composites. Appl. Phys. A 2023, 129, 276. [Google Scholar] [CrossRef]
  10. Liu, X.; Huang, J.; Yang, C.; Wang, P.; Xing, S.; Zhong, D.; Zhou, X. Effects of Graphene and CNTs Reinforcement on the Friction Mechanism of Nitrile Butadiene Rubber under Water Lubrication Conditions. Wear 2022, 500–501, 204334. [Google Scholar] [CrossRef]
  11. Yang, X.; Zhang, Z.; Zhang, T.; Nie, M.; Li, Y. Improved Tribological and Noise Suppression Performance of Graphene/Nitrile Butadiene Rubber Composites via the Exfoliation Effect of Ionic Liquid on Graphene. J Appl Polym Sci 2020, 137, 49513. [Google Scholar] [CrossRef]
  12. Wang, Q. The Heat-Resistant and Tribological Mechanism of Nano-Fe 3 O 4 –Reinforced Nitrile Butadiene Rubber. Journal of Elastomers & Plastics 2013, 45, 289–298. [Google Scholar] [CrossRef]
  13. He, Q.; Zhou, Y.; Qu, W.; Zhang, Y.; Song, L.; Li, Z. Wear Property Improvement by Short Carbon Fiber as Enhancer for Rubber Compound. Polymer Testing 2019, 77, 105879. [Google Scholar] [CrossRef]
  14. Padenko, E.; Berki, P.; Wetzel, B.; Karger-Kocsis, J. Mechanical and Abrasion Wear Properties of Hydrogenated Nitrile Butadiene Rubber of Identical Hardness Filled with Carbon Black and Silica. Journal of Reinforced Plastics and Composites 2016, 35, 81–91. [Google Scholar] [CrossRef]
  15. Jia, Y.; Zhao, Y.; Yan, C.; Wang, G.; Xu, Z.; He, Q. Effects of Alumina Doping on Mechanical and Tribological Properties of Nitrile Butadiene Rubber. Fibers Polym 2021, 22, 3106–3119. [Google Scholar] [CrossRef]
  16. He, Q.; Wang, G.; Zheng, B.; Zhou, W.; Zhang, Y. Impact of WS2 Nanoparticles on Nitrile Butadiene Rubber Properties. Fibers Polym 2020, 21, 1163–1172. [Google Scholar] [CrossRef]
  17. Yang, W.; Wang, C.; Liu, Z.; Tan, J. Curing, Mechanical, and Tribological Properties of Hydrogenated Nitrile Butadiene Rubber Reinforced with Al 2 O 3 Nanoparticles. Polymer Composites 2022, 43, 4588–4599. [Google Scholar] [CrossRef]
  18. Liu, X.; Zhou, X.; Yang, C.; Huang, J.; Kuang, F.; Wang, H. Study on the Effect of Particle Size and Dispersion of SiO2 on Tribological Properties of Nitrile Rubber. Wear 2020, 460–461, 203428. [Google Scholar] [CrossRef]
  19. Liang, Y.R.; Yang, H.X.; Tan, Y.J.; Zhang, T.; Wang, L.Y.; Hu, G. Mechanical and Tribological Properties of Nitrile Rubber Filled with Modified Molybdenum Disulphide. Plastics, Rubber and Composites 2016, 45, 247–252. [Google Scholar] [CrossRef]
  20. Li, Y.; Wang, S.; Arash, B.; Wang, Q. A Study on Tribology of Nitrile-Butadiene Rubber Composites by Incorporation of Carbon Nanotubes: Molecular Dynamics Simulations. Carbon 2016, 100, 145–150. [Google Scholar] [CrossRef]
  21. Wang, M.; Li, Y.; Qian, C.; Zhao, J.; Wang, S. Molecular Dynamics Simulations of Defective Carbon Nanotubes on the Aging and Friction Properties of Nitrile Butadiene Rubber Composites. Polymer Composites 2023, 44, 1228–1239. [Google Scholar] [CrossRef]
  22. Qian, C.; Li, Y.; Zhao, J.; Wang, S.; He, E. Thermal-oxidative Aging and Tribological Properties of Carbon Nanotube/Nitrile Butadiene Rubber Composites with Varying Acrylonitrile Content: Molecular Dynamics Simulations. Polymer Engineering & Sci 2023, 63, 1516–1527. [Google Scholar] [CrossRef]
  23. Qian, C.; Li, Y.; Zhao, J.; Wang, S. Effect of Single-Vacancy- and Vacancy-Adsorbed-Atom-Defective CNTs on the Mechanical and Tribological Properties of NBR Composites: Molecular Dynamics Simulations. J Polym Res 2023, 30, 99. [Google Scholar] [CrossRef]
  24. Cui, J.; Zhao, J.; Wang, S.; Wang, Y.; Li, Y. Effects of Carbon Nanotubes Functionalization on Mechanical and Tribological Properties of Nitrile Rubber Nanocomposites: Molecular Dynamics Simulations. Computational Materials Science 2021, 196, 110556. [Google Scholar] [CrossRef]
  25. Liu, X.; Zhou, X.; Kuang, F.; Zuo, H.; Huang, J. Mechanical and Tribological Properties of Nitrile Rubber Reinforced by Nano-SiO2: Molecular Dynamics Simulation. Tribol Lett 2021, 69, 54. [Google Scholar] [CrossRef]
  26. Liu, X.; Huang, J.; Yang, C.; Xing, S.; Wang, P.; Zhou, X. Molecular Dynamics Simulations Probing the Effects of Interfacial Interactions on the Tribological Properties of Nitrile Butadiene Rubber/Nano-SiO2 under Water Lubrication. Materials Today Communications 2022, 32, 104165. [Google Scholar] [CrossRef]
  27. Cui, J.; Zhao, J.; Wang, S.; Li, Y. A Comparative Study on Enhancement of Mechanical and Tribological Properties of Nitrile Rubber Composites Reinforced by Different Functionalized Graphene Sheets: Molecular Dynamics Simulations. Polymer Composites 2021, 42, 205–219. [Google Scholar] [CrossRef]
  28. He, E.; Wang, S.; Tang, L.; Chen, J. A Study on the Enhancement of the Tribological Properties of Nitrile-Butadiene Rubber Reinforced by Nano-ZnO Particles from an Atomic View. Mater. Res. Express 2021, 8, 095009. [Google Scholar] [CrossRef]
  29. Iijima, S. Helical Microtubules of Graphitic Carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
  30. Ruoff, R.S.; Lorents, D.C. Mechanical and Thermal Properties of Carbon Nanotubes. Carbon 1995, 33, 925–930. [Google Scholar] [CrossRef]
  31. Makowiec, M.E.; Blanchet, T.A. Improved Wear Resistance of Nanotube- and Other Carbon-Filled PTFE Composites. Wear 2017, 374–375, 77–85. [Google Scholar] [CrossRef]
  32. Aili; Zou; Dongsheng; Li Effect of Carbon Nanotube on the Oscillating Wear Behaviour of Metal-PTFE Multilayer Composites. Journal of Wuhan University of Technology Mater.sci.ed 2018. [CrossRef]
  33. Huang, Z. Micromechanical Prediction of Ultimate Strength of Transversely Isotropic Fibrous Composites. International Journal of Solids and Structures 2001, 38, 4147–4172. [Google Scholar] [CrossRef]
  34. Huang, Z.-M. Simulation of the Mechanical Properties of Fibrous Composites by the Bridging Micromechanics Model. Composites Part A: Applied Science and Manufacturing 2001, 32, 143–172. [Google Scholar] [CrossRef]
  35. Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. Journal of Computational Physics 1995, 117, 1–19. [Google Scholar] [CrossRef]
  36. Sun, H. COMPASS: An Ab Initio Force-Field Optimized for Condensed-Phase ApplicationsOverview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
  37. Iljasiepmann, J.; Mcdonald, Ianr. Monte Carlo Simulations of Mixed Monolayers. Molecular Physics 1992, 75, 255–259. [Google Scholar] [CrossRef]
  38. Xu, M.; Wang, Q.; Wang, T.; Tao, L.; Li, S. Molecular Dynamic Simulation Study of Tribological Mechanism of PI Composites Reinforced by CNTs with Different Orientations. Polymer Composites 2022, 43. [Google Scholar] [CrossRef]
  39. Marzari, N.; Ferrari, M. Textural and Micromorphological Effects on the Overall Elastic Response of Macroscopically Anisotropic Composites. Journal of Applied Mechanics 1992, 59, 269–275. [Google Scholar] [CrossRef]
  40. Nackenhorst, U. The ALE-Formulation of Bodies in Rolling Contact. Computer Methods in Applied Mechanics and Engineering 2004, 193, 4299–4322. [Google Scholar] [CrossRef]
  41. Riva, G.; Varriale, F.; Wahlström, J. A Finite Element Analysis (FEA) Approach to Simulate the Coefficient of Friction of a Brake System Starting from Material Friction Characterization. Friction 2021, 9, 191–200. [Google Scholar] [CrossRef]
Preprints 78886 g001
Figure 1. Construction of MD model: (a) NBR matrix; (b) CNT/NBR RVE.
Figure 1. Construction of MD model: (a) NBR matrix; (b) CNT/NBR RVE.
Preprints 78886 g001
Preprints 78886 g002
Figure 2. MD friction simulation of CNT/NBR RVE: (a) relative sliding direction in y-direction; (b) relative sliding direction in x-direction.V.
Figure 2. MD friction simulation of CNT/NBR RVE: (a) relative sliding direction in y-direction; (b) relative sliding direction in x-direction.V.
Preprints 78886 g002
Preprints 78886 g003
Figure 3. Bridging model homogenization process.
Figure 3. Bridging model homogenization process.
Preprints 78886 g003
Preprints 78886 g004
Figure 4. Schematic of the transformation relationship between local and global coordinates.
Figure 4. Schematic of the transformation relationship between local and global coordinates.
Preprints 78886 g004
Preprints 78886 g005
Figure 5. Structure of the FE model.
Figure 5. Structure of the FE model.
Preprints 78886 g005
Preprints 78886 g006
Figure 6. Pressure distribution at the contact interface with three kinds of local grid accuracy：(a) 0.5 mm; (b) 0.3 mm; (c) 0.2 mm.
Figure 6. Pressure distribution at the contact interface with three kinds of local grid accuracy：(a) 0.5 mm; (b) 0.3 mm; (c) 0.2 mm.
Preprints 78886 g006
Preprints 78886 g007
Figure 7. Structure of ring block friction tester.
Figure 7. Structure of ring block friction tester.
Preprints 78886 g007
Preprints 78886 g008
Figure 8. Friction coefficients of Cu-NBR and Cu-CNT/NBR RVE at 0.5 MPa normal pressure and 0.055 m/s relative sliding velocity.
Figure 8. Friction coefficients of Cu-NBR and Cu-CNT/NBR RVE at 0.5 MPa normal pressure and 0.055 m/s relative sliding velocity.
Preprints 78886 g008
Preprints 78886 g009
Figure 9. Friction coefficients of Cu-NBR and Cu-CNT/NBR RVE friction pairs at a compressive load of 0.05-0.9 MPa and a sliding speed of 0.055 m/s.
Figure 9. Friction coefficients of Cu-NBR and Cu-CNT/NBR RVE friction pairs at a compressive load of 0.05-0.9 MPa and a sliding speed of 0.055 m/s.
Preprints 78886 g009
Preprints 78886 g010
Figure 10. Friction coefficients of four CNT/NBR materials with CNTs mass fractions of 0, 1.25%, 2.5% and 5% at a constant speed of 30 rpm (0.055m/s) under 0.5Mpa pressure load.
Figure 10. Friction coefficients of four CNT/NBR materials with CNTs mass fractions of 0, 1.25%, 2.5% and 5% at a constant speed of 30 rpm (0.055m/s) under 0.5Mpa pressure load.
Preprints 78886 g010
Preprints 78886 g011
Figure 11. Comparison of experimental and multi-scale friction model.
Figure 11. Comparison of experimental and multi-scale friction model.
Preprints 78886 g011
Table 1. Structural parameters of copper ring and CNT/NBR block.
Table 1. Structural parameters of copper ring and CNT/NBR block.
Structure member Parameter description Value[mm]
Copper ring Outer diameter 35
Inner diameter 28
Thickness 10
CNT/NBR block Length 16.5
Height 10
Thickness 6.5
Radius of the contact surface 17.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated