Prerpints.org logo
Preprint
Article

Dynamical Behaviours of Matter Wave Positons in Bose-Einstein Condensates

Altmetrics

Downloads

116

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 July 2023

Posted:

06 July 2023

You are already at the latest version

Alerts
Abstract
In this investigation, we explore the existence and intriguing features of matter wave positons in a nonautonomous one-dimensional Bose-Einstein condensate (BEC) system with attractive interatomic interactions. We focus on the Gross-Pitaevskii (GP) equation/nonlinear Schrödinger (NLS)-type equation with time-modulated nonlinearity and trap potential, governing nonlinear wave propagation in the BEC. Our approach involves constructing second- and third-order matter wave positons using a similarity transformation technique. We also identify the constraints on the time-modulated system parameters that give rise to these nonlinear localized profiles. The study considers three distinct forms of modulated nonlinearities: (i) kink-like, (ii) localized or -like, and (iii) periodic. By varying the parameters associated with the nonlinearity strengths, we observe a rich variety of evolution behaviors in the matter wave positon profiles. These behaviors include stretching, curving, oscillating, breathing, collapsing, amplification, and suppression. Our comprehensive studies shed light on the intricate dynamics of matter wave positons in BECs, providing valuable insights into their behavior and characteristics in the presence of time-modulated nonlinearity and trap potential effects.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

Theoretical investigations into the nonlinear collective excitations of matter waves have emerged as a highly intriguing and pertinent field, especially in light of experimental observations of Bose-Einstein condensation (BEC) in vapors of alkali-metal atoms [1,2]. Among the captivating manifestations of localized waves in atomic matter, solitons hold particular interest. The concept of solitons was initially introduced to describe nonlinear solitary waves that exhibit remarkable properties, such as non-dispersive behavior, preserving their localized form and speeds both during propagation and after collisions [3,4,5,6]. These inherent advantages of solitons have sparked significant interest in the study of nonlinear systems across various fields of physics, particularly in high-rate telecommunications involving optical fibers, fluid dynamics, capillary waves, hydrodynamics, plasma physics and so on [4,7,8,9]. In addition to this, BECs exhibit the emergence of Faraday and resonant density waves when subjected to harmonic driving [10]. The characteristics of density waves in dipolar condensates at absolute zero temperature using both mean-field variational and full numerical approaches has been investigated. The breaking of symmetry resulting from the anisotropy of the dipole-dipole interaction was found to be a crucial factor in this phenomenon.
From an experimental perspective, precise control over the existence of matter waves in a BEC system can be achieved by effectively manipulating the nonlinear atom interactions through the Feshbach resonance technique, as well as by varying the external trap potential [11,12,13,14]. This flexibility permits us to consider that the coefficient of nonlinearity and the external potential terms in the Gross-Pitaevskii (GP) equation/generalized nonlinear Schrödinger (NLS) equation can vary as functions of both time and/or space. Consequently, investigating the distinctive features of matter waves (solitons, breathers and rogue waves) becomes highly intriguing, given their spatial and temporal localization, particularly in the context of BEC experiments. Motivated by these achievements, extensive research has been dedicated to investigating localized matter waves within quasi-one-dimensional BECs [14,15,16,17,18,19,20,21]. Furthermore, studies focusing on the varible coefficient NLS equation have unveiled the potential to manipulate and enhance these localized density profiles through the utilization of inhomogeneity parameters [22,23,24,25]. The analysis of soliton propagation in optical and the condensed matter systems with PT -symmetry, particularly in inhomogeneous setups, has gained significant attention. Consequently, considerable efforts have been devoted to showcasing the existence of stable bright solitons, dark solitons, and vortices within the NLS equation featuring PT -symmetric potentials [26,27,28]. In the case of weakly interacting toroidal BECs, the occurrence of rotational fluxons (commonly known as Josephson vortices) is linked to the spontaneous disruption of the rotational symmetry within the tunneling superflows [29]. To explore the impact of controllable symmetry breaking on the resulting state of merged counter-propagating superflows, a weakly dissipative mean-field model was employed. In line with this research trajectory, our aim is to construct an intriguing type of localized solution known as positons within the GP equation. We further endeavor to explore the effects of time-dependent modulation of nonlinearity parameters on the characteristics of positon profiles.
Positons, unlike exponentially decaying soliton solutions, are weakly localized nonlinear waves that hold significant importance in the field of nonlinear physics [30,31,32,33]. These solutions are obtained by constraining degenerate eigenvalues within the widely recognized N-soliton algorithm. For positon solutions, the corresponding eigenvalue in the spectral problem is positive and lies within the continuous spectrum. It has been observed that when two positons collide, they retain their individual identities, whereas the soliton remains unchanged following a collision with a positon. However, the positon experiences an influence from the carrier wave and envelope, resulting in a finite phase shift [34,35]. Notably, Matveev’s positon solution to the Korteweg-de Vries (KdV) equation exhibited a spectral singularity [32]. Building on this pioneering work, positon solutions have been derived for other nonlinear evolution equations successfully [36,37,38,39,40]. Recent efforts by Cen et al. introduced the concept of smooth positons or degenerate soliton solutions by allowing the spectral parameter to take complex values [41,42], thereby eliminating the singularity in the KdV equation. Following these advancements, endeavors have been made to construct smooth positon solutions for various equations including the focusing mKdV equation [43], complex mKdV equation [46], derivative NLS equation [44,45], NLS-Maxwell-Bloch equation [47], higher-order Chen-Lee-Liu equation [49] and Gerdjikov-Ivanov equation [48]. More recently, smooth positons and breather positons have been derived for the generalized NLS equation with higher-order nonlinearity, along with higher-order solutions for an extended NLS equation featuring cubic and quartic nonlinearity [50,51]. Inspired by these advancements in the field of positons, our research aims to construct positon solutions within the GP equation, incorporating time-varying nonlinearity and trap potential.
The crucial step in this attempt involves utilizing the similarity transformation on a meticulously chosen ansatz solution. This transformation effectively converts the variable parameter GP equation into the conventional NLS equation with constant coefficients. By implementing this transformation, the modified variables allow us to derive new solutions for the considered equation by expressing the known positon solutions in the altered coordinate system. By leveraging the combination of known positons of typical NLS equation solutions with similarity transformation functions, one can derive novel (non-autonomous positon) solutions for the GP equation. The integrability requirements, which establish the relationship between variable parameters (modulated nonlinearity and trap potential), and the proposed ansatz solution, serve as the underlying considerations for this procedure. However, despite the associated costs, this approach holds significant value as it not only reveals new analytical solutions for the GP equation but also empowers users to control the outcomes by judiciously selecting appropriate nonlinearity strengths and trap potentials.
Motivated by the experimental feasibility of studying BECs, our research focuses on exploring the dynamical characteristics of positons. To achieve this objective, we construct second- and third-order matter wave positon solutions for the one-dimensional GP equation, considering a variable nonlinearity parameter and an external trap potential. The construction of these solutions involves transforming the time-modulated GP equation into a ccNLS equation using a similarity transformation. We establish that the trapping potential and nonlinearity modulated parameter must satisfy a constraint for the considered equation to be integrable and yield the desired solutions. By leveraging the known smooth positon solutions (second- and third-order) of the constant coefficient NLS equation, we present matter wave smooth positon solutions of the GP equation. We investigate the deformation of positon density profiles with respect to three different forms of variable nonlinearity parameters, namely (i) kink-like nonlinearity R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) , (ii) localized or sech-type nonlinearity R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) , and (iii) periodic nonlineaity R ( t ) = R 0 + R 1 sin ( R 2 t + R 3 ) , where R 0 , R 1 , R 2 and R 3 are arbitrary parameters. Our findings reveal that a range of nonlinear physical phenomena, including stretching, curving, annihilation, breathing, oscillating, enhancement, and suppression, are manifested in the underlying matter wave positon density profiles. When considering a kink-like modulated nonlinearity, the position density profiles of second- and third-order smooth matter wave positions experience stretching, while their amplitudes can either be enhanced or suppressed. It is important to note that these profiles vanish during different time intervals, with disappearance occurring for t < 0 when the parameter R 2 assumes positive values, and for t > 0 when R 2 takes negative values. In the case of a localized or sech-type modulated nonlinearity, the positon density profiles become compressed and curved within the background density of the condensate. For periodic modulated nonlinearity, positons exhibit a periodic behavior, and adjusting the strengths of nonlinearity leads to an increase in their periodicity, as observed in our analysis. This observation provides valuable insights for experimentalists analyzing novel density profiles in BECs.
We structure our work as follows. In Section 2, we take into account the GP equation with time-modulated nonlinearity and trap potentials. The second and third-order smooth positon solutions are deduced for this equation using the similarity transformation. The integrable requirement between the modulated nonlinearity and trap potential is obtained while employing the integrable technique to the considered equation. In Section 3, by suitably choosing the different forms of variable nonlinearity parameter, we explore the various dynamical characteristics in the density of matter wave positon profiles. Finally, in Section 4, we conclude our observations.

2. BEC Model and Similarity transformation

The behavior of a BEC confined within an external potential can be effectively characterized using the renowned NLS equation derived from mean field theory, commonly referred to as the GP equation. In the specific scenario of a cigar-shaped trapping potential, where simplicity and physical significance coincide, the radial degree of freedom in the three-dimensional GP equation can be eliminated through integration, leading to the derivation of a dimensionless quasi-one-dimensional equation [1,2,5,14,17]
i ∂ ψ ∂ t + 1 2 ∂ 2 ψ ∂ x 2 + R ( t ) | ψ | 2 ψ + 1 2 λ 2 ( t ) x 2 ψ = 0 ,
where ψ ( x , t ) is the condensate wave function. In Equation (1), t and x are time and spatial coordinates that are expressed in units ω ⊥ − 1 and a ⊥ = ℏ ( m ω ⊥ ) , m is the atomic mass, respectively. The atom-atom interaction term (scattering length between atoms) denoted by the representation, R ( t ) , is tuneable using the Feshbach resonance (FR). In a series of exquisite experiments using sodium and rubidium condensates, Feshbach resonances were investigated. They have also been employed in a variety of significant experimental studies, such as the creation of bright and dark matter-wave solitons, among others. The time-modulated trap potential is described by λ 2 ( t ) = ω 2 ( t ) ω ⊥ , where ω and ω ⊥ are the trap frequency in the axial direction and the radial trap frequency, respectively. In the study of trapped BECs, the trap frequency along the elongated axis, denoted as ω , has been intentionally selected to vary with time, t, in order to investigate the characteristics of BECs within the trap. As a result, both the coefficient of nonlinearity (R) and the potential parameter ( λ ) can exhibit time dependence. By appropriately choosing these two time-dependent parameters, the GP equation (1) can effectively capture the dynamics and manipulation of BECs. These parameters serve as powerful tools for controlling and manipulating localized matter waves in BECs, achieved through the adjustment of external magnetic fields and the optically controlled interactions using techniques such as the FR method [13,17,20].
To study the matter wave positons in (1), we adopt the similarity transformation mentioned below to map the time-modulated GP equation (1) to the ccNLS equation [5,17,26,28]:
ψ ( x , t ) = s ( t ) ϕ ( η , τ ) exp [ i θ ( x , t ) ] .
In Equation (2), the unknown functions, namely s ( t ) , η ( x , t ) , τ ( t ) and θ ( x , t ) are the amplitude, similarity spatial variable, the dimensionless time and the phase factor, respectively which are to be computed. Upon involving the substitution of (2) into (1), we obtain the following set of partial differential equations that are related to the unknown functions, such as
η x x = 0 , η t + η x θ x = 0 , η x 2 − R ( t ) s 2 ( t ) = 0 , s ′ ( t ) + s ( t ) 1 2 θ x x = 0 , τ ′ ( t ) − R ( t ) s 2 ( t ) = 0 , θ ′ ( t ) + 1 2 θ x 2 − λ 2 ( t ) 2 x 2 = 0 .
The explicit expressions of the unknown functions can be acquired by solving the aforementioned set of equations, and they take the form
s ( t ) = s 0 R ( t ) , η ( x , t ) = s 0 R ( t ) x − b s 0 3 ∫ R 2 ( t ) d t , θ ( x , t ) = − R ( t ) t 2 R ( t ) x 2 + b s 0 2 R ( t ) x − 1 2 b 2 s 0 4 ∫ R 2 ( t ) d t , τ ( t ) = 1 2 s 0 2 ∫ R 2 ( t ) d t .
where b and s 0 are arbitrary constants. Additionally, we have found an integrability condition that imposes a connection between the time-modulated nonlinearity and the trap potential parameter, as shown by: [5,17,28]
d d t R t R − R t R 2 + λ 2 ( t ) = 0 .
Using this equation (5), one can find the λ ( t ) by fixing the R ( t ) and vice versa. In this work, we consider physically intriguing function R ( t ) and determine the λ ( t ) by the expression, that is λ ( t ) = R ′ ( t ) 2 + R ′ ( t ) − R ( t ) R ′ ′ ( t ) R ( t ) .
In Equation (2), the function ϕ ( η , τ ) is found to fulfill the ccNLS equation as
i ∂ ϕ ∂ τ + 1 2 ∂ 2 ϕ ∂ η 2 + | ϕ | 2 ϕ = 0 .
The equation under consideration (6) exhibits a wide range of localized solutions, including solitons, breathers, rogue waves, and their corresponding profiles. In this study, we focus on the positon solutions of the NLS equation to investigate matter wave positons in quasi-one-dimensional BECs.
By selecting an appropriate functional form for the time-modulated nonlinearity function R ( t ) while ensuring the satisfaction of condition (5), we can derive matter wave positon solutions for the GP equation (1) in the following form:
ψ ( x , t ) = s 0 R ( t ) ϕ ( η , τ ) exp i − 1 2 b 2 s 0 4 ∫ R ( t ) 2 d t + b s 0 2 x R ( t ) − x 2 R ′ ( t ) 2 R ( t ) ,
where ϕ ( η , τ ) is the solution of the ccNLS equation (6). The solution (7) has the potential to generate a multitude of novel positon structures that could be experimentally realized. To summarize the current progress, one can generate several solutions (positons) for the GP model (1) by first obtaining solutions for the ccNLS equation (6) while satisfying the mentioned relationships. An intriguing advantage and potential perspective of the similarity transformation is worth emphasizing, as it allows the extension of this approach to models featuring variable nonlinearity and external trap potential coefficients dependent on both longitudinal and spatial coordinates. By appropriately tailoring and imposing constraints, the resulting dynamics of physical systems can be attainable. Consequently, in Sec. III, we construct positon solutions for the ccNLS equation (6) to analyze matter wave positons in quasi-one-dimensional BECs.

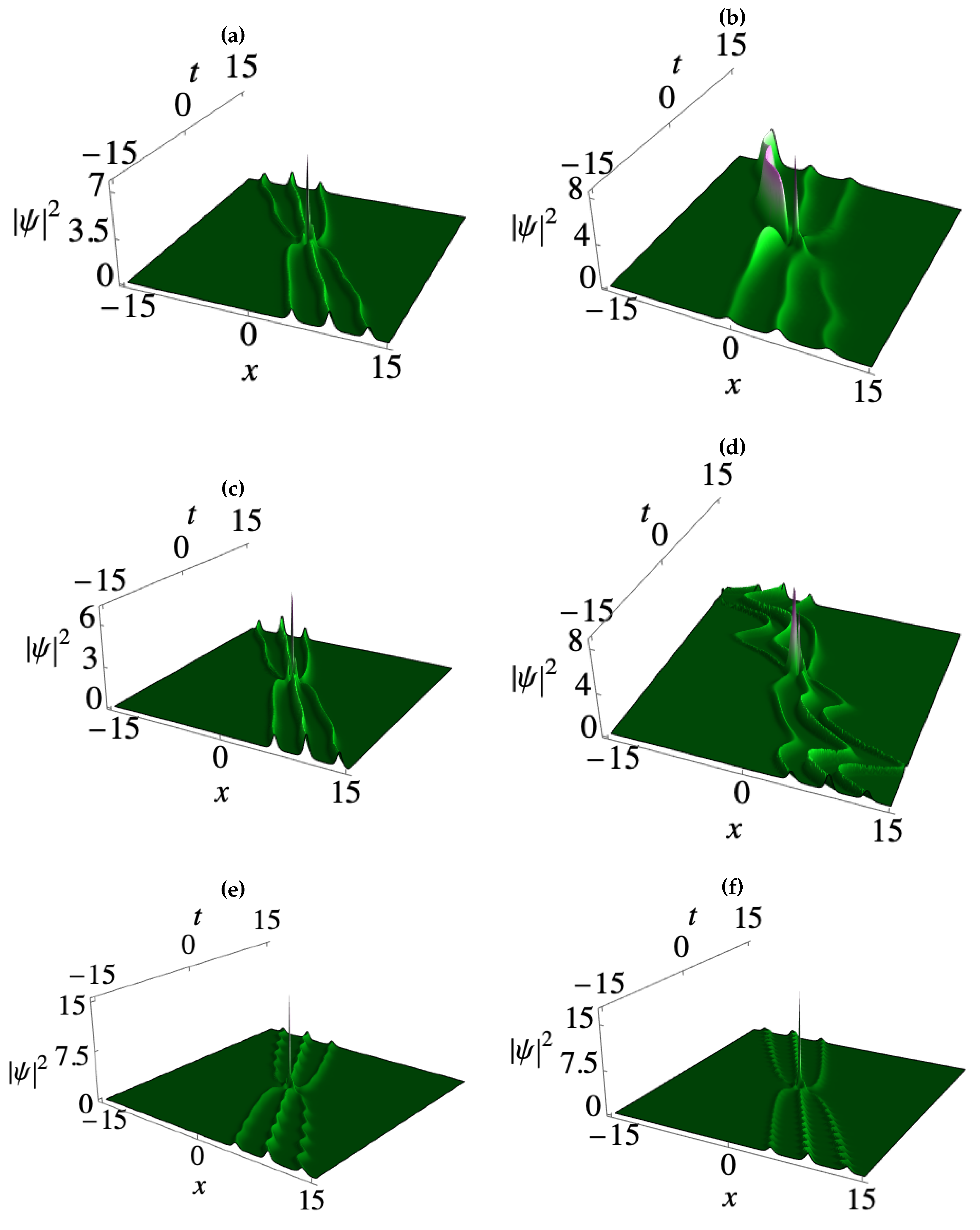
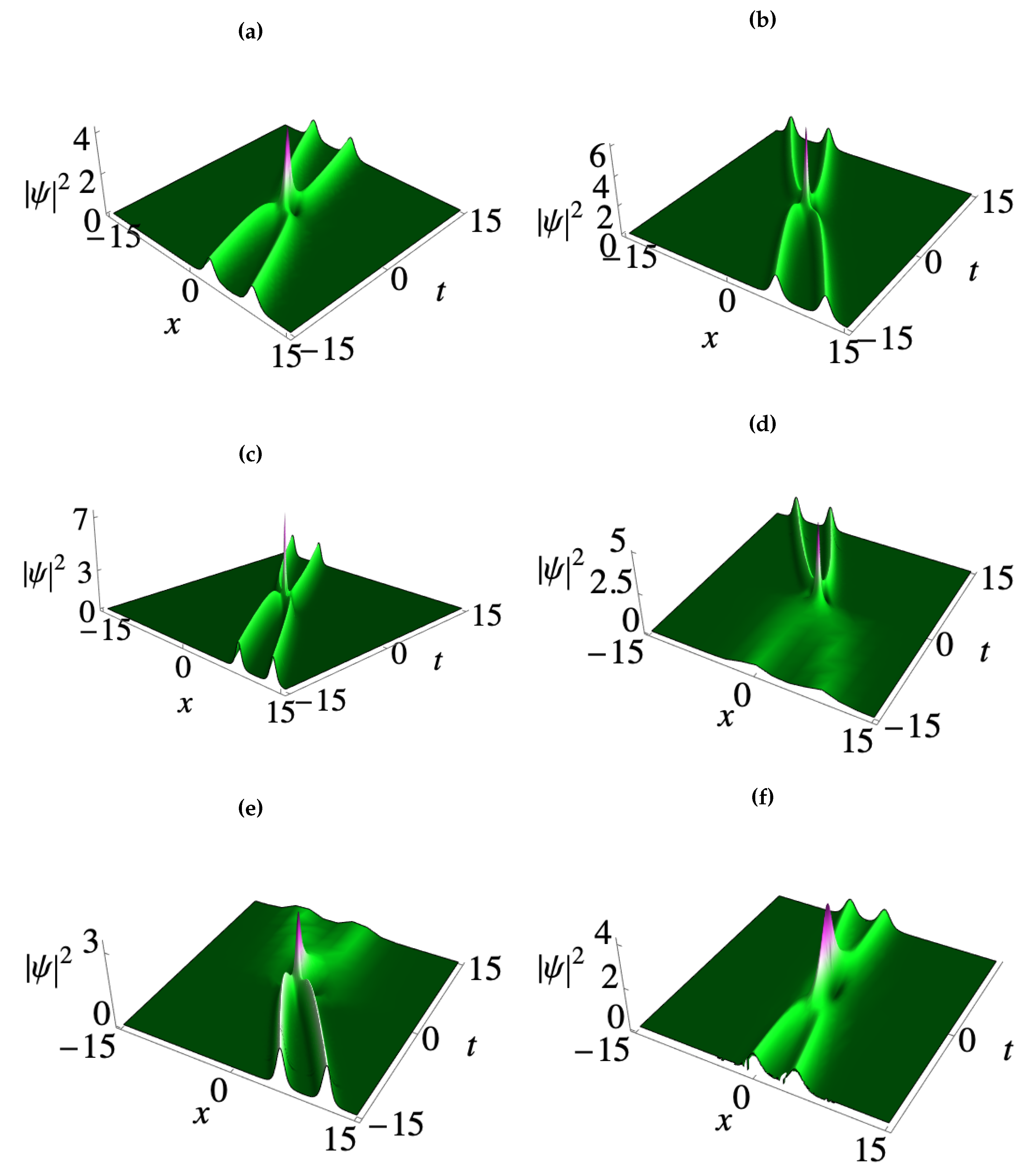
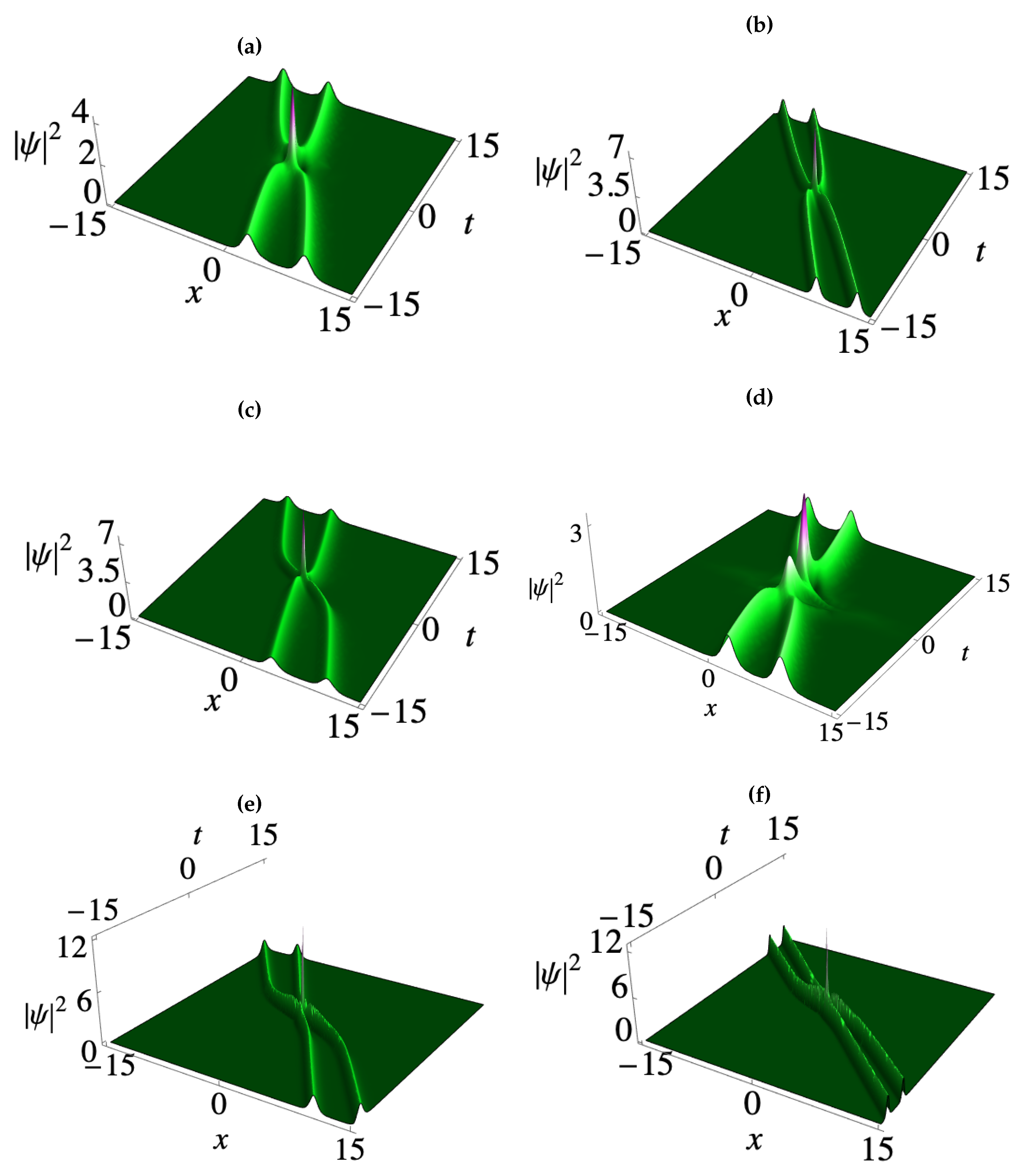
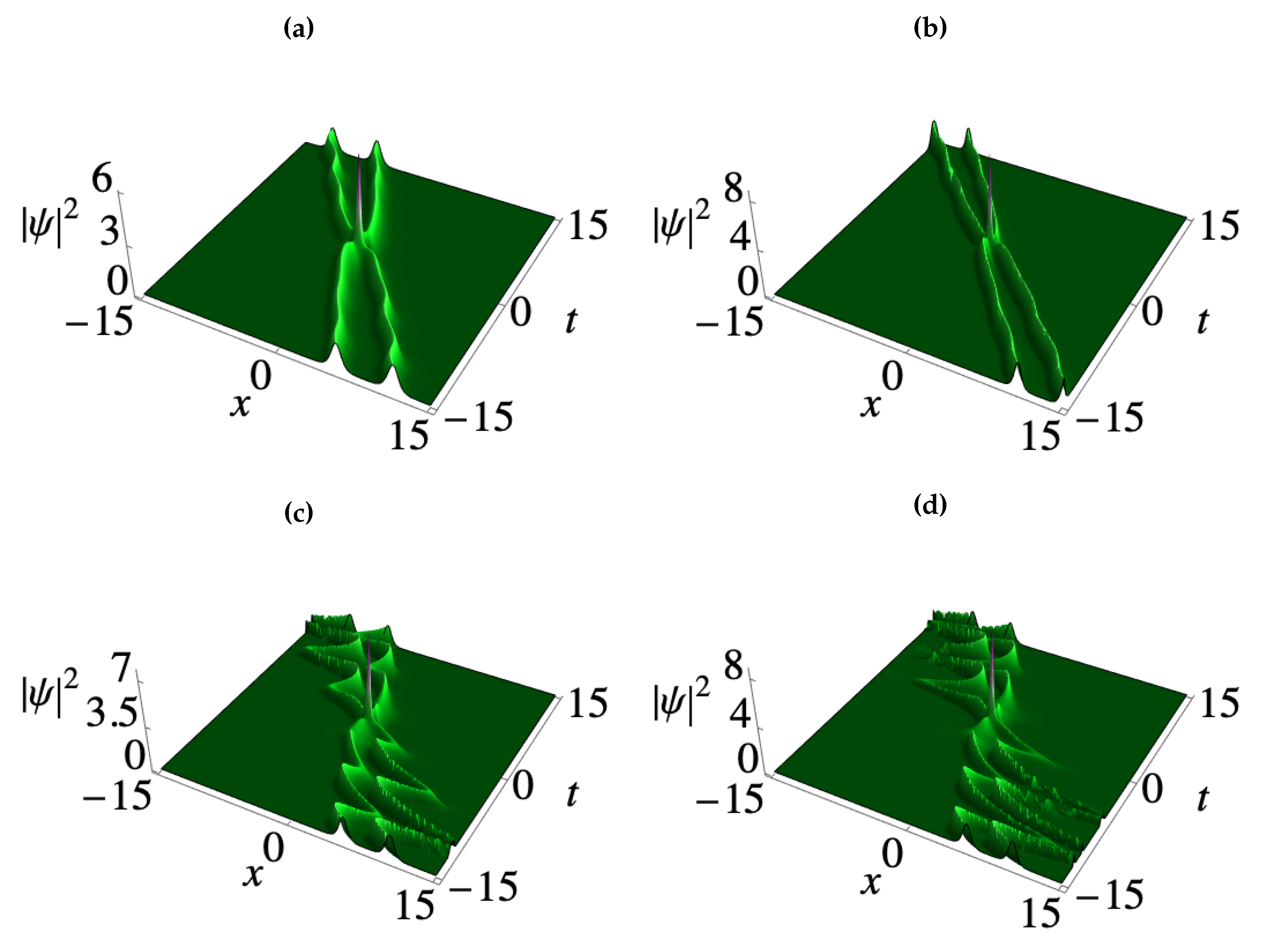
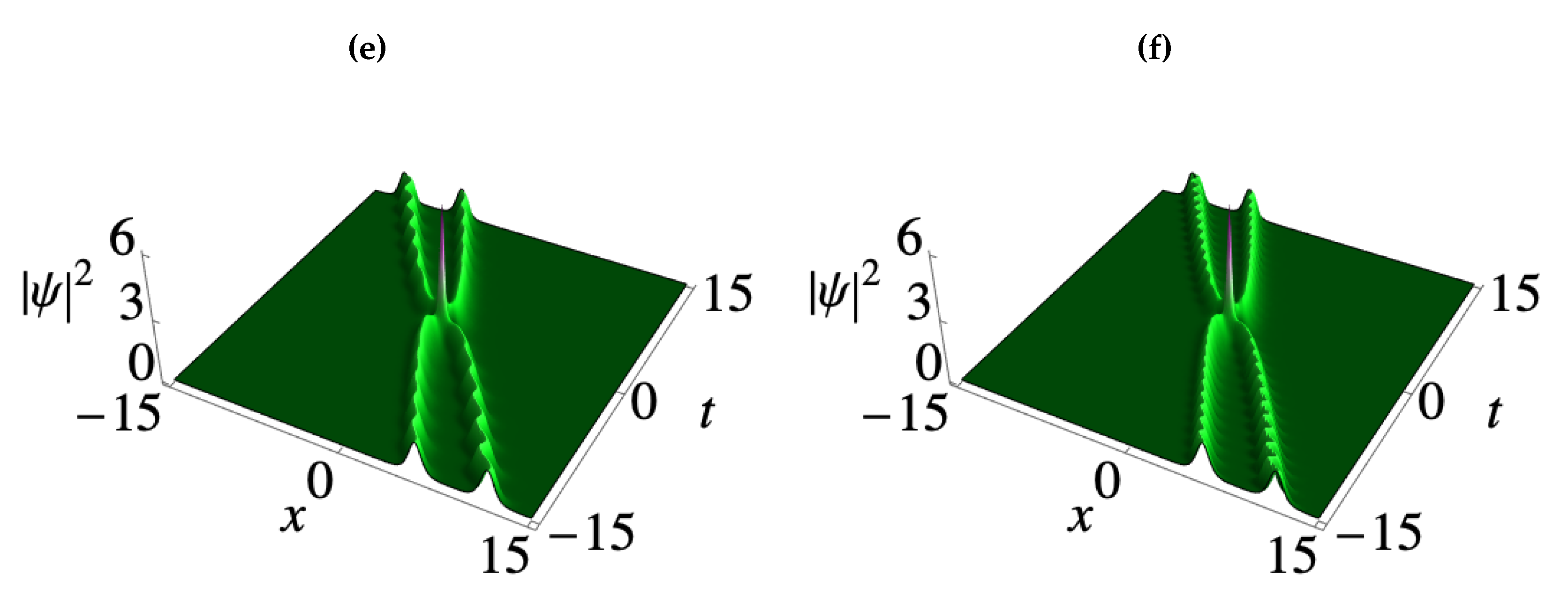
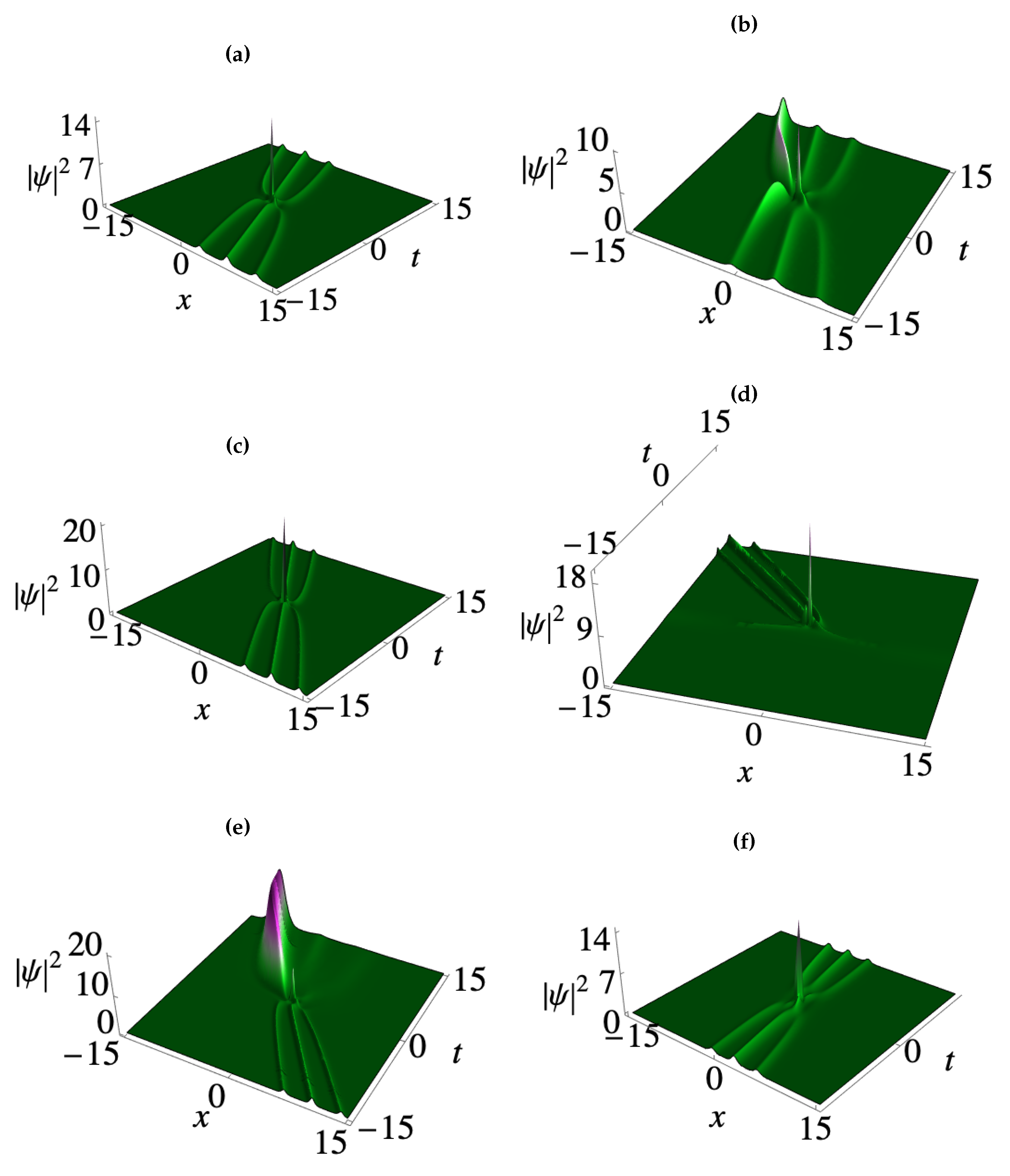
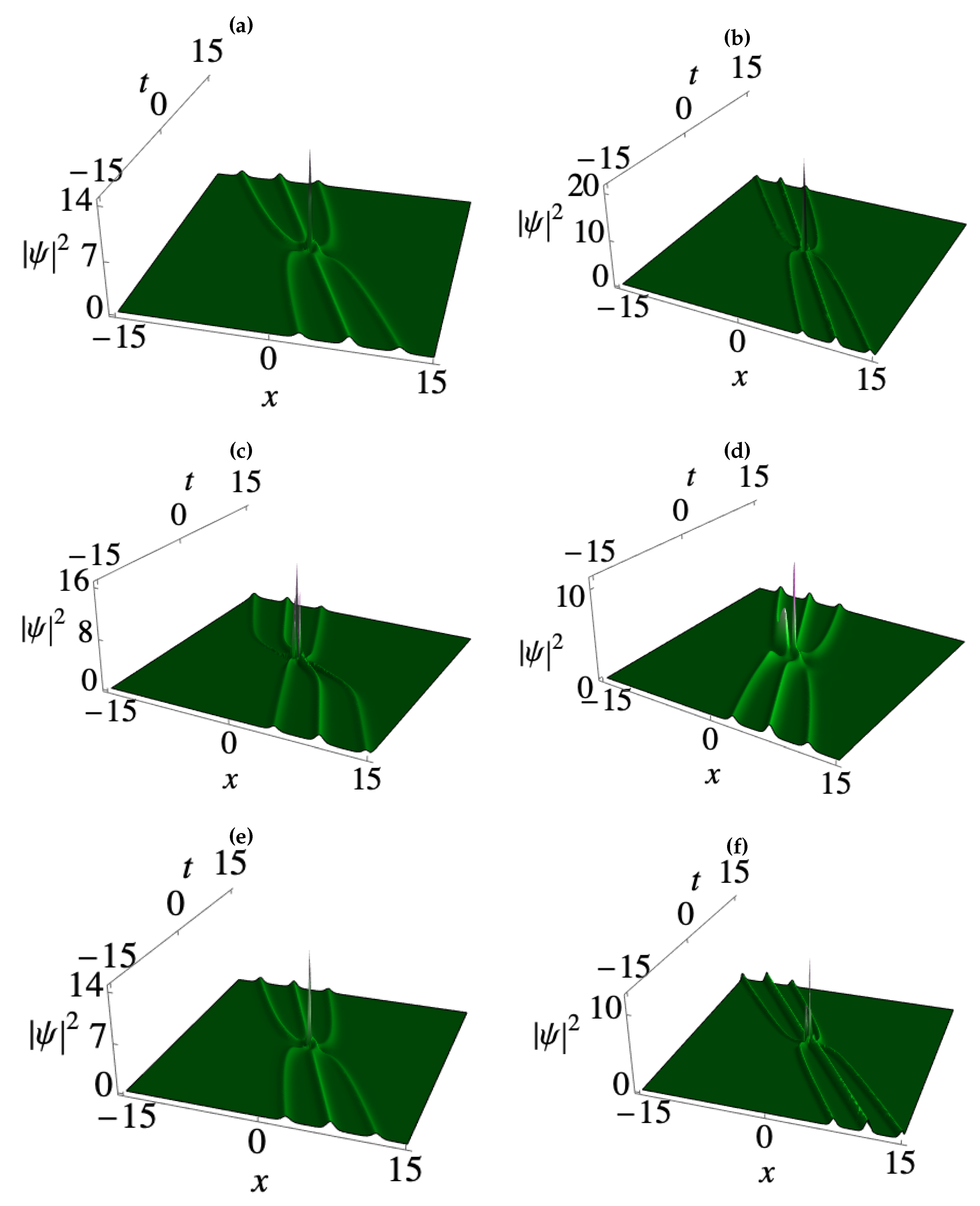
3. Deformation of matter wave positons in BECs

In this section, we intend to investigate the dynamical characteristics of matter wave positons using the solution (7) by considering three different forms of time-varying nonlinearity parameter and the associated trap potentials. For this investigation, in the following, we first derive the second-order and third-order smooth positon solution of the ccNLS equation (6).

3.1. Second-order smooth matter wave positons

Now, we explore the various novel density profiles of second-order smooth matter wave positons in BECs. For this objective, we first derive the second-order smooth positon solution for the ccNLS Equation (6) as [50]
ϕ [ 2 ] = P 11 Q 11 ,
where
P 11 = 4 α 1 − α 1 * e 2 i α 1 2 α 1 τ + η − α 1 η − 4 α 1 * τ + α 1 * η − 4 α 1 2 τ − i + 4 α 1 * − α 1 e 2 i α 1 * 2 α 1 * τ + η − α 1 4 α 1 * τ + η + α 1 * η + 4 α 1 * 2 τ + i , Q 11 = − 2 e 2 i α 1 + α 1 * η + 4 i α 1 2 + α 1 * 2 τ − 1 + 2 α 1 − α 1 * 2 η 2 + 32 α 1 α 1 * α 1 − α 1 * 2 τ 2 + 8 η τ α 1 + α 1 * α 1 − α 1 * 2 + e 4 i α 1 2 α 1 τ + η + e 4 i α 1 * 2 α 1 * τ + η ,
where α 1 is the eigenvalue of the spectral parameter, α 1 * is the complex conjugate of α 1 , η and τ are provided in Equation (4). Substituting this solution into (7) along with the suitable form of R ( t ) , we obtain the second-order smooth matter wave positon solution of (1).
Now, utilizing the above mentioned solution, we move to investigate its dynamical evolutions through three different forms of time-modulated nonlinearity parameter, such as (i) kink-like nonlinearity R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) , (ii) localized or sech-type nonlinearity R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) , and (iii) periodic nonlineaity R ( t ) = R 0 + R 1 sin ( R 2 t + R 3 ) , where R 0 , R 1 , R 2 and R 3 are arbitrary parameters. In the following, we provide a comprehensive demonstration of the impact of modulated nonlinearity parameters on the positon density profiles.
To begin, we take the kink-like nonlinearity parameter, that is R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) to reveal the novel features in BECs. Substituting this nonlinearity term in the generalized solution (7), we find
ψ ( x , t ) = s 0 R 1 tanh R 2 t + R 3 + R 0 ϕ ( η , τ ) exp − i 4 R 2 b 2 s 0 4 − 2 R 1 2 × tanh R 2 t + R 3 + R 0 − R 1 2 log tanh R 2 t + R 3 + 1 − R 0 + R 1 2 × log 1 − tanh R 2 t + R 3 − 4 b s 0 2 x R 1 tanh R 2 t + R 3 + R 0 + 2 R 1 R 2 x 2 sec h 2 R 2 t + R 3 R 1 tanh R 2 t + R 3 + R 0 ,
where ϕ ( η , τ ) is the second-order smooth positon solution of the ccNLS equation (6). Utilizing this solution (10), we examine a thorough analysis of the positon density profiles, investigating their diverse characteristics as we vary the strength of the time-modulated nonlinearity parameter.
Figures 1a-f illustrates the qualitative profile of a second-order smooth matter positon in BECs corresponding to a kink-like nonlinearity modulated parameter R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) . By selecting specific parameter values, R 0 = 1.05 , R 1 = 0.01 , R 2 = 1.05 , and R 3 = 0.5 , we obtain a well-localized second-order smooth positon profile associated with the eigenvalue α 1 = 0.2 + 0.5 i , as depicted in Figure 1a. Notably, the orientation of the smooth positon density profile changes when varying the eigenvalue associated with the solution. For instance, by modifying the eigenvalue to α 1 = 0.3 + 0.6 i , Figure 1b clearly demonstrates a shift in the orientation of the positon profile accompanied by an enhancement in its amplitude. Furthermore, we investigate the effects of adjusting the strengths of the nonlinearity parameters, specifically R 0 , R 1 , and R 2 . For instance, when R 0 is changed to 1.85 , the positon profile’s orientation relocates while experiencing a slight increase in amplitude, as depicted in Figure 1c. Additionally, Figure 1d illustrates that increasing the value of R 1 to 0.5 leads to the collapse of the condensate profile on one side of the positon profile ( t < 0 ). Conversely, when R 1 takes a negative value, such as R 1 = − 0.5 , the reverse phenomenon occurs, resulting in the disappearance of the density profile in the corresponding plane ( t > 0 ) as represented in Figure 1e. Moreover, increasing the value of R 2 to 3.5 yields a well-localized positon profile that exhibits a compression within the condensate density background. Additionally, as depicted in Figure 1f, the width of the crest of the positon profile widens over time.
Next, we consider the localized-type or sech-type nonlinearity, namely R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) for investigating the distortion of positon profiles in the condensate density background. Plugging this form of R ( t ) in (7), we obtain the matter positon solution in the form
ψ ( x , t ) = s 0 R 1 sec h R 2 t + R 3 + R 0 ϕ ( ξ , τ ) exp i 2 R 2 − b 2 s 0 4 R 2 R 0 2 t + R 1 2 tanh R 2 t + R 3 + 2 R 1 R 0 tan − 1 sinh R 2 t + R 3 + b s 0 2 x R 1 sec h R 2 t + R 3 + R 0 + R 1 R 2 x 2 tanh R 2 t + R 3 2 R 0 cosh R 2 t + R 3 + R 1 ,
where ϕ ( η , τ ) is the positon solution of the ccNLS equation (6).
Figure 2a-f represents the density profile of a second-order smooth matter positon with a modulated nonlinearity function given by R ( t ) = R 0 + R 1 Sec h ( R 2 t + R 3 ) . In this study, we consider specific parameter values: R 0 = 1.05 , R 1 = 0.01 , R 2 = 1.05 , and R 3 = 0.5 , aiming to investigate the intriguing properties exhibited by the positon density profiles. With these initial parameter values, we obtain the second-order smooth positon profile as shown in Figure 2a. By increasing R 0 to 1.85 , we observe a stretching of the positon and an enhancement in its amplitude, as depicted in Figure 2b. Similarly, when we tune the parameter R 1 to 0.85 , a curvature appears in the condensate profile, as shown in Figure 2c. Notably, when R 1 takes a negative value, we observe the formation of two peaks at the center ( t = 0 ), accompanied by a suppression in amplitude, as demonstrated in Figure 2d. Additionally, in the case where R 0 = 1.85 and R 1 = 1.75 , we observe a gradual increase in amplitude, further stretching of the positon, and the formation of a curved profile, as shown in Figure 2e. At R 0 = 2.5 and 1.5 , a compressed density profile with an identical amplitude is obtained, as depicted in Figure 2f.
Finally, we investigate the influence of a periodically modulated nonlinearity given by R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) on the positon density profiles. By inserting this R ( t ) in (7), we obtain the explicit form of matter wave positon solution given by
ψ ( x , t ) = s 0 R 1 sin R 2 t + R 3 + R 0 ϕ ( ξ , τ ) exp − i 8 R 2 b 2 s 0 4 4 R 0 2 R 2 t + R 3 + R 1 2 2 R 2 t − sin 2 R 2 t + R 3 + 2 R 3 − 8 R 1 R 0 cos R 2 t + R 3 − 8 b s 0 2 x R 1 sin R 2 t + R 3 + R 0 + 4 R 1 R 2 x 2 cos R 2 t + R 3 R 1 sin R 2 t + R 3 + R 0 ,
where ϕ ( η , τ ) is the positon solution of the ccNLS equation (6).
The second-order smooth matter wave positon density profiles are displayed in Figure 3 for periodic nonlinearity modulated function R ( t ) = R 0 + R 1 sin R 2 t + R 3 in the context of BECs. By appropriately tuning the parameters R 0 , R 1 , and R 2 , we are able to achieve periodic positon solutions. In Figure 3a, using initial parameter values of R 0 = 1.5 , R 1 = 0.05 , R 2 = 1.25 , and R 3 = 0.5 , we observe a periodic behavior in the positon condensate profile. Subsequently, when the nonlinearity strength R 0 is increased to 2.25 , the oscillation of the positon becomes more elongated and the amplitude is raised, as shown in Figure 3b. Moreover, as we increase the value of R 1 to 0.55 , the periodicity of the positon profile increases along with an increase in amplitude which can be seen in 3c. This trend is further amplified when the value of R 1 is increased, as depicted in Figure 3d. When the parameters R 2 = 2.75 and R 3 = 5.25 are chosen, the oscillation in the positon profile increases and retains a similar orientation, as evident in Figure 3e and Figure 3f, respectively.

3.2. Third-order smooth matter wave positons

In the previous sub-section, we investigated the modifications of second-order smooth matter wave positon profiles by varying the distributed coefficients (nonlinearity function) in the GP equation (1). In this sub-section, we delve into the deformations of third-order smooth matter wave positons in condensates as we manipulate the strength of the modulated nonlinearity parameter. To explore these intriguing characteristics, we consider the third-order smooth positon solution for the ccNLS equation (6), which takes the form of [50]
ϕ [ 3 ] = P 2 Q 2 ,
where
P 2 = e − i 2 τ α 1 2 + α 1 * 2 + η ( α 1 + α 1 * ) P 21 e 2 i ( α 1 − α 1 * ) ( η + 2 τ ( α 1 + α 1 * ) ) + P 22 e − 2 i ( α 1 − α 1 * ) ( η + 2 τ ( α 1 + α 1 * ) ) + P 23 ,
with
P 21 = − 4 ( α 1 − α 1 * ) − 3 + 2 η ( 3 i + 8 τ α 1 α 1 − α 1 * + 2 η 2 ( α 1 − α 1 * ) 2 + 32 τ 2 α 1 2 ( α 1 − α 1 * ) 2 − 4 i τ α 1 − α 1 * − 7 α 1 + α 1 * , P 22 = − 4 ( α 1 − α 1 * ) − 3 + 4 i τ ( α 1 − 7 α 1 * ) ( α 1 − α 1 * ) + 2 η 2 ( α 1 − α 1 * ) 2 + 32 τ 2 ( α 1 − α 1 * ) 2 α 1 * 2 − 2 η ( α 1 − α 1 * ) ( 3 i + 8 τ α 1 * ( − α 1 + α 1 * ) , P 23 = 8 ( α 1 − α 1 * ) 3 + 4 η 2 ( α 1 − α 1 * ) 2 − 2 x 4 ( α 1 − α 1 * ) 4 + α 1 2 − 512 τ 4 α 1 2 ( α 1 − α 1 * ) 4 α 1 * 2 + 8 i η α 1 * 3 − 4 η 2 α 1 * 4 − 8 η α 1 3 ( − i + η α 1 * ) − 2 α 1 α 1 * ( − 3 + 4 i η α 1 * + 4 x 2 α 1 * 2 ) + 16 τ ( α 1 − α 1 * ) 2 ( − i + i η 2 ( α 1 − α 1 * ) 2 + η ( α 1 + α 1 * ) − η 3 ( α 1 − α 1 * ) 2 ( α 1 + α 1 * ) ) + 8 τ 3 ( α 1 − α 1 * ) 3 ( α 1 + α 1 * ) ( − i α 1 * + α 1 ( − i + 4 η α 1 * ) ) + 8 τ 2 ( α 1 − α 1 * ) 2 ( α 1 2 − 8 i η α 1 2 α 1 * + η 2 ( 1 + 24 α 1 2 α 1 * 2 ) ) ,
and
Q 2 = 4 e − 3 i α 1 − α 1 * + ( η + 2 τ ( α 1 + α 1 * ) ) 1 + Q 21 e 4 i ( α 1 − α 1 * ) ( η + 2 τ ( α 1 + α 1 * ) ) + Q 22 e 2 i ( α 1 − α 1 * ) ( η + 2 τ ( α 1 + α 1 * ) ) + e 6 i ( α 1 − α 1 * ) ( η + 2 τ ( α 1 + α 1 * ) ) ,
where
Q 21 = 3 + 1024 τ 4 α 1 2 ( α 1 − α 1 * ) 4 α 1 * 2 + 48 τ 2 ( α 1 − α 1 * ) 2 ( α 1 2 − 6 α 1 α 1 * + α 1 * 2 ) + 4 η 4 ( α 1 − α 1 * ) 4 − 128 i τ 3 ( α 1 − α 1 * ) 3 ( α 1 + α 1 * ) ( α 1 2 − 4 α 1 α 1 * + α 1 * 2 ) + 8 η 3 ( α 1 − α 1 * ) 3 ( i + 4 τ ( α 1 2 − α 1 * 2 ) ) + 4 η 2 ( α 1 − α 1 * ) 2 − 3 + 12 i τ ( α 1 2 − α 1 * 2 ) + 16 τ 2 ( α 1 − α 1 * ) 2 ( α 1 2 + 4 α 1 α 1 * + α 1 * 2 − 16 η τ ( α 1 − α 1 * ) 2 3 α 1 * − 32 τ 2 α 1 4 α 1 * + 32 τ 2 α 1 3 α 1 * 2 + 8 τ α 1 2 α 1 * ( − 3 i + 4 τ α 1 * 2 ) + α 1 ( 3 + 24 i τ α 1 * 2 − 32 τ 2 α 1 * 4 ) ,
Q 22 = 3 + 1024 τ 4 α 1 2 ( α 1 − α 1 * ) 4 α 1 * 2 + 48 τ 2 ( α 1 − α 1 * ) 2 ( α 1 2 − 6 α 1 α 1 * + α 1 * 2 ) + 4 η 4 ( α 1 − α 1 * ) 4 + 128 i τ 3 ( α 1 − α 1 * ) 3 ( α 1 + α 1 * ) ( α 1 2 − 4 α 1 α 1 * + α 1 * 2 ) + 8 η 3 ( α 1 − α 1 * ) 3 ( i + 4 τ ( α 1 2 − α 1 * 2 ) ) + 4 η 2 ( α 1 − α 1 * ) 2 − 3 − 12 i τ ( α 1 2 − α 1 * 2 ) + 16 τ 2 ( α 1 − α 1 * ) 2 ( α 1 2 + 4 α 1 α 1 * + α 1 * 2 − 16 η τ ( α 1 − α 1 * ) 2 3 α 1 * − 32 τ 2 α 1 4 α 1 * + 32 τ 2 α 1 3 α 1 * 2 + 8 τ α 1 2 α 1 * ( 3 i + 4 τ α 1 * 2 ) + α 1 ( 3 + 768 i τ 3 α 1 * 6 ) .
By substituting the third-order smooth positon solution of the ccNLS Equation (6), along with the appropriate form of the modulated parameter R ( t ) , into equation (7), we delve into the analysis of the underlying dynamics of GP equation (1).
Figures 4a-f present the condensate profiles of third-order smooth positons with a kink-like nonlinearity modulated function R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) . By considering initial parameters R 0 = 1.25 , R 1 = 0.01 , R 2 = 1.05 , and R 3 = 0.5 , an appropriate third-order positon profile is formed within the condensate density background, as shown in Figure 4a. Notably, a decrease in R 0 leads to a sudden rise in one of the subcrests, as demonstrated in Figure 4b for R 0 = 0.85 . Furthermore, Figure 4c illustrates an increase in amplitude when tuning the value of R 0 to 1.75 . On the other hand, in Figure 4d, when the parameter R 1 is enhanced to 1.25 , the positon tends to disappear within the condensate profile for t < 0 . Interestingly, a reverse scenario occurs when R 1 = − 0.65 , resulting in a higher peak in one of the profiles and an increased amplitude, as depicted in Figure 4e. Similarly, an increase in R 2 to 3.75 yields a compressed three-positon profile with the same amplitude as Figure 4a, as shown in Figure 4f.
In Figures 5a-f, we show density profile of third-order smooth matter positons for sech-like nonlinearity modulated function R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) for the GP model (1). Taking initial parameters R 0 = 1.25 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 , we obtain the conventional smooth three-positon profile, as shown in Figure 5a. By adjusting R 0 to 1.85 , the positon undergoes stretching, resulting in an enhanced amplitude, as depicted in Figure 5b. Similarly, when R 1 is modified to 1.5 , the positon exhibits curvature in one of its wave crest, as seen in Figure 5c. Figure 5d illustrates a decrease in the soliton amplitude when R 1 is set to 0.35 . However, no significant changes are observed in the smooth three-positon profile when altering the value of R2 compared to Figure 5a. This observation is displayed in Figure 5e. Finally, for R 0 = 1.85 and R 1 = 0.8 , the three-positon becomes compressed, accompanied by a decrease in its amplitude, as shown in Figure 5f.
Finally, we investigate the density profile of the third-order smooth matter positon in one-component BECs utilizing a periodic nonlinearity modulated function, denoted as R ( t ) = R 0 + R 1 sin ( R 2 t + R 3 ) . Setting the initial nonlinearity strengths as R 0 = 1.5 , R 1 = 0.05 , R 2 = 0.85 , and R 3 = 0.5 , we aim to obtain an appropriate periodic third-order smooth positon density profile, as illustrated in Figure 6a. Especially, a remarkable change occurs in the profile when the parameter R 0 is selected as 0.85 , resulting in the formation of a sharp ascent on one side of the profile, as depicted in Figure 6b. Similarly, when we increase R 0 to 1.75 , the profile returns to its original position, as displayed in Figure 6c. Furthermore, in Figure 6d, we observe that the periodicity of the positon density profiles increases when R 1 is set to 0.5 . Moreover, raising the value of R 2 to 2.25 leads to an increase in the oscillation amplitude of the positon, as demonstrated in Figure 6e. Finally, when the value of R 2 is further increased to 5.25 , we observe no change in the positon amplitude, but a variation in the oscillation behavior, which is clearly visualized in Figure 6f.

4. Conclusion

In our study, we have derived the second- and third-order smooth matter wave positon solutions of the GP equation. These solutions capture the dynamics of one-component BECs subjected to time-modulated nonlinearity (represented by the effective scattering lengths) and external harmonic trap potentials. Through a similarity transformation technique, we have mapped the time-modulated GP equation onto the ccNLS equation, ensuring an integrability condition between the nonlinearity coefficient and the external trap potential. We have investigated three distinct forms of modulated nonlinearities: (i) kink-like, (ii) localized or sech-like, and (iii) periodic. By varying the parameters associated with the nonlinearity strength, we have observed various nonlinear phenomena in the positon density profiles. These phenomena include stretching, curving, oscillating, breathing, collapsing, amplification, and suppression. In the case of a kink-like modulated nonlinearity, the positon density profiles (represented by the second- and third-order smooth matter wave positons) undergo stretching, while their amplitudes can be enhanced or suppressed. It is noteworthy that these profiles vanish for different time intervals, with disappearance occurring for t < 0 and t > 0 when the parameter R 2 takes positive and negative values, respectively. For the localized or sech-type modulated nonlinearity, the density profiles of positons become compressed and curved within the condensate density background. In the case of periodic modulated nonlinearity, positons exhibit a periodic nature, and we have observed an increase in periodicity as the nonlinearity strengths are adjusted. Our findings contribute to a deeper understanding of the behavior of matter wave positons in BECs under different types of modulated nonlinearities. These results shed light on the intricate interplay between nonlinearity, external trapping potentials, and the corresponding effects on the density profiles of positons. The theoretical findings presented in this study, along with previous research in the literature, offer a valuable groundwork for experimental researchers to explore and validate the deformation of solitons/positons in PT -symmetric systems with spatiotemporal modulation. These investigations can be extended to various fields, such as Bose-Einstein condensates and nonlinear optics, that are currently of great interest. Additionally, as a future direction, this theoretical study can be readily expanded to examine higher-order solitons, breathers, and rogue waves. It can also encompass the exploration of combined spatial and longitudinally varying trap potentials, nonlinear effects, and novel forms of PT -symmetric potentials, potentially leading to the discovery of new applications.

Author Contributions

All authors made equal contributions to the work reported in this paper.

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Data Availability Statement

No data was used for the research described in the article.

Acknowledgments

K.M and D.A are funded by the Center for Computational Modeling, Chennai Institute of Technology, India, vide funding number CIT/CCM/2023/RP-011. N.S was supported by the Ministry of Science and Higher Education of the Republic of Kazakhstan, grant AP19675202.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

  1. Pitaevskii, L.P.; Stringari, S. Bose-Einstein condensation; Clarendon: Oxford, UK, 2003. [Google Scholar]
  2. Kevrekidis, P. G.; Frantzeskakis, D. J. R.; Carretero-González. Emergent Nonlinear Phenomena in Bose-Einstein Condensates; Springer: Berlin, Germany, 2008. [Google Scholar]
  3. Lakshmanan, M.; Rajasekar., S. Nonlinear Dynamics: Integrablity, Chaos and Patterns; Springer: Heidelberg, Germany, 2003. [Google Scholar]
  4. Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM: Philadelphia, 2010. [Google Scholar]
  5. Serkin, V.N.; Hasegawa, A.; Belyaeva, T.L. Solitary waves in nonautonomous nonlinear and dispersive systems: nonautonomous solitons. J. Mod. Opt. 2010, 57, 1456–1472. [Google Scholar] [CrossRef]
  6. Luo, H.G.; Zhao, D.; He, X.G. Exactly controllable transmission of nonautonomous optical solitons. Phys. Rev. A. 2009, 79, 063802. [Google Scholar] [CrossRef]
  7. Shats, M.; Punzmann, H.; Xia, H. Capillary rogue waves. Phys Rev Lett. 2010, 104, 104503. [Google Scholar] [CrossRef] [PubMed]
  8. Ganshin, A.N.; Efimov, V.B.; Kolmakov, G.V. et al. Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys. Rev. Lett. 2008, 101, 065303. [Google Scholar] [CrossRef] [PubMed]
  9. El-Tantawy, S.A.; Salas, A.H.; Albalawi, W. New Localized and Periodic Solutions to a Korteweg-de Vries Equation with Power Law Nonlinearity: Applications to Some Plasma Models. Symmetry. 2022, 14, 197. [Google Scholar] [CrossRef]
  10. Vudragović, D.; Balaž, A. Faraday and Resonant Waves in Dipolar Cigar-Shaped Bose-Einstein Condensates. Symmetry. 2019, 11, 1090. [Google Scholar] [CrossRef]
  11. Inouye, S.; Andrews, M.R.; Stenger, J.; Miesner, H.J.; Stamper-Kurn, D.M.; Ketterle, W. Observation of Feshbach resonances in a Bose-Einstein condensate. Nature. 1998, 392, 151. [Google Scholar] [CrossRef]
  12. Theis, M.; Thalhammer, G.; Winkler, K.; Hellwig, M.; Ruff, G.; Grimm, R.; Denschlag, J.H. Tuning the scattering length with an optically induced Feshbach resonance. Phys. Rev. Lett. 2004, 93, 123001. [Google Scholar] [CrossRef]
  13. Malomed, B.A. Soliton Management in Periodic Systems; Springer: New York, 2006. [Google Scholar]
  14. Wang, D.S.; Liu, J.; Wang, L. Non-autonomous matter-wave solitons in hybrid atomic-molecular Bose-Einstein condensates with tunable interactions and harmonic potential. Phys. Lett. A. 2018, 382, 799–805. [Google Scholar] [CrossRef]
  15. Halder, B.; Ghosh, S.; Basu, P.; Bera, J.; Malomed, B.; Roy, U. Exact Solutions for Solitary Waves in a Bose-Einstein Condensate under the Action of a Four-Color Optical Lattice. Symmetry. 2022, 14, 49. [Google Scholar] [CrossRef]
  16. Bludov, Y.V.; Konotop, V.V.; Akhmediev, N. Matter rogue waves. Phys. Rev. A . 2009, 80, 033610. [Google Scholar] [CrossRef]
  17. Manikandan, K.; Muruganandam, P.; Senthilvelan, M.; Lakshmanan, M. Manipulating matter rogue waves and breathers in Bose-Einstein condensates. Phys Rev E. 2014, 90, 062905. [Google Scholar] [CrossRef] [PubMed]
  18. Wen, L.; Li, L.; Li, Z.-D.; Song, S.-W.; Zhang, X.-F.; Liu, W. M. Matter rogue wave in Bose-Einstein condensates with attractive atomic interaction. Eur. Phys. J. D. 2011, 64, 473. [Google Scholar] [CrossRef]
  19. Hacker, N.; Malomed, B.A. Nonlinear Dynamics of Wave Packets in Tunnel-Coupled Harmonic-Oscillator Traps. Symmetry. 2021, 13, 372. [Google Scholar] [CrossRef]
  20. Triki, H.; Choudhuri, A.; Qin, Z.; Biswas, A.; Alshomrani, A.S. Nonautonomous matter wave bright solitons in a quasi-1D Bose-Einstein condensate system with contact repulsion and dipole-dipole attraction. Applied Mathematics and Computation. 2020, 371, 124951. [Google Scholar] [CrossRef]
  21. Sakaguchi, H.; Malomed, B. Nonlinear Management of Topological Solitons in a Spin-Orbit-Coupled System. Symmetry. 2019, 11, 388. [Google Scholar] [CrossRef]
  22. Yan, Z.Y. Nonautonomous rogons in the inhomogeneous nonlinear Schrödinger equation with variable coefficients. Phys. Lett. A. 2010, 374, 672. [Google Scholar] [CrossRef]
  23. Zhao, L.C. Dynamics of nonautonomous rogue waves in Bose-Einstein condensate. Ann. Phys. 2013, 73, 329. [Google Scholar] [CrossRef]
  24. Wu, X.F.; Hua, G.S.; Ma, Z. Y. Novel rogue waves in an inhomogenous nonlinear medium with external potentials. Commun. Nonlinear Sci. Num. Simulat. 2013, 18, 3325. [Google Scholar] [CrossRef]
  25. He, J.S.; Charalampidis, E.G.; Kevrekidis, P.G.; Frantzeskakis, D.J. Rogue waves in nonlinear Schrödinger models with variable coefficients: application to Bose–Einstein condensates. Phys. Lett. A. 2014, 378, 577. [Google Scholar] [CrossRef]
  26. Konotop, V.V.; Yang, J.; Zezyulin, D.A. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef]
  27. Zezyulin, D.A.; Konotop, V.V. Nonlinear mode in the harmonic PT-symmetric potential. Phys. Rev. A. 2012, 85, 043840. [Google Scholar] [CrossRef]
  28. Manikandan, K.; Sudharsan, J.B.; Senthilvelan, M. Nonlinear tunneling of solitons in a variable coefficients nonlinear Schrödinger equation with PT-symmetric Rosen–Morse potential. Eur. Phys. J. B 2021, 94, 122. [Google Scholar] [CrossRef]
  29. Oliinyk, A.; Yatsuta, I.; Malomed, B.; Yakimenko, A. Symmetry Breaking in Interacting Ring-Shaped Superflows of Bose-Einstein Condensates. Symmetry. 2019, 11, 1312. [Google Scholar] [CrossRef]
  30. Matveev, V.B. Generalized Wronskian formula for solutions of the KdV equations: first applications. Phys. Lett. A. 1992, 166, 205–208. [Google Scholar] [CrossRef]
  31. Matveev, V.B. Positon-positon and soliton-positon collisions: KdV case. Phys. Lett. A. 1992, 166, 209–212. [Google Scholar] [CrossRef]
  32. Matveev, V.B. Positons: Slowly Decreasing Analogues of Solitons. Theor. Math. Phys. 2002, 131, 483. [Google Scholar] [CrossRef]
  33. Kedziora, D.J.; Ankiewicz, A.; Akhmediev, N. Second-order nonlinear Schrödinger equation breather solutions in the degenerate and rogue wave limits. Phys. Rev. E 2012, 85, 066601. [Google Scholar] [CrossRef]
  34. Chow, K.W.; Lai, W.C.; Shek, C.K.; Tso, K. Positon-like Solutions of Nonlinear Evolution Equations in (2+1) Dimensions. Chaos Solitons Fractals 1998, 9, 1901–1912. [Google Scholar] [CrossRef]
  35. Dubard, P.; Gaillard, P.; Klein, C.; Matveev, V.B. On multi-rogue wave solutions of the NLS equation and positon solutions of the KdV equation. Eur. Phys. J. Spec. Top. 2010, 185, 247–258. [Google Scholar] [CrossRef]
  36. Stahlhofen, A.A. Positons of the modified Korteweg-de Vries equation. Ann. Phys. 1992, 504, 554–569. [Google Scholar] [CrossRef]
  37. Maisch, H.; Stahlhofen, A.A. Dynamic properties of positons. Phys. Scr. 1995, 52, 228–236. [Google Scholar] [CrossRef]
  38. Beutler, R. Positon solutions of the sine-Gordon equation. J. Math. Phys. 1993, 34, 3081–3109. [Google Scholar] [CrossRef]
  39. Stahlhofen, A.A.; Matveev, V.B. Positons for the Toda lattice and related spectral problems. J. Phys. A. 1995, 28, 1957–1965. [Google Scholar] [CrossRef]
  40. Hu, H.C.; Liu, Y. New positon, negaton and complexiton solutions for the Hirota–Satsuma coupled KdV system. Phys. Lett. A. 2008, 372, 5795–5798. [Google Scholar] [CrossRef]
  41. Cen, J.; Correa, F.; Fring, A. Time-delay and reality conditions for complex solitons. J. Math. Phys. 2017, 58, 032901. [Google Scholar] [CrossRef]
  42. Cen, J.; Correa, F.; Fring, A. Degenerate multi-solitons in the sine-Gordon equation. J. Phys. A. 2017, 50, 435201. [Google Scholar] [CrossRef]
  43. Xing, Q.; Wu, Z.; Mihalache, D.; He, J.S. Smooth positon solutions of the focusing modified Korteweg-de Vries equation. Nonlinear Dyn. 2017, 89, 2299–2310. [Google Scholar] [CrossRef]
  44. Liu, S.Z.; Zhang, Y.S.; He, J.S. Smooth positons of the second-type derivative nonlinear Schrödinger equation. Commun. Theor. Phys. 2019, 71, 357–361. [Google Scholar] [CrossRef]
  45. Song, W.; Xu, S.; Li, M.; He, J. Generating mechanism and dynamic of the smooth positons for the derivative nonlinear Schrödinger equation. Nonlinear Dyn. 2019, 97, 2135–2145. [Google Scholar] [CrossRef]
  46. Liu, W.; Zhang, Y.S.; He, J.S. Dynamics of the smooth positons of the complex modified KdV equation. Waves Random Complex 2018, 28, 203–214. [Google Scholar] [CrossRef]
  47. Yuan, F. The dynamics of the smooth positon and b-positon solutions for the NLS-MB equations. Nonlinear Dyn. 2020, 102, 1761–1771. [Google Scholar] [CrossRef]
  48. Zhang, Z.; Yang, X.; Li, B. Soliton molecules and dynamics of the smooth positon for the Gerdjikov–Ivanov equation. Appl. Math. Lett. 2020, 103, 106168. [Google Scholar] [CrossRef]
  49. Hu, A.; Li, M.; He, J. Dynamic of the smooth positons of the higher-order Chen–Lee–Liu equation. Nonlinear Dyn. 2021, 104, 4329–4338. [Google Scholar] [CrossRef]
  50. Vishnu Priya, N.; Monisha, S.; Senthilvelan, M.; Rangarajan, G. Nth-order smooth positon and breather-positon solutions of a generalized nonlinear Schrödinger equation. Eur. Phys. J. Plus. 2022, 137, 646. [Google Scholar] [CrossRef]
  51. Monisha, S.; Vishnu Priya, N.; Senthilvelan, M.; Rajasekar, S. Higher order smooth positon and breather positon solutions of an extended nonlinear Schrödinger equation with the cubic and quartic nonlinearity. Chaos, Solitons and Fractals 2022, 162, 112433. [Google Scholar] [CrossRef]
Preprints 78743 g001
Figure 1. Density profile of second-order smooth matter wave positons for (1) with the kink-like nonlinearity modulated function R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.05 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) α 1 = 0.3 + 0.6 i , α 1 * = 0.3 − 0.6 i ; (c) R 0 = 1.85 ; (d) R 1 = 0.5 ; (e) R 1 = − 0.5 ; (f) R 2 = 3.5 . The other parameters are α 1 = 0.2 + 0.5 i , α 1 * = 0.2 − 0.5 i , s 0 = 1.0 , and b = 0.01 .
Figure 1. Density profile of second-order smooth matter wave positons for (1) with the kink-like nonlinearity modulated function R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.05 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) α 1 = 0.3 + 0.6 i , α 1 * = 0.3 − 0.6 i ; (c) R 0 = 1.85 ; (d) R 1 = 0.5 ; (e) R 1 = − 0.5 ; (f) R 2 = 3.5 . The other parameters are α 1 = 0.2 + 0.5 i , α 1 * = 0.2 − 0.5 i , s 0 = 1.0 , and b = 0.01 .
Preprints 78743 g001
Preprints 78743 g002
Figure 2. Density profile of second-order smooth matter positons for (1) with the localized-type modulated nonlinearity R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.05 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) R 0 = 1.85 ; (c) R 1 = 0.85 ; (d) R 1 = − 0.85 ; (e) R 0 = 1.85 , R 1 = 1.75 ; (f) R 0 = 2.5 , R 2 = 1.5 . The other parameters are same as in Figure 1.
Figure 2. Density profile of second-order smooth matter positons for (1) with the localized-type modulated nonlinearity R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.05 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) R 0 = 1.85 ; (c) R 1 = 0.85 ; (d) R 1 = − 0.85 ; (e) R 0 = 1.85 , R 1 = 1.75 ; (f) R 0 = 2.5 , R 2 = 1.5 . The other parameters are same as in Figure 1.
Preprints 78743 g002
Preprints 78743 g003aPreprints 78743 g003b
Figure 3. Density profile of second-order smooth matter wave positons for (1) with the periodic nonlinearity modulated function R ( t ) = R 0 + R 1 sin R 2 t + R 3 . The parameters are (a) R 0 = 1.5 , R 1 = 0.05 , R 2 = 1.25 , R 3 = 0.5 ; (b) R 0 = 2.25 ; (c) R 1 = 0.55 ; (d) R 1 = 0.85 ; (e) R 2 = 2.75 ; (f) R 2 = 5.25 . The other parameters are same as in Figure 1.
Figure 3. Density profile of second-order smooth matter wave positons for (1) with the periodic nonlinearity modulated function R ( t ) = R 0 + R 1 sin R 2 t + R 3 . The parameters are (a) R 0 = 1.5 , R 1 = 0.05 , R 2 = 1.25 , R 3 = 0.5 ; (b) R 0 = 2.25 ; (c) R 1 = 0.55 ; (d) R 1 = 0.85 ; (e) R 2 = 2.75 ; (f) R 2 = 5.25 . The other parameters are same as in Figure 1.
Preprints 78743 g003aPreprints 78743 g003b
Preprints 78743 g004
Figure 4. Density profile of third-order smooth matter positons for (1) with R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.25 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) R 0 = 0.85 ; (c) R 0 = 1.75 ; (d) R 1 = 1.25 ; (e) R 1 = − 0.65 ; (f) R 2 = 3.75 . The other parameters are α 1 = 0.2 + 0.75 i , α 1 * = 0.2 − 0.75 i , s 0 = 1.0 , and b = 0.01 .
Figure 4. Density profile of third-order smooth matter positons for (1) with R ( t ) = R 0 + R 1 tanh ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.25 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) R 0 = 0.85 ; (c) R 0 = 1.75 ; (d) R 1 = 1.25 ; (e) R 1 = − 0.65 ; (f) R 2 = 3.75 . The other parameters are α 1 = 0.2 + 0.75 i , α 1 * = 0.2 − 0.75 i , s 0 = 1.0 , and b = 0.01 .
Preprints 78743 g004
Preprints 78743 g005
Figure 5. Density profile of third-order smooth matter positons for (1) with nonlinearity modulated function R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.25 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) R 0 = 1.85 ; (c) R 1 = 1.5 ; (d) R 1 = 0.35 ; (e) R 2 = 2.75 ; (f) R 0 = 1.85 , R 1 = 0.8 . The other parameters are same as in Figure 4.
Figure 5. Density profile of third-order smooth matter positons for (1) with nonlinearity modulated function R ( t ) = R 0 + R 1 sech ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.25 , R 1 = 0.01 , R 2 = 1.05 , R 3 = 0.5 ; (b) R 0 = 1.85 ; (c) R 1 = 1.5 ; (d) R 1 = 0.35 ; (e) R 2 = 2.75 ; (f) R 0 = 1.85 , R 1 = 0.8 . The other parameters are same as in Figure 4.
Preprints 78743 g005
Preprints 78743 g006
Figure 6. Density profile of third-order smooth matter positons for (1) with nonlinearity modulated function R ( t ) = R 0 + R 1 sin ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.5 , R 1 = 0.05 , R 2 = 0.85 , R 3 = 0.5 ; (b) R 0 = 0.85 ; (c) R 0 = 1.75 ; (d) R 1 = 0.5 ; (e) R 2 = 2.25 ; (f) R 2 = 5.25 . The other parameters are same as in Figure 4.
Figure 6. Density profile of third-order smooth matter positons for (1) with nonlinearity modulated function R ( t ) = R 0 + R 1 sin ( R 2 t + R 3 ) . The parameters are (a) R 0 = 1.5 , R 1 = 0.05 , R 2 = 0.85 , R 3 = 0.5 ; (b) R 0 = 0.85 ; (c) R 0 = 1.75 ; (d) R 1 = 0.5 ; (e) R 2 = 2.25 ; (f) R 2 = 5.25 . The other parameters are same as in Figure 4.
Preprints 78743 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated